Mathematics
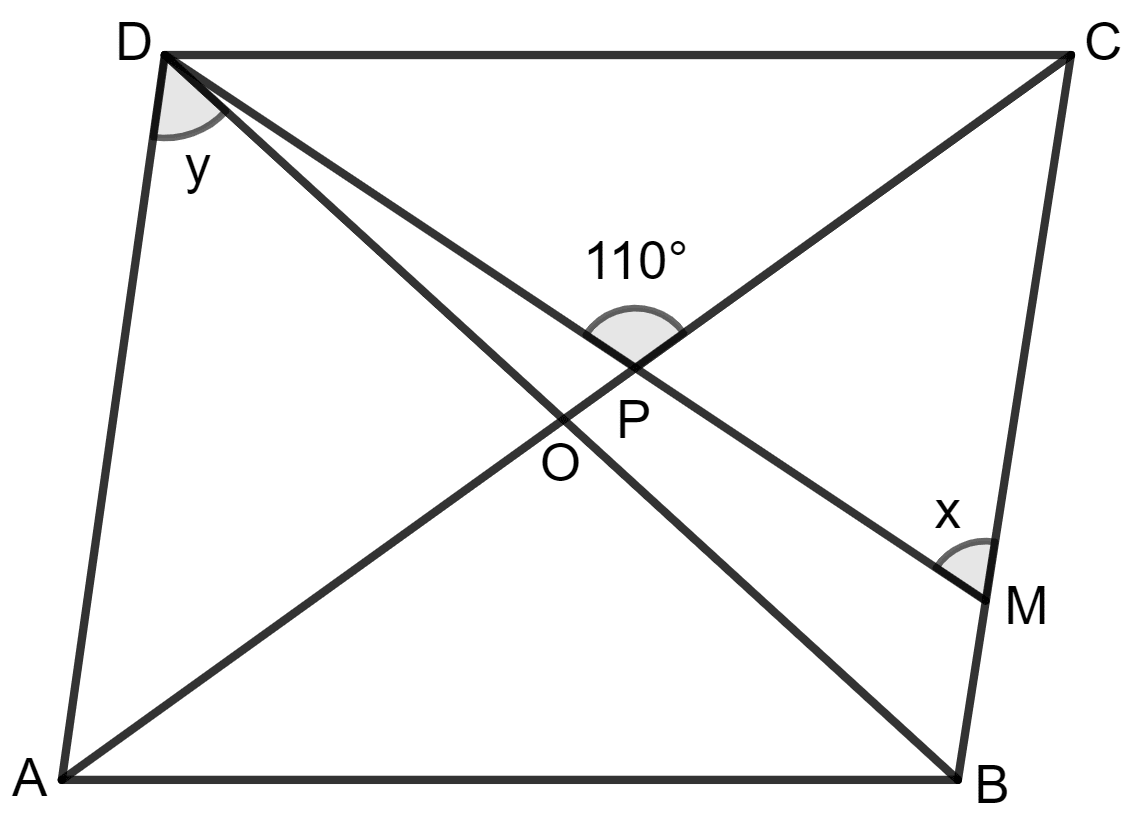
The given figure shows a rhombus ABCD in which angle BCD = 80°. Find angles x and y.
Quadrilaterals
7 Likes
Answer
It is given that in rhombus ABCD, diagonal AC and BD bisect each other at 90° and ∠ BCD = 80°.
Also, ∠BCD = ∠ BAD (opposite angles of rhombus)
⇒ ∠ BAD = 80°
Adjacent angles of a quadrilateral are supplementary.
So, ∠BCD + ∠CDA = 180°
⇒ 80° + ∠CDA = 180°
⇒ ∠CDA = 180° - 80°
⇒ ∠CDA = 100°
And, ∠ ADB = ∠ ADC
⇒ y = 100°
⇒ y = 50°
Also, ∠CDA = ∠ ABC (opposite angles of rhombus)
⇒ ∠ ABC = 100°
Diagonals bisect opposite angles.
∠ OCB or ∠ PCB = ∠ BCD
= 80°
= 40°
Consider triangle PCM,
Exterior angle = sum of opposite interior angles.
∠ CPD = ∠ PCM + ∠ PMC
⇒ 110° = 40° + x
⇒ x = 110° - 40°
⇒ x = 70°
Hence, the value of x = 70° and y = 50°.
Answered By
4 Likes
Related Questions
In a parallelogram ABCD, X and Y are mid-points of opposite sides AB and DC respectively. Prove that:
(i) AX = YC.
(ii) AX is parallel to YC
(iii) AXCY is a parallelogram.
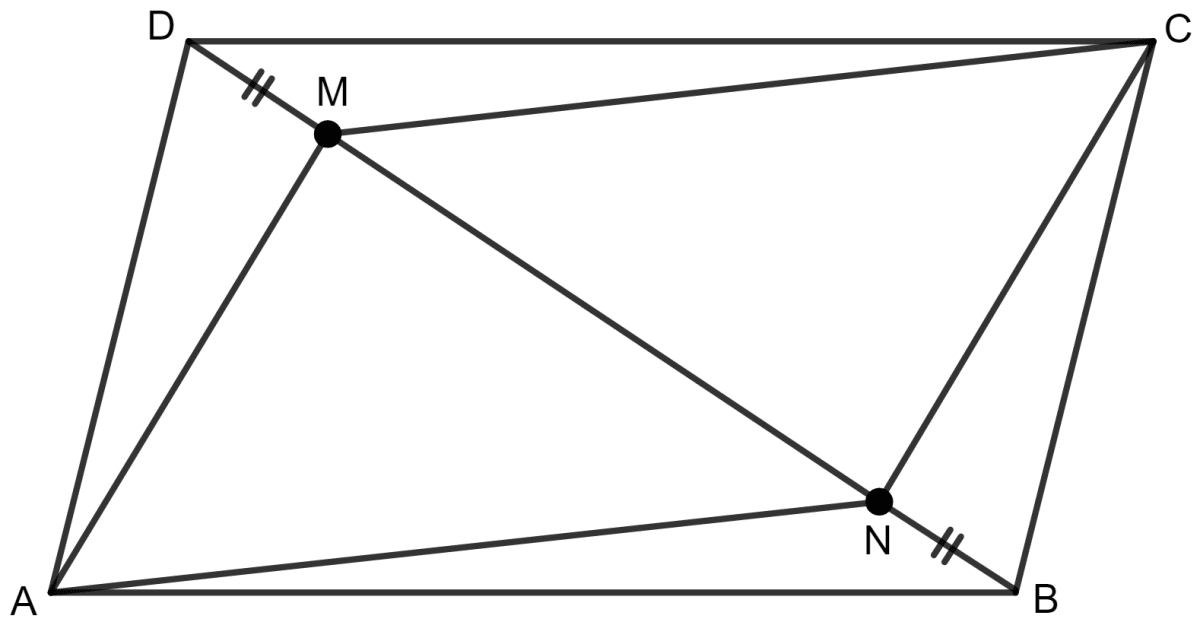
The given figure shows a parallelogram ABCD. Points M and N lie in diagonal BD such that DM = BN. Prove that:
(i) △DMC ≅ △BNA and so CM = AN.
(ii) △AMD ≅ △CNB and so AM = CN.
(iii) ANCM is a parallelogram.
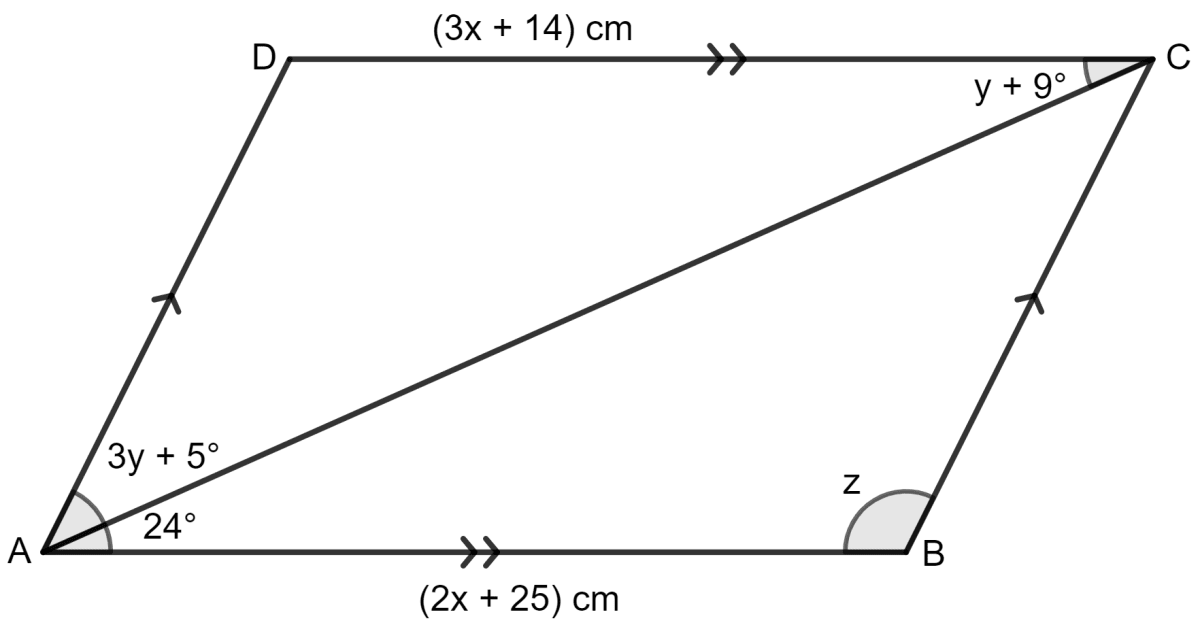
Use the information given in the following diagram to find the values of x, y and z.
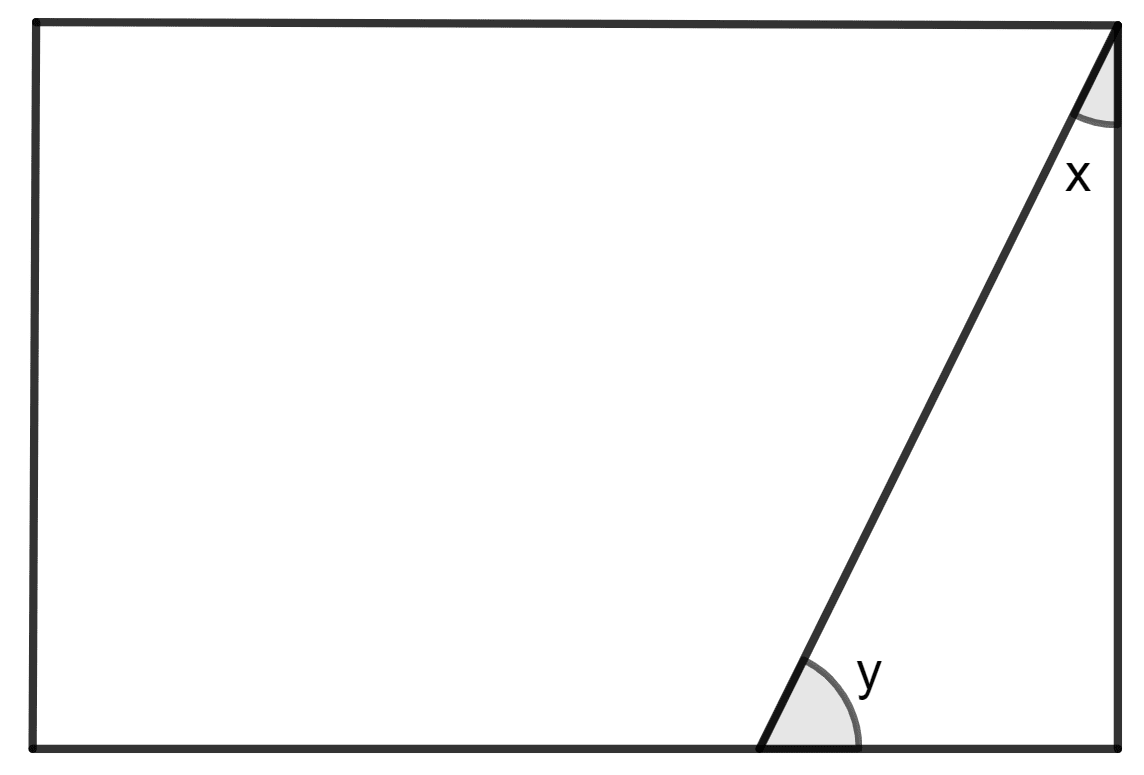
The following figure is a rectangle in which x : y = 3 : 7; find the values of x and y.