Mathematics
The given figure shows a right-angled triangle ABC and an equilateral triangle BCD. Find the area of the shaded portion.
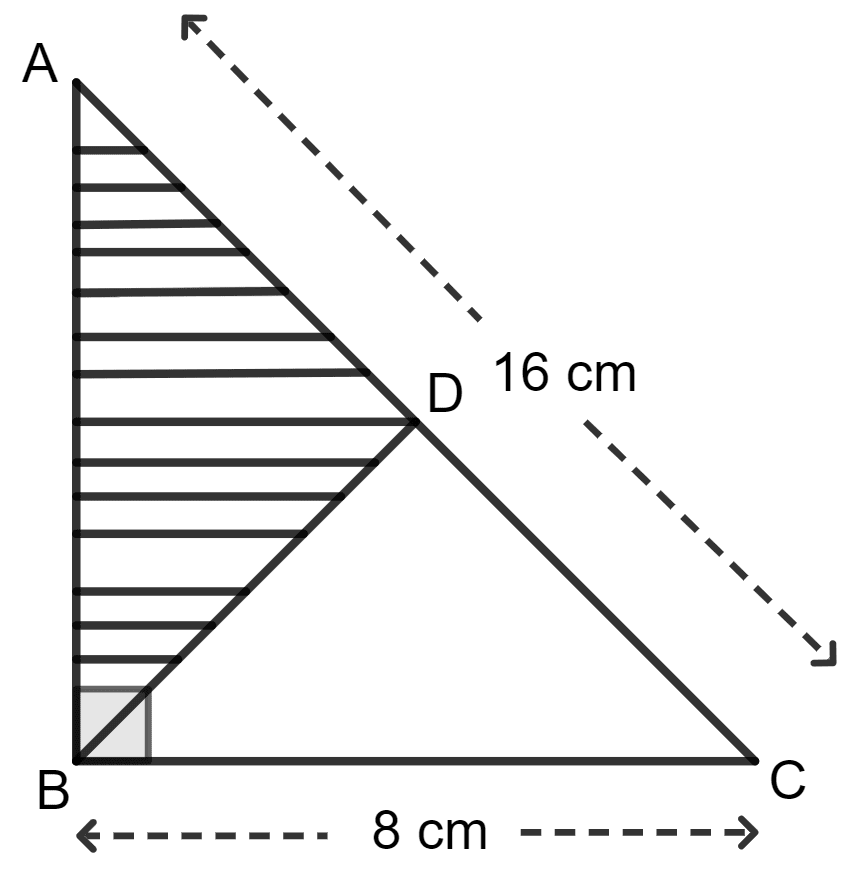
Mensuration
47 Likes
Answer
For triangle ABC (right-angled triangle),
Using the Pythagoras theorem,
Base2 + Height2 = Hypotenuse2
⇒ 82 + height2 = 162
⇒ 64 + height2 = 256
⇒ height2 = 256 - 64
⇒ height2 = 192
⇒ height =
⇒ height = 8
Area of triangle ABC = x base x height
=
=
= cm2
For triangle BCD,
Area of an equilateral triangle = x side2
= x 82
= x 64
= 16 cm2
Area of Δ ABD (shaded portion) = Area of Δ ABC - Area of Δ BDC
= 32 - 16 cm2
= 16 cm2
Hence, the area of the shaded portion is 16 cm2 = 27.712 cm2.
Answered By
29 Likes
Related Questions
Find the area of an isosceles triangle with perimeter 36 cm and base 16 cm.
The base of an isosceles triangle is 24 cm and its area is 192 sq. cm. Find its perimeter.
Find the area and the perimeter of quadrilateral ABCD, given below; if, AB = 8 cm, AD = 10 cm, BD = 12 cm, DC = 13 cm and ∠DBC = 90°.
The base of a triangular field is three times its height. If the cost of cultivating the field at ₹ 36.72 per 100 m2 is ₹ 49,572; find its base and height.