Mathematics
The minute hand of a clock is 8 cm long. Find the area swept by the minute hand between 8.30 a.m. and 9.05 a.m.
Mensuration
20 Likes
Answer
Length of the minute hand (radius of the circle) = 8 cm
Time interval between 9.05 a.m. and 8.30 a.m. = 35 minutes
Area swept by the minute hand in 1 hr = πr2
Area of the circle in 60 minutes = cm2
Area of the circle in 1 minute = cm2
= cm2
Area of the circle in 35 minutes = cm2
= cm2
= cm2
Hence, the area swept by the minute hand between 8:30 a.m. and 9:05 a.m. is cm2.
Answered By
14 Likes
Related Questions
Each wheel of a car is of diameter 80 cm. How many complete revolutions does each wheel make in 10 minutes when the car is travelling at a speed of 66 km per hour ?
An express train is running between two stations with a uniform speed. If the diameter of each wheel of the train is 42 cm and each wheel makes 1200 revolutions per minute, find the speed of the train.
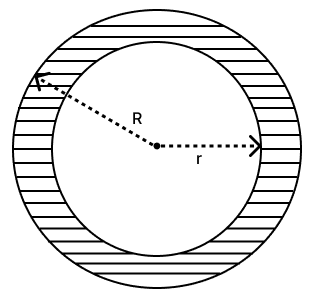
The shaded portion of the figure, given alongside, shows two concentric circles.
If the circumference of the two circles be 396 cm and 374 cm, find the area of the shaded portion.
The base of a right triangle is 8 cm and its hypotenuse is 10 cm; the area of triangle is:
24 cm2
40 cm2
48 cm2
80 cm2