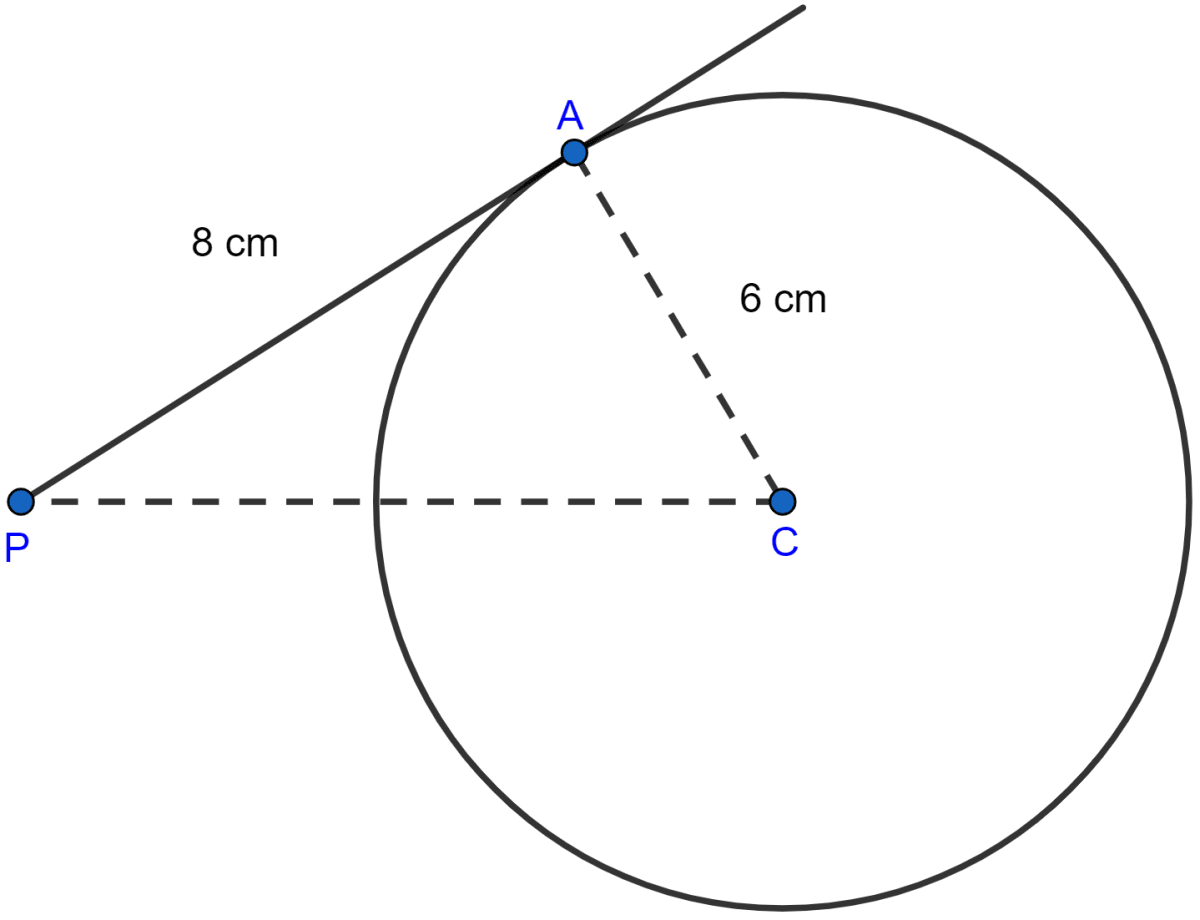
The tangent to a circle of radius 6 cm from an external point P, is of length 8 cm. Calculate the distance of P from the nearest point of the circle.

Since the tangent at any point of a circle and the radius through the point are perpendicular to each other.

So, from figure,

AP ⊥ CP

So, in right angled △CAP by pythagoras theorem,

$\Rightarrow CP^2 = CA^2 + AP^2 \\[1em] \Rightarrow CP^2 = 6^2 + 8^2 \\[1em] \Rightarrow CP^2 = 36 + 64 \\[1em] \Rightarrow CP^2 = 100 \\[1em] \Rightarrow CP = 10\text{ cm}.$

From figure, nearest point to P on the circle is D,

PD = CP - CD = 10 - 6 = 4 cm.

Hence, the distance of P from the nearest point of the circle is 4 cm.