Mathematics
Two parallel chords are drawn in a circle of diameter 30.0 cm. The length of one chord is 24.0 cm and the distance between the two chords is 21.0 cm; find the length of the other chord.
Circles
45 Likes
Answer
Let AB and CD be the two parallel chords.
Given,
Length of one chord is 24.0 cm. Let AB = 24 cm.
Draw OE ⊥ CD and OF ⊥ AB.
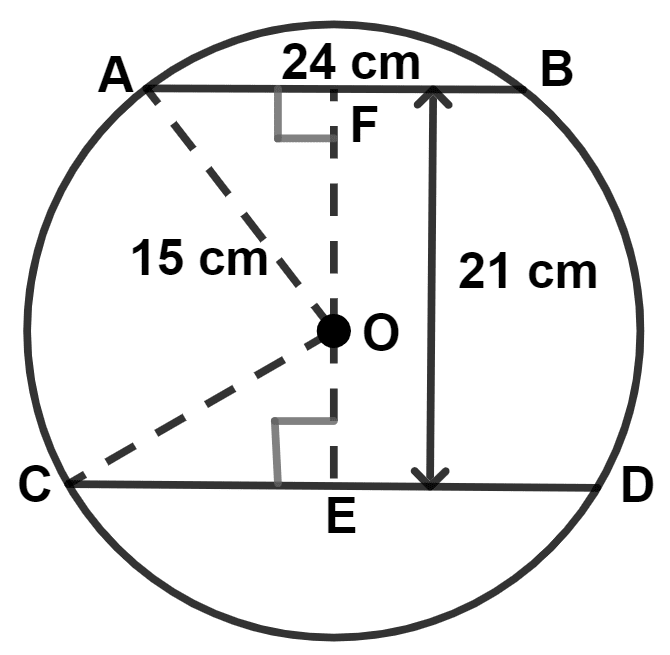
We know that,
Perpendicular from the center to the chord, bisects it.
∴ AF = = 12 cm.
From figure,
OA = OC = radius = = 15 cm.
In right-angled triangle OAF,
By pythagoras theorem,
⇒ Hypotenuse2 = Perpendicular2 + Base2
⇒ OA2 = OF2 + AF2
⇒ 152 = OF2 + 122
⇒ 225 = OF2 + 144
⇒ OF2 = 225 - 144
⇒ OF2 = 81
⇒ OF = = 9 cm.
Given,
Distance between two chords = 21 cm
∴ FE = 21 cm
⇒ OE = FE - OF = 21 - 9 = 12 cm.
In right-angled triangle OCE,
By pythagoras theorem,
⇒ Hypotenuse2 = Perpendicular2 + Base2
⇒ OC2 = OE2 + CE2
⇒ 152 = 122 + CE2
⇒ 225 = 144 + CE2
⇒ CE2 = 225 - 144
⇒ CE2 = 81
⇒ CE = = 9 cm.
As, perpendicular from center to the chord, bisects it.
∴ CD = 2 × CE = 2 × 9 = 18 cm.
Hence, length of other chord = 18 cm.
Answered By
30 Likes
Related Questions
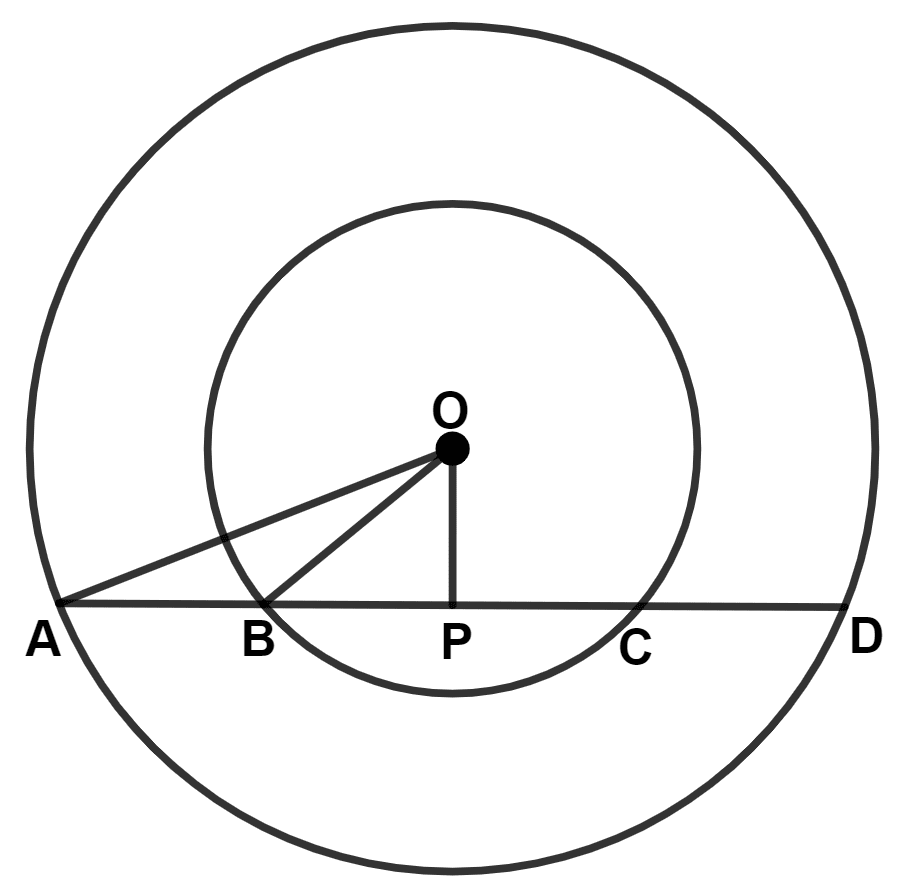
In the following figure, AD is a straight line. OP ⊥ AD and O is the centre of both the circles. If OA = 34 cm, OB = 20 cm and OP = 16 cm; find the length of AB.
In a circle of radius 17 cm, two parallel chords of lengths 30 cm and 16 cm are drawn. Find the distance between the chords, if both the chords are :
(i) on the opposite sides of the center,
(ii) on the same side of the center.
A chord CD of a circle, whose center is O, is bisected at P by a diameter AB.
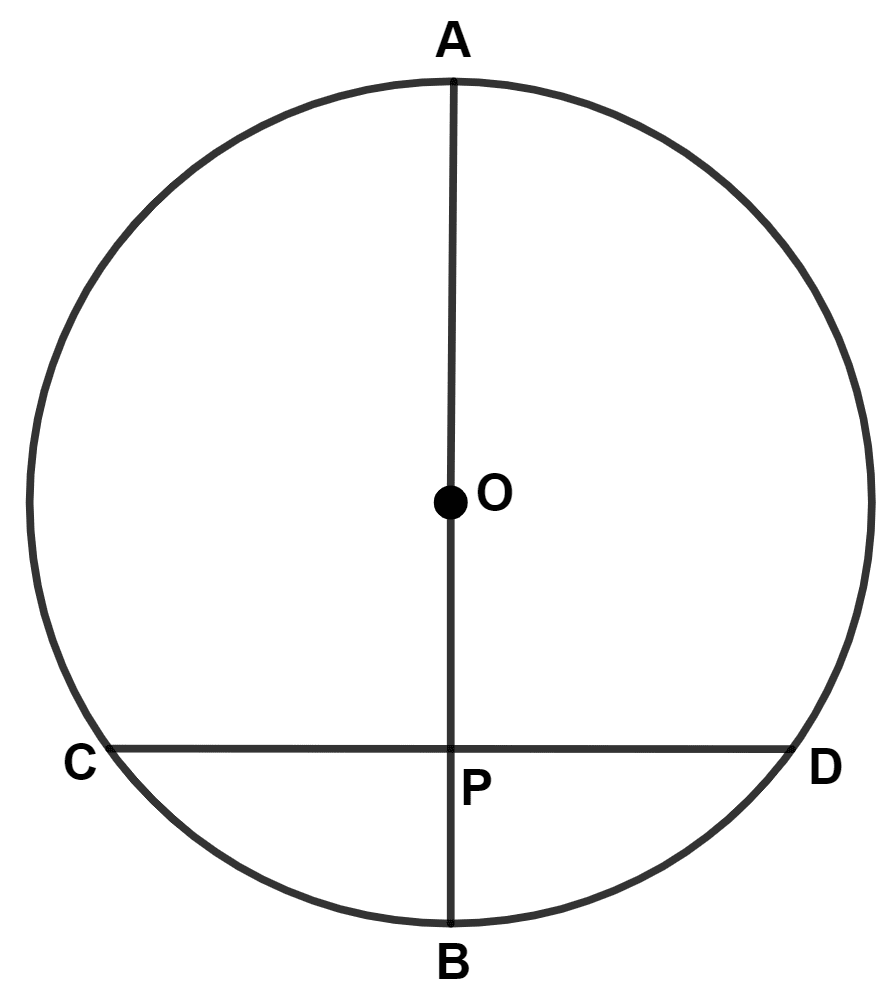
Given OA = OB = 15 cm and OP = 9 cm. Calculate the lengths of :
(i) CD
(ii) AD
(iii) CB.
A straight line is drawn cutting two equal circles and passing through the mid-point M of the line joining their centers O and O'.
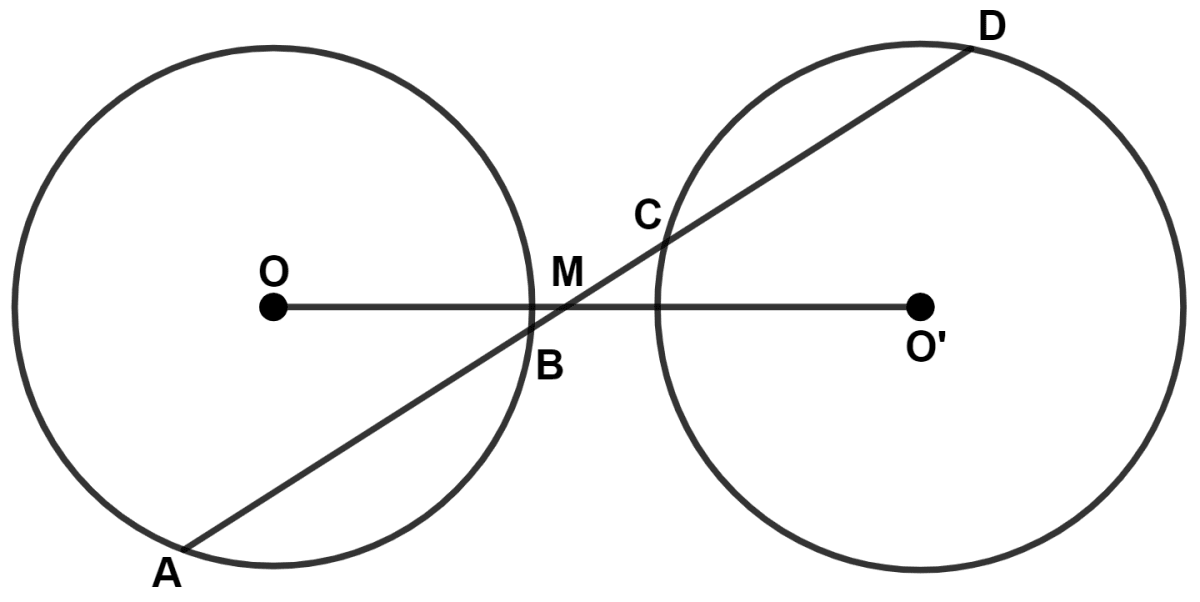
Prove that the chords AB and CD, which are intercepted by the two circles, are equal.