Mathematics
Two parallelogram ABCD and ABEF are equal in area, they lie between the same parallel lines:
Yes
No
Nothing can be said
Answer
If two parallelograms share the same base and are situated between the same parallel lines, their areas will be equal. This is a fundamental property of parallelograms.
Since, area of both the parallelograms are equal and they lie on the same base AB.
Thus, they lie between the same parallel lines.
Hence, option 1 is the correct option.
Related Questions
The area of given parallelogram is:
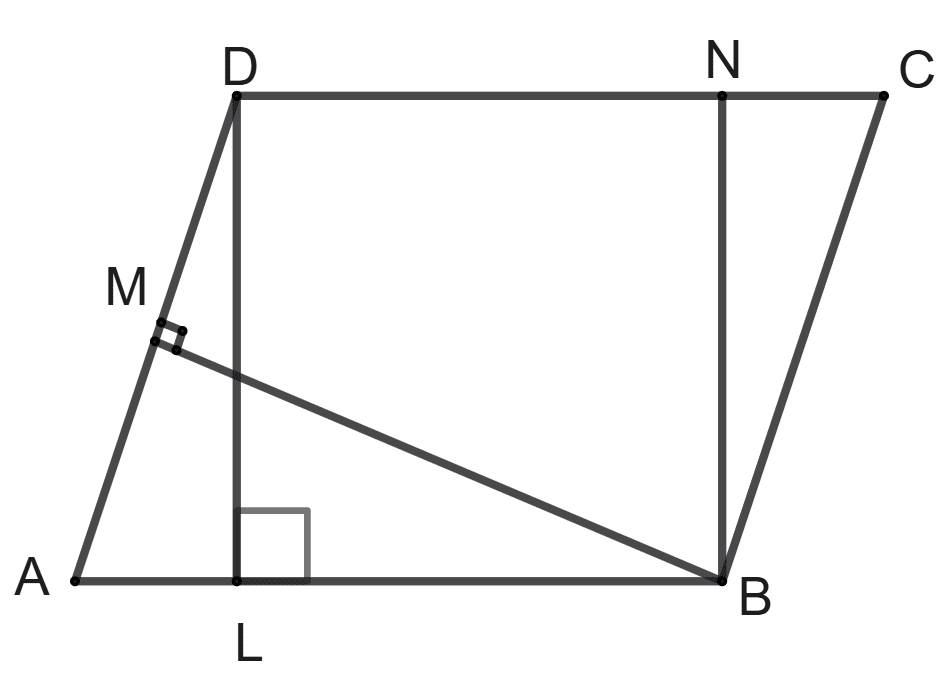
AB x BM
BC x BN
DC x DL
AD x DL
ABCD is a quadrilateral whose diagonals intersect each other at point O. The diagonal AC bisects diagonal BD. Then area of quadrilateral ABCD is :
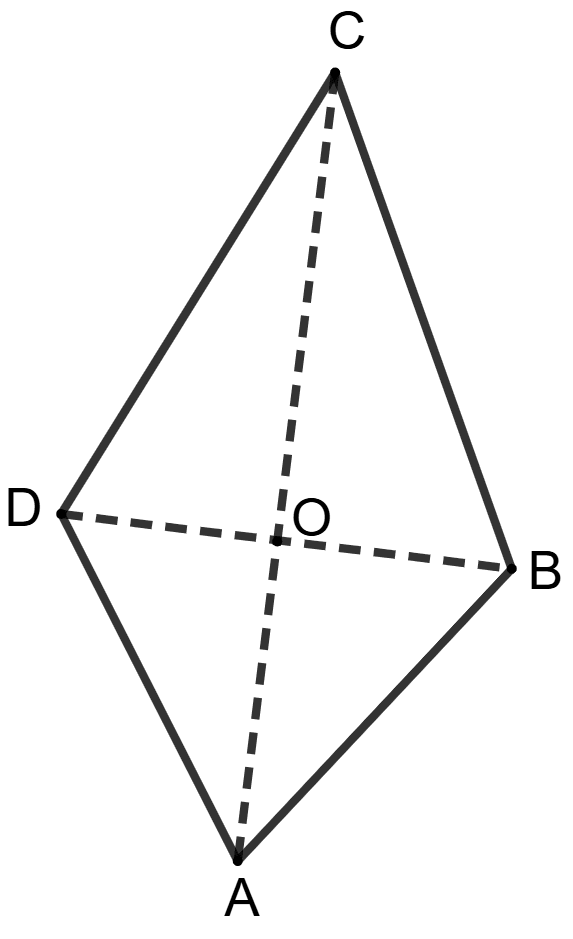
2 x area of ΔABD
2 x area of ΔBCD
4 x area of ΔAOB
2 x area of ΔABC
ABCD is a trapezium with parallel sides AB = a cm and DC = b cm. E and F are the mid-points of the non-parallel sides. The ratio of ar.(ABFE) and ar.(EFCD) is:
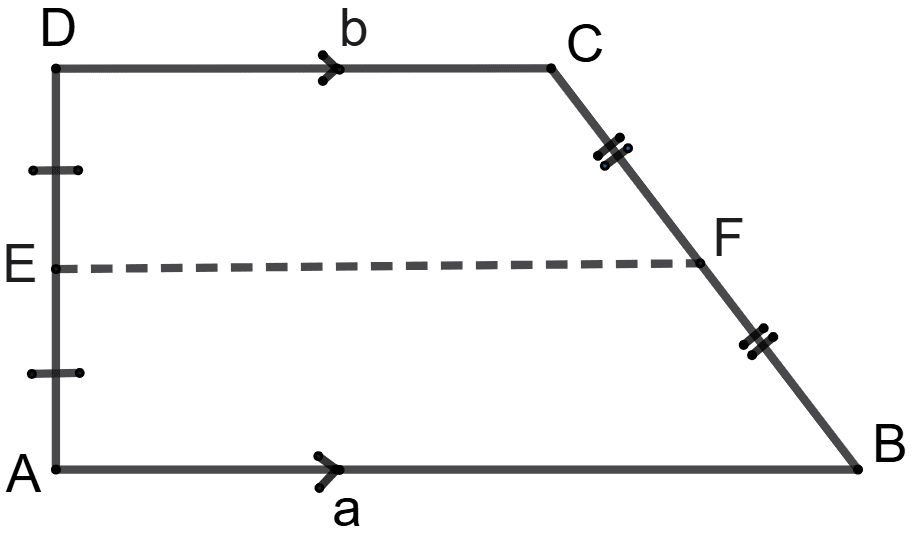
a : b
(3a + b) : (a + 3b)
(a + 3b) : (3a + b)
(2a + b) : (3a + b)
Statement 1: ABCD is a quadrilateral whose diagonal AC divides it into two parts, equal in area.
Statement 2: It is not necessary that the quadrilateral ABCD is a rectangle or a parallelogram or rhombus.
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.