Probability

If A and B are two complementary events then the relation between P(A) and P(B) is :

1. P(A) = P(B)

2. P(A) + P(B) = 0

3. P(A) + P(B) = 1

4. none of these

Answer

We know that,

The probabilities of two complimentary events add up to 1.

∴ P(A) + P(B) = 1

Hence, Option 3 is the correct option.

Out of the vowels of English alphabet, one letter is selected at random. The probability of selecting the letter 'O' is :

1. 1

2. $\dfrac{4}{5}$

3. $\dfrac{1}{26}$

4. $\dfrac{1}{5}$

Answer

Vowels of english alphabet : a, e, i, o, u.

Since, there is one letter 'o' in the vowels.

∴ No. of favourable outcomes = 1

P(selecting the letter 'O') = $\dfrac{\text{No. of favourable outcomes}}{\text{Total no. of possible outcomes}} = \dfrac{1}{5}$.

Hence, Option 4 is the correct option.

When a die is thrown, the probability of getting an even number greater than 4 is :

1. $\dfrac{1}{3}$

2. $\dfrac{2}{3}$

3. $\dfrac{1}{6}$

4. $\dfrac{11}{2}$

Answer

When a dice is thrown, the possible outcomes are 1, 2, 3, 4, 5 and 6.

Even no. greater than 4 is 6.

∴ No. of favourable outcomes = 1

P(getting an even number greater than 4)

= $\dfrac{\text{No. of favourable outcomes}}{\text{Total no. of possible outcomes}} = \dfrac{1}{6}$.

Hence, Option 3 is the correct option.

If a letter is drawn from the letters of English alphabet, then the probability, that it is a letter of the word 'DELHI' is :

1. $\dfrac{1}{5}$

2. $\dfrac{5}{26}$

3. $\dfrac{1}{26}$

4. $\dfrac{21}{26}$

Answer

No. of letters in english alphabet = 26

Letters in the word 'DELHI' are 'D', 'E', 'L', 'H', 'I'.

∴ No. of favourable outcomes = 5

P(drawing a letter of the word 'DELHI')

= $\dfrac{\text{No. of favourable outcomes}}{\text{Total no. of possible outcomes}} = \dfrac{5}{26}$.

Hence, Option 2 is the correct option.

A card is selected at random from a well-shuffled deck of 52 cards. The probability of it being a face card is :

1. $\dfrac{3}{13}$

2. $\dfrac{4}{13}$

3. $\dfrac{6}{13}$

4. $\dfrac{8}{13}$

Answer

No. of face cards in a deck of 52 cards = 12

P(drawing a face card) = $\dfrac{\text{No. of favourable outcomes}}{\text{Total no. of possible outcomes}} = \dfrac{12}{52} = \dfrac{3}{13}$.

Hence, Option 1 is the correct option.

A coin is tossed once. Find the probability of :

(i) getting a tail

(ii) not getting a tail

Answer

In a random experiment of tossing coin once, total number of possible outcomes are 2 which are Head (H) and Tail (T)

(i) Favourable outcome is 'getting a tail'.

∴ Number of favourable outcome = 1.

P(getting a tail) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{1}{2}$.

Hence, the probability of getting a tail = $\dfrac{1}{2}$.

(ii) Favourable outcome is 'not getting a tail' or 'we can say getting a head'.

∴ Number of favourable outcome = 1.

P(not getting a tail) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{1}{2}$.

Hence, the probability of not getting a tail = $\dfrac{1}{2}$.

A bag contains 3 white, 5 black and 2 red balls, all of the same shape and size. A ball is drawn from the bag without looking into it, find the probability that the ball drawn is :

(i) a black ball.

(ii) a red ball.

(iii) a white ball.

(iv) not a red ball.

(v) not a black ball.

Answer

Total number of balls = 3 + 5 + 2 = 10

So, the total number of possible outcomes = 10

(i) There are 5 black balls.

∴ Number of favourable outcomes = 5

P(getting a black ball) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{5}{10} = \dfrac{1}{2}$.

Hence, probability of getting a black ball = $\dfrac{1}{2}$.

(ii) There are 2 red balls.

∴ Number of favourable outcomes = 2.

P(getting a red ball) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{2}{10} = \dfrac{1}{5}$.

Hence, probability of getting a red ball = $\dfrac{1}{5}$.

(iii) There are 3 white balls.

∴ Number of favourable outcomes = 3.

P(getting a white ball) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{3}{10}$.

Hence, probability of getting a white ball = $\dfrac{3}{10}$.

(iv) There are 2 red balls.

∴ 8 (10 - 2) balls which are not red.

∴ Number of favourable outcomes = 8

Thus, P(not getting a red ball) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{8}{10} = \dfrac{4}{5}$.

Hence, the probability of not getting a red ball = $\dfrac{4}{5}$.

(v) There are 3 white + 2 red = 5 balls which are not black

∴ Number of favourable outcomes = 5

Thus, P(not getting a black ball) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{5}{10} = \dfrac{1}{2}$.

Hence, the probability of not getting a black ball = $\dfrac{1}{2}$.

In a single throw of a dice, find the probability of getting a number :

(i) greater than 4.

(ii) less than or equal to 4.

(iii) not greater than 4.

Answer

Here, the sample space = {1, 2, 3, 4, 5, 6}

So, No. of possible outcomes = 6

(i) No. greater than 4 = {5, 6}

∴ Number of favourable outcomes = 2

Thus, P(getting a no. greater than 4) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{2}{6} = \dfrac{1}{3}$.

Hence, the probability of getting a number greater than 4 = $\dfrac{1}{3}$.

(ii) No. less than or equal to 4 = {1, 2, 3, 4}

∴ Number of favourable outcomes = 4

Thus, P(getting a no. less than or equal to 4) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{4}{6} = \dfrac{2}{3}$.

Hence, the probability of getting a number less than or equal to 4 = $\dfrac{2}{3}$.

(iii) Numbers not greater than 4 = {1, 2, 3, 4}

∴ Number of favourable outcomes = 4

Thus, P(getting no. not greater than 4) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{4}{6} = \dfrac{2}{3}$.

Hence, the probability of getting a number not greater than 4 = $\dfrac{2}{3}$.

From a well shuffled deck of 52 cards, one card is drawn. Find the probability that the card drawn will :

(i) be a black card.

(ii) not be a red card.

(iii) be a red card.

(iv) be a face card.

(v) be a face card of red colour.

Answer

We know that,

Total number of cards = 52

So, the total number of outcomes = 52

There are 13 cards of each type. The cards of heart and diamond are red in colour. Spade and clubs are black. Hence, there are 26 red cards and 26 black cards.

(i) Number of black cards in a deck = 26 (13 spade + 13 club)

∴ Number of favourable outcomes = 26

P(of drawing a black card) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{26}{52} = \dfrac{1}{2}$.

Hence, probability of drawing a black card = $\dfrac{1}{2}$.

(ii) Number of red cards in a deck = 26

∴ Number of non-red (black) cards = 52 - 26 = 26.

∴ Number of favourable outcomes = 26

P(of not drawing a red card) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{26}{52} = \dfrac{1}{2}$.

Hence, probability of not drawing a red card = $\dfrac{1}{2}$.

(iii) Number of red cards in a deck = 26.

∴ Number of favourable outcomes = 26

P(of drawing a red card) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{26}{52} = \dfrac{1}{2}$.

Hence, probability of drawing a red card = $\dfrac{1}{2}$.

(iv) There are 12 face cards (4 kings, 4 queens and 4 jacks) in a deck.

∴ Number of favourable outcomes = 12

P(of drawing a face card) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{12}{52} = \dfrac{3}{13}$.

Hence, probability of drawing a face card = $\dfrac{3}{13}$.

(v) There are 26 red cards in a deck, and 6 of these cards are face cards (2 kings, 2 queens and 2 jacks).

∴ Number of favourable outcomes = 6

P(of drawing a red face card) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{6}{52} = \dfrac{3}{26}$.

Hence, probability of drawing a red face card = $\dfrac{3}{26}$.

If A and B are two complementary events then what is the relation between P(A) and P(B)?

Answer

Two complementary events, taken together, include all the outcomes for an experiment and the sum of the probabilities of all outcomes is 1.

∴ P(A) + P(B) = 1

Hence, P(A) + P(B) = 1.

If the probability of happening an event A is 0.46. What will be the probability of not happening of the event A?

Answer

P(A) = 0.46

Let P(A') be the probability of not happening of event A.

Then we know that,

⇒ P(A) + P(A') = 1

⇒ P(A') = 1 - P(A)

⇒ P(A') = 1 - 0.46 = 0.54

Hence, the probability of not happening of event A is 0.54

In a T.T. match between Geeta and Ritu, the probability of the winning of Ritu is 0.73. Find the probability of:

(i) winning of Geeta

(ii) not winning of Ritu.

Answer

(i) Winning of Geeta is a complementary event to winning of Ritu.

∴ P(winning of Ritu) + P(winning of Geeta) = 1

⇒ P(winning of Geeta) = 1 - P(winning of Ritu)

⇒ P(winning of Geeta) = 1 - 0.73

⇒ P(winning of Geeta) = 0.27

Hence, the probability of winning of Geeta = 0.27

(ii) P(not winning of Ritu) = P(winning of Geeta) = 0.27

Hence, the probability of not winning of Ritu = 0.27

In a race between Mahesh and John; the probability that John will loose the race is 0.54. Find the probability of :

(i) winning of Mahesh

(ii) winning of John.

Answer

(i) Since, the race is between Mahesh and John.

We can say that,

P(winning of Mahesh) = P(John loosing the race) = 0.54

Hence, the probability of winning of Mahesh = 0.54

(ii) Winning and loosing of John are complementary events.

∴ P(winning of John) + P(loosing of John) = 1

⇒ P(winning of John) + 0.54 = 1

⇒ P(winning of John) = 1 - 0.54 = 0.46

Hence, the probability of winning of John = 0.46

(i) Write the probability of sure event.

(ii) Write the probability of an even which is impossible.

(iii) For an event E, write a relation representing the range of values of P(E).

Answer

(i) Probability of sure event = 1.

(ii) Since, impossible event cannot occur. Hence, the probability of an impossible event = 0.

(iii) The probability of an event cannot be less than 0 and greater than 1. Hence, 0 ≤ P(E) ≤ 1.

In a single throw of a dice, find the probability of getting :

(i) 5

(ii) 8

(iii) a number less than 8

(iv) a prime number.

Answer

In a single throw of a dice, the possible outcomes are {1, 2, 3, 4, 5, 6}.

∴ No. of possible outcomes = 6.

(i) No. of favourable outcomes (for getting a 5) = 1

P(getting a 5) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{1}{6}$.

Hence, the probability of getting a 5 = $\dfrac{1}{6}$.

(ii) Since, no face as number 8 written on it, there is no outcome favourable to 8.

∴ No. of favourable outcomes = 0.

P(getting a number 8) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{0}{6}$ = 0.

Hence, the probability of getting 8 = 0.

(iii) Out of 1, 2, 3, 4, 5, 6, the numbers less than 8 are 1, 2, 3, 4, 5 and 6.

∴ No. of favourable outcomes = 6.

P(getting a number less than 8) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{6}{6}$ = 1.

Hence, the probability of getting a number less than 8 = 1.

(iv) Out of 1, 2, 3, 4, 5, 6, the prime numbers are 2, 3, 5.

∴ No. of favourable outcomes = 3.

P(getting a prime number) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{3}{6} = \dfrac{1}{2}$.

Hence, the probability of getting a prime number = $\dfrac{1}{2}$.

A dice is thrown once. Find the probability of getting :

(i) an even number

(ii) a number between 3 and 8

(iii) an even number or a multiple of 3.

Answer

In a single throw of dice, the possible outcomes are {1, 2, 3, 4, 5, 6}.

∴ No. of possible outcomes = 6.

(i) Out of 1, 2, 3, 4, 5, 6, the even numbers are 2, 4, 6.

∴ No. of favourable outcomes = 3.

P(getting an even number) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{3}{6} = \dfrac{1}{2}$.

Hence, the probability of getting an even number = $\dfrac{1}{2}$.

(ii) Out of 1, 2, 3, 4, 5, 6, the numbers between 3 and 8 are 4, 5, 6.

∴ No. of favourable outcomes = 3.

P(getting a number between 3 and 8) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{3}{6} = \dfrac{1}{2}$.

Hence, the probability of getting a number between 3 and 8 = $\dfrac{1}{2}$.

(iii) Out of 1, 2, 3, 4, 5, 6, the numbers that are either an even number or a multiple of 3 are 2, 3, 4, 6.

∴ No. of favourable outcomes = 4.

P(getting either an even number or a multiple of 3) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{4}{6} = \dfrac{2}{3}$.

Hence, the probability of getting either an even number or a multiple of 3 = $\dfrac{2}{3}$.

Which of the following cannot be the probability of an event ?

(i) $\dfrac{3}{5}$

(ii) 2.7

(iii) 43%

(iv) -0.6

(v) -3.2

(vi) 0.35

Answer

We know that,

0 ≤ P(Event) ≤ 1.

2.7 cannot be probability of an event as it is greater than 1.

Similarly, -0.6 and -3.2 cannot be as probability cannot be negative.

Hence, (ii), (iv) and (v) cannot be probability of an event.

A bag contains six identical black balls. A child withdraws one ball from the bag without looking into it. What is the probability that he takes out:

(i) a white ball ?

(ii) a black ball ?

Answer

There are six identical black balls.

∴ No. of possible outcomes = 6.

(i) Since, there is no white ball.

∴ No. of favourable outcomes (of getting a white ball) = 0.

P(getting a white ball) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{0}{6}$ = 0.

Hence, the probability of getting a white ball = 0.

(ii) There are 6 identical black balls.

∴ No. of favourable outcomes (of getting a black ball) = 6.

P(getting a black ball) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{6}{6}$ = 1.

Hence, the probability of getting a black ball = 1.

A single letter is selected at random from the word 'Probability'. Find the probability that it is a vowel.

Answer

The word probability has 11 letters.

∴ No. of possible outcomes = 11.

Vowel letters in 'Probability' are 'O', 'A', 'I', 'I'.

No. of favourable outcomes (of getting a vowel) = 4.

P(getting a vowel) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{4}{11}$.

Hence, the probability that letter drawn is a vowel = $\dfrac{4}{11}$.

Ramesh chooses a date at random in January for a party (see the following figure).

Find the probability that he chooses :

(i) a Wednesday

(ii) a Friday

(iii) a Tuesday or a Saturday.

Answer

Since, there are 31 days in January.

∴ No. of possible outcomes = 31.

(i) There is wednesday on 1st, 8th, 15th, 22nd and 29th of January.

∴ No. of favourable outcomes = 5

P(getting a Wednesday) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{5}{31}$.

Hence, the probability of getting a Wednesday = $\dfrac{5}{31}$.

(ii) There is friday on 3rd, 10th, 17th, 24th and 31st of January.

∴ No. of favourable outcomes = 5

P(getting a Friday) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{5}{31}$.

Hence, the probability of getting a Friday = $\dfrac{5}{31}$.

(iii) There is tuesday on 7th, 14th, 21st and 28th of January and Saturday on 4th, 11th, 18th and 25th of January.

∴ No. of favourable outcomes = 8.

P(getting a Tuesday or Saturday) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{8}{31}$.

Hence, the probability of getting a Tuesday or Saturday = $\dfrac{8}{31}$.

A card is drawn from a well-shuffled pack of 52 cards. The probability of the card drawn to be king and jack is :

1. 1

2. 0

3. $\dfrac{1}{2}$

4. $\dfrac{3}{13}$

Answer

A card cannot be a king and a jack simultaneously.

P(drawing a king and jack) = $\dfrac{\text{No. of favourable outcomes}}{\text{Total no. of possible outcomes}} = \dfrac{0}{52}$ = 0.

Hence, Option 2 is the correct option.

The probability that a non-leap year has 53 Sundays is :

1. 1

2. $\dfrac{1}{7}$

3. $\dfrac{1}{365}$

4. $\dfrac{7}{365}$

Answer

There are 365 days in a non-leap year.

No. of weeks = $\dfrac{365}{7}$ = 52 weeks and 1 day.

Since, there is one sunday in a week, and one week has seven days.

So, in order to have 53 sundays the 1 day that remains should also be sunday.

P(that a non-leap year has 53 sundays)

= $\dfrac{\text{No. of favourable outcomes}}{\text{Total no. of possible outcomes}} = \dfrac{1}{7}$.

Hence, Option 2 is the correct option.

Out of 800 identical articles some are selected and remaining are rejected. If the probability of an article to be rejected is 0.425; the number of rejected articles is :

1. 340

2. 800

3. 430

4. 560

Answer

⇒ P(rejecting an item) = $\dfrac{\text{No. of favourable outcomes}}{\text{Total no. of possible outcomes}}$

⇒ 0.425 = $\dfrac{\text{No. of favourable outcomes}}{800}$

⇒ No. of favourable outcomes = 0.425 × 800 = 340.

Hence, Option 1 is the correct option.

A bag contains 24 balls of which 4 are red, 8 are white and remaining are blue. A ball is drawn at random, the probability of it to be blue is :

1. 0.5

2. 1

3. $\dfrac{1}{3}$

4. 2

Answer

No. of blue balls = 24 - 4 - 8 = 12.

P(drawing a blue ball)

= $\dfrac{\text{No. of favourable outcomes}}{\text{Total no. of possible outcomes}} = \dfrac{12}{24} = \dfrac{1}{2}$ = 0.5

Hence, Option 1 is the correct option.

An integer is chosen from integers between 0 and 51, the probability of it to be divisible by 6 is :

1. $\dfrac{3}{25}$

2. $\dfrac{4}{25}$

3. $\dfrac{1}{50}$

4. $\dfrac{1}{25}$

Answer

Integers between 0 and 51 are :

1, 2, 3, ......., 50.

No. of possible outcomes : 50

Integers divisible by 6 between 0 and 51 :

6, 12, 18, 24, 30, 36, 42, 48.

No. of favourable outcomes : 8

P(that a number is divisible by 6) : $\dfrac{\text{No. of favourable outcomes}}{\text{Total no. of possible outcomes}} = \dfrac{8}{50} = \dfrac{4}{25}$.

Hence, Option 2 is the correct option.

Nine cards (identical in all respects) are numbered 2 to 10. A card is selected from them at random. Find the probability that the card selected will be:

(i) an even number

(ii) a multiple of 3

(iii) an even number and a multiple of 3

(iv) an even number or a multiple of 3

Answer

We know that, there are totally 9 cards from which one card is drawn.

Total number of possible outcomes = 9

(i) From numbers 2 to 10, there are 5 even numbers i.e. 2, 4, 6, 8, 10

∴ Favorable number of outcomes = 5

P(selecting a card with an even number) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{5}{9}$.

Hence, the probability that card selected will be an even number = $\dfrac{5}{9}$.

(ii) From numbers 2 to 10, there are 3 numbers which are multiples of 3 i.e. 3, 6, 9.

∴ Favorable number of outcomes = 3

P(selecting a card with multiple of 3) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{3}{9} = \dfrac{1}{3}$.

Hence, the probability that card selected will be a multiple of 3 = $\dfrac{3}{9} = \dfrac{1}{3}$.

(iii) From numbers 2 to 10, there is one number which is an even number as well as multiple of 3 i.e. 6

∴ Number of favourable outcomes = 1

P(selecting a card with even number and multiple of 3) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{1}{9}$.

Hence, the probability of selecting a card with even number and multiple of 3 = $\dfrac{1}{9}$.

(iv) From numbers 2 to 10, there are 7 numbers which are even numbers or a multiple of 3 i.e. 2, 3, 4, 6, 8, 9, 10

∴ Number of favourable outcomes = 7.

P(selecting a card with even number or multiple of 3) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{7}{9}$.

Hence, the probability of selecting a card with even number or multiple of 3 = $\dfrac{7}{9}$.

Hundred identical cards are numbered from 1 to 100. The cards are well shuffled and then a card is drawn. Find the probability that the number on the card drawn is:

(i) a multiple of 5

(ii) a multiple of 6

(iii) between 40 and 60

(iv) greater than 85

(v) less than 48

Answer

We know that, there are 100 cards from which one card is drawn.

Number of possible outcomes = 100

(i) From numbers 1 to 100, there are 20 numbers which are multiple of 5 i.e. {5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 100}

∴ Number of favourable outcomes = 20.

P(selecting a card with a multiple of 5) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{20}{100} = \dfrac{1}{5}$.

Hence, the probability of selecting a card with a multiple of 5 = $\dfrac{1}{5}$.

(ii) From numbers 1 to 100, there are 16 numbers which are multiple of 6 i.e. {6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78, 84, 90, 96}

∴ Number of favourable outcomes = 16.

P(selecting a card with a multiple of 6) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{16}{100} = \dfrac{4}{25}$.

Hence, the probability of selecting a card with a multiple of 6 = $\dfrac{4}{25}$.

(iii) From numbers 1 to 100, there are 19 numbers which are between 40 and 60 i.e. {41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59}

∴ Number of favourable outcomes = 19.

P(selecting a card between 40 and 60) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{19}{100}$.

Hence, the probability of selecting a card between 40 and 60 = $\dfrac{19}{100}$.

(iv) From numbers 1 to 100, there are 15 numbers which are greater than 85 i.e. {86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100}

∴ Number of favourable outcomes = 15.

P(selecting a card with number greater than 85) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{15}{100} = \dfrac{3}{20}$.

Hence, the probability of selecting a card with number greater than 85 = $\dfrac{3}{20}$.

(v) From numbers 1 to 100, there are 47 numbers which are less than 48 i.e. {1, 2, ……….., 46, 47}

∴ Number of favourable outcomes = 47.

P(selecting a card with number less than 48) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{47}{100}$.

Hence, the probability of selecting a card with number less than 47 = $\dfrac{47}{100}$.

From 25 identical cards, numbered 1, 2, 3, 4, 5, ..... , 24, 25; one card is drawn at random. Find the probability that the number on the card drawn is a multiple of :

(i) 3

(ii) 5

(iii) 3 and 5

(iv) 3 or 5

Answer

We know that, there are 25 cards from which one card is drawn.

Number of possible outcomes = 25.

(i) From numbers 1 to 25, there are 8 numbers which are multiple of 3 i.e. {3, 6, 9, 12, 15, 18, 21, 24}

∴ Number of favourable outcomes = 8.

P(selecting a card with a multiple of 3) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{8}{25}$.

Hence, the probability of selecting a card with a multiple of 3 = $\dfrac{8}{25}$.

(ii) From numbers 1 to 25, there are 5 numbers which are multiple of 5 i.e. {5, 10, 15, 20, 25}

∴ Number of favourable outcomes = 5.

P(selecting a card with a multiple of 5) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{5}{25} = \dfrac{1}{5}$.

Hence, the probability of selecting a card with a multiple of 5 = $\dfrac{1}{5}$.

(iii) From numbers 1 to 25, there is only one number which is multiple of 3 and 5 i.e. {15}

∴ Number of favourable outcomes = 1.

P(selecting a card with a multiple of 3 and 5) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{1}{25}$.

Hence, the probability of selecting a card with a multiple of 3 and 5 = $\dfrac{1}{25}$.

(iv) From numbers 1 to 25, there are 12 numbers which are multiple of 3 or 5 i.e. {3, 5, 6, 9, 10, 12, 15, 18, 20, 21, 24, 25}

∴ Number of favourable outcomes = 12.

P(selecting a card with a multiple of 3 or 5) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{12}{25}$.

Hence, the probability of selecting a card with a multiple of 3 or 5 = $\dfrac{12}{25}$.

A dice is thrown once. Find the probability of getting a number :

(i) less than 3

(ii) greater than or equal to 4

(iii) less than 8

(iv) greater than 6

Answer

We know that,

In throwing a dice, total possible outcomes = {1, 2, 3, 4, 5, 6}

No. of favourable outcomes = 6.

(i) On a dice, numbers less than 3 are = {1, 2}

∴ No. of favourable outcomes = 2.

P(getting a number less than 3) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{2}{6} = \dfrac{1}{3}$.

Hence, the probability of getting a number less than 3 = $\dfrac{1}{3}$.

(ii) On a dice, numbers greater than or equal to 4 = {4, 5, 6}

∴ No. of favourable outcomes = 3.

P(getting a number greater than or equal to 4) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{3}{6} = \dfrac{1}{2}$.

Hence, the probability of getting a number greater than or equal to 4 is $\dfrac{1}{2}$.

(iii) On a dice, numbers less than 8 = {1, 2, 3, 4, 5, 6}

∴ No. of favourable outcomes = 6.

P(getting a number less than 8) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{6}{6} = 1$.

Hence, the probability of getting a number less than 8 = 1.

(iv) On a dice, numbers greater than 6 = 0

∴ No. of favourable outcomes = 0.

P(getting a number greater than 6) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{0}{6}$ = 0.

Hence, the probability of getting a number greater than 6 = 0.

A book contains 85 pages. A page is chosen at random. What is the probability that the sum of the digits on the page is 8?

Answer

There are 85 pages.

∴ No. of possible outcomes = 85.

Page numbers whose sum of digits equal to 8 are {08, 17, 26, 35, 44, 53, 62, 71, 80}.

∴ No. of favourable outcomes = 9

P(getting a page with sum of digits equal to 8) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{9}{85}$.

Hence, the probability of getting a page with sum of digits equal to 8 is $\dfrac{9}{85}$.

A pair of dice is thrown. Find the probability of getting a sum of 10 or more, if 5 appears on the first dice.

Answer

When two dice are thrown simultaneously;

Total number of possible outcomes = 6 × 6 = 36.

For obtaining a sum of 10 or more, if 5 appears on the first dice, the favourable outcomes are :

(5, 5) and (5, 6).

∴ No. of favourable outcomes = 2.

P(getting a sum of 10 or more) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{2}{36} = \dfrac{1}{18}$.

Hence, the probability of getting a sum of 10 or more, if 5 appears on the first dice = $\dfrac{1}{18}$.

If two coins are tossed once, what is the probability of getting :

(i) 2 heads ?

(ii) at least one head ?

(iii) both heads or both tails ?

Answer

When two coins are tossed,

Possible outcomes = {HH, HT, TH, TT}.

No. of possible outcomes = 4.

(i) Favourable outcomes for getting 2 heads = {HH}.

No. of favourable outcomes = 1.

P(getting 2 heads) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{1}{4}$.

Hence, the probability of getting 2 heads = $\dfrac{1}{4}$.

(ii) Favourable outcomes for getting at least one head = {HT, TH, HH}.

No. of favourable outcomes = 3.

P(getting at least one head) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{3}{4}$.

Hence, the probability of getting at least one head = $\dfrac{3}{4}$.

(iii) Favourable outcomes for getting both heads or both tails = {HH, TT}.

No. of favourable outcomes = 2.

P(getting both heads or both tails) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{2}{4} = \dfrac{1}{2}$.

Hence, the probability of getting both heads or both tails = $\dfrac{1}{2}$.

Two dice are rolled together. Find the probability of getting :

(i) a total of at least 10.

(ii) a multiple of 2 on one die and an odd number on the other die.

Answer

When two dice are thrown simultaneously;

Total number of possible outcomes = 6 × 6 = 36.

(i) For obtaining a sum of at least 10, the favourable outcomes are :

(4, 6), (5, 5), (5, 6), (6, 4), (6, 5) and (6, 6).

∴ No. of favourable outcomes = 6.

P(getting a total of at least 10) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{6}{36} = \dfrac{1}{6}$.

Hence, the probability of getting a total of at least 10 = $\dfrac{1}{6}$.

(ii) For obtaining a multiple of 2 on one die and an odd number on the other die, the favourable outcomes are :

(1, 2), (1, 4), (1, 6), (2, 1), (2, 3), (2, 5), (3, 2), (3, 4), (3, 6), (4, 1), (4, 3), (4, 5), (5, 2), (5, 4), (5, 6), (6, 1), (6, 3), (6, 5).

∴ No. of favourable outcomes = 18.

P(getting a multiple of 2 on one die and an odd number on the other die) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{18}{36} = \dfrac{1}{2}$.

Hence, the probability of getting a multiple of 2 on one die and an odd number on the other die = $\dfrac{1}{2}$.

A card is drawn from a well-shuffled pack of 52 cards. Find the probability that the card drawn is :

(i) a spade.

(ii) a red card.

(iii) a face card.

(iv) 5 of heart or diamond.

(v) Jack or queen.

(vi) ace and king.

(vii) a red and a king.

(viii) a red or a king.

Answer

There are 52 cards in a deck which are divided into 4 suits of 13 cards each.

∴ No. of possible outcomes = 52.

(i) There are 13 spades in a deck of playing cards.

∴ No. of favourable outcomes = 13.

P(drawing a spade) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{13}{52} = \dfrac{1}{4}$.

Hence, the probability of drawing a spade = $\dfrac{1}{4}$.

(ii) There are 26 red cards (13 hearts and 13 diamonds).

∴ No. of favourable outcomes = 26.

P(drawing a red card) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{26}{52} = \dfrac{1}{2}$.

Hence, the probability of drawing a red card = $\dfrac{1}{2}$.

(iii) There are 12 face cards (4 kings, 4 queens, 4 jacks) in a deck.

∴ No. of favourable outcomes = 12.

P(drawing a face card) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{12}{52} = \dfrac{3}{13}$.

Hence, the probability of drawing a face card = $\dfrac{3}{13}$.

(iv) There are 2 cards one of each heart and diamond with no. 5.

∴ No. of favourable outcomes = 2.

P(drawing a 5 of heart or diamond) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{2}{52} = \dfrac{1}{26}$.

Hence, the probability of drawing a 5 of heart or diamond = $\dfrac{1}{26}$.

(v) There are 4 jacks and 4 queens in a deck.

∴ No. of favourable outcomes = 8.

P(drawing a jack or queen) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{8}{52} = \dfrac{2}{13}$.

Hence, the probability of drawing a jack or queen = $\dfrac{2}{13}$.

(vi) An ace and a king cannot be in a single card.

∴ No. of favourable outcomes = 0.

P(drawing an ace and a king) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}}$ = 0.

Hence, the probability of drawing an ace and a king = 0.

(vii) The king of diamond and heart is red in colour.

∴ No. of favourable outcomes = 2.

P(drawing a red and a king) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{2}{52} = \dfrac{1}{26}$.

Hence, the probability of drawing a red and a king = $\dfrac{1}{26}$.

(viii) There are 26 red (13 hearts + 13 diamonds) and 1 king of each (club and spade).

∴ No. of favourable outcomes = 26 + 1 + 1 = 28.

P(drawing a red or a king) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{28}{52} = \dfrac{7}{13}$.

Hence, the probability of drawing a red or a king = $\dfrac{7}{13}$.

A bag contains 16 coloured balls. Six are green, 7 are red and 3 are white. A ball is chosen, without looking into the bag. Find the probability that the ball chosen is :

(i) red

(ii) not red

(iii) white

(iv) not white

(v) green or red

(vi) white or green

(vii) green or red or white

Answer

There are 16 coloured balls.

∴ No. of possible outcomes = 16.

(i) There are 7 red balls.

∴ No. of favourable outcomes = 7

P(drawing a red ball) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{7}{16}$.

Hence, the probability of drawing a red ball = $\dfrac{7}{16}$.

(ii) There are 9 non red balls (6 green + 3 white).

∴ No. of favourable outcomes = 9

P(not drawing a red ball) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{9}{16}$.

Hence, the probability of not drawing a red ball = $\dfrac{9}{16}$.

(iii) There are 3 white balls.

∴ No. of favourable outcomes = 3

P(drawing a white ball) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{3}{16}$.

Hence, the probability of drawing a white ball = $\dfrac{3}{16}$.

(iv) There are 13 non white balls (6 green + 7 red).

∴ No. of favourable outcomes = 13

P(not drawing a white ball) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{13}{16}$.

Hence, the probability of not drawing a white ball = $\dfrac{13}{16}$.

(v) Since, there are only 3 coloured (red, green and white) balls.

We can say that,

P(drawing a green or red ball) = P(not drawing a white ball) = $\dfrac{13}{16}$.

Hence, the probability of drawing a green or red ball = $\dfrac{13}{16}$.

(vi) Since, there are only 3 coloured (red, green and white) balls.

We can say that,

P(drawing a white or green ball) = P(not drawing a red ball).

From part (ii),

P(not drawing a red ball) = $\dfrac{9}{16}$.

∴ P(drawing a white or green ball) = $\dfrac{9}{16}$.

Hence, the probability of drawing a white or green ball = $\dfrac{9}{16}$.

(vii) There are 6 green, 7 red and 3 white balls.

∴ No. of favourable outcomes = 16.

P(drawing a green or red or white ball) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{16}{16}$ = 1.

Hence, the probability of drawing a green or red or white ball = 1.

A ball is drawn at random from a box containing 12 white, 16 red and 20 green balls. Determine the probability that the ball drawn is :

(i) white

(ii) red

(iii) not green

(iv) red or white

Answer

Box contains 12 white, 16 red and 20 green balls.

∴ No. of possible outcomes = 48.

(i) There are 12 white balls.

∴ No. of favourable outcomes = 12

P(drawing a white ball) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{12}{48} = \dfrac{1}{4}$.

Hence, the probability of drawing a white ball = $\dfrac{1}{4}$.

(ii) There are 16 red balls.

∴ No. of favourable outcomes = 16

P(drawing a red ball) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{16}{48} = \dfrac{1}{3}$.

Hence, the probability of drawing a red ball = $\dfrac{1}{3}$.

(iii) There are 28 non green balls (12 white + 16 red).

∴ No. of favourable outcomes = 28

P(not drawing a green ball) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{28}{48} = \dfrac{7}{12}$.

Hence, the probability of not drawing a green ball = $\dfrac{7}{12}$.

(iv) Since, there are only 3 different colour balls.

We can say that,

P(drawing a red or white ball) = P(not drawing a green ball) = $\dfrac{7}{12}$.

Hence, the probability of drawing a red or white ball = $\dfrac{7}{12}$.

A card is drawn from a pack of 52 cards. Find the probability that the card drawn is :

(i) a red card

(ii) a black card

(iii) a spade

(iv) an ace

(v) a black ace

(vi) ace of diamonds

(vii) not a club

(viii) a queen or a jack.

Answer

In a deck of 52 cards, there are 4 suits of 13 cards each.

No. of possible outcomes = 52.

(i) There are 26 red cards (13 hearts + 13 diamonds).

∴ No. of favourable outcomes = 26.

P(drawing a red card) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{26}{52} = \dfrac{1}{2}$.

Hence, probability of drawing a red card = $\dfrac{1}{2}$.

(ii) There are 26 black cards (13 clubs + 13 spades).

∴ No. of favourable outcomes = 26.

P(drawing a black card) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{26}{52} = \dfrac{1}{2}$.

Hence, probability of drawing a black card = $\dfrac{1}{2}$.

(iii) There are 13 spades in a deck of playing cards.

∴ No. of favourable outcomes = 13.

P(drawing a spade) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{13}{52} = \dfrac{1}{4}$.

Hence, probability of drawing a spade = $\dfrac{1}{4}$.

(iv) There are 4 ace in a deck of playing cards.

∴ No. of favourable outcomes = 4.

P(drawing an ace) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{4}{52} = \dfrac{1}{13}$.

Hence, probability of drawing an ace = $\dfrac{1}{13}$.

(v) There are 2 black ace (1 of club + 1 of spade).

∴ No. of favourable outcomes = 2.

P(drawing a black ace) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{2}{52} = \dfrac{1}{26}$.

Hence, probability of drawing a black ace = $\dfrac{1}{26}$.

(vi) There is 1 ace of diamond.

∴ No. of favourable outcomes = 1.

P(drawing an ace of diamond) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{1}{52}$.

Hence, probability of drawing an ace of diamond = $\dfrac{1}{52}$.

(vii) There are 13 clubs so, there are 39 (52 - 13) non-club cards.

∴ No. of favourable outcomes = 39.

P(drawing a non-club card) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{39}{52} = \dfrac{3}{4}$.

Hence, probability of not drawing a club = $\dfrac{3}{4}$.

(viii) There are 4 queens and 4 jacks.

∴ No. of favourable outcomes = 8.

P(drawing a queen or a jack) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{8}{52} = \dfrac{2}{13}$.

Hence, probability of drawing a queen or a jack = $\dfrac{2}{13}$.

Thirty identical cards are marked with numbers 1 to 30. If one card is drawn at random, find the probability that it is :

(i) a multiple of 4 or 6.

(ii) a multiple of 3 and 5.

(iii) a multiple of 3 or 5.

Answer

Since, there are 30 identical cards.

No. of possible outcomes = 30.

(i) Cards numbered 4, 6, 8, 12, 16, 18, 20, 24, 28, 30 are multiple of either 4 or 6.

∴ No. of favourable outcomes = 10.

P(getting a card which is a multiple of 4 or 6) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{10}{30} = \dfrac{1}{3}$.

Hence, the probability of drawing a card which is a multiple of 4 or 6 = $\dfrac{1}{3}$.

(ii) Cards numbered 15, 30 are multiple of 3 and 5.

∴ No. of favourable outcomes = 2.

P(getting a card which is a multiple of 3 and 5) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{2}{30} = \dfrac{1}{15}$.

Hence, the probability of drawing a card which is a multiple of 3 and 5 = $\dfrac{1}{15}$.

(iii) Cards numbered 3, 5, 6, 9, 10, 12, 15, 18, 20, 21, 24, 25, 27, 30 are multiple of either 3 or 5.

∴ No. of favourable outcomes = 14.

P(getting a card which is a multiple of 3 or 5) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{14}{30} = \dfrac{7}{15}$.

Hence, the probability of drawing a card which is a multiple of 3 or 5 = $\dfrac{7}{15}$.

In a single throw of two dice, find the probability of :

(i) a doublet

(ii) a number less than 3 on each dice

(iii) an odd number as a sum

(iv) a total of atmost 10

(v) an odd number on one dice and a number less than or equal to 4 on other dice.

Answer

When two dice are rolled simultaneously;

Total number of possible outcomes = 6 × 6 = 36.

(i) For obtaining a doublet, the favourable outcomes are : (1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6).

∴ Number of favourable outcomes = 6

P(getting a doublet) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{6}{36} = \dfrac{1}{6}$.

Hence, the probability of getting a doublet = $\dfrac{1}{6}$.

(ii) For obtaining a number less than 3 on each dice, the favourable outcomes are : (1, 1), (1, 2), (2, 1), (2, 2).

∴ Number of favourable outcomes = 4

P(getting a number less than 3 on each dice) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{4}{36} = \dfrac{1}{9}$.

Hence, the probability of getting a number less than 3 on each dice = $\dfrac{1}{9}$.

(iii) For obtaining an odd number as a sum, the favourable outcomes are : (1, 2), (1, 4), (1, 6), (2, 1), (2, 3), (2, 5), (3, 2), (3, 4), (3, 6), (4, 1), (4, 3), (4, 5), (5, 2), (5, 4), (5, 6), (6, 1), (6, 3), (6, 5).

∴ Number of favourable outcomes = 18

P(getting an odd number as a sum) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{18}{36} = \dfrac{1}{2}$.

Hence, the probability of getting an odd number as the sum = $\dfrac{1}{2}$.

(iv) For obtaining a total of atmost 10, the favourable outcomes are : (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (6, 1), (6, 2), (6, 3), (6, 4).

∴ Number of favourable outcomes = 33

P(getting a total of atmost 10) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{33}{36} = \dfrac{11}{12}$.

Hence, the probability of getting a total of atmost 10 = $\dfrac{11}{12}$.

(v) For obtaining an odd number on one dice and a number less than or equal to 4 on other dice, the favourable outcomes are : (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (2, 1), (2, 3), (2, 5), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (4, 1), (4, 3), (4, 5), (5, 1), (5, 2), (5, 3), (5, 4).

∴ Number of favourable outcomes = 20

P(getting an odd number on one dice and a number less than or equal to 4 on other dice) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{20}{36} = \dfrac{5}{9}$.

Hence, the probability of getting an odd number and a number less than or equal to 4 on other dice = $\dfrac{5}{9}$.

Three coins are tossed simultaneously the probability of getting atleast two heads is :

1. $\dfrac{1}{2}$

2. $\dfrac{1}{3}$

3. $\dfrac{1}{4}$

4. $\dfrac{3}{8}$

Answer

When three coins are tossed together; the possible outcomes are :

HHH, HHT, HTH, THH, HTT, THT, TTH and TTT.

i.e., the total number of possible outcomes = 8

Favorable outcomes for getting atleast two heads are : HHH, HHT, HTH, THH.

i.e., the number of favorable outcomes = 4

P(getting atleast two heads) : $\dfrac{\text{No. of favourable outcomes}}{\text{Total no. of possible outcomes}} = \dfrac{4}{8} = \dfrac{1}{2}$.

Hence, Option 1 is the correct option.

A card is drawn from a pack of a well shuffled cards. The probability of getting either a king or a queen is :

1. $\dfrac{1}{13}$

2. $\dfrac{2}{13}$

3. $\dfrac{3}{13}$

4. 0

Answer

No. of kings in a pack of cards = 4 (1 of each suit)

No. of queens in a pack of cards = 4 (1 of each suit)

Total no. of cards in a pack of cards = 52

P(getting either a king or a queen) : $\dfrac{\text{No. of favourable outcomes}}{\text{Total no. of possible outcomes}} = \dfrac{8}{52} = \dfrac{2}{13}$.

Hence, Option 2 is the correct option.

Two dice are rolled together and the product (P) of their scores is obtained :

Event A : P is 6.

Event B : P is an odd number.

Event C : P is 35.

Which of the following event/events has probability equal to 0?

1. Events B and C

2. Events A and B

3. Event B

4. Event C

Answer

When two dice are rolled together, possible outcomes are :

{(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}.

No. of possible outcomes = 36

Maximum product of number on dices = 36 when both the dice have 6 on it.

The product one less than the maximum = 30 when one dice have 5 and the other has 6.

∴ No. of favourable outcomes for getting a product of 35 = 0.

∴ P(event C) = $\dfrac{\text{No. of favourable outcomes}}{\text{Total no. of possible outcomes}} = \dfrac{0}{36}$ = 0.

Hence, Option 4 is the correct option.

A bag contains 20 red balls, 12 blue balls and 8 green balls. Three balls are drawn one by one with replacement, the probability that the third ball being green is :

1. $\dfrac{1}{2}$

2. $\dfrac{2}{5}$

3. $\dfrac{1}{5}$

4. 1.8

Answer

Total no. of balls = 20 + 12 + 8 = 40

No. of green balls = 8

Since, balls are drawn one by one with replacement.

∴ P(third ball drawn be green) = P(ball drawn to be green)

= $\dfrac{\text{No. of favourable outcomes}}{\text{Total no. of possible outcomes}} = \dfrac{8}{40} = \dfrac{1}{5}$.

Hence, Option 3 is the correct option.

Below are given the probabilities A, B, C and D of an event. P(A) : $\dfrac{3}{5}$, P(B) : 1.2, P(C) : -1.2 and P(D) = $1\dfrac{2}{3}$. Which of the above values of the probabilities is possible :

1. Event A

2. Event B

3. Event C

4. Event D

Answer

We know that,

Probability of an event cannot be negative or greater than 1.

∴ Only probability of event A is possible.

Hence, Option 1 is the correct option.

A letter of English alphabet is chosen at random from English alphabets.

Assertion(A): The probability that the chosen letter is not a consonant is 5 : 52.

Reason(R): The probability of an event = $\dfrac{\text{Total number of outcomes}}{\text{Number of favourable outcomes}}$

1. A is true, R is false.

2. A is false, R is true.

3. Both A and R are true and R is correct reason for A.

4. Both A and R are false.

Answer

Given, there are 26 letters in the English alphabet.

There are total 5 (a, e, i, o, u) vowels.

The remaining letters are consonants, (21 consonants).

By formula,

The probability of an event = $\dfrac{\text{Number of favourable outcomes}}{\text{Total number of outcomes}}$

So, reason (R) is false.

Probability that the chosen letter is not a consonant = $\dfrac{Number of vowels}{Total number of english alphabets} = \dfrac{5}{26}$

So, assertion (A) is false.

∴ Both A and R are false.

Hence, option 4 is the correct option.

Number x is chosen from -3, -2, -1, 0, 1, 2 and 3. Also, x² ≤ 5.

Assertion(A): Probability for x² ≤ 5 is $\dfrac{3}{7}$.

Reason(R): Probability = $\dfrac{\text{Favourable outcomes}}{\text{Total number of outcomes}}$.

1. A is true, R is false.

2. A is false, R is true.

3. Both A and R are true and R is correct reason for A.

4. Both A and R are true and R is incorrect reason for A.

Answer

Number x is chosen form -3, -2, -1, 0, 1, 2 and 3. Also, x² ≤ 5.

We need to find the values of x for which x² ≤ 5.

(-3)² = 9 (not favourable)

(-2)² = 4 (favourable)

(-1)² = 1 (favourable)

0² = 0 (favourable)

1² = 1 (favourable)

2² = 4 (favourable)

3² = 9 (not favourable)

The favorable outcomes are -2, -1, 0, 1, 2 in total 5 favourable outcomes.

By formula; the probability for x² ≤ 5 = $\dfrac{\text{Number of favourable outcomes}}{\text{Total number of outcomes}} = \dfrac{5}{7}$.

∴ A is false, R is true.

Hence, option 2 is the correct option.

Face cards of spades are remove from the pack of 52 cards and the remaining cards are well shuffled. Then a card is drawn from the pack.

Statement (1): The probability of drawing a face card is $\dfrac{7}{52}$.

Statement (2): Kings, queens and jacks are the three face card and so the total number of face cards in the pack of 52 card is 3 x 4 = 12.

1. Both the statements are true.

2. Both the statements are false.

3. Statement 1 is true, and statement 2 is false.

4. Statement 1 is false, and statement 2 is true.

Answer

In a standard deck of 52 playing cards, each suit (hearts, diamonds, clubs, spades) contains 3 face cards: Jack, Queen, and King. Therefore, the total number of face cards in the deck is:

3 x 4 = 12

So, statement 2 is true.

After removing the face cards of spades (Jack, Queen, King), we are left with = 12 - 3 = 9 face cards.

The total number of remaining cards in the deck = 52 - 3 = 49.

By formula; the probability of an event = $\dfrac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$

Thus, the probability of drawing a face card from the remaining 49 cards = $\dfrac{9}{49}$.

So, statement 1 is false.

∴ Statement 1 is false, and statement 2 is true.

Hence, option 4 is the correct option.

In a lottery ticket, there are 20 prizes and 25 blanks.

Statement (1): Probability of not getting the prize = 1 - $\dfrac{20}{45}$

Statement (2): P(getting prize) + P(blank) = 1

1. Both the statements are true.

2. Both the statements are false.

3. Statement 1 is true, and statement 2 is false.

4. Statement 1 is false, and statement 2 is true.

Answer

Given, tickets = 20 prizes and 25 blanks

total tickets = 20 + 25 = 45

By formula; the probability of an event = $\dfrac{\text{Number of favourable outcomes}}{\text{Total number of possible outcomes}}$

P(getting prize) = $\dfrac{20}{45}$

P(blank) = $\dfrac{25}{45}$

$\text{P(getting prize) + P(blank) }= \dfrac{20}{45} + \dfrac{25}{45}\\[1em] = \dfrac{20 + 25}{45} \\[1em] = \dfrac{45}{45} \\[1em] = 1.$

Thus, P(getting prize) + P(blank) = 1

So, statement 2 is true.

⇒ P(blank) = 1 - P(getting prize)

⇒ P(blank) = 1 - $\dfrac{20}{45}$

We know that,

P(not getting the prize) = P(blank)

So, statement 1 is true.

∴ Both the statements are true.

Hence, option 1 is the correct option.

From a well-shuffled deck of 52 cards, one card is drawn. Find the probability that the card drawn is :

(i) a face card

(ii) not a face card

(iii) a queen of black colour

(iv) a card with number 5 or 6

(v) a card with number less than 8

(vi) a card with number between 2 and 9

Answer

There are 52 cards in a deck.

We have, the total number of possible outcomes = 52

(i) No. of face cards in a deck of 52 cards = 12 (4 kings, 4 queens and 4 jacks)

∴ No. of favourable outcomes = 12

P(drawing a face card) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{12}{52} = \dfrac{3}{13}$.

Hence, probability of drawing a face card = $\dfrac{3}{13}$.

(ii) As, probability of drawing a face card and a non-face card are complimentary event.

∴ Probability of drawing a face card + Probability of drawing a non-face card = 1

⇒ Probability of not drawing a face card = 1 - Probability of drawing a face card

⇒ Probability of not drawing a face card = $1 - \dfrac{3}{13} = \dfrac{13 - 3}{13} = \dfrac{10}{13}$.

Hence, probability of not drawing a face card = $\dfrac{10}{13}$.

(iii) There are 2 queens of black colour (1 of each club and spade).

∴ No. of favourable outcomes = 2

P(drawing a queen of black colour)

= $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{2}{52} = \dfrac{1}{26}$.

Hence, probability of drawing a queen of black colour = $\dfrac{1}{26}$.

(iv) There are 4 cards (1 of each suit) of each 5 and 6 number.

∴ No. of favourable outcomes = 8

P(drawing a card with number 5 or 6)

= $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{8}{52} = \dfrac{2}{13}$.

Hence, probability of drawing a card with number 5 or 6 = $\dfrac{2}{13}$.

(v) There are {2, 3, 4, 5, 6, 7} numbered cards of each heart, diamond, club and spades.

∴ No. of favourable outcomes = 6 × 4 = 24.

P(getting a card with number less than 8)

= $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{24}{52} = \dfrac{6}{13}$.

Hence, the probability of drawing a card with number less than 8 = $\dfrac{6}{13}$.

(vi) There are {3, 4, 5, 6, 7, 8} numbered cards of each heart, diamond, club and spades.

∴ No. of favourable outcomes = 6 × 4 = 24.

P(getting a card with number between 2 and 9)

= $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{24}{52} = \dfrac{6}{13}$.

Hence, the probability of drawing a card with number between 2 and 9 = $\dfrac{6}{13}$.

In a match between A and B;

(i) the probability of winning of A is 0.83. What is the probability of winning of B?

(ii) the probability of losing the match is 0.49 for B. What is the probability of winning of A?

Answer

(i) Since,the match is between A and B.

∴ Probability of losing of A = Probability of winning of B

We know that,

⇒ Probability of winning of A + Probability of losing of A = 1 (As winning and loosing of A are complimentary events)

⇒ Probability of winning of A + Probability of winning of B = 1

⇒ 0.83 + Probability of winning of B = 1

⇒ Probability of winning of B = 1 - 0.83 = 0.17

Hence, probability of winning of B = 0.17

(ii) Since,the match is between A and B.

∴ Probability of winning of A = Probability of loosing of B

Probability of winning of A = 0.49

A and B are friends. Ignoring the leap year, find the probability that both friends will have:

(i) different birthdays?

(ii) the same birthday?

Answer

Out of the two friends, A’s birthday can be any day of the year. Now, B’s birthday can also be any day of 365 days in the year.

We assume that these 365 outcomes are equally likely.

So,

(i) If A’s birthday is different from B’s, the number of favourable outcomes for his birthday is 365 - 1 = 364

P(A’s birthday is different from B’s birthday) = $\dfrac{\text{364}}{\text{365}}$.

Hence, the probability that both friends will have different birthdays is $\dfrac{364}{365}$

(ii) P(A and B have the same birthday) = 1 - P (both have different birthdays)

= 1 - $\dfrac{364}{365}$

= $\dfrac{365 - 364}{365} = \dfrac{1}{365}$.

Hence, the probability that both friends will have same birthday is $\dfrac{1}{365}$.

A man tosses two different coins (one of ₹ 2 and another of ₹ 5) simultaneously. What is the probability that he gets :

(i) at least one head ?

(ii) at most one head ?

Answer

We know that,

When two coins are tossed simultaneously, the possible outcomes are {(H, H), (H, T), (T, H), (T, T)}

∴ No. of possible outcomes = 4.

(i) The outcomes favourable to event, 'at least one head' are {(H, H), (H, T), (T, H)}.

∴ Number of favourable outcomes = 3

P(getting at least one head) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{3}{4}$.

Hence, the probability that he gets at least one head = $\dfrac{3}{4}$.

(ii) The outcomes favourable to event, 'at most one head' are {(H, T), (T, H), (T, T)}.

∴ Number of favourable outcomes = 3

P(getting at most one head) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{3}{4}$.

Hence, the probability that he gets at most one head = $\dfrac{3}{4}$.

All the three face cards of spades are removed from a well shuffled pack of 52 cards. A card is then drawn at random from the remaining pack. Find the probability of getting :

(i) a black face card

(ii) a queen

(iii) a black card

Answer

We have,

Total number of cards = 52

If 3 face cards of spades are removed

Then, the remaining cards = 49 (52 - 3)

∴ Number of possible outcomes = 49.

(i) There are 3 black face cards of club left.

∴ Number of favourable outcomes = 3.

P(drawing a black face card) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{3}{49}$.

Hence, the probability of drawing a black face card = $\dfrac{3}{49}$

(ii) There are total 4 queens and queen of spade is removed.

Queens left = 3

∴ Number of favourable outcomes = 3.

P(drawing a queen) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{3}{49}$.

Hence, the probability of drawing a queen = $\dfrac{3}{49}$.

(iii) There are 26 black cards and 3 cards of spades are removed which are black.

Number of black cards left = 23 (26 - 3)

∴ Number of favourable outcomes = 23.

P(drawing a black card) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{23}{49}$.

Hence, the probability of drawing a black card = $\dfrac{23}{49}$.

In a musical chairs game, a person has been advised to stop playing the music at any time within 40 seconds after its start. What is the probability that the music will stop within the first 15 seconds ?

Answer

The favourable results = 0 sec to 15 sec and the total results = 0 sec to 40 sec.

∴ Number of favourable outcomes = 15

and

Number of possible outcomes = 40.

P(that music will stop within 15 seconds) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{15}{40} = \dfrac{3}{8}$.

Hence, the probability that the music will stop within the first 15 seconds = $\dfrac{3}{8}$.

In a bundle of 50 shirts, 44 are good, 4 have minor defects and 2 have major defects. What is the probability that :

(i) it is acceptable to a trader who accepts only a good shirt ?

(ii) it is acceptable to a trader who rejects only a shirt with major defects ?

Answer

We have,

Total number of shirts = 50

∴ No. of possible outcomes = 50.

(i) As, trader accepts only good shirts and number of good shirts = 44.

∴ No. of favourable outcomes = 44

P(trader will accept) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{44}{50} = \dfrac{22}{25}$.

Hence, the probability that a shirt is acceptable to a trader who accepts only a good shirt = $\dfrac{22}{25}$.

(ii) As, trader rejects shirts with major defects only and number of shirts with major defects = 2.

No. of shirts that trader will accept = 50 - 2 = 48.

∴ No. of favourable outcomes = 48

P(trader will accept) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{48}{50} = \dfrac{24}{25}$.

Hence, the probability that a shirt is acceptable to a trader who rejects only a shirt with major defects = $\dfrac{24}{25}$.

Two dice are thrown at the same time. Find the probability that the sum of the two numbers appearing on the top of the dice is :

(i) 8

(ii) 13

(iii) less than or equal to 12

Answer

When two dice are thrown simultaneously;

Number of possible outcomes = 6 × 6 = 36.

(i) For obtaining a total of 8, favourable outcomes are : {(2, 6), (3, 5), (4, 4), (5, 3), (6, 2)}.

∴ Number of favourable outcomes = 5.

P(that the sum of the two numbers appearing on the top of the dice is 8) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{5}{36}$.

Hence, the probability that the sum of the two numbers appearing on the top of the dice is 8 = $\dfrac{5}{36}$.

(ii) There is no outcome favourable to obtaining a sum of 13.

∴ Number of favourable outcomes = 0.

P(that the sum of the two numbers appearing on the top of the dice is 13) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}}$ = 0.

Hence, the probability that the sum of the two numbers appearing on the top of the dice is 13 = 0.

(iii) The sum of all the outcomes is either less than or equal to 12.

∴ Number of favourable outcomes = 36.

P(that the sum of the two numbers appearing on the top of the dice is less than or equal to 12) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{36}{36}$ = 1.

Hence, the probability that the sum of the two numbers appearing on the top of the dice is less than or equal to 12 is 1.

The probability that two boys do not have the same birthday is 0.897. What is the probability that the two boys have the same birthday ?

Answer

We know that,

Since, the boys having birthday on same date and different date are complimentary events.

∴ P(do not have the same birthday) + P(having same birthday) = 1

⇒ 0.897 + P(having same birthday) = 1

⇒ P(having same birthday) = 1 - 0.897

⇒ P(having same birthday) = 0.103

Hence, the probability that the two boys have same birthday = 0.103

A bag contains 10 red balls, 16 white balls and 8 green balls. A ball is drawn out of the bag at random. What is the probability that the ball drawn will be :

(i) not red ?

(ii) neither red nor green ?

(iii) white or green ?

Answer

Total number of possible outcomes = 10 + 16 + 8 = 34.

(i) No. of non red balls = 24 (16 white + 8 green)

∴ No. of favourable outcomes = 24.

P(drawing a not red ball) = $\dfrac{\text{No. of favourable outcomes}}{\text{\text{No. of possible outcomes}}} = \dfrac{24}{34} = \dfrac{12}{17}$.

Hence, the probability of drawing a not red ball = $\dfrac{12}{17}$.

(ii) Since, there are only 3 different colour balls in the bag.

∴ P(drawing neither red nor green ball) = P(drawing a white ball)

No. of favourable outcomes (of getting white ball) = 16.

P(drawing a white ball) = $\dfrac{\text{No. of favourable outcomes}}{\text{\text{No. of possible outcomes}}} = \dfrac{16}{34} = \dfrac{8}{17}$.

∴ P(drawing neither red nor green ball) = $\dfrac{8}{17}$.

Hence, the probability that the ball drawn is neither red nor green is $\dfrac{8}{17}$.

(iii) No. of white or green balls = 24 (16 white + 8 green)

∴ No. of favourable outcomes = 24.

P(drawing a white or green ball)

= $\dfrac{\text{No. of favourable outcomes}}{\text{\text{No. of possible outcomes}}} = \dfrac{24}{34} = \dfrac{12}{17}$.

Hence, the probability of drawing a white or green ball = $\dfrac{12}{17}$.

A bag contains twenty ₹ 5 coins, fifty ₹ 2 coins and thirty ₹ 1 coins. If it is equally likely that one of the coins will fall down when the bag is turned upside down, what is the probability that the coin :

(i) will be a ₹ 1 coin ?

(ii) will not be a ₹ 2 coin ?

(iii) will neither be a ₹ 5 coin nor be a ₹ 1 coin ?

Answer

We have,

Total number of coins = 20 + 50 + 30 = 100

So, the total possible outcomes = 100.

(i) Number of ₹ 1 coin = 30

∴ Number of favourable outcomes = 30

P(drawing a ₹ 1 coin) = $\dfrac{\text{No. of favourable outcomes}}{\text{\text{No. of possible outcomes}}} = \dfrac{30}{100} = \dfrac{3}{10}$.

Hence, the probability of drawing a ₹ 1 coin = $\dfrac{3}{10}$.

(ii) Number of ₹ 5 and ₹ 1 coin = 50 (20 + 30)

Hence, no. of coins apart from ₹ 2 coins = 50.

∴ Number of favourable outcomes = 50

P(coin drawn will not be a ₹ 2 coin) = $\dfrac{\text{No. of favourable outcomes}}{\text{\text{No. of possible outcomes}}} = \dfrac{50}{100} = \dfrac{1}{2}$.

Hence, the probability of not drawing a ₹ 2 coin = $\dfrac{1}{2}$.

(iii) No. of ₹ 2 coins = 50

No. of favourable outcomes (for drawing a ₹ 2 coin) = 50

P(drawing a ₹ 2 coin) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of total possible outcomes}} = \dfrac{50}{100} = \dfrac{1}{2}$.

Since, there are only 3 types of coins in the bag.

∴ P(drawing neither ₹ 5 nor ₹ 1 coin) = P(drawing ₹ 2 coin) = $\dfrac{1}{2}$.

Hence, the probability of drawing neither ₹ 5 nor ₹ 1 coin = $\dfrac{1}{2}$.

A game consists of spinning arrow which comes to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12; as shown below.

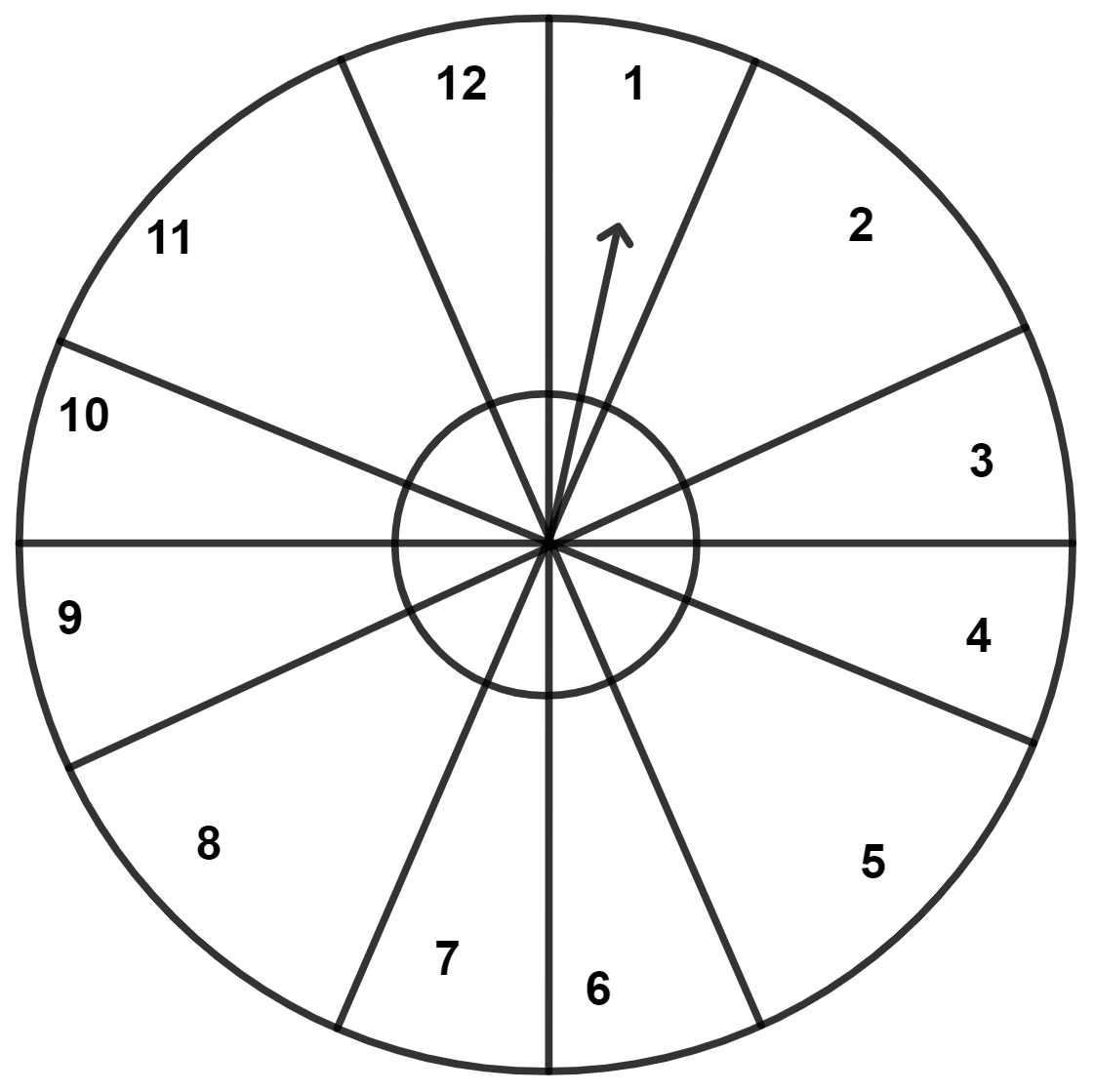
If the outcomes are equally likely, find the probability that the pointer will point at:

(i) 6

(ii) an even number

(iii) a prime number

(iv) a number greater than 8

(v) a number less than or equal to 9

(vi) a number between 3 and 11.

Answer

We have,

Total number of possible outcomes = 12

(i) Number of favorable outcomes for 6 = 1

P(that pointer points at 6) = $\dfrac{\text{No. of favourable outcomes}}{\text{\text{No. of possible outcomes}}} = \dfrac{1}{12}$.

Hence, the probability that pointer points at 6 = $\dfrac{1}{12}$.

(ii) Favorable outcomes for an even number are 2, 4, 6, 8, 10, 12.

∴ Number of favorable outcomes = 6

P(that pointer points at an even number)

= $\dfrac{\text{No. of favourable outcomes}}{\text{\text{No. of possible outcomes}}} = \dfrac{6}{12} = \dfrac{1}{2}$.

Hence, the probability that pointer points at an even number = $\dfrac{1}{2}$.

(iii) Favorable outcomes for a prime number are 2, 3, 5, 7, 11.

∴ Number of favorable outcomes = 5

P(that pointer points at a prime number)

= $\dfrac{\text{No. of favourable outcomes}}{\text{\text{No. of possible outcomes}}} = \dfrac{5}{12}$.

Hence, the probability that pointer points at a prime number = $\dfrac{5}{12}$.

(iv) Favorable outcomes for a number greater than 8 are 9, 10, 11, 12.

∴ Number of favorable outcomes = 4.

P(that pointer points at a number greater than 8)

= $\dfrac{\text{No. of favourable outcomes}}{\text{\text{No. of possible outcomes}}} = \dfrac{4}{12} = \dfrac{1}{3}$.

Hence, the probability that pointer points at a number greater than 8 = $\dfrac{1}{3}$.

(v) Favorable outcomes for a number less than or equal to 9 are 1, 2, 3, 4, 5, 6, 7, 8, 9

∴ Number of favorable outcomes = 9

P(that pointer points at a number less than or equal to 9)

= $\dfrac{\text{No. of favourable outcomes}}{\text{\text{No. of possible outcomes}}} = \dfrac{9}{12} = \dfrac{3}{4}$.

Hence, the probability that pointer points at a number less than or equal to 9 = $\dfrac{3}{4}$.

(vi) Favorable outcomes for a number between 3 and 11 are 4, 5, 6, 7, 8, 9, 10

∴ Number of favorable outcomes = 7

P(that pointer points at a number between 3 and 11)

= $\dfrac{\text{No. of favourable outcomes}}{\text{\text{No. of possible outcomes}}} = \dfrac{7}{12}$.

Hence, the probability that pointer points at a number between 3 and 11 = $\dfrac{7}{12}$.

One card is drawn from a well shuffled deck of 52 cards. Find the probability of getting :

(i) a queen of red color

(ii) a black face card

(iii) the jack or the queen of the hearts

(iv) a diamond

(v) a diamond or a spade

Answer

We have,

Total possible outcomes = 52

(i) Number of queens of red color = 2 (1 of each heart and diamond)

∴ Number of favorable outcomes = 2

P(drawing a queen of red colour)

= $\dfrac{\text{No. of favourable outcomes}}{\text{\text{No. of possible outcomes}}} = \dfrac{2}{52} = \dfrac{1}{26}$.

Hence, the probability of drawing a queen of red colour = $\dfrac{1}{26}$.

(ii) Number of black face cards = 6 (3 of each club and spades)

∴ Number of favorable outcomes = 6

P(drawing a black face card)

= $\dfrac{\text{No. of favourable outcomes}}{\text{\text{No. of possible outcomes}}} = \dfrac{6}{52} = \dfrac{3}{26}$.

Hence, the probability of drawing a black face card = $\dfrac{3}{26}$.

(iii) Favorable outcomes for jack or the queen of hearts = 2 (1 jack + 1 queen)

∴ Number of favorable outcomes = 2

P(drawing a jack or the queen of hearts)

= $\dfrac{\text{No. of favourable outcomes}}{\text{\text{No. of possible outcomes}}} = \dfrac{2}{52} = \dfrac{1}{26}$.

Hence, the probability of drawing a jack or the queen of hearts = $\dfrac{1}{26}$.

(iv) Number of diamond cards = 13

∴ Number of favorable outcomes = 13

P(getting a diamond) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{13}{52} = \dfrac{1}{4}$.

Hence, the probability of getting a diamond = $\dfrac{1}{4}$.

(v) Number of favorable outcomes for a diamond or a spade = 13 + 13 = 26.

P(getting a diamond or spade)

= $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{26}{52} = \dfrac{1}{2}$.

Hence, the probability of getting a diamond or spade = $\dfrac{1}{2}$.

From a deck of 52 cards, all the face cards are removed and then the remaining cards are shuffled. Now one card is drawn from the remaining deck. Find the probability that the card drawn is :

(i) a black card

(ii) 8 of red colour

(iii) a king of black colour.

Answer

There are 12 face cards in a deck.

Remaining cards = 40 (52 - 12)

No. of possible outcomes = 40.

(i) There are 26 black cards in a deck.

Since, face cards are removed and there are 6 black face cards (a king, queen and jack of both club and spades).

No. of black cards left = 26 - 6 = 20.

∴ No. of favourable outcomes = 20.

P(drawing a black card) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{20}{40} = \dfrac{1}{2}$.

Hence, the probability of drawing a black card = $\dfrac{1}{2}$.

(ii) There are 2 number 8 red cards (1 of each heart and diamond).

∴ No. of favourable outcomes = 2.

P(drawing a 8 of red colour) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{2}{40} = \dfrac{1}{20}$.

Hence, the probability of drawing a 8 of red colour = $\dfrac{1}{20}$.

(iii) There is no king left as all face cards are removed.

∴ No. of favourable outcomes = 0.

P(drawing a king of black colour) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{0}{40}$ = 0.

Hence, the probability of drawing a king of black colour = 0.

Seven cards : the eight, the nine, the ten, jack, queen, king and ace of diamonds are well shuffled. One card is then picked up at random.

(i) What is the probability that the card drawn is the eight or the king ?

(ii) If the king is drawn and put aside, what is the probability that the second card picked up is :

(a) an ace ?

(b) a king ?

Answer

There are seven cards.

∴ No. of possible outcomes = 7.

(i) No. of favourable outcomes (of getting a eight or the king) = 2.

P(drawing an eight or the king) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{2}{7}$.

Hence, the probability that the card drawn is the eight or the king = $\dfrac{2}{7}$.

(ii) Since, king is drawn and put aside so, no. of cards left = 7 - 1 = 6.

∴ No. of possible outcomes = 6.

(a) No. of favourable outcomes (of getting an ace) = 1.

P(drawing an ace) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{1}{6}$.

Hence, the probability that the card drawn is an ace = $\dfrac{1}{6}$.

(b) Since, king is drawn aside.

∴ No. of favourable outcomes (of getting a king) = 0.

P(drawing a king) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{0}{6}$ = 0.

Hence, the probability that the card drawn is a king = 0.

(i) 4 defective pens are accidentally mixed with 16 good ones. It is not possible to just look at a pen and tell whether or not it is defective. One pen is drawn at random from the lot. What is the probability that the pen is defective ?

(ii) Suppose the pen drawn in (i) is defective and is not replaced. Now one more pen is drawn at random from the rest. What is the probability that this pen is :

(a) defective ?

(b) not defective ?

Answer

(i) No. of pens = 20 (4 + 16)

∴ No. of possible outcomes = 20.

Since, there are 4 defective pens,

∴ No. of favourable outcomes = 4.

P(drawing a defective pen) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{4}{20} = \dfrac{1}{5}$.

Hence, probability of drawing a defective pen = $\dfrac{1}{5}$.

(ii) Since, pen drawn is defective.

So, no. of pens left = 19 and no. of defective pens left = 3.

(a) No. of favourable outcomes (drawing a defective pen) = 3.

No. of possible outcomes = 19

P(drawing a defective pen) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{3}{19}$.

Hence, probability of drawing a defective pen = $\dfrac{3}{19}$.

(b) No. of favourable outcomes (drawing a good pen) = 16.

No. of possible outcomes = 19

P(drawing a good pen) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{16}{19}$.

Hence, probability of drawing a not defective pen = $\dfrac{16}{19}$.

A bag contains 100 identical marble stones which are numbered from 1 to 100. If one stone is drawn at random from the bag, find the probability that it bears :

(i) a perfect square number.

(ii) a number divisible by 4.

(iii) a number divisible by 5.

(iv) a number divisible by 4 or 5.

(v) a number divisible by 4 and 5.

Answer

There are 100 identical marble stones.

∴ No. of possible outcomes = 100.

(i) Stones containing a perfect square number are numbered :

1, 4, 9, 16, 25, 36, 49, 64, 81, 100.

No. of favourable outcomes = 10.

P(drawing a stone with perfect square number)

= $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{10}{100} = \dfrac{1}{10}$.

Hence, the probability of drawing a stone bearing a perfect square number = $\dfrac{1}{10}$.

(ii) Stones containing a number which is divisible by 4 are numbered :

4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64, 68, 72, 76, 80, 84, 88, 92, 96, 100.

No. of favourable outcomes = 25.

P(drawing a stone with a number divisible by 4)

= $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{25}{100} = \dfrac{1}{4}$.

Hence, the probability of drawing a stone with a number divisible by 4 = $\dfrac{1}{4}$.

(iii) Stones containing a number which is divisible by 5 are numbered :

5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 100.

No. of favourable outcomes = 20.

P(drawing a stone with a number divisible by 5)

= $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{20}{100} = \dfrac{1}{5}$.

Hence, the probability of drawing a stone with a number divisible by 5 = $\dfrac{1}{5}$.

(iv) Stones containing a number which is divisible by 4 or 5 are numbered :

4, 8, 12, 16, 24, 28, 32, 36, 44, 48, 52, 56, 64, 68, 72, 76, 84, 88, 92, 96, 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 100.

No. of favourable outcomes = 40.

P(drawing a stone with a number divisible by 4 or 5)

= $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{40}{100} = \dfrac{2}{5}$.

Hence, the probability of drawing a stone with a number divisible by 4 or 5 = $\dfrac{2}{5}$.

(v) Stones containing a number which is divisible by 4 and 5 are numbered :

20, 40, 60, 80, 100.

No. of favourable outcomes = 5.

P(drawing a stone with a number divisible by 4 and 5)

= $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{5}{100} = \dfrac{1}{20}$.

Hence, the probability of drawing a stone with a number divisible by 4 and 5 = $\dfrac{1}{20}$.

A circle with diameter 20 cm is drawn somewhere on a rectangular piece of paper with length 40 cm and width 30 cm. This paper is kept horizontal on table top and a dice, very small in size, is dropped on the rectangular paper without seeing towards it. If the dice falls and lands on the paper only, find the probability that it will fall and land :

(i) inside the circle.

(ii) outside the circle.

Answer

Diameter of circle drawn = 20 cm

Radius = $\dfrac{\text{Diameter}}{2} = \dfrac{20}{2}$ = 10 cm.

Area of circle = πr²

$= \dfrac{22}{7} \times 10 \times 10 \\[1em] = \dfrac{2200}{7} \text{ cm}^2.$

Length of rectangular piece = 40 cm

Width of rectangular piece = 30 cm

Area of rectangular piece (Total possible outcome) = 40 × 30 = 1200 cm²

(i) No. of favourable outcome for dice landing inside circle = Area of circle = $\dfrac{2200}{7}$ cm².

P(dice lands inside circle)

= $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{\dfrac{2200}{7}}{1200} = \dfrac{2200}{8400} = \dfrac{11}{42}$.

Hence, the probability that dice lands inside the circle = $\dfrac{11}{42}$.

(ii) P(dice lands inside circle) + P(dice lands outside the circle) = 1

P(dice lands outside circle) = 1 - P(dice lands inside the circle)

= 1 - $\dfrac{11}{42}$

= $\dfrac{42 - 11}{42}$

= $\dfrac{31}{42}$.

Hence, the probability that dice lands outside the circle = $\dfrac{31}{42}$.

Two dice (each bearing numbers 1 to 6) are rolled together. Find the probability that the sum of the numbers on the upper-most faces of two dice is :

(i) 4 or 5

(ii) 7, 8 or 9.

(iii) between 5 and 8.

(iv) more than 10.

(v) less than 6.

Answer

When two dice are rolled together;

No. of possible outcomes = 6 × 6 = 36.

(i) Favourable outcomes for sum of numbers on the upper-most faces of two dice to be 4 or 5 are :

(1, 3), (1, 4), (2, 2), (2, 3), (3, 1), (3, 2), (4, 1).

∴ No. of favourable outcomes = 7.

P(getting a sum of 4 or 5) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{7}{36}$.

Hence, the probability of getting sum of numbers on the upper-most faces of two dice to be 4 or 5 = $\dfrac{7}{36}$.

(ii) Favourable outcomes for sum of numbers on the upper-most faces of two dice to be 7, 8 or 9 are :

(1, 6), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6), (4, 3), (4, 4), (4, 5), (5, 2), (5, 3), (5, 4), (6, 1), (6, 2) and (6, 3).

∴ No. of favourable outcomes = 15.

P(getting a sum of 7, 8 or 9) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{15}{36} = \dfrac{5}{12}$.

Hence, the probability of getting sum of numbers on the upper-most faces of two dice to be 7, 8 or 9 = $\dfrac{5}{12}$.

(iii) Favourable outcomes for sum of numbers on the upper-most faces of two dice to be between 5 and 8 are :

(1, 5), (1, 6), (2, 4), (2, 5), (3, 3), (3, 4), (4, 2), (4, 3), (5, 1), (5, 2), (6, 1).

∴ No. of favourable outcomes = 11.

P(getting a sum between 5 and 8) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{11}{36}$.

Hence, the probability of getting sum of numbers on the upper-most faces of two dice between 5 and 8 = $\dfrac{11}{36}$.

(iv) Favourable outcomes for sum of numbers on the upper-most faces of two dice to be more than 10 are :

(5, 6), (6, 5), (6, 6)

∴ No. of favourable outcomes = 3.

P(getting a sum of more than 10) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{3}{36} = \dfrac{1}{12}$.

Hence, the probability of getting sum of numbers on the upper-most faces of more than 10 = $\dfrac{1}{12}$.

(v) Favourable outcomes for sum of numbers on the upper-most faces of two dice to be less than 6 are :

(1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (4, 1).

∴ No. of favourable outcomes = 10.

P(getting a sum of less than 6) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{10}{36} = \dfrac{5}{18}$.

Hence, the probability of getting sum of numbers on the upper-most faces of less than 6 = $\dfrac{5}{18}$.

Three coins are tossed together. Write all the possible outcomes. Now, find the probability of getting :

(i) exactly two heads.

(ii) at least two heads.

(iii) atmost two heads.

(iv) all tails

(v) at least one tail.

Answer

When three coins are tossed simultaneously;

Possible outcomes are : {HHH, TTT, HHT, HTH, THH, TTH, THT, HTT}.

(i) Favourable outcomes for getting exactly two heads are : HHT, HTH, THH.

No. of favourable outcomes = 3

P(getting exactly two heads) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{3}{8}$.

Hence, the probability of getting exactly two heads = $\dfrac{3}{8}$.

(ii) Favourable outcomes for getting at least two heads are : HHT, HTH, THH, HHH.

No. of favourable outcomes = 4

P(getting atleast two heads) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{4}{8} = \dfrac{1}{2}$.

Hence, the probability of getting at least two heads = $\dfrac{1}{2}$.

(iii) Favourable outcomes for getting at most two heads are : TTT, HHT, HTH, THH, TTH, THT, HTT.

No. of favourable outcomes = 7

P(getting atmost two heads) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{7}{8}$.

Hence, the probability of getting at most two heads = $\dfrac{7}{8}$.

(iv) Favourable outcomes for getting all tails is : TTT.

No. of favourable outcomes = 1

P(getting all tails) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{1}{8}$.

Hence, the probability of getting all tails = $\dfrac{1}{8}$.

(v) Favourable outcomes for getting at least one tail is : TTT, HHT, HTH, THH, TTH, THT, HTT.

No. of favourable outcomes = 7

P(getting at least one tail) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{7}{8}$.

Hence, the probability of getting at least one tail is = $\dfrac{7}{8}$.

Two dice are thrown simultaneously. What is the probability that :

(i) 4 will not come up either time ?

(ii) 4 will come up at least once ?

Answer

When two dice are thrown simultaneously;

No. of possible outcomes = 6 × 6 = 36.

(i) Favourable outcomes for 4 not coming on any of the dice are : (1, 1), (1, 2), (1, 3), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 5), (3, 6), (5, 1), (5, 2), (5, 3), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 5), (6, 6).

No. of favourable outcomes = 25

P(such that 4 will not come up either time)

= $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{25}{36}$.

Hence, the probability of not getting 4 any time = $\dfrac{25}{36}$.

(ii) Favorable outcomes for 4 coming up at least once are :

(1, 4), (2, 4), (3, 4), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 4), (6, 4).

No. of favourable outcomes = 11

P(such that 4 will come up at least once)

= $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{11}{36}$.

Hence, the probability of 4 coming up at least once = $\dfrac{11}{36}$.

Offices in Delhi are open for five days in a week (Monday to Friday). Two employees of an office remain absent for one day in the same particular week. Find the probability that they remain absent on :

(i) the same day

(ii) consecutive day

(iii) different days.

Answer

Total number of possible outcomes = 5 × 5 = 25.

Let the five days of the week be denoted as Monday by M, Tuesday by T, Wednesday by W, Thursday by Th and Friday by F; then :

(i) Favourable cases for employees being absent on same day are : MM, TT, WW, Th Th and FF.

No. of favourable cases = 5.

Required probability = $\dfrac{\text{No. of favourable cases}}{\text{No. of possible cases}} = \dfrac{5}{25} = \dfrac{1}{5}$.

Hence, probability that employees remain absent on same day = $\dfrac{1}{5}$.

(ii) Favourable cases for employees being absent on consecutive day are : MT, TM, TW, WT, W Th, Th W, Th F and F Th.

No. of favourable cases = 8.

Required probability = $\dfrac{\text{No. of favourable cases}}{\text{No. of possible cases}} = \dfrac{8}{25}$.

Hence, probability that employees remain absent on consecutive day = $\dfrac{8}{25}$.

(iii) We know that,

Employees being absent on same day and different day are complimentary events.

∴ P(absent on different days) + P(absent on same day) = 1

⇒ P(absent on different days) = 1 - P(absent on same day)

⇒ P(absent on different days) = 1 - $\dfrac{1}{5} = \dfrac{4}{5}$.

Hence, the probability that employees remain absent on different days = $\dfrac{4}{5}$.

A box contains some black balls and 30 white balls. If the probability of drawing a black ball is two-fifths of a white ball; find the number of black balls in the box.

Answer

Let the box contain x black balls.

Total number of balls = x + 30

∴ No. of possible outcomes = x + 30.

No. of favourable outcomes (for drawing a black ball) = x

P(drawing a black ball) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{x}{x + 30}$

No. of favourable outcomes (for drawing a white ball) = 30

P(drawing a white ball) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{30}{x + 30}$

Given,

Probability of drawing a black ball is two-fifths of a white ball,

$\therefore \dfrac{x}{x + 30} = \dfrac{2}{5} \times \dfrac{30}{x + 30} \\[1em] \Rightarrow \dfrac{x}{x + 30} = \dfrac{12}{x + 30} \\[1em] \Rightarrow x = \dfrac{12}{x + 30} \times (x + 30) \\[1em] \Rightarrow x = 12.$

Hence, the number of black balls = 12.

From a pack of 52 playing cards, all cards whose numbers are multiples of 3 are removed. A card is now drawn at random. What is the probability that the card drawn is

(i) a face card (King, Jack or Queen)

(ii) an even numbered red card ?

Answer

Cards whose numbers are multiples of 3 are : 3, 6 and 9 of each heart, club, diamonds and spades.

No. of cards removed = 3 × 4 = 12.

Total cards left = 40 (52 - 12).

∴ No. of possible outcomes = 40.

(i) There are 12 face cards in a deck of 52 playing cards.

∴ No. of favourable outcomes = 12.

P(drawing a face card) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{12}{40} = \dfrac{3}{10}$.

Hence, the probability that the card drawn is a face card = $\dfrac{3}{10}$.

(ii) Favourable outcomes (for an even numbered red card) are 2, 4, 8, 10 of heart and diamond.

∴ No. of favourable outcomes = 8.

P(drawing an even numbered red card)

= $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{8}{40} = \dfrac{1}{5}$.

Hence, the probability that the card drawn is an even numbered red card = $\dfrac{1}{5}$.

A dice has 6 faces marked by the given numbers as shown below :

$\boxed{1} \quad \boxed{2} \quad \boxed{3} \quad \boxed{-1} \quad \boxed{-2} \quad \boxed{-3}$

The dice is thrown once. What is the probability of getting

(i) a positive integer ?

(ii) an integer greater than -3 ?

(iii) the smallest integer ?

Answer

Since, there are 6 faces in a dice.

∴ No. of possible outcomes = 6.

(i) Favourable outcomes for getting a positive integer are 1, 2, 3.

∴ No. of favourable outcomes = 3.

P(getting a positive integer) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{3}{6} = \dfrac{1}{2}$.

Hence, the probability of getting a positive integer = $\dfrac{1}{2}$.

(ii) Favourable outcomes for getting an integer greater than -3 are -2, -1, 1, 2, 3.

∴ No. of favourable outcomes = 5.

P(getting an integer greater than -3)

= $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{5}{6}$.

Hence, the probability of getting an integer greater than -3 = $\dfrac{5}{6}$.

(iii) Favourable outcomes for getting smallest integer is -3.

∴ No. of favourable outcomes = 1.

P(getting smallest integer) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{1}{6}$.

Hence, the probability of getting smallest integer = $\dfrac{1}{6}$.

Sixteen cards are labelled as a, b, c, .........., m, n, o, p. They are put in a box and shuffled. A boy is asked to draw a card from the box. What is the probability that the card drawn is :

(i) a vowel

(ii) a consonant

(iii) none of the letters of the word median ?

Answer

No. of possible outcomes = 16.

(i) Vowels between a, b, c, .........., m, n, o, p are a, e, i, o.

∴ No. of favourable outcomes = 4.

P(that the card drawn is a vowel)

= $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{4}{16} = \dfrac{1}{4}$.

Hence, the probability that the card drawn is a vowel = $\dfrac{1}{4}$.

(ii) Since, there are 4 vowels.

∴ No. of consonants or favourable outcomes = 12 (16 - 4).

P(that the card drawn is a consonant)

= $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{12}{16} = \dfrac{3}{4}$.

Hence, the probability that the card drawn is a consonant = $\dfrac{3}{4}$.

(iii) Letters of the word median are 'm', 'e', 'd', 'i', 'a' and 'n'.

No. of letters left = 16 - 6 = 10.

∴ No. of favourable outcomes = 10.

P(that the card contains none of the letters of the word median)

= $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{10}{16} = \dfrac{5}{8}$.

Hence, the probability that the card drawn contains none of the letters of the word median = $\dfrac{5}{8}$.

A box contains a certain number of balls. On each of 60% balls, letter A is marked. On each of 30% balls, letter B is marked and on each of remaining balls, letter C is marked. A ball is drawn from the box at random. Find the probability that the ball drawn is :

(i) marked C

(ii) A or B

(iii) neither B nor C.

Answer

Given,

On each of 60% balls, letter A is marked. On each of 30% balls, letter B is marked and on each of remaining balls (i.e. 10%), letter C is marked.

Let no. of balls be x.

∴ No. of possible outcomes = x.

No. of balls marked A = $\dfrac{60}{100} \times x = \dfrac{3x}{5}$

No. of balls marked B = $\dfrac{30}{100} \times x = \dfrac{3x}{10}$

No. of balls marked C = $\dfrac{10}{100} \times x = \dfrac{x}{10}$.

(i) No. of balls marked C or favourable outcomes = $\dfrac{x}{10}$

P(drawing a ball marked C) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{\dfrac{x}{10}}{x} = \dfrac{1}{10}$.

Hence, the probability of drawing a ball marked C = $\dfrac{1}{10}$.

(ii) No. of balls marked A or B = $\dfrac{3x}{5} + \dfrac{3x}{10} = \dfrac{6x + 3x}{10} = \dfrac{9x}{10}$.

P(drawing a ball marked A or B) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{\dfrac{9x}{10}}{x} = \dfrac{9}{10}$.

Hence, the probability of drawing a ball marked A or B = $\dfrac{9}{10}$.

(iii) Since, the balls are marked either A, B or C.

So, P(drawing neither B nor C) = P(drawing A marked ball)

No. of A marked balls = $\dfrac{3x}{5}$.

∴ No. of favourable outcomes = $\dfrac{3x}{5}$.

P(drawing a ball marked A) = $\dfrac{\text{No. of favourable outcomes}}{\text{No. of possible outcomes}} = \dfrac{\dfrac{3x}{5}}{x} = \dfrac{3}{5}$.