Find the amount of bill for the following intra-state transaction of goods/services. The rate of GST being 12 % :
| MRP (in ₹) | Discount % |
|---|---|
| 600 | 40 |
| 450 | 32 |
| 900 | 20 |
| 750 | 30 |
Answer
If for the value of any transaction, discount = x %.
It's discounted value = (100 - x)% of its original value.
| MRP (in ₹) | Discount % | Discounted value (Selling price) |
|---|---|---|
| 600 | 40 | 60% of 600 = ₹ 360 |
| 450 | 32 | 68% of 450 = ₹ 306 |
| 900 | 20 | 80% of 900 = ₹ 720 |
| 750 | 30 | 70% of 750 = ₹ 525 |
| Total | ₹ 1911 |
CGST = 6% of ₹ 1911 = = ₹ 114.66
SGST = CGST = ₹ 114.66
Amount of bill = ₹ 1911 + ₹ 114.66 + ₹ 114.66 = ₹ 2140.32
Hence, amount of bill = ₹ 2140.32
Find the amount of bill for the following inter-state transaction of goods/services. The rate of GST being 5 % :
| MRP (in ₹) | Discount % |
|---|---|
| 9600 | 20 |
| 6000 | 50 |
| 10800 | 40 |
| 9000 | 30 |
| 7200 | 40 |
Answer
If for the value of any transaction, discount = x %.
It's discounted value = (100 - x)% of its original value.
| MRP (in ₹) | Discount % | Discounted value (Selling price) |
|---|---|---|
| 9600 | 20 | 80% of 9600 = ₹ 7680 |
| 6000 | 50 | 50% of 6000 = ₹ 3000 |
| 10800 | 40 | 60% of 10800 = ₹ 6480 |
| 9000 | 30 | 70% of 9000 = ₹ 6300 |
| 7200 | 40 | 60% of 7200 = ₹ 4320 |
| Total | ₹ 27780 |
IGST = 5% of ₹ 27780 = = ₹ 1389
Amount of bill = ₹ 27780 + ₹ 1389 = ₹ 29169
Hence, amount of bill = ₹ 29169.
Find the amount of bill for the following transaction of goods/services from Patna (Bihar) to Ajmer (Rajasthan) :
| GST % | MRP (in ₹) | Discount % |
|---|---|---|
| 18 | 12000 | 30 |
| 18 | 15000 | 40 |
| 12 | 5200 | 30 |
| 12 | 8000 | 40 |
Answer
This is a interstate transaction.
∴ GST = IGST.
| MRP (in ₹) | Discount % | Discounted value (Selling price) | GST % | IGST | Amount (in ₹) |
|---|---|---|---|---|---|
| 12000 | 30 | 70% of 12000 = ₹8400 | 18 | 18% of ₹8400 = ₹1512 | 8400 + 1512 = 9912 |
| 15000 | 40 | 60% of 15000 = ₹9000 | 18 | 18% of ₹9000 = ₹1620 | 9000 + 1620 = 10620 |
| 5200 | 30 | 70% of 5200 = ₹3640 | 12 | 12% of ₹3640 = ₹436.80 | 3640 + 436.80 = 4076.80 |
| 8000 | 40 | 60% of 8000 = ₹4800 | 12 | 12% of ₹4800 = ₹576 | 4800 + 576 = 5376 |
| Total | 29984.80 |
Hence, the amount of bill = ₹ 29984.80
Find the amount for the following transaction of goods/services within Gujarat :
| MRP (in ₹)/ item | Number of items | GST% |
|---|---|---|
| 300 | 40 | 12 |
| 600 | 50 | 12 |
| 480 | 70 | 18 |
Answer
This is an intra-state transaction.
GST = CGST + SGST
We know, SGST = CGST
| MRP (in ₹)/ item | Number of items | Total cost of whole quantity (in ₹) | GST % | CGST (in ₹) | SGST (in ₹) | Amount (MRP + CGST + SGST) (in ₹) |
|---|---|---|---|---|---|---|
| 300 | 40 | 12000 | 12 | 6% of 12000 = 720 | 720 | 12000 + 720 + 720 = 13440 |
| 600 | 50 | 30000 | 12 | 6% of 30000 = 1800 | 1800 | 30000 + 1800 + 1800 = 33600 |
| 480 | 70 | 33600 | 18 | 9% of 33600 = 3024 | 3024 | 33600 + 3024 + 3024 = 39648 |
| Total | ₹ 86688 |
Hence, amount of bill = ₹ 86688.
A dealer in Kanpur (U.P.) supplies goods worth ₹ 5000 to a dealer in Meerut (U.P.). The dealer in Meerut supplies the same goods/services to a dealer in Delhi at a profit of ₹ 2000. Find the cost of goods/services in Delhi as per GST system. The rate of GST is 18%.
Answer
When product is sold from Kanpur to Meerut (It is an intra-state transaction)
For dealer in Kanpur :
S.P. = ₹ 5000
CGST = 9% of ₹ 5000 = .
SGST = CGST = ₹ 450.
When product is sold from Meerut to Delhi (It is an inter-state transaction)
For dealer in Meerut :
Input-tax credit (ITC) = ₹ 450 + ₹ 450 = ₹ 900.
C.P. (excluding GST) = ₹ 5000
Profit = ₹ 2000
S.P. = ₹ 5000 + ₹ 2000 = ₹ 7000
IGST = 18% of ₹ 7000 = = ₹ 1260
C.P. in Delhi = S.P. in Meerut + IGST = ₹ 7000 + ₹ 1260 = ₹ 8260.
Hence, cost of goods/services in Delhi = ₹ 8260.
Ashok deposits ₹ 3200 per month in a cumulative deposit account for 3 years at the rate of 9% per annum. Find the maturity value of this account.
Answer
Given,
P = ₹ 3200
r = 9%
Maturity value of recurring deposit = Total sum deposited + Interest on it
= P × n + P ×
where n is time in months.
Time (n) = 3 years = 3 × 12 = 36 months.
Substituting values we get :
Hence, maturity value = ₹ 131184.
Mrs. Karna has a recurring deposit account in Punjab National Bank for 3 years at 8% p.a. If she gets ₹ 9990 as interest at the time of maturity, find :
(i) the monthly instalment
(ii) the maturity value of the account.
Answer
(i) Given,
Time (n) = 3 years = 3 × 12 = 36 months.
Rate = 8%
Let monthly instalment be ₹ P.
By formula,
Interest = P ×
Substituting values we get
Hence, monthly installment = ₹ 2250.
(ii) Maturity value of recurring deposit = Total sum deposited + Interest on it
= P × n + 9990
= 2250 × 36 + 9990
= 81000 + 9990
= ₹ 90990.
Hence, the maturity value of this account = ₹ 90990.
A man has a 5 year recurring deposit account in a bank and deposits ₹ 240 per month. If he recieves ₹ 17,694 at the time of maturity, find the rate of interest.
Answer
Let rate of interest be r%.
Given,
P = ₹ 240
M.V. = ₹ 17694
Time (n) = 5 years = 5 × 12 = 60 months.
Maturity value = P × n + P ×
Substituting values we get :
⇒ 17694 = 240 × 60 + 240 ×
⇒ 17694 = 14400 + 6 ×
⇒ 17694 - 14400 = 6 × 61r
⇒ 3294 = 366r
⇒ r = = 9%.
Hence, rate of interest = 9%.
Sheela has a recurring deposit account in a bank of ₹ 2000 per month at the rate of 10% per annum. If she gets ₹ 83100 at the time of maturity, find the total time (in years) for which the account was held.
Answer
Let time = n months.
Given,
P = ₹ 2000
r = 10%
By formula,
M.V. = P × n + P ×
Substituting values we get :
Since, time cannot be negative.
∴ n = 36 months = 3 years.
Hence, time = 3 years.
A man deposits ₹ 900 per month in a recurring account for 2 years. If he gets ₹ 1800 as interest at the time of maturity, find the rate of interest.
Answer
Let rate of interest be r%.
Given,
P = ₹ 900
Time (n) = 2 years = 24 months.
By formula,
Interest = P ×
Substituting values we get :
Hence, the rate of interest = 8%.
The given diagram represents two sets A and B on real number lines.
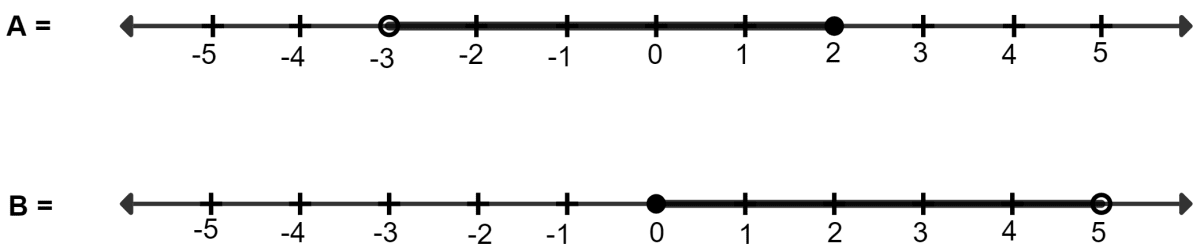
(i) Write down A and B in set-builder form.
(ii) Represent A ∪ B, A ∩ B, A' ∩ B, A - B and B - A on separate number lines.
Answer
(i) From graph,
A = {x ∈ R : -3 < x ≤ 2}, B = {x ∈ R : 0 ≤ x < 5}
(ii) From graph,
A ∪ B = {x ∈ R : -3 < x < 5}

A ∩ B = {x ∈ R : 0 ≤ x ≤ 2}

A' ∩ B = {x ∈ R : -2 < x < 5}
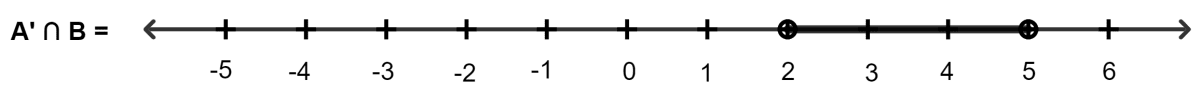
A - B = {x ∈ R : -3 < x < 0}

B - A = {x ∈ R : 2 < x < 5}

Find the values of x, which satisfy the inequation :
; x ∈ N
Graph the solution set on the real number line.

Answer
Solving L.H.S. of the above inequation :
Solving R.H.S. of the inequation :
From (1) and (2),
-2 < x ≤
Since, x ∈ N
∴ x = {1, 2, 3}.
Hence, x = {1, 2, 3}.
State for each of the following statements whether it is true or false :
(a) If (x - a)(x - b) < 0, then x < a and x < b.
(b) If a < 0 and b < 0, then (a + b)2 > 0.
(c) If a and b are any two integers such that a > b, then a2 > b2.
(d) If p = q + 2, then p > q.
(e) If a and b are two negative integers such that a < b, then
Answer
(a) False
Reason — If x < a and x < b, then (x - a)(x - b) will be greater than 0 as multiplication of two negative number generates a positive number.
(b) True
Reason — If a < 0 and b < 0, then (a + b) will be a negative number and square of any negative number is greater than 0, so (a + b)2 is greater than 0.
(c) False
Reason — If a > b, then a2 > b2 is true only if a and b are positive numbers.
(d) True
Reason — If a positive number is added to any number (suppose x), then resultant number is greater than x.
(e) False
Reason — If, a < b and both are two negative integers then on recripocating the numbers the sign will be reversed, so .
Given 20 - 5x < 5(x + 8), find the smallest value of x when :
(i) x ∈ I
(ii) x ∈ W
(iii) x ∈ N
Answer
Solving,
⇒ 20 - 5x < 5(x + 8)
⇒ 20 - 5x < 5x + 40
⇒ 5x + 5x > 20 - 40
⇒ 10x > -20
⇒ x > = -2.
(i) As, x > -2 and x ∈ I.
∴ x = {-1, 0, 1 .......}
The smallest no. = -1.
Hence, smallest value of x = -1, when x is an integer.
(ii) As, x > -2 and x ∈ W.
∴ x = {0, 1, 2 .......}
The smallest no. = 0.
Hence, smallest value of x = 0, when x is a whole number.
(iii) As, x > -2 and x ∈ N.
∴ x = {1, 2 .......}
The smallest no. = 1.
Hence, smallest value of x = 1, when x is a natural number.
If x ∈ Z, solve : 2 + 4x < 2x - 5 ≤ 3x. Also, represent its solution on the real number line.
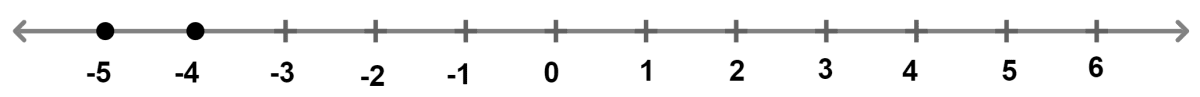
Answer
Given,
⇒ 2 + 4x < 2x - 5 ≤ 3x
Solving L.H.S. of the above inequation :
⇒ 2 + 4x < 2x - 5
⇒ 4x - 2x < - 5 - 2
⇒ 2x < -7
⇒ x <
⇒ x < -3.5 ..........(1)
Solving R.H.S. of the above inequation :
⇒ 2x - 5 ≤ 3x
⇒ 3x - 2x ≥ -5
⇒ x ≥ -5 .............(2)
From (1) and (2), we get :
-5 ≤ x < -3.5; Since, x ∈ Z
Hence, x = {-5, -4}.
If P = {x : 7x - 4 > 5x + 2, x ∈ R} and Q = {x : x - 19 ≥ 1 - 3x, x ∈ R}; find the range of set P ∩ Q and represent it on a number line.
Answer
Solving 7x - 4 > 5x + 2,
⇒ 7x - 5x > 2 + 4
⇒ 2x > 6
⇒ x > 3.
P = {x : x > 3, x ∈ R}
Solving x - 19 ≥ 1 - 3x
⇒ x + 3x ≥ 1 + 19
⇒ 4x ≥ 20
⇒ x ≥ 5.
Q = {x : x ≥ 5, x ∈ R}
P ∩ Q = Numbers common between P and Q
= {x : x ≥ 5, x ∈ R}
P ∩ Q on the number line is :

Find the values of x, which satisfy the inequation , x ∈ W. Graph the solution set on the number line.
Answer
Given,
Solving L.H.S. of the inequation,
Solving R.H.S. of the inequation,
From (i) and (ii) we get,
-2.25 ≤ x < 5
Since, x ∈ W,
∴ Solution set = {0, 1, 2, 3, 4}.
Solution on the number line is :

Solve :
Answer
Solving :
Hence, x = or 5.
Solve :
Answer
Solving :
Hence, x = 1 or 9.
Find the value of k for which the roots of the following equation are real and equal.
k2x2 - 2(2k - 1)x + 4 = 0
Answer
Given,
Equation : k2x2 - 2(2k - 1)x + 4 = 0
The roots of the equation are real and equal, when D = 0.
⇒ b2 - 4ac = 0
⇒ [-2(2k - 1)]2 - 4 × k2 × 4 = 0
⇒ [-4k + 2]2 - 16k2 = 0
⇒ 16k2 + 4 - 16k - 16k2 = 0
⇒ 16k = 4
⇒ k = .
Hence, k = .
Solve :
, when x ≠ 0 and a ≠ 0.
Answer
Solving :
Hence, x = (a + b), -(a + b).
If -5 is a root of the quadratic equation 2x2 + px - 15 = 0 and the quadratic equation p(x2 + x) + k = 0 has equal roots, find the value of k.
Answer
As, -5 is the root of the quadratic equation 2x2 + px - 15 = 0, so it will satisfy the equation.
∴ 2(-5)2 + (-5)p - 15 = 0
⇒ 2 × 25 - 5p - 15 = 0
⇒ 50 - 5p - 15 = 0
⇒ 5p = 35
⇒ p = = 7.
Substituting value of p in p(x2 + x) + k = 0, we get :
⇒ 7(x2 + x) + k = 0
⇒ 7x2 + 7x + k = 0
Since, above equation has real and equal roots.
∴ D = 0
⇒ b2 - 4ac = 0
⇒ (7)2 - 4 × 7 × k = 0
⇒ 49 - 28k = 0
⇒ 28k = 49
⇒ k = .
Hence, k = .
x articles are bought at ₹ (x - 8) each and (x - 2) some other articles are bought at ₹ (x - 3) each. If the total cost of all these articles is ₹ 76, how many articles of first kind were bought ?
Answer
Since,
x articles are bought at ₹ (x - 8) each and (x - 2) some other articles are bought at ₹ (x - 3) each.
Total cost = x(x - 8) + (x - 2)(x - 3).
Given,
Total cost = ₹ 76.
∴ x(x - 8) + (x - 2)(x - 3) = 76
⇒ x2 - 8x + x2 - 3x - 2x + 6 = 76
⇒ 2x2 - 13x + 6 - 76 = 0
⇒ 2x2 - 13x - 70 = 0
⇒ 2x2 - 20x + 7x - 70 = 0
⇒ 2x(x - 10) + 7(x - 10) = 0
⇒ (2x + 7)(x - 10) = 0
⇒ 2x + 7 = 0 or x - 10 = 0
⇒ 2x = -7 or x = 10
⇒ x = - or x = 10.
Since, no. of articles cannot be negative.
∴ x = 10.
Hence, there are 10 articles of first kind.
In a two digit number, the unit's digit exceeds its ten's digit by 2. The product of the given number and the sum of its digits is equal to 144. Find the number.
Answer
Let ten's digit be x.
Unit's digit = x + 2
Number = 10x + x + 2 = 11x + 2
Sum of digits = x + x + 2 = 2x + 2
According to question,
Number × Sum of digits = 144
⇒ (11x + 2)(2x + 2) = 144
⇒ 22x2 + 22x + 4x + 4 = 144
⇒ 22x2 + 26x + 4 = 144
⇒ 22x2 + 26x = 140
⇒ 2(11x2 + 13x) = 140
⇒ 11x2 + 13x = 70
⇒ 11x2 + 13x - 70 = 0
⇒ 11x2 + 35x - 22x - 70 = 0
⇒ x(11x + 35) - 2(11x + 35) = 0
⇒ (x - 2)(11x + 35) = 0
⇒ x - 2 = 0 or 11x + 35 = 0
⇒ x = 2 or x = -
Since, digit cannot be negative.
∴ x = 2.
Number = 11x + 2 = 11(2) + 2
= 22 + 2 = 24.
Hence, number = 24.
The time taken by a person to cover 150 km was 2.5 hours more than the time taken in return journey. If he returned at a speed of 10 km/hour more than the speed of going, what was the speed per hour in each direction ?
Answer
Let speed while going be x km/hour and speed while returning will be (x + 10) km/hour.
Time taken while going = hours.
Time taken while returning = hours.
Given,
Time taken by a person to cover 150 km was 2.5 hours more than the time taken in return journey.
Since, speed cannot be negative.
∴ x = 20 km/hour and (x + 10) = 30 km/hour.
Hence, speed while going = 20 km/hour and speed while returning = 30 km/hour.
A takes 9 days more than B to do a certain piece of work. Together they can do the work in 6 days. How many days will A alone take to do the work ?
Answer
Let A alone takes x days and B alone takes y days.
Given,
A takes 9 days more than B to do a certain piece of work
∴ x = y + 9 .........(1)
As, A takes x days to do a work
So, one day work of A =
As, B takes y days to do a work
So, one day work of B =
As, together they can do work in 6 days.
∴ In one day both of them do th part of work.
Since, days cannot be negative so, y ≠ -6.
x = y + 9 = 18.
Hence, A alone will take 18 days to complete the work.
A man bought a certain number of chairs for ₹ 10000. He kept one for his own use and sold the rest at the rate ₹ 50 more than he gave for one chair. Besides getting his own chair for nothing, he made a profit of ₹ 450. How many chairs did he buy ?
Answer
Given,
Man bought a certain number of chairs for ₹ 10000.
Let no. of chairs bought be x.
∴ Cost of one chair = ₹
S.P. of each chair = ₹
Since, he kept one chair for himself so he sold (x - 1) chairs.
Given,
⇒ Profit = ₹ 450
⇒ S.P. - C.P. = ₹ 450
Since no. of chairs cannot be negative.
∴ x = 20.
Hence, no. of chairs bought = 20.
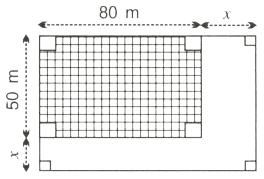
In the given figure; the area of unshaded portion is 75% of the area of the shaded portion. Find the value of x.
Answer
From figure,
Length of larger portion (L) = (80 + x) meters
Breadth of larger portion (B) = (50 + x) meters
Area of larger portion = L × B = (80 + x)(50 + x)
= 4000 + 80x + 50x + x2
= (x2 + 130x + 4000) m2.
Length of smaller portion (l) = 80 meters
Breadth of smaller portion (b) = 50 meters
Area of smaller portion = l × b = 80 × 50 = 4000 m2
Area of unshaded portion = Area of larger portion - Area of smaller portion
= x2 + 130x + 4000 - 4000
= (x2 + 130x) m2.
Given,
Area of unshaded portion is 75% of the area of the shaded portion.
Since, length cannot be negative.
∴ x = 20 meters.
Hence, x = 20 meters.
Solve for x : .
Answer
Applying componendo and dividendo, we get :
Squaring both sides we get :
Again applying componendo and dividendo, we get :
Hence, x = .
If a : b = 2 : 3, b : c = 4 : 5 and c : d = 6 : 7, find a : b : c : d.
Answer
Given,
a : b = 2 : 3
b : c = 4 : 5
c : d = 6 : 7
From (1), (2) and (3), we get :
a : b : c : d = 16 : 24 : 30 : 35
Hence, a : b : c : d = 16 : 24 : 30 : 35.
If = x, prove that x2 - 4ax + 1 = 0.
Answer
Given,
= x.
Applying componendo and dividendo, we get :
Squaring both sides we get,
Applying componendo and dividendo we get :
Hence, proved that x2 - 4ax + 1 = 0.
Find the compounded ratio of :
(i) (a - b) : (a + b) and (b2 + ab) : (a2 - ab)
(ii) (x + y) : (x - y), (x2 + y2) : (x + y)2 and (x2 - y2)2 : (x4 - y4)
(iii) (x2 - 25) : (x2 + 3x - 10); (x2 - 4) : (x2 + 3x + 2) and (x + 1) : (x2 + 2x).
Answer
(i) Calculating the compounded ratio :
Hence, compounded ratio of (a - b) : (a + b) and (b2 + ab) : (a2 - ab) = b : a.
(ii) Calculating the compounded ratio :
Hence, the compounded ratio = 1 : 1.
(iii) Calculating the compounded ratio :
Hence, the compounded ratio = (x - 5) : x(x + 2).
The ratio of the prices of first two fans was 16 : 23. Two years later, when the price of the first fan had risen by 10% and that of the second by ₹ 477, the ratio of their prices became 11 : 20. Find the original prices of the two fans.
Answer
Let price of first fan be f1 and second fan be f2.
Given,
Ratio of the prices of first two fans was 16 : 23.
First fan price after 2 years = .
Second fan price after two years = .
Given,
Ratio of fan's prices becomes 11 : 20 after 2 years.
Substituting value of f1 from (1) in above equation we get :
Substituting value of f2 in equation (1), we get :
Hence, original price of fans are ₹ 848 and ₹ 1219.
If y is the mean proportional between x and z; show that xy + yz is the mean proportional between x2 + y2 and y2 + z2.
Answer
Given,
y is the mean proportional between x and z
To prove,
xy + yz is the mean proportional between x2 + y2 and y2 + z2
Substituting y2 = xz in L.H.S. of (i)
⇒ x2(xz) + x(xz)z + x(xz)z + (xz)z2
⇒ x3z + x2z2 + x2z2 + xz3
⇒ x3z + 2x2z2 + xz3 .........(ii)
Substituting y2 = xz in R.H.S. of (i)
⇒ x2(xz) + x2z2 + (xz)2 + (xz)z2
⇒ x3z + x2z2 + x2z2 + xz3
⇒ x3z + 2x2z2 + xz3 .........(iii)
Since, (ii) = (iii)
Hence, proved that xy + yz is the mean proportional between x2 + y2 and y2 + z2.
Using componendo and dividendo, find value of x :
Answer
Applying componendo and dividendo we get,
Again applying componendo and dividendo we get,
Hence, x = 7.
Given that x + 2 and x - 3 are factors of x3 + ax + b. Calculate the values of a and b. Also, find the remaining factor.
Answer
By factor theorem,
If (x - a) is a factor of polynomial f(x), then remainder f(a) = 0.
⇒ x + 2 = 0
⇒ x = -2.
Since, x + 2 is a factor of x3 + ax + b
∴ Remainder = 0.
⇒ (-2)3 + (-2)a + b = 0
⇒ -8 - 2a + b = 0
⇒ b = 2a + 8 ................(1)
x - 3 = 0
⇒ x = 3.
Since, x - 3 is a factor of x3 + ax + b
∴ Remainder = 0.
⇒ (3)3 + (3)a + b = 0
⇒ 27 + 3a + b = 0
⇒ b = -27 - 3a ................(2)
From (1) and (2), we get:
⇒ 2a + 8 = -27 - 3a
⇒ 2a + 3a = -27 - 8
⇒ 5a = -35
⇒ a =
⇒ a = -7.
Substituting value of a in equation (1), we get :
⇒ b = 2a + 8 = 2 × -7 + 8 = -14 + 8 = -6.
f(x) = x3 + ax + b = x3 - 7x - 6.
Substituting x = -1 in f(x), we get :
⇒ (-1)3 - 7(-1) - 6
⇒ -1 + 7 - 6
⇒ -1 + 1
⇒ 0.
∴ (x + 1) is a factor of x3 - 7x - 6.
Hence, a = -7, b = -6 and (x + 1) is the remaining factor.
Use the remainder theorem to factorise the expression 2x3 + 9x2 + 7x - 6. Hence, solve the equation 2x3 + 9x2 + 7x - 6.
Answer
For x = -2, the value of the given expression
= 2(-2)3 + 9(-2)2 + 7(-2) - 6
= 2 × -8 + 9 × 4 - 14 - 6
= -16 + 36 - 14 - 6
= -36 + 36
= 0.
⇒ x + 2 is a factor of 2x3 + 9x2 + 7x - 6.
Now dividing 2x3 + 9x2 + 7x - 6 by (x + 2),
we get quotient = 2x2 + 5x - 3
∴ 2x3 + 9x2 + 7x - 6 = (x + 2)(2x2 + 5x - 3)
= (x + 2)(2x2 + 6x - x - 3)
= (x + 2)[2x(x + 3) - 1(x + 3)]
= (x + 2)(2x - 1)(x + 3).
∴ (x + 2), (2x - 1) and (x + 3) are the factors of 2x3 + 9x2 + 7x - 6.
⇒ x + 2 = 0
⇒ x = -2
⇒ 2x - 1 = 0
⇒ x =
⇒ x + 3 = 0
⇒ x = -3.
Hence, 2x3 + 9x2 + 7x - 6 = (x + 2)(2x - 1)(x + 3) and x = -2, -3, .
When 2x3 + 5x2 - 2x + 8 is divided by (x - a) the remainder is 2a3 + 5a2. Find the value of a.
Answer
By remainder theorem,
If f(x), a polynomial in x, is divided by (x - a), the remainder = f(a).
∴ On dividing 2x3 + 5x2 - 2x + 8 by (x - a)
Remainder = 2a3 + 5a2 - 2a + 8
Given, remainder = 2a3 + 5a2.
∴ 2a3 + 5a2 - 2a + 8 = 2a3 + 5a2
⇒ -2a + 8 = 0
⇒ 2a = 8
⇒ a = 4.
Hence, a = 4.
What number should be added to x3 - 9x2 - 2x + 3 so that the remainder may be 5 when divided by (x - 2) ?
Answer
Let a be added to x3 - 9x2 - 2x + 3 so that the remainder may be 5 when divided by (x - 2).
By remainder theorem,
If f(x), a polynomial in x, is divided by (x - a), the remainder = f(a).
∴ On dividing x3 - 9x2 - 2x + 3 + a by (x - 2)
Remainder = (2)3 - 9(2)2 - 2(2) + 3 + a
Since, remainder = 5.
∴ 8 - 9(4) - 4 + 3 + a = 5
⇒ 8 - 36 - 1 + a = 5
⇒ a - 29 = 5
⇒ a = 5 + 29 = 34.
Hence, 34 must be added to x3 - 9x2 - 2x + 3 so that the remainder may be 5 when divided by (x - 2).
Let R1 and R2 are remainders when the polynomial x3 + 2x2 - 5ax - 7 and x3 + ax2 - 12x + 6 are divided by (x + 1) and (x - 2) respectively. If 2R1 + R2 = 6; find the value of a.
Answer
On dividing x3 + 2x2 - 5ax - 7 by (x + 1), we get remainder R1 :
∴ R1 = (-1)3 + 2(-1)2 - 5a(-1) - 7
⇒ R1 = -1 + 2 + 5a - 7
⇒ R1 = 5a - 6.
On dividing x3 + ax2 - 12x + 6 by (x - 2), we get remainder R2
∴ R2 = (2)3 + a(2)2 - 12(2) + 6
⇒ R2 = 8 + 4a - 24 + 6
⇒ R2 = 4a - 10.
Given,
⇒ 2R1 + R2 = 6
⇒ 2(5a - 6) + 4a - 10 = 6
⇒ 10a - 12 + 4a - 10 = 6
⇒ 14a - 22 = 6
⇒ 14a = 28
⇒ a = = 2.
Hence, a = 2.
Find matrix B, if matrix A = , matrix C = and AB = 3C.
Answer
Let order of matrix B = m × n
Given,
AB = 3C
Since, the product of matrices is possible, only when the number of columns in the first matrix is equal to the number of rows in the second.
∴ m = 2
Also, the no. of columns of product (resulting) matrix is equal to no. of columns of second matrix.
∴ n = 1
Order of matrix B = m × n = 2 × 1.
Let matrix B =
Substituting matrix in AB = 3C we get,
∴ a + 5b = 6 ........(1)
a + 2b = 3 ........(2)
Subtracting equation (2) from (1), we get :
⇒ a + 5b - (a + 2b) = 6 - 3
⇒ a - a + 5b - 2b = 3
⇒ 3b = 3
⇒ b = 1.
Substituting value of b in (1), we get :
⇒ a + 5(1) = 6
⇒ a + 5 = 6
⇒ a = 1.
B =
Hence, B = .
Find the matrices A and B, if 2A + B = and A - 2B =
Answer
Given,
⇒ 2A + B = .........(1)
⇒ A - 2B = .........(2)
Multiplying equation (1) by 2 and adding in equation (2), we get :
Substituting value of A in equation (1), we get :
Hence,
If A = ; find the matrix X.
Answer
Given,
Substituting value of A and B in above equation we get,
Hence, X =
Given, ; find the matrix X such that AX = B.
Answer
Let order of matrix X = m × n
Given,
AX = B
Since, the product of matrices is possible, only when the number of columns in the first matrix is equal to the number of rows in the second.
∴ m = 2
Also, the no. of columns of product (resulting) matrix is equal to no. of columns of second matrix.
∴ n = 1
Order of matrix X = m × n = 2 × 1.
Let matrix X =
Substituting matrix in AX = B we get,
∴ 3a + 4b = 24 ........(1)
4a - 3b = 7 ........(2)
⇒ 3a + 4b = 24
⇒ 3a = 24 - 4b
⇒ a = ........(3)
Substituting value of a from equation (3) in equation (2), we get :
Substituting value of b in equation (3), we get :
a = = 4.
Hence, X =
Given A = ; find the matrix X such that XA = B.
Answer
Let order of matrix X = m × n
Given,
XA = B
Since, the product of matrices is possible only when the number of columns in the first matrix is equal to the number of rows in the second.
∴ n = 2
Also, the no. of rows of product (resulting) matrix is equal to no. of rows of first matrix.
∴ m = 1
Order of matrix X = m × n = 1 × 2.
Let matrix X =
Substituting matrix in XA = B we get,
∴ 3a - 2b = -2 .........(1)
6a - 8b = 16 .........(2)
⇒ 3a - 2b = -2
⇒ 2(3a - 2b) = 2(-2)
⇒ 6a - 4b = -4 .........(3)
Subtracting equation (2) from (3), we get :
⇒ 6a - 4b - (6a - 8b) = -4 - 16
⇒ 6a - 6a - 4b + 8b = -20
⇒ 4b = -20
⇒ b =
⇒ b = -5.
Substituting value of b in equation (1), we get :
⇒ 3a - 2(-5) = -2
⇒ 3a + 10 = -2
⇒ 3a = -2 - 10
⇒ 3a = -12
⇒ a =
⇒ a = -4.
Hence, X = .
Find the 15th term of the A.P. with second term 11 and common difference 9.
Answer
We know that,
⇒ an = a + (n - 1)d
⇒ a2 = a + (2 - 1)d
⇒ 11 = a + d
⇒ 11 = a + 9
⇒ a = 11 - 9 = 2.
a15 = a + (15 - 1)d
= 2 + 14 × 9
= 2 + 126
= 128.
Hence, 15th term = 128.
How many three digit numbers are divisible by 7 ?
Answer
Three digit numbers which are divisible by 7 are 105, 112, ......., 994.
Let there be n terms.
In above series,
an = 994, a = 105 and d = 7.
By formula,
⇒ an = a + (n - 1)d
⇒ 994 = 105 + (n - 1) × 7
⇒ 994 = 105 + 7(n - 1)
⇒ 994 - 105 = 7(n - 1)
⇒ 889 = 7(n - 1)
⇒ n - 1 =
⇒ n - 1 = 127
⇒ n = 128.
Hence, there are 128 three digit numbers, which are divisible by 7.
Find the sum of terms of the A.P. : 4, 9, 14, ......, 89.
Answer
Let there be n terms in the above series.
From above series,
an = 89, a = 4 and d = 5.
By formula,
⇒ an = a + (n - 1)d
⇒ 89 = 4 + 5(n - 1)
⇒ 85 = 5(n - 1)
⇒ 17 = n - 1
⇒ n = 18.
By formula,
Sum of A.P. =
Substituting values we get,
Hence, sum of A.P. = 837.
Daya gets pocket money from his father every day. Out of the pocket money, he saves ₹ 2.75 on first day, ₹ 3.00 on second day, ₹ 3.25 on third day and so on. Find :
(i) the amount saved by Daya on 14th day
(ii) the amount saved by Daya on 30th day
(iii) the total amount saved by him in 30 days.
Answer
2.75, 3.00, 3.25, ..............
The above A.P. has first term (a) = 2.75 and common difference (d) = 3.00 - 2.75 = 0.25
By formula,
nth term = an = a + (n - 1)d.
(i) The amount saved by Daya on 14th day = 14th term of A.P.
a14 = a + (14 - 1)d
= a + 13d
= 2.75 + 13 × 0.25
= 2.75 + 3.25
= ₹ 6.
Hence, the amount saved by Daya on 14th day = ₹ 6.
(ii) The amount saved by Daya on 30th day = 30th term of A.P.
a30 = a + (30 - 1)d
= a + 29d
= 2.75 + 29 × 0.25
= 2.75 + 7.25
= ₹ 10.
Hence, the amount saved by Daya on 30th day = ₹ 10.
(iii) Sum of A.P. =
Total amount saved by Daya in 30 days = Sum of A.P. upto 30 terms.
Hence, total amount saved by Daya in 30 days = ₹ 191.25
If the sum of first m terms of an A.P. is n and sum of first n terms of the same A.P. is m, show that sum of first (m + n) terms of it is -(m + n).
Answer
Let a be the first term and d be common difference of the A.P.
Given,
Sum of first m terms of an A.P. is n.
⇒ Sm = n
⇒
⇒ m[2a + (m - 1)d] = 2n
⇒ 2am + m(m - 1)d = 2n ..........(1)
Sum of first n terms of an A.P. is m.
⇒ Sn = m
⇒
⇒ n[2a + (n - 1)d] = 2m
⇒ 2an + n(n - 1)d = 2m ..........(2)
Subtracting eq. (2) from (1), we get
Sm + n =
=
= [From (3)]
= -(m + n).
Hence, proved that sum of first (m + n) terms of it is -(m + n).
3rd term of a G.P. is 27 and its 6th term is 729; find the product of its first and 7th terms.
Answer
Let first term of G.P. be a and common ratio be r.
We know that,
nth term of G.P. = arn - 1
Given,
3rd term of a G.P. = 27
∴ ar2 = 27 ..........(1)
Given,
6th term of a G.P. = 729
∴ ar5 = 729 ..........(2)
Dividing equation (2) by (1), we get :
Substituting value of r in equation (1), we get :
⇒ a(3)2 = 27
⇒ 9a = 27
⇒ a =
⇒ a = 3.
7th term = ar6
= 3(3)6
= 3 × 729
= 2187.
Product of first and seventh term = 3 x 2187
= 6561.
Hence, product of first and seventh term = 6561.
Find 5 geometric means between 1 and 27.
Answer
Let a, b, c and d be the 5 geometric means 1 and 27.
∴ 1, a, b, c, d, e and 27 are in G.P.
So, first term (a) = 1 and seventh term = 27.
Let common ratio be r.
∴ ar6 = 27
⇒ (1)r6 = 27
⇒ r6 = 33
⇒ r6 =
⇒ r = .
Second term = ar = ,
Third term = ar2 = ,
Fourth term = ar3 = ,
Fifth term = ar4 = ,
Sixth term = ar5 = .
Hence, 5 geometric means between 1 and 27 = .
Find the sum of the sequence 96 - 48 + 24 ......... upto 10 terms.
Answer
The above sequence is a G.P. with first term (a) = 96 and common ratio (r) = .
By formula,
Sum of G.P. =
Hence, sum of sequence =
Find the sum of first n terms of :
(i) 4 + 44 + 444 + ......
(ii) 0.7 + 0.77 + 0.777 + .......
Answer
(i) Given,
⇒ 4 + 44 + 444 + ...... upto n terms
⇒ 4(1 + 11 + 111 + ....... upto n terms)
⇒ upto n terms)
⇒ upto n terms]
⇒
Above sequence : 10 + 102 + ......... + 10n
It is a G.P. with common term (a) = 10 and common ratio (r) = 10.
By formula,
Sum of G.P. =
⇒
⇒ .
Hence, sum of 4 + 44 + 444 + ...... upto n terms =
(ii) Given,
Above sequence :
It is a G.P. with first term (a) = and common ratio (r) = .
By formula,
Sum of G.P. =
Hence, sum of 0.7 + 0.77 + 0.777 + ....... upto n terms = .
Find (using G.P.) the value of .
Answer
Let, x = .
⇒ x = 0.4232323......
⇒ 10x = 4.232323.......
⇒ 1000x = 423.2323.......
⇒ 1000x - 10x = 423.2323....... - 4.232323.......
⇒ 990x = 419
⇒ x =
Hence, .
If for a G.P., pth, qth and rth terms are a, b and c respectively; prove that :
(q - r)log a + (r - p)log b + (p - q)log c = 0
Answer
Let first term of G.P. be A and common ratio be R.
pth term = a
ARp - 1 = a.
qth term = b
ARq - 1 = b.
rth term = c
ARr - 1 = c.
Hence, proved that
Hence, proved that (q - r)log a + (r - p)log b + (p - q)log c = 0.
If a, b and c are in G.P., prove that :
log a, log b and log c are in A.P.
Answer
Given, a, b and c are in G.P.
∴ b2 = ac .......(i)
For, log a, log b and log c to be in A.P,
log b- log a = log c - log b
log b + log b = log a + log c
2log b = log a + log c
L.H.S. = 2log b = log b2
R.H.S. = log ac
Since, b2 = ac,
L.H.S. = R.H.S.
∴ 2log b = log a + log c
Hence, proved that log a, log b and log c are in A.P.
If each term of a G.P. is raised to the power x, show that the resulting sequence is also a G.P.
Answer
Let a, b and c be in G.P.
∴ b2 = ac
Let, b2 = ac = m ........(i)
Each term be raised to power x.
So, terms = ax, bx and cx.
Terms are in G.P. if common ratio between terms are equal,
Since, L.H.S. = R.H.S.,
Hence, proved that on raising each term of a G.P. to the power x, the resulting sequence is also a G.P.
If a, b and c are in A.P. a, x, b are in G.P. whereas b, y and c are also in G.P.
Show that : x2, b2, y2 are in A.P.
Answer
Given,
a, b, c are in A.P.
⇒ 2b = a + c ........(i)
a, x, b are in G.P.
⇒ x2 = ab ........(ii)
b, y and c are in G.P.
⇒ y2 = bc .........(iii)
Adding (ii) and (iii) we get,
⇒ x2 + y2 = ab + bc
⇒ x2 + y2 = b(a + c)
⇒ x2 + y2 = b.2b (From i)
⇒ x2 + y2 = 2b2.
Hence, proved that x2, b2, y2 are in A.P.
If x, y and z are in G.P., show that x4, y4 and z4 are also in G.P.
Answer
Given, x, y and z are in G.P.
∴ y2 = xz = m (let) .....(1)
New terms = x4, y4 and z4.
For the terms to be in G.P., common ratio between terms must be equal,
Substituting value from equation (1), we get :
⇒ m4 = m4.
Since, L.H.S. = R.H.S.
Hence, proved that x4, y4 and z4 are in G.P.
Find the sum of first n terms of the G.P. , ...........
Answer
Common ratio (r) = .
By formula,
Sum of first n terms of G.P. =
Substituting values we get :
.
Hence, sum of first n terms of the G.P.
Find the values of m and n, in each case; if :
(i) (4, -3) on reflection in x-axis gives (-m, n).
(ii) (m, 5) on reflection in y-axis gives (-5, n - 2)
(iii) (-6, n + 2) on reflection in origin gives (m + 3, -4).
Answer
(i) We know that,
On reflection in x-axis, the sign of y-coordinate changes.
∴ (4, -3) on reflection in x-axis gives (4, 3).
Given,
(4, -3) on reflection in x-axis gives (-m, n)
∴ (-m, n) = (4, 3)
⇒ -m = 4 and n = 3
⇒ m = -4 and n = 3.
Hence, m = -4 and n = 3.
(ii) We know that,
On reflection in y-axis, the sign of x-coordinate changes.
∴ (m, 5) on reflection in y-axis gives (-m, 5).
Given,
(m, 5) on reflection in y-axis gives (-5, n - 2)
∴ (-m, 5) = (-5, n - 2)
⇒ -m = -5 and n - 2 = 5
⇒ m = 5 and n = 7.
Hence, m = 5 and n = 7.
(iii) We know that,
On reflection in origin, the sign of x-coordinate and y-coordinate changes.
∴ (-6, n + 2) on reflection in origin gives [6, -(n + 2)].
Given,
(-6, n + 2) on reflection in origin gives (m + 3, -4)
∴ [6, -(n + 2)] = (m + 3, -4)
⇒ 6 = m + 3 and -(n + 2) = -4
⇒ m = 6 - 3 and -n - 2 = -4
⇒ m = 3 and -n = -4 + 2
⇒ m = 3 and -n = -2
⇒ m = 3 nd n = 2.
Hence, m = 3 and n = 2.
Points A and B have the coordinates (-2, 4) and (-4, 1) respectively. Find :
(i) the co-ordinates of A', the image of A in the line x = 0.
(ii) the coordinates of B', the image of B in the y-axis.
(iii) the coordinates of A", the image of A in the line BB'.

Hence, write the angle between the lines A'A" and BB'. Assign a special name to the figure B'A'BA".
Answer
(i) x = 0 is the y-axis.
On reflection in y-axis,
A(-2, 4) ⇒ A'(2, 4).
Hence, coordinates of A' = (2, 4).
(ii) On reflection in y-axis,
B(-4, 1) ⇒ B'(4, 1).
Hence, coordinates of B' = (4, 1).
(iii) From graph,
On reflection in line BB'
A(-2, 4) ⇒ A"(-2, -2).
Hence, coordinates of A" = (-2, -2).
From graph,
Angle between lines A'A" and BB' = 56° 19' and B'A'BA" is a parallelogram.
Triangle OA1B1 is the reflection of triangle OAB in origin, where A1 (4, -5) is the image of A and B1 (-7, 0) is the image of B.
(i) Write down the co-ordinates of A and B and draw a diagram to represent this information.
(ii) Give a special name to the quadrilateral ABA1B1. Give reason.
(iii) Find the co-ordinates of A2, the image of A under reflection in x-axis followed by reflection in y-axis.
(iv) Find the co-ordinates of B2, the image of B under reflection in y-axis followed by reflection in origin.
Answer
(i) From graph,
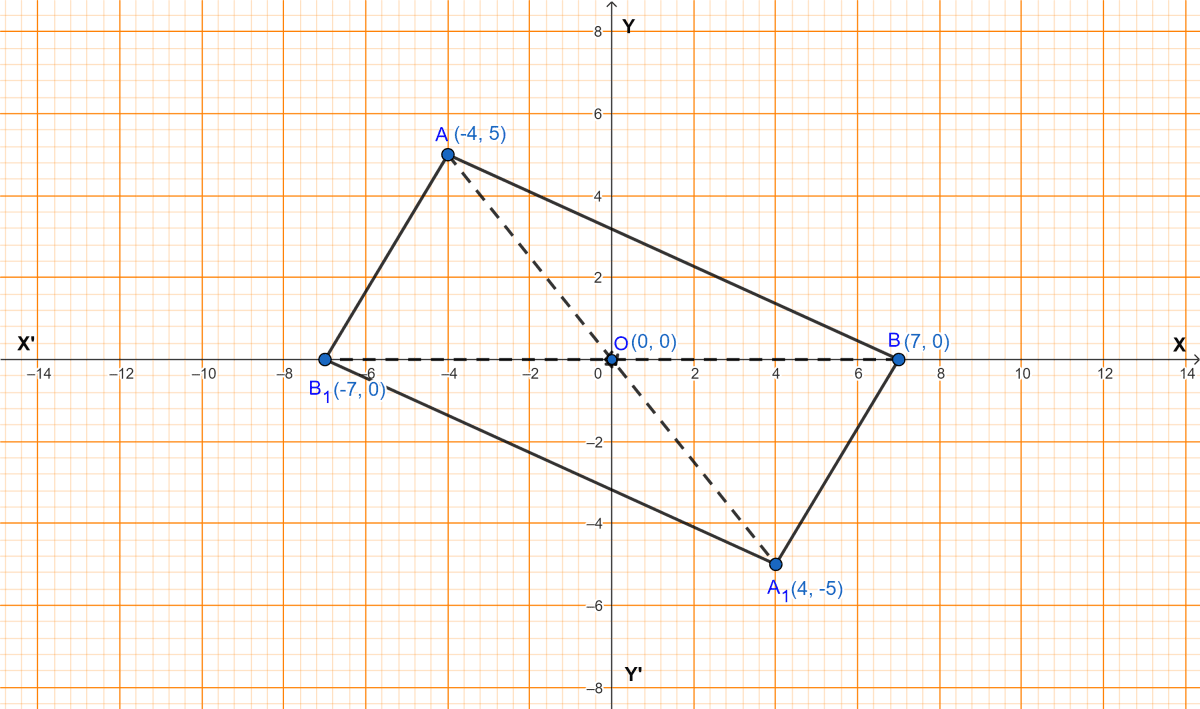
Coordinates of A = (-4, 5) and B = (7, 0).
(ii) By distance formula,
OA = units.
OA1 = units.
OB = OB1 = 7 units.
Since, diagonals bisect each other.
Hence, ABA1B1 is a parallelogram.
(iii) We know that,
On reflection in x-axis, the sign of y-coordinate changes.
∴ (-4, 5) on reflection in x-axis gives (-4, -5).
We know that,
On reflection in y-axis, the sign of x-coordinate changes.
∴ (-4, -5) on reflection in y-axis gives (4, -5).
∴ A2 = (4, -5).
Hence, coordinates of A2 = (4, -5).
(iv) We know that,
On reflection in y-axis, the sign of x-coordinate changes.
∴ (7, 0) on reflection in y-axis gives (-7, 0).
We know that,
On reflection in x-axis, the sign of y-coordinate changes.
∴ (-7, 0) on reflection in x-axis gives (-7, 0).
∴ B2 = (-7, 0).
Hence, coordinates of B2 = (-7, 0).
In what ratio does the point M(p, -1) divide the line segment joining the points A(1, -3) and B(6, 2) ? Hence, find the value of p.

Answer
Let the point M(p, -1) divide the line segment joining the points A(1, -3) and B(6, 2) in ratio k : 1.
By section formula,
Substituting value we get,
⇒ k : 1 = = 2 : 3.
By section formula,
Substituting value we get,
Hence, ratio = 2 : 3 and p = 3.
A(-4, 4), B(x, -1) and C(6, y) are the vertices of △ABC. If the centroid of this triangle ABC is at the origin, find the values of x and y.
Answer
By formula,
Centroid of triangle =
Given,
Centroid of triangle = (0, 0)
Substituting values for x-coordinate we get,
Substituting values for y-coordinate we get,
Hence, x = -2 and y = -3.
A(2, 5), B(-1, 2) and C(5, 8) are the vertices of △ABC. P and Q are points on AB and AC respectively such that AP : PB = AQ : QC = 1 : 2.
(a) Find the coordinates of points P and Q.
(b) Show that BC = 3 × PQ.
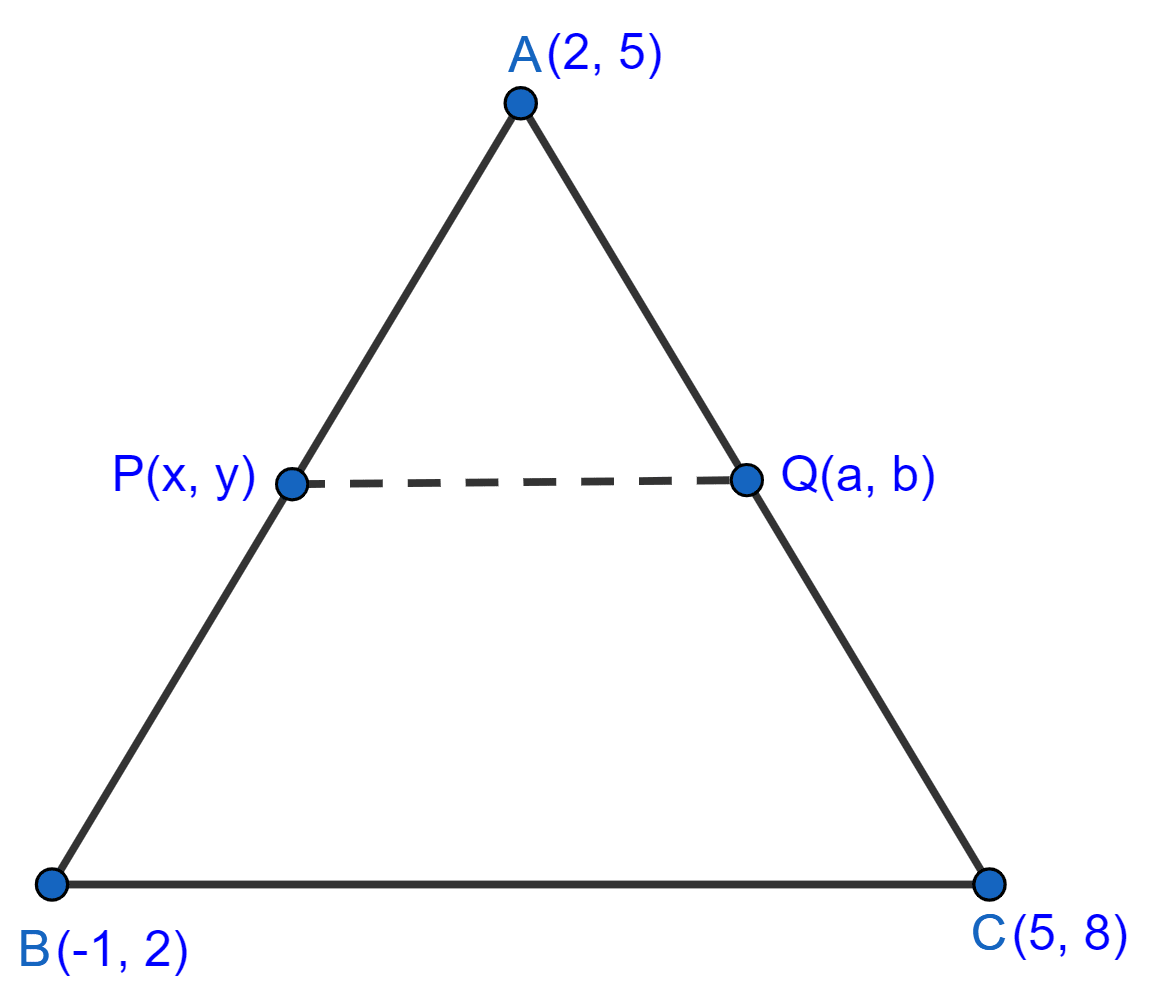
Answer
(a) Let coordinates of P be (x, y)
By section formula,
P(x, y) =
Substituting values we get,
Let coordinates of Q be (a, b)
By section formula,
Q(a, b) =
Substituting values we get,
Hence, coordinates of P = (1, 4) and Q = (3, 6).
(b) By distance formula,
3PQ = 3 × = BC.
Hence, proved that BC = 3PQ.
Show that the points (a, b), (a + 3, b + 4), (a - 1, b + 7) and (a - 4, b + 3) are the vertices of a parallelogram.
Answer
Let the points be A(a, b), B(a + 3, b + 4), C(a - 1, b + 7) and D(a - 4, b + 3).
We know that,
Distance formula =
By distance formula,
Since, AB = BC = CD = DA.
Hence, proved that ABCD are the vertices of a parallelogram.
A(-4, 2), B(0, 2) and C(-2, -4) are vertices of a triangle ABC. P, Q and R are mid-points of sides BC, CA and AB, respectively. Show that the centroid of △PQR is the same as the centroid of △ABC.
Answer
By formula,
Mid-point (M) =

Given,
P is mid-point of BC.
Q is mid-point of CA.
R is mid-point of AB.
Centroid of the triangle is given by (G) =
Let G1 and G2 be centroid of △ABC and △PQR.
Substituting values we get,
Since, G1 = G2.
Hence, proved that the centroid of △PQR is the same as the centroid of △ABC.
Given points A(1, 5), B(-3, 7) and C(15, 9).
(i) Find the equation of a line passing through the mid-point of AC and the point B.
(ii) Find the equation of the line through C and parallel to AB.
(iii) The lines obtained in part (i) and (ii) above, intersect each other at a point P. Find the coordinates of the point P.
(iv) Assign, giving reason, a special name of the figure PABC.
Answer
(i) By formula,
Mid-point (M) =
Let D be the mid-point of AC.
D = = (8, 7).
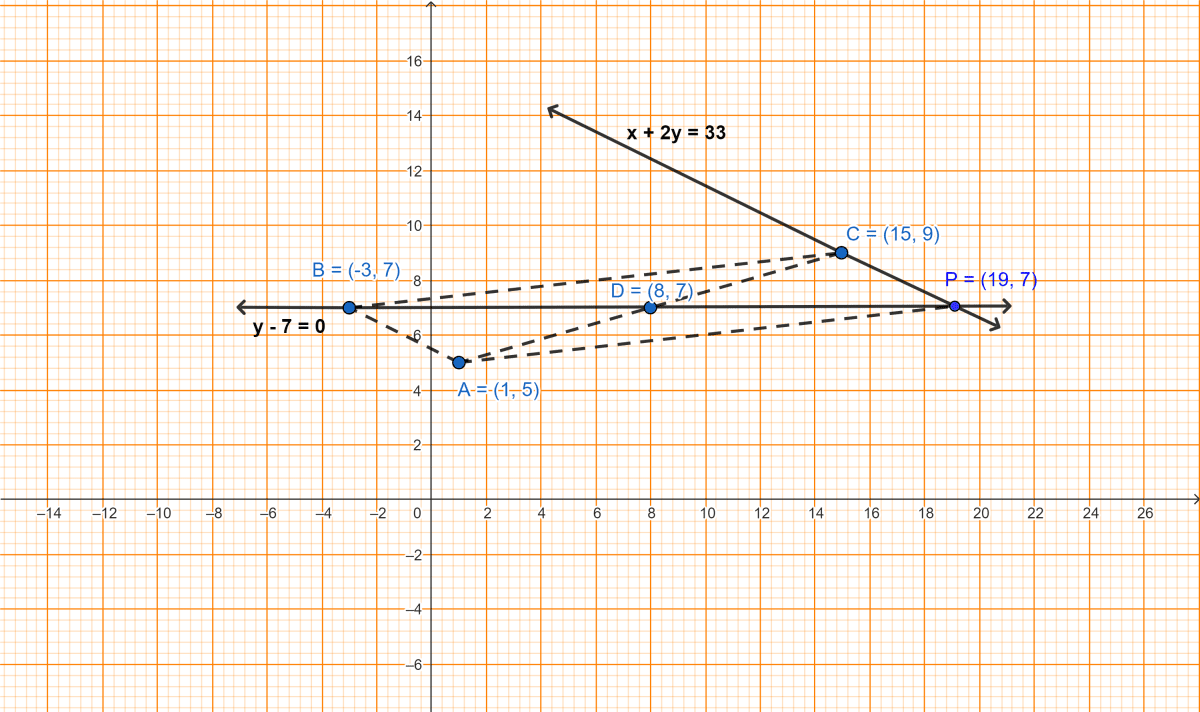
By two-point formula,
Equation of straight line :
⇒ y - y1 = (x - x1)
Equation of BD :
Hence, equation of a line passing through the mid-point of AC and the point B is y - 7 = 0.
(ii) By formula,
Slope =
Slope of AB = .
As, slope of parallel lines are equal.
∴ Slope of line parallel to AB = -.
By point-slope form, equation :
Slope of line through C and parallel to AB.
Hence, equation of the line through C and parallel to AB is x + 2y = 33.
(iii) Equations are :
⇒ y - 7 = 0 ..........(1)
⇒ x + 2y = 33 .........(2)
From equation (1),
⇒ y = 7 ........(3)
Substituting above value of y in equation (2), we get :
⇒ x + 2(7) = 33
⇒ x + 14 = 33
⇒ x = 33 - 14 = 19.
∴ P = (x, y) = (19, 7).
Hence, P = (19, 7).
(iv) Steps :
Mark points A, B, C and P.
Join AB, BC, CP and PA.
From graph, PABC is a trapezium.
Hence, PABC is a trapezium.
The line x - 4y = 6 is the perpendicular bisector of the line segment AB. If B = (1, 3); find the coordinates of point A.
Answer
Given, equation of line,
⇒ x - 4y = 6
⇒ x - 4y - 6 = 0
⇒ 4y = x - 6
⇒ y = .
Comparing with y = mx + c, we get :
Slope = .
Since, given line and AB are perpendicular to each other, so their products = -1. Let slope of line AB be m1.
⇒ m1 = -4.
Now, equation of AB can be found by point slope form,
⇒ y - y1 = m(x - x1)
⇒ y - 3 = -4(x - 1)
⇒ y - 3 = -4x + 4
⇒ 4x + y - 3 - 4 = 0
⇒ 4x + y - 7 = 0.
Since, line x - 4y - 6 = 0 is perpendicular bisector of 4x + y - 7 = 0 hence solving them simultaneously to find point of intersection,
⇒ x - 4y = 6 .........(1)
⇒ 4x + y = 7 ........(2)
Multiplying (2) with 4 and adding with (1), we get :
⇒ 4(4x + y) + x - 4y = 4 × 7 + 6
⇒ 16x + 4y + x - 4y = 28 + 6
⇒ 17x = 34
⇒ x =
⇒ x = 2.
Putting value of x in (1),
⇒ 2 - 4y = 6
⇒ -4y = 4
⇒ y = -1.
Mid-point of AB = (2, -1). Let A be (a, b).
By mid-point formula, coordinates of mid-point of AB are
Hence, coordinates of A = (3, -5).
Find the equation of a line passing through the points (7, -3) and (2, -2). If this line meets x-axis at point P and y-axis at point Q; find the co-ordinates of points P and Q.
Answer
By two-point formula,
Equation of line :
∴ Equation of line passing through (7, -3) and (2, -2) is
Given,
Line meets x-axis at point P. We know that, y-coordinate = 0 at x-axis.
Substituting, y = 0 in x + 5y + 8 = 0, we get :
⇒ x + 5(0) + 8 = 0
⇒ x + 8 = 0
⇒ x = -8.
∴ P = (-8, 0).
Line meets y-axis at point Q. We know that, x-coordinate = 0 at y-axis.
Substituting, x = 0 in x + 5y + 8 = 0, we get :
⇒ 0 + 5y + 8 = 0
⇒ 5y + 8 = 0
⇒ y = -.
∴ Q = .
Hence, equation of line is x + 5y + 8 = 0, P = (-8, 0) and Q = .
A(-3, 1), B(4, 4) and C(1, -2) are the vertices of a triangle ABC. Find :
(i) the equation of median BD,
(ii) the equation of altitude AE.
Answer
(i) D is the mid-point of AC [∵ BD is median]
By mid-point formula,
By two-point formula,
Equation of line :
∴ Equation of line passing through (4, 4) and .
Hence, equation of median BD is 10y = 9x + 4.
(ii) By formula,
Slope =
Slope of BC = = 2.
We know that,
Product of slope of perpendicular lines = -1.
⇒ Slope of BC × Slope of AE = -1
⇒ 2 × Slope of AE = -1
⇒ Slope of AE = -.
By point slope form, equation of AE :
Hence, equation of altitude AE is x + 2y + 1 = 0.
Find equation of perpendicular bisector of the line segment joining the points (4, -3) and (3, 1).
Answer
Mid-point of line segment joining the points (4, -3) and (3, 1) is
Slope of line joining the points (4, -3) and (3, 1) is :
We know that,
⇒ Product of slopes of perpendicular line = -1.
⇒ Slope of line joining the points (4, -3) and (3, 1) × Slope of perpendicular line = -1
⇒ -4 × Slope of perpendicular line = -1
⇒ Slope of perpendicular line = .
Perpendicular bisector of the line segment joining the points (4, -3) and (3, 1) will have slope = and will pass through the point .
By point-slope form, equation of perpendicular bisector is
Hence, equation of perpendicular bisector of the line segment joining the points (4, -3) and (3, 1) is 2x - 8y - 15 = 0.
If (p + 1)x + y = 3 and 3y - (p - 1)x = 4 are perpendicular to each other, find the value of p.
Answer
Given 1st equation,
⇒ (p + 1)x + y = 3
⇒ y = -(p + 1)x + 3
Comparing above equation with y = mx + c, we get :
⇒ Slope (m1) = -(p + 1)
Given 2nd equation,
⇒ 3y - (p - 1)x = 4
⇒ 3y = (p - 1)x + 4
⇒ y =
Comparing above equation with y = mx + c, we get :
⇒ Slope (m2) =
We know that,
Product of slopes of perpendicular lines = -1.
Hence, p = .
If y + (2p + 1)x + 3 = 0 and 8y - (2p - 1)x = 5 are mutually perpendicular, find the value of p.
Answer
Given,
⇒ y + (2p + 1)x + 3 = 0
⇒ y = -(2p + 1)x - 3
Comparing above equation with y = mx + c, we get :
⇒ Slope (m1) = -(2p + 1)
Given,
⇒ 8y - (2p - 1)x = 5
⇒ 8y = (2p - 1)x + 5
⇒ y =
Comparing above equation with y = mx + c, we get :
⇒ Slope (m2) = .
We know that,
Product of slopes of perpendicular lines = -1.
Hence, p = .
The coordinates of the vertex A of a square ABCD is (1, 2) and the equation of diagonal BD is x + 2y = 10. Find the equation of the other diagonal and the co-ordinates of the centre of the square.
Answer
The square is shown in the fig below:
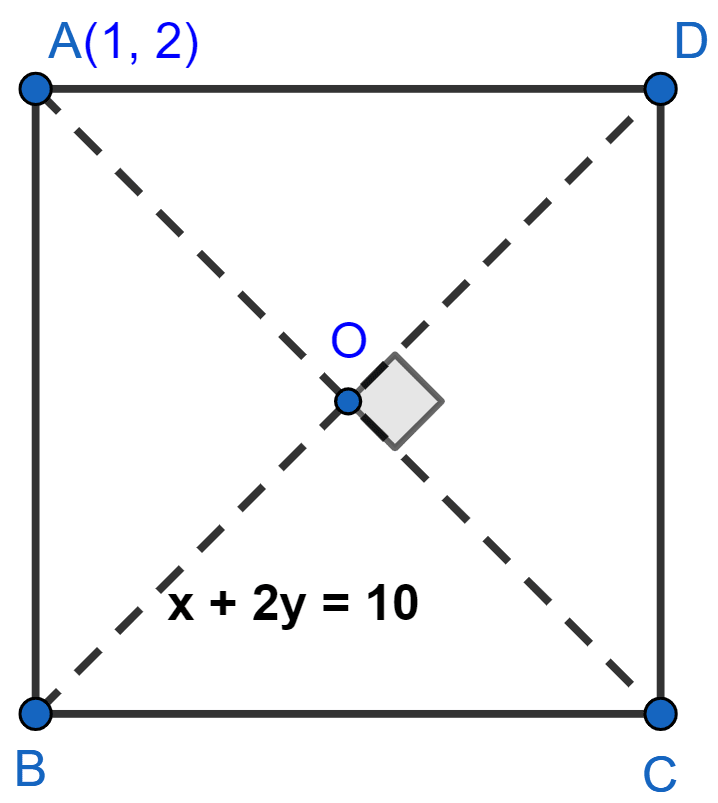
Given,
Equation of diagonal BD is x + 2y = 10
⇒ 2y = -x + 10
⇒ y =
Comparing it with y = mx + c, we get :
Slope (m1) = .
We know that,
Diagonals of a square are perpendicular to each other and product of slopes of perpendicular lines = -1.
Let slope of diagonal AC = m2.
By point-slope form,
Equation of AC is y - y1 = m(x - x1)
⇒ y - 2 = 2(x - 1)
⇒ y - 2 = 2x - 2
⇒ 2x - 2 + 2 = y
⇒ y = 2x.
Since, center of the square is the point of intersection of its diagonals.
Solving,
x + 2y = 10 and y = 2x simultaneously, we get :
⇒ x + 2y = 10 .......(1)
⇒ y = 2x .........(2)
Substituting value of y from eq (2) in (1), we get :
⇒ x + 2(2x) = 10
⇒ x + 4x = 10
⇒ 5x = 10
⇒ x =
⇒ x = 2.
⇒ y = 2x = 2(2) = 4.
Center = (2, 4).
Hence, equation of other diagonal is y = 2x and coordinates of circle = (2, 4).
Find the value of a for which the points A(a, 3), B(2, 1) and C(5, a) are collinear. Hence, find the equation of line.
Answer
Since, points A, B and C are collinear.
∴ Slope of AB = Slope of BC
Let a = -1.
A = (-1, 3) and B = (2, 1).
By point-slope form,
Equation of AB,
⇒ y - y1 = m(x - x1)
⇒ y - 3 = [x - (-1)]
⇒ 3(y - 3) = -2(x + 1)
⇒ 3y - 9 = -2x - 2
⇒ 3y - 9 = -2x - 2
⇒ 2x + 3y = -2 + 9
⇒ 2x + 3y = 7.
Let a = 4.
A = (4, 3) and B = (2, 1).
By point-slope form,
Equation of AB,
⇒ y - y1 = m(x - x1)
⇒ y - 3 = 1[x - 4]
⇒ y - 3 = x - 4
⇒ x - y = -3 + 4
⇒ x - y = 1.
Hence, a = -1 or 4 and equation of line = 2x + 3y = 7 or x - y = 1.
Find the equation of the line which is perpendicular to the line = 1 at the point where this line meets y-axis.
Answer
Let A be the point where the line = 1 meets y-axis.
So, x co-ordinate of point A will be zero.
Substituting x = 0 in equation we get,
A = (0, -b).
The given line equation is,
Comparing above equation with y = mx + c we get,
Slope (m) =
Let slope of perpendicular line be m1.
As product of slope of perpendicular lines is -1,
∴ m × m1 = -1
⇒
⇒ m1 = .
Equation of line through P and slope = is
⇒ y - y1 = m(x - x1)
⇒ y - (-b) = (x - 0)
⇒ b(y + b) = -ax
⇒ by + b2 = -ax
⇒ ax + by + b2 = 0
Hence, equation of required line is ax + by + b2 = 0.
Find :
(i) equation of AB
(ii) equation of CD
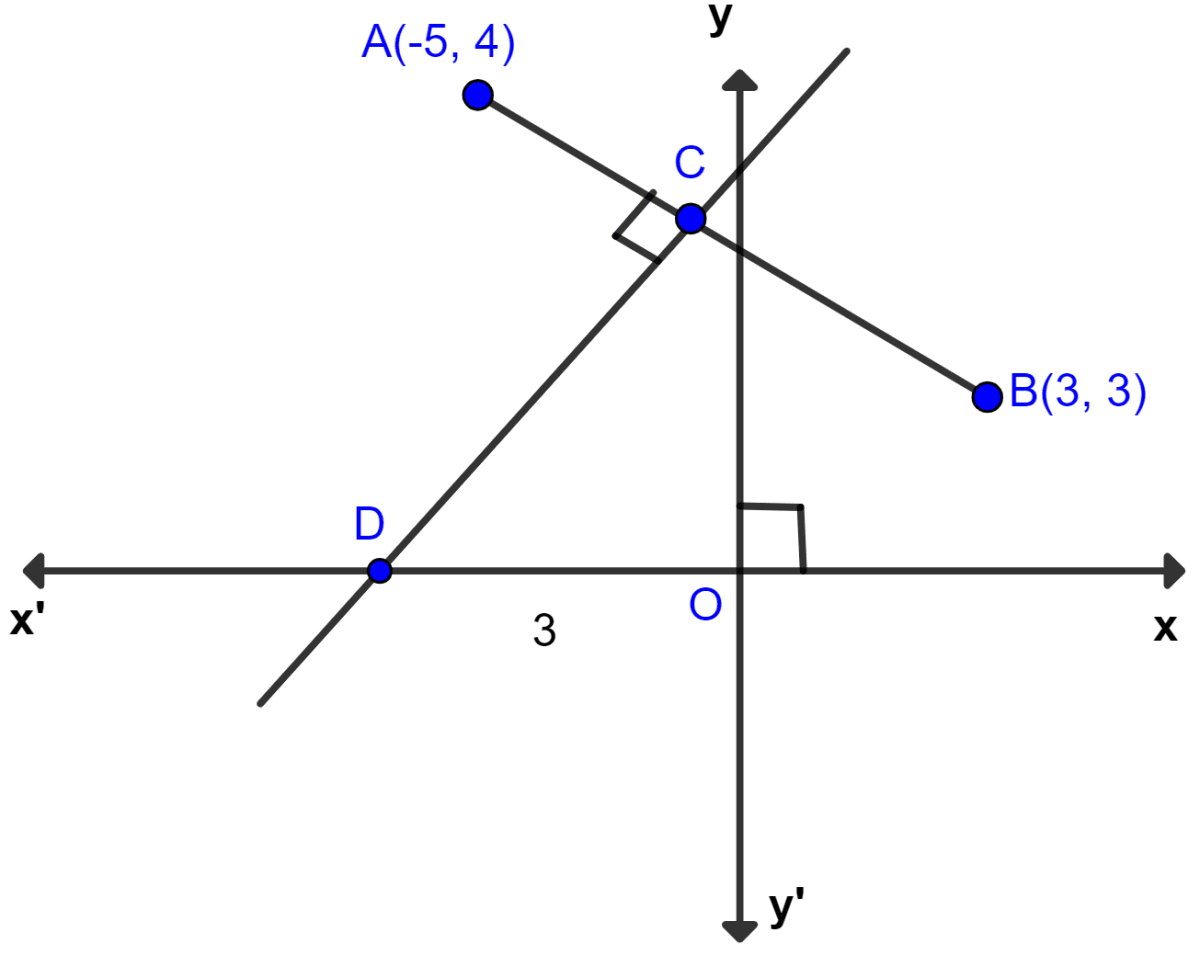
Answer
(i) By formula,
Slope =
Substituting values we get,
By point-slope form,
Equation of AB is :
⇒ y - y1 = m(x - x1)
⇒ y - 4 =
⇒ 8(y - 4) = -1(x + 5)
⇒ 8y - 32 = -x - 5
⇒ x + 8y = -5 + 32
⇒ x + 8y = 27.
Hence, equation of AB is x + 8y = 27.
(ii) From part (i) above,
Slope of AB (m1) =
Let slope of CD be m2.
Since, AB ⊥ CD.
∴ m1 × m2 = -1
⇒
⇒ .
From figure,
D = (-3, 0)
By point-slope form,
Equation of CD is :
⇒ y - y1 = m(x - x1)
⇒ y - 0 = 8[x - (-3)]
⇒ y = 8(x + 3)
⇒ y = 8x + 24.
Hence, equation of CD is y = 8x + 24.
A line through point P(4, 3) meets x-axis at point A and the y-axis at point B. If BP is double of PA, find the equation of AB.
Answer
Let co-ordinates of A be (a, 0) and B be (0, b).
Given,
BP = 2PA
.
∴ P divides AB in the ratio 1 : 2.
By section formula,
A = (a, 0) = (6, 0) and B = (0, b) = (0, 9).
Slope of AB = .
By point-slope form,
Equation of AB is :
⇒ y - y1 = m(x - x1)
⇒ y - 0 = (x - 6)
⇒ 2y = -3(x - 6)
⇒ 2y = -3x + 18
⇒ 3x + 2y = 18.
Hence, equation of AB is 3x + 2y = 18.
M is the mid-point of a line segment AB; AXB and MYB are equilateral triangles on opposite sides of AB; XY cuts AB at Z. Prove that : AZ = 2ZB.
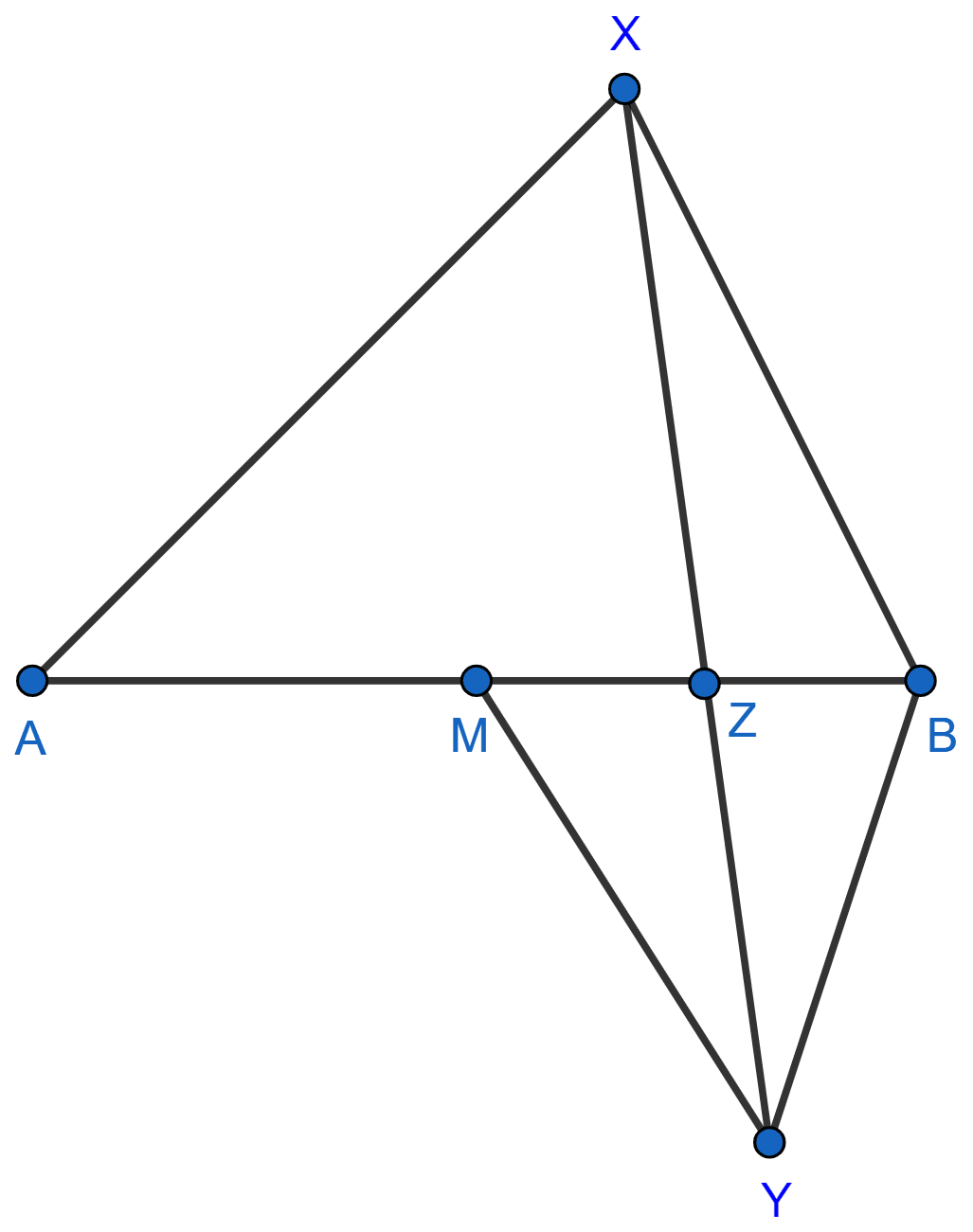
Answer
In △XZB and △MZY,
∠XZB = ∠MZY (Vertically opposite angles are equal)
∠XBZ = ∠YMZ (Each = 60°)
△XZB ~ △MZY [By AA postulate]
In similar triangles,
The ratios between the lengths of corresponding sides are equal.
∴
As sides of equilateral triangle are equal so,
BX = AB
and
MY = MB
∴
∴ ......(1)
As, M is the mid-point of AB.
∴ MB =
From (1),
Hence, proved that AZ = 2ZB.
In the given figure, if AC = 3 cm and CB = 6 cm, find the length of CR.
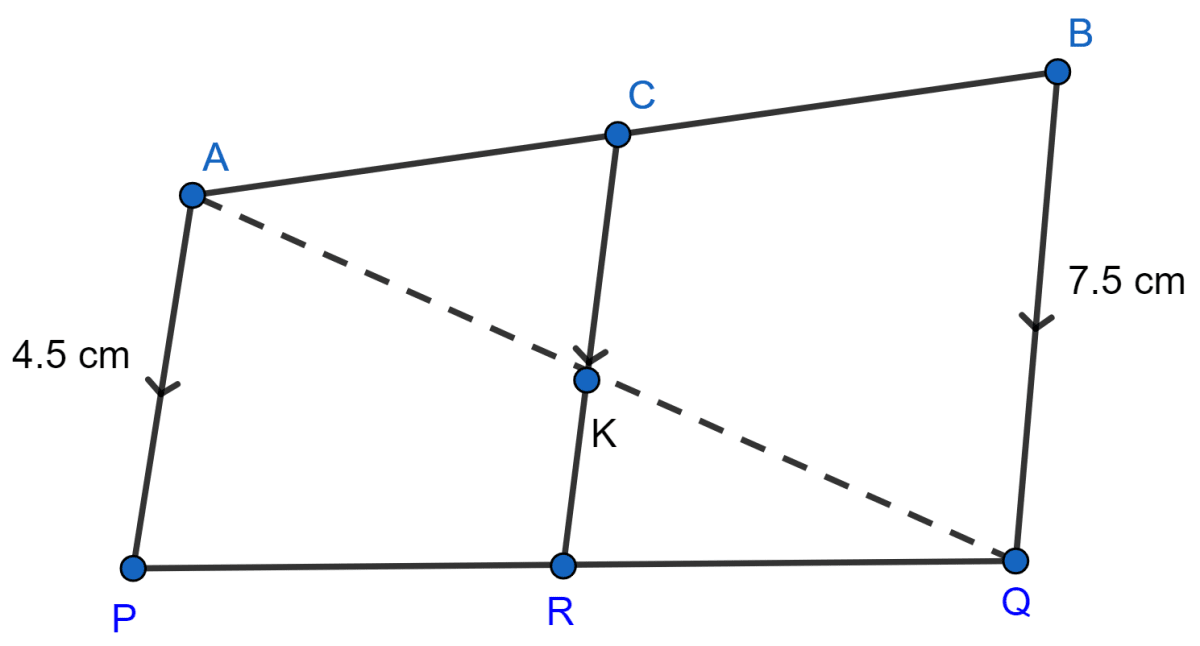
Answer
In △ABQ and △ACK,
CK || BQ
∴ ∠ACK = ∠ABQ [Corresponding angles are equal]
∠KAC = ∠QAB (Common)
∴ △ACK ~ △ABQ
From figure,
AB = AC + CB = 3 + 6 = 9 cm.
In similar triangles,
The ratios between the lengths of corresponding sides are equal.
Also,
In △KRQ and △APQ,
AP || KR
∴ ∠KRQ = ∠APQ [Corresponding angles are equal]
∠KQR = ∠AQP (Common)
∴ △KRQ ~ △APQ
In similar triangles,
The ratios between the lengths of corresponding sides are equal.
From figure,
CR = CK + KR = 2.5 + 3 = 5.5 cm
Hence, CR = 5.5 cm
The given figure shows a trapezium in which AB is parallel to DC and diagonals AC and BD intersect at point O. If BO : OD = 4 : 7, find :
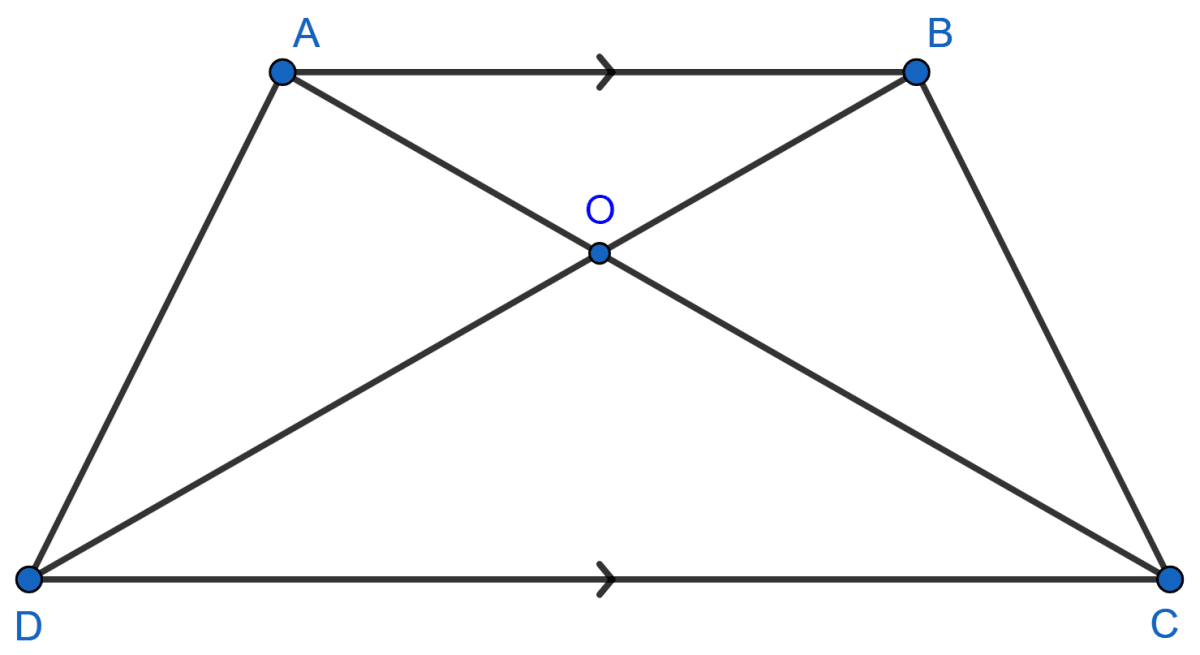
(i) △AOD : △AOB
(ii) △AOB : △ACB
(iii) △DOC : △AOB
(iv) △ABD : △BOC
Answer
(i) Given,
⇒ BO : OD = 4 : 7
⇒ OD : OB = 7 : 4
Since,
△AOD and △AOB have common vertex at A and their bases OD and OB are along the same straight line.
.
Hence, △AOD : △AOB = 7 : 4.
(ii) Since,
△AOB and △ACB have common vertex at A and their bases AO and AC are along the same straight line.
Hence, △AOB : △ACB = 4 : 11.
(iii) Given,
BO : OD = 4 : 7
In △AOB and △DOC
∠AOB = ∠COD [Vertically opposite angles are equal]
∠ABO = ∠ODC [Alternate angles are equal]
∴ △AOB ~ △DOC [By AA axiom]
By area theorem,
Ratio of area of two similar triangles is equal to the square of the ratio of the corresponding sides.
Hence, △DOC : △AOB = 49 : 16.
(iv) Given,
BO : OD = 4 : 7
Since,
△ABD and △BOC have common vertex at B and their bases BD and OB are along the same straight line.
Hence, △ABD : △BOC = 11 : 4.
A model of a ship is made to a scale of 1 : 160. Find :
(i) the length of the ship, if the length of its model is 1.2 m
(ii) the area of the deck of the ship , if the area of deck of its model is 1.2 m2.
(iii) the volume of the ship, if the volume of its model is 1.2 m3.
Answer
Given,
Scale of model = 1 : 160
Scale factor (k) =
(i) By formula,
⇒ Length of model = Scale factor × Length of ship
⇒ 1.2 = × Length of ship
⇒ Length of ship = 1.2 × 160 = 192 m.
Hence, length of ship = 192 m.
(ii) By formula,
⇒ Area of model = (Scale factor)2 × Area of ship
⇒ 1.2 = × Area of ship
⇒ 1.2 = × Area of ship
⇒ Area of ship = 1.2 × 160 × 160 = 30720 m2.
Hence, area of ship = 30720 m2.
(iii) By formula,
⇒ Volume of model = (Scale factor)3 × Volume of ship
⇒ 1.2 = × Volume of ship
⇒ 1.2 = × Volume of ship
⇒ Volume of ship = 1.2 × 160 × 160 × 160 = 49,15,200 m3.
Hence, volume of ship = 49,15,200 m3.
In trapezium ABCD, AB || DC and DC = 2AB. EF drawn parallel to AB cuts AD in F and BC in E such that 4 BE = 3EC. Diagonal DB intersects FE at point G. Prove that : 7EF = 10AB.
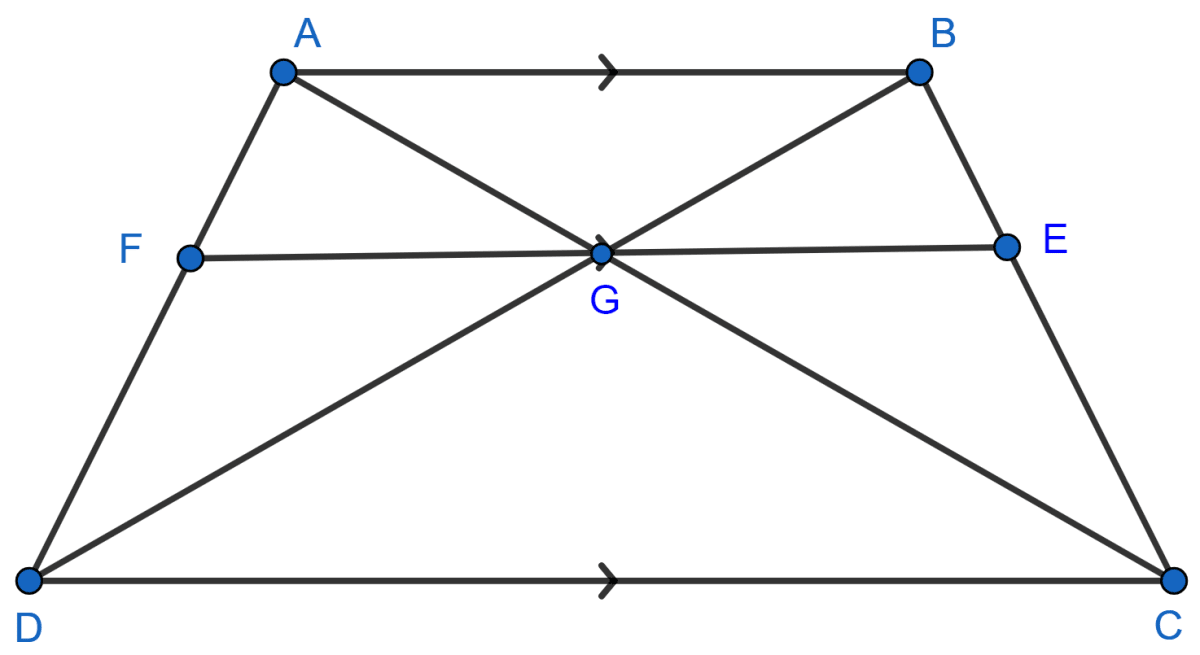
Answer
Given,
⇒ 4BE = 3EC
⇒
In △DFG and △DAB,
⇒ ∠DFG = ∠DAB [As corresponding angles are equal]
⇒ ∠FDG = ∠ADB (Common)
⇒ △DFG ~ △DAB [By AA postulate]
In similar triangles,
The ratios between the lengths of corresponding sides are equal.
..........(1)
In trapezium ABCD, we have
EF || AB || DC
From (1) and (2), we get :
FG = AB .........(3)
In △BEG and △BCD,
⇒ ∠BEG = ∠BCD [As corresponding angles are equal]
⇒ ∠GBE = ∠DBC (Common angle)
⇒ △BEG ~ △BCD [By AA postulate]
In similar triangles,
The ratios between the lengths of corresponding sides are equal.
..............(4)
Given,
Adding equation (3) and (5),
Hence, proved that 7EF = 10AB.
Given : ABCD is a rhombus, DPR and CBR are straight lines.
Prove that :
DP × CR = DC × PR.
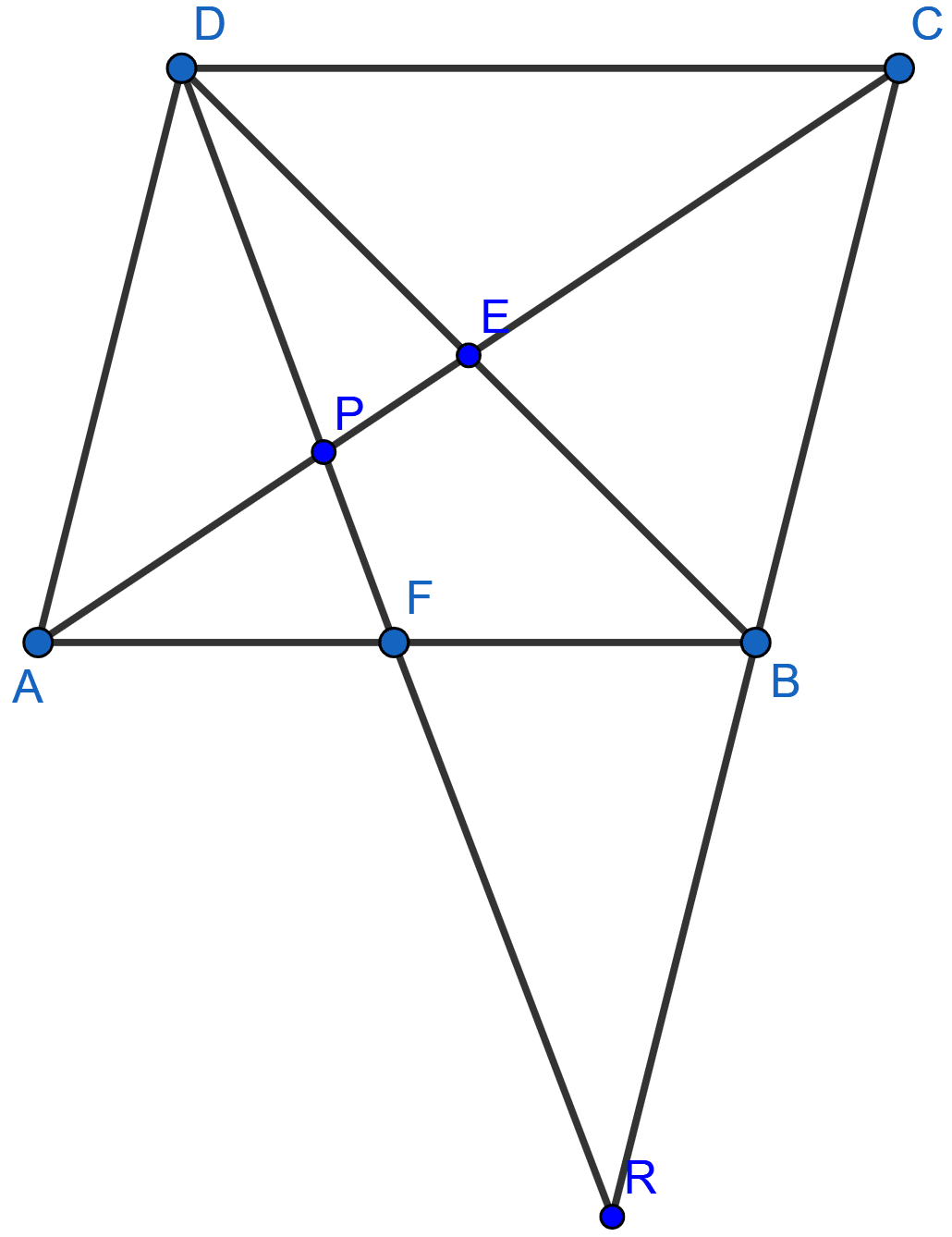
Answer
Since, ABCD is a rhombus.
So, AD || BC.
In △DPA and △RPC,
⇒ ∠DPA = ∠RPC (Vertically opposite angles are equal)
⇒ ∠PAD = ∠PCR [Since, AD || CD and AC is transversal]
∴ △DPA ~ △RPC [By AA]
Since, corresponding sides of similar triangles are proportional we have :
⇒ ..........(1)
In rhombus all sides are equal.
∴ AD = DC
Substituting in (1) we get,
⇒
⇒ DP × CR = DC × PR.
Hence, proved that DP × CR = DC × PR.
Given : FB = FD, AE ⊥ FD and FC ⊥ AD.
Prove that :
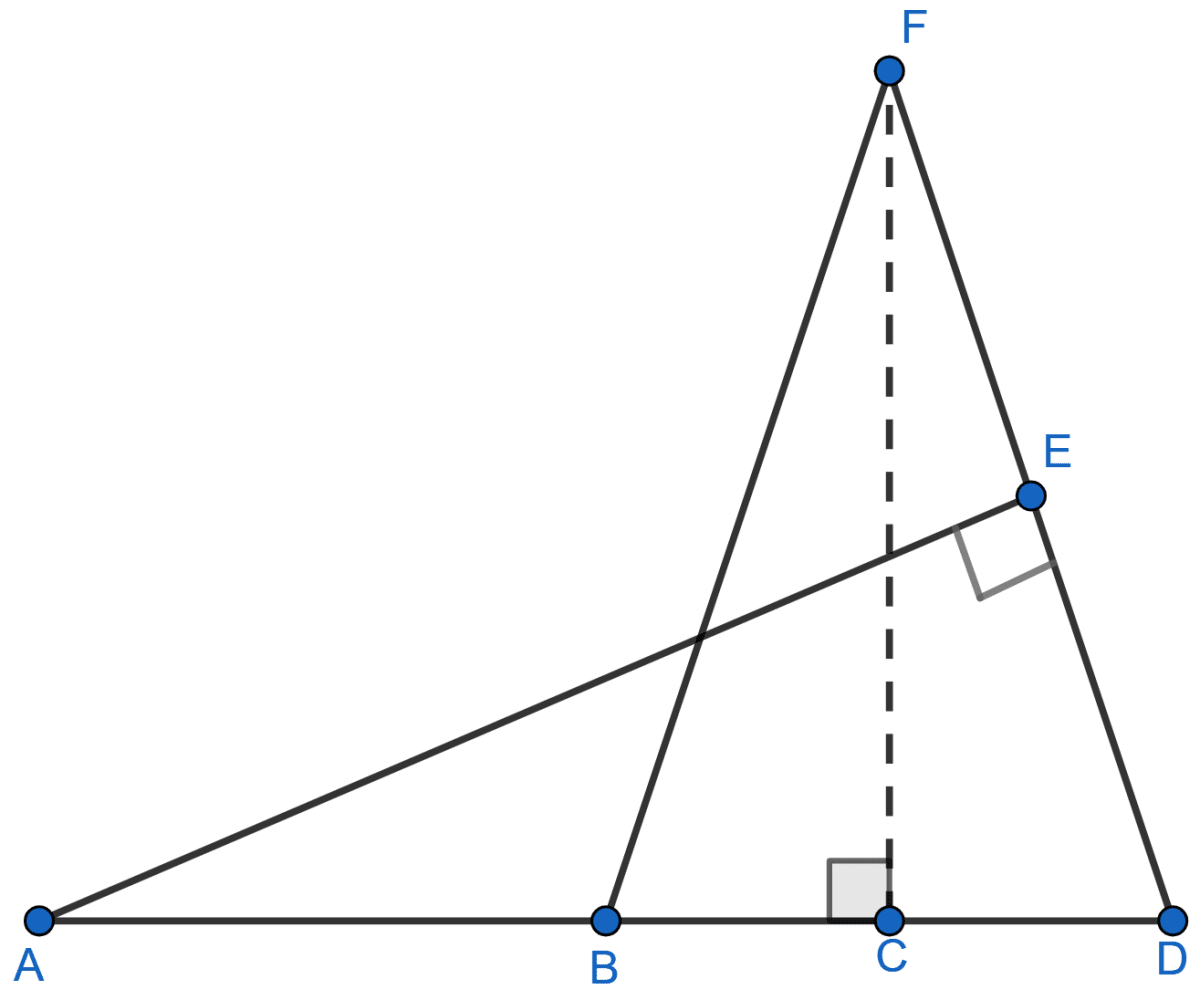
Answer
Given, FB = FD
∴ ∠FBD = ∠FDB [Since, opposite sides of equal angles are equal] ......(1)
In △AED and △FCB,
∠ADE = ∠FBC [From 1]
∠AED = ∠FCB [Both = 90°]
∴ △AED ~ △FCB [By AA]
Since, corresponding sides of similar triangles are proportional we have :
⇒ .
Hence, proved that .
In the figure, QR is parallel to AB and DR is parallel to QB.
Prove that : PQ2 = PD × PA.
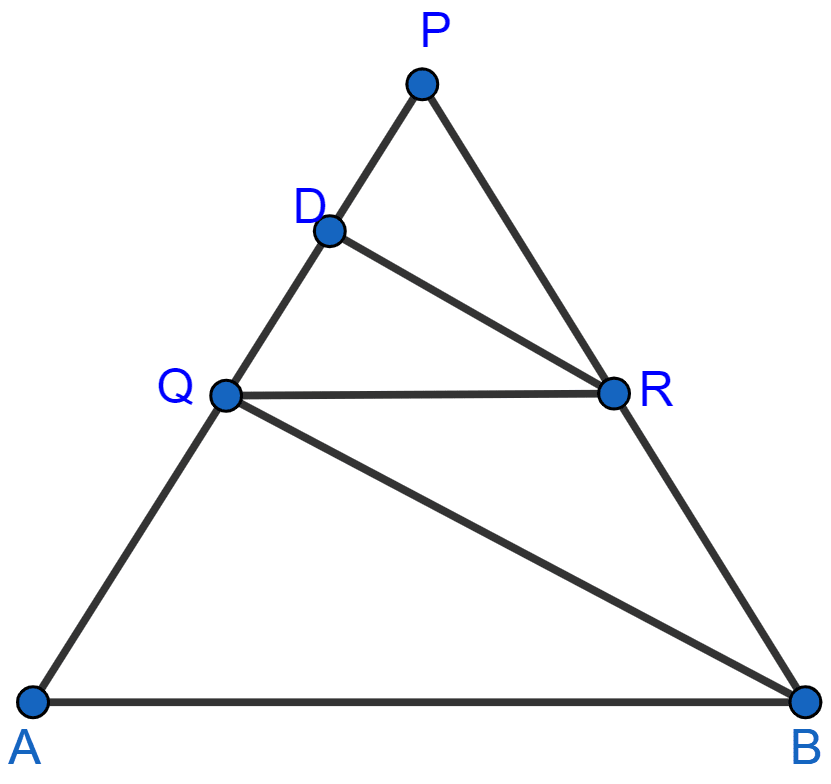
Answer
In △PQR and △PAB,
∠PQR = ∠PAB [Corresponding angles are equal]
∠PRQ = ∠PBA [Corresponding angles are equal]
Hence, △PQR ~ △PAB [By AA]
Since, corresponding sides of similar triangles are proportional to each other.
........(1)
In △PDR and △PQB,
∠PDR = ∠PQB [Corresponding angles are equal]
∠PRD = ∠PBQ [Corresponding angles are equal]
Hence, △PDR ~ △PQB [By AA]
Since, corresponding sides of similar triangles are proportional to each other.
........(2)
From (1) and (2) we get :
Hence, proved that PQ2 = PD × PA.
The given figure shows a trapezium in which AB is parallel to DC and diagonals AC and BD intersect at point P. If AP : CP = 3 : 5.
Find :
(i) △APB : △CPB
(ii) △DPC : △APB
(iii) △ADP : △APB
(iv) △APB : △ADB
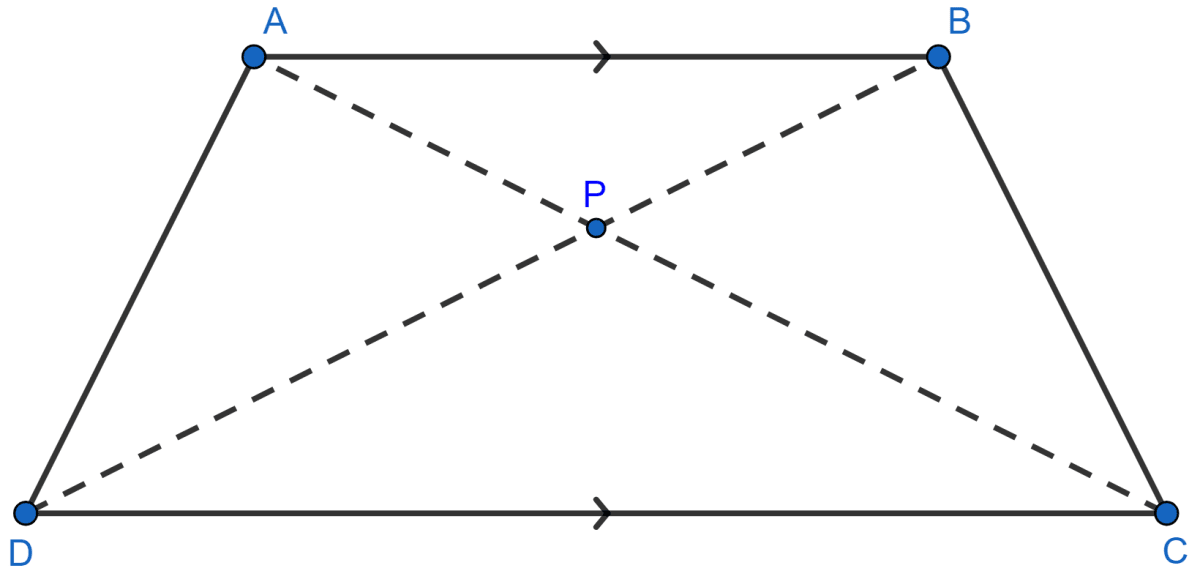
Answer
(i) Since, △APB and △CPB have common vertex at B and their bases AP and PC are along the same straight line AC.
∴ △APB : △CPB = AP : PC = 3 : 5.
Hence, △APB : △CPB = 3 : 5.
(ii) In △DPC and △APB,
∠DPC = ∠APB [Vertically opposite angles are equal]
∠PAB = ∠PCD [Alternate angles are equal]
∴ △DPC ~ △APB.
We know that,
The ratio of the areas of two similar triangles is equal to the ratio of squares of their corresponding sides.
Hence, △DPC : △APB = 25 : 9.
(iii) Since, △DPC ~ △APB,
..........(1)
Since, △ADP and △APB have common vertex at A and their bases DP and PB are along the same straight line.
∴ △ADP : △APB = DP : PB = 5 : 3 .........[From 1]
Hence, △ADP : △APB = 5 : 3.
(iv) From part (iii)
Let PD = 5x and PB = 3x.
From figure,
BD = PD + PB = 5x + 3x = 8x.
Since, △APB and △ADB have common vertex at A and their bases PB and DB are along the same straight line.
∴ △APB : △ADB = PB : BD = 3x : 8x = 3 : 8
Hence, △APB : △ADB = 3 : 8.
In the following diagram, lines l, m and n are parallel to each other. Two transversals p and q intersect the parallel lines at points A, B, C and P, Q, R as shown.
Prove that:
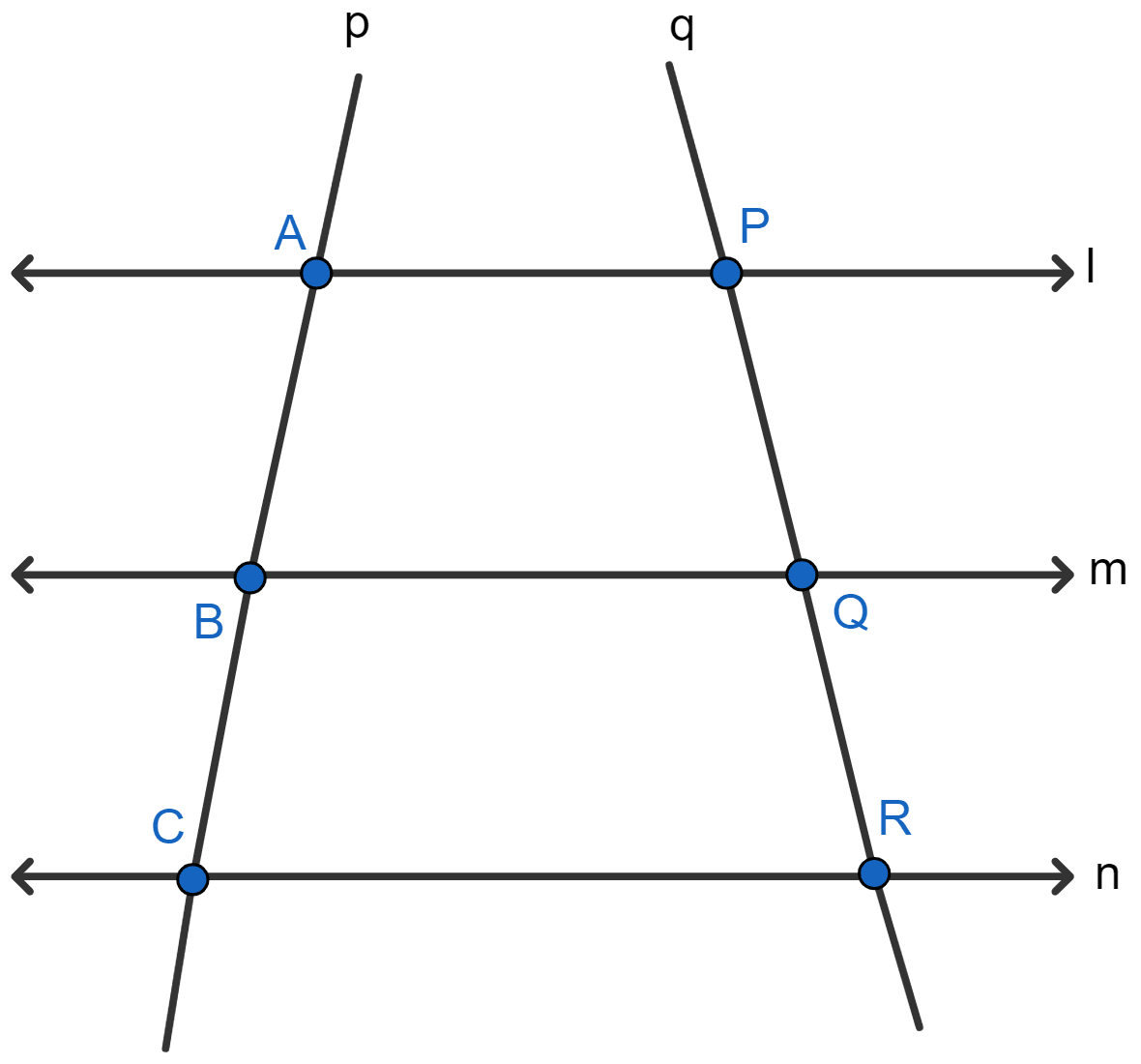
Answer
Join A and R. Let AR meet BQ at point D.
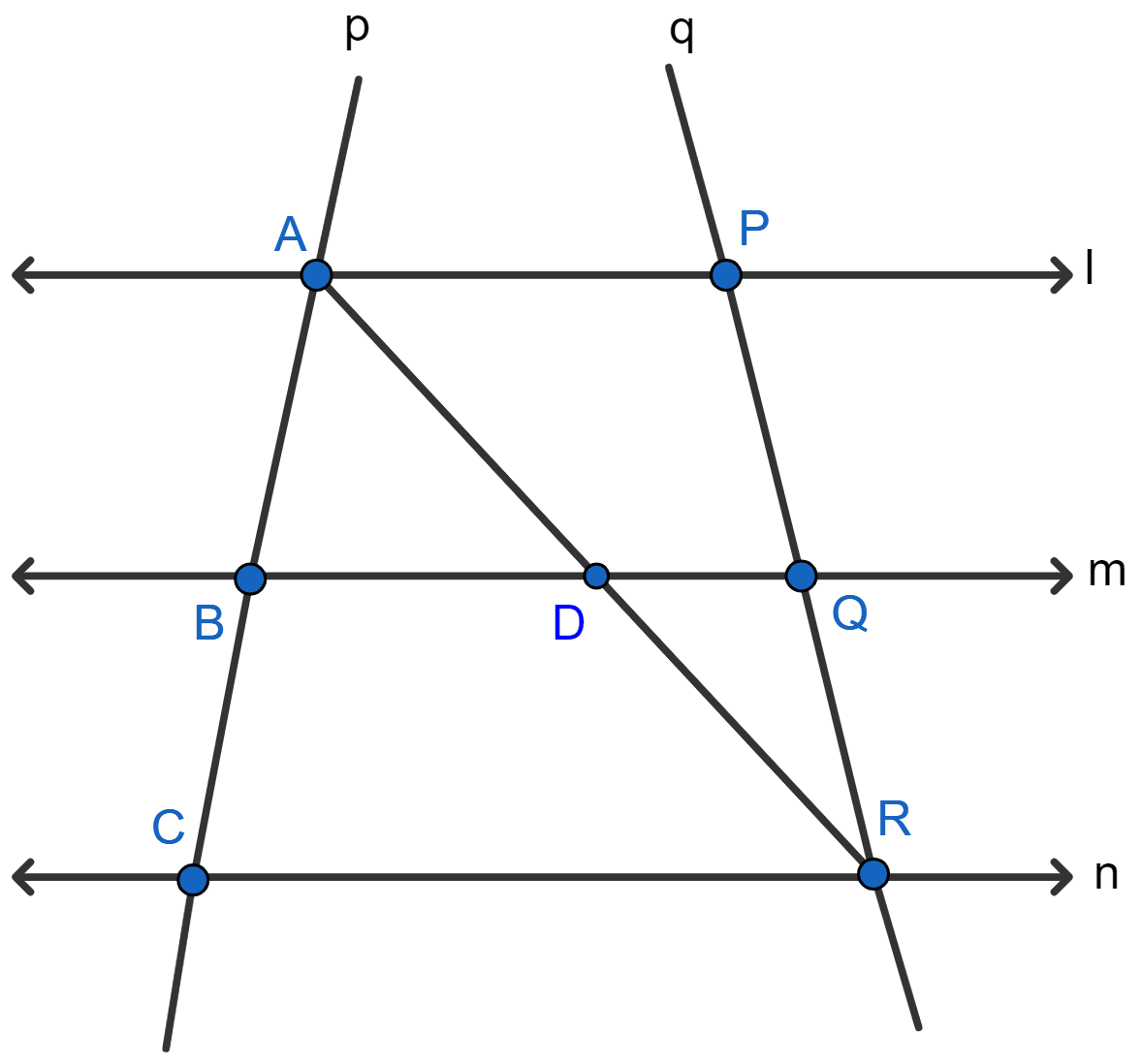
In ∆ACR, BD || CR.
By Basic proportionality theorem, we get
.....(1)
In ∆APR, DQ || AP.
By Basic proportionality theorem, we get
.....(2)
From (1) and (2) we get :
Hence proved that .
The following figure shows a triangle ABC in which AD and BE are perpendiculars to BC and AC respectively.
Show that :
(i) △ADC ~ △BEC
(ii) CA × CE = CB × CD
(iii) △ABC ~ △DEC
(iv) CD × AB = CA × DE
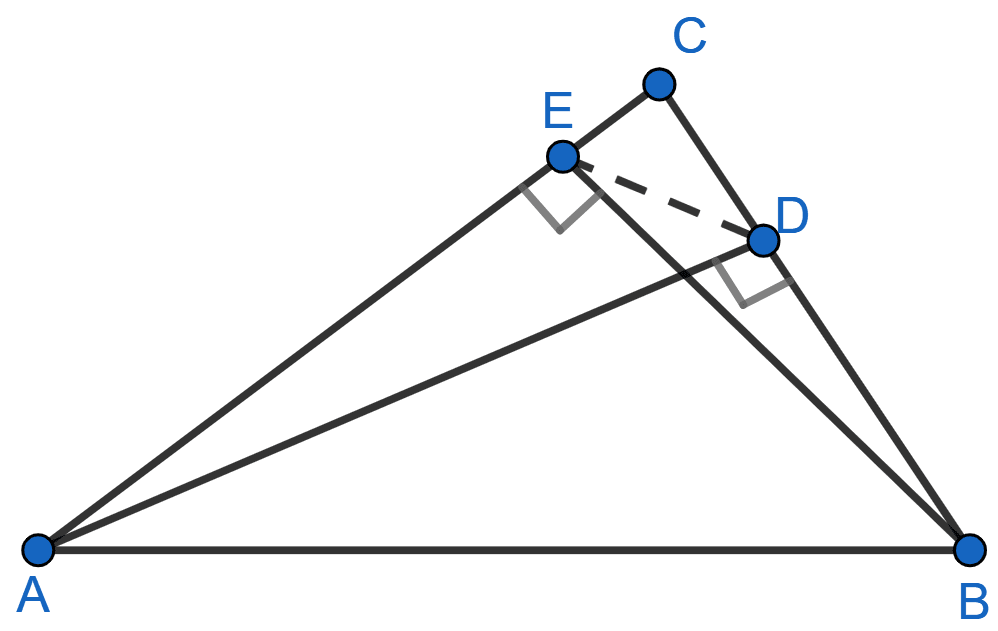
Answer
(i) In △ADC and △BEC,
∠ADC = ∠BEC [Both = 90°]
∠ACD = ∠BCE [Common angle]
∴ △ADC ~ △BEC [By AA].
Hence, proved that △ADC ~ △BEC.
(ii) Since, △ADC ~ △BEC.
We know that,
Corresponding sides of similar triangles are equal.
⇒ CA × CE = CB × CD.
Hence, proved that CA × CE = CB × CD.
(iii) From part (ii) we get,
∠DCE = ∠BCA [Common angle]
∴ △ABC ~ △DEC [By SAS]
Hence, proved that △ABC ~ △DEC.
(iv) Since, △ABC ~ △DEC
We know that,
Corresponding sides of similar triangles are proportional to each other.
⇒
⇒ CD × AB = CA × DE.
Hence, proved that CD × AB = CA × DE.
In triangle ABC, D is mid-point of AB and CD is perpendicular to AB. Bisector of ∠ABC meets CD at E and AC at F. Prove that :
(i) E is equidistant from A and B.
(ii) F is equidistant from AB and BC.
Answer
(i) Join AE.
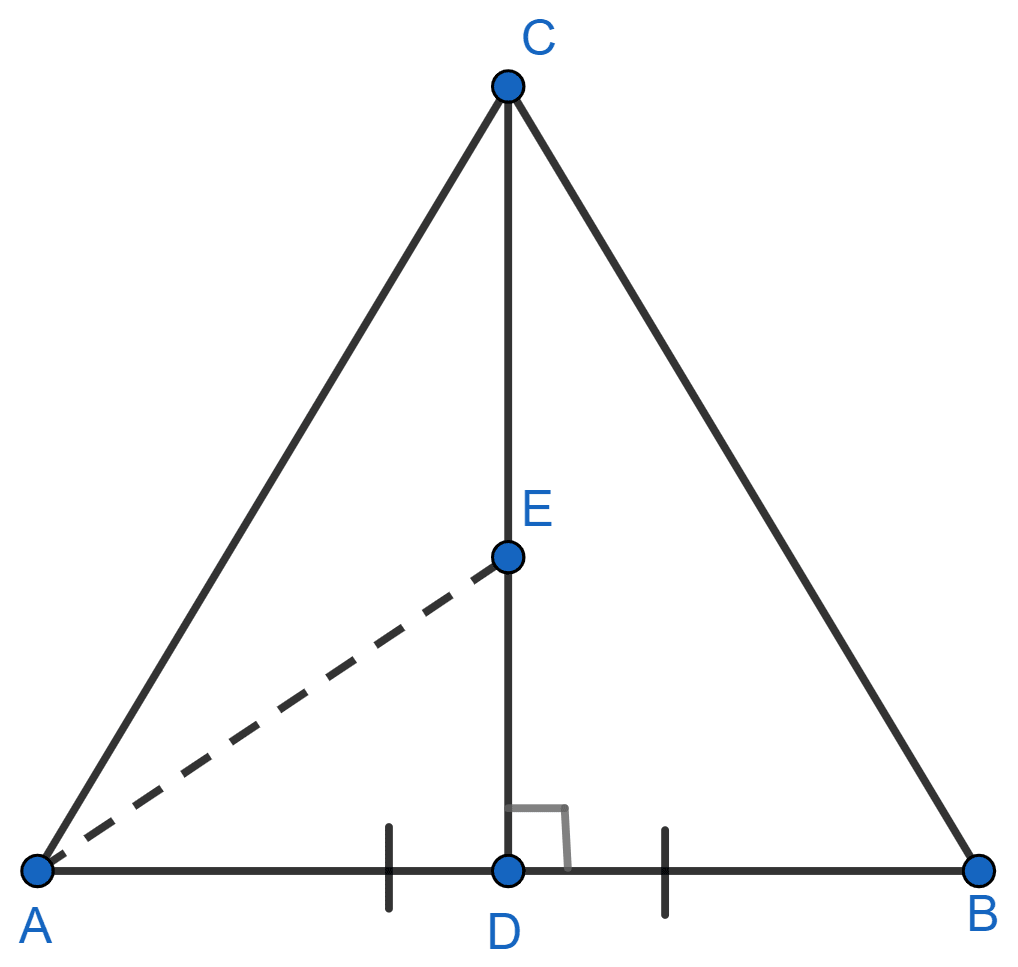
In △EAD and △EBD,
⇒ ED = ED (Common)
⇒ AD = BD (As D is the mid-point of AB)
⇒ ∠EDA = ∠EDB (Both = 90°).
∴ △EAD ≅ △EBD (By SAS axiom)
∴ EA = EB (By C.P.C.T.)
Hence, proved that E is equidistant from A and B.
(ii) Draw FL ⊥ BC and FM ⊥ AB.
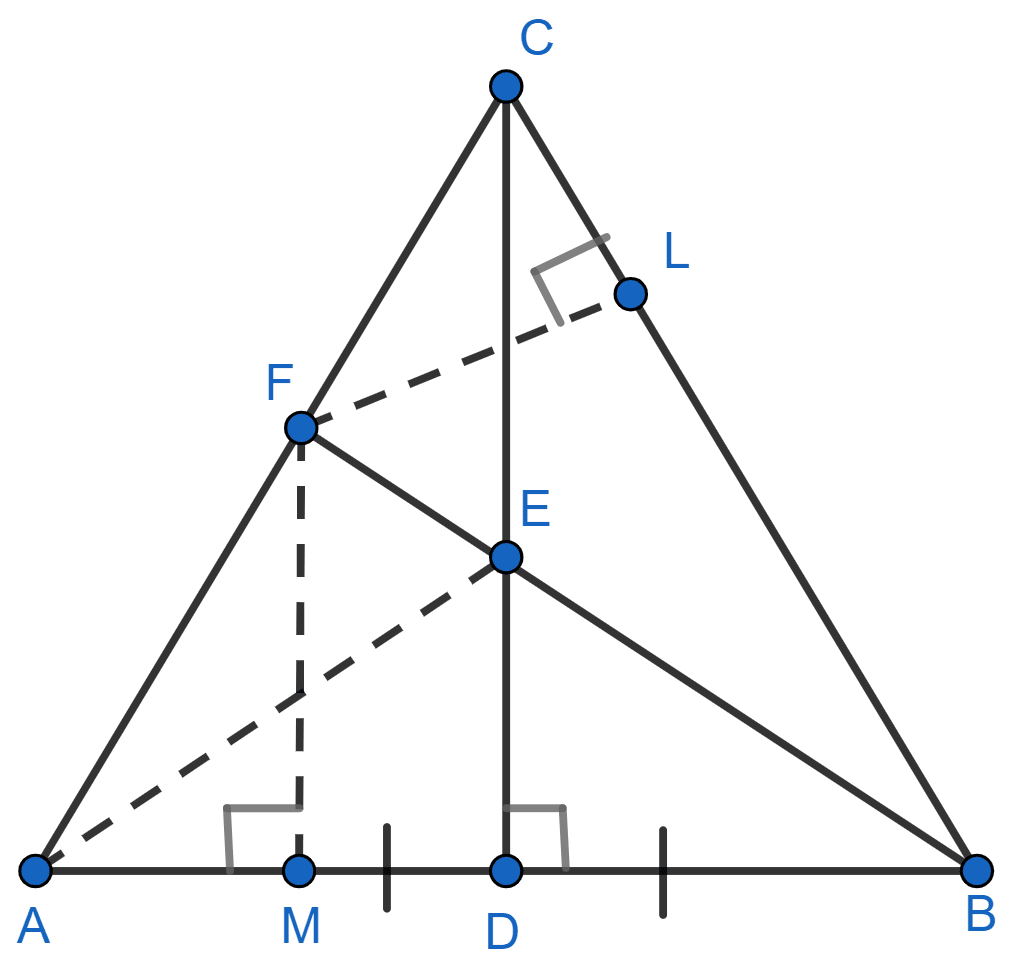
In △BLF and △BMF,
⇒ BF = BF (Common)
⇒ ∠LBF = ∠FBM (As BF is the angle bisector of ∠ABC)
⇒ ∠BLF = ∠BMF (Both = 90°).
∴ △BLF ≅ △BMF (By ASA axiom)
∴ FL = FM (By C.P.C.T.)
Hence, proved that F is equidistant from AB and BC.
Use graph paper for this question. Take 2 cm = 1 unit on both axes.
(i) Plot the points A(1, 1), B(5, 3) and C(2, 7).
(ii) Construct the locus of points equidistant from A and B.
(iii) Construct the locus of points equidistant from AB and AC.
(iv) Locate the point P such that PA = PB and P is equidistant from AB and AC.
(v) Measure and record the length PA in cm.
Answer
Steps of construction :
Plot the points A(1, 1), B(5, 3) and C(2, 7).
Join the points AB, BC, and AC to form a triangle.
Draw DE, perpendicular bisector of AB. (As locus of points equidistant from two points is the perpendicular bisector of line joining them).
Draw AF, angle bisector of A. (As locus of points equidistant from two lines is the angular bisector of angle between them).
Mark point P as the intersection of DE and AF.
Measure AP.

Hence, AP = 2.8 cm.
The speed of sound is 332 meters per second. A gun is fired. Describe the locus of all the people on the earth's surface, who hear the sound exactly after one second.
Answer
Since, speed of sound is 332 m/s.
So, in 1 s it will travel = 332 meters.
Hence, locus of all the people on Earth's surface who will hear sound one second later will be the circumference of a circle whose radius is 332 m and centre is the point where the gun is fired.
In the given figure, ∠ADC = 130° and BC = BE. Find ∠CBE if AB ⊥ CE.
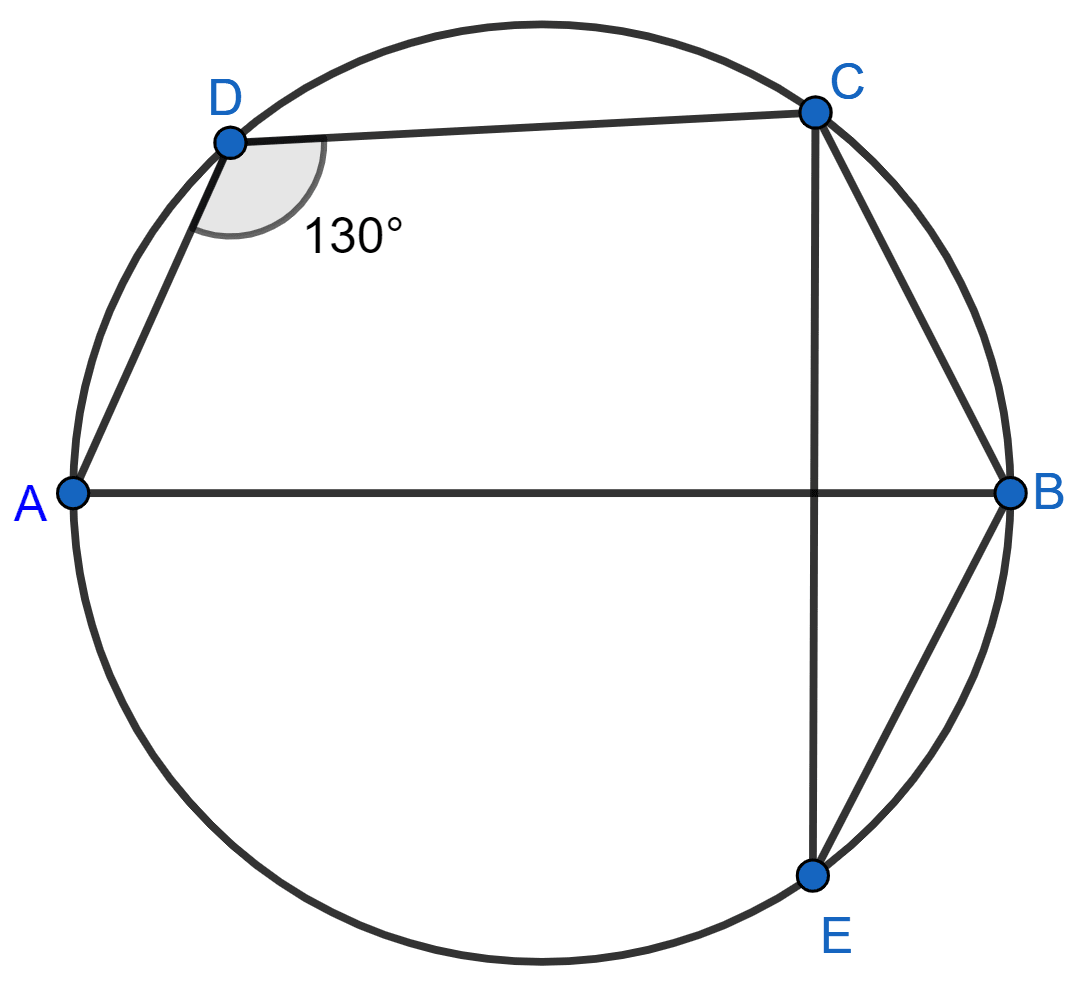
Answer
Since, ABCD is a cyclic quadrilateral and sum of opposite angles in a cyclic quadrilateral = 180°.
∴ ∠ADC + ∠ABC = 180°
⇒ 130° + ∠ABC = 180°
⇒ ∠ABC = 50°.
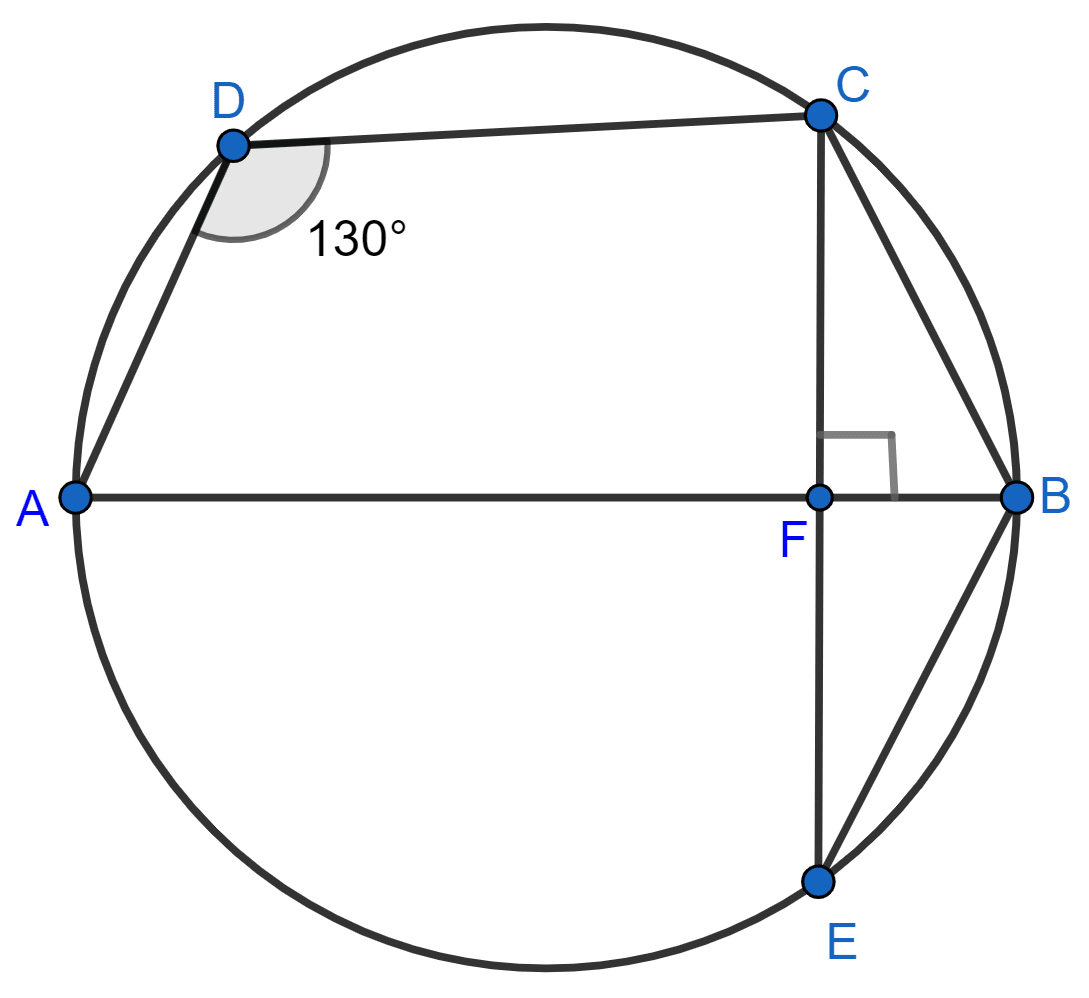
From figure,
⇒ ∠FBC = ∠ABC = 50°.
In △FBC,
By angle sum property of triangle,
⇒ ∠FBC + ∠BCF + ∠CFB = 180°
⇒ 50° + ∠BCF + 90° = 180°
⇒ ∠BCF = 180° - 90° - 50° = 40°.
Given,
BC = BE
In △BCE,
⇒ ∠BEC = ∠BCE = 40°. (As angles opposite to equal sides are equal)
In △FBE,
By angle sum property of triangle,
⇒ ∠BEF + ∠FBE + ∠EFB = 180°
⇒ 40° + ∠FBE + 90° = 180°
⇒ ∠FBE = 180° - 90° - 40° = 50°.
From figure,
∠CBE = ∠FBC + ∠FBE = 50° + 50° = 100°.
Hence, ∠CBE = 100°.
In the given figure, ∠OAB = 30° and ∠OCB = 57°, find ∠BOC and ∠AOC.
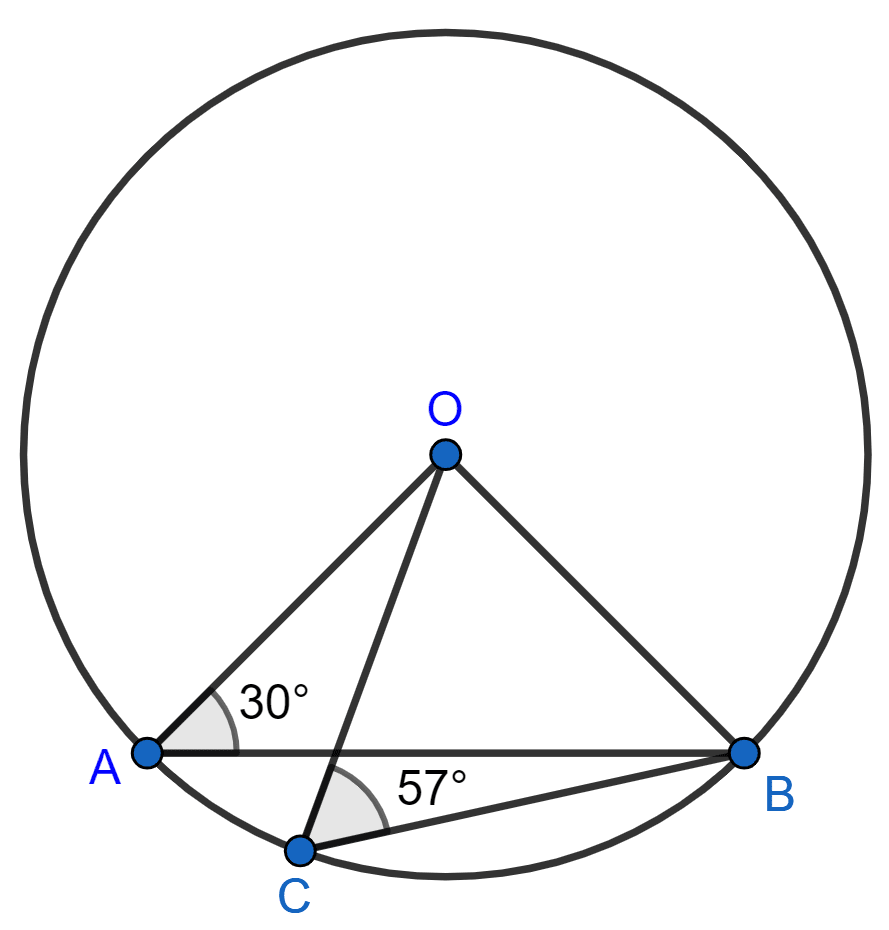
Answer
In △AOB,
⇒ OA = OB [Radius of same circle]
⇒ ∠OBA = ∠BAO = 30° [Angles opposite to equal sides are equal]
Also,
⇒ ∠OBA + ∠BAO + ∠AOB = 180° [By angles sum property of triangle]
⇒ 30° + 30° + ∠AOB = 180°
⇒ ∠AOB = 180° - 60° = 120°
In △OCB,
OC = OB [Radius of same circle]
⇒ ∠OBC = ∠OCB = 57° [Angles opposite to equal sides are equal]
Also,
⇒ ∠OCB + ∠OBC + ∠BOC = 180° [By angles sum property of triangle]
⇒ 57° + 57° + ∠BOC = 180°
⇒ ∠BOC = 180° - 114° = 66°
From figure,
⇒ ∠AOB = ∠AOC + ∠BOC
⇒ 120° = ∠AOC + 66°
⇒ ∠AOC = 120° - 66° = 54°.
Hence, ∠AOC = 54° and ∠BOC = 66°.
In the given figure, O is the center of the circle. If chord AB = chord AC, OP ⊥ AB and OQ ⊥ AC; show that : PB = QC.
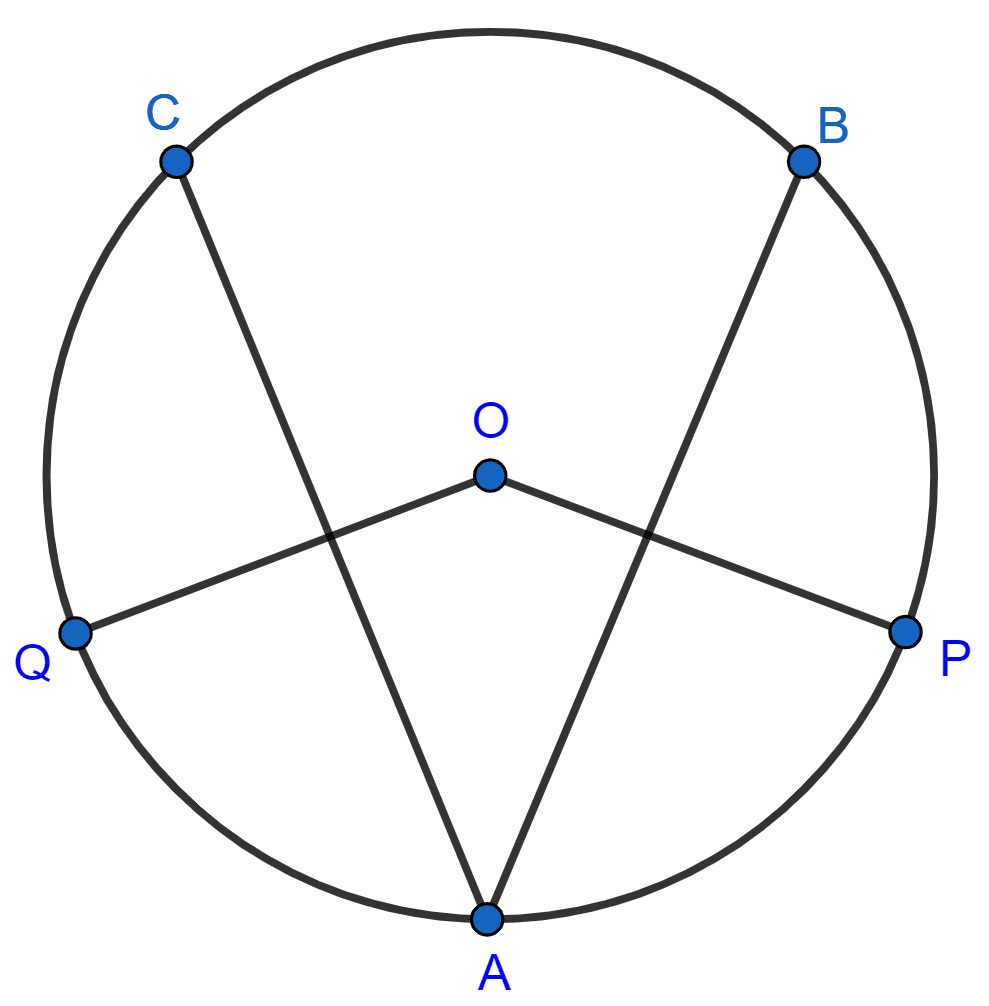
Answer
Let AB = AC = x
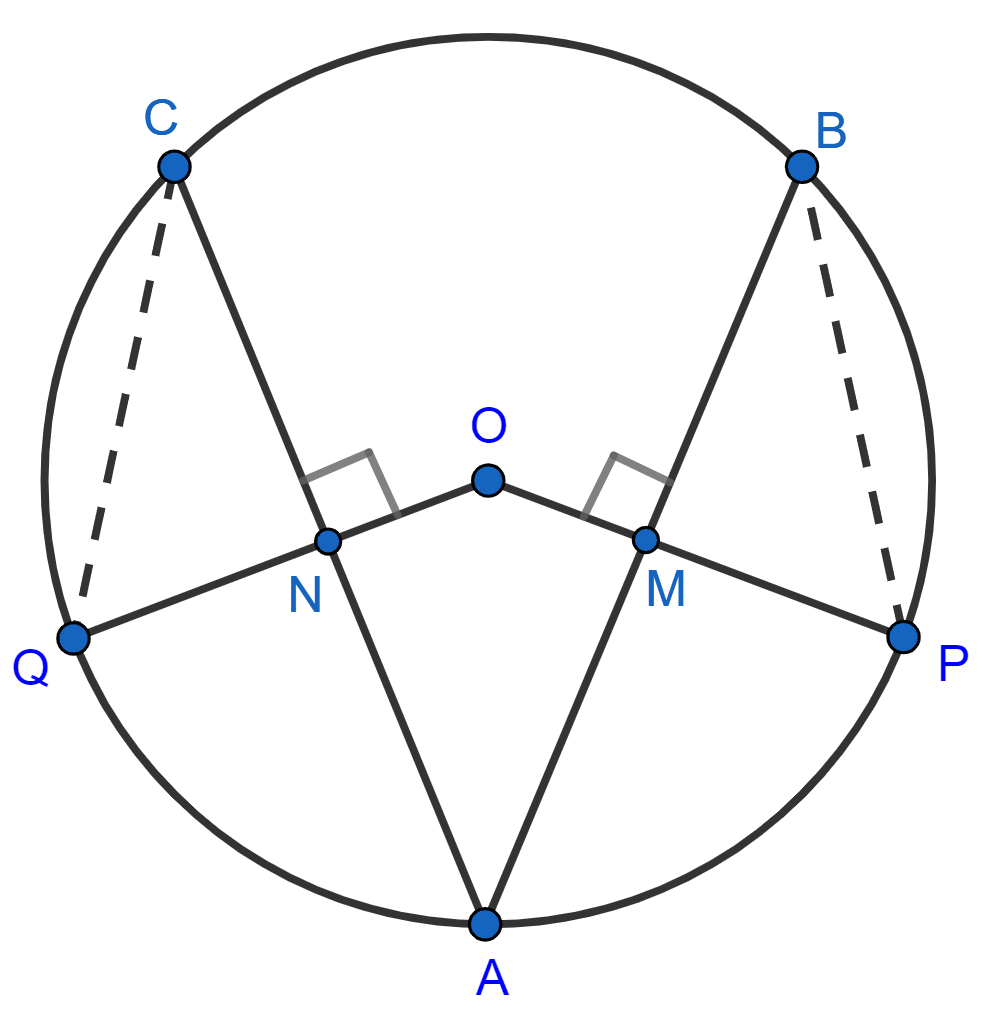
Given,
OP ⊥ AB and OQ ⊥ AC
⇒ OM ⊥ AB and ON ⊥ AC
Since, the perpendicular to a chord from the center of the circle bisects the chord,
∴ AM = MB = and AN = NC =
∴ MB = NC .............(1)
Since, equal chords of a circle are equidistant from the center,
∴ ON = OM = y (let)
Let radius of circle be r.
From figure,
⇒ OQ = OP = r
⇒ QN = OQ - ON = r - y
⇒ PM = OP - OM = r - y
∴ QN = PM .........(2)
In △QNC and △PMB,
⇒ NC = MB [From (1)]
⇒ QN = PM [From (2)]
⇒ ∠QNC = ∠PMB [Both equal to 90°]
∴ △QNC ≅ △∠PMB by SAS axiom.
∴ PB = QC (By C.P.C.T.)
Hence, proved that PB = QC.
In the given figure, AB and XY are diameters of a circle with center O. If ∠APX = 30°, find :
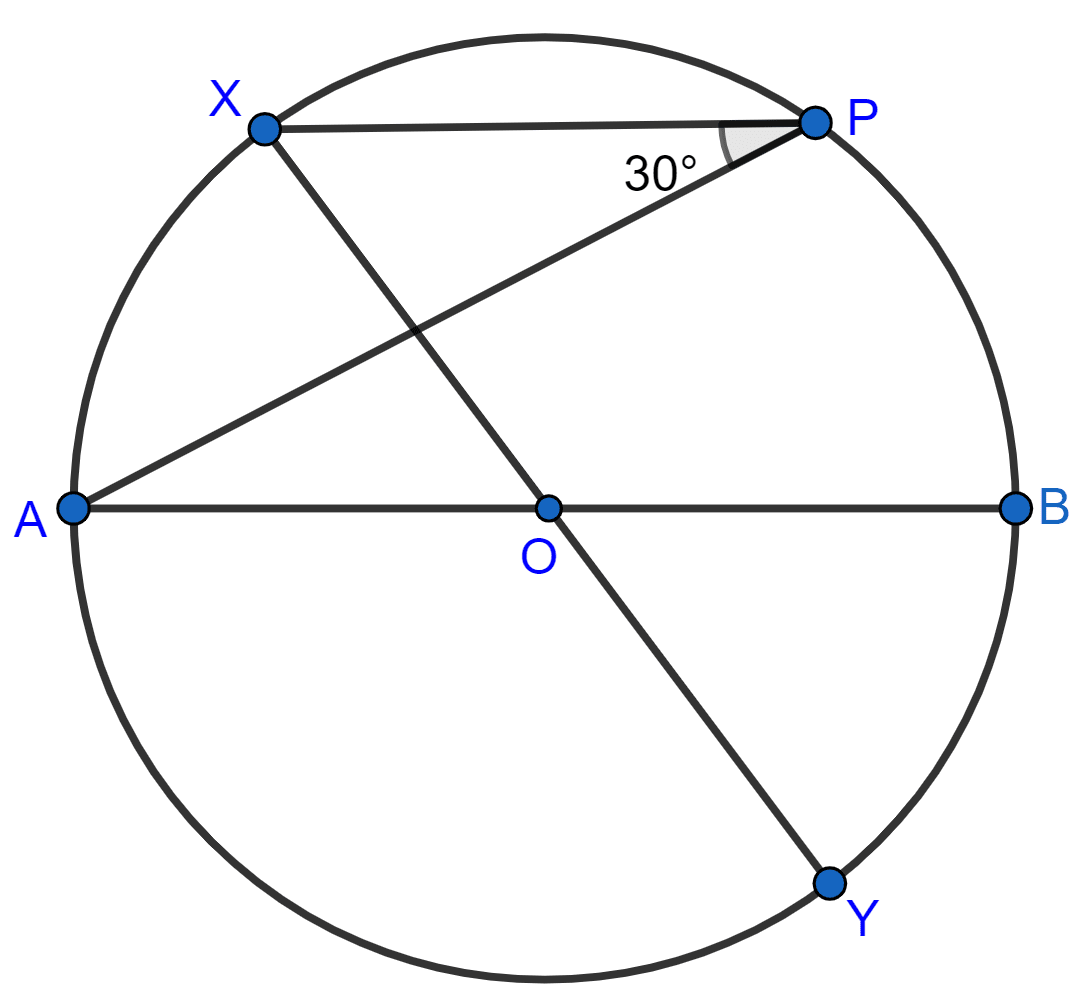
(i) ∠AOX
(ii) ∠APY
(iii) ∠BPY
(iv) ∠OAX
Answer
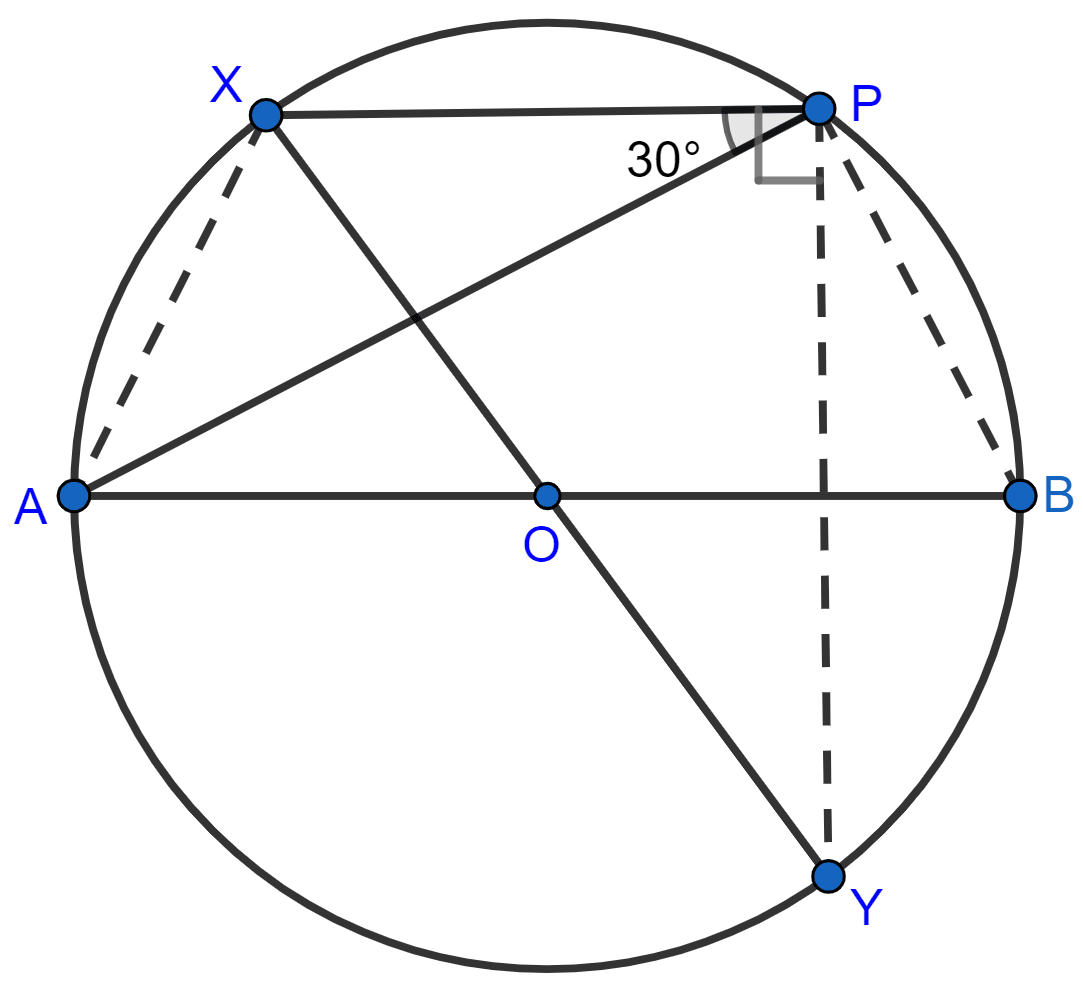
(i) Arc AX subtends ∠AOX at the center and ∠APX at the remaining part of the circle.
⇒ ∠AOX = 2∠APX (∵ angle subtended on center is twice the angle subtended on the remaining part of the circle.)
⇒ ∠AOX = 2 × 30° = 60°.
Hence, the value of ∠AOX = 60°.
(ii) From figure,
∠XPY = 90° [∵ angle in semicircle = 90°]
∴ ∠APY = ∠XPY - ∠APX = 90° - 30° = 60°.
Hence, the value of ∠APY = 60°.
(iii) From figure,
∠APB = 90° [∵ angle in semicircle = 90°]
∴ ∠BPY = ∠APB - ∠APY = 90° - 60° = 30°.
Hence, the value of ∠BPY = 30°.
(iv) In △AOX,
OA = OX (Radius of same circle)
∴ ∠OAX = ∠OXA
Since, sum of angles of a triangle = 180°
∴ ∠AOX + ∠OAX + ∠OXA = 180°
⇒ 60° + ∠OAX + ∠OAX = 180°
⇒ 2∠OAX = 120°
⇒ ∠OAX =
⇒ ∠OAX = 60°.
Hence, the value of ∠OAX = 60°.
In the adjoining figure; AB = AD, BD = CD and ∠DBC = 2∠ABD. Prove that : ABCD is a cyclic quadrilateral.

Answer
In △ABD,
AB = AD
∠ADB = ∠ABD (∵ angles opposite to equal sides are equal) ......(1)
In △BDC,
BD = CD
∠DCB = ∠DBC (∵ angles opposite to equal sides are equal) ......(2)
In △ADB,
⇒ ∠DAB + ∠ADB + ∠ABD = 180° [Angle sum property of triangle]
⇒ ∠DAB + ∠ABD + ∠ABD = 180° [From (1)]
⇒ ∠DAB + 2∠ABD = 180°
⇒ ∠DAB + ∠DBC = 180° [As, ∠DBC = 2∠ABD (Given)]
⇒ ∠DAB + ∠DCB = 180° [From (2)]
Since, ∠DAB and ∠DCB are opposite angles of a quadrilateral and sum of opposite angles in a cyclic quadrilateral = 180°.
Hence, proved that ABCD is a cyclic quadrilateral.
AB is a diameter of a circle with centre O. Chord CD is equal to radius OC. AC and BD produced intersect at P. Prove that : ∠APB = 60°.

Answer

From figure,
∠ADB = 90° [Angle subtended by diameter is a right angle.]
In △COD,
OC = OD [Radius of same circle]
∴ OC = OD = CD.
So, △COD is an equilateral triangle.
∴ ∠COD = 60°.
We know that,
Angle subtended by chord in the center is double the angle in the circumference.
⇒ ∠COD = 2∠CAD
⇒ ∠CAD = ∠COD
⇒ ∠CAD = = 30°.
In △APD,
⇒ ∠PAD = ∠CAD = 30°.
⇒ ∠ADP + ∠ADB = 180° [Linear pair]
⇒ ∠ADP = 180° - ∠ADB = 180° - 90° = 90°.
By angle sum property.
⇒ ∠ADP + ∠APD + ∠PAD = 180°
⇒ 90° + ∠APD + 30° = 180°
⇒ ∠APD + 120° = 180°
⇒ ∠APD = 180° - 120°
⇒ ∠APD = 60°.
From figure,
⇒ ∠APB = ∠APD = 60°.
Hence, proved that ∠APB = 60°.
In the given figure, AC = AB and ∠ABC = 72°. OA and OB are two tangents. Determine :
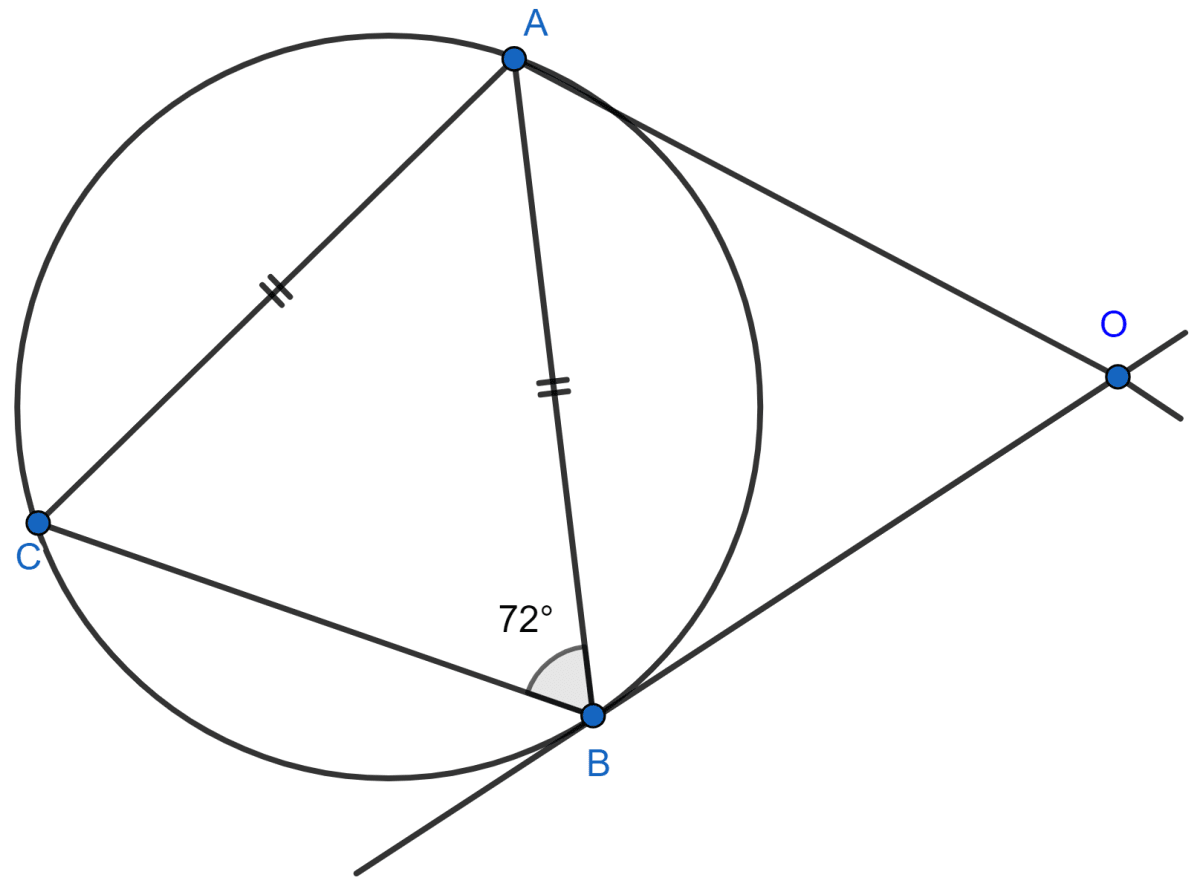
(i) ∠AOB
(ii) angle subtended by the chord AB at the center.
Answer
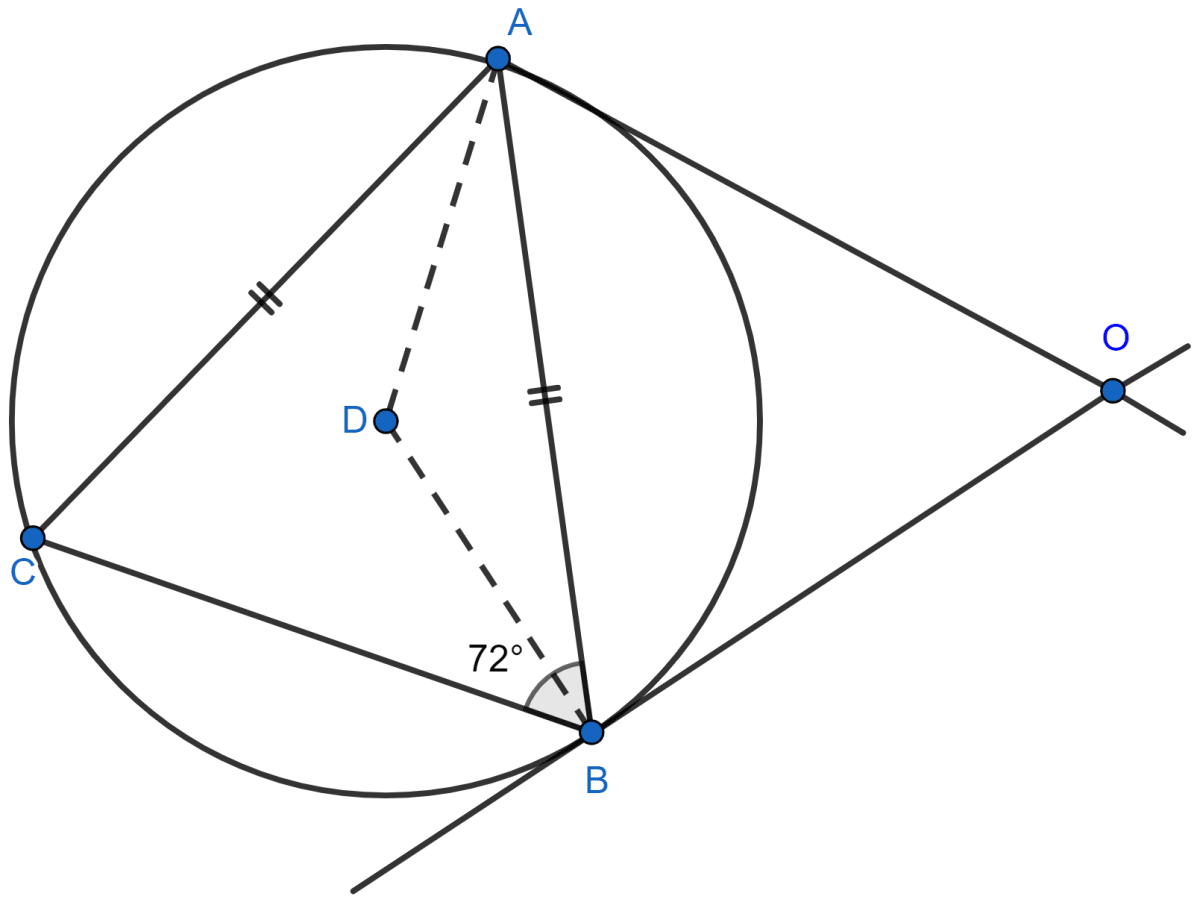
(i) Since,
⇒ AB = AC
⇒ ∠ACB = ∠ABC = 72° [∵ angles opposite to equal sides are equal]
From figure,
⇒ ∠BAO = ∠ACB = 72° [Angles in alternate segment are equal]
⇒ OA = OB [Tangents from a fixed point outside the circle are equal.]
⇒ ∠OBA = ∠BAO = 72° [Since angle opposite to equal sides are equal]
In △ABO,
⇒ ∠BAO + ∠OBA + ∠AOB = 180° [By angle sum property of triangle]
⇒ 72° + 72° + ∠AOB = 180°
⇒ ∠AOB = 180° - 144° = 36°.
Hence, ∠AOB = 36°.
(ii) We know that,
Angle subtended by a chord at the centre of the circle is twice the angle subtended by it at any point of the circumference.
∴ ∠ADB = 2∠ACB = 2 × 72° = 144°.
Hence, angle subtended by AB at the centre of the circle = 144°.
In the given figure, PQ, PR and ST are tangents to the same circle. If ∠P = 40° and ∠QRT = 75°, find a, b and c.
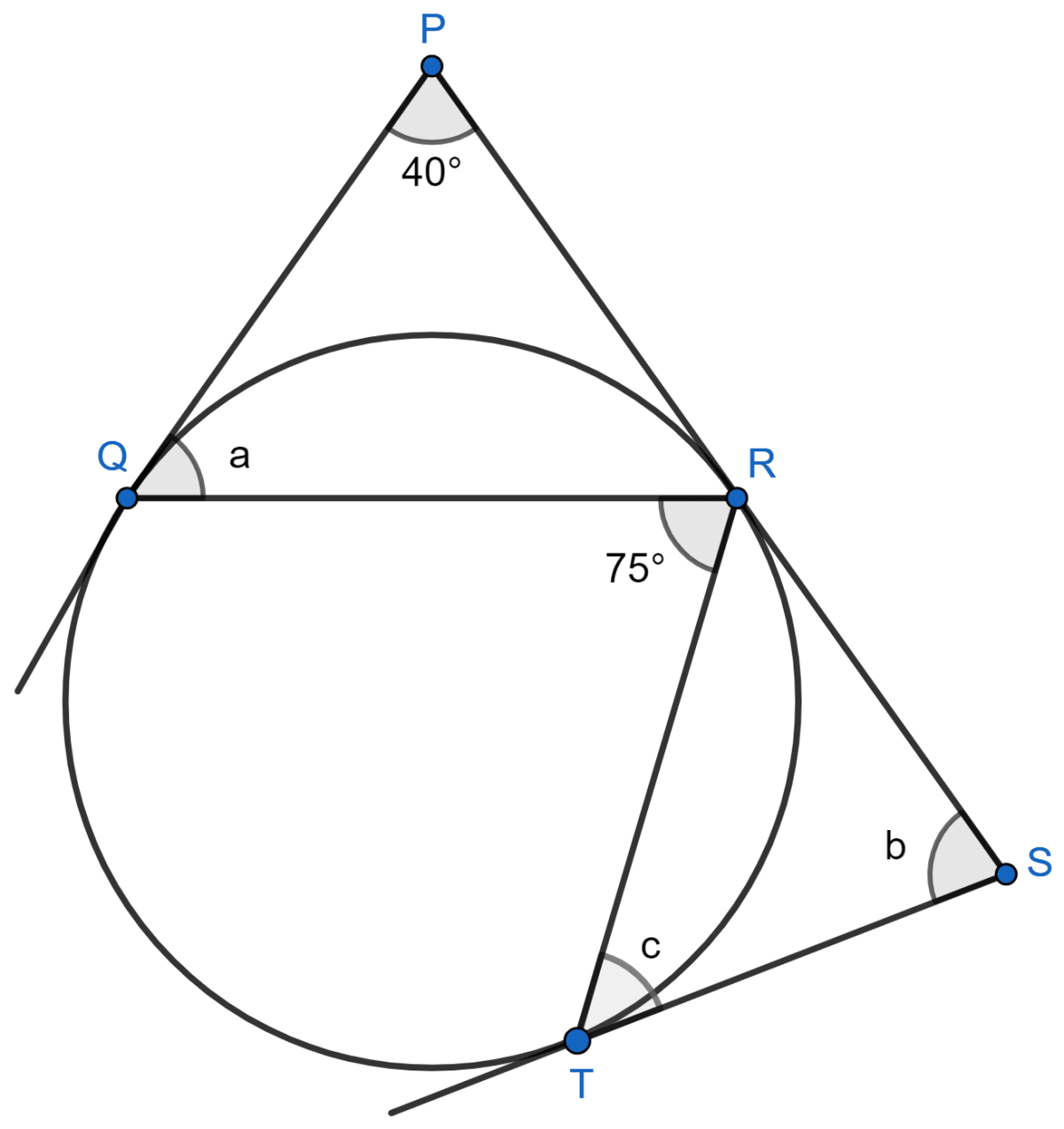
Answer
From figure,
PQ = PR [Tangents from a fixed point outside the circle are equal.]
⇒ ∠PRQ = ∠PQR = a [Since angle opposite to equal sides are equal]
In △PQR,
⇒ ∠QPR + ∠PQR + ∠PRQ = 180° [By angle sum property of triangle]
⇒ 40° + a + a = 180°
⇒ 2a = 180° - 40°
⇒ 2a = 140°
⇒ a =
⇒ a = 70°.
From figure,
⇒ ∠PRQ + ∠QRT + ∠TRS = 180° [Linear pair]
⇒ 70° + 75° + ∠TRS = 180°
⇒ ∠TRS = 180° - 145° = 35°
⇒ SR = ST [Tangents from a fixed point outside the circle are equal.]
⇒ ∠STR = ∠TRS = 35° [Since angle opposite to equal sides are equal]
∴ c = 35°
In △SRT,
⇒ ∠STR + ∠TRS + ∠TSR = 180° [By angle sum property of triangle]
⇒ 35° + 35° + b = 180°
⇒ b = 180° - 70° = 110°.
Hence, a = 70°, b = 110° and c = 35°.
In the given figure, ∠ABC = 90° and BC is diameter of the given circle. Show that :
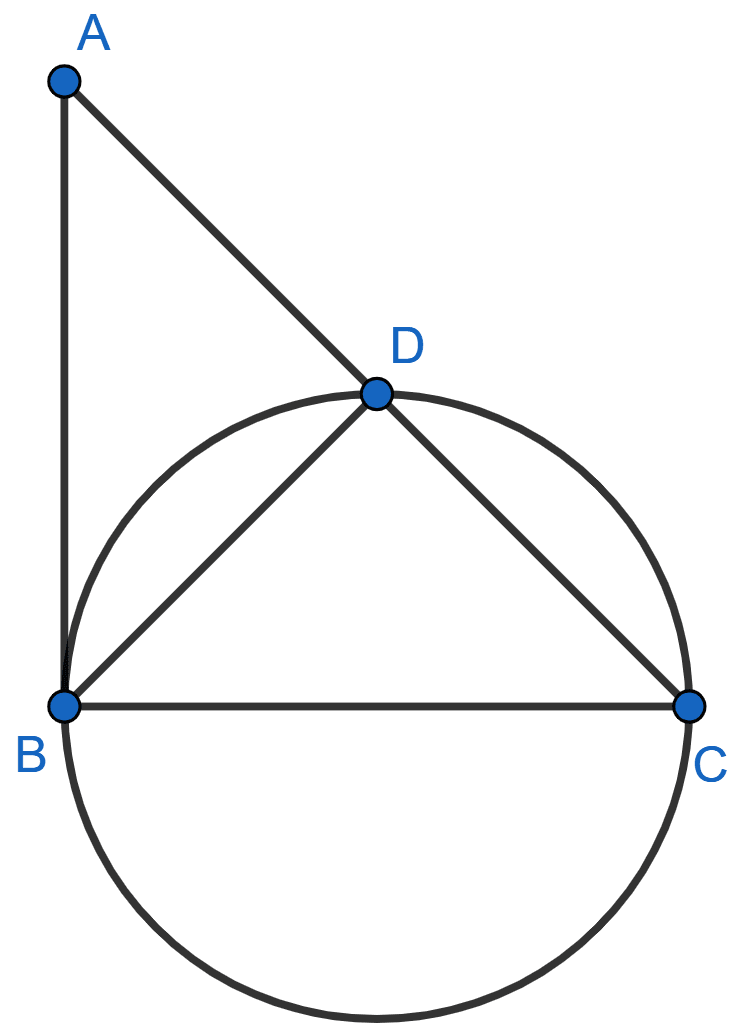
(i) AC × AD = AB2
(ii) AC × CD = BC2
Answer
(i) As, BC is the diameter.
We know that,
Angle in a semicircle is a right angle.
∴ ∠BDC = 90°
From figure,
⇒ ∠BDC + ∠BDA = 180° [Linear Pair]
⇒ 90° + ∠BDA = 180°
⇒ ∠BDA = 180° - 90°
⇒ ∠BDA = 90°.
As, AB is the tangent and BC is diameter and tangent at any point and line from that point to center are perpendicular to each other.
⇒ ∠ABC = 90°
In △ABC and △ABD,
∠ABC = ∠ADB (Both equal to 90°)
∠BAD = ∠BAC (Common)
∴ △ABC ~ △ABD
In similar triangles,
Ratio of corresponding sides are in equal proportion.
Hence, proved that AB2 = AC × AD.
(ii) In △ABC and △BDC,
⇒ ∠ABC = ∠BDC (Both equal to 90°)
⇒ ∠BCA = ∠BCD (Common)
∴ △ABC ~ △BDC
In similar triangles,
Ratio of corresponding sides are in equal proportion.
Hence, proved that BC2 = AD × CD.
In the given figure, AB, BC and CA are tangents to the given circle. If AB = 12 cm, BC = 8 cm and AC = 10 cm, find the lengths of AD, BE and CF.
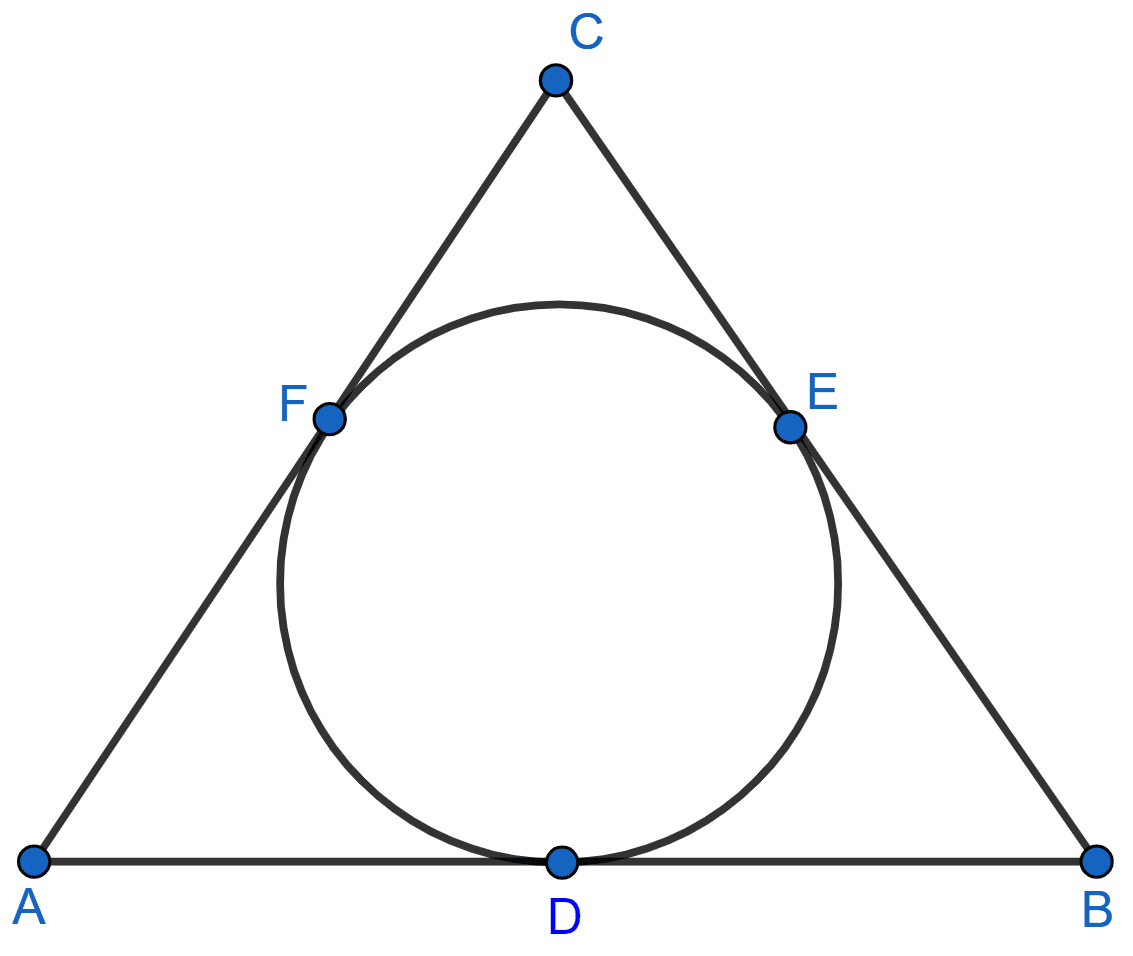
Answer
As, tangents from an exterior fixed point to a circle are equal in length,
Let,
AD = AF = x cm
BD = BE = y cm
CF = CE = z cm
From figure,
⇒ AD + BD = AB
⇒ x + y = 12 .........(1)
⇒ AF + CF = AC
⇒ x + z = 10 ........(2)
⇒ BE + CE = BC
⇒ y + z = 8 ..........(3)
Subtracting eq (3) from (1), we get :
⇒ x + y - (y + z) = 12 - 8
⇒ x - z = 4 ............(4)
Adding equation (2) and (4), we get :
⇒ (x + z) + (x - z) = 10 + 4
⇒ 2x = 14
⇒ x =
⇒ x = 7.
Substituting value of x in equation (1), we get :
⇒ 7 + y = 12
⇒ y = 12 - 7
⇒ y = 5.
Substituting value of y in equation (3), we get :
⇒ y + z = 8
⇒ 5 + z = 8
⇒ z = 8 - 5
⇒ z = 3.
∴ AD = x = 7, BE = y = 5 and CF = z = 3.
Hence, AD = 7 cm, BE = 5 cm and CF = 3 cm.
AB and CD are two chords of a circle intersecting at point P inside the circle. If
(i) AB = 24 cm, AP = 4 cm and PD = 8 cm, determine CP.
(ii) AP = 3 cm, PB = 2.5 cm and CD = 6.5 cm, determine CP.
Answer
(i) From figure,
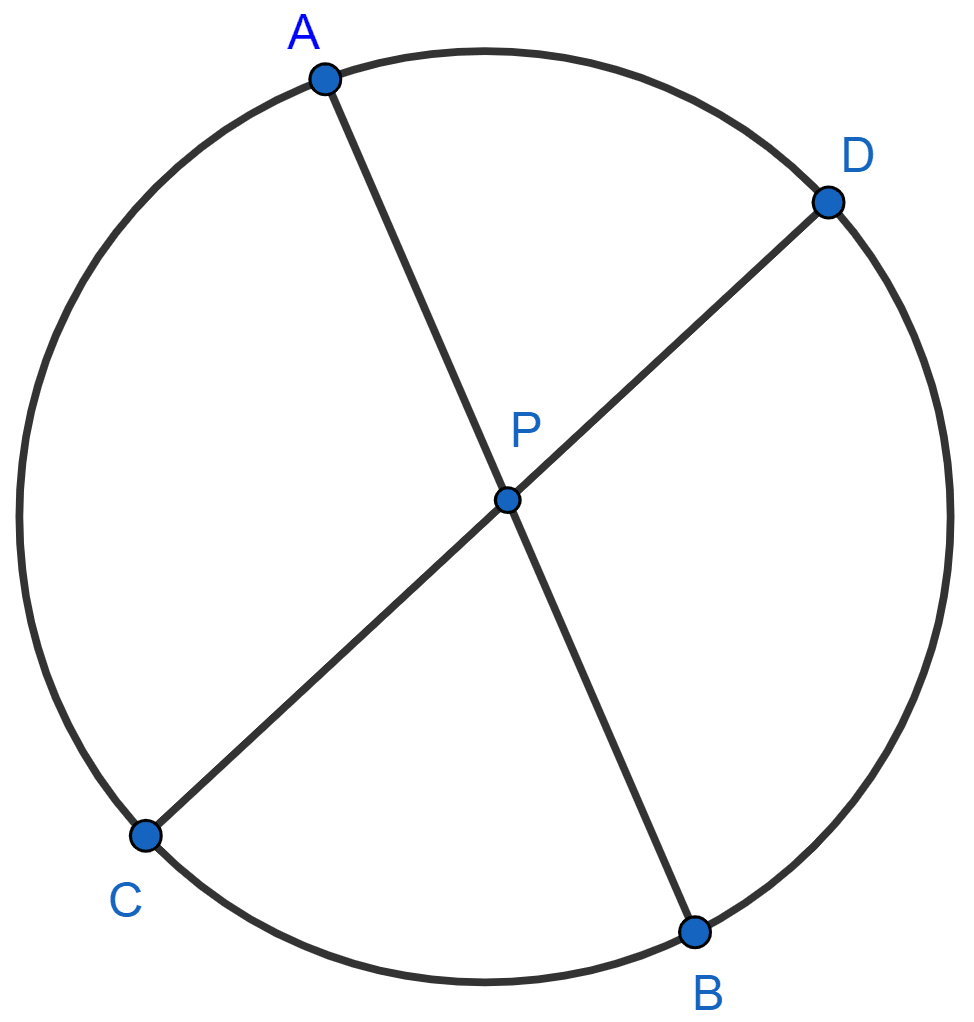
⇒ AB = AP + PB
⇒ 24 = 4 + PB
⇒ PB = 24 - 4
⇒ PB = 20 cm.
We know that,
If two chords intersect in a circle, then the products of the measures of the segments of the chords are equal.
⇒ AP × PB = CP × PD
⇒ 4 × 20 = CP × 8
⇒ 80 = 8CP
⇒ CP = = 10.
Hence, CP = 10 cm.
(ii) Let CP = x, so PD = (6.5 - x).
We know that,
If two chords intersect in a circle , then the products of the measures of the segments of the chords are equal.
⇒ AP × PB = CP × PD
⇒ 3 × 2.5 = x(6.5 - x)
⇒ 7.5 = 6.5x - x2
⇒ x2 - 6.5x + 7.5 = 0
⇒ x2 - 5x - 1.5x + 7.5 = 0
⇒ x(x - 5) - 1.5(x - 5) = 0
⇒ (x - 1.5)(x - 5) = 0
⇒ x - 1.5 = 0 or x - 5 = 0
⇒ x = 1.5 or x = 5.
Hence, CP = 1.5 cm or 5 cm.
AB and CD are two chords of a circle intersecting at point P outside the circle. If
(i) PA = 8 cm, PC = 5 cm and PD = 4 cm, determine AB.
(ii) PC = 30 cm, CD = 14 cm and PA = 24 cm, determine AB.
Answer
(i) We know that,
If two chords of a circle intersect externally, then the product of the lengths of the segments are equal.
⇒ AP × PB = CP × PD
⇒ 8 × PB = 5 × 4
⇒ PB = = 2.5
From figure,
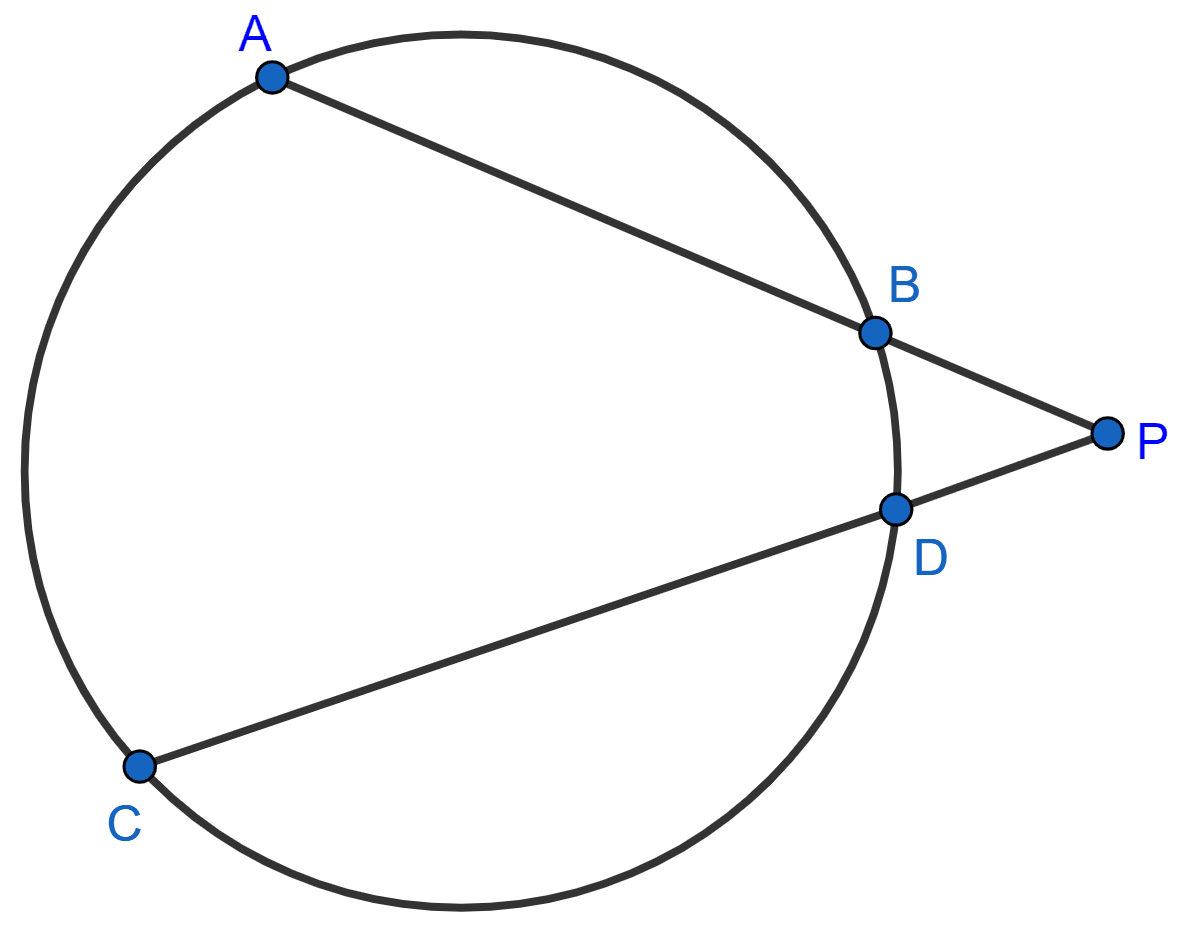
AB = PA - PB = 8 - 2.5 = 5.5 cm.
Hence, AB = 5.5 cm.
(ii) From figure,
⇒ PC = CD + PD
⇒ 30 = 14 + PD
⇒ PD = 16 cm.
We know that,
If two chords of a circle intersect externally, then the product of the lengths of the segments are equal.
⇒ AP × PB = PC × PD
⇒ 24 × PB = 30 × 16
⇒ PB = = 20
From figure,
AB = PA - PB = 24 - 20 = 4 cm.
Hence, AB = 4 cm.
Two circles touch each other internally at a point P. A chord AB of the bigger circle intersects the other circle in C and D. Prove that : ∠CPA = ∠DPB.
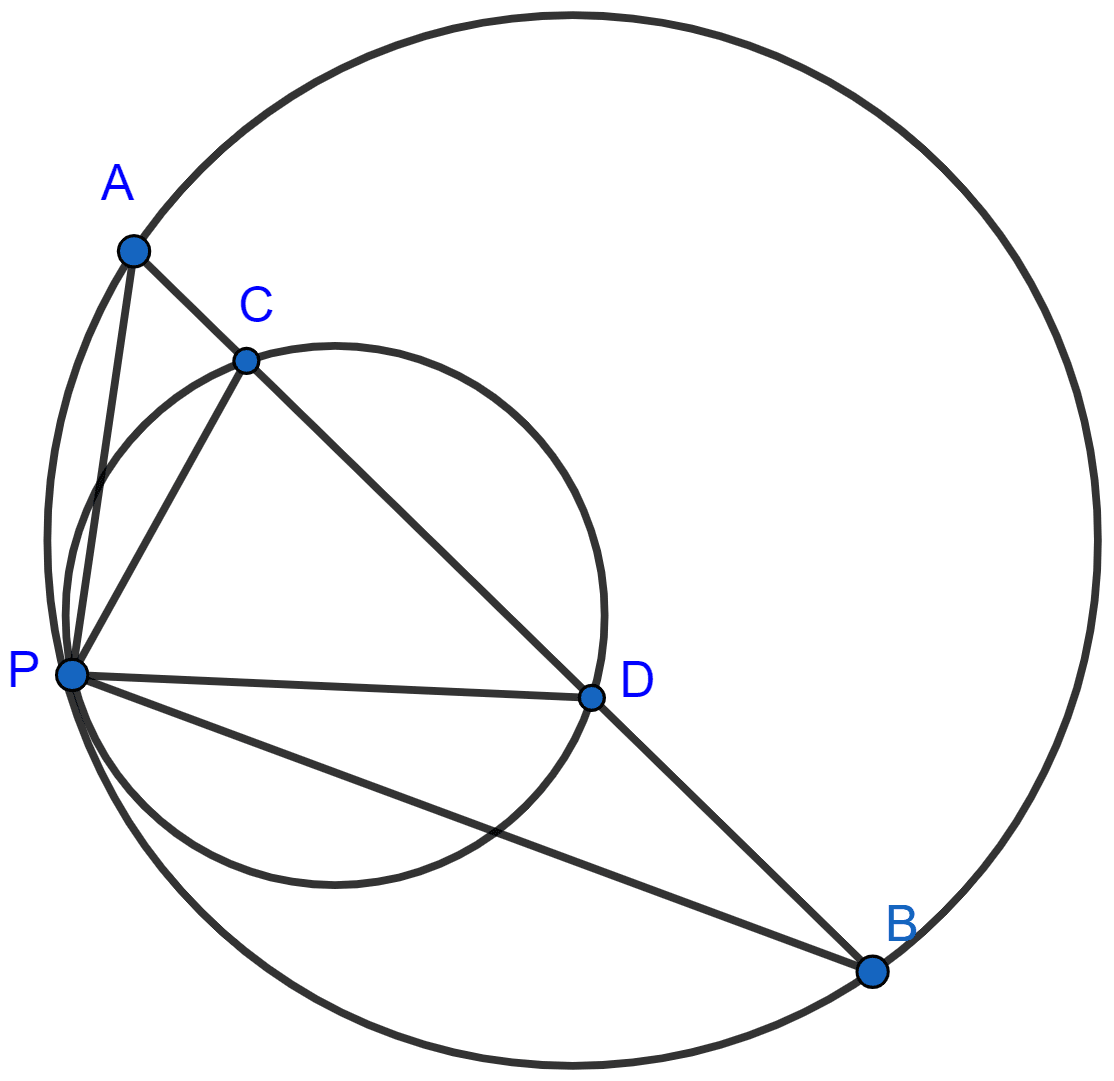
Answer
Draw tangent at point P,
∠PAB = ∠BPS .............(1) [Angles in alternate segments are equal.]
∠PCD = ∠DPS .............(2) [Angles in alternate segments are equal.]
Subtracting (1) from (2), we get :
⇒ ∠PCD - ∠PAB = ∠DPS - ∠BPS ............(3)
In △PAC,
⇒ ∠PCD = ∠PAC + ∠CPA [An exterior angle is equal to sum of two opposite interior angles.]
⇒ ∠PCD = ∠PAB + ∠CPA [From figure, ∠PAC = ∠PAB]
Substituting above value of ∠PCD in (3), we get :
⇒ ∠PAB + ∠CPA - ∠PAB = ∠DPS - ∠BPS
⇒ ∠CPA = ∠DPB [From figure, ∠DPS - ∠BPS = ∠DPB].
Hence, proved that ∠CPA = ∠DPB.
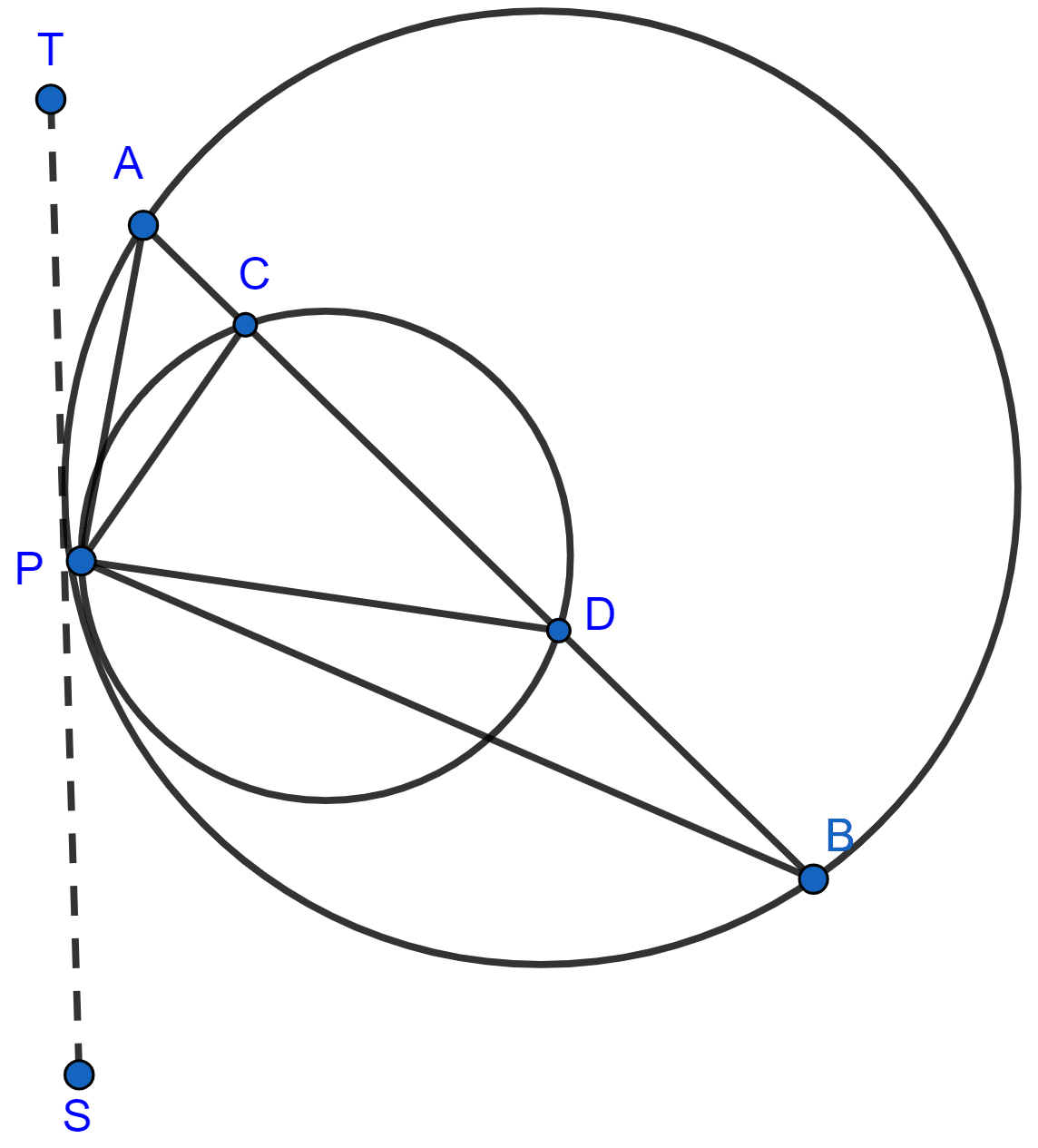
In the given figure, MN is the common chord of two intersecting circles and AB is their common tangent.
Prove that the line NM produced bisects AB at P.

Answer
We know that,
If a chord and a tangent intersect externally, then the product of the lengths of the segments of the chord is equal to the square of the length of the tangent from the point of contact to the point of intersection.
∴ AP2 = PM x PN ..........(1)
From P, PB is the tangent and PMN is the secant for second circle.
∴ PB2 = PM x PN ......... (2)
From (1) and (2), we have
⇒ AP2 = PB2
⇒ AP = PB
Hence, proved that P is the midpoint of AB.
In the given figure, PAT is tangent to the circle with center O, at point A on its circumference and is parallel to chord BC. If CDQ is a line segment, show that :
(i) ∠BAP = ∠ADQ
(ii) ∠AOB = 2∠ADQ
(iii) ∠ADQ = ∠ADB.
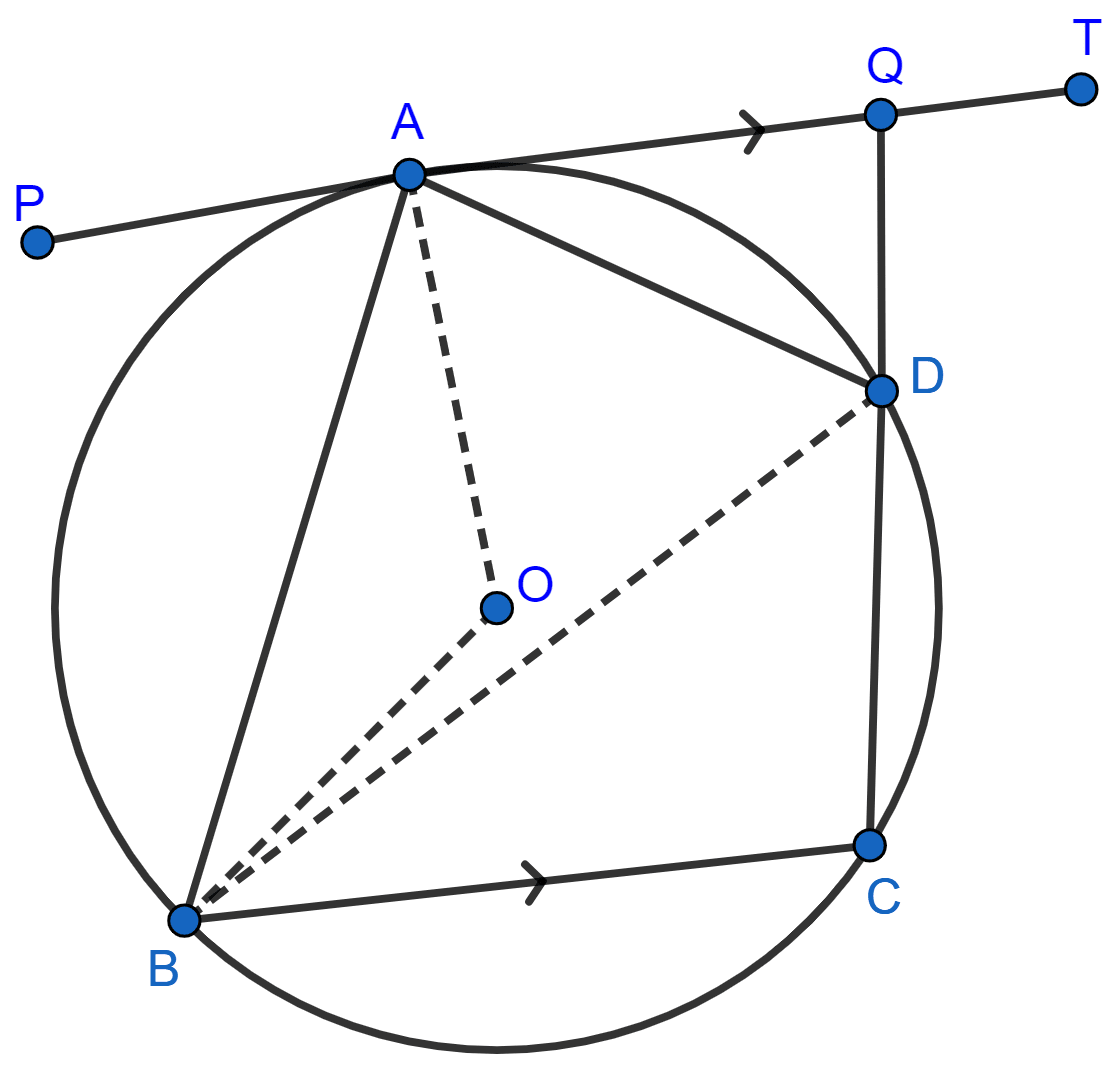
Answer
(i) Since, PAT || BC
∠BAP = ∠ABC [Alternate angles are equal] .........(1)
In cyclic quadrilateral ABCD,
∠ABC + ∠ADC = 180° [Sum of opposite angles in a cyclic quadrilateral = 180°] ................(2)
From figure,
∠ADQ + ∠ADC = 180° [Linear pairs] .........(3)
From (2) and (3), we get :
∠ADQ = ∠ABC ............(4)
From (1) and (4), we get :
∠BAP = ∠ADQ.
Hence, proved that ∠BAP = ∠ADQ.
(ii) We know that,
Angle subtended by an arc at the center is twice the angle subtended at any other point of circumference.
Arc AB subtends ∠AOB at the center and ∠ADB at the remaining part of the circle.
⇒ ∠AOB = 2∠ADB ............(3)
From figure,
∠ADB = ∠PAB [Angles in alternate segment are equal.]
Substituting above value in (3), we get :
⇒ ∠AOB = 2∠PAB
∠PAB = ∠ADQ [Proved above]
⇒ ∠AOB = 2∠ADQ.
Hence, proved that ∠AOB = 2∠ADQ.
(iii) From figure,
∠BAP = ∠ADB [Angles in alternate segment are equal.] .........(4)
∠BAP = ∠ADQ [Proved in part (i)] ...........(5)
From (4) and (5), we get :
∠ADQ = ∠ADB.
Hence, proved that ∠ADQ = ∠ADB.
Construct a triangle ABC in which AC = 5 cm, BC = 7 cm and AB = 6 cm.
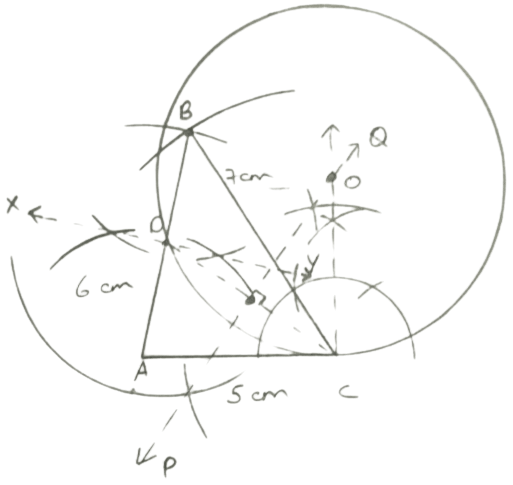
(i) Mark D, the mid-point of AB.
(ii) Construct a circle which touches BC at C and passes through D.
Answer
Steps of construction :
Draw a line segment AC = 5 cm.
From A draw an arc of radius 6 cm and from C draw an arc of radius 7 cm, intersecting each other at point B.
Draw XY, the perpendicular bisector of AB, and mark D as the mid point.
Draw perpendicular bisector of CD.
From C, draw a line segment perpendicular to AC, which intersect the PQ, perpendicular bisector of CD at O.
Take O as centre and OD as radius draw a circle.
Using ruler and compasses only; draw a circle of radius 4 cm. Produce AB, a diameter of this circle, upto point X so that BX = 4 cm. Construct a circle to touch AB at X and to touch the circle, drawn earlier, externally.
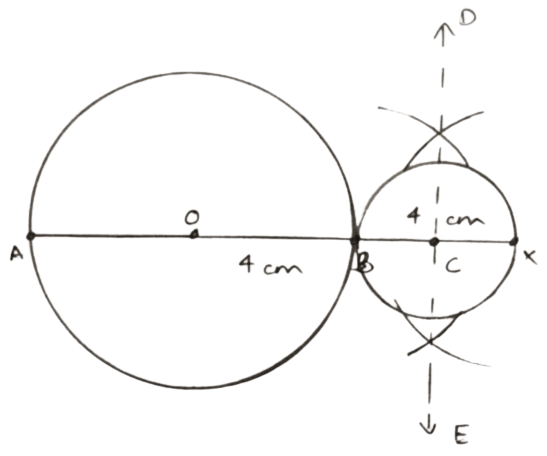
Answer
Steps of construction :
Taking O as center and radius = 4 cm draw a circle.
Draw AB, the diameter of circle with center O.
Produce AB to X such that BX = 4 cm.
Draw DE perpendicular bisector of BX, intersecting BX at C.
From C, as center and CX as radius draw a circle touching circle with center O at B and passing through X.
A cylinder of circumference 8 cm and length 21 cm rolls without sliding for seconds at the rate of 9 complete rounds per second. Find:
(i) distance travelled by the cylinder in seconds, and
(ii) the area covered by the cylinder in seconds
Answer
(i) If distance covered in one revolution is 8 cm, then distance covered in 9 revolutions = 9 x 8 = 72 cm or distance covered in 1 second = 72 cm.
Distance covered in seconds = 72 x 4.5 = 324 cm.
Hence, distance travelled by the cylinder in seconds is 324 cm.

(ii) Given, circumference = 8 cm.
∴ 2πr = 8
⇒
⇒ r = cm.
By formula,
Curved surface area = 2πrh
= 2 x x 21
= 2 x 2 x 2 x 21
= 168 cm2.
So, the area covered in one revolution = 168 cm2,
∴ The area covered in 9 revolutions = 168 x 9 = 1512 cm2,
∴ The area covered in 1 second = 1512 cm2,
Thus, the area covered in seconds = 1512 x 4.5 = 6804 cm2.
Hence, the area covered by cylinder in seconds = 6804 cm2.
A cylindrical bucket 28 cm in diameter and 72 cm high is full of water. The water is emptied into a rectangular tank 66 cm long and 28 cm wide. Find the height of the water level in the tank.
Answer
Given,
Diameter of cylindrical bucket = 28 cm
Radius (r) = = 14 cm.
Height (H) = 72 cm.
Length of rectangular tank (l) = 66 cm
Breadth of rectangular tank (b) = 28 cm.
Let height of water be h cm in the rectangular tank.
Since, water is emptied into a rectangular tank from cylindrical bucket,
∴ Volume of cylindrical bucket = Volume of water in rectangular tank
Hence, height of water level in rectangular tank = 24 cm.
The radius of a solid right circular cylinder increases by 20% and its height decreases by 20%. Find the percentage change in its volume.
Answer
Let the radius of a solid right cylinder be r cm and height be h cm.
∴ Volume of cylinder = πr2h
New radius (r') = r + = 1.2r.
New height (h') = h - = 0.8h.
⇒ New volume of the solid right circular cylinder = πr'2h'
= π x (1.2r)2 x 0.8h
= 1.152 πr2h.
Increase in volume = New volume - Original volume
= 1.152 πr2h - πr2h
= 0.152 πr2h.
By formula,
Percentage change in volume = x 100%
= x 100%
= 15.2 %.
Hence, percentage change in volume = 15.2 %.
The sum of the inner and the outer curved surfaces of a hollow metallic cylinder is 1056 cm2 and the volume of the material is 1056 cm3. Find its internal and external radii. Given that the height of the cylinder is 21 cm.
Answer
Given,
Sum of the inner and the outer curved surfaces of a hollow metallic cylinder = 1056 cm2
∴ 2πrh + 2πRh = 1056
⇒ 2πh(r + R) = 1056
⇒ = 1056
⇒ h(r + R) =
⇒ h(r + R) = 168 ...........(1)
Volume of the material = 1056 cm3
∴ π(R2 - r2)h = 1056
⇒ = 1056
⇒ (R2 - r2)h =
⇒ (R2 - r2)h = 336 .........(2)
Dividing (2) by (1) we get,
Substituting value of height and R in equation (1) we get :
⇒ 21(r + r + 2) = 168
⇒ 21(2r + 2) = 168
⇒ 2r + 2 =
⇒ 2r + 2 = 8
⇒ 2r = 8 - 2
⇒ 2r = 6
⇒ r =
⇒ r = 3 cm.
⇒ R = r + 2 = 3 + 2 = 5 cm.
Hence, internal radius = 3 cm and external radius = 5 cm.
A tent is of the shape of a right circular cylinder upto height of 3 meters and then becomes a right circular cone with a maximum height of 13.5 meters above the ground. Calculate the cost of painting the inner surface of the tent at ₹ 4 per sq. meter, if the radius of the base is 14 meters.
Answer
Given,
Height of cylindrical portion (h) = 3 m
Height of conical part (H) = Maximum height of tent (above ground) - Height of cylindrical portion = 13.5 - 3 = 10.5 m.
Radius of base of cylindrical portion = Radius of conical portion = r = 14 m.
⇒ Curved surface area of tent = Curved surface area of cone + Curved surface area of cylinder
⇒ Curved surface area of tent (C) = πrl + 2πrh .......(1)
We know that,
Substituting values in equation (1), we get :
Given,
Cost of painting the inner surface of the tent at ₹ 4 per sq. meter.
Total cost = Curved surface area of tent × 4
= 1034 × 4 = ₹ 4136.
Hence, cost of painting the inner surface = ₹ 4136.
A copper wire of diameter 6 mm is evenly wrapped on the cylinder of length 18 cm and diameter 49 cm to cover the whole surface. Find :
(i) the length
(ii) the volume of the wire.
Answer
Given,
Diameter of copper wire = 6 mm = 0.6 cm
Length of cylinder (l) = 18 cm
Diameter of cylindrical base = 49 cm
Radius of cylindrical base (r) = = 24.5 cm.
(i) Given,
Copper wire is evenly wrapped on the cylinder to cover the whole surface.
As it is covers the whole length of cylinder.
∴ No. of times it wraps around = = 30.
For each turn, length of copper wire = Circumference of cylinder = 2πr
= 2 × × 24.5
= 154 cm.
Total length = 30 × 154 = 4620 cm = = 46.20 m.
Hence, total length of copper wire = 46.20 m.
(ii) Since, wire is in the form of cylinder.
Height = Length of wire
Given,
Radius of wire (R) = = 0.3 cm.
Volume of wire = πR2 × length
=
= = 1306.8 cm3.
Hence, volume of wire = 1306.8 cm3.
A pool has a uniform circular cross section of radius 5 m and uniform depth 1.4 m. It is filled by a pipe which delivers water at the rate of 20 litres per sec. Calculate, in minutes, the time taken to fill the pool. If the pool is emptied in 42 min. by another cylindrical pipe through which water flows at 2 m per sec, calculate the radius of the pipe in cm.
Answer
Given,
Radius of pool (R) = 5 m,
Depth of pool (H) = 1.4 m.
Since, pool is in the form of cylinder.
Volume of water in pool = πR2H
= = 110 m3
= 110 × 1000 litres = 11 × 104 liters.
Volume of water coming out of filling pipe = 20 litres/sec.
Time taken to fill the tank = second
= minutes
= minutes.
Let radius of pipe be r cm.
Volume of water coming out from draining pipe in 1 sec = Area of cross section × Rate
= πr2 × 2 m/sec
= (200 × πr2) cm3
= (200 × πr2 × 10-3) liters.
Given,
Time required for emptying the pool = 42 min = 42 × 60 seconds.
Hence, time taken to fill the pool = minutes and radius of pipe = cm.
A test tube consists of a hemisphere and a cylinder of the same radius. The volume of water required to fill the whole tube is cm3 and cm3 of water is required to fill the tube to a level which is 2 cm below the top of the tube. Find the radius of the tube and the length of its cylindrical part.

Answer
Let length of cylindrical part be h cm and radius of hemispherical and conical part be r cm.
Given,
Volume of water required to fill whole test tube = cm3.
Volume of water required to fill test tube upto a level which is 2 cm below the top of tube = cm3.
∴ Volume of water above 2 cm part of the test tube = = 77 cm3.
Volume of water in test tube = Volume of cylindrical part + Volume of hemispherical part = cm3.
Hence, radius of tube = 3.5 cm and length of cylindrical part = cm.
A sphere is placed in an inverted hollow conical vessel of base radius 5 cm and vertical height 12 cm. If the highest point of the sphere is at the level of the base of the cone, find the radius of the sphere. Show that the volume of the sphere and the conical vessel are as 40 : 81.
Answer
Given,
Radius of cone (R) = 5 cm.
Height of cone (H) = 12 cm
Let radius of sphere be r cm.
From figure,
FE = FD = r cm
AD = 12 cm, DC = 5 cm
Slant height (AC) =
= = 13 cm.
In △ADC and △AFE,
⇒ ∠ADC = ∠AEF (Both equal to 90°)
⇒ ∠A = ∠A (Common)
∴ △ADC ~ △AFE (By A.A. axiom)
Ratio of corresponding sides of similar triangle are equal.
Ratio of volume of sphere to volume of cone.
Hence, proved that ratio of volume of sphere and conical vessel = 40 : 81.
The difference between the outer and the inner curved surface areas of a hollow cylinder, 14 cm long, is 88 sq. cm. Find the outer and the inner radii of the cylinder, given that the volume of metal used is 176 cu. cm.
Answer
Given,
Height of cylinder (H) = 14 cm
Let outer radius of cylinder be R cm and inner radius be r cm.
Given,
Difference between the outer and the inner curved surface areas of a hollow cylinder is 88 sq. cm.
Given,
Volume of metal = 176 cu. cm
Adding equation (1) and (2), we get :
⇒ R - r + R + r = 1 + 4
⇒ 2R = 5
⇒ R = = 2.5 cm
Substituting value of R in equation (1), we get :
⇒ 2.5 - r = 1
⇒ r = 2.5 - 1 = 1.5 cm
Hence, outer radii = 2.5 cm and inner radii = 1.5 cm.
The surface area of a solid sphere is increased by 21% without changing its shape. Find the percentage increase in its :
(i) radius
(ii) volume
Answer
Let original radius be r units and new radius be R units.
Given,
Surface area of a solid sphere is increased by 21% without changing its shape.
By formula,
Hence, percentage increase in radius = 10%.
(ii) Let original volume be v and new volume be V.
By formula,
Hence, percentage increase in volume = 33.1%.
A wooden toy is in the shape of a cone mounted on a cylinder as shown alongside.
If the height of the cone is 24 cm, the total height of the toy is 60 cm and the radius of the base of the cone = twice the radius of the base of the cylinder = 10 cm; find the total surface area of the toy. [Take π = 3.14]
Answer
Given,
Height of the cone (h) = 24 cm
Height of the cylinder (H) = 60 - 24 = 36 cm
Radius of the cone (r) = 10 cm
Given,
Radius of the base of the cone = Twice the radius of the base of the cylinder.
Radius of base of cylinder (R) = 5 cm.
By formula,
⇒ l2 = r2 + h2
⇒ l2 = 102 + 242
⇒ l2 = 100 + 576
⇒ l2 = 676
⇒ l = = 26 cm.
Total surface area of the toy = Surface area of the conical part + Base area of conical part + Surface area of the cylinder
= πrl + πr2 + 2πRH
= π(rl + r2 + 2RH)
= 3.14 × (10 × 26 + 102 + 2 × 5 × 36)
= 3.14 × (260 + 100 + 360)
= 3.14 × 720
= 2260.8 cm2.
Hence, total surface area of troy = 2260.8 cm2.
The cross-section of a railway tunnel is a rectangle 6 m broad and 8 m high surmounted by a semi-circle as shown in the figure. The tunnel is 35 m long. Find the cost of plastering the internal surface of the tunnel (excluding the floor) at the rate of ₹ 2.25 per m2.

Answer
Given,
Breadth of tunnel (b) = 6 m
Height of tunnel (h) = 8 m
Length of tunnel (l) = 35 m
Let radius of semi-circle be r meters.
From figure,
⇒ 2r = 6
⇒ r = 3 m.
Circumference of semi-circle = πr = m.
Internal surface area of tunnel = Circumference of semi-circle × Length + Area of side interior rectangular walls
= πrl + hl + hl
= πrl + 2hl
=
= 330 + 560
= 890 m2.
Given,
Rate of plastering = ₹ 2.25 per m2.
Total cost = 890 × ₹ 2.25 = ₹ 2002.50.
Hence, cost of plastering internal surface area of tunnel = ₹ 2002.50
Prove that :
Answer
To prove:
Equation : .
Solving L.H.S. of the above equation :
∴ L.H.S. = R.H.S.
Hence, proved that .
Prove that :
Answer
To prove:
Equation : .
Solving L.H.S. of the above equation :
Solving R.H.S. of the above equation :
Since, L.H.S. = R.H.S = 1 + cos A.
Hence, proved that .
Prove that :
sin A(1 + tan A) + cos A(1 + cot A) = sec A + cosec A
Answer
To prove:
Equation : sin A(1 + tan A) + cos A(1 + cot A) = sec A + cosec A.
Solving L.H.S. of the above equation :
By formula,
sin2 A + cos2 A = 1.
∴ L.H.S. = R.H.S.
Hence, proved that sin A(1 + tan A) + cos A(1 + cot A) = sec A + cosec A.
Prove that :
sin2 A tan A + cos2 A cot A + 2 sin A cos A = tan A + cot A
Answer
To prove:
Equation : sin2 A tan A + cos2 A cot A + 2 sin A cos A = tan A + cot A.
Solving L.H.S. of the above equation :
By formula,
sin2 A + cos2 A = 1
.
Solving R.H.S. of the above equation :
Since, L.H.S. = R.H.S. = .
Hence, proved that sin2 A tan A + cos2 A cot A + 2 sin A cos A = tan A + cot A.
Prove that :
cosec A + cot A =
Answer
Solving R.H.S. of the equation :
Multiplying numerator and denominator by (1 + cos A) we get :
By formula,
1 - cos2 A = sin2 A
Since, L.H.S. = R.H.S.
Hence, proved that cosec A + cot A = .
Prove that :
Answer
Solving L.H.S. of the equation :
By formula,
cosec2 A - cot2 A = 1
Since, L.H.S. = R.H.S.
Hence, proved that .
If tan A = 1 and tan B = ; evaluate :
(i) cos A cos B - sin A sin B
(ii) sin A cos B + cos A sin B
Answer
Given,
⇒ tan A = 1
⇒ tan A = tan 45°
⇒ A = 45°.
⇒ tan B =
⇒ tan B = tan 60°
⇒ B = 60°.
(i) Solving,
⇒ cos A cos B - sin A sin B
⇒ cos 45° cos 60° - sin 45° sin 60°
Hence, cos A cos B - sin A sin B =
(ii) Given,
⇒ sin A cos B + cos A sin B
⇒ sin 45° cos 60° + cos 45° sin 60°
Hence, sin A cos B + cos A sin B =
As observed from the top of a 100 m high light house, the angles of depression of two ships approaching it are 30° and 45°. If one ship is directly behind the other, find the distance between the two ships.
Answer
Let AB be the lighthouse and C and D be the position of ships.
From figure,
∠ADC = ∠EAD = 30° (Alternate angles are equal)
∠ACB = ∠EAC = 45° (Alternate angles are equal)
In right angle triangle ABD,
⇒ tan 30° =
⇒
⇒ BD = m.
In right angle triangle ABC,
⇒ tan 45° =
⇒
⇒ BC = AB = 100 m.
From figure,
CD = BD - BC =
= 100 × (1.732 - 1) m.
= 100 × 0.732 = 73.2 m.
Hence, distance between two ships = 73.2 m.
If (2 cos 2A - 1)(tan 3A - 1) = 0; find all possible values of A.
Answer
Given,
⇒ (2 cos 2A - 1)(tan 3A - 1) = 0
⇒ 2 cos 2A - 1 = 0 or tan 3A - 1 = 0
⇒ 2 cos 2A = 1 or tan 3A = 1
⇒ cos 2A = or tan 3A = tan 45°
⇒ cos 2A = cos 60° or tan 3A = tan 45°
⇒ 2A = 60° or 3A = 45°
⇒ A = or A =
⇒ A = 30° or 15°.
Hence, A = 30° or 15°.
If cos A = ; find the value of .
Answer
Given,
cos A = ;
Squaring both sides, we get :
By formula,
tan A = .
Substituting value of sin A and tan A in , we get :
Hence, = 1.
From the top of a light house, it is observed that a ship is sailing directly towards it and the angle of depression of the ship changes from 30° to 45° in 10 minutes. Assuming that the ship is sailing with uniform speed; calculate in how much more time (in minutes) will the ship reach the light house ?
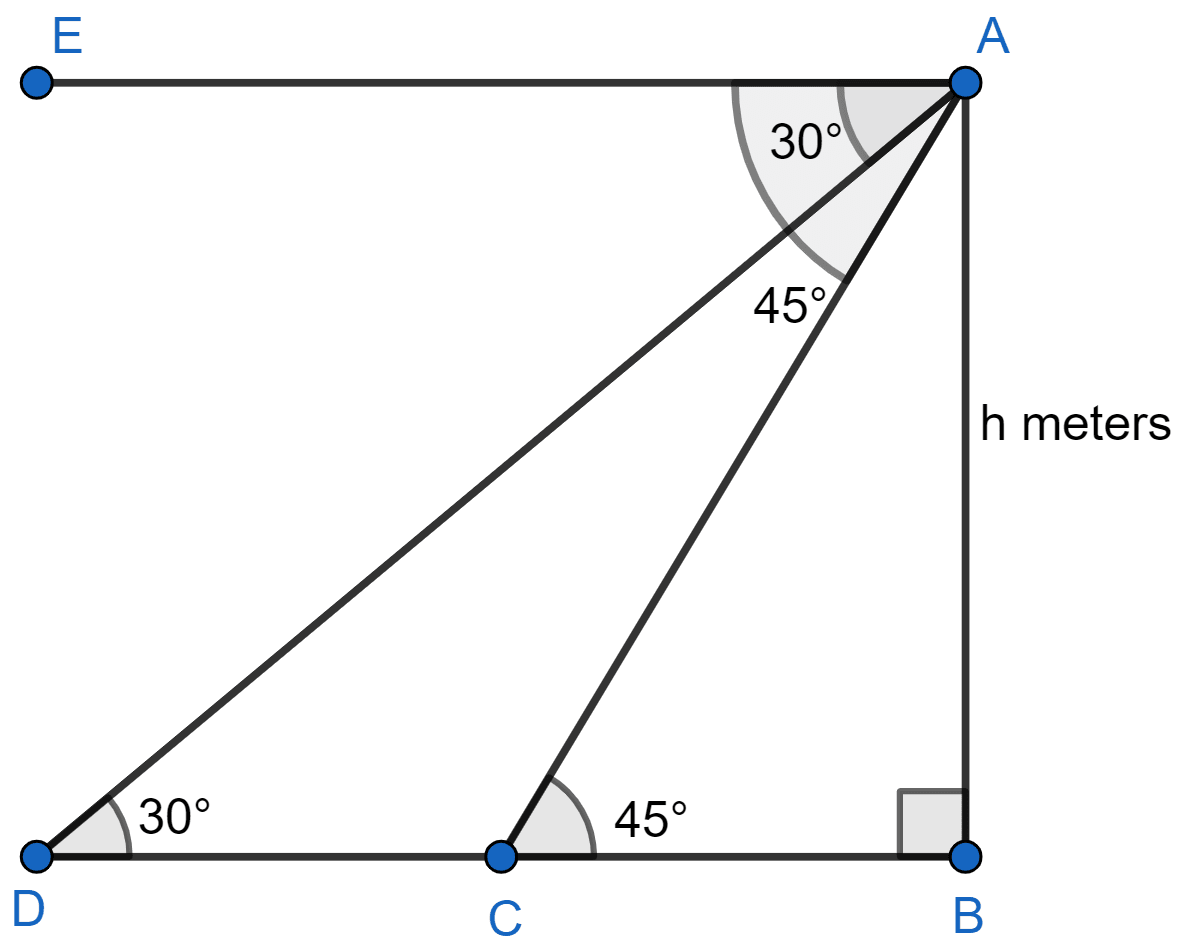
Answer
Let AB be the lighthouse of height h meters and C and D be the position of the ship.
From figure,
∠ADC = ∠EAD = 30° (Alternate angles are equal)
∠ACB = ∠EAC = 45° (Alternate angles are equal)
From figure,
In right angle triangle ADB
⇒ tan 30° =
⇒
⇒ BD = .
In right angle triangle ABC
⇒ tan 45° =
⇒ 1 =
⇒ BC = AB = h.
From figure,
CD = BD - BC = meters.
Given,
Angle of depression of the ship changes from 30° to 45° in 10 minutes.
∴ Ship comes from position D to C in 10 minutes.
∴ Ship covers a distance of CD = in 10 minutes.
Speed of ship = meter/minute.
Time taken by ship to cover (BC = h meters) is
Hence, ship will reach the lighthouse in 13.66 minutes.
The angles of elevation of the top of a tower from two points on the ground at distances a and b meters from the base of the tower and in the same line are complementary. Prove that the height of the tower is meter.
Answer
Let AB be the tower of height h meters, BC = a meters and BD = b meters.
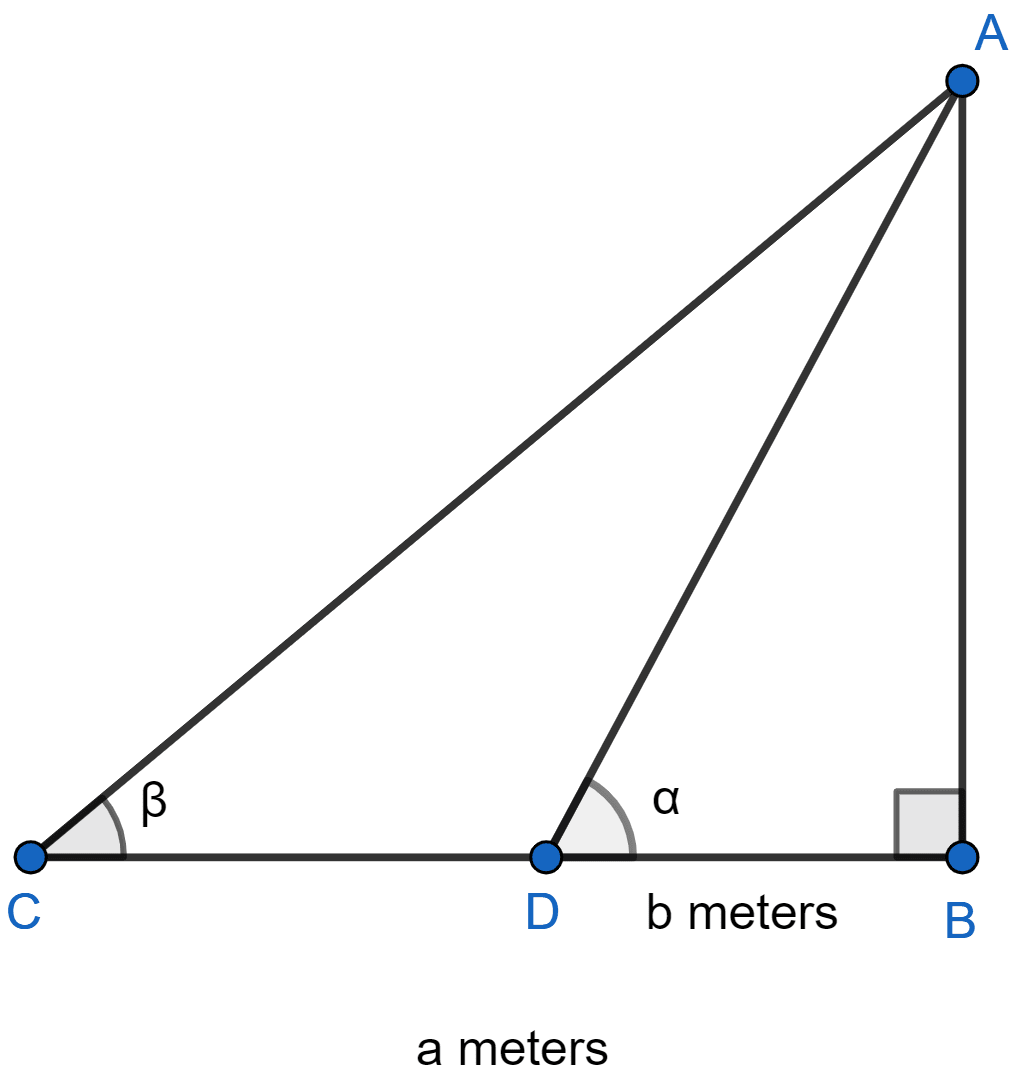
According to question,
⇒ α + β = 90°
⇒ β = 90° - α
From figure,
In △ABD,
In △ABC,
Multiplying (1) by (2) we get,
⇒ tan α cot α =
⇒
⇒ 1 =
⇒ h2 = ab
⇒ h = meters.
Hence, proved that h = meters.
A 20 m high vertical pole and a vertical tower are on the same level ground in such a way that the angle of elevation of the top of the tower, as seen from the foot of the pole, is 60° and the angle of elevation of the top of the pole, as seen from the foot of tower is 30°. Find :
(i) the height of the tower;
(ii) the horizontal distance between the pole and the tower.
Answer
(i) Let CD be the tower and AB be the pole,
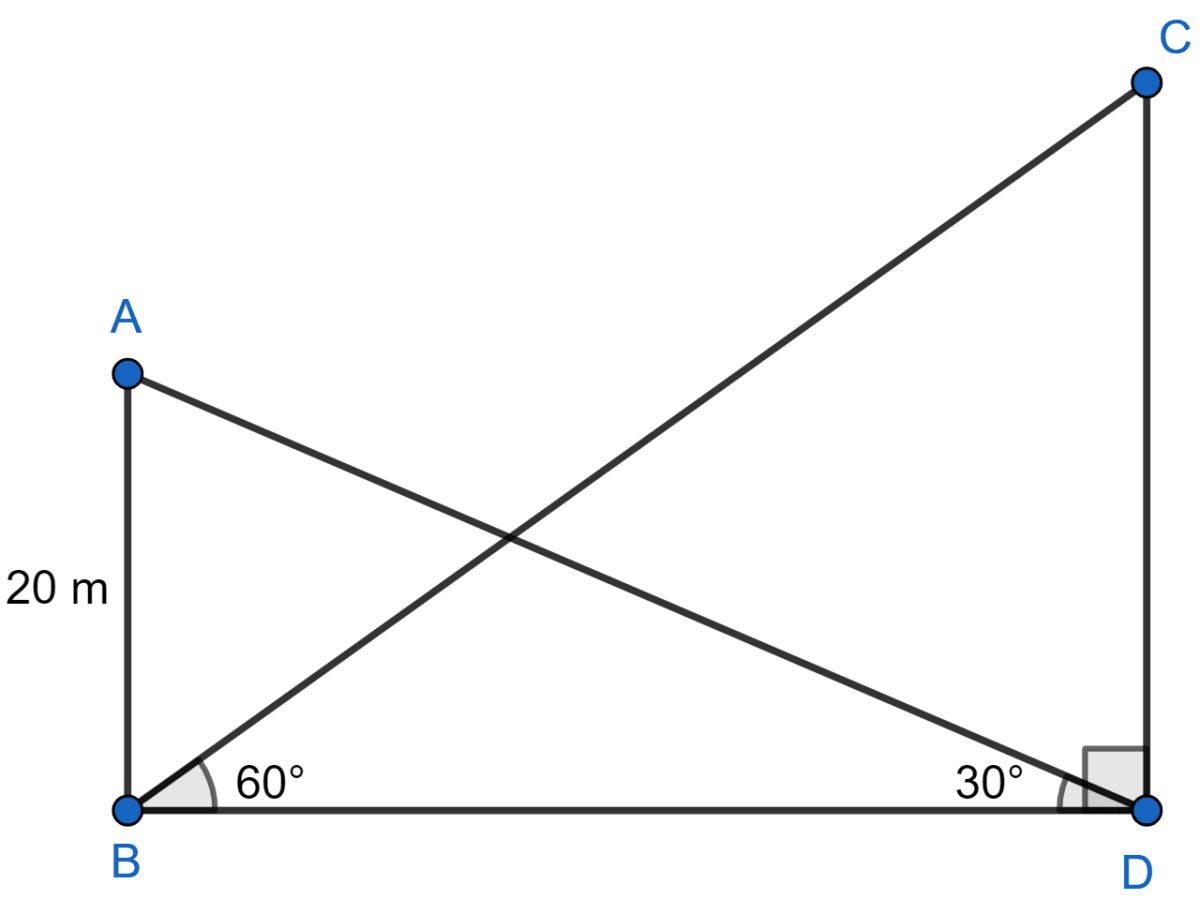
In △ABD,
In △CBD,
Hence, height of tower = 60 meters.
(ii) From part (i),
BD = 34.64 m
Hence, horizontal distance between pole and tower = 34.64 meters.
From a point, 36 m above the surface of a lake, the angle of elevation of a bird is observed to be 30° and the angle of depression of its image in the water of the lake is observed to be 60°. Find the actual height of the bird above the surface of the lake.
Answer
Let DE be the surface of lake and A be the point 36 m above surface of lake and F is the image of bird (B).
Let BC be h meters.
BD = DF (As distance of bird from lake = distance of image of bird in lake from lake)
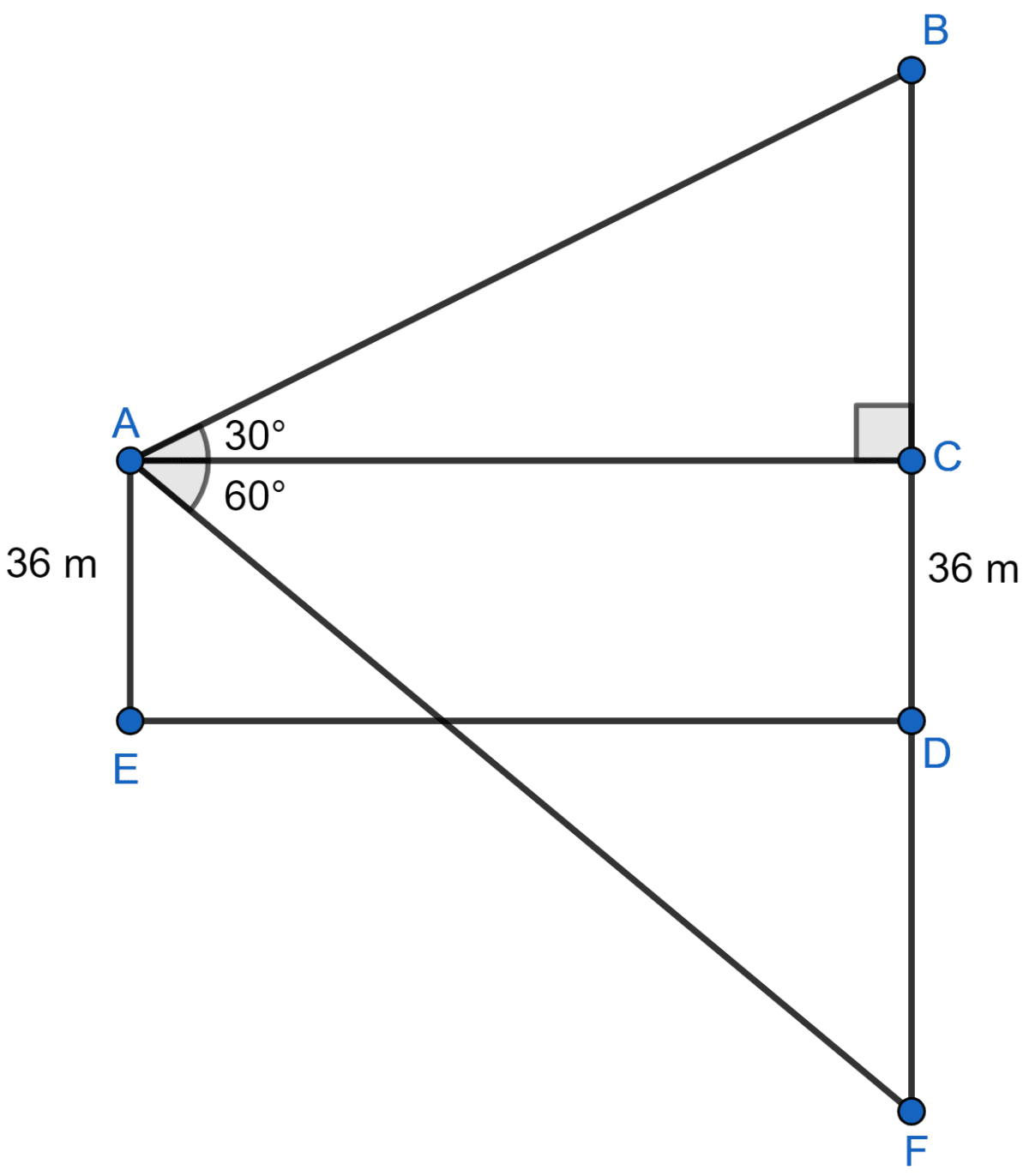
In △ABC,
From figure,
⇒ CF = CD + DF
⇒ CF = CD + BD
⇒ CF = CD + BC + CD
⇒ CF = 36 + h + 36
⇒ CF = h + 72.
In △ACF,
Height of bird from lake = BD = BC + CD = h + 36 = 36 + 36 = 72 m.
Hence, height of bird above surface of lake = 72 meters.
Calculate the mean mark in the distribution given below :
| Marks | Frequency |
|---|---|
| 1 - 10 | 7 |
| 11 - 20 | 9 |
| 21 - 30 | 15 |
| 31 - 40 | 8 |
| 41 - 50 | 6 |
| 51 - 60 | 5 |
Also state :
(i) the median class
(ii) the modal class
Answer
The above distribution is discontinuous converting into continuous distribution, we get :
Adjustment factor = (Lower limit of one class - Upper limit of previous class) / 2
=
= 0.5
Subtract the adjustment factor (0.5) from all the lower limits and add the adjustment factor (0.5) to all the upper limits.
| Marks | Frequency (f) | Cumulative frequency | Class mark (x) | fx |
|---|---|---|---|---|
| 0.5 - 10.5 | 7 | 7 | 5.5 | 38.5 |
| 10.5 - 20.5 | 9 | 16 (9 + 7) | 15.5 | 139.5 |
| 20.5 - 30.5 | 15 | 31 (15 + 16) | 25.5 | 382.5 |
| 30.5 - 40.5 | 8 | 39 (31 + 8) | 35.5 | 284 |
| 40.5 - 50.5 | 6 | 45 (39 + 6) | 45.5 | 273 |
| 50.5 - 60.5 | 5 | 50 (45 + 5) | 55.5 | 277.5 |
| Total | Σf = 50 | Σfx = 1395 |
Mean = = 27.9
Given, total terms = 50.
Since, terms are even.
By formula,
Median = = 25th term.
From table,
15.5 th to 25.5 th term marks lies in the range 20.5 - 30.5.
∴ Median class = 21 - 30.
From table class 21 - 30 has the highest frequency.
∴ Modal class = 21 - 30.
Hence, mean = 27.9, median class = 21 - 30 and modal class = 21 - 30.
Calculate mean, median and mode of the following distribution :
| Marks | Frequency |
|---|---|
| 3 | 3 |
| 4 | 5 |
| 5 | 8 |
| 6 | 7 |
| 7 | 9 |
| 8 | 4 |
| 9 | 3 |
| 10 | 1 |
Answer
Cumulative frequency distribution :
| Marks (x) | Frequency (f) | Cumulative frequency | fx |
|---|---|---|---|
| 3 | 3 | 3 | 9 |
| 4 | 5 | 8 (5 + 3) | 20 |
| 5 | 8 | 16 (8 + 8) | 40 |
| 6 | 7 | 23 (7 + 16) | 42 |
| 7 | 9 | 32 (9 + 23) | 63 |
| 8 | 4 | 36 (4 + 32) | 32 |
| 9 | 3 | 39 (3 + 36) | 27 |
| 10 | 1 | 40 (1 + 39) | 10 |
| Total | Σf = 40 | Σfx = 243 |
By formula,
Mean = = 6.075
Given,
Total terms = 40, which is even.
By formula,
Median = = 20th term.
From table,
Marks of 17th to 23rd term = 6.
∴ Median = 6.
Highest frequency is of 7 marks.
∴ Mode = 7.
Hence, mean = 6.075, median = 6 and mode = 7.
By drawing an ogive; estimate the median for the following frequency distribution :
| Weight (kg) | No. of boys |
|---|---|
| 10 - 15 | 11 |
| 15 - 20 | 25 |
| 20 - 25 | 12 |
| 25 - 30 | 5 |
| 30 - 35 | 2 |
Answer
Cumulative frequency distribution table :
| Weight (kg) | No. of boys (frequency) | Cumulative frequency |
|---|---|---|
| 10 - 15 | 11 | 11 |
| 15 - 20 | 25 | 36 (11 + 25) |
| 20 - 25 | 12 | 48 (36 + 12) |
| 25 - 30 | 5 | 53 (48 + 5) |
| 30 - 35 | 2 | 55 (53 + 2) |
Here, n = 55, which is odd.
By formula,
Median = = 28th term.
Steps of construction of ogive :
Take 2 cm = 5 units on x-axis.
Take 1 cm = 10 units on y-axis.
Plot the point (10, 0), as ogive always starts on x-axis representing the lower limit of the first class.
Plot the points (15, 11), (20, 36), (25, 48), (30, 53) and (35, 55).
Join the points by a free hand curve.
Draw a line parallel to x-axis from point A (frequency) = 28, touching the graph at point B. From point B draw a line parallel to y-axis touching x-axis at point C.

From graph, C = 18.4
Hence, median = 18.4
Estimate the median for the given data by drawing ogive :
| Class | Frequency |
|---|---|
| 0 - 10 | 4 |
| 10 - 20 | 9 |
| 20 - 30 | 15 |
| 30 - 40 | 14 |
| 40 - 50 | 8 |
Answer
Cumulative frequency distribution table :
| Class | Frequency | Cumulative frequency |
|---|---|---|
| 0 - 10 | 4 | 4 |
| 10 - 20 | 9 | 13 (4 + 9) |
| 20 - 30 | 15 | 28 (13 + 15) |
| 30 - 40 | 14 | 42 (28 + 14) |
| 40 - 50 | 8 | 50 (42 + 8) |
Here, n = 50, which is even.
By formula,
Median = = 25th term.
Steps of construction of ogive :
Take 2 cm = 10 units on x-axis.
Take 1 cm = 5 units on y-axis.
Plot the point (0, 0), as ogive always starts on x-axis representing the lower limit of the first class.
Plot the points (10, 4), (20, 13), (30, 28), (40, 42) and (50, 50).
Join the points by a free hand curve.
Draw a line parallel to x-axis from point A (frequency) = 25, touching the graph at point B. From point B draw a line parallel to y-axis touching x-axis at point C.

From graph, C = 28.
Hence, median = 28.
The following distribution represents the height of 160 students of a school.
| Height (in cm) | No. of Students |
|---|---|
| 140 - 145 | 12 |
| 145 - 150 | 20 |
| 150 - 155 | 30 |
| 155 - 160 | 38 |
| 160 - 165 | 24 |
| 165 - 170 | 16 |
| 170 - 175 | 12 |
| 175 - 180 | 8 |
Draw an ogive for the given distribution taking 2 cm = 5 cm of height on one axis and 2 cm = 20 students on the other axis. Using the graph, determine :
(i) the median height.
(ii) the inter-quartile range.
(iii) the number of students whose height is above 172 cm ?
Answer
(i) Cumulative frequency distribution table :
| Height (in cm) | No. of students | Cumulative frequency |
|---|---|---|
| 140 - 145 | 12 | 12 |
| 145 - 150 | 20 | 32 (12 + 20) |
| 150 - 155 | 30 | 62 (32 + 30) |
| 155 - 160 | 38 | 100 (62 + 38) |
| 160 - 165 | 24 | 124 (100 + 24) |
| 165 - 170 | 16 | 140 (124 + 16) |
| 170 - 175 | 12 | 152 (140 + 12) |
| 175 - 180 | 8 | 160 (152 + 8) |
Here, n = 160, which is even.
Median = th term = = 80th term.
Steps of construction :
Take 1 cm = 5 cm on x-axis.
Take 1 cm = 20 students on y-axis.
Since, x axis starts at 140 hence, a kink is drawn at the starting of x-axis. Plot the point (140, 0) as ogive starts on x-axis representing lower limit of first class.
Plot the points (145, 12), (150, 32), (155, 62), (160, 100), (165, 124), (170, 140), (175, 152) and (180, 160).
Join the points by a free-hand curve.
Draw a line parallel to x-axis from point J (no. of students) = 80, touching the graph at point K. From point K draw a line parallel to y-axis touching x-axis at point L.
From graph, L = 157.5
Hence, median = 157.5 cm
(ii) Here, n = 160, which is even.
By formula,
Lower quartile = = 40th term.
Draw a line parallel to x-axis from point P (no. of students) = 40, touching the graph at point Q. From point Q draw a line parallel to y-axis touching x-axis at point R.
From graph, R = 152
Upper quartile = = 120th term.
Draw a line parallel to x-axis from point M (no. of students) = 120, touching the graph at point N. From point N draw a line parallel to y-axis touching x-axis at point O.
From graph, O = 164
Inter quartile range = Upper quartile - Lower quartile
= 164 - 152 = 12.
Hence, inter quartile range = 12.
(iii) Draw a line parallel to y-axis from point S (height) = 172 cm, touching the graph at point T. From point T draw a line parallel to x-axis touching y-axis at point U.
From graph, U = 144.
∴ 144 students have height less than or equal to 172 cm.
No. of students whose height is more than 172 cm = 160 - 144 = 16.

Hence, no. of students whose height is more than 172 cm = 16.
Draw an ogive for the data given below and from the graph determine :
(i) the median marks,
(ii) the number of students who obtained more than 75% marks ?
| Marks | No. of students |
|---|---|
| 10 - 19 | 14 |
| 20 - 29 | 16 |
| 30 - 39 | 22 |
| 40 - 49 | 26 |
| 50 - 59 | 18 |
| 60 - 69 | 11 |
| 70 - 79 | 6 |
| 80 - 89 | 4 |
| 90 - 99 | 3 |
Answer
(i) The above distribution is discontinuous, converting into continuous distribution, we get :
Adjustment factor = (Lower limit of one class - Upper limit of previous class) / 2
=
= 0.5
Subtract the adjustment factor (0.5) from all the lower limits and add the adjustment factor (0.5) to all the upper limits.
Cumulative frequency distribution table :
| Marks | No. of students | Cumulative frequency distribution |
|---|---|---|
| 9.5 - 19.5 | 14 | 14 |
| 19.5 - 29.5 | 16 | 30 (14 + 16) |
| 29.5 - 39.5 | 22 | 52 (30 + 22) |
| 39.5 - 49.5 | 26 | 78 (52 + 26) |
| 49.5 - 59.5 | 18 | 96 (78 + 18) |
| 59.5 - 69.5 | 11 | 107 (96 + 11) |
| 69.5 - 79.5 | 6 | 113 (107 + 6) |
| 79.5 - 89.5 | 4 | 117 (113 + 4) |
| 89.5 - 99.5 | 3 | 120 (117 + 3) |
Here, n = 120, which is even.
Median = th term
= = 60th term.
Steps of construction :
Since, the scale on x-axis starts at 9.5, a break (kink) is shown near the origin on x-axis to indicate that the graph is drawn to scale beginning at 9.5
Take 1 cm along x-axis = 10 units.
Take 1 cm along y-axis = 20 units.
Plot the point (9.5, 0) as ogive starts on x-axis representing lower limit of first class.
Plot the points (19.5, 14), (29.5, 30), (39.5, 52), (49.5, 78), (59.5, 96), (69.5, 107), (79.5, 113), (89.5, 117) and (99.5, 120).
Join the points by a free-hand curve.
Draw a line parallel to x-axis from point O (no. of students) = 60, touching the graph at point P. From point P draw a line parallel to y-axis touching x-axis at point Q.
From graph, Q = 42.5 or 43
Hence, median = 42.5 or 43.
(ii) Total marks = 100.
75% marks = = 75.
Draw a line parallel to y-axis from point R (marks) = 75, touching the graph at point S. From point S draw a line parallel to x-axis touching y-axis at point T.
From graph, T = 111.
∴ 111 students score less than or equal to 75%.
Students scoring above than 75% = 120 - 111 = 9.

Hence, 9 students score more than 75%.
The incomes of the parents of 100 students in a class in a certain university are tabulated below.
| Income (in thousand ₹) | No. of students |
|---|---|
| 0 - 8 | 8 |
| 8 - 16 | 35 |
| 16 - 24 | 35 |
| 24 - 32 | 14 |
| 32 - 40 | 8 |
(i) Draw a cumulative frequency curve to estimate the median income.
(ii) If 15% of the students are given freeships on the basis of the income of their parents, find the annual income of parents, below which the freeships will be awarded.
(iii) Calculate the Arithmetic mean.
Answer
(i) Cumulative frequency distribution table :
| Income (in thousand ₹) | No. of students(frequency) | Cumulative frequency |
|---|---|---|
| 0 - 8 | 8 | 8 |
| 8 - 16 | 35 | 43 (8 + 35) |
| 16 - 24 | 35 | 78 (43 + 35) |
| 24 - 32 | 14 | 92 (78 + 14) |
| 32 - 40 | 8 | 100 (92 + 8) |
Here, n = 100, which is even.
Median = = 50th term.
Steps of construction of ogive :
Take 2 cm = 8 thousand on x-axis.
Take 1 cm = 10 students on y-axis.
Plot the point (0, 0) as ogive starts from x-axis representing the lower limit of first class.
Plot the points (8, 8), (16, 43), (24, 78), (32, 92) and (40, 100).
Join the points by a free hand curve.
Draw a line parallel to x-axis from point G (no. of students) = 50, touching the graph at point H. From point H draw a line parallel to y-axis touching x-axis at point I.
From graph, I = 17.6 (thousands)
Hence, median = 17.6 thousands.
(ii) 15% of 100 students = = 15.
Draw a line parallel to x-axis from point J (no. of students) = 15, touching the graph at point K. From point K draw a line parallel to y-axis touching x-axis at point L.
From graph,
L = 9.6 thousands.
Hence, the annual income of parents, below which the freeships will be awarded is 9.6 thousands.
(iii)
| Income (in thousand ₹) | Class mean (x) | No. of students (f) | fx |
|---|---|---|---|
| 0 - 8 | 4 | 8 | 32 |
| 8 - 16 | 12 | 35 | 420 |
| 16 - 24 | 20 | 35 | 700 |
| 24 - 32 | 28 | 14 | 392 |
| 32 - 40 | 36 | 8 | 288 |
| Total | Σf = 100 | Σfx = 1832 |
Mean = = 18.32 (thousands)
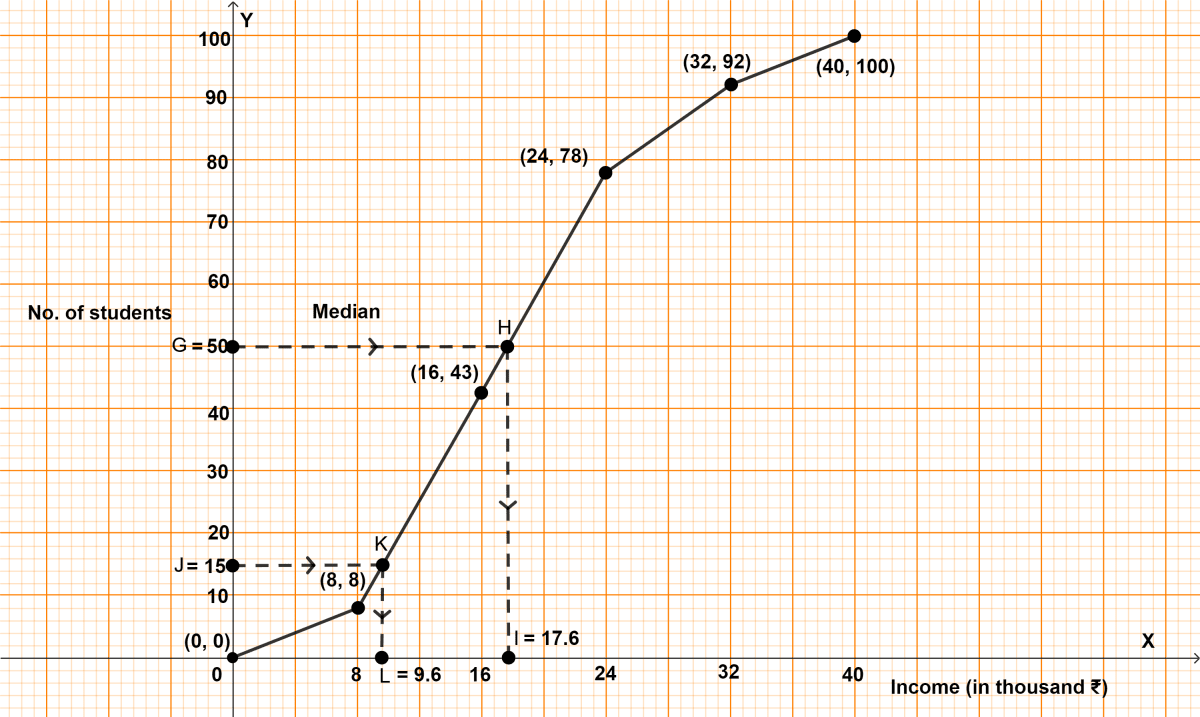
Hence, mean = 18.32 (thousands).
Draw an ogive for the following distribution :
| Income in ₹ | No. of employees |
|---|---|
| 120 - 140 | 30 |
| 140 - 160 | 72 |
| 160 - 180 | 90 |
| 180 - 200 | 80 |
| 200 - 220 | 70 |
| 220 - 240 | 28 |
Use the ogive drawn to determine :
(i) the median income,
(ii) the number of employees whose income exceeds ₹ 190.
Answer
Cumulative frequency distribution table :
| Income in ₹ | No. of employees | Cumulative frequency |
|---|---|---|
| 120 - 140 | 30 | 30 |
| 140 - 160 | 72 | 102 (30 + 72) |
| 160 - 180 | 90 | 192 (102 + 90) |
| 180 - 200 | 80 | 272 (192 + 80) |
| 200 - 220 | 70 | 342 (272 + 70) |
| 220 - 240 | 28 | 370 (342 + 28) |
(i) Here, n = 370, which is even,
Median = = 185.
Steps of construction :
Take 2 cm = ₹ 20 on x-axis.
Take 1 cm = 50 employees on y-axis.
A kink is shown near x-axis as it starts from 120. Plot the point (120, 0) as ogive starts on x-axis representing lower limit of first class.
Plot the points (140, 30), (160, 102), (180, 192), (200, 272), (220, 342) and (240, 370).
Join the points by a free-hand curve.
Draw a line parallel to x-axis from point H (no. of employees) = 185, touching the graph at point I. From point I draw a line parallel to y-axis touching x-axis at point J.
From graph, J = 179
Hence, median wage = ₹ 179.
(ii) Steps :
- Draw a line parallel to y-axis from point K (income) = ₹ 190, touching the graph at point L. From point L draw a line parallel to x-axis touching y-axis at point M.
From graph, M = 232
It means that,
232 employees have income less than or equal to ₹ 190.
∴ No. of employees having income more than ₹ 190 = 370 - 232 = 138.
Hence, no. of employees having income more than ₹ 190 = 138.
The result of a examination is tabulated below :
| Marks (less than) | No. of candidates |
|---|---|
| 10 | 0 |
| 20 | 25 |
| 30 | 42 |
| 40 | 65 |
| 50 | 95 |
| 60 | 120 |
| 70 | 128 |
| 80 | 135 |
| 90 | 148 |
| 100 | 150 |
Draw the ogive for the above data and from it determine :
(i) the number of candidates who got marks less than 45.
(ii) the number of candidates who got marks more than 75.
Answer
The above table can be written as :
| Marks | No. of candidates |
|---|---|
| 0 - 10 | 0 |
| 10 - 20 | 25 |
| 20 - 30 | 42 |
| 30 - 40 | 65 |
| 40 - 50 | 95 |
| 50 - 60 | 120 |
| 60 - 70 | 128 |
| 70 - 80 | 135 |
| 80 - 90 | 148 |
| 90 - 100 | 150 |
Steps of construction :
Take 1 cm = 10 marks on x-axis.
Take 1 cm = 20 students on y-axis.
Plot the point (0, 0) as ogive starts on x-axis representing lower limit of first class.
Plot the points (10, 0), (20, 25), (30, 42), (40, 65), (50, 95), (60, 120), (70, 128), (80, 135), (90, 148) and (100, 150).
Join the points by a free-hand curve.
Draw a line parallel to y-axis from point L (marks) = 45, touching the graph at point M. From point M draw a line parallel to x-axis touching y-axis at point N.
From graph, N = 80
Hence, no. of students having marks less than 45 = 80.
(ii) Steps :
- Draw a line parallel to y-axis from point O (marks) = 75, touching the graph at point P. From point P draw a line parallel to x-axis touching y-axis at point Q.
From graph, Q = 131
It means that,
131 students have marks less than or equal to 75.
∴ No. of students having marks more than 75 = 150 - 131 = 19.
Hence, no. of students having marks more than 75 = 19.
Marks obtained by 200 students in an examination are given below :
| Marks | No. of students |
|---|---|
| 0 - 10 | 5 |
| 10 - 20 | 11 |
| 20 - 30 | 10 |
| 30 - 40 | 20 |
| 40 - 50 | 28 |
| 50 - 60 | 37 |
| 60 - 70 | 40 |
| 70 - 80 | 29 |
| 80 - 90 | 14 |
| 90 - 100 | 6 |
Draw an ogive for the given distribution taking 2 cm = 10 marks on one axis and 2 cm = 20 students on the other axis. Using the graph, determine :
(i) The median marks
(ii) The number of students who failed if minimum marks required to pass is 40 ?
(iii) If scoring 85 and more marks is considered as grade one, find the number of students who secured grade one in the examination ?
Answer
(i) Cumulative frequency distribution table :
| Marks | No. of students | Cumulative frequency |
|---|---|---|
| 0 - 10 | 5 | 5 |
| 10 - 20 | 11 | 16 |
| 20 - 30 | 10 | 26 |
| 30 - 40 | 20 | 46 |
| 40 - 50 | 28 | 74 |
| 50 - 60 | 37 | 111 |
| 60 - 70 | 40 | 151 |
| 70 - 80 | 29 | 180 |
| 80 - 90 | 14 | 194 |
| 90 - 100 | 6 | 200 |
Here, n = 200, which is even.
By formula,
Median = th term
= = 100th term.
Steps of construction :
Take 1 cm along x-axis = 10 marks.
Take 1 cm along y-axis = 20 students.
Plot the point (0, 0) as ogive starts from x-axis representing lower limit of first class.
Plot the points (10, 5), (20, 16), (30, 26), (40, 46), (50, 74), (60, 111), (70, 151), (80, 180), (90, 194) and (100, 200).
Join the points by a free hand curve.
Draw a line parallel to x-axis from point L (no. of students) = 100, touching the graph at point M. From point M draw a line parallel to y-axis touching x-axis at point N.
From graph, N = 57
Hence, median = 57.
(ii) Minimum marks required to pass = 40.
Draw a line parallel to y-axis from point O (marks) = 40, touching the graph at point Q. From point Q draw a line parallel to x-axis touching y-axis at point P.
From graph,
P = 46.
∴ 46 students scored less than 40 marks.
Hence, 46 students failed the examination.
(iii) 85 or more marks is considered grade one.
Draw a line parallel to y-axis from point Q (marks) = 85, touching the graph at point R. From point R draw a line parallel to x-axis touching y-axis at point S.
From graph,
S = 188.
∴ 188 students scored less than 85 marks.
∴ 12 (200 - 188) students scored more than 85 marks.
Hence, 12 students secured grade one.
Marks obtained by 40 students in a short assessment is given below, where a and b are two missing data.
| Marks | Number of students |
|---|---|
| 5 | 6 |
| 6 | a |
| 7 | 16 |
| 8 | 13 |
| 9 | b |
If the mean of the distribution is 7.2, find a and b.
Answer
| Marks (x) | Number of students (f) | fx |
|---|---|---|
| 5 | 6 | 30 |
| 6 | a | 6a |
| 7 | 16 | 112 |
| 8 | 13 | 104 |
| 9 | b | 9b |
| Total | Σf = a + b + 35 | Σfx = 246 + 6a + 9b |
Total 40 students.
∴ a + b + 35 = 40
⇒ a + b = 40 - 35
⇒ a + b = 5
⇒ a = 5 - b ........(1)
Given, mean = 7.2
Substituting value of a from (1) in above equation :
a = 5 - b = 5 - 4 = 1.
Hence, a = 1 and b = 4.
The marks obtained by 100 students in a mathematics test are given below :
| Marks | No. of students |
|---|---|
| 0 - 10 | 3 |
| 10 - 20 | 7 |
| 20 - 30 | 12 |
| 30 - 40 | 17 |
| 40 - 50 | 23 |
| 50 - 60 | 14 |
| 60 - 70 | 9 |
| 70 - 80 | 6 |
| 80 - 90 | 5 |
| 90 - 100 | 4 |
Draw an ogive for the given distribution on a graph sheet. Use a scale of 2 cm = 10 units on both the axes.
Use the ogive to estimate :
(i) median
(ii) lower quartile
(iii) number of students who obtained more than 85% marks in the test.
(iv) number of students failed, if the pass percentage was 35.
Answer
(i) Cumulative frequency distribution table :
| Marks | No. of students | Cumulative frequency |
|---|---|---|
| 0 - 10 | 3 | 3 |
| 10 - 20 | 7 | 10 |
| 20 - 30 | 12 | 22 |
| 30 - 40 | 17 | 39 |
| 40 - 50 | 23 | 62 |
| 50 - 60 | 14 | 76 |
| 60 - 70 | 9 | 85 |
| 70 - 80 | 6 | 91 |
| 80 - 90 | 5 | 96 |
| 90 - 100 | 4 | 100 |
Here, n = 100, which is even.
Median = th term
= = 50th term.
Steps of construction of ogive :
Take 1 cm = 10 marks on x-axis.
Take 1 cm = 20 students on y-axis.
Plot the point (0, 0) as ogive starts from x-axis representing lower limit of first class.
Plot the points (10, 3), (20, 10), (30, 22), (40, 39), (50, 62), (60, 76), (70, 85), (80, 91), (90, 96) and (100, 100).
Join the points by a free hand curve.
Draw a line parallel to x-axis from point L (no. of students) = 50, touching the graph at point M. From point M draw a line parallel to y-axis touching x-axis at point N.
From graph, N = 45
Hence, median = 45.
(ii) Here, n = 100, which is even.
By formula,
Lower quartile = = 25th term.
Draw a line parallel to x-axis from point O (no. of students) = 25, touching the graph at point P. From point P draw a line parallel to y-axis touching x-axis at point Q.
From graph, Q = 32
Hence, lower quartile = 32.
(iii) Total marks = 100.
85% of 100 marks = = 85.
Draw a line parallel to y-axis from point R (marks) = 85, touching the graph at point S. From point S draw a line parallel to x-axis touching y-axis at point T.
From graph, T = 94.
It means that 94 students scored either less or equal to 85% marks.
No. of students left = 100 - 94 = 6.
Hence, no. of students scoring more than 85% marks = 6.
(iv) Total marks = 100.
35% of 100 marks = = 35.
Draw a line parallel to y-axis from point U (marks) = 35, touching the graph at point V. From point V draw a line parallel to x-axis touching y-axis at point W.
From graph, W = 28.
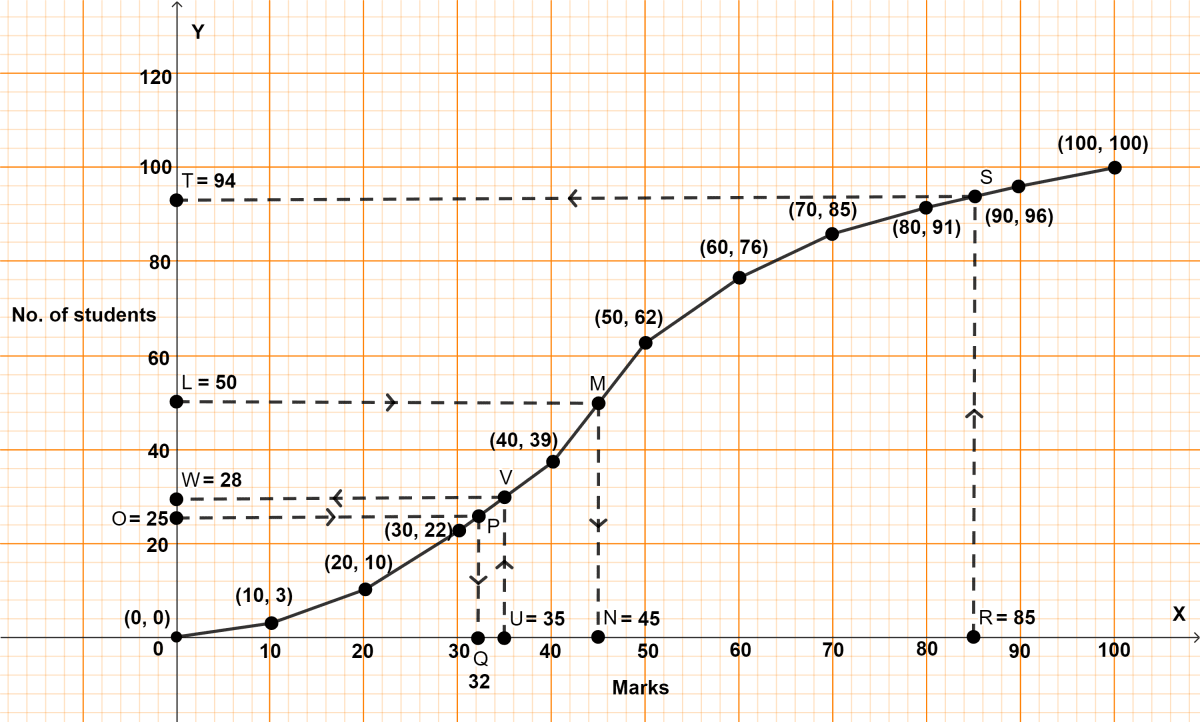
Hence, 28 students fail if pass percentage was 35%.
A bag contains a red ball, a blue ball and a yellow ball, all the balls being of the same size. If a ball is drawn from the bag, without looking into it, find the probability that the ball drawn is :
(i) yellow
(ii) red
(iii) blue
Answer
No. of possible outcomes = 3 (1 red + 1 blue + 1 yellow)
(i) No. of yellow balls = 1.
∴ No. of favourable outcomes = 1
P(drawing a yellow ball) = .
Hence, probability of drawing a yellow ball = .
(ii) No. of red balls = 1.
∴ No. of favourable outcomes = 1
P(drawing a red ball) = .
Hence, probability of drawing a red ball = .
(iii) No. of blue balls = 1.
∴ No. of favourable outcomes = 1
P(drawing a blue ball) = .
Hence, probability of drawing a blue ball = .
A bag contains 6 red balls, 8 blue balls and 10 yellow balls, all the balls being of the same size. If a ball is drawn from the bag, without looking into it, find the probability that the ball drawn is :
(i) yellow
(ii) red
(iii) blue
(iv) not yellow
(v) not blue
Answer
No. of possible outcomes = 24 (6 red + 8 blue + 10 yellow)
(i) No. of yellow balls = 10.
∴ No. of favourable outcomes = 10
P(drawing a yellow ball) = .
Hence, probability of drawing a yellow ball = .
(ii) No. of red balls = 6.
∴ No. of favourable outcomes = 6
P(drawing a red ball) = .
Hence, probability of drawing a red ball = .
(iii) No. of blue balls = 8.
∴ No. of favourable outcomes = 8
P(drawing a blue ball) = .
Hence, probability of drawing a blue ball = .
(iv) No. of balls that are not yellow = 14 (6 red + 8 blue)
∴ No. of favourable outcomes = 14
P(not drawing a yellow ball) = .
Hence, probability of not drawing a yellow ball = .
(v) No. of balls that are not blue = 16 (6 red + 10 yellow)
∴ No. of favourable outcomes = 16
P(not drawing a blue ball) = .
Hence, probability of not drawing a blue ball = .
Two dice are thrown at the same time. Write down all the possible outcomes. Find the probability of getting the sum of two numbers appearing on the top of the dice as :
(i) 13
(ii) less than 13
(iii) 10
(iv) less than 10
Answer
When two dice are thrown, simultaneously.
Possible outcomes = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}.
No. of possible outcomes = 6 × 6 = 36.
(i) Favourable outcomes for getting a sum of 13 = 0.
∴ No. of favourable outcomes = 0
P(getting a sum of 13) = = 0.
Hence, probability of getting a sum of 13 = 0.
(ii) Favourable outcomes for getting a sum less than 13 = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}.
∴ No. of favourable outcomes = 36
P(getting a sum less than 13) = = 1.
Hence, probability of getting a sum less than 13 = 1.
(iii) Favourable outcomes for getting a sum of 10 = {(4, 6), (5, 5), (6, 4)}.
∴ No. of favourable outcomes = 3
P(getting a sum of 10) = .
Hence, probability of getting a sum of 10 = .
(iv) Favourable outcomes for getting a sum less than 10 = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (5, 1), (5, 2), (5, 3), (5, 4), (6, 1), (6, 2), (6, 3)}.
∴ No. of favourable outcomes = 30
P(getting a sum less than 10) = .
Hence, probability of getting a sum less than 10 = .
Five cards :- the ten, jack, queen, king and ace of diamonds are well-shuffled with their face downwards. One card is then picked up at random.
(i) What is the probability that the card is the queen ?
(ii) If the queen is drawn and put aside, what is the probability that the second card picked up is (a) an ace ? (b) a queen ?
Answer
There are five cards.
∴ No. of possible outcomes = 5.
(i) No. of queens = 1
∴ No. of favourable outcomes = 1
P(getting a queen) = .
Hence, probability of drawing a queen = .
(ii) Since, queen is drawn and put aside.
∴ No. of cards left = 5 - 1 = 4
∴ No. of possible outcomes = 4.
(a) No. of ace cards = 1
∴ No. of favourable outcomes = 1
P(getting an ace) = .
Hence, probability of drawing an ace = .
(b) No. of queen left = 0
∴ No. of favourable outcomes = 0
P(getting a queen) = = 0.
Hence, probability of getting a queen = 0.
(i) A lot of 20 bulbs contains 4 defective bulbs. One bulb is drawn at random from the lot. What is the probability that this bulb is defective ?
(ii) Suppose the bulb drawn in (i) is not defective and is not replaced. Now one bulb is drawn at random from the rest. What is the probability that this bulb is not defective?
Answer
No. of defective bulbs = 4.
∴ No. of favourable outcomes = 4
P(getting a defective ball) = .
Hence, probability of getting a defective bulb = .
(ii) Since, one bulb is drawn at random and is not defective and is not replaced.
∴ No. of possible outcomes = 19.
∴ No. of good bulbs present = 15 (16 - 1)
∴ No. of favourable outcomes = 15
P(not getting a defective ball) = .
Hence, probability of not getting a defective bulb = .