Using the given information, find the value of x in the following Figure :

Answer
∠ADB = ∠ACB = 50° (∵ angles in same segment are equal.)
We know that sum of angles in a triangle is 180°.
Considering △ADB,
⇒ ∠ADB + ∠DAB + ∠ABD = 180°
⇒ 50° + 42° + x° = 180°
⇒ x° + 92° = 180°
⇒ x° = 180° - 92°
⇒ x° = 88°
Hence, the value of x = 88°.
Using the given information, find the value of x in the following figure :

Answer
From figure,
∠ACB = ∠ADB = 45° (∵ angles in same segment are equal.)
∴ ∠DCB = 32° + 45° = 77°.
Since, sum of opposite angles of a parallelogram = 180°.
∴ ∠DCB + x° = 180°
⇒ 77° + x° = 180°
⇒ x° = 180° - 77°
⇒ x° = 103°.
Hence, the value of x = 103°.
Using the given information, find the value of x in the following figure :

Answer
Considering △ABC and △ADC,
∠ABC = ∠ADC = 20° (∵ angles in same segment are equal.)
∠DOC = ∠DOB = 90° (As DA is perpendicular to BC)
We know that sum of angles in a triangle is 180°.
Considering △DOC,
⇒ ∠ODC + ∠DOC + ∠OCD = 180°
⇒ 20° + 90° + x° = 180°
⇒ x° + 110° = 180°
⇒ x° = 180° - 110°
⇒ x° = 70°
Hence, the value of x = 70°.
Using the given information, find the value of x in the following figure :

Answer
Considering △ABC and △DBC,
∠BAC = ∠BDC = x° (∵ angles in same segment are equal.)
We know that sum of angles in a triangle is 180°.
Considering △ABC,
⇒ ∠BAC + ∠ABC + ∠BCA = 180°
⇒ x° + 69° + 31° = 180°
⇒ x° + 100° = 180°
⇒ x° = 180° - 100°
⇒ x° = 80°
Hence, the value of x = 80°.
Using the given information, find the value of x in the following figure :

Answer
Considering △ACB and △CDB,
∠CAB = ∠CDB = x° (∵ angles in same segment are equal.)
Considering △ACP,
∠CPB = ∠APD = 120° (∵ vertically opposite angles are equal.)
Since exterior angle in a triangle is equal to the sum of the opposite interior angles,
⇒ ∠CAP + ∠ACP = ∠APD
⇒ x° + 70° = 120°
⇒ x° = 120° - 70°
⇒ x° = 50°
Hence, the value of x = 50°.
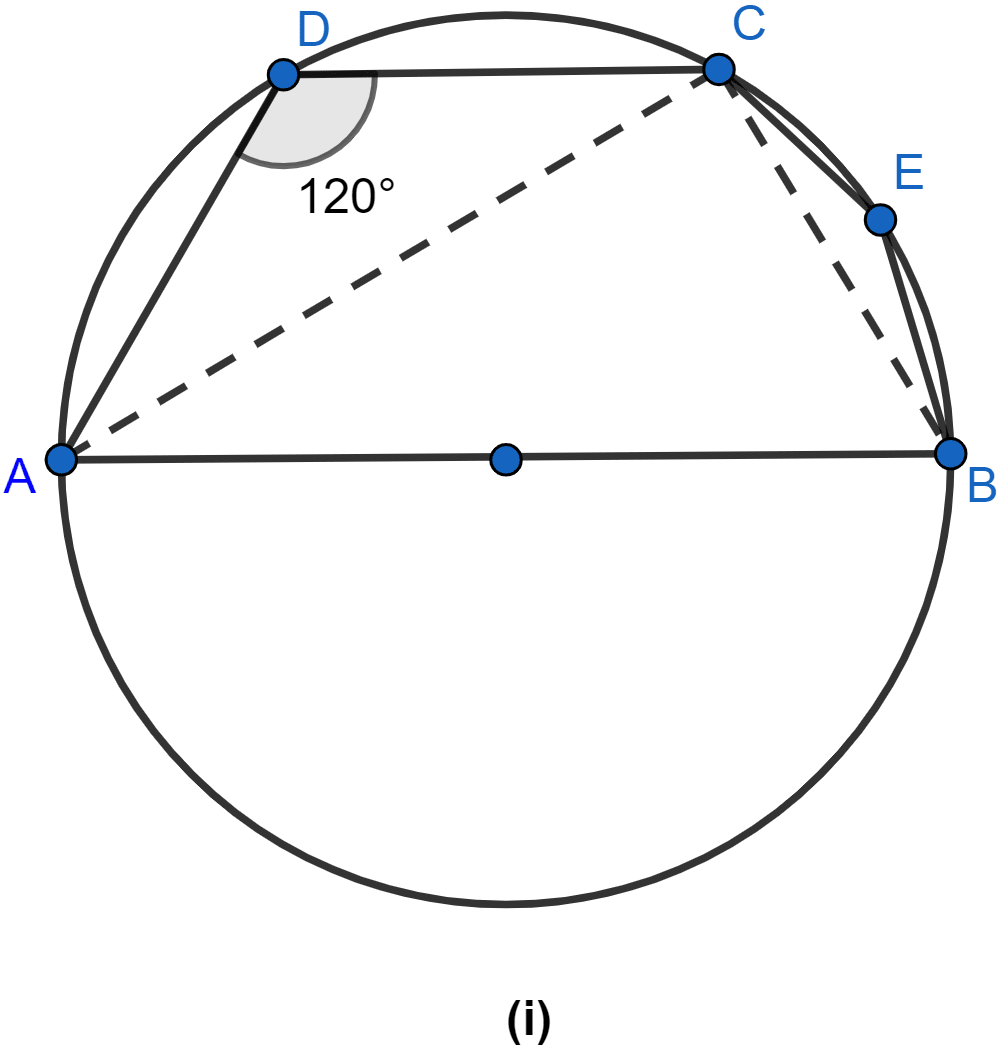
Using the given information, find the value of x in the following figure :

Answer
From figure,
∠DAB = ∠BCD = 25° (∵ angles in same segment are equal)
In △DAP,
Exterior angle ∠CDA = ∠DAP + ∠DPA ....(i)
From figure,
∠DAP = ∠DAB = 25°.
Putting values in equation (i),
⇒ x° = 25° + 35°
⇒ x° = 60°.
Hence, the value of x = 60°.
If O is the center of the circle, find the value of x in the following figure (using the given information) :

Answer
Considering △ACB and △ADB,
∠ACB = ∠ADB = x° (∵ angles in same segment are equal.)
Considering △ACB,
∠ABC = 90° (∵ angle in semicircle is 90°.)
Since sum of angles in a triangle is equal to 180°.
⇒ ∠BAC + ∠ACB + ∠ABC = 180°.
⇒ 40° + x° + 90° = 180°
⇒ x° + 130° = 180°
⇒ x° = 50°.
Hence, the value of x = 50°.
If O is the center of the circle, find the value of x in the following figure (using the given information) :

Answer
∠ADB = ∠ACB = x° (∵ angles in same segment are equal.)
Considering △AOD,
∠ODA = ∠OAD = 62° (∵ OD = OA, and angles of equal sides are equal.)
∴ x = 62°.
Hence, the value of x = 62°.
If O is the center of the circle, find the value of x in the following figure (using the given information) :
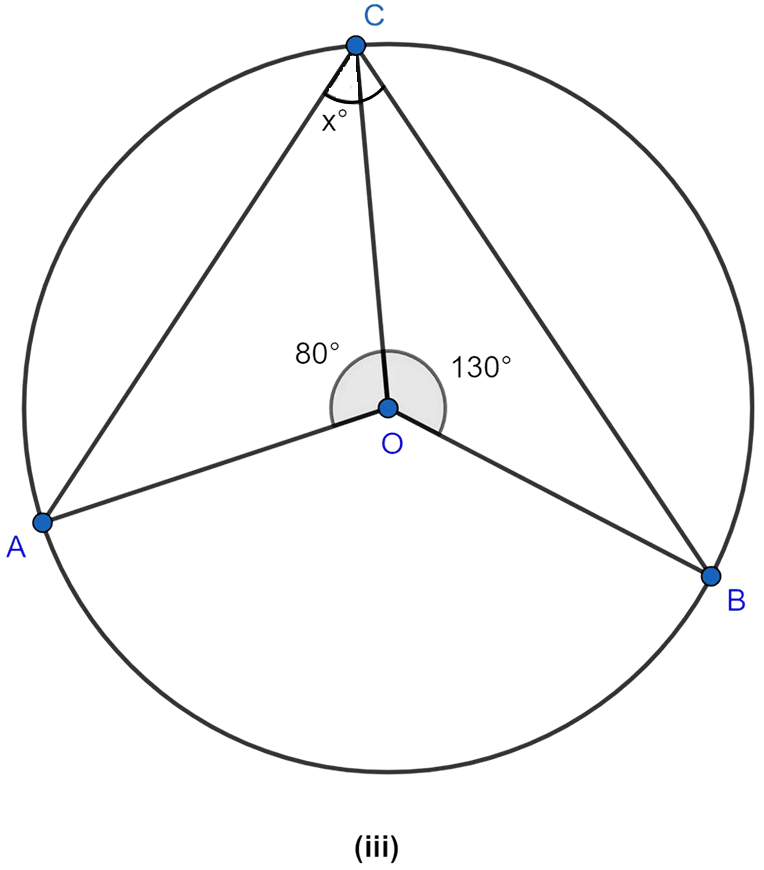
Answer
Angle of a circle is 360°.
⇒ ∠AOB + ∠AOC + ∠BOC = 360°
⇒ ∠AOB + 80° + 130° = 360°
⇒ ∠AOB + 210° = 360°
⇒ ∠AOB = 360° - 210°
⇒ ∠AOB = 150°.
From figure,
⇒ ∠AOB = 2∠ACB (∵ angle subtended by an arc at the center = double the angle subtended by it any point on the remaining part of the circle.)
⇒ 150° = 2∠ACB
⇒ ∠ACB =
⇒ ∠ACB = 75°
⇒ x° = 75°.
Hence, the value of x = 75°.
If O is the center of the circle, find the value of x in the following figure (using the given information) :

Answer
AC subtends reflex angle ∠AOC at center and ∠ABC at point B. Since angle subtended at center is double the angle subtended at any other part of the circle.
⇒ Reflex ∠AOC = 2∠ABC .....(i)
From figure,
∠ABC + ∠CBD = 180° (As they are linear pair.)
∠ABC + 75° = 180°
∠ABC = 180° - 75°
∠ABC = 105°.
Putting value of ∠ABC = 105° in (i)
x° = 2(105°)
x° = 210°
Hence, the value of x = 210.
If O is the center of the circle, find the value of x in the following figure (using the given information) :

Answer
From figure,
⇒ ∠AOC + ∠COB = 180°
⇒ ∠COB = 180° - ∠AOC
⇒ ∠COB = 180° - 135°
⇒ ∠COB = 45°.
BC subtends ∠COB = 45° at center and ∠CDB = x° at point D. Since angle subtended at center is double the angle subtended at any other part of the circle.
⇒ ∠COB = 2∠CDB
⇒ 45° = 2x°
⇒ x° =
Hence, the value of x = .
If O is the center of the circle, find the value of x in the following figure (using the given information) :

Answer
Label the points as shown in the figure below:

Arc AD subtends ∠AOD = 70° at center.
⇒ ∠AOD = 2∠ABD (∵ angle subtended by an arc at the center = double the angle subtended by it any point on the remaining part of the circle.)
⇒ 70° = 2∠ABD
⇒ ∠ABD =
⇒ ∠ABD = 35°
∠ABM = ∠ABD.
Considering △ABM,
Since sum of angles in a triangle is equal to 180°.
⇒ ∠AMB + ∠ABM + ∠BAM = 180°.
⇒ 90° + 35° + x° = 180°
⇒ x° + 125° = 180°
⇒ x° = 55°.
Hence, the value of x = 55.
In the figure (i) given below, AD || BC. If ∠ACB = 35°. Find the measurement of ∠DBC.

Answer
From figure,
∠DAC = ∠ACB = 35° (∵ alternate angles are equal.)
∠DAC = ∠DBC = 35° (∵ angles in same segment are equal.)
Hence, the value of ∠DBC = 35°.
In the figure (ii) given below, it is given that O is the center of the circle and ∠AOC = 130°. Find ∠ABC.

Answer
From figure,
⇒ ∠AOC + Reflex ∠AOC = 360°
⇒ 130° + Reflex ∠AOC = 360°
⇒ Reflex ∠AOC = 360° - 130°
⇒ Reflex ∠AOC = 230°.
Arc AC subtends Reflex ∠AOC at center and ∠ABC at another point of circle.
⇒ Reflex ∠AOC = 2 ∠ABC
⇒ 2∠ABC = 230°
⇒ ∠ABC =
⇒ ∠ABC = 115°.
Hence, the value of ∠ABC = 115°.
In the figure (i) given below, calculate the values of x and y.

Answer
In the figure,

ABCD is a cyclic quadrilateral.
⇒ ∠B + ∠D = 180°
⇒ 40° + 45° + y = 180°
⇒ 85° + y = 180°
⇒ y = 180° - 85°
⇒ y = 95°.
Considering △ABD and △ACD,
∠ABD = ∠ACD = 40° (∵ angles in same segment are equal.)
x = 40°.
Hence, the value of x = 40° and y = 95°.
In the figure (ii) given below, O is the center of the circle. Calculate the values of x and y.

Answer
From figure,
⇒ ∠AOB + Reflex ∠AOB = 360°
⇒ 120° + Reflex ∠AOB = 360°
⇒ Reflex ∠AOB = 360° - 120°
⇒ Reflex ∠AOB = 240°.
Arc AB subtends Reflex ∠AOB at center and ∠ADB at point D of circle.
⇒ Reflex ∠AOB = 2 ∠ADB
⇒ 2∠ADB = 240°
⇒ ∠ADB =
⇒ ∠ADB = 120°
⇒ y° = 120°
Arc AB subtends ∠AOB at center and ∠ACB at point C of circle.
⇒ ∠AOB = 2 ∠ACB
⇒ 2∠ACB = 120°
⇒ ∠ACB =
⇒ ∠ACB = 60°
⇒ x° = 60°
Hence, the value of x = 60 and y = 120.
In the figure (i) given below, M, A, B, N are points on a circle having center O. AN and MB cut at Y. If ∠NYB = 50° and ∠YNB = 20°, find ∠MAN and the reflex angle MON.

Answer
Considering △YBN,
Since sum of angles in a triangle is equal to 180°.
⇒ ∠NYB + ∠YNB + ∠YBN = 180°.
⇒ 50° + 20° + ∠YBN = 180°
⇒ 70° + ∠YBN = 180°
⇒ ∠YBN = 180° - 70°
⇒ ∠YBN = 110°.
From figure,
∠MBN = ∠YBN = 110°.
Considering △MAN and △MBN,
∠MAN = ∠MBN = 110° (∵ angles in same segment are equal.)
MN subtends Reflex ∠MON at center and ∠MAN at point A of circle.
⇒ Reflex ∠MON = 2 ∠MAN = 2 × 110° = 220°.
Hence, ∠MAN = 110° and Reflex ∠MON = 220°.
In the figure (ii) given below, O is the center of the circle. If ∠AOB = 140° and ∠OAC = 50°, find
(i) ∠ACB
(ii) ∠OBC
(iii) ∠OAB
(iv) ∠CBA.
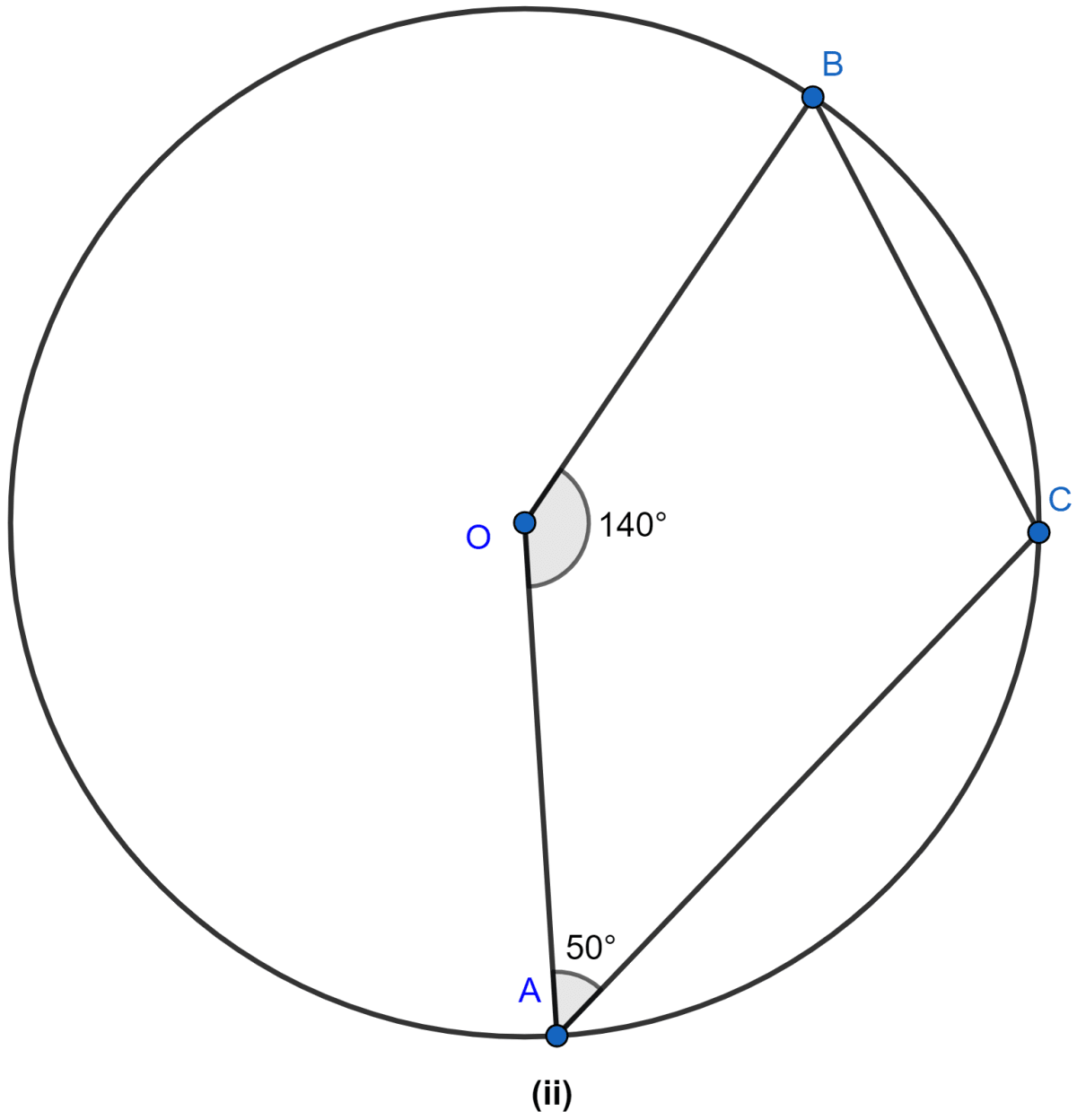
Answer
(i) From figure,
⇒ ∠AOB + Reflex ∠AOB = 360°
⇒ 140° + Reflex ∠AOB = 360°
⇒ Reflex ∠AOB = 360° - 140°
⇒ Reflex ∠AOC = 220°.
Arc AB subtends Reflex ∠AOB at center and ∠ACB at point C of circle.
⇒ Reflex ∠AOB = 2 ∠ACB
⇒ 2∠ACB = 220°
⇒ ∠ACB =
⇒ ∠ACB = 110°.
Hence, the value of ∠ACB = 110°.
(ii) In Quadrilateral OABC,
⇒ ∠OAC + ∠ACB + ∠BOA + ∠OBC = 360°
⇒ 50° + 110° + 140° + ∠OBC = 360°
⇒ 300° + ∠OBC = 360°
⇒ ∠OBC = 360° - 300°
⇒ ∠OBC = 60°
Hence, the value of ∠OBC = 60°.
(iii) In △OAB,
OA = OB (Radius of the circle)
∠OAB = ∠OBA = x (∵ angles of equal sides in isosceles triangle are equal.)
Sum of angles in a triangle are equal,
⇒ ∠AOB + ∠OAB + ∠OBA = 180°.
⇒ 140° + x + x = 180°
⇒ 140° + 2x = 180°
⇒ 2x = 40°
⇒ x = 20°.
Hence, the value of ∠OAB = 20°.
(iv) ∠CBA = ∠OBC - ∠OBA
⇒ ∠CBA = 60° - 20° ⇒ ∠CBA = 40°
Hence, the value of ∠CBA = 40°.
In the figure (i) given below, A, B, C and D are points on the circle with center O. Given that ∠ABC = 62°, find
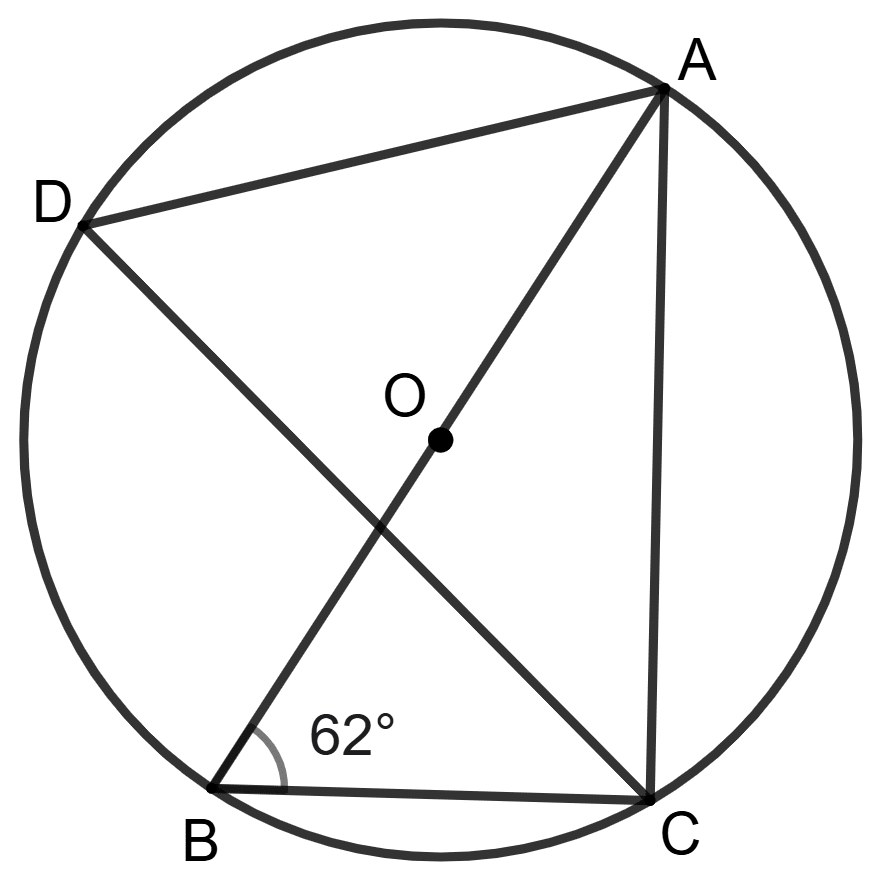
(i) ∠ADC
(ii) ∠CAB
Answer
(i) From figure,
⇒ ∠ADC = ∠ABC (Angles in same segment are equal)
⇒ ∠ADC = 62°.
Hence, ∠ADC = 62°.
(ii) We know that,
Angle in a semi-circle is a right angle.
∠ACB = 90°
Using angle sum property,
⇒ ∠CAB + ∠ACB + ∠ABC = 180°
⇒ ∠CAB + 90° + 62° = 180°
⇒ ∠CAB + 152° = 180°
⇒ ∠CAB = 180° - 152°
⇒ ∠CAB = 28°.
Hence, ∠CAB = 28°.
In the figure (ii) given below, AB is a diameter of the circle whose center is O. Given that ∠ECD = ∠EDC = 32°, calculate
(i) ∠CEF
(ii) ∠COF

Answer
(i) In △EDC,
∠ECD = ∠EDC = 32° (Given)
Since sum of angles of triangle = 180°.
⇒ ∠DEC + ∠ECD + ∠EDC = 180°
⇒ ∠DEC + 32° + 32° = 180°
⇒ ∠DEC = 180° - 64°
⇒ ∠DEC = 116°.
Since, ∠CEF and ∠DEC are linear pair,
∴ ∠CEF + ∠DEC = 180°
⇒ ∠CEF + 116° = 180°
⇒ ∠CEF = 180° - 116°
⇒ ∠CEF = 64°
Hence, ∠CEF = 64°.
(ii) ∠FDC = ∠EDC = 32°. (From figure)
Arc FC subtends ∠COF at center and ∠FDC at point D of circle so,
⇒ ∠COF = 2 ∠FDC
⇒ ∠COF = 2 × 32°
⇒ ∠COF = 64°
Hence, the value of ∠COF = 64°.
In the figure (i) given below, AB is a diameter of the circle APBR. APQ and RBQ are straight lines, ∠A = 35°, ∠Q = 25°. Find :
(i) ∠PRB
(ii) ∠PBR
(iii) ∠BPR

Answer
(i) ∠PRB = ∠PAB = 35° (∵ angles in same segment are equal.)
Hence, the value of ∠PRB = 35°
(ii) From figure,
∠APB = 90° (∵ angle in semicircle is 90°.)
⇒ ∠APB + ∠BPQ = 180° (∵ angles form a linear pair).
⇒ 90° + ∠BPQ = 180°
⇒ ∠BPQ = 90°.
Exterior angle in a triangle is equal to the sum of opposite two interior angles.
In △PBQ,
Ext. ∠PBR = ∠PQB + ∠BPQ = 25° + 90° = 115°.
Hence, the value of ∠PBR = 115°
(iii) In △PRQ,
Ext. ∠APR = ∠PRQ + ∠PQR = ∠PRB + ∠PQR = 35° + 25° = 60°.
∠APB = 90° (∵ angle in semicircle is 90°.)
From figure,
∠BPR = ∠APB - ∠APR = 90° - 60° = 30°.
Hence, the value of ∠BPR = 30°
In the figure (ii) given below, it is given that ∠ABC = 40° and AD is a diameter of the circle. Calculate ∠DAC.

Answer
Consider △ABC and △ADC,
∠ABC = ∠ADC = 40° (∵ angles in same segment are equal.)
In △ADC,
∠DCA = 90° (∵ angle in semicircle is 90°.)
We know that sum of angles of a triangle is 180°.
⇒ ∠DAC + ∠ADC + ∠DCA = 180°.
⇒ ∠DAC + 40° + 90° = 180°
⇒ ∠DAC + 130° = 180°
⇒ ∠DAC = 180° - 130°
⇒ ∠DAC = 50°.
Hence, the value of ∠DAC = 50°.
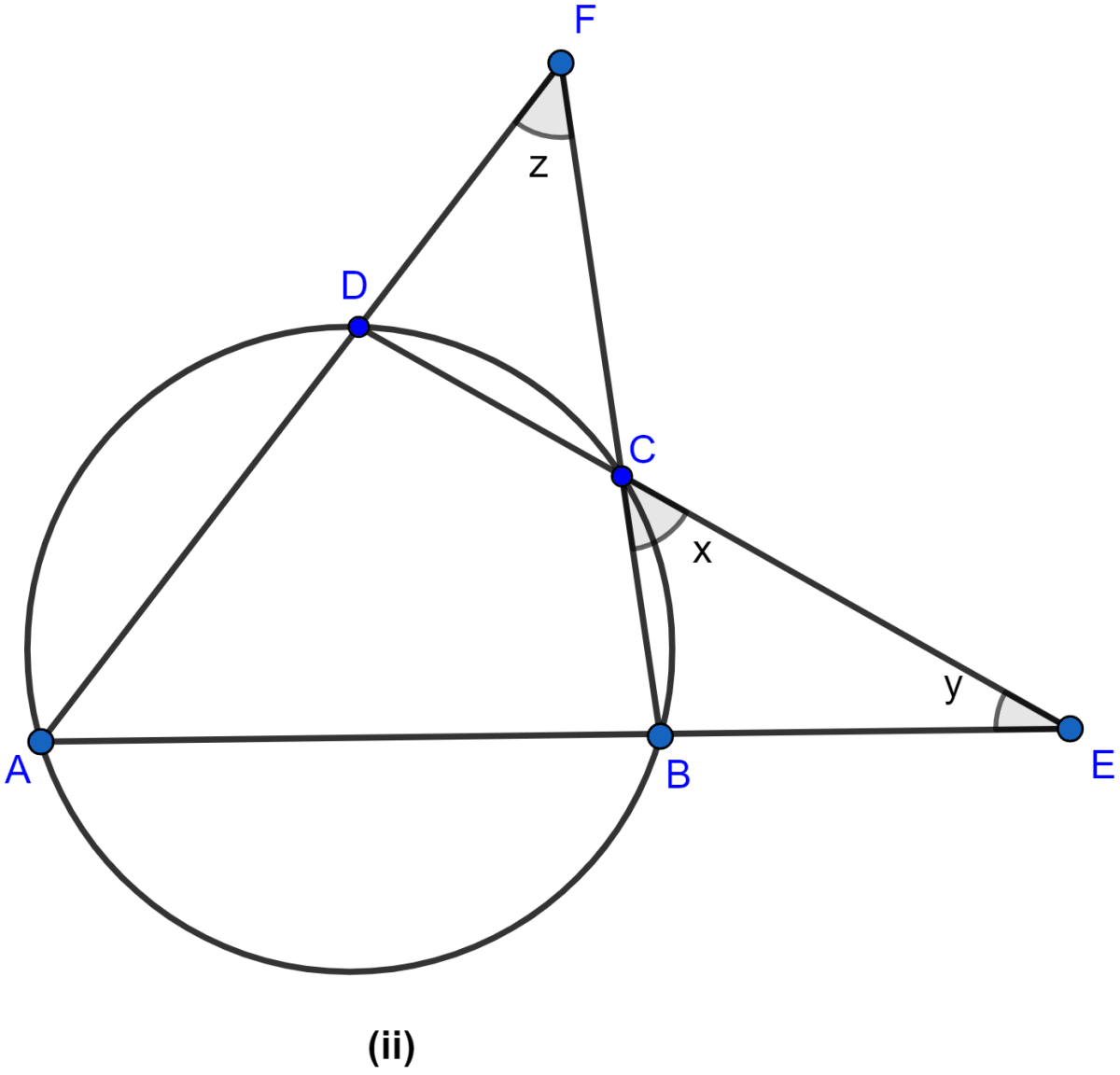
In the figure (i) given below, P and Q are centers of two circles intersecting at B and C. ACD is a straight line. Calculate the value of x.

Answer
Arc AB subtends ∠APB at center and ∠ACB at the point C on the circle.
∴ ∠APB = 2∠ACB
⇒ ∠APB = 2∠ACB
⇒ 130° = 2∠ACB
⇒ ∠ACB = 65°.
From figure,
∠ACB + ∠BCD = 180°. (∵ both angles form a linear pair)
⇒ 65° + ∠BCD = 180°
⇒ ∠BCD = 180° - 65°
⇒ ∠BCD = 115°.
In circle with center Q,
⇒ ∠BQD + Reflex ∠BQD = 360°
⇒ x° + Reflex ∠BQD = 360°
⇒ Reflex ∠BQD = 360° - x°.
Arc BD subtends reflex ∠BQD at center and ∠BCD at the point C on the circle.
∴ Reflex ∠BQD = 2∠BCD
⇒ 360° - x° = 2 × 115°
⇒ 360° - x° = 230°
⇒ x° = 360° - 230°
⇒ x° = 130°.
Hence, the value of x = 130.
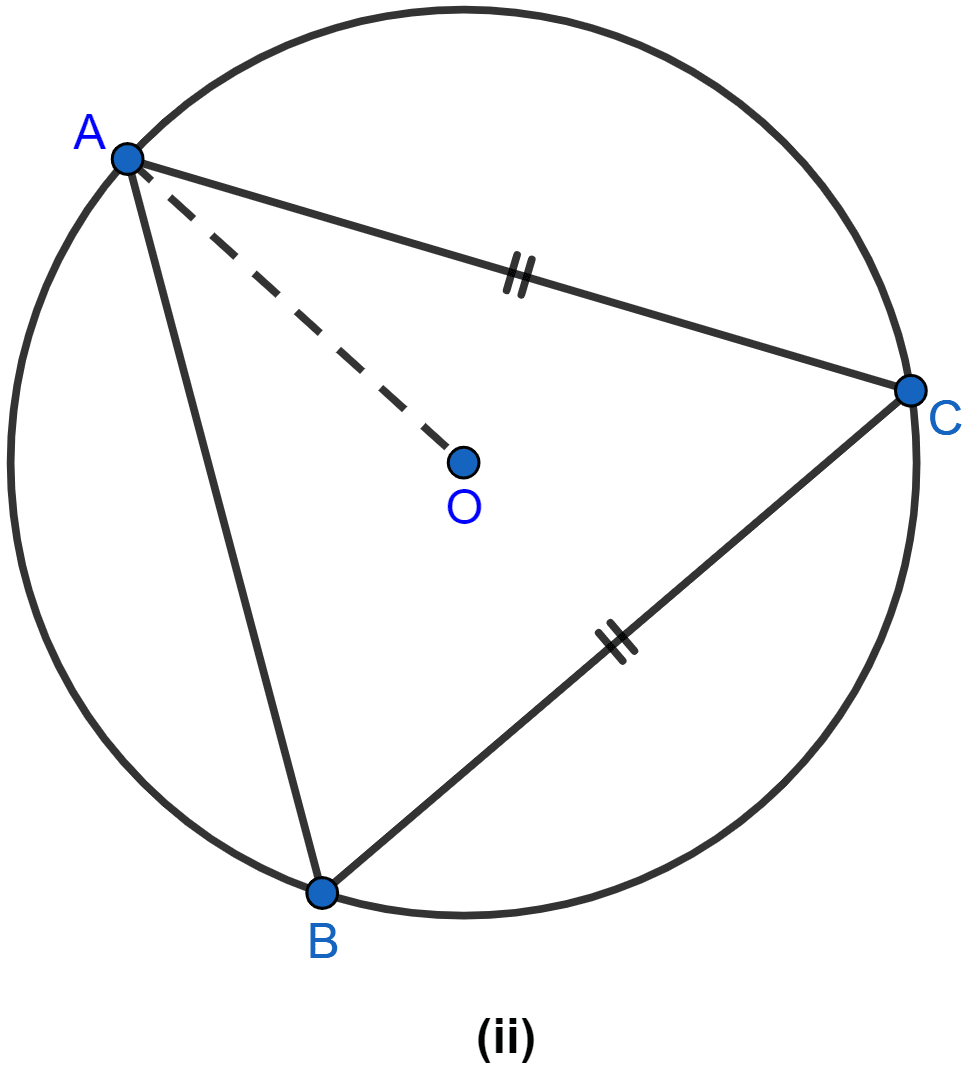
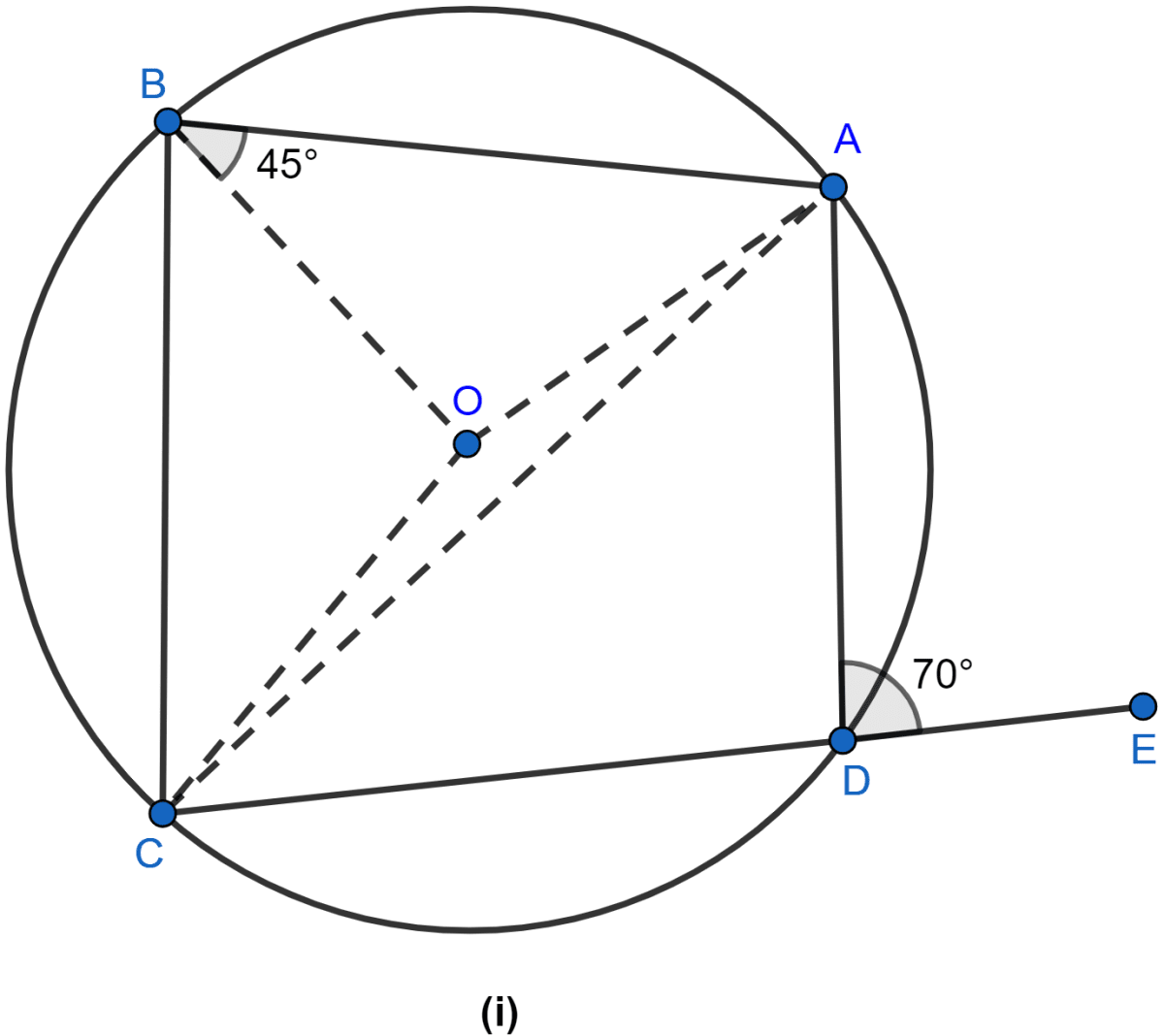
In the figure (ii) given below, O is the circumcenter of triangle ABC in which AC = BC. Given that ∠ACB = 56°, calculate
(i) ∠CAB
(ii) ∠OAC.
Answer
(i) From figure,
AC = BC so,
∠CBA = ∠CAB (As angles of equal sides are equal)
In △ABC,
∠CAB + ∠CBA + ∠ACB = 180°
2∠CAB + 56° = 180°
2∠CAB = 180° - 56°
2∠CAB = 124°
∠CAB = 62°.
Hence, ∠CAB = 62°.
(ii) OC is the radius of the circle. OC bisects ∠ACB.
∠OCA = ∠ACB = 56° = 28°.
Now in △OCA,
OA = OC (Radius of the same circle)
∠OAC = ∠OCA = 28°.
Hence, ∠OAC = 28°.
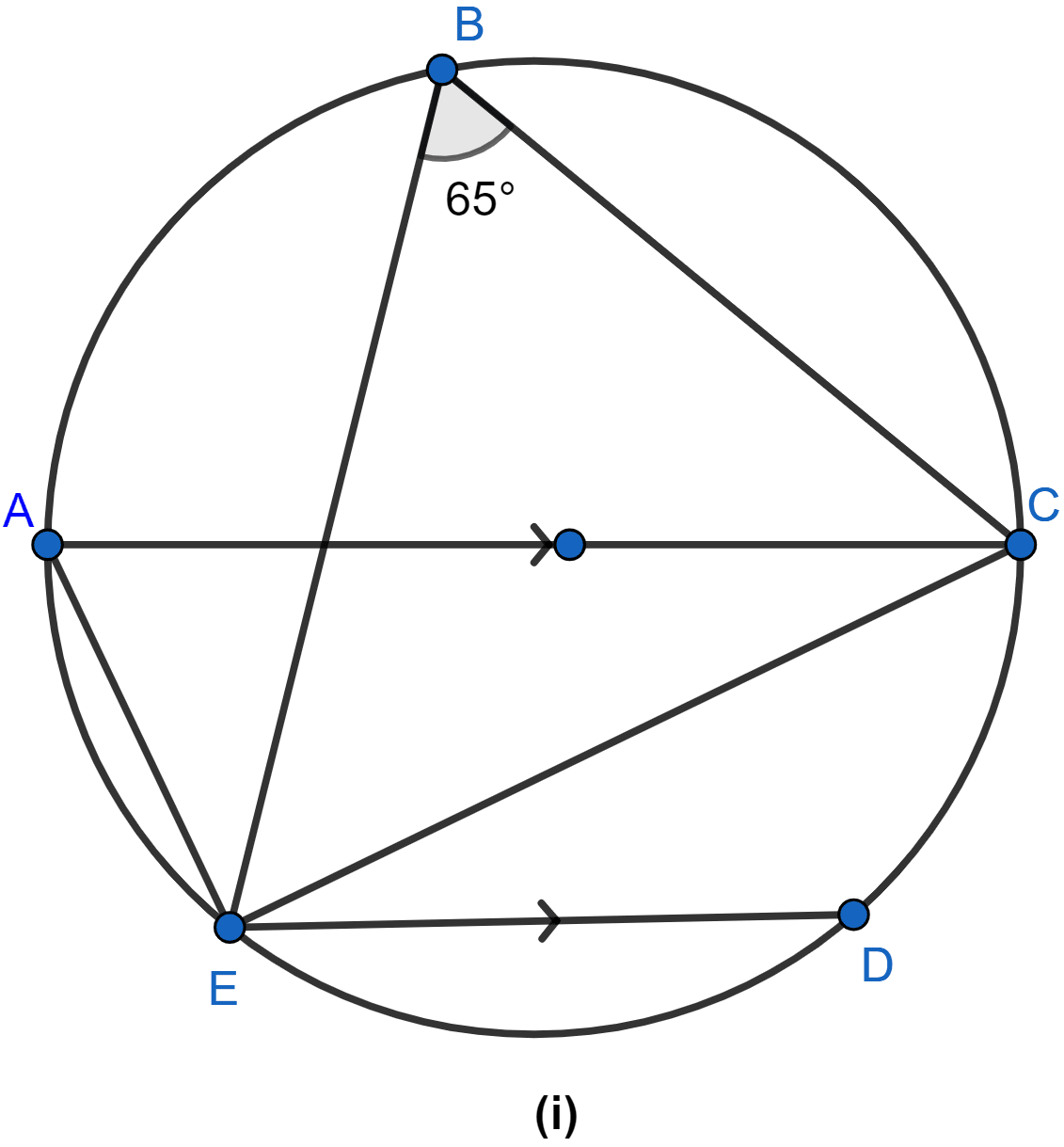
In the figure (i) given below, chord ED is parallel to the diameter AC of the circle. Given ∠CBE = 65°, calculate ∠DEC.
Answer
Consider △AEC and △EBC,
∠EAC = ∠EBC = 65° (∵ angles in same segment are equal.)
In △AEC,
∠AEC = 90° (∵ angle in semicircle is 90°.)
We know that sum of angles of a triangle is 180°.
⇒ ∠AEC + ∠EAC + ∠ACE = 180°.
⇒ 90° + 65° + ∠ACE = 180°
⇒ ∠ACE + 155° = 180°
⇒ ∠ACE = 180° - 155°
⇒ ∠ACE = 25°.
Hence, the value of ∠ACE = 25°.
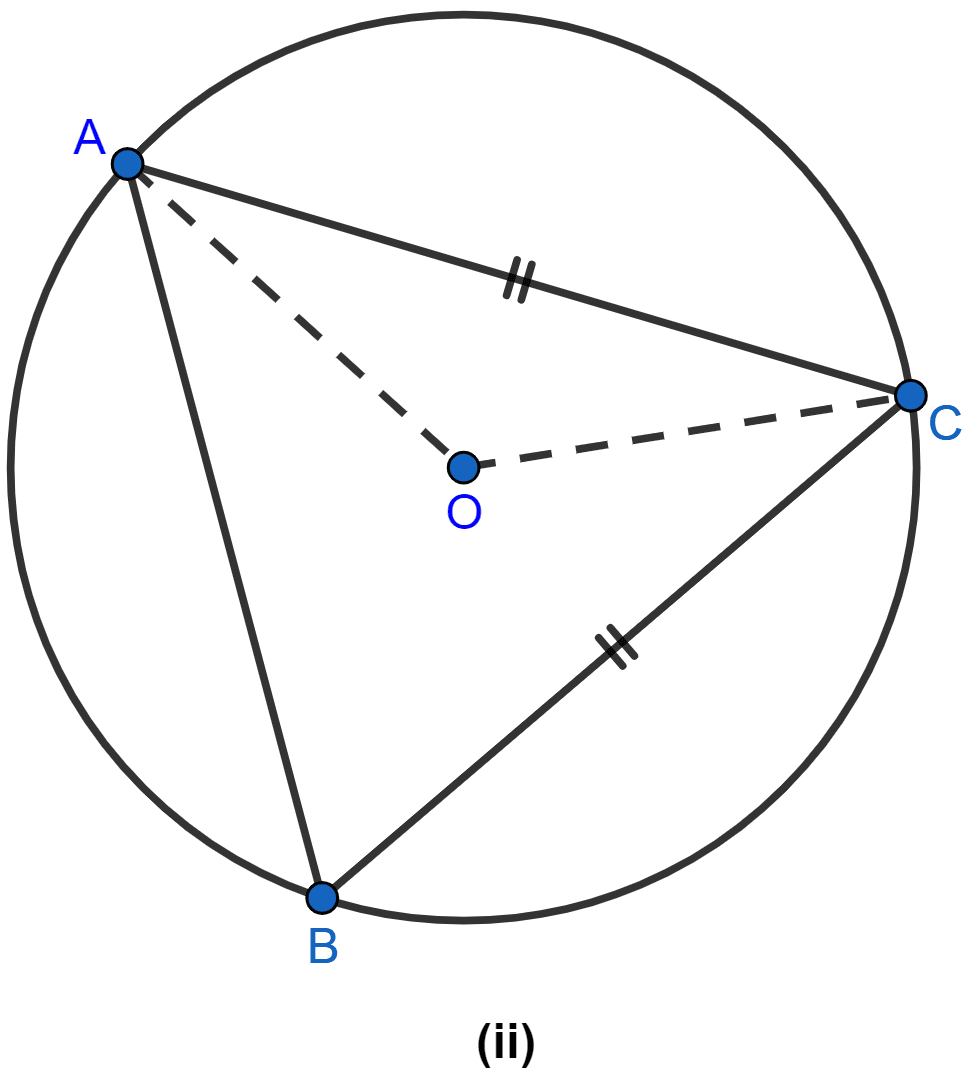
In the figure (ii) given below, C is a point on the minor arc AB of the circle with centre O. Given ∠ACB = p°, ∠AOB = q°, express q in terms of p. Calculate p if OACB is a parallelogram.
Answer
From figure,
⇒ ∠AOB + Reflex ∠AOB = 360°
⇒ q° + Reflex ∠AOB = 360°
⇒ Reflex ∠AOB = 360° - q°.
Arc AB subtends reflex ∠AOB at center and ∠ACB at the point C on the circle.
∴ Reflex ∠AOB = 2∠ACB
⇒ 360° - q° = 2 × p°
⇒ 360° - q° = 2p°
⇒ 2p° + q° = 360°
⇒ q° = 360° - 2p°
⇒ q° = 2(180° - p°)
⇒ q = 2(180 - p).
Given, OABC is a parallelogram, then
Opposite angles are equal.
∴ ∠AOB = ∠ACB
⇒ p° = q°
⇒ p° = 360° - 2p°
⇒ 3p° = 360°
⇒ p° = 120°.
Hence, q = 2(180 - p) and the value of p = 120.
In the figure (i) given below, straight lines AB and CD pass through the center O of a circle. If ∠OCE = 40° and ∠AOD = 75°, find the number of degrees in
(i) ∠CDE
(ii) ∠OBE.

Answer
(i) In △CED,
∠CED = 90° (∵ angle in semicircle is 90°.)
We know that sum of angles of a triangle is 180°.
⇒ ∠CED + ∠DCE + ∠CDE = 180°.
⇒ 90° + 40° + ∠CDE = 180°
⇒ ∠CDE + 130° = 180°
⇒ ∠CDE = 180° - 130°
⇒ ∠CDE = 50°.
Hence, the number of degrees in ∠CDE = 50.
(ii) From figure,
∠AOD + ∠DOB = 180° (∵ they form linear pair)
⇒ 75° + ∠DOB = 180°
⇒ ∠DOB = 180° - 75°
⇒ ∠DOB = 105°.
In △DOB,
∠ODB = ∠CDE = 50°
We know that sum of angles of a triangle is 180°.
⇒ ∠DOB + ∠ODB + ∠DBO = 180°.
⇒ 105° + 50° + ∠DBO = 180°
⇒ ∠DBO + 155° = 180°
⇒ ∠DBO = 180° - 155°
⇒ ∠DBO = 25°.
From figure,
∠OBE = ∠DBO
∴ ∠OBE = 25°.
Hence, the number of degrees in ∠OBE = 25.
In the figure (ii) given below, I is the incentre of △ABC. AI produced meets the circumcircle of △ABC at D. Given that ∠ABC = 55° and ∠ACB = 65°, calculate
(i) ∠BCD
(ii) ∠CBD
(iii) ∠DCI
(iv) ∠BIC.
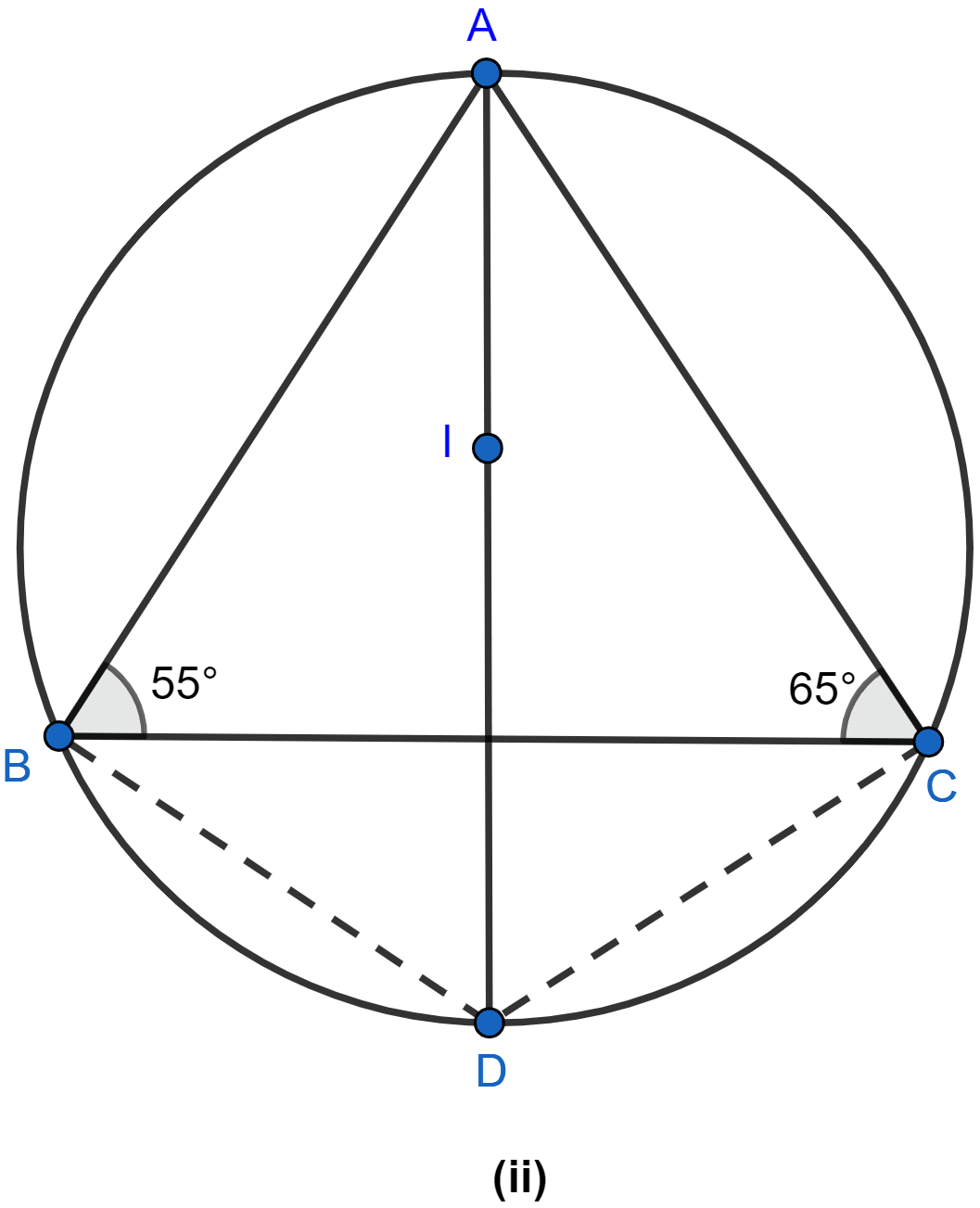
Answer
(i) Join BI and CI as shown in the figure below:
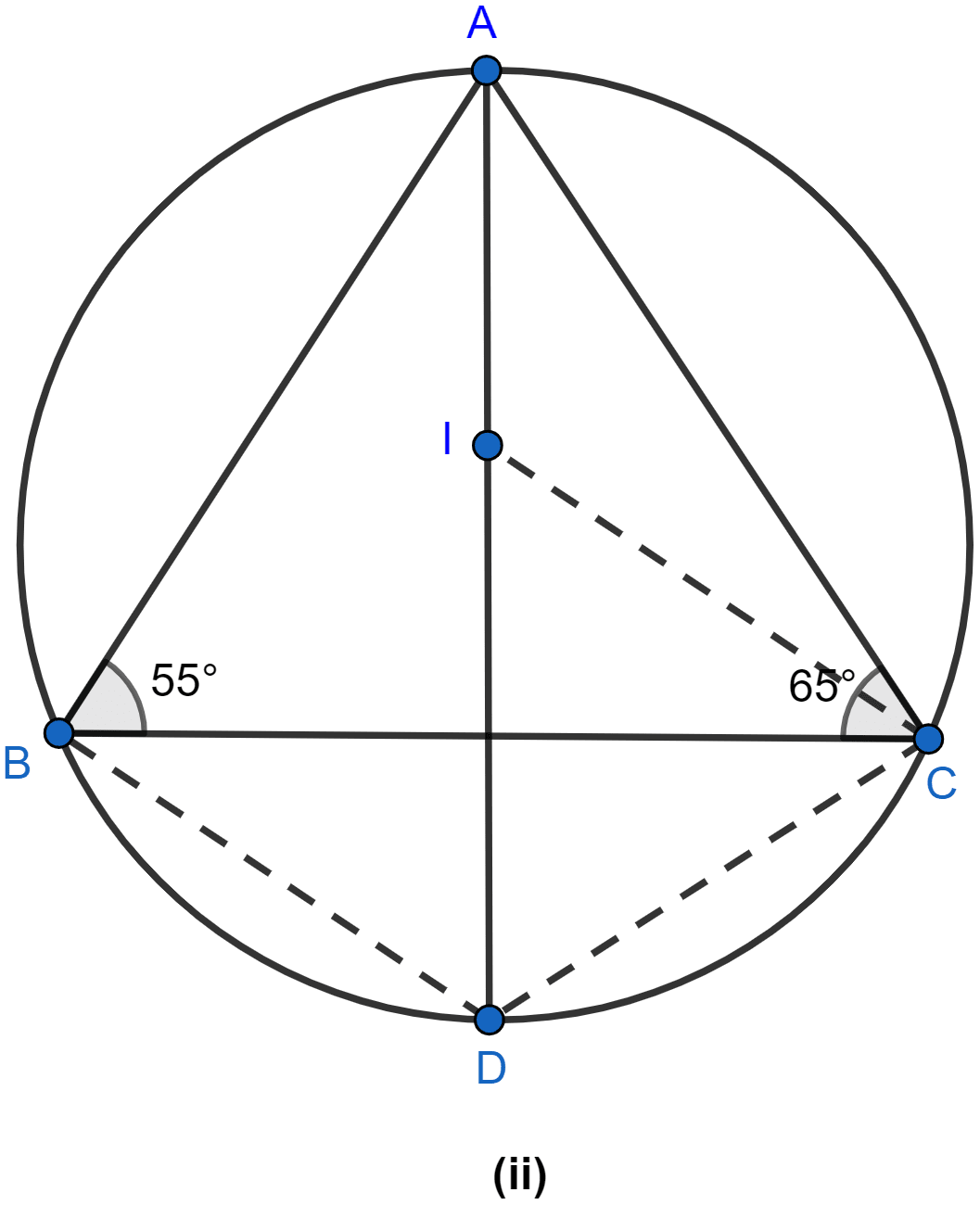
In △ABC,
⇒ ∠BAC + ∠ABC + ∠ACB = 180° (∵ sum of angles = 180°.)
⇒ ∠BAC + 55° + 65° = 180°
⇒ ∠BAC + 120° = 180°
⇒ ∠BAC = 180° - 120°
⇒ ∠BAC = 60°.
I is the incentre,
∴ I lies on the bisectors of angle of the △ABC,
∴ ∠BAD = ∠CAD = = 30°.
∠BCD = ∠BAD = 30°. (∵ angles in same segment are equal.)
Hence, the value of ∠BCD = 30°
(ii) Similarly,
∠CBD = ∠CAD = 30°. (∵ angles in same segment are equal.)
Hence, the value of ∠CBD = 30°
(iii) The line CI bisects ∠C (∵ I lies on the bisectors of angle of the △ABC).
∴ ∠BCI = .
From figure,
∠DCI = ∠BCD + ∠BCI = .
Hence, the value of ∠DCI = .
(iv) ∠IBC =
∠ICB =
∠BIC = 180° - (∠IBC + ∠ICB)
Hence, the value of ∠BIC = 120°.
O is the circumcentre of the triangle ABC and D is mid-point of the base BC. Prove that ∠BOD = ∠A.
Answer
From the below figure:
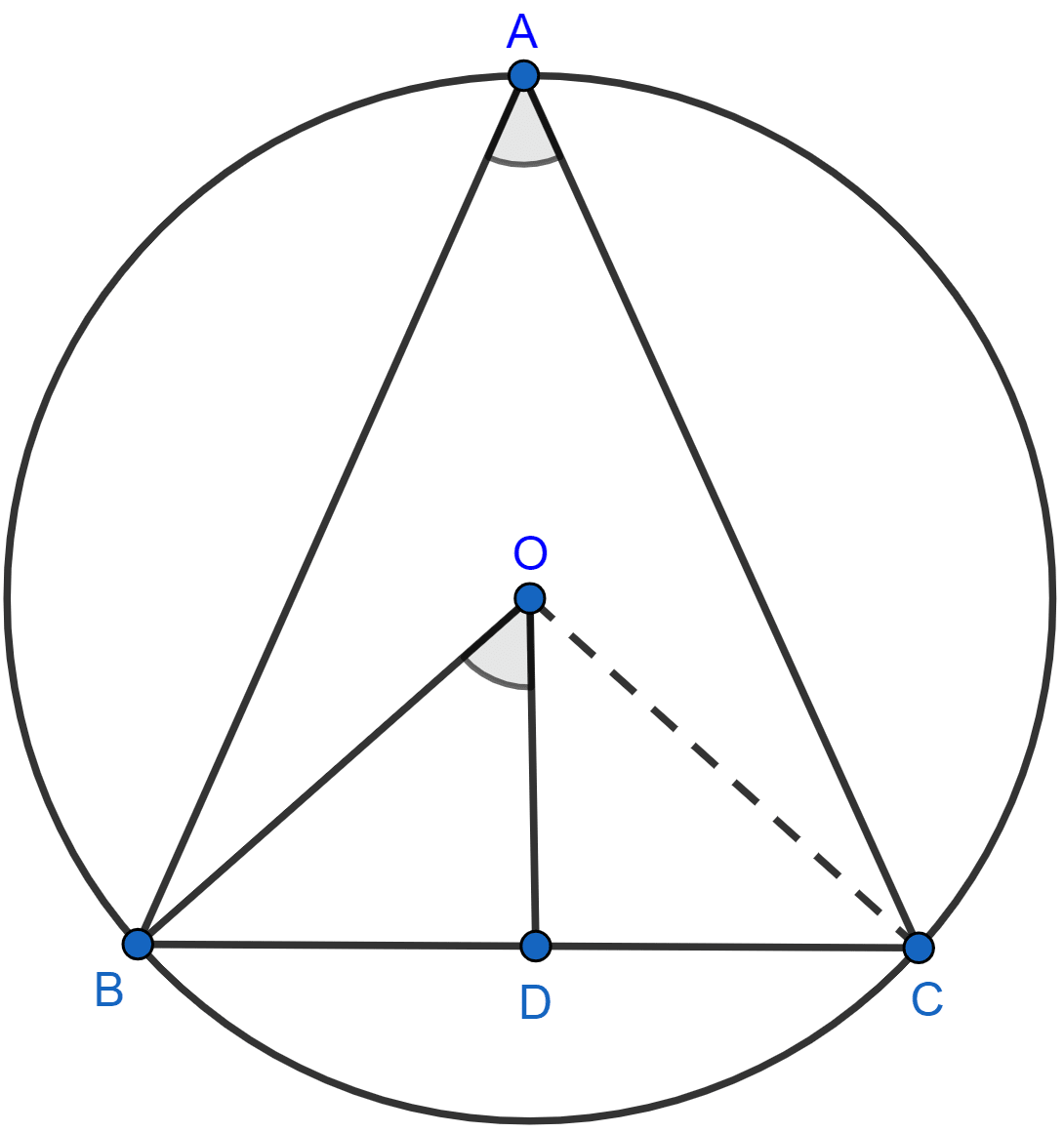
Arc BC subtends ∠BOC at center and ∠BAC at the point A on the circle.
∴ ∠BOC = 2∠A
In △OBD and △ODC,
OD = OD (Common side)
BD = CD (As D is the mid-point of BC)
OB = OC (Radius of the same circle)
∴ △OBD ≅ △ODC (SSS rule of congruency).
∴ ∠BOD = ∠COD (As corresponding part of congruent triangles are congruent.)
Since, ∠BOD = ∠COD so,
∠BOD = ∠BOC ....(i)
∠BOC = 2∠A
∠A = ∠BOC .....(ii)
From (i) and (ii) we get,
∠BOD = ∠A
Hence, proved that ∠BOD = ∠A.
In the adjoining figure, AB and CD are equal chords. AD and BC intersects at E. Prove that AE = CE and BE = DE.
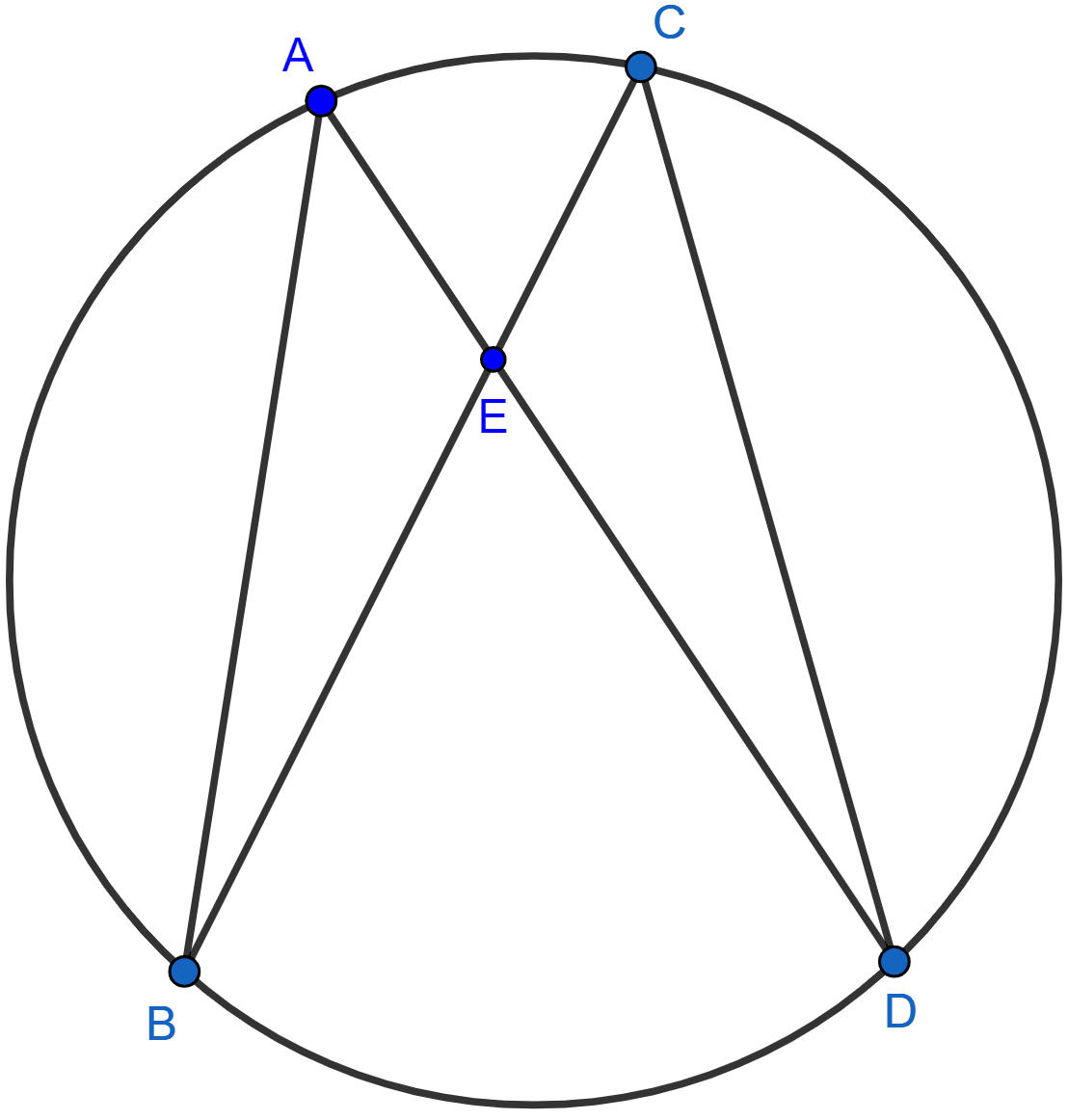
Answer
In △AEB and △CED,
∠A = ∠C (∵ angles in same segment of a circle are equal.)
∠B = ∠D (∵ angles in same segment of a circle are equal.)
AB = CD (Given)
∴ △AEB ≅ △CED (By ASA axiom)
As corresponding part of congruent triangles are congruent hence,
AE = CE and BE = DE.
Hence, proved that AE = CE and BE = DE.
In the figure (i) given below, AB is a diameter of a circle with center O. AC and BD are perpendiculars on a line PQ. BD meets the circle at E. Prove that AC = ED.
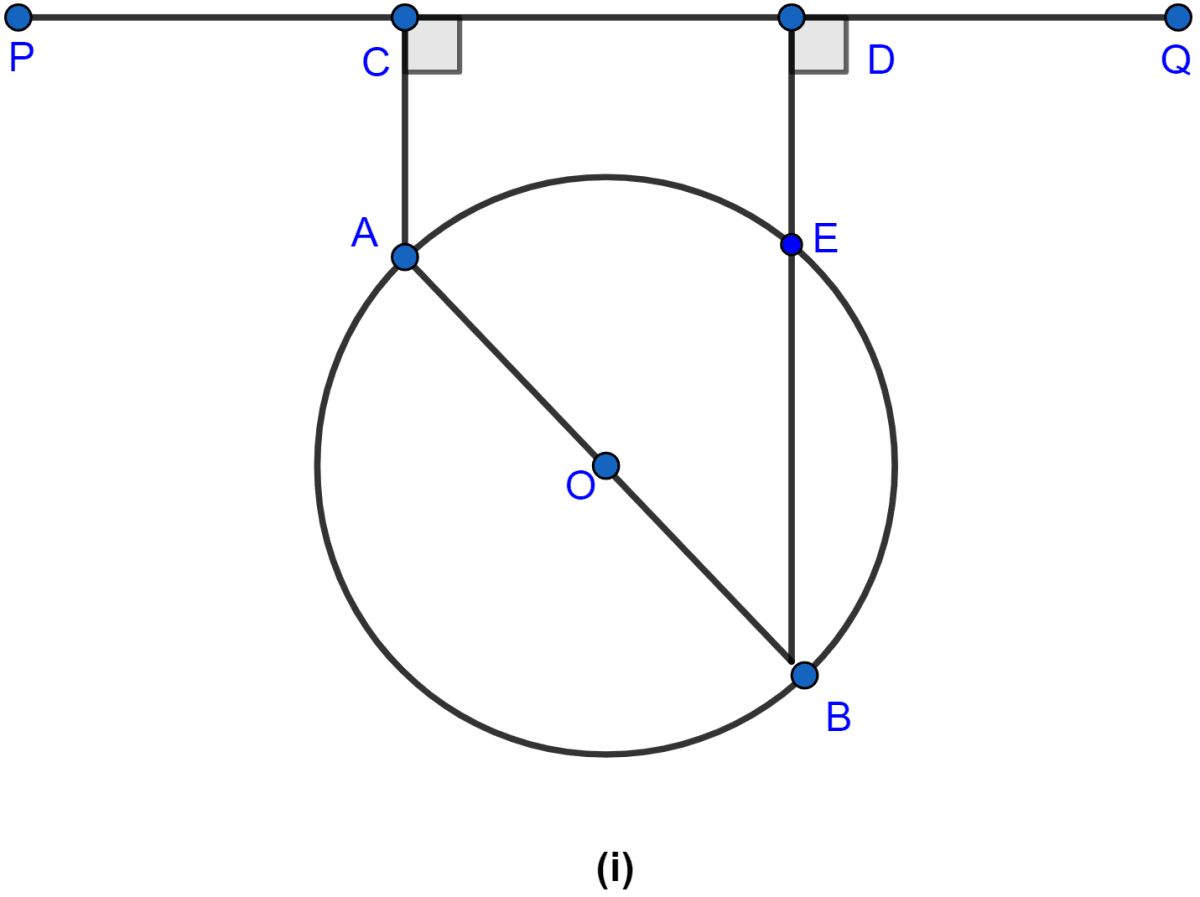
Answer
Join AE.
∠AEB = 90° (∵ angle in semicircle is 90°.)
∠AED = 90° (∵ ∠AEB and ∠AED form a linear pair.)
Hence, we can say that,
DE is also perpendicular to AE, since DE is also perpendicular to PQ hence,
AE || PQ.
Since, CA and DE both are perpendicular to PQ hence,
CA || DE.
Hence, proved that ACDE is a rectangle.
In rectangle opposite sides are equal so,
AC = DE.
Hence, proved that AC = DE.
In the figure (ii) given below, O is the centre of a circle. Chord CD is parallel to the diameter AB. If ∠ABC = 25°, calculate ∠CED.
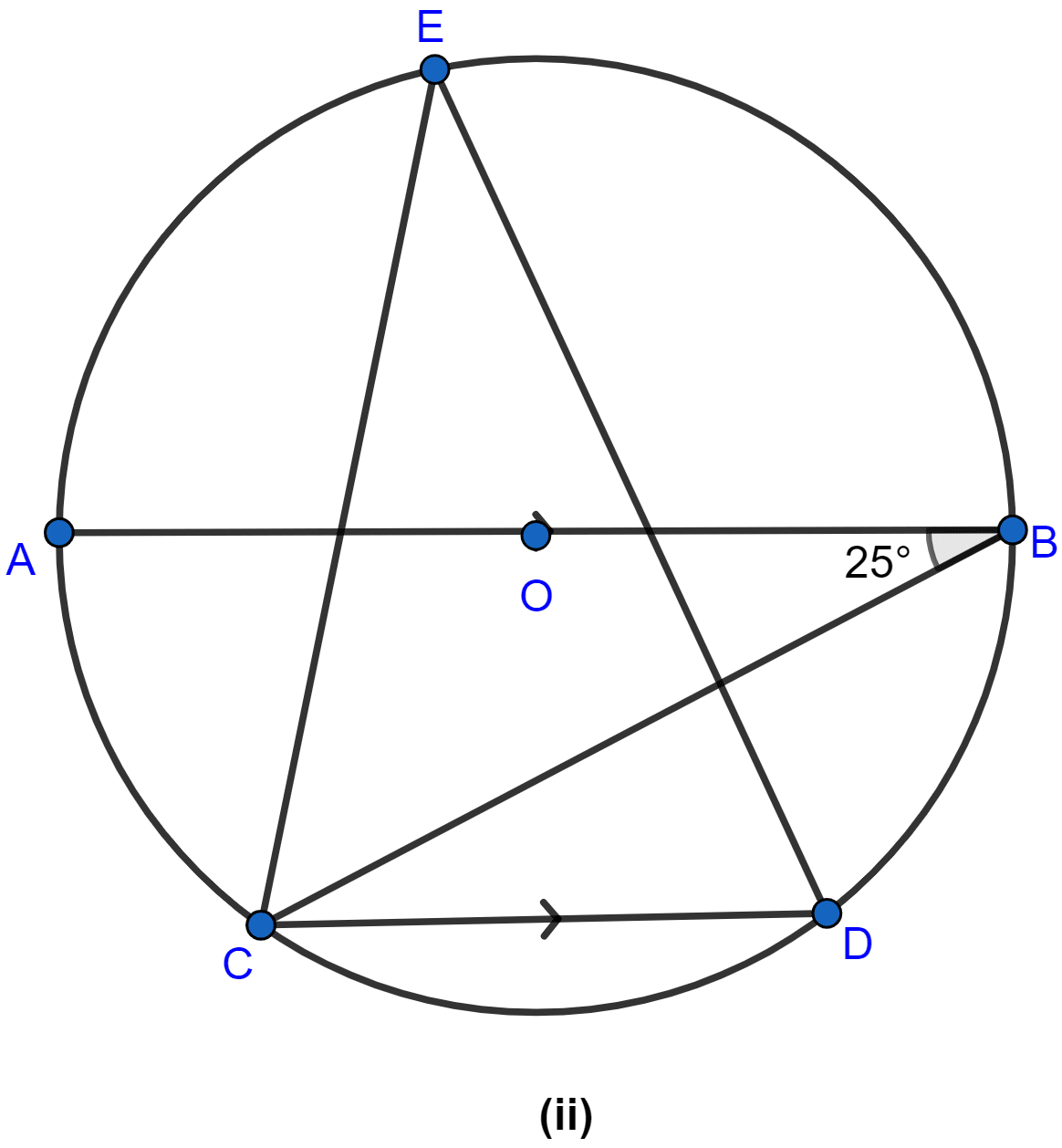
Answer
Join OC and OD as shown in the figure below:
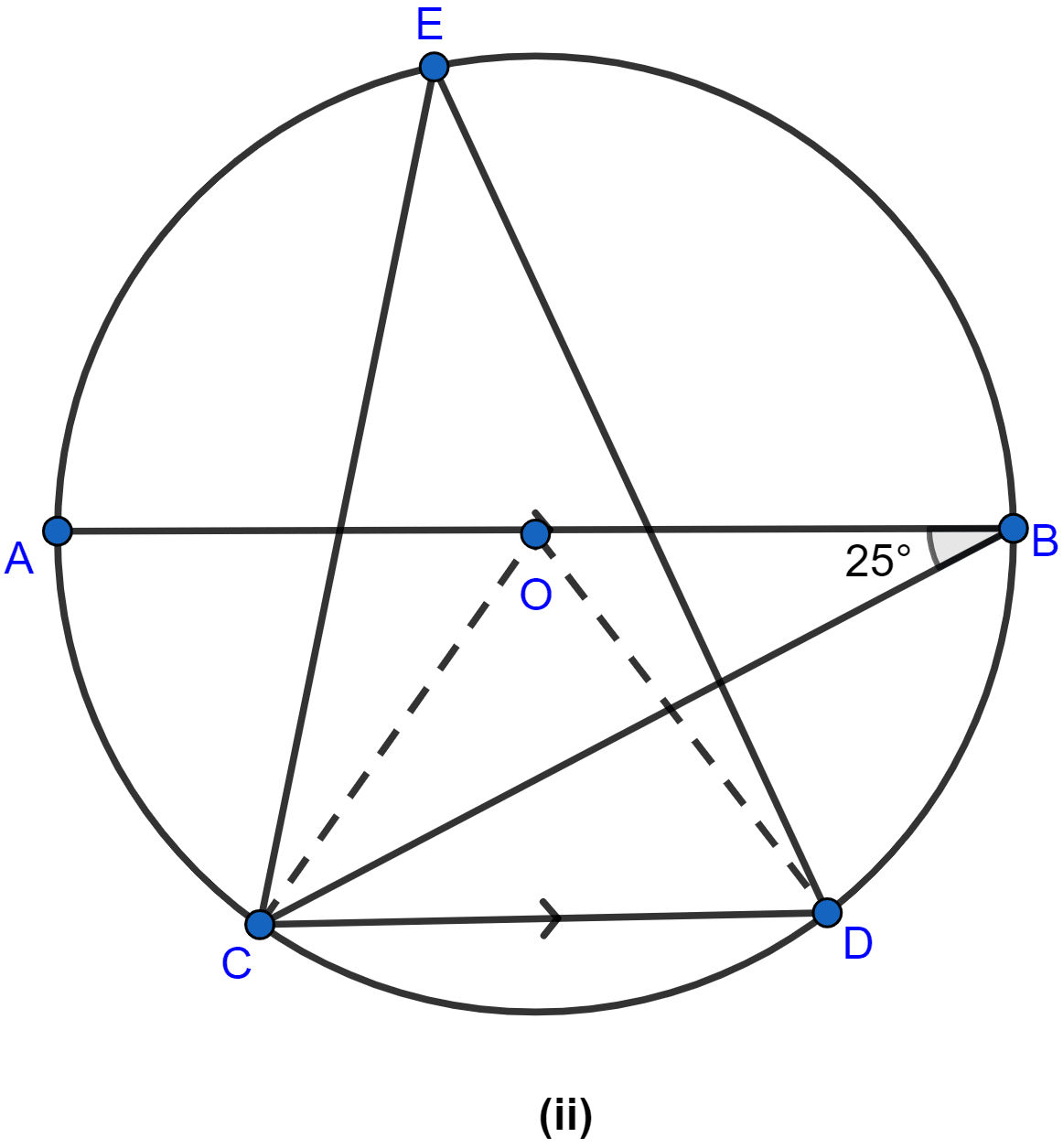
AC subtends angle AOC at centre and ∠ABC at point B.
∴ ∠AOC = 2∠ABC = 2 × 25° = 50°.
From figure,
∠OCD = ∠AOC (Alternate angles)
Hence, ∠OCD = 50°.
In △OCD,
OC = OD (Both are radius of the circle)
so, ∠ODC = ∠OCD.
Since, sum of angles of a triangle is 180°.
⇒ ∠COD + ∠OCD + ∠ODC = 180°
⇒ ∠COD + 50° + 50° = 180°
⇒ ∠COD + 100° = 180°
⇒ ∠COD = 80°.
CD subtends ∠COD at center and ∠CED at point E of the circle.
∴ ∠COD = 2∠CED
⇒ 80° = 2∠CED
⇒ ∠CED = 40°.
Hence, ∠CED = 40°.
In the adjoining figure, O is the center of the given circle and OABC is a parallelogram. BC is produced to meet the circle at D. Prove that ∠ABC = 2∠OAD.
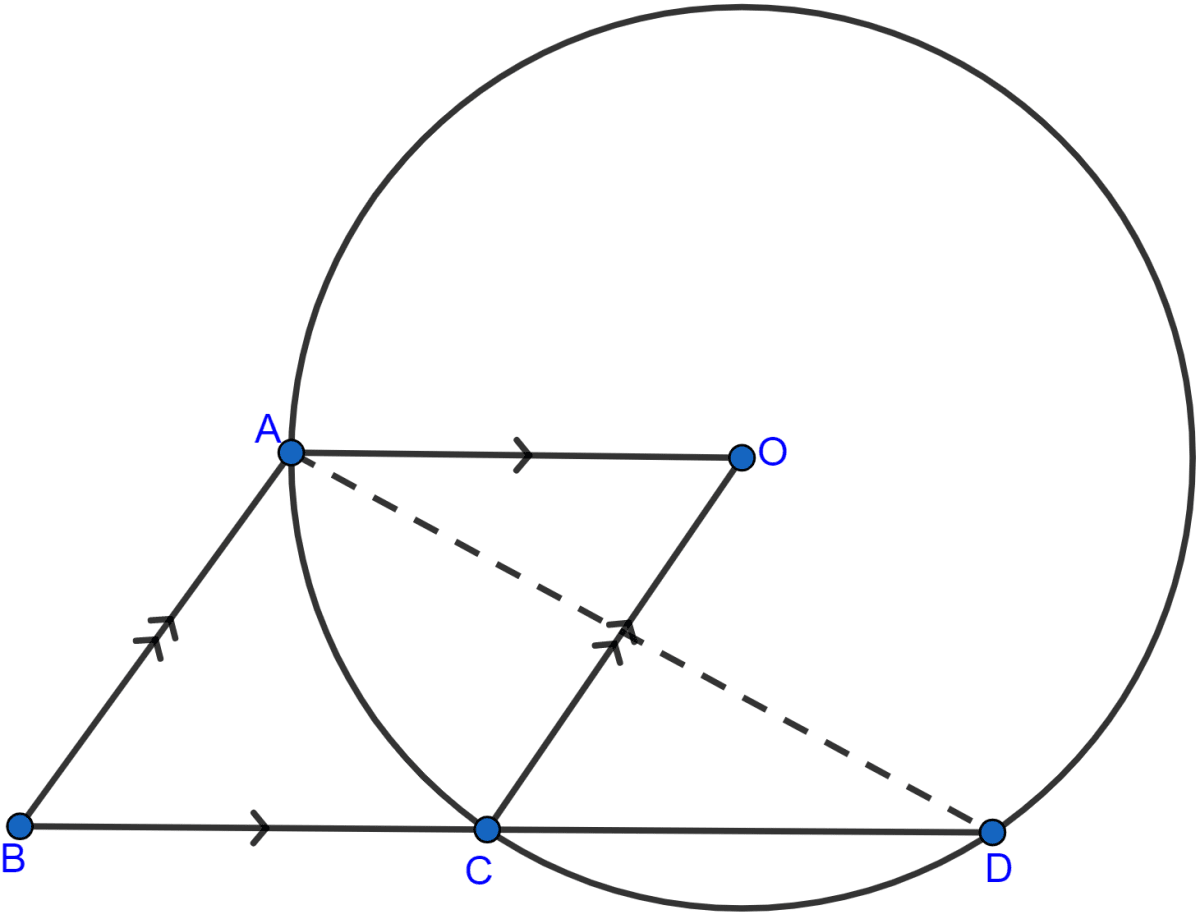
Answer
Join AD.
Arc AC subtends ∠AOC at the center and ∠ADC at the point D of the circle.
∴ ∠AOC = 2∠ADC (As angle at center = double the angle at the remaining part of the circle)
∠OAD = ∠ADC (∵ alternate angles are equal.)
∴ ∠AOC = 2∠OAD .....(i)
Since, opposite angles are equal in parallelogram,
∴ ∠ABC = ∠AOC
Putting values of ∠AOC in eqn (i) we get,
∠ABC = 2∠OAD.
Hence, proved that ∠ABC = 2∠OAD.
In figure (i) given below, P is the point of intersection of the chords BC and AQ such that AB = AP. Prove that CP = CQ.
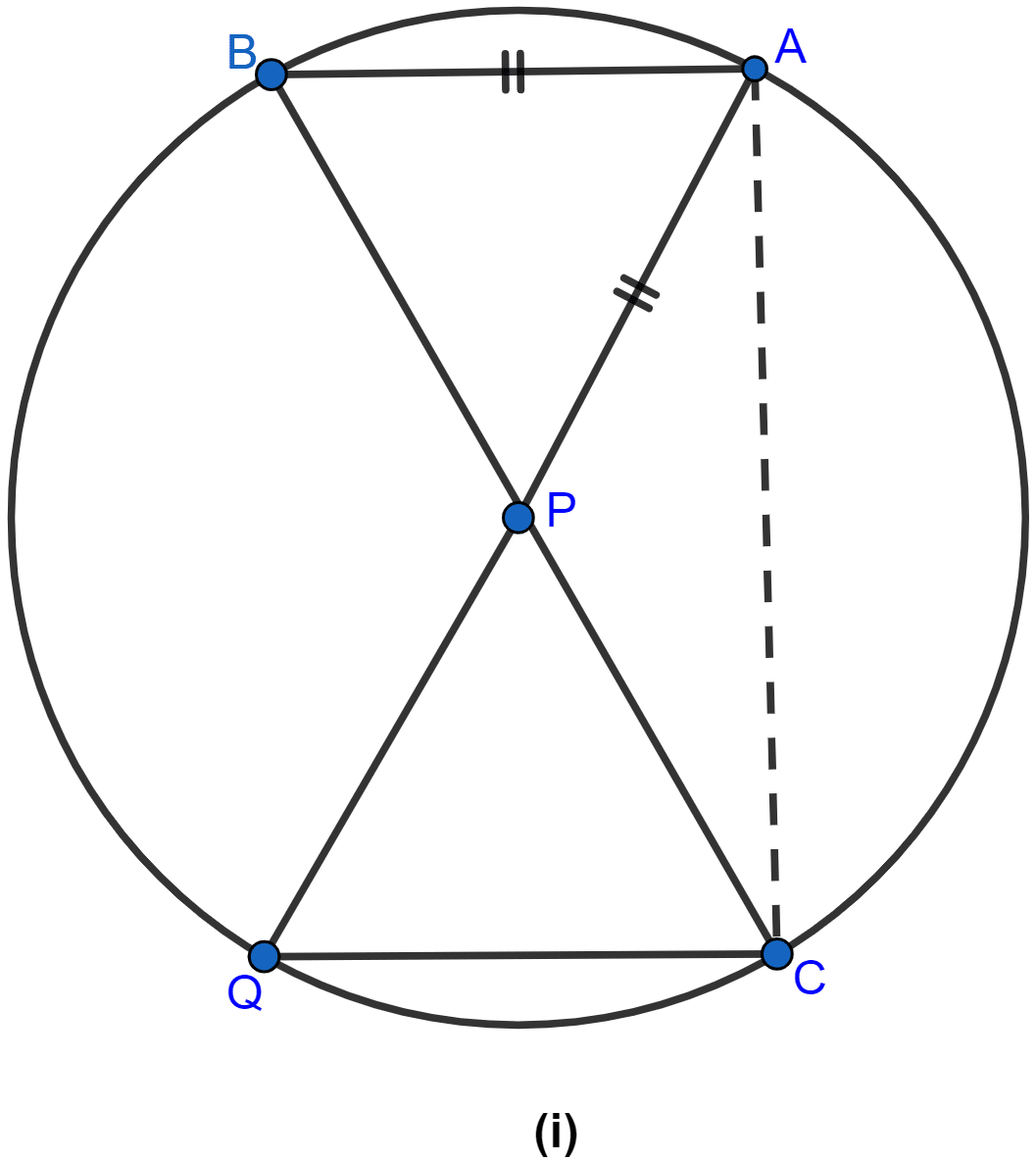
Answer
Given, two chords AQ and BC intersect each other at P inside the circle. AB and CQ are joined and AB = AP.
To prove : CP = CQ
Construction : Join AC.
Proof :
In △ABP and △CQP
∠B = ∠Q (∵ angles in same segment are equal)
∠BAP = ∠PCQ (∵ angles in same segment are equal)
∠BPA = ∠CPQ (∵ vertically opposite angles are equal.)
∴ △ABP ~ △CQP (By AAA axiom of similarity.)
Since, triangles are similar hence, the ratio of the corresponding sides are equal.
We know, AB = AP,
Hence, proved that CQ = CP.
In the figure (ii) given below, AB = AC = CD, ∠ADC = 38°. Calculate
(i) ∠ABC
(ii) ∠BEC.
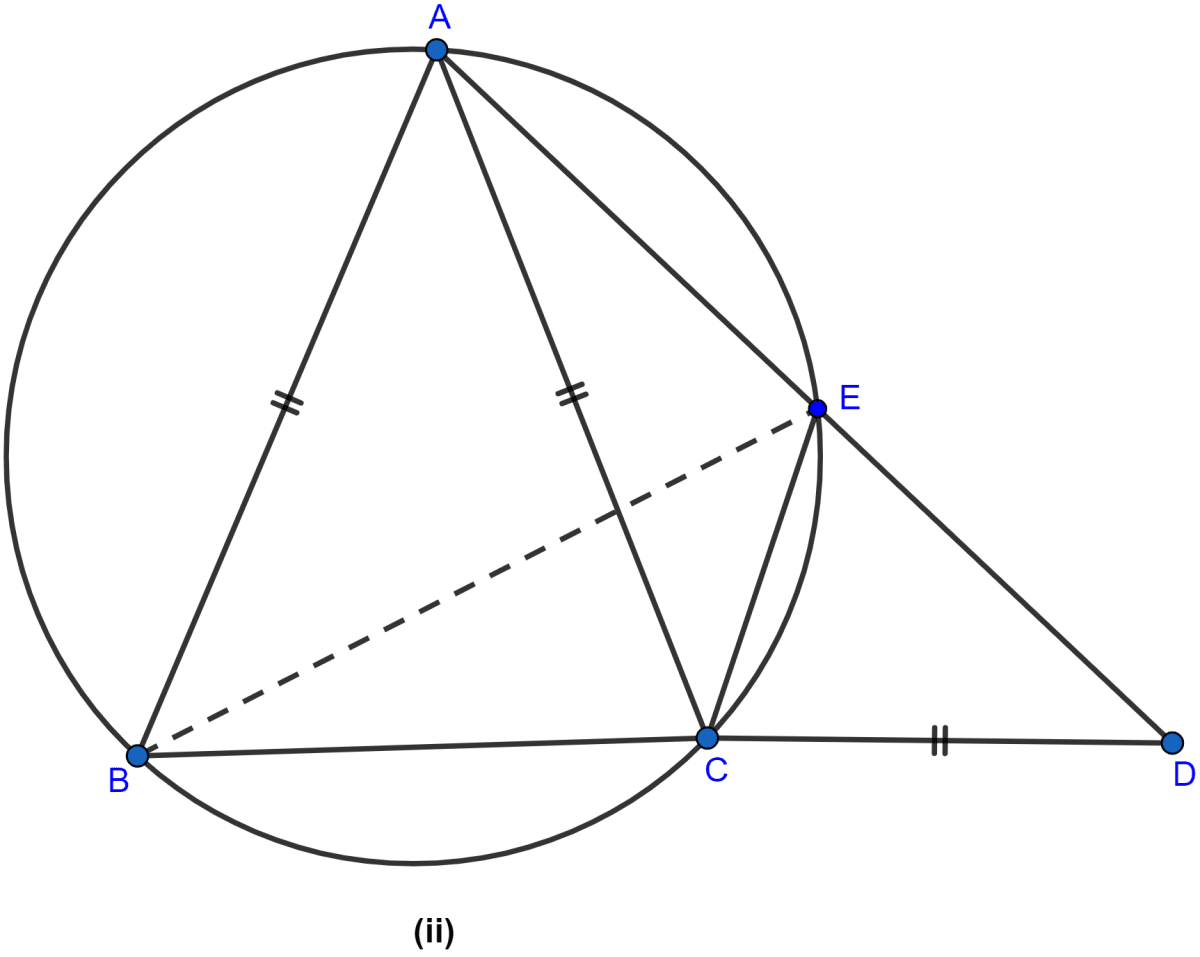
Answer
(i) In △ACD,
AC = CD
∴ ∠CAD = ∠ADC = 38° (∵ angles of equal sides in triangle are equal)
∠ACB = ∠CAD + ∠ADC = 38° + 38° = 76° (∵ exterior angle = sum of two opposite interior angles.)
In △ABC,
AB = AC
∴ ∠ABC = ∠ACB = 76° (As angles of equal sides in triangle are equal)
Hence, the value of ∠ABC = 76°.
(ii) We know that sum of angles in a triangle = 180°.
⇒ ∠BAC + ∠ABC + ∠ACB = 180°
⇒ ∠BAC + 76° + 76° = 180°
⇒ ∠BAC + 152° = 180°
⇒ ∠BAC = 180° - 152°
⇒ ∠BAC = 28°.
∠BEC = ∠BAC (∵ angles in same segment are equal.)
∠BEC = 28°.
Hence, the value of ∠BEC = 28°.
In the figure (i) given below, CP bisects ∠ACB. Prove that DP bisects ∠ADB.

Answer
From figure,
∠ACB = ∠ADB (∵ angles in same segment are equal.) ....(i)
∠ACP = ∠ADP (∵ angles in same segment are equal.) ....(ii)
We know,
∠ACP = ∠ACB (∵ CP bisects ∠ACB.) .....(iii)
Using values from eq (i) and eq (ii) and putting in eq (iii) we get,
∠ADP = ∠ADB
Hence, proved that DP bisects ∠ADB.
In the figure (ii) given below, BD bisects ∠ABC. Prove that .
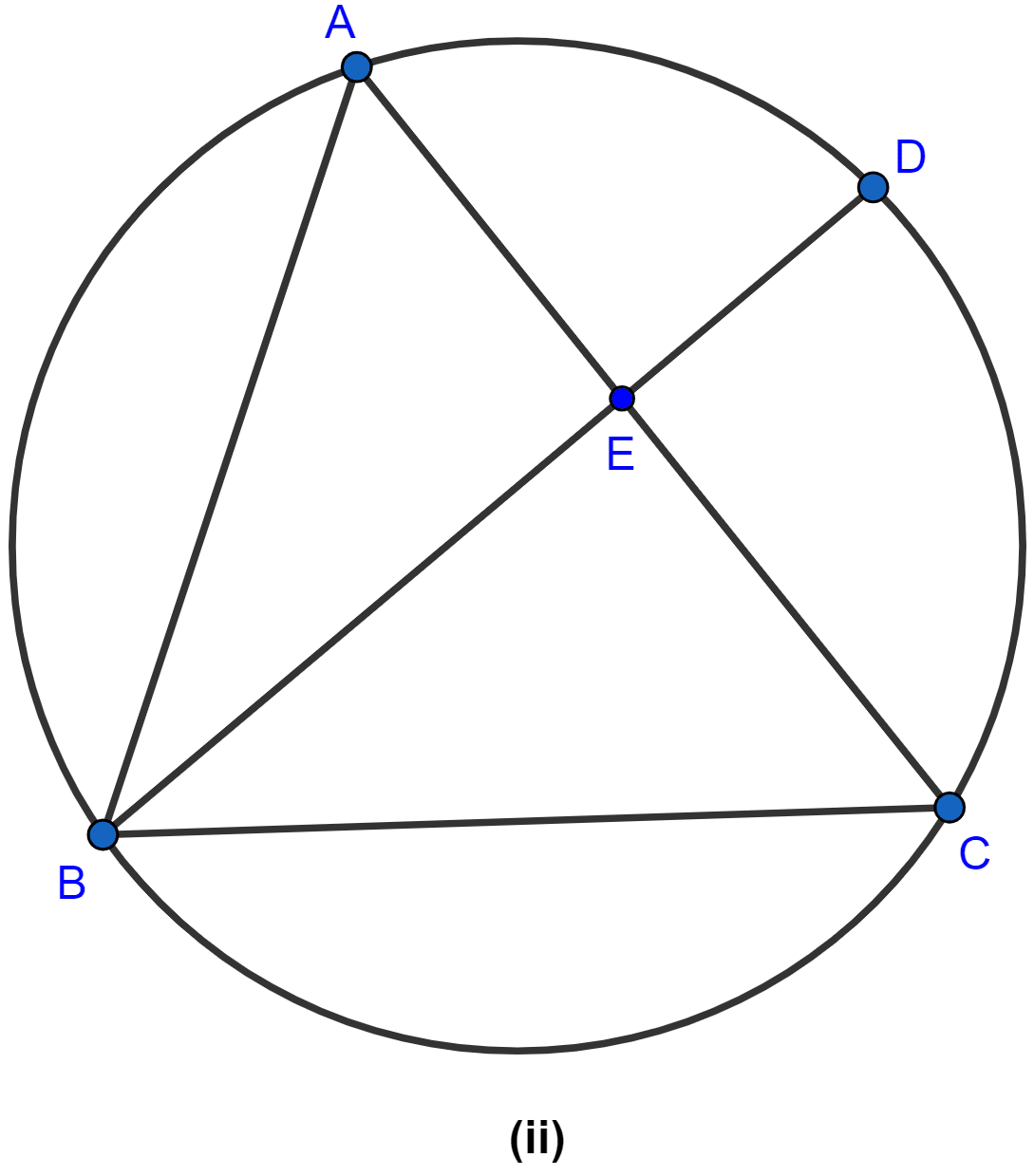
Answer
Join CD as shown in the figure below:
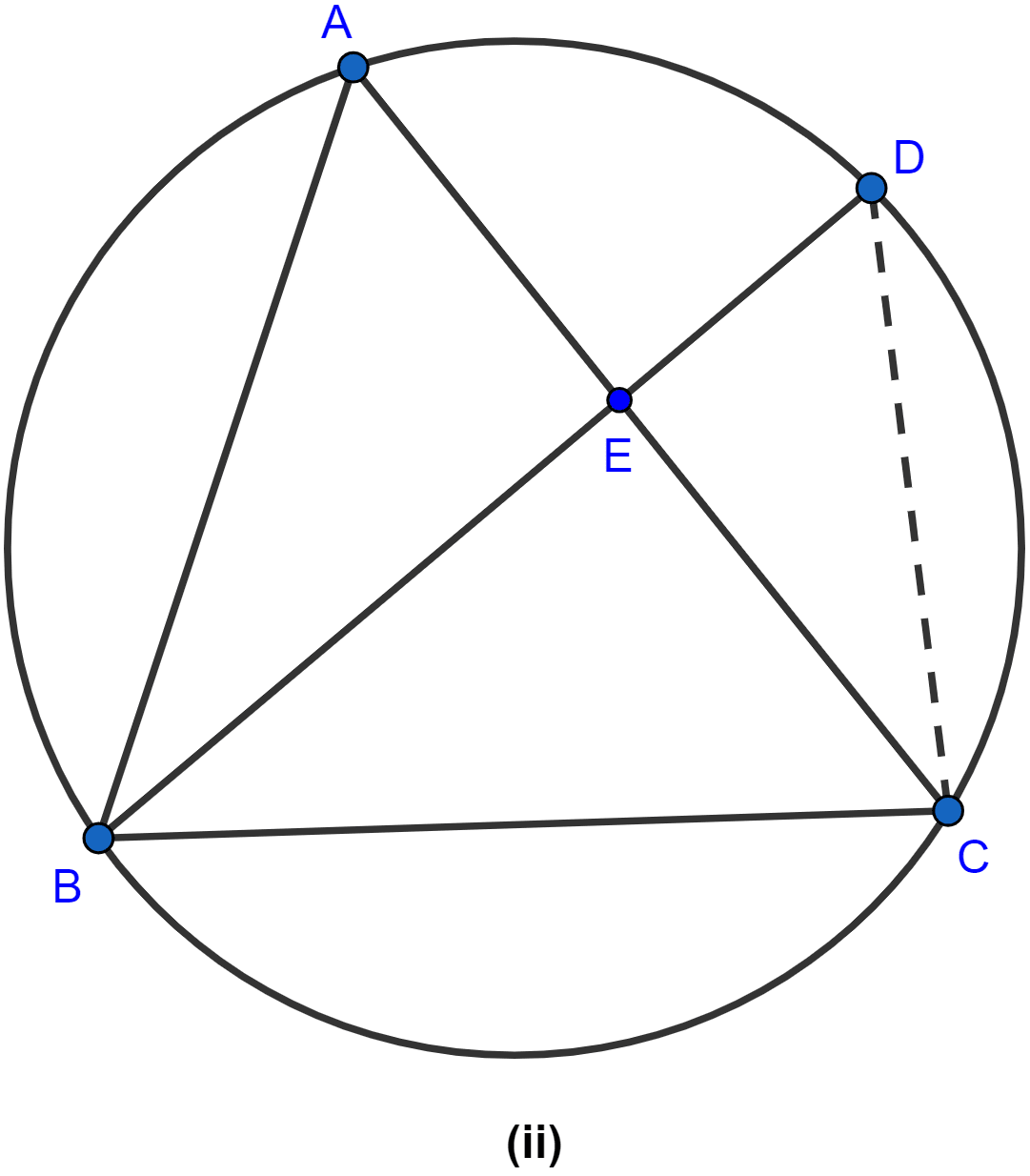
In △ABE and △BCD,
∠A = ∠D (∵ angles in same segment are equal.)
∠ABE = ∠DBC (As BD is bisector of ∠ABC)
△ABE ~ △BCD (AA rule of similarity).
Since, ratio of corresponding sides of similar triangles are equal,
∴
Hence, proved.
In the figure (i) given below, chords AB and CD of a circle intersect at E.
(i) Prove that triangles ADE and CBE are similar.
(ii) Given DC = 12 cm, DE = 4 cm and AE = 16 cm, calculate the length of BE.

Answer
(i) In △CBE and △ADE,
∠B = ∠D (∵ angles in same segment are equal.)
∠BEC = ∠DEA (∵ vertically opposite angles are equal.)
△CBE ~ △ADE. (By AA axiom)
Hence, proved that △CBE ~ △ADE.
(ii) Given, DC = 12 cm.
From figure,
⇒ DC = DE + EC
⇒ 12 = 4 + EC
⇒ EC = 12 - 4
⇒ EC = 8 cm.
Chords AB and CD intersect each other at E.
Considering △BEC and △AED,
∠BEC = ∠DEA (∵ vertically opposite angles are equal.)
∠CBE = ∠EDA (∵ both angles are subtended on circle by arc AC and angles in same segment are equal.)
Hence, △BEC ~ △AED.
Since triangles are similar hence the ratio of the corresponding sides are equal.
Hence, the length of BE = 2 cm.
In the figure (ii) given below, AB and CD are two intersecting chords of a circle. Name two triangles which are similar. Hence, calculate CP given that AP = 6 cm, PB = 4 cm, and CD = 14 cm (PC > PD).
Answer
In △APD and △CPB,
∠DAB = ∠DCB (∵ angles in same segment are equal.)
∠APD = ∠CPB (∵ vertically opposite angles are equal.)
△APD ~ △CPB. (By AA axiom)
Hence, proved that △APD ~ △CPB.
Chords AB and CD intersect each other at P.
Since △APD ~ △CPB, Hence, the ratio of corresponding sides are equal.
∴ AP × PB = CP × PD .....(i)
From figure,
CD = CP + PD
Let CP = x cm.
⇒ 14 = x + PD
⇒ PD = (x - 14) cm.
Putting values in eq (i)
⇒ 6 × 4 = x × (x - 14)
⇒ 24 = x2 - 14x
⇒ x2 - 14x - 24 = 0
⇒ x2 - 12x - 2x - 24 = 0
⇒ x(x - 12) -2(x - 12) = 0
⇒ (x - 2)(x - 12) = 0
⇒ x - 2 = 0 or x - 12 = 0
⇒ x = 2 or x = 12
Since, given PC > PD so, CP = 12 cm.
Hence, the length of CP = 12 cm.
In the adjoining figure, AE and BC intersect each other at point D. If ∠CDE = 90°, AB = 5 cm, BD = 4 cm and CD = 9 cm, find DE.
Answer
Join A and B as shown in the figure below:
From figure,
Since, ∠CDE = 90° so, ∠ADB = 90° (∵ vertically opposite angles are equal.)
In right angle triangle △ADB, by pythagoras theorem,
Chords AE and CB intersect each other at D.
In △ADB and △CDE,
∠BAD = ∠DCE (∵ angles in same segment are equal.)
∠ADB = ∠CDE (∵ vertically opposite angles are equal.)
△ADB ~ △CDE. (By AA axiom)
Since △ADB ~ △CDE, Hence, the ratio of corresponding sides are equal.
∴ AD × DE = CD × BD
⇒ 3 × DE = 9 × 4
⇒ DE =
⇒ DE = 12 cm.
Hence, the length of DE = 12 cm.
In the figure (i) given below, PR is a diameter of the circle, PQ = 7 cm, QR = 6 cm and RS = 2 cm. Calculate the perimeter of the cyclic quadrilateral PQRS.
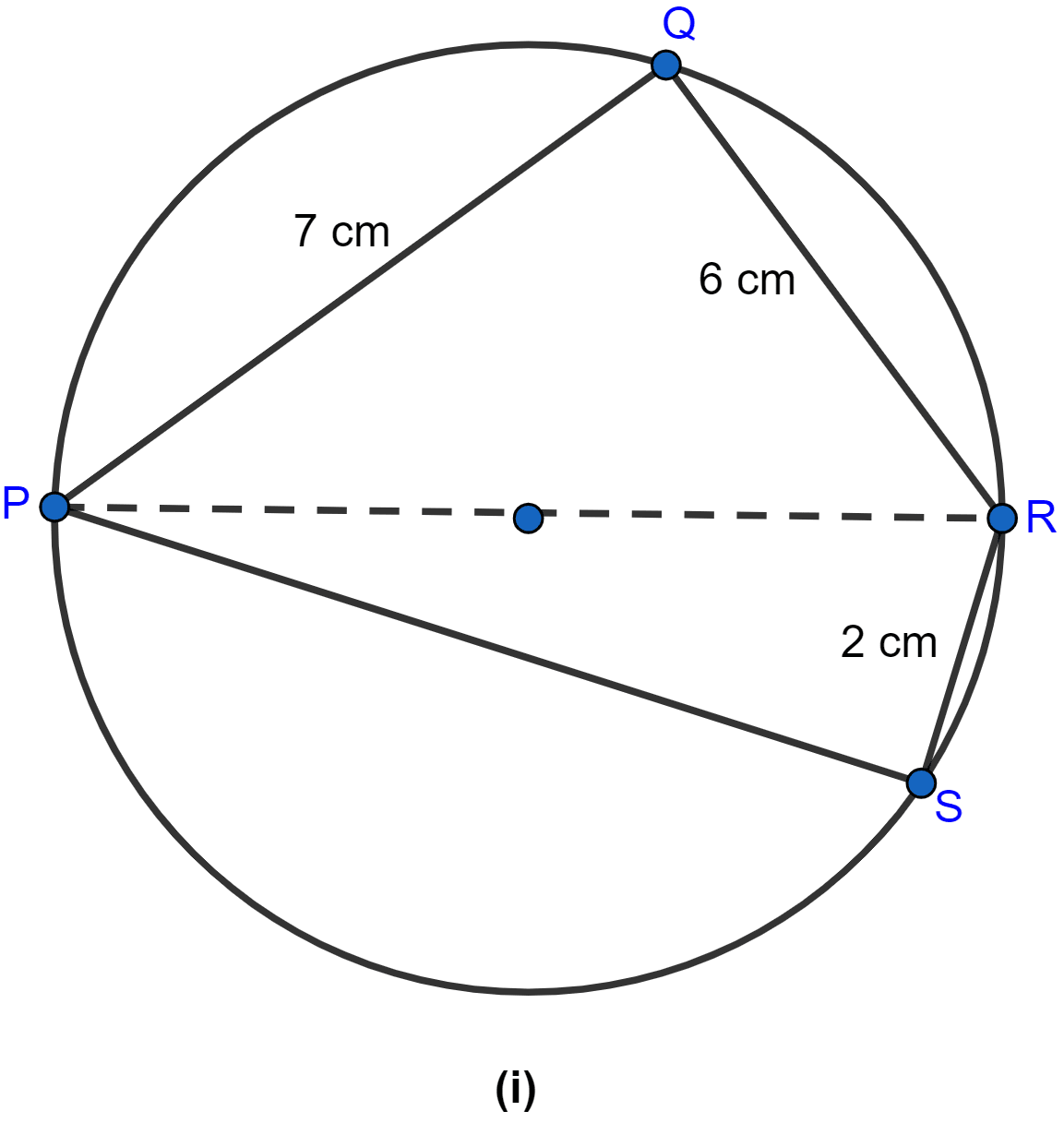
Answer
We know that ∠PQR = 90° as angle in semicircle is equal to 90°.
So, △PQR is a right angled triangle.
By pythagoras theorem,
In △PRS,
∠PSR = 90° as angle in semicircle is equal to 90°.
So, △PRS is a right angled triangle.
By pythagoras theorem,
Perimeter of PQRS = PQ + QR + RS + SP = 7 + 6 + 2 + 9 = 24 cm.
Hence, the perimeter of cyclic quadrilateral is 24 cm.
In the figure (ii) given below, the diagonals of a cyclic quadrilateral ABCD intersect in P and the area of the triangle APB is 24 cm2. If AB = 8 cm and CD = 5 cm, calculate the area of △DPC.
Answer
In △ABP and △DPC,
∠APB = ∠DPC (∵ vertically opposite angles are equal.)
∠ABP = ∠DCP (∵ angles in same segment are equal.)
△APB ~ △DPC. (By AA axiom)
We know that ratio of the area of similar triangles is the ratio of their corresponding sides.
Hence, the area of △DPC = cm2.
In adjoining figure, AB = 9 cm, PA = 7.5 cm and PC = 5 cm. Chords AD and BC intersect at P.
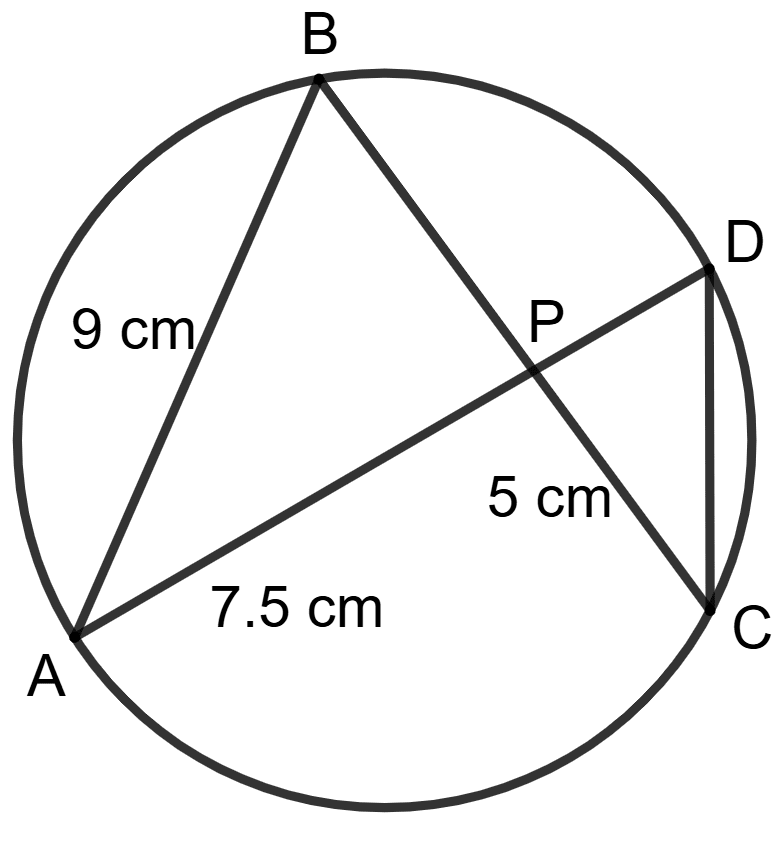
(i) Prove that Δ PAB ∼ Δ PCD.
(ii) Find the length of CD.
(iii) Find the area of Δ PAB : area of Δ PCD.
Answer
(i) As we know that,
If two chords of a circle intersect internally or externally, then the products of the lengths of segments are equal.
∴ PA.PD = PB.PC
⇒ ∠APB = ∠CPD (Vertically opposite angles)
If the corresponding sides of two triangles are proportional and one angle are equal, then the two triangles are similar.
Hence, proved that Δ PAB ∼ Δ PCD (By SAS rule of similarity).
(ii) Since, Δ PAB ∼ Δ PCD
Substituting the values, we get :
Hence, the length of CD = 6 cm.
(iii) As we know that,
The ratio of the areas of two similar triangles is equal to the ratio of the squares of their corresponding sides.
Hence, the area of ΔPAB : area of ΔPCD = 9 : 4.
In the figure (i) given below, QPX is the bisector of ∠YXZ of the triangle XYZ. Prove that XY : XQ = XP : XZ.
Answer
In △XYQ and △XPZ,
∠Q = ∠Z (∵ angles in same segment are equal as arc XY subtends both the angles at the circle.)
∠YXQ = ∠PXZ (∵ QPX is the bisector of ∠YXZ hence it divides the angle in two equal halves.)
△XYQ ~ △XPZ. (By AA axiom)
Since triangles are similar hence, the ratio of corresponding sides are similar,
Hence, proved that XY : XQ = XP : XZ.
In the figure (ii) given below, chords BA and DC of a circle meet at P. Prove that
(i) ∠PAD = ∠PCB
(ii) PA × PB = PC × PD.

Answer
(i) From figure,
∠PAD + ∠DAB = ∠PCB + ∠BCD (∵ both are equal to 180°)....(i)
∠DAB = ∠BCD (∵ angles in same segment are equal.)
Putting this value of ∠DAB in (i) we get,
⇒ ∠PAD + ∠BCD = ∠PCB + ∠BCD
⇒ ∠PAD = ∠PCB + ∠BCD - ∠BCD
⇒ ∠PAD = ∠PCB
Hence, proved that ∠PAD = ∠PCB.
(ii) In △PBC and △PAD,
∠PAD = ∠PCB (Proved above.)
∠P = ∠P (Common angle.)
△PBC ~ △PAD. (By AA axiom)
Since triangles are similar hence, the ratio of corresponding sides are similar,
Hence proved that PA × PB = PC × PD.
If O is the center of the circle find the value of x in the following figure (using the given information) :

Answer
From figure,

ABCD is a cyclic quadrilateral.
By property of cyclic quadrilateral — An exterior angle of cyclic quadrilateral is equal to opposite interior angle.
We get,
∠BAD = ∠DCE = x°
Arc BD subtends ∠BOD on center and ∠BAD at point A of the circle.
∴ ∠BOD = 2∠BAD (∵ as angle subtended on center of circle is double the angle subtended on any other part.)
⇒ 150° = 2x°
⇒ x° =
⇒ x° = 75°.
Hence, the value of x = 75.
If O is the center of the circle find the value of x in the following figure (using the given information) :

Answer
From figure,

ABCD is a cyclic quadrilateral.
By property of cyclic quadrilateral — An exterior angle of cyclic quadrilateral is equal to opposite interior angle.
We get,
∠BAD = ∠DCE = 80°
Arc BD subtends ∠BOD on center and ∠BAD at point A of the circle.
From figure,
∠BOD = 360° - x°
∴ ∠BOD = 2∠BAD (∵ as angle subtended on center of circle is double the angle subtended on any other part.)
⇒ 360° - x° = 2 × 80°
⇒ x° = 360° - 160°
⇒ x° = 200°.
Hence, the value of x = 200.
If O is the center of the circle find the value of x in the following figure (using the given information) :

Answer
From figure,
ABCD is a cyclic quadrilateral.
∠ACB = 90°. (∵ angle in semi circle is 90°)
Since sum of angles in triangle is 180°.
∴ In △ABC
⇒ ∠CAB + ∠ACB + ∠ABC = 180°
⇒ 25° + 90° + ∠ABC = 180°
⇒ 115° + ∠ABC = 180°
⇒ ∠ABC = 65°.
Since opposite angles sum is 180° in cyclic quadrilateral
⇒ ∠ABC + ∠ADC = 180°
⇒ 65° + x° = 180°
⇒ x° = 180° - 65°
⇒ x° = 115°.
Hence, the value of x = 115.
In the figure (i) given below, O is the center of the circle. If ∠AOC = 150°, find
(i) ∠ABC
(ii) ∠ADC.

Answer
(i) Arc AC subtends ∠AOC on center and ∠ABC at point B of the circle.
∴ ∠AOC = 2∠ABC (∵ as angle subtended on center of circle is double the angle subtended on any other part.)
⇒ 150° = 2∠ABC
⇒ ∠ABC =
⇒ ∠ABC = 75°.
Hence, the value of ∠ABC = 75°.
(ii) From figure,
ABCD is a cyclic quadrilateral.
Since opposite angles sum is 180° in cyclic quadrilateral
⇒ ∠ABC + ∠ADC = 180°
⇒ 75° + x° = 180°
⇒ x° = 180° - 75°
⇒ x° = 105°.
Hence, the value of ∠ADC = 105°.
In the figure (ii) given below, AC is a diameter of the given circle and ∠BCD = 75°. Calculate the size of
(i) ∠ABC
(ii) ∠EAF
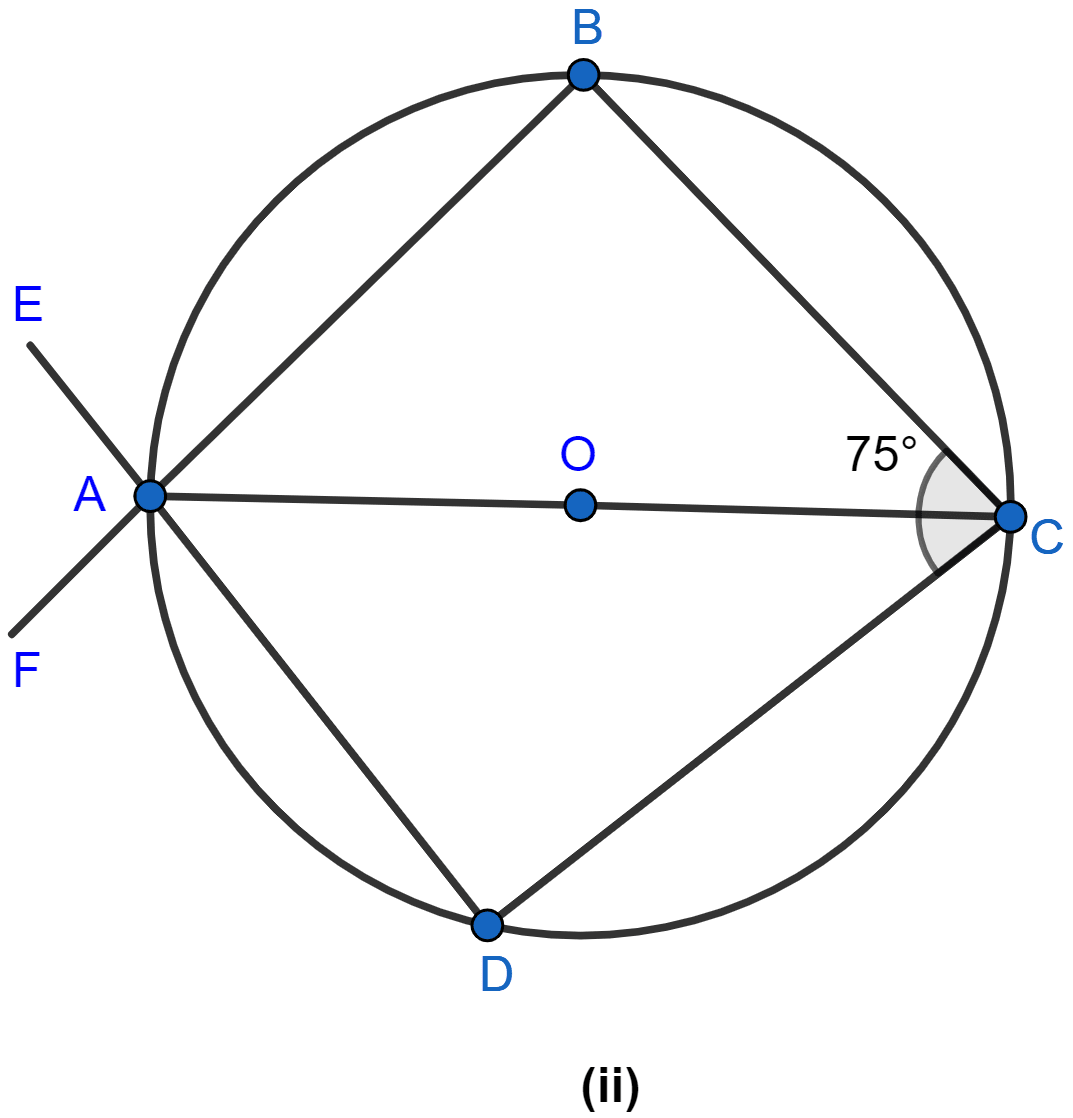
Answer
(i) From figure,
∠ABC = 90° (∵ angle in semicircle is equal to 90°)
Hence, the value of ∠ABC = 90°.
(ii) Since opposite angles sum is 180° in cyclic quadrilateral
⇒ ∠BAD + ∠BCD = 180°
⇒ ∠BAD + 75° = 180°
⇒ ∠BAD = 180° - 75°
⇒ ∠BAD = 105°.
From figure,
∠EAF = ∠BAD = 105°.
Hence, the value of ∠BAD = 105°.
In the figure (i) given below, if ∠DCB = 58° and BD is a diameter of the circle, calculate
(i) ∠BDC
(ii) ∠BEC
(iii) ∠BAC

Answer
(i) Given,
∠DBC = 58°
From figure,
∠BCD = 90° (∵ angle in semicircle is equal to 90°.)
Since sum of angles in triangle is 180°.
∴ In △BCD
⇒ ∠DBC + ∠BCD + ∠BDC = 180°
⇒ 58° + 90° + ∠BDC = 180°
⇒ 148° + ∠BDC = 180°
⇒ ∠BDC = 180° - 148°
⇒ ∠BDC = 32°.
Hence, the value of ∠BDC = 32°.
(ii) Considering quadrilateral BDCE.
From figure,
BDCE is a cyclic quadrilateral.
Since opposite angles sum is 180° in cyclic quadrilateral
⇒ ∠BDC + ∠BEC = 180°
⇒ 32° + ∠BEC = 180°
⇒ ∠BEC = 180° - 32°
⇒ ∠BEC = 148°.
Hence, the value of ∠BEC = 148°.
(iii) From figure,
∠BAC = ∠BDC (∵ angles in same segment are equal.)
∴ ∠BAC = 32°.
Hence, the value of ∠BAC = 32°.
In the figure (ii) given below, AB is parallel to DC, ∠BCE = 80° and ∠BAC = 25°. Find :
(i) ∠CAD
(ii) ∠CBD
(iii) ∠ADC

Answer
(i) ABCD is a cyclic quadrilateral.
Since exterior angle of a cyclic quadrilateral is equal to the opposite interior angle.
∴ ∠BCE = ∠DAB
⇒ ∠BCE = ∠CAD + ∠BAC
⇒ 80° = ∠CAD + 25°
⇒ ∠CAD = 80° - 25°
⇒ ∠CAD = 55°.
Hence, the value of ∠CAD = 55°.
(ii) From figure,
∠CBD = ∠CAD (∵ angles in same segment are equal.)
∠CBD = 55°.
Hence, the value of ∠CBD = 55°.
(iii) ∠BAC = ∠BDC (∵ angles in same segment are equal.)
∠BDC = 25°.
Now AB || DC and BD is the transversal
∠ABD = ∠BDC (∵ ∵ alternate angles are equal.)
⇒ ∠ABD = 25°
From figure,
∠ABC = ∠ABD + ∠CBD = 25° + 55° = 80°.
Since, sum of opposite angles of a cyclic quadrilateral is 180°.
⇒ ∠ABC + ∠ADC = 180°
⇒ 80° + ∠ADC = 180°
⇒ ∠ADC = 180° - 80°
⇒ ∠ADC = 100°.
Hence, the value of ∠ADC = 100°.
In the figure (i) given below, ABCD is a cyclic quadrilateral. If ∠ADC = 80° and ∠ACD = 52°, find the values of ∠ABC and ∠CBD.

Answer
In the given figure,
ABCD is a cyclic quadrilateral.
Since, sum of opposite angles of a cyclic quadrilateral is 180°.
⇒ ∠ABC + ∠ADC = 180°
⇒ ∠ABC + 80° = 180°
⇒ ∠ABC = 180° - 80°
⇒ ∠ABC = 100°.
From figure,
∠DBA = ∠DCA = 52°. (∵ angles in same segment are equal.)
⇒ ∠ABC = ∠DBA + ∠CBD
⇒ 100° = 52° + ∠CBD
⇒ ∠CBD = 100° - 52°
⇒ ∠CBD = 48°.
Hence, ∠ABC = 100° and ∠CBD = 48°.
In the figure (ii) given below, O is the center of the circle. ∠AOE = 150°, ∠DAO = 51°. Calculate the sizes of ∠BEC and ∠EBC.
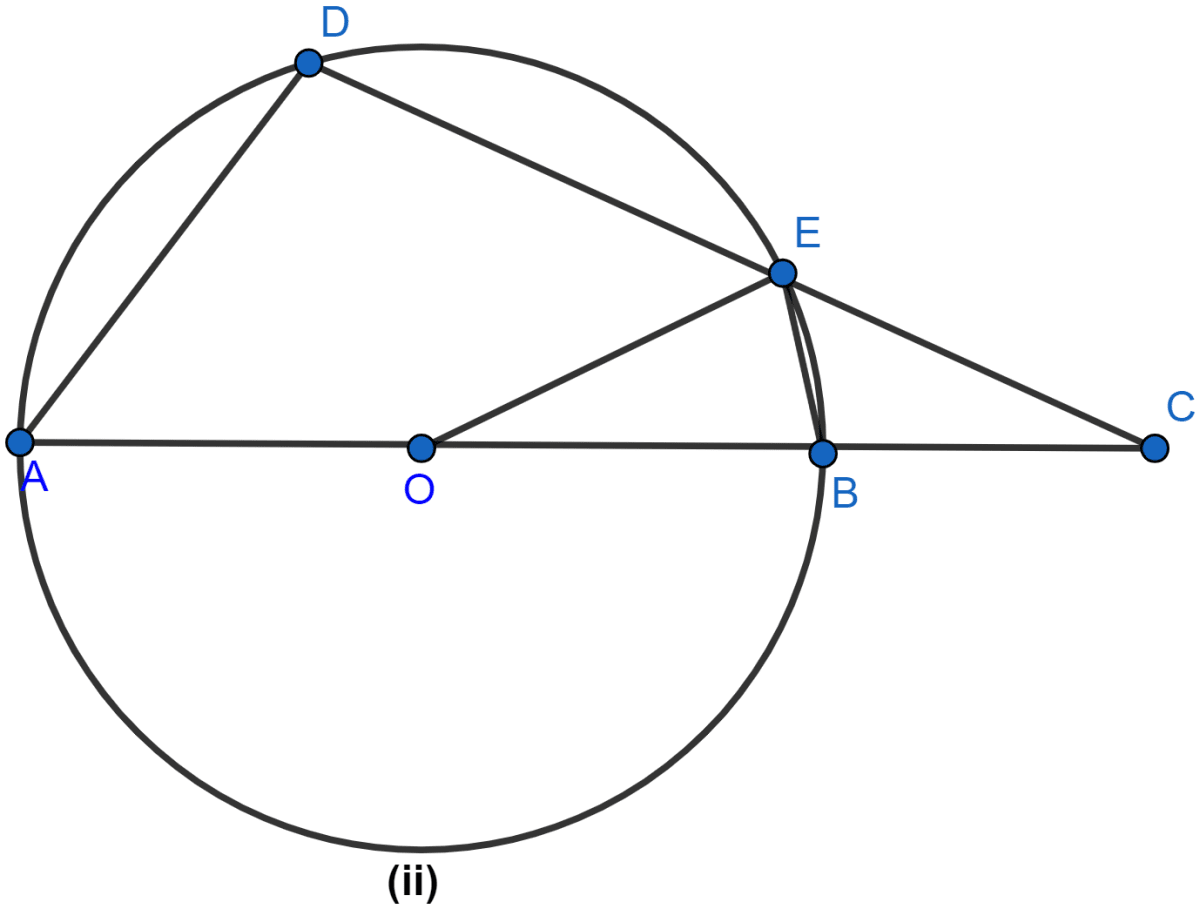
Answer
From figure,
∠DAB = ∠DAO = 51°.
ABED is a cyclic quadrilateral as all vertices lie on the circumference of the circle.
∠BEC = ∠DAB = 51° (∵ exterior angle of a cyclic quadrilateral is equal to the opposite interior angle.)
Reflex ∠AOE = 360° - ∠AOE = 360° - 150° = 210°.
Arc AE subtends ∠ADE at point D and Reflex ∠AOE at center.
Reflex ∠AOE = 2∠ADE (∵ angle subtended by an arc at center is double the angle subtended at any other point of the circle.)
210° = 2∠ADE
∠ADE =
∠ADE = 105°.
∠EBC = ∠ADE = 105° (∵ exterior angle of a cyclic quadrilateral is equal to the opposite interior angle.)
Hence, ∠BEC = 51° and ∠EBC = 105°.
In the figure (i) given below, ABCD is a parallelogram. A circle passes through A and D and cuts AB at E and DC at F. Given that ∠BEF = 80°, find ∠ABC.

Answer
ADFE is a cyclic quadrilateral as all vertices lie on the circumference of the circle.
∠ADF = ∠FEB = 80° (∵ exterior angle of a cyclic quadrilateral is equal to the opposite interior angle.)
As opposite angles of a parallelogram are equal.
∠ABC = ∠ADC
From figure,
∠ADC = ∠ADF = 80°.
∴ ∠ABC = 80°.
Hence, the value of ∠ABC = 80°.
In the figure (ii) given below, ABCD is a cyclic trapezium in which AD is parallel to BC and ∠B = 70°, find
(i) ∠BAD
(ii) ∠BCD

Answer
(i) In trapezium sum of angles on same side = 180°.
⇒ ∠ABC + ∠BAD = 180°
⇒ 70° + ∠BAD = 180°
⇒ ∠BAD = 180° - 70°
⇒ ∠BAD = 110°
Hence, the value of ∠BAD = 110°.
(ii) ABCD is a cyclic quadrilateral as all vertices lie on the circumference of the circle.
Sum of opposite angles of cyclic quadrilateral = 180°
⇒ ∠BAD + ∠BCD = 180°
⇒ 110° + ∠BCD = 180°
⇒ ∠BCD = 180° - 110°
⇒ ∠BCD = 70°.
Hence, the value of ∠BCD = 70°.
In the figure (i) given below, O is the center of the circle. If ∠BAD = 30°, find the values of p, q and r.

Answer
From figure,
ABCD is a cyclic quadrilateral as all vertices lie on the circumference of the circle.
Sum of opposite angles of cyclic quadrilateral = 180°
⇒ ∠A + ∠C = 180°
⇒ 30° + p = 180°
⇒ p = 180° - 30°
⇒ p = 150°.
∠BAD = ∠BED (∵ angles in same segment are equal.)
⇒ r = 30°.
Arc BD subtends ∠BAD at point A and ∠BOD at center.
∠BOD = 2∠BAD (∵ angle subtended by an arc at center is double the angle subtended at any other point of the circle.)
q = 2 × 30°
q = 60°.
Hence, the value of p = 150°, q = 60° and r = 30°.
In the figure (ii) given below, two circles intersect at points P and Q. If ∠A = 80° and ∠D = 84°, calculate
(i) ∠QBC
(ii) ∠BCP

Answer
Join PQ as shown in the figure below:

PQAD is a cyclic quadrilateral as all vertices lie on the circumference of the circle.
Sum of opposite angles of cyclic quadrilateral = 180°
⇒ ∠DAQ + ∠DPQ = 180°
⇒ 80° + ∠DPQ = 180°
⇒ ∠DPQ = 180° - 80°
⇒ ∠DPQ = 100°.
Also,
⇒ ∠PDA + ∠PQA = 180°
⇒ 84° + ∠PQA = 180°
⇒ ∠PQA = 180° - 84°
⇒ ∠PQA = 96°.
Since exterior angle of a cyclic quadrilateral is equal to the opposite interior angle.
∠QBC = ∠DPQ = 100°
∠BCP = ∠PQA = 96°.
Hence, the value of ∠QBC = 100° and ∠BCP = 96°.
In the figure (i) given below, PQ is a diameter. Chord SR is parallel to PQ. Given ∠PQR = 58°, calculate
(i) ∠RPQ
(ii) ∠STP
(T is a point on the minor arc SP)
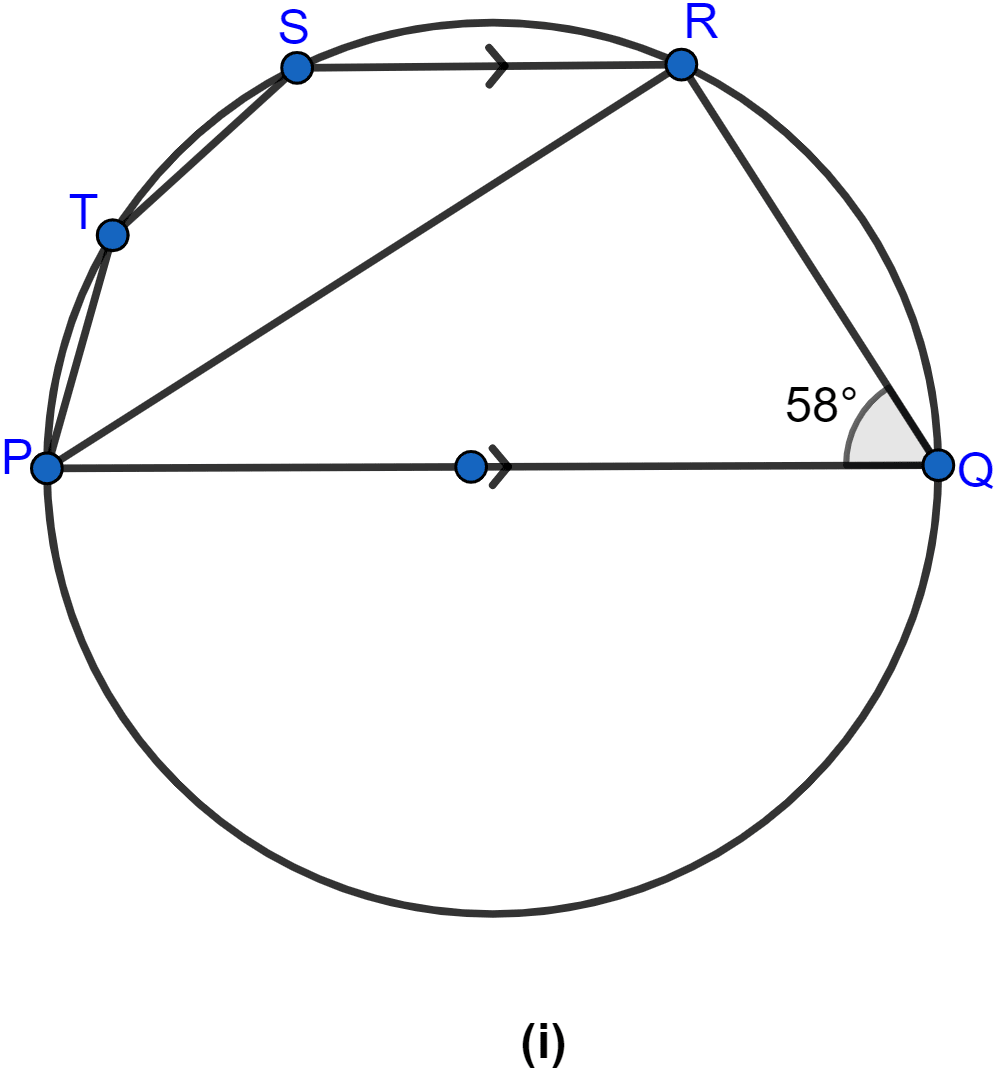
Answer
(i) From figure,
∠PRQ = 90° (∵ angle in semicircle is equal to 90°.)
Since sum of angles in triangle is 180°.
⇒ ∠PRQ + ∠RQP + ∠RPQ = 180°
⇒ 90° + 58° + ∠RPQ = 180°
⇒ ∠RPQ + 148° = 180°
⇒ ∠RPQ = 180° - 148
⇒ ∠RPQ = 32°.
Hence, the value of ∠RPQ = 32°.
(ii) From figure,
∠SRP = ∠RPQ = 32° (∵ alternate angles are equal.)
Since, PTSR is a cyclic quadrilateral so sum of its opposite angles is equal to 180°.
⇒ ∠SRP + ∠STP = 180°
⇒ 32° + ∠STP = 180°
⇒ ∠STP = 180° - 32°
⇒ ∠STP = 148°.
Hence, the value of ∠STP = 148°.
In the figure (ii) given below, if ∠ACE = 43° and ∠CAF = 62°, find the values of a, b and c.
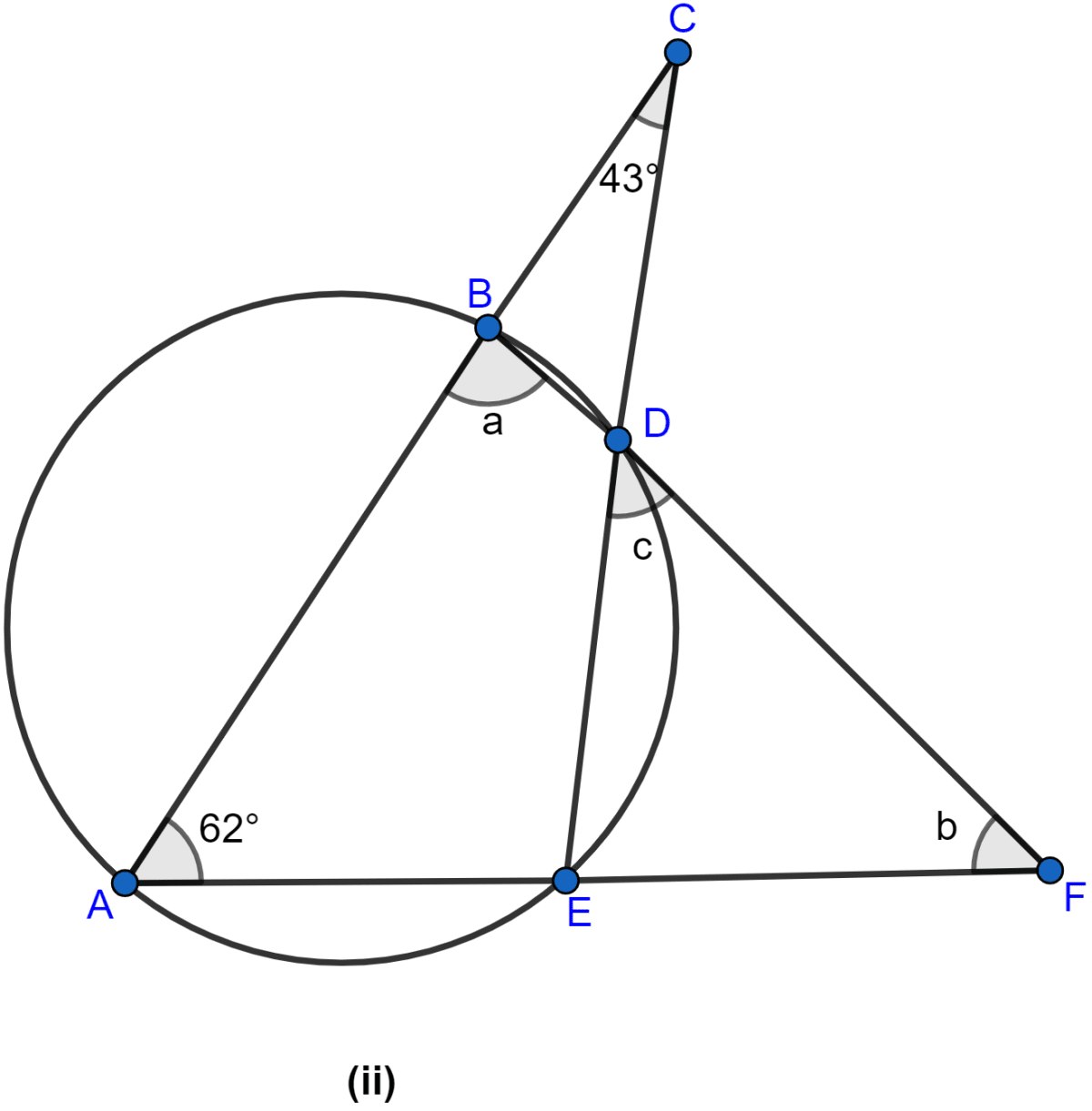
Answer
From figure,
∠CAE = ∠CAF = 62°
Since sum of angles in triangle is 180°.
In △ACE,
⇒ ∠CAE + ∠ACE + ∠CEA = 180°
⇒ 62° + 43° + ∠CEA = 180°
⇒ ∠CEA + 105° = 180°
⇒ ∠CEA = 180° - 105°
⇒ ∠CEA = 75°.
From figure,
⇒ ∠CEA + ∠DEF = 180° (As they are linear pair.)
⇒ 75° + ∠DEF = 180°
⇒ ∠DEF = 180° - 75°
⇒ ∠DEF = 105°.
ABDE is a cyclic quadrilateral as all of its vertices lie on the circumference of the circle.
Since exterior angle of a cyclic quadrilateral is equal to the opposite interior angle.
⇒ ∠ABD = ∠DEF = 105°
⇒ a = 105°.
Since sum of angles in triangle is 180°.
In △ABF,
⇒ ∠BAF + ∠ABF + ∠BFA = 180°
⇒ 62° + a + b = 180°
⇒ 62° + 105° + b = 180°
⇒ b + 167° = 180°
⇒ b = 180° - 167°
⇒ b = 13°
Since exterior angle of a cyclic quadrilateral is equal to the opposite interior angle.
⇒ ∠EDF = ∠BAE = 62°
⇒ c = 62°.
Hence, the value of a = 105°, b = 13° and c = 62°.
In the figure (i) given below, AB is a diameter of the circle. If ∠ADC = 120°, find ∠CAB.
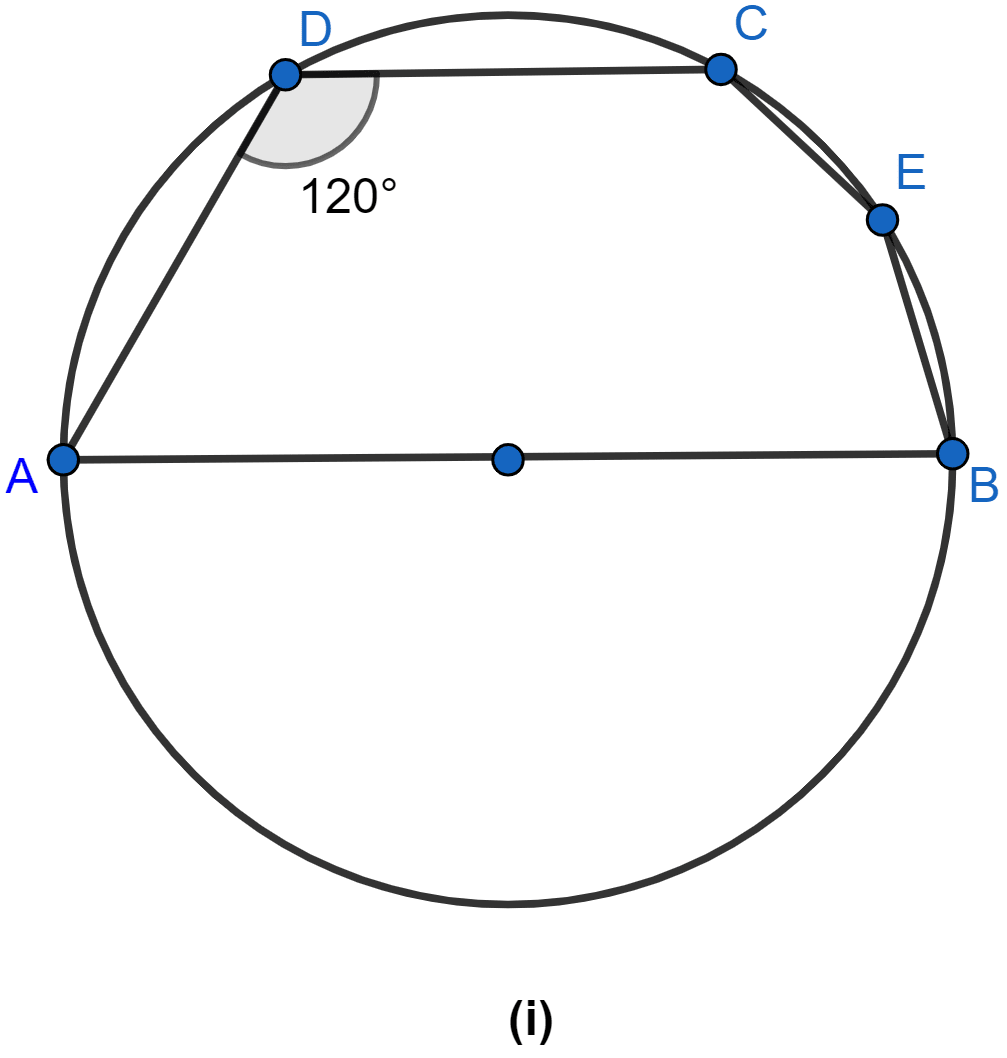
Answer
Join CB as shown in the figure below:
So, ABCD becomes a cyclic quadrilateral.
Sum of opposite angles of cyclic quadrilateral = 180°
⇒ ∠CBA + ∠ADC = 180°
⇒ ∠CBA + 120° = 180°
⇒ ∠CBA = 180° - 120°
⇒ ∠CBA = 60°.
Join AC.
In △ABC
∠ACB = 90° (∵ angle in semicircle is equal to 90°.)
Sum of angles of triangle = 180°
⇒ ∠CAB + ∠ACB + ∠CBA = 180°
⇒ ∠CAB + 90° + 60° = 180°
⇒ ∠CAB + 150° = 180°
⇒ ∠CAB = 180° - 150°
⇒ ∠CAB = 30°.
Hence, the value of ∠CAB = 30°.
In the figure (ii) given below, sides AB and DC of a cyclic quadrilateral ABCD are produced to meet at E, the sides AD and BC are produced to meet at F. If x : y : z = 3 : 4 : 5, find the values of x, y and z.
Answer
In figure,
ABCD is a cyclic quadrilateral.
∠DAB = ∠BCE = x (Property of cyclic quadrilateral by which an exterior angle = opposite interior angle.)
In △BCE
∠CBE = 180° - (x° + y°)
From figure,
∠CBE and ∠CBA are linear pairs.
So,
⇒ ∠CBE + ∠CBA = 180°
⇒ 180° - (x° + y°) + ∠CBA = 180°
⇒ ∠CBA = 180° - 180° + (x° + y°)
⇒ ∠CBA = x° + y°
In △ABF,
So,
∠BAF + ∠ABF + ∠AFB = 180°
x + (x + y) + z = 180° (∵ From figure, ∠BAF = ∠DAB and ∠ABF = ∠CBA)
Given x : y : z = 3 : 4 : 5 , so x = 3k, y = 4k and z = 5k
3k + (3k + 4k) + 5k = 180°
15k = 180°
k = 12°
Hence, x = 3k = 3 × 12° = 36°, y = 4k = 4 × 12° = 48° and z = 5k = 5 × 12° = 60°.
Hence, the value of x = 36°, y = 48° and z = 60°.
In the figure (i) given below, ABCD is a quadrilateral inscribed in a circle with centre O. CD is produced to E. If ∠ADE = 70° and ∠OBA = 45°, calculate
(i) ∠OCA
(ii) ∠BAC
Answer
Join OA, OB, OC and AC as shown in the figure below:
(i) ABCD is a cyclic quadrilateral as all the vertices lie on the circumference.
Since exterior angle of a cyclic quadrilateral is equal to the opposite interior angle.
⇒ ∠ADE = ∠ABC = 70°.
Arc AC subtends ∠AOC at center and ∠ABC at point B,
∠AOC = 2∠ABC (∵ angle subtended by an arc at centre is double the angle subtended at any other point of the circle.)
⇒ ∠AOC = 2 × 70° = 140°.
From figure,
OA = OC = Radius of the circle.
So, ∠OCA = ∠OAC = x.
Since sum of angles of triangle = 180°
In △OCA,
⇒ ∠AOC + ∠OCA + ∠OAC = 180°
⇒ 140° + x + x = 180°
⇒ 140° + 2x = 180°
⇒ 2x = 180° - 140°
⇒ 2x = 40°
⇒ x = 20°.
Hence, the value of ∠OCA = 20°.
(ii) From above solution,
∠ABC = 70°
From figure,
∠ABC = ∠OBA + ∠OBC
70° = 45° + ∠OBC
∠OBC = 70° - 45°
∠OBC = 25°.
As, OB = OC = radius of the circle.
∴ ∠OCB = ∠OBC = 25°.
From figure,
⇒ ∠ACB = ∠OCB + OCA
⇒ ∠ACB = 25° + 20° = 45°
Since sum of angles of triangle = 180°
In △ABC,
⇒ ∠ABC + ∠ACB + ∠BAC = 180°
⇒ 70° + 45° + ∠BAC = 180°
⇒ 115° + ∠BAC = 180°
⇒ ∠BAC = 180° - 115°
⇒ ∠BAC = 65°
Hence, the value of ∠BAC = 65°.
In figure (ii) given below, ABF is a straight line and BE || DC. If ∠DAB = 92° and ∠EBF = 20°, find
(i) ∠BCD
(ii) ∠ADC
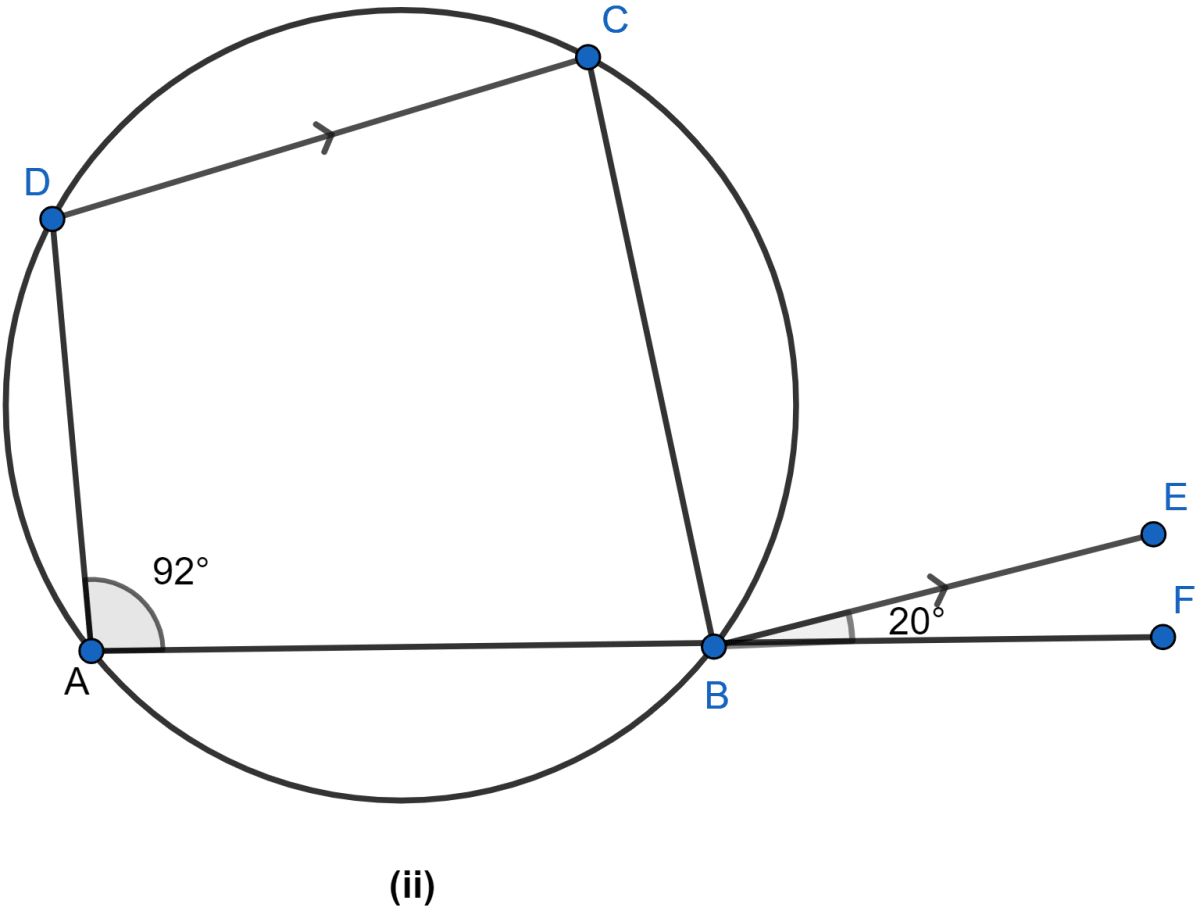
Answer
(i) Sum of opposite angles of cyclic quadrilateral = 180°
⇒ ∠DAB + ∠BCD = 180°
⇒ 92° + ∠BCD = 180°
⇒ ∠BCD = 180° - 92°
⇒ ∠BCD = 88°.
Hence, the value of ∠BCD = 88°.
(ii) ∠CBE = ∠BCD = 88° (∵ ∠CBE and ∠BCD are alternate angles)
∵ exterior angle of a cyclic quadrilateral is equal to the opposite interior angle.
⇒ ∠ADC = ∠CBF
⇒ ∠ADC = ∠CBE + ∠EBF
⇒ ∠ADC = 88° + 20°
⇒ ∠ADC = 108°.
Hence, the value of ∠ADC = 108°.
In the figure (i) given below, PQRS is a cyclic quadrilateral in which PQ = QR and RS is produced to T. If ∠QPR = 52°, calculate ∠PST.

Answer
Given, ∠QPR = 52°.
Since PQ = PR so, ∠QRP = ∠QPR = 52°.
Since sum of angles of triangle = 180°
In △PQR
⇒ ∠QPR + ∠QRP + ∠PQR = 180°
⇒ 52° + 52° + ∠PQR = 180°
⇒ 104° + ∠PQR = 180°
⇒ ∠PQR = 180° - 104°
⇒ ∠PQR = 76°.
∵ exterior angle of a cyclic quadrilateral is equal to the opposite interior angle.
∠PST = ∠PQR = 76°
Hence, the value of ∠PST = 76°
In the figure (ii) given below, O is the center of the circle. If ∠OAD = 50°, find the values of x and y.

Answer
From figure,
ABCD is a cyclic quadrilateral as all vertices lie on the circumference of the circle.
Sum of opposite angles of cyclic quadrilateral = 180°
⇒ ∠BCD + ∠BAD = 180°
⇒ x + 50° = 180°
⇒ x = 180° - 50°
⇒ x = 130°.
OA = OD = radius of the circle.
So, in △ODA,
∠ODA = ∠OAD = 50°.
In triangle exterior angle is equal to the sum of the opposite two interior angle.
y = ∠ODA + ∠OAD = 50° + 50° = 100°.
Hence, the value of x = 130° and y = 100°.
In the figure (i) given below, O is the center of the circle. If ∠COD = 40° and ∠CBE = 100°, then find :
(i) ∠ADC
(ii) ∠DAC
(iii) ∠ODA
(iv) ∠OCA

Answer
(i) ABCD is a cyclic quadrilateral.
∵ exterior angle of a cyclic quadrilateral is equal to the opposite interior angle.
∠ADC = ∠CBE = 100°.
Hence, the value of ∠ADC = 100°
(ii) Arc DC subtends ∠DOC at center and ∠DAC at point A.
⇒ ∠DOC = 2∠DAC (∵ angle subtended on center by an arc is double the angle subtended on the remaining part of circle.)
⇒ 40° = 2∠DAC
⇒ ∠DAC = 20°
Hence, the value of ∠DAC = 20°.
(iii) In △COD, OC = OD = radius of the same circle.
∠CDO = ∠DCO = x
Since sum of angles of triangle = 180°
In △COD
⇒ ∠CDO + ∠DCO + ∠COD = 180°
⇒ x + x + 40° = 180°
⇒ 40° + 2x = 180°
⇒ 2x = 180° - 40°
⇒ 2x = 140°
⇒ x = 70°.
From figure,
⇒ ∠ADC = ∠ODA + ∠CDO
⇒ 100° = ∠ODA + 70°
⇒ ∠ODA = 100° - 70° = 30°.
Hence, the value of ∠ODA = 30°.
(iv) Since sum of angles of triangle = 180°
In △ADC
⇒ ∠ADC + ∠DAC + ∠ACD = 180°
⇒ 100° + 20° + ∠ACD = 180°
⇒ 120° + ∠ACD = 180°
⇒ ∠ACD = 180° - 120°
⇒ ∠ACD = 60°.
From figure,
∠OCA = ∠DCO - ∠ACD = 70° - 60° = 10°.
Hence, the value of ∠OCA = 10°.
In the figure (ii) given below, O is the center of the circle. If ∠BAD = 75° and BC = CD, find:
(i) ∠BOD
(ii) ∠BCD
(iii) ∠BOC
(iv) ∠OBD
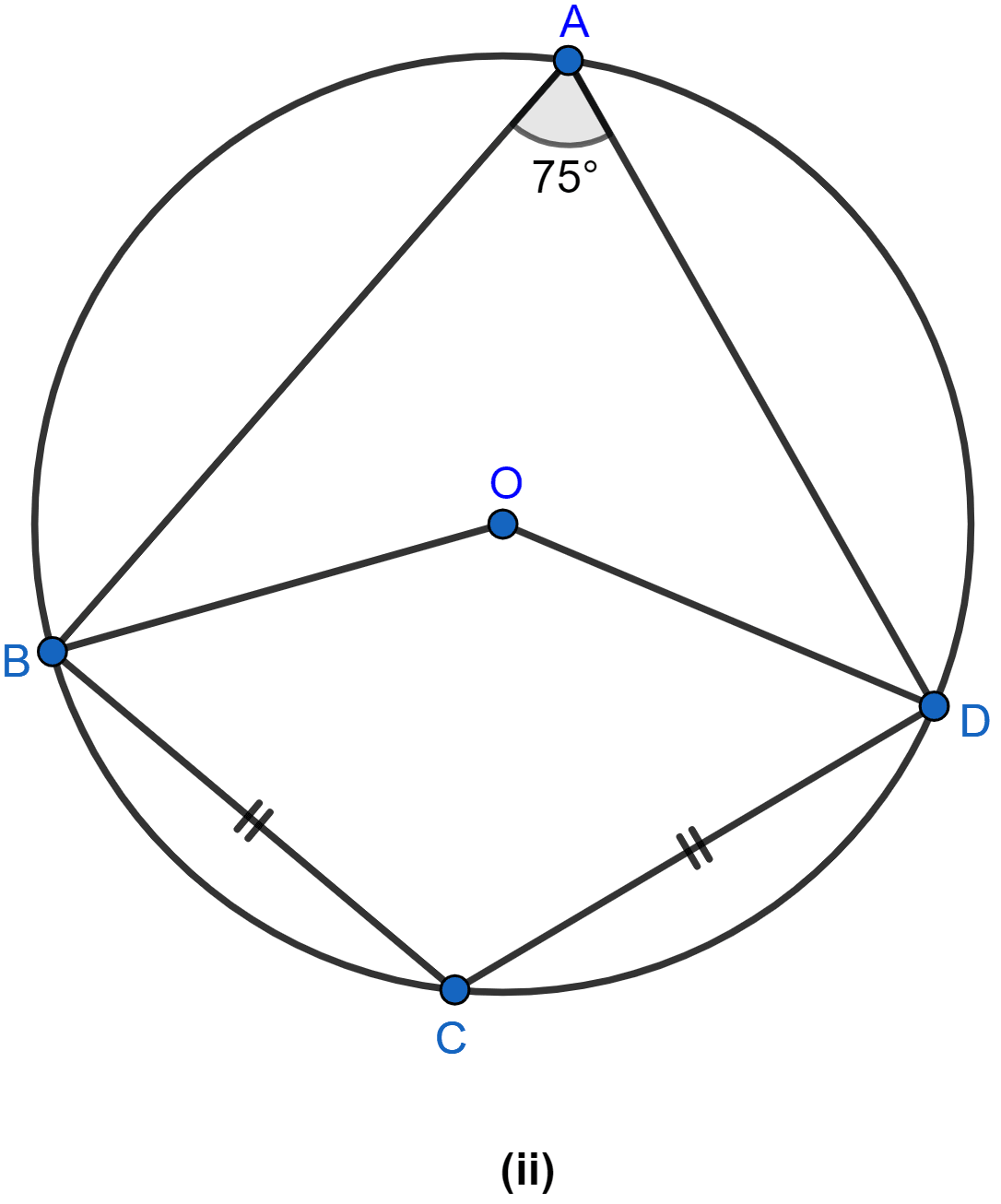
Answer
Join OC and BD as shown in the figure below:
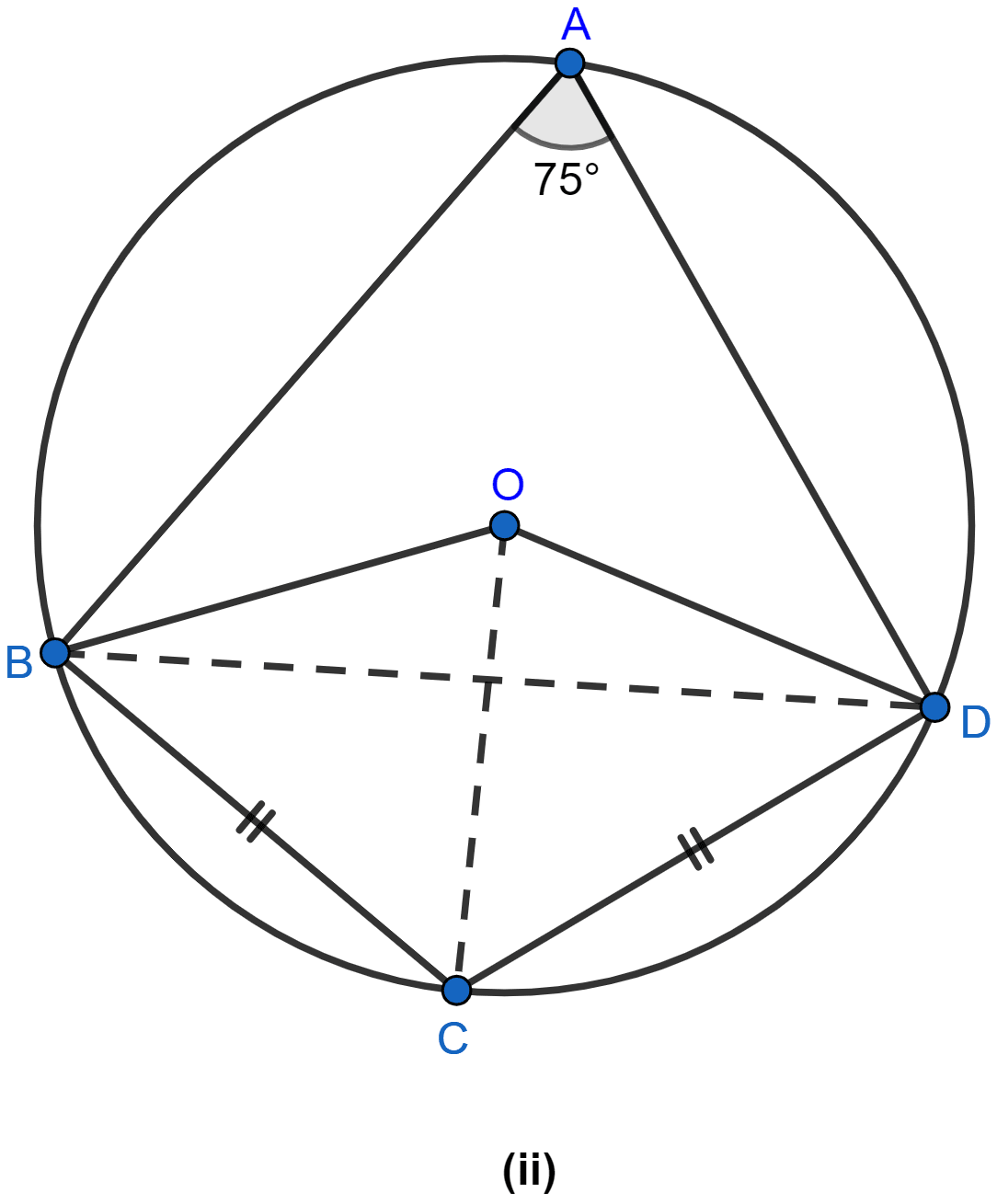
(i) ∠BOD = 2 × ∠BAD (∵ angle subtended by an arc at center is double the angle subtended at any point on the remaining part of the circle.)
∠BOD = 2 × 75° = 150°.
Hence, the value of ∠BOD = 150°.
(ii) ABCD is a cyclic quadrilateral as all of its vertices lie on the circumference of the circle.
We know that sum of opposite angles of a cyclic quadrilateral = 180°.
⇒ ∠BCD + ∠BAD = 180°
⇒ ∠BCD + 75° = 180°
⇒ ∠BCD = 180° - 75°
⇒ ∠BCD = 105°.
Hence, the value of ∠BCD = 105°.
(iii) Join OC.
As equal chords of a circle subtend equal angles at the center and chord BC = chord CD, so ∠BOC = ∠COD.
∠BOC = ∠BOD = = 75°.
Hence, the value of ∠BOC = 75°.
(iv) Join BD.
Since, OB = OD
∴ ∠OBD = ∠ODB = x
Since sum of angles of triangle = 180°
In △OBD
⇒ ∠BOD + ∠OBD + ∠ODB = 180°
⇒ 150° + x + x = 180°
⇒ 150° + 2x = 180°
⇒ 2x = 180° - 150°
⇒ 2x = 30°
⇒ x = 15°.
Hence, the value of ∠OBD = 15°.
In the adjoining figure, O is the center and AOE is the diameter of the semicircle ABCDE. If AB = BC and ∠AEB = 50°, find :
(i) ∠CBE
(ii) ∠CDE
(iii) ∠AOB.
Prove that OB is parallel to EC.
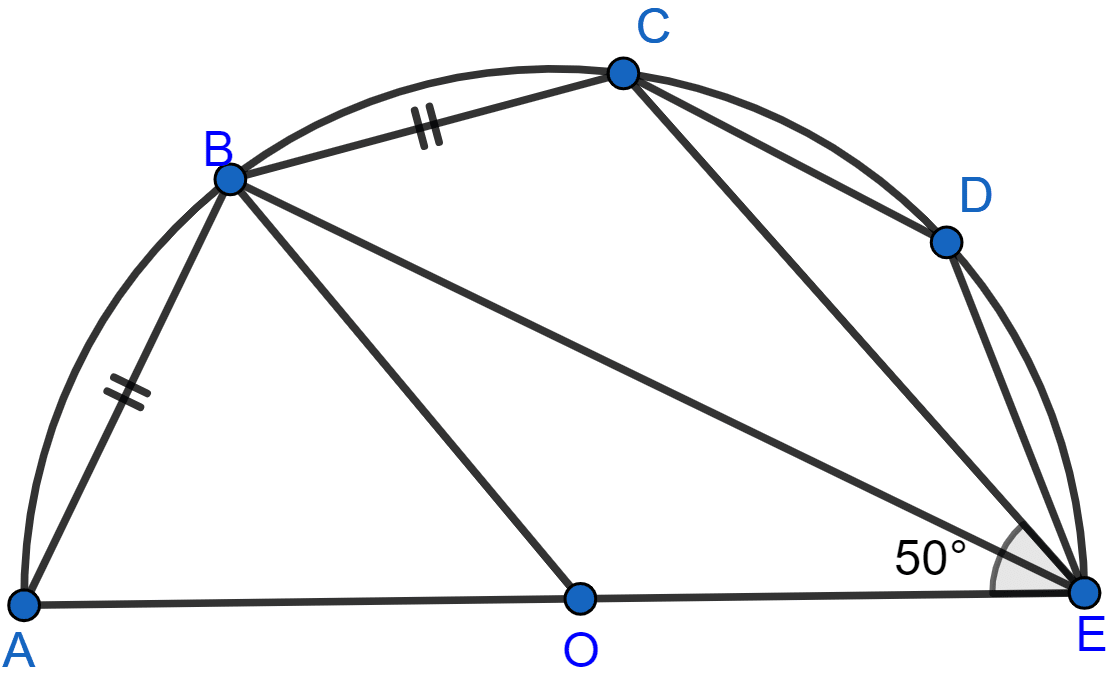
Answer
(i) AECB is a cyclic quadrilateral as all of its vertices lie on the circumference of the circle.
From figure,
∠ABE = 90° (∵ angle in semicircle is 90°.)
We know that sum of opposite angles of a cyclic quadrilateral = 180°.
⇒ ∠AEC + ∠ABC = 180°
⇒ ∠AEC + ∠ABE + ∠CBE = 180°
⇒ 50° + 90° + ∠CBE = 180°
⇒ ∠CBE + 140° = 180°
⇒ ∠CBE = 180° - 140° = 40°.
Hence, the value of ∠CBE = 40°.
(ii) BEDC is a cyclic quadrilateral as all of its vertices lie on the circumference of the circle.
We know that sum of opposite angles of a cyclic quadrilateral = 180°.
⇒ ∠CBE + ∠CDE = 180°
⇒ 40° + ∠CDE = 180°
⇒ ∠CDE = 180° - 40° = 140°.
Hence, the value of ∠CDE = 140°.
(iii) Given,
AB = BC
∴ ∠AEB = ∠BEC = ∠AEC = (∵ equal chords subtend equal angle at circumference.)
In △OBE,
OB = OE = radius of the same circle
∴ ∠OBE = ∠OEB = 25°.
In triangle exterior angle is equal to the sum of opposite two interior angles.
∠AOB = ∠OBE + ∠OEB = 25° + 25° = 50°.
Hence, the value of ∠AOB = 50°.
∠AOB = ∠OEC (∵ both are equal to 50°)
Since these angles are corresponding angles and are equal which is property of parallel lines.
Hence proved that OB || EC.
In the figure (i) given below, ED and BC are two parallel chords of the circle and ABE, ACD are two st. lines. Prove that AED is an isosceles triangle.
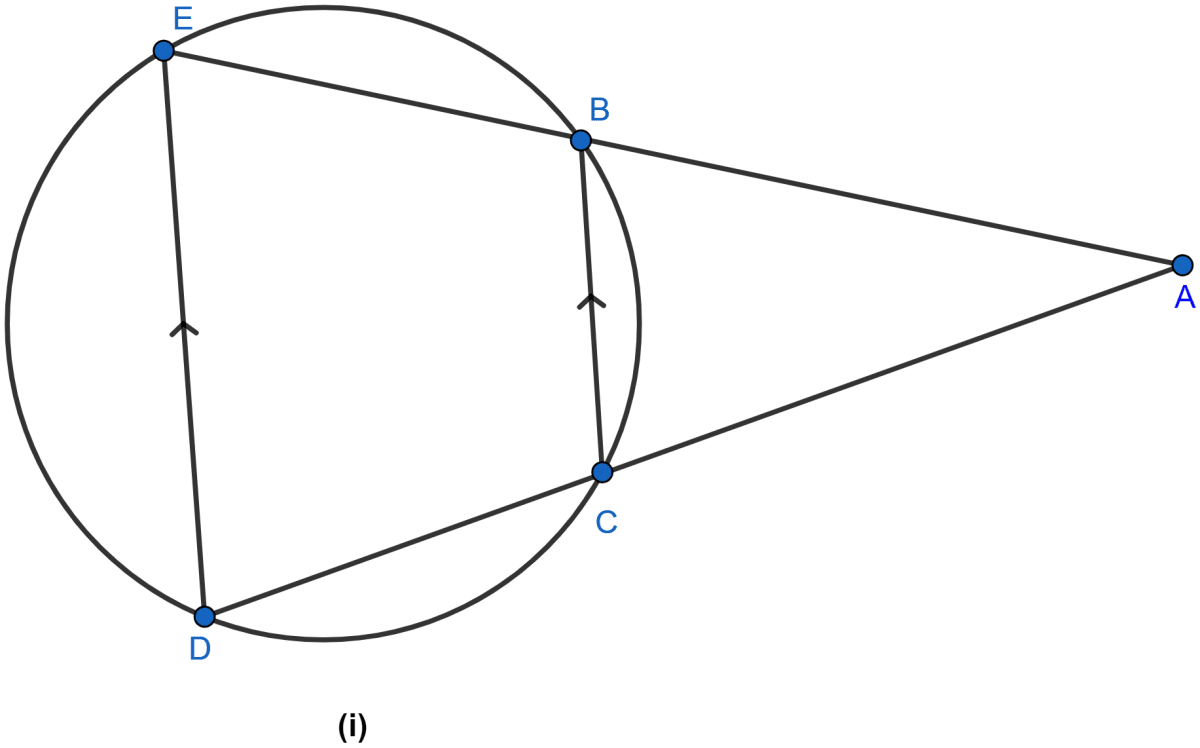
Answer
BEDC is a cyclic quadrilateral as all of its vertices lie on the circumference of the circle.
∵ exterior angle of a cyclic quadrilateral is equal to the opposite interior angle.
∠ABC = ∠D ....(i)
From figure, as ED is parallel to BC, ∠ABC and ∠E are corresponding angles,
∴ ∠ABC = ∠E ....(ii)
From (i) and (ii)
∠D = ∠E
In △AED,
∠D = ∠E,
∴ AE = AD. (As sides opposite to equal angles are equal)
Hence, proved that △AED is an isosceles triangle.
In the figure (ii) given below, SP is the bisector of ∠RPT and PQRS is a cyclic quadrilateral. Prove that SQ = RS.
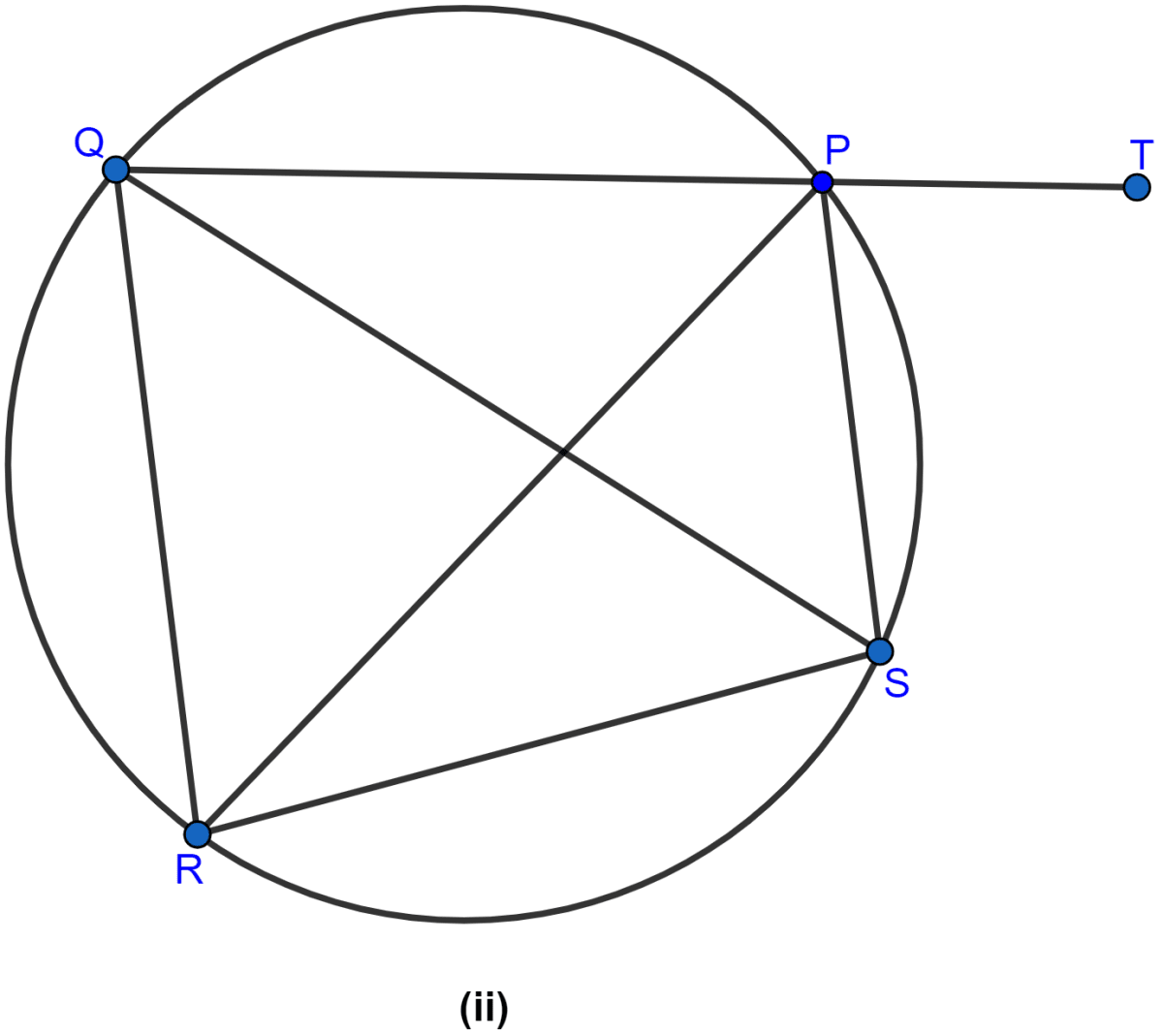
Answer
Since, SP is the bisector of the angle ∠RPT.
So, ∠RPS = ∠SPT
From figure,
∠RPS = ∠RQS (As angle in same segment are equal)
Given, PQRS is a cyclic quadrilateral.
∵ exterior angle of a cyclic quadrilateral is equal to the opposite interior angle.
∠QRS = ∠SPT
∴ ∠QRS = ∠RPS
or,
∠QRS = ∠RQS
In △QRS,
∠QRS = ∠RQS
∴ SQ = RS (As sides opposite to equal angles are equal.)
Hence, proved that SQ = RS.
In the adjoining figure, ABC is an isosceles triangle in which AB = AC and circle passing through B and C intersects sides AB and AC at points D and E. Prove that DE || BC.
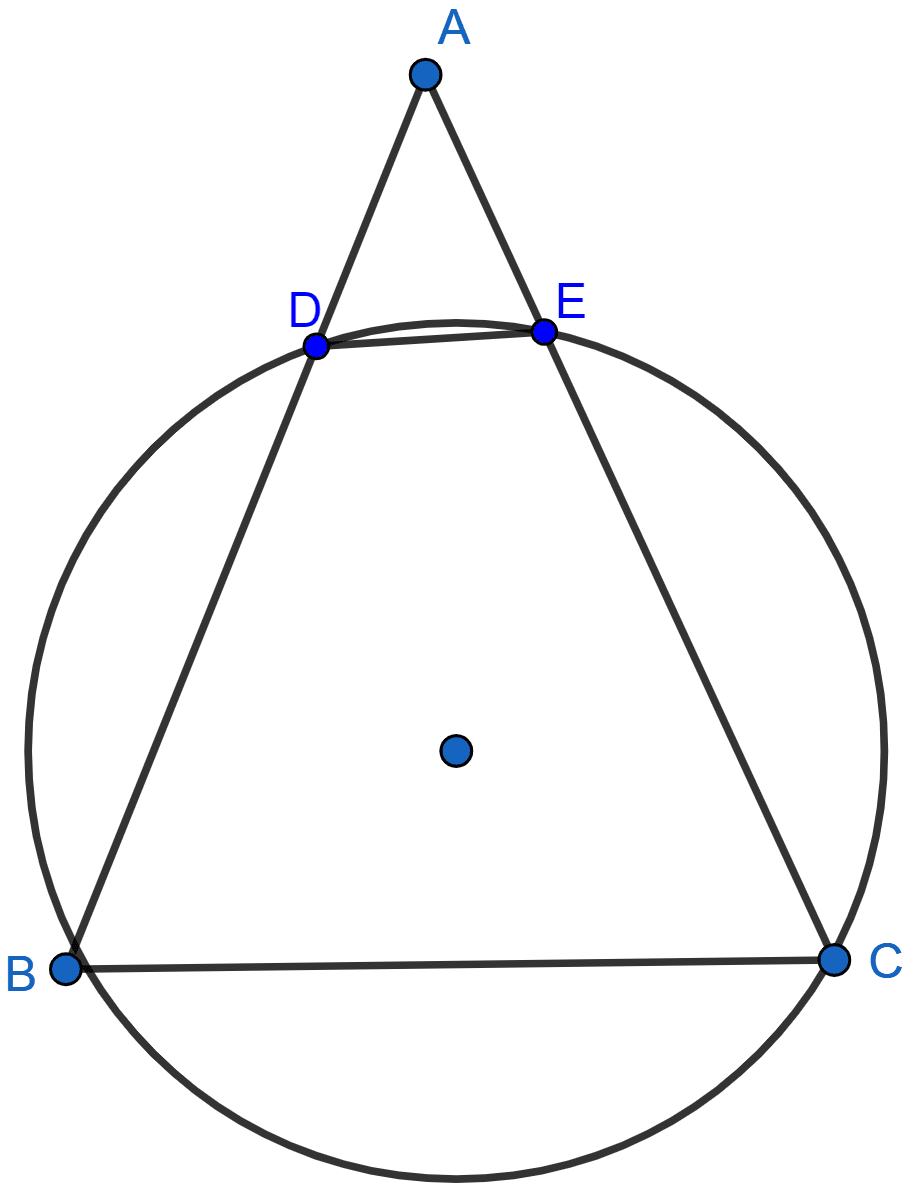
Answer
Given, AB = AC
∴ ∠ABC = ∠ACB (As angles opposite to equal sides are equal)
As BCED is a cyclic quadrilateral,
∠ADE = ∠BCE (∵ exterior angle of a cyclic quadrilateral is equal to the opposite interior angle.)
∴ ∠ADE = ∠ABC
Since these angles are equal and are corresponding this is the property of parallel lines,
∴ DE || BC.
Hence, proved that DE || BC.
Prove that a cyclic parallelogram is a rectangle.
Answer
Let ABCD be a cyclic parallelogram.
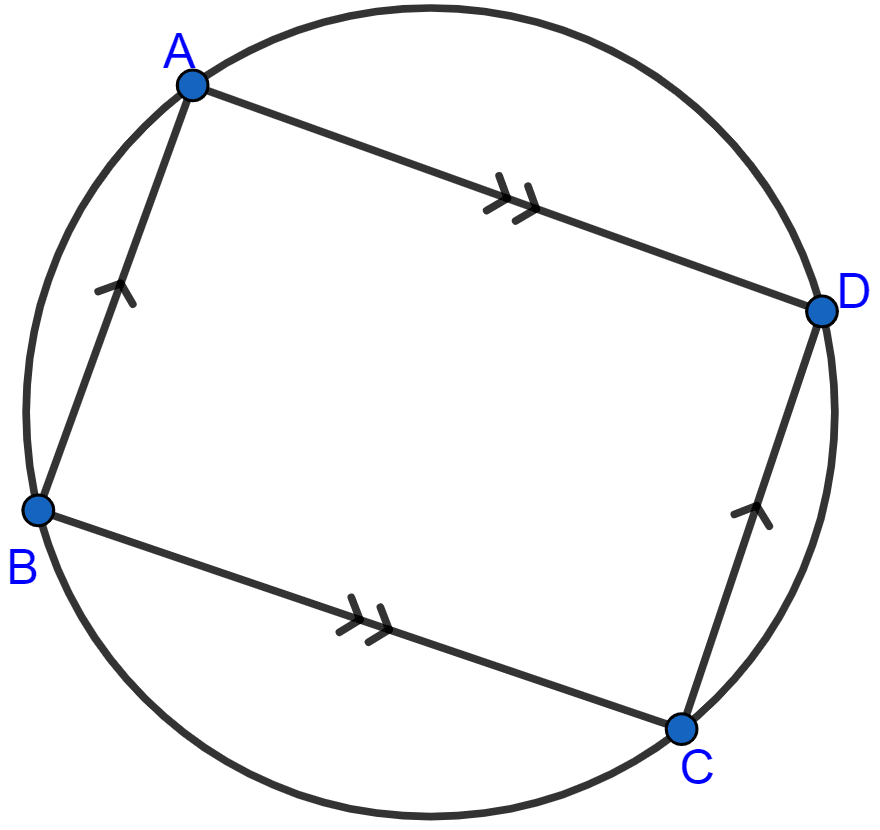
In parallelogram opposite angles are equal.
∴ ∠A = ∠C and ∠B = ∠D.
Sum of opposite angles of a cyclic quadrilateral is 180°
⇒ ∠A + ∠C = 180°
⇒ ∠A + ∠A = 180°
⇒ 2∠A = 180°
⇒ ∠A = 90°.
∴ ∠C = 90°.
Similarly,
⇒ ∠B + ∠D = 180°
⇒ ∠B + ∠B = 180°
⇒ 2∠B = 180°
⇒ ∠B = 90°.
∴ ∠D = 90°.
Hence, ∠A = ∠B = ∠C = ∠D = 90°.
In parallelogram opposite sides are equal i.e. AD = BC and AB = CD.
Hence, ABCD is a rectangle as opposite sides are equal and all the angles are equal to 90°.
Prove that a cyclic rhombus is a square.
Answer
Let ABCD be a cyclic rhombus.

In rhombus opposite angles are equal.
∴ ∠A = ∠C and ∠B = ∠D.
Sum of opposite angles of a cyclic quadrilateral is 180°
⇒ ∠A + ∠C = 180°
⇒ ∠A + ∠A = 180°
⇒ 2∠A = 180°
⇒ ∠A = 90°.
∴ ∠C = 90°.
Similarly,
⇒ ∠B + ∠D = 180°
⇒ ∠B + ∠B = 180°
⇒ 2∠B = 180°
⇒ ∠B = 90°.
∴ ∠D = 90°.
Hence, ∠A = ∠B = ∠C = ∠D = 90°.
In rhombus all sides are equal i.e. AD = BC = AB = CD.
Hence, ABCD is a square as all sides are equal and all the angles are equal to 90°.
In the adjoining figure, chords AB and CD of the circle are produced to meet at O. Prove that triangles ODB and OAC are similar. Given that CD = 2 cm, DO = 6 cm and BO = 3 cm, calculate AB. Also find

Answer
In △ODB and △OAC,
∠ODB = ∠C
∠O = ∠O (Common)
∴ △ODB ~ △OAC (AA axiom)
Since, in similar triangles the ratio of the corresponding sides are equal.
AB = OA - OB = 16 - 3 = 13 cm.
Since, △ODB ~ △OAC
Subtracting 1 from both sides we get,
Dividing (ii) by (i),
Hence, the length of AB = 13 cm and
Find the length of the tangent drawn to a circle of radius 3 cm, from a point distant 5 cm from the centre.
Answer
Let tangent be drawn from point P.
In a circle with centre O and radius = 3 cm and P is at a distance of 5 cm.

OT = 3 cm and OP = 5 cm
OT ⊥ PT
In right angle △OTP,
By pythagoras theorem,
Hence, the length of tangent = 4 cm.
A point P is at a distance 13 cm from the centre C of a circle, and PT is a tangent to the given circle. If PT = 12 cm, find the radius of the circle.
Answer
The below diagram shows the circle and the tangent:
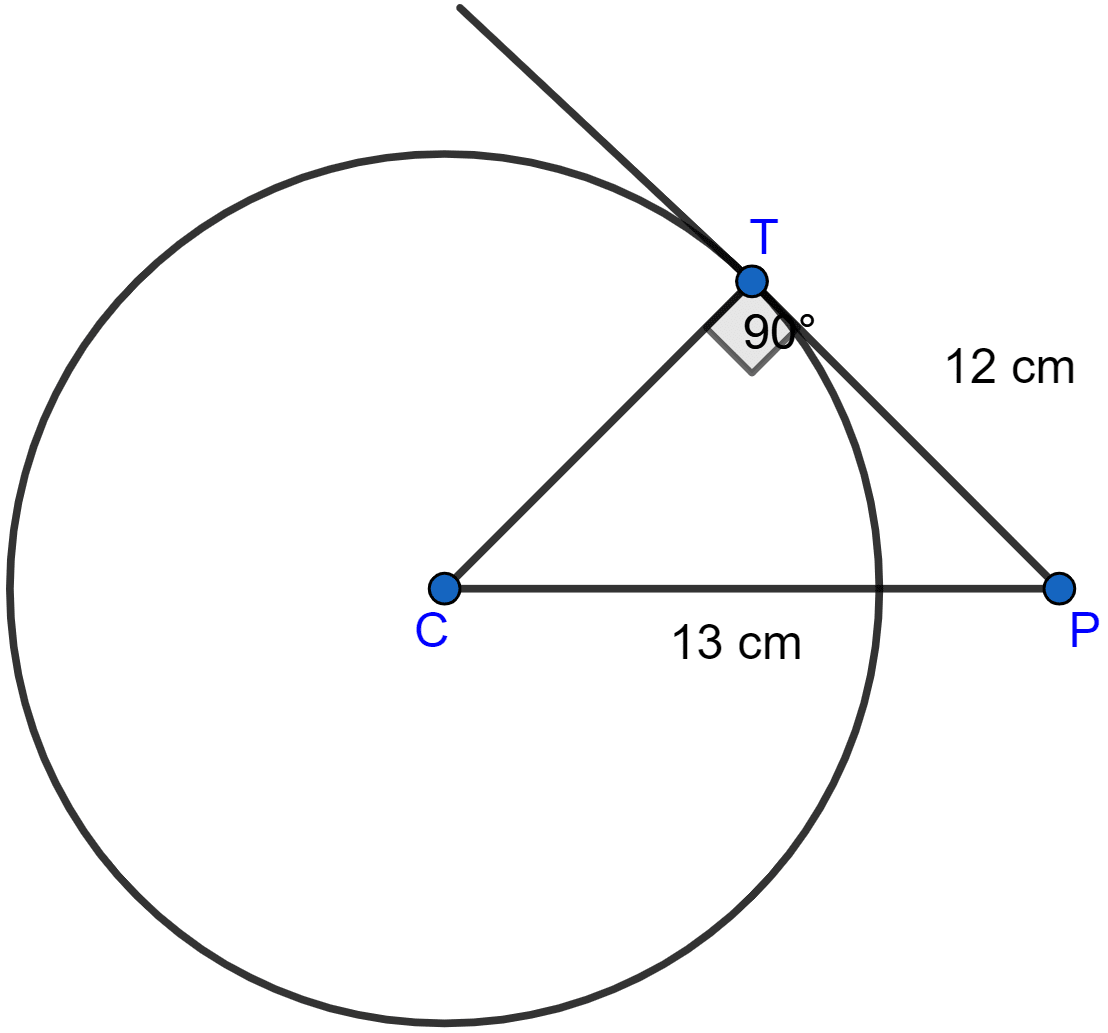
Given point P is 13 cm away from centre C, so CP = 13 cm.
PT = 12 cm
CT = radius of the circle.
Since the tangent at any point of a circle and the radius through the point are perpendicular to each other.
So, CT ⊥ PT
So, in right angled △CPT by pythagoras theorem,
Hence, radius of circle = 5 cm.
The tangent to a circle of radius 6 cm from an external point P, is of length 8 cm. Calculate the distance of P from the nearest point of the circle.
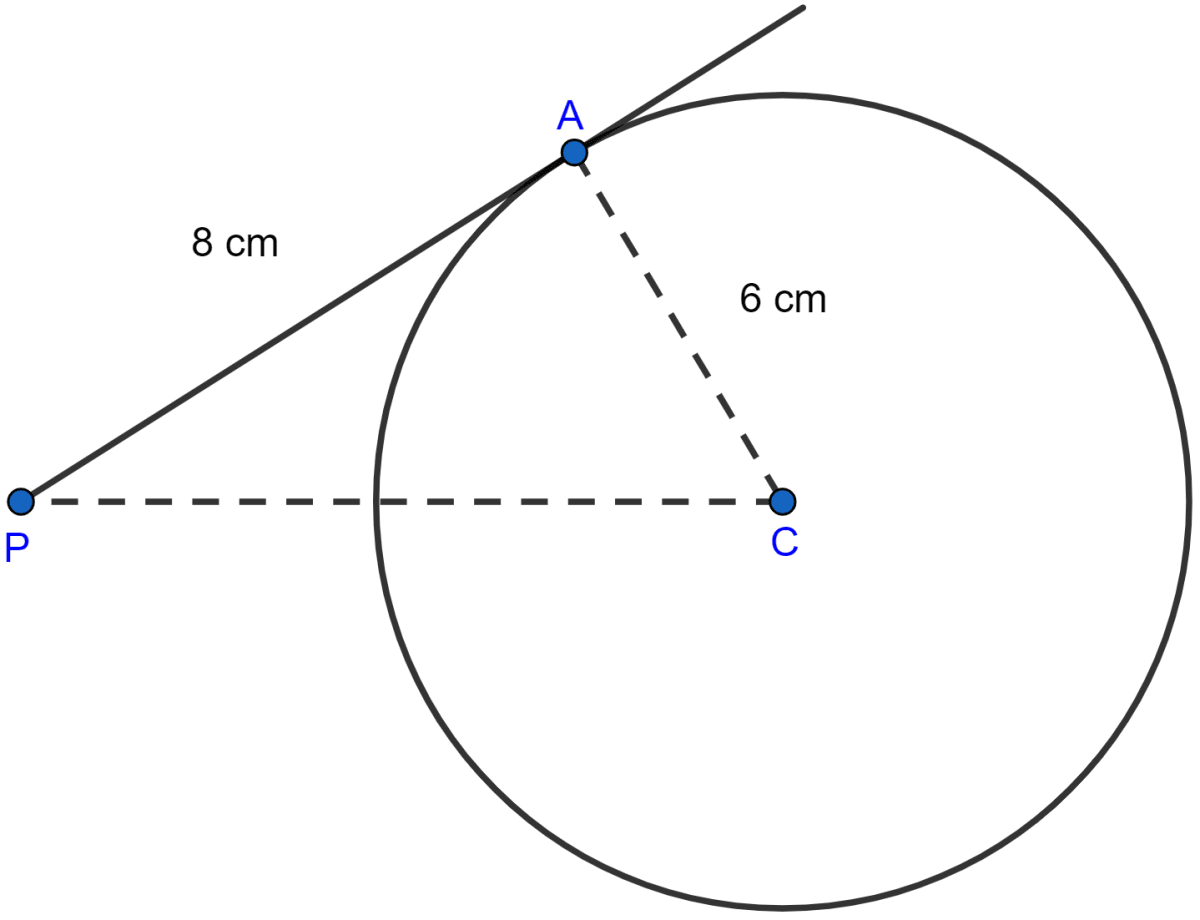
Answer
Since the tangent at any point of a circle and the radius through the point are perpendicular to each other.
So, from figure,
AP ⊥ CP
So, in right angled △CAP by pythagoras theorem,
From figure, nearest point to P on the circle is D,
PD = CP - CD = 10 - 6 = 4 cm.
Hence, the distance of P from the nearest point of the circle is 4 cm.
The figure shows a circle of radius 9 cm with O as the centre. The diameter AB produced meets the tangent PQ at P. If PA = 24 cm, find the length of tangent PQ.

Answer
Given,
Radius of circle (r) = OA = OB = 9 cm
From figure,
AB = OA + OB = 9 + 9 = 18 cm
PB = PA - AB = 24 - 18 = 6 cm
We know that,
If a secant segment and tangent segment are drawn to a circle from the same external point, the length of the tangent segment is the geometric mean between the length of the secant segment and the length of the external part of the secant segment.
⇒ PQ2 = PB × PA
⇒ PQ2 = 6 × 24
⇒ PQ2 = 144
⇒ PQ = = 12 cm.
Hence, length of tangent PQ = 12 cm.
Two concentric circles are of radii 13 cm and 5 cm. Find the length of the chord of the outer circle which touches the inner circle.
Answer
From figure,
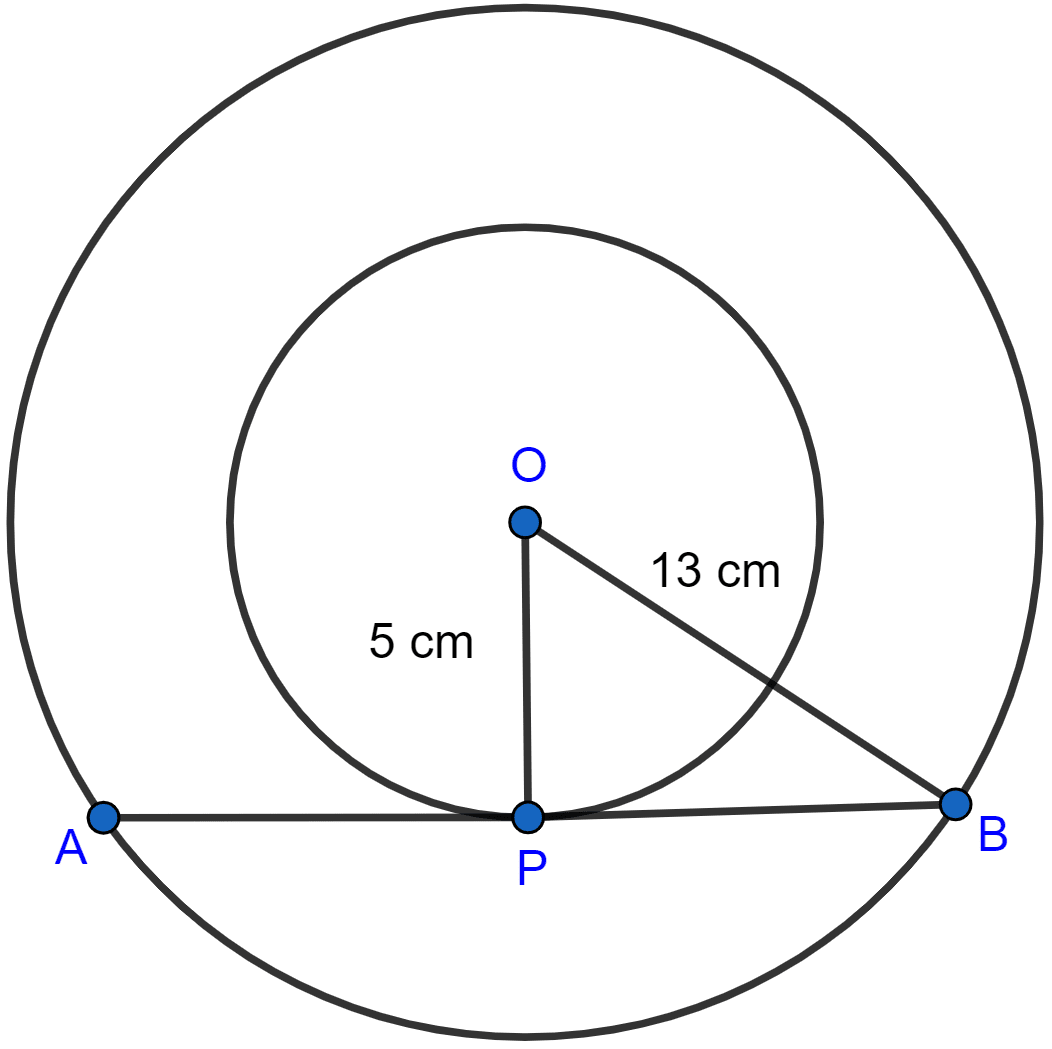
AB is the chord of the outer circle which touches the inner circle at P.
OP is the radius of the inner circle and APB is the tangent to the inner circle.
In the right angled triangle OPB, by pythagoras theorem,
As perpendicular line from centre bisects the chord of the circle so,
AP = PB = 12 cm.
AB = AP + PB = 12 + 12 = 24 cm.
Hence, the length of chord = 24 cm.
Two circles of radii 5 cm and 2.8 cm touch each other. Find the distance between their centres if they touch
(i) Externally
(ii) Internally
Answer
(i) From figure,
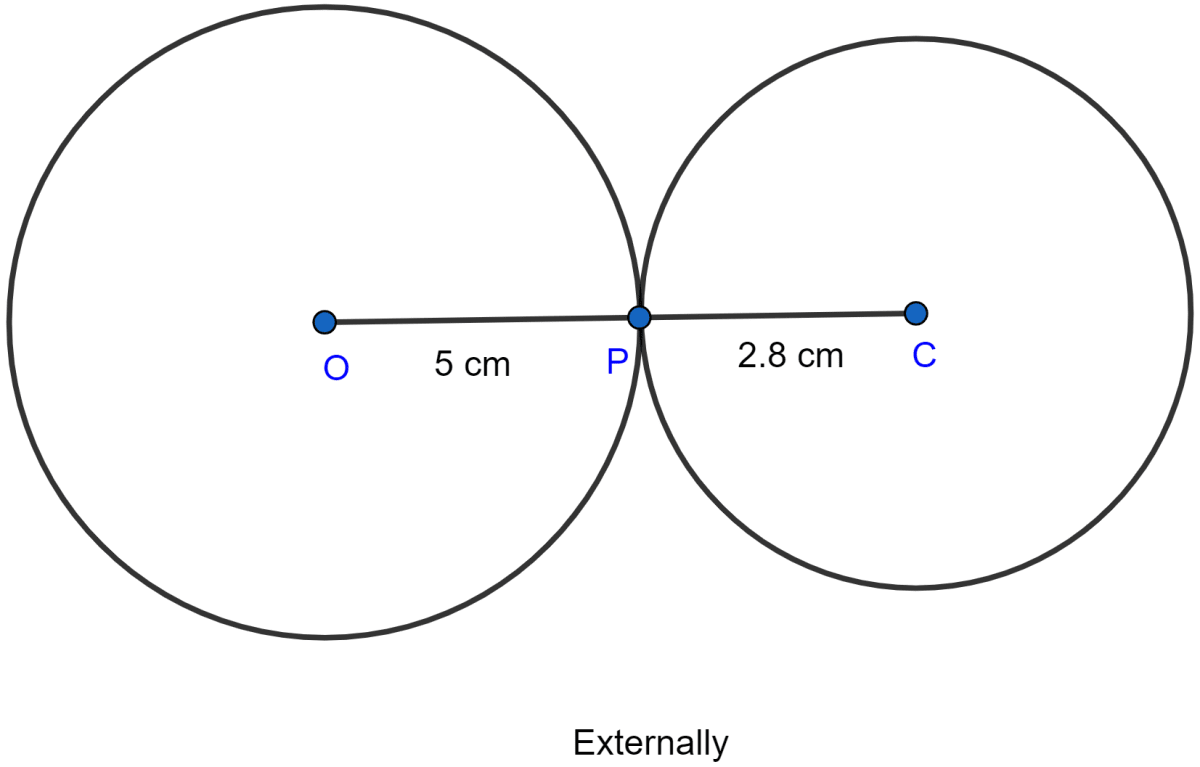
OC = OP + PC = 5 + 2.8 = 7.8 cm
Hence, the distance between centres of circle = 7.8 cm when circles touch externally.
(ii) From figure,

OC = OP - CP = 5 - 2.8 = 2.2 cm.
Hence, the distance between centres of circle = 2.2 cm when circles touch internally.
In figure (i) given below, triangle ABC is circumscribed, find x.

Answer
From figure, AP and AQ are the tangents to the circle.
∴ AQ = AP = 4 cm. (∵ if two tangents are drawn to a circle from an external point then the tangents have equal lengths.)
From figure, BP and BR are the tangents to the circle.
∴ BR = BP = 6 cm. (∵ if two tangents are drawn to a circle from an external point then the tangents have equal lengths.)
From figure,
CQ = CA - AQ = 12 - 4 = 8 cm.
From figure, CQ and CR are the tangents to the circle.
∴ CR = CQ = 8 cm. (∵ if two tangents are drawn to a circle from an external point then the tangents have equal lengths.)
From figure,
x = BR + CR = 6 + 8 = 14 cm.
Hence, the value of x = 14 cm.
In figure (ii) given below, quadrilateral ABCD is circumscribed, find x.

Answer
From A, AP and AQ are the tangents to the circle.
∴ AP = AQ = 5 cm. (∵ if two tangents are drawn to a circle from an external point then the tangents have equal lengths.)
From C, CR and CS are the tangents to the circle.
∴ CS = CR = 3 cm. (∵ if two tangents are drawn to a circle from an external point then the tangents have equal lengths.)
From figure,
BS = BC - CS = 7 - 3 = 4 cm.
From B, BS and BP are the tangents to the circle.
∴ BP = BS = 4 cm. (∵ if two tangents are drawn to a circle from an external point then the tangents have equal lengths.)
From figure,
x = BP + AP = 4 + 5 = 9 cm.
Hence, the value of x = 9 cm.
In figure (i) given below, quadrilateral ABCD is circumscribed ; find the perimeter of quadrilateral ABCD.
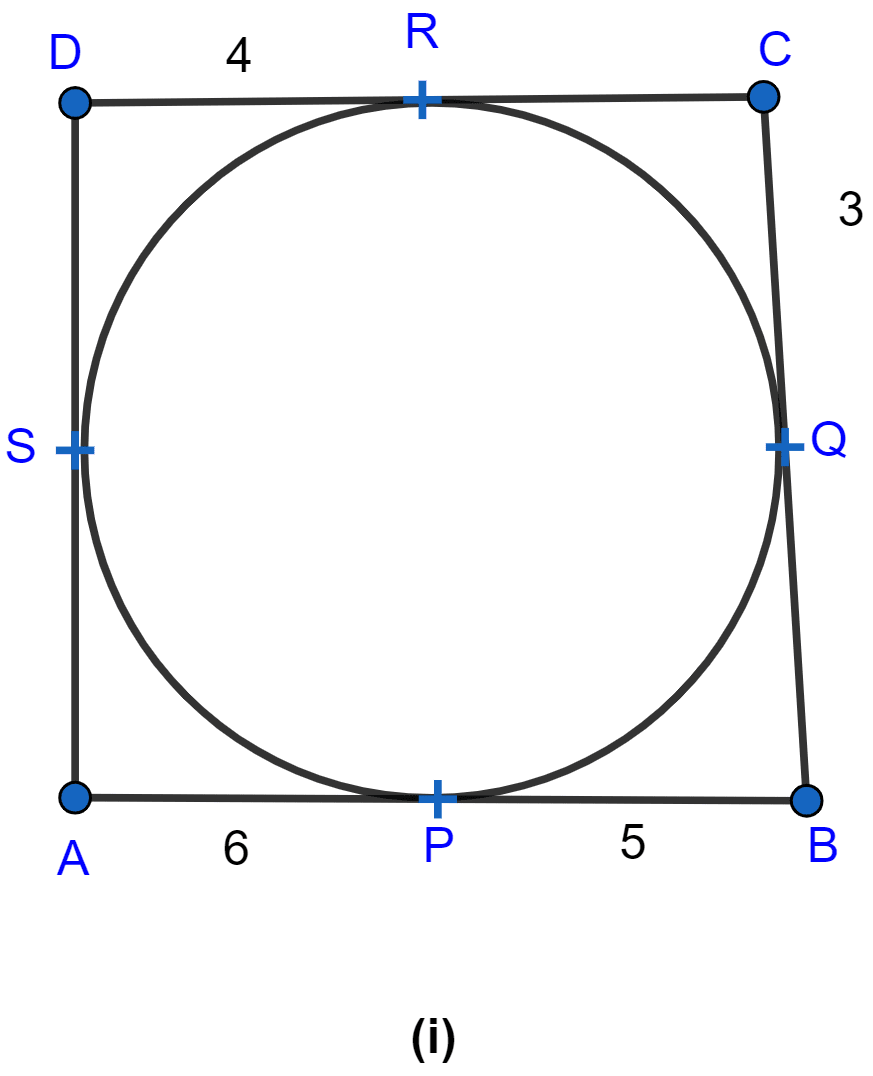
Answer
From A, AP and AS are the tangents to the circle.
∴ AS = AP = 6 cm. (∵ if two tangents are drawn to a circle from an external point then the tangents have equal lengths.)
From B, BP and BQ are the tangents to the circle.
∴ BQ = BP = 5 cm. (∵ if two tangents are drawn to a circle from an external point then the tangents have equal lengths.)
From C, CQ and CR are the tangents to the circle.
∴ CR = CQ = 3 cm. (∵ if two tangents are drawn to a circle from an external point then the tangents have equal lengths.)
From D, DS and DR are the tangents to the circle.
∴ DS = DR = 4 cm. (∵ if two tangents are drawn to a circle from an external point then the tangents have equal lengths.)
Therefore, perimeter of the quadrilateral ABCD
Hence, the perimeter of ABCD = 36 cm.
In Figure (ii) given below, quadrilateral ABCD is circumscribed and AD ⊥ DC; find x if radius of incircle is 10 cm.
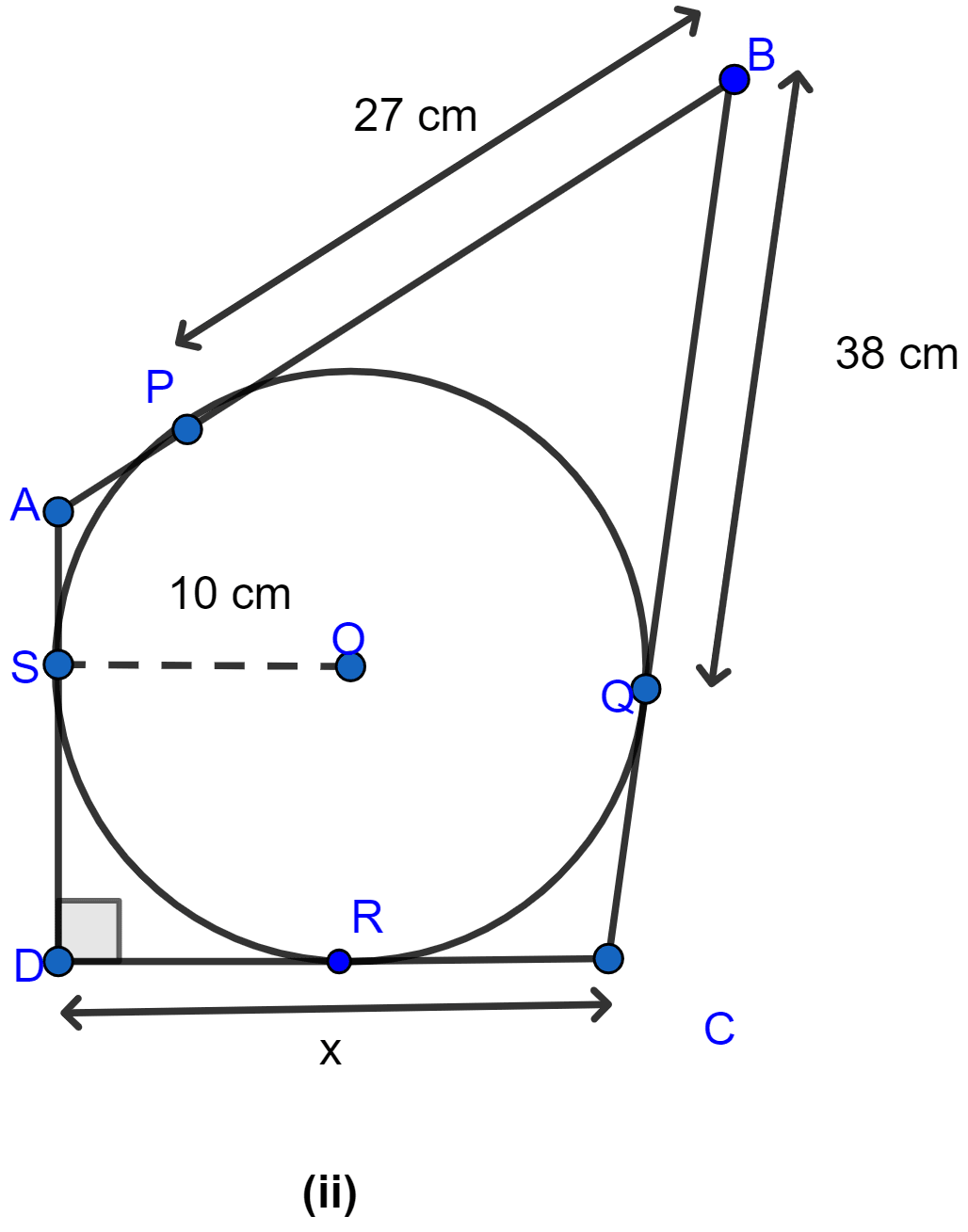
Answer
Join OR as shown in the figure below:
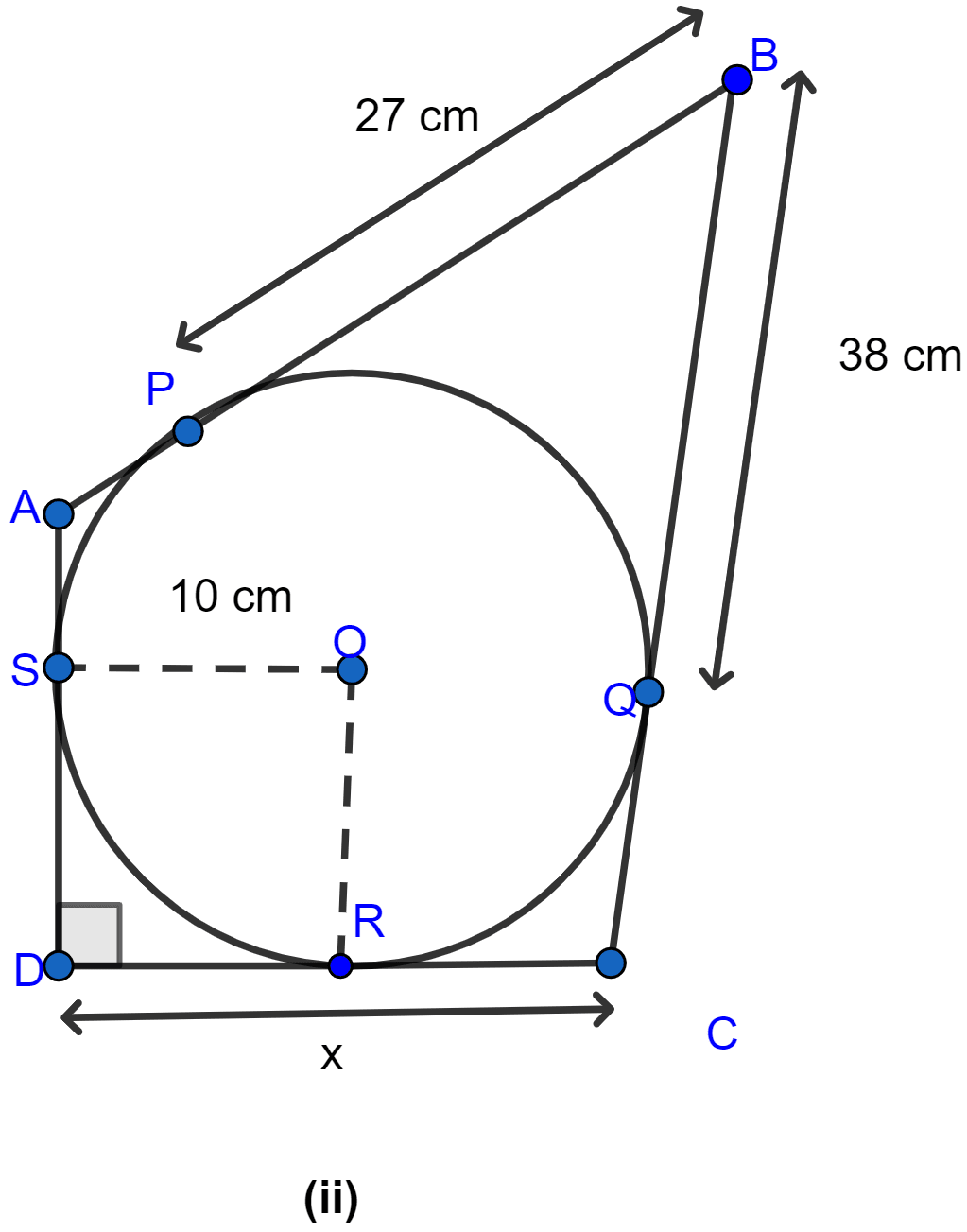
From figure,
OS = OR (As both are radius of circle.)
SD = OR (As OSDR form a square.)
∴ SD = OS.
From D, DS and DR are the tangents to the circle.
∴ DR = DS = 10 cm. (∵ if two tangents are drawn to a circle from an external point then the tangents have equal lengths.)
From B, BP and BQ are the tangents to the circle.
∴ BQ = BP = 27 cm. (∵ if two tangents are drawn to a circle from an external point then the tangents have equal lengths.)
From figure,
CQ = BC - BQ = 38 - 27 = 11 cm.
Now from C, CQ and CR are the tangents to the circle
CR = CQ = 11 cm.
⇒ DC = x = DR + CR = 10 + 11 = 21 cm.
Hence, the length of x = 21 cm.
In figure (i) given below, O is the centre of the circle and AB is a tangent at B. If AB = 15 cm and AC = 7.5 cm, find the radius of the circle.

Answer
Since the tangent at any point of a circle and the radius through the point are perpendicular to each other.
So, from figure,
OB ⊥ AB
In right angled △OBA,
Hence, radius of the circle = 11.25 cm.
In the figure (ii) given below, from an external point P, tangents PA and PB are drawn to a circle. CE is a tangent to the circle at D. If AP = 15 cm, find the perimeter of the triangle PEC.

Answer
From P, PA and PB are the tangents to the circle.
∴ PA = PB = 15 cm. (∵ if two tangents are drawn to a circle from an external point then the tangents have equal lengths.)
From E, EA and ED are the tangents to the circle.
∴ EA = ED (∵ if two tangents are drawn to a circle from an external point then the tangents have equal lengths.)
From C, BC and CD are the tangents to the circle.
∴ BC = CD (∵ if two tangents are drawn to a circle from an external point then the tangents have equal lengths.)
Now perimeter of triangle PEC,
Hence, perimeter of triangle PEC = 30 cm.
If a, b, c are the sides of a right angled triangle where c is the hypotenuse, prove that the radius r of the circle which touches the sides of the triangle is given by r = .
Answer
Let the circle touch the sides BC, CA and AB of the right triangle ABC at points D, E and F respectively,
where BC = a, CA = b and AB = c (as shown in the given figure).
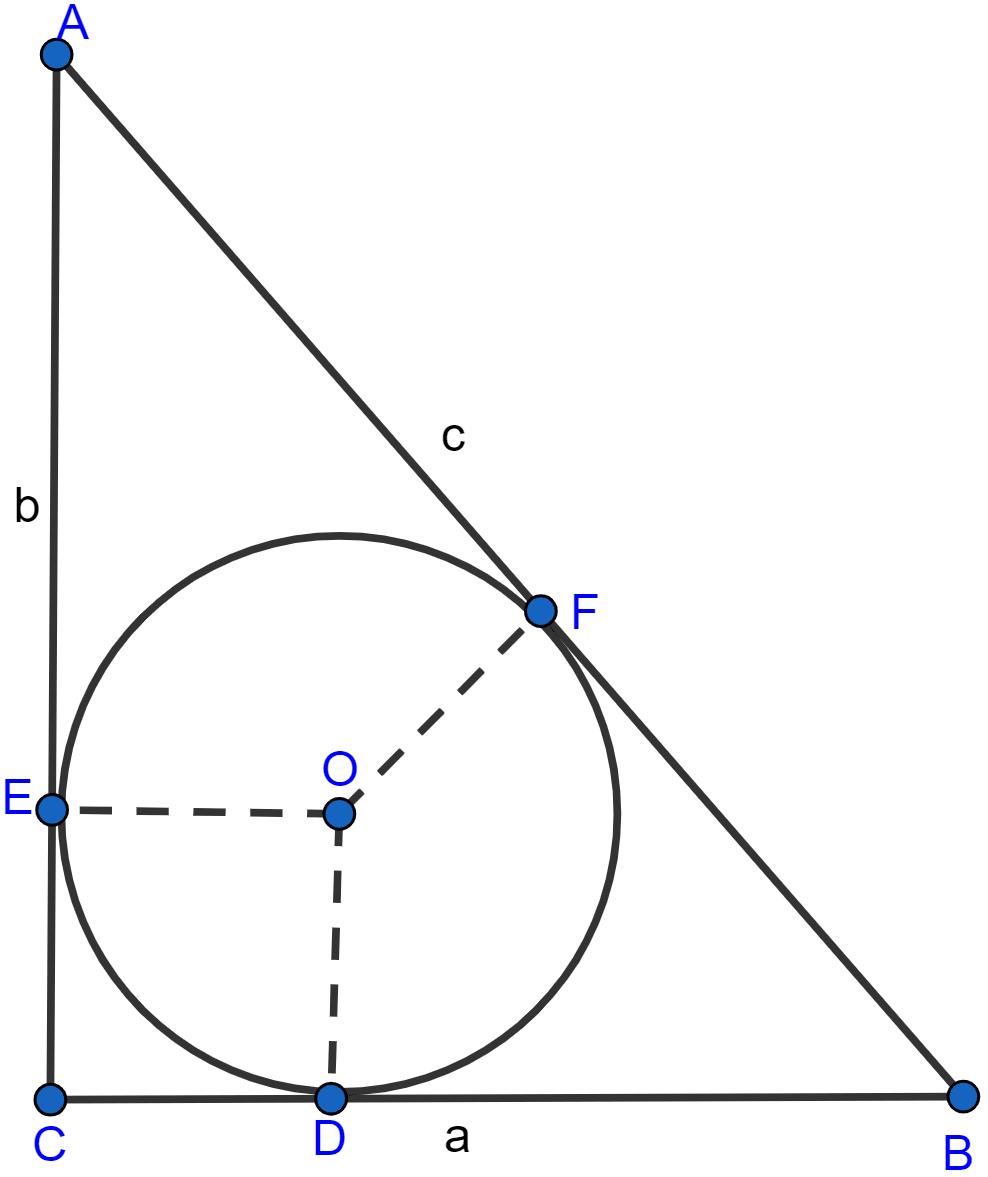
As the lengths of tangents drawn from an external point to a circle are equal
AE = AF, BD = BF and CD = CE
OD ⊥ BC and OE ⊥ CA (∵ tangents is ⊥ to radius)
ODCE is a square of side r
DC = CE = r
AF = AE = AC - EC = b - r and,
BF = BD = BC - DC = a - r
Now,
AB = AF + BF
⇒ c = (b - r) + (a - r)
⇒ c = b + a - 2r
⇒ 2r = a + b - c
⇒ r = .
Hence, proved that r =
In the given figure, PB is a tangent to a circle with centre O at B. AB is a chord of length 24 cm at a distance of 5 cm from the centre. If the length of the tangent is 20 cm, find the length of OP.

Answer
Join OB as shown in figure below:

OM = 5 cm
OM ⊥ AB and M is mid-point of AB,
MB = 12 cm.
In right-angled triangle △OMB,
As BP is tangent to circle at B, OB ⊥ BP.
In right-angled triangle △OBP,
Hence, the length of OP = cm.
Three circles of radii 2 cm, 3 cm and 4 cm touch each other externally. Find the perimeter of the triangle obtained on joining the centres of these circles.
Answer
Three circles with centres A, B and C touch each other externally and the radii of these circles are 2 cm, 3 cm and 4 cm respectively.
From figure,

By joining the centres of circles, triangle ABC is formed in which,
AB = 2 + 3 = 5 cm
BC = 3 + 4 = 7 cm
CA = 4 + 2 = 6 cm.
Therefore, perimeter of the triangle ABC = AB + BC + CA = 5 + 7 + 6 = 18 cm.
Hence, the perimeter of triangle ABC = 18 cm.
In the figure (i) given below, the sides of the quadrilateral touch the circle. Prove that AB + CD = BC + DA.
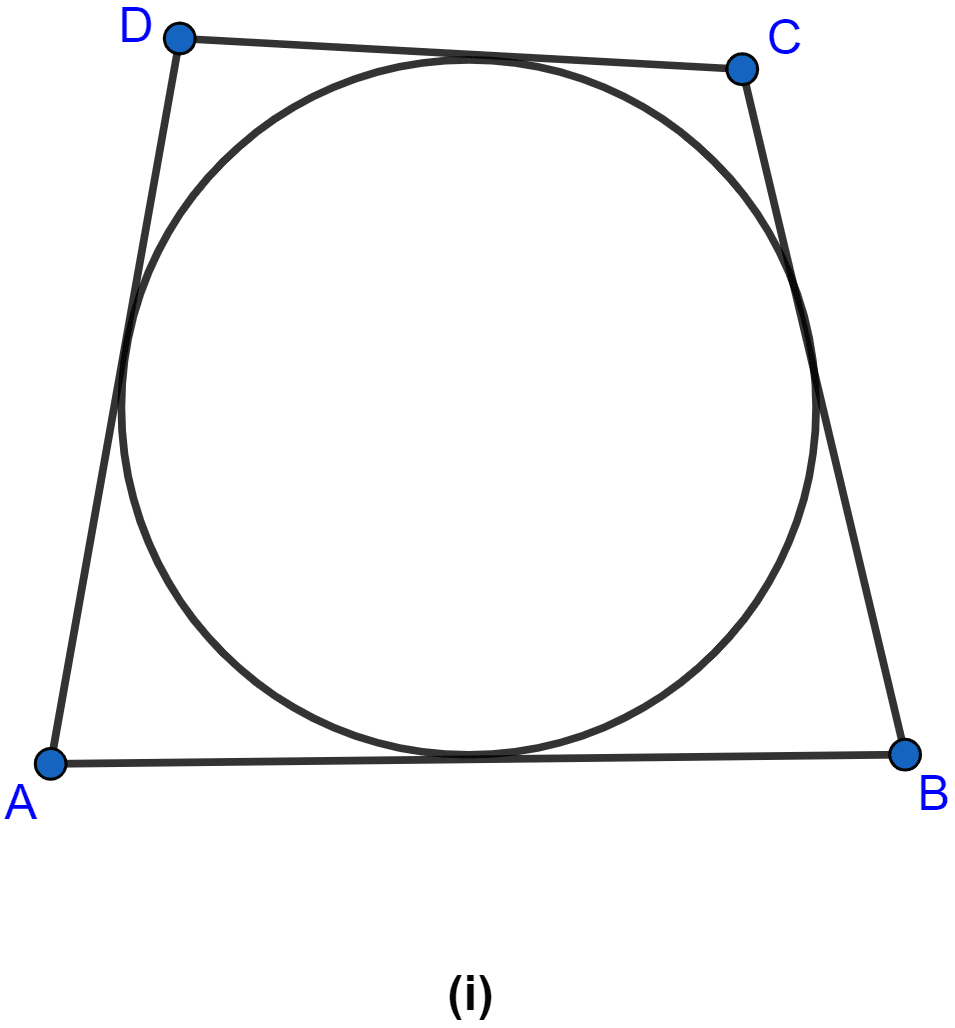
Answer
Let p, Q, R, S be the points where the circle touches the sides of the quadrilateral as shown in the figure below:
From A, AP and AS are the tangents to the circle.
∴ AP = AS ...(i) (∵ if two tangents are drawn to a circle from an external point then the tangents have equal lengths.)
From B, BP and BQ are the tangents to the circle.
∴ PB = BQ ....(ii) (∵ if two tangents are drawn to a circle from an external point then the tangents have equal lengths.)
From C, CR and CQ are the tangents to the circle.
∴ CR = CQ ....(iii) (∵ if two tangents are drawn to a circle from an external point then the tangents have equal lengths.)
From D, DR and DS are the tangents to the circle.
∴ DR = DS ....(iv) (∵ if two tangents are drawn to a circle from an external point then the tangents have equal lengths.)
Adding L.H.S. and R.H.S. of equations (i), (ii), (iii) and (iv) we get,
⇒ AP + PB + CR + DR = AS + BQ + CQ + DS
⇒ AB + CD = BC + DA
Hence, proved that AB + CD = BC + DA.
In the figure (ii) given below, ABC is a triangle with AB = 10 cm, BC = 8 cm and AC = 6 cm (not drawn to scale). Three circles are drawn touching each other with vertices A, B and C as their centres. Find the radii of the three circles.
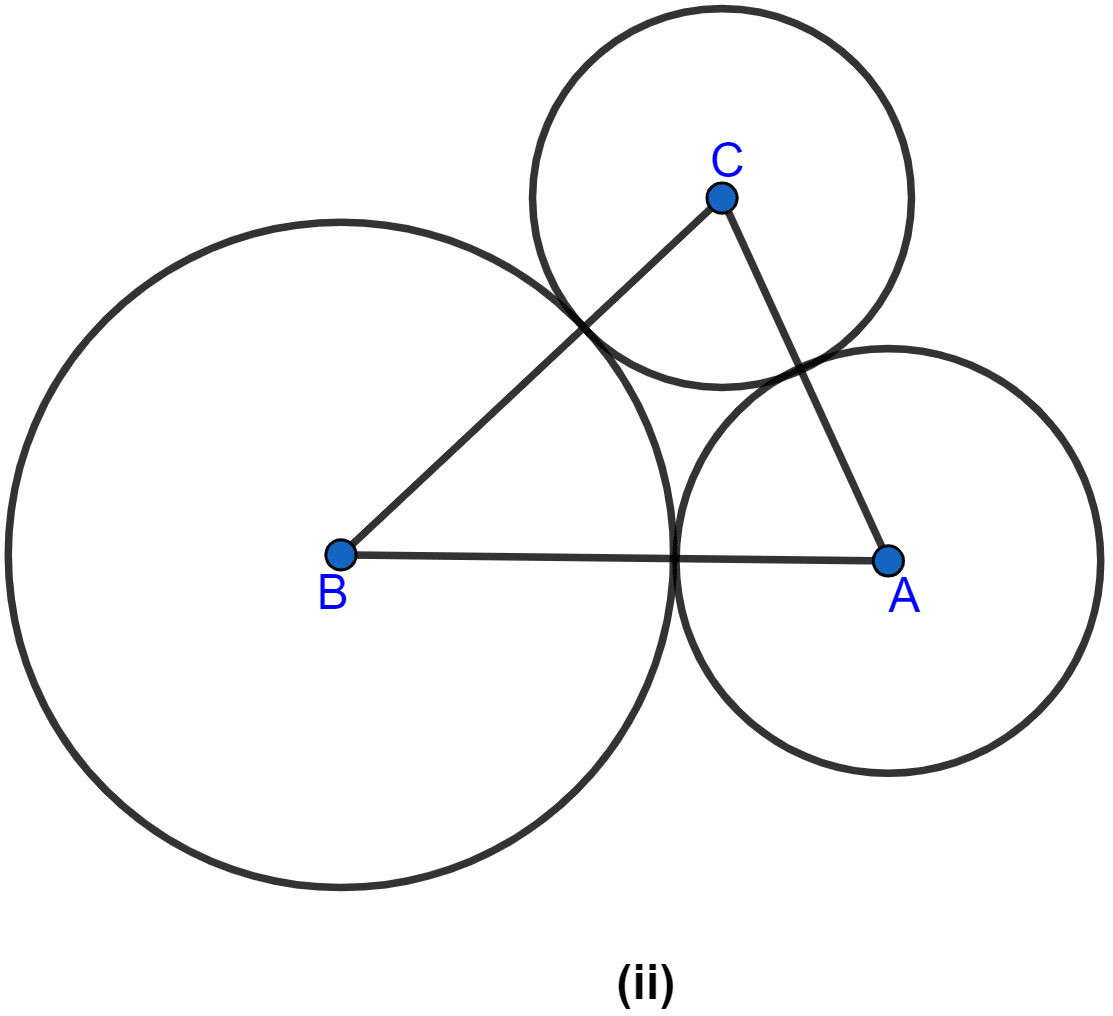
Answer
Given, AB = 10 cm, BC = 8 cm, AC = 6 cm
Let the radius of the circles with centre A, B and C be x cm, y cm and z cm.
From figure,
AB = 10 cm.
⇒ x + y = 10 cm ....(i)
BC = 8 cm.
⇒ y + z = 8 cm ....(ii)
AC = 6 cm.
⇒ x + z = 6 cm .....(iii)
Adding eqn. (i), (ii) and (iii) we get,
⇒ x + y + y + z + x + z = (10 + 8 + 6) cm
⇒ 2x + 2y + 2z = 24 cm
⇒ 2(x + y + z) = 24 cm
⇒ x + y + z = 12 cm .....(iv)
Now, (iv) - (i) we get,
⇒ x + y + z - (x + y) = (12 - 10) cm
⇒ x + y + z - x - y = 2 cm
⇒ z = 2 cm.
Also, by (iv) - (ii) we get,
⇒ x + y + z - (y + z) = (12 - 8) cm
⇒ x + y + z - y - z = 4 cm
⇒ x = 4 cm
Also, by (iv) - (iii) we get,
⇒ x + y + z - (x + z) = (12 - 6) cm
⇒ x + y + z - x - z = 6 cm
⇒ y = 6 cm.
Hence, the radius of the circle with centre A, B and C are 4 cm, 6 cm and 2 cm.
In the figure (i) given below, PQ = 24 cm, QR = 7 cm and ∠PQR = 90°. Find the radius of the inscribed circle of △PQR.
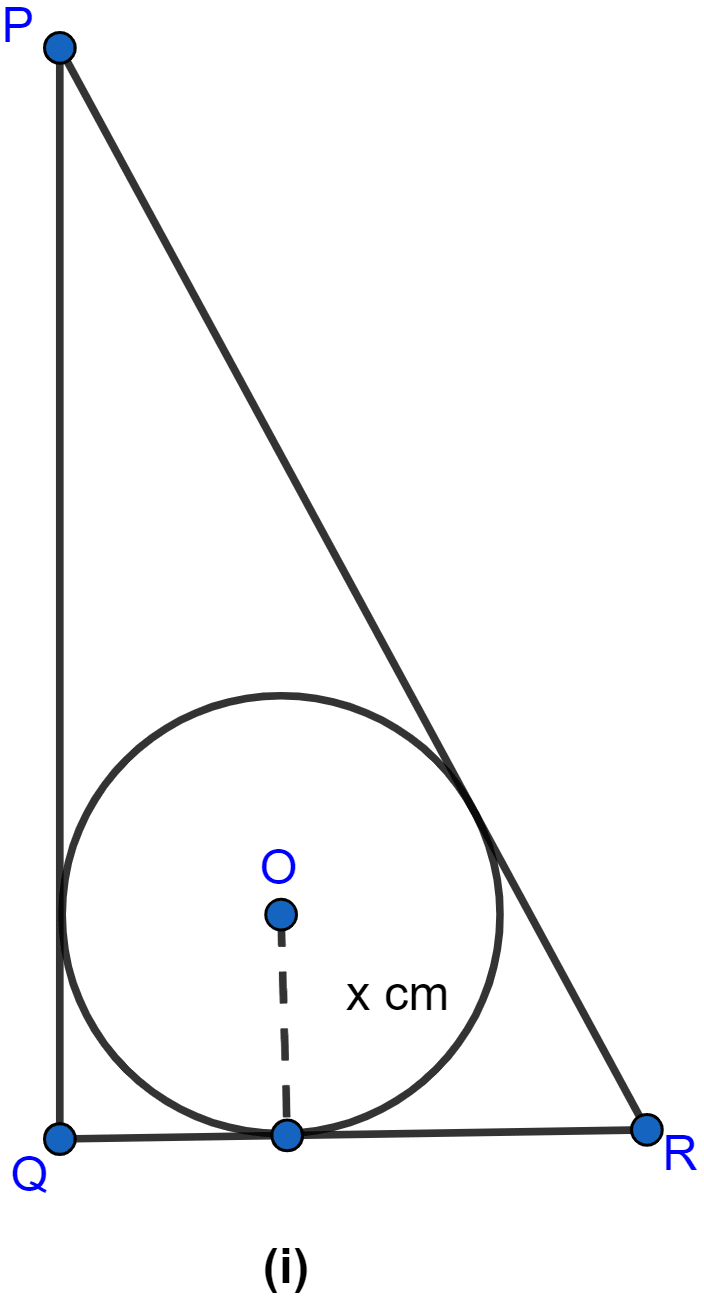
Answer
Let the sides of triangle PQ, QR and PR meet the circle at L, M and N respectively.
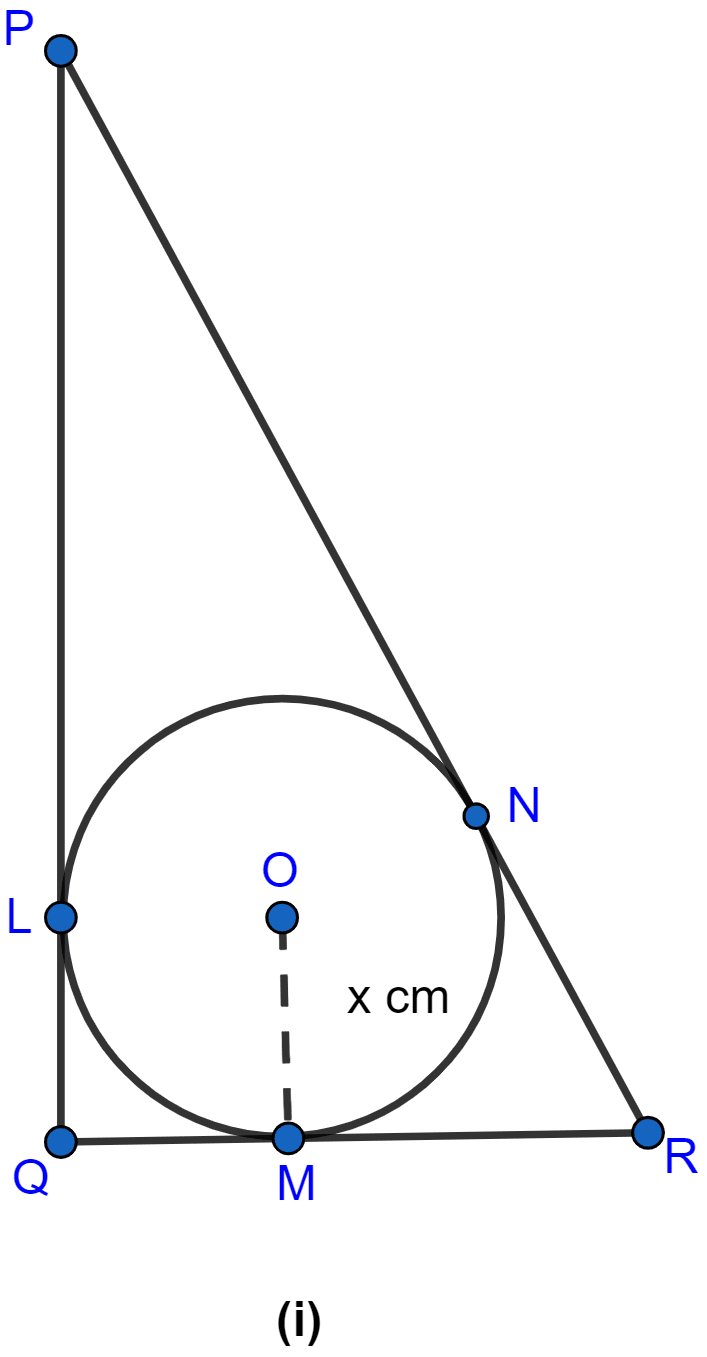
In right-angled triangle PQR
From figure,
RM = RN = (∵ tangents drawn from a common external point to a circle are equal.)
RM = RQ - QM = (7 - x) cm.
PL = PN = (∵ tangents drawn from a common external point to a circle are equal.)
PL = PQ - QL = (24 - x) cm.
We can see,
PR = PN + RN = PL + RM.
⇒ 25 = 24 - x + 7 - x
⇒ 25 = 31 - 2x
⇒ 2x = 31 - 25
⇒ 2x = 6
⇒ x = 3.
Hence, the radius of the inscribed circle is 3 cm.
In the figure (ii) given below, two concentric circles with centre O are of radii 5 cm and 3 cm. From an external point P, tangents PA and PB are drawn to these circles. If AP = 12 cm, find BP.
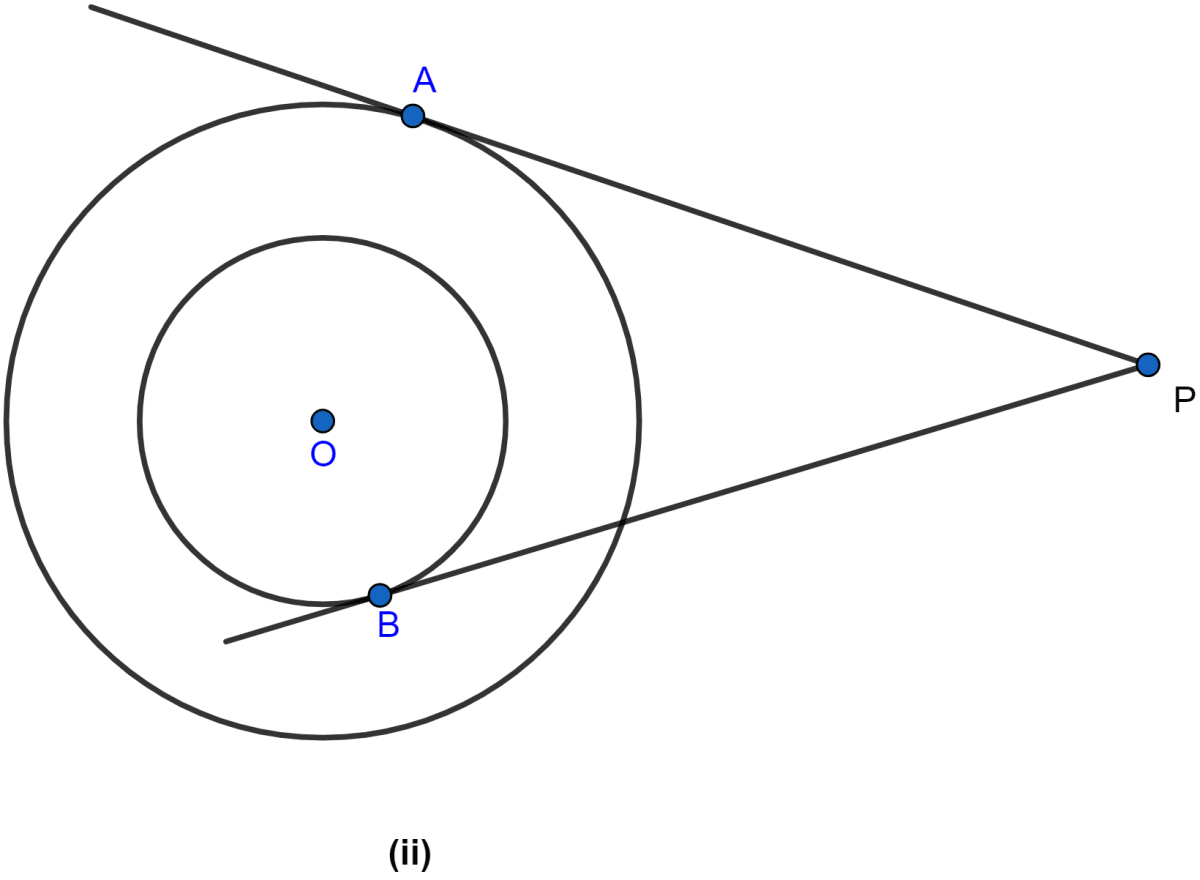
Answer
Join OA and OB.
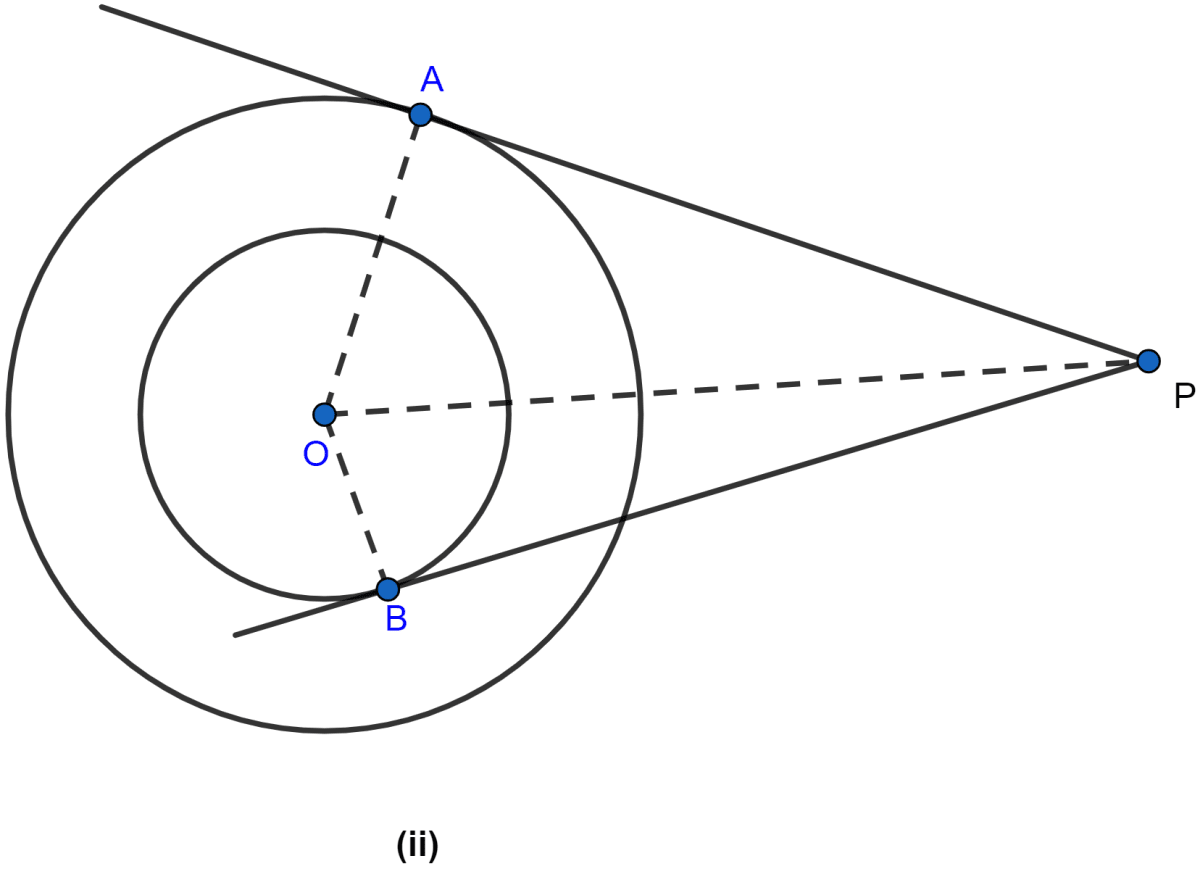
OA ⊥ AP. (∵ tangent at a point and radius through the point are perpendicular to each other.)
So, in right angled triangle OAP,
OB ⊥ BP. (∵ tangent at a point and radius through the point are perpendicular to each other.)
So, in right angled triangle OBP,
Hence, the length of BP = cm.
In the figure (i) given below, AB = 8 cm and M is mid-point of AB. Semicircles are drawn on AB, AM and MB as diameters. A circle with centre C touches all three semicircles as shown, find its radius.
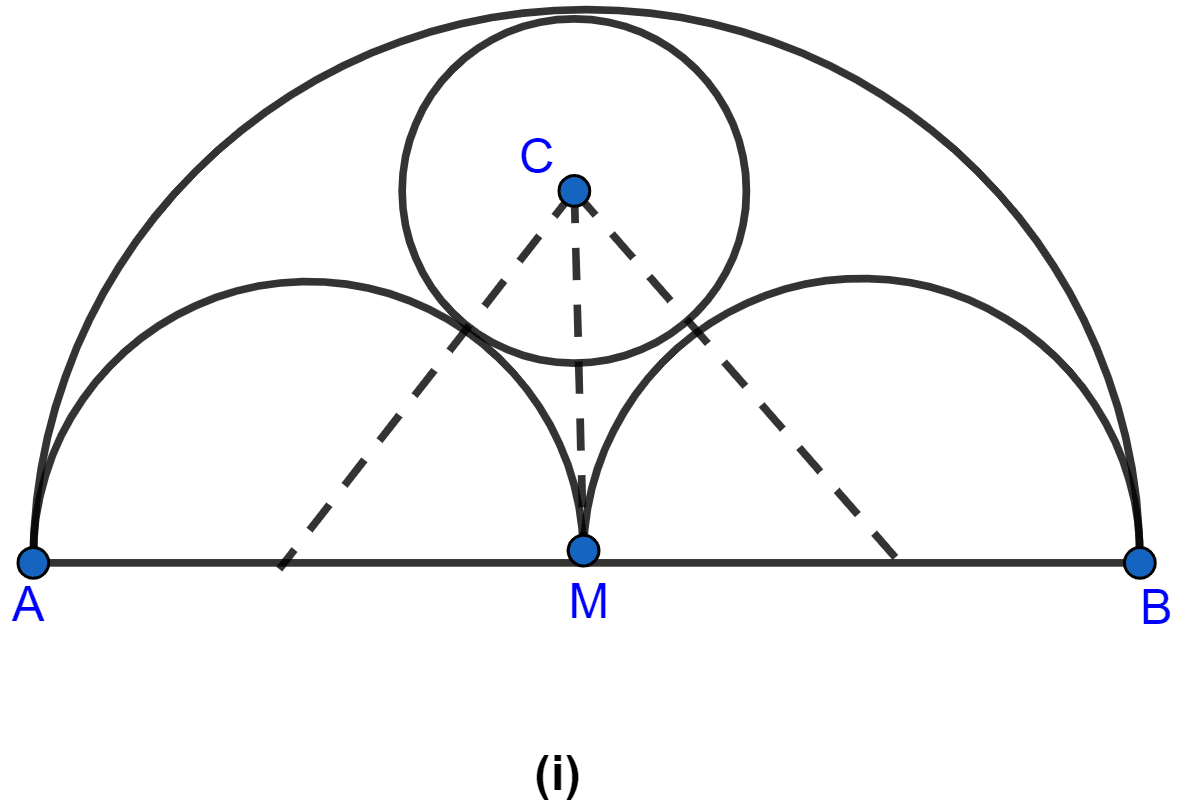
Answer
Let x be the radius of the circle with centre C.
Since M is the mid-point of AB hence, AM = MB = 4 cm.
Two semicircles are thus drawn on AB with diameters as AM and MB.
Since radius = .
Hence, radius of both the semicircles with diameters AM and MB = 2 cm.
From figure,
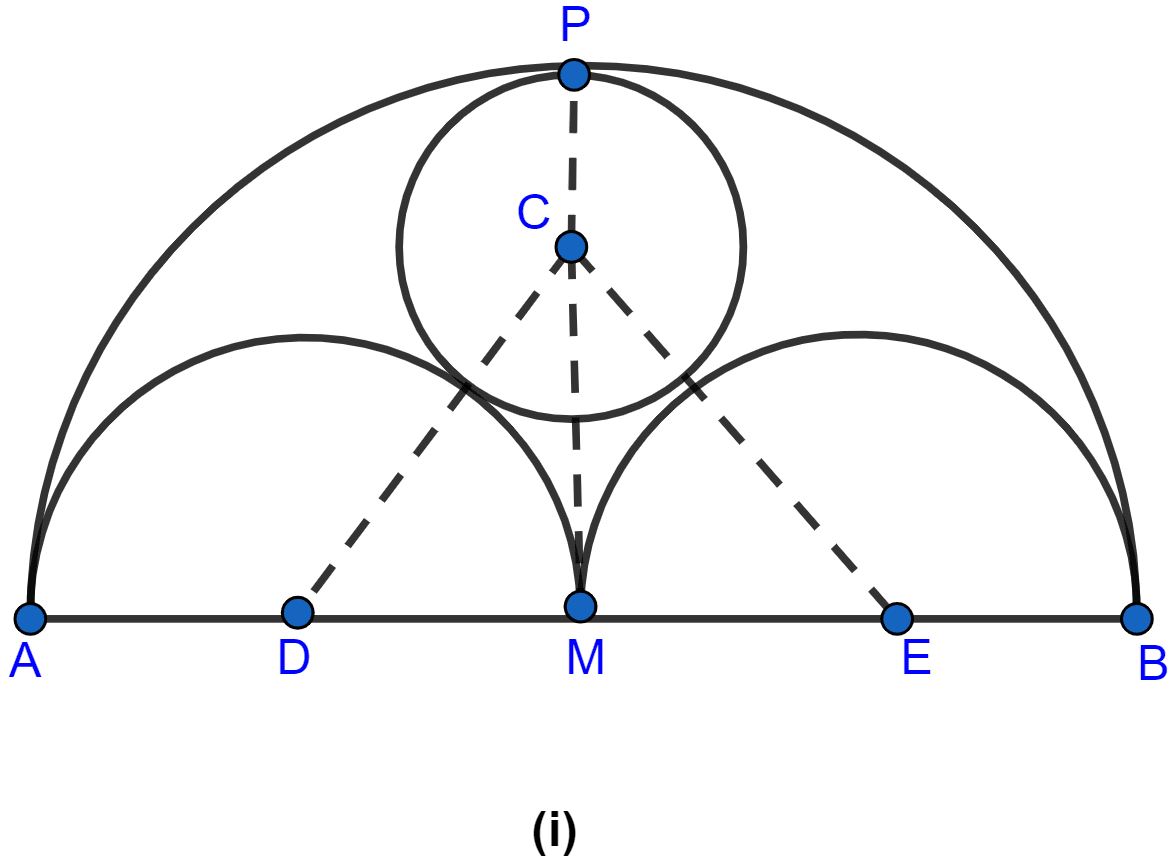
CM = MP - PC = (4 - x) cm.
In right angled triangle CMD,
Hence, the radius of small circle = cm.
In the figure (ii) given below, equal circles with centres O and O' touch each other at X. OO' is produced to meet a circle O' at A. AC is tangent to the circle whose centre is O. O'D is perpendicular to AC. Find the value of
(i)
(ii)
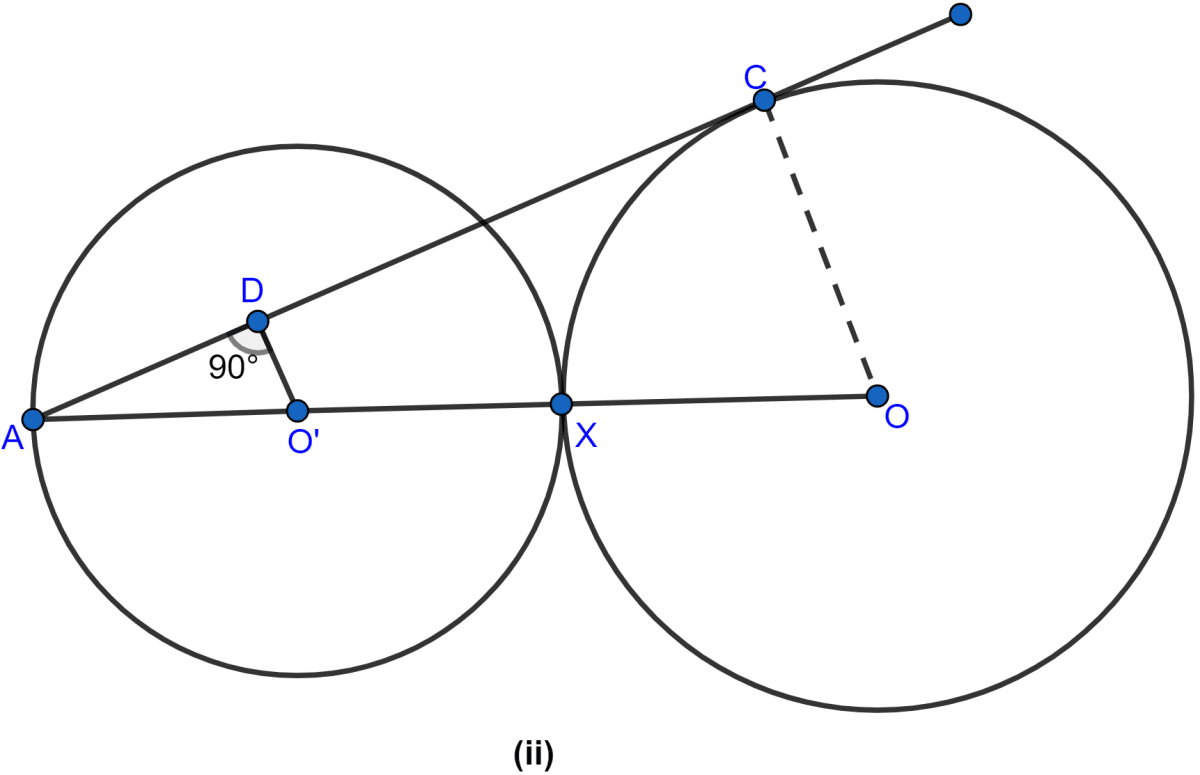
Answer
From figure,
OC is radius and AC is tangent, then OC ⊥ AC.
Let radius of each equal circle = r.
(i) From figure,
AO = AO' + O'X + XO and AO' = O'X = XO = r (radius of circle)
AO = r + r + r = 3r.
Hence, the value of .
(ii) Considering △ADO' and △ACO
∠A = ∠A (Common angles)
∠D = ∠C (Both are equal to 90°)
∴ By AA axiom △ADO' ~ △ACO.
Since triangles are similar hence the ratio of their areas is equal to the ratio of the square of the corresponding sides.
Hence, the value of
The length of the direct common tangent to two circles of radii 12 cm and 4 cm is 15 cm. Calculate the distance between their centres.
Answer
Let there be two circles with center A and B and radius 12 and 4 cm respectively.
From figure,
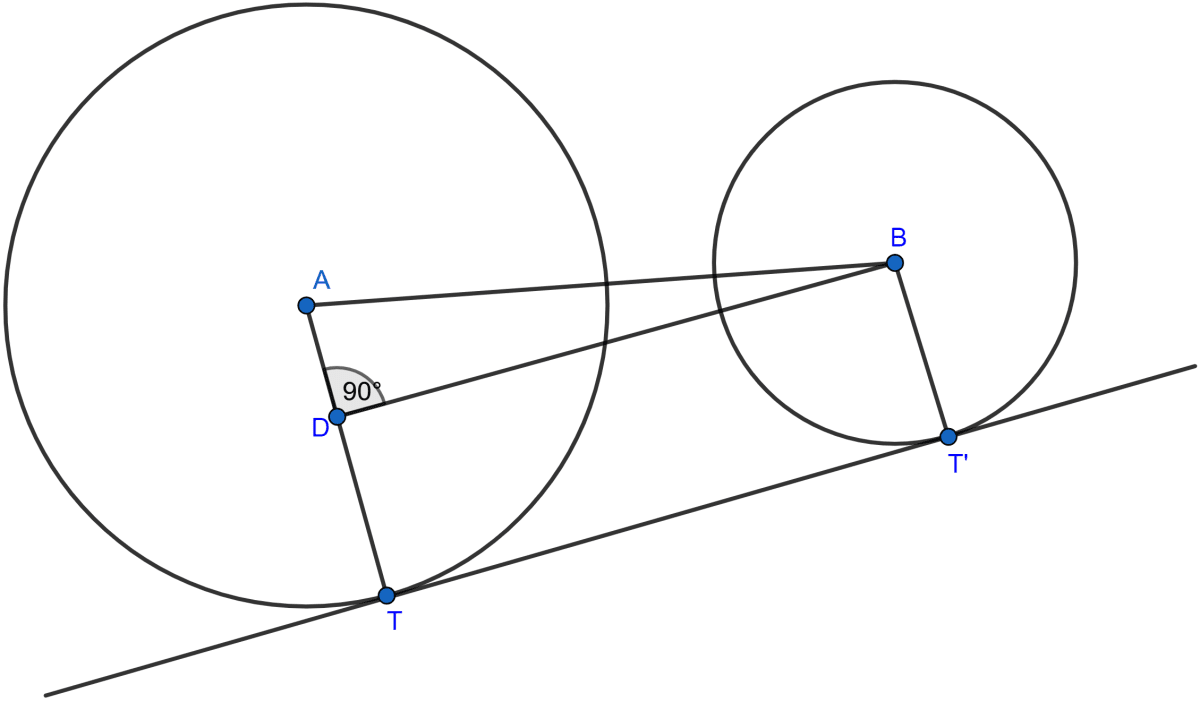
TT' is the common tangent.
DT = BT' = 4 cm.
DB = TT' = 15 cm.
In right angled triangle ADB
AD = AT - DT = 12 - 4 = 8 cm
Hence, the distance between two centres = 17 cm.
Calculate the length of a direct common tangent to two circles of radii 3 cm and 8 cm with their centres 13 cm apart.
Answer
Let there be two circles with centre A and B with radius 8 cm and 3 cm respectively.
Let TT' be the length of common tangent.
From figure,

DT = BT' = 3cm.
AD = AT - DT = 8 - 3 = 5 cm.
In right angled triangle ADB
Since, TDBT' is a rectangle,
So, TT' = DB = 12 cm.
Hence, the length of direct common tangent is 12 cm.
In the given figure, AC is a transverse common tangent to two circles with centres P and Q and of radii 6 cm and 3 cm respectively. Given that AB = 8 cm, calculate PQ.
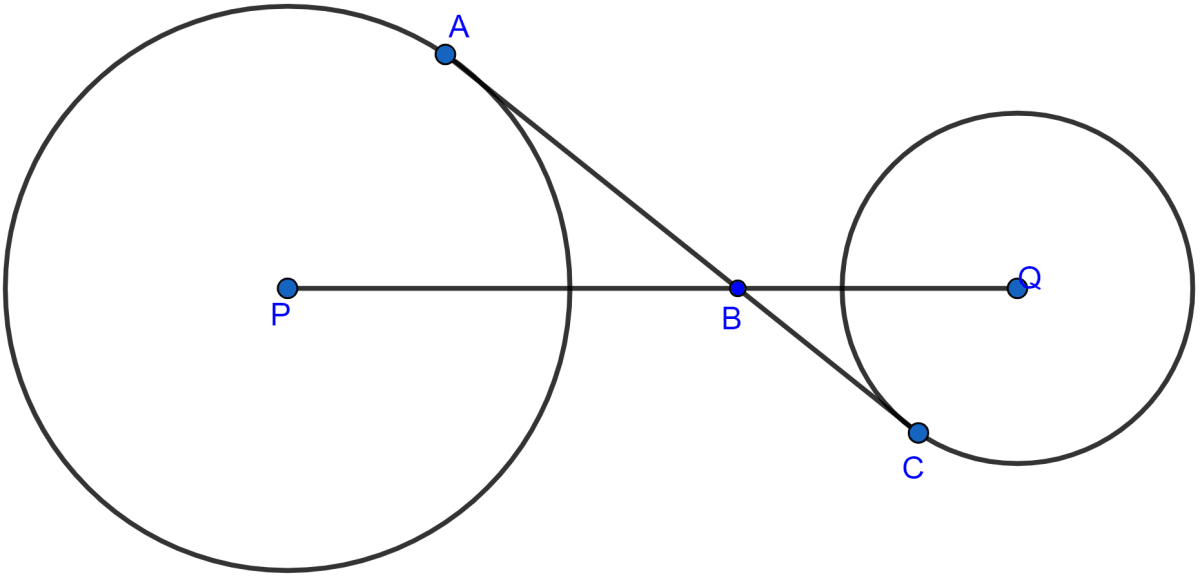
Answer
Join AP and CQ.
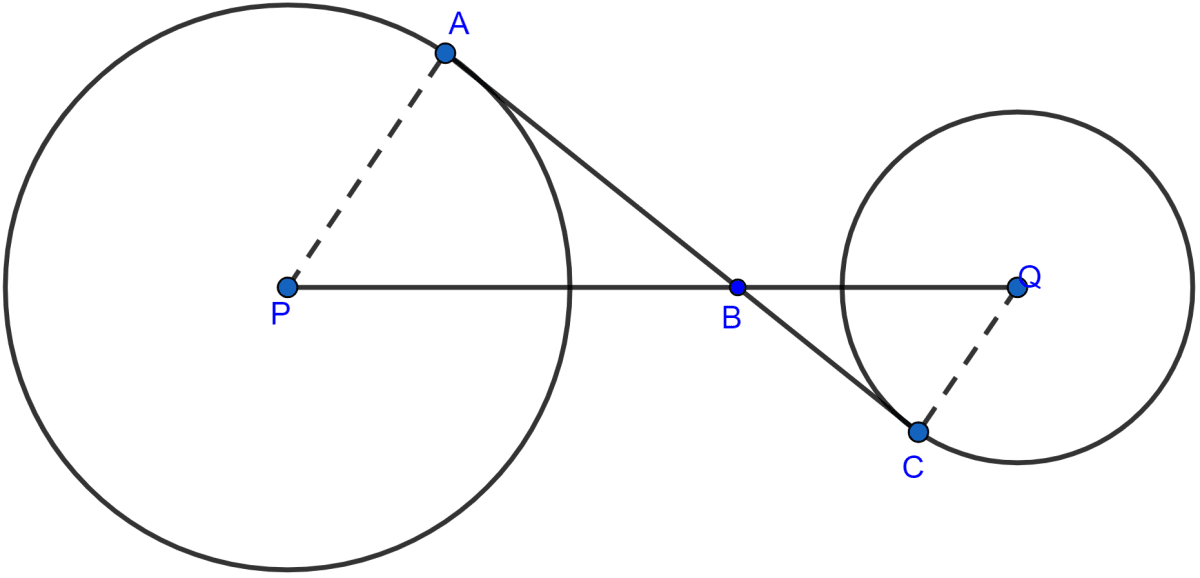
AB ⊥ AP (∵ tangent at a point and radius through the point are perpendicular to each other.)
In right angled triangle PAB.
Considering △PAB and △BCQ,
∠A = ∠C (Each are equal to 90°)
∠ABP = ∠CBQ (Vertically opposite angles are equal)
△PAB ~ △BCQ by AA axiom.
Since triangles are similar hence, the ratio of their corresponding sides are equal.
From figure,
PQ = PB + BQ = 10 + 5 = 15 cm.
Hence, the length of PQ = 15 cm.
Two circles with centres A, B are of radii 6 cm and 3 cm respectively. If AB = 15 cm, find the length of a transverse common tangent to these circles.
Answer
The two circles with centres A, B are of radii 6 cm and 3 cm and AB = 15 cm are shown in the figure below:
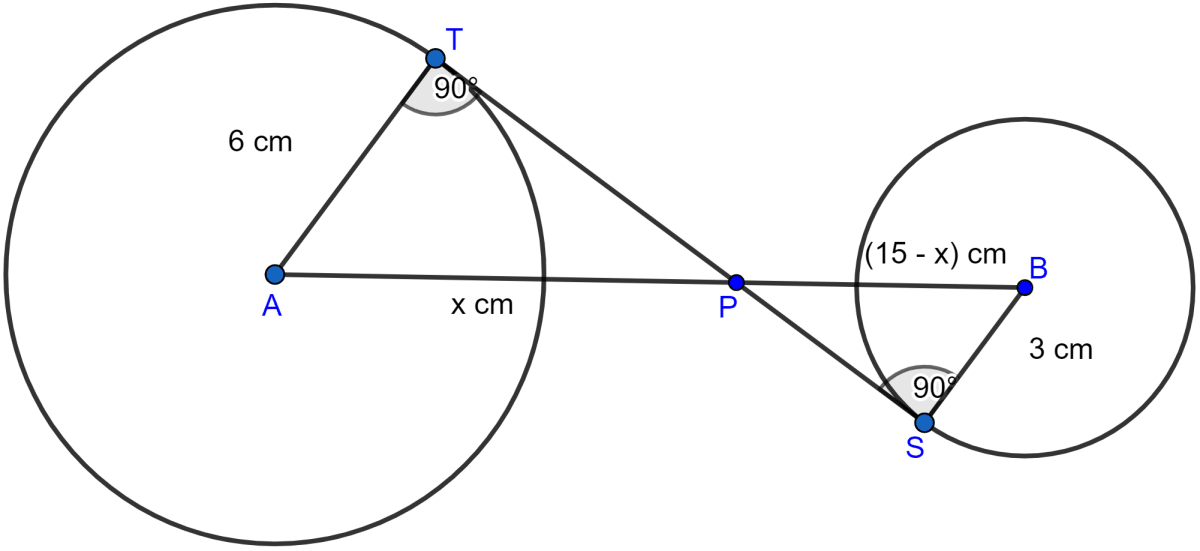
Given, AB = 15 cm.
Let AP = x, then PB = 15 - x
Considering △ATP and △SBP,
∠T = ∠S (Each are equal to 90°)
∠APT = ∠BPS (Vertically opposite angles are equal)
△ATP ~ △SBP by AA axiom.
Since triangles are similar hence, the ratio of their corresponding sides are equal.
∴ AP = 10 cm,
From figure,
PB = AB - AP = 15 - 10 = 5 cm.
Now in right-angled triangle ATP,
Similarly in right angled triangle PSB,
Hence, TS = TP + PS = 8 + 4 = 12 cm.
Hence, the length of a transverse common tangent to these circles are 12 cm.
In the figure (i) given below, PA and PB are tangents at the points A and B respectively of a circle with centre O. Q and R are points on the circle If ∠APB = 70°, find
(i) ∠AOB
(ii) ∠AQB
(iii) ∠ARB

Answer
AP and BP are tangents to the circle and OA and OB are radius of the circle.
∴ OA ⊥ AP and OB ⊥ BP.
∴ ∠OAP = ∠OBP = 90°
Sum of angles of a quadrilateral = 360°.
Hence, in quadrilateral OAPB,
⇒ ∠APB + ∠OAP + ∠OBP + ∠AOB = 360°
⇒ 70° + 90° + 90° + ∠AOB = 360°
⇒ 250° + ∠AOB = 360°
⇒ ∠AOB = 360° - 250°
⇒ ∠AOB = 110°.
Hence, the value of ∠AOB = 110°.
(ii) Arc AB subtends ∠AOB at centre and ∠AQB at remaining part of circle.
∴ ∠AOB = 2∠AQB (As angle at centre is double the angle subtended at remaining part of circle.)
⇒ 2∠AQB = 110°
⇒ ∠AQB = = 55°.
Hence, the value of ∠AQB = 55°.
(iii) Reflex ∠AOB = 360° - ∠AOB = 360° - 110° = 250°.
Arc AB subtends Reflex ∠AOB at centre and ∠ARB at remaining part of circle.
∴ Reflex ∠AOB = 2∠ARB (As angle at centre is double the angle subtended at remaining part of circle.)
⇒ 2∠ARB = 250°
⇒ ∠ARB = = 125°.
Hence, the value of ∠ARB = 125°.
In the figure (ii) given below, two circles touch internally at P from an external point Q on the common tangent at P, two tangents QA and QB are drawn to the two circles. Prove that QA = QB.
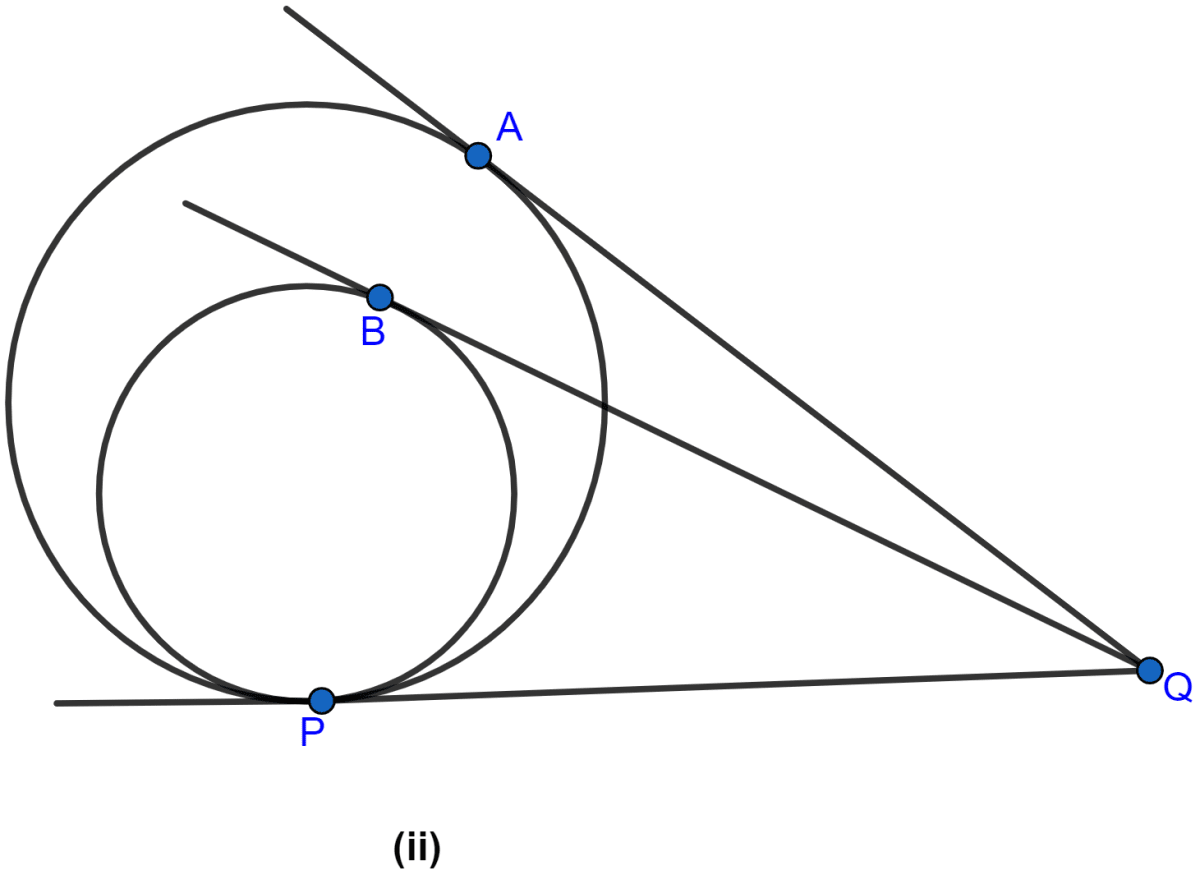
Answer
From figure,
QA and QP are the tangents to the outer circle.
∴ QA = QP .....(i) (∵ the length of the different tangents to a circle from a single point are equal.)
Similarly, from Q, QB and QP are the tangents to the inner circle.
∴ QB = QP .....(ii) (∵ the length of the different tangents to a circle from a single point are equal.)
From (i) and (ii),
QA = QB.
Hence, proved that QA = QB.
In the given figure, AD is a diameter of a circle with centre O and AB is tangent at A. C is a point on the circle such that DC produced intersects the tangent at B. If ∠ABC = 50°, find ∠AOC.
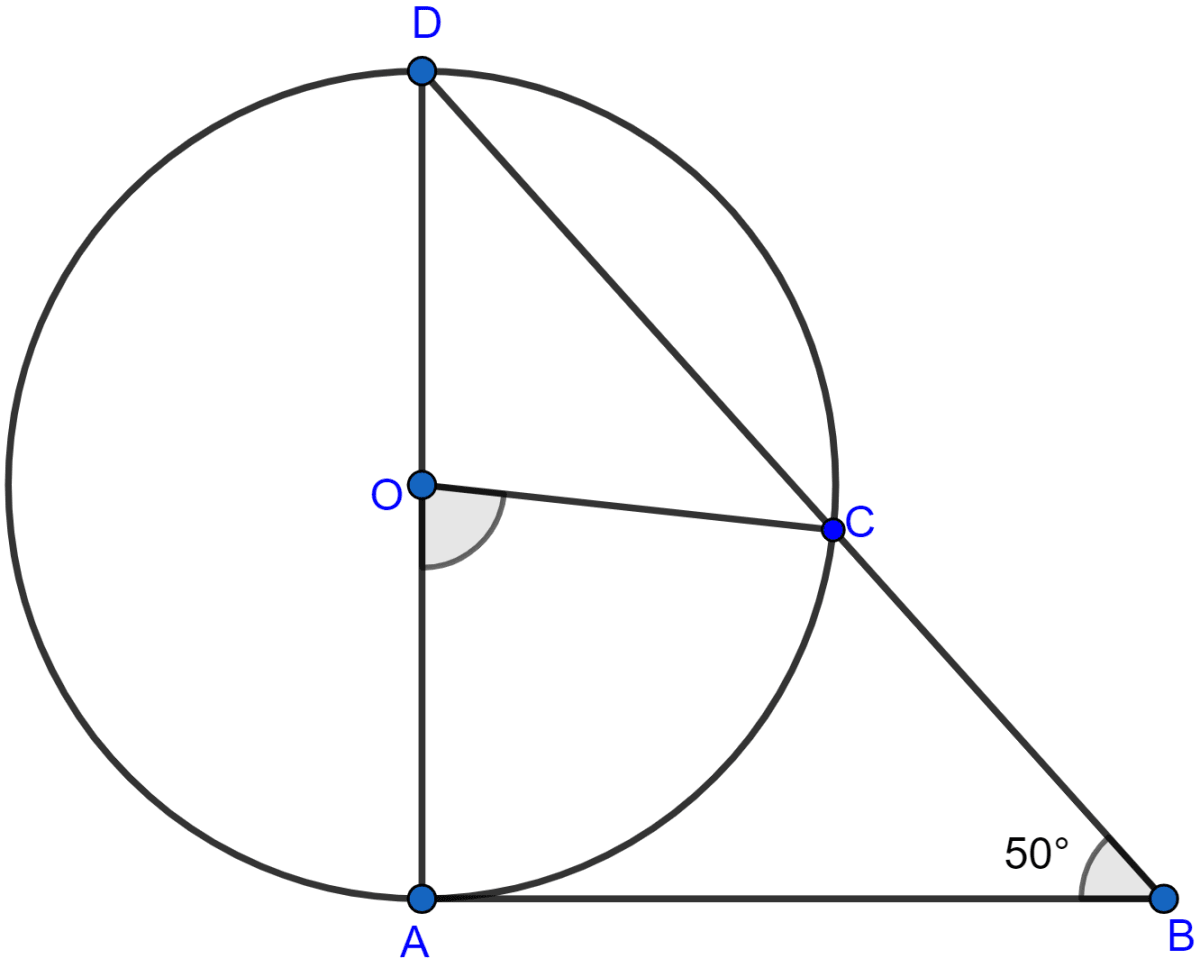
Answer
In the figure,
AB ⊥ AD. (∵ tangent at a point and radius through the point are perpendicular to each other.)
From figure,
∠ABD = ∠ABC = 50°
In △ABD,
∠ABD + ∠BDA + ∠DAB = 180°
⇒ 50° + ∠BDA + 90° = 180°
⇒ ∠BDA + 140° = 180°
⇒ ∠BDA = 180° - 140°
⇒ ∠BDA = 40°.
From figure,
∠ADC = ∠BDA = 40°.
Arc AC subtends ∠AOC at the centre and ∠ADC on point D.
∴ ∠AOC = 2∠ADC (∵ angle subtended at centre by an arc is double the angle subtended at remaining part of circle.)
∠AOC = 2 × 40° = 80°.
Hence, value of ∠AOC = 80°.
In the given figure, tangents PQ and PR are drawn from an external point P to a circle such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find ∠RQS.

Answer
Given,
RS || PQ,
∠TRS = ∠RPQ = 30° (∵ Corresponding angles are equal)
∠RQS = ∠TRS = 30° (∵ Angles in alternate segments are equal.)
Hence, value of ∠RQS = 30°.
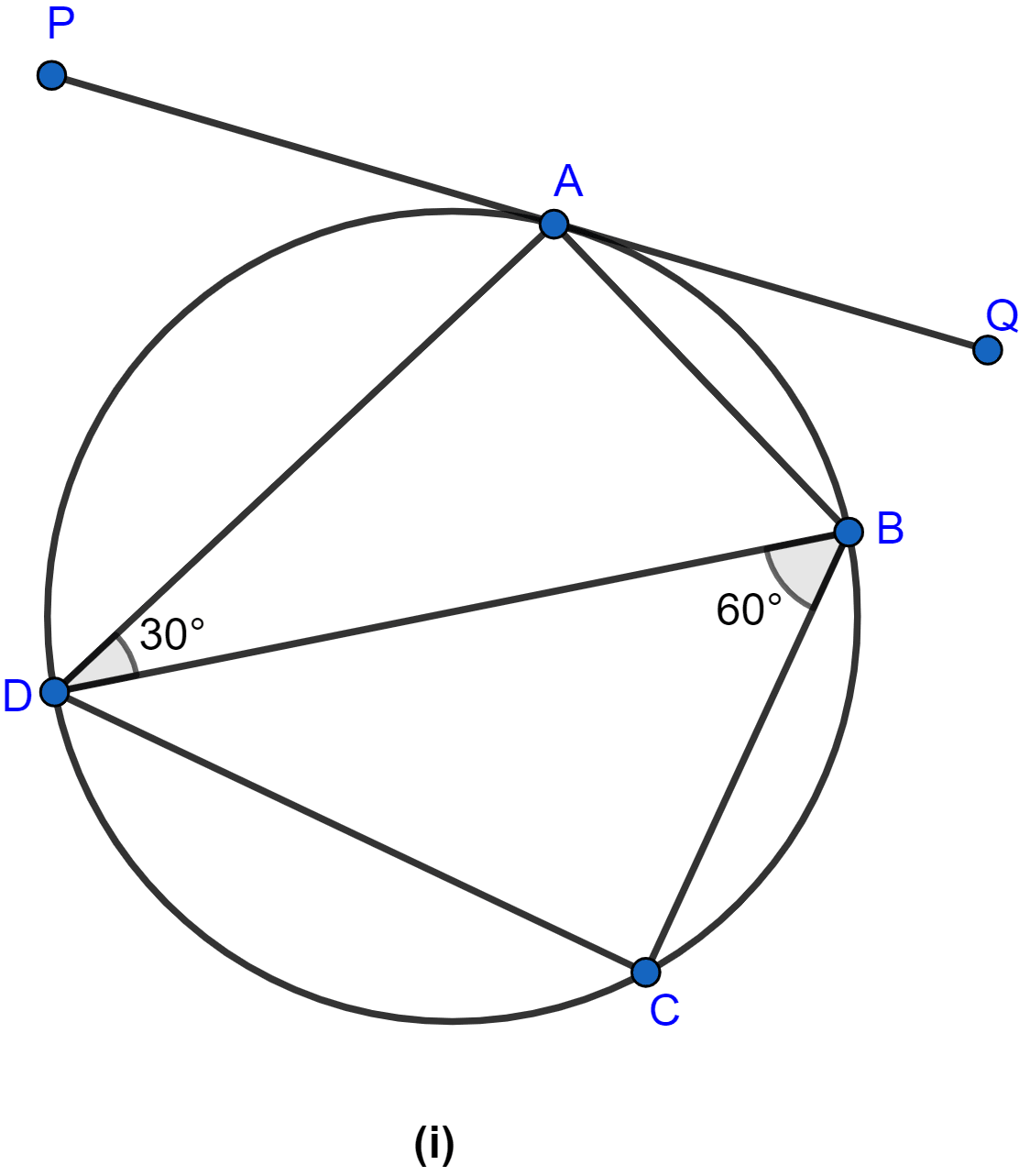
In the figure (i) given below, PQ is a tangent to the circle at A, DB is a diameter, ∠ADB = 30° and ∠CBD = 60°, calculate
(i) ∠QAB
(ii) ∠PAD
(iii) ∠CDB.
Answer
(i) ∠QAB = ∠BDA (∵ angles in alternate segment are equal.)
∴ ∠QAB = 30°.
Hence, the value of ∠QAB = 30°.
(ii) In △ADB,
∠DAB = 90° (∵ angle in semi-circle is 90°.)
Since, sum of angles in a triangle is 180°.
⇒ ∠ABD + ∠ADB + ∠DAB = 180°
⇒ ∠ABD + 30° + 90° = 180°
⇒ ∠ABD + 120° = 180°
⇒ ∠ABD = 60°.
From figure,
∠PAD = ∠ABD = 60° (∵ angles in alternate segment are equal)
Hence, the value of ∠PAD = 60°.
(iii) In △BCD,
∠BCD = 90° (As angle in semi-circle is 90°.)
∠CBD = 60°
Since, sum of angles in a triangle is 180°.
⇒ ∠BCD + ∠CBD + ∠CDB = 180°
⇒ 90° + 60° + ∠CDB = 180°
⇒ ∠CDB + 150° = 180°
⇒ ∠CDB = 30°.
Hence, the value of ∠CDB = 30°.
In the figure (ii) given below, ABCD is a cyclic quadrilateral. The tangent to the circle at B meets DC produced at F. If ∠EAB = 85° and ∠BFC = 50°, find ∠CAB.
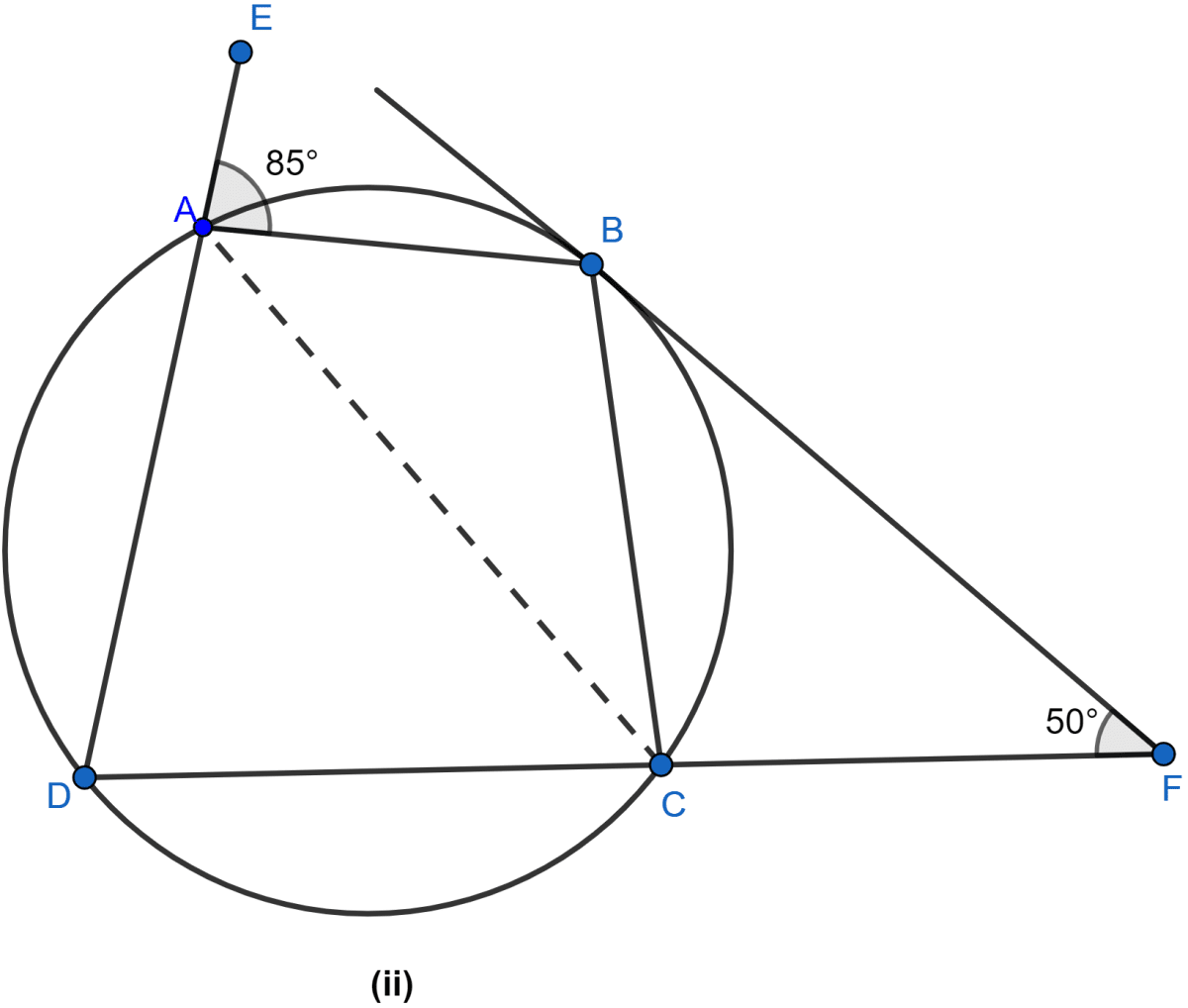
Answer
ABCD is a cyclic quadrilateral.
In cyclic quadrilateral, the exterior angle = opposite interior angle.
∴ ∠BCD = ∠EAB = 85°
From figure,
⇒ ∠BCD + ∠BCF = 180° (∵ both are linear pair)
⇒ ∠BCF + 85° = 180°
⇒ ∠BCF = 95°.
Now in △BCF,
Since, sum of angles in a triangle is 180°.
⇒ ∠BCF + ∠BFC + ∠CBF = 180°
⇒ 95° + 50° + ∠CBF = 180°
⇒ ∠CBF + 145° = 180°
⇒ ∠CBF = 35°.
We know, BF is a tangent and BC is a chord.
∴ ∠CAB = ∠CBF = 35° (∵ angles in alternate segment are equal.)
⇒ ∠CAB = 35°.
Hence, the value of ∠CAB = 35°.
In the figure (i) given below, O is the centre of the circle and SP is a tangent. If ∠SRT = 65°, find the values of x, y and z.

Answer
From figure,
In △SRT,
SR ⊥ ST (∵ tangent is perpendicular to radius from that point.)
so, ∠TSR = 90°
Since, sum of angles in a triangle = 180°
⇒ ∠TSR + ∠SRT + ∠STR = 180°
⇒ 90° + 65° + x = 180°
⇒ x + 155° = 180°
⇒ x = 25°.
SQ subtends ∠SOQ at the centre and ∠STQ on point D.
∴ ∠SOQ = 2∠STQ (∵ angle subtended at centre by an arc is double the angle subtended at remaining part of circle.)
y = 2x = 2 × 25° = 50°.
In △OSP,
Since, sum of angles in a triangle = 180
⇒ ∠OSP + ∠SOP + ∠SPO = 180°
⇒ 90° + y + z = 180°
⇒ 90° + 50° + z = 180°
⇒ z + 140° = 180°
⇒ z = 180° - 140° = 40°.
Hence, the value of x = 25°, y = 50° and z = 40°.
In the figure (ii) given below, O is the centre of the circle. PS and PT are tangents and ∠SPT = 84°. Calculate the sizes of the angles TOS and TQS.
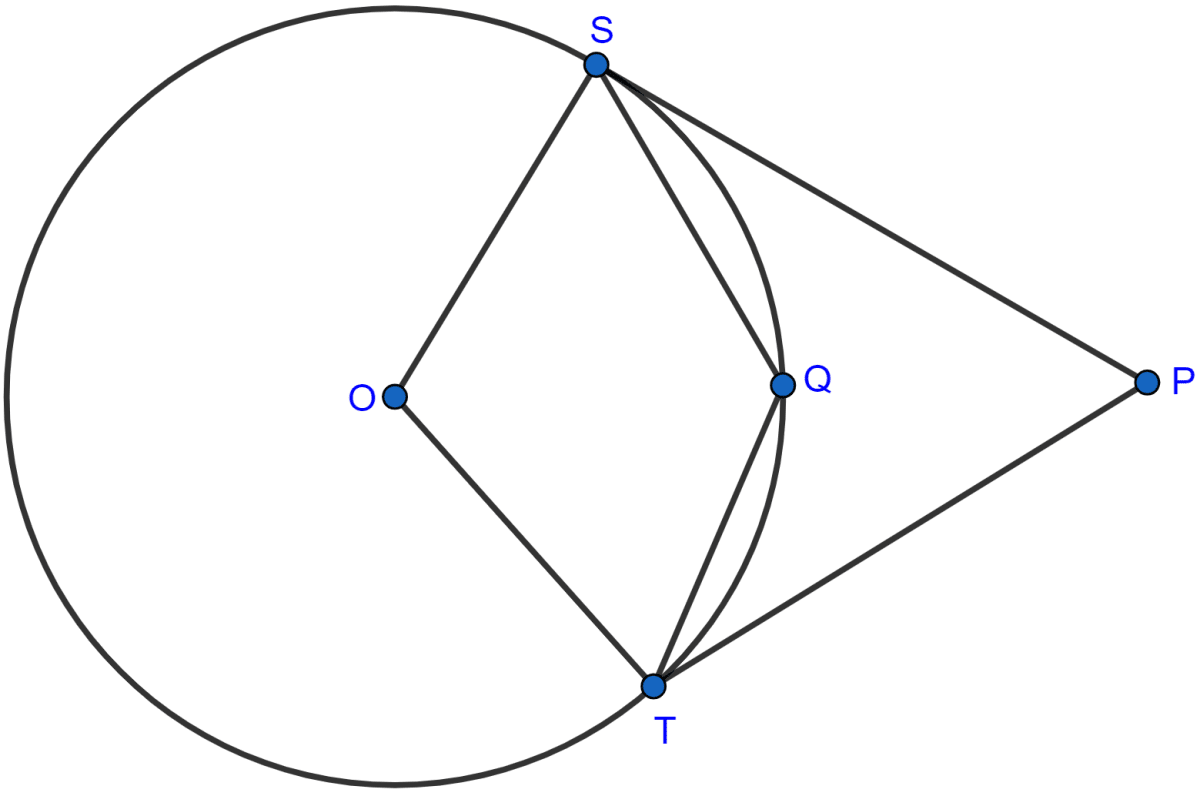
Answer
Since PS and PT are tangents on the circle. So,
∠OSP = ∠OTP = 90°.
Since, sum of angles in a quadrilateral = 360
∠TOS + ∠OTP + ∠SPT + ∠OSP = 360°
∠TOS + 90° + 84° + 90° = 360°
∠TOS + 264° = 360°
∠TOS = 360° - 264°
∠TOS = 96°.
Reflex ∠TOS = 360° - ∠TOS = 360° - 96° = 264°.
Arc ST subtends reflex ∠TOS at the centre and ∠TQS at the remaining part of the circle.
∴ Reflex ∠TOS = 2∠TQS
∠TQS = x Reflex ∠TOS = x 264° = 132°.
Hence, the value of ∠TOS = 96° and ∠TQS = 132°.
In the adjoining figure, O is the centre of the circle. Tangents to the circle at A and B meet at C. If ∠ACO = 30°, find
(i) ∠BCO
(ii) ∠AOB
(iii) ∠APB

Answer
(i) ∠BCO = ∠ACO = 30° (∵ C is the intersecting point of tangent AC and BC. So, OC divides ∠ACB in two halves.)
Hence, the value of ∠BCO = 30°.
(ii) We know that the tangent at any point of a circle and the radius through the point are perpendicular to each other.
∴ ∠OAC = ∠OBC = 90°.
∴ ∠AOC = ∠BOC (∵ tangents are equally inclined to the line joining the point and the centre of the circle.)
Since sum of angles in a triangle = 180.
In AOC
⇒ ∠AOC + ∠OAC + ∠ACO = 180°
⇒ ∠AOC + 90° + 30° = 180°
⇒ ∠AOC + 120° = 180°
⇒ ∠AOC = 180° - 120° = 60°.
∴ ∠BOC = 60°.
From figure,
∠AOB = ∠AOC + ∠BOC = 60° + 60° = 120°.
Hence, the value of ∠AOB = 120°.
(iii) Arc AB subtends ∠AOB at the centre and ∠APB at the remaining part of the circle.
∴ ∠AOB = 2∠APB (∵ angle subtended at centre by an arc is double the angle subtended at remaining point of the circle.)
∠APB = x ∠AOB = x 120° = 60°.
Hence, the value of ∠APB = 60°.
In the figure (i) given below, O is the centre of the circle. The tangents at B and D meet at P. If AB is parallel to CD and ∠ABC = 55°, find
(i) ∠BOD
(ii) ∠BPD.
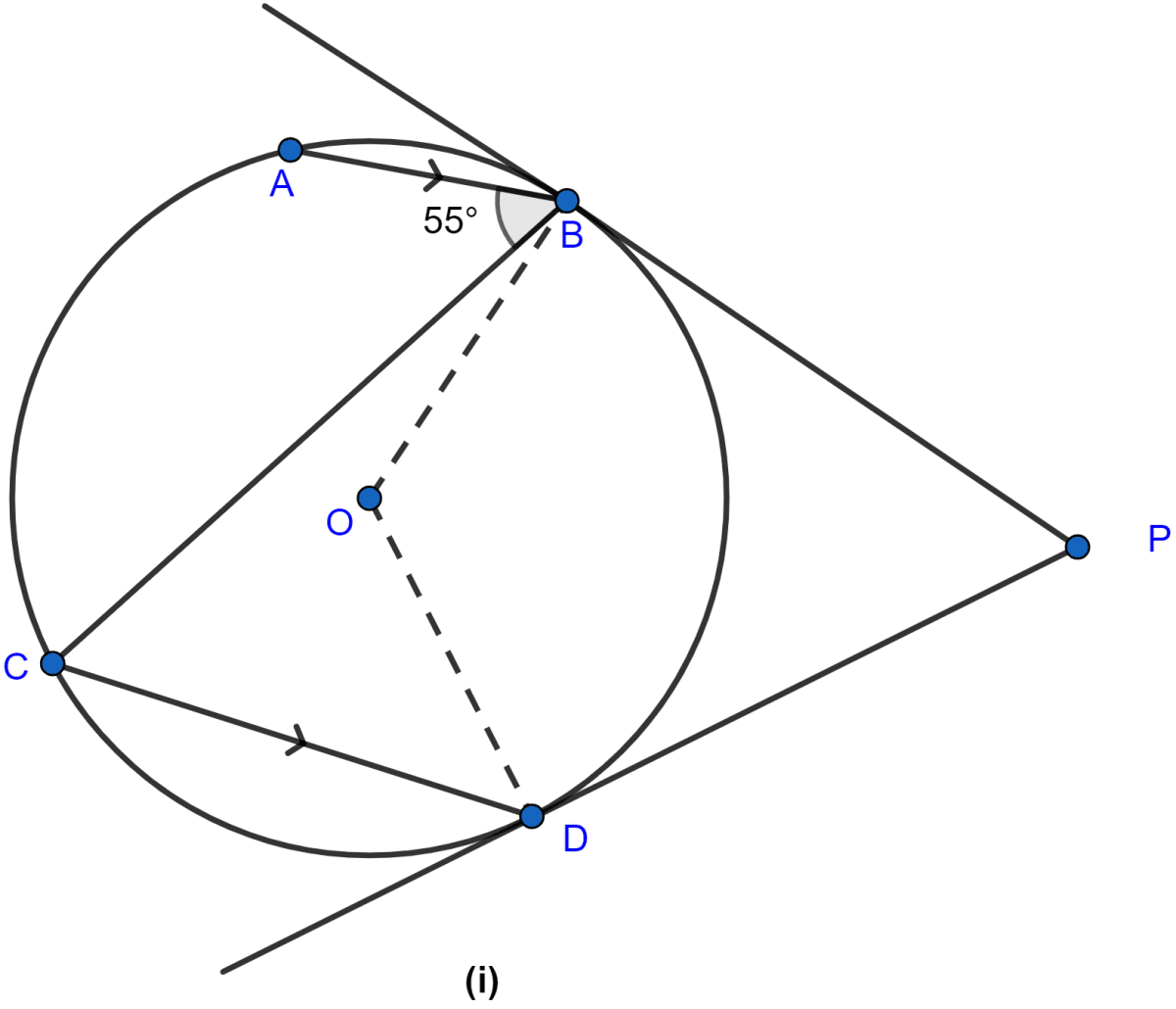
Answer
(i) From figure,
∠BCD = ∠ABC (∵ alternate angles are equal)
∠BCD = 55°.
Arc BD subtends ∠BOD at the centre and ∠BCD at the remaining part of the circle.
∴ ∠BOD = 2∠BCD (∵ angle subtended at centre by an arc is double the angle subtended at remaining point of circle.)
∠BOD = 2 × 55° = 110°.
Hence, the value of ∠BOD = 110°
(ii) OB and OD are radius and, BP and DP are tangents to the circle.
∴ OB ⊥ BP and OD ⊥ DP.
In quadrilateral OBPD, sum of angles = 360°
∠BOD + ∠ODP + ∠OBP + ∠BPD = 360°
110° + 90° + 90° + ∠BPD = 360°
290° + ∠BPD = 360°
∠BPD = 360° - 290°
∠BPD = 70°.
Hence, the value of ∠BPD = 70°.
In the figure (ii) given below, O is the centre of the circle. AB is a diameter, TPT' is a tangent to the circle at P. If ∠BPT' = 30°, calculate
(i) ∠APT
(ii) ∠BOP

Answer
From figure,
∠APB = 90° (∵ angles in semicircle is equal to 90)
From figure,
∠APT + ∠APT' = 180° (∵ they form linear pair)
⇒ ∠APT + ∠APB + ∠BPT' = 180°
⇒ ∠APT + 90° + 30° = 180°
⇒ ∠APT + 120° = 180°
⇒ ∠APT = 180° - 120°
⇒ ∠APT = 60°.
Hence, the value of ∠APT = 60°.
(ii) From figure,
BAP = BPT' = 30. (∵ angles in alternate segment are equal.)
Arc BP subtends ∠BOP at the centre and ∠BAP at the remaining part of the circle.
∴ ∠BOP = 2∠BAP (∵ angle subtended at centre by an arc is double the angle subtended at remaining part of circle.)
∠BOP = 2 × 30° = 60°.
Hence, the value of ∠BOP = 60°.
In the adjoining figure, ABCD is a cyclic quadrilateral. The line PQ is the tangent to the circle at A. If ∠CAQ : ∠CAP = 1 : 2, AB bisects ∠CAQ and AD bisects ∠CAP, then find the measures of the angles of the cyclic quadrilateral. Also prove that BD is a diameter of the circle.
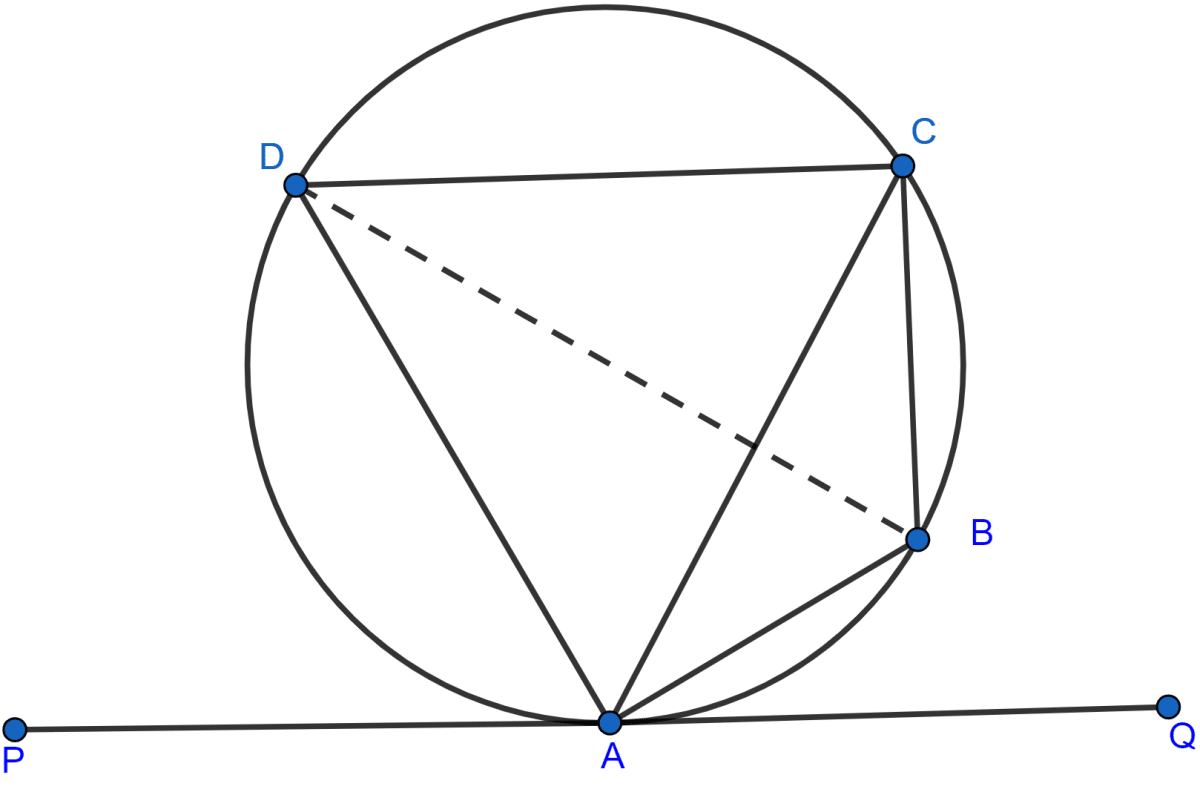
Answer
Given,
AB and AD are bisectors of ∠CAQ and ∠CAP respectively.
Let AB bisects ∠CAQ in two halves of each value x.
∴ ∠CAB = x and ∠BAQ = x.
Let AD bisects ∠CAP in two halves of each value y.
∴ ∠CAD = y and ∠DAP = y.
Since, ∠CAQ and ∠CAP are linear pair so,
⇒ ∠CAQ + ∠CAP = 180°
⇒ ∠CAB + ∠BAQ + ∠CAD + ∠DAP = 180°
⇒ x + x + y + y = 180°
⇒ 2x + 2y = 180°
⇒ x + y =
⇒ x + y = 90°.
∴ ∠CAB + ∠CAD = 90° ⇒ ∠BAD = 90°.
Since angle in semicircle is equal to 90°.
Hence, proved BD is the diameter of the circle.
Given, ∠CAQ : ∠CAP = 1 : 2.
Let ∠CAQ = k so ∠CAP = 2k.
Since ∠CAQ and ∠CAP are linear pair so,
⇒ ∠CAQ + ∠CAP = 180°
⇒ k + 2k = 180°
⇒ 3k = 180°
⇒ k = 60°.
∠CAQ = 60° and ∠CAP = 2 × 60° = 120°.
From figure,
∠ADC = ∠CAQ = 60° (∵ angles in alternate segments are equal)
∠ABC = ∠CAP = 120° (∵ angles in alternate segments are equal)
Since sum of opposite angles in cyclic quadrilateral is 180°.
⇒ ∠D + ∠B = 180°
⇒ 60° + ∠B = 180°
⇒ ∠B = 180° - 60°
⇒ ∠B = 120°.
Similarly,
⇒ ∠A + ∠C = 180°
⇒ 90° + ∠C = 180°
⇒ ∠C = 180° - 90°
⇒ ∠C = 90°.
Hence, the angles of cyclic quadrilateral are ∠A = 90°, ∠B = 120°, ∠C = 90° and ∠D = 60°.
In a triangle ABC, the incircle (centre O) touches BC, CA and AB at P, Q and R respectively. Calculate :
(i) ∠QOR
(ii) ∠QPR, given that ∠A = 60°.
Answer
(i) From figure,

OQ ⊥ AC and OR ⊥ AB (∵ OQ and OR are the radii and AC and AB are tangents.)
Now in quadrilateral AROQ,
∠A = 60°, ∠ORA = 90° and ∠OQA = 90°.
∠A + ∠ORA + ∠OQA + ∠QOR = 360°
60° + 90° + 90° + ∠QOR = 360°
240° + ∠QOR = 360°
∠QOR = 360° - 240°
∠QOR = 120°.
Hence, the value of ∠QOR = 120°.
(ii) Arc QR subtends ∠QOR at the centre and ∠QPR at the remaining part of the circle.
∴ ∠QOR = 2∠QPR (∵ angle subtended at centre by an arc is double the angle subtended at remaining part of circle)
120° = 2∠QPR
∠QPR = = 60°.
Hence, the value of ∠QPR = 60°.
In the figure (i) given below, AB is a diameter. The tangent at C meets AB produced at Q, ∠CAB = 34°. Find :
(i) ∠CBA
(ii) ∠CQA
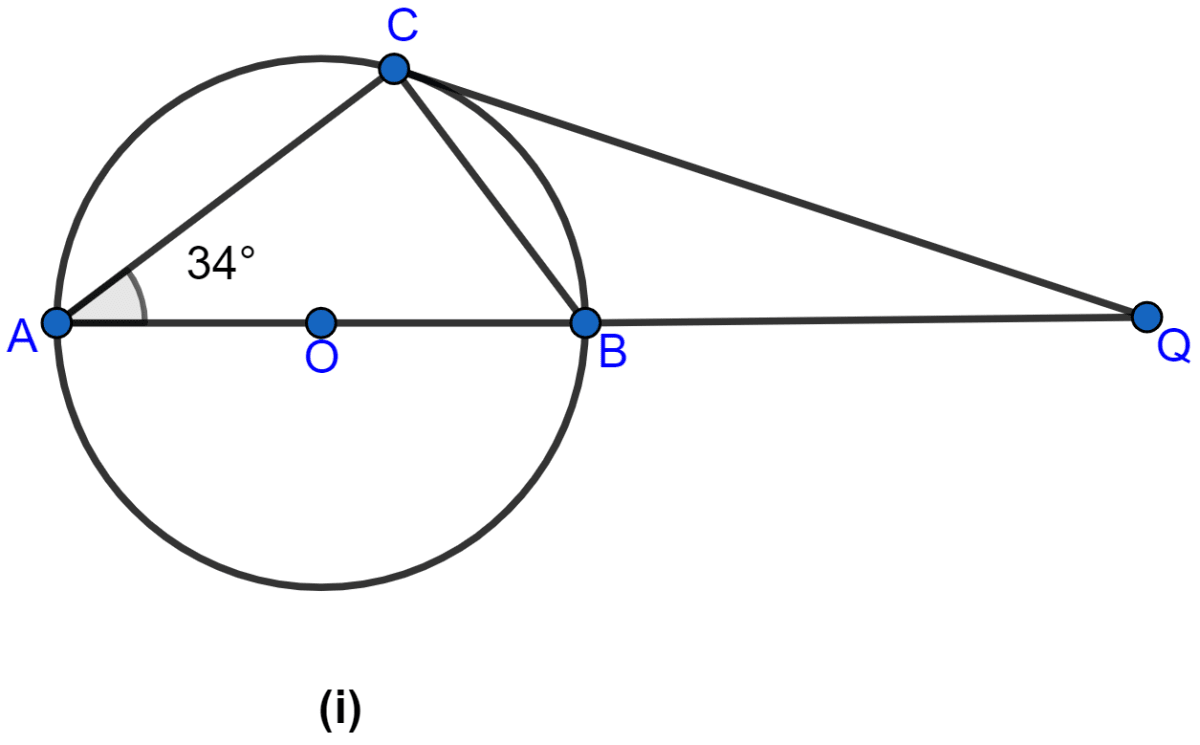
Answer
From figure,
∠ACB = 90 (∵ angles in semicircle is equal to 90.)
Since sum of angles in a triangle = 180.
In △ABC,
⇒ ∠CAB + ∠ACB + ∠CBA = 180°
⇒ 34° + 90° + ∠CBA = 180°
⇒ 124° + ∠CBA = 180°
⇒ ∠CBA = 180° - 124°
⇒ ∠CBA = 56°.
Hence, the value of ∠CBA = 56°.
(ii) From figure,
∠BCQ = ∠CAB = 34°. (∵ angles in alternate segments are equal.)
∠ACQ = ∠ACB + ∠BCQ = 90° + 34° = 124°.
Since sum of angles in a triangle = 180°.
In △ACQ,
⇒ ∠CAQ + ∠ACQ + ∠CQA = 180°
⇒ 34° + 124° + ∠CQA = 180°
⇒ 158° + ∠CQA = 180°
⇒ ∠CQA = 180° - 158°
⇒ ∠CQA = 22°.
Hence, the value of ∠CQA = 22°.
In the figure (ii) given below, AP and BP are tangents to the circle with centre O. Given ∠APB = 60°, calculate :
(i) ∠AOB
(ii) ∠OAB
(iii) ∠ACB

Answer
(i) From figure,
OA ⊥ AP and OB ⊥ BP (∵ OA and OB are the radii and AP and BP are tangents.)
Now in quadrilateral AOBP,
∠P = 60°, ∠OAP = 90° and ∠OBP = 90°.
∠P + ∠OAP + ∠OBP + ∠AOB = 360°
60° + 90° + 90° + ∠AOB = 360°
240° + ∠AOB = 360°
∠AOB = 360° - 240°
∠AOB = 120°.
Hence, the value of ∠AOB = 120°.
(ii) Join AB as shown in the figure below:

Considering △OAB,
The triangle is isosceles as OA = OB = radii of the circle so, ∠OAB = ∠OBA = x.
Since sum of angles in a triangle = 180.
In △OAB,
⇒ ∠AOB + ∠OAB + ∠OBA = 180°
⇒ 120° + x + x = 180°
⇒ 120° + 2x = 180°
⇒ 2x = 180° - 120°
⇒ 2x = 60°
⇒ x = 30°
Hence, the value of ∠OAB = 30°.
(iii) Arc AB subtends ∠AOB at the centre and ∠ACB at the remaining part of the circle.
∴ ∠AOB = 2∠ACB (∵ angle subtended at centre by an arc is double the angle subtended at remaining part of circle)
120° = 2∠ACB
∠ACB = = 60°.
Hence, the value of ∠ACB = 60°.
In the figure (i) given below, O is the centre of the circumcircle of triangle XYZ. Tangents at X and Y intersect at T. Given ∠XTY = 80° and ∠XOZ = 140°, calculate the value of ∠ZXY.
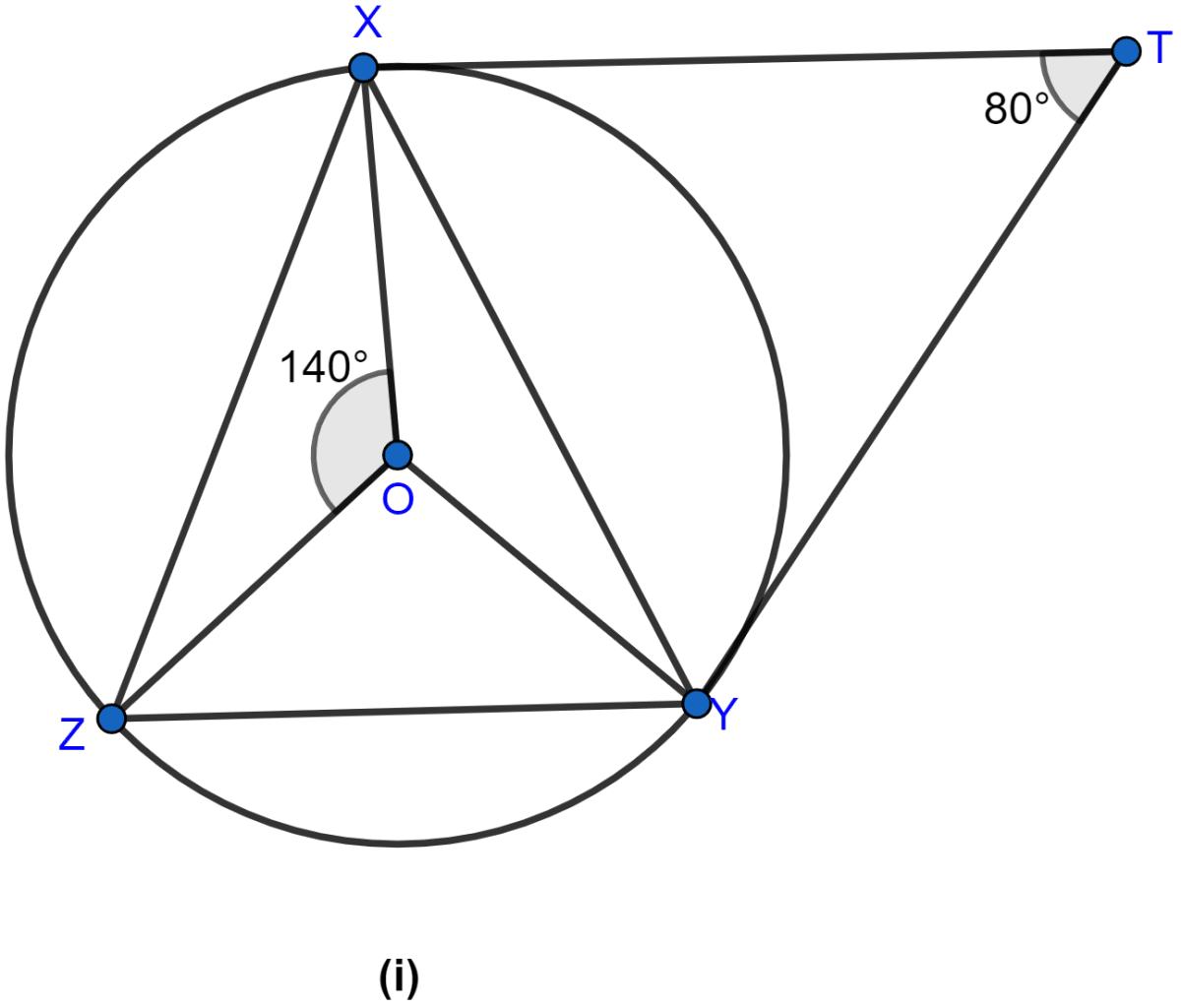
Answer
From figure,
XT = YT (∵ tangents from an external point to a circle are of equal length.)
So, △XTY is an isosceles triangle with
∠YXT = ∠XYT = a.
Since sum of angles in a triangle = 180°.
In △XTY,
⇒ ∠YXT + ∠XYT + ∠XTY = 180°
⇒ a + a + 80° = 180°
⇒ 2a + 80° = 180°
⇒ 2a = 180° - 80°
⇒ 2a = 100°
⇒ a = 50°.
From figure,
OX = OZ = radius of the circle
So, △OXZ is an isosceles triangle with
∠OXZ = ∠OZX = b.
Since sum of angles in a triangle = 180°.
In △OXZ,
⇒ ∠OXZ + ∠OZX + ∠XOZ = 180°
⇒ b + b + 140° = 180°
⇒ 2b + 140° = 180°
⇒ 2b = 180° - 140°
⇒ 2b = 40°
⇒ b = 20°.
From figure,
OX ⊥ XT (∵ tangent at a point and radius through the point are perpendicular to each other.)
∴ ∠OXT = 90°
∠OXY + ∠YXT = 90°
∠OXY + 50° = 90°
∠OXY = 90° - 50°
∠OXY = 40°.
From figure,
∠ZXY = ∠OXZ + ∠OXY = 20° + 40° = 60°.
Hence, the value of ∠ZXY = 60°.
In the figure (ii) given below, O is the center of the circle and PT is the tangent to the circle at P. Given ∠QPT = 30°, calculate
(i) ∠PRQ
(ii) ∠POQ.
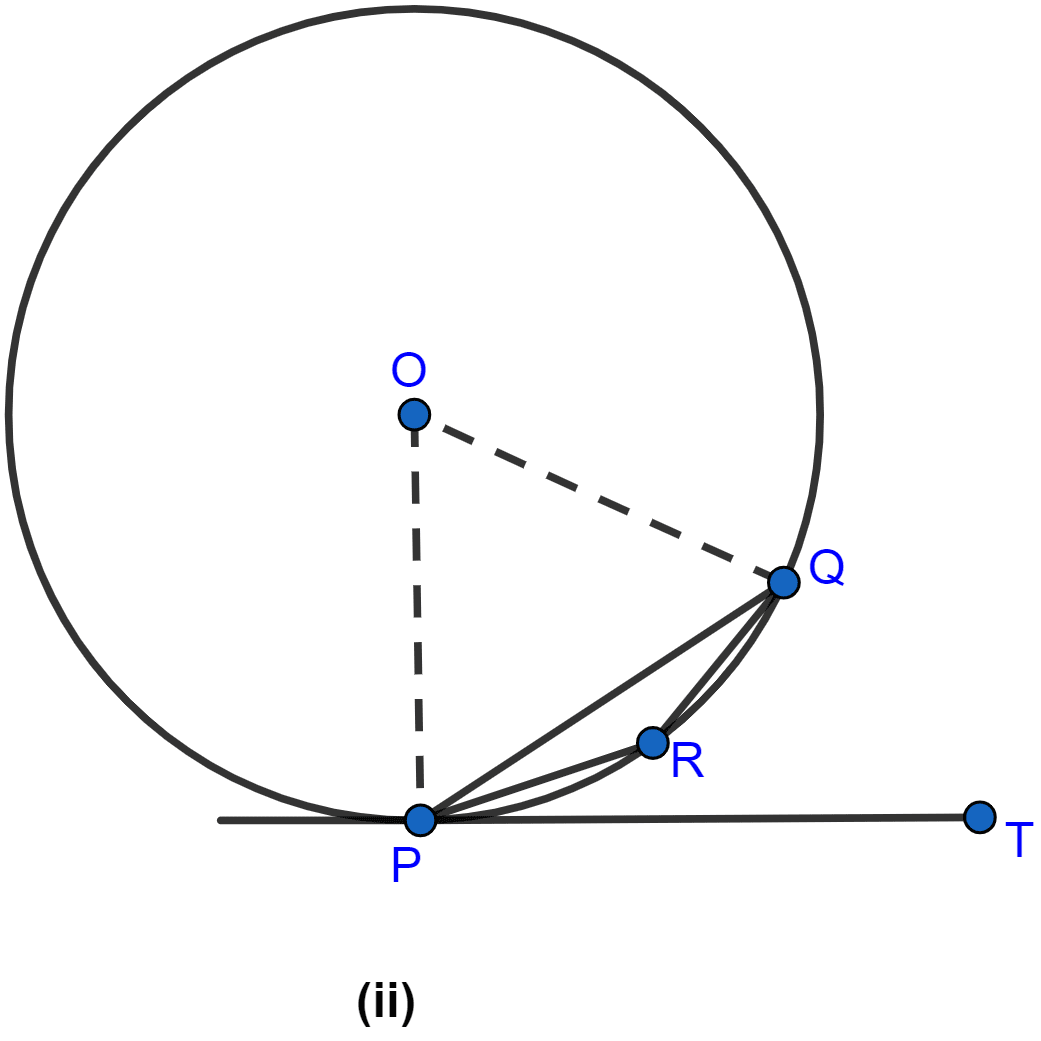
Answer
From figure,
OP ⊥ PT (∵ tangent at a point and radius through the point are perpendicular to each other.)
∴ ∠OPT = 90°.
Given, ∠QPT = 30°.
From figure,
∠OPT = 90°
∠OPQ + ∠QPT = 90°
∠OPQ + 30° = 90°
∠OPQ = 90° - 30° = 60°.
In △OPQ,
OP = OQ (∵ both are equal to radius of the circle.)
So, the triangle is isosceles. So,
∠OQP = OPQ = 60°.
Since sum of angles in a triangle = 180°.
In △OPQ,
⇒ ∠OQP + ∠OPQ + ∠POQ = 180°
⇒ 60 + 60 + ∠POQ = 180°
⇒ 120 + ∠POQ = 180°
⇒ ∠POQ = 180° - 120°
⇒ ∠POQ = 60°
Reflex ∠POQ = 360° - ∠POQ = 360° - 60° = 300°.
Arc PQ subtends Reflex ∠POQ at the centre and ∠PRQ at the remaining part of the circle.
∴ Reflex ∠POQ = 2∠PRQ (∵ angle subtended at centre by an arc is double the angle subtended at remaining part of circle)
300° = 2° × ∠PRQ
∠PRQ = = 150°.
(i) Hence, the value of ∠PRQ = 150°.
(ii) Hence, the value of ∠POQ = 60°.
Two chords AB, CD of a circle intersect internally at a point P. If
(i) AP = 6 cm, PB = 4 cm and PD = 3 cm, find PC.
(ii) AB = 12 cm, AP = 2 cm, PC = 5 cm, find PD.
(iii) AP = 5 cm, PB = 6 cm and CD = 13 cm, find CP.
Answer
We know that when two chords of a circle intersect internally or externally, then the products of the lengths of segments are equal.
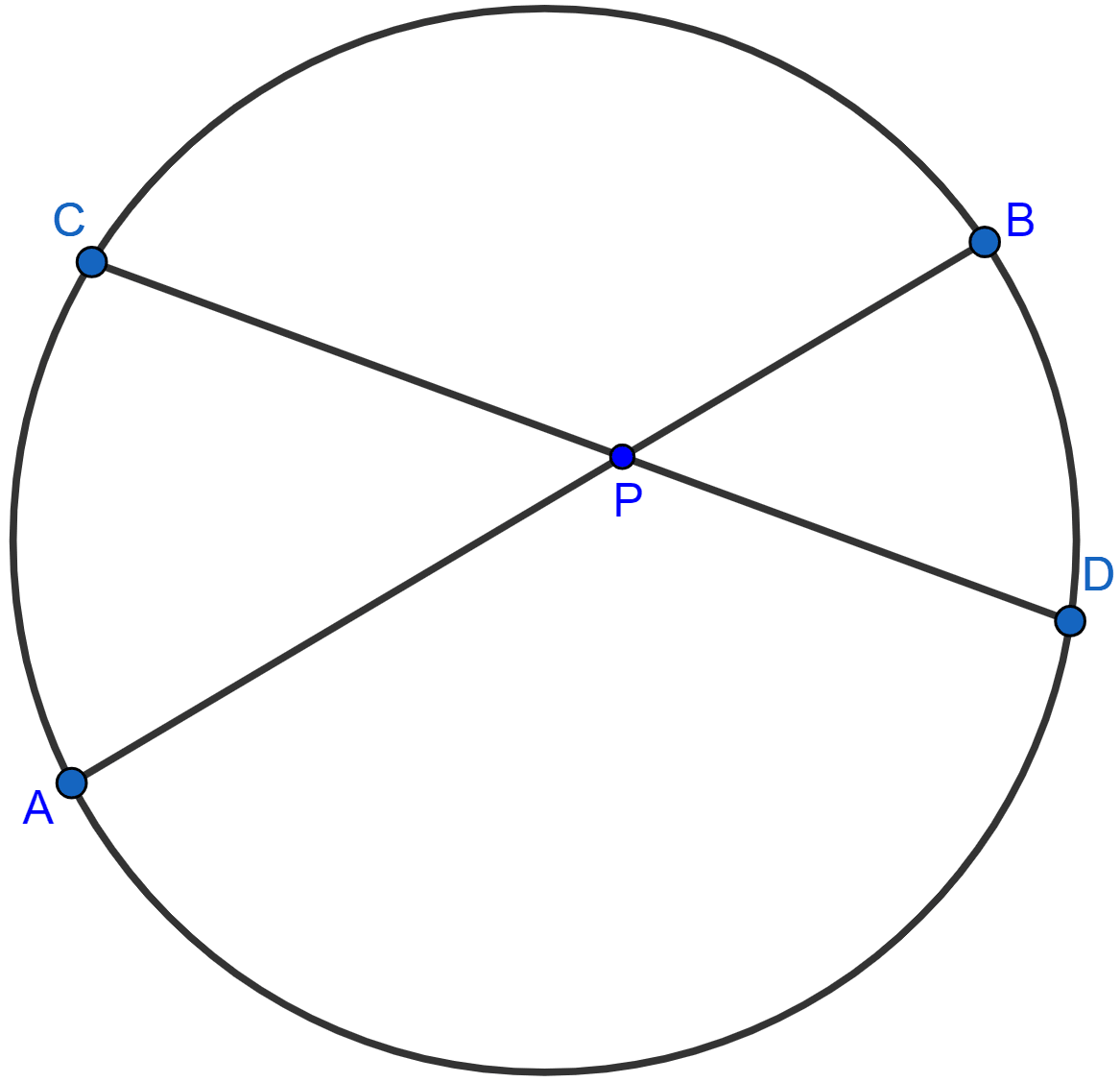
Given, chords AB and CD of a circle intersect internally at a point P. So,
PA.PB = PC.PD
(i) Given, AP = 6 cm, PB = 4 cm and PD = 3 cm.
We know that,
PA.PB = PC.PD
⇒ 6 × 4 = PC × 3
⇒ 24 = 3PC
⇒ PC = = 8 cm.
Hence, the length of PC = 8 cm.
(ii) Given, AB = 12 cm, AP = 2 cm, PC = 5 cm
PB = AB - AP = 12 - 2 = 10 cm.
We know that,
PA.PB = PC.PD
⇒ 2 × 10 = 5 × PD
⇒ 20 = 5PD
⇒ PD = = 4 cm.
Hence, the length of PD = 4 cm.
(iii) Given, AP = 5 cm, PB = 6 cm and CD = 13 cm
Let PC = x, so PD = 13 - x
We know that,
PA.PB = PC.PD
⇒ 5 × 6 = x(13 - x)
⇒ 30 = 13x - x2
⇒ x2 - 13x + 30 = 0
⇒ x2 - 10x - 3x + 30 = 0
⇒ x(x - 10) - 3(x - 10) = 0
⇒ (x - 3)(x - 10) = 0
⇒ x - 3 = 0 or x - 10 = 0
⇒ x = 3 or x = 10.
Hence, PC = 3 cm or 10 cm.
In the figure (i) given below, PT is a tangent to the circle. Find TP if AT = 16 cm and AB = 12 cm.

Answer
We know that,
If a chord and a tangent intersect externally, then the product of lengths of the segments of the chord is equal to the square of the length of the tangent from the point of contact to the point of intersection.
∴ TP2 = AT × BT
From figure,
BT = AT - AB = 16 - 12 = 4 cm.
Putting values we get,
⇒ TP2 = 16 × 4
⇒ TP2 = 64
⇒ TP =
⇒ TP = 8 cm.
Hence, the length of TP = 8 cm.
In the figure (ii) given below, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find :
(i) AB
(ii) the length of tangent PT.

Answer
We know that,
If a chord and a tangent intersect externally, then the product of lengths of the segments of the chord is equal to the square of the length of the tangent from the point of contact to the point of intersection.
∴ TP2 = PC × PD
From figure,
PC = PD + CD
= 5 + 7.8
= 12.8 cm.
⇒ TP2 = 12.8 × 5
⇒ TP2 = 64
⇒ TP =
⇒ TP = 8 cm.
Similarly,
⇒ TP2 = AP × BP
⇒ 82 = AP × 4
⇒ 64 = 4AP
⇒ AP =
⇒ AP = 16 cm.
(i) From figure,
AB = AP - BP = 16 - 4 = 12 cm.
Hence, the length of AB = 12 cm.
(ii) The length of tangent PT = 8 cm.
PAB is a secant and PT is tangent to a circle. If
(i) PT = 8 cm and PA = 5 cm, find the length of AB.
(ii) PA = 4.5 cm and AB = 13.5 cm, find the length of PT.
Answer
We know that,
If a chord and a tangent intersect externally, then the product of lengths of the segments of the chord is equal to the square of the length of the tangent from the point of contact to the point of intersection.
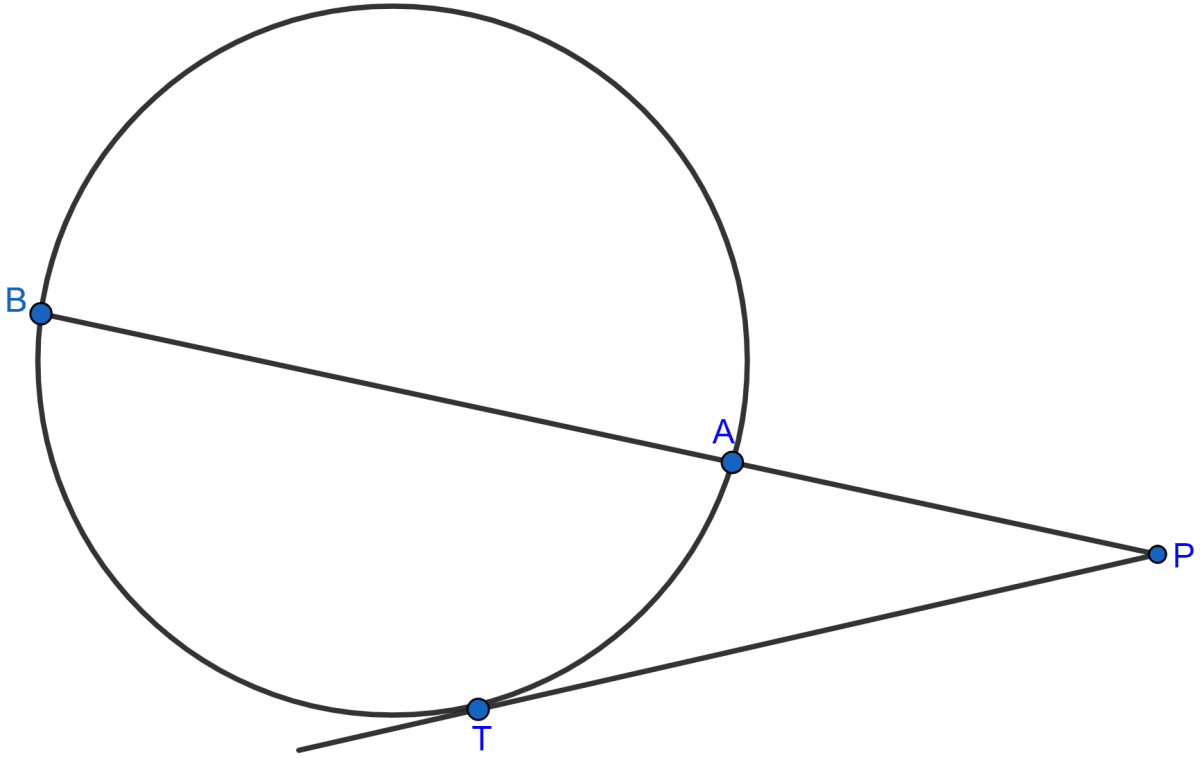
∴ PT2 = PA × PB
(i) Putting values in above equation:
⇒ 82 = 5 × PB
⇒ 82 = 5PB
⇒ PB =
⇒ PB = 12.8 cm.
AB = PB - PA = 12.8 - 5 = 7.8 cm.
Hence, the length of AB = 7.8 cm.
(ii) We know,
PB = AB + PA = 13.5 + 4.5 = 18 cm.
PT2 = PA × PB
⇒ PT2 = 4.5 × 18
⇒ PT2 = 81
⇒ PT =
⇒ PT = 9 cm.
Hence, the length of PT = 9 cm.
In the adjoining figure, CBA is a secant and CD is tangent to the circle. If AB = 7 cm and BC = 9 cm, then
(i) Prove that △ACD ~ △DCB
(ii) find the length of CD.
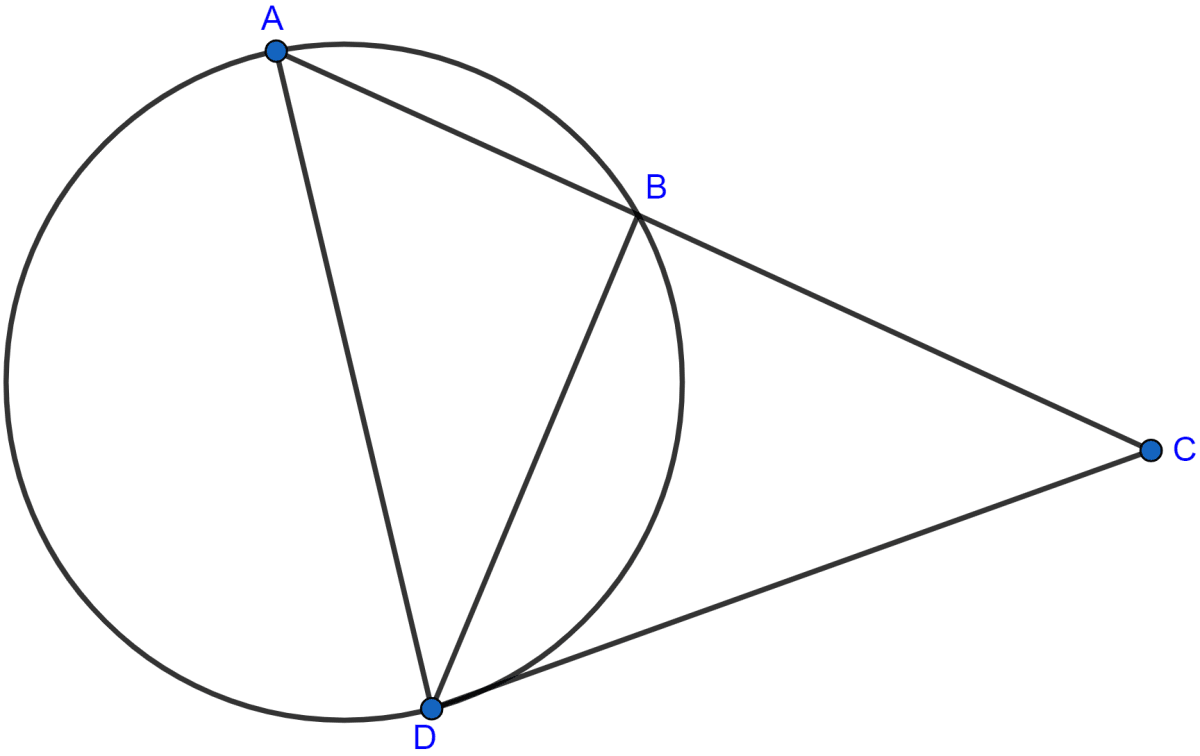
Answer
(i) In △ACD and △DCB
∠C = ∠C (Common angles)
∠CAD = ∠CDB (Angles in alternate segments are equal)
∴ △ACD ~ △DCB (By AA axiom.)
Hence, proved that △ACD ~ △DCB.
(ii) Since triangles are similar hence, the ratio of their corresponding sides are equal.
Hence, the length of DC = 12 cm.
In the figure (i) given below, PAB is a secant and PT is tangent to a circle. If PA : AB = 1 : 3 and PT = 6 cm, find the length of PB.

Answer
Given, PA : AB = 1 : 3.
Let PA = k, so AB = 3k.
PB = PA + AB = k + 3k = 4k.
We know that,
If a chord and a tangent intersect externally, then the product of lengths of the segments of the chord is equal to the square of the length of the tangent from the point of contact to the point of intersection.
∴ PT2 = PA × PB
⇒ 62 = k × 4k
⇒ 36 = 4k2
⇒ k2 =
⇒ k = cm
⇒ k = 3 cm.
PB = 4k = 4(3) = 12 cm.
Hence, the length of PB = 12 cm.
In the figure (ii) given below, ABC is an isosceles triangle in which AB = AC and Q is mid-point of AC. If APB is a secant and AC is tangent to the circle at Q, prove that AB = 4AP.
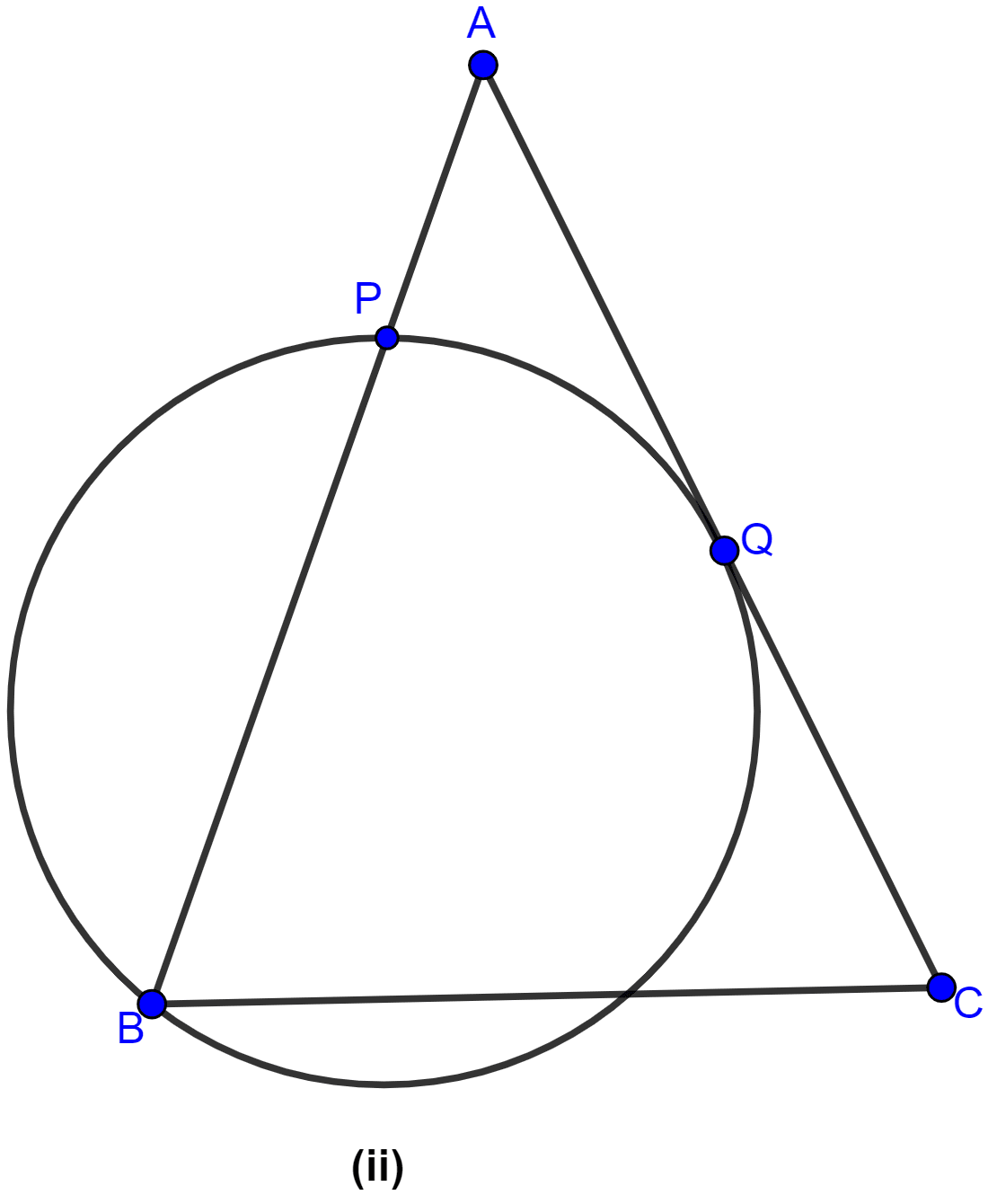
Answer
We know that,
If a chord and a tangent intersect externally, then the product of lengths of the segments of the chord is equal to the square of the length of the tangent from the point of contact to the point of intersection.
∴ AQ2 = AP × AB .....(Eq. 1)
Given Q is mid-point of AC, so AQ = .
Since, AC = AB.
Dividing both sides by AB,
AB = 4 x AP.
Hence, proved that AB = 4AP.
Two chords AB, CD of a circle intersect externally at a point P. If PA = PC, prove that AB = CD.
Answer
We know that when two chords of a circle intersect internally or externally, then the products of the lengths of segments are equal.
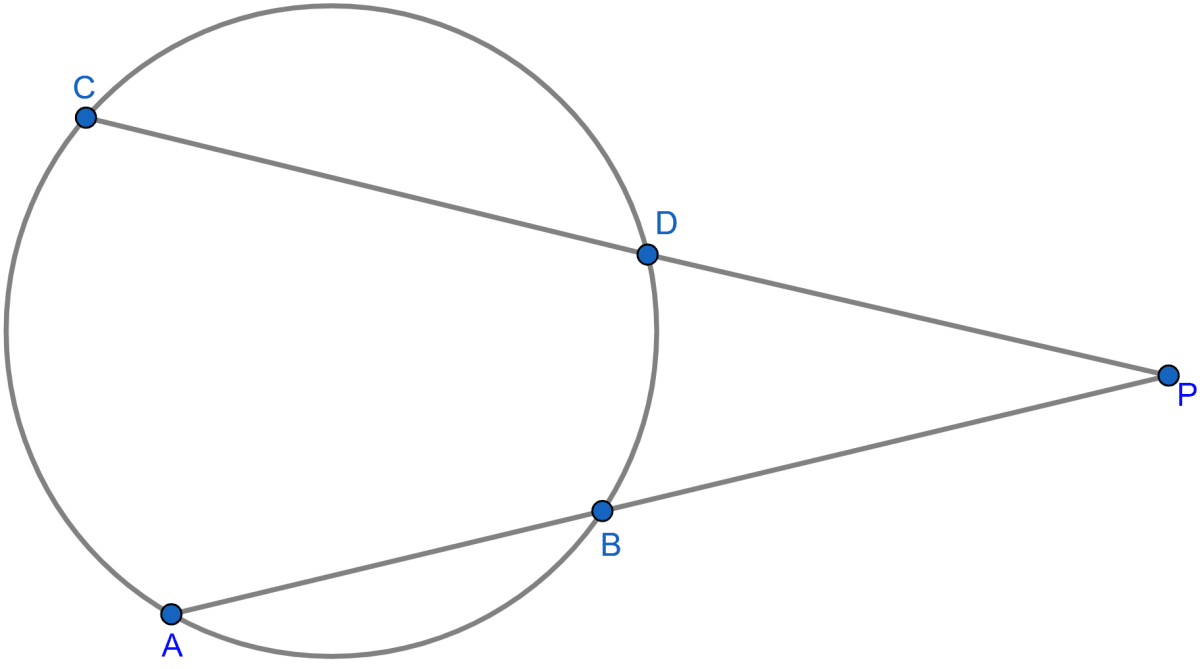
Given, chords AB and CD of a circle intersect externally at a point P. So,
PA.PB = PC.PD .....(Eq. 1)
Let PA = a, so PC = a. (∵ PA = PB)
Putting these value in Eq. 1 we get,
a.PB = a.PD
Dividing both sides by a we get,
PB = PD.
Let PB = PD = b
From figure,
AB = PA - PB = a - b.
CD = PC - PD = a - b.
Hence, proved that AB = CD.
In the figure (i) given below, AT is tangent to a circle at A. If ∠BAT = 45° and ∠BAC = 65°, find ∠ABC.

Answer
From figure,
∠ACB = ∠BAT = 45° (∵ angles in alternate segments are equal)
Since sum of angles in a triangle = 180°.
In △ABC,
⇒ ∠ACB + ∠CAB + ∠ABC = 180°
⇒ 45° + 65° + ∠ABC = 180°
⇒ 110° + ∠ABC = 180°
⇒ ∠ABC = 180° - 110°
⇒ ∠ABC = 70°.
Hence, the value of ∠ABC = 70°.
In the figure (ii) given below, A, B and C are three points on a circle. The tangent at C meets BA produced at T. Given that ∠ATC = 36° and ∠ACT = 48°, calculate the angle subtended by AB at the centre of the circle.
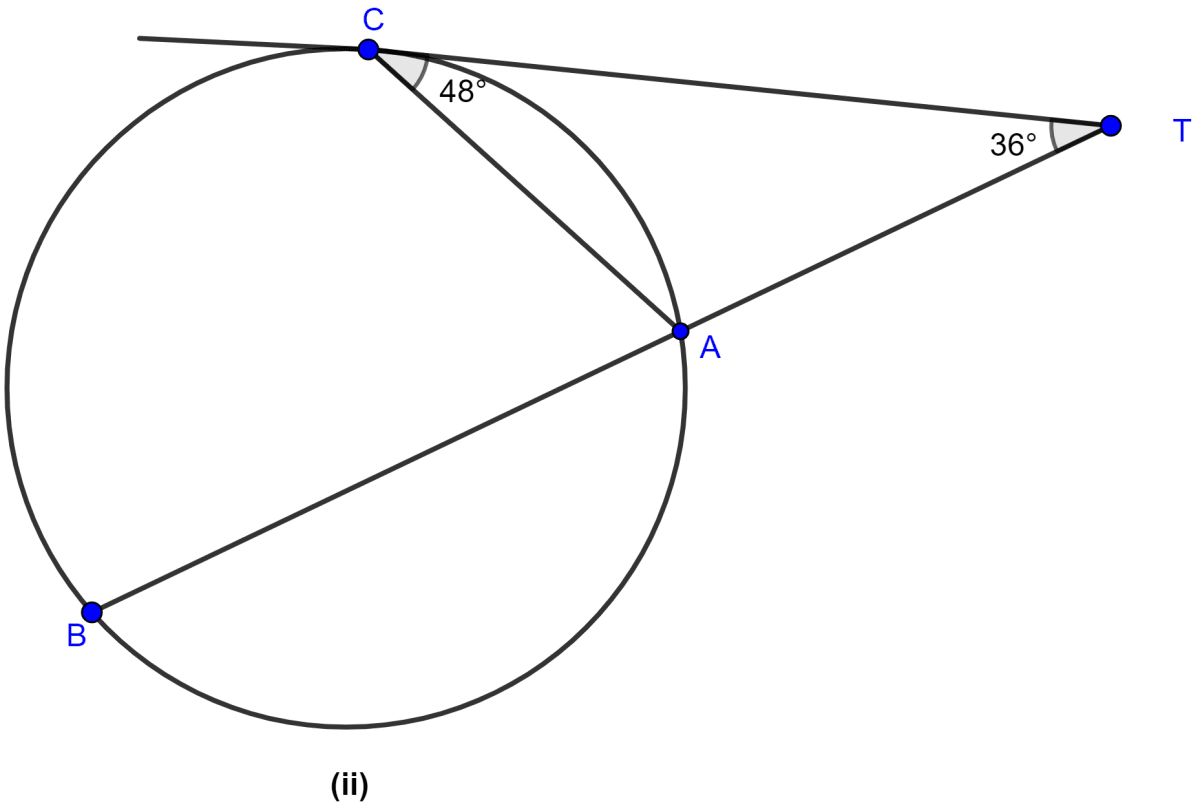
Answer
Join OA, OB and CB. In △ATC,
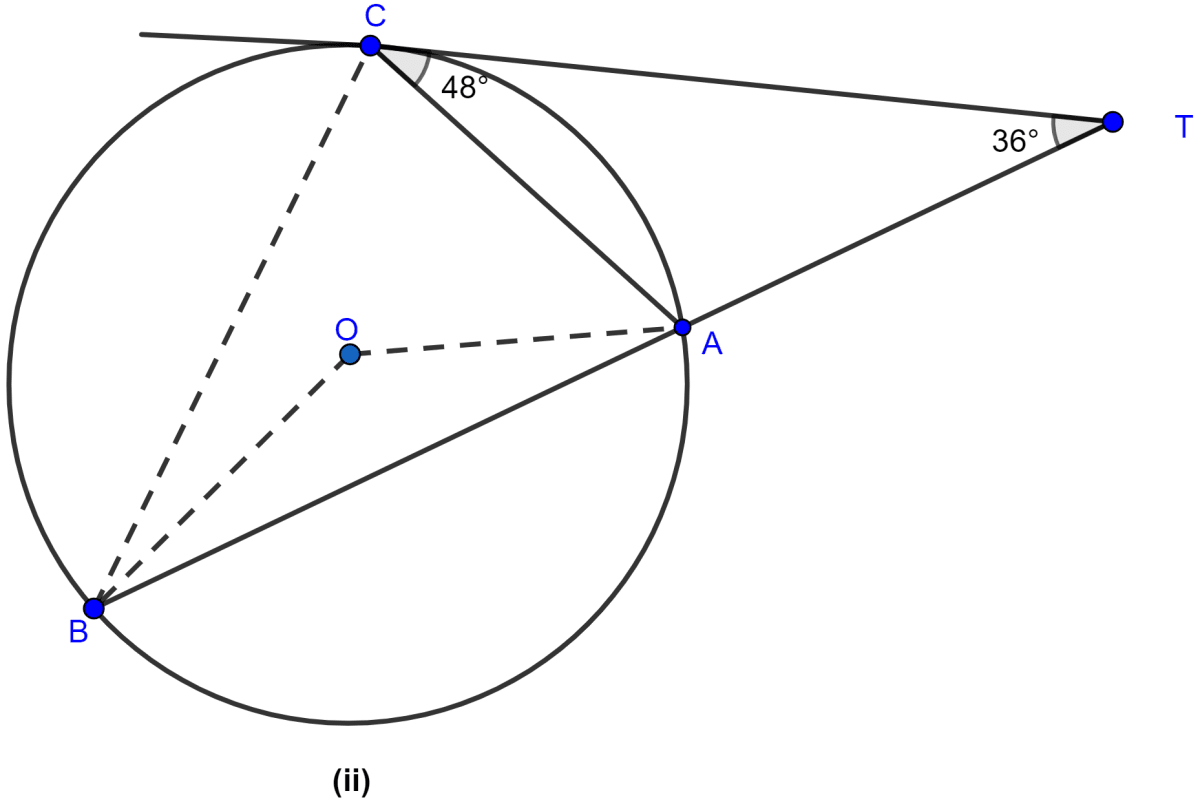
Ext. ∠CAB = ∠ATC + TCA (∵ external angle in a triangle is equal to the sum of opposite interior angles.)
Ext. ∠CAB = 36° + 48° = 84°.
From figure,
∠ABC = ∠TCA = 48° (∵ angles in alternate segment are equal.)
Since sum of angles in a triangle = 180°.
In △ABC,
⇒ ∠ABC + ∠BAC + ∠ACB = 180°
⇒ 48° + 84° + ∠ACB = 180°
⇒ 132° + ∠ACB = 180°
⇒ ∠ACB = 180° - 132°
⇒ ∠ACB = 48°.
Arc AB subtends ∠AOB at the centre and ∠ACB at the remaining part of the circle.
∴ ∠AOB = 2∠ACB (∵ angle subtended at centre is double the angle subtended at remaining part of the circle.)
∠AOB = 2 × 48° = 96°.
Hence, the angle subtended by AB at the center of the circle is 96°.
In the adjoining figure, △ABC is isosceles with AB = AC. Prove that the tangent at A to the circumcircle of △ABC is parallel to BC.

Answer
In △ABC,
AB = AC (Given)
∴ ∠C = ∠B (∵ angles opposite to equal sides are equal.)
From figure,
∠TAC = ∠B (∵ angles in alternate segment are equal.)
But ∠B = ∠C
∴ ∠TAC = ∠C
But angles ∠TAC and ∠C are alternate angles. Since, they are equal
Hence, proved that AT || BC.
If the sides of a rectangle touch a circle, prove that the rectangle is a square.
Answer
The figure below shows a rectangle ABCD with its sides touching the circle at points P, Q, R and S.
We know that,
Length of tangents from an external point to the circle are equal.
Hence,
AP = AS .....(Eq. 1)
BP = BQ .....(Eq. 2)
CR = CQ .....(Eq. 3)
DR = DS .....(Eq. 4)
Adding the above 4 equations,
⇒ AP + BP + CR + DR = AS + BQ + CQ + DS
⇒ AB + CD = AD + BC
But AB = CD and AD = BC (As opposite sides of a rectangle are equal.)
⇒ AB + AB = BC + BC
⇒ 2AB = 2BC
⇒ AB = BC.
∴ AB = BC = CD = DA.
Hence, proved that ABCD is a square.
In the figure (i) given below, two circles intersect at A, B. From a point P on one of these circles, two line segments PAC and PBD are drawn, intersecting the other circles at C and D respectively. Prove that CD is parallel to the tangent at P.

Answer
From figure,
PT is a tangent and PA is chord.
∠APT = ∠ABP (∵ angles in alternate segments are equal.) ...(i)
BDCA is a cyclic quadrilateral as all the vertices lie on the circumference of the circle.
In cyclic quadrilateral the exterior angle is equal to the opposite interior angle.
∴ ∠ABP = ∠ACD ....(ii)
From (i) and (ii),
∠APT = ∠ACD
The angles ∠APT and ∠ACD are alternate angles, but since they are equal,
Hence, proved that CD || PT.
In the figure (ii) given below, two circles with centres C, C' intersect at A, B and the point C lies on the circle with C'. PQ is a tangent to the circle with centre C' at A. Prove that AC bisects ∠PAB.

Answer
In △ACB,
AC = BC (Radius of the same circle)
∴ ∠BAC = ∠ABC ....(i)
PAQ is tangent and AC is the chord of the circle.
∠PAC = ∠ABC (∵ angles in alternate segment are equal) ....(i)
From (i) and (ii)
∠BAC = ∠PAC
Hence, proved that AC bisects ∠PAB.
In the figure (i) given below, AB is a chord of the circle with centre O, BT is tangent to the circle. If ∠OAB = 32°, find the values of x and y.
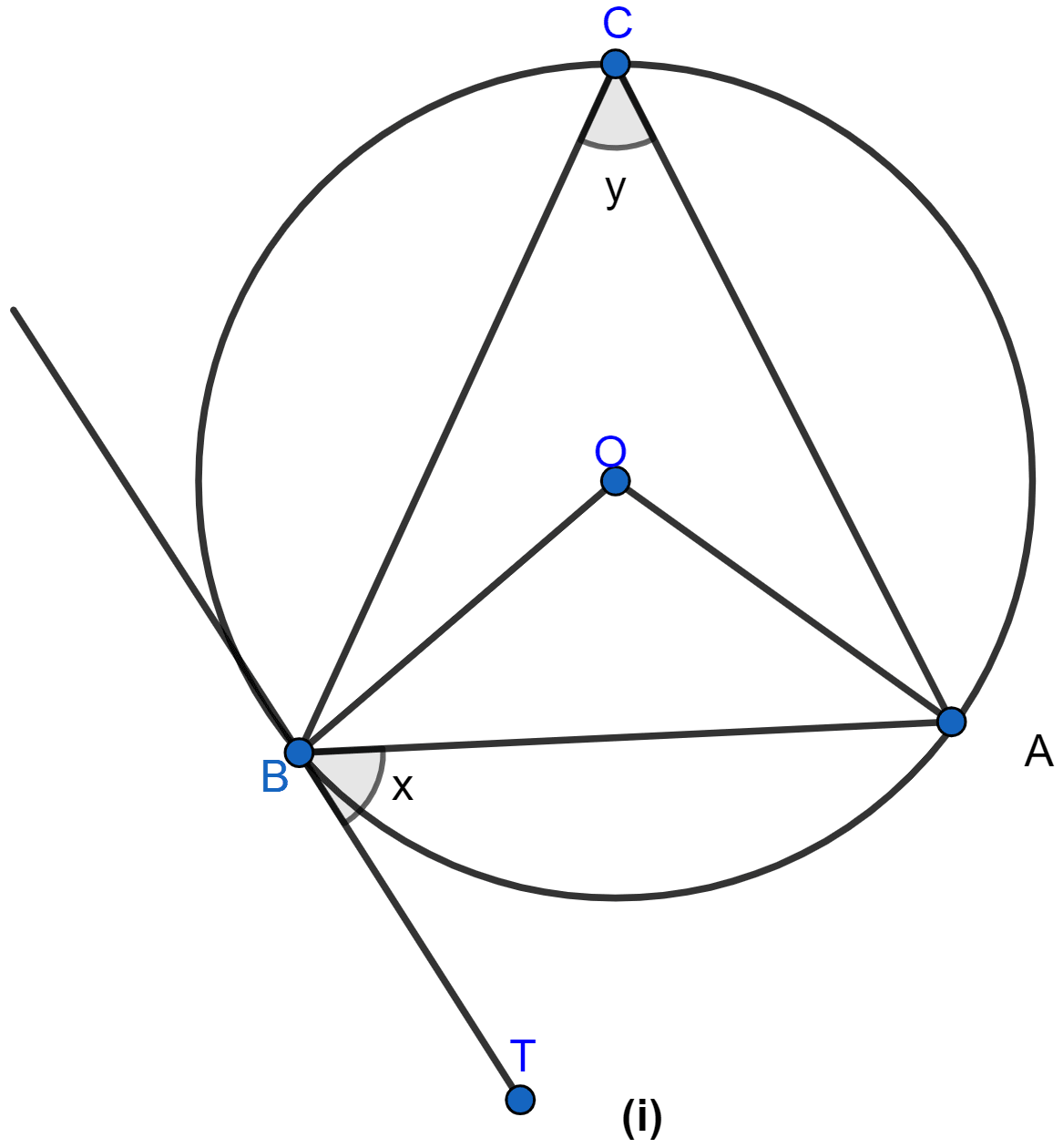
Answer
In △OAB,
OA = OB (∵ both are radius of the common circle.)
So, △OAB is a isosceles triangle with,
∠OBA = ∠OAB = 32°.
Since sum of angles in a triangle = 180°.
In △OAB,
⇒ ∠OBA + ∠OAB + ∠AOB = 180°
⇒ 32° + 32° + ∠AOB = 180°
⇒ 64° + ∠AOB = 180°
⇒ ∠AOB = 180° - 64°
⇒ ∠AOB = 116°.
Arc AB subtends ∠AOB at centre and ∠ACB at remaining part of circle.
∴ ∠AOB = 2∠ACB (∵ angle subtended at centre is double the angle subtended at remaining part of the circle.)
⇒ 116° = 2y
⇒ y =
⇒ y = 58°.
From figure,
∠ABT = ∠ACB = 58° (∵ angles in alternate segments are equal.)
∴ x = 58°.
Hence, the value of x = 58° and y = 58°.
In the figure (ii) given below, O and O' are centres of two circles touching each other externally at the point P. The common tangent at P meets a direct common tangent AB at M. Prove that,
(i) M bisects AB.
(ii) ∠APB = 90°.

Answer
(i) From figure,
From M, MA and MP are the tangents.
∴ MA = MP.....(i) (∵ length of the different tangents to a circle from a single point are equal.)
Similarly,
From M, MB and MP are the tangents.
∴ MB = MP.....(ii) (∵ length of the different tangents to a circle from a single point are equal.)
From (i) and (ii),
MA = MB.
Hence, proved that M bisects AB.
(ii) Since MA = MP
Hence in triangle APM,
∠MAP = ∠MPA ....(i) (∵ angles opposite to equal sides are equal.)
Since MB = MP
Hence in triangle BPM,
∠MPB = ∠MBP ....(ii) (∵ angles opposite to equal sides are equal.)
Adding equations (i) and (ii)
⇒ ∠MAP + ∠MPB = ∠MPA + ∠MBP
⇒ ∠MAP + ∠MBP = ∠APB
Since sum of angles in a triangle = 180°
In triangle APB
⇒ ∠APB + ∠MAP + ∠MBP = 180°
Putting value of ∠MAP + ∠MBP = ∠APB in above equation
⇒ ∠APB + ∠APB = 180°
⇒ 2∠APB = 180°
⇒ ∠APB = = 90°.
Hence, proved that ∠APB = 90°.
In adjoining figure, P and Q are the centers of two circles touching externally at R and CD is the common tangent.
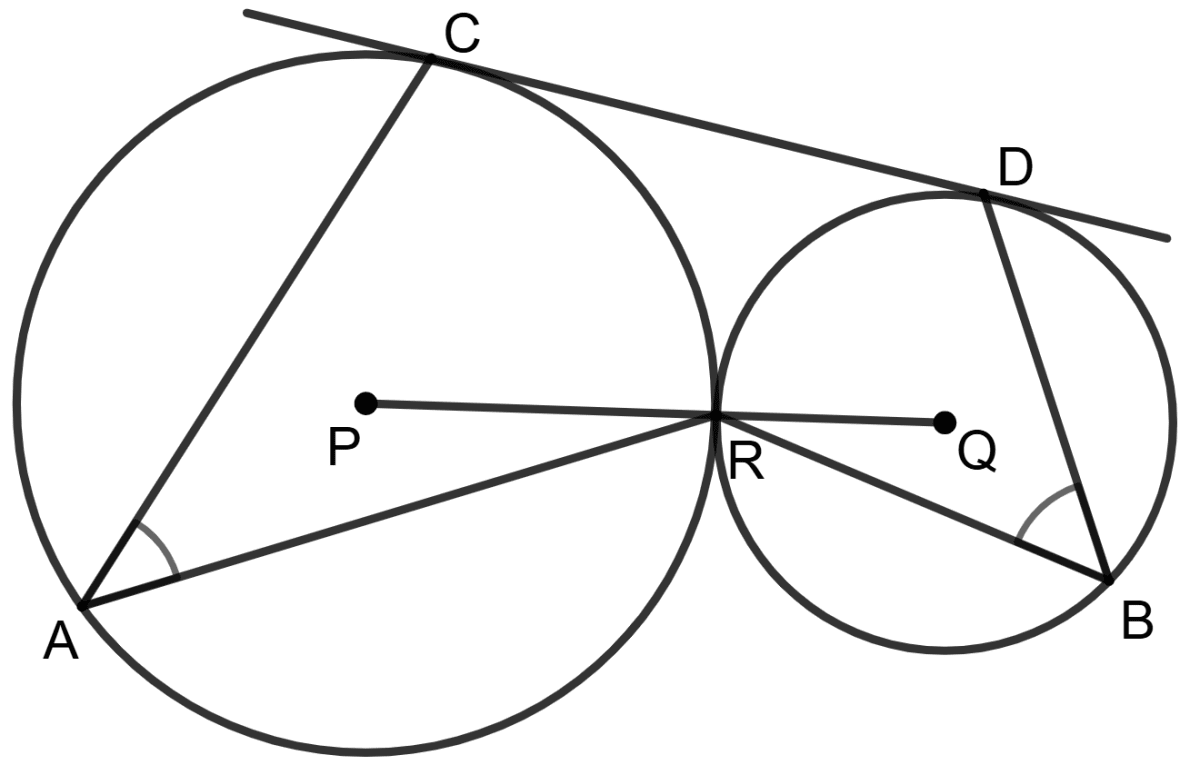
If ∠CAR = 38°, then find ∠DBR.
Answer
Join PC and QD.
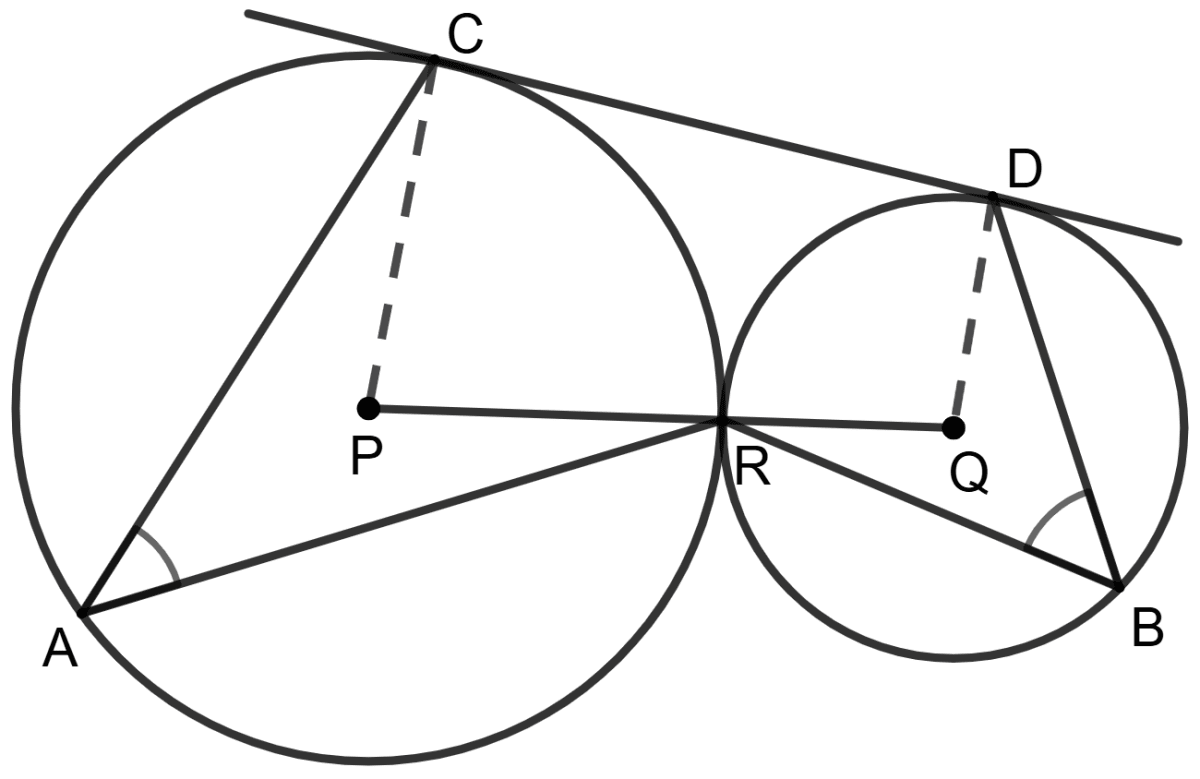
We know that,
The tangent at any point of a circle is perpendicular to the radius through the point of contact.
∴ PC ⊥ CD and QD ⊥ CD
⇒ ∠PCD = 90° and ∠QDC = 90°
The angle subtended by an arc of a circle at the center is double the angle subtended by it at any point on the remaining part of the circle.
⇒ ∠CPR = 2 x ∠CAR = 2 x 38° = 76°
⇒ ∠CPR = ∠CPQ = 76°
CDQP is quadrilateral.
∴ ∠PCD + ∠QDC + ∠DQP + ∠CPQ = 360°
⇒ 90° + 90° + ∠DQP + 76° = 360°
⇒ 256° + ∠DQP = 360°
⇒ ∠DQP = 360° - 256°
⇒ ∠DQP = 104°
From figure,
⇒ ∠DQR = ∠DQP
⇒ ∠DQR = 104°
The angle subtended by an arc of a circle at the center is double the angle subtended by it at any point on the remaining part of the circle.
⇒ ∠DQR = 2 x ∠DBR
⇒ 104° = 2 x ∠DBR
⇒ ∠DBR =
⇒ ∠DBR = 52°.
Hence, ∠DBR = 52°.
In the adjoining figure, O is the centre of the circle. If ∠OAB = 40°, then ∠ACB is equal to
50°
40°
60°
70°

Answer
From figure,
OA = OB (Radius of the circle.)
So, △OAB is an isosceles triangle with ∠OBA = ∠OAB (As angles opposite to equal sides are equal.)
∠OBA = 40°.
Since, sum of angles in a triangle = 180°.
⇒ ∠OAB + ∠OBA + ∠AOB = 180°
⇒ 40° + 40° + ∠AOB = 180°
⇒ 80° + ∠AOB = 180°
⇒ ∠AOB = 180° - 80°
⇒ ∠AOB = 100°.
Arc AB subtends ∠AOB at centre and ∠ACB at remaining part of circle.
∠AOB = 2∠ACB (∵ angle subtended at centre is double the angle subtended at remaining part of circle.)
100° = 2∠ACB
∠ACB = = 50°.
Hence, Option 1 is the correct option.
ABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and ∠ADC = 140°, then ∠BAC is equal to
80°
50°
40°
30°
Answer
Cyclic quadrilateral ABCD is shown in the figure below:
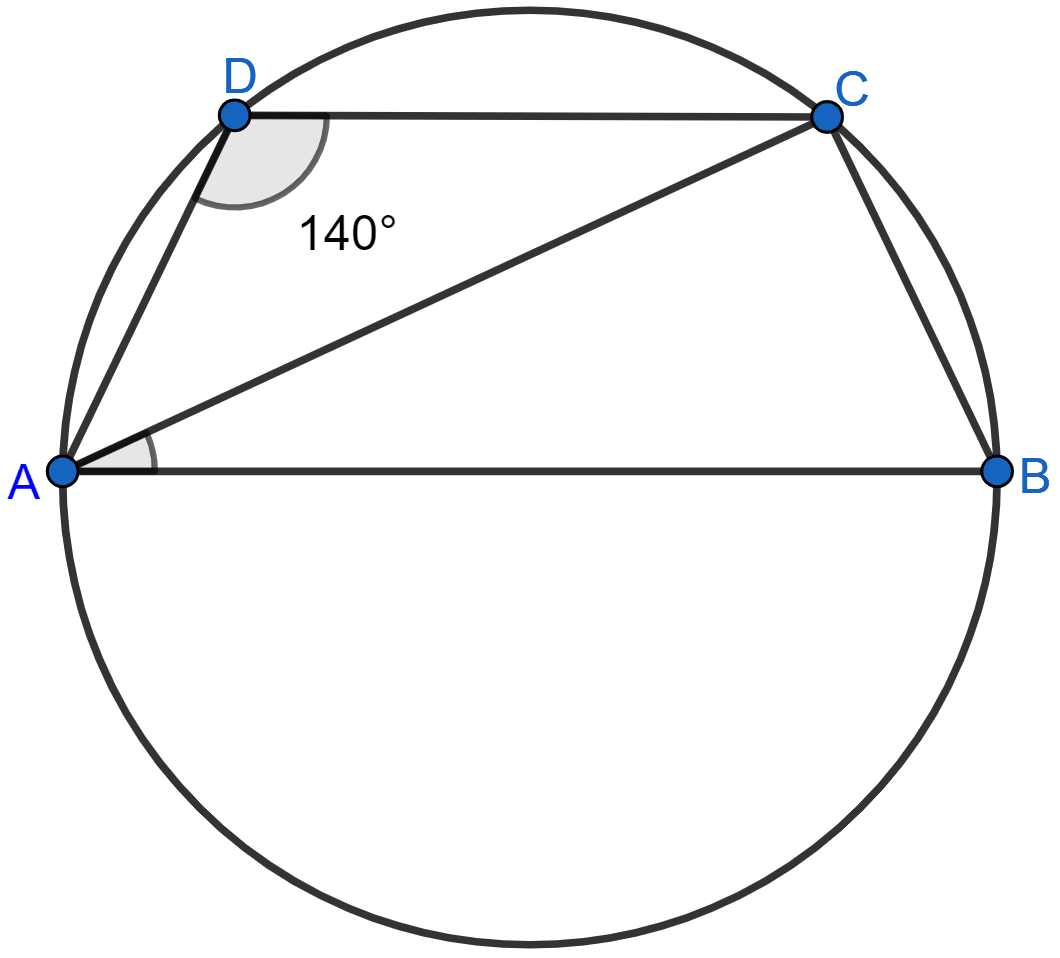
The sum of opposite angles in a quadrilateral = 180°.
∴ ∠ADC + ∠ABC = 180°
140° + ∠ABC = 180°
∠ABC = 180° - 140° = 40°.
In △ABC,
∠ACB = 90° (∵ angles in semicircle = 90°.)
Since, sum of angles in a triangle = 180°.
In △ABC,
⇒ ∠ABC + ∠ACB + ∠BAC = 180°
⇒ 40° + 90° + ∠BAC = 180°
⇒ 130° + ∠BAC = 180°
⇒ ∠BAC = 180° - 130°
⇒ ∠BAC = 50°.
Hence, Option 2 is the correct option.
In the adjoining figure, O is the centre of the circle. If ∠BAO = 60°, then ∠ADC is equal to
30°
45°
60°
120°

Answer
In the figure,
OA = OB (Radius of the circle.)
So, △OAB is an isosceles triangle with ∠OBA = ∠BAO (∵ angles opposite to equal sides are equal.)
∠OBA = 60°.
In a triangle the exterior angle is equal to the sum of opposite interior angle.
∴ ∠AOC = ∠BAO + ∠OBA = 60° + 60° = 120°.
Arc AC subtends ∠AOC at centre and ∠ADC at remaining part of circle.
∠AOC = 2∠ADC (∵ angle subtended at centre is double the angle subtended at remaining part of circle.)
120° = 2∠ADC
∠ADC = = 60°.
Hence, Option 3 is the correct option.
In the adjoining figure, O is the centre of the circle. If the length of the chord PQ is equal to the radius of the circle, then ∠PRQ is
60°
45°
30°
15°
Answer
From figure,
In △OPQ,
OP = OQ = PQ = (Radius of the circle.)
Hence, △OPQ is an equilateral triangle.
∴ ∠POQ = 60° (∵ all angles of an equilateral triangle = 60°.)
Arc PQ subtends ∠POQ at centre and ∠PRQ at remaining part of circle.
∠POQ = 2∠PRQ (∵ angle subtended at centre is double the angle subtended at remaining part of circle.)
60° = 2∠PRQ
∠PRQ = = 30°.
Hence, Option 3 is the correct option.
In the adjoining figure, if O is the centre of the circle then the value of x is
18°
20°
24°
36°

Answer
From figure,
∠ADB = ∠ACB = 2x (∵ ∵ angles in same segment are equal.)
Join OA as shown in the figure below:

Arc AB subtends ∠AOB at centre and ∠ADB at remaining part of circle.
∠AOB = 2∠ADB = 2(2x) = 4x (∵ angle subtended at centre is double the angle subtended at remaining part of circle.)
In △OAB,
OA = OB (Radius of the circle.)
So, △OAB is an isosceles triangle with ∠OBA = ∠OAB (∵ angles opposite to equal sides are equal.)
∠OAB = 3x.
Since, sum of angles in a triangle = 180°.
⇒ ∠OAB + ∠OBA + ∠AOB = 180°
⇒ 3x + 3x + 4x = 180°
⇒ 10x = 180°
⇒ x = 18°
Hence, Option 1 is the correct option.
From a point which is at a distance of 13 cm from the centre O of a circle of radius 5 cm, the pair of tangents PQ and PR to the circle are drawn. Then the area of the quadrilateral PQOR is
60 cm2
65 cm2
30 cm2
32.5 cm2
Answer
Given, the point P is 13 cm from O, the centre of the circle as shown in the figure below:
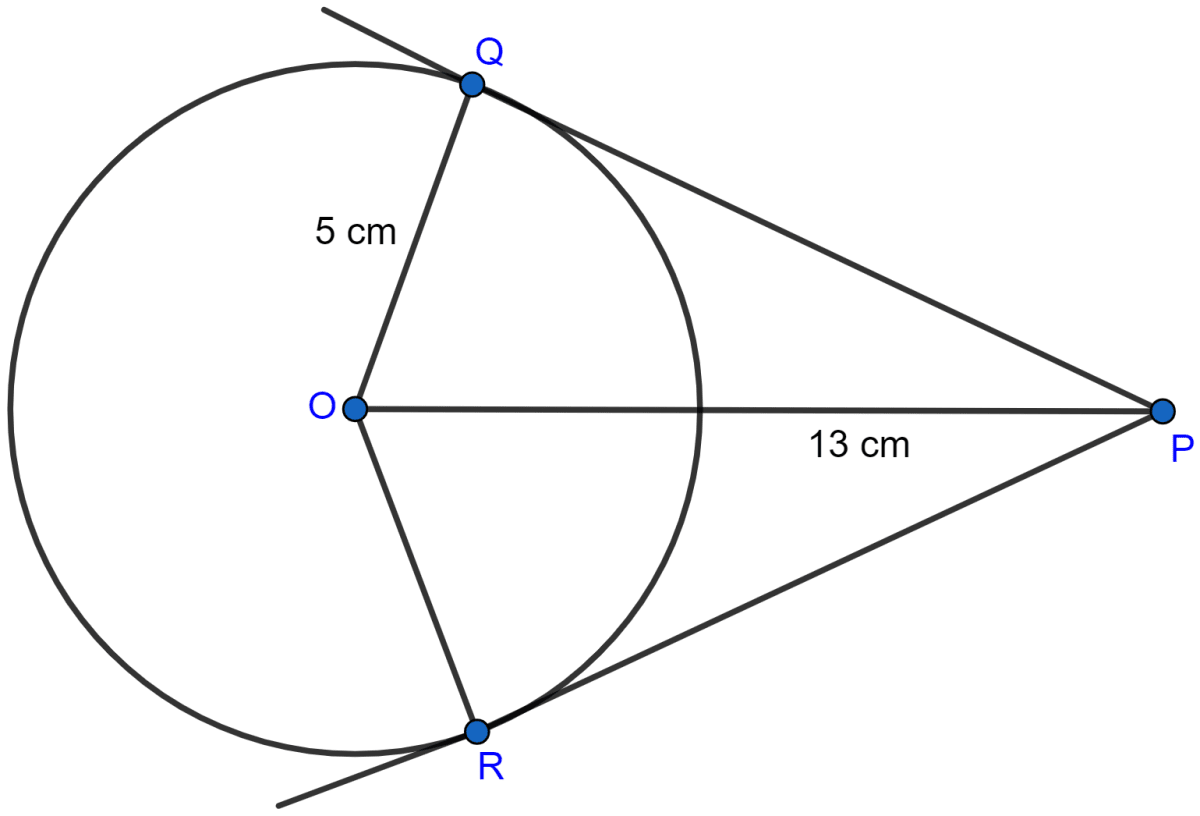
Radius of the circle (OQ) = 5 cm
PQ and PR are tangents from P to the circle.
PQ ⊥ OQ (∵ radius of a circle and tangent through that point are perpendicular to each other.)
∴ OQP = 90°.
So, in △OQP,
Area of △OPQ = = cm2.
Similarly,
PR ⊥ OR (∵ radius of a circle and tangent through that point are perpendicular to each other.)
∴ ∠ORP = 90°.
So, in △ORP,
Area of △POR = = cm2.
Area of quadrilateral PQOR = Area of △POR + Area of △OPQ = 30 + 30 = 60 cm2.
Hence, Option 1 is the correct option.
In the adjoining figure, ABCD is a cyclic quadrilateral. If ∠BAD = (2x + 5)° and ∠BCD = (x + 10)°, then x is equal to
65
45
55
50
Answer
Since, ABCD is a cyclic quadrilateral.
We know that,
The sum of opposite angles of a cyclic quadrilateral is 180°.
⇒ ∠BAD + ∠BCD = 180°
⇒ (2x + 5)° + (x + 10)° = 180°
⇒ 3x° + 15° = 180°
⇒ 3x° = 180° - 15°
⇒ 3x° = 165°
⇒ x° =
⇒ x° = 55°
⇒ x = 55.
Hence, Option 3 is the correct option.
In the adjoining figure, PQ and PR are tangents from P to a circle with centre O. If ∠POR = 55°, then ∠QPR is
35°
55°
70°
80°
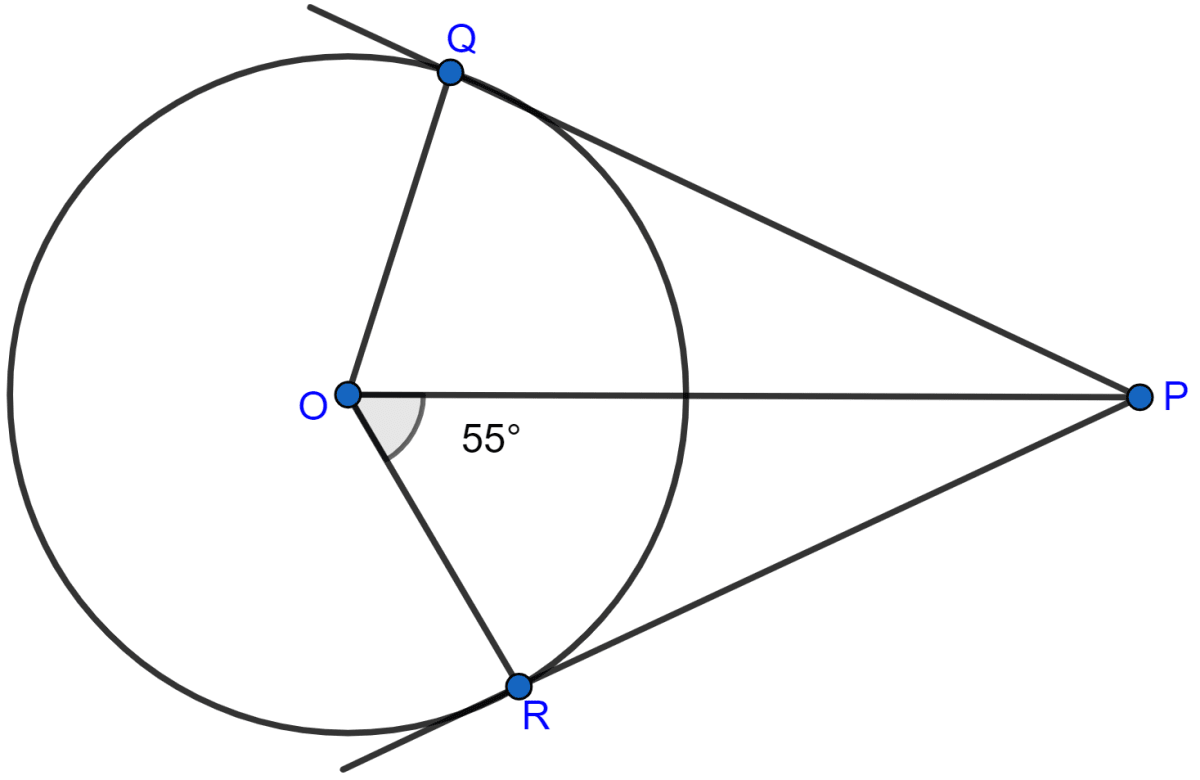
Answer
OR ⊥ PR (∵ radius of a circle and tangent through that point are perpendicular to each other.)
∴ ∠ORP = 90°.
Since, sum of angles in a triangle = 180°.
⇒ ∠ORP + ∠POR + ∠OPR = 180°
⇒ 90° + 55° + ∠OPR = 180°
⇒ 145° + ∠OPR = 180°
⇒ ∠OPR = 180° - 145°
⇒ ∠OPR = 35°.
∠QPO = ∠OPR = 35° (∵ the tangents are equally inclined to the line joining the point and the centre of the circle.)
From figure,
∠QPR = ∠OPR + ∠QPO = 35° + 35° = 70°.
Hence, Option 3 is the correct option.
In the adjoining figure, PA and PB are tangents from point P to a circle with centre O. If the radius of the circle is 5 cm and PA ⊥ PB, then the length OP is equal to
5 cm
10 cm
7.5 cm
5√2 cm

Answer
Join OA as shown in the figure below:

OA ⊥ PA (∵ radius of a circle and tangent through that point are perpendicular to each other.)
∴ ∠OAP = 90°.
Given, PA ⊥ PB
∴ ∠APB = 90°.
∵ the tangents are equally inclined to the line joining the point and the centre of the circle.
∠APO = x ∠APB = 45°.
Since, sum of angles in a triangle = 180°.
In △OAP,
⇒ ∠APO + ∠OAP + ∠AOP = 180°
⇒ 45° + 90° + ∠AOP = 180°
⇒ 135° + ∠AOP = 180°
⇒ ∠AOP = 180° - 135°
⇒ ∠AOP = 45°.
Since, ∠AOP = ∠APO hence, △OAP is an isosceles triangle with OA = AP = 5 cm.
In right angled triangle △OAP,
Hence, Option 4 is the correct option.
At one end A of a diameter AB of a circle of radius 5 cm, tangent XAY is drawn to the circle. The length of the chord CD parallel to XY and at a distance 8 cm from A is
4 cm
5 cm
6 cm
8 cm
Answer
The figure is shown below:

Since tangent and radius at point of contact of a circle are perpendicular to each other. Hence,
XAY ⊥ AO
Given XAY || to CD hence,
CD ⊥ AB.
In right angled triangle OEC,
OE = AE - AO = 8 - 5 = 3 cm.
⇒ OC2 = OE2 + CE2 (By pythagoras theorem)
⇒ 52 = 32 + CE2
⇒ CE2 = 25 - 9
⇒ CE2 = 16
⇒ CE = 4 cm.
Similarly in right angled triangle OED,
⇒ OD2 = OE2 + ED2 (By pythagoras theorem)
⇒ 52 = 32 + ED2
⇒ ED2 = 25 - 9
⇒ ED2 = 16
⇒ ED = 4 cm.
⇒ CD = CE + ED = 4 + 4 = 8 cm.
Hence, Option 4 is the correct option.
If radii of two concentric circles are 4 cm and 5 cm, then the length of each chord of one circle which is tangent to the other is
3 cm
6 cm
9 cm
1 cm
Answer
From figure,
AB is chord to the bigger circle which is tangent to the smaller circle at C.
OC ⊥ AC (∵ radius of a circle and tangent through that point are perpendicular to each other.)
∴ ∠ACO = 90°.
In △ACO,
Length of chord AB = 2 × AC = 2 × 3 = 6 cm.
Hence, Option 2 is the correct option.
In the adjoining diagram, RT is a tangent touching the circle at S. If ∠PST = 30° and ∠SPQ = 60° then ∠PSQ is equal to
40°
30°
60°
90°
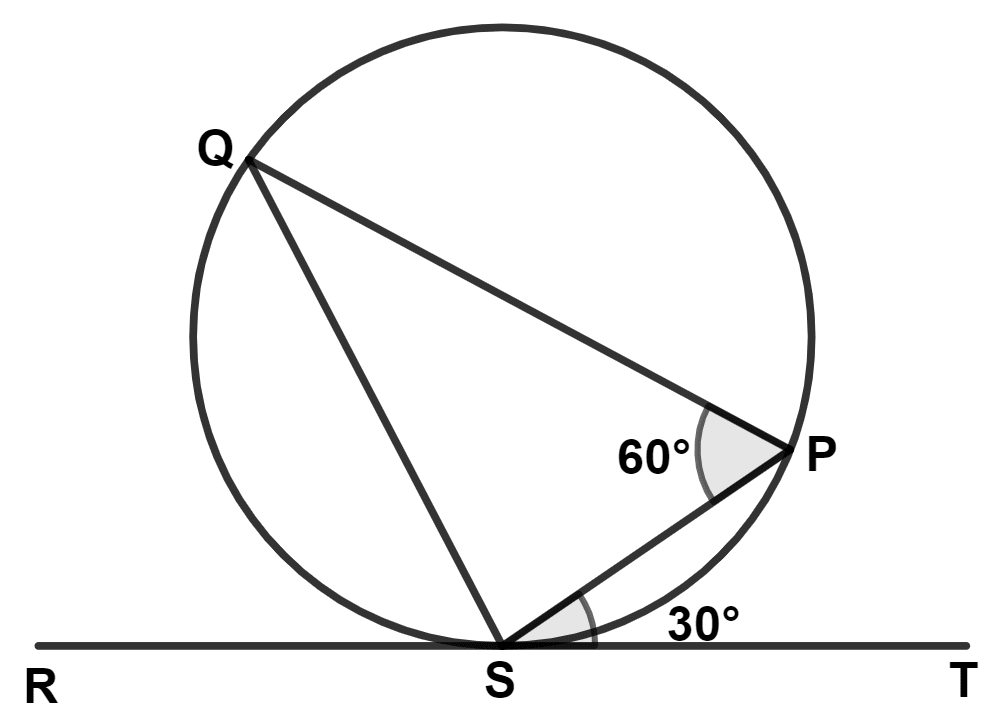
Answer
We know that,
Angle between tangent and the chord at the point of contact is equal to angle of the alternate segment.
∴ ∠PQS = ∠PST = 30°
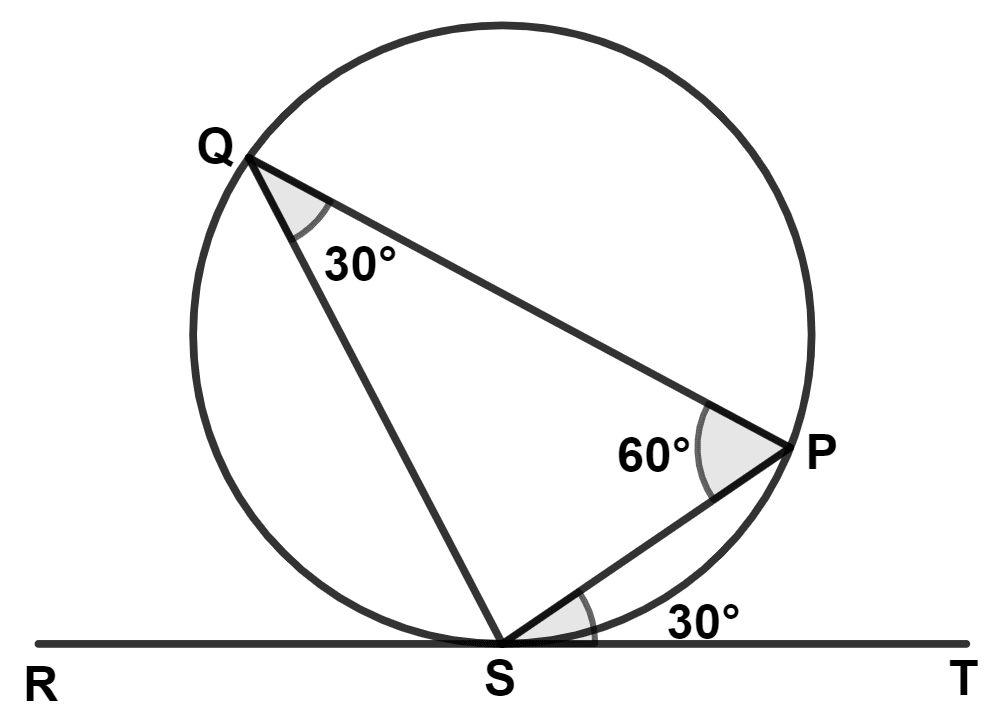
In △ PQS,
By angle sum property of triangle,
⇒ ∠PQS + ∠QPS + ∠PSQ = 180°
⇒ 30° + 60° + ∠PSQ = 180°
⇒ ∠PSQ + 90° = 180°
⇒ ∠PSQ = 180° - 90° = 90°.
Hence, Option 4 is the correct option.
In the adjoining figure, PA and PB are tangents to a circle with centre O. If ∠APB = 50°, then ∠OAB is equal to
25°
30°
40°
50°
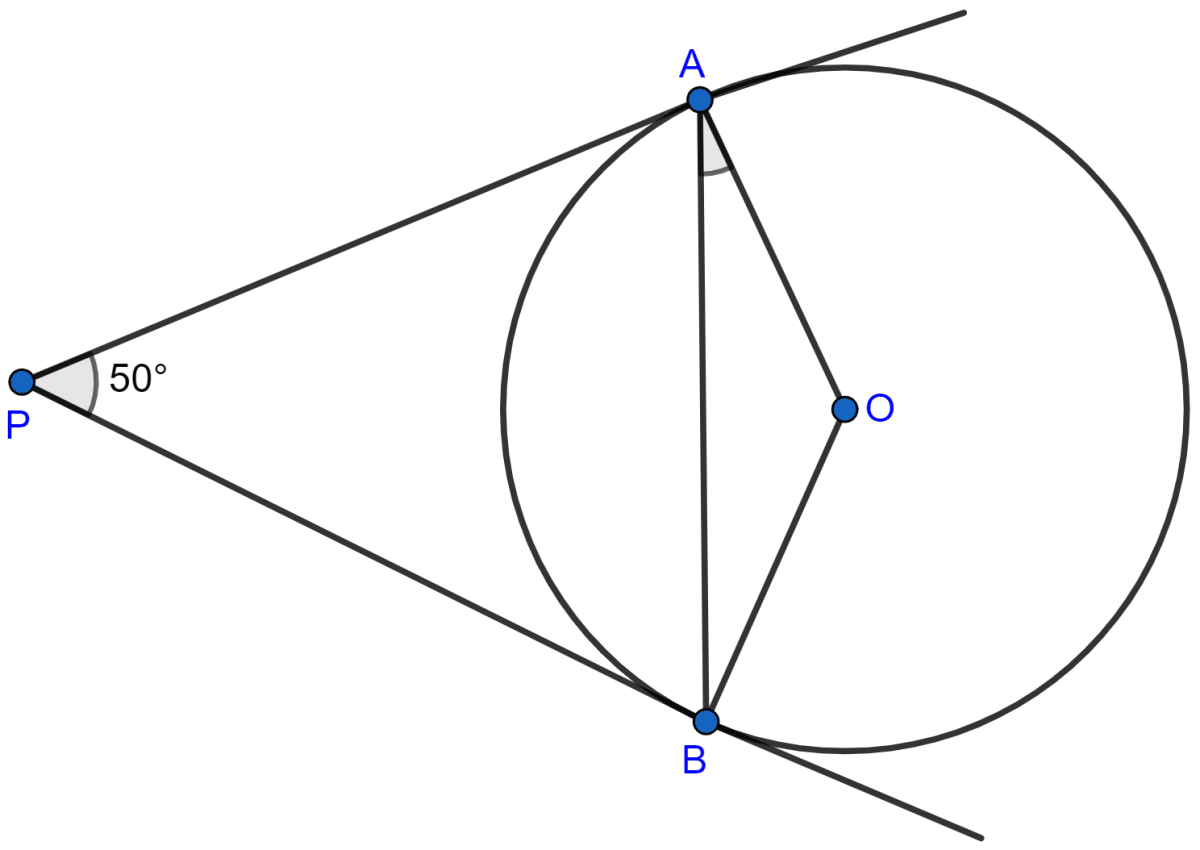
Answer
In the given figure,
PA and PB are tangents to the circle with centre O.
∠APB = 50°
Since sum of opposite angles of quadrilateral = 180°.
∴ ∠AOB + ∠APB = 180°
⇒ ∠AOB + 50° = 180°
⇒ ∠AOB = 180° - 50° = 130°.
In △OAB,
OA = OB (Radius of the same circle)
Hence, △OAB is an isosceles triangle with ∠OAB = ∠OBA.
Since, sum of angles of a triangle = 180°.
In △OAB,
⇒ ∠OAB + ∠OBA + ∠AOB = 180°
⇒ ∠OAB + ∠OAB + 130° = 180°
⇒ 2∠OAB = 180° - 130°
⇒ 2∠OAB = 50°
⇒ ∠OAB = 25°.
Hence, Option 1 is the correct option.
In the adjoining figure, sides BC, CA and AB of △ABC touch a circle at point D, E and F respectively. If BD = 4 cm, DC = 3 cm and CA = 8 cm, then the length of side AB is
12 cm
11 cm
10 cm
9 cm

Answer
We know that if two tangents are drawn from an external point to a circle then, the lengths of the tangents are equal.
∴ BF = BD = 4 cm, CE = CD = 3 cm and AF = AE.
Given, CA = 8 cm.
From figure,
⇒ CA = AE + CE
⇒ 8 = AE + 3
⇒ AE = 8 - 3 = 5 cm.
We know AF = AE = 5cm.
From figure,
AB = AF + BF = 5 + 4 = 9 cm.
Hence, Option 4 is the correct option.
In the adjoining figure, sides BC, CA and AB of △ABC touch a circle at the points P, Q and R respectively. If PC = 5 cm, AR = 4 cm and RB = 6 cm, then the perimeter of △ABC is
60 cm
45 cm
30 cm
15 cm

Answer
We know that if two tangents are drawn from an external point to a circle then, the lengths of the tangents are equal.
∴ BP = BR = 6 cm, CQ = CP = 5 cm and AQ = AR = 4 cm.
Perimeter of △ABC ⇒ AB + BC + CA
⇒ AR + BR + BP + CP + AQ + CQ
⇒ 4 + 6 + 6 + 5 + 4 + 5
⇒ 30 cm.
Hence, Option 3 is the correct option.
PQ is a tangent to a circle at point P. Centre of circle is O. If △OPQ is an isosceles triangle, then ∠QOP is equal to
30°
60°
45°
90°
Answer
The circle with centre O and PQ as tangent is shown in the figure below:

We know that,
OP ⊥ PQ (∵ tangent through a point and radius from that point are perpendicular to each other)
Given, △OPQ is an isosceles triangle.
Since, ∠OPQ = 90° hence, the other two angles will be equal to each other.
∴ ∠QOP = ∠OQP
We know that sum of angles in a triangle = 180°.
In △OPQ,
⇒ ∠OPQ + ∠QOP + ∠OQP = 180°
⇒ ∠OPQ + ∠QOP + ∠QOP = 180°
⇒ 90° + 2∠QOP = 180°
⇒ 2∠QOP = 180° - 90
⇒ ∠QOP =
⇒ ∠QOP = 45°.
Hence, Option 3 is the correct option.
In the adjoining figure, PA and PB are tangents at points A and B respectively to a circle with centre O. If C is a point on the circle and ∠APB = 40°, then ∠ACB is equal to
80°
70°
90°
140°
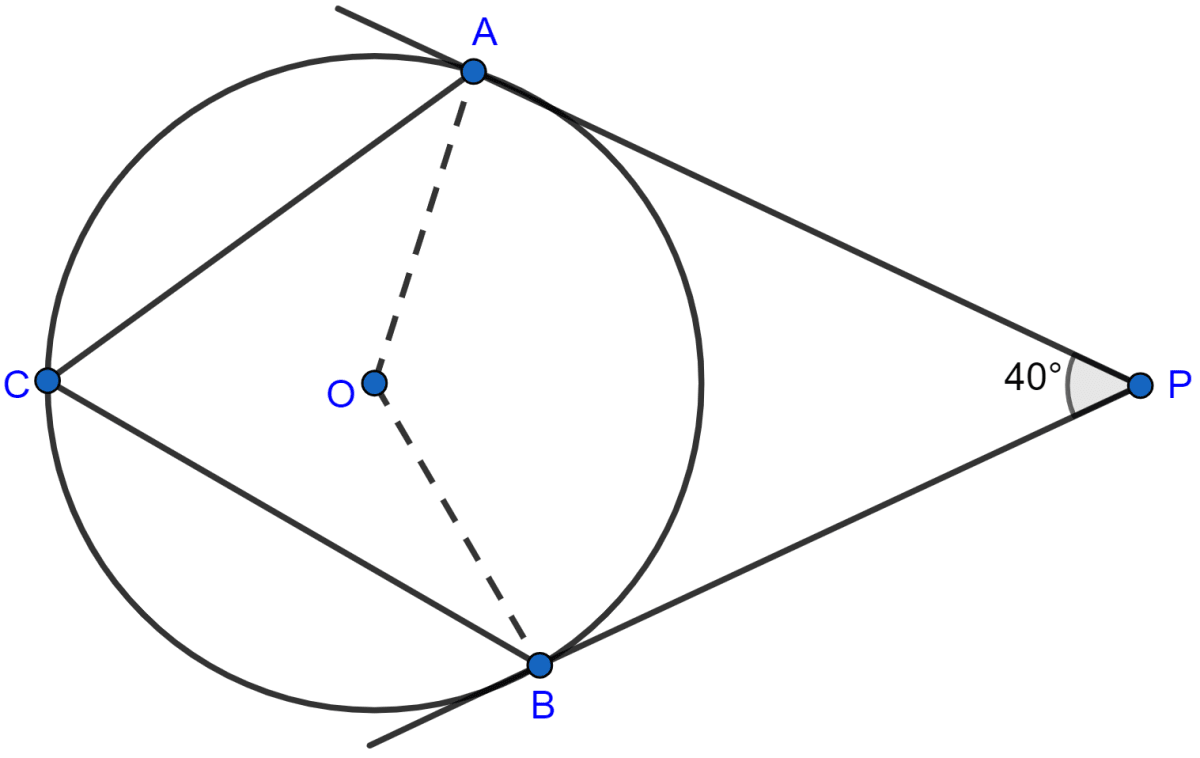
Answer
Join OP.
We know that the tangents are equally inclined to the line joining the point and the centre of the circle.
∴ ∠APO = = 20°.
AP ⊥ OA.
∴ ∠OAP = 90°.
In right angle triangle OAP,
⇒ ∠APO + ∠AOP + ∠OAP = 180°
⇒ 20° + ∠AOP + 90° = 180°
⇒ ∠AOP + 110° = 180°
⇒ ∠AOP = 180° - 110° = 70°.
As the tangents subtends equal angles at centre.
∴ ∠BOP = ∠AOP = 70°.
∠AOB = ∠AOP + ∠BOP = 70° + 70° = 140°.
Arc AB subtends ∠AOB at center and ∠ACB on the remaining part of the circle.
∴ ∠AOB = 2∠ACB
⇒ ∠ACB = ∠AOB
⇒ ∠ACB =
⇒ ∠ACB = 70°.
Hence, Option 2 is the correct option.
In the adjoining figure, two circles touch each other at A. BC and AP are common tangents to these circles. If BP = 3.8 cm, then the length of BC is equal to
7.6 cm
1.9 cm
11.4 cm
5.7 cm

Answer
We know that if two tangents are drawn from an external point to a circle then, the lengths of the tangents are equal.
From figure,
PA and PB are the tangents to the first circle.
∴ PA = PB = 3.8 cm
PA and PC are tangents to the second circle.
∴ PC = PA = 3.8 cm
From figure,
BC = PB + PC = 3.8 + 3.8 = 7.6 cm.
Hence, Option 1 is the correct option.
In the adjoining figure, if sides PQ, QR, RS and SP of a quadrilateral PQRS touch a circle at points A, B, C and D respectively, then PD + BQ is equal to
PQ
QR
PS
SR

Answer
We know that if two tangents are drawn from an external point to a circle then, the lengths of the tangents are equal.
From figure,
PA and PD are the tangents to the circle from P.
∴ PA = PD
QB and QA are the tangents to the circle from Q.
∴ QB = QA
Hence,
⇒ PD + BQ
⇒ PA + QA
⇒ PQ.
Hence, Option 1 is the correct option.
In the adjoining figure, PQR is a tangent at Q to a circle. If AB is a chord parallel to PR and ∠BQR = 70°, then ∠AQB is equal to
20°
40°
35°
45°

Answer
From figure,
BQ is chord and PQR is a tangent.
∠BQR = ∠A (∵ angles in alternate segment are equal.)
As AB || PQR
∠BQR = ∠B (∵ alternate angles are equal)
∴ ∠A = ∠B = 70°
We know that sum of angles in a triangle = 180°.
In △AQB,
⇒ ∠A + ∠B + ∠AQB = 180°
⇒ 70° + 70° + ∠AQB = 180°
⇒ 140° + ∠AQB = 180°
⇒ ∠AQB = 180° - 140°
⇒ ∠AQB = 40°.
Hence, Option 2 is the correct option.
Two chords AB and CD of a circle intersect externally at a point P. If PC = 15 cm, CD = 7 cm and AP = 12 cm, then AB is
2 cm
4 cm
6 cm
none of these

Answer
We know that if two chords of a circle intersect internally or externally, then the products of the lengths of segments are equal.
Hence, from figure,
PA.PB = PC.PD .....(i)
Given,
PC = 15 cm and CD = 7 cm
From figure,
PD = PC - CD = 15 - 7 = 8 cm.
Let BP = x cm then AB = (12 - x) cm
Putting values in equation (i),
⇒ PA.PB = PC.PD
⇒ 12.x = 15.8
⇒ 12x = 120
⇒ x = = 10 cm.
AB = 12 - x = 12 - 10 = 2 cm.
Hence, Option 1 is the correct option.
In a circle with radius R, the shortest distance between two parallel tangents is equal to :
R
2R
2πR
πR
Answer
Let l and m be tangents to circle with center O, touching the circle at point A and B.

From figure,
Shortest distance between tangents = OA + OB = R + R = 2R.
Hence, Option 2 is the correct option.
In the given diagram, PS and PT are the tangents to the circle. SQ || PT and ∠SPT = 80°. The value of ∠QST is :
140°
90°
80°
50°

Answer
In △ PST,
⇒ PS = PT (Tangents from an external point to a circle are equal in length)
⇒ ∠PST = ∠PTS = a (let) (Angles opposite to equal sides are equal)
By angle sum property of triangle,
⇒ ∠PST + ∠PTS + ∠SPT = 180°
⇒ a + a + 80° = 180°
⇒ 2a = 180° - 80°
⇒ 2a = 100°
⇒ a = = 50°.
From figure,
⇒ ∠QST = ∠STP = 50° (Alternate angles are equal)
Hence, Option 4 is the correct option.
The circumcentre of a triangle is the point which is ∶
at equal distance from the three sides of the triangle.
at equal distance from the three vertices of the triangle.
the point of intersection of the three medians.
the point of intersection of the three altitudes of the triangle.
Answer
The circumcenter of a triangle is defined as the point equidistant from the three vertices of the triangle.
Hence, Option 2 is the correct option.
The three vertices of a scalene triangle are always equidistant from a fixed point. The point is :
Orthocenter of the triangle
Incenter of the triangle
Circumcenter of the triangle
Centroid of the triangle
Answer
Let ABC be the triangle and O is the circumcenter of triangle.

Circumcenter is the center of circle which passes through all vertices of triangle.
∴ OA = OB = OC (Radius of circle)
Hence, Option 3 is the correct option.
In the adjoining figure, AC is a diameter of the circle, AP = 3 cm and PB = 4 cm and QP ⊥ AB. If the area of △ APQ is 18 cm2, then the area of shaded portion QPBC is :
32 cm2
49 cm2
80 cm2
98 cm2
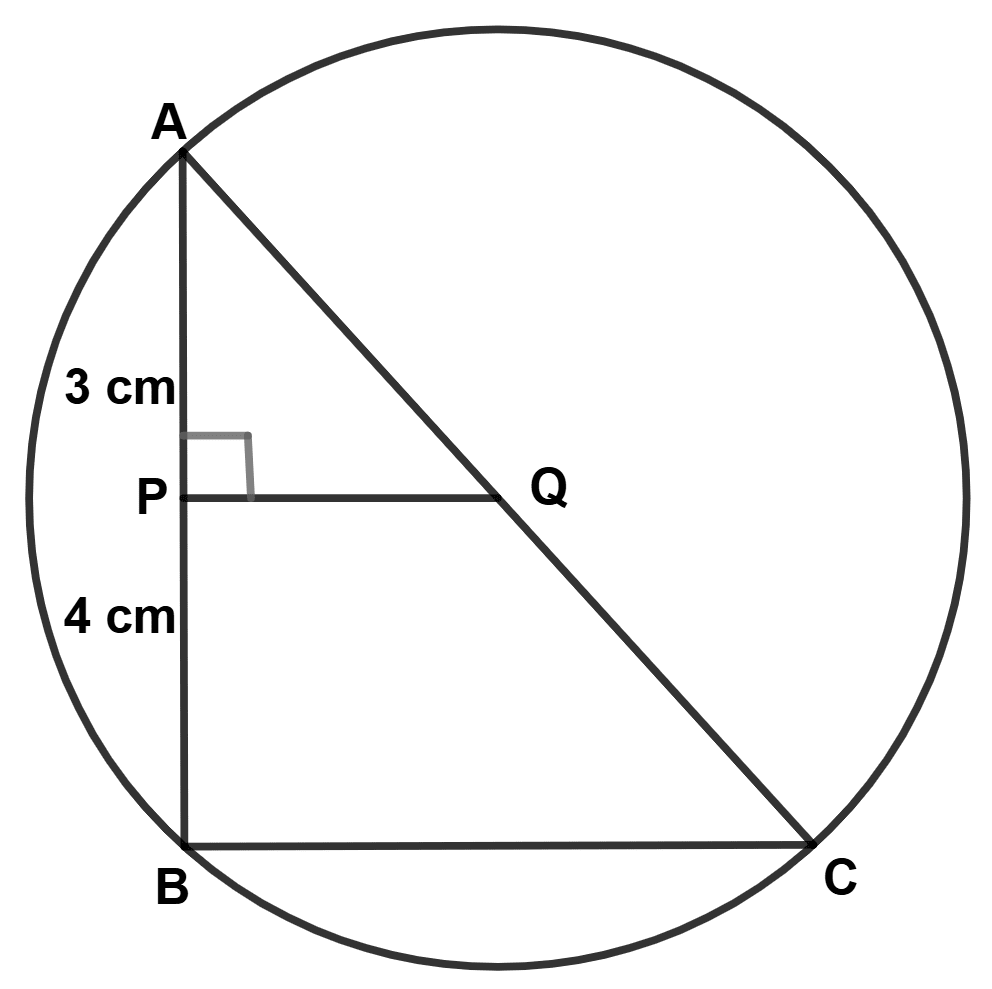
Answer
We know that,
Angle in a semi-circle is a right angle.
∴ ∠ABC = 90°.
In △ APQ and △ ABC,
⇒ ∠APQ = ∠ABC (Both equal to 90°)
⇒ ∠PAQ = ∠BAC (Common angles)
∴ △ APQ ~ △ ABC (By A.A. axiom)
We know that,
The ratio of area of similar triangles is equal to the ratio of the square of the corresponding sides.
From figure,
Area of QPBC = Area of △ ABC - Area of △ APQ = 98 - 18 = 80 cm2.
Hence, Option 3 is the correct option.
In the adjoining diagram, O is the center of the circle and PT is a tangent. The value of x is :
20°
40°
55°
70°
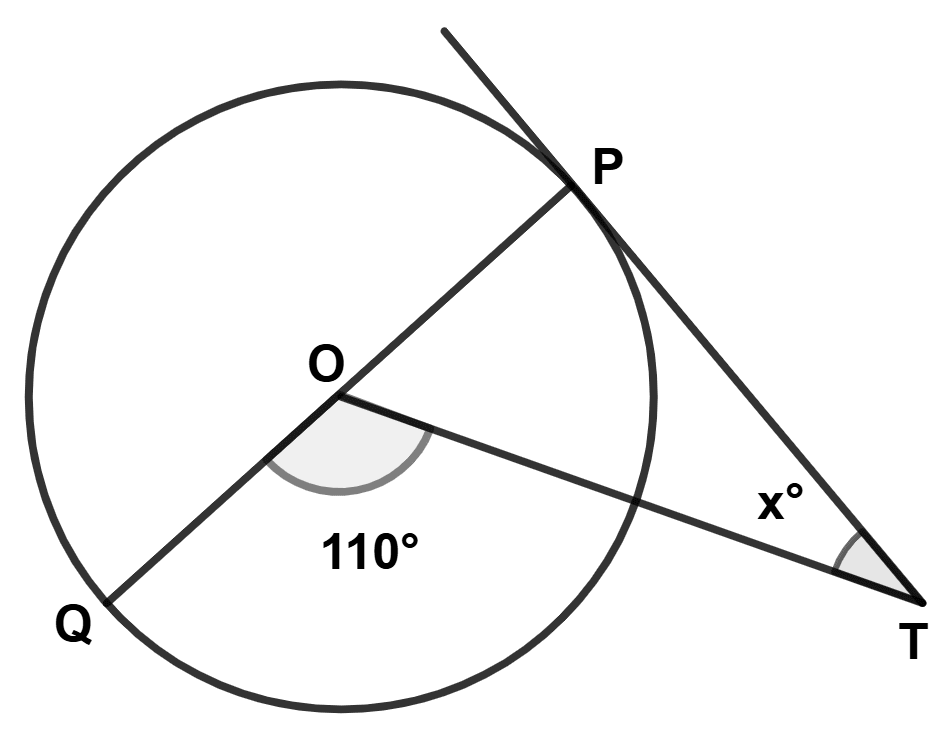
Answer
From figure,
⇒ ∠QOT + ∠TOP = 180° (Linear Pair)
⇒ 110° + ∠TOP = 180°
⇒ ∠TOP = 180° - 110° = 70°.
⇒ ∠OPT = 90° (Tangent is perpendicular to radius at point of intersection)
In △ TOP,
⇒ ∠OPT + ∠TOP + ∠PTO = 180°
⇒ 90° + 70° + x°= 180°
⇒ x° + 160° = 180°
⇒ x° = 180° - 160° = 20°.
Hence, Option 1 is the correct option.
The adjacent figure shows a circle with center O and while OABC is a quadrilateral.
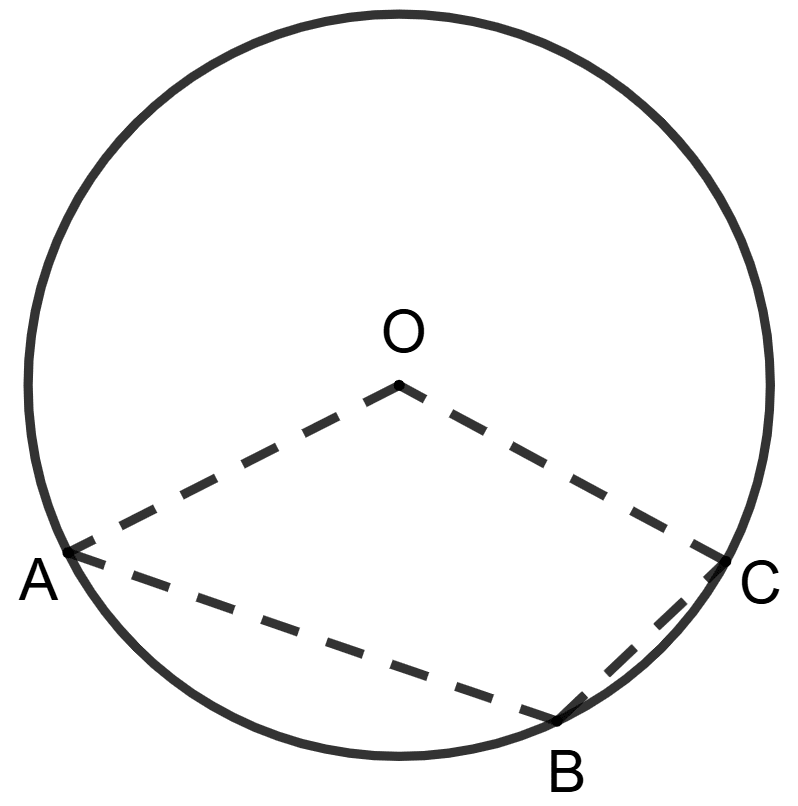
Assertion (A): OABC is a cyclic quadrilateral.
Reason (R): A quadrilateral inscribed in a circle is a cyclic quadrilateral.
Assertion (A) is true, but Reason (R) is false.
Assertion (A) is false, but Reason (R) is true.
Both Assertion (A) and Reason (R) are correct, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are correct, and Reason (R) is incorrect reason for Assertion (A).
Answer
A cyclic quadrilateral is defined as a quadrilateral whose all four vertices lie on the circumference of a circle. In other words, it is a quadrilateral that is inscribed in a circle.
So, reason (R) is true.
In the given figure, O is center of the circle. Hence, it does not lie on the circumference of the circle.
Therefore, OABC is not a cyclic quadrilateral.
So, assertion (A) is false.
Thus, Assertion (A) is false, but Reason (R) is true.
Hence, option 2 is the correct option.
Assertion (A): In the adjoining figure, AB is a diameter of the circle. If P is any point on the circle, then AB2 = AP2 + BP2.
Reason (R): Angle in a semicircle is 90°.
Assertion (A) is true, but Reason (R) is false.
Assertion (A) is false, but Reason (R) is true.
Both Assertion (A) and Reason (R) are correct, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are correct, and Reason (R) is incorrect reason for Assertion (A).
Answer
Given,
AB is the diameter of the circle.
We know that,
Angle in a semi-circle is a right angle.
So, reason (R) is true.
∠APB = 90°
We know that,
Side opposite to 90° is hypotenuse.
Thus, in triangle APB, AB is the hypotenuse.
Using pythagoras theorem in ΔAPB,
⇒ Hypotenuse2 = Base2 + Perpendicular2
⇒ AB2 = BP2 + AP2
So, assertion (A) is true.
Thus, both Assertion (A) and Reason (R) are correct, and Reason (R) is the correct reason for Assertion (A).
Hence, option 3 is the correct option.
Assertion (A): In the adjoining figure, ABCD is a cyclic quadrilateral. If ∠CBE = 108°, then ∠ADC = 108°.
Reason (R): In a cyclic quadrilateral, opposite angles are supplementary.
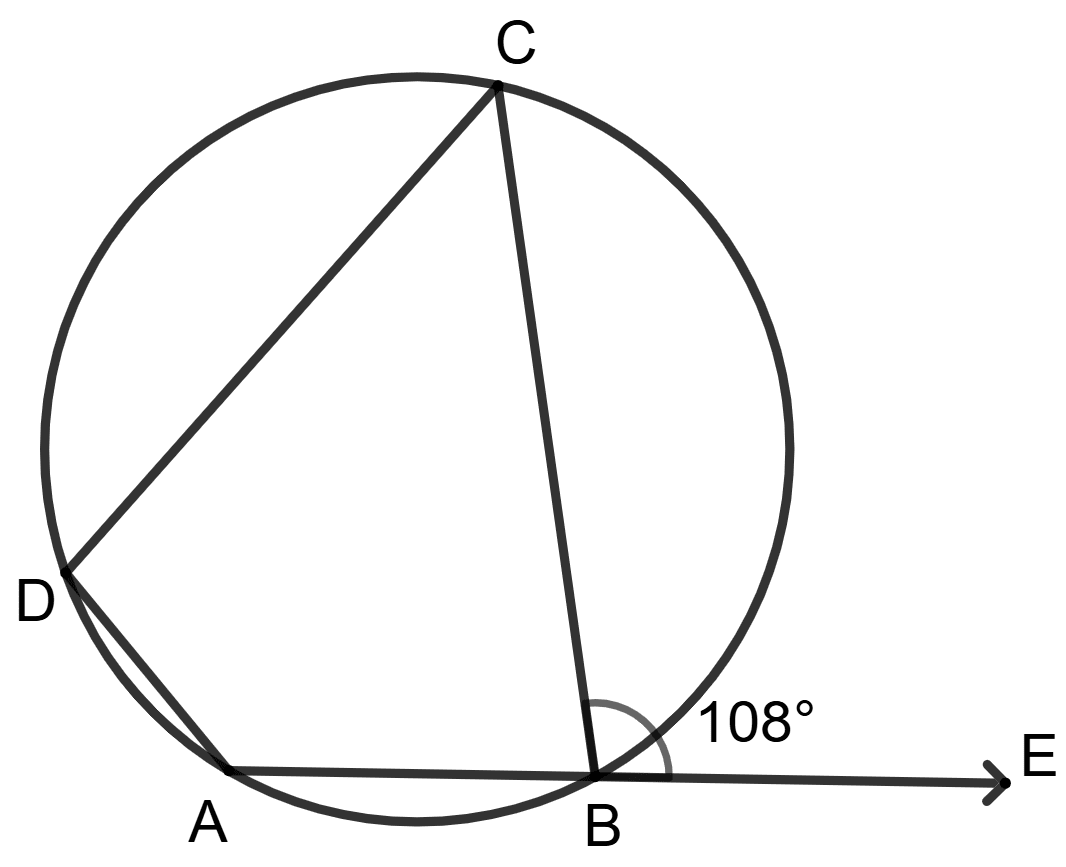
Assertion (A) is true, but Reason (R) is false.
Assertion (A) is false, but Reason (R) is true.
Both Assertion (A) and Reason (R) are correct, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are correct, and Reason (R) is incorrect reason for Assertion (A).
Answer
From figure,
∠CBE and ∠CBA forms a linear pair.
⇒ ∠CBE + ∠CBA = 180°
⇒ 108° + ∠CBA = 180°
⇒ ∠CBA = 180° - 108°
⇒ ∠CBA = 72°
ABCD is a cyclic quadrilateral, opposite angles are supplementary.
So, reason (R) is true.
⇒ ∠CBA + ∠ADC = 180°
⇒ 72° + ∠ADC = 180°
⇒ ∠ADC = 180° - 72°
⇒ ∠ADC = 108°.
So, assertion (A) is true.
Thus, both Assertion (A) and Reason (R) are correct, and Reason (R) is the correct reason for Assertion (A).
Hence, option 3 is the correct option.
Assertion (A): An exterior angle of a cyclic quadrilateral is equal to an interior angle.
Reason (R): If an exterior angle of a quadrilateral is equal to opposite interior angle, then the quadrilateral is cyclic.
Assertion (A) is true, but Reason (R) is false.
Assertion (A) is false, but Reason (R) is true.
Both Assertion (A) and Reason (R) are correct, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are correct, and Reason (R) is incorrect reason for Assertion (A).
Answer
We know that,
In a cyclic quadrilateral, an exterior angle is equal to the opposite interior angle.
So, reason (R) is true.
In case of assertion (A) : An exterior angle of a cyclic quadrilateral is equal to an interior angle.
This statement is incorrectly stated as the exterior angle is equal to the opposite interior angle.
So, assertion (A) is false.
Thus, Assertion (A) is false, but Reason (R) is true.
Hence, option 2 is the correct option.
In the adjoining figure P, Q and R the points of the circle, PT is the tangent to the circle at point P.
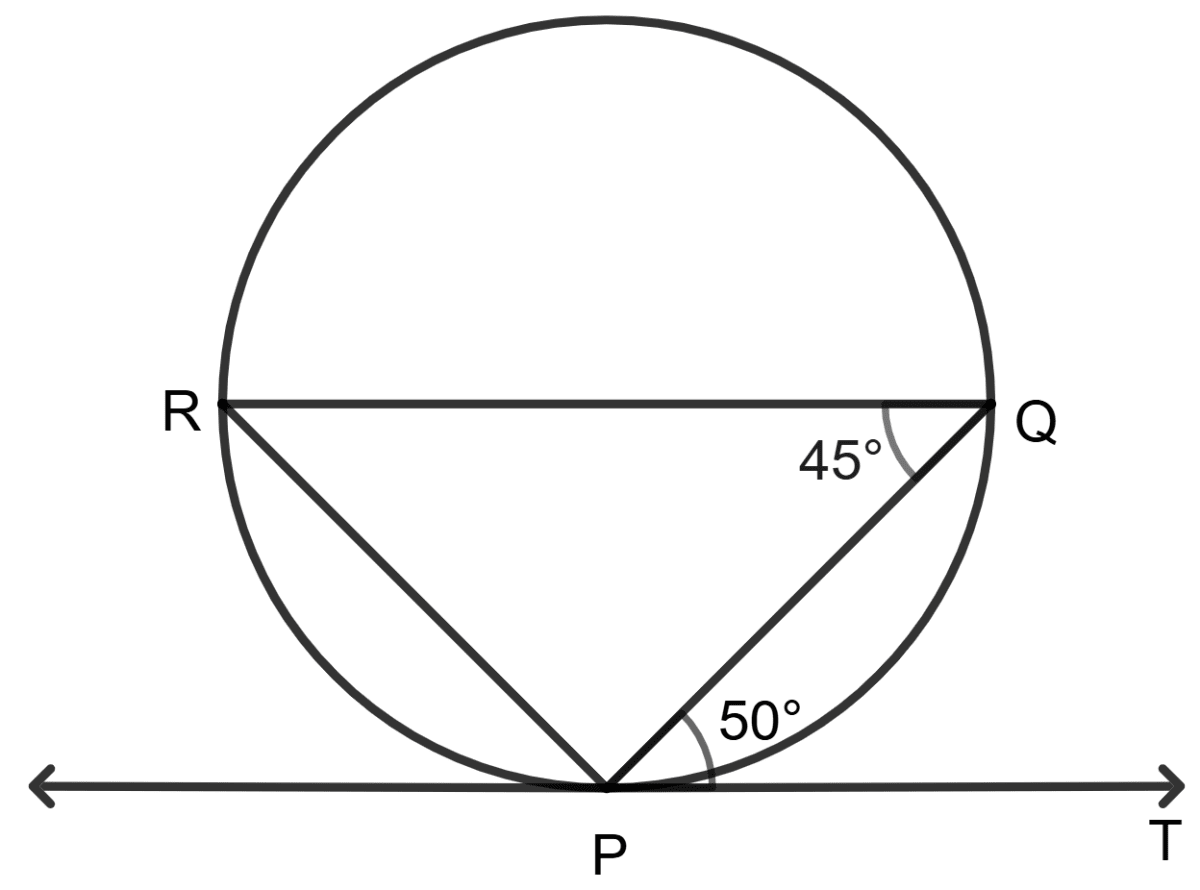
Assertion (A): If ∠QPT = 50° and ∠PQR = 45°, then ∠QPR = 95°.
Reason (R): Angles in alternate segments are equal.
Assertion (A) is true, but Reason (R) is false.
Assertion (A) is false, but Reason (R) is true.
Both Assertion (A) and Reason (R) are correct, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are correct, and Reason (R) is incorrect reason for Assertion (A).
Answer
According to alternate Segment theorem,
The angle between a tangent to a circle and a chord drawn from the point of contact is equal to the angle subtended by the chord in the alternate segment of the circle.
So, reason (R) is true.
∴ ∠QRP = ∠QPT (By alternate segment theorem)
⇒ ∠QRP = 50°
In ΔPQR, according to angle sum property,
∴ ∠PQR + ∠PRQ + ∠QPR = 180°
⇒ 45° + 50° + ∠QPR = 180°
⇒ 95° + ∠QPR = 180°
⇒ ∠QPR = 180° - 95°
⇒ ∠QPR = 85°
So, assertion (A) is false.
Thus, Assertion (A) is false, but Reason (R) is true.
Hence, option 2 is the correct option.
In the adjoining figure, O is the centre of the circle. If QR = OP and ∠ORP = 20°, find the value of 'x' giving reasons.
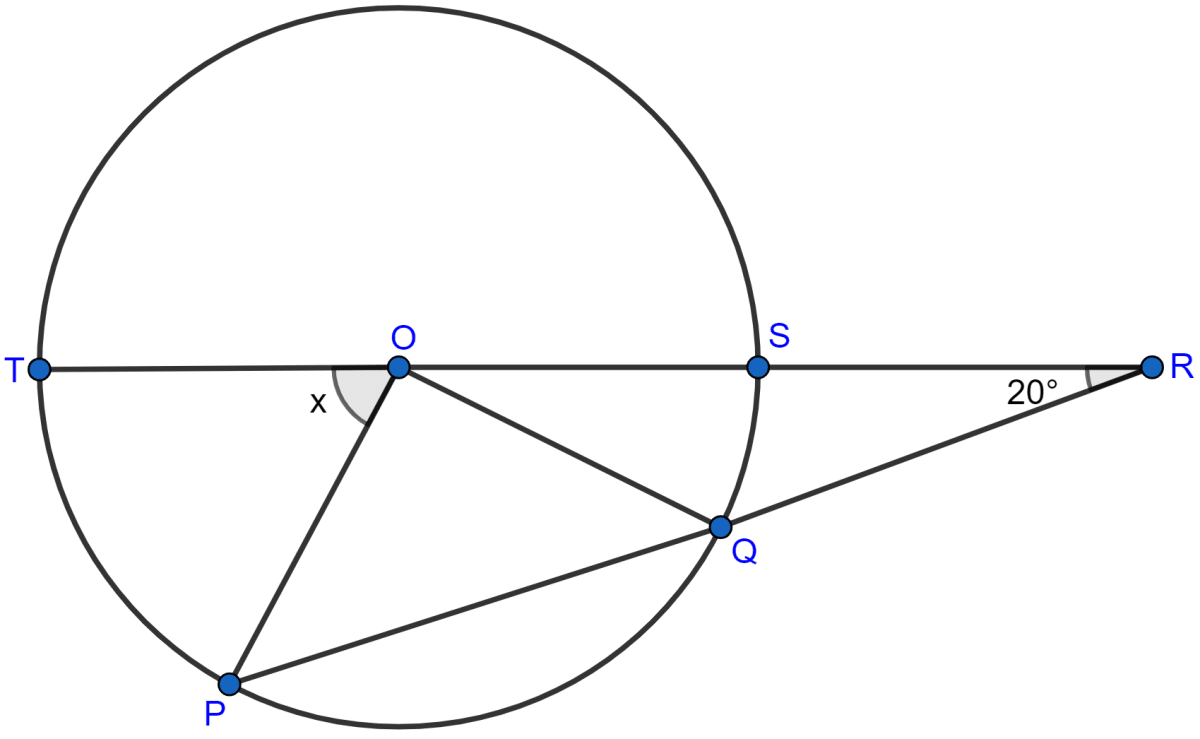
Answer
Given,
QR = OP ⇒ QR = OQ
⇒ ∠QOR = ∠ORQ = 20° (∵ angles opposite equal sides of a triangle are equal)
Exterior angle in a triangle is equal to the sum of two opposite interior angles.
∴ ∠OQP = ∠QOR + ∠ORQ = 20° + 20° = 40°.
As OP = OQ, ∠OPQ = ∠OQP
⇒ ∠OPQ = 40°
⇒ ∠OPR = 40°.
Exterior angle in a triangle is equal to the sum of two opposite interior angles.
∴ x = ∠TOP = ∠OPR + ∠ORP = 40° + 20° = 60°.
Hence, the value of x = 60°.
In the figure (i) given below, triangle ABC is equilateral. Find ∠BDC and ∠BEC.

Answer
Since ABC is an equilateral triangle so,
∠A = ∠B = ∠C = 60°.
From figure,
∠BDC = ∠BAC (∵ angles in alternate segments are equal.)
∴ ∠BDC = 60°.
BDCE is a cyclic quadrilateral. Hence, sum of the opposite angles = 180°.
⇒ ∠BDC + ∠BEC = 180°
⇒ 60° + ∠BEC = 180°
⇒ ∠BEC = 180° - 60° = 120°.
Hence, the value of ∠BDC = 60° and ∠BEC = 120°.
In the figure (ii) given below, AB is a diameter of a circle with centre O. OD is perpendicular to AB and C is a point on the arc DB. Find ∠BAD and ∠ACD.
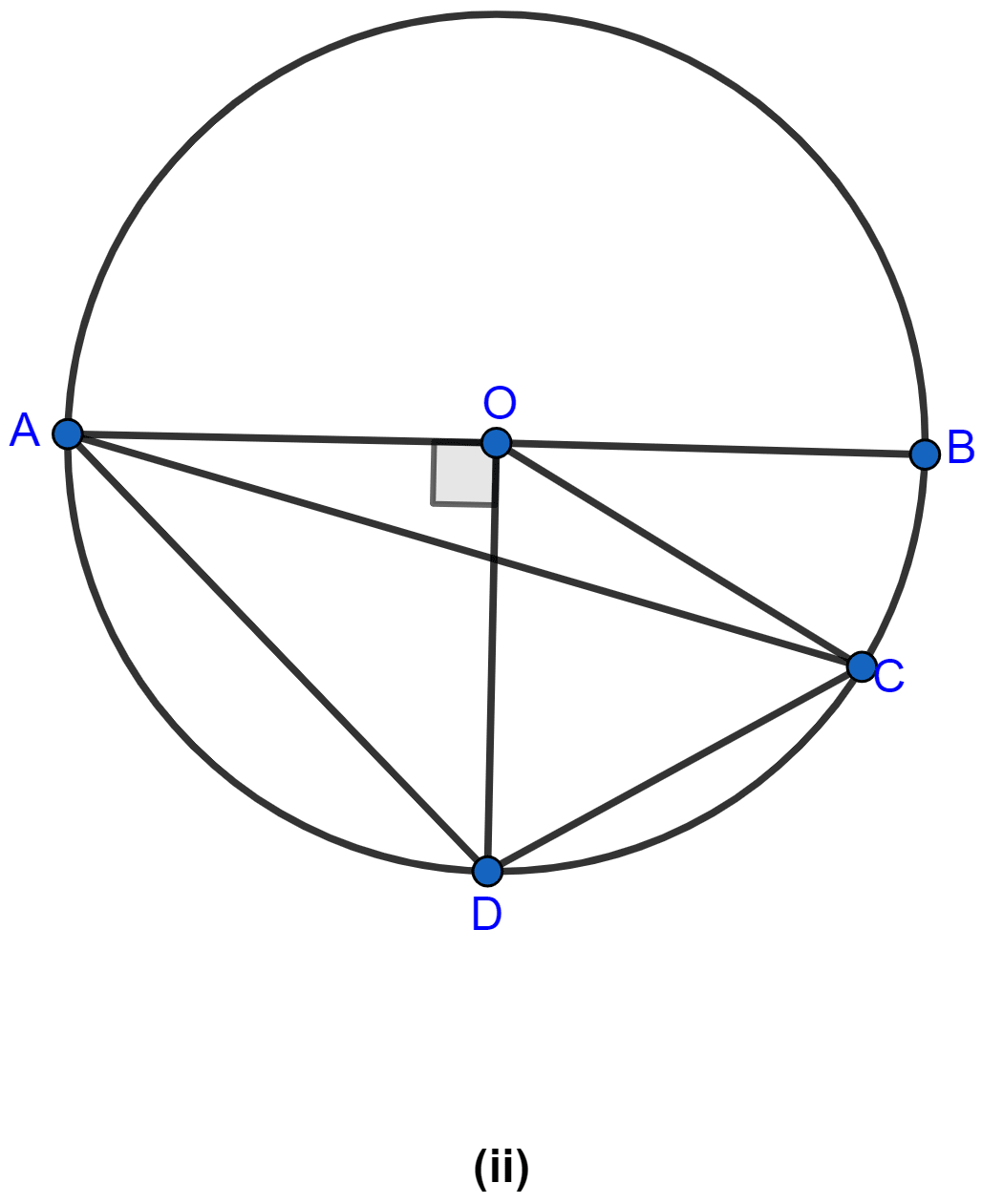
Answer
In △AOD, ∠AOD = 90°.
OA = OD (Radii of the semi-circle)
∠OAD = ∠ODA (∵ angles opposite equal side are equal.)
We know that sum of angles in a triangle = 180°.
In △OAD,
⇒ ∠AOD + ∠OAD + ∠ODA = 180°
⇒ 90° + ∠OAD + ∠OAD = 180°
⇒ 90° + 2∠OAD = 180°
⇒ 2∠OAD = 180° - 90°
⇒ ∠OAD = = 45°.
From figure,
∠BAD = ∠OAD = 45°.
Arc AD subtends ∠AOD at the centre and ∠ACD at the remaining part of the circle.
∠AOD = 2∠ACD (∵ angle subtended on centre is double the angle subtended at remaining part of the circle.)
⇒ 90° = 2∠ACD
⇒ ∠ACD = = 45°.
Hence, the value of ∠BAD = 45° and ∠ACD = 45°.
In the figure (i) given below, AC is a tangent to the circle with centre O. If ∠ADB = 55°, find x and y. Give reasons for your answers.
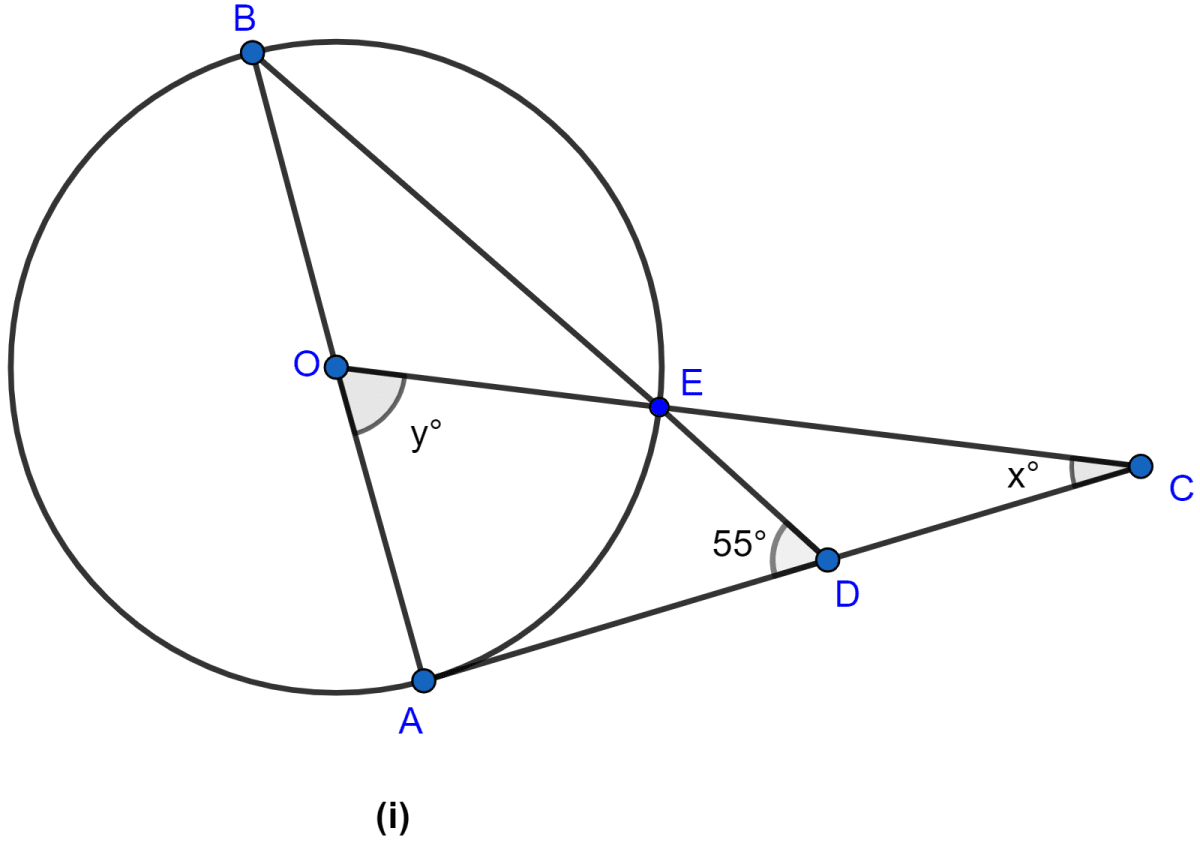
Answer
We know that angle between the radius and tangent at the point of contact is right angle.
∴ ∠A = 90°.
Also in △OBE, OB = OE = radius of the circle.
∴ ∠B = ∠OEB .....(i)
In △ABD,
⇒ ∠A + ∠B + ∠ADB = 180°
⇒ 90° + ∠B + 55° = 180°
⇒ ∠B + 145° = 180°
⇒ ∠B = 180° - 145° = 35°.
∴ ∠OEB = 35°.
From figure,
∠DEC = ∠OEB = 35° (∵ vertically opposite angles are equal.)
∠EDC + ∠ADE = 180° (∵ both form a linear pair)
∠EDC + 55° = 180°
∠EDC = 180° - 55°
∠EDC = 125°.
In △EDC,
⇒ ∠DEC + ∠EDC + ∠DCE = 180°
⇒ 35° + 125° + x° = 180°
⇒ x° + 160° = 180°
⇒ x° = 180° - 160° = 20°.
In △AOC,
⇒ ∠AOC + ∠OAC + ∠ACO = 180°
⇒ y° + 90° + x° = 180°
⇒ y° + 90° + 20° = 180°
⇒ y° + 110° = 180°
⇒ y° = 180° - 110° = 70°.
Hence, the value of x = 20 and y = 70.
In the figure (ii) given below, AB is a diameter of the semicircle ABCDE with centre O. If AE = ED and ∠BCD = 140°, find ∠AED and ∠EBD. Also prove that OE is parallel to BD.
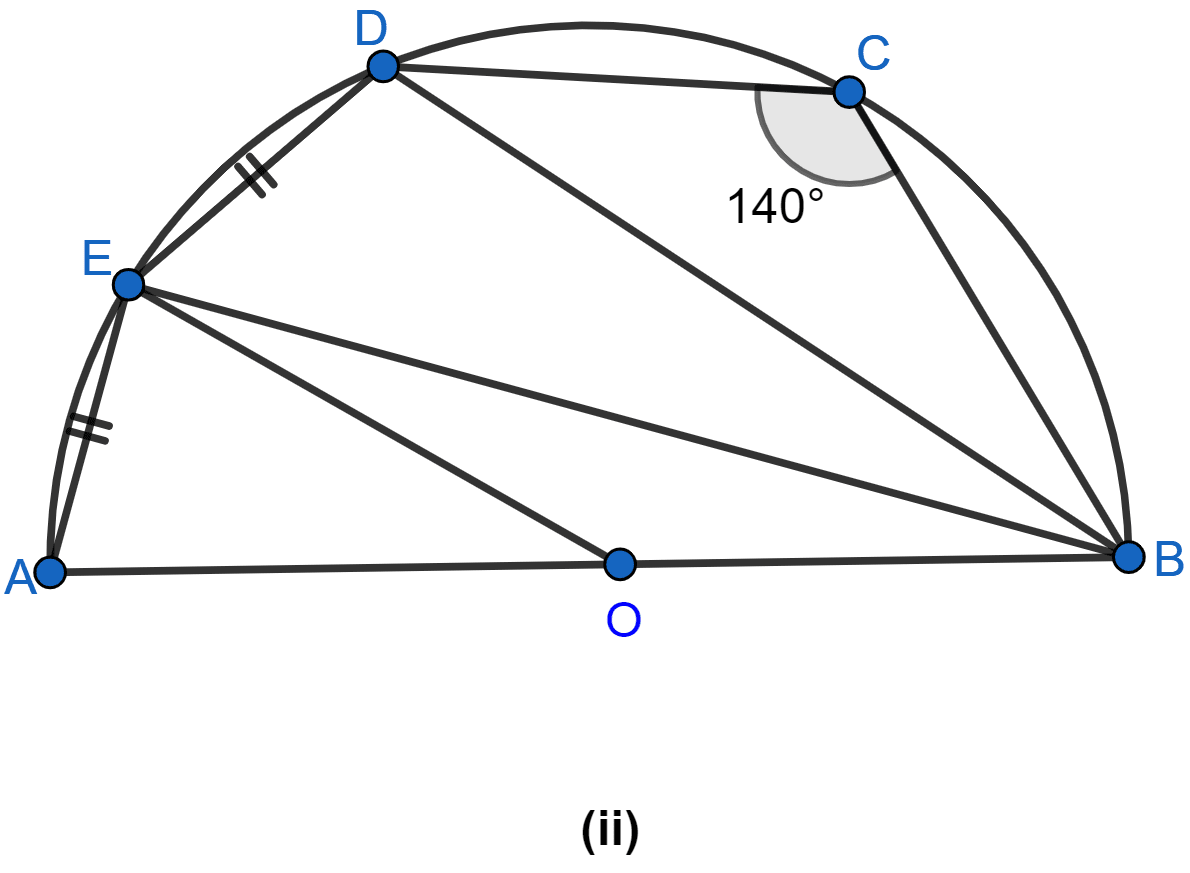
Answer
We know that in a cyclic quadrilateral the sum of opposite interior angles = 180°.
In cyclic quadrilateral BCDE,
⇒ ∠BCD + ∠BED = 180°
⇒ 140° + ∠BED = 180°
⇒ ∠BED = 180° - 140° = 40°.
∠AEB = 90°. (∵ angle in semicircle = 90°.)
From figure,
∠AED = ∠AEB + ∠BED = 90° + 40° = 130°.
In cyclic quadrilateral AEDB,
⇒ ∠AED + ∠DBA = 180°
⇒ 130° + ∠DBA = 180°
⇒ ∠DBA = 180° - 130° = 50°.
Given chord AE = ED
∴ ∠DBE = ∠EBA
From figure,
⇒ ∠DBA = ∠DBE + ∠EBA
⇒ 50 = ∠DBE + ∠DBE
⇒ 2∠DBE = 50°
⇒ ∠DBE = = 25°.
or, ∠EBD = 25°.
In △OEB, OE = OB (Radii of the same circle.)
∠OEB = ∠EBO = ∠DBE
But these are alternate angles.
∴ OE || BD.
Hence, the value of ∠AED = 130° and ∠EBD = 25°.
In the figure (i) given below, O is the centre of the circle. Prove that ∠AOC = 2(∠ACB + ∠BAC).
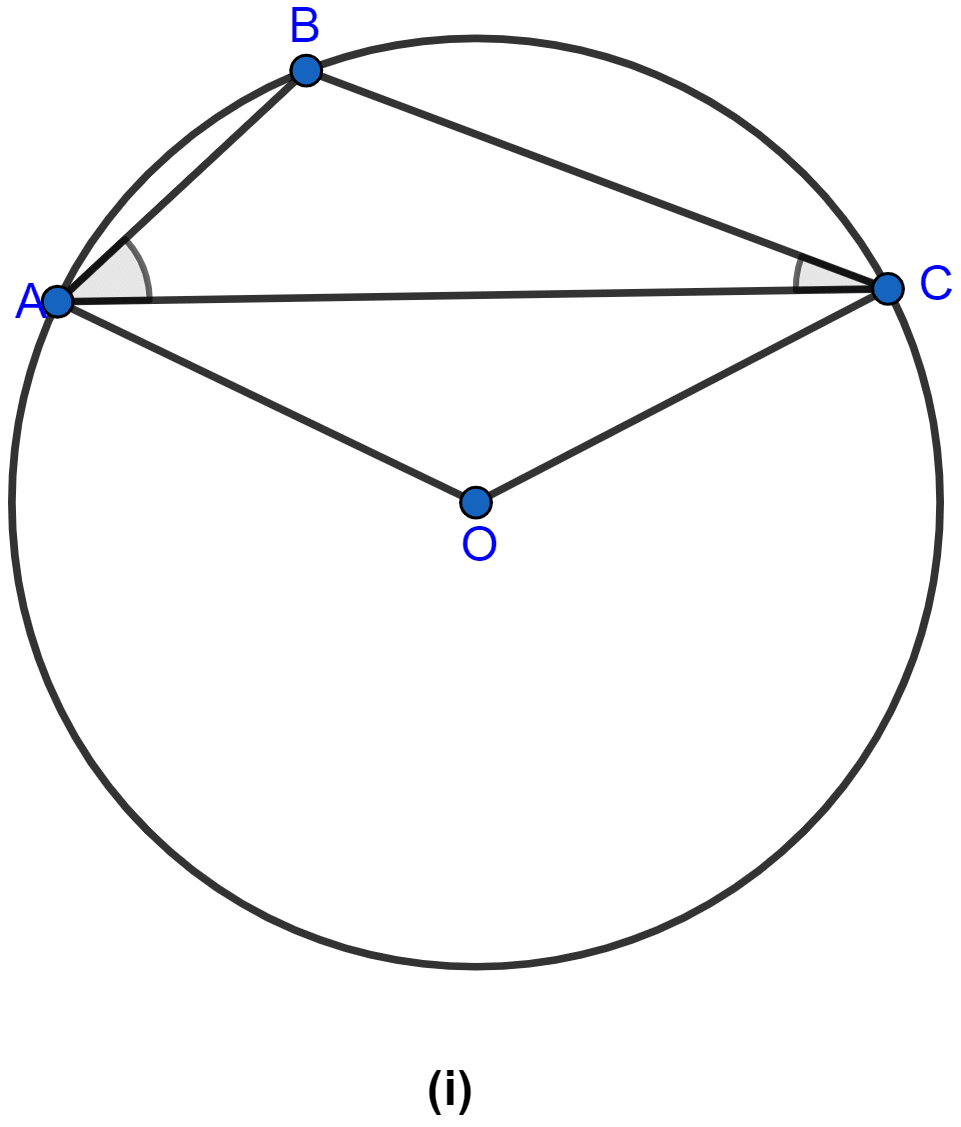
Answer
We know that sum of angles in a triangle = 180°.
In △ABC,
∠ACB + ∠BAC + ∠ABC = 180°
∠ABC = 180° - (∠ACB + ∠BAC) .....(i)
In the circle arc AC subtends Reflex ∠AOC at centre and ∠ABC at remaining part of the circle.
∴ Reflex ∠AOC = 2∠ABC (∵ angle subtended on centre is double the angle subtended at remaining part of the circle.)
From (i)
Reflex ∠AOC = 2(180° - (∠ACB + ∠BAC))
We know
Reflex ∠AOC = 360° - ∠AOC.
or,
360° - ∠AOC = 2(180° - (∠ACB + ∠BAC))
360° -∠AOC = 360° - 2(∠ACB + ∠BAC)
∠AOC = 360° - (360° - 2(∠ACB + ∠BAC))
∠AOC = 2(∠ACB + ∠BAC).
Hence, proved that ∠AOC = 2(∠ACB + ∠BAC).
In the figure (ii) given below, O is the centre of the circle. Prove that x + y = z.
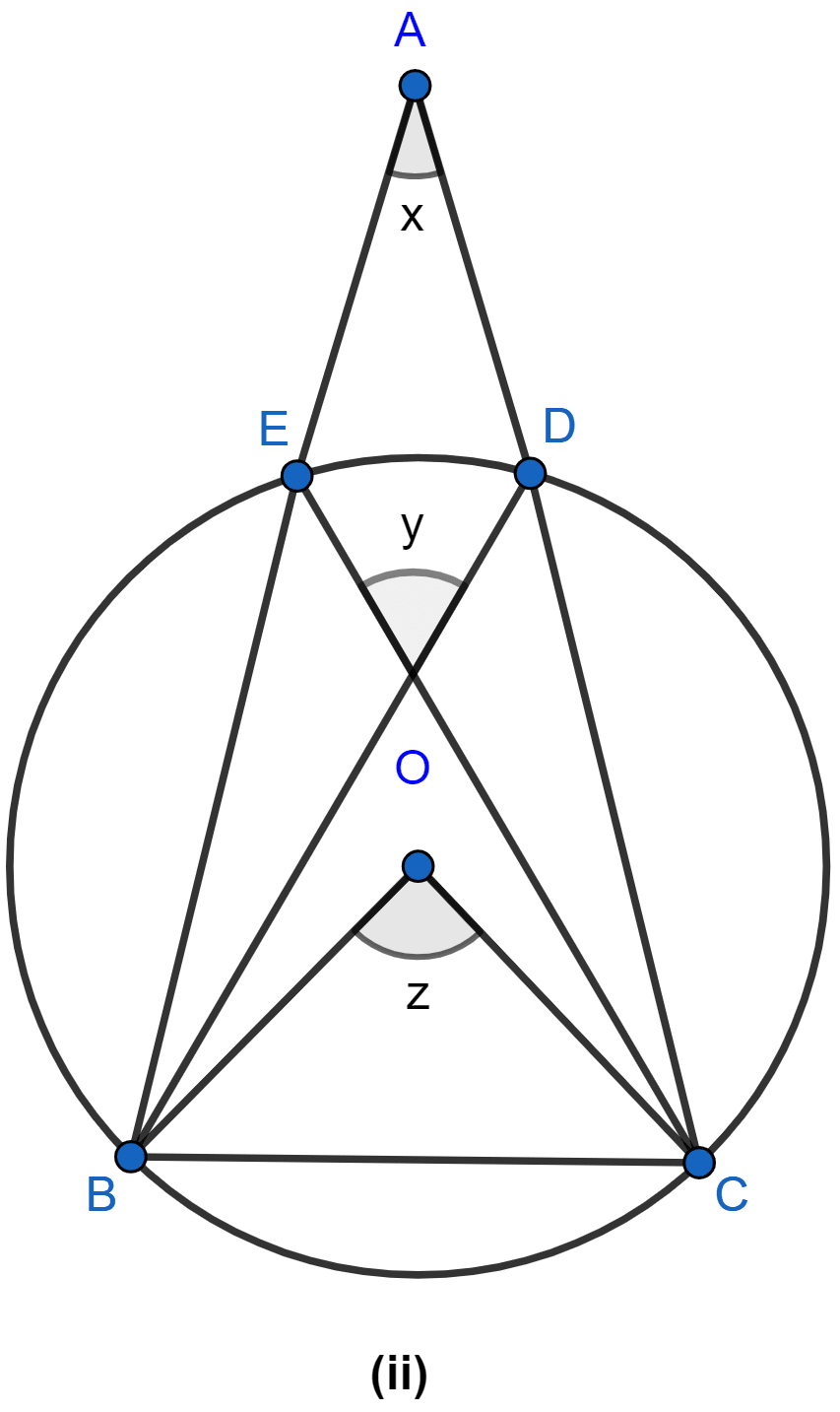
Answer
From figure,
∠BEC = ∠BDC (∵ angles in same segment are equal)
Arc BC subtends ∠BOC at the centre and ∠BEC at the remaining part of the circle.
∴ ∠BOC = 2∠BEC (∵ angle subtended on centre is double the angle subtended at remaining part of the circle.)
⇒ ∠BOC = ∠BEC + ∠BEC = ∠BEC + ∠BDC
⇒ ∠BOC = ∠BEC + ∠BDC .....(i)
In △OBE,
⇒ ∠EOD = ∠EBO + ∠BEO ....(ii) (∵ exterior angle is equal to the sum of two opposite interior angles.)
From figure,
∠EBO = ∠EBD and ∠BEO = ∠BEC and Exterior angle ∠EOD = y.
Putting these values in eqn (ii) we get,
⇒ y = ∠EBD + ∠BEC
⇒ ∠BEC = y - ∠EBD .....(iii)
In △ABD,
∠BDC = ∠BAD + ∠ABD ....(iv) (∵ exterior angle is equal to the sum of two opposite interior angles.)
From figure,
∠ABD = ∠EBD and ∠BAD = x.
Putting these values in eqn (iv) we get,
∠BDC = x + ∠EBD ......(v)
Putting value of ∠BEC and ∠BDC from eqn (iii) and (v) respectively in (i) we get,
⇒ ∠BOC = ∠BEC + ∠BDC
⇒ ∠BOC = y - ∠EBD + x + ∠EBD
⇒ ∠BOC = x + y
From figure,
∠BOC = z.
∴ z = x + y.
Hence, proved that x + y = z.
In the figure (i) given below, AB is diameter of a circle. If DC is parallel to AB and ∠CAB = 25°, find (i) ∠ADC (ii) ∠DAC.
Answer
(i) Join AD.
From figure,
∠BDC = ∠BAC = 25°. (∵ angles in same segment are equal.)
∠ADB = 90° (∵ angle in semicircle = 90°.)
∠ADC = ∠ADB + ∠BDC = 90° + 25° = 115°.
Hence, the value of ∠ADC = 115°.
(ii) ∠ACD = ∠CAB = 25° (∵ alternate angles are equal)
Since sum of angles in a triangle = 180°.
In △ADC,
⇒ ∠ADC + ∠DAC + ∠ACD = 180°
⇒ 115° + ∠DAC + 25° = 180°
⇒ ∠DAC + 140° = 180°
⇒ ∠DAC = 180° - 140° = 40°.
Hence, the value of ∠DAC = 40°.
In the figure (ii) given below, sides AB and DC of a cyclic quadrilateral are produced to meet at a point P and the sides AD and BC produced to meet at a point Q. If ∠ADC = 75° and ∠BPC = 50°, find ∠BAD and ∠CQD.

Answer
Since sum of angles in a triangle = 180°.
In △ADP,
⇒ ∠ADP + ∠DAP + ∠DPA = 180°
⇒ 75° + ∠DAP + 50° = 180°
⇒ ∠DAP + 125° = 180°
⇒ ∠DAP = 180° - 125° = 55°.
From figure,
∠BAD = ∠DAP = 55°.
In cyclic quadrilateral sum of opposite angles = 180°
In ABCD,
∴ ∠ADC + ∠CBA = 180°
⇒ 75° + ∠CBA = 180°
⇒ ∠CBA = 180° - 75° = 105°.
In △ABQ,
⇒ ∠ABQ + ∠BAQ + ∠AQB = 180°
From figure, ∠BAQ = ∠BAD and ∠ABQ = ∠CBA or,
⇒ 105° + 55° + ∠AQB = 180°
⇒ ∠AQB + 160° = 180°
⇒ ∠AQB = 180° - 160° = 20°.
From figure,
∠CQD = ∠AQB = 20°.
Hence, the value of ∠BAD = 55° and ∠CQD = 20°.
In the figure (i) given below, ABDC is a cyclic quadrilateral. If AB = CD, prove that AD = BC.
Answer
Join AC and BD.
In △ABD and △CBD,
AB = CD (Given)
BD = BD (Common side)
∠BAD = ∠BCD (∵ angles in same segment are equal.)
∴ △ABD ≅ △CBD. (By SSA axiom of congruency.)
∴ BC = AD (As corresponding parts of congruent triangles are congruent.)
Hence, proved that BC = AD.
In the figure (ii) given below, ABC is an isosceles triangle with AB = AC. If ∠ABC = 50°, find ∠BDC and ∠BEC.

Answer
Since, AB = AC.
Hence, in △ABC,
∠ACB = ∠ABC = 50°.
Since sum of angles in a triangle = 180°.
In △ABC,
⇒ ∠ABC + ∠ACB + ∠BAC = 180°
⇒ 50° + 50° + ∠BAC = 180°
⇒ ∠BAC + 100° = 180°
⇒ ∠BAC = 180° - 100° = 80°.
From figure,
∠BDC = ∠BAC = 80° (∵ angles in same segment are equal.)
In cyclic quadrilateral sum of opposite angles = 180°,
Hence in BDCE,
⇒ ∠BDC + ∠BEC = 180°
⇒ 80° + ∠BEC = 180°
⇒ ∠BEC = 180° - 80° = 100°.
Hence, the value of ∠BDC = 80° and ∠BEC = 100°.
A point P is 13 cm from the centre of a circle. The length of the tangent drawn from P to the circle is 12 cm. Find the distance of P from the nearest point of the circle.
Answer
Let T be the point of contact of the tangent from point P to the circle with centre O.
From figure,

OT ⊥ PT (As tangent and radius from point of contact are perpendicular to each other.)
In right-angled triangle OPT
⇒ OP2 = OT2 + PT2
⇒ 132 = OT2 + 122
⇒ 169 - 144 = OT2
⇒ OT2 = 25
⇒ OT = 5 cm.
From figure,
⇒ OA = OT = 5 cm (Radius of the circle.)
⇒ PA = OP - OA = 13 - 5 = 8 cm.
Hence, the distance of P from the nearest point of circle = 8 cm.
Two circles touch each other internally. Prove that the tangents drawn to the two circles from any point on the common tangent are equal in length.
Answer
Let two circles touch each other at point P and T is a point on common tangent as shown in the figure below:
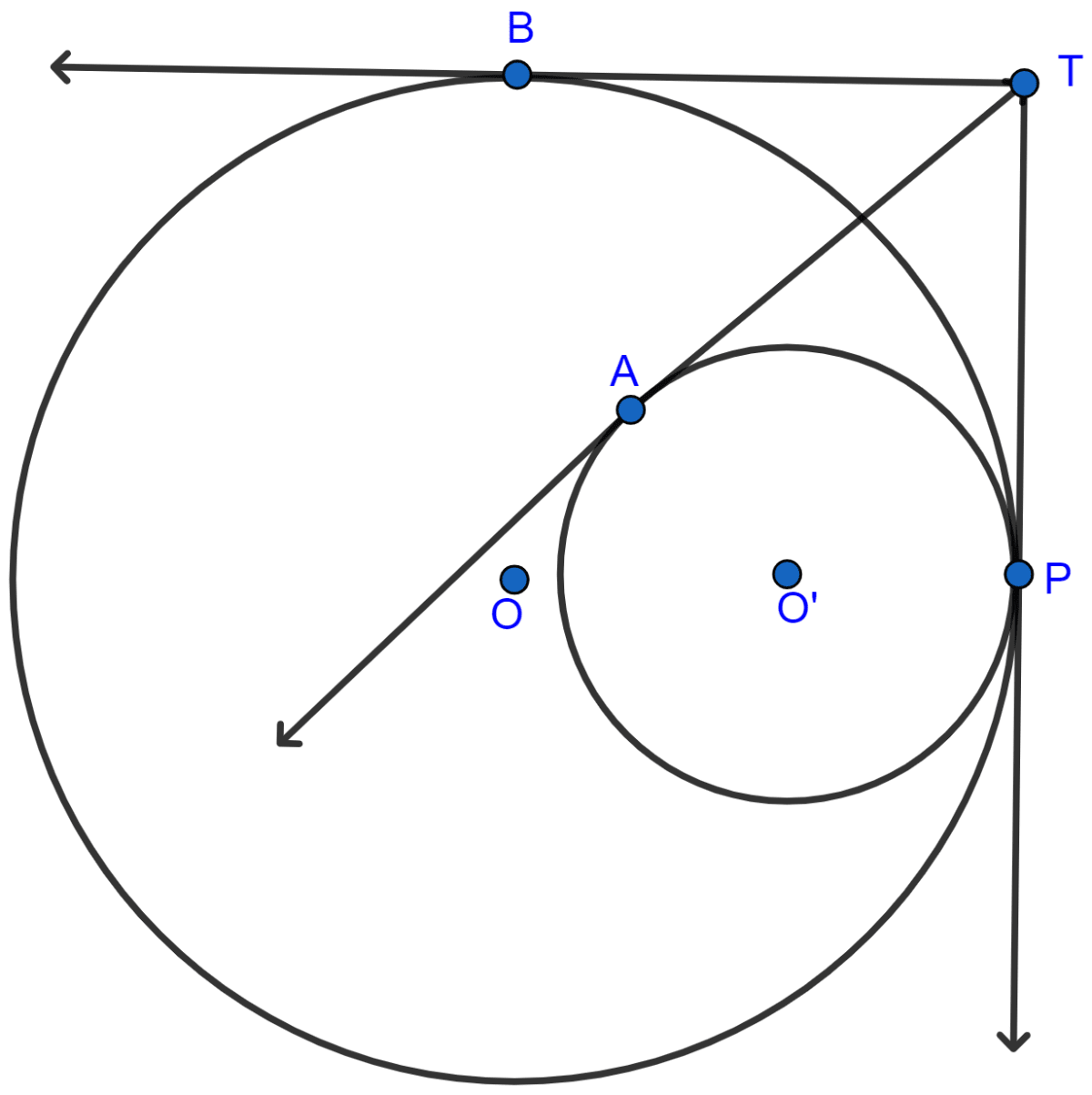
As tangents drawn from an external point to a circle are equal in length.
From T, TA and TP are tangents to the circle with centre O'.
TA = TP .....(i)
From T, TB and TP are tangents to the circle with centre O.
TB = TP .....(ii)
From (i) and (ii),
TA = TB.
Hence, proved that tangents drawn to two circles from any point on common tangent are equal in length.
From a point outside a circle, with centre O, tangents PA and PB are drawn. Prove that
(i) ∠AOP = ∠BOP
(ii) OP is the perpendicular bisector of the chord AB.
Answer
The figure is shown below:
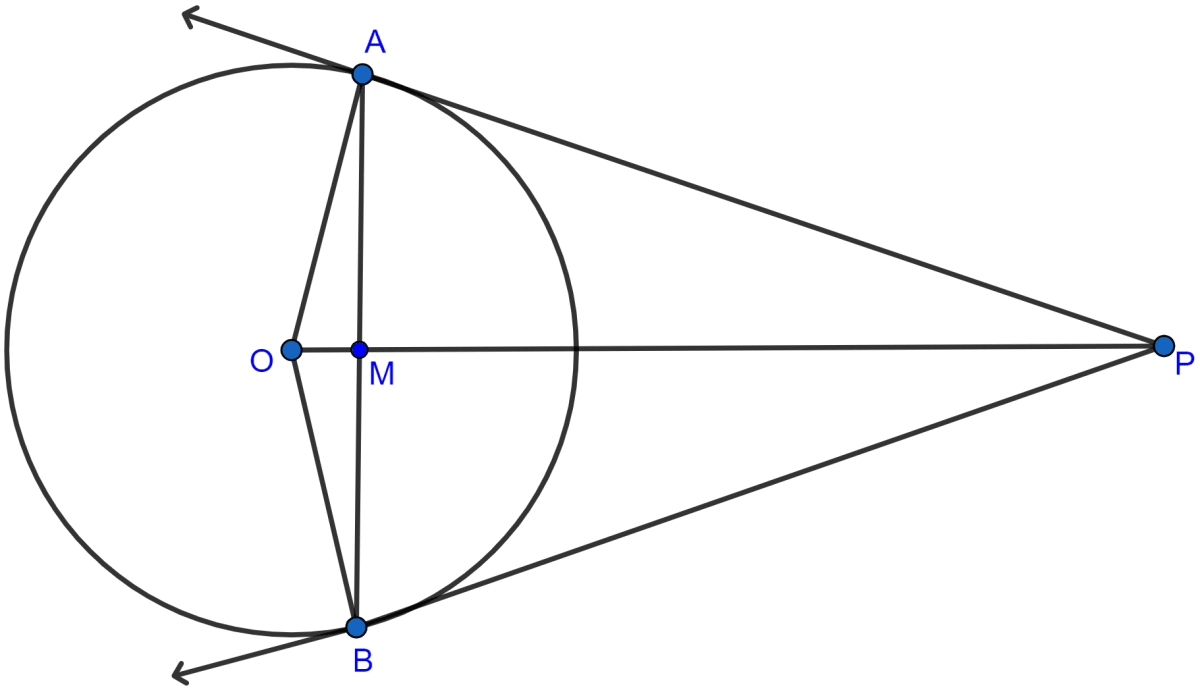
(i) In △AOP and △BOP,
OP = OP (Common sides)
OA = OB (Radius of the circle)
∠OAP = ∠OBP (Both are equal to 90° as tangents and radius on point of contact are perpendicular to each other.)
∴ △OAP ≅ △OBP (S.A.S. axiom of congruency)
(As Corresponding parts of congruent triangles are congruent)
∴ ∠AOP = ∠BOP and ∠APO = ∠BPO.
Hence, proved that ∠AOP = ∠BOP.
(ii) In △APM and △BPM,
PM = PM (Common side)
∠APM = ∠BPM (Proved above)
AP = BP (∵ tangents from an exterior point to a circle are equal in length)
∴ △APM ≅ △BPM (S.A.S. axiom of congruency)
(Congruent parts of congruent triangles are congruent.)
∴ AM = BM and ∠AMP = ∠BMP
But ∠AMP + ∠BMP = 180°
∴ ∠AMP = ∠BMP = 90°.
Hence, proved that OP is perpendicular bisector of AB at M.
The figure given below shows two circles with centres A, B and a transverse common tangent to these circles meet the straight line AB in C. Prove that :
AP : BQ = PC : CQ.
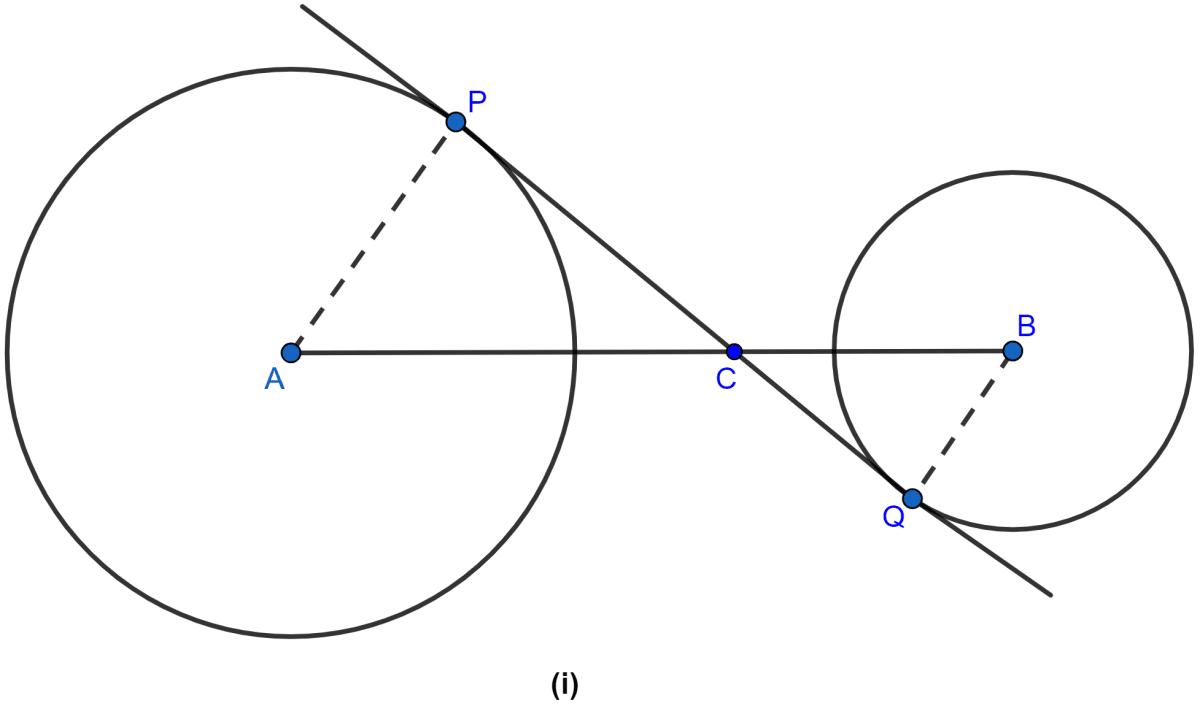
Answer
In △APC and △BQC
∠PCA = ∠QCB (∵ vertically opposite angles are equal)
∠APC = ∠BQC (∵ both are equal to 90 as radius and tangent to a circle at the point of contact are perpendicular to each other.)
∴ △APC ~ △BQC (By AA axiom of similarity)
Since triangles are similar hence the ratio of their corresponding sides are equal.
Hence, proved that AP : BQ = PC : CQ
In the figure (ii) given below, PQ is a tangent to the circle with centre O and AB is a diameter of the circle. If QA is parallel to PO, prove that PB is tangent to the circle.
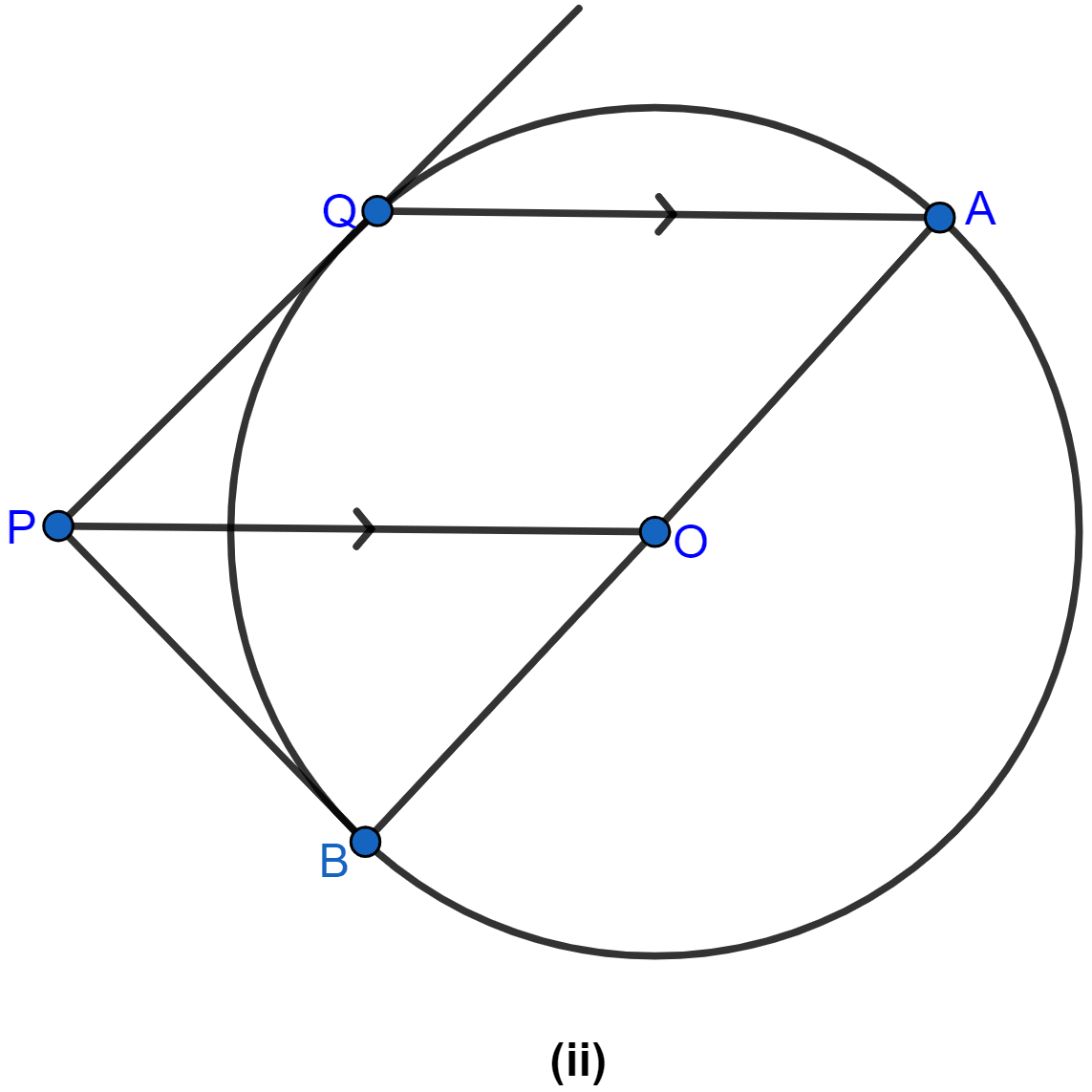
Answer
Join OQ as shown in the figure below:
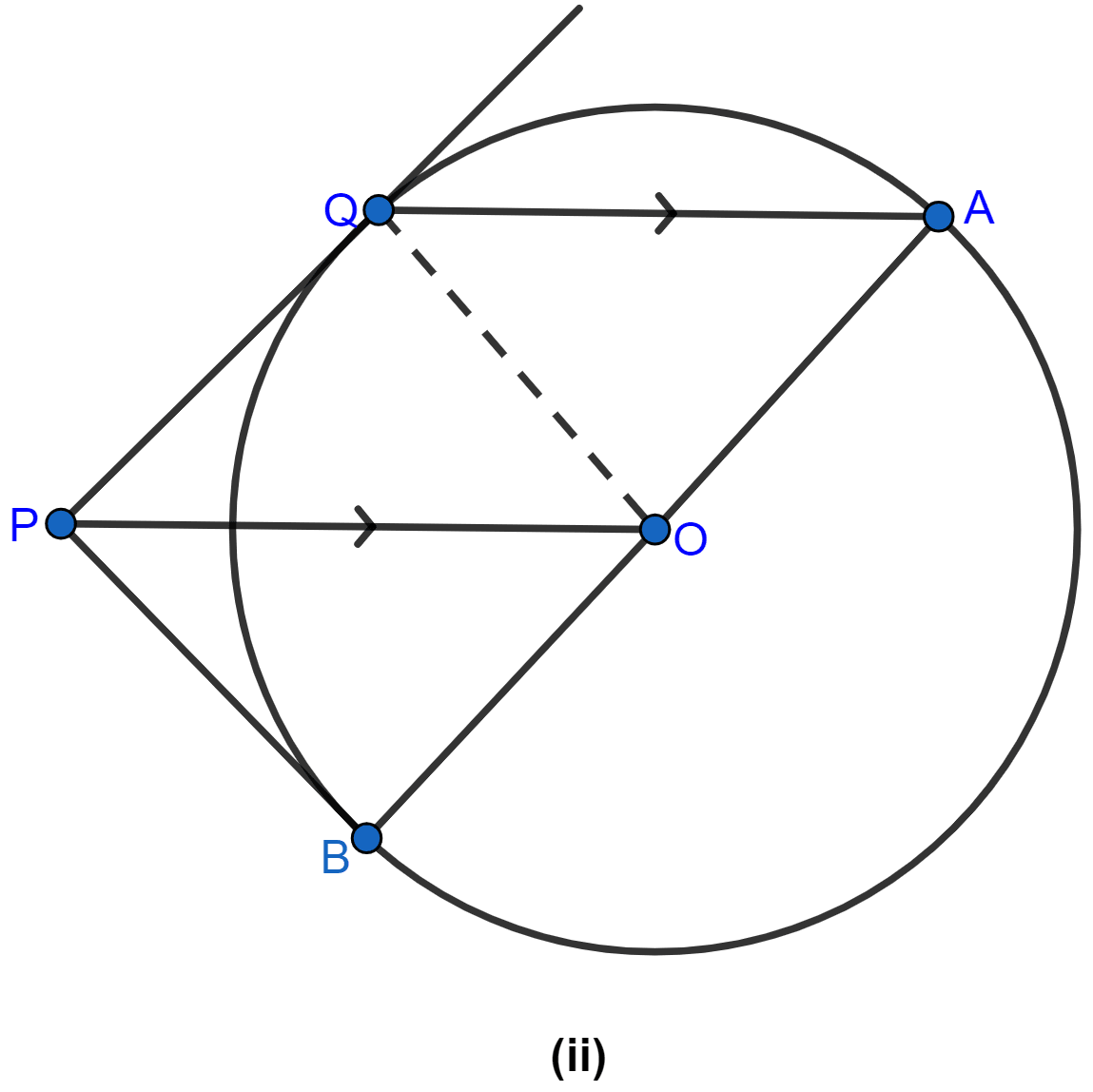
In △OAQ,
OA = OQ (Radius of the same circle.)
∠OAQ = ∠OQA.
Given QA || PO
∴ ∠OAQ = ∠POB (∵ corresponding angles are equal.)
and ∠OQA = ∠QOP (∵ alternate angles are equal.)
But ∠OAQ = ∠OQA,
∴ ∠POB = ∠QOP
Now in △OPQ and △OBP
OP = OP (Common sides)
OQ = OB (Radius of the same circle.)
∠QOP = ∠POB
∴ △OPQ ≅ △OBP (S.A.S. axiom of congruency)
As corresponding parts of congruent triangles are congruent,
∴ ∠OQP = ∠OBP
But ∠OQP = 90°
∴ ∠OBP = 90°
∴ PB is the tangent of the circle.
Hence, proved that PB is the tangent of the circle.
In the figure given below, two circles with centres A and B touch externally. PM is a tangent to the circle with centre A and QN is a tangent to the circle with centre B. If PM = 15 cm, QN = 12 cm, PA = 17 cm and QB = 13 cm, then find the distance between the centres A and B of the circles.
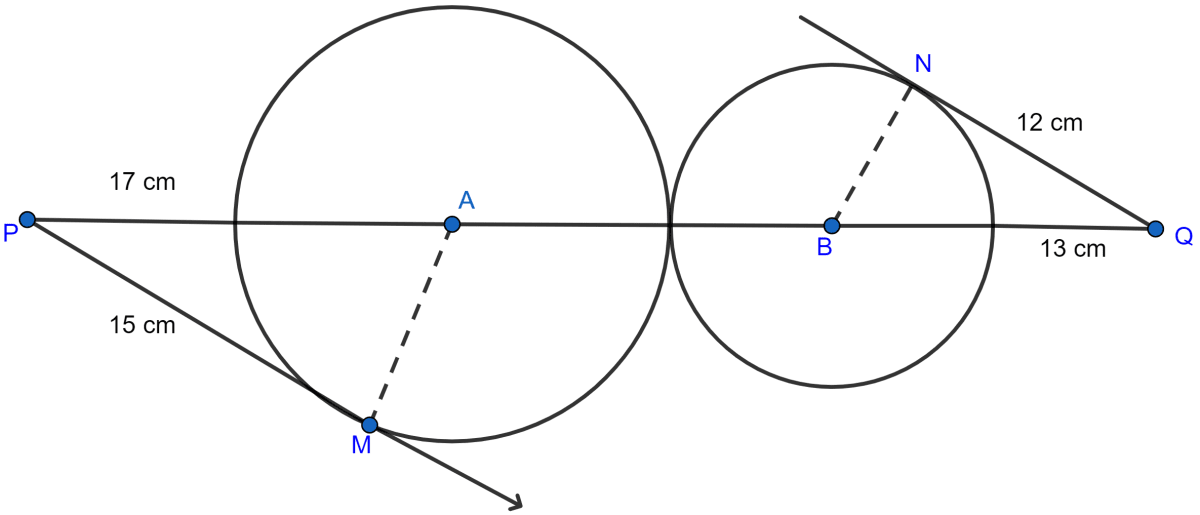
Answer
Since radius and tangent at the point of contact of a circle are perpendicular to each other.
∴ ∠AMP = ∠BNQ = 90°.
In right angled triangle △AMP
AP2 = AM2 + PM2 (By pythagoras theorem)
⇒ AM2 = AP2 - PM2
⇒ AM2 = 172 - 152
⇒ AM2 = 289 - 225
⇒ AM2 = 64
⇒ AM =
⇒ AM = 8 cm.
Similarly in right angled triangle △BNQ
BQ2 = BN2 + NQ2 (By pythagoras theorem)
⇒ BN2 = BQ2 - NQ2
⇒ BN2 = 132 - 122
⇒ BN2 = 169 - 144
⇒ BN2 = 25
⇒ BN =
⇒ BN = 5 cm.
From figure the distance between A and B is equal to the sum of their radius = 8 + 5 = 13 cm.
Two chords AB, CD of a circle intersect externally at a point P. If PB = 7 cm, AB = 9 cm and PD = 6 cm, find CD.
Answer
We know that,
If two chords of a circle intersect externally, then the products of the length of segments are equal.
From figure,
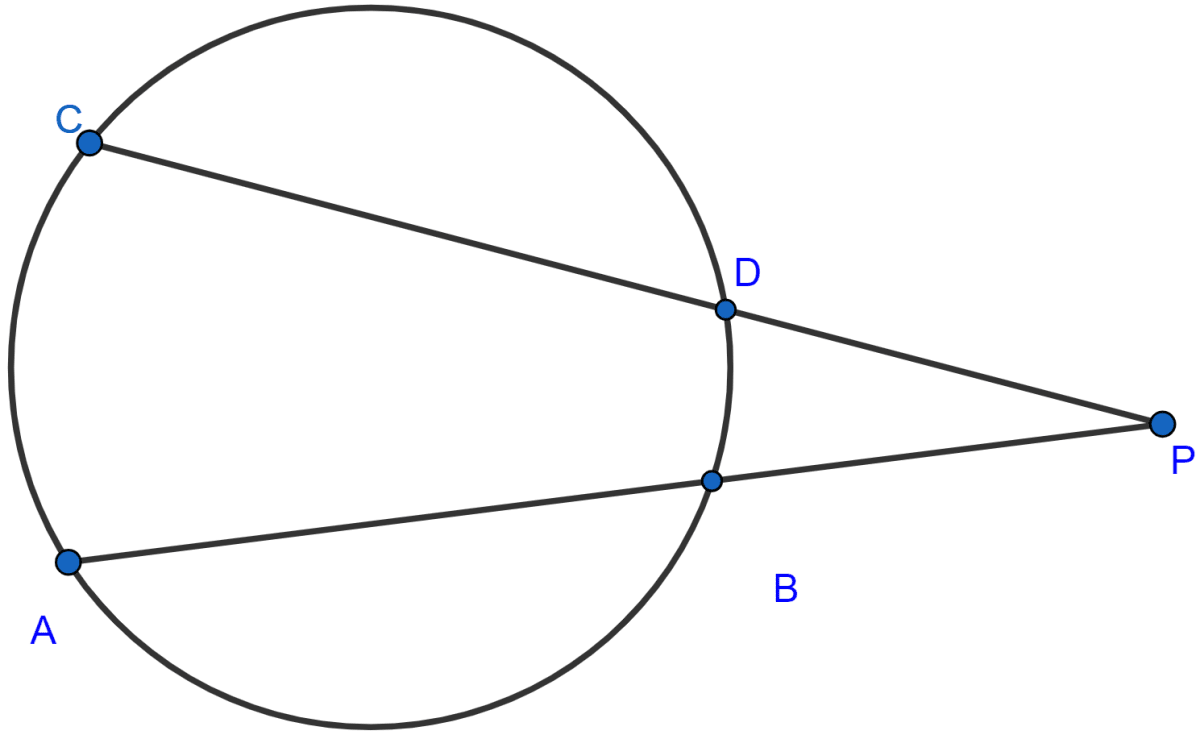
PA.PB = PC.PD .....(i)
PA = PB + AB = 7 + 9 = 16 cm.
Putting values in equation (i) we get,
⇒ 16 × 7 = PC × 6
⇒ 112 = PC × 6
⇒ PC =
⇒ PC = .
From figure,
CD = PC - PD =
Hence, the value of CD = cm.
In the figure (i) given below, chord AB and diameter CD of a circle with centre O meet at P. PT is tangent to the circle at T. If AP = 16 cm, AB = 12 cm and DP = 2 cm, find the length of PT and the radius of the circle.

Answer
We know that if a chord and a tangent intersect externally, then the product of the lengths of the segments of the chord is equal to the square of the length of the tangent from the point of contact to the point of intersection.
∴ PA.PB = PT2 .....(i)
From figure,
PB = PA - AB = 16 - 12 = 4 cm.
Putting values in equation (i),
16 x 4 = PT2
PT2 = 64
PT = = 8 cm.
Join OT as shown in the figure below:

In △OTP,
OT ⊥ TP (∵ tangents and radius at the point of contact are perpendicular to each other.)
In right angled triangle OTP,
OP2 = OT2 + PT2 (By pythagoras theorem)
(OD + DP)2 = OT2 + PT2
Since, OD = OT = radius of circle = r.
(r + 2)2 = r2 + 82
r2 + 4 + 4r = r2 + 64
r2 - r2 + 4r = 64 - 4
4r = 60
r = 15 cm.
Hence, the length of PT = 8 cm and radius of circle = 15 cm.
In the figure (ii) given below, chord AB and diameter CD of a circle meet at P. If AB = 8 cm, BP = 6 cm and PD = 4 cm, find the radius of the circle. Also find the length of the tangent drawn from P to the circle.

Answer
We know that if a chord and a tangent intersect externally, then the product of the lengths of the segments of the chord is equal to the square of the length of the tangent from the point of contact to the point of intersection.
∴ PA.PB = PT2 .....(i)
From figure,
PA = AB + PB = 8 + 6 = 14 cm.
Putting values in equation (i),
14 x 6 = PT2
PT2 = 84
PT = cm.
Joining OT as shown in the figure below:

In △OTP,
OT ⊥ TP (∵ tangents and radius at a point of contact are perpendicular to each other.)
In right angled triangle OTP,
Since, OD = OT = radius of circle = r.
Hence, the radius of the circle = 8.5 cm and length of tangent = cm.
In the adjoining figure, chord AB and diameter PQ of a circle with centre O meet at X. If BX = 5 cm, OX = 10 cm and the radius of the circle is 6 cm, compute the length of AB. Also find the length of tangent drawn from X to the circle.
Answer
From figure,
OP = OQ = radius of circle = 6 cm.
XP = XO + OP = 10 + 6 = 16 cm.
XQ = XO - OQ = 10 - 6 = 4 cm.
We know that,
If two chords of a circle intersect externally, then the products of the length of segments are equal.
From figure,
XA XB = XP XQ
5 XA = 16 4
XA = = 12.8 cm.
AB = XA - XB = 12.8 - 5 = 7.8 cm
Let XT be the tangent to the circle as shown in the figure below:
We know that if a chord and a tangent intersect externally, then the product of the lengths of the segments of the chord is equal to the square of the length of the tangent from the point of contact to the point of intersection.
∴ XP.XQ = XT2 .....(i)
XT2 = 16 x 4 = 64
XT = = 8 cm.
Hence, the length of AB = 7.8 cm and length of tangent = 8 cm.
In the figure (i) given below, ∠CBP = 40°, ∠CPB = q° and ∠DAB = p°. Obtain an equation connecting p and q. If AC and BD meet at Q so that ∠AQD = 2q° and the points C, P, B and Q are concyclic, find the values of p and q.
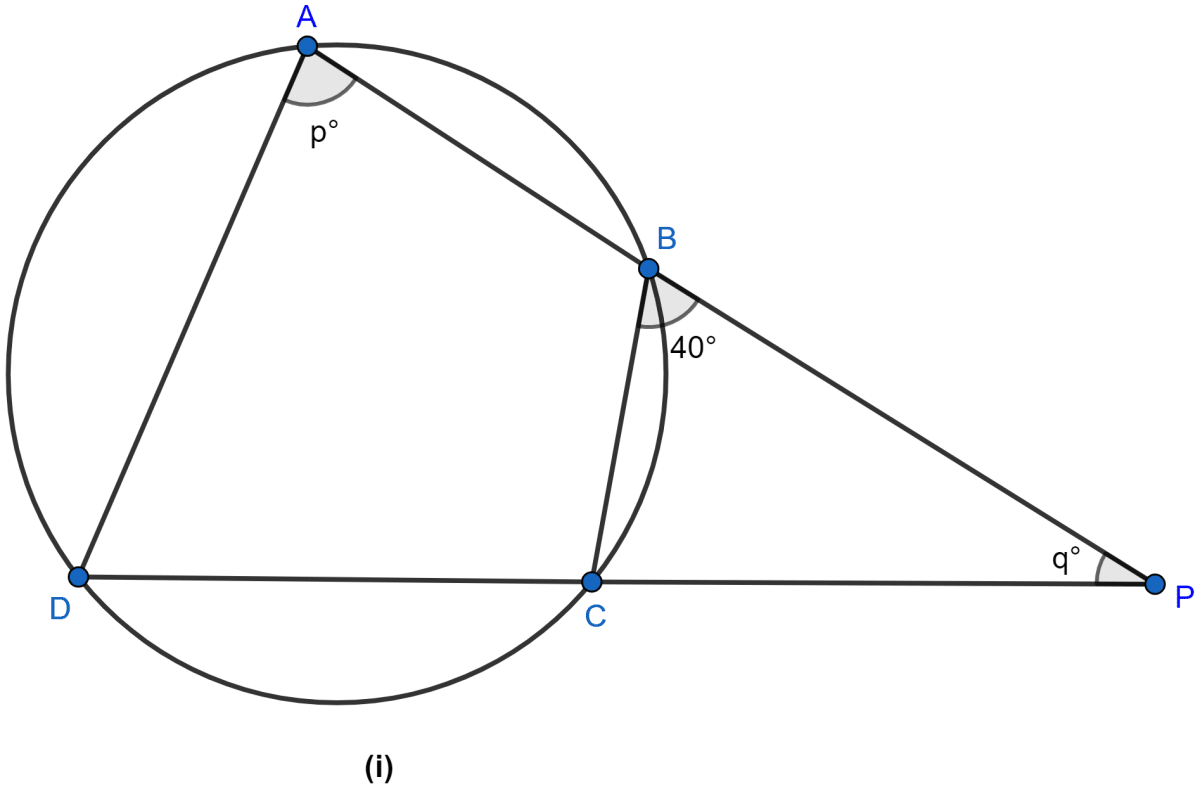
Answer
From figure,
∠ADC = ∠CBP = 40°. (∵ angles in alternate segments are equal.)
Since sum of angles in a triangle = 180°.
In △ADP,
∠DAP + ∠APD + ∠ADP = 180°
From figure, ∠ADP = ∠ADC = 40°.
⇒ p° + q° + 40° = 180°
⇒ p° + q° = 180° - 40°
⇒ p° + q° = 140° .....(i)
Join AC and BD as shown in the figure below:
∠CQB = ∠AQD = 2q° (∵ vertically opposite angles are equal.)
Given C, P, B, Q are concyclic.
∴ ∠CPB + ∠CQB = 180°
⇒ q° + 2q° = 180°
⇒ 3q° = 180°
⇒ q° = 60°.
Putting value of q in equation (i) we get,
⇒ p° + 60° = 140°
⇒ p° = 140° - 60° = 80°.
Hence, the value of p = 80 and q = 60 and the relation between p and q is p + q = 140.
In the figure (ii) given below, AC is a diameter of the circle with centre O. If CD || BE, ∠AOB = 130° and ∠ACE = 20°, find :
(i) ∠BEC
(ii) ∠ACB
(iii) ∠BCD
(iv) ∠CED.
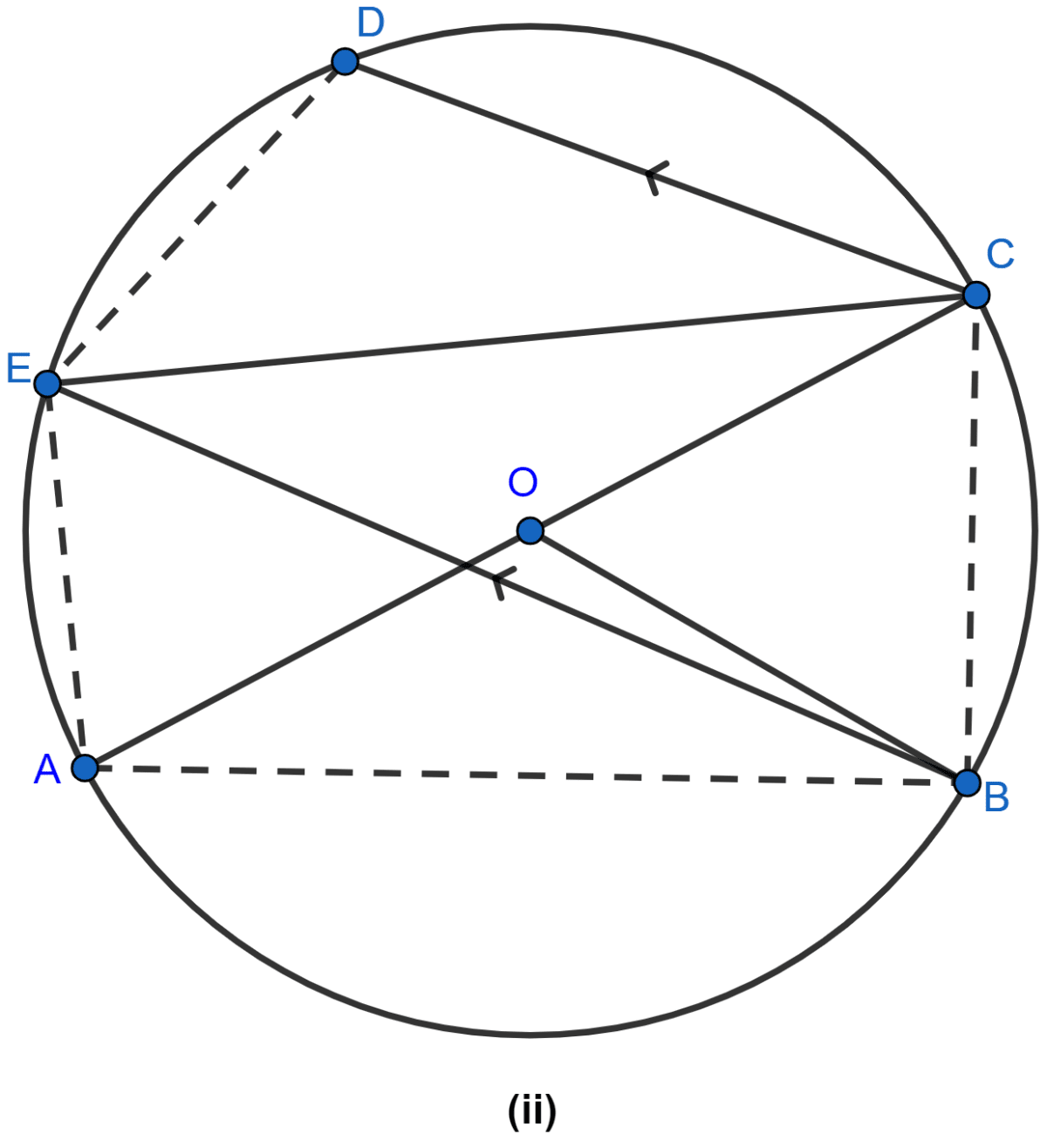
Answer
∠AOB = 130°.
∠AOB + ∠BOC = 180° (∵ these angles form linear pair.)
130° + ∠BOC = 180°
∠BOC = 180° - 130° = 50°.
(i) Arc BC subtends ∠BOC at the centre and ∠BEC at the remaining part of the circle.
∠BOC = 2∠BEC (∵ angle subtended on centre is twice the angle subtended on the remaining part of the circle).
⇒ 50° = 2∠BEC
⇒ ∠BEC =
Hence, the value of ∠BEC = 25°.
(ii) Arc AB subtends ∠AOB at the centre and ∠ACB at the remaining part of the circle.
⇒ ∠AOB = 2∠ACB (∵ angle subtended on centre is twice the angle subtended on the remaining part of the circle).
⇒ 130° = 2∠ACB
⇒ ∠ACB =
Hence, the value of ∠ACB = 65°.
(iii) Given, CD || EB,
∠ECD = ∠CEB = 25°. (∵ alternate angles are equal.)
From figure,
∠BCD = ∠ACB + ∠ACE + ∠ECD = 65° + 20° + 25° = 110°.
Hence, the value of ∠BCD = 110°.
(iv) EBCD is a cyclic quadrilateral hence the sum of opposite interior angles = 180°.
∴ ∠BED + ∠BCD = 180°
⇒ ∠BEC + ∠CED + ∠BCD = 180°
⇒ 25° + ∠CED + 110° = 180°
⇒ ∠CED + 135° = 180°
⇒ ∠CED = 180° - 135° = 45°.
Hence, the value of ∠CED = 45°.
In the figure (i) given below, chords AB, BC and CD of a circle with center O are equal. If ∠BCD = 120°, find
(i) ∠BDC
(ii) ∠BEC
(iii) ∠AEB
(iv) ∠AOB.
Hence, prove that △OAB is equilateral.

Answer
(i) In △BCD, BC = CD
∴ ∠CBD = ∠BDC (∵ angles opposite to equal sides are equal.)
Since sum of angles in a triangle = 180°.
In △BCD,
∠BCD + ∠CBD + ∠CDB = 180°
⇒ 120° + ∠CBD + ∠CBD = 180°
⇒ 120° + 2∠CBD = 180°
⇒ 2∠CBD = 180° - 120°
⇒ ∠CBD = = 30°.
As ∠CBD = ∠BDC,
∴ ∠BDC = 30°.
Hence, the value of ∠BDC = 30°.
(ii) From figure,
∠BDC = ∠BEC (∵ angles in same segment are equal.)
∴ ∠BEC = 30°
Hence, the value of ∠BEC = 30°.
(iii) Given AB = CB
∴ ∠BEC = ∠AEB (∵ equal chords subtend equal angles.)
∴ ∠AEB = 30°
Hence, the value of ∠AEB = 30°.
(iv) Arc AB subtends ∠AOB at the centre and ∠AEB at the remaining part of the circle.
⇒ ∠AOB = 2∠AEB (∵ angle subtended on centre is twice the angle subtended on the remaining part of the circle).
⇒ ∠AOB = 2 × 30°
⇒ ∠AOB = 60°.
Hence, the value of ∠AOB = 60°.
In the figure (i) given below, AB and XY are diameters of a circle with centre O. If ∠APX = 30°, find
(i) ∠AOX
(ii) ∠APY
(iii) ∠BPY
(iv) ∠OAX.

Answer
(i) Arc AX subtends ∠AOX at the centre and ∠APX at the remaining part of the circle.
⇒ ∠AOX = 2∠APX (∵ angle subtended on centre is twice the angle subtended on the remaining part of the circle).
⇒ ∠AOX = 2 × 30°
⇒ ∠AOX = 60°.
Hence, the value of ∠AOX = 60°.
(ii) From figure,
∠XPY = 90° (∵ angle in semicircle = 90°.)
∴ ∠APY = ∠XPY - ∠APX = 90° - 30° = 60°.
Hence, the value of ∠APY = 60°.
(iii) From figure,
∠APB = 90° (∵ angle in semicircle = 90°.)
∴ ∠BPY = ∠APB - ∠APY = 90° - 60° = 30°.
Hence, the value of ∠BPY = 30°.
(iv) In △AOX,
OA = OX (Radius of the same circle.)
∴ ∠OAX = ∠OXA
Since sum of angles of a triangle = 180°
∴ ∠AOX + ∠OAX + ∠OXA = 180°
⇒ 60° + ∠OAX + ∠OAX = 180°
⇒ 2∠OAX = 180° - 60°
⇒ 2∠OAX = 120°
⇒ ∠OAX = 60°.
Hence, the value of ∠OAX = 60°.
In the figure (ii) given below, AP and BP are tangents to the circle with centre O. If ∠CBP = 25° and ∠CAP = 40°, find
(i) ∠ADB
(ii) ∠AOB
(iii) ∠ACB
(iv) ∠APB.
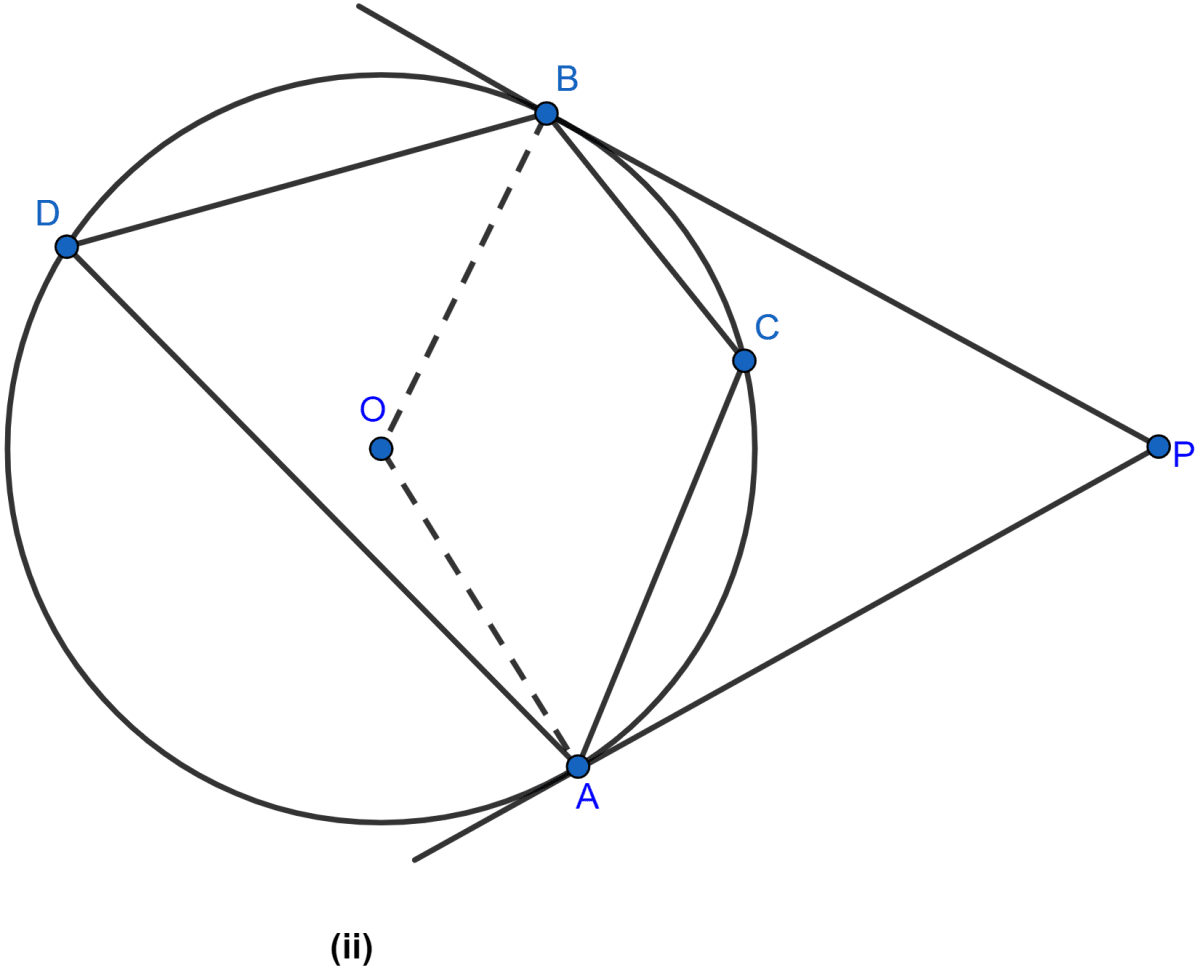
Answer
(i) ∠CDB = ∠CBP (∵ angles in alternate segments are equal.)
∴ ∠CDB = 25° ....(i)
Similarly, ∠CDA = ∠CAP = 40° (∵ angles in alternate segments are equal.)
∴ ∠ADB = ∠CDA + ∠CDB = 40° + 25° = 65°.
Hence, the value of ∠ADB = 65°.
(ii) Arc AB subtends ∠AOB at the centre and ∠ADB at the remaining part of the circle.
⇒ ∠AOB = 2∠ADB (As angle subtended on centre is twice the angle subtended on the remaining part of the circle).
⇒ ∠AOB = 2 × 65°
⇒ ∠AOB = 130°.
Hence, the value of ∠AOB = 130°.
(iii) ACBD is a cyclic quadrilateral.
∴ ∠ACB + ∠ADB = 180° (∵ sum of opposite angles = 180°.)
⇒ ∠ACB + 65° = 180°
⇒ ∠ACB = 180° - 65° = 115°.
Hence, the value of ∠ACB = 115°.
(iv) From figure,
⇒ ∠AOB + ∠APB = 180°
⇒ 130° + ∠APB = 180°
⇒ ∠APB = 180° - 130° = 50°.
Hence, the value of ∠APB = 50°.
In the given figure AC is the diameter of the circle with center O. CD is parallel to BE. ∠AOB = 80° and ∠ACE = 20°. Calculate :
(a) ∠BEC
(b) ∠BCD
(c) ∠CED
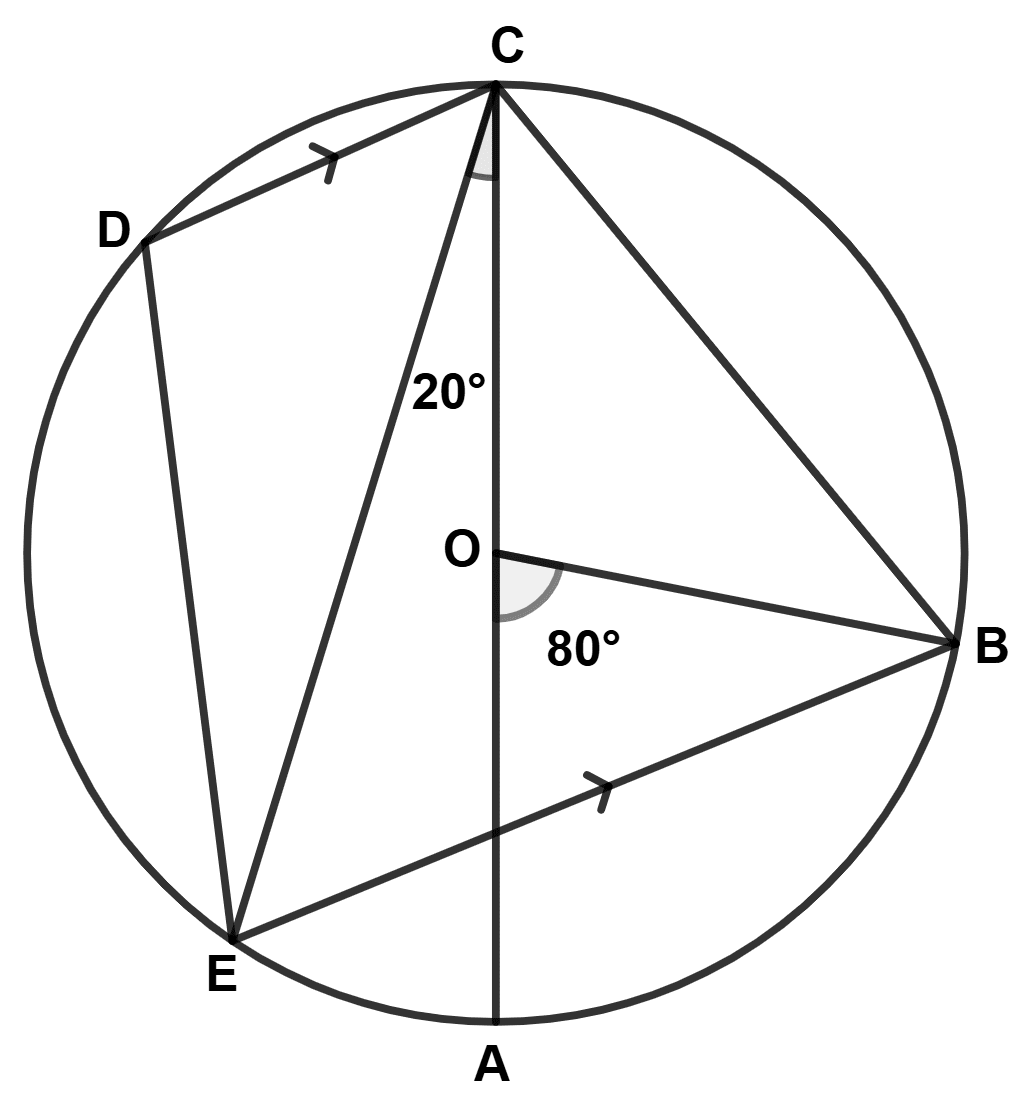
Answer
(a) Join AE.
We know that,
The angle subtended by a chord at the centre is twice the angle subtended on the circumference.
∴ ∠AOB = 2∠AEB
⇒ 80° = 2∠AEB
⇒ ∠AEB = = 40°.
We know that,
Angle in a semi-circle is a right angle.
⇒ ∠AEC = 90°
From figure,
⇒ ∠BEC = ∠AEC - ∠AEB = 90° - 40° = 50°.
Hence, ∠BEC = 50°.
(b) From figure,
⇒ ∠ECD = ∠CEB = 50° (Alternate angles are equal)
We know that,
The angle subtended by a chord at the centre is twice the angle subtended on the circumference.
⇒ ∠AOB = 2∠BCA
⇒ 80° = 2∠BCA
⇒ ∠BCA = = 40°.
From figure,
⇒ ∠BCD = ∠BCA + ∠ACE + ∠ECD = 40° + 20° + 50° = 110°.
Hence, ∠BCD = 110°.
(c) As sum of opposite angles of cyclic quadrilateral = 180°.
⇒ ∠BED + ∠BCD = 180°
⇒ ∠BED = 180° - ∠BCD = 180° - 110° = 70°.
From figure,
⇒ ∠BED = ∠BEC + ∠CED
⇒ 70° = 50° + ∠CED
⇒ ∠CED = 70° - 50° = 20°.
Hence, ∠CED = 20°.
In the given figure (drawn not to scale) chords AD and BC intersect at P, where AB = 9 cm, PB = 3 cm and PD = 2 cm.
(a) Prove that △ APB ~ △ CPD
(b) Find the length of CD
(c) Find area △ APB : area △ CPD.
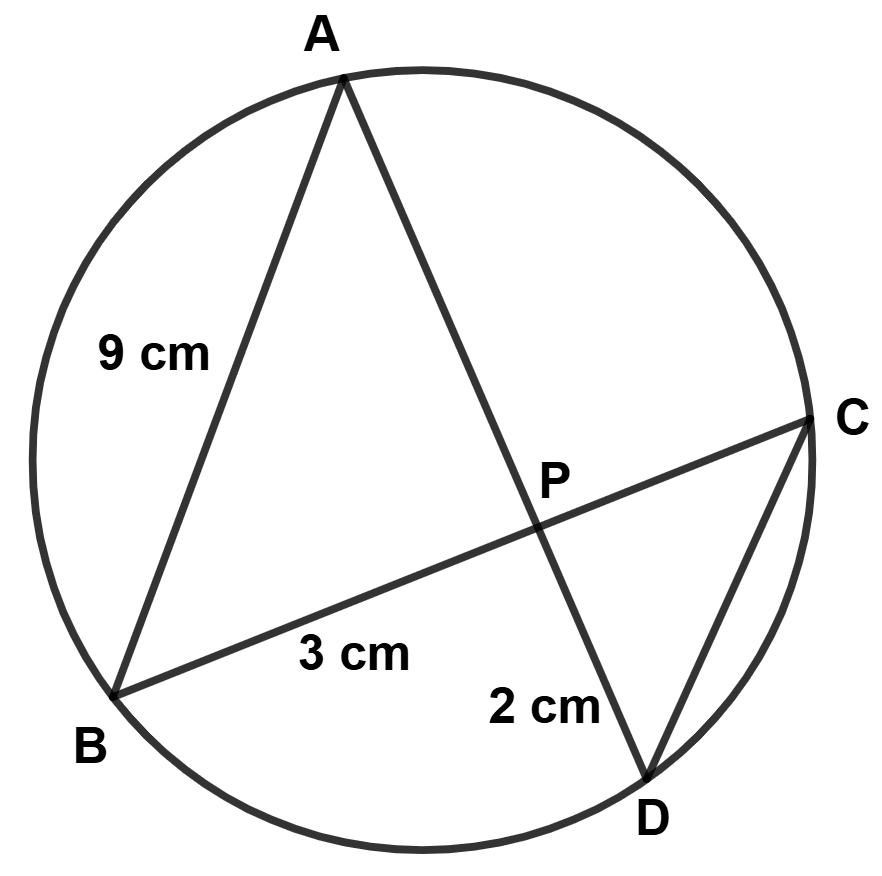
Answer
(a) In △ APB and △ CPD,
⇒ ∠APB = ∠CPD (Vertically opposite angles are equal)
⇒ ∠BAP = ∠DCP (Angles in same segment are equal)
∴ △ APB ~ △ CPD (By A.A. axiom)
Hence, proved that △ APB ~ △ CPD.
(b) We know that,
Corresponding sides of similar triangles are proportional.
Hence, CD = 6 cm.
(c) We know that,
Ratio of area of similar triangles is equal to the ratio of square of the corresponding sides.
Hence, area △ APB : area △ CPD = 9 : 4.
In the given figure PT is a tangent to the circle. Chord BA produced meets the tangent PT at P. Given PT = 20 cm and PA = 16 cm.
(a) Prove △ PTB ~ △ PAT
(b) Find the length of AB.
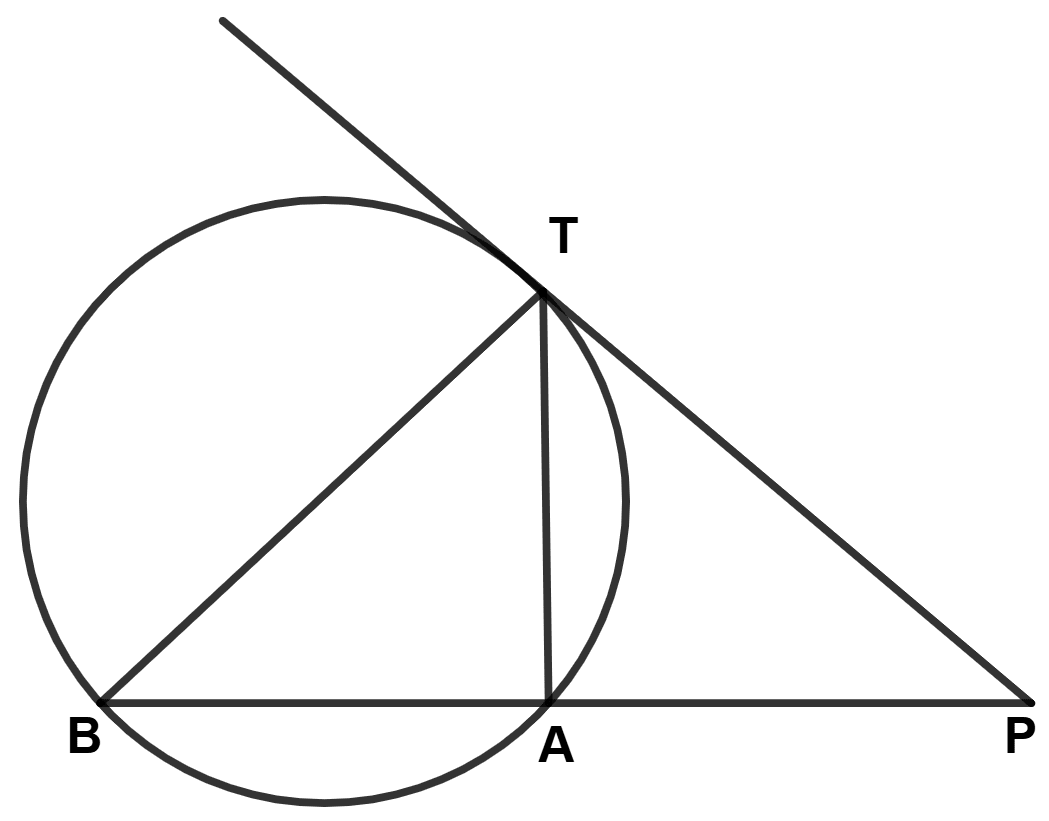
Answer
(a) In △ PTB and △ PAT,
⇒ ∠PTA = ∠PBT (Alternate segment theorem)
⇒ ∠TPA = ∠BPT (Common angle)
∴ △ PTB ~ △ PAT (By A.A. axiom)
Hence, proved that △ PTB ~ △ PAT.
(b) We know that,
If a chord and a tangent intersect externally, then the product of the lengths of segments of the chord is equal to the square of the length of the tangent from the point of contact to the point of intersection.
⇒ PA × PB = PT2
⇒ PA × (PA + AB) = PT2
⇒ 16 × (16 + AB) = 202
⇒ 16 × (16 + AB) = 400
⇒ 16 + AB = 25
⇒ AB = 25 - 16 = 9 cm.
Hence, AB = 9 cm.
Prove that any four vertices of a regular pentagon are concyclic.
Answer
Let the regular pentagon be ABCDE.
Since it's regular, and all interior angles are equal to 108°.
∴ ∠ABC = ∠BCD = ∠CDE = ∠DEA = ∠EAB
Interior angle of a regular polygon is given by :
So, each interior angle of a regular pentagon = - 108°.
In triangle AED,
AE = ED [Sides of a regular pentagon are equal]
∴ ∠EAD = ∠EDA [Angles opposite to equal sides are equal] ......(1)
⇒ ∠AED + ∠EAD + ∠EDA = 180°
⇒ 108° + ∠EAD + ∠EAD = 180°
⇒ 2∠EAD = 180° - 108°
⇒ 2∠EAD = 72°
⇒ ∠EAD =
⇒ ∠EAD = 36°
∴ ∠EDA = 36°.
From figure,
⇒ ∠BAD = ∠BAE - ∠EAD = 108° - 36° = 72°.
In quadrilateral ABCD,
∠BAD + ∠BCD = 72° + 108° = 180°.
Since, sum of opposite angles = 180°,
which is possible when the quadrilateral is cyclic quadrilateral.
Hence, proved that any four vertices of a regular pentagon are concylic.