Locus

A point moves such that its distance from a fixed line AB is always the same. What is the relation between AB and the path traveled by P?

Answer

Let point P move in such a way that it is at a fixed distance from the fixed line AB.

∴ It is a set of two lines parallel to AB, drawn on either side of it at equal distance from it as shown in the figure below.

Hence, the path consists of a pair of straight lines parallel to AB.

A point P moves so that its perpendicular distances from two given lines AB and CD are equal. State the locus of point P.

Answer

There can be two cases :

(i) When two lines AB and CD are parallel

In this case the locus of the point P which is equidistant from AB and CD is a line in the midway of AB and CD and parallel to them.

(ii) When AB and CD are intersecting lines,

In this case the locus of the point P will be a pair of straight lines l and m which bisect the angles between the given lines AB and CD.

P is a fixed point and a point Q moves such that the distance PQ is constant. What is the locus of the path traced out by the point Q?

Answer

Given, P is a fixed point and Q is a moving point such that it is always at an equidistant from P.

∴ P is the centre of the path of Q which is a circle and distance PQ is the radius of the circle.

Hence, the locus of point Q is a circle with P as centre.

AB is a fixed line. State the locus of point P so that ∠APB = 90°.

Answer

We know that the angle in a semi-circle is always equal to 90°.

Hence, the locus of point P will be the circle whose diameter is AB.

A, B are fixed points. State the locus of P so that ∠APB = 60°.

Answer

The locus of P will be arc of the circle with AB as chord.

Draw and describe the locus of points at a distance 2.5 cm from the fixed line.

Answer

From graph we see that,

The locus of point will be a pair of straight lines parallel to the fixed line and at perpendicular distance of 2.5 cm from it.

Draw and describe the locus of vertices of all isosceles triangles having a common base.

Answer

△ABC is an isosceles triangle in which AB = AC.

From A, draw AD perpendicular to BC.

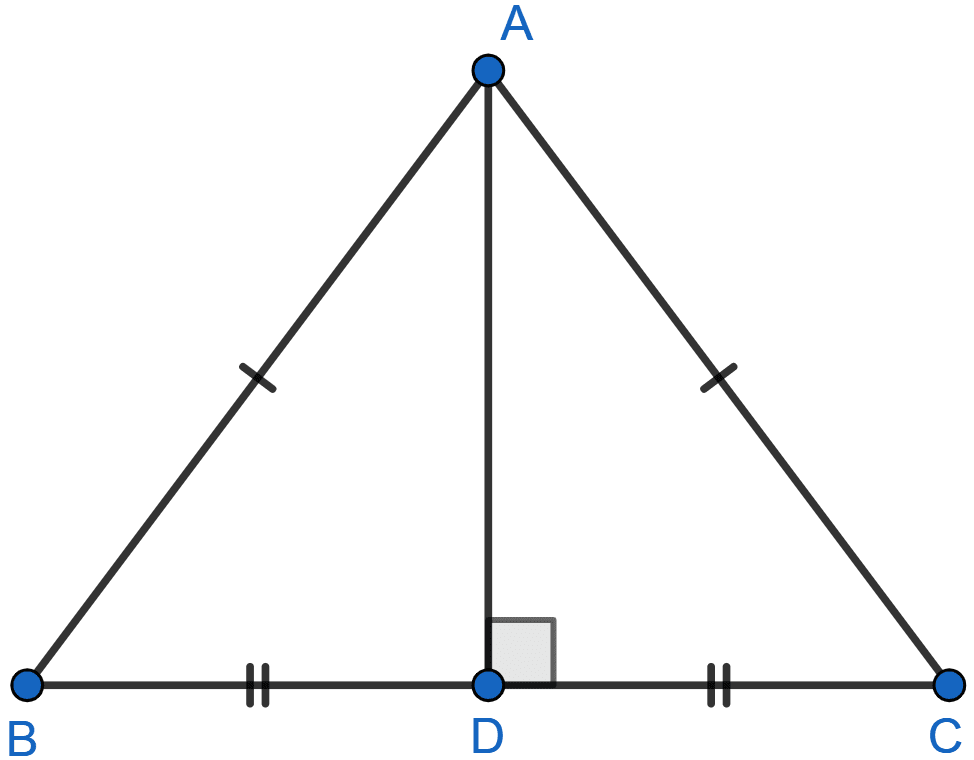
In △ABD and △ACD

AD = AD (Common sides)
AB = AC (Since, triangle is isosceles)
∠ADB = ∠ADC (90°)

Hence, by SAS axiom △ABD ~ △ACD. Since, triangles are similar so the ratio of the corresponding sides will be equal,

$\dfrac{BD}{DC} = \dfrac{AB}{AC} \\[1em] \dfrac{BD}{DC} = \dfrac{AC}{AC} \qquad [\because \text{AB = AC}] \\[1em] \dfrac{BD}{DC} = 1 \\[1em] BD = DC.$

Since, BD = DC so AD can be said as the perpendicular bisector of BC.

Hence, the locus of vertices will be the perpendicular bisector of the base.

Draw and describe the locus of points inside a circle and equidistant from two fixed points on the circle.

Answer

Let the two points on circle be A and B. Draw a perpendicular bisector of AB which passes from centre (O) and meets the circle at C and E. This CE will be the locus of the points.

Hence, the locus of the points will be the diameter of circle which is perpendicular to the chord of the circle joining the given points.

Draw and describe the locus of centres of all circles passing through two fixed points.

Answer

Let the two fixed points be A and B, and C₁, C₂, C₃ be the centres of circles passing through A and B.

From figure we see that,

The locus of the centres of the circles passing through two points will be the perpendicular bisector of the line segment joining two fixed points.

Draw and describe the locus of a point in rhombus ABCD which is equidistant from AB and AD.

Answer

Let ABCD be a rhombus.

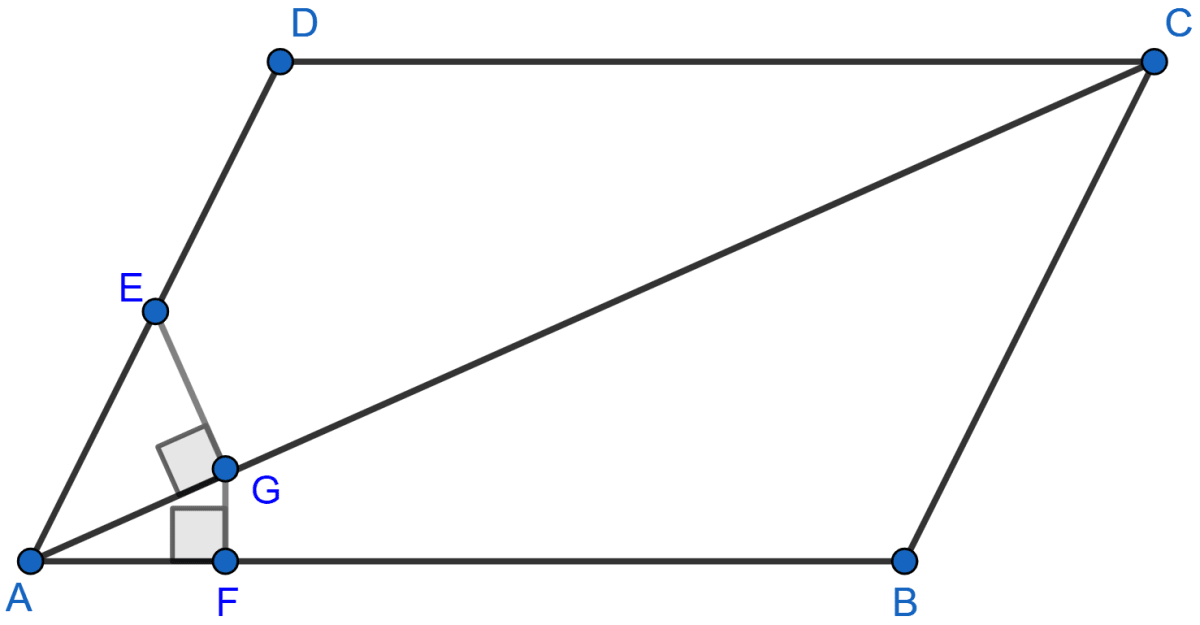
AC is diagonal of rhombus which will bisect angle A. As rhombus bisects the vertices angle.

∴ AC bisects ∠A

Let there be a point E and F on the sides AD and AB respectively. Draw a line perpendicular to AC from both the points.

Considering △AEG and △AFG

∠AGE = ∠AFG (Both are equal to 90°)
∠EAG = ∠FAG (Both are equal to half of ∠DAB.)

Hence, by AA axiom △AEG ~ △AFG.

Since triangles are similar so the ratio of their corresponding sides will be similar.

$\therefore \dfrac{EG}{FG} = \dfrac{AG}{AG} \\[1em] \Rightarrow \dfrac{EG}{FG} = 1 \\[1em] \Rightarrow EG = FG.$

Since, distance from AD and AB is similar,

Hence, the locus of point is the diagonal AC of the rhombus ABCD.

Draw and describe the locus of a point in the rhombus ABCD which is equidistant from the points A and C.

Answer

Let ABCD be the rhombus.

So, AC and BD will be the diagonal of rhombus. They meet at O.

Since, diagonals bisects each other so, OA = OC.

Since, BD passes through O so it will be also equidistant from A and C.

Hence, locus will be the diagonal BD of the rhombus ABCD.

Describe completely the locus of mid-point of radii of a circle.

Answer

Let radius = r.

The distance between midpoint of radius and centre = $\dfrac{r}{2}$.

Hence, the locus of the midpoints of the radii of the circle will be another concentric circle with half the radius.

Describe completely the locus of centre of a ball, rolling along a straight line on a level floor.

Answer

Suppose a ball moves from A to B. Initially the ball will be at A and finally at B. Figure for the same is shown below:

Hence, the locus of centre of ball will be a parallel line to the floor at a height equal to radius of the ball.

Describe completely the locus of point in a plane equidistant from a given line.

Answer

Let the given line be AB, and point P and P' be two points on both sides of AB at an equal distance,

Draw a line CD and EF from P and P' respectively parallel to AB.

Hence, the locus is a pair of lines parallel to the given line.

Describe completely the locus of point in a plane, at a constant distance of 5 cm from a fixed point (in the plane).

Answer

Let the fixed point be O and another point P be such that OP = 5 cm.

By taking O as centre and radius OP, draw a circle.

Thus this circle is the locus of point P.

Hence, the locus will be a circle with fixed point as centre and radius 5 cm.

Describe completely the locus of centre of a circle of varying radius and touching two arms of ∠ABC.

Answer

Let there be two circles with centre O and O' and BD be the angle bisector of ∠ABC.

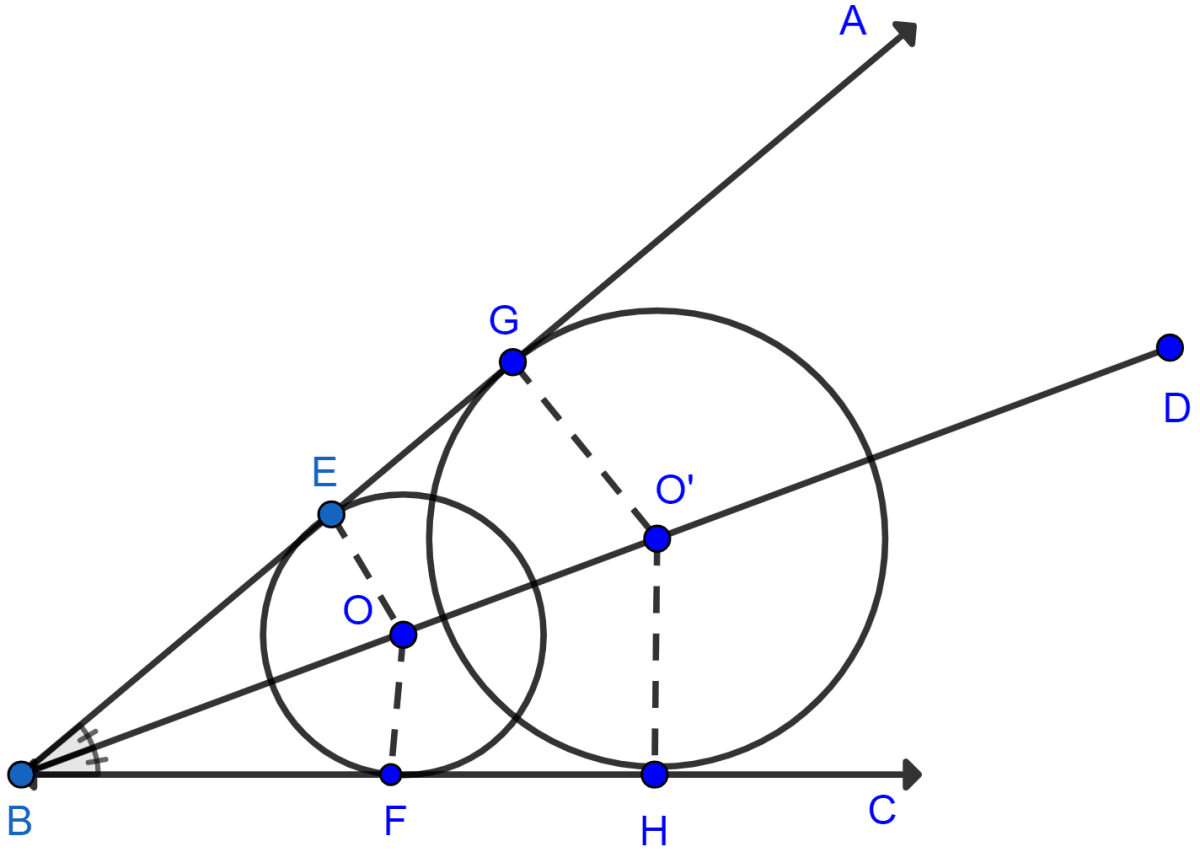
AB and BC are two tangents to the circle.

We know that radius and tangent make 90°.

From graph,

∠OEB = ∠OFB (Both are equal to 90)

∠OBE = ∠OBF (Since, BX is the angle bisector of ∠ABC.)

Hence, by AA axiom △OEB ~ △OFB.

Since triangles are similar hence, the ratio of their corresponding sides are similar.

$\therefore \dfrac{OE}{OB} = \dfrac{OF}{OB} \\[1em] \Rightarrow OE = \dfrac{OF}{OB} \times OB \\[1em] \Rightarrow OE = OF \\[1em]$

Since, O is the centre hence, we can say that OE = OF = radius. Thus circle with centre O is at equal distance from both arms of angle.

Similarly,

From graph,

∠O'GB = ∠O'HB (Both are equal to 90)

∠O'BG = ∠O'BH (Since, BX is the angle bisector of ∠ABC.)

Hence, by AA axiom △O'GB ~ △O'HB.

Since triangles are similar hence, the ratio of their corresponding sides are similar.

$\therefore \dfrac{O'G}{O'B} = \dfrac{O'H}{O'B} \\[1em] \Rightarrow O'G = \dfrac{O'H}{O'B} \times O'B \\[1em] \Rightarrow O'G = O'H \\[1em]$

Since, O' is the centre hence, we can say that O'G = O'H = radius. Thus circle with centre O' is at equal distance from both arms of angle.

Hence, the locus is the bisector of the ∠ABC.

Describe completely the locus of centre of a circle of radius 2 cm and touching a fixed circle of radius 3 cm with centre O.

Answer

From the figure,

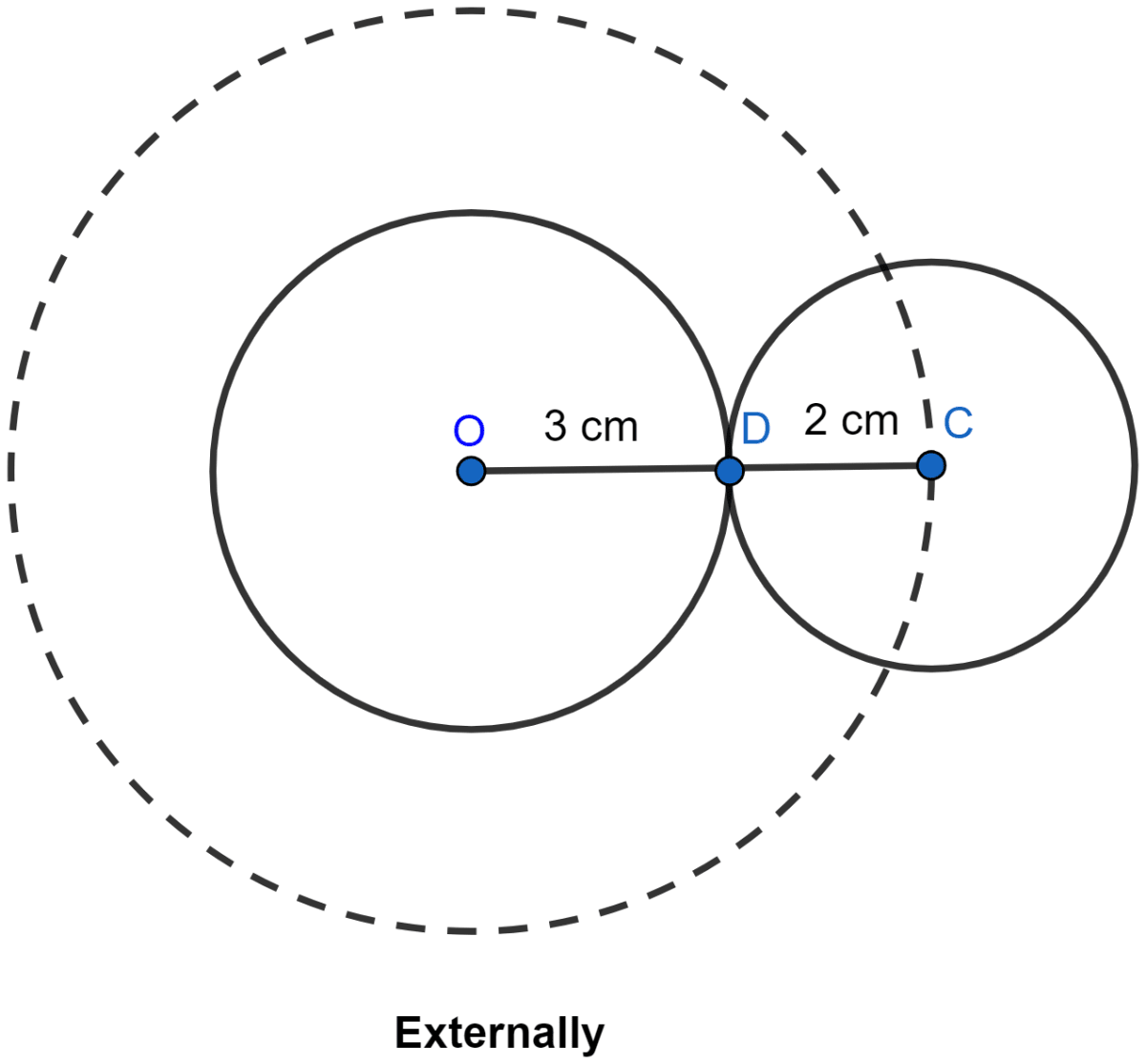
If the circle with 2 cm as radius touches the given circle externally then the locus of the centre of the circle will be a concentric circle with radius (3 + 2) = 5 cm.

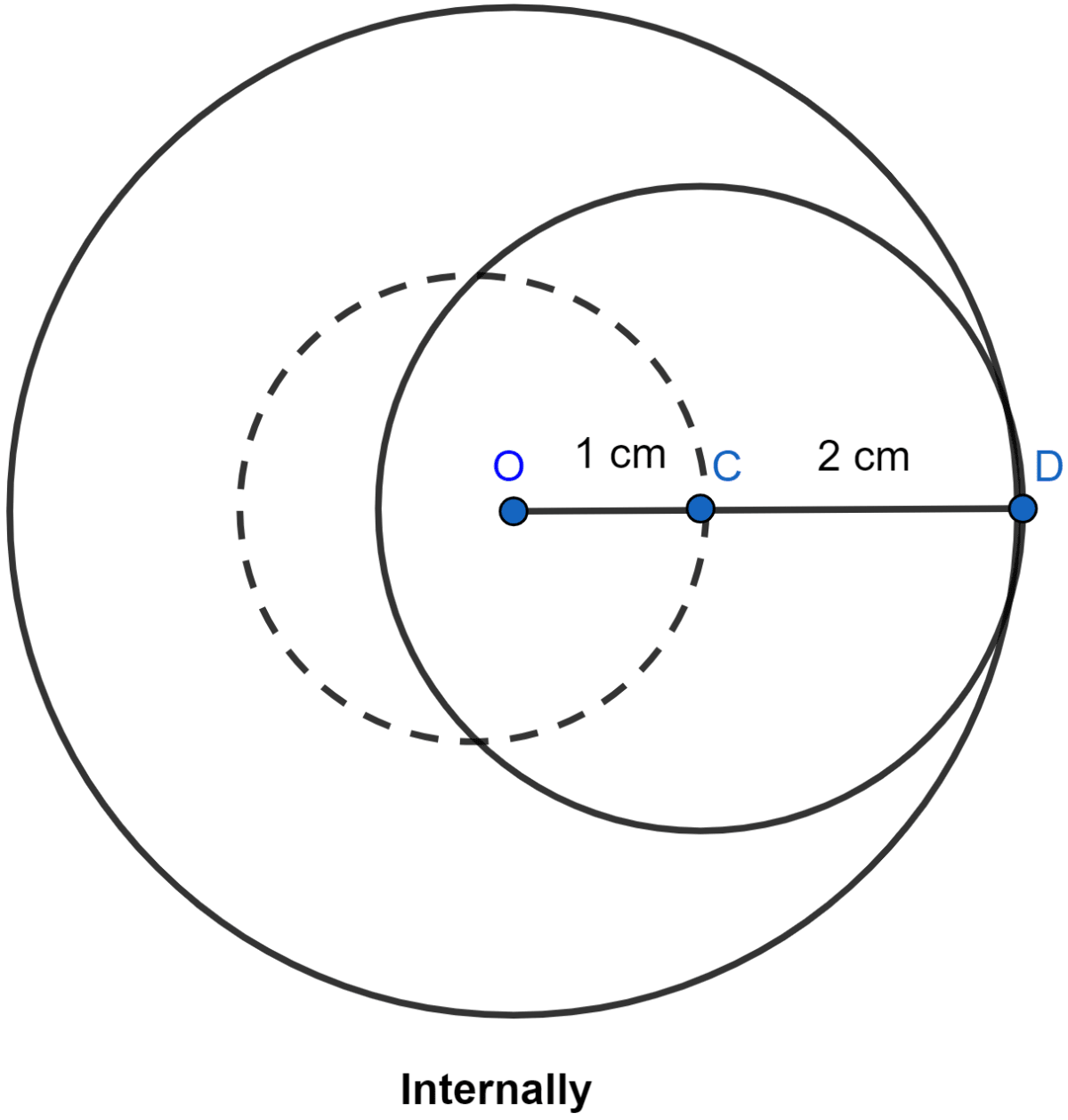
If the circle with 2 cm as radius touches the given circle with 3 cm as radius internally, then the locus of the centre of the circle will be a concentric circle with radius (3 - 2) = 1 cm.

Using ruler and compasses, construct

(i) a triangle ABC in which AB = 5.5 cm, BC = 3.4 cm and CA = 4.9 cm.

(ii) the locus of points equidistant from A and C.

Answer

(i) The figure below shows the constructed triangle ABC:

(ii) From figure we can see,

The locus of points A and C will be the perpendicular bisector of the line segment joining A and C.

Construct triangle ABC, with AB = 7 cm, BC = 8 cm and ∠ABC = 60°. Locate by construction the point P such that :

(i) P is equidistant from B and C and

(ii) P is equidistant from AB and BC.

(iii) Measure and record the length of PB.

Answer

Construct the △ABC with the given data:

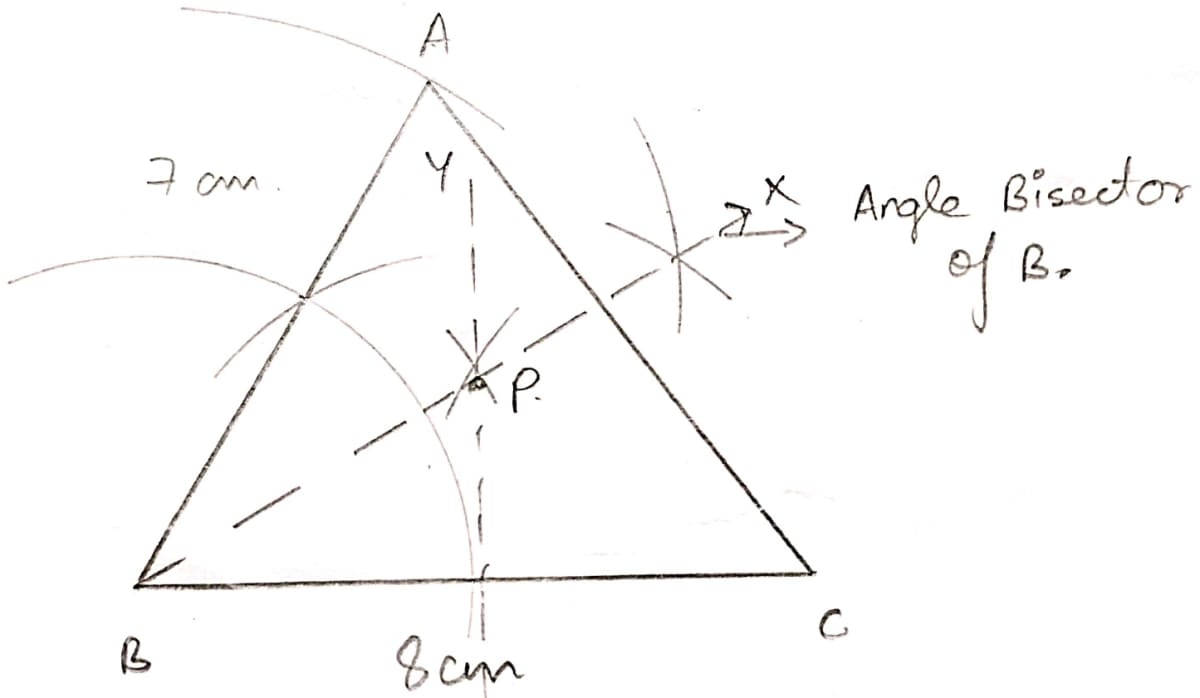
(i) Since, P is equidistant from B and C hence, it will be a point on the perpendicular bisector of BC i.e. YZ.

(ii) Since, P is also equidistant from AB and BC, so, it will be a point on angle bisector of B i.e. BX.

Hence, the intersection of BX and YZ is point P.

(iii) The length of PB is 4.6 cm.

A line segment AB is 8 cm long. Locate by construction the locus of a point which is :

(i) Equidistant from A and B.

(ii) Always 4 cm from the line AB.

(iii) Mark two points X and Y, which are 4 cm from AB and equidistant from A and B. Name the figure AXBY.

Answer

The figure is shown below:

(i) The locus of a point equidistant from A and B will be perpendicular bisector of AB.

(ii) Let the perpendicular bisector bisect AB at O. Cut an arc of 4 cm from O on CD (perpendicular bisector) on both sides. Mark these points as X and Y.

Hence, locus will be point on perpendicular bisector of AB at a distance of 4 cm on both sides.

(iii) Joining the points A, B, X and Y.

Hence, the figure formed ABXY is a square.

Use ruler and compasses only for this question.

(i) Construct △ABC, where AB = 3.5 cm, BC = 6 cm and ∠ABC = 60°.

(ii) Construct the locus of points inside the triangle which are equidistant from BA and BC.

(iii) Construct the locus of points inside the triangle which are equidistant from B and C.

(iv) Mark the point P which is equidistant from AB, BC and also equidistant from B and C. Measure and record the length of PB.

Answer

(i) The constructed triangle is shown below in the figure:

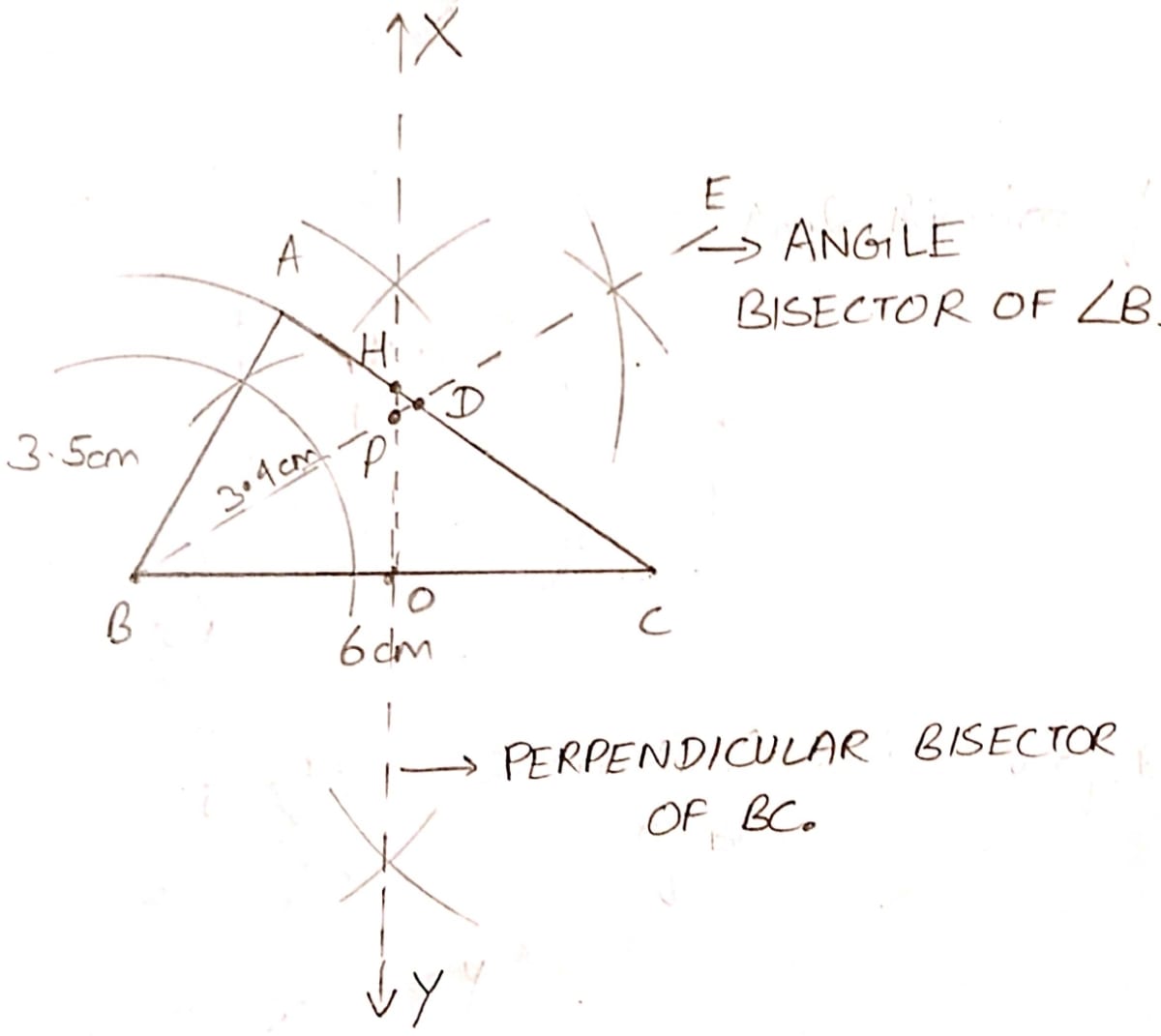
(ii) We know that locus of a point which is equidistant from two lines is the angle bisector between two lines.

From figure,

BE = angle bisector of B, which meets triangle at point D.

Hence, BD is the locus of points inside the triangle which are equidistant from BA and BC.

(iii) We know that locus of a point which is equidistant from two points is the perpendicular bisector joining two points.

From figure,

XY = perpendicular bisector of BC, which meets AC at point H and BC at point O.

Hence, OH is the locus of points inside the triangle which are equidistant from B and C.

(iv) From figure,

Point P is the intersection point of BE and XY. Hence, it is equidistant from AB, BC and also equidistant from B and C.

The length of PB = 3.4 cm.

Construct a triangle ABC with AB = 5.5 cm, AC = 6 cm and ∠BAC = 105°.

Hence,

(i) Construct the locus of points equidistant from BA and BC.

(ii) Construct the locus of points equidistant from B and C.

(iii) Mark the point which satisfies the above two loci as P. Measure and write the length of PC.

Answer

The figure is shown below:

(i) We know that the locus of points equidistant from two lines is equal to the perpendicular bisector of angle between the lines.

From figure,

The locus of points equidistant from BA and BC is angle bisector of ABC i.e. BX.

(ii) We know that the locus of points equidistant from two points is the perpendicular bisector of the line joining the two points

From figure,

The locus of points equidistant from B and C is the perpendicular bisector of BC i.e. YZ.

(iii) From figure,

YZ and BX meet at point P.

Hence, P is the point which satisfies above two loci and PC = 5.1 cm.

Points A, B and C represent position of three towers such that AB = 60 m, BC = 73 m and CA = 52 m. Taking a scale of 10 m to 1 cm, make an accurate drawing of △ABC. Find by drawing, the location of a point which is equidistant from A, B and C, and its actual distance from any of the towers.

Answer

Construct the triangle ABC with given conditions.

Construct perpendicular bisectors of all the three sides of triangle.

From figure we see,

FG = Perpendicular bisector of AB.

DE = Perpendicular bisector of AC.

HI = Perpendicular bisector of BC.

These bisectors meet each other at point P. Hence, point P is at equal distance from point A,B and C.

By measuring BP = 37 m.

Hence, the distance of each tower is nearly 37 m.

Draw two intersecting lines to include an angle of 30°. Use ruler and compasses to locate points which are equidistant from these lines and also 2 cm away from their point of intersection. How many such point exist ?

Answer

Let two intersecting lines be AB and CD making angles of 30° and 150°. Let these lines intersect at O.

We know that locus of points equidistant from two lines is the angle bisector of angle between them.

From figure,

EF and GH are angular bisectors of AB and CD.

Construct a circle taking O as centre and radius as 2 cm. This circle meet the bisectors at four points P, Q, R and S.

Hence, there are 4 points that are equidistant from two intersecting lines and 2 cm away from their point of intersection.

Without using set square or protractor, construct the quadrilateral ABCD in which ∠BAD = 45°, AD = AB = 6 cm, BC = 3.6 cm and CD = 5 cm.

(i) Measure ∠BCD.

(ii) Locate the point P on BD which is equidistant from BC and CD.

Answer

Draw AB = 6 cm as base. Construct 90° from point A and bisect the angle and cut off AD = 6cm, such that ∠BAD = 45°.

From D cut an arc of 5 cm and from B cut an arc of 3.6 cm. C will be their point of intersection. Join the points forming quadrilateral ABCD.

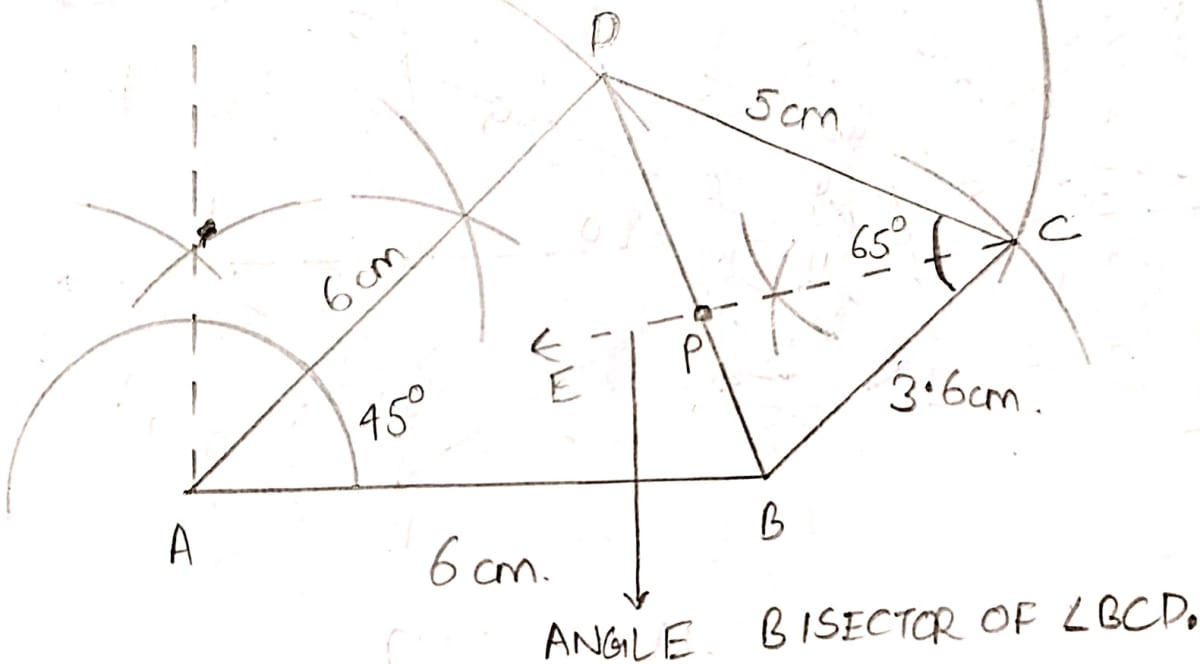
(i) Measuring angle BCD from the figure we get,

∠BCD = 65°.

(ii) We know that locus of points equidistant from two lines is the angle bisector of angle between them.

From the figure,

CE is the angular bisector of ∠BCD, hence it will be equidistant from CD and BC.

CE meets BD at point P as marked in the figure.

Without using set square or protractor, construct rhombus ABCD with sides of length 4 cm and diagonal AC of length 5 cm. Measure ∠ABC. Find the point R on AD such that RB = RC. Measure the length of AR.

Answer

Draw AB = 4 cm as base of rhombus. From A cut an arc of 5 cm and from B cut an arc of 4 cm. Take their point of intersection as point C. From C cut an arc of 4 cm and from A also, take their point of intersection as point D. Join the points to form rhombus ABCD, and AC to form diagonal.

On measuring ∠ABC, it is equal to 78°.

We want to find a point R such that, RB = RC.

We know that locus of point equidistant from two points is the perpendicular bisector of the line segment joining them.

From figure,

PQ is the perpendicular bisector of BC and meets AD at point R, such that AR = 1.2 cm.

Hence, ∠ABC = 78° and AR = 1.2 cm.

Without using set square or protractor construct :

(i) Triangle ABC, in which AB = 5.5 cm, BC = 3.2 cm and CA = 4.8 cm.

(ii) Draw the locus of a point which moves so that it is always 2.5 cm from B.

(iii) Draw the locus of a point which moves so that it is equidistant from the sides BC and CA.

(iv) Mark the point of intersection of the loci with the letter P and measure PC.

Answer

(i) Steps of Construction :

1. Draw BC = 3.2 cm as base.

2. From B cut an arc of of 5.5 cm and from C cut an arc of 4.8 cm. Take their intersection as point A.

3. Join the points to form triangle ABC.

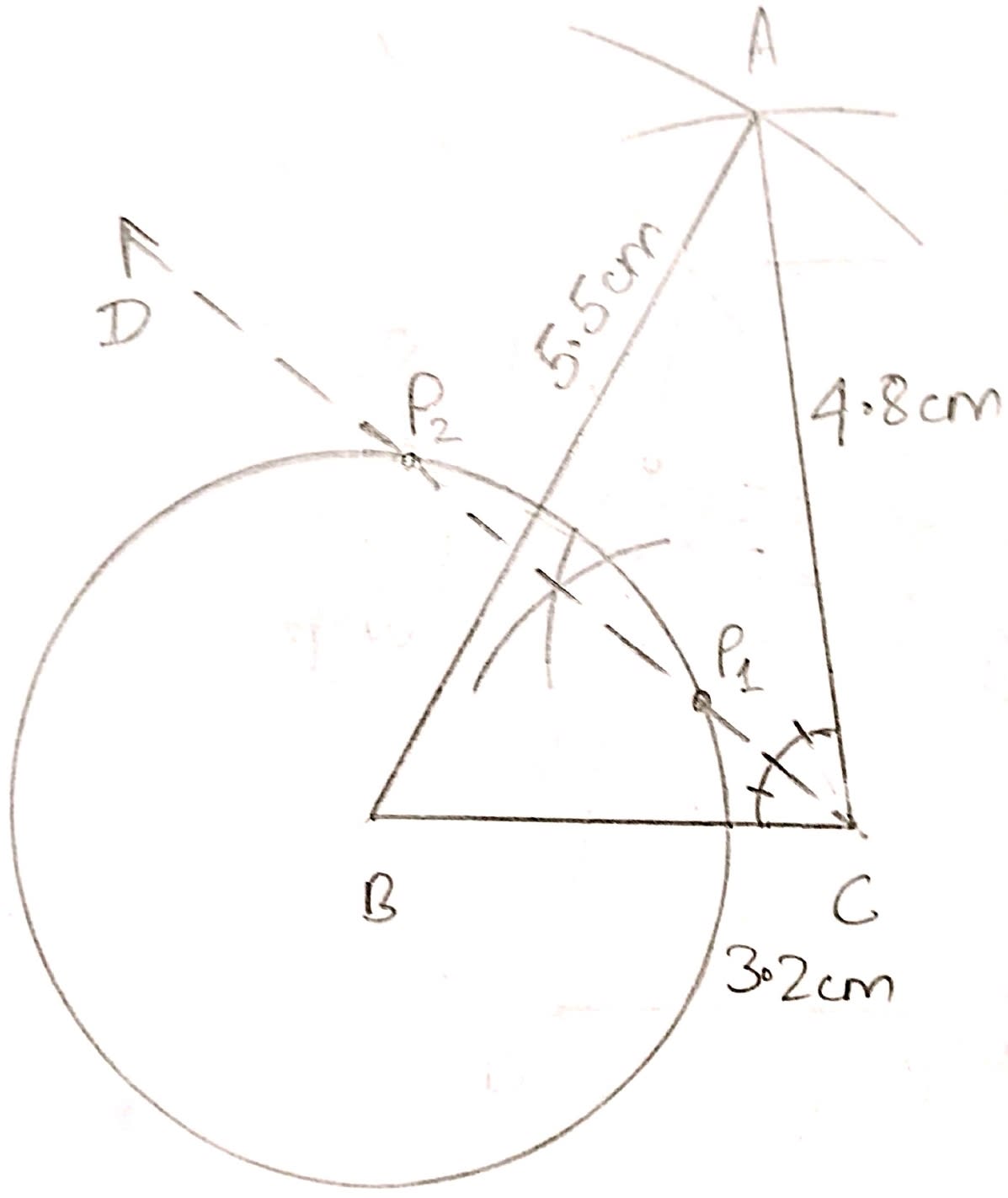
(ii) The locus of point that is always 2.5 cm from point B will be a circle with center as B and radius 2.5 cm.

(iii) We know that locus of points equidistant from two lines is the angle bisector of angle between them.

From figure,

CD is the angular bisectors of ACB, hence it will be equidistant from CA and BC.

(iv) There are two points P₁ and P₂ which intersect the circle.

On measuring we get,

P₁C = 1.1 cm and P₂C = 3.6 cm.

By using ruler and compasses only, construct an isosceles triangle ABC in which BC = 5 cm, AB = AC and ∠BAC = 90°. Locate the point P such that

(i) P is equidistant from the sides BC and AC.

(ii) P is equidistant from the points B and C.

Answer

Steps of construction :

1. Make BC = 5 cm as base.

2. Create a semicircle with BC as diameter.

3. Make right bisector of BC and mark it as D.

4. Make angle bisector of ∠ACB. From graph, CE is the abgle bisector.

5. Mark point P where angle bisector ∠ACB i.e CE meets perpendicular bisector of BC i.e. AD.

6. Draw perpendicular from point P and it meets semicircle at point A.

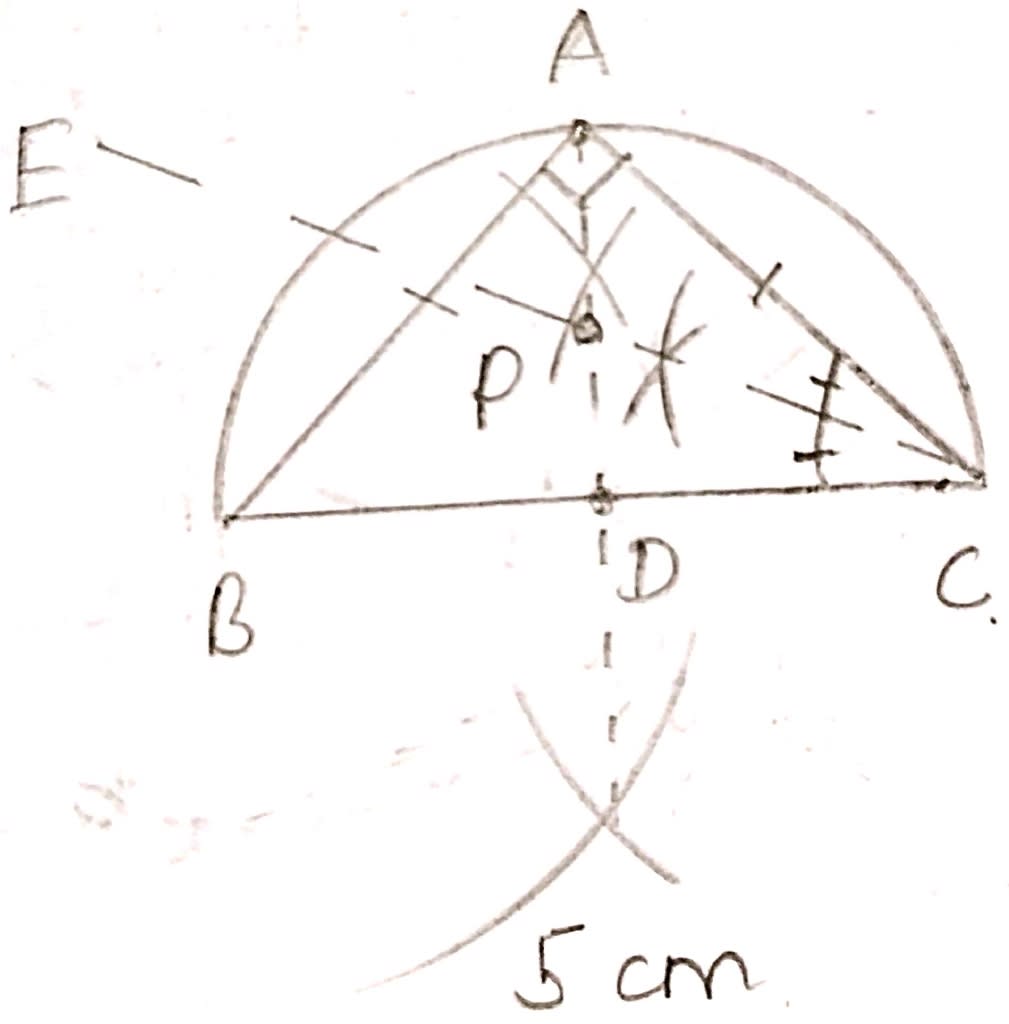
(i) We know that locus of points equidistant from two lines is the angle bisector of angle between them.

From figure,

CE is the angular bisector of ∠ACB, hence it will be equidistant from AC and BC.

(ii) We know that locus of points equidistant from two points is the perpendicular bisector of line segment joining them.

From figure,

AD is the perpendicular bisector of BC, hence it will be equidistant from B and C.

Both AD and CE meet at point P, so P is equidistant from BC and CA and also from B and C.

Using ruler and compass only, construct a semicircle with diameter BC = 7 cm. Locate a point P on the circumference of the semicircle such that A is equidistant from B and C. Completely the cyclic quadrilateral ABCD such that D is equidistant from AB and BC. Measure ∠ADC and write it down.

Answer

Steps of construction :

1. Draw a line segment BC = 7 cm.

2. Create a semicircle with BC as diameter.

3. Make right bisector of BC and construct perpendicular from it such that it meets the semicircle at A as shown in figure.

4. Construct angle bisector of ∠ABC, and let it meet the semicircle at point D.

5. Join the points to form quadrilateral ABCD.

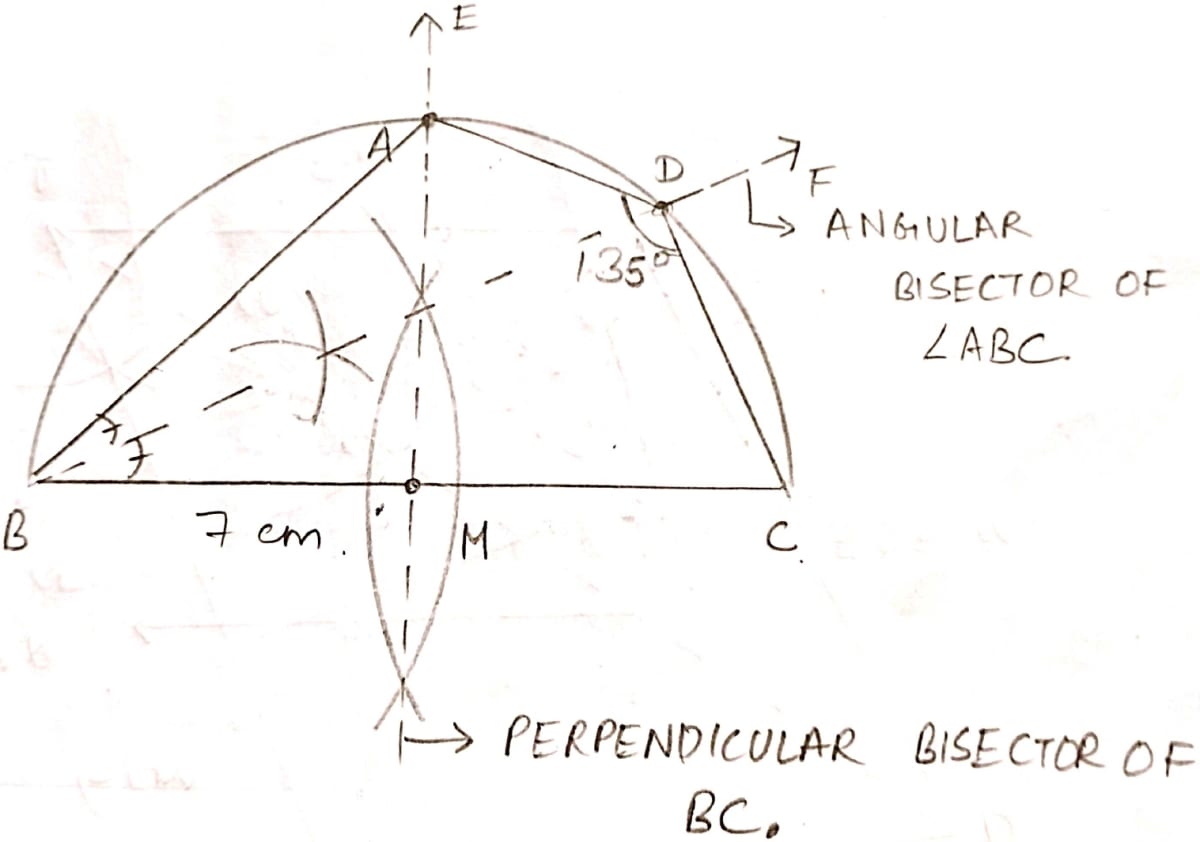
On, measuring we get ∠ADC = 135°.

Using ruler and compasses only, construct a quadrilateral ABCD in which AB = 6 cm, BC = 5 cm, ∠B = 60°, AD = 5 cm and D is equidistant from AB and BC. Measure CD.

Answer

Steps of construction :

1. Draw BC = 5 cm as base.

2. Make angle 60° at B.

3. Cut off an arc of 6 cm from B at the angle and mark it A as in figure.

4. Since, D is equidistant from AB and BC hence, it will lie on angle bisector of ∠ABC.

5. Make an arc of 5 cm from point A take point D where the arc cuts angle bisector BE.

6. Join, the points A, B, C and D to form quadrilateral ABCD.

On measuring we get, CD = 5.25 approximately.

Construct an isosceles triangle ABC such that AB = 6 cm, BC = AC = 4 cm. Bisect ∠C internally and mark a point P on this bisector such that CP = 5 cm. Find the points Q and R which are 5 cm from P and also 5 cm from the line AB.

Answer

Steps of construction :

1. Draw AB = 6 cm as base.

2. Make an arc of 4 cm from A and B. Take the point of intersection as C.

3. Join the points A, B and C to form △.

4. Make the angle bisector of C as in the figure.

5. Cut an arc from CZ of 5 cm and mark point P such that CP = 5 cm.

6. Make a line XY parallel to AB at a distance of 5 cm.

7. From point P make an arc of 5 cm cutting XY at Q and R.

Use ruler and compasses only for this question. Draw a circle of radius 4 cm and mark two chords AB and AC of the circle of length 6 cm and 5 cm respectively.

(i) Construct the locus of points, inside the circle, that are equidistant from A and C. Prove your construction.

(ii) Construct the locus of points, inside the circle, that are equidistant from AB and AC.

Answer

Steps of construction :

1. Construct a circle with center as O and radius 4 cm.

2. Take a point A on the circle. From A make arcs of radius 6 cm and 5 cm and where they intersect the circle mark those points as B and C respectively.

(i) We know that locus of points that are equidistant from two points is the perpendicular bisector of line segment joining those points.

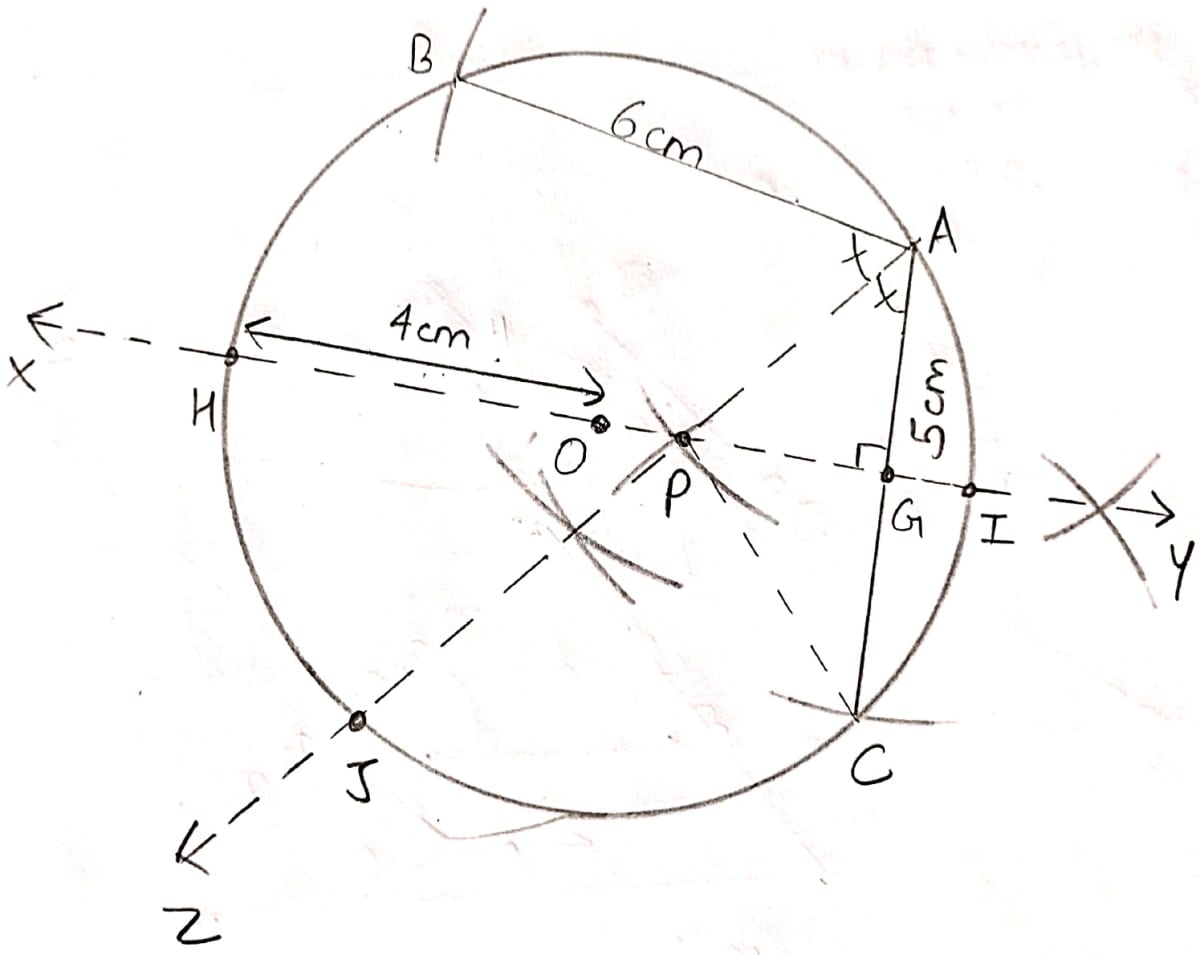
So from figure,

IH is the locus of points inside the circle, that are equidistant from A and C.

Hence, the locus is the diameter of the circle which is perpendicular to the chord AC.

Proof:

Consider △GPA and △GPC.

∠PGC = ∠PGA (Both are equal to 90°)

PG = PG (Common side)

CG = AG (They are equal as GH bisects AC).

Hence, by SAS axiom △GPA ~ △GPC.

Since triangles are similar, hence the ratio of their corresponding sides are equal.

$\therefore \dfrac{AP}{PG} = \dfrac{PC}{PG} \\[1em] \Rightarrow AP = \dfrac{PC}{PG} \times PG \\[1em] \Rightarrow AP = PC.$

Hence, proved that AP = PC.

(ii) We know that locus of points that are equidistant from two lines is the angular bisector of the lines.

So, from figure,

AZ is the angular bisector of angle between AB and AC.

Hence, locus is the chord of the circle bisecting ∠BAC.

Ruler and compasses only may be used in this question. All construction lines and arcs must be clearly shown, and be of sufficient length and clarity to permit the assessment.

(i) Construct a triangle ABC, in which BC = 6 cm, AB = 9 cm, and ∠ABC = 60°.

(ii) Construct the locus of all points, inside △ABC, which are equidistant from B and C.

(iii) Construct the locus of the vertices of the triangles with BC as base, which are equal in area to △ABC.

(iv) Mark the point Q, in your construction, which would make △QBC equal in area to △ABC, and isosceles.

(v) Measure and record the length of CQ.

Answer

(i) Steps of construction :

1. Draw BC = 6 cm as base.

2. Construct ∠ABC = 60° and make an arc from B such as AB = 9 cm.

3. Join points A, B and C such that ABC forms a triangle.

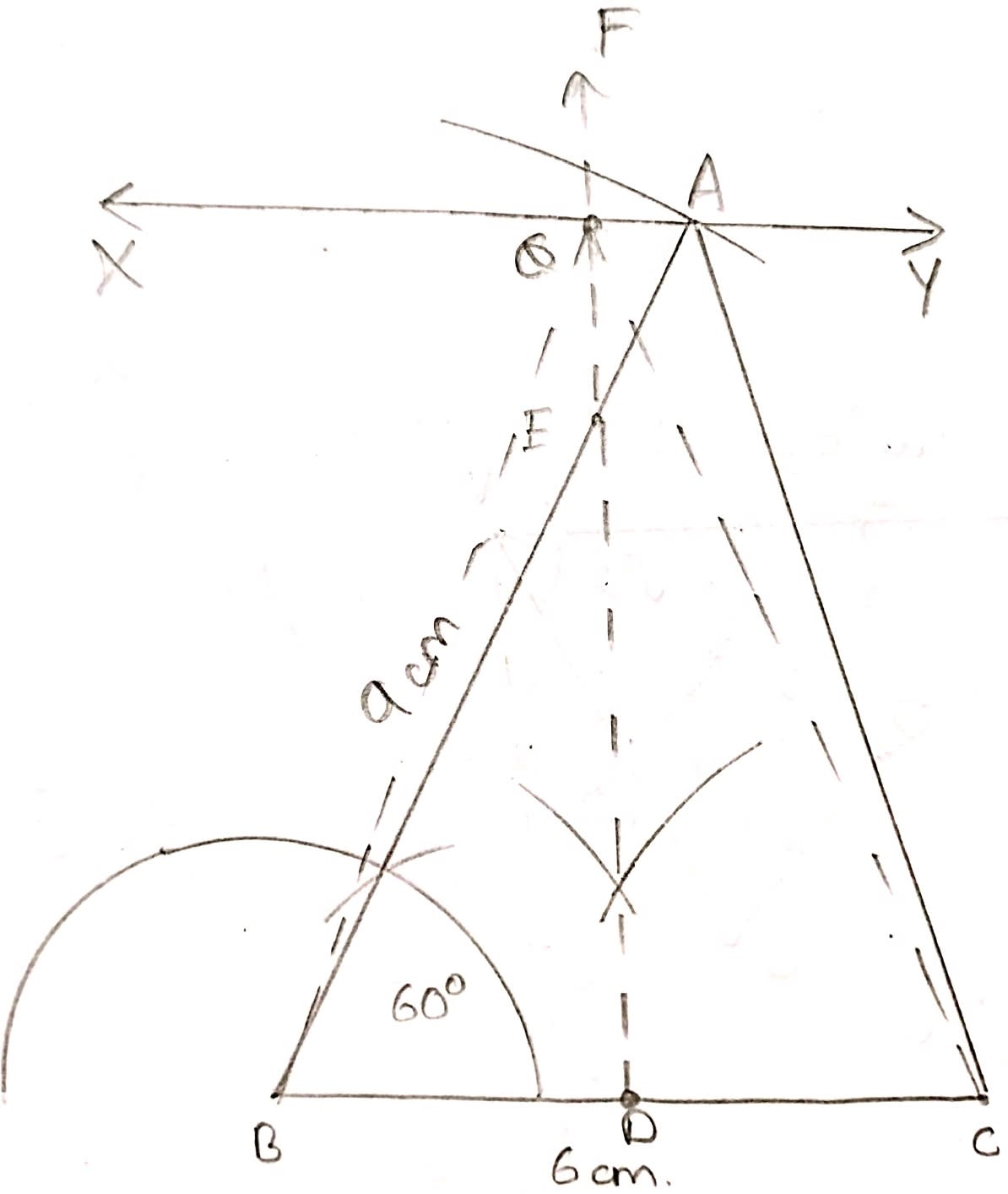
(ii) We know that locus of points equidistant from two points is the perpendicular bisector of the line segment joining two points.

From figure,

Right bisector of BC (i.e. DE in figure) inside △ABC.

(iii) The locus of the vertices of the triangles with BC as base, which are equal in area to △ABC is a straight line through A and parallel to BC, the area will be same as triangles will be on same base and between same parallel lines.

(iv) Q is the point of intersection of right bisector of BC and the straight line through A parallel to BC.

(v) On measuring,

CQ = 8.2 cm approximately.

Draw a straight line AB of length 8cm. Draw the locus of all points which are equidistant from A and B. Prove your statement.

Answer

We know that locus of point equidistant from two points is the perpendicular bisector of the line segment joining them.

From figure,

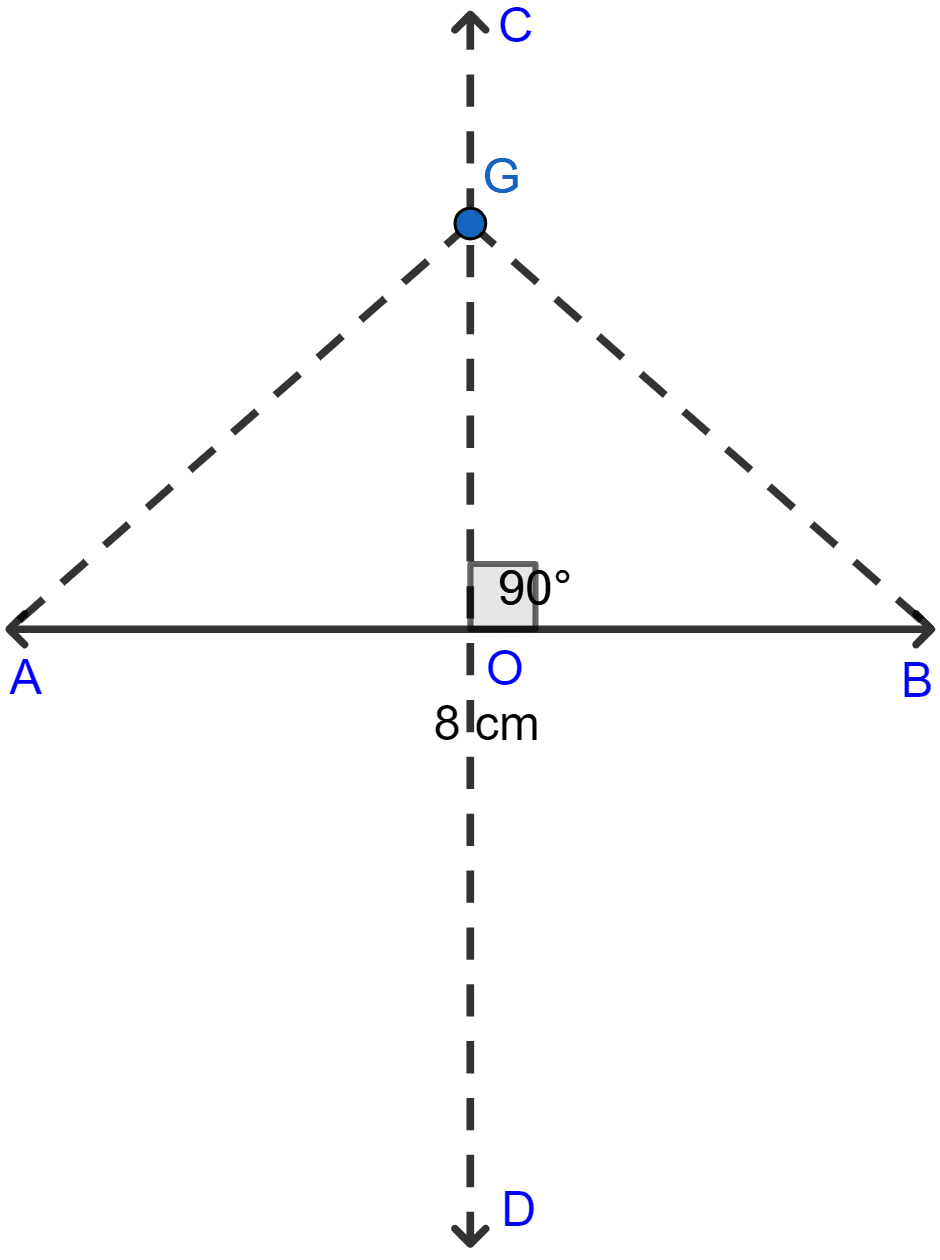
CD is the locus of all points which are equidistant from A and B.

Proof :

Consider △GOA and △GOB.

∠GOA = ∠GOB (Both are equal to 90°)

OG = OG (Common side)

AO = OB (They are equal as CD bisects AB at O).

Hence, by SAS axiom △GOA ~ △GOB.

Since triangles are similar, hence the ratio of their corresponding sides are equal.

$\therefore \dfrac{AG}{OG} = \dfrac{BG}{OG} \\[1em] \Rightarrow AG = \dfrac{BC}{OG} \times OG \\[1em] \Rightarrow AG = BG.$

Hence, proved that AG = BG. Thus proved that any point on CD is equidistant from A and B.

A point P is allowed to travel in space. State the locus of P so that it always remains at a constant distance from a fixed point C.

Answer

Since, the point P is allowed to travel in space hence, the point can be any dimension.

Hence, the locus will be a sphere with C as center and constant distance as radius.

Draw a line segment AB of length 7 cm. Construct the locus of a point P such that area of triangle PAB is 14 cm².

Answer

Let the height of triangle PAB = h cm.

So, area of triangle = $\dfrac{1}{2}$ × base × height

$\Rightarrow 14 = \dfrac{1}{2} \times 7 \times h \\[1em] \Rightarrow \dfrac{14 \times 2}{7} = h \\[1em] \Rightarrow h = \dfrac{28}{7} \\[1em] \Rightarrow h = 4 \text{cm}$

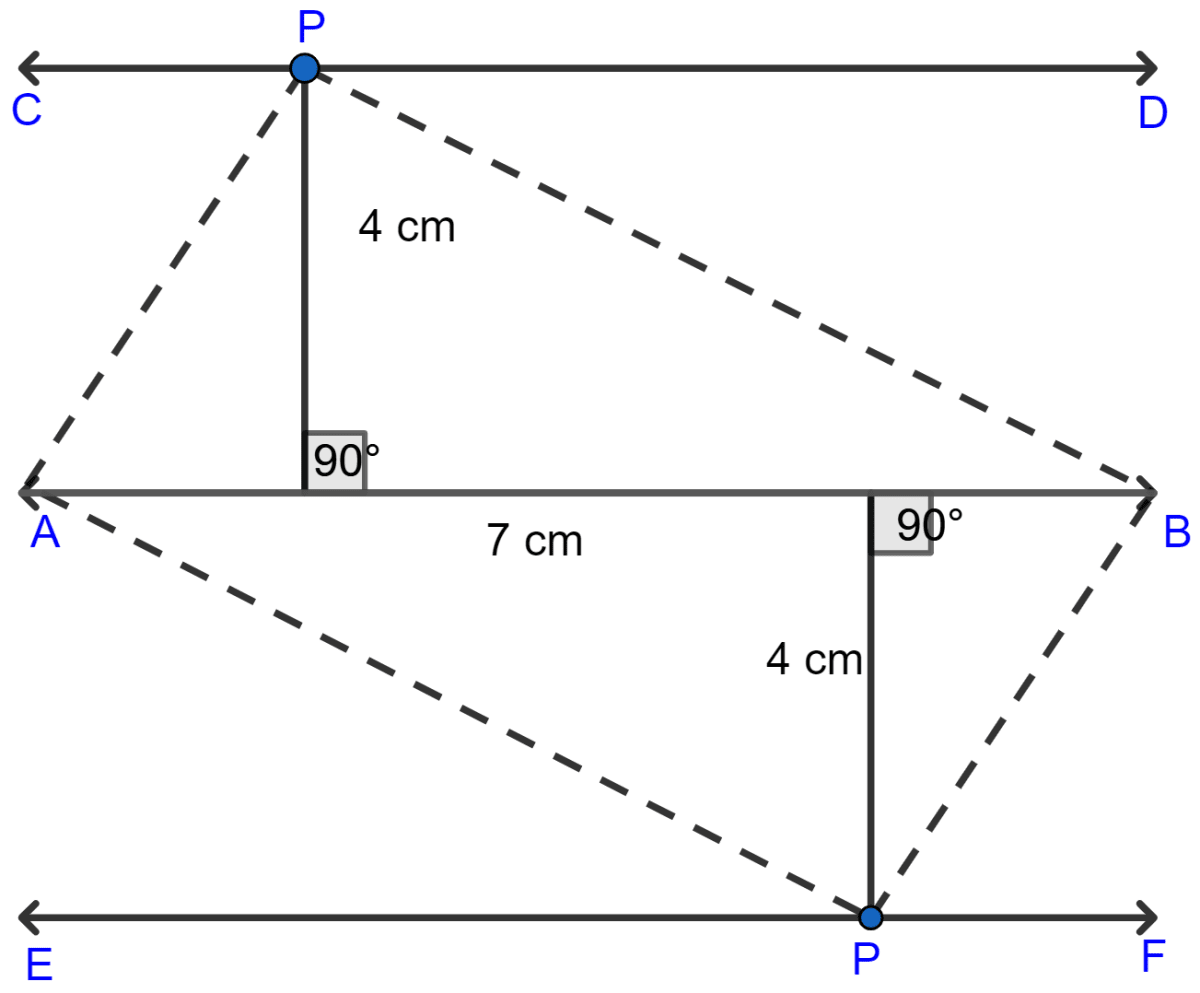
Hence, the locus of point P will be a pair of straight lines (CD and EF in figure) at a distance of 4 cm from AB.

Draw a line segment AB of length 12 cm. Mark M, the mid-point of AB. Draw and describe the locus of a point which is

(i) at a distance of 3 cm from AB.

(ii) at a distance of 5 cm from the point M.

Mark the points P, Q, R, S which satisfy both the above conditions. What kind of quadrilateral is PQRS ? Compute the area of quadrilateral PQRS.

Answer

The figure is shown below:

(i) Draw the line segment CD and EF parallel to AB, at a distance of 3 cm from it.

Hence, the locus is a pair of straight lines at a distance of 3 cm from AB.

(ii) Mark M as the mid-point of AB. Take M as center and radius 5 cm draw a circle.

Hence, the locus is a circle with center M and radius 5 cm.

(iii) The circle meets the segments CD and EF at P, Q, R and S.

P, Q, R and S are joined to form a rectangle.

Area of rectangle = Length × Breadth = PQ × PR.

On measuring PQ = 8cm.

So, Area = 8 × 6 = 48 cm².

Hence, PQRS is a square and area is 48 cm².

AB and CD are two intersecting lines. Find the position of a point which is at a distance of 2 cm from AB and 1.6 cm from CD.

Answer

As shown in figure,

1. Draw EF at a distance of 2 cm and parallel to AB.

2. Draw GH at a distance of 1.6 cm and parallel to CD.

The point M is the point of intersection of EF and GH.

Hence, point M is the position of point which is at a distance of 2cm from AB and 1.6 cm from CD.

Two straight roads PQ and PK cross each other at P at an angle of 75°. S is a stone on the road PQ, 800 m from P towards Q. By drawing a figure to scale 1 cm = 100m, locate the position of a flag staff X, which is equidistant from P and S, and is also equidistant from the roads.

Answer

Scale given 1 cm = 100m so, 800m = 8 cm.

Two roads PK and PQ are drawn with an angle of 75°.

We know that locus of point equidistant from two lines is the angle bisector between them.

From figure we see that,

PR is the angle bisector of ∠KPQ.

We know that locus of point equidistant from two points is the perpendicular bisector of line segment joining the points.

From figure we see that,

AB is the perpendicular bisector of PS.

AB and PR intersects at X.

Hence, point X is equidistant from P and S also from roads PK and PQ.

Construct a rhombus PQRS whose diagonals PR, QS are 8 cm and 6 cm respectively. Find by construction a point X equidistant from PQ, PS and equidistant from R, S. Measure XR.

Answer

Steps of construction :

1. Draw QS = 6 cm and PR = 8 cm as diagonals. Join the points to form rhombus PQRS.

2. Since, diagonals of rhombus bisects vertices, hence, PR is angular bisector of SPQ.

3. Draw CD, the perpendicular bisector of RS.

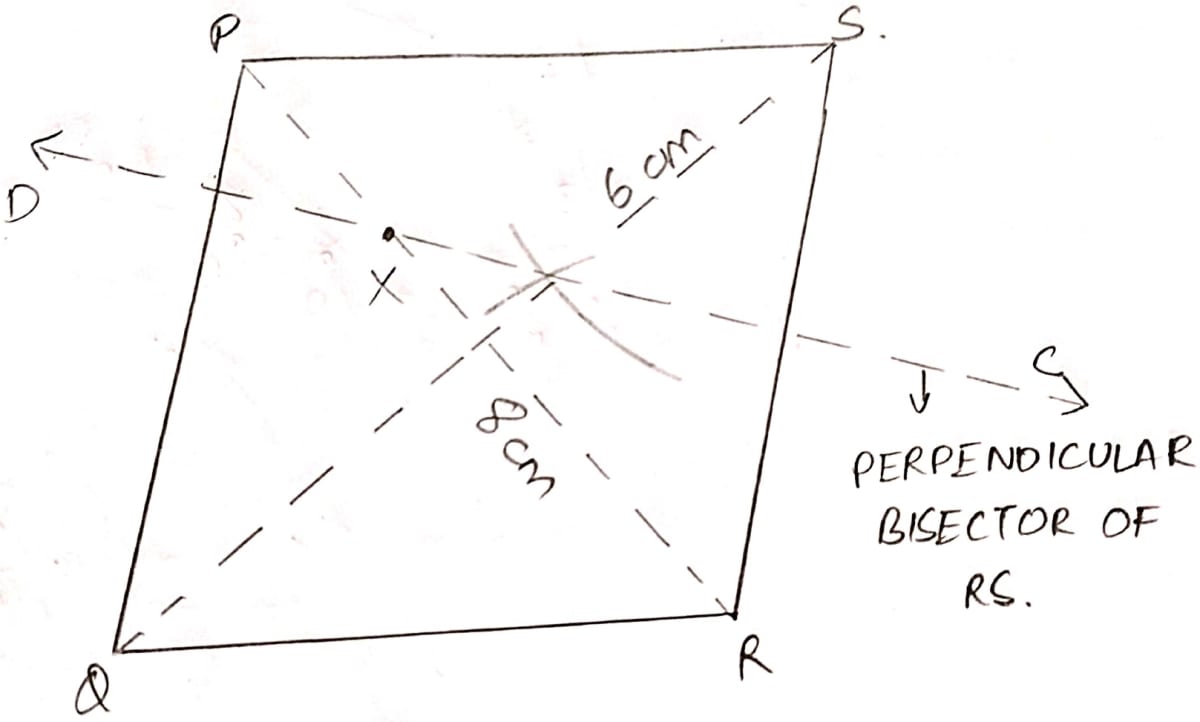
The intersection of CD and PR is the point X which satisfies both i.e. it is equidistant from PQ, PS and R and S also.

On measuring we get, XR = 3.15 cm.

Without using set square or protractor, construct the parallelogram ABCD in which AB = 5.1 cm, the diagonal AC = 5.6 cm and the diagonal BD = 7 cm. Locate the point P on DC, which is equidistant from AB and BC.

Answer

Steps of construction :

1. Draw AB = 5.1 cm as base.

2. At A, with radius 2.8 cm and at B with radius 3.5 cm draw two arcs intersecting each other at O.

3. Join AO and produce it till C such that OC = AO = 2.8 cm and join BO and produce it till D such that OD = BO = 3.5 cm.

4. Join A, B, C and D forming parallelogram ABCD.

We know that locus of point equidistant from two lines is the angle bisector of the two lines.

From figure,

BE is the angle bisector of ∠ABC which meets DC at P.

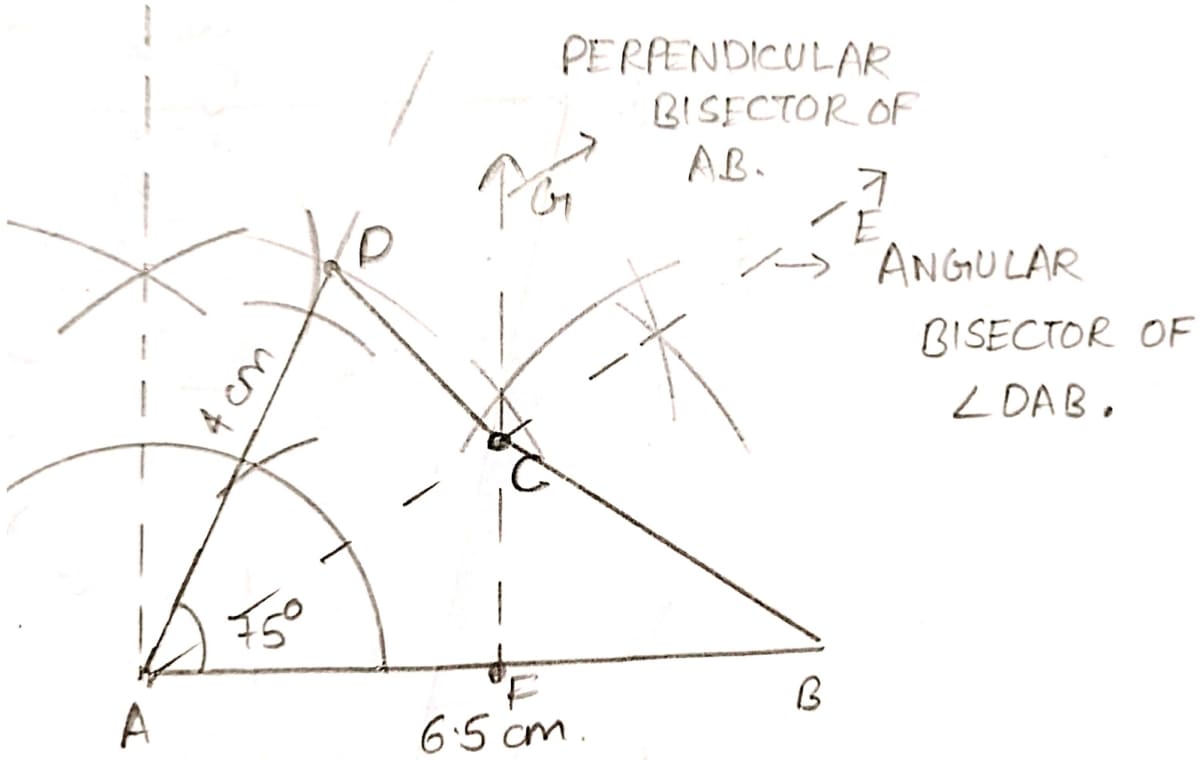
By using ruler and compasses only, construct a quadrilateral ABCD in which AB = 6.5 cm, AD = 4 cm and ∠DAB = 75°. C is equidistant from the sides AB and AD, also C is equidistant from the points A and B.

Answer

Steps of construction :

1. Draw AB = 6.5 cm as base.

2. At A, construct angle ∠DAB = 75° and cut an arc from A on it and mark point D such that AD = 4 cm.

3. Since, C is equidistant from the sides AB and AD, also C is equidistant from the points A and B hence it will be the intersection point of perpendicular bisector of AB i.e. FG and angle bisector of ∠DAB i.e. AE.

4. Join A, B, C and D forming quadrilateral ABCD.

Use ruler and compass to answer this question. Construct ∠ABC = 90°, where AB = 6 cm, BC = 8 cm.

(a) Construct the locus of points equidistant from B and C.

(b) Construct the locus of points equidistant from A and B.

(c) Mark the point which satisfies both the conditions (a) and (b) as O. Construct the locus of points keeping a fixed distance OA from the fixed point O.

(d) Construct the locus of points which are equidistant from BA and BC.

Answer

Steps of construction :

1. Draw a line segment BC = 8 cm

2. Construct ∠ABC = 90°, such that AB = 6 cm.

3. Draw XY, the perpendicular bisector of BC.

4. Draw PQ, the perpendicular bisector of AB.

5. Mark point O, the intersection of segment XY and PQ.

6. Draw BZ, the angle bisector of AB and BC.

We know that,

Locus of points equidistant from two points is the perpendicular bisector of the line joining the two points segment.

(a) Locus of points equidistant from B and C is XY.

(b) Locus of points equidistant from A and B is PQ.

We know that,

Locus of points equidistant from two sides is the angular bisector of angle between them.

(d) Locus of points which are equidistant from BA and BC is BZ.