Angle & Cyclic Properties of a Circle

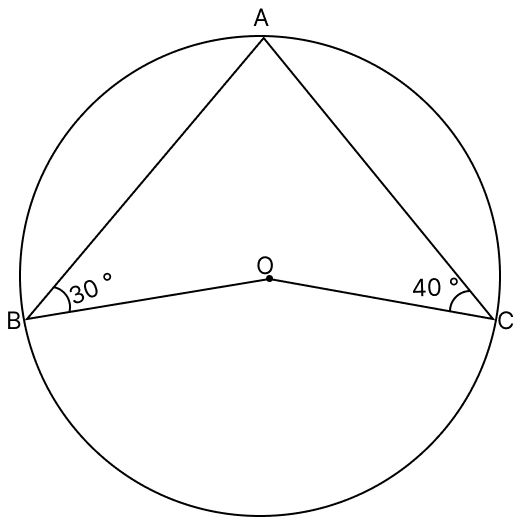
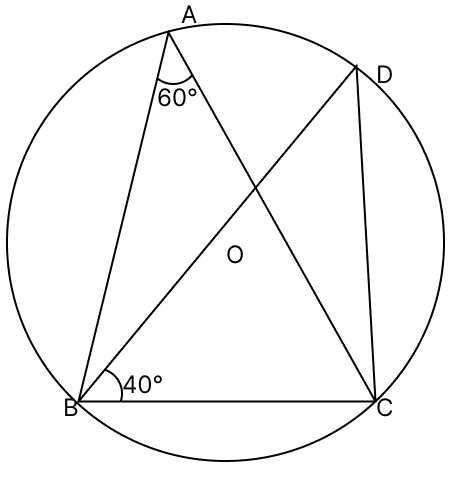
In the given figure, O is the centre of a circle, ∠OAB = 30° and ∠OCB = 40°. Calculate ∠AOC.

Answer

Join AC.

As, OA = OC = radius of circle.

Let ∠OAC = ∠OCA = x (As angles opposite to equal sides are equal)

We know that,

Sum of angles of triangle = 180°

∴ ∠OAC + ∠OCA + ∠AOC = 180°

⇒ x + x + ∠AOC = 180°

⇒ ∠AOC = 180° - 2x

From figure,

⇒ ∠BAC = ∠BAO + OAC = 30° + x

⇒ ∠BCA = ∠BCO + OCA = 40° + x

Now, in ∆ABC

⇒ ∠ABC = 180° - ∠BAC - ∠BCA [Angle sum property of a triangle]

= 180° - (30° + x) - (40° + x)

= 180° - 30° - x - 40° - x

= 180° - 70° - 2x

= 110° - 2x.

We know that,

Angle which an arc subtends at the center is double that which it subtends at any point on the remaining part of the circumference.

∴ ∠AOC = 2∠ABC

⇒ 180° - 2x = 2(110° - 2x)

⇒ 180° - 2x = 220° - 4x

⇒ -2x + 4x = 220° - 180°

⇒ 2x = 40°

⇒ x = 20°.

Thus, ∠AOC = 180° - 2x = 180° - 2(20°)

= 180° - 40° = 140°.

Hence, ∠AOC = 140°.

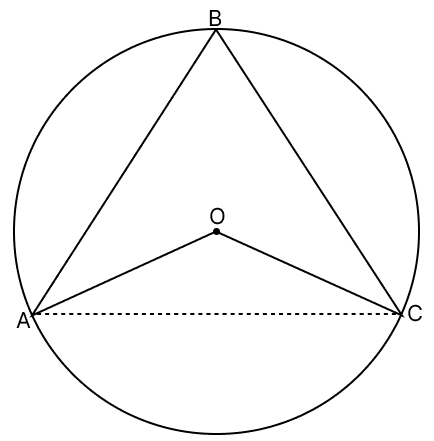
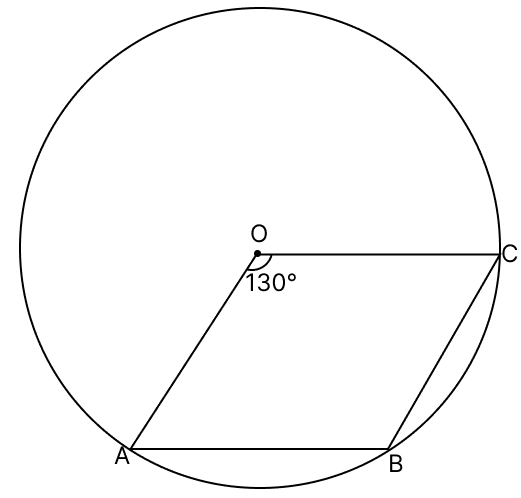
In the given figure, O is the centre of the circle and ∠AOC = 130°. Find ∠ABC.

Answer

From figure,

⇒ ∠AOC + Reflex ∠AOC = 360°

⇒ 130° + Reflex ∠AOC = 360°

⇒ Reflex ∠AOC = 360° - 130°

⇒ Reflex ∠AOC = 230°.

Arc AC subtends Reflex ∠AOC at center and ∠ABC at another point of circle.

⇒ Reflex ∠AOC = 2 ∠ABC

⇒ 2∠ABC = 230°

⇒ ∠ABC = $\dfrac{230^{\circ}}{2}$

⇒ ∠ABC = 115°.

Hence, the value of ∠ABC = 115°.

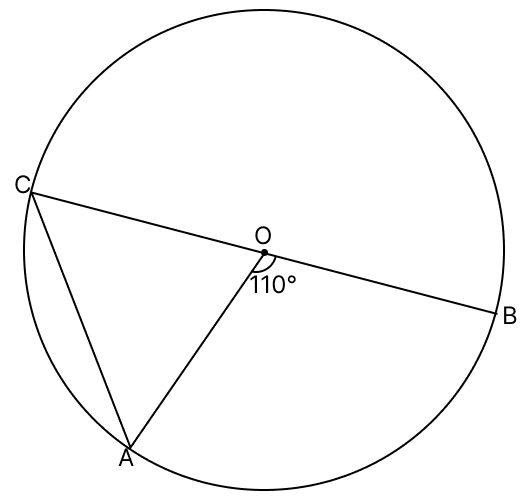
In the given figure, O is the centre of the circle and ∠AOB = 110°. Calculate:

(i) ∠ACO

(ii) ∠CAO.

Answer

(i) We know that,

Angle which an arc subtends at the center is double that which it subtends at any point on the remaining part of the circumference.

⇒ ∠AOB = 2∠ACO

⇒ 110° = 2∠ACO

⇒ ∠ACO = $\dfrac{110^{\circ}}{2}$

⇒ ∠ACO = 55°

Hence, ∠ACO = 55°.

(ii) From figure,

⇒ ∠COA + ∠AOB = 180° [Linear pair]

⇒ ∠COA + 110° = 180°

⇒ ∠COA = 180° - 110°

⇒ ∠COA = 70°

The sum of the three interior angles of any triangle is always 180°.

In ΔABC,

⇒ ∠COA + ∠ACO + ∠CAO = 180°

⇒ 70° + 55° + ∠CAO = 180°

⇒ 125° + ∠CAO = 180°

⇒ ∠CAO = 180° - 125°

⇒ ∠CAO = 55°.

Hence, ∠CAO = 55°.

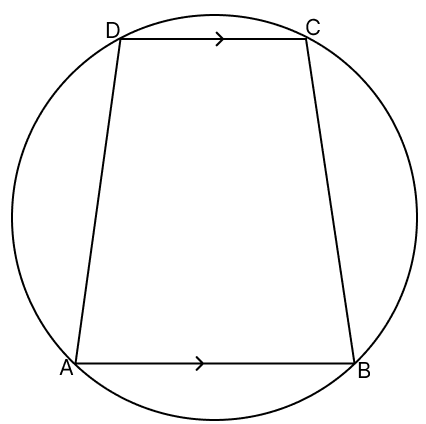
In the given figure, AB ∥ DC and ∠BAD = 100°. Calculate :

(i) ∠BCD

(ii) ∠ADC

(iii) ∠ABC.

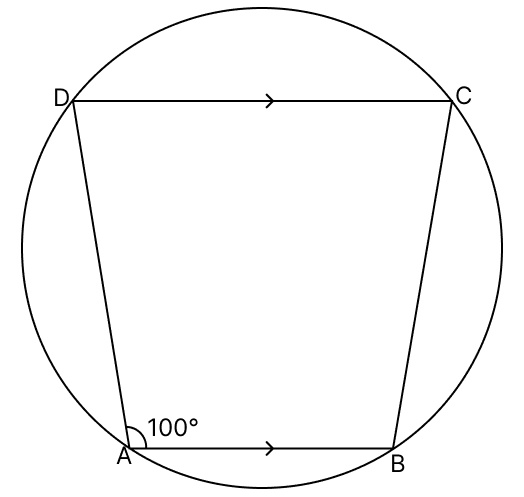
Answer

(i) We know that:

Sum of opposite angles of a cyclic quadrilateral is 180°.

⇒ ∠BAD + ∠BCD = 180°

⇒ ∠BCD = 180° - 100°

⇒ ∠BCD = 80°.

Hence, ∠BCD = 80°.

(ii) Since AB ∥ DC, the angles ∠BAD and ∠ADC are consecutive interior angles along the transversal AD.

Therefore,

⇒ ∠BAD + ∠ADC = 180°

⇒ 100° + ∠ADC = 180°

⇒ ∠ADC = 180° - 100°

⇒ ∠ADC = 80°.

Hence, ∠ADC = 80°.

(iii) We know that:

Sum of opposite angles of a cyclic quadrilateral is 180°.

⇒ ∠ABC + ∠ADC = 180°

⇒ ∠ABC + 80° = 180°

⇒ ∠ABC = 180° - 80°

⇒ ∠ABC = 100°.

Hence, ∠ABC = 100°.

In the given figure, ∠ACB = 52° and= ∠BDC = 43°. Calculate

(i) ∠ADB

(ii) ∠BAC

(iii) ∠ABC.

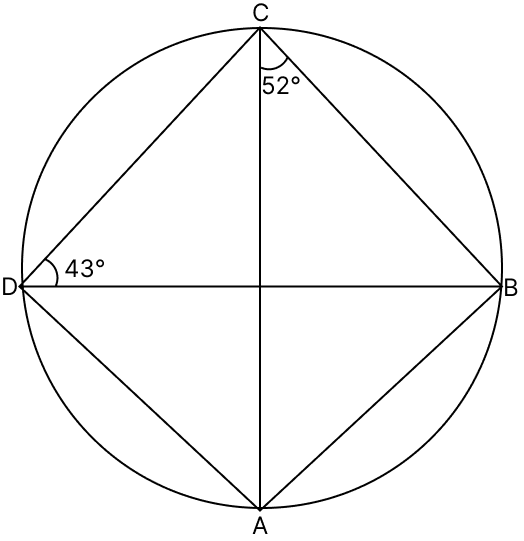
Answer

(i) From figure,

∠ADB = ∠ACB = 52° [Angles in the same segment are equal]

∠ADB = 52°.

Hence, ∠ADB = 52°.

(ii) From figure,

∠BAC = ∠BDC = 43° [Angles in the same segment are equal]

∠BAC = 43°.

Hence, ∠BAC = 43°.

(iii) We know that,

The sum of the three interior angles of any triangle is always 180°.

⇒ ∠BAC + ∠ABC + ∠ACB = 180°

⇒ 43° + ∠ABC + 52° = 180°

⇒ ∠ABC + 95° = 180°

⇒ ∠ABC = 180° - 95°

⇒ ∠ABC = 85°.

Hence, ∠ABC = 85°.

In the given figure, O is the centre of the circle. If ∠AOB = 140° and ∠OAC = 50°, find :

(i) ∠ABC

(ii) ∠BCO

(iii) ∠OAB

(iv) ∠BCA

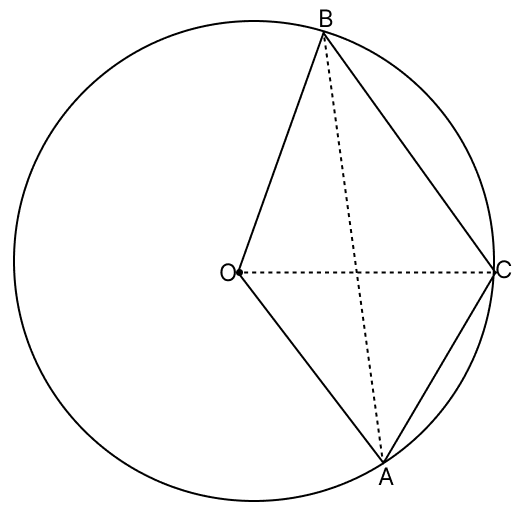
Answer

(i) From figure,

OA = OC [Radius of same circle]

In Δ AOC,

∠OCA = ∠OAC = 50° (As angles opposite to equal sides in a triangle are equal)

We know that,

The sum of the three interior angles of any triangle is always 180°.

∠AOC + ∠OCA + ∠OAC = 180°

∠AOC + 50° + 50° = 180°

∠AOC = 180° − 50° − 50° = 80°.

We know that,

Angle at the center is double the angle at the circumference subtended by the same chord.

∠ABC = $\dfrac{1}{2}$ ∠AOC

∠ABC = $\dfrac{1}{2}$ 80°

∠ABC = 40°.

Hence, ∠ABC = 40°.

(ii) From figure,

∠BOC = ∠AOB − ∠AOC = 140° − 80° = 60°.

OB = OC (Radius of same circle)

Let ∠OBC = ∠OCB = x (As angles opposite to equal sides are equal)

We know that,

The sum of the three interior angles of any triangle is always 180°.

⇒ ∠OBC + ∠OCB + ∠BOC = 180°

⇒ x + x + 60° = 180°

⇒ 2x = 180° - 60°

⇒ 2x = 120°

⇒ x = $\dfrac{120^{\circ}}{2}$

⇒ x = 60°.

Hence, ∠BCO = 60°.

(iii) In ∆AOB, we have

OA = OB (radius of same circle)

So, ∠OBA = ∠OAB (As angles opposite to equal sides are equal)

By angle sum property of a triangle we get,

⇒ ∠OBA + ∠OAB + ∠AOB = 180°

⇒ 2∠OAB + 140° = 180°

⇒ 2∠OAB = 40°

⇒ ∠OAB = $\dfrac{40^{\circ}}{2}$

⇒ ∠OAB = 20°.

Hence, ∠OAB = 20°.

(iv) We know that,

⇒ ∠BCO = 60°

⇒ ∠OCA = 50°

From figure,

⇒ ∠BCA = ∠BCO + ∠OCA

⇒ ∠BCA = 60° + 50°

⇒ ∠BCA = 110°.

Hence, ∠BCA = 110°.

In the given figure, ∠BAD = 70°, ∠ABD = 50° and ∠ADC = 80°. Calculate :

(i) ∠BDC

(ii) ∠BCD

(iii) ∠BCA.

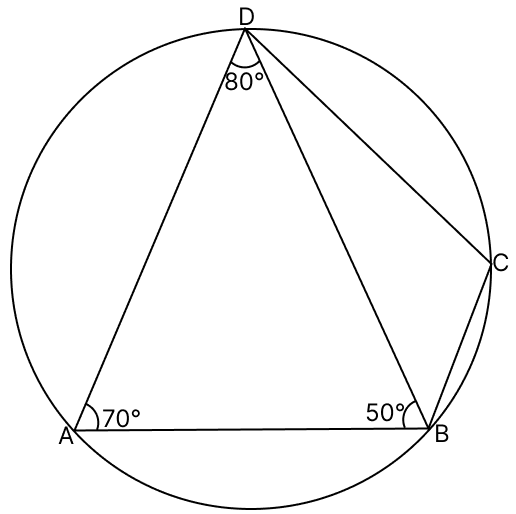
Answer

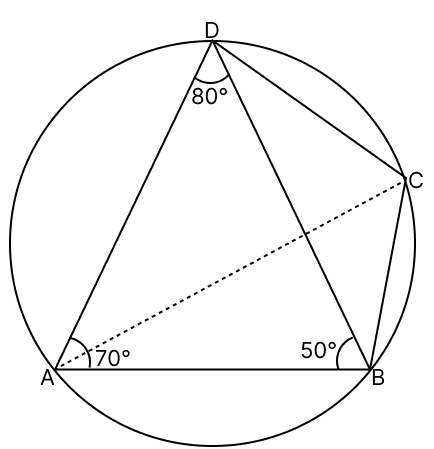
(i) By angle sum property of a triangle we get,

In ΔABD,

⇒ ∠BAD + ∠ABD + ∠ADB = 180°

⇒ 70° + 50° + ∠ADB = 180°

⇒ 120° + ∠ADB = 180°

⇒ ∠ADB = 180° - 120°

⇒ ∠ADB = 60°.

From figure,

⇒ ∠BDC = ∠ADC - ∠ADB

⇒ ∠BDC = 80° - 60°

⇒ ∠BDC = 20°.

Hence, ∠BDC = 20°.

(ii) We know that,

Sum of opposite angles of a cyclic quadrilateral is 180°.

⇒ ∠BAD + ∠BCD = 180°

⇒ 70° + ∠BCD = 180°

⇒ ∠BCD = 180° - 70°

⇒ ∠BCD = 110°.

Hence, ∠BCD = 110°.

(iii) We know that,

Angles in the same segment of a circle are equal.

⇒ ∠BCA = ∠ADB

⇒ ∠BCA = 60°.

Hence, ∠BCA = 60°.

In the given figure, O is the centre of the circle. If ∠ADC = 140°, find ∠BAC.

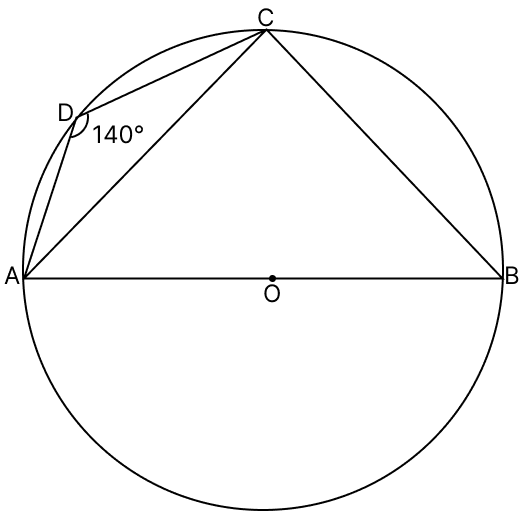
Answer

From figure,

∠ACB = 90° [Angle in a semicircle is a right angle]

We know that,

In a cyclic quadrilateral, the sum of opposite angles is 180°.

⇒ ∠ABC + ∠ADC = 180°

⇒ ∠ABC + 140° = 180°

⇒ ∠ABC = 180° - 140°

⇒ ∠ABC = 40°.

By angle sum property of a triangle we get,

⇒ ∠BAC + ∠ABC + ∠ACB = 180°

⇒ ∠BAC + 40° + 90° = 180°

⇒ ∠BAC + 130° = 180°

⇒ ∠BAC = 180° - 130°

⇒ ∠BAC = 50°.

Hence, ∠BAC = 50°.

PQRS is a cyclic quadrilateral. Given ∠QPS = 73°, ∠PQS = 55° and ∠PSR = 82°, calculate ∠QRS, ∠RQS and ∠PRQ.

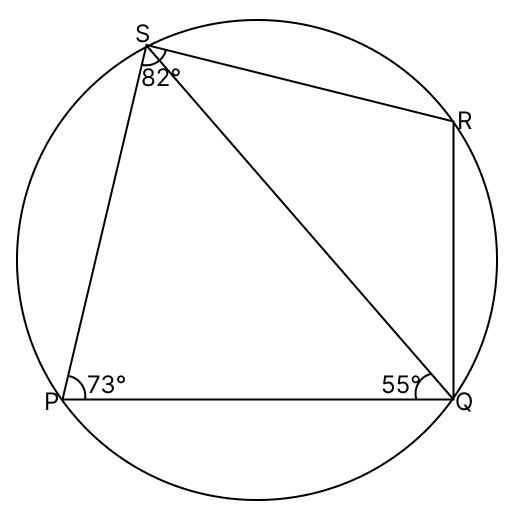
Answer

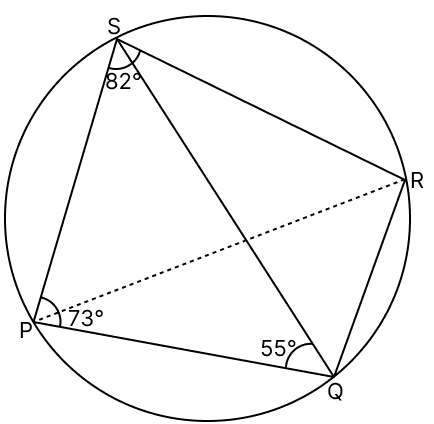
We know that,

In a cyclic quadrilateral, the sum of opposite angles is 180°.

⇒ ∠QPS + ∠QRS = 180°

⇒ 73° + ∠QRS = 180°

⇒ ∠QRS = 180° - 73°

⇒ ∠QRS = 107°.

From figure,

⇒ ∠PSR + ∠PQR = 180°

⇒ ∠PSR + ∠PQS + ∠RQS = 180°

⇒ 82° + 55° + ∠RQS = 180°

⇒ 137° + ∠RQS = 180°

⇒ ∠RQS = 180° - 137°

⇒ ∠RQS = 43°.

By angle sum property of a triangle we get,

⇒ ∠PSQ + ∠PQS + ∠QPS = 180°

⇒ ∠PSQ + 55° + 73° = 180°

⇒ ∠PSQ + 128° = 180°

⇒ ∠PSQ = 180° - 128°

⇒ ∠PSQ = 52°.

∠PSQ = ∠PRQ = 52° [Angles in the same segment]

Hence, ∠QRS = 107°, ∠RQS = 43° and ∠PRQ = 52°.

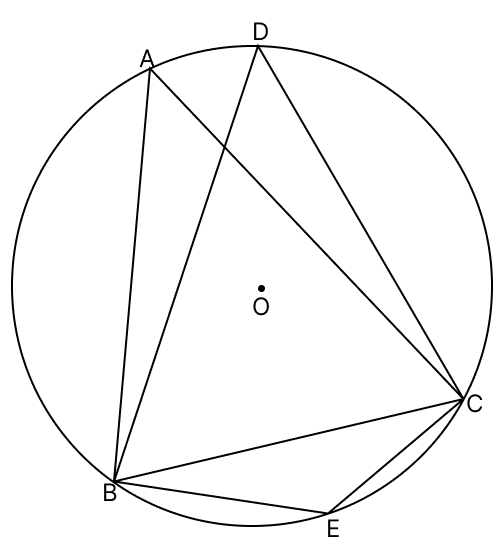
In the given figure, O is the centre of the circle and ΔABC is equilateral. Find :

(i) ∠BDC

(ii) ∠BEC.

Answer

(i) Since ABC is an equilateral triangle so,

∠A = ∠B = ∠C = 60°.

From figure,

∠BDC = ∠BAC (Angles in same segment are equal.)

∴ ∠BDC = 60°.

Hence, ∠BDC = 60°.

(ii) BDCE is a cyclic quadrilateral. Hence, sum of the opposite angles = 180°.

⇒ ∠BDC + ∠BEC = 180°

⇒ 60° + ∠BEC = 180°

⇒ ∠BEC = 180° - 60° = 120°.

Hence, ∠BEC = 120°.

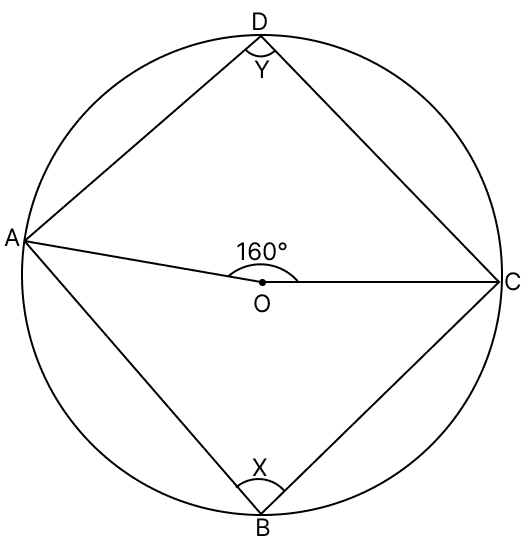
In the given figure, O is the centre of the circle and ∠AOC = 160°. Prove that 3∠y − 2∠x = 140°.

Answer

We know that,

Angle at the center is double the angle at the circumference subtended by the same chord.

∠AOC = 2∠ABC

∠AOC = 2x

∠x = $\dfrac{1}{2}$ ∠AOC = $\dfrac{160^{\circ}}{2}$ = 80°.

In a cyclic quadrilateral, the sum of opposite angles is 180°.

In quadrilateral ABCD,

⇒ ∠ABC + ∠ADC = 180°

⇒ ∠x + ∠y = 180°

⇒ 80° + ∠y = 180°

⇒ ∠y = 100°.

Substitute values in L.H.S of equation 3∠y − 2∠x = 140° :

= 3(100°) − 2(80°)

= 300° − 160°

= 140°.

As, L.H.S = R.H.S

Hence, proved that 3∠y − 2∠x = 140°.

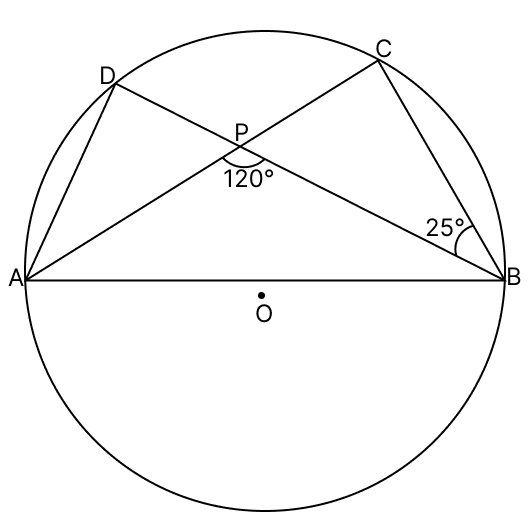
In the given figure, O is the centre of the circle. If ∠CBD = 25° and ∠APB = 120°, find ∠ADB.

Answer

From figure,

⇒ ∠CPB + ∠APB = 180° [Linear pair]

⇒ ∠CPB = 180° - ∠APB

⇒ ∠CPB = (180° − 120°) = 60°.

By angle sum property of a triangle we get,

⇒ ∠PCB + ∠CPB + ∠PBC = 180°

⇒ ∠PCB + 60° + 25° = 180°

⇒ ∠PCB + 85° = 180°

⇒ ∠PCB = 180° - 85°

⇒ ∠PCB = 95°

⇒ ∠ADB = ∠ACB = 95° [Angles in same segment of a circle are equal]

Hence, the value of ∠ADB = 95°.

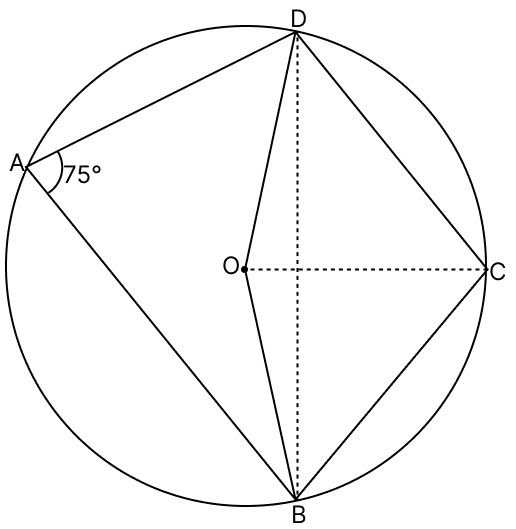
In the given figure, O is the centre of the circle, ∠BAD = 75° and chord BC = chord CD. Find : (i) ∠BOC (ii) ∠OBD (iii) ∠BCD

Answer

(i) As equal chords of a circle subtend equal angles at the center and chord BC = chord CD, so ∠BOC = ∠COD.

∠BOD = 2 × ∠BAD

∠BOD = 2 × 75°

∠BOD = 150°

∠BOC = $\dfrac{1}{2}$ ∠BOD

= $\dfrac{1}{2}$ × 150° = 75°.

Hence, the value of ∠BOC = 75°.

(ii) Join BD.

Since, OB = OD

∴ ∠OBD = ∠ODB = x

Since sum of angles of triangle = 180°

In △OBD

⇒ ∠BOD + ∠OBD + ∠ODB = 180°

⇒ 150° + x + x = 180°

⇒ 150° + 2x = 180°

⇒ 2x = 180° - 150°

⇒ 2x = 30°

⇒ x = 15°.

Hence, the value of ∠OBD = 15°.

(iii) ABCD is a cyclic quadrilateral as all of its vertices lie on the circumference of the circle.

We know that sum of opposite angles of a cyclic quadrilateral = 180°.

⇒ ∠BCD + ∠BAD = 180°

⇒ ∠BCD + 75° = 180°

⇒ ∠BCD = 180° - 75°

⇒ ∠BCD = 105°.

Hence, the value of ∠BCD = 105°.

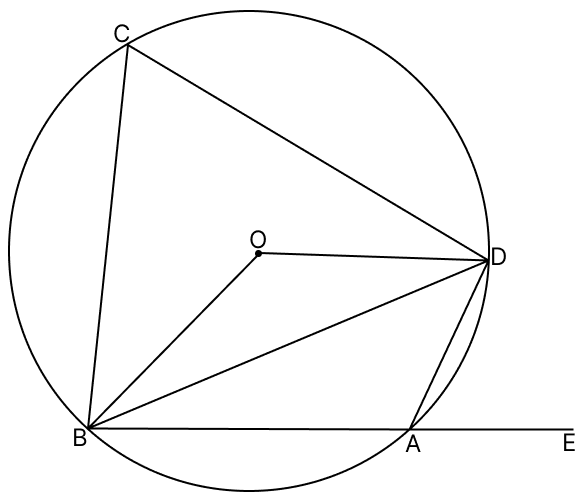
In the figure given, O is the centre of the circle. ∠DAE = 70°, find giving suitable reasons, the measure of :

(i) ∠BCD

(ii) ∠BOD

(iii) ∠OBD

Answer

(i) Given,

∠DAE = 70°

From figure,

⇒ ∠DAE + ∠BAD = 180° [Linear pairs]

⇒ 70° + ∠BAD = 180°

⇒ ∠BAD = 180° - 70° = 110°.

We know that,

Sum of opposite angles in a cyclic quadrilateral = 180°

⇒ ∠BCD + ∠BAD = 180°

⇒ ∠BCD + 110° = 180°

⇒ ∠BCD = 180° - 110° = 70°.

Hence, ∠BCD = 70°.

(ii) We know that,

Angle which an arc subtends at the centre is double that which it subtends at any point on the remaining part of the circumference.

⇒ ∠BOD = 2∠BCD = 2 × 70° = 140°.

Hence, ∠BOD = 140°.

(iii) In △OBD,

OB = OD [Radius of same circle]

∠OBD = ∠ODB = x.

⇒ ∠OBD + ∠ODB + ∠BOD = 180°

⇒ x + x + 140° = 180°

⇒ 2x = 180° - 140°

⇒ 2x = 40°

⇒ x = $\dfrac{40^{\circ}}{2}$ = 20°.

∴ ∠OBD = 20°.

Hence, ∠OBD = 20°.

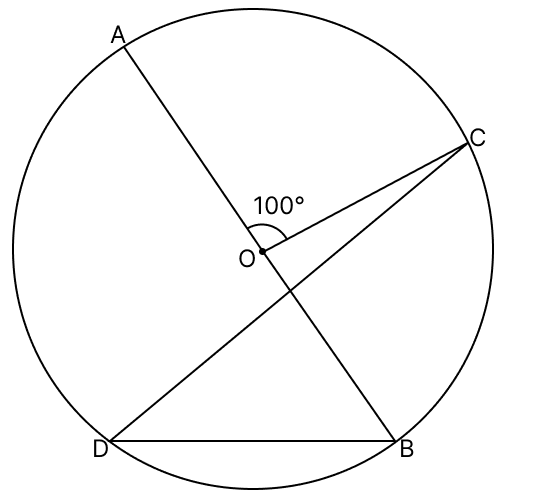
In the given figure, AOB is a diameter of the circle with centre O and ∠AOC = 100°, find ∠BDC.

Answer

From figure,

∠AOC + ∠BOC = 180° [Linear pair]

100° + ∠BOC = 180°

∠BOC = 180° - 100°

∠BOC = 80°.

We know that,

Angle which an arc subtends at the centre is double that which it subtends at any point on the remaining part of the circumference.

⇒ ∠BOC = 2∠BDC

⇒ 80° = 2∠BDC

⇒ ∠BDC = $\dfrac{80^{\circ}}{2}$ = 40°

Hence, ∠BDC = 40°.

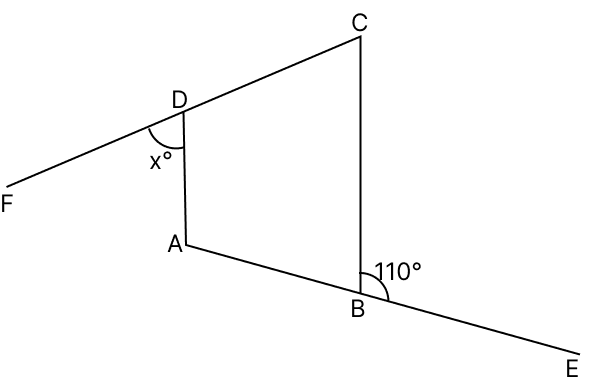
In the given figure, find whether the points A, B, C, D are concyclic when:

(i) x = 70

(ii) x = 80

Answer

From the figure,

∠ABC + ∠CBE = 180° [Linear pair]

∠ABC + 110° = 180°

∠ABC = 70°

For the points A, B, C, D to be concyclic, ∠ABC + ∠ADC must be equal to 180°.

(i) When x = 70

x° + ∠ADC = 180° [Linear pair]

∠ADC = 180° − x° = 180° - 70° = 110°.

∠ABC + ∠ADC = 70° + 110° = 180°

Since the sum of opposite angles is 180°, the points A, B, C, D are concyclic when x = 70.

Hence, yes the points A, B, C, D are concyclic when x = 70.

(ii) When x = 80

x° + ∠ADC = 180° [Linear pair]

∠ADC = 180° − 80° = 100°

Check for con-cyclicity,

∠ABC + ∠ADC = 70° + 100° = 170°

Since the sum of opposite angles is not 180°, the points A, B, C, D are not concyclic when x = 80.

Hence, no the points A, B, C, D are not concyclic when x = 80.

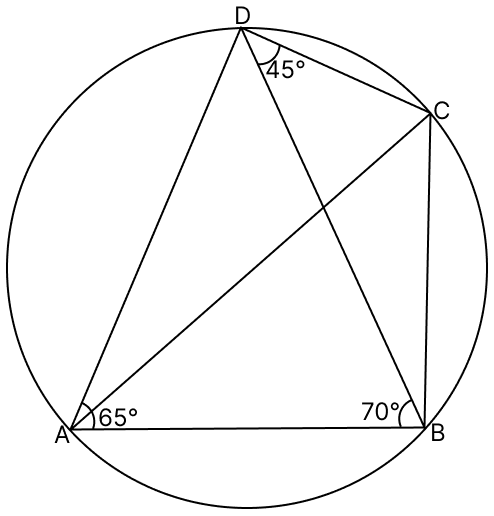
In the adjoining figure, ∠BAD = 65°, ∠ABD = 70° and ∠BDC = 45°. Find: (i) ∠BCD (ii) ∠ADB Hence, show that AC is a diameter.

Answer

(i) We know that,

Sum of opposite angles in a cyclic quadrilateral = 180°.

In cyclic quadrilateral ABCD,

∴ ∠BCD + ∠BAD = 180°

⇒ ∠BCD + 65° = 180°

⇒ ∠BCD = 180° - 65° = 115°.

Hence, ∠BCD = 115°.

(ii) In △ABD,

⇒ ∠ADB + ∠BAD + ∠DBA = 180° [Angle sum property of triangle]

⇒ ∠ADB + 65° + 70° = 180°

⇒ ∠ADB + 135° = 180°

⇒ ∠ADB = 180° - 135° = 45°.

We know that,

Angles in same segment are equal.

∴ ∠ACB = ∠ADB = 45°.

From figure,

∠ADC = ∠ADB + ∠BDC = 45° + 45° = 90°.

Since, angle in a semi-circle is a right angle. Thus, AC is the diameter.

Hence, ∠ADB = 45° and proved that AC is a diameter.

In the given figure, ABCD is a cyclic quadrilateral in which ∠CAD = 25°, ∠ADB = 35° and ∠ABD = 50°. Calculate:

(i) ∠CBD

(ii) ∠CAB

(iii) ∠ACB

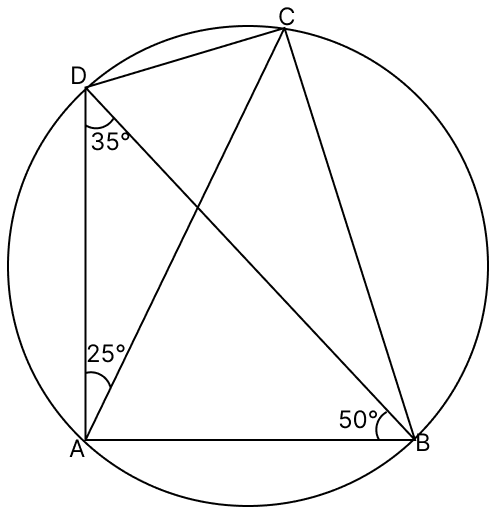
Answer

(i) We know that,

Angles in same segment are equal.

∠CBD = ∠CAD = 25°

Hence, ∠CBD = 25°.

(ii) We know that,

Angles in same segment are equal.Therefore,

⇒ ∠ACD = ∠ABD = 50°

⇒ ∠ACB = ∠ADB = 35°

From figure

⇒ ∠BCD = ∠ACD + ∠ACB

⇒ ∠BCD = 35° + 50°

⇒ ∠BCD = 85°.

We know that,

Sum of opposite angles in a cyclic quadrilateral = 180°.

⇒ ∠DAB + ∠DCB = 180°

⇒ ∠DAB = 180° - 85°

⇒ ∠DAB = 95°.

From figure,

⇒ ∠CAB = ∠DAB - ∠DAC

= 95° - 25°

= 70°.

Hence, ∠CAB = 70°.

(iii) Angles in same segment are equal. Therefore,

∠ACB = ∠ADB = 35°

Hence, ∠ACB = 35°.

In the figure, AB is parallel to DC, ∠BCE = 80° and ∠BAC = 25°. Find :

(i) ∠CAD

(ii) ∠CBD

(iii) ∠ADC

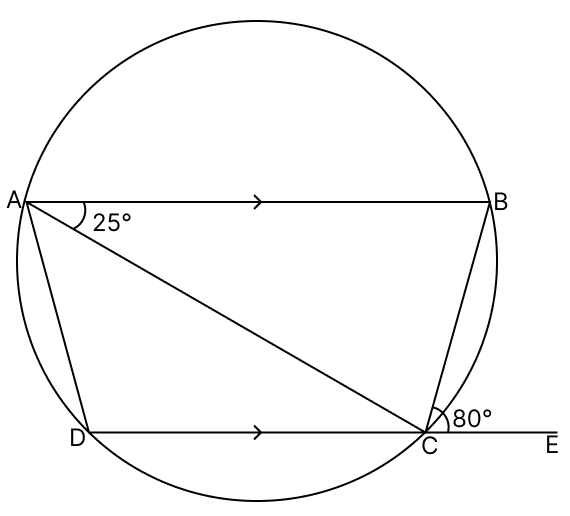
Answer

(i) We know that,

Exterior angle of a cyclic quadrilateral is equal to interior opposite angle.

∠BAD = Exterior ∠BCE = 80°.

From figure,

∠CAD = ∠BAD - ∠BAC = 80° - 25° = 55°.

Hence, ∠CAD = 55°.

(ii) We know that,

Angles in same segment are equal.

∴ ∠CBD = ∠CAD = 55°.

Hence, ∠CBD = 55°.

(iii) Since, AB ∥ DC,

∠ACD = ∠BAC = 25° [Alternate angles are equal]

In triangle ADC,

By angle sum property of triangle,

⇒ ∠ADC + ∠CAD + ∠ACD = 180°

⇒ ∠ADC + 55° + 25° = 180°

⇒ ∠ADC + 80° = 180°

⇒ ∠ADC = 180° - 80°

⇒ ∠ADC = 100°.

Hence, ∠ADC = 100°.

In the given figure, ABCD is a cyclic quadrilateral whose side CD has been produced to E. If BA = BC and ∠BAC = 40°, find ∠ADE.

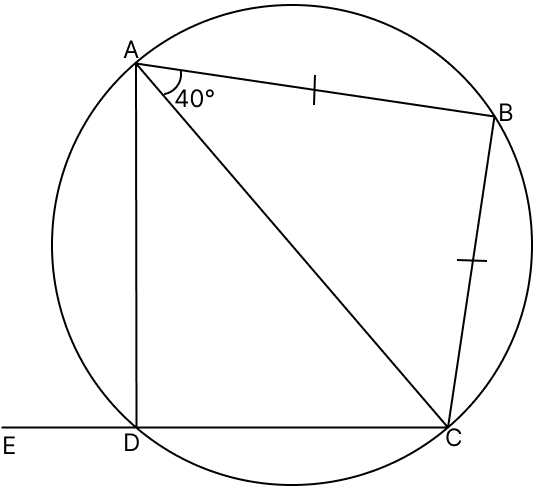
Answer

Given,

Quadrilateral ABCD is a cyclic quadrilateral.

∠ACB = ∠CAB = 40° [Angles opposite to equal sides are equal]

By angle sum property of a triangle we get,

In ΔABC,

⇒ ∠CAB + ∠CBA + ∠ACB = 180°

⇒ 40° + ∠CBA + 40° = 180°

⇒ ∠CBA + 80° = 180°

∴ ∠CBA = 100°

∠CBA + ∠CDA = 180° [Sum of opposite angles in a cyclic quadrilateral = 180°]

⇒ 100° + ∠CDA = 180°

⇒ ∠CDA = 80°

∴ ∠CDA + ∠ADE = 180° [Linear pairs]

⇒ 80° + ∠ADE = 180°

⇒ ∠ADE = 100°.

Hence, the value of ∠ADE is 100°.

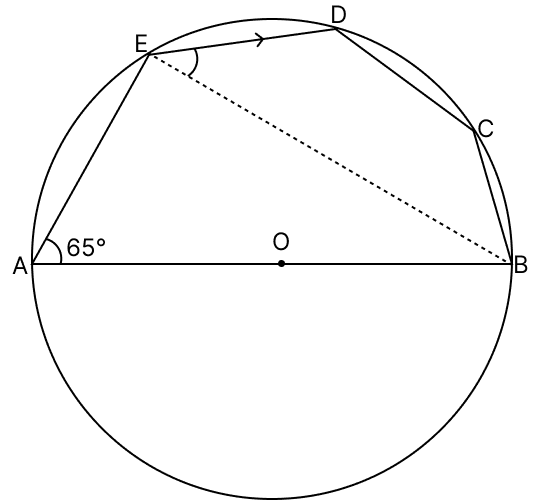
In the given figure, AB is a diameter of a circle with centre O and chord ED is parallel to AB and ∠EAB = 65°. Calculate : (i) ∠EBA (ii) ∠BED (iii) ∠BCD

Answer

(i) We know that,

Angle in semi-circle is a right angle.

∴ ∠AEB = 90°.

In △AEB,

⇒ ∠AEB + ∠EBA + ∠EAB = 180°

⇒ 90° + ∠EBA + 65° = 180°

⇒ 155° + ∠EBA = 180°

⇒ ∠EBA = 180° - 155° = 25°.

Hence, ∠EBA = 25°.

(ii) ∠BED = ∠EBA = 25° Alternate interior angles ED ∥ AB, EB as a transversal

Hence, ∠BED = 25°.

(iii) As, AB ∥ ED

∴ ∠DEB = ∠EBA = 25° [Alternate angles]

BCDE is a cyclic quadrilateral.

∴ ∠DEB + ∠BCD = 180° [Sum of opposite angles in a cyclic quadrilateral = 180°.]

⇒ 25° + ∠BCD = 180°

⇒ ∠BCD = 180° - 25° = 155°.

Hence, ∠BCD = 155°.

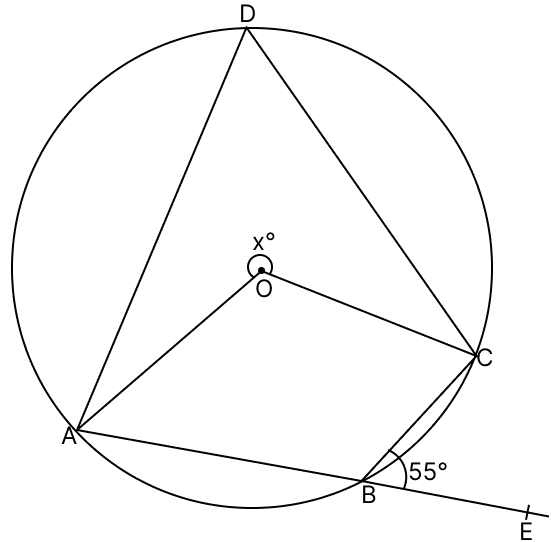
In the given figure, O is the centre of a circle and ABE is a straight line. If ∠CBE = 55°, find :

(i) ∠ADC

(ii) ∠ABC

(iii) the value of x.

Answer

(i) We know that,

In a cyclic quadrilateral, the exterior angle is equal to the interior opposite angle.

∠ADC = ∠CBE = 55°

Hence, ∠ADC = 55°.

(ii) From figure,

∠CBE + ∠ABC = 180° [Linear pairs]

∠ABC = 180° - 55°

∠ABC = 125°.

Hence, ∠ABC = 125°.

(iii) We know that,

Angle which an arc subtends at the centre is double that which it subtends at any point on the remaining part of the circumference.

∠AOC = 2∠ADC

∠AOC = 2(55°)

∠AOC = 110°

The reflex angle AOC,

x° = 360° - angle AOC

x° = 360° - 110°

x° = 250°.

Hence, x = 250.

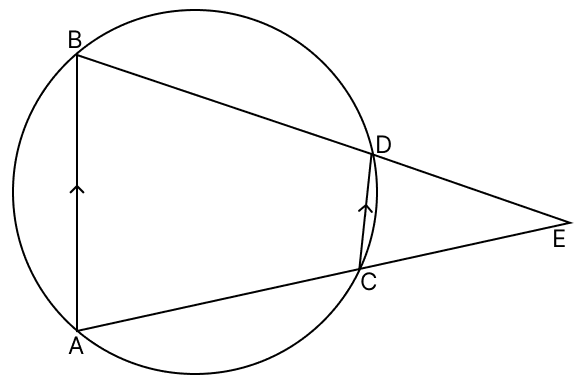
In the given figure AB and CD are two parallel chords of a circle. If BDE and ACE are straight lines, intersecting at E, prove that Δ AEB is isosceles.

Answer

We know that,

Exterior angle of a cyclic quadrilateral is equal to interior opposite angle.

∠EDC = ∠A ....(i)

∠DCE = ∠B ....(ii)

AB ∥ CD

∠EDC = ∠B [Corresponding angles] ......(iii)

∠DCE = ∠A [Corresponding angles] .......(iv)

From (i), (ii), (iii) and (iv) we get :

∴ ∠A = ∠B

BE = AE [Sides opposite to equal angles are equal]

Hence, proved that ΔAEB is isosceles.

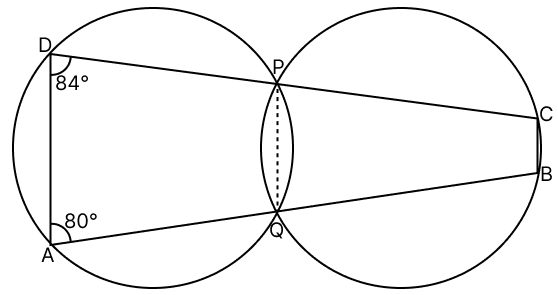
In the given figure, the two circles intersect at P and Q. If ∠A = 80° and ∠D = 84°, calculate :

(i) ∠QBC

(ii) ∠BCP

Answer

PQAD is a cyclic quadrilateral as all vertices lie on the circumference of the circle.

Sum of opposite angles of cyclic quadrilateral = 180°

⇒ ∠DAQ + ∠DPQ = 180°

⇒ 80° + ∠DPQ = 180°

⇒ ∠DPQ = 180° - 80°

⇒ ∠DPQ = 100°.

Also,

⇒ ∠PDA + ∠PQA = 180°

⇒ 84° + ∠PQA = 180°

⇒ ∠PQA = 180° - 84°

⇒ ∠PQA = 96°.

Since exterior angle of a cyclic quadrilateral is equal to the opposite interior angle.

(i) ∠QBC = ∠DPQ = 100°.

Hence, ∠QBC = 100°.

(ii) ∠BCP = ∠PQA = 96°.

Hence, ∠BCP = 96°.

In the given figure, O is the centre of the circle. If ∠AOD = 140° and ∠CAB = 50°, calculate :

(i) ∠EDB

(ii) ∠EBD

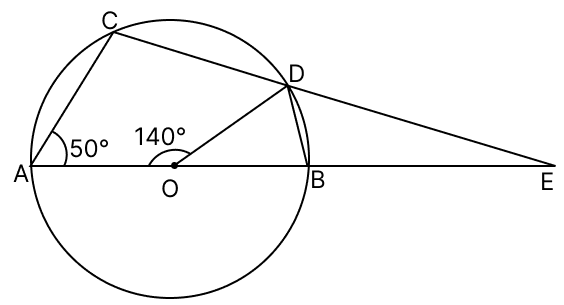
Answer

(i) We know that,

An Exterior angle of a cyclic quadrilateral is equal to the interior opposite angle. ∠EDB is the exterior angle at vertex D. The interior opposite angle is ∠CAB.

⇒ ∠EBD = ∠CAB = 50°

Hence, the value of ∠EDB = 50°.

(ii) We know that,

⇒ OD = OB [radii of same circle]

From figure,

⇒ ∠AOD + ∠DOB = 180° [Linear pairs]

⇒ 140° + ∠DOB = 180°

⇒ ∠DOB = 180° - 140°

⇒ ∠DOB = 40°

In ΔODB,

By angle sum property of triangle,

⇒ ∠DOB + ∠ODB + ∠OBD = 180°

⇒ 40° + 2∠OBD = 180°

⇒ 2∠OBD = 180° - 40°

⇒ 2∠OBD = 140°

⇒ ∠OBD = $\dfrac{180^{\circ}}{2}$

⇒ ∠OBD = 70°

From figure,

⇒ ∠OBD + ∠EBD = 180° [Linear pairs]

⇒ 70° + ∠EBD = 180°

⇒ ∠EBD = 180° - 70°

⇒ ∠EBD = 110°

Hence, the value of ∠EBD = 110°.

In the given figure, AB is a diameter of a circle with centre O. If ADF and CBF are straight lines, meeting at F such that ∠BAD = 35° and ∠BFD = 25°, find :

(i) ∠DCB

(ii) ∠DBC

(iii) ∠BDC

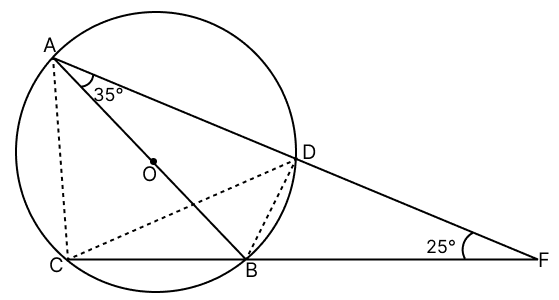
Answer

(i) We know that,

Angles in same segment are equal.

∠DCB = ∠BAD = 35°

Hence, the value of ∠DCB = 35°.

(ii) From figure,

∠ADB = 90° (∵ Angle in semicircle is 90°.)

∴ ∠BDF = 90°

In △DBF,

⇒ ∠DBF + ∠DFB + ∠BDF = 180° (∵ By angle sum triangle property).

⇒ ∠DBF = 180° - (∠DFB + ∠BDF)

⇒ ∠DBF = 180° - (90° + 25°)

⇒ ∠DBF = 65°.

⇒ ∠DBF + ∠DBC = 180° (Linear pairs)

⇒ ∠DBC = 180° - 65°

⇒ ∠DBC = 115°.

Hence, the value of ∠DBC = 115°.

(iii) In △DCB,

⇒ ∠DCB + ∠CBD + ∠BDC = 180° (∵ By angle sum triangle property).

⇒ ∠BDC = 180° - (∠DCB + ∠CBD)

⇒ ∠BDC = 180° - (35° + 115°)

⇒ ∠BDC = 180° - (35° + 115°)

⇒ ∠BDC = 30°.

Hence, the value of ∠BDC = 30°.

In the given figure, the straight lines AB and CD pass through the centre O of the circle. If ∠AOD = 75° and ∠OCE = 40°, find :

(i) ∠CDE

(ii) ∠OBE.

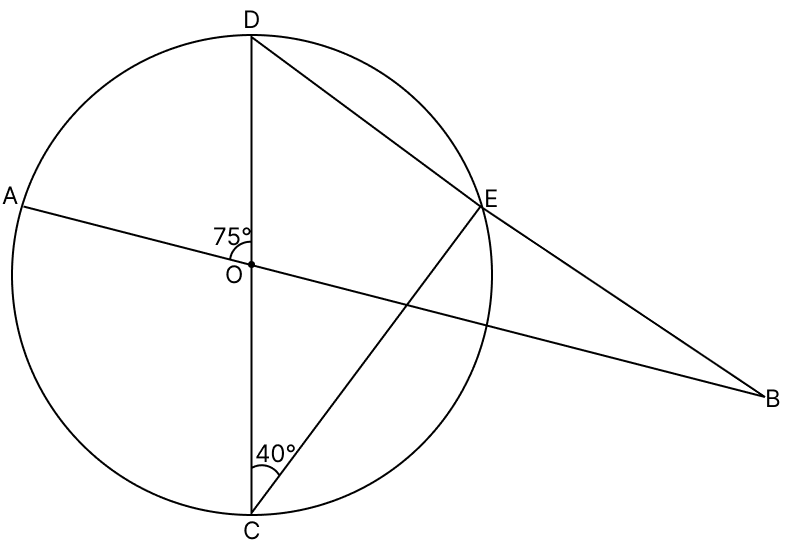
Answer

(i) Since, AB and CD pass through the center, thus they are the diameters of circle.

In △CED,

∠CED = 90° (∵ angle in semicircle is 90°.)

We know that sum of angles of a triangle is 180°.

⇒ ∠CED + ∠DCE + ∠CDE = 180°.

⇒ 90° + 40° + ∠CDE = 180°

⇒ ∠CDE + 130° = 180°

⇒ ∠CDE = 180° - 130°

⇒ ∠CDE = 50°.

Hence, ∠CDE = 50°.

(ii) From figure,

⇒ ∠AOD + ∠DOB = 180° (Linear pairs)

⇒ 75° + ∠DOB = 180°

⇒ ∠DOB = 180° - 75°

⇒ ∠DOB = 105°.

In △DOB,

∠ODB = ∠CDE = 50°

We know that,

Sum of angles of a triangle is 180°.

⇒ ∠DOB + ∠ODB + ∠DBO = 180°.

⇒ 105° + 50° + ∠DBO = 180°

⇒ ∠DBO + 155° = 180°

⇒ ∠DBO = 180° - 155°

⇒ ∠DBO = 25°.

From figure,

∠OBE = ∠DBO

∴ ∠OBE = 25°.

Hence, ∠OBE = 25°.

In the adjoining figure, AB = AC = CD and ∠ADC = 35°. Calculate :

(i) ∠ABC

(ii) ∠BEC

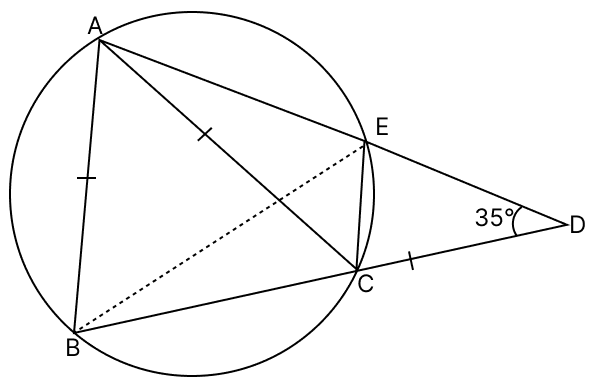
Answer

(i) Given,

AC = CD

In triangle ACD,

∠DAC = ∠ADC = 35° [Angles opposite to equal sides in a triangle are equal]

In △ACD,

⇒ ∠DAC + ∠ADC + ∠ACD = 180°

⇒ 35° + 35° + ∠ACD = 180°

⇒ 70° + ∠ACD = 180°

⇒ ∠ACD = 180° - 70° = 110°.

From figure,

⇒ ∠ACB + ∠ACD = 180° [Linear pair]

⇒ ∠ACB + 110° = 180°

⇒ ∠ACB = 180° - 110° = 70°.

Given,

AB = AC

∴ ∠ABC = ∠ACB = 70°. [As angles opposite to equal sides are equal]

Hence, ∠ABC = 70°.

(ii) In △ABC,

⇒ ∠BAC + ∠ACB + ∠ABC = 180° [Angle sum property of triangle]

⇒ ∠BAC + 70° + 70° = 180°

⇒ ∠BAC + 140° = 180°

⇒ ∠BAC = 180° - 140° = 40°.

We know that,

Angles in same segment are equal.

⇒ ∠BEC = ∠BAC = 40°.

Hence, ∠BEC = 40°.

The exterior angles B and C in ΔABC are bisected to meet at a point P. Prove that ∠BPC = 90° − $\dfrac{A}{2}$. Is ABPC a cyclic quadrilateral ?

Answer

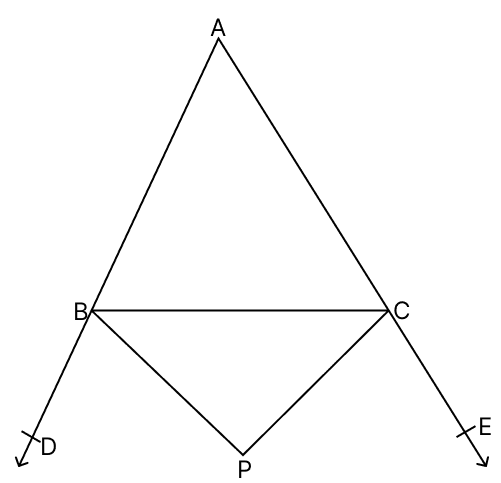
We know that,

An exterior angle of a triangle equals to the sum of the two interior opposite angles.

∠CBD = ∠A + ∠C

∠BCE = ∠A + ∠B.

Since BP bisects the exterior angle ∠CBD :

∠PBC = $\dfrac{1}{2}$ ∠CBD

Similarly, since CP bisects the exterior angle ∠BCE :

∠PCB = $\dfrac{1}{2}$ ∠BCE

In △BPC,

By angle sum property of triangle,

$\Rightarrow ∠PBC + ∠PCB + ∠BPC = 180^{\circ} \\[1em] \Rightarrow \dfrac{1}{2}∠CBD + \dfrac{1}{2}∠BCE + ∠BPC = 180^{\circ} \\[1em] \Rightarrow \dfrac{1}{2}(∠A + ∠C) + \dfrac{1}{2}(∠A + ∠B) + ∠BPC = 180^{\circ} \\[1em] \Rightarrow ∠A + \dfrac{1}{2}(∠C + ∠B) + ∠BPC = 180^{\circ} \\[1em] \Rightarrow \dfrac{1}{2}(∠B + ∠C) + ∠BPC = 180^{\circ} - A \\[1em] \Rightarrow \dfrac{1}{2}(180^{\circ} - A) + ∠BPC = 180^{\circ} - A \\[1em] \Rightarrow 90^{\circ} - \dfrac{A}{2} + ∠BPC = 180^{\circ} - A \\[1em] \Rightarrow ∠BPC = 180^{\circ} - A - \Big[90^{\circ} - \dfrac{A}{2}\Big] \\[1em] \Rightarrow ∠BPC = 180^{\circ} - A - 90^{\circ} + \dfrac{A}{2}\\[1em] \Rightarrow ∠BPC = 90^{\circ} - \dfrac{A}{2}.$

For A, B, P, C to be concyclic we would need ∠A + ∠BPC = 180° But:

∵ ∠A + ∠BPC = ∠A + $90^{\circ} - \dfrac{∠A}{2} = 90^{\circ} + \dfrac{∠A}{2}$

Hence, proved that $∠BPC = 90° - \dfrac{∠A}{2}$ and ABPC is not cyclic.

In the given figure, O is the centre of the circle. If QR = OP and ∠ORP = 20°, find the value of x giving reasons.

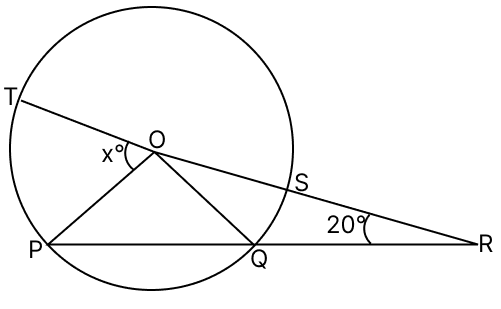
Answer

Given,

⇒ QR = OP

⇒ QR = OQ (As, OP = OQ = Radius of circle)

⇒ ∠QOR = ∠ORQ = 20° (Angles opposite to equal sides of a triangle are equal)

Exterior angle in a triangle is equal to the sum of two opposite interior angles.

∴ ∠OQP = ∠QOR + ∠ORQ = 20° + 20° = 40°.

As OP = OQ, ∠OPQ = ∠OQP

⇒ ∠OPQ = 40°

⇒ ∠OPR = 40°.

Exterior angle in a triangle is equal to the sum of two opposite interior angles.

In triangle OPR,

∴ x° = ∠OPR + ∠ORP = 40° + 20° = 60°.

Hence, the value of x = 60.

In the given figure, I is the incentre of Δ ABC. Here AI produced meets the circumcircle of Δ ABC at D. If ∠ABC = 55° and ∠ACB = 65°, calculate :

(i) ∠BCD

(ii) ∠CBD

(iii) ∠DCI

(iv) ∠BIC

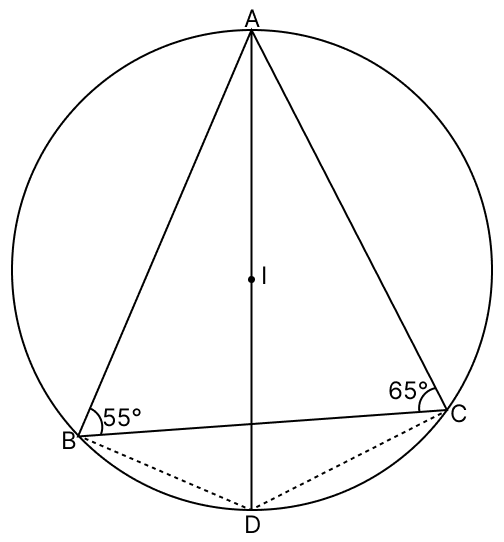
Answer

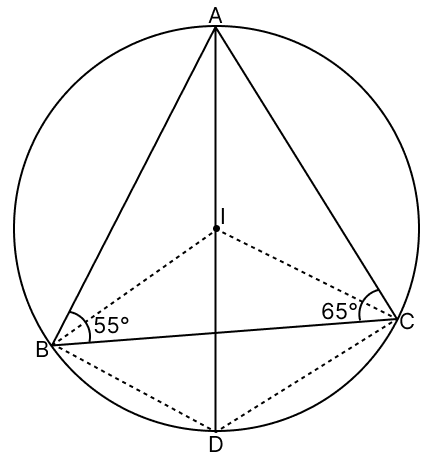
(i) Join BI and CI.

In △ABC,

⇒ ∠BAC + ∠ABC + ∠ACB = 180° (∵ sum of angles = 180°.)

⇒ ∠BAC + 55° + 65° = 180°

⇒ ∠BAC + 120° = 180°

⇒ ∠BAC = 180° - 120°

⇒ ∠BAC = 60°.

I is the incentre,

∴ I lies on the bisectors of angle of the △ABC,

∴ ∠BAD = ∠CAD = $\dfrac{60^{\circ}}{2}$ = 30°.

∠BCD = ∠BAD = 30°. (∵ angles in same segment are equal.)

Hence, the value of ∠BCD = 30°.

(ii) Similarly,

∠CBD = ∠CAD = 30°. (∵ angles in same segment are equal.)

Hence, the value of ∠CBD = 30°.

(iii) The line CI bisects ∠C (∵ I lies on the bisectors of angle of the △ABC).

∴ ∠BCI = $\dfrac{65^{\circ}}{2} = 32 \dfrac{1}{2}^{\circ}$.

From figure,

∠DCI = ∠BCD + ∠BCI = 30° + $32 \dfrac{1}{2}^{\circ}$

= 62.5°.

Hence, the value of ∠DCI = 62.5°.

(iv) ∠IBC = $\dfrac{55}{2}^{\circ}$ = 27.5°

∠ICB = $\dfrac{65}{2}^{\circ}$ = 32.5°

In triangle BIC,

By angle sum property of triangle,

∠BIC + ∠IBC + ∠ICB = 180°

∠BIC = 180° - (∠IBC + ∠ICB)

= 180° - (27.5° + 32.5°)

= 180° - 60°

= 120°.

Hence, the value of ∠BIC = 120°.

In the given figure, ∠DBC = 58° and BD is a diameter of the circle. Calculate :

(i) ∠BDC

(ii) ∠BEC

(iii) ∠BAC

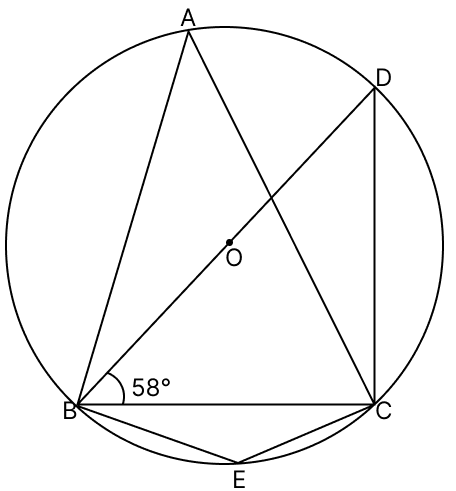
Answer

(i) Given that BD is a diameter of the circle.

We know that,

Angle in a semicircle is a right angle.

So, ∠BCD = 90°

Also given that,

∠DBC = 58°

In ∆BDC,

⇒ ∠DBC + ∠BCD + ∠BDC = 180° [Angle sum property of triangle]

⇒ 58° + 90° + ∠BDC = 180°

⇒ 148° + ∠BDC = 180°

⇒ ∠BDC = 180° - 148° = 32°.

Hence, ∠BDC = 32°.

(ii) We know that, the opposite angles of a cyclic quadrilateral are supplementary.

So, in cyclic quadrilateral BECD

⇒ ∠BEC + ∠BDC = 180°

⇒ ∠BEC + 32° = 180°

⇒ ∠BEC = 180° - 32° = 148°

Hence, ∠BEC = 148°.

(iii) In cyclic quadrilateral ABEC,

⇒ ∠BAC + ∠BEC = 180° [Sum of opposite angles of a cyclic quadrilateral = 180°]

⇒ ∠BAC + 148° = 180°

⇒ ∠BAC = 180° - 148° = 32°.

Hence, ∠BAC = 32°.

In the given figure, ABCDE is a pentagon inscribed in a circle such that AC is a diameter and side BC ∥ AE. If ∠BAC = 50°, find giving reasons :

(i) ∠ACB

(ii) ∠EDC

(iii) ∠BEC

Hence prove that BE is also a diameter.

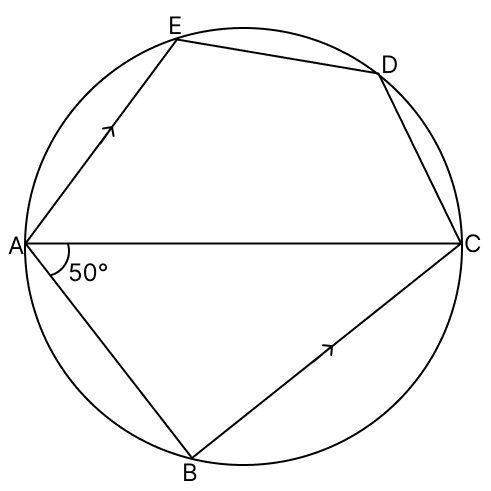
Answer

(i) ∠ABC = 90° [Angle in semicircle]

In ∆ABC,

⇒ ∠ABC + ∠BAC + ∠ACB = 180° [Angle sum property of triangle]

⇒ 90° + 50° + ∠ACB = 180°

⇒ 140° + ∠ACB = 180°

⇒ ∠ACB = 40°

Hence, ∠ACB = 40°.

(ii) ∠EAC = ∠ACB = 40° [Alternate angles, AC transversal to parallel lines AE and BC]

∠EAC + ∠EDC = 180° [Sum of opposite angles of a cyclic quadrilateral = 180°]

40° + ∠EDC = 180°

∠EDC = 140°

Hence, ∠EDC = 140°.

(iii) ∠EBC + ∠EDC = 180° [Sum of opposite angles of a cyclic quadrilateral = 180°]

140° + ∠EBC = 180°

∠EBC = 40°

In ∆EBC,

⇒ ∠BEC + ∠ECB + ∠EBC = 180° [Angle sum property of triangle]

⇒ ∠BEC + 90° + 40° = 180°

⇒ ∠BEC = 180° - 130°

⇒ ∠BEC = 50°

In ∆EAB,

⇒ ∠EAB = ∠EAC + ∠BAC

= 40° + 50° = 90°

We know that, if an angle of a triangle in a circle is 90° then, the hypotenuse must be the diameter of the circle.

Hence, ∠BEC = 50° and BE is the diameter of the circle.

In the given figure, O is the centre of the circle and AB is a diameter. If AC = BD and ∠AOC = 72°, find:

(i) ∠ABC

(ii) ∠BAD

(iii) ∠ABD

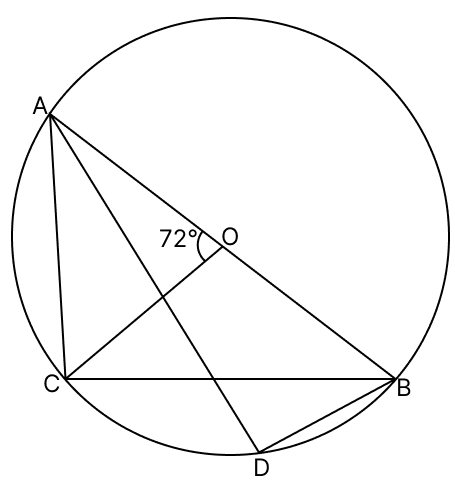
Answer

(i) We know that,

Angle which an arc subtends at the centre is double that which it subtends at any point on the remaining part of the circumference.

∠ABC = $\dfrac{1}{2}$ ∠AOC

∠ABC = $\dfrac{72^{\circ}}{2}$ = 36°

Hence, ∠ABC = 36°.

(ii) Given,

AC = BD

∠BAC = ∠ABC = 36° [Angles opposite to equal sides are equal]

Hence, ∠BAC = 36°.

(iii) In ∆ABD,

∠ABD + ∠BAD + ∠ADB = 180° [Angle sum property of triangle]

∠ABD + 36° + 90° = 180°

∠ABD + 126° = 180°

∠ABD = 180° - 126°

∠ABD = 54°

Hence, ∠ABD = 54°.

In the given figure, A, C, B, D are points on the circle with centre O. Given ∠ABC = 62°. Find :

(i) ∠ADC

(ii) ∠CAB

Answer

(i) From figure,

⇒ ∠ADC = ∠ABC (Angles in same segment are equal)

⇒ ∠ADC = 62°.

Hence, ∠ADC = 62°.

(ii) We know that,

Angle in a semi-circle is a right angle.

∠ACB = 90°

Using angle sum property,

⇒ ∠CAB + ∠ACB + ∠ABC = 180°

⇒ ∠CAB + 90° + 62° = 180°

⇒ ∠CAB + 152° = 180°

⇒ ∠CAB = 180° - 152°

⇒ ∠CAB = 28°.

Hence, ∠CAB = 28°.

The angle in a semi-circle is :

1. an acute angle

2. an obtuse angle

3. a right angle

4. can be either acute or obtuse

Answer

The angle in semi-circle is always a right angle.

Hence, option 3 is the correct option.

The angle subtended by an arc of a circle at any point on the remaining part of the circle is ______ of the angle subtended by it at the centre.

1. double

2. half

3. equal

4. triple

Answer

The angle subtended by an arc of a circle at any point on the remaining part of the circle is half of the angle subtended by it at the centre.

Hence, option 2 is the correct option.

The sum of the opposite angles of a cyclic quadrilateral is :

1. 90°

2. 150°

3. 180°

4. 360°

Answer

The sum of the opposite angles of a cyclic quadrilateral is 180°.

Hence, option 3 is the correct option.

If a pair of opposite angles of a quadrilateral are supplementary, then the quadrilateral is :

1. a rectangle

2. a parallelogram

3. a square

4. a cyclic quadrilateral

Answer

If a pair of opposite angles of a quadrilateral are supplementary, then the quadrilateral is a cyclic quadrilateral.

Hence, option 4 is the correct option.

The exterior angle of a cyclic quadrilateral is equal to :

1. 90°

2. the interior opposite angle

3. the interior adjacent angle

4. any of the interior angles

Answer

The exterior angle of a cyclic quadrilateral is equal to the interior opposite angle.

Hence, option 2 is the correct option.

Any two angles formed in the same segment of a circle are :

1. complementary

2. supplementary

3. each right angle

4. equal

Answer

Any two angles formed in the same segment of a circle are equal.

Hence, option 4 is the correct option.

Every cyclic parallelogram is a/an :

1. square

2. rhombus

3. rectangle

4. isosceles trapezium

Answer

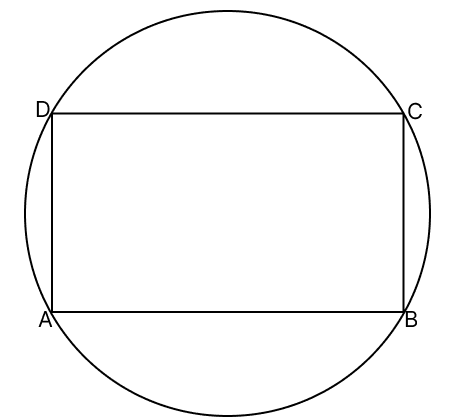
Given,

ABCD is a cyclic parallelogram.

∠ABC = ∠ADC [Opposite angles of parallelogram are equal]

∠ABC + ∠ADC = 180° [Sum of opposite angles of cyclic quadrilateral is 180°]

∠ABC + ∠ABC = 180°

2∠ABC = 180°

∠ABC = $\dfrac{180^{\circ}}{2}$

∠ABC = ∠ADC = 90°

A parallelogram one of whose angle is 90° is a rectangle.

Hence, Every cyclic parallelogram is a rectangle.

Hence, option 3 is the correct option.

An isosceles trapezium is always :

1. a parallelogram

2. a square

3. a rectangle

4. a cyclic quadrilateral

Answer

Given,

ABCD is an isosceles trapezium with AB ∥ CD and AD = BC.

∠A + ∠D = 180° [Interior angles on the same side of a transversal are supplementary]

In an isosceles trapezium,

∠A = ∠B and ∠C = ∠D [Base angles are equal]

So,

∠A + ∠C = 180°

Since a pair of opposite angles of quadrilateral ABCD is supplementary,

ABCD is a cyclic quadrilateral.

Hence, an isosceles trapezium is always a cyclic quadrilateral.

Hence, option 4 is the correct option.

Which of the following quadrilaterals is not always a cyclic quadrilateral?

1. square

2. rhombus

3. rectangle

4. an isosceles trapezium

Answer

Given,

ABCD is a rhombus.

In a rhombus,

All sides are equal, but angles are not necessarily equal to 90°.

Opposite angles of a rhombus are equal.

So,

∠A = ∠C and ∠B = ∠D

But,

∠A + ∠C ≠ 180° (always)

Hence, opposite angles of a rhombus are not always supplementary.

Therefore, a rhombus is not always a cyclic quadrilateral.

Hence, option 2 is the correct option.

The quadrilateral formed by angle bisectors of a cyclic quadrilateral is :

1. cyclic

2. square

3. rectangle

4. parallelogram

Answer

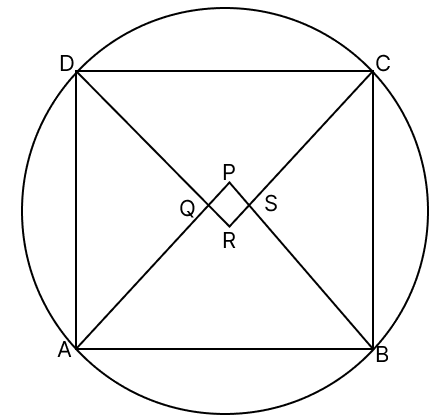
Given,

ABCD is a cyclic quadrilateral in which AP, BP, CR and DR are the angle bisectors of ∠A, ∠B, ∠C and ∠D respectively, forming quadrilateral PQRS.

In ΔPAB,

∠APB + ∠PAB + ∠PBA = 180° [Sum of the angles of a triangle is 180°]

But,

∠PAB = $\dfrac{1}{2}$∠A and ∠PBA = $\dfrac{1}{2}$∠B [AP and BP are angle bisectors]

So,

∠APB + $\dfrac{1}{2}$∠A + $\dfrac{1}{2}$∠B = 180° …(i)

Similarly, in ΔRCD,

∠CRD + ∠RCD + ∠RDC = 180° [Sum of the angles of a triangle is 180°]

But,

∠RCD = $\dfrac{1}{2}$∠C and ∠RDC = $\dfrac{1}{2}$∠D [CR and DR are angle bisectors]

So,

∠CRD + $\dfrac{1}{2}$∠C + $\dfrac{1}{2}$∠D = 180° …(ii)

Adding (i) and (ii),

∠APB + ∠CRD + $\dfrac{1}{2}$ (∠A + ∠B + ∠C + ∠D) = 360°

But,

∠A + ∠B + ∠C + ∠D = 360° [Sum of angles of a quadrilateral]

So,

∠APB + ∠CRD + $\dfrac{1}{2}$ × 360° = 360°

∠APB + ∠CRD + 180° = 360°

∠APB + ∠CRD = 180°

Since a pair of opposite angles of quadrilateral PQRS is supplementary,

PQRS is a cyclic quadrilateral.

Hence, option 1 is the correct option.

In the given figure, O is the centre of the circle and ∠ACB = 30°. Then, ∠AOB = ?

1. 15°

2. 30°

3. 60°

4. 90°

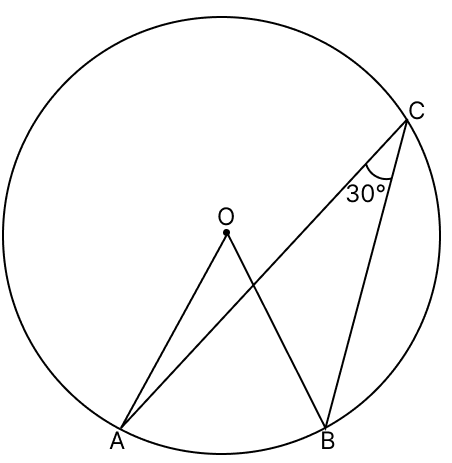
Answer

We know that,

Angle which an arc subtends at the center is double that which it subtends at any point on the remaining part of the circumference.

⇒ ∠AOB = 2∠ACB

⇒ ∠AOB = 2 × 30°

⇒ ∠AOB = 60°.

Hence, option 3 is the correct option.

In the given figure, O is the centre of the circle. If ∠OAB = 35° and C is a point on the circle, then ∠ACB = ?

1. 35°

2. 55°

3. 45°

4. 75°

Answer

Given,

Since O is the centre of the circle, OA and OB are both radii. OA = OB Therefore,

∠OBA = ∠OAB = 35° [Angles opposite to equal sides of a triangle are equal]

In ΔAOB,

By angle sum property of triangle,

∠OBA + ∠OAB + ∠AOB = 180°

35° + 35° + ∠AOB = 180°

∠AOB = 180° - 35° - 35°

∠AOB = 110°.

We know that,

Angle which an arc subtends at the center is double that which it subtends at any point on the remaining part of the circumference.

⇒ ∠AOB = 2∠ACB

⇒ 110° = 2∠ACB

⇒ ∠ACB = $\dfrac{110^{\circ}}{2}$

⇒ ∠ACB = 55°.

Hence, option 2 is the correct option.

In the given figure, ∠ABC and ∠DBC are inscribed in a circle such that ∠BAC = 60° and ∠DBC = 40°. Then, ∠BCD = ?

1. 60°

2. 40°

3. 100°

4. 80°

Answer

Given,

Points A and D are on the circle, and both form angles with the chord BC.

∠BDC = ∠BAC = 60° [Angles in same segment are equal]

In ΔBCD,

By angle sum property of triangle,

∠BCD + ∠DBC + ∠BDC = 180°

∠BCD = 180° - ∠DBC - ∠BDC

∠BCD = 180° - 40° - 60°

∠BCD = 80°.

Hence, option 4 is the correct option.

In the given figure, O is the centre of the circle. If ∠OAC = 55°, then ∠OBD = ?

1. 55°

2. 35°

3. 45°

4. 70°

Answer

In ΔOAC,

OA = OC [Radii of same circle]

Since, two sides are equal it is isosceles triangle and opposite sides are also equal:

∠OCA = ∠OAC = 55°

In ΔOBD,

OB = OD [Radii of same circle]

Since, two sides are equal it is isosceles triangle and opposite sides are also equal:

∠OBD = ∠ODB

∠AOC = ∠BOD [vertically opposite angles]

In ΔOAC,

By angle sum property of triangle,

∠AOC + ∠OAC + ∠OCA = 180°

∠AOC + 55° + 55° = 180°

∠AOC + 110° = 180°

∠AOC = 180° - 110°

∠AOC = 70°

∠AOC = ∠BOD = 70°

In ΔOBD,

By angle sum property of triangle,

∠BOD + ∠OBD + ∠ODB = 180°

70° + 2∠OBD = 180°

2∠OBD = 180° - 70°

2∠OBD = 110°

∠OBD = $\dfrac{110^{\circ}}{2}$

∠OBD = 55°.

Hence, option 1 is the correct option.

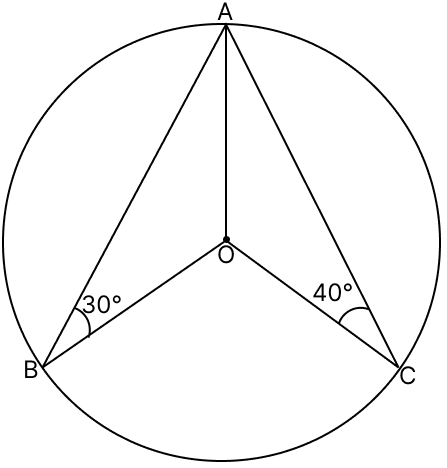
In the given figure, O is the centre of the circle in which ∠OBA = 30° and ∠OCA = 40°. Then, ∠BOC = ?

1. 70°

2. 100°

3. 120°

4. 140°

Answer

Join BC.

In △BOC,

Since,

OB = OC (Radius of same circle)

∴ ∠OBC = ∠OCB = x (let)

By angle sum property of triangle,

⇒ ∠OBC + ∠OCB + ∠BOC = 180°

⇒ x + x + ∠BOC = 180°

⇒ ∠BOC = 180° - 2x

In △AOC,

By angle sum property of triangle,

⇒ ∠BAC + ∠CBA + ∠ACB = 180°

⇒ ∠BAC + (30° + x) + (40° + x) = 180°

⇒ ∠BAC + 70° + 2x = 180°

⇒ ∠BAC = 180° - 70° - 2x

⇒ ∠BAC = 110° - 2x

We know that,

The angle which an arc subtends at the center is double that which it subtends at any point on the remaining part of the circumference.

∴ ∠BOC = 2∠BAC

⇒ 180° - 2x = 2(110° - 2x)

⇒ 180° - 2x = 220° - 4x

⇒ 4x - 2x = 220° - 180°

⇒ 2x = 40°

⇒ x = $\dfrac{40^{\circ}}{2}$ = 20°

⇒ ∠BOC = 180° - 2x

⇒ ∠BOC = 180° - 2(20°) = 180° - 40° = 140°.

Hence, option 4 is the correct option.

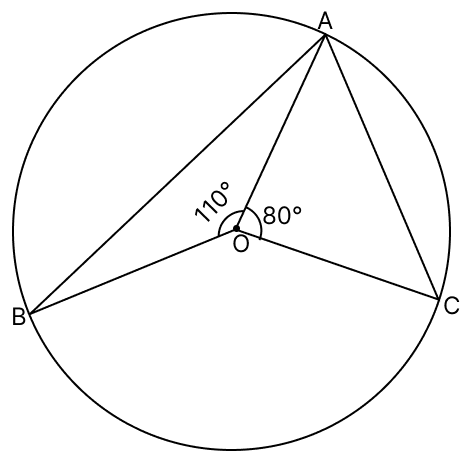
In the given figure, O is the centre of the circle.
If ∠AOB = 110° and ∠AOC = 80°, then ∠BAC = ?

1. 75°

2. 80°

3. 85°

4. 95°

Answer

From figure,

∠BOC = 360° - (∠AOB + ∠AOC)

∠BOC = 360° - (110° + 80°)

= 360° - 190°

= 170°.

We know that,

The angle which an arc subtends at the center is double that which it subtends at any point on the remaining part of the circumference.

∴ BOC = 2∠BAC

∴ ∠BAC = $\dfrac{1}{2}$ ∠BOC

= $\dfrac{170^{\circ}}{2}$ = 85°.

Hence, option 3 is the correct option.

In the given figure, O is the centre of the circle and ∠OPQ = 30°. Then, ∠PAQ = ?

1. 60°

2. 70°

3. 80°

4. 75°

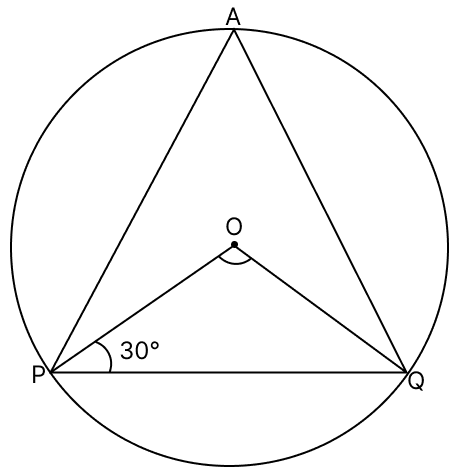
Answer

From figure,

OP = OQ (Radii of same circle)

∠OQP = ∠OPQ = 30° (As angles opposite to equal sides are equal)

In △POQ,

By angle sum property of triangle,

∠POQ + ∠OQP + ∠OPQ = 180°

∠POQ = 180° - ∠OQP - ∠OPQ

∠POQ = 180° - 30° - 30°

∠POQ = 120°.

We know that,

The angle which an arc subtends at the center is double that which it subtends at any point on the remaining part of the circumference.

∴ ∠POQ = 2∠PAQ

∴ ∠PAQ = $\dfrac{1}{2}$ ∠POQ

= $\dfrac{120^{\circ}}{2}$ = 60°.

Hence, option 1 is the correct option.

In the given figure, O is the centre of the circle and ∠AOB = 150°. Then, ∠ACB = ?

1. 75°

2. 105°

3. 85°

4. 115°

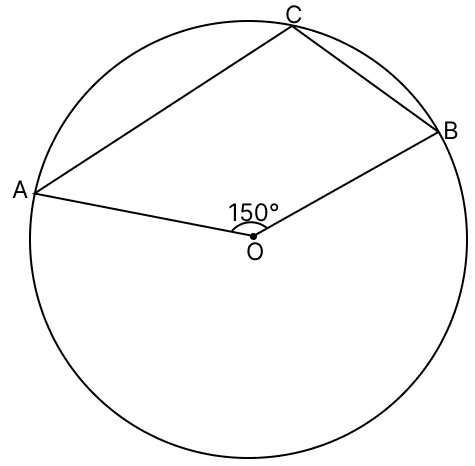
Answer

We know that,

The angle which an arc subtends at the center is double that which it subtends at any point on the remaining part of the circumference.

∴ ∠ACB = $\dfrac{1}{2}$ Reflex∠AOB

= $\dfrac{360^{\circ} - 150^{\circ}}{2}$ = 105°.

Hence, option 2 is the correct option.

In the given figure, ABCD is a cyclic quadrilateral. The measure of its greatest angle is :

1. 135°

2. 140°

3. 150°

4. 160°

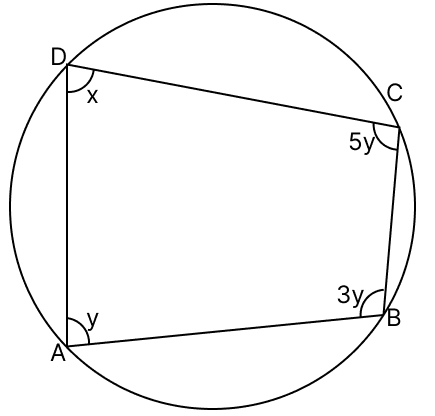
Answer

The sum of the opposite angles of a cyclic quadrilateral is 180°.

∠A + ∠C = 180°

y + 5y = 180°

6y = 180°

y = 30°

∠B + ∠D = 180°

3x + x = 180°

4x = 180°

x = 45°

∠A = y = 30°

∠C = 5y = 150°

∠D = x = 45°

∠B = 3x = 135°

Hence, option 3 is the correct option.

In the given figure, O is the centre of the circle.
If ∠PQR = 35°, then ∠POR is equal to :

1. 17.5°

2. 35°

3. 60°

4. 70°

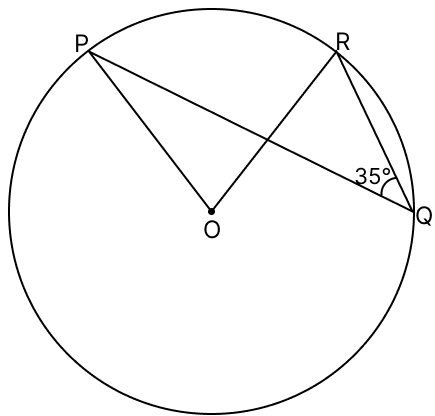
Answer

We know that,

The angle which an arc subtends at the center is double that which it subtends at any point on the remaining part of the circumference.

∴ ∠POR = 2∠PQR = 2 × 35° = 70°.

Hence, option 4 is the correct option.

In the given figure, O is the centre of the circle and ∠BDC = 36°. The measure of ∠ACB is :

1. 36°

2. 54°

3. 72°

4. 46°

Answer

We know that,

The angle which an arc subtends at the center is double that which it subtends at any point on the remaining part of the circumference.

∴ ∠BOC = 2∠BDC

∠BOC = 2(36°) = 72°

∠AOB + ∠BOC = 180°

∠AOB = 180° - ∠BOC

∠AOB = 180°- 72° = 108°

∴ ∠ACB = $\dfrac{1}{2}$ ∠AOB

∠ACB = $\dfrac{108^{\circ}}{2}$ = 54°.

Hence, option 2 is the correct option.

ABCD is a cyclic quadrilateral such that AC is a diameter of the circle. If ∠BAC = 58° and ∠DAC = 65°, then ∠BCD is equal to :

1. 57°

2. 123°

3. 90°

4. 60°

Answer

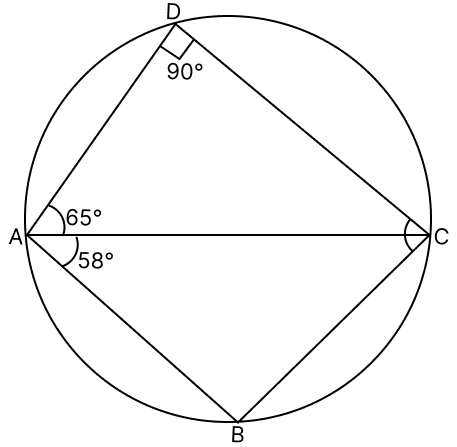
∠ADC = 90° and ∠ADC = 90° [Angle in semicircle is a right angle]

In △ABC,

∠BAC = 58°

∠ABC = 90°

By angle sum property of triangle,

∠BCA + ∠BAC + ∠ABC = 180°

∠BCA = 180° - (∠BAC + ∠ABC)

∠BCA = 180° - (90° + 58°) = 32°

In △ABC :

∠DAC = 65° and ∠ADC = 90°

By angle sum property of triangle,

∠DCA + ∠DAC + ∠ADC = 180°

∠DCA = 180° - (∠DAC + ∠ADC)

∠DCA = 180° - (90° + 65°) = 25°

From figure,

∠BCD = ∠DCA + ∠BCA = 32° + 25° = 57°.

Hence, option 1 is the correct option.

The angle formed in a minor segment of a circle is :

1. an acute angle

2. an obtuse angle

3. a right angle

4. either an acute or an obtuse angle

Answer

A minor segment is the smaller of the two regions created when a chord divides a circle. The corresponding arc is the minor arc.

The angle formed in a minor segment of a circle is an obtuse angle.

Hence, option 2 is the correct option.

The angle formed in a major segment of a circle is :

1. an acute angle

2. an obtuse angle

3. a right angle

4. either an acute or an obtuse angle

Answer

A major segment is the larger of the two regions created when a chord divides a circle. The corresponding arc is the major arc.

The angle formed in a major segment of a circle is an acute angle.

Hence, option 1 is the correct option.

An equilateral triangle ABC is inscribed in a circle with centre O. The measure of ∠BOC is :

1. 120°

2. 60°

3. 90°

4. 30°

Answer

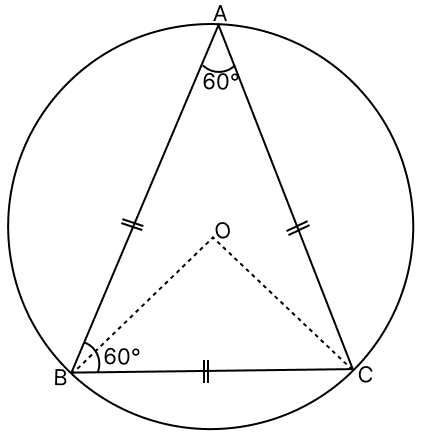
In equilateral triangle ABC,

∠BAC = 60°

We know that,

The angle which an arc subtends at the center is double that which it subtends at any point on the remaining part of the circumference.

∴ ∠BOC = 2∠BAC = 2(60°) = 120°.

Hence, option 1 is the correct option.

If two diameters of a circle intersect each other at right angles, then the quadrilateral formed by joining their end points is a :

1. rhombus

2. square

3. rectangle

4. parallelogram

Answer

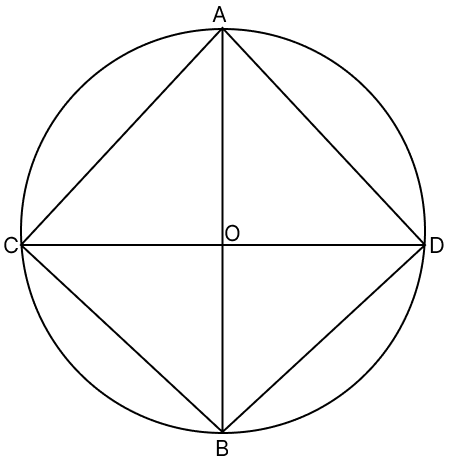
Let the two diameters AB and CD intersect at the centre O at right angles.

The quadrilateral formed by joining the end points in order is ACBD.

In ΔAOC, ΔCOB, ΔBOD, ΔDOA , we have two sides which are radii and an included angles as 90°. Therefore, by SAS theorem, all triangles are congruent.

Thus, all four sides are equal AC = CB = BD = DA.

Each interior angle of the quadrilateral (e.g., ∠ACB) is an angle inscribed in a semicircle. Thus, each interior angle equals to 90°.

A quadrilateral with all sides equal, and all angles equal to 90° is a square.

Hence, option 2 is the correct option.

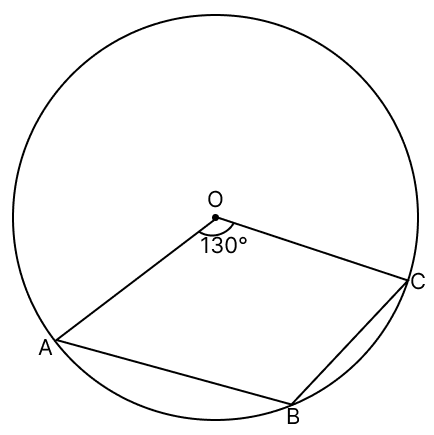
In the given figure, O is the centre of the circle such that ∠AOC = 130°, then ∠ABC is equal to :

1. 65°

2. 90°

3. 105°

4. 115°

Answer

Reflex ∠AOC = 360° - 130° = 230°

We know that,

The angle which an arc subtends at the center is double that which it subtends at any point on the remaining part of the circumference.

∴ ∠ABC = $\dfrac{1}{2}$ Reflex ∠AOC

∠ABC = $\dfrac{230^{\circ}}{2}$ = 115°.

Hence, option 4 is the correct option.

A chord of a circle is equal to its radius. The angle subtended by this chord at the minor arc of the circle is :

1. 60°

2. 90°

3. 120°

4. 150°

Answer

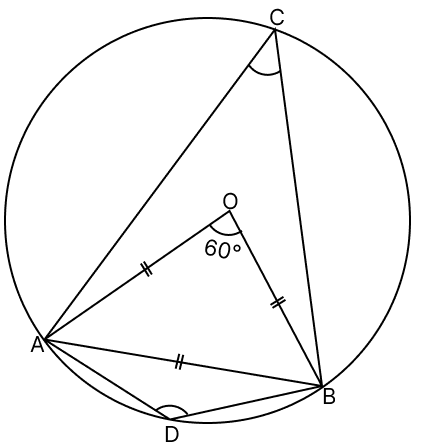
If chord length AB = radius(OA, OB), then the triangle OAB formed by two radii and the chord is equilateral.

Central angle subtended by the chord = ∠AOB = 60°

∠ACB = $\dfrac{1}{2}$ ∠AOB = $\dfrac{1}{2}$ (60°) = 30°.

Opposite angles of a cyclic quadrilateral ADBC are supplementary.

∠ACB + ∠ADB = 180°

∠ADB = 180° - 30°

∠ADB = 150°.

Thus, angle subtended by this chord at the minor arc of the circle is 150°.

Hence, option 4 is the correct option.

ABCD is a cyclic quadrilateral such that ∠ADB = 45° and ∠DCA = 55°, then ∠DAB is equal to :

1. 55°

2. 45°

3. 100°

4. 80°

Answer

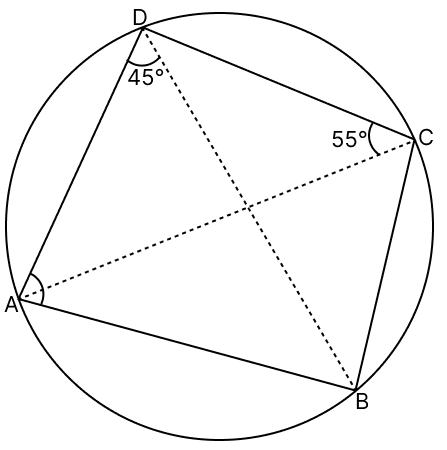
∠ACB = ∠ADB = 45° [Angles in the same segment]

From figure,

∠BCD = ∠ACD + ∠ACB

∠BCD = 55° + 45° = 100°

In a cyclic quadrilateral, the sum of opposite angles is 180°.

∠DAB + ∠BCD = 180°

∠DAB = 180° - ∠BCD

∠DAB = 180° - 100° = 80°.

Hence, option 4 is the correct option.

In the given figure, if ∠ACD = 30° and ∠BPD = 100°, then ∠CDB is equal to :

1. 30°

2. 40°

3. 50°

4. 60°

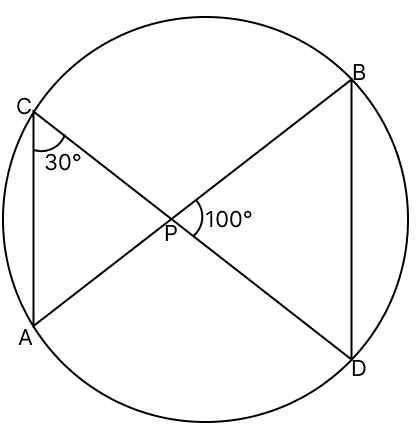
Answer

∠ABD = ∠ACD = 30° [Angles in the same segment]

From figure,

∠PBD = ∠ABD = 30°

In ΔPBD,

By angle sum property,

∠PBD + ∠BPD + ∠PDB = 180°

30° + 100° + ∠PDB = 180°

∠PDB = 180° - 130°

∠PDB = 50°.

From figure,

∠CDB = ∠PDB = 50°.

Hence, option 3 is the correct option.

If an arc of a circle subtends a right angle at any point on the remaining part of the circle, then the arc is a :

1. minor arc

2. major arc

3. semi-circle

4. none of these

Answer

An angle subtended by an arc at a point on the remaining part of the circle is an angle at the circumference.

An angle in a semicircle is a right angle.

Hence, option 3 is the correct option.

ABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and ∠ADC = 125°, then ∠BAC is equal to :

1. 35°

2. 40°

3. 45°

4. 55°

Answer

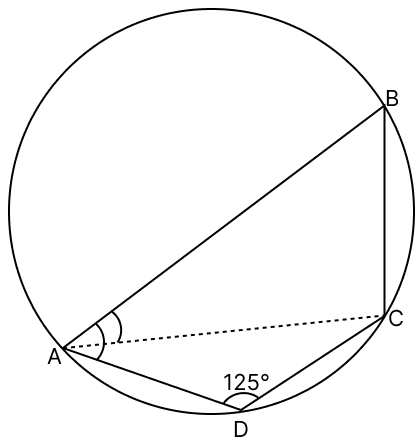
Opposite angles of a cyclic quadrilateral are supplementary.

So,

∠ABC + ∠ADC = 180°

∠ABC = 180° − 125° = 55°.

∠ACB = 90° [Angle in semicircle is a right angle]

In △ABC,

By angle sum property of triangle,

∠BAC + ∠ABC + ∠ACB = 180°

∠BAC + 55° + 90° = 180°

∠BAC = 180° − 145° = 35°.

Hence, option 1 is the correct option.

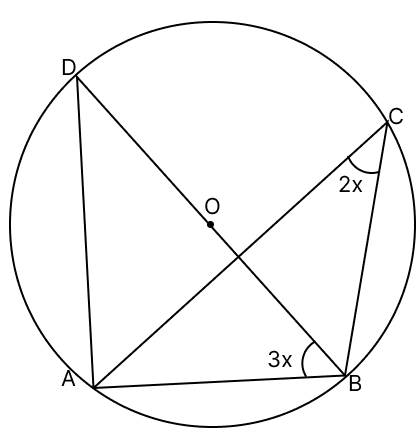
In the given figure, if O is the centre of the circle, then the value of x is :

1. 15°

2. 18°

3. 20°

4. 24°

Answer

From figure,

∠DAB = 90° [Angle in the semicircle is a right angle]

In the figure, both ∠ADB and ∠ACB are subtended by the same arc AB. Therefore:

∠ADB = ∠ACB = 2x

In triangle ADB,

∠DAB + ∠ADB + ∠ABD = 180°

90° + 2x + 3x = 180°

5x = 90°

x = 18°.

Hence, option 2 is the correct option.

In the given figure, O is the centre of the circle.
If the length of chord AB is equal to the radius of the circle; then ∠ACB is equal to :

1. 30°

2. 45°

3. 60°

4. 40°

Answer

If the length of chord AB is equal to the radius of the circle; then △AOB is equilateral triangle.

∠AOB = 60°

We know that,

The angle which an arc subtends at the center is double that which it subtends at any point on the remaining part of the circumference.

∴ ∠ACB = $\dfrac{1}{2}$ ∠AOB

∠ACB = $\dfrac{60^{\circ}}{2}$ = 30°.

Hence, option 1 is the correct option.

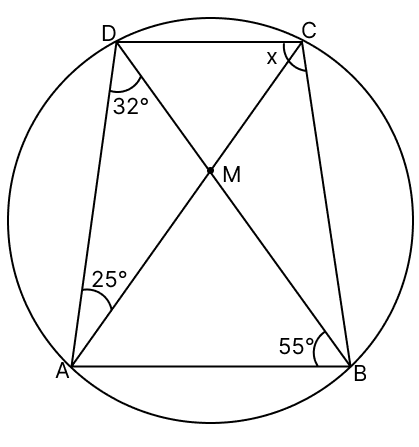
The value of x in the following figure is :

1. 80°

2. 57°

3. 87°

4. 96°

Answer

Arc AD subtends ∠ABD and ∠ACD. Therefore,

∠ABD = ∠ACD = 55° [From Figure]

Arc AB subtends ∠BCA and ∠BDA. Therefore,

∠BCA = ∠BDA = 32° [From Figure]

From figure,

∠BCD = ∠BCA + ∠ACD

∠BCD = 32° + 55°

∠BCD = 87°.

Hence, option 3 is the correct option.

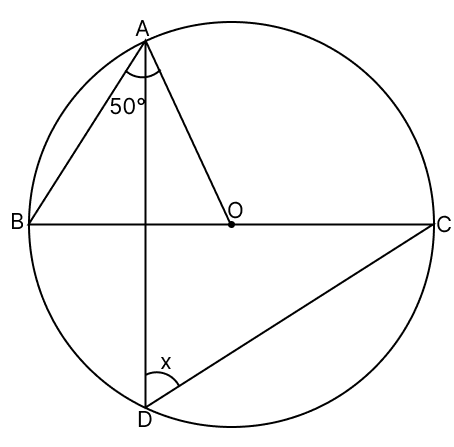
In the given figure, if O is the centre of the circle, then the value of x is :

1. 40°

2. 50°

3. 70°

4. 30°

Answer

Join AC and BD.

∠BDC = 90° (Angle in semicircle is right angle)

OA = OB (Radii of same circle)

∠OBA = ∠OAB = 50° (Angles opposite to equal sides are equal in a triangle)

In triangle OAB,

∠AOB + ∠OAB + ∠OBA = 180°

∠AOB = 180° - (∠OAB + ∠OBA)

∠AOB = 180° - (50° + 50°)

∠AOB = 80°.

The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.

∠ACB = $\dfrac{1}{2}$ ∠AOB

∠ACB = $\dfrac{80°}{2}$

∠ACB = 40°

∠ADB = ∠ACB = 40° [Angle in same segment are equal]

From figure,

∠BDC = ∠ADB + x

90° = 40° + x

x = 50°.

Hence, option 2 is the correct option.

In the given figure, O is centre of the circle.
If ∠AOC = 130°, then the value of x is :

1. 25°

2. 50°

3. 65°

4. 40°

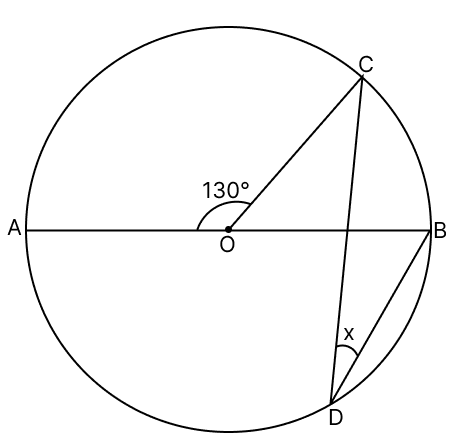
Answer

Join AD.

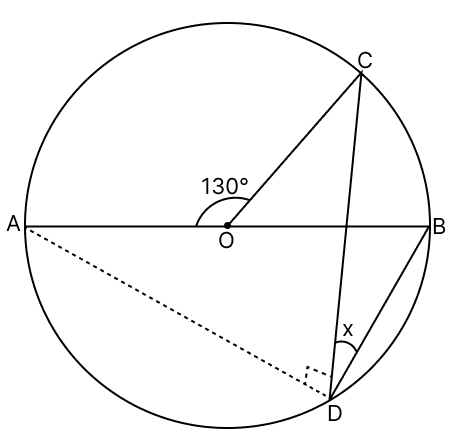
∠AOC = 130°

∠ADB = 90°

We know that,

The angle which an arc subtends at the center is double that which it subtends at any point on the remaining part of the circumference.

∴ ∠ADC = $\dfrac{1}{2}$ ∠AOC

∠ADC = $\dfrac{130^{\circ}}{2}$ = 65°

At point D,

∠ADB = ∠ADC + ∠CDB

90° = 65° + x

x = 25°

Hence, option 1 is the correct option.

In the given figure, O is the centre of the circle, ∠AOB = 40° and ∠BDC = 100°. The measure of ∠OBC is :

1. 40°

2. 80°

3. 60°

4. 20°

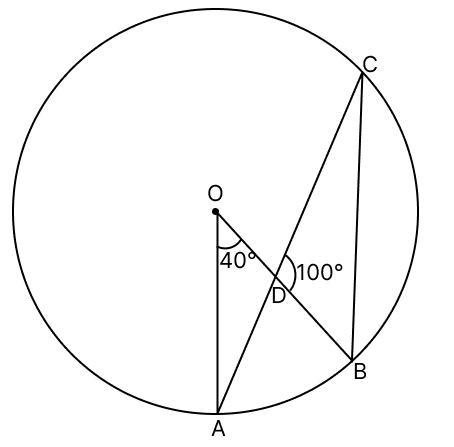
Answer

We know that,

The angle subtended by an arc at the center is double the angle subtended by it at any point on the remaining part of the circle.

∴ ∠ACB = $\dfrac{1}{2}$ ∠AOB

∠ACB = $\dfrac{40^{\circ}}{2}$ = 20°

In ΔBDC, the sum of all angles is 180°

∠OBC + ∠BDC + ∠ACB = 180°

∠OBC + 100° + 20° = 180°

∠OBC = 180° - 120°

∠OBC = 60°

Hence, option 3 is the correct option.

ABCD is a cyclic quadrilateral. If ∠BAD = (2x + 5)° and ∠BCD = (x + 10)°, then x is equal to :

1. 65°

2. 45°

3. 55°

4. 5°

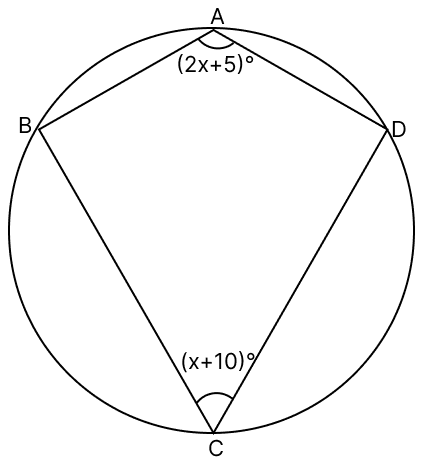
Answer

In a cyclic quadrilateral, opposite angles are supplementary.

Since ∠BAD and ∠BCD are opposite angles,

(2x + 5)° + (x + 10)° = 180°

3x + 15 = 180°

3x = 165°

x = 55°

Hence, option 3 is the correct option.

Assertion (A): In the given figure, if O is the centre of the circle, then ∠ACB = 40°.

Reason (R): Angle at the centre is double the angle at the remaining part of the circle.

1. A is true, R is false

2. A is false, R is true

3. Both A and R are true

4. Both A and R are false

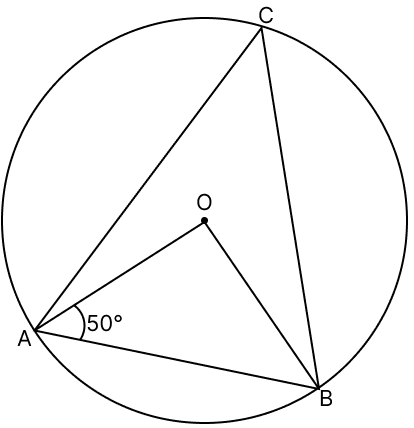
Answer

From figure,

OA = OB (Radii of same circle)

∠OBA = ∠OAB = 50° (As angles opposite to equal sides in a triangle are equal)

∠OBA + ∠OAB + ∠AOB = 180° [Angle sum property of a triangle]

50° + 50° + ∠AOB = 180°

100° + ∠AOB = 180°'

∠AOB = 180° - 100°

∠AOB = 80°.

We know that,

Angle which an arc subtends at the center is double that which it subtends at any point on the remaining part of the circumference.

So, reason (R) is true.

∠AOB = 2∠ACB

∠ACB = $\dfrac{80°}{2}$ = 40°.

So, Assertion (A) is true.

Both A and R are true.

Hence, option 3 is the correct option.

Assertion (A): In the figure, ∠ACB = 70°.

Reason (R): Opposite angles of a cyclic quadrilateral are equal.

1. A is true, R is false

2. A is false, R is true

3. Both A and R are true

4. Both A and R are false

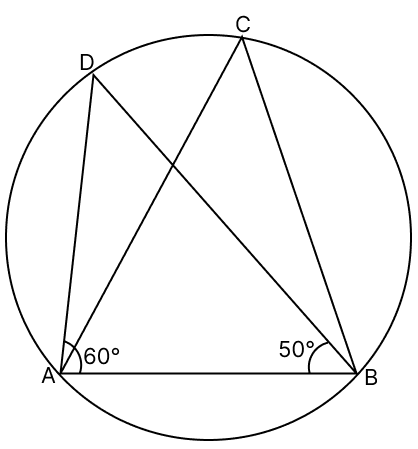
Answer

In triangle ABD,

∠DAB = 60°

∠DBA = 50°

From figure,

⇒ ∠DAB + ∠DBA + ∠ADB = 180° [Angle sum property of a triangle]

⇒ 60° + 50° + ∠ADB = 180°

⇒ 110° + ∠ADB = 180°

⇒ ∠ADB = 180° - 110°

⇒ ∠ADB = 70°

Angle in same segment are equal.

∠ADB = ∠ACB = 70°

So, assertion (A) is true.

We know that,

In cyclic quadrilateral opposite angles are supplementary (sum = 180°), not equal.

So, reason (R) is false.

A is true, R is false.

Hence, option 1 is the correct option.

Assertion (A): In the figure, if AB is a diameter of the circle, then ∠BAC = 50°.

Reason (R): Sum of two angles of a cyclic quadrilateral is always 180°.

1. A is true, R is false

2. A is false, R is true

3. Both A and R are true

4. Both A and R are false

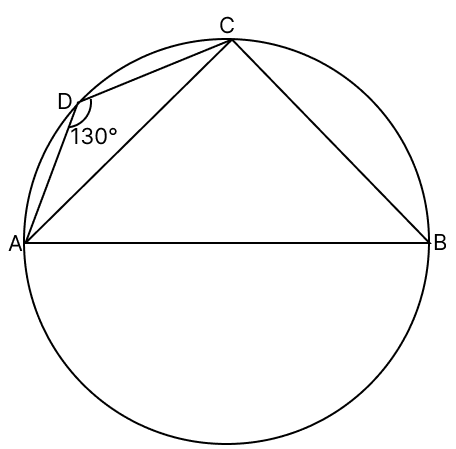
Answer

In △ABC,

∠BCA = 90° [Angle in the semicircle]

Since ABCD is cyclic quadrilateral the sum of opposite angles is 180°,

∠ADC + ∠ABC = 180°

∠ABC = 180° - 130°

∠ABC = 50°

In triangle ABC,

∠ABC + ∠BAC + ∠ACB = 180°

∠BAC = 180° - (∠ABC + ∠ACB)

∠BAC = 180° - (50° + 90°)

∠BAC = 40°.

So, assertion (A) is false.

We know that,

Sum of opposite angles of a cyclic quadrilateral is always 180°. But the sum of two angles of a cyclic quadrilateral is not always 180°.

So, reason (R) is false.

A is false, R is false.

Hence, option 4 is the correct option.

Assertion (A): In the figure, if O is the centre of the circle, then ∠BCD = 80°.

Reason (R): Exterior angle of a cyclic quadrilateral is equal to the interior opposite angle.

1. A is true, R is false

2. A is false, R is true

3. Both A and R are true

4. Both A and R are false

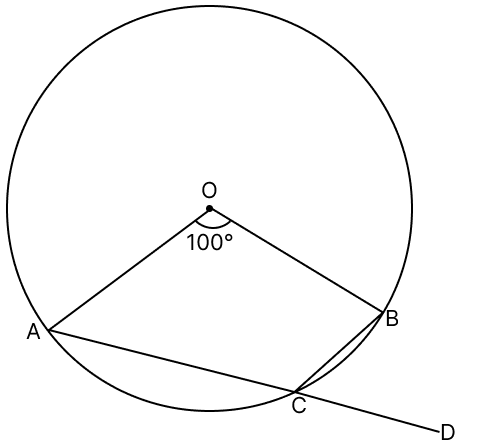
Answer

From figure,

The angle subtended by an arc at the center is double the angle subtended by it at any point on the remaining part of the circle.

Reflex AOB = 360° - 100° = 260°

∠ACB = $\dfrac{1}{2}$ Reflex ∠AOB

∠ACB = $\dfrac{260 ^{\circ}}{2}$

∠ACB = 130°

∠ACB + ∠BCD = 180° [Linear pair]

∠BCD = 180° - 130°

∠BCD = 50°

So assertion (A) is false.

We know that,

In, cyclic quadrilaterals if one side is extended, the exterior angle formed is equal to the interior opposite angle.

So, reason (R) is true.

A is false, R is true

Hence, option 2 is the correct option.