Tangent Properties of Circles

Find the length of the tangent drawn to a circle of radius 8 cm, from a point which is at a distance of 10 cm from the centre of the circle.

Answer

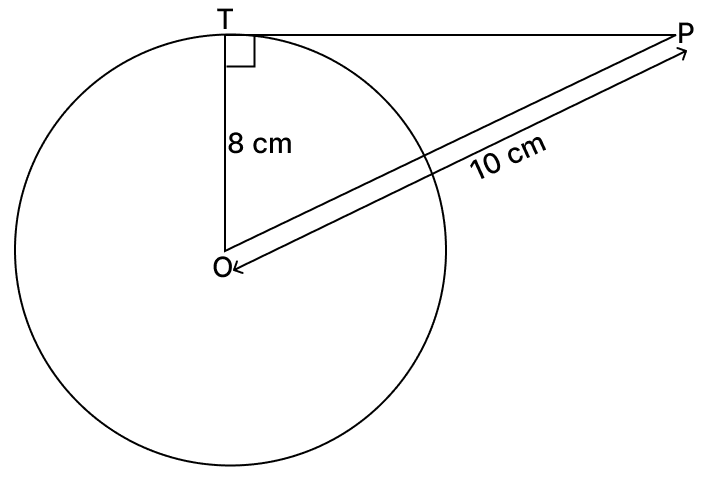
Consider a circle with centre O and radius 8 cm.

Let P be an external point from where a tangent is drawn to meet the circle at T. Join OT.

∴ OP = 10 cm and OT = 8 cm

We know that,

The tangent at any point of a circle and the radius through this point are perpendicular to each other.

In right angled ∆OTP, we have

⇒ OP² = OT² + PT²

⇒ 10² = 8² + PT²

⇒ PT² = 100 - 64 = 36

⇒ PT = 6 cm

Hence, the length of tangent = 6 cm.

A point P is 17 cm away from the centre of the circle and the length of the tangent drawn from P to the circle is 15 cm. Find the radius of the circle.

Answer

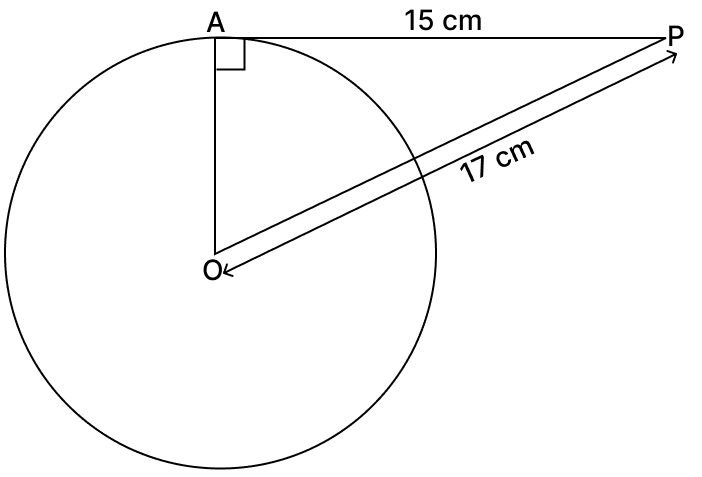
Consider a circle with centre O,

Let P be an external point from where a tangent is drawn to meet the circle at A.

∴ OP = 17 cm and AP = 15 cm

We know that,

The tangent at any point of a circle and the radius through this point are perpendicular to each other.

In right angled ∆OAP, we have

⇒ OP² = OA² + AP²

⇒ 17² = OA² + 15²

⇒ 289 = OA² + 225

⇒ OA² = 289 - 225

⇒ OA² = 64

⇒ OA = $\sqrt{64}$

⇒ OA = 8 cm

Hence, the radius of circle is 8 cm.

There are two concentric circles, each with centre O and of radii 10 cm and 26 cm respectively. Find the length of the chord AB of the outer circle which touches the inner circle at P.

Answer

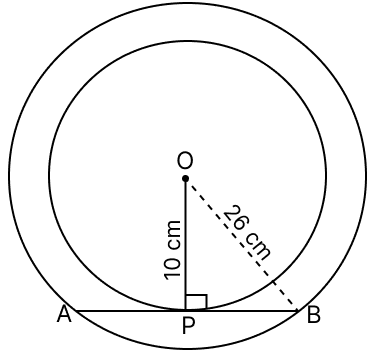
AB is the chord of the outer circle which touches the inner circle at P.

OP is the radius of the inner circle and APB is the tangent to the inner circle.

In the right angled triangle OPB, by pythagoras theorem,

⇒ OB² = OP² + PB²

⇒ 26² = 10² + PB²

⇒ 676 = 100 + PB²

⇒ PB² = 676 - 100

⇒ PB² = 576

⇒ PB = $\sqrt{576}$

⇒ PB = 24 cm

As perpendicular line from centre bisects the chord of the circle so,

AP = PB = 24 cm.

AB = AP + PB = 24 + 24 = 48 cm.

Hence, the length of chord (AB) = 48 cm.

A and B are centres of circles of radii 9 cm and 2 cm such that AB = 17 cm and C is the centre of the circle of radius r cm which touches the above circles externally. If ∠ACB = 90°, write an equation in r and solve it.

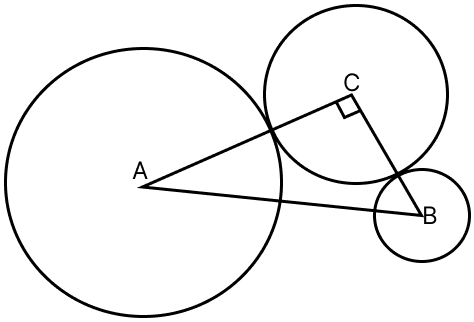
Answer

From figure,

In △ABC,

By pythagoras theorem,

⇒ AB² = AC² + BC²

⇒ 17² = (r + 9)² + (r + 2)²

⇒ 289 = r² + 81 + 18r + r² + 4 + 4r

⇒ 289 = 2r² + 85 + 22r

⇒ 2r² + 22r + 85 - 289 = 0

⇒ 2r² + 22r - 204 = 0

⇒ 2(r² + 11r - 102) = 0

⇒ r² + 11r - 102 = 0

⇒ r² + 17r - 6r - 102 = 0

⇒ r(r + 17) - 6(r + 17) = 0

⇒ (r - 6)(r + 17) = 0

⇒ r - 6 = 0 or r + 17 = 0

⇒ r = 6 or r = -17.

Since, radius cannot be negative.

⇒ r = 6 cm.

Hence, equation is r² + 11r - 102 = 0 and r = 6 cm.

Two circles touch each other externally at a point C and P is a point on the common tangent at C. If PA and PB are tangents to the two circles, prove that PA = PB.

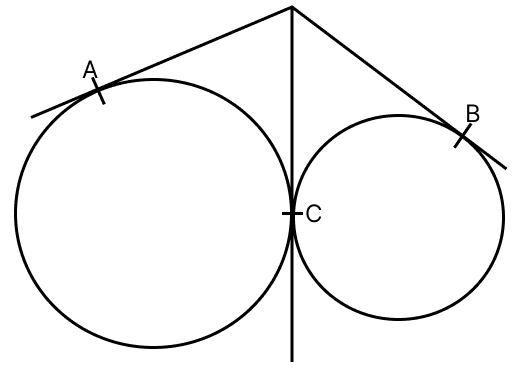
Answer

The tangents from a point outside the circle are equal.

The point P is also external to the right circle. The segments PB and PC are tangents drawn from P to this circle.

PB = PC .........(1)

The point P is external to the left circle. The segments PA and PC are tangents drawn from P to this circle.

PA = PC .........(2)

From (1) and (2), we get :

∴ PA = PB.

Hence, proved that PA = PB.

Two circles touch each other internally. Prove that the tangents drawn to the two circles from any point on the common tangent are equal in length.

Answer

As tangents drawn from an external point to a circle are equal in length.

From T, TA and TP are tangents to the circle with centre O.

TA = TP .....(1)

From T, TB and TP are tangents to the circle with centre O'.

TB = TP ........(2)

From (1) and (2),

TA = TB.

Hence, proved that tangents drawn to two circles from any point on common tangent are equal in length.

Two circles of radii 18 cm and 8 cm touch externally. Find the length of a direct common tangent to the two circles.

Answer

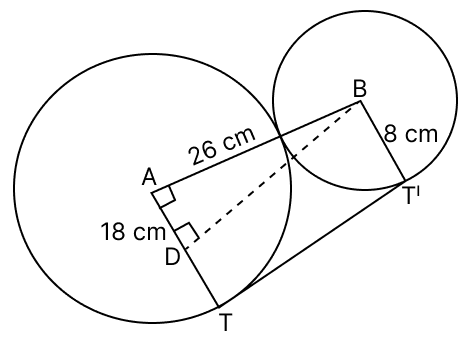
Let there be two circles with centre A and B with radius 18 cm and 8 cm respectively.

Let TT' be the length of common tangent.

Construct a right-angled triangle Δ ADB by drawing a line from center B parallel to TT' to intersect radius AT at D.

From figure,

DT = BT' = 8cm.

AD = AT - DT = 18 - 8 = 10 cm.

AB = 18 + 8 = 26 cm

In right angled triangle ADB,

⇒ AB² = AD² + DB²

⇒ 26² = 10² + DB²

⇒ 676 = 100 + DB²

⇒ DB² = 676 - 100

⇒ DB² = 576

⇒ DB = 24 cm

Since, TDBT' is a rectangle,

So, TT' = DB = 24 cm.

Hence, the length of direct common tangent is 24 cm.

Two circles of radii 8 cm and 3 cm have their centres 13 cm apart. Find the length of a direct common tangent to the two circles.

Answer

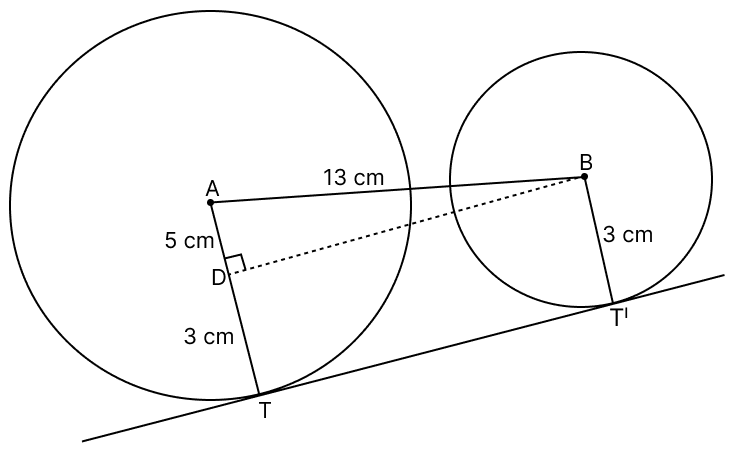
Let there be two circles with centre A and B with radius 8 cm and 3 cm respectively.

Let TT' be the length of common tangent.

Construct a right-angled triangle ΔADB by drawing a line from center B parallel to TT' to intersect radius AT at D.

From figure,

DT = BT' = 3cm.

AD = AT - DT = 8 - 3 = 5 cm.

In right angled triangle ADB,

⇒ AB² = AD² + DB²

⇒ 13² = 5² + DB²

⇒ DB² = 13² - 5²

⇒ DB² = 169 - 25

⇒ DB² = 144

⇒ DB = 12 cm

Since, TDBT' is a rectangle,

So, TT' = DB = 12 cm.

Hence, the length of direct common tangent is 12 cm.

Two circles of radii 8 cm and 3 cm have a direct common tangent of length 10 cm. Find the distance between their centres, up to two places of decimal.

Answer

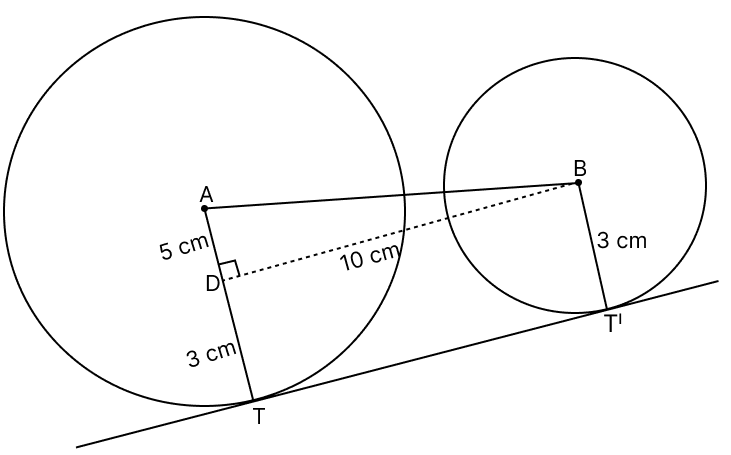
Let there be two circles with centre A and B with radius 8 cm and 3 cm respectively.

Let TT' be the length of common tangent.

Construct a right-angled triangle Δ ADB by drawing a line from center B parallel to TT' to intersect radius AT at D.

From figure,

⇒ TT' = BD = 10 cm

⇒ DT = BT' = 3 cm.

⇒ AD = AT - DT = 8 - 3 = 5 cm.

In right angled triangle ADB,

⇒ AB² = AD² + DB²

⇒ AB² = 10² + 5²

⇒ AB² = 100 + 25

⇒ AB² = 125

⇒ AB = $\sqrt{125}$

⇒ AB = 11.18 cm.

Hence, the distance between the centres 11.18 cm.

With the vertices of Δ PQR as centres, three circles are described, each touching the other two externally. If the sides of the triangle are 7 cm, 8 cm and 11 cm, find the radii of the three circles.

Answer

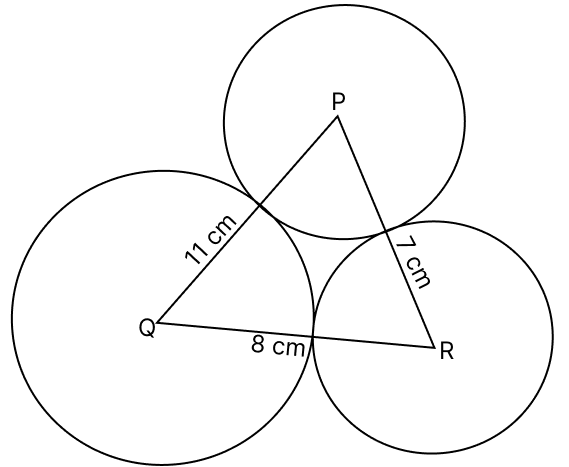
Let radius of circles with center P, Q and R be r₁, r₂ and r₃.

⇒ PQ = r₁ + r₂ = 7 …………(1)

⇒ PR = r₁ + r₃ = 8 …………(2)

⇒ QR = r₂ + r₃ = 11 ………….(3)

Adding all the above equations, we get

⇒ r₁ + r₂ + r₁ + r₃ + r₂ + r₃ = 7 + 8 + 11

⇒ 2(r₁ + r₂ + r₃) = 26

⇒ r₁ + r₂ + r₃ = $\dfrac{26}{2}$ ​ ⇒ r₁ + r₂ + r₃ = 13 cm ………..(4)

Substituting value of r₂ + r₃ = 11 in equation (4) we get :

⇒ r₁ + 11 = 13

⇒ r₁ = 13 - 11

⇒ r₁ = 2 cm.

Substituting value of r₁ + r₂ = 7 in equation (4) we get :

⇒ 7 + r₃ = 13

⇒ r₃ = 13 - 7

⇒ r₃ = 6 cm.

Substituting value of r₁ + r₃ = 8 in equation (4) we get :

⇒ 8 + r₂ = 13

⇒ r₂ = 13 - 8

⇒ r₂ = 5 cm.

Hence, the radii of the circles with center P, Q and R are 2 cm, 5 cm and 6 cm.

ΔABC is a right-angled triangle in which ∠A = 90°, AC = 12 cm and BC = 13 cm. A circle with centre O has been inscribed inside the triangle. Calculate the value of x, the radius of the inscribed circle.

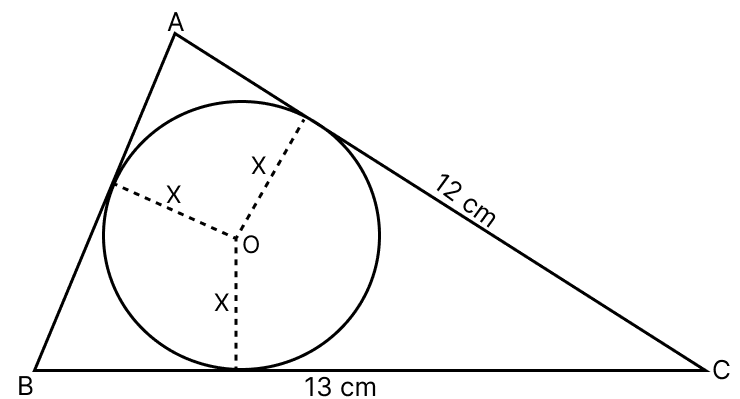
Answer

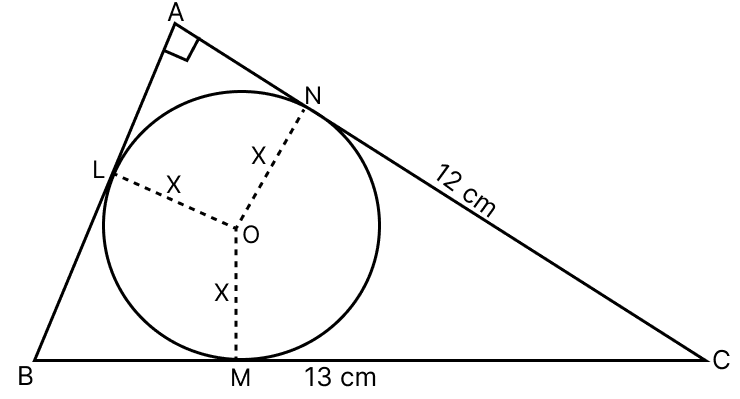
Let AB touches the circle at L, AC at N and BC at M.

From figure,

ANLO is a square

AL = LO = ON = AN = x

NC = AC - AN = (12 - x) cm

NC = MC = (12 - x) cm [∵ Tangents from exterior point are equal in length.]

Since, ABC is a right angled triangle,

∴ BC² = AC² + AB² [By pythagoras theorem]

⇒ 13² = 12² + AB²

⇒ AB² = 13² - 12²

⇒ AB² = 169 - 144

⇒ AB² = 25

⇒ AB = $\sqrt{25}$

⇒ AB = 5 cm.

From figure,

LB = AB - AL = (5 - x) cm.

LB = BM = (5 - x) cm.[∵ Tangents from exterior point are equal in length.]

Then,

⇒ BC = BM + CM

⇒ 13 = (5 - x) + (12 - x)

⇒ 13 = 17 - 2x

⇒ 2x = 17 - 13

⇒ 2x = 4

⇒ x = $\dfrac{4}{2}$

⇒ x = 2 cm.

Hence, x = 2 cm.

PQR is a right-angled triangle with PQ = 3 cm and QR = 4 cm. A circle which touches all the sides of the triangle is inscribed in the triangle. Calculate the radius of the circle.

Answer

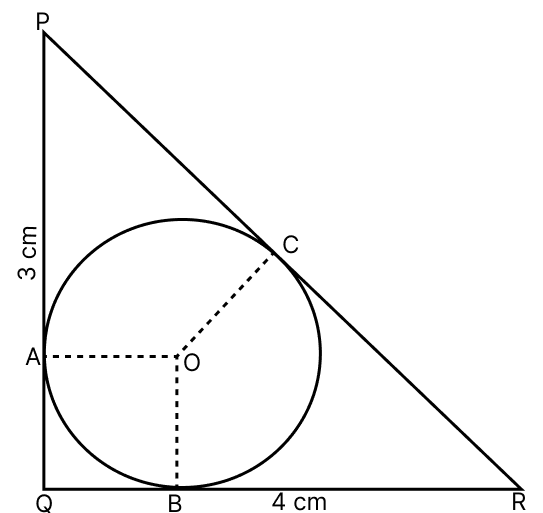
Let the inscribed circle touch the sides PQ, QR and PR at A, B and C respectively.

PQR is a right-angled triangle with PQ = 3 cm and QR = 4 cm.

By pythagoras theorem,

⇒ PR² = PQ² + QR²

⇒ PR² = 3² + 4²

⇒ PR² = 9 + 16

⇒ PR² = 25

⇒ PR = 5 cm.

By tangent property we have,

∠OAQ = ∠OBQ = 90°

∠AQB = 90°

Since, all the angles of OAQB equals to 90°.

From figure,

OAQB is a square.

OA = OB = AQ = BQ = x (let)

PA = PQ - AQ = (3 - x) cm

PA = PC = (3 - x) cm.[∵ Tangents from exterior point are equal in length.]

RB = RQ - QB = (4 - x) cm

RC = RB = (4 - x) cm.[∵ Tangents from exterior point are equal in length.]

PR = PC + RC = 3 - x + 4 - x = 7 - 2x

5 = 7 - 2x

2x = 7 - 5

2x = 2

x = 1 cm.

Hence, radius of the circle inscribed in the triangle equals to 1 cm.

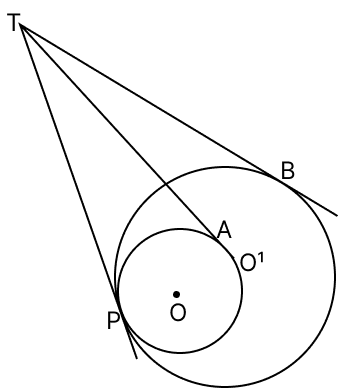
In the given figure, O is the centre of each one of two concentric circles of radii 4 cm and 6 cm respectively. PA and PB are tangents to outer and inner circle respectively. If PA = 10 cm, find the length of PB, upto two places of decimal.

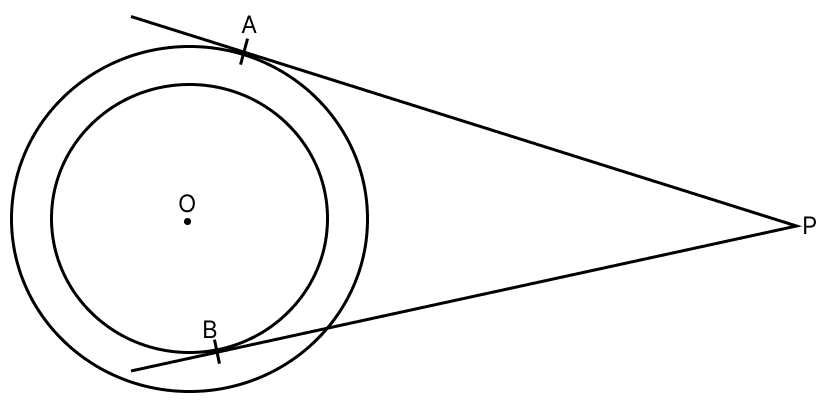
Answer

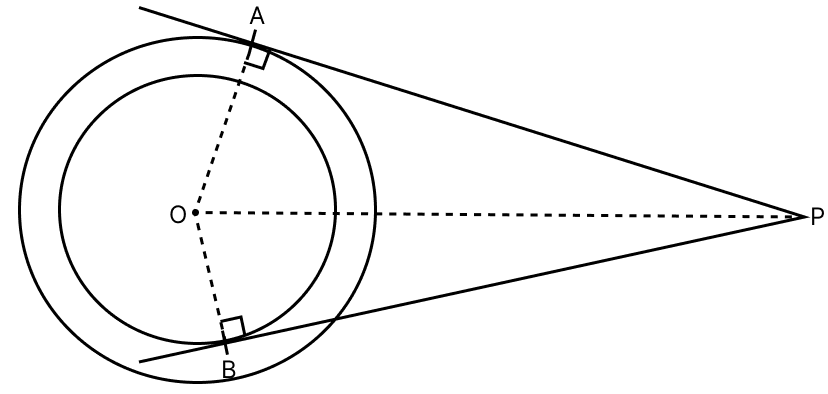
Given,

O is the centre of two concentric circles of radii OA = 6 cm and OB = 4 cm.

PA and PB are the two tangents to the outer and inner circles respectively and PA = 10 cm.

We know that,

The tangent at any point of a circle and the radius through this point are perpendicular to each other.

∠OAP = ∠OBP = 90°

Since, OAP is a right angled triangle,

∴ OP² = OA² + PA² [By pythagoras theorem]

⇒ OP² = 6² + 10²

⇒ OP² = 36 + 100

⇒ OP² = 136

⇒ OP = $\sqrt{136}$

Since, OBP is a right angled triangle,

⇒ OP² = OB² + PB²

⇒ PB² = OP² - OB²

⇒ PB² = $(\sqrt{136})^2 - 4^2$

⇒ PB² = 136 - 16

⇒ PB² = 120

⇒ PB = $\sqrt{120}$

⇒ PB = 10.95 cm

Hence, length of PB is 10.95 cm.

In the given figure, ΔABC is circumscribed. The circle touches the sides AB, BC and CA at P, Q, R respectively. If AP = 5 cm, BP = 7 cm, AC = 14 cm and BC = x cm, find the value of x.

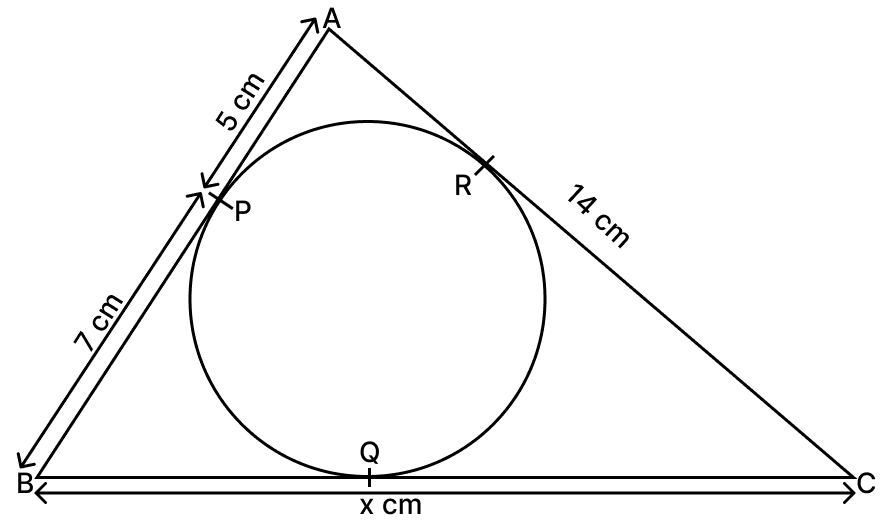
Answer

We know that,

Tangents from an exterior point to a circle are equal in length.

From A,

⇒ AP = AR = 5 cm

From figure,

⇒ AC = AR + RC

⇒ 14 = 5 + RC

⇒ RC = 14 - 5 = 9 cm

From B,

BP = BQ = 7 cm

From C,

CQ = CR = 9 cm

From figure,

⇒ BC = BQ + QC = 7 + 9 = 16 cm

⇒ x = 16 cm.

Hence, x = 16 cm.

In the given figure, quadrilateral ABCD is circumscribed. The circle touches the sides AB, BC, CD and DA at P, Q, R, S respectively. If AP = 9 cm, BP = 7 cm, CQ = 5 cm and DR = 6 cm, find the perimeter of quadrilateral ABCD.

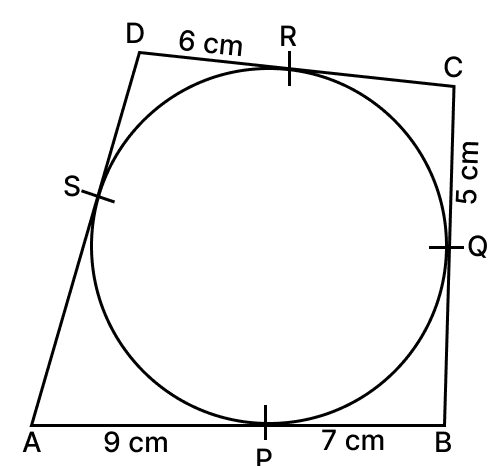
Answer

We know that,

Tangents from an exterior point to a circle are equal in length.

From A,

AP = AS = 9 cm

From B,

BP = BQ = 7 cm

From C,

CQ = CR = 5 cm

From D,

DR = DS = 6 cm

From figure,

⇒ AB = AP + PB = 9 + 7 = 16 cm

⇒ BC = BQ + QC = 7 + 5 = 12 cm

⇒ CD = CR + RD = 5 + 6 = 11 cm

⇒ DA = AS + SD = 9 + 6 = 15 cm

Perimeter of ABCD = AB + BC + CD + DA

= 16 + 12 + 11 + 15

= 54 cm.

Hence, perimeter of ABCD = 54 cm.

In the given figure, the circle touches the sides AB, BC, CD and DA of a quadrilateral ABCD at the points P, Q, R and S respectively. If AB = 11 cm, BC = x cm, CR = 4 cm and AS = 6 cm, find the value of x.

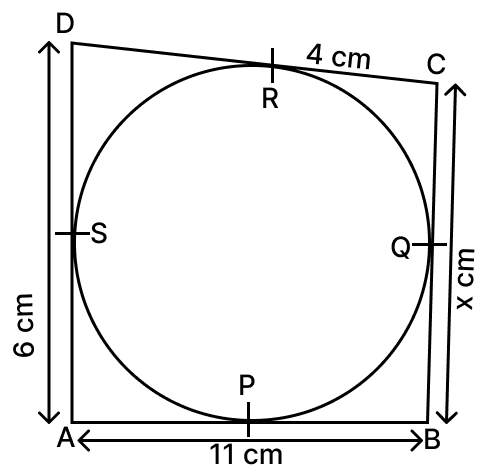
Answer

We know that,

Tangents from an exterior point to a circle are equal in length.

From A,

⇒ AP = AS = 6 cm

From C,

⇒ CR = CQ = 4 cm

⇒ BP = AB - AP = 11 - 6 = 5 cm.

From B,

⇒ BQ = BP = 5 cm

From figure,

BC = BQ + CQ = 5 + 4 = 9 cm

x = 9 cm

Hence, x = 9 cm.

In the given figure, a circle touches the side BC of ΔABC at P and AB and AC produced at Q and R respectively. If AQ = 15 cm, find the perimeter of ΔABC.

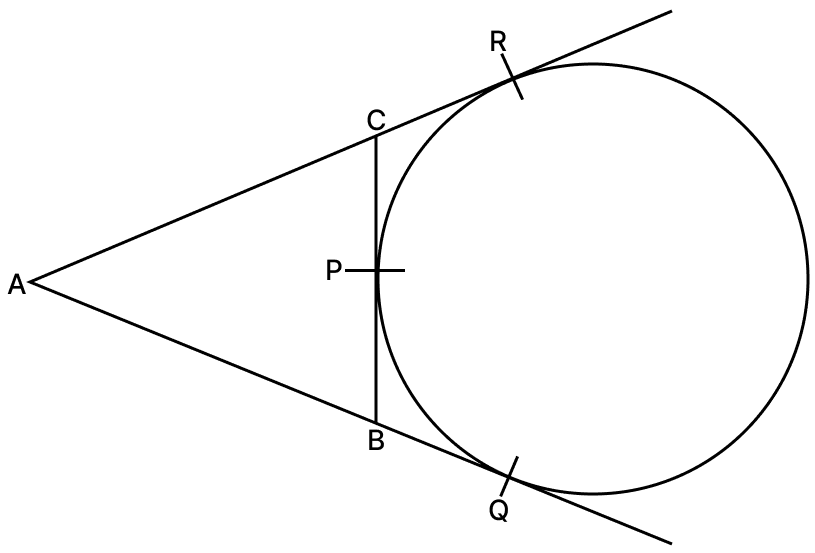
Answer

We know that,

Tangents from an exterior point to a circle are equal in length.

From A,

⇒ AQ = AR ....(1)

From B,

⇒ BQ = BP ....(2)

From C,

⇒ CP = CR .....(3)

Perimeter of triangle ABC = AB + BC + CA

= AB + (BP + PC) + (AR - CR)

= (AB + BP) + PC + (AQ - CP)    ...[From equation (1) and (3)]

= (AB + BQ) + PC + (AQ - CP)    ...[From equation (2)]

= AQ + PC + AQ - PC

= 2AQ

= 2(15)

= 30 cm.

Hence, perimeter of triangle ABC = 30 cm.

In the given figure, PA and PB are two tangents to the circle with centre O. If ∠APB = 40°, find ∠AQB and ∠AMB.

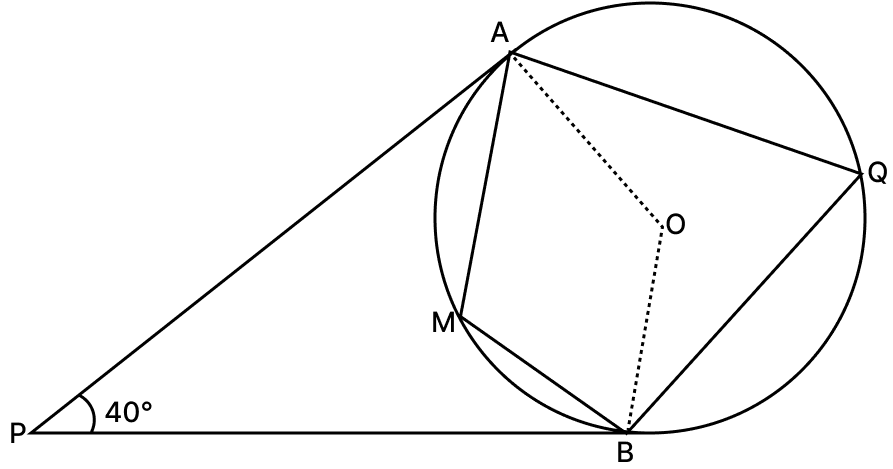
Answer

Join OA and OB.

We know that,

The tangent at any point of a circle and the radius through this point are perpendicular to each other.

∠PAO = ∠PBO = 90°

In quadrilateral AOPB, By angle sum property of quadrilateral,

⇒ ∠OAP + ∠APB + ∠PBO + ∠AOB = 360°

⇒ 90° + 40° + 90° + ∠AOB = 360°

⇒ 220° + ∠AOB = 360°

⇒ ∠AOB = 360° - 220°

⇒ ∠AOB = 140°.

Arc AB subtends ∠AOB at center and ∠AQB on the remaining part of the circle.

⇒ ∠AQB = $\dfrac{1}{2}$ ∠AOB

⇒ ∠AQB = $\dfrac{140°}{2}$

⇒ ∠AQB = 70°.

Sum of opposite angles in cyclic quadrilateral is 180°.

⇒ ∠AQB + ∠AMB = 180°

⇒ 70° + ∠AMB = 180°

⇒ ∠AMB = 180° - 70°

⇒ ∠AMB = 110°.

Hence, ∠AMB = 110° and ∠AQB = 70°.

In the given figure, PA and PB are two tangents to the circle with centre O. If ∠APB = 50°, find :

(i) ∠AOB

(ii) ∠OAB

(iii) ∠ACB

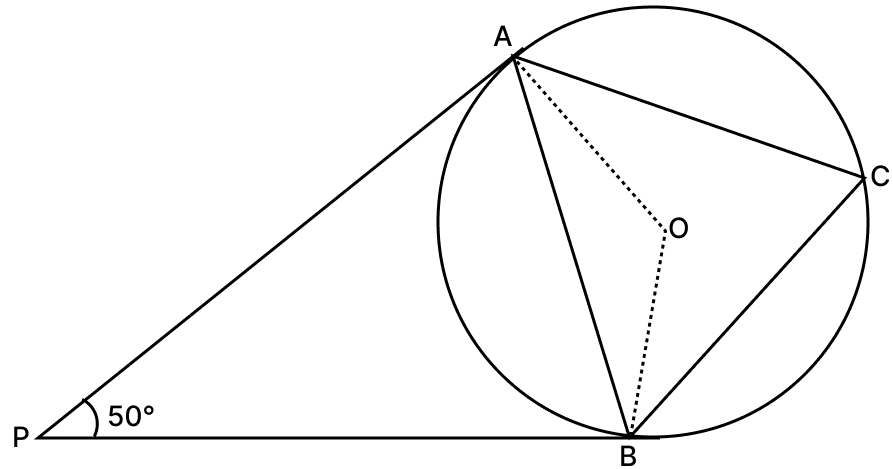
Answer

(i) We know that,

The tangent at any point of a circle and the radius through this point are perpendicular to each other.

∠OBP = ∠OAP = 90°

In quadrilateral AOPB, By angle sum property of quadrilateral,

⇒ ∠OBP + ∠OAP + ∠AOB + ∠APB = 360°

⇒ 90° + 90° + ∠AOB + 50° = 360°

⇒ 230° + ∠AOB = 360°

⇒ ∠AOB = 360° - 230°

⇒ ∠AOB = 130°.

Hence, ∠AOB = 130°.

(ii) From figure,

OA = OB (Radii)

In triangle OAB,

∠OBA = ∠OAB [Angles opposite to equal sides]

In triangle OAB,

⇒ ∠OBA + ∠OAB + ∠AOB = 180°

⇒ 2∠OAB + 130° = 180°

⇒ 2∠OAB = 180° - 130°

⇒ 2∠OAB = 50°

⇒ ∠OAB = 25°.

Hence, ∠OAB = 25°.

(iii) Arc AB subtends ∠AOB at center and ∠ACB on the remaining part of the circle.

⇒ ∠ACB = $\dfrac{1}{2}$ ∠AOB

⇒ ∠ACB = $\dfrac{130°}{2}$

⇒ ∠ACB = 65°.

Hence, ∠ACB = 65°.

In the given figure, PQ is a diameter of a circle with centre O and PT is a tangent at P. QT meets the circle at R. If ∠POR = 72°, find ∠PTR.

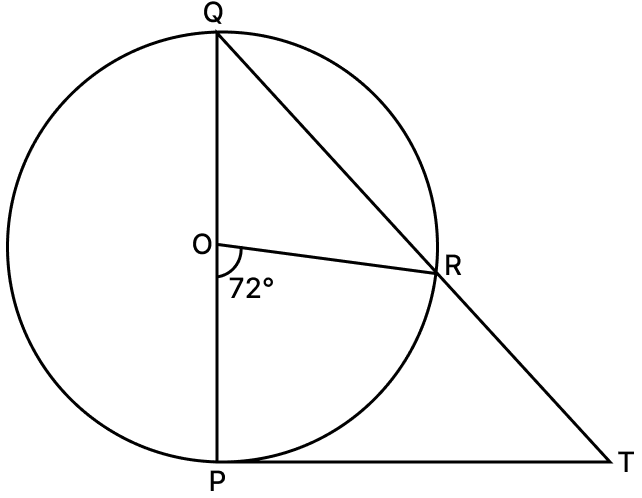
Answer

Arc PR subtends ∠POR at center and ∠PQR on the remaining part of the circle.

⇒ ∠PQR = $\dfrac{1}{2}$ ∠POR

⇒ ∠PQR = $\dfrac{72°}{2}$

⇒ ∠PQR = 36°.

We know that,

The tangent at any point of a circle and the radius through this point are perpendicular to each other.

∠QPT = 90°

In triangle QPT,

⇒ ∠QPT + ∠PQR + ∠PTR = 180°

⇒ 90° + 36° + ∠PTR = 180°

⇒ 126° + ∠PTR = 180°

⇒ ∠PTR = 180° - 126°

⇒ ∠PTR = 54°.

Hence, ∠PTR = 54°.

In the given figure, O is the centre of the circumcircle of ΔABC. Tangents at A and B intersect at T. If ∠ATB = 80° and ∠AOC = 130°, calculate ∠CAB.

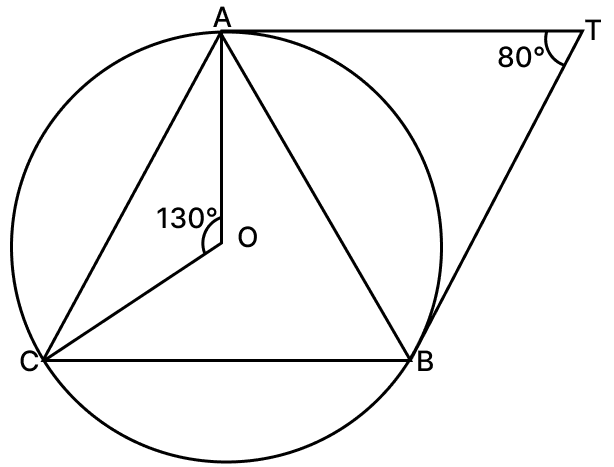
Answer

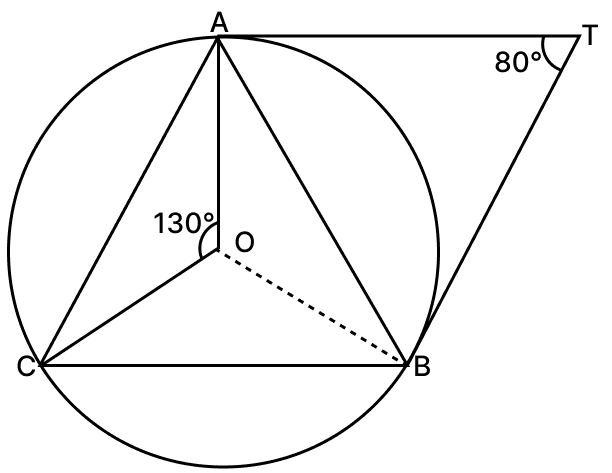
From figure,

TA and TB are the tangents.

∴ OA ⊥ TA and OB ⊥ TB

In quadrilateral AOBT,

By angle sum property,

⇒ ∠ATB + ∠TAO + ∠TBO + ∠AOB = 360°

⇒ ∠ATB + ∠AOB + 90° + 90° = 360°

⇒ ∠ATB + ∠AOB = 180°

⇒ 80° + ∠AOB = 180°

⇒ ∠AOB = 180° - 80°

⇒ ∠AOB = 100°.

From figure,

∠BOC = 360° - (∠AOC + ∠AOB)

= 360° - (130° + 100°)

= 360° - 230° = 130°.

We know that,

The angle at the centre of a circle is twice the angle at the circumference, subtended by the same arc.

Now arc BC subtends ∠COB at the centre and ∠CAB at the remaining part of the circle.

∴ ∠CAB = $\dfrac{1}{2}$ ∠COB

= $\dfrac{1}{2}$ × 130° = 65°.

Hence, ∠CAB = 65°.

In the given figure, PA and PB are tangents to a circle with centre O and ΔABC has been inscribed in the circle such that AB = AC. If ∠BAC = 72°, calculate

(i) ∠AOB

(ii) ∠APB.

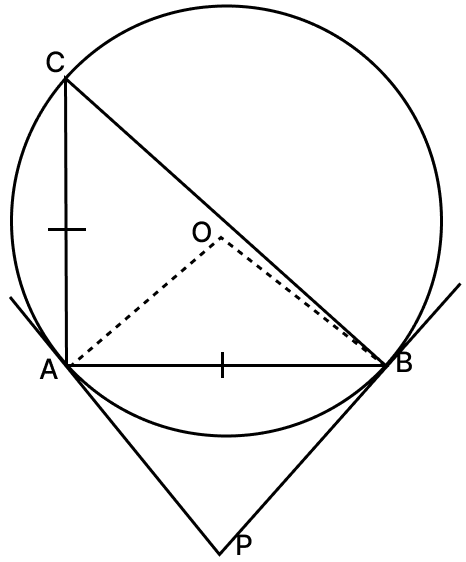
Answer

(i) AB = AC [ABC is a isosceles triangle]

∠BAC = 72°

∠ABC = ∠ACB [Angles opposite to equal sides in a triangle are equal]

Sum of angles of a triangle :

⇒ ∠ABC + ∠ACB + ∠BAC = 180°

⇒ 2∠ABC + 72° = 180°

⇒ 2∠ABC = 108°

⇒ ∠ABC = 54°

⇒ ∠ABC = ∠ACB = 54°.

Arc AB subtends ∠AOB at center and ∠ACB on the remaining part of the circle.

⇒ ∠AOB = 2∠ACB = 2(54°) = 108°.

Hence, ∠AOB = 108°.

(ii) ∠A = ∠B = 90° [∵The tangent at any point of a circle is perpendicular to the radius through the point of contact.]

⇒ ∠AOB + ∠OAP + ∠OBP + ∠APB = 360° [Angle Sum Property of a Quadrilateral]

⇒ 108° + 90° + 90° + ∠APB = 360°

⇒ 288° + ∠APB = 360°

⇒ ∠APB = 360° - 288°

⇒ ∠APB = 72°.

Hence, ∠APB = 72°.

Show that the tangent lines at the end points of a diameter of a circle are parallel.

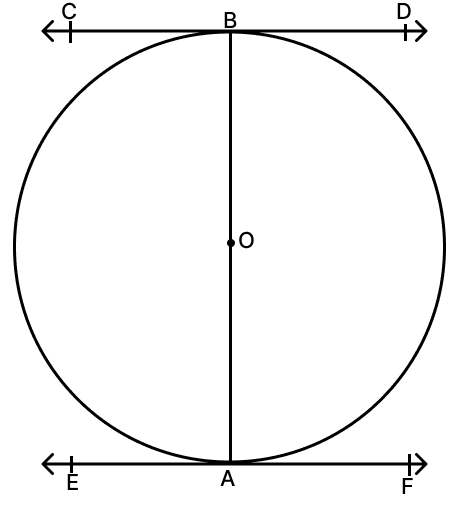
Answer

The tangent at any point of a circle is perpendicular to the radius through the point of contact.

Thus, OA ⊥ EF and OB ⊥ CD

Since the tangents are perpendicular to the radius,

⇒ ∠CBO = 90°, ∠EAO = 90°

⇒ ∠FAO = 90°, ∠OBD = 90°

∴ ∠DBO = ∠OAE, ∠CBO = ∠OAF

These are pair of alternate interior angles.

If the alternate interior angles are equal, then lines CD and EF should be parallel.

CD and EF are the tangents drawn to the circle at the ends of the diameter AB.

Hence, proved that tangents drawn at the ends of a diameter of a circle are parallel.

Prove that the tangents at the extremities of any chord make equal angles with the chord.

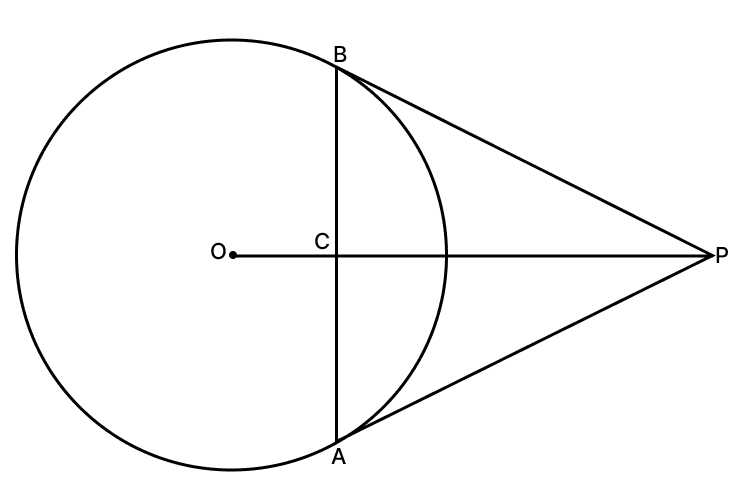
Answer

Let AB be a chord of a circle with centre O, and AP, BP be the tangents at A and B respectively.

From figure,

PA = PB [∵ Tangents from an external point to a circle are equal]

In triangle PAB,

∠PAB = ∠PBA [Angles opposite to equal sides in a triangle are equal]

∴ ∠PAC = ∠PBC.

Hence, proved any chord make equal angles with the chord.

Show that the line segment joining the points of contact of two parallel tangents passes through the centre.

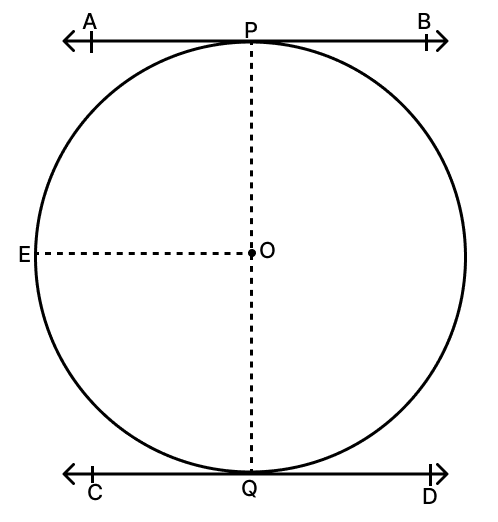
Answer

Let AB and CD are parallel tangents of circle with centre O.

The tangent at any point of a circle is perpendicular to the radius through the point of contact.

∠APO = 90°

⇒ ∠APO + ∠EOP = 180° (sum of adjacent interior angles)

⇒ ∠EOP = 180° - 90°

⇒ ∠EOP = 90°

Similarly,

⇒ ∠EOQ + ∠CQO = 180° (sum of adjacent interior angles)

⇒ ∠EOQ = 180° - 90°

⇒ ∠EOQ = 90°

∠EOP + ∠EOQ = 90° + 90° = 180°

∴ POQ is a straight line.

Hence, line segment joining the points of contact of two parallel tangents passes through the centre.

In the given figure, PQ is a transverse common tangent to two circles with centres A and B and of radii 5 cm and 3 cm respectively. If PQ intersects AB at C such that CP = 12 cm, calculate AB.

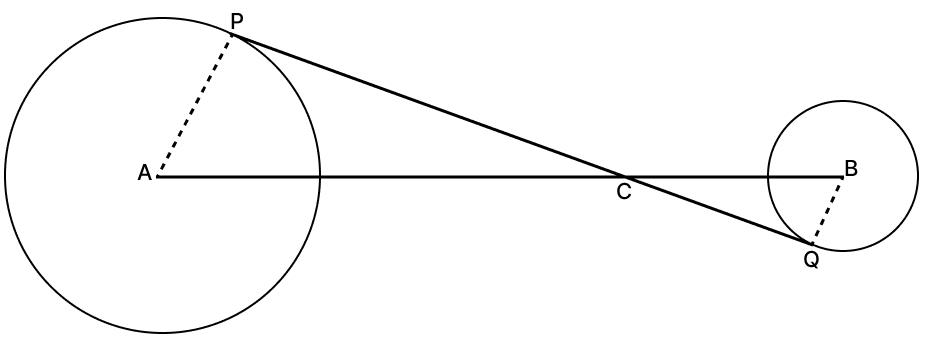
Answer

From figure,

AP ⊥ PQ (∵ tangent at a point and radius through the point are perpendicular to each other.)

In right angled triangle PAC.

⇒ CA² = PC² + AP²

⇒ CA² = 12² + 5²

⇒ CA² = 144 + 25

⇒ CA² = 169

⇒ CA = $\sqrt{169}$

⇒ CA = 13 cm.

Considering triangles PAC and BCQ,

⇒ ∠APC = ∠BQC = 90°

⇒ ∠PCA = ∠QCB (Vertically opposite angles are equal)

△PAC ~ △QBC by AA axiom.

Since triangles are similar hence, the ratio of their corresponding sides are equal.

$\dfrac{CA}{CB} = \dfrac{PA}{QB} = \dfrac{5}{3}$

$\dfrac{13}{CB} = \dfrac{5}{3}$

⇒ CB = 7.8 cm.

From figure,

AB = AC + CB = 13 + 7.8 = 20.8 cm

Hence, AB = 20.8 cm.

ΔABC is an isosceles triangle in which AB = AC, circumscribed about a circle. Prove that the base is bisected by the point of contact.

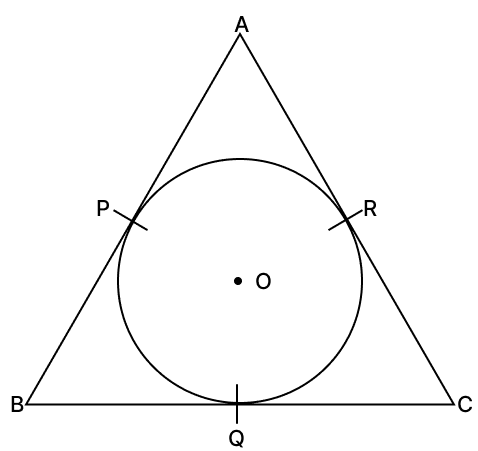
Answer

We know that,

Tangents from exterior point are equal in length.

We have,

AR = AP, BQ = BP and CQ = CR

Now, AB = AC

⇒ AP + PB = AR + RC

⇒ AR + PB = AR + RC [∵ AR = AP]

⇒ PB = RC

⇒ BQ = CQ.

It means BC is bisected at point Q.

Hence, proved that the base is bisected by the point of contact.

In the given figure, quadrilateral ABCD is circumscribed and AD ⟂ AB. If the radius of the incircle is 10 cm, find the value of x.

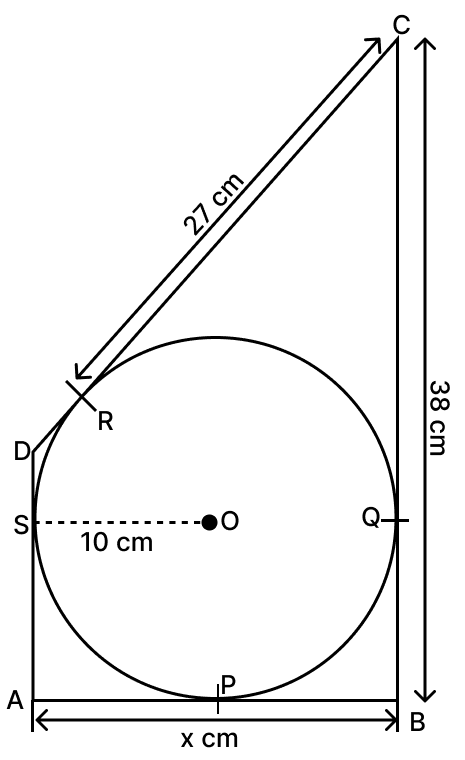
Answer

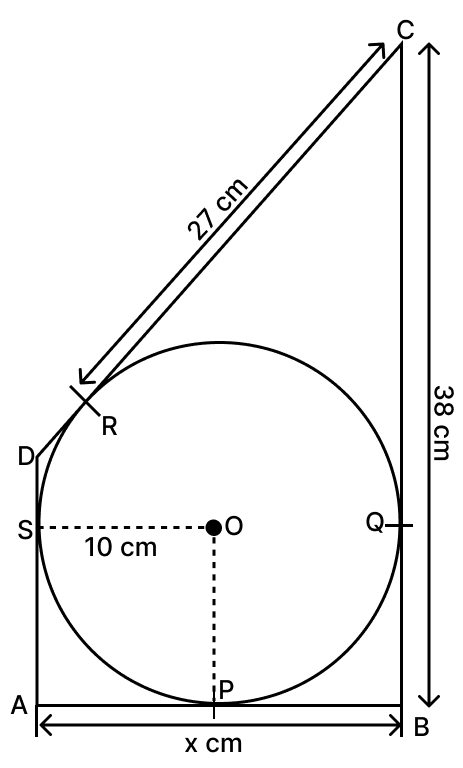
From figure,

OS = OP (As both are radius of circle.)

Since,

Adjacent sides are equal and each angle is a right angle.

∴ AP = OS.

From A, AS and AP are the tangents to the circle.

∴ AP = AS = 10 cm. (∵ if two tangents are drawn to a circle from an external point then the tangents have equal lengths.)

From C, CR and CQ are the tangents to the circle.

∴ CQ = CR = 27 cm. (∵ if two tangents are drawn to a circle from an external point then the tangents have equal lengths.)

From figure,

BQ = BC - CQ = 38 - 27 = 11 cm.

Now from B, BQ and BP are the tangents to the circle

BP = BQ = 11 cm.

⇒ AB = x = AP + BP = 10 + 11 = 21 cm.

Hence, x = 21 cm.

In the given figure, a circle is inscribed in quadrilateral ABCD. If BC = 38 cm, BQ = 27 cm, DC = 25 cm and AD ⟂ DC, find the radius of the circle.

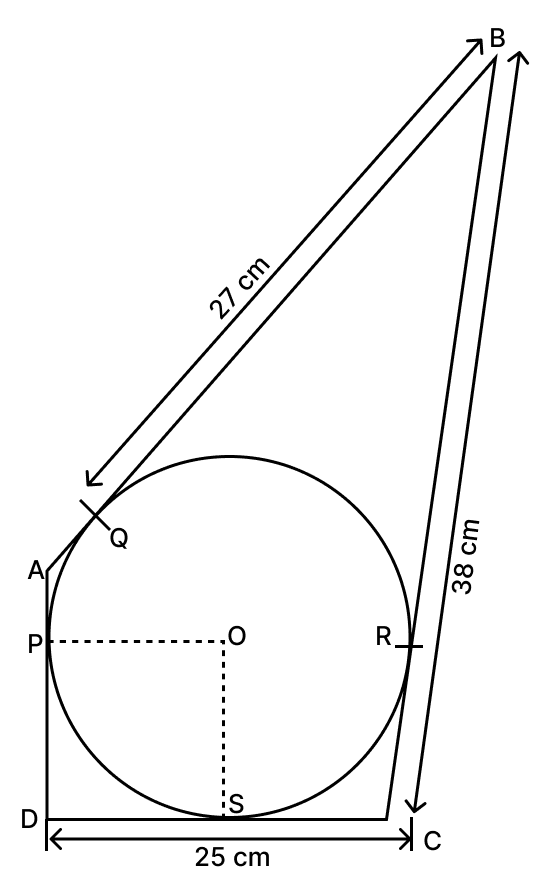
Answer

From figure,

⇒ BR = BQ = 27 cm [∵ Length of tangents form an external point to a circle are equal.]

⇒ CR = BC - BR = 38 - 27 = 11 cm.

⇒ CR = CS = 11 cm [∵ Length of tangents form an external point to a circle are equal.]

⇒ DS = DC - CS = 25 - 11 = 14 cm.

In quadrilateral DSOP,

⇒ ∠SDP + ∠DPO + ∠OSD + ∠POS = 360°

⇒ 90° + 90° + 90° + ∠POS = 360°

⇒ ∠POS = 360° - 270° = 90°.

Since, all angles are 90° and OS = OP [∵ Both equal to radius of same circle]

Hence, proved that DPOS is a square.

OP = DS = 14 cm.

Hence, radius of circle = 14 cm.

In the given figure, O is the centre of the circle and SP is a tangent. If ∠SRT = 65°, find the values of x, y and z.

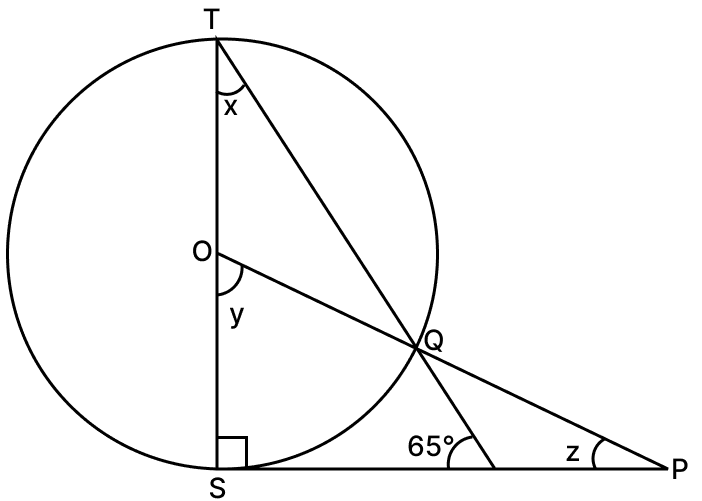
Answer

From figure,

In △SRT,

SP ⊥ ST (∵ tangent is perpendicular to radius from that point.)

so, ∠TSR = 90°

Since, sum of angles in a triangle = 180°

⇒ ∠TSR + ∠SRT + ∠STR = 180°

⇒ 90° + 65° + x = 180°

⇒ x + 155° = 180°

⇒ x = 25°.

SQ subtends ∠SOQ at the centre and ∠STQ on point T.

∴ ∠SOQ = 2∠STQ (∵ angle subtended at centre by an arc is double the angle subtended at remaining part of circle.)

y = 2x = 2 × 25° = 50°.

In △OSP,

Since, sum of angles in a triangle = 180°

⇒ ∠OSP + ∠SOP + ∠SPO = 180°

⇒ 90° + y + z = 180°

⇒ 90° + 50° + z = 180°

⇒ z + 140° = 180°

⇒ z = 180° - 140° = 40°.

Hence, the value of x = 25°, y = 50° and z = 40°.

In the given figure, TP and TQ are two tangents to the circle with centre O, touching at A and C respectively. If ∠BCQ = 55° and ∠BAP = 60°, find :

(i) ∠OBA and ∠OBC

(ii) ∠AOC

(iii) ∠ATC

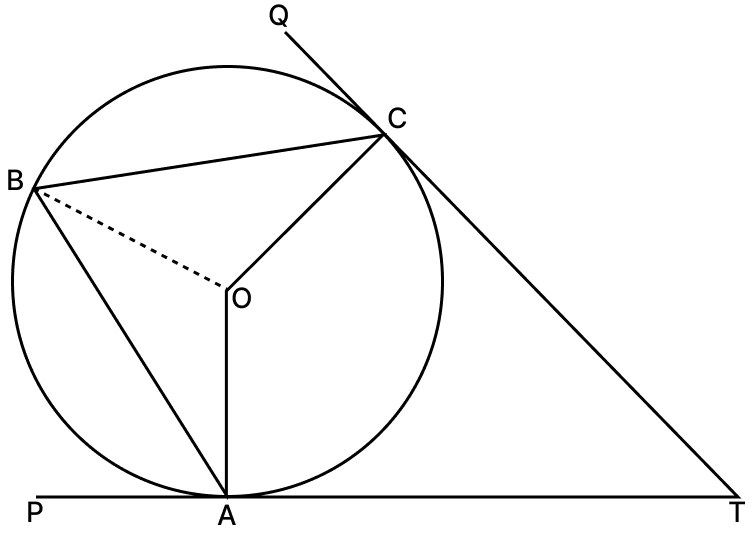
Answer

(i) ∠OAP = 90° [As TP is tangent at point A]

From figure,

⇒ ∠OAB = ∠OAP - ∠BAP = 90° - 60° = 30°.

⇒ OA = OB (Radius of same circle)

⇒ ∠OBA = ∠OAB = 30° (Angles opposite to equal sides are equal)

∠OCQ = 90° [As TQ is tangent at point C]

From figure,

∠OCB = ∠OCQ - ∠BCQ = 90° - 55° = 35°.

⇒ OB = OC (Radius of same circle)

⇒ ∠OBC = ∠OCB = 35° (Angles opposite to equal sides are equal)

Hence, ∠OBA = 30° and ∠OBC = 35°.

(ii) We know that,

The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.

⇒ ∠AOC = 2∠ABC

⇒ ∠AOC = 2(∠OBA + ∠OBC)

⇒ ∠AOC = 2(30° + 35°)

⇒ ∠AOC = 2 × 65° = 130°.

Hence, ∠AOC = 130°.

(iii) In quadrilateral OATC,

⇒ ∠AOC + ∠OAT + ∠OCT + ∠ATC = 360°

⇒ 130° + 90° + 90° + ∠ATC = 360°

⇒ 310° + ∠ATC = 360°

⇒ ∠ATC = 360° - 310° = 50°.

Hence, ∠ATC = 50°.

In the given figure, O is the centre of the circle. PQ and PR are tangents and ∠QPR = 70°. Calculate :

(i) ∠QOR

(ii) ∠QSR

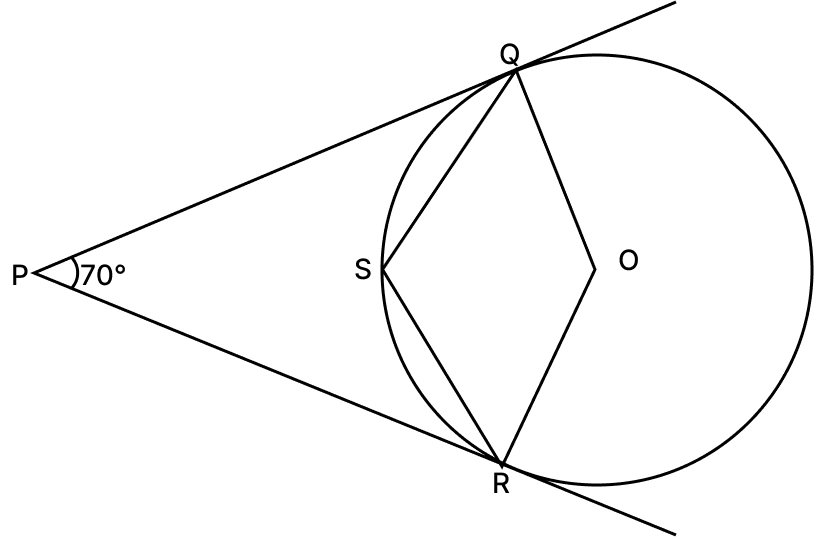
Answer

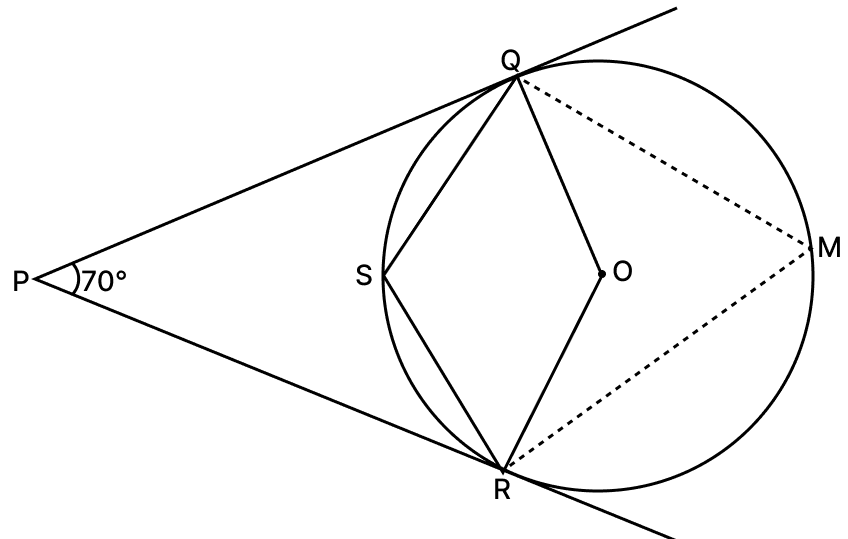
(i) We know that,

The tangent at any point of a circle and the radius through this point are perpendicular to each other.

In quadrilateral ORPQ,

∠OQP = ∠ORP = 90° [∵ The tangent at any point of a circle and the radius through this point are perpendicular to each other]

∠QPR = 70° [Given]

⇒ ∠OQP + ∠ORP + ∠QPR + ∠QOR = 360° [By angle sum property of quadrilateral]

⇒ 90° + 90° + 70° + ∠QOR = 360°

⇒ 250° + ∠QOR = 360°

⇒ ∠QOR = 110°.

Hence, ∠QOR = 110°.

(ii) Let M be a point on circumference of circle.

We know that,

The angle subtended by an arc at the centre is twice the angle subtended at the circumference.

⇒ ∠QMR = $\dfrac{1}{2}$ ∠QOR

= $\dfrac{110°}{2}$

= 55°.

Sum of opposite angles in cyclic quadrilateral is 180°.

⇒ ∠QSR + ∠QMR = 180°.

⇒ ∠QSR = 180° - 55°

⇒ ∠QSR = 125°.

Hence, ∠QSR = 125°.

In the given figure, O is the centre of the circle. CE is a tangent to the circle at A. If ∠ABD = 26°, then find :

(i) ∠BDA

(ii) ∠BAD

(iii) ∠CAD

(iv) ∠ODB

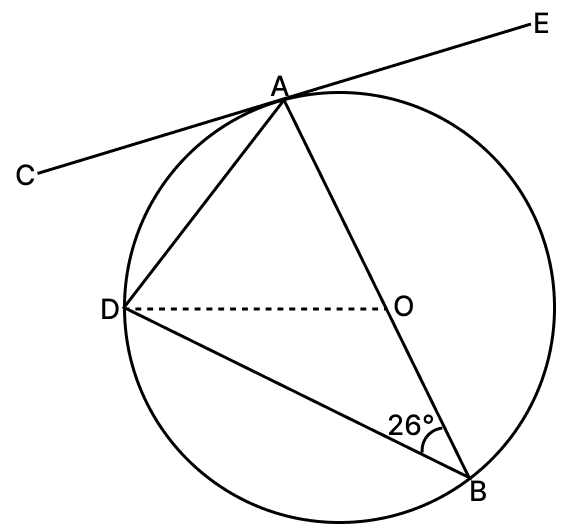
Answer

(i) We know that,

Angle in a semi-circle is a right angle.

∴ ∠BDA = 90°.

Hence, ∠BDA = 90°.

(ii) In △ BAD,

By angle sum property of triangle,

⇒ ∠BDA + ∠BAD + ∠ABD = 180°

⇒ 90° + ∠BAD + 26° = 180°

⇒ ∠BAD + 116° = 180°

⇒ ∠BAD = 180° - 116° = 64°.

Hence, ∠BAD = 64°.

(iii) From figure,

CE is tangent to the circle.

Angle between tangent and radius of the circle is 90°.

From figure,

⇒ ∠CAB = 90°

⇒ ∠CAD + ∠BAD = 90°

⇒ ∠CAD + 64° = 90°

⇒ ∠CAD = 90° - 64° = 26°.

Hence, ∠CAD = 26°.

(iv) In △ OBD,

⇒ OD = OB (Radius of same circle)

We know that,

Angles opposite to equal sides are equal.

⇒ ∠ODB = ∠OBD = 26°.

Hence, ∠ODB = 26°.

(i)

(ii)

(iii)

(iv)

(v)

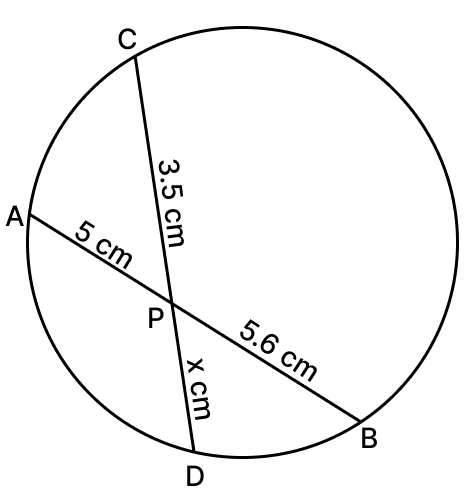
Find the unknown length x in each of the following figures.

Answer

We know that,

If two chords of a circle intersect internally, then the products of the length of segments are equal.

(i) PA × PB = PC × PD

5 × 5.6 = 3.5 × x

x = $\dfrac{28}{3.5}$

x = 8 cm.

Hence, x = 8 cm.

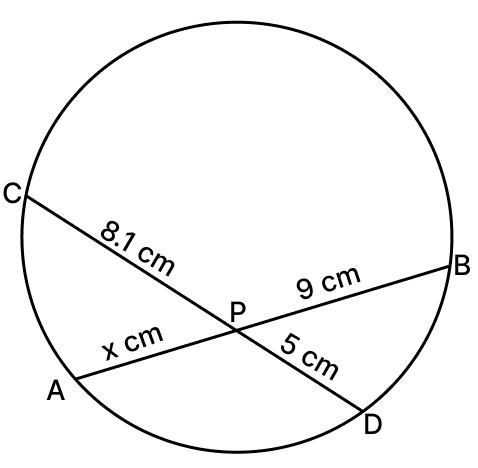
(ii) PA × PB = PC × PD

x × 9 = 8.1 × 5

x = $\dfrac{40.5}{9}$

x = 4.5 cm

Hence, x = 4.5 cm.

We know that,

If two chords of a circle intersect externally, then the products of the length of segments are equal.

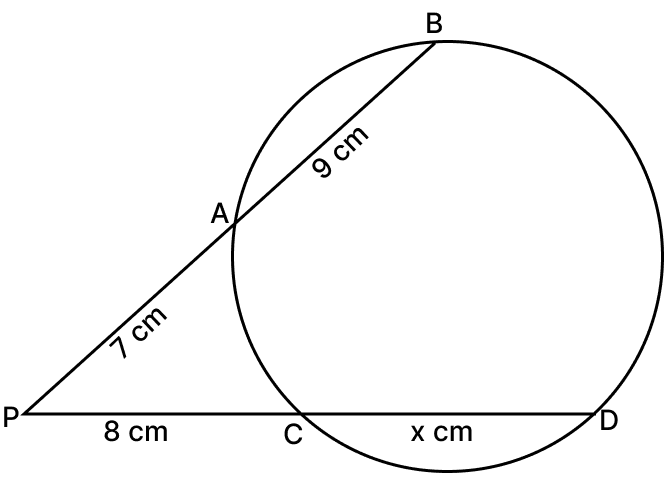
(iii) PA × PB = PC × PD

⇒ PB = PA + AB = 7 + 9 = 16

⇒ PD = PC + CD = 8 + x

⇒ 7 × 16 = 8 × (8 + x)

⇒ 112 = 64 + 8x

⇒ 8x = 112 - 64

⇒ x = $\dfrac{48}{8}$

⇒ x = 6 cm.

Hence, x = 6 cm.

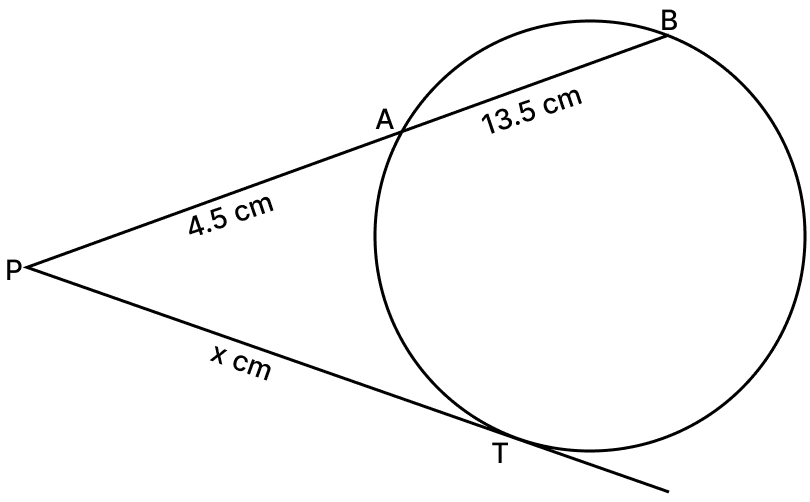
(iv) We know that,

If a chord and a tangent intersect externally, then the product of lengths of the segments of the chord is equal to the square of the length of the tangent from the point of contact to the point of intersection.

∴ PT² = AP × BP

x² = 4.5 × 18

x² = 81

x = 9 cm.

Hence, x = 9 cm.

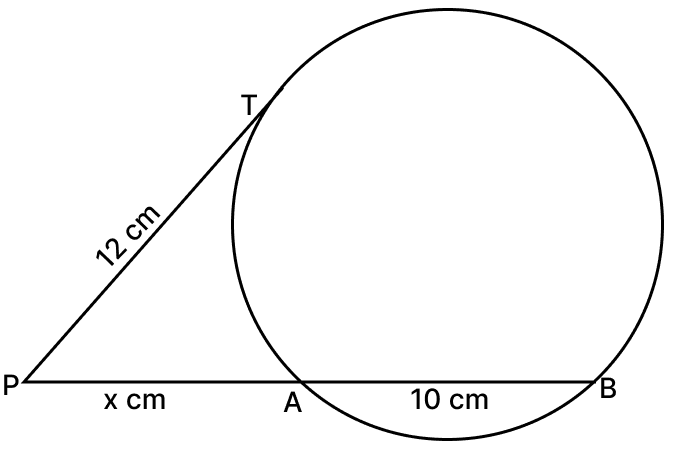
(v) We know that,

If a chord and a tangent intersect externally, then the product of lengths of the segments of the chord is equal to the square of the length of the tangent from the point of contact to the point of intersection.

∴ PT² = AP × BP

⇒ BP = AP + AB = x + 10

⇒ 12² = x × (x + 10)

⇒ 144 = x² + 10x

⇒ x² + 10x - 144 = 0

⇒ x² + 18x - 8x - 144 = 0

⇒ x(x + 18) - 8(x + 18) = 0

⇒ (x - 8)(x + 18) = 0

⇒ (x - 8) = 0 or (x + 18) = 0      [Using Zero-product rule]

⇒ x = 8 or x = -18

∴ x = 8 because length cannot be negative.

Hence, x = 8 cm.

Two chords AB and CD of a circle intersect externally at E. If EC = 2 cm, EA = 3 cm and AB = 5 cm, find the length of CD.

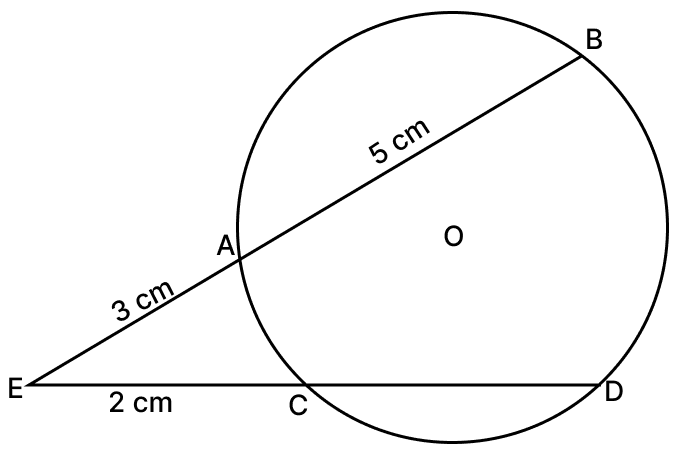
Answer

We know that,

If two chords of a circle intersect externally, then the products of the length of segments are equal.

From figure,

EA × EB = EC × ED ....(1)

EB = EA + AB = 3 + 5 = 8 cm

Substituting values in equation (1) we get,

⇒ 3 × 8 = 2 × ED

⇒ 24 = 2 × ED

⇒ ED = $\dfrac{24}{2}$

⇒ ED = 12 cm.

⇒ CD = ED - EC = 12 - 2 = 10 cm

Hence, CD = 10 cm.

In the adjoining figure, PT is a tangent to the circle. Find PT, if AP = 16 cm and AB = 12 cm.

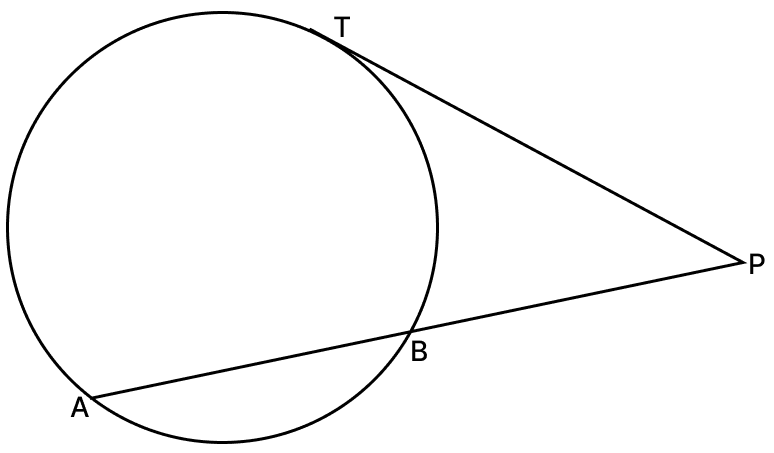
Answer

We know that,

If a chord and a tangent intersect externally, then the product of lengths of the segments of the chord is equal to the square of the length of the tangent from the point of contact to the point of intersection.

∴ PT² = AP × BP

From figure,

BP = AP - AB = 16 - 12 = 4 cm.

Substituting values we get,

PT² = 16 × 4

PT² = 64

PT = $\sqrt{64}$

PT = 8 cm.

Hence, PT = 8 cm.

Two chords AB and CD of a circle intersect at a point P inside the circle such that AB = 12 cm, AP = 2.4 cm and PD = 7.2 cm. Find CD.

Answer

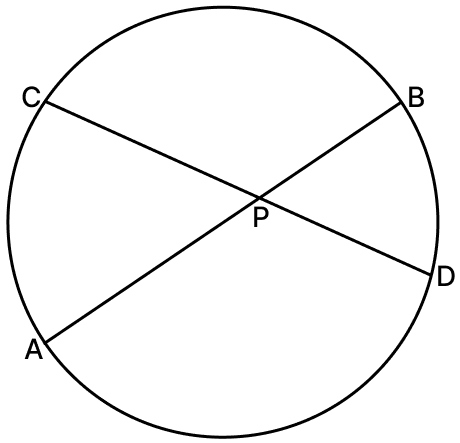
We know that,

If two chords of a circle intersect internally, then the products of the length of segments are equal.

AP × PB = CP × PD

PB = AB - AP = 12 - 2.4 = 9.6 cm

Substituting values we get,

⇒ 2.4 × 9.6 = CP × 7.2

⇒ CP = $\dfrac{23.04}{7.2}$

⇒ CP = 3.2 cm

⇒ CD = CP + PD = 3.2 + 7.2 = 10.4 cm

Hence, CD = 10.4 cm.

If AB and CD are two chords of a circle which when produced meet at a point P outside the circle such that PA = 12 cm, AB = 4 cm and CD = 10 cm, find PD.

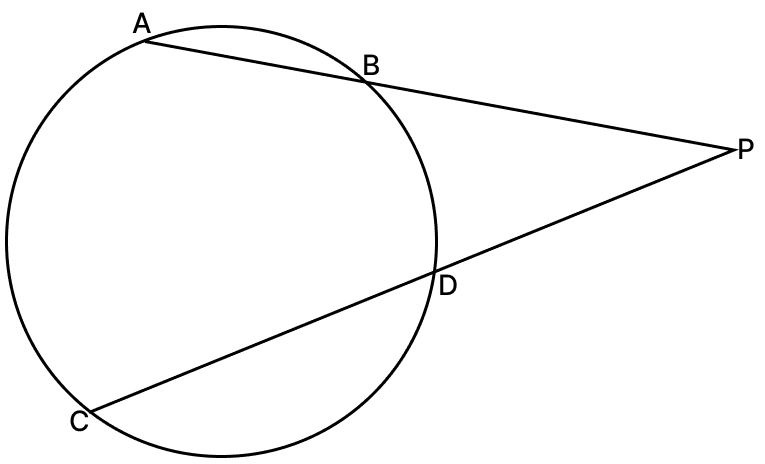
Answer

We know that,

If two chords of a circle intersect externally, then the products of the length of segments are equal.

PA × PB = CP × PD ........(1)

PB = PA - AB

PB = 12 - 4 = 8 cm

Let length of PD be x.

PC = x + CD = x + 10

Substituting values in equation (1) we get,

⇒ 12 × 8 = (x + 10) × x

⇒ 96 = x² + 10x

⇒ x² + 10x - 96 = 0

⇒ x² + 16x - 6x - 96 = 0

⇒ x(x + 16) - 6(x + 16) = 0

⇒ (x - 6)(x + 16) = 0

⇒ x = 6 [Length cannot be negative]

⇒ PD = 6 cm.

Hence, PD = 6 cm.

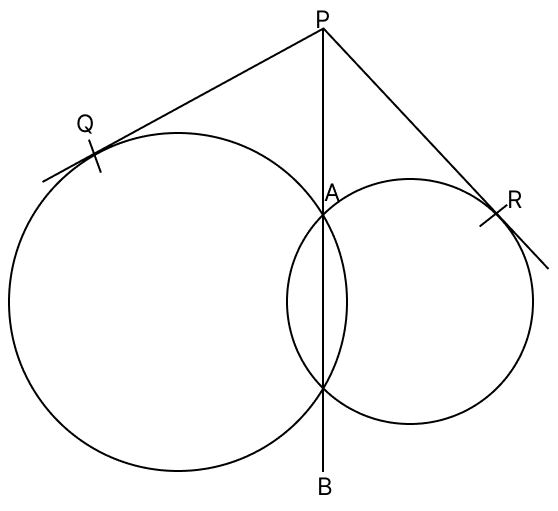
In the given figure, two circles intersect each other at the points A and B. If PQ and PR are tangents to these circles from a point P on AB produced, show that PQ = PR.

Answer

We know that,

If a chord and a tangent intersect externally, then the product of lengths of the segments of the chord is equal to the square of the length of the tangent from the point of contact to the point of intersection.

For circle 1:

∴ PQ² = PA × PB

For circle 2:

∴ PR² = PA × PB

Thus,

PQ² = PR²

Taking square root on both sides,

PQ = PR

Hence, proved that PQ = PR.

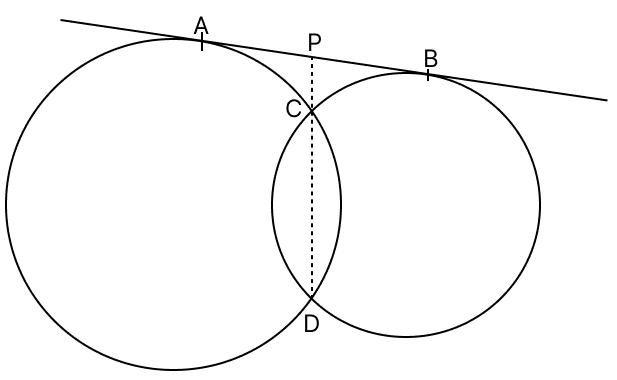
In the given figure, AB is a direct common tangent to two intersecting circles. Their common chord when produced intersects AB at P. Prove that P is the mid-point of AB.

Answer

We know that,

If a chord and a tangent intersect externally, then the product of lengths of the segments of the chord is equal to the square of the length of the tangent from the point of contact to the point of intersection.

For circle 1:

∴ PA² = PC × PD

For circle 2:

∴ PB² = PC × PD

Thus,

PA² = PB²

Taking square root on both sides,

PA = PB

Point P divides AB into two equal parts.

Hence, proved P is the mid-point of AB.

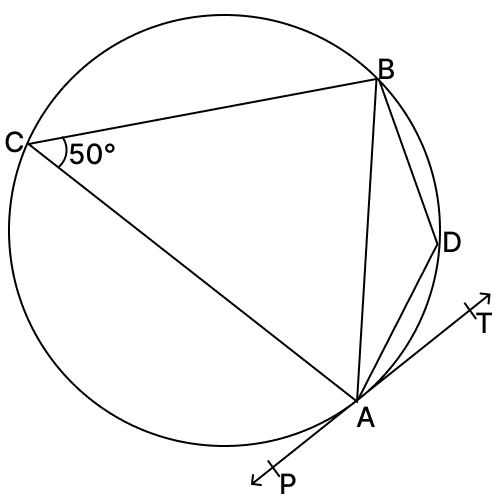
In the given figure, PAT is tangent at A. If ∠ACB = 50°, find :

(i) ∠TAB

(ii) ∠ADB

Answer

(i) ∠TAB = ∠ACB = 50° [Angles in the alternate segment are equal]

Hence, ∠TAB = 50°.

(ii) ∠ADB + ∠ACB = 180° [Opposite angles of cyclic quadrilateral]

∠ADB = 180° - 50°

∠ADB = 130°.

Hence, ∠ADB = 130°.

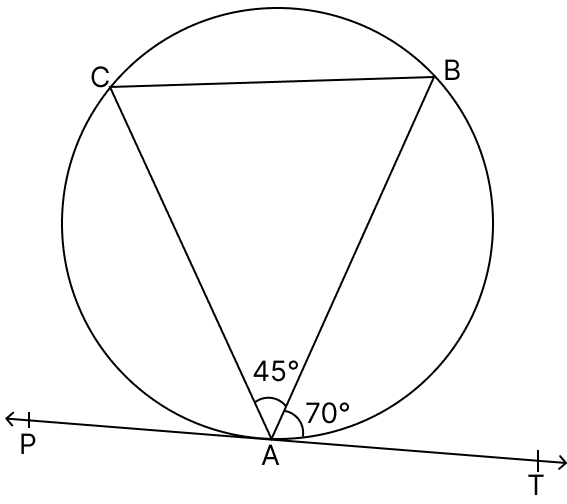
In the given figure, PAT is tangent at A. If ∠TAB = 70° and ∠BAC = 45°, find ∠ABC.

Answer

From figure,

∠ACB = ∠TAB = 70° [Angles in the alternate segment are equal]

In ΔABC,

⇒ ∠ACB + ∠BAC + ∠ABC = 180° [By angle sum property of triangle]

⇒ ∠ABC = 180° - (∠BAC + ∠ACB)

⇒ ∠ABC = 180° - (45° + 70°)

⇒ ∠ABC = 65°.

Hence, ∠ABC = 65°.

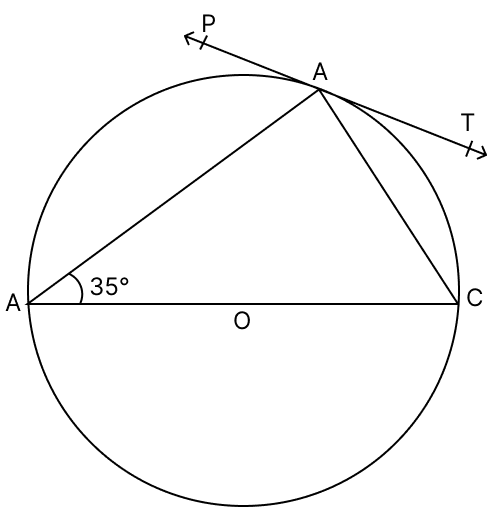
In the given figure, PAT is tangent at A to the circle with centre O. If ∠ABC = 35°, find :

(i) ∠TAC

(ii) ∠PAB

Answer

(i) ∠TAC = ∠ABC = 35° [Angles in the alternate segment are equal]

Hence, ∠TAC = 35°.

(ii) Since BC is a diameter, ∠BAC is an angle in a semicircle.Therefore, ∠BAC = 90°

⇒ ∠ACB + ∠BAC + ∠ABC = 180°

⇒ ∠ACB + 90° + 35° = 180°

⇒ ∠ACB = 180° - 90° - 35°

⇒ ∠ACB = 55°

⇒ ∠PAB = ∠ACB [Angles in the alternate segment are equal]

⇒ ∠PAB = 55°

Hence, ∠PAB = 55°.

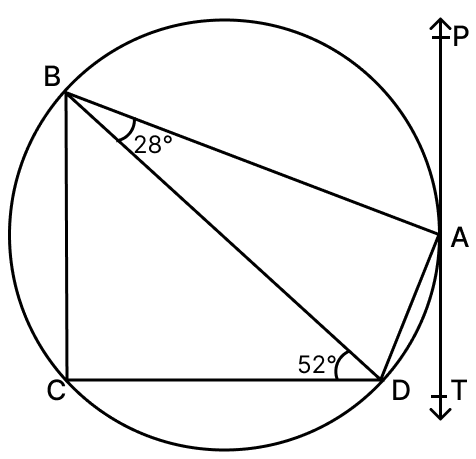
In the given figure, PAT is tangent at A and BD is a diameter of the circle. If ∠ABD = 28° and ∠BDC = 52°, find :

(i) ∠TAD

(ii) ∠BAD

(iii) ∠PAB

(iv) ∠CBD

Answer

(i) ∠TAD = ∠ABD = 28° [Angles in the alternate segment are equal]

Hence, ∠TAD = 28°.

(ii) ∠BAD = 90° [Angle in the semicircle]

Hence, ∠BAD = 90°.

(iii) ∠PAB = ∠ADB [Angles in the alternate segment]

By angle sum property of triangle :

⇒ ∠ADB + ∠ABD + ∠BAD = 180°

⇒ ∠ADB + 28° + 90° = 180°

⇒ ∠ADB = 180° - (28° + 90°)

⇒ ∠ADB = 62°

⇒ ∠PAB = 62°.

Hence, ∠PAB = 62°.

(iv) In ΔBCD, since BD is the diameter ∠BCD = 90°.

By angle sum property of triangle,

⇒ ∠CBD + ∠BCD + ∠BDC = 180°

⇒ ∠CBD + 90° + 52° = 180°

⇒ ∠CBD = 180° - 90° - 52°

⇒ ∠CBD = 38°.

Hence, ∠CBD = 38°.

In the given figure, PQ and PR are two equal chords of a circle. Show that the tangent at P is parallel to QR.

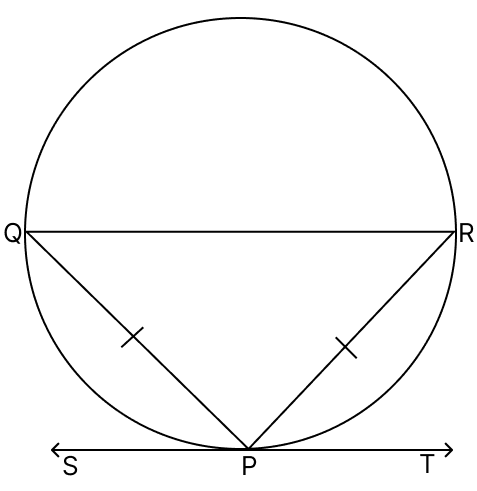
Answer

Given,

PQ = PR

∠PRQ = ∠PQR [Angles opposite to equal sides in a triangle are equal]

∠TPR = ∠PQR [Angles in alternate segment]

∴ ∠PRQ = ∠TPR

These are pair of alternate interior angles.

If the alternate interior angles are equal, then lines P and QR should be parallel.

Hence, proved tangent at P is parallel to QR.

In the given figure, AB is a chord of the circle with centre O and BT is a tangent to the circle. If ∠OAB = 35°, find the values of x and y.

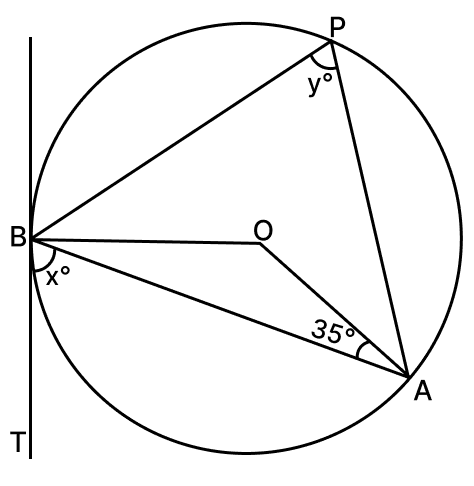
Answer

In △OAB,

OA = OB (∵ both are radius of the common circle.)

So, △OAB is a isosceles triangle with,

∠OBA = ∠OAB = 35°.

Since sum of angles in a triangle = 180°.

In △OAB,

⇒ ∠OBA + ∠OAB + ∠AOB = 180°

⇒ 35° + 35° + ∠AOB = 180°

⇒ 70° + ∠AOB = 180°

⇒ ∠AOB = 180° - 70°

⇒ ∠AOB = 110°.

Arc AB subtends ∠AOB at centre and ∠ACB at remaining part of circle.

∴ ∠AOB = 2∠ACB (∵ angle subtended at centre is double the angle subtended at remaining part of the circle.)

⇒ 110° = 2y

⇒ y = $\dfrac{110}{2}$

⇒ y = 55°.

From figure,

∠ABT = ∠ACB = 55° (∵ Angles in alternate segments are equal.)

∴ x = 55°.

Hence, the value of x = 55 and y = 55.

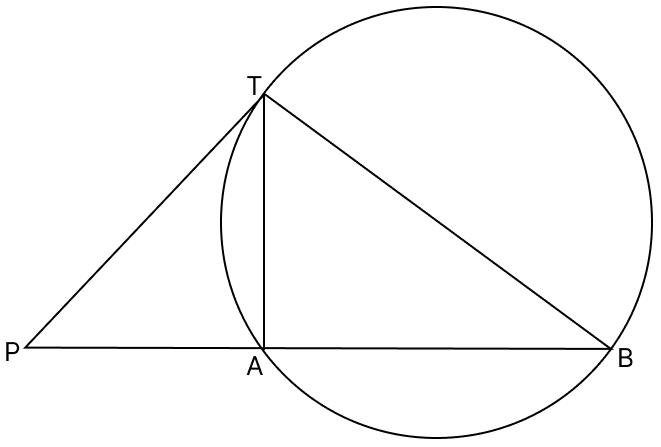
In the given figure, PAB is a secant to the circle and PT is a tangent at T. Prove that:

(i) ∠PAT ∼ ∠PTB

(ii) PA × PB = PT²

Answer

(i) In △PAT and △PTB:

⇒ ∠TPA = ∠BPT [Common angles]

⇒ ∠PTA = ∠PBT [Angles in the alternate segment]

△PAT ∼ △PTB [By AA similarity]

Hence, proved △PAT ∼ △PTB.

(ii) Since, corresponding sides of similar triangle are proportional to each other.

$\dfrac{PA}{PT} = \dfrac{PT}{PB}$

PT² = PA × PB

Hence, proved that PT² = PA × PB.

In a right-angled ΔABC, the perpendicular BD on hypotenuse AC is drawn. Prove that :

(i) AC × AD = AB²

(ii) AC × CD = BC²

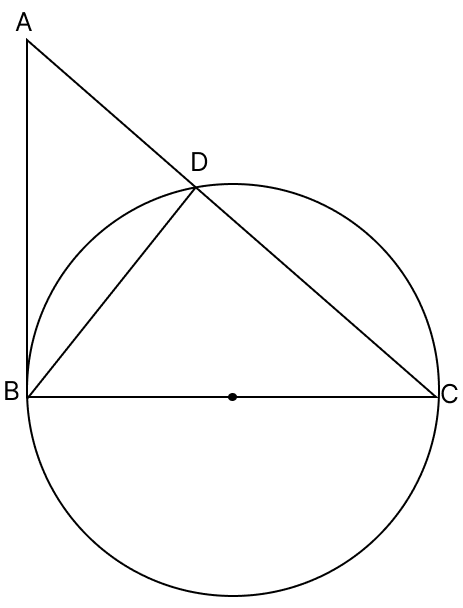
Answer

(i) In ΔABC and ΔADB,

⇒ ∠ABC = ∠ADB = 90°

⇒ ∠BAC = ∠DAB [Common angles]

△ABC ∼ △ADB [By AA similarity]

Since, corresponding sides of similar triangle are proportional to each other.

$\dfrac{AB}{AD} = \dfrac{AC}{AB}$

AB² = AC × AD

Hence, AB² = AC × AD.

(ii) In ΔABC and ΔBDC

⇒ ∠ABC = ∠CDB = 90°

⇒ ∠C [Common angles]

△ABC ∼ △BDC [By AA similarity]

$\dfrac{BC}{CD} = \dfrac{AC}{BC}$

BC² = AC × CD

Hence, BC² = AC × CD.

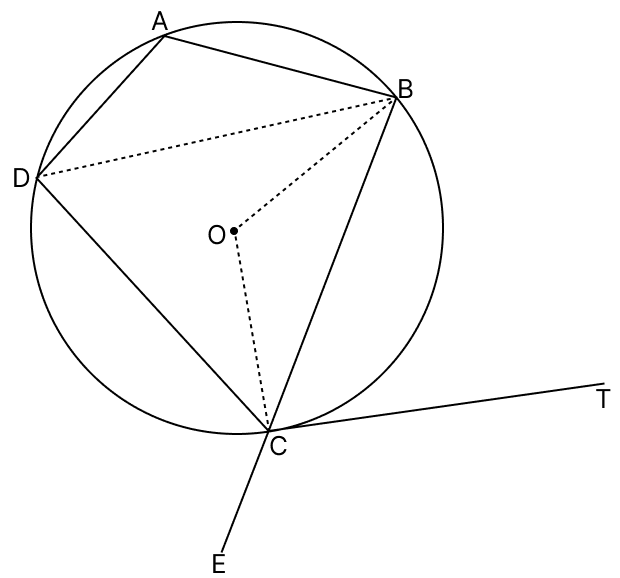
In the given figure, ABCD is a cyclic quadrilateral in which CB = CD and TC is a tangent to the circle at C. If O is the centre of the circle and BC is produced to E such that ∠DCE = 110°, find:

(i) ∠DCT

(ii) ∠BOC

Answer

(i) From figure,

⇒ ∠DCE + ∠DCB = 180° [Linear pair]

⇒ ∠DCB = 180° - ∠DCE

⇒ ∠DCB = 180° - 110°

⇒ ∠DCB = 70°.

Given,,

CB = CD

∠BDC = ∠DBC = 55° [Angles opposite to equal sides in a triangle are equal]

Arc BC subtends ∠BOC at center and ∠BDC on the remaining part of the circle.

⇒ ∠BOC = 2(∠BDC)

⇒ ∠BOC = 2(55°) = 110°

⇒ ∠BCT = ∠BDC = 55° [Angles in alternate segments]

From figure,

⇒ ∠DCT = ∠DCB + ∠BCT

⇒ ∠DCT = 70° + 55° = 125°.

Hence, ∠DCT = 125°.

(ii) From part (i), we get :

∠BOC = 110°

Hence, ∠BOC = 110°.

In the given figure, AC is a tangent to the circle with centre O. If ∠ADB = 55°, find x and y. Give reasons.

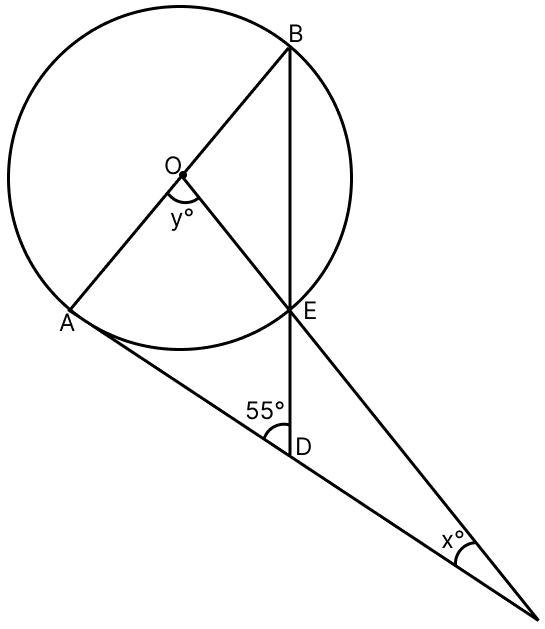
Answer

We know that,

Angle between the radius and tangent at the point of contact is right angle.

∴ ∠A = 90°.

Also in △OBE, OB = OE = radius of the circle.

∴ ∠B = ∠OEB …..(i)

In △ABD,

⇒ ∠A + ∠B + ∠ADB = 180°

⇒ 90° + ∠B + 55° = 180°

⇒ ∠B + 145° = 180°

⇒ ∠B = 180° - 145° = 35°.

∴ ∠OEB = 35°.

From figure,

∠DEC = ∠OEB = 35° (∵ vertically opposite angles are equal.)

∠EDC + ∠ADE = 180° (∵ both form a linear pair)

∠EDC + 55° = 180°

∠EDC = 180° - 55°

∠EDC = 125°.

In △EDC,

⇒ ∠DEC + ∠EDC + ∠DCE = 180°

⇒ 35° + 125° + x° = 180°

⇒ x° + 160° = 180°

⇒ x° = 180° - 160° = 20°.

In △AOC,

⇒ ∠AOC + ∠OAC + ∠ACO = 180°

⇒ y° + 90° + x° = 180°

⇒ y° + 90° + 20° = 180°

⇒ y° + 110° = 180°

⇒ y° = 180° - 110° = 70°.

Hence, the value of x = 20° and y = 70°.

In two concentric circles, a chord of larger circle which is ________ to smaller circle is bisected at the point of contact.

1. secant

2. tangent

3. chord

4. diameter

Answer

In two concentric circles, a chord of larger circle which is tangent to smaller circle is bisected at the point of contact.

Hence, option 2 is the correct option.

The length of the tangent drawn to a circle of radius 8 cm, from a point which is at a distance of 10 cm from the centre of the circle is :

1. 6 cm

2. 7 cm

3. 9 cm

4. 2 cm

Answer

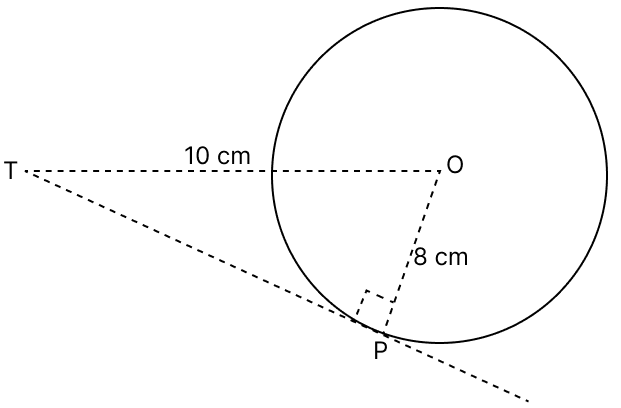
We know that,

The tangent at any point of a circle and the radius through this point are perpendicular to each other.

In right ∆OTP, we have

OT² = PT² + OP²

PT² = OT² - OP²

PT² = 100 - 64

PT² = 36

PT = $\sqrt{36}$ = 6 cm.

Hence, option 1 is the correct option.

There are ________ two tangents to a circle passing through a point lying outside the circle.

1. at least

2. at most

3. exactly

4. maximum

Answer

A standard theorem in circle states:

From a point lying outside a circle, exactly two tangents can be drawn to the circle.

Hence, option 3 is the correct option.

If two tangents are drawn from an external point to a circle, then the tangents are equally inclined to the line joining the point and the centre of the circle, i.e., the centre lies on the ________ of the angle between the two tangents.

1. perpendicular

2. bisector

3. perpendicular bisector

4. none of these

Answer

When two tangents are drawn from an external point to a circle, the line joining the external point and the centre of the circle bisects the angle between the two tangents.

Hence, option 2 is the correct option.

From a point M, the length of the tangent to a circle is 24 cm and the distance of M from the centre is 25 cm. The radius of the circle is :

1. 7 cm

2. 12 cm

3. 24.5 cm

4. 12.5 cm

Answer

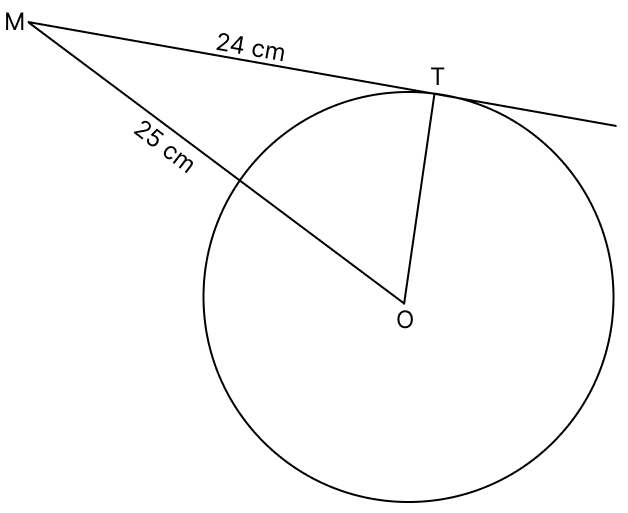
We know that,

The tangent at any point of a circle and the radius through this point are perpendicular to each other.

In right ∆MOT, we have

MO² = MT² + OT²

OT² = MO² - MT²

OT² = 25² - 24²

OT² = 625 - 576

OT² = 49

OT = $\sqrt{49}$

OT = 7 cm.

Hence, option 1 is the correct option.

PQ is a tangent to a circle at point P. Centre of the circle is O. If ΔOPQ is an isosceles triangle, then ∠QOP =

1. 30°

2. 60°

3. 45°

4. 90°

Answer

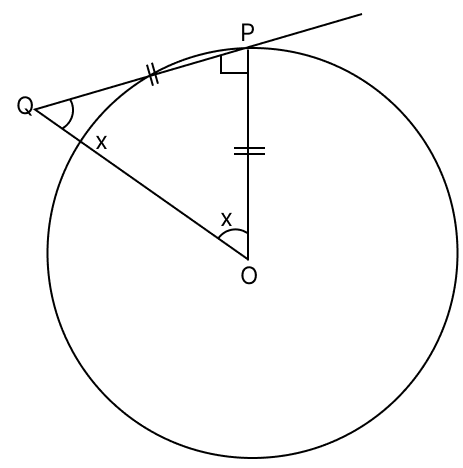
Let QP = OP

We know that,

The tangent at any point of a circle and the radius through this point are perpendicular to each other.

∠OPQ = 90°

∠QOP = ∠OQP = x [Anglers opposite to equal sides are equal in a triangle]

By angles sum triangle property,

x + x + 90° = 180°

2x + 90° = 180°

2x = 180° - 90°

2x = 90°

x = $\dfrac{90°}{2}$

x = 45°

∠QOP = 45°

Hence, option 3 is the correct option.

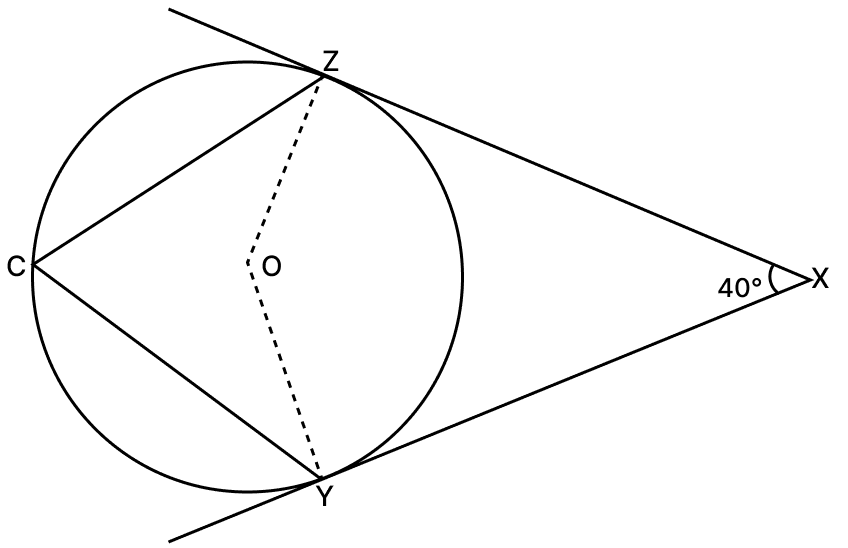
In the figure XY and XZ are tangents at points Y and Z respectively to a circle with centre O. If C is a point on the circle and ∠ZXY = 40°, then ∠ZCY = ?

1. 80°

2. 70°

3. 140°

4. 40°

Answer

From figure,

The tangent at any point of a circle and the radius through this point are perpendicular to each other.

∠OZX = 90°

∠OYX = 90°

∠ZXY + ∠ZOY + ∠OZX + ∠OYX = 360° [Angle sum property of quadrilateral]

40° + 90° + 90° + ∠ZOY = 360°

220° + ∠ZOY = 360°

∠ZOY = 360° - 220°

∠ZOY = 140°.

We know that,

Angle at the centre is double the angle at a point on the remaining part of the circle.

∠ZCY = $\dfrac{1}{2}$ ∠ZOY

∠ZCY = $\dfrac{140°}{2}$

∠ZCY = 70°.

Hence, option 2 is the correct option.

In the given figure, if sides AB, BC, CD and DA of a quadrilateral ABCD touch a circle at points P, Q, R and S respectively, then CR + PB =

1. BC

2. AB

3. CD

4. AD

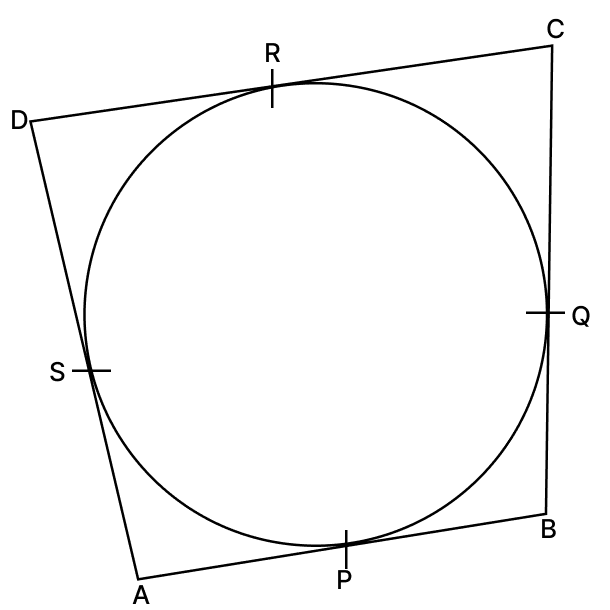
Answer

Tangents drawn from the same external point to a circle are equal.

From B,

BP = BQ ........(1)

From C,

CR = CQ ..........(2)

Adding equation (1) and (2), we get :

∴ CR + PB = CQ + BQ = BC

Hence, option 1 is the correct option.

In the figure, sides MN, NL and LM of ΔLMN touch a circle at the points A, B and C respectively. If AN = 5 cm, CL = 4 cm and CM = 6 cm, then the perimeter of ΔLMN is :

1. 30 cm

2. 45 cm

3. 60 cm

4. 15 cm

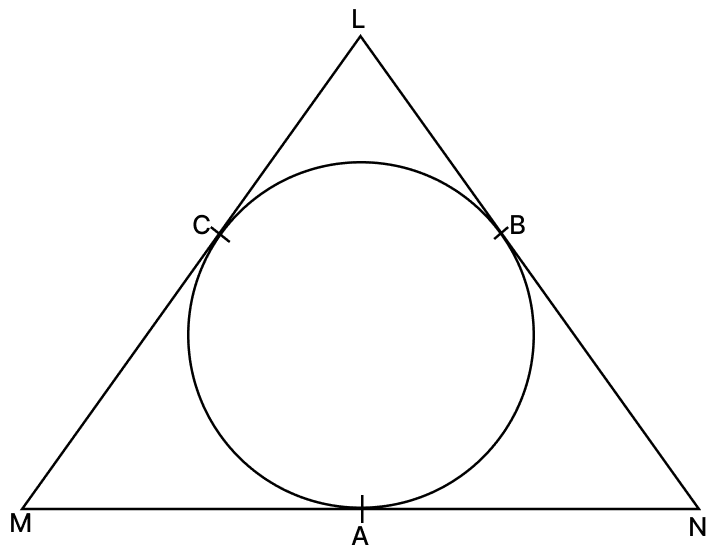
Answer

Tangents drawn from the same external point to a circle are equal.

From M,

MA = CM = 6 cm

From N,

NA = NB = 5 cm

From L,

LB = LC = 4 cm

MN = MA + AN = 6 + 5 = 11

NL = NB + BL = 5 + 4 = 9

LM = LC + CM = 4 + 6 = 10

Perimeter of ΔLMN = MN + LN + LM

= 11 + 9 + 10

= 30 cm.

Hence, option 1 is the correct option.

In the figure, two circles touch each other at X. YZ and PX are common tangents to these circles. If YP = 3.8 cm, then YZ = ?

1. 1.9 cm

2. 11.4 cm

3. 7.6 cm

4. 7 cm

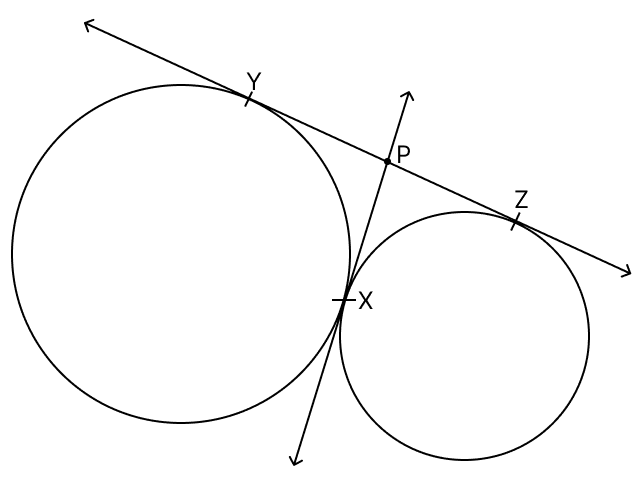
Answer

We know that if two tangents are drawn from an external point to a circle then, the lengths of the tangents are equal.

From figure,

PX and PY are the tangents to the first circle.

∴ PX = PY = 3.8 cm

PX and PZ are tangents to the second circle.

∴ PZ = PX = 3.8 cm

From figure,

YZ = PZ + PY = 3.8 + 3.8 = 7.6 cm.

Hence, option 3 is the correct option.

In the figure, AB is a chord of the circle such that ∠AXB = 50°. If AP is tangent to the circle at point A, then ∠BAP = ?

1. 65°

2. 50°

3. 40°

4. can’t be determined

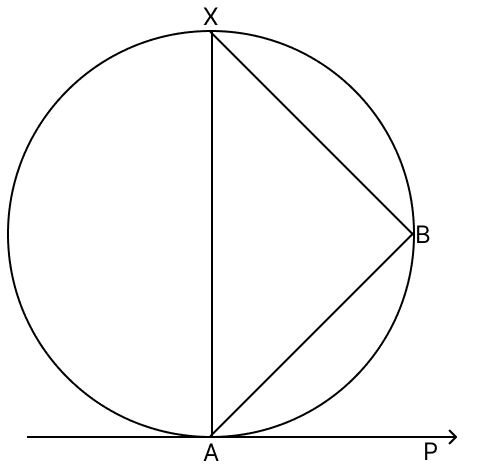
Answer

From figure,

∠BAP = ∠AXB = 50° [Angle in alternate segment are equal]

Hence, option 2 is the correct option.

In the given figure, RT is a tangent touching the circle at S. If ∠PST = 30° and ∠SPQ = 60°, then ∠PSQ is :

1. 40°

2. 30°

3. 60°

4. 90°

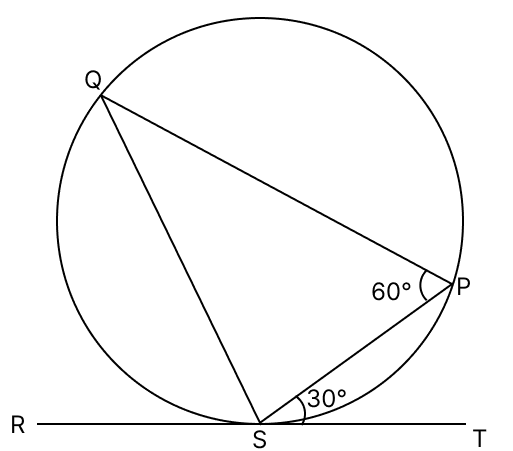
Answer

We know that,

Angle between tangent and the chord at the point of contact is equal to angle of the alternate segment.

∴ ∠PQS = ∠PST = 30°

In △ PQS,

By angle sum property of triangle,

⇒ ∠PQS + ∠QPS + ∠PSQ = 180°

⇒ 30° + 60° + ∠PSQ = 180°

⇒ ∠PSQ + 90° = 180°

⇒ ∠PSQ = 180° - 90° = 90°.

Hence, option 4 is the correct option.

In the given figure, O is the centre of the circle and AB is a chord. If the tangent AM at A makes an angle of 50° with AB, then ∠AOB = ?

1. 100°

2. 75°

3. 80°

4. 150°

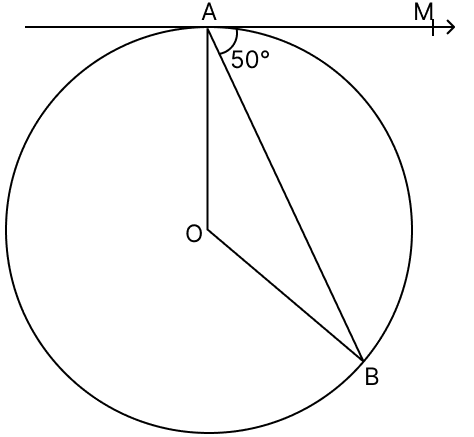
Answer

In a circle, radius through the point of contact is perpendicular to the tangent.

∠OAM = 90°

∠OAB + ∠BAM = 90°

∠OAB + 50° = 90°

∠OAB = 90° - 50°

∠OAB = 40°

OA = OB (Radii of same circle)

∠OBA = ∠OAB = 40° [Angles opposite to equal sides in a triangle are equal]

In △AOB,

By angle sum property of triangle,

⇒ ∠OBA + ∠OAB + ∠AOB = 180°

⇒ 40° + 40° + ∠AOB = 180°

⇒ ∠AOB + 80° = 180°

⇒ ∠AOB = 180° - 80° = 100°.

Hence, option 1 is the correct option.

In the figure, XY is a tangent at X to the circle with centre O. If ∠XYO = 25°, then x = ?

1. 25°

2. 115°

3. 65°

4. 60°

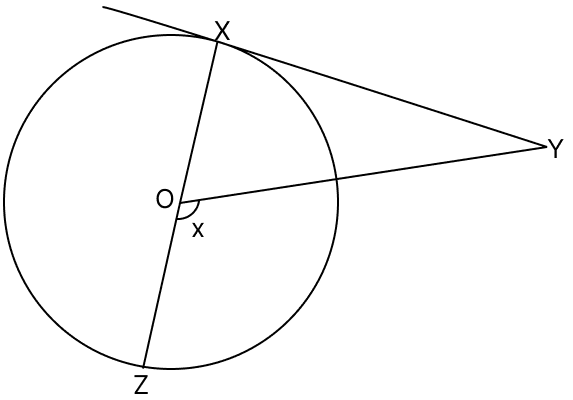
Answer

∠XYO = 25°

In a circle, radius through the point of contact is perpendicular to the tangent.

∠OXY = 90°

In △ XOY,

By angle sum property of triangle,

⇒ ∠XYO + ∠OXY + ∠XOY = 180°

⇒ 25° + 90° + ∠XOY = 180°

⇒ ∠XOY + 115° = 180°

⇒ ∠XOY = 180° - 115° = 65°.

From figure,

∠XOY + x = 180° [Linear pairs]

x = 180° - 65°

x = 115°.

Hence, option 2 is the correct option.

In the given figure, XQY is a tangent at Q to a circle. If PM is a chord parallel to XY and ∠MQY = 70°, then ∠PQM = ?

1. 20°

2. 35°

3. 40°

4. 70°

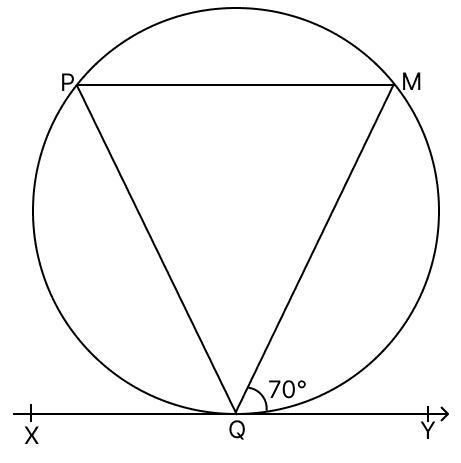
Answer

From figure,

MQ is chord and XQY is a tangent.

∠P = ∠MQY (∵ angles in alternate segment are equal.)

As PM || XQY

∠MQY = ∠M (∵ alternate angles are equal)

∴ ∠P = ∠M = 70°

We know that sum of angles in a triangle = 180°.

In △PQM,

⇒ ∠P + ∠M + ∠PQM = 180°

⇒ 70° + 70° + ∠PQM = 180°

⇒ 140° + ∠PQM = 180°

⇒ ∠PQM = 180° - 140°

⇒ ∠PQM = 40°.

Hence, option 3 is the correct option.

Assertion (A): In the figure, AB, AC and DE are tangents to the circle. If AC = 7 cm, then perimeter of ΔADE is 14 cm.

Reason (R): The lengths of tangents to a circle from an exterior point are equal.

1. A is true, R is false

2. A is false, R is true

3. Both A and R are true

4. Both A and R are false

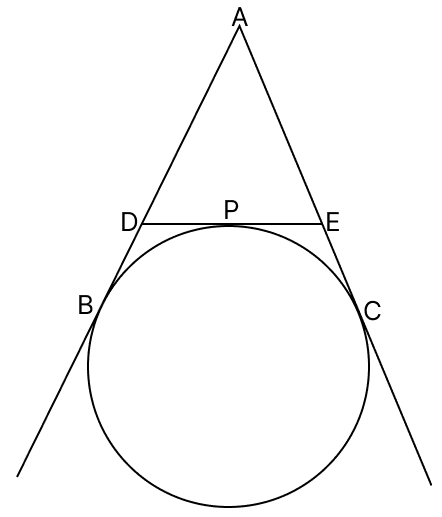
Answer

The lengths of tangents to a circle from an exterior point are equal.

∴ Reason (R) is true.

∴ AB = AC = 7 cm

⇒ Perimeter of ΔADE = AD + AE + DE

We can write DE as (DP + PE)

⇒ Perimeter of ΔADE = AD + AE + (DP + PE)

Substituting DP with DB and PE with EC:

⇒ Perimeter of ΔADE = AD + AE + (DB + EC)

⇒ Perimeter of ΔADE = (AD + DB) + (AE + EC)

⇒ Perimeter of ΔADE = AB + AC

⇒ Perimeter of ΔADE = 7 + 7

⇒ Perimeter of ΔADE = 14 cm.

Assertion (A) is true.

Hence, option 3 is the correct option.

Assertion (A): From a point P, 10 cm away from the centre of a circle, a tangent PT of length 8 cm is drawn, then the radius of the circle is 5 cm.

Reason (R): In a circle, radius through the point of contact is perpendicular to the tangent.

1. A is true, R is false

2. A is false, R is true

3. Both A and R are true

4. Both A and R are false

Answer

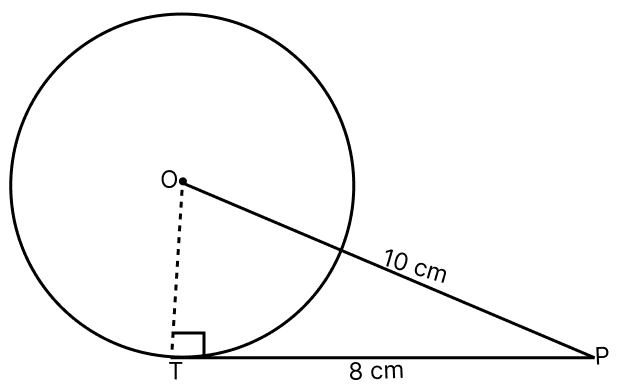
In a circle, radius through the point of contact is perpendicular to the tangent.

In right angled triangle OPT,

OP² = OT² + PT²

10² = OT² + 8²

OT² = 100 - 64

OT² = 36

OT = 6 cm.

Assertion (A) is false.

In a circle, the radius through the point of contact is perpendicular to the tangent is true.

Reason (R) is true.

A is false, R is true

Hence, option 2 is the correct option.

Assertion (A): In two concentric circles, the chord of the larger circle, which touches the smaller circle, is bisected at the point of contact.

Reason (R): A line joining centre to any point of a chord of a circle bisects the chord.

1. A is true, R is false

2. A is false, R is true

3. Both A and R are true

4. Both A and R are false

Answer

In concentric circles, a chord of the larger circle touching the smaller circle is bisected at the point of contact.

Assertion (A) is true.

A line from the centre bisects a chord only when it is perpendicular to the chord, not to any point on the chord.

Reason (R) is false.

A is true, R is false.

Hence, option 1 is the correct option.