Draw a line AB = 5 cm. Mark a point C on AB such that AC = 3 cm. Using a ruler and a compass only construct:
(i) A circle of radius 2.5 cm passing through A and C.
(ii) Construct two tangents to the circle from the external point B.
Measure and record the lengths of the tangents.
Answer
Steps of construction :
Draw a line segment AB = 5 cm.
With A as center cut an arc of 3 cm on AB to obtain C.
With A as center and radius = 2.5 cm draw an arc.
With C as center and radius = 2.5 cm draw an arc cutting the previous arc and mark the point O.
With O as center and radius = 2.5 cm draw a circle.
Join OB.
Draw the perpendicular bisector of OB, let it meet OB at point M.
With M as center and radius equal to OM, draw a circle to cut the previous circle at points P and Q.
Join PB and QB. Hence, PB and QB are required tangents.
Measure PB and QB.
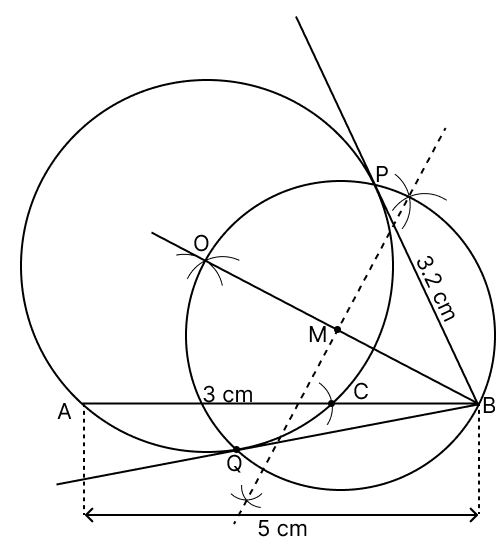
On measuring, PB = QB = 3.2 cm.
Hence, length of each tangent = 3.2 cm.
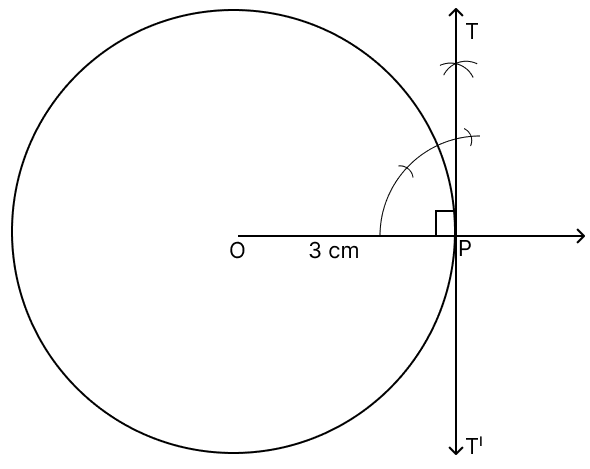
Draw a circle of radius 3 cm. Take a point P on it. Using ruler and compasses only construct a tangent to the circle at the point P.
Answer
Steps of Construction :
Draw a circle of radius = 3 cm with centre as O.
Extend the radius of the circle on one the side and mark point P, Join OP.
At point P, construct a line perpendicular to OP and name it as TT'.
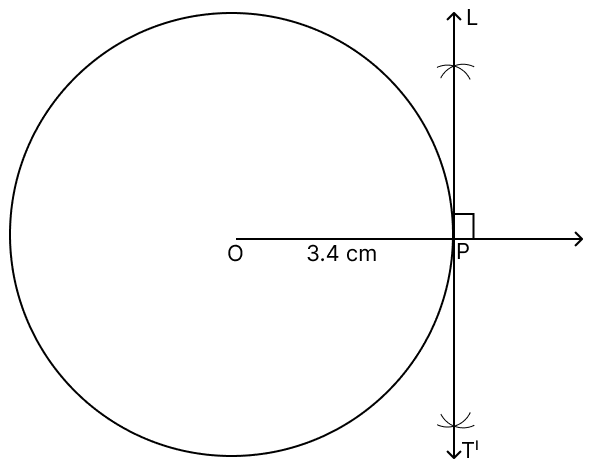
Draw a circle of radius 3.4 cm. Take a point P on it. Without using the centre of the circle, construct a tangent to the circle at the point P.
Answer
Steps of Construction :
Draw a circle of radius = 3.4 cm with centre as O.
Extend the radius of the circle on one the side and mark point P, Join OP.
At point P, construct a line perpendicular to OP and name it as L.
Draw a circle of radius 2.7 cm. Mark its centre as O. Take a point P at a distance of 5.3 cm from O. From the point P, draw two tangents to the circle. Measure the length of each.
Answer
Steps of Construction :
Draw a circle of radius = 2.7 cm with centre as O.
Mark a point P at a distance of 5.3 cm from O. Join OP. Draw its perpendicular bisector to meet OP at M.
With M as centre and OM as radius, draw a circle. Let this circle intersect the given circle with centre as O at points A and B.
Join PA and PB.
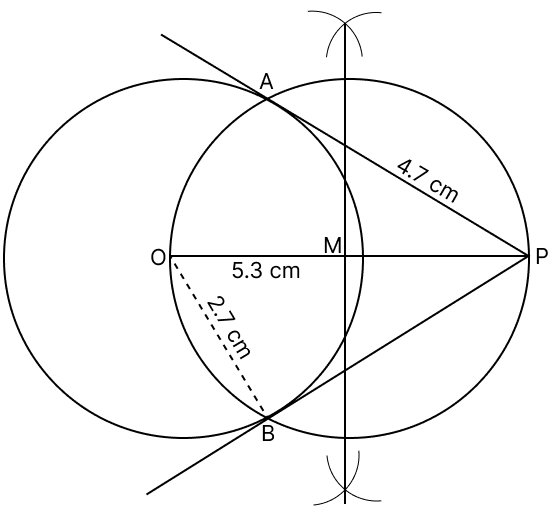
On measuring we get : PA = PB = 4.7 cm.
Hence, the length of each tangent = 4.7 cm.
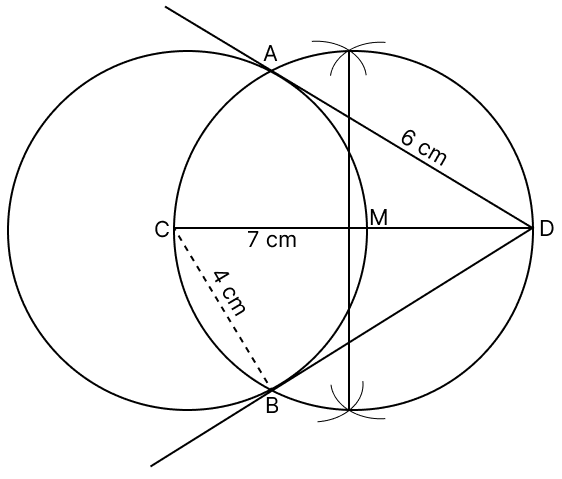
Draw a circle of radius 4 cm. Mark its centre as C and mark a point D such that CD = 7 cm. Using ruler and compasses only but not using the centre of the circle, construct two tangents from D.
Answer
Steps of construction :
Construct a circle with centre as C and radius = 4 cm.
Mark a point D at a distance of 7 cm from the centre. Join CD. Draw its perpendicular bisector to meet CD at M.
With M as centre and CM (or MD) as radius, draw a circle. Let this circle intersect the given circle with centre as C at points A and B.
Join DA and DB.
Draw a circle of radius 3.2 cm. Draw two tangents to it inclined at an angle of 60° with each other.
Answer
Steps of Construction :
Draw a circle with center O, radius = 3.2 cm and BC as diameter.
Draw arcs making an angle of 120° at O such that ∠AOB = 120°.
At A and B, draw two rays making an angle of 90° at each point which meet other at point P.
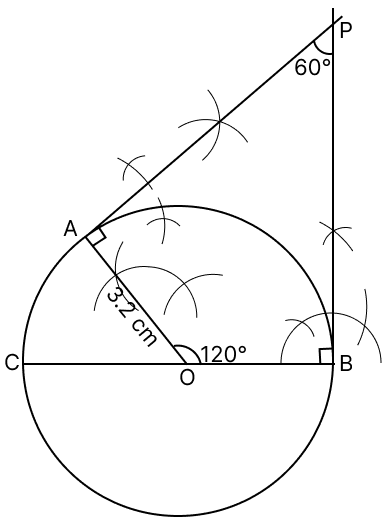
Hence, AP and BP are required tangents making an angle of 60° with each other.
Draw a circle of radius 2.5 cm. Draw two tangents to it inclined at an angle of 45° to each other.
Answer
Steps of Construction :
Draw a circle with center O, radius = 2.5 cm and BC as diameter.
Draw arcs making an angle of 135° (180° - 45°) at O such that ∠AOB = 135°.
At A and B, draw two rays making an angle of 90° at each point which meet other at point P.
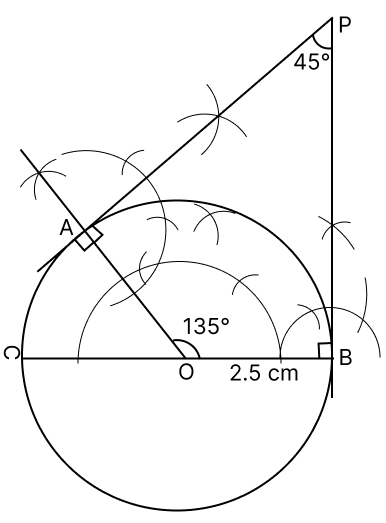
Hence, AP and BP are required tangents making an angle of 45° with each other.
Draw a circle of radius 3.5 cm. Mark a point P outside the circle at a distance of 6 cm from the centre. Construct two tangents from P to the given circle. Measure the length of one tangent.
Answer
Steps of construction :
With O as center and radius = 3.5 cm draw a circle.
Take a point P such that OP = 6 cm.
Draw perpendicular bisector of OP, cutting OP at M.
With center M and radius OM, draw a circle which intersects the circle with center O at A and B.
Join AP and BP. Measure AP and BP.
Hence, AP and BP are required tangents.
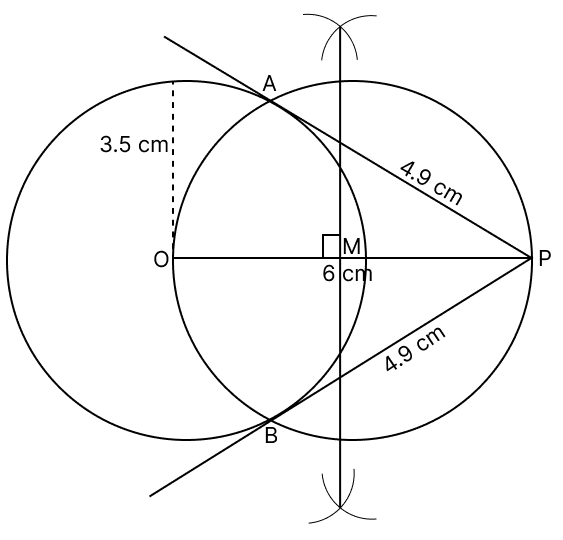
On measuring,
AP = BP = 4.9 cm.
Hence, length of each tangent = 4.9 cm.
Use ruler and compasses only for answering this question. Draw a circle of radius 4 cm. Mark the centre as O. Mark a point P outside the circle at a distance of 7 cm from the centre. Construct two tangents to the circle from the external point P. Measure and write down the length of any one tangent.
Answer
Steps of construction :
Construct a circle with centre as O and radius = 4 cm.
Mark a point P at a distance of 7 cm from the centre. Join OP. Draw its perpendicular bisector to meet OP at M.
With M as centre and OM (or MP) as radius, draw a circle. Let this circle intersect the given circle with centre as O at points A and B.
Join PA and PB.
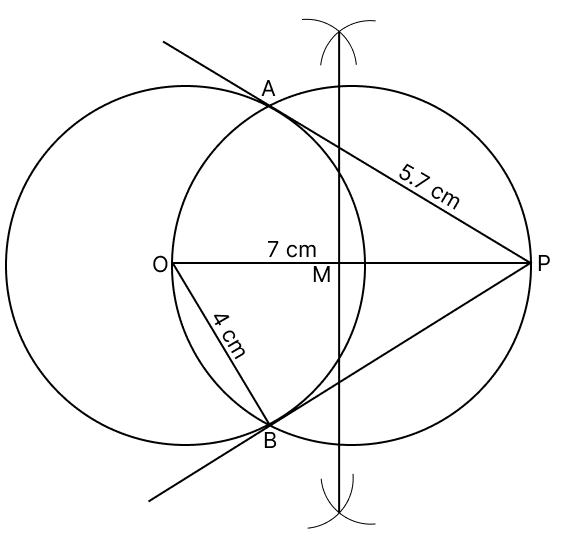
On measuring, PA = PB = 5.7 cm
Hence, the length of each tangent = 5.7 cm.
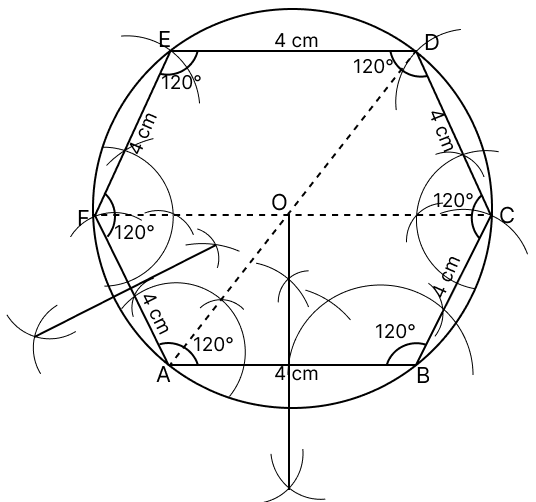
Construct a regular hexagon of side 4 cm. Construct a circle circumscribing the hexagon.
Answer
We know that each angle in a regular hexagon = 120°.
Steps of construction :
Draw a regular hexagon ABCDEF with each side equal to 4 cm and each interior angle = 120°.
Draw the perpendicular bisectors of AB and AF which intersect each other at O.
With O as center and OA as radius draw a circle which will pass through all the vertices of the regular hexagon.
Hence, above is the required circumcircle of regular hexagon.
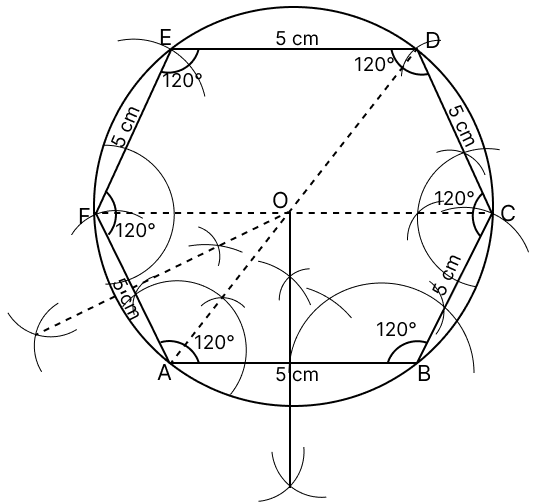
Construct a regular hexagon of side 5 cm. Construct a circle circumscribing the hexagon.
Answer
Steps of construction :
Draw a regular hexagon ABCDEF with each side equal to 5 cm and each interior angle = 120°.
Draw the perpendicular bisectors of AB and AF which intersect each other at O.
With O as center and OA as radius draw a circle which will pass through all the vertices of the regular hexagon.
Hence, above is the required circumcircle of regular hexagon.
Construct a ΔABC with BC = 6.5 cm, AB = 5.5 cm and AC = 5 cm. Construct the incircle of the triangle. Measure the radius of the incircle.
Answer
Steps of construction :
Draw a line segment BC = 6.5 cm.
Cut an arc from C of 5 cm and an arc of 5.5 cm from B.
Mark the point as A where the arcs from B and C intersect.
Join A, B and C. Hence, the △ABC is formed.
Draw the (internal) bisectors of ∠B and ∠C. Let these bisectors meet at point I.
From I, draw IN perpendicular to the side BC.
With I as centre and radius equal to IN, draw a circle. The circle so drawn touches all the sides of the △ABC, and is the required incircle of △ABC.
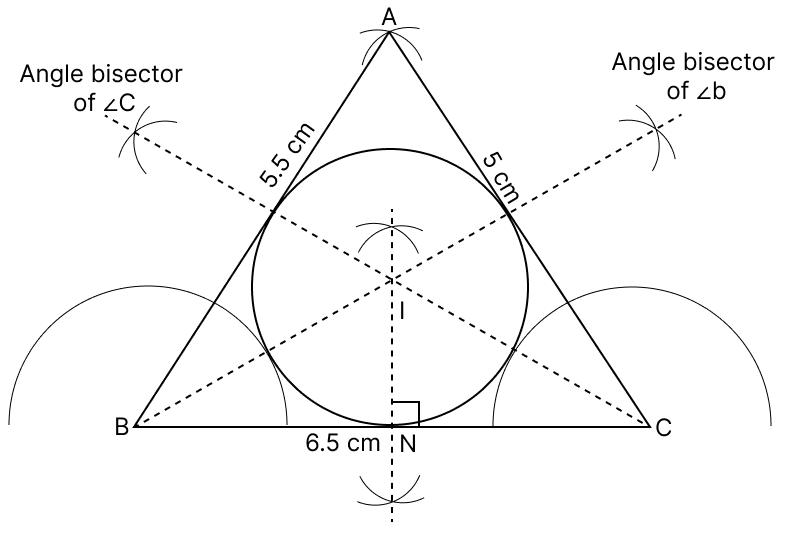
On measuring IN, we get the radius of the incircle.
Hence, the radius of incircle is 1.5 cm.
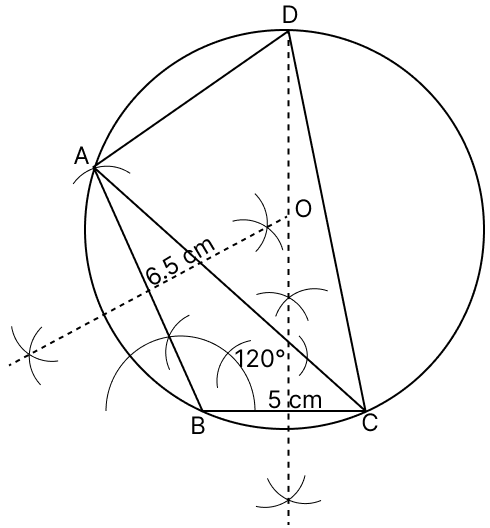
(i) Construct a ΔABC in which BC = 5 cm, AB = 6.5 cm and ∠ABC = 120°.
(ii) Construct a circle circumscribing ΔABC.
(iii) Draw a cyclic quadrilateral ABCD so that D is equidistant from B and C.
Answer
Steps of construction :
Draw a line segment BC = 5 cm.
From B construct angle 120° and extend the line such that AB = 6.5 cm.
Join points A, B and C. Hence, the △ABC is formed.
Draw the perpendicular bisector of AB and BC. Let these bisectors meet at the point O.
With O as center and radius equal to OA, draw a circle. The circle so drawn passes through the points A, B and C, and is required circumcircle of △ABC.
Extend perpendicular bisector of BC, until it intersect circle and mark it as D.
Join AD and CD.
Using ruler and compasses only, draw an equilateral triangle of side 4.5 cm and draw its circumscribed circle. Measure the radius of the circle.
Answer
Steps of Construction :
Draw a line segment BC = 4.5 cm.
With centers B and C, draw two arcs of radius 4.5 cm which intersect each other at A.
Join AC and AB.
Draw perpendicular bisectors of AC and BC intersecting each other at O.
With center O, and radius OA or OB or OC draw a circle which pass through A, B and C. Measure OC.
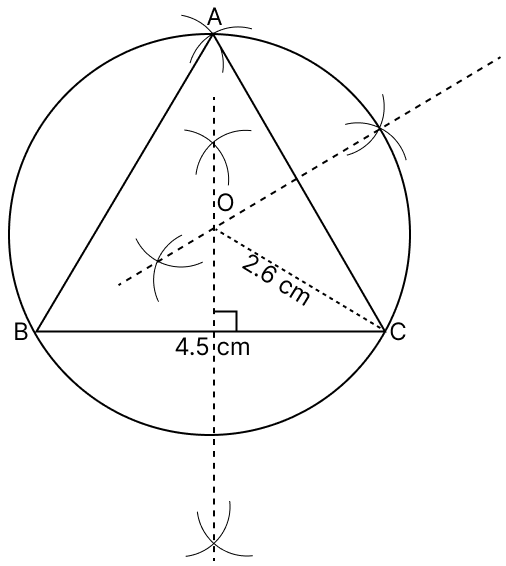
On measuring, OC = 2.6 cm.
Hence, above is the required circumcircle with radius = 2.6 cm.
Using ruler and compasses only, draw an equilateral triangle of height 6 cm and draw its inscribed circle. Measure the radius of the circle.
Answer
Steps of construction :
Draw a line XY.
Construct perpendicular bisector of XY, let bisector intersect XY at point M.
From point M, draw an arc with radius 6 cm, mark the point of intersection of arc and perpendicular bisector as A.
Construct ∠MAB = 30° and ∠MAC = 30°.
Draw angle bisectors of ∠B and ∠C intersecting each other at O.
Draw OM perpendicular to BC. With O as center and OM as radius draw a circle, touching sides of △ABC. Measure OM.
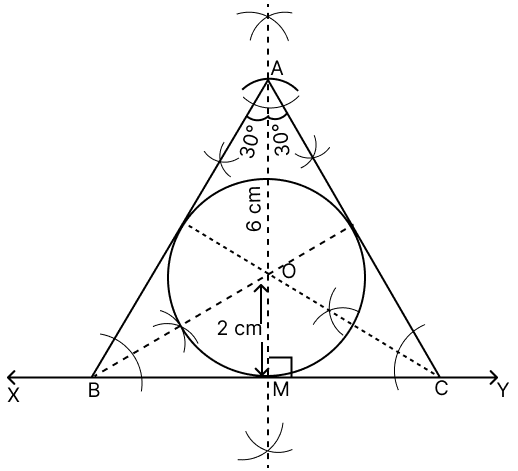
On measuring,
OM = 2 cm.
Hence, radius of the circle = 2 cm.
Construct a triangle with sides 5 cm, 4 cm and 3 cm. Draw its circumcircle and measure its radius.
Answer
Steps of construction :
Draw a line segment BC = 4 cm.
From B cut an arc of 3 cm and from C cut an arc of 5 cm.
Mark the point as A where the arcs meet.
Join the points A, B and C. Hence, the △ABC is formed.
Draw the perpendicular bisector of AB and BC. Let these bisectors meet at the point O.
With O as center and radius equal to OA, draw a circle. The circle so drawn passes through the points A, B and C, and is the required circumcircle of △ABC.
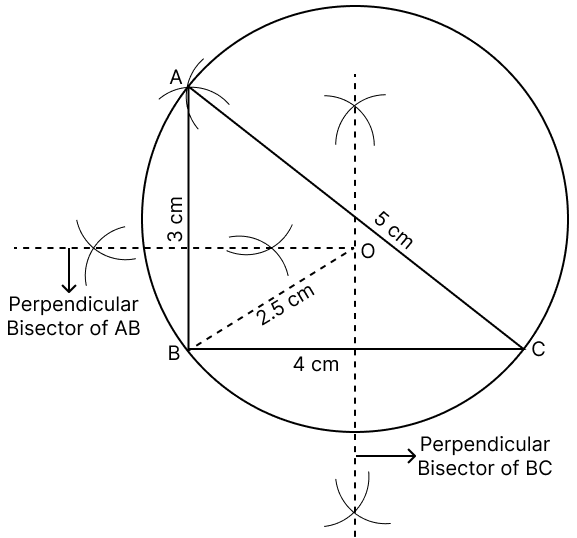
Measuring OB we get the radius of the circumcircle.
Hence,the radius of the circumcircle = 2.5 cm.
(ii) Using a ruler and a pair of compasses only, construct:
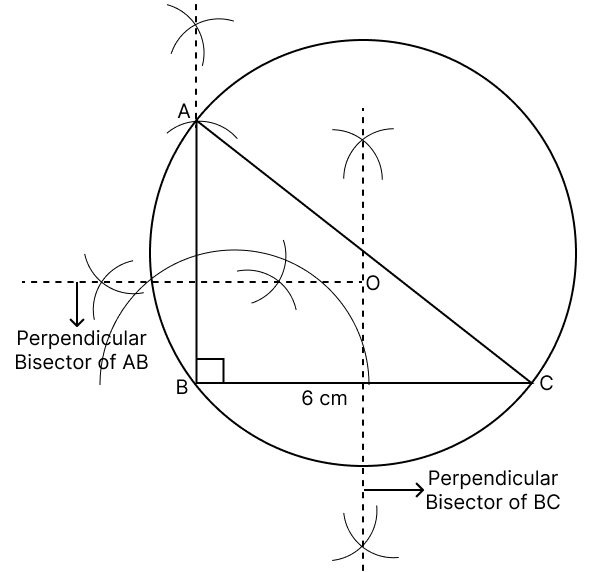
(a) a triangle ABC, given AB = 4 cm, BC = 6 cm and ∠ABC = 90°.
(b) a circle which passes through the points A, B and C and mark its centre as O.
Answer
Steps of construction :
Draw a line segment BC = 6 cm.
Draw the perpendicular from point B and cut AB from that perpendicular such that AB = 4 cm.
Join points A, B and C.
In the above triangle, draw the perpendicular bisector of AB and BC. Let these bisectors meet at the point O.
With O as center and radius equal to OA, draw a circle. The circle so drawn passes through the points A, B and C, and is required circumcircle of △ABC.
Using a ruler and a compass construct a triangle ABC in which AB = 7 cm, ∠CAB = 60° and AC = 5 cm. Construct the locus of:
(i) Points equidistant from AB and AC.
(ii) Points equidistant from BA and BC.
Hence, construct a circle touching the three sides of the triangle internally.
Answer
Steps of construction :
Draw a line segment AB = 7 cm.
Construct AX such that ∠XAB = 60°.
With A as center and radius = 5 cm cut arc on AX and mark it as point C.
Join BC. ABC is the required triangle.
Draw AY and BZ, angle bisector of A and B.
Let AY and BZ meet at point O.
Draw OD ⊥ AB.
With O as center and OD as radius draw a circle.
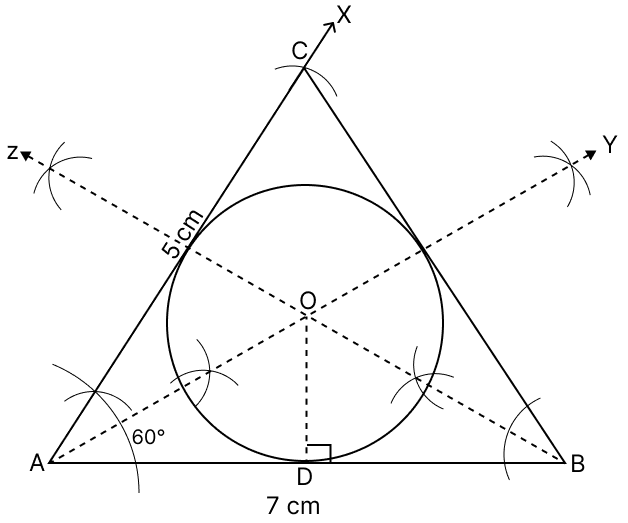
(i) Hence, AY is the locus of points equidistant from AB and AC.
(ii) Hence, BZ is the locus of points equidistant from BA and BC.
Draw a right-angled ΔABC in which hypotenuse BC = 6.4 cm and the altitude from A on BC is 2.5 cm. Draw the circumcircle of the triangle and measure its radius.
Answer
Steps of construction :
Draw BC = 6.4 cm.
Draw PQ, the right bisector of BC and draw a circle with PB as radius.
Along PQ, cut off PR = 2.5 cm.
Through R, draw AA′ ∥ BC meeting the circle at A and A′.
Join AB and AC. Draw AT perpendicular to BC, AT = 2.5 cm.
Mid-point of BC is circumcentre and radius = BC.
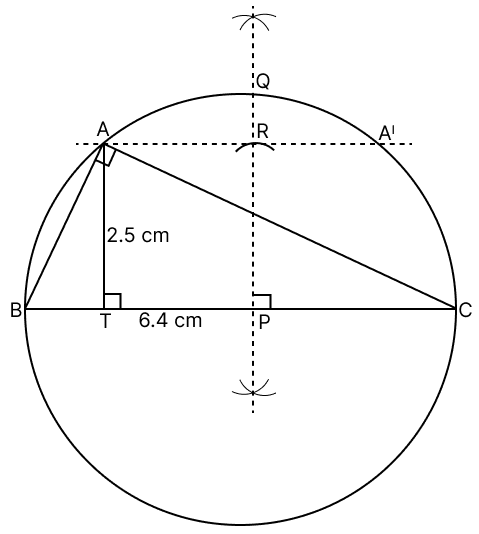
Hence, radius PQ = 3.2 cm.
Construct a ΔABC in which AB = 4.5 cm, BC = 7 cm and median AD = 4 cm. Draw the inscribed circle of the triangle and measure its radius.
Answer
Steps of construction :
Draw BC = 7 cm. Mark its mid-point as D.
With B as centre and radius 4.5 cm, draw an arc.
With D as centre and 4 cm as radius, draw another arc, cutting the first arc at A.
Join AB and AC.
Construct the angle bisectors BH and CE of ∠ABC and ∠ACB.
Let the two angle bisectors intersect at point I.
Draw IP perpendicular to BC.
With I as centre and IP as radius, draw a circle.
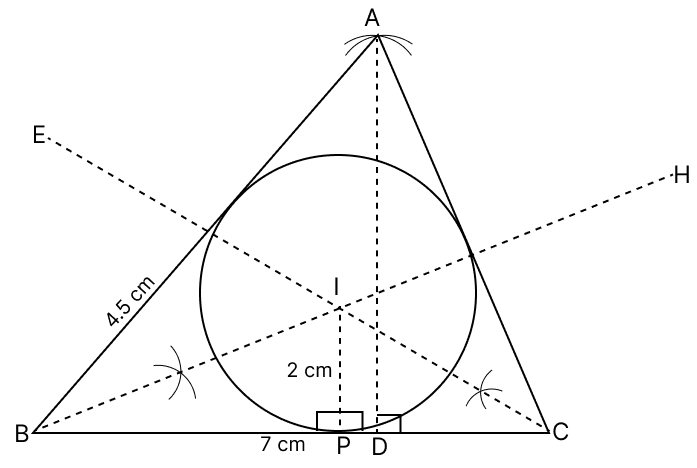
Hence, radius IP = 2 cm.
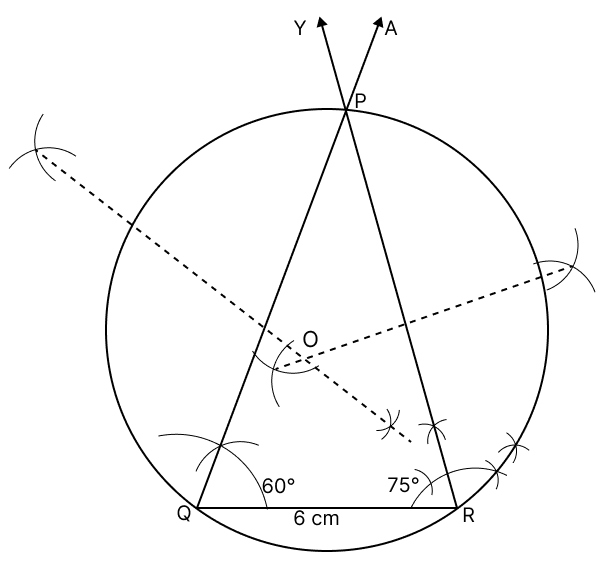
Using ruler and compasses only construct a ΔPQR in which QR = 6 cm, ∠Q = 60° and ∠R = 75°. Draw the circumcircle of the triangle.
Answer
Steps of construction :
Draw a line segment QR = 6 cm.
At point Q, draw ray QA, such that ∠Q = 60°.
At point R, draw ray RY, such that ∠R = 75°.
The rays QA and RY intersect at point P.
Δ PQR is the required triangle.
Draw the perpendicular bisector of PQ and PR. Let these bisectors intersect at O.
With O as centre and OQ as radius, draw a circle, which is the required circumcircle of triangle PQR.
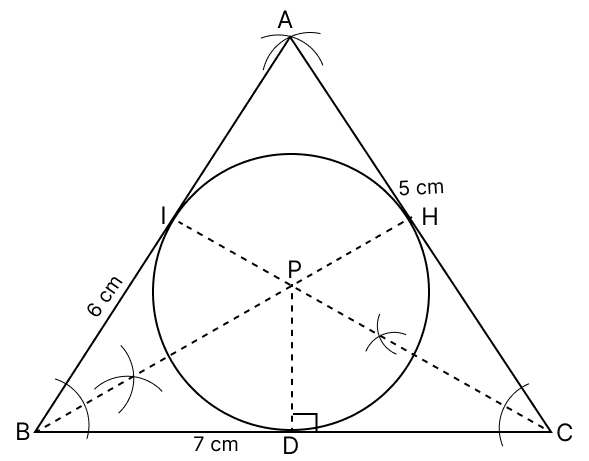
Using compasses and ruler, construct a ΔABC in which AB = 6 cm, BC = 7 cm and AC = 5 cm. Draw a circle inside the triangle touching its sides.
Answer
Steps of construction :
Draw BC = 7 cm.
With B as centre, draw an arc of radius 6 cm.
With C as the centre, draw an arc of radius 5 cm.
Join AB and AC to form ΔABC.
Construct the angle bisector BH and CI of ∠ABC and ∠ACB respectively.
Let the two angle bisectors intersect at point P.
Draw PD perpendicular to BC. With P as centre and PD as radius, draw a circle.
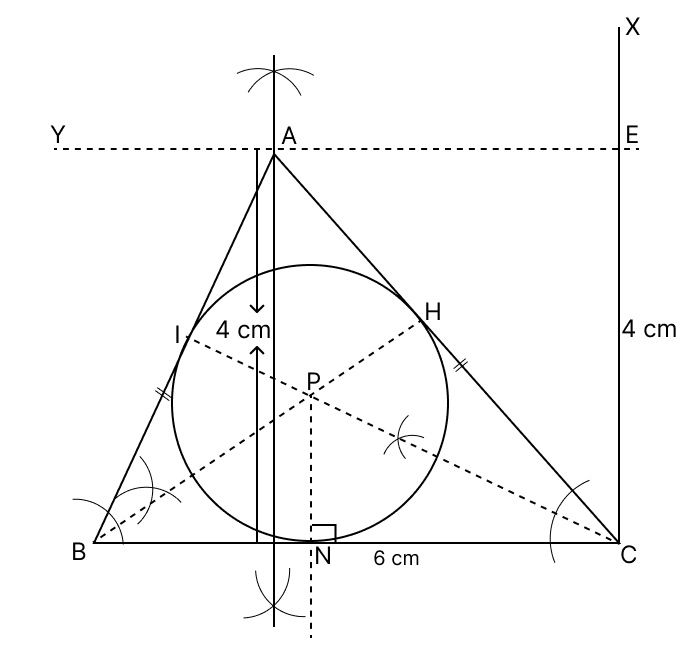
Draw an isosceles ΔABC in which base BC = 6 cm and the altitude from vertex to the base is 4 cm. Draw its inscribed circle.
Answer
Steps of construction :
Draw BC = 6 cm as base.
At C, draw a perpendicular line CX and from it, cut off CE = 4 cm.
From E, draw EY, perpendicular to CX.
Draw perpendicular bisector of BC that intersects EY at A, such that AB = AC.
Join AB and AC to form △ABC.
Construct the angle bisector BH and IC of ∠ABC and ∠ACB respectively.
Let the two angle bisectors intersect at point P.
From P, draw PN perpendicular to the side BC.
With P as centre and radius equal to PN, draw a circle. The circle so drawn touches all the sides of the △ABC, and is the required incircle of △ABC.
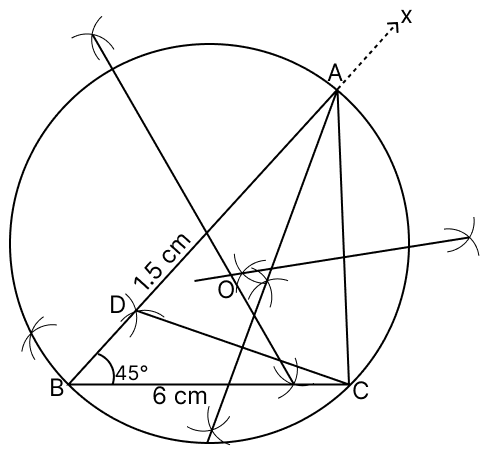
Draw a ΔABC in which BC = 6 cm, ∠B = 45° and (AB − AC) = 1.5 cm. Draw the circumcircle of the triangle. Use ruler and compasses only.
Answer
Draw BC = 6 cm.
At point B, Construct an angle of 45°, ∠XBC = 45°.
Let D be a point on the ray XB such that BD = 1.5 cm.
Join CD. Draw the perpendicular bisector of CD such that bisector intersect ray XB at point A.
Join AB and AC. ΔABC is the required triangle.
Draw the perpendicular bisector of AB and AC. Let these bisectors intersect at O.
With O as centre and OA as radius, draw a circle.
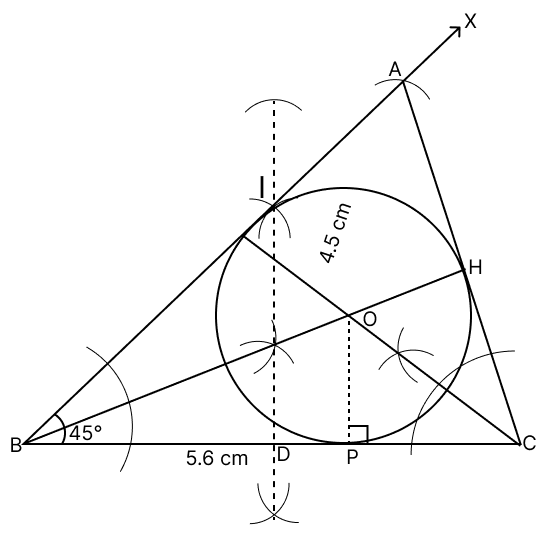
Using ruler and compasses only construct a ΔABC having base = 5 cm, vertical angle = 45° and median through vertex equal to 4 cm. Draw the incircle of the triangle.
Answer
Steps of construction :
Draw a line segment BC = 5 cm.
Construct perpendicular bisector of BC.
At point B, construct an angle of 45°, ∠XBC = 45°.
Let this ray XB intersect the perpendicular bisector of BC at O. With a radius of OB draw major arc.
From M, draw an arc of radius 4 cm, that intersects the major arc and label it as A.
Join AB and AC. Hence, ABC is the required triangle.
Construct the angle bisector BH and CI of ∠ABC and ∠ACB respectively.
Let the two angle bisectors intersect at point P.
Draw PD perpendicular to BC. With P as centre and PD as radius, draw a circle.
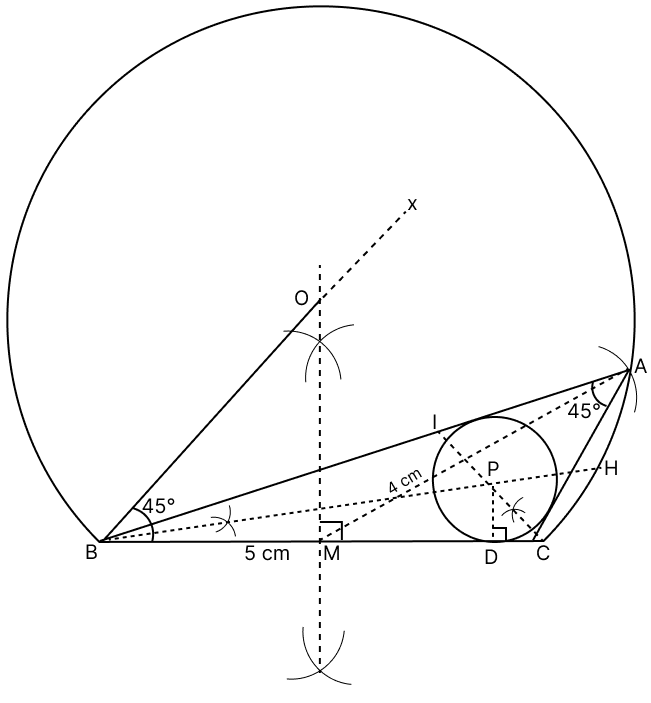
Using ruler and compasses only construct a ΔABC in which BC = 6.2 cm, ∠A = 60° and the altitude through A is 2.6 cm. Draw the incircle of the triangle.
Answer
Steps of construction :
Draw a line segment BC = 6.2 cm.
Construct perpendicular bisector of BC, intersecting BC at point M.
At point B and C, construct an angle of 30°, ∠XBC = 30° and ∠YCB = 30°.
Let this rays XB and CY intersect at O. With center as O and radius as OB, draw major arc.
From M, draw an arc of radius 2.6 cm on perpendicular bisector of BC mark it as E.
Draw a line parallel to BC passing through E, which intersect major arc at A.
Join AB and AC. Hence, ABC is the required triangle.
Construct the angle bisector BH and CI of ∠ABC and ∠ACB respectively.
Let the two angle bisectors intersect at point P.
Draw PD perpendicular to BC. With P as centre and PD as radius, draw a circle.
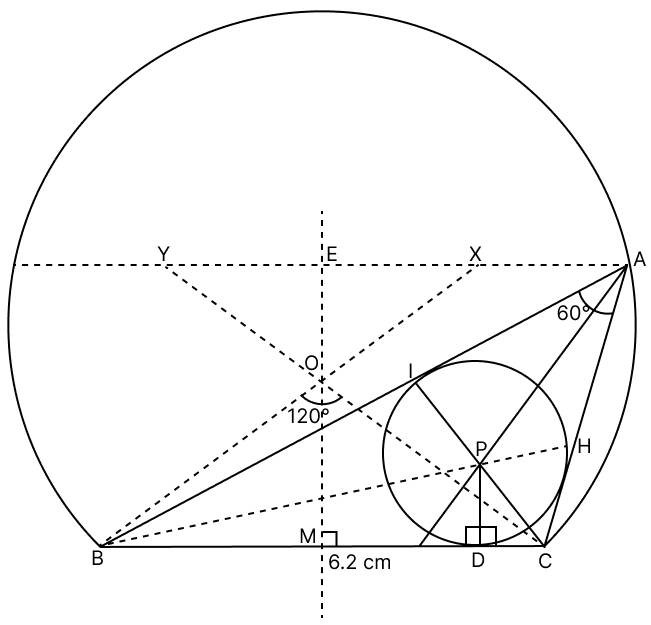
Draw a ΔABC in which BC = 5.6 cm, ∠B = 45° and the median AD from A to BC is 4.5 cm. Inscribe a circle in it.
Answer
Steps of construction :
Draw a line segment BC = 5.6 cm.
Construct perpendicular bisector of BC which intersect BC at D.
At B, construct angle ∠XBC = 45°.
From D, with radius 4.5 cm draw an arc that intersect BX, mark it as A.
Join AB and AC. Hence, ABC is the required triangle.
Construct the angle bisector BH and CI of ∠ABC and ∠ACB respectively.
Let the two angle bisectors intersect at point O.
Draw OP perpendicular to BC. With O as centre and OP as radius, draw a circle.
Draw a regular hexagon of side 2.4 cm. Circumscribe a circle to it.
Answer
Steps of construction :
We know that each angle in a regular hexagon = 120°.
Draw a line segment AB = 2.4 cm.
At A and B draw rays making an angle of 120° each and cut off AF = BC = 2.4 cm.
At F and C, draw rays making angle of 120° each and cut off EF = CD = 2.4 cm.
Join ED. Hence, ABCDEF is the required hexagon.
Draw the perpendicular bisectors of AB and AF which intersect each other at O.
With O as center and OA as radius draw a circle which will pass through all the vertices of the regular hexagon.
Hence, above is the required circumcircle of regular hexagon.
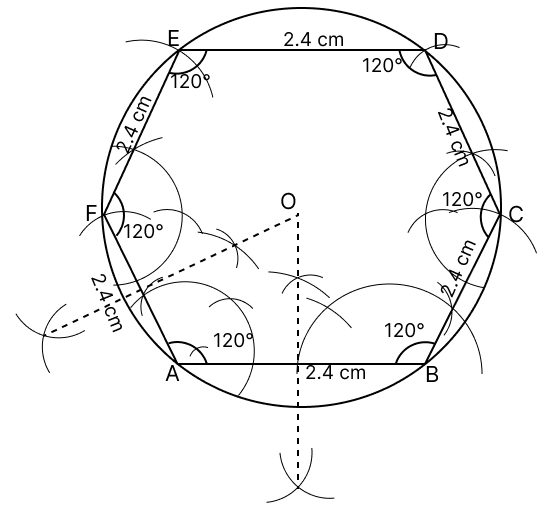
Hence, ABCDEF is the required hexagon.
Draw a regular hexagon of side 2.2 cm. Inscribe a circle in it.
Answer
We know that each angle in a regular hexagon = 120°.
Draw a line segment AB = 2.2 cm.
At A and B draw rays making an angle of 120° each and cut off AF = BC = 2.2 cm.
At F and C, draw rays making angle of 120° each and cut off EF = CD = 2.2 cm.
Join ED. Hence, ABCDEF is the required hexagon.
Draw the angle bisectors of A and B which intersect each other at O.
Draw OL ⊥ AB.
With centre O and radius OL, draw a circle which touches the sides of hexagon. This is the required incircle of hexagon ABCDEF.
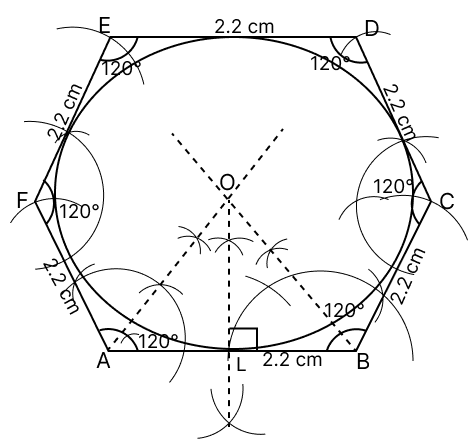
Hence, ABCDEF is required hexagon.
Using ruler and compass, construct a triangle ABC, where AB = 3 cm, BC = 4 cm and ∠ABC = 90°. Hence, construct a circle circumscribing the triangle ABC. Measure and write down the radius of the circle.
Answer
Steps of construction :
Draw a line segment AB = 3 cm.
From B, draw a ray BX such that ∠XBA = 90°.
From B draw an arc of 4 cm cutting XB at C.
Join AC. ABC is the required triangle.
Construct perpendicular bisectors of AB and AC, such that they intersect at O.
With O as center and OA as radius draw a circle passing through A, B and C.
Measure OA.
Hence, above is the required circumcircle of triangle ABC.
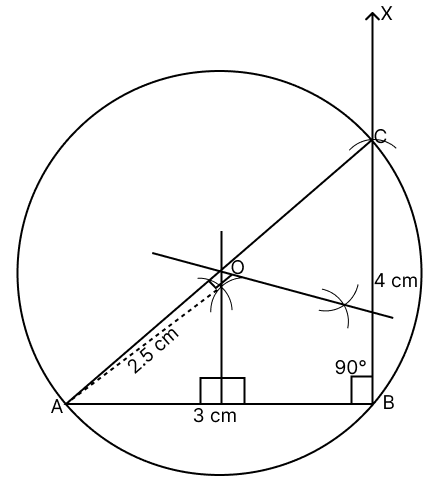
On measuring we get OA = 2.5 cm.
Hence,the length of the radius of the circle = 2.5 cm.