Loci

Describe and construct each of the following loci:

(i) The locus of the tip of a minute hand of a watch.

(ii) The locus of the tip of the pendulum of a clock.

(iii) The locus of a point 5 cm from a fixed point O.

(iv) The locus of a point at a distance of 3 cm from a fixed line AB.

(v) The locus of a point equidistant from the arms OA and OB of ∠AOB.

(vi) The locus of the centres of all circles, each of radius 1 cm and touching externally a fixed circle with centre O and radius 3 cm.

(vii) The locus of the centres of all circles to which both the arms of an angle ∠AOB are tangents.

(viii) The locus of a point 1 cm from the circumference of a fixed circle towards the centre O, whose radius is 3 cm.

(ix) The locus of a point 1 cm from the centre of a circle of radius 2.5 cm.

(x) The locus of a stone dropped from a tower.

(xi) AB is a fixed line. State the locus of a point P such that ∠APB = 90°.

Answer

(i) Let radius of minute hand be r units.

The minute hand rotates around a fixed center. The distance from the tip to the center remains constant, forming a circle.

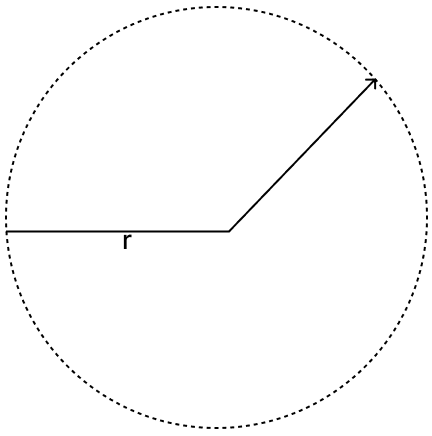
Hence, the locus of the tip of a minute hand of a watch is the circumference of a circle with radius equal to the length of minute hand.

(ii) A pendulum swings in an arc from a fixed pivot, always at a constant distance from the pivot.

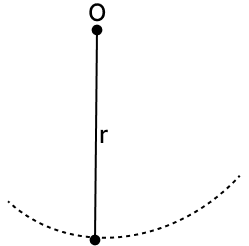
Hence, the locus of the tip of the pendulum of a clock is an arc of a circle whose radius is equal to length of pendulum.

(iii) All points 5 cm from one point form a circle.

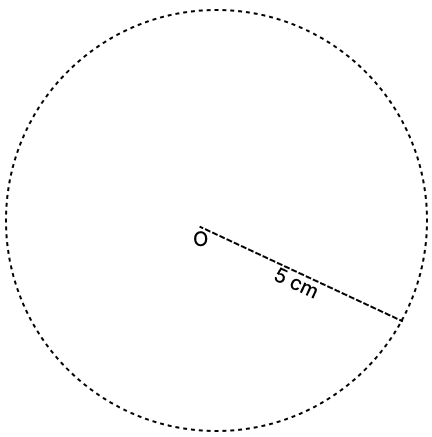
Hence, the locus of a point 5 cm from a fixed point O is the circumference of a circle with center O and radius 5 cm.

(iv) All points 3 cm from a line lie on two lines parallel to the original line.

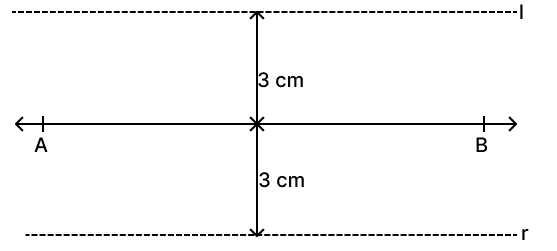
Hence, the locus of a point at a distance of 3 cm from a fixed line AB are two parallel lines, 3 cm away from AB.

(v) Points equidistant from two intersecting lines lie on the angle bisector.

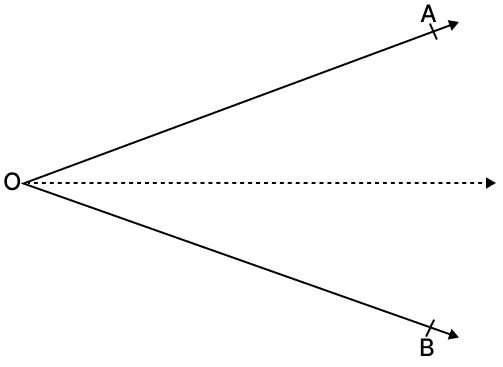
Hence, the locus of a point equidistant from the arms OA and OB of ∠AOB is the bisector of ∠AOB.

(vi) The locus of centres of all circles of radius 1 cm touching externally a fixed circle of radius 3 cm. Distance between centers = 3 + 1 = 4 cm, forming a concentric circle.

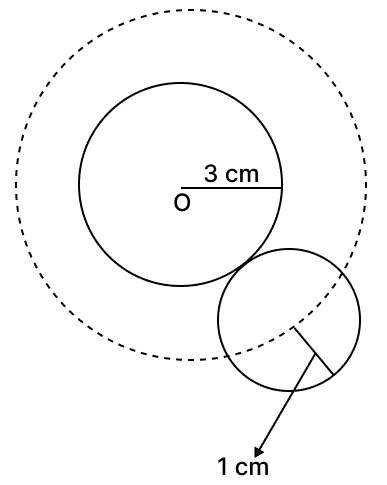
Hence, the locus of the centres of all such circles is a circle with center O and radius 4 cm.

(vii) The locus of centres of all circles tangent to both arms of ∠AOB. The center must be equidistant from both arms i.e. angle bisector of the angle between OA and OB.

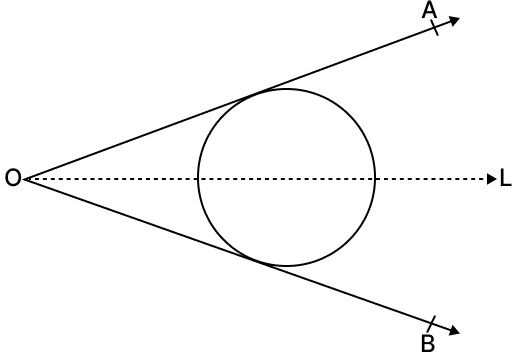
Hence, the locus of the centres of all circles to which both the arms of an angle ∠AOB are tangents is the bisector of ∠AOB.

(viii) The locus of a point 1 cm from the circumference of a circle of radius 3 cm, towards the centre will be a circle with same center and radius equal to 2 cm (3 - 1).

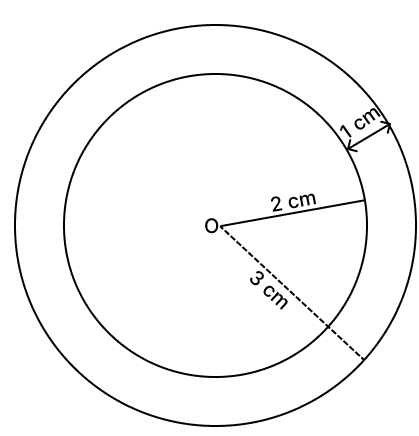
Hence, the locus of a point is a circle concentric with the fixed circle, having center O and radius 2 cm.

(ix) The locus of a point 1 cm from the centre of a circle of radius 2.5 cm. The radius of the original circle is irrelevant. Distance from center is fixed at 1 cm.

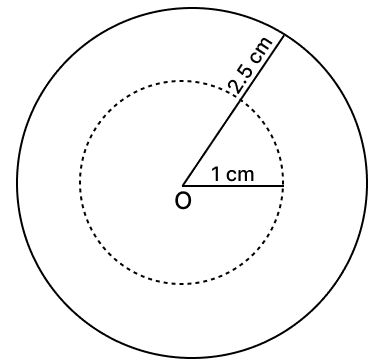
Hence, the locus of a point 1 cm from the centre of a circle is the circumference of a circle with center O and radius 1 cm.

(x) The locus of a stone dropped from a tower is a straight line parallel to tower.

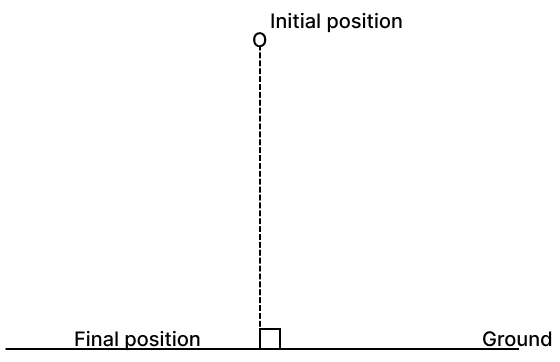
Hence, the locus of a stone dropped from a tower is a straight vertical line segment.

(xi) We know that the angle in a semi-circle is always equal to 90°.

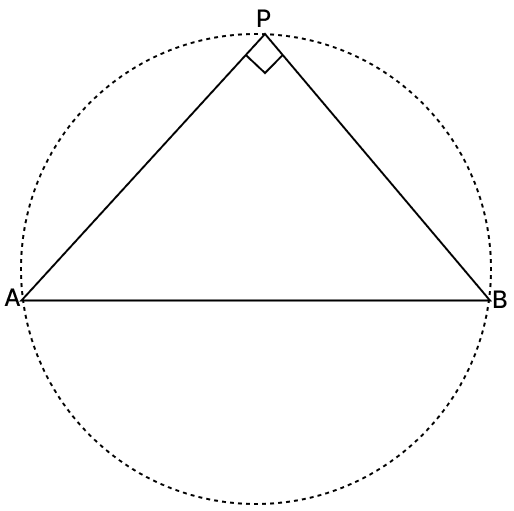
Hence, the locus of point P will be the circle whose diameter is AB.

Describe the locus of a point in a rhombus ABCD which is equidistant from

(i) AB and AD

(ii) A and C

Answer

(i) Locus of a point equidistant from AB and AD

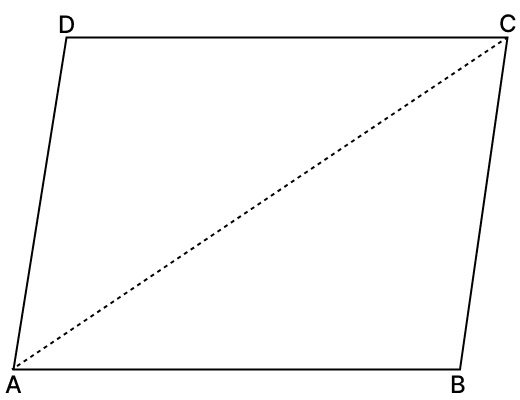
The locus of a point equidistant from two intersecting lines AB and AD is the angle bisector of the angle formed by those lines i.e. angle bisector of ∠DAB.

Since, diagonals of rhombus bisect the interior angles.

Hence, locus of a point in rhombus ABCD equidistant from AB and AD is the bisector of ∠DAB, i.e., diagonal AC.

(ii) Locus of a point equidistant from A and C

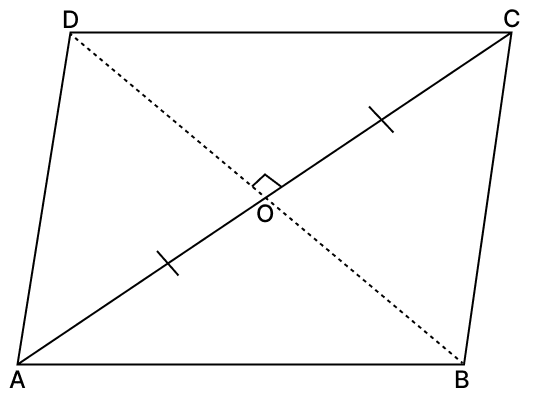
The locus of a point equidistant from two fixed points A and C is the perpendicular bisector of the line segment joining the two points AC.

Since, diagonals of a rhombus always bisect each other at right angles.

Hence, locus of a point in rhombus ABCD equidistant from A and C is the perpendicular bisector of AC, i.e., diagonal BD.

Construct a ΔABC in which BC = 5.3 cm, CA = 4.8 cm and AB = 4 cm. Find by construction a point P which is equidistant from BC and AB and also equidistant from B and C.

Answer

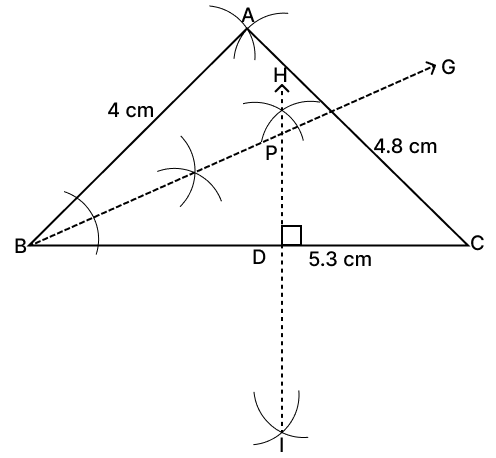
Steps of construction:

1. Draw base BC of length 5.3 cm.

2. With B as the center and a radius of 4 cm, draw an arc.

3. With C as the center and a radius of 4.8 cm, draw a second arc intersecting previous arc at A. Join ABC to get required triangle.

4. Draw BG angle bisector of ∠ABC.

5. Draw HI, the perpendicular bisector of BC.

The intersection of the angle bisector BG and the perpendicular bisector HI is the required point P.

Construct ∠AOB = 60°. Mark a point P equidistant from OA and OB such that its distance from another given line CD is 3 cm.

Answer

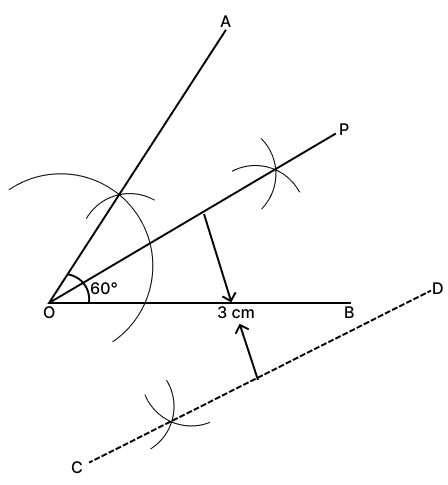
Steps of construction:

1. Draw base OB.

2. Make angle 60° at O, ∠AOB = 60°.

3. Draw OP the angle bisector of ∠AOB.

4. Draw line parallel to OP 3 cm away from CD.

ABC is an equilateral triangle of side 3.2 cm. Find the points on AB and AB produced which are 2 cm from BC.

Answer

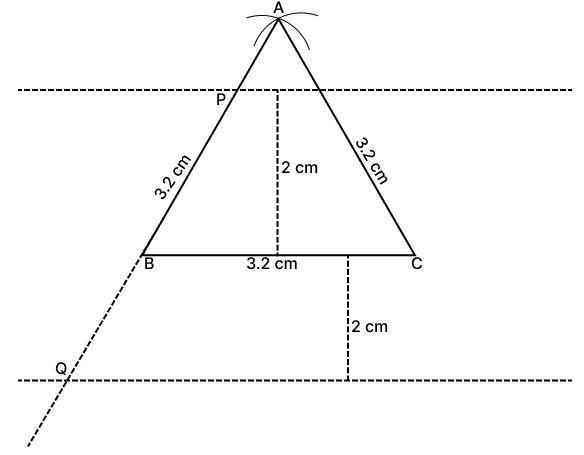
Steps of construction:

1. Draw base BC = 3.2 cm.

2. With B and C as center draw arcs of radius 3.2 cm intersecting at point A.

3. Join ABC, ΔABC is required triangle.

4. Draw two parallel lines on opposite sides of BC at a distance of 2 cm from it.

5. Mark the points of intersection at AB and AB produced as P and Q respectively.

Using ruler and compasses only, construct a ΔABC such that AB = 4.6 cm, BC = 3 cm and ∠ABC = 30°. Complete the rhombus ABDE such that C is equidistant from AB and BD. Locate the point Q on BC such that Q is equidistant from A and B.

Answer

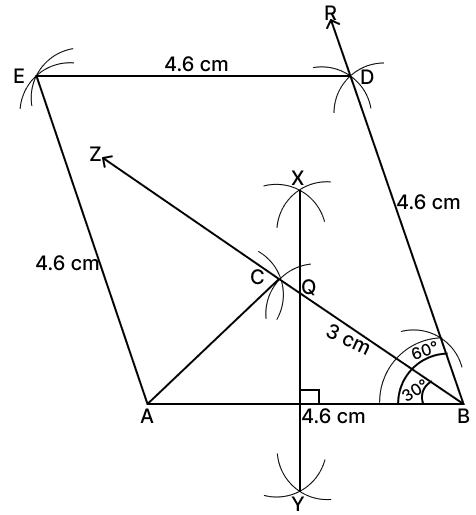
Steps of construction:

1. Draw a line segment AB = 4.6 cm.

2. Draw BZ such that ∠ABZ = 30°.

3. From BZ cut off BC = 3 cm, ∠ABC = 30°.

4. Join AC.

Since, C is equidistant from AB and BD, thus it will lie on the angle bisector of angle between AB and BD. Since, ∠ABC = 30°.

∴ ∠ABR = 60°

6. Draw ∠ABR = 60°.

7. From BR cut off BD = 4.6 cm, ∠ABD = 60° .

8. With D and A as center draw arcs of 4.6 cm cutting each other at point E.

9. Join DE and AE. Complete the rhombus ABDE .

10. Draw XY, the perpendicular bisector of AB.

11. Mark point Q as the intersection point of BC and XY.

AB and CD are two intersecting lines. Find the position of the point distant 2 cm from AB and 1.8 cm from CD.

Answer

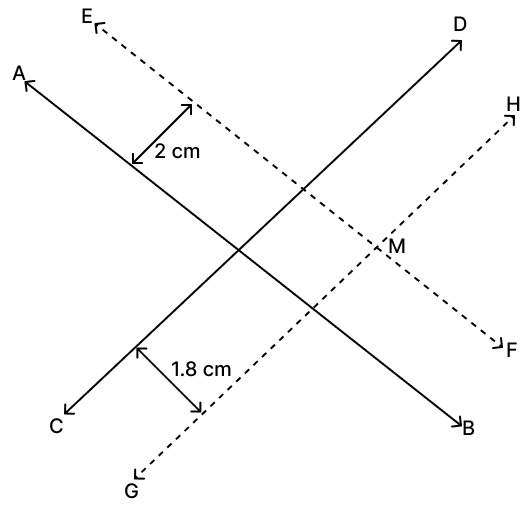
Steps of construction:

1. Draw EF at a distance of 2 cm and parallel to AB.

2. Draw GH at a distance of 1.8 cm and parallel to CD.

3. The point M is the point of intersection of EF and GH.

Hence, point M is the position of point which is at a distance of 2 cm from AB and 1.8 cm from CD.

Using ruler and compasses only, construct a rhombus ABCD whose diagonals AC and BD are 8 cm and 6 cm long respectively. Find by construction a point P equidistant from AB and AD and also equidistant from C and D. Measure PC.

Answer

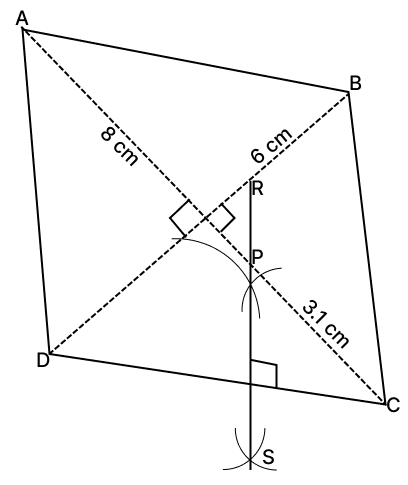
Steps of construction :

1. Draw AC = 8 cm and BD = 6 cm as diagonals perpendicular and bisecting each other. Join the points to form rhombus ABCD.

2. Since, diagonals of rhombus bisects vertices, hence, AC is angular bisector of BAD.

3. Draw RS, the perpendicular bisector of CD.

4. The intersection of RS and AC is the point P which satisfies both i.e. it is equidistant from AD, AB and C and D also.

On measuring we get, CP = 3.1 cm.

Using ruler and compasses only, construct a ΔABC in which AB = 4 cm, BC = 5 cm and ∠ABC = 120°.

(i) Locate the point P such that ∠BAP = 90° and BP = CP.

(ii) Measure the length of BP.

Answer

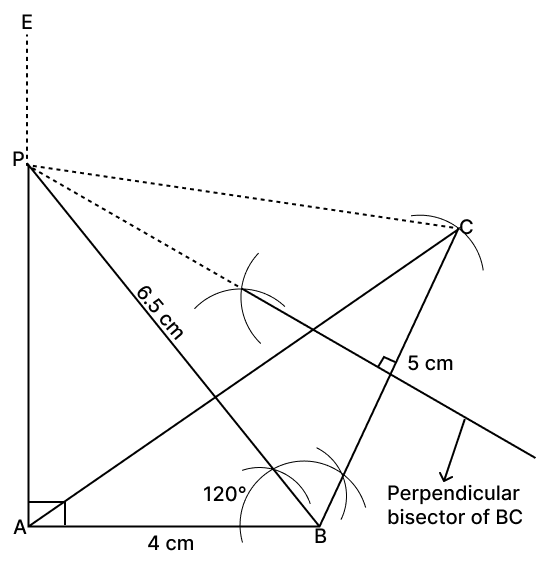
Steps of construction:

1. Draw AB of length 4 cm.

2. Make angle 120° at B, draw an arc of radius 5 cm from point B on this angle. Join BC and AC.

3. At point A, draw a line AE ⟂ AB.

4. Draw perpendicular bisector of BC

(i) Mark the point of intersection of bisector and AE as P. Thus BP = CP, as point P lies on perpendicular bisector of BC.

(ii) On measuring, BP = 6.5 cm.

Using ruler and compasses only, construct a ΔABC in which AB = 6 cm, BC = 3.5 cm and CA = 4.6 cm.

(i) Draw the locus of a point P which moves so that it is always 3 cm from B.

(ii) Draw the locus of a point which moves so that it is equidistant from BC and CA.

(iii) Mark the point of intersection of the two loci obtained above. Measure PC.

Answer

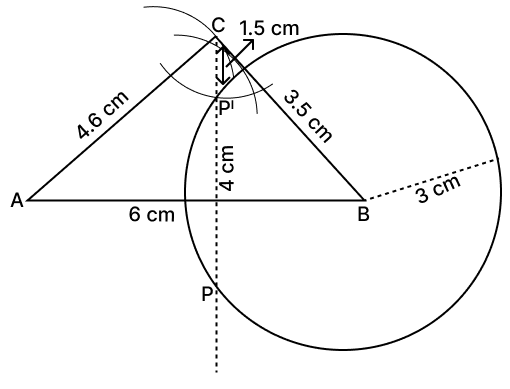
Steps of construction :

1. Draw a line segment AB = 6 cm.

2. With B as the center and a radius of 3.5 cm, draw an arc.

3. With A as the center and a radius of 4.6 cm, draw a second arc intersecting the first arc at C.

4. Join ABC, ABC is required triangle.

5. With B as the center and a radius of 3 cm, draw a circle.

6. Draw the angle bisector of C.

7. Mark the point where bisector meets circle as P and P'. Measure CP and CP'.

On measuring PC = 4 cm and CP' = 1.5 cm.

Using ruler and compasses only, construct an isosceles ΔABC in which BC = 5 cm, AB = AC and ∠BAC = 90°. Locate the point P such that :

(i) P is equidistant from BC and AC.

(ii) P is equidistant from B and C.

Answer

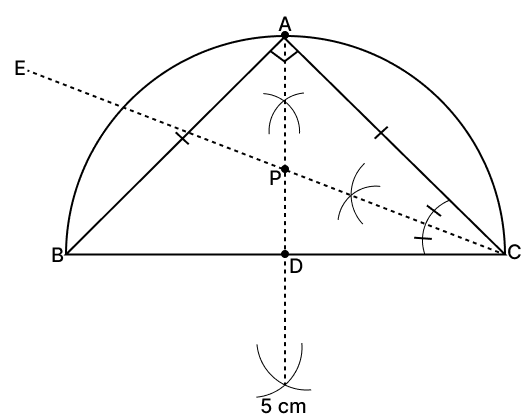
Steps of construction :

1. Make BC = 5 cm as base.

2. Create a semicircle with BC as diameter.

3. Make right bisector of BC and mark it's intersection and BC as D and the semicircle as A. Join AB and AC.

4. Make angle bisector of ∠ACB. From graph, CE is the angle bisector.

5. Mark point P where angle bisector ∠ACB i.e CE meets perpendicular bisector of BC i.e. AD.

(i) We know that locus of points equidistant from two lines is the angle bisector of angle between them.

From figure,

CE is the angular bisector of ∠ACB, hence it will be equidistant from AC and BC.

(ii) We know that locus of points equidistant from two points is the perpendicular bisector of line segment joining them.

From figure,

AD is the perpendicular bisector of BC, hence it will be equidistant from B and C.

Using ruler and compasses only, construct a quadrilateral ABCD in which AB = 6 cm, BC = 5 cm, ∠B = 60°, AD = 5 cm and D is equidistant from AB and BC.

Answer

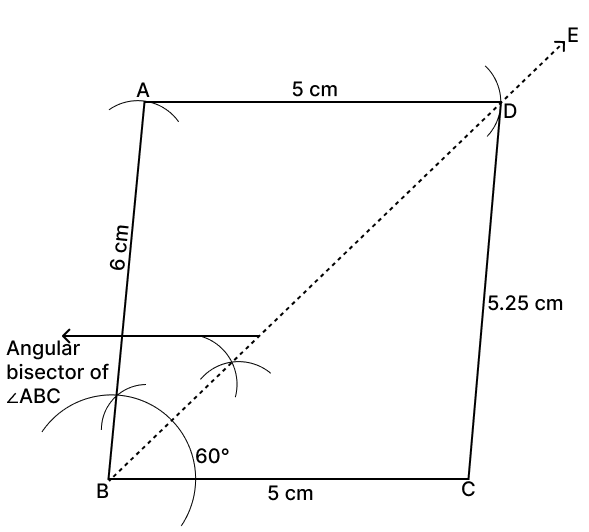
Steps of construction :

1. Draw BC = 5 cm as base.

2. Make angle 60° at B.

3. Cut off an arc of 6 cm from B at the angle and mark it A as in figure.

4. Since, D is equidistant from AB and BC hence, it will lie on angle bisector of ∠ABC i.e. on BE.

5. Make an arc of 5 cm from point A take point D where the arc cuts BE.

6. Join, the points A, B, C and D to form quadrilateral ABCD.

Using ruler and compasses only, construct a parallelogram ABCD in which AB = 5.1 cm, diagonal AC = 5.6 cm and diagonal BD = 7 cm. Locate the point P on DC, which is equidistant from AB and BC.

Answer

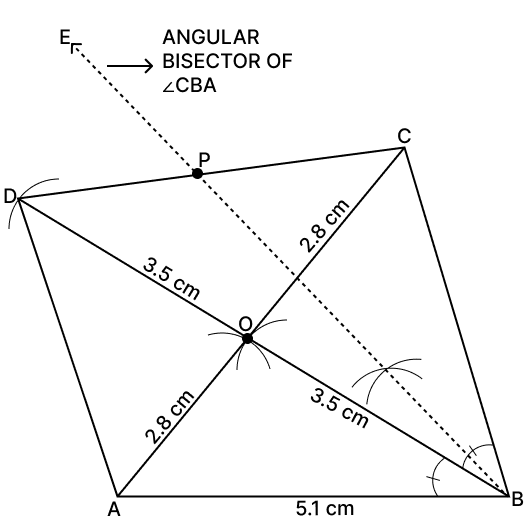
Steps of construction :

1. Draw AB = 5.1 cm as base.

2. At A, with radius 2.8 cm and at B with radius 3.5 cm draw two arcs intersecting each other at O.

3. Join AO and produce it till C such that OC = AO = 2.8 cm and join BO and produce it till D such that OD = BO = 3.5 cm.

4. Join A, B, C and D forming parallelogram ABCD.

5. We know that locus of point equidistant from two lines is the angle bisector of the two lines.

From figure,

BE is the angle bisector of ∠ABC which meets DC at P.

Draw a circle of radius 4 cm and mark two chords AB and AC of the circle of length 6 cm and 5 cm respectively.

(i) Construct the locus of points inside the circle, that are equidistant from A and C.

(ii) Construct the locus of points, inside the circle, that are equidistant from AB and AC.

Answer

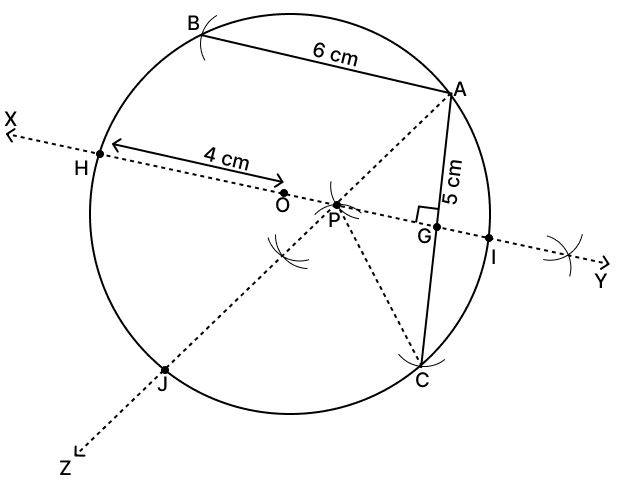
Steps of construction :

1. Construct a circle with center as O and radius 4 cm.

2. Take a point A on the circle. From A make arcs of radius 6 cm and 5 cm and where they intersect the circle mark those points as B and C respectively.

(i) We know that locus of points that are equidistant from two points is the perpendicular bisector of line segment joining those points.

So from figure,

IH is the locus of points inside the circle, that are equidistant from A and C.

Hence, the locus is the diameter of the circle which is perpendicular to the chord AC.

Proof:

Consider △GPA and △GPC.

∠PGC = ∠PGA (Both are equal to 90°)

PG = PG (Common side)

CG = AG (They are equal as GH bisects AC).

Hence, by SAS axiom △GPA congruent to △GPC.

Since triangles are similar, hence the ratio of their corresponding sides are equal.

$\therefore \dfrac{AP}{PG} = \dfrac{PC}{PG} \\[1em] \Rightarrow AP = \dfrac{PC}{PG} \times PG \\[1em] \Rightarrow AP = PC$

Hence, proved that AP = PC.

(ii) We know that locus of points that are equidistant from two lines is the angular bisector of the lines.

So, from figure,

AZ is the angular bisector of angle between AB and AC.

AJ is the locus of points equidistant from AB and AC inside the circle.

Hence, locus is the chord of the circle bisecting ∠BAC.

A and B are fixed points 5 cm apart. The locus of the point P is the set of those points for which AP = 4 cm and the locus of Q is the set of those points for which BQ = 3.5 cm.
Construct the loci of P and Q and the points of intersection of the two loci. How many such points are there?

Answer

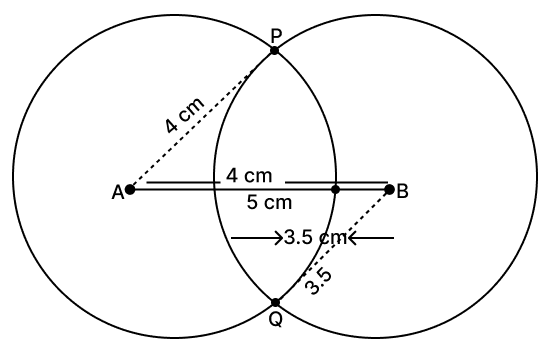
Steps of construction :

1. Draw a line segment AB = 5 cm.

2. With A as the center and a radius of 4 cm, draw the circle.

3. With B as the center and a radius of 3.5 cm, draw the circle.

4. Mark the two points where the circle intersect as P and Q.

The loci of point P is a circle with center as point A and loci of point Q is a circle with centre as point B.

The two circles intersect at two distinct points.

Using only a ruler and compasses, construct ∠ABC = 120°, where AB = BC = 5 cm.

(a) Mark two points D and E which satisfy the condition that they are equidistant from both BA and BC.

(b) In the above figure, join AE and EC. Describe the figures.

(i) ABCD
(ii) BD
(iii) ABE

Answer

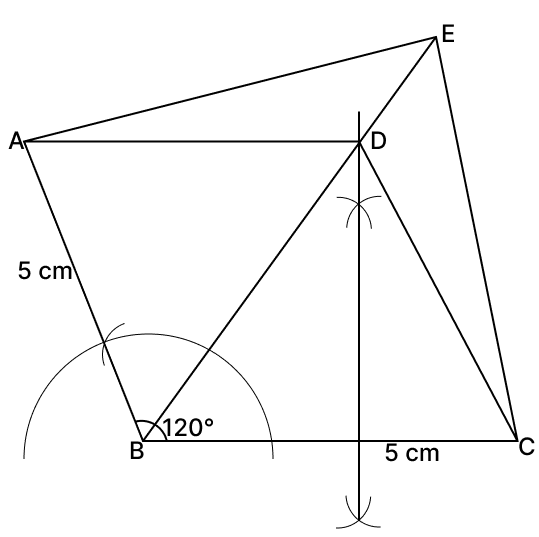
Steps of construction :

1. Draw a straight line segment BC = 5 cm.

2. From B with radius 5cm mark an arc as A.Construct ∠ABC = 120° .

3. Join AB, so that ∠ABC = 120° and AB = 5 cm.

4. Construct the angle bisector BE of ∠ABC.

5. Draw perpendicular bisector of BC. Mark the point of intersection of bisectors as D.

6. Join AD and DC.

7. E lies on the angle bisector of ∠ABC.

8. Join AE and CE.

(i) ABCD is a rhombus.

(ii) BD is angle bisector of ∠ABC.

(iii) ABE is a triangle.

Using ruler and compasses only,

(i) Construct a ΔABC in which BC = 6 cm, ∠ABC = 120° and AB = 3.5 cm.

(ii) In the above figure, draw a circle with BC as diameter. Find a point P on the circumference of the circle which is equidistant from AB and BC. Measure ∠BCP.

Answer

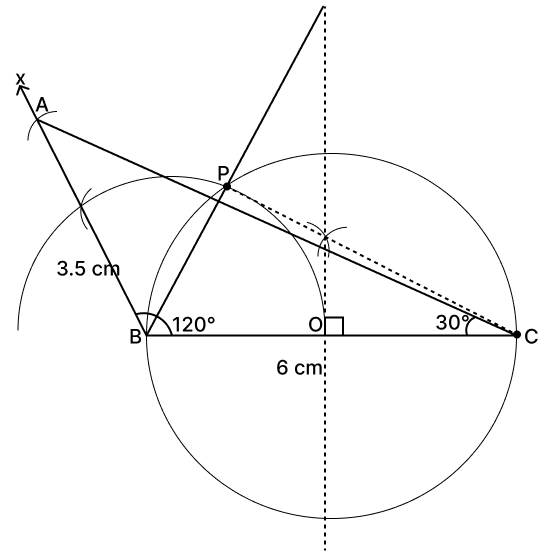
Steps of construction :

1. Draw a line BC = 6 cm.

2. At B, draw a ray BX making an angle of 120° with BC. With B as center and radius 3.5 cm, cut off AB = 3.5 cm.

3. Join AC. ABC is the required triangle.

4. Draw perpendicular bisector of BC which cuts BC at point O. With O as center and radius = OB, draw a circle.

5. Draw angle bisector of ∠ABC which meets the circle at point P. Thus, point P is equidistant from AB and BC.

6. Measure ∠BCP.

On measuring, ∠BCP = 30°.

Use a ruler and a pair of compasses to construct ΔABC in which BC = 4.2 cm, ∠ABC = 60° and AB = 5 cm. Construct a circle of radius 2 cm to touch both the arms of ∠ABC of ΔABC.

Answer

Steps of construction:

1. Draw BC of length 4.2 cm.

2. Make angle 60° at B.

3. With B as center and radius 5 cm, cut off AB = 5 cm.

4. Join AC, ΔABC required triangle.

5. Draw BD angle bisector of ∠ABC.

6. Draw EF || BC at 2 cm from BC, intersects BD at O.

7. Taking O as centre and 2 cm as radius draw required circle.

Using ruler and compasses construct

(i) a triangle ABC in which AB = 5.5 cm, BC = 3.4 cm and CA = 4.9 cm.

(ii) the locus of points equidistant from A and C.

(iii) a circle touching AB at A and passing through C.

Answer

(i) The figure below shows the constructed triangle ABC:

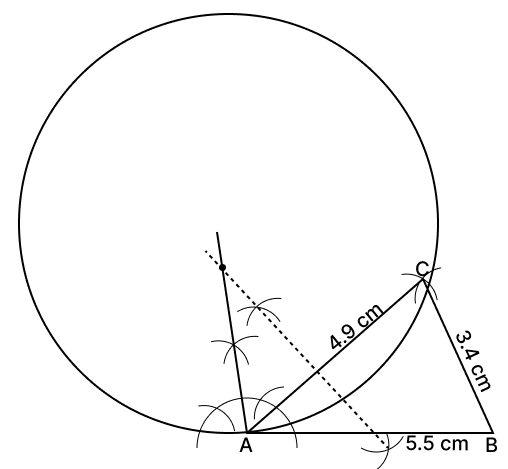
Steps of construction,

1. Draw AB = 5.5 cm.

2. With A as centre and 4.9 cm radius draw an arc.

3. With B as centre and 3.4 cm radius cut the previous arc. Mark point of intersection as C.

4. Draw a right angle at A and perpendicular bisector to AC.

5. Mark point of intersection as O. With OA as radius draw a circle.

(ii) From figure we can see,

The locus of points A and C will be the perpendicular bisector of the line segment joining A and C.

The locus of a point which moves in a plane in such a way that its distance from a fixed point is always constant, is known as :

1. a square

2. an equilateral triangle

3. a circle

4. a parallelogram

Answer

The locus of a point that moves in a plane such that its distance from a fixed point is always constant, is known as a circle.

The fixed point is the center of the circle, and the constant distance is the radius of the circle.

Hence, option 3 is the correct option.

The locus of a point which is equidistant from two given fixed points, is the ______ of the line segment joining the given fixed points.

1. median

2. angle bisector

3. altitude

4. perpendicular bisector

Answer

The perpendicular bisector of a line segment is the set of all points that maintain equal distance from the two endpoints of that segment.

Hence, option 4 is the correct option.

The locus of a point which is equidistant from two intersecting lines is the ______ formed by the given lines.

1. pair of lines bisecting the angles

2. pair of parallel lines

3. pair of perpendicular lines

4. none of these

Answer

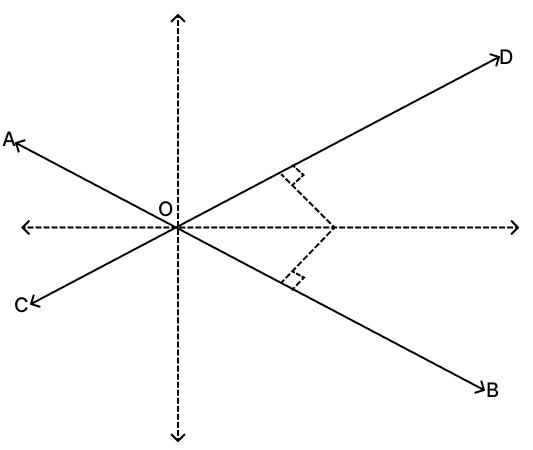
Let AB and CD meet at point O.

For two intersecting lines, the points that are equidistant from both lines lie on the lines that bisect the angles formed at their intersection, every point maintains equal perpendicular distance from the two intersecting lines.

Hence, option 1 is the correct option.

If A and B are two fixed points, then the locus of a point P such that ∠APB = 90°, is the:

1. square

2. rectangle

3. circle

4. rhombus

Answer

All points P that satisfy ∠APB = 90° lie on a circle for which AB is the diameter.

This is because a right angle is subtended only by the diameter of a circle.

So, the locus is a circle.

Hence, option 3 is the correct option.

A point P moves such that its distance from a fixed line AB is always the same. What is the relation between AB and the path traveled by P ?

1. It is a set of two lines perpendicular to AB.

2. It is a set of two lines parallel to AB drawn on either side at equal distance from it.

3. It is a set of two concentric circles.

4. It is a set of two intersecting lines with AB bisecting the angle between them.

Answer

If a point moves so that its distance from a fixed line remains constant, it must stay on two lines that maintain that same constant distance on both sides of the given line. These lines are parallel to the original line AB.

So the path is two parallel lines, each at the given fixed distance from AB.

Hence, option 2 is the correct option.

A point P moves so that its perpendicular distance from two given parallel lines AB and CD are equal. Then, the locus of the point P is:

1. a line l anywhere in between AB and CD and parallel to them.

2. a line l perpendicular to both AB and CD.

3. a line l in the midway of AB and CD and parallel to them.

4. none of these

Answer

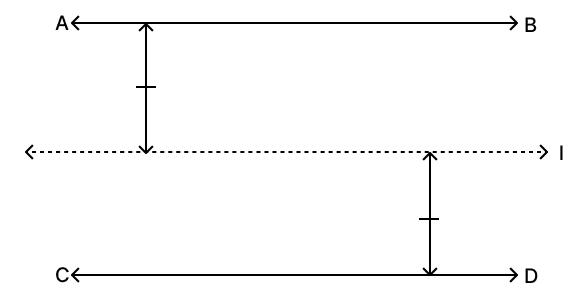
If the perpendicular distances of a moving point from two parallel lines are equal, then the point must lie exactly halfway between them.

The set of all such points forms a single line parallel to both AB and CD, drawn exactly midway between them.

Hence, option 3 is the correct option.

The locus of a point equidistant from two concentric circles is:

1. a circle concentric with the given circles and inside the smaller circle.

2. a circle concentric with the given circles and outside the larger circle.

3. a circle concentric with the given circles and midway between them.

4. the common centre of the two circles.

Answer

For concentric circles, every point’s distance from each circle is measured along the same radial direction because the centre is common.

A point that is equidistant from both circles must lie at a radius that is exactly midway between the two radii.

Hence, option 3 is the correct option.

The locus of a point which is equidistant from a given circle consists of:

1. a pair of circles concentric with the given circle.

2. a circle concentric with the given circle and inside it.

3. a circle concentric with the given circle and outside it.

4. a pair of lines parallel to each other on either side of the centre.

Answer

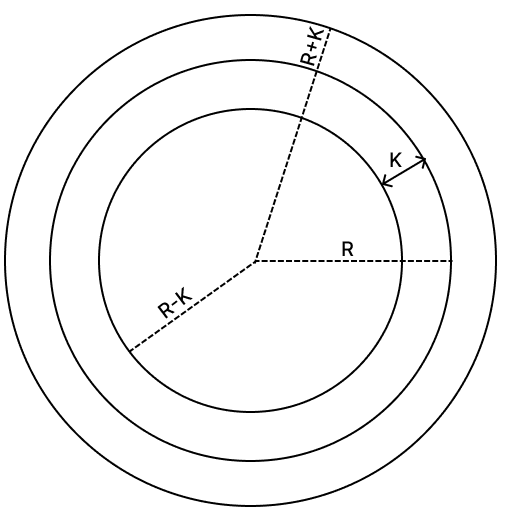
If a point stays at a constant distance (let k) from a given circle, then:

One set of such points lies outside the circle at distance k, forming a circle of radius (R + k).

Another set lies inside the circle at distance k, forming a circle of radius (R − k).

Hence, option 1 is the correct option.

A and B are two fixed points in a plane. Then, the locus of a point P which moves in such a way that PA² + PB² = AB², is:

1. a square with AB as one of its sides.

2. a rectangle with AB as one of its sides.

3. a rhombus with AB as one of its diagonal.

4. the circumference of a circle with AB as its diameter.

Answer

The condition PA² + PB² = AB² is exactly the Pythagorean relation.

This holds only when ∠APB = 90°.

All points that subtend a right angle at AB lie on a circle with AB as its diameter.

Therefore, the locus of point P is the circle having AB as its diameter.

Hence, option 4 is the correct option.

The locus of the tip of the pendulum of a clock is:

1. a circle

2. a chord of a circle

3. an arc of a circle

4. a diameter of a circle

Answer

Let the fixed pivot be O and the constant length be "r"

A pendulum swings back and forth from a fixed pivot. Its length remains constant, so its tip moves along a portion of a circle, not the full circle.

Therefore, the path traced is an arc of a circle.

Hence, option 3 is the correct option.

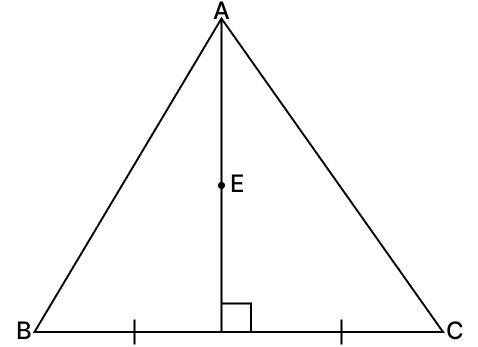
Assertion (A): In the figure, D is the mid-point of BC and AD ⟂ BC. If E lies on AD, then BE = CE.

Reason (R): Every point on the perpendicular bisector of a line segment is equidistant from its end points.

1. A is true, R is false

2. A is false, R is true

3. Both A and R are true

4. Both A and R are false

Answer

The point E lies on the perpendicular bisector of BC i.e. AD.

∴ BE = CE

So, Assertion (A) is true.

We know that,

The locus of a point equidistant from two fixed points is the perpendicular bisector of the line segment connecting those two points.

So, Reason (R) is true.

Both (A) and (R) are true.

Hence, option 3 is the correct option.

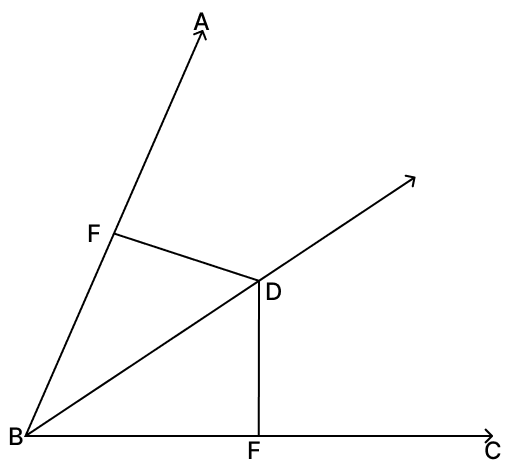
Assertion (A): In the figure, ∠ABD = ∠CBD, so DE = DF.

Reason (R): Every point on the angle bisector of two intersecting lines is equidistant from the lines.

1. A is true, R is false

2. A is false, R is true

3. Both A and R are true

4. Both A and R are false

Answer

We know that,

Every point on the angle bisector of two intersecting lines is equidistant from the lines.

∴ Reason (R) is true.

Since,

∠ABD = ∠CBD only tells us that BD is the angle bisector of ∠ABC.

From the figure, DE and DF are not shown as perpendiculars to BA and BC respectively. Equality of distances from the sides is guaranteed only for perpendicular distances.

Therefore, concluding DE = DF is not justified.

∴ Assertion (A) is false.

Thus, A is false, R is true.

Hence, option 2 is the correct option.