In the given figure, XY || BC. Given that AX = 3 cm, XB = 1.5 cm and BC = 6 cm.
(i) Calculate .
(ii) Calculate XY.
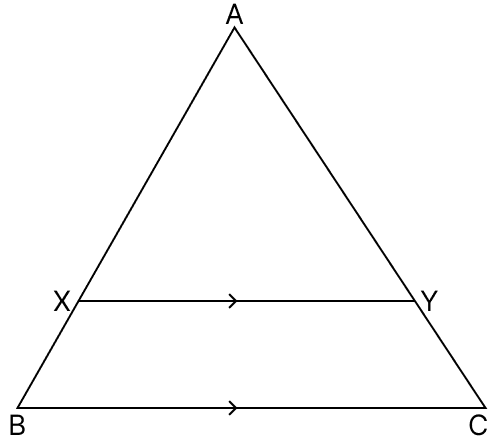
Answer
(i) By basic proportionality theorem,
A line drawn parallel to a side of triangle divides the other two sides proportionally.
Since, XY || BC
Hence, .
(ii) In ΔAXY and ΔABC,
∠AXY = ∠ABC [Corresponding angles are equal]
∠XAY = ∠BAC [Common ]
∴ ΔAXY ∼ ΔABC.
Since, corresponding sides of similar triangle are proportional to each other.
Hence, XY = 4 cm.
In the given figure, DE || BC.
(i) If AD = 3.6 cm, AB = 9 cm and AE = 2.4 cm, find EC.
(ii) If and AC = 5.6 cm, find AE.
(iii) If AD = x cm, DB = (x − 2) cm, AE = (x + 2) cm and EC = (x − 1) cm, find the value of x.
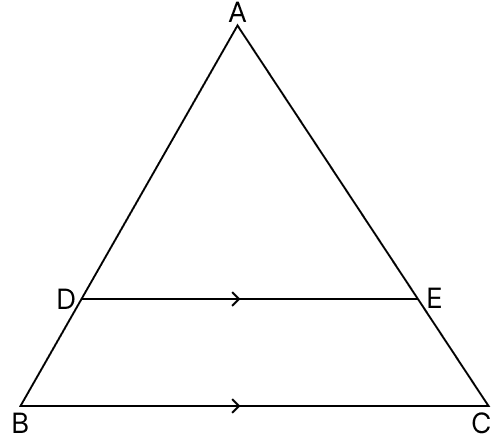
Answer
By basic proportionality theorem,
A line drawn parallel to a side of triangle divides the other two sides proportionally.
(i) Given,
AD = 3.6 cm
AB = 9 cm
AE = 2.4 cm
Since, DE || BC by basic proportionality theorem,
Hence, EC = 3.6 cm.
(ii) Given,
AC = 5.6 cm
Since, DE || BC by basic proportionality theorem,
Hence, AE = 2.1 cm.
(iii) Given,
AD = x cm
DB = (x − 2) cm
AE = (x + 2) cm
EC = (x − 1) cm
Since, DE || BC by basic proportionality theorem,
Hence, x = 4 cm.
D and E are points on the sides AB and AC respectively of ΔABC. For each of the following cases, state whether DE ∥ BC :
(i) AD = 5.7 cm, BD = 9.5 cm, AE = 3.6 cm and EC = 6 cm.
(ii) AB = 5.6 cm, AD = 1.4 cm, AC = 9.6 cm and EC = 2.4 cm.
(iii) AB = 11.7 cm, BD = 5.2 cm, AE = 4.4 cm and AC = 9.9 cm.
(iv) AB = 10.8 cm, BD = 4.5 cm, AC = 4.8 cm and AE = 2.8 cm.
Answer
By basic proportionality theorem,
A line drawn parallel to a side of triangle divides the other two sides proportionally.
(i) Given,
AD = 5.7 cm
BD = 9.5 cm
AE = 3.6 cm
EC = 6 cm.
Check for proportionality,
We conclude that DE is parallel to BC
Hence, DE is parallel to BC.
(ii) Given,
AB = 5.6 cm
AD = 1.4 cm
AC = 9.6 cm
EC = 2.4 cm.
From figure,
DB = AB - AD = 5.6 - 1.4 = 4.2 cm
AE = AC - EC = 9.6 - 2.4 = 7.2 cm
Check for proportionality,
We conclude that DE is not parallel to BC
Hence, DE is not parallel to BC.
(iii) Given,
AB = 11.7 cm
BD = 5.2 cm
AE = 4.4 cm
AC = 9.9 cm.
From figure,
AD = AB - BD = 11.7 - 5.2 = 6.5 cm
EC = AC - AE = 9.9 - 4.4 = 5.5 cm
Check for proportionality,
We conclude that DE is not parallel to BC
Hence, DE is not parallel to BC.
(iv) Given,
AB = 10.8 cm
BD = 4.5 cm
AC = 4.8 cm
AE = 2.8 cm.
AD = AB - BD = 10.8 - 4.5 = 6.3 cm
EC = AC - AE = 4.8 - 2.8 = 2 cm
Check for proportionality,
We conclude that DE is parallel to BC
Hence, DE is parallel to BC.
In the given figure, it is given that ∠ABD = ∠CDB = ∠PQB = 90°. If AB = x units, CD = y units and PQ = z units, prove that .
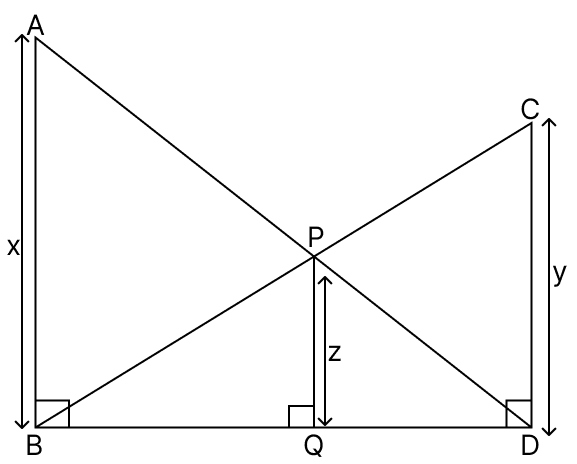
Answer
In ΔPQD and ΔABD,
∠ABD = ∠PQD = 90° [From figure]
∠ADB = ∠PDQ [Common angles]
∴ ΔPQD ∼ ΔABD (By A.A. axiom)
Corresponding sides of similar triangles are proportional.
In ΔPQB and ΔCDB,
∠CDB = ∠PQB = 90° [Given]
∠CBD = ∠PBQ [Common angles]
∴ ΔPQB ∼ ΔCDB (By A.A. axiom)
Corresponding sides of similar triangles are proportional.
Add equations (1) and (2) we get,
Hence, proved that .
In ΔABC, AD is the bisector of ∠A. If BC = 10 cm, BD = 6 cm and AC = 6 cm, find AB.
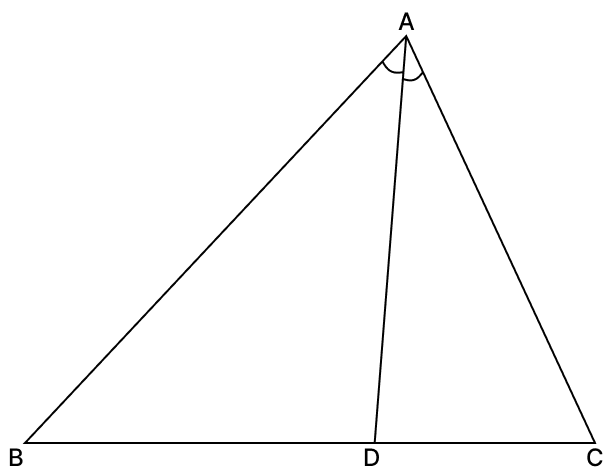
Answer
Construction: Draw a line through C parallel to AD, meeting BA produced at E.
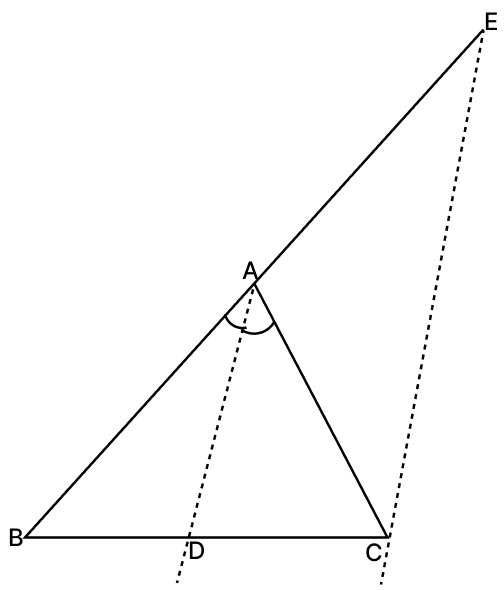
In ΔBCE,
Since AD ∥ CE, by Basic Proportionality Theorem:
...(i)
Also, since AD ∥ CE:
∠BAD = ∠AEC [Corresponding angles are equal]
∠DAC = ∠ACE [Alternate interior angles are equal]
Since AD is bisector of ∠A, ∠BAD = ∠DAC.
Therefore, ∠AEC = ∠ACE.
In ΔACE, sides opposite to equal angles are equal:
AE = AC ...(ii)
Substitute (ii) into (i):
Given,
AC = 6 cm
BC = 10 cm
BD = 6 cm
DC = BC - BD [from figure]
DC = 10 - 6 = 4 cm
Let length of AB be x,
Hence, length of AB is 9 cm.
In the given figure, AC ∥ DE ∥ BF. If AC = 24 cm, EG = 8 cm, GB = 16 cm, BF = 30 cm.
(i) Prove that ΔGED ∼ ΔGBF.
(ii) Find DE.
(iii) Find DB : AB.
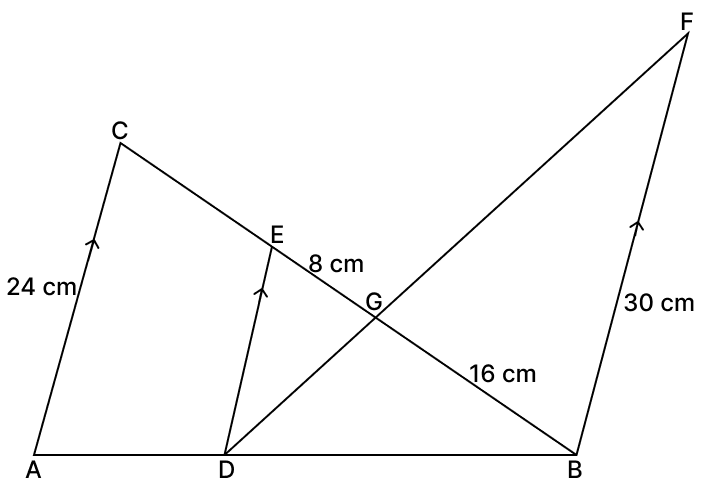
Answer
(i) In ΔGED and ΔGBF,
∠DGE = ∠BGF [Vertically opposite angles are equal]
∠GED = ∠GBF [Alternate angles are equal]
∴ ΔGED ∼ ΔGBF (By A.A. axiom)
Hence, proved ΔGED ∼ ΔGBF.
(ii) We know that,
Corresponding sides of similar triangles are proportional.
Hence, DE = 15 cm.
(iii) In ΔDBE and ΔABC,
∠EBD = ∠CBA [Common angles]
∠BDE = ∠BAC [Corresponding angles are equal, Since AC ∥ DE]
ΔDBE ∼ ΔABC (By A.A. axiom)
Corresponding sides of similar triangles are proportional.
Hence, DB : AB = 5 : 8.
In the adjoining figure, ABCD is a parallelogram, P is a point on side BC and DP when produced meets AB produced at L. Prove that :
(i) DP : PL = DC : BL.
(ii) DL : DP = AL : DC.
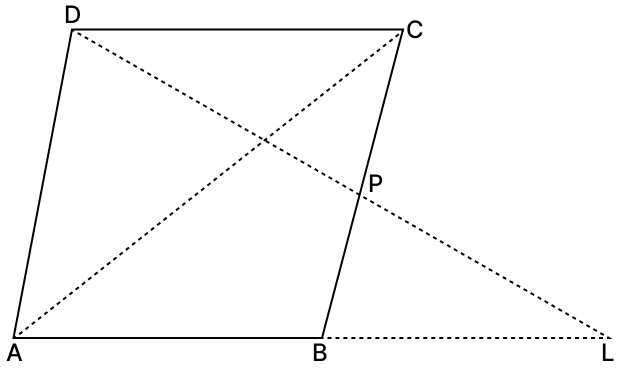
Answer
(i) Given,
ABCD is a parallelogram.
∴ AB || DC and AD || BC
In ΔDPC and ΔLPB,
∠PDC = ∠PLB [Alternate angles are equal]
∠DPC = ∠LPB [Vertically opposite angles are equal]
∴ ΔDPC ∼ ΔLPB (By A.A. axiom)
Corresponding sides of similar triangles are proportional.
DP : PL = DC : BL
Hence, proved DP : PL = DC : BL.
(ii) In ΔALD and ΔCPD,
∠ALD = ∠PDC [Alternate interior angles, AB || DC]
∠DAL = ∠PCD [Opposite angles of a parallelogram are equal]
∴ ΔLAD ∼ ΔDCP (By A.A. axiom)
Corresponding sides of similar triangles are proportional.
DL : DP = AL : DC
Hence, proved DL : DP = AL : DC.
In the given figure, ABCD is a parallelogram, E is a point on BC and the diagonal BD intersects AE at F.
Prove that DF × FE = FB × FA.
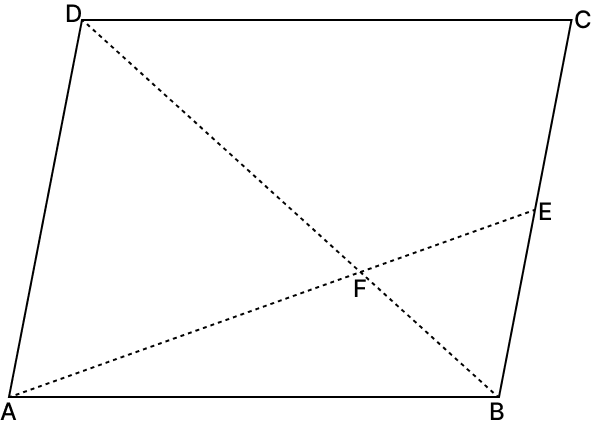
Answer
Since, ABCD is a || gm
∴ AD || BC
In ΔADF and ΔEBF,
∠ADF = ∠EBF [Alternate angles are equal]
∠AFD = ∠EFB [Vertically opposite angles are equal]
∴ ΔADF ∼ ΔEBF (By A.A. axiom)
Corresponding sides of similar triangles are proportional.
DF × FE = FB × FA
Hence, proved that DF × FE = FB × FA.
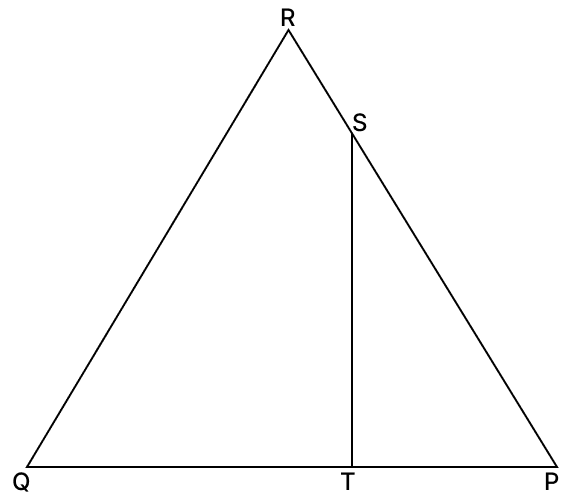
In the adjoining figure (not drawn to scale), PS = 4 cm, SR = 2 cm, PT = 3 cm and QT = 5 cm.
(i) Show that ΔPQR ∼ ΔPST.
(ii) Calculate ST, if QR = 5.8 cm.
Answer
(i) Given,
PS = 4 cm, SR = 2 cm, PT = 3 cm and QT = 5 cm.
PR = PS + SR = 4 + 2 = 6 cm
PQ = PT + TQ = 3 + 5 = 8 cm
In ΔPQR and ΔPST,
∠QPR = ∠SPT [Common angle]
∴ ΔPQR ∼ ΔPST [By S.A.S. axiom]
Hence, ΔPQR ∼ ΔPST.
(ii) We know that,
Corresponding sides of similar triangles are proportional.
Hence, ST = 2.9 cm.
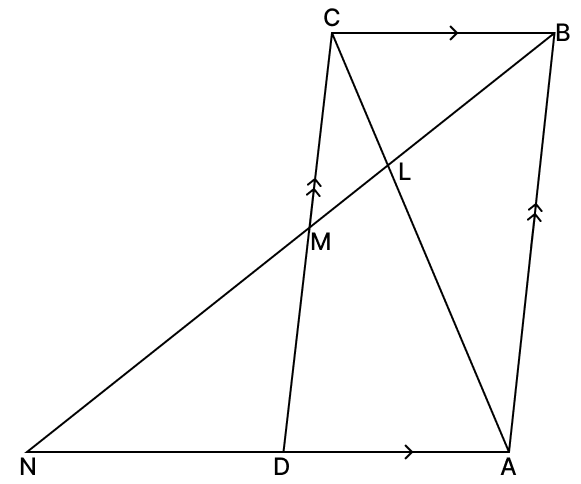
In the adjoining figure, ABCD is a parallelogram in which AB = 16 cm, BC = 10 cm and L is a point on AC such that CL : LA = 2 : 3. If BL produced meets CD at M and AD produced at N, prove that :
(i) ΔCLB ∼ ΔALN.
(ii) ΔCLM ∼ ΔALB.
Answer
(i) In ΔCLB and ΔALN,
∠CBL = ∠ANL [Alternate angles are equal]
∠CLB = ∠ALN [Vertically opposite angles are equal]
∴ ΔCLB ∼ ΔALN (By A.A. axiom)
Hence, proved that ΔCLB ∼ ΔALN.
(ii) In ΔCLM and ΔALB,
∠LMC = ∠LAB [Alternate angles, since CM ∥ AB, transversal LM]
∠CLM = ∠ALB [Vertically opposite angles are equal]
∴ ΔCLM ∼ ΔALB (By A.A. axiom)
Hence, proved that ΔCLM ∼ ΔALB.
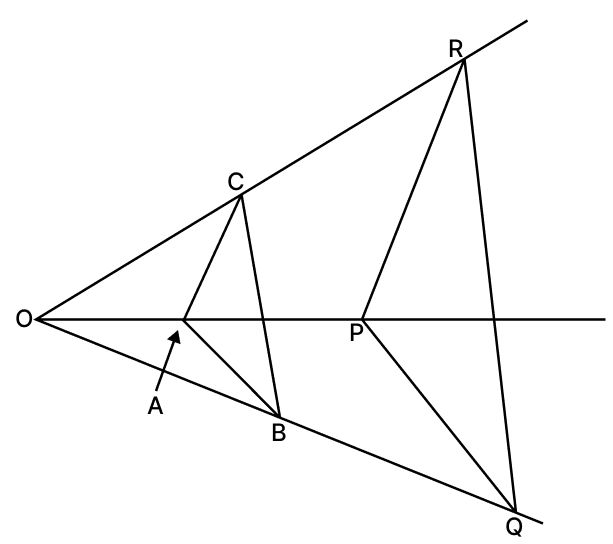
In the given figure, AB ∥ PQ and AC ∥ PR. Prove that BC ∥ QR.
Answer
In ΔOPQ,
AB ∥ PQ [Given]
By Basic Proportionality Theorem,
.... (i)
In ΔOPR,
AC ∥ PR [Given]
By Basic Proportionality Theorem,
.... (ii)
From (i) and (ii), we get:
In ΔOQR,
Since
By Converse of Basic Proportionality Theorem,
BC ∥ QR
Hence, proved that BC ∥ QR.
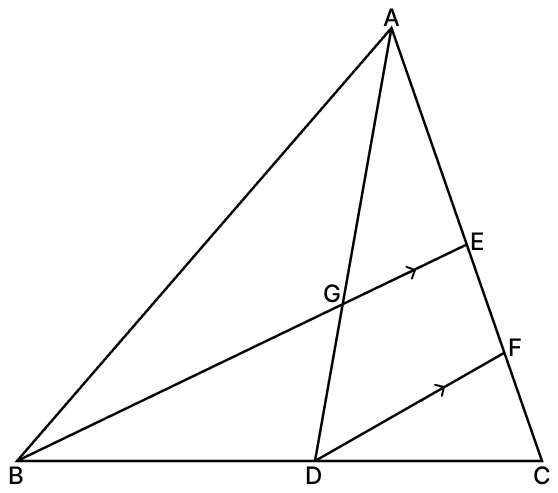
In the given figure, medians AD and BE of ΔABC meet at G and DF ∥ BE. Prove that :
(i) EF = FC.
(ii) AG : GD = 2 : 1.
Answer
(i) In ∆CFD and ∆CEB,
∠CDF = ∠CBE [Corresponding angles are equal]
∠FCD = ∠ECB [Common]
∴ ∆CFD ∼ ∆CEB (By A.A. axiom)
Since, corresponding sides of similar triangles are proportional.
From figure,
⇒ CE = CF + FE
⇒ 2CF = CF + FE
⇒ CF = FE.
Hence, proved that EF = FC.
(ii) In ∆AFD,
GE ∥ DF
By basic proportionality theorem we have,
.....(1)
Now, AE = EC [∵ BE is media,n so E is the mid-point of AC]
As, AE = EC = 2EF [As, EF = FC].
Substituting value of AE in (1) we get,
Hence, proved that AG : GD = 2 : 1.
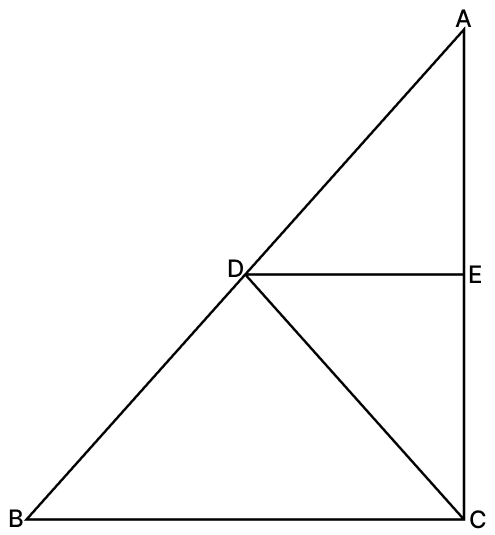
In the given figure, DE ∥ BC and BD = DC.
(i) Prove that DE bisects ∠ADC.
(ii) If AD = 4.5 cm, AE = 3.9 cm and DC = 7.5 cm, find CE.
(iii) Find the ratio AD : DB.
Answer
(i) Given, DE ∥ BC.
⇒ ∠ADE = ∠DBC [Corresponding angles are equal] ... (1)
⇒ ∠EDC = ∠DCB [Alternate interior angles are equal] ... (2)
Given, BD = DC.
⇒ ∠DBC = ∠DCB [Angles opposite to equal sides are equal] ... (3)
From (1), (2), and (3), we get:
∠ADE = ∠EDC
Thus, DE bisects ∠ADC.
Hence, DE bisects ∠ADC.
(ii) Given,
AD = 4.5 cm, AE = 3.9 cm, DC = 7.5 cm
Given,
BD = DC = 7.5 cm
By basic proportionality theorem we have,
Hence, CE = 6.5 cm.
(iii) By basic proportionality theorem,
Hence, the ratio AD : DB is 3 : 5.
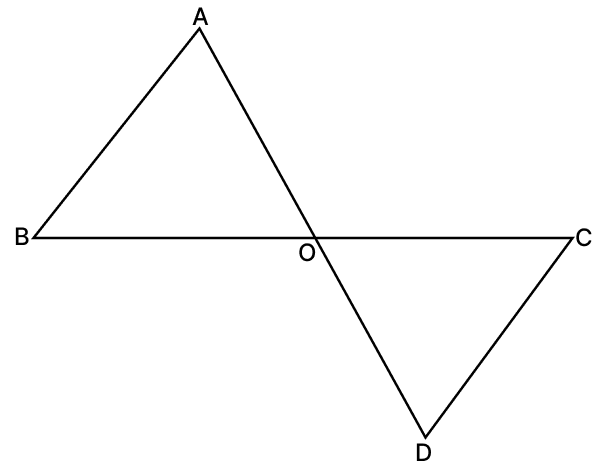
In the given figure, BA ∥ DC. Show that ΔOAB ∼ ΔODC. If AB = 4 cm, CD = 3 cm, OC = 5.7 cm and OD = 3.6 cm, find OA and OB.
Answer
Considering ΔAOB and ΔDOC,
∠AOB = ∠COD [Vertically opposite angles are equal]
∠A = ∠D [Alternate angles are equal]
∴ ΔAOB ∼ ΔDOC (By A.A. axiom)
We know that,
Corresponding sides of similar triangles are proportional.
Considering,
Considering,
Hence, OA = 4.8 cm and OB = 7.6 cm.
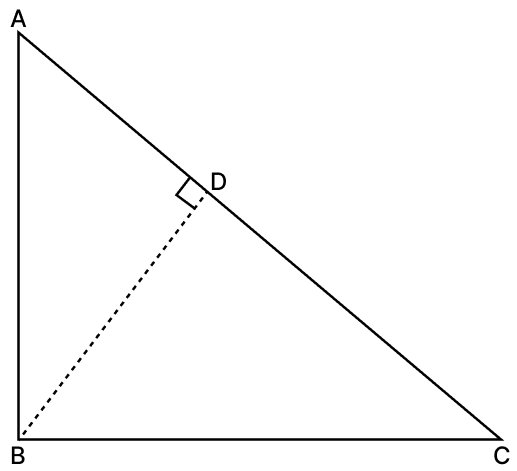
In the given figure, ∠ABC = 90° and BD ⟂ AC. If AB = 5.7 cm, BD = 3.8 cm and CD = 5.4 cm, find BC.
Answer
We have, ∠ABC = 90° and BD ⟂ AC
In ΔABC and ΔBDC,
∠ABC = ∠BDC [Each 90°]
∠ACB = ∠BCD [Common]
∴ ΔABC ∼ ΔBDC (By A.A. axiom)
We know that,
Corresponding sides of similar triangles are proportional.
Hence, BC = 8.1 cm.
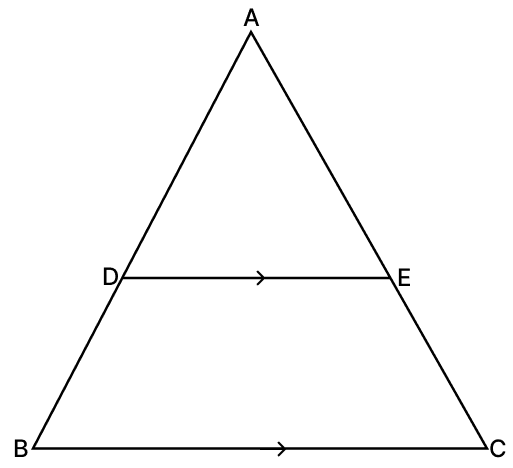
In the given figure, DE ∥ BC.
(i) Prove that ΔADE ∼ ΔABC.
(ii) Given that AD = DB, calculate DE, if BC = 4.5 cm.
(iii) Find .
(iv) Find .
Answer
(i) Considering ΔADE and ΔABC,
∠BAC = ∠DAE [Common angles]
∠ADE = ∠ABC [Corresponding angles are equal]
∴ ΔADE ∼ ΔABC (By A.A. axiom)
Hence, proved that ΔADE ∼ ΔABC.
(ii) Given,
Since triangles ADE and ABC are similar so, ratio of their corresponding sides will be equal.
Hence, the length of DE = 1.5 cm.
(iii) We know that,
The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
Hence, .
(iv) From figure,
Area of trap.(BCED) = area(Δ ABC) - area(Δ ADE)
Hence, .
Given that ΔABC ∼ ΔPQR.
(i) If ar(ΔABC) = 49 cm2 and ar(ΔPQR) = 25 cm2 and AB = 5.6 cm, find the length of PQ.
(ii) If ar(ΔABC) = 28 cm2 and ar(ΔPQR) = 63 cm2 and PR = 8.4 cm, find the length of AC.
(iii) If BC = 4 cm, QR = 5 cm and ar(ΔABC) = 32 cm2 determine ar(ΔPQR).
Answer
(i) Given,
ΔABC ∼ ΔPQR
ar(ΔABC) = 49 cm2
ar(ΔPQR) = 25 cm2
AB = 5.6 cm
We know that,
The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
Hence, PQ = 4 cm.
(ii) Given,
ΔABC ∼ ΔPQR
ar(ΔABC) = 28 cm2
ar(ΔPQR) = 63 cm2
PR = 8.4 cm
We know that,
The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
Hence, AC = 5.6 cm.
(iii) Given,
ΔABC ∼ ΔPQR
BC = 4 cm
QR = 5 cm
ar(ΔABC) = 32 cm2
We know that,
The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
Hence, ar(ΔPQR) = 50 cm2.
The areas of two similar triangles are 48 cm2 and 75 cm2 respectively. If the altitude of the first triangle is 3.6 cm, find the corresponding altitude of the other.
Answer
Let the length of altitude of other triangle be x cm
We know that, the ratio of the areas of two similar triangles is equal to the ratio of the square of their corresponding altitudes.
Hence, the length of altitude of other triangle = 4.5 cm.
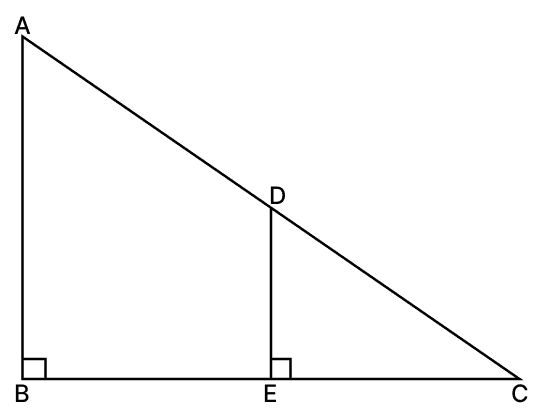
In the given figure, AB ⟂ BC and DE ⟂ BC. If AB = 9 cm, DE = 3 cm and AC = 24 cm, calculate AD.
Answer
Given,
AB ⟂ BC and DE ⟂ BC
Thus AB ∥ DE.
∠ABC = ∠DEC [Given]
∠ACB = ∠DCE [Common angle in both triangles]
∴ ΔABC ∼ ΔDEC (By A.A. axiom)
From figure,
DC = AC - AD = 24 - AD
We know that,
Corresponding sides of similar triangles are proportional.
Hence, AD = 16 cm.
In the given figure, DE || BC. If DE = 4 cm, BC = 6 cm and ar(ΔADE) = 20 cm2, find the area of ΔABC.

Answer
Considering ΔADE and ΔABC,
∠A = ∠A [Common angles]
∠ADE = ∠ABC [Corresponding angles are equal]
∴ ΔADE ∼ ΔABC (By A.A. axiom)
We know that,
The ratio of the areas of two similar triangles is equal to the ratio of the square of their corresponding sides.
Let the area of ΔABC be x cm2.
Hence, area of ΔABC = 45 cm2.
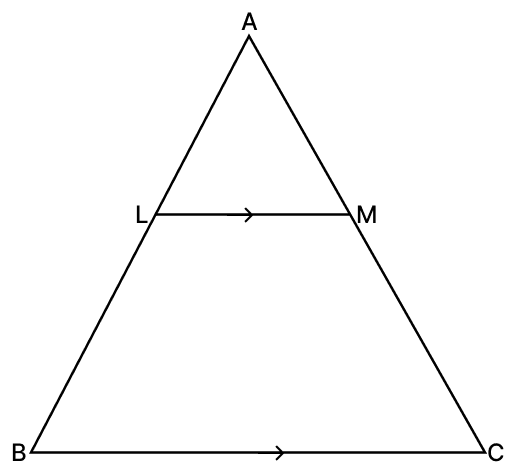
In the given figure, LM ∥ BC. If AB = 6 cm, AL = 2 cm and AC = 9 cm, calculate :
(i) the length of CM,
(ii) Find the value of .
Answer
(i) Given,
AB = 6 cm
AL = 2 cm
LB = AB - AL = 6 - 2 = 4 cm
AC = AM + MC
AM = AC - MC
AM = 9 - MC
In ΔAML and ΔABC,
∠AML = ∠ACB [Corresponding angles are equal]
∠LAM = ∠BAC [Common angle]
ΔAML ∼ ΔABC [By AA similarity]
We know that,
Corresponding sides of similar triangles are proportional.
Hence, CM = 6 cm.
(ii) Given
In ΔALM and ΔABC,
∠AML = ∠ACB [Corresponding angles are equal]
∠LAM = ∠BAC [Common angle]
ΔAML ∼ ΔABC [By AA similarity]
We know that,
The ratio of the areas of two similar triangles is equal to the ratio of the square of their corresponding sides.
Let ar(ΔALM) = x, then ar(ΔABC) = 9x.
From figure,
ar(trap. LBCM) = ar(ΔABC) - ar(ΔALM)
= 9x - x
= 8x.
.
Hence, .
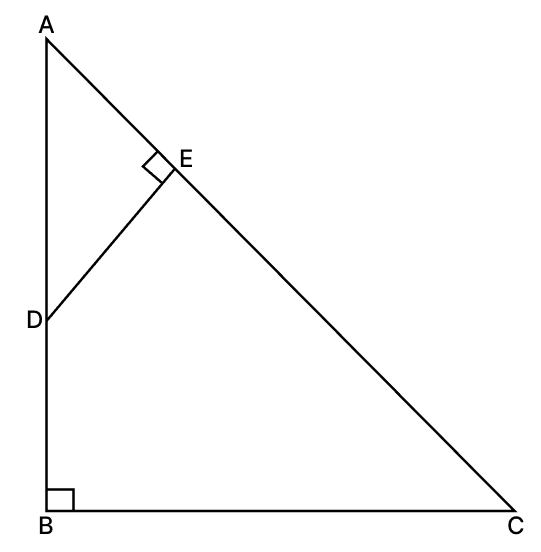
In ΔABC, it is given that AB = 12 cm, ∠B = 90° and AC = 15 cm. If D and E are points on AB and AC respectively such that ∠AED = 90° and DE = 3 cm, prove that :
(i) ΔABC ∼ ΔAED.
(ii) ar(ΔAED) = 6 cm2.
(iii) ar(quad BCED) : ar(ΔABC) = 8 : 9.
Answer
(i) Given,
∠ABC = ∠AED = 90° [Given]
∠BAC = ∠DAE [Common angle]
∴ ΔABC ∼ ΔAED (By A.A. axiom)
Hence, proved that ΔABC ∼ ΔAED.
(ii) ΔABC is right-angled triangle, applying pythagoras theorem,
⇒ AC2 = AB2 + BC2
⇒ BC2 = AC2 - AB2
⇒ BC2 = (15)2 - (12)2
⇒ BC2 = 225 - 144
⇒ BC2 = 81
⇒ BC =
⇒ BC = 9 cm
Area of ΔABC = × Base × height
= × 12 × 9
= 54 cm2
Since, ΔABC ∼ ΔAED,
We know that,
The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
Hence, proved that ar(ΔAED) = 6 cm2.
(iii) From figure,
ar(quad. BCED) = ar(ΔABC) - ar(ΔAED)
ar(quad. BCED) = 54 - 6
ar(quad. BCED) = 48 cm2.
.
Hence, proved that ar(quad BCED) : ar(ΔABC) = 8 : 9.
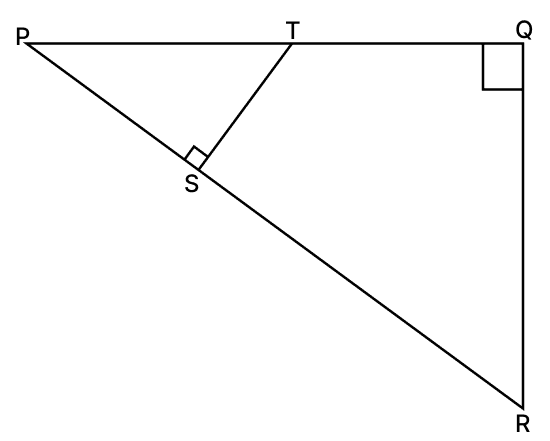
In the given figure, ∠PQR = ∠PST = 90°, PQ = 5 cm and PS = 2 cm.
(i) Prove that ΔPQR ∼ ΔPST.
(ii) Find area of ΔPQR : Area of quadrilateral SRQT.
Answer
(i) Considering ΔPQR and ΔPST.
∠P = ∠P [Common angles]
∠PQR = ∠PST [Both are equal to 90°]
∴ ΔPQR ∼ ΔPST (By A.A. axiom)
Hence, proved that ΔPQR ∼ ΔPST.
(ii) We know that,
The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
Hence, area of ΔPQR : Area of quadrilateral SRQT = 25 : 21.
In a ΔPQR, L and M are two points on the base QR such that ∠LPQ = ∠RQP and ∠RPM = ∠RQP. Prove that
(i) ΔPQL ∼ ΔRPM.
(ii) QL × RM = PL × PM.
(iii) PQ2 = QL × QR.
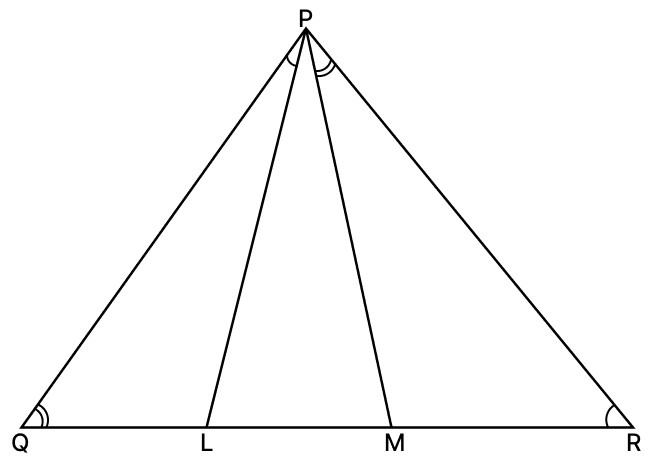
Answer
(i) In ΔPQL and ΔRPM
∠LPQ = ∠MRP [Given]
∠LQP = ∠RPM [Given]
∴ ΔPQL ∼ ΔRPM (y A.A. axiom)
Hence, proved that ΔPQL ∼ ΔRPM.
(ii) Since, ΔPQL ∼ ΔRPM and corresponding sides of similar triangle are proportional to each other.
Hence, proved that QL × RM = PL × PM.
(iii) In ΔPQL and ΔRQP
∠LPQ = ∠QRP [Given ]
∠Q = ∠Q [Common]
∴ ΔPQL ∼ ΔRQP (By A.A. axiom)
Since, corresponding sides of similar triangle are proportional to each other.
Hence, proved that PQ2 = QR x QL.
In the adjoining figure, the medians BD and CE of a ΔABC meet at G. Prove that :
(i) ΔEGD ∼ ΔCGB.
(ii) BG = 2 × GD.
Answer
(i) Since, BD and CE are medians.
So, E is mid-point of AB and D is mid-point of AC.
By mid-point theorem,
ED ∥ BC and ED = BC [By mid-point theorem]
.....(1)
In triangle EGD and BGC,
∠EGD = ∠BGC [Vertically opposite angles are equal]
∠DEG = ∠GCB [Alternate angles are equal]
∴ ΔEGD ∼ ΔCGB by (By A.A. axiom)
Hence, proved that ΔEGD ∼ ΔCGB.
(ii) Since, corresponding sides of similar triangle are proportional to each other.
Hence, proved that BG = 2GD.
In the adjoining figure, PQRS is a parallelogram with PQ = 15 cm and RQ = 10 cm. If L is a point on RP such that RL : PL = 2 : 3 and QL produced meets RS at M and PS produced at N, find the lengths of PN and RM.
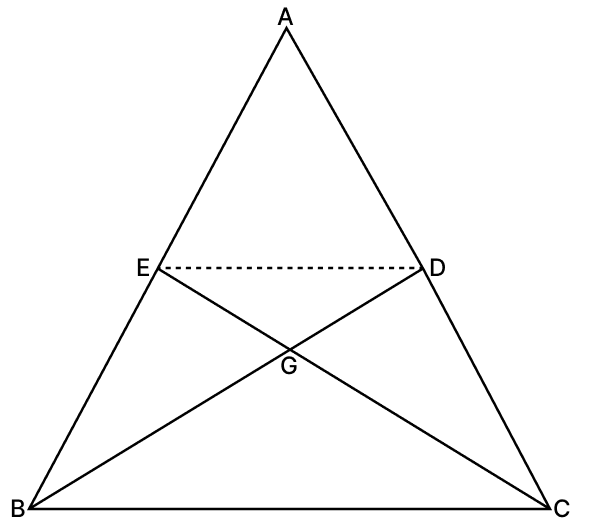
Answer
In ΔRLQ and ΔPLN,
⇒ ∠RLQ = ∠PLN [Vertically opposite angles are equal]
⇒ ∠LRQ = ∠LPN [Alternate angles are equal]
∴ ΔRLQ ∼ ΔPLN (By A.A. axiom)
Since, corresponding sides of similar triangles are proportional we have :
In ΔRLM and ΔPLQ,
⇒ ∠RLM = ∠PLQ [Vertically opposite angles are equal]
⇒ ∠LRM = ∠LPQ [Alternate angles are equal]
∴ ΔRLM ∼ ΔPLQ (By A.A. axiom)
Since, corresponding sides of similar triangles are proportional we have :
Hence, PN = 15 cm and RM = 10 cm.
In the given figure, ΔABC ∼ ΔPQR, AM and PN are altitudes, whereas AX and PY are medians. Prove that .
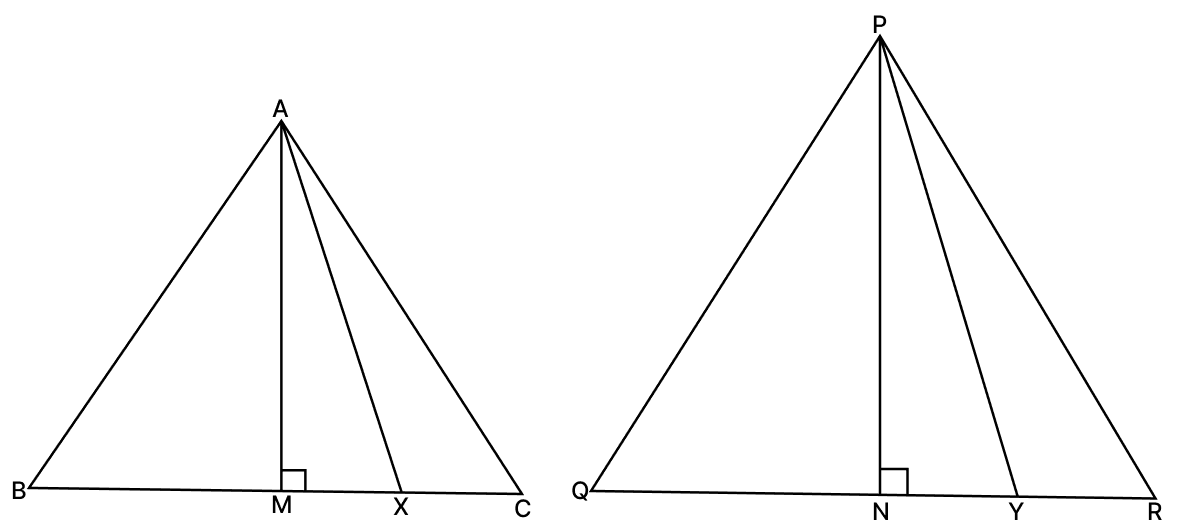
Answer
Since ΔABC ∼ ΔPQR
So, their respective sides will be in proportion
Also, ∠A = ∠P, ∠B = ∠Q, ∠C = ∠R
In ΔABM and ΔPQN,
∠ABM = ∠PQN [Since, ABC and PQR are similar]
∠AMB = ∠PNQ = 90° [Given ]
∴ ΔΑΒΜ ∼ ΔPQN by AA similarity
.....(1)
Since, AX and PY are medians so they will divide their opposite sides.
BX = and QY =
Therefore, we have:
∠ABC = ∠PQR
So, we had observed that two respective sides are in same proportion in both triangles and also angle included between them is respectively equal.
Hence, ∆ABX ∼ ∆PQY (by SAS similarity rule).So,
.....(2)
From (1) and (2),
Hence, proved that
In the given figure, BC ∥ DE, area (ΔABC) = 25 cm2, area (trap. BCED) = 24 cm2 and DE = 14 cm. Calculate the length of BC.
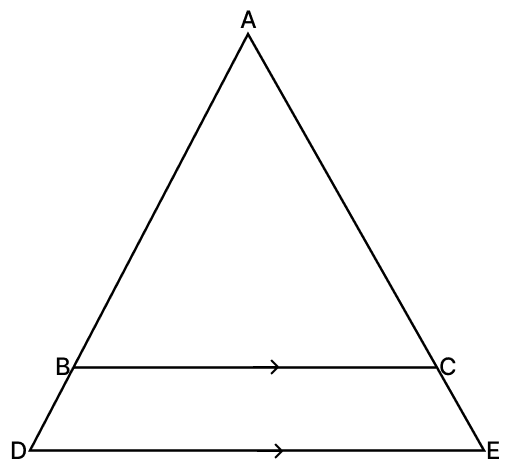
Answer
Area of ΔADE = Area of ΔABC + Area of trapezium BCED = 25 + 24 = 49 cm2.
Given,
BC ∥ DE.
In ΔABC and ΔADE,
∠ABC = ∠ADE [Corresponding angles are equal]
∠ACB = ∠AED [Corresponding angles are equal]
∴ ΔABC ∼ ΔADE by (By A.A. axiom)
We know that,
The ratio of the areas of two similar triangles is equal to the ratio of squares of their corresponding sides.
Hence, BC = 10 cm.
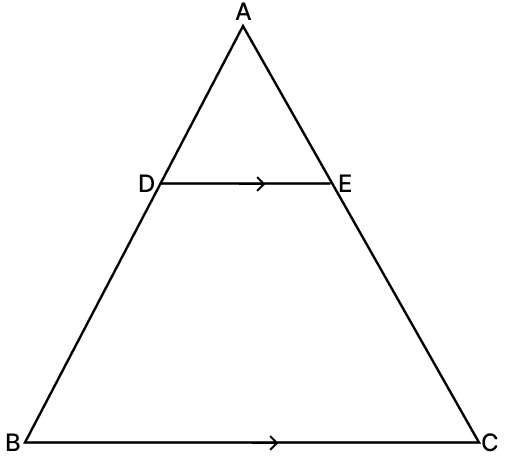
In the given figure, DE ∥ BC and DE : BC = 3 : 5. alculate ar(ΔADE) : ar(trap. BCED).
Answer
It is given that DE ∥ BC.
∠ADE = ∠ABC [Corresponding angles are equal]
∠AED = ∠ACB [Corresponding angles are equal]
∴ ΔADE ∼ ΔАВС (By A.A. axiom)
We know that,
The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
Subtracting 1 from both sides, we get:
Hence, ar(ΔADE) : ar(trap. BCED) = 9 : 16.
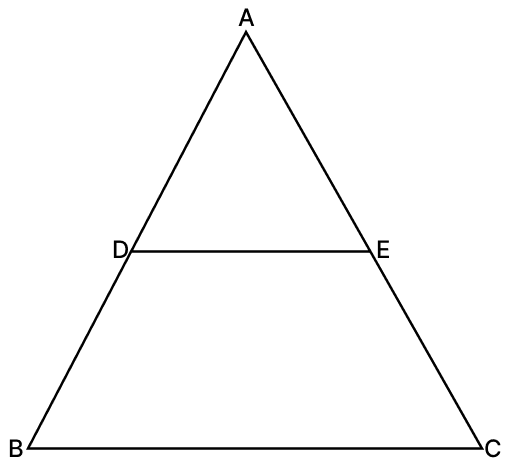
In ΔABC, D and E are mid-points of AB and AC respectively.
Find: ar(ΔADE) : ar(ΔABC).
Answer
We know that,
The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and is half of the third side.
Given,
In Δ ABC,
D is mid-point of side AB and E is the mid-point of the side AC.
∴ DE ∥ BC and DE = BC
D is mid-point of side AB.
∴ AB = 2AD
Let us consider ΔADE and ΔABC
∠DAE = ∠BAC [Common angle]
∠ADE = ∠ABC [Corresponding angle are equal]
∴ ΔADE ∼ ΔABC by AA similarity.
Hence, ar(ΔADE) : ar(ΔABC) = 1 : 4.
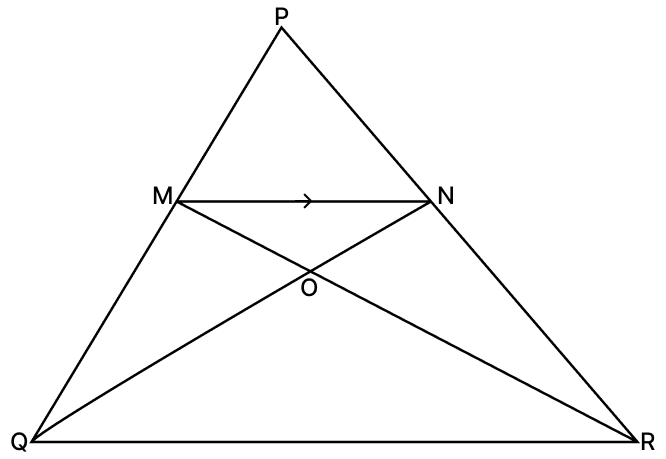
In ΔPQR, MN is parallel to QR and .
(i) Find .
(ii) Prove that ΔOMN and ΔORQ are similar.
(iii) Find: Area of ΔOMN : Area of ΔORQ.
Answer
(i) Considering ΔPMN and ΔPQR,
∠P = ∠P [Common angles]
∠PMN = ∠PQR [Corresponding angles are equal]
∴ ΔPMN ∼ ΔPQR by AA similarity.
Given,
Since triangles are similar hence the ratio of the corresponding sides will be equal,
.
Hence,
(ii) Considering ΔOMN and ΔORQ,
∠MON = ∠QOR (Vertically opposite angles are equal)
∠OMN = ∠ORQ (Alternate angles are equal)
Hence, by AA similarity ΔOMN ∼ ΔORQ.
(iii) We know that, the ratio of the areas of two similar triangles is equal to the ratio of the square of their corresponding sides.
Hence, the ratio of the Area of ΔOMN : Area of ΔORQ = 4 : 25.
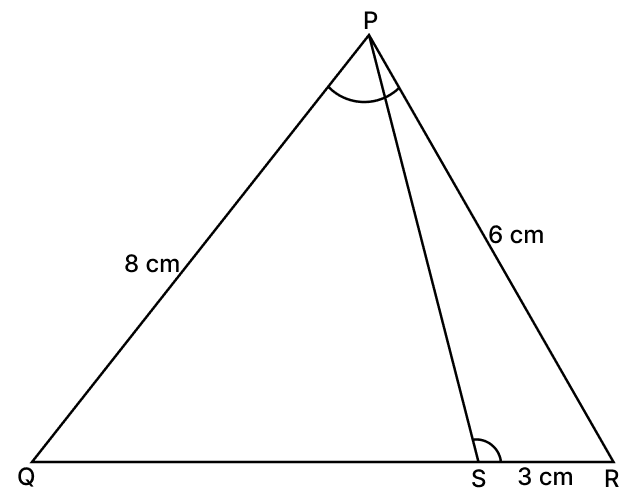
PQR is a triangle, S is a point on the side QR of ΔPQR such that ∠PSR = ∠QPR. Given QP = 8 cm, PR = 6 cm and SR = 3 cm.
(i) Prove ΔPQR ∼ ΔSPR.
(ii) Find the length of QR and PS.
(iii) Find .
Answer
(i) In ΔPQR and ΔSPR,
⇒ ∠PSR = ∠QPR [Given ]
⇒ ∠PRQ = ∠PRS [Common angle]
∴ ΔPQR ∼ ΔSPR by AA similarity.
Hence, proved that ΔPQR ∼ ΔSPR.
(ii) Since, ΔPQR ∼ ΔSPR and corresponding sides of similar triangle are proportional to each other.
Also,
Hence, QR = 12 cm and PS = 4 cm.
(iii) We know that,
Ratio of areas of two similar triangles is same as the square of the ratio between their corresponding sides.
Hence,
If ΔABC and ΔDEF are similar triangles in which ∠A = 47° and ∠E = 83°, then ∠C equals :
50°
60°
70°
80°
Answer
Given,
ΔABC ∼ ΔDEF.
Thus, corresponding angles are equal.
∠B = ∠E = 83°
We know that, sum of all angles in triangle is equal to 180°.
∠A + ∠B + ∠C = 180°
47° + 83° + ∠C = 180°
130° + ∠C = 180°
∠C = 180° - 130°
∠C = 50°.
Hence, option 1 is the correct option.
If ΔABC ∼ ΔQRP, then the corresponding proportional sides are :
Answer
Given,
ΔABC ∼ ΔQRP.
Hence, option 4 is the correct option.
If in ΔABC and ΔPQR, we have , then:
ΔPQR ∼ ΔCAB
ΔPQR ∼ ΔABC
ΔBCA ∼ ΔPQR
ΔCBA ∼ ΔPQR
Answer
Given,
The two triangles are ΔABC and ΔPQR.
By SSS similarity criterion, if the sides of one triangle are proportional to the sides of another triangle, then their corresponding angles are equal and the triangles are similar.
To find the correspondence of vertices:
The side AB corresponds to QR. The vertex opposite to AB is C, and opposite to QR is P.
C = P
The side BC corresponds to PR. The vertex opposite to BC is A, and opposite to PR is Q.
A = Q
The side CA corresponds to PQ. The vertex opposite to CA is B, and opposite to PQ is R.
B = R
∴ΔPQR ∼ ΔCAB
Hence, option 1 is the correct option.
In the given figure, AB = 24 cm, AC = 18 cm, DE = 12 cm, DF = 9 cm and ∠BAC = ∠EDF. Then ΔABC ∼ ΔEDF by the condition :
AAA
SAS
SSS
AAS
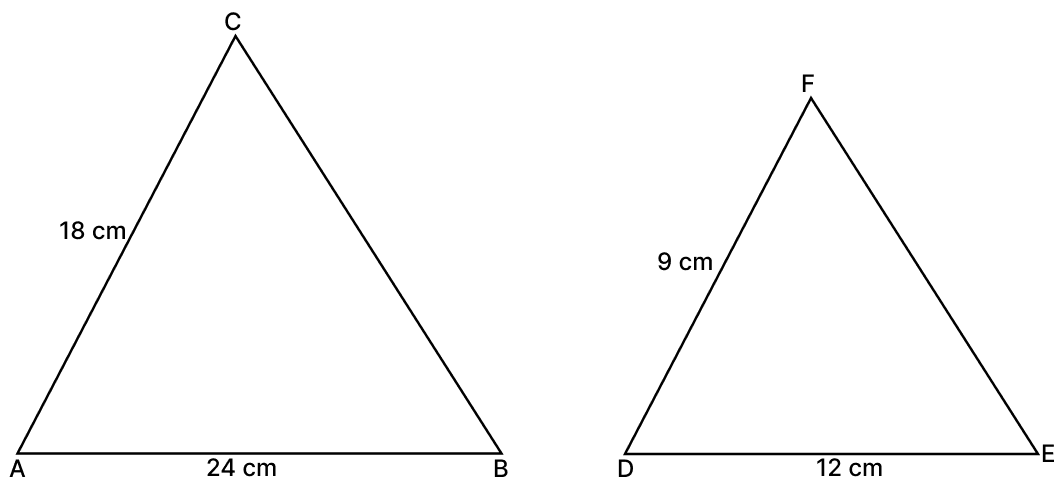
Answer
Thus,
∠BAC = ∠EDF [Given ]
∴ ΔABC ∼ ΔEDF (By S.A.S. axiom)
Hence, option 2 is the correct option.
If ΔABC and ΔDEF are so related that , then which of the following is true?
∠A = ∠E and ∠B = ∠D
∠B = ∠F and ∠C = ∠D
∠A = ∠F and ∠B = ∠D
∠C = ∠F and ∠A = ∠D
Answer
Given,
∴ ΔABC ∼ ΔDEF BY SSS theorem.
Side AB corresponds to side FD. Therefore, vertex A corresponds to vertex F and vertex B corresponds to vertex D.
Side BC corresponds to side DE. Therefore, vertex B corresponding to D. It also implies vertex C corresponds to vertex E.
Since the triangles are similar, the corresponding angles are also similar,
∠A = ∠F and ∠B = ∠D
Hence, option 3 is the correct option.
In the given figure, PQ is parallel to TR, then by using condition of similarity:
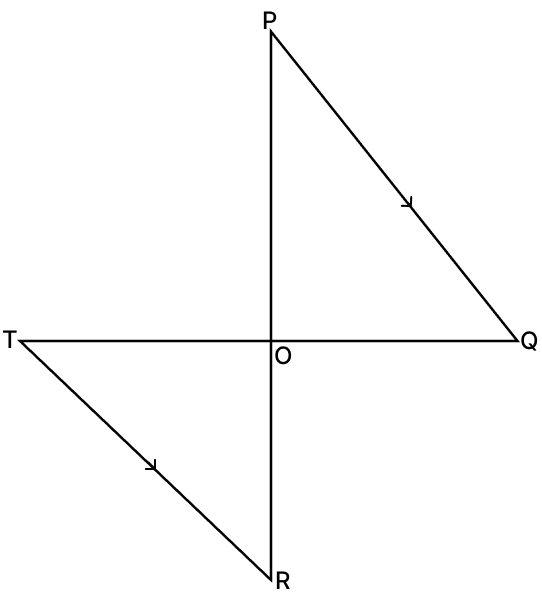
Answer
Given,
ΔPOQ and ΔROT
∠POQ = ∠TOR [vertically opposite angles are equal]
∠OPQ = ∠ORT [Alternate interior angles are equal]
∴ ΔPOQ ∼ ΔROT (By A.A. axiom)
We know that,
The ratio of corresponding sides in similar triangles are proportional.
Hence, option 2 is the correct option.
D and E are points on the sides AB and AC respectively of ΔABC. In which of the following cases DE ∥ BC?
AD = 3 cm, BD = 8 cm, AC = 8 cm, AE = 3 cm
AD = 5 cm, BD = 6 cm, AE = 6 cm, CE = 5 cm
AB = 18 cm, AD = 8 cm, AE = 12 cm, EC = 15 cm
none of these
Answer
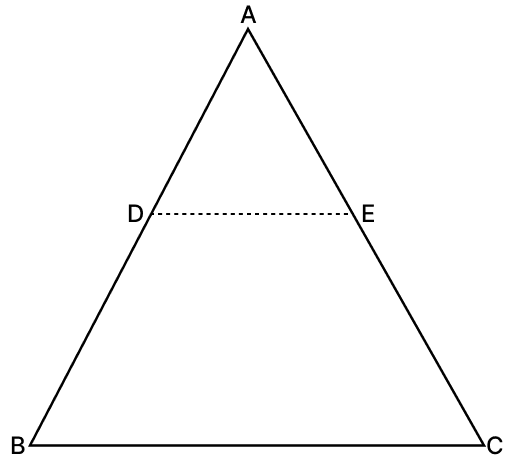
Checking option 3,
Given,
In ΔABC, DE is parallel to BC if and only if it divides the sides AB and AC in the same ratio
From figure,
DB = AB - AD = 18 - 8 = 10 cm
AB = 18 cm, AD = 8 cm, AE = 12 cm, EC = 15 cm DE is parallel to BC holds true.
Hence, option 3 is the correct option.
In ΔABC, DE ∥ BC such that . If AC = 5.6 cm, then AE = ?
2.1 cm
2.8 cm
3.1 cm
4.2 cm

Answer
By basic proportionality theorem,
If a line is drawn parallel to one side of a triangle intersecting the other two sides, it divides those two sides in the same ratio.
Since DE ∥ BC in ΔABC,
Hence, option 1 is the correct option.
In ΔABC, DE ∥ BC so that AD = (7x − 4) cm, AE = (5x − 2) cm, DB = (3x + 4) cm and EC = (3x) cm.
Then x equals:
2.5
3
4
5

Answer
By basic proportionality theorem,
If a line is drawn parallel to one side of a triangle intersecting the other two sides, it divides those two sides in the same ratio.
Since DE ∥ BC in ΔABC,
x cannot be as it yields negative AD and AE values. Therefore x = 4.
Hence, option 3 is the correct option.
It is given that ΔABC ∼ ΔDFE. If ∠A = 30°, ∠C = 50°, AB = 5 cm, AC = 8 cm and DF = 7.5 cm, then which of the following is true?
DE = 12 cm, ∠F = 50°
DE = 12 cm, ∠F = 100°
EF = 12 cm, ∠D = 100°
EF = 12 cm, ∠D = 30°
Answer
Given,
∠A = 30°
∠C = 50°
In triangle ABC,
∠A + ∠B + ∠C = 180°
∠B = 180° - (∠A + ∠C)
∠B = 180° - (30° + 50°)
∠B = 180° - 80°
∠B = 100°.
As the triangles are similar, the corresponding angles will be equal.
So, ∠F = ∠B = 100°
Since the triangles are similar, the ratio of corresponding sides is proportional,
DE = 12 cm, ∠F = 100°
Hence, option 2 is the correct option.
In ΔDEF and ΔPQR, it is given that ∠D = ∠Q and ∠R = ∠E, then which of the following is not true?
Answer
Given, in ΔDEF and ΔPQR:
∠D = ∠Q
∠E = ∠R
∴ ΔDEF ∼ ΔQRP by AA similarity.
The ratio of corresponding sides is:
do not hold true.
Hence, option 1 is the correct option.
In ΔABC, D and E are points on AB and AC respectively such that DE ∥ BC. If AE = 2 cm, EC = 3 cm and BC = 10 cm, then DE is equal to:
4 cm
5 cm
cm
15 cm
Answer
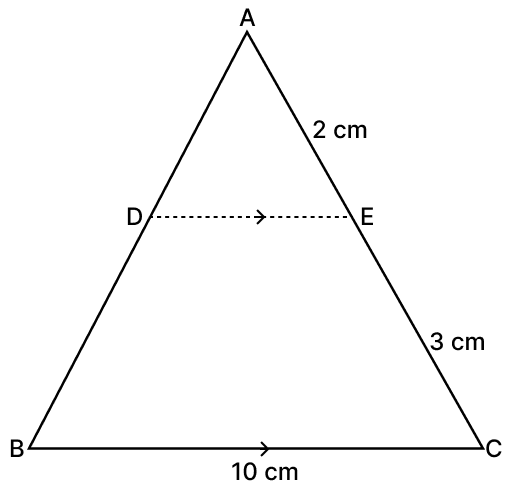
From figure,
AC = AE + EC = 2 + 3 = 5 cm.
In ΔABC and ΔADE,
∠A = ∠A [Common angle]
∠ABC = ∠ADE [Corresponding angles are equal]
∴ ΔABC ∼ ΔADE (By A.A. axiom).
In similar triangles, ratios of corresponding sides are equal.
Hence, option 1 is the correct option.
ΔABC is such that AB = 3 cm, BC = 2 cm and CA = 2.5 cm. ΔDEF ∼ ΔABC. If EF = 4 cm, then the perimeter of ΔDEF is :
7.5 cm
15 cm
22.5 cm
30 cm
Answer
Given,
ΔDEF ∼ ΔABC
Perimeter of ΔABC = AB + BC + CA = 3 + 2 + 2.5 = 7.5 cm
Since the two triangles are similar, we can write:
Hence, option 2 is the correct option.
In ΔABC, DE is drawn parallel to BC cutting the other two sides at D and E. If AB = 3.6 cm, AC = 2.4 cm and AD = 2.1 cm, then AE is equal to:
1.05 cm
1.2 cm
1.4 cm
1.8 cm
Answer
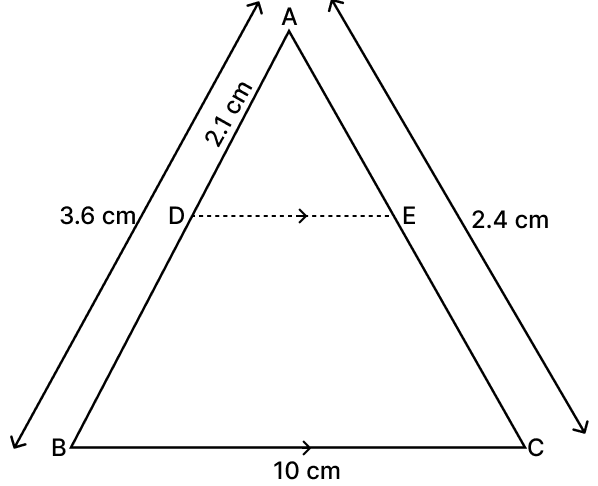
Given,
In ΔABC and ΔADE,
∠A = ∠A [Common angle]
∠ABC = ∠ADE [Corresponding angles are equal]
∴ ΔABC ∼ ΔADE (By A.A. axiom).
We know that,
Corresponding sides of similar triangle are proportional.
Hence, option 3 is the correct option.
In the given figure, ∠BAP = ∠DCP = 70°, PC = 6 cm and CA = 4 cm, then PD : DB is equal to:
5 : 3
3 : 5
3 : 2
2 : 3
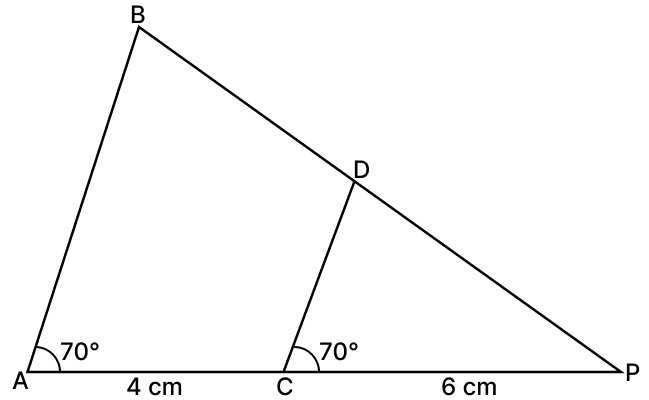
Answer
Given,
∠BAP = ∠DCP = 70°
From figure,
∠BAP and ∠DCP are corresponding angles and since they are equal.
∴ AB ∥ CD.
By basic proportionality theorm,
Hence, option 3 is the correct option.
In the adjoining figure, DE ∥ BC. If AD : DB = 3 : 1 and EA = 3.3 cm, then AC equals:
1.1 cm
4 cm
4.4 cm
5.5 cm

Answer
Since, DE // BC,
By basic proportionality theorem,
From figure,
AC = AE + EC
AC = 3.3 + 1.1 = 4.4 cm.
Hence, option 3 is the correct option.
In the adjoining figure, ∠ADE = ∠ABC, AE = 8 cm, EB = 7 cm, BC = 9 cm, AD = 10 cm and DC = 2 cm. Then the length of DE is:
6 cm
6.75 cm
7.8 cm
13.5 cm
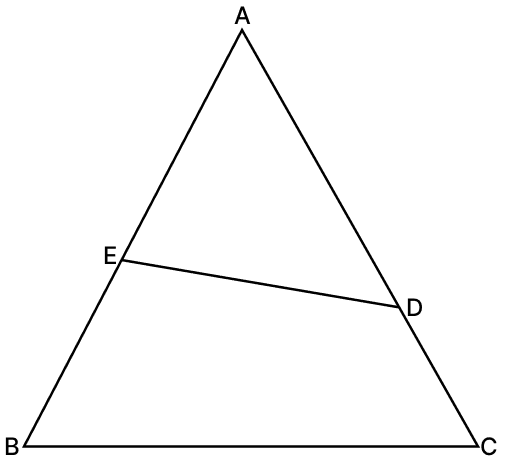
Answer
From figure,
AB = AE + EB = 8 + 7 = 15 cm
AC = AD + DC = 10 + 2 = 12 cm
In ΔABC and ΔADE
∠BAC = ∠DAE [Common angle]
∠ABC = ∠ADE [Given]
∴ ΔABC ∼ ΔADE (By A.A. axiom).
We know that,
In similar triangles the ratio of corresponding sides are equal.
Hence, option 1 is the correct option.
In ΔABC, it is given that AB = 9 cm, BC = 6 cm and CA = 7.5 cm. Also ΔDEF is given such that EF = 8 cm and ΔDEF ∼ ΔABC. Then the perimeter of ΔDEF is:
22.5 cm
25 cm
27 cm
30 cm
Answer
Given,
ΔDEF ∼ ΔABC
Perimeter of ΔABC = AB + BC + CA = 9 + 6 + 7.5 = 22.5 cm.
Since the triangles are similar,
Hence, option 4 is the correct option.
In a ΔABC, AB = 10 cm, AC = 14 cm and BC = 6 cm. If AD is the internal bisector of ∠A, then CD is equal to:
3.5 cm
4.8 cm
7 cm
10.5 cm
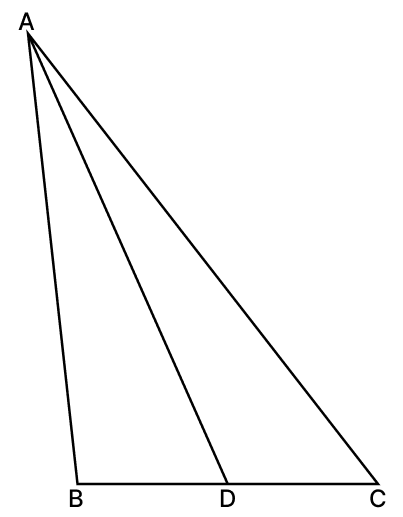
Answer
Construction: Draw a line through C parallel to AD, meeting BA produced at E.
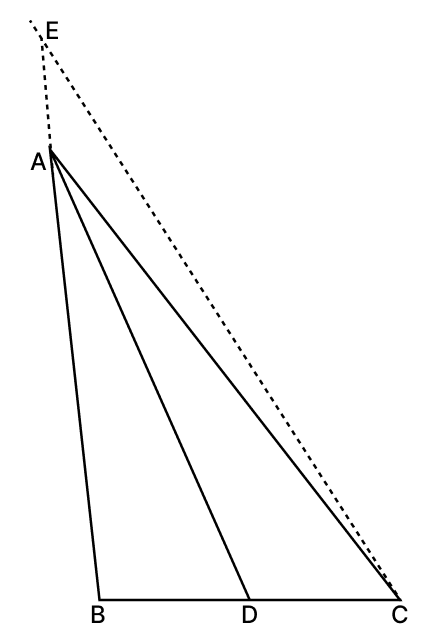
Since AD ∥ EC and BE is the transversal:
∠BAD = ∠AEC [Corresponding angles are equal]
Since AD ∥ EC and AC is the transversal:
∠DAC = ∠ACE [Alternate interior angles]
Given AD is the bisector of ∠A:
∠BAD = ∠DAC
∴ ∠AEC = ∠ACE
In ΔACE, sides opposite to equal angles are equal.
∴ AE = AC = 14 cm
Let DC be x,
Now, in ΔBCE, we have AD ∥ EC. By Basic Proportionality Theorem,
Let CD = x.
Then BD = BC - CD = 6 - x.
Substituting these values into the ratio:
Thus, CD = 3.5 cm.
Hence, option 1 is the correct option.
In the given figure, two line segments AC and BD intersect each other at point P such that PA = 6 cm, PB = 3 cm, PC = 2.5 cm, PD = 5 cm, ∠APB = 50° and ∠CDP = 30°. Then ∠PBA = ?
30°
50°
60°
100°
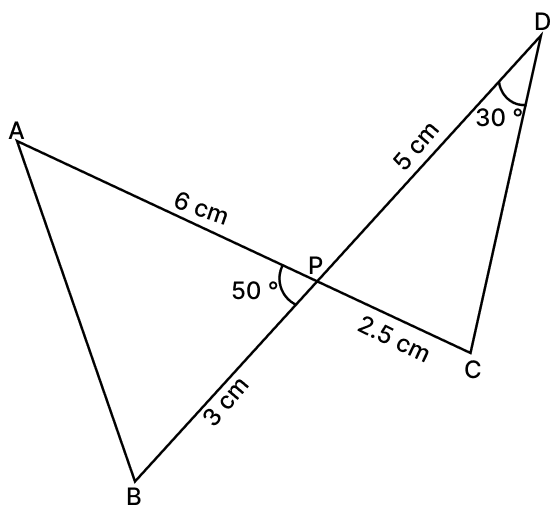
Answer
Considering ΔAPB and ΔCPD,
∠APB = ∠CPD [Vertically opposite angles are equal]
∴ ΔAPB ∼ ΔDPC (By SAS similarity)
Hence, ∠PAB = ∠PDC = 30°
⇒ ∠PBA = 180° - (∠PAB + ∠APB)
⇒ ∠PBA = 180° - (30° + 50°)
⇒ ∠PBA = 180° - 80°
⇒ ∠PBA = 100°.
Hence, option 4 is the correct option.
ABCD is a trapezium with AB parallel to DC. Then the triangle similar to ΔAOB is:
ΔACB
ΔADB
ΔCOB
ΔCOD
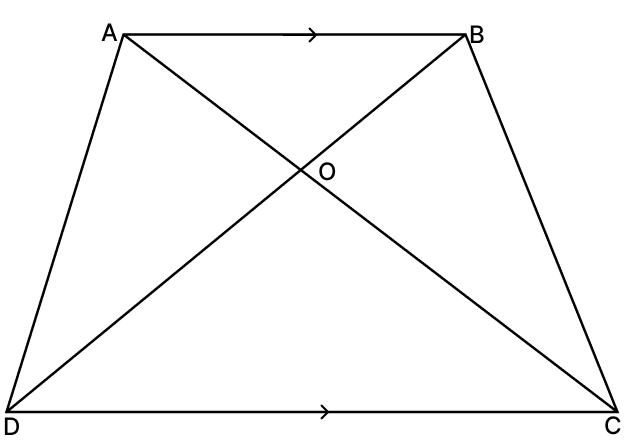
Answer
Given,
Consider ΔAOB and ΔCOD
∠AOB = ∠COD [Vertically opposite angles are equal]
∠OBA = ∠ODC [Alternate angles are equal]
Therefore, by AA rule of similarity ΔAOB ~ ΔCOD.
Hence, option 4 is the correct option.
The ratio of the corresponding sides of two similar triangles is 1 : 3. The ratio of their corresponding heights is :
1 : 3
1 : 9
3 : 1
9 : 1
Answer
Given,
The ratio of corresponding sides be 1 : 3.
Heights are linear measures corresponding to sides, so the ratio of the heights will also be 1 : 3.
Hence, option 1 is the correct option.
If in triangles ABC and DEF, ∠A = ∠E = 40°, AB : ED = AC : EF and ∠F = 65°, then ∠B is equal to :
35°
65°
75°
85°
Answer
Given,
ΔABC and ΔDEF
∠A = ∠E = 40° [Equal angles]
AB : ED = AC : EF [Corresponding sides are equal]
∴ ΔABC ∼ ΔEDF by SAS similarity. Therefore,
⇒ ∠A = ∠E = 40°
⇒ ∠B = ∠D = x
⇒ ∠C = ∠F = 65°
The sum of all the angles in a triangle is 180°:
⇒ ∠A + ∠B + ∠C = 180°
⇒ 40° + x + 65° = 180°
⇒ x = 180° - 40° - 65°
⇒ x = 75°
⇒ ∠B = ∠D = 75°.
Hence, option 3 is the correct option.
In the given figure, AB ∥ CD and OA = (2x + 4) cm, OB = (9x − 21) cm, OC = (2x − 1) cm and OD = 3 cm. Then x equals:
2.1
3
4
6
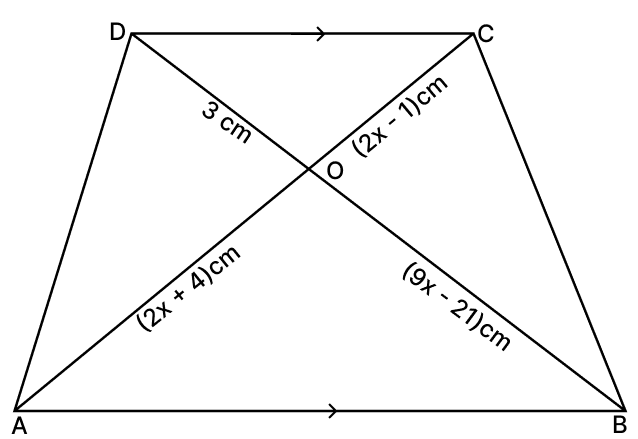
Answer
Given,
OA = (2x + 4) cm
OB = (9x − 21) cm
OC = (2x − 1) cm
OD = 3 cm
In ΔOAB and ΔOCD
∠COD = ∠AOB [Vertically Opposite Angles are equal]
∠OAB = ∠OCD [alternate interior angles are equal]
∴ ΔOAB ∼ ΔOCD by AA similarity. Then ratios of corresponding sides are equal :
x cannot be as it yields negative OB and OC values. Therefore x = 3.
Hence, option 2 is the correct option.
The shadow of a 5 m long stick is 2 m long. At the same time the length of the shadow of a 12.5 m high tree is:
3 m
3.5 m
4.5 m
5 m
Answer
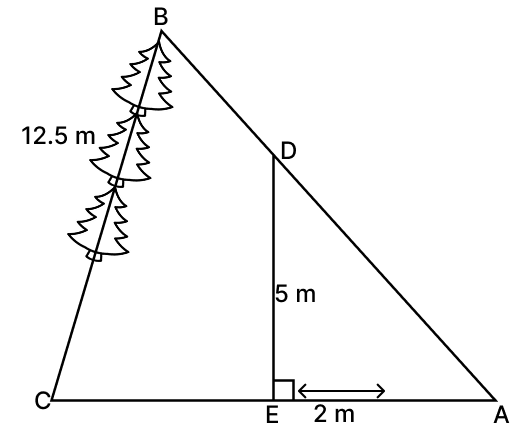
Given,
Suppose DE is a 5 m long stick and BC is a 12.5 m high tree.
Suppose EA and CA are the shadows of DE and BC respectively.
Now, In ΔABC and ΔADE,
∠ACB = ∠AED = 90°
∠A = ∠A [Common]
∴ ΔABC ∼ ΔADE by AA similarity.Then ratios of corresponding sides are equal:
Hence, option 4 is the correct option.
In a right-angled ΔABC, right-angled at A, if AD ⟂ BC such that AD = p, BC = a, CA = b and AB = c, then:
p2 = b2 + c2
p2 = b2 c2
Answer
Given,
Area of a right angled triangle =
Area of triangle ABC =
Area of triangle ABC = .......(1)
Also,
Area of triangle ABC =
Area of triangle ABC = .....(2)
From equation (1) and (2), we get :
bc = ap
bc = ap
a =
Applying Pythogoras theorem to right-angled triangle ABC:
Hence, option 4 is the correct option.
In a right-angled ΔABC in which ∠A = 90°, if AD ⟂ BC, then which of the following statements is correct?
AB = BD × AD
AB2 = BC × BD
AB2 = BD × DC
AB2 = BC × DC

Answer
Given,
In ΔABC and ΔDBA,
∠ADC = ∠ADB = 90°
∠B = ∠B [Common]
ΔABC ∼ ΔDBA [By AA similarity]
From the similarity ΔABC ∼ ΔDBA, the ratio of corresponding sides is equal:
Hence, option 2 is the correct option.
In the adjoining figure, XY is parallel to BC. If XY divides the triangle into two equal parts, then equals:
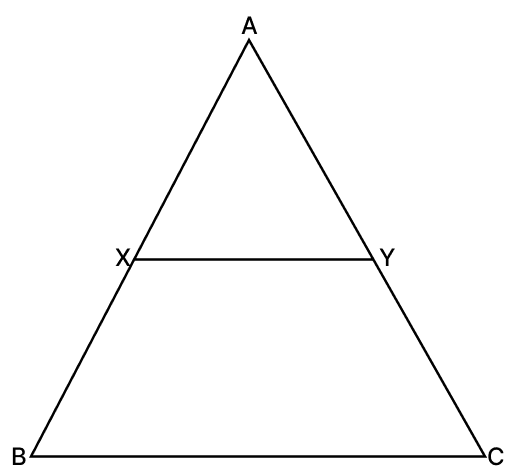
Answer
Given,
In ΔABC and ΔAXY
∠BAC = ∠XAY [Common angle]
∠AXY = ∠ABC [Corresponding angles are equal]
∴ ΔABC ∼ ΔAXY (By A.A. axiom)
The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
.....(1)
X and Y divides triangle ABC into two equal parts. Therefore,
Area of ΔAXY = Area of ΔABC
.....(2)
Equating Eqn(1) and Eqn(2) :
Hence, option 1 is the correct option.
Which of the following is true in the given figure, where AD is the altitude to the hypotenuse of a right-angled ΔABC?
(I) ΔABD ∼ ΔCAD
(II) ΔADB ≅ ΔCDA
(III) ΔADB ∼ ΔCAB
I and II
II and III
I and III
I, II and III
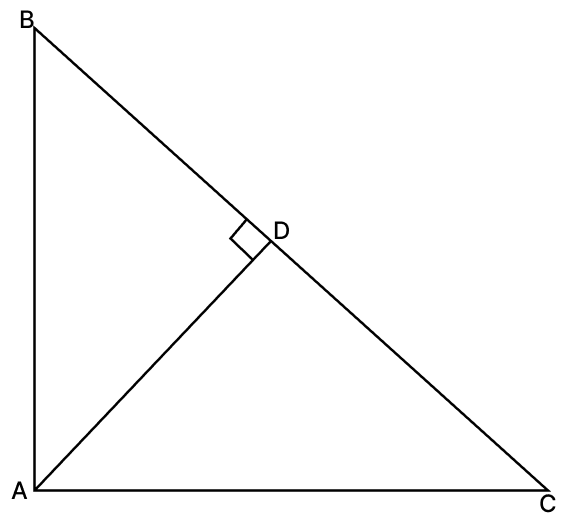
Answer
In ΔABD,
∠B + ∠BAD = 90°
∠BAD = 90° - ∠B ........(1)
In ΔABC,
Since, BC is the hypotenuse, thus angle A = 90°
From figure,
∠DAC = ∠BAC - ∠BAD
∠DAC = 90° - ∠BAD
Substituting value of ∠BAD from equation (1) in above equation, we get :
∠DAC = 90° - (90° - ∠B) = ∠B.
In ΔABD and ΔCAD,
∠DAC = ∠B (Proved above)
∠ADB = ∠ADC (Both equal to 90°)
∴ ΔABD ∼ ΔCAD by AA similarity.
Thus, (I) is true.
or we can say that ΔADB ∼ ΔCDA.
Thus, (II) is true.
In ΔADB and ΔCAB,
∠ADB = ∠CAB = 90°
∠ABD = ∠CBA [Common angle]
∴ ΔADB ∼ ΔCAB by AA similarity.
Thus, (III) is true.
Hence, option 4 is the correct option.
The areas of two similar triangles are 49 cm2 and 64 cm2 respectively. The ratio of their corresponding sides is:
7 : 8
49 : 64
8 : 7
64 : 49
Answer
Given,
Let, A1 and A2 be the areas of two triangle. s1 and s2 be the length of their corresponding sides.
Since the triangles are similar, the ratios of Areas of triangles is equal to squares of corresponding sides.
Ratio between sides = 7 : 8.
Hence, option 1 is the correct option.
The areas of two similar triangles are 12 cm2 and 48 cm2 respectively. If the height of the smaller one is 2.1 cm, then the corresponding height of the bigger one is:
0.525 cm
4.2 cm
4.41 cm
8.4 cm
Answer
Given,
Let, A1 and A2 be the areas of two triangle. h1 and h2 be the height of their corresponding sides.
Since the triangles are similar, the ratios of Areas of triangles is equal to squares of corresponding heights.
Hence, option 2 is the correct option.
The areas of two similar triangles are 81 cm2 and 144 cm2. If the largest side of the smaller triangle is 27 cm, then largest side of the larger triangle is:
24 cm
36 cm
48 cm
none of these
Answer
Given,
Let, A1 and A2 be the areas of two triangle. s1 and s2 be the length of their corresponding sides.
Since the triangles are similar, the ratios of Areas of triangles is equal to squares of corresponding sides.
Hence, option 2 is the correct option.
ΔABC and ΔDEF are similar to each other. If the ratio of side AB to side DE is , then the ratio of area of ΔABC to that of ΔDEF is:
Answer
Given,
ΔABC and ΔDEF are similar to each other.
Since the triangles are similar, the ratios of Areas of triangles is equal to squares of corresponding sides.
Area of triangle ABC : Area of triangle DEF = .
Hence, option 1 is the correct option.
If ΔABC ∼ ΔQRP, , AB = 18 cm and BC = 15 cm, then PR = ?
cm
8 cm
10 cm
12 cm
Answer
Given,
AB = 18 cm
BC = 15 cm
Since the triangles are similar, the ratios of Areas of triangles is equal to the ratio of the squares of corresponding sides.
Hence, option 3 is the correct option.
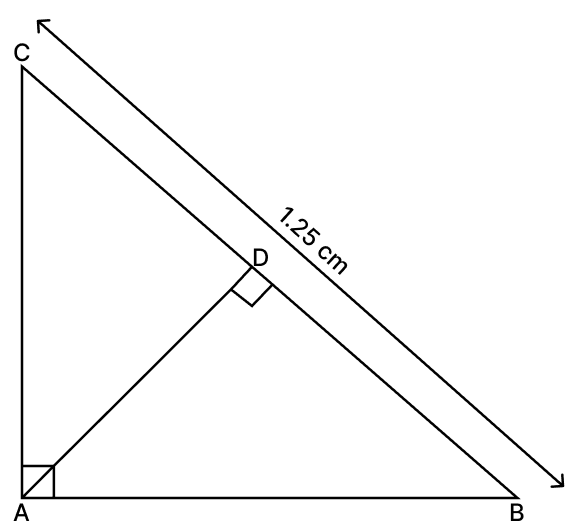
In the given figure, ∠CAB = 90° and AD ⟂ BC. If AC = 75 cm, AB = 1 m and BC = 1.25 m, then AD equals:
50 cm
60 cm
65 cm
70 cm
Answer
Given,
∠CAB = 90°
AC = 75 cm = 0.75 m
AB = 1 m
BC = 1.25 m
In ΔCAB and ΔADB,
∠CAB = ∠ADB = 90° [AD ⟂ BC]
∠CBA = ∠ABD [Common angle]
∴ ΔCAB ∼ ΔADB by AA similarity. Then ratios of corresponding sides are equal:
AD = 0.6 m = 60 cm.
Hence, option 2 is the correct option.
A street lamp is fixed on a lamp-post at a height of 3.3 m from the ground. A boy 110 cm tall walks away from the base of this lamp post at a speed of 0.8 m/s. The length of the shadow of the boy after 4 seconds is:
1.1 m
1.6 m
2.1 m
2.6 m
Answer
Let AB = 3.3 m be the lamp post and QP = 1.1 m be the position of boy after 4 seconds.
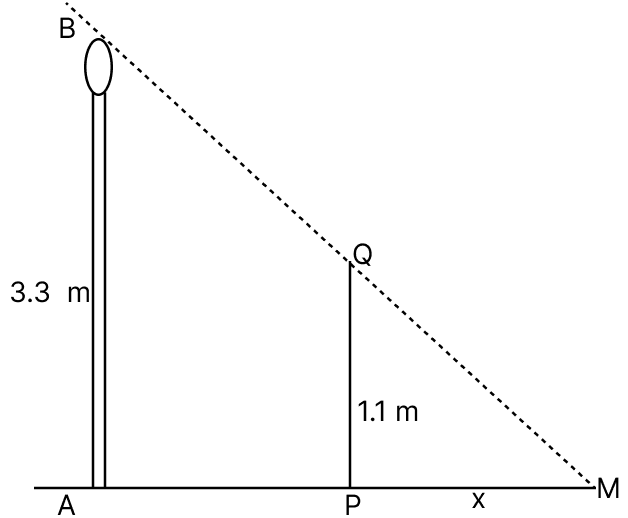
AP is the distance moved in 4s at 0.8m/s = 4(0.8) = 3.2 m
PM is the length of the shadow of boy.
In triangle AMB and PMQ,
∠MAB = ∠MPQ = 90°
∠AMB = ∠PMQ [Common angle]
∴ ΔAMB ∼ ΔPMQ [By AA similarity].
Then ratios of corresponding sides of similar triangles are equal.
Hence, option 2 is the correct option.
The lengths of the sides of triangle P are 3, 4 and 5 units. Another triangle Q, which is similar to P, has one side of length 60 units, what is the smallest possible perimeter of triangle Q?
120 units
144 units
180 units
240 units
Answer
Given,
Triangle P is similar to triangle Q
Perimeter of Triangle P = 3 + 4 + 5 = 12 units
Since the triangles are similar, the corresponding sides have a scale factor of k . One of the length of side of triangle Q is 60 units. The Corresponding scale factors will be:
Case 1 :
k = = 20
Case 2 :
k = = 15
Case 3 :
k = = 12
Among the three cases, smallest sclae factor = 12.
Smallest possible perimeter of Triangle (Q) = 12 × 12 = 144 units.
Hence, option 2 is the correct option.
Which of the following is correct?
If D is a point on side AB of ΔABC such that AD : DB = 5 : 2 and E is a point on BC such that DE ∥ AC, then ar(ΔABC) : ar(ΔDBE) = 9 : 4.
If the areas of two similar triangles are in the ratio 25 : 64, then their perimeters are in the ratio 5 : 8.
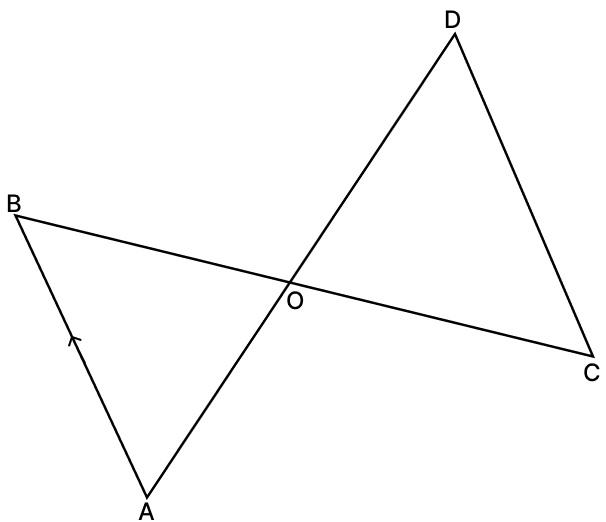
In the adjoining figure if AB ∥ CD, then ΔAOB ∼ ΔCOD.
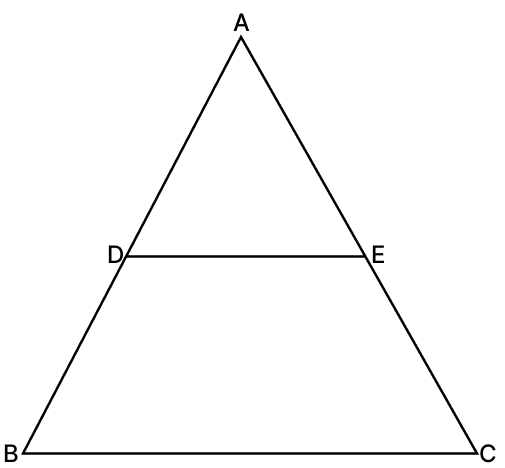
In the adjoining figure, if D and E are the mid-points of AB and AC respectively, then ar(ΔADE) = × ar(ΔABC).
Answer
Solving option 2,
Since the triangles are similar,
The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides (or perimeters).
Hence proved.
Hence, option 2 is the correct option.
In the given figure, D, E and F are the mid-points of the sides BC, AC and AB respectively of ΔABC. Then which of the following does not hold true?
ΔAFE ∼ ΔABC
ΔFBD ∼ ΔABC
ΔEDC ∼ ΔABC
ΔDFE ∼ ΔABC
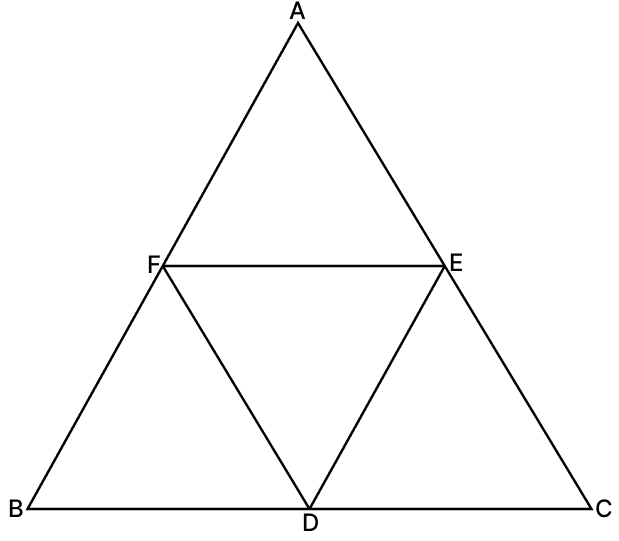
Answer
Given,
Since D, E, F are midpoints of BC, AC and AB respectively.
According to the Mid-point Theorem, the segment joining the mid-points of two sides of a triangle is parallel to the third side and is half its length.
Thus, by mid-point theorem,
DE ∥ AB
DE = AB
EF ∥ BC
EF = BC
FD ∥ AC
DF = AC
Ratios can be written as,
∴ ΔDFE ∼ ΔACB is true, but ΔDFE ≁ ΔABC.
Hence, option 4 is the correct option.
A triangle with sides 6, 9 and 12 units has area A sq. units. What is the area (in sq. units) of a triangle with sides 8, 12 and 16 units in terms of A?
A
A
A
A
Answer
We compare the ratios of the corresponding sides of the first triangle with sides 6, 9, 12 and the second triangle with sides 8, 12, 16.
k = .
Therefore, the two triangles are similar with scale factor of k = . The ratio of Areas of two triangle is equal to square of it's scale factor.
Hence, option 3 is the correct option.
Directions (Q. 41 to 44): These questions are based on the following information :
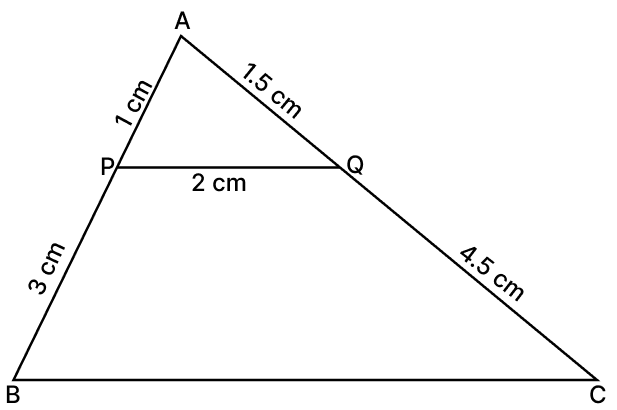
In the given figure, ABC is a triangle and PQ is a straight line meeting AB in P and AC in Q. It is given that AP = 1 cm, PB = 3 cm, AQ = 1.5 cm, QC = 4.5 cm and PQ = 2 cm.
The perimeter of ΔABC is:
12 cm
16 cm
18 cm
24 cm
Answer
From figure,
AB = AP + PB = 1 + 3 = 4 cm
AC = AQ + QC = 1.5 + 4.5 = 6 cm
In ΔAPQ and ΔABC,
∠PAQ = ∠BAC [Common angles]
ΔAPQ ∼ ΔABC [By SAS Similarity]
Since, corresponding sides of similar triangle are proportional to each other.
Perimeter = AB + AC + BC
= 4 + 6 + 8
= 18 cm.
Hence, option 3 is the correct option.
The ratio of the areas of ΔAPQ and ΔABC is:
1 : 3
1 : 4
1 : 9
1 : 16
Answer
We know that,
The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
Hence, option 4 is the correct option.
Which of the following holds true?
ΔAPQ ∼ ΔABC
ΔAQP ∼ ΔABC
ΔAPQ ∼ ΔACB
none of these
Answer
In ΔAPQ and ΔABC,
∠PAQ = ∠BAC [Common angles]
∴ ΔAPQ ∼ ΔABC by SAS Similarity.
Hence, option 1 is the correct option.
Which axiom of similarity applies in the above case?
AAA
AA
SSS
SAS
Answer
Two pairs of corresponding sides are proportional () and icluded angle is also equal (angle A).
This is the S.A.S. (Side-Angle-Side) Similarity Axiom.
Hence, option 4 is the correct option.
Directions (Q. 45 to 48): Using the given diagram answer the following questions.
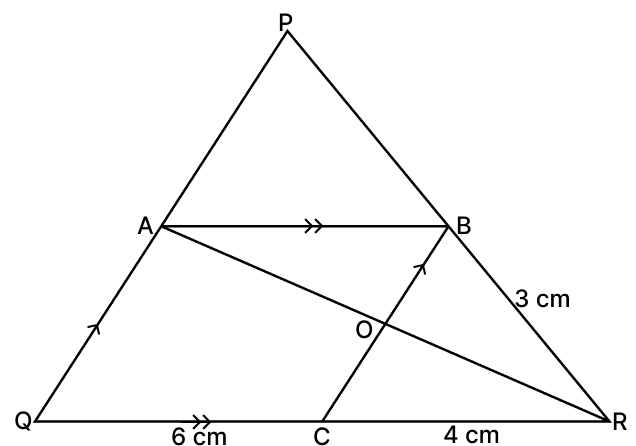
In ΔPQR, AB ∥ QR, QP ∥ CB and AR intersects CB at O.
The triangle similar to ΔARQ is:
ΔORC
ΔARP
ΔOBR
ΔQRP
Answer
In ΔARQ and ΔORC,
∠BRC = ∠ARQ [Common angle]
∠AQR = ∠BCR [Corresponding angles, AB ∥ QR, BC is the transversal]
ΔARQ ∼ ΔORC [By AA Similarity]
Hence, option 1 is the correct option.
ΔPQR ∼ ΔBCR by axiom:
SAS
AAA
SSS
AAS
Answer
In ΔPQR and ΔBCR,
∠PRQ = ∠BRC [Common angle]
∠PQR = ∠BCR [Corresponding angles, CB ∥ QP, BC is the transversal]
ΔPQR ∼ ΔBCR [By AA or AAA similarity]
Hence, option 2 is the correct option.
If QC = 6 cm, CR = 4 cm, BR = 3 cm, then the length of RP is:
4.5 cm
5 cm
7.5 cm
8 cm
Answer
RQ = RC + CQ = 4 + 6 = 10 cm.
RB = 3 cm
RC = 4 cm
From 46 que we have ΔPQR ∼ ΔBCR,
Since, corresponding sides of similar triangle are proportional to each other.
Hence, option 3 is the correct option.
The ratio PQ : BC is:
2 : 3
3 : 2
2 : 5
5 : 2
Answer
Using ΔPQR ∼ ΔBCR,
Hence, option 4 is the correct option.
Directions (Q. 49 to 52): Answer these questions on the basis of the following information:
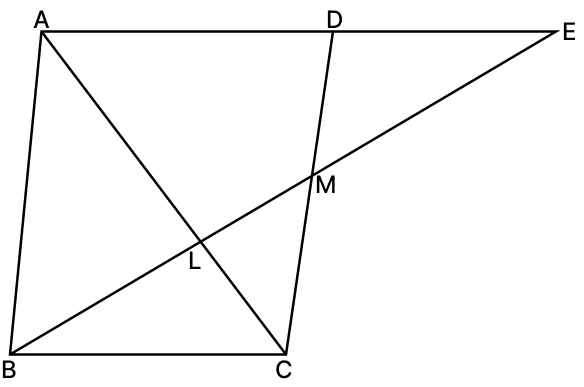
Through the mid-point M of the side CD of a ∥gm ABCD, the line BM is drawn, intersecting AC on L and AD produced in E.
Which of the following is true for triangles BMC and EMD ?
I. They are similar to each other.
II. They are congruent to each other.
III. Their areas are equal.
IV. Their perimeters are equal.
I and II
II and III
I and III
I, II, III and IV
Answer
In ΔBMC and ΔEMD,
∠EDM = ∠MCB [Alternate angles are equal]
∠EMD = ∠BMC [Vertically opposite angles are equal]
CM = DM (As M is the mid-point of CD)
ΔBMC ≅ ΔEMD [By A.A. axiom]
Congruent triangles are similar, have equal areas and perimeters.
∴ All statements are correct
Hence, option 4 is the correct option.
ΔAEL is similar to:
ΔCBL
ΔCML
ΔDME
ΔBMC
Answer
In ΔAEL and ΔCBL,
∠EAL = ∠BCL[Alternate angles are equal]
∠ALE = ∠CLB [Vertical opposite angles are equal]
ΔAEL ∼ ΔCBL [By A.A. axiom]
Hence, option 1 is the correct option.
By which axiom are the above triangles similar?
AA
SSS
SAS
ASA
Answer
The similarity ΔAEL ∼ ΔCBL was established by using two pairs of corresponding angles.
Hence, option 1 is the correct option.
EL : BL is equal to :
1 : 2
2 : 1
1 : 3
3 : 1
Answer
AD = BC [ABCD is a parallelogram]
BC = DE [ΔBMC ≅ ΔEMD]
From figure,
AE = AD + DE
AE = BC + BC
AE = 2BC
Using ΔAEL ∼ ΔCBL,
Since, corresponding sides of similar triangle are proportional to each other.
Hence, option 2 is the correct option.
Directions (Q. 53 to 56): Study the following diagram carefully and answer the given questions:
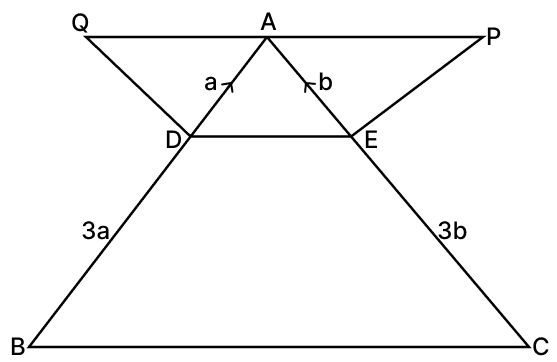
In ΔABC, D and E are points on AB and AC respectively such that AD = a, DB = 3a, AE = b and EC = 3b. DQ ∥ EA and EP ∥ DA are drawn. QP is joined.
ΔADE is similar to which of the following triangles?
I. ΔABC
II. ΔDAQ
III. ΔADQ
IV. ΔEPA
V. ΔEAP
I, II and IV only
I, III and V only
I, II and V only
I, III and IV only
Answer
In ΔADE and ΔABC,
∠A is common.
By SAS Similarity of Triangles, ΔADE ∼ ΔABC.
In ΔADE and ΔDAQ,
∠DQA = ∠ADE [Corresponding angle]
∠QDA = ∠DAE [Alternate Interior Angle]
∴ ΔADE ∼ ΔDAQ by AA similarity
In ΔADE and ΔEPA,
∠EPA = ∠ADE [Corresponding angle]
∠PEA = ∠DAE [Alternate Interior Angle]
∴ ΔADE ∼ ΔEPA by AA similarity
Hence, option 1 is the correct option.
If DE = 2 cm, then BC is equal to:
4 cm
6 cm
7 cm
8 cm
Answer
Since ΔADE ∼ ΔABC, corresponding sides are proportional.
Given AD = a and DB = 3a, so AB = 4a.
Hence, option 4 is the correct option.
The ratio of the perimeters of ΔADE and ΔABC is:
1 : 2
1 : 3
1 : 4
1 : 6
Answer
Hence, option 3 is the correct option.
The ratio of the areas of ΔADE and trapezium DBCE is:
1 : 8
1 : 9
1 : 15
1 : 16
Answer
Hence, option 3 is the correct option.
Directions (Q. 57 to 60): Study the given information and answer the questions that follow:
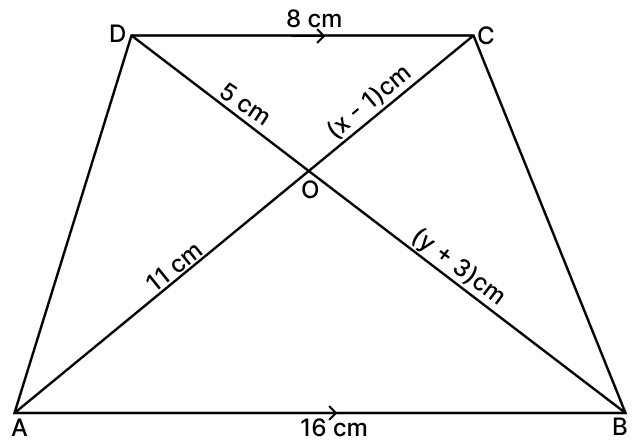
In the given figure ABCD is a trapezium in which DC is parallel to AB. AB = 16 cm and DC = 8 cm, OD = 5 cm, OB = (y + 3) cm, OA = 11 cm and OC = (x − 1) cm.
From the given figure name the pair of similar triangles :
ΔAOD, ΔOBC
ΔCOD, ΔAOB
ΔADB, ΔACB
ΔCOD, ΔCOB
Answer
Given,
In ΔAOB and ΔCOD,
∠AOB = ∠COD [Vertically opposite angle are equal]
∠OAB = ∠OCD [Alternate interior angle are equal]
∴ ΔAOB ∼ ΔCOD (By A.A. axiom)
Hence, option 2 is the correct option.
The corresponding proportional sides with respect to the pair of similar triangles obtained above is :
Answer
Given,
ΔAOB ∼ ΔCOD.Since the triangles are similar, the ratios of the corresponding sides are equal,
Hence, option 1 is the correct option.
The ratio of the sides of the pair of similar triangles is:
1 : 3
1 : 2
2 : 3
3 : 1
Answer
Given,
ΔAOB ∼ ΔCOD. Since the triangles are similar, the ratios the corresponding sides are equal,
Ratio = = 1 : 2.
Hence, option 2 is the correct option.
Using the ratio of sides of the pair of similar triangles, the values of x and y are respectively :
x = 4.6, y = 7
x = 7, y = 7
x = 6.5, y = 7
x = 6.5, y = 2
Answer
Given,
ΔAOB ∼ ΔCOD. Since the triangles are similar, the ratios the corresponding sides are equal,
Solving,
Substituting values we get :
Solving,
Substituting values we get :
x = 6.5, y = 7
Hence, option 3 is the correct option.
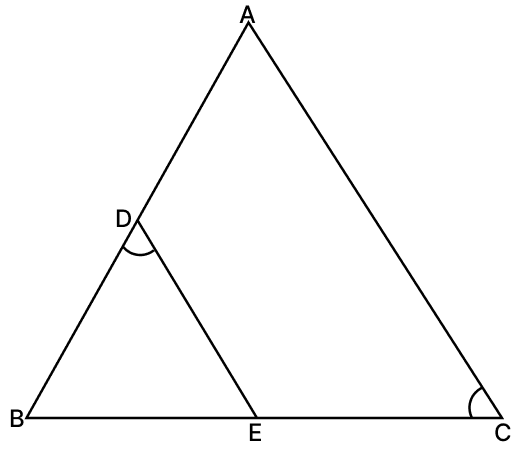
Assertion (A): In the figure, if ∠EDB = ∠ACB, BE = 6 cm, EC = 4 cm and BD = 5 cm, then the length of AB is 12 cm.
Reason (R): If two triangles have two pairs of corresponding angles equal, then the triangles are similar.
A is true, R is false.
A is false, R is true.
Both A and R are true.
Both A and R are false.
Answer
In ΔEDB and ΔACB,
∠EDB = ∠ACB (Given)
∠EBD = ∠ABC [Common angles]
∴ ΔEDB ∼ ΔACB [By AA axiom]
From figure,
BC = BE + EC = 6 + 4 = 10 cm.
Since, corresponding sides of similar triangle are proportional to each other.
So, Assertion (A) is true.
We know that,
If two triangles have two pairs of corresponding angles equal, then the triangles are similar, by A.A. axiom.
Reason (R) is true.
Both A and R are true.
Hence, option 3 is the correct option.
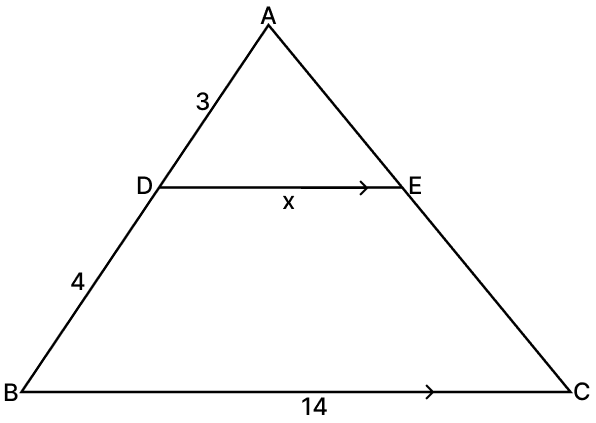
Assertion (A): In the figure, if DE ∥ BC, then the value of x is 6 units.
Reason (R): Two similar triangles are always congruent.
A is true, R is false.
A is false, R is true.
Both A and R are true.
Both A and R are false.
Answer
Given,
DE ∥ BC,
In ΔADE and ΔABC,
∠ADE = ∠ABC (Corresponding angles are equal)
∠DAE = ∠BAC (Common angle)
∴ ΔADE ~ ΔABC
AD = 3 units
DB = 4 units
From figure,
AB = AD + DB = 3 + 4 = 7 units.
We know that,
Corresponding sides of similar triangle are proportional to each other.
Assertion (A) is true.
Congruent triangles must have all corresponding sides and angles equal.
Similar triangles only require corresponding angles to be equal and corresponding sides to be proportional.
Similar triangles are not always congruent.
Reason (R) is false.
A is true, R is false
Hence, option 1 is the correct option.
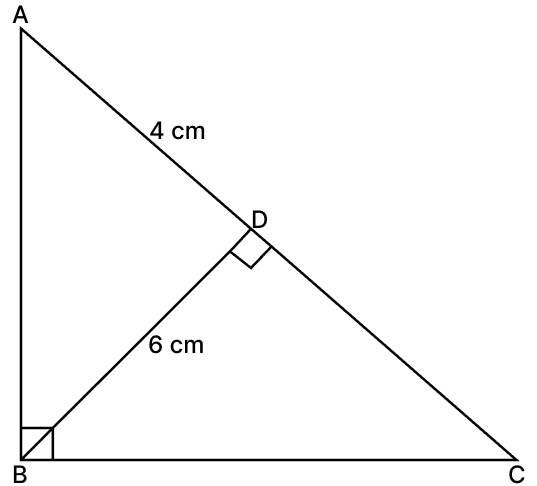
Assertion (A): In the figure, ∠ABC = ∠BDC = 90°.
If AD = 4 cm, BD = 6 cm, then area of ΔABC is 40 cm2.
Reason (R): Areas of two similar triangles are proportional to the squares of their corresponding sides.
A is true, R is false
A is false, R is true
Both A and R are true
Both A and R are false
Answer
In ΔADB and ΔBDC,
∠ADB = ∠BDC = 90°
∠DBA = ∠DCB [Angles complementary to ∠DBC]
∴ ΔADB ∼ ΔBDC [By A.A. axiom]
Since, corresponding sides of similar triangle are proportional to each other.
From figure,
AC = AD + DC = 4 + 9 = 13 cm.
Height BD = 6 cm.
Area of ΔABC = × Base × Height
The Assertion states Area is 40 cm2, which is incorrect.
So, Assertion (A) is false.
Areas of two similar triangles are proportional to the squares of their corresponding sides.
Reason (R) is true
A is false, R is true.
Hence, option 2 is the correct option.
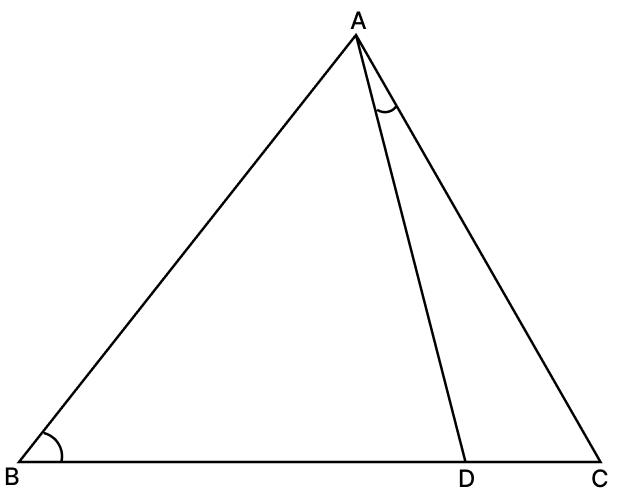
Assertion (A): In ΔABC, if ∠ABC = ∠DAC, AB = 8 cm, AC = 4 cm, AD = 5 cm, then BC = 3.5 cm.
Reason (R): SAS and ASS both are valid criteria for similarity of two triangles.
A is true, R is false
A is false, R is true
Both A and R are true
Both A and R are false
Answer
In ΔABC and ΔDAC,
∠ABC = ∠DAC (Given)
∠BCA = ∠DCA [Common angles]
ΔABC ∼ ΔDAC [By A.A. axiom]
Since, corresponding sides of similar triangle are proportional to each other.
Assertion (A) is false.
SAS and ASS both are valid criteria for similarity of two triangles.
The SAS (Side-Angle-Side) criterion is a valid test for similarity.
The ASS (Angle-Side-Side) criterion is not a valid test for similarity.
Since the statement claims both are valid
Reason (R) is false.
Both A and R are false.
Hence, option 4 is the correct option.