Similarity (As a Size Transformation)

Δ ABC with sides AB = 3.6 cm, BC = 4.5 cm and CA = 6 cm is enlarged to Δ A'B'C' such that the largest side of the enlarged triangle is 10 cm. Find the scale factor and use it to find the lengths of the other sides of Δ A'B'C'.

Answer

Longest side in Δ ABC (CA) = 6 cm

Longest side in Δ A'B'C' (C'A') = 10 cm

Let scale factor be k.

C'A' = k × CA

k = $\dfrac{C'A'}{CA} = \dfrac{10}{6} = \dfrac{5}{3}$.

∴ The scale factor is, k = $\dfrac{5}{3}$

Now,

A'B' = k × (AB) = $\dfrac{5}{3} \times 3.6$ = 6 cm

B'C' = k × (BC) = $\dfrac{5}{3} \times 4.5$ = 7.5 cm

Hence, scale factor = $\dfrac{5}{3}$, A'B' = 6 cm and B'C' = 7.5 cm.

A Δ ABC with sides AB = 16 cm, BC = 12 cm and CA = 18 cm is reduced to Δ A'B'C' such that the smallest side of the image triangle is 4.8 cm. Find the scale factor and use it to find the lengths of the other sides of Δ A'B'C'.

Answer

Smallest side in Δ ABC (BC) = 12 cm

Smallest side in Δ A'B'C' (B'C') = 4.8 cm

Let scale factor be k.

B'C' = k × BC

k = $\dfrac{B'C'}{BC} = \dfrac{4.8}{12} = \dfrac{2}{5}$

∴ The scale factor is, k = $\dfrac{2}{5}$.

Now,

⇒ A'B' = k × (AB) = $\dfrac{2}{5} \times 16$ = 6.4 cm

⇒ A'C' = k × (AC) = $\dfrac{2}{5} \times 18$ = 7.2 cm

Hence, scale factor = $\dfrac{2}{5}$, A'B' = 6.4 cm and A'C' = 7.2 cm.

A Δ PQR is reduced by a scale factor 0.72. If the area of Δ PQR is 62.5 cm², find the area of its image.

Answer

We know that,

Area of image = k² × Area of the actual triangle Δ PQR

= (0.72)² × 62.5

= 0.5184 × 62.5

= 32.4 cm².

Hence, area of image of Δ PQR = 32.4 cm².

A rectangle having an area of 60 cm² is transformed under enlargement about a point in space. If the area of its image is 135 cm², find the scale factor of the enlargement.

Answer

Let scale factor be k.

We know that,

Area of the image = k² × (Area of the rectangle)

$\Rightarrow 135 = k^2 \times 60 \\[1em] \Rightarrow k^2 = \dfrac{135}{60} \\[1em] \Rightarrow k^2 = \dfrac{9}{4} \\[1em] \Rightarrow k = \sqrt{\dfrac{9}{4}} \\[1em] \Rightarrow k = \dfrac{3}{2} = 1.5$

Hence, scale factor of enlargement = 1.5

On a map drawn to a scale of 1 : 25000, a triangular plot LMN of land has the following measurements :

LM = 6 cm, MN = 8 cm and ∠LMN = 90°. Calculate :

(i) the actual lengths of MN and LN in kilometers,

(ii) the actual area of the plot in sq. km.

Answer

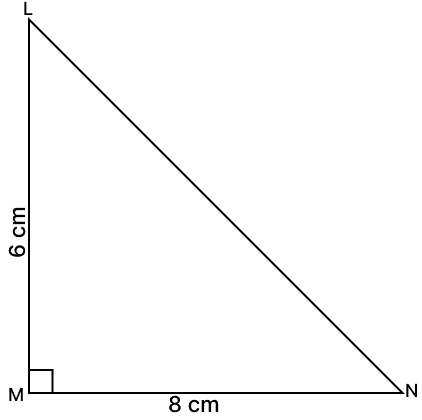
(i) Since, the model of the triangular plot is made to the scale of 1 : 25000.

k = $\dfrac{1}{25000}$.

Length of MN in model = k × (Actual length of MN)

8 = $\dfrac{1}{25000}$ × Actual length of MN

Actual length of MN = 8 × 25000

= 200000 cm.

= $\dfrac{200000}{100000}$ km.

= 2 km.

Length of LM in model = k × (Actual length of LM)

6 = $\dfrac{1}{25000}$ × Actual length of LM

Actual length of LM = 6 × 25000

= 150000 cm.

= $\dfrac{150000}{100000}$ km.

= 1.5 km.

Using pythagoras theorem:

LN² = LM² + MN²

LN² = (1.5)² + 2²

LN² = 2.25 + 4

LN² = 6.25

LN = $\sqrt{6.25}$

LN = 2.5 km

Hence, MN = 2 km and LN = 2.5 km.

(ii) We know that,

Area of triangle = $\dfrac{1}{2}$ × Base × Height

= $\dfrac{1}{2}$ × LM × MN

= $\dfrac{1}{2}$ × 1.5 × 2

= 1.5 km².

Hence, actual area of the plot = 1.5 sq.km.

The scale of a map is 1 : 200000. A plot of land of area 10 km² is to be represented on the map. Find :

(i) the length in km on the ground, represented by 1 cm on the map,

(ii) the area in km² that can be represented by 3 cm² on the map,

(iii) the area on the map representing the plot of land.

Answer

(i) Since, the scale of map is 1 : 200000.

1 cm on map = 200000 cm on ground

200000 cm = $\dfrac{200000}{100000}$ = 2km

Hence, 1 cm on map represents 2 km on ground.

(ii) Given,

Area of plot on map = 3 cm²

Area of plot on map = k² × Area of actual plot

3 = $\Big(\dfrac{1}{200000}\Big)^2$ × Area of actual plot

Area of actual plot = 3 × 200000 × 200000 cm²

= $\dfrac{3 \times 200000 \times 200000}{100000 \times 100000}$ km²

= 12 km^2.

Hence, required area = 12 km².

(iii) Area of plot on map = k² × Area of actual plot

Area of plot on map = $\Big(\dfrac{1}{200000}\Big)^2 \times 10$ km²

Area of plot on map = $\dfrac{10 \times 100000 \times 100000}{200000 \times 200000}$ cm²

= 2.5 cm².

Hence, area on the map representing the plot of land is 2.5 cm².

On a map drawn to a scale of 1 : 20000, a rectangular plot of land ABCD has AB = 32 cm and BC = 24 cm. Calculate :

(i) the diagonal distance of the plot in km,

(ii) the area of the plot in sq. km.

Answer

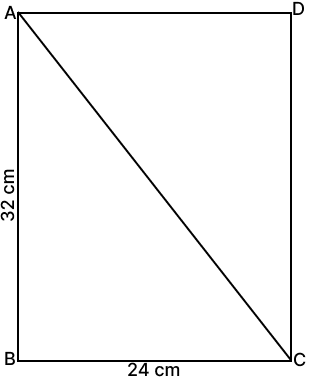
(i) By pythagoras theorem,

⇒ AC² = AB² + BC²

⇒ AC² = 32² + 24²

⇒ AC² = 1024 + 576

⇒ AC² = 1600

⇒ AC = $\sqrt{1600}$ = 40 cm.

Given,

Scale of map = $\dfrac{1}{20000}$

Length of diagonal distance in map = k × Actual length of diagonal of plot

40 = $\dfrac{1}{20000}$ × Actual length of diagonal of plot

Actual length of diagonal of plot = 40 × 20000 = 800000 cm

= $\dfrac{800000}{100000}$ = 8 km.

Hence, diagonal distance of plot = 8 km.

(ii) Area of plot on map = AB × BC = 24 × 32 = 768 cm²

Area of plot on map = k² × Area of actual plot

768 = $\Big(\dfrac{1}{20000}\Big)^2$ × Area of actual plot

Area of actual plot = 768 × 20000 × 20000 cm²

= $\dfrac{768 \times 20000 \times 20000}{100000 \times 100000}$ km²

= 30.72 km²

Hence, area of plot = 30.72 km².

The dimensions of the model of a multistorey building are 1 m × 60 cm × 1.25 m. If the model is drawn to a scale 1 : 60, find the actual dimensions of the building in meters. Find:

(i) the floor area of a room of the building, whose area in the model is 250 cm²,

(ii) the volume of the room in the model, whose actual volume is 648 cubic metres.

Answer

(i) Given,

Scale factor (k) = 1 : 60 = $\dfrac{1}{60}$

Dimensions of model = l × b × h = 1 m × 60 cm × 1.25 m.

= 1 m × 0.60 m × 1.25 m.

We know that,

Model dimensions = k × Actual dimension

$\text{Actual length} = \dfrac{\text{ Model length}}{k} \\[1em] = \dfrac{1}{\dfrac{1}{60}} \\[1em] = 60 \text{ m}. \\[1em] \text{Actual breadth} = \dfrac{\text{ Model breadth}}{k} \\[1em] = \dfrac{0.60}{\dfrac{1}{60}} \\[1em] = 0.60 \times 60\\[1em] = 36 \text{ m}. \\[1em] \text{Actual height} = \dfrac{\text{ Model height}}{k} \\[1em] = \dfrac{1.25}{\dfrac{1}{60}} \\[1em] = 1.25 \times 60 \\[1em] = 75 \text{ m}.$

Actual dimensions (in meters) = 60 m × 36 m × 75 m.

By formula,

Floor area of model room = k² × Floor area of building room

250 = $\dfrac{1}{60} \times \dfrac{1}{60}$ × Floor area of building room

Floor area of building room = 60 × 60 × 250 cm²

= 900000 cm²

= $\dfrac{900000}{10000}$ m².

= 90 m².

Hence, length = 60m, breadth = 36 m, height = 75m, floor area of a room of the building = 90 m².

(ii) By formula,

Volume of a room of model = k³ × Volume of a room of building

= $\dfrac{1}{60} \times \dfrac{1}{60} \times \dfrac{1}{60} \times 648$

= $\dfrac{1}{60} \times \dfrac{1}{60} \times \dfrac{1}{60} \times 648$ m³

= 0.003 x 100 x 100 x 100 cm³

= 3000 cm³.

Hence, volume of a room in model = 3000 cm³.

A model of a ship is made to a scale of 1 : 250. Find :

(i) the length of the ship, if the length of its model is 1.2 m.

(ii) the area of the deck of the ship, if the area of the deck of its model is 1.6 m².

(iii) the volume of its model, when the volume of the ship is 1 cubic kilometer.

Answer

(i) Since, the model of the ship is made to the scale of 1 : 250.

∴ K = $\dfrac{1}{250}$.

Length of model = k × (Actual length of the ship)

1.2 = $\dfrac{1}{250}$ × Actual length of the ship

Actual length of the ship = 1.2 × 250 = 300 m.

Hence, the length of the ship is 300 m.

(ii) Area of the deck of the model = k² × (Area of the deck of the ship)

1.6 = $\Big(\dfrac{1}{250}\Big)^2$ x Area of the deck of the ship

1.6 = $\dfrac{1}{62500}$ x Area of the deck of the ship

Area of the deck of the ship = 62500 x 1.6 = 100000 m²

Hence, the area of the deck of the ship is 100000 m².

(iii) Given,

Volume of ship = 1 km³ = (1000)³ m³

Let the volume of the model be x.

Volume of the model = k³ × (Volume of the ship)

⇒ x = $\Big(\dfrac{1}{250}\Big)^3$ × 1000³

⇒ x = $\dfrac{1000 \times 1000 \times 1000}{250 \times 250 \times 250}$

⇒ x = 4 × 4 × 4

⇒ x = 64 m³.

Hence, the volume of the model of the ship is 64 m³.

A model of a ship is made to a scale of 1 : 200.

(i) If the length of the model is 4 m, calculate the length of the ship.

(ii) If the area of the deck of the ship is 160000 m², find the area of the deck of the model.

(iii) If the volume of the model is 200 litres, calculate the volume of the ship in cubic metres.

Answer

(i) Since, the model of the ship is made to the scale of 1 : 200.

∴ K = $\dfrac{1}{200}$.

Length of model ship = k × (Actual length of the ship)

4 = $\dfrac{1}{200}$ × Actual length of the ship

Actual length of the ship = 4 × 200 = 800 m.

Hence, the length of the ship is 800 m.

(ii) Area of the deck of the model = k² × (Area of the deck of the ship)

Let area of deck of model be x.

⇒ x = $\Big(\dfrac{1}{200}\Big)^2$ × (160000)

⇒ x = $\dfrac{1}{40000}$ × (160000)

⇒ x = 4 m².

Hence, the area of the deck of model is 4 m².

(iii) Given,

Volume of model = 200 litres = $\dfrac{200}{1000} \text{ m}^3 = 0.2 \text{ m}^3$

Volume of the model = k³ × (Volume of the ship)

0.2 = $\Big(\dfrac{1}{200}\Big)^3$ × Volume of the ship

0.2 = $\dfrac{1}{8000000}$ × Volume of the ship

Volume of the ship = 8000000 × 0.2 = 1600000.

Hence, the volume of the ship is 1600000 m³.

Figures which have exactly the same shape, but not necessarily the same ............... are said to be similar.

1. angle

2. side

3. size

4. volume

Answer

Figures are said to be similar if: their shapes are identical,but their sizes may differ.

Hence, option 3 is the correct option.

All regular polygons having the same number of ............... are similar.

1. sides

2. angles

3. diagonals

4. centric

Answer

All regular polygons with the same number of sides are always similar, regardless of their size.

Hence, option 1 is the correct option.

Two circles are always :

1. congruent

2. similar

3. enlarged

4. concentric

Answer

Two circles are always similar because similarity means that the figures have the same shape but possibly different sizes.

Hence, option 2 is the correct option.

In size transformation, the given figure is called an object and the resulting figure is called its :

1. pre-image

2. image

3. post-image

4. enlarge object

Answer

The resulting figure, after the transformation is applied, is called the image.

Hence, option 2 is the correct option.

Let k be the scale factor of a given size transformation. Then k < 1 as the transformation is a/an :

1. enlargement

2. identity transformation

3. reduction

4. preserved

Answer

If the transformation is a reduction, the image is smaller than the object, meaning the scale factor k is between 0 and 1: 0 < k < 1.

Hence, option 3 is the correct option.

Each side of the resulting figure = ............... times the corresponding side of the given figure, where k is the scale factor.

1. k²

2. k

3. k³

4. 2k

Answer

The length of any side in the resulting figure (the image) is equal to the length of the corresponding side in the given figure (the object) multiplied by the scale factor k.

Hence, option 2 is the correct option.

The transformation is a/an ..............., if k = 1, where k is the scale factor of a given size transformation.

1. identity transformation

2. reduction

3. enlargement

4. map

Answer

If k = 1, the resulting figure (image) is congruent to the original figure (object), meaning it has the same size and the same shape. This specific transformation is called an identity transformation because it maps the object onto itself.

Hence, option 1 is the correct option.

In case of solids, we have volume of the resulting figure = ............... × (volume of the given figure), where k is the scale factor.

1. k

2. k²

3. k³

4. 3k

Answer

Volume of the resulting figure = k³ × (the volume of given figure)

Hence, option 3 is the correct option.

If scale factor, k = $\dfrac{1}{p}$, then area of the model = ............... × (area of the actual figure).

1. k²

2. k

3. k³

4. $\dfrac{1}{p}$

Answer

We know that,

If scale factor = k, then :

Area of model = k² × (Area of actual figure)

Hence, option 1 is the correct option.

Let the map of a plane figure be drawn to the scale 1 : p. Then scale factor, k = ..............., length in the map = k × (Actual length).

1. $\dfrac{p}{1}$

2. $\dfrac{1}{p}$

3. $\dfrac{1}{k}$

4. k

Answer

Given,

Scale = 1 : p = $\dfrac{1}{p}$.

Hence, option 2 is the correct option.

Assertion (A) : Two circles are always similar.

Reason (R) : Similar shapes have same shape and size.

1. A is true, R is false

2. A is false, R is true

3. Both A and R are true

4. Both A and R are false

Answer

Two circles are always similar. This is True. Similarity means having the same shape but not necessarily the same size. All circles have the same characteristic shape.

Thus, A is true, R is false.

Hence, option 1 is the correct option.

Assertion (A) : In a size transformation, if the scale factor k is greater than 1 then it is a reduction.

Reason (R) : Size transformation is a process in which a given figure is reduced by a certain scale factor.

1. A is true, R is false

2. A is false, R is true

3. Both A and R are true

4. Both A and R are false

Answer

If k is greater than 1, the resulting image is larger than the object, which is an enlargement.

Assertion is false.

A size transformation (or dilation) is a general process that can result in an enlargement (k > 1), or reduction (0 < k < 1), or an identity transformation (k = 1).

Reason is false.

Both A and R are false

Hence, option 4 is the correct option.