KnowledgeBoat Logo
|
OPEN IN APP

Chapter 14

Equation of A Straight Line

Class - 10 RS Aggarwal Mathematics Solutions

Exercise 14A

Question 1

Find the slope of the line passing through the points:

(i) A(–2, 1) and B(3, –4)

(ii) A(0, –3) and B(2, 1)

(iii) A(4, –9) and B(–2, –1)

(iv) A(2, 5) and B(–4, –4)

Answer

(i) A(-2, 1) and B(3, -4)

By formula,

Slope (m) = y2−y1x2−x1\dfrac{y_2 - y_1}{x_2 - x_1}

Substituting values we get,

⇒m=−4−13−(−2)=−53+2=−55=−1.\Rightarrow m = \dfrac{-4 - 1}{3 - (-2)} \\[1em] = \dfrac{-5}{3 + 2} \\[1em] = \dfrac{-5}{5} \\[1em] = -1.

Hence, slope is -1.

(ii) A(0, –3) and B(2, 1)

By formula,

Slope (m) = y2−y1x2−x1\dfrac{y_2 - y_1}{x_2 - x_1}

Substituting values we get,

⇒m=1−(−3)2−0=1+32=42=2.\Rightarrow m = \dfrac{1 - (-3)}{2 - 0} \\[1em] = \dfrac{1 + 3}{2} \\[1em] = \dfrac{4}{2} \\[1em] = 2.

Hence, slope is 2.

(iii) A(4, –9) and B(–2, –1)

By formula,

Slope (m) = y2−y1x2−x1\dfrac{y_2 - y_1}{x_2 - x_1}

Substituting values we get,

⇒m=−1−(−9)−2−4=−1+9−6=8−6=−43.\Rightarrow m = \dfrac{-1 - (-9)}{-2 - 4} \\[1em] = \dfrac{-1 + 9}{-6} \\[1em] = \dfrac{8}{-6} \\[1em] = -\dfrac{4}{3}.

Hence, slope is −43-\dfrac{4}{3}.

(iv) A(2, 5) and B(–4, –4)

By formula,

Slope (m) = y2−y1x2−x1\dfrac{y_2 - y_1}{x_2 - x_1}

Substituting values we get,

⇒m=−4−5−4−2=−9−6=32.\Rightarrow m = \dfrac{-4 - 5}{-4 - 2} \\[1em] = \dfrac{-9}{-6} \\[1em] = \dfrac{3}{2}.

Hence, slope is 32\dfrac{3}{2}.

Question 2

If the slope of the line joining P(k, 3) and Q(8, –6) is −34\dfrac{-3}{4}, find the value of k.

Answer

Given,

P(k, 3) and Q(8, –6)

Slope = −34\dfrac{-3}{4}

By formula,

Slope (m) = y2−y1x2−x1\dfrac{y_2 - y_1}{x_2 - x_1}

Substituting values we get,

⇒Slope of PQ=−6−38−k⇒−34=−6−38−k⇒−34=−98−k⇒3(8−k)=4(9)⇒24−3k=36⇒−3k=36−24⇒−3k=12⇒k=12−3⇒k=−4.\Rightarrow \text{Slope of PQ} = \dfrac{-6 - 3}{8 - k} \\[1em] \Rightarrow -\dfrac{3}{4} = \dfrac{-6 - 3}{8 - k} \\[1em] \Rightarrow -\dfrac{3}{4} = \dfrac{-9}{8 - k} \\[1em] \Rightarrow 3(8 - k) = 4(9) \\[1em] \Rightarrow 24 -3k = 36 \\[1em] \Rightarrow -3k = 36 - 24 \\[1em] \Rightarrow -3k = 12 \\[1em] \Rightarrow k = \dfrac{12}{-3} \\[1em] \Rightarrow k = -4.

Hence, k = -4.

Question 3

Without using the distance formula, prove that the points A(1, 4), B(3, –2) and C(–3, 16) are collinear.

Answer

To prove that the points A(1, 4), B(3, –2), and C(–3, 16) are collinear we must show that the slope between any pair of points is the same.

By formula,

Slope (m) = y2−y1x2−x1\dfrac{y_2 - y_1}{x_2 - x_1}

Substituting values we get,

⇒Slope of AB=−2−43−1=−62=−3.⇒Slope of BC=16−(−2)−3−3=16+2−6=18−6=−3.\Rightarrow \text{Slope of AB} = \dfrac{-2 - 4}{3 - 1} \\[1em] = \dfrac{-6}{2} \\[1em] = -3. \\[1em] \Rightarrow \text{Slope of BC} = \dfrac{16 -(-2)}{-3 - 3} \\[1em] = \dfrac{16 + 2}{-6} \\[1em] = \dfrac{18}{-6} \\[1em] = -3.

Slope of AB = Slope of BC

Hence, proved points A, B and C are collinear.

Question 4

Find the value of k such that the points P(k, 1), Q(2, –5) and R(k - 2, –3) are collinear.

Answer

Given,

Points P, Q and R are collinear.

Thus, the slope of PQ equal to the slope of QR.

By formula,

Slope (m) = y2−y1x2−x1\dfrac{y_2 - y_1}{x_2 - x_1}

Substituting values we get,

⇒Slope of PQ=−5−12−k=−62−k⇒Slope of QR=−3−(−5)(k−2)−2=−3+5k−4=2k−4.\Rightarrow \text{Slope of PQ} = \dfrac{-5 - 1}{2 - k} \\[1em] = \dfrac{-6}{2 - k} \\[1em] \Rightarrow \text{Slope of QR} = \dfrac{-3 -(-5)}{(k - 2) - 2} \\[1em] = \dfrac{-3 + 5}{k - 4} \\[1em] = \dfrac{2}{k - 4}.

Slope of PQ = Slope of QR

⇒−62−k=2k−4\Rightarrow \dfrac{-6}{2 - k} = \dfrac{2}{k - 4}

⇒ -6(k - 4) = 2(2 - k)

⇒ -6k + 24 = 4 - 2k

⇒ 24 - 4 = -2k + 6k

⇒ 20 = 4k

⇒ k = 204\dfrac{20}{4}

⇒ k = 5

Hence, k = 5.

Question 5

Find the equation of a line parallel to the x-axis and passing through the point (–3, 2).

Answer

We know that the equation of straight line parallel to x-axis is

y = a

Since the line passes through the point (-3,2), we get

a = 2

∴ Equation of the line

⇒ y = 2 or y - 2 = 0.

Hence, equation of the line is y = 2.

Question 6

Find the equation of a line parallel to the y-axis and passing through the point (–7, 5).

Answer

We know that the equation of straight line parallel to y-axis is x = a.

Since the line passes through the point (-7, 5), we get

a = -7

∴ Equation of the line

⇒ x = -7 or x + 7 = 0.

Hence, equation of the line is x + 7 = 0.

Question 7

Find the equation of a line whose inclination is 30° and whose y-intercept is –2.

Answer

Given,

θ = 30° and c = -2.

We know that,

m = tan θ = tan 30° = 13\dfrac{1}{\sqrt3}.

Substituting values of m and c in equation y = mx + c, we get :

⇒y=13x+(−2)⇒3y=x−23⇒3y−x+23=0.\Rightarrow y = \dfrac{1}{\sqrt3} x + (-2) \\[1em] \Rightarrow \sqrt3y = x - 2\sqrt{3} \\[1em] \Rightarrow \sqrt3y - x + 2\sqrt{3} = 0.

Hence, equation of the line is 3y−x+23\sqrt3y - x + 2\sqrt{3}.

Question 8

Find the equation of a line whose:

(i) Slope = 34\dfrac{3}{4} and y-intercept = –4

(ii) Gradient = 3\sqrt{3} and y-intercept = −23\dfrac{-2}{3}

Answer

(i) The equation of the straight line is given by, y = mx + c, we get where m is the slope and c is the y-intercept.

Given slope = 34\dfrac{3}{4} and y-intercept = -4. Substituting values in equation we get,

⇒ y = 34\dfrac{3}{4}x - 4.

⇒ y = 3x−164\dfrac{3x - 16}{4}

⇒ 4y = 3x - 16

⇒ 3x - 4y = 16.

Hence, equation of the line is 3x - 4y = 16.

(ii) The equation of straight line is given by y = mx + c, where m is the slope and c is the y-intercept.

Given slope = 3\sqrt{3} and y-intercept = −23\dfrac{-2}{3}.

Substituting values in equation we get,

⇒y=3x+(−23)⇒y=33x−23⇒3y=33x−2⇒33x−3y−2=0.\Rightarrow y = \sqrt{3}x + \Big(\dfrac{-2}{3}\Big) \\[1em] \Rightarrow y = \dfrac{3\sqrt{3}x -2}{3} \\[1em] \Rightarrow 3y = 3\sqrt{3}x - 2 \\[1em] \Rightarrow 3\sqrt{3}x -3y - 2 = 0.

Hence, equation of the line is 33x−3y−2=03\sqrt{3}x -3y - 2 = 0.

Question 9

Find the equation of a line which makes an angle of 60° with the positive direction of the x-axis and passes through the point P(0, –3).

Answer

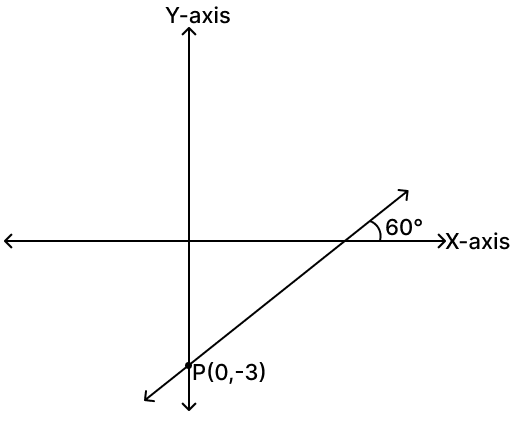
Find the equation of a line which makes an angle of 60° with the positive direction of the x-axis and passes through the point P(0, –3). Equation of a Straight line, RSA Mathematics Solutions ICSE Class 10.

m = tan θ = tan 60° = 3\sqrt3

By point-slope form,

Equation of line : y - y1 = m(x - x1)

Substituting values we get,

⇒y−(−3)=3(x−0)⇒y+3=3x⇒3x−y=3.\Rightarrow y - (-3) = \sqrt3(x - 0) \\[1em] \Rightarrow y + 3 = \sqrt3x \\[1em] \Rightarrow \sqrt3x - y = 3.

Hence, equation of the line is 3x−y=3\sqrt3x - y = 3.

Question 10

Find the equation of a line:

(i) Whose slope is 4 and which passes through the point (3, 7)

(ii) Whose slope is –3 and which passes through the point (–2, 3)

Answer

(i) By point-slope form,

Equation of line : y - y1 = m(x - x1)

Substituting values we get,

⇒ y - 7 = 4(x - 3)

⇒ y - 7 = 4x - 12

⇒ y = 4x - 12 + 7

⇒ y = 4x - 5

⇒ 4x - y = 5.

Hence, equation of the line is 4x - y = 5.

(ii) By point-slope form,

Equation of line : y - y1 = m(x - x1)

Substituting values we get,

⇒ y - 3 = -3(x - (-2))

⇒ y - 3 = -3(x + 2)

⇒ y - 3 = -3x - 6

⇒ y = -3x - 6 + 3

⇒ y = -3x - 3

⇒ 3x + y + 3 = 0

Hence, equation of the line is 3x + y + 3 = 0.

Question 11

Find the gradient and the y-intercept of each of the following lines:

(i) 5x – 10y = 3

(ii) x6+y9=1\dfrac{x}{6} + \dfrac{y}{9} = 1

(iii) x + 4 = 0

(iv) y = 6

Answer

(i) Given,

⇒ 5x – 10y = 3

Converting 5x – 10y = 3 in the form y = mx + c we get,

⇒ -10y = 3 - 5x

⇒ y = −310−5x−10-\dfrac{3}{10} - \dfrac{5x}{-10}

⇒ y = −310+x2-\dfrac{3}{10} + \dfrac{x}{2}

⇒ y = 12x−310\dfrac{1}{2}x - \dfrac{3}{10}

The equation of straight line is given by, y = mx + c, where m is the slope and c is the y-intercept.

Comparing, y = mx + c with y = 12x−310\dfrac{1}{2}x - \dfrac{3}{10}, we get:

m = slope = 12\dfrac{1}{2}

c = y-intercept = −310-\dfrac{3}{10}

Hence, slope = 12,y-intercept=−310\dfrac{1}{2}, \text{y-intercept} = -\dfrac{3}{10}.

(ii) Converting x6+y9=1\dfrac{x}{6} + \dfrac{y}{9} = 1 in the form y = mx + c we get,

⇒x6+y9=1⇒y9=1−x6⇒y=9(1−x6)⇒y=(9−9x6)⇒y=−3x2+9.\Rightarrow \dfrac{x}{6} + \dfrac{y}{9} = 1 \\[1em] \Rightarrow \dfrac{y}{9} = 1 - \dfrac{x}{6} \\[1em] \Rightarrow y = 9 \Big(1 - \dfrac{x}{6}\Big) \\[1em] \Rightarrow y = \Big(9 - \dfrac{9x}{6}\Big) \\[1em] \Rightarrow y = -\dfrac{3x}{2} + 9.

The equation of straight line is given by,

y = mx + c, where m is the slope and c is the y-intercept.

Comparing y = mx + c with y=−3x2+9y = -\dfrac{3x}{2} + 9, we get:

m = slope = −32-\dfrac{3}{2}

c = y-intercept = 9

Hence, slope = −32-\dfrac{3}{2}, y-intercept = 9.

(iii) Given,

x + 4 = 0

x = -4

This is a vertical line parallel to the y-axis, passing through the x-axis at x = -4.

We know that the inclination of a line parallel to y-axis is 90°.

∴ Slope of y-axis = tan 90° = infinity, which is not defined.

Since the line is parallel to the y-axis and passes through a negative x-value, it never crosses the y-axis. There is no y-intercept.

Hence, slope is not defined and line has no y-intercept.

(iv) Given,

y = 6

This is a horizontal line parallel to the x-axis, passing through the y-axis at y = 6.

We know that the inclination of a line parallel to x-axis is 0°.

∴ Slope of a line parallel to x-axis = tan 0° = 0.

y-intercept = 6

Hence, slope = 0 and y-intercept = 6.

Question 12

Find the gradient and the equation of the line passing through the points:

(i) A(–2, 1) and B(3, –4)

(ii) A(4, –2) and B(2, –3)

Answer

(i) Slope of AB = y2−y1x2−x1\dfrac{y_2 - y_1}{x_2 - x_1}

= −4−13−(−2)\dfrac{-4 - 1}{3 - (-2)}

= −55\dfrac{-5}{5}

= -1.

Equation : y - y1 = m(x - x1)

⇒ y - 1 = -1(x - (-2))

⇒ y - 1 = -1(x + 2)

⇒ y - 1 = -x - 2

⇒ x + y - 1 + 2 = 0

⇒ x + y + 1 = 0.

Hence, slope = -1, equation of AB is x + y + 1 = 0.

(ii) Slope of AB = y2−y1x2−x1\dfrac{y_2 - y_1}{x_2 - x_1}

= −3−(−2)2−4\dfrac{-3 - (-2)}{2 - 4}

= −1−2\dfrac{-1}{-2}

= 12\dfrac{1}{2}.

Equation : y - y1 = m(x - x1)

⇒ y - (-2) = 12\dfrac{1}{2} (x - 4)

⇒ 2(y + 2) = (x - 4)

⇒ 2y + 4 = x - 4

⇒ x - 2y - 4 - 4 = 0

⇒ x - 2y - 8 = 0.

Hence, slope = 12\dfrac{1}{2}, equation of AB is x - 2y - 8 = 0.

Question 13

A straight line passes through the points P(–1, 4) and Q(5, –2). It intersects x-axis and y-axis at the points A and B respectively and M is the mid-point of AB. Find :

(i) the equation of the line

(ii) the co-ordinates of A and B

(iii) the co-ordinates of M

Answer

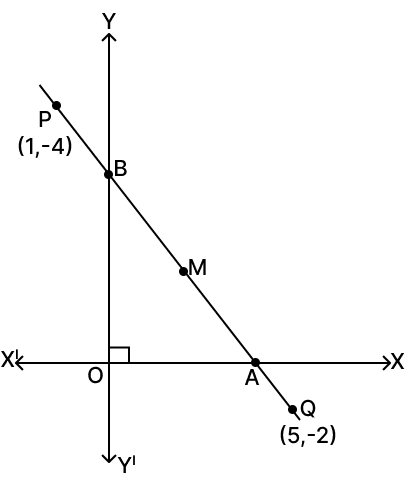
A straight line passes through the points P(–1, 4) and Q(5, –2). It intersects x-axis and y-axis at the points A and B respectively and M is the mid-point of AB. Find : Equation of a Straight line, RSA Mathematics Solutions ICSE Class 10.

(i) Given points, P(-1, 4) and Q(5, -2)

⇒ Slope of PQ =y2−y1x2−x1=−2−45−(−1)=−66=−1.\Rightarrow \text{ Slope of PQ } = \dfrac{y_2 - y_1}{x_2 - x_1} \\[1em] = \dfrac{-2 - 4}{5 - (-1)} \\[1em] = \dfrac{-6}{6} = -1.

By point-slope form,

Equation of the line PQ, y - y1 = m(x - x1)

⇒ y - 4 = -1[x - (-1)]

⇒ y - 4 = -1[x + 1]

⇒ y - 4 = -x - 1

⇒ x + y = -1 + 4

⇒ x + y - 3 = 0.

Hence, equation of line is x + y - 3 = 0.

(ii) For point A (on x-axis), y = 0.

So, putting y = 0 in the equation of PQ, we have

⇒ x + 0 = 3

⇒ x = 3.

∴ A = (3, 0).

For point B (on y-axis), x = 0.

So, putting x = 0 in the equation of PQ, we have

⇒ 0 + y = 3

⇒ y = 3

∴ B = (0, 3).

Hence, co-ordinates of A = (3, 0) and B = (0, 3).

(iii) M is the mid-point of AB.

∴ M = (x1+x22,y1+y22)\Big(\dfrac{x_1 + x_2}{2}, \dfrac{y_1 + y_2}{2}\Big)

= (3+02,0+32)\Big(\dfrac{3 + 0}{2}, \dfrac{0 + 3}{2}\Big)

= (32,32)\Big(\dfrac{3}{2}, \dfrac{3}{2}\Big)

Hence, mid-point of AB = (32,32)\Big(\dfrac{3}{2}, \dfrac{3}{2}\Big).

Question 14

A(2, 3) and B(–2, 5) are two given points. Find :

(i) the gradient of AB

(ii) the equation of AB

(iii) the co-ordinates of the point, where AB intersects x-axis.

Answer

(i) Given points, A(2, 3) and B(–2, 5)

⇒ Slope of AB =y2−y1x2−x1=5−3−2−2=2−4=−12.\Rightarrow \text{ Slope of AB } = \dfrac{y_2 - y_1}{x_2 - x_1} \\[1em] = \dfrac{5 - 3}{-2 -2} \\[1em] = \dfrac{2}{-4} = -\dfrac{1}{2}.

Hence, slope = −12-\dfrac{1}{2}.

(ii) By point-slope form,

Equation of the line AB, y - y1 = m(x - x1)

⇒ y - 3 = −12-\dfrac{1}{2}(x - 2)

⇒ 2(y - 3) = -1(x - 2)

⇒ 2y - 6 = -x + 2

⇒ x + 2y = 6 + 2

⇒ x + 2y = 8.

Hence, equation of line is x + 2y = 8.

(iii) The line intersects the x-axis when y = 0. Substituting y = 0 into the equation of the line, x + 2y = 8, we get :

⇒ x + 2(0) = 8

⇒ x = 8

Hence, coordinates of the point where AB intersects the x-axis are (8, 0).

Question 15

A straight line passes through the points A(2, –4) and B(5, –2). Find :

(i) the slope of the line AB

(ii) the equation of the line AB

(iii) the value of k, if AB passes through the point P(k + 3, k – 4)

Answer

(i) Given points, A(2, –4) and B(5, –2)

⇒ Slope of AB =y2−y1x2−x1=−2−(−4)5−2=23.\Rightarrow \text{ Slope of AB } = \dfrac{y_2 - y_1}{x_2 - x_1} \\[1em] = \dfrac{-2 - (-4)}{5 - 2} \\[1em] = \dfrac{2}{3}.

Hence, slope = 23\dfrac{2}{3}.

(ii) By point-slope form,

Equation of the line AB, y - y1 = m(x - x1)

⇒ y - (-4) = 23\dfrac{2}{3}(x - 2)

⇒ 3(y + 4) = 2(x - 2)

⇒ 3y + 12 = 2x - 4

⇒ 3y - 2x + 12 + 4 = 0

⇒ 3y - 2x + 16 = 0

Hence, equation of line is 3y - 2x + 16 = 0.

(iii) Since the line AB passes through the point P(k + 3, k - 4), the coordinates of P must satisfy the equation of the line, x - 2y - 10 = 0.

⇒ 3(k - 4) - 2(k + 3) + 16 = 0

⇒ 3k - 12 - 2k - 6 + 16 = 0

⇒ (3k - 2k) + (-12 - 6 + 16) = 0

⇒ k - 2 = 0

⇒ k = 2.

Hence, k = 2.

Question 16(i)

If A(3, 4), B(7, –2) and C(–2, –1) are the vertices of a ΔABC, write down the equation of the median through the vertex C.

Answer

Let median through C be CX.

We know that, the median, CX through C will bisect the line AB.

By Mid-point formula,

Mid-point = (x1+x22,y1+y22)\Big(\dfrac{x_1 + x_2}{2}, \dfrac{y_1 + y_2}{2}\Big)

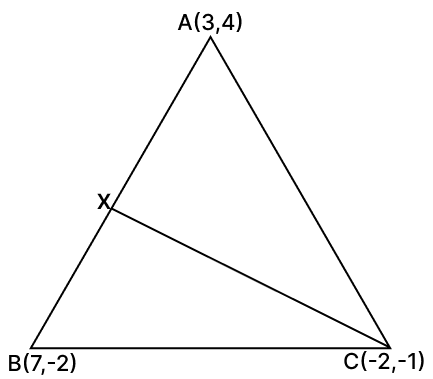
If A(3, 4), B(7, –2) and C(–2, –1) are the vertices of a ΔABC, write down the equation of the median through the vertex C. Equation of a Straight line, RSA Mathematics Solutions ICSE Class 10.

The co-ordinates of point X are

(3+72,4+(−2)2)=(102,22)\Big(\dfrac{3 + 7}{2}, \dfrac{4 + (-2)}{2}\Big) = \Big(\dfrac{10}{2}, \dfrac{2}{2}\Big) = (5, 1).

By formula,

Slope = y2−y1x2−x1\dfrac{y_2 - y_1}{x_2 - x_1}

Substituting values we get,

Slope of CX = 1−(−1)5−(−2)=27\dfrac{1 - (-1)}{5 - (-2)} = \dfrac{2}{7}.

Then, the required equation of the median CX is given by :

⇒ y - y1 = m(x - x1)

⇒ y - (-1) = 27\dfrac{2}{7}[x - (2)]

⇒ 7(y + 1) = 2(x + 2)

⇒ 7y + 7 = 2x + 4

⇒ 7y = 2x + 4 - 7

⇒ 2x - 7y - 3 = 0

Hence, equation of line is 2x - 7y - 3 = 0.

Question 16(ii)

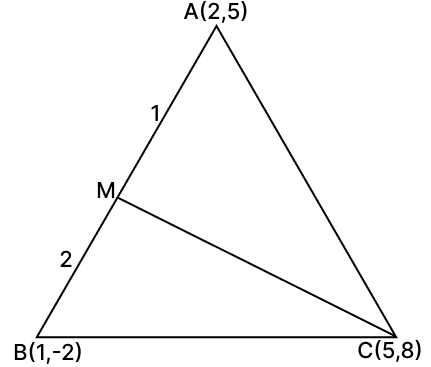
A(2, 5), B(–1, 2) and C(5, 8) are the vertices of a ΔABC, M is a point on AB such that AM : MB = 1 : 2. Find the co-ordinates of M. Hence, find the equation of the line passing through the points C and M.

Answer

Given AM : MB = 1 : 2. By section-formula the coordinates of M are,

(m1x2+m2x1m1+m2,m1y2+m2y1m1+m2)\Big(\dfrac{m_1x_2 + m_2x_1}{m_1 + m_2}, \dfrac{m_1y_2 + m_2y_1}{m_1 + m_2} \Big)

A(2, 5), B(–1, 2) and C(5, 8) are the vertices of a ΔABC, M is a point on AB such that AM : MB = 1 : 2. Find the co-ordinates of M. Hence, find the equation of the line passing through the points C and M. Equation of a Straight line, RSA Mathematics Solutions ICSE Class 10.

Substituting values we get,

M=(1(−1)+2(2)1+2,1(2)+2(5)1+2)=(−1+43,2+103)=(33,123)=(1,4).M = \Big(\dfrac{1(-1) + 2(2)}{1 + 2}, \dfrac{1(2) + 2(5)}{1 + 2} \Big) \\[1em] = \Big(\dfrac{-1 + 4}{3}, \dfrac{2 + 10}{3} \Big) \\[1em] = \Big(\dfrac{3}{3}, \dfrac{12}{3} \Big) \\[1em] = (1, 4).

Equation of line CM can be given by two-point formula i.e.,

y−y1=y2−y1x2−x1(x−x1)y - y_1 = \dfrac{y_2 - y_1}{x_2 - x_1}(x - x_1)

Substituting values we get,

⇒ y − 8 = 4−81−5\dfrac{4 - 8}{1 - 5}(x − 5)

⇒ y − 8 = −4−4\dfrac{-4}{-4}(x − 5)

⇒ y − 8 = 1(x − 5)

⇒ y − 8 = x − 5

⇒ x − y − 5 + 8 = 0

⇒ x − y + 3 = 0.

Hence, the equation of CM is x - y + 3 = 0 and the coordinates of M are (1, 4).

Question 17

The vertices of a ΔABC are A(2, –11), B(2, 13) and C(–12, 1). Find the equations of its sides.

Answer

Given,

Coordinates A(2, −11) and B(2, 13)

Slope = y2−y1x2−x1\dfrac{y_2 - y_1}{x_2 - x_1}

Substituting values we get,

Slope of AB = 13−(−11)2−2=13+110=240\dfrac{13 - (-11)}{2 - 2} = \dfrac{13 + 11}{0} =\dfrac{24}{0}

Slope is not defined.

The line AB is a vertical line parallel to the y-axis.

Points have the same x-coordinate, x = 2.

Equation of line AB: x = 2

Given, Points: B(2,13), C(−12,1)

By formula,

Slope = y2−y1x2−x1\dfrac{y_2 - y_1}{x_2 - x_1}

Substituting values we get,

Slope of BC = 1−(13)−12−2=−12−14=67\dfrac{1 - (13)}{-12 - 2} = \dfrac{-12}{-14} =\dfrac{6}{7}

By point-slope form,

Equation of the line BC, y - y1 = m(x - x1)

⇒ y - 13 = 67\dfrac{6}{7} (x - 2)

⇒ 7(y - 13) = 6(x - 2)

⇒ 7y - 91 = 6x - 12

⇒ 7y - 6x = -12 + 91

⇒ 7y - 6x = 79

Equation of BC: 7y - 6x = 79

Given, Points: C(−12,1), A(2,−11)

By formula,

Slope = y2−y1x2−x1\dfrac{y_2 - y_1}{x_2 - x_1}

Substituting values we get,

Slope of CA = −11−12−(−12)=−1214=−67\dfrac{-11 - 1}{2 - (-12)} = \dfrac{-12}{14} =-\dfrac{6}{7}

By point-slope form,

Equation of the line CA, y - y1 = m(x - x1)

⇒ y - 1 = −67-\dfrac{6}{7} (x + 12)

⇒ 7(y - 1) = -6(x + 12)

⇒ 7y - 7 = -6x - 72

⇒ 7y + 6x - 7 + 72 = 0

⇒ 7y + 6x + 65 = 0

Equation of the line CA: 7y + 6x + 65 = 0

Hence, the equation of AB, BC and CA are x = 2, 7y - 6x = 79, 7y + 6x + 65 = 0 respectively.

Question 18

ABC is a triangle whose vertices are A(1, –1), B(0, 4) and C(–6, 4). D is the mid-point of BC. Find the :

(i) co-ordinates of D

(ii) equation of the median AD

Answer

(i) By formula,

Mid-point (M) = = (x1+x22,y1+y22)\Big(\dfrac{x_1 + x_2}{2}, \dfrac{y_1 + y_2}{2}\Big)

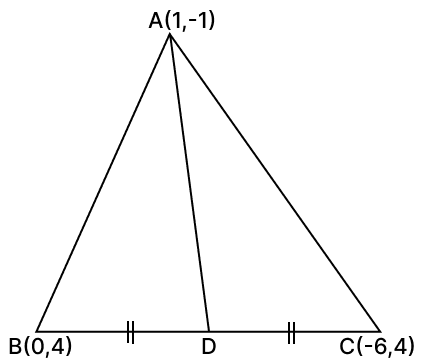
ABC is a triangle whose vertices are A(1, –1), B(0, 4) and C(–6, 4). D is the mid-point of BC. Find the : Equation of a Straight line, RSA Mathematics Solutions ICSE Class 10.

Given,

D is the mid-point of BC.

∴ Co-ordinates of D

=(0+(−6)2,4+42)=(−62,82)=(−3,4).= \Big(\dfrac{0 + (-6)}{2}, \dfrac{4 + 4}{2}\Big) \\[1em] = \Big(\dfrac{-6}{2}, \dfrac{8}{2}\Big) \\[1em] = (-3, 4).

Hence, coordinates of D = (-3, 4).

(ii) Slope = y2−y1x2−x1=4−(−1)(−3)−1=−54\dfrac{y_2 - y_1}{x_2 - x_1} = \dfrac{4 - (-1)}{(-3) - 1} = -\dfrac{5}{4}

Equation of a line :

y - y1 = m(x - x1)

Substituting values we get :

Equation of AD :

⇒ y - (-1) = −54-\dfrac{5}{4} (x - 1)

⇒ -4(y + 1) = 5(x - 1)

⇒ -4y - 4 = 5x - 5

⇒ 5x + 4y = -4 + 5

⇒ 5x + 4y - 1 = 0.

Hence, equation of median AD is 5x + 4y - 1 = 0.

Question 19

Find the equation of a line passing through the point (2, 3) and intersecting the line 2x – 3y = 6 on the y-axis.

Answer

On the y-axis,

x = 0.

Substitute x = 0 into 2x − 3y = 6:

⇒ 2(0) − 3y = 6

⇒ −3y = 6

⇒ y = −2

So, the line 2x − 3y = 6 meets the y-axis at (0, -2).

Calculating slope for points (2, 3) and (0, -2).

By formula,

Slope = y2−y1x2−x1\dfrac{y_2 - y_1}{x_2 - x_1}

m = 3−(−2)2−0=52\dfrac{3 -(-2)}{2 - 0} = \dfrac{5}{2}

By two-point form :

Equation of a line :

y - y1 = m(x - x1)

Substituting values we get :

⇒ y - (-2) = 52\dfrac{5}{2} (x - 0)

⇒ 2(y + 2) = 5x

⇒ 2y + 4 = 5x

⇒ 5x - 2y - 4 = 0

Hence, equation of line 5x - 2y = 4.

Question 20

Find the equation of a line with x-intercept = 5 and passing through the point (4, –3).

Answer

When x-intercept = 5; corresponding point on the x-axis = (5, 0).

By formula,

Slope = y2−y1x2−x1\dfrac{y_2 - y_1}{x_2 - x_1}

Slope of the line through (5, 0) and (4, -3) = −3−04−5=−3−1=3\dfrac{-3 - 0}{4 - 5} = \dfrac{-3}{-1} = 3

By point-slope form,

⇒ y - y1 = m(x - x1)

⇒ y - 0 = 3(x − 5)

⇒ y = 3x - 15

⇒ 3x - y = 15.

Hence, equation of line is 3x - y = 15.

Question 21

Find the equations of the diagonals of a rectangle whose sides are: x = –1, x = 4, y = –1 and y = 2.

Answer

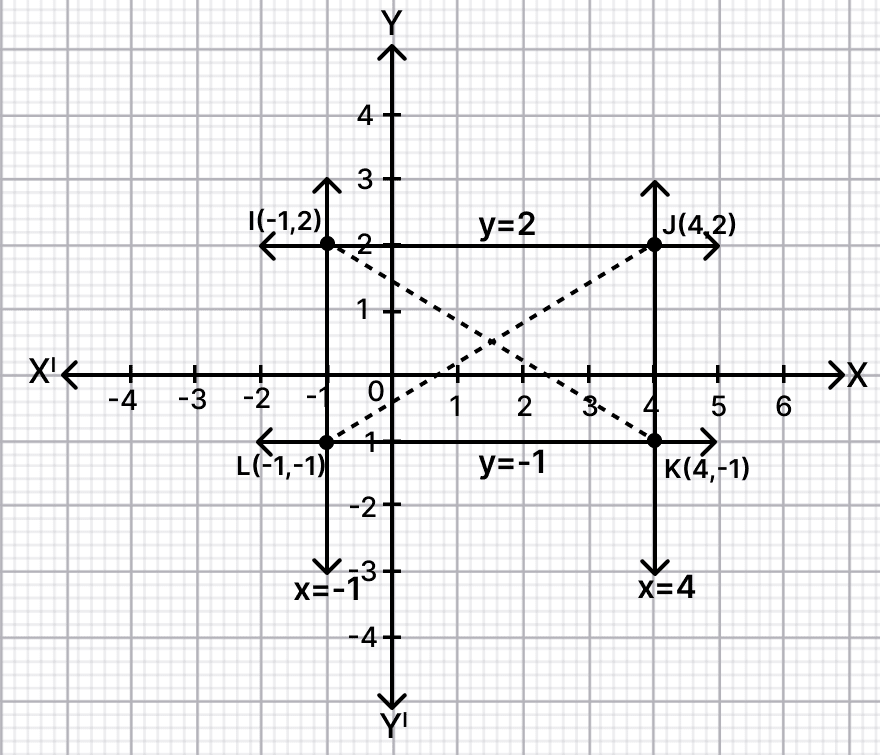
Find the equations of the diagonals of a rectangle whose sides are: x = –1, x = 4, y = –1 and y = 2. Equation of a Straight line, RSA Mathematics Solutions ICSE Class 10.

From figure,

The lines intersect at point I, J, K and L.

By two point formula,

Equation of line : y−y1=y2−y1x2−x1(x−x1)y - y_1 = \dfrac{y_2 - y_1}{x_2 - x_1}(x - x_1)

Equation of diagonal IK is

⇒y−2=−1−24−(−1)[x−(−1)]⇒y−2=−35[x+1]⇒5(y−2)=−3[x+1]⇒5y−10=−3x−3⇒5y+3x−10+3=0⇒3x+5y−7=0⇒3x+5y=7.\Rightarrow y - 2 = \dfrac{-1 - 2}{4 - (-1)}[x - (-1)] \\[1em] \Rightarrow y - 2 = -\dfrac{3}{5}[x + 1] \\[1em] \Rightarrow 5(y - 2) = -3[x + 1] \\[1em] \Rightarrow 5y - 10 = -3x -3 \\[1em] \Rightarrow 5y + 3x -10 + 3 = 0 \\[1em] \Rightarrow 3x + 5y - 7 = 0 \\[1em] \Rightarrow 3x + 5y = 7.

Equation of diagonal LJ is

⇒ y - (-1) = 2−(−1)4−(−1)\dfrac{2 - (-1)}{4 - (-1)} [x - (-1)]

⇒ y - (-1) = 35\dfrac{3}{5} [x - (-1)]

⇒ 5(y + 1) = 3[x + 1]

⇒ 5y + 5 = 3x + 3

⇒ 5y − 3x + 5 − 3 = 0

⇒ 5y - 3x + 2 = 0

⇒ 3x - 5y = 2.

Hence, equation of diagonals are 3x - 5y = 2 and 3x + 5y = 7.

Question 22

Find the equation of the line passing through the point (3, 2) and making positive equal intercepts on axes. Find the length of each intercept.

Answer

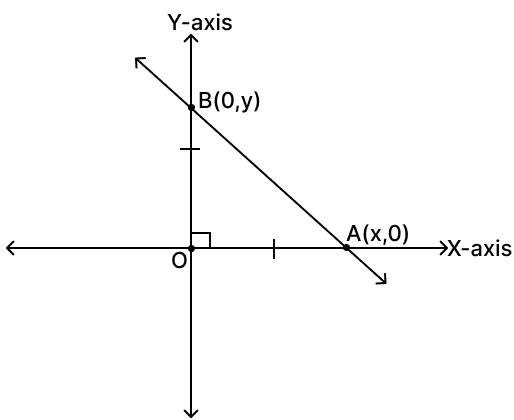
Find the equation of the line passing through the point (3, 2) and making positive equal intercepts on axes. Find the length of each intercept. Equation of a Straight line, RSA Mathematics Solutions ICSE Class 10.

Let the line containing the point (3, 2) passes through x-axis at A(x, 0) and y-axis at B(0, y).

Given, the intercepts made on both the axes are equal.

∴ x = y

Slope of the line

m=y2−y1x2−x1=0−yx−0=−yx=−xx=−1.m = \dfrac{y_2 - y_1}{x_2 - x_1} \\[1em] = \dfrac{0 - y}{x - 0} \\[1em] = \dfrac{-y}{x} \\[1em] = \dfrac{-x}{x} \\[1em] = -1.

Hence, the equation of the line will be

⇒ y - y1 = m(x - x1)

⇒ y - 2 = -1(x - 3)

⇒ y - 2 = -x + 3

⇒ y + x - 2 - 3 = 0

⇒ y = -x + 5.

Comparing above equation with y = mx + c, we get :

c = 5.

Thus, y-intercept = 5.

∴ x-intercept = 5.

Hence, equation of line is x + y = 5 and length of x and y intercept is 5 units.

Question 23

Find the equation of the line passing through the origin and the point of intersection of the lines 5x + 7y = 3 and 2x – 3y = 7.

Answer

⇒ 5x + 7y = 3 ….(1)

⇒ 2x - 3y = 7 ….(2)

Multiplying equation (1) by 3, we get :

⇒ 3(5x + 7y) = 3.3

⇒ 15x + 21y = 9 ….(3)

Multiplying equation (2) by 7, we get :

⇒ 7(2x - 3y) = 7.7

⇒ 14x - 21y = 49 ….(4)

Adding equations (3) and (4) we get,

⇒ 15x + 21y + 14x - 21y = 9 + 49

⇒ 29x = 58

⇒ x = 5829\dfrac{58}{29}

⇒ x = 2.

Substituting x = 2 in (1), we get :

⇒ 5(2) + 7y = 3

⇒ 10 + 7y = 3

⇒ 7y = 3 - 10

⇒ 7y = -7

⇒ y = −77\dfrac{-7}{7}

⇒ y = -1.

Hence, the point of intersection of lines is (2, -1).

The equation of the line joining (2, -1) and (0, 0) will be given by two-point form i.e.,

y−y1=y2−y1x2−x1(x−x1)y - y _1 = \dfrac{y_2 - y_1}{x_2 - x_1} (x - x_1)

Substituting values in above equation we get,

⇒ y - (-1) = 0−(−1)0−2\dfrac{0 - (-1)}{0 - 2} (x - 2)

⇒ y + 1 = 1−2\dfrac{1}{-2} (x - 2)

⇒ -2(y + 1) = (x - 2)

⇒ -2y - 2 = x - 2

⇒ x + 2y - 2 + 2 = 0

⇒ x + 2y = 0.

Hence, equation of line is x + 2y = 0.

Question 24

M and N are two points on the x-axis and y-axis respectively. P(3, 2) divides the line segment MN in the ratio 2 : 3. Find :

(i) the co-ordinates of M and N

(ii) slope of the line MN

Answer

M and N are two points on the x-axis and y-axis respectively. P(3, 2) divides the line segment MN in the ratio 2 : 3. Find : Equation of a Straight line, RSA Mathematics Solutions ICSE Class 10.

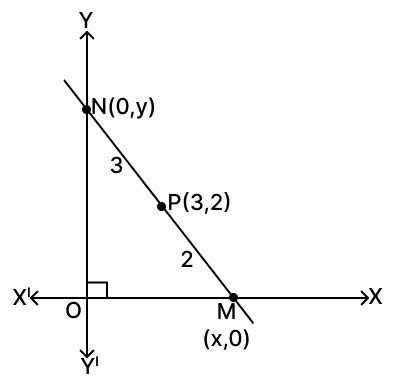
(i) Let the coordinates of M and N be (x, 0) and (0, y).

By section formula the coordinates of P are,

⇒(m1x2+m2x1m1+m2,m1y2+m2y1m1+m2)=(2(0)+3x2+3,2y+3(0)2+3)=(3x5,2y5)\Rightarrow \Big(\dfrac{m_1x_2 + m_2x_1}{m_1 + m_2}, \dfrac{m_1y_2 + m_2y_1}{m_1 + m_2}\Big) \\[1em] = \Big(\dfrac{2(0) + 3x}{2 + 3}, \dfrac{2y + 3(0)}{2 + 3}\Big) \\[1em] = \Big(\dfrac{3x}{5}, \dfrac{2y}{5}\Big)

Given, P(3, 2). Comparing two values of P we get,

⇒ 3 = 3x5\dfrac{3x}{5} and 2 = 2y5\dfrac{2y}{5}

⇒ 3x = 15 and 2y = 10

⇒ x = 5 and y = 5.

Hence, the coordinates of M and N are (5, 0) and (0, 5) respectively.

(ii) Slope of line MN can be given by y2−y1x2−x1\dfrac{y_2 - y_1}{x_2 - x_1}

Substituting value in above equation we get slope,

= 5−00−5\dfrac{5 - 0}{0 - 5}

= 5−5\dfrac{5}{-5}

= -1.

Hence, the slope of the line is -1.

Question 25

In what ratio does the line x – 5y + 15 = 0 divide the join of A(2, 1) and B(–3, 6)? Also, find the co-ordinates of their point of intersection.

Answer

Let P divides line AB in the ratio m : n.

By section formula,

⇒P(x,y)=(mx2+nx1m+n,my2+ny1m+n)=(m(−3)+n(2)m+n,m(6)+n(1)m+n)=(−3m+2nm+n,6m+nm+n).\Rightarrow P(x, y) = \Big(\dfrac{mx_2 + nx_1}{m + n}, \dfrac{my_2 + ny_1}{m + n}\Big) \\[1em] = \Big(\dfrac{m(-3) + n(2)}{m + n}, \dfrac{m(6) + n(1)}{m + n}\Big) \\[1em] = \Big(\dfrac{-3m + 2n}{m + n}, \dfrac{6m + n}{m + n}\Big).

Since, point P lies on line x - 5y + 15 = 0, substituting values we get :

⇒−3m+2nm+n−5(6m+nm+n)+15=0⇒−3m+2n−5(6m+n)+15(m+n)(m+n)=0⇒−3m+2n−30m−5n+15m+15n=0⇒−18m+12n=0⇒6(−3m+2n)=0⇒−3m+2n=0⇒2n=3m⇒mn=23.\Rightarrow \dfrac{-3m + 2n}{m + n} - 5 \Big(\dfrac{6m + n}{m + n}\Big) + 15 = 0 \\[1em] \Rightarrow \dfrac{-3m + 2n - 5(6m + n) + 15(m + n)}{(m + n)} = 0 \\[1em] \Rightarrow -3m + 2n - 30m - 5n + 15m + 15n = 0 \\[1em] \Rightarrow -18m + 12n = 0 \\[1em] \Rightarrow 6(-3m + 2n) = 0 \\[1em] \Rightarrow -3m + 2n = 0 \\[1em] \Rightarrow 2n = 3m \\[1em] \Rightarrow \dfrac{m}{n} = \dfrac{2}{3}.

By section formula,

⇒(x,y)=(mx2+nx1m+n,my2+ny1m+n)⇒(x,y)=(2(−3)+3(2)2+3,2(6)+3(1)2+3)⇒(x,y)=(−6+65,12+35)⇒(x,y)=0,155⇒(x,y)=(0,3).\Rightarrow (x, y) = \Big(\dfrac{mx_2 + nx_1}{m + n}, \dfrac{my_2 + ny_1}{m + n}\Big) \\[1em] \Rightarrow (x, y) = \Big(\dfrac{2(-3) + 3(2)}{2 + 3}, \dfrac{2(6) + 3(1)}{2 + 3}\Big) \\[1em] \Rightarrow (x, y) = \Big(\dfrac{-6 + 6}{5}, \dfrac{12 + 3}{5}\Big) \\[1em] \Rightarrow (x, y) = 0, \dfrac{15}{5} \\[1em] \Rightarrow (x, y) = (0, 3).

Hence, the line x – 5y + 15 = 0 divides AB in the ratio 2 : 3 and the co-ordinates of their point of intersection are (0, 3).

Question 26

Find the equations of the medians of ΔABC whose vertices are A(–1, 2), B(2, 1) and C(0, 4). Hence, find the co-ordinates of the centroid of ΔABC.

Answer

By using Midpoint formula,

(x, y) = (x1+x22,y1+y22)\Big(\dfrac{x_1 + x_2}{2}, \dfrac{y_1 + y_2}{2}\Big)

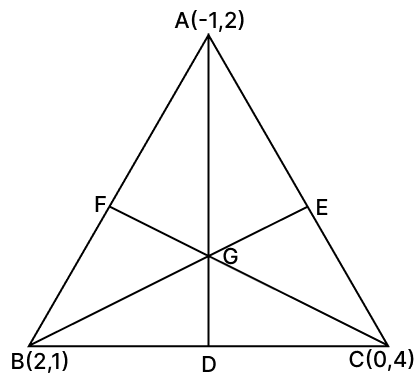
Find the equations of the medians of ΔABC whose vertices are A(–1, 2), B(2, 1) and C(0, 4). Hence, find the co-ordinates of the centroid of ΔABC. Equation of a Straight line, RSA Mathematics Solutions ICSE Class 10.

D (Midpoint of BC): B(2, 1)and C(0, 4)

D = (2+02,1+42)=(1,52)\Big(\dfrac{2 + 0}{2}, \dfrac{1 + 4}{2}\Big) = \Big(1, \dfrac{5}{2})

E (Midpoint of AC): A(-1, 2) and C(0, 4)

E = (−1+02,2+42)=(−12,3)\Big(\dfrac{-1 + 0}{2}, \dfrac{2 + 4}{2}\Big) = \Big(-\dfrac{1}{2}, 3\Big)

F (Midpoint of AB): A(-1, 2) and B(2, 1)

F = (−1+22,2+12)=(12,32)\Big(\dfrac{-1 + 2}{2}, \dfrac{2 + 1}{2}\Big) = \Big(\dfrac{1}{2}, \dfrac{3}{2}\Big)

Median AD through A(-1, 2) and D(1,52)D\Big(1, \dfrac{5}{2}\Big)

By slope formula:

m=y2−y1x2−x1m = \dfrac{y_2 - y_1}{x_2 - x_1}

Substitute values we get:

mAD=52−21−(−1)=122=14m_{AD} = \dfrac{\dfrac{5}{2} - 2}{1 - (-1)} = \dfrac{\dfrac{1}{2}}{2} = \dfrac{1}{4}

The equation of the line will be given by two-point form i.e.,

y - y1 = m(x - x1)

Substituting values in above equation we get,

⇒ y - 2 = 14\dfrac{1}{4} (x + 4)

⇒ 4(y - 2) = (x + 1)

⇒ 4y - 8 = x + 1

⇒ x - 4y + 9 = 0

Median BE through B(2, 1) and E(−12,3)E\Big(-\dfrac{1}{2}, 3\Big)

mBE=3−1−12−2=2−52=−45m_{BE} = \dfrac{3 - 1}{-\dfrac{1}{2} - 2} = \dfrac{2}{-\dfrac{5}{2}} = -\dfrac{4}{5}

The equation of the line will be given by two-point form i.e.,

⇒ y - 1 = −45-\dfrac{4}{5} (x - 2)

⇒ 5(y - 1) = 4(x - 2)

⇒ 5y - 5 = 4x - 8

⇒ 4x + 5y - 13 = 0

Median CF through C(0, 4) and F(12,32)F\Big(\dfrac{1}{2}, \dfrac{3}{2}\Big)

mCF=32−412−0=−5212=−5m_{CF} = \dfrac{\dfrac{3}{2} - 4}{\dfrac{1}{2} - 0} = \dfrac{-\dfrac{5}{2}}{\dfrac{1}{2}} = -5

Since C(0, 4) is the y-intercept, we use y = mx + c:

⇒ y = -5x + 4

⇒ 5x + y - 4 = 0

By using centroid formula,

G=(x1+x2+x33,y1+y2+y33)G = \Big(\dfrac{x_1 + x_2 + x_3}{3}, \dfrac{y_1 + y_2 + y_3}{3}\Big)

Using A(-1, 2), B(2, 1), and C(0, 4):

⇒G=(−1+2+03,2+1+43)=(−1+2+03,2+1+43)=(13,73).\Rightarrow G = \Big(\dfrac{-1 + 2 + 0}{3}, \dfrac{2 + 1 + 4}{3}\Big) \\[1em] = \Big(\dfrac{-1 + 2 + 0}{3}, \dfrac{2 + 1 + 4}{3}\Big) \\[1em] = \Big(\dfrac{1}{3}, \dfrac{7}{3}\Big).

Hence, equations of medians are x - 4y + 9 = 0, 4x + 5y - 13 = 0 and 5x + y - 4 = 0, coordinates of centroid (13,73)\Big(\dfrac{1}{3}, \dfrac{7}{3}\Big).

Question 27

Three vertices of a parallelogram ABCD taken in order are A(3, 6), B(5, 10) and C(3, 2). Find :

(i) the co-ordinates of the fourth vertex D

(ii) length of diagonal BD

(iii) equation of side AB of the parallelogram ABCD

Answer

The parallelogram ABCD is shown in the figure below:

(i) We know that the diagonals of a parallelogram bisect each other. Let (x, y) be the coordinates of D.

Mid-point of diagonal AC = x1+x22,y1+y22=3+32,6+22=(3,4)\dfrac{x_1 + x_2}{2}, \dfrac{y_1 + y_2}{2} = \dfrac{3 + 3}{2}, \dfrac{6 + 2}{2} = (3, 4)

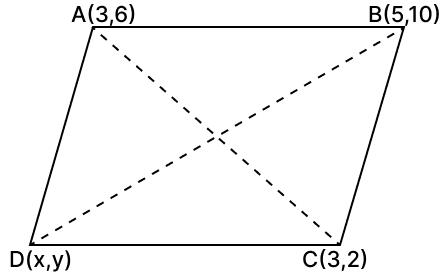
Three vertices of a parallelogram ABCD taken in order are A(3, 6), B(5, 10) and C(3, 2). Find : Equation of a Straight line, RSA Mathematics Solutions ICSE Class 10.

Mid-point of diagonal BD = 5+x2,10+y2\dfrac{5 + x}{2}, \dfrac{10 + y}{2}

These two should be same. On equating we get,

5+x2=3,10+y2=4\dfrac{5 + x}{2} = 3, \dfrac{10 + y}{2} = 4

⇒ 5 + x = 6 and 10 + y = 8

⇒ x = 6 − 5 and y = 8 − 10

⇒ x = 1 and y = −2.

Hence, coordinates of D are (1, -2).

(ii) By distance formula the distance between B(5, 10) and D(1, -2) is given by (x2−x1)2+(y2−y1)2\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}

Substituting values we get BD,

=(1−5)2+(−2−10)2=(−4)2+(−12)2=16+144=160=410= \sqrt{(1 - 5)^2 + (-2 - 10)^2} \\[1em] = \sqrt{(-4)^2 + (-12)^2} \\[1em] = \sqrt{16 + 144} \\[1em] = \sqrt{160} \\[1em] = 4\sqrt{10}

Hence, the length of diagonal BD is 4104\sqrt{10} units.

(iii) Equation of side AB can be given by two point formula i.e.,

y−y1=y2−y1x2−x1(x−x1)y - y_1 = \dfrac{y_2 - y_1}{x_2 - x_1} (x - x_1)

Substituting values we get,

⇒ y − 6 = 10−65−3\dfrac{10 - 6}{5 - 3} (x - 3)

⇒ y − 6 = 42\dfrac{4}{2} (x - 3)

⇒ (y − 6) = 2(x - 3)

⇒ (y − 6) = 2x - 6

⇒ 2x - y -6 + 6 = 0

⇒ 2x - y = 0

Hence, equation of the line is 2x - y = 0.

Question 28

In the given figure, ABC is a triangle and BC is parallel to the y-axis. AB and AC intersect the y-axis at P and Q respectively. Find :

(i) the co-ordinates of A

(ii) the length of AB and AC

(iii) the ratio in which Q divides AC

(iv) the equation of the line AC

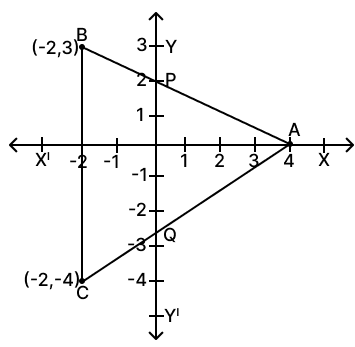
In the given figure, ABC is a triangle and BC is parallel to the y-axis. AB and AC intersect the y-axis at P and Q respectively. Find. Equation of a Straight line, RSA Mathematics Solutions ICSE Class 10.

Answer

(i) From figure,

The co-ordinates of A = (4, 0).

(ii) By distance formula,

D = (x2−x1)2+(y2−y1)2\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}

Substituting values we get,

AB=(−2−4)2+(3−0)2=(−6)2+(3)2=36+9=45=35.AC=(−2−4)2+(−4−0)2=(−6)2+(−4)2=36+16=52=213.AB = \sqrt{(-2 - 4)^2 + (3 - 0)^2} \\[1em] = \sqrt{(-6)^2 + (3)^2} \\[1em] = \sqrt{36 + 9} \\[1em] = \sqrt{45} \\[1em] = 3\sqrt{5}. \\[1em] AC = \sqrt{(-2 - 4)^2 + (-4 - 0)^2} \\[1em] = \sqrt{(-6)^2 + (-4)^2} \\[1em] = \sqrt{36 + 16} \\[1em] = \sqrt{52} \\[1em] = 2\sqrt{13}.

Hence, length of AB=35 and AC=213AB = 3\sqrt{5}\text{ and } AC = 2\sqrt{13}.

(iii) From figure,

Q lies on y-axis.

∴ x co-ordinate of Q = 0.

Let co-ordinate of Q are (0, a).

Let ratio in which Q divides AC be k : 1.

By section-formula,

Q=(m1x2+m2x1m1+m2,m1y2+m2y1m1+m2)Q = \Big(\dfrac{m_1x_2 + m_2x_1}{m_1 + m_2}, \dfrac{m_1y_2 + m_2y_1}{m_1 + m_2}\Big)

Comparing x-coordinate we get :

⇒0=k×−2+1×4k+1⇒0=−2k+4⇒2k=4⇒k=2.\Rightarrow 0 = \dfrac{k \times -2 + 1 \times 4}{k + 1} \\[1em] \Rightarrow 0 = -2k + 4 \\[1em] \Rightarrow 2k = 4 \\[1em] \Rightarrow k = 2.

k : 1 = 2 : 1.

Hence, Q divides AC in the ratio 2 : 1.

(iv) By formula,

Slope = y2−y1x2−x1\dfrac{y_2 - y_1}{x_2 - x_1}

Slope of AC = −4−0−2−4=−4−6=23\dfrac{-4 - 0}{-2 - 4} = \dfrac{-4}{-6} = \dfrac{2}{3}

By point-slope form,

Equation of AC is :

⇒ y - y1 = m (x - x1)

⇒ y - 0 = 23\dfrac{2}{3} (x - 4)

⇒ 3y = 2x - 8

⇒ 2x - 3y = 8

Hence, equation of AC is 2x - 3y = 8.

Exercise 14B

Question 1

If A(2, –3), B(–5, 1), C(7, –1) and D(0, k) be four points such that AB is parallel to CD, find the value of k.

Answer

AB is parallel to line segment CD means they must have the same gradient

By using slope formula,

m = y2−y1x2−x1\dfrac{y_2 - y_1}{x_2 - x_1}

Given, points A(2, –3), B(–5, 1)

Substituting values we get,

mAB=1−(−3)−5−2=1+3−7=−47m_{AB} = \dfrac{1 - (-3)}{-5 - 2} = \dfrac{1 + 3}{-7} = -\dfrac{4}{7}

Given, points C(7, –1) and D(0, k)

Substituting values we get,

mCD=k−(−1)0−7=k+1−7m_{CD} = \dfrac{k - (-1)}{0 - 7} = \dfrac{k + 1}{-7}

Equate the Gradients:

⇒−47=k+1−7⇒−47×−7=k+1⇒k+1=4⇒k=4−1⇒k=3.\Rightarrow -\dfrac{4}{7} = \dfrac{k + 1}{-7} \\[1em] \Rightarrow -\dfrac{4}{7} \times -7 = k + 1 \\[1em] \Rightarrow k + 1 = 4 \\[1em] \Rightarrow k = 4 - 1 \\[1em] \Rightarrow k = 3.

Hence, value of k = 3.

Question 2

Show that the lines x + 2y – 5 = 0 and 2x + 4y + 9 = 0 are parallel.

Answer

Given,

⇒ x + 2y – 5 = 0

Converting x + 2y - 5 = 0 in the form y = mx + c we get,

⇒ 2y = -x + 5

⇒ y = −x2+52\dfrac{-x}{2} + \dfrac{5}{2}

The equation of straight line is given by,

y = mx + c, where m is the slope and c is the y-intercept.

Comparing y = mx + c with y = −x2+52\dfrac{-x}{2} + \dfrac{5}{2}, we get:

⇒ m1 = −12-\dfrac{1}{2}

Given,

⇒ 2x + 4y + 9 = 0

Converting 2x + 4y + 9 = 0 in the form y = mx + c we get,

⇒ 4y = -2x - 9

⇒ y = −2x4−94\dfrac{-2x}{4} - \dfrac{9}{4}

⇒ y = −1x2−94\dfrac{-1x}{2} - \dfrac{9}{4}

Comparing y = mx + c with y = −1x2−94\dfrac{-1x}{2} - \dfrac{9}{4}, we get:

⇒ m2 = −12-\dfrac{1}{2}

Since the gradient of the first line is equal to the gradient of the second line.

The lines are parallel to each other.

Hence, proved that lines are parallel.

Question 3

Find the value of k for which the lines kx + 2y + 3 = 0 and 8x + ky – 1 = 0 are parallel.

Answer

Since, the lines are parallel they have same gradient.

Given, kx + 2y + 3 = 0

Converting kx + 2y + 3 = 0 in the form y = mx + c, we get :

⇒ 2y = -kx - 3

⇒ y = −k2x−32-\dfrac{k}{2}x - \dfrac{3}{2}

The equation of straight line is given by,

y = mx + c, where m is the slope and c is the y-intercept.

Comparing y = mx + c with y = −k2x−32-\dfrac{k}{2}x - \dfrac{3}{2}, we get :

⇒ m1 = −k2-\dfrac{k}{2}

Given,

8x + ky - 1 = 0

Converting 8x + ky - 1 = 0 in the form y = mx + c we get,

⇒ ky = -8x + 1

⇒ y = −8xk+1k\dfrac{-8x}{k} + \dfrac{1}{k}

Comparing y = mx + c with y = −8xk+1k\dfrac{-8x}{k} + \dfrac{1}{k}, we get :

⇒ m2 = −8k-\dfrac{8}{k}

Since, lines are parallel, equating the gradients :

⇒−k2=−8k⇒k(k)=8(2)⇒k2=16⇒k=16⇒k=±4.\Rightarrow -\dfrac{k}{2} = -\dfrac{8}{k} \\[1em] \Rightarrow k(k) = 8(2) \\[1em] \Rightarrow k^2 = 16 \\[1em] \Rightarrow k = \sqrt{16} \\[1em] \Rightarrow k = \pm 4.

Hence, value of k = ± 4.

Question 4

If the lines 2x – by + 5 = 0 and ax + 3y = 2 are parallel, find the relation connecting a and b.

Answer

Converting 2x - by + 5 = 0 in the form y = mx + c we get,

⇒ 2x - by + 5 = 0

⇒ by = 2x + 5

⇒ y = 2bx+5b\dfrac{2}{b}x + \dfrac{5}{b}

m1 = 2b\dfrac{2}{b}

Converting ax + 3y = 2 in the form y = mx + c we get,

⇒ ax + 3y = 2

⇒ 3y = -ax + 2

⇒ y = −a3x+23-\dfrac{a}{3}x + \dfrac{2}{3}

m2 = −a3-\dfrac{a}{3}

Given, two lines are parallel so their slopes will be equal,

m1 = m2

⇒ 2b=−a3\dfrac{2}{b} = -\dfrac{a}{3}

⇒ 3 × 2 = −a × b

⇒ 6 = −ab

⇒ ab + 6 = 0

⇒ ab = −6.

Hence, the relation connecting a and b is ab = -6.

Question 5

Prove that the line through A(–2, 6) and B(4, 8) is perpendicular to the line through C(8, 12) and D(4, 24).

Answer

The slope of the line passing through two points (x1, y1) and (x2, y2) is given by

Slope = y2−y1x2−x1\dfrac{y_2 - y_1}{x_2 - x_1}

Slope (m1) of line joining (-2, 6) and (4, 8) is,

= 8−64−(−2)=26=13\dfrac{8 - 6}{4 - (-2)} = \dfrac{2}{6} = \dfrac{1}{3}

Slope (m2) of line joining (8, 12) and (4, 24) is,

=24−124−8=12−4=−3\dfrac{24 - 12}{4 - 8} = \dfrac{12}{-4} = -3

m1 × m2 = 13×−3\dfrac{1}{3} \times -3 = -1.

Product of slopes = -1.

Hence, the lines are perpendicular to each other.

Question 6

If A(2, –5), B(–2, 5), C(k, 3) and D(1, 1) be four points such that AB and CD are perpendicular to each other, find the value of k.

Answer

By using slope formula,

m = y2−y1x2−x1\dfrac{y_2 - y_1}{x_2 - x_1}

Given, points A(2, –5), B(–2, 5)

Substituting values we get,

mAB=5−(−5)−2−2=5+5−4=−104=−52m_{AB} = \dfrac{5 - (-5)}{-2 - 2} = \dfrac{5 + 5}{-4} = -\dfrac{10}{4} = -\dfrac{5}{2}

Given, points C(k, 3) and D(1, 1)

Substituting values we get,

mCD=1−31−k=−21−km_{CD} = \dfrac{1 - 3}{1 - k} = \dfrac{-2}{1 - k}

Since the lines are perpendicular the product of the gradients is equal to -1:

⇒(−52)×(−21−k)=−1⇒(102(1−k))=−1⇒(51−k)=−1⇒5=−1(1−k)⇒5=−1+k⇒k=5+1⇒k=6.\Rightarrow \Big(-\dfrac{5}{2}\Big) \times \Big(\dfrac{-2}{1 - k}\Big) = -1 \\[1em] \Rightarrow \Big(\dfrac{10}{2(1 - k)}\Big) = -1 \\[1em] \Rightarrow \Big(\dfrac{5}{1 - k}\Big) = -1 \\[1em] \Rightarrow 5 = -1(1 - k) \\[1em] \Rightarrow 5 = -1 + k \\[1em] \Rightarrow k = 5 + 1 \\[1em] \Rightarrow k = 6.

Hence, value of k = 6.

Question 7

Prove that the lines 2x + 3y + 8 = 0 and 27x – 18y + 10 = 0 are perpendicular to each other.

Answer

Converting 2x + 3y + 8 = 0 in the form y = mx + c we get,

⇒ 3y = -2x - 8

⇒ y = −23x−83-\dfrac{2}{3}x - \dfrac{8}{3}

Comparing, we get slope of this line : m1 = −23-\dfrac{2}{3}

Converting 27x – 18y + 10 = 0 in the form y = mx + c we get,

⇒ -18y = -27x - 10

⇒ y = −27x−18−10−18\dfrac{-27x}{-18} - \dfrac{10}{-18}

⇒ y = 3x2+59\dfrac{3x}{2} + \dfrac{5}{9}

Comparing, we get slope of this line : m2 = 32\dfrac{3}{2}

Product of Gradients

m1 × m2 = −23×32-\dfrac{2}{3} \times \dfrac{3}{2}

= −66-\dfrac{6}{6}

= -1

Since the product of the gradients is -1. The lines are perpendicular to each other.

Hence, proved that lines 2x + 3y + 8 = 0 and 27x – 18y + 10 = 0 are perpendicular to each other.

Question 8(i)

If the lines y = 3x + 7 and 2y + px = 3 are perpendicular to each other, find the value of p.

Answer

Given lines,

⇒ y = 3x + 7 and 2y + px = 3

⇒ y = 3x + 7 and 2y = -px + 3

⇒ y = 3x + 7 and y = −p2x+32-\dfrac{p}{2}x + \dfrac{3}{2}

Comparing above equations with y = mx + c we get,

Slope of 1st line = 3

Slope of 2nd line = −p2-\dfrac{p}{2}

Since,

Product of slopes of perpendicular lines = -1.

∴3×−p2=−1⇒−p=−1×23⇒−p=−23⇒p=23.\therefore 3 \times -\dfrac{p}{2} = -1 \\[1em] \Rightarrow -p = \dfrac{-1 \times 2}{3} \\[1em] \Rightarrow -p = \dfrac{-2}{3} \\[1em] \Rightarrow p = \dfrac{2}{3}.

Hence, p = 23\dfrac{2}{3}.

Question 8(ii)

If the straight lines 3x – 5y = 7 and 4x + ay + 9 = 0 are perpendicular to each other, find the value of a.

Answer

Converting 3x - 5y + 7 = 0 in the form y = mx + c we get,

⇒ 3x - 5y + 7 = 0

⇒ 5y = 3x + 7

⇒ y = 35x+75\dfrac{3}{5}x + \dfrac{7}{5}

Comparing, we get slope of first line = m1 = 35\dfrac{3}{5}

Converting 4x + ay + 9 = 0 in the form y = mx + c we get,

⇒ 4x + ay + 9 = 0

⇒ ay = -4x - 9

⇒ y = −4ax−9a-\dfrac{4}{a}x - \dfrac{9}{a}

Comparing, we get slope of second line = m2 = −4a-\dfrac{4}{a}

Given, two lines are perpendicular so product of their slopes will be equal to -1,

⇒m1⋅m2=−1⇒35×−4a=−1⇒−125a=−1⇒a=125.\Rightarrow m_1 \cdot m_2 = -1 \\[1em] \Rightarrow \dfrac{3}{5} \times -\dfrac{4}{a} = -1 \\[1em] \Rightarrow -\dfrac{12}{5a} = -1 \\[1em] \Rightarrow a = \dfrac{12}{5}.

Hence,the value of a = 125\dfrac{12}{5}.

Question 9

Without using Pythagoras Theorem, prove that the points A(1, 3), B(3, –1) and C(–5, –5) are the vertices of a right-angled triangle.

Answer

By using slope formula,

m = y2−y1x2−x1\dfrac{y_2 - y_1}{x_2 - x_1}

Given, points A(1, 3), B(3, –1)

Substituting values we get,

mAB=−1−33−1=−42=−2m_{AB} = \dfrac{-1 - 3}{3 - 1} = -\dfrac{4}{2} = -2

Given, points B(3, –1) and C(–5, –5)

Substituting values we get,

mBC=−5−(−1)−5−3=−5+1−8=−4−8=12m_{BC} = \dfrac{-5 - (-1)}{-5 - 3} = \dfrac{-5 + 1}{-8} = \dfrac{-4}{-8} = \dfrac{1}{2}

Check for perpendicularity,

⇒mAB×mBC=−2×12=−1.\Rightarrow m_{AB} \times m_{BC} = -2 \times \dfrac{1}{2} = -1.

Since the product of the gradients of AB and BC is -1, the side AB is perpendicular to the side BC.

∠ABC = 90°.

Hence, proved the points A(1, 3), B(3, –1) and C(–5, –5) are the vertices of a right-angled triangle.

Question 10

Without using distance formula, show that the points A(1, –2), B(3, 6), C(5, 10) and D(3, 2) are the vertices of a parallelogram.

Answer

By using slope formula,

m = y2−y1x2−x1\dfrac{y_2 - y_1}{x_2 - x_1}

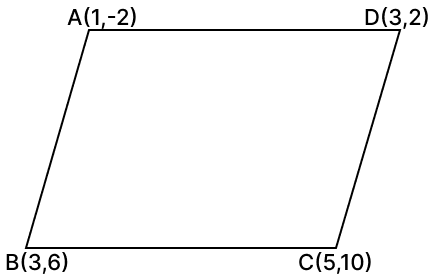
Without using distance formula, show that the points A(1, –2), B(3, 6), C(5, 10) and D(3, 2) are the vertices of a parallelogram. Equation of a Straight line, RSA Mathematics Solutions ICSE Class 10.

Given, points A(1, –2), B(3, 6)

Substituting values we get,

mAB=6−(−2)3−1=82=4m_{AB} = \dfrac{6 - (-2)}{3 - 1} = \dfrac{8}{2} = 4

Given, points C(5, 10) and D(3, 2)

Substituting values we get,

mDC=10−25−3=82=4m_{DC} = \dfrac{10 - 2}{5 - 3} = \dfrac{8}{2} = 4

Given, points B(3, 6), C(5, 10)

Substituting values we get,

mBC=10−65−3=42=2m_{BC} = \dfrac{10 - 6}{5 - 3} = \dfrac{4}{2} = 2

Given, points A(1, –2), D(3, 2)

Substituting values we get,

mAD=2−(−2)3−1=42=2m_{AD} = \dfrac{2 - (-2)}{3 - 1} = \dfrac{4}{2} = 2

mAB = mCD and mBC = mAD

∴ AB is parallel to CD and BC is parallel to AD

Since both pairs of opposite sides are parallel, the quadrilateral ABCD is a parallelogram.

Hence, proved that ABCD is a parallelogram.

Question 11

Given that A(5, 4), B(–3, –2) and C(1, –8) are the vertices of a ΔABC. Find:

(i) the slope of median AD

(ii) the slope of altitude BM

Answer

(i) Since, AD is median. So, D is the mid-point of BC.

By using formula,

(x, y) = (x1+x22,y1+y22)\Big(\dfrac{x_1 + x_2}{2}, \dfrac{y_1 + y_2}{2}\Big)

Substitute values we get,

D = (−3+12,−2+(−8)2)=(−22,−102)=(−1,−5)\Big(\dfrac{-3 + 1}{2}, \dfrac{-2 + (-8)}{2}\Big) = \Big(\dfrac{-2}{2}, \dfrac{-10}{2}\Big) = (-1, -5)

By using slope formula,

m = y2−y1x2−x1\dfrac{y_2 - y_1}{x_2 - x_1}

Slope of AD = −5−4−1−5=−9−6=32\dfrac{-5 - 4}{-1 - 5} = \dfrac{-9}{-6} = \dfrac{3}{2}

Hence, slope of the median AD = 32\dfrac{3}{2}.

(ii) The altitude BM is perpendicular to the side AC. Therefore, the product of their slopes is -1.

Slope of AC = −8−41−5=−12−4=3\dfrac{-8 - 4}{1 - 5} = \dfrac{-12}{-4} = 3

mBM × 3 = -1

mBM = −13\dfrac{-1}{3}

Hence, slope of the BM = −13-\dfrac{1}{3}.

Question 12(i)

Find the equation of the line parallel to the line 3x + 2y = 8 and passing through the point (0, 1).

Answer

Given,

⇒ 3x + 2y = 8

Converting 3x + 2y = 8 in the form y = mx + c we get,

⇒ 2y = -3x + 8

⇒ y = −32x+82-\dfrac{3}{2}x + \dfrac{8}{2}

Comparing above equations with y = mx + c we get,

Slope = −32-\dfrac{3}{2}

Since, parallel lines have equal slope.

∴ Slope of line parallel to 3x + 2y = 8 is −32-\dfrac{3}{2}

By point-slope form,

⇒ y - y1 = m(x - x1)

Thus, equation of line with slope −32-\dfrac{3}{2} and passing through (0, 1) is :

⇒ y - 1 = −32-\dfrac{3}{2}(x - 0)

⇒ 2(y - 1) = -3x

⇒ 2y - 2 = -3x

⇒ 3x + 2y = 2 .

Hence, equation of the line passing through (0, 1) and parallel to 3x + 2y = 8 is 3x + 2y = 2.

Question 12(ii)

Find the equation of a line parallel to the line 2x + y – 7 = 0 and passing through the intersection of the lines x + y – 4 = 0 and 2x – y = 8.

Answer

Simultaneously solving equations :

⇒ x + y - 4 = 0 …….(1)

⇒ 2x - y = 8 ……..(2)

Solving equation (1), we get :

⇒ x = 4 - y ………..(3)

Substituting value of x from (3) in (2), we get :

⇒ 2(4 - y) - y = 8

⇒ 8 - 2y - y = 8

⇒ 8 - 3y = 8

⇒ 3y = 0

⇒ y = 0.

Substituting value of y in (3), we get :

⇒ x = 4 - 0 = 4.

Point of intersection = (4, 0).

Given,

Equation :

⇒ 2x + y - 7 = 0

⇒ y = -2x + 7

Comparing above equation with y = mx + c, we get :

⇒ m = -2.

We know that,

Slope of parallel lines are equal.

∴ Slope of line parallel to 2x + y - 7 = -2.

By point-slope formula,

Equation of line :

⇒ y - y1 = m(x - x1)

Thus, equation of line with slope = -2 and passing through (4, 0).

⇒ y - 0 = -2(x - 4)

⇒ y = -2x + 8

⇒ 2x + y - 8 = 0.

Hence, the equation of required line is 2x + y - 8 = 0.

Question 13

A(–1, 3), B(4, 2) and C(3, –2) are the vertices of a triangle.

(i) Find the co-ordinates of the centroid G of the triangle.

(ii) Find the equation of the line through G and parallel to AC.

Answer

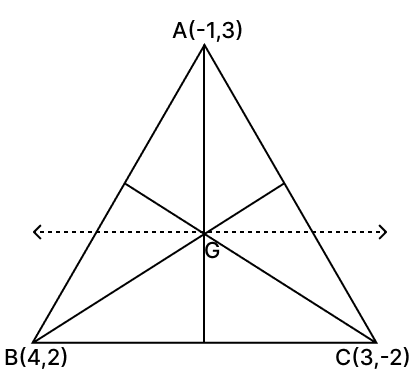
A(–1, 3), B(4, 2) and C(3, –2) are the vertices of a triangle. Equation of a Straight line, RSA Mathematics Solutions ICSE Class 10.

(i) Centroid of the triangle is given by,

G=(x1+x2+x33,y1+y2+y33)=(−1+4+33,3+2−23)=(63,33)=(2,1).G = \Big(\dfrac{x_1 + x_2 + x_3}{3}, \dfrac{y_1 + y_2 + y_3}{3}\Big) \\[1em] = \Big(\dfrac{-1 + 4 + 3}{3}, \dfrac{3 + 2 - 2}{3}\Big) \\[1em] = \Big(\dfrac{6}{3}, \dfrac{3}{3}\Big) \\[1em] = (2, 1).

Hence, the coordinates of the centroid G of the triangle is (2, 1).

(ii) Slope of AC = y2−y1x2−x1=−2−33−(−1)=−54\dfrac{y_2 - y_1}{x_2 - x_1} = \dfrac{-2 - 3}{3 - (-1)} = -\dfrac{5}{4}

So, the slope of the line parallel to AC is also −54-\dfrac{5}{4}. and it passes through (2, 1). Hence, its equation can be given by point-slope form i.e.,

⇒ y - y1 = m(x - x1)

⇒ y - 1 = −54-\dfrac{5}{4}(x - 2)

⇒ 4(y − 1) = −5(x − 2)

⇒ 4y − 4 = −5x + 10

⇒ 4y + 5x = 14

⇒ 5x + 4y − 14 = 0.

Hence, the equation of the required line is 5x + 4y - 14 = 0.

Question 14

Find the equation of a line passing through the point P(–2, 1) and parallel to the line joining the points A(4, –3) and B(–1, 5).

Answer

Since the required line is parallel to the line segment AB, they must have the same gradient.

Slope of AB = y2−y1x2−x1=5−(−3)−1−4=−85\dfrac{y_2 - y_1}{x_2 - x_1} = \dfrac{5 - (-3)}{-1 - 4} = -\dfrac{8}{5}

Using the point-slope form,

⇒ y - y1 = m(x - x1)

⇒ y - 1 = −85-\dfrac{8}{5}[x - (-2)]

⇒ 5(y - 1) = -8(x + 2)

⇒ 5y - 5 = -8x - 16

⇒ 8x + 5y - 5 + 16 = 0

⇒ 8x + 5y + 11 = 0

Hence, the equation of the required line is 8x + 5y + 11 = 0.

Question 15

Find the equation of the line passing through the origin and perpendicular to the line y + 5x = 3.

Answer

Converting y + 5x = 3 in the form y = mx + c we get,

⇒ y = -5x + 3

Comparing above equation with y = mx + c we get, m = -5

For two lines to be perpendicular, the product of their gradients must be -1.

Let slope of required line be m2, then :

⇒ -5 × m2 = -1

⇒ m2 = −1−5\dfrac{-1}{-5}

⇒ m2 = 15\dfrac{1}{5}

Using the slope-intercept form y = mx + c. Since the line passes through the origin, the y-intercept is 0.

⇒ y = 15\dfrac{1}{5}x + 0

⇒ 5y = x

⇒ x - 5y = 0.

Hence, the equation of the required line is x - 5y = 0.

Question 16

Find the equation of a line passing through the origin and parallel to the line 3x – 2y + 4 = 0.

Answer

Converting 3x - 2y + 4 = 0 in the form y = mx + c we get,

⇒ -2y = -3x - 4

⇒ y = −3x−2−4−2\dfrac{-3x}{-2} - \dfrac{4}{-2}

⇒ y = 3x2\dfrac{3x}{2} + 2

Comparing above equation with y = mx + c we get, m = 32\dfrac{3}{2}

Since the required line is parallel to the given line, they must have the same gradient:

⇒ Slope of parallel line = 32\dfrac{3}{2}

Using the slope-intercept form y = mx + c. Since the line passes through the origin, the y-intercept is 0.

⇒ y = 32\dfrac{3}{2}x + 0

⇒ 2y = 3x

⇒ 3x - 2y = 0.

Hence, the equation of the required line is 3x - 2y = 0.

Question 17

Find the equation of the line that has x-intercept –3 and is perpendicular to the line 3x + 5y = 1.

Answer

Let point where line touches x-axis be A. So, A = (-3, 0)

Given equation of line,

⇒ 3x + 5y = 1

⇒ 5y = -3x + 1

⇒ y = −35x+15-\dfrac{3}{5}x + \dfrac{1}{5}

Comparing above equation with y = mx + c we get, m1 = −35-\dfrac{3}{5}

Let slope of line perpendicular to 3x + 5y = 1 be m2

⇒ m1 × m2 = -1

⇒ −35×m2=−1-\dfrac{3}{5} \times m_2 = -1

⇒ m2=53m_2 = \dfrac{5}{3}

By point-slope form,

Equation of line with slope = 53\dfrac{5}{3}and passing through (-3, 0) is :

⇒ y - y1 = m(x - x1)

⇒ y - 0 = 53\dfrac{5}{3}[x - (-3)]

⇒ 3y = 5[x + 3]

⇒ 3y = 5x + 15

⇒ 5x - 3y + 15 = 0.

Hence, equation of required line is 5x - 3y + 15 = 0.

Question 18

Find the equation of the line passing through (2, 4) and perpendicular to x-axis.

Answer

A line perpendicular to the x-axis, has equation x = k.

Since, line passes through (2, 4).

∴ Equation : x = 2.

Hence, equation of required line is x = 2.

Question 19

Find the equation of the perpendicular dropped from the point (–1, 2) onto the line joining the points (1, 4) and (2, 3).

Answer

Let P = (-1, 2)

Let A and B be the points (1, 4) and (2, 3).

Slope of AB = y2−y1x2−x1=3−42−1=−11=−1\dfrac{y_2 - y_1}{x_2 - x_1} = \dfrac{3 - 4}{2 - 1} = \dfrac{-1}{1} = -1

We know that,

Product of slope of perpendicular lines is -1.

Let slope of line through P and perpendicular to AB be m.

∴ m × Slope of AB = -1

⇒ m × -1 = -1

⇒ -m = -1

⇒ m = 1.

By point-slope form,

Equation of line through P,

⇒ y - y1 = m(x - x1)

⇒ y - 2 = 1[x - (-1)]

⇒ y - 2 = 1(x + 1)

⇒ y - 2 = x + 1

⇒ y - x = 1 + 2

⇒ y - x = 3

⇒ x - y + 3 = 0.

Hence, equation of the perpendicular dropped from the point (-1, 2) onto the line joining the points (1, 4) and (2, 3) is x - y + 3 = 0.

Question 20

Find the equation of the line passing through the point of intersection of the lines 5x – 8y + 23 = 0 and 7x + 6y – 71 = 0 and perpendicular to the line 4x – 2y = 3.

Answer

Given line equations are,

⇒ 7x + 6y - 71 = 0

⇒ 7x + 6y = 71 .......(1)

and

⇒ 5x - 8y + 23 = 0

⇒ 5x - 8y = -23 .......(2)

Multiplying (1) by 4, we get :

⇒ 28x + 24y = 284 .......(3)

Multiplying (2) by 3, we get :

⇒ 15x – 24y = -69 .......(4)

On adding (3) and (4), we get :

⇒ 28x + 24y + 15x - 24y = 284 + (-69)

⇒ 28x + 15x + 24y - 24y = 284 - 69

⇒ 43x = 215

⇒ x = 21543\dfrac{215}{43}

⇒ x = 5.

Substituting value of x in equation (2), we get :

⇒ 5.5 - 8y = -23

⇒ 25 - 8y = -23

⇒ 8y = 25 + 23

⇒ 8y = 48

⇒ y = 6.

Hence, the required line passes through the point (5, 6).

Given,

⇒ 4x – 2y = 3

⇒ 2y = 4x – 3

⇒ y = 2x – 32\dfrac{3}{2}.

Comparing above equation with y = mx + c we get,

Slope (m) = 2

Let slope of required line be m1.

As, the lines are perpendicular to each other so product of their slopes = -1.

⇒ m × m1 = -1

⇒ 2 × m1 = -1

⇒ m1 = −12-\dfrac{1}{2}.

Thus, equation of the line with slope −12-\dfrac{1}{2} and passing through (5, 6) is :

⇒ y – y1 = m(x – x1)

⇒ y – 6 = −12-\dfrac{1}{2}(x – 5)

⇒ 2(y – 6) = -1(x - 5)

⇒ 2y - 12 = -x + 5

⇒ 2y + x = 5 + 12

⇒ x + 2y = 17.

Hence, equation of required line is x + 2y = 17.

Question 21

A line through origin meets the line 2x = 3y + 13 at right angles at point Q. Find the co-ordinates of Q.

Answer

Let the line passing through the origin O(0, 0) be L1 and slope m1, and the given line be L2 : 2x = 3y + 13 and slope be m2.

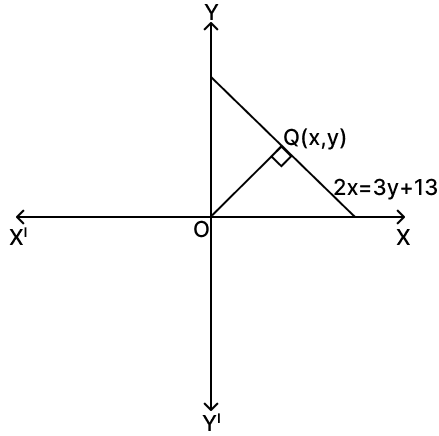
A line through origin meets the line 2x = 3y + 13 at right angles at point Q. Find the co-ordinates of Q. Equation of a Straight line, RSA Mathematics Solutions ICSE Class 10.

Given equation of line,

⇒ 2x = 3y + 13

⇒ 3y = 2x - 13

⇒ y = 23x−133\dfrac{2}{3}x - \dfrac{13}{3}

Comparing above equation with y = mx + c we get, Slope (m2) = 23\dfrac{2}{3}.

Since L1 is perpendicular to L2, the product of their slopes is -1.

⇒ m1 × m2 = -1

⇒ m1 × 23\dfrac{2}{3} = -1

⇒ m1 = −32-\dfrac{3}{2}.

The equation of the line L1 having slope m1 and passing through the origin can be given by point-slope form i.e.,

⇒ y - y1 = m(x - x1)

⇒ y - 0 = −32-\dfrac{3}{2}(x - 0)

⇒ y = −3x2-\dfrac{3x}{2}

⇒ 2y = -3x

⇒ 2y + 3x = 0.

For finding the coordinates of the foot of the perpendicular which is the point of intersection of the lines.

-3y + 2x - 13 = 0 .......(i)

2y + 3x = 0 ..........(ii)

On multiplying equation (i) by 2, we get :

-6y + 4x - 26 = 0 ..........(iii)

On multiplying equation (ii) by 3 we get,

6y + 9x = 0 .........(iv)

Adding (iii) and (iv) we get,

⇒ -6y + 4x - 26 + 6y + 9x = 0

⇒ 13x - 26 = 0

⇒ 13x = 26

⇒ x = 2613\dfrac{26}{13}

⇒ x = 2.

Substituting value of x in (ii), we get :

⇒ 2y + 3(2) = 0

⇒ 2y + 6 = 0

⇒ 2y = -6

⇒ y = −62\dfrac{-6}{2}

⇒ y = -3.

∴ Coordinates = (2, -3)

Hence, coordinates of Q = (2, -3).

Question 22

Find the equation of the perpendicular from the point P(1, –2) on the line 4x – 3y – 5 = 0. Also, find the co-ordinates of the foot of the perpendicular.

Answer

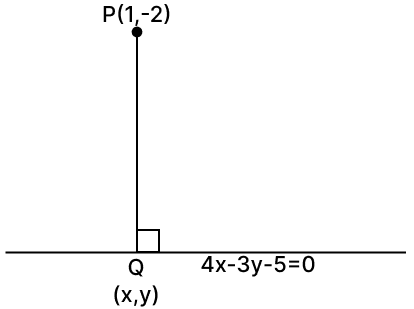
Find the equation of the perpendicular from the point P(1, –2) on the line 4x – 3y – 5 = 0. Also, find the co-ordinates of the foot of the perpendicular. Equation of a Straight line, RSA Mathematics Solutions ICSE Class 10.

Solving,

⇒ 4x - 3y - 5 = 0

⇒ 3y = 4x - 5

⇒ y = 43x−53\dfrac{4}{3}x - \dfrac{5}{3}

Comparing above equation with y = mx + c we get, Slope of the line (m1) = 43\dfrac{4}{3}

Let the slope of the line perpendicular to 4x - 3y - 5 = 0 be m2.

Then,

⇒m1×m2=−1⇒43×m2=−1⇒m2=−34.\Rightarrow m_1 × m_2 = -1 \\[1em] \Rightarrow \dfrac{4}{3} × m_2 = -1 \\[1em] \Rightarrow m_2 = -\dfrac{3}{4}.

The equation of the line having slope m2 and passing through the point (1, -2) can be given by point-slope form i.e.,

⇒ y - y1 = m(x - x1)

⇒ y - (-2) = −34(x−1)-\dfrac{3}{4}(x - 1)

⇒ 4(y + 2) = −3(x − 1)

⇒ 4y + 8 = −3x + 3

⇒ 3x + 4y + 5 = 0.

For finding the coordinates of the foot of the perpendicular which is the point of intersection of the lines. Let point of intersection of lines be Q.

4x - 3y - 5 = 0 .......(1)

3x + 4y + 5 = 0 ........(2)

On multiplying equation (1) by 4, we get :

16x - 12y - 20 = 0 ...........(3)

On multiplying equation (2) by 3, we get :

9x + 12y + 15 = 0 ..........(4)

Adding equations (3) and (4) we get,

⇒ 16x - 12y - 20 + 9x + 12y + 15 = 0

⇒ 25x - 5 = 0

⇒ x = 525\dfrac{5}{25}

⇒ x = 15\dfrac{1}{5}.

Substituting value of x in (1), we get :

⇒4×15−3y−5=0⇒45−3y−5=0⇒3y=45−255⇒3y=−215⇒y=−75.\Rightarrow 4\times \dfrac{1}{5} - 3y - 5 = 0 \\[1em] \Rightarrow \dfrac{4}{5} - 3y - 5 = 0 \\[1em] \Rightarrow 3y = \dfrac{4}{5} - \dfrac{25}{5} \\[1em] \Rightarrow 3y = -\dfrac{21}{5} \\[1em] \Rightarrow y = -\dfrac{7}{5}.

∴ Q = (15,−75)\Big(\dfrac{1}{5}, -\dfrac{7}{5}\Big)

Hence, the equation of the new line is 3x + 4y + 5 = 0 and coordinates of the foot of perpendicular are (15,−75)\Big(\dfrac{1}{5}, -\dfrac{7}{5}\Big).

Question 23

Find the equation of the line which is perpendicular to the line xa−yb=1\dfrac{x}{a} - \dfrac{y}{b} = 1 at the point where the given line meets y-axis.

Answer

Let A be the point where the line xa−yb=1\dfrac{x}{a} - \dfrac{y}{b} = 1 meets y-axis.

So, x-co-ordinate of point A will be zero.

Substituting x = 0 in equation we get,

⇒0a−yb=1⇒−yb=1⇒y=−b\Rightarrow \dfrac{0}{a} - \dfrac{y}{b} = 1 \\[1em] \Rightarrow -\dfrac{y}{b} = 1 \\[1em] \Rightarrow y = -b

A = (0, -b).

The given line equation is,

⇒xa−yb=1⇒yb=xa−1⇒y=bxa−b\Rightarrow \dfrac{x}{a} - \dfrac{y}{b} = 1 \\[1em] \Rightarrow \dfrac{y}{b} = \dfrac{x}{a} - 1 \\[1em] \Rightarrow y= \dfrac{bx}{a} - b

Comparing above equation with y = mx + c we get,

Slope (m) = ba\dfrac{b}{a}

Let slope of perpendicular line be m1.

As product of slope of perpendicular lines is -1,

∴ m × m1 = -1

⇒ ba\dfrac{b}{a} × m1 = -1

⇒ m1 = −ab-\dfrac{a}{b}

Equation of line through A (0, -b) and slope = −ab-\dfrac{a}{b} is :

⇒ y - y1 = m(x - x1)

⇒ y - (-b) = −ab-\dfrac{a}{b}(x - 0)

⇒ b(y + b) = -ax

⇒ by + b2 = -ax

⇒ ax + by + b2 = 0

Hence, equation of required line is ax + by + b2 = 0.

Question 24

The points B(7, 3) and D(0, –4) are two opposite vertices of a rhombus ABCD. Find the equation of diagonal AC.

Answer

The points B(7, 3) and D(0, –4) are two opposite vertices of a rhombus ABCD. Find the equation of diagonal AC. Equation of a Straight line, RSA Mathematics Solutions ICSE Class 10.

Slope of the line BD (m1),

m1=y2−y1x2−x1=−4−30−7=−7−7=1.m_1 = \dfrac{y_2 - y_1}{x_2 - x_1} \\[1em] = \dfrac{-4 - 3}{0 - 7} \\[1em] = \dfrac{-7}{-7} \\[1em] = 1.

Diagonals of rhombus bisect each other at right angles.

∴ BD is perpendicular to AC. Let slope of AC be m2.

⇒ m1 × m2 = -1

⇒ 1 × m2 = -1

⇒ m2 = -1

Let O be the mid-point of diagonals. It's coordinates are given by,

O=(x1+x22,y1+y22)=(7+02,3+(−4)2)=(72,−12).O = \Big(\dfrac{x_1 + x_2}{2}, \dfrac{y_1 + y_2}{2}\Big) \\[1em] = \Big(\dfrac{7 + 0}{2}, \dfrac{3 + (-4)}{2}\Big) \\[1em] = \Big(\dfrac{7}{2}, -\dfrac{1}{2}\Big).

Equation of AC can be given by point slope form i.e.,

⇒y−y1=m(x−x1)⇒y−(−12)=−1[x−(72)]⇒y+(12)=[−x+(72)]⇒(2y+12)=(−2x+72)⇒2y+1=−2x+7⇒2y+2x−6=0⇒2(y+x−3)=0⇒x+y−3=0⇒x+y=3.\Rightarrow y - y_1 = m(x - x_1) \\[1em] \Rightarrow y - \Big(-\dfrac{1}{2}\Big) = -1 \Big[x - \Big(\dfrac{7}{2}\Big)\Big] \\[1em] \Rightarrow y + \Big(\dfrac{1}{2}\Big) = \Big[-x + \Big(\dfrac{7}{2}\Big)\Big] \\[1em] \Rightarrow \Big(\dfrac{2y + 1}{2}\Big) = \Big(\dfrac{-2x + 7}{2}\Big) \\[1em] \Rightarrow 2y + 1 = −2x + 7 \\[1em] \Rightarrow 2y + 2x − 6 = 0 \\[1em] \Rightarrow 2(y + x − 3) = 0 \\[1em] \Rightarrow x + y - 3 = 0 \\[1em] \Rightarrow x + y = 3.

Hence, the equation of the required line is x + y = 3.

Question 25

The points A(1, 3) and C(6, 8) are two opposite vertices of a square ABCD. Find the equation of the diagonal BD.

Answer

Given,

A(1, 3) and C(6, 8)

mAC=y2−y1x2−x1=8−36−1=55=1.m_{AC}= \dfrac{y_2 - y_1}{x_2 - x_1} = \dfrac{8 - 3}{6 - 1} = \dfrac{5}{5} = 1.

We know that diagonal AC is a perpendicular bisector of diagonal BD.

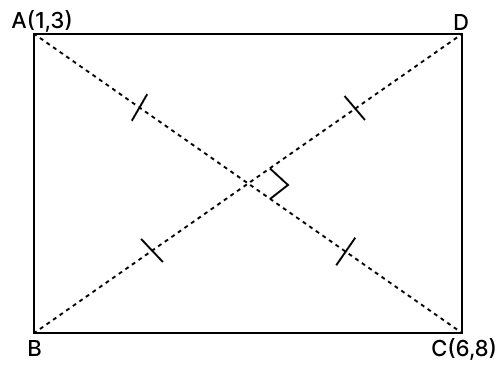
The points A(1, 3) and C(6, 8) are two opposite vertices of a square ABCD. Find the equation of the diagonal BD. Equation of a Straight line, RSA Mathematics Solutions ICSE Class 10.

⇒ mAC × mBD = -1

⇒ 1 × mBD = -1

⇒ mBD = -1

Let O be the point of intersection of diagonals, which is the mid-point of both the diagonals.

O=(x1+x22,y1+y22)=(1+62,3+82)=(72,112).O = \Big(\dfrac{x_1 + x_2}{2}, \dfrac{y_1 + y_2}{2}\Big) \\[1em] = \Big(\dfrac{1 + 6}{2}, \dfrac{3 + 8}{2}\Big) \\[1em] = \Big(\dfrac{7}{2}, \dfrac{11}{2}\Big).

By point-slope formula equation of AC is

⇒y−y1=m(x−x1)⇒y−(112)=−1[x−(72)]⇒y−112=−x+72⇒y+x−112−72=0⇒y+x−182=0⇒x+y−9=0.\Rightarrow y - y_1 = m(x - x_1) \\[1em] \Rightarrow y - \Big(\dfrac{11}{2}\Big) = -1 \Big[x - \Big(\dfrac{7}{2}\Big)\Big] \\[1em] \Rightarrow y - \dfrac{11}{2} = -x + \dfrac{7}{2} \\[1em] \Rightarrow y + x - \dfrac{11}{2} - \dfrac{7}{2} = 0 \\[1em] \Rightarrow y + x - \dfrac{18}{2} = 0 \\[1em] \Rightarrow x + y - 9 = 0.

Hence, the equation of the required line is x + y - 9 = 0.

Question 26

A(1, 4), B(3, 2) and C(7, 5) are the vertices of a ΔABC. Find :

(i) the co-ordinates of the centroid G of ΔABC

(ii) the equation of a line through G and parallel to AB

Answer

(i) By formula,

Centroid of triangle = (x1+x2+x33,y1+y2+y33)\Big(\dfrac{x_1 + x_2 + x_3}{3}, \dfrac{y_1 + y_2 + y_3}{3}\Big)

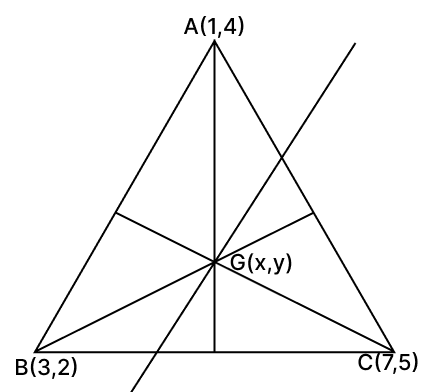
A(1, 4), B(3, 2) and C(7, 5) are the vertices of a ΔABC. Find.Equation of a Straight line, RSA Mathematics Solutions ICSE Class 10.

Substituting values we get,

Centroid = (1+3+73,4+2+53)=(113,113)\Big(\dfrac{1 + 3 + 7}{3}, \dfrac{4 + 2 + 5}{3}\Big) = \Big(\dfrac{11}{3}, \dfrac{11}{3}\Big)

Hence, centroid of triangle = (113,113)\Big(\dfrac{11}{3}, \dfrac{11}{3}\Big).

(ii) Calculating,

Slope of AB = y2−y1x2−x1=2−43−1=−22=−1\dfrac{y_2 - y_1}{x_2 - x_1} = \dfrac{2 - 4}{3 - 1} = \dfrac{-2}{2} = -1

Slope of line parallel to AB will also be equal to -1, as slope of parallel lies are equal.

By point-slope form,

Equation of a line, through the centroid and parallel to AB,

⇒ y - y1 = m(x - x1)

⇒ y - (113)=−1[x−(113)]\Big(\dfrac{11}{3}\Big) = -1 \Big[x - \Big(\dfrac{11}{3}\Big)\Big]

⇒ (3y−113)=−1(3x−113)\Big(\dfrac{3y - 11}{3}\Big) = -1 \Big(\dfrac{3x - 11}{3}\Big)

⇒ 3y − 11 = −1(3x − 11)

⇒ 3y − 11 = −3x + 11

⇒ 3y + 3x = 11 + 11

⇒ 3x + 3y = 22.

Hence, the equation of a line, through the centroid and parallel to AB is 3x + 3y = 22.

Question 27

A(–4, 2), B(6, 4) and C(2, –2) are the vertices of ΔABC. Find :

(i) the equation of median AD

(ii) the equation of altitude BM

(iii) the equation of right bisector of AB

(iv) the co-ordinates of centroid of ΔABC

Answer

(i) Slope of AD = y2−y1x2−x1=1−24−(−4)=−18\dfrac{y_2 - y_1}{x_2 - x_1} = \dfrac{1 - 2}{4 - (-4)} = \dfrac{-1}{8}

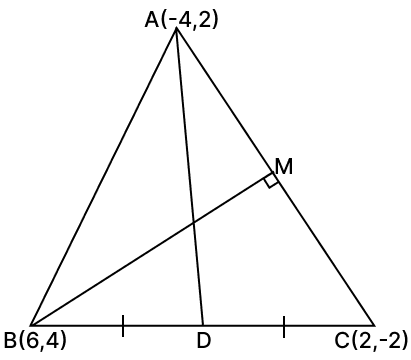
A(–4, 2), B(6, 4) and C(2, –2) are the vertices of ΔABC. Find. Equation of a Straight line, RSA Mathematics Solutions ICSE Class 10.

A median joins a vertex to the midpoint of the opposite side. D is the midpoint of BC.

=(x1+x22,y1+y22)=(6+22,4+(−2)2)=(82,22)=(4,1).= \Big(\dfrac{x_1 + x_2}{2}, \dfrac{y_1 + y_2}{2}\Big) \\[1em] = \Big(\dfrac{6 + 2}{2}, \dfrac{4 + (-2)}{2}\Big) \\[1em] = \Big(\dfrac{8}{2}, \dfrac{2}{2}\Big) = (4, 1).

By point-slope form,

Equation of a median AB, given by:

⇒ y - y1 = m(x - x1)

⇒ y - 2 = −18\dfrac{-1}{8} [x - (-4)]

⇒ 8(y - 2) = -1(x + 4)

⇒ 8y - 16 = -x - 4

⇒ x + 8y - 12 = 0

Hence, the equation of a line AD x + 8y - 12 = 0.

(ii) Slope of AC = y2−y1x2−x1=−2−22−(−4)=−46=−23\dfrac{y_2 - y_1}{x_2 - x_1} = \dfrac{-2 - 2}{2 - (-4)} = \dfrac{-4}{6} = -\dfrac{2}{3}

We know that altitude BM is a perpendicular AC.

Let the slope of BM be m1,

⇒ mAC × m2 = -1

⇒ −23-\dfrac{2}{3} × m1 = -1

⇒ m1 = 32\dfrac{3}{2}

Equation of a line BM,

⇒ y - y1 = m(x - x1)

⇒ y - 4 = 32\dfrac{3}{2} (x - 6)

⇒ 2(y - 4) = 3(x - 6)

⇒ 2y - 8 = 3x - 18

⇒ 3x - 2y - 10 = 0

Hence, the equation of a line BM 3x - 2y - 10 = 0.

(iii) Slope of AB = y2−y1x2−x1=4−26−(−4)=210=15\dfrac{y_2 - y_1}{x_2 - x_1} = \dfrac{4 - 2}{6 - (-4)} = \dfrac{2}{10} = \dfrac{1}{5}

Right bisector of AB is perpendicular to AB

Let the slope of Right bisector of AB be m2,

⇒ mAB × m2 = -1

⇒ 15\dfrac{1}{5} × m2 = -1

⇒ m2 = -5

Coordinates of Midpoint of AB

=(x1+x22,y1+y22)=(−4+62,2+42)=(22,62)=(1,3).= \Big(\dfrac{x_1 + x_2}{2}, \dfrac{y_1 + y_2}{2}\Big) \\[1em] = \Big(\dfrac{-4 + 6}{2}, \dfrac{2 + 4}{2}\Big) \\[1em] = \Big(\dfrac{2}{2}, \dfrac{6}{2}\Big) = (1, 3).

Equation of a line BM,

⇒ y - y1 = m(x - x1)

⇒ y - 3 = -5 (x - 1)

⇒ (y - 3) = -5x + 5

⇒ 5x + y - 8 = 0

Hence, the equation of right bisector of AB 5x + y - 8 = 0.

(iv) Centroid of triangle ABC = (x1+x2+x33,y1+y2+y33)\Big(\dfrac{x_1 + x_2 + x_3}{3}, \dfrac{y_1 + y_2 + y_3}{3}\Big)

Substitute values we get,

=(−4+6+23,2+4+(−2)3)=(43,43)= \Big(\dfrac{-4 + 6 + 2}{3}, \dfrac{2 + 4 + (-2)}{3}\Big) = \Big(\dfrac{4}{3}, \dfrac{4}{3}\Big)

Hence, coordinates of centroid are (43,43)\Big(\dfrac{4}{3}, \dfrac{4}{3}\Big).

Question 28

Find the equation of the perpendicular drawn from the point P(2, 3) on the line y = 3x + 4. Find the co-ordinates of the foot of the perpendicular.

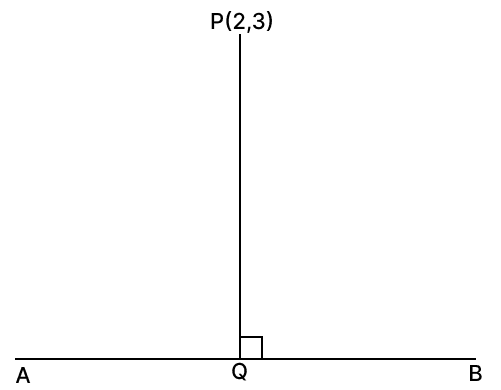
Find the equation of the perpendicular drawn from the point P(2, 3) on the line y = 3x + 4. Find the co-ordinates of the foot of the perpendicular. Equation of a Straight line, RSA Mathematics Solutions ICSE Class 10.

Answer

Given line y = 3x + 4...(1)

Comparing above equation with y = mx + c we get m1 = 3

Since line is perpendicular to y = 3x + 4, the product of their gradients must be -1.

Let the slope of required line be m 2

⇒ m1 × m2 = -1

⇒ 3 × m2 = -1

⇒ m2 = −13-\dfrac{1}{3}

By point slope formula,

Equation of a line,

⇒ y - y1 = m(x - x1)

⇒ y - 3 = −13-\dfrac{1}{3} (x - 2)

⇒ 3(y - 3) = -1(x - 2)

⇒ 3y - 9 = -x + 2

⇒ x + 3y - 11 = 0...(2)

The equation of the perpendicular drawn from P(2, 3) is x + 3y - 11 = 0.

Substitute y into x + 3y - 11 = 0:

⇒ x + 3(3x + 4) - 11 = 0

⇒ x + 9x + 12 - 11 = 0

⇒ 10x + 1 = 0

⇒ 10x = -1

⇒ x = −110-\dfrac{1}{10}

Substitute value of x in y = 3x + 4:

⇒ y = 3 (−110)\Big(-\dfrac{1}{10}\Big) + 4

⇒ y = (−310+4010)\Big(-\dfrac{3}{10} + \dfrac{40}{10}\Big)

⇒ y = 3710\dfrac{37}{10}

Hence, equation of required line is x + 3y - 11 = 0 and coordinates of foot of perpendicular (−110,3710)\Big(-\dfrac{1}{10}, \dfrac{37}{10}\Big).

Question 29

A(1, 2), B(2, 3) and C(4, 3) are the vertices of a ΔABC. Find :

(i) the equation of altitude through B

(ii) the equation of altitude through C

(iii) the co-ordinates of the orthocentre of ΔABC

Answer

(i) Slope of AC = y2−y1x2−x1=3−24−1=13\dfrac{y_2 - y_1}{x_2 - x_1} = \dfrac{3 - 2}{4 - 1} = \dfrac{1}{3}

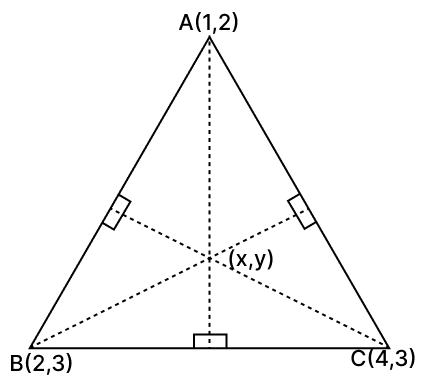
A(1, 2), B(2, 3) and C(4, 3) are the vertices of a ΔABC. Find. Equation of a Straight line, RSA Mathematics Solutions ICSE Class 10.

The altitude through B is perpendicular to the side AC.

Let the slope of altitude be m1,

⇒ mAC × m2 = -1

⇒ 13\dfrac{1}{3} × m1 = -1

⇒ m1 = -3

By point slope formula,

Equation of altitude B,

⇒ y - 3 = -3(x - 2)

⇒ y - 3 = -3x + 6

⇒ 3x + y - 9 = 0 ...(1)

Hence, the equation of the altitude through B is 3x + y - 9 = 0.

(ii) Slope of AB = y2−y1x2−x1=3−22−1=11=1\dfrac{y_2 - y_1}{x_2 - x_1} = \dfrac{3 - 2}{2 - 1} = \dfrac{1}{1} = 1

The altitude through C is perpendicular to the side AB.

Let the slope of altitude be m2,

⇒ mAB × m2 = -1

⇒ 1 × m2 = -1

⇒ m2 = -1

By point slope formula,

Equation of altitude B,

⇒ y - y1 = m(x - x1)

⇒ y - 3 = -1(x - 4)

⇒ y - 3 = -x + 4

⇒ x + y - 7 = 0 ...(2)

Hence, the equation of the altitude through C is x + y - 7 = 0.

(iii) Subtract Equation (2) from Equation (1):

⇒ (3x + y - 9) - (x + y - 7) = 0 - 0

⇒ 3x + y - 9 - x - y + 7 = 0 - 0

⇒ 3x - x + y - y - 9 + 7 = 0

⇒ 2x - 2 = 0

⇒ 2x = 2

⇒ x = 1

Substitute x = 1 into Equation (2):

⇒ 1 + y - 7 = 0

⇒ y - 6 = 0

⇒ y = 6.

Hence, the co-ordinates of the orthocentre of ΔABC are (1, 6).

Question 30

A(1, 2), B(3, –4) and C(5, –6) are the vertices of ΔABC. Find :

(i) the equation of the right bisector of BC

(ii) the equation of the right bisector of CA

(iii) the co-ordinates of the circumcentre of ΔABC

Answer

(i) Slope of BC = y2−y1x2−x1=−6−(−4)5−3=−22=−1\dfrac{y_2 - y_1}{x_2 - x_1} = \dfrac{-6 - (-4)}{5 - 3} = \dfrac{-2}{2} = -1

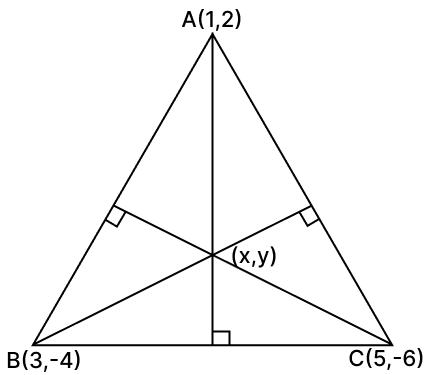
A(1, 2), B(3, –4) and C(5, –6) are the vertices of ΔABC. Find. Equation of a Straight line, RSA Mathematics Solutions ICSE Class 10.

The right bisector is perpendicular to BC.

Let the slope of right bisector be m1,

⇒ mAB × m1 = -1

⇒ -1 × m1 = -1

⇒ m1 = 1

The right bisector (perpendicular bisector) passes through the midpoint of BC

x,y=(x1+x22,y1+y22)=(3+52,−4+(−6)2)=(82,−102)=(4,−5).x, y = \Big(\dfrac{x_1 + x_2}{2}, \dfrac{y_1 + y_2}{2}\Big) \\[1em] = \Big(\dfrac{3 + 5}{2}, \dfrac{-4 + (-6)}{2}\Big) \\[1em] = \Big(\dfrac{8}{2}, \dfrac{-10}{2}\Big) = (4, -5).

By point slope formula,

Equation of right bisector of BC,

⇒ y - y1 = m(x - x1)

⇒ y - (-5) = 1(x - 4)

⇒ y + 5 = x - 4

⇒ x - y - 9 = 0....(1)

Hence, equation of right bisector of BC is x - y - 9 = 0.

(ii) Slope of CA = y2−y1x2−x1=2−(−6)1−5=8−4=−2\dfrac{y_2 - y_1}{x_2 - x_1} = \dfrac{2 - (-6)}{1 - 5} = \dfrac{8}{-4} = -2

The right bisector is perpendicular to CA.

Let the slope of right bisector of CA be m2,

⇒ mCA × m2 = -1

⇒ -2 × m2 = -1

⇒ m2 = 12\dfrac{1}{2}

Midpoint of CA

x,y=(x1+x22,y1+y22)=(5+12,−6+22)=(62,−42)=(3,−2).x, y = \Big(\dfrac{x_1 + x_2}{2}, \dfrac{y_1 + y_2}{2}\Big) \\[1em] = \Big(\dfrac{5 + 1}{2}, \dfrac{-6 + 2 }{2}\Big) \\[1em] = \Big(\dfrac{6}{2}, \dfrac{-4}{2}\Big) = (3, -2).

By point slope formula,

Equation of right bisector of CA,

⇒ y - y1 = m(x - x1)

⇒ y - (-2) = 12\dfrac{1}{2} (x - 3)

⇒ 2(y + 2) = (x - 3)

⇒ 2y + 4 = (x - 3)

⇒ x - 2y - 7 = 0 ...(2)

Hence, equation of right bisector of AC is x - 2y - 7 = 0.

(iii) Subtract Equation (2) from Equation (1):

⇒ (x - y) - (x - 2y) = 9 - 7

⇒ x - x - y + 2y = 2

⇒ y = 2.

Substitute y = 2 into Equation (1):

⇒ x - 2 = 9

⇒ x = 11.

Hence, coordinates of the circumcenter are (11, 2).

Question 31

(i) Is the line passing through the points A(–2, 3) and B(4, 1) perpendicular to the line 3x – y = 1?

(ii) Does the line 3x – y = 1 bisect the join of A(–2, 3) and B(4, 1)?

Answer

(i) Equation of line through (-2, 3) and (4, 1) can be given by two-point form i.e.,

y - y1 = y2−y1x2−x1\dfrac{y_2 - y_1}{x_2 - x_1} (x - x1)

Substituting values we get,

⇒y−3=1−34−(−2)[x−(−2)]⇒y−3=−26[x+2]⇒y−3=−13[x+2]⇒y=−x3−23+3⇒y=−x3−2+93⇒y=−x3−113.\Rightarrow y - 3 = \dfrac{1 - 3}{4 - (-2)} [x - (-2)] \\[1em] \Rightarrow y - 3 = \dfrac{-2}{6} [x + 2] \\[1em] \Rightarrow y - 3 = \dfrac{-1}{3} [x + 2] \\[1em] \Rightarrow y = \dfrac{-x}{3} - \dfrac{2}{3} + 3 \\[1em] \Rightarrow y = \dfrac{-x}{3} - \dfrac{2 + 9}{3} \\[1em] \Rightarrow y = \dfrac{-x}{3} - \dfrac{11}{3}.

Comparing the above equation with y = mx + c we get,

Slope = m1 = −13-\dfrac{1}{3}

The other equation is 3x = y + 1 or y = 3x - 1, comparing this with y = mx + c we get,

slope = m2 = 3

Product of slopes,

= m1 × m2

= −13-\dfrac{1}{3} × 3

= -1.

Since, the product of slopes is -1 hence, the lines are perpendicular to each other.

Hence, the line joining A(–2, 3) and B(4, 1) is perpendicular to the line 3x – y = 1.

(ii) Mid-point of (-2, 3) and (4, 1) can be given by mid-point formula i.e.,

(x,y)=(x1+x22,y1+y22)=(−2+42,3+12)=(1,2).(x, y) = \Big(\dfrac{x_1 + x_2}{2}, \dfrac{y_1 + y_2}{2}\Big) = \Big(\dfrac{-2 + 4}{2}, \dfrac{3 + 1}{2}\Big) = (1, 2).

Line 3x = y + 1 bisects the line joining (-2, 3) and (4, 1) if the mid-point i.e., (1, 2) satisfies the equation.

Substituting (1, 2) in 3x = y + 1.

L.H.S. = 3x = 3(1) = 3.

R.H.S. = y + 1 = 2 + 1 = 3.

Since, L.H.S. = R.H.S. hence, (1, 2) satisfies 3x = y + 1.

Hence, the line 3x – y = 1 bisects the join of A(–2, 3) and B(4, 1).

Question 32

A line segment AB meets x-axis at A and y-axis at B. P(4, –1) divides AB in the ratio 1 : 2.

(i) Find the co-ordinates of A and B.

(ii) Find the equation of the line through P and perpendicular to AB.

Answer

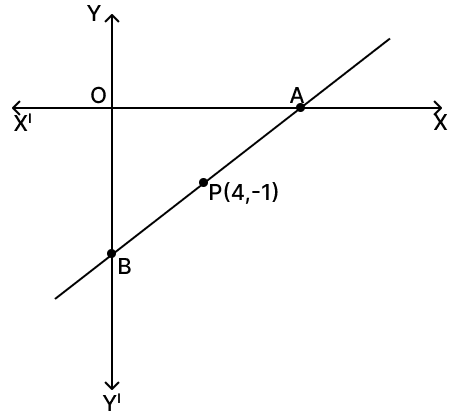
A line segment AB meets x-axis at A and y-axis at B. P(4, –1) divides AB in the ratio 1 : 2. Equation of a Straight line, RSA Mathematics Solutions ICSE Class 10.

(i) As A lies on x-axis let its co-ordinates be (a, 0) and B lies on y-axis so, co-ordinates = (0, b).

By section-formula,

⇒P=(m1x2+m2x1m1+m2,m1y2+m2y1m1+m2)⇒(4,−1)=(1(0)+2a1+2,1(b)+2(0)1+2)⇒(4,−1)=(2a3,b3)⇒2a3=4 and b3=−1⇒a=122=6 and b=−3.\Rightarrow P = \Big(\dfrac{m_1x_2 + m_2x_1}{m_1 + m_2}, \dfrac{m_1y_2 + m_2y_1}{m_1 + m_2} \Big) \\[1em] \Rightarrow (4, -1) = \Big(\dfrac{1(0) + 2a}{1 + 2}, \dfrac{1(b) + 2(0)}{1 + 2} \Big) \\[1em] \Rightarrow (4, -1) = \Big(\dfrac{2a}{3}, \dfrac{b}{3} \Big) \\[1em] \Rightarrow \dfrac{2a}{3} = 4 \text{ and } \dfrac{b}{3} = -1 \\[1em] \Rightarrow a = \dfrac{12}{2} = 6 \text{ and } b = -3.

Hence, A = (6, 0) and B = (0, -3).

(ii) By formula,

Slope of AB = y2−y1x2−x1=−3−00−6=−3−6=12.\dfrac{y_2 - y_1}{x_2 - x_1} = \dfrac{-3 - 0}{0 - 6} = \dfrac{-3}{-6} = \dfrac{1}{2}.

Let slope of perpendicular line be m.

Since the product of the slopes of perpendicular lines = -1.

⇒ m × Slope of AB = -1

⇒ m × 12\dfrac{1}{2} = -1

⇒ m = -2.

By point-slope from,

Equation of line passing through P and slope = -2 is :

⇒ y - y1 = m(x - x1)

⇒ y - (-1) = -2(x - 4)

⇒ y + 1 = -2x + 8

⇒ 2x + y = 7.

Hence, equation of required line is 2x + y = 7.

Question 33

The vertices of a ΔABC are A(3, 8), B(–1, 2) and C(6, –6). Find :

(i) Slope of BC.

(ii) Equation of a line perpendicular to BC and passing through A.

Answer

(i) Let the slope of BC be m1. Slope of BC is given by,

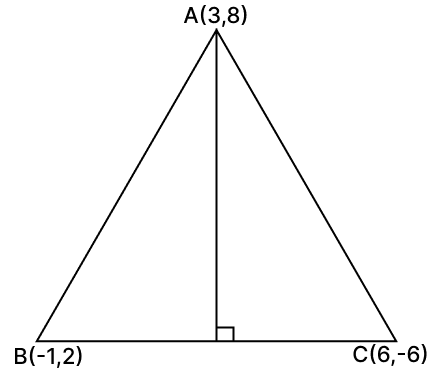
The vertices of a ΔABC are A(3, 8), B(–1, 2) and C(6, –6). Find. Equation of a Straight line, RSA Mathematics Solutions ICSE Class 10.

m1=y2−y1x2−x1=−6−26−(−1)=−87.m_1 = \dfrac{y_2 - y_1}{x_2 - x_1} \\[1em] = \dfrac{-6 - 2}{6 - (-1)} \\[1em] = \dfrac{-8}{7}.

Hence, the slope of BC is −87-\dfrac{8}{7}.

(ii) Let slope of line perpendicular to BC be m2

So,m1 × m2 = -1

⇒ −87-\dfrac{8}{7} × m2 = -1

⇒ m2 = 78\dfrac{7}{8}

Equation of the line having the slope = 78\dfrac{7}{8} and passing through A(3, 8) can be given bu point slope formula i.e.,

⇒ y - y1 = m(x - x1)

⇒ y - 8 = 78\dfrac{7}{8} (x - 3)

⇒ 8(y − 8) = 7(x − 3)

⇒ 8y − 64 = 7x − 21

⇒ 7x − 8y − 21 + 64 = 0

⇒ 7x − 8y + 43 = 0.

Hence, the equation of the required line is 7x - 8y + 43 = 0.

Question 34

Line AB is perpendicular to CD. Coordinates of B, C and D are respectively (4, 0), (0, –1) and (4, 3). Find :

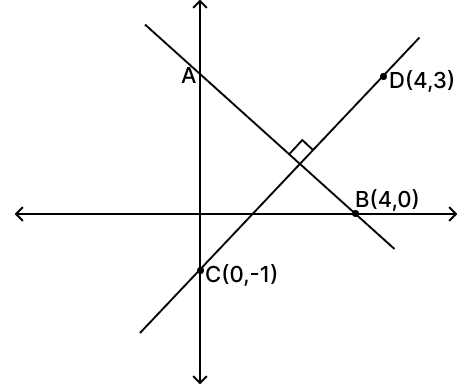
The coordinates of a point which divides a line segment joining the points (-3, 4) and (7, -6) in the ratio 1 : 2. Equation of a Straight line, RSA Mathematics Solutions ICSE Class 10.

(i) Slope of CD.

(ii) Equation of AB.

Answer

(i) By formula,

Slope of a line = y2−y1x2−x1\dfrac{y_2 - y_1}{x_2 - x_1}

Substituting values we get :

Slope of CD = 3−(−1)4−0=44=1\dfrac{3 - (-1)}{4 - 0} = \dfrac{4}{4} = 1

Hence, slope of CD = 1.

(ii) We know that,

The product of slope of two perpendicular lines equals to -1.

∴ Slope of AB × Slope of CD = -1

⇒ Slope of AB × 1 = -1

⇒ Slope of AB = -1.

By point-slope formula,

Equation of line

⇒ y - y1 = m(x - x1)

Equation of AB :

⇒ y - 0 = -1(x - 4)

⇒ y = -x + 4

⇒ x + y = 4.

Hence, equation of AB is x + y = 4.

Question 35

A and B are two points on the x-axis and y-axis respectively.

A and B are two points on the x-axis and y-axis respectively. Equation of a Straight line, RSA Mathematics Solutions ICSE Class 10.

(i) Write down the coordinates of A and B.

(ii) P is a point on AB such that AP : PB = 3 : 1. Using section formula, find the coordinates of point P.

(iii) Find the equation of a line passing through P and perpendicular to AB.

Answer

(i) From figure,

A = (4, 0) and B = (0, 4).

(ii) Let coordinates of P be (x, y).

By section formula,

(x, y) = (m1x2+m2x1m1+m2,m1y2+m2y1m1+m2)\Big(\dfrac{m_1x_2 + m_2x_1}{m_1 + m_2}, \dfrac{m_1y_2 + m_2y_1}{m_1 + m_2}\Big)

Substituting values we get :

⇒(x,y)=(3(0)+1(4)3+1,3(4)+1(0)3+1)=(0+44,12+04)=(44,124)=(1,3).\Rightarrow (x, y) = \Big(\dfrac{3(0) + 1(4)}{3 + 1}, \dfrac{3(4) + 1(0)}{3 + 1}\Big) \\[1em] = \Big(\dfrac{0 + 4}{4}, \dfrac{12 + 0}{4}\Big) \\[1em] = \Big(\dfrac{4}{4}, \dfrac{12}{4}\Big) \\[1em] = (1,3).

Hence, coordinates of P = (1, 3).

(iii) By formula,

Slope = y2−y1x2−x1\dfrac{y_2 - y_1}{x_2 - x_1}

Substituting values we get :

Slope of AB = 4−00−4=4−4=−1\dfrac{4 - 0}{0 - 4} = \dfrac{4}{-4} = -1

We know that,

Product of slope of perpendicular lines = -1.

∴ Slope of AB × Slope of line perpendicular to AB = -1

⇒ -1 × Slope of line perpendicular to AB = -1

⇒ Slope of line perpendicular to AB = −1−1=1\dfrac{-1}{-1} = 1

Line passing through P and perpendicular to AB :

⇒ y - y1 = m(x - x1)

⇒ y - 3 = 1(x - 1)

⇒ y - 3 = x - 1

⇒ y = x - 1 + 3

⇒ x - y + 2 = 0

Hence, required equation is x - y + 2 = 0.

Multiple Choice Questions

Question 1

The inclination of every line parallel to the x-axis is:

  1. 0°

  2. 90°

  3. 180°

  4. none of these

Answer

The angle that a horizontal line makes with the x-axis is 0°.

The angle between the line and the x-axis is 0°.

Hence, option 1 is the correct option.

Question 2

The inclination of y-axis is:

  1. 0°

  2. 45°

  3. 90°

  4. 180°

Answer

A vertical line makes a right angle with the horizontal x-axis.

Therefore, the angle of inclination of the y-axis is 90°.

Hence, option 3 is the correct option.

Question 3

The slope of a line whose inclination is 30°, is:

  1. 12\dfrac{1}{2}

  2. 3\sqrt{3}

  3. 1

  4. 13\dfrac{1}{\sqrt{3}}

Answer

The slope (m) of a line is related to its inclination (θ) by the formula:

m = tan θ

m = tan 30° = 13\dfrac{1}{\sqrt3}.

Hence, option 4 is the correct option.

Question 4

The slope of a horizontal line is:

  1. 0

  2. 1

  3. 2

  4. not defined

Answer

A horizontal line is a line parallel to the x-axis.

Thus θ = 0°

We know that,

m = tan θ

m = tan 0° = 0

Hence, option 1 is the correct option.

Question 5

The slope of a vertical line is:

  1. 0

  2. 1

  3. 90

  4. not defined

Answer

A vertical line is perpendicular to x-axis.

Thus, θ = 90°.

We know that,

m = tan θ

m = tan 90° = not defined

Hence, option 4 is the correct option.

Question 6

The slope of a line passing through two given points A(x1, y1) and B(x2, y2) is given by:

  1. m=x2−x1y2−y1m = \dfrac{x_2 - x_1}{y_2 - y_1}

  2. m=y2×y1x2×x1m = \dfrac{y_2 \times y_1}{x_2 \times x_1}

  3. m=x2×x1y2×y1m = \dfrac{x_2 \times x_1}{y_2 \times y_1}

  4. m=y2−y1x2−x1m = \dfrac{y_2 - y_1}{x_2 - x_1}

Answer

The correct formula for slope is: m=y2−y1x2−x1m = \dfrac{y_2 - y_1}{x_2 - x_1}

Hence, option 4 is the correct option.

Question 7

A line which is neither parallel to x-axis nor parallel to y-axis, is called

  1. a transverse line

  2. an oblique line

  3. a horizontal line

  4. a vertical line

Answer

Any straight line that is neither horizontal (parallel to the x-axis) nor vertical (parallel to the y-axis) is an oblique line.

Hence, option 2 is the correct option.

Question 8

Which of the following lines does not have x-intercept?

  1. A horizontal line

  2. A vertical line

  3. An oblique line

  4. None of these

Answer

A horizontal line has equation : y = c.

It does not crosses x-axis at any point, thus x-intercept = 0.

Hence, option 1 is the correct option.

Question 9

Which of the following lines does not have y-intercept?

  1. A horizontal line

  2. A vertical line

  3. y-axis

  4. A transverse line

Answer

A y-intercept is the point where a line crosses the y-axis.

A vertical line: A vertical line has the equation x = a.

If a = 0 , it has an infinite number of y-intercepts.

If a ≠ 0 , the line is parallel to the y-axis and never crosses it. Therefore, it has no y-intercept.

Hence, option 2 is the correct option.

Question 10

The equation of x-axis is:

  1. x = 0

  2. y = 0

  3. x = a

  4. y = a

Answer

The equation of x-axis is :

y = 0

Every point on the x-axis has a y-coordinate of 0, regardless of its x-coordinate.

Hence, option 2 is the correct option.

Question 11

The equation of y-axis is :

  1. x = 0

  2. y = 0

  3. x = a

  4. y = a

Answer

The equation of y-axis is:

x = 0

Every point on the y-axis has an x-coordinate of 0, regardless of its y-coordinate.

Hence, option 1 is the correct option.

Question 12

The equation of a line parallel to x-axis and at a distance of 5 units below it, is:

  1. x – 5 = 0

  2. x + 5 = 0

  3. y – 5 = 0

  4. y + 5 = 0

Answer

Any line parallel to the x-axis is a horizontal line and has the equation of form y = k.

The distance is 5 units below x-axis, thus the y-coordinate (k) of every point on the line is -5.

y = -5

y + 5 = 0.

Hence, option 4 is the correct option.

Question 13

The equation of a line parallel to y-axis and at a distance of 8 units to the right of it, is:

  1. x – 8 = 0

  2. x + 8 = 0

  3. y – 5 = 0

  4. y + 5 = 0

Answer

Any line parallel to the y-axis is a vertical line and has the equation form x = k.

The distance is 8 units to the right, thus the x-coordinate (k) of every point on the line is +8.

x = 8

x - 8 = 0

Hence, option 1 is the correct option.

Question 14

The equation of a line with slope m and y-intercept c is given by:

  1. x = my + c

  2. cy = mx

  3. y = mx + c

  4. none of these

Answer

y = mx + c, is the standard form of a linear equation known as the slope-intercept form.

Hence, option 3 is the correct option.

Question 15

The slope m of a line whose inclination is α, is given by :

  1. sin α

  2. cos α

  3. tan α

  4. cot α

Answer

The slope (m) of a line is defined as the tangent of its angle of inclination.

m = tan α

Hence, option 3 is the correct option.

Question 16

The equation of a line with slope m and passing through a point P(a, b), is given by :

  1. (y – a) = m(x – b)

  2. (x – b) = m(y – a)

  3. (x – a) = m(y – b)

  4. (y – b) = m(x – a)

Answer

By point-slope form,

Equation of line :

y - y1 = m (x - x1)

Thus, equation of line passing through (a, b) and slope m is :

y - b = m(x - a)

Hence, option 4 is the correct option.

Question 17

The equation of a line passing through two points A(x1, y1) and B(x2, y2) is given by:

  1. (x – x1) = y2−y1x2−x1\dfrac{y_2 - y_1}{x_2 - x_1} (y – y1)

  2. (y – y1) = x2−x1y2−y1\dfrac{x_2 - x_1}{y_2 - y_1} (x – x1)

  3. (y – y1) = y2−y1x2−x1\dfrac{y_2 - y_1}{x_2 - x_1} (x – x1)

  4. (y – y1) = y1−y2x2−x1\dfrac{y_1 - y_2}{x_2 - x_1} (x – x1)

Answer

By two-point formula,

Equation of line :

(y – y1) = y2−y1x2−x1\dfrac{y_2 - y_1}{x_2 - x_1} (x – x1)

Hence, option 3 is the correct option.

Question 18

The equation of a line with slope m and passing through (0, 0) is :

  1. x = my

  2. y = mx

  3. m = y – x

  4. m = y + x

Answer

We know that,

Equation of line:

y - y1 = m (x - x1)

Substituting values in equation :

y - 0 = m(x - 0)

y = mx.

Hence, option 2 is the correct option.

Question 19

The gradient of the line passing through the points A(–3, 4) and B(2, –6) is:

  1. –12\dfrac{1}{2}

  2. –2

  3. 2

  4. 12\dfrac{1}{2}

Answer

We know that,

m=y2−y1x2−x1mAB=−6−42−(−3)=−105=−2.m = \dfrac{y_2 - y_1}{x_2 - x_1} \\[1em] m_{AB} = \dfrac{-6 - 4}{2-(-3)} \\[1em] = \dfrac{-10}{5} = -2.

Hence, option 2 is the correct option.

Question 20

The equation of a straight line whose inclination with x-axis is 30° and whose y-intercept is –4, is:

  1. 3x−y−43=0\sqrt{3}x - y - 4\sqrt{3} = 0

  2. x+3y−43=0x + \sqrt{3}y - 4\sqrt{3} = 0

  3. x−3y−43=0x - \sqrt{3}y - 4\sqrt{3} = 0

  4. 3x+y−43=0\sqrt{3}x + y - 4\sqrt{3} = 0

Answer

The slope m is determined by the inclination θ = 30°.

m = tan θ

m = tan 30°

m = 13\dfrac{1}{\sqrt3}

Slope-intercept form:

y = mx + c

⇒y=13x−4⇒3y=x−43⇒x−3y−43=0.\Rightarrow y = \dfrac{1}{\sqrt3}x - 4 \\[1em] \Rightarrow \sqrt3y = x - 4\sqrt3 \\[1em] \Rightarrow x - \sqrt3y - 4\sqrt3 = 0.

Hence, option 3 is the correct option.

Question 21

The slope of the straight line passing through the points A(3, –2) and B(3, –4) is:

  1. 0

  2. 1

  3. –2

  4. not defined

Answer

We know that,

Slope = y2−y1x2−x1\dfrac{y_2 - y_1}{x_2 - x_1}

mAB=−4−(−2)3−3=−4+20=−20.m_{AB} = \dfrac{-4 - (-2)}{3 - 3} \\[1em] = \dfrac{-4 + 2}{0} \\[1em] = \dfrac{-2}{0}.

Slope is not defined.

Hence, option 4 is the correct option.

Question 22

The inclination of the line y = 3\sqrt{3} x – 5 is:

  1. 0°

  2. 30°

  3. 45°

  4. 60°

Answer

Comparing equation, y = 3\sqrt{3} x – 5 with y = mx + c, we get :

⇒ m = 3\sqrt3

⇒ tan θ = 3\sqrt{3}

⇒ tan θ = tan 60°

⇒ θ = 60°.

Hence, option 4 is the correct option.

Question 23

If the slope of the line passing through the points (2, 5) and (k, 3) is 2, then the value of k is:

  1. 0

  2. –1

  3. 1

  4. 2

Answer

We know that,

m = y2−y1x2−x1\dfrac{y_2 - y_1}{x_2 - x_1}

Substitute values we get:

⇒2=3−5k−2⇒2=−2k−2⇒2(k−2)=−2⇒(k−2)=−22⇒(k−2)=−1⇒k=−1+2⇒k=1.\Rightarrow 2 = \dfrac{3 - 5}{k - 2} \\[1em] \Rightarrow 2 = \dfrac{-2}{k - 2} \\[1em] \Rightarrow 2(k - 2) = -2 \\[1em] \Rightarrow (k - 2) = \dfrac{-2}{2} \\[1em] \Rightarrow (k - 2) = -1 \\[1em] \Rightarrow k = -1 + 2 \\[1em] \Rightarrow k = 1.

Hence, option 3 is the correct option.

Question 24

What can be said regarding a straight line if its slope is negative?

  1. Inclination, θ is an acute angle.

  2. Inclination, θ is an obtuse angle.

  3. Either the line is x-axis or it is parallel to the x-axis.

  4. Either the line is y-axis or it is parallel to the y-axis.

Answer

If the slope is negative, then tan θ must be negative.

tan θ < 0

This happens only when the angle θ made with the positive x-axis is between 90° and 180°.

And angles between 90° and 180° are called obtuse angles.

Hence, option 2 is the correct option.

Question 25

The equation of a straight line passing through the point (–6, 8) and parallel to the x-axis is:

  1. x – 6 = 0

  2. x + 6 = 0

  3. y – 8 = 0

  4. y + 8 = 0

Answer

The equation of horizontal line is of the form y = c.

Since the line must pass through the point (-6, 8), its y-coordinate must be equal to 8.

y = 8

y - 8 = 0.

Hence, option 3 is the correct option.

Question 26

The slope of the line, 3x – 22y2\sqrt2y – 4 = 0 is:

  1. 322\dfrac{3\sqrt{2}}{2}

  2. −322\dfrac{-3\sqrt{2}}{2}

  3. 324\dfrac{3\sqrt{2}}{4}

  4. −324-\dfrac{3\sqrt{2}}{4}

Answer

Solving,

⇒3x−22y−4=0⇒−22y=−3x+4⇒y=−3−22x+4−22⇒y=322x−22.\Rightarrow 3x - 2\sqrt{2}y - 4 = 0 \\[1em] \Rightarrow -2\sqrt{2}y = -3x + 4 \\[1em] \Rightarrow y = \dfrac{-3}{-2\sqrt{2}}x + \dfrac{4}{-2\sqrt{2}} \\[1em] \Rightarrow y = \dfrac{3}{2\sqrt{2}}x - \dfrac{2}{\sqrt{2}}.

Comparing above equation with y = mx + c, we get :

m = 322\dfrac{3}{2\sqrt2}

Rationalizing the Denominator,

m=322×22=322×2=324.m = \dfrac{3}{2\sqrt{2}} \times \dfrac{\sqrt{2}}{\sqrt{2}} \\[1em] = \dfrac{3\sqrt{2}}{2 \times 2} \\[1em] = \dfrac{3\sqrt{2}}{4}.

Hence, option 3 is the correct option.

Question 27

The equation of the line passing through the points A(4, 3) and B(–2, 6) is :

  1. x + 2y – 10 = 0

  2. x – 2y – 6 = 0

  3. x – 3y + 8 = 0

  4. x + 2y – 6 = 0

Answer

We know that,

m=y2−y1x2−x1mAB=6−3−2−4=3−6=−12.m = \dfrac{y_2 - y_1}{x_2 - x_1} \\[1em] m_{AB} = \dfrac{6 - 3}{-2 - 4} \\[1em] = \dfrac{3}{-6} \\[1em] = -\dfrac{1}{2}.

By point-slope form :

⇒ y - y1 = m(x - x1)

⇒ y - 3 = −12-\dfrac{1}{2} (x - 4)

⇒ 2(y - 3) = -1(x - 4)

⇒ 2y - 6 = -x + 4

⇒ x + 2y - 6 - 4 = 0

⇒ x + 2y - 10 = 0.

Hence, option 1 is the correct option.

Question 28

The equation of a line passing through the point (5, –3) and having the y-intercept of 8 units below the x-axis is:

  1. x + y – 8 = 0

  2. x – y – 8 = 0

  3. 2x + y – 4 = 0

  4. x – 2y – 8 = 0

Answer

The line intersects the y-axis 8 units below the x-axis. This means the line intersect y-axis at (0, -8).

Thus, y-intercept of lie (c) = -8

Thus, line passes through (0, -8) and (5, -3).

We know that,

m=y2−y1x2−x1=−3−(−8)5−0=55=1.m = \dfrac{y_2 - y_1}{x_2 - x_1} \\[1em] = \dfrac{-3 - (-8)}{5 - 0} \\[1em] = \dfrac{5}{5} \\[1em] = 1.

Substitute m = 1 and c = -8 into y = mx + c, we get :

⇒ y = 1.x + (-8)

⇒ y = x - 8

⇒ x - y - 8 = 0.

Hence, option 2 is the correct option.

Question 29

The value of m such that the points A(5, –2), B(8, –3) and C(m, –12) are collinear, is:

  1. 29

  2. 33

  3. 35

  4. 41

Answer

For three points A, B, and C to be collinear.

mAB = mBC

We know that,

m = y2−y1x2−x1\dfrac{y_2 - y_1}{x_2 - x_1}

Using A(5, -2) and B(8, -3) :

mAB=−3−(−2)8−5=−13.m_{AB} = \dfrac{-3 - (-2)}{8 - 5} \\[1em] = \dfrac{-1}{3}.

Using B(8, -3) and C(m, -12):

mBC=−12−(−3)m−8=−9m−8m_{BC} = \dfrac{-12 - (-3)}{m - 8} \\[1em] = \dfrac{-9}{m - 8}

mAB = mBC

⇒ −13=−9m−8\dfrac{-1}{3} = \dfrac{-9}{m - 8}

⇒ -1(m - 8) = -9 × 3

⇒ -m + 8 = -27

⇒ -m = -27 - 8

⇒ -m = -35

⇒ m = 35.

Hence, option 3 is the correct option.

Question 30

The equation of the straight line passing through the point (9, –9) and parallel to the y-axis is:

  1. y – 9 = 0

  2. y + 9 = 0

  3. x + 9 = 0

  4. x – 9 = 0

Answer

The equation of line parallel to y-axis is :

x = c

Since the line must pass through the point (9, -9), its x-coordinate must be x = 9.

x - 9 = 0

Hence, option 4 is the correct option.

Question 31

Two non-vertical lines with slopes m1 and m2 are parallel to each other, if:

  1. m1m2 = 1

  2. m1m2 = –1

  3. m1 = –m2

  4. m1 = m2

Answer

Two distinct non-vertical lines are parallel if and only if their slopes are equal.

m1 = m2

Hence, option 4 is the correct option.

Question 32

Two non-vertical lines with slopes m1 and m2 are perpendicular to each other, if:

  1. m1.m2 = 1

  2. m1.m2 = –1

  3. m1 = –m2

  4. m1 = m2

Answer

Two non-vertical lines are perpendicular if and only if the product of their slopes is -1.

m1.m2 = –1

Hence, option 2 is the correct option.

Question 33

The slope of a line parallel to the line passing through the points A(3, –7) and B(5, –7) is:

  1. 2

  2. 1

  3. –1

  4. 0

Answer

Given, points A(3, –7) and B(5, –7)

Slope = y2−y1x2−x1\dfrac{y_2 - y_1}{x_2 - x_1}

Substitute values we get,

mAB=−7−(−7)5−3=−7+72=02=0.m_{AB} = \dfrac{-7 - (-7)}{5 - 3} \\[1em] = \dfrac{-7 + 7}{2} \\[1em] = \dfrac{0}{2} = 0.

As, slope of parallel lines are equal.

Thus, slope of line parallel to AB = 0.

Hence, option 4 is the correct option.

Question 34

The slope of a line perpendicular to the line passing through the points P(3, –4) and Q(1, –8) is:

  1. −12\dfrac{-1}{2}

  2. 2

  3. 12\dfrac{1}{2}

  4. –2

Answer

Slope of the line passing through P(3, –4) and Q(1, –8).

mPQ=y2−y1x2−x1=−8−(−4)1−3=−8+4−2=−4−2=2.m_{PQ} = \dfrac{y_2 - y_1}{x_2 - x_1} \\[1em] = \dfrac{-8 - (-4)}{1 - 3} \\[1em] = \dfrac{-8 + 4}{-2} \\[1em] = \dfrac{-4}{-2} = 2.

Since the required line is perpendicular to line PQ, the product of their slopes must be -1.

Let slope of required line be m.

⇒ mPQ × m = -1

⇒ 2 × m = -1

⇒ m = −12\dfrac{-1}{2}

Hence, option 1 is the correct option.

Question 35

The slope of a line parallel to the line, 3x – 5y + 8 = 0, is:

  1. −53\dfrac{-5}{3}

  2. 53\dfrac{5}{3}

  3. –35–\dfrac{3}{5}

  4. 35\dfrac{3}{5}

Answer

Solving,

⇒ 3x - 5y + 8 = 0

⇒ 3x + 8 = 5y

⇒ y=35x+85y = \dfrac{3}{5}x + \dfrac{8}{5}.

The slope of the given line is m=35m = \dfrac{3}{5}.

Since the required line is parallel, its slope must be the same as m.

Let slope of required line be m1,

m1 = m = 35\dfrac{3}{5}.

Hence, option 4 is the correct option.

Question 36

The slope of a line perpendicular to the line, 3x = 4y – 10, is :

  1. 43\dfrac{4}{3}

  2. –43–\dfrac{4}{3}

  3. 34\dfrac{3}{4}

  4. −34\dfrac{-3}{4}

Answer

Solving,

⇒ 3x = 4y - 10

⇒ 4y = 3x + 10

⇒y=34x+104\Rightarrow y = \dfrac{3}{4}x + \dfrac{10}{4}.

The slope of the given line is m=34m = \dfrac{3}{4}.

Since the required line is perpendicular, the product of the slopes must be -1.

Let slope of required line be a, then :

⇒ m × a = -1

⇒ 34\dfrac{3}{4} × a = -1

⇒ a = −43\dfrac{-4}{3}.

Hence, option 2 is the correct option.

Question 37

If the lines 2x + 3y = 5 and kx – 6y = 7 are parallel, then the value of k is:

  1. –4

  2. –14–\dfrac{1}{4}

  3. 4

  4. –5

Answer

For two lines to be parallel, their slopes must be equal.

Line 1 : 2x + 3y = 5

First, convert the equation 2x + 3y = 5 into the slope-intercept form, y = mx + c, to find its slope, m.

3y=−2x+5y=−23x+53m1=−233y = -2x + 5 \\[1em] y = -\dfrac{2}{3}x + \dfrac{5}{3} \\[1em] m_1 = -\dfrac{2}{3}

Line 2: kx - 6y = 7

First, convert the equation kx - 6y = 7 into the slope-intercept form, y = mx + c, to find its slope, m.

−6y=−kx+7y=−k−6x+7−6=k6x−76m2=k6-6y = -kx + 7 \\[1em] y = \dfrac{-k}{-6}x + \dfrac{7}{-6} = \dfrac{k}{6}x - \dfrac{7}{6} \\[1em] m_2 = \dfrac{k}{6}

The slopes of parallel lines are equal:

⇒m1=m2⇒−23=k6⇒k=−2×63⇒k=−123⇒k=−4.\Rightarrow m_1 = m_2 \\[1em] \Rightarrow -\dfrac{2}{3} = \dfrac{k}{6} \\[1em] \Rightarrow k = -\dfrac{2 \times 6}{3} \\[1em] \Rightarrow k = -\dfrac{12}{3} \\[1em] \Rightarrow k = -4.

Hence, option 1 is the correct option.

Question 38

If the lines x – my + 3 = 0 and 2x + 3y – 7 = 0 are perpendicular to each other, then the value of m is:

  1. –23–\dfrac{2}{3}

  2. 23\dfrac{2}{3}

  3. –32–\dfrac{3}{2}

  4. 32\dfrac{3}{2}

Answer

For two lines to be perpendicular, the product of their slopes must be -1.

Line 1: x - my + 3 = 0

First, convert the equation x - my + 3 = 0 into the slope-intercept form, y = mx + c, to find its slope, m.

−my=−x−3y=−1−mx+−3−m=1mx+3mm1=1m.-my = -x - 3 \\[1em] y = \dfrac{-1}{-m}x + \dfrac{-3}{-m} = \dfrac{1}{m}x + \dfrac{3}{m} \\[1em] m_1 = \dfrac{1}{m}.

Line 2: 2x + 3y - 7 = 0

First, convert the equation 2x + 3y - 7 = 0 into the slope-intercept form, y = mx + c, to find its slope, m.

3y=−2x+7y=−23x+73m2=−233y = -2x + 7 \\[1em] y = -\dfrac{2}{3}x + \dfrac{7}{3} \\[1em] m_2 = -\dfrac{2}{3}

The product of slopes of perpendicular lines is equal to -1:

⇒m1×m2=−1⇒(1m)×(−23)=−1⇒−23m=−1⇒−2=−3m⇒m=23.\Rightarrow m_1 \times m_2 = -1 \\[1em] \Rightarrow \Big(\dfrac{1}{m}\Big) \times \Big(-\dfrac{2}{3}\Big) = -1 \\[1em] \Rightarrow \dfrac{-2}{3m} = -1 \\[1em] \Rightarrow -2 = -3m \\[1em] \Rightarrow m = \dfrac{2}{3}.

Hence, option 2 is the correct option.

Question 39

The equation of the straight line passing through the point (1, 2) and parallel to the line y = 3x + 1, is:

  1. x – 3y + 1 = 0

  2. 3x + y + 1 = 0

  3. 3x – y – 1 = 0

  4. 3x – y + 1 = 0

Answer

The given line is y=3x+1y = 3x + 1, so its slope is m = 3.

Since the required line is parallel, its slope is also m = 3.

Using the point-slope form y - y1 = m(x - x1) with the point (x1, y1) = (1, 2) and m=3:

y - 2 = 3(x - 1)

y - 2 = 3x - 3

Rearranging the equation to the standard form (Ax + By + C = 0):

0 = 3x - y - 3 + 2

3x - y - 1 = 0

Hence, option 3 is the correct option.

Question 40

The slope of the line, ax + by + c = 0, is:

  1. −ab-\dfrac{a}{b}

  2. −ba-\dfrac{b}{a}

  3. cb\dfrac{c}{b}

  4. ba\dfrac{b}{a}

Answer

Convert the general linear equation ax + by + c = 0 into the slope-intercept form, y = mx + c, to find the slope, m.

by = -ax - c

y=(−ab)x−cby = \Big(\dfrac{-a}{b}\Big)x - \dfrac{c}{b}

The slope, m, is the coefficient of x.

m = −ab-\dfrac{a}{b}

Hence, option 1 is the correct option.

Question 41

If two lines are perpendicular to one another, then the relation between their slopes m1 and m2 is:

  1. m1 = m2

  2. m1=1m2m_1 = \dfrac{1}{m_2}

  3. m1 = –m2

  4. m1 × m2 = -1

Answer

If two lines are perpendicular, then the product of their slopes must be -1.

m1 × m2 = -1.

Hence, option 4 is the correct option.

Assertion Reason Questions

Question 1

Assertion (A): The slope of the line passing through the points (3, –2) and (–7, –2) is 0.

Reason (R): The gradient (slope) of a line passing through the points (x1, y1) and (x2, y2) is x2−x1y2−y1\dfrac{x_2 - x_1}{y_2 - y_1}.

  1. A is true, R is false

  2. A is false, R is true

  3. Both A and R are true

  4. Both A and R are false

Answer

By formula,

Slope = y2−y1x2−x1=−2−(−2)−7−3=0−10=0\dfrac{y_2 - y_1}{x_2 - x_1} = \dfrac{-2 - (-2)}{-7 - 3} = \dfrac{0}{-10} = 0

The Assertion (A) is True and Reason (R) is false.

A is true, R is false

Hence, option 1 is the correct option.

Question 2

Assertion (A): The angle of inclination of the line y = x3\dfrac{x}{\sqrt{3}} – 5 is 60°.

Reason (R): The gradient m of a line is given by m = tan θ.

  1. A is true, R is false

  2. A is false, R is true

  3. Both A and R are true

  4. Both A and R are false

Answer

y = 13\dfrac{1}{\sqrt3}x - 5

Comparing above equation with y = mx + c, we get: m = 13\dfrac{1}{\sqrt3}

tan⁡θ=13\tan \theta = \dfrac{1}{\sqrt{3}}

tan θ = tan 30°

θ = 30°.

Assertion (A) is False.

The gradient (m) of a line is given by m = tan θ, where θ is the angle of inclination. This formula is the correct definition of the slope in relation to the angle of inclination.

Reason (R) is True.

A is false, R is true.

Hence, option 2 is the correct option.

Question 3

Assertion (A): The slope of the line perpendicular to the line passing through the points (2, 5) and (–3, 6) is given by 5.

Reason (R): The product of the slopes of two perpendicular lines is always –1.

  1. A is true, R is false

  2. A is false, R is true

  3. Both A and R are true

  4. Both A and R are false

Answer

Slope (m1) = y2−y1x2−x1=6−5−3−2=−15\dfrac{y_2 - y_1}{x_2 - x_1} = \dfrac{6 - 5}{-3 -2} = -\dfrac{1}{5}

The product of the slopes of two perpendicular lines is always –1. Let slope of perpendicular line be m2.

⇒ m1 × m2 = -1

⇒ −15-\dfrac{1}{5} × m2 = -1

⇒ m2 = 5.

Both A and R are true

Hence, option 3 is the correct option.

Question 4

Assertion (A): The equation of the line whose inclination is 45° and which intersects the y-axis at the point (0, –4) is x – y = 4.

Reason (R): The equation of the line having slope m and y-intercept c is given by y = cx + m.

  1. A is true, R is false

  2. A is false, R is true

  3. Both A and R are true

  4. Both A and R are false

Answer

The slope is m = tan θ

m = tan 45° = 1

The line intersects the y-axis at (0, -4), so the y-intercept is c = -4.

By Slope-intercept form,

Equation of line :

⇒ y = mx + c

⇒ y = 1x + (-4)

⇒ y = x - 4

⇒ x - y = 4

Assertion (A) is True.

The correct slope-intercept form is y = mx + c, where m is the slope (gradient) and c is the y-intercept.

Reason (R) is False.

A is true, R is false.

Hence, option 1 is the correct option.

Question 5

Assertion (A): A line is parallel to the line 2x – 3y = 7 and it passes through the point (0, 4). The equation of this line is 2x – 3y – 12 = 0.

Reason (R): If two lines are parallel, then sum of their slopes is equal to 1.

  1. A is true, R is false

  2. A is false, R is true

  3. Both A and R are true

  4. Both A and R are false

Answer

A line is parallel to 2x − 3y = 7 and passes through (0, 4).

⇒ 2x - 3y = 7

⇒ -3y = -2x + 7

⇒ y = 23x−73\dfrac{2}{3}x - \dfrac{7}{3}

Comparing above equation with y = mx + c, we get: m = 23\dfrac{2}{3}

Since the lines are parallel, the slope of parallel line = 23\dfrac{2}{3}.

The required line passes through (0, 4), so its y-intercept is c = 4.

Using the slope-intercept form y = mx + c:

⇒ y = 23\dfrac{2}{3}x + 4

⇒ 3y = 2x + 12

⇒ 2x - 3y + 12 = 0

Assertion (A) is False.

The condition for two lines to be parallel is that their slopes are equal m1 = m2.

Reason (R) is False.

Hence, option 4 is the correct option.

PrevNext