In equation 2x - 5 = 0; ordinate is :
0
2
-5
1
Answer
In the equation 2x − 5 = 0, we need to find the ordinate, which means the y-coordinate of a point on the graph of this equation.
2x - 5 = 0
⇒ 2x = 5
⇒ x =
⇒ x = 2.5
Notice that this equation only involves x and has no y-term. This tells us that the equation represents a vertical line parallel to y-axis at x = 2.5. Hence, ordinate = 0 (i.e., y = 0).
Hence, option 1 is the correct option.
In equation , the independent variable is :
y
x
Answer
Given:
In the above equation, the value of y depends on the value of x, so y is said to be dependent variable and x is said to be independent variable.
Hence, option 2 is the correct option.
If (2x - 1, y + 5) = (3, 10), the values of x and y are :
x = 4, y = 5
x = 8, y = 5
x = 2, y = 5
x = 1, y = 5
Answer
Since two ordered pairs are equal, their first components are equal and their second components are separately equal.
(2x - 1, y + 5) = (3, 10)
⇒ 2x - 1 = 3 and y + 5 = 10
⇒ 2x = 3 + 1 and y = 10 - 5
⇒ 2x = 4 and y = 5
⇒ x = and y = 5
⇒ x = 2 and y = 5
Hence, option 3 is the correct option.
(5, -7) belongs to :
1st quadrant
2nd quadrant
3rd quadrant
4th quadrant
Answer
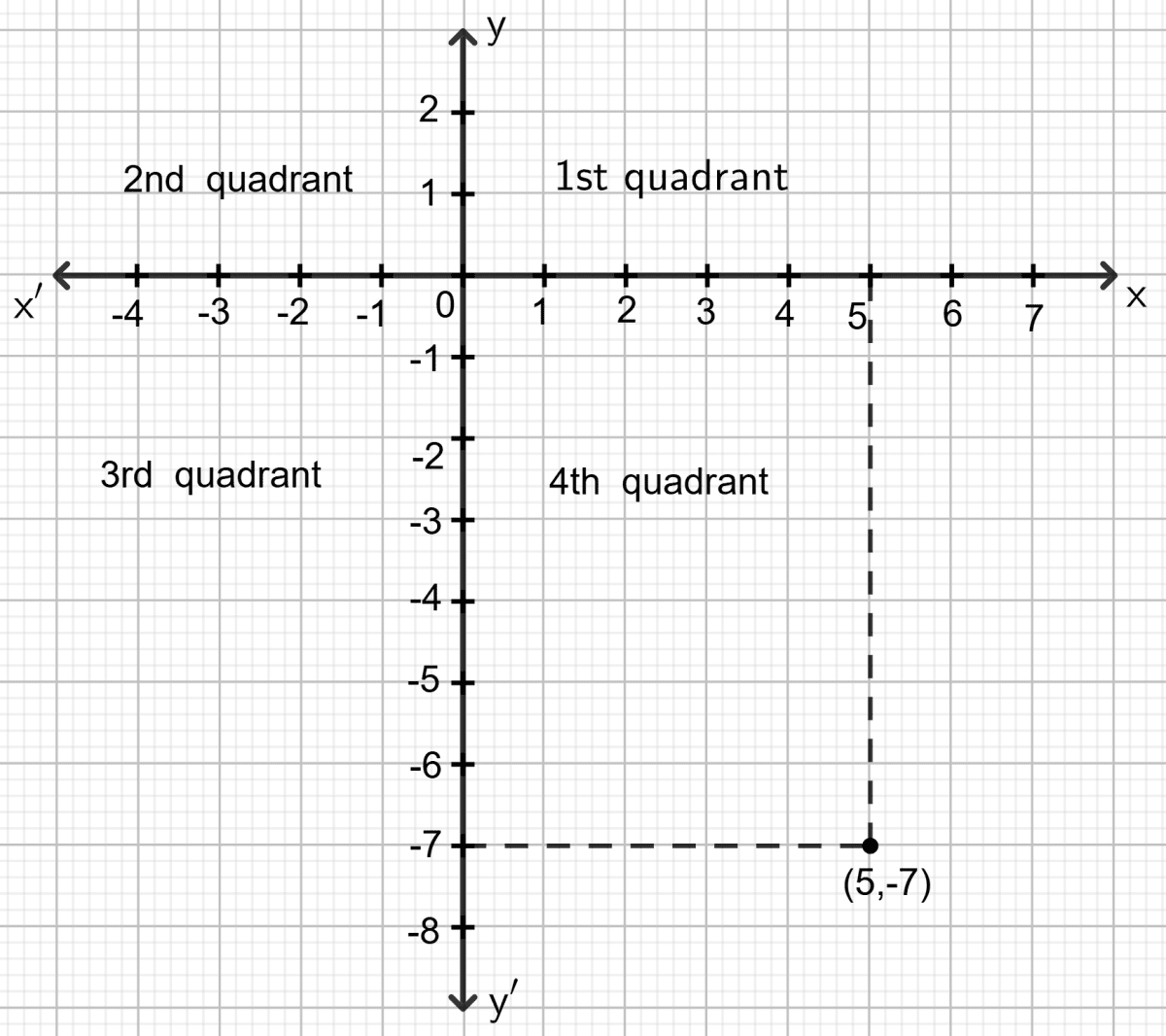
The point (5, -7) has a positive x-coordinate and a negative y-coordinate. This places it in the 4th quadrant.
Hence, option 4 is the correct option.
Abscissa of a point is the solution of equation 3x - 2 = 7 and its ordinate is the solution of equation 8 - 3y = 2. The point is :
(3, 2)
(-3, 2)
(3, -2)
(-3, -4)
Answer
Given:
3x - 2 = 7
⇒ 3x = 7 + 2
⇒ 3x = 9
⇒ x =
⇒ x = 3
And, 8 - 3y = 2
⇒ 3y = 8 - 2
⇒ 3y = 6
⇒ y =
⇒ y = 2
Therefore, the co-ordinates of the point = (3, 2).
Hence, option 1 is the correct option.
For each equation given below; name the dependent and independent variables.
(i)
(ii) x = 9y + 4
(iii)
(iv)
Answer
(i)
In the above equation, the value of y depends on the value of x, so y is said to be dependent variable and x is said to be independent variable.
Hence, x = independent variable and y = dependent variable.
(ii) x = 9y + 4
In the above equation, the value of x depends on the value of y, so x is said to be dependent variable and y is said to be independent variable.
Hence, x = dependent and y = independent.
(iii)
In the above equation, the value of x depends on the value of y, so x is said to be dependent variable and y is said to be independent variable.
Hence, x = dependent and y = independent.
(iv)
In the above equation, the value of y depends on the value of x, so y is said to be dependent variable and x is said to be independent variable.
Hence, x = independent and y = dependent.
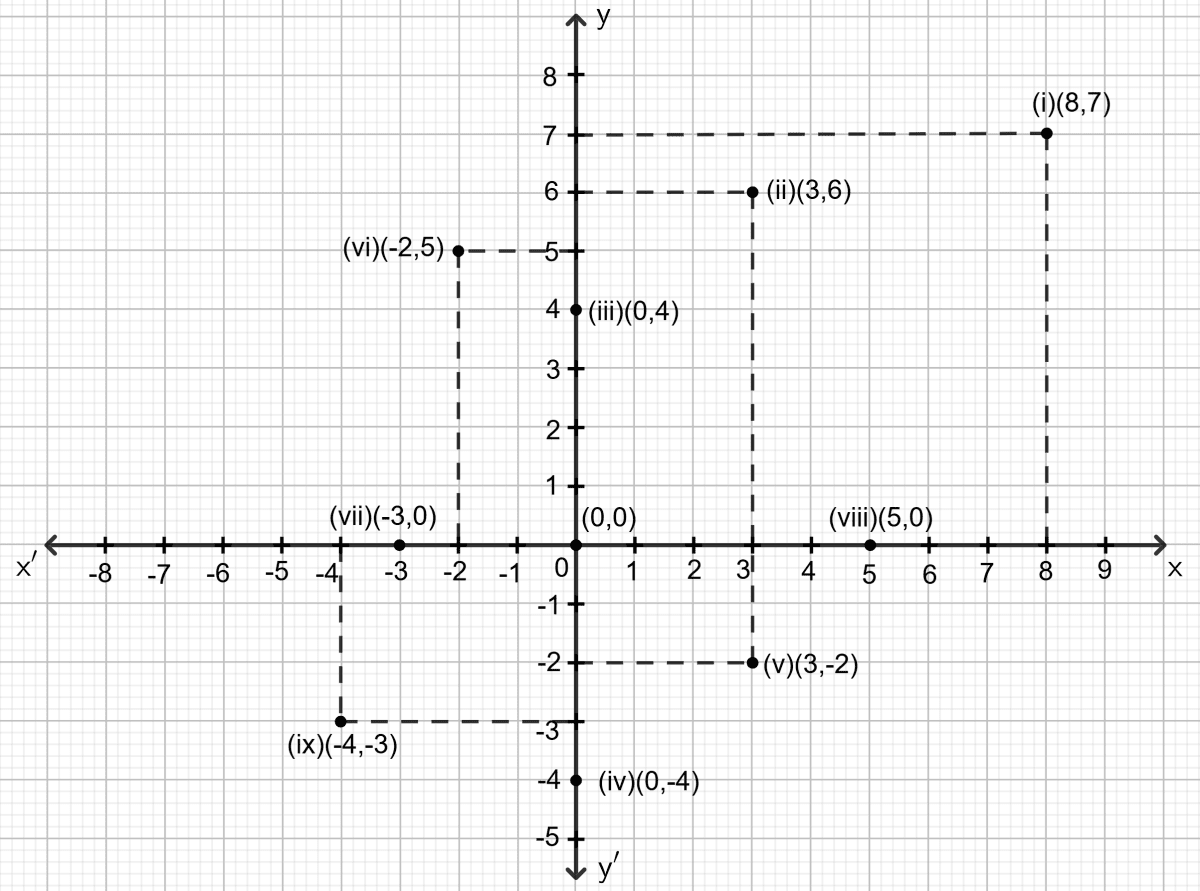
Plot the following points on the same graph paper :
(i) (8, 7)
(ii) (3, 6)
(iii) (0, 4)
(iv) (0, -4)
(v) (3, -2)
(vi) (-2, 5)
(vii) (-3, 0)
(viii) (5, 0)
(ix) (-4, -3)
Answer
Find the values of x and y if :
(i) (x - 1, y + 3) = (4, 4)
(ii) (3x + 1, 2y - 7) = (9, - 9)
(iii) (5x - 3y, y - 3x) = (4, - 4)
Answer
Since two ordered pairs are equal, their first components are equal and their second components are separately equal.
(i) (x - 1, y + 3) = (4, 4)
⇒ x - 1 = 4 and y + 3 = 4
⇒ x = 4 + 1 and y = 4 - 3
⇒ x = 5 and y = 1
Hence, x = 5 and y = 1.
(ii) (3x + 1, 2y - 7) = (9, - 9)
⇒ 3x + 1 = 9 and 2y - 7 = -9
⇒ 3x = 9 - 1 and 2y = -9 + 7
⇒ 3x = 8 and 2y = -2
⇒ x = and y = -
⇒ x = and y = -1
Hence, x = and y = -1.
(iii) (5x - 3y, y - 3x) = (4, - 4)
⇒ 5x - 3y = 4 ................(1)
And, y - 3x = - 4
⇒ y = -4 + 3x ................(2)
Putting the value of y in (1), we get
⇒ 5x - 3(-4 + 3x) = 4
⇒ 5x + 12 - 9x = 4
⇒ 5x - 9x = 4 - 12
⇒ - 4x = - 8
⇒ x =
⇒ x = 2
Putting the value of x in (2),
y = - 4 + 3x
⇒ y = - 4 + 3 x 2
⇒ y = - 4 + 6
⇒ y = 2
Hence, x = 2 and y = 2.
Use the graph given below, to find the co-ordinates of the point (s) satisfying the given conditions :
(i) the abscissa is 2.
(ii) the ordinate is 0.
(iii) the ordinate is 3.
(iv) the ordinate is - 4.
(v) the abscissa is 5.
(vi) the abscissa is equal to the ordinate.
(vii) the ordinate is half of the abscissa.

Answer
(i) The abscissa is 2.
The abscissa represents the x-coordinate, so x = 2.
Observing the graph, the y-coordinate for this point is also 2.
Hence, the point is A = (2, 2).
(ii) The ordinate is 0.
The ordinate represents the y-coordinate, so y = 0.
Observing the graph, the x-coordinate for this point is 5.
Hence, the point is B = (5, 0).
(iii) The ordinate is 3.
The ordinate represents the y-coordinate, so y = 3.
Observing the graph, the x-coordinates for this point are -4 and 6.
Hence, the points are C = (-4, 3) and E = (6, 3).
(iv) The ordinate is - 4.
The ordinate represents the y-coordinate, so y = - 4.
Observing the graph, the x-coordinate for this point is 2.
Hence, the point is D = (2, -4).
(v) The abscissa is 5.
The abscissa represents the x-coordinate, so x = 5.
Observing the graph, the y-coordinates for this point are 0, 5 and -3.
Hence, the points are B = (5, 0), H = (5, 5) and G = (5, -3).
(vi) The abscissa is equal to the ordinate.
The abscissa represents the x-coordinate, and ordinate represents the y-coordinate so x = y.
Observing the graph, the points are (2,2), (5, 5) and (4, 4).
Hence, the points are A = (2, 2), H = (5, 5) and I = (4, 4).
(vii) The ordinate is half of the abscissa.
The abscissa represents the x-coordinate, and ordinate represents the y-coordinate so y = .
Observing the graph, the point is (6, 3).
Hence, the point is E = (6, 3).
State, true or false :
(i) The ordinate of a point is its x-co-ordinate.
(ii) The origin is in the first quadrant.
(iii) The y-axis is the vertical number line.
(iv) Every point is located in one of the four quadrants.
(v) If the ordinate of a point is equal to its abscissa; the point lies either in the first quadrant or in the second quadrant.
(vi) The origin (0, 0) lies on the x-axis.
(vii) The point (a, b) lies on the y-axis if b = 0.
Answer
(i) False
Reason :
The ordinate is the y-co-ordinate of a point.
(ii) False
Reason :
The origin (0, 0) is the point where the x-axis and y-axis intersect.
(iii) True
Reason :
The y-axis is the vertical number line and the x-axis is the horizontal number line in the coordinate plane.
(iv) False
Reason :
Points that lie on the x-axis or y-axis are not located in any of the four quadrants.
(v) False
Reason :
If the ordinate (y-coordinate) equals the abscissa (x-coordinate), (x = y), the point lies either in the first quadrant (x > 0, y > 0) or the third quadrant (x < 0, y < 0).
(vi) True
Reason :
The origin (0, 0) lies on both the x-axis and y-axis, as it is the intersection point of the two axes.
(vii) False
Reason :
The point (a, b) lies on the y-axis if the x-coordinate a = 0, not b = 0.
In each of the following, find the co-ordinates of the point whose abscissa is the solution of the first equation and ordinate is the solution of the second equation :
(i) 3 - 2x = 7; 2y + 1 = 10 - .
(ii)
(iii)
Answer
(i) 3 - 2x = 7
⇒ 2x = 3 - 7
⇒ 2x = - 4
⇒ x = -
⇒ x = - 2
2y + 1 = 10 -
⇒ 2y + = 10 - 1
⇒ = 9
⇒ = 9
⇒ y =
⇒ y = 2
Hence, the co-ordinates of the point = (-2, 2).
(ii)
Hence, the co-ordinates of the point = (6, 2).
(iii)
Hence, the co-ordinates of the point = .
In each of the following, the co-ordinates of the three vertices of a rectangle ABCD are given. By plotting the given points; find, in each case, the co-ordinates of the fourth vertex :
(i) A (2, 0), B (8, 0) and C (8, 4).
(ii) A (4, 2), B (-2, 2) and D (4, -2).
(iii) A (- 4, - 6), C (6, 0) and D (- 4, 0)
(iv) B (10, 4), C (0, 4) and D (0, - 2).
Answer
(i) After plotting the given points A(2, 0), B(8, 0) and C(8, 4) on a graph paper, join A with B and B with C. From the graph, it is clear that the vertical distance between the points B(8, 0) and C(8, 4) is 4 units. Therefore, the vertical distance between points A(2, 0) and D must be 4 units.
Now, complete the rectangle ABCD and read the coordinates of point D. As shown on the graph, D = (2, 4).

Hence, D = (2, 4).
(ii) After plotting the given points A(4, 2), B(-2, 2) and D(4, -2) on a graph paper, join A with B and A with D.
From the graph it is clear that the vertical distance between the points A(4, 2) and D(4, -2) is 4 units and the horizontal distance between the points A(4, 2) and B(-2, 2) is 6 units. Therefore, the vertical distance between points B(-2, 2) and C must be 4 units and the horizontal distance between points B(-2, 2) and C must be 6 units.
Now, complete the rectangle ABCD and read the coordinates of point C. As shown on the graph, C = (-2, 2).

Hence, C = (-2, 2).
(iii) After plotting the given points A(-4, -6), C(6, 0) and D(-4, 0) on a graph paper, join A with D and C with D.
From the graph it is clear that the vertical distance between the points A(-4, -6) and D(-4, 0) is 6 units and the horizontal distance between the points C(6, 0) and D(-4, 0) is 10 units. Therefore, the vertical distance between the points A(-4, -6) and B must be 10 units and the horizontal distance between the points C(6, 0) and B must be 10 units.
Now complete the rectangle ABCD and read the coordinates of point B. As shown on the graph, B = (6, -6).

Hence, B = (6, -6).
(iv) After plotting the given points B (10, 4), C (0, 4) and D (0, - 2) on a graph paper, join B with C and C with D.
From the graph it is clear that the vertical distance between the points C(0, 4) and D(0, -2) is 6 units and the horizontal distance between the points C(0, 4) and D(0, -2) is 10 units. Therefore, the vertical distance between the points B(10, 4) and A must be 6 units and the horizontal distance between the points D(0, -2) and B must be 10 units.
Now complete the rectangle ABCD and read the coordinates of point A. As shown on the graph, A = (10, -2).

Hence, A = (10, -2).
A (-2, 2), B (8, 2) and C (4, -4) are the vertices of a parallelogram ABCD. By plotting the given points on a graph paper; find the co-ordinates of the fourth vertex D.
Also, from the same graph, state the co-ordinates of the mid-points of the sides AB and CD.
Answer
Plot the points A (-2, 2), B (8, 2) and C (4, -4) on the graph paper. Join point A with B and B with C.
From the graph, it is clear that the horizontal distance between the points A (-2, 2) and B (8, 2) is 10 units and the vertical distance between the points B (8, 2) and C (4, -4) is 6 units. Therefore, the vertical distance between the points A (-2, 2) and D must be 6 units and the horizontal distance between the points C (4, -4) and D must be 10 units.
Now, complete the parallelogram ABCD and read the coordinates of point D. As shown on the graph, D = (-6, -4).
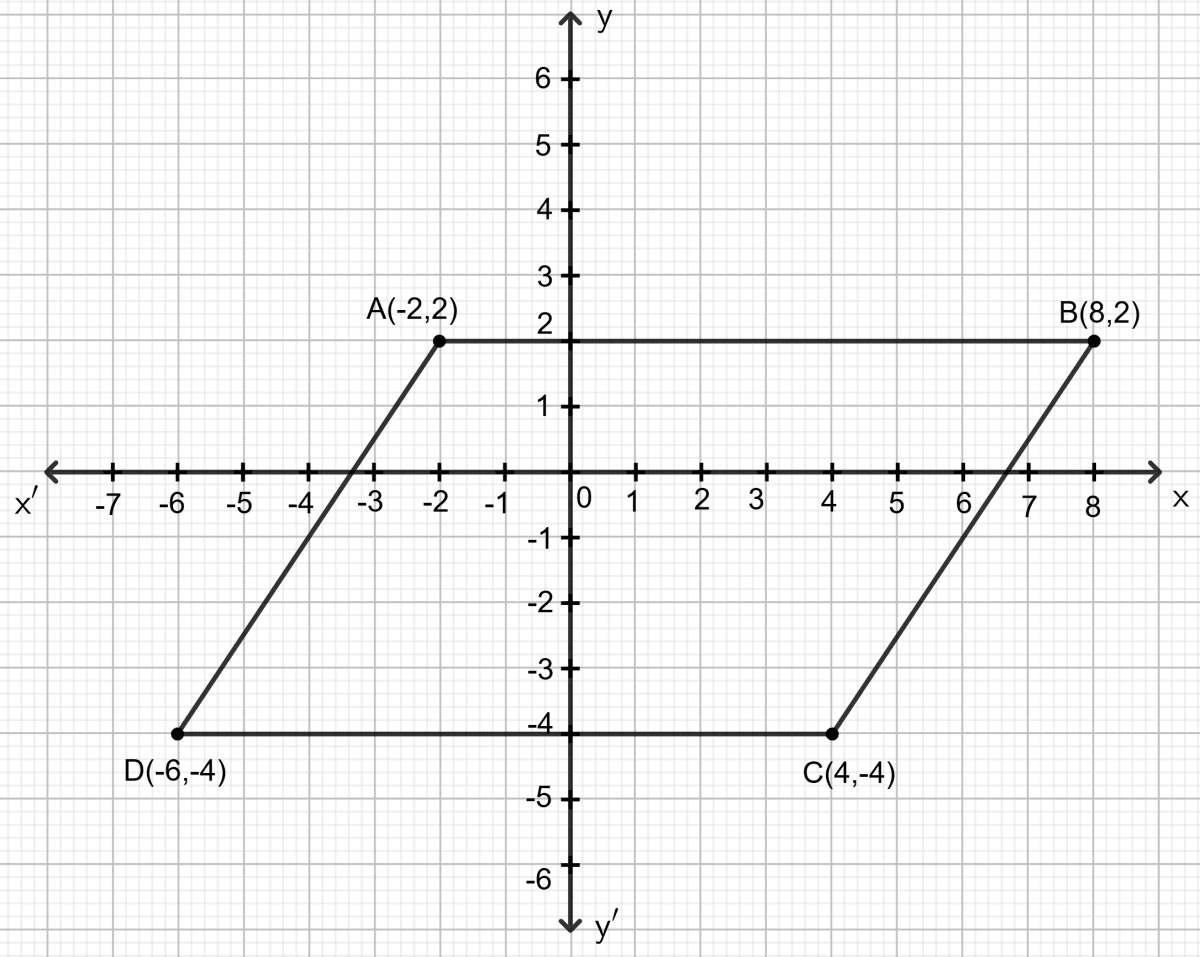
The midpoint of AB lies exactly halfway between A(-2, 2) and B(8, 2). On the graph, this midpoint is at (3, 2), as it is 5 units from both A and B.
The midpoint of CD lies exactly halfway between C (4, -4) and B (-6, -4). On the graph, this midpoint is at (-1, -4), as it is 5 units from both C and D.
Hence, D = (-6, -4) and mid point of AB = (3, 2) and CD = (-1, -4).
A (- 2, 4), C (4, 10) and D (- 2, 10) are the vertices of a square ABCD. Use the graphical method to find the co-ordinates of the fourth vertex B. Also, find :
(i) the co-ordinates of the mid-point of BC;
(ii) the co-ordinates of the mid-point of CD and
(iii) the co-ordinates of the point of intersection of the diagonals of the square ABCD.
Answer
Plot the points A (- 2, 4), C (4, 10) and D (- 2, 10) on the graph paper. Join point A with D and D with C.
From the graph, it is clear that the horizontal distance between the points C (4, 10) and D (-2, 10) is 6 units and the vertical distance between the points A (-2, 4) and D (-2, 10) is 6 units. Therefore, the vertical distance between the points C (4, 10) and B must be 6 units and the horizontal distance between the points A (-2, 4) and B must be 6 units.
Now, complete the square ABCD and read the coordinates of point B, as shown on the graph, B = (4, 4).
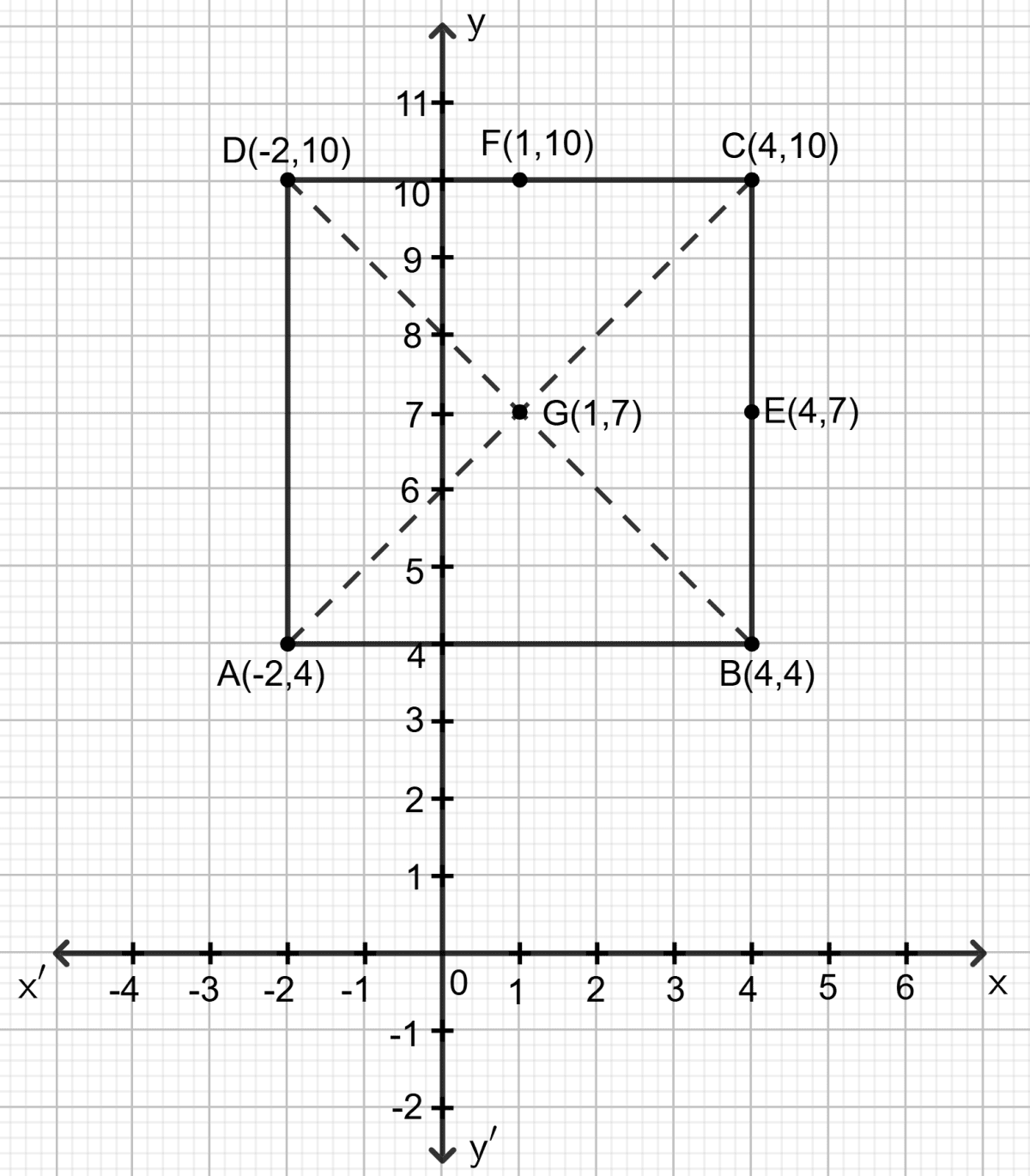
The midpoint of BC lies exactly halfway between B(4, 4) and C(4, 10). On the graph, this midpoint is at E(4, 7), as it is 3 units from both B and C.
The midpoint of CD lies exactly halfway between C(4, 10) and D(-2, 10). On the graph, this midpoint is at F(1, 10), as it is 3 units from both C and D.
The coordinates of the midpoint of diagonals of the square is G = (1, 7).
Hence, the co-ordinates of the mid-point of BC = (4, 7), the co-ordinates of the mid-point of CD = (1, 10) and the co-ordinates of the point of intersection of the diagonals of the square ABCD = (1, 7).
Line y + 7 = 0 is :
parallel to x-axis
parallel to y-axis
not parallel to x-axis
not parallel to y-axis
Answer
Given:
y + 7 = 0
⇒ y = -7
The graph of y = -7 is a straight line that is parallel to the x-axis and at a distance of -7 units from it.
Hence, option 1 is the correct option.
A line is parallel to y-axis and at a distance of 5 units on the positive side of the x-axis. The equation of the line is :
y = 5
y + 5 = 0
x = 5
x + 5 = 0
Answer
A line is parallel to y-axis means the equation of the line is in the form x = + a or -a units, where a is the distance from the y-axis.
If the line is at a distance of 5 units from the y-axis on the positive side, the equation will be x = 5.
Hence, option 3 is the correct option.
6x - 5y = 7 is the equation of a line. If x = 2 then the value of y will be :
1
-1
5
-5
Answer
Given:
6x - 5y = 7
If x = 2,
⇒ 6 2 - 5y = 7
⇒ 12 - 5y = 7
⇒ 12 - 7 = 5y
⇒ 5 = 5y
⇒ y =
⇒ y = 1
Hence, option 1 is the correct option.
For equation = 1, the value of y for x = 9 is :
-4
6
4
-6
Answer
Given:
When x = 9,
Hence, option 3 is the correct option.
Lines x - 4 = 0 and 3y = 1 intersect each other at point P. The co-ordinates of point P are:
Answer
x - 4 = 0 ⇒ x = 4
This line represents a vertical line parallel to y-axis.
3y = 1 ⇒ y =
This represents a horizontal line parallel to x-axis.
Since the first line has x = 4 and the second line has y = , the point od intersection P is (4, ).
Hence, option 2 is the correct option.
Draw the graph for the linear equation given below :
x = 3
Answer
x = 3
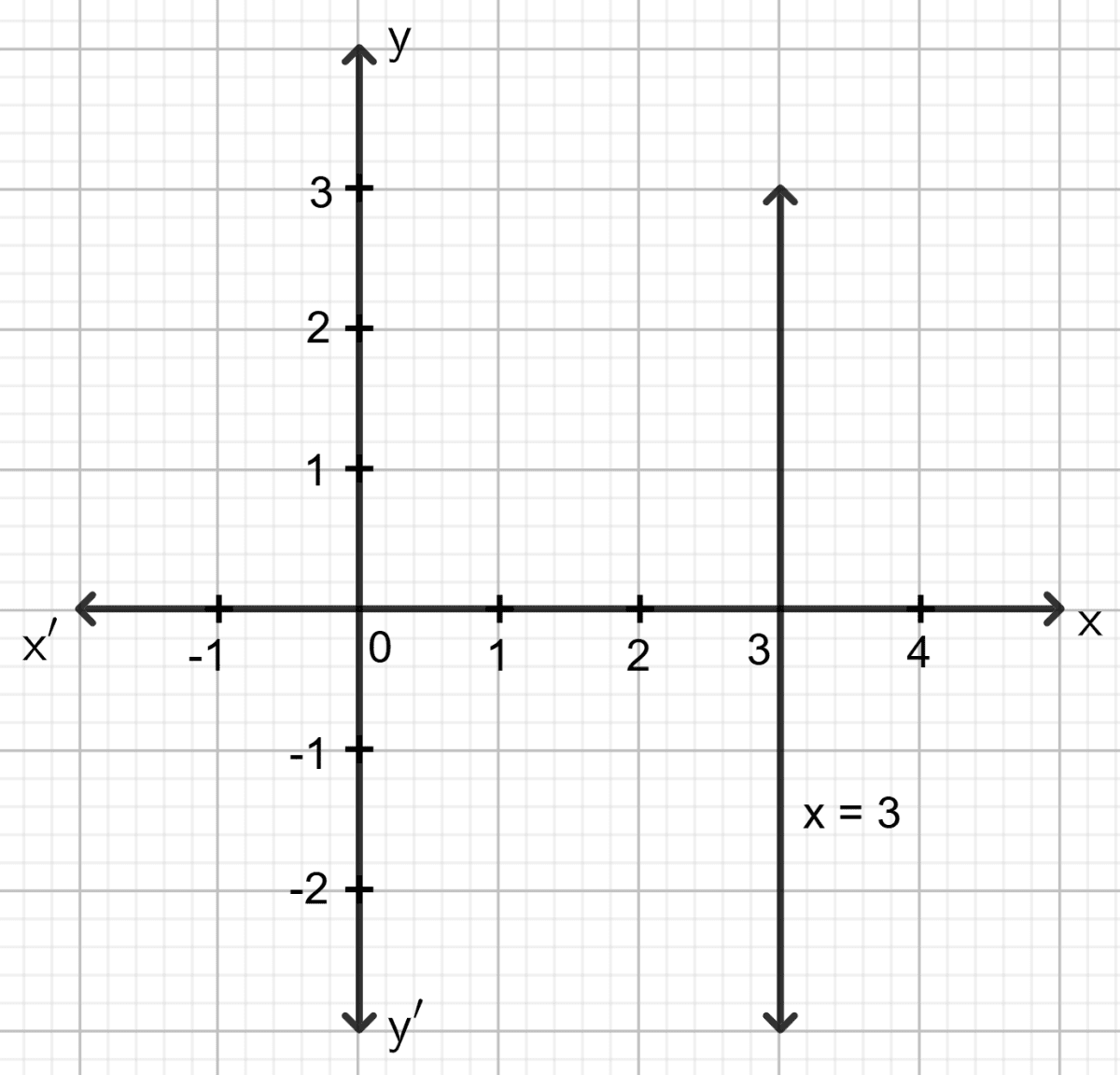
The graph of x = 3 is the straight line which is parallel to the y-axis at a distance of 3 units from it.
Draw the graph for the linear equation given below :
x + 3 = 0
Answer
x + 3 = 0
⇒ x = -3
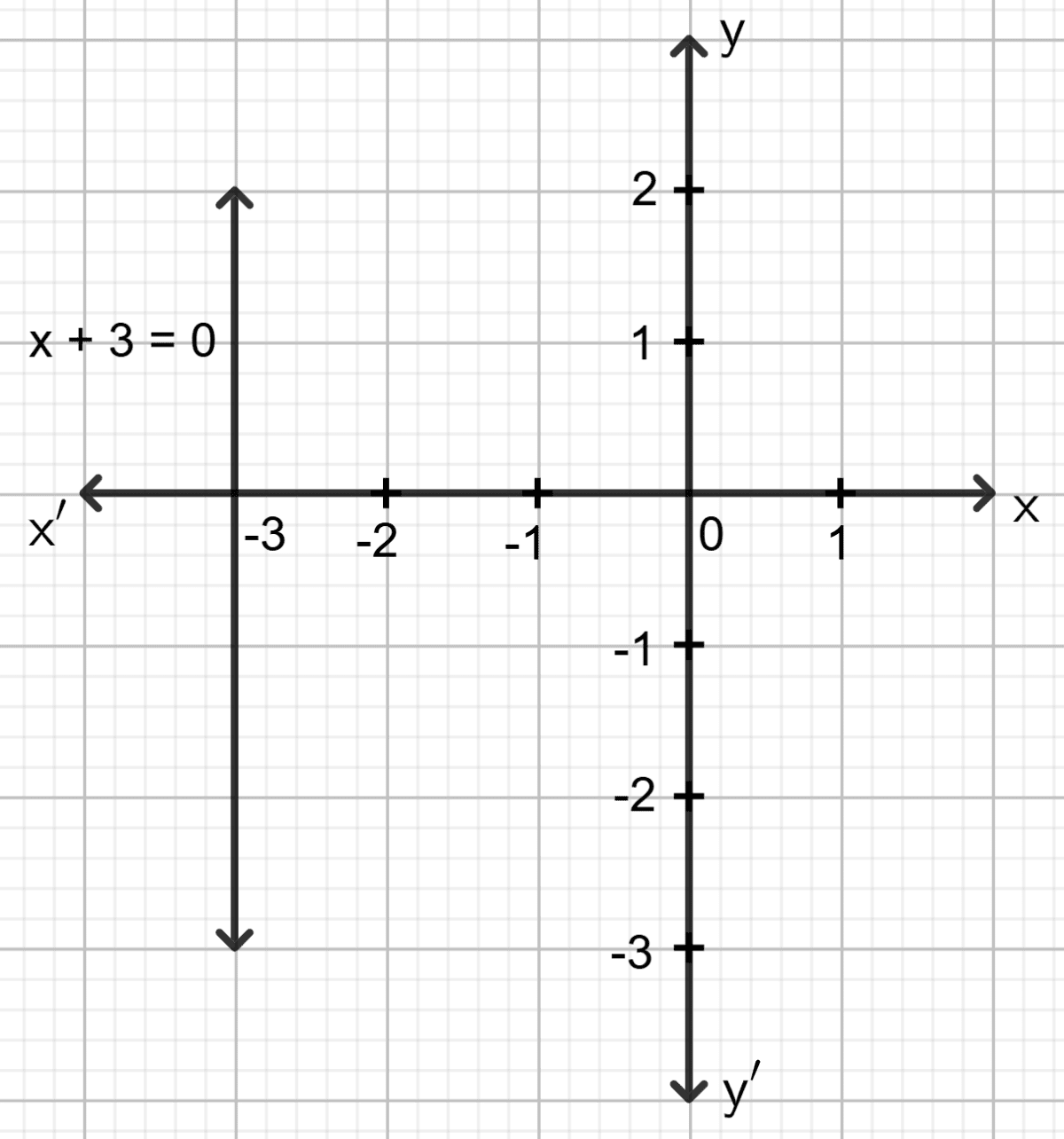
The graph of x + 3 = 0 is the straight line which is parallel to the y-axis at a distance of -3 units from it.
Draw the graph for the linear equation given below :
x - 5 = 0
Answer
x - 5 = 0
⇒ x = 5
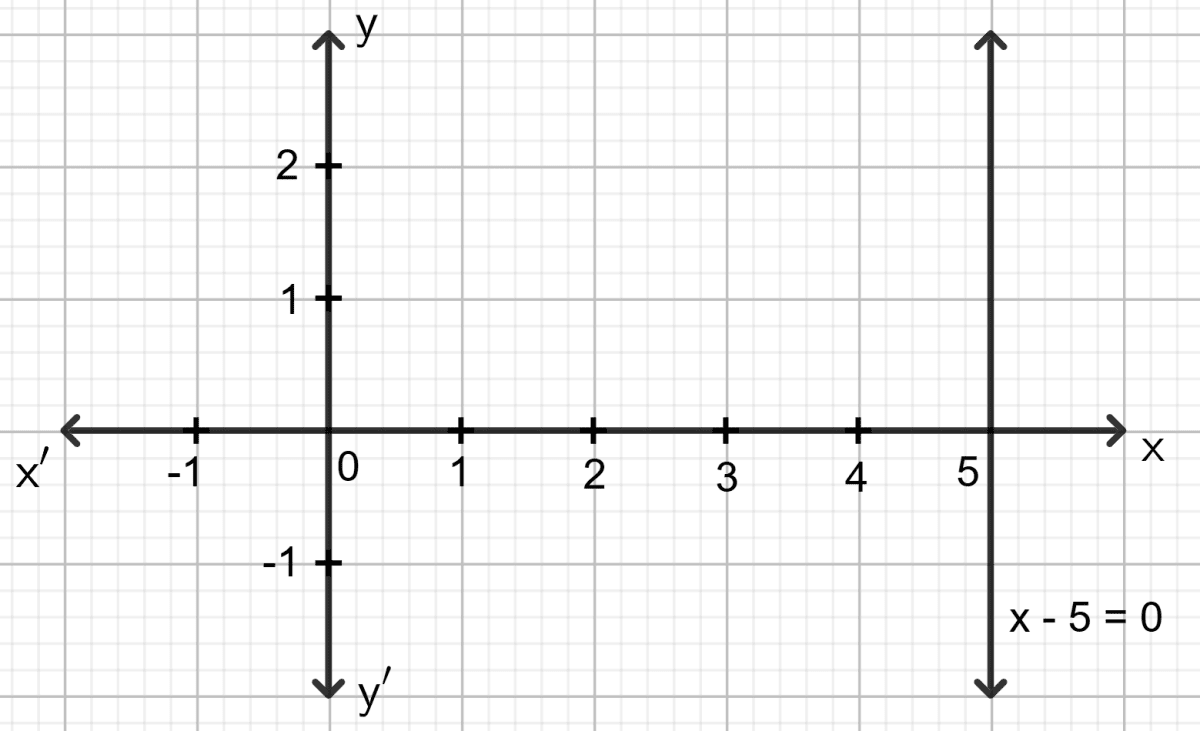
The graph of x - 5 = 0 is the straight line which is parallel to the y-axis at a distance of 5 units from it.
Draw the graph for the linear equation given below :
2x - 7 = 0
Answer
2x - 7 = 0
⇒ 2x = 7
⇒ x =
⇒ x = 3.5
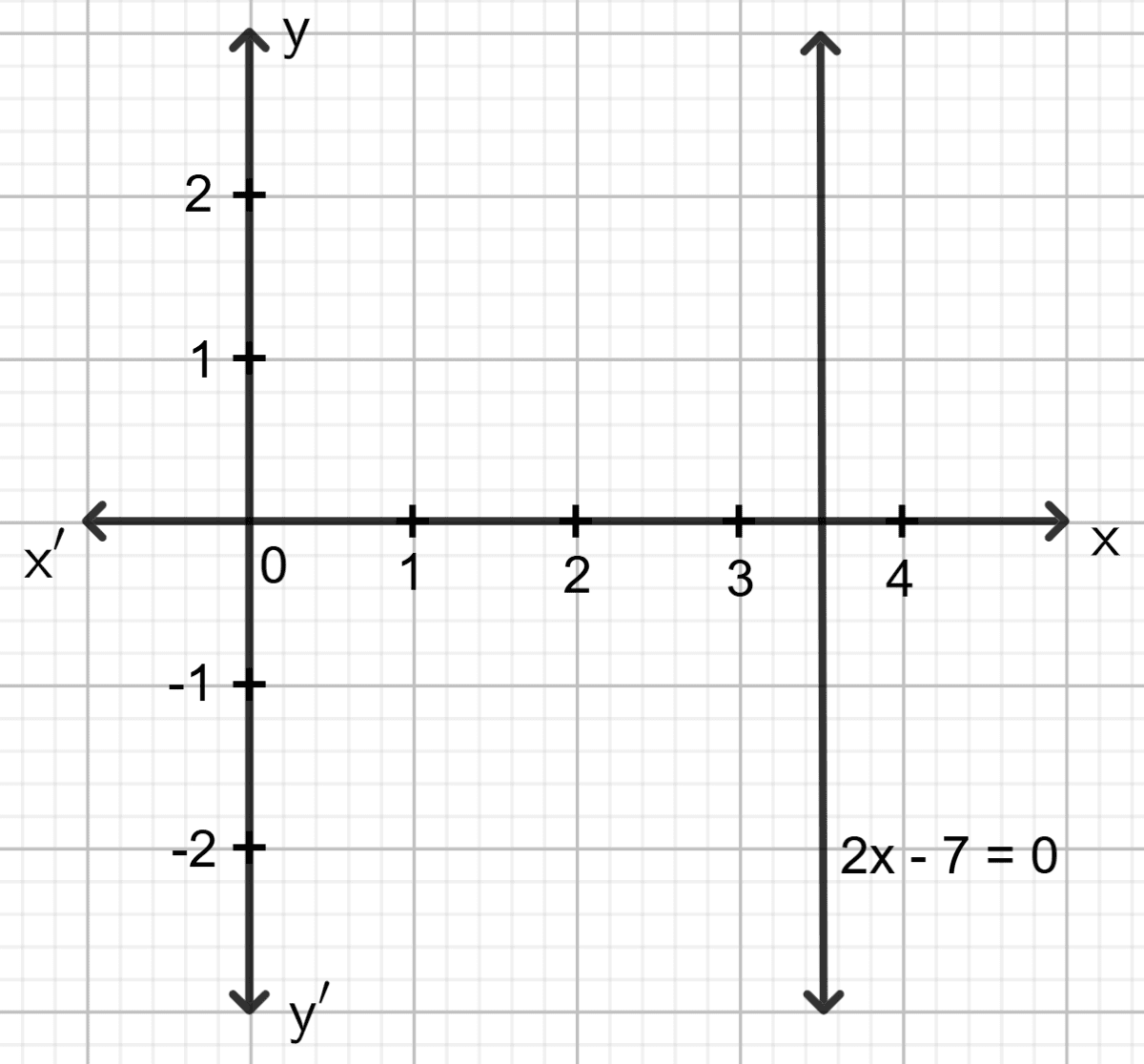
The graph of 2x - 7 = 0 is the straight line which is parallel to the y-axis at a distance of 3.5 units from it.
Draw the graph for the linear equation given below :
y = 4
Answer
y = 4

The graph of y = 4 is the straight line which is parallel to the x-axis at a distance of 4 units from it.
Draw the graph for the linear equation given below :
y + 6 = 0
Answer
y + 6 = 0
⇒ y = - 6
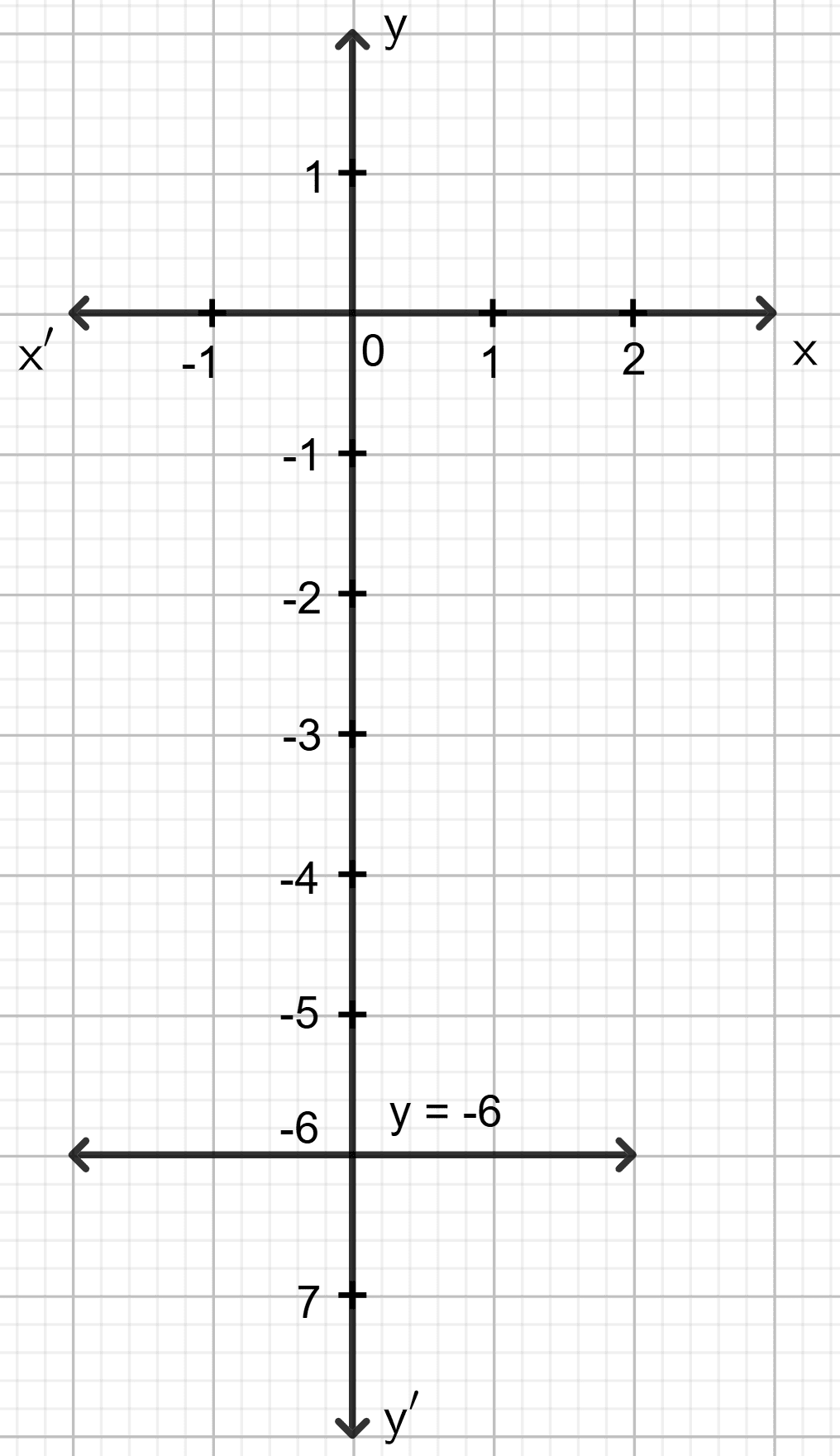
The graph of y + 6 = 0 is the straight line which is parallel to the x-axis at a distance of -6 units from it.
Draw the graph for the linear equation given below :
y - 2 = 0
Answer
y - 2 = 0
⇒ y = 2
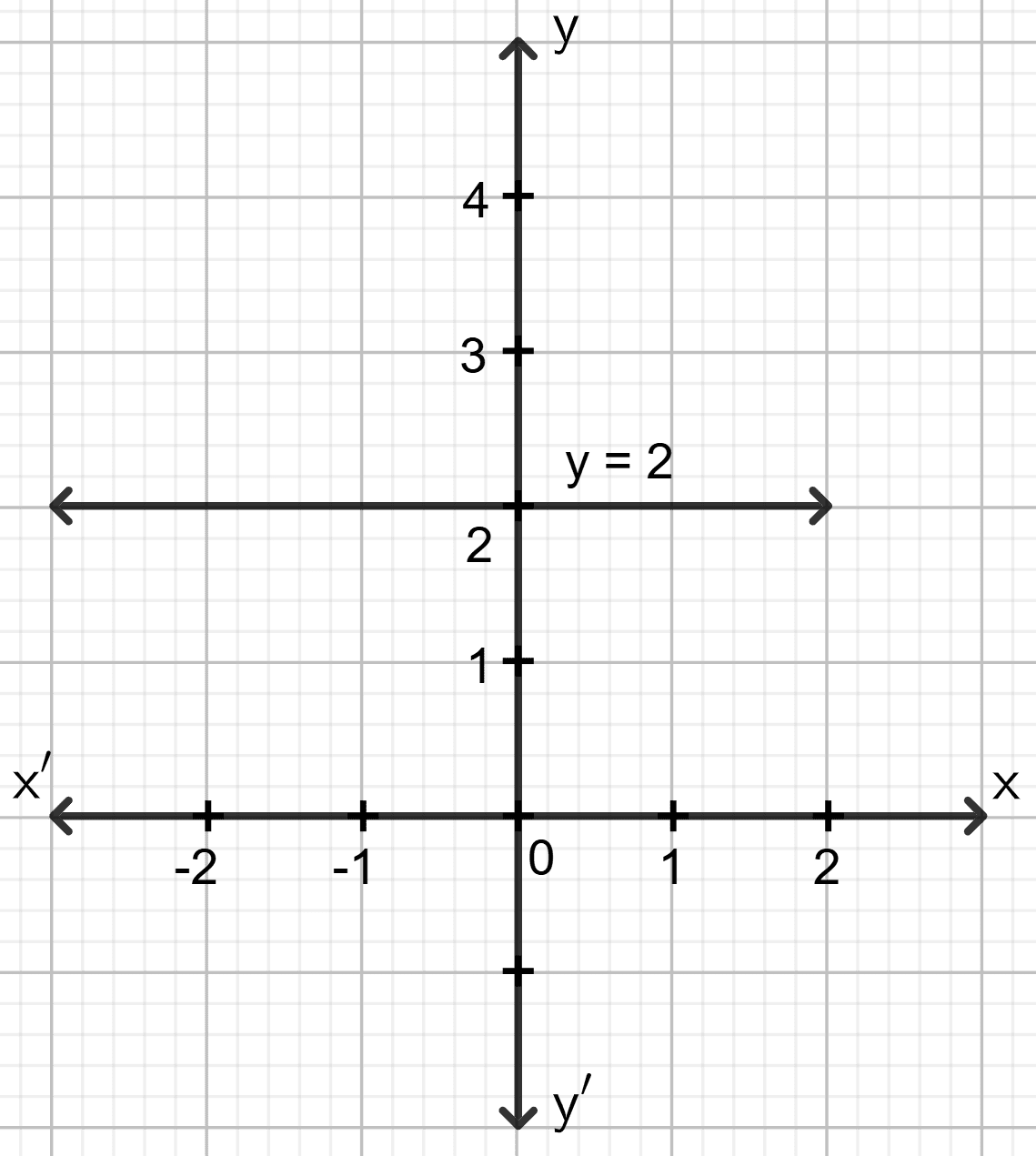
The graph of y - 2 = 0 is the straight line which is parallel to the x-axis at a distance of 2 units from it.
Draw the graph for the linear equation given below :
3y + 5 = 0
Answer
3y + 5 = 0
⇒ 3y = - 5
⇒ y = -
⇒ y = - 1.6
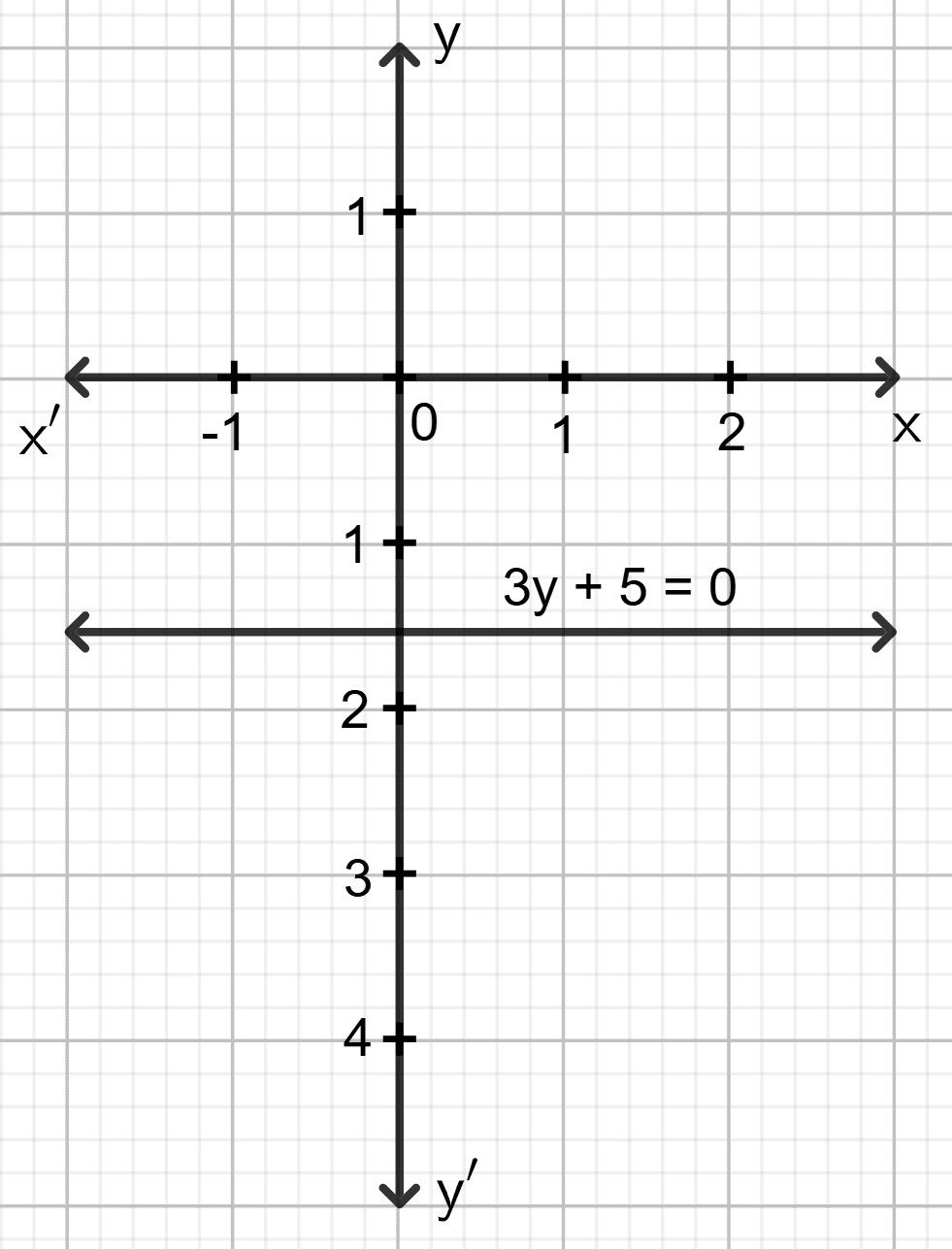
The graph of 3y + 5 = 0 is the straight line which is parallel to the x-axis at a distance of - 1.6 units from it.
Draw the graph for the linear equation given below :
2y - 5 = 0
Answer
2y - 5 = 0
⇒ 2y = 5
⇒ y =
⇒ y = 2.5
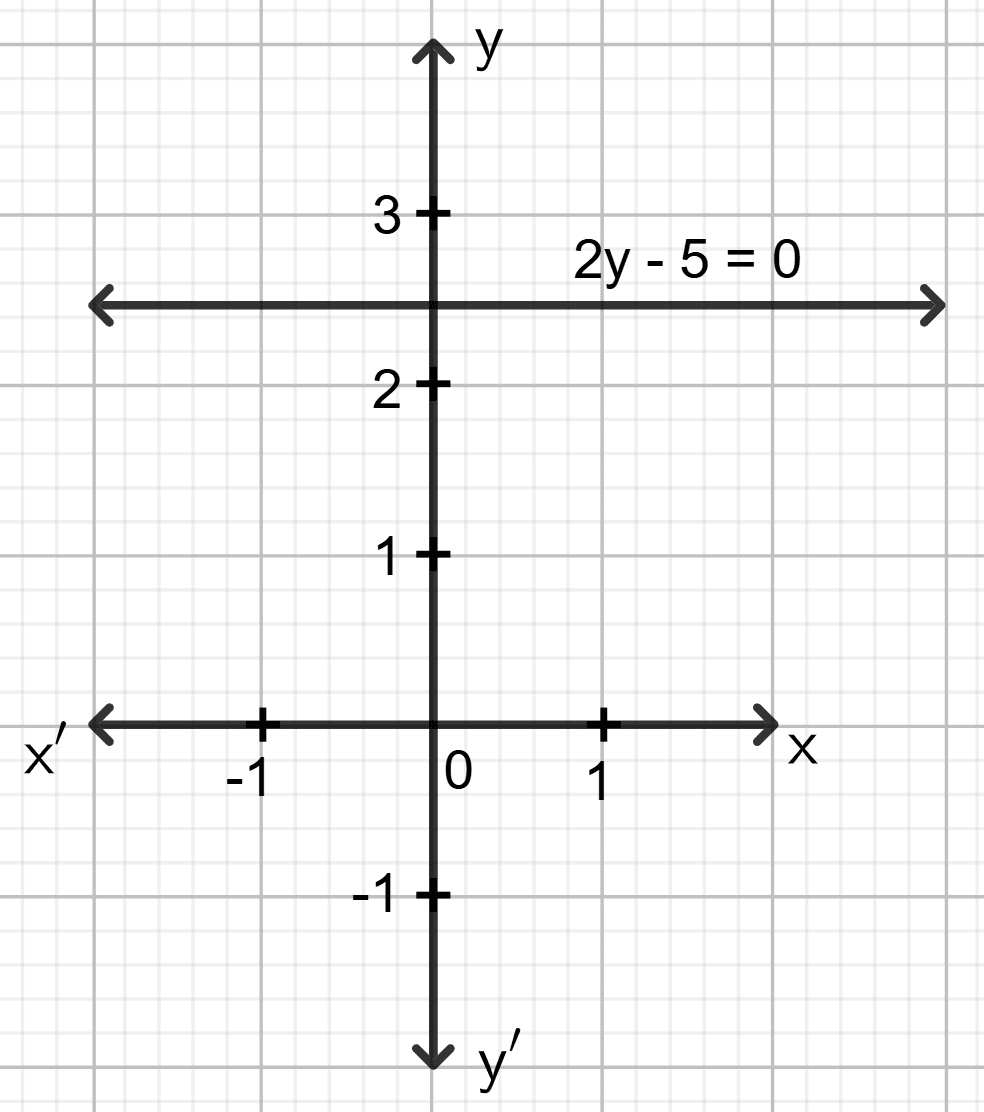
The graph of 2y - 5 = 0 is the straight line which is parallel to the x-axis at a distance of 2.5 units from it.
Draw the graph for the linear equation given below :
y = 0
Answer
y = 0
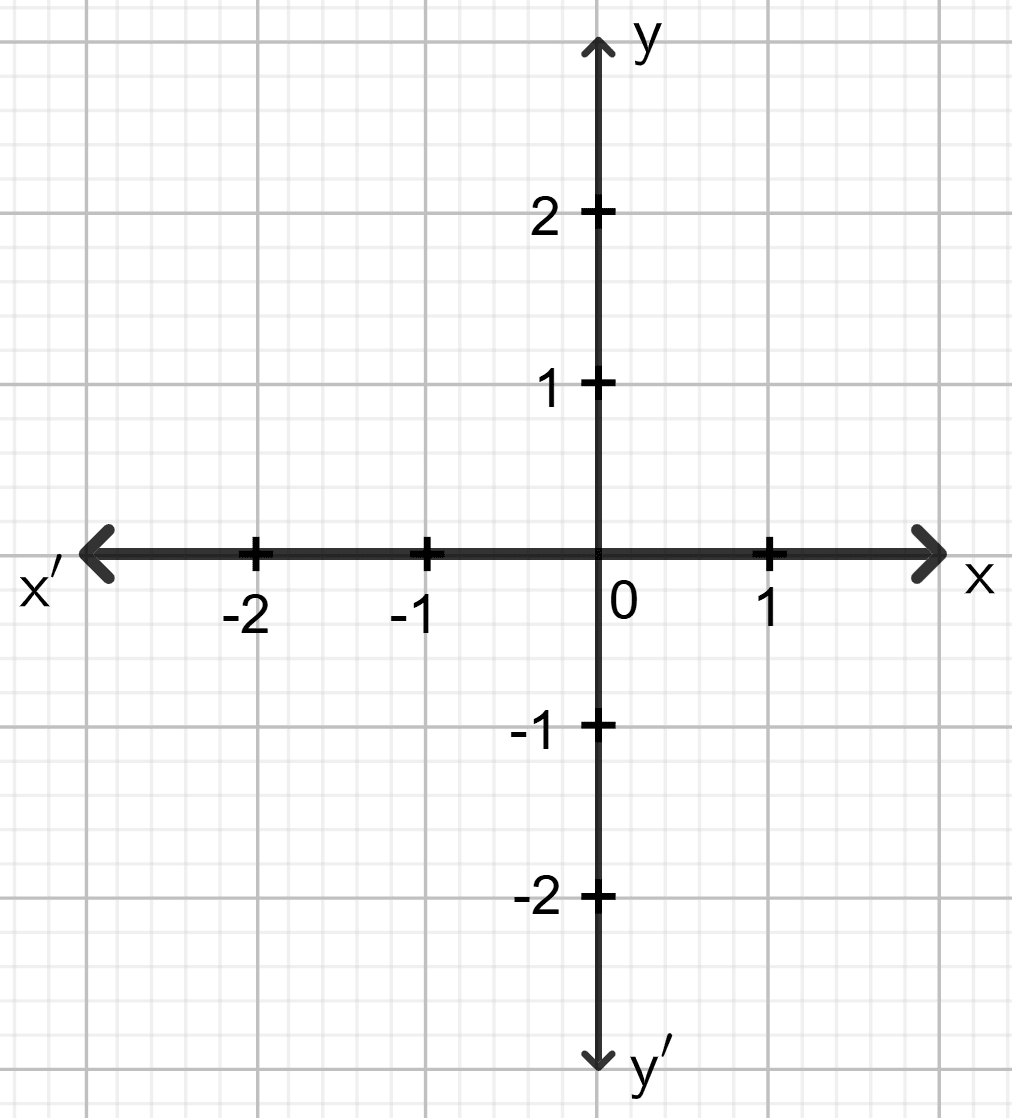
The graph of y = 0 is the straight line which is on x-axis.
Draw the graph for the linear equation given below :
x = 0
Answer
x = 0
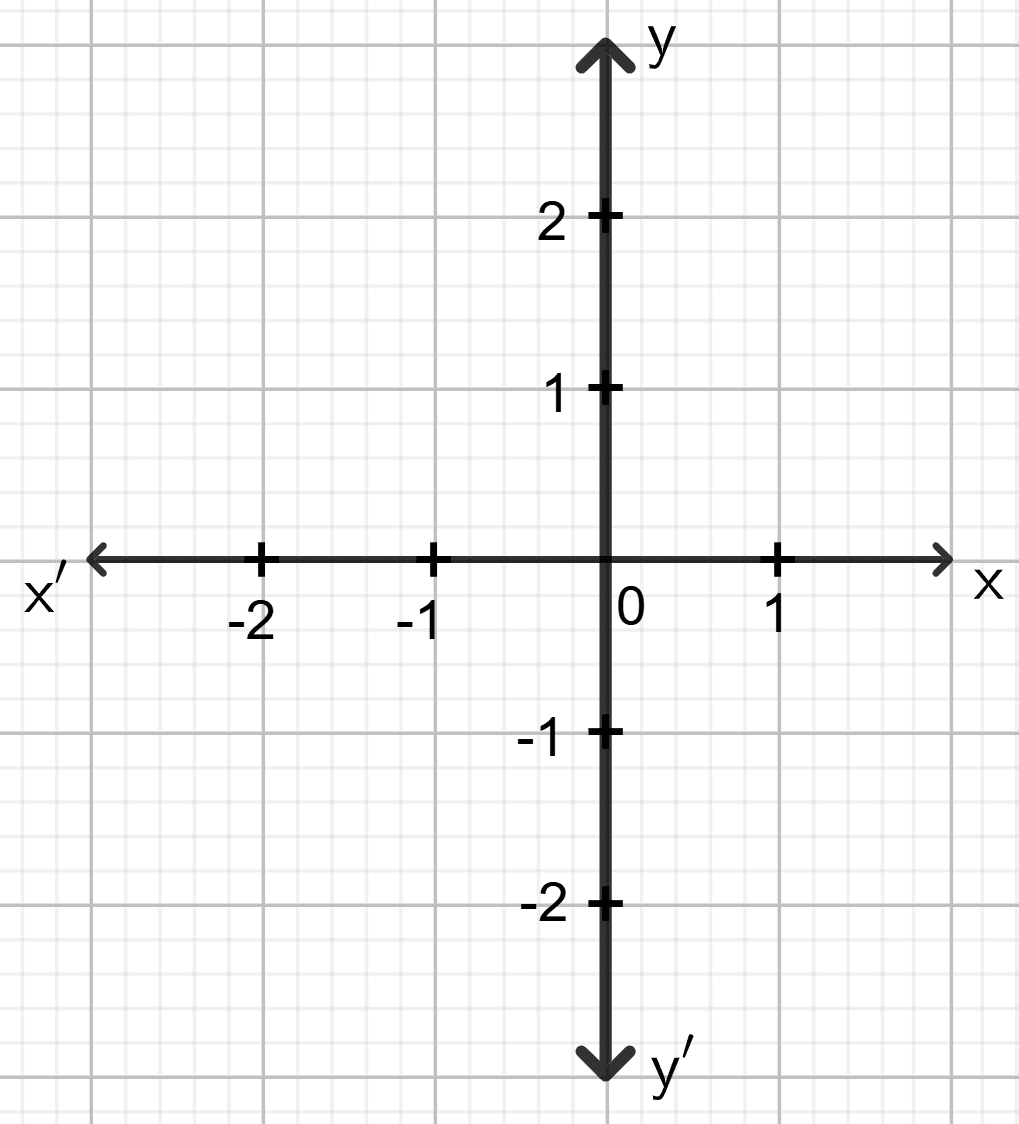
The graph of x = 0 is the straight line which is on y-axis.
Draw the graph for the linear equation given below :
y = 3x
Answer
y = 3x
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -1, then y = 3 (-1) = -3
Let x = 0, then y = 3 0 = 0
Let x = 1, then y = 3 1 = 3
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -1 | 0 | 1 |
|---|---|---|---|
| y | -3 | 0 | 3 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
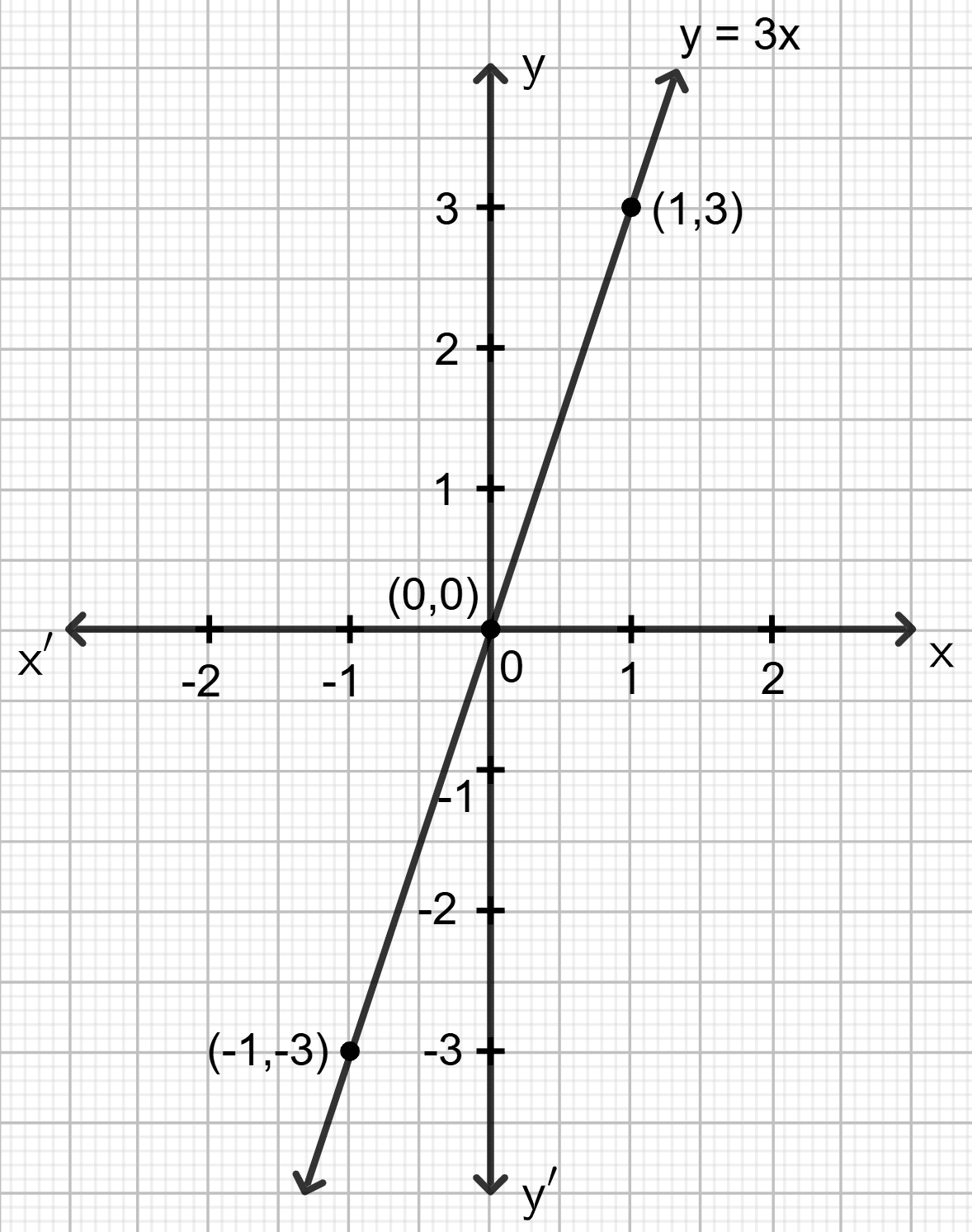
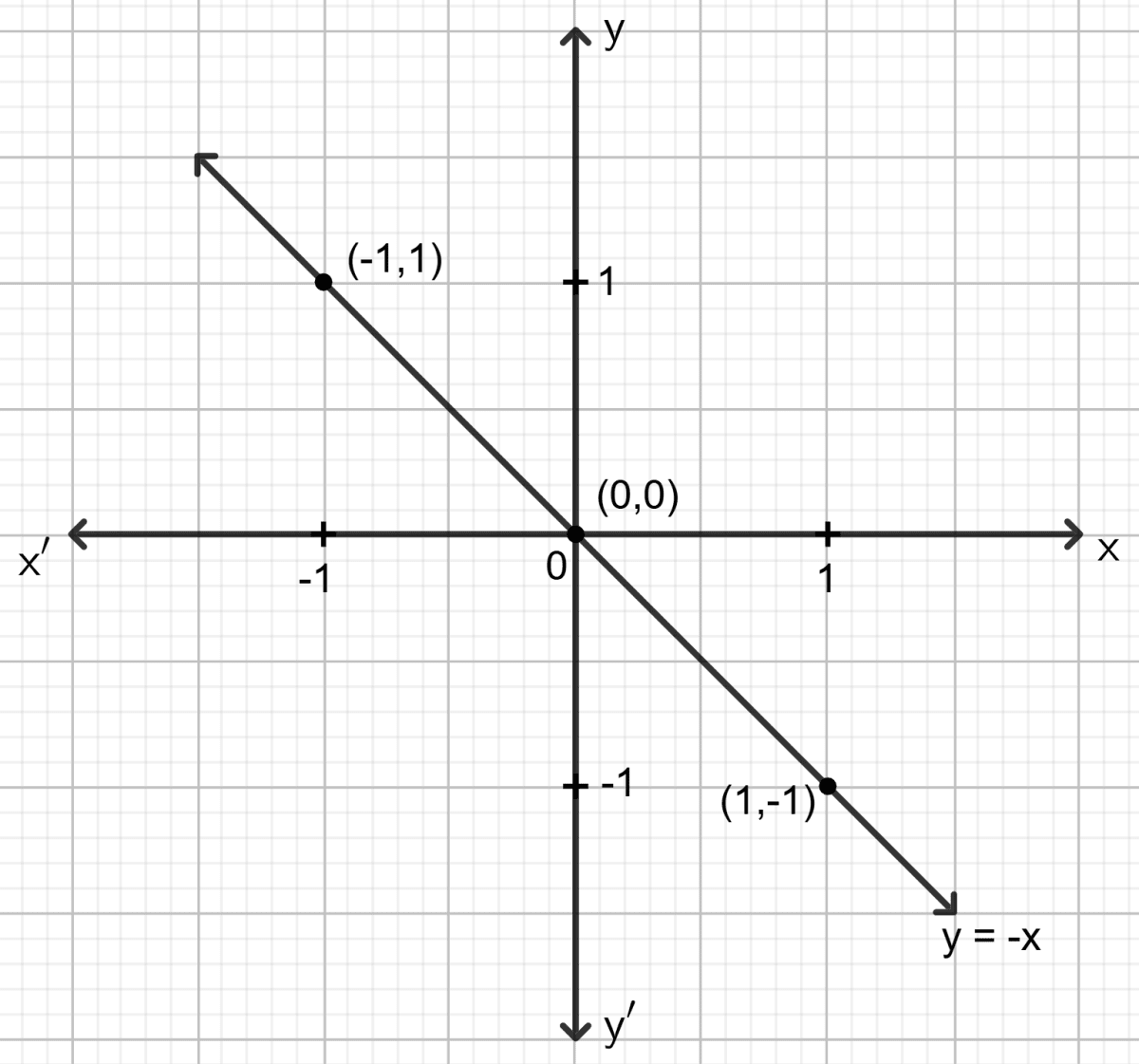
Draw the graph for the linear equation given below :
y = - x
Answer
y = - x
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -1, then y = - (-1) = 1
Let x = 0, then y = 0 = 0
Let x = 1, then y = - 1 = - 1
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -1 | 0 | 1 |
|---|---|---|---|
| y | 1 | 0 | -1 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
Draw the graph for the linear equation given below :
y = - 2x
Answer
y = - 2x
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -1, then y = - 2 (-1) = 2
Let x = 0, then y = - 2 0 = 0
Let x = 1, then y = - 2 1 = - 2
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -1 | 0 | 1 |
|---|---|---|---|
| y | 2 | 0 | -2 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
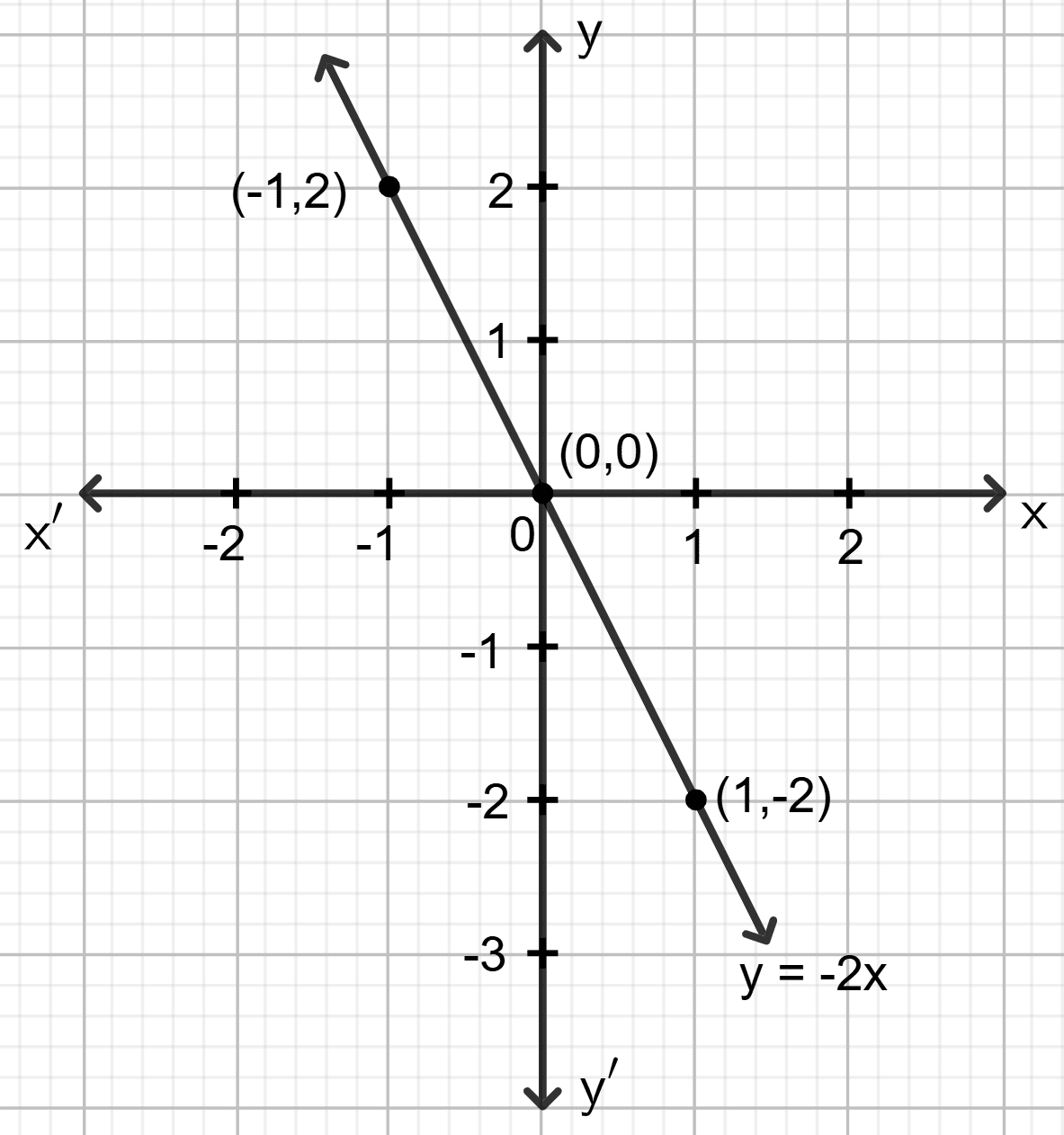
Draw the graph for the linear equation given below :
y = x
Answer
y = x
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -1, then y = -1
Let x = 0, then y = 0
Let x = 1, then y = 1
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -1 | 0 | 1 |
|---|---|---|---|
| y | -1 | 0 | 1 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
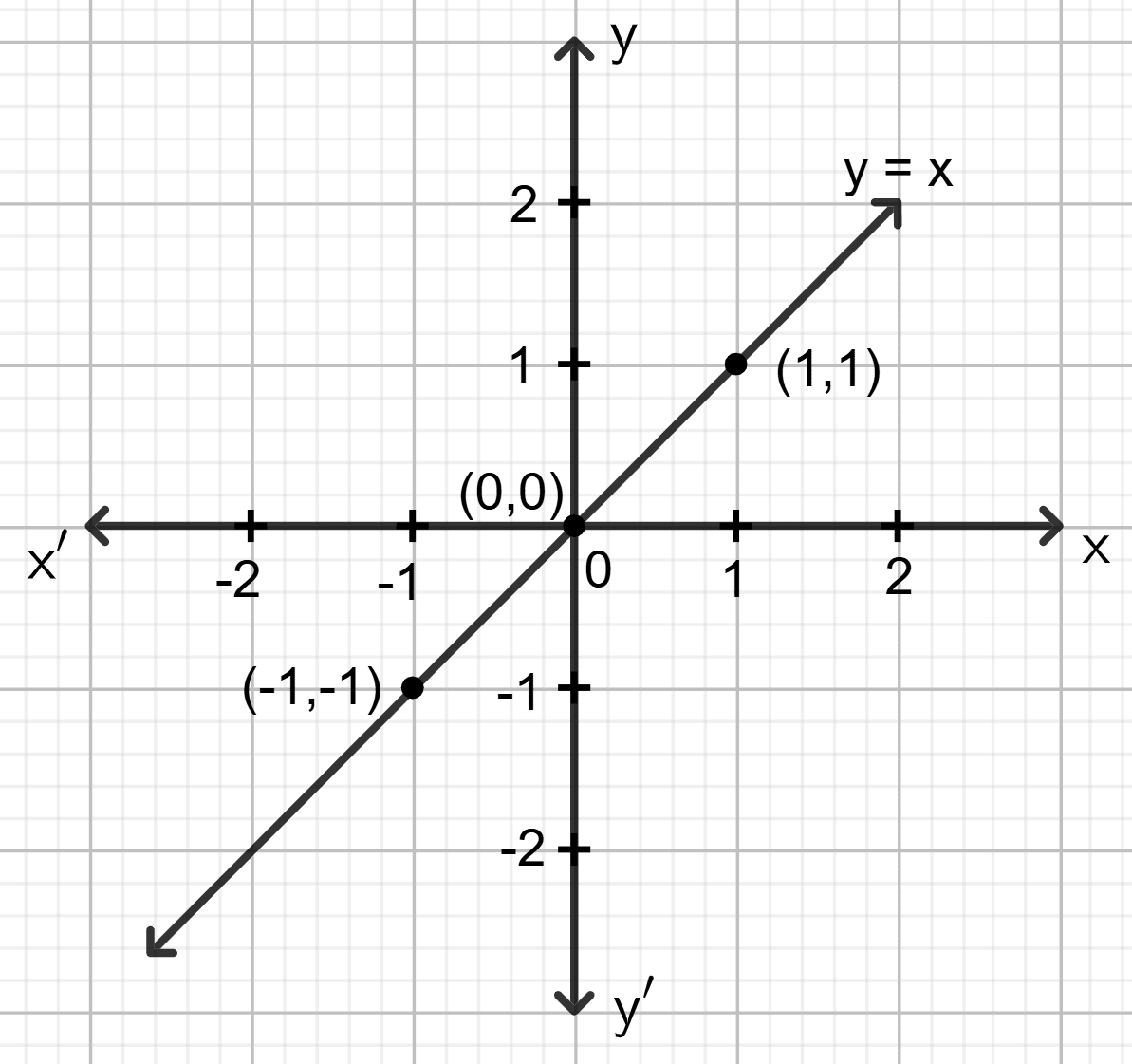
Draw the graph for the linear equation given below :
5x + y = 0
Answer
5x + y = 0
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -1, then 5 (-1) + y = 0 ⇒ y = 5
Let x = 0, then 5 0 + y = 0 ⇒ y = 0
Let x = 1, then 5 1 + y = 0 ⇒ y = -5
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -1 | 0 | 1 |
|---|---|---|---|
| y | 5 | 0 | -5 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
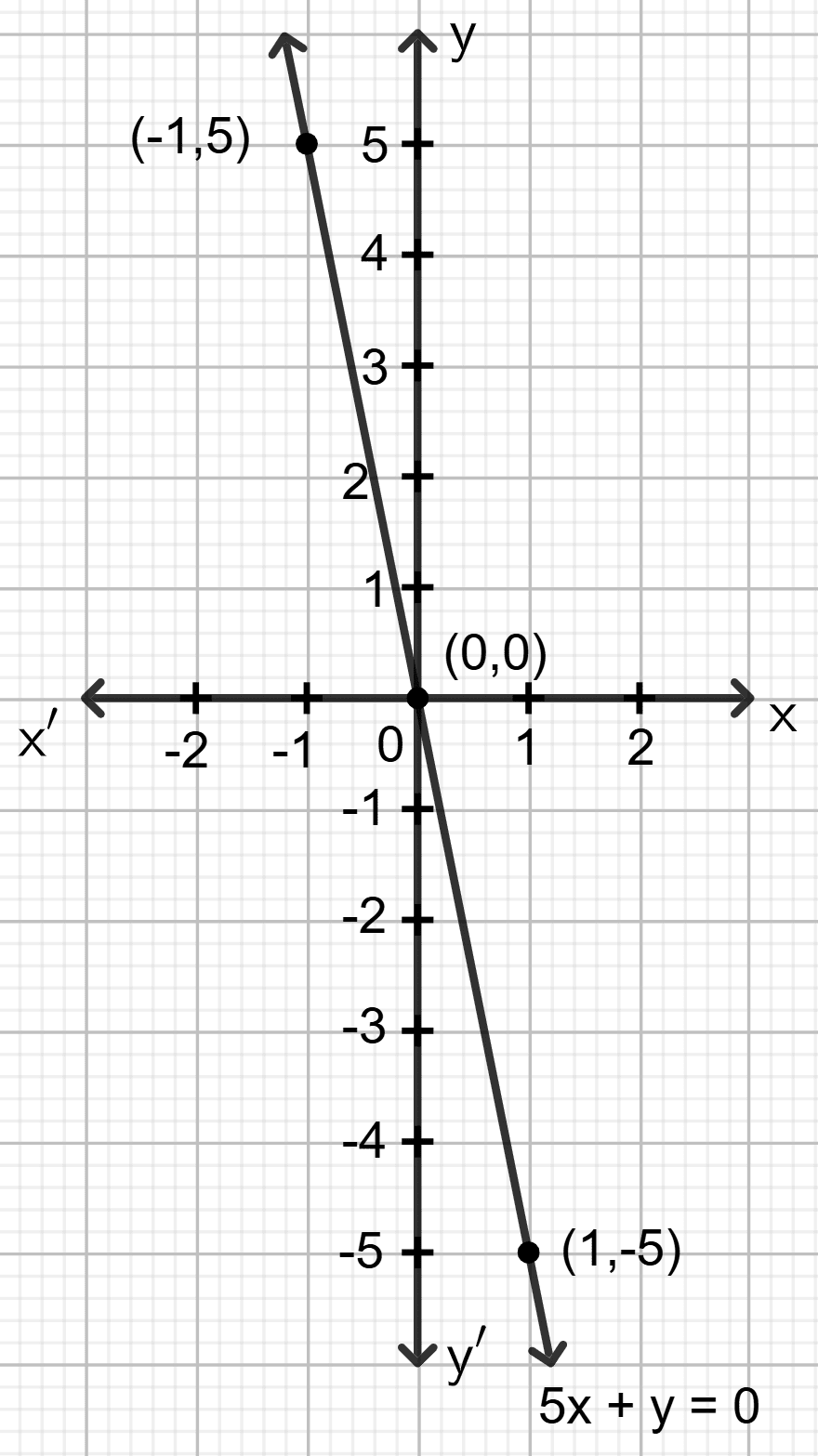
Draw the graph for the linear equation given below :
x + 2y = 0
Answer
x + 2y = 0
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -1, then (-1) + 2y = 0 ⇒ y = 0.5
Let x = 0, then 0 + 2y = 0 ⇒ y = 0
Let x = 1, then 1 + 2y = 0 ⇒ y = -0.5
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -1 | 0 | 1 |
|---|---|---|---|
| y | 0.5 | 0 | -0.5 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
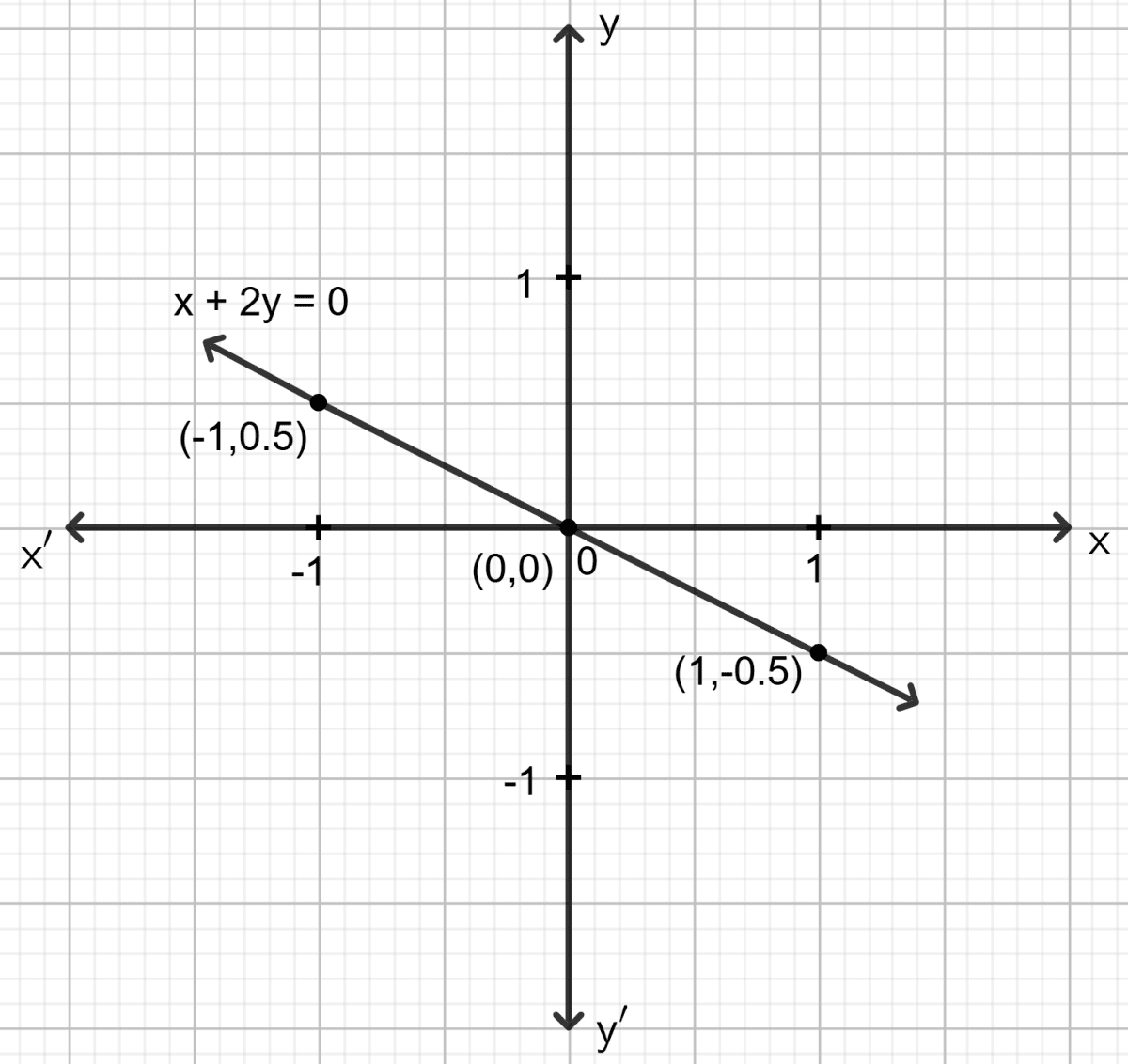
Draw the graph for the linear equation given below :
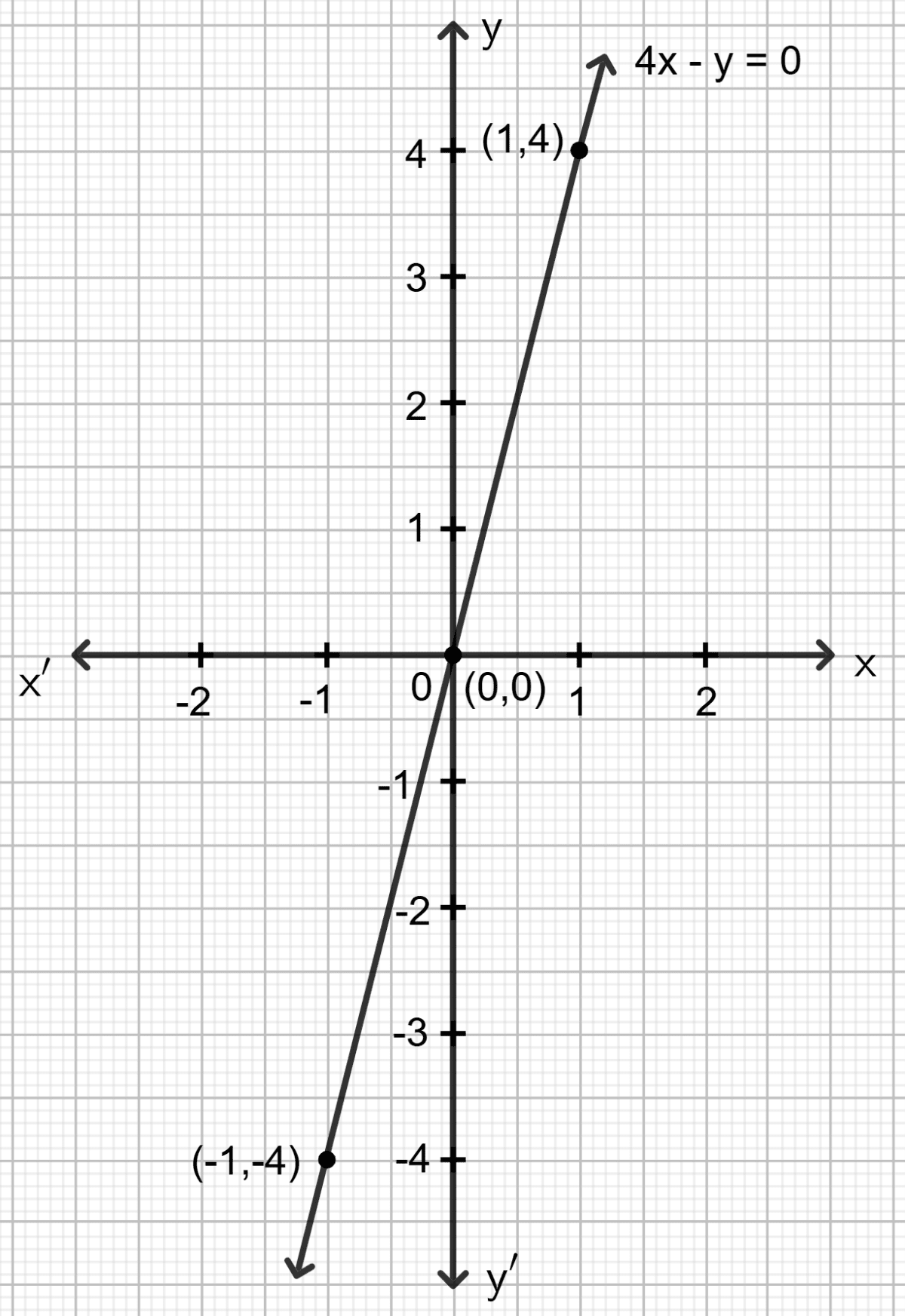
4x - y = 0
Answer
4x - y = 0
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -1, then 4 (-1) - y = 0 ⇒ y = -4
Let x = 0, then 4 0 - y = 0 ⇒ y = 0
Let x = 1, then 4 1 - y = 0 ⇒ y = 4
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -1 | 0 | 1 |
|---|---|---|---|
| y | -4 | 0 | 4 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
Draw the graph for the linear equation given below :
3x + 2y = 0
Answer
3x + 2y = 0
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -1, then 3 (-1) + 2y = 0 ⇒ y = 1.5
Let x = 0, then 3 0 + 2y = 0 ⇒ y = 0
Let x = 1, then 3 1 + 2y = 0 ⇒ y = -1.5
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -1 | 0 | 1 |
|---|---|---|---|
| y | 1.5 | 0 | -1.5 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
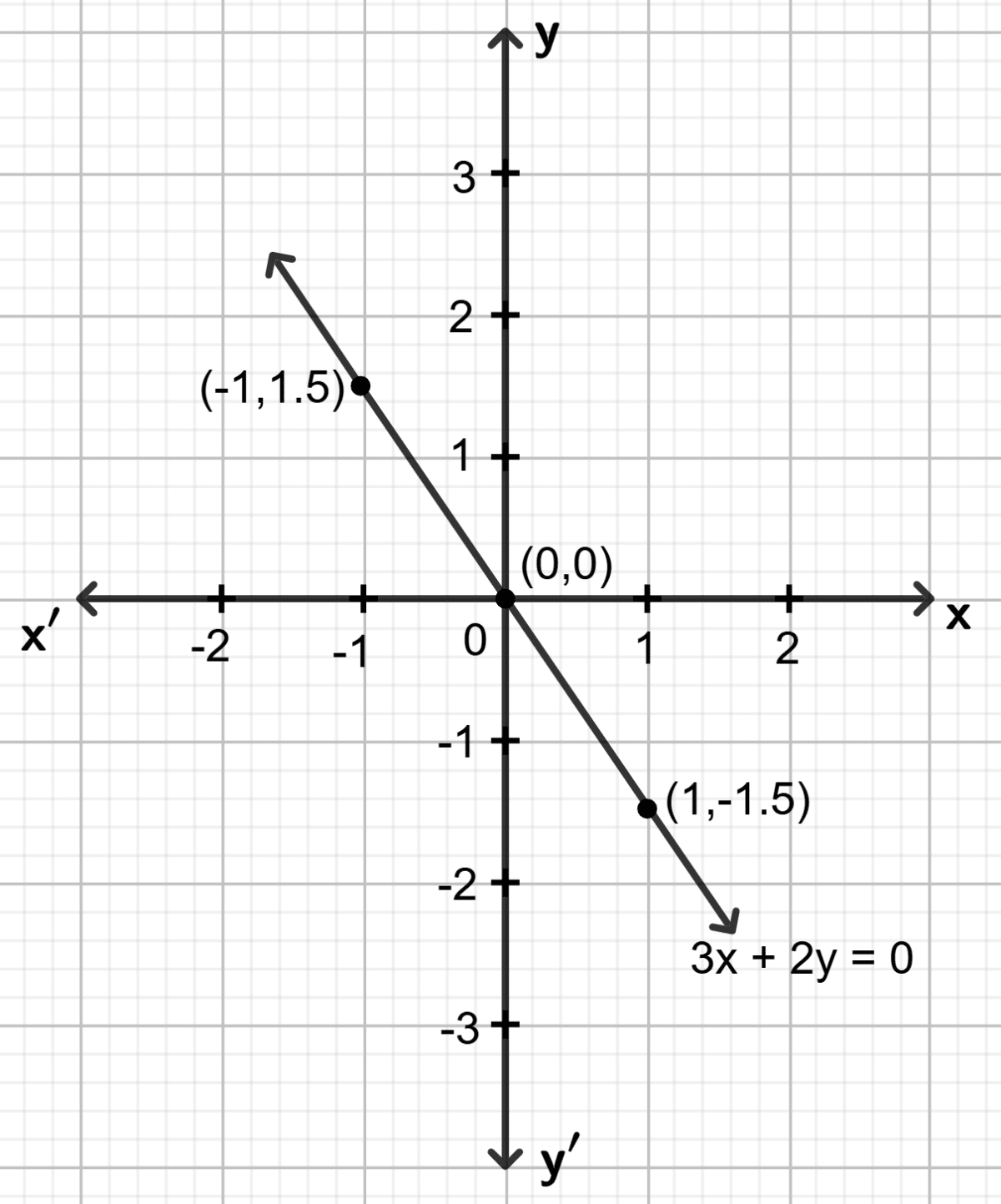
Draw the graph for the linear equation given below :
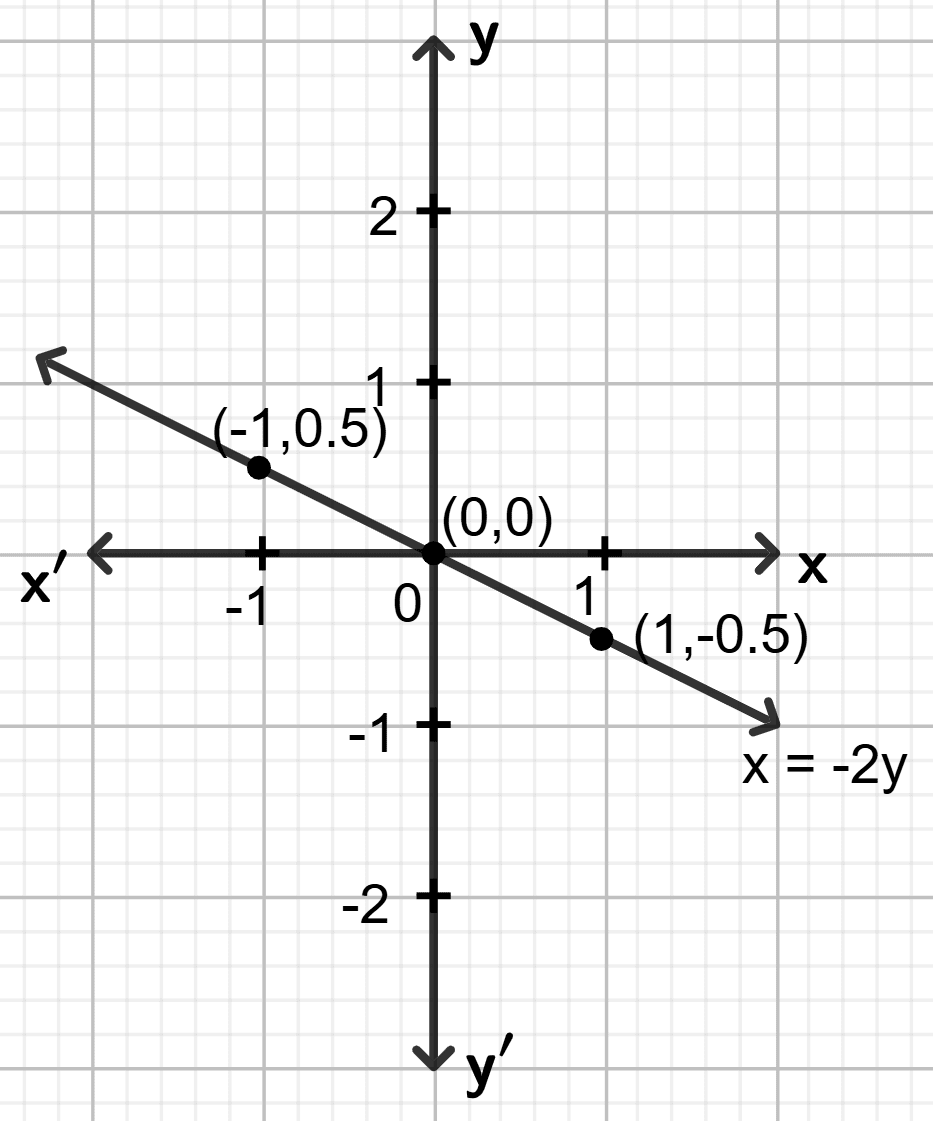
x = - 2y
Answer
x = - 2y
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -1, then (-1) = - 2y ⇒ y = 0.5
Let x = 0, then 0 = - 2y ⇒ y = 0
Let x = 1, then 1 = - 2y ⇒ y = - 0.5
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -1 | 0 | 1 |
|---|---|---|---|
| y | 0.5 | 0 | -0.5 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
Draw the graph for the linear equation given below :
y = 2x + 3
Answer
y = 2x + 3
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -1, then y = 2 (-1) + 3 ⇒ y = 1
Let x = 0, then y = 2 0 + 3 ⇒ y = 3
Let x = 1, then y = 2 1 + 3 ⇒ y = 5
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -1 | 0 | 1 |
|---|---|---|---|
| y | 1 | 3 | 5 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
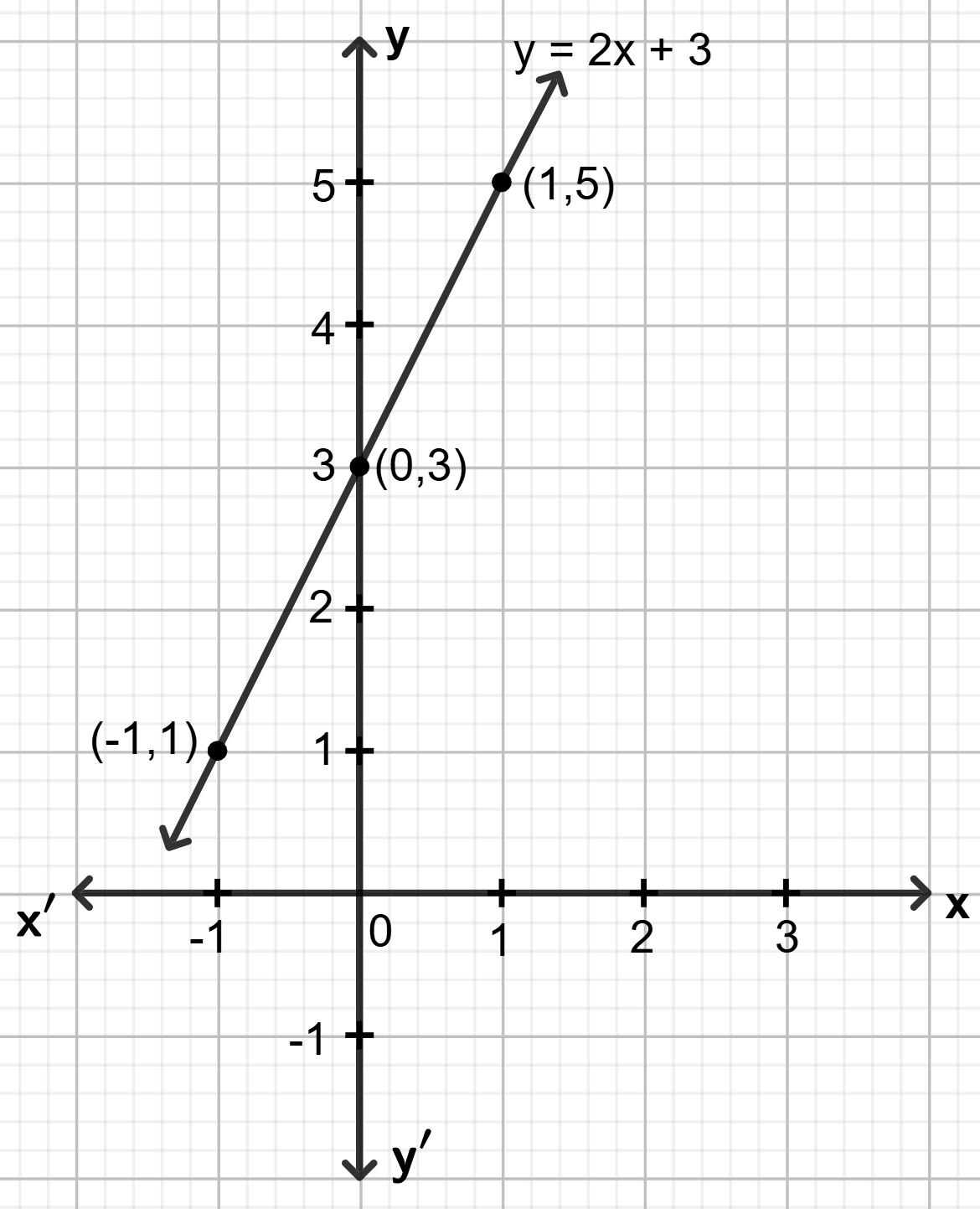
Draw the graph for the linear equation given below :
Answer
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -3, then
Let x = 0, then
Let x = 3, then
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -3 | 0 | 3 |
|---|---|---|---|
| y | -3 | -1 | 1 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
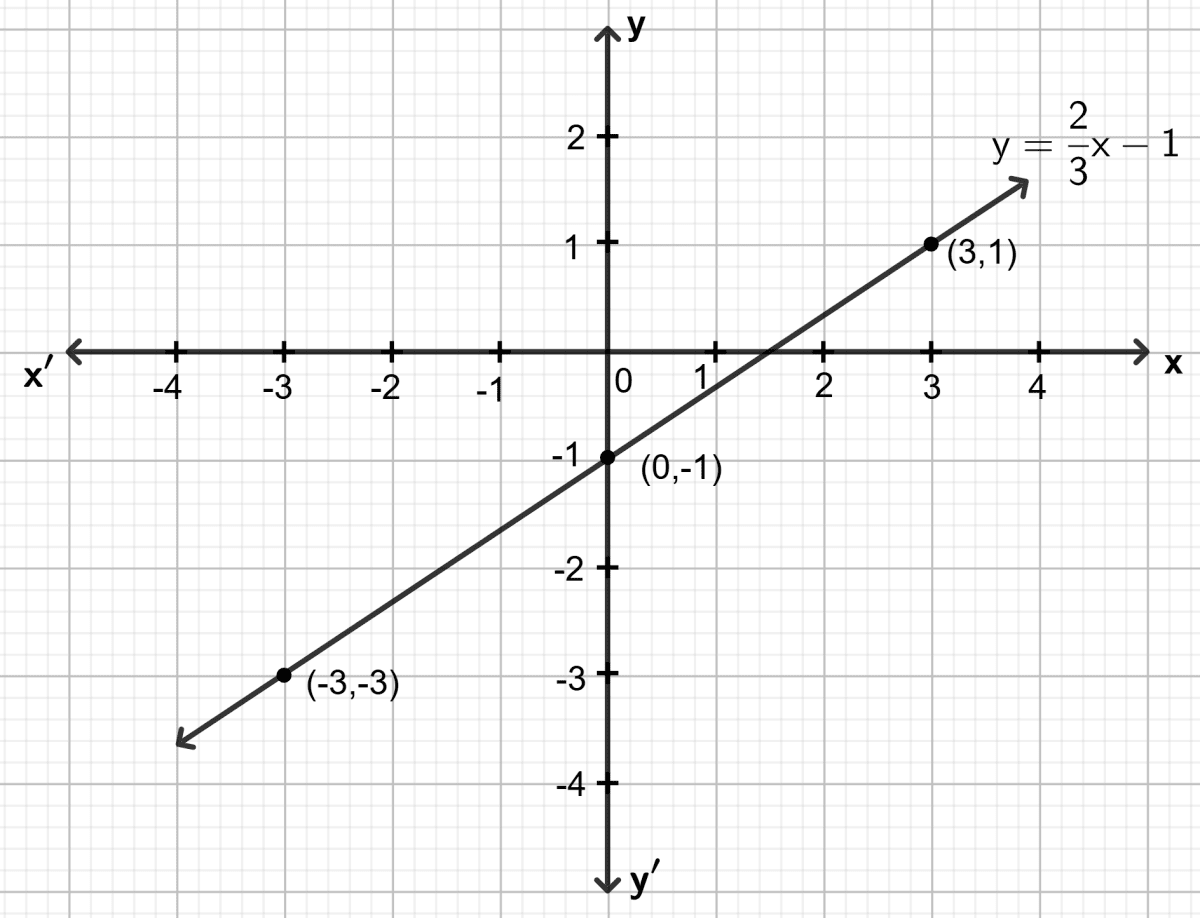
Draw the graph for the linear equation given below :
y = -x + 4
Answer
y = -x + 4
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -1, then y = -(-1) + 4 ⇒ y = 5
Let x = 0, then y = 0 + 4 ⇒ y = 4
Let x = 1, then y = -1 + 4 ⇒ y = 3
Step 2:
Make a table i(as given below) for the different pairs of the values of x and y:
| x | -1 | 0 | 1 |
|---|---|---|---|
| y | 5 | 4 | 3 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
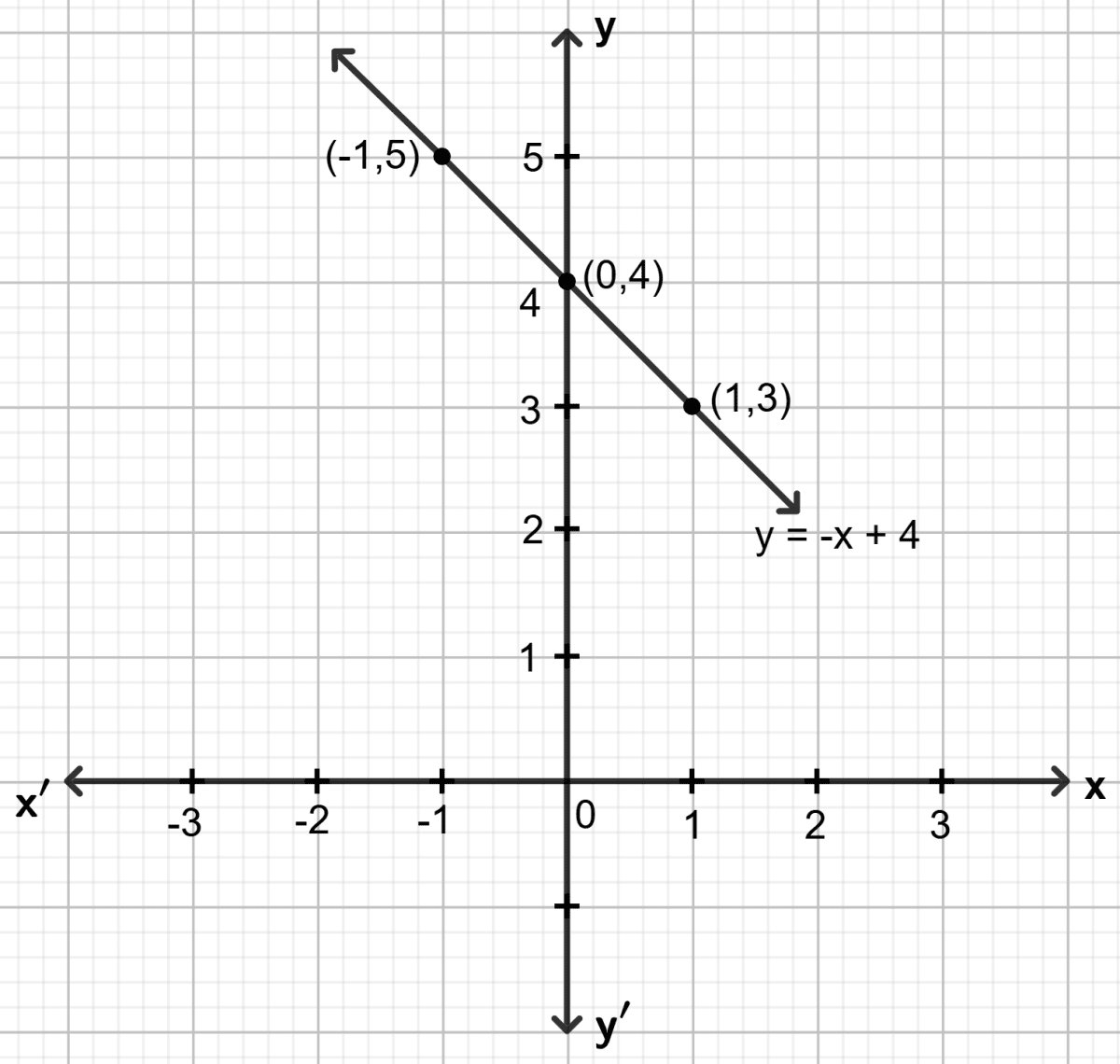
Draw the graph for the linear equation given below :
Answer
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -, then
Let x = , then
Let x = , then
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -1.5 | 0.5 | 1.5 |
|---|---|---|---|
| y | -8.5 | -0.5 | 3.5 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
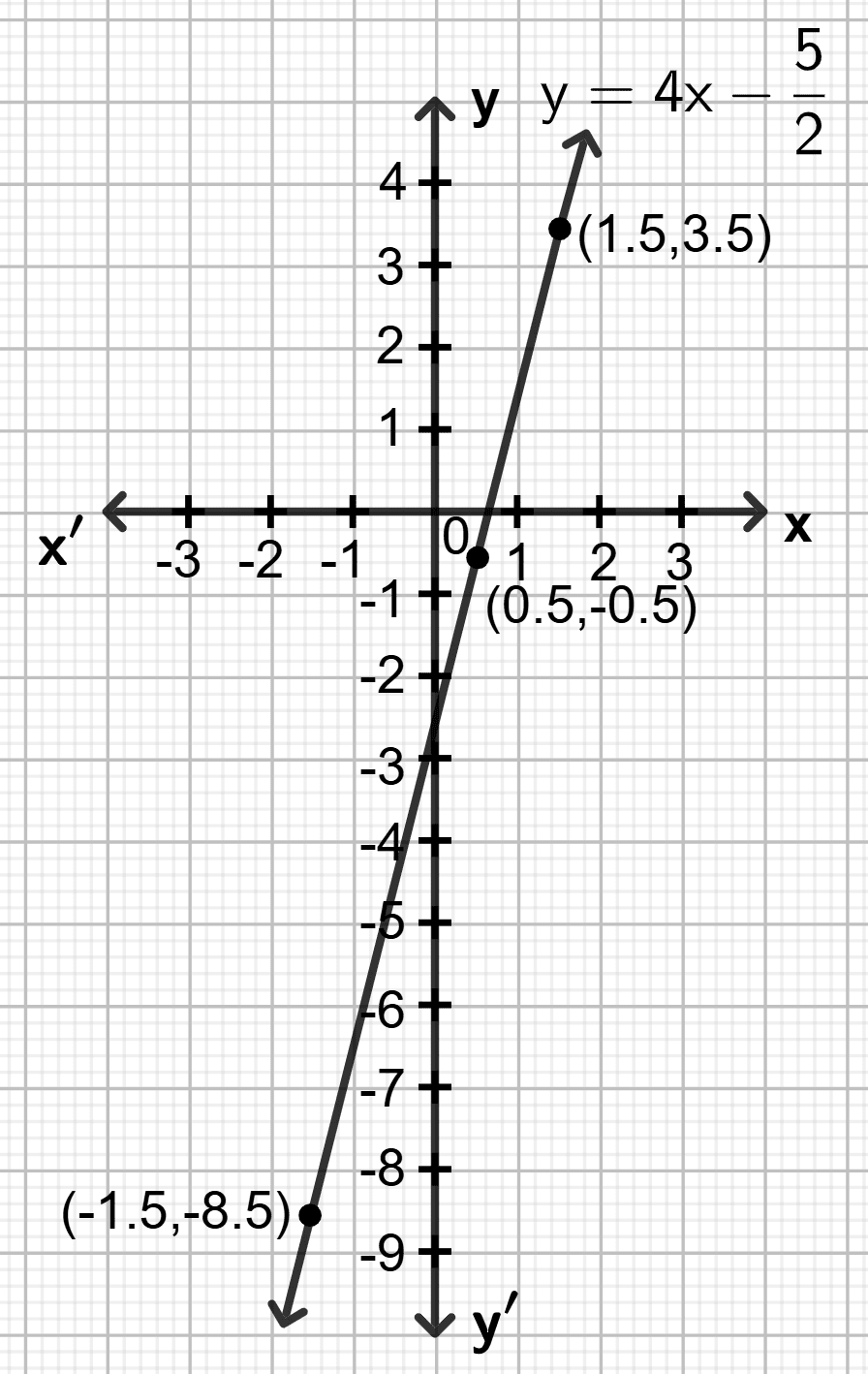
Draw the graph for the linear equation given below :
Answer
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -2, then
Let x = 0, then
Let x = 2, then
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -2 | 0 | 2 |
|---|---|---|---|
| y | -2.3 | 0.6 | 3.6 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
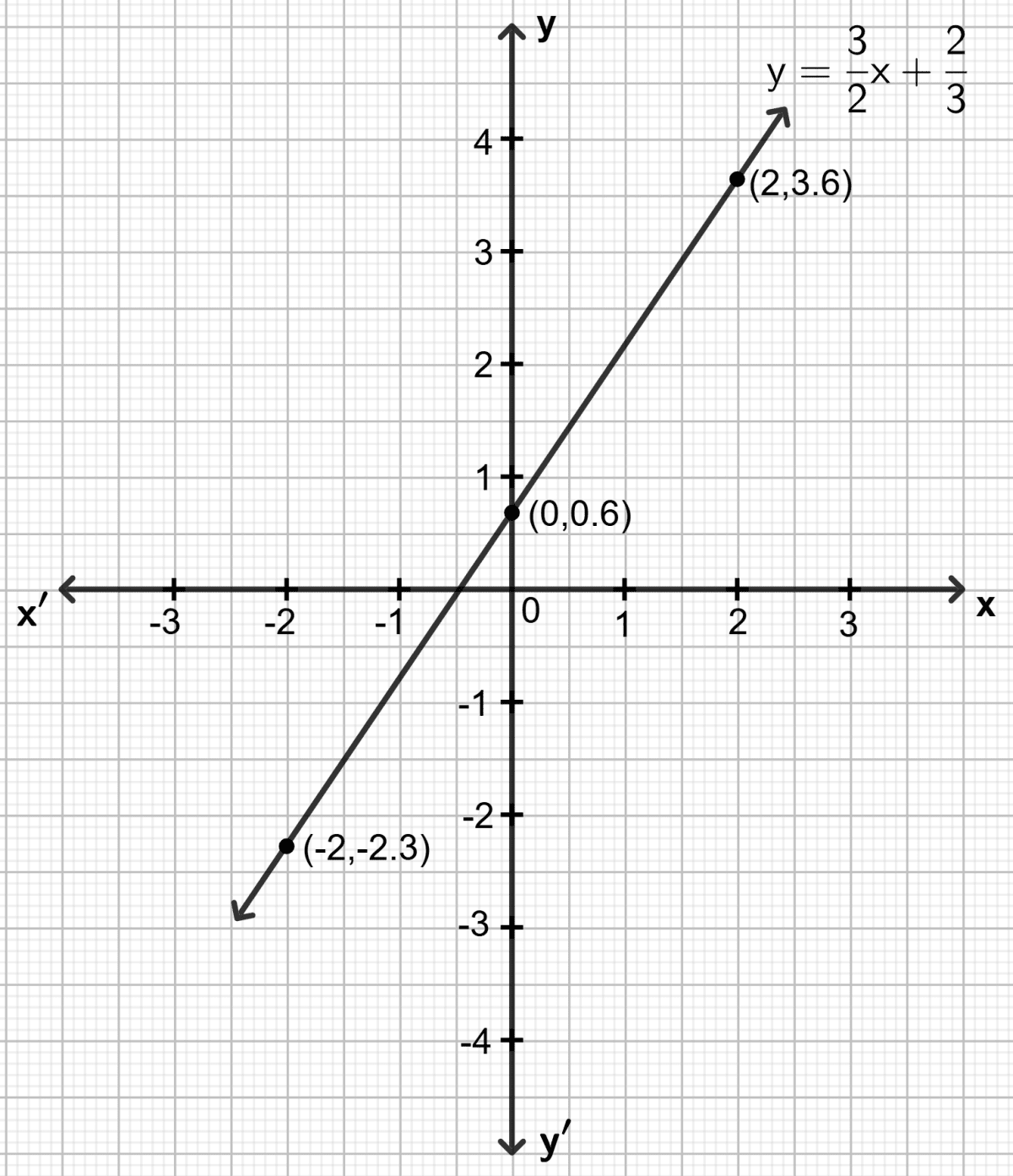
Draw the graph for the linear equation given below :
2x - 3y = 4
Answer
2x - 3y = 4
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -4, then 2 (-4) - 3y = 4 ⇒ y = -4
Let x = 2, then 2 2 - 3y = 4 ⇒ y = 0
Let x = 5, then 2 5 - 3y = 4 ⇒ y = 2
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -4 | 2 | 5 |
|---|---|---|---|
| y | -4 | 0 | 2 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
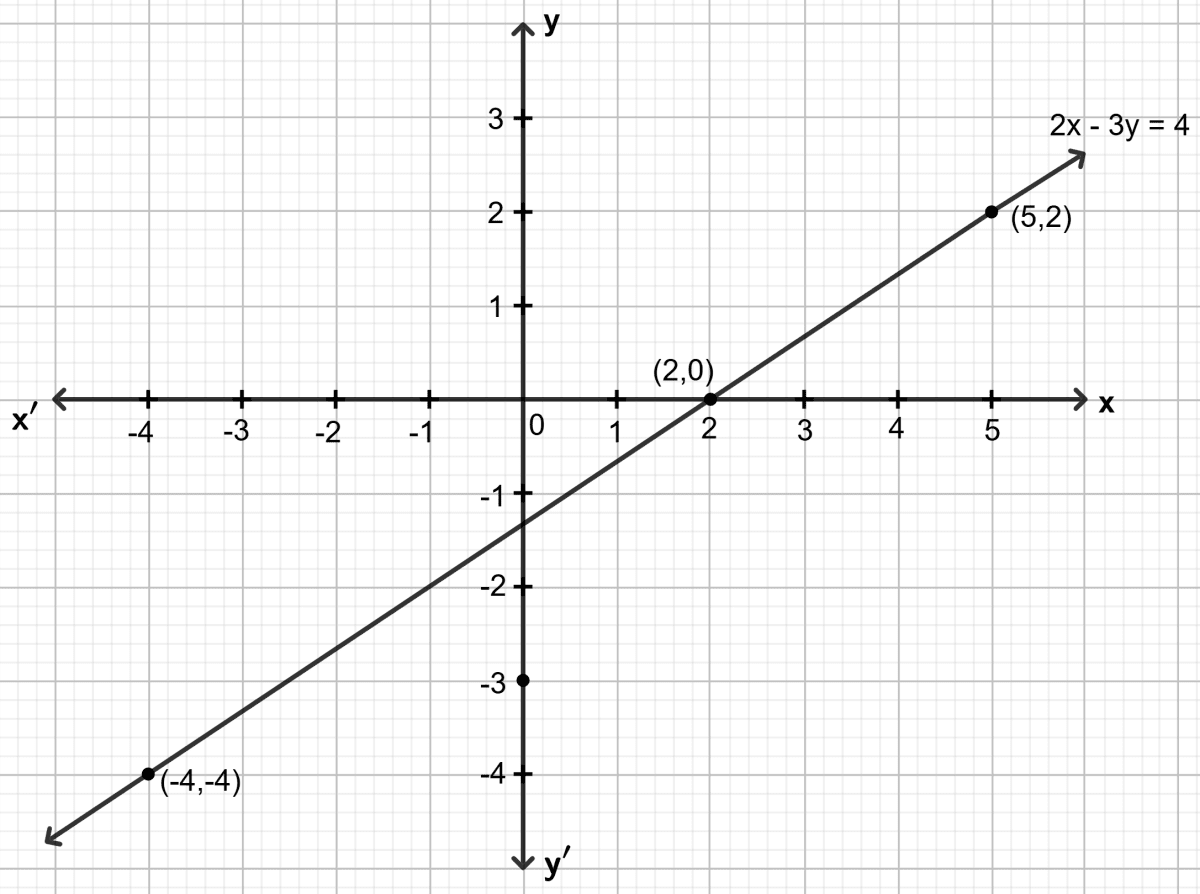
Draw the graph for the linear equation given below :
Answer
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -5, then
Let x = 1, then
Let x = 4, then
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -5 | 1 | 4 |
|---|---|---|---|
| y | -6 | -2 | 0 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
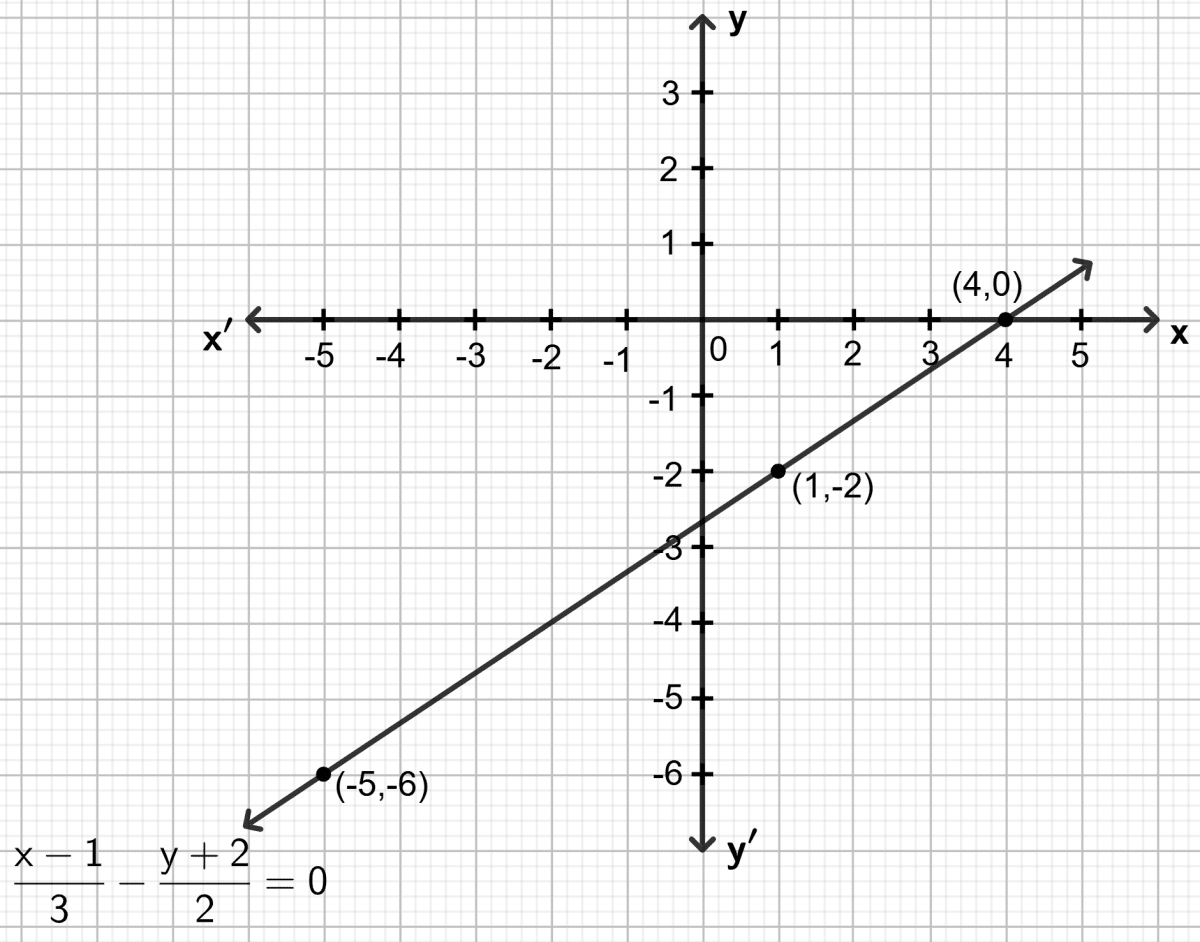
Draw the graph for the linear equation given below :
Answer
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = 0, then
Let x = 1, then
Let x = 3, then
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | 0 | 1 | 3 |
|---|---|---|---|
| y | -8.5 | -6 | -1 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
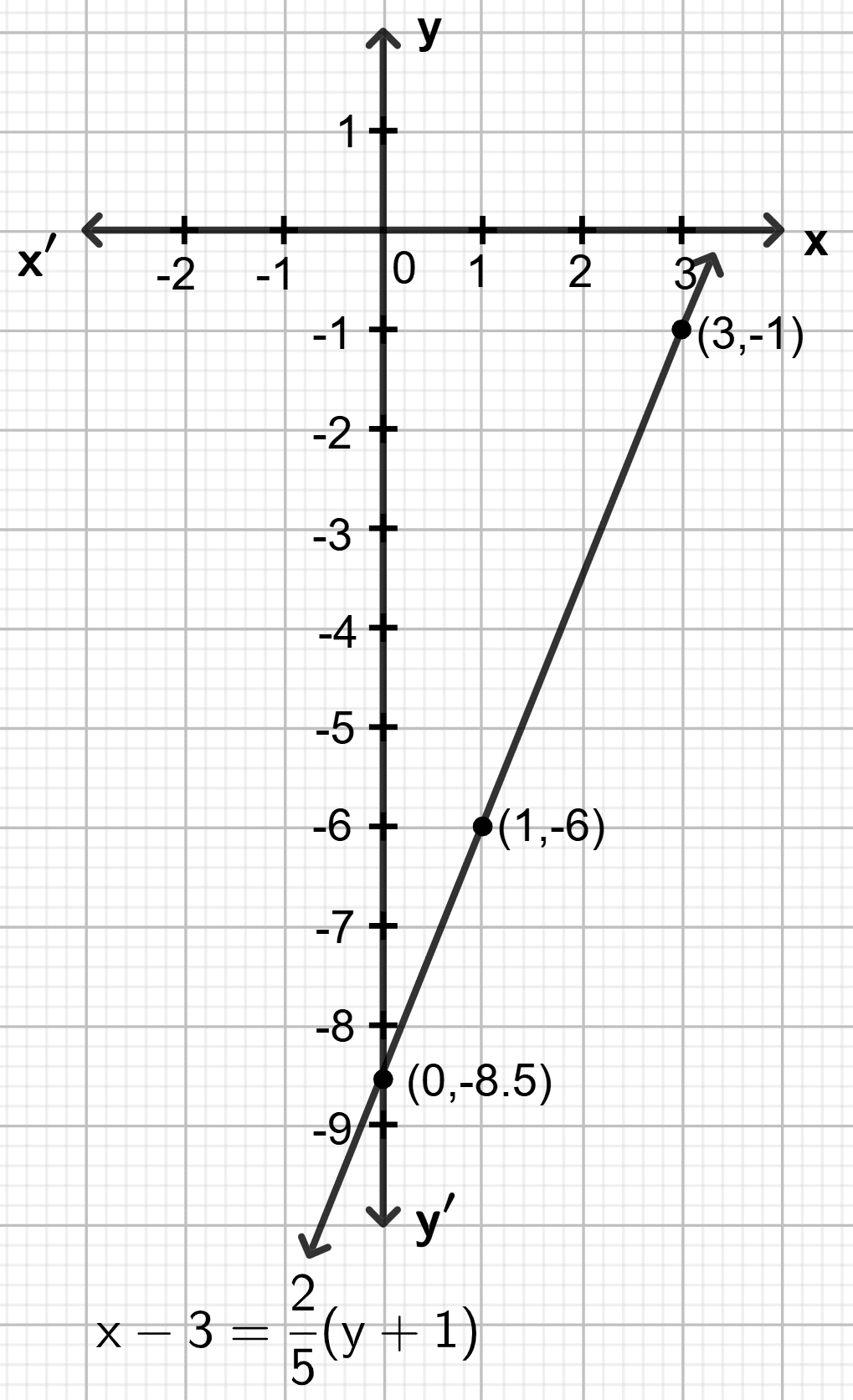
Draw the graph for the linear equation given below :
x + 5y + 2 = 0
Answer
x + 5y + 2 = 0
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -2, then -2 + 5y + 2 = 0 ⇒ y = 0
Let x = 0, then 0 + 5y + 2 = 0 ⇒ y = - 0.4
Let x = 2, then 2 + 5y + 2 = 0 ⇒ y = - 0.8
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -2 | 0 | 2 |
|---|---|---|---|
| y | 0 | -0.4 | -0.8 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
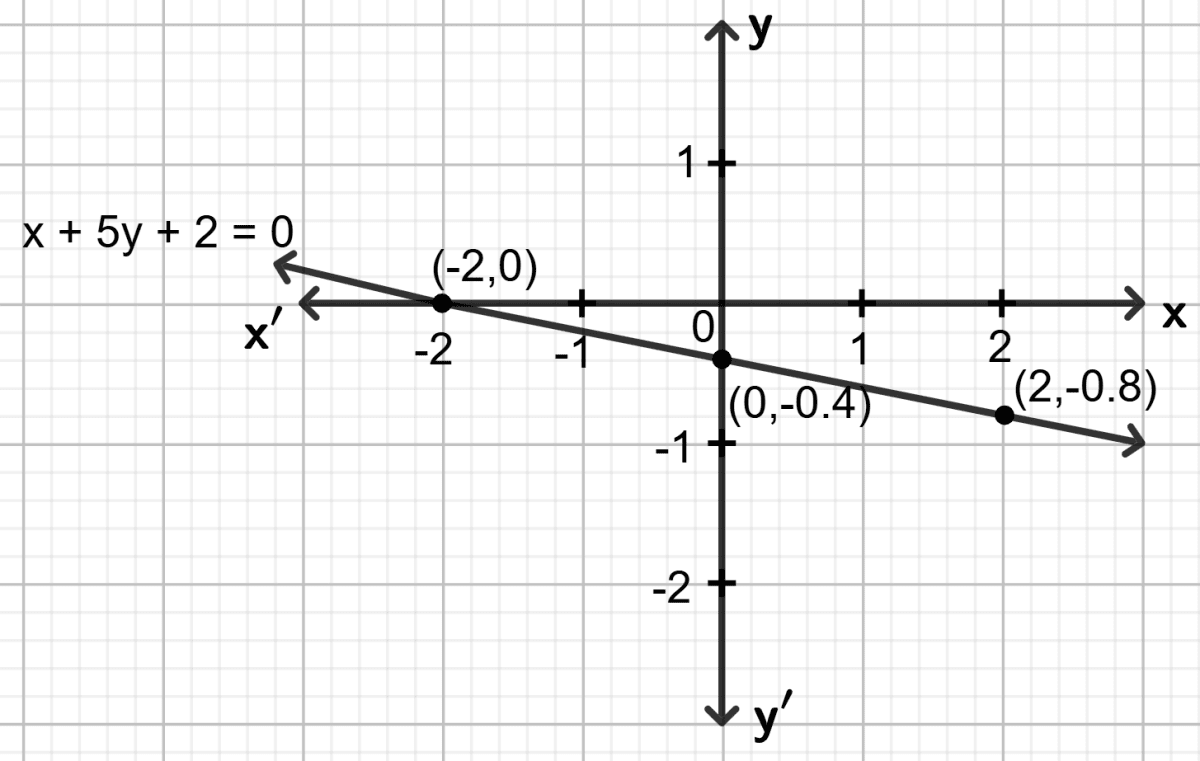
Draw the graph for the equation given below :
3x + 2y = 6
Find the co-ordinates of the points where the graph (line) drawn meets the co-ordinate axes.
Answer
3x + 2y = 6
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -1, then 3 (-1) + 2y = 6 ⇒ y =
Let x = 0, then 3 0 + 2y = 6 ⇒ y =
Let x = 1, then 3 1 + 2y = 6 ⇒ y =
Step 2: Make a table (as given below) for the different pairs of the values of x and y:
| x | -1 | 0 | 1 |
|---|---|---|---|
| y | 4.5 | 3 | 1.5 |
Step 3: Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
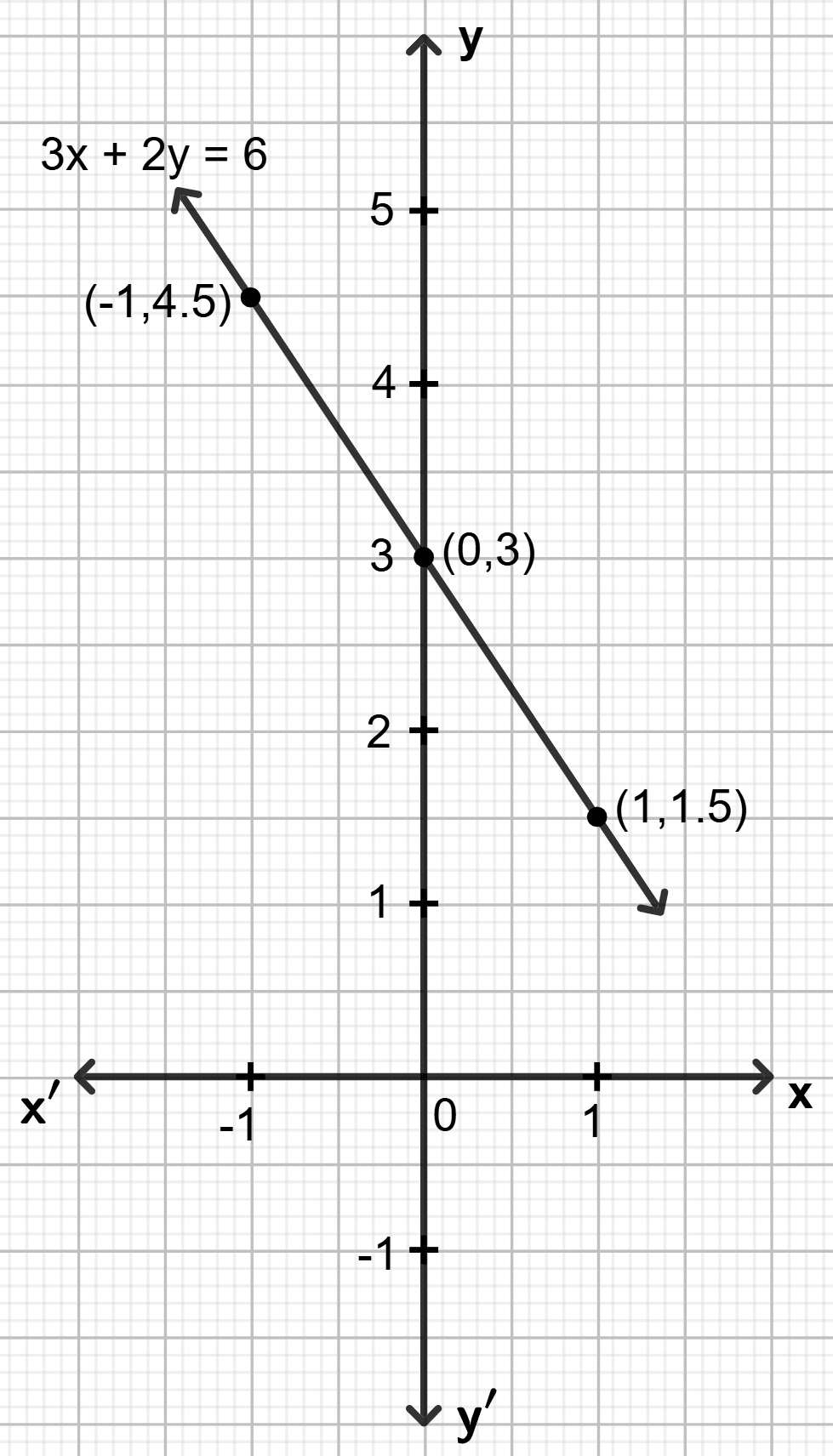
Draw the graph for the equation given below :
2x - 5y = 10
Find the co-ordinates of the points where the graph (line) drawn meets the co-ordinate axes.
Answer
2x - 5y = 10
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -1, then 2 (-1) - 5y = 10 ⇒ y =
Let x = 0, then 2 0 - 5y = 10 ⇒ y =
Let x = 1, then 2 1 - 5y = 10 ⇒ y =
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -1 | 0 | 1 |
|---|---|---|---|
| y | -2.4 | -2 | -1.6 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
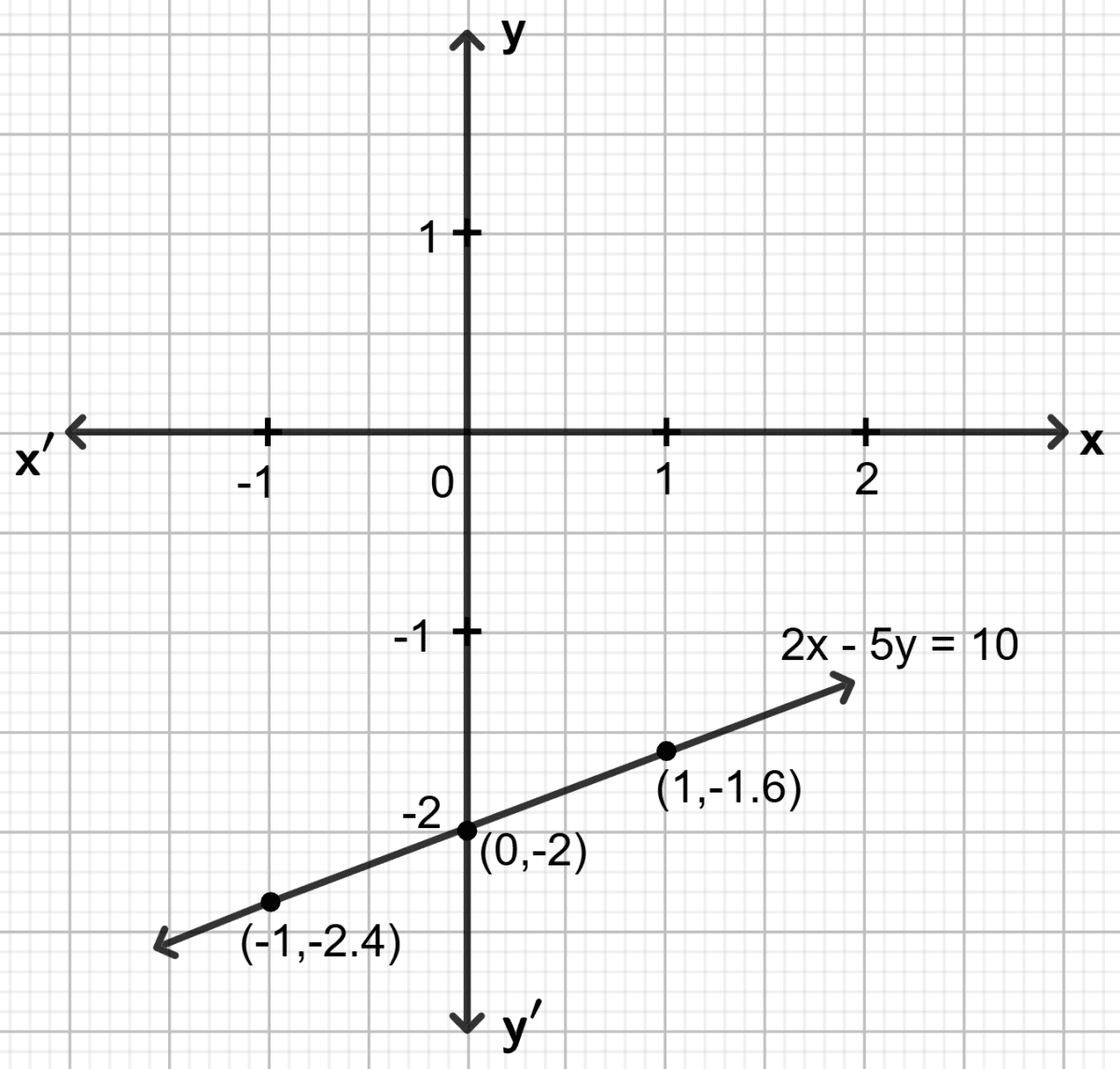
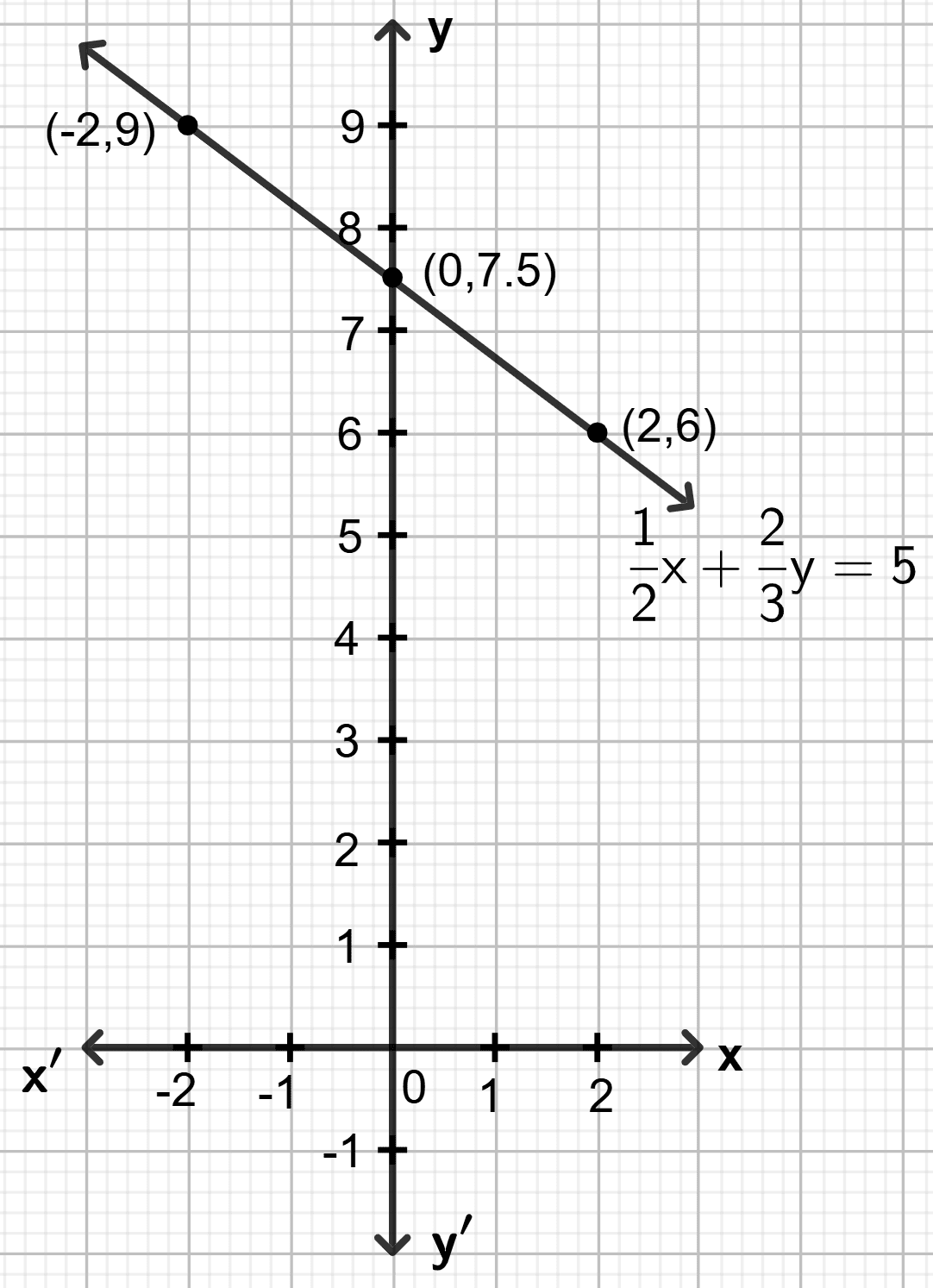
Draw the graph for the equation given below :
Find the co-ordinates of the points where the graph (line) drawn meets the co-ordinate axes.
Answer
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -2, then
Let x = 0, then
Let x = 2, then
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -2 | 0 | 2 |
|---|---|---|---|
| y | 9 | 7.5 | 6 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
Draw the graph for the equation given below :
Find the co-ordinates of the points where the graph (line) drawn meets the co-ordinate axes.
Answer
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -1, then
Let x = 0, then
Let x = 1, then
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -1 | 0 | 1 |
|---|---|---|---|
| y | -3 | 0.3 | 3.6 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
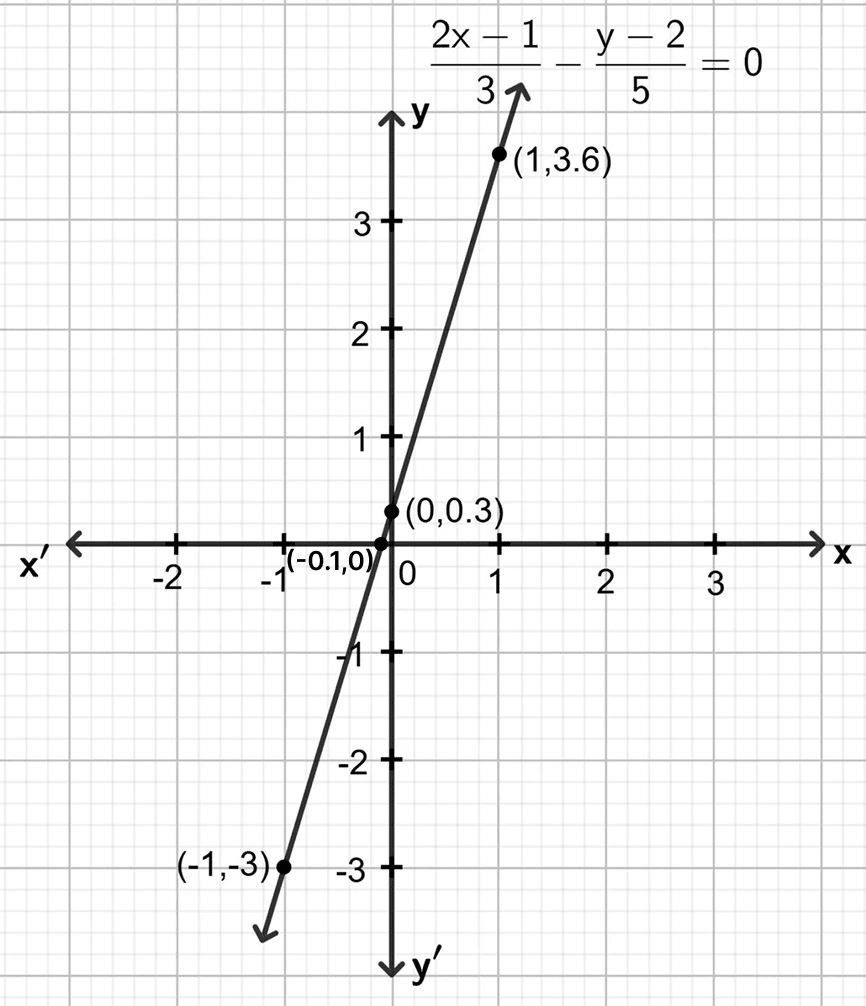
From the graph we get that the line meets x-axis at (-0.1, 0) and y-axis at (0, 0.3)
For the linear equation, given below, draw the graph and then use the graph drawn to find the area of a triangle enclosed by the graph and the co-ordinate axes :
3x - (5 - y) = 7
Answer
3x - (5 - y) = 7
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -1, then 3 (-1) - (5 - y) = 7 ⇒ y = 15
Let x = 0, then 3 0 - (5 - y) = 7 ⇒ y = 12
Let x = 1, then 3 1 - (5 - y) = 7 ⇒ y = 9
Let x = 4, then 3 4 - (5 - y) = 7 ⇒ y = 0
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -1 | 0 | 1 | 4 |
|---|---|---|---|---|
| y | 15 | 12 | 9 | 0 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
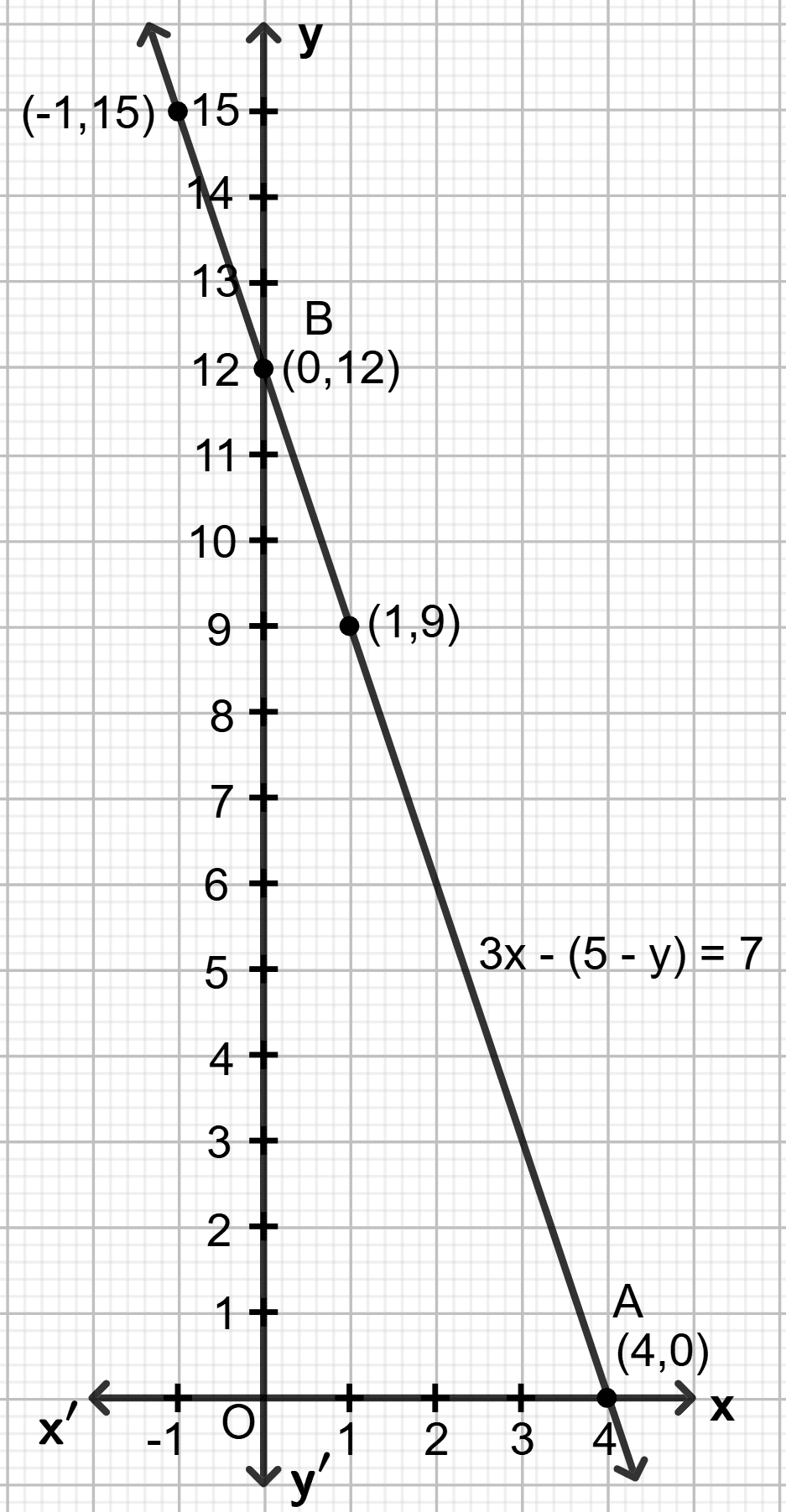
The area of the triangle ABO will be = altitude
= OB
= 12 square unit
= 24 square unit
Hence, the area of triangle = 24 square unit.
For the linear equation, given below, draw the graph and then use the graph drawn to find the area of a triangle enclosed by the graph and the co-ordinate axes :
7 - 3 (1 - y) = - 5 + 2x.
Answer
7 - 3 (1 - y) = - 5 + 2x
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = 0, then 7 - 3 (1 - y) = - 5 + 2 0 ⇒ y = -3
Let x = 4.5, then 7 - 3 (1 - y) = - 5 + 2 4.5 ⇒ y = 0
Let x = 6, then 7 - 3 (1 - y) = - 5 + 2 6 ⇒ y = 1
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | 0 | 4.5 | 6 |
|---|---|---|---|
| y | -3 | 0 | 1 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
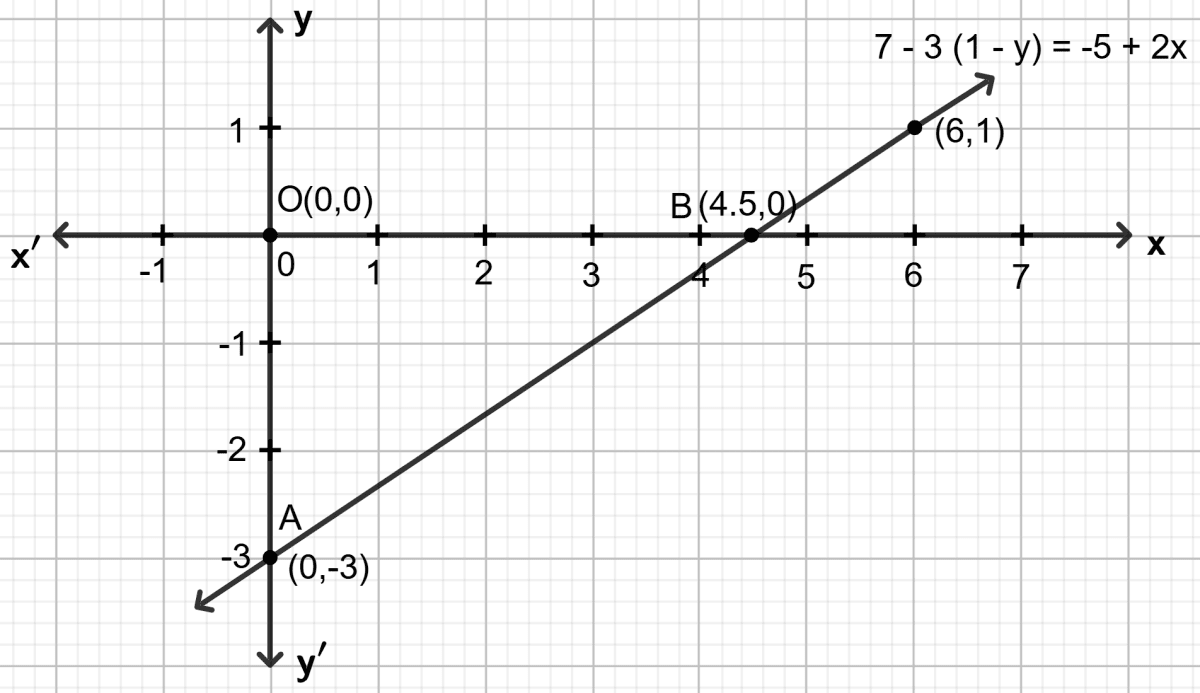
The area of the triangle ABO will be = altitude
= \times\times\dfrac{1}{2} 3 4.5
= 6.75 square unit
Hence, the area of triangle = 6.75 square unit.
For the pair of linear equations given below, draw graphs and then state, whether the lines drawn are parallel or perpendicular to each other.
y = 3x - 1
y = 3x + 2
Answer
First equation = y = 3x - 1
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -1, then y = 3 (-1) - 1 ⇒ y = -4
Let x = 0, then y = 3 0 - 1 ⇒ y = -1
Let x = 1, then y = 3 1 - 1 ⇒ y = 2
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -1 | 0 | 1 |
|---|---|---|---|
| y | -4 | -1 | 2 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
Second equation = y = 3x + 2
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -2, then y = 3 (-2) + 2 ⇒ y = -4
Let x = -1, then y = 3 (-1) + 2 ⇒ y = -1
Let x = 0, then y = 3 0 + 2 ⇒ y = 2
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -2 | -1 | 0 |
|---|---|---|---|
| y | -4 | -1 | 2 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
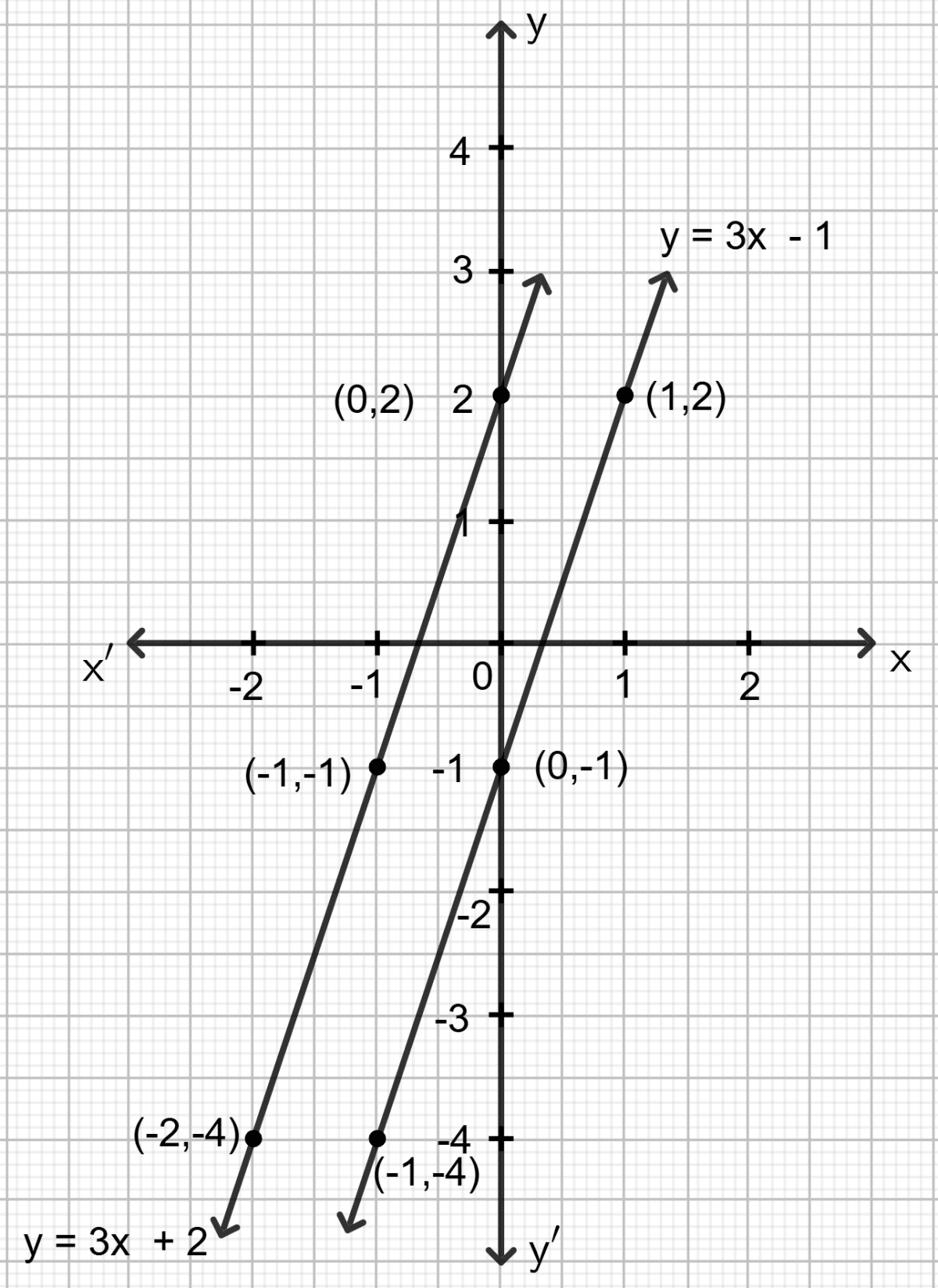
Hence, the two lines are parallel to each other.
For the pair of linear equations given below, draw graphs and then state, whether the lines drawn are parallel or perpendicular to each other.
y = x - 3
y = - x + 5
Answer
First equation = y = x - 3
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -1, then y = (-1) - 3 ⇒ y = - 4
Let x = 0, then y = 0 - 3 ⇒ y = - 3
Let x = 1, then y = 1 - 3 ⇒ y = - 2
Let x = 4, then y = 4 - 3 ⇒ y = 1
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -1 | 0 | 1 | 4 |
|---|---|---|---|---|
| y | -4 | -3 | -2 | 1 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
Second equation = y = - x + 5
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -1, then y = - (-1) + 5 ⇒ y = 6
Let x = 0, then y = - 0 + 5 ⇒ y = 5
Let x = 1, then y = - 1 + 5 ⇒ y = 4
Let x = 4, then y = - 4 + 5 ⇒ y = 1
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -1 | 0 | 1 | 4 |
|---|---|---|---|---|
| y | 6 | 5 | 4 | 1 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.

Hence, the two lines are perpendicular to each other.
For the pair of linear equations given below, draw graphs and then state, whether the lines drawn are parallel or perpendicular to each other.
2x - 3y = 6
Answer
First equation = 2x - 3y = 6
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -1, then 2 (-1) - 3y = 6 ⇒ y = - 2.6
Let x = 0, then 2 (0) - 3y = 6 ⇒ y = - 2
Let x = 1, then 2 1 - 3y = 6 ⇒ y = - 1.3
Let x = 3, then 2 3 - 3y = 6 ⇒ y = 0
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -1 | 0 | 1 | 3 |
|---|---|---|---|---|
| y | -2.6 | -2 | -1.3 | 0 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
Second equation =
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -1, then ⇒ y = 4.5
Let x = 0, then ⇒ y = 3
Let x = 1, then ⇒ y = 1.5
Let x = 2, then ⇒ y = 0
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -1 | 0 | 1 | 2 |
|---|---|---|---|---|
| y | 4.5 | 3 | 1.5 | 0 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.

Hence, the two lines are perpendicular to each other.
For the pair of linear equations given below, draw graphs and then state, whether the lines drawn are parallel or perpendicular to each other.
3x + 4y = 24
Answer
First equation = 3x + 4y = 24
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -2, then 3 (-2) + 4y = 24 ⇒ y = 7.5
Let x = 0, then 3 0 + 4y = 24 ⇒ y = 6
Let x = 2, then 3 2 + 4y = 24 ⇒ y = 4.5
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -2 | 0 | 2 |
|---|---|---|---|
| y | 7.5 | 6 | 4.5 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
Second equation =
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -1, then ⇒ y = 3.7
Let x = 0, then ⇒ y = 3
Let x = 1, then ⇒ y = 2.2
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -1 | 0 | 1 |
|---|---|---|---|
| y | 3.7 | 3 | 2.2 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.

Hence, the two lines are parallel to each other.
On the same graph paper, plot the graph of y = x - 2, y = 2x + 1 and y = 4 from x = -4 to 3.
Answer
The given equations are y = x - 2, y = 2x + 1 and y = 4.
Make a table (as given below) for the different pairs of the values of x and y:
| x | -4 | 0 | 3 |
|---|---|---|---|
| y = x - 2 | -6 | -2 | 1 |
| y = 2x + 1 | -7 | 1 | 7 |
| y = 4 | 4 | 4 | 4 |
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
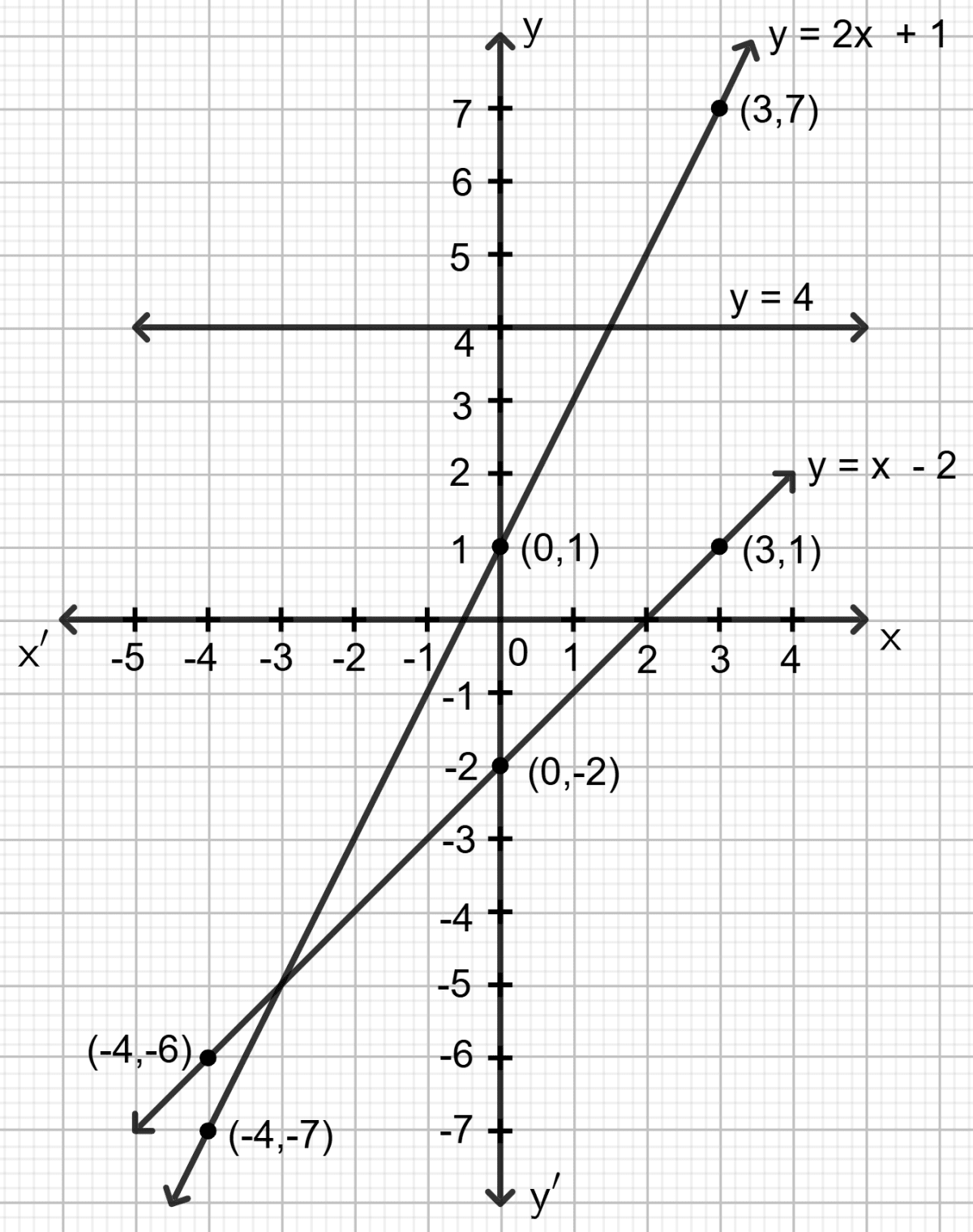
On the same graph paper, plot the graphs of y = 2x - 1, y = 2x and y = 2x + 1 from x = - 2 to x = 4. Are the graphs (lines) drawn parallel to each other ?
Answer
The given equations are y = 2x - 1, y = 2x and y = 2x + 1.
Make a table (as given below) for the different pairs of the values of x and y:
| x | -2 | 0 | 4 |
|---|---|---|---|
| y = 2x - 1 | -5 | -1 | 7 |
| y = 2x | -4 | 0 | 8 |
| y = 2x + 1 | -3 | 1 | 9 |
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
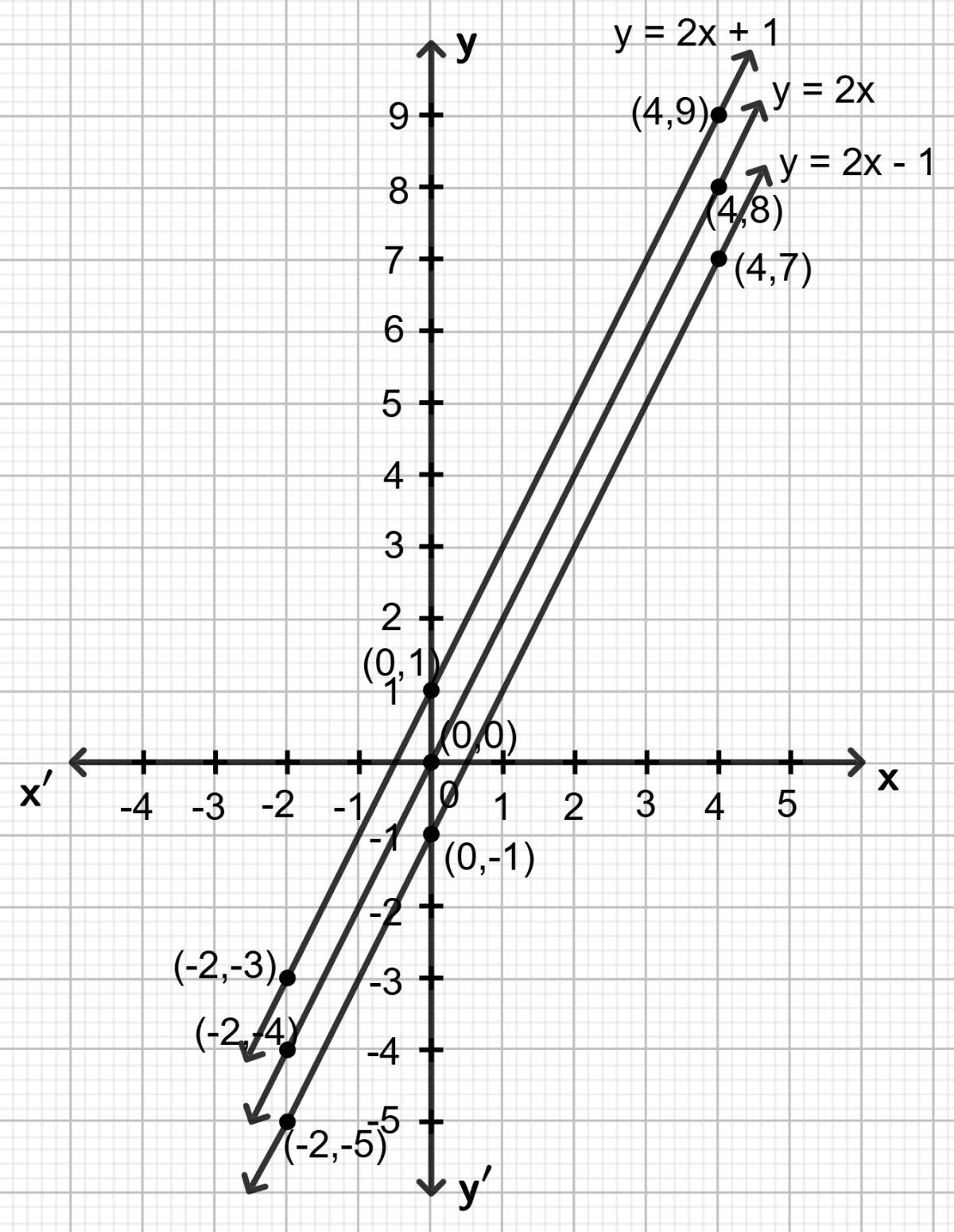
Yes, the lines drawn are parallel to each other.
The graph of 3x + 2y = 6 meets the x-axis at point P and the y-axis at point Q. Use the graphical method to find the co-ordinates of points P and Q.
Answer
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -2, then 3 (-2) + 2y = 6 ⇒ y = 6
Let x = -1, then 3 (-1) + 2y = 6 ⇒ y = 4.5
Let x = 0, then 3 0 + 2y = 6 ⇒ y = 3
Let x = 1, then 3 1 + 2y = 6 ⇒ y = 1.5
Let x = 2, then 3 2 + 2y = 6 ⇒ y = 0
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -2 | -1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| y | 6 | 4.5 | 3 | 1.5 | 0 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
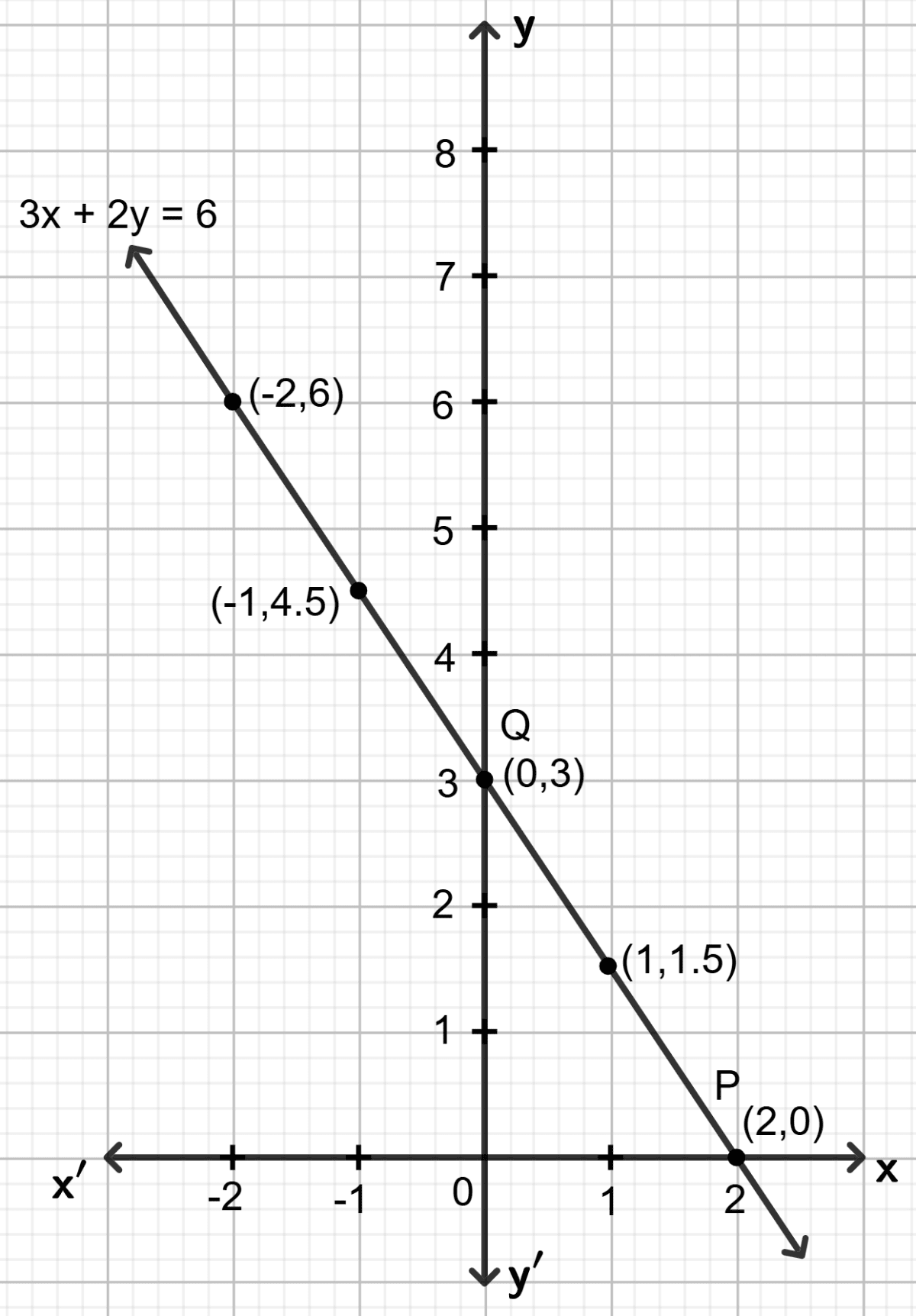
The graph intersects the x-axis at P(2,0).
The graph intersects the y-axis at Q(0,3).
Hence, the coordinates of P = (2, 0) and Q = (0, 3).
The inclination of a point is 60°. The slope of the line is :
Answer
The inclination of a point is 60°, then θ = 60°.
The slope of the line = m = tan 60° =
Hence, option 3 is the correct option.
For the equation 2x - 5y = 8; slope is :
5
8
Answer
⇒ 2x - 5y = 8
⇒ - 5y = 8 - 2x
⇒ 5y = 2x - 8
⇒ y =
∴ Slope = coefficient of x =
Hence, option 4 is the correct option.
For the equation 5x - 6y = 9, the y-intercept is :
Answer
⇒ 5x - 6y = 9
⇒ -6y = 9 - 5x
⇒ 6y = 5x - 9
⇒ y =
∴ y-intercept = constant term = -
Hence, option 4 is the correct option.
If the slope of a line is -2 and its y-intercept is -7, the equation of the line is:
2x + y + 7 = 0
2x - y + 7 = 0
2x - y - 7 = 0
2x + y - 7 = 0
Answer
slope = -2 ⇒ m = -2
y-intercept = -7 ⇒ c = -7
∴ Equation is : y = mx + c
⇒ y = (-2)x + (-7)
⇒ y = -2x - 7
⇒ 2x + y + 7 = 0
Hence, option 1 is the correct option.
For the equation x - y + 1 = 0; the values of slope (m) and y-intercept (c) are :
m = 1, c = 1
m = -1, c = 1
m = 1, c = -1
m = -1, c = -1
Answer
The given equation : x - y + 1 = 0
⇒ y = x + 1
General form of equation: y = mx + c
m = 1, c = 1
Hence, option 1 is the correct option.
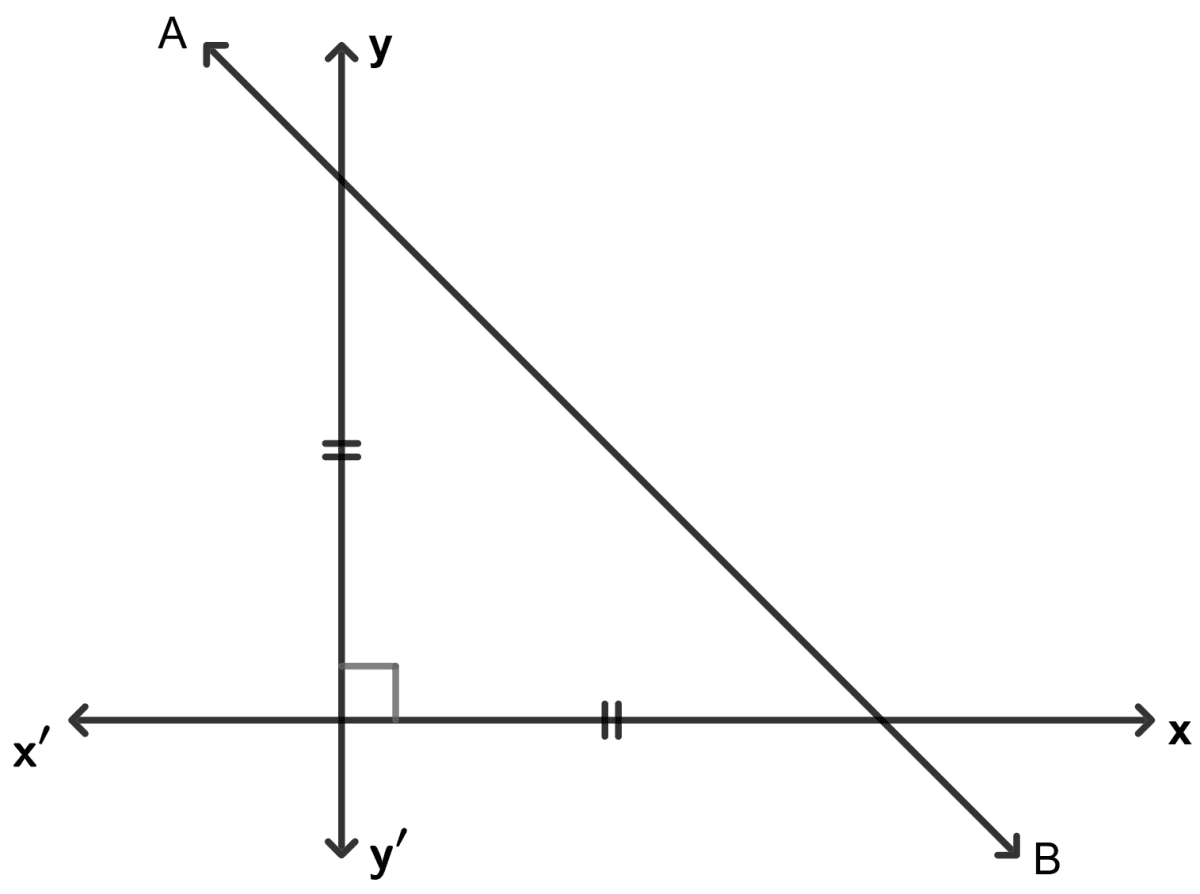
In the following, find the inclination of line AB :
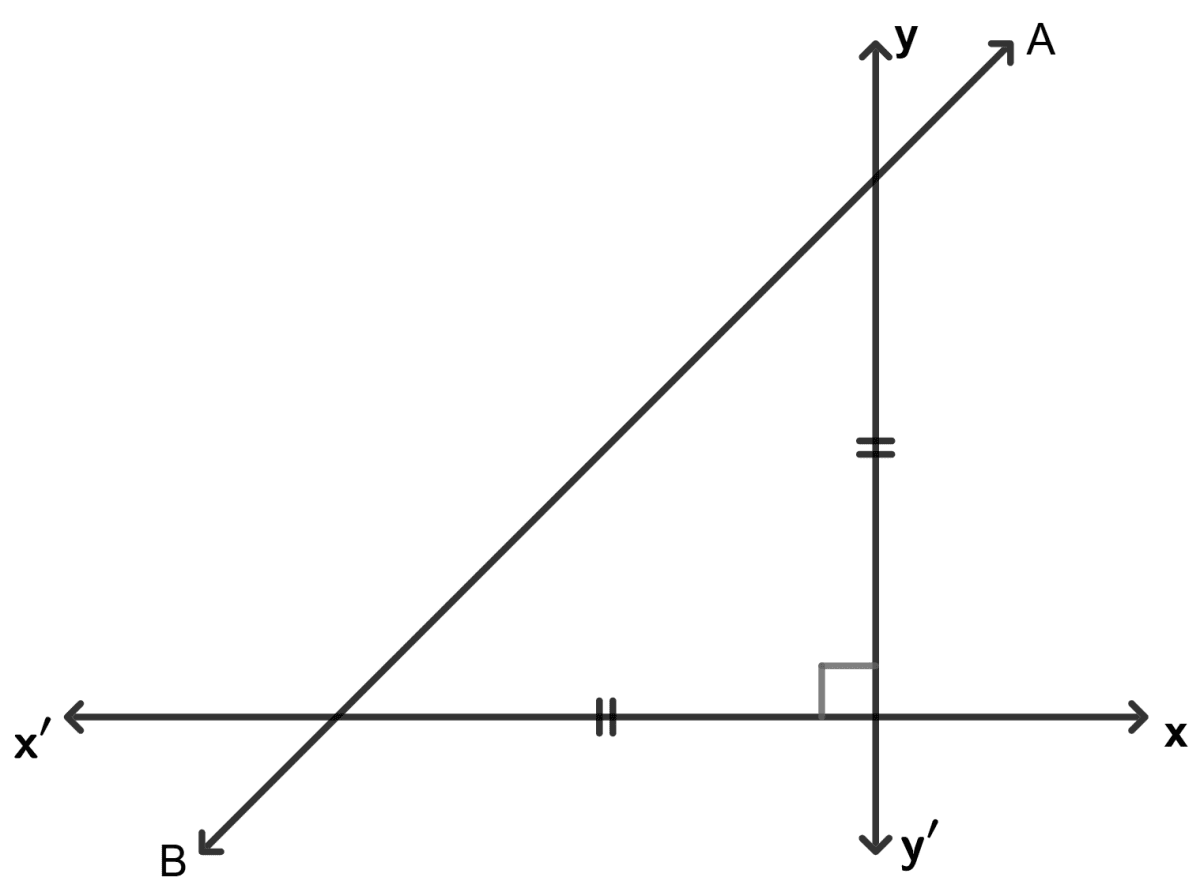
Answer
MO = NO
∠ NMO = ∠ MNO
∠ MON = 90°
Let ∠ MNO = ∠ NMO = x.
As we know that sum of all angles of triangle = 180°
⇒ ∠ NMO + ∠ MNO + ∠ MON = 180°
⇒ x + x + 90° = 180°
⇒ 2x = 180° - 90°
⇒ x =
⇒ x = 45°
Hence, the inclination = 45°.
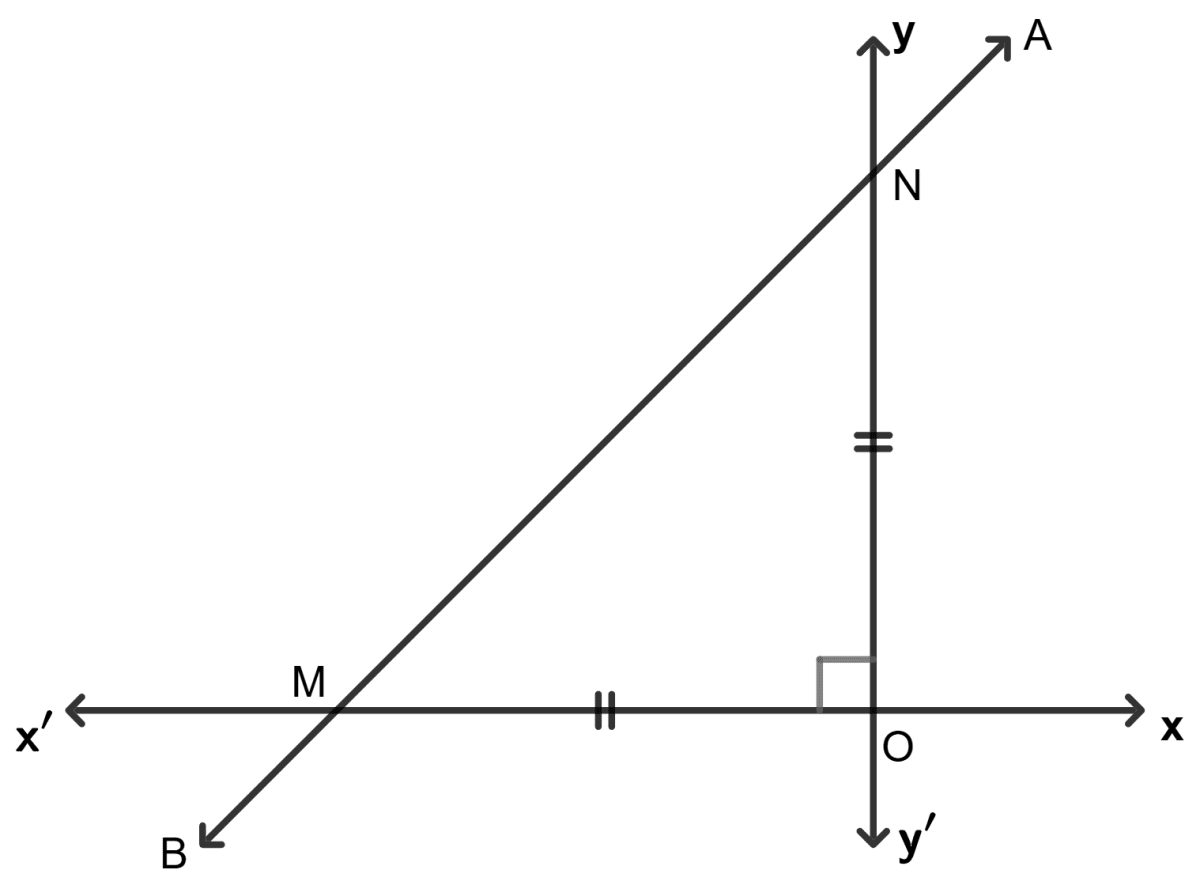
In the following, find the inclination of line AB :
Answer
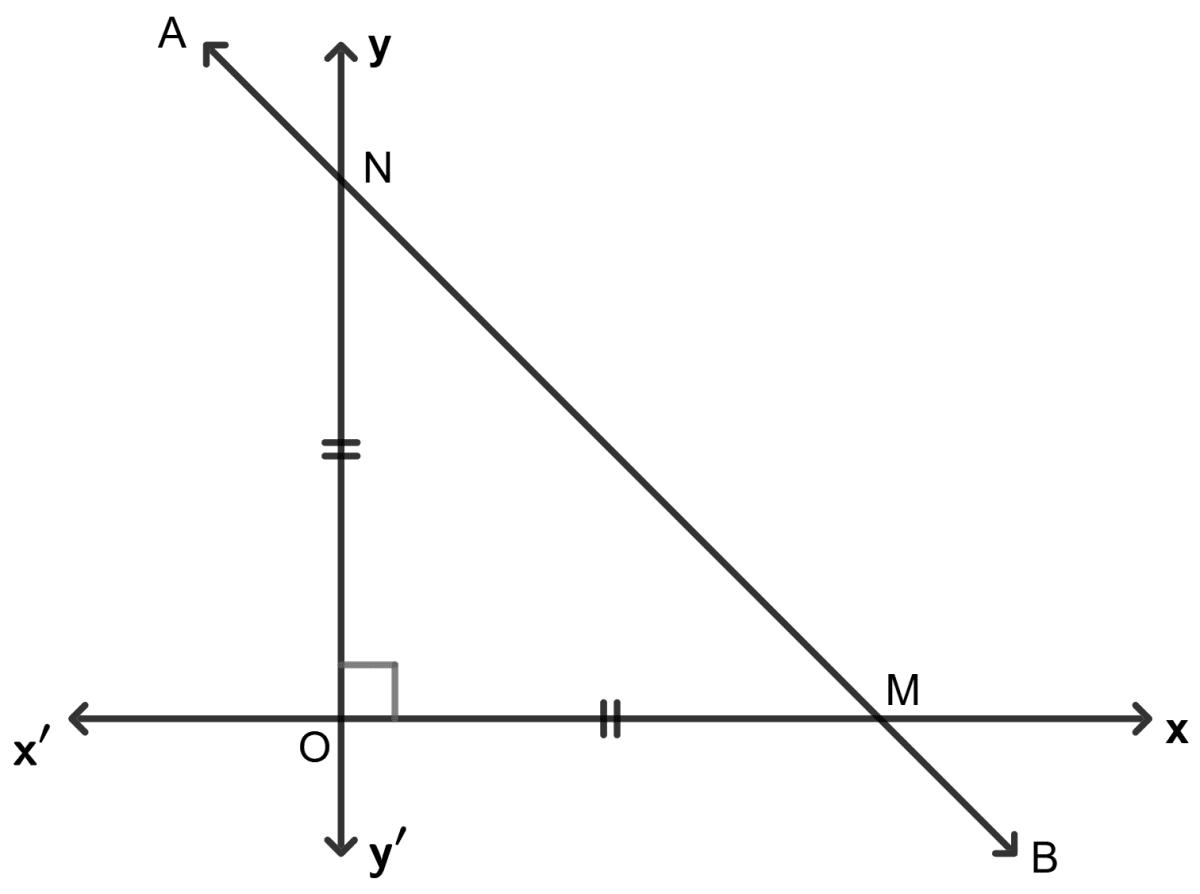
MO = NO
∠ NMO = ∠ MNO
∠ MON = 90°
Let ∠ MNO = ∠ NMO = x.
As we know that sum of all angles of triangle = 180°
⇒ ∠ NMO + ∠ MNO + ∠ MON = 180°
⇒ x + x + 90° = 180°
⇒ 2x = 180° - 90°
⇒ x =
⇒ x = 45°
Inclination = 180° - 45° = 135°
Hence, the inclination = 135°.
In the following, find the inclination of line AB :
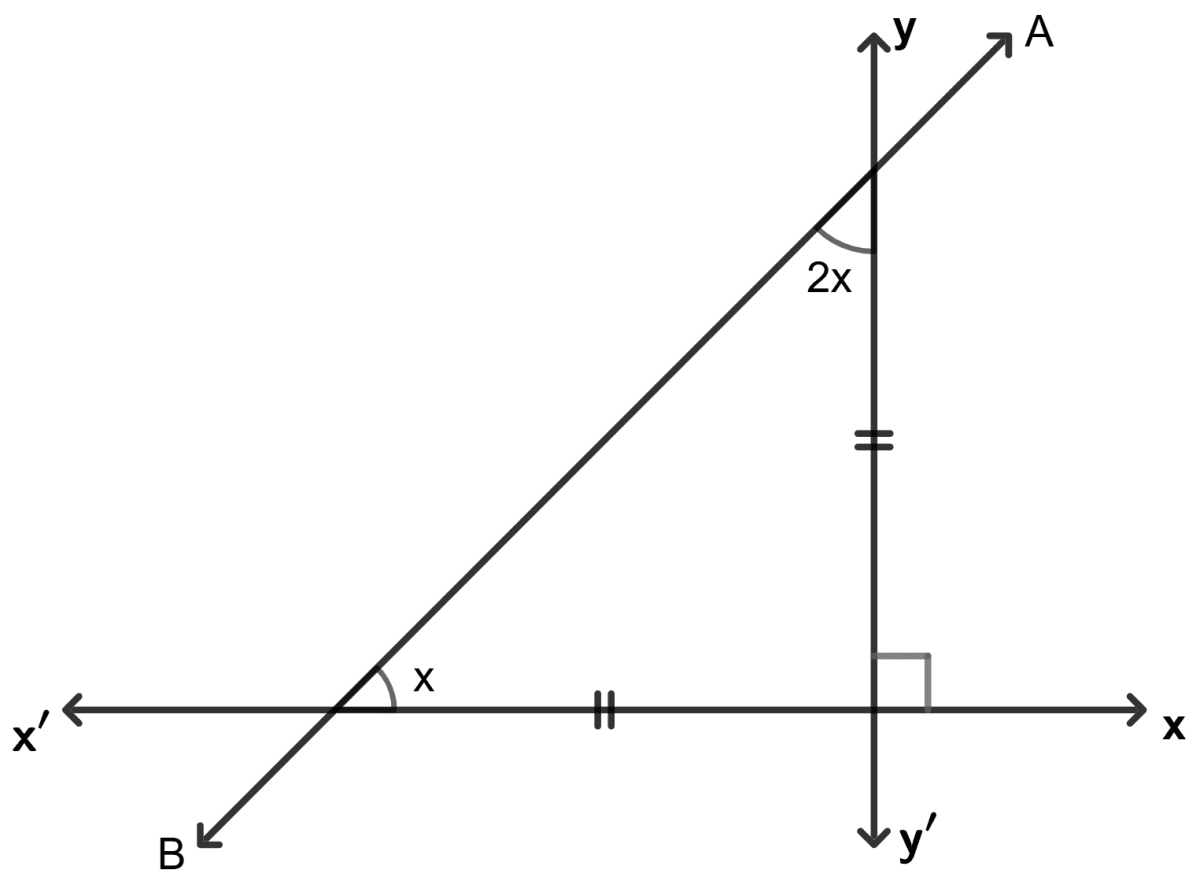
Answer

∠ NMO = 2x
∠ MNO = x
∠ MON = 90°
As we know that sum of all angles of triangle = 180°
⇒ ∠ NMO + ∠ MNO + ∠ MON = 180°
⇒ 2x + x + 90° = 180°
⇒ 3x = 180° - 90°
⇒ x =
⇒ x = 30°
Hence, the inclination = 30°.
Write the inclination of a line which is :
(i) parallel to x-axis.
(ii) perpendicular to x-axis.
(iii) parallel to y-axis.
(iv) perpendicular to y-axis.
Answer
(i) A line parallel to the x-axis has an inclination of 0°, as it does not make an angle with the x-axis.
Hence, the inclination of the line = 0°.
(ii) A line perpendicular to the x-axis is parallel to the y-axis and makes a 90° angle with the x-axis.
Hence, the inclination of the line = 90°.
(iii) A line parallel to the y-axis is perpendicular to the x-axis, so its inclination is 90°.
Hence, the inclination of the line = 90°.
(iv) A line perpendicular to the y-axis is parallel to the x-axis, so its inclination is 0°.
Hence, the inclination of the line = 0°.
Write the slope of the line whose inclination is:
(i) 0°
(ii) 30°
(iii) 45°
(iv) 60°
Answer
(i) 0°
The inclination of a line is 0°, then θ = 0°.
The slope of the line = m = tan 0° = 0
Hence, the slope of the line whose inclination is 0° is 0.
(ii) 30°
The inclination of a line is 30°, then θ = 30°.
The slope of the line = m = tan 30° =
Hence, the slope of the line whose inclination is 30° is .
(iii) 45°
The inclination of a line is 45°, then θ = 45°.
The slope of the line = m = tan 45° = 1
Hence, the slope of the line whose inclination is 45° is 1.
(iv) 60°
The inclination of a line is 60°, then θ = 60°.
The slope of the line = m = tan 60° =
Hence, the slope of the line whose inclination is 60° is .
Find the inclination of the line whose slope is:
(i) 0
(ii) 1
(iii)
(iv)
Answer
(i) The slope of the line = m = 0 ⇒ tan θ = 0
⇒ tan θ = tan 0°
⇒ θ = 0°
Hence, the inclination is 0°.
(ii) The slope of the line = m = 1 ⇒ tan θ = 1
⇒ tan θ = tan 45°
⇒ θ = 45°
Hence, the inclination is 45°.
(iii) The slope of the line = m = ⇒ tan θ = .
⇒ tan θ = tan 60°
⇒ θ = 60°
Hence, the inclination is 60°.
(iv) The slope of the line = m = ⇒ tan θ =
⇒ tan θ = tan 30°
⇒ θ = 30°
Hence, the inclination is 30°.
Write the slope of the line which is :
(i) parallel to x-axis.
(ii) perpendicular to x-axis.
(iii) parallel to y-axis.
(iv) perpendicular to y-axis.
Answer
(i) A line parallel to the x-axis has an inclination of 0°, as it does not make an angle with the x-axis.
Therefore, the inclination of the line is 0°.
The slope of the line = m = tan θ = tan 0° = 0
Hence, the slope of the line is 0.
(ii) A line perpendicular to the x-axis is parallel to the y-axis and makes a 90° angle with the x-axis.
Therefore, the inclination of the line is 90°.
The slope of the line = m = tan θ = tan 90° = not defined
Hence, the slope of the line is not defined.
(iii) A line parallel to the y-axis is perpendicular to the x-axis, so its inclination is 90°.
Therefore, the inclination of the line is 90°.
The slope of the line = m = tan θ = tan 90° = not defined
Hence, the slope of the line is not defined.
(iv) A line perpendicular to the y-axis is parallel to the x-axis, so its inclination is 0°.
Therefore, the inclination of the line is 0°.
The slope of the line = m = tan θ = tan 0° = 0
Hence, the slope of the line is 0.
For each of the equations given below, find the slope and the y-intercept :
(i) x + 3y + 5 = 0
(ii) 3x - y - 8 = 0
(iii) 5x = 4y + 7
(iv) x = 5y - 4
(v) y = 7x - 2
(vi) 3y = 7
(vii) 4y + 9 = 0
Answer
(i) x + 3y + 5 = 0
⇒ 3y = -x - 5
⇒ y = -
∴ Slope = coefficient of x =
And, y-intercept = constant term =
Hence, the slope = and y-intercept = .
(ii) 3x - y - 8 = 0
⇒ y = 3x - 8
∴ Slope = coefficient of x = 3
And, y-intercept = constant term = -8
Hence, the slope = 3 and y-intercept = -8.
(iii) 5x = 4y + 7
⇒ 4y = 5x - 7
⇒ y = x -
∴ Slope = coefficient of x =
And, y-intercept = constant term =
Hence, the slope = and y-intercept = .
(iv) x = 5y - 4
⇒ 5y = x + 4
⇒ y = x +
∴ Slope = coefficient of x =
And, y-intercept = constant term =
Hence, the slope = and y-intercept = .
(v) y = 7x - 2
∴ Slope = coefficient of x = 7
And, y-intercept = constant term = -2
Hence, the slope = 7 and y-intercept = -2.
(vi) 3y = 7
⇒ 3y = 0 x + 7
⇒ y = 0 x +
∴ Slope = coefficient of x = 0
And, y-intercept = constant term =
Hence, the slope = 0 and y-intercept = .
(vii) 4y + 9 = 0
⇒ 4y = 0 x - 9
⇒ y = 0 x -
∴ Slope = coefficient of x = 0
And, y-intercept = constant term =
Hence, the slope = 0 and y-intercept = .
Find the equation of the line, whose :
(i) slope = 2 and y-intercept = 3
(ii) slope = 5 and y-intercept = - 8
(iii) slope = - 4 and y-intercept = 2
(iv) slope = - 3 and y-intercept = - 1
(v) slope = 0 and y-intercept = - 5
(vi) slope = 0 and y-intercept = 0
Answer
(i) slope = 2 ⇒ m = 2
y-intercept = 3 ⇒ c = 3
∴ Equation is : y = mx + c
⇒ y = 2x + 3
Hence, the equation of the line is y = 2x + 3.
(ii) slope = 5 ⇒ m = 5
y-intercept = -8 ⇒ c = -8
∴ Equation is : y = mx + c
⇒ y = 5x - 8
Hence, the equation of the line is y = 5x - 8.
(iii) slope = -4 ⇒ m = -4
y-intercept = 2 ⇒ c = 2
∴ Equation is : y = mx + c
⇒ y = -4x + 2
⇒ 4x + y = 2
Hence, the equation of the line is 4x + y = 2.
(iv) slope = -3 ⇒ m = -3
y-intercept = -1 ⇒ c = -1
∴ Equation is : y = mx + c
⇒ y = -3x - 1
⇒ 3x + y + 1 = 0
Hence, the equation of the line is 3x + y + 1 = 0.
(v) slope = 0 ⇒ m = 0
y-intercept = - 5 ⇒ c = - 5
∴ Equation is : y = mx + c
⇒ y = 0 x - 5
⇒ y + 5 = 0
Hence, the equation of the line is y + 5 = 0.
(vi) slope = 0 ⇒ m = 0
y-intercept = 0 ⇒ c = 0
∴ Equation is : y = mx + c
⇒ y = 0 x + 0
⇒ y = 0
Hence, the equation of the line is y = 0.
Draw the line 3x + 4y = 12 on a graph paper. From the graph paper, read the y-intercept of the line.
Answer
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = 0, then 3 0 + 4y = 12 ⇒ y = 3
Let x = 1, then 3 1 + 4y = 12 ⇒ y = 2.2
Let x = 4, then 3 4 + 4y = 12 ⇒ y = 0
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | 0 | 1 | 4 |
|---|---|---|---|
| y | 3 | 2.2 | 0 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
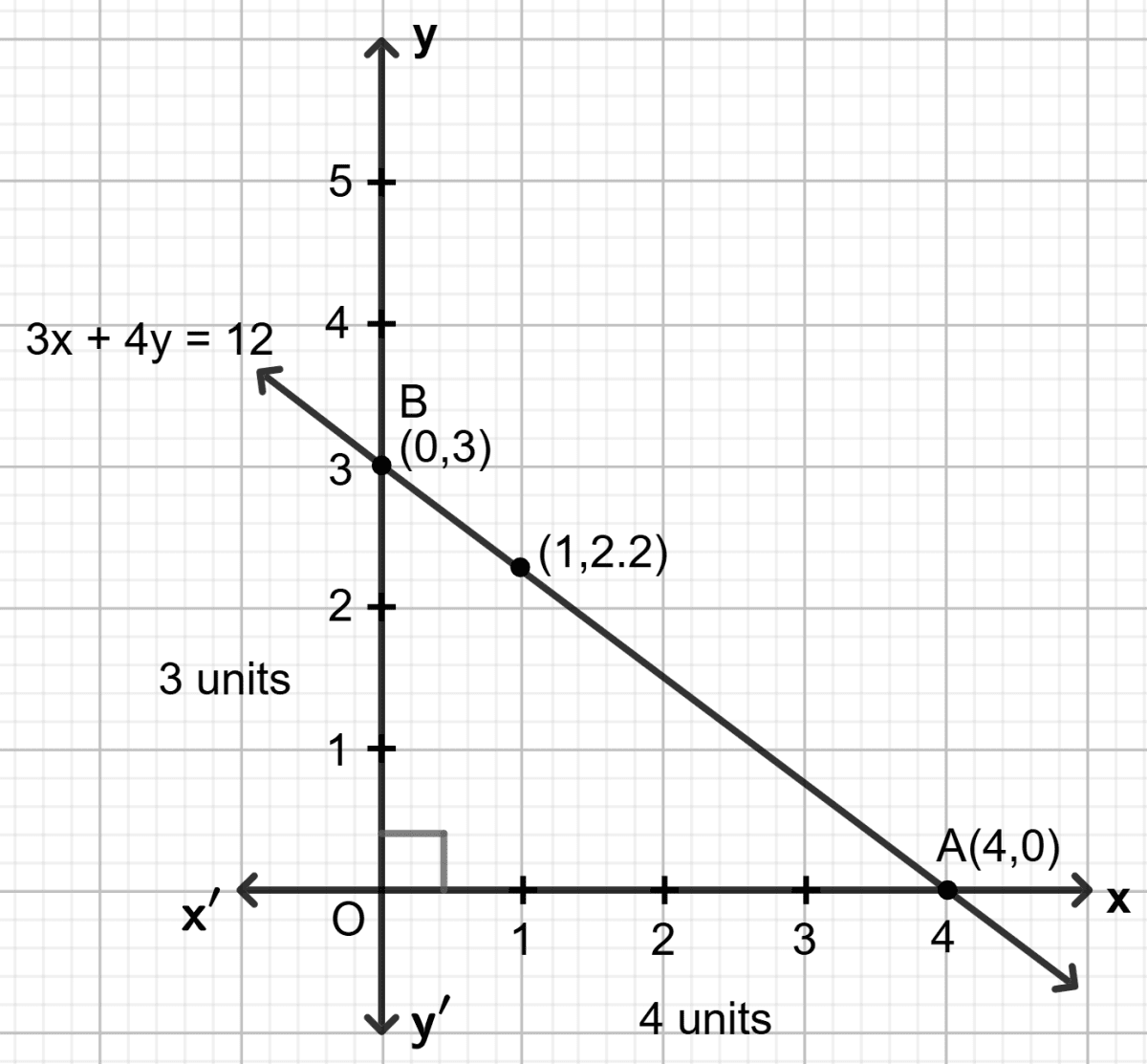
From the graph, y-intercept of the line = OB = 3.
Hence, y-intercept of the line = 3.
Draw the line 2x - 3y - 18 = 0 on a graph paper. From the graph paper, read the y-intercept of the line.
Answer
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = 0, then 2 0 - 3y - 18 = 0 ⇒ y = -6
Let x = 3, then 2 3 - 3y - 18 = 0 ⇒ y = -4
Let x = 6, then 2 6 - 3y - 18 = 0 ⇒ y = -2
Let x = 9, then 2 9 - 3y - 18 = 0 ⇒ y = 0
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | 0 | 3 | 6 | 9 |
|---|---|---|---|---|
| y | -6 | -4 | -2 | 0 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
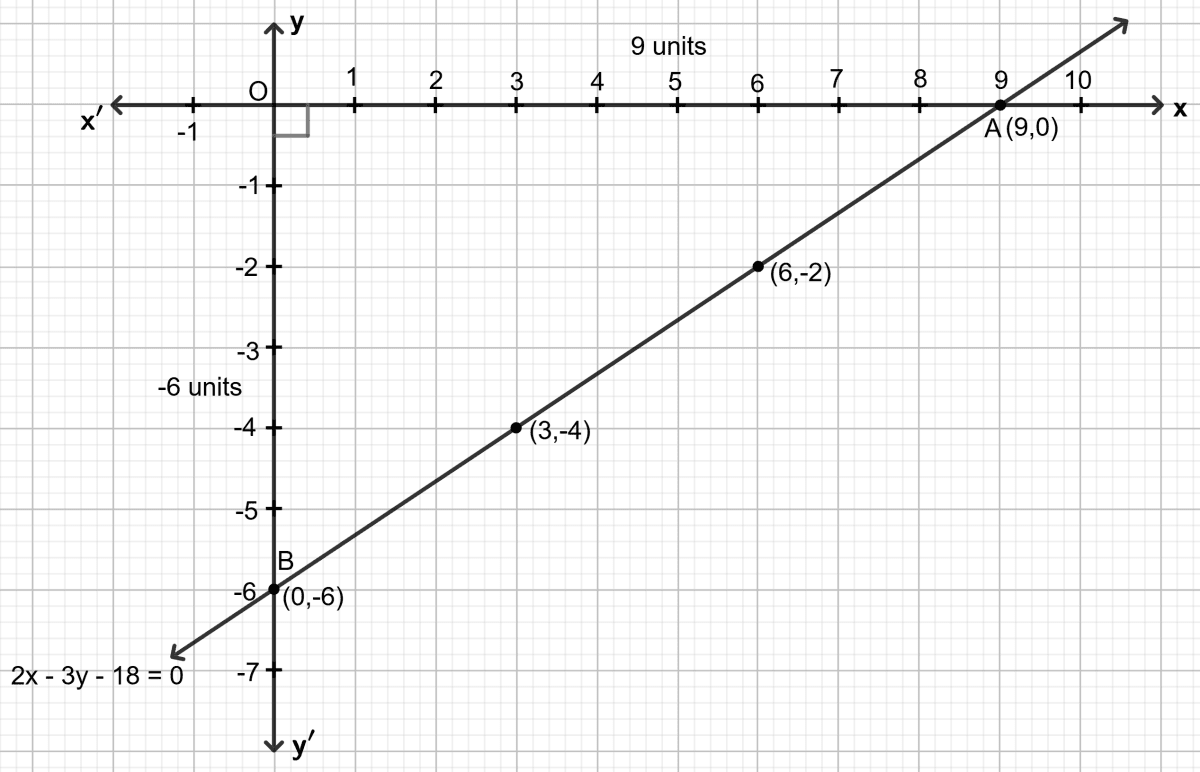
From the graph, y-intercept of the line = OB = -6.
Hence, y-intercept of the line = -6.
For point P(-5, 4):
abscissa = 4, ordinate = -5
ordinate = 4, abscissa = -5
abscissa = ordinate = -5
abscissa = ordinate = 4
Answer
Given, point P(-5, 4)
Abscissa (x-coordinate): -5
Ordinate (y-coordinate): 4
Hence, option 2 is the correct option.
If the perpendicular distance of a point P from the x-axis is 5 unit then the point P has
x-co-ordinate = -5
y-co-ordinate = 5 only
y-co-ordinate = -5 only
y-co-ordinate = 5 or -5
Answer
As we know that the distance of a point from the X-axis is the absolute value of its y-coordinate.
So, if perpendicular distance of a point from the x-axis is 5 units. Then the y-coordinate can be 5 or -5.
Hence, option 4 is the correct option.
A point lies on y-axis at a distance of 2 unit from x-axis. Its co-ordinates are :
(2, 0) only
(0, 2) only
(2, 2)
(0, 2) or (0, -2)
Answer
If a point lies on the y‑axis, its x‑coordinate is 0.
If it’s at a distance of 2 units from the x‑axis, that means its y-coordinate is either +2 or −2 (since distance ignores sign).
Its co-ordinates are (0, 2) or (0, -2).
Hence, option 4 is the correct option.
Three vertices of a square ABCD are A(2, 0), B(-3, 0) and C(-3, -5). Its fourth vertex D is:
(2, 5)
(2, -5)
(-2, 5)
(-2, -5)
Answer
The points are shown on the graph below:
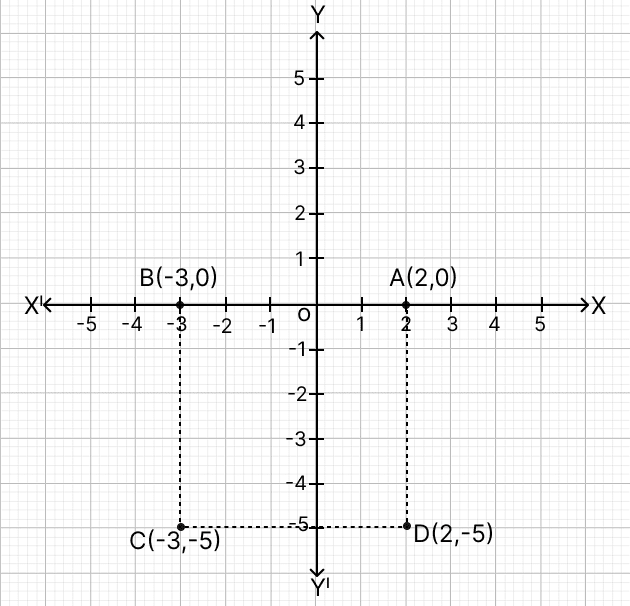
Steps of construction :
Plot points A(2, 0), B(-3, 0) and C(-3, -5) on graph.
Measure AB.
Mark point D such that it is at a distance AB from points A and C.
Join AB, BC, CD and DA.
From graph,
The co-ordinates of fourth vertex D is (2, -5).
Hence, option 2 is the correct option.
Statement 1: In the given diagram, OAB is an equilateral triangle.
Co-ordinates of the vertex B = (4, 4)
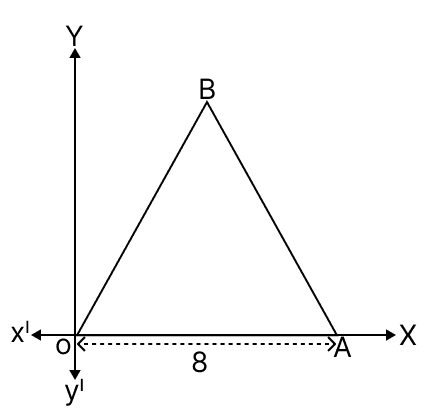
Statement 2: B = (4, )
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Answer
Given equilateral triangle OAB.
OA = OB = AB = 8 units.
Draw BD ⊥ OA.
In an equilateral triangle, a perpendicular drawn from one of the vertices to the opposite side bisects the side.
∴ OD = x OA = x 8 = 4.
In right angle triangle OBD,
By pythagoras theorem,
⇒ OB2 = OD2 + BD2
⇒ 82 = 42 + BD2
⇒ 64 = 16 + BD2
⇒ BD2 = 64 - 16
⇒ BD2 = 48
⇒ BD =
⇒ BD =
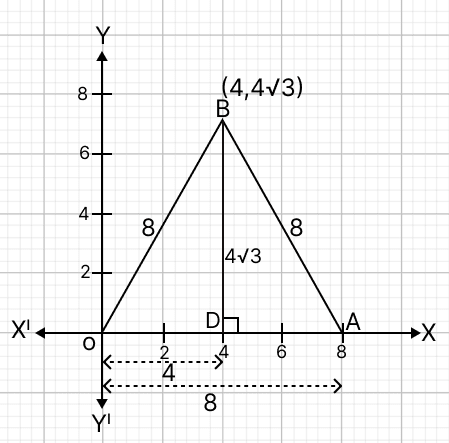
From graph,
Co-ordinates of O = (0, 0)
Co-ordinates of A = (8, 0)
As, OD = 4 units and BD = units.
Co-ordinates of B = (4, ).
∴ Statement 1 is false, and statement 2 is true.
Hence, option 4 is the correct option.
Statement 1: The vertex B of square OABC with each side 4 units lies in the fourth quadrant and its side are along the co-ordinate axes. The co-ordinate of vertex B are (4, -4).
Statement 2: B = (4, 4)
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Answer
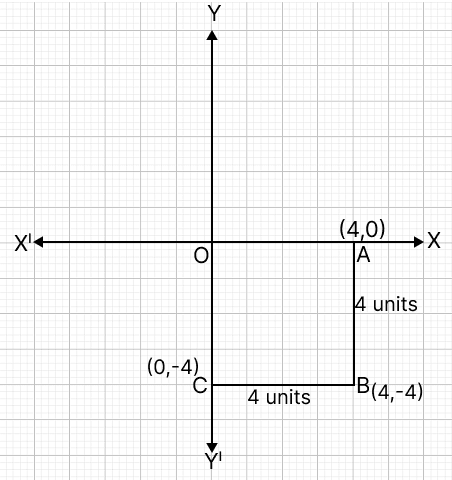
Vertex B lies in the fourth quadrant. The square's sides are along the coordinate axes, so one vertex, O, is at the origin (0, 0).
The side length is 4 units.
With O at (0, 0), the other two vertices on the axes must be A (4, 0) on the positive x-axis and C (0, -4) on the negative y-axis.
The fourth quadrant is where the x-coordinates are positive and the y-coordinates are negative.
Vertex B is located at the point where the line extending 4 units to the right from C (0, -4) intersects with the line extending 4 units down from A (4, 0), which is (4, -4).
⇒ B = (4, –4).
∴ Statement 1 is true, and statement 2 is false.
Hence, option 3 is the correct option.
Assertion (A): PQR is an equilateral triangle. The co-ordinates of point Q are (0, ).
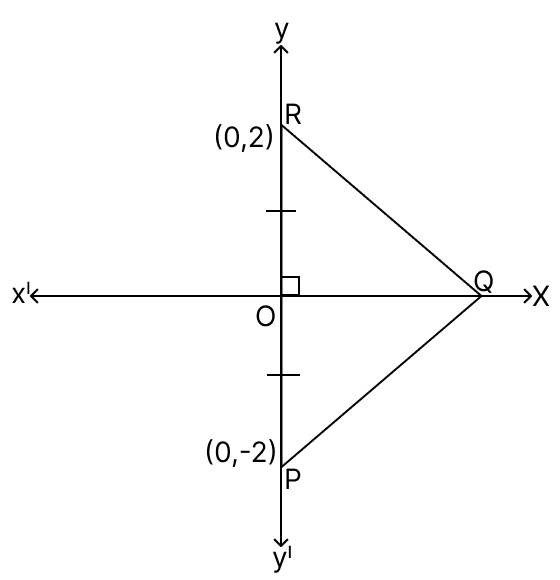
Reason (R): In ΔOPQ,
OQ2 = PQ2 - OP2 = 42 - 22 = 12.
A is true, but R is false.
A is false, but R is true.
Both A and R are true, and R is the correct reason for A.
Both A and R are true, and R is the incorrect reason for A.
Answer
The coordinates of R(0, 2) and P(0, -2).
Using distance formula,
Distance between two points =
PR = units.
Given equilateral triangle PQR.
∴ PQ = QR = PR = 4 units.
In an equilateral triangle, a perpendicular drawn from one of the vertices to the opposite side bisects the side.
∴ OP = x PR = x 4 = 2 units.
In right angle triangle OPQ,
By pythagoras theorem,
⇒ QP2 = OP2 + OQ2
⇒ OQ2 = QP2 - OP2
⇒ OQ2 = 42 - 22
⇒ OQ2 = 16 - 4
⇒ OQ2 = 12
⇒ OQ =
⇒ OQ =
Since, OQ = units and Q lies on x-axis.
Co-ordinates of Q = (, 0).
∴ A is false, but R is true.
Hence, option 2 is the correct option.
Assertion (A): (2x - 3y, 8) = (2, x + 2y)
⇒ x = 1 and y = -2
Reason (R): 2x - 3y = 2 and 8 = x + 2y
A is true, but R is false.
A is false, but R is true.
Both A and R are true, and R is the correct reason for A.
Both A and R are true, and R is the incorrect reason for A.
Answer
Given, (2x - 3y, 8) = (2, x + 2y)
Thus,
2x - 3y = 2 ........(1)
x + 2y = 8 ........(2)
So, reason (R) is true.
Multiplying equation (2) by 2, we get :
⇒ 2(x + 2y) = 2 × 8
⇒ 2x + 4y = 16 ........(3)
Subtracting equation (1) from (3), we get :
⇒ 2x + 4y - (2x - 3y) = 16 - 2
⇒ 2x - 2x + 4y + 3y = 14
⇒ 7y = 14
⇒ y = = 2.
Substituting the value y = 2 in first equation,
⇒ 2x - 3 x 2 = 2
⇒ 2x - 6 = 2
⇒ 2x = 2 + 6
⇒ 2x = 8
⇒ x = = 4.
Hence, the value of x = 4 and y = 2.
∴ A is false, but R is true.
Hence, option 2 is the correct option.
By plotting the following points on the same graph paper, check whether they are collinear or not :
(3, 5), (1, 1) and (0, -1)
Answer
(3, 5), (1, 1) and (0, -1)
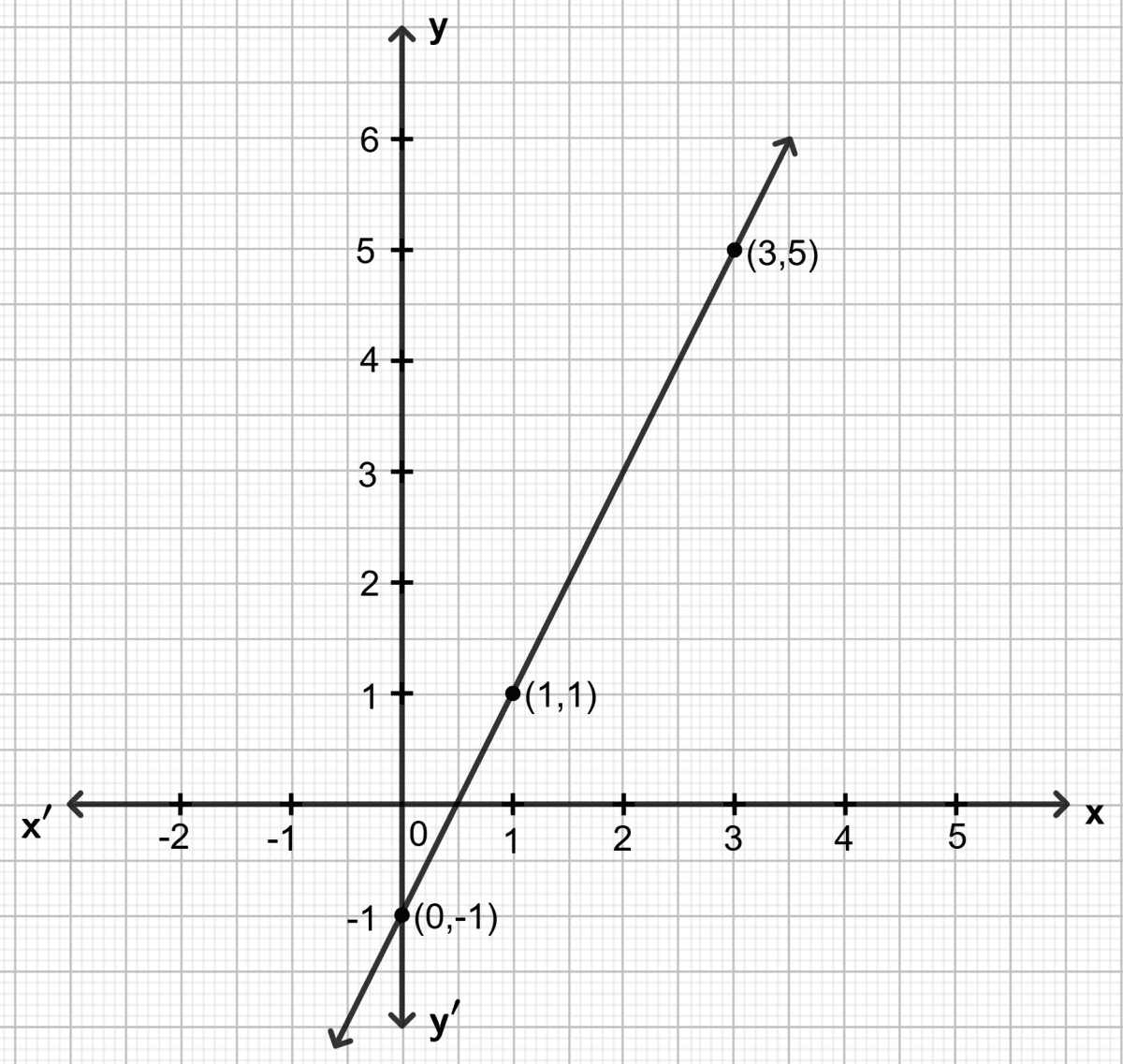
As shown in the figure, all three points lie on the same straight line.
Hence, the points are collinear.
By plotting the following points on the same graph paper, check whether they are collinear or not :
(-2, -1), (-1, -4) and (-4, 1)
Answer
(-2, -1), (-1, -4) and (-4, 1)
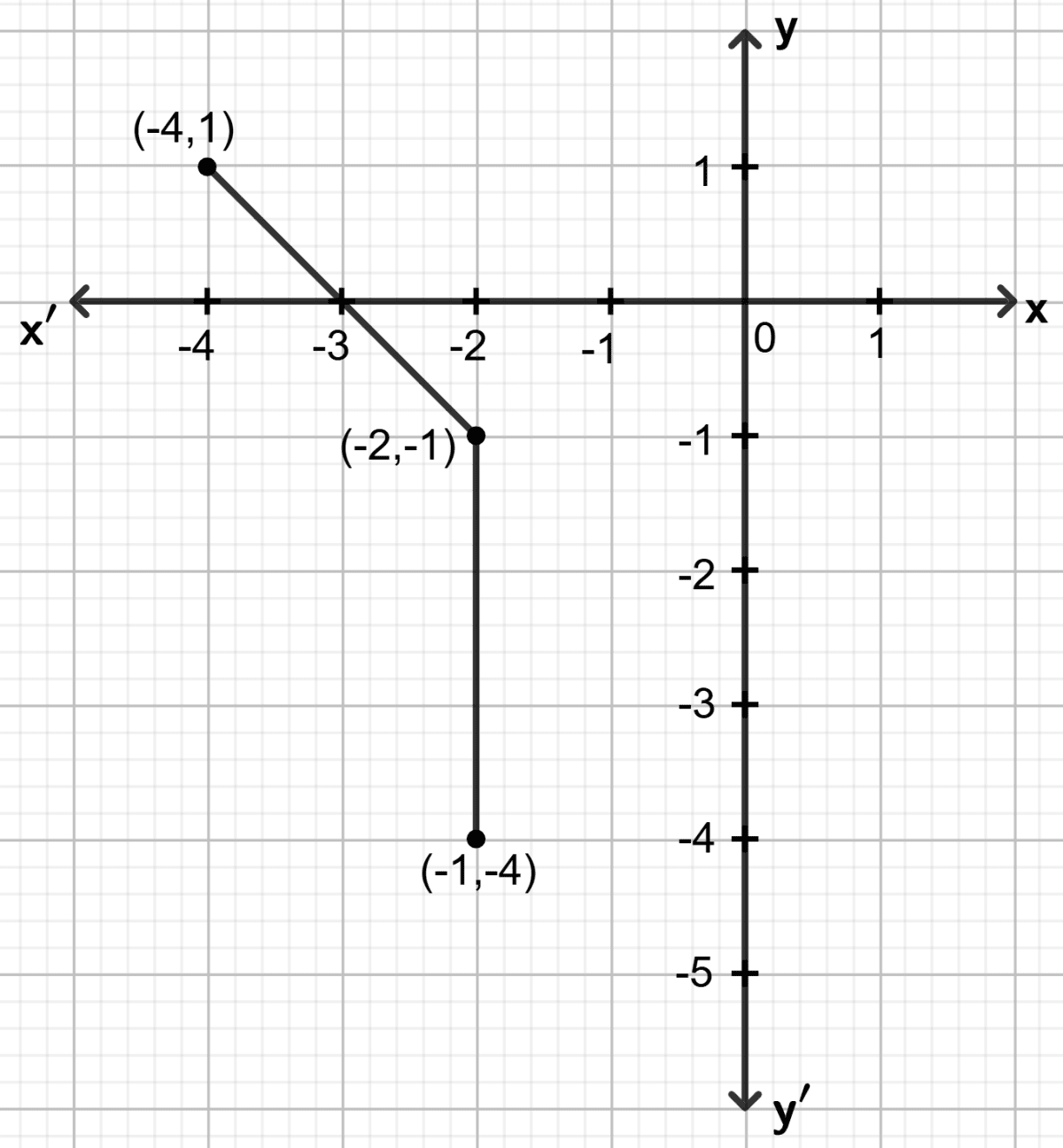
As shown in the figure, all three points do not lie on the same straight line.
Hence, the points are not collinear.
Plot the point A (5, -7). From point A, draw AM perpendicular to x-axis and AN perpendicular to y-axis. Write the co-ordinates of points M and N.
Answer
Given point : A (5, -7)
AM is perpendicular to the x-axis.
AN is perpendicular to the y-axis.
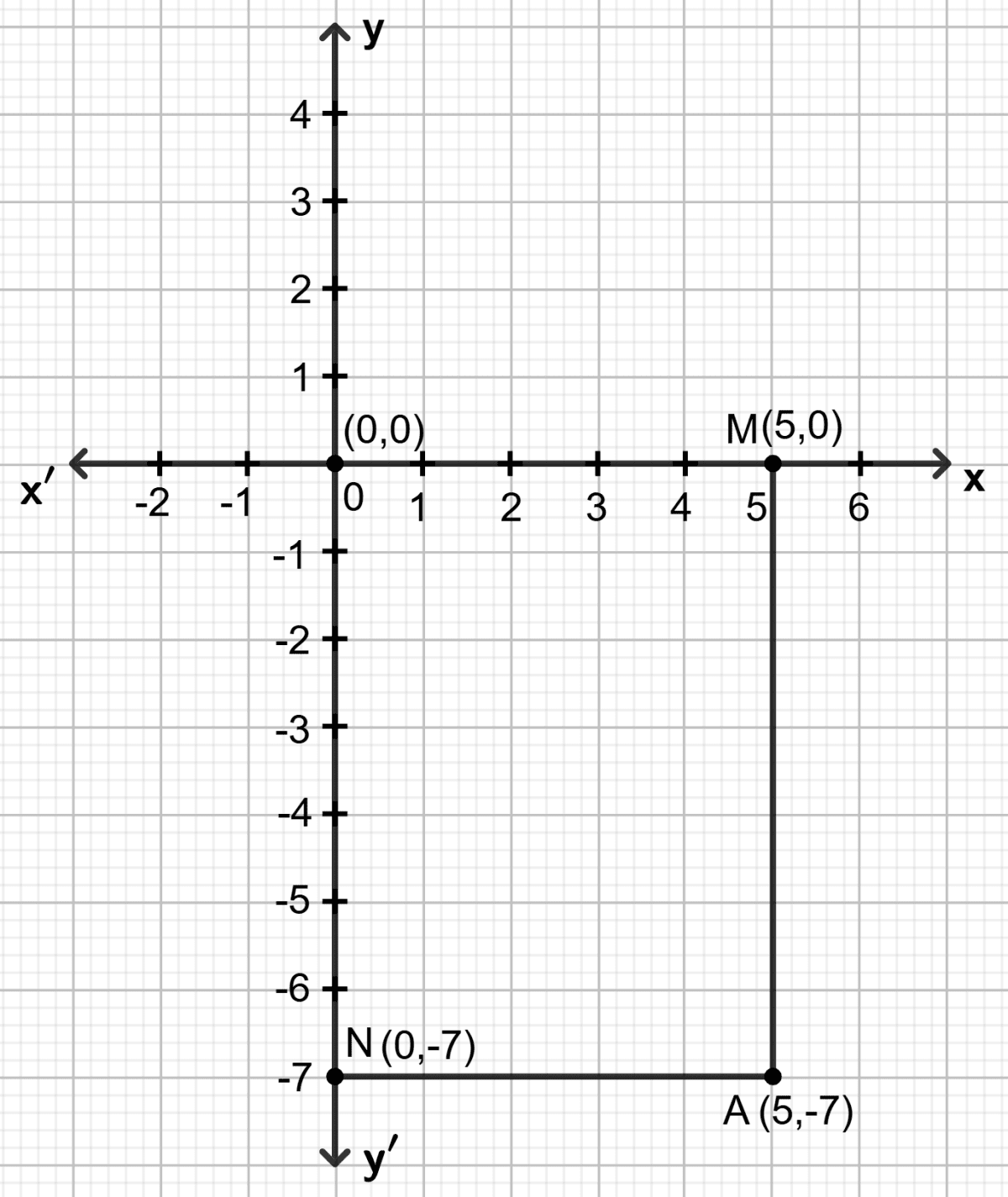
The graph intersects the x-axis at M(5, 0).
The graph intersects the y-axis at N(0, -7).
Hence, the coordinates of the points are M = (5, 0) and N = (0, -7).
In square ABCD; A = (3, 4), B = (-2, 4) and C = (-2, -1). By plotting these points on a graph paper, find the co-ordinates of vertex D. Also, find the area of the square.
Answer
Plot the points A = (3, 4), B = (-2, 4) and C = (-2, -1) on the graph paper. Join point A with B and B with C.
From the graph, it is clear that the horizontal distance between the points A (3, 4) and B (-2, 4) is 5 units and the vertical distance between the points B (-2, 4) and C (-2, -1) is 5 units. Therefore, the vertical distance between the points A (3, 4) and D must be 5 units and the horizontal distance between the points C (-2, -1) and D must be 5 units.
Now, complete the square ABCD and read the coordinates of point D, as shown on the graph, D = (3, -1).
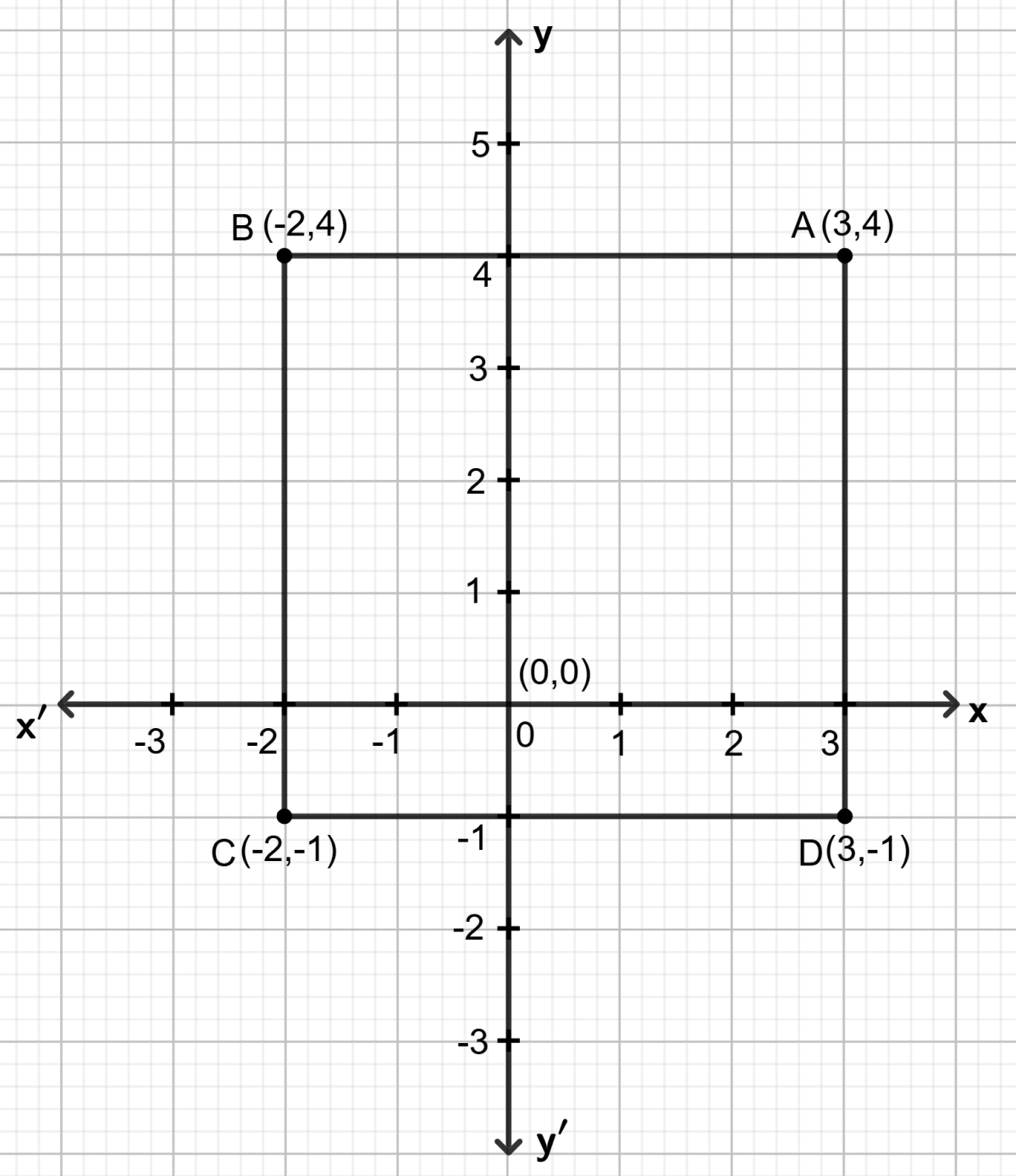
Area of the square ABCD = AD x CD
= 5 x 5 square units
= 25 square units
Hence, the coordinates of D = (3, -1) and the area of the square = 25 square units.
In rectangle OABC; point O is the origin, OA = 10 units along x-axis and AB = 8 units. Find the co-ordinates of vertices A, B and C.
Answer
Given that in rectangle OABC, point O is the origin and OA = 10 units along x-axis, therefore we have O(0, 0) and A(10, 0).
It is also given that AB = 8 units. Since AB is perpendicular to OA (as OABC is a rectangle), the line through A is a vertical line and it meets B at B(10, 8).
Through point B, draw a horizontal line (parallel to x-axis) that meets the y-axis at y = 8. This gives the coordinates of point C: (0, 8).
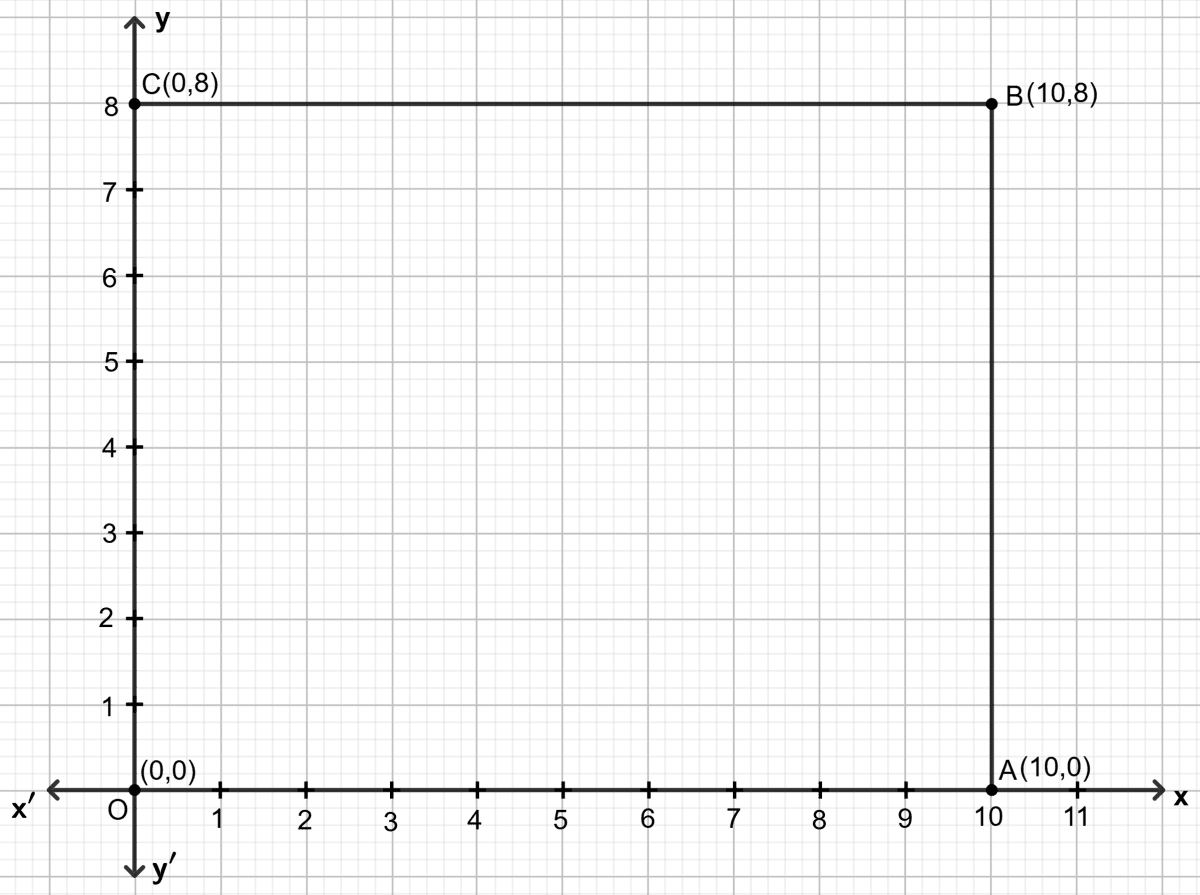
Thus, the vertices of rectangle OABC are: O(0, 0), A(10, 0), B(10, 8) and C(0, 8)
Hence, the coordinates of the vertices are A = (10, 0), B = (10, 8) and C = (0, 8).
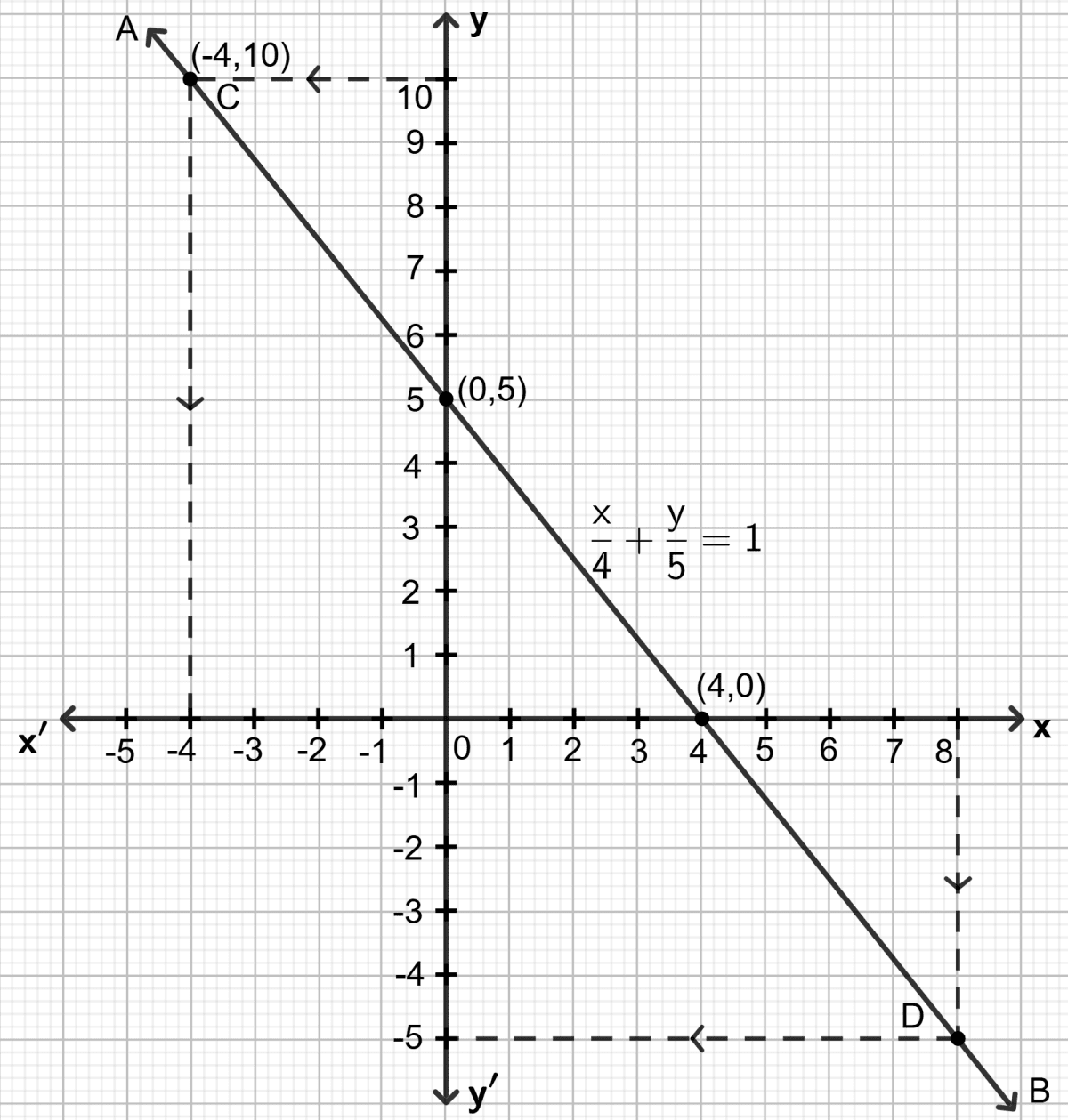
Draw the graph of equation x + 2y - 3 = 0. From the graph, find :
(i) x1, the value of x, when y = 3
(ii) x2, the value of x, when y = -2.
Answer
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -1, then (-1) + 2y - 3 = 0 ⇒ y = 2
Let x = 0, then 0 + 2y - 3 = 0 ⇒ y = 1.5
Let x = 1, then 1 + 2y - 3 = 0 ⇒ y = 1
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -1 | 0 | 1 |
|---|---|---|---|
| y | 2 | 1.5 | 1 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line AB passing through the points plotted on the graph.
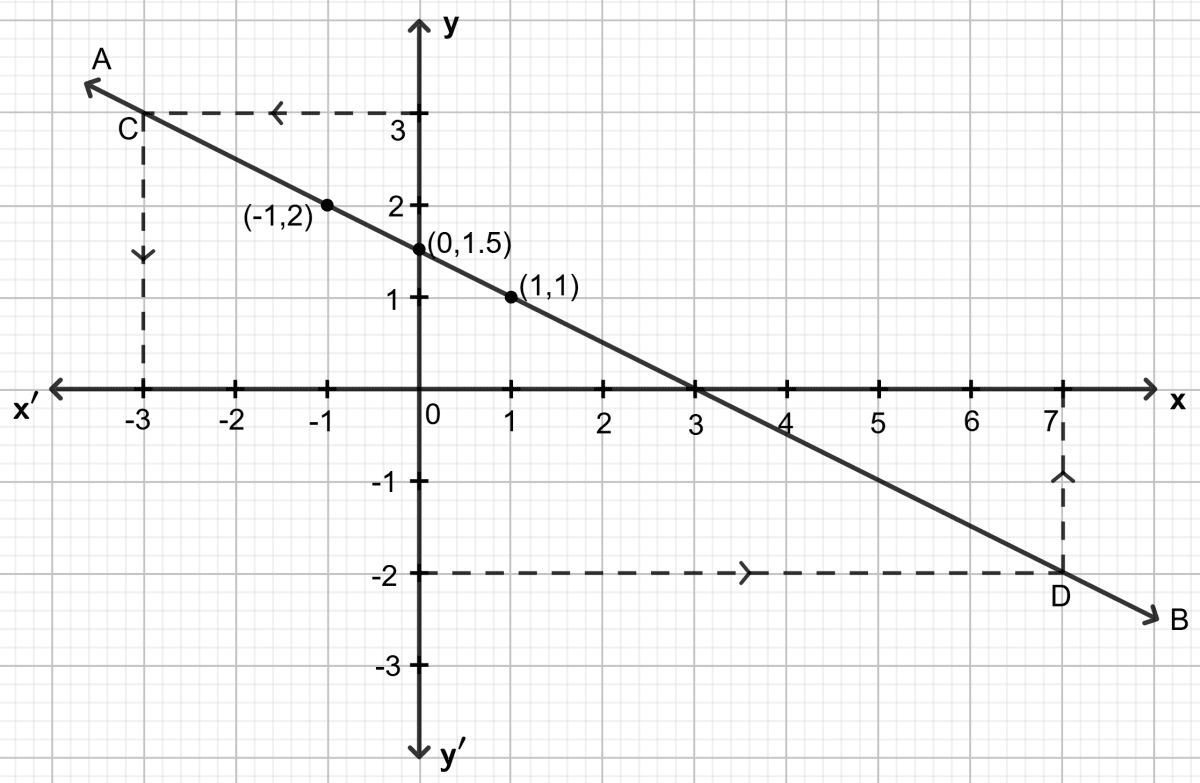
(i) To find x1, the value of x, when y = 3:
Through the point y = 3, draw a horizontal straight line which meets the line AB at point C. Through point C, draw a vertical line which meets the x-axis at x = -3.
Hence, the value of x, when y = 3 is -3 , i.e, x1 = -3.
(ii) To find x2, the value of x, when y = -2:
Through the point y = -2, draw a horizontal straight line which meets the line AB at point D. Now, through point D, draw a vertical line which meets the y-axis at x = 7.
Hence, the value of x, when y = -2 is 7 , i.e, x2 = 7.
Draw the graph of equation 3x - 4y = 12. Use the graph drawn to find :
(i) y1, the value of y, when x = 4
(ii) y2, the value of y, when x = 0.
Answer
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -2, then 3 (-2) - 4y = 12 ⇒ y = -4.5
Let x = 1, then 3 1 - 4y = 12 ⇒ y = -2.2
Let x = 2, then 3 2 - 4y = 12 ⇒ y = -1.5
Let x = 4, then 3 4 - 4y = 12 ⇒ y = 0
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -2 | 1 | 2 | 4 |
|---|---|---|---|---|
| y | -4.5 | -2.2 | -1.5 | 0 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
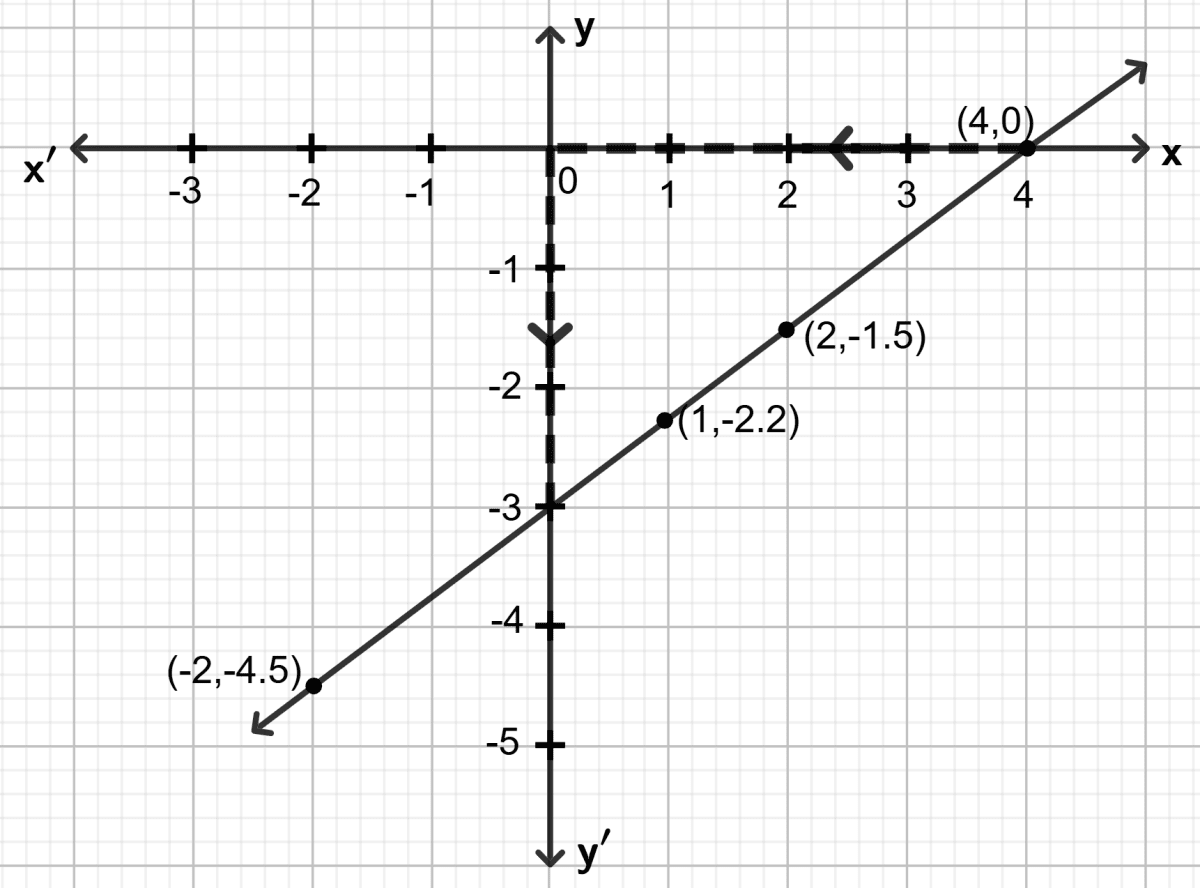
(i) To find y1, the value of y, when x = 4:
Through the point x = 4, draw a horizontal line which meets the y-axis at y = 0.
Hence, the value of y, when x = 4 is 0 , i.e, y1 = 0.
(ii) To find y2, the value of y, when x = 0:
Through the point x = 0, draw a vertical line which meets the y-axis at x = -3.
Hence, the value of y, when x = 0 is -3 , i.e, y2 = -3.
Draw the graph of equation . Use the graph drawn to find :
(i) x1, the value of x, when y = 10
(ii) y1, the value of y, when x = 8.
Answer
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -4, then ⇒ y = 10
Let x = 0, then ⇒ y = 5
Let x = 4, then ⇒ y = 0
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | - 4 | 0 | 4 |
|---|---|---|---|
| y | 10 | 5 | 0 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line AB passing through the points plotted on the graph.
(i) To find x1, the value of x, when y = 10:
Through the point y = 10, draw a horizontal straight line which meets the line AB at point C.
Through point C, draw a vertical line which meets the x-axis at x = -4.
Hence, the value of x, when y = 10 is -4 , i.e, x1 = -4.
(ii) To find y1, the value of y, when x = 8:
Through the point x = 8, draw a vertical line which meets the line AB at point D.
Now, through point D, draw a horizontal line which meets the y-axis at y = -5.
Hence, the value of y, when x = 8 is -5 , i.e, y1 = -5.
Use the graphical method to show that the straight lines given by the equations and pass through the same point.
Answer
First equation : x + y = 2
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -1, then (-1) + y = 2 ⇒ y = 3
Let x = 0, then 0 + y = 2 ⇒ y = 2
Let x = 1, then 1 + y = 2 ⇒ y = 1
Let x = 3, then 3 + y = 2 ⇒ y = -1
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -1 | 0 | 1 | 3 |
|---|---|---|---|---|
| y | 3 | 2 | 1 | -1 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
Second equation : x - 2y = 5
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -1, then (-1) - 2y = 5 ⇒ y = -3
Let x = 0, then 0 - 2y = 5 ⇒ y = -2.5
Let x = 1, then 1 - 2y = 5 ⇒ y = -2
Let x = 3, then 3 - 2y = 5 ⇒ y = -1
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -1 | 0 | 1 | 3 |
|---|---|---|---|---|
| y | -3 | -2.5 | -2 | -1 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
Third equation :
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -3, then ⇒ y = 1
Let x = 0, then ⇒ y = 0
Let x = 3, then ⇒ y = -1
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -3 | 0 | 3 |
|---|---|---|---|
| y | 1 | 0 | -1 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
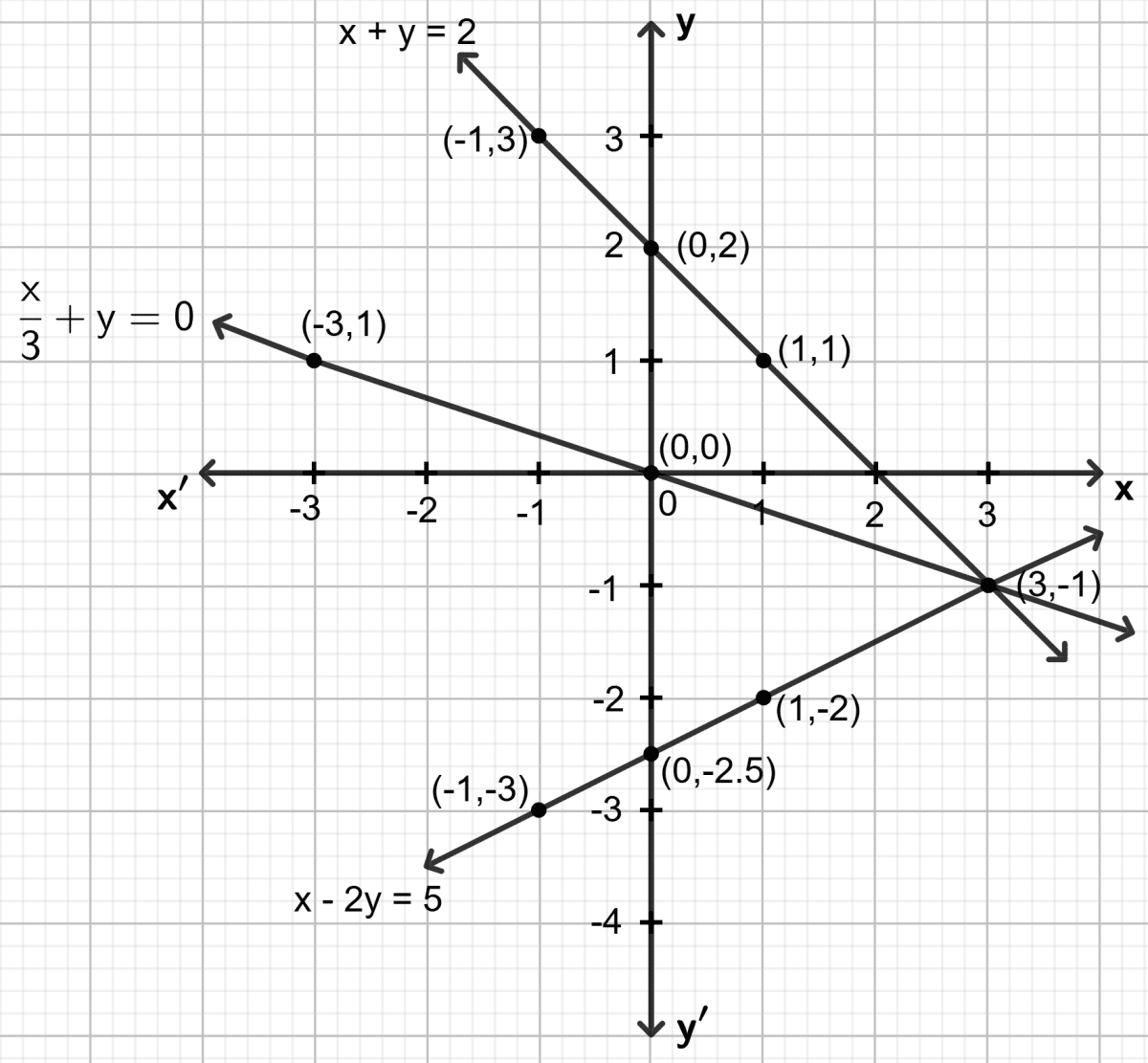
Hence, the three straight lines pass through the same point.
Draw the graph of line x + y = 5. Use the graph paper drawn to find the inclination and the y-intercept of the line.
Answer
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = (-1), then (-1) + y = 5 ⇒ y = 6
Let x = 0, then 0 + y = 5 ⇒ y = 5
Let x = 1, then 1 + y = 5 ⇒ y = 4
Let x = 5, then 5 + y = 5 ⇒ y = 0
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -1 | 0 | 1 | 5 |
|---|---|---|---|---|
| y | 6 | 5 | 4 | 0 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
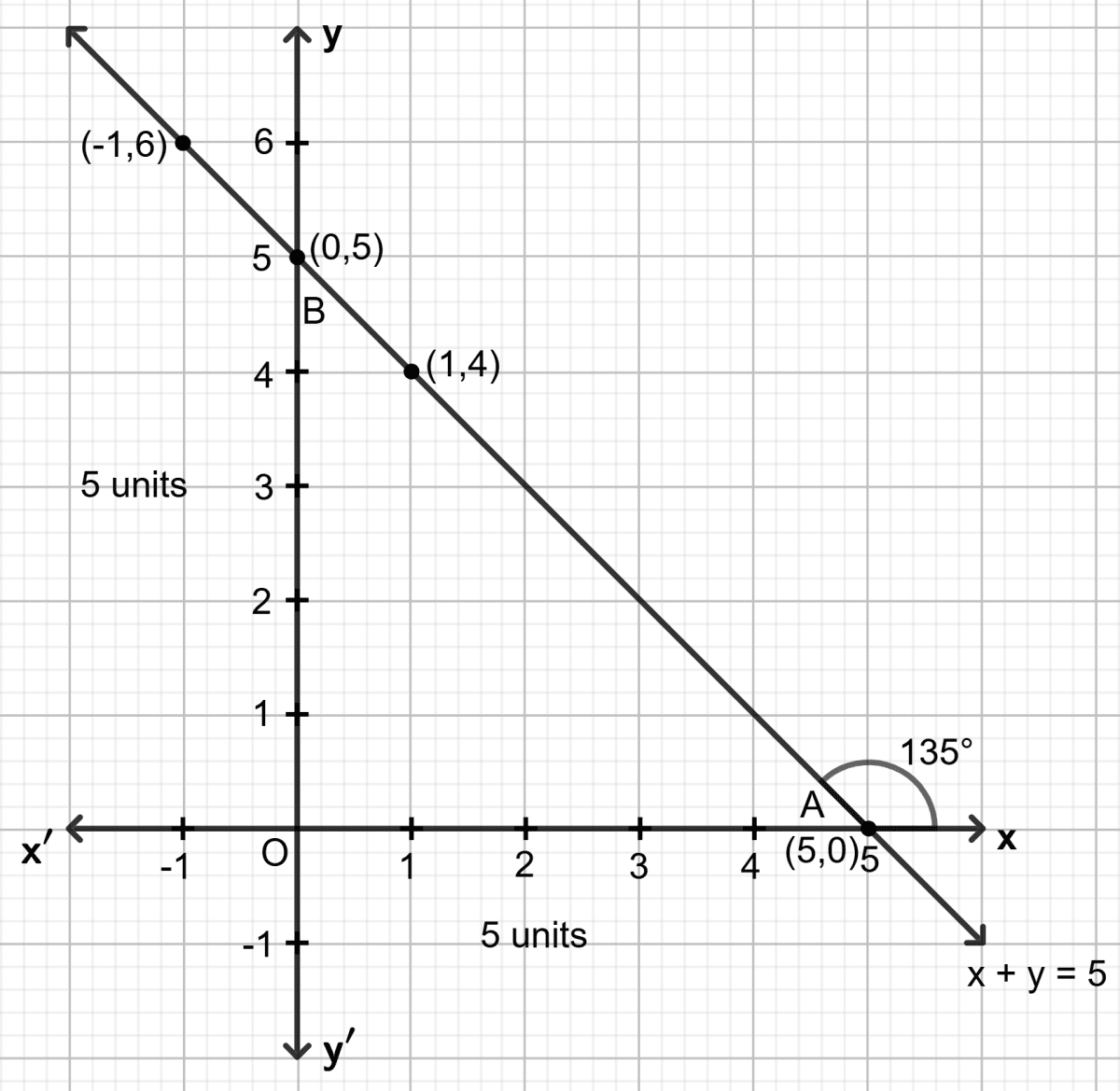
From the graph, inclination of the line = θ = 135° and y-intercept of the line = OB = 5.
Hence, inclination = 135° and y-intercept of the line = 5.
Draw the graph of line 2x + y = 5.
Answer
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -1, then 2 (-1) + y = 5 ⇒ y = 7
Let x = 0, then 2 0 + y = 5 ⇒ y = 5
Let x = 1, then 2 1 + y = 5 ⇒ y = 3
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -1 | 0 | 1 |
|---|---|---|---|
| y | 7 | 5 | 3 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
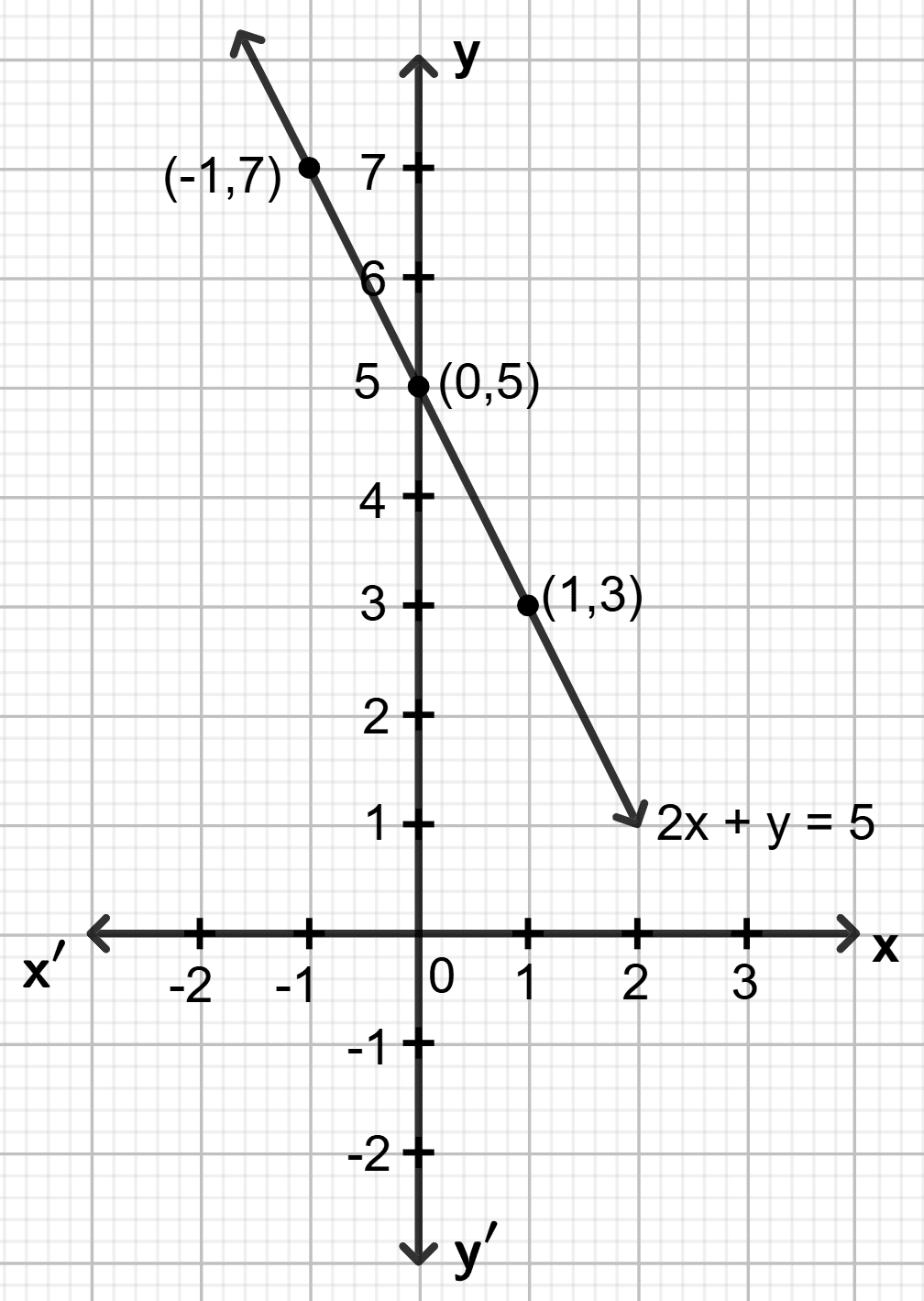
Draw the graph of line 4x - y = 5. Use this graph to find :
(i) x1, the value of x when y = 3.
(ii) y1, the value of y, when x = 3.
Answer
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = 4, then 4 (4) - y = 5 ⇒ y = 11
Let x = 3.5, then 4 3.5 - y = 5 ⇒ y = 9
Let x = 1, then 4 1 - y = 5 ⇒ y = -1
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | 4 | 3.5 | 3 |
|---|---|---|---|
| y | 11 | 9 | 7 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line AB passing through the points plotted on the graph.
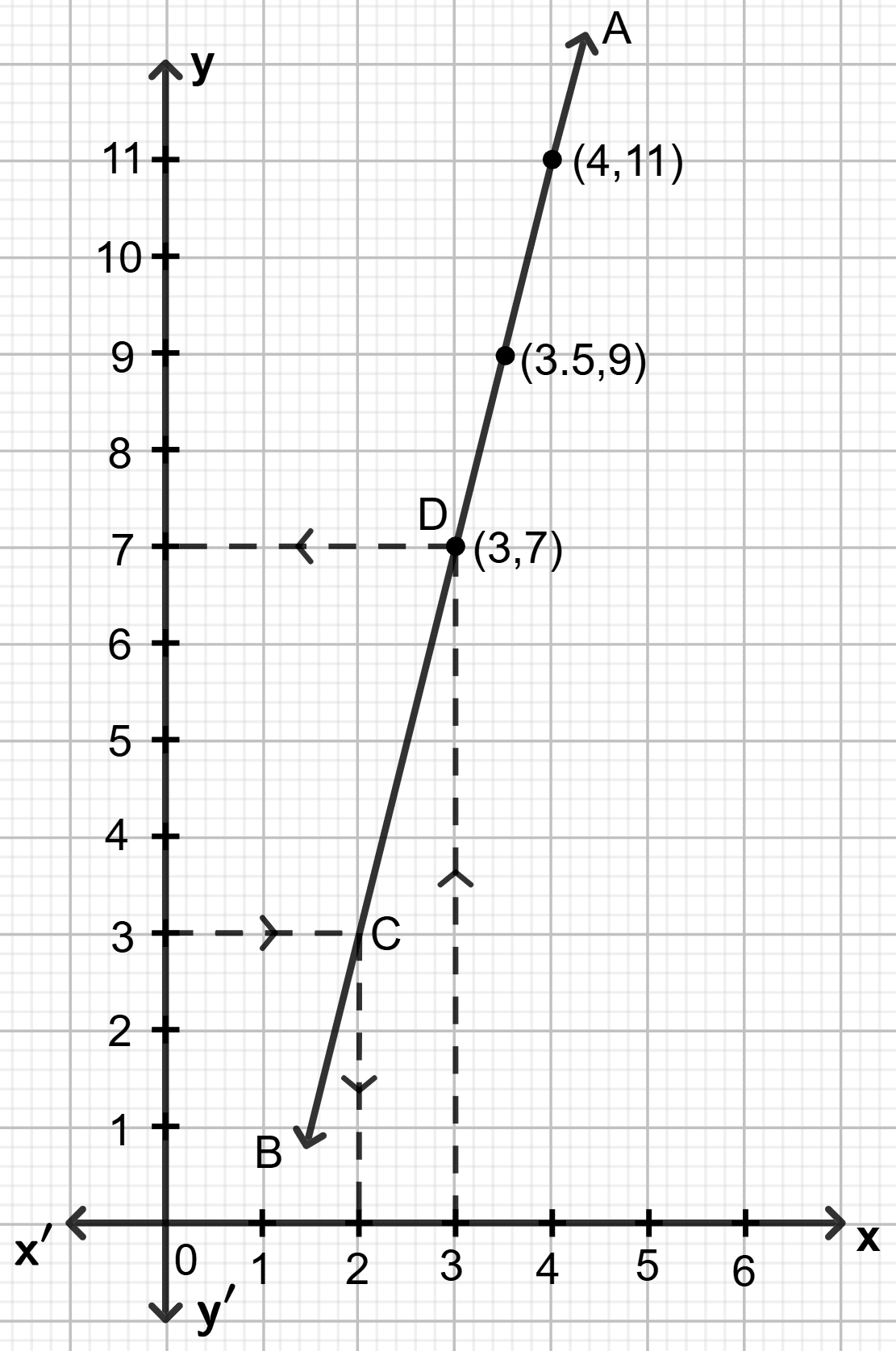
(i) To find x1, the value of x, when y = 3:
Through the point y = 3, draw a horizontal straight line which meets the line AB at point C.
Through point C, draw a vertical line which meets the x-axis at x = 2.
Hence, the value of x, when y = 3 is 2 , i.e, x1 = 2.
(ii) To find y1, the value of y, when x = 3:
Through the point x = 3, draw a vertical line which meets the line AB at point D.
Through point D, draw a horizontal line which meets the y-axis at y = 7.
Hence, the value of y, when x = 3 is 7 , i.e, y1 = 7.