Point (k, 2) lies on the line x - 4y = 2; the value of k is :
10
-6
-10
6
Answer
Given that the point (k, 2) lies on the line x - 4y = 2, substitute x = k and y = 2 into the equation:
⇒ k - 4 2 = 2
⇒ k - 8 = 2
⇒ k = 2 + 8
⇒ k = 10
Hence, option 1 is the correct option.
The line y = mx - 8 passes through the point (5, 2); the value of m is :
1
2
-2
-1
Answer
Since the line y = mx - 8 passes through the point (5, 2), substitute x = 5 and y = 2 into the equation:
⇒ 2 = m 5 - 8
⇒ 2 = 5m - 8
⇒ 5m = 2 + 8
⇒ 5m = 10
⇒ m =
⇒ m = 2
Hence, option 2 is the correct option.
The line 5x - 2y - 10 = 0 intersects x-axis at point P. The co-ordinates of point P are:
(0, 2)
(0, -2)
(2, 0)
(-2, 0)
Answer
It is given that the line 5x - 2y - 10 = 0 intersects x-axis at point P.
At the x-axis, the y-coordinate is 0. Let P = (a, 0), where x = a and y = 0.
⇒ 5 a - 2 0 - 10 = 0
⇒ 5a - 0 - 10 = 0
⇒ 5a = 10
⇒ a =
⇒ a = 2
The coordinates of point P are (2, 0).
Hence, option 3 is the correct option.
The line 5x - 4y - 20 = 0 intersects y-axis at point A. The co-ordinates of point A are :
(-5, 0)
(5, 0)
(0, 5)
(0, -5)
Answer
It is given that the line 5x - 4y - 20 = 0 intersects y-axis at point A.
At the y-axis, the x-coordinate is 0. Let A = (0, b) means x = 0 and y = b.
⇒ 5 0 - 4 b - 20 = 0
⇒ 0 - 4b - 20 = 0
⇒ 4b + 20 = 0
⇒ 4b = - 20
⇒ b = -
⇒ b = - 5
A = (0, -5)
Hence, option 4 is the correct option.
The point (0, 0) lies on :
x-axis
y-axis
x-axis or y-axis
x-axis and y-axis both
Answer
The axes are two perpendicular lines (x-axis and y-axis) that intersect at the origin. The point (0,0), known as the origin, lies on both the x-axis and the y-axis because:
The x-coordinate of (0,0) is 0, which satisfies the condition for a point on the y-axis.
The y-coordinate of (0,0) is 0, which satisfies the condition for a point on the x-axis.
Thus, the point (0,0) lies on both the x-axis and y-axis.
Hence, option 4 is the correct option.
Draw the graph for each equation, given below :
(i) x = 5
(ii) x + 5 = 0
(iii) y = 7
(iv) y + 7 = 0
(v) 2x + 3y = 0
(vi) 3x + 2y = 6
(vii) x - 5y + 4 = 0
(viii) 5x + y + 5 = 0
Answer
(i) x = 5
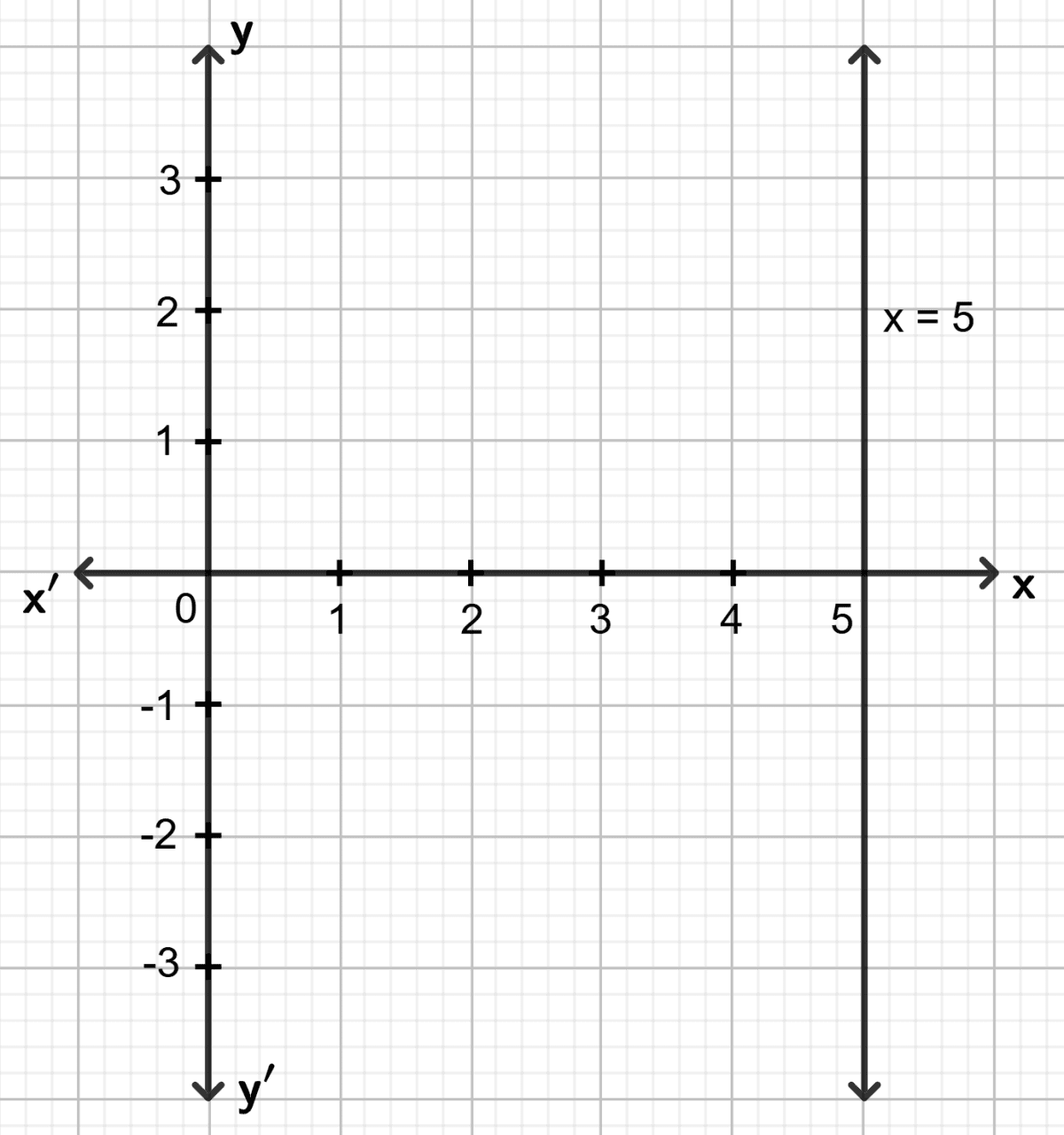
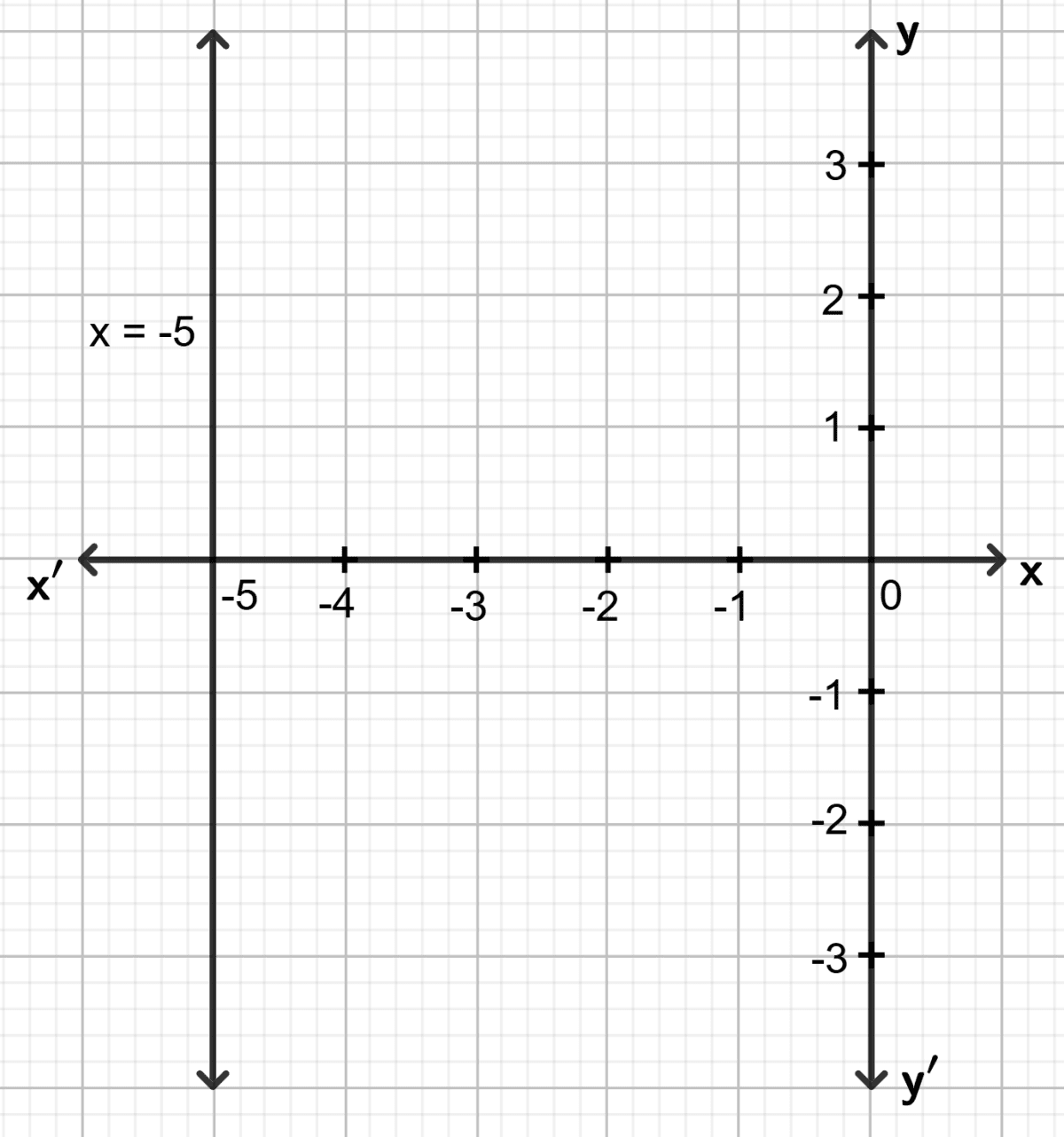
(ii) x + 5 = 0
x = -5
(iii) y = 7
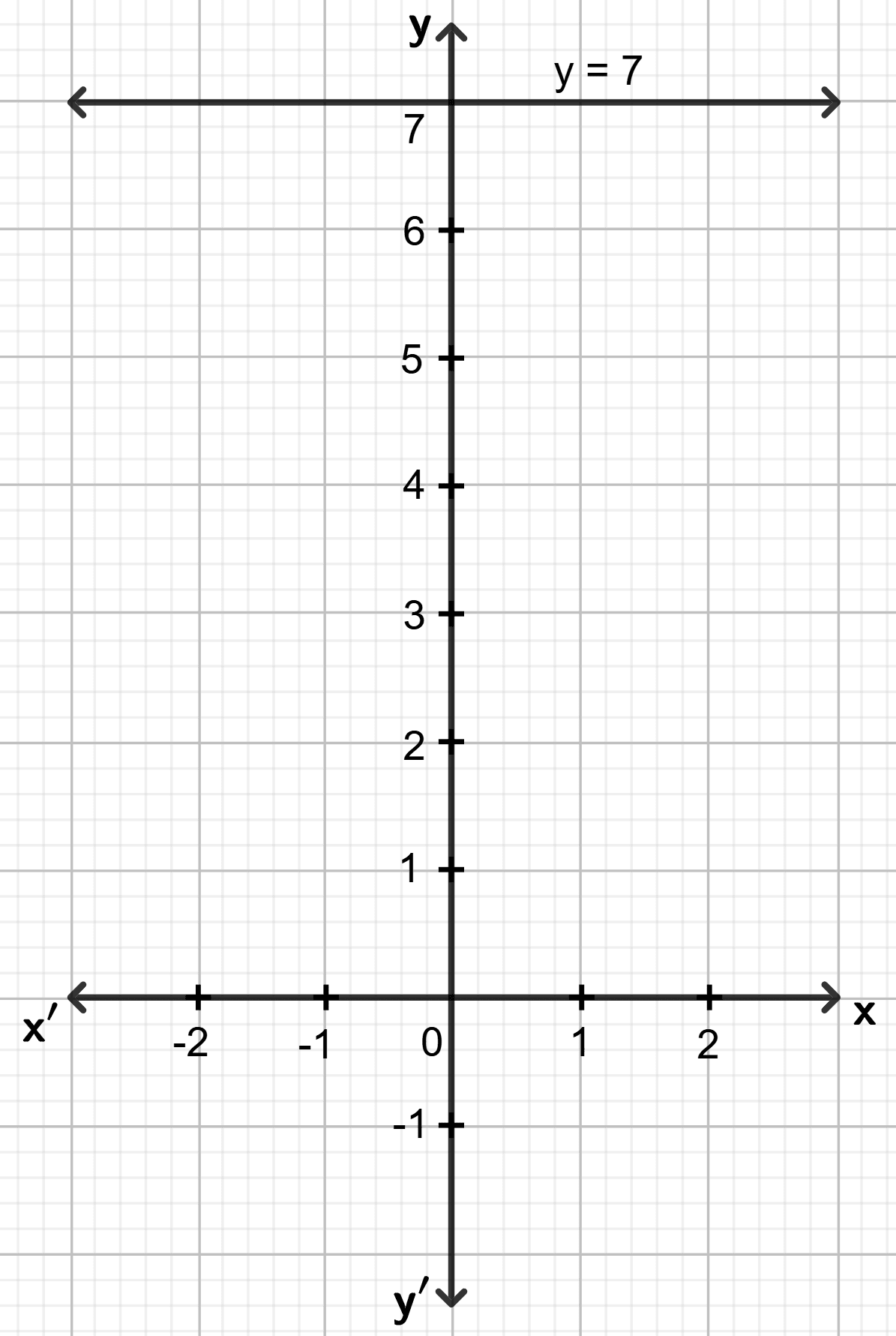
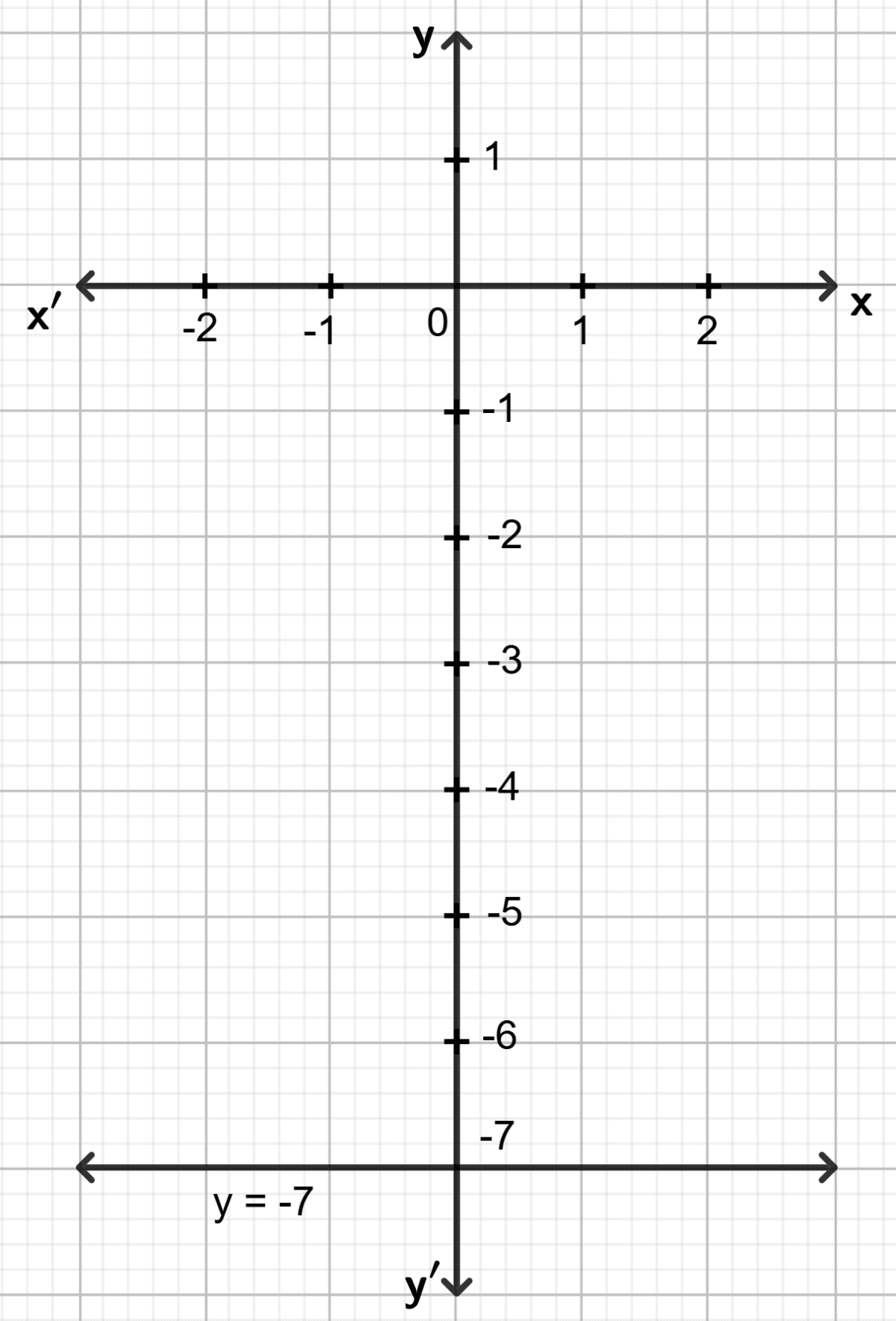
(iv) y + 7 = 0
y = -7
(v) 2x + 3y = 0
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -1, then 2 (-1) + 3y = 0 ⇒ y = 0.6
Let x = 0, then 2 0 + 3y = 0 ⇒ y = 0
Let x = 1, then 2 1 + 3y = 0 ⇒ y = - 0.6
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -1 | 0 | 1 |
|---|---|---|---|
| y | 0.6 | 0 | -0.6 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
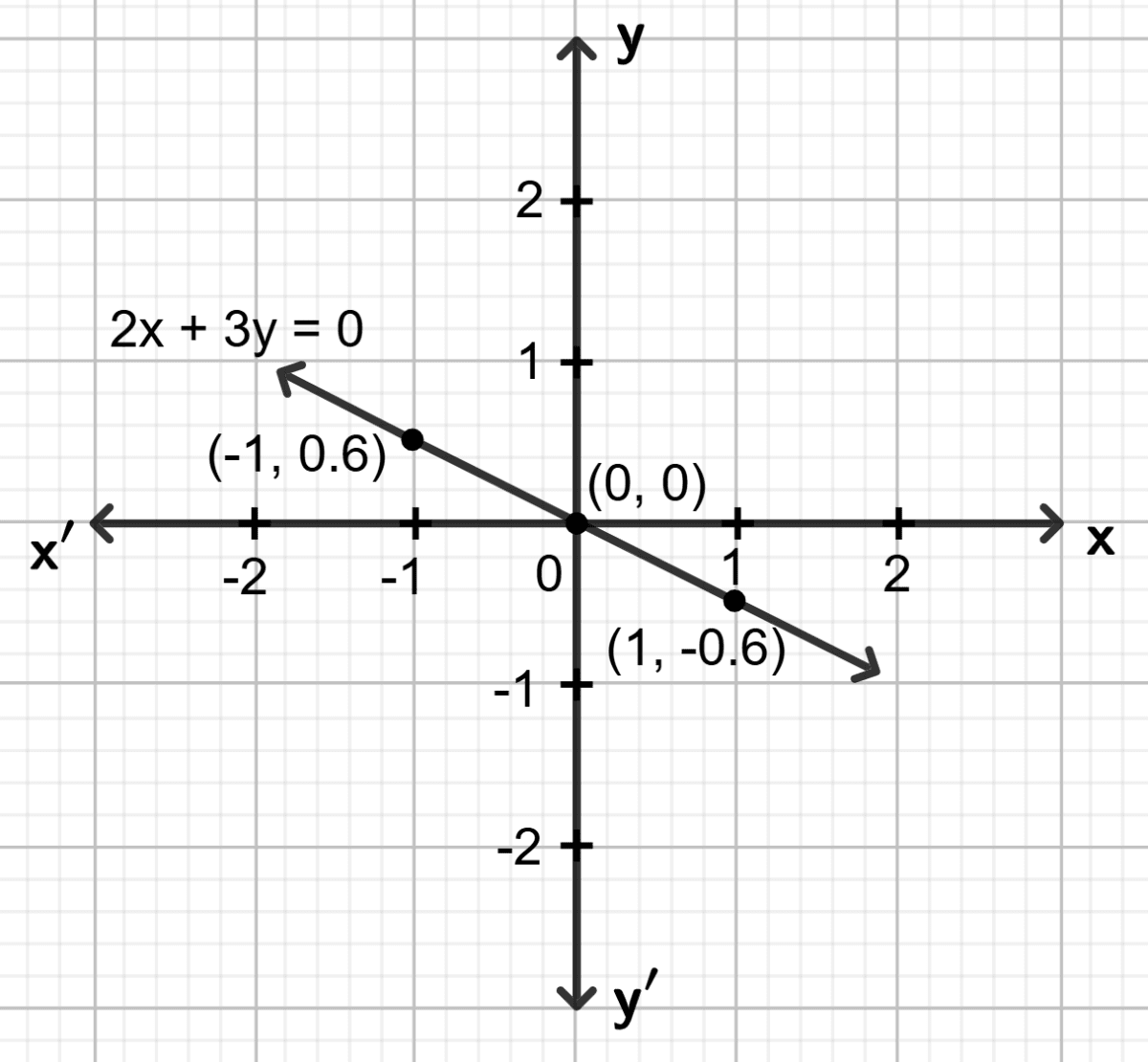
(vi) 3x + 2y = 6
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -1, then 3 (-1) + 2y = 6 ⇒ y = 4.5
Let x = 0, then 3 0 + 2y = 6 ⇒ y = 3
Let x = 1, then 3 1 + 2y = 6 ⇒ y = 1.5
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -1 | 0 | 1 |
|---|---|---|---|
| y | 4.5 | 3 | 1.5 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
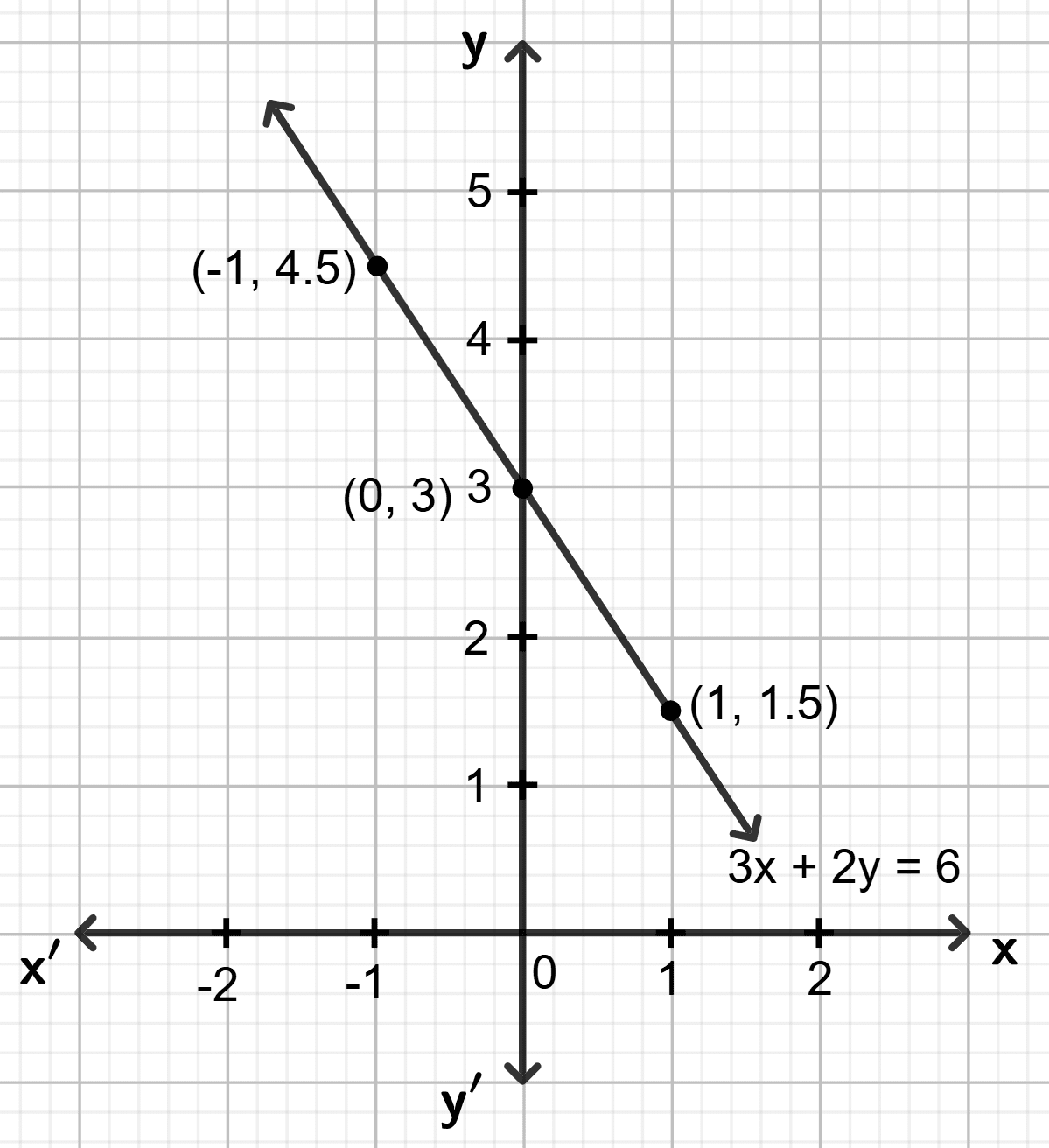
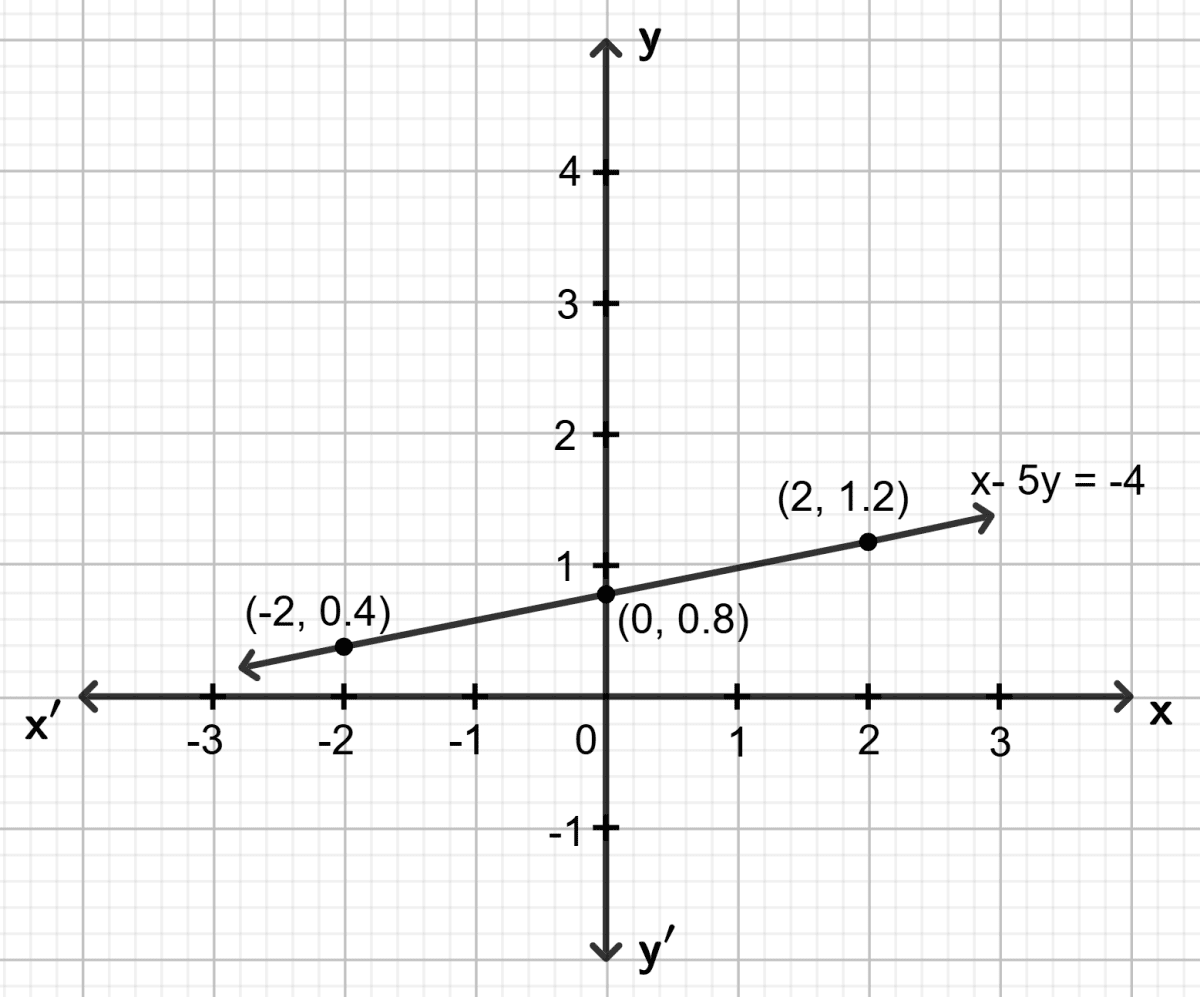
(vii) x - 5y + 4 = 0
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -2, then (-2) - 5y + 4 = 0 ⇒ y = 0.4
Let x = 0, then 0 - 5y + 4 = 0 ⇒ y = 0.8
Let x = 2, then 2 - 5y + 4 = 0 ⇒ y = 1.2
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -2 | 0 | 2 |
|---|---|---|---|
| y | 0.4 | 0.8 | 1.2 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
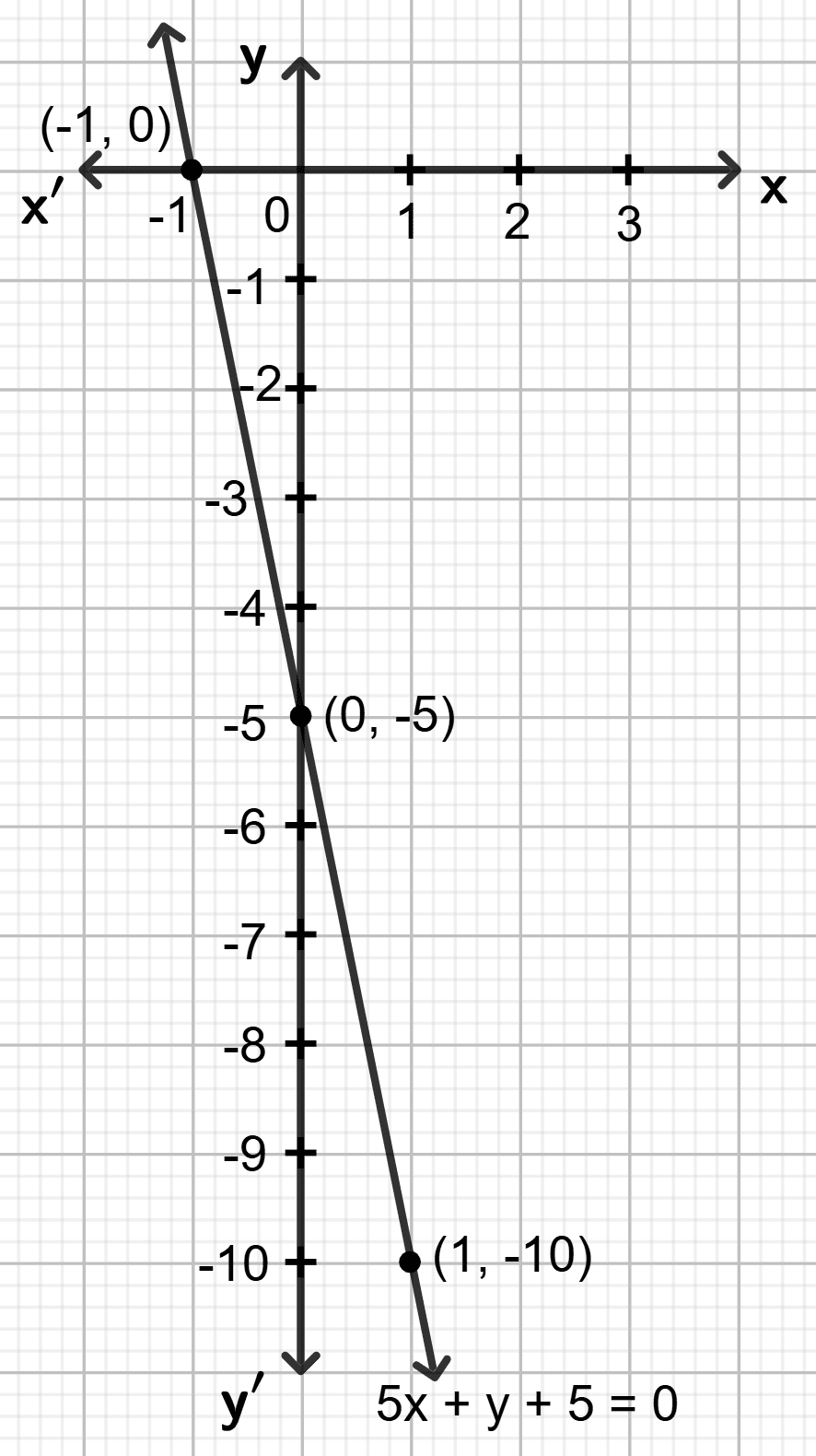
(viii) 5x + y + 5 = 0
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -1, then 5 (-1) + y + 5 = 0 ⇒ y = 0
Let x = 0, then 5 0 + y + 5 = 0 ⇒ y = -5
Let x = 1, then 5 1 + y + 5 = 0 ⇒ y = -10
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -1 | 0 | 1 |
|---|---|---|---|
| y | 0 | -5 | -10 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
Draw the graph for each equation given below; hence find the co-ordinates of the points where the graph drawn meets the co-ordinate axes :
(i)
(ii)
Answer
(i)
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -3, then ⇒ y = 10
Let x = 0, then ⇒ y = 5
Let x = 3, then ⇒ y = 0
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -3 | 0 | 3 |
|---|---|---|---|
| y | 10 | 5 | 0 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
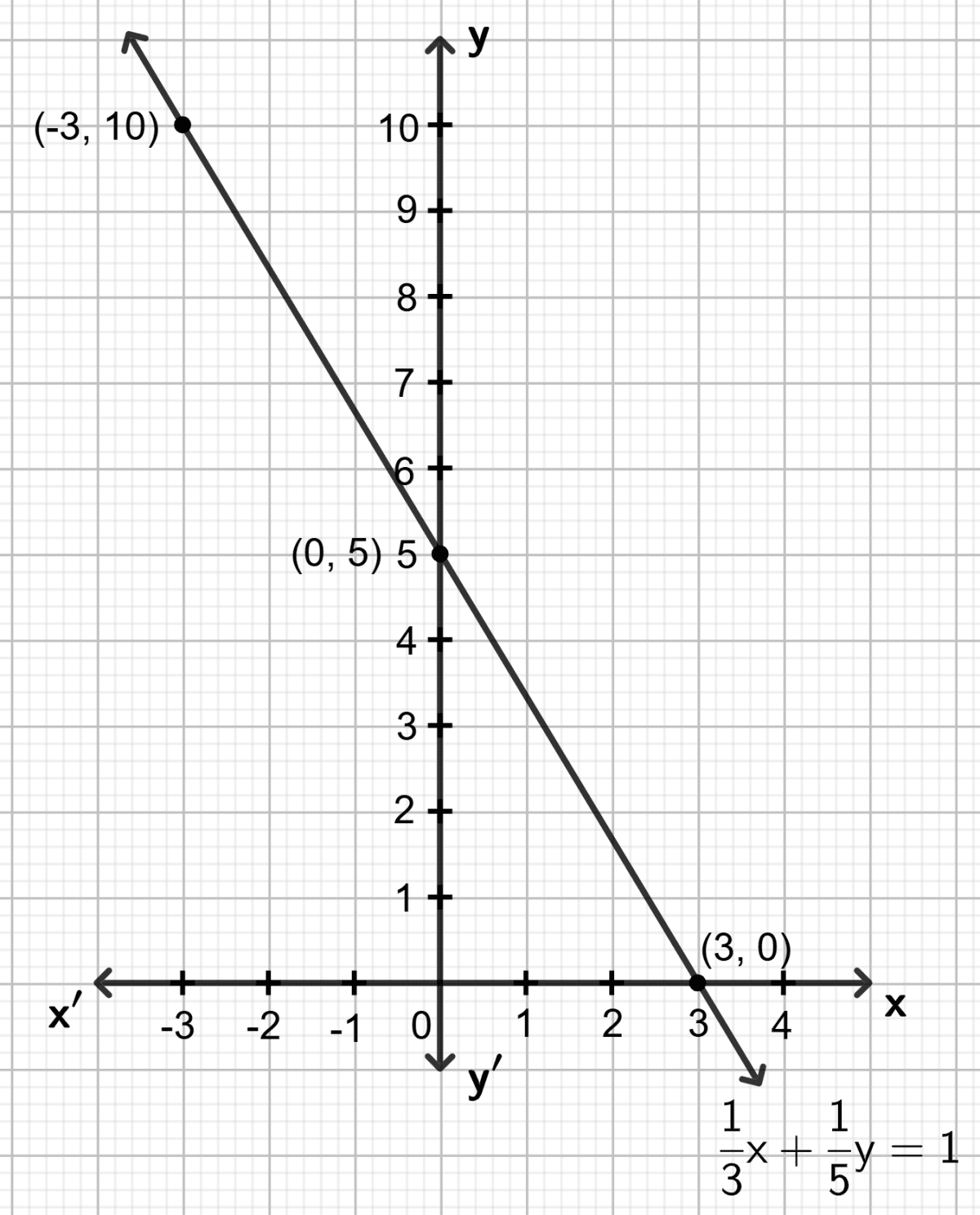
Hence, the co-ordinates of the points where the graph drawn meets the co-ordinate axes are (0, 5) and (3, 0).
(ii)
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -9, then ⇒ y = 0
Let x = -3, then ⇒ y = 4
Let x = 0, then ⇒ y = 6
Let x = 3, then ⇒ y = 8
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -9 | -3 | 0 | 3 |
|---|---|---|---|---|
| y | 0 | 4 | 6 | 8 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
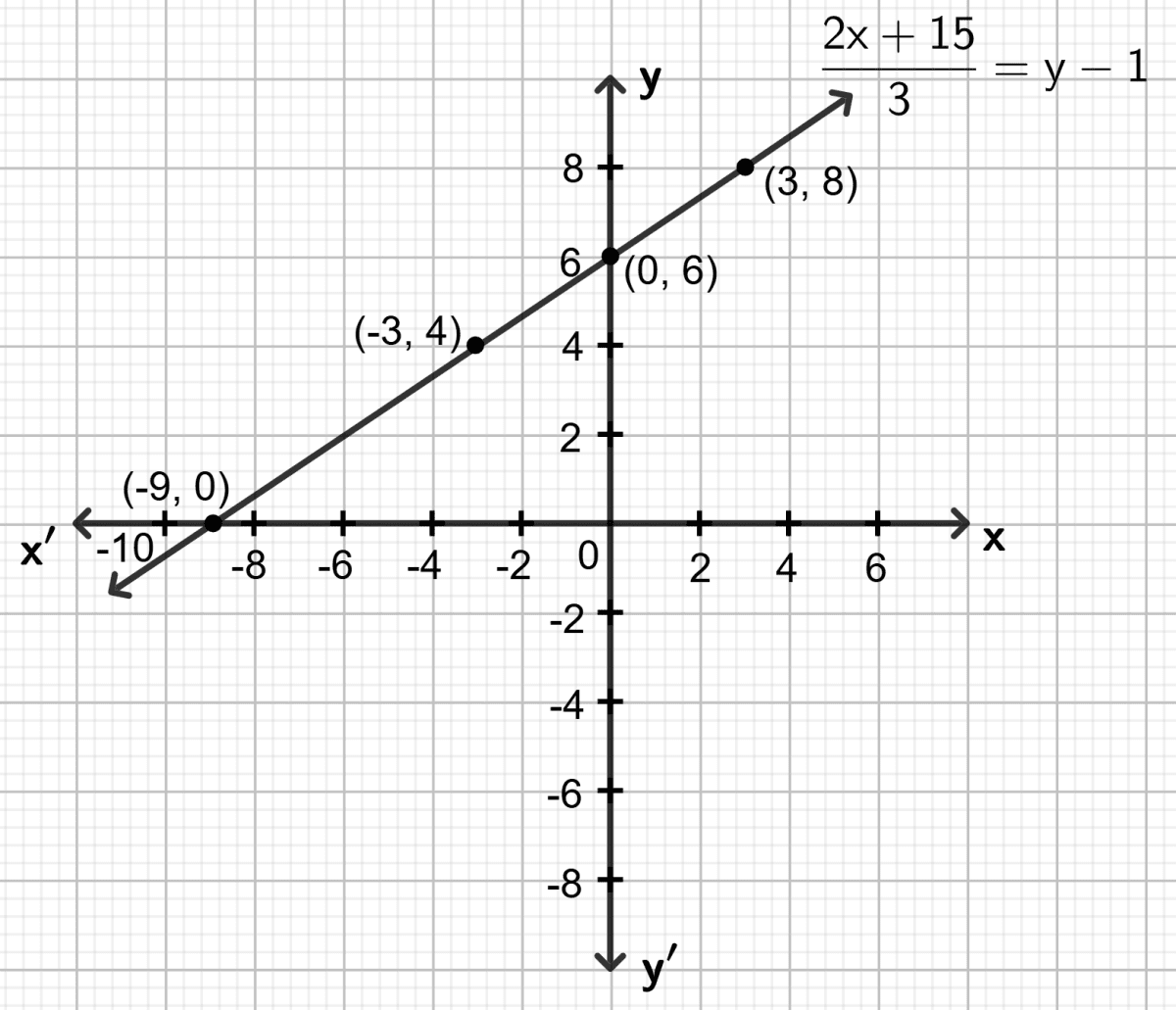
Hence, the co-ordinates of the points where the graph drawn meets the co-ordinate axes are (0, 6) and (-9, 0).
Draw the graph of the straight line given by the equation 4x - 3y + 36 = 0
Calculate the area of the triangle formed by the line drawn and the co-ordinate axes.
Answer
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -9, then 4 (-9) - 3y + 36 = 0 ⇒ y = 0
Let x = -6, then 4 (-6) - 3y + 36 = 0 ⇒ y = 4
Let x = -3, then 4 (-3) - 3y + 36 = 0 ⇒ y = 8
Let x = 0, then 4 0 - 3y + 36 = 0 ⇒ y = 12
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -9 | -6 | -3 | 0 |
|---|---|---|---|---|
| y | 0 | 4 | 8 | 12 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
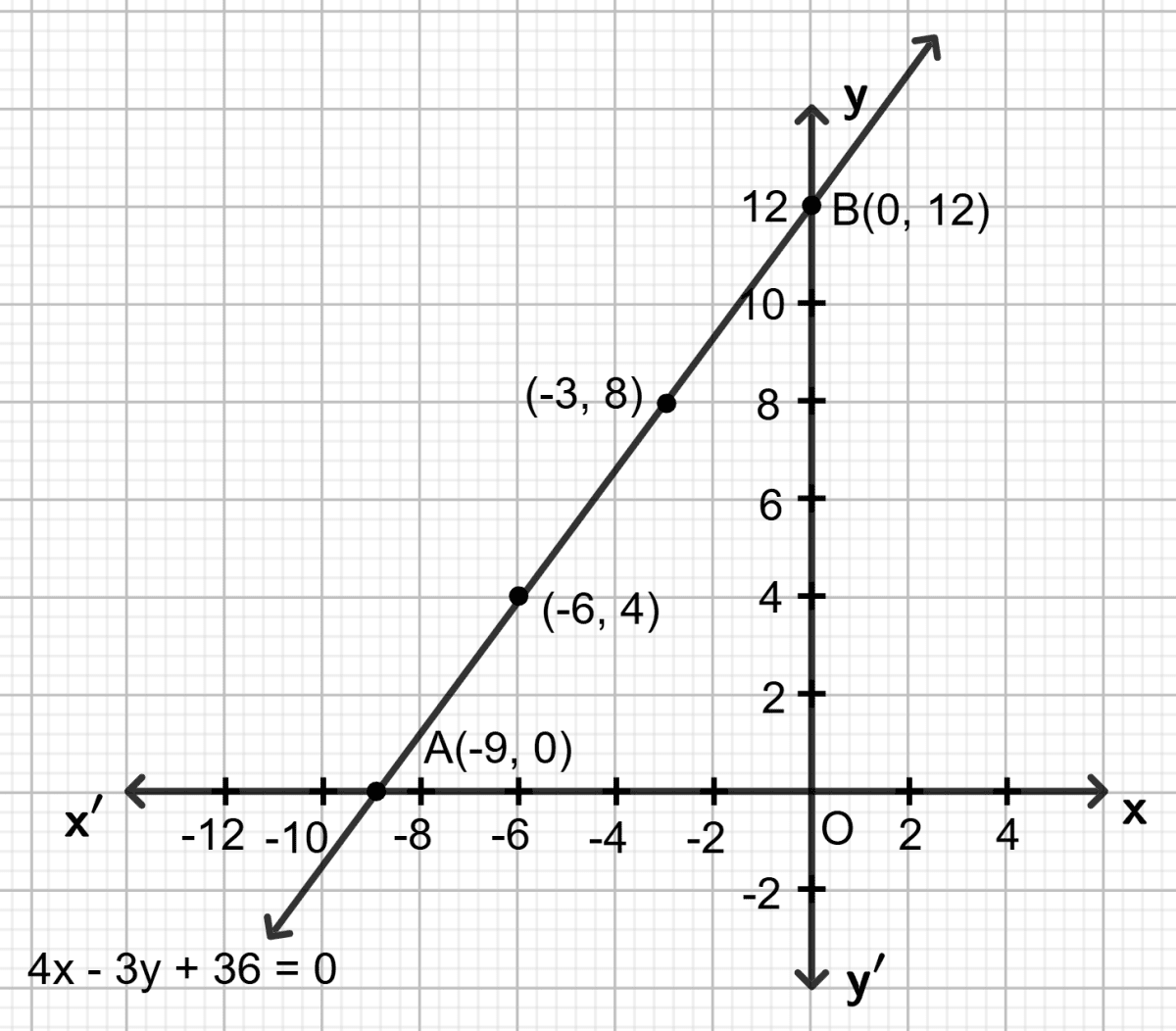
Area of triangle OAB = OA x OB
= x 9 x 12 square units
= x 108 square units
= 54 square units
Hence, area of triangle = 54 sq. units.
Draw the graph of the equation
2x - 3y - 5 = 0
From the graph, find :
(i) x1, the value of x, when y = 7
(ii) x2, the value of x, when y = -5
Answer
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -2, then 2 (-2) - 3y - 5 = 0 ⇒ y = -3
Let x = 0, then 2 0 - 3y - 5 = 0 ⇒ y = -1.6
Let x = 2, then 2 2 - 3y - 5 = 0 ⇒ y = -0.3
Let x = 5, then 2 5 - 3y - 5 = 0 ⇒ y = 1.6
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -2 | 0 | 2 | 5 |
|---|---|---|---|---|
| y | -3 | -1.6 | -0.3 | 1.6 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line AB passing through the points plotted on the graph.
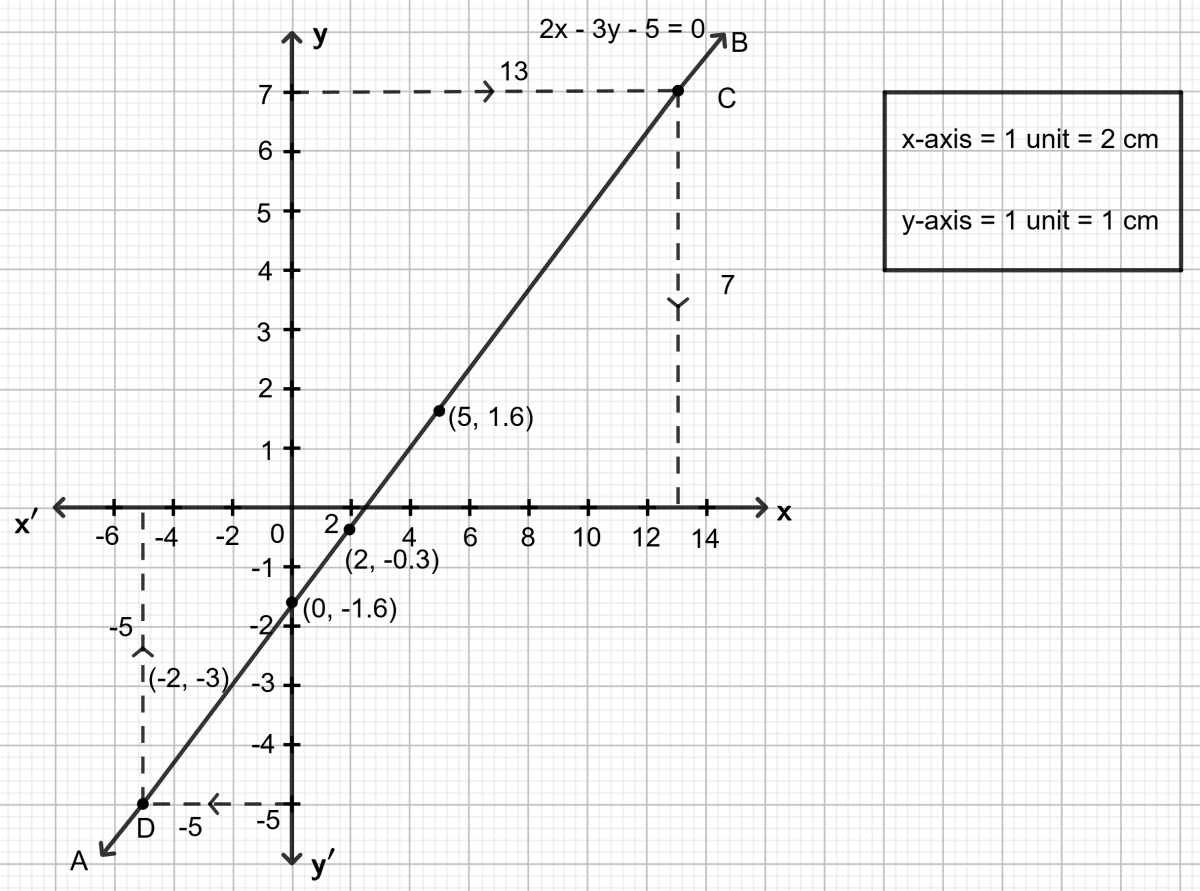
(i) To find x1, the value of x, when y = 7:
Through the point y = 7, draw a horizontal straight line which meets the line AB at point C.
Through point C, draw a vertical line which meets the x-axis at x = 13.
Hence, the value of x, when y = 7 is 13 , i.e, x1 = 13.
(ii) To find x2, the value of x, when y = -5:
Through the point y = -5, draw a horizontal straight line which meets the line AB at point D.
Through point D, draw a vertical line which meets the x - axis at x = -5.
Hence, the value of x, when y = -5 is -5, i.e, x2 = -5.
Draw the graph of the equation
4x + 3y + 6 = 0
From the graph, find :
(i) y1, the value of y, when x = 12
(ii) y2, the value of y, when x = -6
Answer
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -3, then 4 (-3) + 3y + 6 = 0 ⇒ y = 2
Let x = 0, then 4 0 + 3y + 6 = 0 ⇒ y = -2
Let x = 3, then 4 3 + 3y + 6 = 0 ⇒ y = -6
Let x = 8, then 4 8 + 3y + 6 = 0 ⇒ y = -12.6
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -3 | 0 | 3 | 8 |
|---|---|---|---|---|
| y | 2 | -2 | -6 | -12.6 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line AB passing through the points plotted on the graph.
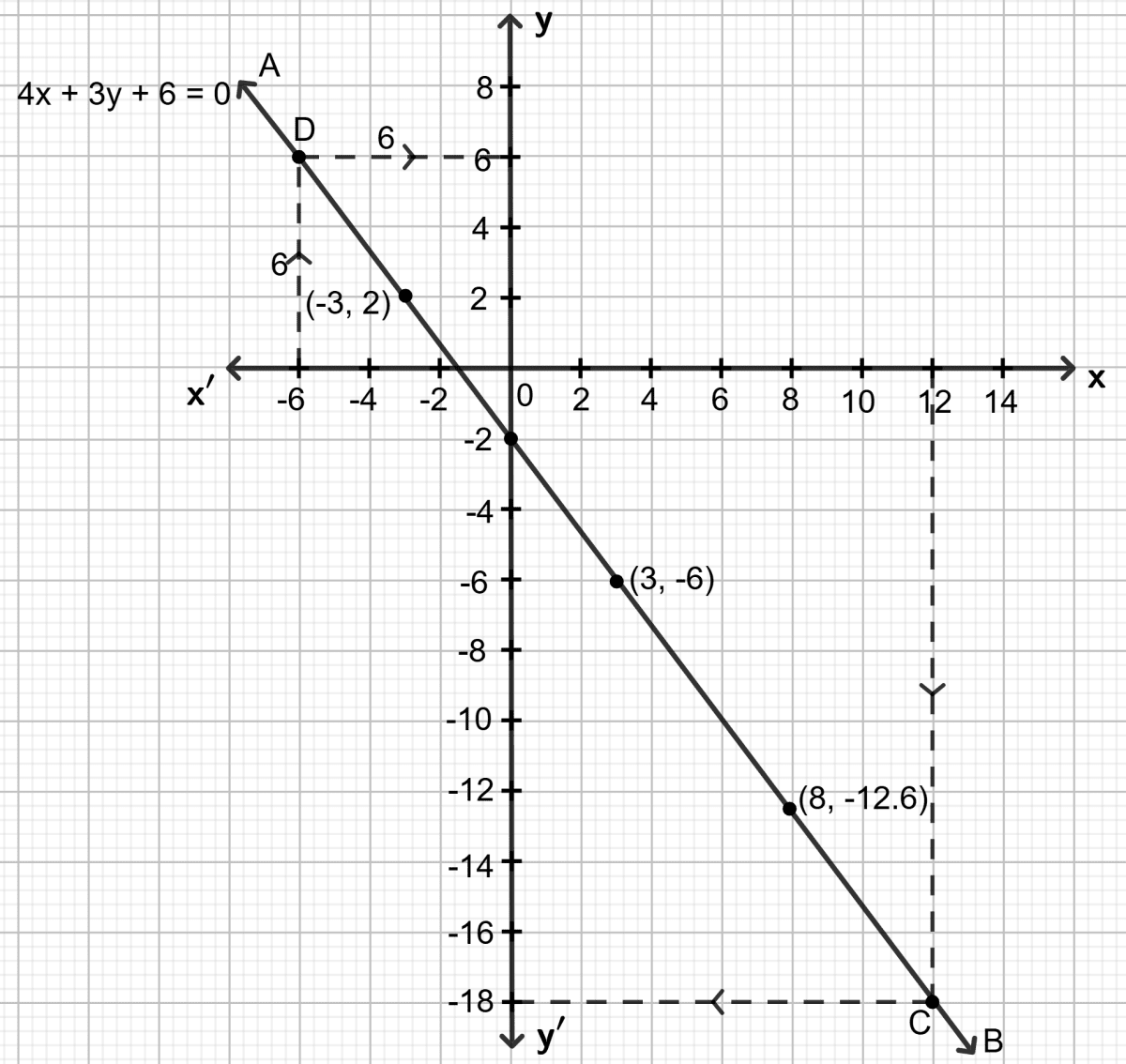
(i) To find y1, the value of y, when x = 12:
Through the point x = 12, draw a vertical straight line which meets the line AB at point C.
Through point C, draw a horizontal line which meets the y-axis at y = -18.
Hence, the value of y, when x = 12 is -18 , i.e, y1 = -18.
(ii) To find y2, the value of y, when x = -6:
Through the point x = -6, draw a vertical straight line which meets the line AB at point D.
Through point D, draw a horizontal line which meets the y-axis at y = 6.
Hence, the value of x, when y = -5 is 6, i.e, y2 = 6.
Use the table given below to draw the graph.
| x | -5 | -1 | 3 | b | 13 |
|---|---|---|---|---|---|
| y | -2 | a | 2 | 5 | 7 |
From your graph, find the values of 'a' and 'b'. State a linear relation between the variables x and y.
Answer
Plot the given points (-5, -2), (3, 2) and (13, 7) on a graph paper.
Draw a straight line passing through these points.
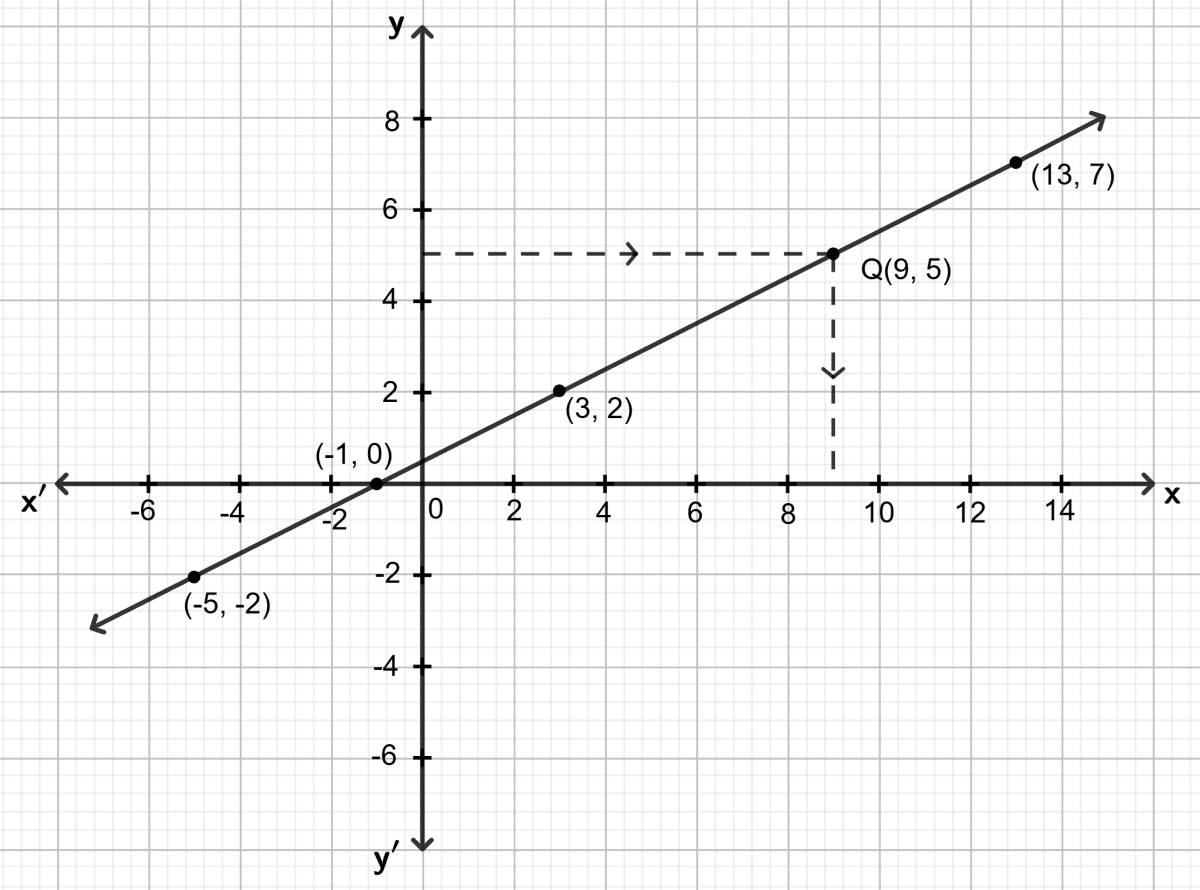
To find the value of 'a':
From the graph, y = 0 when x = −1.
∴ a = 0
To find the value of 'b':
Through y = 5, draw a horizontal line which meets the graph at a point, say Q. Through Q, draw a vertical line which meets the x-axis at x = 9.
∴ b = 9
Let the linear relation between the variable x and y be y = mx + c.
Since, the graph passes through the point (-5, -2); substitute x = -5 and y = -2 in y = mx + c.
This gives -2 = -5m + c ...............(1)
Again, the graph passes through the point (3, 2); substitute x = 3 and y = 2 in y = mx + c
This gives 2 = 3m + c ...............(2)
Subtracting (2) from (1),
-2 - 2 = -5m + c -3m - c
⇒ -4 = -8m
⇒ m =
⇒ m =
substituting the value of m in equation (1),
-2 = -5 + c
⇒-2 = + c
⇒-2 + = c
⇒ = c
⇒ c =
∴ Required relation is : y = mx + c i.e. y =
Hence, a = 0 and b = 9. Linear relation : y = .
Draw the graph obtained from the table below :
| x | a | 3 | -5 | 5 | c | -1 |
|---|---|---|---|---|---|---|
| y | -1 | 2 | b | 3 | 4 | 0 |
Use the graph to find the values of a, b and c. State a linear relation between the variables x and y.
Answer
Plot the given points (3, 2), (5, 3) and (-1, 0) on a graph paper.
Draw a straight line passing through these points.
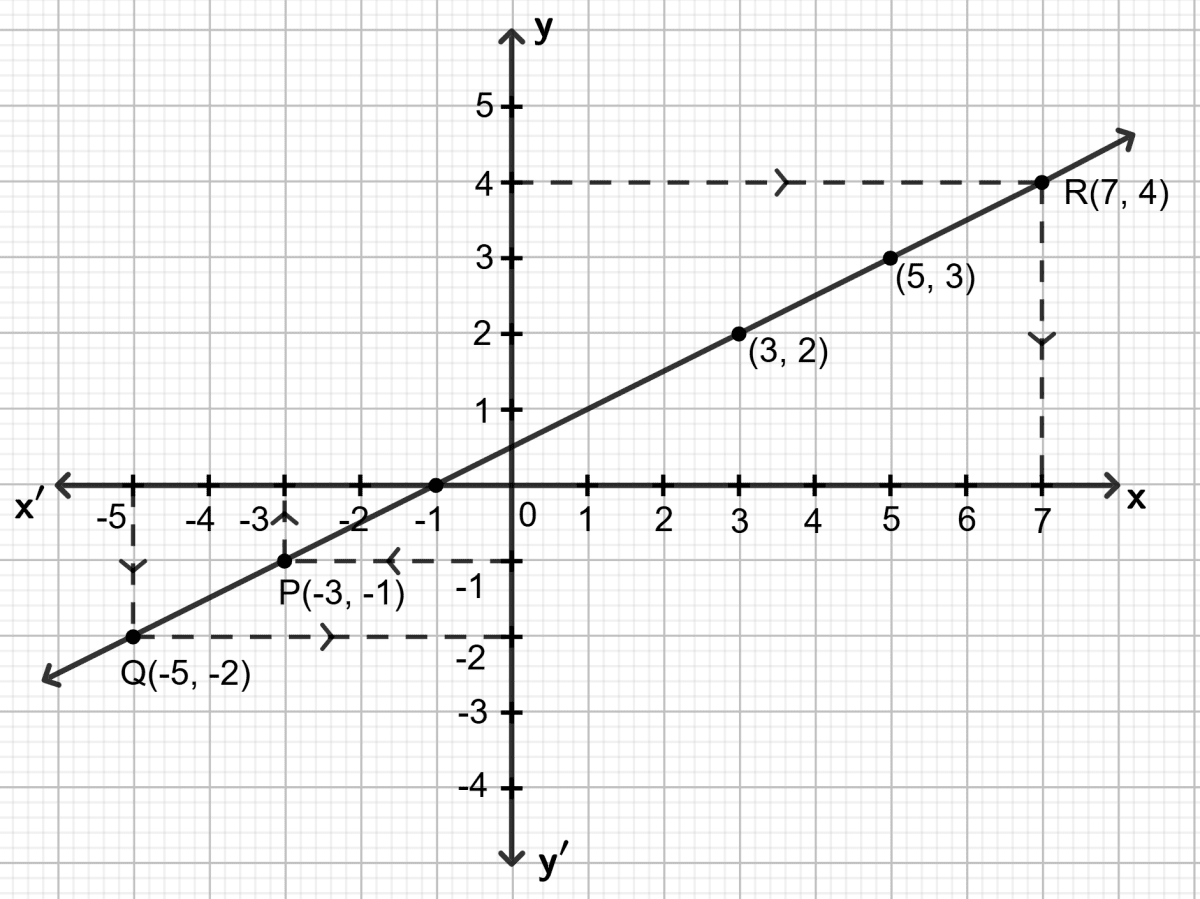
To find the value of 'a':
Through y = -1, draw a horizontal line which meets the graph at a point, say P. Through P, draw a vertical line which meets the x-axis at x = -3.
∴ a = -3
To find the value of 'b':
Similarly, through x = -5, draw a vertical line which meets the graph at a point, say Q. Through Q, draw a horizontal line which meets the y-axis at y = -2.
∴ b = -2
To find the value of 'c':
Similarly, through y = 4, draw a horizontal line which meets the graph at a point, say R. Through R, draw a vertical line which meets the x-axis at x = 7.
∴ c = 7
Let the linear relation between the variable x and y be y = mx + c.
Since, the graph passes through the point (3, 2); substitute x = 3 and y = 2 in y = mx + c.
This gives 2 = 3m + c ...............(1)
Again, the graph passes through the point (5, 3); substitute x = 5 and y = 3 in y = mx + c
This gives 3 = 5m + c ...............(2)
Subtracting (2) from (1),
2 - 3 = 3m + c -5m - c
⇒ -1 = -2m
⇒ m =
Substituting the value of m in equation (1),
2 = 3 + c
⇒2 = + c
⇒2 - = c
⇒ = c
⇒ c =
∴ Required relation is : y = mx + c i.e. x = 2y - 1
Hence, a = -3, b = -2 and c = 7. Linear relation : x = 2y - 1.
A straight line passes through the points (2, 4) and (5, -2). Taking 1 cm = 1 unit; mark these points on a graph paper and draw the straight line through these points. If points (m, -4) and (3, n) lie on the line drawn; find the values of m and n.
Answer
Plot the given points (2, 4) and (5, -2) on a graph paper.
Draw a straight line AB passing through these points.
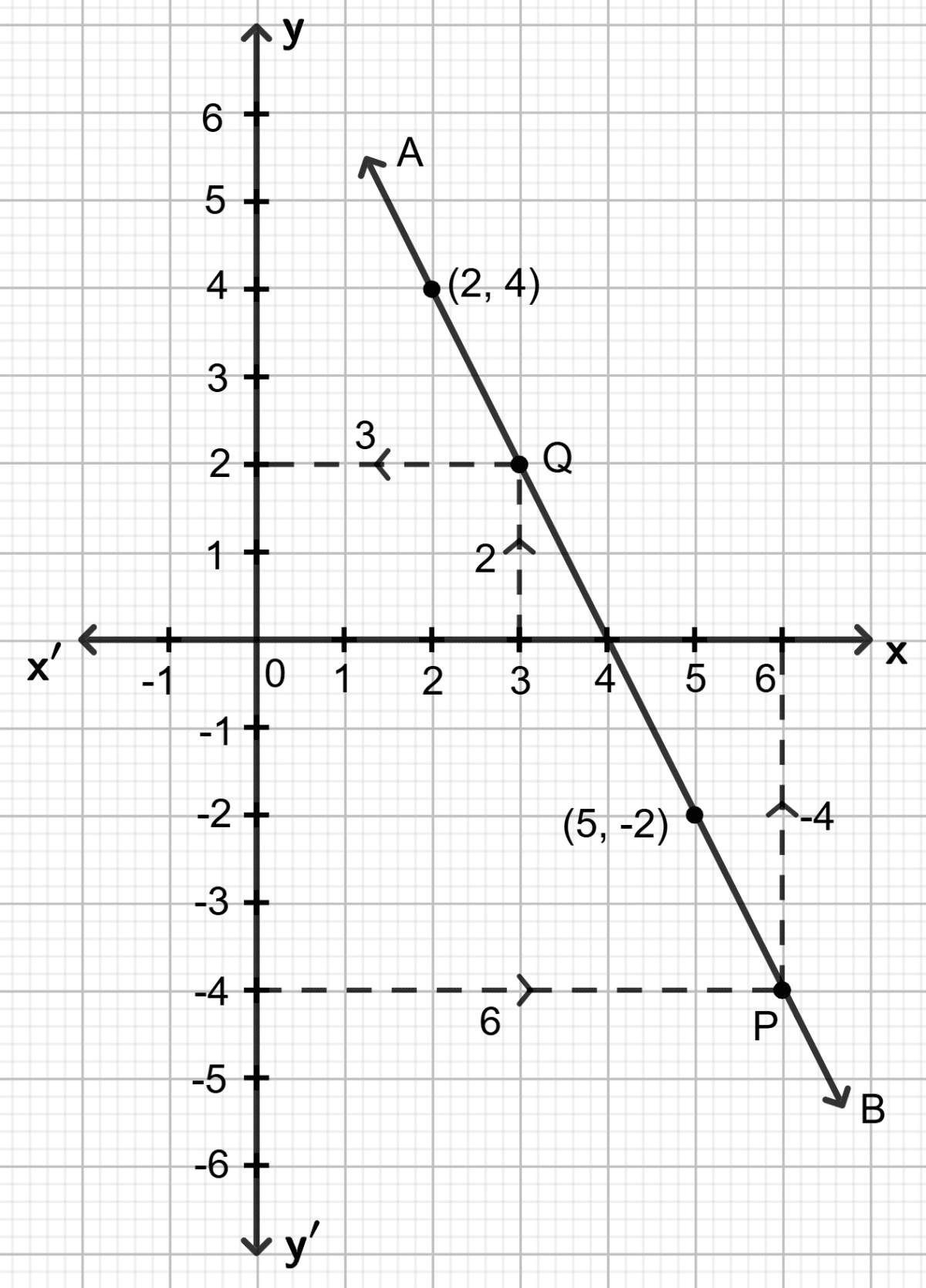
Since, point (m, -4) lies on the straight line drawn, through y = -4 draw a horizontal line which meets the straight line AB at point P. Through P, draw a vertical line which meets the x-axis at point 6.
∴ m = 6
Also, as (3, n) lies on the straight line drawn, through x = 3, draw a vertical line which meets the straight line at point Q. Through point Q, draw a horizontal line which meets the y-axis at point 2.
∴ n = 2
Hence, m = 6 and n = 2.
Draw the graph (straight line) given by equation x - 3y = 18. If the straight line drawn passes through the points (m, -5) and (6, n); find the values of m and n.
Answer
Given equation: x - 3y = 18
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = 0, then 0 - 3y = 18 ⇒ y = - 6
Let x = 3, then 3 - 3y = 18 ⇒ y = - 5
Let x = 6, then 6 - 3y = 18 ⇒ y = - 4
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | 0 | 3 | 6 |
|---|---|---|---|
| y | -6 | -5 | -4 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
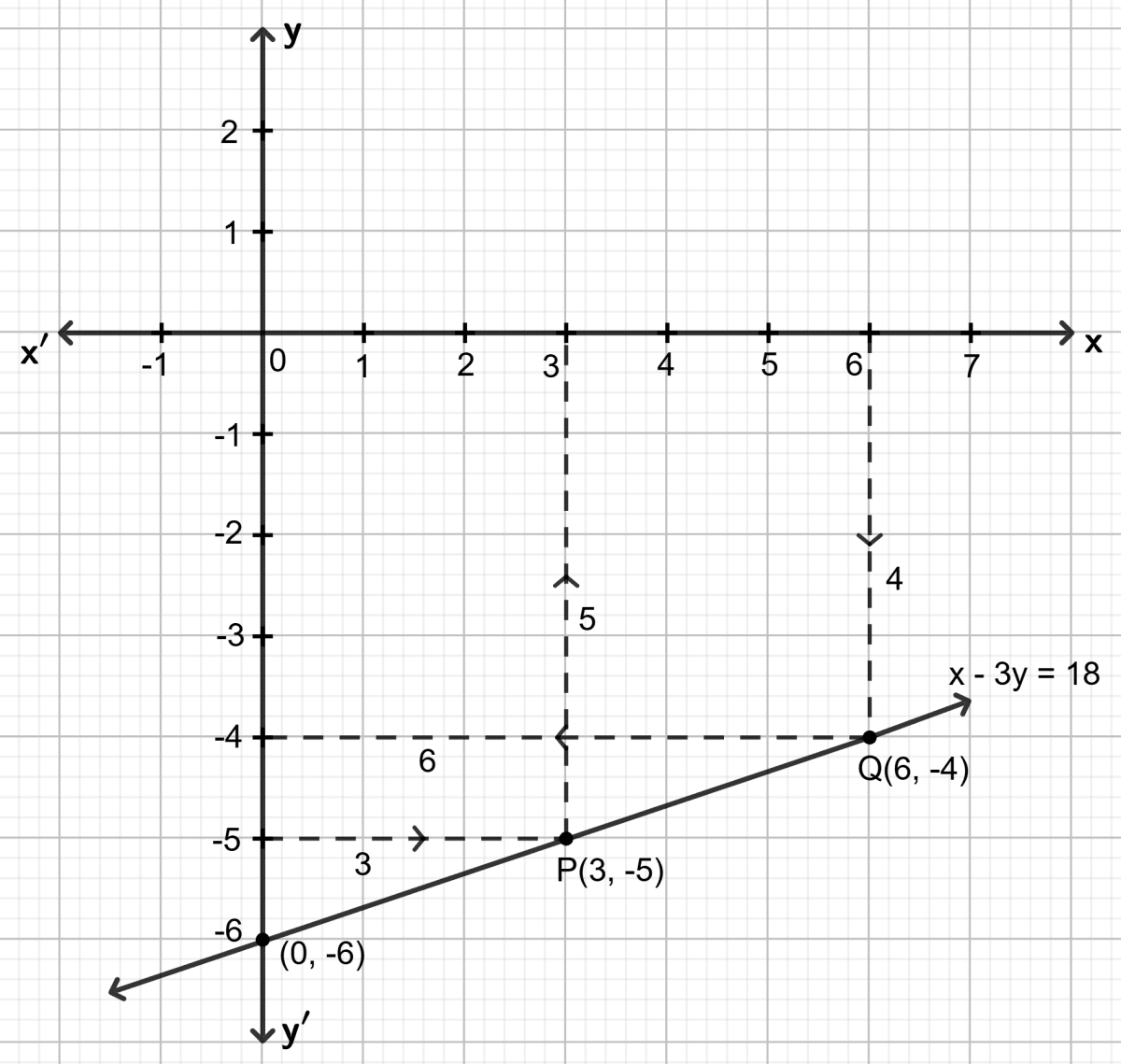
Since, point (m, -5) lies on the straight line drawn, through y = -5, draw a horizontal line which meets the graph at a point, say P. Through P, draw a vertical line which meets the x-axis at x = 3.
Also, (6, n) also lies on the straight line drawn, through x = 6, draw a vertical line which meets the graph at a point, say Q. Through Q, draw a horizontal line which meets the y-axis at x = -4.
Hence, m = 3 and n = -4.
The point of intersection of lines x = 8 and y - 8 = 0 is :
(8, 8)
(8, -8)
(-8, 8)
(-8, -8)
Answer
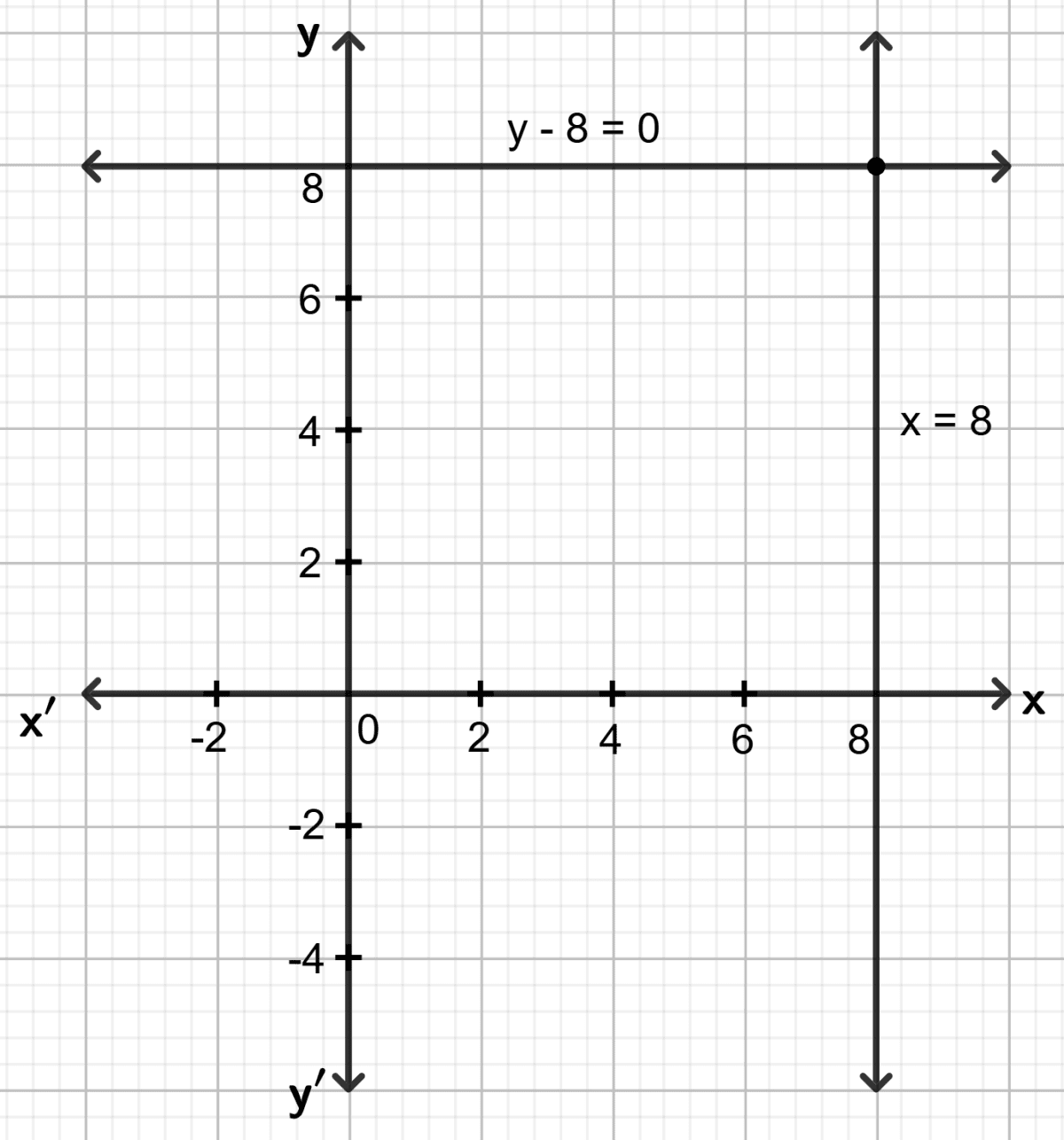
The lines x = 8 and y = 8 intersect at point (8, 8).
Hence, option 1 is the correct option.
For line y = 20 + 2x, if x = 20, the value of y is :
40
60
80
0
Answer
Given equation: y = 20 + 2x
When x = 20
y = 20 + 2 20
= 20 + 40
= 60
Hence, option 2 is the correct option.
A point that lies on the line 2x - 3y = 4 can be taken as :
(-5, -2)
(-5, 2)
(5, 2)
(5, -2)
Answer
Given equation: 2x - 3y = 4
1. For (-5, -2):
Substitute x = -5 and y = -2
L.H.S. : 2 (-5) - 3 (-2)
= -10 + 6
= -4
R.H.S. = 4
Since, L.H.S. ≠ R.H.S., (-5, -2) does not lie on the line.
2. For (-5, 2):
Substitute x = -5 and y = 2
L.H.S. : 2 (-5) - 3 2
= -10 - 6
= - 16
R.H.S. = 4
Since, L.H.S. ≠ R.H.S., (-5, 2) does not lie on the line.
3. For (5, 2):
Substitute x = 5 and y = 2
L.H.S. : 2 5 - 3 2
= 10 - 6
= 4
R.H.S. = 4
Since, L.H.S. = R.H.S., (5, 2) lies on the line.
4. For (5, -2):
Substitute x = 5 and y = -2
L.H.S. : 2 5 - 3 (-2)
= 10 + 6
= 16
R.H.S. = 4
Since, L.H.S. ≠ R.H.S., (5, -2) does not lie on the line.
Hence, option 3 is the correct option.
The line x + 5 = 0 :
is parallel to x-axis
is parallel to y-axis
passes through (0, 0)
passes through (5, 0)
Answer
x + 5 = 0
⇒ x = - 5
This equation represents a vertical line that is parallel to the y-axis, where the x-coordinate is always −5.
Hence, option 2 is the correct option.
The lines y - 2 = 0 and 2x + 3y = 12 cut each other at point :
(-3, 2)
(3, -2)
(-3, -2)
(3, 2)
Answer
y - 2 = 0
⇒ y = 2
And, 2x + 3y = 12
⇒ 2x + 3 x 2 = 12
⇒ 2x + 6 = 12
⇒ 2x = 12 - 6
⇒ 2x = 6
⇒ x =
⇒ x = 3
Hence, the lines y - 2 = 0 and 2x + 3y = 12 cut each other at point (3, 2).
Hence, option 4 is the correct option.
Solve, graphically, the following pairs of equations :
(i)
x - 5 = 0
y + 4 = 0
(ii)
2x + y = 23
4x - y = 19
(iii)
3x + 7y = 27
(iv)
Answer
(i) x - 5 = 0
⇒ x = 5
and, y + 4 = 0
⇒ y = - 4
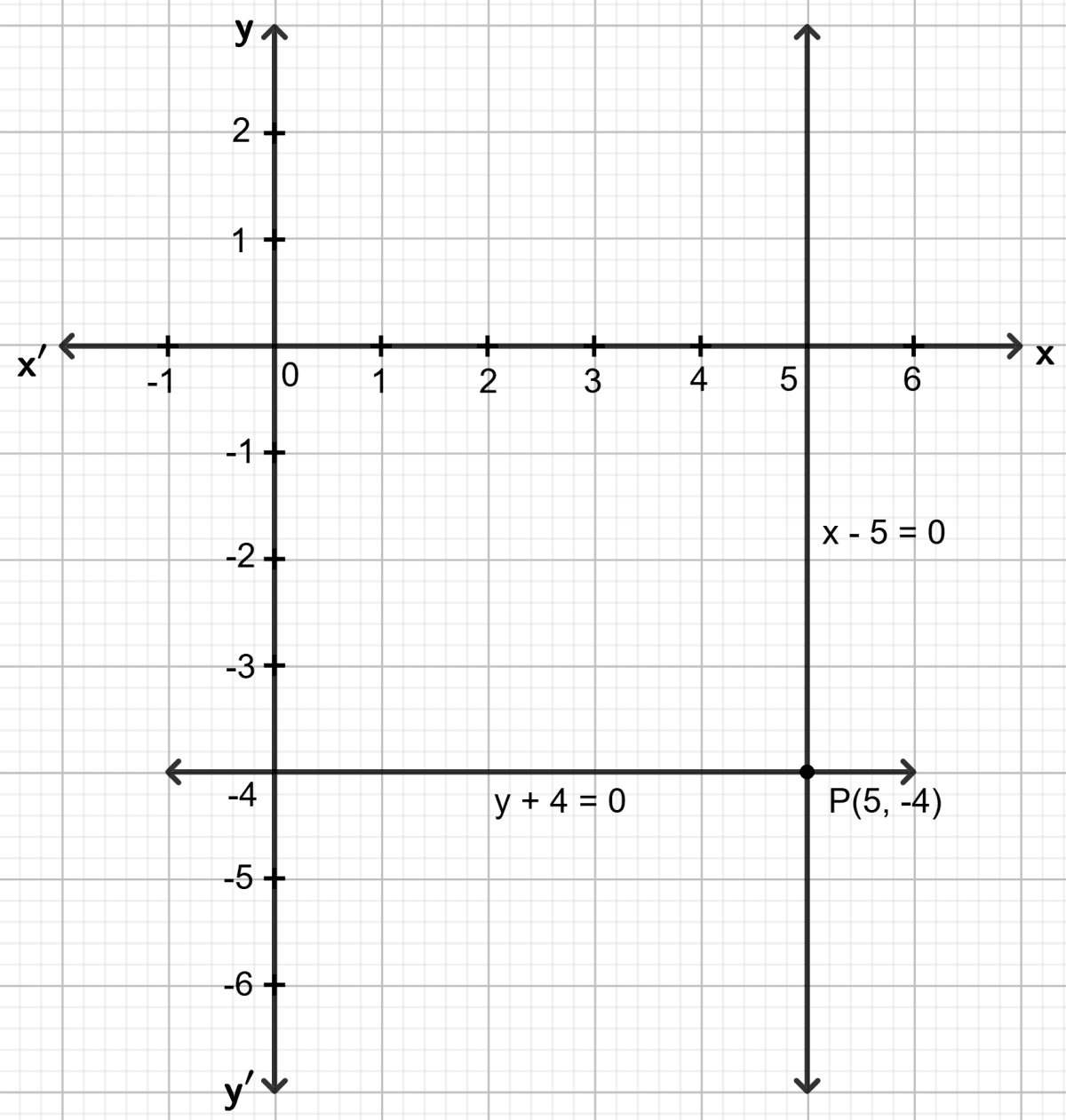
On the same graph paper, draw the graph for each given equation.
Both the straight lines drawn meet at point P. As it is clear from the graph, co-ordinates of the common point are (5, -4).
Solution of the given equations is : x = 5 and y = -4.
(ii)
First equation : 2x + y = 23
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = 2, then 2 2 + y = 23 ⇒ y = 19
Let x = 4, then 2 4 + y = 23 ⇒ y = 15
Let x = 6, then 2 6 + y = 23 ⇒ y = 11
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | 2 | 4 | 6 |
|---|---|---|---|
| y | 19 | 15 | 11 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
Second equation : 4x - y = 19
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = 4, then 4 4 - y = 19 ⇒ y = -3
Let x = 6, then 4 6 - y = 19 ⇒ y = 5
Let x = 8, then 4 8 - y = 19 ⇒ y = 13
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | 4 | 6 | 8 |
|---|---|---|---|
| y | -3 | 5 | 13 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
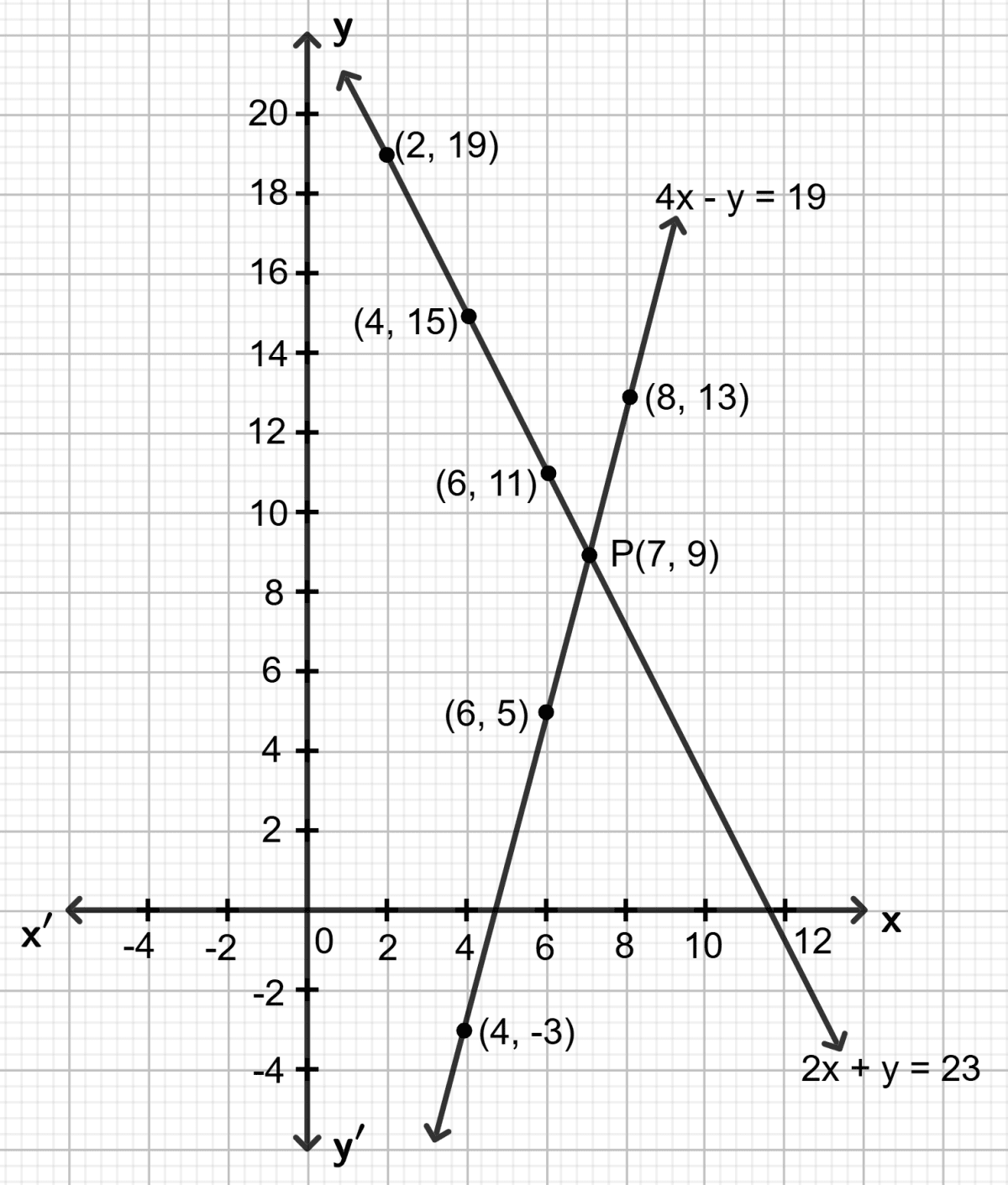
On the same graph paper, draw the graph for each given equation.
Both the straight lines drawn meet at point P. As it is clear from the graph, co-ordinates of the common point are (7, 9).
Solution of the given equations is : x = 7 and y = 9.
(iii)
First equation : 3x + 7y = 27
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = 0, then 3 0 + 7y = 27 ⇒ y = 3.8
Let x = 2, then 3 2 + 7y = 27 ⇒ y = 3
Let x = 4, then 3 4 + 7y = 27 ⇒ y = 2.1
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | 0 | 2 | 4 |
|---|---|---|---|
| y | 3.8 | 3 | 2.1 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
Second equation :
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = 0, then ⇒ y = 8
Let x = 1, then ⇒ y = 5.5
Let x = 2, then ⇒ y = 3
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | 0 | 1 | 2 |
|---|---|---|---|
| y | 8 | 5.5 | 3 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
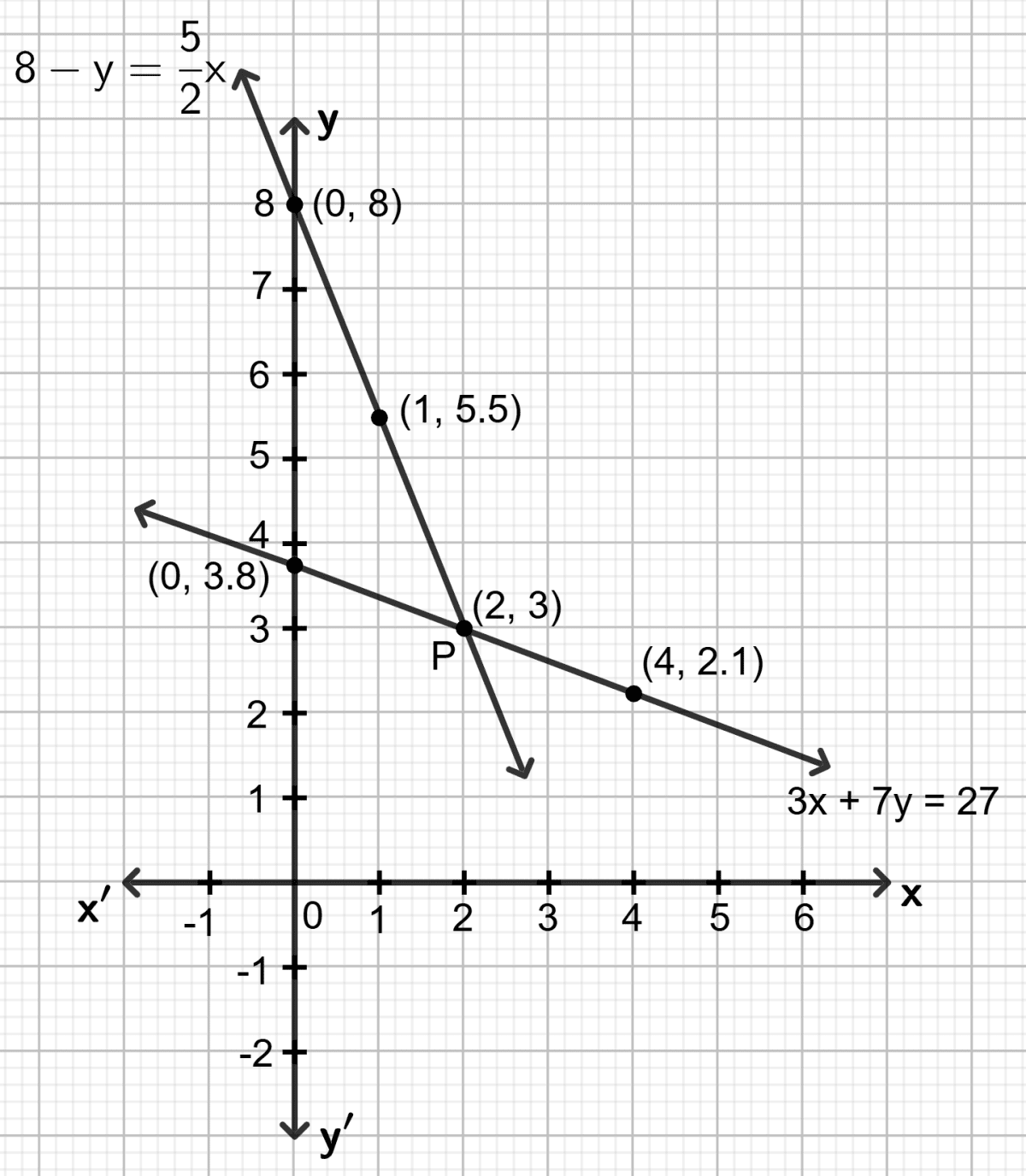
On the same graph paper, draw the graph for each given equation.
Both the straight lines drawn meet at point P. As it is clear from the graph, co-ordinates of the common point are (2, 3).
Solution of the given equations is : x = 2 and y = 3.
(iv)
First equation :
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = 0, then ⇒ y = 0.3
Let x = 3, then ⇒ y = -0.2
Let x = 7, then ⇒ y = -1
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | 0 | 3 | 7 |
|---|---|---|---|
| y | 0.3 | -0.2 | -1 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
Second equation :
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = 0, then ⇒ y = -1.6
Let x = 7, then ⇒ y = -1
Let x = 14, then ⇒ y = -0.4
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | 0 | 7 | 14 |
|---|---|---|---|
| y | -1.6 | -1 | -0.4 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
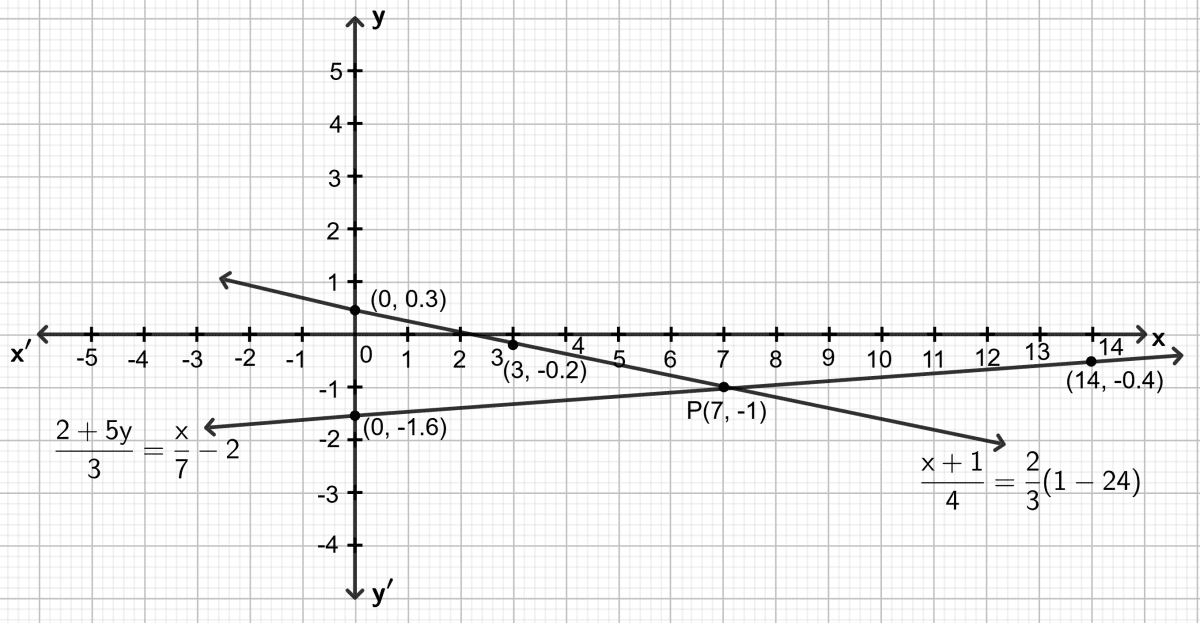
On the same graph paper, draw the graph for each given equation.
Both the straight lines drawn meet at point P. As it is clear from the graph, co-ordinates of the common point are (7, -1).
Solution of the given equations is : x = 7 and y = -1.
Solve graphically the simultaneous equations given below. Take the scale as 2 cm = 1 unit on both the axes.
x - 2y - 4 = 0
2x + y = 3
Answer
First equation: x - 2y - 4 = 0
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = 0, then 0 - 2y - 4 = 0 ⇒ y = -2
Let x = 2, then 2 - 2y - 4 = 0 ⇒ y = -1
Let x = 4, then 4 - 2y - 4 = 0 ⇒ y = 0
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | 0 | 2 | 4 |
|---|---|---|---|
| y | -2 | -1 | 0 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
Second equation: 2x + y = 3
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = 0, then 2 0 + y = 3 ⇒ y = 3
Let x = 2, then 2 2 + y = 3 ⇒ y = -1
Let x = 4, then 2 4 + y = 3 ⇒ y = -5
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | 0 | 2 | 4 |
|---|---|---|---|
| y | 3 | -1 | -5 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
On the same graph paper, draw the graph for each given equation.
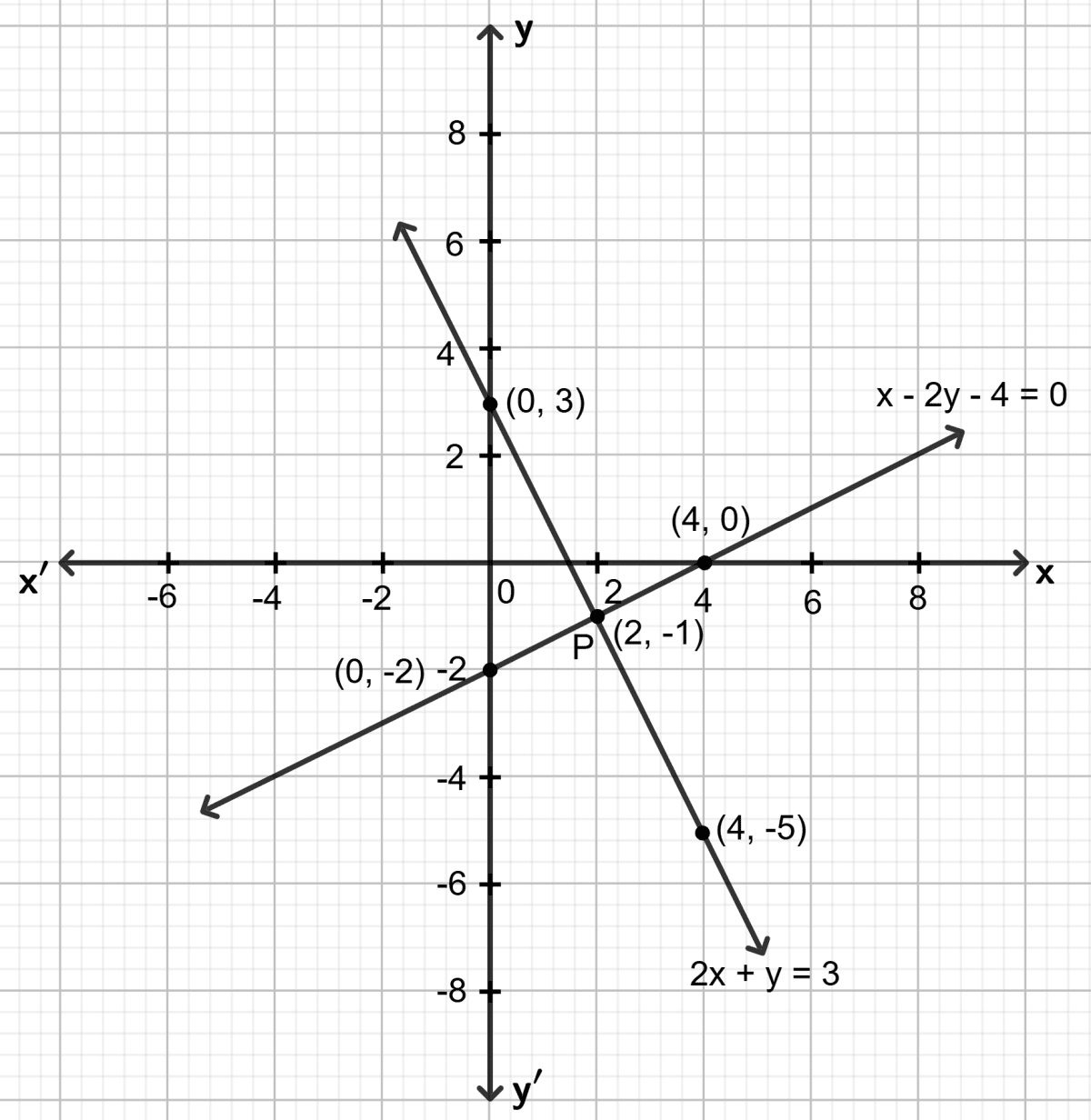
Both the straight line drawn meet the point P. As it is clear from the graph, co-ordinates of the common point P are (2, -1).
Solution of the given equation x = 2 and y = -1.
Use graph paper for this question. Draw the graph of 2x - y - 1 = 0 and 2x + y = 9 on the same axes. Use 2 cm = 1 unit on both axes and plot only 3 points per line.
Write down the co-ordinates of the point of intersection of the two lines.
Answer
First equation: 2x - y - 1 = 0
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = 0, then 2 0 - y - 1 = 0 ⇒ y = -1
Let x = 2, then 2 2 - y - 1 = 0 ⇒ y = 3
Let x = 4, then 2 4 - y - 1 = 0 ⇒ y = 7
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | 0 | 2 | 4 |
|---|---|---|---|
| y | -1 | 3 | 7 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
Second equation: 2x + y = 9
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = 0, then 2 0 + y = 9 ⇒ y = 9
Let x = 2, then 2 2 + y = 9 ⇒ y = 5
Let x = 4, then 2 4 + y = 9 ⇒ y = 1
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | 0 | 2 | 4 |
|---|---|---|---|
| y | 9 | 5 | 1 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.

On the same graph paper, draw the graph for each given equation.
Both the straight line drawn meet the point P. As it is clear from the graph, co - ordinate of the common point P are (2.5, 4).
Solution of the given equation x = 2.5 and y = 4.
Hence, point of intersection = (2.5, 4).
Use graph paper for this question. Take 2 cm = 2 units on x-axis and 2 cm = 1 unit on y-axis.
Solve graphically the following equations :
3x + 5y = 12; 3x - 5y + 18 = 0
(Plot only three points per line)
Answer
First equation: 3x + 5y = 12
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = 0, then 3 0 + 5y = 12 ⇒ y = 2.4
Let x = 2, then 3 2 + 5y = 12 ⇒ y = 1.2
Let x = 4, then 3 4 + 5y = 12 ⇒ y = 0
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | 0 | 2 | 4 |
|---|---|---|---|
| y | 2.4 | 1.2 | 0 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
Second equation: 3x - 5y + 18 = 0
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -2, then 3 (-2) - 5y + 18 = 0 ⇒ y = 2.4
Let x = 0, then 3 0 - 5y + 18 = 0 ⇒ y = 3.6
Let x = 2, then 3 2 - 5y + 18 = 0 ⇒ y = 4.8
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -2 | 0 | 2 |
|---|---|---|---|
| y | 2.4 | 3.6 | 4.8 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
On the same graph paper, draw the graph for each given equation.
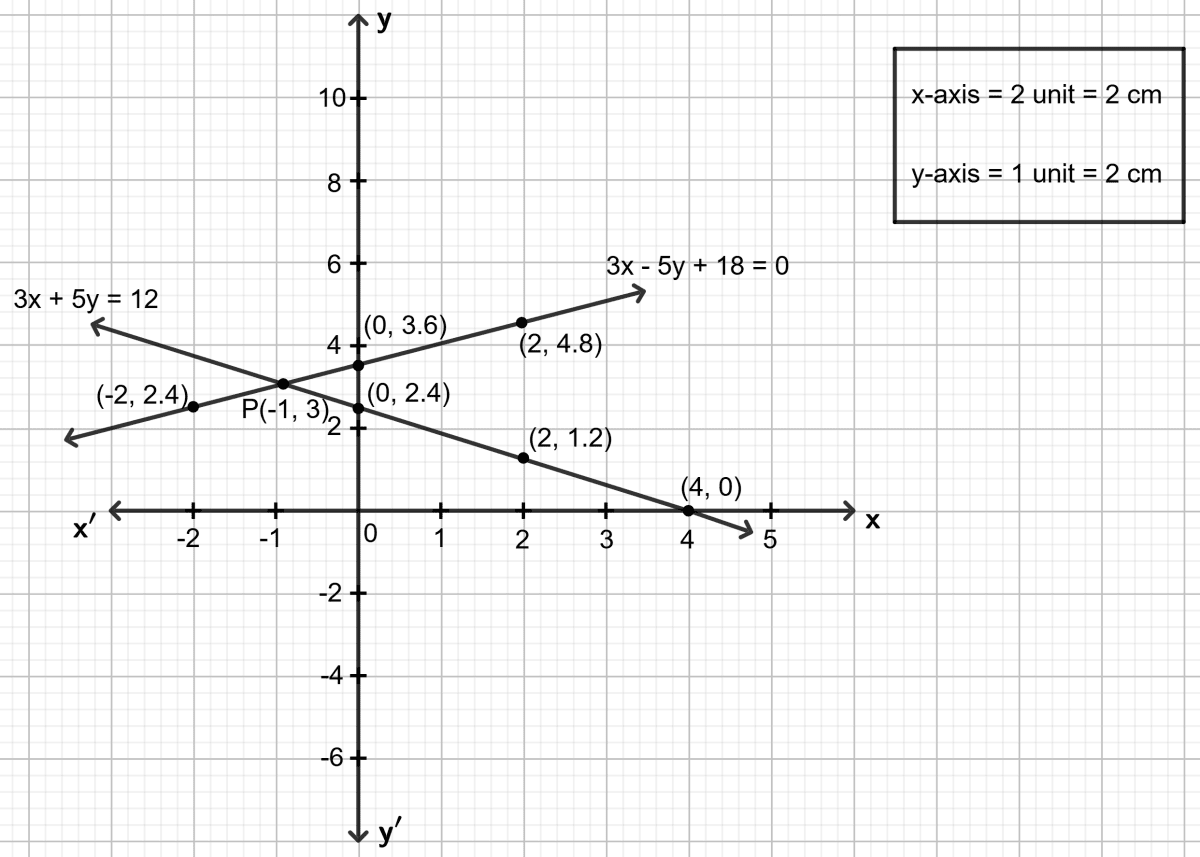
Both the straight line drawn meet the point P. As it is clear from the graph, co-ordinates of the common point P are (-1, 3).
Solution of the given equation x = -1 and y = 3.
Use graph paper for this question. Take 2 cm = 1 unit on both the axes.
(i) Draw the graphs of x + y + 3 = 0 and 3x - 2y + 4 = 0. Plot only three points per line.
(ii) Write down the co-ordinates of the point of intersection of the lines.
(iii) Measure and record the distance of the point of intersection of the lines from the origin in cm.
Answer
(i)
First equation: x + y + 3 = 0
Step 1:
Give three suitable values to the variable x and find the corresponding values of y.
Let x = 0, then 0 + y + 3 = 0 ⇒ y = -3
Let x = -4, then -4 + y + 3 = 0 ⇒ y = 1
Let x = -6, then -6 + y + 3 = 0 ⇒ y = 3
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | 0 | -4 | -6 |
|---|---|---|---|
| y | -3 | 1 | 3 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
Second equation: 3x - 2y + 4 = 0
Step 1:
Give three suitable values to the variable x and find the corresponding values of y.
Let x = 0, then 3 0 - 2y + 4 = 0 ⇒ y = 2
Let x = 2, then 3 2 - 2y + 4 = 0 ⇒ y = 5
Let x = 4, then 3 4 - 2y + 4 = 0 ⇒ y = 8
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | 0 | 2 | 4 |
|---|---|---|---|
| y | 2 | 5 | 8 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
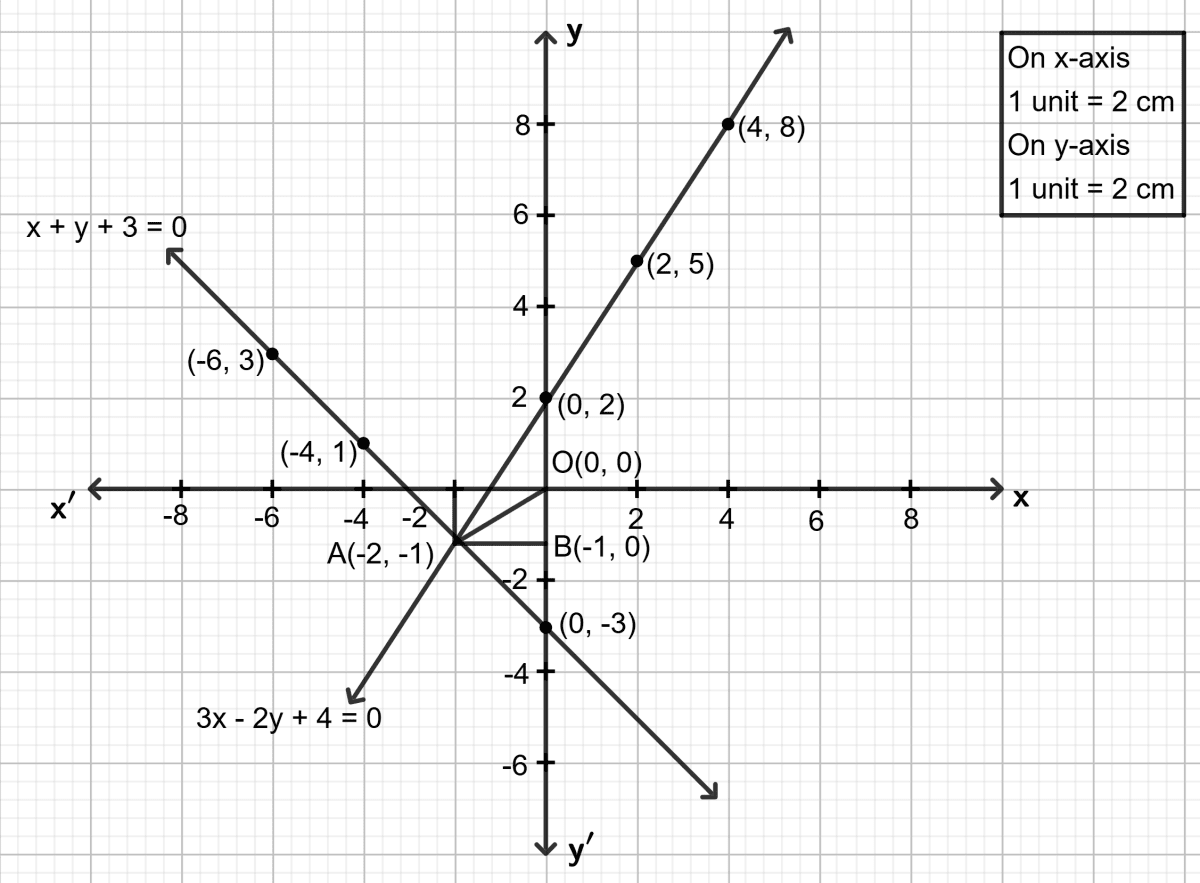
(ii) Both the straight line drawn meet at the point A. As it is clear from the graph, co-ordinates of the common point A are (-2, -1).
Hence, co-ordinates of the point of intersection of the lines are (-2, -1).
(iii) In triangle OAB,
Using pythagoras theorem,
OA2 = AB2 + OB2
= 22 + 12
= 4 + 1
= 5
OA =
OA = 2.2 cm
Hence, the distance of the point of intersection of the lines from the origin is 2.2 cm.
The sides of a triangle are given by the equations y - 2 = 0; y + 1 = 3 (x - 2) and x + 2y = 0.
Find, graphically :
(i) the area of triangle;
(ii) the co-ordinates of the vertices of the triangle.
Answer
(i)
First equation: y - 2 = 0
y = 2
Second equation: y + 1 = 3 (x - 2)
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = 0, then y + 1 = 3 (0 - 2) ⇒ y = -7
Let x = 2, then y + 1 = 3 (2 - 2) ⇒ y = -1
Let x = 4, then y + 1 = 3 (4 - 2) ⇒ y = 5
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | 0 | 2 | 4 |
|---|---|---|---|
| y | -7 | -1 | 5 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
Third equation: x + 2y = 0
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = 0, then 0 + 2y = 0 ⇒ y = 0
Let x = 2, then 0 + 2y = 0 ⇒ y = -1
Let x = 4, then 4 + 2y = 0 ⇒ y = -2
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | 0 | 2 | 4 |
|---|---|---|---|
| y | 0 | -1 | -2 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
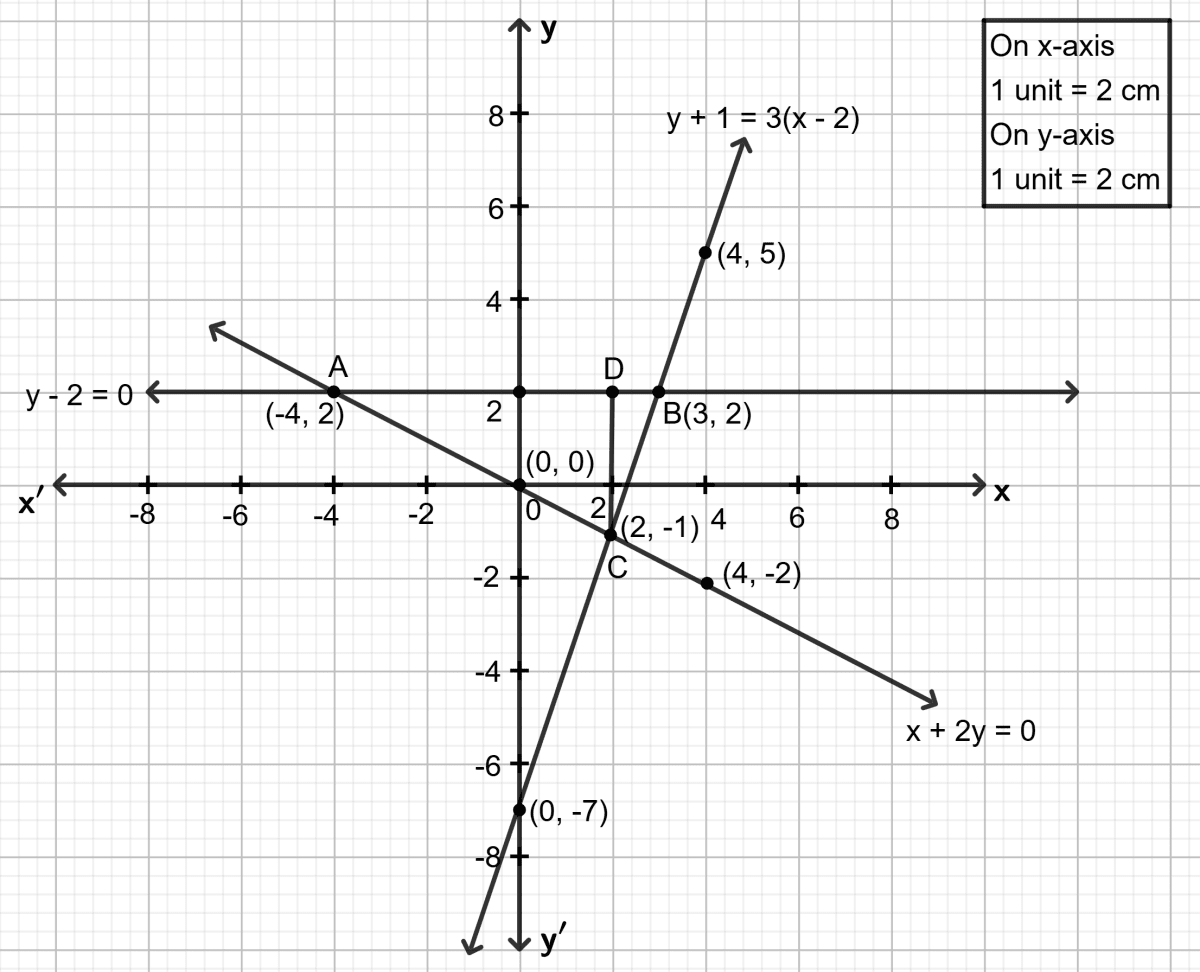
(i) The area of the triangle formed by the lines = x base x height
= x AB x CD
= x 7 x 3
=
= 10.5 sq. units
Hence, area of triangle = 10.5 sq. units.
(ii) The co-ordinates of A = (-4, 2)
The co-ordinates of B = (3, 2)
The co-ordinates of C = (2, -1)
Hence, the co-ordinates of the vertices of the triangle are (-4, 2), (3, 2) and (2, -1).
By drawing a graph for each of the equations 3x + y + 5 = 0; 3y - x = 5 and 2x + 5y = 1 on the same graph paper; show that the lines given by these equations are concurrent (i.e. they pass through the same point).
Take 2 cm = 1 unit on both the axes.
Answer
First equation: 3x + y + 5 = 0
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -3, then 3 (-3) + y + 5 = 0 ⇒ y = 4
Let x = -2, then 3 (-2) + y + 5 = 0 ⇒ y = 1
Let x = 1, then 3 1 + y + 5 = 0 ⇒ y = -8
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -3 | -2 | 1 |
|---|---|---|---|
| y | 4 | 1 | -8 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
Second equation: 3y - x = 5
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -2, then 3y - (-2) = 5 ⇒ y = 1
Let x = 1, then 3y - 1 = 5 ⇒ y = 2
Let x = 7, then 3y - 7 = 5 ⇒ y = 4
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -2 | 1 | 7 |
|---|---|---|---|
| y | 1 | 2 | 4 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
Third equation: 2x + 5y = 1
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -7, then 2 (-7) + 5y = 1 ⇒ y = 3
Let x = -2, then 2 (-2) + 5y = 1 ⇒ y = 1
Let x = 3, then 2 3 + 5y = 1 ⇒ y = -1
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -7 | -2 | 3 |
|---|---|---|---|
| y | 3 | 1 | -1 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph. 3
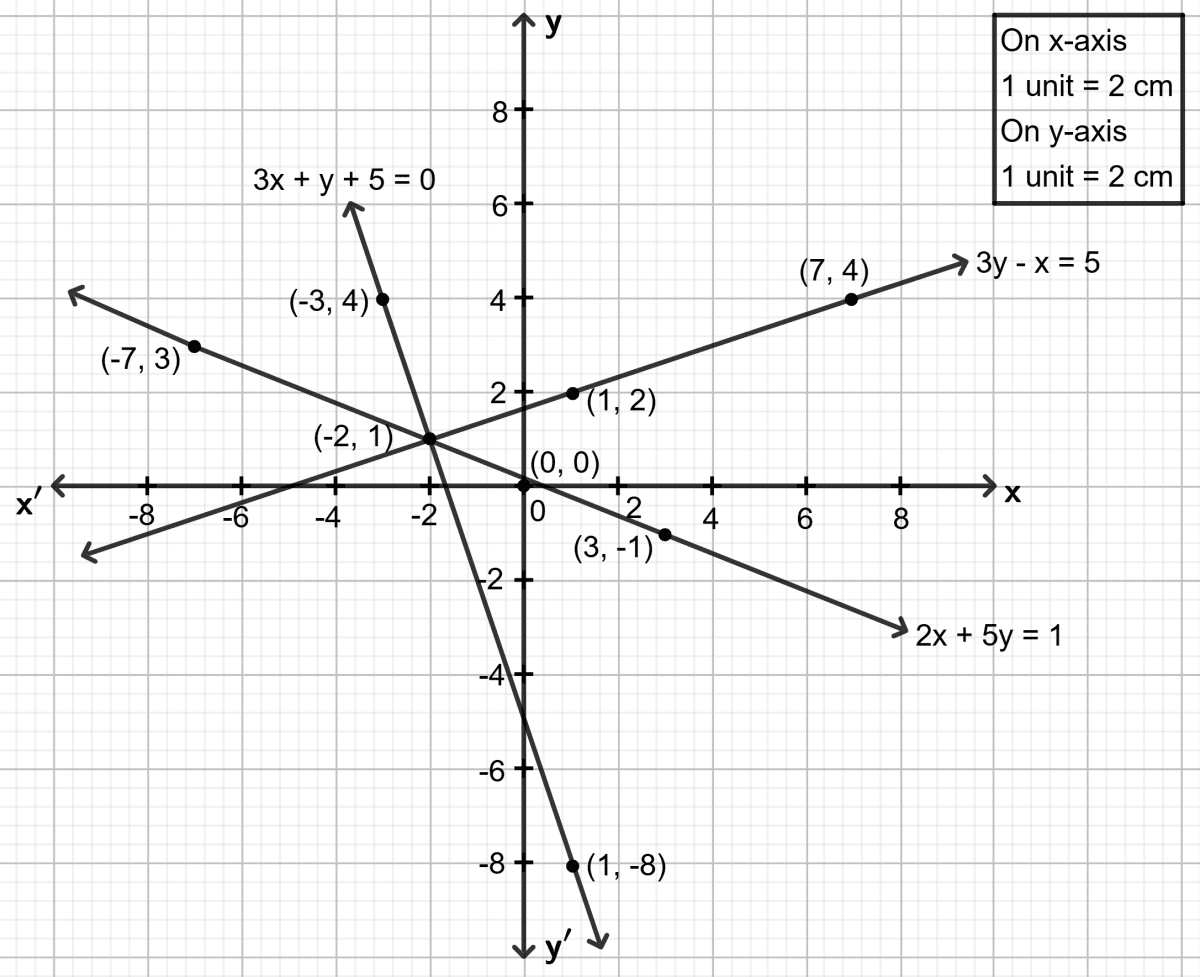
From the graph, it is clear that all three lines intersect at a common point (-2, 1), confirming that the lines are concurrent.
Using a scale of 1 cm to 1 unit for both the axes, draw the graphs of the following equations : 6y = 5x + 10, y = 5x - 15.
From the graph find :
(i) the co-ordinates of the point where the two lines intersect;
(ii) the area of the triangle between the lines and the x-axis.
Answer
First equation: 6y = 5x + 10
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -8, then 6y = 5 (-8) + 10 ⇒ y = -5
Let x = -2, then 6y = 5 (-2) + 10 ⇒ y = 0
Let x = 4, then 6y = 5 4 + 10 ⇒ y = 5
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -8 | -2 | 4 |
|---|---|---|---|
| y | -5 | 0 | 5 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
Second equation: y = 5x - 15
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = 3, then y = 5 3 - 15 ⇒ y = 0
Let x = 4, then y = 5 4 - 15 ⇒ y = 5
Let x = 5, then y = 5 5 - 15 ⇒ y = 10
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | 3 | 4 | 5 |
|---|---|---|---|
| y | 0 | 5 | 10 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
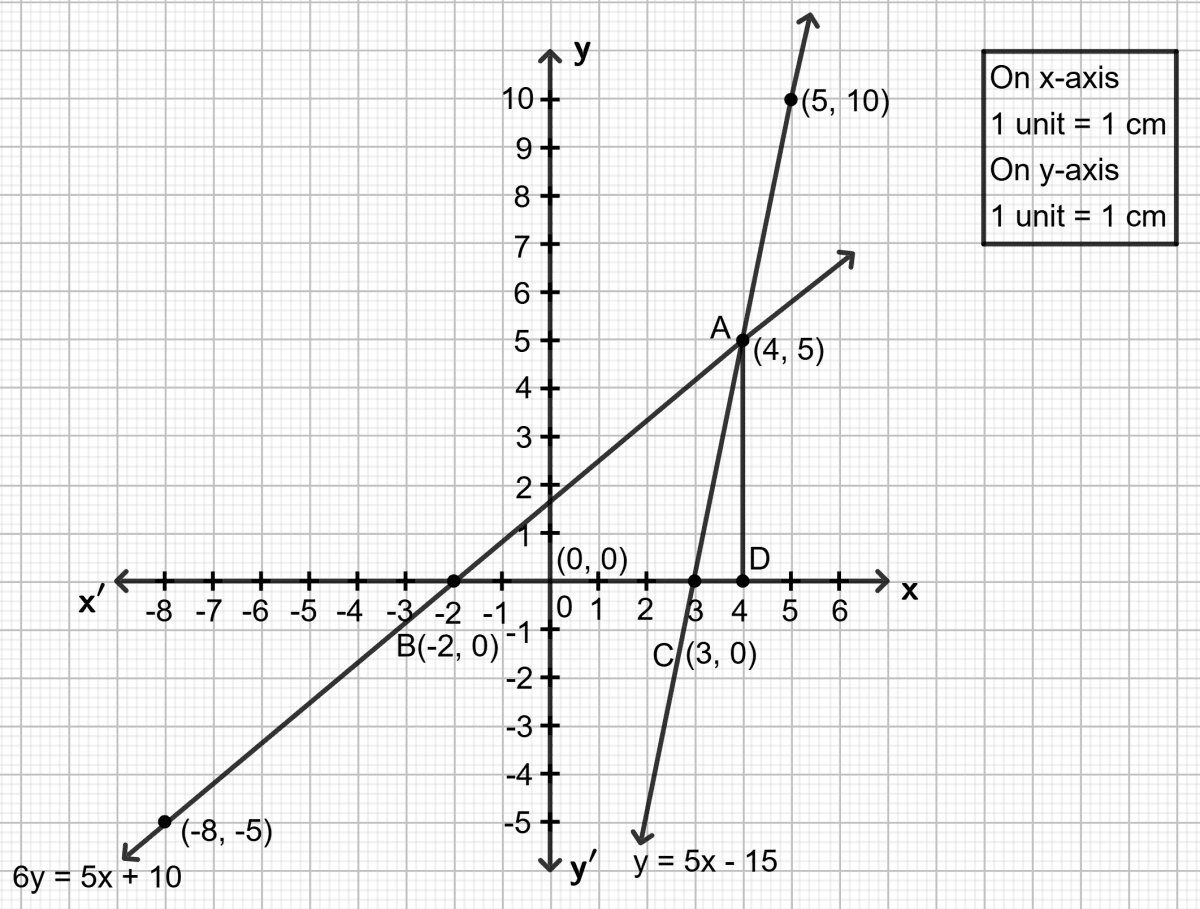
(i) Both the straight line drawn meet at the point A. As it is clear from the graph, co-ordinates of the common point A are (4, 5).
Hence, the co-ordinates of the point where the two lines intersect = (4, 5).
(ii) The area of the triangle = x base x height
= x BC x AD
= x 5 x 5
= sq. units
= 12.5 sq. units
Hence, the area of the triangle between the lines and the x-axis = 12.5 sq. units.
The cost of manufacturing x articles is ₹ (50 + 3x). The selling price of x articles is ₹ 4x.
On a graph sheet, with the same axes, and taking suitable scales draw two graphs, first for the cost of manufacturing against no. of articles and the second for the selling price against number of articles.
Use your graph to determine :
(i) No. of articles to be manufactured and sold to breakeven point (no profit and no loss),
(ii) The profit or loss made when
(a) 30
(b) 60 articles are manufactured and sold.
Answer
Given:
The cost of manufacturing x articles = ₹ (50 + 3x).
C.P. = ₹ (50 + 3x)
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of C.P.
Let x = 0, then C.P. = ₹ (50 + 3 0) ⇒ C.P. = ₹ 50
Let x = 20, then C.P. = ₹ (50 + 3 20) ⇒ C.P. = ₹ 110
Let x = 40, then C.P. = ₹ (50 + 3 40) ⇒ C.P. = ₹ 170
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | 0 | 20 | 40 |
|---|---|---|---|
| C.P. | 50 | 110 | 170 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
And, the selling price of x articles is ₹ 4x
S.P. = ₹ 4x
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of S.P.
Let x = 0, then S.P. = ₹ 4 0 ⇒ S.P. = ₹ 0
Let x = 20, then S.P. = ₹ 4 20 ⇒ S.P. = ₹ 80
Let x = 40, then S.P. = ₹ 4 40 ⇒ S.P. = ₹ 160
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | 0 | 20 | 40 |
|---|---|---|---|
| S.P. | 0 | 80 | 160 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
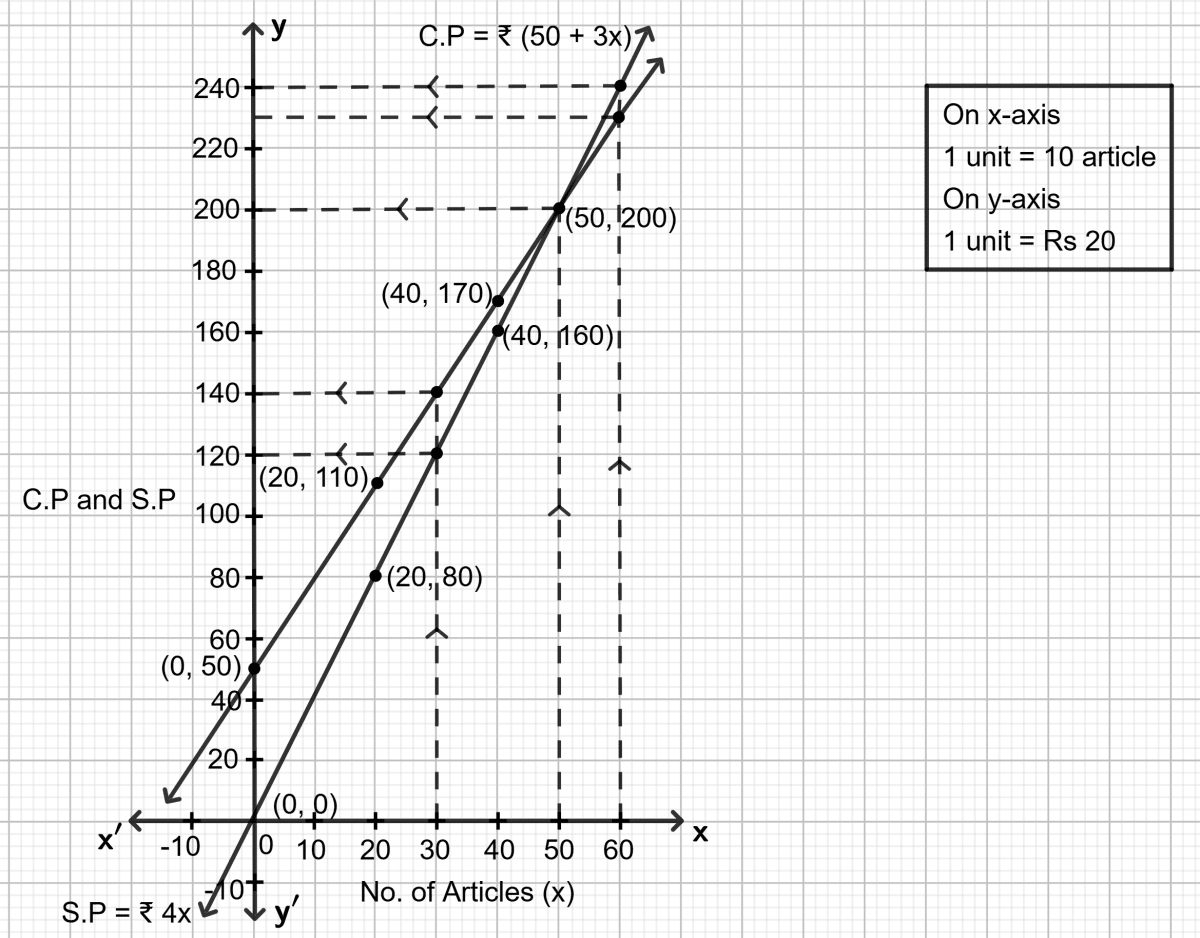
(i) The above figure shows the graphs of C.P. and S.P. Since the two straight lines meet at x = 50, it shows that the C.P. of 50 articles is the same as their selling price.
Hence, No. of articles to be manufactured and sold to breakeven point (no profit and no loss) = 0.
(ii)
(a) Draw the vertical line through x = 30, which meets graph for C.P. at ₹ 140 and graph for S.P. at ₹ 120.
C.P. > S.P.
Therefore, loss = C.P. - S.P.
= ₹ 140 - ₹ 120
= ₹ 20
Hence, the loss = ₹ 20.
(b) Draw the vertical line through x = 60, which meets graph for C.P. at ₹ 230 and graph for S.P. at ₹ 240.
C.P. = ₹ 230 and S.P. = ₹ 240
S.P. > C.P.
Therefore, profit = S.P. - C.P.
= ₹ 240 - ₹ 230
= ₹ 10
Hence, the profit = ₹ 10.
For the line 2x - y = 7 and for x = 3 the value of y is :
1
-1
5
-5
Answer
Given, equation of lines 2x - y = 7 and x = 3
Substituting x = 3 in 2x - y = 7, we get :
⇒ 2 x 3 - y = 7
⇒ 6 - y = 7
⇒ y = 6 - 7
⇒ y = -1.
Hence, option 2 is the correct option.
The line x + 3y + 2 = 0 passes through the point (4, k); then the value of k is;
2
1
-1
-2
Answer
If the line x + 3y + 2 = 0 passes through the point (4, k), then substituting x = 4 and y = k into the equation of the line,
⇒ 4 + 3 x k + 2 = 0
⇒ 6 + 3k = 0
⇒ 3k = -6
⇒ k =
⇒ k = -2.
Hence, option 4 is the correct option.
Line x - 5 = 0 and y + 3 = 0 intersect each other at point:
(5, 3)
(5, -3)
(-5, 3)
(-5, -3)
Answer
⇒ x - 5 = 0
⇒ x = 5
This line represents a vertical line parallel to y-axis.
⇒ y + 3 = 0
⇒ y = -3
This represents a horizontal line parallel to x-axis.
Point of intersection of lines x = 5 and y = -3 is (5, -3).
Hence, option 2 is the correct option.
For the line 4x - 7y + 6 = 0 if x = 2; the value of y is :
2
-2
1
-1
Answer
Given,
equation of line 4x - 7y + 6 = 0
Substitute the given value of x (which is 2) into the equation:
⇒ 4 x 2 - 7y + 6 = 0
⇒ 8 - 7y + 6 = 0
⇒ 14 - 7y = 0
⇒ 7y = 14
⇒ y =
⇒ y = 2.
Hence, option 1 is the correct option.
Statement 1: The graph of 2x - 5 = 0 is a line parallel to y-axis.
Statement 2: When the equations of line are of the form x = ± k (a constant), the lines are parallel to y-axis.
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Answer
Given,
⇒ 2x - 5 = 0
⇒ 2x = 5
⇒ x =
This represents a vertical line (parallel to the y-axis) at a distance of units.
This line is at a distance of units to the right of the y-axis because the x-coordinate of every point on the line is .
∴ Statement 1 is true.
For equations of the form x = ± k.
These represent vertical lines (parallel to the y-axis) because the value of x remains constant at k or -k for all values of y.
∴ Statement 2 is true.
∴ Both the statements are true.
Hence, option 1 is the correct option.
Statement 1: The lines of the form ax ± by = 0 always pass through the origin.
Statement 2: On substituting x = 0 and y = 0; we get a x 0 ± b x 0 = 0.
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Answer
A line passes through the origin (0, 0) if the coordinates of the origin satisfy the equation of the line.
Substituting x = 0 and y = 0 in L.H.S. of the equation ax ± by = 0, we get :
⇒ a(0) ± b(0)
⇒ 0, which is equal to R.H.S.
Since, (0, 0) satisfies the equation ax ± by = 0, thus lines of the form ax ± by = 0 always pass through the origin.
∴ Both the statements are true.
Hence, option 1 is the correct option.
Assertion (A): y + 5 = 0 is the equation of line parallel to x-axis and at the distance of 5 unit in the negative direction from it.
Reason (R): For all the points on the y = a (a constant), the value of abscissa is a.
A is true, but R is false.
A is false, but R is true.
Both A and R are true, and R is the correct reason for A.
Both A and R are true, and R is the incorrect reason for A.
Answer
⇒ y + 5 = 0
⇒ y = -5
This represents a horizontal line (parallel to the x-axis) because the y-coordinate remains constant at -5 for all values of x. The line is 5 units below the x-axis since the y-coordinate of every point is −5, which is 5 units in the negative direction from the x-axis.
∴ Assertion (R) is true.
For all points on the line y = a, the value of ordinate (y-coordinate) = a.
∴ Reason (R) is false.
∴ A is true, but R is false.
Hence, option 1 is the correct option.
Assertion (A): For the line 3x + 4y = 7, the abscissa is .
Reason (R): 3x + 4y = 7
⇒ 3x = 7
and x = .
A is true, but R is false.
A is false, but R is true.
Both A and R are true, and R is the correct reason for A.
Both A and R are true, and R is the incorrect reason for A.
Answer
Given, equation of line : 3x + 4y = 7
When, y = 0
⇒ 3x + 4 x 0 = 7
⇒ 3x = 7
⇒ x =
∴ Reason (R) is true.
So, the abscissa is .
∴ Assertion (A) is false.
∴ A is false, but R is true.
Hence, option 2 is the correct option.
Find the distance of point (8, -4) from y-axis.
Answer
Plot the point (8, -4) on the graph paper.
Draw a perpendicular line from the point (8, -4) to the y-axis.
From graph it is clear that the distance between the point (8,−4) and the y-axis is 8 units.
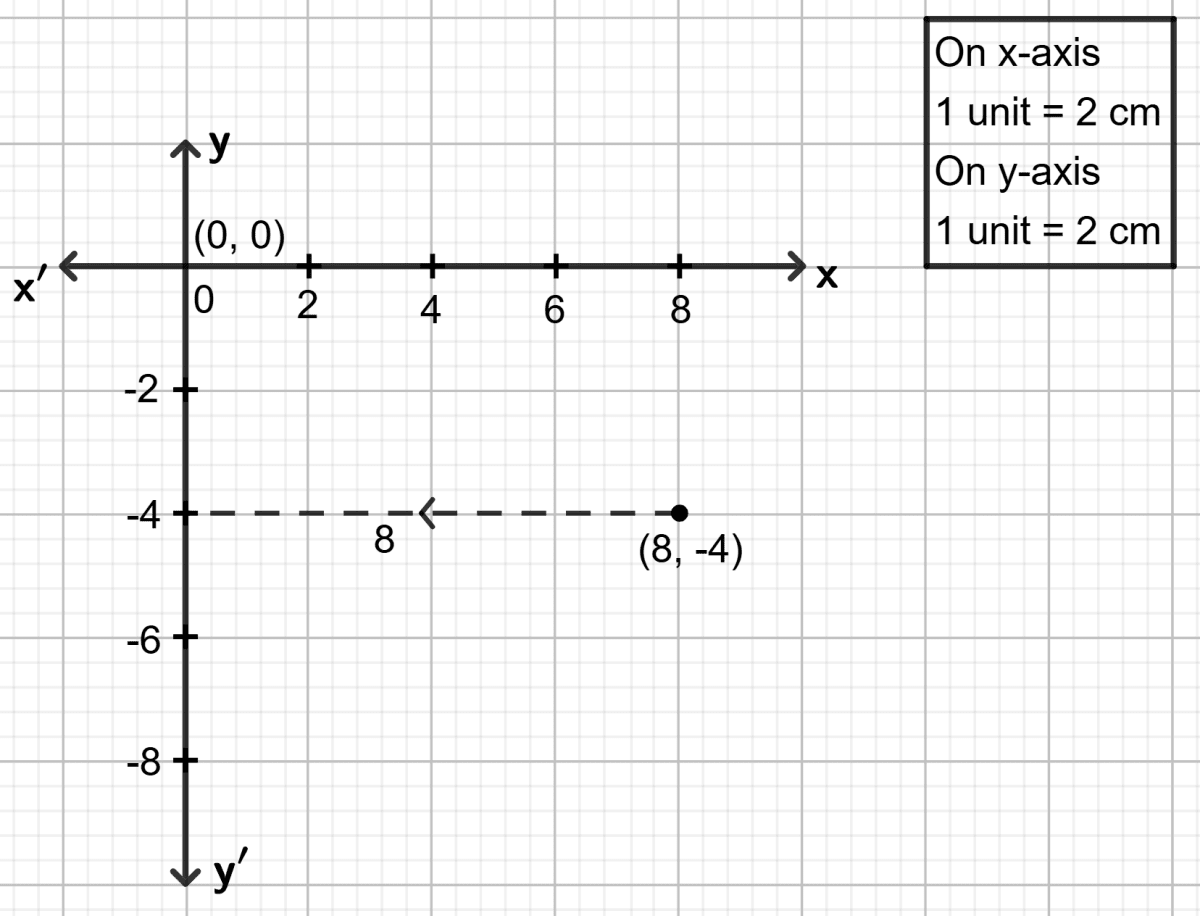
Hence, the distance of point (8, -4) from y-axis is 8 units.
Three vertices of parallelogram ABCD are A(-5, -1), B(3, -1) and C(1, -6). Use graphical method to find the co-ordinates of fourth vertex D.
Answer
Plot the points A(-5, -1), B(3, -1) and C(1, -6) on the graph paper. Join point A with B and B with C.
From the graph, it is clear that the horizontal distance between the points A (-5, -1) and B (3, -1) is 8 units and the vertical distance between the points B (3, -1) and C (1, -6) is 5 units. Therefore, the vertical distance between the points A (-5, -1) and D must be 5 units and the horizontal distance between the points C (1, -6) and D must be 8 units.
Now, complete the parallelogram ABCD and read the coordinates of point D. As shown on the graph, D = (-7, -6).
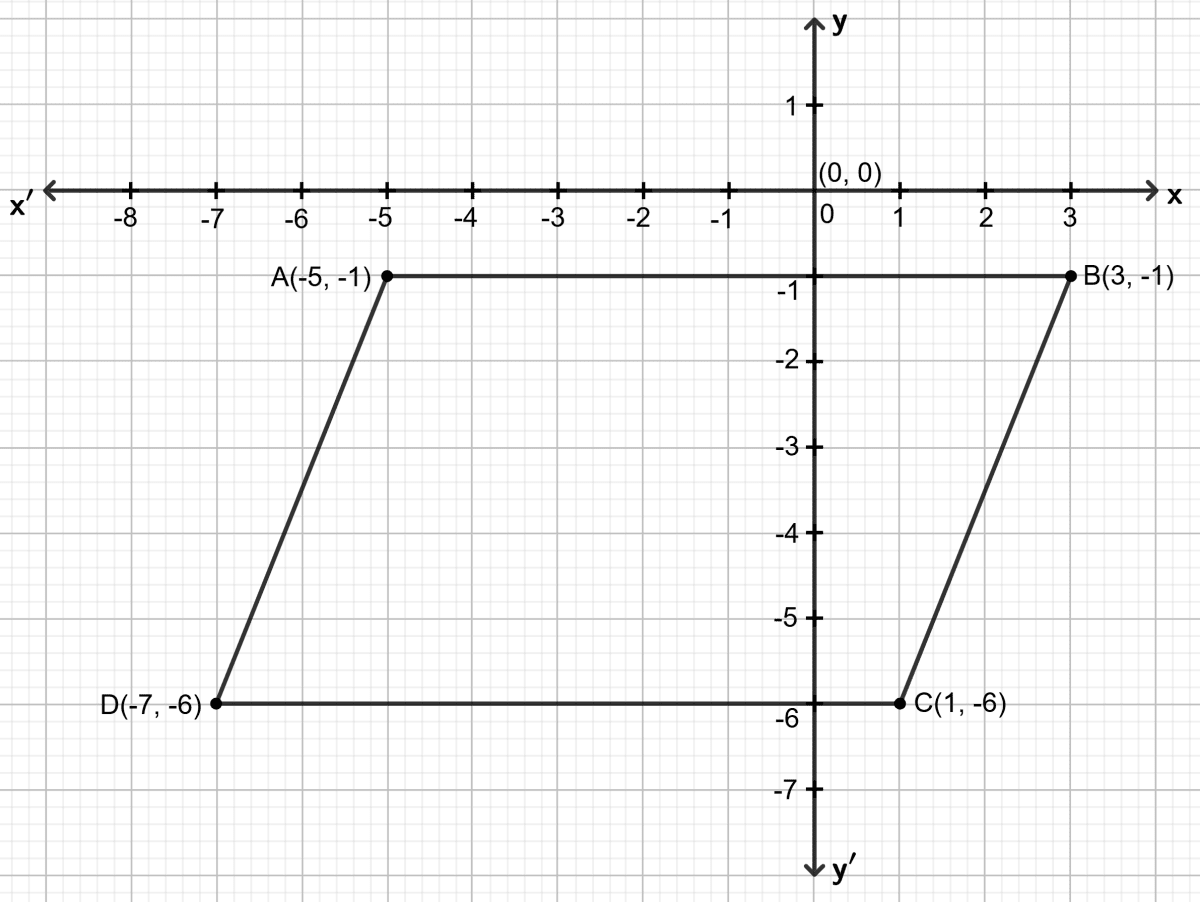
Hence, the co-ordinates of fourth vertex D are (-7, -6).
In the given figure, ABC is an equilateral triangle. Find the co-ordinates of A.
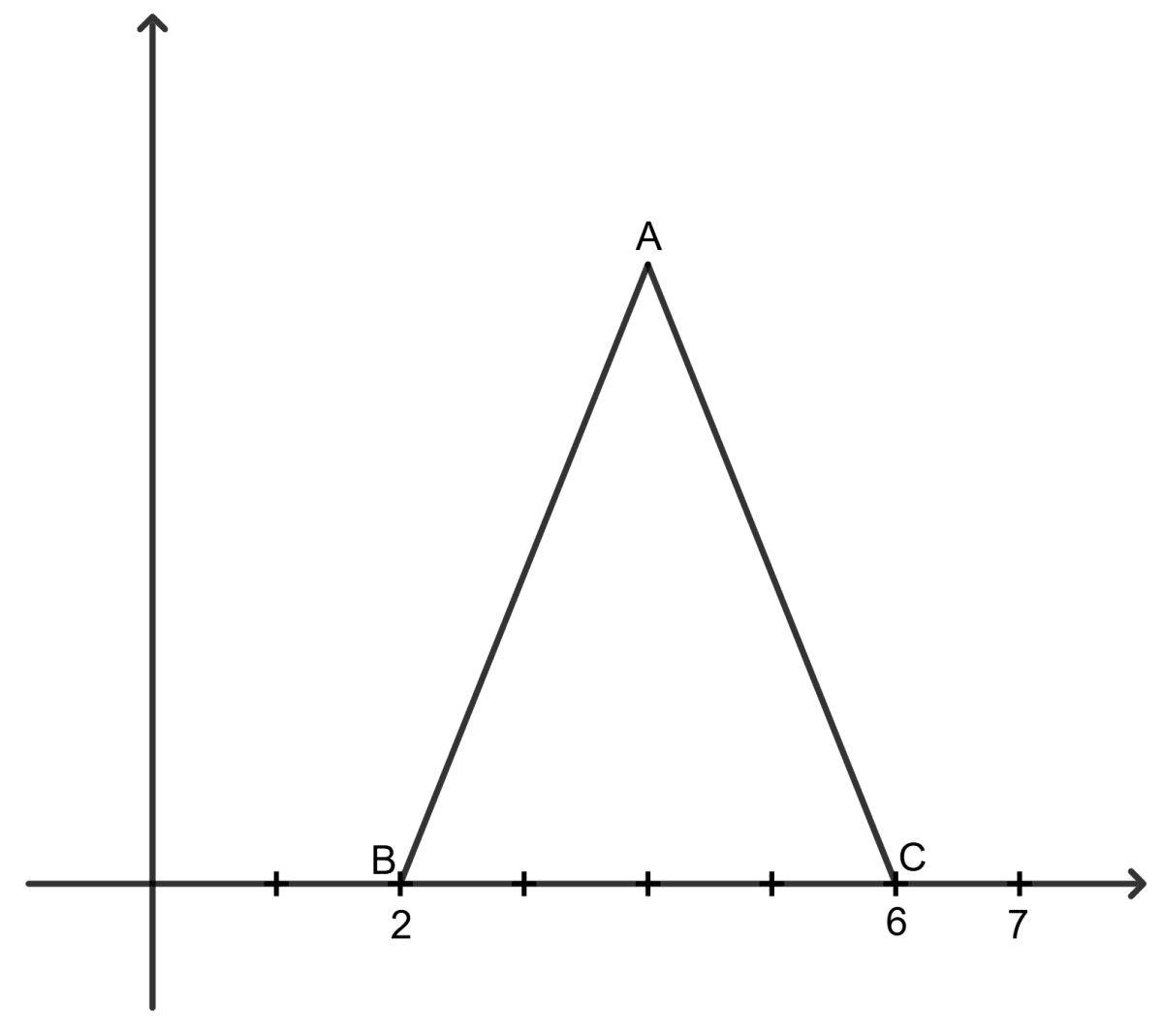
Answer
Given:
The co-ordinates of B = (2, 0)
The co-ordinates of C = (6, 0)
So, the length of BC = 6 - 2 = 4 units
Since ABC is an equilateral triangle,
The height of the triangle =
=
= 2 units
The mid-point of BC =
= (4, 0)
Since Δ ABC is equilateral, and BC lies on the x-axis:
The abscissa (x-coordinate) of A is the same as the midpoint of BC, i.e., x=4.
The ordinate (y-coordinate) of A is the height of the triangle, .
Hence, the co-ordinates of A are (4, 2 ).
Draw the graph of 3x + 2y = 6. Use the graph drawn to find the area of triangle formed by the line drawn and the co-ordinate axes.
Answer
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = 0, then 3 0 + 2y = 6 ⇒ y = 3
Let x = 2, then 3 2 + 2y = 6 ⇒ y = 0
Let x = 4, then 3 4 + 2y = 6 ⇒ y = -3
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | 0 | 2 | 4 |
|---|---|---|---|
| y | 3 | 0 | -3 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
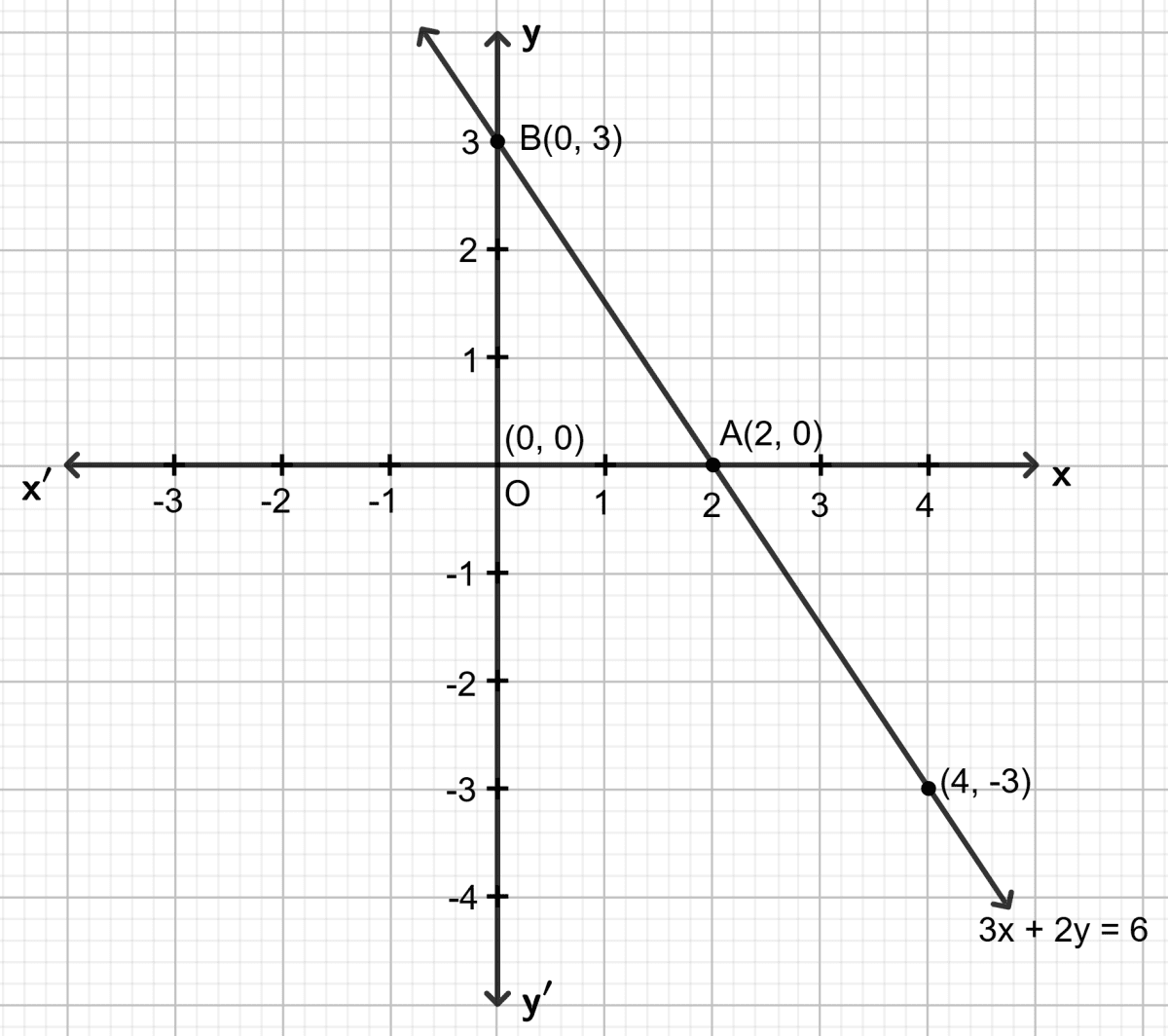
The area of the triangle = x base x height
= x OA x OB
= x 2 x 3
= sq. units
= 3 sq. units
Hence, the area of triangle formed by the line drawn and the co-ordinate axes is 3 sq. units.
Use the graphical method to find the value of k, if :
(i) (k, -3) lies on the straight line 2x + 3y = 1
(ii) (5, k - 2) lies on the straight line x - 2y + 1 = 0
Answer
(i) 2x + 3y = 1
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = 0, then 2 0 + 3y = 1 ⇒ y = 0.3
Let x = 2, then 2 2 + 3y = 1 ⇒ y = -1
Let x = 4, then 2 4 + 3y = 1 ⇒ y = -2.3
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | 0 | 2 | 4 |
|---|---|---|---|
| y | 0.3 | -1 | -2.3 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
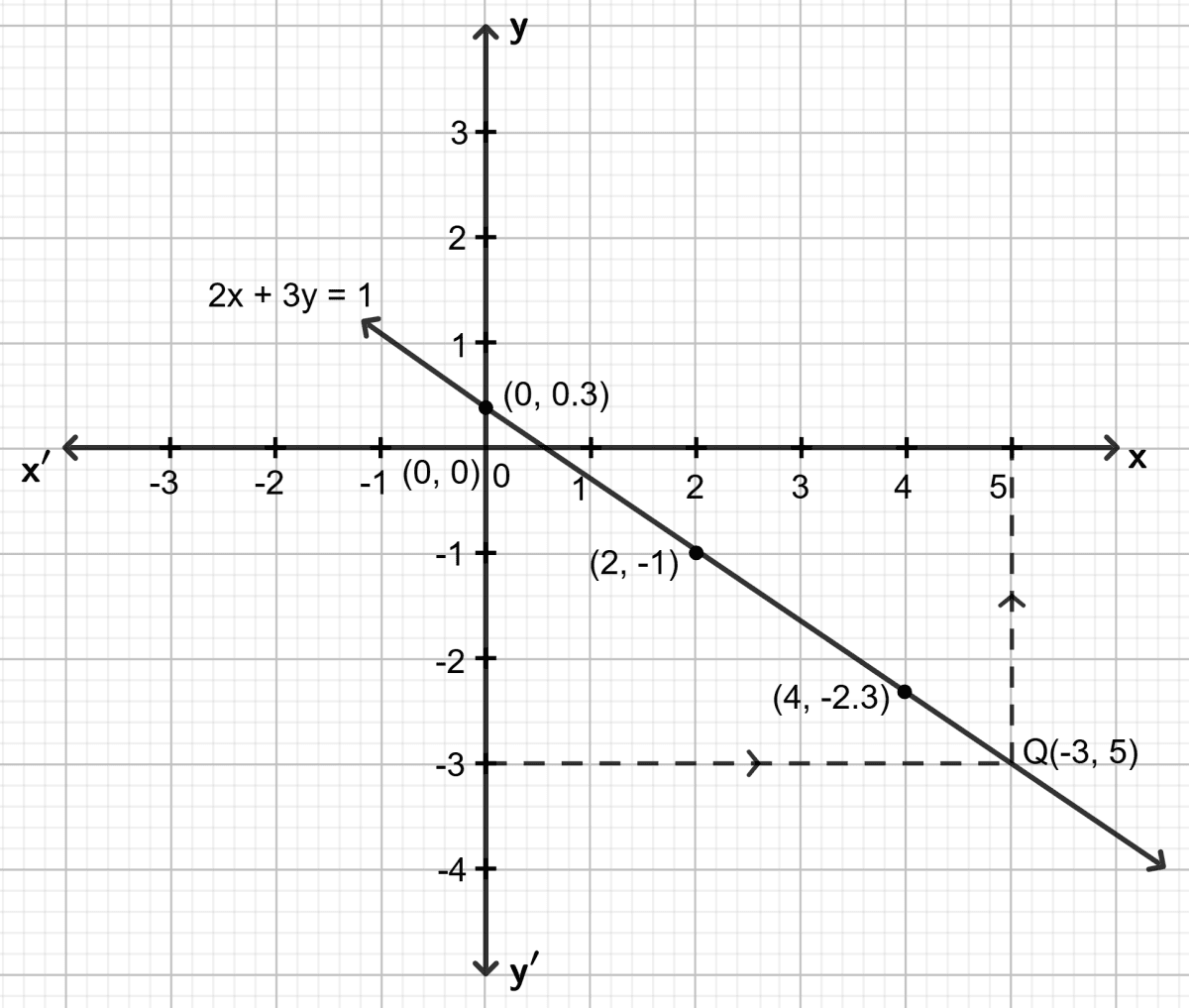
Since, point (k, -3) lies on the straight line drawn, through y = -3, draw a horizontal line which meets the straight line at point, say Q. Through point Q, draw a vertical line which meets the x-axis at 5.
Hence, the value of k = 5.
(ii) x - 2y + 1 = 0
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -1, then -1 - 2y + 1 = 0 ⇒ y = 0
Let x = 0, then 0 - 2y + 1 = 0 ⇒ y = 0.5
Let x = 1, then 1 - 2y + 1 = 0 ⇒ y = 1
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -1 | 0 | 1 |
|---|---|---|---|
| y | 0 | 0.5 | 1 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
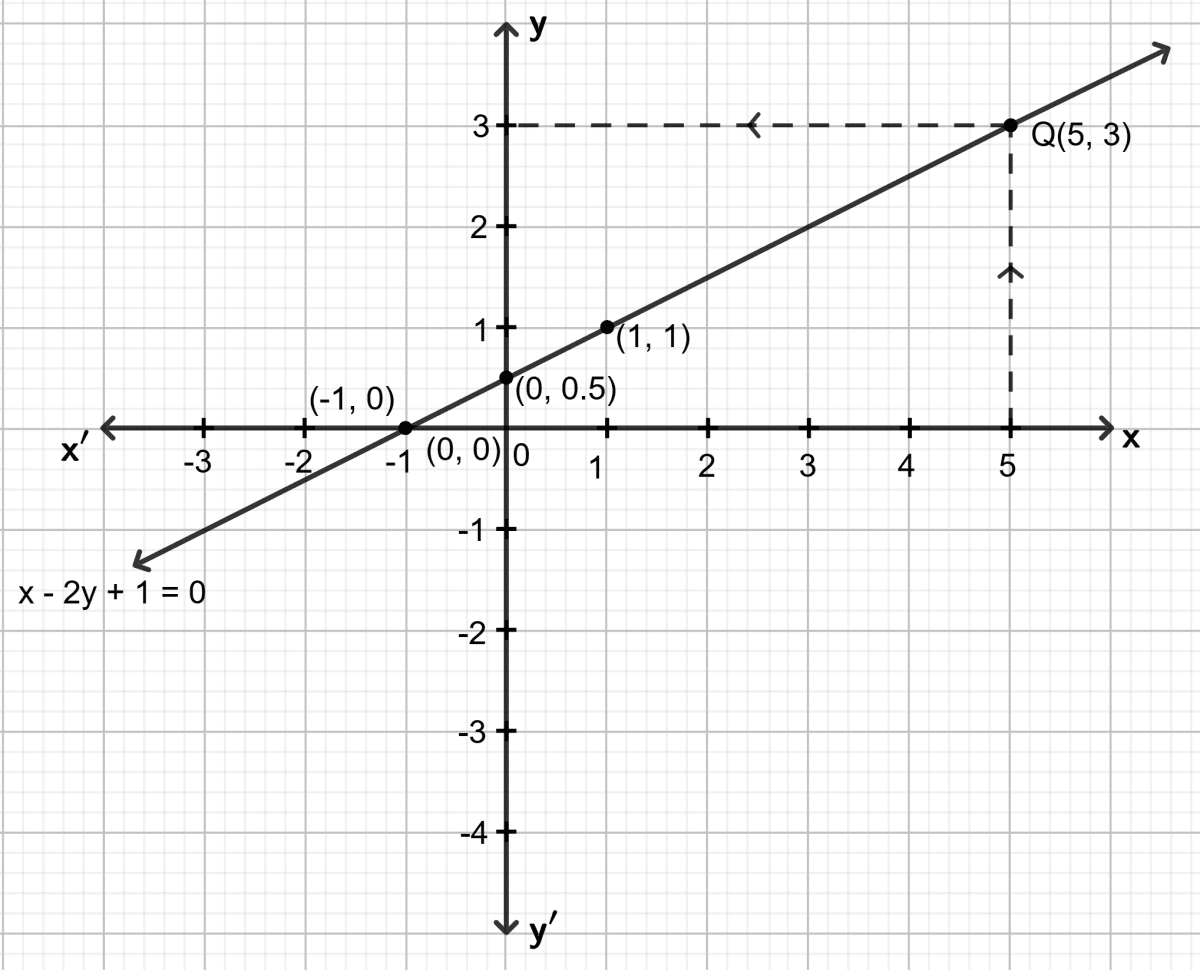
Since, point (5, k - 2) lies on the straight line drawn, through x = 5, draw a vertical line which meets the graph at a point, say Q. Through point Q, draw a horizontal line which meets the y-axis at point 3.
k - 2 = 3
⇒ k = 3 + 2
⇒ k = 5
Hence, the value of k = 5.
Find graphically, the vertices of the triangle whose sides have the equations 2y - x = 8; 5y - x = 14 and y - 2x = 1 respectively.
Take 1 cm = 1 unit on both the axes.
Answer
First equation: 2y - x = 8
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -4, then 2y - (-4) = 8 ⇒ y = 2
Let x = -2, then 2y - (-2) = 8 ⇒ y = 3
Let x = 0, then 2y - 0 = 8 ⇒ y = 4
Let x = 2, then 2y - 2 = 8 ⇒ y = 5
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -4 | -2 | 0 | 2 |
|---|---|---|---|---|
| y | 2 | 3 | 4 | 5 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
Second equation: 5y - x = 14
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -4, then 5y - (-4) = 14 ⇒ y = 2
Let x = 0, then 5y - 0 = 14 ⇒ y = 2.8
Let x = 2, then 5y - 2 = 14 ⇒ y = 3.2
Let x = 4, then 5y - 4 = 14 ⇒ y = 3.6
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -4 | 0 | 2 | 4 |
|---|---|---|---|---|
| y | 2 | 2.8 | 3.2 | 3.6 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
Third equation: y - 2x = 1
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = 0, then y - 2 0 = 1 ⇒ y = 1
Let x = 2, then y - 2 2 = 1 ⇒ y = 5
Let x = 4, then y - 2 4 = 1 ⇒ y = 9
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | 0 | 2 | 4 |
|---|---|---|---|
| y | 1 | 5 | 9 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
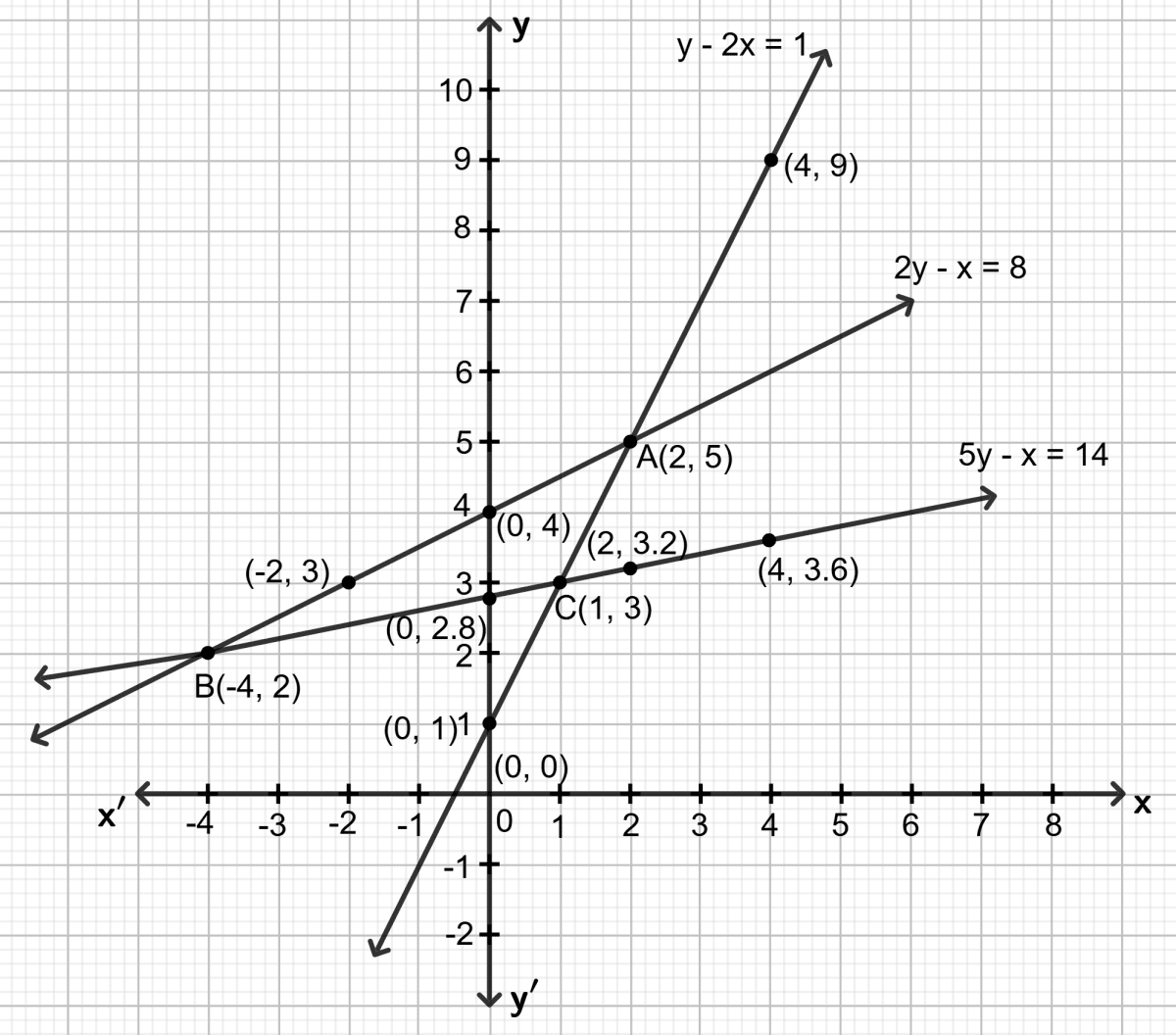
The vertices of the triangle are:
The coordinate of A = (2, 5)
The coordinate of B = (-4, 2)
The coordinate of C = (1, 3)
Hence, the coordinates of the vertices of triangle = (1, 3), (-4, 2) and (2, 5).
Using the same axes of co-ordinates and the same unit, solve graphically :
x + y = 0 and 3x - 2y = 10.
(Take at least 3 points for each line drawn).
Answer
First equation: x + y = 0
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = 0, then 0 + y = 0 ⇒ y = 0
Let x = 1, then 1 + y = 0 ⇒ y = -1
Let x = 2, then 2 + y = 0 ⇒ y = -2
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | 0 | 1 | 2 |
|---|---|---|---|
| y | 0 | -1 | -2 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
Second equation: 3x - 2y = 10
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = 0, then 3 0 - 2y = 10 ⇒ y = -5
Let x = 1, then 3 1 - 2y = 10 ⇒ y = -3.5
Let x = 2, then 3 2 - 2y = 10 ⇒ y = -2
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | 0 | 1 | 2 |
|---|---|---|---|
| y | -5 | -3.5 | -2 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
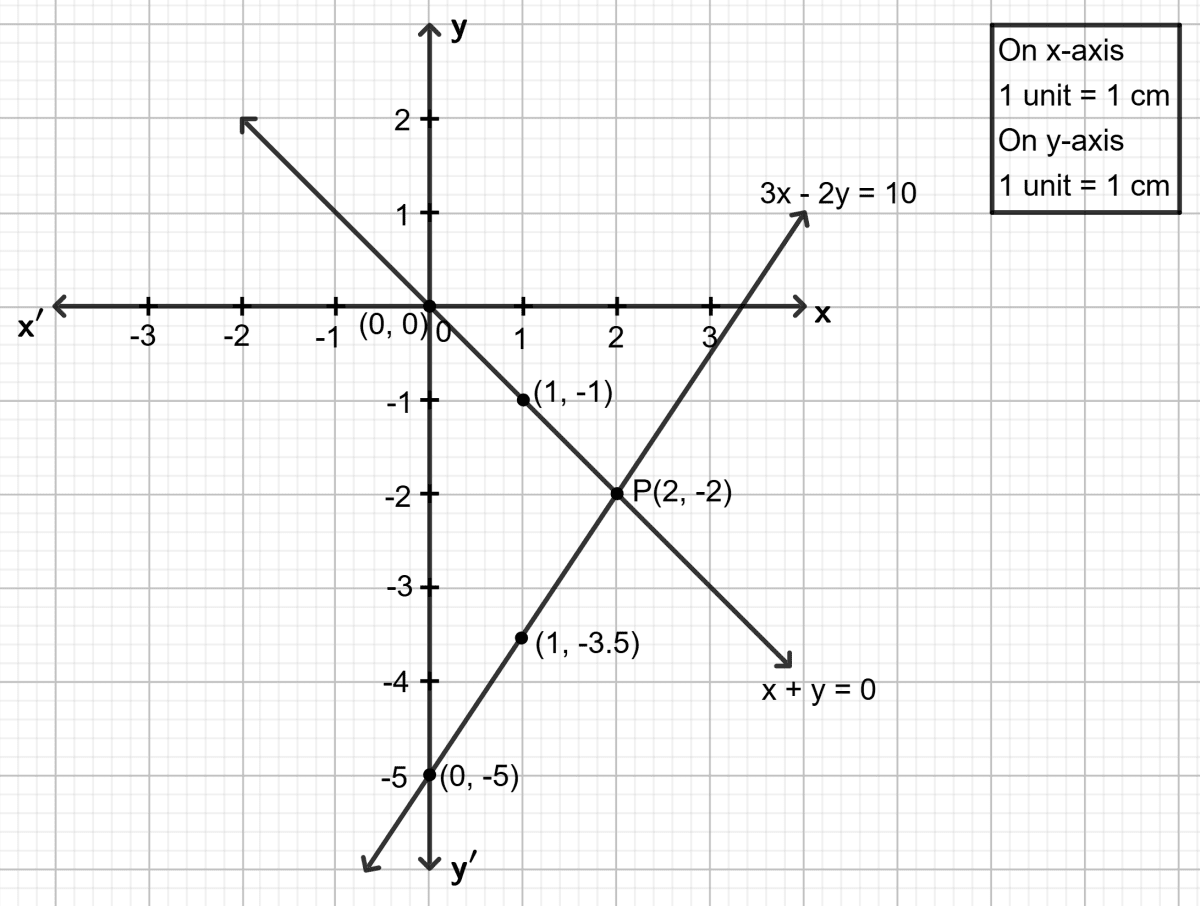
Both the straight line drawn meet the point P. As it is clear from the graph, co-ordinates of the common point P are (2, -2).
Solution of the given equation x = 2 and y = -2.
Solve graphically, the following equations.
x + 2y = 4; 3x - 2y = 4.
Take 2 cm = 1 unit on each axis.
Also, find the area of the triangle formed by the lines and the x-axis.
Answer
First equation: x + 2y = 4
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = 0, then 0 + 2y = 4 ⇒ y = 2
Let x = 2, then 2 + 2y = 4 ⇒ y = 1
Let x = 4, then 4 + 2y = 4 ⇒ y = 0
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | 0 | 2 | 4 |
|---|---|---|---|
| y | 2 | 1 | 0 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
Second equation: 3x - 2y = 4
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = 0, then 3 0 - 2y = 4 ⇒ y = -2
Let x = 2, then 3 2 - 2y = 4 ⇒ y = 1
Let x = 4, then 3 4 - 2y = 4 ⇒ y = 4
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | 0 | 2 | 4 |
|---|---|---|---|
| y | -2 | 1 | 4 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.

Both the straight line drawn meet the point A. As it is clear from the graph, co-ordinates of the common point A are (2, 1).
Solution of the given equation x = 2 and y = 1.
The area of the triangle = x base x height
= x BC x AD
= x 2.6 x 1
= 1.3 sq. units
Hence, the area of the triangle formed between the lines and the x-axis = 1.3 sq. units.
Use the graphical method to find the value of 'x' for which the expressions and are equal.
Answer
First equation: y =
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -4, then y = ⇒ y = -5
Let x = -2, then y = ⇒ y = -2
Let x = 2, then y = ⇒ y = 4
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -4 | -2 | 2 |
|---|---|---|---|
| y | -5 | -2 | 4 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
Second equation: y =
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -4, then y = ⇒ y = -5
Let x = 4, then y = ⇒ y = 1
Let x = 8, then y = ⇒ y = 4
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -4 | 4 | 8 |
|---|---|---|---|
| y | -5 | 1 | 4 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
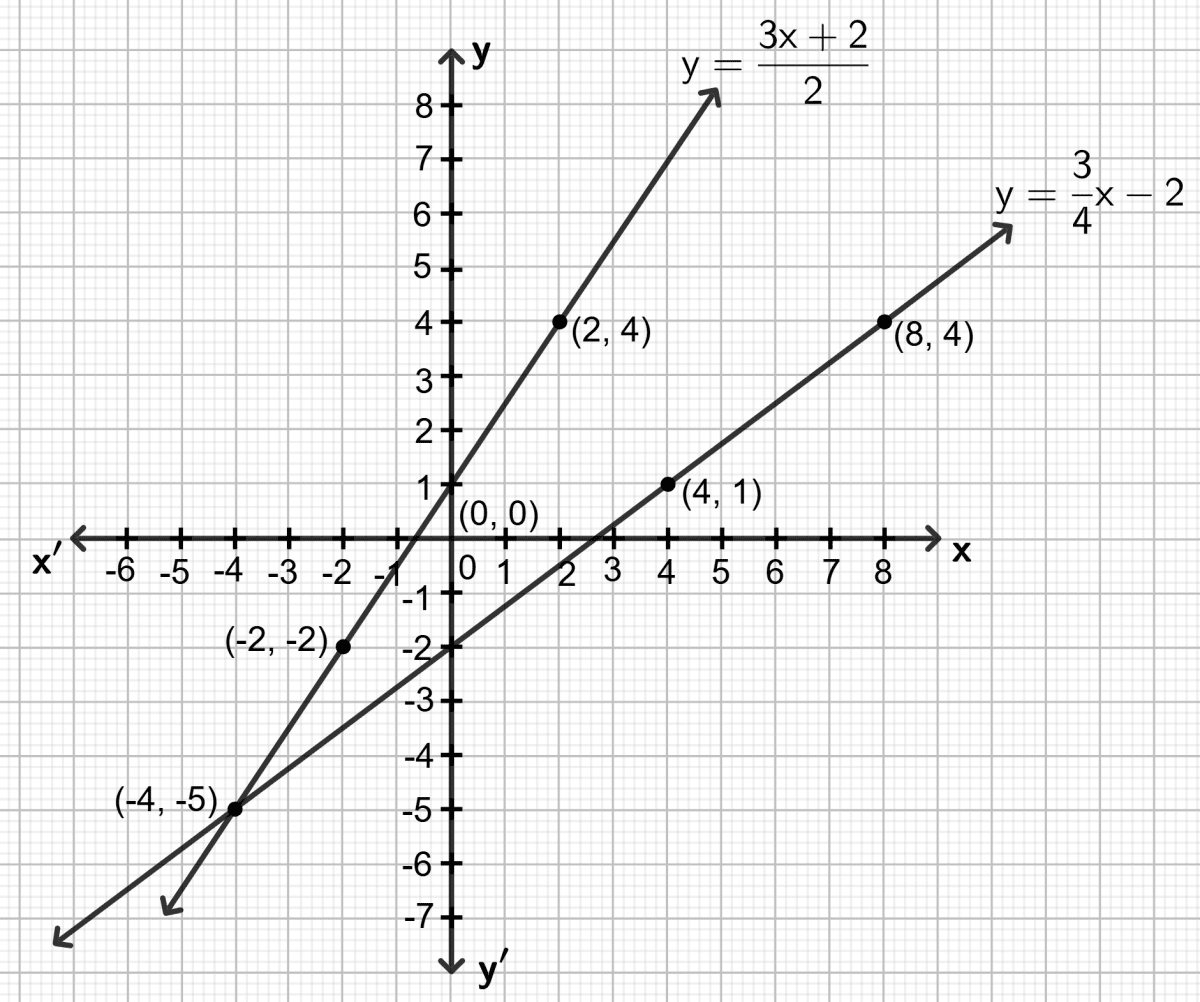
After plotting both lines on the graph, observe where the two lines intersect. The intersection point represents the value of x where both equations are equal.
From the graph, we see that the lines intersect at x = -4.
Hence, the value of x for which the two equations are equal is -4.
The course of an enemy submarine, as plotted on rectangular co-ordinate axes, gives the equation 2x + 3y = 4. On the same axes, a destroyer's course is indicated by the graph x - y = 7. Use the graphical method to find the point at which the paths of the submarine and the destroyer intersect.
Answer
Enemy equation: 2x + 3y = 4
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = -4, then 2 (-4) + 3y = 4 ⇒ y = 4
Let x = -1, then 2 (-1) + 3y = 4 ⇒ y = 2
Let x = 5, then 2 5 + 3y = 4 ⇒ y = -2
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | -4 | -1 | 5 |
|---|---|---|---|
| y | 4 | 2 | -2 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
Destroyer equation: x - y = 7
Step 1:
Give at least three suitable values to the variable x and find the corresponding values of y.
Let x = 5, then 5 - y = 7 ⇒ y = -2
Let x = 9, then 9 - y = 7 ⇒ y = 2
Let x = 11, then 11 - y = 7 ⇒ y = 4
Step 2:
Make a table (as given below) for the different pairs of the values of x and y:
| x | 5 | 9 | 11 |
|---|---|---|---|
| y | -2 | 2 | 4 |
Step 3:
Plot the points, from the table, on a graph paper and then draw a straight line passing through the points plotted on the graph.
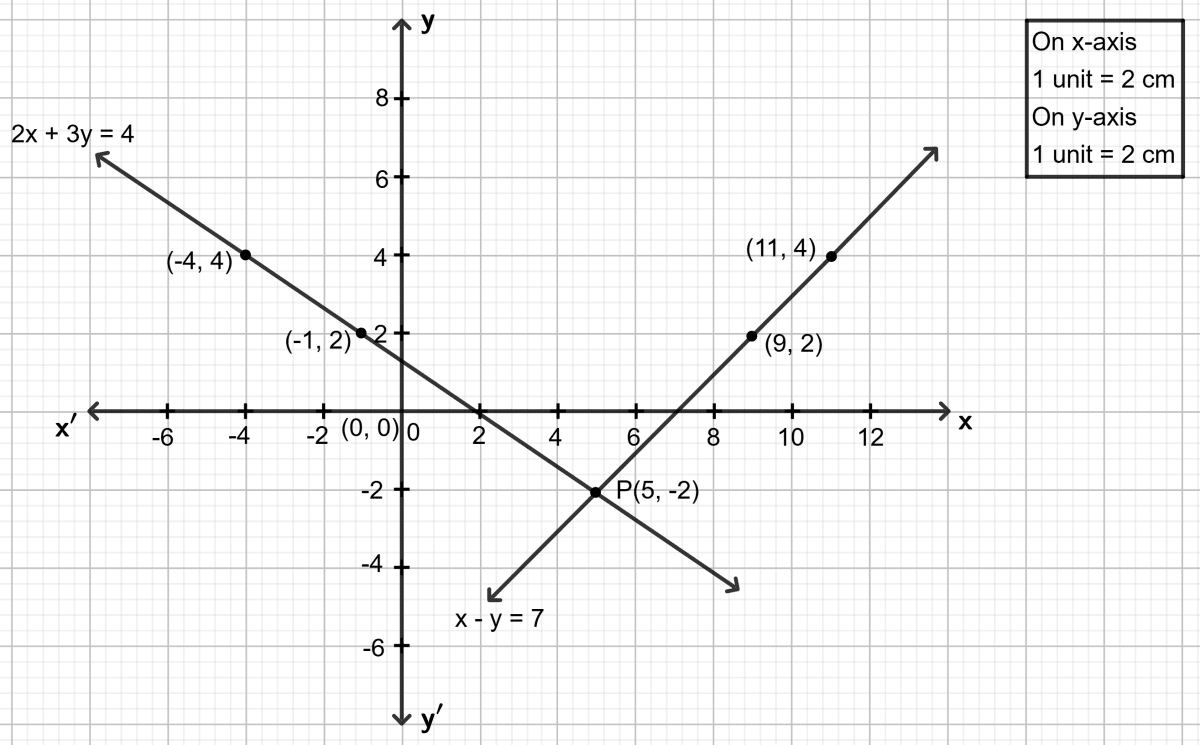
Both the straight lines intersect at point P. As it is clear from the graph, co-ordinates of point P are (-2, -1).
Hence, (5, -2) is the point at which the paths of the submarine and the destroyer intersect.