Length of a side and corresponding altitude of a triangle is doubled. The area of triangle will become :
double
half
four times
one-fourth
Answer
The area of a triangle is given by:
Area = x length x altitude
When the length of the side and the corresponding altitude of the triangle are doubled:
Area1 = x 2 x length x 2 x altitude
=
= 4 x Area
Area1 = 4 x Area
Thus, the new area of triangle becomes four times the original area.
Hence, option 3 is the correct option.
If each side of an equilateral triangle is halved, its area will be :
halved
four times
unaltered
one-fourth
Answer
Area of equilateral triangle =
If each side of the equilateral triangle is halved, then the new area will be:
New area =
=
= x Original area
Therefore, the new area of the equilateral triangle will be one-fourth of the original area.
Hence, option 4 is the correct option.
The area of a triangle is 37.5 cm2. If its base is 12.5 cm; the corresponding altitude is :
3 cm
25 cm
6 cm
12 cm
Answer
Given:
Area = 37.5 cm2
Base = 12.5 cm
Let h be the altitude of triangle.
Area of triangle = x base x altitude
⇒ 37.5 = x 12.5 x h
⇒ h =
⇒ h =
⇒ h = 6 cm
Hence, option 3 is the correct option.
ABC is a triangle with AB = AC = 12 cm and ∠A = 90°, the area of the triangle ABC is :
144 cm2
36 cm2
72 cm2
108 cm2
Answer
Given:
AB = AC = 12 cm
∠A = 90°
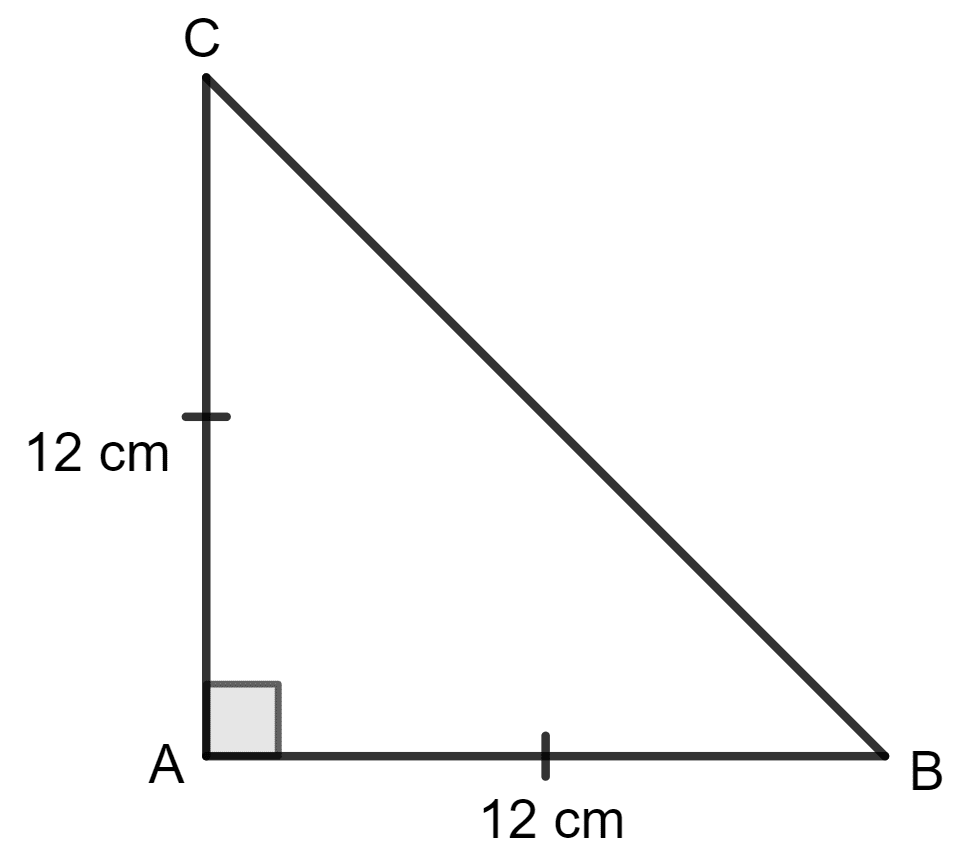
Area of triangle = x base x altitude
= x 12 x 12 cm2
= x 144 cm2
= 72 cm2
Hence, option 3 is the correct option.
The sides of a triangle are 9 cm, 12 cm and 15 cm; the area of the triangle is :
54 cm2
96 cm2
108 cm2
135 cm2
Answer
Let the sides of the triangle be:
a = 9 cm, b = 12 cm and c = 15 cm.
The semi-perimeter s:
∵ Area of triangle =
= cm2
= cm2
= cm2
= 54 cm2
Hence, option 1 is the correct option.
Find the area of a triangle whose sides are 18 cm, 24 cm and 30 cm.
Also, find the length of altitude corresponding to the largest side of the triangle.
Answer
Let the sides of the triangle be:
a = 18 cm, b = 24 cm and c = 30 cm.
The semi-perimeter s:
∵ Area of triangle =
= cm2
= cm2
= cm2
= 216 cm2
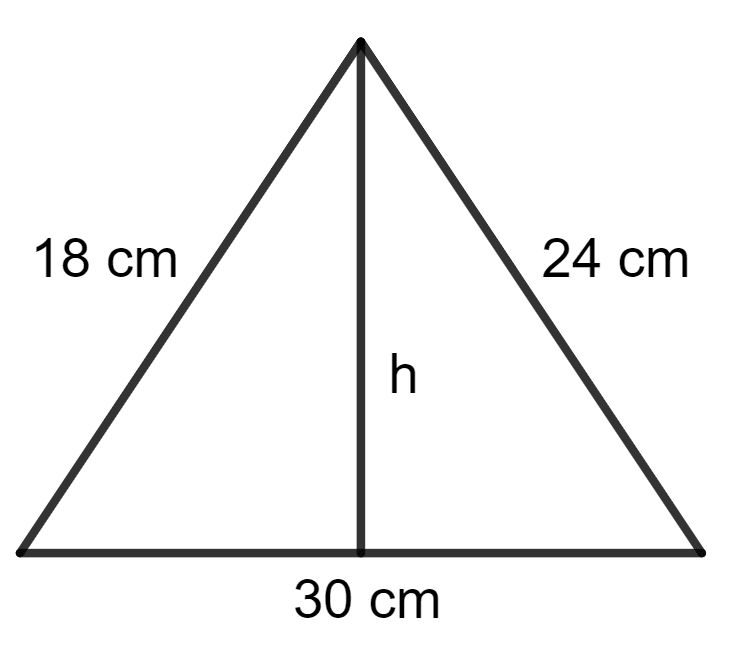
Using the area formula to find the altitude corresponding to the largest side (base = 30 cm):
Area = x base x altitude
Let h be the altitude:
⇒ 216 = x 30 x h
⇒ 216 = 15 x h
⇒ h =
⇒ h = 14.4 cm
Hence, the area of the triangle is 216 cm2 and the length of altitude corresponding to the largest side is 14.4 cm.
The lengths of the sides of a triangle are in the ratio 3 : 4 : 5. Find the area of the triangle if its perimeter is 144 cm.
Answer
It is given that the lengths of the sides of a triangle are in the ratio 3 : 4 : 5.
Let the lengths of the sides be 3a, 4a and 5a.
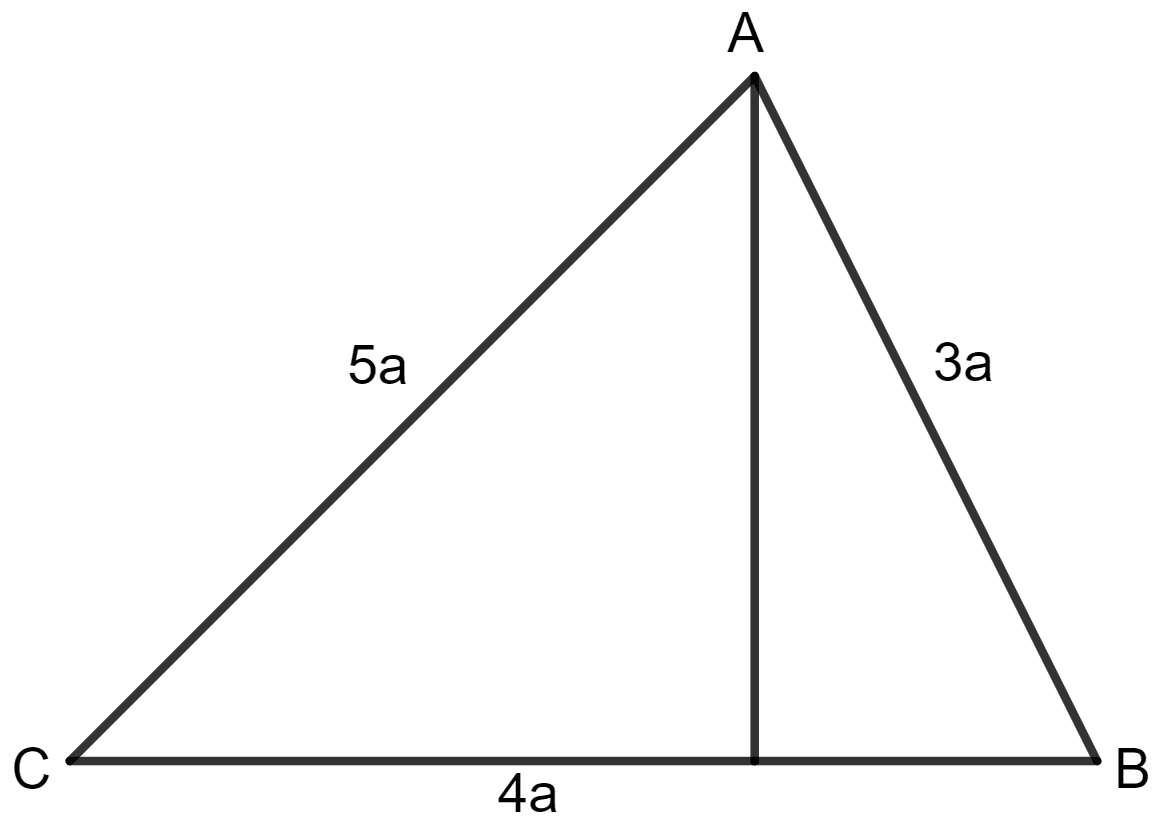
The perimeter of the triangle is 144 cm.
Perimeter = sum of all sides of triangle
⇒ 144 = 3a + 4a + 5a
⇒ 144 = 12a
⇒ a =
⇒ a = 12
So, the sides of triangle = 3a, 4a and 5a
= 3 x 12, 4 x 12 and 5 x 12
= 36, 48 and 60
Let a = 36 cm, b = 48 cm and c = 60 cm.
The semi-perimeter s:
∵ Area of triangle =
= cm2
= cm2
= cm2
= 864 cm2
Hence, the area of the triangle is 864 cm2.
ABC is a triangle in which AB = AC = 4 cm and ∠A = 90°. Calculate :
(i) the area of Δ ABC,
(ii) the length of perpendicular from A to BC.
Answer
(i) Given:
AB = AC = 4 cm
∠A = 90°
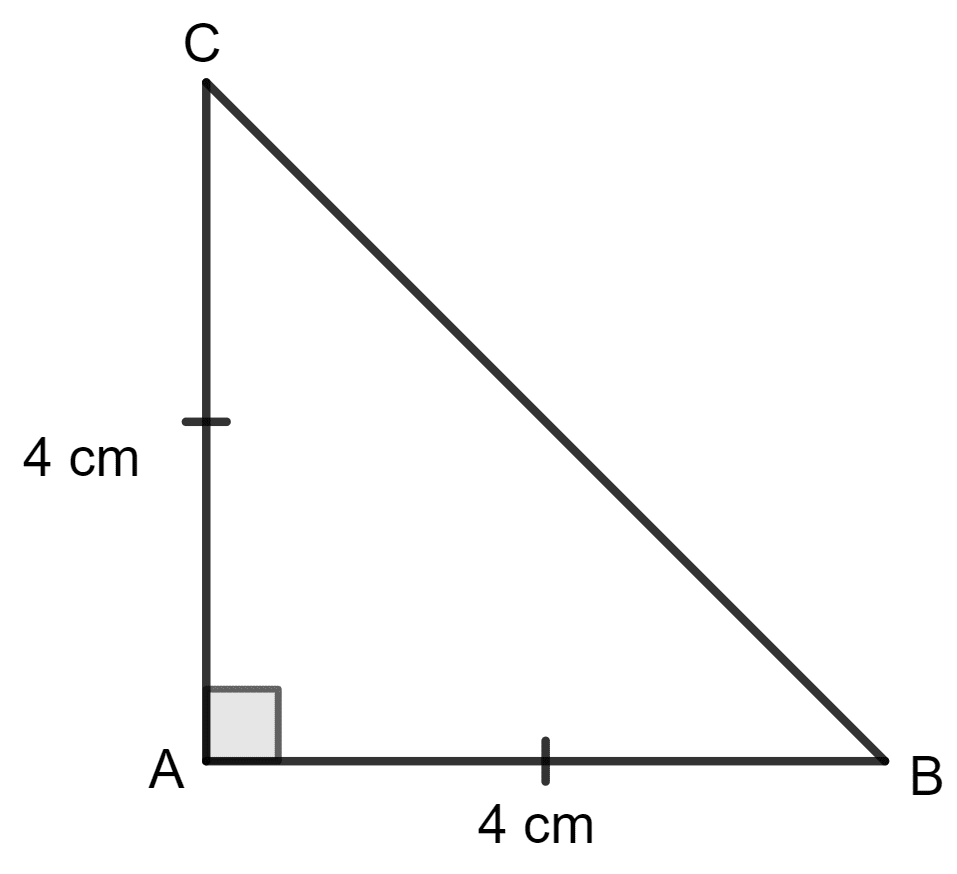
Area = x base x height
= x 4 x 4 cm2
= x 16 cm2
= 8 cm2
(ii) By using the Pythagoras theorem,
AB2 + AC2 = BC2
⇒ (4)2 + (4)2 = BC2
⇒ 16 + 16 = BC2
⇒ BC2 = 32
⇒ BC =
⇒ BC = 4 cm
Now considering BC as the base of the triangle, altitude AD will be its height.
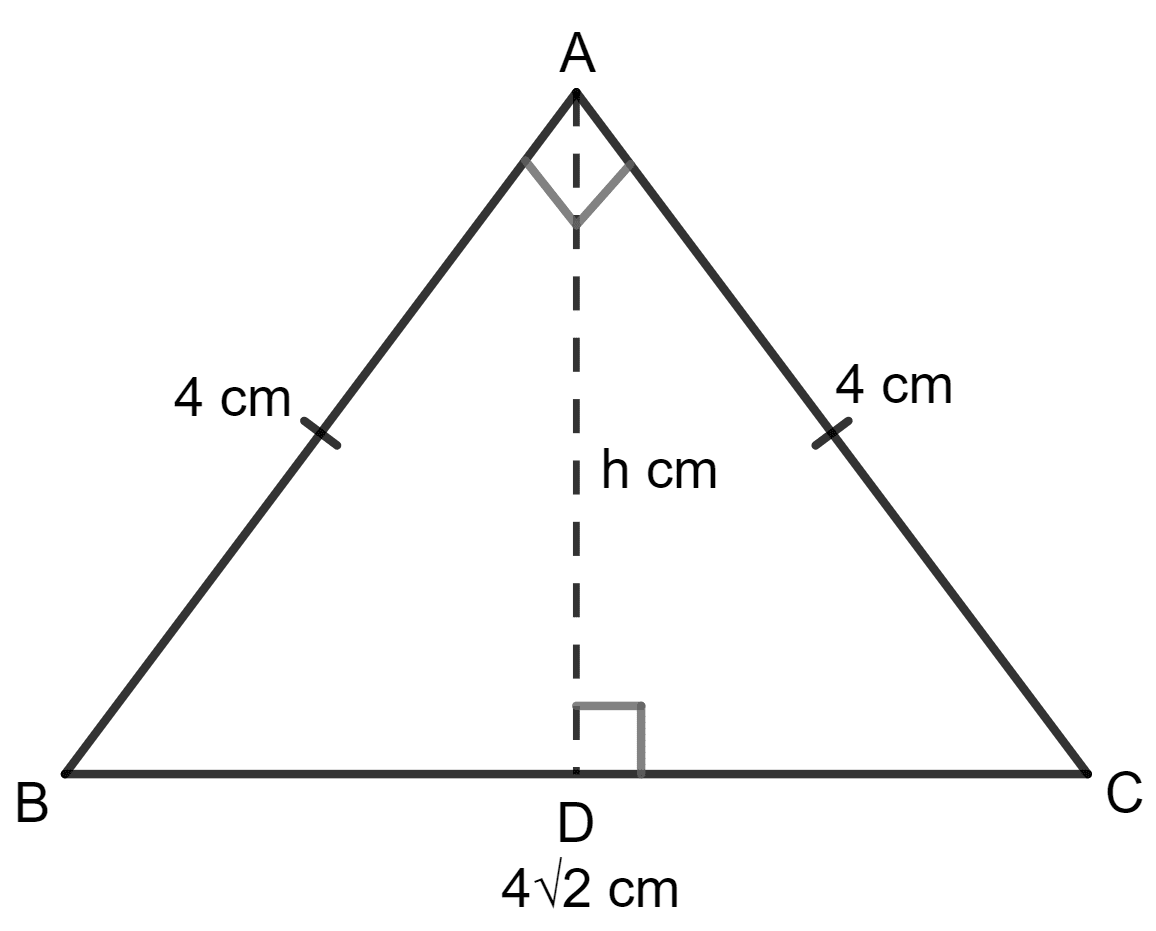
Area of the triangle will remain the same as before i.e., 8 cm2.
Let h be the altitude of triangle
Area = x base x height
∴ 8 = x BC x AD
⇒ 8 = x x h
⇒ 8 = x h
⇒ h =
⇒ h =
⇒ h = 2.83 cm
Hence, the length of perpendicular from A to BC is 2.83 cm.
The area of an equilateral triangle is . Find its perimeter.
Answer
Given:
Area =
Let s be the side of equilateral triangle.
Area of equilateral triangle =
Perimeter = 3 x side
= 3 x 12 cm
= 36 cm
Hence, the perimeter is 36 cm.
Find the area of an isosceles triangle with perimeter 36 cm and base 16 cm.
Answer
Given:
Perimeter = 36 cm
Base = 16 cm
Let a be the length of the equal sides of the triangle.
Perimeter = 2 x Equal side + Base
⇒ 36 = 2a + 16
⇒ 2a = 36 - 16
⇒ 2a = 20
⇒ a =
⇒ a = 10 cm
Thus, the triangle has two equal sides, each 10 cm long, and a base of 16 cm.
a = 10 cm, b = 10 cm and c = 16 cm.
The semi-perimeter is:
∵ Area of triangle =
= cm2
= cm2
= cm2
= 48 cm2
Hence, the area is 48 cm2.
The base of an isosceles triangle is 24 cm and its area is 192 sq. cm. Find its perimeter.
Answer
Given:
Base (b) = 24 cm
Area = 192 cm2
Let s be the length of the equal sides of the triangle.
Area of an isosceles triangle =
Perimeter = sum of all sides of triangle
= 20 + 20 + 24 cm
= 64 cm
Hence, the perimeter is 64 cm.
The given figure shows a right-angled triangle ABC and an equilateral triangle BCD. Find the area of the shaded portion.
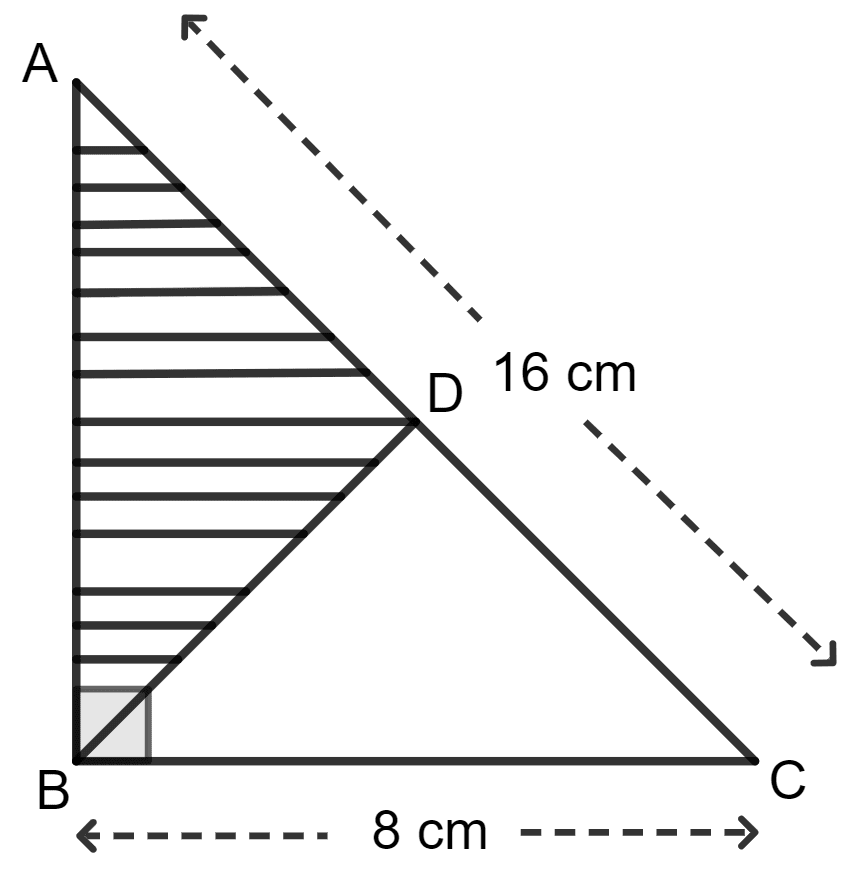
Answer
For triangle ABC (right-angled triangle),
Using the Pythagoras theorem,
Base2 + Height2 = Hypotenuse2
⇒ 82 + height2 = 162
⇒ 64 + height2 = 256
⇒ height2 = 256 - 64
⇒ height2 = 192
⇒ height =
⇒ height = 8
Area of triangle ABC = x base x height
=
=
= cm2
For triangle BCD,
Area of an equilateral triangle = x side2
= x 82
= x 64
= 16 cm2
Area of Δ ABD (shaded portion) = Area of Δ ABC - Area of Δ BDC
= 32 - 16 cm2
= 16 cm2
Hence, the area of the shaded portion is 16 cm2 = 27.712 cm2.
Find the area and the perimeter of quadrilateral ABCD, given below; if, AB = 8 cm, AD = 10 cm, BD = 12 cm, DC = 13 cm and ∠DBC = 90°.
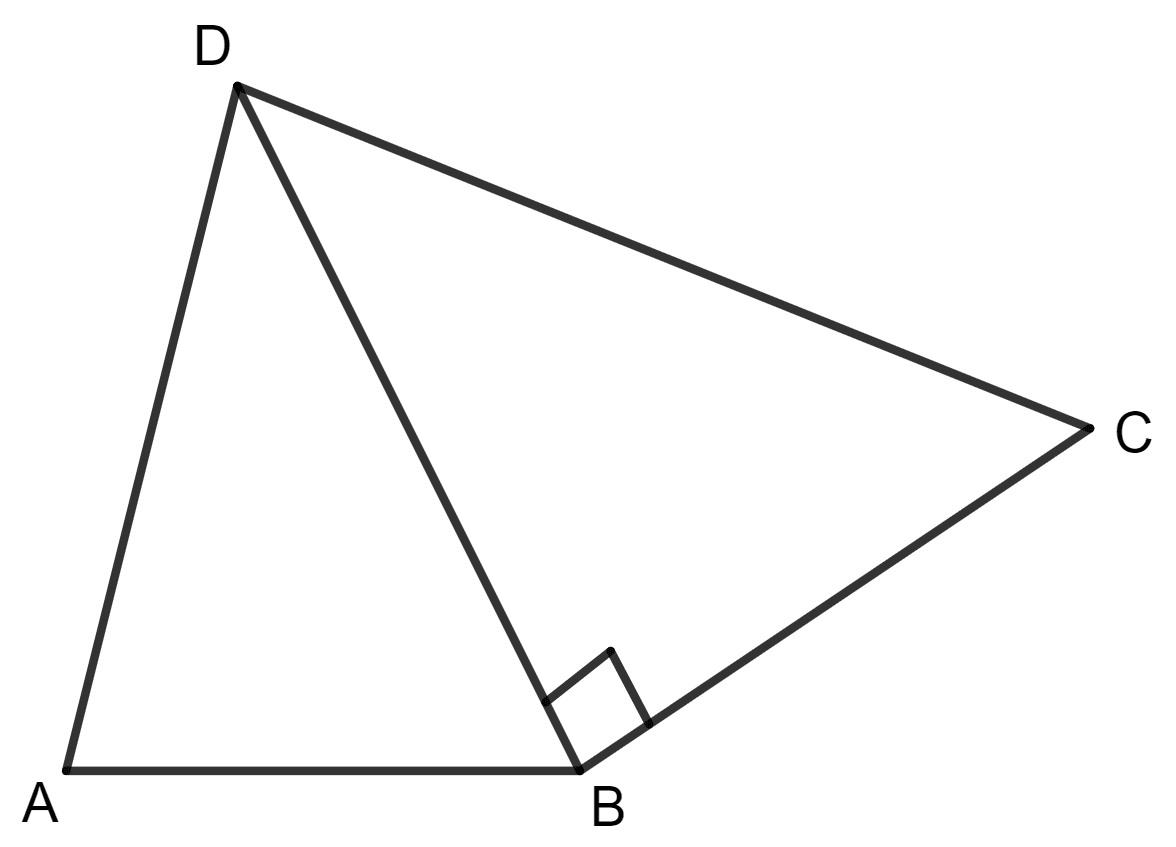
Answer
Given:
AB = 8 cm, AD = 10 cm, BD = 12 cm, DC = 13 cm and ∠DBC = 90°
In Δ BCD,
By using the Pythagoras theorem,
Base2 + Height2 = Hypotenuse2
⇒ BC2 + 122 = 132
⇒ BC2 + 144 = 169
⇒ BC2 = 169 - 144
⇒ BC2 = 25
⇒ BC =
⇒ BC = 5 cm
Area of Δ BCD = x base x height
= x 12 x 5 cm2
= x 60 cm2
= 30 cm2
For Δ ABD,
Let AD = a = 10 cm, BD = b = 12 cm and AB = c = 8 cm.
∵ Area of triangle =
= cm2
= cm2
= cm2
= 39.7 cm2
Area of quadrilateral ABCD = Area of Δ ABD + Area of Δ BCD
= 39.5 + 30 cm2
= 69.5 cm2
Perimeter of quadrilateral ABCD = Sum of all sides of quadrilateral
= AB + BC + CD + DA
= 8 + 10 + 13 + 5
= 36 cm
Hence, the area of quadrilateral is 69.7 cm2 and the perimeter is 36 cm.
The base of a triangular field is three times its height. If the cost of cultivating the field at ₹ 36.72 per 100 m2 is ₹ 49,572; find its base and height.
Answer
Given:
Cost of cultivating the field = ₹ 36.72 per 100 m2
Total cost = ₹ 49,572
Total cost = Area x Cost of cultivating per 100 m2
Area =
Let the height of the triangle be h.
Since the base of the field is three times its height, we have:
Base = 3h
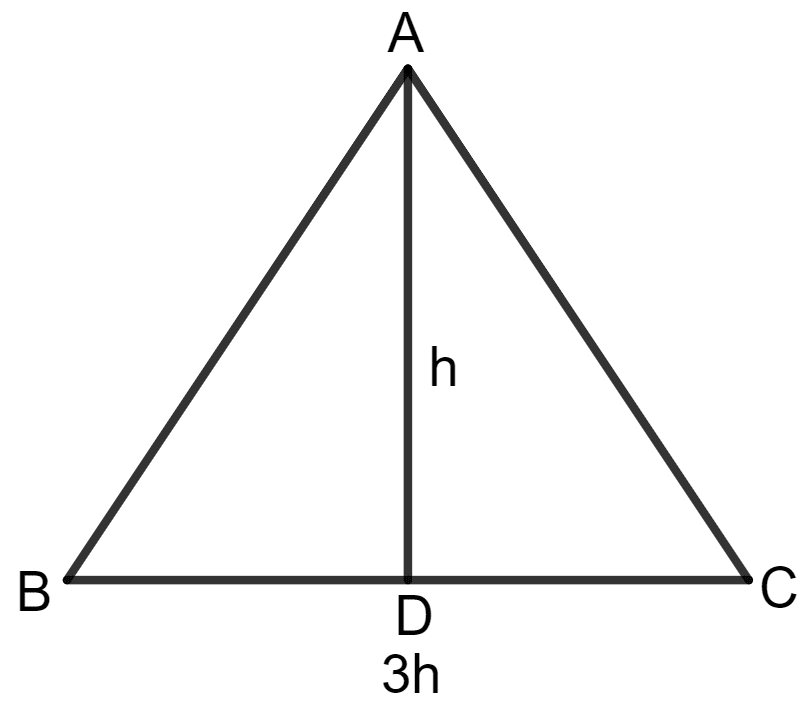
Area = x base x height
Thus, the height of the triangle is 300 m.
Base = 3 x height = 3 x 300 m = 900 m
Hence, the height is 300 m and the base is 900m.
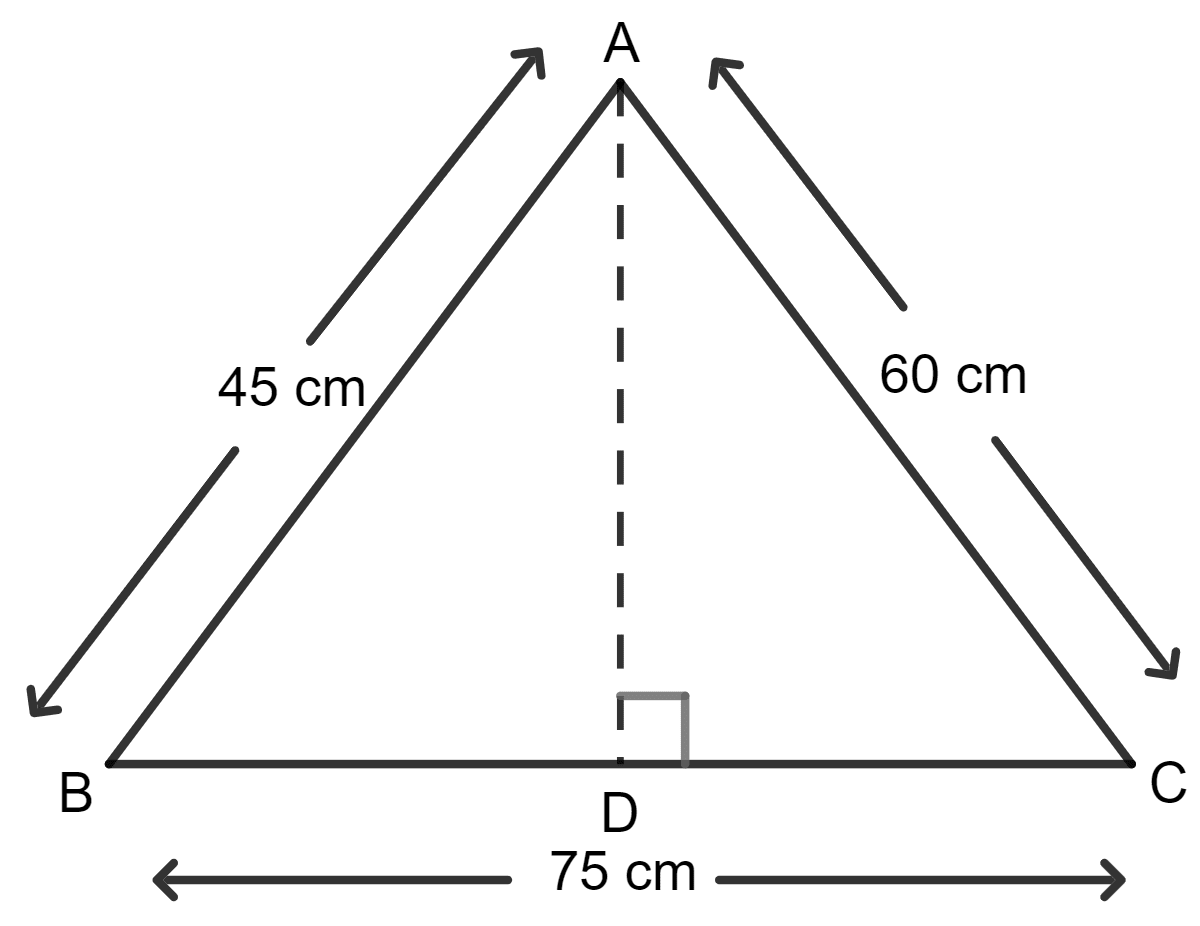
The sides of a triangular field are in the ratio 5 : 3 : 4 and its perimeter is 180 m. Find :
(i) its area.
(ii) altitude of the triangle corresponding to its largest side.
(iii) the cost of levelling the field at the rate of ₹ 10 per square metre.
Answer
(i) Given:
The sides of a triangular field are in the ratio 5 : 3 : 4.
Perimeter = 180 m
Let the sides of field be 5a, 3a and 4a.
Perimeter = Sum of all sides of triangular field
⇒ 180 = 5a + 3a + 4a
⇒ 180 = 12a
⇒ a =
⇒ a = 15
Thus, sides of field = 5a , 3a and 4a
= 5 x 15, 3 x 15 and 4 x 15
= 75 m, 45 m and 60 m
Let a = 75 m, b = 45 m and c = 60 m.
∵ Area of triangle =
= m2
= m2
= m2
= 1,350 m2
Hence, the area is 1,350 m2.
(ii) Area = x base x altitude
Base = 75 m
Let h be the altitude of triangle corresponding to the largest side 75 m,
⇒ 1350 = x 75 x h
⇒ h =
⇒ h =
⇒ h = 36 m
Hence, the altitude of the triangle corresponding to its largest side is 36 m.
(iii) Cost of levelling = ₹ 10 per square metre
Total cost = Area x Cost of levelling
= ₹ 1,350 x 10
= ₹ 13,500
Hence, the total cost of levelling is ₹ 13,500.
Each of equal sides of an isosceles triangle is 4 cm greater than its height. If the base of the triangle is 24 cm; calculate the perimeter and the area of the triangle.
Answer
Each of equal sides of an isosceles triangle is 4 cm greater than its height.
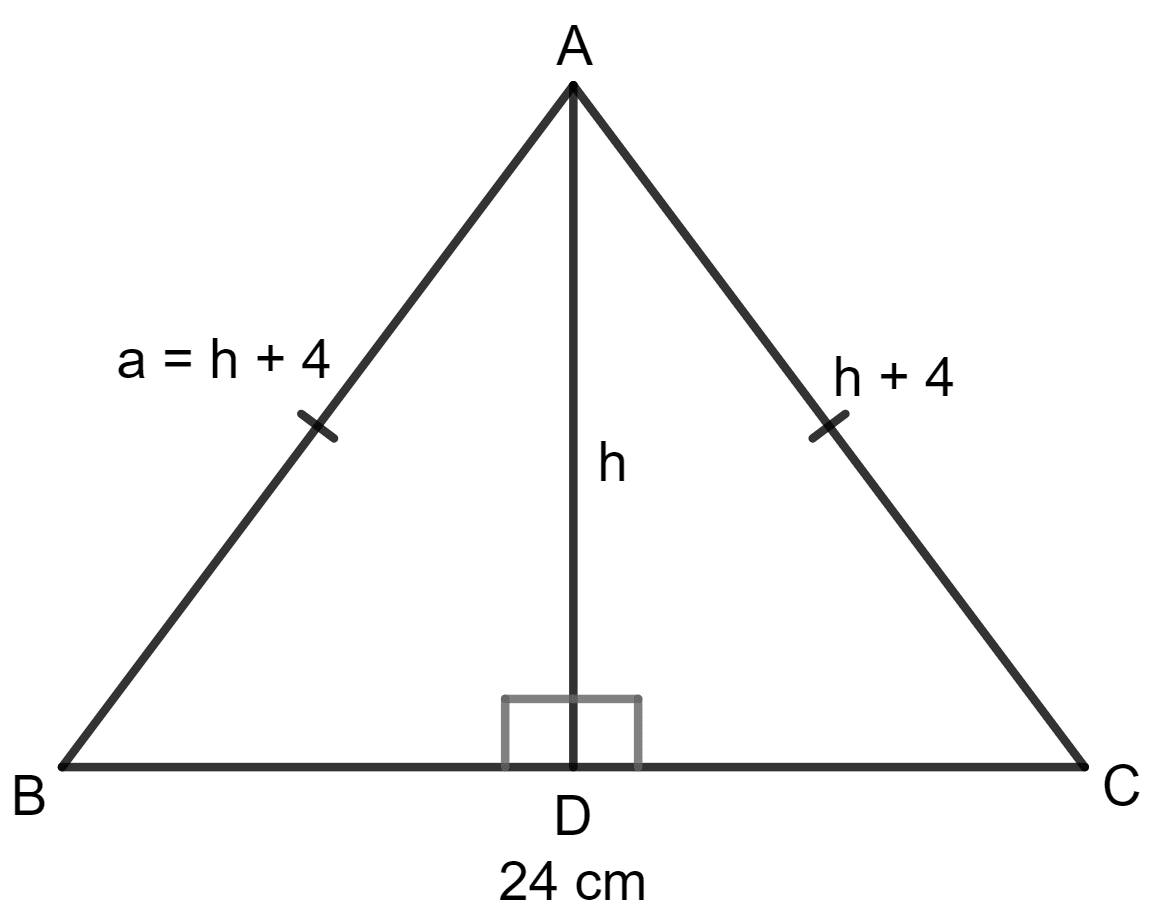
Let h be the height of the triangle.
Equal sides: AB = AC = h + 4
Base: BC = 24 cm
In Δ ABD and Δ ACD,
AD = AD [∵ Common Side]
∠ ADB = ∠ ADC [∵ Both are 90°]
AB = AC [∵ Δ ABC is isosceles]
∴ Δ ABD ≅ Δ ACD [RHS axiom]
∴ BD = CD [C.P.C.T]
∴ BD = CD = = = 12 cm
By using the Pythagoras theorem in Δ ABD,
BD2 + AD2 = AB2
⇒ 122 + h2 = (h + 4)2
⇒ 144 + h2 = h2 + 42 + 2 x h x 4
⇒ 144 + = + 16 + 8h
⇒ 144 - 16 = 8h
⇒ 128 = 8h
⇒ h =
⇒ h = 16 cm
⇒ a = h + 4 = 16 + 4 = 20 cm
Perimeter of triangle = Sum of all sides
= AB + AC + BC
= (20 + 20 + 24) cm
= 64 cm
Area of triangle = x base x height
= x 24 x 16
= 12 x 16
= 192 cm2
Hence, the perimeter is 64 cm and the area is 192 cm2.
Calculate the area and the height of an equilateral triangle whose perimeter is 60 cm.
Answer
Given:
Perimeter = 60 cm
Let a be the sides of equilateral triangle.
Perimeter = Sum of all sides
⇒ 60 = a + a + a
⇒ 60 = 3a
⇒ a =
⇒ a = 20 cm
Area of equilateral triangle =
Height of equilateral triangle =
Hence, the area is 173.2 cm2 and the height is 17.32 cm.
In triangle ABC; angle A = 90°, side AB = x cm, AC = (x + 5) cm and area = 150 cm2. Find the sides of the triangle.
Answer
Δ ABC is shown in the figure below:
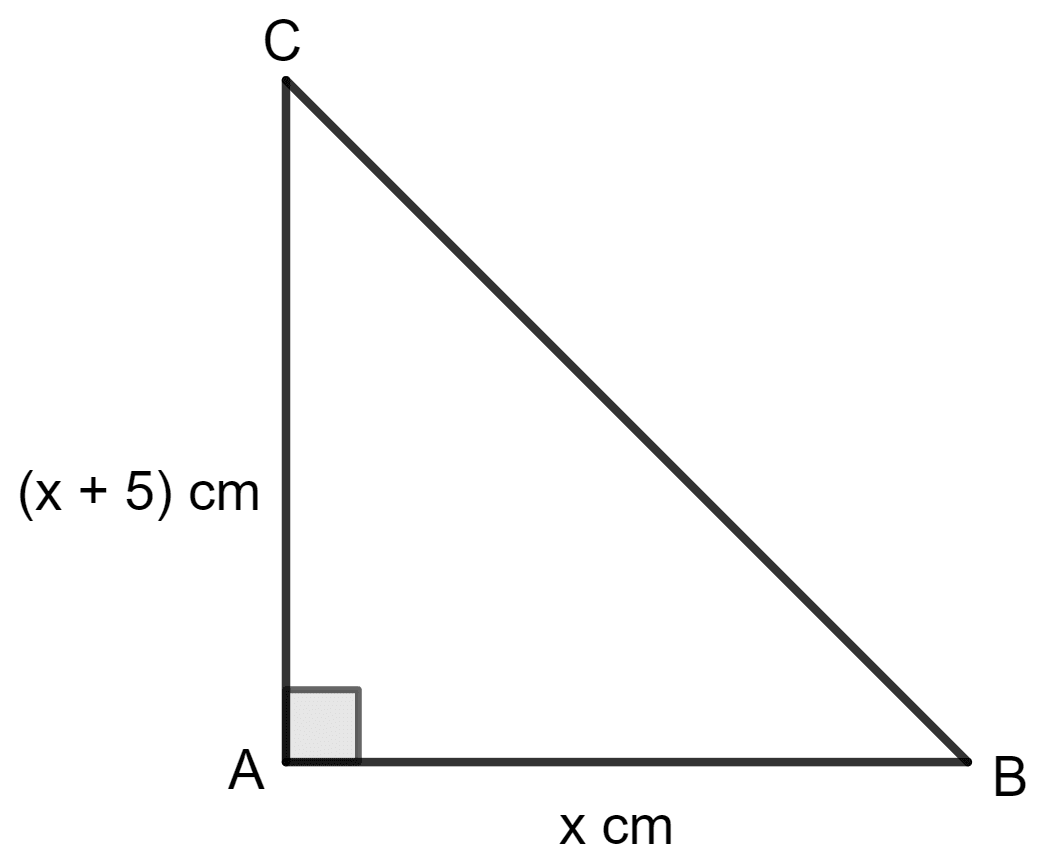
Given:
Area = 150 cm2
Area = base height
Since length cannot be negative, AB = 15 cm.
Thus, AC = x + 5 = 15 + 5 cm = 20 cm
By using the Pythagoras theorem,
AB2 + AC2 = BC2
⇒ 152 + 202 = BC2
⇒ 225 + 400 = BC2
⇒ 625 = BC2
⇒ BC =
⇒ BC = 25
Hence, the sides of the triangle are 15 cm, 20 cm and 25 cm.
If the difference between the sides of a right angled triangle is 3 cm and its area is 54 cm2; find its perimeter.
Answer
Given:
Area = 54 cm2
Let the two sides of the right-angled triangle be x cm and (x - 3) cm.
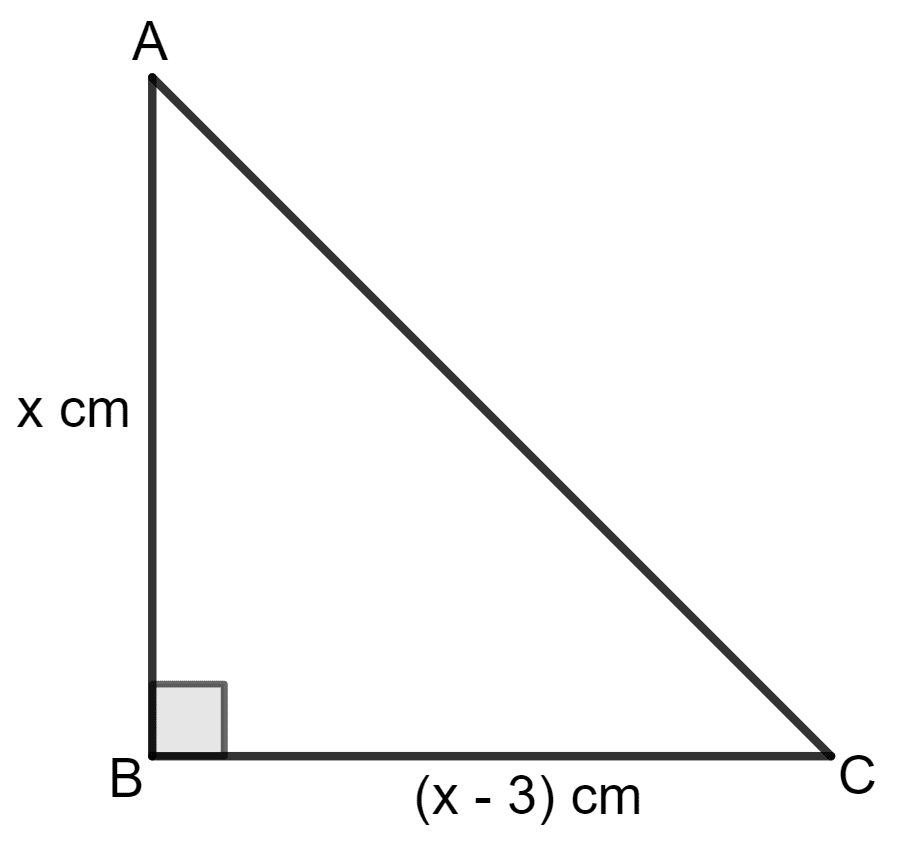
Area = x base x height
⇒ 54 = x BC x AB
⇒ 54 = (x - 3) x
⇒ 54 2 = (x - 3) x
⇒ 108 = x2 - 3x
⇒ x2 - 3x - 108 = 0
⇒ x2 - 12x + 9x - 108 = 0
⇒ x(x - 12) + 9(x - 12) = 0
⇒ (x - 12)(x + 9) = 0
⇒ x = 12 or -9
Since length cannot be negative, AB is 12 cm.
BC = (x - 3) cm = 12 - 3 cm = 9 cm
By using the Pythagoras theorem,
AB2 + BC2 = AC2
⇒ 122 + 92 = AC2
⇒ 144 + 81 = AC2
⇒ 225 = AC2
⇒ AC =
⇒ AC = 15
Perimeter of right angled triangle = AB + BC + AC
= 12 + 9 + 15 cm
= 36 cm
Hence, the perimeter of the triangle is 36 cm.
The area of the given figure is :
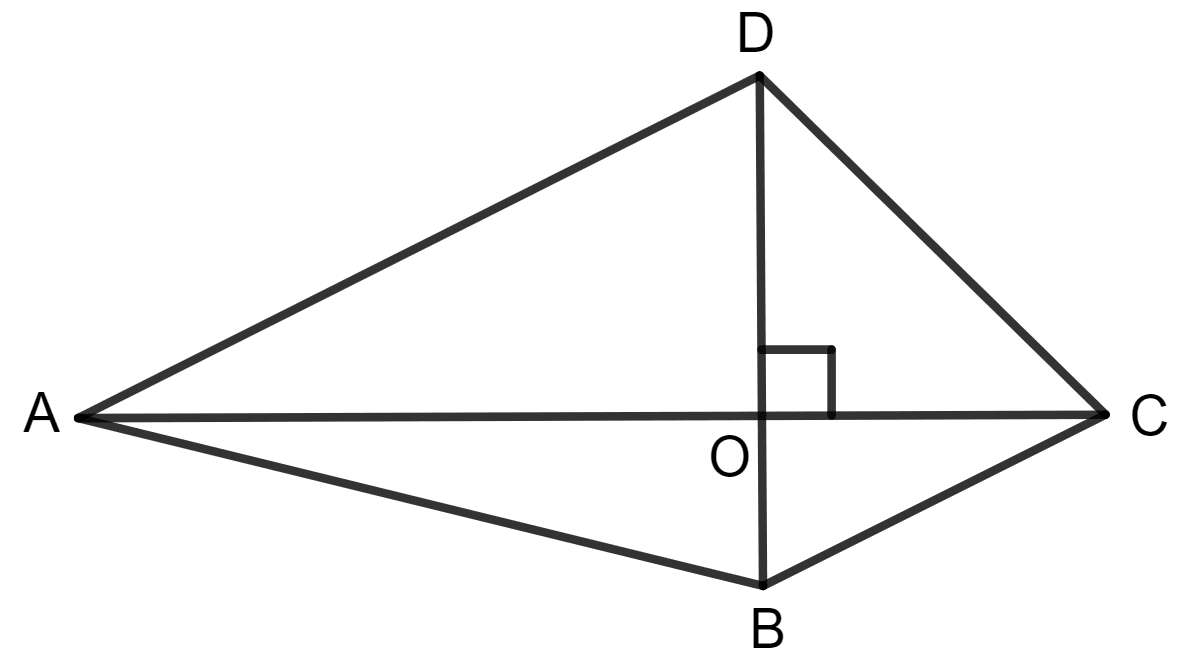
AC x BD
Answer
Area of triangle = x base x height
For Δ ABD,
Area = x BD x AO
For Δ CBD,
Area = x BD x CO
Area of quadrilateral ABCD = Area of Δ ABD + Area of Δ CBD
= x BD x AO + x BD x CO
= x BD x (AO + CO)
= x BD x AC
Hence, option 2 is the correct option.
If two adjacent sides and a diagonal of a rectangle are x, y and d respectively. The area of the rectangle is :
Answer
Given:
Adjacent sides of rectangle = x and y
Area of rectangle = base x height
=
Hence, option 1 is the correct option.
A square DEFG of side 8 cm is inscribed in a rectangle of adjacent sides 20 cm and 16 cm as shown in the figure.
The area of the shaded portion is :
64 cm2
128 cm2
256 cm2
320 cm2
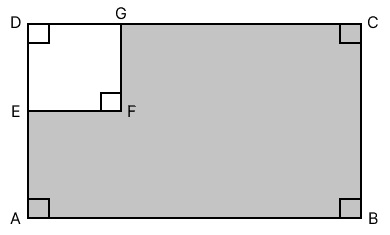
Answer
Area of shaded portion = Area of rectangle ABCD - Area of square DEFG
Area of square = Side2
Area of rectangle = Base x Height
Area of shaded portion = 20 x 16 - 82 cm2
= 320 - 64 cm2
= 256 cm2
Hence, option 3 is the correct option.
The perimeter of a square is 72 cm, its area is :
324 cm2
356 cm2
Answer
Given:
Perimeter = 72 cm
Let s be the side of square.
Perimeter = 4 x side
⇒ 4 x s = 72
⇒ s =
⇒ s = 18 cm
Area = Side2
= 182 cm2
= 324 cm2
Hence, option 3 is the correct option.
Area of a rhombus is 360 cm2. If one diagonal of it is 20 cm; the other diagonal is :
24 cm
18 cm
40 cm
36 cm
Answer
Given:
Area = 360 cm2.
One diagonal = 20 cm
Let d be the other diagonal.
Area of rhombus = x product of diagonals
⇒ x 20 x d = 360
⇒ 10 x d = 360
⇒ d =
⇒ d = 36 cm
Hence, option 4 is the correct option.
Find the area of a quadrilateral one of whose diagonals is 30 cm long and the perpendiculars from the other two vertices are 19 cm and 11 cm respectively.
Answer
The quadrilateral is shown in the figure below:
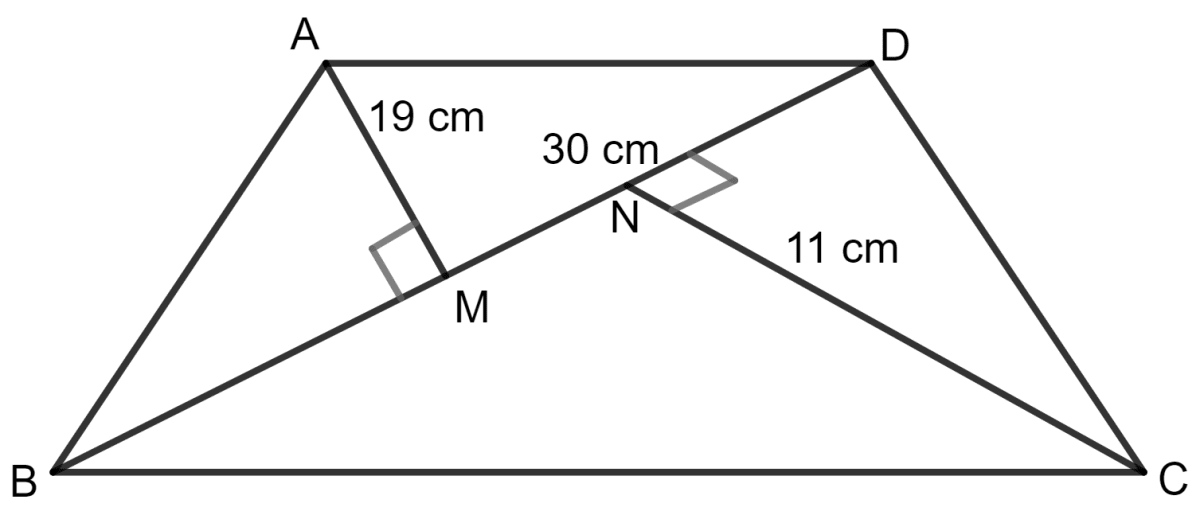
Area of triangle = x base x height
For Δ ABD,
Area = x BD x AM
= x 30 x 19 cm2
= 15 x 19 cm2
= 285 cm2
For Δ CBD,
Area = x BD x CN
= x 30 x 11 cm2
= 15 x 11 cm2
= 165 cm2
Area of quadrilateral ABCD = Area of Δ ABD + Area of Δ CBD
= 285 + 165 cm2
= 450 cm2
Hence, the area of quadrilateral is 450 cm2.
The diagonals of a quadrilateral are 16 cm and 13 cm. If they intersect each other at right angles; find the area of the quadrilateral.
Answer
Since the diagonals of the quadrilateral intersect at right angles, the area of the quadrilateral is given by:
Area = x Product of diagonals
= x 16 x 13 cm2
= 8 x 13 cm2
= 104 cm2
Hence, the area of the quadrilateral is 104 cm2.
Calculate the area of quadrilateral ABCD, in which ∠ABD = 90°, triangle BCD is an equilateral triangle of side 24 cm and AD = 26 cm.
Answer
For Δ ABD,
By using the Pythagoras theorem,
Base2 + Height2 = Hypotenuse2
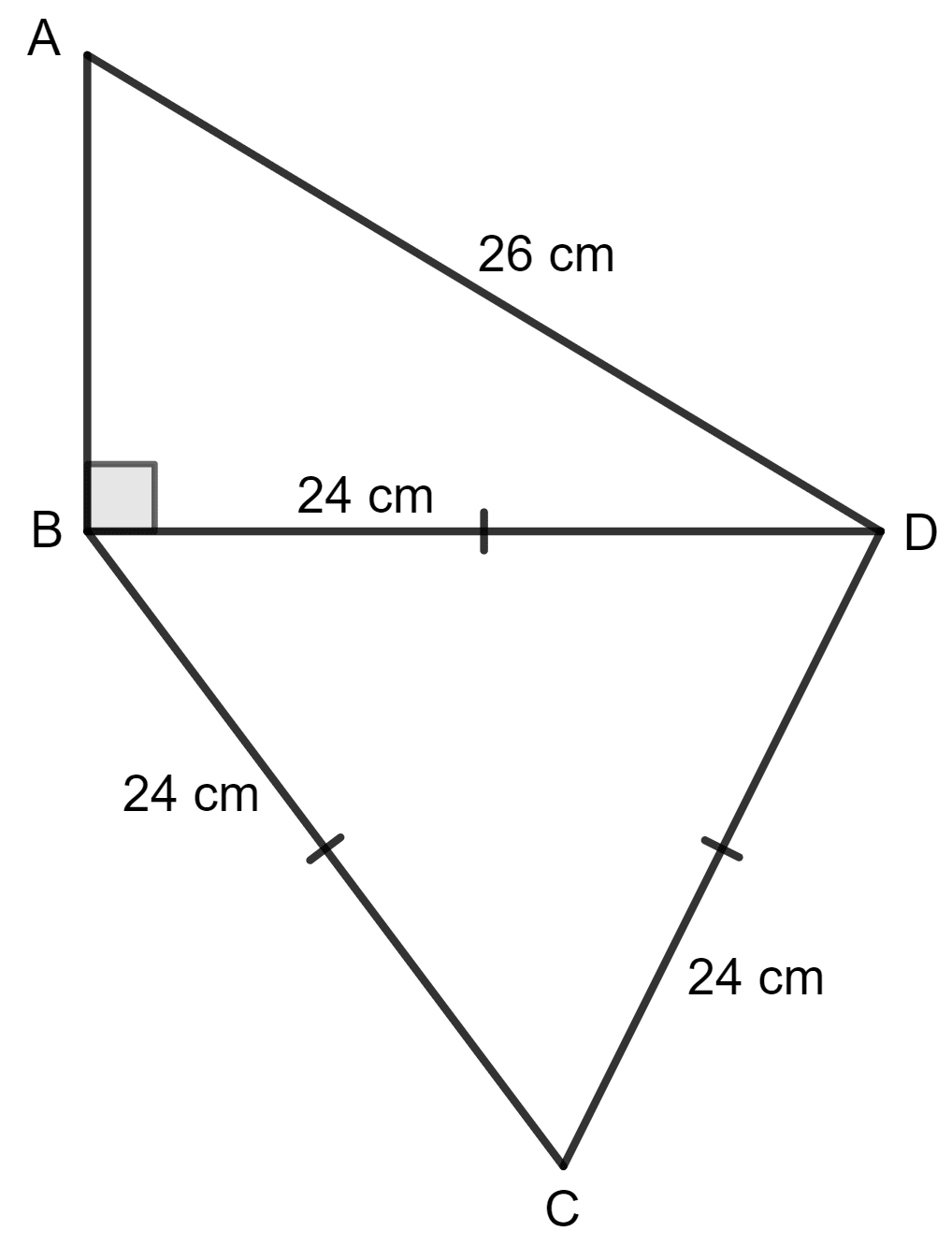
⇒ AB2 + BD2 = AD2
⇒ AB2 + (24)2 = (26)2
⇒ AB2 + 576 = 676
⇒ AB2 = 676 - 576
⇒ AB2 = 100
⇒ AB =
⇒ AB = 10 cm
Area of Δ ABD = x AB x BD
= x 10 x 24 cm2
= 5 x 24 cm2
= 120 cm2
Area of equilateral triangle BCD = x side2
= x 242
= x 576
= 144 cm2
= 249.41 cm2
Total area of quadrilateral ABCD = Δ ABD + Δ BCD
= 120 + 249.41 cm2
= 369.41 cm2
Hence, the area of quadrilateral ABCD is 369.41 cm2.
Calculate the area of quadrilateral ABCD in which AB = 32 cm, AD = 24 cm, ∠A = 90° and BC = CD = 52 cm.
Answer
Quadrilateral ABCD is shown in the figure below:
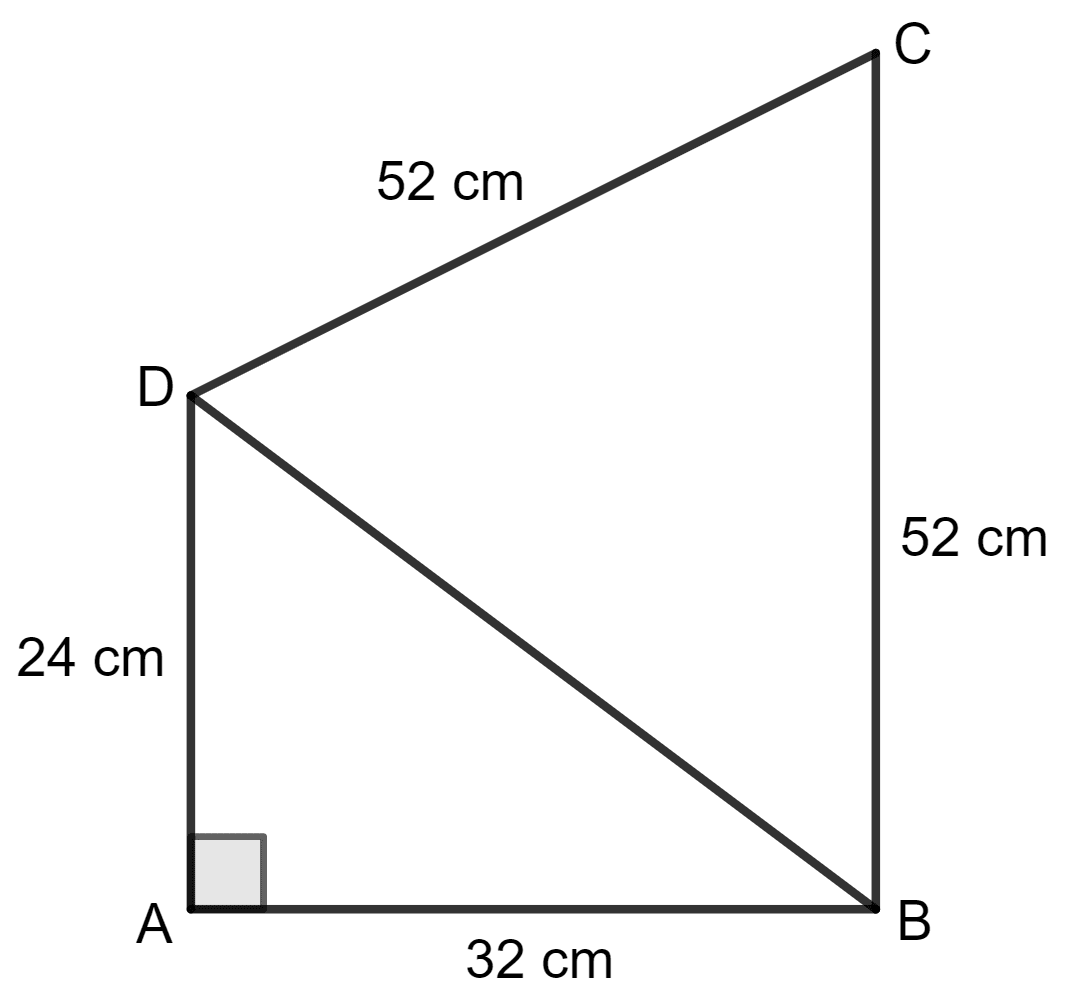
Area of Δ DAB = x base x height
= x DA x AB
= x 24 x 32 cm2
= 12 x 32 cm2
= 384 cm2
By using the Pythagoras theorem,
AD2 + AB2 = BD2
⇒ 242 + 322 = BD2
⇒ 576 + 1,024 = BD2
⇒ 1,600 = BD2
⇒ BD =
⇒ BD = 40 cm
In triangle BCD,
Let the sides of the triangle be:
a = 40 cm, b = 52 cm and c = 52 cm.
The semi-perimeter s:
∵ Area of Δ BCD =
= cm2
= cm2
= cm2
= 960 cm2
Therefore, area of quadrilateral ABCD = Area of Δ DAB + Area of triangle BCD
= 384 + 960 cm2
= 1344 cm2
Hence, the area of quadrilateral ABCD is 1344 cm2.
The perimeter of a rectangular field is km. If the length of the field is twice its width; find the area of the rectangle in sq. metres.
Answer
Given:
Perimeter = km.
Length of the field = Twice its width.
Let a be the width of the field.
So, the length = 2a
Perimeter of a rectangle = 2(length + width)
Thus, width = km
= m
= 100 m
Length = 2a = 2 x 100 m
= 200 m
Area = length x width
= 200 x 100 m2
= 20,000 m2
Hence, the area of the rectangle is 20,000 m2.
A rectangular plot 85 m long and 60 m broad is to be covered with grass leaving 5 m all around. Find the area to be laid with grass.
Answer
Given:
The length of the rectangular field is 85 m.
The breadth of the rectangular field is 60 m.
The width of the path to be covered with grass is 5 m.
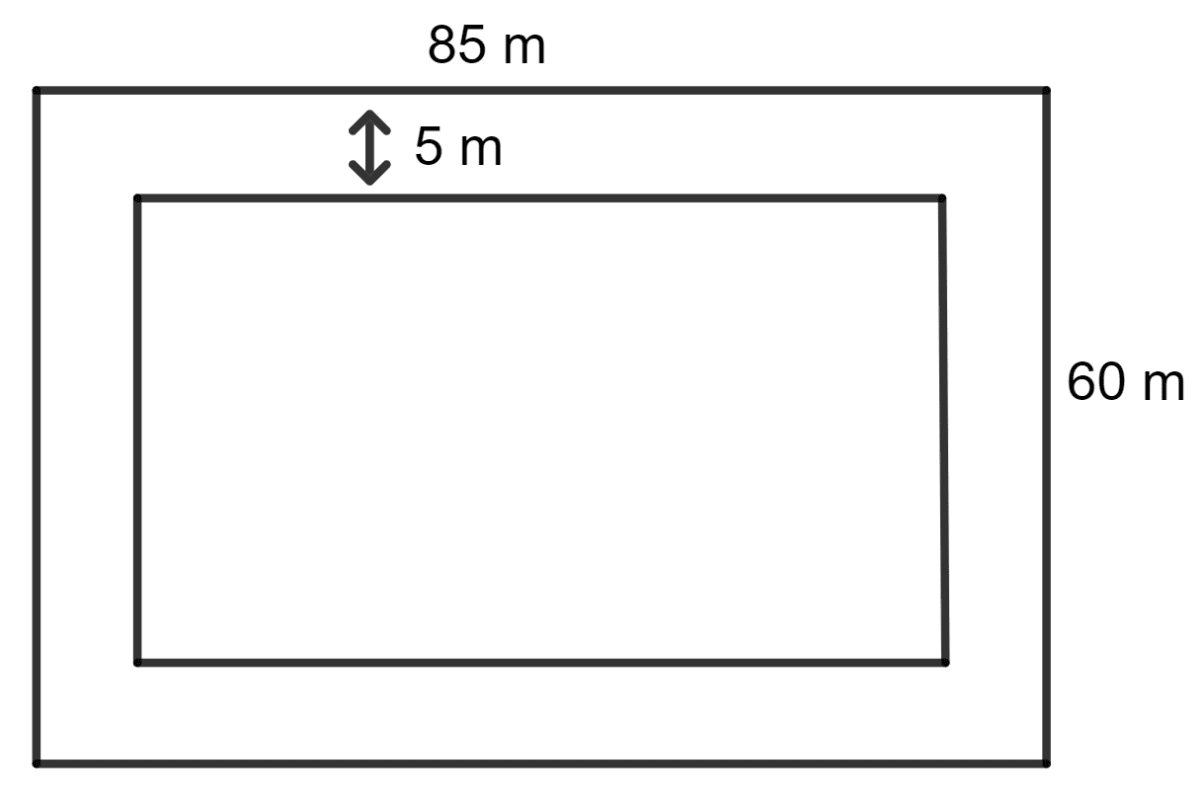
The length of the inner rectangular field = 85 m - 5 m - 5 m = 75 m
The breadth of the inner rectangular field = 60 m - 5 m - 5 m = 50 m
The area of a rectangle = length x breadth
⇒ Area of the inner field = 75 x 50 m2 = 3,750 m2
Hence, the area to be covered with grass is 3,750 m2.
The length and the breadth of a rectangle are 6 cm and 4 cm respectively. Find the height of a triangle whose base is 6 cm and area is 3 times that of the rectangle.
Answer
Given:
Length of the rectangle = 6 cm
Breadth of the rectangle = 4 cm
Area of the rectangle = length x breadth
= 6 x 4 cm2
= 24 cm2
Let h be the height of the triangle.
Base of the triangle = 6 cm
It is given that area of triangle is 3 times the area of the rectangle.
Area of triangle = x base x height
⇒ 3 x 24 = x 6 x h
⇒ 3 x 24 = 3 x h
⇒ x 24 = x h
⇒ h = 24 cm
Hence, the height of the triangle is 24 cm.
How many tiles, each of area 400 cm2, will be needed to pave a footpath which is 2 m wide and surrounds a grass plot 25 m long and 13 m wide ?
Answer
Given:
Dimensions of grass plot (ABCD) = 25 x 13 m
Width of footpath = 2 m
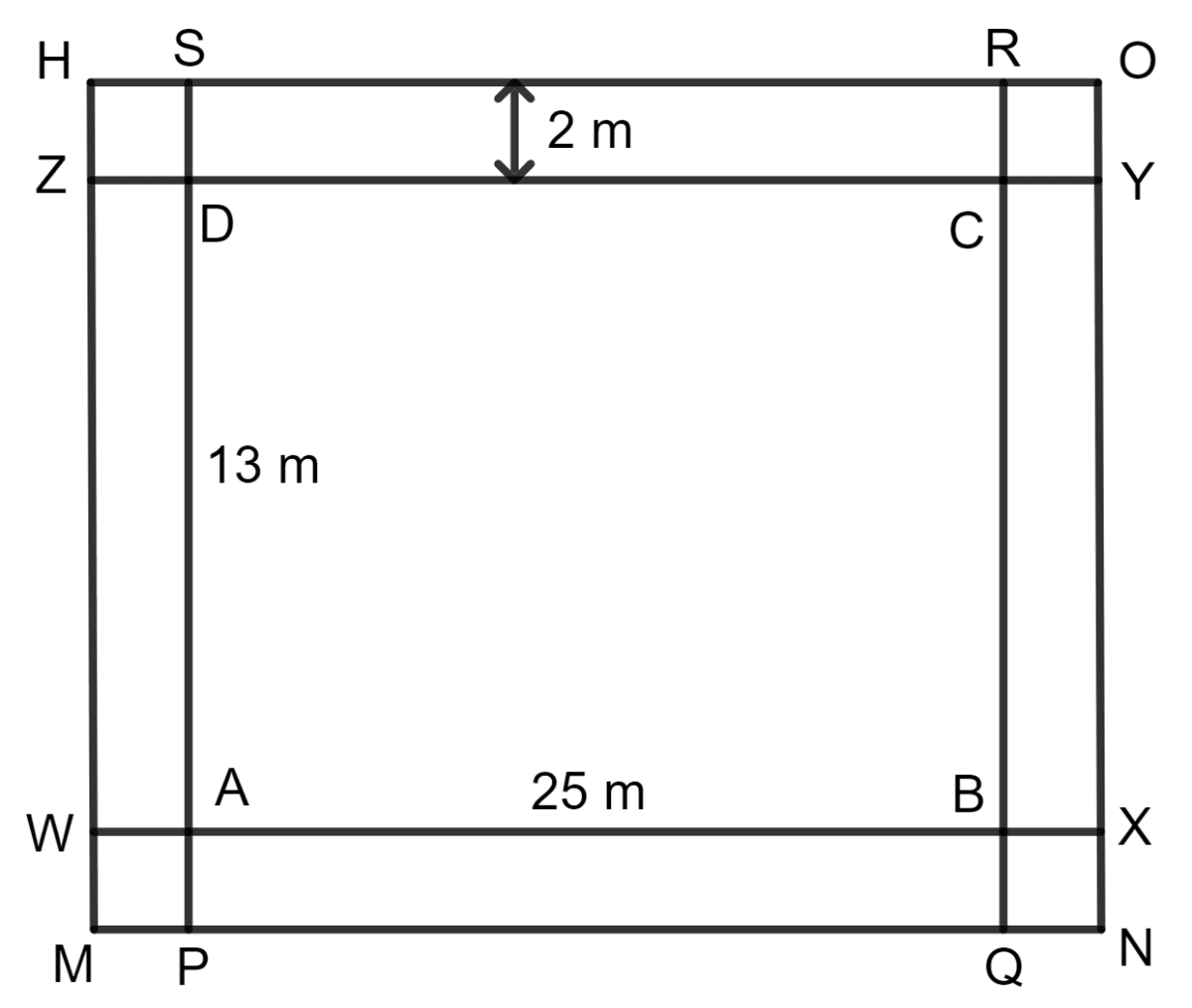
Area of footpath = Area of ABQP + Area of QNOR + Area of RCDS + Area of SHMP
= 2Area of ABQP + 2Area of QNOR
= 2(Area of ABQP + Area of QNOR)
Area of ABQP = l x b = AB x AP
= 25 x 2 m2
= 50 m2
Area of QNOR = l x b = DN x QN
= 17 x 2 m2
= 34 m2
Area of footpath = 2(50 + 34) m2
= 2 x 84 m2
= 168 m2
= 1680000 sq. cm
Total area = Number of tiles x Area covered by 1 tiles
⇒ 1680000 = Number of tiles x 400
⇒ Number of tiles =
= 4200
Hence, the number of tiles = 4200.
The cost of enclosing a rectangular garden with a fence all round, at the rate of 75 paise per metre, is ₹ 300. If the length of the garden is 120 metres, find the area of the field in square metres.
Answer
Given:
Length of the garden = 120 m
Cost of fencing = 75 paise per metre = ₹ 0.75 per m
Total cost = ₹ 300
Total cost of fencing = Perimeter x Cost per metre
⇒ ₹ 300 = Perimeter x ₹ 0.75
⇒ Perimeter = m
⇒ Perimeter = m
⇒ Perimeter = 400 m

Let b be the breadth of the garden.
Perimeter = 2(l + b)
⇒ 2(120 + b) = 400
⇒ 120 + b =
⇒ 120 + b = 200
⇒ b = 200 - 120
⇒ b = 80 m
Area of the rectangular garden = Length x Breadth
= 120 x 80 m2
= 9600 m2
Hence, the area of the garden is 9600 sq. m.
The width of a rectangular room is of its length, x, and its perimeter is y. Write an equation connecting x and y. Find the length of the room when the perimeter is 4400 cm.
Answer
Given:
Length = x
Width = of the length =
Perimeter =
Perimeter of a rectangle = 2(l + b)
The length when y = 4400 cm,
Hence, the equation connecting x and y is and the length of the room is 14 m.
The length of a rectangular verandah is 3 m more than its breadth. The numerical value of its area is equal to the numerical value of its perimeter.
(i) Taking x as the breadth of the verandah, write an equation in x that represents the above statement.
(ii) Solve the equation obtained in (i) above and hence find the dimensions of the verandah.
Answer
(i) Given:
Breadth of the verandah = x
Length of the verandah = x + 3
It is also given that the numerical value of the area is equal to the numerical value of the perimeter.
⇒ l x b = 2(l + b)
⇒ x(x + 3) = 2(x + x + 3)
⇒ x2 + 3x = 2(2x + 3)
⇒ x2 + 3x = 4x + 6
⇒ x2 + 3x - 4x - 6 = 0
⇒ x2 - x - 6 = 0
Hence, the equation is x2 - x - 6.
(ii) From (i),
⇒ x2 - x - 6 = 0
⇒ x2 - 3x + 2x - 6 = 0
⇒ x(x - 3) + 2(x - 3) = 0
⇒ (x - 3)(x + 2) = 0
⇒ x = 3 or - 2
Since breadth cannot be negative, x = 3 m.
Length = x + 3 = 3 + 3 m = 6 m
Hence, length = 6 m and breadth = 3 m.
The diagram, given below, shows two paths drawn inside a rectangular field 80 m long and 45 m wide. The widths of the two paths are 8 m and 15 m as shown. Find the area of the shaded portion.
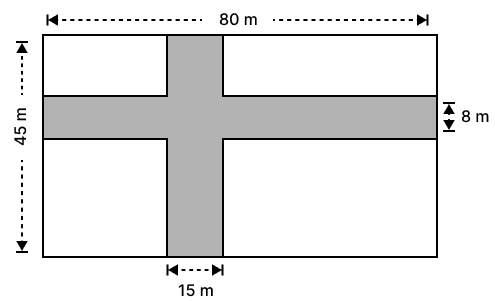
Answer
Given:
Length of the rectangular field = 80 m
Width of the rectangular field = 45 m
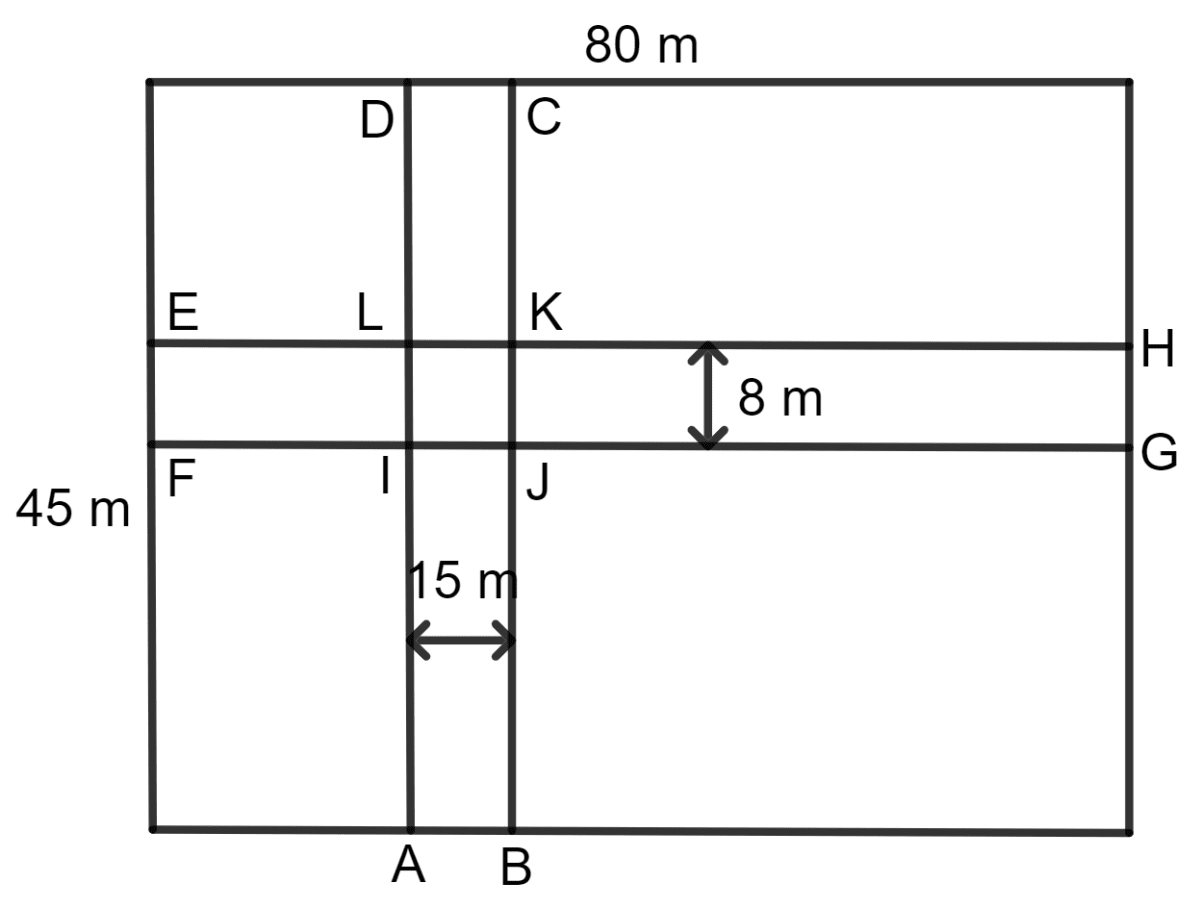
Area of shaded path = Area of path ABCD + Area of cross path EFGH - Area of path IJKL
Area of path ABCD = l x b = AB x BC
= 15 x 45 m2
= 675 m2
Area of path EFGH = l x b = EF x FG
= 8 x 80 m2
= 640 m2
Area of path IJKL = l x b = IJ x KL
= 15 x 8 m2
= 120 m2
Area of shaded path = 675 + 640 - 120 m2
= 1,195 m2
Hence, the area of shaded portion is 1,195 m2.
The rate for a 1.20 m wide carpet is ₹ 40 per metre; find the cost of covering a hall 45 m long and 32 m wide with this carpet. Also, find the cost of carpeting the same hall if the carpet, 80 cm wide, is at ₹ 25 per metre.
Answer
Given:
Dimensions of the hall = 45 m x 32 m
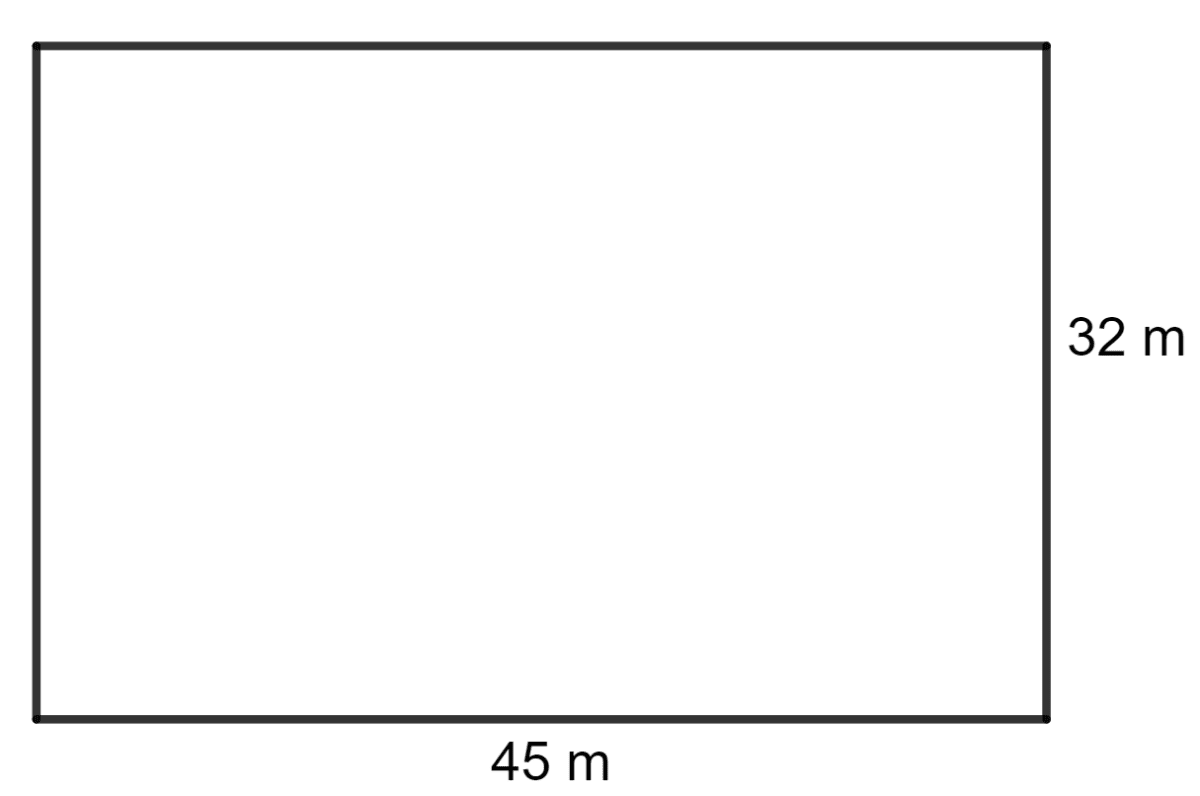
Area = l x b
= 45 x 32 m2
= 1,440 m2
Cost per metre of carpet = ₹40
Width of the carpet = 1.20 m
Cost per square metre = = = ₹ 33.33
Total cost = Cost per square metre x area of hall
= 33.33 x 1440
= ₹ 48,000
Width of the carpet in metres: 80 cm = 0.8 m
Cost per metre of carpet = ₹25
Cost per square metre = = = ₹ 31.25
Total cost = Cost per square metre x area of hall
= 31.25 x 1440
= ₹ 45,000
Hence, the cost of covering the hall with a 1.20 m wide carpet at ₹ 40 per metre is ₹ 48,000 and the cost of carpeting the hall with an 80 cm wide carpet at ₹ 25 per metre is ₹ 45,000.
Find the area and perimeter of a square plot of land, the length of whose diagonal is 15 metres. Give your answer correct to 2 places of decimals.
Answer
Given:
Diagonal of the square = 15 m
Let a be the length of side of the square.
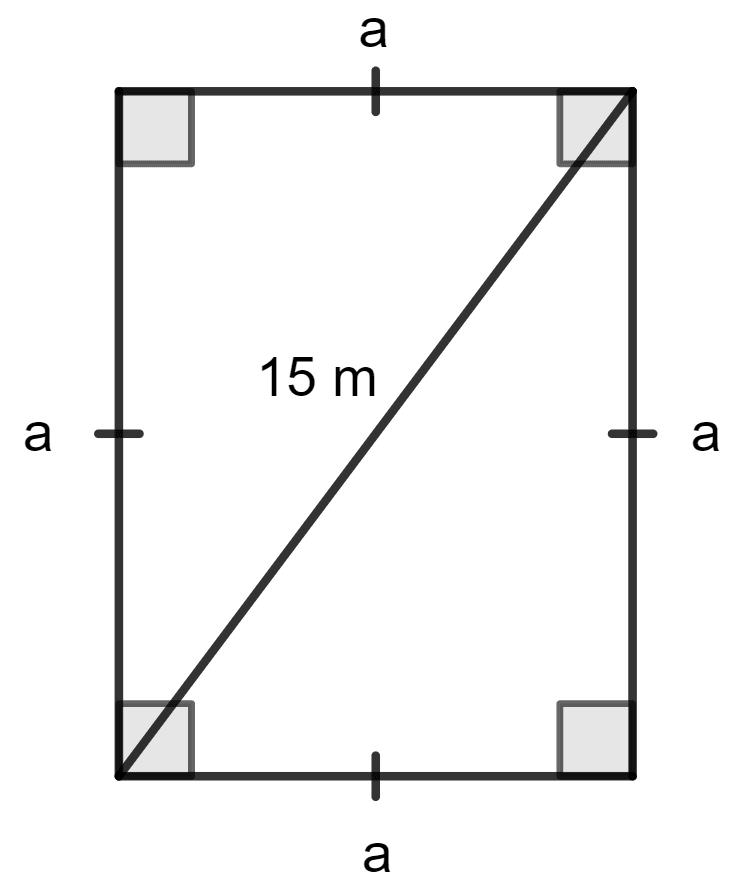
Using the Pythagoras theorem for a square,
⇒ Side2 + Side2 = Diagonal2
⇒ 2 x Side2 = Diagonal2
⇒ 2 x a2 = 152
⇒ 2a2 = 225
⇒ a2 =
⇒ a2 = 112.5
⇒ a =
⇒ a = 10.61 m
Area of square = side2
= 10.612 m2
= 112.5 m2
Perimeter of square = 4 x side
= 4 x 10.60 m
= 42.43 m
Hence, the area of the square plot is 112.5 m2 and the perimeter is 42.43 m.
The shaded region of the given diagram represents the lawn in the form of a house. On the three sides of the lawn there are flower-beds having a uniform width of 2 m.
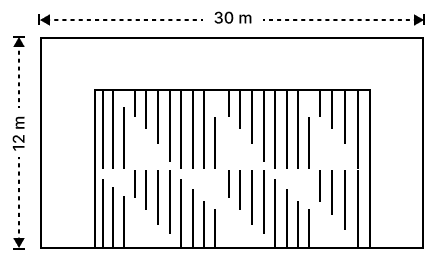
(i) Find the length and the breadth of the lawn.
(ii) Hence, or otherwise, find the area of the flower-beds.
Answer
Given:
Length of the lawn = 30 m
Breadth of the lawn = 12 m
Width of flowerbed = 2 m
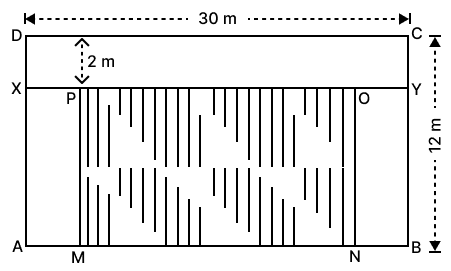
New length of lawn = 30 - 2 - 2 m = 30 - 4 m = 26 m
New breadth of lawn = 12 - 2 m = 10 m
Hence, the length of lawn = 26 m and the breadth of lawn = 10 m.
(ii) Area of flowerbed = Area of AMPX + Area of XDCY + Area of NBYO
Area of AMPX = l x b = AM x MP
= 10 x 2 m2
= 20 m2
Area of XDCY = l x b = XD x DC
= 30 x 2 m2
= 60 m2
Area of NBYO = l x b = NB x BY
= 10 x 2 m2
= 20 m2
Area of flowerbed = 20 + 60 + 20 m2
= 100 m2
Hence, the area of flowerbed is 100 m2.
A floor which measures 15 m x 8 m is to be laid with tiles measuring 50 cm x 25 cm. Find the number of tiles required.
Further, if a carpet is laid on the floor so that a space of 1 m exists between its edges and the edges of the floor, what fraction of the floor is left uncovered.
Answer
Given:
Dimensions of the floor = 15 m x 8 m
Dimensions of the tile = 50 cm x 25 cm = 0.5 m x 0.25 m
Area of floor = l x b
= 15 x 8 m2
= 120 m2
Area of tile = ltile x btile
= 0.5 x 0.25 m2
= 0.125 m2
Let n be the number of tiles.
Area of floor = Area of tile x Number of tiles
⇒ 120 = 0.125 x n
⇒ n =
⇒ n =
⇒ n = 960
Now, a carpet is laid on the floor, leaving a space of 1 m between its edges and the edges of the floor.
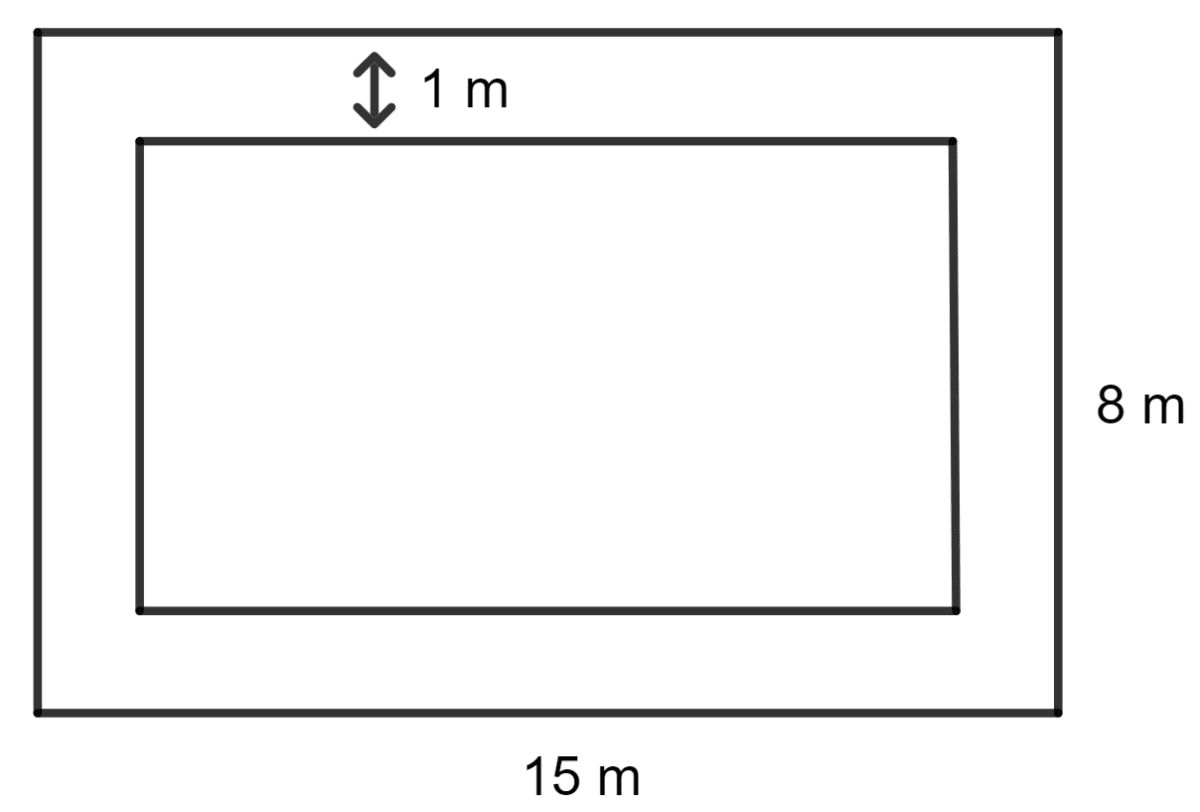
Length of the carpet = 15 - 1 - 1 m = 13 m
Breadth of the carpet = 8 - 1 - 1 m = 6 m
Area of uncovered floor = Area of floor - Area of carpet
= 15 x 8 - 13 x 6 m2
= 120 - 78 m2
= 42 m2
Fraction of floor left uncovered = =
Hence, the number of tiles needed is 960 and the fraction of the floor left uncovered is .
Two adjacent sides of parallelogram are 24 cm and 18 cm. If the distance between the longer sides is 12 cm; find the distance between the shorter sides.
Answer
Step 1 Finding the area of the parallelogram.
Length of one side of the parallelogram (longer side) = 24 cm
Length of the adjacent side (shorter side) = 18 cm
The distance between the longer sides = 12 cm
Area of parallelogram = base x height
= AB x DE
= 24 x 12 cm2
= 288 cm2
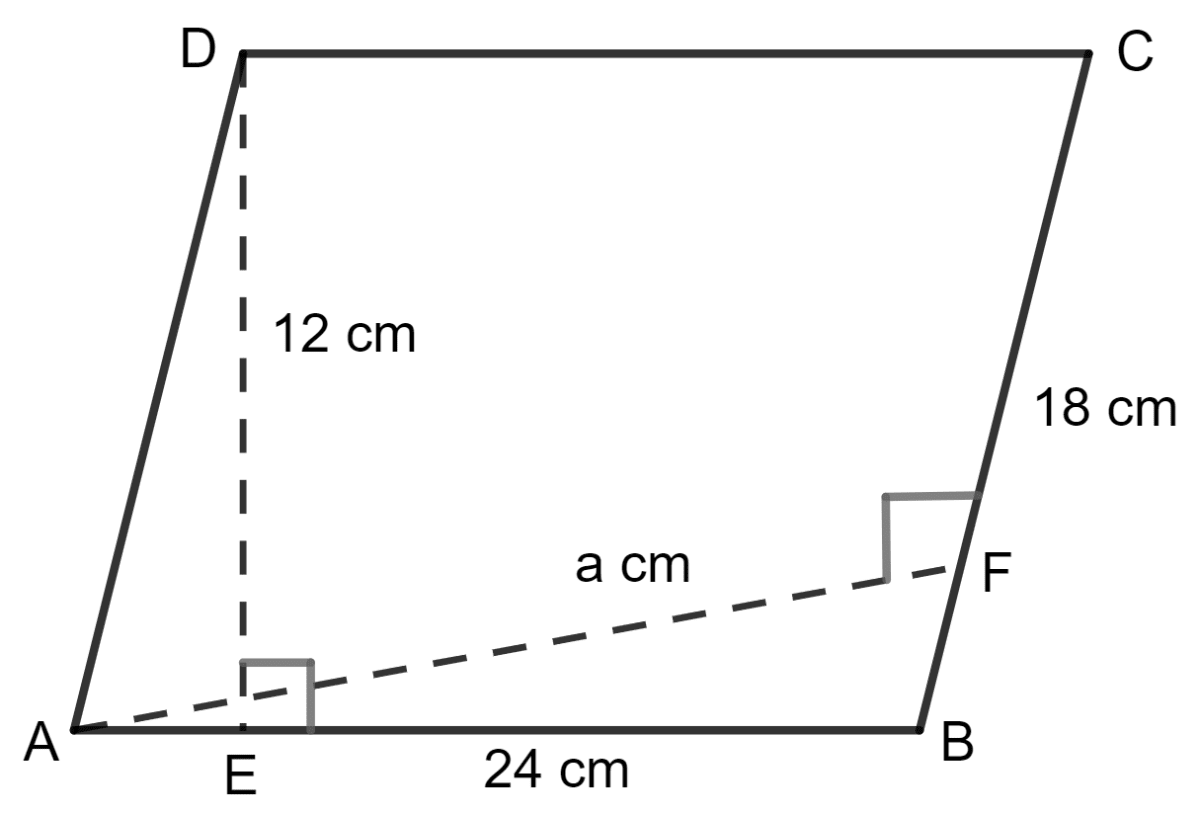
Step 2 Finding the sides of the parallelogram.
Let a be the distance between the shorter sides.
Area = base x height
= BC x AF
= 18 x a
Since area of the parallelogram will be same, if we consider AB as the base or BC as the base.
⇒ AB x DE = BC x AF
⇒ 288 = 18 x a
⇒ a =
⇒ a = 16 cm
Hence, the distance between the shorter sides of the parallelogram is 16 cm.
Two adjacent sides of a parallelogram are 28 cm and 26 cm. If one diagonal of it is 30 cm long; find the area of the parallelogram. Also, find the distance between its shorter sides.
Answer
By joining diagonal BD, the parallelogram is divided into two triangles. Let the sides of Δ ABD be:
a = 28 cm, b = 26 cm and c = 30 cm.
The semi-perimeter s:
∵ Area of triangle =
= cm2
= cm2
= cm2
= 336 cm2
Area of parallelogram ABCD = 2 x area of Δ ABD
= 2 x 336 cm2
= 672 cm2
Let h be the distance between the shorter sides.
Area of the parallelogram = base x height
⇒ 26 x h = 672
⇒ h =
⇒ h = 25.84 cm
Hence, the area of the parallelogram is 672 cm2 and the distance between the shorter sides is 25.84 cm.
The area of a rhombus is 216 sq. cm. If its one diagonal is 24 cm; find :
(i) length of its other diagonal,
(ii) length of its side,
(iii) perimeter of the rhombus.
Answer
(i) Given:
Area of rhombus = 216 sq. cm
One diagonal = 24 cm
Let d be the other diagonal of rhombus.
Area = x product of diagonals
⇒ 216 = x 24 x d
⇒ 216 = 12 x d
⇒ d =
⇒ d = 18
Hence, the length of other diagonal is 18 cm.
(ii) The rhombus is shown in the figure below:
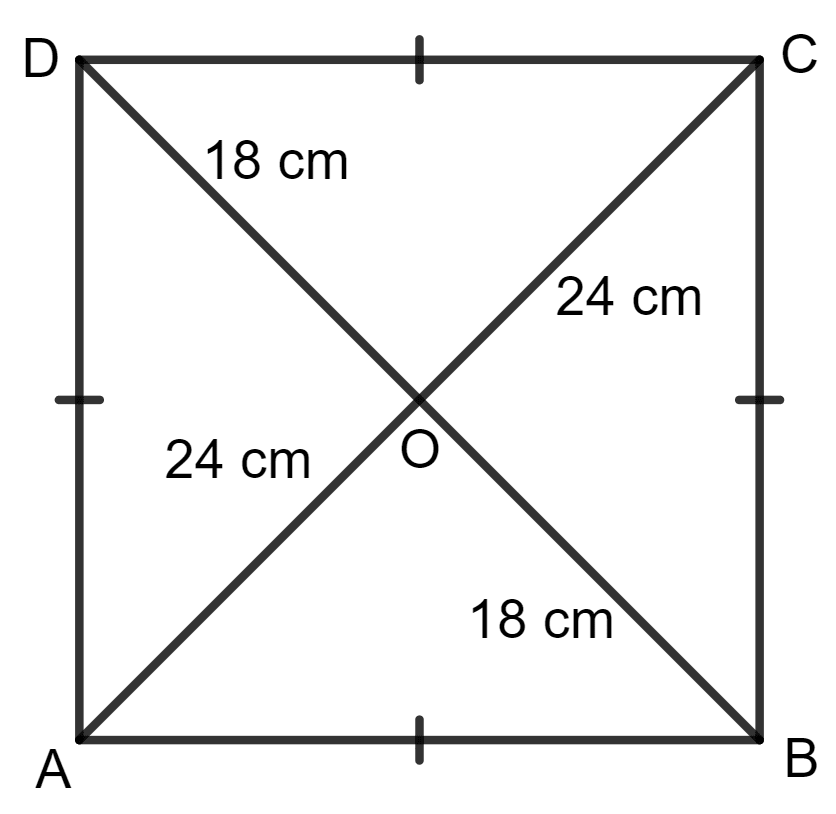
Diagonal AC = 24 cm
Then, OA = OC = = 12 cm
Diagonal BD = 18 cm
Then, OB = OD = = 9 cm
Since the diagonals of a rhombus bisect at 90°.
Applying pythagoras theorem in Δ AOB, we get:
AB2 = OA2 + OB2
⇒ AB2 = (12)2 + (9)2
⇒ AB2 = 144 + 81
⇒ AB2 = 225
⇒ AB =
⇒ AB = 15 cm
Hence, the length of each side of the rhombus is 15 cm.
(iii) Perimeter of the rhombus = 4 x side
= 4 x 15 cm
= 60 cm
Hence, the perimeter of the rhombus 60 cm.
The perimeter of a rhombus is 52 cm. If one diagonal is 24 cm; find :
(i) the length of its other diagonal,
(ii) its area.
Answer
(i) Given:
Perimeter of the rhombus = 52 cm
One diagonal BD = 24 cm
Let a be the length of a side of the rhombus.
Perimeter of a rhombus = 4 x Side
⇒ 4 x a = 52
⇒ a =
⇒ a = 13 cm
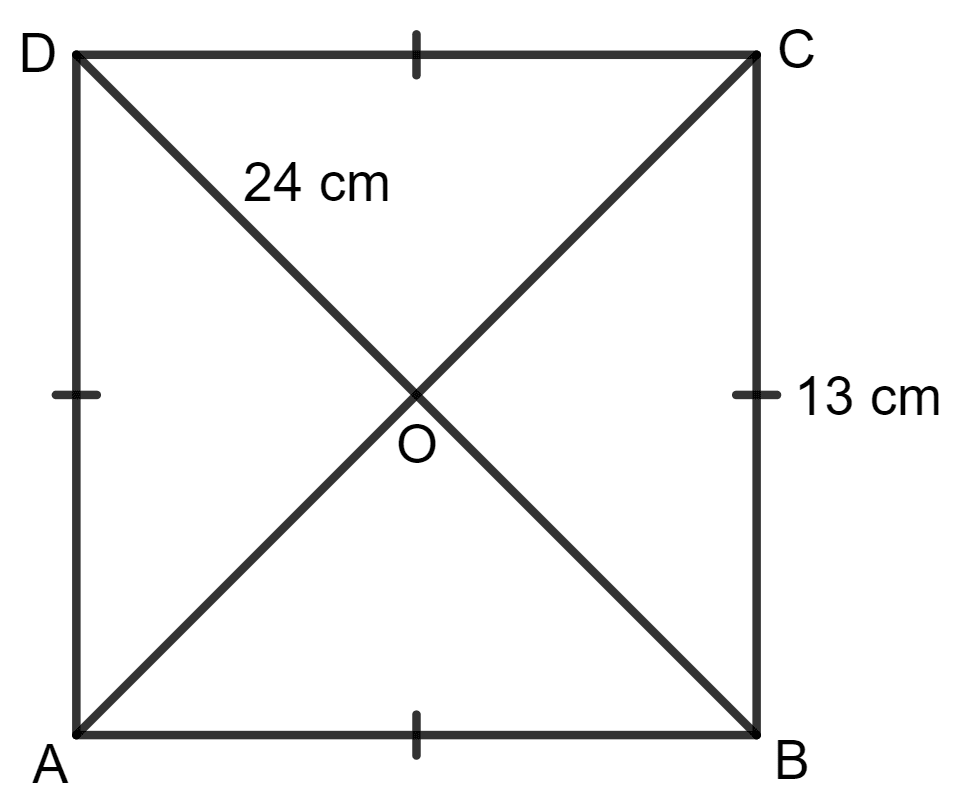
BD = 24 cm
Then, OB = OD = = 12 cm
Since the diagonals of a rhombus bisect at 90°.
Applying pythagoras theorem in triangle AOB, we get:
AB2 = OA2 + OB2
⇒ (13)2 = OA2 + (12)2
⇒ 169 = OA2 + 144
⇒ OA2 = 169 - 144
⇒ OA2 = 25
⇒ OA =
⇒ OA = 5 cm
AC = 2 x OA = 2 x 5 cm = 10 cm
Hence, the length of the other diagonal is 10 cm.
(ii) Area = x product of diagonals
= x 24 x 10 cm2
= 12 x 10 cm2
= 120 cm2
Hence, the area of the rhombus is 120 cm2.
The perimeter of a rhombus is 46 cm. If the height of the rhombus is 8 cm; find its area.
Answer
Given:
Perimeter of the rhombus = 46 cm
Height of the rhombus = 8 cm
Let a be the length of a side of the rhombus.
Perimeter = 4 x Side
⇒ 46 = 4 x a
⇒ a =
⇒ a = 11.5 cm
Area = base x height
= 11.5 x 8 cm2
= 92 cm2
Hence, the area of the rhombus is 92 cm2.
The given figure shows the cross-section of a concrete structure. Calculate the area of cross-section if AB = 1.8 m, CD = 0.6 m, DE = 0.8 m, EF = 0.3 m and AF = 1.2 m.
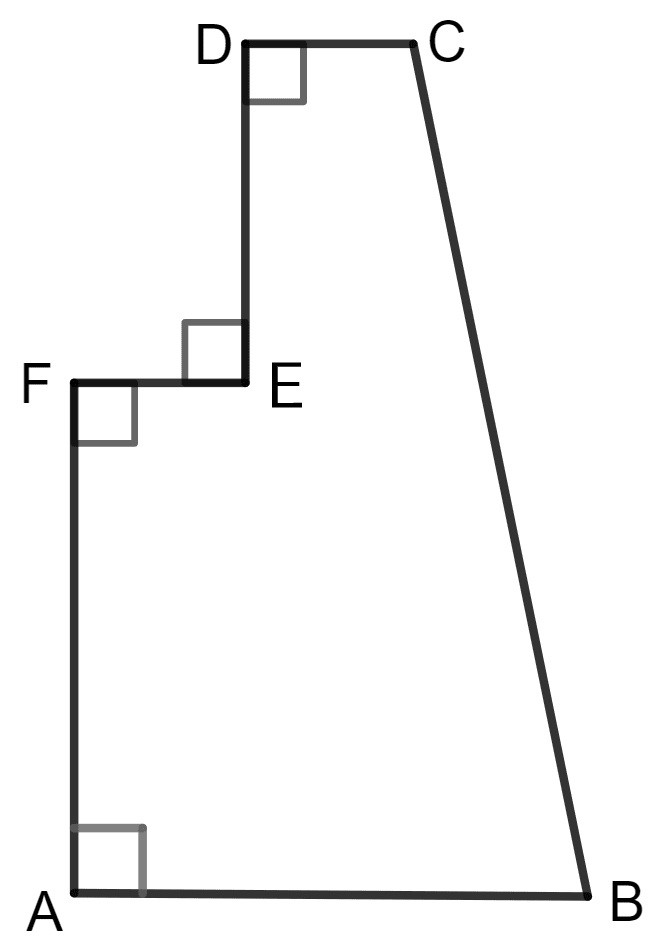
Answer
Given:
AB = 1.8 m, CD = 0.6 m, DE = 0.8 m, EF = 0.3 m and AF = 1.2 m
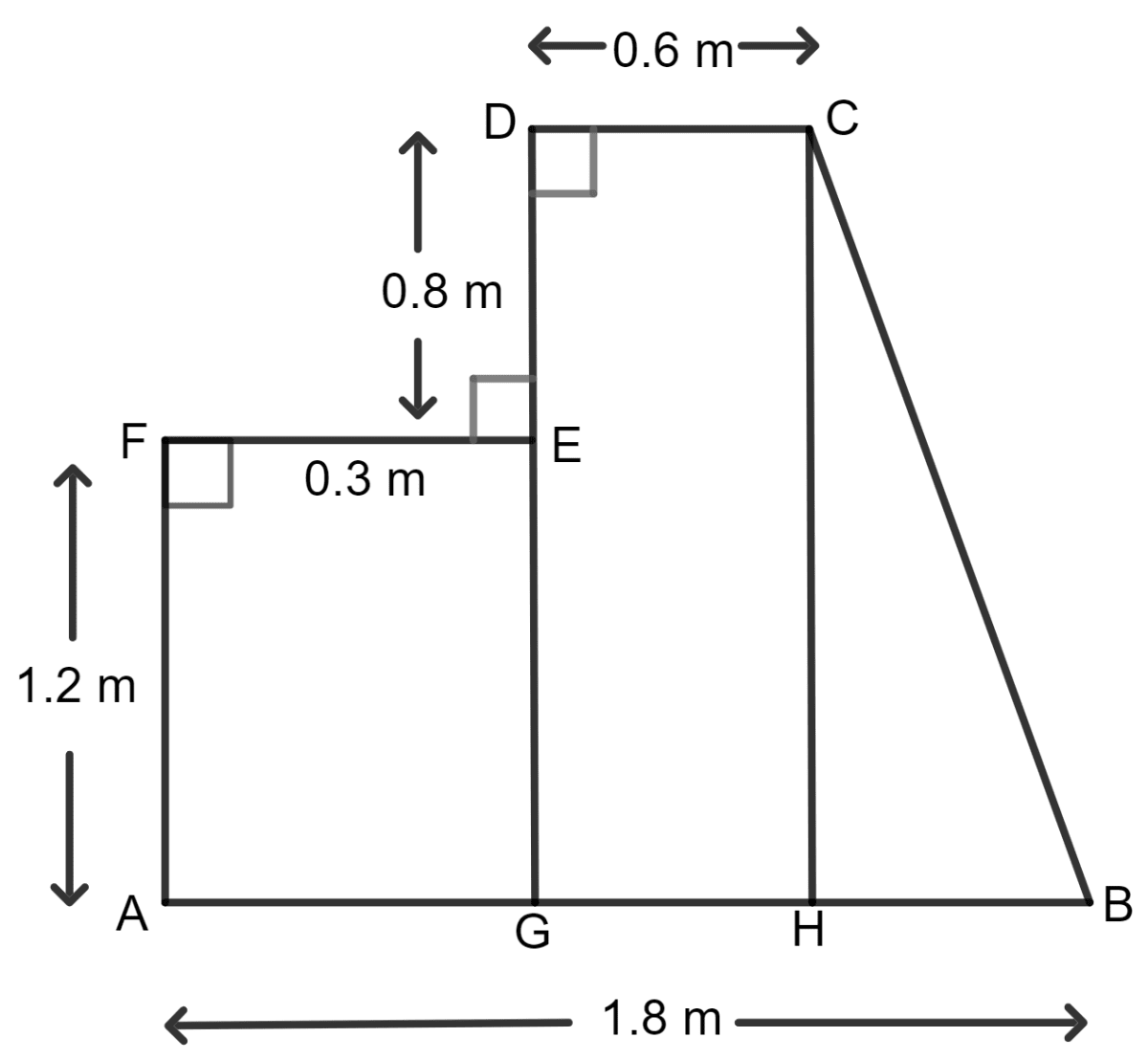
Area of ABCDEF = Area of rectangle AGEF + Area of rectangle GHCD + Area of triangle HBC.
Area of rectangle AGEF = l x b = AF x EF
= 1.2 x 0.3 m2
= 0.36 m2
Area of rectangle GHCD = l x b = GH x HC
= 0.6 x 2 m2 (HC = AF + ED = 1.2 + 0.8 = 2 cm)
= 1.2 m2
Area of triangle HBC = x b x h = x HB x HC
= x 0.9 x 2 m2 (HB = AB - AH = 1.8 - 0.9 = 0.9)
= 0.9 x 1 m2
= 0.9 m2
Now, area of ABCDEF = 0.36 m2 + 1.2 m2 + 0.9 m2
= 2.46 m2
Hence, the area of cross-section is 2.46 sq. m.
Calculate the area of the figure given below which is not drawn to scale.
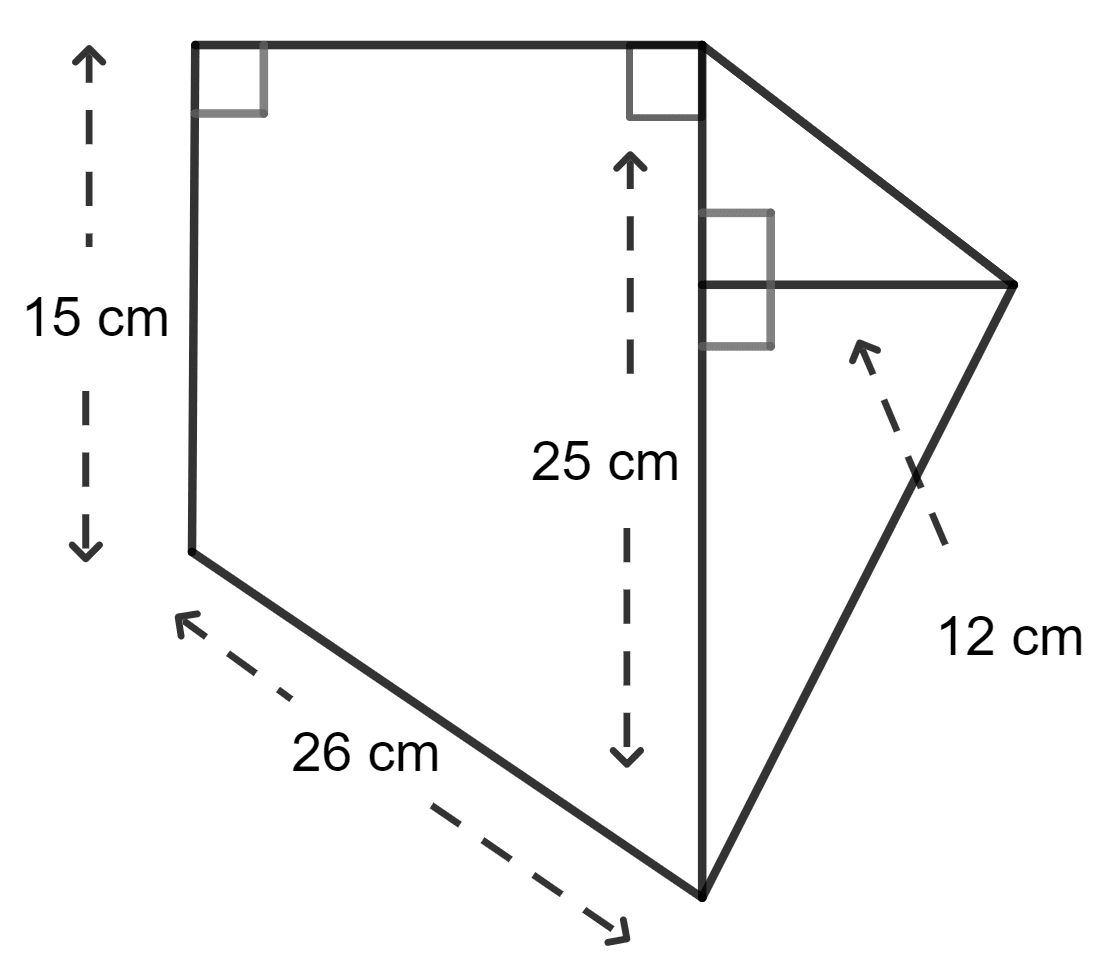
Answer
Area of figure ABCEF = Area of trapezium ABCF + Area of triangle CEF
Area of triangle CEF = x b x h = x CF x DE
= x 25 x 12 m2
= 25 x 6 m2
= 150 m2
In triangle BGC,
Base2 + Height2 = Hypotenuse2
⇒ CG2 + BG2 = CB2
Let h be the length of BG.
⇒ 102 + h2 = 262 (∵CG = CF - GF = CF - BA = 25 - 15 = 10)
⇒ 100 + h2 = 676
⇒ h2 = 676 - 100
⇒ h2 = 576
⇒ h =
⇒ h = 24 cm
Area of trapezium = (sum of parallel sides) x distance between the parallel sides
= (AB + CF) x BG
= (15 + 25) x 24 m2
= x 40 x 24 m2
= 20 x 24 m2
= 480 m2
So, total area of figure ABCEF = 150 + 480 m2
= 630 m2
Hence, the area is 630 m2.
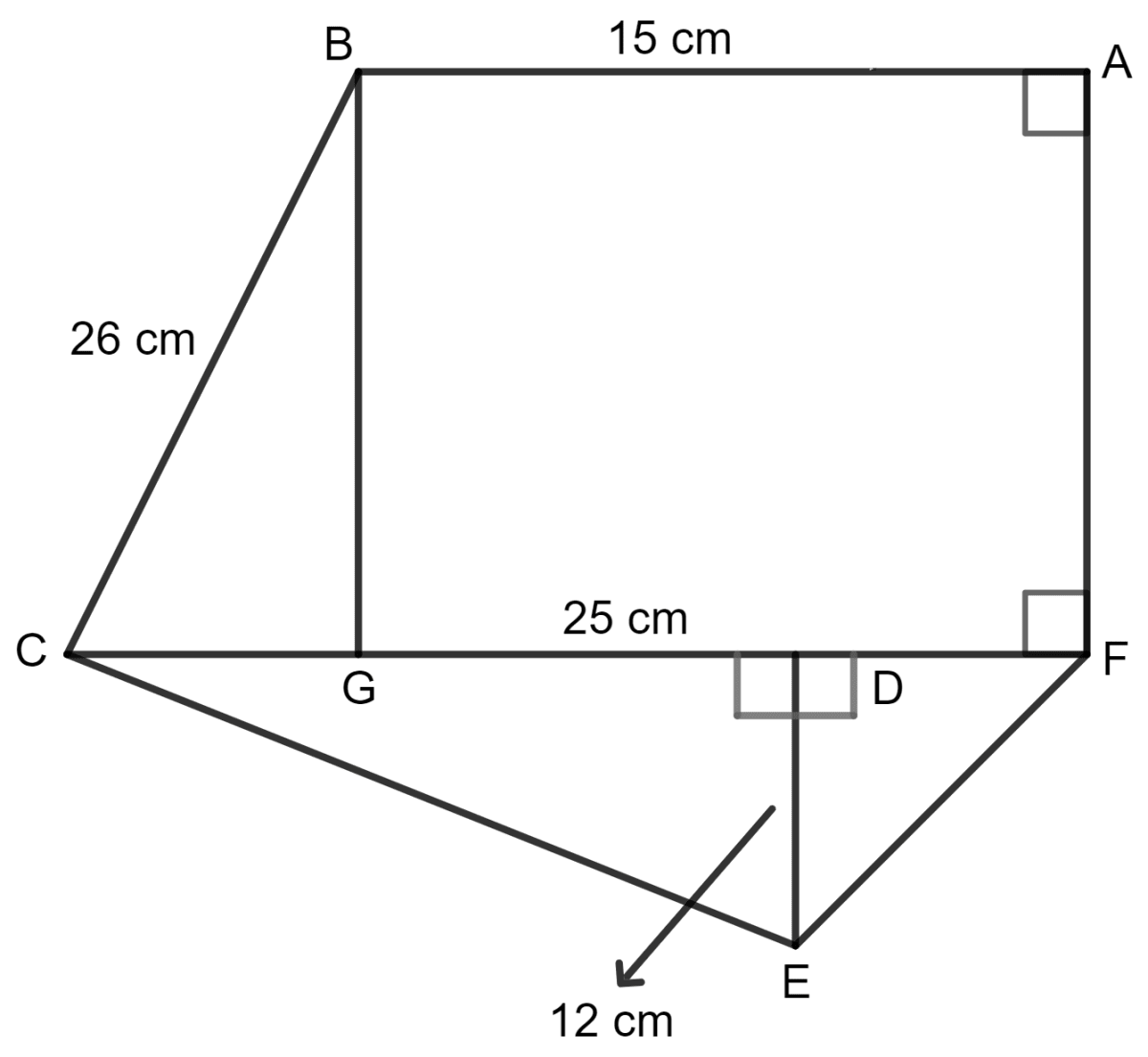
The following diagram shows a pentagonal field ABCDE in which the lengths of AF, FG, GH and HD are 50 m, 40 m, 15 m and 25 m respectively; and the lengths of perpendiculars BF, CH and EG are 50 m, 25 m and 60 m respectively. Determine the area of the field.
Answer
Area of figure ABCDE = Area of Δ ABF + Area of Δ AED + Area of Δ DHC + Area of trapezium BFHC
Area of Δ ABF = x b x h = x AF x BF
= x 50 x 50 m2
= 25 x 50 m2
= 1250 m2
Area of Δ AED = x b x h = x AD x GE
= x (AF + FG + GH + HD) x GE
= x (50 + 40 + 15 + 25) x 60 m2
= 130 x 30 m2
= 3900 m2
Area of Δ DHC = x b x h = x HD x CH
= x 25 x 25 m2
= 12.5 x 25 m2
= 312.5 m2
Area of trapezium BFHC = (sum of parallel sides) x distance between the parallel sides
= (BF + CH) x FH
= (BF + CH) x (FH + GH)
= (50 + 25) x (40 + 15) m2
= x 75 x 55 m2
= 37.5 x 55 m2
= 2062.5 m2
Thus, area of figure ABCDE = 1250 + 3900 + 312.5 + 2062.5 m2
= 7525 m2
Hence, the area is 7525 sq. m.
In the given figure, AB = BC, ∠ABC = 90°, AC = 14 cm and BPC (shaded portion) is semi-circle. If , the area of shaded portion is :
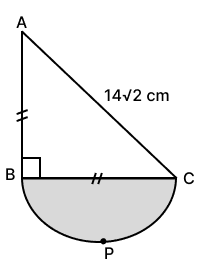
77 cm2
308 cm2
231 cm2
154 cm2
Answer
Let AB = BC = a cm and triangle ABC is a right triangle,
Using the Pythagoras theorem,
Base2 + Height2 = Hypotenuse2
⇒ BC2 + AB2 = AC2
⇒ a2 + a2 = ()2
⇒ 2a2 = 392
⇒ a2 =
⇒ a2 = 196
⇒ a =
⇒ a = 14 cm
Thus, AB = BC = 14 cm.
The diameter of the semicircle is BC = 14 cm, so the radius r is:
r = = = 7 cm
Area of semi-circle = πr2
Thus, the area of the shaded portion (the semicircle) is 77 cm2.
Hence, option 1 is the correct option.
The diameter of a circle is 14 cm. If it is doubled, the perimeter of the resulting circle will become:
four times
doubled
halved
three times
Answer
Given:
Diameter of the original circle = 14 cm
Radius of the original circle = r = = = 7 cm
Perimeter of the original circle = 2πr
When diameter is doubled, new diameter = 2 x 14 cm = 28 cm
New radius, r = = = 14 cm
New perimeter of circle:
Thus, the new perimeter is doubled compared to the original perimeter.
Hence, option 2 is the correct option.
In the given figure, OABC is a square of side 14 cm. Taking , the area of the shaded portion is :
154 cm2
196 cm2
42 cm2
52 cm2
Answer
Side of the square = Radius of the circle = 14 cm
Area of shaded portion = Area of square - Area of quarter circle
The area of the shaded portion is 42 cm2.
Hence, option 3 is the correct option.
If the radius of a circle is doubled, then its area will become :
doubled
halved
four times
three times
Answer
Let r be the radius of circle.
Area of circle = πr2
When the radius is doubled, new radius = 2r
Area of new circle = π x (2r)2
= π x 4r2
= 4πr2
The new area is four times the area of the original circle.
Hence, option 3 is the correct option.
The radii of two circles are 14 cm and 28 cm. If the area of the shaded portion is :
1848 cm2
1644 cm2
486 cm2
702 cm2
Answer
Area of shaded portion = Area of bigger circle - Area of smaller circle
The area of shaded portion is 1848 cm2.
Hence, option 1 is the correct option.
The diameter of a circle is 28 cm. Find its :
(i) circumference
(ii) area
Answer
Given:
Diameter = d = 28 cm
Radius = r = = = 14 cm
(i) Circumference of a circle = 2πr
Hence, the circumference of a circle is 88 cm.
(ii) Area of a circle = πr2
Hence, the area of a circle is 616 cm2.
The circumference of a circular field is 308 m. Find its :
(i) radius
(ii) area.
Answer
(i) Let r be the radius of the circle.
The circumference of a circle = 308 m
As we know, the circumference of a circle = 2πr
Hence, the radius of a circle is 49 m.
(ii) Area of a circle = πr2
Hence, the area of a circle is 7,546 m2.
The sum of the circumference and diameter of a circle is 116 cm. Find its radius.
Answer
Given:
Circumference of a circle + Diameter of a circle = 116 cm
Hence, the radius of a circle is 14 cm.
The radii of two circles are 25 cm and 18 cm. Find the radius of the circle which has circumference equal to the sum of circumferences of these two circles.
Answer
Circumference of a circle = 2πr
For the first circle,
r1 = 25 cm
Circumference1 = 2 x π x 25 = 50π cm
For the second circle,
r2 = 18 cm
Circumference2 = 2 x π x 18 = 36π cm
Total circumference = Circumference1 + Circumference2
= 50π + 36π
= 86π cm
Let the radius of the new circle be R.
Circumference of the new circle = 2πR
86π = 2πR
86 = 2R
R =
R = 43 cm
Hence, the radius of the new circle is 43 cm.
The radii of two circles are 48 cm and 13 cm. Find the area of the circle which has its circumference equal to the difference of the circumferences of the given two circles.
Answer
Circumference of a circle = 2πr
For the first circle,
r1 = 48 cm
Circumference1 = 2 x π x 48 = 96π cm
For the second circle,
r2 = 13 cm
Circumference2 = 2 x π x 13 = 26π cm
Total circumference = Circumference1 - Circumference2
= 96π - 26π
= 70π cm
Let the radius of the new circle be R.
Circumference of the new circle = 2πR
70π = 2πR
70 = 2R
R =
R = 35 cm
And, area of the new circle = πr2
Hence, the area of new circle is 3,850 cm2.
The diameters of two circles are 32 cm and 24 cm. Find the radius of the circle having its area equal to sum of the areas of the two given circles.
Answer
For the first circle,
d1 = 32 cm
r1 = = = 16 cm
Area1 = π x 162 = 256π cm2
For the second circle,
d2 = 24 cm
r2 = = = 12 cm
Area2 = π x 122 = 144π cm2
Total area = Area1 + Area2
= 256π + 144π
= 400π cm
Let the radius of the new circle be R.
Area of the new circle = πR2
400π = πR2
400 = R2
R =
R = 20 cm
Hence, the radius of the new circle is 20 cm.
The radius of a circle is 5 m. Find the circumference of the circle whose area is 49 times the area of the given circle.
Answer
Given:
Radius of original circle = r = 5 m
Area of new circle = 49 times area of original circle.
Let R be the radius of new circle.
Circumference of new circle = 2πR
Hence, the circumference of new circle is 220 m.
A circle of largest area is cut from a rectangular piece of card-board with dimensions 55 cm and 42 cm. Find the ratio between the area of the circle cut and the area of the remaining card-board.
Answer
Given:
The dimensions of rectangular piece of card-board are:
Length = 55 cm
Width = 42 cm
The largest circle that can be cut from the rectangle will have a diameter equal to the shorter side of the rectangle.
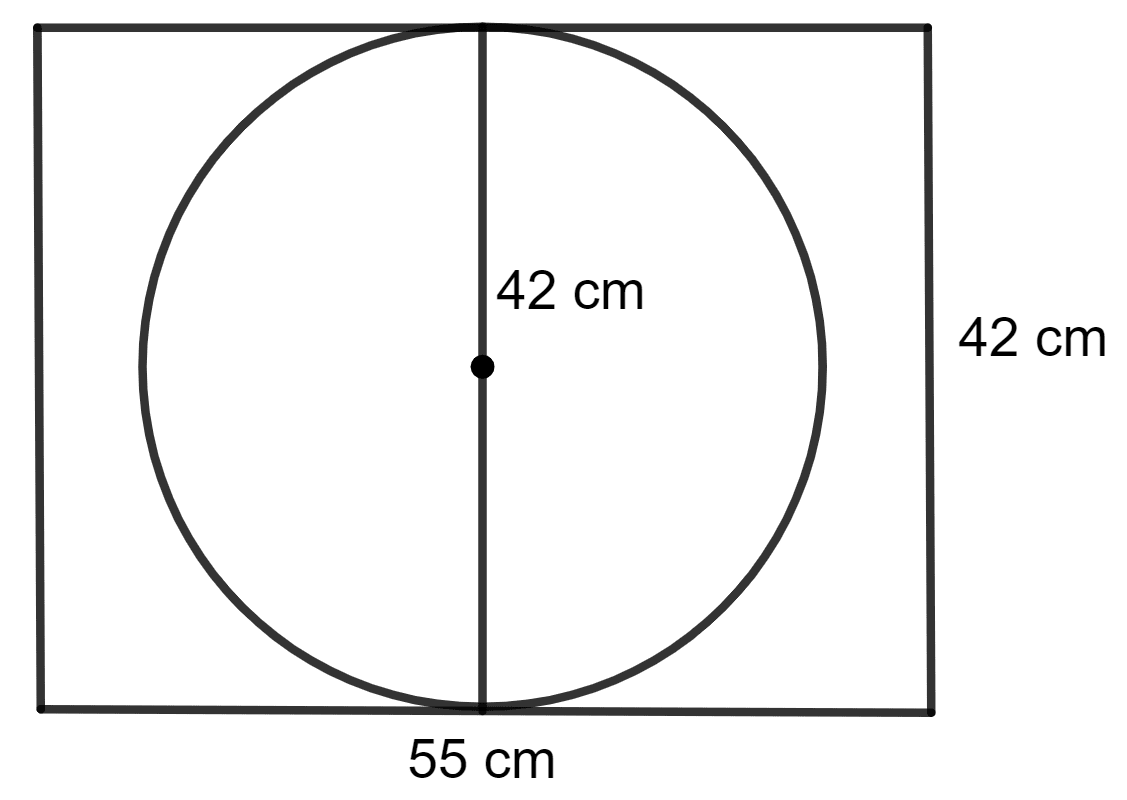
Diameter = Width = 42 cm
∵ Radius = r = = = 21 cm
Area of the circle = πr2
Area of the rectangular piece of cardboard = 55 x 42 cm2
= 2,310 cm2
Therefore, area of remaining cardboard = Area of rectangle - Area of circle
= (2,310 - 1,386) cm2
= 924 cm2
So, the ratio between the area of the circle cut and the area of the remaining card-board = 1,386 : 924
= 231 : 154
= 3 : 2
Hence, the ratio between the area of the circle cut and the area of the remaining cardboard is 3 : 2.
The following figure shows a square card-board ABCD of side 28 cm. Four identical circles of largest possible size are cut from this card as shown below.
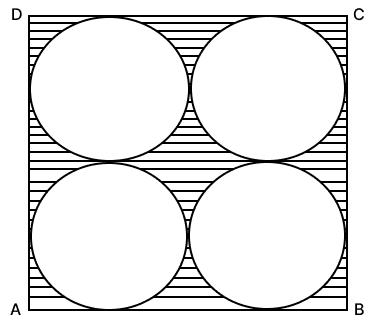
Find the area of the remaining card-board.
Answer
Given:
Side of square ABCD = 28 cm
Side of square = 2 x diameter of circle
Diameter of circle = = 14 cm
Radius of circle = = = 7 cm
Area of the remaining card-board = Area of square - 4 x Area of 1 circle
= side2 - 4 x πr2
Hence, the area of remaining cardboard is 168 cm2.
The radii of two circles are in the ratio 3 : 8. If the difference between their areas is 2695 π cm2, find the area of the smaller circle.
Answer
Let the two radii of two circles be 3a and 8a.
The difference between their areas = 2695 π cm2
⇒ π x (8a)2 - π x (3a)2 = 2695 π
⇒ π x 64a2 - π x 9a2 = 2695 π
⇒ π x (64a2 - 9a2) = 2695 π
⇒ x (64a2 - 9a2) = 2695
⇒ 64a2 - 9a2 = 2695
⇒ 55a2 = 2695
⇒ a2 =
⇒ a2 = 49
⇒ a =
⇒ a = 7 cm
The radii are 3a and 8a = 3 x 7 cm and 8 x 7 cm = 21 cm and 56 cm
Area of smaller circle = π x (21)2
Hence, the area of smaller circle is 1,386 cm2.
The diameters of three circles are in the ratio 3 : 5 : 6. If the sum of the circumferences of these circles be 308 cm; find the difference between the areas of the largest and the smallest of these circles.
Answer
Let the diameters of the three circles be 3a, 5a and 6a.
Radius of three circles = , and
Circumference of a circle = 2πr
For the first circle,
r1 = cm
Circumference1 = 2 x π x = 3aπ cm
For the second circle,
r2 = cm
Circumference2 = 2 x π x = 5aπ cm
For the third circle,
r2 = cm
Circumference2 = 2 x π x = 6aπ cm
Total circumference = Circumference1 + Circumference2 + Circumference3
⇒ 3aπ + 5aπ + 6aπ = 308
⇒ 14aπ = 308
⇒ 14 x a x = 308
⇒ 2 x a x 22 = 308
⇒ 44a = 308
⇒ a =
⇒ a = 7 cm
Radius of three circles = x 7 cm, x 7 cm and x 7 cm
= 10.5 cm, 17.5 cm and 21 cm
Difference between the area of the largest and the smallest circles = π(21)2 - π(10.5)2
= 441π - 110.25π cm2
= 330.75π cm2
= 330.75 x cm2
= 47.25 x 22 cm2
= 1039.5 cm2
Hence, the difference in the area = 1039.5 cm2.
Find the area of a ring shaped region enclosed between two concentric circles of radii 20 cm and 15 cm.
Answer
Given:
r1 = 20 cm
r2 = 15 cm
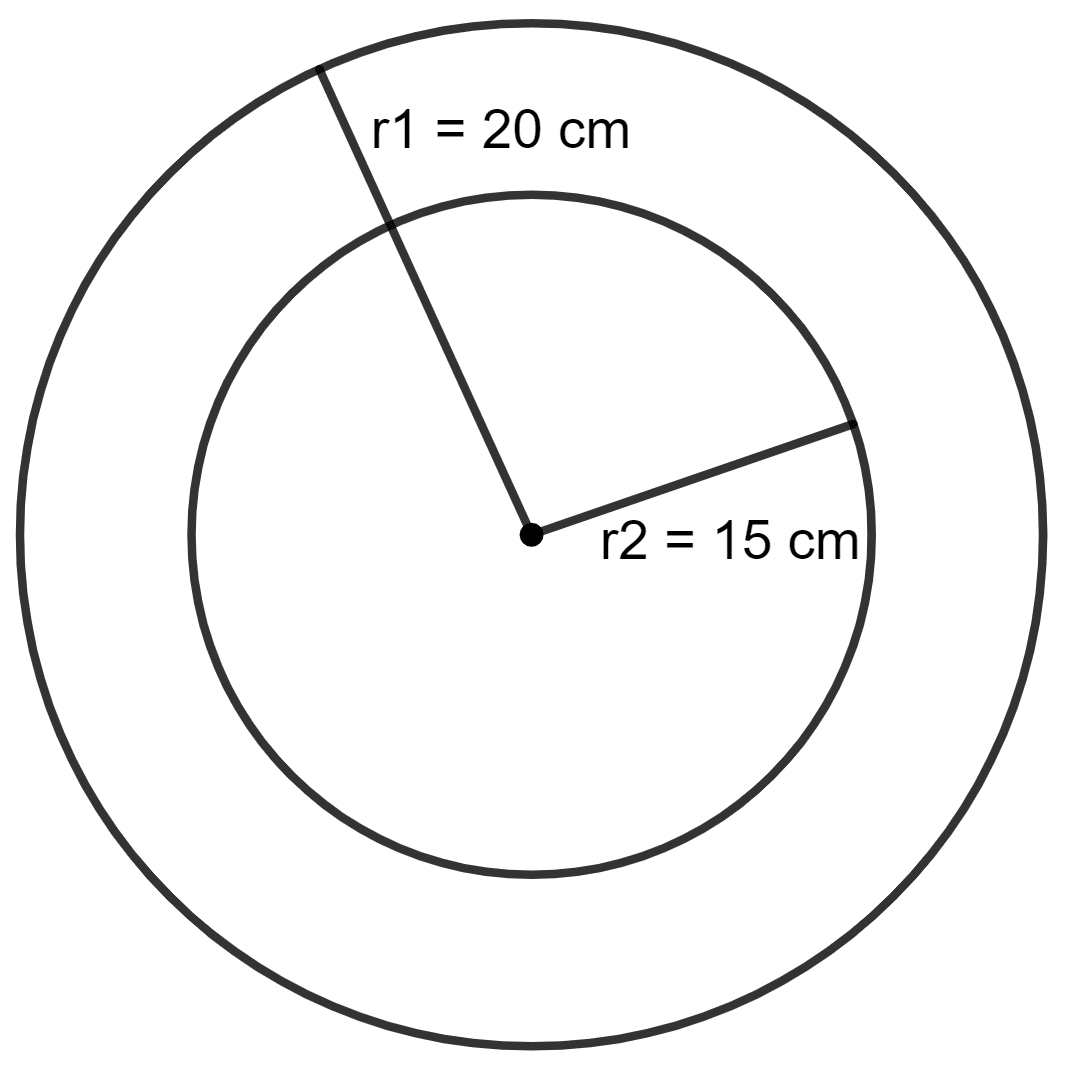
Area of ring shaped region = π(r12 - r22)
= π(202 - 152) cm2
= π(400 - 225) cm2
= π x 175 cm2
= x 175 cm2
= 22 x 25 cm2
= 550 cm2
Hence, the area of ring shaped region is 550 cm2.
The circumference of a given circular park is 55 m. It is surrounded by a path of uniform width 3.5 m. Find the area of the path.
Answer
Let r be the radius of the circular park.
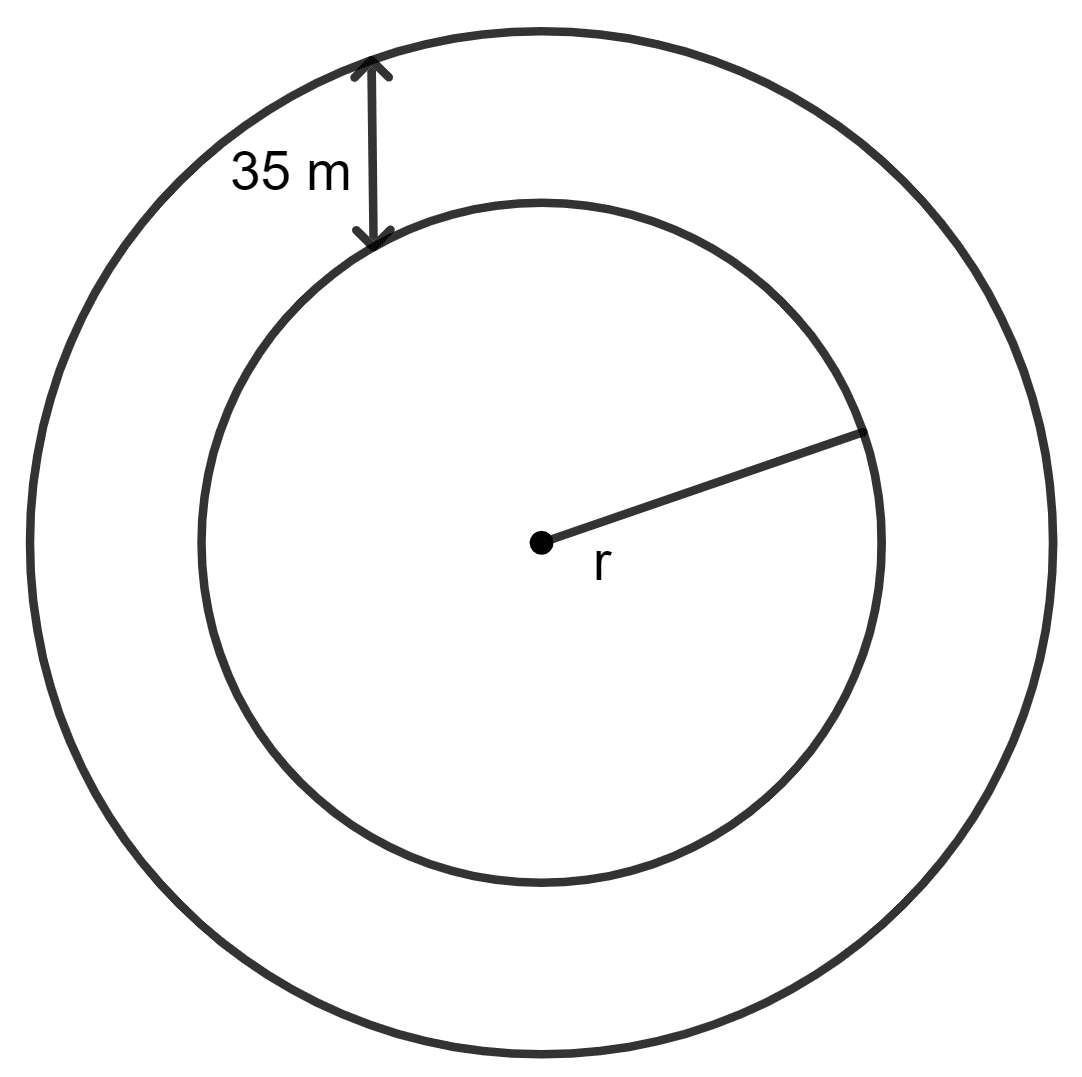
Circumference = 2πr
⇒ 2πr = 55
⇒ 2 x x r = 55
⇒ x r = 55
⇒ r =
⇒ r =
⇒ r =
⇒ r = 8.75 m
Radius of outer park = radius of park + width of the path
= 8.75 + 3.5 m
= 12.25 m
Area of the path = Area of outer park - Area of circular park
= π (12.25)2 - π (8.75)2 m2
= 150.0625π - 76.5625π m2
= 73.5 π m2
= 73.5 x m2
= 10.5 x 22 m2
= 231 m2
Hence, the area of the path is 231 m2.
There are two circular gardens A and B. The circumference of garden A is 1.760 km and the area of garden B is 25 times the area of garden A. Find the circumference of garden B.
Answer
Let r be the radius of the circular garden A.
Circumference of garden A = 2πr
⇒ 2πr = 1.760 km
⇒ 2πr = 1760 m
⇒ 2 x x r = 1760 m
⇒ x r = 1760 m
⇒ r = m
⇒ r = 7 x 40 m
⇒ r = 280 m
Area of garden A = πr2
= π x (280)2
= 78400π
Let R be the radius of garden B.
It is given that the area of garden B is 25 times the area of garden A.
⇒ πR2 = 25 x πr2
⇒ πR2 = 25 x 78400π
⇒ R2 = 25 x 78400
⇒ R2 = 25 x 78400
⇒ R2 = 1960000
⇒ R =
⇒ R = 1400 m
Circumference of garden B = 2πR
= 2 x x 1400 m
= 2 x 22 x 200 m
= 8800 m = 8.8 km
Hence, the circumference of garden B is 8.8 km.
A wheel has diameter 84 cm. Find how many complete revolutions must it make to cover 3.168 km.
Answer
Diameter of the wheel = 84 cm
Radius of the wheel = = = 42 cm
Circumference of the wheel = 2πr
Let the wheel make n revolutions.
Total distance traveled by the wheel = n x Circumference of the wheel
⇒ 3.168 km = n x 264 cm
⇒ 316,800 cm = n x 264 cm
⇒ n =
⇒ n = 1200
Hence, the wheel makes 1,200 revolutions.
Each wheel of a car is of diameter 80 cm. How many complete revolutions does each wheel make in 10 minutes when the car is travelling at a speed of 66 km per hour ?
Answer
Diameter of wheel = 80 cm
Radius of the wheel = = = 40 cm
Circumference of the wheel = 2πr
Let the wheel make n number of revolutions.
Speed of the car = 66 km per hour
Time = 10 min
Total distance = Speed x Time
= x 10 cm
= 11 x 100,000 cm
= 1,100,000
Total distance = Number of revolutions x Circumference of the wheel
⇒ 1,100,000 cm = n x cm
⇒ n =
⇒ n =
⇒ n = 4,375
Hence, the wheel makes 4,375 complete revolutions.
An express train is running between two stations with a uniform speed. If the diameter of each wheel of the train is 42 cm and each wheel makes 1200 revolutions per minute, find the speed of the train.
Answer
Diameter of wheel = 42 cm
Radius of wheel = = = 21 cm
Circumference of wheel = 2πr
Total distance covered by one wheel in 1 minute = Number of revolutions x Circumference of wheel
= 1,200 x 132 cm
= 158,400 cm
= 1.584 km
Speed of the train =
=
=
= 95.04 km/hr
Hence, the speed of the train is 95.04 km/hr.
The minute hand of a clock is 8 cm long. Find the area swept by the minute hand between 8.30 a.m. and 9.05 a.m.
Answer
Length of the minute hand (radius of the circle) = 8 cm
Time interval between 9.05 a.m. and 8.30 a.m. = 35 minutes
Area swept by the minute hand in 1 hr = πr2
Area of the circle in 60 minutes = cm2
Area of the circle in 1 minute = cm2
= cm2
Area of the circle in 35 minutes = cm2
= cm2
= cm2
Hence, the area swept by the minute hand between 8:30 a.m. and 9:05 a.m. is cm2.
The shaded portion of the figure, given alongside, shows two concentric circles.
If the circumference of the two circles be 396 cm and 374 cm, find the area of the shaded portion.
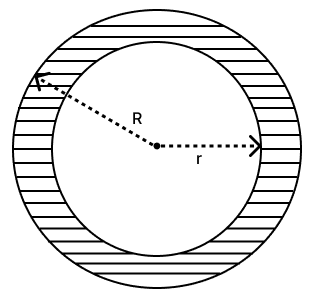
Answer
Circumference of the circle = 2πr
For outer circle,
For inner circle,
Area of shaded portion = π(R2 - r2)
= π(632 - 59.52) cm2
= π(3,969 - 3,540.25) cm2
= π x 428.75 cm2
= x 428.75 cm2
= 22 x 61.25 cm2
= 1,347.5 cm2
Hence, the area of the shaded portion is 1,347.5 cm2.
The base of a right triangle is 8 cm and its hypotenuse is 10 cm; the area of triangle is:
24 cm2
40 cm2
48 cm2
80 cm2
Answer
Given:
Base of the triangle = 8 cm
Hypotenuse of the triangle = 10 cm
Let h be the height of the triangle.
In a right-angled triangle, using the Pythagoras theorem,
⇒ Base2 + Height2 = Hypotenuse2
⇒ (8)2 + h2 = (10)2
⇒ 64 + h2 = 100
⇒ h2 = 100 - 64
⇒ h2 = 36
⇒ h =
⇒ h = 6 cm.
By formula,
Area of the triangle = x base x height
= x 8 x 6 cm2
= 24 cm2.
Hence, option 1 is the correct option.
The area of an equilateral triangle is cm2, its perimeter is :
16 cm
4 cm
12 cm
8 cm
Answer
Given,
Area of equilateral triangle = cm2
By formula,
Area of the equilateral triangle = x side2
By formula,
Perimeter of equilateral triangle = 3 x side
= 3 x 4 cm
= 12 cm.
Hence, option 3 is the correct option.
If the perimeter of a square is 80 cm, its area is 80 cm2.
true
false
none of these two
Answer
Given,
Perimeter of a square = 80 cm
⇒ 4 x side = 80
⇒ side =
⇒ side = 20 cm
By formula,
Area of square = side2
= 202 cm2
= 400 cm2.
So, given area is false.
Hence, option 2 is the correct option.
If the area of a trapezium is 32 cm2 and distance between its parallel sides is 8 cm; the sum of length of its parallel side is :
4 cm
16 cm
8 cm
12 cm
Answer
Given, area of a trapezium = 32 cm2
Distance between its parallel sides = 8 cm
By formula,
Area of trapezium = x (sum of parallel sides) x distance between the parallel sides
⇒ 32 = x (Sum of parallel sides) x 8
⇒ 32 = Sum of parallel sides x 4
⇒ Sum of parallel sides =
⇒ Sum of parallel sides = 8 cm.
Hence, option 3 is the correct option.
Statement 1: The side of a triangular board are 8 cm, 6 cm and 10 cm; the cost of painting it at the rate of ₹ 10 per square cm is x 6 x 8 x ₹ 10.
Statement 2: 102 = 82 + 62
⇒ Sides of the triangle are 8 cm and 6 cm.
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Answer
Given,
Sides of a triangular board are 8 cm, 6 cm and 10 cm.
⇒ 102 = 100, 82 = 64 and 62 = 36.
⇒ 100 = 64 + 36
⇒ 102 = 82 + 62
This confirms the triangle with sides 6 cm, 8 cm, and 10 cm is a right triangle, where 10 cm is the hypotenuse.
Thus, sides of the triangle are 8 cm and 6 cm.
So, statement 2 is true.
Area of triangle = x base x height
= x 8 x 6
Rate of painting = ₹ 10 per square cm
Cost of painting = Area x rate of painting
= x 8 x 6 x ₹ 10
So, statement 1 is true.
∴ Both the statements are true.
Hence, option 1 is the correct option.
Statement 1: A rhombus shaped sheet with perimeter 40 cm has one diagonal 12 cm and the other diagonal is 16 cm.
Statement 2: If the other diagonal of this rhombus = x cm, x = 102 - 62.
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Answer
Given,
The perimeter of a rhombus = 40 cm.
One diagonal = 12 cm.
As we know, the perimeter of the rhombus = 4 x side
⇒ 4 x side = 40 cm
⇒ side = cm
⇒ side = 10 cm

Let ABCD be a rhombus. From figure,
AB = 10 cm
Let diagonal AC = 12 cm
We know that,
Diagonals of rhombus bisect each other.
Then, OA = OC = = 6 cm
Let OB be a cm.
Since the diagonal of a rhombus bisect at 90°.
Applying pythagoras theorem in triangle AOB, we get:
⇒ AB2 = OA2 + OB2
⇒ (10)2 = (6)2 + a2
⇒ a2 = (10)2 - (6)2
⇒ a2 = 100 - 36
⇒ a2 = 64
⇒ a =
⇒ a = 8
So, OB = 8 cm
BD = 2 x OB = 2 x 8 cm = 16 cm.
∴ Statement 1 is true.
As solved above,
If the other diagonal of this rhombus = x cm,
Then will be equal to 102 - 62.
∴ Statement 2 is false.
∴ Statement 1 is true, and statement 2 is false.
Hence, option 3 is the correct option.
Assertion (A): The perimeter of the adjoining figure is (32 + x) cm.
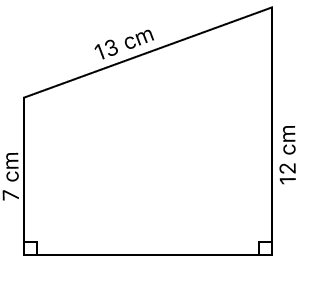
Reason (R): x2 = 132 - 52 = 144 and x = 12 cm.
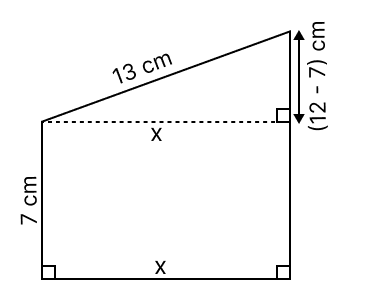
Perimeter = (32 + 12) cm
A is true, but R is false.
A is false, but R is true.
Both A and R are true, and R is the correct reason for A.
Both A and R are true, and R is the incorrect reason for A.
Answer
Perimeter of the figure = sum of all the sides
= 7 + 13 + 12 + x
= (32 + x) cm
So, assertion (A) is true.
From figure,
AB = AC - BC = 12 - 7 = 5 cm
Since, ABE is a right angled triangle. Using pythagoras theorem,
⇒ AE2 = AB2 + BE2
⇒ 132 = 52 + x2
⇒ 169 = 25 + x2
⇒ x2 = 169 - 25
⇒ x2 = 144
⇒ x =
⇒ x = 12 cm
Perimeter = (32 + x) = (32 + 12) cm.
∴ Both A and R are true, and R is the correct reason for A.
Hence, option 3 is the correct option.
Assertion (A): If BC = 14 cm, AB = 14 x 4 cm
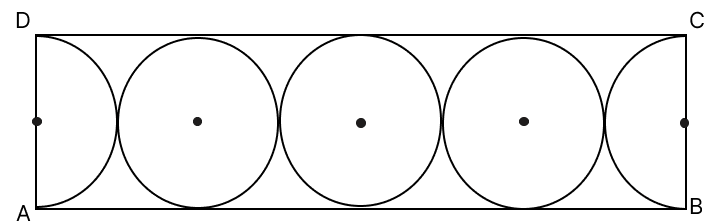
Reason (R): AB = 4 x 2r = 4 x 14 cm
A is true, but R is false.
A is false, but R is true.
Both A and R are true, and R is the correct reason for A.
Both A and R are true, and R is the incorrect reason for A.
Answer
Given, BC = 14 cm
From figure,
Diameter (d) = 2r = 14 cm
AB has 4 circles (3 circles and 2 semi-circles).
AB = 4 x diameter of one circle = 4 x 2r = 4 x 14 cm = 56 cm.
∴ Both A and R are true, and R is the correct reason for A.
Hence, option 3 is the correct option.
AD is altitude of an isosceles triangle ABC in which AB = AC = 30 cm and BC = 36 cm. A point O is marked on AD in such a way that ∠BOC = 90°. Find the area of quadrilateral ABOC.
Answer
ΔABC is shown in the figure below:
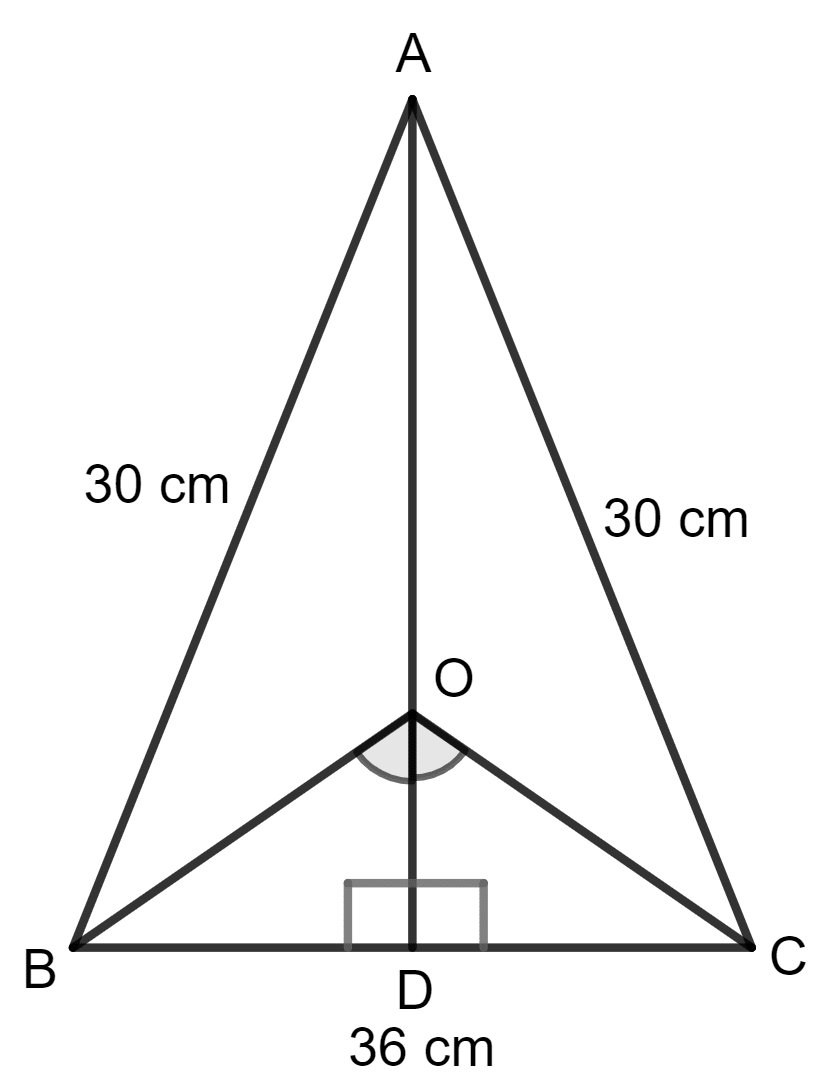
Area of isosceles triangle ABC =
∠ BOC = ∠ COD = 45° (∵ AD divide ∠ BOC in 2 equal halves)
Let OB = OC = x.
In Δ BOC, by using the Pythagoras theorem,
OB2 + OC2 = BC2
⇒ x2 + x2 = (36)2
⇒ 2x2 = 1,296
⇒ x2 =
⇒ x2 = 648
⇒ x =
⇒ x = 18
Now the area of triangle BOC = x base x height
Area of quadrilateral ABOC = Area of Δ ABC - Area of Δ BOC
= 432 - 324 cm2
= 108 cm2
Hence, the area of quadrilateral ABOC is 108 cm2.
A footpath of uniform width runs all around the outside of a rectangular field 30 m long and 24 m wide. If the path occupies an area of 360 m2, find its width.
Answer
Given:
The length of the rectangular field = 30 m
The breadth of the rectangular field = 24 m
Area of path = 360 m2
Let the width of the path be x m.
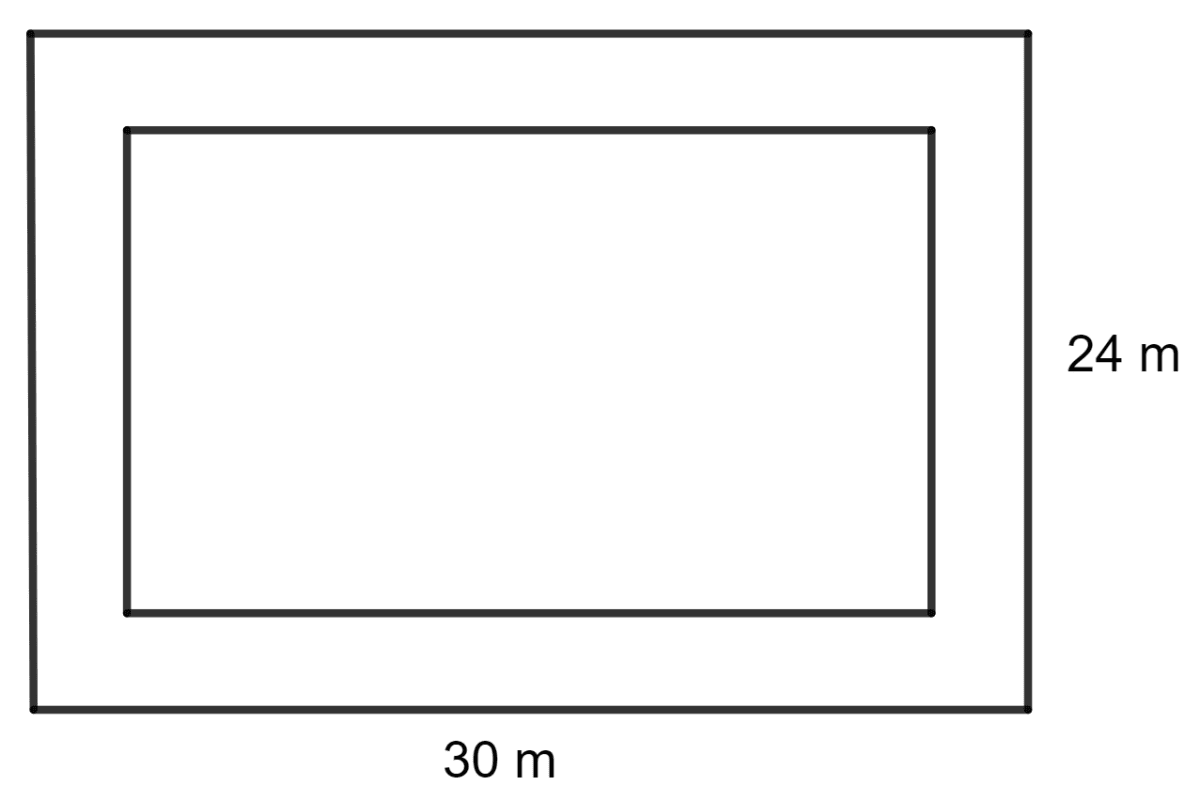
The length of the smaller rectangular field = 30 m - x m - x m
= 30 - 2x m
The breadth of the smaller rectangular field = 24 m - x m - x m
= 24 - 2x m
As we know, the area of a rectangle = length x breadth
⇒ Area of the larger rectangular field = 30 x 24 m2
= 720 m2
⇒ Area of the smaller rectangular field = (30 - 2x) x (24 - 2x) m2
= (720 - 108x - 4x2) m2
Area of the path = Area of larger rectangular field - Area of smaller rectangular field
⇒ 360 = 720 - (720 - 108x - 4x2)
⇒ 360 = 720 - 720 + 108x + 4x2
⇒ 4x2 + 108x - 360 = 0
⇒ x2 + 27x - 90 = 0
⇒ x2 + 30x - 3x - 90 = 0
⇒ x(x + 30) - 3(x + 30) = 0
⇒ (x + 30)(x - 3) = 0
⇒ x = - 30 or 3
Since the width of the path cannot be negative,
x = 3 m
Hence, the width of the path is 3 m.
A wire when bent in the form of a square encloses an area of 484 m2. Find the largest area enclosed by the same wire when bent to form :
(i) an equilateral triangle.
(ii) a rectangle of breadth 16 m.
Answer
(i) Area of the square = 484 m2
Let a be the length of side of the square.
⇒ a2 = 484
⇒ a =
⇒ a = 22 m
Total length of the wire = Perimeter of the square = 4 x 22m = 88 m
Perimeter of the square = Perimeter of equilateral triangle.
⇒ 3 x side = 88 m
⇒ side = m
⇒ side = 29.3 m
Area of equilateral triangle = x side2
= x (29.3)2 m2
= x 858.49 m2
= 372.57 m2
Hence, the area of the equilateral triangle is 372.57 sq. m.
(ii) Given:
Length of the rectangle = 16 m
Let b be the breadth of the rectangle.
Perimeter of the rectangle = Perimeter of the square
⇒ 2(l + b) = 88 m
⇒ 2(16 + b) = 88 m
⇒ 16 + b = m
⇒ 16 + b = 44 m
⇒ b = 44 - 16 m
⇒ b = 28 m
Area of the rectangle = l x b
= 16 x 28 m2
= 448 m2
Hence, the area of the rectangle is 448 sq. m.
For the trapezium given below; find its area.
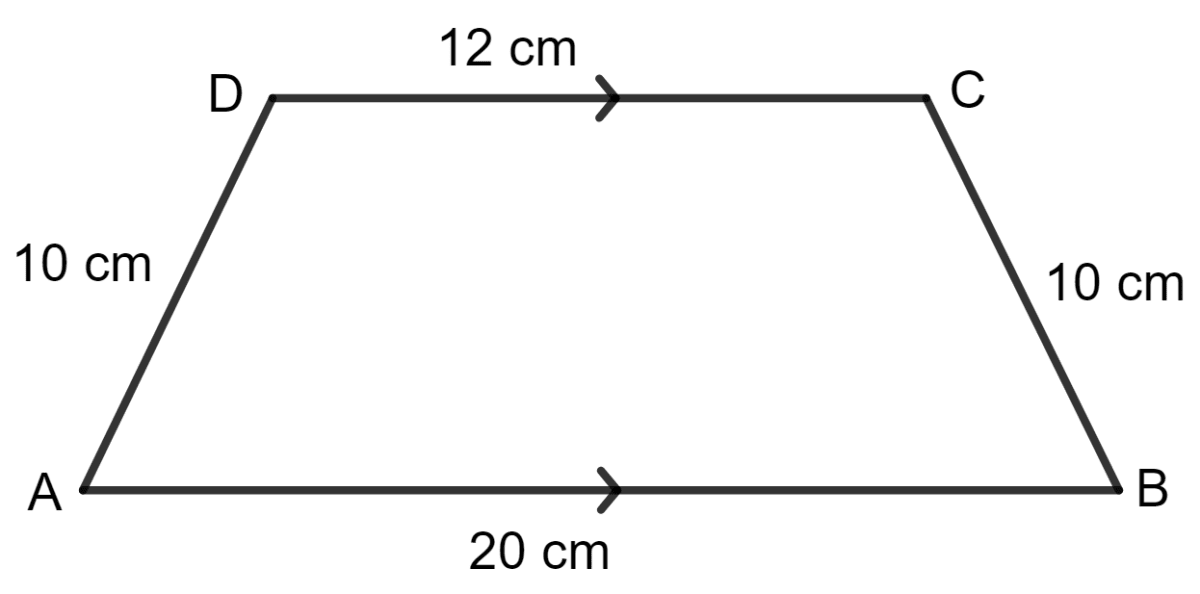
Answer
Draw CE parallel to DA which meets AB at point E.
Since, AB || DC thus AE || DC and DA || CE.
Since, opposite sides are parallel, thus AECD is a parallelogram.
Opposite sides of a parallelogram are equal, thus CE = AD = 10 cm and AE = DC = 12 cm.
In isosceles triangle EBC,
Draw CF ⊥ EB.
In an isosceles triangle, the perpendicular from the common vertex to the base, bisects it.
Thus, EF = = 4 cm.
In right triangle CEF,
By pythagoras theorem,
Hypotenuse2 = Perpendicular2 + Base2
EC2 = CF2 + EF2
102 = CF2 + 42
100 = CF2 + 16
CF2 = 100 - 16
CF2 = 84
CF = = 9.16 cm
By formula,
Area of trapezium = x sum of parallel sides x distance between them
Area of trapezium ABCD =
Hence, area of trapezium ABCD = 146.56 cm2.
For the trapezium given below; find its area.
Answer
Draw CO such that CO is perpendicular to AB.
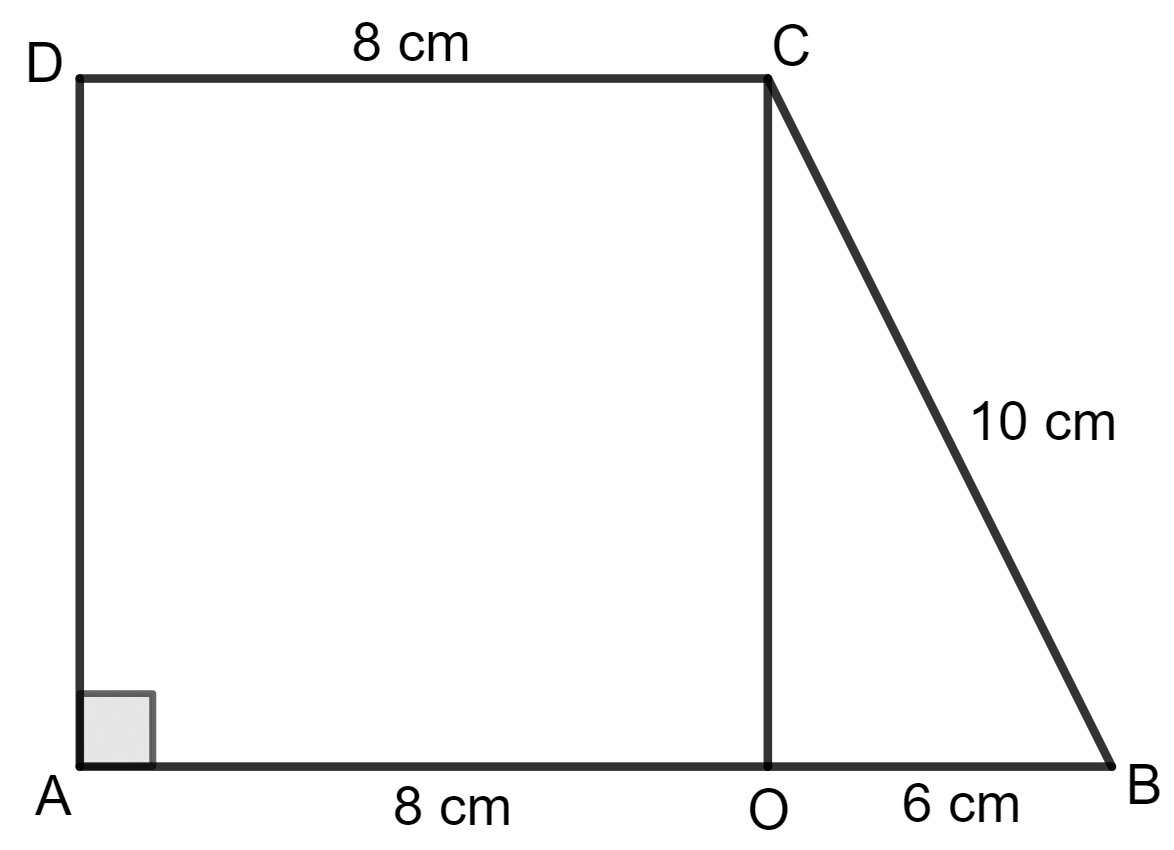
AO = DC = 8 cm
AB = AO + OB
⇒ 14 = 8 + OB
⇒ OB = 14 - 8 = 6 cm
Area of trapezium ABCD = x (sum of parallel sides) x height
In triangle BCO, by using the Pythagoras theorem,
Base2 + Height2 = Hypotenuse2
⇒ (6)2 + Height2 = 102
⇒ 36 + Height2 = 100
⇒ Height2 = 100 - 36
⇒ Height2 = 64
⇒ Height =
⇒ Height = 8 cm
Area of trapezium ABCD = x (8 + 14) x 8
= x 22 x 8 sq. cm
= 11 x 8 sq. cm
= 88 sq. cm
Hence, the area of trapezium ABCD is 88 sq. cm.
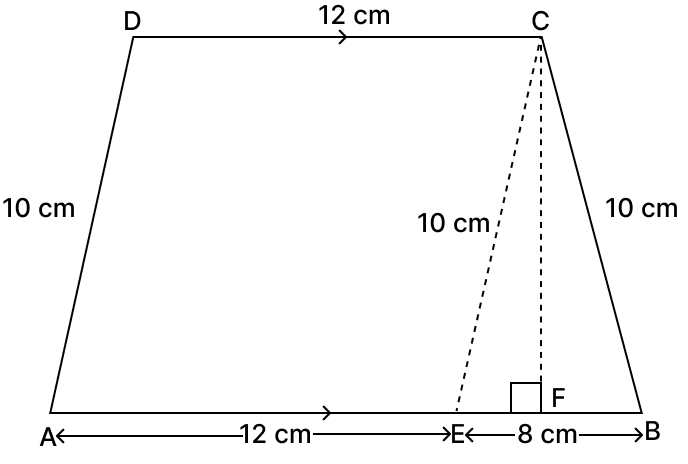
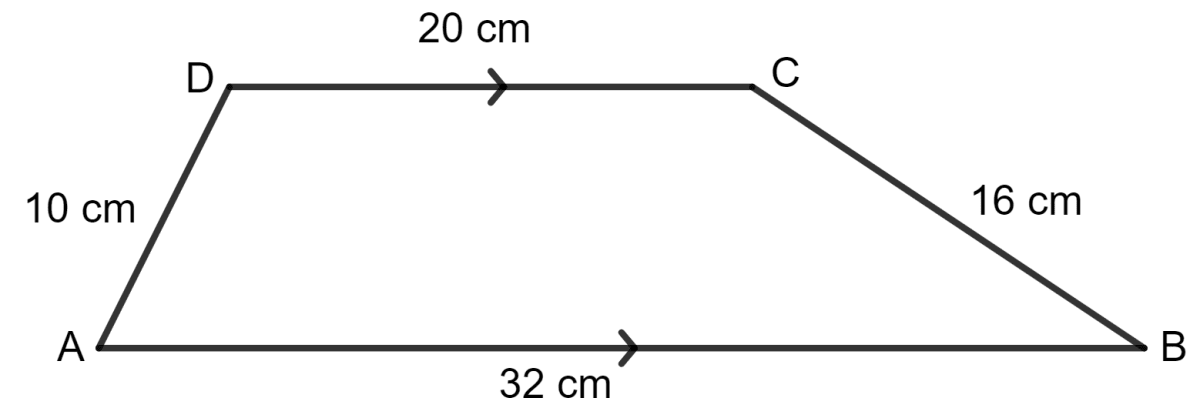
For the trapezium given below; find its area.
Answer
Draw CE parallel to DA which meets AB at point E.
AE = DC = 20 cm
AB = AE + EB
⇒ 32 = 20 + EB
⇒ EB = 32 - 20 = 12 cm
And, DA = CE = 10 cm
For the Δ EBC,
Let the sides of the triangle be:
a = 10 cm, b = 12 cm and c = 16 cm.
The semi-perimeter s:
∵ Area of triangle EBC =
= cm2
= cm2
= cm2
= 59.9 cm2
Let h be the height of Δ EBC,
Area of Δ EBC = x base x height
⇒ x 12 x height = 59.9
⇒ 6 x height = 59.9
⇒ height =
⇒ height = 9.98 cm
Area of trapezium ABCD = x (sum of parallel sides) x height
= x (20 + 32) x 9.98
= x 52 x 9.98 sq. cm
= 26 x 9.98 sq. cm
= 259.65 sq. cm
Hence, the area of trapezium ABCD is 259.65 sq. cm.
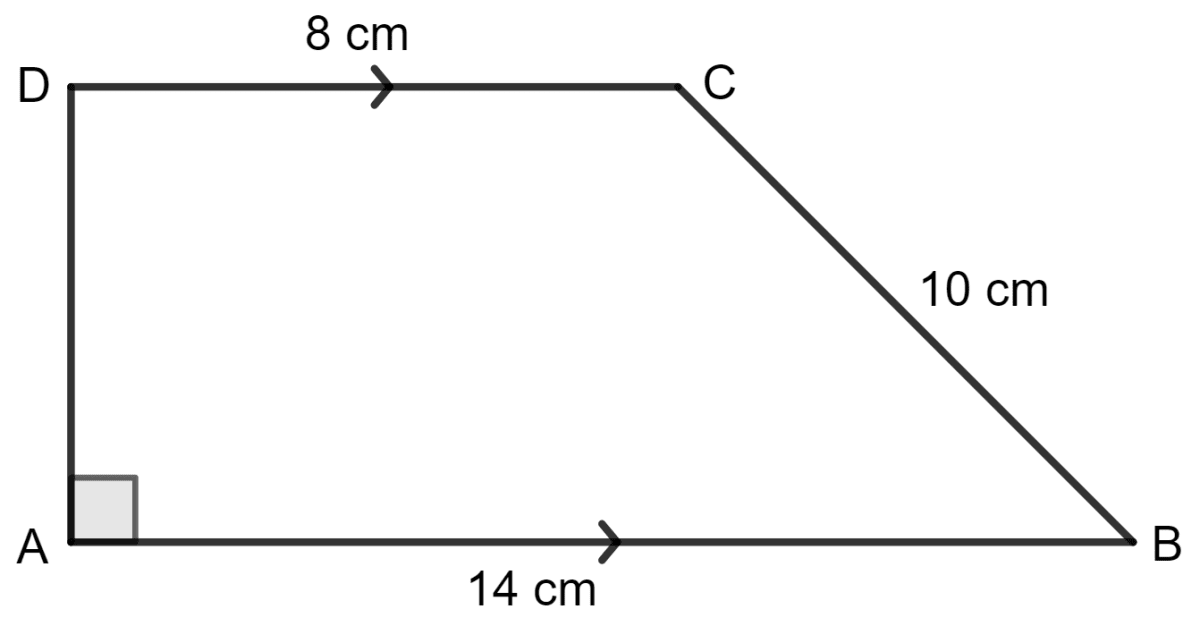
For the trapezium given below; find its area.
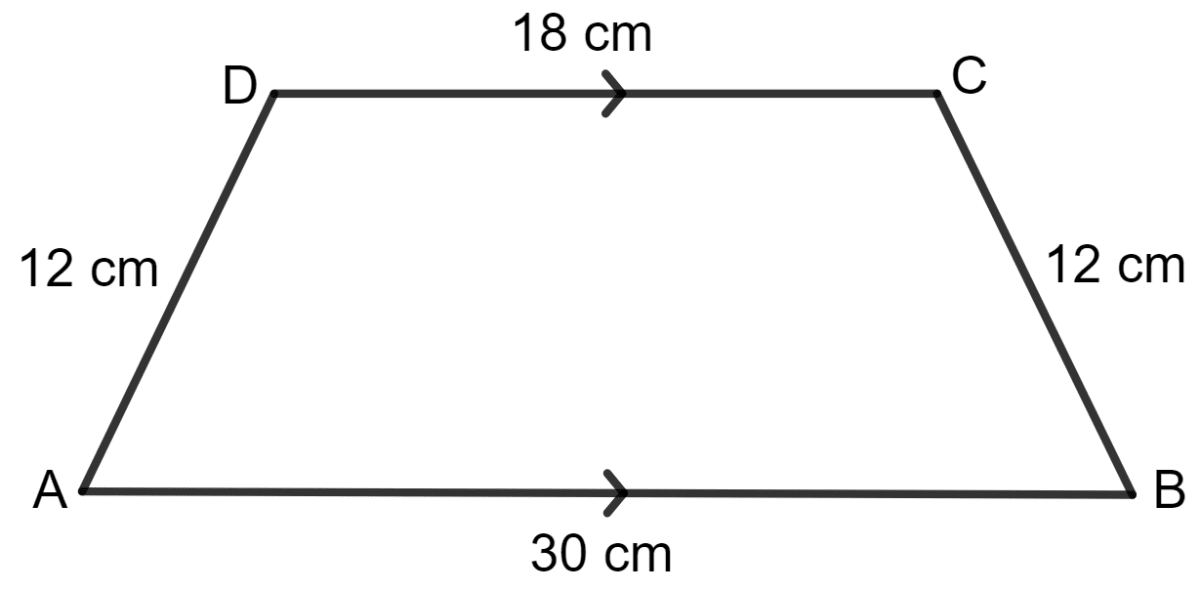
Answer
Draw DE and CF perpendicular to AB.
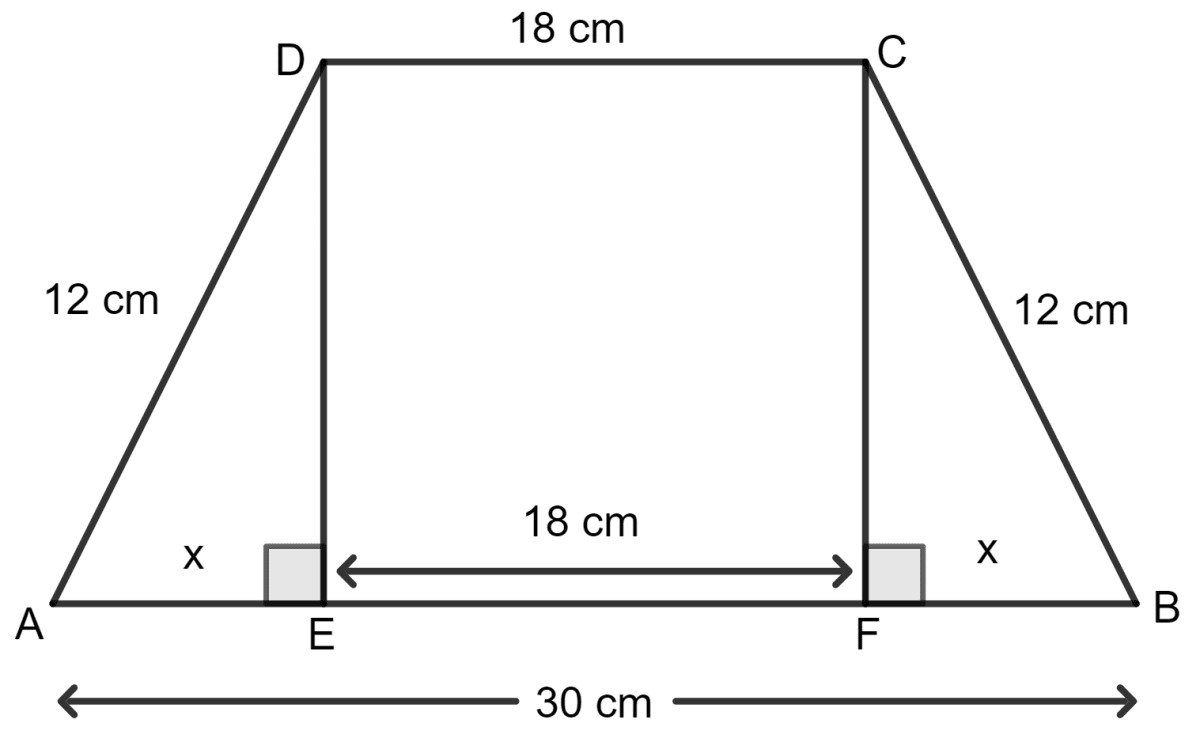
ABCD is an isosceles trapezium.
Let EF = FB = x cm
DC = EF = 18 cm
AB = AE + EF + FB
⇒ 30 = x + 18 + x
⇒ 30 = 2x + 18
⇒ 2x = 30 - 18
⇒ 2x = 12
⇒ x =
⇒ x = 6 cm
As EDA is a right angled triangle, by using the Pythagoras theorem,
Base2 + Height2 = Hypotenuse2
⇒ (6)2 + height2 = 122
⇒ 36 + height2 = 144
⇒ height2 = 144 - 36
⇒ height2 = 108 cm
⇒ height = cm
⇒ height = 10.39 cm
Area of trapezium ABCD = x (sum of parallel sides) x height
= x (18 + 30) x 10.39
= x 48 x 10.39 sq. cm
= 24 x 10.39 sq. cm
= 249.41 sq. cm
Hence, the area of trapezium ABCD is 249.41 sq. cm.
The perimeter of a rectangular board is 70 cm. Taking its length as x cm, find its width in terms of x.
If the area of the rectangular board is 300 cm2; find its dimensions.
Answer
Given:
Perimeter of the rectangular board = 70 cm
Length = x cm
Let b be the width of the rectangular board.
Perimeter of a rectangle = 2(l + b)
⇒ 2(x + b) = 70
⇒ x + b =
⇒ x + b = 35
⇒ b = 35 - x
Area = l x b
⇒ x (35 - x) = 300
⇒ 35x - x2 = 300
⇒ 35x - x2 - 300 = 0
⇒ x2 - 35x + 300 = 0
⇒ x2 - 20x - 15x + 300 = 0
⇒ x(x - 20) - 15(x - 20) = 0
⇒ (x - 20)(x - 15) = 0
⇒ x = 20 or 15
Therefore, b = (35 - x)
b = 15 or 20
Hence, the width of rectangular board is (35 - x) and the dimensions of the board are 20 cm and 15 cm.
The area of a rectangle is 640 m2. Taking its length as x m; find, in terms of x, the width of the rectangle. If the perimeter of the rectangle is 104 m; find its dimensions.
Answer
Given:
Area of the rectangle = 640 m2
Length = x meters
Let b be the width of the rectangle.
Area of the rectangle = l x b
⇒ x × b = 640
⇒ b = m
By formula,
Perimeter of the rectangle = 2(l + b)
⇒ = 104
⇒
⇒ = 52
⇒ x2 + 640 = 52x
⇒ x2 - 52x + 640 = 0
⇒ x2 - 32x - 20x + 640 = 0
⇒ x(x - 32) - 20(x - 32) = 0
⇒ (x - 20)(x - 32) = 0
⇒ x - 20 = 0 or x - 32 = 0
⇒ x = 20 m or x = 32 m.
Now,
⇒ b =
Case 1 : x = 20 m
⇒ b = = 32 m.
Case 2 : x = 32 m
⇒ b = = 20 m.
Hence, the width of rectangle is and the dimensions of the rectangle are 20 m and 32 m.
The length of a rectangle is twice the side of a square and its width is 6 cm greater than the side of the square. If area of the rectangle is three times the area of the square; find the dimensions of each.
Answer
Given:
Let s be the side of the square.
Length of the rectangle = 2 x Side of the square
⇒ l = 2s
Width of the rectangle = Side of the square + 6
⇒ w = s + 6
Area of the rectangle = 3 x area of the square
⇒ l x w = 3s2
⇒ 2s x (s + 6) = 3s2
⇒ 2s2 + 12s = 3s2
⇒ 2s2 + 12s - 3s2 = 0
⇒ - s2 + 12s = 0
⇒ s2 - 12s = 0
⇒ s(s - 12) = 0
⇒ s = 0 or 12
Since the side cannot be zero, s = 12 cm.
The dimensions of the rectangle:
l = 2 x s = 2 x 12 cm = 24 cm
w = s + 6 = 12 + 6 = 18 cm
Hence, the length and width of the rectangle are 24 cm and 18 cm, and the side of the square is 12 cm.
ABCD is a square with each side 12 cm. P is a point on BC such that area of Δ ABP : area of trapezium APCD = 1 : 5. Find the length of CP.
Answer
Square ABCD is shown in the figure below:
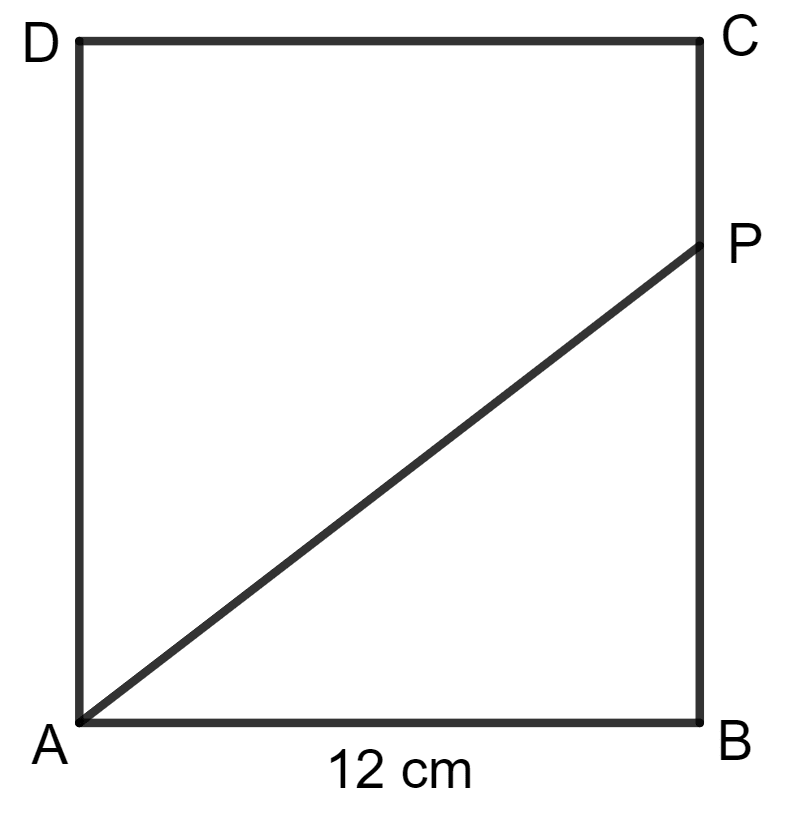
Given:
Area of Δ ABP = x base x height
= x 12 x (12 - CP)
Area of trapezium APCD = x (sum of parallel sides) x height
= x (12 + CP) x 12
Hence, the length of CP is 8 cm.
A rectangular plot of land measures 45 m x 30 m. A boundary wall of height 2.4 m is built all around the plot at a distance of 1 m from the plot. Find the area of the inner surface of the boundary wall.
Answer
Given:
The boundary wall is built all around the rectangular plot at a distance of 1 meter, which means the wall forms a larger rectangle around the plot as shown in the figure below:
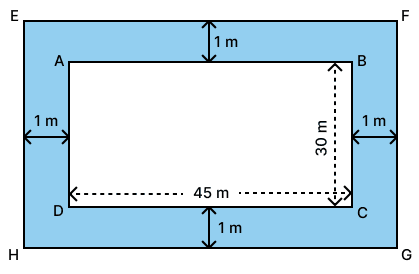
Dimensions of the outer rectangle (including the boundary wall):
Length of the outer rectangle = (45 + 1 + 1) m = 47 m
Width of the outer rectangle = (30 + 1 + 1) m = 32 m
Perimeter of the outer rectangle = 2(length + breadth)
= 2(47 + 32)
= 2 x 79 = 158 m
Area of the inner surface of the boundary wall is the perimeter of the outer rectangle multiplied by the height of the wall.
Inner surface area of boundary wall = Perimeter of outer rectangle x height of wall
= 158 m x 2.4 m
= 379.2 m2
Hence, the area of the inner surface of the boundary wall is 379.2 m2.
A wire when bent in the form of a square encloses an area = 576 cm2. Find the largest area enclosed by the same wire when bent to form:
(i) an equilateral triangle.
(ii) a rectangle whose adjacent sides differ by 4 cm.
Answer
(i) Area of the square = 576 cm2
Let a be the length of side of the square.
⇒ a2 = 576
⇒ a =
⇒ a = 24 cm
Total length of the wire = Perimeter of the square = 4 x 24 cm = 96 cm
Perimeter of the square = Perimeter of equilateral triangle.
⇒ 3 x side = 96 cm
⇒ side = cm
⇒ side = 32 cm
Area of equilateral triangle = x side2
= x (32)2 cm2
= x 1,024 cm2
= 256 cm2
Hence, the area of equilateral triangle is 256 cm2.
(ii) Given:
Let l be the length and b be the breadth of the rectangle.
l - b = 4 ...............(1)
Perimeter of rectangle = Perimeter of square
⇒ 2(l + b) = 96 cm
⇒ 2(l + b) = 96 cm
⇒ l + b = cm
⇒ l + b = 48 cm ...............(2)
Add equation (1) and (2), we get
⇒ (l - b) + (l + b) = 4 + 48
⇒ l - b + l + b = 52
⇒ 2l = 52
⇒ l =
⇒ l = 26 cm
So, b = l - 4 = 26 - 4 = 22 cm
Area of rectangle = l x b
= 26 x 22 cm2
= 572 cm2
Hence, the area of rectangle is 572 cm2.
The area of a parallelogram is y cm2 and its height is h cm. The base of another parallelogram is x cm more than the base of the first parallelogram and its area is twice the area of the first. Find, in terms of y, h and x, the expression for the height of the second parallelogram.
Answer
Given:
Area of the first parallelogram = y cm2
Height of the first parallelogram = h cm
Area of the first parallelogram = base x height
⇒ y = base x h
⇒ base of the first parallelogram = cm
The base of the second parallelogram = cm
Area of the second parallelogram = base x height
⇒ x height
⇒ height =
Hence, the height of the second parallelogram is .
The distance between parallel sides of a trapezium is 15 cm and the length of the line segment joining the mid-points of its non-parallel sides is 26 cm. Find the area of the trapezium.
Answer
Given:
Let the given trapezium be as shown in the figure below:

The distance between parallel sides of a trapezium, (i.e., height) = 15 cm
The length of the line segment joining the mid-points of its non-parallel sides, EF = 26 cm
Since EF is half of the sum of the lengths of the parallel sides.
EF = x (AD + BC)
⇒ x (AD + BC) = 26
⇒ AD + BC = 26 x 2 cm = 52 cm
Area of trapezium = x (Sum of parallel sides) x height
= x (AD + BC) x height
= x 52 x 15
= 26 x 15
= 390 cm2
Hence, the area of the trapezium is 390 cm2.
The diagonal of a rectangular plot is 34 m and its perimeter is 92 m. Find its area.
Answer
Given:
Diagonal of the rectangular plot = 34 m
Perimeter of the rectangular plot = 92 m
Let l be the length and b be the breadth of the rectangular plot.
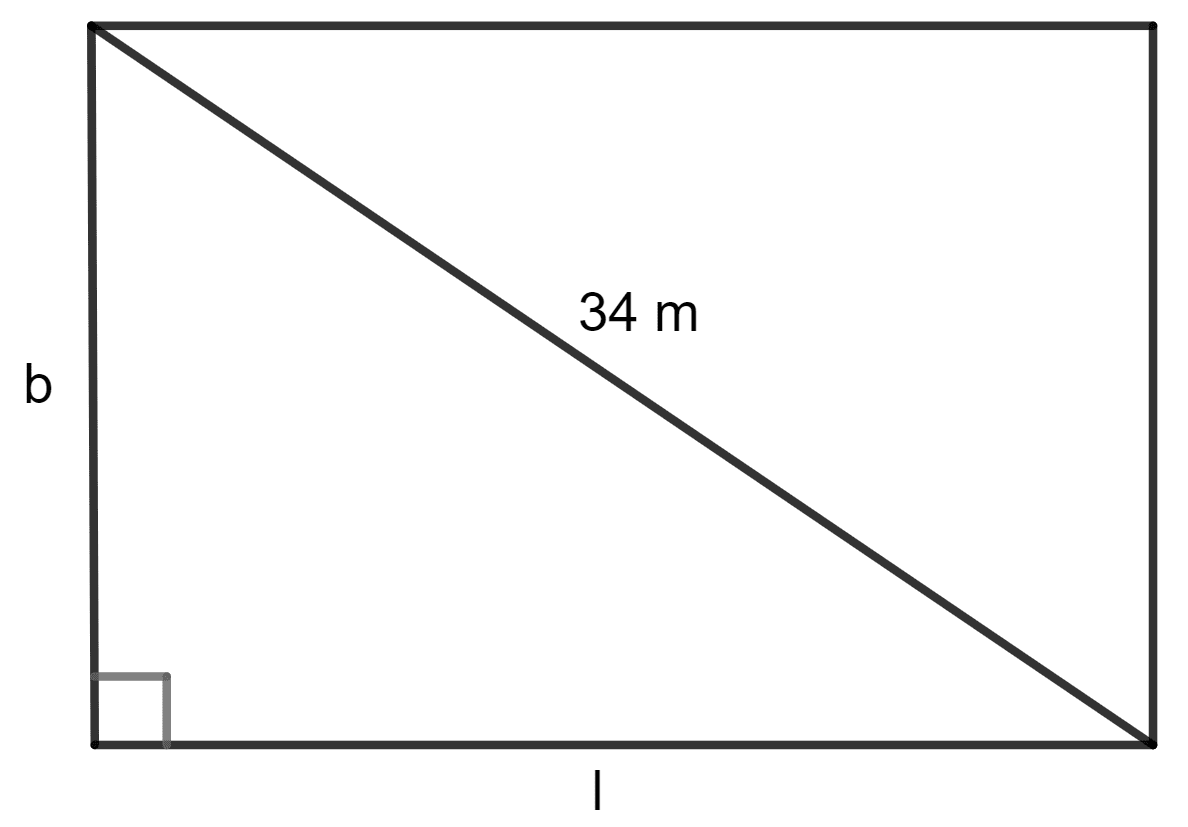
Perimeter = 2(l + b)
⇒ 2(l + b) = 92
⇒ l + b =
⇒ l + b = 46
Squaring both side,
⇒ (l + b)2 = 462
⇒ l2 + b2 + 2lb = 2,116 ...............(1)
As all the angles of rectangle are 90°, we can use the Pythagoras theorem,
Base2 + Height2 = Hypotenuse2
⇒ l2 + b2 = 342
⇒ l2 + b2 = 1,156
Using equation (1), we get
⇒ 2,116 - 2lb = 1,156
⇒ 2,116 - 1,156 = 2lb
⇒ 960 = 2lb
⇒ lb =
⇒ lb = 480
Hence, the area of the rectangular plot is 480 m2.
The cost of fencing a circular field at the rate of ₹ 240 per metre is ₹ 52,800. The field is to be ploughed at the rate of ₹ 12.50 per m2. Find the cost of ploughing the field.
Answer
Given:
Rate of fencing = ₹ 240 per metre
Total cost = ₹ 52,800
Let r be the radius of the field.
Total cost = Circumference of field x Rate of fencing
Area of the field = πr2
Rate of ploughing = ₹ 12.50 per m2
Total cost of ploughing = Area of the field x Rate of ploughing
= 3,850 x 12.50
= ₹ 48,125
Hence, the total cost of ploughing is ₹ 48,125.
Two circles touch each other externally. The sum of their areas is 58π cm2 and the distance between their centres is 10 cm. Find the radii of the two circles.
Answer
Let r1 and r2 be the radii of the two circles.
Sum of the areas = 58π
⇒ A1 + A2 = 58π
⇒ πr12 + πr22 = 58π
⇒ π(r12 + r22) = 58π
⇒ (r12 + r22) = 58
⇒ r12 + r22 = 58 ...............(1)
Also, since the circles touch externally, the sum of their radii equals the distance between their centers.
r1 + r2 = 10
⇒ r1 = 10 - r2
Substituting the value of r1 in equation (1),
⇒ (10 - r2)2 + r22 = 58
⇒ 102 + r22 - 2 x 10 x r2 + r22 = 58
⇒ 100 + 2r22 - 20r2 = 58
⇒ 100 + 2r22 - 20r2 - 58 = 0
⇒ 2r22 - 20r2 - 42 = 0
⇒ r22 - 10r2 - 21 = 0
⇒ r22 - 3r2 - 7r2 - 21 = 0
⇒ r2(r2 - 3) - 7(r2 - 3) = 0
⇒ (r2 - 3)(r2 - 7) = 0
⇒ r2 = 3 cm or 7 cm
Using equation (1), we find r1:
If r2 = 3, then r1 = 10 - 3 = 7 cm
If r2 = 7, then r1 = 10 - 7 = 3 cm
Hence, the radii of the two circles are 7 cm and 3 cm.
The given figure shows a rectangle ABCD inscribed in a circle as shown alongside.
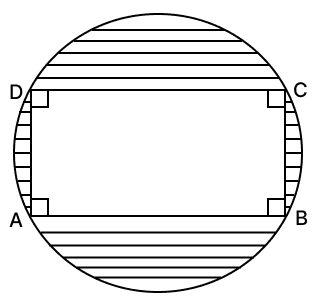
If AB = 28 cm and BC = 21 cm, find the area of the shaded portion of the given figure.
Answer
ABCD is a rectangle. So, ∠ABC = 90°.
By using the Pythagoras theorem,
Let h be the diagonal of the rectangle.
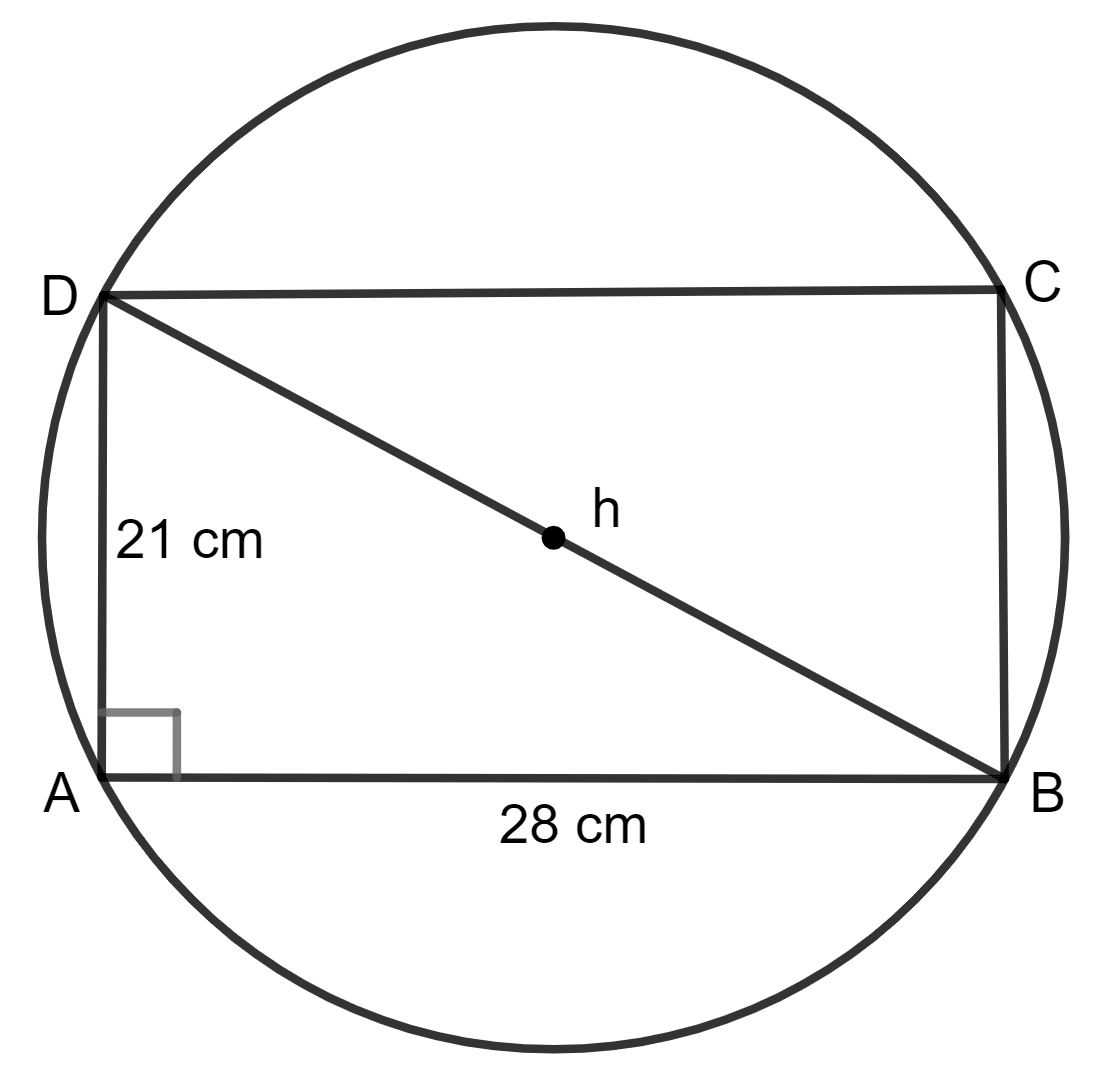
Base2 + Height2 = Diagonal2
⇒ 282 + 212 = h2
⇒ 784 + 441 = h2
⇒ 1,225 = h2
⇒ h =
⇒ h = 35 cm
Diagonal of rectangle = Diameter of circle.
Radius = = = 17.5 cm
Area of shaded portion = Area of circle - Area of rectangle
= πr2 - lb cm2
= x 17.52 - 28 x 21 cm2
= x 306.25 - 28 x 21 cm2
= 22 x 43.75 - 588 cm2
= 962.5 - 588 cm2
= 374.5 cm2
Hence, area of the shaded portion = 374.5 cm2.
A square is inscribed in a circle of radius 7 cm. Find the area of the square.
Answer
Diagonal of the square = Diameter of the circle.
Radius of circle = 7 cm
Diameter of circle = 2 x 7 cm = 14 cm
Diagonal of square = 14 cm
Let s be the side of square.
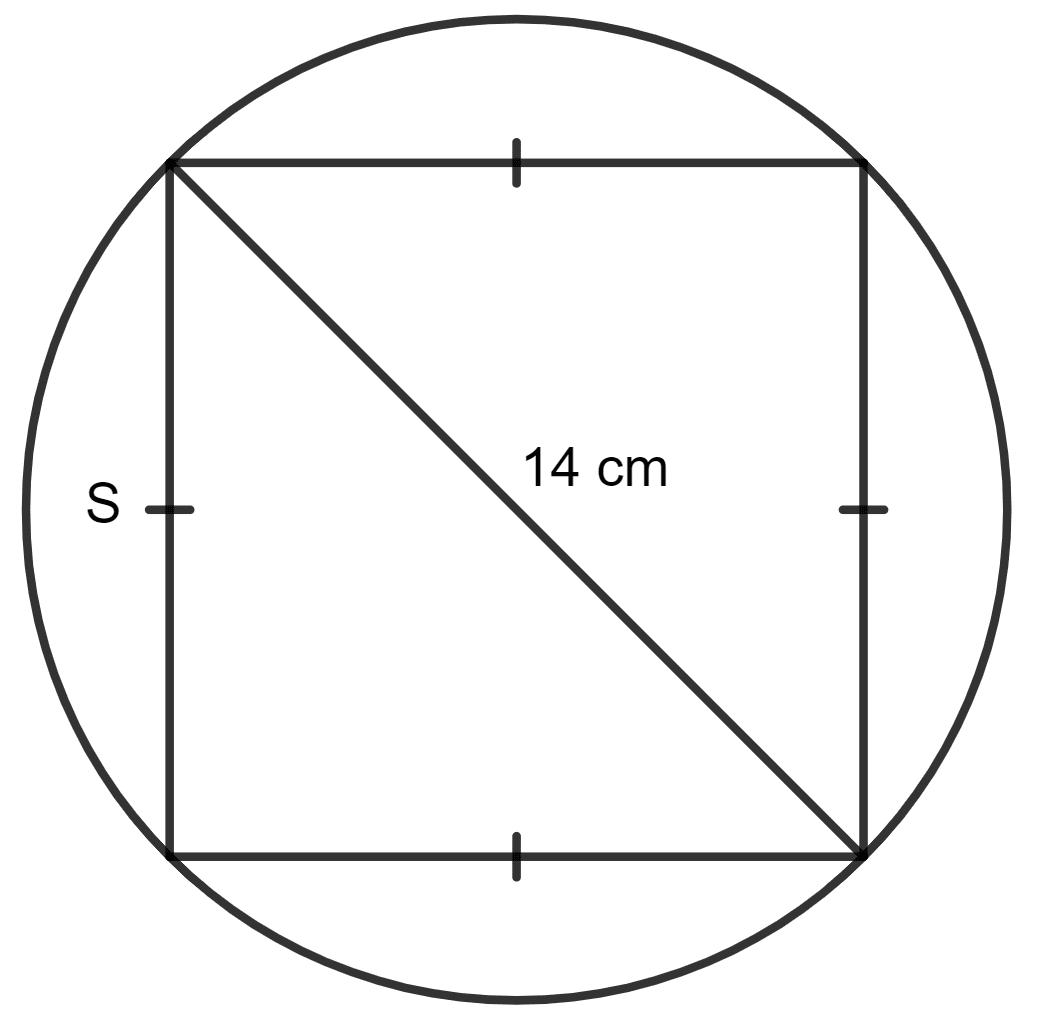
By using the Pythagoras theorem,
Base2 + Height2 = Hypotenuse2
⇒ s2 + s2 = 142
⇒ 2s2 = 196
⇒ s2 =
⇒ s2 = 98 cm
⇒ s = cm
Area of square = Side2
= cm2
= 98 cm2
Hence, the area of the square is 98 cm2.
A metal wire, when bent in the form of an equilateral triangle of largest area, encloses an area of . If the same wire is bent into the form of a circle of largest area, find the area of this circle.
Answer
Given:
Area of the equivalent triangle =
Let a be the length of the equivalent triangle.
Area of equivalent triangle =
Perimeter of the triangle = 3 x side
= 3 x 44 cm = 132 cm
Perimeter of triangle = Circumference of circle
Area of circle = πr2
Hence, the area of the circle is 1,386 cm2.
The perimeter of a triangle is 450 m and its sides are in the ratio 12 : 5 : 13. Find the area of the triangle.
Answer
Given:
Perimeter of the triangle = 450 m
Ratio of the sides = 12 : 5 : 13.
Let the sides of triangle be 12a, 5a and 13a.
Perimeter of the triangle = Sum of sides of the triangle
⇒ 12a + 5a + 13a = 450
⇒ 30a = 450
⇒ a =
⇒ a = 15
Thus, sides are 12 x 15, 5 x 15 and 13 x 15 m
= 180 m, 75 m and 195 m
The sides of the triangle are:
a = 180 m, b = 75 m and c = 195 m.
The semi-perimeter s:
∵ Area of triangle =
= m2
= m2
= m2
= 6,750 m2
Hence, the area of the triangle is 6,750 m2.
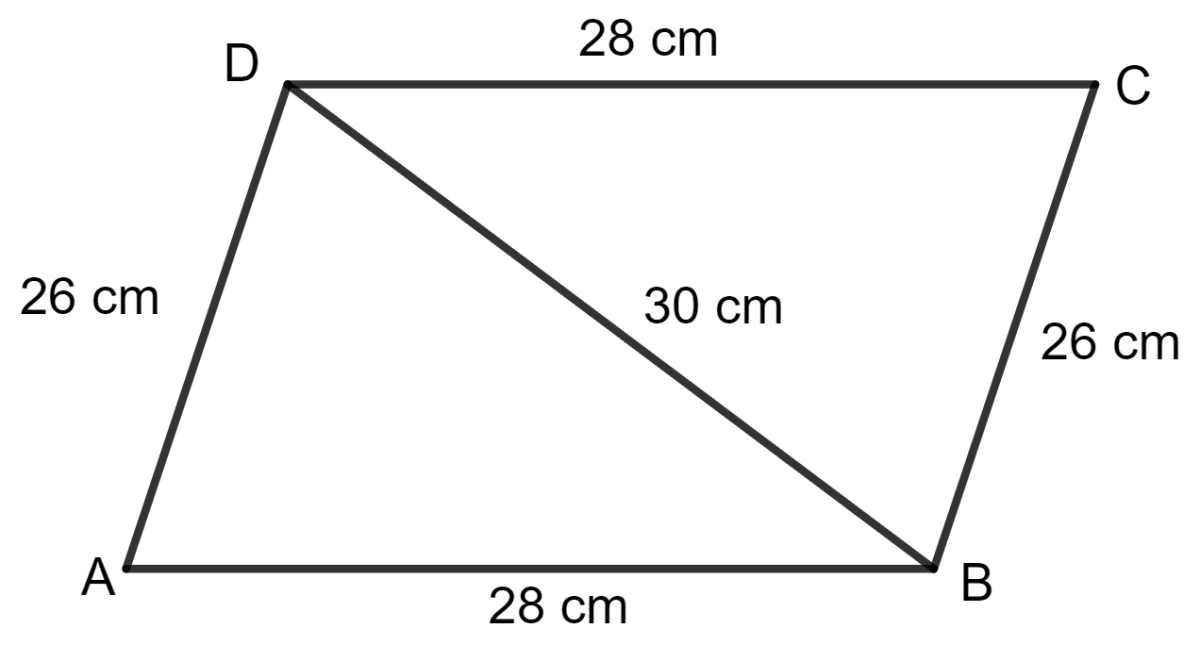
A triangle and a parallelogram have the same base and the same area. If the sides of the triangle are 26 cm, 28 cm and 30 cm and the parallelogram stands on the base 28 cm, find the height of the parallelogram.
Answer
Let the sides of the triangle be:
a = 26 cm, b = 28 cm and c = 30 cm.
The semi-perimeter s of the triangle is:
∵ Area of triangle =
= cm2
= cm2
= cm2
= 336 cm2
Area of triangle = Area of parallelogram
(∵ Area of parallelogram = base x height)
Let h be the height of parallelogram.
⇒ 336 = 28 x h
⇒ h =
⇒ h = 12 cm
Hence, the height of the parallelogram is 12 cm.
Using the information in the following figure, find the area of the trapezium.
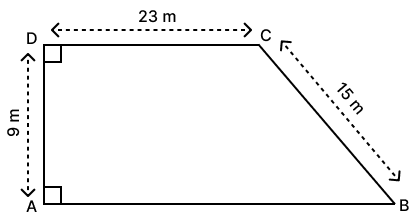
Answer
Draw a perpendicular line CP on AB, such that CP = 9 m and AP = 23 m.
Let PB = a m
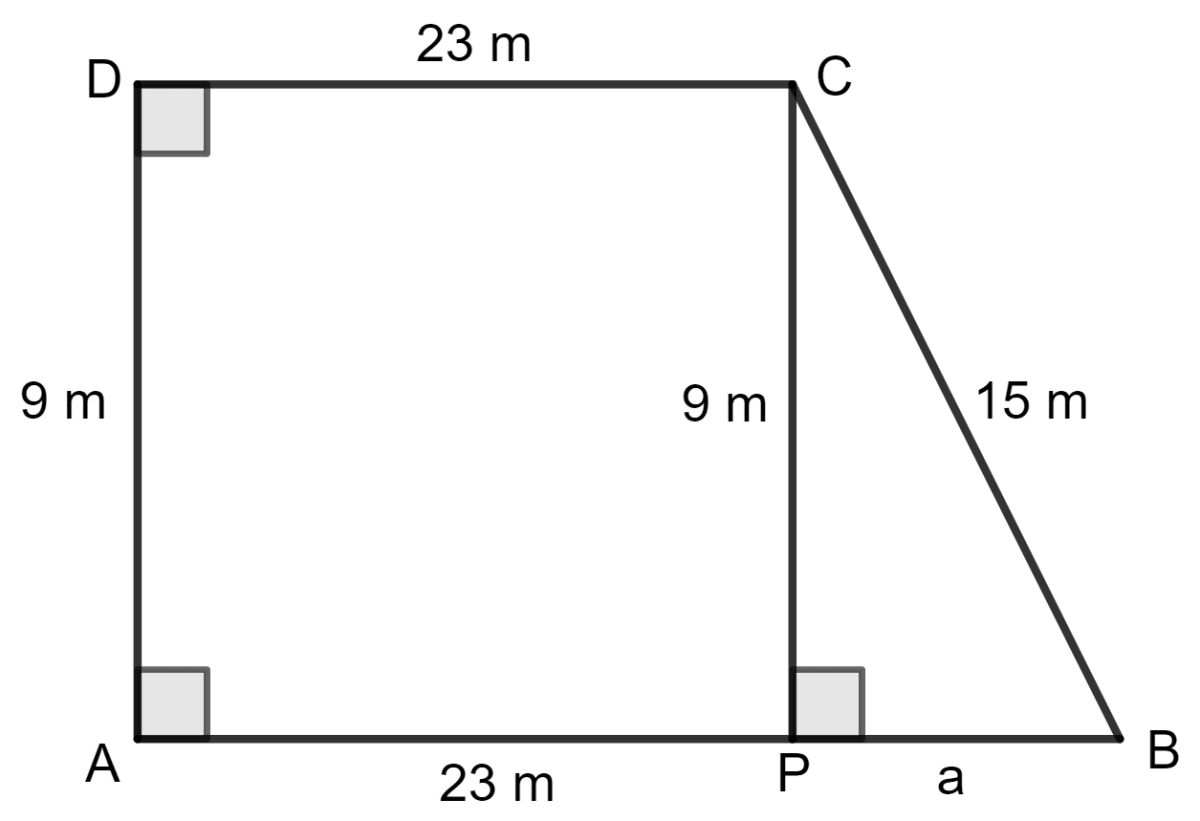
In Δ CPB, by using the Pythagoras theorem,
Base2 + Height2 = Hypotenuse2
⇒ a2 + (9)2 = (15)2
⇒ a2 + 81 = 225
⇒ a2 = 225 - 81
⇒ a2 = 144
⇒ a2 = 144
⇒ a =
⇒ a = 12 m
So, AB = AP + PB = 23 + 12 = 35 m
Area of trapezium = (sum of parallel sides) x height
= (23 + 35) x 9
= x 58 x 9
= 29 x 9
= 261 m2
Hence, the area of the trapezium is 261 m2.
Sum of the areas of two squares is 400 cm2. If the difference of their perimeters is 16 cm, find the sides of the two squares.
Answer
Given:
Sum of the areas of two squares = 400 cm2.
The difference of their perimeters = 16 cm
Let a and b be the sides of 2 square.
Sum of Areas,
⇒ a2 + b2 = 400 ...............(1)
Difference of Perimeters,
⇒ 4a - 4b = 16
⇒ 4(a - b) = 16
⇒ a - b =
⇒ a - b = 4
⇒ a = 4 + b
Substituting the value of a in equation (1), we get
⇒ (4 + b)2 + b2 = 400
⇒ 42 + b2 + 2 x 4 x b + b2 = 400
⇒ 16 + b2 + 8b + b2 = 400
⇒ 16 + 2b2 + 8b - 400 = 0
⇒ 2b2 + 8b - 384 = 0
⇒ b2 + 4b - 192 = 0
⇒ b2 + 16b - 12b - 192 = 0
⇒ b(b + 16) - 12(b + 16) = 0
⇒ (b + 16)(b - 12) = 0
⇒ b = - 16 or 12
Since the side of a square cannot be negative, b = 12 cm.
So, a = 4 + b = 16 cm
Hence, the sides of the squares are 16 cm and 12 cm.
Find the area and the perimeter of a square with diagonal 24 cm.
[Take = 1.41].
Answer
Diagonal of the square = 24 cm
Let a be the side of square.
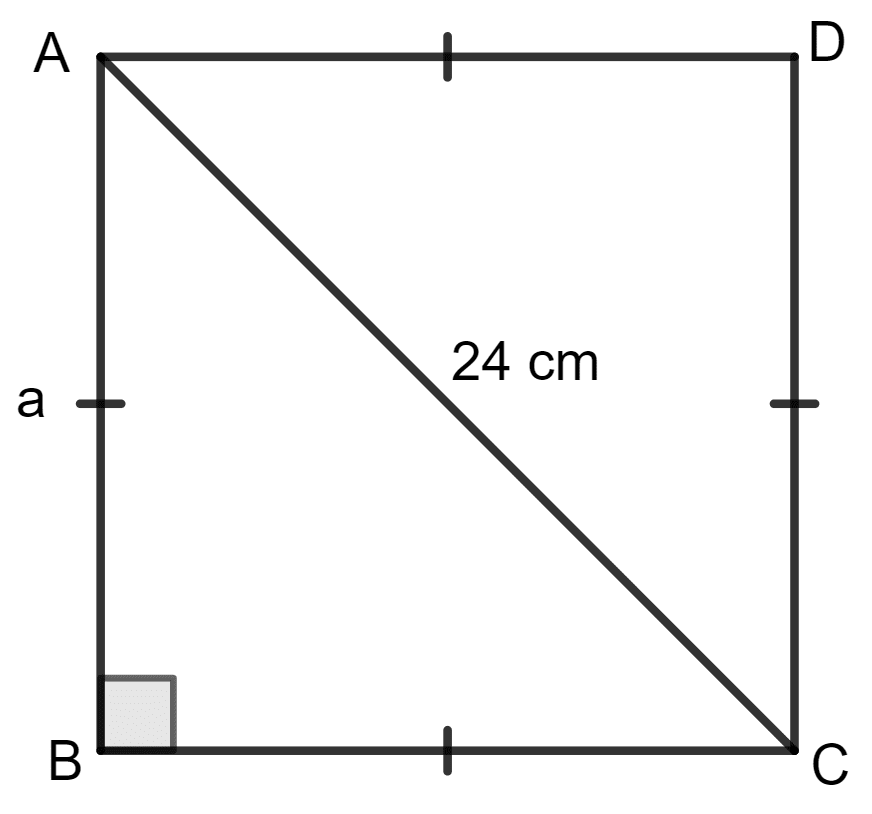
By using the Pythagoras theorem,
AB2 + BC2 = AC2
⇒ a2 + a2 = (24)2
⇒ 2a2 = 576
⇒ a2 =
⇒ a2 = 288
⇒ a =
⇒ a = 12
⇒ a = 12 x 1.41 = 16.92 cm
Area of the square = side2
= ()2 cm2
= 288 cm2
Perimeter of the square = 4 x side
= 4 x 16.92 cm
= 67.68 cm
Hence, the area of the square is 288 cm2 and the perimeter is 67.68 cm.
A steel wire, when bent in the form of a square, encloses an area of 121 cm2. The same wire is bent in the form of a circle. Find area of the circle.
Answer
Given:
Area of the square = 121 cm2
Let s be the side of the square.
As we know, the area of the square = side2
⇒ s2 = 121
⇒ s =
⇒ s = 11
Total length of the wire = Perimeter of the square
As we know, the perimeter of the square = 4 x side
= 4 x 11
= 44 cm
Perimeter of the square = Circumference of the circle
Let r be the radius of the circle.
⇒ 2πr = 44
Area of the circle = πr2
Hence, the area of the circle is 154 cm2.
The perimeter of a semicircular plate is 108 cm, find its area.
Answer
Given:
Perimeter of the semicircular plate = 108 cm
Let r be the radius of the plate.
The perimeter of the semicircular plate includes the curved part (half the circumference of a circle) and the diameter. So,
⇒ πr + 2r = Perimeter
⇒ πr + 2r = 108
⇒ r(π + 2) = 108
⇒ r = 108
⇒ r = 108
⇒ r = 108
⇒ r = 108
⇒ r =
⇒ r = 7 x 3 = 21 cm
Area of semicircular plate = πr2
Hence, the area of the semicircular plate is 693 cm2.
Two circles touch externally. The sum of their areas is 130π sq. cm and the distance between their centres is 14 cm. Find the radii of the circles.
Answer
Given:
Sum of areas of two circles = 130π cm2
The distance between their centres = 14 cm
Let and be the radii of 2 circles.
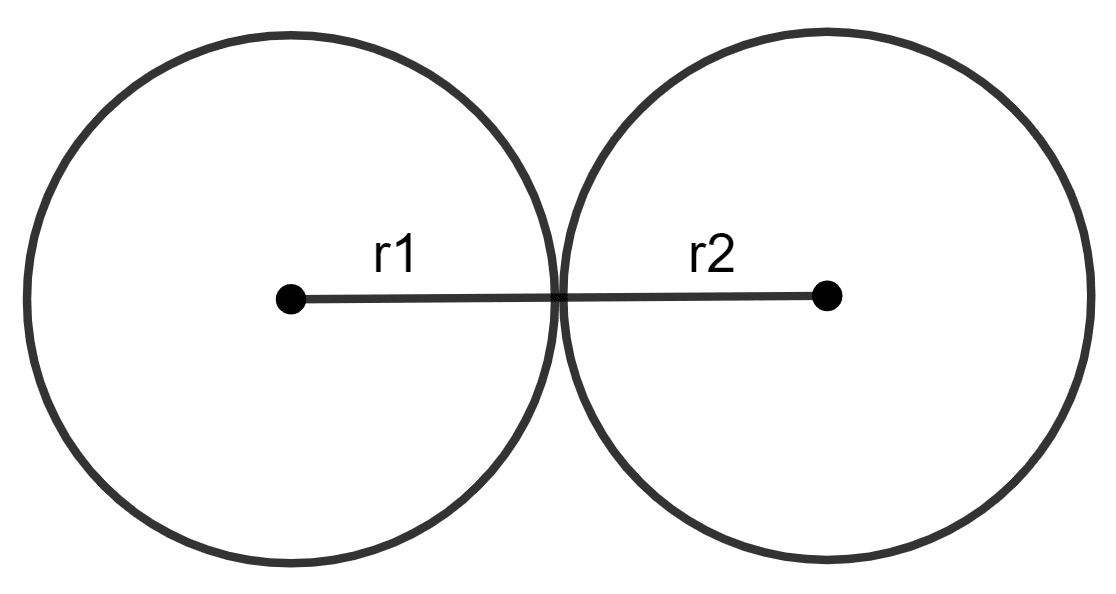
Area of the first circle + Area of the second circle = 130π
⇒ A1 + A2 = 130π
⇒ πr12 + πr22 = 130π
⇒ π(r12 + r22) = 130π
⇒ (r12 + r22) = 130
⇒ r12 + r22 = 130 ...............(1)
Also, since the circles touch externally, the sum of their radii equals the distance between their centers.
r1 + r2 = 14
⇒ r1 = 14 - r2
Putting the value of r1 in equation (1),
⇒ (14 - r2)2 + r22 = 130
⇒ 142 + r22 - 2 x 14 x r2 + r22 = 130
⇒ 196 + 2r22 - 28r2 = 130
⇒ 196 + 2r22 - 28r2 - 130 = 0
⇒ 2r22 - 28r2 + 66 = 0
⇒ r22 - 14r2 + 33 = 0
⇒ r22 - 11r2 - 3r2 + 33 = 0
⇒ r2(r2 - 11) - 3(r2 - 11) = 0
⇒ (r2 - 11)(r2 - 3) = 0
⇒ r2 = 11 cm or 3 cm
Using equation (1), we find r1:
If r2 = 11, then r1 = 14 - 11 = 3cm
If r2 = 3, then r1 = 14 - 3 = 11cm
Hence, the radii of the two circles are 11 cm and 3 cm.
The diameters of the front and the rear wheels of a tractor are 63 cm and 1.54 m respectively. The rear wheel is rotating at revolutions per minute. Find :
(i) the revolutions per minute made by the front wheel.
(ii) the distance travelled by the tractor in 40 minutes.
Answer
(i) Given:
Diameter of the rear wheel = 1.54 m
Diameter of the front wheel = 0.63 m
Radius of the rear wheel = = = 0.77 m
Radius of the front wheel = = = 0.315 m
Distance travelled by the tractor in 1 revolution of the rear wheel = Circumference of the rear wheel
= 2πr
The number of revolutions per minute for the rear wheel is = =
So, the distance traveled by the rear wheel in one minute is = 4.84 x
= 0.44 x 270
= 118.8 m
Let x be the number of revolutions made by the front wheel.
The total distance travelled by tractor in 1 min = Number of revolutions made by the front wheel in 1 min x Circumference of wheel
Hence, the number of revolutions made by the front wheel is 60.
(ii) Distance travelled by the tractor in 40 minutes = Number of revolutions made by the rear wheel in 40 min x Circumference of the rear wheel
Hence, the distance travelled by the tractor in 40 minutes is 4,752 m = 4.752 km.
Two circles touch each other externally. The sum of their areas is 74π cm2 and the distance between their centres is 12 cm. Find the diameters of the circle.
Answer
Given:
Sum of area = 740π cm2
The distance between their centres = 12 cm
Let and be the radius of 2 circles.
⇒ A1 + A2 = 74π
⇒ πr12 + πr22 = 74π
⇒ π(r12 + r22) = 74π
⇒ (r12 + r22) = 74
⇒ r12 + r22 = 74 ...............(1)
And, r1 + r2 = 12
⇒ r1 = 12 - r2
Putting the value of r1 in equation (1),
⇒ (12 - r2)2 + r22 = 74
⇒ 122 + r22 - 2 x 12 x r2 + r22 = 74
⇒ 144 + 2r22 - 24r2 = 74
⇒ 144 + 2r22 - 24r2 - 74 = 0
⇒ 2r22 - 24r2 + 70 = 0
⇒ r22 - 12r2 + 35 = 0
⇒ r22 - 7r2 - 5r2 + 35 = 0
⇒ r2(r2 - 7) - 5(r2 - 7) = 0
⇒ (r2 - 7)(r2 - 5) = 0
⇒ r2 = 7 cm or 5 cm
⇒ r1 = 12 - r2 = 12 - 7 or 12 - 5 = 5 cm or 7 cm
Hence, the radius of 2 circles = 7 cm and 5 cm.
If a square is inscribed in a circle, find the ratio of the areas of the circle and the square.
Answer
Let a be the side of the square.
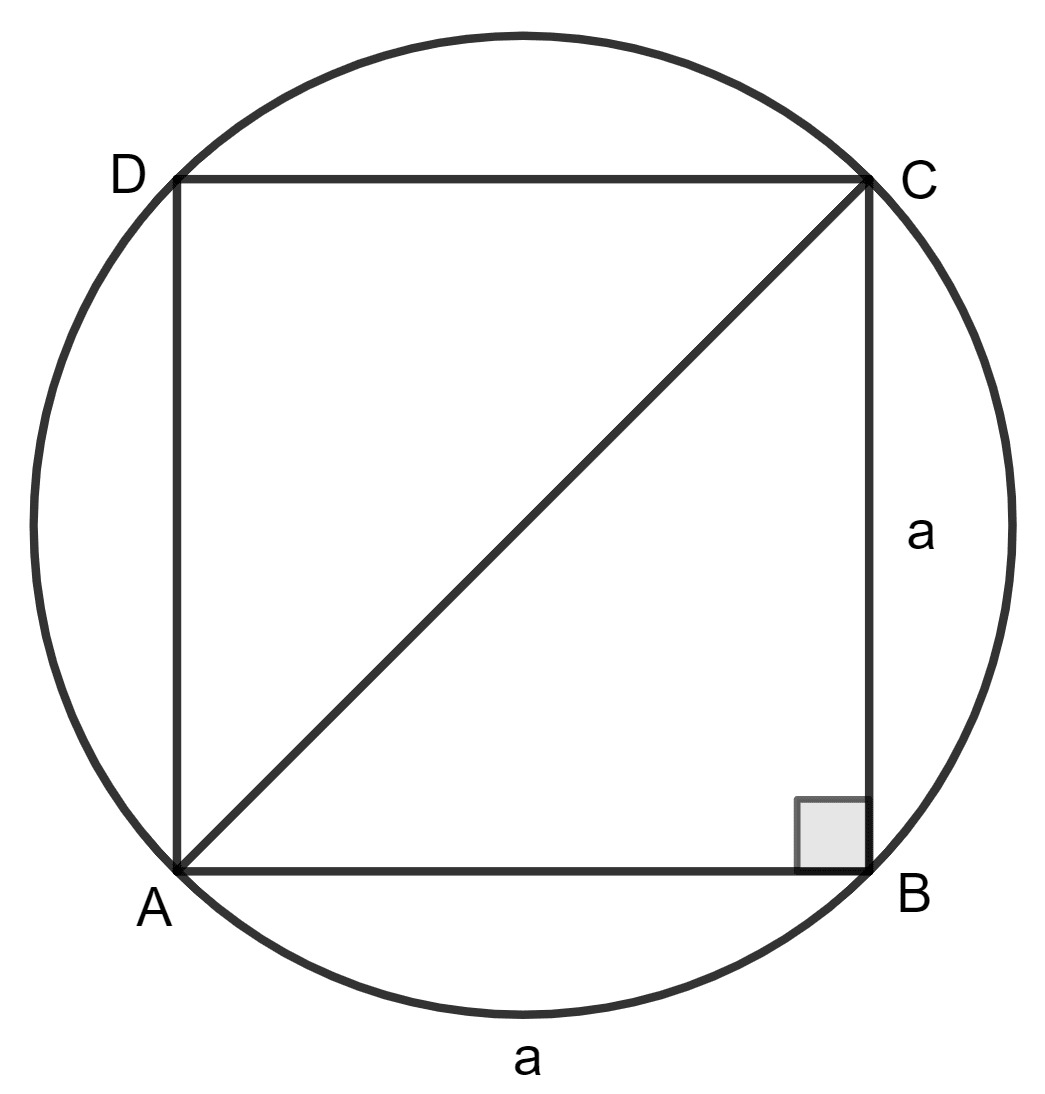
By using the Pythagoras theorem,
AB2 + BC2 = AC2
⇒ a2 + a2 = AC2
⇒ AC2 = 2a2
⇒ AC = a
Diagonal of the square = Diameter of the circle
d = a
Radius, r = =
Now, the ratio of the area of the circle to the area of the square is:
Hence, the ratio of the area of the circle to the area of the square is 11 : 7.