Solids

The area of a square on the diagonal of a cube is 48 cm². Each edge of the cube is :

1. 2 cm

2. 4 cm

3. 6 cm

4. 8 cm

Answer

Given:

Area of the square = 48 cm²

Let a be the Side of square.

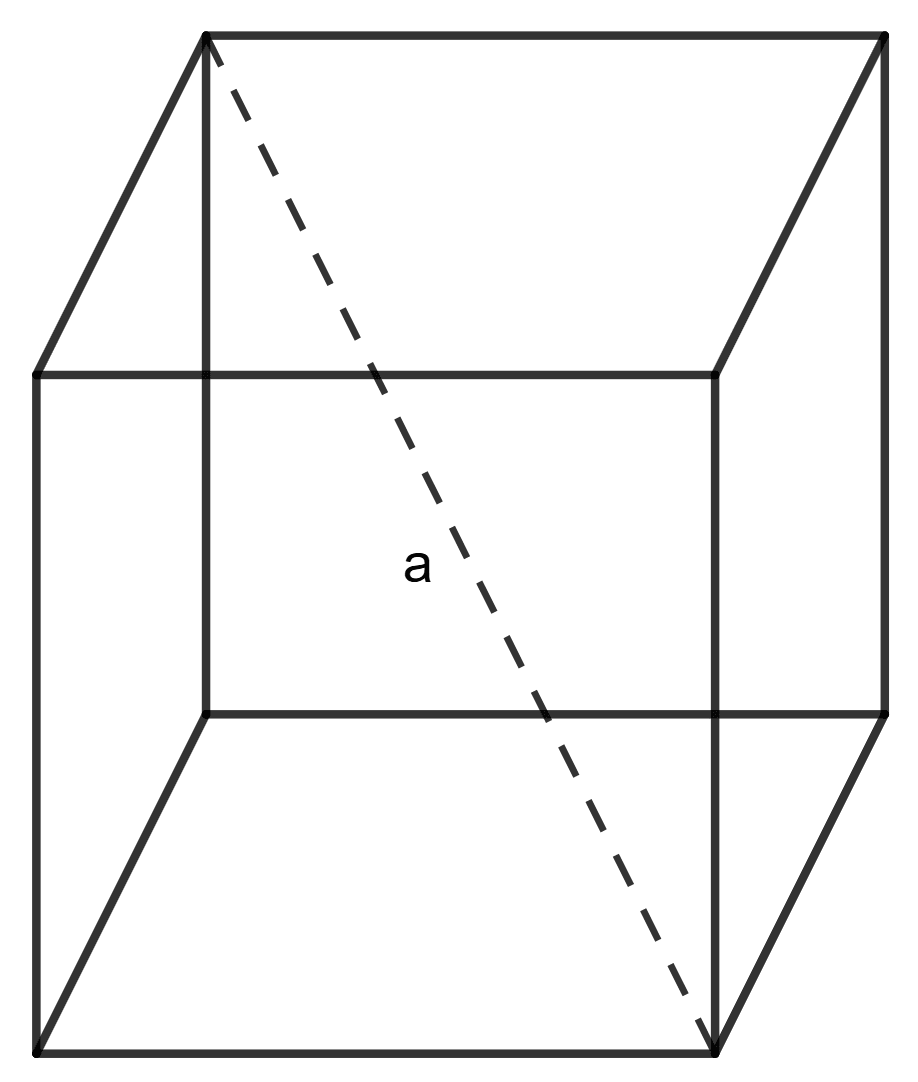
Area of square = side²

⇒ a² = 48 cm²

⇒ a = $\sqrt{48}$ cm

⇒ a = $\sqrt{16 \times 3}$ cm

⇒ a = 4 $\sqrt{3}$ cm

Let s be the side of cube.

Diagonal of cube = side $\sqrt{3}$

⇒ Side of square = Diagonal of cube

⇒ s $\sqrt{3}$ = 4 $\sqrt{3}$ cm

⇒ s $\cancel{\sqrt{3}}$ = 4 $\cancel{\sqrt{3}}$ cm

⇒ side = 4 cm

Each edge of the cube is 4 cm.

Hence, option 2 is the correct option.

A cuboid has length = 4 cm, breadth = 3 cm and diagonal = 13 cm. The volume of the cuboid is :

1. 156 cm³

2. 288 cm³

3. 144 cm³

4. 78 cm³

Answer

Given:

Length of cuboid = 4 cm

Breadth of cuboid = 3 cm

Diagonal of cuboid = 13 cm

Let h be the height of cuboid.

Length of diagonal of cuboid = $\sqrt{l^2 + b^2 + h^2}$

⇒ $\sqrt{4^2 + 3^2 + h^2}$ = 13

⇒ $\sqrt{16 + 9 + h^2}$ = 13

Squaring both sides, we get

⇒ $({\sqrt{16 + 9 + h^2}})^2$ = (13)²

⇒ 16 + 9 + h² = 169

⇒ 25 + h² = 169

⇒ h² = 169 - 25

⇒ h² = 144

⇒ h = $\sqrt{144}$

⇒ h = 12 cm

Volume of cuboid = l x b x h

= 4 x 3 x 12 cm²

= 144 cm²

Volume of cuboid is 144 cm².

Hence, option 3 is the correct option.

A cuboid with dimensions 12 cm x 9 cm x 2 cm is made of a metal. It is melted and recast into a solid cube. The edge of the cube is :

1. 6 cm

2. 12 cm

3. 15 cm

4. 8 cm

Answer

Given:

Dimensions of cuboid = 12 cm x 9 cm x 2 cm

Let s be the side of cube.

Volume of cuboid = Volume of cube

⇒ side³ = l x b x h

⇒ s³ = 12 x 9 x 2 cm³

⇒ s³ = 216 cm³

⇒ s = $\sqrt[3]{216}$ cm

⇒ s = 6 cm

The edge of the cube is 6 cm.

Hence, option 1 is the correct option.

The dimensional ratio of the sides of a cuboid is 3 : 2 : 1. If its volume is 1296 cm³; the actual dimensions of the cuboid are :

1. 12 cm, 12 cm and 8 cm

2. 8 cm, 8 cm and 12 cm

3. 12 cm, 12 cm and 12 cm

4. 18 cm, 12 cm and 6 cm

Answer

Given:

Volume of cuboid = 1296 cm³

Dimensions of cuboid = 3 : 2 : 1

Let the sides of cuboid be 3a, 2a and a.

Volume of cuboid = l x b x h

⇒ 3a x 2a x a = 1296 cm³

⇒ 6a³ = 1296 cm³

⇒ a³ = $\dfrac{1296}{6}$ cm³

⇒ a³ = 216 cm³

⇒ a = $\sqrt[3]{216}$ cm

⇒ a = 6 cm

Sides are 3a, 2a and a = 3 x 6 cm, 2 x 6 cm and 6 cm

= 18 cm, 12 cm and 6 cm

Hence, option 4 is the correct option.

A tank with dimensions 12 m, 10 m and 8 m is dug and the soil taken out of it is spread uniformly on a field of length = 40 m and breadth = 32 m. The rise in level of the field is :

1. 7.5 m

2. 7.5 cm

3. 75 cm

4. 75 m

Answer

Given:

Dimensions of tank = 12 m, 10 m and 8 m

Dimensions of field = 40 m, 32 m

Let h be the height of field.

Volume of tank = Volume of soil spread on the field

⇒ l_tank x b_tank x h_tank = l_field x b_field x h_field

⇒ 12 x 10 x 8 = 40 x 32 x h

⇒ 960 = 1,280 x h

⇒ h = $\dfrac{960}{1,280}$ m

⇒ h = 0.75 m = 75 cm

The rise in level of the field is 75 cm.

Hence, option 3 is the correct option.

Through the pipe of uniform cross-section (12 cm²) water flows with the speed of 20 cm/s. The volume of water that flows in 1 minute is :

1. 0.0144 m³

2. 0.144 m³

3. 144 cm³

4. 240 cm³

Answer

Given:

Area of cross section = 12 cm²

Speed of water = 20 cm/s

Volume of water flowing out per second = Area of cross section x speed of water

= 12 x 20 cm³

= 240 cm³/s

Volume of water flowing out per minute = 240 x 60 cm³

= 14,400 cm³

= 0.0144 m³

The total volume of water flowing out in one minute is 0.0144 m³.

Hence, option 1 is the correct option.

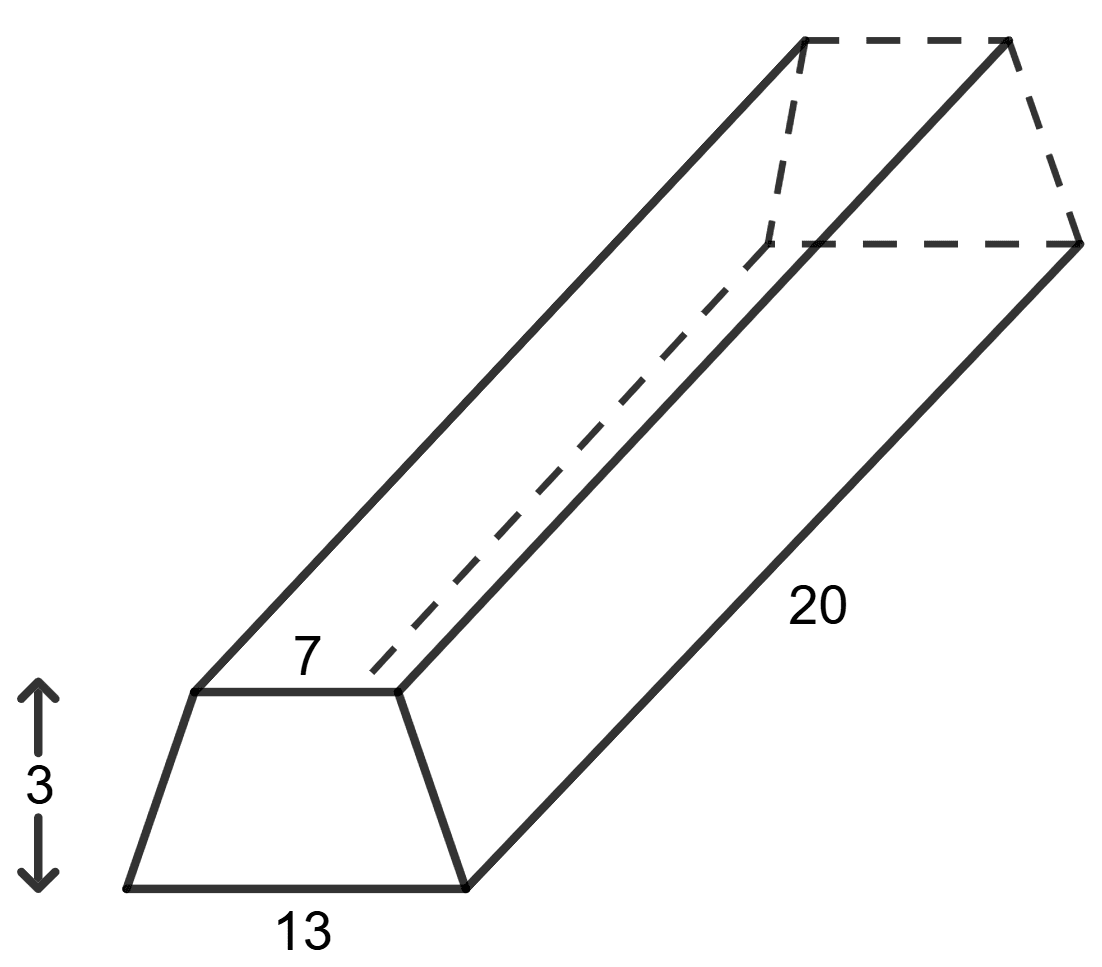
In the given figure, all the dimensions are given in cm. The volume of the solid is :

1. 7 cm x 13 cm x 20 cm

2. (7 + 13) x 20 x 3 cm³

3. $\dfrac{1}{4}(7 + 13)$ x 3 x 20 cm³

4. $\dfrac{1}{2}(7 + 13)$ x 3 x 20 cm³

Answer

Volume of solid = Area of base x height

Area of base = Area of trapezium = $\dfrac{1}{2}$ x (sum of parallel side) x height

= $\dfrac{1}{2}$ x (7 + 13) x 3

Volume of solid = $\dfrac{1}{2}$ x (7 + 13) x 3 x 20

Hence, option 4 is the correct option.

The length, breadth and height of a rectangular solid are in the ratio 5 : 4 : 2. If the total surface area is 1216 cm², find the length, the breadth and the height of the solid.

Answer

Given:

Total surface area = 1216 cm²

Ratio of dimensions = 5 : 4 : 2

Let the sides of rectangular solid be 5a, 4a and 2a.

Total surface area = 2(lb + bh + hl)

⇒ 2(5a x 4a + 4a x 2a + 2a x 5a) = 1216 cm²

⇒ 2(20a² + 8a² + 10a²) = 1216 cm²

⇒ 2 x 38a² = 1216 cm²

⇒ 76a² = 1216 cm²

⇒ a² = $\dfrac{1216}{76}$ cm²

⇒ a² = 16 cm²

⇒ a = $\sqrt{16}$ cm

⇒ a = 4 cm

Dimensions of rectangular solid are:

Length = 5a = 5 x 4 cm = 20 cm

Breadth = 4a = 4 x 4 cm = 16 cm

Height = 2a = 2 x 4 cm = 8 cm

Hence, length, breadth and height of rectangular solid are 20 cm, 16 cm and 8 cm, respectively.

The volume of a cube is 729 cm³. Find its total surface area.

Answer

Given:

Volume of a cube = 729 cm³

Let a be the side of cube.

Volume of a cube = side³

⇒ a³ = 729 cm³

⇒ a = $\sqrt{729}$ cm

⇒ a = 9 cm

Total surface area of a cube = 6a²

= 6 x 9² cm²

= 6 x 81 cm²

= 486 cm²

Hence, the total surface area of a cube is 486 cm².

The dimensions of a Cinema Hall are 100 m, 60 m and 15 m. How many persons can sit in the hall, if each requires 150 m³ of air ?

Answer

Given:

Dimensions of hall = 100 m, 60 m and 15 m

Volume of hall = l x b x h

= 100 x 60 x 15 m³

= 90,000 m³

Let n be the number of persons.

Volume of air = Number of person x Air required by each person

⇒ 90,000 m³ = n x 150 m³

⇒ n = $\dfrac{90,000}{150}$

⇒ n = 600

Hence, the number of people that can sit in the Cinema Hall is 600.

75 persons can sleep in a room 25 m by 9.6 m. If each person requires 16 m³ of air; find the height of the room.

Answer

Given:

Number of persons that can sleep in the room = 75

Air required by each person = 16 m³

Let h be the height of the room.

Dimensions of room = 25 m x 9.6 m x h m

Volume of air in the room = Number of persons x Air required by each person

⇒ 25 x 9.6 x h = 75 x 16

⇒ 240 x h = 75 x 16

⇒ 240 x h = 1,200

⇒ h = $\dfrac{1,200}{240}$

⇒ h = 5 m

Hence, the height of the room is 5 m.

The edges of three cubes of metal are 3 cm, 4 cm and 5 cm. They are melted and formed into a single cube. Find the edge of the new cube.

Answer

Given:

Edges of three cubes:

Cube 1: s₁ = 3 cm
Cube 2: s₂ = 4 cm
Cube 3: s₃ = 5 cm

Volume of new cube formed = Total volume of the 3 melted cubes

Let S be the edge of the new cube formed from the melted material.

Total Volume of the Three Cubes = V₁ + V₂ + V₃

⇒ s₁³ + s₂³ + s₃³ = S³

⇒ 3³ + 4³ + 5³ = S³

⇒ 27 + 64 + 125 = S³

⇒ S³ = 216

⇒ S = $\sqrt[3]{216}$

⇒ S = 6 cm

Hence, the edge of the new cube is 6 cm.

Three cubes, whose edges are x cm, 8 cm and 10 cm respectively, are melted and recast into a single cube of edge 12 cm. Find 'x'.

Answer

Given:

Edges of three cubes:

Cube 1: s₁ = x cm
Cube 2: s₂ = 8 cm
Cube 3: s₃ = 10 cm

Edge of the new cube formed from the melted material = 12 cm

Total Volume of the Three Cubes = V₁ + V₂ + V₃

⇒ s₁³ + s₂³ + s₃³ = S³

⇒ x³ + 8³ + 10³ = 12³

⇒ x³ + 512 + 1,000 = 1,728

⇒ x³ + 1,512 = 1,728

⇒ x³ = 1,728 - 1,512

⇒ x³ = 216

⇒ x = $\sqrt[3]{216}$

⇒ x = 6 cm

Hence, x = 6 cm.

Three equal cubes are placed adjacently in a row. Find the ratio of the total surface area of the resulting cuboid to that of the sum of the total surface areas of the three cubes.

Answer

Given:

Let a be the side of each cube.

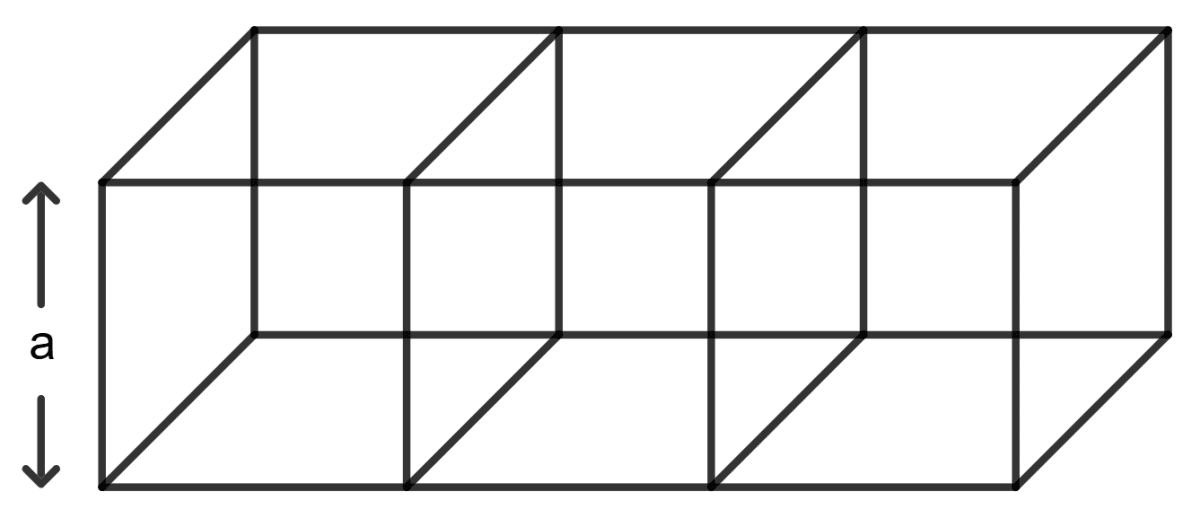
When the cubes are placed adjacently, they form a cuboid with the following dimensions:

Length of cuboid = a + a + a = 3a

Breadth of cuboid = a

Height of cuboid = a

The ratio = $\dfrac{\text{Tot. surface area of cuboid}}{\text{Sum of tot. surface areas of 3 cubes}}$

$= \dfrac{2(lb + bh + hl)}{6 \times side^2 + 6 \times side^2 + 6 \times side^2}\\[1em] = \dfrac{2(3a \times a + a \times a + a \times 3a)}{3 \times 6a^2}\\[1em] = \dfrac{2(3a^2 + a^2 + 3a^2)}{18a^2}\\[1em] = \dfrac{2 \times 7a^2}{18a^2}\\[1em] = \dfrac{14a^2}{18a^2}\\[1em] = \dfrac{14 \cancel{a^2}}{18 \cancel{a^2}}\\[1em] = \dfrac{14}{18}\\[1em] = \dfrac{7}{9}\\[1em]$

Hence, the ratio of the total surface area of the resulting cuboid to that of the sum of the total surface areas of the three cubes is 7:9.

The cost of papering the four walls of a room at 75 paise per square metre is ₹ 240. The height of the room is 5 metres. Find the length and the breadth of the room, if they are in the ratio 5 : 3.

Answer

Given:

Total cost = ₹ 240

Cost of papering = 75 paise per sq. m. = ₹ 0.75 per sq. m.

Height of the room = 5 m

Ratio of length to breadth = 5 : 3

Let the length and breadth of room be 5a and 3a.

Area of the four walls = 2(l + b)h

= 2(5a + 3a)5

= 2 x 8a x 5 sq. m.

= 80a sq. m.

Total cost = Area of the four walls x Cost of papering

⇒ 240 = 80a x 0.75

⇒ 240 = 60a

⇒ a = $\dfrac{240}{60}$

⇒ a = 4 m

The length and breadth of room are 5a and 3a = 5 x 4 m and 3 x 4 m

= 20 m and 12 m

Hence, the length and breadth of the room are 20 m and 12 m, respectively.

The area of a playground is 3650 m². Find the cost of covering it with gravel 1.2 cm deep, if the gravel costs ₹ 6.40 per cubic metre.

Answer

Given:

Area of playground = 3650 m²

Depth of gravel = 1.2 cm = 0.012 m

Cost of gravel = ₹ 6.40 per cubic metre

Volume of Gravel Needed = Area of playground x Depth

= 3,650 x 0.012 m³

= 43.8 m³

Total cost of the gravel = Volume of Gravel Needed x Cost per cubic metre

= 43.8 x 6.40

= ₹ 280.32

Hence, the cost of covering the playground with gravel is ₹ 280.32.

A square plate of side 'x' cm is 8 mm thick. If its volume is 2880 cm³; find the value of x.

Answer

Given:

Volume of the square plate = 2880 cm³

Thickness of the square plate = 8 mm = 0.8 cm

Side of the square plate = x cm

Volume of the square plate = side x side x thickness

⇒ 2,880 = x $\times$ x $\times$ 0.8

⇒ 2,880 = x² $\times$ 0.8

⇒ x² = $\dfrac{2,880}{0.8}$

⇒ x² = 3600

⇒ x = $\sqrt{3600}$

⇒ x = 60 cm

Hence, the value of x is 60 cm.

The external dimensions of a closed wooden box are 27 cm, 19 cm and 11 cm. If the thickness of the wood in the box is 1.5 cm; find :

(i) volume of the wood in the box;

(ii) the cost of the box, if wood costs ₹ 1.20 per cm³;

(iii) number of 4 cm cubes that could be placed into the box.

Answer

(i) Given:

External dimensions of wooden box = 27 cm, 19 cm and 11 cm.

Thickness of the wood = 1.5 cm

External volume of box = l x b x h

= 27 x 19 x 11

= 5,643 cm ³

Internal volume of box = l x b x h

= (27 - 2 x 1.5) x (19 - 2 x 1.5) x (11 - 2 x 1.5)

= (27 - 3) x (19 - 3) x (11 - 3)

= 24 x 16 x 8

= 3,072 cm ³

Volume of wood = External volume of box - Internal volume of box

= 5,643 cm ³ - 3,072 cm ³

= 2,571 cm ³

Hence, volume of wood in the box is 2,571 cm ³.

(ii) Cost of wood = ₹ 1.20 per cm³

Total cost = Volume of wood x Cost of wood

= ₹ 2,571 x 1.20

= ₹ 3,085.20

Hence, total cost of the box is ₹ 3,085.20.

(iii) Side of cube = 4 cm

Let n be the number of cubes.

Internal volume of box = Number of cubes x Volume of cube

⇒ 3,072 = n x side³

⇒ 3,072 = n x 4³

⇒ 3,072 = n x 64

⇒ n = $\dfrac{3,072}{64}$

⇒ n = 48

Hence, the number of 4 cm cubes that could be placed into the box is 48.

A tank 20 m long, 12 m wide and 8 m deep is to be made of iron sheet. It is open at the top. Determine the cost of iron-sheet, at the rate of ₹ 12.50 per metre, if the sheet is 2.5 m wide.

Answer

Given:

Dimensions of the tank = 20 m x 12 m x 8 m

Width of the iron sheet = 2.5 m

Rate of iron sheet = ₹ 12.50 per metre

Area of sheet = Surface area of the tank

⇒ Length_sheet x Width_sheet = Area of 4 walls of the tank + Area of base

⇒ Length_sheet x 2.5 m = 2(l + b)h + l x b

⇒ Length_sheet x 2.5 m = 2(20 + 12)8 + 20 x 12 m²

⇒ Length_sheet x 2.5 m = 2 x 32 x 8 + 240 m²

⇒ Length_sheet x 2.5 m = 512 + 240 m²

⇒ Length_sheet x 2.5 m = 752 m²

⇒ Length_sheet = $\dfrac{752}{2.5}$ m

⇒ Length_sheet = 300.8 m

Cost of the sheet = Length of the sheet x Rate of iron sheet

= 300.8 x 12.50

= ₹ 3,760

Hence, the total cost of the iron sheet is ₹ 3,760.

A closed rectangular box is made of wood of 1.5 cm thickness. The exterior length and breadth are respectively 78 cm and 19 cm, and the capacity of the box is 15 cubic decimetres. Calculate the exterior height of the box.

Answer

Given:

External length of the box = 78 cm

External breadth of the box = 19 cm

Thickness of the wood = 1.5 cm

Volume of the box = 15 dm³ = 15,000 cm³

Let h be the external height of the box.

Volume of the box = l x b x h

⇒ (78 - 2 x 1.5) x (19 - 2 x 1.5) x (h - 2 x 1.5) cm³ = 15,000 cm³

⇒ (78 - 3) x (19 - 3) x (h - 3) cm³ = 15,000 cm³

⇒ 75 x 16 x (h - 3) cm³ = 15,000 cm³

⇒ 1,200 x (h - 3) cm³ = 15,000 cm³

⇒ (h - 3) = $\dfrac{15,000}{1,200}$ cm

⇒ h - 3 = 12.5 cm

⇒ h = 12.5 + 3 cm

⇒ h = 15.5 cm

Hence, the exterior height of the box is 15.5 cm.

The square on the diagonal of a cube has an area of 1875 sq. cm. Calculate :

(i) the side of the cube.

(ii) the total surface area of the cube.

Answer

(i) Given:

Area of the square = 1875 cm²

Let a be the side of the square.

Let s be the side of cube.

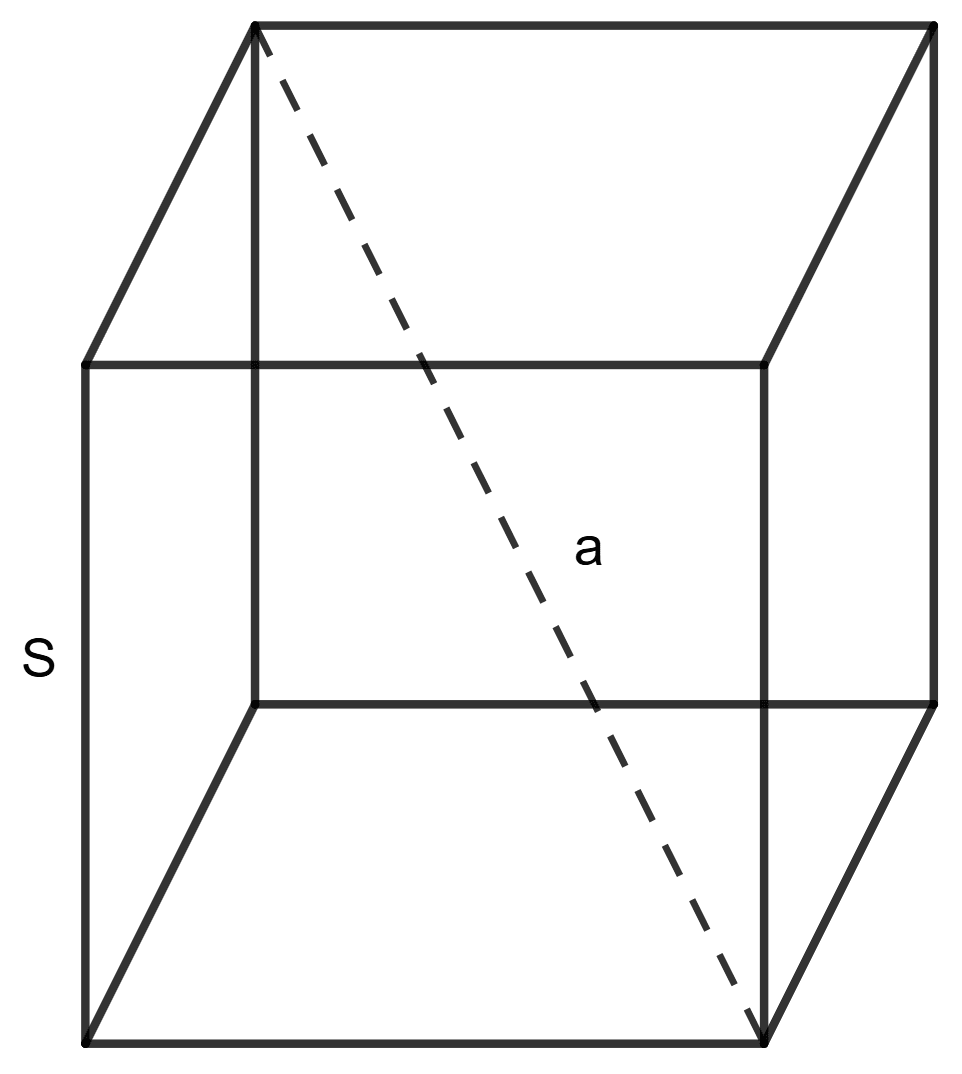
Area of the square = side²

⇒ a² = 1875 cm²

⇒ a = $\sqrt{1875}$ cm

⇒ a = 25 $\sqrt{3}$ cm

Side of the square = Diagonal of the cube

Diagonal of the cube = side $\sqrt{3}$

⇒ s $\sqrt{3}$ = 25 $\sqrt{3}$ cm

⇒ side $\cancel{\sqrt{3}}$ = 25 $\cancel{\sqrt{3}}$ cm

⇒ side = 25 cm

Hence, the side of the cube is 25cm.

(ii) Total surface area of the cube = 6 x side²

= 6 x (25)² cm²

= 6 x 625 cm²

= 3,750 cm²

Hence, the total surface area of the cube is 3,750 cm².

The following figure shows a solid of uniform cross-section. Find the volume of the solid. All measurements are in centimetres. Assume that all angles in the figure are right angles.

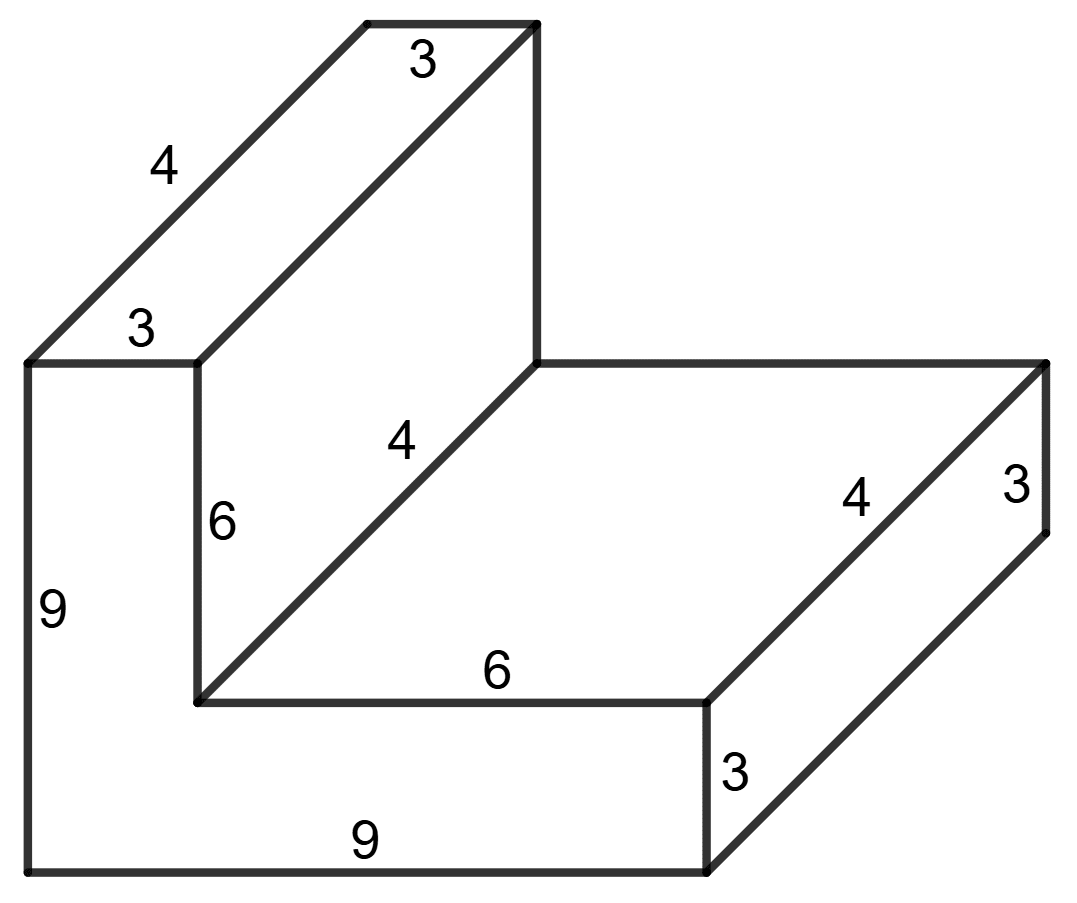
Answer

The solid can be divided into two cuboids.

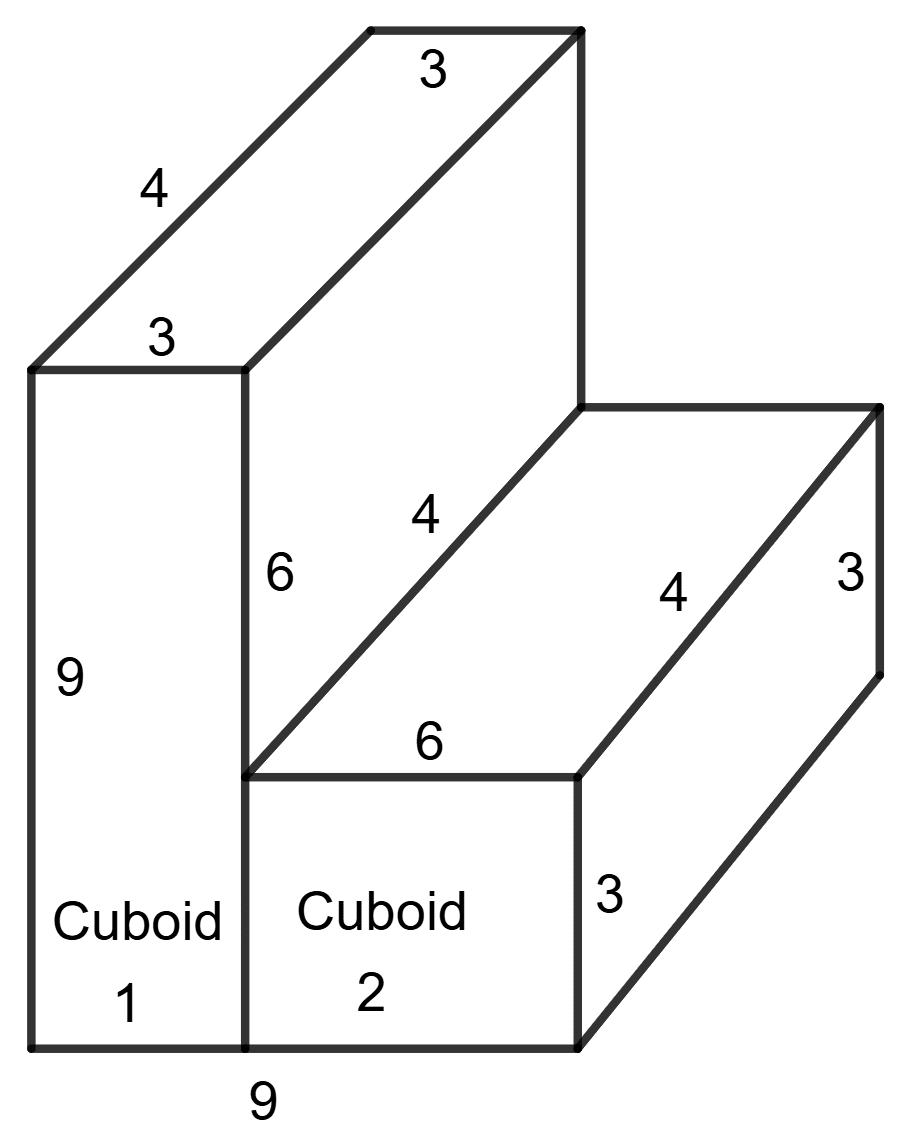
Dimensions of cuboid 1:

Length(l₁) = 9 cm Breadth(b₁) = 4 cm Height(h₁) = 3 cm

Dimension of cuboid 2:

Length(l₂) = 6 cm Breadth(b₂) = 4 cm Height(h₂) = 3 cm

Volume of solid = V₁ + V₂

= l₁b₁h₁ + l₂b₂h₂

= 9 x 4 x 3 + 6 x 4 x 3 cm³

= 108 + 72 cm³

= 180 cm³

Hence, the volume of the solid is 180 cm³.

A swimming pool is 40 m long and 15 m wide. Its shallow and deep ends are 1.5 m and 3 m deep respectively. If the bottom of the pool slopes uniformly, find the amount of water in litres required to fill the pool.

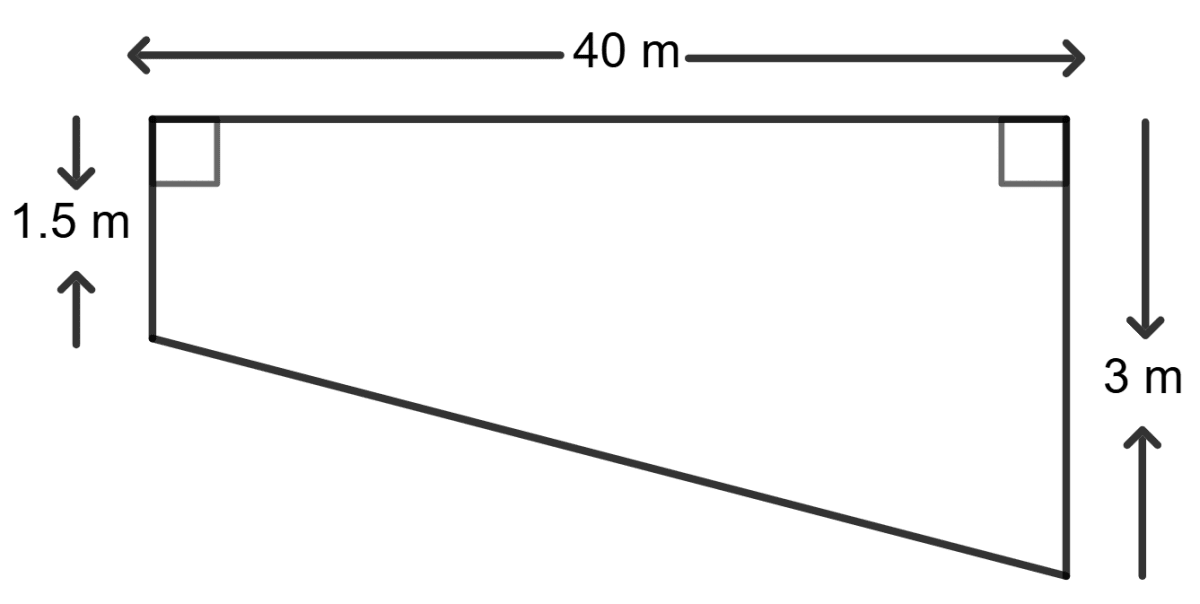
Answer

Length of the pool (L) = 40 m

Width of the pool (W) = 15 m

Depth at the shallow end = 1.5 m

Depth at the deep end = 3 m

The cross-section of the pool is a trapezium with:

Parallel sides (depths) as 1.5 m and 3 m.

Height of the trapezium equal to the width of the pool (15 m).

Area of the trapezium = $\dfrac{1}{2}$ x (sum of parallel lines) x height

= $\dfrac{1}{2}$ x (1.5 + 3) x 15 m²

= $\dfrac{1}{2}$ x 4.5 x 15 m²

= $\dfrac{1}{2}$ x 67.5 m²

= 33.75 m²

Volume of the pool = Area of the trapezium x length

= 33.75 x 40 m³

= 1350 m³ = 13,50,000 litres

Hence, the amount of water required to fill the swimming pool is 13,50,000 litres.

The cross-section of a tunnel perpendicular to its length is a trapezium ABCD as shown in the following figure; also given that : AM = BN; AB = 7 m; CD = 5 m. The height of the tunnel is 2.4 m. The tunnel is 40 m long. Calculate :

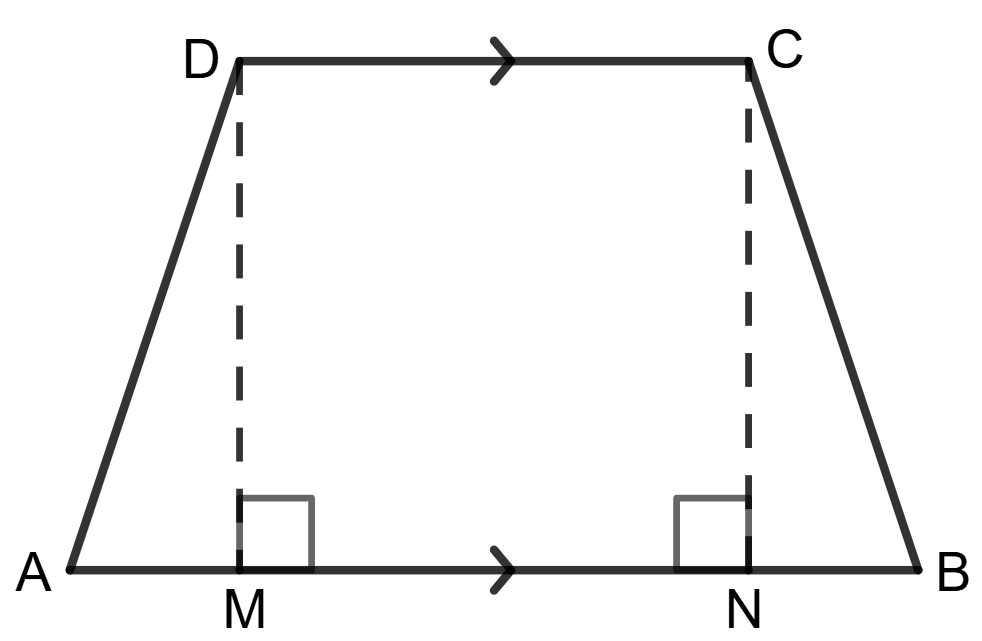
(i) the cost of painting the internal surface of the tunnel (excluding the floor) at the rate of ₹ 5 per m² (sq. metre).

(ii) the cost of paving the floor at the rate of ₹ 18 per m².

Answer

(i) Length of the tunnel = 40 m

Height of the tunnel = 2.4 m

Cross-section dimensions: AB = 7 m, CD = 5 m

AM = BN = $\dfrac{AB - CD}{2}$ = $\dfrac{7 - 5}{2}$ = $\dfrac{2}{2}$ = 1 m

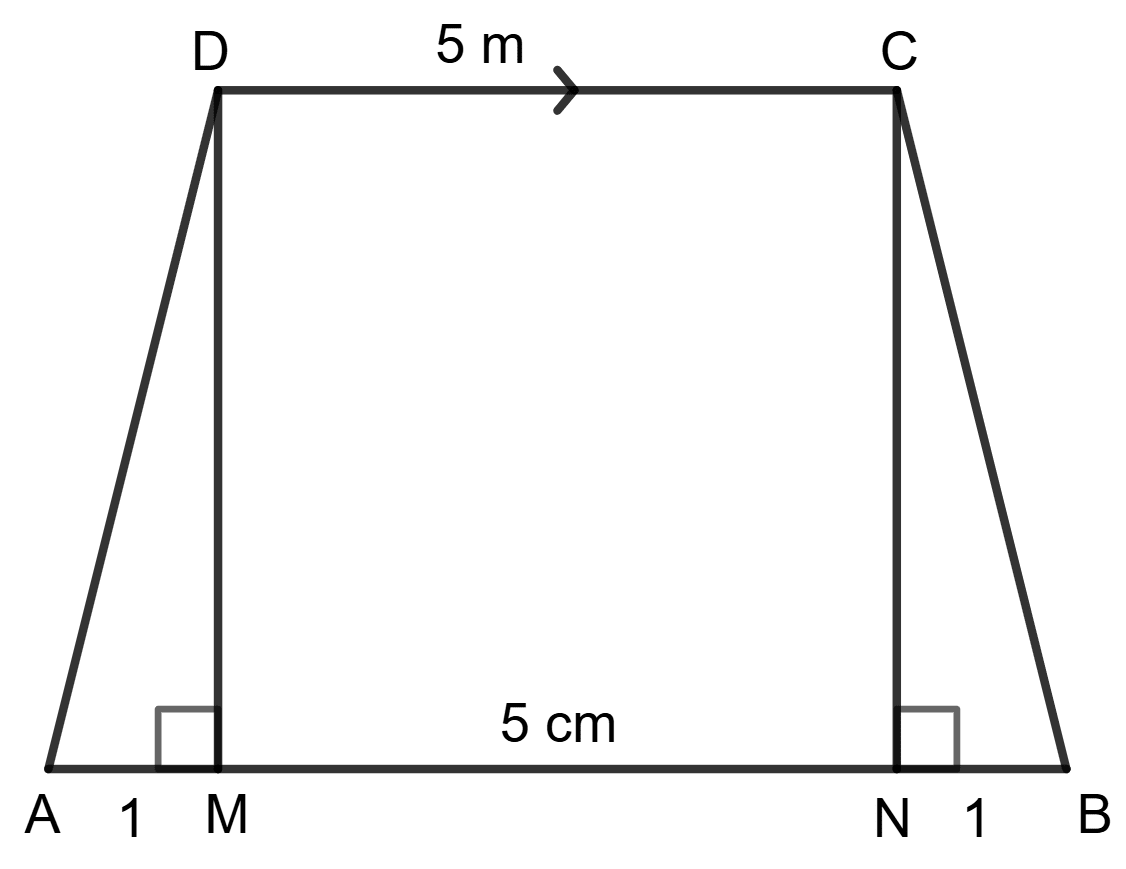
In Δ ADM,

Using the pythagorean theorem in triangle ADM,

Base² + Height² = Hypotenuse²

⇒ AM² + DM² = AD²

⇒ 1² + (2.4)² = AD²

⇒ 1 + 5.76 = AD²

⇒ 6.76 = AD²

⇒ AD = $\sqrt{6.76}$

⇒ AD = 2.6 m

Area of the internal surface of the tunnel (excluding the floor) = Area of vertical walls - Area of floor

= 2.6 x 40 + 5 x 40 + 2.6 x 40 m²

= 104 + 200 + 104 m²

= 408 m²

Total cost of painting = Area of vertical walls x Cost of painting

= ₹ 408 x 5

= ₹ 2,040

Hence, total cost of painting the internal surface = ₹ 2,040.

(ii) Area of floor = 7 x 40 m²

= 280 m²

Total cost of paving = Area of floor x rate of paving

= ₹ (280 x 18)

= ₹ 5,040

Hence, total cost of paving = ₹ 5,040.

Water is discharged from a pipe of cross-section area 3.2 cm² at the speed of 5m/s. Calculate the volume of water discharged :

(i) in cm³ per sec.

(ii) in litres per minute.

Answer

(i) Cross-sectional area = 3.2 cm²

Speed of water = 5 m/s = 500 cm/s

Volume of water discharged per second = Cross-sectional area x Speed

= 3.2 x 500

= 1,600

Hence, the volume of water discharged per second is 1600 cm^3.

(ii) Volume of water discharged per min = 1600 x 60

= 96,000 cm³

= $\dfrac{96,000}{1,000}$ = 96 litres

Hence, the volume of water discharged per minute is 96 litres.

A hose-pipe of cross-section area 2 cm² delivers 1500 litres of water in 5 minutes. What is the speed of water in m/s through the pipe ?

Answer

Given:

Cross-sectional area of the hose-pipe = 2 cm²

Volume of water = 1,500 liters = 1,500,000 cm³

Time = 5 minutes = 5 x 60 seconds = 300 seconds

Volume of water flowing per second = $\dfrac{1,500,000}{300}$

= 5,000 cm³/ sec

Volume of water flowing per second = Area of cross-section x Speed of water

⇒ 5,000 = 2 x Speed of water

⇒ Speed of water = $\dfrac{5,000}{2}$

⇒ Speed of water = 2,500 cm/s = 25 m/s

Hence, the speed of water through the pipe is 25 m/s.

The cross-section of a piece of metal 4 m in length is shown below. Calculate :

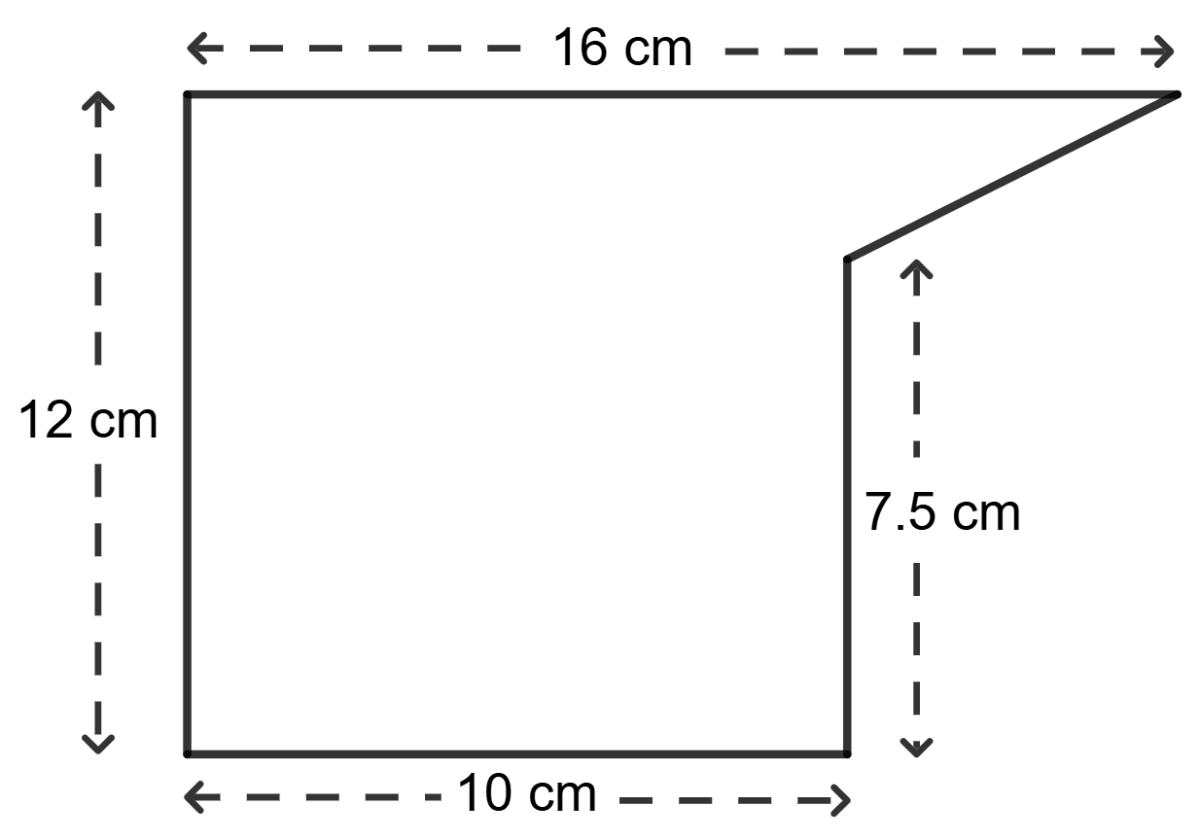
(i) the area of the cross-section;

(ii) the volume of the piece of metal in cubic centimetres.

If 1 cubic centimetre of the metal weighs 6.6 g, calculate the weight of the piece of metal to the nearest kg.

Answer

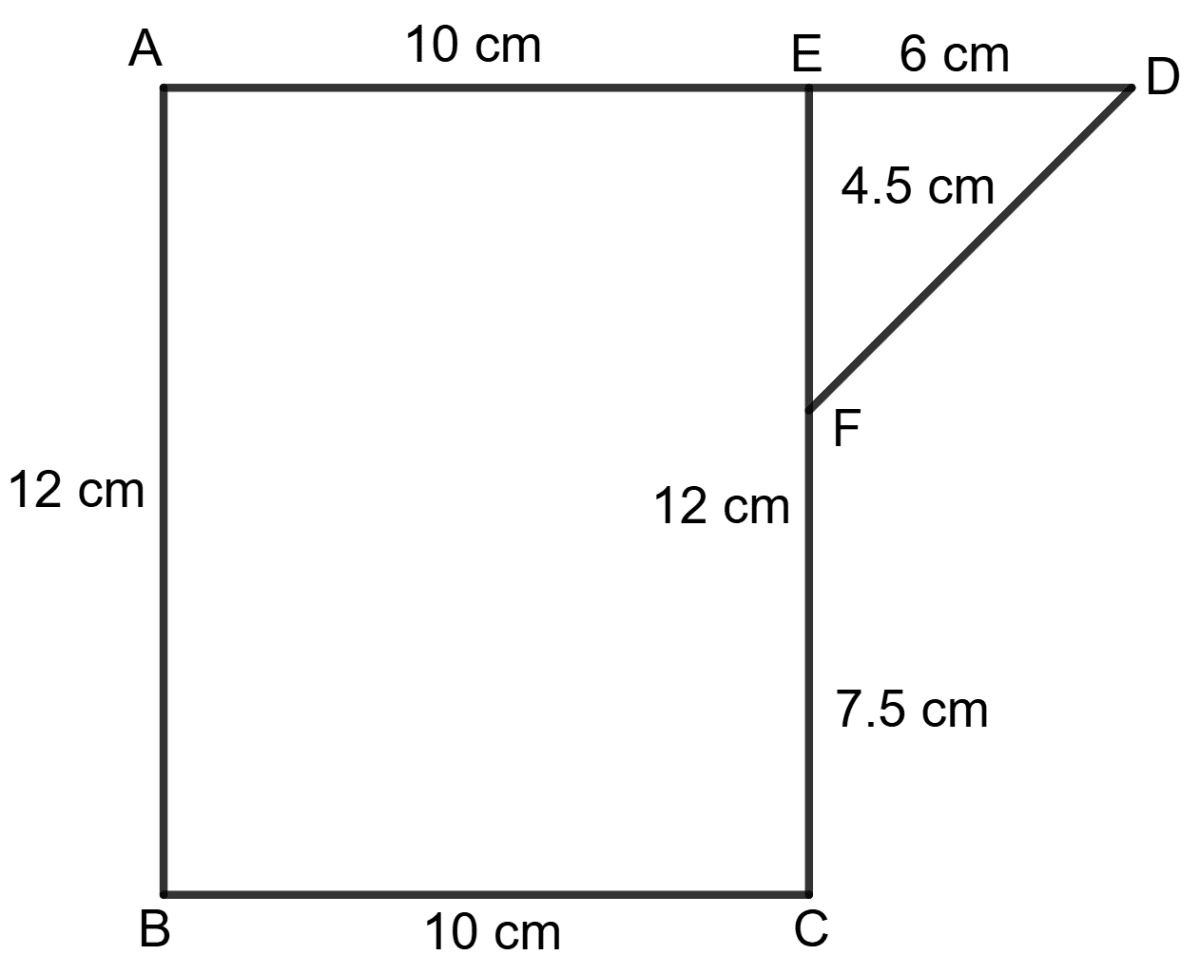
(i) Area of cross-section = Area of rectangle ABCE + Area of Δ DEF

= length x breadth + $\dfrac{1}{2}$ x base x height

= 12 x 10 + $\dfrac{1}{2}$ x (16 - 10) x (12 - 7.5) m²

= 120 + $\dfrac{1}{2}$ x 6 x 4.5 m²

= 120 + 3 x 4.5 m²

= 120 + 13.5 m²

= 133.5 m²

Hence, the area of cross-section is 133.5 m².

(ii) Length of the piece of metal = 4 m = 400 cm

Volume of the piece of metal = Area of cross-section x length

= 133.5 x 400 cm³

= 53,400 cm³

Weight of 1 cubic cm of metal = 6.6 g

Weight of 53,400 cubic cm metal = 6.6 x 53,400 g

= $\dfrac{352,440}{1000}$ kg = 352.44 kg

Hence, the volume of the piece of metal is 53,400 cm³ and weight of the piece of metal is 352.44 kg.

A rectangular water-tank measuring 80 cm x 60 cm x 60 cm is filled from a pipe of cross-sectional area 1.5 cm², the water emerging at 3.2 m/s. How long does it take to fill the tank?

Answer

Given:

Dimensions of the rectangular tank = 80 cm x 60 cm x 60 cm

Cross-sectional area of the pipe = 1.5 cm²

Speed of water = 3.2 m/s = 3.2 × 100 cm/s = 320 cm/s

Volume of the rectangular tank = 80 x 60 x 60 cm³

= 2,88,000 cm³

Volume of water flowing per second = Cross-sectional area x Speed of water

= 1.5 x 320 cm³/s

= 480 cm³/s

Volume of water flowing per minute = 480 x 60 cm³

= 28,800 cm³/min

Total time required to fill the tank = $\dfrac{\text{Volume of tank}}{\text{Volume per minute}}$

= $\dfrac{288,000}{28,800}$ min

= 10 minutes

Hence, the time taken by the pipe to fill the tank is 10 minutes.

The radius of a sphere is 2r, then its volume is equal to :

1. $\dfrac{4}{3}$ πr³

2. 4πr³

3. $\dfrac{8πr^3}{3}$

4. $\dfrac{32πr^3}{3}$

Answer

Given:

Radius of a sphere = 2r

By formula,

Volume of sphere = $\dfrac{4}{3}$ π(radius)³

= $\dfrac{4}{3}$ x π x (2r)³

= $\dfrac{4}{3}$ x π x 8r³

= $\dfrac{4 \times 8}{3}$ πr³

= $\dfrac{32}{3}$ πr³

Hence, option 4 is the correct option.

The total surface area of a cube is 96 cm². The volume of the cube is:

1. 8 cm³

2. 512 cm³

3. 64 cm³

4. 27 cm³

Answer

Given,

Total surface area of a cube = 96 cm²

By formula,

Total surface area of a cube = 6 x side²

⇒ 6 x side² = 96

⇒ side² = $\dfrac{96}{6}$

⇒ side² = 16

⇒ side = $\sqrt{16}$

⇒ side = 4 cm.

Volume of cube = side³

= 4³

= 64 cm³.

Hence, option 3 is the correct option.

If a solid cube of side 16 cm is cut into eight identical cubes. The side of each cube is:

1. 2 cm

2. 4 cm

3. 6 cm

4. 8 cm

Answer

Given,

Side of the original cube = 16 cm

Let s be the side of each smaller cube.

As we know,

Volume of a cube = side³

Volume of the original cube = Volume of 8 identical cubes

⇒ (16)³ = 8 x s³

⇒ 4096 = 8 x s³

⇒ s³ = $\dfrac{4096}{8}$

⇒ s³ = 512

⇒ s = $\sqrt[3]{512}$

⇒ s = 8 cm.

Hence, option 4 is the correct option.

The diameters of two solid spheres are in the ratio 5 : 7. The ratio between areas of their curved surfaces is :

1. 5 : 7

2. 7 : 5

3. 49 : 25

4. 25 : 49

Answer

Given,

The diameters of two solid spheres are in the ratio 5 : 7.

Let the diameters of two spheres be 5a and 7a.

So, their radius will be r₁ = $\dfrac{5a}{2}$ and r₂ = $\dfrac{7a}{2}$

By formula,

Curved surface area of sphere = 4πr²

$\text{Ratio of their curved surfaces areas }= \dfrac{4πr_1^2}{4πr_2^2}\\[1em] = \dfrac{4 \times π \times \Big(\dfrac{5a}{2}\Big)^2}{4 \times π \times \Big(\dfrac{7a}{2}\Big)^2}\\[1em] = \dfrac{\Big(\dfrac{5a}{2}\Big)^2}{\Big(\dfrac{7a}{2}\Big)^2}\\[1em] = \dfrac{\Big(\dfrac{25a^2}{4}\Big)}{\Big(\dfrac{49a^2}{4}\Big)}\\[1em] = \dfrac{25}{49}\\[1em] = 25 : 49.$

Hence, option 4 is the correct option.

The radius of a cylinder is doubled and its curved surface area is kept as same, the height of the cylinder is:

1. same

2. doubled

3. halved

4. none of these

Answer

Let the original radius and height of a cylinder be r and h units, respectively.

Given, radius of the cylinder is doubled.

∴ New radius = 2r

Let H be the new height of the cylinder.

By formula,

Curved surface area = 2π x radius x height

Original curved surface area = 2πrh

New curved surface area = 2π x (2r) x H = 4πrH

Given,

Curved surface area remains same.

⇒ 2πrh = 4πrH

⇒ H = $\dfrac{2πr}{4πr}h = \dfrac{h}{2}$.

Hence, option 3 is the correct option.

Statement 1: Each side of a cuboid is doubled, its total surface area is also doubled.

Statement 2: The surface area of resulting cuboid is 2 x 2 x 2 times the original area.

1. Both the statements are true.

2. Both the statements are false.

3. Statement 1 is true, and statement 2 is false.

4. Statement 1 is false, and statement 2 is true.

Answer

Let the original cuboid have length l, breadth b, and height h.

So, sides of new cuboid = 2l, 2b and 2h.

As we know that surface area of the cuboid = 2(lb + bh + hl)

The surface area of new cuboid = 2[(2l) x (2b) + (2b) x (2h) + (2h) x (2l)]

= 2(4lb + 4bh + 4hl)

= 2 x 2 x [2(lb + bh + hl)]

= 4 x surface area of the cuboid

= 2 x 2 x surface area of the cuboid

∴ Both the statements are false.

Hence, option 2 is the correct option.

Assertion (A): The radius of a hemisphere increases from r cm to 2r cm. The ratio between the surface area of the original hemisphere and the resulting hemisphere is 1 : 4.

Reason (R): Surface area of the first case = πr² + 2πr²

Surface area of the second case = π(2r)² + 2π(2r)²

1. A is true, but R is false.

2. A is false, but R is true.

3. Both A and R are true, and R is the correct reason for A.

4. Both A and R are true, and R is the incorrect reason for A.

Answer

Let A₁ be the surface area of the original hemisphere.

A₁ = πr² + 2πr² = 3πr².

Let A₂ be the surface area of the resulting hemisphere.

A₂ = π(2r)² + 2π(2r)²

= 3π(2r)²

= 3π x 4r²

= 12πr².

Ratio between the surface area of the original hemisphere and the resulting hemisphere is :

$\text{Ratio } = \dfrac{A_1}{A_2}\\[1em] = \dfrac{3πr^2}{12πr^2}\\[1em] = \dfrac{3}{12}\\[1em] = \dfrac{1}{4}.$

∴ Both A and R are true, and R is the correct reason for A.

Hence, option 3 is the correct option.

Assertion (A): A sphere is inscribed in a cylinder the ratio of the volume of the cylinder to the volume of the sphere is 1 : 4.

Reason (R): Required ratio = πr² x 2r : $\dfrac{4}{3}$ πr³

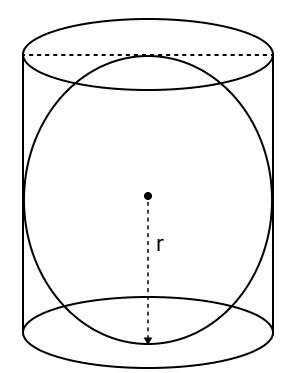
1. A is true, but R is false.

2. A is false, but R is true.

3. Both A and R are true, and R is the correct reason for A.

4. Both A and R are true, and R is the incorrect reason for A.

Answer

Let r be the radius of the sphere. 

From figure,

The radius of the cylinder is also r and the height of the cylinder is 2r.

By formula,

Volume of a cylinder (V_cylinder) = πr²h

= πr²(2r)

= 2πr³.

By formula,

Volume of a sphere (V_sphere) = $\dfrac{4}{3}$ πr³

Ratio of the volume of the cylinder to the volume of the sphere :

$\text{Ratio} = \dfrac{V_{cylinder}}{V_{sphere}}\\[1em] = \dfrac{2πr^3}{\dfrac{4}{3} πr^3}\\[1em] = \dfrac{2}{\dfrac{4}{3}}\\[1em] = \dfrac{2 \times 3}{4}\\[1em] = \dfrac{6}{4}\\[1em] = \dfrac{3}{2} \\[1em] = 3 : 2.$

∴ A is false, but R is true.

Hence, option 2 is the correct option.

A hollow square-shaped tube open at both ends is made of iron. The internal square is of 5 cm side and the length of the tube is 8 cm. There are 192 cm³ of iron in this tube. Find its thickness.

Answer

Given:

Volume of iron = 192 cm³

Length of the tube = 8 cm

Internal side of the square = 5 cm

Let x be the thickness of the tube.

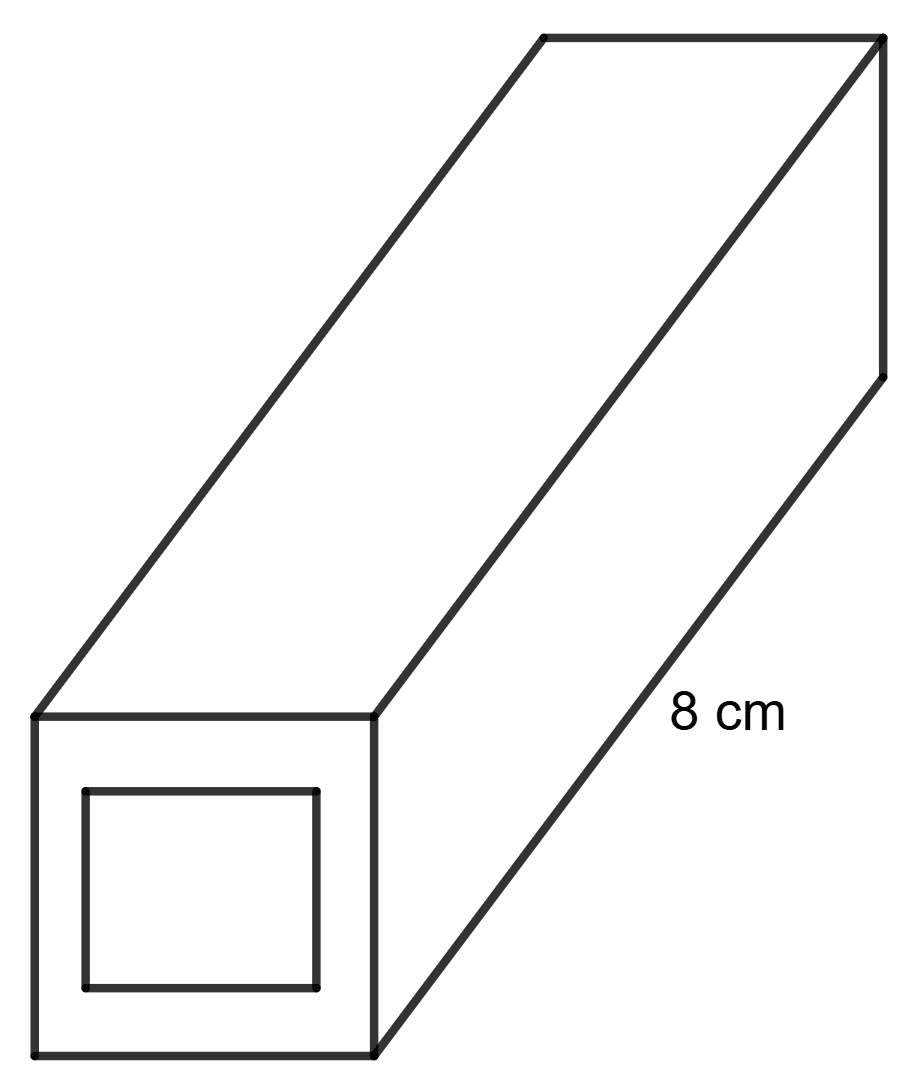
External side of the square = (5 + 2x) cm

Internal volume of the tube = Internal Side x Internal Side x length

= 5 x 5 x 8 cm³

= 200 cm³

External volume of the tube = External side x External side x length

= (5 + 2x) x (5 + 2x) x 8 cm³

= (4x² + 20x + 25) x 8 cm³

= 32x² + 160x + 200 cm³

Volume of iron = External volume - Internal volume

⇒ (32x² + 160x + 200) - 200 cm³ = 192 cm³

⇒ 32x² + 160x + 200 - 200 - 192 = 0

⇒ 32x² + 160x - 192 = 0

Divide through by 32:

⇒ x² + 5x - 6 = 0

⇒ x² + 6x - 1x - 6 = 0

⇒ x(x + 6) - 1(x + 6) = 0

⇒ (x + 6)(x - 1) = 0

⇒ x = - 6 or 1

Since thickness cannot be negative, x = 1.

Hence, the thickness of the pipe is 1 cm.

Four identical cubes are joined end to end to form a cuboid. If the total surface area of the resulting cuboid is 648 cm²; find the length of edge of each cube.

Also, find the ratio between the surface area of the resulting cuboid and the surface area of a cube.

Answer

Given:

Total surface area of the cuboid = 648 cm²

Let a be the side of each cube.

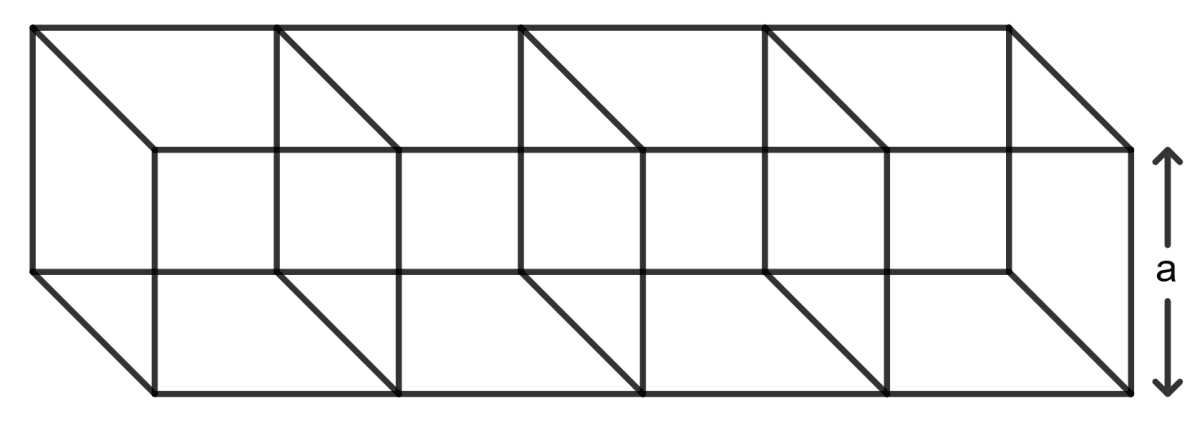
When four identical cubes are placed adjacently, the cuboid's dimensions are:

Length = a + a + a + a = 4a

Breadth = a

Height = a

Total surface area of the cuboid = 2(lb + bh + hl)

⇒ 2(4a x a + a x a + a x 4a) = 648

⇒ 2(4a² + a² + 4a²) = 648

⇒ 2 x 9a² = 648

⇒ 18a² = 648

⇒ a² = $\dfrac{648}{18}$

⇒ a² = 36

⇒ a = $\sqrt{36}$

⇒ a = 6

Thus, the length of the edge of each cube is 6 cm.

$\text{The ratio} = \dfrac{\text{Total surface area of the cuboid}}{\text{Surface Area of one cube}}$

$= \dfrac{648}{6 \times side^2}\\[1em] = \dfrac{648}{6 \times 6^2}\\[1em] = \dfrac{648}{6 \times 36}\\[1em] = \dfrac{648}{216}\\[1em] = \dfrac{3}{1}\\[1em]$

Hence, the edge of each cube is 6 cm, and the ratio of the surface area of the resulting cuboid to that of one cube is 3:1.

A rectangular card-board sheet has length 32 cm and breadth 26 cm. Squares each of side 3 cm, are cut from the corners of the sheet and the sides are folded to make a rectangular container. Find the capacity of the container formed.

Answer

Given:

Length of the sheet = 32 cm

Breadth of the sheet = 26 cm

Side of square = 3 cm

Inner length of the sheet = 32 - 3 - 3 cm = 26 cm

Inner breadth of the sheet = 26 - 3 - 3 cm = 20 cm

Height of the container (equal to the side of the square) = 3 cm

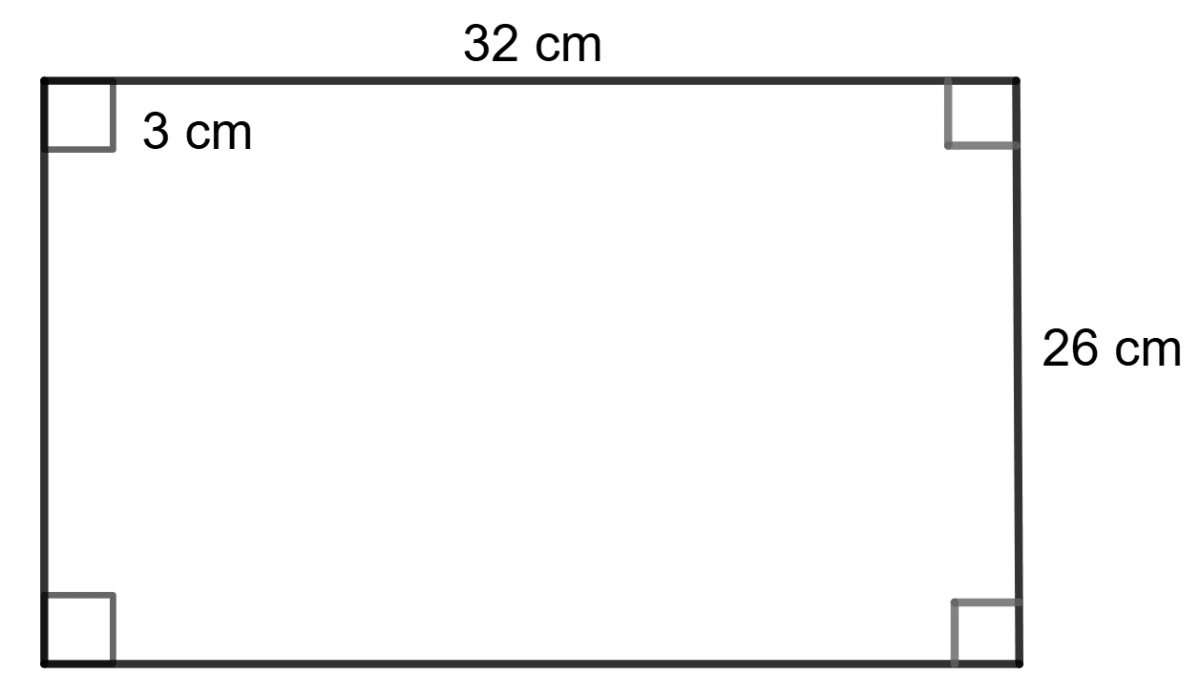
Volume of container = l x b x h

= 26 x 20 x 3 cm³

= 1,560 cm³

Hence, the volume of the container is 1,560 cm³.

A swimming pool is 18 m long and 8 m wide. Its deep and shallow ends are 2 m and 1.2 m respectively. Find the capacity of the pool, assuming that the bottom of the pool slopes uniformly.

Answer

Given:

Length of the pool = 18 m

Width of the pool = 8 m

Depth at the deep end = 2 m

Depth at the shallow end = 1.2 m

Volume of the pool = Area of base x width

Area of base(ABCD) = Area of trapezium = $\dfrac{1}{2}$ x (sum of parallel side) x height

∵ Height (Length of pool) = 18 m

= $\dfrac{1}{2}$ x (2 + 1.2) x 18 m²

= $\dfrac{1}{2}$ x 3.2 x 18 m²

= 1.6 x 18 m²

= 28.8 m²

Volume of the pool = 28.8 x 8 m³

= 230.4 m³

Hence, the capacity of the pool is 230.4 m³.

The following figure shows a closed victory-stand whose dimensions are given in cm.

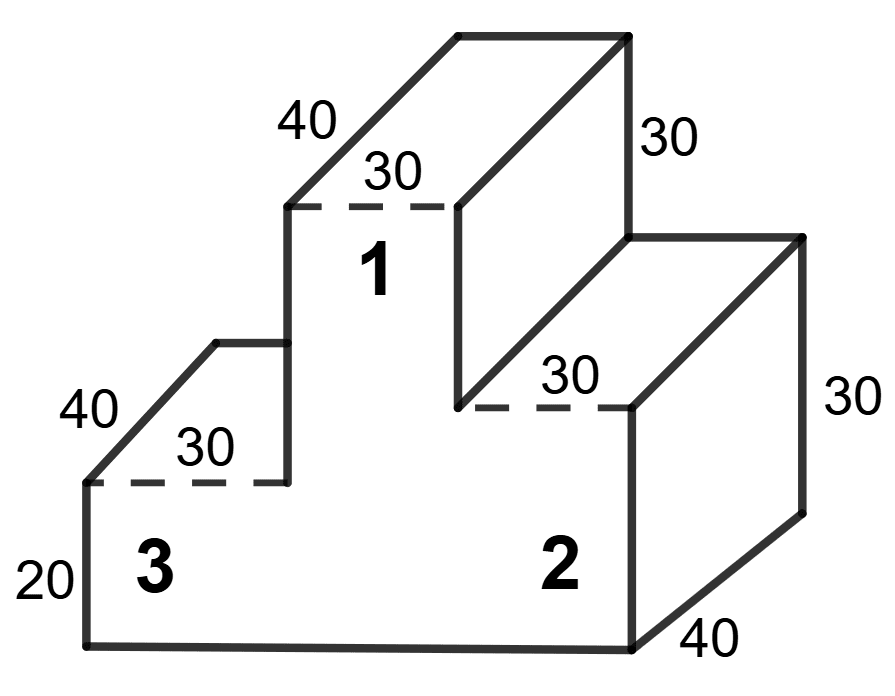
Find the volume and the surface area of the victory stand.

Answer

Given:

The dimensions of step 1 = 30 cm x 40 cm x (30 + 30) cm

The dimensions of step 2 = 40 cm x 30 cm x 30 cm

The dimensions of step 3 = 40 cm x 30 cm x 20 cm

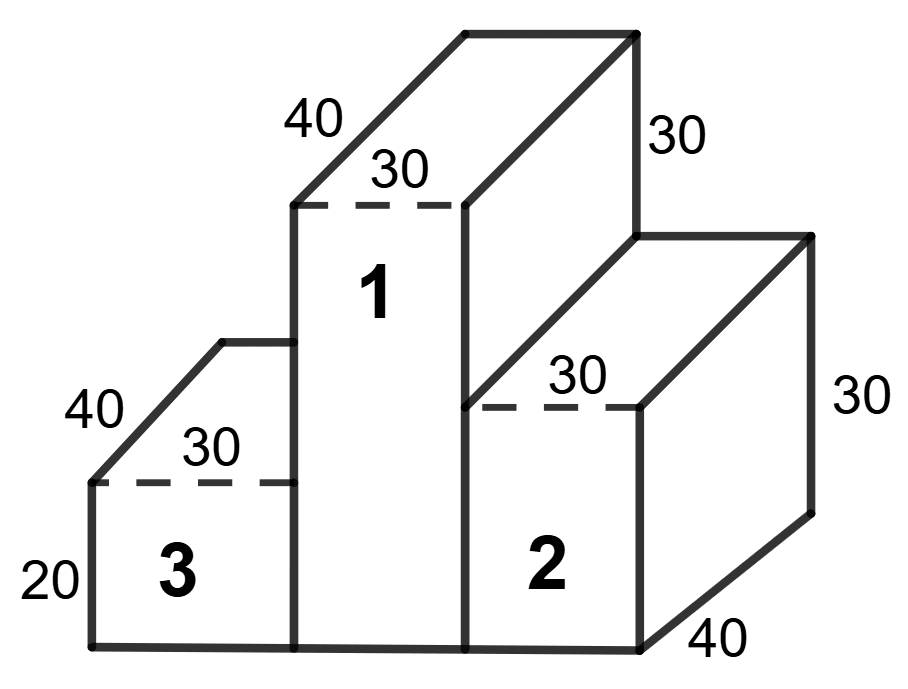
Total volume of victory stand = Volume of step 1 + Volume of step 2 + Volume of step 3

(∵ Volume of cuboid = l x b x h)

Total volume of victory stand = 40 x 30 x 60 + 40 x 30 x 30 + 40 x 30 x 20 cm³

= 72,000 + 36,000 + 24,000 cm³

= 1,32,000 cm³

We know that

Total surface area = Area of front and back + Area of vertical faces + Area of top faces

Putting the values, we get

= 2(30 x 20 + 30 x 60 + 30 x 30) + (20 x 40 + 40 x 40 + 30 x 40 + 30 x 40) + 3(30 x 40) cm²

= 2(600 + 1,800 + 900) + (800 + 1,600 + 1,200 + 1,200) + 3 x 1,200 cm²

= 2 x 3,300 + 4,800 + 3,600 cm²

= 6,600 + 4,800 + 3,600 cm²

= 15,000 cm²

Hence, the volume of the victory stand is 1,32,000 cm³ and the surface area is 15,000 cm².

Each face of a cube has perimeter equal to 32 cm. Find its surface area and its volume.

Answer

Given:

Perimeter of each face = 32 cm

Perimeter of square = 4 x side

⇒ 4 x side = 32 cm

⇒ side = $\dfrac{32}{4}$ cm

⇒ side = 8 cm

Surface area of cube = 6 x side²

= 6 x (8)² cm²

= 6 x 64 cm²

= 384 cm²

Volume of cube = side³

= 8³ cm³

= 512 cm³

Hence, the surface area is 384 cm² and the volume is 512 cm³.

A school auditorium is 40 m long, 30 m broad and 12 m high. If each student requires 1.2 m² of the floor area; find the maximum number of students that can be accommodated in this auditorium. Also, find the volume of air available in the auditorium, for each student.

Answer

Given:

Dimension of the auditorium = 40 m x 30 m x 12 m

Area of the floor = l x b

= 40 x 30 m²

= 1,200 m²

Each student requires 1.2 m² of floor area.

Thus, maximum number of students = $\dfrac{1,200}{1.2}$

= 1,000

Volume of auditorium = l x b x h

= 40 x 30 x 12 m³

= 14,400 m³

Air available per student = $\dfrac{14,400}{1000}$ = 14.4 m³

Hence, the maximum number of students that can be accommodated in the auditorium = 1,000 and the volume of air available per student = 14.4 m³.

The internal dimensions of a rectangular box are 12 cm $\times$ x cm $\times$ 9 cm. If the length of the longest rod that can be placed in this box is 17cm; find x.

Answer

Given:

Dimensions of the box = 12 cm $\times$ x cm $\times$ 9 cm

Length of longest diagonal = $\sqrt{l^2 + b^2 + h^2}$

$⇒ \sqrt{12^2 + x^2 + 9^2} = 17\\[1em] ⇒ \Big[\sqrt{12^2 + x^2 + 9^2}\Big]^2 = (17)^2\\[1em] ⇒ 12^2 + x^2 + 9^2 = 289\\[1em] ⇒ 144 + x^2 + 81 = 289\\[1em] ⇒ 225 + x^2 = 289\\[1em] ⇒ x^2 = 289 - 225\\[1em] ⇒ x^2 = 64\\[1em] ⇒ x = \sqrt{64}\\[1em] ⇒ x = 8$

Hence, the value of x is 8 cm.

The internal length, breadth and height of a box are 30 cm, 24 cm and 15 cm. Find the largest number of cubes which can be placed inside this box if the edge of each cube is

(i) 3 cm

(ii) 4 cm

(iii) 5 cm

Answer

(i) Given:

Dimensions of box = 30 cm x 24 cm x 15 cm

Edge of cube = 3 cm

Number of cubes which can be placed along length = $\dfrac{30}{3}$ = 10

Number of cubes which can be placed along breadth = $\dfrac{24}{3}$ = 8

Number of cubes which can be placed along height = $\dfrac{15}{3}$ = 5

The total number of cubes placed = 10 x 8 x 5 = 400

Hence, the number of cubes = 400.

(ii) Given:

Dimensions of box = 30 cm x 24 cm x 15 cm

Edge of cube = 4 cm

Number of cubes which can be placed along length = $\dfrac{30}{4}$ = 7.5 = 7 (taking only integer value)

Number of cubes which can be placed along breadth = $\dfrac{24}{4}$ = 6

Number of cubes which can be placed along height = $\dfrac{15}{4}$ = 3.75 = 3 (taking only integer value)

The total number of cubes placed = 7 x 6 x 3 = 126

Hence, the number of cubes = 126.

(iii) Given:

Dimensions of box = 30 cm x 24 cm x 15 cm

Edge of cube = 5 cm

Number of cubes which can be placed along length = $\dfrac{30}{5}$ = 6

Number of cubes which can be placed along breadth = $\dfrac{24}{5}$ = 4.8 = 4 (taking only integer value)

Number of cubes which can be placed along height = $\dfrac{15}{5}$ = 3

The total number of cubes placed = 6 x 4 x 3 = 72

Hence, the number of cubes = 72.

A rectangular field is 112 m long and 62 m broad. A cubical tank of edge 6 m is dug at each of the four corners of the field and the earth so removed is evenly spread on the remaining field. Find the rise in level.

Answer

Given:

Dimensions of the rectangular field = 112 m x 62 m

Edge of each cubical tank = 6 m

Let h be the rise in level.

Volume of 4 tanks = Volume of the removed earth

4 x Volume of 1 tank = (Area of field - 4 x Area of tank) x Rise in level

⇒ 4 x (6)³ = (112 x 62 - 4 x 6²) x h

⇒ 4 x 216 = (6,944 - 4 x 36) x h

⇒ 864 = (6,944 - 144) x h

⇒ 864 = 6,800 x h

⇒ h = $\dfrac{864}{6,800}$

⇒ h = 0.127 m

⇒ h = 12.7 cm

Hence, the rise in level of the field is 12.7 cm.

When length of each side of a cube is increased by 3 cm, its volume is increased by 2457 cm³. Find its side. How much will its volume decrease, if length of each side of it is reduced by 20% ?

Answer

Let a be the side of the original cube.

Side of the new cube = a + 3

Volume of the new cube = a³ + 2457

⇒ a³ + 2457 = (a + 3)³

⇒ a³ + 2457 = a³ + 3³ + 3 x a² x 3 + 3 x a x 3²

⇒ $\cancel{a^3}$+ 2457 = $\cancel{a^3}$+ 27 + 9a² + 27a

⇒ 2457 = 27 + 9a² + 27a

⇒ 9a² + 27a - 2457 + 27 = 0

⇒ 9a² + 27a - 2430 = 0

⇒ a² + 3a - 270 = 0

⇒ a² + 18a - 15a - 270 = 0

⇒ a(a + 18) - 15(a + 18) = 0

⇒ (a + 18)(a - 15) = 0

⇒ a = -18 or 15

Since the side cannot be negative, the side of the original cube, a = 15 cm.

Volume of original cube = side³

= (15)³ cm³

= 3375 cm³

When the length of side is reduced by 20%.

New side of the cube = side - 20% of side

= 15 - $\dfrac{20}{100}$ x 15

= 15 - $\dfrac{1}{5}$ x 15

= 15 - 3

= 12 cm

New volume of the cube = side³

= (12)³ cm³

= 1728 cm³

Decrease in volume = 3375 - 1728 cm³

= 1647 cm³

Hence, the side of the original cube is 15 cm and the decrease in volume is 1647 cm³.

A rectangular tank 30 cm x 20 cm x 12 cm contains water to a depth of 6 cm. A metal cube of side 10 cm is placed in the tank with its one face resting on the bottom of the tank. Find the volume of water, in litres, that must be poured in the tank so that the metal cube is just submerged in the water.

Answer

Given:

Dimensions of the tank = 30 cm x 20 cm x 12 cm

Side of the cube = 10 cm

Initial depth of water in the tank = 6 cm

Initial volume of water in tank = 30 x 20 x 6 = 3600 cm³

Volume of cube = side cm³ = 10 x 10 x 10 = 1000 cm³

Volume of water required to fill the tank to a depth of 10 cm = 30 x 20 x 10 = 6000 cm³

Additional volume of water required to just submerge the cube = Volume of water at 10 cm depth - Volume of water at 6 cm depth - Volume of cube

= 6000 - 3600 - 1000

= 1400 cm³ = 1.4 litre

Hence, the volume of water that must be poured into the tank so that the metal cube is just submerged is 1.4 litre.

The dimensions of a solid metallic cuboid are 72 cm x 30 cm x 75 cm. It is melted and recast into identical solid metal cubes with each of edge 6 cm. Find the number of cubes formed.

Also, find the cost of polishing the surfaces of all the cubes formed at the rate ₹ 150 per sq.m.

Answer

Given:

Dimensions of the solid cuboid = 72 cm x 30 cm x 75 cm

Side of the cube = 6 cm

Let n be the number of cubes.

Volume of solid cuboid = Number of cubes x Volume of one cube

⇒ l x b x h = n x side³

⇒ 72 x 30 x 75 = n x (6)³

⇒ 162,000 = n x 216

⇒ n = $\dfrac{162,000}{216}$

⇒ n = 750

Total surface area of one cube = 6 x side²

= 6 x (6)² cm²

= 216 cm²

Total surface area of 750 cubes = 750 x 216 cm²

= 162,000 cm²

= 16.2 m²

Rate of polishing = ₹ 150 per sq.m

Total cost = Total surface area x Rate of polishing

= ₹ 16.2 x 150

= ₹ 2,430

Hence, the number of cubes formed = 750 and the total cost of polishing = ₹ 2,430.

The dimensions of a car petrol tank are 50 cm x 32 cm x 24 cm, which is full of petrol. If a car's average consumption is 15 km per litre, find the maximum distance that can be covered by the car.

Answer

Given:

Dimensions of tank = 50 cm x 32 cm x 24 cm

Volume of tank = 50 x 32 x 24 cm³

= 38,400 cm³

= 38.4 litre (∵ 100 cm³ = 1 litre)

Average consumption of car = 15 km per litre

Maximum distance covered by car = Volume of tank x Average consumption of car

= 38.4 x 15

= 576 km

Hence, the maximum distance that can be covered by the car is 576 km.

The dimensions of a rectangular box are in the ratio 4 : 2 : 3. The difference between cost of covering it with paper at 12 per m² and with paper at the rate of 13.50 per m² is ₹ 1,248. Find the dimensions of the box.

Answer

Given:

The ratio of dimensions of the rectangular box = 4 : 2 : 3

Let the dimension be 4a, 2a and 3a.

Total surface area of box = 2(lb + bh + hl)

= 2(4a x 2a + 2a x 3a + 3a x 4a)

= 2(8a² + 6a² + 12a²)

= 2 x 26a²

= 52a²

The difference between cost of covering it with paper at 12 per m² and with paper at the rate of 13.50 per m² = ₹ 1,248

⇒ Total surface area x 13.5 per m² - Total surface area x 12 per m² = ₹ 1,248

⇒ 52a² x 13.5 - 52a² x 12 = ₹ 1,248

⇒ 52a² (13.5 - 12) = ₹ 1,248

⇒ 52a² x 1.5 = ₹ 1,248

⇒ 78a² = ₹ 1,248

⇒ a² = $\dfrac{1,248}{78}$

⇒ a² = 16

⇒ a = $\sqrt{16}$

⇒ a = 4 m

So, the dimensions are 4a, 2a and 3a

= 4 x 4 m, 2 x 4 m and 3 x 4 m

= 16 m, 8 m and 12 m

Hence, the dimensions of the box are 16 m , 8 m and 12 m.