Rectilinear Figures [Quadrilaterals : Parallelogram, Rectangle, Rhombus, Square and Trapezium]

One angle of a seven-sided polygon is 114° and each of the other six angles is x°. Then the magnitude of x is :

1. 131°c

2. 132°

3. 135°

4. 130°

Answer

By Formula,

Sum of interior angles of an 'n' sided polygon = (2n - 4) × 90°.

∴ Sum of interior angles of a seven-sided polygon = (2 × 7 - 4) × 90°

= (14 - 4) × 90°

= 10 × 90° = 900°.

Given,

One angle of a seven-sided polygon is 114° and each of the other six angles is x°.

∴ 114° + 6x = 900°

⇒ 6x = 900° - 114°

⇒ 6x = 786°

⇒ x = $\dfrac{786°}{6}$ = 131°.

Hence, Option 1 is the correct option.

In a parallelogram ABCD, ∠A - ∠C is equal to :

1. 90°

2. 120°

3. 0°

4. 180°

Answer

We know that,

Opposite angles of a parallelogram are equal.

∴ ∠A = ∠C = x (let)

∴ ∠A - ∠C = x - x = 0°.

Hence, Option 3 is the correct option.

If each interior angle of a polygon is 144°; the number of sides in it is :

1. 5

2. 10

3. 6

4. 7

Answer

By formula,

Each interior angle of a regular polygon = $\dfrac{(2n - 4) \times 90°}{n}$

$\therefore \dfrac{(2n - 4) \times 90°}{n} = 144° \\[1em] \Rightarrow 180°.n - 360° = 144°.n \\[1em] \Rightarrow 180°.n - 144°.n = 360° \\[1em] \Rightarrow 36°.n = 360° \\[1em] \Rightarrow n = \dfrac{360°}{36°} = 10.$

Hence, Option 2 is the correct option.

The sum of the interior angles of a regular polygon is equal to six times the sum of its exterior angles. The number of sides of the polygon is :

1. 14

2. 10

3. 12

4. 16

Answer

Let n be the number of sides of the polygon.

By formula,

Sum of interior angles of an 'n' sided regular polygon = (2n - 4) × 90°.

Sum of exterior angles of a regular polygon = 360°.

Given,

The sum of the interior angles of a regular polygon is equal to six times the sum of its exterior angles.

∴ (2n - 4) × 90° = 6 × 360°

⇒ 2n - 4 = $\dfrac{6 \times 360°}{90°}$

⇒ 2n - 4 = 6 × 4

⇒ 2n - 4 = 24

⇒ 2n = 24 + 4

⇒ 2n = 28

⇒ n = $\dfrac{28}{2}$ = 14.

Hence, Option 1 is the correct option.

An exterior angle and an interior angle of a regular polygon are in the ratio 2 : 7. The number of sides in the polygon is :

1. 12

2. 6

3. 4

4. 9

Answer

Let n be the number of sides of the polygon.

Given,

An exterior angle and an interior angle of a regular polygon are in the ratio 2 : 7.

By formula,

Each interior angle of a regular polygon = $\dfrac{(2n - 4) × 90°}{n}$

Each exterior angle of a regular polygon = $\dfrac{360°}{n}$

$\Rightarrow \dfrac{\dfrac{360°}{n}}{\dfrac{(2n - 4) × 90°}{n}} = \dfrac{2}{7} \\[1em] \Rightarrow \dfrac{360° \times n}{(2n - 4) \times 90° \times n} = \dfrac{2}{7} \\[1em] \Rightarrow \dfrac{4}{2n - 4} = \dfrac{2}{7} \\[1em] \Rightarrow 2(2n - 4) = 28 \\[1em] \Rightarrow 4n - 8 = 28 \\[1em] \Rightarrow 4n = 28 + 8 \\[1em] \Rightarrow 4n = 36 \\[1em] \Rightarrow n = \dfrac{36}{4} = 9.$

Hence, Option 4 is the correct option.

The sum of the interior angles of a polygon is four times the sum of its exterior angles. Find the number of sides in the polygon.

Answer

Let n be the number of sides of the polygon.

By formula,

Sum of interior angles of an 'n' sided polygon = (2n - 4) × 90°.

Sum of exterior angles of a polygon = 360°.

Given,

The sum of the interior angles of a polygon is four times the sum of its exterior angles.

⇒ (2n - 4) × 90° = 4 × 360°

⇒ (2n - 4) = $\dfrac{4 \times 360°}{90°}$

⇒ (2n - 4) = 4 × 4

⇒ 2n - 4 = 16

⇒ 2n = 16 + 4

⇒ 2n = 20

⇒ n = $\dfrac{20}{2}$ = 10.

Hence, number of sides in polygon = 10.

The angles of a pentagon are in the ratio 4 : 8 : 6 : 4 : 5. Find each angle of the pentagon.

Answer

By formula,

Sum of interior angles of an 'n' sided polygon = (2n - 4) × 90°.

Sum of interior angles of a pentagon = [2 × 5 - 4] × 90°

= [10 - 4] × 90°

= 6 × 90°

= 540°.

Given,

The angles of a pentagon are in the ratio 4 : 8 : 6 : 4 : 5.

Let angles be 4x, 8x, 6x, 4x and 5x.

⇒ 4x + 8x + 6x + 4x + 5x = 540°

⇒ 27x = 540°

⇒ x = $\dfrac{540°}{27}$ = 20°.

⇒ 4x = 4(20°) = 80°, 8x = 8(20°) = 160°, 6x = 6(20°) = 120°, 4x = 4(20°) = 80° and 5x = 5(20°) = 100°.

Hence, angles of pentagon are 80°, 160°, 120°, 80° and 100°.

One angle of a six-sided polygon is 140° and the other angles are equal. Find the measure of each equal angle.

Answer

By formula,

Sum of interior angles of an 'n' sided polygon = (2n - 4) × 90°.

Sum of interior angles of a six-sided polygon = [2 × 6 - 4] × 90°

= [12 - 4] × 90°

= 8 × 90°

= 720°.

Given,

One angle of a six-sided polygon is 140° and the other angles are equal.

∴ 140° + 5x = 720°

⇒ 5x = 720° - 140°

⇒ 5x = 580°

⇒ x = $\dfrac{580°}{5}$ = 116°.

Hence, each equal angle of a six-sided polygon = 116°.

In a polygon, there are 5 right angles and the remaining angles are equal to 195° each. Find the number of sides in the polygon.

Answer

Let n be the number of sides of the polygon.

By formula,

Sum of interior angles of an 'n' sided polygon = (2n - 4) × 90°.

Given,

In the polygon, there are 5 right angles and the remaining angles are equal to 195° each.

∴ 5 × 90° + (n - 5) × 195° = (2n - 4) × 90°

⇒ 450° + 195°.n - 975° = 180°.n - 360°

⇒ 195°.n - 180°.n = 975° - 450° - 360°

⇒ 15°.n = 165°

⇒ n = $\dfrac{165°}{15°}$ = 11.

Hence, no. of sides in the polygon = 11.

Three angles of a seven sided polygon are 132° each and remaining four angles are equal. Find the value of each equal angle.

Answer

By formula,

Sum of interior angles of an 'n' sided polygon = (2n - 4) × 90°.

Sum of interior angles of 7 sided polygon = [2 × 7 - 4] × 90°

= [14 - 4] × 90°

= 10 × 90°

= 900°.

Given,

Three angles of a seven sided polygon are 132° each and remaining four angles are equal. Let each equal angle be x.

⇒ 3 × 132° + 4x = 900°

⇒ 396° + 4x = 900°

⇒ 4x = 900° - 396°

⇒ 4x = 504°

⇒ x = $\dfrac{504°}{4}$ = 126°.

Hence, each equal angle = 126°.

Two angles of an eight sided polygon are 142° and 176°. If the remaining angles are equal to each other; find the magnitude of each of the equal angles.

Answer

By formula,

Sum of interior angles of an 'n' sided polygon = (2n - 4) × 90°.

Sum of interior angles of 8 sided polygon = [2 × 8 - 4] × 90°

= [16 - 4] × 90°

= 12 × 90°

= 1080°.

Given,

Two angles of an eight sided polygon are 142° and 176° and remaining angles are equal. Let each equal angle be x.

⇒ 142° + 176° + 6x = 1080°

⇒ 318° + 6x = 1080°

⇒ 6x = 1080° - 318°

⇒ 6x = 762°

⇒ x = $\dfrac{762°}{6}$ = 127°.

Hence, each equal angle = 127°.

In a pentagon ABCDE, AB is parallel to DC and ∠A : ∠E : ∠D = 3 : 4 : 5. Find angle E.

Answer

By formula,

Sum of interior angles of an 'n' sided polygon = (2n - 4) × 90°.

Sum of interior angles of 5 sided polygon = [2 × 5 - 4] × 90°

= [10 - 4] × 90°

= 6 × 90°

= 540°.

We know that,

Sum of interior angles on the same side of transversal are supplementary.

∴ ∠B + ∠C = 180°.

Given,

∠A : ∠E : ∠D = 3 : 4 : 5

Let ∠A = 3x, ∠E = 4x and ∠D = 5x.

∴ ∠A + ∠B + ∠C + ∠D + ∠E = 540°

⇒ 3x + 180° + 5x + 4x = 540°

⇒ 12x = 540° - 180°

⇒ 12x = 360°

⇒ x = $\dfrac{360°}{12}$ = 30°.

⇒ ∠E = 4x = 4(30°) = 120°.

Hence, ∠E = 120°.

AB, BC and CD are the three consecutive sides of a regular polygon. If ∠BAC = 15°; find,

(i) each interior angle of the polygon.

(ii) each exterior angle of the polygon.

(iii) number of sides of the polygon.

Answer

(i) In △ ABC,

⇒ AB = BC (As, ABCD is a regular polygon)

⇒ ∠BCA = ∠BAC = 15° (In a triangle angles opposite to equal sides are equal)

By angle sum property of triangle,

⇒ ∠BCA + ∠BAC + ∠ABC = 180°

⇒ 15° + 15° + ∠ABC = 180°

⇒ 30° + ∠ABC = 180°

⇒ ∠ABC = 180° - 30° = 150°.

Since, each interior angle of a regular polygon are equal.

Hence, each interior angle of a regular polygon = 150°.

(ii) We know that,

At each vertex of every polygon,

⇒ Exterior angle + Interior angle = 180°

⇒ Exterior angle + 150° = 180°

⇒ Exterior angle = 180° - 150° = 30°.

Hence, each exterior angle of a regular polygon = 30°.

(iii) Let n be the number of sides in the polygon.

By formula,

Sum of interior angles of an 'n' sided polygon = (2n - 4) × 90°.

∴ 150°.n = (2n - 4) × 90°

⇒ 150°.n = 180°.n - 360°

⇒ 180°.n - 150°.n = 360°

⇒ 30°.n = 360°

⇒ n = $\dfrac{360°}{30°}$ = 12.

Hence, no. of sides in polygon = 12.

The ratio between an exterior angle and an interior angle of a regular polygon is 2 : 3. Find the number of sides in the polygon.

Answer

Given,

Ratio between an exterior angle and an interior angle of a regular polygon is 2 : 3.

Let exterior angle be 2x and interior angle be 3x.

We know that,

At each vertex of every polygon,

⇒ Exterior angle + Interior angle = 180°

⇒ 2x + 3x = 180°

⇒ 5x = 180°

⇒ x = $\dfrac{180°}{5}$ = 36°.

⇒ 2x = 2 × 36° = 72°, 3x = 3 × 36° = 108°.

By formula,

If each exterior angle of a regular polygon is x°, the number of sides in it = $\dfrac{360°}{x°}$

No. of sides in a regular polygon with exterior angle = 72° is $\dfrac{360°}{72°}$ = 5.

Hence, no. of sides in polygon = 5.

A quadrilateral ABCD is a trapezium, if :

1. AB = DC

2. AD = BC

3. ∠A + ∠C = 180°

4. ∠B + ∠C = 180°

Answer

We know that,

Sum of adjacent angles in a trapezium equals to 180°.

∴ ∠B + ∠C = 180°.

Hence, Option 4 is the correct option.

If the diagonals of a square ABCD intersect each other at point O, the triangle OAB is :

1. an equilateral triangle.

2. a right-angled but not an isosceles triangle.

3. an isosceles but not a right-angled triangle.

4. an isosceles right-angled triangle.

Answer

In a square,

Diagonals are equal and bisect each other.

∴ AC = BD

⇒ $\dfrac{AC}{2} = \dfrac{BD}{2}$

⇒ OA = OB.

Diagonals intersect at right angle.

∴ ∠AOB = 90°.

∴ △ AOB is an isosceles right-angled triangle.

Hence, Option 4 is the correct option.

A quadrilateral in which the diagonals are equal and bisect each other at right angles is a :

1. rectangle which is not a square.

2. rhombus which is not a square.

3. square.

4. kite which is not a square.

Answer

In a square,

Diagonals are equal and bisect each other at right angles.

Hence, Option 3 is the correct option.

Which of the following is not true for a parallelogram :

1. opposite sides are equal

2. opposite angles are equal

3. opposite angles are bisected by the diagonals

4. diagonals bisect each other

Answer

In a parallelogram,

Opposite sides and angles are equal, and diagonals bisect each other.

Hence, Option 3 is the correct option.

If the diagonals of a quadrilateral bisect each other at right angle, the quadrilateral is :

1. square

2. rhombus

3. parallelogram

4. rectangle

Answer

Diagonals of rhombus and square bisect each other at right angle.

Each square is a rhombus, but not each rhombus is a square.

Hence, Option 2 is the correct option.

State, 'true' or 'false' :

(i) The diagonals of a rectangle bisect each other.

(ii) The diagonals of a quadrilateral bisect each other.

(iii) The diagonals of a parallelogram bisect each other at right angle.

(iv) Each diagonal of a rhombus bisects it.

(v) The quadrilateral, whose four sides are equal, is a square.

(vi) Every rhombus is a parallelogram.

(vii) Every parallelogram is a rhombus.

(viii) Diagonals of a rhombus are equal.

(ix) If two adjacent sides of a parallelogram are equal, it is a rhombus.

(x) If the diagonals of a quadrilateral bisect each other at right angle, the quadrilateral is a square.

Answer

(i) True

(ii) False

Reason — Not all the quadrilateral's diagonals bisect each other, for example : diagonals of trapezium do not bisect each other.

(iii) False

Reason — The diagonals of parallelogram bisect each other at right angle only if it is a rhombus or a square.

(iv) True

(v) False

Reason — The quadrilateral, whose four sides are equal, can be a square or a rhombus.

(vi) True

(vii) False

Reason — Every rhombus is a parallelogram.

(viii) False

Reason — A rhombus with equal diagonals is a square.

(ix) True

(x) False

Reason — If the diagonals of a quadrilateral bisect each other at right angle, then the quadrilateral can be a square or a rhombus.

In the figure, given alongside, AM bisects angle A and DM bisects angle D of parallelogram ABCD. Prove that : ∠AMD = 90°.

Answer

In a parallelogram,

Sum of consecutive angles equal to 180°.

∴ ∠A + ∠D = 180° .......(1)

Given,

AM bisects angle A and DM bisects angle D of parallelogram ABCD.

∴ ∠MDA = $\dfrac{∠D}{2}$ and ∠DAM = $\dfrac{∠A}{2}$

In △ AMD,

By angle sum property of triangle,

⇒ ∠MDA + ∠DAM + ∠AMD = 180°

⇒ $\dfrac{∠D}{2} + \dfrac{∠A}{2}$ + ∠AMD = 180°

⇒ $\dfrac{∠A + ∠D}{2}$ + ∠AMD = 180°

⇒ $\dfrac{180°}{2}$ + ∠AMD = 180° [From equation (1)]

⇒ 90° + ∠AMD = 180°

⇒ ∠AMD = 180° - 90° = 90°.

Hence, proved that ∠AMD = 90°.

In the following figure, AE and BC are equal and parallel and the three sides AB, CD and DE are equal to one another. If angle A is 102°. Find angles AEC and BCD.

Answer

Join EC.

Since, AE = BC and AE || BC.

∴ AECB is a parallelogram.

In a parallelogram,

Consecutive angles are supplementary.

In a parallelogram AECB,

⇒ ∠BAE + ∠AEC = 180°

⇒ 102° + ∠AEC = 180°

⇒ ∠AEC = 180° - 102° = 78°.

In a parallelogram,

Opposite sides are equal.

∴ EC = AB ..........(1)

Given,

AB = ED = CD .........(2)

From equations (1) and (2), we get :

⇒ EC = ED = CD.

In △ CDE,

⇒ EC = ED = CD

∴ CDE is an equilateral triangle.

∴ Each angle of triangle CDE equals to 60°.

From figure,

⇒ ∠BCD = ∠BCE + ∠ECD

⇒ ∠BCD = ∠BAE + ∠ECD (∠BAE = ∠BCE, as opposite angles of parallelogram are equal)

⇒ ∠BCD = 102° + 60° = 162°.

Hence, ∠AEC = 78° and ∠BCD = 162°.

In a square ABCD, diagonals meet at O. P is a point on BC, such that OB = BP. Show that :

(i) ∠POC = $\Big(22\dfrac{1}{2}\Big)^{°}$

(ii) ∠BDC = 2 ∠POC

(iii) ∠BOP = 3 ∠COP

Answer

(i) Let ∠POC = x°.

We know that,

Each interior angle equals to 90°. Diagonals of square bisect the interior angles.

From figure,

⇒ ∠OCP = ∠OBP = $\dfrac{90°}{2}$ = 45°.

We know that,

In a triangle, an exterior angle is equal to sum of two opposite interior angles.

∴ ∠OPB = ∠OCP + ∠POC

⇒ ∠OPB = 45° + x° .........(1)

In △ OBP,

⇒ OB = BP (Given)

⇒ ∠OPB = ∠BOP (Angles opposite to equal sides are equal) .........(2)

From equation (1) and (2), we get :

⇒ ∠BOP = 45° + x° ............(3)

We know that,

Diagonals of square are perpendicular to each other.

∴ ∠BOC = 90°

⇒ ∠BOP + ∠POC = 90°

⇒ 45° + x° + x° = 90°

⇒ 2x° = 90° - 45°

⇒ 2x° = 45°

⇒ x° = $\dfrac{45°}{2}$

⇒ x° = $\Big(22\dfrac{1}{2}\Big)^{°}$

⇒ ∠POC = $\Big(22\dfrac{1}{2}\Big)^{°}$.

Hence, proved that ∠POC = $\Big(22\dfrac{1}{2}\Big)^{°}$.

(ii) From figure,

⇒ ∠BDC = 45° (Diagonals of a square bisect the interior angles)

⇒ ∠BDC = 2 × $\Big(22\dfrac{1}{2}\Big)^{°}$

⇒ ∠BDC = 2 × ∠POC

⇒ ∠BDC = 2 ∠POC.

Hence, proved that ∠BDC = 2 ∠POC.

(iii) From equation (3),

⇒ ∠BOP = 45° + x°

⇒ ∠BOP = 45° + 22.5°

⇒ ∠BOP = 67.5°

⇒ ∠BOP = 3 × 22.5°

⇒ ∠BOP = 3 × ∠POC

⇒ ∠BOP = 3 ∠POC.

Hence, proved that ∠BOP = 3 ∠COP.

The given figure shows a square ABCD and an equilateral triangle ABP. Calculate :

(i) ∠AOB

(ii) ∠BPC

(iii) ∠PCD

(iv) reflex ∠APC

Answer

(i) Given,

ABP is an equilateral triangle.

∴ ∠PAB = 60°

From figure,

⇒ ∠OAB = ∠PAB = 60°.

We know that,

Each interior angle of a square equals 90° and diagonals bisect interior angles.

∴ ∠DBA = $\dfrac{90°}{2}$ = 45°.

From figure,

⇒ ∠OBA = ∠DBA = 45°.

In △ AOB,

By angle sum property of triangle,

⇒ ∠OBA + ∠OAB + ∠AOB = 180°

⇒ 45° + 60° + ∠AOB = 180°

⇒ ∠AOB + 105° = 180°

⇒ ∠AOB = 180° - 105° = 75°.

Hence, ∠AOB = 75°.

(ii) From figure,

⇒ ∠PBA = 60° [Each angle of an equilateral triangle equals to 60°.]

⇒ ∠CBP = ∠CBA - ∠PBA = 90° - 60° = 30°.

We know that,

⇒ BP = AB (Sides of equilateral triangle) .........(1)

⇒ AB = BC (Sides of square ABCD are equal) ........(2)

From equation (1) and (2), we get :

⇒ BP = BC.

In △ BPC,

⇒ BP = BC

⇒ ∠BCP = ∠BPC = x (let) [Angles opposite to equal sides are equal]

By angle sum property of triangle,

⇒ ∠BCP + ∠BPC + ∠CBP = 180°

⇒ x + x + 30° = 180°

⇒ 2x = 180° - 30°

⇒ 2x = 150°

⇒ x = $\dfrac{150°}{2}$ = 75°.

Hence, ∠BPC = 75°.

(iii) As,

⇒ ∠BCP = ∠BPC = 75°

From figure,

⇒ ∠C = ∠BCP + ∠PCD

⇒ 90° = 75° + ∠PCD

⇒ ∠PCD = 90° - 75° = 15°.

Hence, ∠PCD = 15°.

(iv) From figure,

⇒ ∠APC = ∠APB + ∠BPC

⇒ ∠APC = 60° + 75° = 135°

⇒ Reflex ∠APC = 360° - ∠APC = 360° - 135° = 225°.

Hence, reflex ∠APC = 225°.

In the given figure; ABCD is a rhombus with angle A = 67°. If DEC is an equilateral triangle, calculate :

(i) ∠CBE

(ii) ∠DBE

Answer

(i) In rhombus ABCD,

⇒ ∠C = ∠A = 67° (Opposite angles of rhombus are equal)

From figure,

⇒ ∠BCD = ∠C = 67°.

⇒ ∠A + ∠B = 180°

⇒ 67° + ∠B = 180°

⇒ ∠B = 180° - 67° = 113°.

In △ DBC,

⇒ DC = CB (Sides of rhombus are equal in length) .........(1)

⇒ ∠CDB = ∠CBD = x (let) (In a triangle angles opposite to equal sides are equal.)

By angle sum property of triangle,

⇒ ∠CDB + ∠CBD + ∠BCD = 180°

⇒ x + x + ∠BCD = 180°

⇒ 2x + 67° = 180°

⇒ 2x = 180° - 67°

⇒ 2x = 113°

⇒ x = $\dfrac{113°}{2}$ = 56.5°

⇒ ∠CDB = ∠CBD = 56.5°

Given,

DEC is an equilateral triangle, so all the sides of triangle are equal.

∴ DC = EC ..........(2)

From equations (1) and (2), we get :

⇒ CB = EC

⇒ ∠CEB = ∠CBE = y (let) [Angles opposite to equal sides are equal]

By angle sum property of triangle,

⇒ ∠CEB + ∠CBE + ∠ECB = 180°

⇒ y + y + (∠ECD + ∠BCD) = 180°

⇒ 2y + (60° + 67°) = 180°

⇒ 2y + 127° = 180°

⇒ 2y = 180° - 127°

⇒ 2y = 53°

⇒ y = $\dfrac{53°}{2}$ = 26.5°

⇒ ∠CBE = 26.5° or 26° 30'

Hence, ∠CBE = 26.5° or 26° 30'.

(ii) From figure,

⇒ ∠DBE = ∠CBD - ∠CBE

⇒ ∠DBE = 56.5° - 26.5° = 30°.

Hence, ∠DBE = 30°.

In each of the following figures, ABCD is a parallelogram.

(i)

(ii)

In each case, given above, find the values of x and y.

Answer

(i) We know that,

Opposite sides of parallelogram are equal.

∴ AB = CD and AD = BC

⇒ AB = CD

⇒ 4x = 6y + 2

⇒ x = $\dfrac{6y + 2}{4}$ ........(1)

⇒ AD = BC

⇒ 4y = 3x - 3

⇒ 3x = 4y + 3

⇒ x = $\dfrac{4y + 3}{3}$ ..........(2)

From equation (1) and (2), we get :

⇒ $\dfrac{6y + 2}{4} = \dfrac{4y + 3}{3}$

⇒ 3(6y + 2) = 4(4y + 3)

⇒ 18y + 6 = 16y + 12

⇒ 18y - 16y = 12 - 6

⇒ 2y = 6

⇒ y = $\dfrac{6}{2}$ = 3.

Substituting value of y in equation (1), we get :

⇒ x = $\dfrac{6y + 2}{4} = \dfrac{6 \times 3 + 2}{4} = \dfrac{18 + 2}{4} = \dfrac{20}{4}$ = 5.

Hence, x = 5 and y = 3.

(ii) We know that,

Opposite angles of parallelogram are equal.

∴ ∠B = ∠D

⇒ 7y = 6x + 3y - 8°

⇒ 7y - 3y = 6x - 8°

⇒ 4y = 6x - 8°

⇒ y = $\dfrac{6x - 8°}{4}$ ..........(1)

We know that,

Consecutive angles of a parallelogram are supplementary.

⇒ ∠A + ∠C = 180°

⇒ 4x + 20° + 7y = 180°

⇒ 4x + 7y = 180° - 20°

⇒ 4x + 7y = 160°

⇒ 7y = 160° - 4x

⇒ y = $\dfrac{160° - 4x}{7}$ ...........(2)

From equation (1) and (2), we get :

⇒ $\dfrac{6x - 8°}{4} = \dfrac{160° - 4x}{7}$

⇒ 7(6x - 8°) = 4(160° - 4x)

⇒ 42x - 56° = 640° - 16x

⇒ 42x + 16x = 640° + 56°

⇒ 58x = 696°

⇒ x = $\dfrac{696°}{58}$ = 12°.

Substituting value of x in equation (1), we get :

⇒ y = $\dfrac{6x - 8°}{4} = \dfrac{6 \times 12° - 8°}{4} = \dfrac{72° - 8°}{4} = \dfrac{64°}{4}$ = 16°.

Hence, x = 12° and y = 16°.

The angles of a quadrilateral are in the ratio 3 : 4 : 5 : 6. Show that the quadrilateral is a trapezium.

Answer

Let ABCD be the quadrilateral.

Given,

Angles of a quadrilateral are in the ratio 3 : 4 : 5 : 6.

Let angles of quadrilateral be ∠A = 3x, ∠B = 4x, ∠C = 5x and ∠D = 6x.

We know that,

Sum of angles of a quadrilateral is 360°.

∴ 3x + 4x + 5x + 6x = 360°

⇒ 18x = 360°

⇒ x = $\dfrac{360°}{18}$ = 20°.

⇒ ∠A = 3x = 3 × 20° = 60°,

⇒ ∠B = 4x = 4 × 20° = 80°,

⇒ ∠C = 5x = 5 × 20° = 100° and

⇒ ∠D = 6x = 6 × 20° = 120°.

⇒ ∠A + ∠D = 60° + 120° = 180°,

⇒ ∠B + ∠C = 80° + 100° = 180°.

Since, ∠A and ∠D are supplementary and ∠B and ∠C are supplementary.

∴ AB || CD.

Since, one of the opposite sides of quadrilateral ABCD is parallel and all interior angles are unequal.

Hence, proved that quadrilateral is a trapezium.

In a parallelogram ABCD, AB = 20 cm and AD = 12 cm. The bisector of angle A meets DC at E and BC produced at F. Find the length of CF.

Answer

Given,

Bisector of angle A meets DC at E.

∴ AE bisects angle A.

∴ ∠DAE = ∠BAF = x (let)

From figure,

⇒ ∠AFB = ∠DAE = x (Alternate angles are equal)

In △ ABF,

⇒ ∠AFB = ∠BAF (Both equal to x)

∴ BF = AB = 20 cm (Sides opposite to equal angles are equal)

⇒ BF = BC + CF

⇒ BF = AD + CF (BC = AD, opposite sides of a parallelogram are equal)

⇒ 20 = 12 + CF

⇒ CF = 20 - 12 = 8 cm.

Hence, CF = 8 cm.

If the opposite sides of a quadrilateral are equal, the quadrilateral is :

1. rectangle

2. parallelogram

3. not a square

4. rhombus

Answer

If the opposite sides of a quadrilateral are equal, the quadrilateral is a parallelogram.

Hence, Option 2 is the correct option.

If the opposite angles of a quadrilateral are equal, the quadrilateral is :

1. rectangle

2. parallelogram

3. square

4. rhombus

Answer

If the opposite angles of a quadrilateral are equal, the quadrilateral is a parallelogram.

Hence, Option 2 is the correct option.

If three angles of a quadrilateral are equal to 90° each, then the quadrilateral is :

1. rectangle

2. square

3. parallelogram

4. rhombus

Answer

Given,

Three angles of a quadrilateral are equal to 90° each.

We know that,

Sum of angles of a quadrilateral = 360°.

Let fourth angle be x.

∴ 3 × 90° + x = 360°

⇒ 270° + x = 360°

⇒ x = 360° - 270° = 90°.

We know that,

Each interior angle of a rectangle and square equals to 90°.

Each square is a rectangle but not each rectangle is a square.

Hence, Option 1 is the correct option.

If three angles of a quadrilateral are equal, then the quadrilateral is :

1. rectangle

2. rhombus

3. not a parallelogram

4. parallelogram

Answer

If three angles of a quadrilateral are equal, then the quadrilateral is not a parallelogram.

Hence, Option 3 is the correct option.

BEC is an equilateral triangle inside the square ABCD. The value of angle ECD is :

1. 60°

2. 30°

3. 75°

4. 45°

Answer

Given,

BEC is an equilateral triangle.

∴ ∠BCE = 60°.

From figure,

⇒ ∠ECD = ∠BCD - ∠BCE = 90° - 60° = 30°.

Hence, Option 2 is the correct option.

E is the mid-point of side AB and F is the mid point of side DC of parallelogram ABCD. Prove that AEFD is a parallelogram.

Answer

We know that,

Opposite sides of parallelogram are equal.

∴ AB = CD

⇒ $\dfrac{AB}{2} = \dfrac{CD}{2}$

⇒ AE = FD.

Also,

Opposite sides of parallelogram are parallel.

∴ AB || CD

⇒ AE || FD.

∴ AE = FD and AE || FD.

Since, one pair of opposite side of quadrilateral AEFD is parallel.

Hence, proved that AEFD is a parallelogram.

The diagonal BD of a parallelogram ABCD bisects angles B and D. Prove that ABCD is a rhombus.

Answer

Since, opposite angles of a parallelogram are equal.

∴ ∠ABC = ∠ADC = x (let)

Given,

BD bisects ∠B.

∴ ∠ABD = ∠CBD = $\dfrac{1}{2} ∠ABC = \dfrac{x}{2}$

BD bisects ∠D.

∴ ∠ADB = ∠BDC = $\dfrac{1}{2} ∠ADC = \dfrac{x}{2}$

⇒ ∠ABD = ∠ADB and ∠CBD = ∠CDB

In △ ABD,

⇒ ∠ABD = ∠ADB

∴ AB = AD (Sides opposite to equal angles are equal) ......(1)

In △ CBD,

⇒ ∠CBD = ∠CDB

∴ CD = BC (Sides opposite to equal angles are equal) .........(2)

As, ABCD is a parallelogram.

Thus, opposite sides are equal.

∴ AB = CD .........(3)

∴ AD = BC ..........(4)

From equations (1), (2), (3) and (4), we get :

⇒ AB = BC = CD = AD.

Since, all sides of quadrilateral ABCD are equal.

Hence, proved that ABCD is a rhombus.

The alongside figure shows a parallelogram ABCD in which AE = EF = FC. Prove that :

(i) DE is parallel to FB

(ii) DE = FB

(iii) DEBF is a parallelogram.

Answer

Join BD. Let BD intersect AC at point O.

(i) We know that,

Diagonals of parallelogram bisect each other.

∴ OB = OD and OA = OC.

From figure,

⇒ OA = OC

⇒ OA - AE = OC - FC (As, AE = FC)

⇒ OE = OF.

In quadrilateral DEBF,

⇒ OB = OD and OE = OF.

Since, diagonals of quadrilateral DEBF bisect each other,

∴ DEBF is a parallelogram.

∴ DE || FB (Opposite sides of parallelogram are parallel.)

Hence, proved that DE || FB.

(ii) We know that,

Opposite sides of parallelogram are equal.

In parallelogram DEBF,

∴ DE = FB.

Hence, proved that DE = FB.

(iii) Since, one pair of opposite sides of quadrilateral DEBF is equal and parallel,

i.e. DE || FB and DE = FB,

∴ DEBF is a parallelogram.

Hence, proved that DEBF is a parallelogram.

In the alongside figure, ABCD is a parallelogram in which AP bisects angle A and BQ bisects angle B. Prove that :

(i) AQ = BP

(ii) PQ = CD

(iii) ABPQ is a parallelogram

Answer

(i) Let ∠A = 2x.

We know that,

Sum of consecutive angles in a parallelogram equals to 180°.

⇒ ∠A + ∠B = 180°

⇒ 2x + ∠B = 180°

⇒ ∠B = 180° - 2x.

⇒ ∠PAB = $\dfrac{∠A}{2} = \dfrac{2x}{2}$ = x.

⇒ ∠QBA = $\dfrac{∠B}{2} = \dfrac{180° - 2x}{2}$ = 90° - x.

In △ ABP,

⇒ ∠PAB + ∠ABP + ∠BPA = 180° (By angle sum property of triangle)

⇒ x + 180° - 2x + ∠BPA = 180°

⇒ 180° - x + ∠BPA = 180°

⇒ ∠BPA = 180° - 180° + x = x.

∴ ∠BPA = ∠PAB (Both equal to x)

∴ AB = BP (In a triangle sides opposite to equal angles are equal) ..........(1)

In △ ABQ,

⇒ ∠QBA + ∠BAQ + ∠AQB = 180° (By angle sum property of triangle)

⇒ 90° - x + 2x + ∠AQB = 180°

⇒ 90° + x + ∠AQB = 180°

⇒ ∠AQB = 180° - 90° - x = 90° - x.

∴ ∠AQB = ∠QBA (Both equal to 90° - x)

∴ AB = AQ (In a triangle sides opposite to equal angles are equal) ..........(2)

From equation (1) and (2), we get :

⇒ AQ = BP.

Hence, proved that AQ = BP.

(ii) Given,

ABCD is a parallelogram.

We know that,

Opposite sides of parallelogram are equal and parallel.

∴ AB = CD ............(1)

∴ AD || BC.

Since, AD || BC

∴ AQ || BP

Join PQ.

We know that,

AQ = BP (Proved above)

In quadrilateral ABPQ,

AQ = BP and AQ || BP.

Since, one of the pair of opposite sides of quadrilateral ABPQ are equal and parallel.

∴ ABPQ is a parallelogram.

∴ AB = PQ [Opposite sides of parallelogram are equal] .........(2)

From (1) and (2), we get :

PQ = CD.

Hence, proved that PQ = CD.

(iii) In quadrilateral ABPQ,

AQ || BP and AQ = BP.

∴ ABPQ is a parallelogram (Since, one of the pair of opposite sides of quadrilateral ABPQ are equal and parallel.)

Hence, proved that ABPQ is a parallelogram.

In the given figure, ABCD is a parallelogram. Prove that : AB = 2BC.

Answer

Given,

ABCD is a parallelogram.

∴ AB || CD (Opposite sides of parallelogram are parallel)

From figure,

AE is the transversal.

⇒ ∠BAE = ∠AED (Alternate angles are equal) ........(1)

⇒ ∠DAE = ∠BAE (Since, AE is the bisector of angle A) .........(2)

From equations (1) and (2), we get :

⇒ ∠AED = ∠DAE.

In △ DAE,

⇒ ∠AED = ∠DAE

⇒ AD = DE (In a triangle, sides opposite to equal angles are equal) .......(3)

From figure,

BE is the transversal.

⇒ ∠CEB = ∠EBA (Alternate angles are equal) ........(4)

⇒ ∠CBE = ∠EBA (Since, BE is the bisector of angle B) .........(5)

From equations (4) and (5), we get :

⇒ ∠CEB = ∠CBE.

In △ CBE,

⇒ ∠CEB = ∠CBE

⇒ BC = CE (In a triangle, sides opposite to equal angles are equal) .......(6)

In parallelogram ABCD,

⇒ AB = CD (Opposite sides of parallelogram are equal)

⇒ AB = DE + EC

⇒ AB = AD + BC [From equation (3) and (6)]

⇒ AB = BC + BC (AD = BC, as opposite sides of parallelogram are equal)

⇒ AB = 2 BC.

Hence, proved that AB = 2 BC.

Prove that the bisectors of opposite angles of a parallelogram are parallel.

Answer

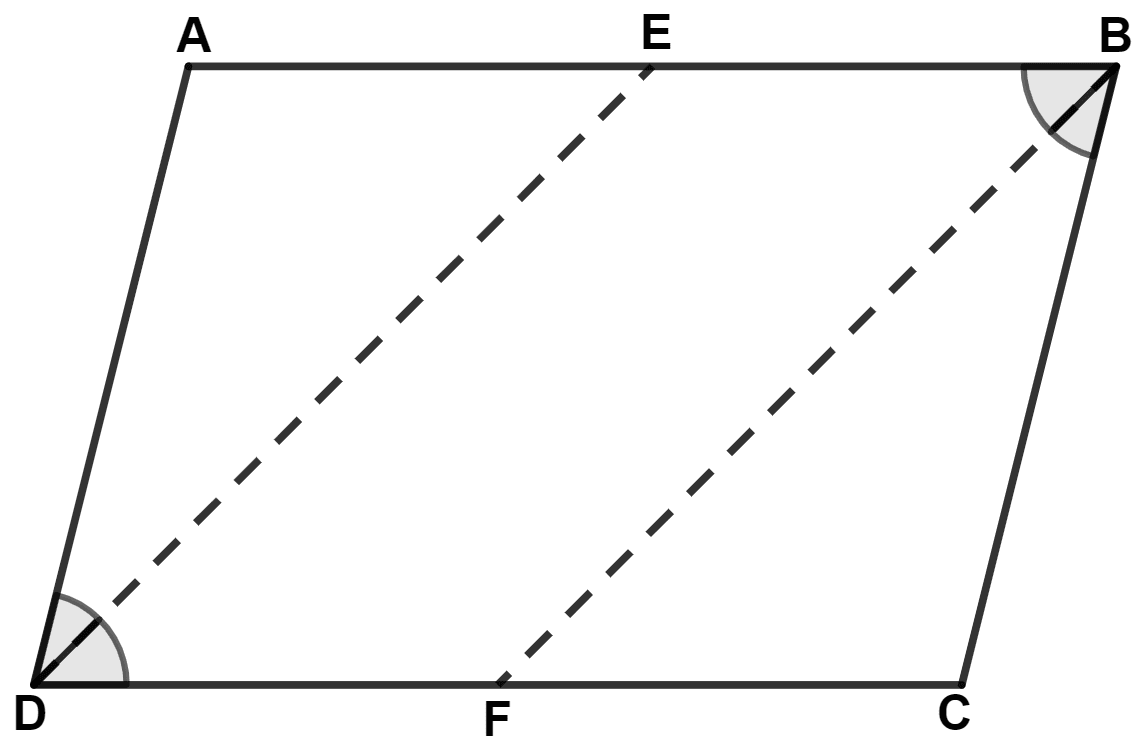
From figure,

DE and BF are bisectors of angles D and B respectively.

In parallelogram ABCD,

⇒ ∠B = ∠D (Opposite angles of || gm are equal)

⇒ $\dfrac{∠B}{2} = \dfrac{∠D}{2}$

⇒ ∠FBC = ∠ADE.

In △ ADE and △ CBF,

⇒ ∠ADE = ∠FBC (Proved above)

⇒ AD = BC (Opposite sides of || gm ABCD are equal)

⇒ ∠DAE = ∠BCF (Opposite angles of || gm ABCD are equal)

∴ △ ADE ≅ △ CBF (By A.S.A. axiom)

We know that,

Corresponding sides of congruent triangle are equal.

∴ AE = CF

Since, AE = CF and AB = CD,

∴ BE = DF

In parallelogram ABCD,

⇒ AB || CD

⇒ BE || DF

Since,

BE = DF and BE || DF

In quadrilateral BEDF, one of the pair of opposite sides are equal and parallel.

∴ BEDF is a parallelogram.

∴ DE || BF.

Hence, proved that bisectors of opposite angles of a parallelogram are parallel.

Prove that the bisectors of interior angles of a parallelogram form a rectangle.

Answer

Let ABCD be the parallelogram.

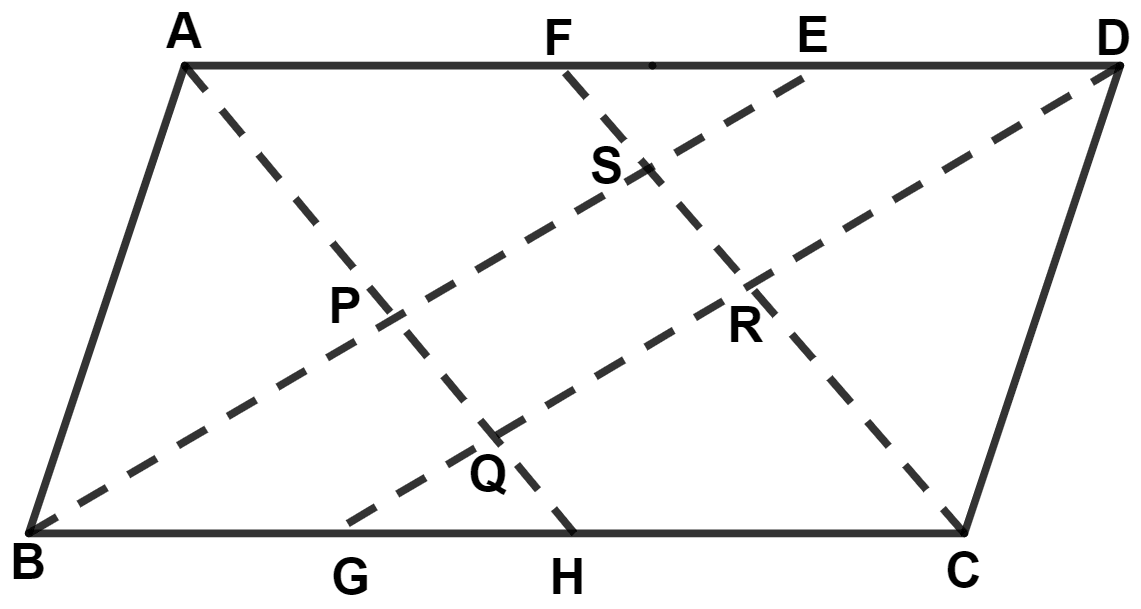
From figure,

AH, BE, CF and DG are bisectors of ∠A, ∠B, ∠C and ∠D respectively.

We know that,

Consecutive angles of parallelogram are supplementary.

Considering ∠A + ∠B = 180°,

⇒ $\dfrac{∠A + ∠B}{2} = \dfrac{180°}{2}$

⇒ $\dfrac{∠A + ∠B}{2}$ = 90°

⇒ $\dfrac{∠A}{2} + \dfrac{∠B}{2}$ = 90° ............(1)

Considering ∠B + ∠C = 180°,

⇒ $\dfrac{∠B + ∠C}{2} = \dfrac{180°}{2}$

⇒ $\dfrac{∠B + ∠C}{2}$ = 90°

⇒ $\dfrac{∠B}{2} + \dfrac{∠C}{2}$ = 90° ............(2)

Considering ∠C + ∠D = 180°,

⇒ $\dfrac{∠C + ∠D}{2} = \dfrac{180°}{2}$

⇒ $\dfrac{∠C + ∠D}{2}$ = 90°

⇒ $\dfrac{∠C}{2} + \dfrac{∠D}{2}$ = 90° .........(3)

Considering ∠D + ∠A = 180°,

⇒ $\dfrac{∠D + ∠A}{2} = \dfrac{180°}{2}$

⇒ $\dfrac{∠D + ∠A}{2}$ = 90°

⇒ $\dfrac{∠D}{2} + \dfrac{∠A}{2}$ = 90° .........(4)

In △ PAB,

By angle sum property of triangle,

⇒ ∠PAB + ∠ABP + ∠BPA = 180°

⇒ $\dfrac{∠A}{2} + \dfrac{∠B}{2}$ + ∠BPA = 180°

⇒ 90° + ∠BPA = 180° [From equation (1)]

⇒ ∠BPA = 180° - 90° = 90°.

From figure,

⇒ ∠SPQ = ∠BPA = 90° (Vertically opposite angles are equal)

In △ BSC,

By angle sum property of triangle,

⇒ ∠SBC + ∠SCB + ∠BSC = 180°

⇒ $\dfrac{∠B}{2} + \dfrac{∠C}{2}$ + ∠BSC = 180°

⇒ 90° + ∠BSC = 180° [From equation (2)]

⇒ ∠BSC = 180° - 90° = 90°.

From figure,

⇒ ∠PSR = ∠BSC = 90°.

In △ DRC,

By angle sum property of triangle,

⇒ ∠RCD + ∠CDR + ∠DRC = 180°

⇒ $\dfrac{∠C}{2} + \dfrac{∠D}{2}$ + ∠DRC = 180°

⇒ 90° + ∠DRC = 180° [From equation (3)]

⇒ ∠DRC = 180° - 90° = 90°.

From figure,

⇒ ∠SRQ = ∠DRC = 90° (Vertically opposite angles are equal)

In △ AQD,

By angle sum property of triangle,

⇒ ∠QAD + ∠ADQ + ∠DQA = 180°

⇒ $\dfrac{∠A}{2} + \dfrac{∠D}{2}$ + ∠DQA = 180°

⇒ 90° + ∠DQA = 180° [From equation (4)]

⇒ ∠DQA = 180° - 90° = 90°.

From figure,

⇒ ∠RQP = ∠DQA = 90°.

Since, all the interior angles of quadrilateral PQRS equals to 90°.

∴ PQRS is a rectangle.

Hence, proved that bisectors of interior angles of a parallelogram form a rectangle.

Prove that the bisectors of the interior angles of a rectangle form a square.

Answer

In rectangle,

All the interior angles equal to 90°. So, bisectors divide interior angles into two 45° angles.

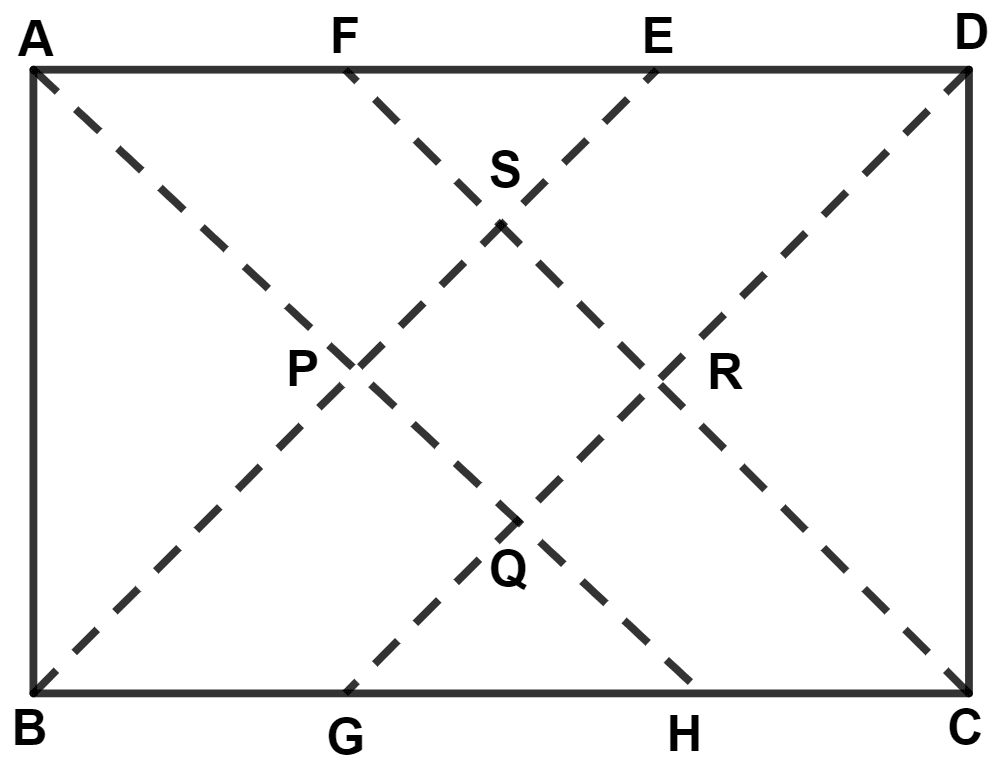
In △ BSC,

By angle sum property of triangle,

⇒ ∠SBC + ∠SCB + ∠BSC = 180°

⇒ $\dfrac{∠B}{2} + \dfrac{∠C}{2}$ + ∠BSC = 180°

⇒ 45° + 45° + ∠BSC = 180°

⇒ ∠BSC = 180° - 90° = 90°.

Since,

⇒ ∠SBC = ∠SCB

∴ BS = SC (Sides opposite to equal angles are equal) .....(1)

From figure,

⇒ ∠PSR = ∠BSC = 90°.

In △ APB and △ DRC,

⇒ ∠PAB = ∠RDC (Both equal to 45°)

⇒ ∠PBA = ∠RCD (Both equal to 45°)

⇒ AB = CD (Opposite sides of rectangle are equal)

∴ △ APB ≅ △ DRC (By A.S.A. axiom)

We know that,

Corresponding parts of congruent triangle are equal.

∴ BP = CR .........(2)

Subtracting equation (2) from (1), we get :

⇒ BS - BP = SC - CR

⇒ PS = SR .............(3)

In △ DRC,

By angle sum property of triangle,

⇒ ∠RCD + ∠CDR + ∠DRC = 180°

⇒ $\dfrac{∠C}{2} + \dfrac{∠D}{2}$ + ∠DRC = 180°

⇒ 45° + 45° + ∠DRC = 180°

⇒ ∠DRC = 180° - 90° = 90°.

From figure,

⇒ ∠SRQ = ∠DRC = 90° (Vertically opposite angles are equal)

In △ PAB,

By angle sum property of triangle,

⇒ ∠PAB + ∠ABP + ∠BPA = 180°

⇒ $\dfrac{∠A}{2} + \dfrac{∠B}{2}$ + ∠BPA = 180°

⇒ 45° + 45° + ∠BPA = 180°

⇒ ∠BPA = 180° - 90° = 90°.

From figure,

⇒ ∠SPQ = ∠BPA = 90° (Vertically opposite angles are equal)

In △ AQD,

By angle sum property of triangle,

⇒ ∠DAQ + ∠QDA + ∠AQD = 180°

⇒ $\dfrac{∠A}{2} + \dfrac{∠D}{2}$ + ∠AQD = 180°

⇒ 45° + 45° + ∠AQD = 180°

⇒ ∠AQD = 180° - 90° = 90°.

Since,

⇒ ∠DAQ = ∠QDA

∴ AQ = QD (Sides opposite to equal angles are equal) .....(4)

From figure,

⇒ ∠PQR = ∠AQD = 90°.

Since, △ APB ≅ △ DRC

∴ AP = DR .........(5)

Subtracting equation (5) from (4), we get :

⇒ AQ - AP = QD - DR

⇒ PQ = QR ...........(6)

In △ BSC and △ AQD,

⇒ ∠B = ∠A (Both equal to 45°)

⇒ ∠C = ∠D (Both equal to 45°)

⇒ ∠S = ∠Q (Both equal to 90°)

∴ △ BSC ≅ △ AQD (By A.A.A. axiom)

We know that,

Corresponding parts of congruent triangle are equal.

∴ BS = AQ .........(7)

In △ AQD,

⇒ ∠A = ∠D (Both equal to 45°)

⇒ DQ = AQ (Sides opposite to equal angles are equal) .........(8)

From equation (7) and (8), we get :

⇒ BS = DQ .........(9)

In △ CDR,

⇒ ∠C = ∠D (Both equal to 45°)

⇒ DR = CR (Sides opposite to equal angles are equal) .........(10)

From equation (2) and (10), we get :

⇒ BP = DR .....(11)

Subtracting equation (11) from (9), we get :

⇒ BS - BP = DQ - DR

⇒ PS = QR .........(12)

From equation (3), (6) and (12), we get :

⇒ PQ = QR = RS = PS.

Since, all sides of quadrilateral PQRS are equal and each interior angle equals to 90°.

∴ PQRS is a square.

Hence, proved that bisectors of the interior angles of a rectangle form a square.

In parallelogram ABCD, the bisectors of angle A meets DC at P and AB = 2AD.

Prove that :

(i) BP bisects angle B.

(ii) Angle APB = 90°.

Answer

(i) Let AD = x.

Given,

AB = 2AD = 2x.

Given,

AP is the bisector of angle A,

∴ ∠1 = ∠2 .............(1)

From figure,

⇒ ∠2 = ∠5 [Alternate angles are equal] ......(2)

From equation (1) and (2), we get :

⇒ ∠1 = ∠5

In △ ADP,

⇒ ∠1 = ∠5

⇒ DP = AD = x (Sides opposite to equal angles are equal)

From figure,

⇒ AB = CD (Opposite sides of parallelogram are equal)

⇒ CD = 2x

⇒ DP + PC = 2x

⇒ x + PC = 2x

⇒ PC = 2x - x = x.

Also,

⇒ BC = AD = x (Opposite sides of parallelogram are equal)

In △ BCP,

⇒ BC = PC (Both equal to x)

⇒ ∠6 = ∠4 (Angles opposite to equal sides are equal) ......(3)

⇒ ∠6 = ∠3 (Alternate angles are equal) ..........(4)

From equation (3) and (4), we get :

⇒ ∠3 = ∠4.

∴ BP is the bisector of angle B.

Hence, proved that BP bisects angle B.

(ii) We know that,

Consecutive angles of parallelogram are supplementary.

Considering ∠A + ∠B = 180°,

⇒ $\dfrac{∠A + ∠B}{2} = \dfrac{180°}{2}$

⇒ $\dfrac{∠A + ∠B}{2}$ = 90°

⇒ $\dfrac{∠A}{2} + \dfrac{∠B}{2}$ = 90° ............(1)

In △ PAB,

By angle sum property of triangle,

⇒ ∠PAB + ∠ABP + ∠APB = 180°

⇒ $\dfrac{∠A}{2} + \dfrac{∠B}{2}$ + ∠APB = 180°

⇒ 90° + ∠APB = 180° [From equation (1)]

⇒ ∠APB = 180° - 90° = 90°.

Hence, proved that ∠APB = 90°.

Points M and N are taken on the diagonal AC of a parallelogram ABCD such that AM = CN. Prove that BMDN is a parallelogram.

Answer

Join BD. Let BD intersect AC at point O.

In parallelogram ABCD,

Diagonals of || gm bisect each other.

⇒ OA = OC .........(1)

⇒ OB = OD

Given,

⇒ AM = CN .........(2)

Subtracting equation (2) from (1), we get :

⇒ OA - AM = OC - CN

⇒ OM = ON.

In quadrilateral BMDN,

⇒ OM = ON and OB = OD.

∴ Diagonals of quadrilateral BMDN bisect each other.

∴ BMDN is a parallelogram.

Hence, proved that BMDN is a parallelogram.

In the following figure, ABCD is a parallelogram. Prove that :

(i) AP bisects angle A

(ii) BP bisects angle B

(iii) ∠DAP + ∠CBP = ∠APB

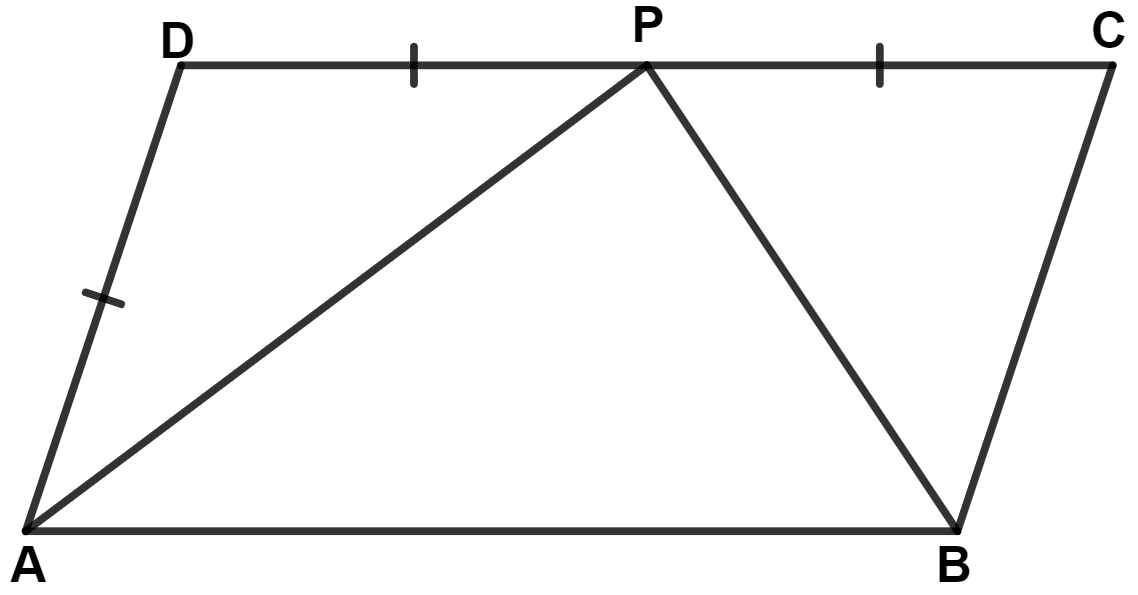
Answer

(i) In △ ADP,

⇒ AD = DP (Given)

∴ ∠APD = ∠PAD (Angles opposite to equal sides are equal) .......(1)

In parallelogram ABCD,

AB || DC and AP is the transversal.

∴ ∠APD = ∠PAB (Alternate angles are equal) ........(2)

From equation (1) and (2), we get :

⇒ ∠PAD = ∠PAB.

∴ AP bisects angle A.

Hence, proved that AP bisects angle A.

(ii) In || gm ABCD,

⇒ BC = AD (Opposite sides of || gm are equal)

∴ BC = PC

∴ ∠BPC = ∠PBC (Angles opposite to equal sides are equal) .......(3)

In parallelogram ABCD,

AB || DC and BP is the transversal.

∴ ∠BPC = ∠PBA (Alternate angles are equal) ........(4)

From equation (1) and (2), we get :

⇒ ∠PBC = ∠PBA.

∴ BP bisects angle B.

Hence, proved that BP bisects angle B.

(iii) We know that,

Consecutive angles of a || gm are supplementary.

∴ ∠A + ∠B = 180°,

⇒ $\dfrac{∠A + ∠B}{2} = \dfrac{180°}{2}$

⇒ $\dfrac{∠A + ∠B}{2}$ = 90°

⇒ $\dfrac{∠A}{2} + \dfrac{∠B}{2}$ = 90°

⇒ ∠PAB + ∠PBA = 90° .........(1)

In △ APB,

⇒ ∠PAB + ∠PBA + ∠APB = 180°

⇒ 90° + ∠APB = 180°

⇒ ∠APB = 180° - 90°

⇒ ∠APB = 90° ........(2)

From figure,

⇒ ∠PAB = ∠DAP (As, AP bisects ∠A)

⇒ ∠PBA = ∠CBP (As, BP bisects ∠B)

Substituting value of ∠PAB and ∠PBA in equation (1), we get :

⇒ ∠DAP + ∠CBP = 90° .........(3)

From equation (3) and (4), we get :

⇒ ∠DAP + ∠CBP = ∠APB.

Hence, proved that ∠DAP + ∠CBP = ∠APB.

ABCD is a square. A is joined to a point P on BC and D is joined to a point Q on AB. If AP = DQ; prove that AP and DQ are perpendicular to each other.

Answer

Let AP and DQ intersect at point O.

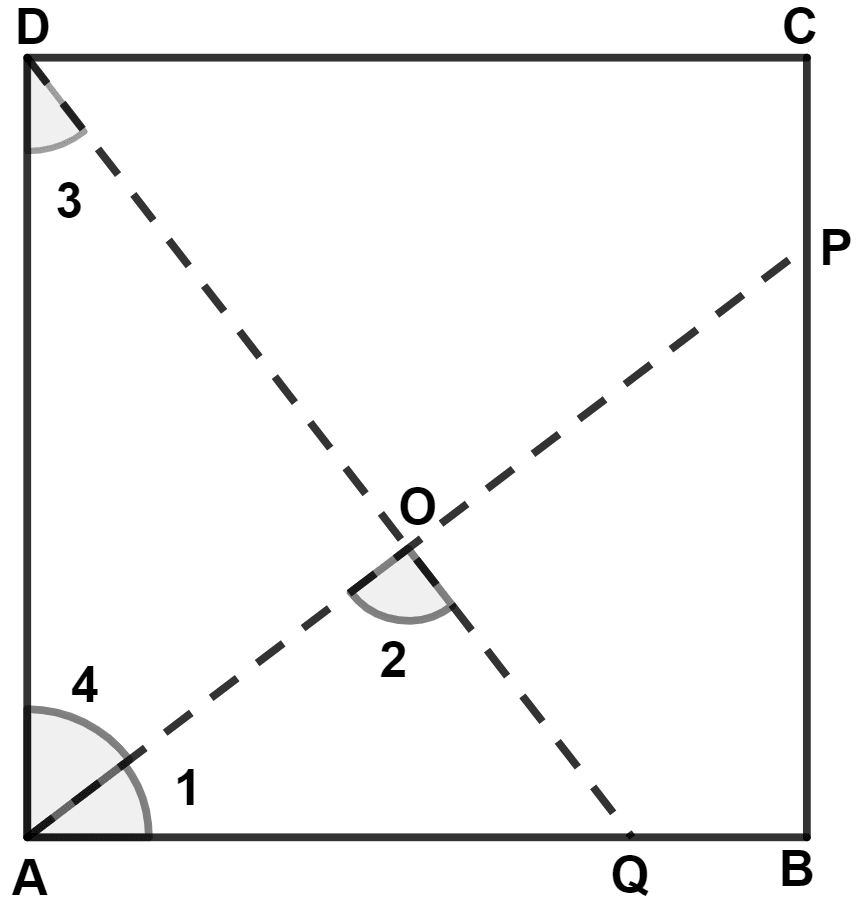
In △ DAQ and △ ABP,

⇒ ∠DAQ = ∠ABP (Interior angle of square equal to 90°)

⇒ DQ = AP (Given)

⇒ AD = AB (Each side of square equal in length)

∴ △ DAQ ≅ △ ABP (By R.H.S. congruence rule)

We know that,

Corresponding parts of congruent triangle are equal.

∴ ∠3 = ∠1 ........(1)

From figure,

⇒ ∠1 + ∠4 = 90°

Substituting value of ∠1 from equation (1) in above equation, we get :

⇒ ∠3 + ∠4 = 90°

In triangle AOD,

By angle sum property of triangle,

⇒ ∠ODA + ∠OAD + ∠AOD = 180°

⇒ ∠3 + ∠4 + ∠AOD = 180°

⇒ 90° + ∠AOD = 180°

⇒ ∠AOD = 180° - 90° = 90°.

∴ AP ⊥ DQ.

Hence, proved that AP and DQ are perpendicular to each other.

In a quadrilateral ABCD, AB = AD and CB = CD. Prove that :

(i) AC bisects angle BAD.

(ii) AC is perpendicular bisector of BD.

Answer

(i) In △ ABC and △ ADC,

⇒ AB = AD (Given)

⇒ BC = CD (Given)

⇒ AC = AC (Common side)

∴ △ ABC ≅ △ ADC (By S.S.S. axiom)

We know that,

Corresponding parts of congruent triangle are equal.

⇒ ∠BAC = ∠DAC

∴ AC bisects ∠BAD.

Hence, proved that AC bisects angle BAD.

(ii) Since, AC bisects ∠BAD

∴ ∠BAO = ∠DAO

In △ AOB and △ AOD,

⇒ AB = AD (Given)

⇒ AO = AO (Common side)

⇒ ∠BAO = ∠DAO (Proved above)

∴ △ AOB ≅ △ AOD (By S.A.S. axiom)

We know that,

Corresponding parts of congruent triangle are equal.

⇒ ∠BOA = ∠DOA ........(1)

From figure,

⇒ ∠BOA + ∠DOA = 180° (Linear pair)

⇒ ∠BOA + ∠BOA = 180° [From equation (1)]

⇒ 2∠BOA = 180°

⇒ ∠BOA = $\dfrac{180°}{2}$ = 90°.

∴ AC is perpendicular bisector of BD.

Hence, proved that AC is perpendicular bisector of BD.

The angles of a pentagon are in the ratio 2 : 5 : 6 : 4 : 3. The largest angle is:

1. 54°

2. 135°

3. 162°

4. 108°

Answer

According to the properties of polygons, if a polygon has n sides, then the sum of its interior angles is (2n - 4) x 90°.

A pentagon have 5 sides.

Sum of its interior angles = (2 x 5 - 4) x 90°

= (10 - 4) x 90°

= 6 x 90°

= 540°.

It is given that the interior angles of the pentagon are in the ratio 2 : 5 : 6 : 4 : 3.

So,

⇒ 2a + 5a + 6a + 4a + 3a = 540°

⇒ 20a = 540°

⇒ a = $\dfrac{540°}{20}$

⇒ a = 27°

The angles are:

⇒ 2a = 2 x 27° = 54°

⇒ 5a = 5 x 27° = 135°

⇒ 6a = 6 x 27° = 162°

⇒ 4a = 4 x 27° = 108°

⇒ 3a = 3 x 27° = 81°

Thus, the largest angle = 162°.

Hence, option 3 is the correct option.

At a vertex of a regular polygon, exterior angle is 120°. Then the number of sides of this polygon is:

1. 3

2. 4

3. 5

4. 6

Answer

Given, exterior angle = 120°.

The sum of the exterior angles of any convex polygon is 360°. For a regular polygon, all exterior angles are equal.

Let the number of sides of polygon be n.

By formula,

For a regular polygon,

Number of sides in it = $\dfrac{360°}{\text{Each exterior angle}} = \dfrac{360°}{120°}$ = 3.

Hence, option 1 is the correct option.

A quadrilateral ABCD is a trapezium if:

1. AB = DC

2. AD = BC

3. ∠A + ∠C = 180°

4. ∠B + ∠C = 180°

Answer

In a trapezium the sum of co-interior adjacent angles = 180°.

From figure,

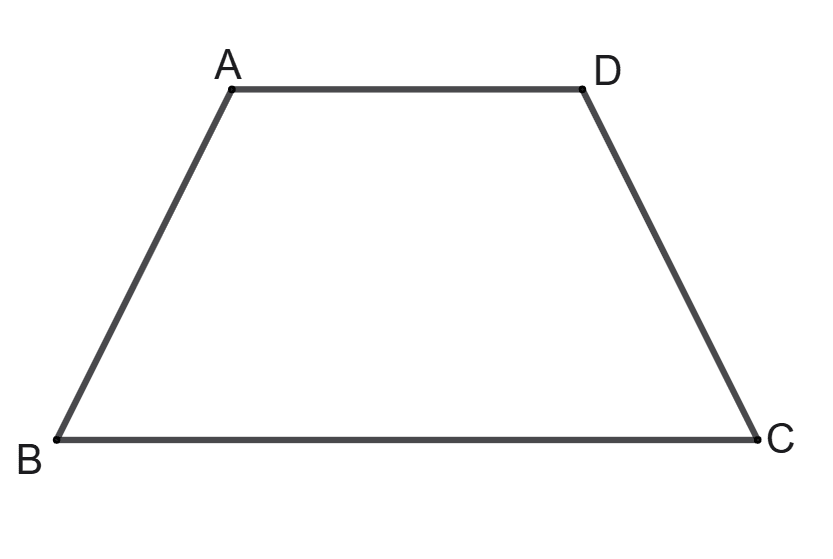
∠B and ∠C are adjacent angles.

∴ ∠B + ∠C = 180°

Hence, option 4 is the correct option.

In parallelogram ABCD, diagonal AC and BD intersect each other at point O. Then:

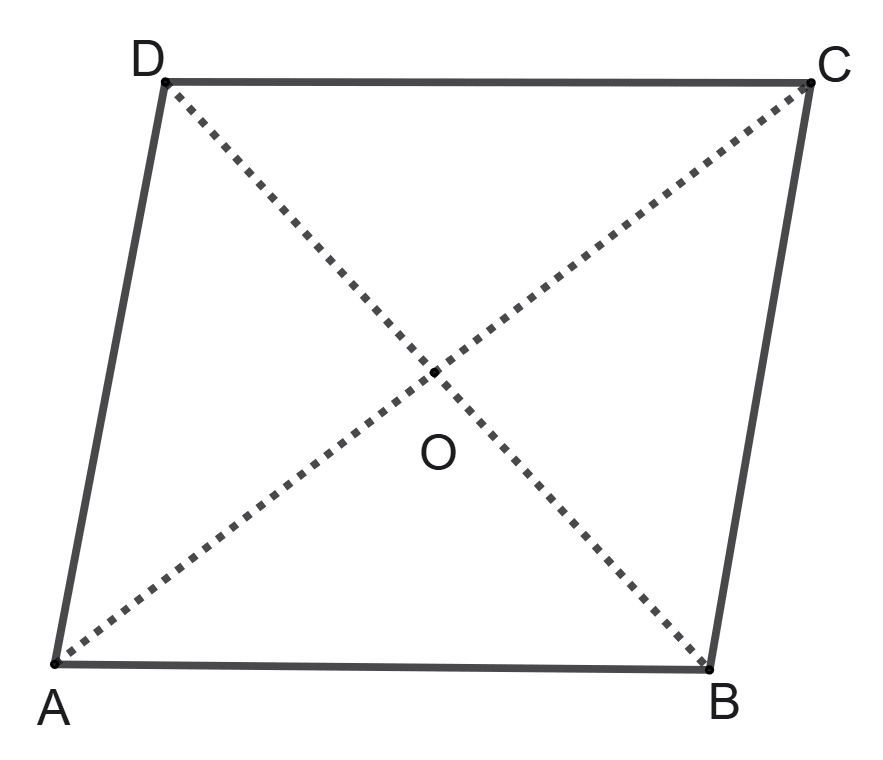
1. AC = BD

2. ∠AOB = 90°

3. The four triangles formed are congruent

4. AC and BD bisect each other

Answer

Given; ABCD is a parallelogram in which AC and BD are the diagonals of the parallelogram.

As we know that in a parallelogram, opposite sides are parallel and equal in length, opposite angles are equal and consecutive angles are supplementary.

Option 1: AC = BD is true only for rectangles or squares, not all parallelograms.

Option 2: ∠AOB = 90° is true only for rhombuses or squares, not all parallelograms.

Option 3: The four triangles formed are congruent is true only for rhombuses or squares, not all parallelograms.

Option 4: AC and BD bisect each other is a fundamental property of all parallelograms.

Hence, option 4 is the correct option.

Statement 1: The sum of the interior angles of a regular polygon is twice of the sum of its exterior angles.

Statement 2: Number of sides(n) of the polygon is 6.

1. Both the statements are true.

2. Both the statements are false.

3. Statement 1 is true, and statement 2 is false.

4. Statement 1 is false, and statement 2 is true.

Answer

It is given that the sum of interior angles of a regular polygon is twice the sum of its exterior angles.

Sum of all exterior angles of any polygon (regular or irregular) is always 360°.

Sum of all interior angles of an n-sided polygon (regular or irregular) is (n - 2) x 180°.

According to statement 1,

⇒ (n - 2) x 180° = 2 x 360°

⇒ (n - 2) x 180° = 720°

⇒ 180°n - 360° = 720°

⇒ 180°n = 720° + 360°

⇒ 180°n = 1080°

⇒ n = $\dfrac{1080°}{180°}$ = 6

Thus, the number of sides is 6.

∴ Both the statements are true.

Hence, option 1 is the correct option.

Statement 1: Through a vertex of a polygon, 3 diagonals can be drawn.

Statement 2: The polygon is hexagon.

1. Both the statements are true.

2. Both the statements are false.

3. Statement 1 is true, and statement 2 is false.

4. Statement 1 is false, and statement 2 is true.

Answer

It is possible through a vertex of a polygon, to draw 3 diagonals.

The number of diagonals from a single vertex in a polygon with n sides is n - 3.

3 = n - 3

n = 3 + 3 = 6.

A polygon with 6 sides is a hexagon.

∴ Both the statements are true.

Hence, option 1 is the correct option.

Assertion (A): The diagonal of a quadrilateral bisect each other at right angle.

Reason (R): The quadrilateral is square.

1. A is true, but R is false.

2. A is false, but R is true.

3. Both A and R are true, and R is the correct reason for A.

4. Both A and R are true, and R is the incorrect reason for A.

Answer

Let quadrilateral be ABCD.

Since, diagonals bisect each other at 90°.

∴ Assertion (A) is true.

∴ ∠AOB = ∠BOC = ∠COD = ∠DOA = 90°.

From figure,

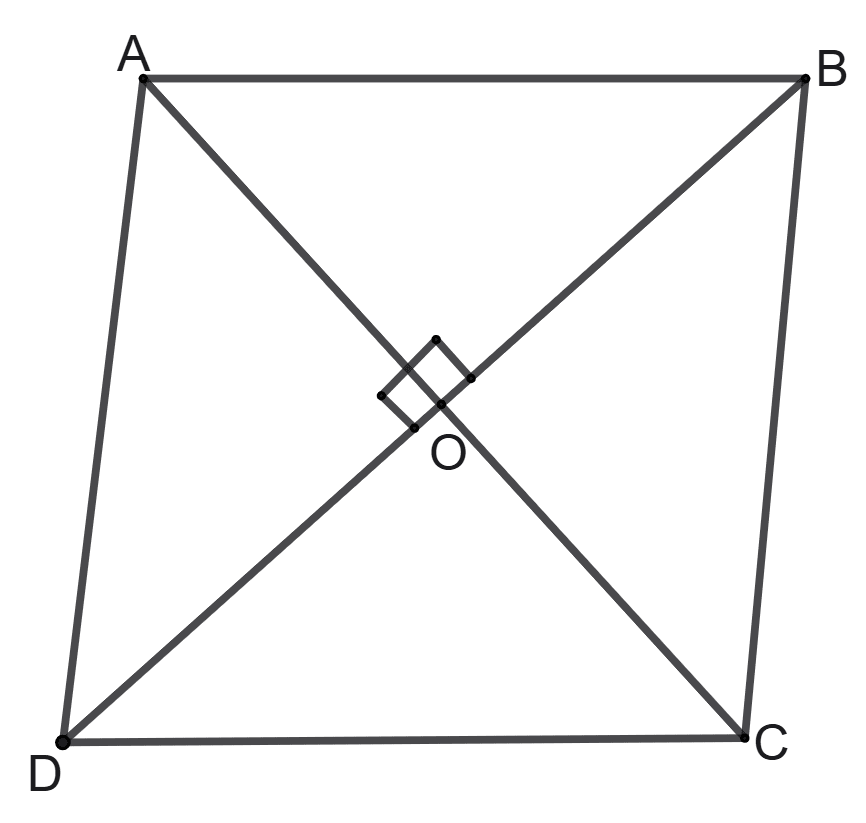
Considering △OAB and △OCD we have,

⇒ OA = OC (As diagonals bisect each other)

⇒ OB = OD (As diagonals bisect each other)

⇒ ∠AOB = ∠COD (Both equal to 90°)

Hence, △OAB ≅ △OCD by SAS axiom.

AB = CD (By C.P.C.T.) .........................(1)

∴ ∠OAB = ∠OCD (By C.P.C.T.)

The above angles are alternate angles.

Hence, we can say that AB || CD.

Considering △OAD and △OCB we have,

⇒ OA = OC (As diagonals bisect each other)

⇒ OB = OD (As diagonals bisect each other)

⇒ ∠AOD = ∠COB (Both equal to 90°)

Hence, △OAD ≅ △OCB by SAS axiom.

AD = BC (By C.P.C.T.) .....................(2)

∠OAD = ∠OCB (By C.P.C.T.)

The above angles are alternate angles.

Hence, we can say that AD || BC.

Considering △AOB and △AOD we have,

⇒ AO = AO (Common side)

⇒ OB = OD (As diagonals bisect each other)

⇒ ∠AOD = ∠AOB (Both equal to 90°)

Hence, △AOB ≅ △AOD by SAS axiom.

AB = AD (By C.P.C.T.) .....................(3)

From (i), (ii) and (iii) we get,

AB = BC = CD = AD.

Since, all the sides are equal and diagonals bisect each other.

Thus, we can say that the quadrilateral is rhombus.

∴ A is true, but R is false.

Hence, option 1 is the correct option.

Assertion (A): In parallelogram ABCD, PD bisects ∠ADC and PC bisects angle DCB, then ∠DPC = 90°.

Reason (R): ∠PDC = $\dfrac{1}{2}$ x ∠ADC

∠PCD = $\dfrac{1}{2}$ x ∠BCD

∠PDC + ∠PCD = $\dfrac{1}{2}$ x (∠ADC + ∠BCD)

1. A is true, but R is false.

2. A is false, but R is true.

3. Both A and R are true, and R is the correct reason for A.

4. Both A and R are true, and R is the incorrect reason for A.

Answer

We know that consecutive angles of a parallelogram are supplementary.

ABCD is a parallelogram.

∴ ∠ADC + ∠BCD = 180° .....................(1)

PD bisects ∠ADC.

⇒ ∠PDC = $\dfrac{∠ADC}{2}$ ...............(2)

PC bisects ∠BCD.

⇒ ∠PCD = $\dfrac{∠BCD}{2}$ ...............(3)

Adding equations (2) and (3), we get :

⇒ ∠PDC + ∠PCD = $\dfrac{∠ADC}{2}$ + $\dfrac{∠BCD}{2} = \dfrac{1}{2}$ (∠ADC + ∠BCD)

= $\dfrac{1}{2}$ x 180°

= 90°.

In ΔPCD, according to angle sum property,

⇒ ∠PDC + ∠PCD + ∠DPC = 180°

⇒ 90° + ∠DPC = 180°

⇒ ∠DPC = 180° - 90°

⇒ ∠DPC = 90°

∴ Both A and R are true, and R is the correct reason for A.

Hence, option 3 is the correct option.

The difference between an exterior angle of (n - 1) sided regular polygon and an exterior angle of (n + 2) sided regular polygon is 6°. Find the value of n.

Answer

Exterior angle of (n - 1) sided regular polygon = $\dfrac{360°}{n - 1}$

Exterior angle of (n + 2) sided regular polygon = $\dfrac{360°}{n + 2}$

Given,

Difference between an exterior angle of (n - 1) sided regular polygon and an exterior angle of (n + 2) sided regular polygon is 6°.

$\therefore \dfrac{360°}{n - 1} - \dfrac{360°}{n + 2} = 6° \\[1em] \Rightarrow \dfrac{360°(n + 2) - 360°(n - 1)}{(n - 1)(n + 2)} = 6° \\[1em] \Rightarrow \dfrac{360°.n + 720° - 360°.n + 360°}{n^2 + 2n - n - 2} = 6° \\[1em] \Rightarrow \dfrac{1080°}{n^2 + n - 2} = 6° \\[1em] \Rightarrow 1080° = 6°(n^2 + n - 2) \\[1em] \Rightarrow n^2 + n - 2 = \dfrac{1080°}{6°} \\[1em] \Rightarrow n^2 + n - 2 = 180 \\[1em] \Rightarrow n^2 + n - 2 - 180 = 0 \\[1em] \Rightarrow n^2 + n - 182 = 0 \\[1em] \Rightarrow n^2 + 14n - 13n - 182 = 0 \\[1em] \Rightarrow n(n + 14) - 13(n + 14) = 0 \\[1em] \Rightarrow (n - 13)(n + 14) = 0 \\[1em] \Rightarrow n - 13 = 0 \text{ or } n + 14 = 0 \\[1em] \Rightarrow n = 13 \text{ or } n = -14.$

Since, no. of sides cannot be negative.

∴ n = 13.

Hence, n = 13.

Two alternate sides of a regular polygon, when produced, meet at right angle. Find :

(i) the value of each exterior angle of the polygon;

(ii) the number of sides in the polygon.

Answer

(i) Let AB and CD be the alternate sides of regular polygon.

Given,

Two alternate sides of a regular polygon, when produced, meet at right angle.

We know that,

Interior angles of regular polygon are equal.

∴ ∠ABC = ∠BCD

⇒ 180° - ∠ABC = 180° - ∠BCD

⇒ ∠PBC = ∠BCP = x

In △ PBC,

⇒ ∠PBC + ∠BCP + ∠BPC = 180°

⇒ x + x + 90° = 180°

⇒ 2x = 180° - 90°

⇒ 2x = 90°

⇒ x = $\dfrac{90°}{2}$

⇒ x = 45°.

∴ ∠PBC = ∠BCP = 45°.

Hence, value of each exterior angle of the polygon = 45°.

(ii) By formula,

Number of sides in polygon = $\dfrac{360°}{\text{Exterior angle}} = \dfrac{360°}{45°}$ = 8.

Hence, number of sides in the polygon = 8.

In parallelogram ABCD, AP and AQ are perpendiculars from vertex of obtuse angle A as shown. If ∠x : ∠y = 2 : 1; find the angles of the parallelogram.

Answer

Given,

∠x : ∠y = 2 : 1

Let ∠x = 2a and ∠y = a.

From figure,

AQCP is a quadrilateral.

∴ ∠A + ∠P + ∠C + ∠Q = 360° (Sum of interior angles of a quadrilateral equals)

⇒ y + 90° + x + 90° = 360°

⇒ a + 90° + 2a + 90° = 360°

⇒ 3a + 180° = 360°

⇒ 3a = 360° - 180°

⇒ 3a = 180°

⇒ a = $\dfrac{180°}{3}$

⇒ a = 60°.

⇒ ∠x = 2 × 60° = 120° and ∠y = 60°.

From figure,

⇒ ∠C = ∠x = 120°,

⇒ ∠A = ∠C = 120° (Opposite angles of parallelogram are equal),

⇒ ∠B + ∠C = 180° (Sum of adjacent angles of a parallelogram equals to 180°)

⇒ ∠B + 120° = 180°

⇒ ∠B = 180° - 120° = 60°

⇒ ∠D = ∠B = 60° (Opposite angles of parallelogram are equal).

Hence, ∠DAB = ∠C = 120° and ∠B = ∠D = 60°.

In the given figure, AP is bisector of ∠A and CQ is bisector of ∠C of parallelogram ABCD. Prove that APCQ is a parallelogram.

Answer

Join AC.

Let AC intersect BD at point O.

As, AP is the bisector of ∠A and CQ is bisector of ∠C.

∴ ∠DAP = $\dfrac{∠A}{2}$ and ∠BCQ = $\dfrac{∠C}{2}$.

In || gm ABCD,

⇒ ∠A = ∠C (Opposite angles of || gm are equal)

⇒ $\dfrac{∠A}{2} = \dfrac{∠C}{2}$

⇒ ∠DAP = ∠BCQ.

In △ ADP and △ CBQ,

⇒ ∠DAP = ∠BCQ

⇒ AD = BC (Opposite sides of || gm are equal)

⇒ ∠ADP = ∠QBC (Alternate angles are equal)

∴ △ ADP ≅ △ CBQ (By A.S.A. axiom)

We know that,

Corresponding sides of congruent triangle are equal.

∴ DP = QB ........(1)

We know that,

Diagonals of parallelogram bisect each other.

⇒ OD = OB .......(2)

⇒ OA = OC.

Subtracting equation (1) from (2), we get :

⇒ OD - DP = OB - QB

⇒ OP = OQ.

In quadrilateral APCQ,

⇒ OP = OQ and OA = OC.

Since, diagonals of quadrilateral APCQ bisect each other.

∴ APCQ is a parallelogram.

Hence, proved that APCQ is a parallelogram.

In case of a parallelogram prove that :

(i) the bisectors of any two adjacent angles intersect at 90°.

(ii) the bisectors of opposite angles are parallel to each other.

Answer

(i) Let ABCD be the parallelogram. AO and DO be the bisector of angles A and D respectively.

∴ ∠DAO = $\dfrac{∠A}{2}$ and ∠ADO = $\dfrac{∠D}{2}$.

We know that,

In a parallelogram, consecutive angles are supplementary.

∴ ∠A + ∠D = 180°

⇒ $\dfrac{∠A}{2} + \dfrac{∠D}{2} = \dfrac{180°}{2}$

⇒ ∠DAO + ∠ADO = 90° .........(1)

In △ AOD,

By angle sum property of triangle,

⇒ ∠DAO + ∠ADO + ∠AOD = 180°

⇒ 90° + ∠AOD = 180°

⇒ ∠AOD = 180° - 90° = 90°.

Hence, bisectors of any two adjacent angles intersect at 90°.

(ii)

From figure,

DE and BF are bisectors of angles D and B respectively.

In parallelogram ABCD,

⇒ ∠B = ∠D (Opposite angles of || gm are equal)

⇒ $\dfrac{∠B}{2} = \dfrac{∠D}{2}$

⇒ ∠FBC = ∠ADE.

In △ ADE and △ CBF,

⇒ ∠ADE = ∠FBC (Proved above)

⇒ AD = BC (Opposite sides of || gm ABCD are equal)

⇒ ∠DAE = ∠BCF (Opposite angles of || gm ABCD are equal)

∴ △ ADE ≅ △ CBF (By A.S.A. axiom)

We know that,

Corresponding sides of congruent triangle are equal.

∴ AE = CF

Since, AE = CF and AB = CD,

∴ BE = DF

In parallelogram ABCD,

⇒ AB || CD

⇒ BE || DF

Since,

BE = DF and BE || DF

In quadrilateral BEDF, one of the pair of opposite sides are equal and parallel.

∴ BEDF is a parallelogram.

∴ DE || BF.

Hence, proved that bisectors of opposite angles of a parallelogram are parallel.

The diagonals of a rectangle intersect each other at right angles. Prove that the rectangle is a square.

Answer

Let ABCD be the rectangle.

Since, opposite sides of rectangle are equal.

∴ AB = DC ........(1)

∴ AD = BC .........(2)

Given,

Diagonals intersect at right angle.

∴ ∠AOB = 90°, ∠AOD = 90°.

In △ AOB and △ AOD,

⇒ AO = AO (Common side)

⇒ ∠AOB = ∠AOD (Both equal to 90°)

⇒ OB = OD (Diagonals of rectangle bisect each other)

∴ △ AOB ≅ △ AOD (By S.A.S. axiom)

We know that,

Corresponding parts of congruent triangle are equal.

∴ AD = AB .......(3)

From equations (1), (2) and (3), we get :

⇒ AB = BC = CD = AD.

Since, all sides are equal and diagonals intersect at right angle.

Hence, proved that the rectangle is a square.

In the following figure, ABCD and PQRS are two parallelograms such that ∠D = 120° and ∠Q = 70°. Find the value of x.

Answer

In parallelogram ABCD,

⇒ ∠A = ∠C and ∠B = ∠D = 120° (Opposite angles of a parallelogram are equal)

⇒ ∠A + ∠B + ∠C + ∠D = 360° (By angle sum property)

⇒ ∠C + ∠D + ∠C + ∠D = 360°

⇒ 2∠C + 120° + 120° = 360°

⇒ 2∠C + 240° = 360°

⇒ 2∠C = 360° - 240°

⇒ 2∠C = 120°

⇒ ∠C = $\dfrac{120°}{2}$ = 60°.

In parallelogram PQRS,

⇒ ∠S = ∠Q = 70° (Opposite angles of a parallelogram are equal)

In △ OSC,

By angle sum property of triangle,

⇒ ∠S + ∠C + ∠O = 180°

⇒ 70° + 60° + x = 180°

⇒ 130° + x = 180°

⇒ x = 180° - 130° = 50°.

Hence, x = 50°.

In the following figure, ABCD is a rhombus and DCFE is a square.

If ∠ABC = 56°, find :

(i) ∠DAE

(ii) ∠FEA

(iii) ∠EAC

(iv) ∠AEC

Answer

(i) In rhombus ABCD,

⇒ ∠CDA = ∠CBA = 56° (Opposite angles of rhombus are equal.)

In square DCFE,

⇒ ∠CDE = 90° (Each interior angle of a square equals to 90°)

From figure,

⇒ AD = CD (Each side of rhombus are equal) .........(1)

⇒ CD = ED (Each side of square are equal) .........(2)

From equation (1) and (2), we get :

⇒ AD = ED.

In △ ADE,

⇒ AD = ED (Proved above)

⇒ ∠AED = ∠DAE

By angle sum property of triangle,

⇒ ∠DAE + ∠AED + ∠ADE = 180°

⇒ ∠DAE + ∠DAE + (∠CDA + ∠CDE) = 180°

⇒ 2∠DAE + (56° + 90°) = 180°

⇒ 2∠DAE + 146° = 180°

⇒ 2∠DAE = 180° - 146°

⇒ 2∠DAE = 34°

⇒ ∠DAE = $\dfrac{34°}{2}$ = 17°.

Hence, ∠DAE = 17°.

(ii) From figure,

⇒ ∠FED = 90° (Each interior angle of square equals 90°)

⇒ ∠AED = ∠DAE = 17°.

⇒ ∠FEA = ∠FED - ∠AED

⇒ ∠FEA = 90° - 17° = 73°.

Hence, ∠FEA = 73°.

(iii) In rhombus ABCD,

By angle sum property,

⇒ ∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°

⇒ ∠ABC + ∠DAB + ∠CDA + ∠DAB = 360° (∠BCD = ∠DAB, as opposite angles of rhombus are equal)

⇒ 56° + 2∠DAB + 56° = 360°

⇒ 112° + 2∠DAB = 360°

⇒ 2∠DAB = 360° - 112°

⇒ 2∠DAB = 248°

⇒ ∠DAB = $\dfrac{248°}{2}$ = 124°.

From figure,

⇒ ∠DAC = $\dfrac{∠DAB}{2}$ (As, diagonals of rhombus bisect interior angles)

⇒ ∠DAC = $\dfrac{124°}{2}$ = 62°.

From figure,

⇒ ∠EAC = ∠DAC - ∠DAE = 62° - 17° = 45°.

Hence, ∠EAC = 45°.

(iv) Join EC.

From figure,

⇒ ∠DEC = $\dfrac{∠DEF}{2}$ (As, diagonals of square bisect interior angles)

⇒ ∠DEC = $\dfrac{90°}{2}$ = 45°.

From figure,

⇒ ∠AEC = ∠DEC - ∠DEA = 90° - 17° = 73°.

Hence, ∠AEC = 73°.

In parallelogram ABCD, E is the mid-point of side AB and CE bisects angle BCD. Prove that :

(i) AE = AD

(ii) DE bisects angle ADC

(iii) angle DEC is a right angle

Answer

(i) In parallelogram ABCD,

AB || DC (Opposite sides are parallel)

CE is the transversal.

∴ ∠CED = ∠BCE (Alternate angles are equal)

∴ BC = EB (In triangle, side opposite to equal angles are equal) ..........(1)

From figure,

⇒ BC = AD (Opposite sides of parallelogram are equal) ........(2)

Given,

⇒ AE = EB (As, E is the mid-point of AB) ........(3)

From equation (1), (2) and (3), we get :

⇒ AE = AD.

Hence, proved that AE = AD.

(ii) In △ AED,

⇒ AD = AE (Proved above)

⇒ ∠AED = ∠ADE (Angles opposite to equal sides are equal.) .......(4)

From figure,

⇒ ∠EDC = ∠AED (Alternate angles are equal.) ..........(5)

From equations (4) and (5), we get :

⇒ ∠ADE = ∠EDC.

Hence, proved that DE bisects angle ADC.

(iii) We know that,

Sum of consecutive angles in a parallelogram equal to 180°.

∴ ∠D + ∠C = 180°

⇒ $\dfrac{∠D + ∠C}{2} = \dfrac{180°}{2}$

⇒ $\dfrac{∠D}{2} + \dfrac{∠C}{2}$ = 90°

⇒ ∠EDC + ∠ECD = 90° [As, DE and CE are bisectors of angle D and C] ...........(1)

In △ DEC,

By angle sum property of triangle,

⇒ ∠EDC + ∠ECD + ∠DEC = 180°

⇒ 90° + ∠DEC = 180°

⇒ ∠DEC = 180° - 90° = 90°.

Hence, proved that DEC is a right angle.

In parallelogram ABCD, X and Y are mid-points of opposite sides AB and DC respectively. Prove that :

(i) AX = YC

(ii) AX is parallel to YC

(iii) AXCY is a parallelogram

Answer

(i) We know that,

Opposite sides of || gm are equal.

∴ AB = CD

⇒ $\dfrac{AB}{2} = \dfrac{CD}{2}$

⇒ AX = CY (As, X and Y are mid-points of AB and CD respectively)

Hence, proved that AX = YC.

(ii) We know that,

Opposite sides of || gm are parallel.

∴ AB || DC

∴ AX || YC.

Hence, proved that AX || YC.

(iii) From figure,

AX = YC and AX || YC.

Since, one pair of opposite sides of quadrilateral AXCY are equal and parallel.

∴ AXCY is a || gm.

Hence, proved that AXCY is a parallelogram.