Construction of Polygons [Using Ruler and Compass Only]

A quadrilateral can be constructed, if its :

1. three sides and one angle are known

2. four sides and one angle are known

3. two sides and two angles are known

4. four sides are known

Answer

A quadrilateral can be constructed if its four sides and one angle are known.

Hence, Option 2 is the correct option.

A parallelogram can be constructed, if its :

1. all the four sides are known

2. opposite sides are known

3. opposite angles are known

4. two adjacent sides and contained angle are known

Answer

A parallelogram can be constructed if its two adjacent sides and contained angle are known.

Hence, Option 4 is the correct option.

A parallelogram can be constructed, if its :

1. both the diagonals and included angle are given

2. both the diagonals and one angle are given

3. both the diagonals are given

4. one side and one diagonal are given

Answer

A parallelogram can be constructed if its both the diagonals and included angle are given.

Hence, Option 1 is the correct option.

A trapezium can be constructed, if its :

1. parallel sides are given

2. non-parallel sides are given

3. both the non-parallel sides and both the parallel sides are given

4. four sides are given

Answer

A trapezium can be constructed if its both the non-parallel sides and both the parallel sides are given.

Hence, Option 3 is the correct option.

A rhombus can be constructed, if its :

1. one side is given

2. one side and one diagonal are given

3. one of the diagonals is given

4. opposite angles are given

Answer

A rhombus can be constructed if its one side and one diagonal are given.

Hence, Option 2 is the correct option.

Construct a quadrilateral ABCD, when :

AB = 3.2 cm, BC = 5.2 cm, CD = 6.2 cm, DA = 4.2 cm and BD = 5.2 cm.

Answer

Steps of construction :

1. Draw a line segment BC = 5.2 cm.

2. With B and C as center and radii equal to 5.2 cm and 6.2 cm respectively draw arcs cutting each other at D.

3. Join BD and CD.

4. With B and D as center and radii equal to 3.2 cm and 4.2 cm respectively draw arcs cutting each other at A.

5. Join AB and AD.

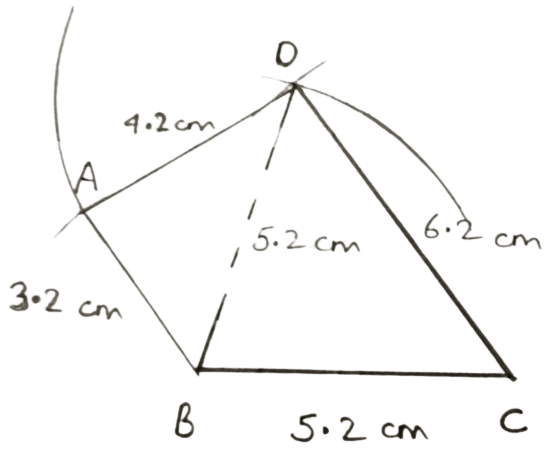
Hence, ABCD is the required quadrilateral.

AB = 7.2 cm, BC = 5.8 cm, CD = 6.3 cm, AD = 4.3 cm and angle A = 75°.

Answer

Steps of construction :

1. Draw a line segment AB = 7.2 cm.

2. Through A, draw AX such that ∠A = 75°.

3. From AX, cut AD = 4.3 cm.

4. With B and D as centers and radii 5.8 cm and 6.3 cm respectively, draw arcs cutting each other at C.

5. Join BC and CD.

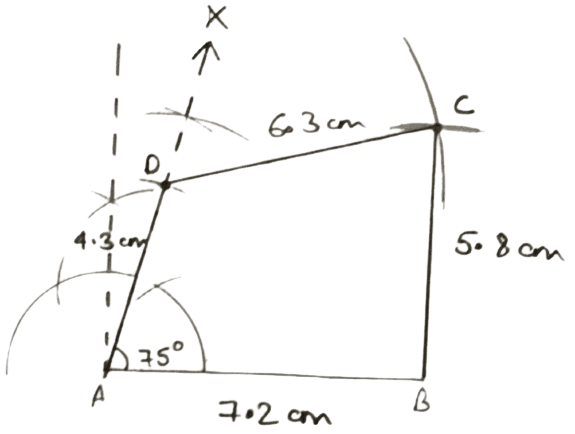
Hence, ABCD is the required quadrilateral.

Angle A = 90°, AB = 4.6 cm, BD = 6.4 cm, AC = 6.0 cm and CD = 4.2 cm.

Answer

Steps of construction :

1. Draw a line segment AB = 4.6 cm.

2. Through A, draw AP such that ∠A = 90°.

3. With B as center and radius 6.4 cm draw an arc cutting AP at D. Join AD and BD.

4. With D and A as centers and radii 4.2 cm and 6.0 cm respectively, draw arcs cutting each other at C.

5. Join DC, BC and AC.

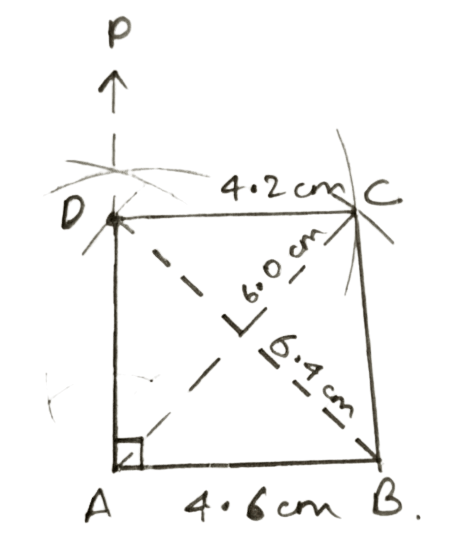
Hence, ABCD is the required quadrilateral.

AB = 3.8 cm, AC = 4.8 cm, AD = 2.8 cm, angle A = 105° and angle B = 60°.

Answer

Steps of construction :

1. Draw a line segment AB = 3.8 cm.

2. Through A, draw AX such that ∠A = 105°.

3. Through B, draw BY such that ∠B = 60°.

4. From AX, cut AD = 2.8 cm.

5. With A as center and radius 4.8 cm draw an arc cutting BY at C. Join BC and CD.

6. Join AC.

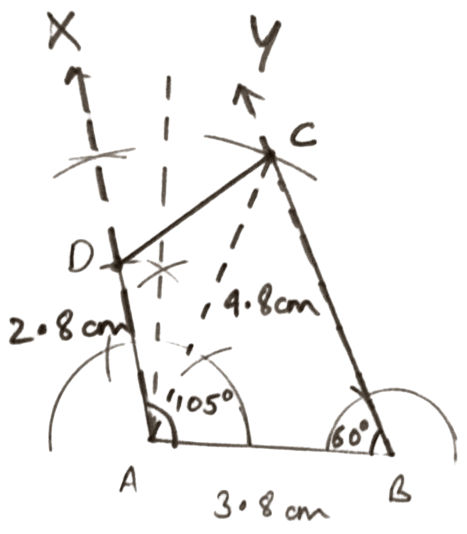
Hence, ABCD is the required quadrilateral.

BC = 7.5 cm, AC = 5.8 cm, AD = 3.6 cm, CD = 4.2 cm and angle A = 120°.

Answer

Steps of construction :

1. Draw a line segment AD = 3.6 cm.

2. Through A, draw AP such that ∠A = 120°.

3. With D and A as centers and radii 4.2 cm and 5.8 cm respectively, draw arcs cutting each other at C. Join AC and CD.

4. With C as center and radius 7.5 cm draw an arc cutting AP at B.

5. Join AB and BC.

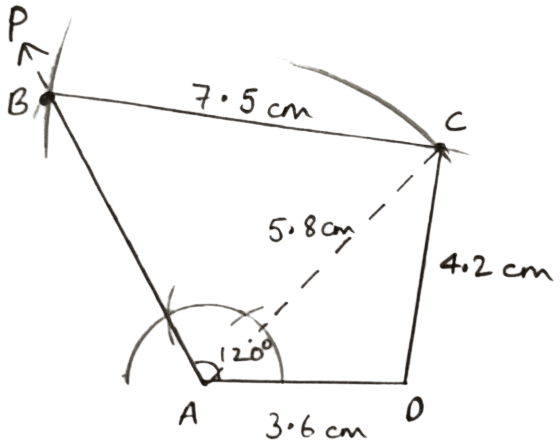
Hence, ABCD is the required quadrilateral.

AD = AB = 4 cm, BC = 2.8 cm, CD = 2.5 cm and angle BAD = 45°.

Answer

Steps of construction :

1. Draw a line segment AD = 4 cm.

2. Draw AP, such that ∠A = 45°.

3. With A as center and radius equal to 4 cm draw an arc cutting AP at B.

4. With B and D as centers and radii 2.8 cm and 2.5 cm respectively, draw arcs cutting each other at C.

5. Join BC and CD.

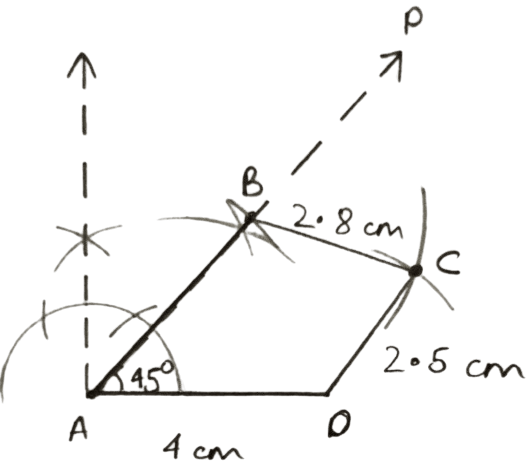
Hence, ABCD is the required quadrilateral.

AB = 6.3 cm, BC = CD = 4.2 cm and ∠ABC = ∠BCD = 90°.

Answer

Steps of construction :

1. Draw a line segment AB = 6.3 cm.

2. Draw BP, such that ∠ABP = 90°.

3. With B as center and radius equal to 4.2 cm draw an arc cutting BP at C. Join BC.

4. With C as center, draw a line CD, such that ∠BCD = 90°.

5. Join AD.

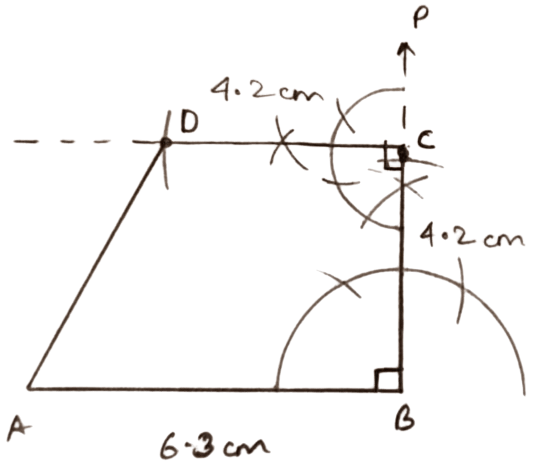
Hence, ABCD is the required quadrilateral.

Construct a parallelogram ABCD, when :

AB = 4.4 cm, AD = 6.2 cm and AC = 4.8 cm.

Answer

In parallelogram,

Opposite sides are equal.

∴ CD = AB = 4.4 cm and BC = AD = 6.2 cm

Steps of construction :

1. Draw a line segment AD = 6.2 cm.

2. With A and D as centers and radii 4.8 cm and 4.4 cm respectively, draw arcs cutting each other at C. Join AC and CD.

3. With A and C as centers and radii 4.4 cm and 6.2 cm respectively, draw arcs cutting each other at B.

4. Join AB and BC.

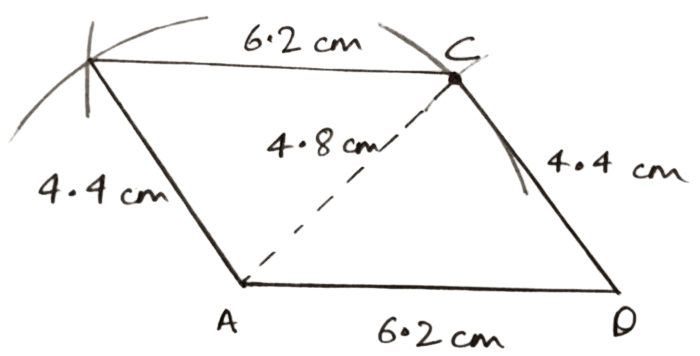
Hence, ABCD is the required parallelogram.

Diagonal AC = 6.4 cm, diagonal BD = 8.2 cm and angle between the diagonals = 60°.

Answer

Steps of construction :

1. Draw a line segment AC = 6.4 cm and locate its mid-point O.

2. Draw line BOD such that ∠DOC = 60° and OB = OD = $\dfrac{1}{2} BD = \dfrac{1}{2} \times 8.2$ cm = 4.1 cm.

3. Join AB, BC, CD and DA.

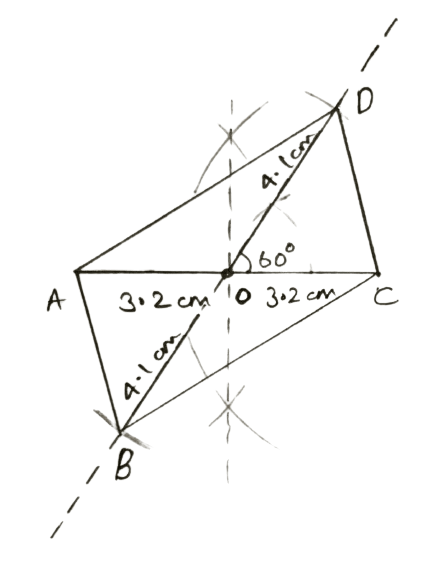
Hence, ABCD is the required parallelogram.

AB = 5.8 cm, diagonal AC = 8.2 cm and diagonal BD = 6.2 cm.

Answer

Steps of construction :

1. Draw a line segment AB = 5.8 cm

2. Since diagonals of a parallelogram bisect each other; construct triangle OBC, such that :

OB = $\dfrac{1}{2}BD = \dfrac{1}{2} \times 6.2$ = 3.1 cm

OA = $\dfrac{1}{2}AC = \dfrac{1}{2} \times 8.2$ = 4.1 cm

3. Produce BO upto D, such that OD = OB = 3.1 cm and produce AO upto C, such that OC = OA = 4.1 cm.

4. Join BC, CD and AD.

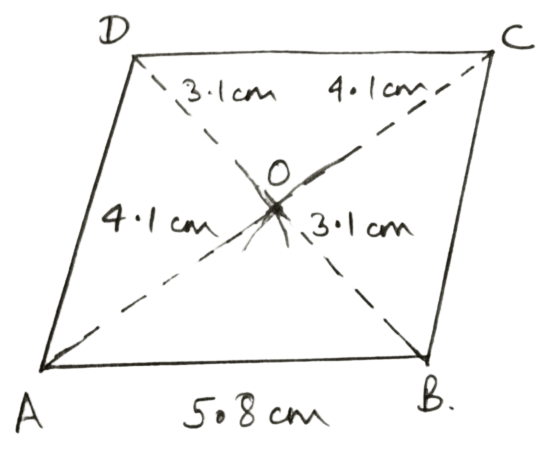
Hence, ABCD is the required parallelogram.

AB = 6.0 cm, AD = 5.0 cm and ∠A = 45°.

Answer

In parallelogram,

Opposite sides are equal.

∴ BC = AD = 5.0 cm and CD = AB = 6.0 cm

Steps of construction :

1. Draw a line segment AB = 6.0 cm.

2. Draw AP, such that ∠A = 45°.

3. With A as center and radius equal to 5 cm draw an arc cutting AP at D.

4. With B and D as centers and radii 5.0 cm and 6.0 cm respectively, draw arcs cutting each other at C.

5. Join BC and CD.

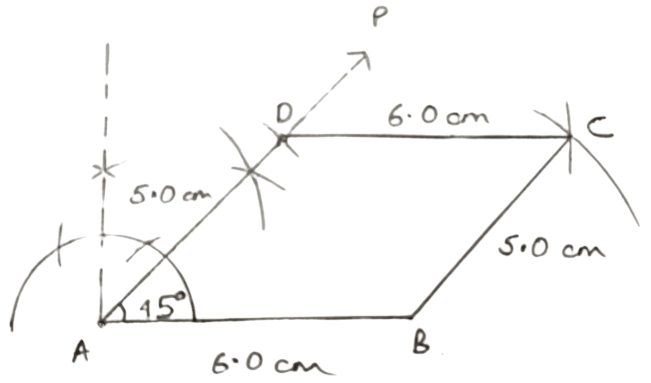
Hence, ABCD is the required parallelogram.

Base AB = 6.5 cm, BC = 4 cm and the altitude corresponding to AB = 3.1 cm.

Answer

Steps of construction :

1. Draw a line segment AB = 6.5 cm.

2. At B, draw BP ⊥ AB.

3. From BP, cut BE = 3.1 cm.

4. Through E draw a perpendicular to BP to get QR parallel to AB.

5. With B as center and radius = 4 cm, draw an arc that cuts QR at C.

6. With A as center and radius = AD = 4 cm, draw an arc that cuts QR at D.

7. Join AD, BC and CD.

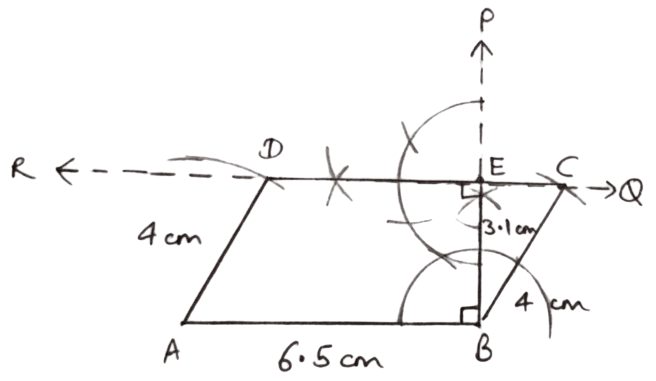
Hence, ABCD is the required parallelogram.

AB = 4.5 cm, ∠B = 120° and the distance between AB and DC = 3.0 cm.

Answer

Steps of construction :

1. Draw a line segment AB = 4.5 cm.

2. At B, draw BP ⊥ AB.

3. From BP, cut BE = 3 cm.

4. Through E draw a perpendicular to BP to get QR parallel to AB.

5. Draw BY, such that ∠B = 120°.

6. Let BY intersect QR at C.

7. With A as center and radius = BC, draw an arc cutting QR at D.

8. Join AD, BC and CD.

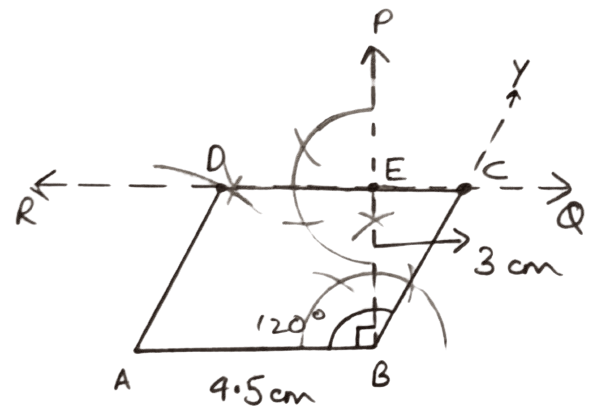
Hence, ABCD is the required parallelogram.

Base BC = 5.6 cm, diagonal BD = 6.5 cm and altitude = 3.2 cm.

Answer

Steps of construction :

1. Draw a line segment BC = 5.6 cm.

2. At C, draw CX ⊥ BC.

3. From CX, cut CY = 3.2 cm.

4. Through Y draw a straight line PQ parallel to BC.

5. With B as center and radius 6.5 cm draw an arc to meet PQ at D.

6. With D as center and radius 5.6 cm draw an arc to meet PQ at A.

7. Join AB, BD, AD and CD.

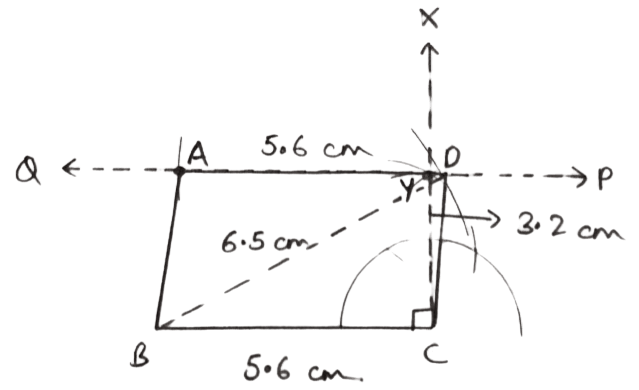
Hence, ABCD is the required parallelogram.

Construct a rectangle ABCD, when :

Its sides are 6.0 cm and 7.2 cm.

Answer

Steps of construction :

1. Let adjacent side AB = 6.0 cm and BC = 7.2 cm.

2. Draw a line segment BC = 7.2 cm.

3. Draw BX ⊥ BC and CY ⊥ BC.

4. With B as center and radius equal to 6 cm draw arc cutting BX at A.

5. With C as center and radius equal to 6 cm draw arc cutting CY at D.

6. Join AD.

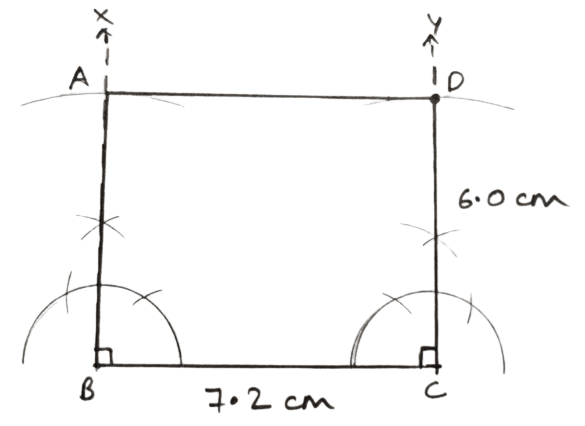
Hence, ABCD is the required rectangle.

One side = 4 cm and one diagonal is 5 cm. Measure the length of other side.

Answer

In rectangle ABCD,

Let side AB = 4 cm and AC = 5 cm.

Steps of construction :

1. Draw a line segment AB = 4 cm.

2. Draw BX ⊥ AB.

3. With A as center and radius equal to 5 cm draw an arc cutting BX at C.

4. Join AC and BC. Measure BC.

5. With C and A as center and radii 4 cm and BC respectively draw arcs cutting each other at D.

6. Join AD and CD.

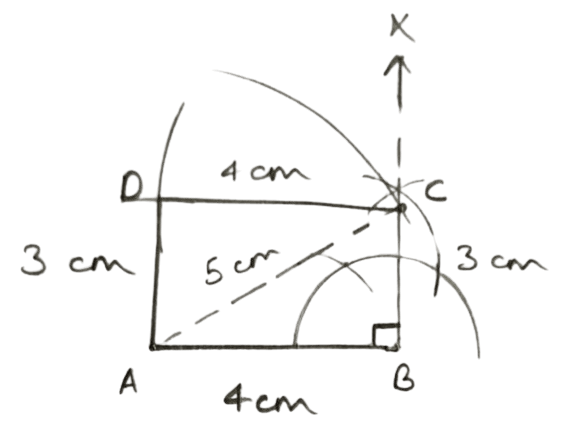
Hence, ABCD is the required rectangle.

One diagonal = 6.0 cm and the acute angle between the diagonals = 45°.

Answer

Steps of construction :

1. Draw a line segment AC = 6 cm.

2. Mark mid-point of AC as O.

3. From point O draw QR, at an angle of 45°.

4. With O as center and radius equal to 3 cm cut off OB and OD from QR.

5. Join BC, CD, AD and AB.

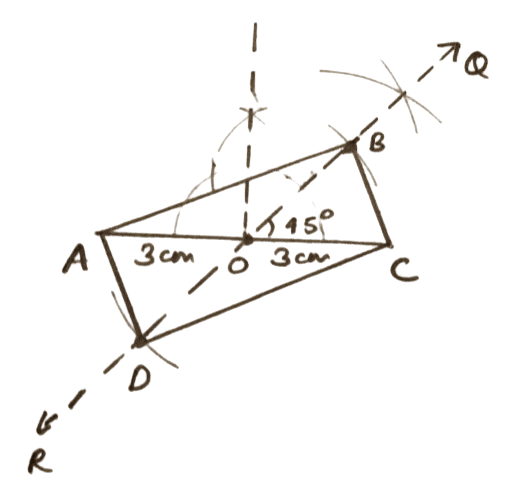
Hence, ABCD is the required rectangle.

Area = 24 cm² and base = 4.8 cm.

Answer

We know that,

⇒ Area of rectangle = Base × Height

⇒ 24 = 4.8 × Height

⇒ Height = $\dfrac{24}{4.8}$ = 5 cm.

Steps of construction :

1. Let adjacent sides AB = 4.8 cm and BC = 5 cm.

2. Draw a line segment AB = 4.8 cm.

3. Draw AX ⊥ AB and BY ⊥ AB.

4. With A as center and radius equal to 5 cm draw arc cutting AX at D.

5. With B as center and radius equal to 5 cm draw arc cutting BY at C.

6. Join CD.

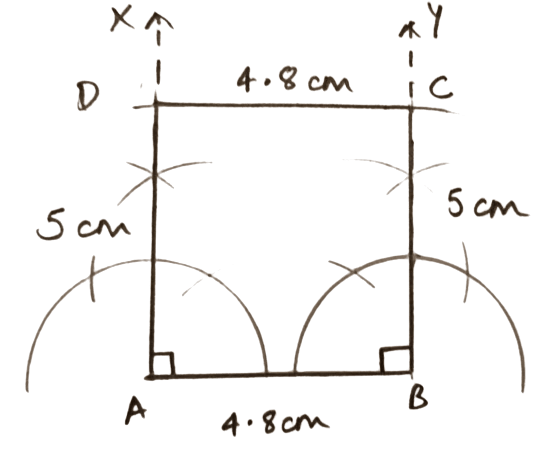
Hence, ABCD is the required rectangle.

Area = 36 cm² and height = 4.5 cm.

Answer

We know that,

⇒ Area of rectangle = Base × Height

⇒ 36 = Base × 4.5

⇒ Base = $\dfrac{36}{4.5}$ = 8 cm.

Steps of construction :

1. Let adjacent sides AB = 4.5 cm and BC = 8 cm.

2. Draw a line segment BC = 8 cm.

3. Draw BX ⊥ BC and CY ⊥ BC.

4. With B as center and radius equal to 4.5 cm draw arc cutting BX at A.

5. With C as center and radius equal to 4.5 cm draw arc cutting CY at D.

6. Join AD.

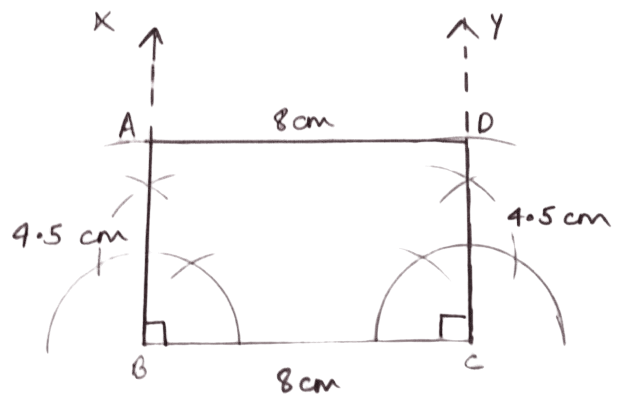
Hence, ABCD is the required rectangle.

Construct a trapezium ABCD, when :

AB = 4.8 cm, BC = 6.8 cm, CD = 5.4 cm, angle B = 60° and AD // BC.

Answer

Steps of construction :

1. Draw a line segment BC = 6.8 cm.

2. Draw BX, such that ∠XBC = 60°.

3. From BX, cut BA = 4.8 cm.

4. From point A draw QR || BC.

5. With C as center and radius equal to 5.4 cm draw an arc cutting QR at D.

6. Join CD and AD.

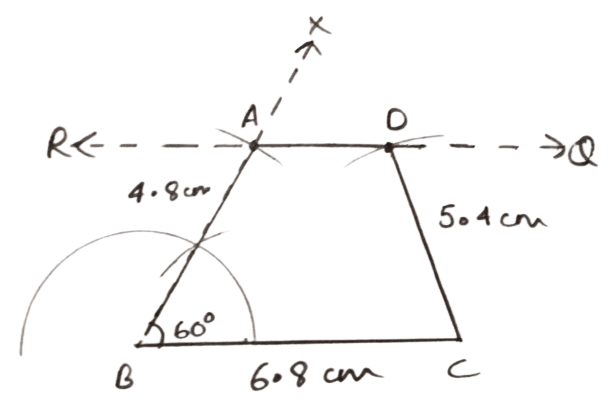
Hence, ABCD is the required trapezium.

AB = CD = 3.2 cm, BC = 6.0 cm, AD = 4.4 cm and AD // BC.

Answer

Steps of construction :

1. Draw a line segment BC = 6 cm.

2. From BC, cut BE = AD = 4.4 cm.

3. Draw triangle DEC, such that DE = AB = 3.2 cm and CD = 3.2 cm.

4. Taking B and D as centers and radii 3.2 cm and 4.4 cm respectively, draw arcs cutting each other at A.

5. Join AB and AD.

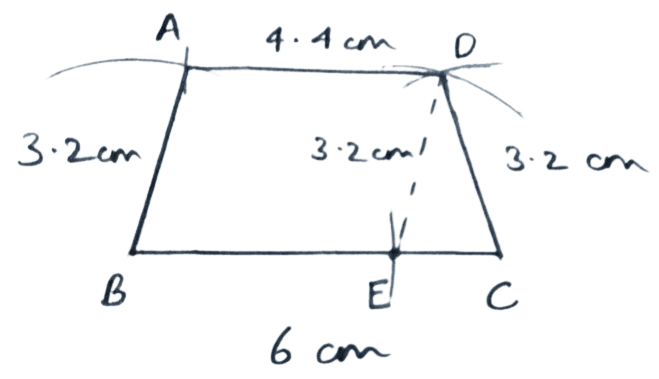
Hence, ABCD is the required trapezium.

Construct a rhombus ABCD, when :

Its one side = 6 cm and ∠A = 60°.

Answer

We know that,

Sum of consecutive angles of rhombus = 180°.

∴ ∠A + ∠B = 180°

⇒ 60° + ∠B = 180°

⇒ ∠B = 180° - 60° = 120°.

Steps of construction :

1. Draw a line segment AB = 6 cm.

2. At A, construct ∠BAP = 60°.

3. From AP, cut off AD = 6 cm.

4. Through D, draw XY parallel to AB.

5. At B, construct ∠ABQ = 120°, intersecting XY at C.

6. Join CD.

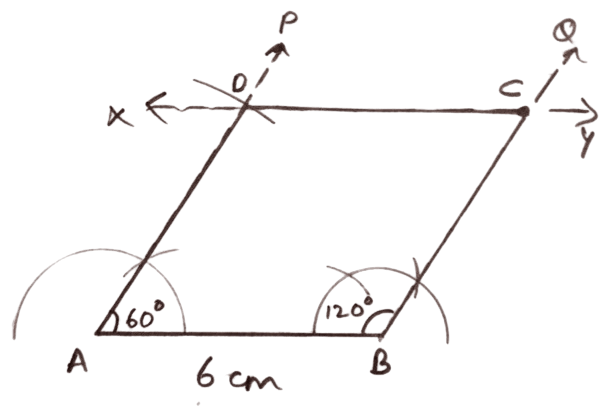
Hence, ABCD is the required rhombus.

One side = 5.4 cm and one diagonal is 7.0 cm.

Answer

Steps of construction :

1. Draw a line segment AC = 7 cm.

2. With A as center and radius equal to 5.4 cm, we draw an arc extending on both sides of AC.

3. With C as center and radius equal to 5.4 cm, we draw an arc extending on both sides of AC to the cut first arc at B and D.

4. Join AB, BC, CD and DA.

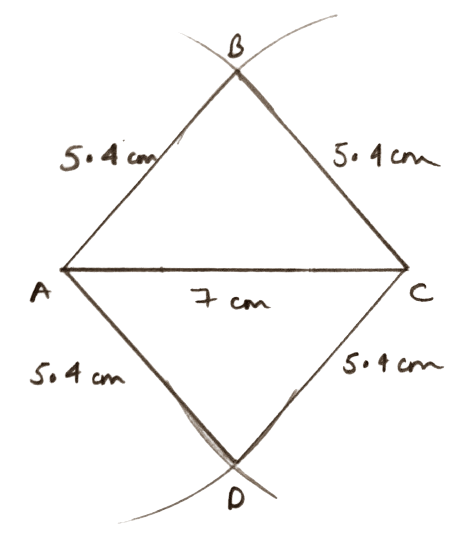
Hence, ABCD is the required rhombus.

Diagonal AC = 6.3 cm and diagonal BD = 5.8 cm

Answer

Steps of construction :

1. Draw a line segment AC = 6.3 cm

2. Draw perpendicular bisector of AC, which cuts AC at O.

3. From perpendicular bisector cut OD and OB such that,

OD = OB = $\dfrac{1}{2}BD = \dfrac{1}{2} \times 5.8$ = 2.9 cm.

4. Join AB, BC, CD and DA.

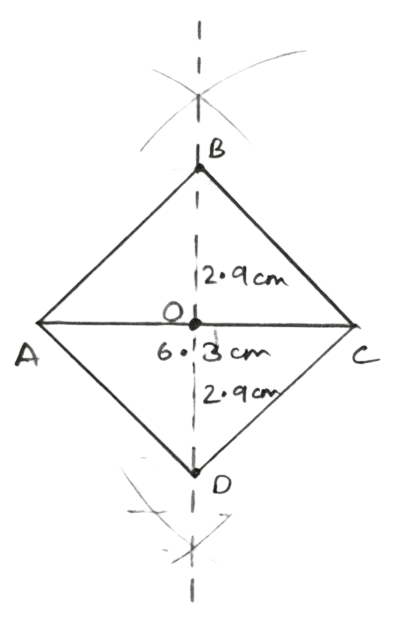
Hence, ABCD is the required rhombus.

One side = 5.0 cm and height = 2.6 cm.

Answer

Steps of construction :

1. Draw a line segment AB = 5 cm.

2. At B, draw BP ⊥ AB.

3. From BP, cut BE = 2.6 cm.

4. Through E, draw QR, perpendicular to BP, such that QR || AB.

5. With A and B as centers and radii 5 cm draw arcs cutting QR at D and C.

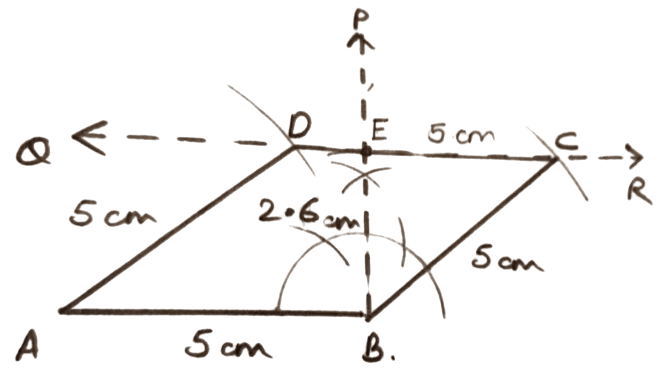
Hence, ABCD is the required rhombus.

∠A = 60° and height = 3.0 cm.

Answer

Steps of construction :

1. Draw a line segment AP.

2. Draw a line AF such that ∠A = 60°.

3. Take a point S on AP, at S draw a perpendicular SE of length 3 cm such that it cuts AF at D.

4. Through D draw a line QR || AP.

5. With A as center and radius equal to AD draw an arc cutting AP at B.

6. With B and D as centers and radii equal to AD draw arcs cutting each other at C.

7. Join BC and CD.

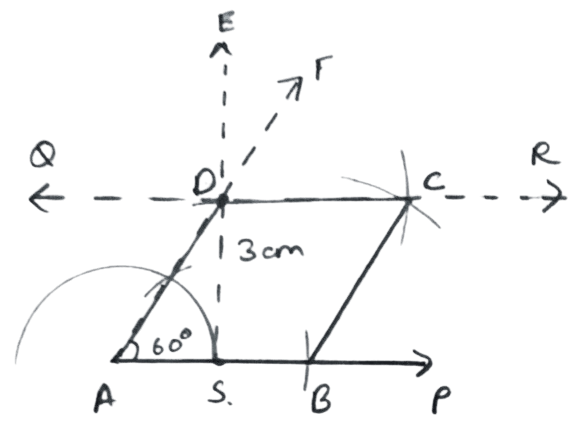
Hence, ABCD is the required rhombus.

Diagonal AC = 6.0 cm and height = 3.5 cm.

Answer

Steps of construction :

1. Draw a line segment AP.

2. Draw PX ⊥ AP.

3. From PX, cut PZ = 3.5 cm.

4. Through Z, draw EF || AP.

5. With A as center and radius equal to 6 cm draw an arc cutting EF at C.

6. Draw QR, perpendicular bisector of AC meeting AP at B.

7. Join BC.

8. With A and C as center and radius equal to BC in both cases draw arcs cutting each other at D.

9. Join AD and CD.

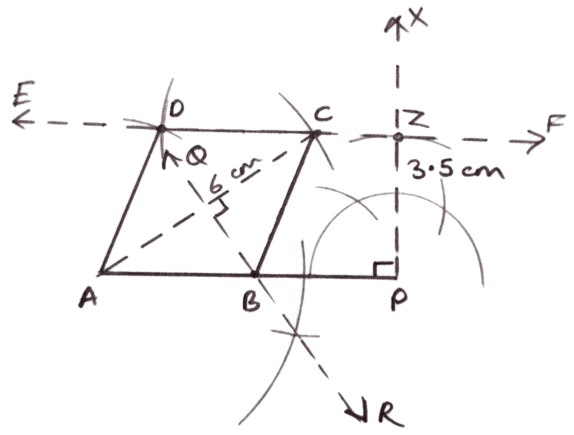
Hence, ABCD is the required rhombus.

Construct a square ABCD, when :

One side = 4.5 cm.

Answer

Steps of construction :

1. Draw a line segment AB = 4.5 cm.

2. Draw AP ⊥ AB.

3. From AP cut off AD = 4.5 cm.

4. With B as a center and radius 4.5 cm draw an arc.

5. With D as center and radius 4.5 cm draw another arc cutting the former arc at C.

6. Join BC and CD.

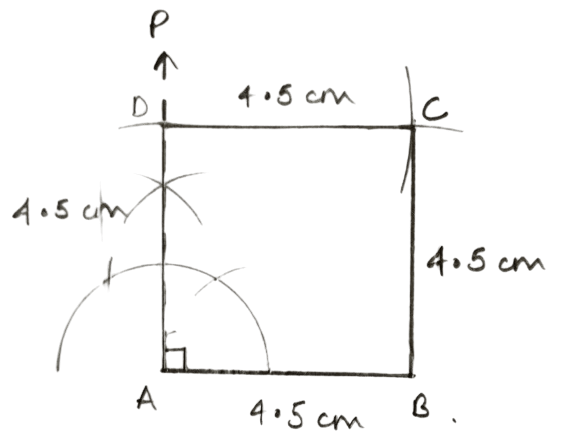
Hence, ABCD is the required square.

One diagonal = 5.4 cm.

Answer

Steps of construction :

1. Draw AC = 5.4 cm.

2. Draw XY, the perpendicular bisector of AC, meeting AC at O.

3. With O as center and radius equal to $\dfrac{5.4}{2}$ = 2.7 cm, draw an arc cutting XY at B and D.

4. Join AB, BC, CD, and DA.

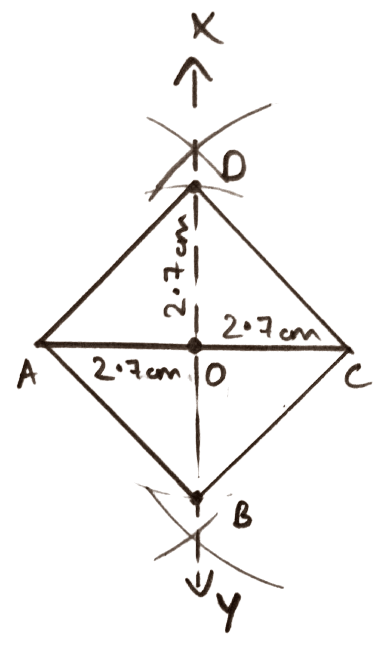
Hence, ABCD is the required square.

Perimeter = 24 cm.

Answer

We know that,

Perimeter of square = 4 × side

⇒ 24 = 4 × side

⇒ Side = $\dfrac{24}{4}$ = 6 cm.

Steps of construction :

1. Draw a line segment AB = 6 cm.

2. Draw AP ⊥ AB.

3. From AP cut off AD = 6 cm.

4. With B as a center and radius 6 cm draw an arc.

5. With D as center and radius 6 cm draw another arc cutting the former arc at C.

6. Join BC and CD.

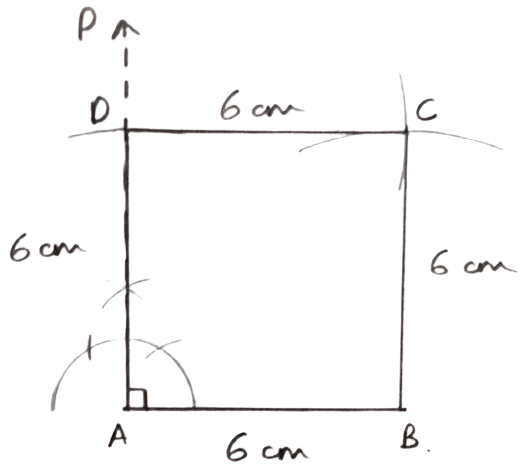
Hence, ABCD is the required square.

Construct a rhombus, having given one side = 4.8 cm and one angle = 75°.

Answer

Steps of construction :

1. Draw a line segment AB = 4.8 cm.

2. At A draw AX such that ∠BAX = 75°.

3. With A as center and radius equal to 4.8 cm draw an arc cutting AX at D.

4. Using the same radius taking D and B as centers cut off arcs, which will intersect at C.

5. Join CD and BC.

Hence, ABCD is the required rhombus.

Construct a regular hexagon of side

(i) 2.5 cm

(ii) 3.2 cm

Answer

(i) Steps of construction :

1. Draw a circle of radius 2.5 cm.

2. Taking any point A on the circumference of the circle as centre, draw arcs of same radii which cut the circumference at B and F.

3. With B and F as centers, again draw two arcs of same radii (2.5 cm) which cut the circumference at C and E respectively.

4. With C or E as center, draw one more arc of the same radius which cuts the circumference at point D.

5. Join AB, BC, CD, DE, EF and FA.

Hence, ABCDEF is the required regular hexagon.

(ii) Steps of construction :

1. Draw a circle of radius 3.2 cm.

2. Taking any point A on the circumference of the circle as centre, draw arcs of same radii which cut the circumference at B and F.

3. With B and F as centers, again draw two arcs of same radii (3.2 cm) which cut the circumference at C and E respectively.

4. With C or E as center, draw one more arc of the same radius which cuts the circumference at point D.

5. Join AB, BC, CD, DE, EF and FA.

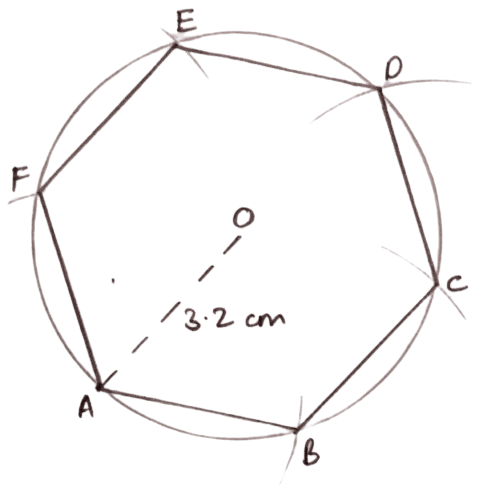
Hence, ABCDEF is the required regular hexagon.

Is it possible to construct a quadrilateral with sides 5 cm, 6 cm, 7 cm, 8 cm and one of the diagonal 15 cm.

1. Yes

2. No

3. Nothing can be said

Answer

A quadrilateral with a diagonal forms two triangles. Let the diagonal be 15 cm.

Consider one triangle with sides 5 cm, 6 cm, and 15 cm.

Consider the other triangle with sides 7 cm, 8 cm, and 15 cm.

The Triangle Inequality Theorem states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.

Check if the sum of any two sides is greater than the third side for the triangle with sides 5 cm, 6 cm, and 15 cm.

Sum of 5 cm and 6 cm: 5 + 6 = 11.

Compare to the third side: 11 < 15.

Sum of 6 cm and 11 cm: 6 + 11 = 17.

Compare to the third side: 17 > 5.

Sum of 5 cm and 11 cm: 5 + 11 = 16.

Compare to the third side: 16 > 6.

Since 11 < 15, the Triangle Inequality Theorem is violated for the first triangle.

Therefore, a triangle with sides 5 cm, 6 cm, and 15 cm cannot be formed.

Thus, the quadrilateral cannot be constructed.

Hence, option 2 is the correct option.

In a regular hexagon, leading diagonal of it, is twice of its side.

1. Yes

2. No

3. Nothing can be said

Answer

A regular hexagon has six equal sides and six equal interior angles, each measuring 120 degrees.

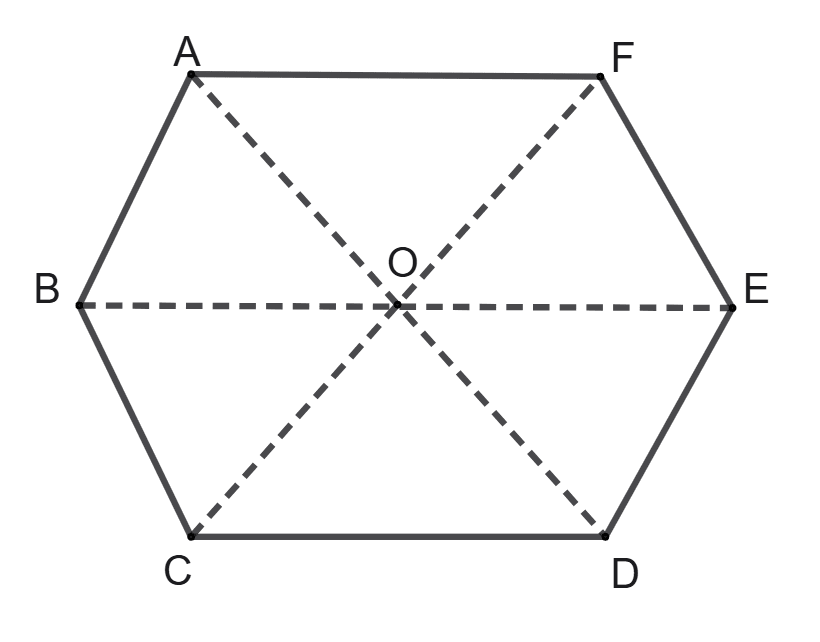
We know that,

Each regular hexagon can be divided into six equilateral triangles, with each side equal to the side of hexagon.

Let ABCDEF be a regular hexagon with O as the center and side of length x units.

From figure,

CF (Diagonal) = CO + OF = x + x = 2x.

Thus leading diagonal is twice the side of regular hexagon.

Hence, option 1 is the correct option.

Statement 1: In a quadrilateral ABCD; AB = BC = CD = DA = 8 cm.

Statement 2: It is possible to construct the quadrilateral.

1. Both the statements are true.

2. Both the statements are false.

3. Statement 1 is true, and statement 2 is false.

4. Statement 1 is false, and statement 2 is true.

Answer

In a quadrilateral ABCD; AB = BC = CD = DA = 8 cm

This is true, such a quadrilateral can exist. When all four sides are equal, the quadrilateral can be a rhombus or a square.

So, statement 1 is true.

Construction typically requires just one extra piece of information either a diagonal length or a specific angle.

No, it is not possible to construct the quadrilateral.

So, statement 2 is false.

∴ Statement 1 is true, and statement 2 is false.

Hence, option 3 is the correct option.

Assertion (A): The diagonals and one side of the parallelograms are given.

Reason (R): Is it possible to construct parallelogram as the diagonals bisect each other.

1. A is true, but R is false.

2. A is false, but R is true.

3. Both A and R are true, and R is the correct reason for A.

4. Both A and R are true, and R is the incorrect reason for A.

Answer

In a parallelogram, a fundamental property is that the diagonals bisect each other — i.e. each diagonal is split into two equal segments at their intersection.

Since, one side is known and diagonals are known we can create triangles, and thus completely constructing the parallelogram.

∴ Both A and R are true, and R is the correct reason for A.

Hence, option 3 is the correct option.

Construct a quadrilateral ABCD with AB = 7 cm, BC = CD = 5 cm and ∠ABC = ∠BCD = 90°.

Answer

Steps of construction :

1. Draw a line segment BC = 5 cm.

2. Draw BX ⊥ BC and CY ⊥ BC.

3. From BX, cut BA = 7 cm.

4. From CY, cut CD = 5 cm.

5. Join AD.

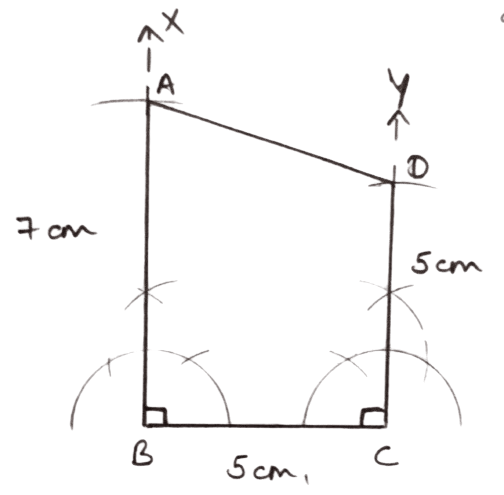
Hence, ABCD is the required quadrilateral.

Construct a trapezium ABCD in which AD // BC, AB = CD = 3.6 cm, BC = 5 cm and AD = 4.5 cm.

Answer

Steps of construction :

1. Draw a line segment BC = 5 cm.

2. From BC, cut BE = AD = 4.5 cm.

3. Draw triangle DEC, such that DE = AB = 3.6 cm and CD = 3.6 cm.

4. Taking B and D as centers and radii 3.6 cm and 4.5 cm respectively, draw arcs cutting each other at A.

5. Join AB and AD.

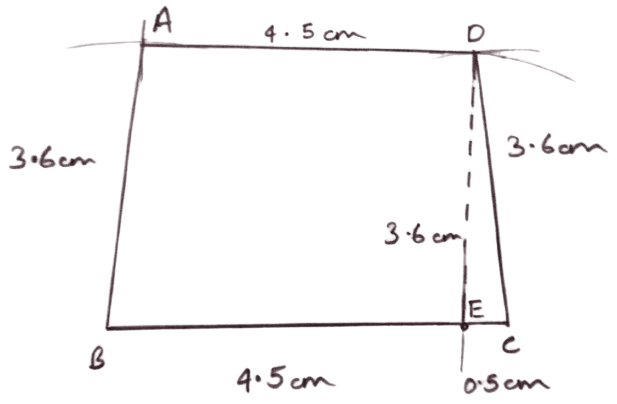
Hence, ABCD is the required trapezium.

Using ruler and compasses, construct a rectangle ABCD, with AB = 5 cm and AD = 3.6 cm.

Answer

Steps of construction :

1. Draw a line segment AB = 5 cm.

2. Draw AX ⊥ AB and BY ⊥ AB.

3. With B as center and radius equal to 3.6 cm draw arc cutting BY at C.

4. With A as center and radius equal to 3.6 cm draw arc cutting AX at D.

5. Join CD.

Hence, ABCD is the required rectangle.

Using ruler and compasses only, construct the quadrilateral ABCD, having given AB = 5 cm, BC = 2.5 cm, CD = 6 cm, angle BAD = 90° and the diagonal AC = 5.5 cm.

Answer

Steps of construction :

1. Draw a line segment AB = 5 cm.

2. Draw AX ⊥ AB.

3. With A and B as center and radii equal to 5.5 cm and 2.5 cm respectively draw arcs cutting each other at C. Join AC and BC.

4. With C as center and radius equal to 6 cm draw arc cutting AX at D.

5. Join AD and CD.

Hence, ABCD is the required quadrilateral.

Using ruler and compasses only, construct a trapezium ABCD, in which the parallel sides AB and DC are 3.3 cm apart; AB = 4.5 cm, angle A = 120°, BC = 3.6 cm and angle B is obtuse.

Answer

Steps of construction :

1. Draw a line segment AB = 4.5 cm.

2. Draw ∠BAS = 120° and AE ⊥ AB.

3. From AE, cut AX = 3.3 cm.

4. Through X, draw a line PQ parallel to AB and cutting AS at D.

5. With B as center and radius equal to 3.6 cm draw an arc cutting PQ on C.

6. Join BC and CD.

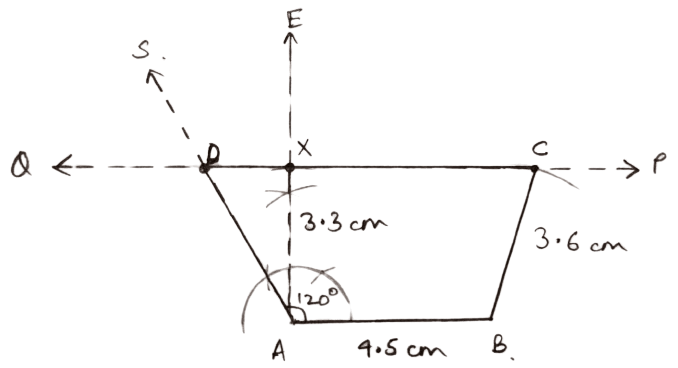
Hence, ABCD is the required trapezium.

Using ruler and compasses only, construct the quadrilateral ABCD, having given AB = 5 cm, BC = 2.5 cm, CD = 6 cm, ∠BAD = 90° and diagonal BD = 5.5 cm.

Answer

Steps of construction :

1. Draw a line segment AB = 5 cm.

2. Draw AX ⊥ AB.

3. With B as center and radius equal to 5.5 cm draw an arc cutting AX at D. Join BD.

4. With D and B as center and radii equal to 6 cm and 2.5 cm respectively draw arcs cutting each other at C.

5. Join DC and BC.

Hence, ABCD is the required quadrilateral.

Using ruler and compasses only, construct a parallelogram ABCD using the following data :

AB = 6 cm, AD = 3 cm and ∠DAB = 45°. If the bisector of ∠DAB meets DC at P, prove that ∠APB is a right angle.

Answer

Steps of construction :

1. Draw a line segment AB = 6 cm.

2. With A as center draw a line AX such that ∠BAX = 45°.

3. From AX, cut AD = 3 cm.

4. With B and D as center and radii equal to 3 cm and 6 cm draw arc cutting each other at point C.

5. Join BC and CD.

6. Draw AY, the angular bisector of angle A intersecting CD at point P.

7. Join BP. Measure ∠APB.

On measuring ∠APB = 90°.

Hence, ABCD is the required parallelogram.

The perpendicular distances between the pair of opposite sides of a parallelogram, are 3 cm and 4 cm, and one of its angles measures 60°. Using ruler and compasses only, construct the parallelogram.

Answer

Steps of construction :

1. Draw a straight line PQ, take a point A on it.

2. At A, construct ∠QAF = 60°.

3. At A, draw AE ⊥ PQ, from AE cut off AN = 3 cm.

4. Through N draw a straight line parallel to PQ to meet AF at D.

5. At A, draw AG ⊥ AD, from AG cut off AM = 4 cm.

6. Through M, draw a straight line parallel to AD to meet AQ at B and ND at C.

7. Join AB, BC, CD and DA.

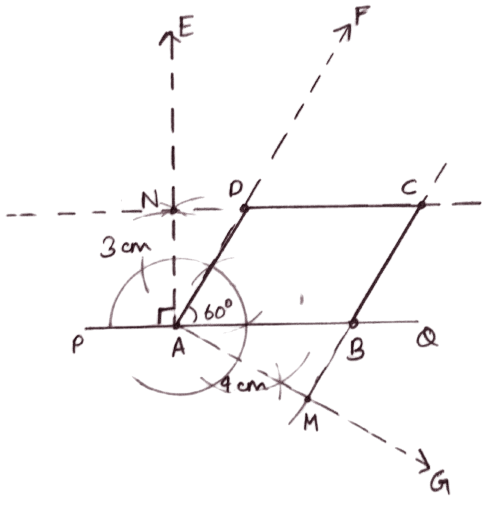
Hence, ABCD is the required parallelogram.

Draw parallelogram ABCD with the following data :

AB = 6 cm, AD = 5 cm and ∠DAB = 45°.

Let AC and DB meet in O and let E be the mid-point of BC. Join OE. Prove that :

(i) OE // AB

(ii) OE = $\dfrac{1}{2}$ AB

Answer

In parallelogram,

Opposite sides are equal.

∴ BC = AD = 5.0 cm and CD = AB = 6.0 cm

Steps of construction :

1. Draw a line segment AB = 6.0 cm.

2. Draw AP, such that ∠A = 45°.

3. With A as center and radius equal to 5 cm draw an arc cutting AP at D.

4. With B and D as centers and radii 5.0 cm and 6.0 cm respectively, draw arcs cutting each other at C.

5. Join BC and CD.

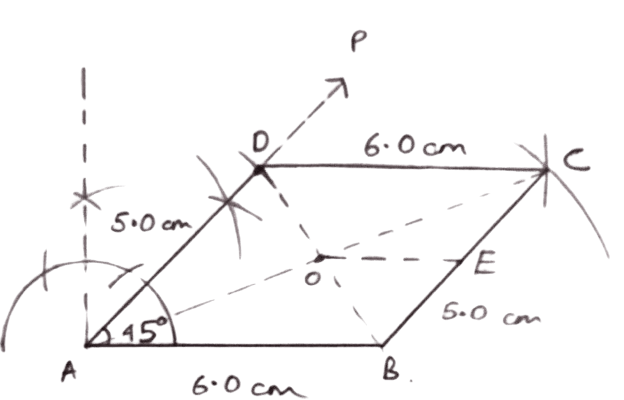
Hence, ABCD is the required parallelogram.

(i) In △ ABC,

O is the mid-point of AC (As diagonals of || gm bisect each other).

E is the mid-point of BC (Given).

By mid-point theorem,

If a line segment joins the mid-point of any two sides of a triangle, then the line segment is said to be parallel to the remaining third side and its measure will be half of the third side.

⇒ OE // AB.

Hence, proved that OE // AB.

(ii) In △ ABC,

O is the mid-point of AC (As diagonals of || gm bisect each other).

E is the mid-point of BC (Given).

By mid-point theorem,

If a line segment joins the mid-point of any two sides of a triangle, then the line segment is said to be parallel to the remaining third side and its measure will be half of the third side.

⇒ OE = $\dfrac{1}{2}AB$.

Hence, proved that OE = $\dfrac{1}{2}AB$.

Using ruler and compasses only, construct a rectangle each of whose diagonals measure 6 cm and the diagonals intersect at an angle of 45°.

Answer

Steps of construction :

1. Draw a line segment AC = 6 cm.

2. Bisect AC at O.

3. At O, draw a ray XY making an angle of 45° at O.

4. From XY, cut off OB = OD = $\dfrac{6}{2}$ = 3 cm each.

5. Join AB, BC, CD and DA.

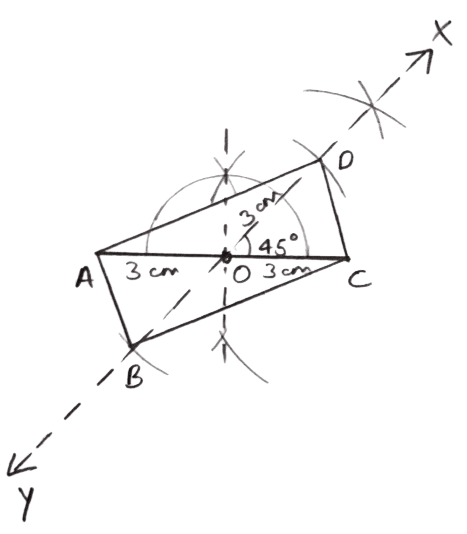
Hence, ABCD is the required rectangle.