Area Theorems [Proof and Use]

In the given figure, BD : DC = 3 : 5, then area of △ ABD : area of △ ACD is :

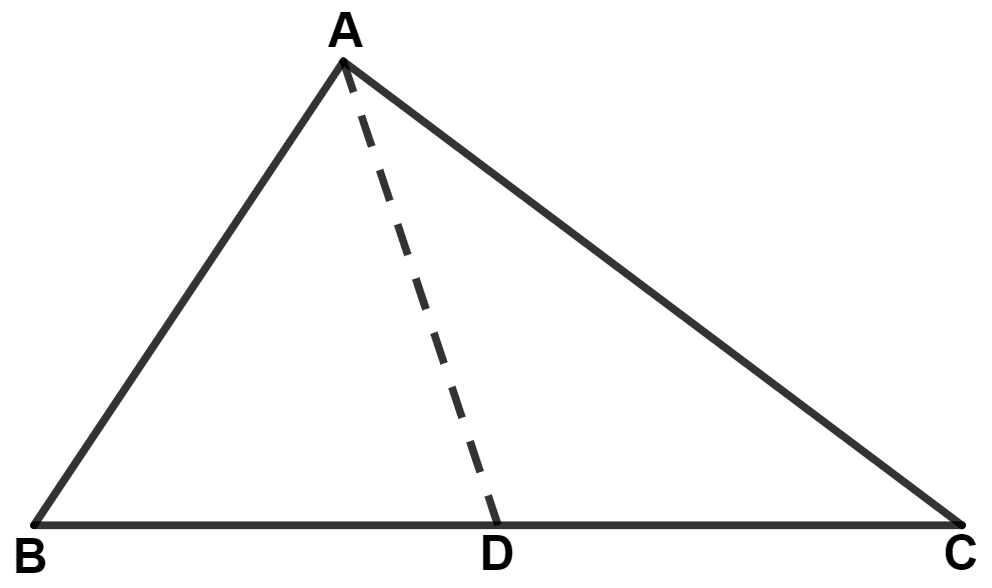
1. 5 : 3

2. 3 : 5

3. 25 : 9

4. 9 : 25

Answer

In the given figure,

△ ABD and △ ACD has same vertex A and bases along the same straight line BC.

∴ $\dfrac{\text{Area of △ ABD}}{\text{Area of △ ACD}} = \dfrac{BD}{DC} = \dfrac{3}{5}$

∴ area of △ ABD : area of △ ACD = 3 : 5.

Hence, Option 2 is the correct option.

A median of a triangle divides it into two :

1. triangles of equal areas

2. congruent triangles

3. triangles of areas in the ratio 2 : 1

4. right triangles

Answer

A median of a triangle divides it into two triangles of equal areas.

Hence, Option 1 is the correct option.

In the given figure, AB is parallel to DC and AB ≠ DC, the area of △ AOD is equal to area of triangle :

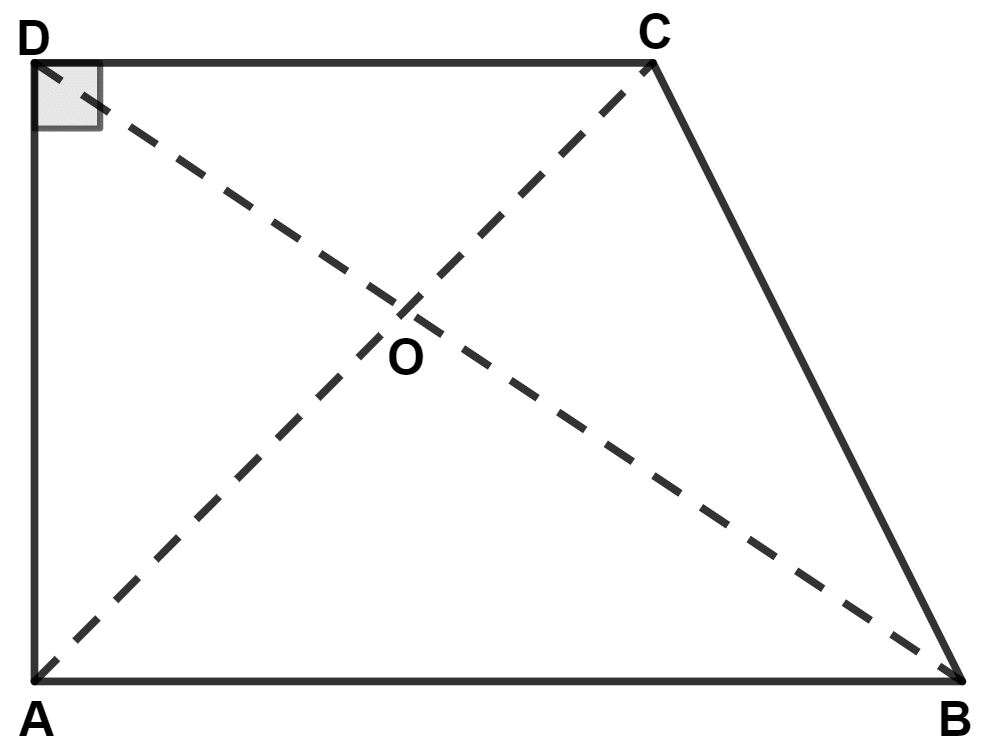
1. AOB

2. COD

3. ACB

4. BOC

Answer

We know that,

The area of triangles lying on same base and between same parallel lines are equal.

From figure,

△ ADC and △ BCD lie on same base CD and between same parallel lines AB and CD.

∴ Area of △ ADC = Area of △ BCD

⇒ Area of △ ADC - Area of △ COD = Area of △ BCD - Area of △ BOC

⇒ Area of △ AOD = Area of △ BOC.

Hence, Option 4 is the correct option.

In the given figure, AF // BE and PQ // RS, FC and ED are perpendiculars to RS. The area of parallelogram ABEF is equal to :

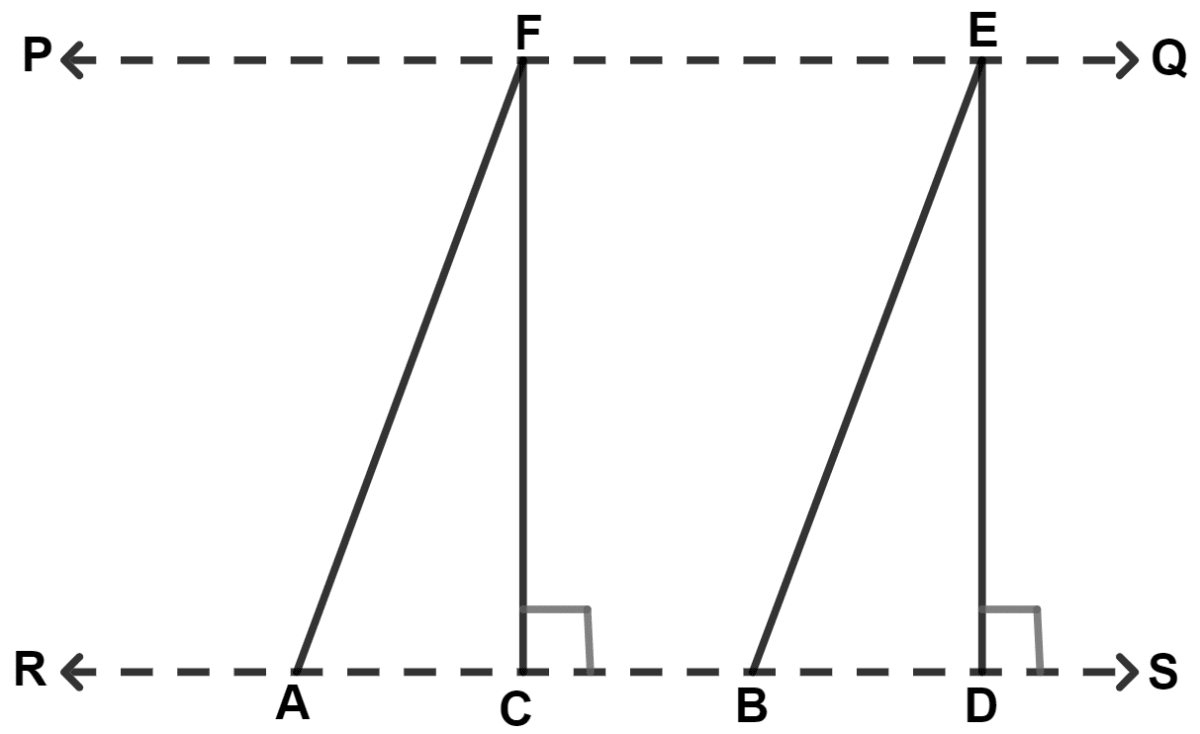
1. rect. CDEF

2. quad. CBEF

3. 2 × △ACF

4. 2 × △EBD

Answer

We know that,

Parallelogram on equal bases and between the same parallel are equal in area.

A rectangle is also a parallelogram.

From figure,

Parallelogram ABEF and rectangle CDEF lie on same base FE and between same parallel lines PQ and RS.

∴ Area of parallelogram ABEF = Area of rectangle CDEF.

Hence, Option 1 is the correct option.

In the given figure, D is mid-point of side BC, the area of triangle BEA is equal to area of triangle :

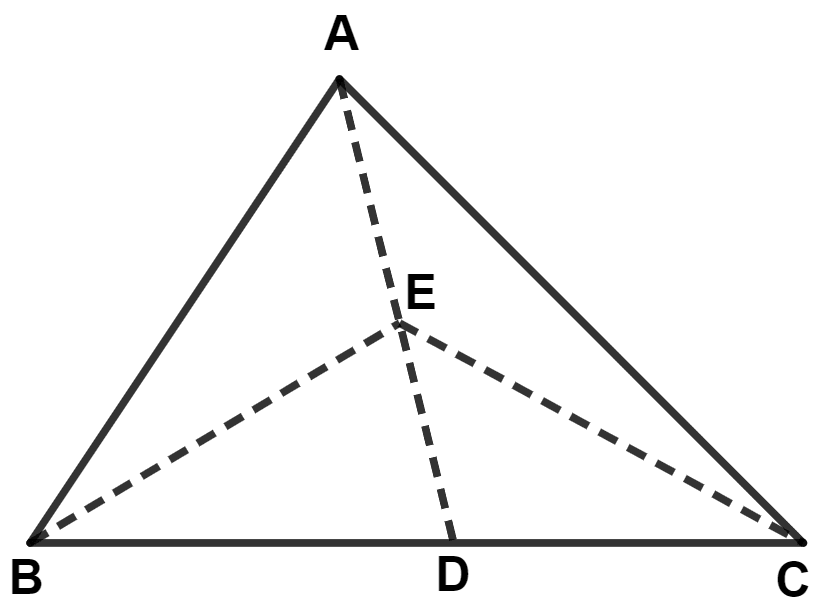
1. BED

2. CED

3. CEA

4. ACD

Answer

In △ ABC,

Since, D is the mid-point of side BC.

∴ AD is the median of BC.

∴ Area of △ ABD = Area of △ ACD (As, median of a triangle divides it into two triangles of equal areas.) ...........(1)

In △ EBC,

Since, D is the mid-point of side BC.

∴ ED is the median of BC.

∴ Area of △ EBD = Area of △ ECD (As, median of a triangle divides it into two triangles of equal areas.) .........(2)

Subtracting equation (2) from (1), we get :

⇒ Area of △ ABD - Area of △ EBD = Area of △ ACD - Area of △ ECD

⇒ Area of △ BEA = Area of △ CEA.

Hence, Option 3 is the correct option.

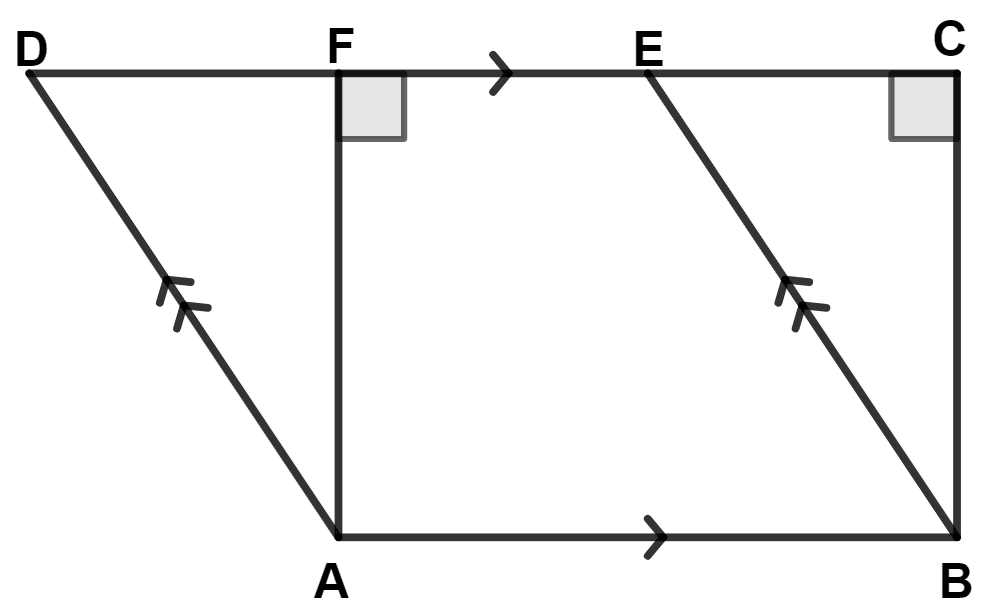
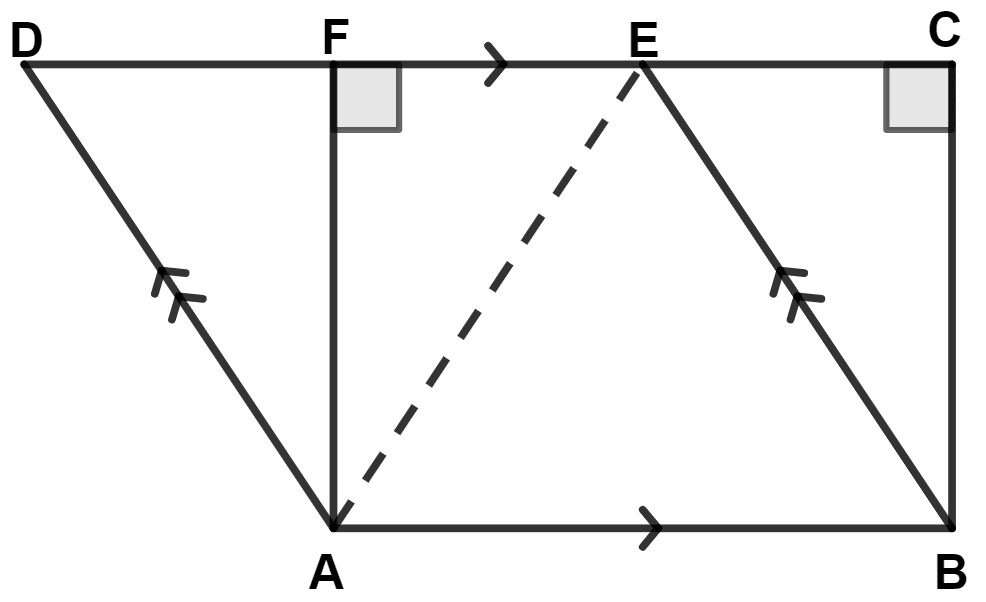
In the given figure, if area of triangle ADE is 60 cm²; state, giving reason, the area of :

(i) parallelogram ABED;

(ii) rectangle ABCF;

(iii) triangle ABE.

Answer

(i) We know that,

Area of triangle is half that of a parallelogram, on the same base and between the same parallels.

From figure,

△ ADE and parallelogram ABED lies on same base DE and between same parallel lines AB and DE.

∴ Area of △ ADE = $\dfrac{1}{2}$ Area of parallelogram ABED

⇒ Area of parallelogram ABED = 2 × Area of △ ADE

⇒ Area of parallelogram ABED = 2 × 60 = 120 cm².

Hence, area of parallelogram ABED = 120 cm².

(ii) We know that,

Area of parallelogram is equal to area of a rectangle on the same base and between same parallel lines.

From figure,

Parallelogram ABED and rectangle ABCF lie on lie on same base AB and between same parallel lines AB and CD.

∴ Area of rectangle ABCF = Area of parallelogram ABED = 120 cm².

Hence, area of rectangle ABCF = 120 cm².

(iii) We know that,

Area of a triangle is half that of a parallelogram on the same base and between the same parallels.

∴ Area of triangle ABE = $\dfrac{1}{2}$ Area of parallelogram ABED

= $\dfrac{1}{2} \times 120$ = 60 cm².

Hence, area of triangle ABE = 60 cm².

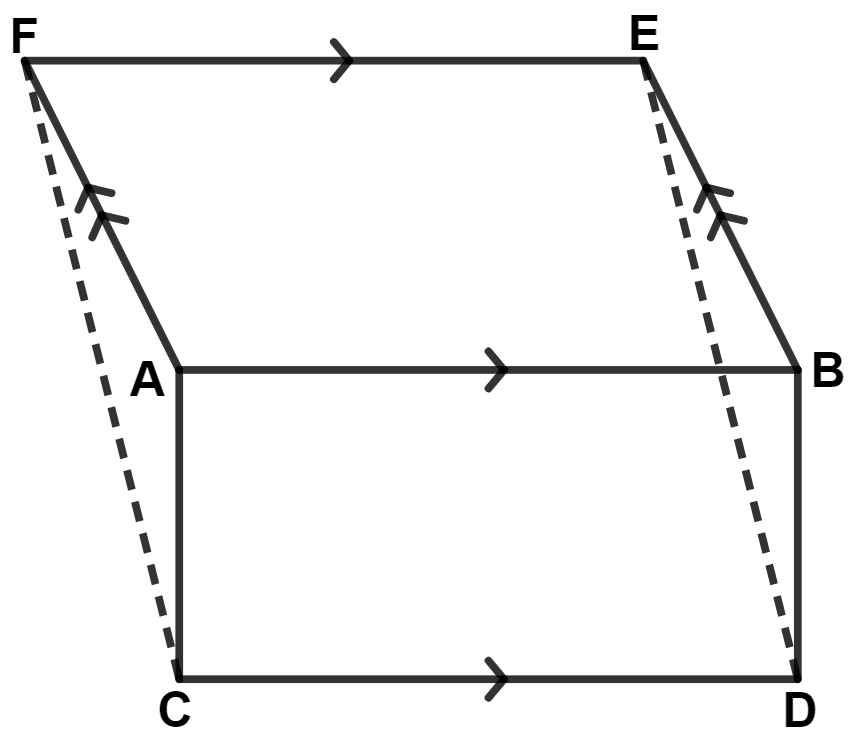
The given figure shows a rectangle ABDC and a parallelogram ABEF; drawn on opposite sides of AB. Prove that :

(i) quadrilateral CDEF is a parallelogram

(ii) Area of quad. CDEF = Area of rect. ABDC + Area of // gm ABEF

Answer

(i) Given,

ABCD is a rectangle.

∴ AB = CD (Opposite sides of rectangle are equal) ...............(1)

Given,

ABEF is a rectangle.

∴ AB = FE (Opposite sides of parallelogram are equal) ...............(2)

From equations (1) and (2), we get :

⇒ CD = FE.

From figure,

CD || FE

Since, one pair of opposite sides of quadrilateral CDEF are equal and parallel.

∴ CDEF is a parallelogram.

Hence, proved that CDEF is a parallelogram.

(ii) In △ AFC and △ BED,

⇒ AF = BE (Opposite sides of parallelogram ABEF)

⇒ AC = BD (Opposite sides of rectangle ABCD)

⇒ CF = ED (Opposite sides of parallelogram CDEF)

∴ △ AFC ≅ △ BED (By S.S.S. axiom)

We know that,

Area of congruent triangle are equal.

∴ Area of △ AFC = Area of △ BED ..........(1)

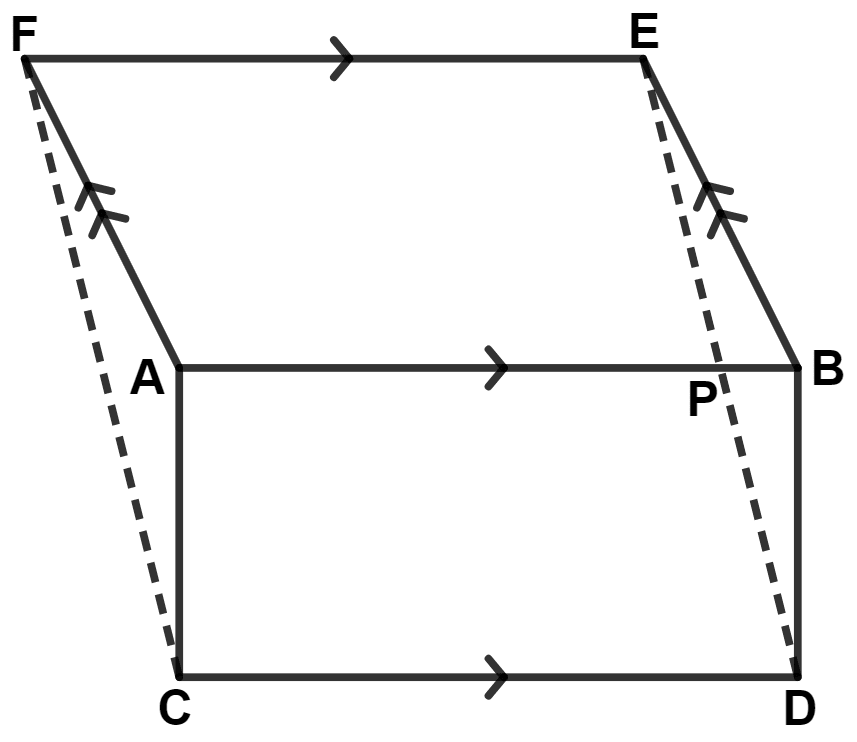
From figure,

⇒ Area of quadrilateral CDEF = Area of △ ACF + Area of ACDPEF

⇒ Area of quadrilateral CDEF = Area of △ BED + Area of ACDPEF [From equation (1)]

⇒ Area of quadrilateral CDEF = Area of CDBEPA

⇒ Area of quadrilateral CDEF = Area of rect. ABDC + Area of // gm ABEF.

Hence, proved that Area of quadrilateral CDEF = Area of rect. ABDC + Area of // gm ABEF.

In the given figure, diagonals PR and QS of the parallelogram PQRS intersect at point O and LM is parallel to PS. Show that :

(i) 2 Area (△ POS) = Area (// gm PMLS)

(ii) Area (△ POS) + Area (△ QOR) = $\dfrac{1}{2}$ Area (//gm PQRS)

(iii) Area (△ POS) + Area (△ QOR) = Area (△ POQ) + Area (△ SOR)

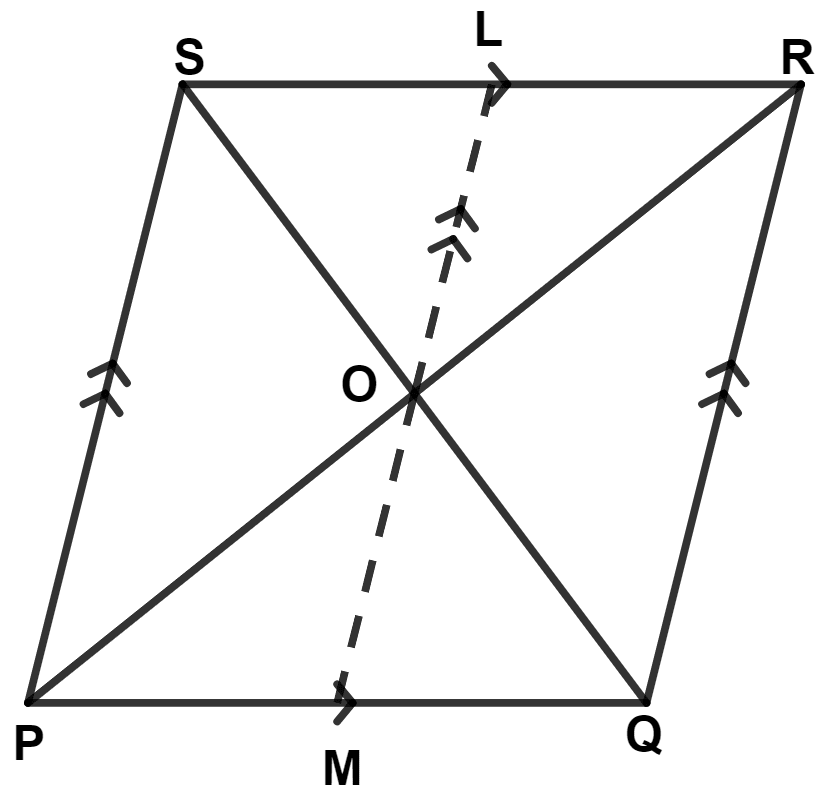
Answer

(i) We know that,

Area of a triangle is half that of a parallelogram on the same base and between the same parallels.

From figure,

Triangle POS and parallelogram PMLS lie on same base PS and between same parallel lines PS and ML.

∴ Area of triangle POS = $\dfrac{1}{2}$ Area of parallelogram PMLS

⇒ Area of parallelogram PMLS = 2 (Area of triangle POS)

Hence, proved that 2 area (△ POS) = area (// gm PMLS).

(ii) We know that,

Area of a triangle is half that of a parallelogram on the same base and between the same parallels.

From figure,

Triangle POS and parallelogram PMLS lie on same base PS and between same parallel lines PS and ML.

∴ Area of triangle POS = $\dfrac{1}{2}$ Area of parallelogram PMLS ..........(1)

Triangle QOR and parallelogram MQRL lie on same base QR and between same parallel lines QR and ML.

∴ Area of triangle QOR = $\dfrac{1}{2}$ Area of parallelogram MQRL ..........(2)

Adding equations (1) and (2), we get :

⇒ Area of triangle POS + Area of triangle QOR = $\dfrac{1}{2}$ Area of parallelogram PMLS + $\dfrac{1}{2}$ Area of parallelogram MQRL

⇒ Area of triangle POS + Area of triangle QOR = $\dfrac{1}{2}$ (Area of parallelogram PMLS + Area of parallelogram MQRL)

⇒ Area of triangle POS + Area of triangle QOR = $\dfrac{1}{2}$ Area of parallelogram PQRS.

Hence, proved that area (△ POS) + area (△ QOR) = $\dfrac{1}{2}$ area (//gm PQRS).

(iii) We know that,

In a parallelogram diagonals bisect each other.

∴ OS = OQ

In △ PQS,

O is the mid-point of QS.

∴ OP is the median.

We know that,

Median of a triangle divides it into two triangles of equal areas.

∴ Area of △ POS = Area of △ POQ .........(3)

In △ QSR,

O is the mid-point of QS.

∴ OR is the median.

We know that,

Median of a triangle divides it into two triangles of equal areas.

∴ Area of △ QOR = Area of △ SOR .........(4)

Adding equations (3) and (4), we get :

⇒ Area of △ POS + Area of △ QOR = Area of △ POQ + Area of △ SOR.

Hence, proved that area (△ POS) + area (△ QOR) = area (△ POQ) + area (△ SOR).

In parallelogram ABCD, P is a point on side AB and Q is a point on side BC. Prove that :

(i) △ CPD and △ AQD are equal in area.

(ii) Area (△ AQD) = Area (△ APD) + Area (△ CPB)

Answer

We know that,

Area of a triangle is half that of a parallelogram on the same base and between the same parallels.

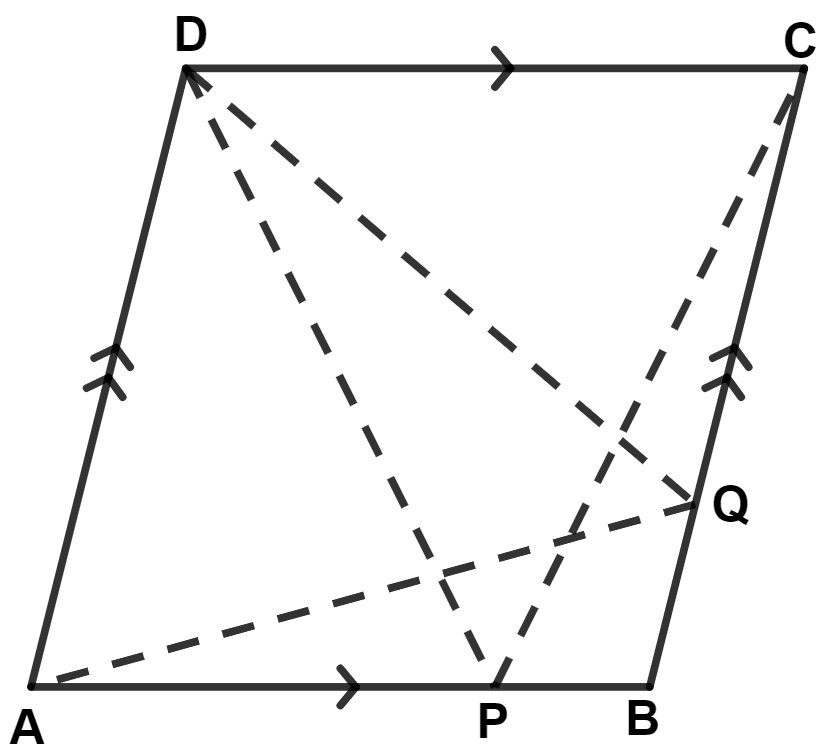
(i) From figure,

△ CPD and || gm ABCD are on the same base CD and between the same parallel lines AB and CD.

∴ Area of triangle CPD = $\dfrac{1}{2}$ Area of parallelogram ABCD ........(1)

△ AQD and || gm ABCD are on the same base AD and between the same parallel lines AD and BC.

∴ Area of triangle AQD = $\dfrac{1}{2}$ Area of parallelogram ABCD ........(2)

From equations (1) and (2), we get :

Area of triangle CPD = Area of triangle AQD.

Hence, proved that area of triangle CPD = area of triangle AQD.

(ii) From part (i), we get :

⇒ Area of △ CPD = $\dfrac{1}{2}$ Area of parallelogram ABCD

∴ Area of || gm ABCD - Area of △ CPD = $\dfrac{1}{2}$ Area of parallelogram ABCD ........(3)

From figure,

⇒ Area of || gm ABCD - Area of △ CPD = Area of △ APD + Area of △ CPB ............(4)

From equations (3) and (4), we get :

⇒ Area of △ APD + Area of △ CPB = $\dfrac{1}{2}$ Area of || gm ABCD ........(5)

Since,

⇒ Area of △ ADQ = $\dfrac{1}{2}$ Area of || gm ABCD [From eqn. 2]

Substituting value of $\dfrac{1}{2}$ Area of || gm ABCD from above equation in equation (5), we get :

⇒ Area of △ APD + Area of △ CPB = Area of △ ADQ.

Hence, proved that area (△ AQD) = area (△ APD) + area (△ CPB).

In the given figure, M and N are the mid-points of the sides DC and AB respectively of the parallelogram ABCD.

If the area of parallelogram ABCD is 48 cm²;

(i) state the area of the triangle BEC.

(ii) name the parallelogram which is equal in area to the triangle BEC.

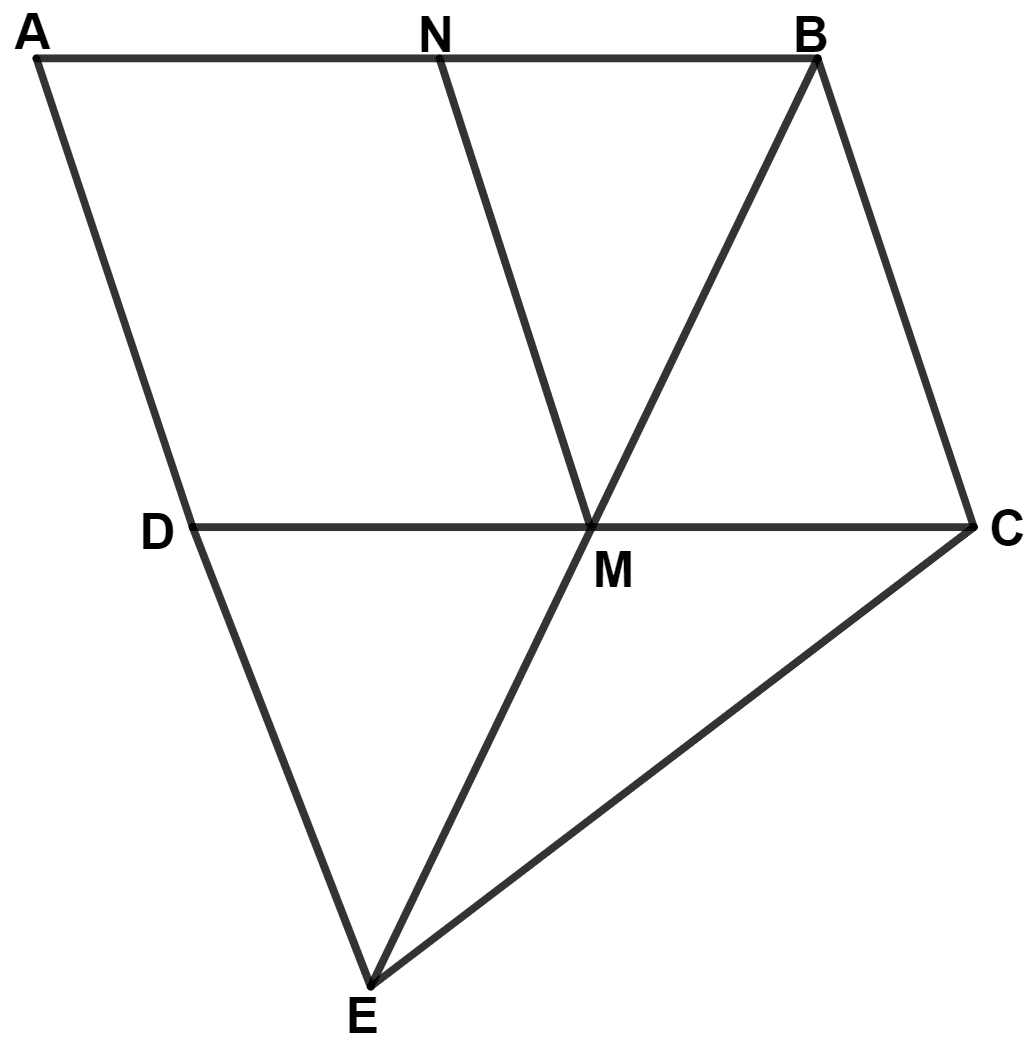
Answer

(i) We know that,

Area of a triangle is half that of a parallelogram on the same base and between the same parallels.

Since, triangle BEC and parallelogram ABCD are on the same base BC and between the same parallels AE and BC.

∴ Area of △ BEC = $\dfrac{1}{2}$ Area of || gm ABCD = $\dfrac{1}{2} \times 48$ = 24 cm².

Hence, the area of the triangle BEC = 24 cm².

(ii) Since, M and N are the mid-points of the sides DC and AB respectively.

∴ Area of || gm ANMD = Area of || gm NBCM = $\dfrac{1}{2}$ Area of || gm ABCD .........(1)

From part (i), we get :

Area of △ BEC = $\dfrac{1}{2}$ Area of || gm ABCD ........(2)

From equation (1) and (2), we get :

Area of || gm ANMD = Area of || gm NBCM = Area of △ BEC.

Hence, parallelograms ANMD and NBCM are equal in area to triangle BEC.

In the following figure, CE is drawn parallel to diagonal DB of the quadrilateral ABCD which meets AB produced at point E.

Prove that △ ADE and quadrilateral ABCD are equal in area.

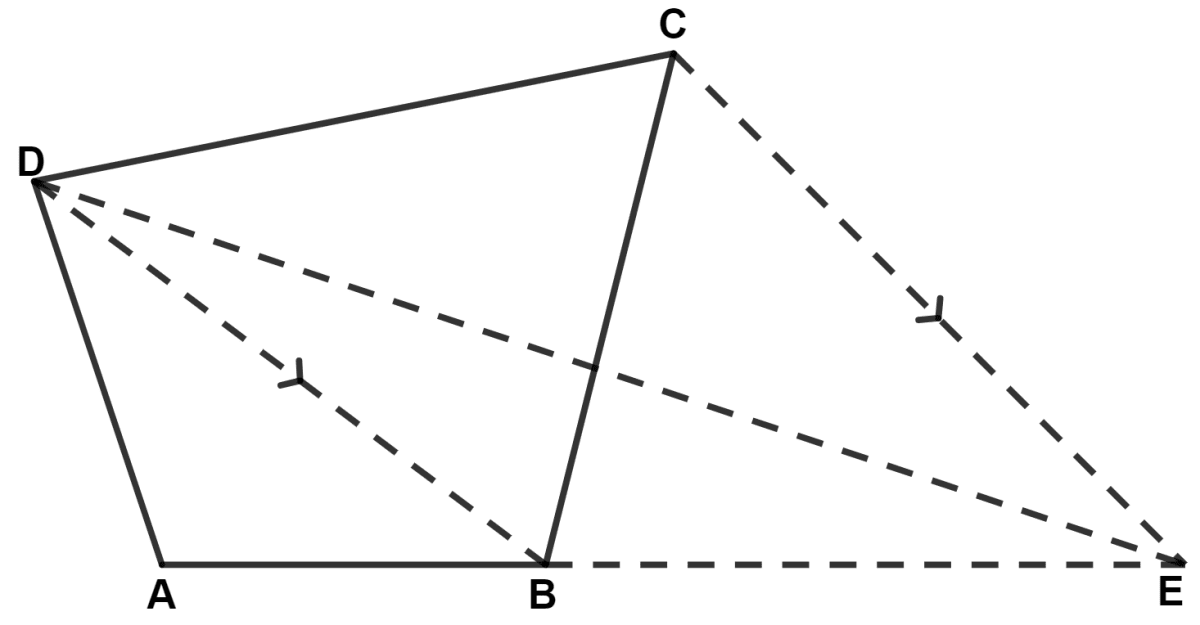
Answer

We know that,

Triangles on the same base and between the same parallel lines are equal in area.

△ BDE and △ BDC lie on the same base BD and along the same parallel lines DB and CE.

∴ Area of △ BDE = Area of △ BDC ..........(1)

From figure,

⇒ Area of △ ADE = Area of △ ADB + Area of △ BDE

⇒ Area of △ ADE = Area of △ ADB + Area of △ BDC [From equation (1)]

⇒ Area of △ ADE = Area of quadrilateral ABCD.

Hence, proved that △ ADE and quadrilateral ABCD are equal in area.

ABCD is a parallelogram, a line through A cuts DC at point P and BC produced at Q. Prove that triangle BCP is equal in area to triangle DPQ.

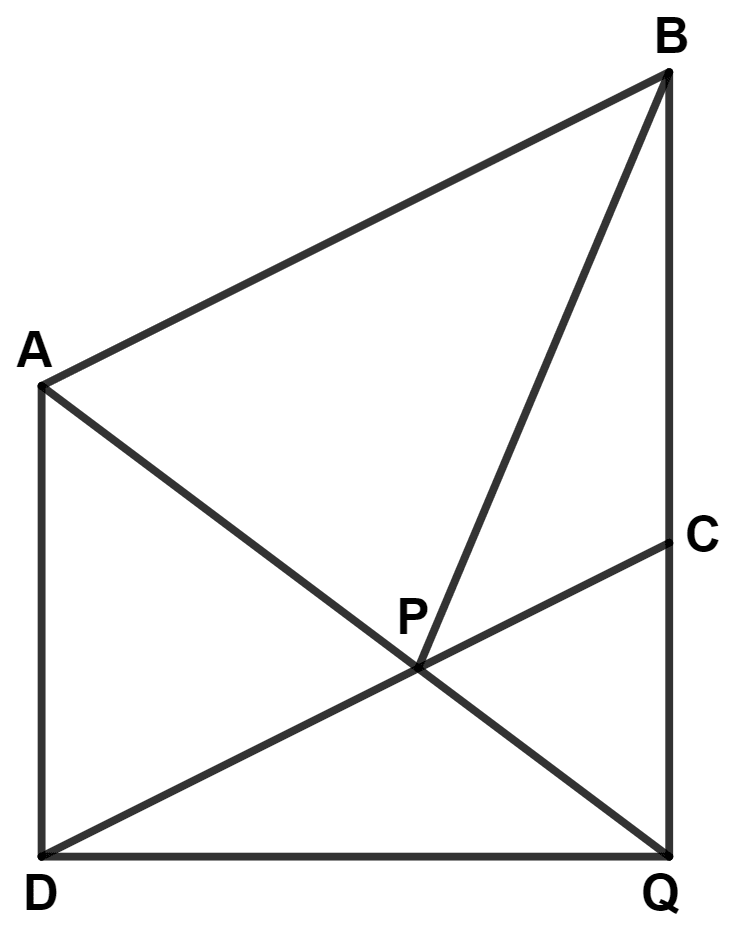
Answer

We know that,

Area of a triangle is half that of a parallelogram on the same base and between the same parallels.

Since, triangle APB and parallelogram ABCD are on the same base AB and between the same parallels AB and DC.

∴ Area of △ APB = $\dfrac{1}{2}$ Area of || gm ABCD ........(1)

Since, triangle ADQ and parallelogram ABCD are on the same base AD and between the same parallels AD and BQ.

∴ Area of △ ADQ = $\dfrac{1}{2}$ Area of || gm ABCD ........(2)

Adding equations (1) and (2), we get :

⇒ Area of △ APB + Area of △ ADQ = $\dfrac{1}{2}$ Area of || gm ABCD + $\dfrac{1}{2}$ Area of || gm ABCD

⇒ Area of △ APB + Area of △ ADQ = Area of || gm ABCD ...........(3)

From figure,

⇒ Area of △ APB + Area of △ ADQ = Area of quadrilateral ADQB - Area of △ BPQ ..............(4)

From equation (3) and (4), we get :

⇒ Area of quadrilateral ADQB - Area of △ BPQ = Area of || gm ABCD

⇒ Area of quadrilateral ADQB - Area of △ BPQ = Area of quadrilateral ADQB - Area of △ DCQ

⇒ Area of △ BPQ = Area of △ DCQ

⇒ Area of △ BPQ - Area of △ PCQ = Area of △ DCQ - Area of △ PCQ

⇒ Area of △ BCP = Area of △ DPQ.

Hence, proved that area of △ BCP = area of △ DPQ.

The given figure shows a pentagon ABCDE. EG drawn parallel to DA meets BA produced at G and CF drawn parallel to DB meets AB produced at F. Prove that the area of pentagon ABCDE is equal to the area of triangle GDF.

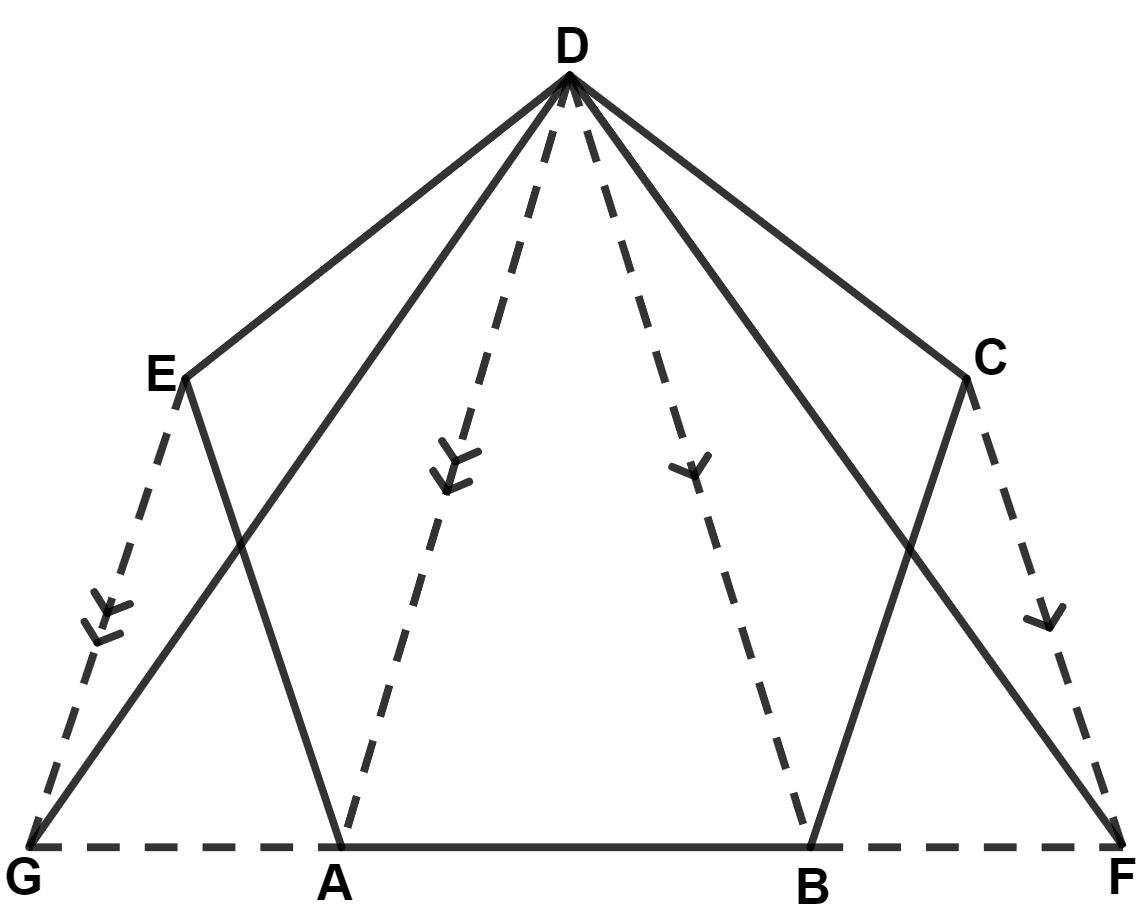
Answer

We know that,

Triangles on the same base and between the same parallel lines are equal in area.

Since, triangle EDG and EGA lie on the same base EG and between the same parallel lines EG and DA.

∴ Area of △ EDG = Area of △ EGA

Subtracting △ EOG from both sides, we get :

⇒ Area of △ EDG - Area of △ EOG = Area of △ EGA - Area of △ EOG

⇒ Area of △ EOD = Area of △ GOA .........(1)

Since, triangle FDC and FBC lie on the same base FC and between the same parallel lines DB and CF.

∴ Area of △ FDC = Area of △ FBC

Subtracting △ FPC from both sides, we get :

⇒ Area of △ FDC - Area of △ FPC = Area of △ FBC - Area of △ FPC

⇒ Area of △ DPC = Area of △ BPF .........(2)

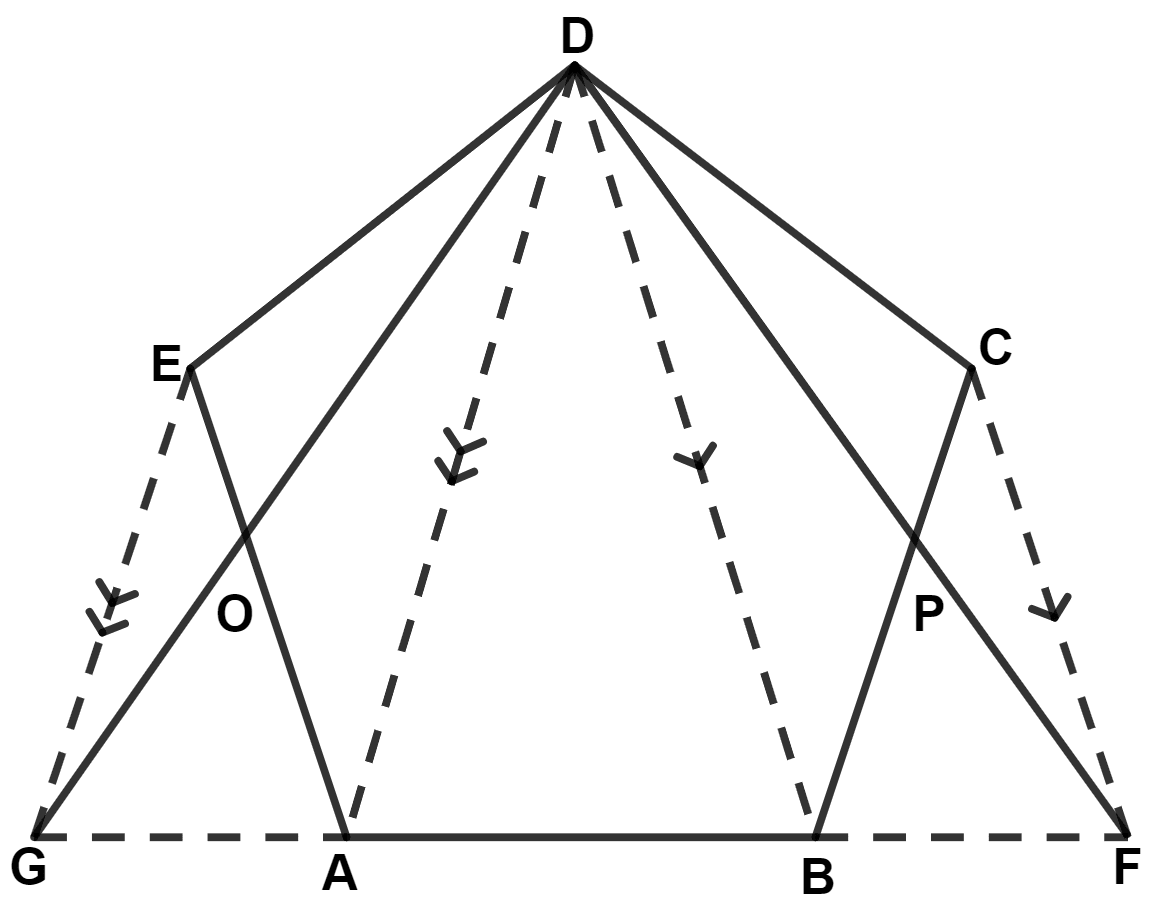
From figure,

⇒ Area of △ GDF = Area of △ GOA + Area of △ BPF + Area of pentagon ABPDO

⇒ Area of △ GDF = Area of △ EOD + Area of △ DPC + Area of pentagon ABPDO

⇒ Area of △ GDF = Area of pentagon ABCDE.

Hence, proved that area of pentagon ABCDE is equal to the area of triangle GDF.

In the given figure, AP is parallel to BC, BP is parallel to CQ. Prove that the areas of triangles ABC and BQP are equal.

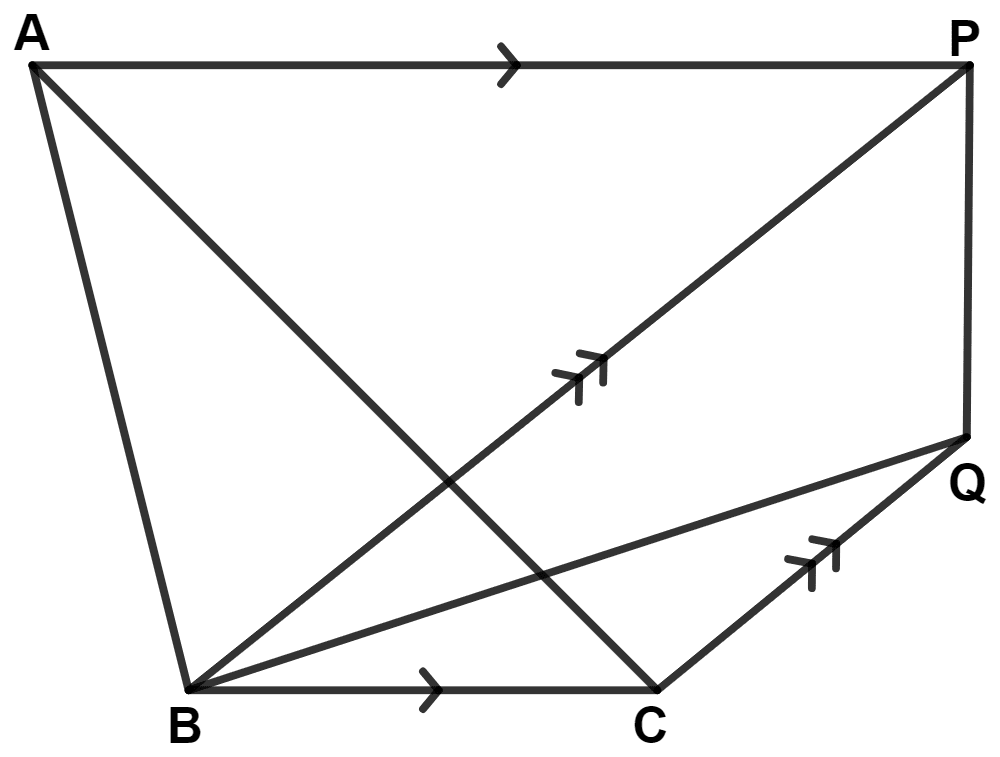
Answer

We know that,

Triangles on the same base and between the same parallel lines are equal in area.

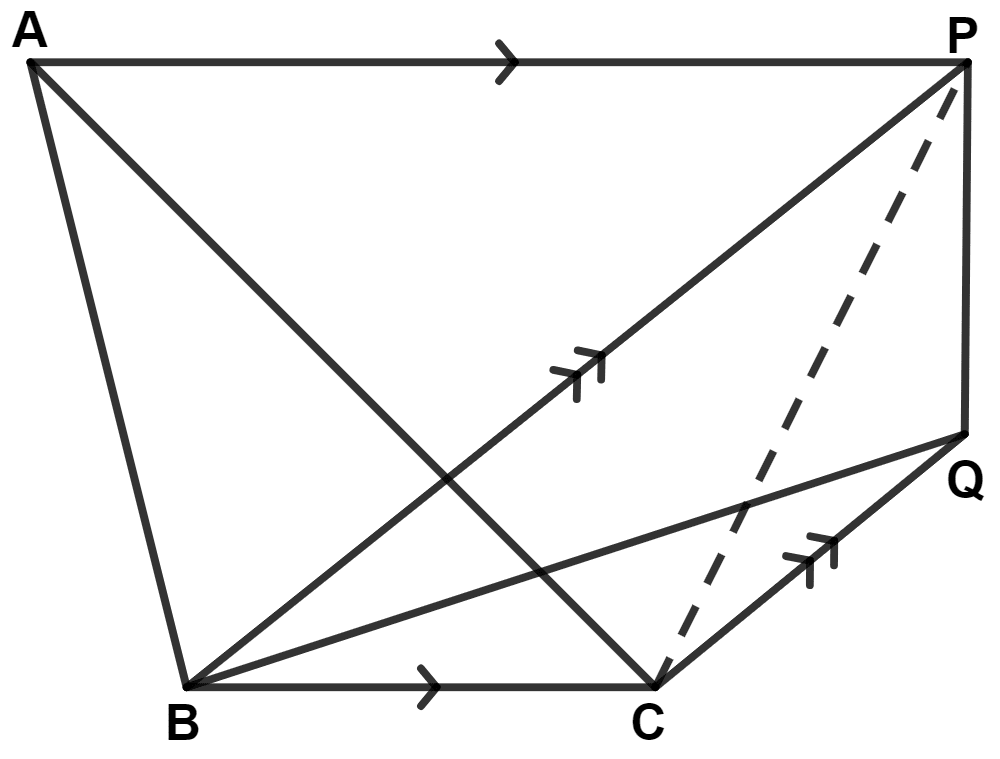
Since, triangle ABC and BPC lie on the same base BC and between the same parallel lines AP and BC.

∴ Area of △ ABC = Area of △ BPC .........(1)

Since, triangle BPC and BQP lie on the same base BP and between the same parallel lines BP and CQ.

∴ Area of △ BPC = Area of △ BQP .........(2)

From equations (1) and (2), we get :

Area of △ ABC = Area of △ BQP.

Hence, proved that area of △ ABC = area of △ BQP.

In the figure given alongside, squares ABDE and AFGC are drawn on the side AB and the hypotenuse AC of the right triangle ABC.

If BH is perpendicular to FG, prove that :

(i) △ EAC ≅ △ BAF

(ii) Area of the square ABDE = Area of the rectangle ARHF.

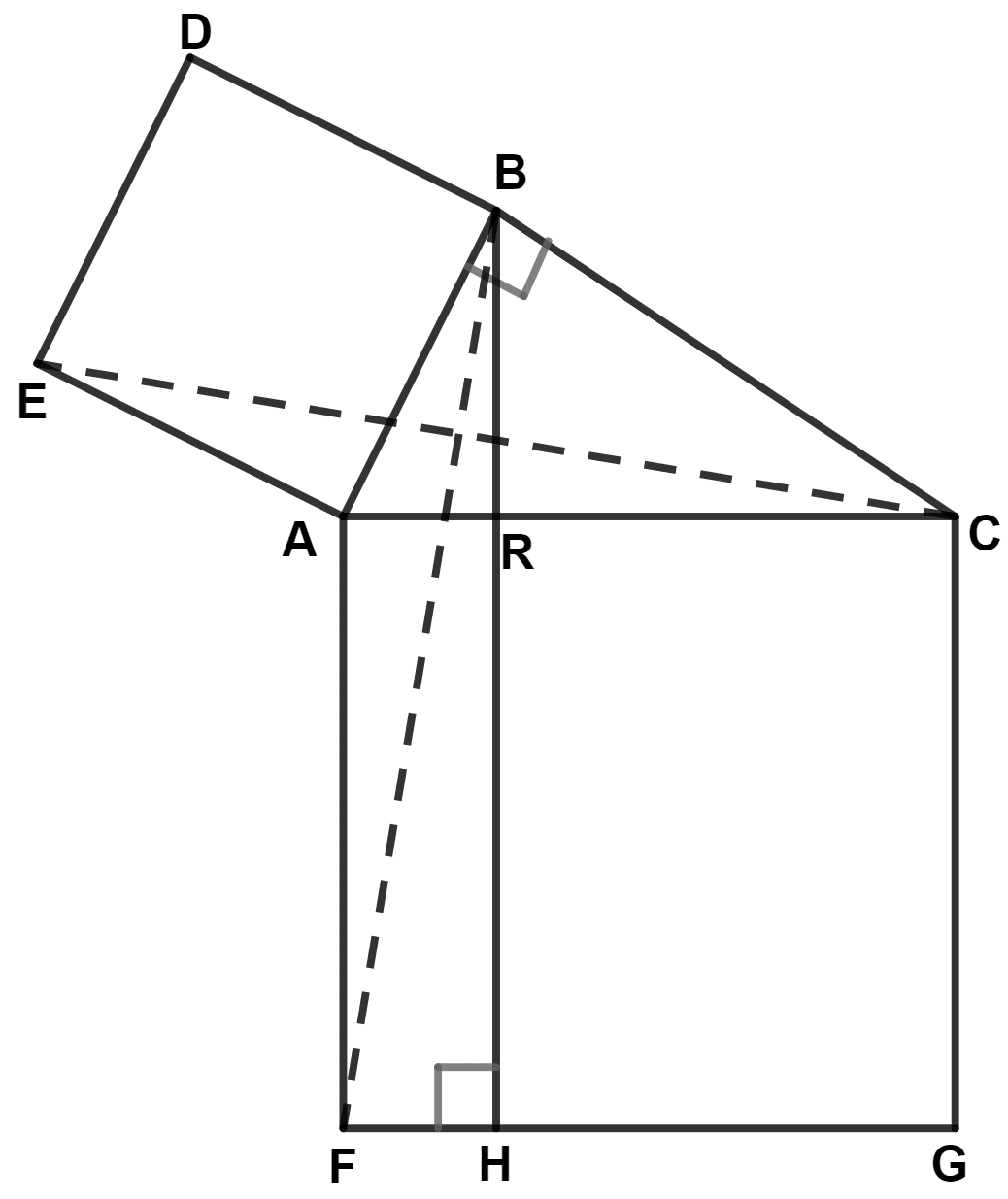
Answer

(i) From figure,

⇒ ∠EAC = ∠EAB + ∠BAC

⇒ ∠EAC = 90° + ∠BAC (As, ABDE is a square and each angle of square equal to 90°) ........(1)

Also,

⇒ ∠BAF = ∠FAC + ∠BAC

⇒ ∠BAF = 90° + ∠BAC (As, AFGC is a square and each angle of square equal to 90°) ............(2)

From equation (1) and (2),

⇒ ∠EAC = ∠BAF

In △ EAC and △ BAF,

⇒ EA = BA (Sides of square ABDE)

⇒ ∠EAC = ∠BAF (Proved above)

⇒ AC = AF (Sides of square AFGC)

∴ △ EAC ≅ △ BAF (By S.A.S. axiom)

Hence, proved that △ EAC ≅ △ BAF.

(ii) From figure,

ABC is a right angled triangle.

⇒ AC² = AB² + BC² [By pythagoras theorem]

⇒ AB² = AC² - BC²

⇒ AB² = (AR + RC)² - (BR² + RC²)

⇒ AB² = AR² + RC² + 2.AR.RC - BR² - RC²

⇒ AB² = AR² + RC² + 2.AR.RC - (AB² - AR²) - RC² [Using pythagoras theorem in △ ABR]

⇒ AB² = AR² + RC² + 2.AR.RC - AB² + AR² - RC²

⇒ AB² + AB² = AR² + AR² + RC² - RC² + 2.AR.RC

⇒ 2AB² = 2AR² + 2.AR.RC

⇒ 2AB² = 2AR(AR + RC)

⇒ AB² = AR(AR + RC)

⇒ AB² = AR.AC

⇒ AB² = AR.AF (As, AC = AF, sides of same sqaure)

∴ Area of square ABDE = Area of rectangle ARFH.

Hence, proved that area of square ABDE = area of rectangle ARFH.

In the following figure, DE is parallel to BC. Show that :

(i) Area (△ ADC) = Area (△ AEB)

(ii) Area (△ BOD) = Area (△ COE)

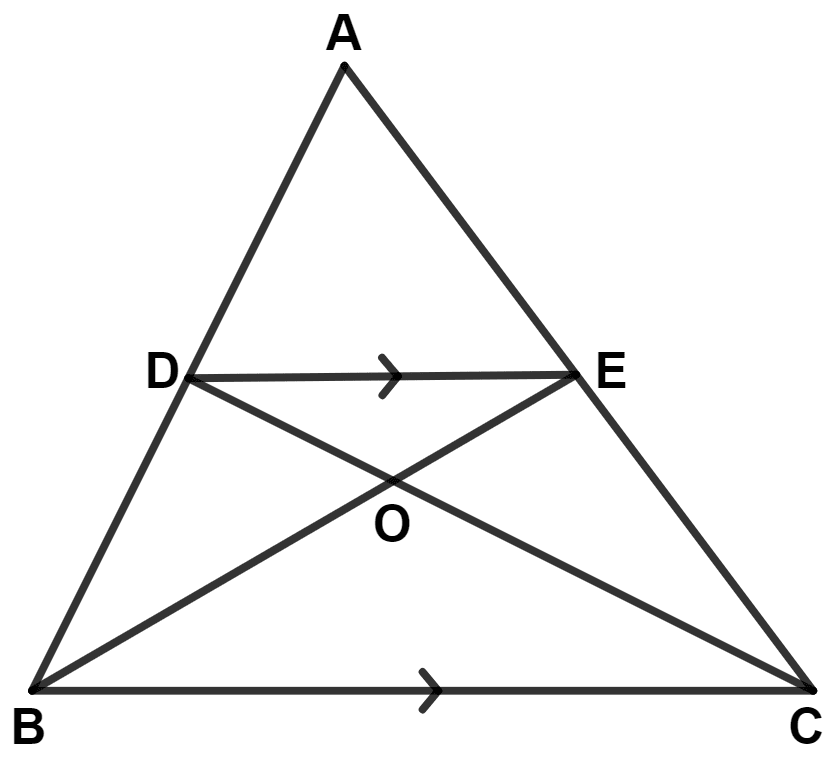
Answer

We know that,

Triangles on the same base and between the same parallel lines are equal in area.

Since, triangle DEB and DEC lie on the same base DE and between the same parallel lines DE and BC.

∴ Area of △ DEC = Area of △ DEB .........(1)

(i) Adding area of △ ADE in both sides of the equation (1), we get :

⇒ Area of △ DEC + Area of △ ADE = Area of △ DEB + Area of △ ADE

⇒ Area of △ ADC = Area of △ AEB.

Hence, proved that area of △ ADC = area of △ AEB.

(ii) Subtracting area of △ DOE in both sides of the equation (1), we get :

⇒ Area of △ DEC - Area of △ DOE = Area of △ DEB - Area of △ DOE

⇒ Area of △ COE = Area of △ BOD.

Hence, proved that area of △ BOD = area of △ COE.

Show that :

(i) a diagonal divides a parallelogram into two triangles of equal area.

(ii) the ratio of the areas of two triangles of the same height is equal to the ratio of their bases.

(iii) the ratio of the areas of two triangles on the same base is equal to the ratio of their heights.

Answer

(i) Suppose ABCD is the parallelogram and diagonal AC divides it into two triangles ABC and ADC.

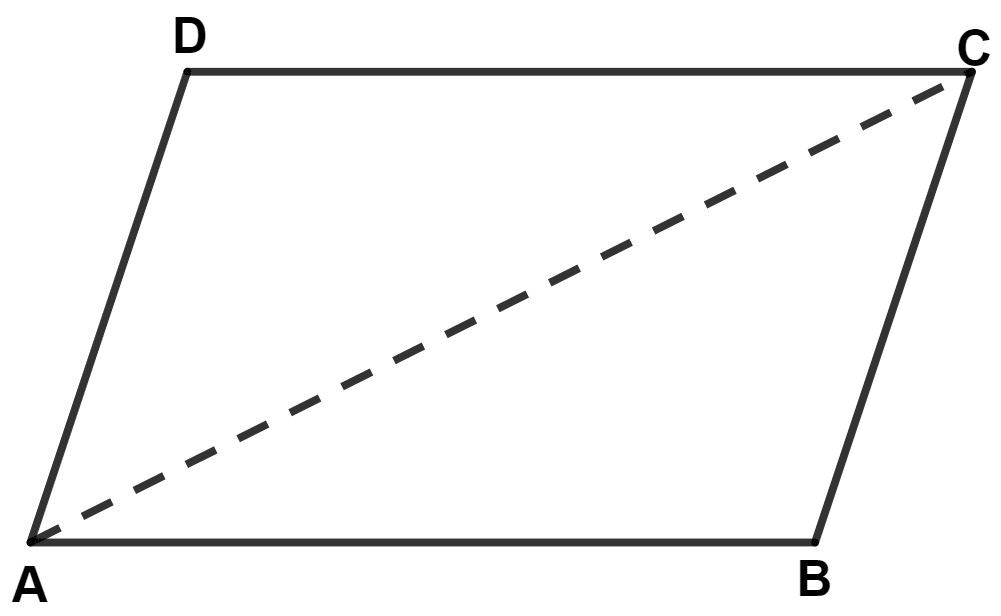
In △ ABC and △ ADC,

⇒ AB = CD (Opposite sides of parallelogram are equal)

⇒ AD = BC (Opposite sides of parallelogram are equal)

⇒ AC = AC (Common side)

∴ △ ABC ≅ △ ADC (By S.S.S. axiom)

We know that,

Area of congruent triangle are equal.

∴ Area of △ ABC = Area of △ ADC.

Hence, proved that a diagonal divides a parallelogram into triangles of equal area.

(ii) From figure,

AQ and PQ are the altitude of triangle ABC and PRZ respectively wheres bases of both the triangles are equal i.e. BC = RZ = k (let).

We know that,

⇒ Area of triangle = $\dfrac{1}{2}$ × base × height

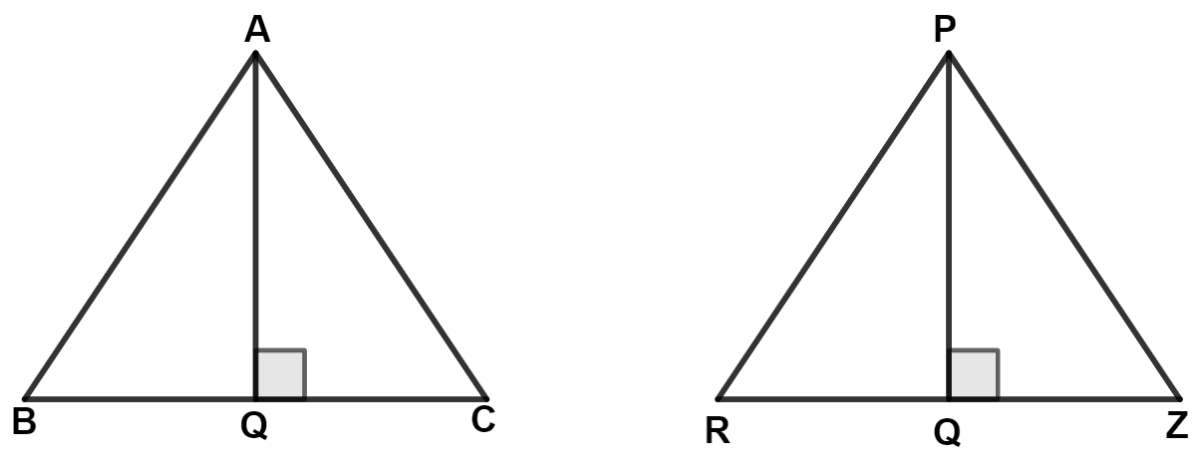
⇒ Area of △ ABC = $\dfrac{1}{2}$ × BC × AQ

⇒ Area of △ ABC = $\dfrac{1}{2} \times k \times AQ$ ........(1)

⇒ Area of △ PRZ = $\dfrac{1}{2}$ × RZ × PQ

⇒ Area of △ PRZ = $\dfrac{1}{2} \times k \times PQ$ ........(2)

Dividing equation (2) by (1), we get :

$\Rightarrow \dfrac{\text{Area of △ PRZ}}{\text{Area of △ ABC}} = \dfrac{\dfrac{1}{2} × k × PQ}{\dfrac{1}{2} × k × AQ} = \dfrac{PQ}{AQ}$.

Hence, proved that the ratio of the areas of two triangles of the same height is equal to the ratio of their bases.

(iii) We know that,

⇒ Area of triangle = $\dfrac{1}{2}$ × base × height

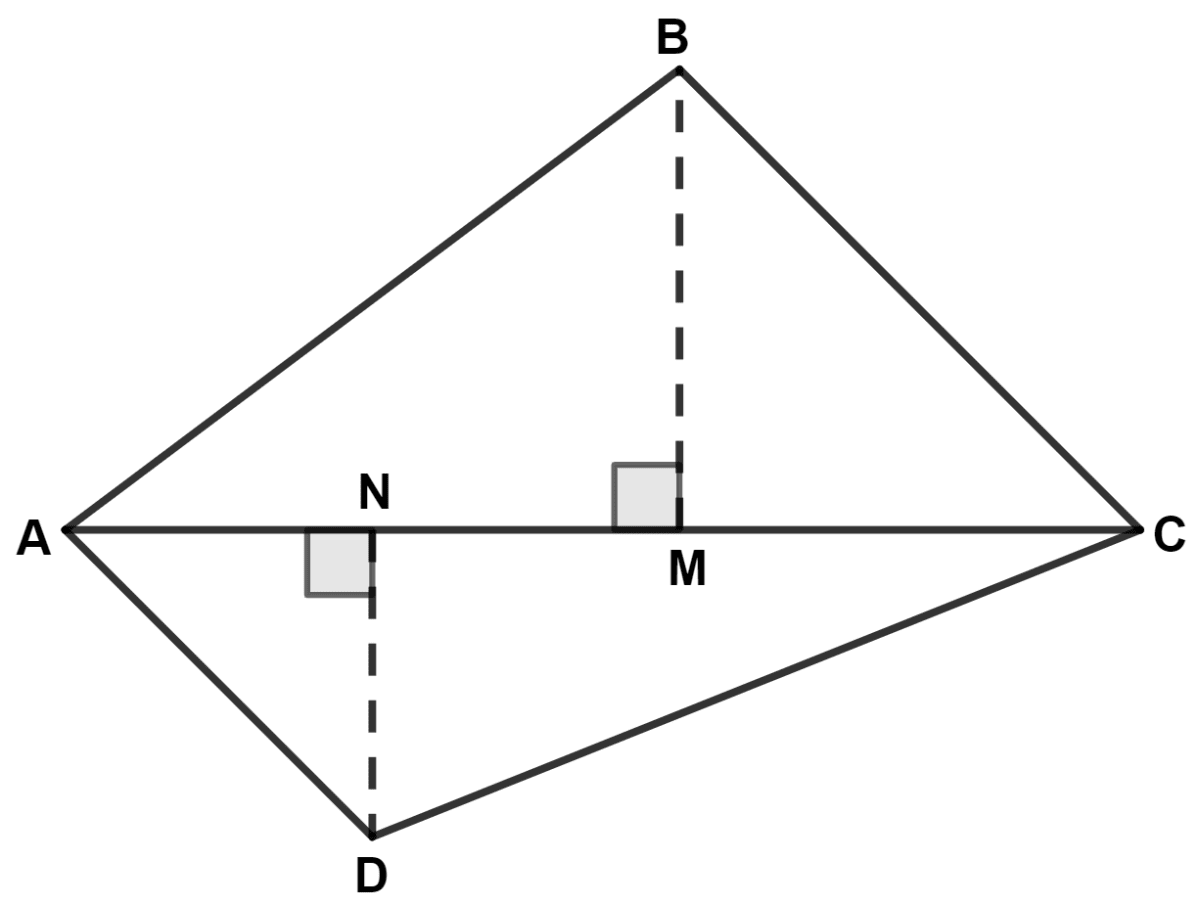
From figure,

⇒ Area of △ ABC = $\dfrac{1}{2}$ × AC × BM ........(1)

⇒ Area of △ ADC = $\dfrac{1}{2}$ × AC × DN ........(2)

Dividing equation (2) by (1), we get :

$\Rightarrow \dfrac{\text{Area of △ ADC}}{\text{Area of △ ABC}} = \dfrac{\dfrac{1}{2} × AC × DN}{\dfrac{1}{2} × AC × BM} = \dfrac{DN}{BM}$.

Hence, proved that the ratio of the areas of two triangles on the same base is equal to the ratio of their heights.

In the given figure; AD is median of △ ABC and E is any point on median AD. Prove that Area (△ ABE) = Area (△ ACE).

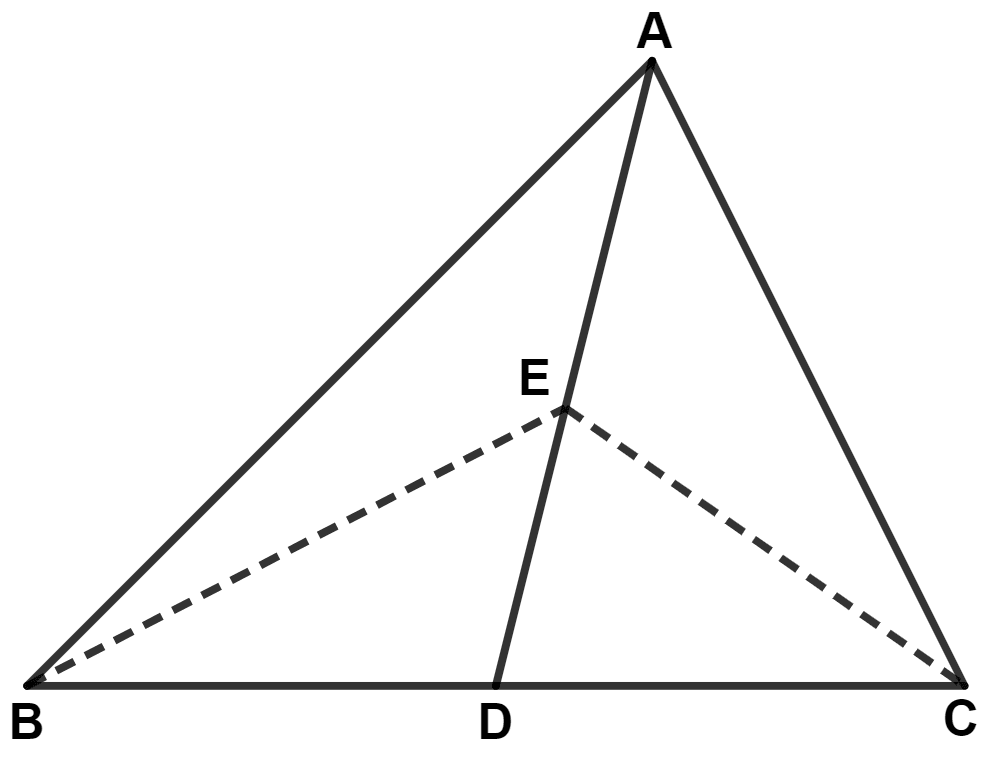
Answer

We know that,

Median of a triangle divides it into two triangles of equal area.

Given,

AD is the median of △ ABC.

∴ Area of △ ABD = Area of △ ACD ..........(1)

Since, E is a point on median AD.

∴ ED is median of △ EBC.

∴ Area of △ EBD = Area of △ ECD ..........(2)

Subtracting equation (2) from (1), we get :

⇒ Area of △ ABD - Area of △ EBD = Area of △ ACD - Area of △ ECD

⇒ Area of △ ABE = Area of △ ACE.

Hence, proved that area (△ ABE) = area (△ ACE).

In the figure of question 14, if E is the mid point of median AD, then prove that :

Area (△ ABE) = $\dfrac{1}{4}$ Area (△ ABC).

Answer

We know that,

Median of a triangle divides it into two triangles of equal area.

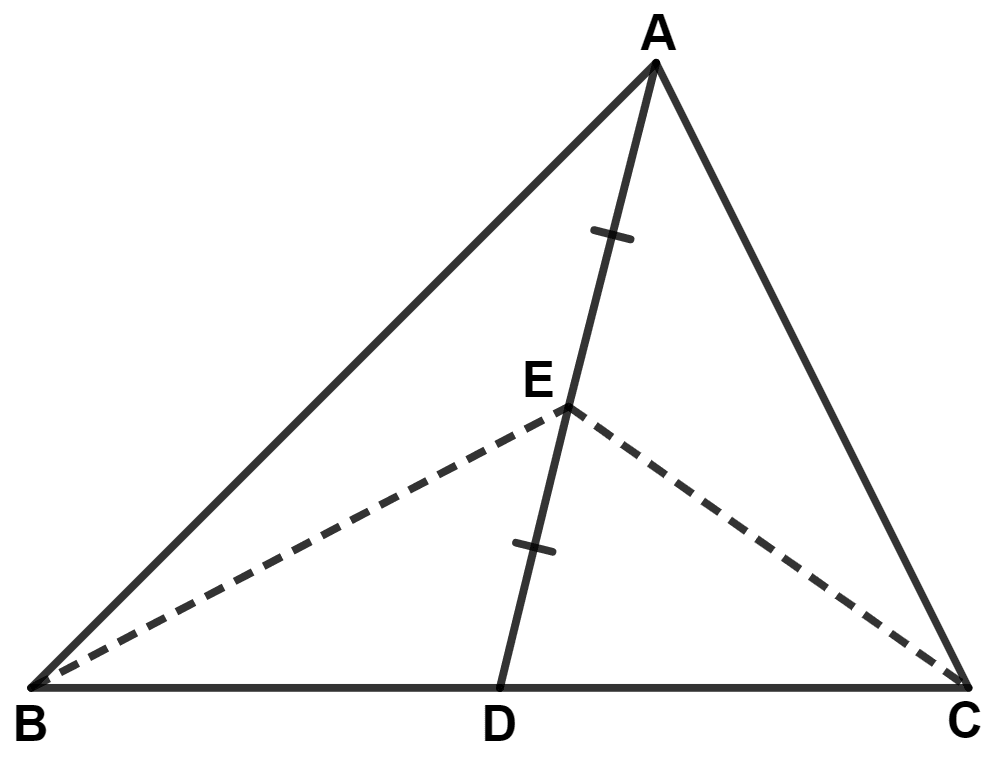
From figure,

AD is the median of Δ ABC, so it will divide Δ ABC into two equal triangles.

∴ Area of Δ ABD = Area of Δ ADC = $\dfrac{1}{2}$ Area of Δ ABC

⇒ Area of Δ ABD = $\dfrac{1}{2}$ Area of Δ ABC .........(1)

In Δ ABD,

Since, E is mid-point of AD,

∴ BE is the median.

∴ BE will divide Δ ABD into two equal triangles.

∴ Area of Δ ABE = Area of Δ BED = $\dfrac{1}{2}$ Area of Δ ABD

⇒ Area of Δ ABE = $\dfrac{1}{2}$ Area of Δ ABD .........(2)

Substituting value of Area of Δ ABD from equation (1) in (2), we get :

⇒ Area of Δ ABE = $\dfrac{1}{2} \times \dfrac{1}{2}$ Area of Δ ABC

⇒ Area of Δ ABE = $\dfrac{1}{4}$ Area of Δ ABC.

Hence, proved that area of Δ ABE = $\dfrac{1}{4}$ area of Δ ABC.

ABCD is a parallelogram. P and Q are the mid-points of sides AB and AD respectively. Prove that area of triangle APQ = $\dfrac{1}{8}$ of the area of parallelogram ABCD.

Answer

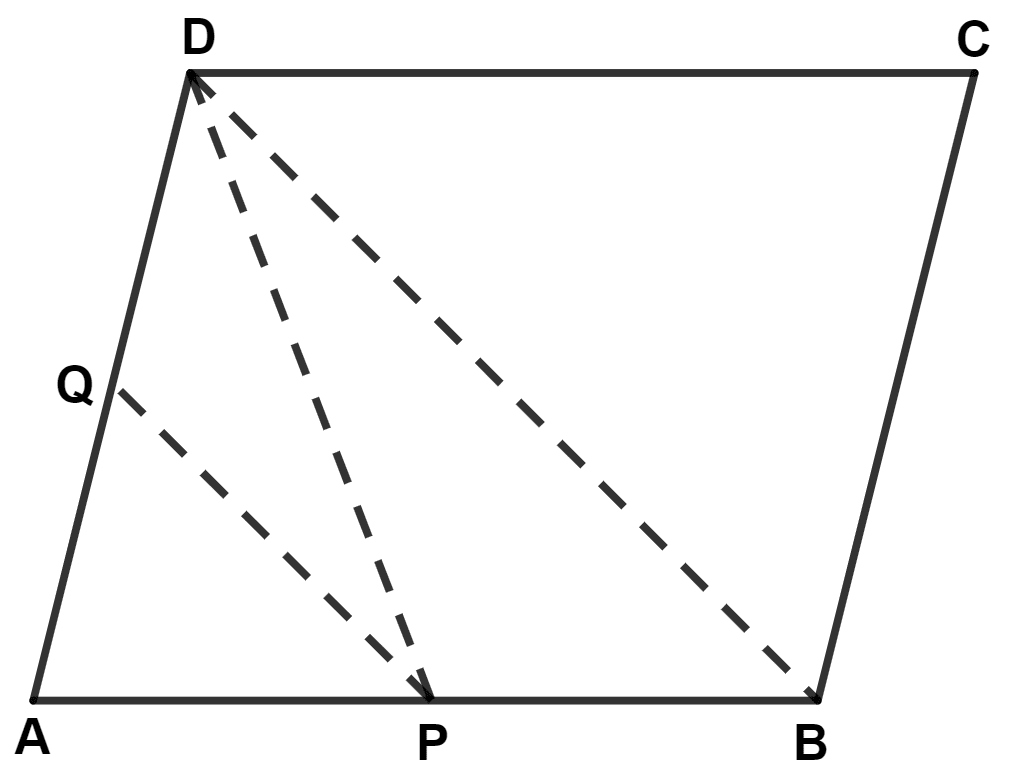
From figure,

ABCD is the parallelogram and BD is the diagonal of the parallelogram.

∴ BD divides || gm ABCD into two triangles of equal area.

∴ Area of Δ ABD = Area of Δ DBC = $\dfrac{1}{2}$ Area of || gm ABCD ..........(1)

Since, P is the mid-point of AB,

∴ DP is the median of Δ ABD.

∴ Area of Δ APD = Area of Δ DPB = $\dfrac{1}{2}$ Area of Δ ABD (Median divides triangle into two triangles of equal area)

⇒ Area of Δ APD = $\dfrac{1}{2}$ Area of Δ ABD

⇒ Area of Δ APD = $\dfrac{1}{2} \times \dfrac{1}{2}$ Area of || gm ABCD [From equation (1)]

⇒ Area of Δ APD = $\dfrac{1}{4}$ Area of || gm ABCD .......(2)

In Δ APD,

Q is the mid-point of AD.

∴ PQ is the median.

∴ Area of Δ APQ = Area of Δ DPQ = $\dfrac{1}{2}$ Area of Δ APD

⇒ Area of Δ APQ = $\dfrac{1}{2}$ Area of Δ APD

⇒ Area of Δ APQ = $\dfrac{1}{2} \times \dfrac{1}{4}$ Area of || gm ABCD [From equation (2)]

⇒ Area of Δ APQ = $\dfrac{1}{8}$ Area of || gm ABCD.

Hence, proved that area of Δ APQ = $\dfrac{1}{8}$ area of || gm ABCD.

The base BC of triangle ABC is divided at D so that BD = $\dfrac{1}{2}$ DC.

Prove that the area of Δ ABD = $\dfrac{1}{3}$ of the area of Δ ABC.

Answer

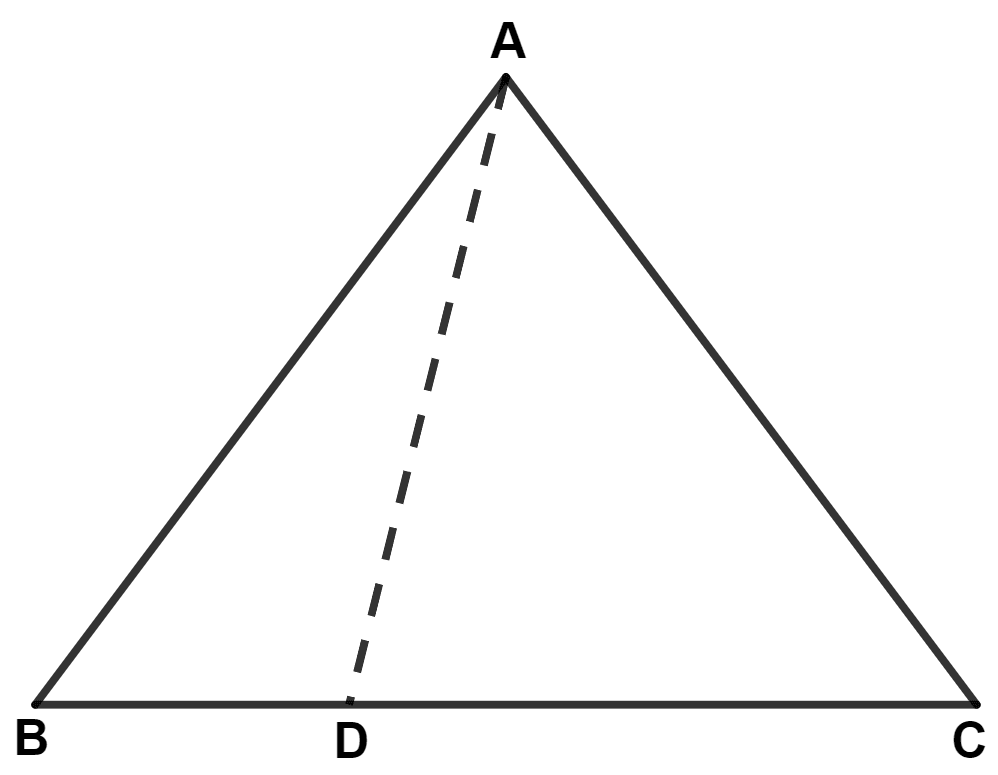
In △ ABC,

⇒ BD = $\dfrac{1}{2}$ DC

⇒ $\dfrac{BD}{DC} = \dfrac{1}{2}$

We know that,

Ratio of the area of triangles with same vertex and bases along the same line is equal to the ratio of their respective bases.

$\Rightarrow \dfrac{\text{Area of Δ ABD}}{\text{Area of Δ ADC}} = \dfrac{BD}{DC} \\[1em] \Rightarrow \dfrac{\text{Area of Δ ABD}}{\text{Area of Δ ADC}} = \dfrac{1}{2} \\[1em] \Rightarrow \text{Area of Δ ADC} = \text{2 Area of Δ ABD}.$

From figure,

⇒ Area of Δ ABC = Area of Δ ABD + Area of Δ ADC

⇒ Area of Δ ABC = Area of Δ ABD + 2 Area of Δ ABD

⇒ Area of Δ ABC = 3 Area of Δ ABD

⇒ Area of Δ ABD = $\dfrac{1}{3}$ Area of Δ ABC.

Hence, proved that area of Δ ABD = $\dfrac{1}{3}$ area of Δ ABC.

In a parallelogram ABCD, point P lies in DC such that DP : PC = 3 : 2. If area of Δ DPB = 30 sq.cm, find the area of the parallelogram ABCD.

Answer

Given,

DP : PC = 3 : 2

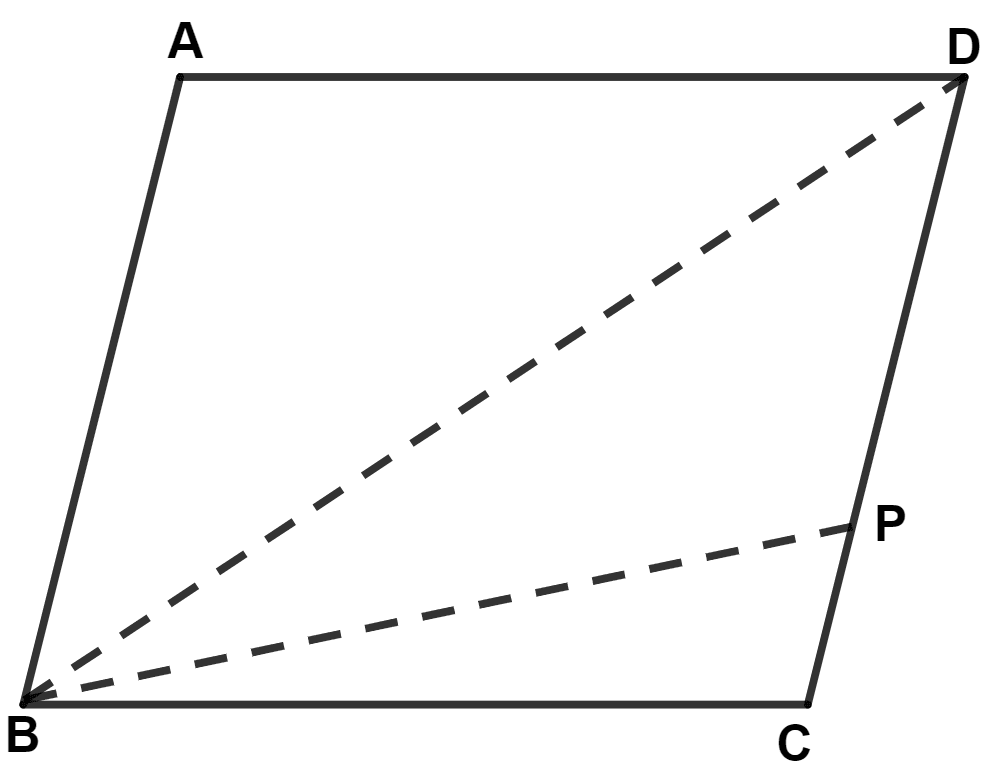
We know that,

Ratio of the area of triangles with same vertex and bases along the same line is equal to the ratio of their respective bases.

$\Rightarrow \dfrac{\text{Area of Δ DPB}}{\text{Area of Δ PCB}} = \dfrac{DP}{PC} \\[1em] \Rightarrow \dfrac{\text{Area of Δ DPB}}{\text{Area of Δ PCB}} = \dfrac{3}{2} \\[1em] \Rightarrow \text{Area of Δ PCB} = \dfrac{2}{3} \times \text{Area of Δ DPB} \\[1em] \Rightarrow \text{Area of Δ PCB} = \dfrac{2}{3} \times 30 \\[1em] \Rightarrow \text{Area of Δ PCB} = 20 \text{ cm}^2.$

From figure,

Area of Δ CDB = Area of Δ PCB + Area of Δ DPB = 20 + 30 = 50 cm².

Since, diagonal divides a || gm into two triangles of equal area.

∴ Area of || gm ABCD = 2 Area of Δ CDB = 2 × 50 = 100 cm².

Hence, area of \\ gm ABCD = 100 cm².

The median of a triangle divides it into two:

1. triangles of equal area

2. congruent triangles

3. right triangles

4. isosceles triangles

Answer

We know that,

A median of a triangle divides it into two triangles of equal area.

Hence, option 1 is the correct option.

The area of given parallelogram is:

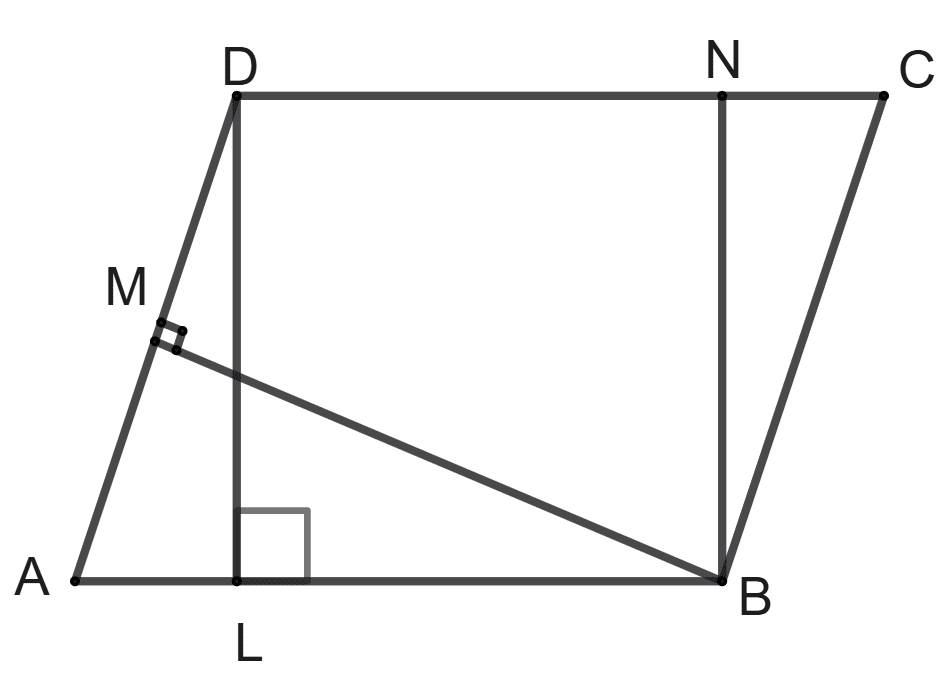
1. AB x BM

2. BC x BN

3. DC x DL

4. AD x DL

Answer

Since the opposite sides of a parallelogram are parallel and equal to each other.

∴ AB ∥ DC and AD ∥ BC

∴ AB = DC and AD = BC

Area of parallelogram = base x height = AB x DL = DC x DL.

Hence, option 3 is the correct option.

ABCD is a quadrilateral whose diagonals intersect each other at point O. The diagonal AC bisects diagonal BD. Then area of quadrilateral ABCD is :

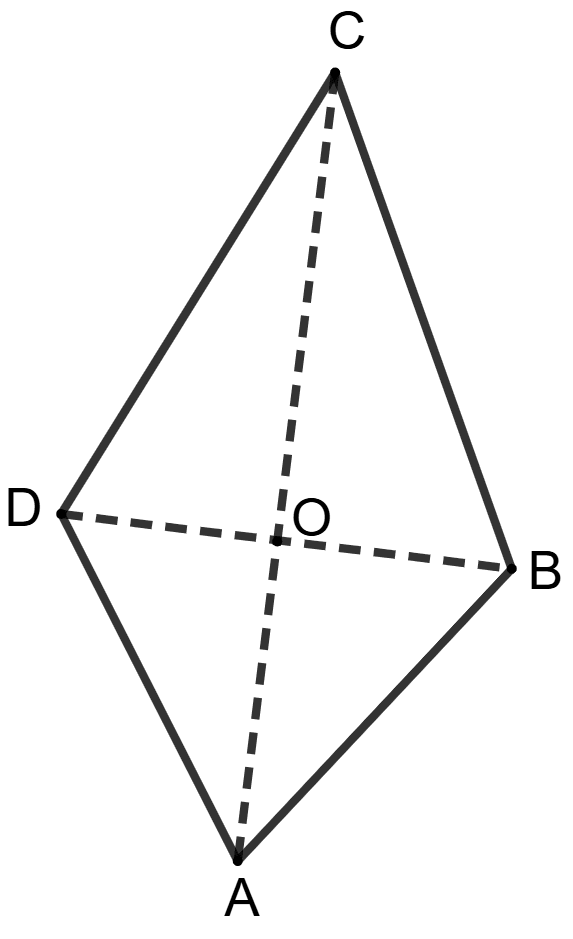
1. 2 x area of ΔABD

2. 2 x area of ΔBCD

3. 4 x area of ΔAOB

4. 2 x area of ΔABC

Answer

ABCD is a quadrilateral. Diagonals AC and BD intersect at point O. Diagonal AC bisects diagonal BD.

Since AC bisects BD at O. O is the midpoint of BD. 

Using the property, a median of a triangle divides it into two triangles of equal area.

⇒ AO is a median of ΔABD and CO is a median of ΔCBD. 

⇒ Area of (ΔAOD) = Area of (ΔAOB) as AO is a median to BD in ΔABD.

⇒ Area of (ΔCOD) = Area of (ΔCOB) as CO is a median to BD in ΔCBD.

As we know that Area of quadrilateral ABCD = Area of (ΔABD) + Area of (ΔBCD)

⇒ Area of quadrilateral ABCD = [Area of (ΔAOD) + Area of (ΔAOB)] + [Area of (ΔCOD) + Area of (ΔCOB)]

⇒ Area of quadrilateral ABCD = [Area of (ΔAOB) + Area of (ΔAOB)] + [Area of (ΔCOB) + Area of (ΔCOB)]

⇒ Area of quadrilateral ABCD = 2Area of (ΔAOB) + 2Area of (ΔCOB)

⇒ Area of quadrilateral ABCD = 2[Area of (ΔAOB) + Area of (ΔCOB)]

⇒ Area of quadrilateral ABCD = 2 x Area of (ΔABC).

Hence, option 4 is the correct option.

Two parallelogram ABCD and ABEF are equal in area, they lie between the same parallel lines:

1. Yes

2. No

3. Nothing can be said

Answer

If two parallelograms share the same base and are situated between the same parallel lines, their areas will be equal. This is a fundamental property of parallelograms.

Since, area of both the parallelograms are equal and they lie on the same base AB.

Thus, they lie between the same parallel lines.

Hence, option 1 is the correct option.

ABCD is a trapezium with parallel sides AB = a cm and DC = b cm. E and F are the mid-points of the non-parallel sides. The ratio of ar.(ABFE) and ar.(EFCD) is:

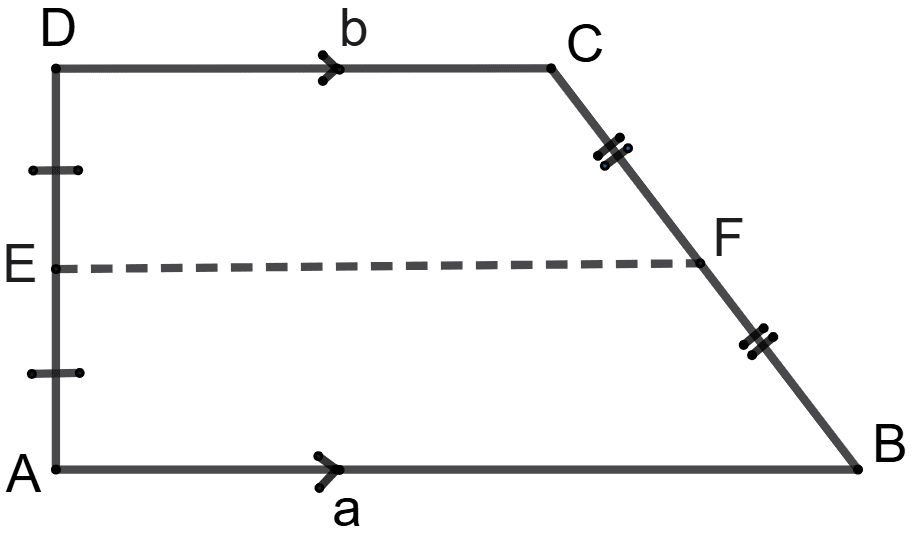
1. a : b

2. (3a + b) : (a + 3b)

3. (a + 3b) : (3a + b)

4. (2a + b) : (3a + b)

Answer

We know that,

The line segment connecting the midpoints of the non-parallel sides of a trapezium is parallel to the parallel sides and its length is half the sum of the lengths of the parallel sides.

AB || EF || DC

EF = $\dfrac{1}{2}(AB + DC) = \dfrac{1}{2}(a + b)$

By formula,

Area of trapezium = $\dfrac{1}{2}$ × Sum of parallel sides × Distance between them

From figure,

E is the mid-point of AD, so AE = ED = x (let)

Area of trapezium ABFE = $\dfrac{1}{2}$ × (AB + EF) × AE .......(1)

Area of trapezium EFCD = $\dfrac{1}{2}$ × (EF + CD) × DE .......(2)

Dividing equation (1) from (2), we get :

$\Rightarrow \dfrac{\text{Area of trapezium ABFE}}{\text{Area of trapezium EFCD}} = \dfrac{\dfrac{1}{2} \times (AB + FE) \times AE}{\dfrac{1}{2} \times (EF + CD) \times DE} \\[1em] = \dfrac{\Big[a + \dfrac{1}{2}(a + b)\Big] \times x}{\Big[b + \dfrac{1}{2}(a + b)\Big] \times x} \\[1em] = \dfrac{\dfrac{2a + a + b}{2}}{\dfrac{2b + a + b}{2}} \\[1em] = \dfrac{3a + b}{3b + a}.$

Area of trapezium ABFE : Area of trapezium EFCD = (3a + b) : (3b + a).

Hence, option 2 is the correct option.

Statement 1: ABCD is a quadrilateral whose diagonal AC divides it into two parts, equal in area.

Statement 2: It is not necessary that the quadrilateral ABCD is a rectangle or a parallelogram or rhombus.

1. Both the statements are true.

2. Both the statements are false.

3. Statement 1 is true, and statement 2 is false.

4. Statement 1 is false, and statement 2 is true.

Answer

Let ABCD be a quadrilateral such that each diagonal divides it into triangles of equal areas, then

Area of △ABC = $\dfrac{1}{2}$ Area of ABCD, ...................(1)

Area of △ADC = $\dfrac{1}{2}$ Area of ABCD, ...................(2)

From (1) and (2) we get,

Area of △ABC = Area of △ADC.

So, statement 1 is true.

The condition that a diagonal divides a quadrilateral into two parts of equal area does not restrict the quadrilateral to be a rectangle, parallelogram, or rhombus.

∴ Statement 2 is true.

∴ Both the statements are true.

Hence, option 1 is the correct option.

Assertion (A): PQRS a parallelogram whose area is 180 cm² and A is any point on the diagonal PR. The area of triangle ASR = 30 cm².

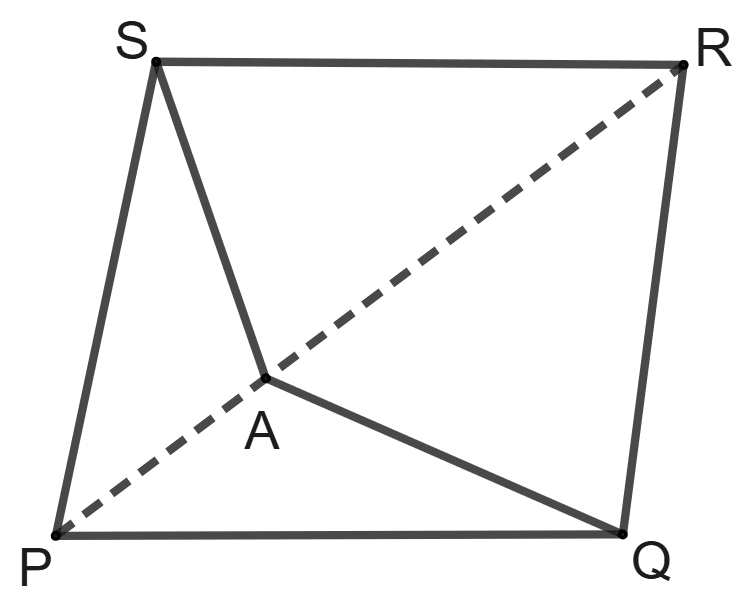
Reason (R): A is not the mid-point of diagonal PR.

1. A is true, but R is false.

2. A is false, but R is true.

3. Both A and R are true, and R is the correct reason for A.

4. Both A and R are true, and R is the incorrect reason for A.

Answer

Given,

Area of parallelogram PQRS = 180 cm².

We know that,

Diagonal of a parallelogram divides it into two triangles of equal area.

So, area of ΔPRS = $\dfrac{180}{2}$ = 90 cm²

Now, A is any point on PR.

So, area of ΔASR < area of ΔPRS.

i.e., area of ΔASR < 90 cm².

But the area of triangle ASR = 30 cm² is not necessarily true based solely on the fact that A is any point on PR.

∴ Assertion (A) is false.

From figure,

A does not lies on the diagonal QS.

Since, diagonals of || gm bisect each other.

Thus, A is not the mid-point of diagonal PR.

∴ Reason (R) is true.

∴ A is false, but R is true.

Hence, option 2 is the correct option.

Assertion (A): ABCD is a square. E is mid-point of side AB and F is mid-point of side DC. If DA = 16 cm, the area of triangle COF is 32 cm².

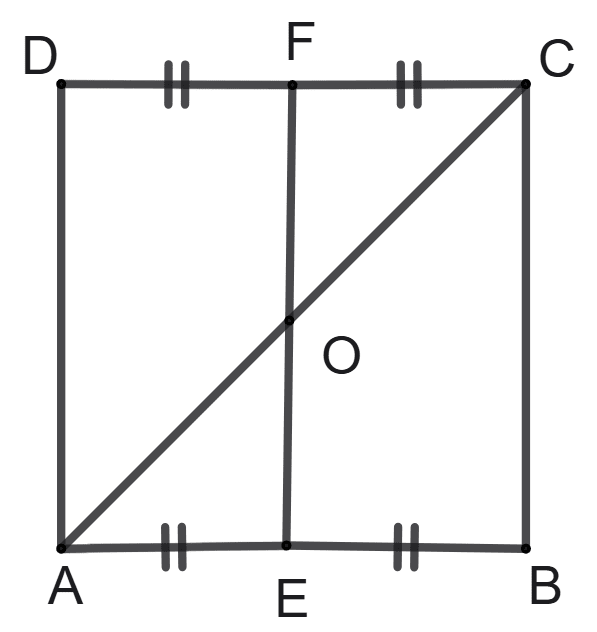
Reason (R): EF is ⊥ to DC and OF = $\dfrac{1}{2} \text{EF} = \dfrac{1}{2}$ DA = 8 cm.

Area of COF = $\dfrac{1}{2}$ x CF x OF

1. A is true, but R is false.

2. A is false, but R is true.

3. Both A and R are true, and R is the correct reason for A.

4. Both A and R are true, and R is the incorrect reason for A.

Answer

Given, ABCD is a square. DA = 16 cm.

∴ AB = BC = CD = DA = 16 cm

F is mid-point of DC.

CF = $\dfrac{1}{2}$ x DC = $\dfrac{1}{2}$ x 16 = 8 cm.

If EF is ⊥ to DC, then OF is perpendicular to DC.

Area of ΔCOF = $\dfrac{1}{2}$ x base x height

= $\dfrac{1}{2}$ x CF x OF

= $\dfrac{1}{2}$ x 8 x 8

= 4 x 8

= 32 cm².

∴ Both A and R are true, and R is the correct reason for A.

Hence, option 3 is the correct option.

ABCD and BCFE are parallelograms. If area of triangle EBC = 480 cm², AB = 30 cm and BC = 40 cm; Calculate :

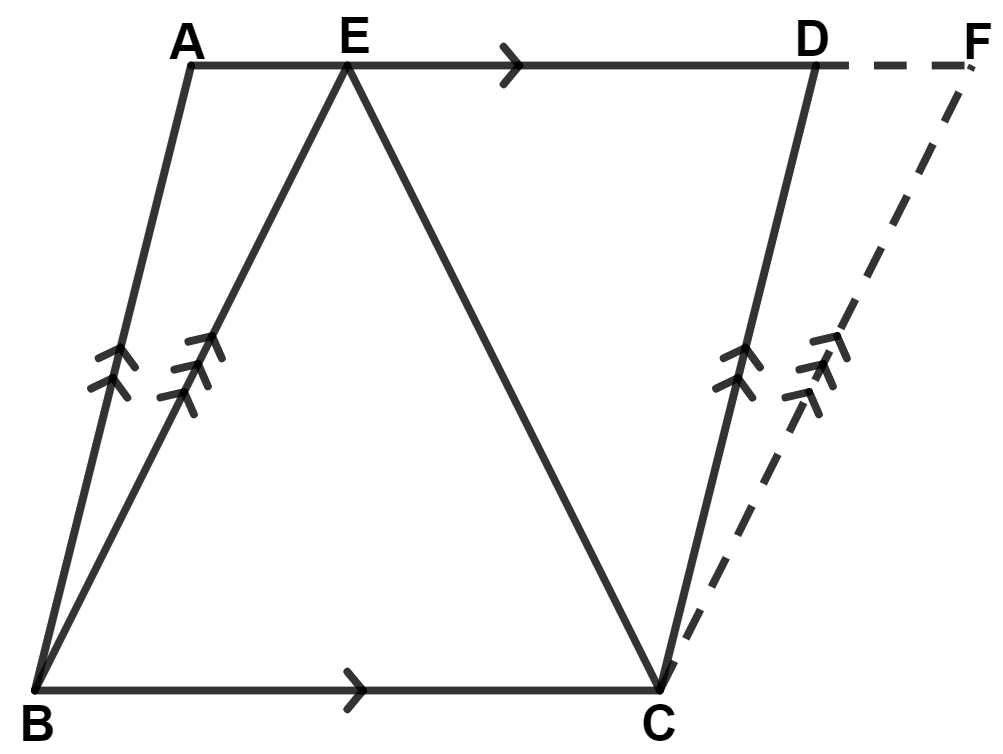
(i) area of parallelogram ABCD;

(ii) area of the parallelogram BCFE;

(iii) length of altitude from A on CD;

(iv) area of triangle ECF.

Answer

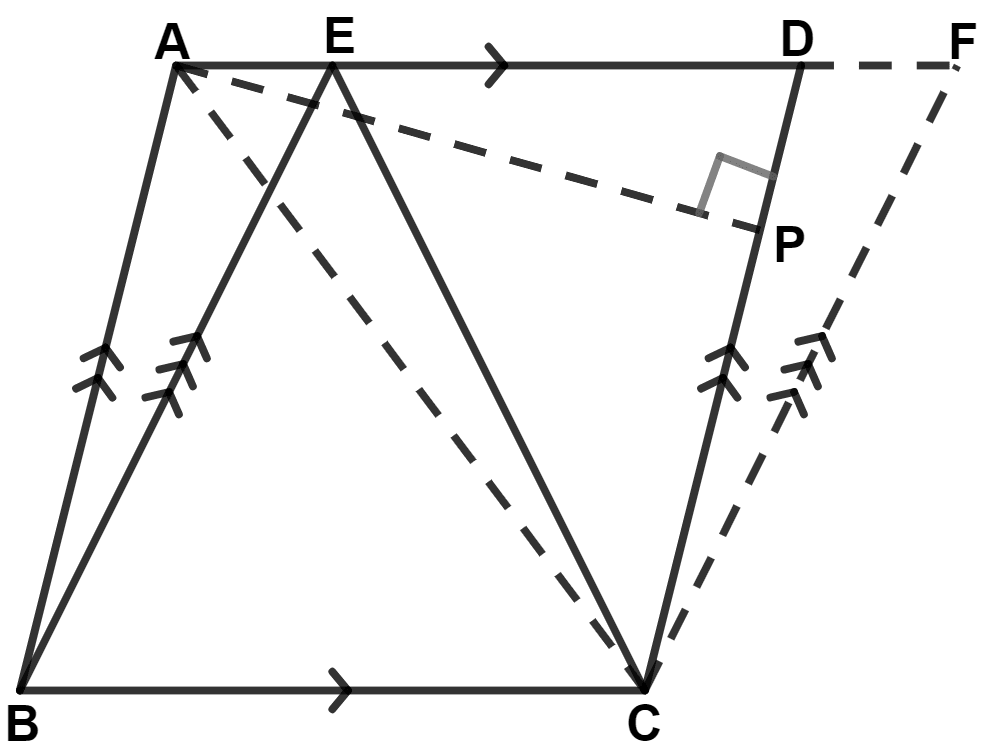
(i) We know that,

The area of a triangle is half that of a parallelogram on the same base and between the same parallels.

From figure,

△ EBC and || gm ABCD lie on same base BC and between same parallel lines AD and BC.

∴ Area of △ EBC = $\dfrac{1}{2} \times$ Area of || gm ABCD

⇒ 480 = $\dfrac{1}{2} \times$ Area of || gm ABCD

⇒ Area of || gm ABCD = 2 × 480 = 960 cm².

Hence, area of || gm ABCD = 960 cm².

(ii) We know that,

Parallelograms on equal bases and between the same parallels are equal in area.

From figure,

Parallelogram ABCD and BCFE lie on same base BC and between same parallel lines AF and BC.

∴ Area of || gm BCFE = Area of || ABCD = 960 cm².

Hence, area of || gm BCFE = 960 cm².

(iii) We know that,

The area of a triangle is half that of a parallelogram on the same base and between the same parallels.

From figure,

△ ACD and || gm ABCD lie on same base AD and between same parallel lines AD and BC.

∴ Area of △ ACD = $\dfrac{1}{2} \times$ Area of || gm ABCD

⇒ Area of △ ACD = $\dfrac{1}{2} \times 960$ = 480 cm².

Since, opposite sides of parallelogram are equal.

∴ CD = AB = 30 cm.

By formula,

⇒ Area of triangle = $\dfrac{1}{2}$ × base × height

⇒ Area of triangle ACD = $\dfrac{1}{2} \times CD \times AP$

⇒ 480 = $\dfrac{1}{2} \times 30 \times AP$

⇒ AP = $\dfrac{480 \times 2}{30}$ = 32 cm.

Hence, length of altitude from A on CD = 32 cm.

(iv) We know that,

The area of a triangle is half that of a parallelogram on the same base and between the same parallels.

From figure,

△ EFC and || gm BCFE lie on same base EF and between same parallel lines EF and BC.

∴ Area of △ EFC = $\dfrac{1}{2} \times$ Area of || gm BCFE

⇒ Area of △ EFC = $\dfrac{1}{2} \times 960$ = 480 cm².

Hence, area of triangle ECF = 480 cm².

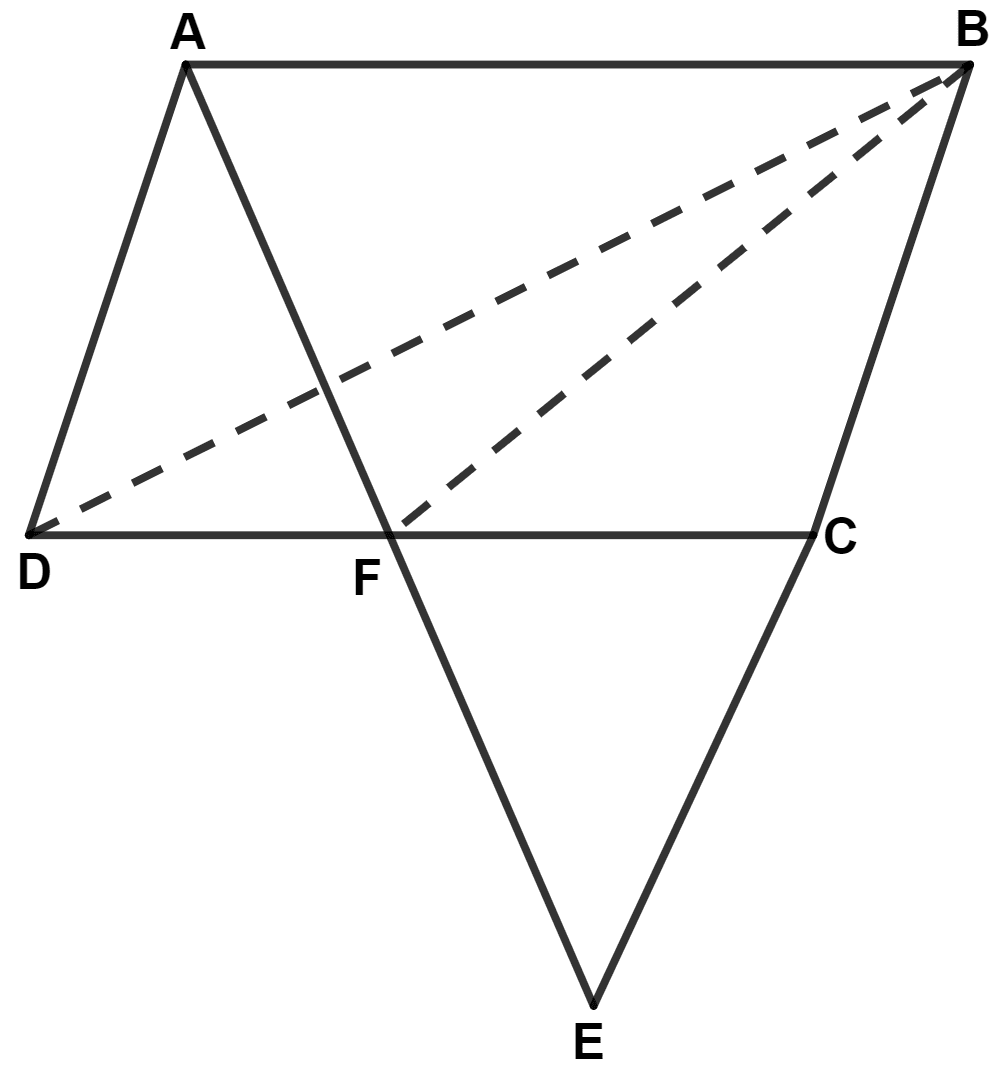
In the given figure, D is mid-point of side AB of △ ABC and BDEC is a parallelogram.

Prove that :

Area of △ ABC = Area of // gm BDEC.

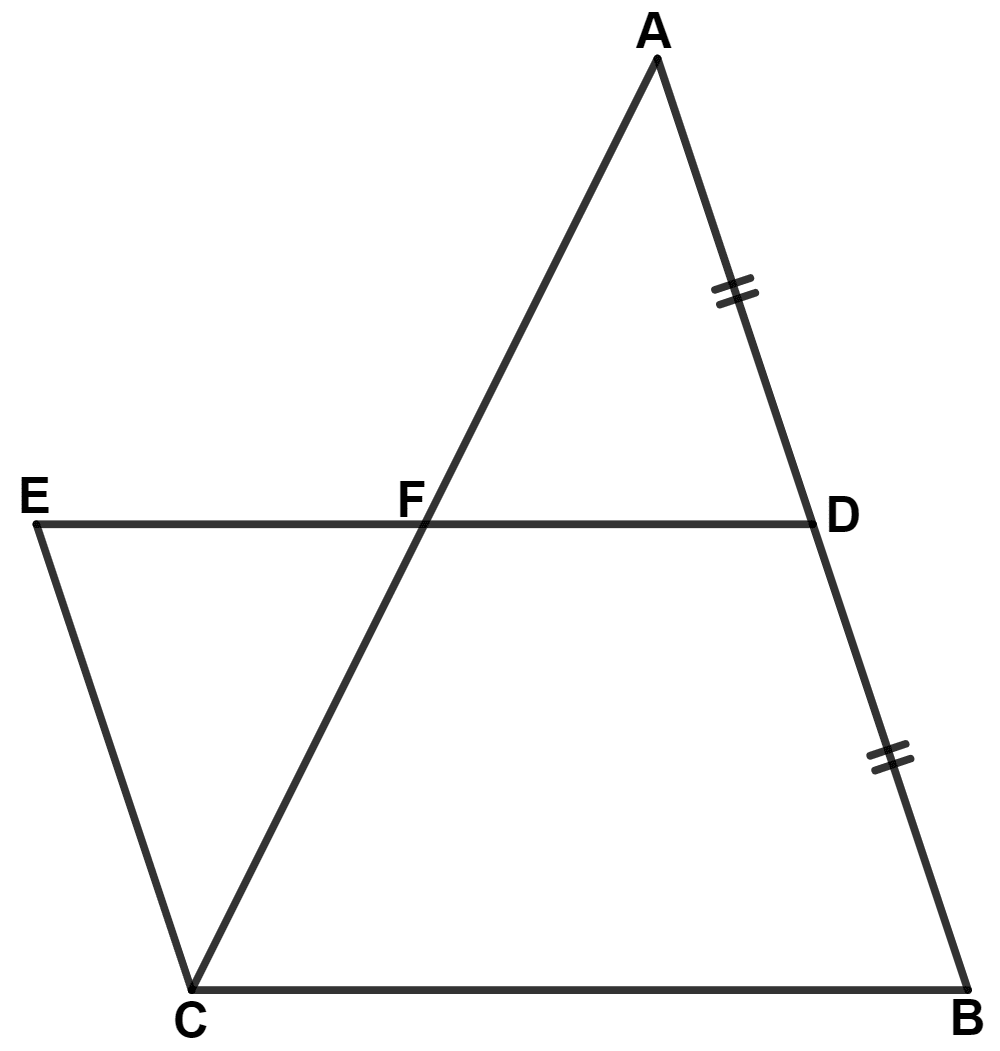
Answer

Given,

⇒ AD = DB ........(1)

⇒ EC = DB (Opposite side of parallelogram are equal) ........(2)

From equation (1) and (2), we get :

⇒ AD = EC

In △ EFC and △AFD,

⇒ ∠EFC = ∠AFD (Vertically opposite angles are equal)

⇒ AD = EC (Proved above)

⇒ ∠ECF = ∠FAD (Alternate angles are equal)

∴ △ EFC ≅ △ AFD (By A.A.S. axiom)

We know that,

Area of congruent triangles are equal.

∴ Area of △ EFC = Area of △ AFD

Adding area of quadrilateral CBDF on both sides of above equation, we get:

⇒ Area of △ EFC + Area of quad.CBDF = Area of △ AFD + Area of quad. CBDF

⇒ Area of || gm BDEC = Area of △ ABC.

Hence, proved that area of △ ABC = area of // gm BDEC.

In the following figure, AC // PS // QR and PQ // DB // SR.

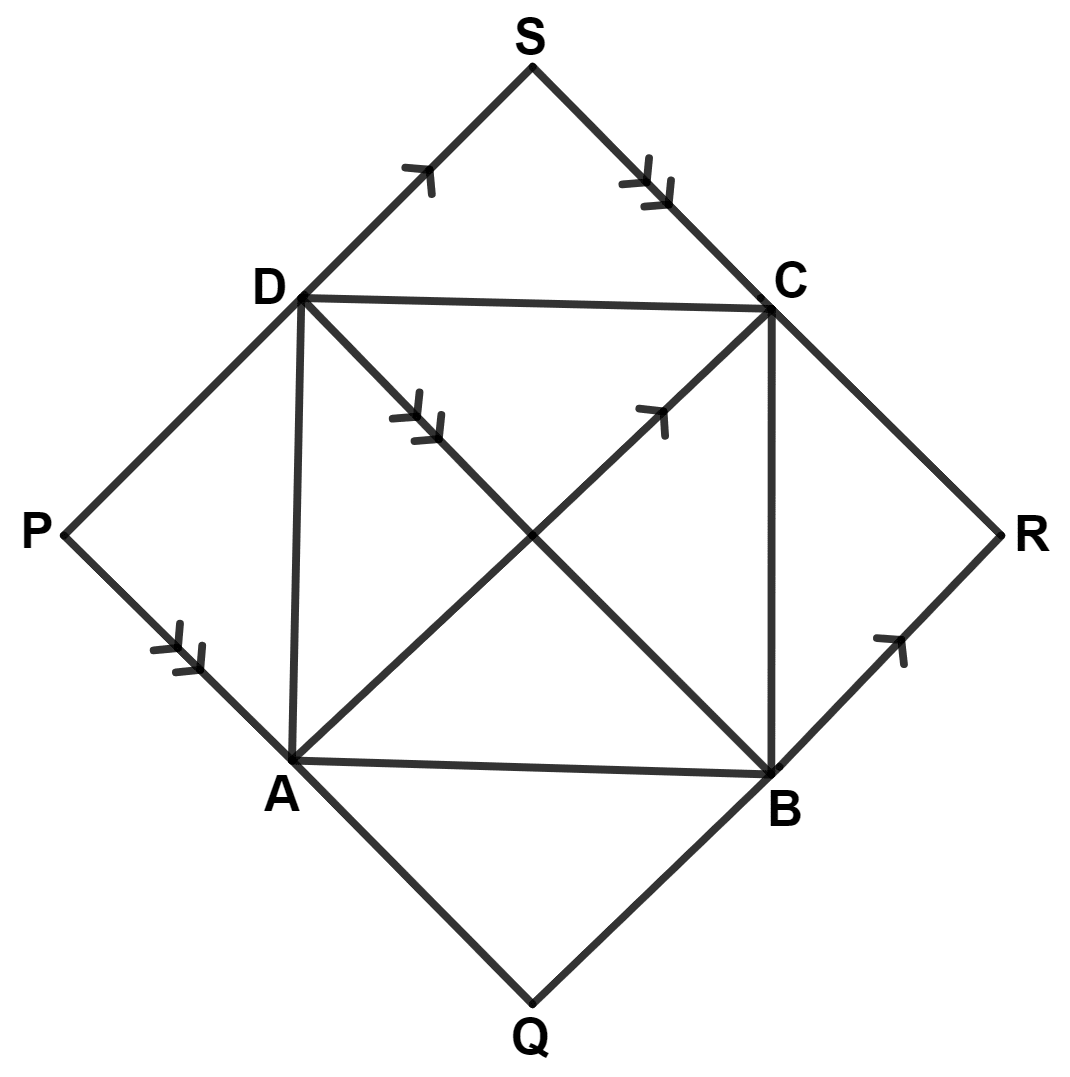
Prove that :

Area of quadrilateral PQRS = 2 × Area of quad.ABCD.

Answer

From figure,

PQRS is a parallelogram.

Given,

AC // PS // QR and PQ // DB // SR.

∴ AQRC and APSC are also parallelograms.

We know that,

The area of a triangle is half that of a parallelogram on the same base and between the same parallels.

From figure,

△ ABC and || gm AQRC lie on same base AC and between same parallel lines AC and QR.

∴ Area of △ ABC = $\dfrac{1}{2} \times$ Area of || gm AQRC ............(1)

△ ADC and || gm ACSP lie on same base AC and between same parallel lines AC and PS.

∴ Area of △ ADC = $\dfrac{1}{2} \times$ Area of || gm ACSP ............(2)

Adding equations (1) and (2), we get :

⇒ Area of △ ABC + Area of △ ADC = $\dfrac{1}{2} \times$ Area of || gm AQRC + $\dfrac{1}{2} \times$ Area of || gm ACSP

⇒ Area of quadrilateral ABCD = $\dfrac{1}{2}$ (Area of || gm AQRC + Area of || gm ACSP)

⇒ Area of quadrilateral ABCD = $\dfrac{1}{2}$ Area of || PQRS

⇒ Area of || gm PQRS = 2 × Area of quadrilateral ABCD.

Hence, proved that area of quadrilateral PQRS = 2 × area of quad. ABCD.

ABCD is a trapezium with AB // DC. A line parallel to AC intersects AB at point M and BC at point N. Prove that :

area of △ ADM = area of △ ACN.

Answer

We know that,

Area of triangles on the same base and between same parallel lines are equal.

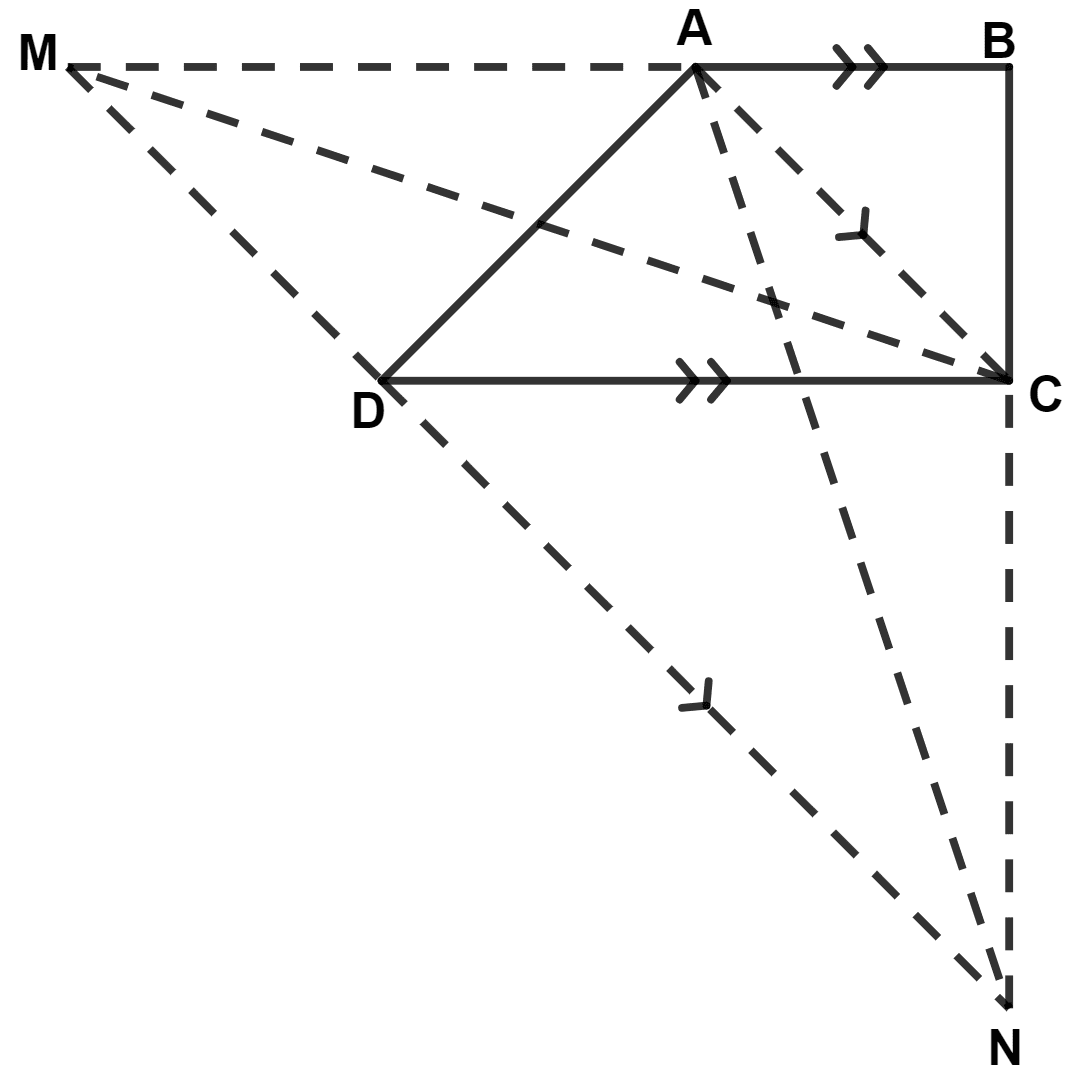
From figure,

△ ADM and △ AMC lie on same base AM and between same parallel lines MB and DC.

∴ Area of △ ADM = Area of △ AMC ...........(1)

△ AMC and △ ACN lie on same base AC and between same parallel lines MN and AC.

∴ Area of △ AMC = Area of △ ACN ...........(2)

From equation (1) and (2), we get :

⇒ Area of △ ADM = Area of △ ACN.

Hence, proved that Area of △ ADM = Area of △ ACN.

In the given figure, AD // BE // CF. Prove that :

area (△ AEC) = area (△ DBF)

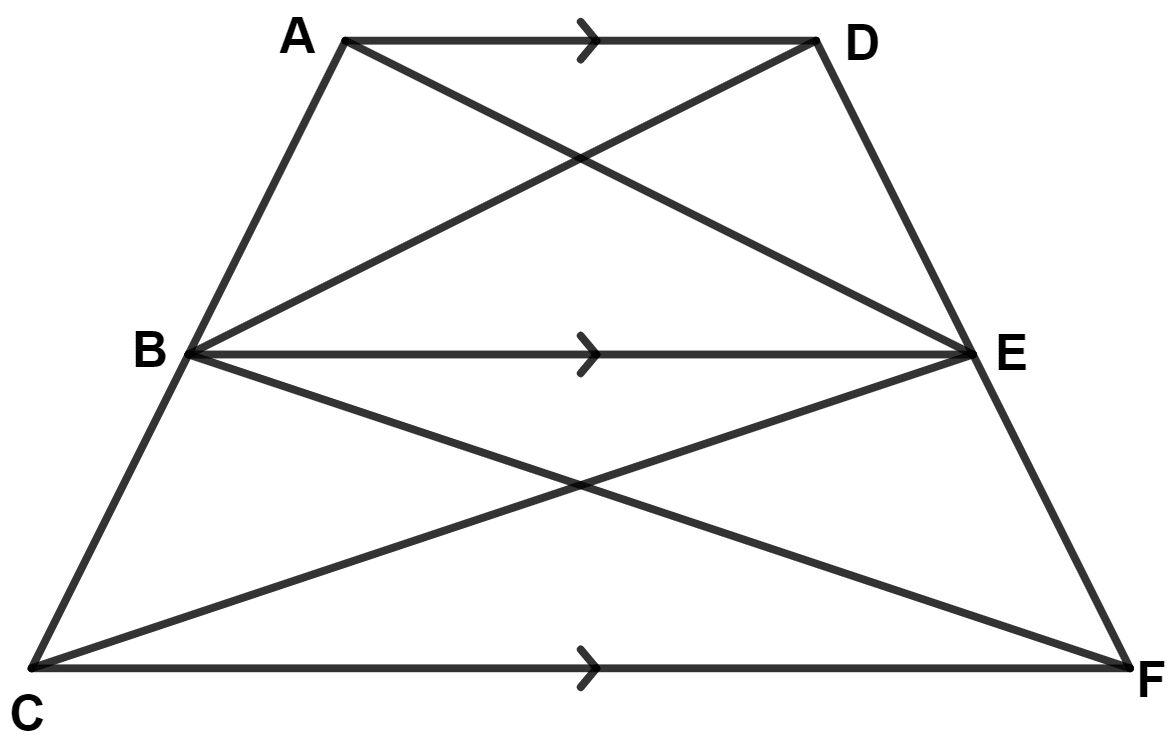
Answer

We know that,

Area of triangles on the same base and between the same parallels lines are equal.

From figure,

△ BDE and △ ABE lie on same base BE and between same parallel lines AD and BE.

∴ Area of △ ABE = Area of △ BDE ...........(1)

△ BEC and △ BEF lie on same base BE and between same parallel lines CF and BE.

∴ Area of △ BEC = Area of △ BEF ............(2)

Adding equations (1) and (2), we get :

⇒ Area of △ ABE + Area of △ BEC = Area of △ BDE + Area of △ BEF

⇒ Area of △ AEC = Area of △ DBF.

Hence, proved that area (△ AEC) = area (△ DBF).

In the given figure, ABCD is a parallelogram. BC is produced to point X. Prove that :

area (△ ABX) = area (quad.ACXD)

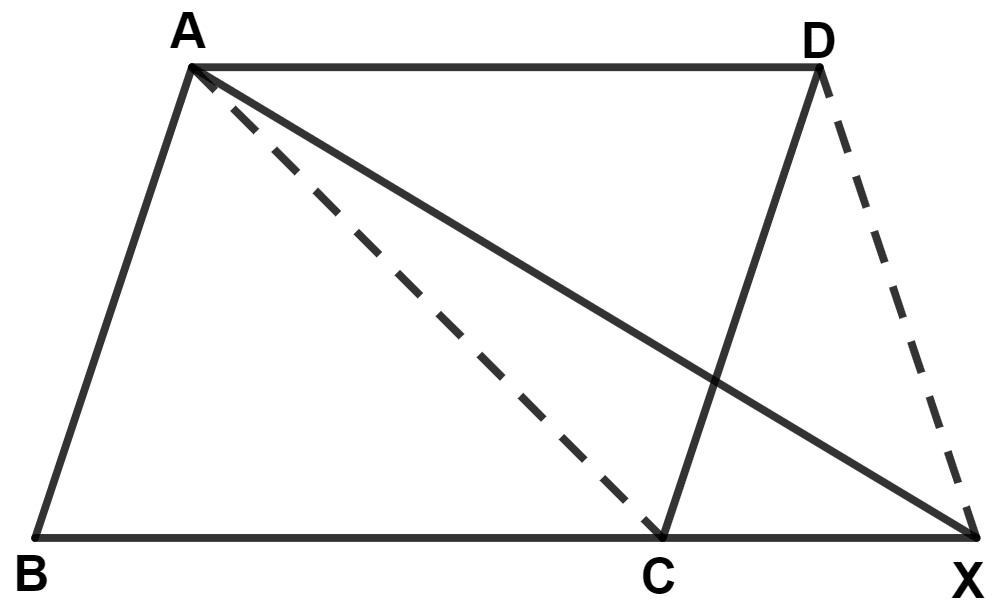
Answer

Since, ABCD is a parallelogram.

∴ AD // BC (Opposite sides of parallelogram are parallel)

We know that,

Area of triangles on the same base and between the same parallels lines are equal.

△ ABC and △ ADC lie on same base AC and between same parallel lines AD and BC.

∴ Area of △ ABC = Area of △ ACD ........(1)

△ ACX and △ CXD lie on same base CX and between same parallel lines AD and BX.

∴ Area of △ ACX = Area of △ CXD ........(2)

From figure,

⇒ Area of △ ABX = Area of △ ABC + Area of △ ACX

⇒ Area of △ ABX = Area of △ ACD + Area of △ CXD [From equation (1) and (2)]

⇒ Area of △ ABX = Area of quadrilateral ACXD.

Hence, proved that area (△ ABX) = area (quad.ACXD).

The given figure shows parallelograms ABCD and APQR. Show that these parallelograms are equal in area.

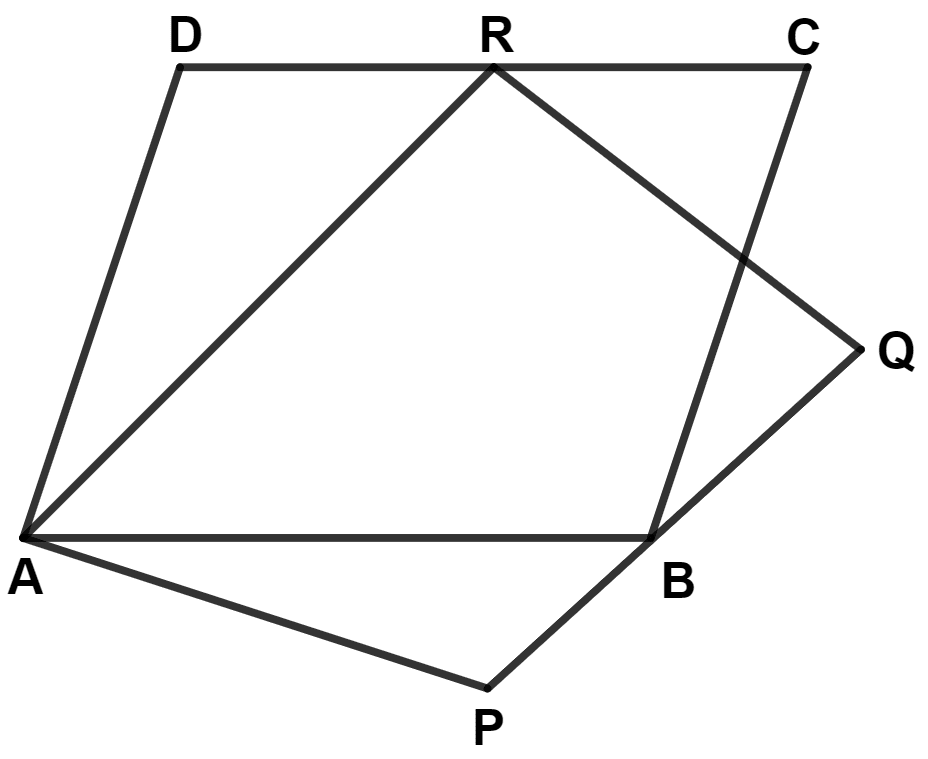
Answer

We know that,

Opposite sides of || gm are equal and parallel.

∴ AB || DC and AR || PQ.

We know that,

The area of triangle is half that of a parallelogram on the same base and between the same parallels.

From figure,

|| gm ABCD and △ ABR lies on same base AB and between same parallel lines AB and DC.

∴ Area of △ ABR = $\dfrac{1}{2}$ Area of || gm ABCD

⇒ Area of || gm ABCD = 2 Area of △ ABR .......(1)

We know that,

Area of triangles on the same base and between the same parallels lines are equal.

△ ABR and △ APR lie on same base AR and between same parallel lines AR and PQ.

∴ Area of △ ABR = Area of △ APR ........(2)

From equations (1) and (2), we get :

⇒ Area of || gm ABCD = 2 Area of △ APR .........(3)

Also, || gm APQR and △ APR lies on same base AR and between same parallel lines AR and PQ.

∴ Area of △ APR = $\dfrac{1}{2}$ Area of || gm APQR .......(4)

Using value of area of △ APR from equation (4) in (3), we get :

⇒ Area of || gm ABCD = $2 \times \dfrac{1}{2}$ Area of || gm APQR

⇒ Area of || gm ABCD = Area of || gm APQR.

Hence, proved that the parallelograms ABCD and APQR are equal in area.

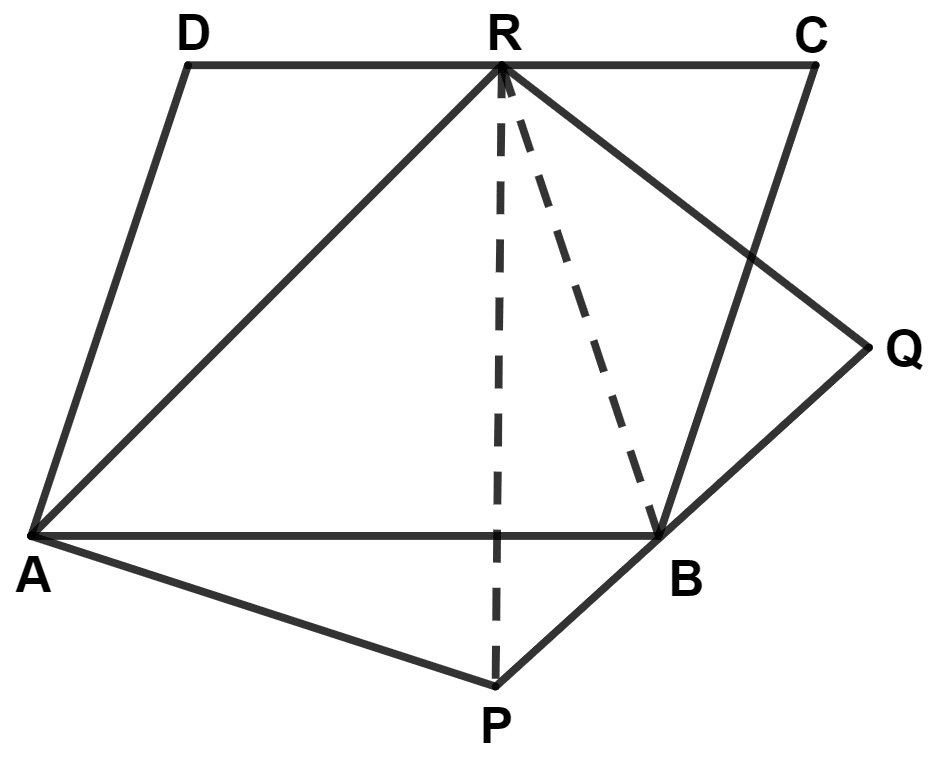
ABCD is a parallelogram in which BC is produced to E such that CE = BC and AE intersects CD at F. If ar.(△ DFB) = 30 cm²; find the area of parallelogram.

Answer

We know that,

Area of triangles on the same base and between the same parallel lines are equal.

△ ADF and △ DFB lie on same base DF and between same parallel lines AB and DC.

∴ Area of △ ADF = Area of △ DFB = 30 cm²

By converse of mid-point theorem,

If a line is drawn through the midpoint of one side of a triangle, and parallel to the other side, it bisects the third side.

In △ ABE,

C is the mid-point of BE and CF || AB.

∴ F is the mid-point of AE. (By converse of mid-point theorem)

∴ EF = AF.

In △ ADF and △ EFC,

⇒ ∠AFD = ∠EFC (Vertically opposite angles are equal)

⇒ EF = AF (Proved above)

⇒ ∠DAF = ∠CEF (Alternate interior angles are equal)

∴ △ ADF ≅ △ EFC (By A.S.A. axiom)

We know that,

Area of congruent triangles are equal.

∴ Area of △ EFC = Area of △ ADF = 30 cm².

In △ BFE,

Since, C is the mid-point of BE.

∴ CF is the mid-point of median of triangle.

We know that,

Median of triangle divides it into two triangles of equal areas.

∴ Area of △ BFC = Area of △ EFC = 30 cm².

From figure,

⇒ Area of △ BDC = Area of △ BDF + Area of △ BFC

⇒ Area of △ BDC = 30 + 30 = 60 cm².

We know that,

The area of triangle is half that of a parallelogram on the same base and between the same parallels.

From figure,

|| gm ABCD and △ BDC lies on same base DC and between same parallel lines AB and DC.

∴ Area of △ BDC = $\dfrac{1}{2}$ Area of || gm ABCD

⇒ Area of || gm ABCD = 2 × Area of △ BDC

⇒ Area of || gm ABCD = 2 × 60 = 120 cm².

Hence, area of || gm ABCD = 120 cm².

The following figure shows a triangle ABC in which P, Q and R are mid-points of sides AB, BC and CA respectively. S is mid-point of PQ. Prove that :

ar.(△ ABC) = 8 × ar.(△ QSB)

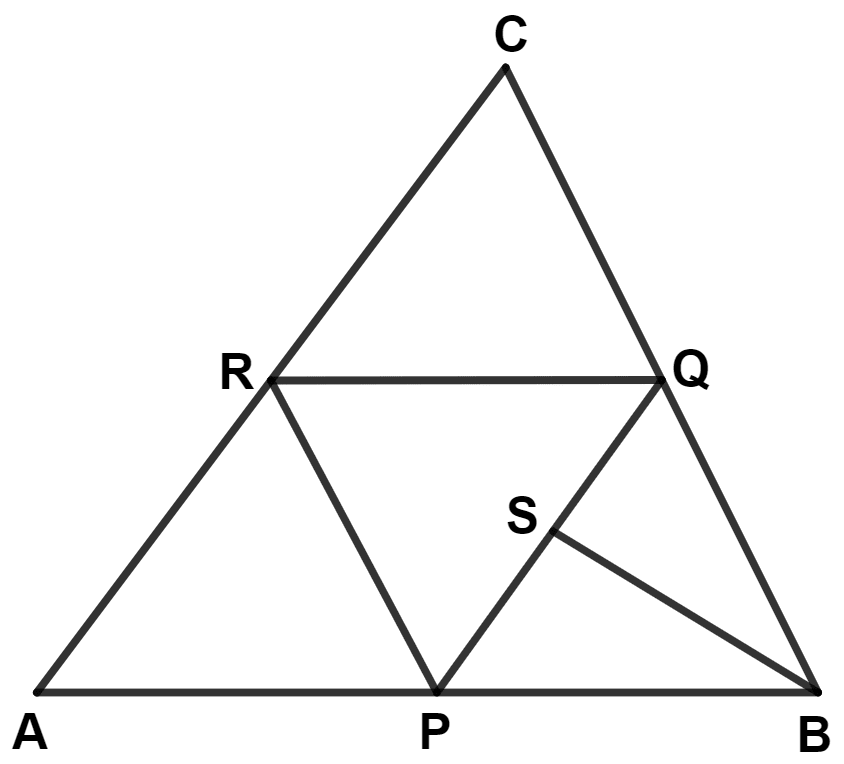
Answer

In △ ABC,

R and Q are mid-points of AC and BC respectively.

∴ RQ || AB (By mid-point theorem)

We know that,

Area of triangles on the same base and between the same parallel lines are equal.

△ PBQ and △ PAR lie on same base (AP = BP) and between same parallel lines RQ and AB.

∴ Area of △ PBQ = Area of △ APR ...............(1)

P and R are mid-points of AB and AC respectively.

∴ PR || BC (By mid-point theorem)

∴ PR || BQ

∴ PBQR is a parallelogram.

PQ is the diagonal.

⇒ Area of △ PBQ = Area of △ PQR (Diagonal of parallelogram divides it into two triangles of equal areas.) .........(2)

From equation (1) and (2), we get :

⇒ Area of △ PBQ = Area of △ PQR = Area of △ APR ........(3)

P and Q are mid-points of AB and BC respectively.

∴ PQ || AC (By mid-point theorem)

∴ PQ || RC

∴ PQCR is a parallelogram.

RQ is the diagonal.

⇒ Area of △ PQR = Area of △ RQC (Diagonal of parallelogram divides it into two triangles of equal areas.) .........(4)

From equation (3) and (4), we get :

⇒ Area of △ PBQ = Area of △ PQR = Area of △ APR = Area of △ RQC = x (let).

From figure,

⇒ Area of △ PBQ + Area of △ PQR + Area of △ APR + Area of △ RQC = Area of △ ABC

⇒ x + x + x + x = Area of △ ABC

⇒ 4x = Area of △ ABC

⇒ x = $\dfrac{1}{4}$ Area of △ ABC

⇒ Area of △ PBQ = $\dfrac{1}{4}$ Area of △ ABC ........(5)

In △ PBQ,

S is the mid-point of PQ and BS is median.

⇒ Area of △ QSB = Area of △ PSB (Median divides triangle into two triangles of equal area)

⇒ Area of △ QSB = $\dfrac{1}{2}$ Area of △ PBQ

⇒ Area of △ PBQ = 2 Area of △ QSB ..........(6)

Substituting value of area of △ PBQ from equation (6) in (5), we get :

⇒ 2 Area of △ QSB = $\dfrac{1}{4}$ Area of △ ABC

⇒ Area of △ QSB = $\dfrac{1}{8}$ Area of △ ABC.

Hence, proved that area of △ QSB = $\dfrac{1}{8}$ area of △ ABC.

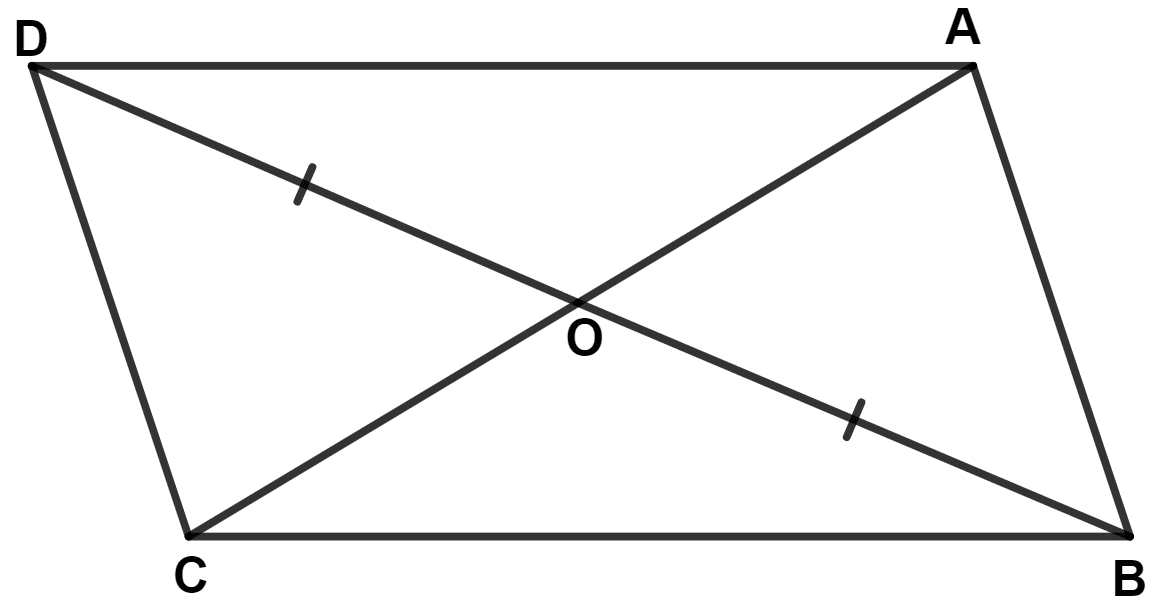
In the given figure, the diagonals AC and BD intersect at point O. If OB = OD and AB // DC, prove that :

(i) Area of (△ DOC) = Area of (△ AOB)

(ii) Area of (△ DCB) = Area of (△ ACB)

(iii) ABCD is a parallelogram.

Answer

(i) In △ DOC and △ AOB,

⇒ ∠DOC = ∠AOB (Vertically opposite angles are equal)

⇒ OD = OB (Given)

⇒ ∠DCO = ∠OAB (Alternate angles are equal)

∴ △ DOC ≅ △ AOB (By A.A.S. axiom)

We know that,

Area of congruent triangles are equal.

∴ Area of (△ DOC) = Area of (△ AOB).

Hence, proved that area of (△ DOC) = area of (△ AOB).

(ii) From part (i),

⇒ Area of (△ DOC) = Area of (△ AOB)

⇒ Area of (△ DOC) + Area of (△ BOC) = Area of (△ AOB) + Area of (△ BOC)

⇒ Area of (△ DCB) = Area of (△ ACB).

Hence, proved that area of (△ DCB) = area of (△ ACB).

(iii) We know that,

Area of triangles on same base and between same parallel lines are equal.

Triangles DCB and ACB lie on same base BC and are equal in area.

∴ They lie between same parallel lines.

∴ AD // BC

Also,

AB // DC (Given)

Since, both pairs of opposite sides are parallel,

∴ ABCD is a parallelogram.

Hence, proved that ABCD is a parallelogram.

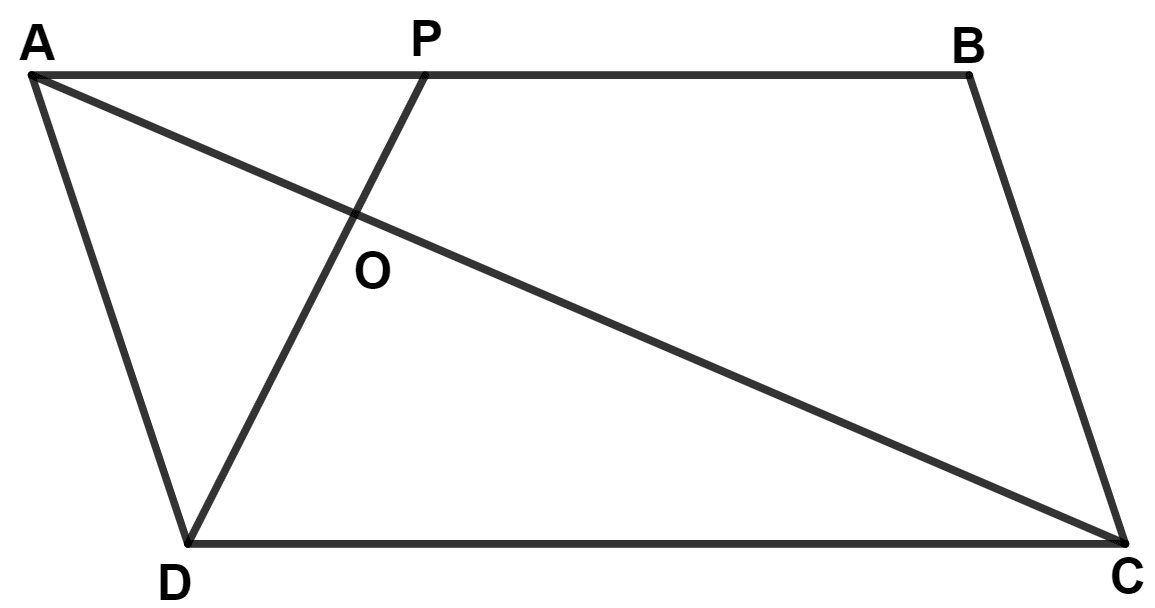
The given figure shows a parallelogram ABCD with area 324 sq.cm. P is a point in AB such that AP : PB = 1 : 2. Find the area of △ APD.

Answer

Join BD.

We know that,

Ratio of the area of triangles with same vertex and bases along the same line is equal to the ratio of their respective bases.

$\therefore \dfrac{\text{Area of △ APD}}{\text{Area of △ BPD}} = \dfrac{AP}{BP} \\[1em] \Rightarrow \dfrac{\text{Area of △ APD}}{\text{Area of △ BPD}} = \dfrac{1}{2} \\[1em] \Rightarrow \text{Area of △ BPD} = 2\text{Area of △ APD}.$

We know that,

The area of triangle is half that of a parallelogram on the same base and between the same parallels.

△ ABD and || gm ABCD lie on same base AB and between same parallel lines AB and DC.

∴ Area of △ ABD = $\dfrac{1}{2}$ Area of || gm ABCD = $\dfrac{1}{2} \times 324$ = 162 cm².

From figure,

⇒ Area of △ ABD = Area of △ APD + Area of △ BPD

⇒ 162 = Area of △ APD + 2 Area of △ APD

⇒ 3 Area of △ APD = 162

⇒ Area of △ APD = $\dfrac{162}{3}$ = 54 cm².

Hence, area of △ APD = 54 cm².

In △ ABC, E and F are mid-points of sides AB and AC respectively. If BF and CE intersect each other at point O, prove that the △ OBC and quadrilateral AEOF are equal in area.

Answer

By mid-point theorem,

The line segment in a triangle joining the midpoint of any two sides of the triangle is said to be parallel to its third side and is also half of the length of the third side.

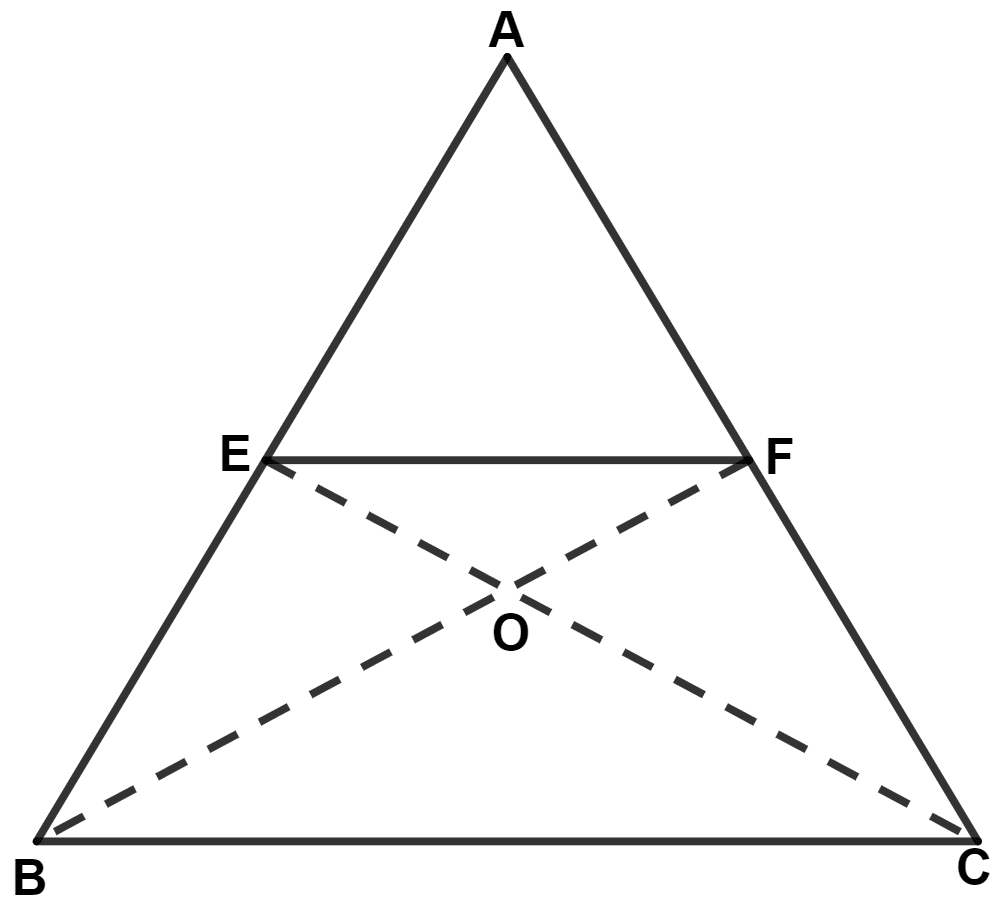
In △ ABC,

Since, E and F are mid-points of sides AB and AC respectively.

∴ EF || BC.

We know that,

The areas of two triangles lying on same base and between same parallel lines are equal.

From figure,

△ BEF and △ CEF lie on same base EF and between same parallel lines EF and BC.

∴ Area of △ BEF = Area of △ CEF

⇒ Area of △ BEF - Area of △ EOF = Area of △ CEF - Area of △ EOF

⇒ Area of △ BOE = Area of △ COF .......(1)

Since, F is the mid-point of AC.

∴ BF is the median of triangle.

We know that,

Median of triangle divides the triangle into two triangles of equal area.

∴ Area of △ ABF = Area of △ CBF

⇒ Area of △ ABF - Area of △ BOE = Area of △ CBF - Area of △ BOE

⇒ Area of △ ABF - Area of △ BOE = Area of △ CBF - Area of △ COF [From equation (1)]

⇒ Area of quadrilateral AEOF = Area of △ OBC.

Hence, proved that △ OBC and quadrilateral AEOF are equal in area.

In parallelogram ABCD, P is mid-point of AB. CP and BD intersect each other at point O. If area of △ POB = 40 cm² and OP : OC = 1 : 2, find :

(i) Areas of △ BOC and △ PBC

(ii) Area of △ ABC and parallelogram ABCD.

Answer

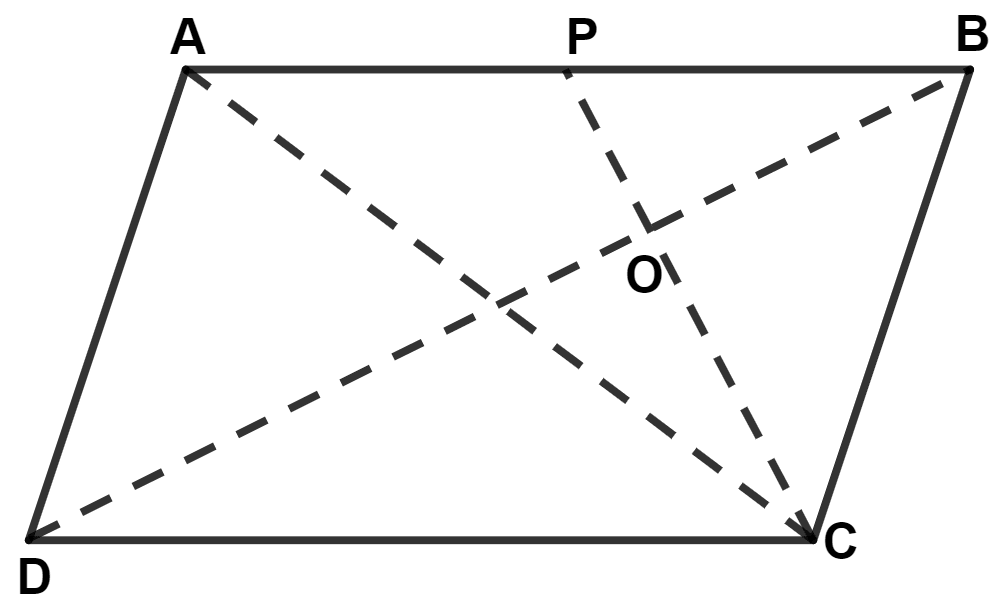
(i) Given,

OP : OC = 1 : 2

We know that,

Ratio of the area of triangles with same vertex and bases along the same line is equal to the ratio of their respective bases.

$\Rightarrow \dfrac{\text{Area of △ POB}}{\text{Area of △ BOC}} = \dfrac{OP}{OC} \\[1em] \Rightarrow \dfrac{40}{\text{Area of △ BOC}} = \dfrac{1}{2} \\[1em] \Rightarrow \text{Area of △ BOC} = 2 \times 40 = 80 \text{ cm}^2.$

From figure,

Area of △ PBC = Area of △ BOC + Area of △ POB = 80 + 40 = 120 cm².

Hence, area of △ BOC = 80 cm² and area of △ PBC = 120 cm².

(ii) Given,

P is the mid-point of AB.

∴ CP is the median of △ ABC.

We know that,

Median of triangle divides it into two triangles of equal area.

∴ Area of △ APC = Area of △ PBC = 120 cm².

From figure,

⇒ Area of △ ABC = Area of △ APC + Area of △ BPC = 120 + 120 = 240 cm².

We know that,

The area of triangle is half that of a parallelogram on the same base and between the same parallels.

Since, △ ABC and || gm ABCD lies on same base AB and between same parallel lines AB and DC.

∴ Area of △ ABC = $\dfrac{1}{2}$ Area of || gm ABCD

⇒ Area of || gm ABCD = 2 Area of △ ABC = 2 × 240 = 480 cm².

Hence, area of △ ABC = 240 cm² and || gm ABCD = 480 cm².

The medians of a triangle ABC intersect each other at point G. If one of its medians is AD, prove that :

(i) Area (△ ABD) = 3 × Area (△ BGD)

(ii) Area (△ ACD) = 3 × Area (△ CGD)

(iii) Area (△ BGC) = $\dfrac{1}{3}$ × Area (△ ABC)

Answer

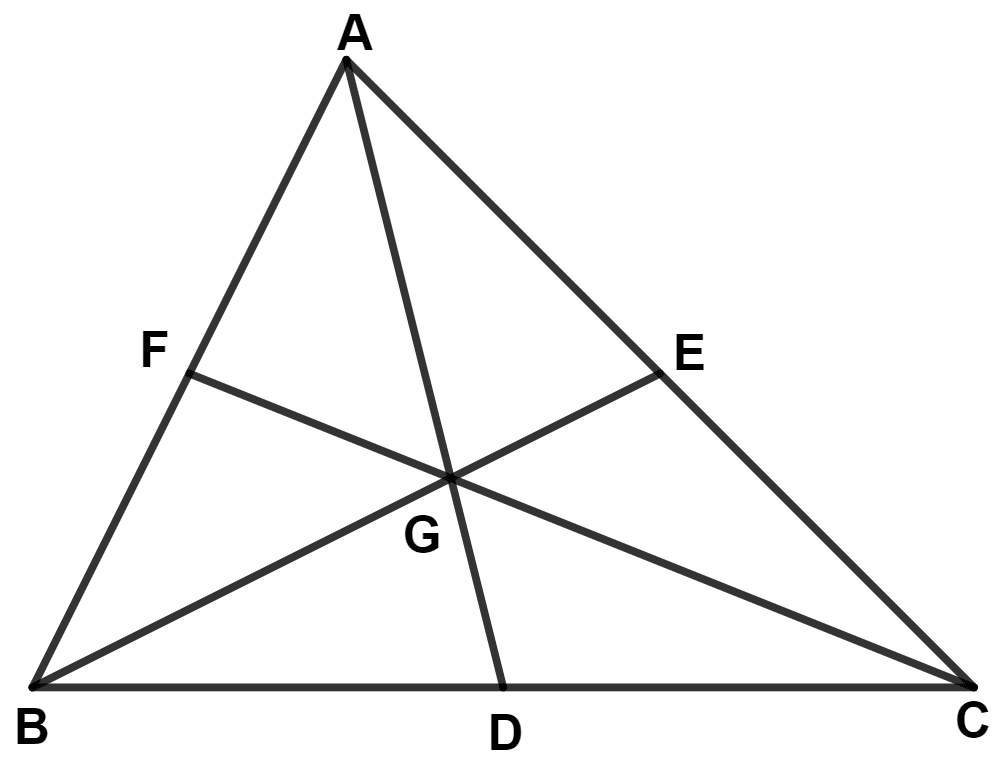
(i) Given,

Medians of a triangle ABC intersect each other at point G.

We know that,

Medians intersect at centroid, also the centroid divides medians in the ratio 2 : 1.

∴ AG : GD = 2 : 1.

We know that,

Ratio of the area of triangles with same vertex and bases along the same line is equal to the ratio of their respective bases.

$\Rightarrow \dfrac{\text{Area of △ AGB}}{\text{Area of △ BGD}} = \dfrac{AG}{GD} \\[1em] \Rightarrow \dfrac{\text{Area of △ AGB}}{\text{Area of △ BGD}} = \dfrac{2}{1} \\[1em] \Rightarrow \text{Area of △ AGB} = 2 \text{ Area of △ BGD}.$

From figure,

⇒ Area of △ ABD = Area of △ AGB + Area of △ BGD

⇒ Area of △ ABD = 2 Area of △ BGD + Area of △ BGD

⇒ Area of △ ABD = 3 Area of △ BGD.

Hence, proved that area of △ ABD = 3 area of △ BGD.

(ii) We know,

AG : GD = 2 : 1

Ratio of the area of triangles with same vertex and bases along the same line is equal to the ratio of their respective bases.

$\Rightarrow \dfrac{\text{Area of △ AGC}}{\text{Area of △ CGD}} = \dfrac{AG}{GD} \\[1em] \Rightarrow \dfrac{\text{Area of △ AGC}}{\text{Area of △ CGD}} = \dfrac{2}{1} \\[1em] \Rightarrow \text{Area of △ AGC} = 2 \text{ Area of △ CGD}.$

From figure,

⇒ Area of △ ACD = Area of △ AGC + Area of △ CGD

⇒ Area of △ ACD = 2 Area of △ CGD + Area of △ CGD

⇒ Area of △ ACD = 3 Area of △ CGD.

Hence, proved that area of △ ACD = 3 area of △ CGD.

(iii) From part (i),

⇒ Area of △ ABD = 3 Area of △ BGD ........(1)

From part (ii),

⇒ Area of △ ACD = 3 Area of △ CGD ..........(2)

Adding equations (1) and (2), we get :

⇒ Area of △ ABD + Area of △ ACD = 3 Area of △ BGD + 3 Area of △ CGD

⇒ Area of △ ABC = 3(Area of △ BGD + Area of △ CGD)

⇒ Area of △ ABC = 3 Area of △ BGC

⇒ Area of △ BGC = $\dfrac{1}{3}$ Area of △ BGC

Hence, proved that area of △ BGC = $\dfrac{1}{3}$ area of △ BGC.

The perimeter of a triangle ABC is 37 cm and the ratio between the lengths of its altitudes be 6 : 5 : 4. Find the lengths of its sides.

Answer

Let the sides be x cm, y cm and (37 - x - y) cm. Also, the length of altitudes be 6a, 5a and 4a cm.

By formula,

Area of triangle = $\dfrac{1}{2} \times$ base × height

Area of triangle ABC = $\dfrac{1}{2} \times x \times 6a = \dfrac{1}{2} \times y \times 5a = \dfrac{1}{2} \times (37 - x - y) \times 4a$

Solving L.H.S. of the equation :

$\Rightarrow \dfrac{1}{2} \times x \times 6a = \dfrac{1}{2} \times y \times 5a \\[1em] \Rightarrow 3ax = \dfrac{5ay}{2} \\[1em] \Rightarrow 6ax = 5ay \\[1em] \Rightarrow 6x = 5y \\[1em] \Rightarrow x = \dfrac{5y}{6} \text{ .........(1)}$

Solving L.H.S. of the equation :

$\Rightarrow \dfrac{1}{2} \times y \times 5a = \dfrac{1}{2} \times (37 - x - y) \times 4a \\[1em] \Rightarrow 5ay = 4a(37 - x - y) \\[1em] \Rightarrow 5y = 4(37 - x - y) \\[1em] \Rightarrow 5y = 148 - 4x - 4y \\[1em] \Rightarrow 148 - 4x - 4y - 5y = 0 \\[1em] \Rightarrow 148 - 4x - 9y = 0$

Substituting value of x from equation (1) in above equation, we get :

$\Rightarrow 148 - 4 \times \dfrac{5y}{6} - 9y = 0 \\[1em] \Rightarrow 148 - \dfrac{10y}{3} - 9y = 0 \\[1em] \Rightarrow \dfrac{444 - 10y - 27y}{3} = 0 \\[1em] \Rightarrow 444 - 37y = 0 \\[1em] \Rightarrow 37y = 444 \\[1em] \Rightarrow y = \dfrac{444}{37} = 12.$

Substituting value of y in equation (1), we get :

$\Rightarrow x = \dfrac{5y}{6} \\[1em] \Rightarrow x = \dfrac{5 \times 12}{6} \\[1em] \Rightarrow x = \dfrac{60}{6} = 10.$

Sides : x = 10 cm, y = 12 cm, (37 - x - y) = (37 - 10 - 12) = 15 cm.

Hence, sides of triangle ABC are 10 cm, 12 cm and 15 cm.

In parallelogram ABCD, E is a point in AB and DE meets diagonal AC at point F. If DF : FE = 5 : 3 and area of △ ADF is 60 cm²; find :

(i) area of △ ADE

(ii) if AE : EB = 4 : 5, find the area of △ ADB.

(iii) also, find area of parallelogram ABCD.

Answer

We know that,

Ratio of the area of triangles with same vertex and bases along the same line is equal to the ratio of their respective bases.

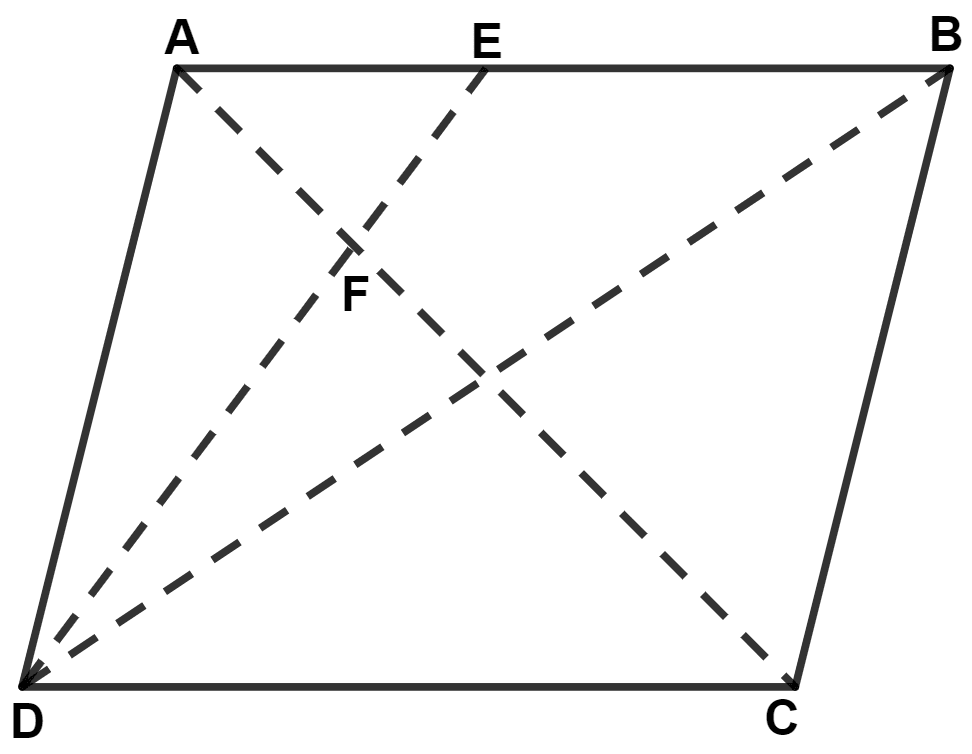
(i) △ ADF and △ AFE have same vertex A and their bases are on the same straight line DE.

$\therefore \dfrac{\text{Area of △ ADF}}{\text{Area of △ AFE}} = \dfrac{DF}{FE} \\[1em] \Rightarrow \dfrac{60}{\text{Area of △ AFE}} = \dfrac{5}{3} \\[1em] \Rightarrow \text{Area of △ AFE} = \dfrac{60 \times 3}{5} = \dfrac{180}{5} = 36 \text{ cm}^2.$

From figure,

Area of △ ADE = Area of △ ADF + Area of △ AFE = 60 + 36 = 96 cm².

Hence, area of △ ADE = 96 cm².

(ii) △ ADE and △ EDB have same vertex D and their bases are on the same straight line AB.

$\therefore \dfrac{\text{Area of △ ADE}}{\text{Area of △ EDB}} = \dfrac{AE}{EB} \\[1em] \Rightarrow \dfrac{96}{\text{Area of △ EDB}} = \dfrac{4}{5} \\[1em] \Rightarrow \text{Area of △ EDB} = \dfrac{96 \times 5}{4} = \dfrac{480}{4} = 120 \text{ cm}^2.$

From figure,

Area of △ ADB = Area of △ ADE + Area of △ EDB = 96 + 120 = 216 cm².

Hence, area of △ ADB = 216 cm².

(iii) We know that,

Diagonal of a parallelogram divides it into two triangles of equal area.

Area of parallelogram ABCD = 2 × Area of △ ADB = 2 × 216 = 432 cm².

Hence, area of || gm ABCD = 432 cm².

In the following figure, BD is parallel to CA, E is mid-point of CA and BD = $\dfrac{1}{2}$ CA.

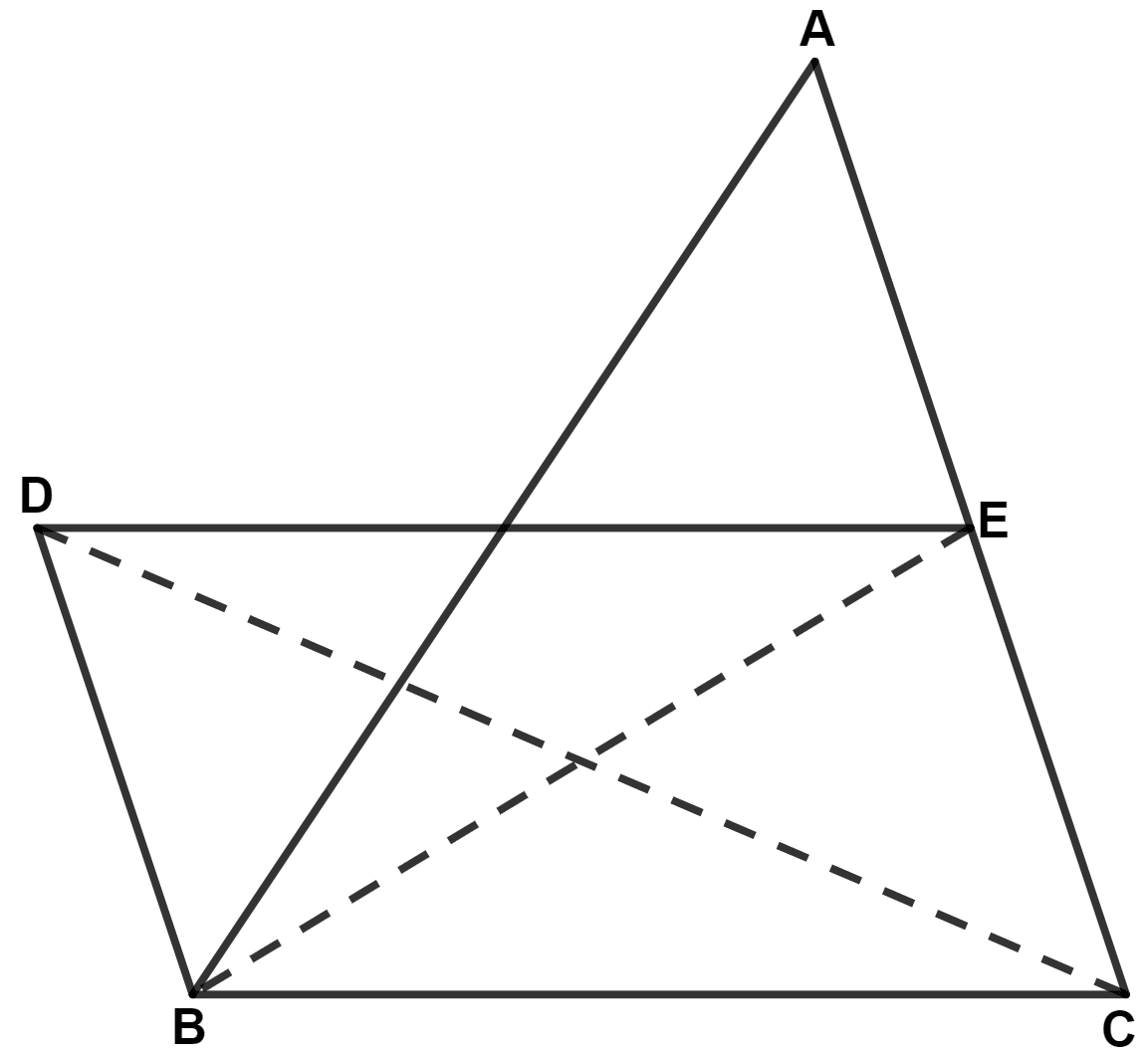
Prove that : ar.(△ ABC) = 2 × ar.(△ DBC)

Answer

Since,

⇒ BD || CA

∴ BD || CE

Also,

BD = CE.

Since, BD = CE and BD || CE,

∴ BCED is a parallelogram.

We know that,

The area of triangle on same base and between the same parallels are equal in area.

△ DBC and △ EBC lie on the same base BC and between same parallel lines BC and ED.

∴ Area of △ DBC = Area of △ EBC ............(1)

In △ ABC,

E is the mid-point of AC.

∴ BE is the median of triangle.

∴ Area of △ EBC = Area of △ ABE ..........(2)

From figure,

⇒ Area of △ ABC = Area of △ EBC + Area of △ ABE

⇒ Area of △ ABC = Area of △ EBC + Area of △ EBC [From equation (2)]

⇒ Area of △ ABC = 2 Area of △ EBC

⇒ Area of △ ABC = 2 Area of △ DBC. [From equation (1)]

Hence, proved that area of △ ABC = 2 area of △ DBC.

In the following figure, OAB is a triangle and AB // DC.

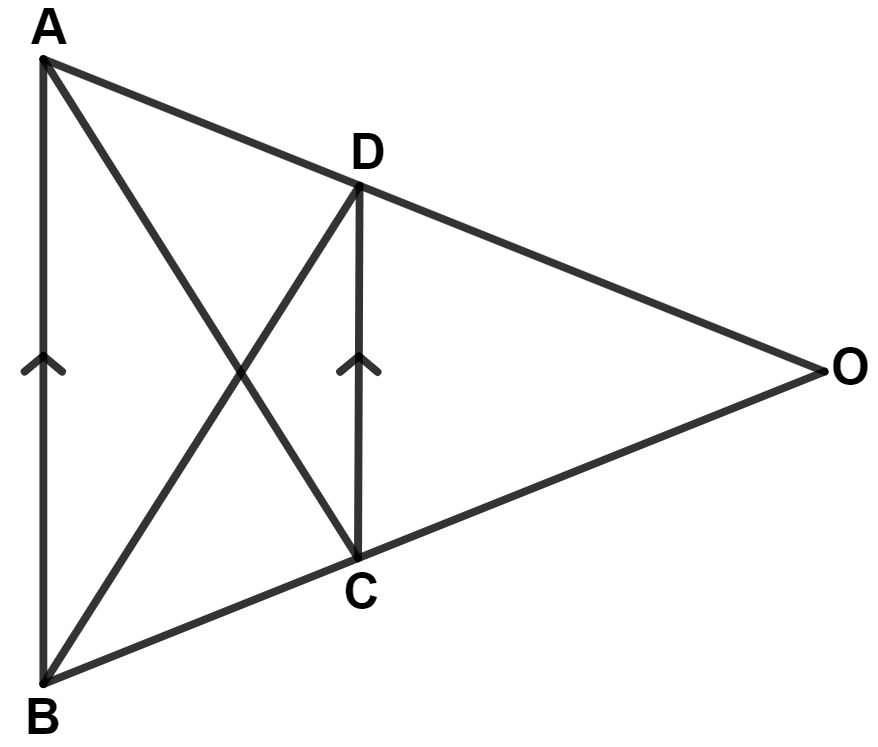
If the area of △ CAD = 140 cm² and the area of △ ODC = 172 cm², find

(i) the area of △ DBC

(ii) the area of △ OAC

(iii) the area of △ ODB

Answer

(i) We know that,

The area of triangles on the same base and between the same parallel lines are equal.

Since, △ DBC and △ CAD have same base CD and between the same parallel lines BA and CD.

∴ Area of △ DBC = Area of △ CAD = 140 cm².

Hence, area of △ DBC = 140 cm².

(ii) From figure,

⇒ Area of △ OAC = Area of △ CAD + Area of △ ODC

⇒ Area of △ OAC = 140 + 172 = 312 cm².

Hence, area of △ OAC = 312 cm².

(iii) From figure,

⇒ Area of △ ODB = Area of △ DBC + Area of △ ODC

⇒ Area of △ ODB = 140 + 172 = 312 cm².

Hence, area of △ ODB = 312 cm².

E, F, G and H are the mid-points of the sides of a parallelogram ABCD. Show that area of quadrilateral EFGH is half of the area of parallelogram ABCD.

Answer

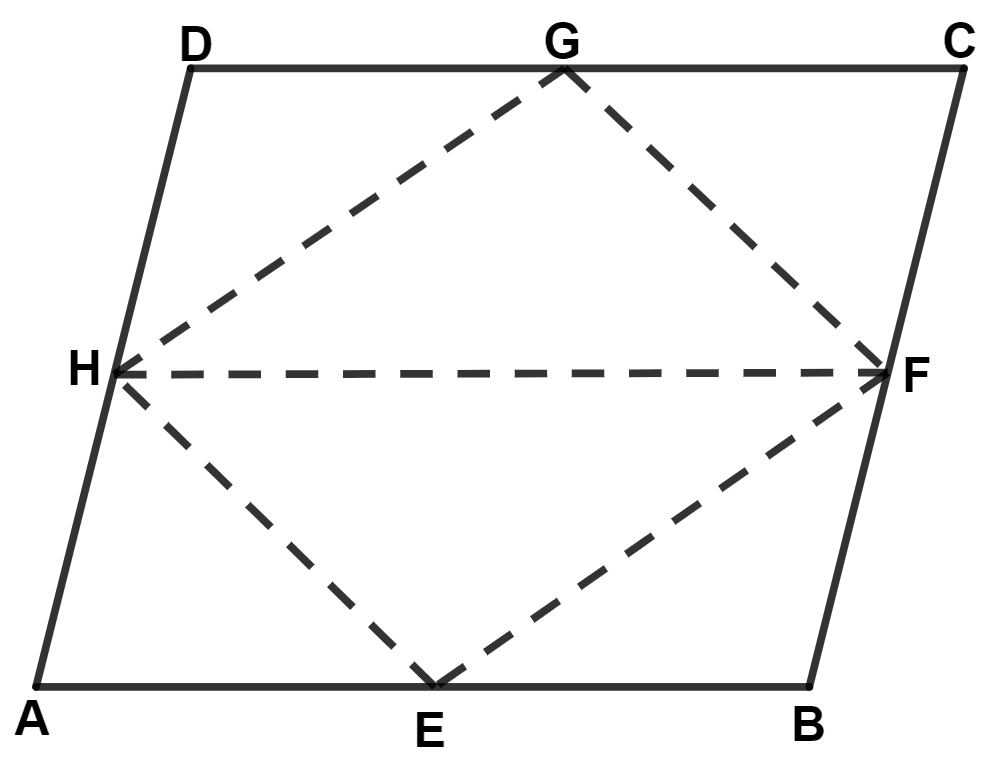
Since, H and F are mid-points of AD and BC respectively.

∴ AH = $\dfrac{1}{2}AD$ and BF = $\dfrac{1}{2}BC$

Since, ABCD is a parallelogram.

∴ AD = BC and AD || BC (Opposite sides of parallelogram are equal)

⇒ $\dfrac{AD}{2} = \dfrac{BC}{2}$ and AD || BC

⇒ AH = BF and AH || BF.

Since, one pair of opposite sides are equal and parallel.

∴ ABFH is a || gm.

We know that,

The area of a triangle is half that of a parallelogram on the same base and between the same parallels.

Since, || gm ABFH and triangle HEF are on the same base FH and between the same parallel lines HF and AB.

∴ Area of △ HEF = $\dfrac{1}{2}$ Area of || gm ABFH ..........(1)

Since, || gm HFCD and triangle HGF are on the same base FH and between the same parallel lines HF and DC.

∴ Area of △ HGF = $\dfrac{1}{2}$ Area of || gm HFCD ..........(2)

Adding equations (1) and (2), we get :

⇒ Area of △ HEF + Area of △ FGH = $\dfrac{1}{2}$ Area of || gm ABFH + $\dfrac{1}{2}$ Area of || gm HFCD

⇒ Area of quadrilateral EFGH = $\dfrac{1}{2}$ (Area of || gm ABFH + Area of || gm HFCD)

⇒ Area of quadrilateral EFGH = $\dfrac{1}{2}$ Area of || gm ABCD.

Hence, proved that area of quadrilateral EFGH is half of the area of parallelogram ABCD.