Circle

A chord of length 6 cm is drawn in a circle of diameter 10 cm, its distance from the center of the circle is :

1. 6 cm

2. 8 cm

3. 4 cm

4. 10 cm

Answer

Let AB be the chord of the circle with center O.

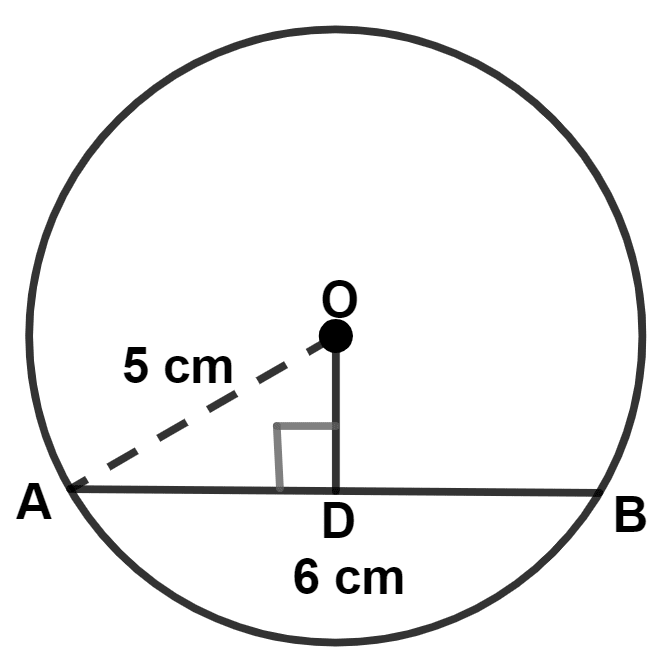
Given,

Diameter = 10 cm

Radius = $\dfrac{\text{Diameter}}{2} = \dfrac{10}{2}$ = 5 cm.

We know that,

Perpendicular from center to chord, bisects the chord.

∴ AD = $\dfrac{AB}{2} = \dfrac{6}{2}$ = 3 cm.

In right angled triangle OAD,

By pythagoras theorem,

⇒ Hypotenuse² = Perpendicular² + Base²

⇒ OA² = OD² + AD²

⇒ 5² = OD² + 3²

⇒ OD² = 5² - 3²

⇒ OD² = 25 - 9

⇒ OD² = 16

⇒ OD = $\sqrt{16}$ = 4 cm.

Hence, Option 3 is the correct option.

The given figure shows two concentric circles and AD is a chord. The relation between AB and CD is :

1. AB = CD

2. AB > CD

3. AB < CD

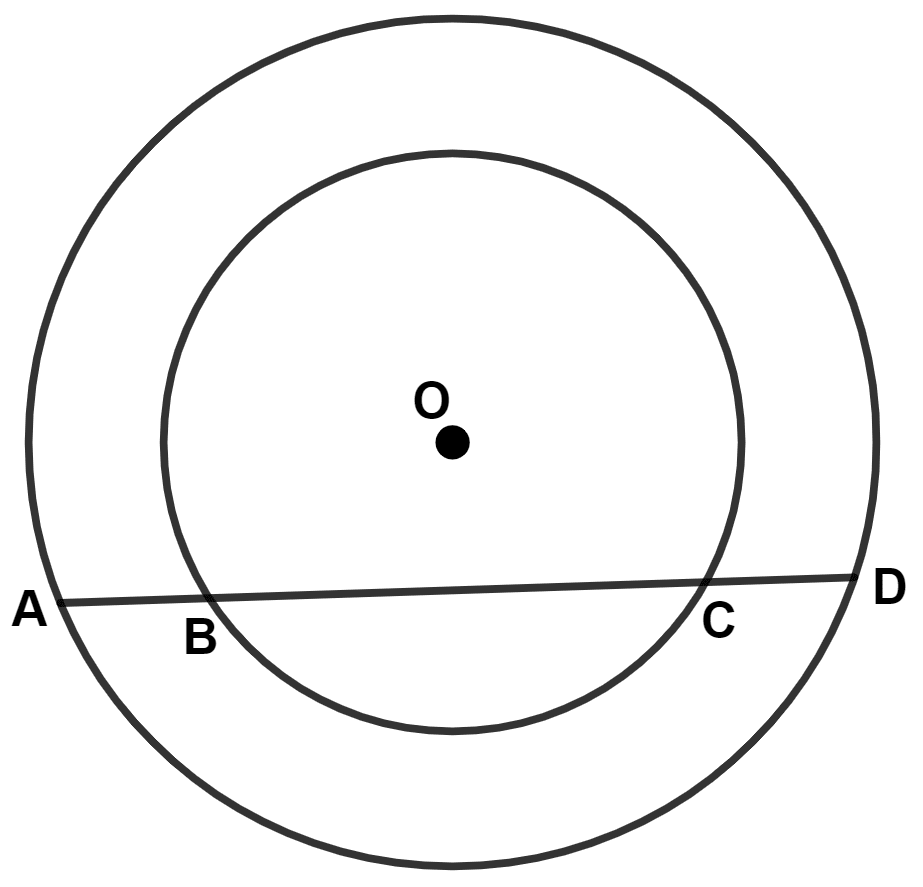
4. AB ≠ CD

Answer

Draw OE ⊥ AD.

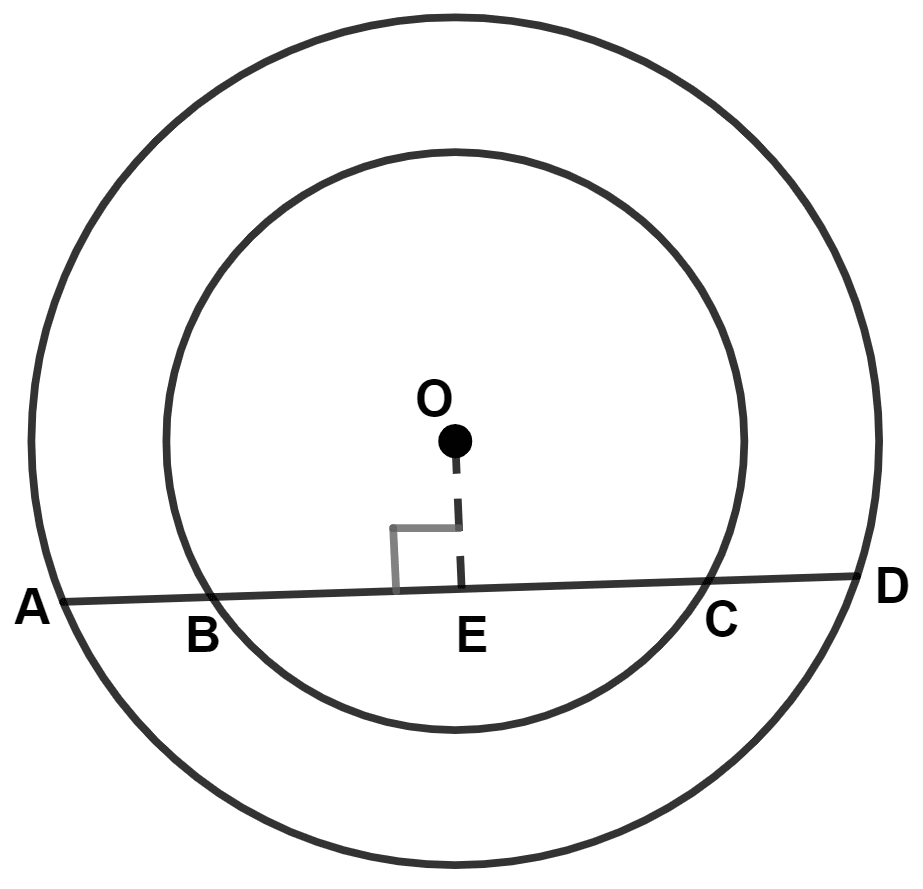
We know that,

Perpendicular from center to chord, bisects the chord.

In smaller circle,

⇒ BE = EC ...........(1)

In larger circle,

⇒ AE = ED ............(2)

Subtracting equation (1) from (2), we get :

⇒ AE - BE = ED - EC

⇒ AB = CD.

Hence, Option 1 is the correct option.

In the given figure, chord AB is larger than chord CD. The relation between OM and ON is :

1. OM = ON

2. OM < ON

3. OM > ON

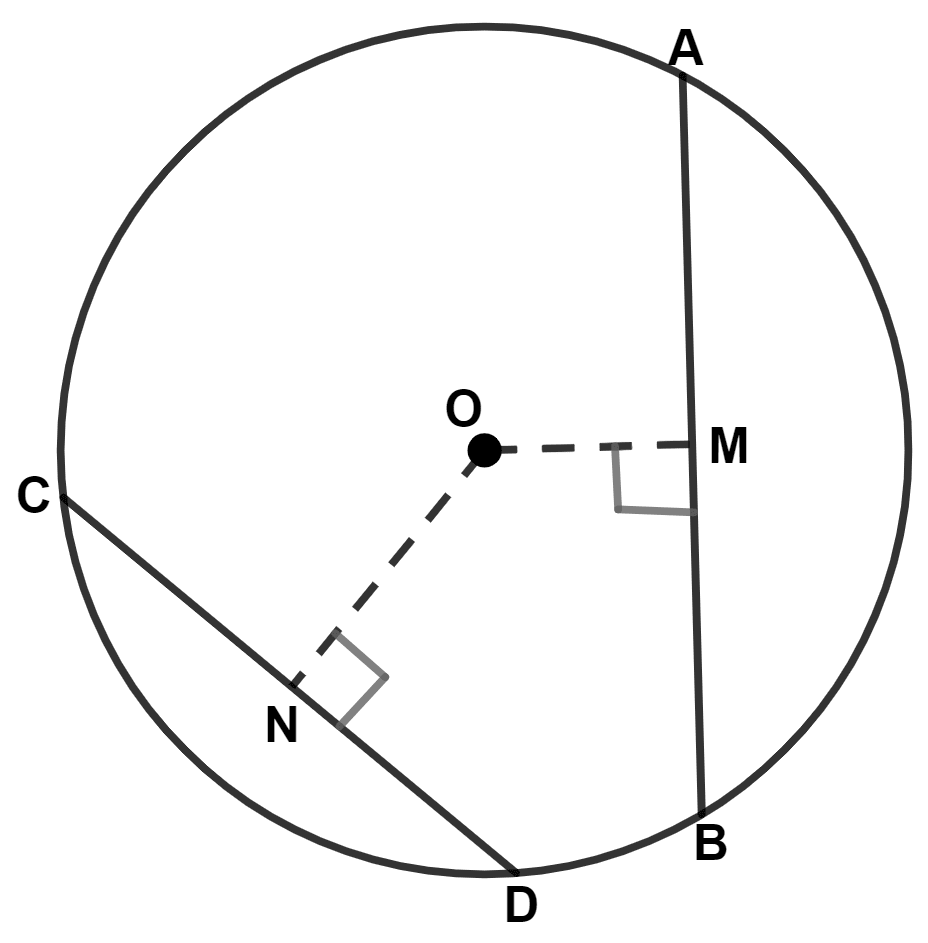
4. OM + ON = AB

Answer

Join OC and OB.

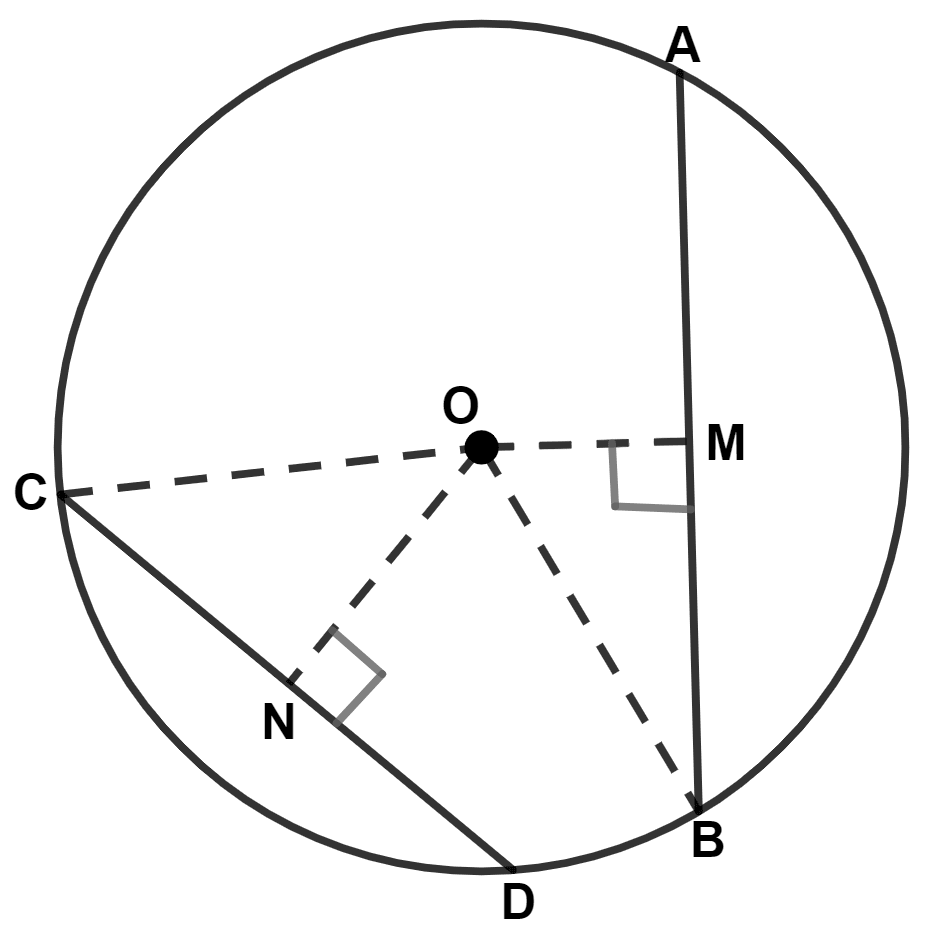
Given,

⇒ AB > CD

⇒ $\dfrac{AB}{2} \gt \dfrac{CD}{2}$

⇒ BM > CN

From figure,

OC = OB = radius = r.

In right angle triangle ONC,

By pythagoras theorem,

⇒ Hypotenuse² = Perpendicular² + Base²

⇒ OC² = ON² + CN²

⇒ r² = ON² + CN²

⇒ ON² = r² - CN²

⇒ ON = $\sqrt{r^2 - CN^2}$

In right angle triangle OMB,

By pythagoras theorem,

⇒ Hypotenuse² = Perpendicular² + Base²

⇒ OB² = OM² + BM²

⇒ r² = OM² + BM²

⇒ OM² = r² - BM²

⇒ OM = $\sqrt{r^2 - BM^2}$

Since, BM > CN

∴ r² - BM² < r² - CN²

⇒ $\sqrt{r^2 - BM^2} \lt \sqrt{r^2 - CN^2}$

⇒ OM < ON.

Hence, Option 2 is the correct option.

The line joining the mid-points of two chords of a circle passes through its center, then the chords are :

1. not parallel to each other

2. equal to each other

3. parallel to each other

4. not equal to each other

Answer

The line from centre of circle to the midpoint of any chord is also the perpendicular bisector of the chord.

∴ The two chords are parallel as they are both perpendicular to the line through the centre.

Hence, Option 3 is the correct option.

In the given figure, O and O' are centers of two circles, AB // CD // OO', then which of the following is not true :

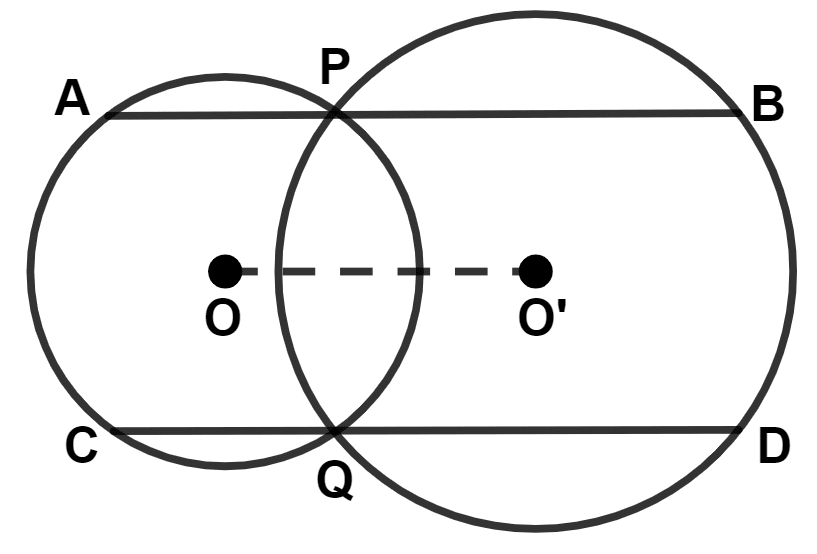
1. AB = 2 × OO'

2. CD = 2 × OO'

3. AB = CD

4. AB ≠ CD

Answer

Draw ON and O'M perpendicular to AB.

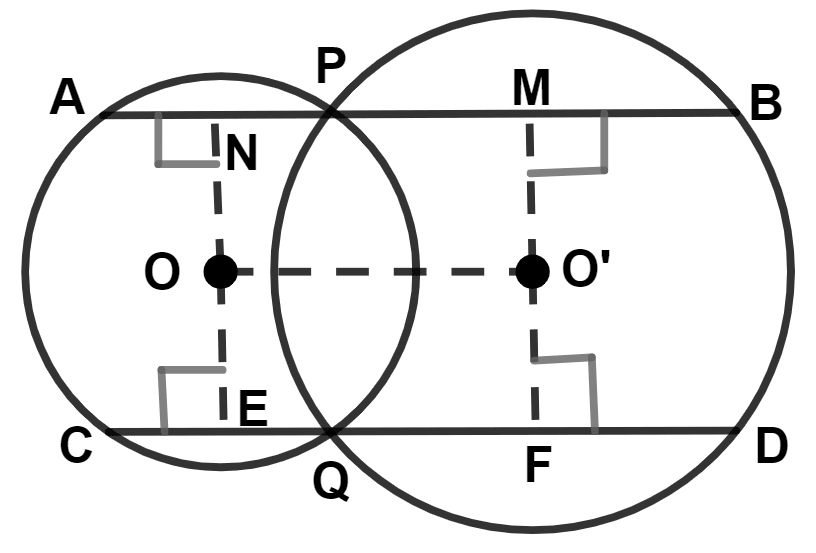
We know that,

Perpendicular from center to the chord bisects it.

∴ AN = NP and MP = MB

From figure,

⇒ AB = AN + PN + MP + MB

⇒ AB = PN + PN + MP + MP

⇒ AB = 2PN + 2MP

⇒ AB = 2(PN + MP)

⇒ AB = 2NM

⇒ AB = 2OO' ............(1)

Draw OE and O'F perpendicular to CD.

We know that,

Perpendicular from center to the chord bisects it.

∴ CE = EQ and QF = FD

From figure,

⇒ CD = CE + EQ + QF + FD

⇒ CD = EQ + EQ + QF + QF

⇒ CD = 2EQ + 2QF

⇒ CD = 2(EQ + QF)

⇒ CD = 2EF

⇒ CD = 2OO' ............(2)

From equation (1) and (2), we get :

⇒ AB = CD.

Hence, Option 4 is the correct option.

A chord of length 8 cm is drawn at a distance of 3 cm from the center of a circle. Calculate the radius of the circle.

Answer

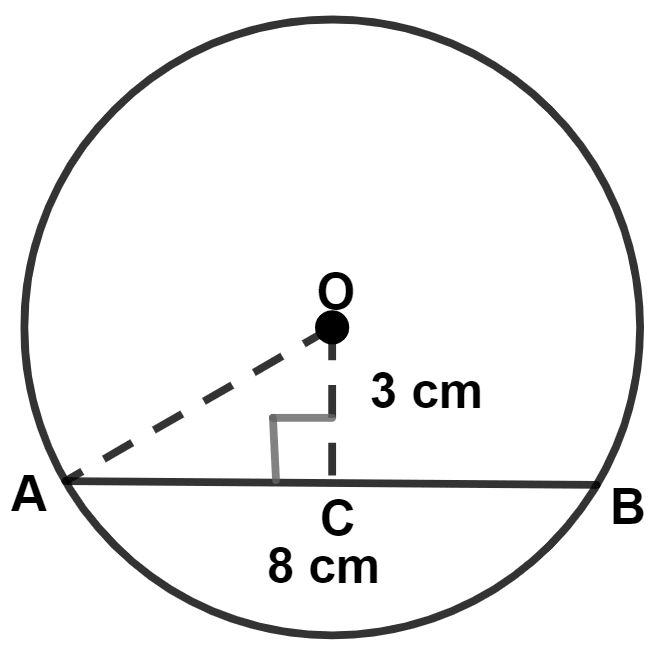
Let AB = 8 cm be the chord of the circle with center O.

We know that,

Perpendicular from center to chord, bisects the chord.

∴ AC = $\dfrac{AB}{2} = \dfrac{8}{2}$ = 4 cm.

In right angled triangle OAC,

By pythagoras theorem,

⇒ Hypotenuse² = Perpendicular² + Base²

⇒ OA² = OC² + AC²

⇒ OA² = 3² + 4²

⇒ OA² = 9 + 16

⇒ OA² = 25

⇒ OA = $\sqrt{25}$ = 5 cm.

Hence, radius of circle = 5 cm.

The radius of a circle is 17.0 cm and the length of perpendicular drawn from its center to a chord is 8.0 cm. Calculate the length of the chord.

Answer

Let AB be the chord of the circle with center O and OC be the perpendicular from center to the chord.

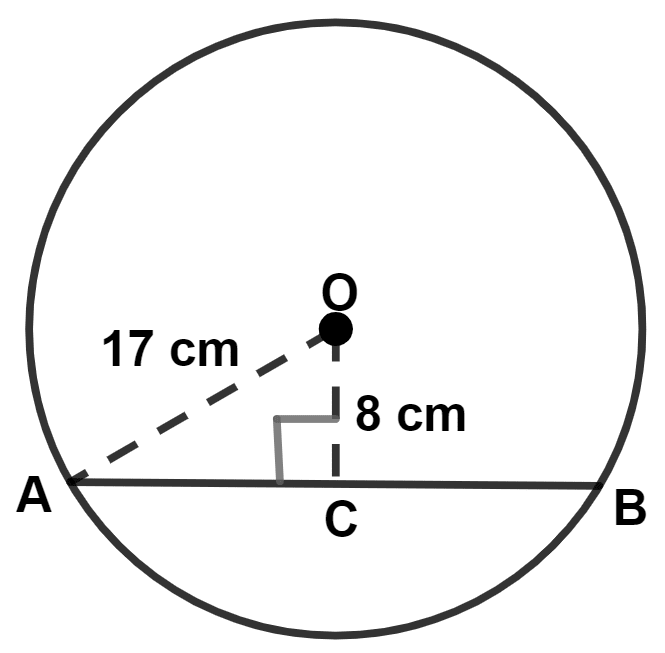
Given,

Radius (OA) = 17 cm

In right angled triangle OAC,

By pythagoras theorem,

⇒ Hypotenuse² = Perpendicular² + Base²

⇒ OA² = OC² + AC²

⇒ 17² = 8² + AC²

⇒ AC² = 17² - 8²

⇒ AC² = 289 - 64

⇒ AC² = 225

⇒ AC = $\sqrt{225}$ = 15 cm.

We know that,

Perpendicular from center to chord, bisects the chord.

∴ AB = 2 × AC = 2 × 15 = 30 cm.

Hence, length of chord = 30 cm.

A chord of length 24 cm is at a distance of 5 cm from the center of the circle. Find the length of the chord of the same circle which is at a distance of 12 cm from the centre.

Answer

Let AB be the chord of the circle with center O at the distance of 5 cm from the center of the circle.

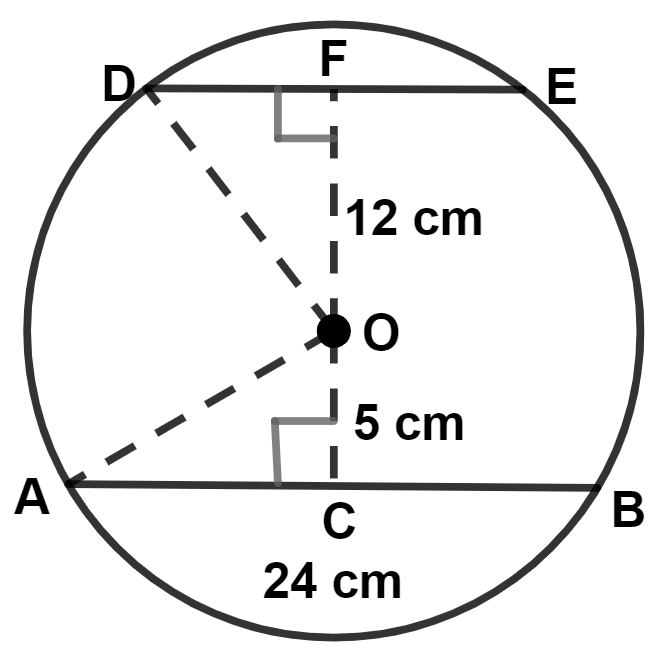
We know that,

Perpendicular from center to chord, bisects the chord.

∴ AC = $\dfrac{AB}{2} = \dfrac{24}{2}$ = 12 cm.

In right angled triangle OAC,

By pythagoras theorem,

⇒ Hypotenuse² = Perpendicular² + Base²

⇒ OA² = OC² + AC²

⇒ OA² = 5² + 12²

⇒ OA² = 25 + 144

⇒ OA² = 169

⇒ OA = $\sqrt{169}$ = 13 cm.

From figure,

OD = OA = 13 cm (Radius of same circle)

Let chord DE be at the distance of 12 cm from the center.

In right angled triangle OFD,

By pythagoras theorem,

⇒ Hypotenuse² = Perpendicular² + Base²

⇒ OD² = OF² + FD²

⇒ 13² = 12² + FD²

⇒ FD² = 13² - 12²

⇒ FD² = 169 - 144

⇒ FD² = 25

⇒ FD = $\sqrt{25}$ = 5 cm.

⇒ DE = 2 × FD = 2 × 5 = 10 cm.

Hence, length of chord at a distance of 12 cm from the centre equals to 10 cm.

In the following figure, AD is a straight line. OP ⊥ AD and O is the centre of both the circles. If OA = 34 cm, OB = 20 cm and OP = 16 cm; find the length of AB.

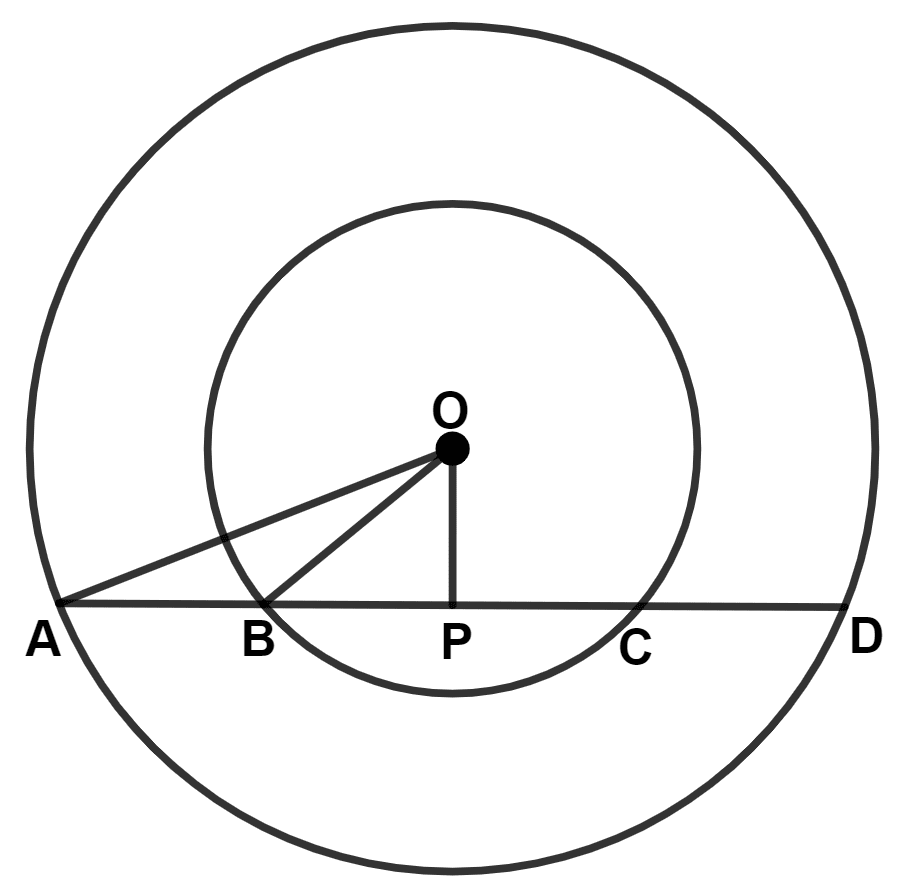
Answer

From figure,

In right-angled triangle OBP,

By pythagoras theorem,

⇒ Hypotenuse² = Perpendicular² + Base²

⇒ OB² = OP² + BP²

⇒ 20² = 16² + BP²

⇒ 400 = 256 + BP²

⇒ BP² = 400 - 256

⇒ BP² = 144

⇒ BP = $\sqrt{144}$ = 12 cm.

In right-angled triangle AOP,

⇒ Hypotenuse² = Perpendicular² + Base²

⇒ OA² = OP² + AP²

⇒ 34² = 16² + AP²

⇒ 1156 = 256 + AP²

⇒ AP² = 1156 - 256

⇒ AP² = 900

⇒ AP = $\sqrt{900}$ = 30 cm.

From figure,

AB = AP - BP = 30 - 12 = 18 cm.

Hence, AB = 18 cm.

In a circle of radius 17 cm, two parallel chords of lengths 30 cm and 16 cm are drawn. Find the distance between the chords, if both the chords are :

(i) on the opposite sides of the center,

(ii) on the same side of the center.

Answer

(i) Let AB and CD be chords on opposite side of the center of the circle.

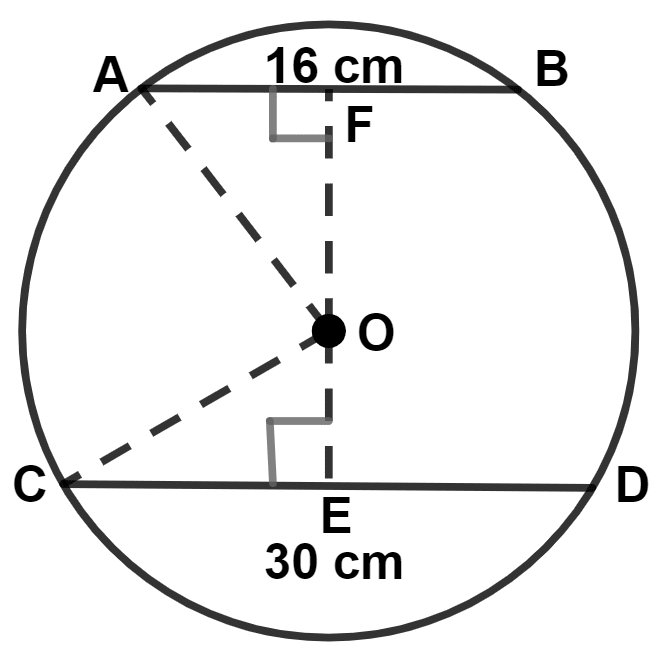
We know that,

Perpendicular from the center to the chord, bisects it.

∴ AF = $\dfrac{AB}{2} = \dfrac{16}{2}$ = 8 cm, CE = $\dfrac{CD}{2} = \dfrac{30}{2}$ = 15 cm.

From figure,

OA = OC = radius = 17 cm.

In right-angled triangle OCE,

By pythagoras theorem,

⇒ Hypotenuse² = Perpendicular² + Base²

⇒ OC² = OE² + CE²

⇒ 17² = OE² + 15²

⇒ 289 = OE² + 225

⇒ OE² = 289 - 225

⇒ OE² = 64

⇒ OE = $\sqrt{64}$ = 8 cm.

In right-angled triangle OAF,

By pythagoras theorem,

⇒ Hypotenuse² = Perpendicular² + Base²

⇒ OA² = OF² + AF²

⇒ 17² = OF² + 8²

⇒ 289 = OF² + 64

⇒ OF² = 289 - 64

⇒ OF² = 225

⇒ OF = $\sqrt{225}$ = 15 cm.

From figure,

⇒ EF = OE + OF = 8 + 15 = 23 cm.

Hence, distance between the chords = 23 cm.

(ii) Let AB and CD be chords on same side of the center of the circle.

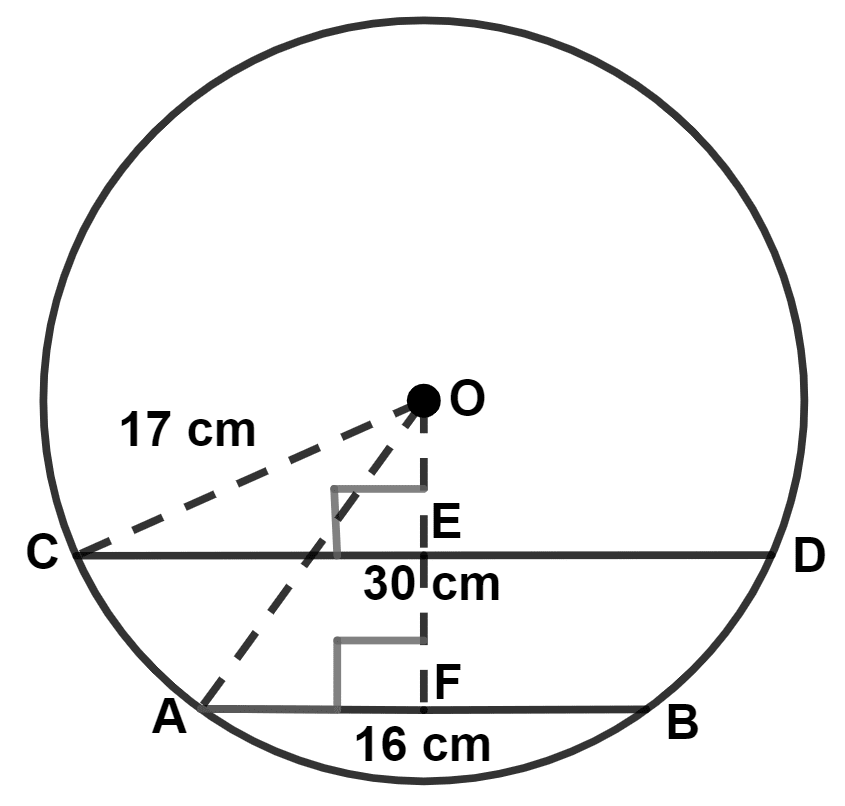
We know that,

Perpendicular from the center to the chord, bisects it.

∴ AF = $\dfrac{AB}{2} = \dfrac{16}{2}$ = 8 cm, CE = $\dfrac{CD}{2} = \dfrac{30}{2}$ = 15 cm.

From figure,

OA = OC = radius = 17 cm.

In right-angled triangle OCE,

By pythagoras theorem,

⇒ Hypotenuse² = Perpendicular² + Base²

⇒ OC² = OE² + CE²

⇒ 17² = OE² + 15²

⇒ 289 = OE² + 225

⇒ OE² = 289 - 225

⇒ OE² = 64

⇒ OE = $\sqrt{64}$ = 8 cm.

In right-angled triangle OAF,

By pythagoras theorem,

⇒ Hypotenuse² = Perpendicular² + Base²

⇒ OA² = OF² + AF²

⇒ 17² = OF² + 8²

⇒ 289 = OF² + 64

⇒ OF² = 289 - 64

⇒ OF² = 225

⇒ OF = $\sqrt{225}$ = 15 cm.

From figure,

⇒ EF = OF - OE = 15 - 8 = 7 cm.

Hence, distance between the chords = 7 cm.

Two parallel chords are drawn in a circle of diameter 30.0 cm. The length of one chord is 24.0 cm and the distance between the two chords is 21.0 cm; find the length of the other chord.

Answer

Let AB and CD be the two parallel chords.

Given,

Length of one chord is 24.0 cm. Let AB = 24 cm.

Draw OE ⊥ CD and OF ⊥ AB.

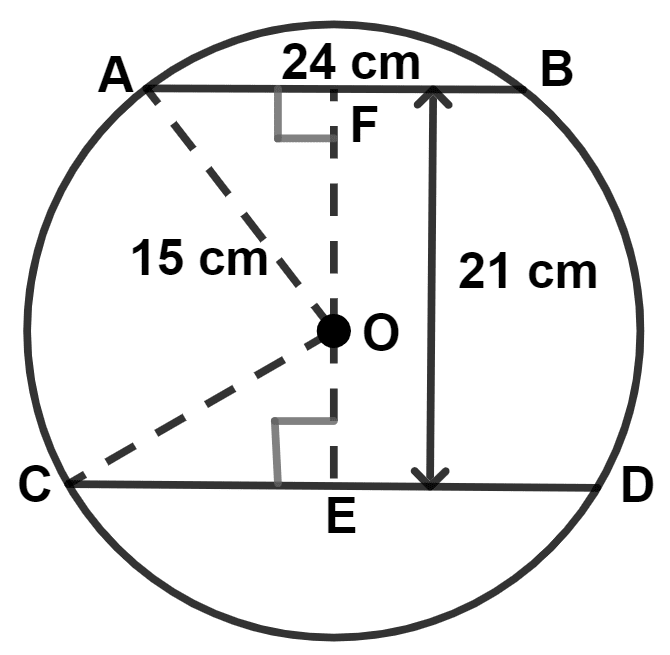
We know that,

Perpendicular from the center to the chord, bisects it.

∴ AF = $\dfrac{AB}{2} = \dfrac{24}{2}$ = 12 cm.

From figure,

OA = OC = radius = $\dfrac{\text{Diameter}}{2} = \dfrac{30}{2}$ = 15 cm.

In right-angled triangle OAF,

By pythagoras theorem,

⇒ Hypotenuse² = Perpendicular² + Base²

⇒ OA² = OF² + AF²

⇒ 15² = OF² + 12²

⇒ 225 = OF² + 144

⇒ OF² = 225 - 144

⇒ OF² = 81

⇒ OF = $\sqrt{81}$ = 9 cm.

Given,

Distance between two chords = 21 cm

∴ FE = 21 cm

⇒ OE = FE - OF = 21 - 9 = 12 cm.

In right-angled triangle OCE,

By pythagoras theorem,

⇒ Hypotenuse² = Perpendicular² + Base²

⇒ OC² = OE² + CE²

⇒ 15² = 12² + CE²

⇒ 225 = 144 + CE²

⇒ CE² = 225 - 144

⇒ CE² = 81

⇒ CE = $\sqrt{81}$ = 9 cm.

As, perpendicular from center to the chord, bisects it.

∴ CD = 2 × CE = 2 × 9 = 18 cm.

Hence, length of other chord = 18 cm.

A chord CD of a circle, whose center is O, is bisected at P by a diameter AB.

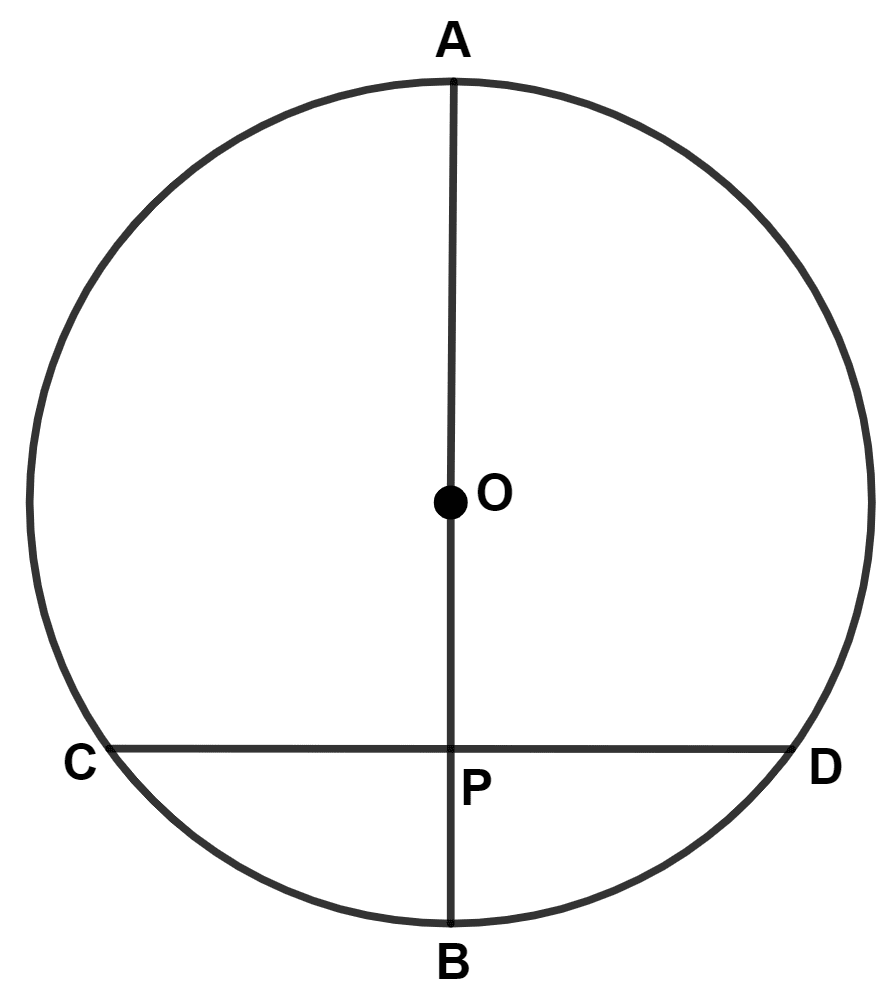
Given OA = OB = 15 cm and OP = 9 cm. Calculate the lengths of :

(i) CD

(ii) AD

(iii) CB.

Answer

We know that,

A straight line drawn from the center of a circle to bisect a chord is at right angles to the chord.

∴ OP ⊥ CD.

Join OC, AD and BC.

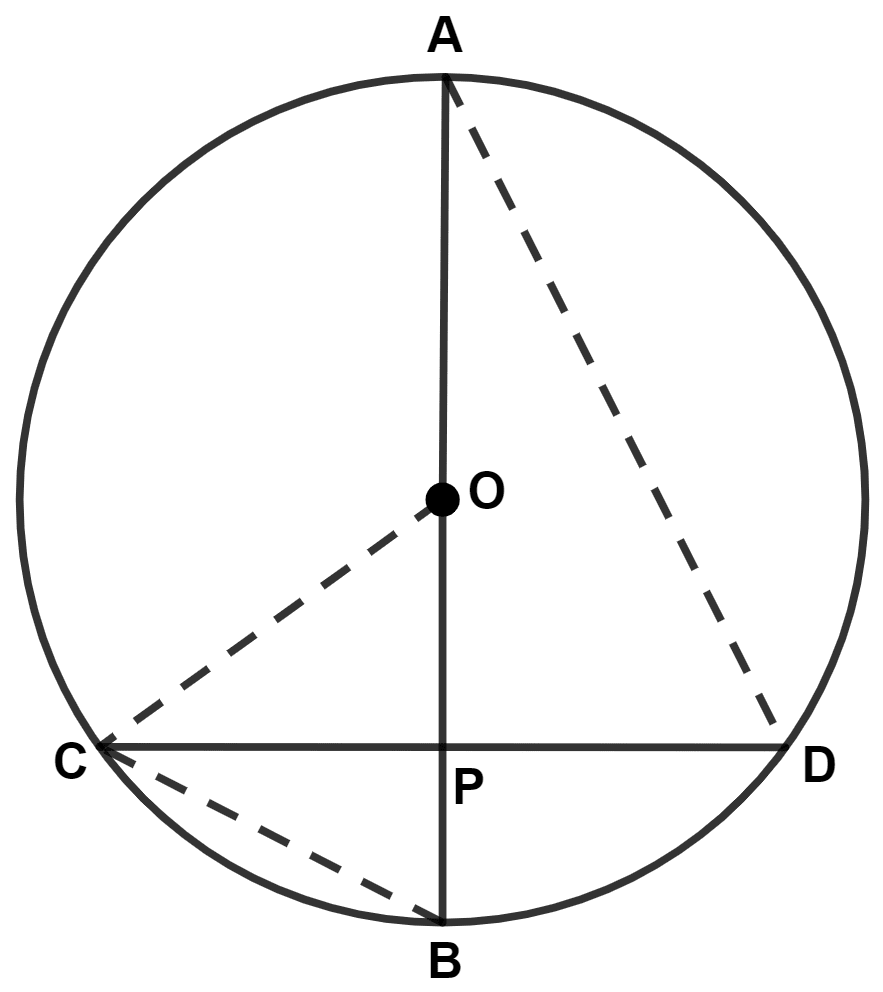
Given,

OA = OB = 15 cm

∴ Radius of circle = 15 cm.

∴ OC = 15 cm.

(i) In right-angled triangle OCP,

By pythagoras theorem,

⇒ Hypotenuse² = Perpendicular² + Base²

⇒ OC² = OP² + CP²

⇒ 15² = 9² + CP²

⇒ 225 = 81 + CP²

⇒ CP² = 225 - 81

⇒ CP² = 144

⇒ CP = $\sqrt{144}$ = 12 cm.

Since, chord CD is bisected at point P.

∴ CD = 2 × CP = 2 × 12 = 24 cm.

Hence, CD = 24 cm.

(ii) Since, chord CD is bisected at point P.

∴ PD = CP = 12 cm.

From figure,

⇒ AP = OA + OP = 15 + 9 = 24 cm.

In right-angled triangle APD,

By pythagoras theorem,

⇒ Hypotenuse² = Perpendicular² + Base²

⇒ AD² = AP² + PD²

⇒ AD² = 24² + 12²

⇒ AD² = 576 + 144

⇒ AD² = 720

⇒ AD = $\sqrt{720}$ = 26.83 cm.

Hence, AD = 26.83 cm.

(iii) From figure,

AB is the diameter of the circle.

∴ AB = 2 × OA = 2 × 15 = 30 cm.

⇒ PB = AB - AP = 30 - 24 = 6 cm.

In right-angled triangle CPB,

By pythagoras theorem,

⇒ Hypotenuse² = Perpendicular² + Base²

⇒ CB² = CP² + PB²

⇒ CB² = 12² + 6²

⇒ CB² = 144 + 36

⇒ CB² = 180

⇒ CB = $\sqrt{180}$ = 13.42 cm.

Hence, CB = 13.42 cm.

A straight line is drawn cutting two equal circles and passing through the mid-point M of the line joining their centers O and O'.

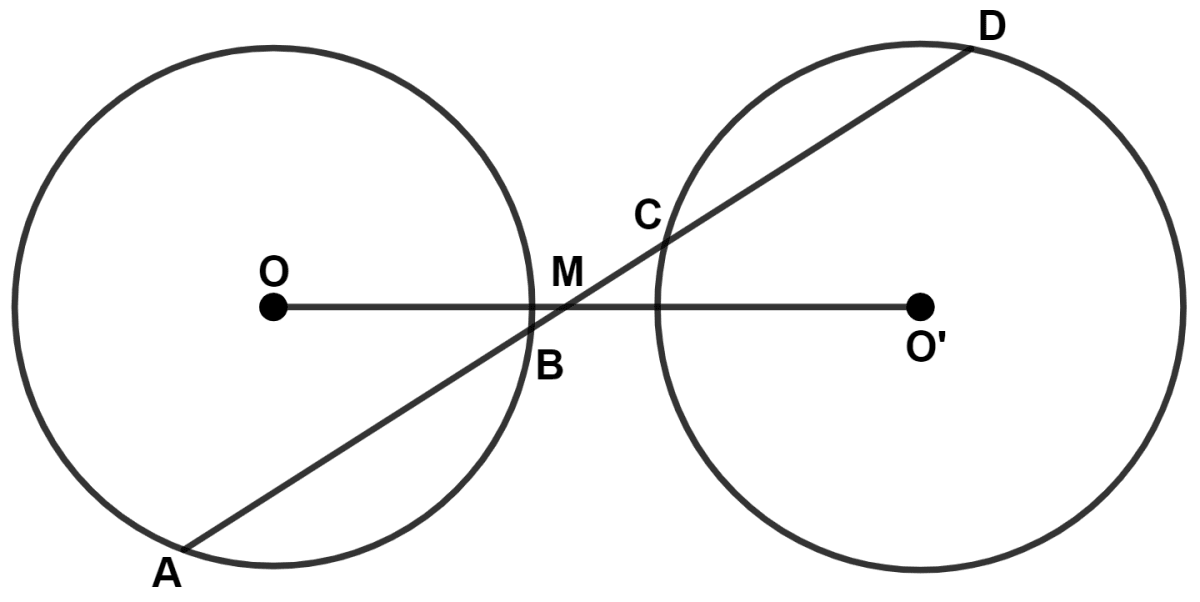
Prove that the chords AB and CD, which are intercepted by the two circles, are equal.

Answer

Draw OP ⊥ AB and O'Q ⊥ CD.

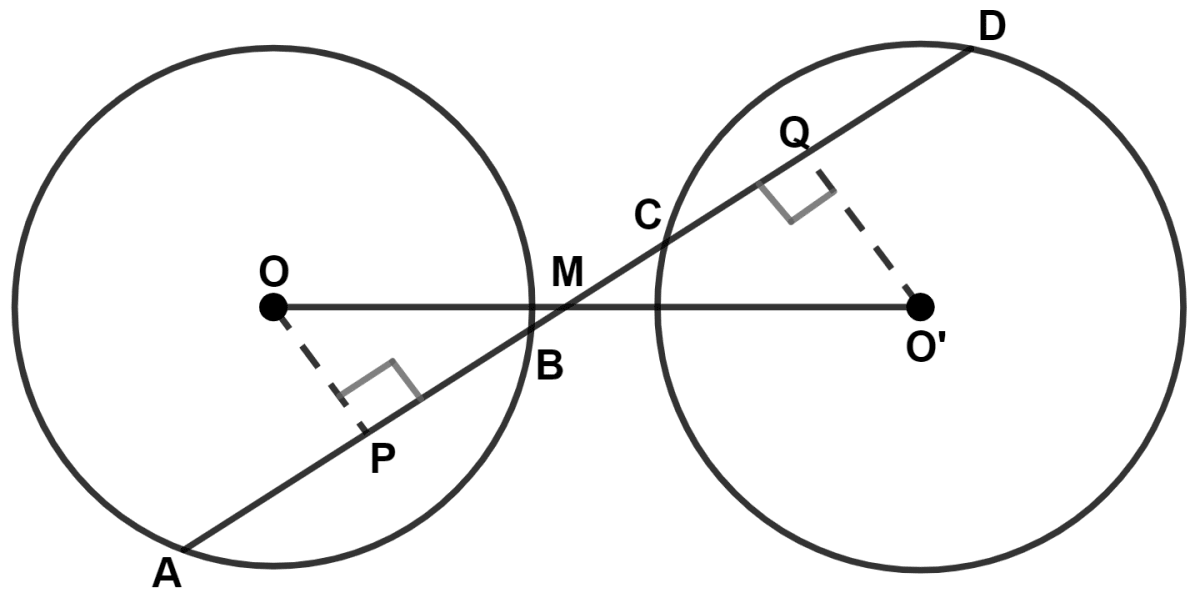
In △ OMP and △ O'MQ,

⇒ ∠OMP = ∠O'MQ (Vertically opposite angles are equal)

⇒ ∠OPM = ∠O'QM (Both equal to 90°)

⇒ OM = O'M (As, M is the mid-point of OO')

∴ △ OMP ≅ △ O'MQ (By A.A.S. axiom)

We know that,

Corresponding parts of congruent triangle are equal.

∴ OP = O'Q.

We know that,

Two chords of a circle or equal circles which are equidistant from the center are equal.

∴ AB = CD.

Hence, proved that AB = CD.

M and N are the mid-points of two equal chords AB and CD respectively of a circle with center O. Prove that :

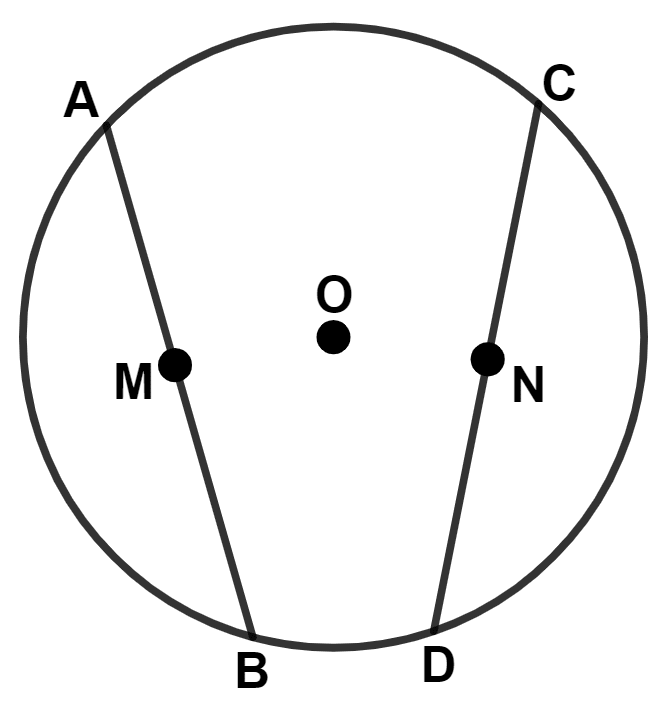
(i) ∠BMN = ∠DNM

(ii) ∠AMN = ∠CNM.

Answer

Join OM, ON, OB and OD.

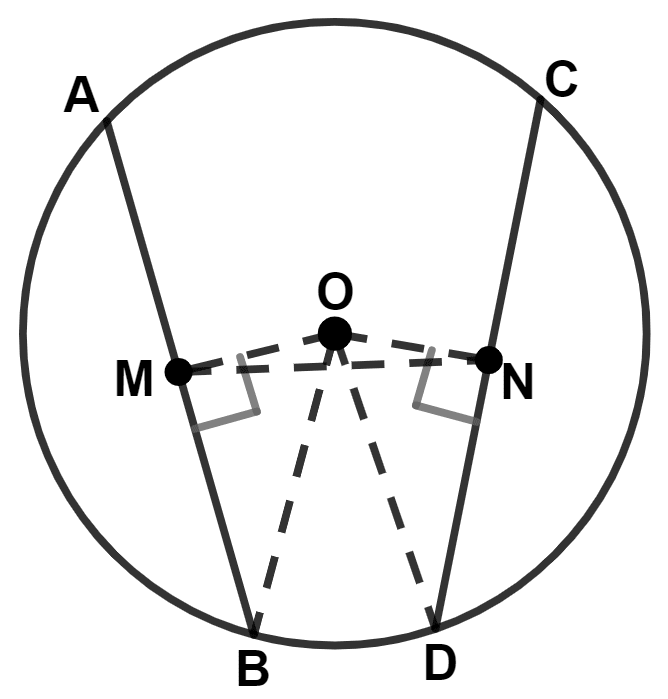
Given,

M and N are the mid-points of two equal chords AB and CD.

∴ BM = $\dfrac{1}{2}AB$ and DN = $\dfrac{1}{2}CD$

Since, AB and CD are equal chords.

∴ BM = DN ..........(1)

We know that,

A straight line drawn from the center of a circle to bisect a chord, which is not a diameter, is at right angles to the chord.

∴ OM ⊥ AB and ON ⊥ CD.

∴ ∠OMB = ∠OND (Both equal to 90°) ........(2)

(i) In triangle OMN,

⇒ ON = OM (Equal chords of a circle are equidistant from the center.)

⇒ ∠OMN = ∠ONM (Angles opposite to equal sides are equal) ........(3)

Subtracting equation (2) from (3), we get :

⇒ ∠OMB - ∠OMN = ∠OND - ∠ONM

⇒ ∠BMN = ∠DNM.

Hence, proved that ∠BMN = ∠DNM.

(ii) From figure,

⇒ ∠OMA = ∠ONC (Both equal to 90°) ...............(4)

Adding equation (3) and (4), we get :

⇒ ∠OMA + ∠OMN = ∠ONC + ∠ONM

⇒ ∠AMN = ∠CNM.

Hence, proved that ∠AMN = ∠CNM.

Two equal chords AB and CD of a circle with center O, intersect each other at point P inside the circle. Prove that :

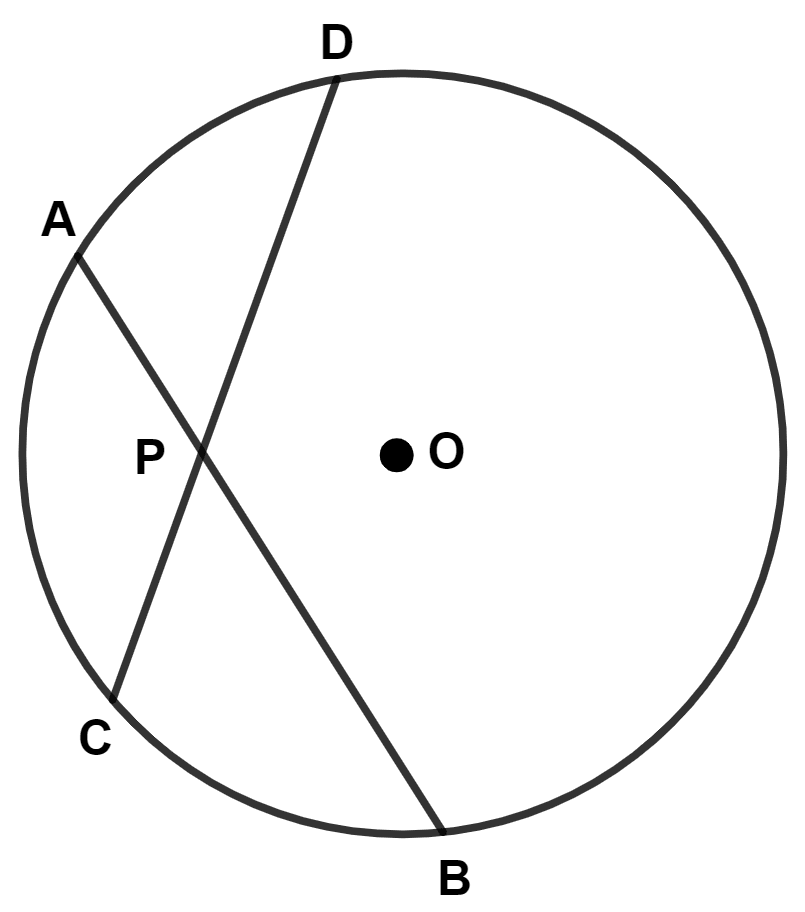
(i) AP = CP

(ii) BP = DP

Answer

Draw, OM ⊥ AB and ON ⊥ CD.

Join OP, OB and OD.

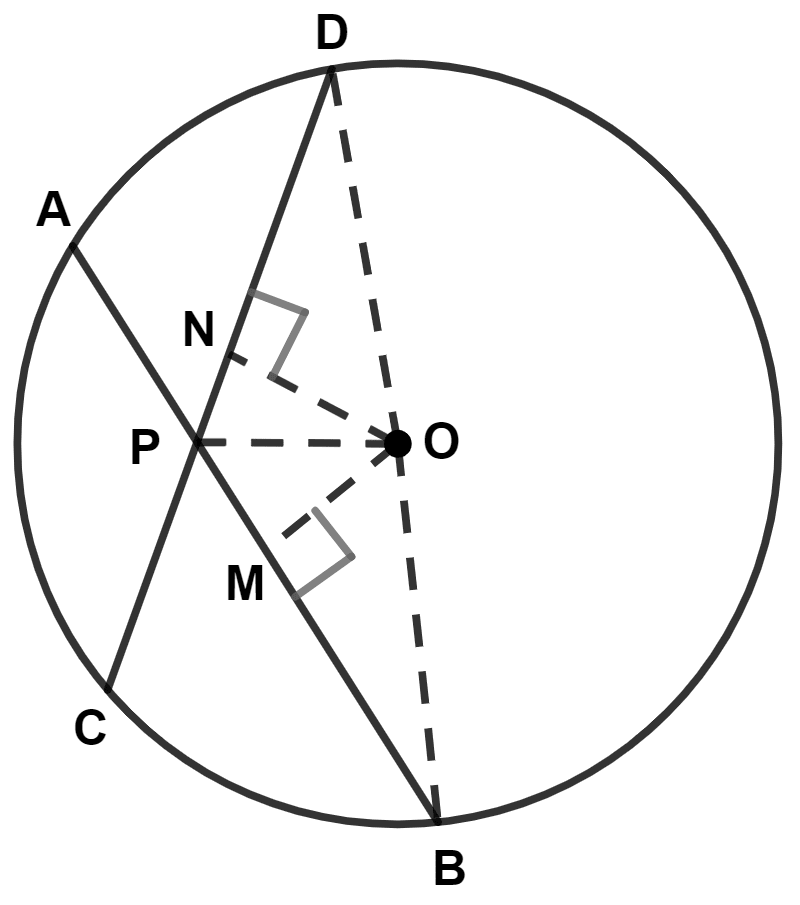
We know that,

Perpendicular to a chord, from the center of the circle, bisects the chord.

∴ OM and ON bisects AB and CD respectively.

Given,

Two chords are equal.

∴ AB = CD = x (let)

∴ MB = $\dfrac{1}{2}AB = \dfrac{1}{2}x$ and ND = $\dfrac{1}{2}CD = \dfrac{1}{2}x$,

∴ MB = ND = x (let) ..............(1)

From figure,

OB = OD = y (Radius of same circle)

In right-angled triangle OMB,

By pythagoras theorem,

⇒ Hypotenuse² = Perpendicular² + Base²

⇒ OB² = OM² + MB²

⇒ OM² = OB² - MB²

⇒ OM² = y² - x²

⇒ OM = $\sqrt{y^2 - x^2}$ ........(2)

In right-angled triangle OND,

By pythagoras theorem,

⇒ Hypotenuse² = Perpendicular² + Base²

⇒ OD² = ON² + ND²

⇒ ON² = OD² - ND²

⇒ ON² = y² - x²

⇒ ON = $\sqrt{y^2 - x^2}$ ........(3)

From equation (2) and (3), we get :

⇒ OM = ON

In △ OPM and △ OPN,

⇒ ∠OMP = ∠ONP (Both equal to 90°)

⇒ OP = OP (Common side)

⇒ OM = ON (Proved above)

∴ △ OPM ≅ △ OPN (By R.H.S. axiom)

We know that,

Corresponding parts of congruent triangles are equal.

∴ PM = PN.

Adding equation (1) to both the sides, we get :

⇒ MB + PM = ND + PN

⇒ PB = PD ...........(4)

Given,

⇒ AB = CD .........(5)

Subtracting equation (4) from (5), we get :

⇒ AB - PB = CD - PD

⇒ AP = CP.

Hence, proved that AP = CP and PB = CD.

In the following figure, OABC is a square. A circle is drawn with O as center which meets OC at P and OA at Q. Prove that :

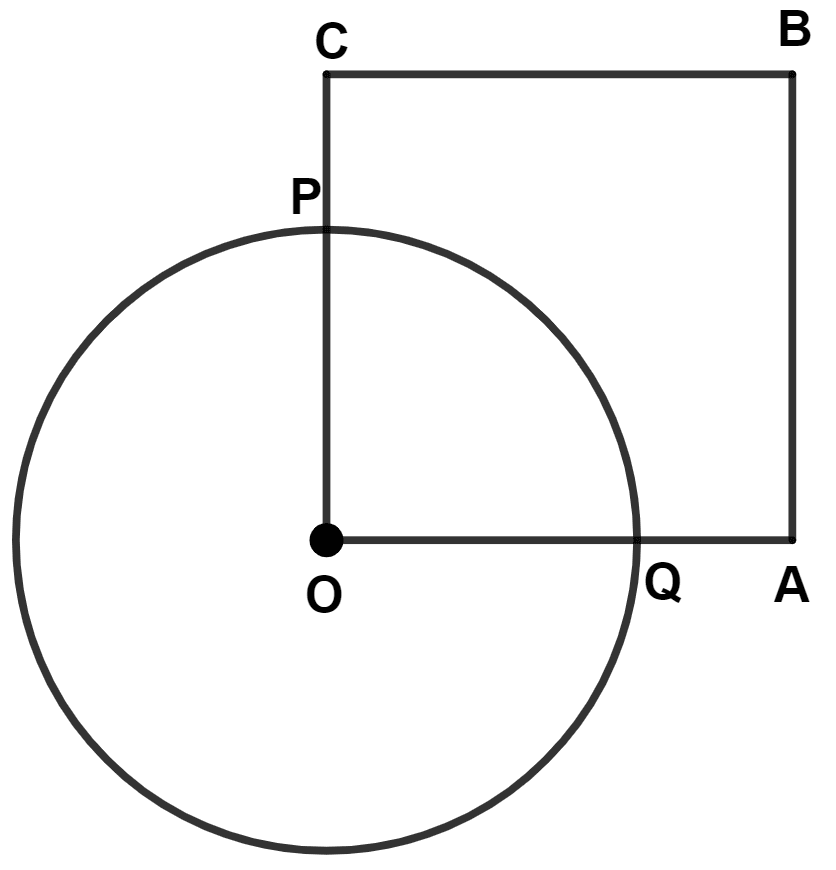
(i) △ OPA ≅ △ OQC

(ii) △ BPC ≅ △ BQA

Answer

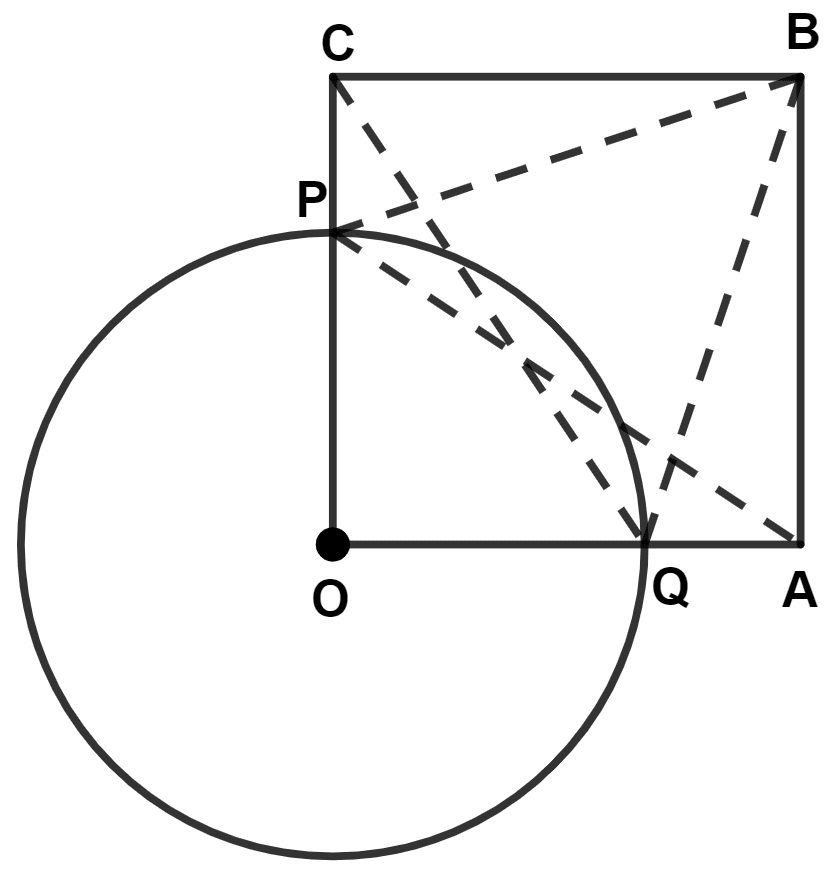
(i) In △ OPA and △ OQC,

⇒ OP = OQ (Radius of same circle)

⇒ ∠AOP = ∠COQ (Both equal to 90°)

⇒ OA = OC (Sides of square)

∴ △ OPA ≅ △ OQC (By S.A.S. axiom)

Hence, proved that △ OPA ≅ △ OQC.

(ii) Proved above,

⇒ OC = OA ...........(1)

⇒ OP = OQ ...........(2)

Subtracting equation (2) from (1),

⇒ OC - OP = OA - OQ

⇒ CP = QA

In △ BPC and △ BQA,

⇒ BC = BA (Sides of square)

⇒ ∠PCB = ∠QAB (Both equal to 90°)

⇒ CP = QA (Proved above)

∴ △ BPC ≅ △ BQA (By S.A.S. axiom)

Hence, proved that △ BPC ≅ △ BQA.

The length of common chord of two intersecting circles is 30 cm. If the diameters of these two circles be 50 cm and 34 cm, calculate the distance between their centers.

Answer

Let O be the center of the circle with diameter 50 cm and O' be the center of the circle with diameter 34 cm.

Let AB be the common chord.

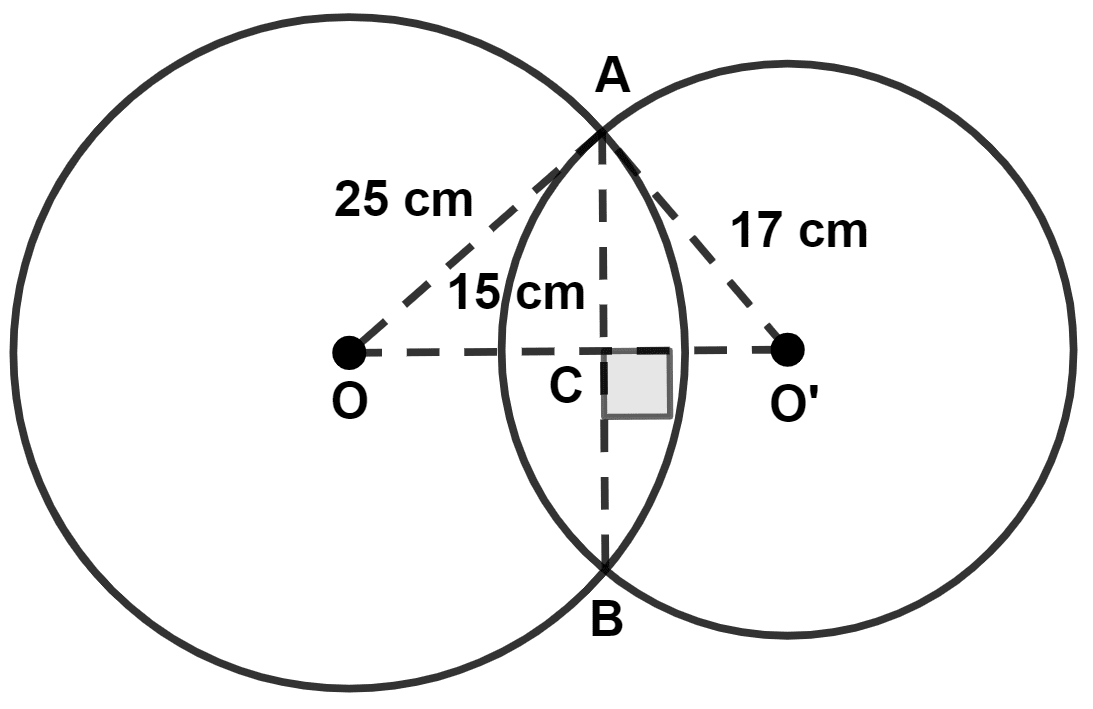
Radius = $\dfrac{\text{Diameter}}{2}$

Radius of circle with center O = $\dfrac{50}{2}$ = 25 cm,

Radius of circle with center O' = $\dfrac{34}{2}$ = 17 cm.

We know that,

Perpendicular from center to chord, bisects the chord.

∴ AC = BC = $\dfrac{AB}{2} = \dfrac{30}{2}$ = 15 cm.

In right-angled triangle AOC,

By pythagoras theorem,

⇒ AO² = AC² + OC²

⇒ 25² = 15² + OC²

⇒ 625 = 225 + OC²

⇒ OC² = 625 - 225

⇒ OC² = 400

⇒ OC = $\sqrt{400}$ = 20 cm.

In right-angled triangle AO'C,

By pythagoras theorem,

⇒ AO'² = AC² + O'C²

⇒ 17² = 15² + O'C²

⇒ 289 = 225 + O'C²

⇒ O'C² = 289 - 225

⇒ O'C² = 64

⇒ O'C = $\sqrt{64}$ = 8 cm.

From figure,

OO' = OC + O'C = 20 + 8 = 28 cm.

Hence, distance between centers = 28 cm.

The line joining the mid-points of two chords of a circle passes through its center. Prove that the chords are parallel.

Answer

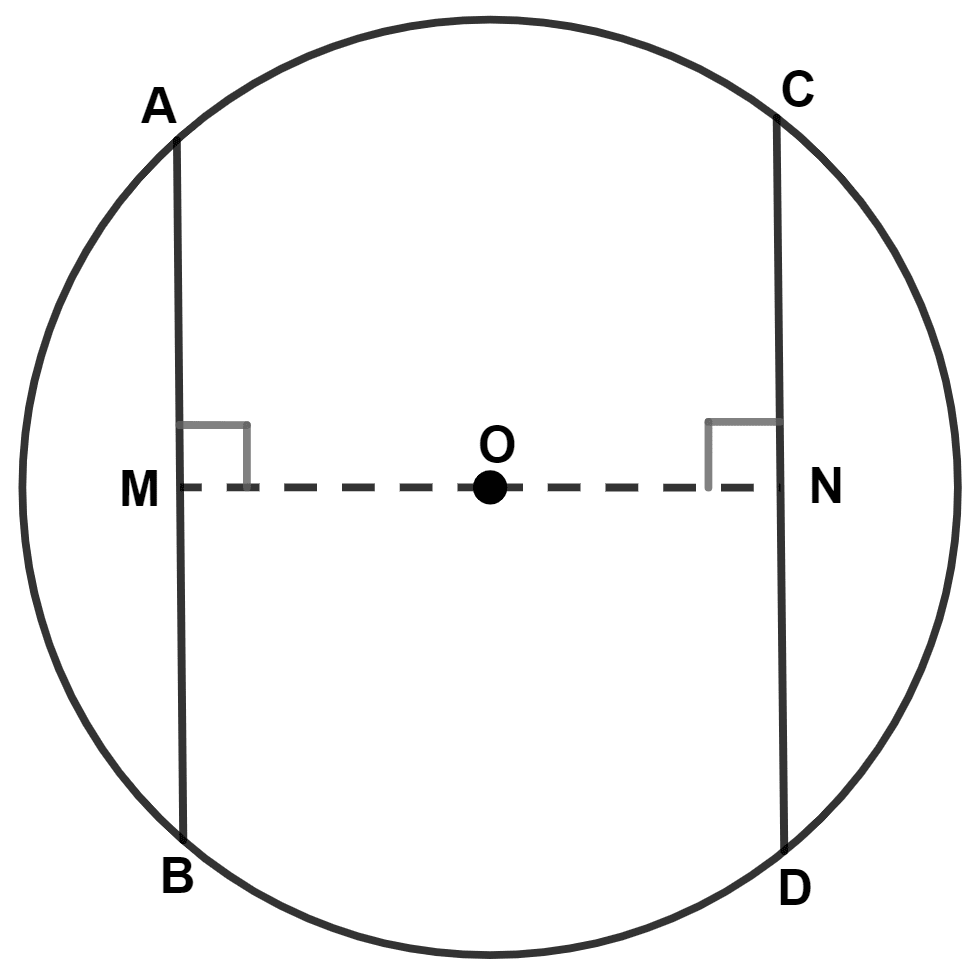
Since, the straight line drawn from the center of a circle to bisect a chord is perpendicular to the chord,

∴ OM ⊥ AB and ON ⊥ CD.

So,

⇒ ∠OMA = ∠OMB = 90° and ∠ONC = ∠OND = 90°

Since,

⇒ ∠OMA = ∠OND = 90° (Alternate angles are equal)

⇒ ∠OMB = ∠ONC = 90° (Alternate angles are equal)

Hence, proved that AB || CD.

In the following figure, the line ABCD is perpendicular to PQ; where P and Q are the centers of the circles. Show that :

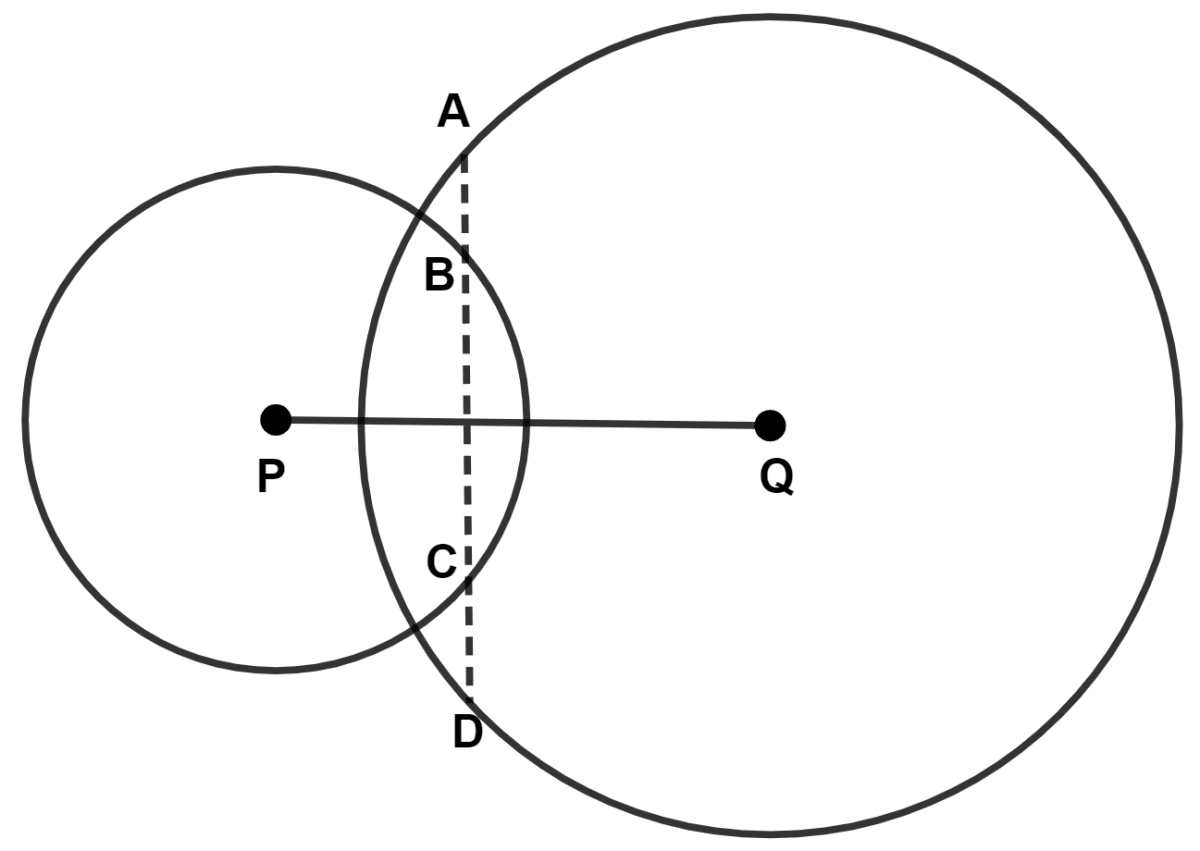
(i) AB = CD

(ii) AC = BD

Answer

We know that,

Perpendicular from center to chord, bisects the chord.

Since, ABCD is perpendicular to PQ.

∴ OA = OD ............(1)

Also,

⇒ OB = OC ..............(2)

(i) Subtracting equation (2) from (1), we get :

⇒ OA - OB = OD - OC

⇒ AB = CD.

Hence, proved that AB = CD.

(ii) We know that,

⇒ AB = CD

Adding BC to both sides of above equation, we get :

⇒ AB + BC = CD + BC

⇒ AC = BD.

Hence, proved that AC = BD.

In the given figure, arc APB = arc CQD, then :

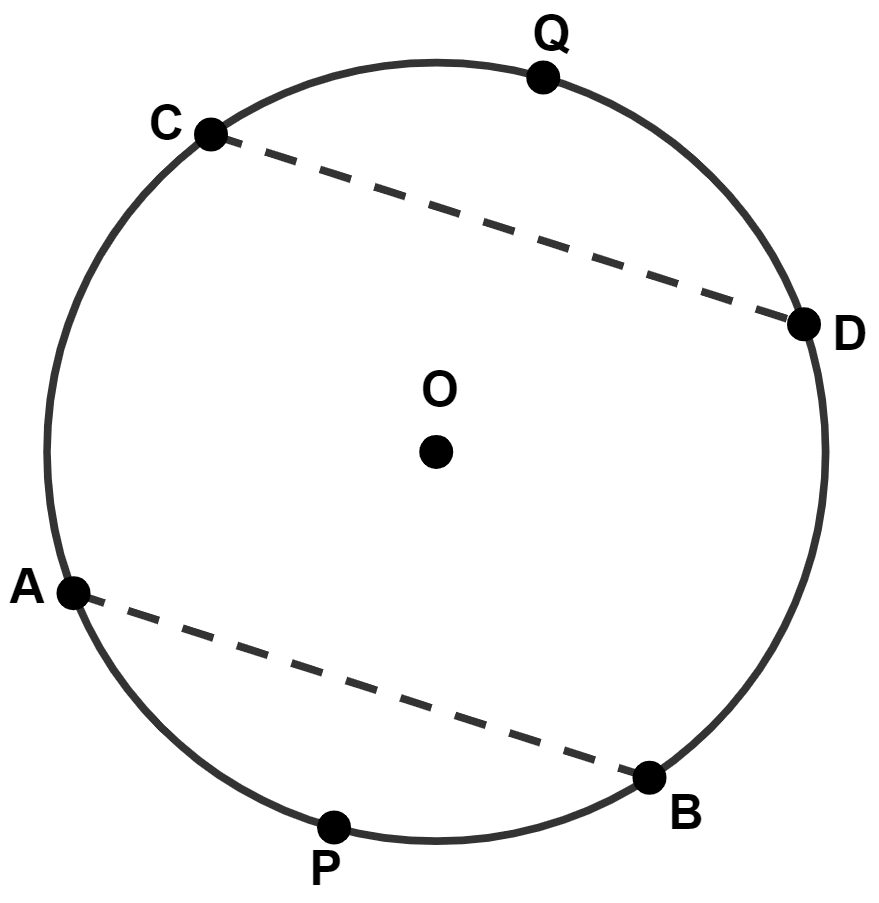
1. AB = CD

2. AB > CD

3. AB < CD

4. none of the above

Answer

We know that,

Equal arcs subtends equal chords.

Given,

⇒ arc APB = arc CQD

⇒ AB = CD.

Hence, Option 1 is the correct option.

In the given figure, O is center of the circle and ∠COD is greater than ∠AOB, then :

1. AB > CD

2. AB < CD

3. AB = CD

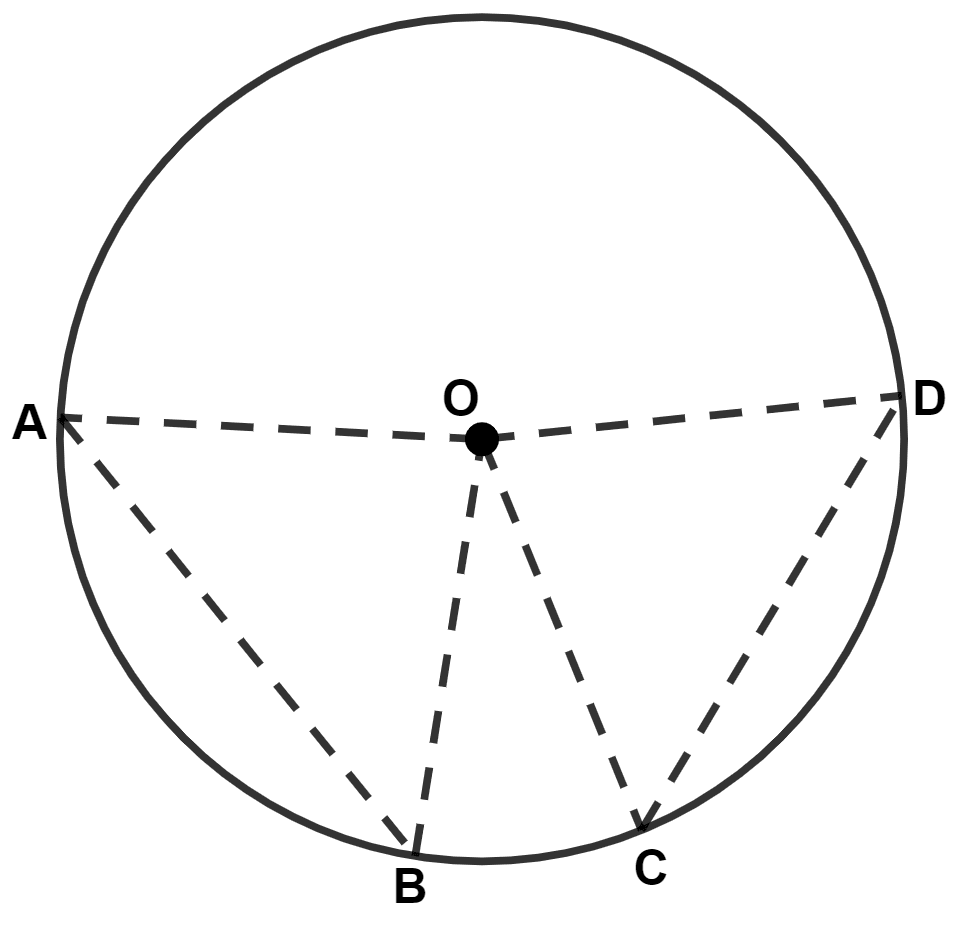
4. AB + CD = AD

Answer

We know that,

Greater the chord, greater is the angle subtended by it at the center.

Given,

⇒ ∠AOB < ∠COD

⇒ AB < CD

Hence, Option 2 is the correct option.

In a circle, O is its center and AB, CD are its two chords. If AB : CD = 3 : 2, then ratio between ∠AOB and ∠COD is :

1. 1 : 1

2. 3 : 2

3. 2 : 5

4. 3 : 5

Answer

Ratio of the angles subtended by the chords on the center is equal to the ratio of the chords.

⇒ $\dfrac{∠AOB}{∠COD} = \dfrac{AB}{CD} = \dfrac{3}{2}$

⇒ ∠AOB : ∠COD = 3 : 2.

Hence, Option 2 is the correct option.

In the given figure, O is the center of the circle and ABC is an equilateral triangle, then ∠AOB is equal to :

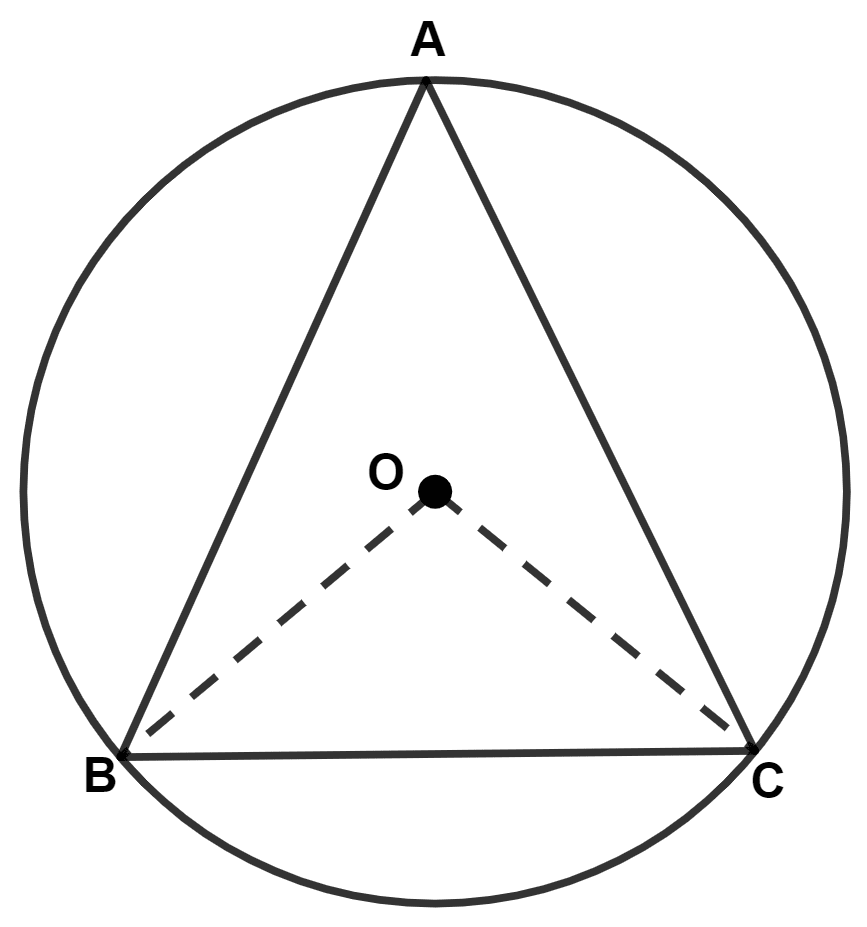
1. 105°

2. 90°

3. 60°

4. 120°

Answer

Since, ABC is an equilateral triangle.

∴ AB = BC = AC.

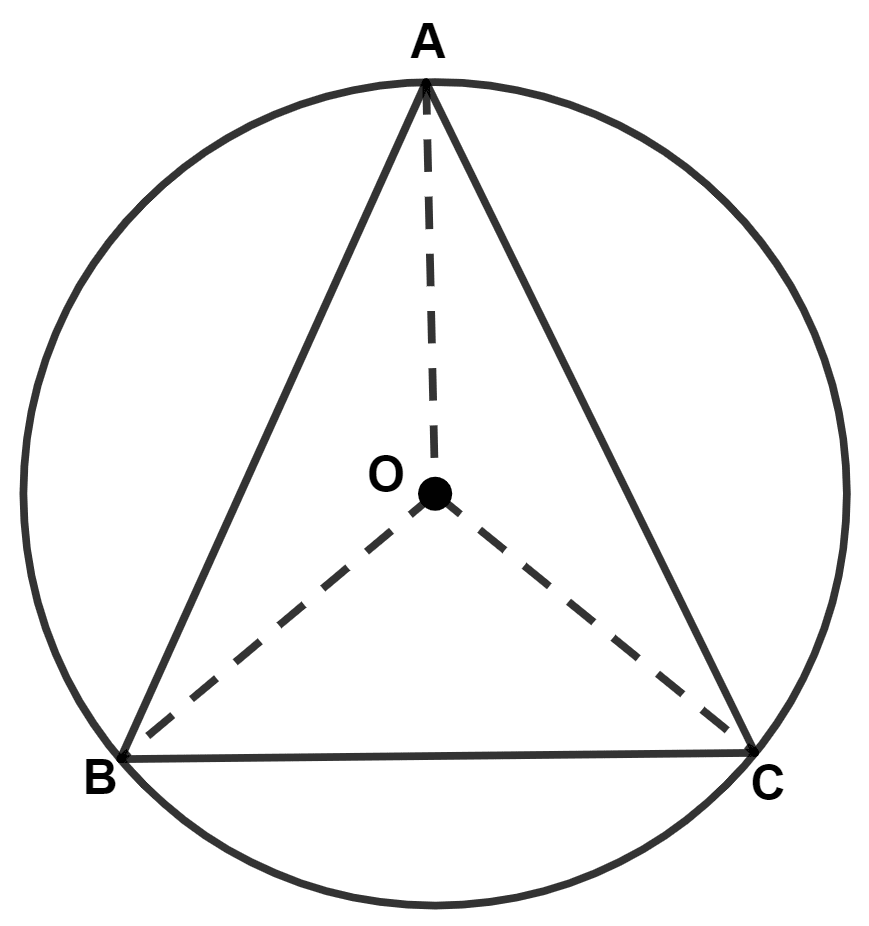
We know that,

Equal chords subtend equal angles at the center.

∴ ∠AOB = ∠BOC = ∠COA = x (let)

We know that,

Angles around a point add to 360 °.

∴ ∠AOB + ∠BOC + ∠COA = 360°

⇒ x + x + x = 360°

⇒ 3x = 360°

⇒ x = $\dfrac{360°}{3}$ = 120°

⇒ ∠AOB = 120°.

Hence, Option 4 is the correct option.

In the given figure, O is the center of the circle and chord AB : chord CD = 5 : 3. If angle DOC = 60°; then ∠AOB is :

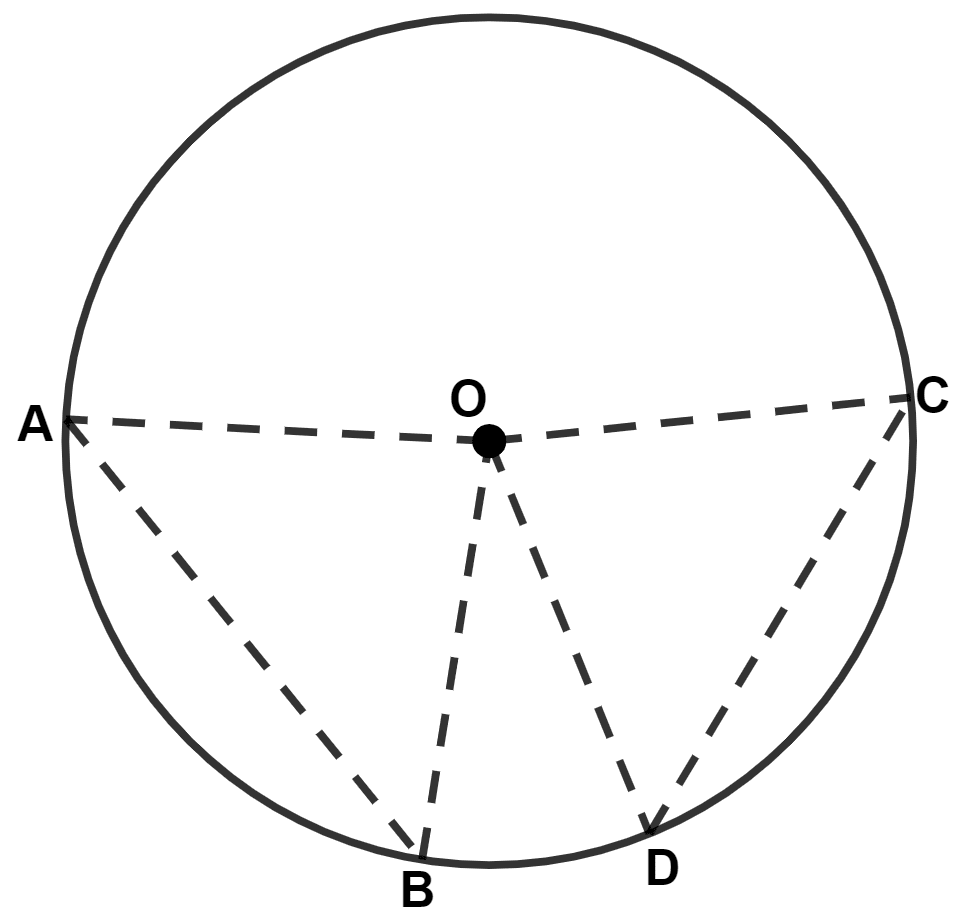
1. 120°

2. 75°

3. 100°

4. 80°

Answer

Ratio of the angles subtended by the chords on the center is equal to the ratio of the chords.

$\Rightarrow \dfrac{∠AOB}{∠COD} = \dfrac{AB}{CD} \\[1em] \Rightarrow \dfrac{∠AOB}{60°} = \dfrac{5}{3} \\[1em] \Rightarrow ∠AOB = \dfrac{5}{3} \times 60° = \dfrac{300°}{3} = 100°.$

Hence, Option 3 is the correct option.

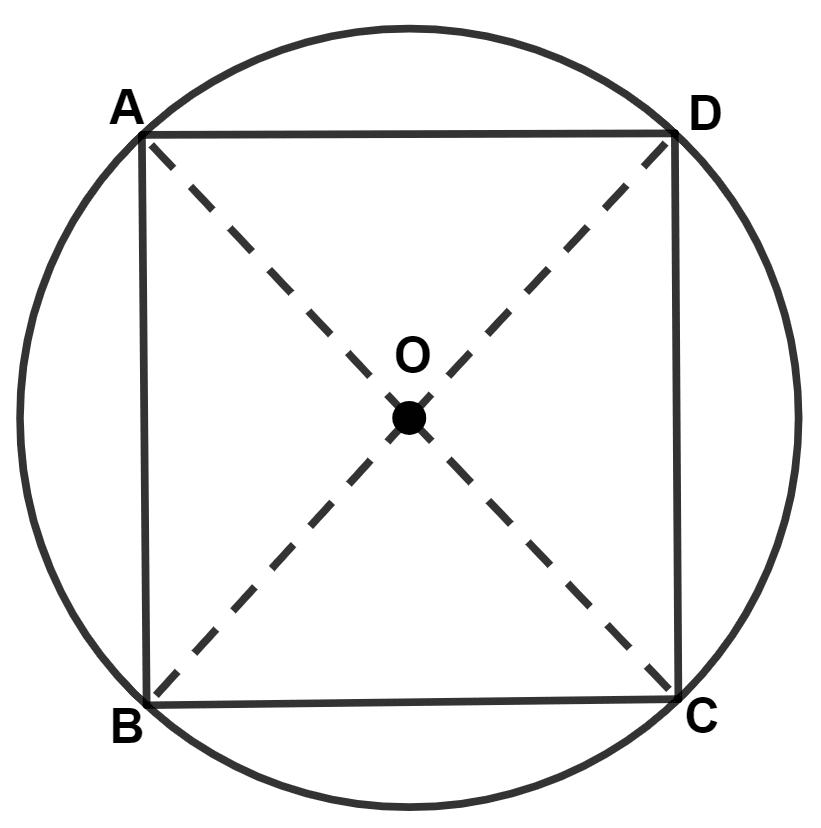
In the given figure, a square is inscribed in a circle with center O. Find :

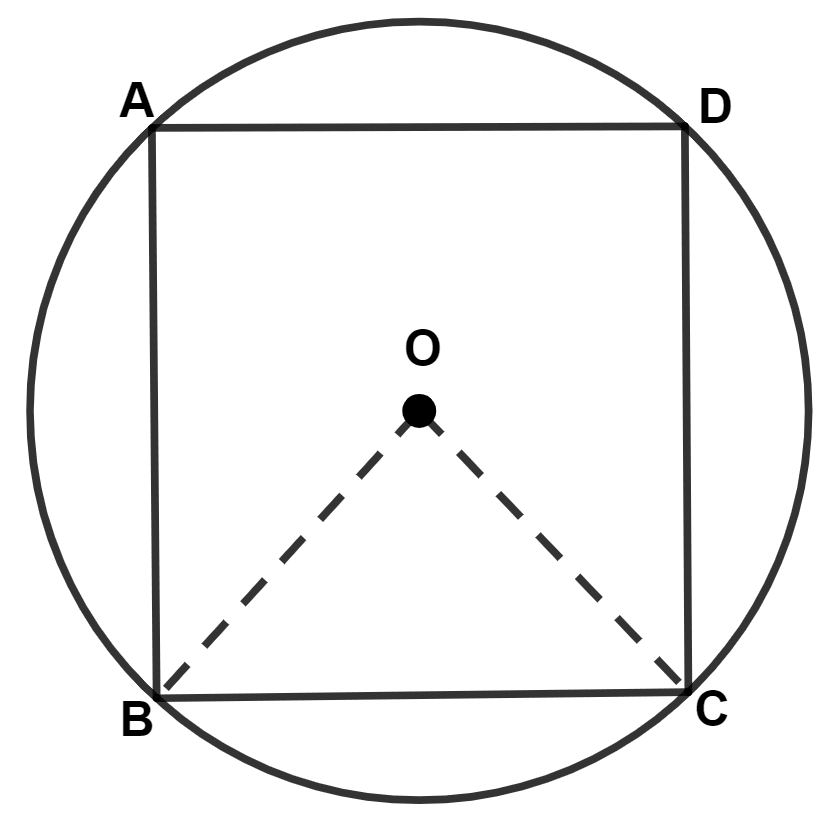
(i) ∠BOC

(ii) ∠OCB

(iii) ∠COD

(iv) ∠BOD

Is BD a diameter of the circle?

Answer

Join OA and OD.

(i) We know that,

Diagonals of a square bisect each other at 90°.

∴ ∠BOC = 90°.

Hence, ∠BOC = 90°.

(ii) From figure,

OB and OC are the radius of the circle.

In △ OBC,

⇒ OB = OC

⇒ ∠OCB = ∠OBC = x (let) [Angle opposite to equal sides are equal]

By angle sum property of triangle,

⇒ ∠OCB + ∠OBC + ∠BOC = 180°

⇒ x + x + 90° = 180°

⇒ 2x + 90° = 180°

⇒ 2x = 180° - 90°

⇒ 2x = 90°

⇒ x = $\dfrac{90°}{2}$

⇒ x = 45°

⇒ ∠OCB = 45°.

Hence, ∠OCB = 45°.

(iii) We know that,

Diagonals of a square bisect each other at 90°.

∴ ∠COD = 90°.

Hence, ∠COD = 90°.

(iv) From figure,

⇒ ∠BOD = ∠BOC + ∠COD = 90° + 90° = 180°.

Hence, ∠BOD = 180° and BD is the diameter of the circle.

In the given figure, AB is a side of a regular pentagon and BC is a side of a regular hexagon.

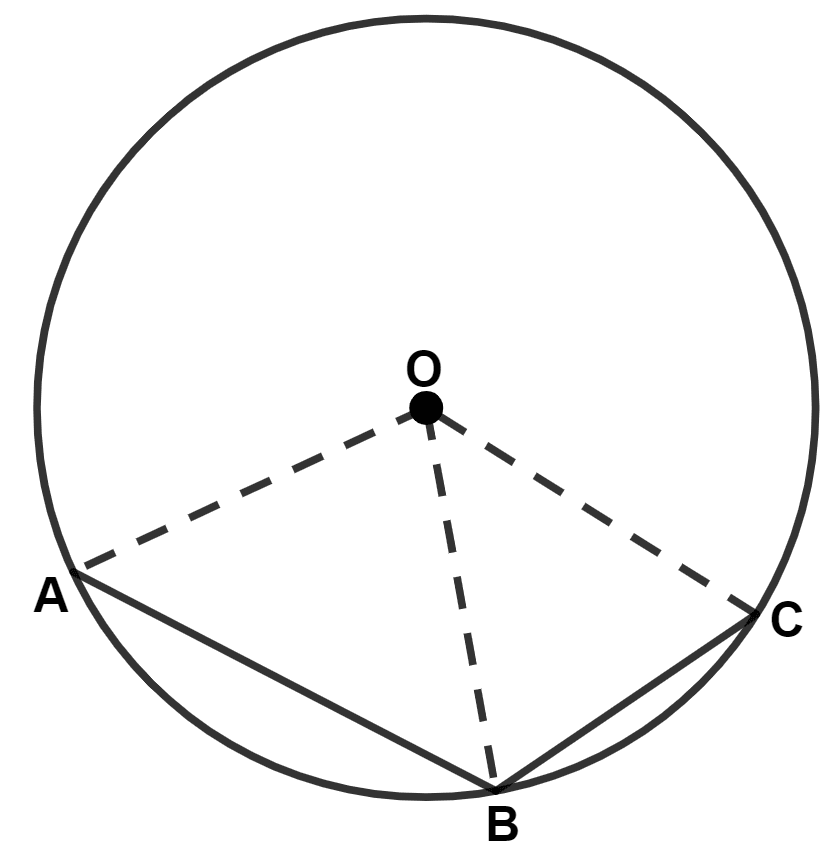
(i) ∠AOB

(ii) ∠BOC

(iii) ∠AOC

(iv) ∠OBA

(v) ∠OBC

(vi) ∠ABC

Answer

We know that,

The angle subtended by each side of an n-sided regular polygon at the center of circle = $\dfrac{360°}{n}$.

(i) Given,

AB is the side of the pentagon.

Angle subtended by each arm of the pentagon at the center of the circle is $\dfrac{360°}{5}$ = 72°.

Hence, ∠AOB = 72°.

(ii) Given,

BC is the side of the hexagon.

Angle subtended by each arm of the hexagon at the center of the circle is $\dfrac{360°}{6}$ = 60°.

Hence, ∠BOC = 60°.

(iii) From figure,

⇒ ∠AOC = ∠AOB + ∠BOC = 72° + 60° = 132°.

Hence, ∠AOC = 132°.

(iv) In △ OAB,

⇒ OA = OB

⇒ ∠OBA = ∠OAB = x (let) [Angle opposite to equal sides are equal]

By angle sum property of triangle,

⇒ ∠OAB + ∠OBA + ∠AOB = 180°

⇒ x + x + 72° = 180°

⇒ 2x + 72° = 180°

⇒ 2x = 180° - 72°

⇒ 2x = 108°

⇒ x = $\dfrac{108°}{2}$

⇒ x = 54°

⇒ ∠OBA = 54°.

Hence, ∠OBA = 54°.

(v) In △ OBC,

⇒ OC = OB

⇒ ∠OBC = ∠OCB = y (let) [Angle opposite to equal sides are equal]

By angle sum property of triangle,

⇒ ∠OBC + ∠OCB + ∠BOC = 180°

⇒ y + y + 60° = 180°

⇒ 2y + 60° = 180°

⇒ 2y = 180° - 60°

⇒ 2y = 120°

⇒ y = $\dfrac{120°}{2}$

⇒ y = 60°

⇒ ∠OBC = 60°.

Hence, ∠OBC = 60°.

(vi) From figure,

⇒ ∠ABC = ∠OBA + ∠OBC = 54° + 60° = 114°.

Hence, ∠ABC = 114°.

In the given figure, arc AB and arc BC are equal in length.

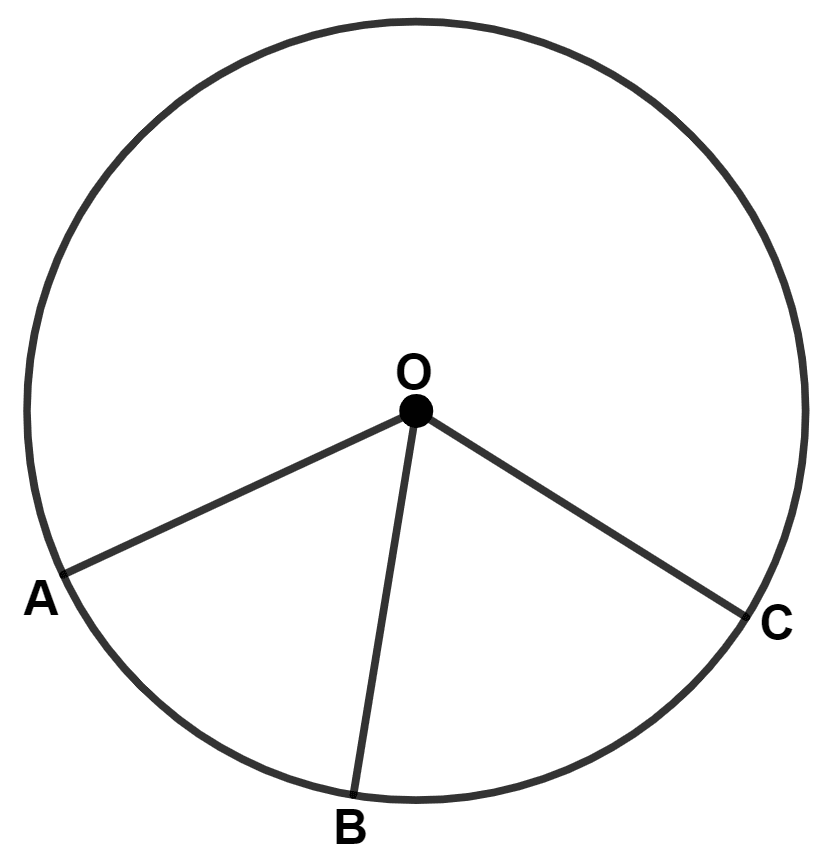
If ∠AOB = 48°, find :

(i) ∠BOC

(ii) ∠OBC

(iii) ∠AOC

(iv) ∠OAC

Answer

(i) We know that,

If two arcs are of a circle are equal, they subtend equal angles at the center.

∴ ∠BOC = ∠AOB = 48°.

Hence, ∠BOC = 48°.

(ii) Join BC.

In △ OBC,

⇒ OC = OB (Radius of same circle)

⇒ ∠OBC = ∠OCB = y (let) [Angle opposite to equal sides are equal]

By angle sum property of triangle,

⇒ ∠OBC + ∠OCB + ∠BOC = 180°

⇒ y + y + 48° = 180°

⇒ 2y + 48° = 180°

⇒ 2y = 180° - 48°

⇒ 2y = 132°

⇒ y = $\dfrac{132°}{2}$

⇒ y = 66°

⇒ ∠OBC = 66°.

Hence, ∠OBC = 66°.

(iii) From figure,

⇒ ∠AOC = ∠AOB + ∠BOC = 48° + 48° = 96°.

Hence, ∠AOC = 96°.

(iv) Join AC.

In △ AOC,

⇒ OC = OA (Radius of same circle)

⇒ ∠OAC = ∠OCA = x (let) [Angle opposite to equal sides are equal]

By angle sum property of triangle,

⇒ ∠OAC + ∠OCA + ∠AOC = 180°

⇒ x + x + 96° = 180°

⇒ 2x + 96° = 180°

⇒ 2x = 180° - 96°

⇒ 2x = 84°

⇒ x = $\dfrac{84°}{2}$

⇒ x = 42°

⇒ ∠OAC = 42°.

Hence, ∠OAC = 42°.

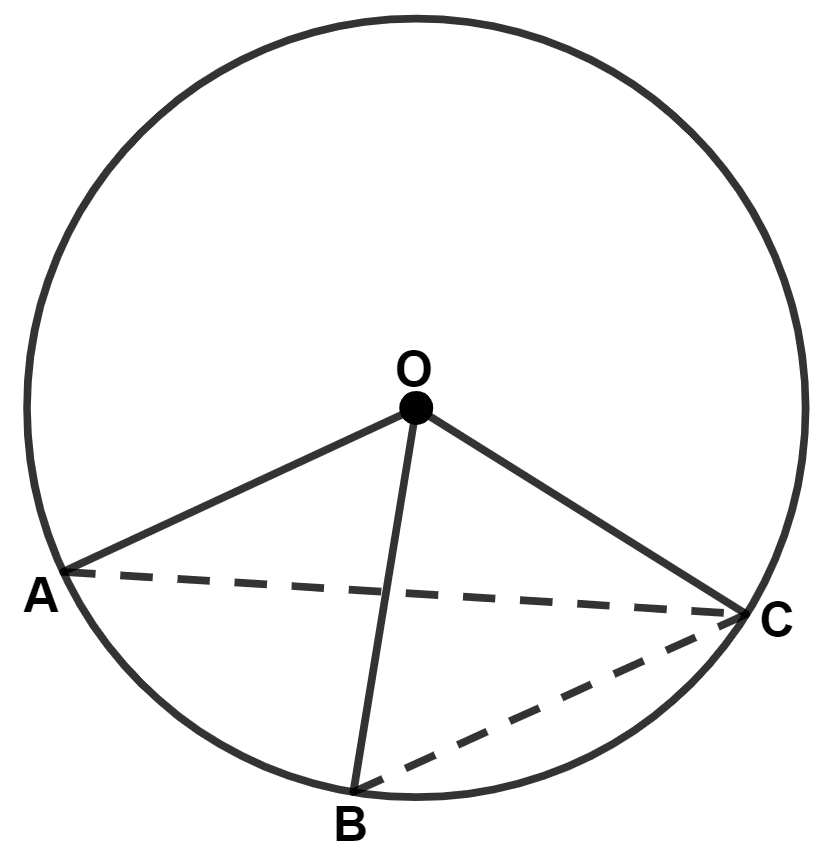
In the given figure, the lengths of arcs AB and BC are in the ratio 3 : 2.

If ∠AOB = 96°, find :

(i) ∠BOC

(ii) ∠ABC

Answer

(i) We know that,

Ratio of the angles subtended by the chords on the center is equal to the ratio of the chords.

$\Rightarrow \dfrac{∠AOB}{∠BOC} = \dfrac{AB}{BC} \\[1em] \Rightarrow \dfrac{96°}{∠BOC} = \dfrac{3}{2} \\[1em] \Rightarrow ∠BOC = \dfrac{2}{3} \times 96° = 2 \times 32° = 64°.$

Hence, ∠BOC = 64°.

(ii) In △ AOB,

⇒ OA = OB (Radius of same circle)

⇒ ∠OBA = ∠OAB = x (let) [Angle opposite to equal sides are equal]

By angle sum property of triangle,

⇒ ∠OAB + ∠OBA + ∠AOB = 180°

⇒ x + x + 96° = 180°

⇒ 2x + 96° = 180°

⇒ 2x = 180° - 96°

⇒ 2x = 84°

⇒ x = $\dfrac{84°}{2}$

⇒ x = 42°

⇒ ∠OBA = 42°.

In △ BOC,

⇒ OB = OC (Radius of same circle)

⇒ ∠OCB = ∠OBC = y (let) [Angle opposite to equal sides are equal]

By angle sum property of triangle,

⇒ ∠OCB + ∠OBC + ∠BOC = 180°

⇒ y + y + 64° = 180°

⇒ 2y + 64° = 180°

⇒ 2y = 180° - 64°

⇒ 2y = 116°

⇒ y = $\dfrac{116°}{2}$

⇒ y = 58°

⇒ ∠OBC = 58°.

From figure,

⇒ ∠ABC = ∠OBA + ∠OBC = 42° + 58° = 100°.

Hence, ∠ABC = 100°.

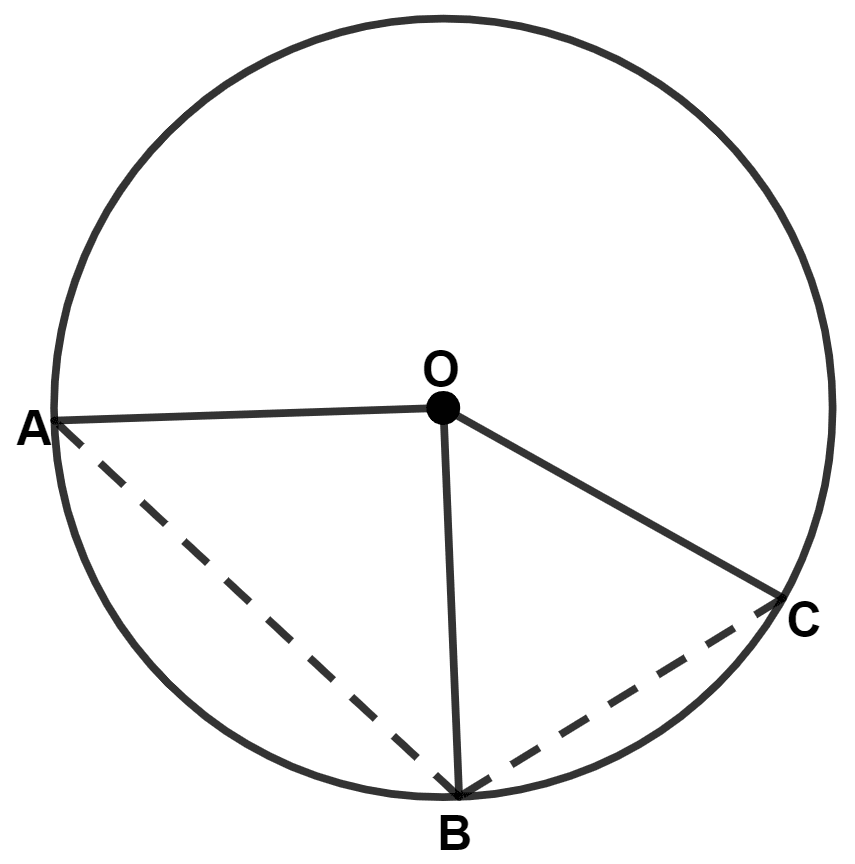
In the given figure, AB = BC = DC and ∠AOB = 50°. Find :

(i) ∠AOC

(ii) ∠AOD

(iii) ∠BOD

(iv) ∠OAC

(v) ∠ODA

Answer

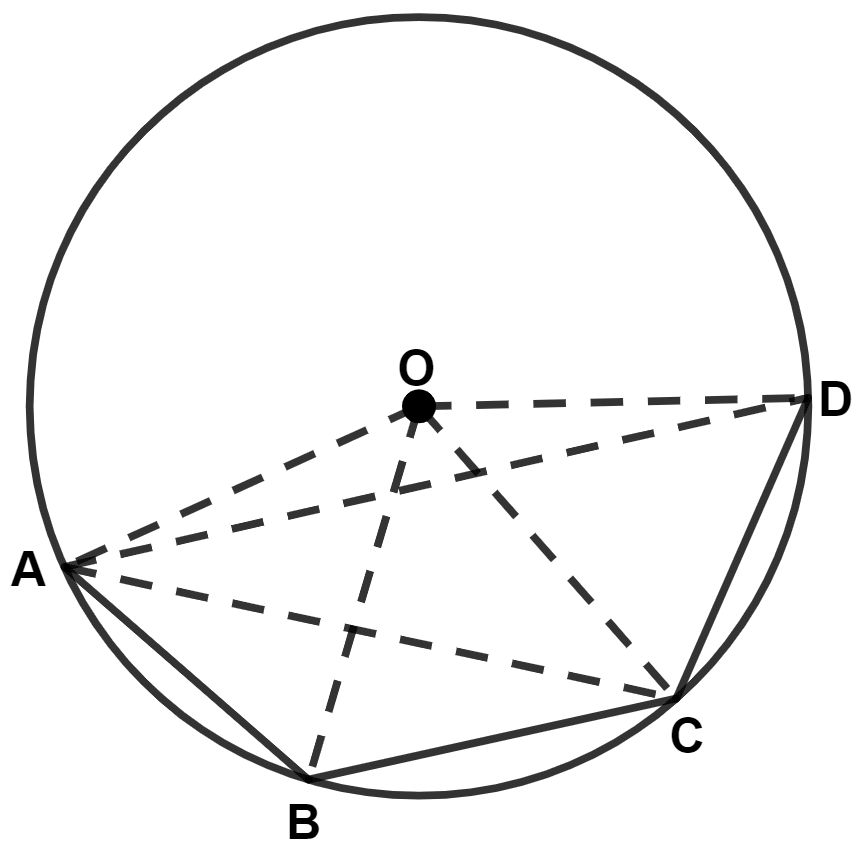
(i) We know that,

Equal chords subtend equal angles at the center.

Since, AB = BC = DC

∴ ∠BOC = ∠AOB = 50°.

From figure,

⇒ ∠AOC = ∠BOC + ∠AOB = 50° + 50° = 100°.

Hence, ∠AOC = 100°.

(ii) We know that,

Equal chords subtend equal angles at the center.

Since, AB = BC = DC

∴ ∠DOC = ∠AOB = 50°.

From figure,

⇒ ∠AOD = ∠AOC + ∠DOC = 100° + 50° = 150°.

Hence, ∠AOD = 150°.

(iii) From figure,

⇒ ∠BOD = ∠BOC + ∠DOC = 50° + 50° = 100°.

Hence, ∠BOD = 100°.

(iv) Join AC.

In △ AOC,

⇒ OA = OC (Radius of same circle)

⇒ ∠OAC = ∠OCA = y (let) [Angle opposite to equal sides are equal]

By angle sum property of triangle,

⇒ ∠OAC + ∠OCA + ∠AOC = 180°

⇒ y + y + 100° = 180°

⇒ 2y + 100° = 180°

⇒ 2y = 180° - 100°

⇒ 2y = 80°

⇒ y = $\dfrac{80°}{2}$

⇒ y = 40°

⇒ ∠OAC = 40°.

Hence, ∠OAC = 40°.

(v) Join AD.

In △ OAD,

⇒ OA = OD (Radius of same circle)

⇒ ∠ODA = ∠OAD = x (let) [Angle opposite to equal sides are equal]

By angle sum property of triangle,

⇒ ∠OAD + ∠ODA + ∠AOD = 180°

⇒ x + x + 150° = 180°

⇒ 2x + 150° = 180°

⇒ 2x = 180° - 150°

⇒ 2x = 30°

⇒ x = $\dfrac{30°}{2}$

⇒ x = 15°

⇒ ∠ODA = 15°.

Hence, ∠OAD = 15°.

In the given figure, AB is a side of a regular hexagon and AC is a side of regular eight sided polygon. Find :

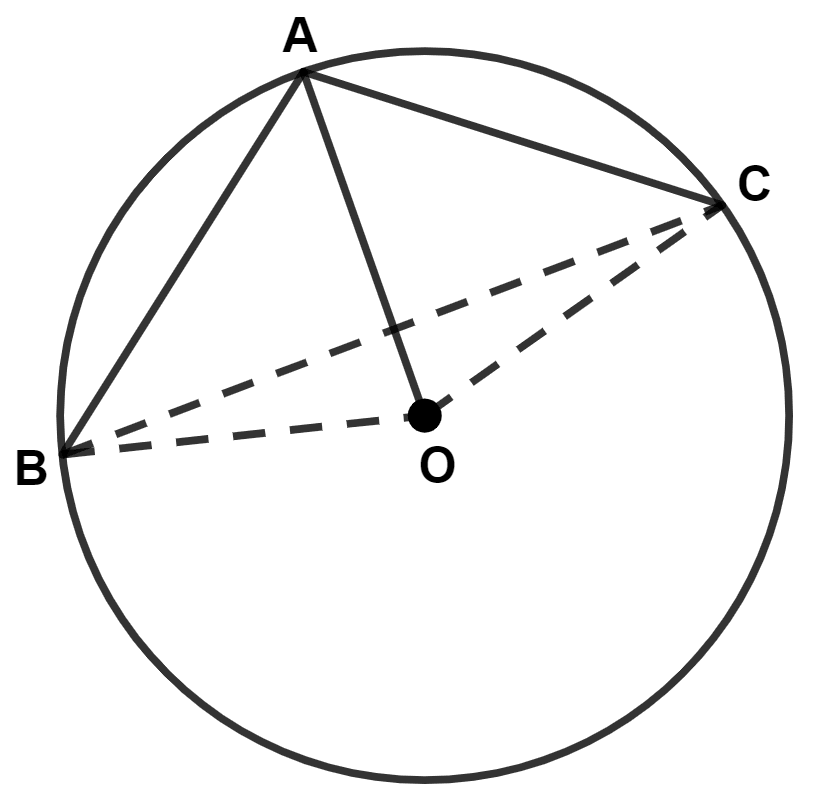
(i) ∠AOB

(ii) ∠AOC

(iii) ∠BOC

(iv) ∠OBC

Answer

We know that,

The angle subtended by each side of an n-sided regular polygon at the center of circle = $\dfrac{360°}{n}$.

(i) Given,

AB is the side of the hexagon.

Angle subtended by each arm of the hexagon at the center of the circle is $\dfrac{360°}{6}$ = 60°.

Hence, ∠AOB = 60°.

(ii) Given,

AC is the side of a regular eight sided polygon.

Angle subtended by each arm of the regular eight sided polygon at the center of the circle is $\dfrac{360°}{8}$ = 45°.

Hence, ∠AOC = 45°.

(iii) From figure,

⇒ ∠BOC = ∠AOB + ∠AOC = 60° + 45° = 105°.

Hence, ∠BOC = 105°.

(iv) In △ OBC,

⇒ OB = OC (Radius of same circle)

⇒ ∠OBC = ∠OCB = x (let) [Angle opposite to equal sides are equal]

By angle sum property of triangle,

⇒ ∠OBC + ∠OCB + ∠BOC = 180°

⇒ x + x + 105° = 180°

⇒ 2x + 105° = 180°

⇒ 2x = 180° - 105°

⇒ 2x = 75°

⇒ x = $\dfrac{75°}{2}$

⇒ x = 37.5°

⇒ ∠OBC = 37.5°.

Hence, ∠OBC = 37.5°=37°30'.

In the given figure, O is the centre of the circle and the length of arc AB is twice the length of arc BC.

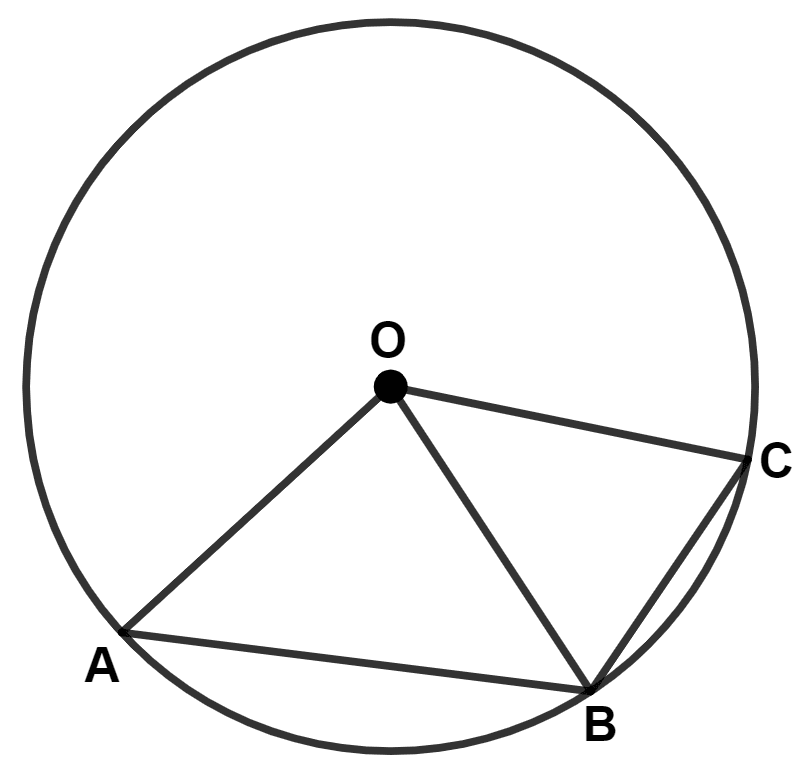
If ∠AOB = 100°, find :

(i) ∠BOC

(ii) ∠OAC

Answer

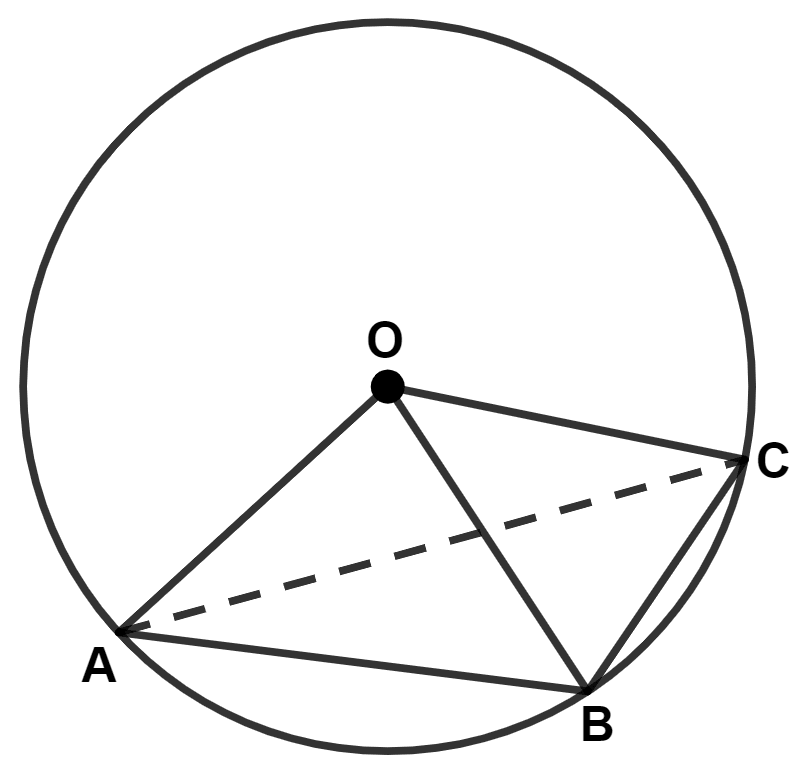
(i) We know that,

Ratio of the angles subtended by the chords on the center is equal to the ratio of the chords.

$\Rightarrow \dfrac{∠AOB}{∠BOC} = \dfrac{AB}{BC} \\[1em] \Rightarrow \dfrac{100°}{∠BOC} = \dfrac{2}{1} \\[1em] \Rightarrow ∠BOC = \dfrac{1}{2} \times 100° = 50°.$

Hence, ∠BOC = 50°.

(ii) Join AC.

From figure,

⇒ ∠AOC = ∠AOB + ∠BOC = 100° + 50° = 150°.

In △ OAC,

⇒ OA = OC (Radius of same circle)

⇒ ∠OCA = ∠OAC = x (let) [Angle opposite to equal sides are equal]

By angle sum property of triangle,

⇒ ∠OAC + ∠OCA + ∠AOC = 180°

⇒ x + x + 150° = 180°

⇒ 2x + 150° = 180°

⇒ 2x = 180° - 150°

⇒ 2x = 30°

⇒ x = $\dfrac{30°}{2}$

⇒ x = 15°

⇒ ∠OAC = 15°.

Hence, ∠OAC = 15°.

In a circle with center at point O, chord AB is a side of a square and chord BC is a side of regular hexagon. Then angle AOC is equal to:

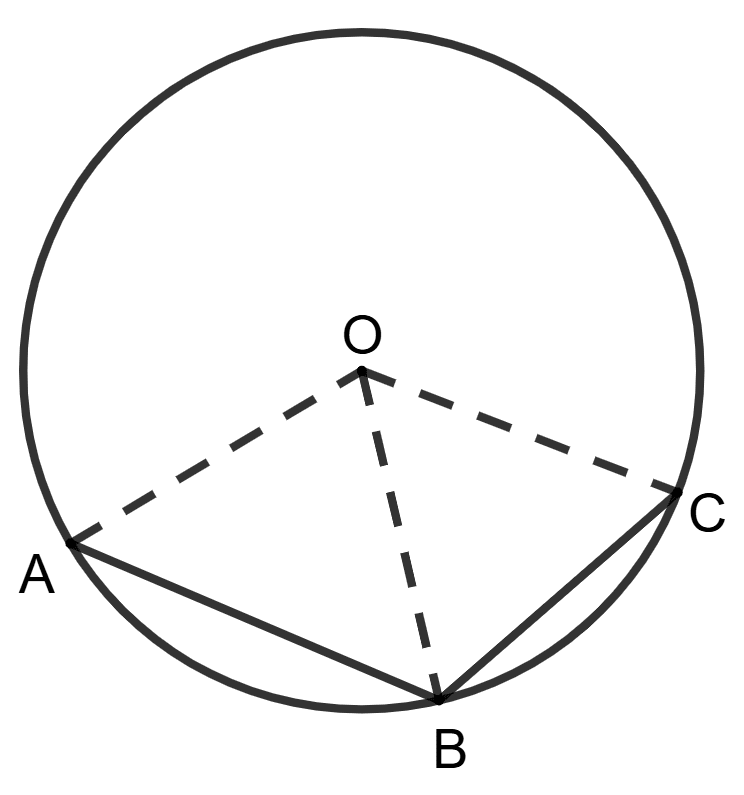
1. 120°

2. 150°

3. 90°

4. none of these

Answer

We know that,

The angle subtended by each side of an n-sided regular polygon at the center of circle = $\dfrac{360°}{n}$

Given, AB is the side of the square.

Angle subtended by each arm of the square at the center of the circle is $\dfrac{360°}{4}$ = 90°.

⇒ ∠AOB = 90°.

BC is the side of the hexagon.

Angle subtended by each arm of the hexagon at the center of the circle is $\dfrac{360°}{6}$ = 60°.

⇒ ∠BOC = 60°.

From figure,

∠AOC = ∠AOB + ∠BOC = 90° + 60° = 150°.

Hence, option 2 is the correct option.

AB (= 20 cm) is diameter of the given circle and AP (= 16 cm). The distance of chord AP from center O is:

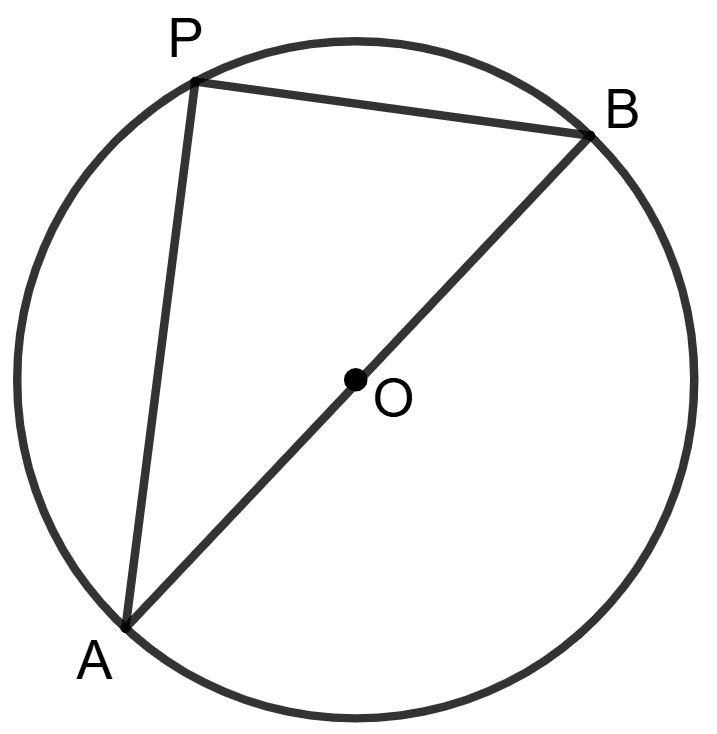
1. 12 cm

2. 18 cm

3. 9 cm

4. 6 cm

Answer

Given:

Length of the chord AP = 16 cm.

Diameter of the circle AB = 20 cm.

Radius of the circle, r = $\dfrac{20}{2}$ = 10 cm.

Construction: Draw OC ⊥ AP, where O is the center of the circle.

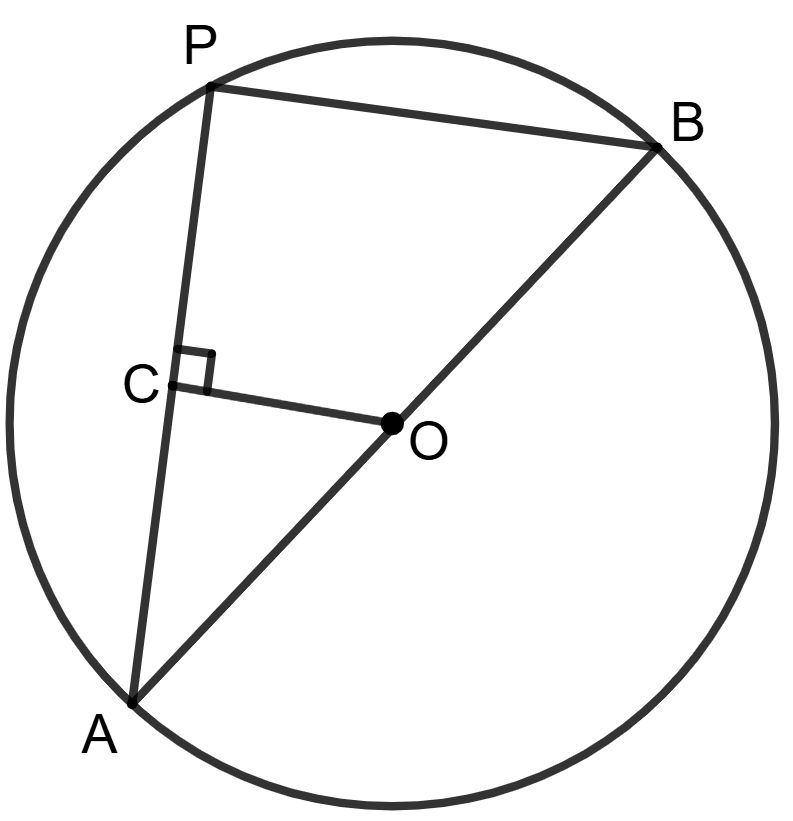
Since, perpendicular drawn from the center of a circle to a chord bisects it.

∴ OC bisects AP

AC = $\dfrac{1}{2}$ x AP = $\dfrac{1}{2}$ x 16 = 8 cm.

In Δ OAC, ∠C = 90°

Using Pythagoras theorem,

∴ OA² = OC² + AC²

⇒ (10)² = OC² + (8)²

⇒ 100 = OC² + 64

⇒ OC² = 100 - 64

⇒ OC² = 36

⇒ OC = ​$\sqrt{36}$

⇒ OC = 6 cm.

So, the distance of the chord from the center of the circle is 6 cm.

Hence, option 4 is the correct option.

Given O is center of the circle with chord AB = 8 cm, OA = 5 cm and OD ⊥ AB. The length of CD is :

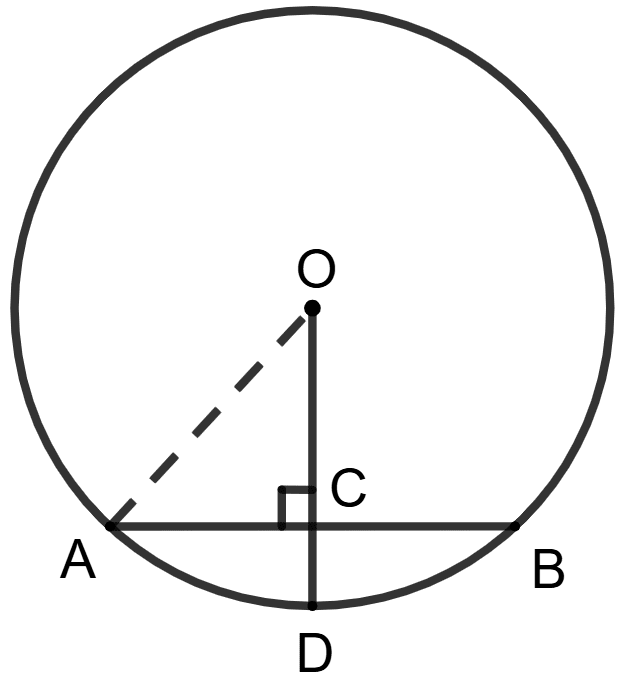
1. 3 cm

2. 5 cm

3. 2 cm

4. none of these

Answer

Given, the length of chord AB = 8 cm.

OD ⊥ AB.

Since, perpendicular drawn from the center of a circle to a chord bisects it.

∴ OC bisects AB.

⇒ AC = $\dfrac{AB}{2} = \dfrac{8}{2}$ = 4 cm

Radius of the circle, OA = 5 cm.

In Δ OAC, ∠C = 90°

Using Pythagoras theorem,

∴ OA² = OC² + AC²

⇒ 5² = OC² + 4²

⇒ 25 = OC² + 16

⇒ OC² = 25 - 16

⇒ OC² = 9

⇒ OC = $\sqrt{9}$

⇒ OC = 3 cm

Since, OD = OA (Radii of the circle)

From figure,

⇒ CD = OD - OC = 5 - 3 = 2 cm.

Hence, option 3 is the correct option.

AB and CD are the chords of a circle with centre O, ∠AOB = 60° and angles ∠COD = 45°; the ratio between the length of the chords AB and CD is

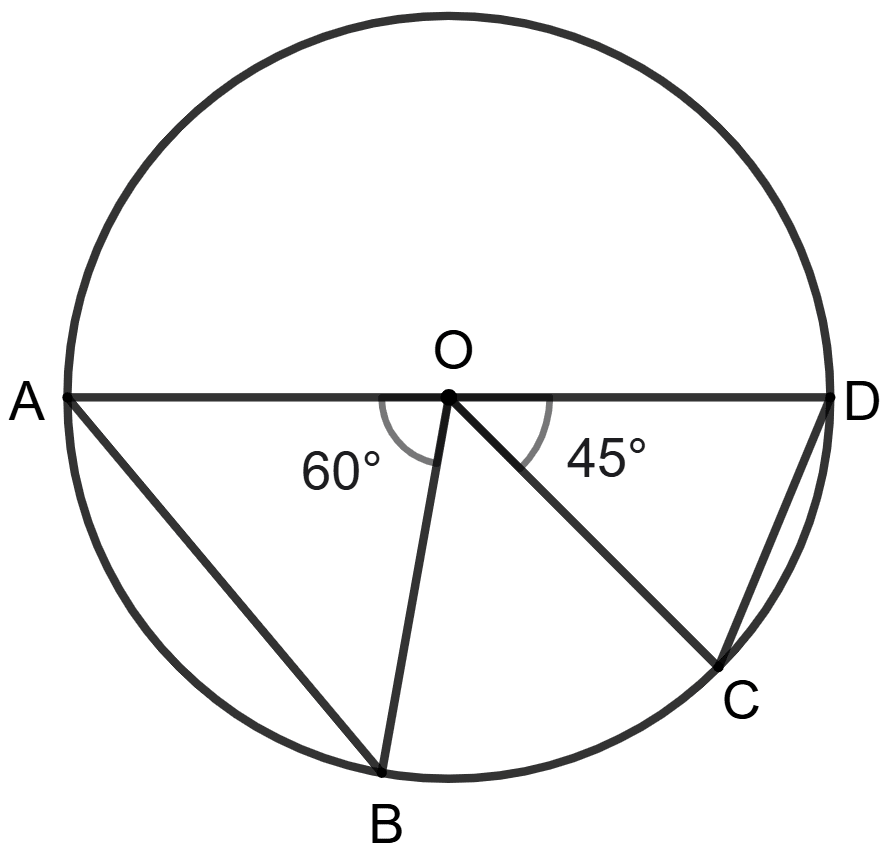
1. 3 : 4

2. 4 : 3

3. 7 : 4

4. 7 : 3

Answer

We know that,

Ratio of the angles subtended by the chords on the center is equal to the ratio of the length of the chords.

$\therefore \dfrac{\text{∠AOB}}{\text{∠COD}} = \dfrac{\text{AB}}{\text{CD}} \\[1em] \Rightarrow \dfrac{60°}{45°} = \dfrac{\text{AB}}{\text{CD}} \\[1em] \Rightarrow \dfrac{4}{3} = \dfrac{\text{AB}}{\text{CD}}$

So, ratio between the length of the chords AB and CD is 4 : 3.

Hence, option 2 is the correct option.

Statement 1: O and O' are centres of two equal circles and ABCD is a straight line.

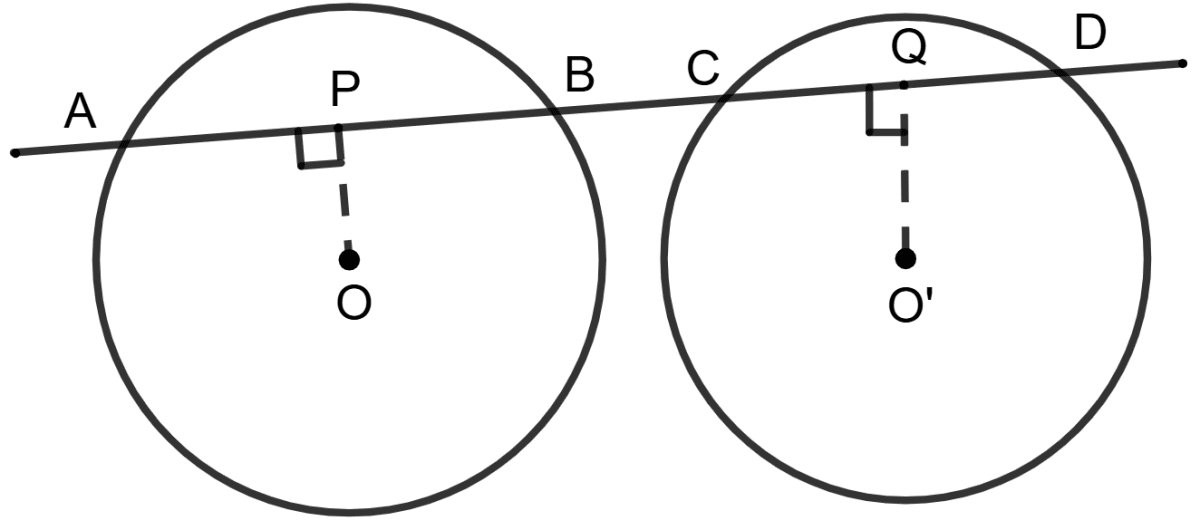
Statement 2: If OP ⊥ AB, O'Q ⊥ CD and O'Q is greater than OP, then CD > AB.

1. Both the statements are true.

2. Both the statements are false.

3. Statement 1 is true, and statement 2 is false.

4. Statement 1 is false, and statement 2 is true.

Answer

O and O' are centres of two equal circles means they are having same radius.

The points A, B, C and D are shown aligned horizontally forming a single, continuous line.

∴ Statement 1 is true.

According to fundamental property of a circle, in two same circles, the chord that is farther from the center is shorter, and the chord that is closer to the center is longer.

Given, OP ⊥ AB, O'Q ⊥ CD and O'Q > OP.

⇒ CD < AB

∴ Statement 2 is false.

∴ Statement 1 is true, and statement 2 is false.

Hence, option 3 is the correct option.

Statement 1: In a circle with center O, chord AB : chord BC = 1 : 3. If angle AOC is 160° ⇒ angle BOC = 120°.

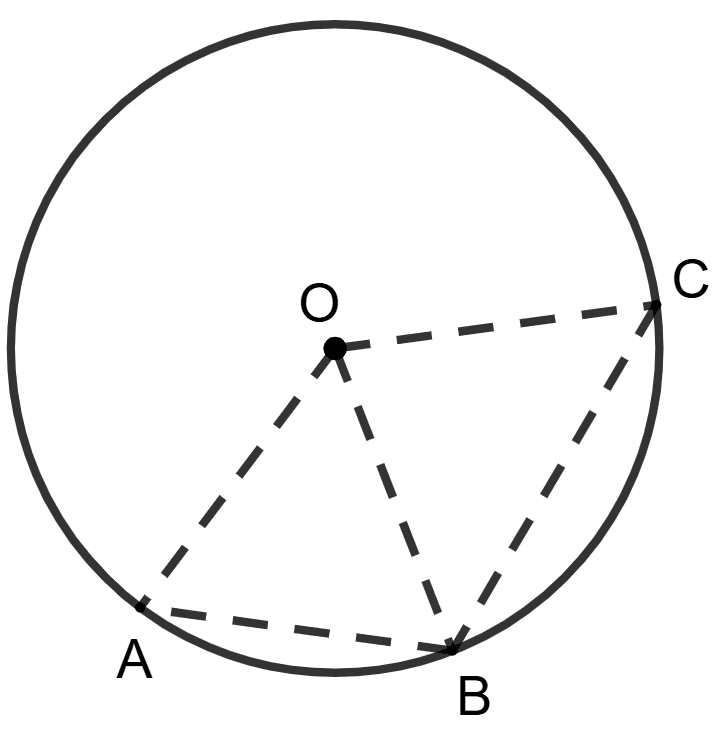
Statement 2: AB : BC = 1 : 3

⇒ ∠AOC = 3 x ∠AOB

1. Both the statements are true.

2. Both the statements are false.

3. Statement 1 is true, and statement 2 is false.

4. Statement 1 is false, and statement 2 is true.

Answer

We know that,

Ratio of the angles subtended by the chords on the center is equal to the ratio of the length of the chords.

$\therefore \dfrac{\text{∠AOB}}{\text{∠BOC}} = \dfrac{\text{AB}}{\text{BC}}\\[1em] \Rightarrow \dfrac{\text{∠AOB}}{\text{∠BOC}} = \dfrac{1}{3}\\[1em] \Rightarrow 3 \times \text{∠AOB} = \text{∠BOC}.$

So, statement 2 is false.

From figure,

⇒ ∠AOC = ∠AOB + ∠BOC

⇒ 160° = ∠AOB + 3∠AOB

⇒ 160° = 4∠AOB

⇒ ∠AOB = $\dfrac{160°}{4}$

⇒ ∠AOB = 40° and, ∠BOC = 3 x 40° = 120°.

So, statement 1 is true.

∴ Statement 1 is true, and statement 2 is false.

Hence, option 3 is the correct option.

Assertion (A): In the given figure, chord AB = 8 cm, diameter CD = 20 cm, then length of OP = 10 cm.

Reason (R): OP = $\sqrt{OA^2 - AP^2}$

and CP = OC + OP

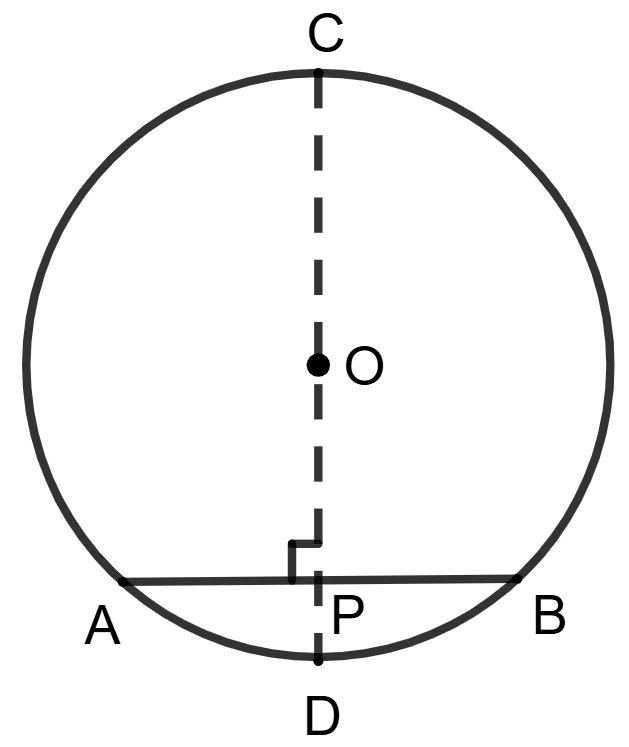
1. A is true, but R is false.

2. A is false, but R is true.

3. Both A and R are true, and R is the correct reason for A.

4. Both A and R are true, and R is the incorrect reason for A.

Answer

Given:

Length of the chord AB = 8 cm.

Diameter of the circle CD = 20 cm.

As we know that the radius of a circle is exactly half its diameter.

Radius of the circle, r = $\dfrac{20}{2}$ = 10 cm.

Construction: Join OA.

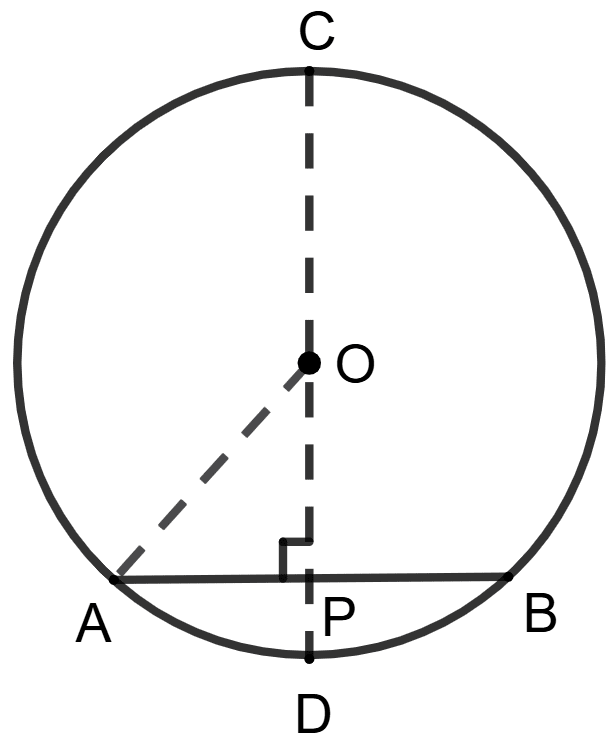
OP ⊥ AB.

Since, perpendicular drawn from the center of a circle to a chord bisects it.

∴ OP bisects AB

⇒ AP = $\dfrac{1}{2}$ x AB = $\dfrac{1}{2}$ x 8 = 4 cm

⇒ OA = 10 cm

In Δ OAP, ∠P = 90°

Using Pythagoras theorem,

∴ OA² = OP² + AP²

⇒ OP² = OA² - AP²

$\Rightarrow OP = \sqrt{OA^2 - AP^2}\\[1em] \Rightarrow OP = \sqrt{10^2 - 4^2}\\[1em] \Rightarrow OP = \sqrt{100 - 16}\\[1em] \Rightarrow OP = \sqrt{84}\\[1em] \Rightarrow OP = 2\sqrt{21} \text{ cm}$

∴ Assertion (A) is false.

From figure, CP = CO + OP = 10 + 2 $\sqrt{21}$ cm

∴ Reason (R) is true.

∴ A is false, but R is true.

Hence, option 2 is the correct option.

The figure, given below, shows a circle with center O in which diameter AB bisects the chord CD at point E. If CE = ED = 8 cm and EB = 4 cm, find the radius of the circle.

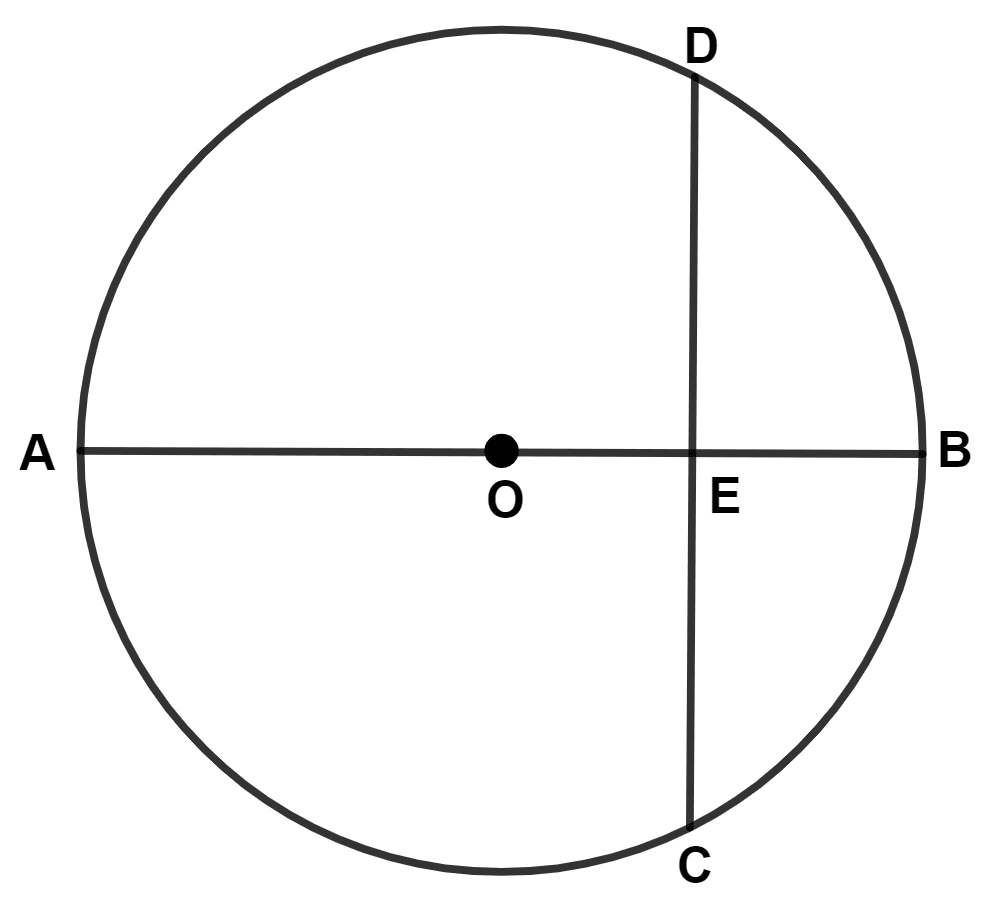
Answer

Join OD.

Let radius of circle be x cm.

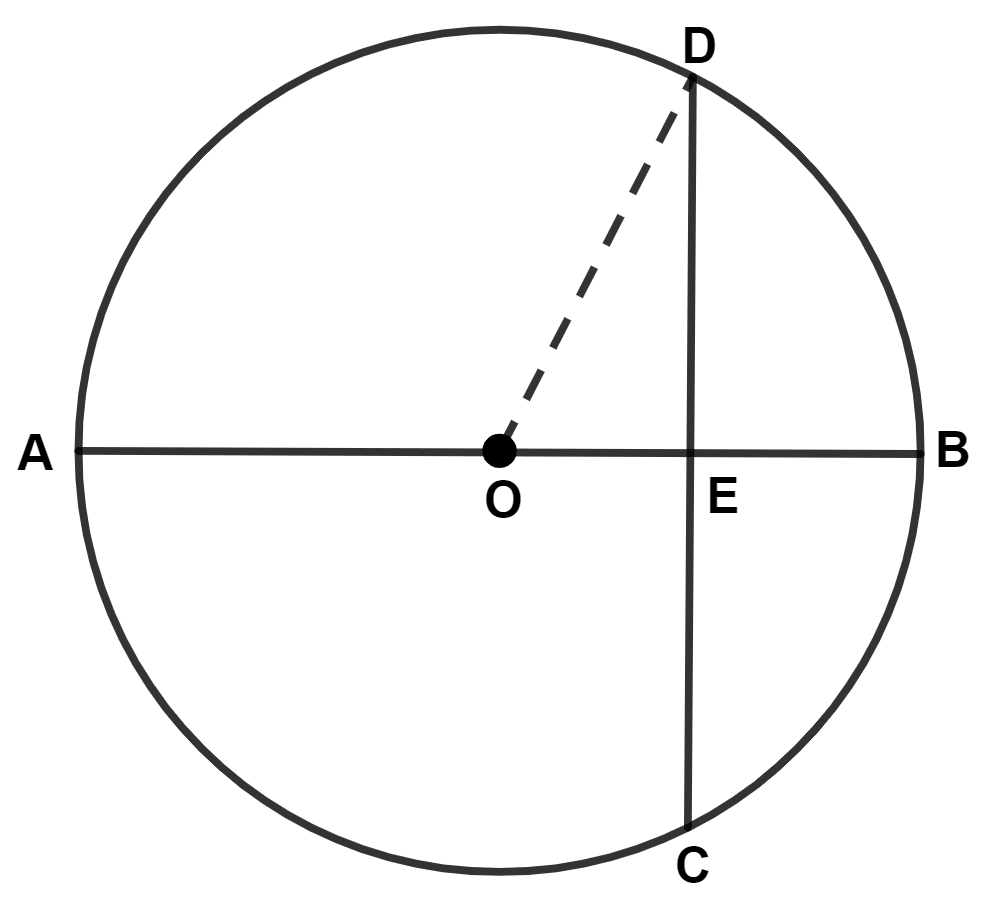
From figure,

Radius = OB = OD = x cm

⇒ OE = OB - EB = (x - 4) cm.

We know that,

A straight line drawn from the center of a circle to bisect a chord, is perpendicular to the chord.

∴ OE ⊥ CD

In right-angled triangle OED,

By pythagoras theorem,

⇒ Hypotenuse² = Perpendicular² + Base²

⇒ OD² = OE² + ED²

⇒ x² = (x - 4)² + 8²

⇒ x² = x² + 4² - 2 × x × 4 + 64

⇒ x² = x² + 16 - 8x + 64

⇒ x² - x² + 8x = 80

⇒ 8x = 80

⇒ x = $\dfrac{80}{8}$ = 10 cm.

Hence, radius of circle = 10 cm.

In the given figure, O is the center of the circle. AB and CD are two chords of the circle. OM is perpendicular to AB and ON is perpendicular to CD. AB = 24 cm, OM = 5 cm, ON = 12 cm. Find the :

(i) the radius of the circle

(ii) length of chord CD.

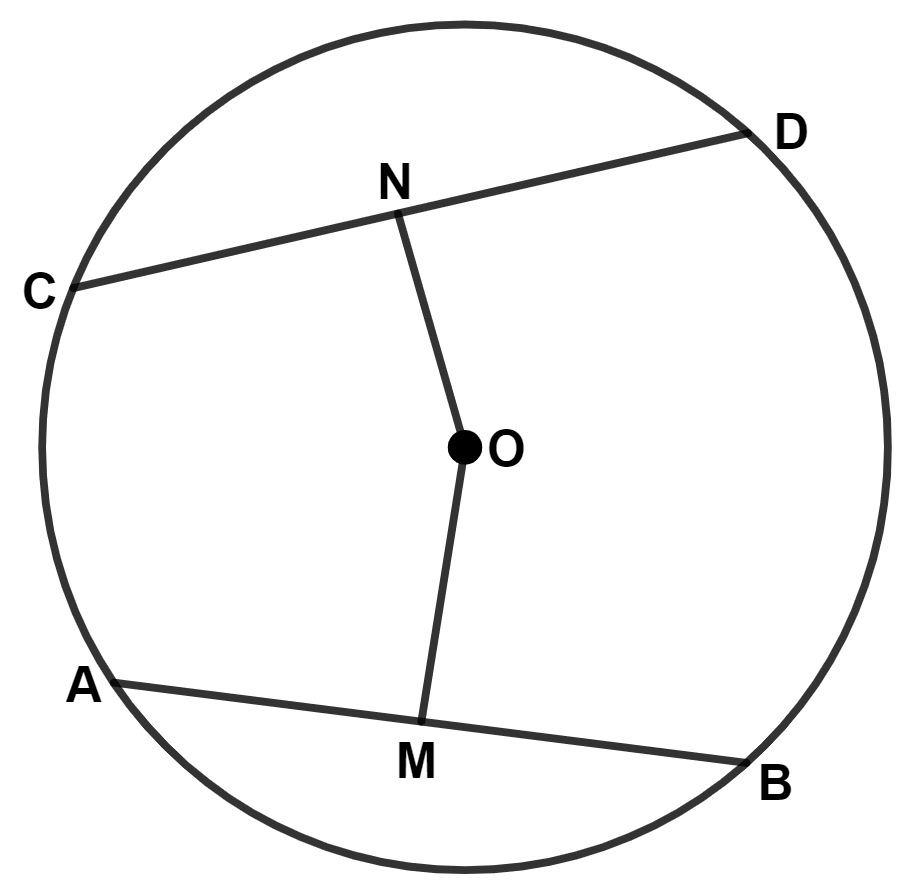
Answer

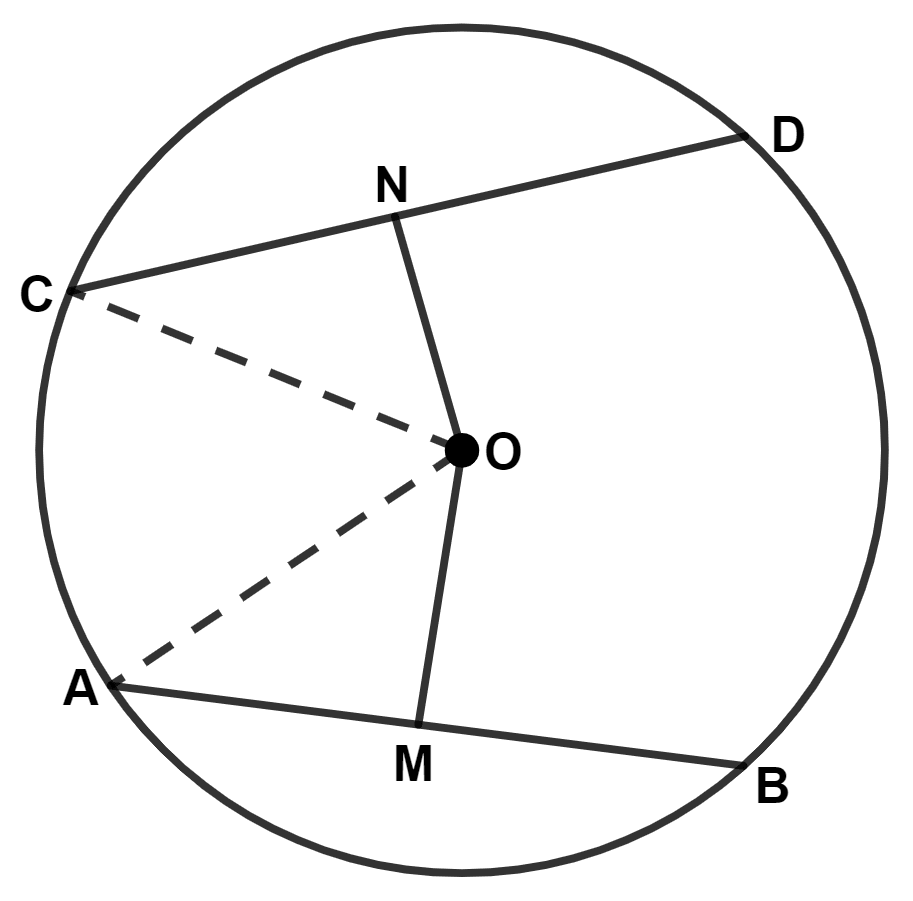
(i) Join OA.

We know that,

Perpendicular from center to chord, bisects the chord.

As, OM ⊥ AB

∴ AM = $\dfrac{AB}{2} = \dfrac{24}{2}$ = 12 cm.

In △ OAM,

By pythagoras theorem,

⇒ Hypotenuse² = Perpendicular² + Base²

⇒ OA² = OM² + AM²

⇒ OA² = 5² + 12²

⇒ OA² = 25 + 144

⇒ OA² = 169

⇒ OA = $\sqrt{169}$ = 13 cm.

Hence the radius of circle = 13 cm.

(ii) We know that,

Perpendicular from center of the circle to chord, bisects the chord.

As, ON ⊥ CD

∴ CN = $\dfrac{CD}{2}$

⇒ CD = 2CN .............(1)

Join OC.

In △ OCN,

By pythagoras theorem,

⇒ Hypotenuse² = Perpendicular² + Base²

⇒ OC² = ON² + NC²

⇒ 13² = 12² + CN²

⇒ CN² = 13² - 12²

⇒ CN² = 169 - 144

⇒ CN² = 25

⇒ CN = $\sqrt{25}$ = 5 cm.

Substituting value of CN in equation (1), we get :

⇒ CD = 2 × 5 = 10 cm.

Hence, length of chord CD = 10 cm.

AB and CD are two equal chords of a circle with center O which intersect each other at right angle at point P. If OM ⊥ AB and ON ⊥ CD; show that OMPN is a square.

Answer

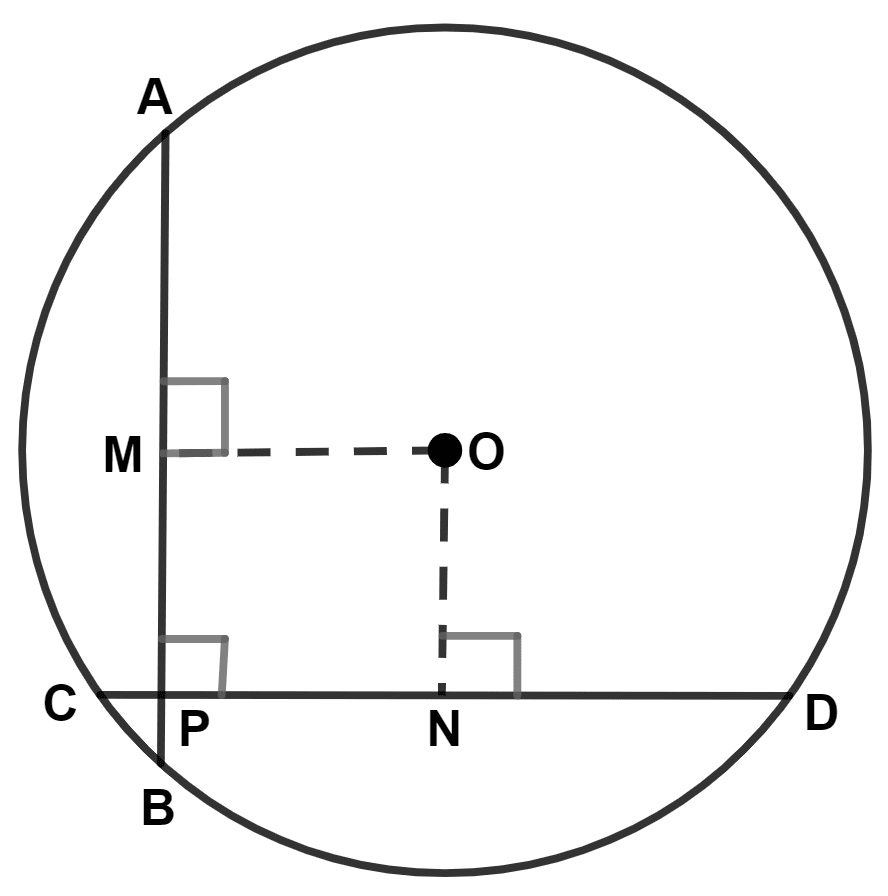
Since, OM ⊥ AB and ON ⊥ CD.

∴ ∠OMP = ∠ONP = 90°.

Given,

AB and CD intersect at right angle.

∴ ∠MPN = 90°.

We know that,

Sum of angles of quadrilateral equal to 360°.

∴ ∠OMP + ∠ONP + ∠MPN + ∠MON = 360°

⇒ 90° + 90° + 90° + ∠MON = 360°

⇒ 270° + ∠MON = 360°

⇒ ∠MON = 360° - 270° = 90°.

Given,

AB = CD

We know that,

Equal chords are equidistant from the center.

∴ OM = ON = x (let) ............(1)

Since,

⇒ AB ⊥ CD and ON ⊥ CD

∴ AB || ON

∴ MP || ON.

⇒ OM ⊥ AB and CD ⊥ AB

∴ OM || CD

∴ OM || PN.

Since, in quadrilateral OMPN opposite sides are parallel.

∴ OMPN is parallelogram.

We know that,

Opposite sides of parallelogram are equal.

∴ MP = ON = x and OM = PN = x

∴ MP = ON = OM = PN.

Since, all sides of quadrilateral OMPN are equal and each interior angle to 90°.

Hence, proved that OMPN is a square.

The radius of a circle is 13 cm and the length of one of its chords is 24 cm. Find the distance of the chord from the centers.

Answer

Let AB be the chord of the circle with center O. Draw OC ⊥ AB.

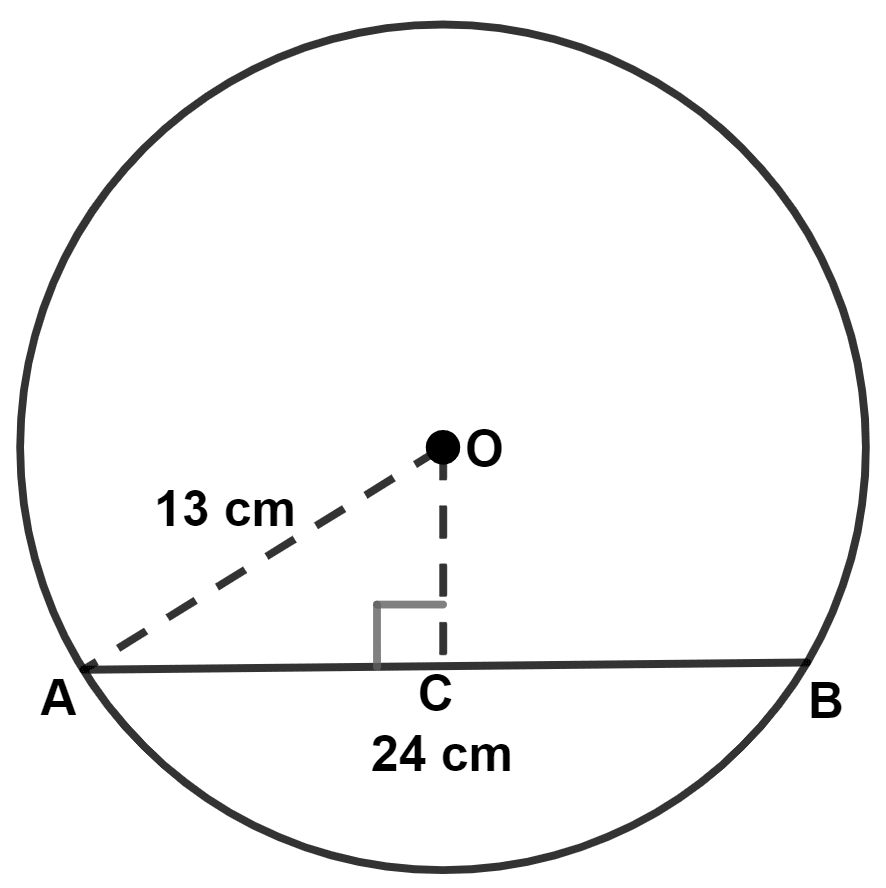
We know that,

Perpendicular from the center of circle to the chord, bisects the chord.

∴ AC = $\dfrac{AB}{2} = \dfrac{24}{2}$ = 12 cm.

In right-angled triangle OAC,

⇒ OA² = OC² + AC²

⇒ 13² = OC² + 12²

⇒ 169 = OC² + 144

⇒ OC² = 169 - 144

⇒ OC² = 25

⇒ OC = $\sqrt{25}$ = 5 cm.

Hence, the distance of the chord from the center = 5 cm.

Prove that equal chords of congruent circles subtend equal angles at their centers.

Answer

We know that,

Congruent circles have equal radius.

Let there be two congruent circles with center O and O' and radius equal to r units.

Let there be two equal chords AB and CD.

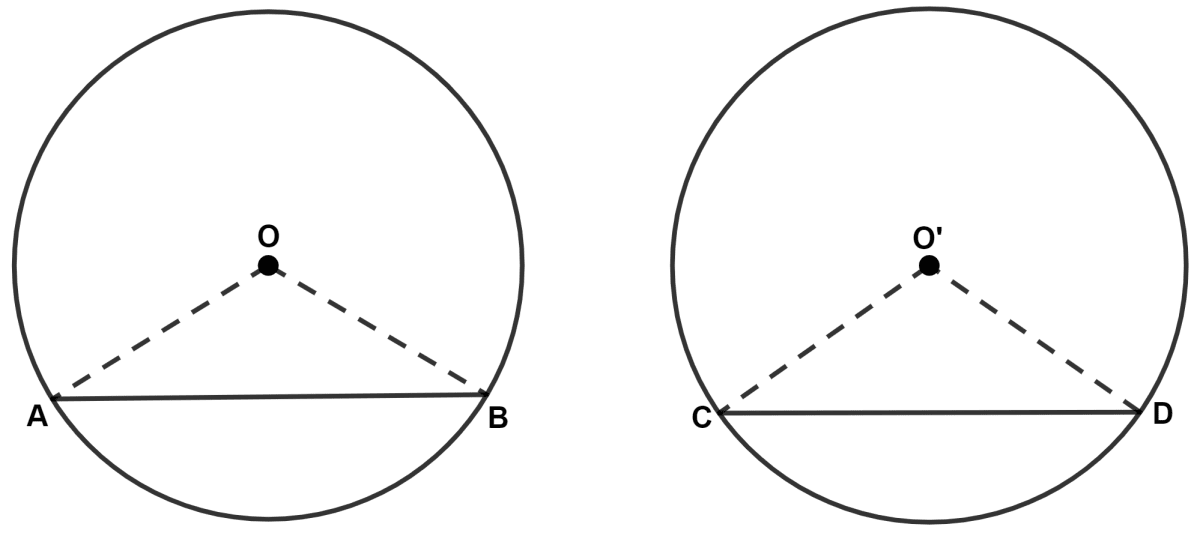
In △ AOB and △ CO'D,

⇒ OA = O'C (Both equal to r units)

⇒ OB = O'D (Both equal to r units)

⇒ AB = CD (Given)

⇒ △ AOB ≅ △ CO'D (By S.S.S. axiom)

We know that,

Corresponding parts of congruent triangles are equal.

∴ ∠AOB = ∠CO'D.

Hence, proved that equal chords of congruent circles subtend equal angles at their centers.

Draw two circles of different radii. How many points these circles can have in common? What is the maximum number of common points ?

Answer

Let there be two circles of different radii with centers A and C.

There can be four cases with two circles of different radii :

(i) No point of intersection when circles are away from each other.

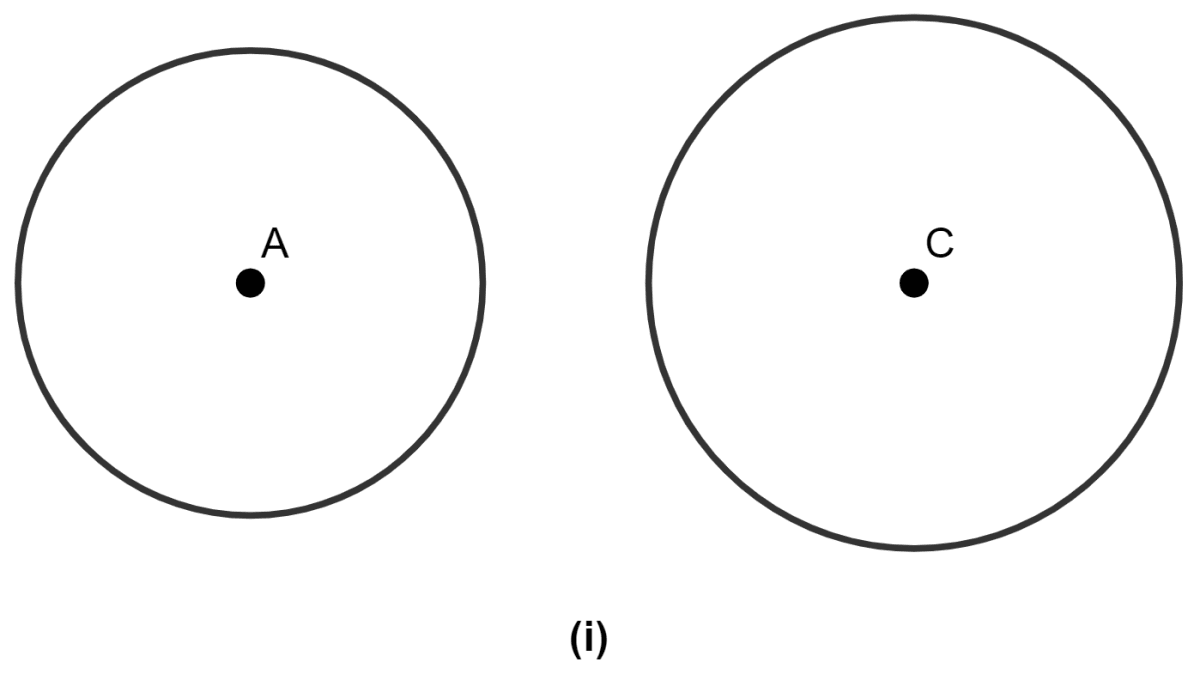
(ii) One point of intersection when circles touch each other.

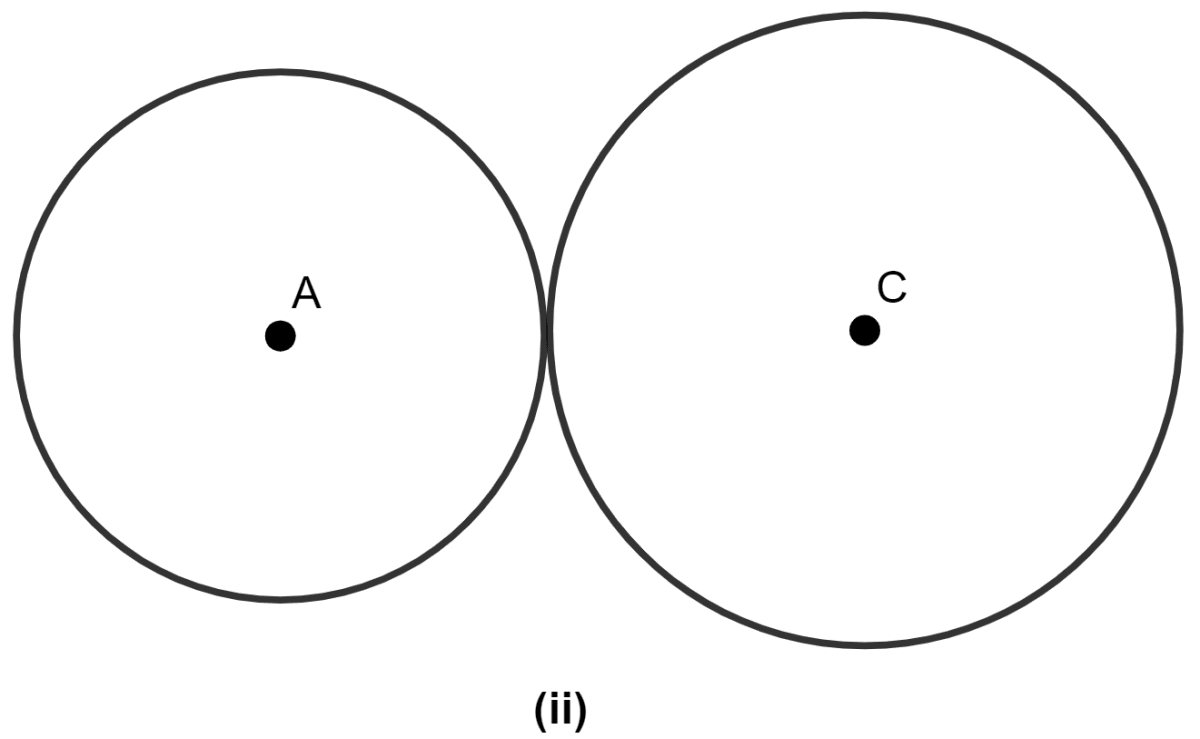
(iii) Two points of intersection when circles intersect each other.

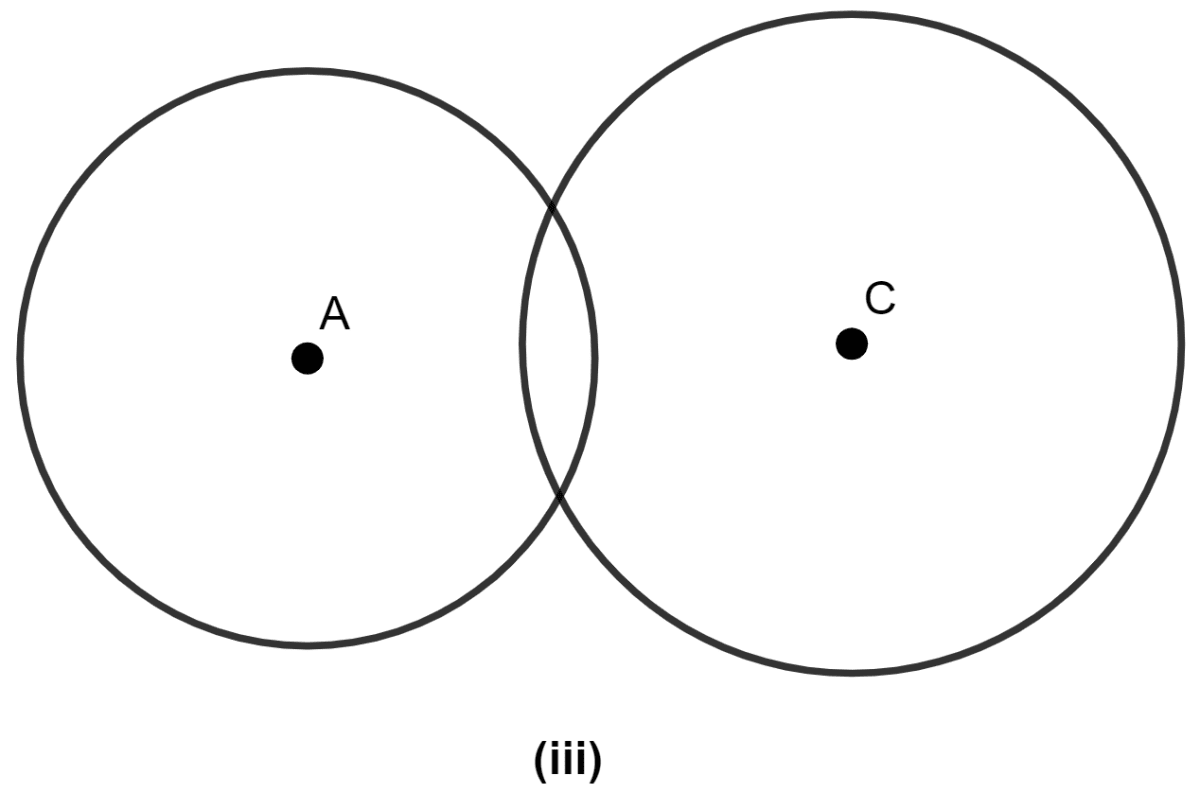
(iv) Infinite, when one circle is completely inside the other and centers are concurrent.

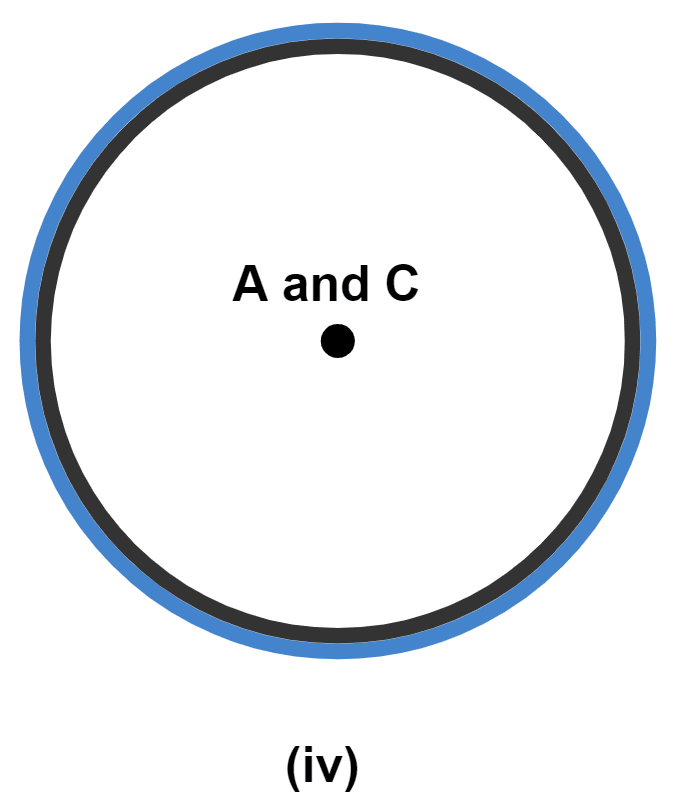
Hence, maximum number of common points are infinite.

Suppose you are given a circle. Describe a method by which you can find the center of this circle.

Answer

Steps of construction :

1. Draw two chords AB and CD in the given circle.

2. Draw XY, the perpendicular bisector of chord AB and MN, the perpendicular bisector of chord CD.

3. Mark point O, the intersection of perpendicular bisectors of both the chords.

Point O, is the center of the circle

Given two equal chords AB and CD of a circle, with center O, intersecting each other at point P. Prove that :

(i) AP = CP

(ii) BP = DP

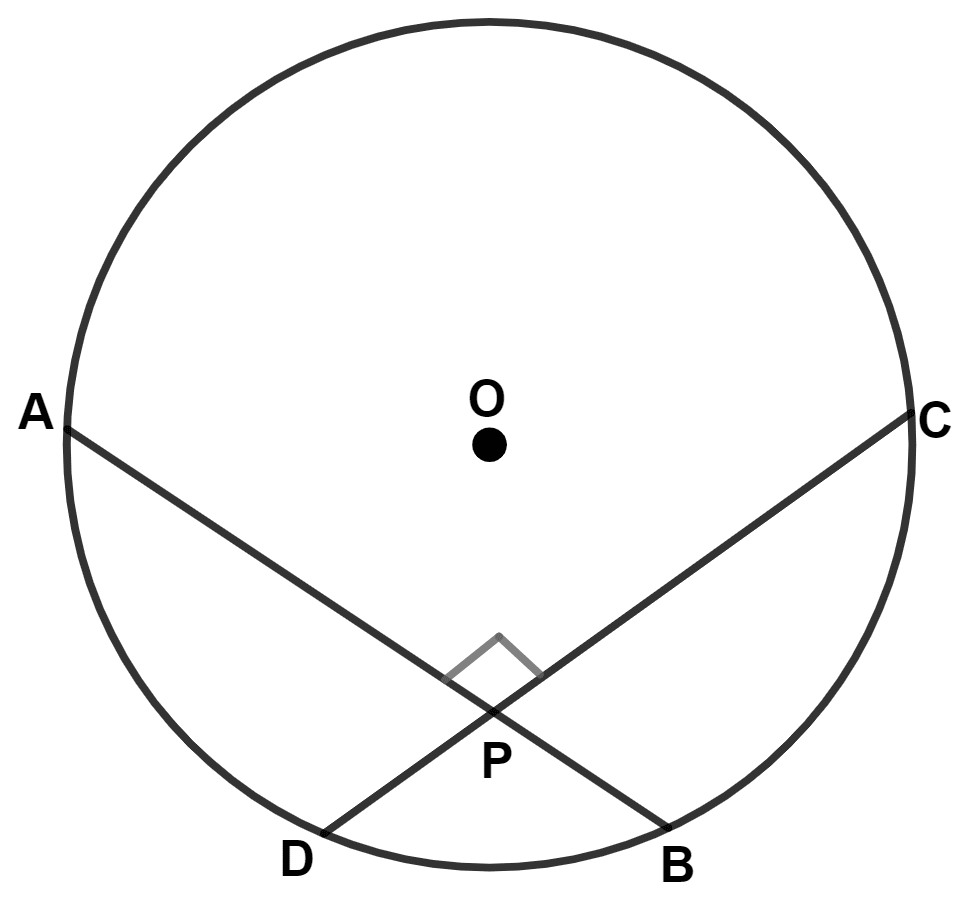
Answer

Draw, OM ⊥ AB and ON ⊥ CD.

Join OP, OB and OD.

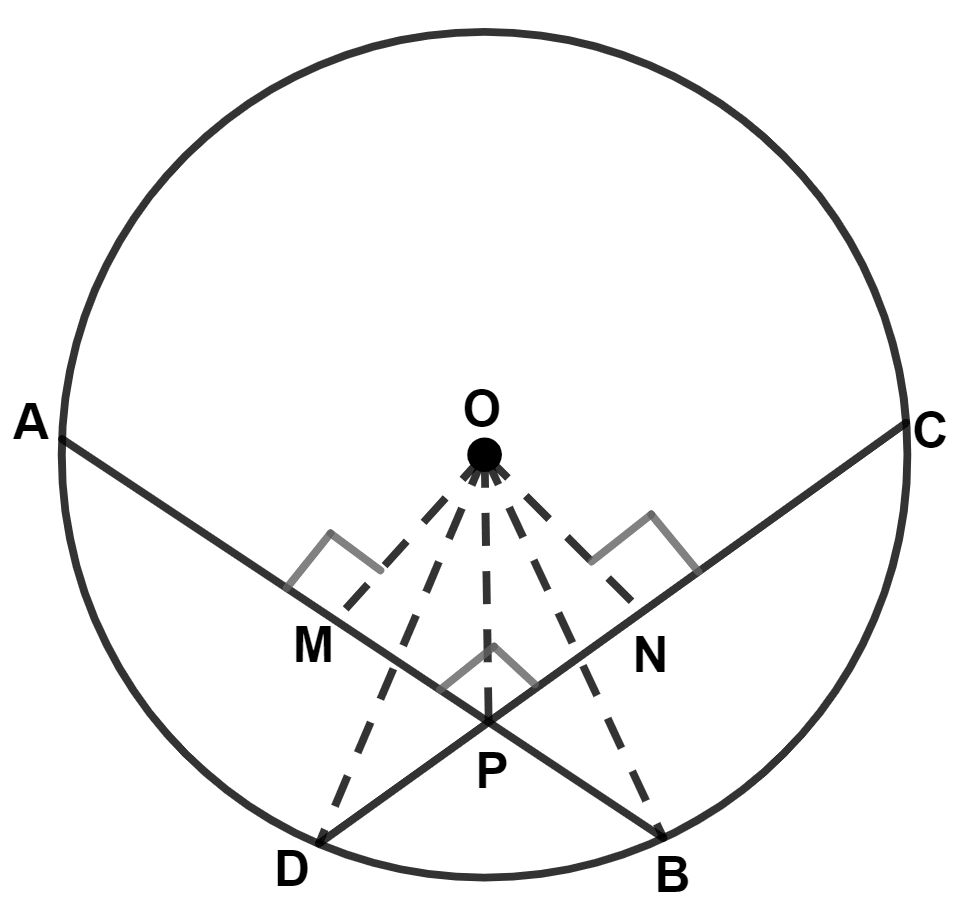
We know that,

Perpendicular to a chord, from the center of the circle, bisects the chord.

∴ OM and ON bisects AB and CD respectively.

Given,

Two chords are equal.

∴ AB = CD = x (let)

∴ MB = $\dfrac{1}{2}AB = \dfrac{1}{2}x$ and ND = $\dfrac{1}{2}CD = \dfrac{1}{2}x$,

∴ MB = ND ..............(1)

Let, MB = ND = x.

From figure,

OB = OD = y (Radius of same circle)

In right-angled triangle OMB,

By pythagoras theorem,

⇒ Hypotenuse² = Perpendicular² + Base²

⇒ OB² = OM² + MB²

⇒ OM² = OB² - MB²

⇒ OM² = y² - x²

⇒ OM = $\sqrt{y^2 - x^2}$ ........(2)

In right-angled triangle OND,

By pythagoras theorem,

⇒ Hypotenuse² = Perpendicular² + Base²

⇒ OD² = ON² + ND²

⇒ ON² = OD² - ND²

⇒ ON² = y² - x²

⇒ ON = $\sqrt{y^2 - x^2}$ ........(3)

From equation (2) and (3), we get :

⇒ OM = ON

In △ OPM and △ OPN,

⇒ ∠OMP = ∠ONP (Both equal to 90°)

⇒ OP = OP (Common side)

⇒ OM = ON (Proved above)

∴ △ OPM ≅ △ OPN (By R.H.S. axiom)

We know that,

Corresponding parts of congruent triangles are equal.

∴ PM = PN ..........(2)

Subtracting equation (2) from (1), we get :

⇒ MB - PM = ND - PN

⇒ PB = PD ...........(4)

Given,

⇒ AB = CD .........(5)

Subtracting equation (4) from (5), we get :

⇒ AB - PB = CD - PD

⇒ AP = CP.

Hence, proved that AP = CP and BP = DP.

In a circle of radius 10 cm, AB and CD are two parallel chords of lengths 16 cm and 12 cm respectively. Calculate the distance between the chords, if they are on :

(i) the same side of the center

(ii) the opposite side of the center

Answer

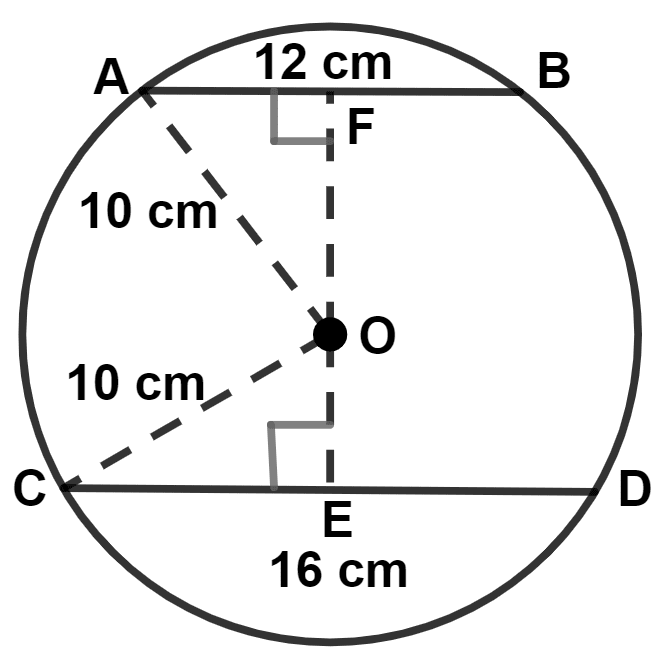
(i) Let AB and CD be chords on same side of the center of the circle.

We know that,

Perpendicular from the center to the chord, bisects it.

∴ AF = $\dfrac{AB}{2} = \dfrac{12}{2}$ = 6 cm, CE = $\dfrac{CD}{2} = \dfrac{16}{2}$ = 8 cm.

From figure,

OA = OC = radius = 10 cm.

In right-angled triangle OCE,

By pythagoras theorem,

⇒ Hypotenuse² = Perpendicular² + Base²

⇒ OC² = OE² + CE²

⇒ 10² = OE² + 8²

⇒ 100 = OE² + 64

⇒ OE² = 100 - 64

⇒ OE² = 36

⇒ OE = $\sqrt{36}$ = 6 cm.

In right-angled triangle OAF,

By pythagoras theorem,

⇒ Hypotenuse² = Perpendicular² + Base²

⇒ OA² = OF² + AF²

⇒ 10² = OF² + 6²

⇒ 100 = OF² + 36

⇒ OF² = 100 - 36

⇒ OF² = 64

⇒ OF = $\sqrt{64}$ = 8 cm.

From figure,

⇒ EF = OF - OE = 8 - 6 = 2 cm.

Hence, distance between the chords = 2 cm.

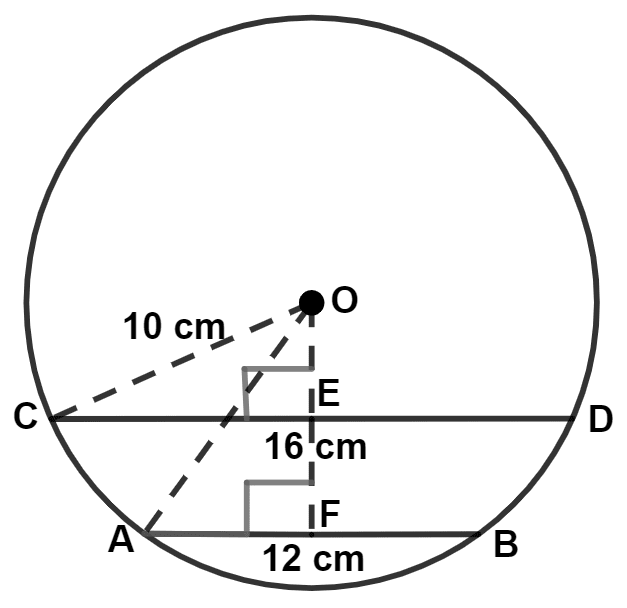
(ii) Let AB and CD be chords on opposite side of the center of the circle.

We know that,

Perpendicular from the center to the chord, bisects it.

∴ AF = $\dfrac{AB}{2} = \dfrac{12}{2}$ = 6 cm, CE = $\dfrac{CD}{2} = \dfrac{16}{2}$ = 8 cm.

From figure,

OA = OC = radius = 10 cm.

In right-angled triangle OCE,

By pythagoras theorem,

⇒ Hypotenuse² = Perpendicular² + Base²

⇒ OC² = OE² + CE²

⇒ 10² = OE² + 8²

⇒ 100 = OE² + 64

⇒ OE² = 100 - 64

⇒ OE² = 36

⇒ OE = $\sqrt{36}$ = 6 cm.

In right-angled triangle OAF,

By pythagoras theorem,

⇒ Hypotenuse² = Perpendicular² + Base²

⇒ OA² = OF² + AF²

⇒ 10² = OF² + 6²

⇒ 100 = OF² + 36

⇒ OF² = 100 - 36

⇒ OF² = 64

⇒ OF = $\sqrt{64}$ = 8 cm.

From figure,

⇒ EF = OE + OF = 6 + 8 = 14 cm.

Hence, distance between the chords = 14 cm.

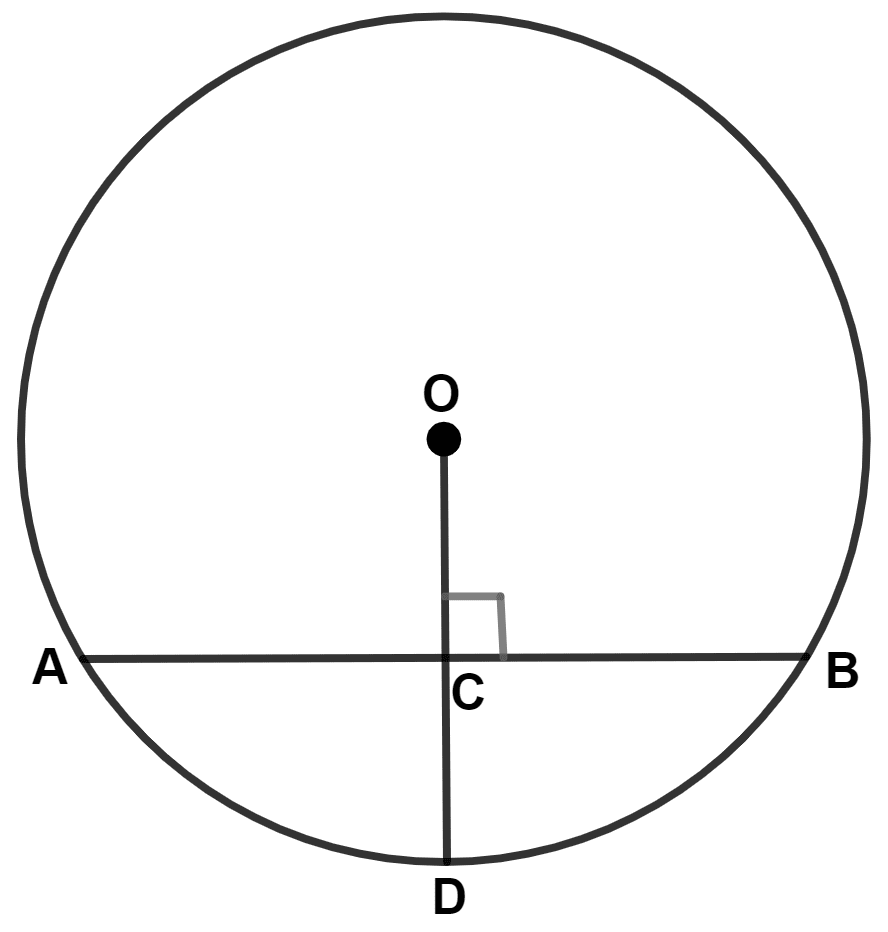
In the given figure, O is the center of the circle with radius 20 cm and OD is perpendicular to AB.

If AB = 32 cm, find the length of CD.

Answer

Join OA.

We know that,

Perpendicular from centre to the chord, bisects the chord.

∴ AC = $\dfrac{AB}{2} = \dfrac{32}{2}$ = 16 cm.

In right-angled triangle OAC,

By pythagoras theorem,

⇒ Hypotenuse² = Perpendicular² + Base²

⇒ OA² = OC² + AC²

⇒ 20² = OC² + 16²

⇒ 400 = OC² + 256

⇒ OC² = 400 - 256

⇒ OC² = 144

⇒ OC = $\sqrt{144}$ = 12 cm.

From figure,

CD = OD - OC = 20 - 12 = 8 cm.

Hence, CD = 8 cm.

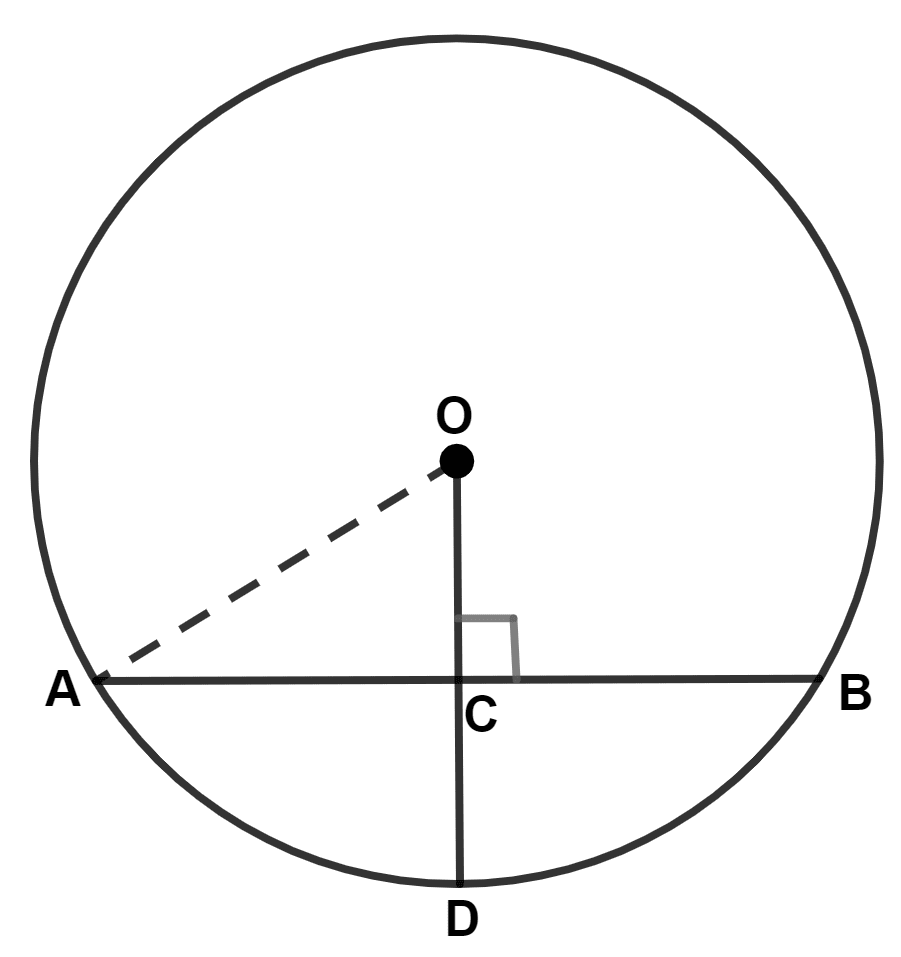
In the given figure, AB and CD are two equal chords of a circle, with center O.

If P is the mid-point of chord AB. Q is the mid-point of chord CD and ∠POQ = 150°, find ∠APQ.

Answer

We know that,

Equal chords are equidistant from the center.

∴ OP = OQ

In △ OPQ,

⇒ OP = OQ

⇒ ∠OQP = ∠OPQ = x (let) (Angles opposite to equal sides are equal)

By angle sum property of triangle,

⇒ ∠OQP + ∠OPQ + ∠POQ = 180°

⇒ x + x + 150° = 180°

⇒ 2x = 180° - 150°

⇒ 2x = 30°

⇒ x = $\dfrac{30°}{2}$ = 15°.

We know that,

A straight line drawn from the center of the circle to bisect the chord, which is not a diameter, is at right angles to the chord.

∴ ∠OPA = 90°

From figure,

⇒ ∠APQ = ∠OPA - ∠OPQ = 90° - x = 90° - 15° = 75°.

Hence, ∠APQ = 75°.

In the given figure, AOC is the diameter of the circle, with center O. If arc AXB is half of arc BYC, find ∠BOC.

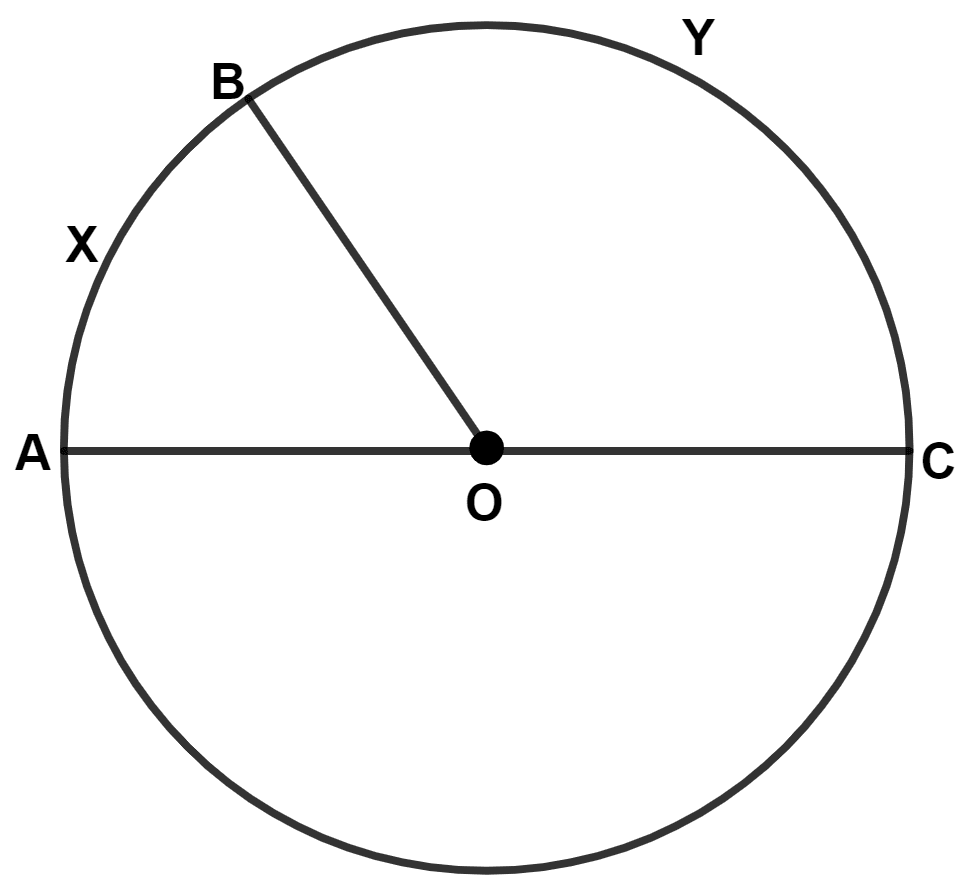
Answer

We know that,

Ratio of the angles subtended by the arcs on the center is equal to the ratio of the arcs.

$\Rightarrow \dfrac{∠AOB}{∠BOC} = \dfrac{AXB}{BYC} \\[1em] \Rightarrow \dfrac{∠AOB}{∠BOC} = \dfrac{1}{2} \\[1em] \Rightarrow ∠AOB = \dfrac{∠BOC}{2}.$

From figure,

⇒ ∠AOB + ∠BOC = 180°

⇒ $\dfrac{∠BOC}{2}$ + ∠BOC = 180°

⇒ $\dfrac{2∠BOC + ∠BOC}{2}$ = 180°

⇒ $\dfrac{3∠BOC}{2}$ = 180°

⇒ ∠BOC = $\dfrac{2}{3} \times 180° = \dfrac{360°}{3}$ = 120°.

Hence, ∠BOC = 120°.

The circumference of a circle, with center O, is divided into three arcs APB, BQC and CRA such that :

$\dfrac{\text{arc APB}}{2} = \dfrac{\text{arc BQC}}{3} = \dfrac{\text{arc CRA}}{4}$

Find ∠BOC.

Answer

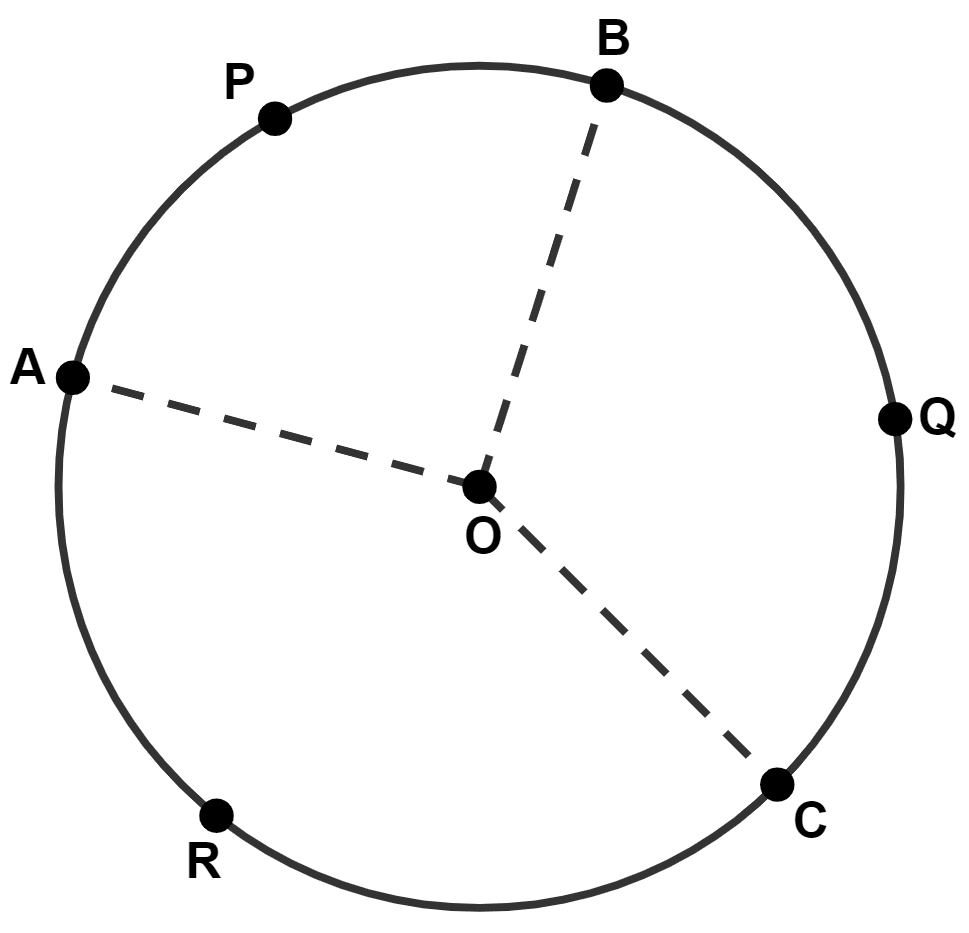
Given,

⇒ $\dfrac{\text{arc APB}}{2} = \dfrac{\text{arc BQC}}{3} = \dfrac{\text{arc CRA}}{4}$ = k (let)

⇒ arc APB = 2k, arc BQC = 3k and arc CRA = 4k.

We know that,

Ratio of the angles subtended by the arcs on the center is equal to the ratio of the arcs.

⇒ ∠AOB : ∠BOC : ∠COA = 2k : 3k : 4k

⇒ ∠AOB : ∠BOC : ∠COA = 2 : 3 : 4

⇒ ∠AOB = 2x°, ∠BOC = 3x°, ∠COA = 4x°.

From figure,

⇒ ∠AOB + ∠BOC + ∠COA = 360°

⇒ 2x° + 3x° + 4x° = 360°

⇒ 9x° = 360°

⇒ x° = $\dfrac{360°}{9}$ = 40°.

⇒ ∠AOB = 2x° = 2(40°) = 80°,

⇒ ∠BOC = 3x° = 3(40°) = 120°,

⇒ ∠COA = 4x° = 4(40°) = 160°.

Hence, ∠BOC = 120°.