Which of the following variables are discrete?
daily temperature of your city
sizes of shoes
distance travelled by a man
time
Answer
A discrete variable is a variable which is incapable of taking all possible numerical values.
From the given options, only shoe sizes are considered discrete variables, whereas daily temperature in your city, distance traveled by a person, and time are continuous variables.
Hence, option 2 is the correct option.
The marks obtained by 15 students in a test (out of hundred) are given below :
81, 72, 90, 90, 80, 55, 72, 66, 69, 80, 36, 54, 62, 56 and 58
The range of data is :
46
54
90
100
Answer
Range is defined as the difference between the highest and lowest values in the data.
From the given data, highest value = 90.
Lowest value = 36
Range = 90 - 36
= 54
Hence, option 2 is the correct option.
The class-mark of the class 35-45 is :
35
45
40
42
Answer
Class-mark is the value midway between its actual lower limit and actual upper limit.
Lower class limit = 35
Upper class limit = 45
Hence, option 3 is the correct option.
In the class-intervals 1-10, 11-20, 21-30; the class 11-20 after adjustment is :
0.5-10.5
20.5-30.5
10.5-30.5
10.5-20.5
Answer
The adjustment factor is
The adjusted class would then be as follows:
| Class interval before adjustment | Class interval after adjustment |
|---|---|
| 1 - 10 | 0.5 - 10.5 |
| 11 - 20 | 10.5 - 20.5 |
| 21 - 30 | 20.5 - 30.5 |
The class 11-20 after adjustment is 10.5-20.5.
Hence, option 4 is the correct option.
The class marks of a frequency distribution are 10, 15, 20, 25, ............... The class corresponding to the class mark 15 is :
12.5-17.5
10-20
10.25-17
14-16
Answer
The given class marks are 10, 15, 20, 25, ........
The class width is the difference between any two consecutive class marks.
Class width = 15 - 10 = 5
If a is the class mark of a class interval of width h, then the lower and upper limits of the class interval are:
Lower limit = a - upper limit = a +
So, a = 15 and h = 5
Class interval =
= (15 - 2.5) to (15 + 2.5)
= 12.5 to 17.5
Hence, the class corresponding to the class mark 15 is 12.5-17.5.
Hence, option 1 is the correct option.
State, which of the following variables are continuous and which are discrete :
(a) number of children in your class.
(b) distance travelled by a car.
(c) sizes of shoes.
(d) time.
(e) number of patients in a hospital.
Answer
(a) Discrete variable
Reason
A discrete variable is a variable which is incapable of taking all possible numerical values. In this case, the number of children is a finite, whole number.
(b) Continuous variable
Reason
Continuous variable is a variable which can take any numerical value within a certain range. The distance can be measured in infinitely small increments.
(c) Discrete variable
Reason
A discrete variable is a variable which is incapable of taking all possible numerical values. Sizes of shoes are represented by specific values.
(d) Continuous variable
Reason
Continuous variable is a variable which can take any numerical value within a certain range. Time can take on an infinite number of values within a range.
(e) Discrete variable
Reason
A discrete variable is a variable which is incapable of taking all possible numerical values. The number of patients is countable and can only be whole numbers
Given below are the marks obtained by 30 students in an examination :
08 17 33 41 47 23 20 34
09 18 42 14 30 19 29 11
36 48 40 24 22 02 16 21
15 32 47 44 33 01
Taking class intervals 1-10, 11-20, ..............., 41-50; make a frequency table for the above distribution.
Answer
The frequency table for the given distribution is :
| Marks | Tally marks | Frequency |
|---|---|---|
| 1 - 10 | IIII | 4 |
| 11 - 20 | 8 | |
| 21 - 30 | 6 | |
| 31 - 40 | 6 | |
| 41 - 50 | 6 |
The marks of 24 candidates in the subject mathematics are given below :
45 48 15 23 30 35 40 11
29 0 3 12 48 50 18 30
15 30 11 42 23 2 3 44
The maximum marks are 50. Make a frequency distribution taking class intervals 0-10, 10-20, ............... .
Answer
The frequency table for the given distribution is :
| Marks | Tally marks | Frequency |
|---|---|---|
| 0 - 10 | IIII | 4 |
| 10 - 20 | 6 | |
| 20 - 30 | III | 3 |
| 30 - 40 | IIII | 4 |
| 40 - 50 | 7 |
Fill in the blanks :
(a) A quantity which can vary from one individual to another is called a ...............
(b) Sizes of shoes are ............... variables.
(c) Daily temperature is ............... variable.
(d) The range of the data 7, 13, 6, 25, 18, 20, 16 is ...............
Range of the data is the difference between the highest and the lowest values.
(e) In the class interval 35-46; the lower limit is ............... and upper limit is ...............
(f) The class mark of class interval 22 - 29 is ...............
Answer
(i) A quantity which can vary from one individual to another is called a variable.
(ii) Sizes of shoes are distinct variables.
(iii) Daily temperature is continuous variable.
(iv) The range of the data 7, 13, 6, 25, 18, 20, 16 is (25-6) = 19.
Range of the data is the difference between the highest and the lowest values.
(v) In the class interval 35 - 46; the lower limit is 35 and upper limit is 46.
(vi) The class mark of class interval 22 - 29 is 25.5.
Find the actual lower class limits, upper class limits and the mid-values of the classes :
10-19, 20-29, 30-39 and 40-49.
Answer
| Class limit | Exclusive class limit |
|---|---|
| 10 - 19 | 9.5 - 19.5 |
| 20 - 29 | 19.5 - 29.5 |
| 30 - 39 | 29.5 - 39.5 |
| 40 - 49 | 39.5 - 49.5 |
In case of frequency 10-19 the lower class limit is 9.5, the upper class limit is 19.5 and the mid value is
In case of frequency 20-29 the lower class limit is 19.5, the upper class limit is 29.5 and the mid value is
In case of frequency 30-39 the lower class limit is 29.5, the upper class limit is 39.5 and the mid value is
In case of frequency 40-49 the lower class limit is 39.5, the upper class limit is 49.5 and the mid value is
Find the actual lower and upper class limits and also the class marks of the classes :
1.1-2.0, 2.1-3.0 and 3.1-4.0.
Answer
| Class limit | Exclusive class limit |
|---|---|
| 1.1 - 2.0 | 1.05 - 2.05 |
| 2.1 - 3.0 | 2.05 - 3.05 |
| 3.1 - 4.0 | 3.05 - 4.05 |
In case of frequency 1.1-2.0 the lower class limit is 1.05, the upper class limit is 2.05 and the class mark is
In case of frequency 2.1-3.0 the lower class limit is 2.05, the upper class limit is 3.05 and the class mark is
In case of frequency 3.1-4.0 the lower class limit is 3.05, the upper class limit is 4.05 and the class mark is
Use the table given below to find :
(a) The actual class limits of the fourth class.
(b) The class boundaries of the sixth class.
(c) The class mark of the third class.
(d) The upper and lower limits of the fifth class.
(e) The size of the third class.
| Class Interval | Frequency |
|---|---|
| 30 - 34 | 7 |
| 35 - 39 | 10 |
| 40 - 44 | 12 |
| 45 - 49 | 13 |
| 50 - 54 | 8 |
| 55 - 59 | 4 |
Answer
| Class Interval | Exclusive class Interval | Frequency |
|---|---|---|
| 30 - 34 | 29.5 - 34.5 | 7 |
| 35 - 39 | 34.5 - 39.5 | 10 |
| 40 - 44 | 39.5 - 44.5 | 12 |
| 45 - 49 | 44.5 - 49.5 | 13 |
| 50 - 54 | 49.5 - 54.5 | 8 |
| 55 - 59 | 54.5 - 59.5 | 4 |
(i) The actual class limits of the fourth class is 44.5-49.5.
(ii) The class boundaries of the sixth class is 54.5-59.5.
(iii) The class mark of the third class
(iv) The upper and lower limits of the fifth class (50-54) is 54 and 50, respectively.
(v) Interval of third class = 40-44
The size of class = Upper limit - lower limit + 1
The size of third class = 44 - 40 + 1
= 4 + 1
= 5
Hence, the size of third class is 5.
Construct a cumulative frequency distribution table from the frequency table given below :
(i)
| Class Interval | Frequency |
|---|---|
| 0 - 8 | 9 |
| 8 - 16 | 13 |
| 16 - 24 | 12 |
| 24 - 32 | 7 |
| 32 - 40 | 15 |
(ii)
| Class Interval | Frequency |
|---|---|
| 1 - 10 | 12 |
| 11 - 20 | 18 |
| 21 - 30 | 23 |
| 31 - 40 | 15 |
| 41 - 50 | 10 |
Answer
(i) The cumulative frequency distribution table is:
| Class Interval | Frequency | Cumulative frequency |
|---|---|---|
| 0 - 8 | 9 | 9 |
| 8 - 16 | 13 | 9 + 13 = 22 |
| 16 - 24 | 12 | 9 + 13 + 12 = 34 |
| 24 - 32 | 7 | 9 + 13 + 12 + 7 = 41 |
| 32 - 40 | 15 | 9 + 13 + 12 + 7 + 15 = 56 |
(ii) The cumulative frequency distribution table is -
| Class Interval | Frequency | Cumulative frequency |
|---|---|---|
| 1 - 10 | 12 | 12 |
| 11 - 20 | 18 | 12 + 18 = 30 |
| 21 - 30 | 23 | 12 + 18 + 23 = 53 |
| 31 - 40 | 15 | 12 + 18 + 23 + 15 = 68 |
| 41 - 50 | 10 | 12 + 18 + 23 + 15 + 10 = 78 |
Construct a frequency distribution table from the following cumulative frequency distribution:
(i)
| Class Interval | Cumulative Frequency |
|---|---|
| 10 - 19 | 8 |
| 20 - 29 | 19 |
| 30 - 39 | 23 |
| 40 - 49 | 30 |
(ii)
| C.I. | C.F. |
|---|---|
| 5 - 10 | 18 |
| 10 - 15 | 30 |
| 15 - 20 | 46 |
| 20 - 25 | 73 |
| 25 - 30 | 90 |
Answer
(i) The frequency distribution table is
| Class Interval | Cumulative Frequency | Frequency |
|---|---|---|
| 10 - 19 | 8 | 8 |
| 20 - 29 | 19 | 19 - 8 = 11 |
| 30 - 39 | 23 | 23 -19 = 4 |
| 40 - 49 | 30 | 30 -23 = 7 |
(ii) The frequency distribution table is
| Class Interval | Cumulative Frequency | Frequency |
|---|---|---|
| 5 - 10 | 18 | 18 |
| 10 - 15 | 30 | 30 - 18 = 12 |
| 15 - 20 | 46 | 46 - 30 = 16 |
| 20 - 25 | 73 | 73 - 46 = 27 |
| 25 - 30 | 90 | 90 -73 = 17 |
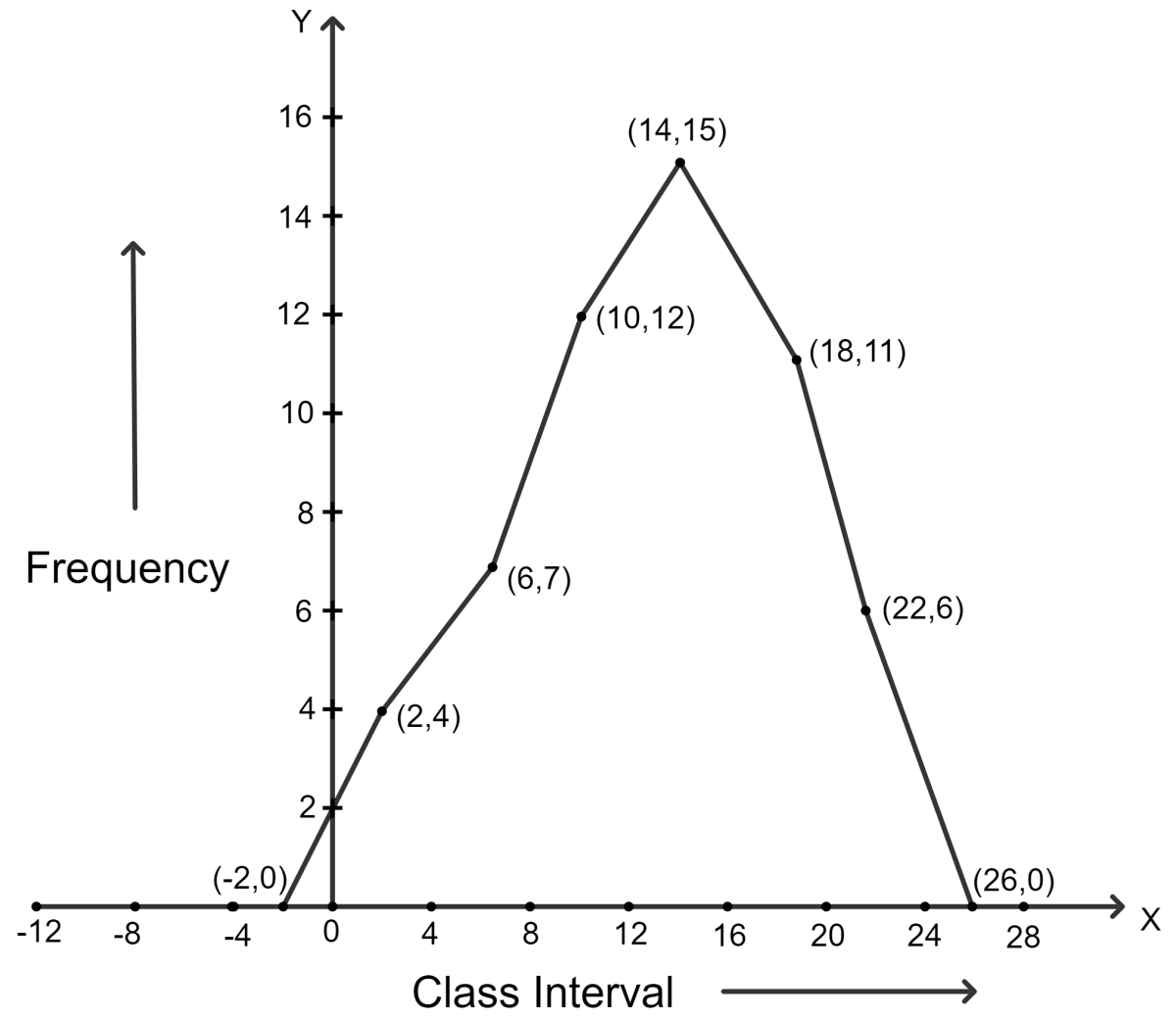
Construct a frequency polygon for the following distribution :
| Class-intervals | 0 - 4 | 4 - 8 | 8 - 12 | 12 - 16 | 16 - 20 | 20 - 24 |
|---|---|---|---|---|---|---|
| Frequency | 4 | 7 | 10 | 15 | 11 | 6 |
Answer
| Class intervals | Frequency | Class mark |
|---|---|---|
| -4 - 0 | 0 | |
| 0 - 4 | 4 | |
| 4 - 8 | 7 | |
| 8 - 12 | 12 | |
| 12 - 16 | 15 | |
| 16 - 20 | 11 | |
| 20 - 24 | 6 | |
| 24 - 28 | 0 |
Steps:
Find the class-mark (mid-value) of each given class-interval.
Class-mark = mid-value =
On a graph paper, mark class-marks along x-axis and frequencies along y-axis.
On this graph paper, mark points taking values of class-marks along x-axis and the values of their corresponding frequencies along y-axis.
Draw line segments joining the consecutive points marked in step (3) above.
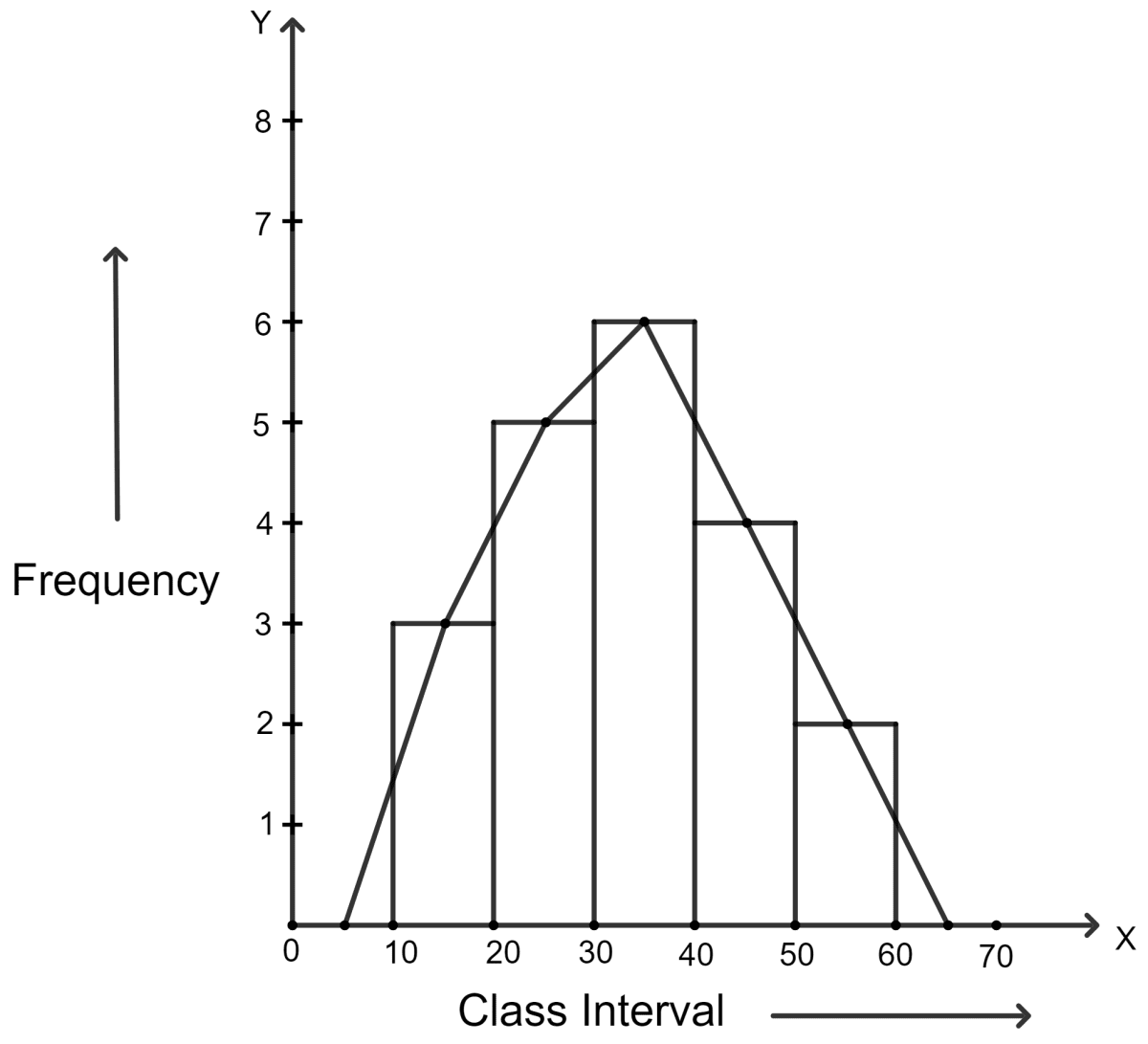
Construct a combined histogram and frequency polygon for the following frequency distribution :
| Class-intervals | 10 - 20 | 20 - 30 | 30 - 40 | 40 - 50 | 50 - 60 |
|---|---|---|---|---|---|
| Frequency | 3 | 5 | 6 | 4 | 2 |
Answer
Steps:
Draw a histogram for the given data.
Mark the mid-point at the top of each rectangle of the histogram drawn.
Also, mark the mid-point of the immediately lower class-interval (in the given question, the immediately lower class-interval is 0 - 10) and mid-point of the immediately higher class-interval (in the given question the immediate upper class-interval is 60 - 70).
Join the consecutive mid-points marked by straight lines to obtain the required frequency polygon.
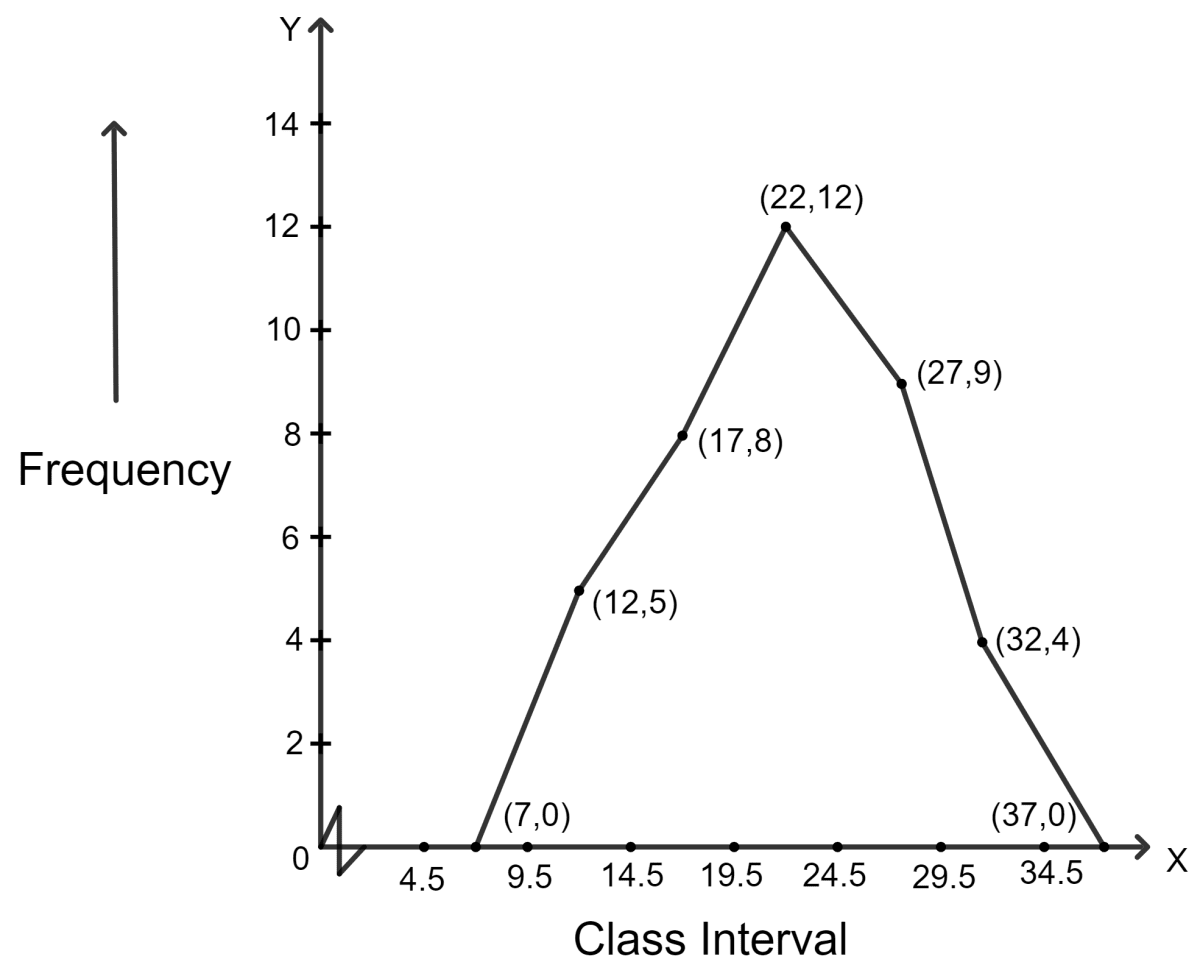
Construct a frequency polygon for the following data :
| Class-intervals | 10 - 14 | 15 - 19 | 20 - 24 | 25 - 29 | 30 - 34 |
|---|---|---|---|---|---|
| Frequency | 5 | 8 | 12 | 9 | 4 |
Answer
The given class interval are inclusive. For constructing polygon we will first convert them into the exclusive form.
| Class - intervals | Frequency | Class marks |
|---|---|---|
| 4.5 - 9.5 | 0 | |
| 9.5 - 14.5 | 5 | |
| 14.5 - 19.5 | 8 | |
| 19.5 - 24.5 | 12 | |
| 24.5 - 29.5 | 9 | |
| 29.5 - 34.5 | 4 | |
| 34.5 - 39.5 | 0 |
Steps:
Find the class-mark (mid-value) of each given class-interval.
Class-mark = mid-value =
On a graph paper, mark class-marks along x-axis and frequencies along y-axis.
On this graph paper, mark points taking values of class-marks along x-axis and the values of their corresponding frequencies along y-axis.
Draw line segments joining the consecutive points marked in step (3) above.
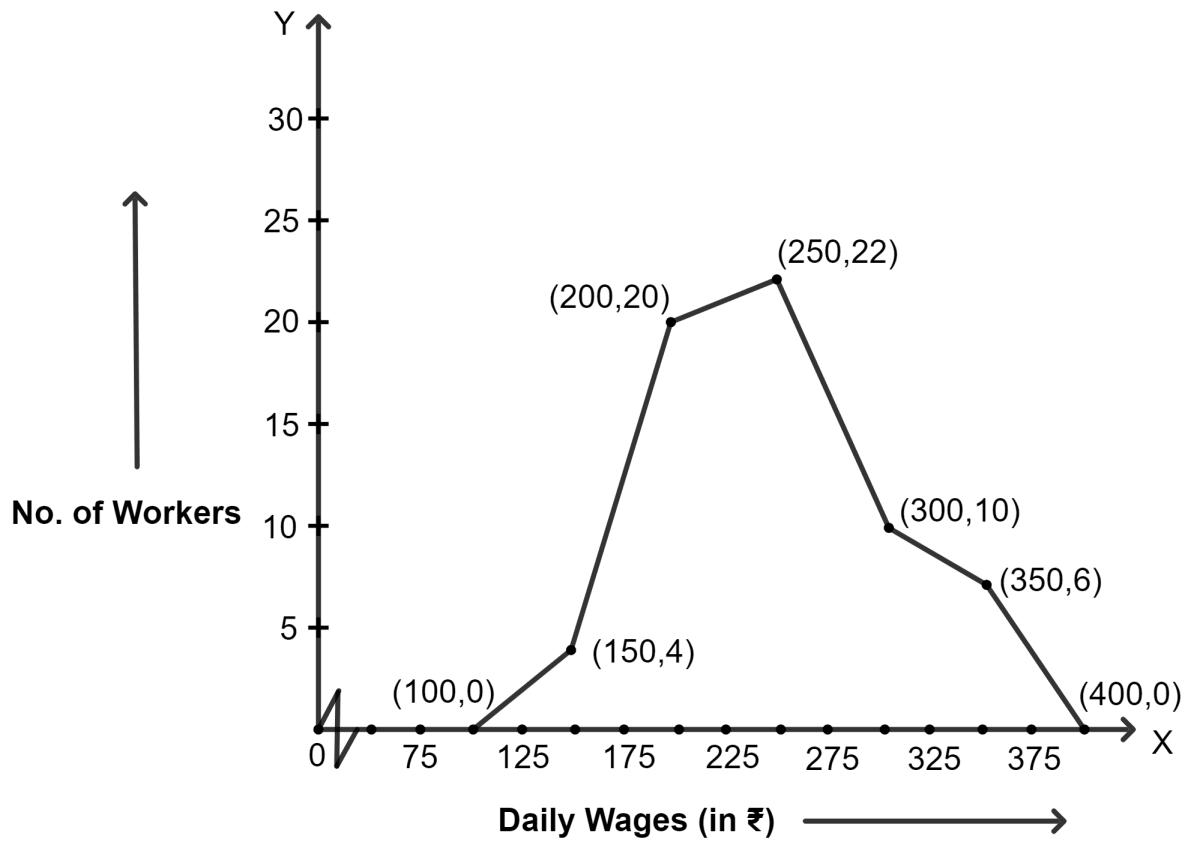
The daily wages in a factory are distributed as follows :
| Daily wages (in ₹) | 125 - 175 | 175 - 225 | 225 - 275 | 275 - 325 | 325 - 375 |
|---|---|---|---|---|---|
| Number of workers | 4 | 20 | 22 | 10 | 6 |
Draw a frequency polygon for this distribution.
Answer
| Daily wages (in ₹) | No. of workers | Class marks |
|---|---|---|
| 75 - 125 | 0 | |
| 125 - 175 | 4 | |
| 175 - 225 | 20 | |
| 225 - 275 | 22 | |
| 275 - 325 | 10 | |
| 325 - 375 | 6 | |
| 375 - 425 | 0 |
Steps:
Find the class-mark (mid-value) of each given class-interval.
Class-mark mid-value =
On a graph paper, mark class-marks along x-axis and frequencies along y-axis.
On this graph paper, mark points taking values of class-marks along x-axis and the values of their corresponding frequencies along y-axis.
Draw line segments joining the consecutive points marked in step (3) above.
The class-mark of class 19 - 30 is:
Answer
By formula, class-mark =
Substituting the values, we get :
Class-mark of class 19 - 30 =
Hence, option 1 is the correct option.
In a frequency distribution, mid-values of the class is 10 and width of the class is 6, the lower limit of the class is :
6
7
8
9
Answer
Lower limit of class = Mid value -
= 10 -
= 10 - 3
= 7.
Hence, option 2 is the correct option.
Statement 1: Let m be the mid-value and x be the upper limit of a class in the continuous frequency distribution, then the lower limit of this class is 2m - x.
Statement 2: For a given class: = mid-value of the class
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Answer
Given, mid-value = m
Upper limit of a class = x
As we know,
Mid-value =
So, statement 2 is true.
⇒ m =
⇒ 2m = lower class-limit + x
⇒ Lower class-limit = 2m - x
So, statement 1 is true.
∴ Both the statements are true.
Hence, option 1 is the correct option.
Assertion (A): 30 children were asked about the number of hours they watched TV program everyday. The results are recorded as under.
| Number of hours | Frequency |
|---|---|
| 0 - 5 | 8 |
| 5 - 10 | 16 |
| 10 - 15 | 4 |
| 15 - 20 | 2 |
Then the number of children who watched TV for 10 or more hours a day is 22.
Reason (R): The assertion is not correct as the required number is 4 + 2 = 6.
A is true, but R is false.
A is false, but R is true.
Both A and R are true, and R is the correct reason for A.
Both A and R are true, and R is the incorrect reason for A.
Answer
10 or more hours covers the 10 – 15 and 15 – 20 classes.
4 students are there in 10 - 15 class.
2 students are there in 15 - 20 class.
Total students = 4 + 2 = 6
∴ A is false, but R is true.
Hence, option 2 is the correct option.
Construct a frequency table from the following data :
| Marks | No. of students |
|---|---|
| less than 10 | 6 |
| less than 20 | 15 |
| less than 30 | 30 |
| less than 40 | 39 |
| less than 50 | 53 |
| less than 60 | 70 |
Answer`
The frequency table for the given distribution is :
| Marks | Tally marks | No. of students |
|---|---|---|
| 0 - 10 | 6 | |
| 10 - 20 | 9 | |
| 20 - 30 | 15 | |
| 30 - 40 | 9 | |
| 40 - 50 | 14 | |
| 50 - 60 | 17 |
Construct the frequency distribution table from the following cumulative frequency table:
| Ages | No. of students |
|---|---|
| Below 4 | 0 |
| Below 7 | 85 |
| Below 10 | 140 |
| Below 13 | 243 |
| Below 16 | 300 |
(i) State the number of students in the age group 10-13.
(ii) State the age-group which has the least number of students.
Answer
The frequency table for the given distribution is :
| Ages | Cumulative frequency | No. of students |
|---|---|---|
| 0 - 4 | 0 | 0 |
| 4 - 7 | 85 | 85 - 0 = 85 |
| 7 - 10 | 140 | 140 - 85 = 55 |
| 10 - 13 | 243 | 243 - 140 = 103 |
| 13 - 16 | 300 | 300 - 243 = 57 |
(i) There are 103 students in the age group 10-13.
(ii) The age group 7-10 has the least number of students.
Fill in the blanks in the following table:
| Class Interval | Frequency | Cumulative Frequency |
|---|---|---|
| 25 - 34 | ............... | 15 |
| 35 - 44 | ............... | 28 |
| 45 - 54 | 21 | ............... |
| 55 - 64 | 16 | ............... |
| 65 - 74 | 73 | |
| 75 - 84 | 12 | ............... |
Answer
| Class Interval | Frequency | Cumulative Frequency |
|---|---|---|
| 25 - 34 | 15 | 15 |
| 35 - 44 | 28 - 15 =13 | 28 |
| 45 - 54 | 21 | 15 + 13 + 21 = 49 |
| 55 - 64 | 16 | 15 + 13 + 21 + 16 = 65 |
| 65 - 74 | 73 - 65 = 8 | 73 |
| 75 - 84 | 12 | 15 + 13 + 21 + 16 + 8 + 12 = 85 |
The value of π upto 50 decimal places is :
3.14159265358979323846264338327950288419716939937510
(i) Make a frequency distribution table of the digits from 0 to 9 after the decimal place.
(ii) Which are the most and the least occurring digits ?
Answer
(i) The frequency distribution table of the digits from 0 to 9 after the decimal place is :
| Digit | Tally marks | Frequency |
|---|---|---|
| 0 | II | 2 |
| 1 | 5 | |
| 2 | 5 | |
| 3 | 8 | |
| 4 | IIII | 4 |
| 5 | 5 | |
| 6 | IIII | 4 |
| 7 | IIII | 4 |
| 8 | 5 | |
| 9 | 8 | |
| Total | 50 |
(ii) From the frequency distribution table, the frequency of digit 9 and 3 is maximum (8) and the frequency of digit 0 is minimum (2).
Hence, the most occurring digits are 9 and 3 and the least occurring digit is 0.
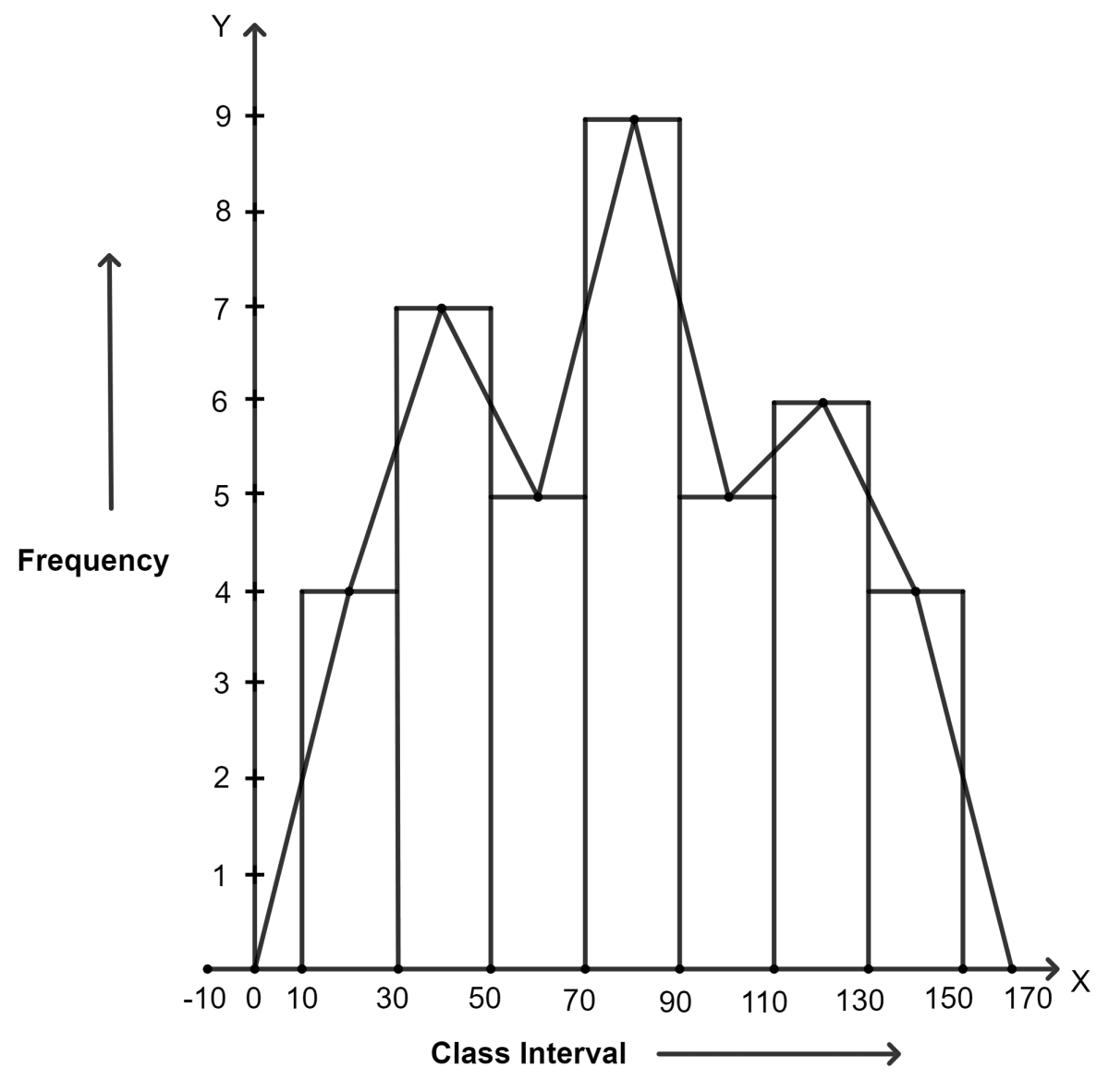
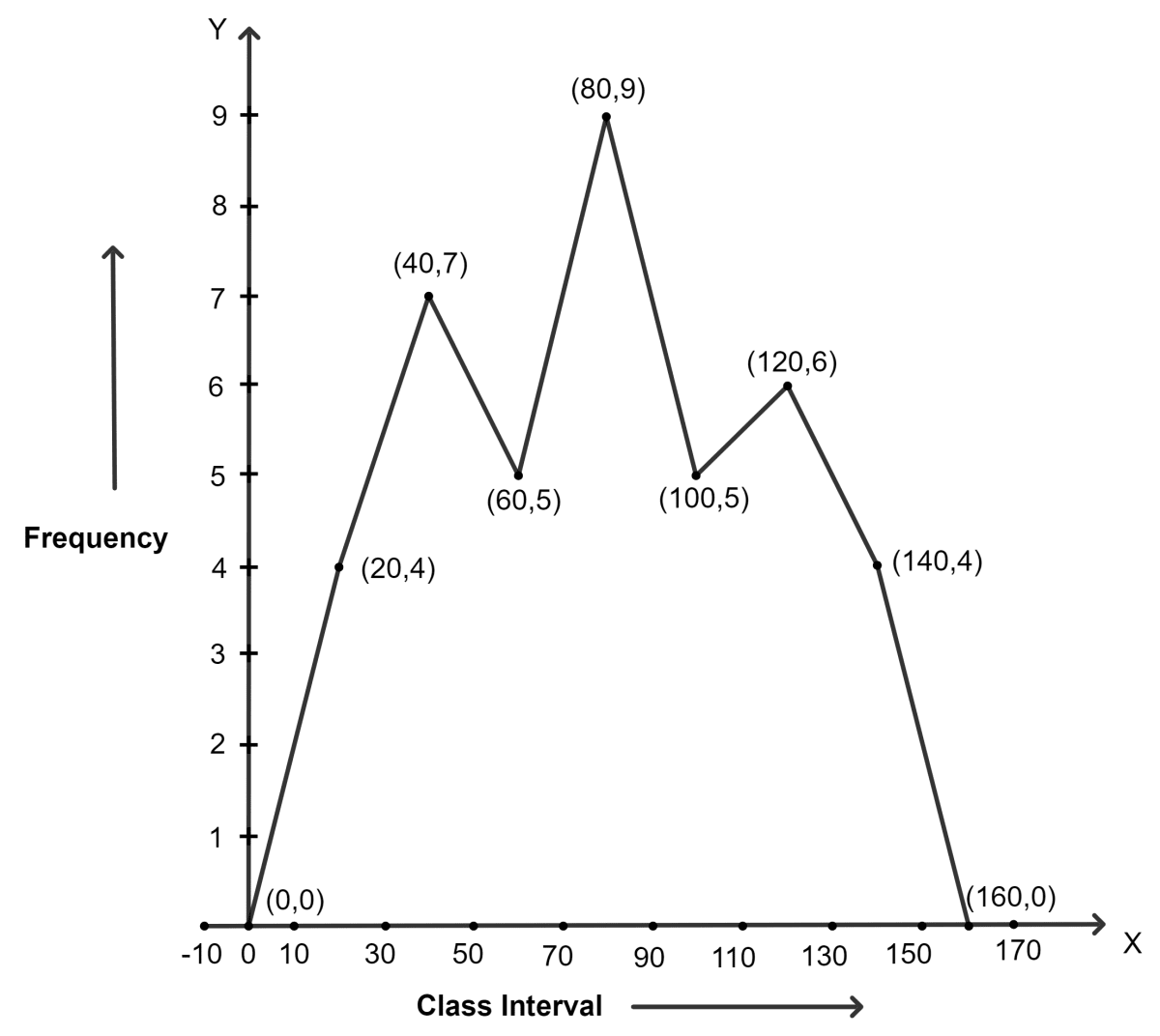
Draw frequency polygons for the following frequency distribution :
(a) using histogram
(b) without using histogram.
| C.I. | 10 - 30 | 30 - 50 | 50 - 70 | 70 - 90 | 90 - 110 | 110 - 130 | 130 - 150 |
|---|---|---|---|---|---|---|---|
| f | 4 | 7 | 5 | 9 | 5 | 6 | 4 |
Answer
(a) Using histogram
Steps:
Draw a histogram for the given data.
Mark the mid-point at the top of each rectangle of the histogram drawn.
Also, mark the mid-point of the immediately lower class-interval (in the given question, the immediately lower class-interval is -10 - 10) and mid-point of the immediately higher class-interval (in the given question the immediate upper class-interval is 150 - 170).
Join the consecutive mid-points marked by straight lines to obtain the required frequency polygon.
(b) Without using histogram
Steps:
Find the class-mark (mid-value) of each given class-interval.
Class-mark = mid-value =
On a graph paper, mark class-marks along x-axis and frequencies along y-axis
On this graph paper, mark points taking values of class-marks along x-axis and the values of their corresponding frequencies along y-axis.
Draw line segments joining the consecutive points marked in step (3) above.
| C.I. | f | Class mark |
|---|---|---|
| -10 - 10 | 0 | = 0 |
| 10 - 30 | 4 | = 20 |
| 30 - 50 | 7 | = 40 |
| 50 - 70 | 5 | = 60 |
| 70 - 90 | 9 | = 80 |
| 90 - 110 | 5 | = 100 |
| 110 - 130 | 6 | = 120 |
| 130 - 150 | 4 | = 140 |
| 150 - 170 | 0 | = 160 |
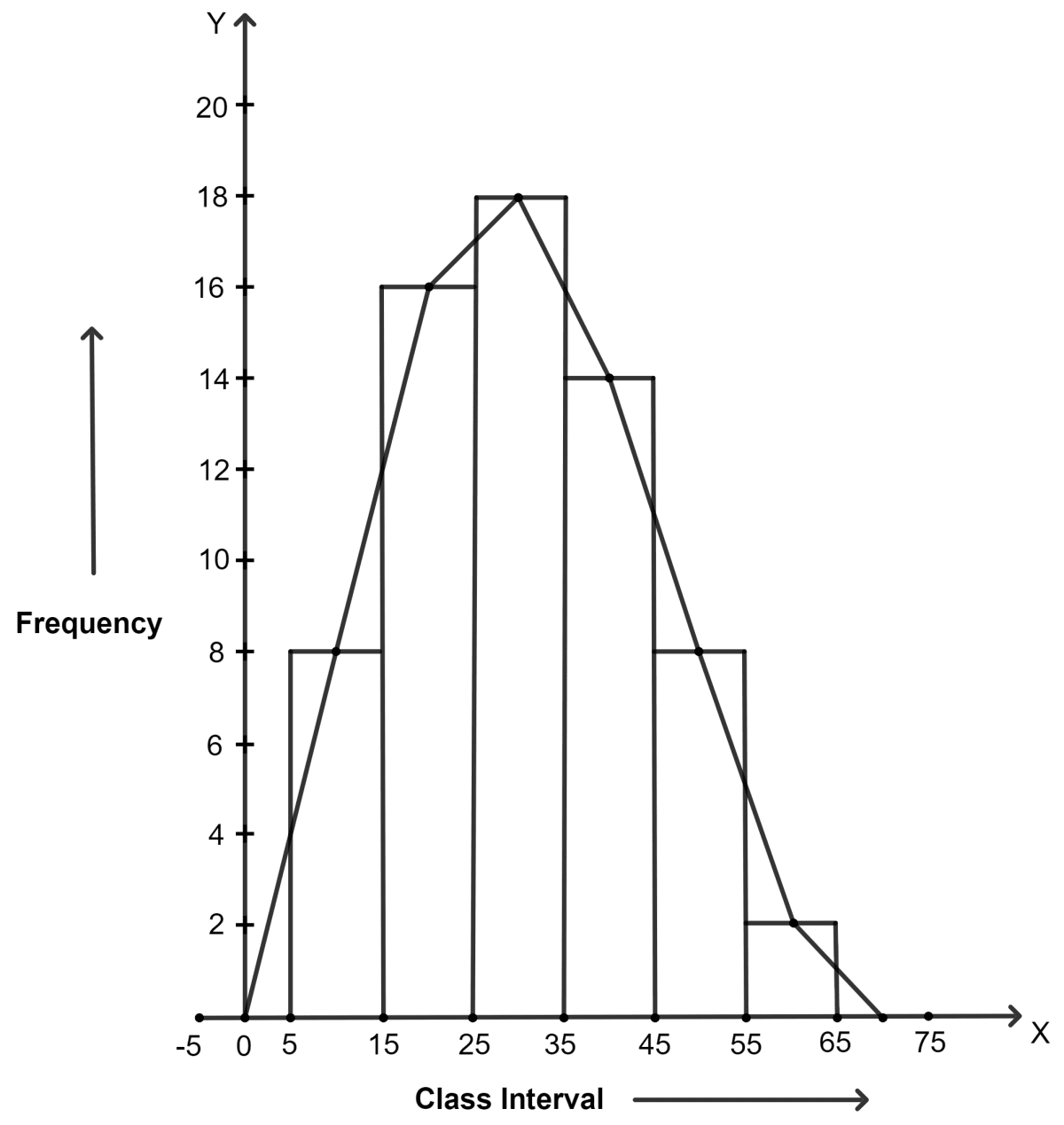
Draw frequency polygons for the following frequency distribution :
(a) using histogram
(b) without using histogram.
| C.I. | 5 - 15 | 15 - 25 | 25 - 35 | 35 - 45 | 45 - 55 | 55 - 65 |
|---|---|---|---|---|---|---|
| f | 8 | 16 | 18 | 14 | 8 | 2 |
Answer
(a) Using histogram
Steps:
Draw a histogram for the given data.
Mark the mid-point at the top of each rectangle of the histogram drawn.
Also, mark the mid-point of the immediately lower class-interval (in the given question, the immediately lower class-interval is 0 - 5) and mid-point of the immediately higher class-interval (in the given question the immediate upper class-interval is 65 - 75).
Join the consecutive mid-points marked by straight lines to obtain the required frequency polygon.
(b) Without using histogram
Steps:
Find the class-mark (mid-value) of each given class-interval.
Class-mark = mid-value =
On a graph paper, mark class-marks along x-axis and frequencies along y-axis
On this graph paper, mark points taking values of class-marks along x-axis and the values of their corresponding frequencies along y-axis.
Draw line segments joining the consecutive points marked in step (3) above.
| C.I. | f | Class mark |
|---|---|---|
| -5 - 5 | 0 | = 0 |
| 5 - 15 | 8 | = 10 |
| 15 - 25 | 16 | = 20 |
| 25 - 35 | 18 | = 30 |
| 35 - 45 | 14 | = 40 |
| 45 - 55 | 8 | = 50 |
| 55 - 65 | 2 | = 60 |
| 65 - 75 | 0 | = 70 |
Using the class intervals 0-9, 10-19, 20-29, ............... , construct the frequency distribution for :
15, 8, 12, 7, 13, 16, 22, 29, 35, 49, 37 and 48.
Answer
The frequency table for the given distribution is :
| Class intervals | Tally marks | Frequency |
|---|---|---|
| 0 - 9 | II | 2 |
| 10 - 19 | IIII | 4 |
| 20 - 29 | II | 2 |
| 30 - 39 | II | 2 |
| 40 - 49 | II | 2 |
Construct the cumulative frequency table for :
| Marks | 20 - 29 | 30 - 39 | 40 - 49 | 50 - 59 |
|---|---|---|---|---|
| No. of students | 18 | 23 | 36 | 42 |
Answer
The cumulative frequency table for the given distribution is :
| Marks | No. of students | Cumulative frequency |
|---|---|---|
| 20 - 29 | 18 | 18 |
| 30 - 39 | 23 | 18 + 23 = 41 |
| 40 - 49 | 36 | 18 + 23 + 36 = 77 |
| 50 - 59 | 42 | 18 + 23 + 36 + 42 = 119 |
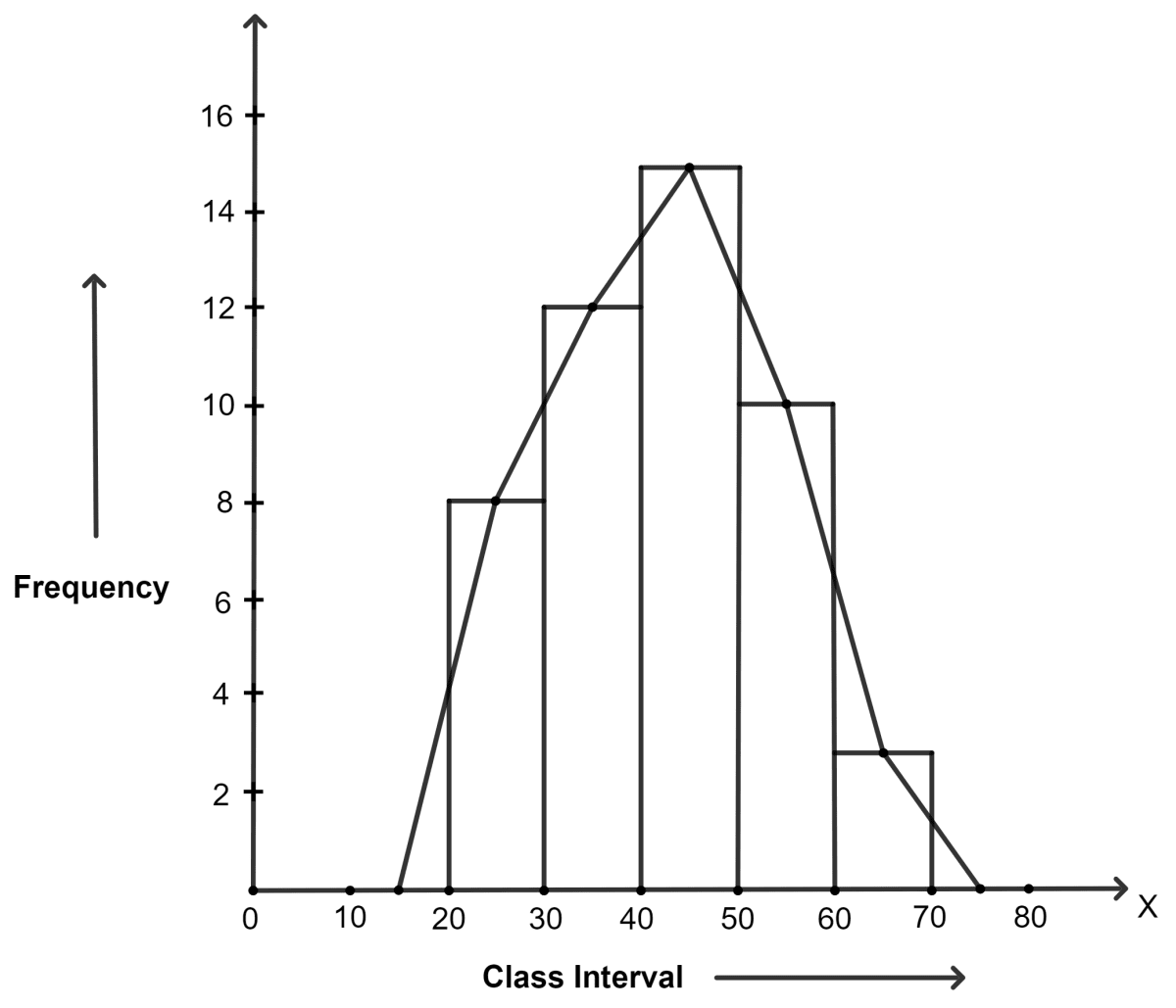
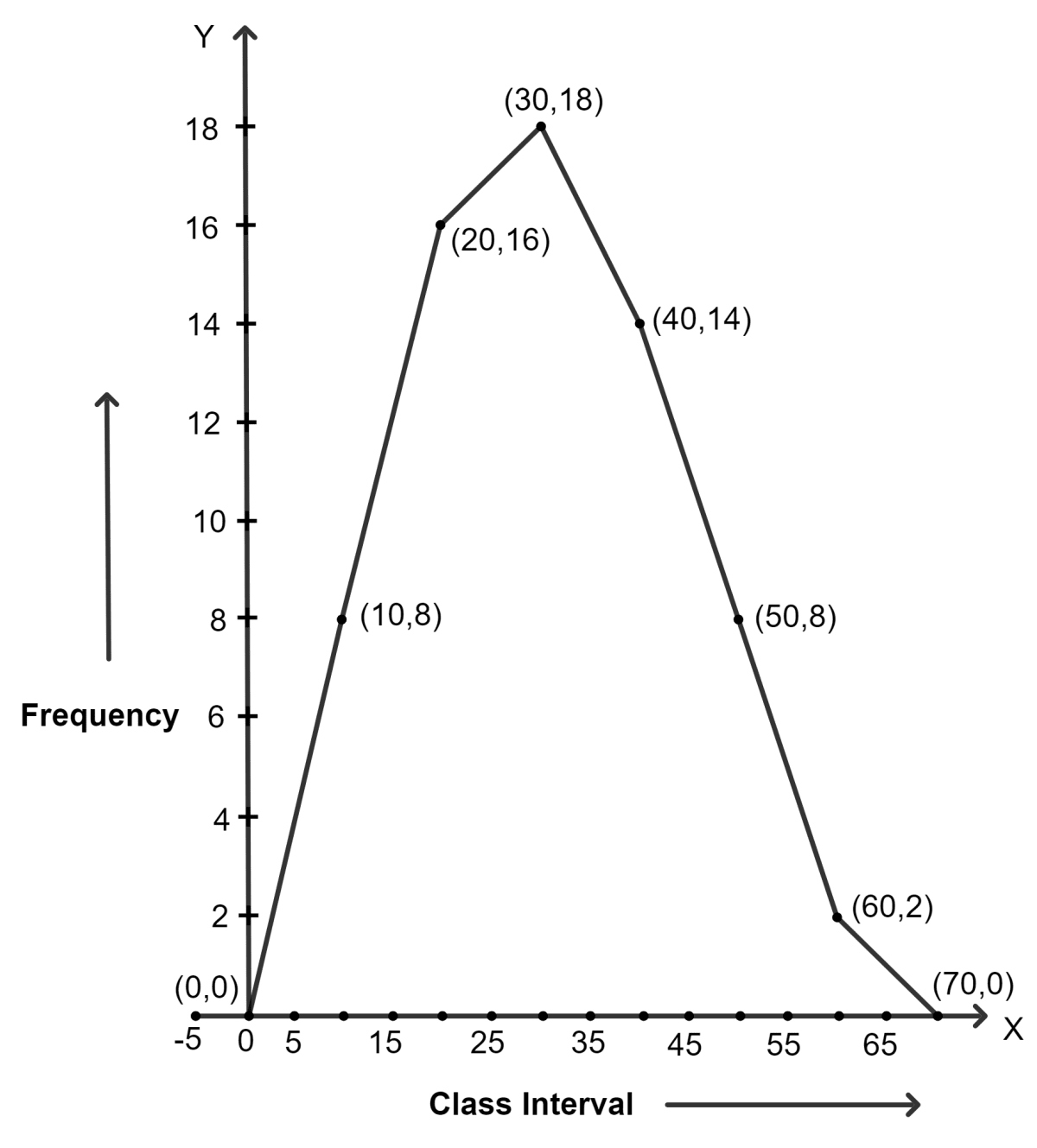
Construct a combined histogram and frequency polygon for the following frequency distribution :
| Class-intervals | 20 - 30 | 30 - 40 | 40 - 50 | 50 - 60 | 60 - 70 |
|---|---|---|---|---|---|
| Frequency | 8 | 12 | 15 | 10 | 3 |
Answer
Steps:
Draw a histogram for the given data.
Mark the mid-point at the top of each rectangle of the histogram drawn.
Also, mark the mid-point of the immediately lower class-interval (in the given question, the immediately lower class-interval is 10 - 20) and mid-point of the immediately higher class-interval (in the given question the immediate upper class-interval is 70 - 80).
Join the consecutive mid-points marked by straight lines to obtain the required frequency polygon.