Mid-point Theorem and its Converse [Including Intercept Theorem]

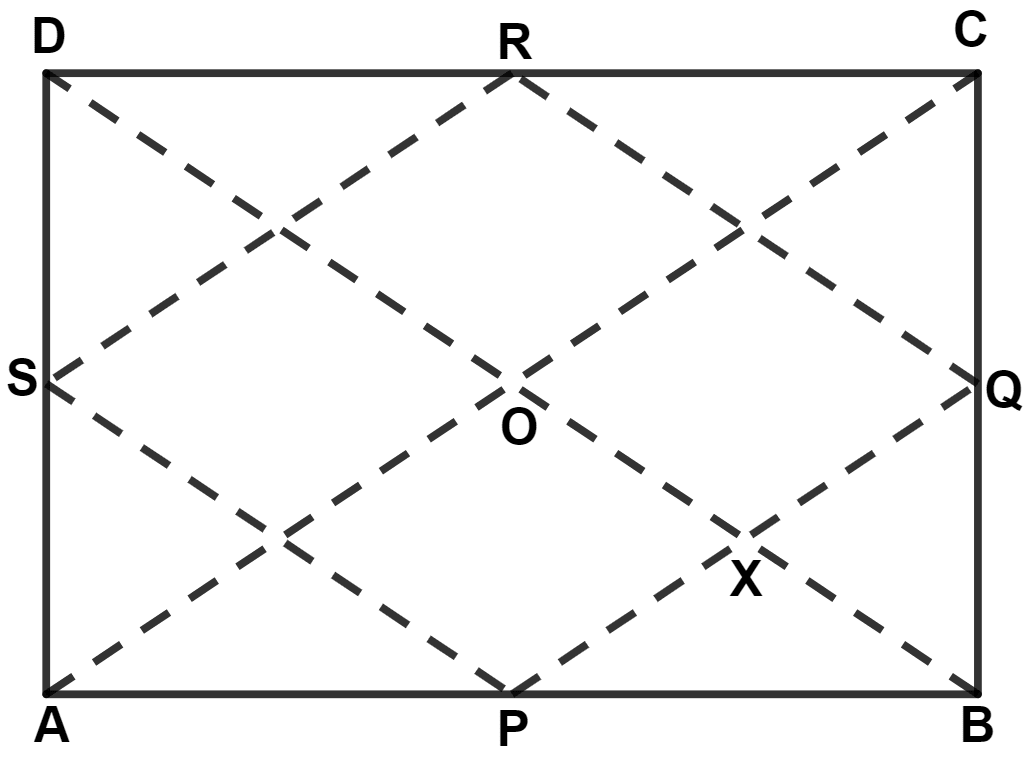
In the given figure, ABCD is a rectangle. As per the given information, the length of PQ is :

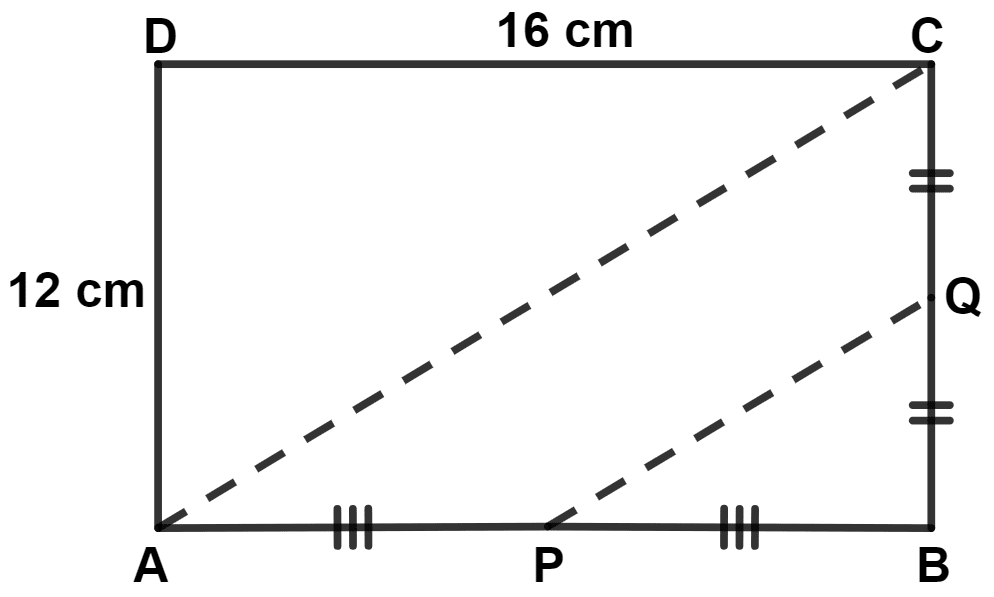
1. 12 cm

2. 14 cm

3. 20 cm

4. 10 cm

Answer

From figure,

AP = PB and BQ = QC.

∴ P is the mid-point of AB and Q is the mid-point of BC.

In △ ADC,

⇒ AD² + CD² = AC² (By pythagoras theorem)

⇒ 12² + 16² = AC²

⇒ 144 + 256 = AC²

⇒ AC² = 400

⇒ AC = $\sqrt{400}$ = 20 cm.

By mid-point theorem,

The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and is equal to half of it.

∴ PQ = $\dfrac{1}{2} AC = \dfrac{1}{2} \times 20$ = 10 cm.

Hence, Option 4 is the correct option.

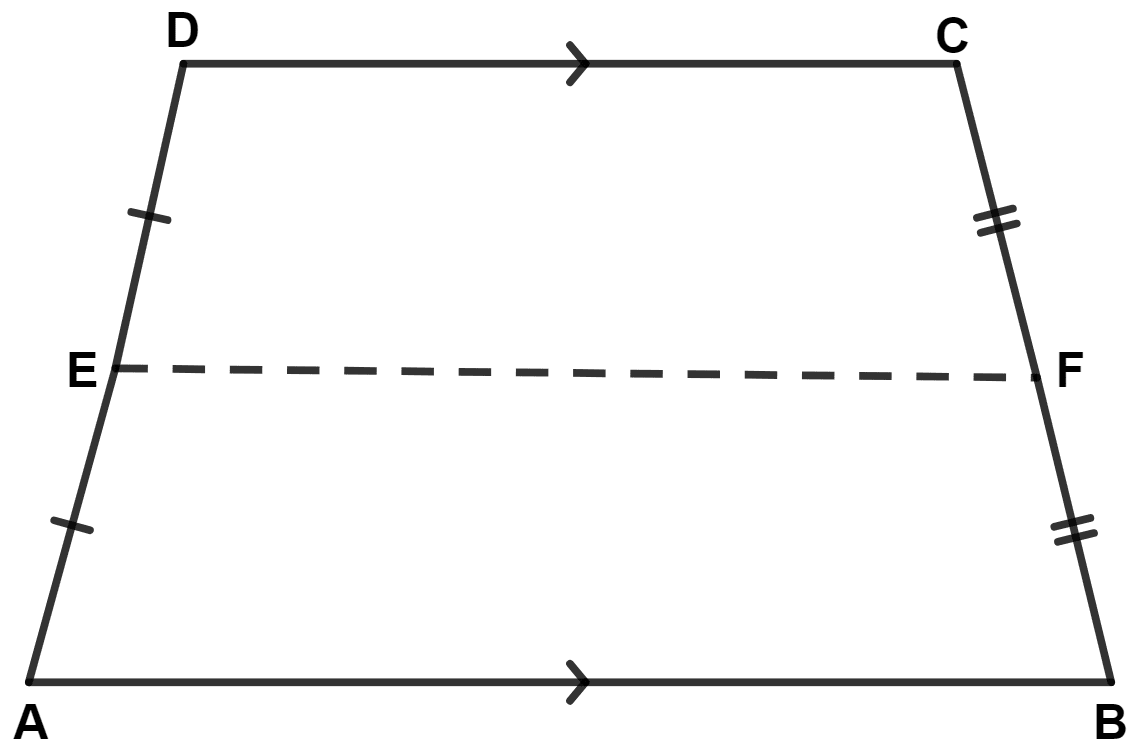
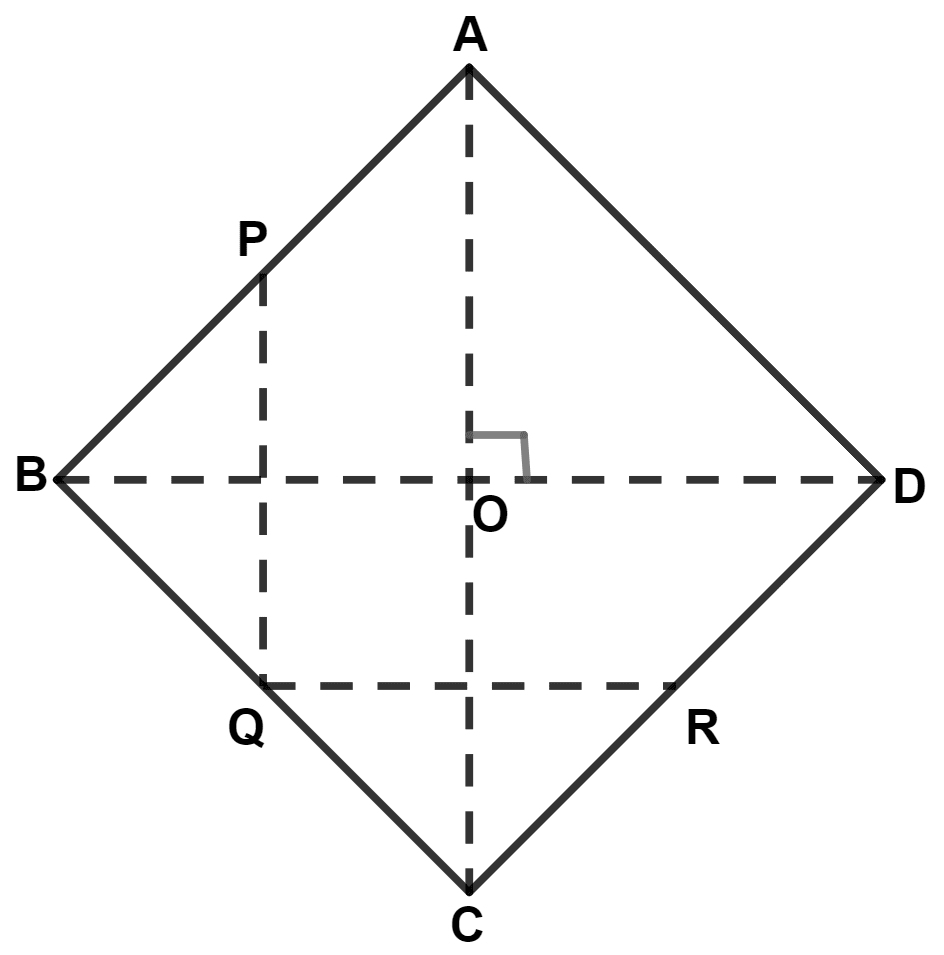
The quadrilateral obtained by joining the mid-points (in order) of the sides of quadrilateral ABCD is :

1. rectangle

2. rhombus

3. parallelogram

4. square

Answer

Let ABCD be the quadrilateral. P, Q, R and S are the mid-points of sides AB, BC, CD and DA.

Join PQRS, AC and BD.

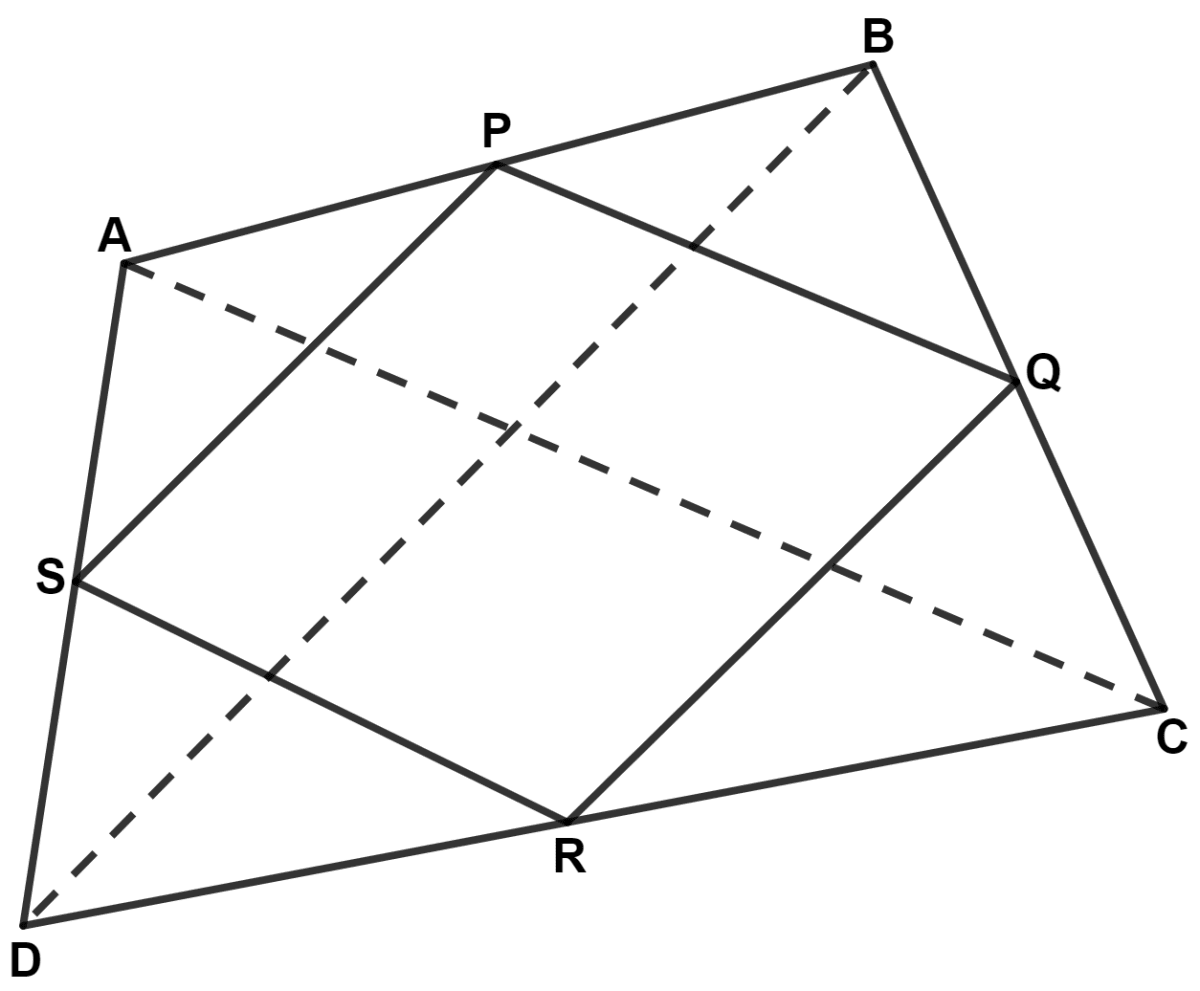
By mid-point theorem,

The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and is equal to half of it.

In △ ABC,

P and Q are mid-points of sides AB and BC respectively.

∴ PQ || AC and PQ = $\dfrac{1}{2}AC$ (By mid-point theorem) .......(1)

In △ ADC,

S and R are mid-points of sides AD and DC respectively.

∴ SR || AC and SR = $\dfrac{1}{2}AC$ (By mid-point theorem) ........(2)

From equations (1) and (2), we get :

⇒ PQ = SR and PQ || SR.

In △ ABD,

P and S are mid-points of sides AB and AD respectively.

∴ SP || BD and SP = $\dfrac{1}{2}BD$ (By mid-point theorem) .......(3)

In △ CBD,

Q and R are mid-points of sides BC and DC respectively.

∴ QR || BD and QR = $\dfrac{1}{2}BD$ (By mid-point theorem) ........(4)

From equations (3) and (4), we get :

⇒ SP = QR and SP || QR.

Since, opposite sides are parallel and equal.

∴ PQRS is a parallelogram.

Hence, Option 3 is the correct option.

If BC = 12 cm, AB = 14.8 cm, AC = 12.8 cm, the perimeter of quadrilateral BCYX is :

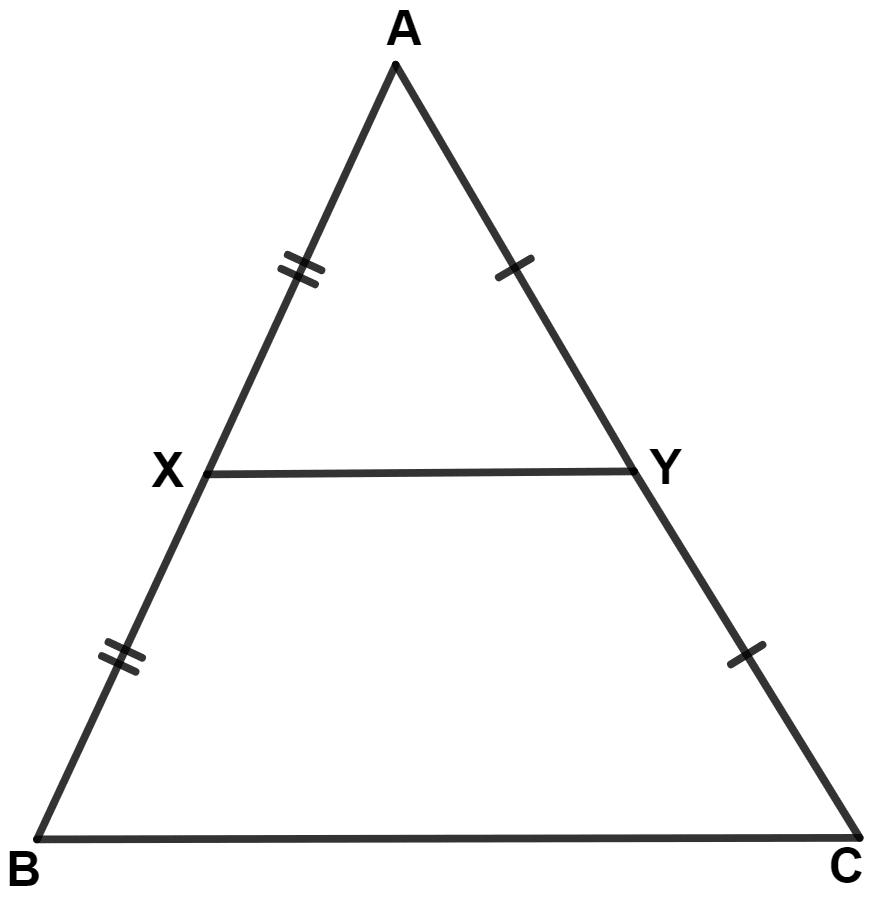
1. 31.8 cm

2. 15.9 cm

3. 29.8 cm

4. 32.8 cm

Answer

From figure,

X and Y are the mid-point of AB and AC respectively.

∴ BX = $\dfrac{AB}{2} = \dfrac{14.8}{2}$ = 7.4 cm and CY = $\dfrac{AC}{2} = \dfrac{12.8}{2}$ = 6.4 cm.

By mid-point theorem,

The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and is equal to half of it.

In △ ABC,

∴ XY = $\dfrac{1}{2}BC = \dfrac{1}{2} \times 12$ = 6 cm.

Perimeter of BCYX = BC + CY + XY + BX = 12 + 6.4 + 6 + 7.4 = 31.8 cm

Hence, Option 1 is the correct option.

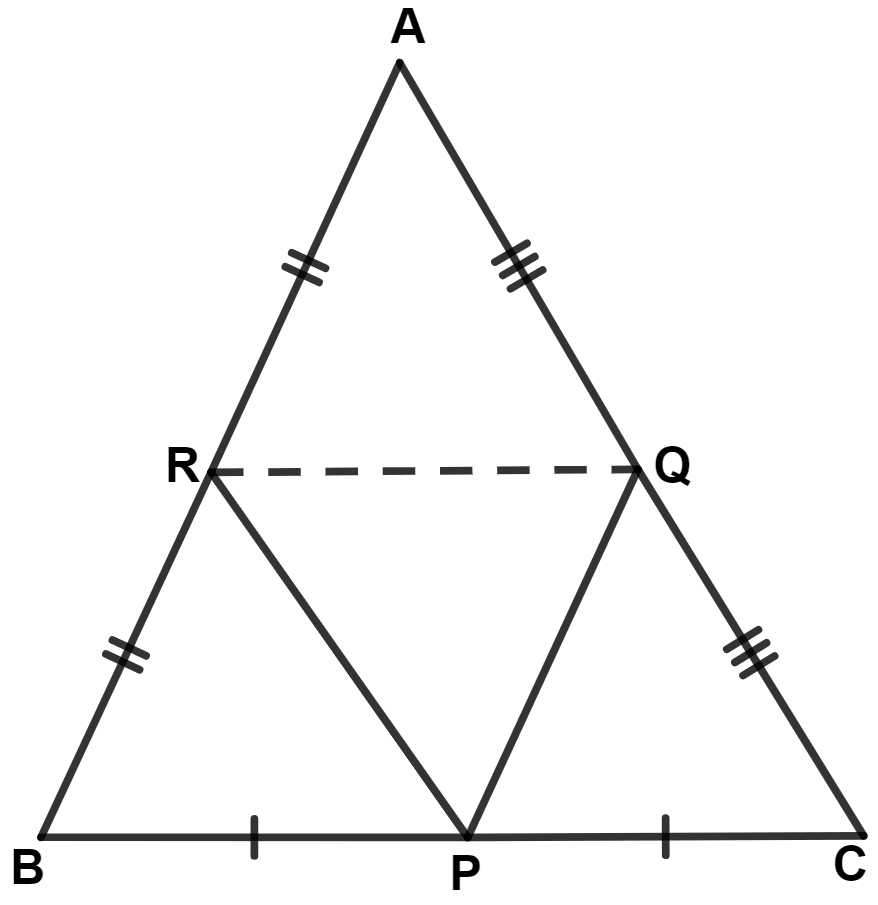
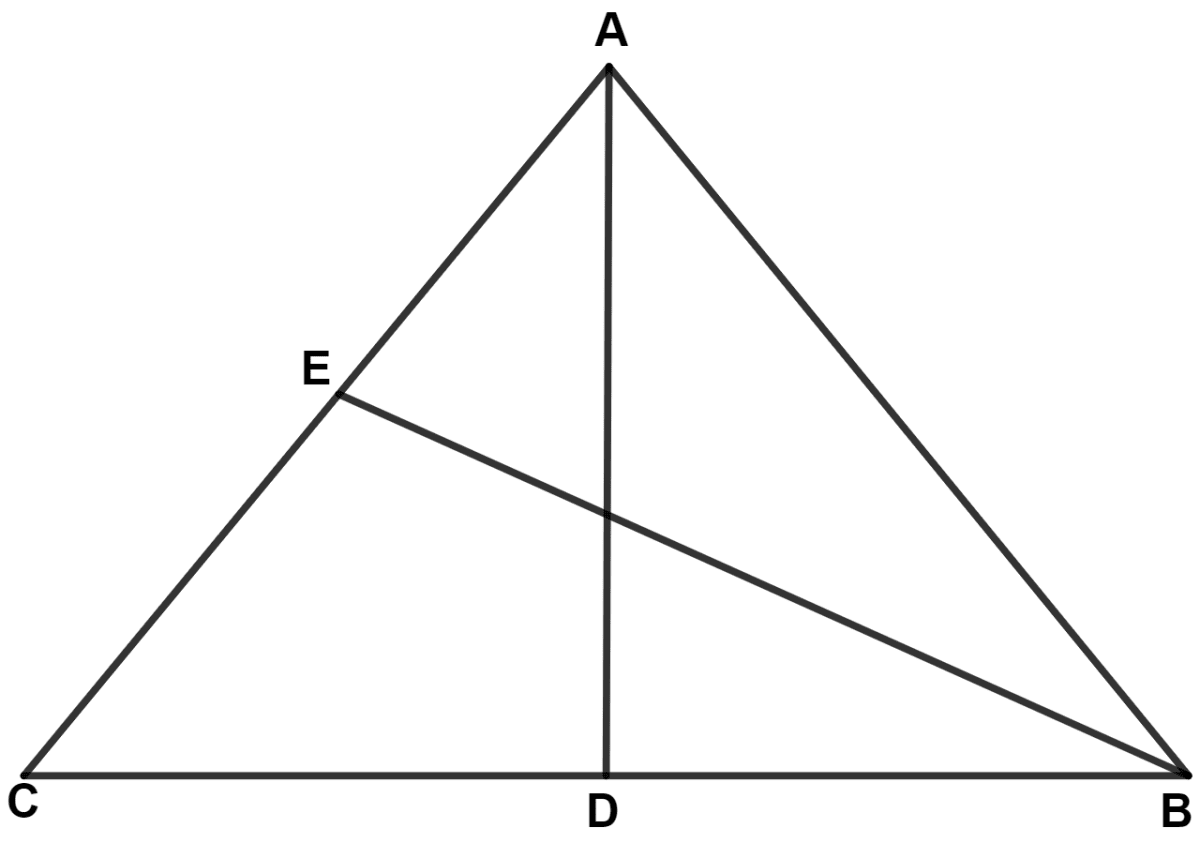
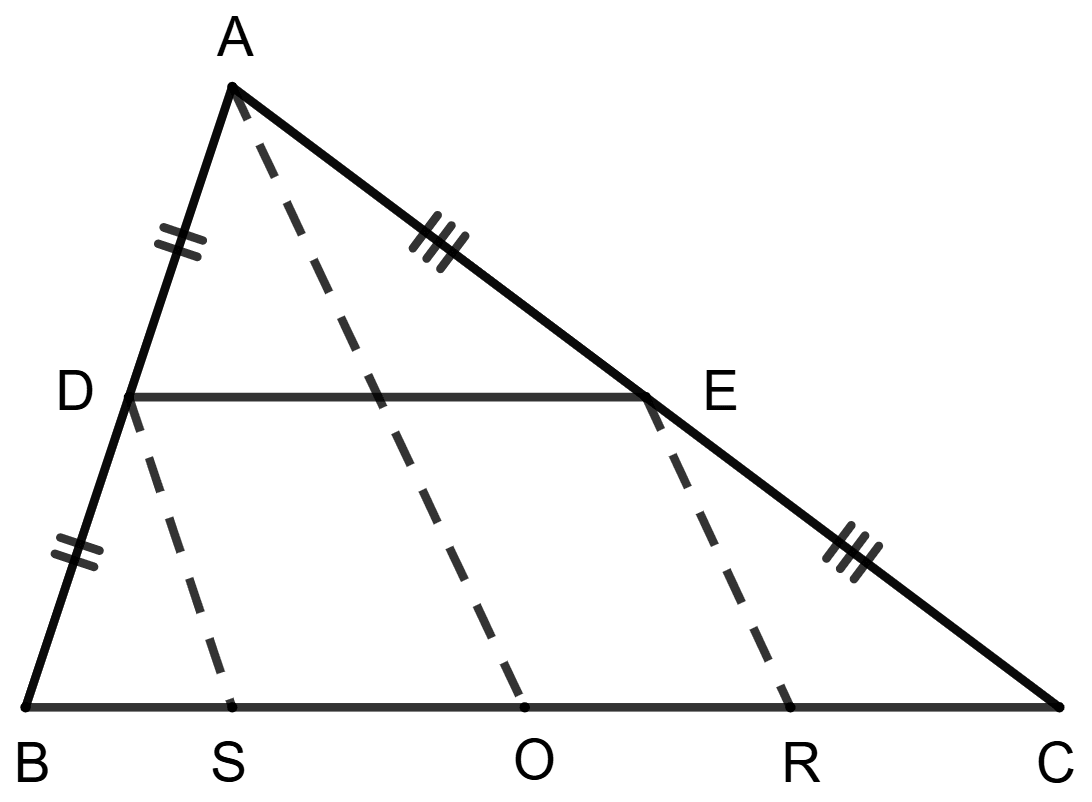
In the given figure, AB = AC, P, Q and R are mid-points of sides BC, CA and AB respectively, then △ PQR is :

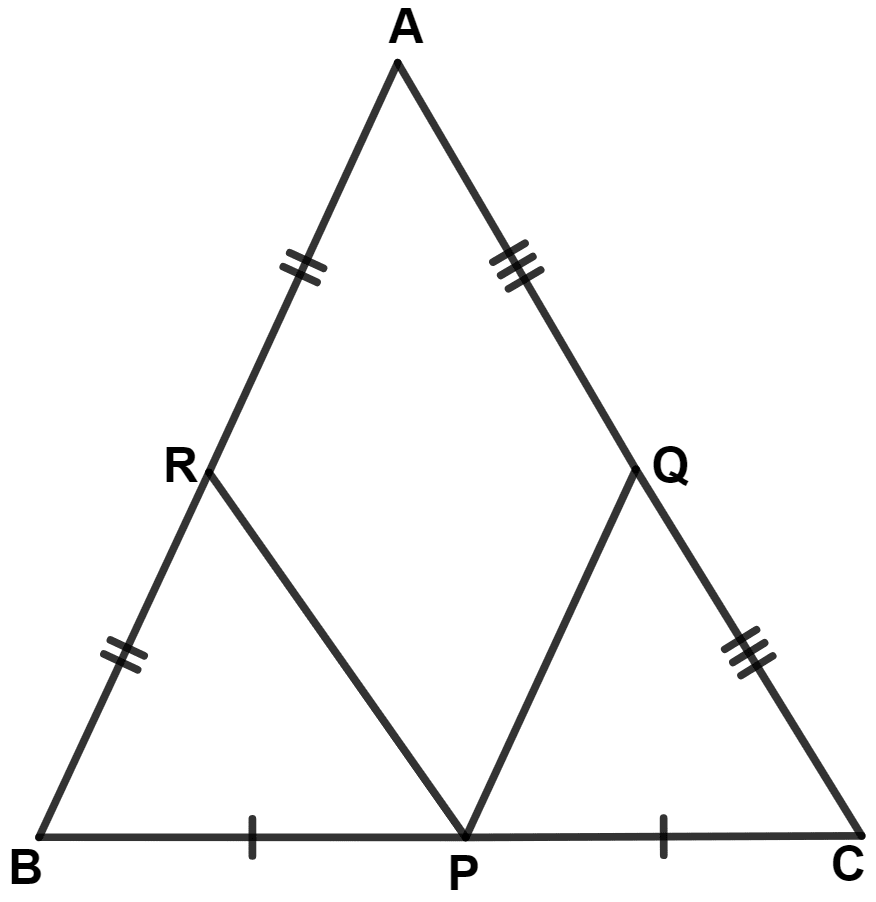
1. scalene

2. isosceles

3. equilateral

4. obtuse angled

Answer

Given,

AB = AC = x (let)

From figure,

AR = RB, BP = PC and AQ = QC.

∴ R, P and Q are mid-points of sides AB, BC and AC respectively.

Join QR.

By mid-point theorem,

The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and is equal to half of it.

∴ PQ = $\dfrac{1}{2}AB = \dfrac{x}{2}$, PR = $\dfrac{1}{2}AC = \dfrac{x}{2}$ and QR = $\dfrac{1}{2}BC$.

In △ PQR,

PQ = PR.

∴ △ PQR is an isosceles triangle.

Hence, Option 2 is the correct option.

P, Q, R and S are the mid-points of sides AB, BC, CD and DA respectively of rectangle ABCD, then quadrilateral PQRS is :

1. rectangle

2. rhombus

3. square

4. parallelogram

Answer

By mid-point theorem,

The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and is equal to half of it.

Join AC and BD.

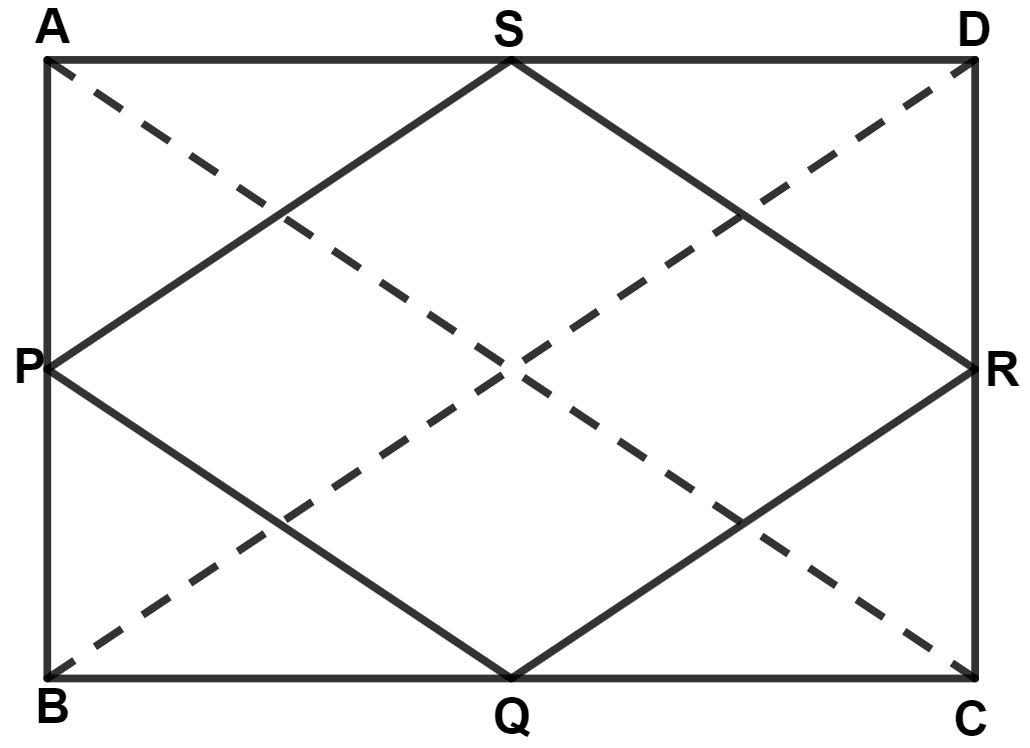
We know that,

Diagonals of a rectangle are equal.

∴ AC = BD = x (let)

In Δ ABC, P and Q are the mid-points of sides AB and BC respectively.

∴ PQ || AC and PQ = $\dfrac{1}{2}AC = \dfrac{1}{2}x$ (By mid-point theorem) ........(1)

In Δ ADC, S and R are mid-points of sides AD and CD respectively.

∴ SR || AC and SR = $\dfrac{1}{2}AC = \dfrac{1}{2}x$ (By mid-point theorem) .........(2)

From equations (1) and (2), we get :

PQ || SR and PQ = SR

In Δ ABD, P and S are the mid-points of sides AB and AD respectively.

∴ PS || BD and PS = $\dfrac{1}{2}BD = \dfrac{1}{2}x$ (By mid-point theorem) ........(3)

In Δ BDC, Q and R are mid-points of sides BC and CD respectively.

∴ QR || BD and QR = $\dfrac{1}{2}BD = \dfrac{1}{2}x$ (By mid-point theorem) .........(4)

From equations (3) and (4), we get :

PQ || SR and PS = QR

By using equation (1), (2), (3) and (4), we get :

⇒ PQ = QR = SR = PS

∴ PQRS is a rhombus.

Hence, Option 2 is the correct option.

In triangle ABC, M is the mid-point of AB and a straight line through M and parallel to BC cuts AC at N. Find the lengths of AN and MN, if BC = 7 cm and AC = 5 cm.

Answer

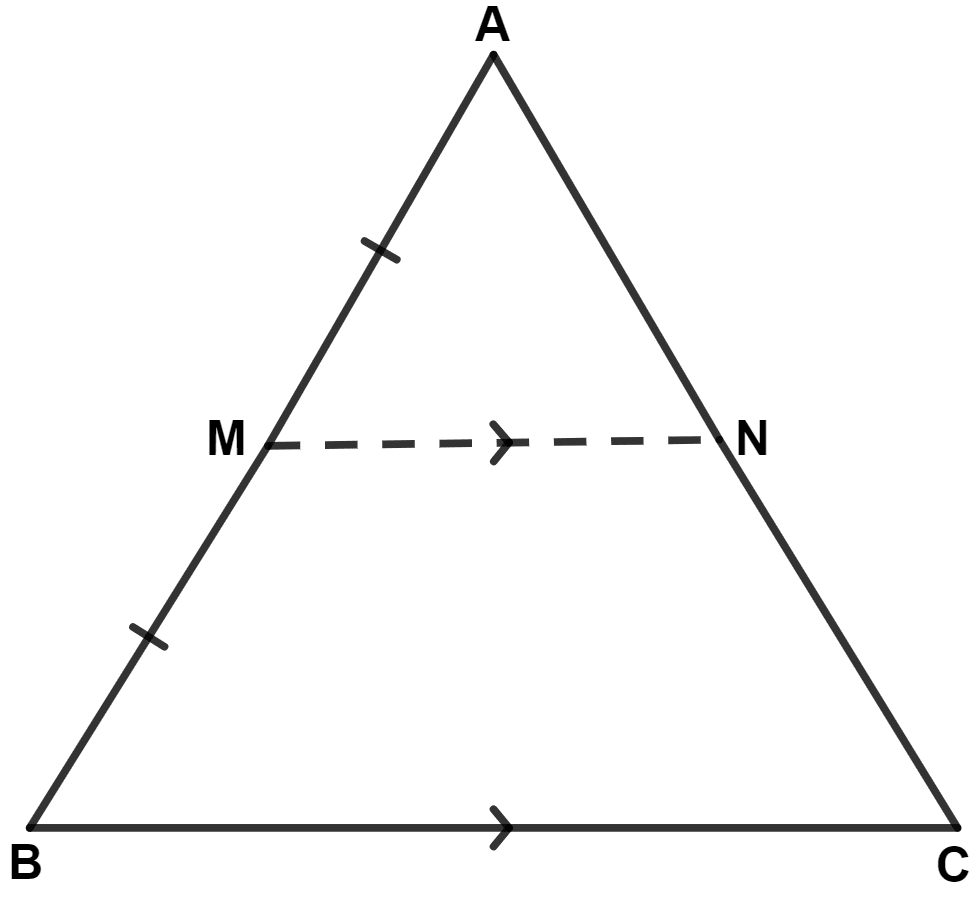
By converse of mid-point theorem,

The straight line drawn through the mid-point of one side of a triangle parallel to another, bisects the third side.

∴ N bisects AC.

∴ AN = $\dfrac{AC}{2} = \dfrac{5}{2}$ = 2.5 cm.

By mid-point theorem,

The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and is equal to half of it.

∴ MN = $\dfrac{1}{2}BC = \dfrac{1}{2} \times 7$ = 3.5 cm.

Hence, AN = 2.5 cm and MN = 3.5 cm.

Prove that the figure obtained by joining the mid-points of the adjacent sides of a rectangle is a rhombus.

Answer

Let ABCD be the rectangle and P, Q, R and S be the mid-points of sides AB, BC, CD and DA respectively. Join PQRS.

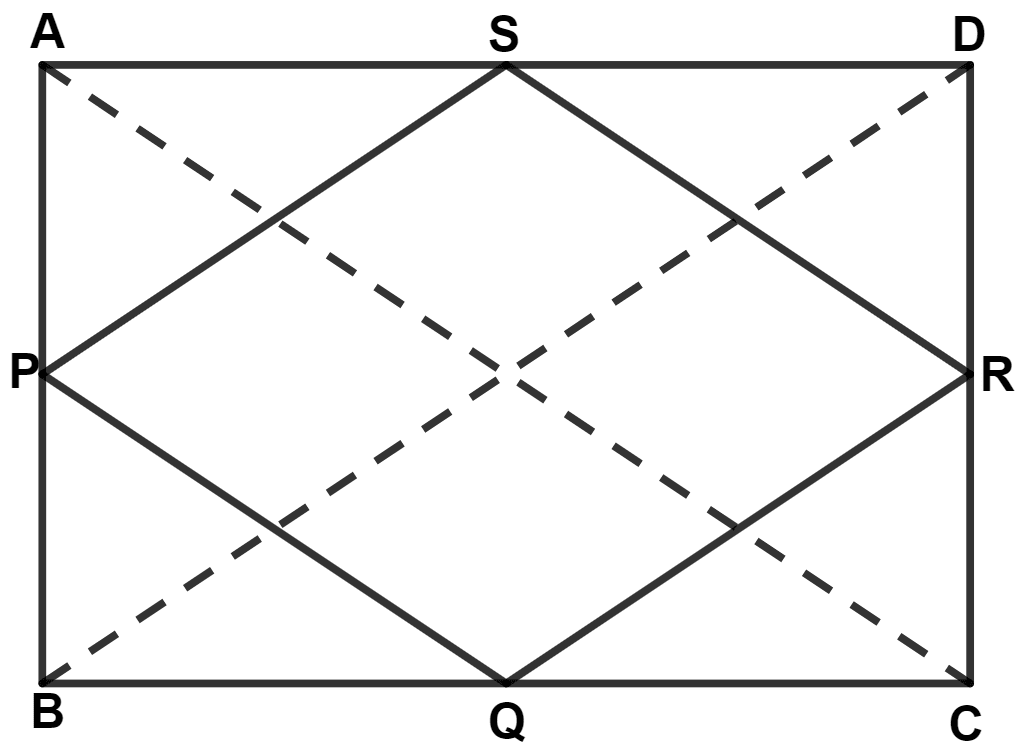
By mid-point theorem,

The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and is equal to half of it.

Join AC and BD.

We know that,

Diagonals of a rectangle are equal.

∴ AC = BD = x (let)

In Δ ABC, P and Q are the mid-points of sides AB and BC respectively.

∴ PQ || AC and PQ = $\dfrac{1}{2}AC = \dfrac{1}{2}x$ (By mid-point theorem) ........(1)

In Δ ADC, S and R are mid-points of sides AD and CD respectively.

∴ SR || AC and SR = $\dfrac{1}{2}AC = \dfrac{1}{2}x$ (By mid-point theorem) .........(2)

From equations (1) and (2), we get :

PQ || SR and PQ = SR

In Δ ABD, P and S are the mid-points of sides AB and AD respectively.

∴ PS || BD and PS = $\dfrac{1}{2}BD = \dfrac{1}{2}x$ (By mid-point theorem) ........(3)

In Δ BDC, Q and R are mid-points of sides BC and CD respectively.

∴ QR || BD and QR = $\dfrac{1}{2}BD = \dfrac{1}{2}x$ (By mid-point theorem) .........(4)

From equations (3) and (4), we get :

PQ || SR and PS = QR

By using equation (1), (2), (3) and (4), we get :

⇒ PQ = QR = SR = PS

Since, opposite sides are parallel and all the sides are equal.

∴ PQRS is a rhombus.

Hence, proved that the figure obtained by joining the mid-points of the adjacent sides of a rectangle is a rhombus.

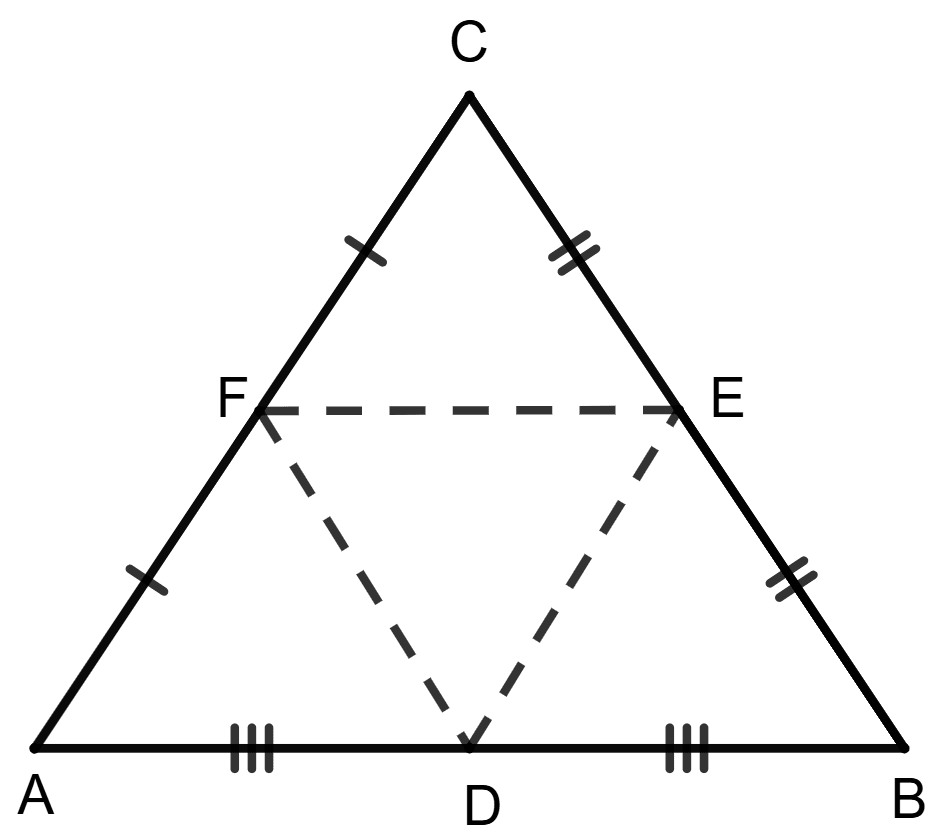
D, E and F are the mid-points of the sides AB, BC and CA of an isosceles △ ABC in which AB = BC. Prove that △ DEF is also isosceles.

Answer

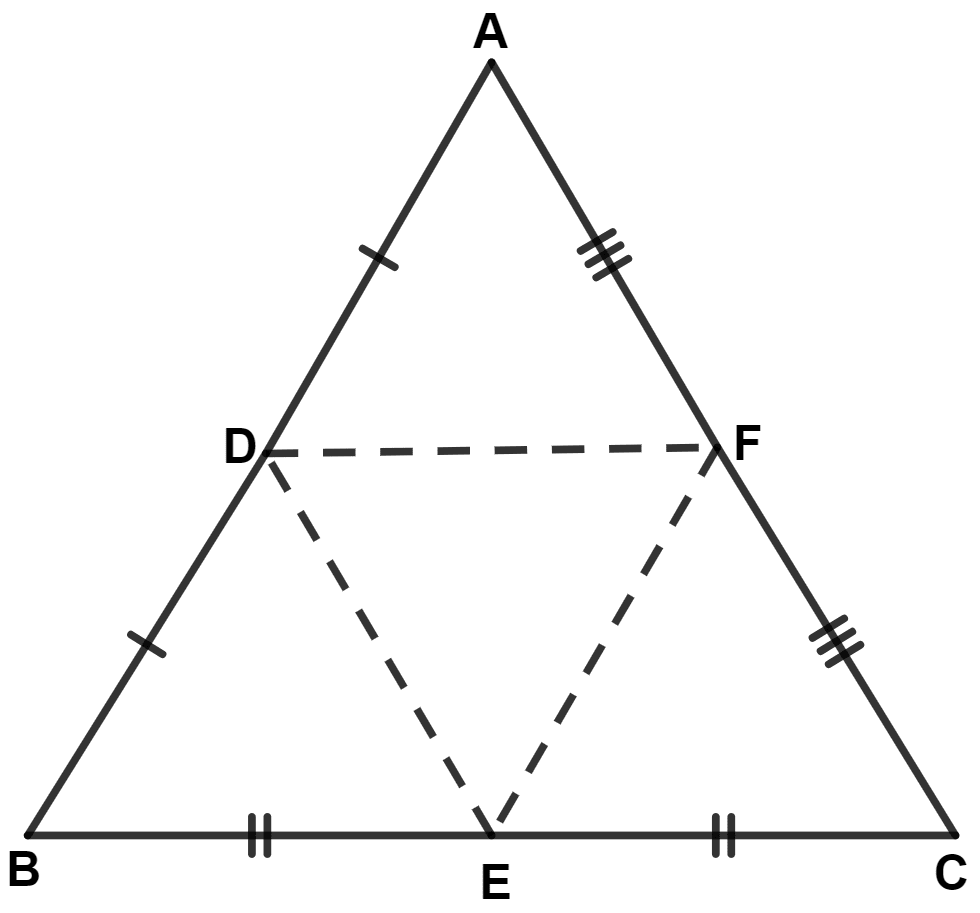
Join D, E and F.

Given,

AB = BC = x (let)

Given,

D, E and F are mid-points of sides AB, BC and AC respectively.

By mid-point theorem,

The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and is equal to half of it.

∴ DF = $\dfrac{1}{2}BC = \dfrac{x}{2}$, FE = $\dfrac{1}{2}AB = \dfrac{x}{2}$ and DE = $\dfrac{1}{2}AC$.

In △ DEF,

DF = FE.

∴ △ DEF is an isosceles triangle.

Hence, proved that DEF is an isosceles triangle.

The following figure shows a trapezium ABCD in which AB // DC. P is the mid-point of AD and PR // AB. Prove that :

PR = $\dfrac{1}{2}$ (AB + CD)

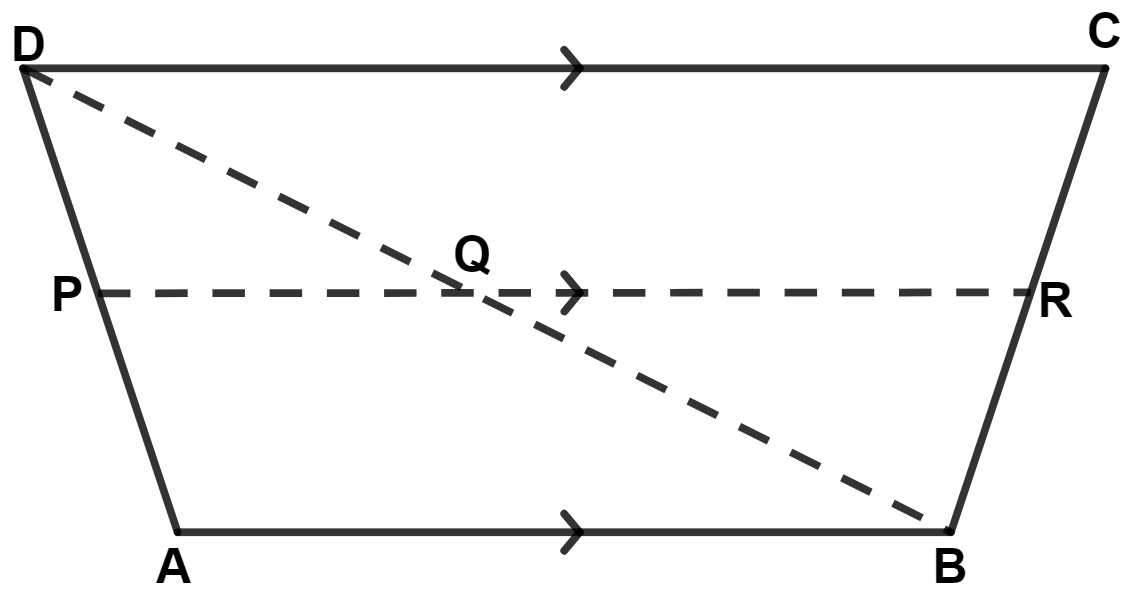
Answer

By mid-point theorem,

The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and is equal to half of it.

By converse of mid-point theorem,

The straight line drawn through the mid-point of one side of a triangle parallel to another, bisects the third side.

Given,

⇒ PR // AB

⇒ PQ // AB

In △ ABD,

P is mid-point of AD and PQ // AB.

∴ Q is mid-point of BD. (By converse of mid-point theorem)

∴ PQ = $\dfrac{1}{2}AB$ (By mid-point theorem) ..........(1)

Given,

⇒ PR // DC

⇒ QR // DC

In △ BCD,

Q is mid-point of BD and QR // DC.

∴ R is mid-point of BC. (By converse of mid-point theorem)

∴ QR = $\dfrac{1}{2}CD$ (By mid-point theorem) ..........(2)

Adding equations (1) and (2), we get :

⇒ PQ + QR = $\dfrac{1}{2}AB + \dfrac{1}{2}CD$

⇒ PR = $\dfrac{1}{2}(AB + CD)$.

Hence, proved that PR = $\dfrac{1}{2}(AB + CD)$.

The figure, given below, shows a trapezium ABCD. M and N are the mid-points of the non-parallel sides AD and BC respectively. Find :

(i) MN, if AB = 11 cm and DC = 8 cm.

(ii) AB, if DC = 20 cm and MN = 27 cm.

(iii) DC, if MN = 15 cm and AB = 23 cm.

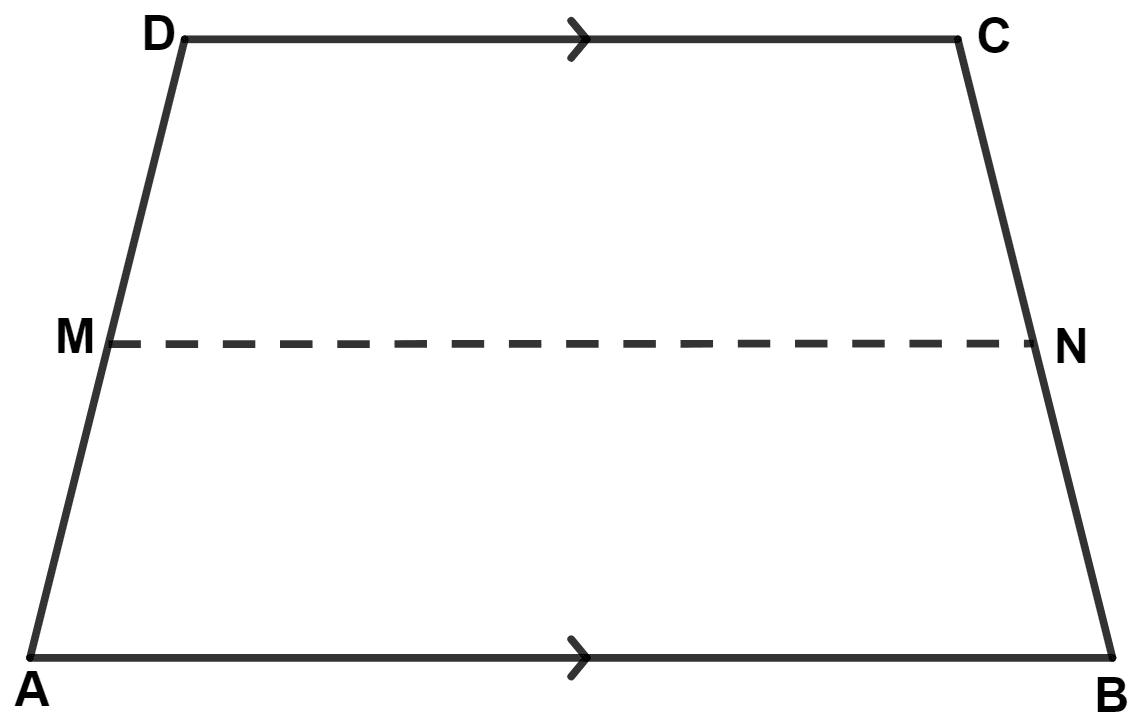
Answer

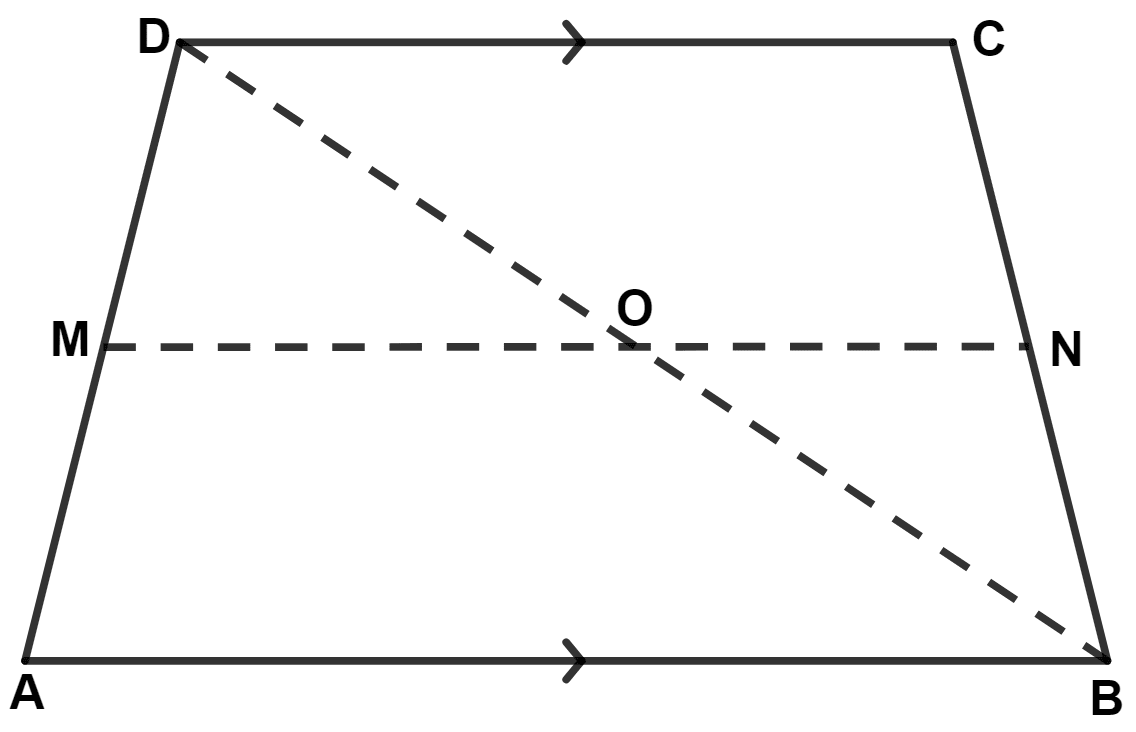
Join BD. Let BD intersects MN at point O.

We know that,

In trapezium the line joining the mid-points of non-parallel sides are parallel to the parallel sides of trapezium.

∴ MN || AB || DC.

By mid-point theorem,

The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and is equal to half of it.

By converse of mid-point theorem,

The straight line drawn through the mid-point of one side of a triangle parallel to another, bisects the third side.

Given,

⇒ MN || AB

⇒ MO || AB

In △ ABD,

M is mid-point of AD and MO || AB.

∴ O is mid-point of BD. (By converse of mid-point theorem)

∴ MO = $\dfrac{1}{2}AB$ (By mid-point theorem) ..........(1)

Given,

⇒ MN || DC

⇒ ON || DC

In △ BCD,

O is mid-point of BD and N is mid-point of BC.

∴ ON = $\dfrac{1}{2}CD$ (By mid-point theorem) ..........(2)

Adding equations (1) and (2), we get :

⇒ MO + ON = $\dfrac{1}{2}AB + \dfrac{1}{2}CD$

⇒ MN = $\dfrac{1}{2}(AB + CD)$ ..........(3)

(i) Given,

⇒ AB = 11 cm

⇒ DC = 8 cm

Substituting values in equation (3), we get :

$\Rightarrow MN = \dfrac{1}{2}(AB + CD) \\[1em] \Rightarrow MN = \dfrac{1}{2} \times (11 + 8) \\[1em] \Rightarrow MN = \dfrac{1}{2} \times 19 \\[1em] \Rightarrow MN = 9.5 \text{ cm}.$

Hence, MN = 9.5 cm

(ii) Given,

⇒ MN = 27 cm

⇒ DC = 20 cm

Substituting values in equation (3), we get :

$\Rightarrow MN = \dfrac{1}{2}(AB + CD) \\[1em] \Rightarrow 27 = \dfrac{1}{2} \times (AB + 20) \\[1em] \Rightarrow 27 \times 2 = AB + 20 \\[1em] \Rightarrow AB + 20 = 54 \\[1em] \Rightarrow AB = 54 - 20 = 34 \text{ cm}.$

Hence, AB = 34 cm.

(iii) Given,

⇒ MN = 15 cm

⇒ AB = 23 cm

Substituting values in equation (3), we get :

$\Rightarrow MN = \dfrac{1}{2}(AB + CD) \\[1em] \Rightarrow 15 = \dfrac{1}{2} \times (23 + DC) \\[1em] \Rightarrow 15 \times 2 = 23 + DC \\[1em] \Rightarrow 23 + DC = 30 \\[1em] \Rightarrow DC = 30 - 23 = 7 \text{ cm}.$

Hence, DC = 7 cm.

The diagonals of a quadrilateral intersect at right angles. Prove that the figure obtained by joining the mid-points of the adjacent sides of the quadrilateral is a rectangle.

Answer

By mid-point theorem,

The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and is equal to half of it.

Let ABCD be a quadrilateral where P, Q, R and S are the mid-point of AB, BC, CD and DA.

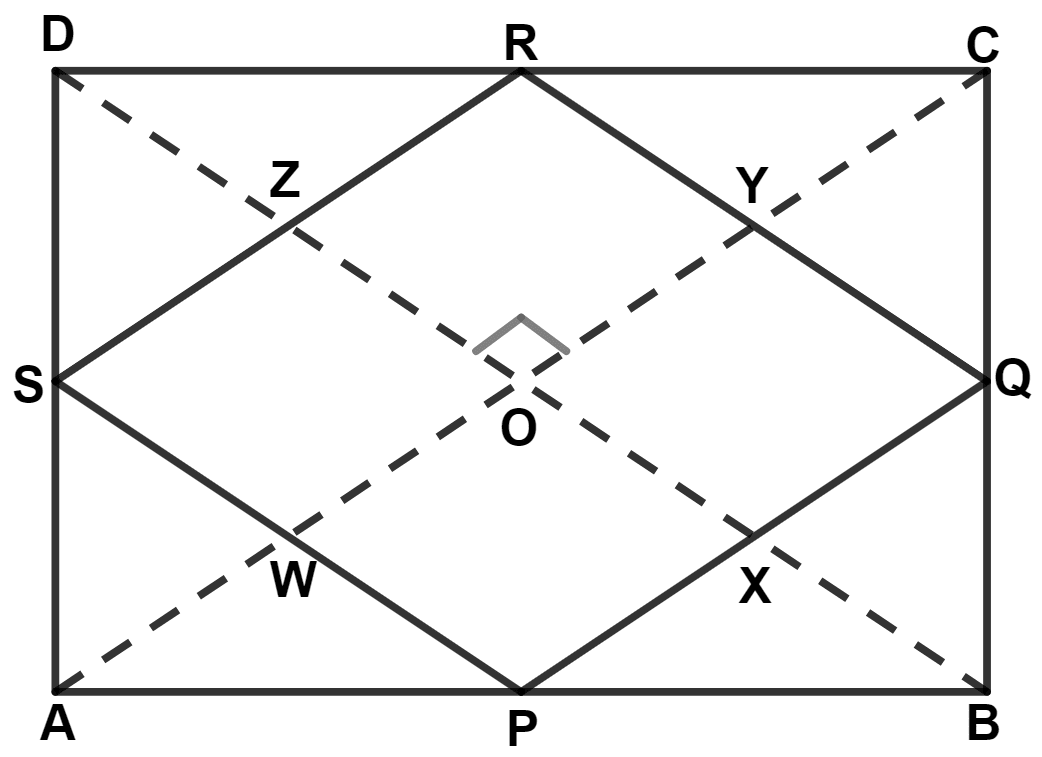
In △ ABC,

P and Q are mid-points of AB and BC respectively.

⇒ PQ = $\dfrac{1}{2}AC$ and PQ || AC. [By mid-point theorem] .......(1)

In △ ADC,

S and R are mid-points of AD and CD respectively.

⇒ SR = $\dfrac{1}{2}AC$ and SR || AC. [By mid-point theorem] .......(2)

From (1) and (2), we get :

PQ = SR and PQ || SR.

In △ BCD,

R and Q are mid-points of CD and BC respectively.

⇒ QR = $\dfrac{1}{2}BD$ and QR || BD. [By mid-point theorem] .......(3)

In △ ABD,

S and P are mid-points of AD and AB respectively.

⇒ PS = $\dfrac{1}{2}BD$ and PS || BD. [By mid-point theorem] .......(4)

From (3) and (4), we get :

QR = PS and QR || PS.

Since, diagonals of quadrilateral intersect at right angle.

∴ ∠AOD = ∠COD = AOB = ∠BOC = 90°.

From figure,

PQ || AC

∴ ∠PXO = ∠AOD = 90° (Corresponding angles are equal)

∴ ∠QXO = ∠COD = 90° (Corresponding angles are equal)

SR || AC

∴ ∠SZO = ∠AOB = 90° (Corresponding angles are equal)

∴ ∠RZO = ∠BOC = 90° (Corresponding angles are equal)

PS || BD

∴ ∠S = ∠RZO = 90° (Corresponding angles are equal)

∴ ∠P = ∠QXO = 90° (Corresponding angles are equal)

QR || BD

∴ ∠R = ∠SZO = 90° (Corresponding angles are equal)

∴ ∠Q = ∠PXO = 90° (Corresponding angles are equal)

Since, in quadrilateral PQRS,

Each interior angle equal to 90° and opposite sides are parallel and equal.

∴ PQRS is a rectangle.

Hence, proved that the the figure obtained by joining the mid-points of the adjacent sides of the quadrilateral is a rectangle.

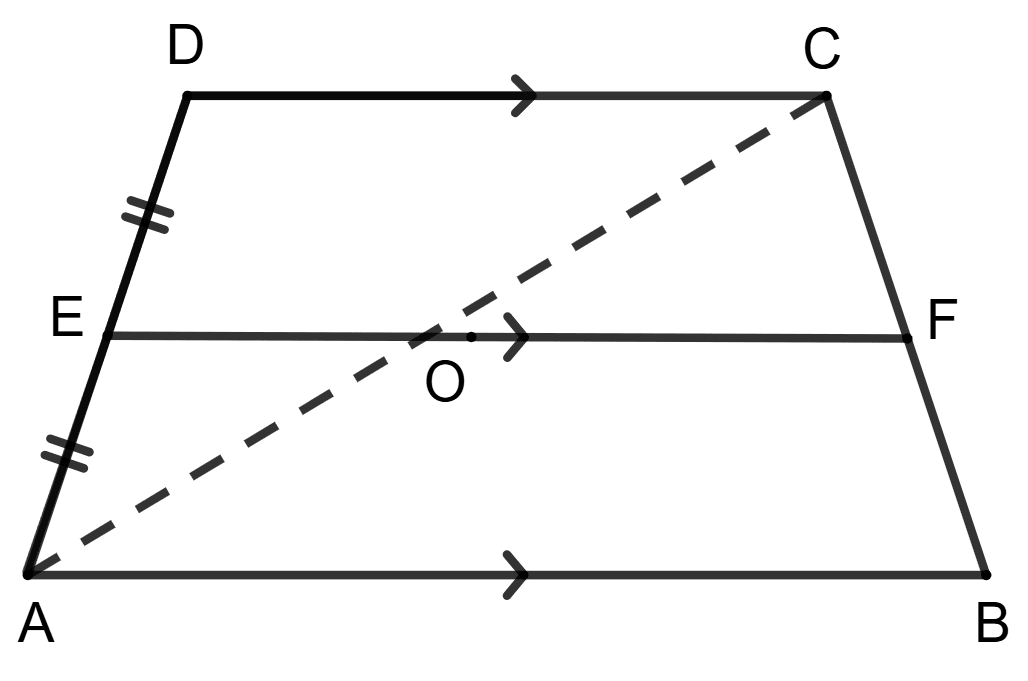
L and M are the mid-points of sides AB and DC respectively of parallelogram ABCD. Prove that segments DL and BM trisect diagonal AC.

Answer

From figure,

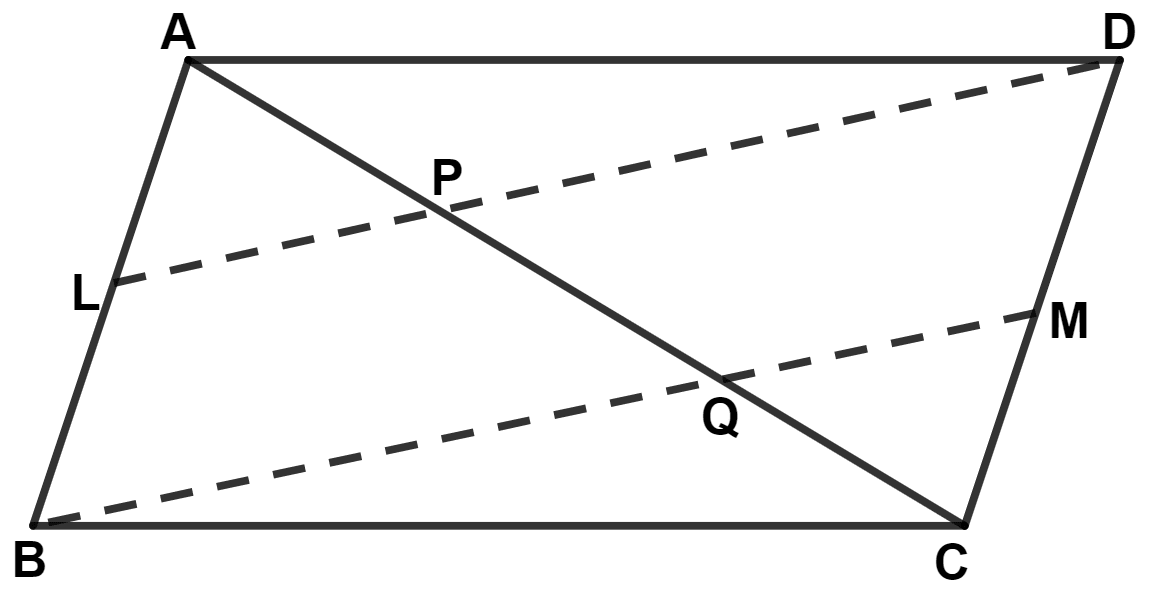
As, ABCD is a parallelogram.

∴ AB = CD

⇒ $\dfrac{AB}{2} = \dfrac{CD}{2}$

⇒ BL = DM

As, AB || CD

∴ BL || DM

Since, in quadrilateral DLBM,

BL = DM and BL || DM

∴ DLBM is a parallelogram.

So we get, DL parallel to MB.

Suppose DL and BM intersect AC at P and Q respectively.

By converse of mid-point theorem,

The straight line drawn through the mid-point of one side of a triangle parallel to another, bisects the third side.

In triangle ABQ,

⇒ PL || QB (As, DL || MB)

⇒ Given, L is the midpoint of AB.

∴ P is the mid point of AQ (By converse of mid-point theorem)

∴ AP = PQ ........(1)

In triangle CDP,

⇒ QM || PD (As, BM || DL)

⇒ Given, M is the midpoint of CD.

∴ Q is the mid point of CP (By converse of mid-point theorem)

∴ PQ = CQ ........(2)

From equations (1) and (2), we get,

⇒ AP = PQ = CQ.

Hence, proved that DL and BM trisect the diagonal AC.

ABCD is a quadrilateral in which AD = BC. E, F, G and H are the mid-points of AB, BD, CD and AC respectively. Prove that EFGH is a rhombus.

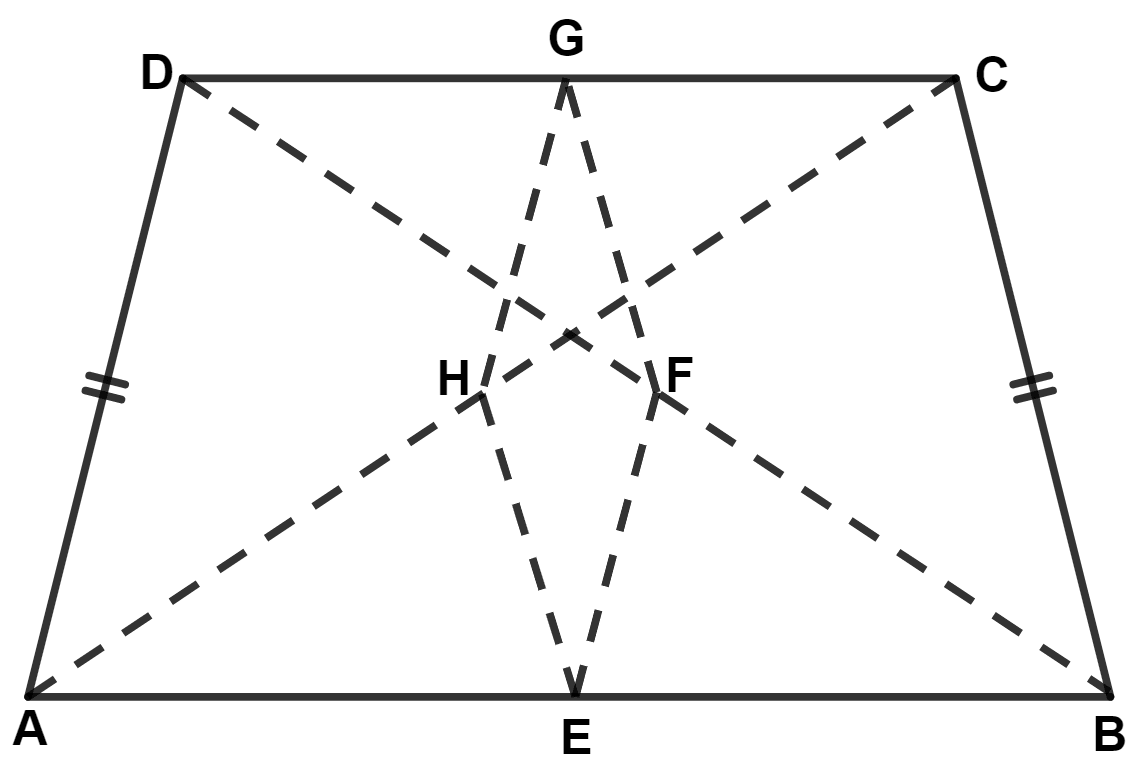
Answer

By mid-point theorem,

The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and is equal to half of it.

In △ ADC,

G and H are mid-points of sides CD and AC respectively.

⇒ GH = $\dfrac{1}{2}AD$

⇒ AD = 2GH .........(1)

In △ ABD,

E and F are mid-points of sides AB and BD respectively.

⇒ EF = $\dfrac{1}{2}AD$

⇒ AD = 2EF .........(2)

From equations (1) and (2), we get :

⇒ AD = 2GH = 2EF ........(3)

In △ BCD,

G and F are mid-points of sides CD and BD respectively.

⇒ GF = $\dfrac{1}{2}BC$

⇒ BC = 2GF .........(4)

In △ ABC,

E and H are mid-points of sides AB and AC respectively.

⇒ EH = $\dfrac{1}{2}BC$

⇒ BC = 2EH .........(5)

From equations (4) and (5), we get :

⇒ BC = 2GF = 2EH ........(6)

Given,

⇒ AD = BC .............(7)

From equations (3), (6) and (7), we get :

⇒ 2GH = 2EF = 2GF = 2EH

⇒ GH = EF = GF = EH.

Since, all sides of quadrilateral EFGH are equal.

∴ EFGH is a rhombus.

Hence, proved that EFGH is a rhombus.

A parallelogram ABCD has P the mid-point of DC and Q a point of AC such that CQ = $\dfrac{1}{4}AC$. PQ produced meets BC at R.

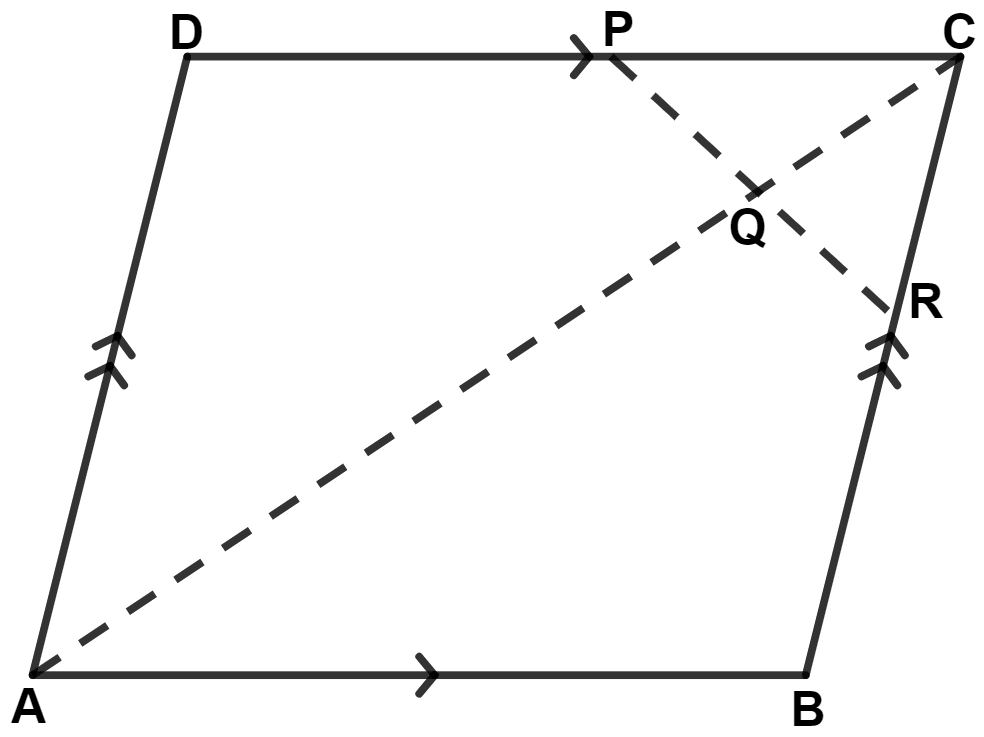
Prove that :

(i) R is the mid-point of BC,

(ii) PR = $\dfrac{1}{2}DB$.

Answer

By mid-point theorem,

The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and is equal to half of it.

By converse of mid-point theorem,

The straight line drawn through the mid-point of one side of a triangle parallel to another, bisects the third side.

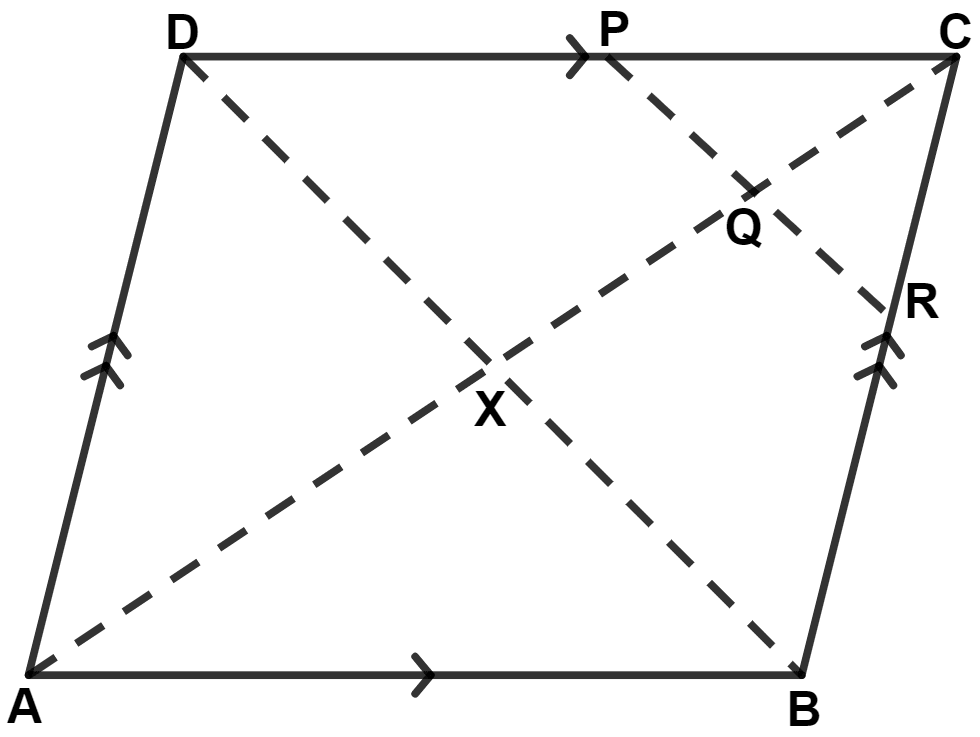
We know that,

Diagonals of parallelogram bisect each other.

∴ AX = CX and BX = DX.

Given,

⇒ CQ = $\dfrac{1}{4}AC$

⇒ CQ = $\dfrac{1}{4} \times (AX + CX)$

⇒ CQ = $\dfrac{1}{4} \times (CX + CX) = \dfrac{1}{4} \times 2CX = \dfrac{CX}{2}$.

∴ Q is the mid-point of CX.

(i) In △ CDX,

P and Q are mid-point of sides CD and CX.

∴ PQ || DX (By mid-point theorem)

Since, DXB and PQR are straight line.

∴ PR || DB

∴ QR || XB.

In △ CXB,

Q is the mid-point of CX and QR || XB.

∴ R is the mid-point of BC (By converse of mid-point theorem).

Hence, proved that R is the mid-point of BC.

(ii) In △ BCD,

P and R are mid-point of sides CD and BC.

∴ PR || BD and PR = $\dfrac{1}{2}BD$.

Hence, proved that PR = $\dfrac{1}{2}BD$.

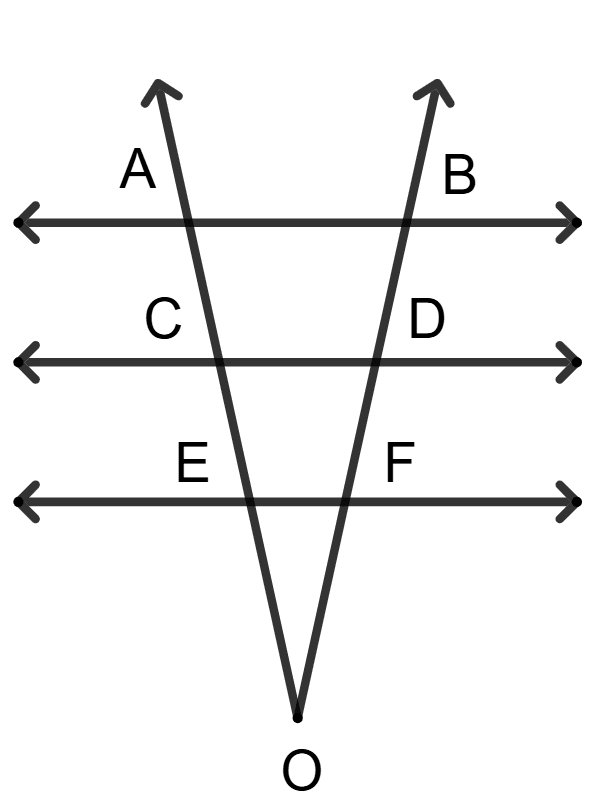
In the given figure, l // m // n and D is mid-point of CE. If AE = 12.6 cm, then BD is :

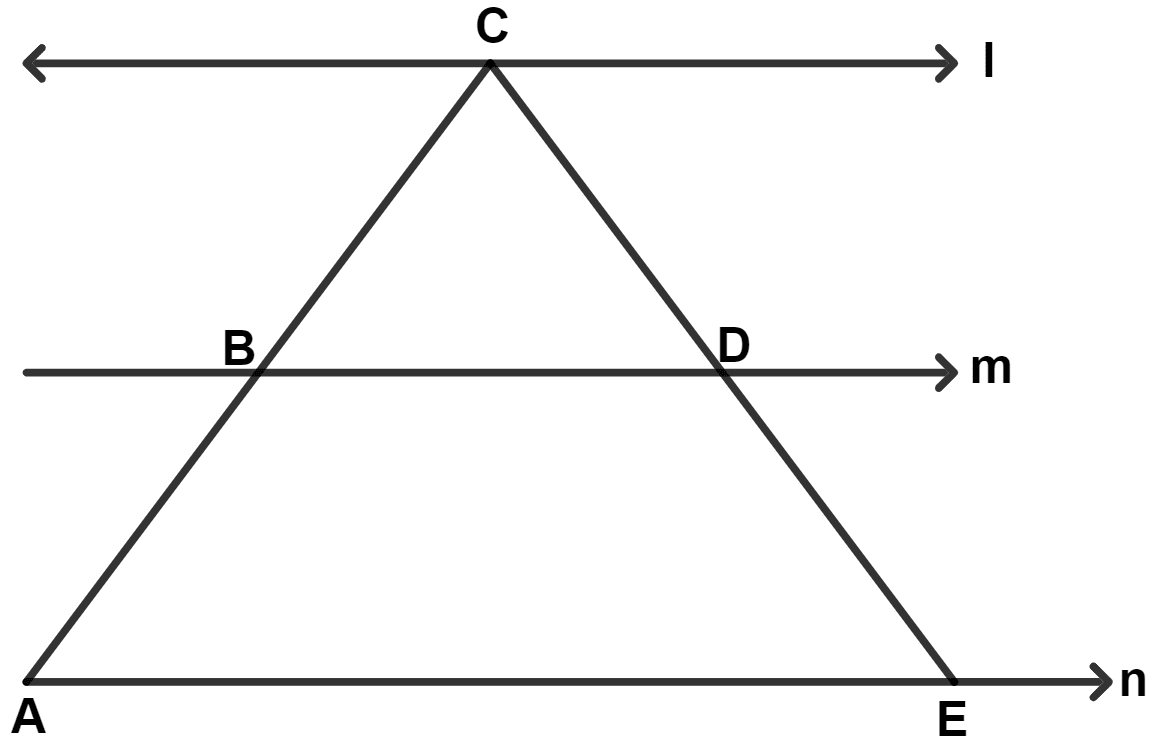
1. 12.6 cm

2. 25.2 cm

3. 6.3 cm

4. 18.9 cm

Answer

By mid-point theorem,

The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and is equal to half of it.

By converse of mid-point theorem,

The straight line drawn through the mid-point of one side of a triangle parallel to another, bisects the third side.

In △ AEC,

Given,

⇒ m // n

∴ BD // AE.

D is mid-point of CE.

∴ B is the mid-point of AC. (By converse of mid-point theorem)

Also,

⇒ BD = $\dfrac{1}{2}AE = \dfrac{1}{2} \times 12.6$ = 6.3 cm

Hence, Option 3 is the correct option.

In a trapezium ABCD, AB // DC, E is mid-point of AD and F is mid-point of BC, then :

1. 2EF = $\dfrac{1}{2}(AB + DC)$

2. 2EF = AB + DC

3. EF = AB + DC

4. EF = $\dfrac{1}{2} \times AB \times DC$

Answer

Join AC. Let AC intersects EF at point O.

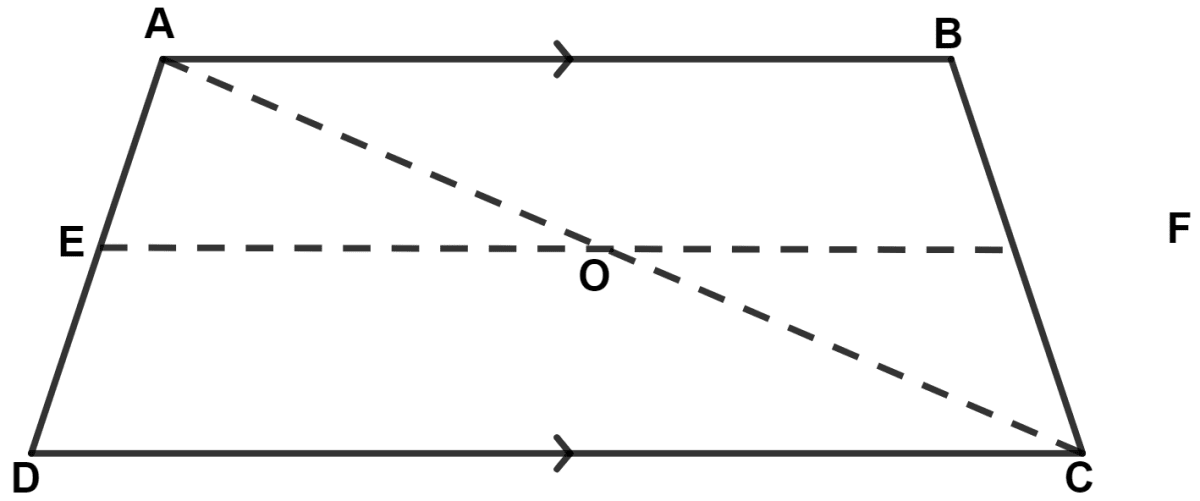
We know that,

In trapezium the line joining the mid-points of non-parallel sides are parallel to the parallel sides of trapezium.

∴ AB || EF || DC.

By mid-point theorem,

The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and is equal to half of it.

By converse of mid-point theorem,

The straight line drawn through the mid-point of one side of a triangle parallel to another, bisects the third side.

Given,

⇒ EF || DC

⇒ EO || DC

In △ ADC,

E is mid-point of AD and EO || DC.

∴ O is mid-point of AC. (By converse of mid-point theorem)

∴ EO = $\dfrac{1}{2}DC$ (By mid-point theorem) ..........(1)

Given,

⇒ EF || AB

⇒ OF || AB

In △ ABC,

O is mid-point of AC and F is mid-point of BC.

∴ OF = $\dfrac{1}{2}AB$ (By mid-point theorem) ..........(2)

Adding equations (1) and (2), we get :

⇒ EO + OF = $\dfrac{1}{2}DC + \dfrac{1}{2}AB$

⇒ EF = $\dfrac{1}{2}(DC + AB)$

⇒ 2EF = AB + DC.

Hence, Option 2 is the correct option.

The given figure shows a parallelogram ABCD in which E is mid-point of AD and DL // EB. Then, BF is equal to :

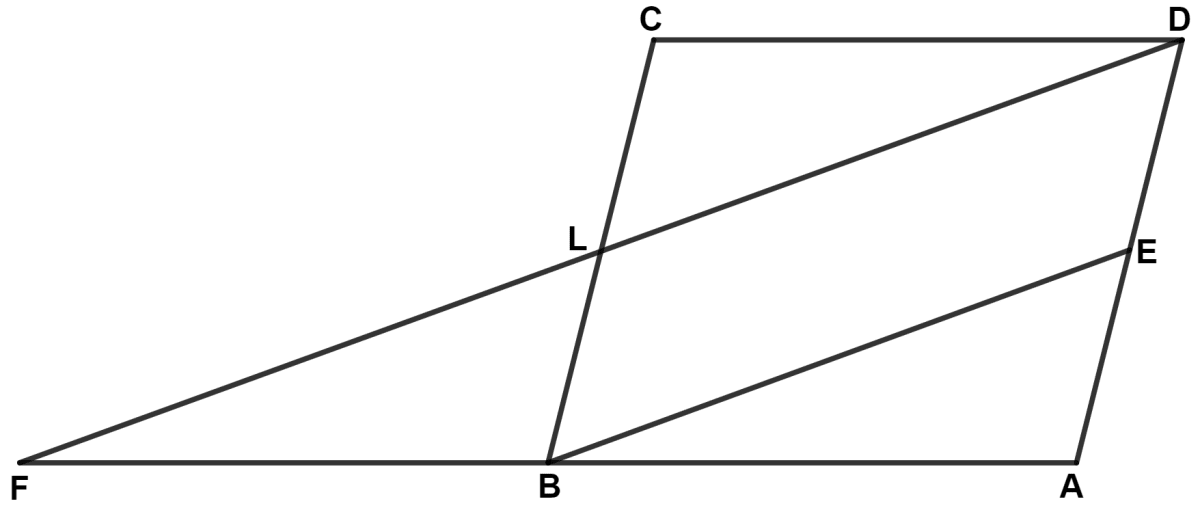
1. AD

2. BE

3. AE

4. AB

Answer

By equal intercept theorem,

If a transversal makes equal intercepts on three or more parallel lines, then any other line cutting them will also make equal intercepts.

In parallelogram ABCD,

DL || EB

Since, E is mid-point of AD.

∴ AE = ED

∴ BL = LC (By equal intercept theorem)

In △ BLF and △ DLC,

⇒ ∠BLF = ∠DLC (Vertically opposite angles are equal)

⇒ BL = LC (Proved above)

⇒ ∠LBF = ∠LCD (Alternate angles are equal)

∴ △ BLF ≅ △ DLC (By A.S.A. axiom)

We know that,

Corresponding parts of congruent triangle are equal.

∴ BF = CD .........(1)

We know that,

Opposite sides of parallelogram are equal.

∴ AB = CD .........(2)

From equation (1) and (2), we get :

⇒ BF = AB.

Hence, Option 4 is the correct option.

In the given figure AD and BE are medians, then ED is equal to :

1. 2AB

2. $\dfrac{1}{2}AB$

3. $\dfrac{1}{4}AB$

4. $\dfrac{1}{8}AB$

Answer

Join ED.

By mid-point theorem,

The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and is equal to half of it.

Since, AD and BE are medians.

∴ D is mid-point of BC and E is mid-point of AC.

In △ ABC,

∴ ED = $\dfrac{1}{2}AB$ (By mid-point theorem)

Hence, Option 2 is the correct option.

In the quadrilateral ABCD, if AB // CD, E is mid-point of side AD and F is mid-point of BC. If AB = 20 cm and EF = 16 cm, the length of side DC is :

1. 18 cm

2. 12 cm

3. 24 cm

4. 32 cm

Answer

Join BD. Let BD intersect EF at point O.

We know that,

In trapezium the line joining the mid-points of non-parallel sides are parallel to the parallel sides of trapezium.

∴ AB || EF || DC.

By mid-point theorem,

The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and is equal to half of it.

By converse of mid-point theorem,

The straight line drawn through the mid-point of one side of a triangle parallel to another, bisects the third side.

Given,

⇒ EF || AB

⇒ EO || AB

In △ ABD,

E is mid-point of AD and EO || AB.

∴ O is mid-point of BD. (By converse of mid-point theorem)

∴ EO = $\dfrac{1}{2}AB$ (By mid-point theorem) ..........(1)

Given,

⇒ EF || DC

⇒ OF || DC

In △ BCD,

O is mid-point of BD and F is mid-point of BC.

∴ OF = $\dfrac{1}{2}CD$ (By mid-point theorem) ..........(2)

Adding equations (1) and (2), we get :

⇒ EO + OF = $\dfrac{1}{2}AB + \dfrac{1}{2}CD$

⇒ EF = $\dfrac{1}{2}(AB + CD)$

Substituting values we get :

$\Rightarrow 16 = \dfrac{1}{2}(20 + CD) \\[1em] \Rightarrow 16 \times 2 = 20 + CD \\[1em] \Rightarrow 32 = 20 + CD \\[1em] \Rightarrow CD = 32 - 20 = 12\text{ cm}.$

Hence, Option 2 is the correct option.

Use the following figure to find :

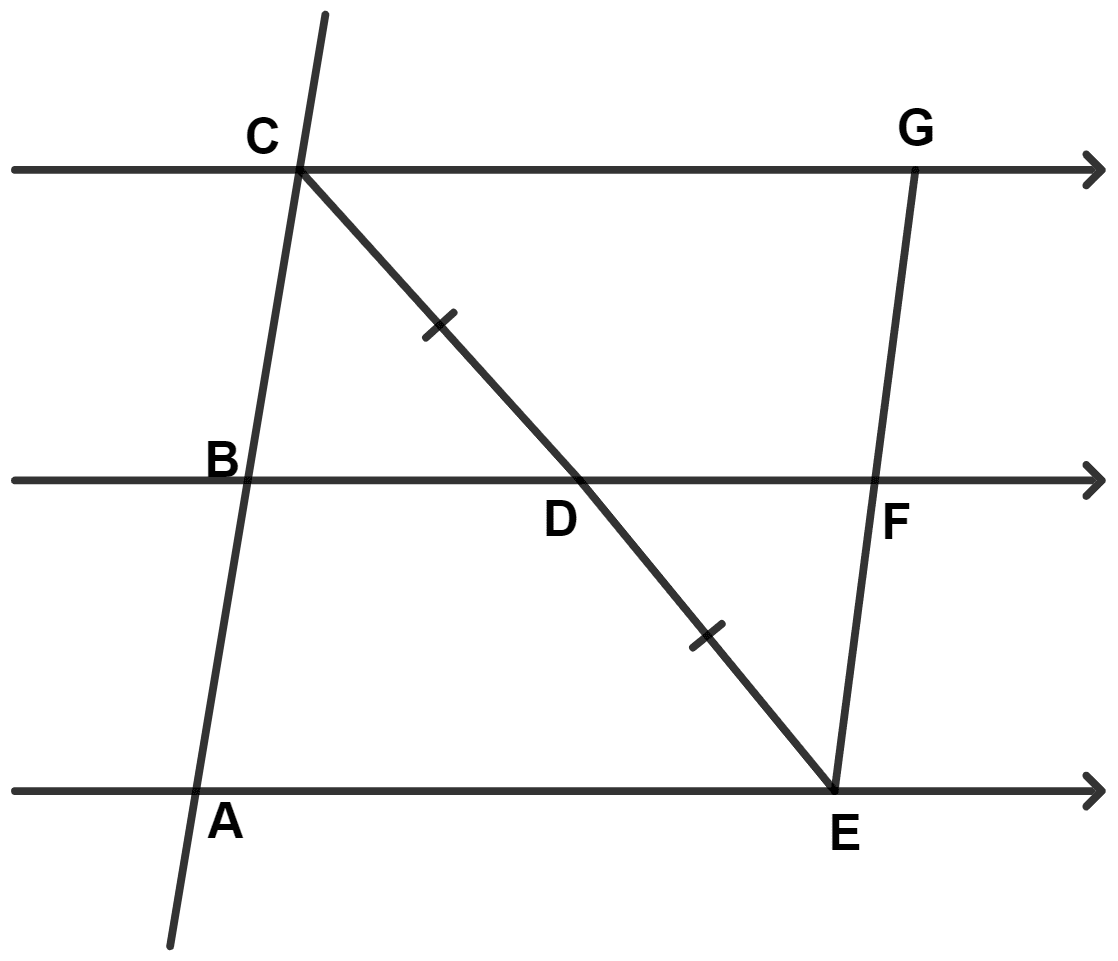
(i) BC, if AB = 7.2 cm.

(ii) GE, if FE = 4 cm.

(iii) AE, if BD = 4.1 cm.

(iv) DF, if CG = 11 cm.

Answer

By equal intercept theorem,

If a transversal makes equal intercepts on three or more parallel lines, then any other line cutting them will also make equal intercepts.

(i) From figure,

CG || BF || AE

Since, CD = DE

∴ BC = AB = 7.2 cm (By equal intercept theorem)

Hence, BC = 7.2 cm.

(ii) From figure,

CG || BF || AE

Since, CD = DE

∴ FG = FE = 4 cm (By equal intercept theorem)

From figure,

⇒ GE = FG + FE = 4 + 4 = 8 cm.

Hence, GE = 8 cm.

(iii) By mid-point theorem,

The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and is equal to half of it.

By converse of mid-point theorem,

The straight line drawn through the mid-point of one side of a triangle parallel to another, bisects the third side.

In △ AEC,

D is mid-point of CE

⇒ BF || AE

∴ BD || AE.

∴ B is mid-point of AC. (By converse of mid-point theorem)

∴ BD = $\dfrac{1}{2}AE$ (By mid-point theorem)

⇒ AE = 2BD = 2 × 4.1 = 8.2 cm

Hence, AE = 8.2 cm.

(iv) In △ EGC,

D is mid-point of CE.

⇒ BF || CG

∴ DF || CG.

∴ F is mid-point of GE. (By converse of mid-point theorem)

∴ DF = $\dfrac{1}{2}CG$ (By mid-point theorem)

⇒ DF = $\dfrac{1}{2} \times 11$ = 5.5 cm

Hence, DF = 5.5 cm.

In the figure, given below, 2AD = AB, P is mid-point of AB, Q is mid-point of DR and PR // BS. Prove that :

(i) AQ // BS

(ii) DS = 3RS

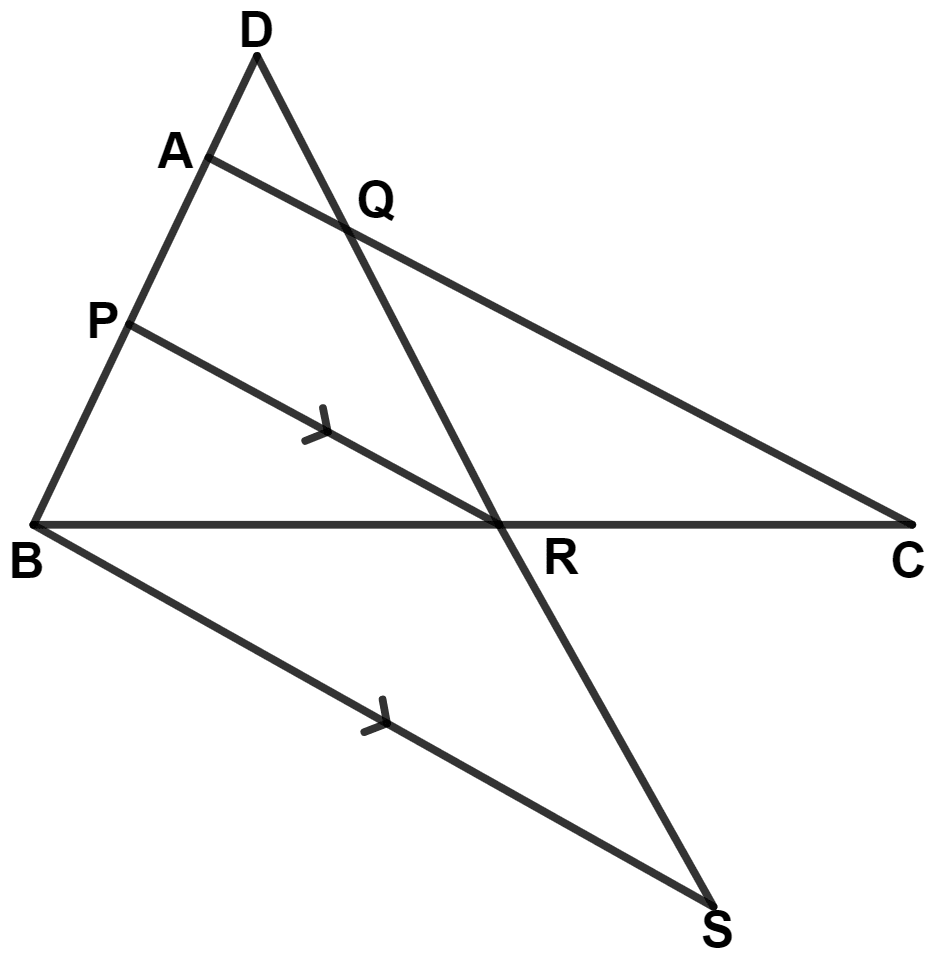
Answer

Given,

P is mid-point of AB.

∴ AP = PB

Since, 2AD = AB

∴ AD = $\dfrac{AB}{2}$

∴ AP = AB = AD.

(i) By mid-point theorem,

The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and is equal to half of it.

In △ DPR,

A and Q are mid-points of DP and DR respectively.

∴ AQ || PR [By mid-point theorem] .......(1)

Given,

⇒ PR || BS ...........(2)

From equations (1) and (2), we get :

⇒ AQ || BS.

Hence, proved that AQ || BS.

(ii) By equal intercept theorem,

If a transversal makes equal intercepts on three or more parallel lines, then any other line cutting them will also make equal intercepts.

From figure,

PR || BS

Since, AD = AP = PB

∴ DQ = QR = RS .........(3)

From figure,

⇒ DS = DQ + QR + RS

⇒ DS = RS + RS + RS [From equation (3)]

⇒ DS = 3RS.

Hence, proved that DS = 3RS.

The side AC of a triangle ABC is produced to point E so that CE = $\dfrac{1}{2}AC$. D is the mid-point of BC and ED produced meets AB at F. Lines through D and C are drawn parallel to AB which meet AC at point P and EF at point R respectively. Prove that :

(i) 3DF = EF

(ii) 4CR = AB.

Answer

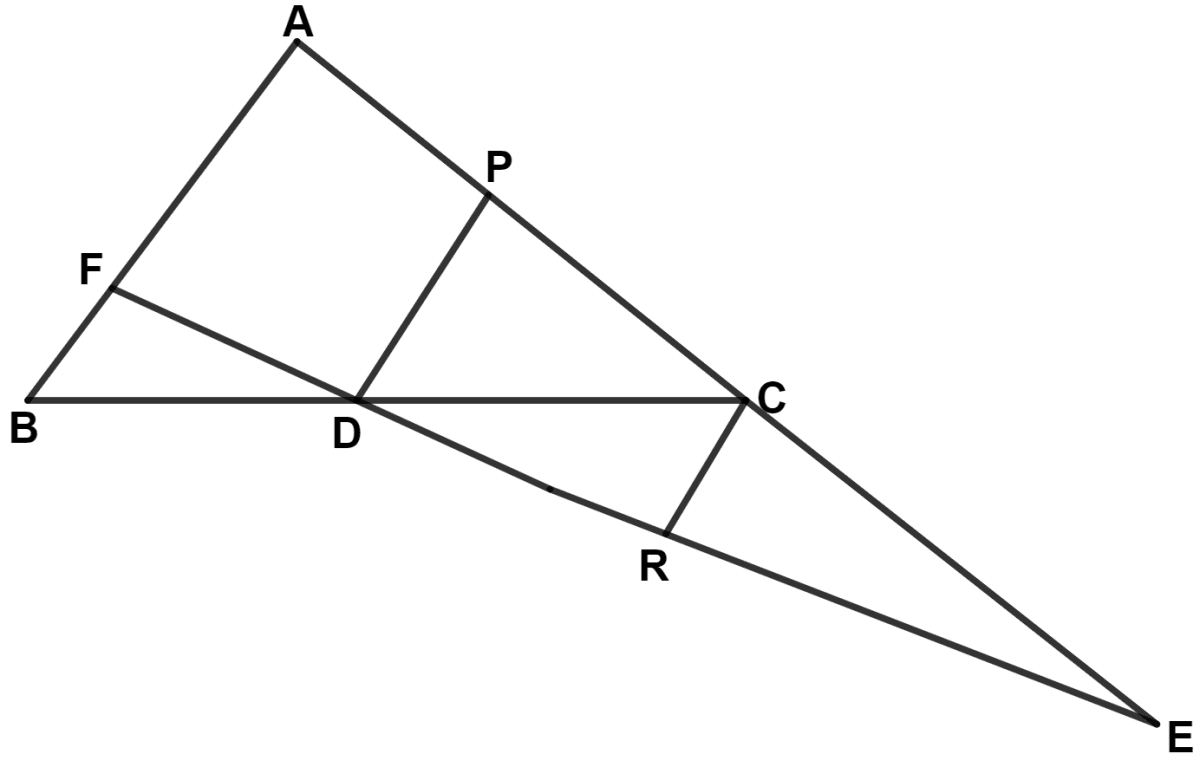
By mid-point theorem,

The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and is equal to half of it.

By converse of mid-point theorem,

The straight line drawn through the mid-point of one side of a triangle parallel to another, bisects the third side.

By equal intercept theorem,

If a transversal makes equal intercepts on three or more parallel lines, then any other line cutting them will also make equal intercepts.

(i) In △ ABC,

D is the mid-point of BC and DP || AB.

∴ P is the mid-point of AC. (By converse of mid-point theorem)

∴ AP = PC

Given,

⇒ CE = $\dfrac{1}{2}AC$

∴ CE = PC

Since, AP = PC and CE = PC,

∴ AP = PC = CE.

Since,

⇒ AB || DP || CR

⇒ AF || DP || CR (Since, point F lies on straight line AB)

In △ AEF,

AF || PD || CR and AP = PC = CE

∴ DF = DR = RE = x (let) [By equal intercept theorem]

From figure,

⇒ EF = DF + DR + RE = x + x + x = 3x = 3DF.

Hence, proved that 3DF = EF.

(ii) In △ ABC,

D is mid-point of BC and DP || AB.

∴ P is the mid-point of AC. (By converse of mid-point theorem)

∴ PD = $\dfrac{1}{2}AB$ (By mid-point theorem) .........(1)

In △ PED,

Given,

⇒ CE = $\dfrac{1}{2}AC$

⇒ CE = PC (Since, P is mid-point of AC)

∴ C is the mid-point of PE.

C is mid-point of PE and DP || CR.

∴ R is the mid-point of DE. (By converse of mid-point theorem)

∴ CR = $\dfrac{1}{2}PD$ (By mid-point theorem) .........(2)

Substituting value of PD from equation (1) in equation (2), we get :

⇒ CR = $\dfrac{1}{2} \times \dfrac{1}{2}AB$

⇒ CR = $\dfrac{1}{4}AB$

⇒ 4CR = AB.

Hence, proved that 4CR = AB.

In triangle ABC, the medians BP and CQ are produced upto points M and N respectively such that BP = PM and CQ = QN. Prove that :

(i) M, A and N are collinear.

(ii) A is the mid-point of MN.

Answer

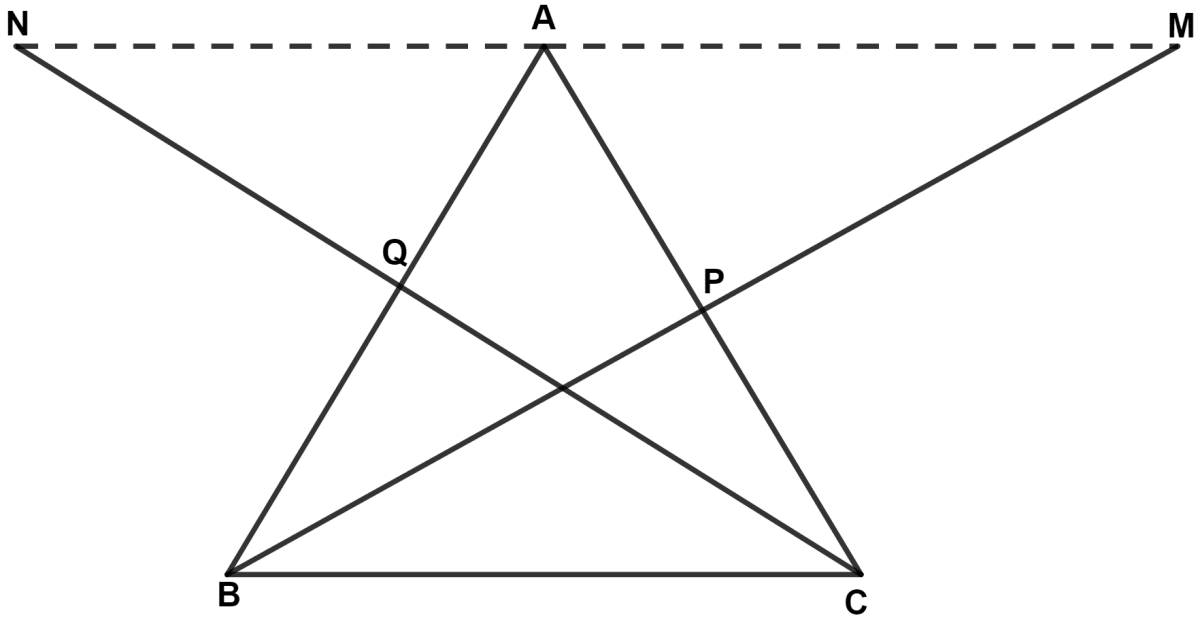
In △ AQN and △ BQC,

⇒ AQ = BQ (Since, CQ is the median)

⇒ QN = CQ (Given)

⇒ ∠AQN = ∠CQB (Vertically opposite angles are equal)

∴ △ AQN ≅ △ BQC (By S.A.S. axiom)

We know that,

Corresponding parts of congruent triangle are equal.

⇒ ∠QAN = ∠QBC ........(1)

⇒ BC = AN ..........(2)

In △ APM and △ CPB,

⇒ AP = CP (Since, BP is the median)

⇒ PM = BP (Given)

⇒ ∠APM = ∠CPB (Vertically opposite angles are equal)

∴ △ APM ≅ △ CPB (By S.A.S. axiom)

⇒ ∠PAM = ∠PCB [By C.P.C.T.C.] ........(3)

⇒ BC = AM [By C.P.C.T.C.] ..........(4)

(i) In △ ABC,

By angle sum property of triangle,

⇒ ∠ABC + ∠ACB + ∠BAC = 180°

⇒ ∠QBC + ∠PCB + ∠BAC = 180°

⇒ ∠QAN + ∠PAM + ∠BAC = 180° [From equations (1) and (3)]

Since, the sum of above angles equal to 180°.

∴ N, A and M lies in a straight line.

Hence, proved that M, A and N are collinear.

(ii) From equations (2) and (4), we get :

⇒ AM = AN.

Hence, proved that A is the mid-point of MN.

In triangle ABC, angle B is obtuse. D and E are mid-points of sides AB and BC respectively and F is a point on side AC such that EF is parallel to AB. Show that BEFD is a parallelogram.

Answer

By mid-point theorem,

The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and is equal to half of it.

By converse of mid-point theorem,

The straight line drawn through the mid-point of one side of a triangle parallel to another, bisects the third side.

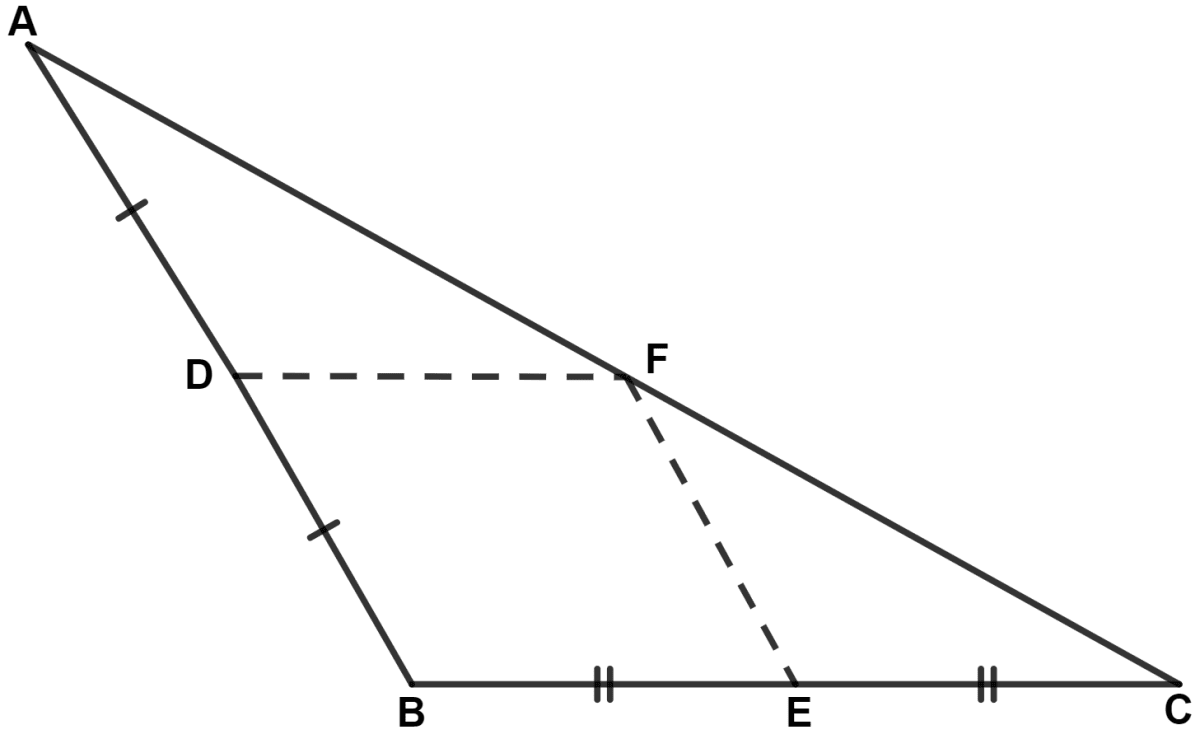
In △ ABC,

E is the mid-point of BC and FE || AB.

∴ F is the mid-point of AC. (By converse of mid-point theorem)

Since,

⇒ FE || AB

∴ FE || BD.

D and F are mid-point of sides AB and AC respectively.

∴ DF || BC (By mid-point theorem)

∴ DF || BE.

Since, opposite sides of quadrilateral BEFD are parallel.

Hence, proved that BEFD is a parallelogram.

In parallelogram ABCD, E and F are mid-points of the sides AB and CD respectively. The line segments AF and BF meet the line segments ED and EC at points G and H respectively. Prove that :

(i) triangles HEB and FHC are congruent;

(ii) GEHF is a parallelogram.

Answer

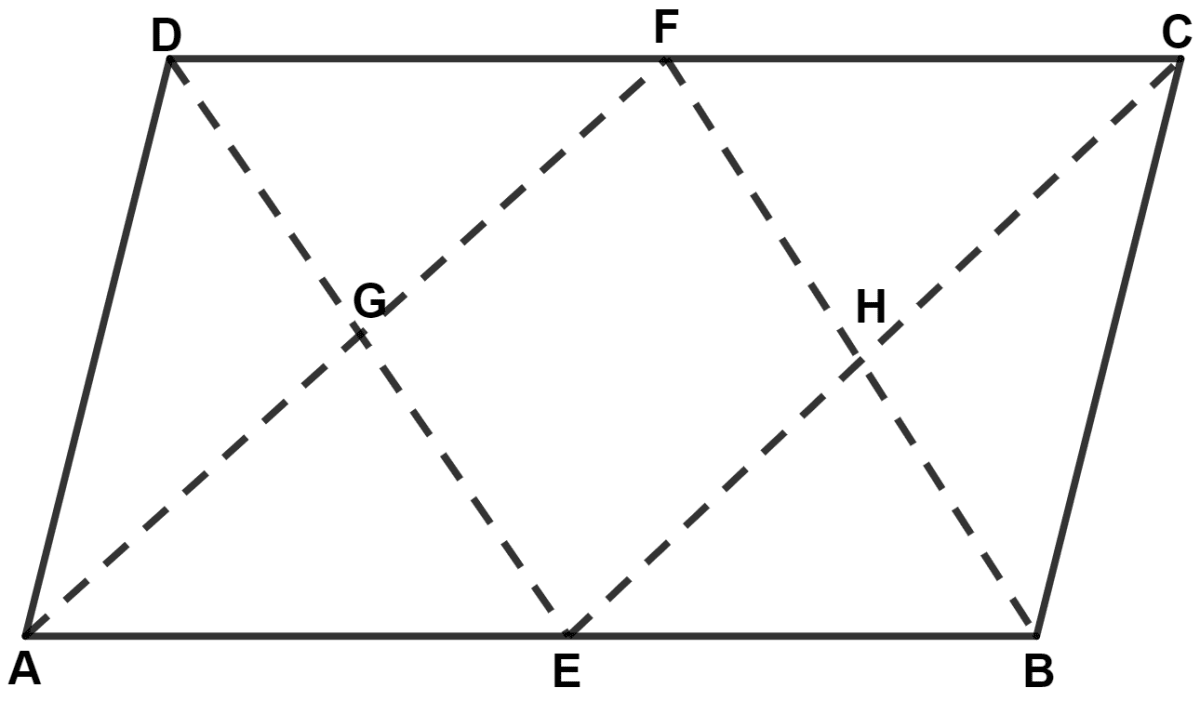
(i) In △ HEB and △ FHC,

⇒ BE = CF (Since, opposite sides of parallelogram are equal i.e. AB = CD and E and F are mid-points of AB and CD respectively)

⇒ ∠HBE = ∠HFC (Alternate angles are equal)

⇒ ∠EHB = ∠FHC (Vertically opposite angles are equal)

∴ △ HEB ≅ △ FHC (By A.A.S. axiom)

Hence, proved that triangles HEB and FHC are congruent.

(ii) Since,

△ HEB ≅ △ FHC

We know that,

Corresponding parts of congruent triangle are equal.

⇒ EH = CH and BH = FH.

⇒ H is the mid-point of BF and CE.

In △ AGE and △ DGF,

⇒ AE = DF (Since, opposite sides of parallelogram are equal i.e. AB = CD and E and F are mid-points of AB and CD respectively)

⇒ ∠GEA = ∠GDF (Alternate angles are equal)

⇒ ∠AGE = ∠DGF (Vertically opposite angles are equal)

∴ △ AGE ≅ △ DGF (By A.A.S. axiom)

∴ AG = GF and EG = DG [By C.P.C.T.C.]

⇒ G is the mid-point of DE and AF.

In △ ECD,

F and H are mid-points of sides CD and EC respectively.

∴ FH || DE [By mid-point theorem]

⇒ FH || GE

F and G are mid-points of sides CD and ED respectively.

∴ GF || EC [By mid-point theorem]

⇒ GF || EH

Since, opposite sides of quadrilateral GEFH are parallel.

Hence, proved that GEHF is a parallelogram.

In triangle ABC, D and E are points on side AB such that AD = DE = EB. Through D and E, lines are drawn parallel to BC which meet side AC at points F and G respectively. Through F and G, lines are drawn parallel to AB which meet side BC at points M and N respectively. Prove that : BM = MN = NC.

Answer

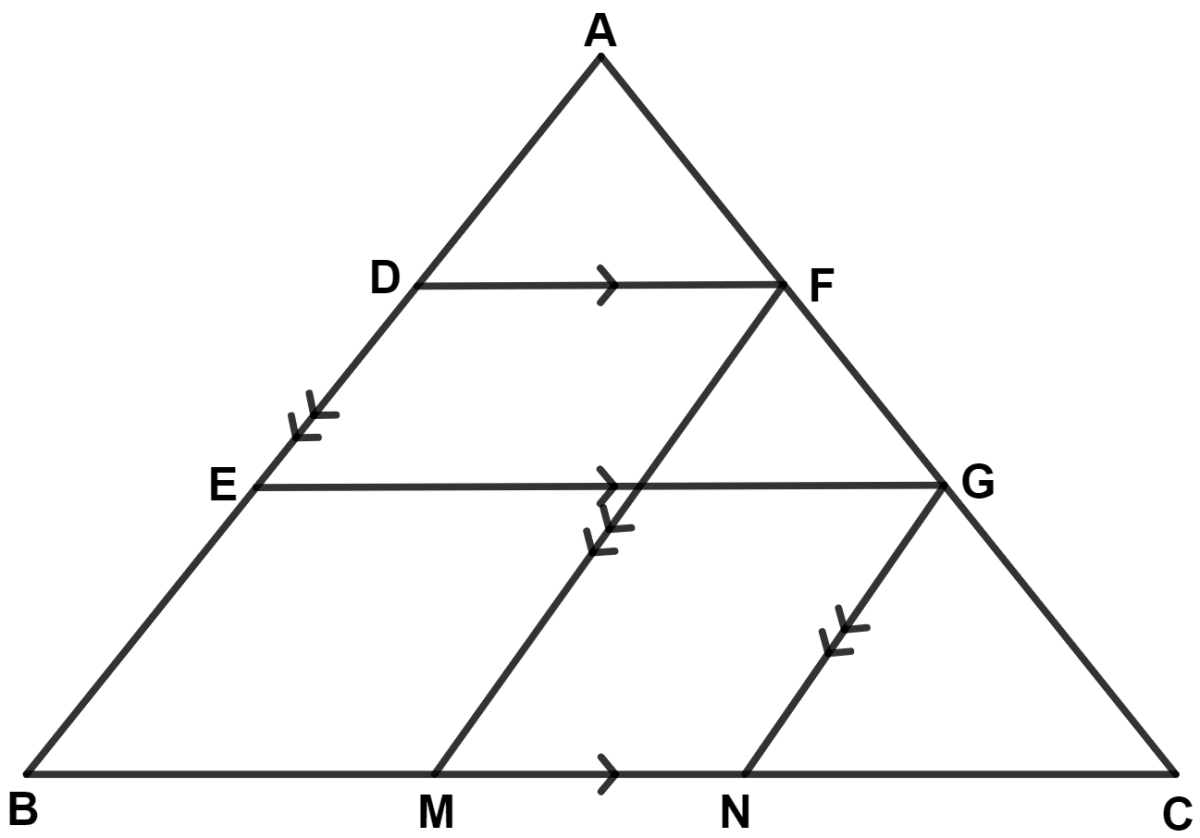
By mid-point theorem,

The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and is equal to half of it.

By converse of mid-point theorem,

The straight line drawn through the mid-point of one side of a triangle parallel to another, bisects the third side.

By equal intercept theorem,

If a transversal makes equal intercepts on three or more parallel lines, then any other line cutting them will also make equal intercepts.

In △ AEG,

D is the mid-point of AE and DF || EG.

∴ F is mid-point of AG (By converse of mid-point theorem)

∴ AF = FG .........(1)

Since,

DF || EG || BC and DE || BE

∴ FG = GC [By equal intercept theorem]...........(2)

From equation (1) and (2), we get :

⇒ AF = FG = GC

Since, AB || FM || GN and AF = FG = GC

∴ BM = MN = NC [By equal intercept theorem]

Hence, proved that BM = MN = NC.

In triangle ABC; M is the mid-point of AB, N is mid-point of AC and D is any point in base BC. Use intercept theorem to show that MN bisects AD.

Answer

Let MN intersects at AD at point X.

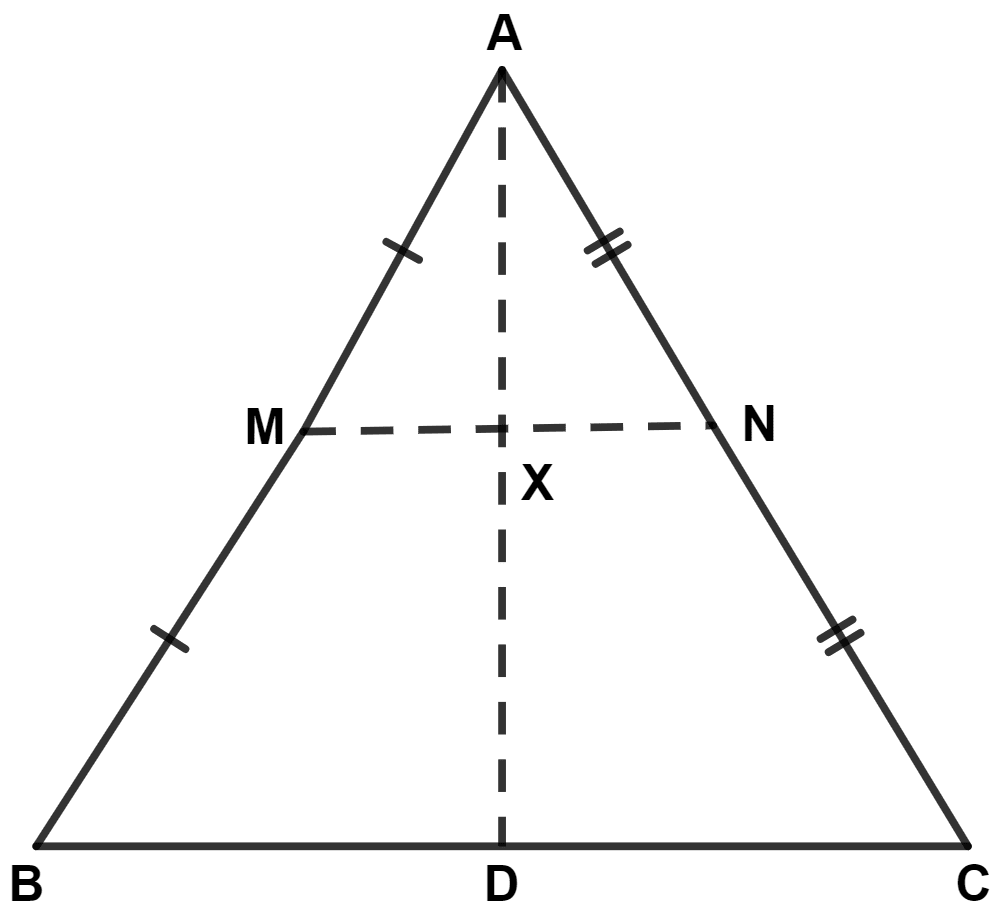
By mid-point theorem,

The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and is equal to half of it.

In △ ABC,

M is mid-point of AB and N is mid-point of AC.

∴ MN || BC (By mid-point theorem)

By equal intercept theorem,

If a transversal makes equal intercepts on three or more parallel lines, then any other line cutting them will also make equal intercepts.

Since,

M is mid-point of AB.

∴ AM = MB

N is mid-point of AC.

∴ AN = CN

From figure,

MN || BC, AM = BM and AN = CN

∴ AX = DX (By equal intercept theorem)

Hence, proved that MN bisects AD.

If the quadrilateral formed by joining the mid-points of the adjacent sides of quadrilateral ABCD is a rectangle, show that the diagonals AC and BD intersect at right angle.

Answer

Let ABCD be a quadrilateral and P, Q, R and S are the mid-point of AB, BC, CD and DA.

Diagonal AC and BD intersect at point O.

By mid-point theorem,

The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and is equal to half of it.

In △ ABC,

P and Q are mid-points of AB and BC.

∴ PQ || AC (By mid-point theorem)

From figure,

⇒ ∠AOD = ∠PXO (Corresponding angles are equal) ............(1)

In △ BCD,

R and Q are mid-points of CD and BC.

∴ QR || BD (By mid-point theorem)

Interior angles of a rectangle equals to 90°.

⇒ ∠RQX = ∠Q = 90°.

From figure,

⇒ ∠PXO = ∠RQX = 90° (Corresponding angles are equal) ............(2)

From (1) and (2), we get :

⇒ ∠AOD = ∠PXO = 90°.

Hence, AC and BD intersect at right angles.

The midpoint of the side of a triangle are joined together to get four triangles. These four triangles are:

1. not equal to each other

2. congruent to each other

3. not congruent to each other

4. none of these

Answer

From figure,

In △ABC,

D, E and F are mid-points of AB, BC and CA respectively.

Now join DE, EF and FD.

To prove :

△ADF ≅ △DBE ≅ △ECF ≅ △DEF

In △ABC,

D and E are midpoints of AB and BC.

∴ DE || AC (By, mid-point theorem) or,

DE || FC ........(1)

DE || AF ........(2)

D and F are midpoints of AB and AC.

∴ DF || BC (By, mid-point theorem) or,

DF || EC ........(3)

DF || BE ......(4)

F and E are midpoints of AC and BC.

∴ FE || AB (By, mid-point theorem) or,

FE || AD .........(5)

FE || DB .........(6)

From (1) and (3) we get,

DE || FC and DF || EC.

Since, opposite sides of a parallelogram are parallel.

∴ DECF is a parallelogram

We know that,

Diagonal of || gm divides it into two congruent triangles.

Diagonal FE divides the parallelogram DECF in two congruent triangles DEF and CEF.

∴ △DEF ≅ △ECF .........(7)

From (2) and (5) we get,

DE || AF and FE || AD.

Since, opposite sides of a parallelogram are parallel.

∴ ADEF is a parallelogram.

We know that,

Diagonal of || gm divides it into two congruent triangles.

Diagonal FD divides the parallelogram in two congruent triangles DEF and AFD.

∴ △DEF ≅ △AFD .........(8)

From (4) and (6) we get,

DF || BE and FE || DB.

∴ DBEF is a parallelogram.

We know that,

Diagonal DE divides the parallelogram in two congruent triangles DEF and DBE.

∴ △DEF ≅ △DBE .........(9)

From equations 7, 8 and 9 we get,

△AFD ≅ △DBE ≅ △ECF ≅ △DEF.

Thus, the four triangles formed are congruent to each other.

Hence, option 2 is the correct option.

In the given figure, AB || CD || EF. If AC = 7 cm, AE = 14 cm and BF = 20 cm, then DF is equal to:

1. 7 cm

2. 14 cm

3. 10 cm

4. 16 cm

Answer

Given, AB || CD || EF, AC = 7 cm, AE = 14 cm and BF = 20 cm.

Let the length of DF be x cm.

According to equal intercept theorem,

If a transversal makes equal intercepts on three or more parallel lines, then any other line cutting them will also make equal intercepts.

From figure,

⇒ AE = AC + CE

⇒ 14 = 7 + CE

⇒ CE = 7 cm.

Since, OA makes equal intercept, so OB will also make equal intercepts.

∴ BD = DF = x (let)

From figure,

⇒ BF = BD + DF

⇒ 20 = x + x

⇒ 2x = 20

⇒ x = $\dfrac{20}{2}$ = 10 cm.

Hence, option 3 is the correct option.

In the given figure, AB || CD || EF and E is the mid-point of side AD, then :

1. OE : OF = 1 : 3

2. OE = OF

3. OF = 2 x OE

4. CF = FB

Answer

Given,

E is mid-point of AD.

Since, EF || DC ⇒ EO || DC

According to converse of the mid-point theorem, in any triangle, a straight line through the midpoint of one side that is parallel to a second side, then that line bisects the third side.

⇒ OA = OC

⇒ O is the mid-point of AC.

Since, EF || AB ⇒ OF || AB

According to converse of the mid-point theorem,

F will be the mif-point of BC.

⇒ CF = FB

Hence, option 4 is the correct option.

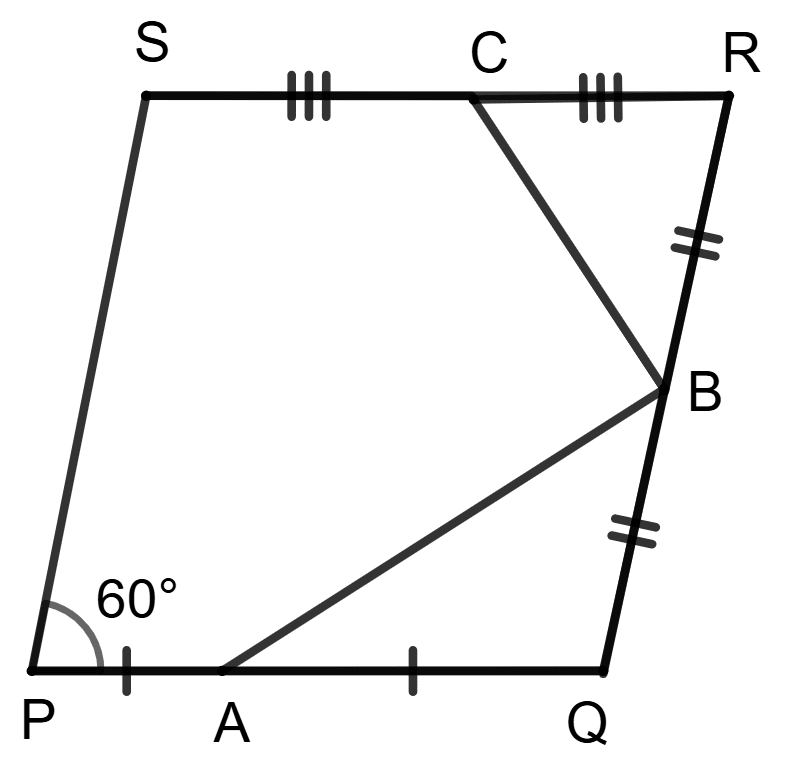
In rhombus PQRS; A, B and C are mid-points of sides PQ, QR and RS respectively. If ∠P = 60°, the angle PQR is equal to:

1. 60°

2. 90°

3. 120°

4. none of these

Answer

Given, ∠P = 60°

∠P and ∠PQR are consecutive angles in the rhombus.

The sum of consecutive angles in a rhombus is 180°.

⇒ ∠P + ∠PQR = 180°

⇒ 60° + ∠PQR = 180°

⇒ ∠PQR = 180° - 60°

⇒ ∠PQR = 120°.

Hence, option 3 is the correct option.

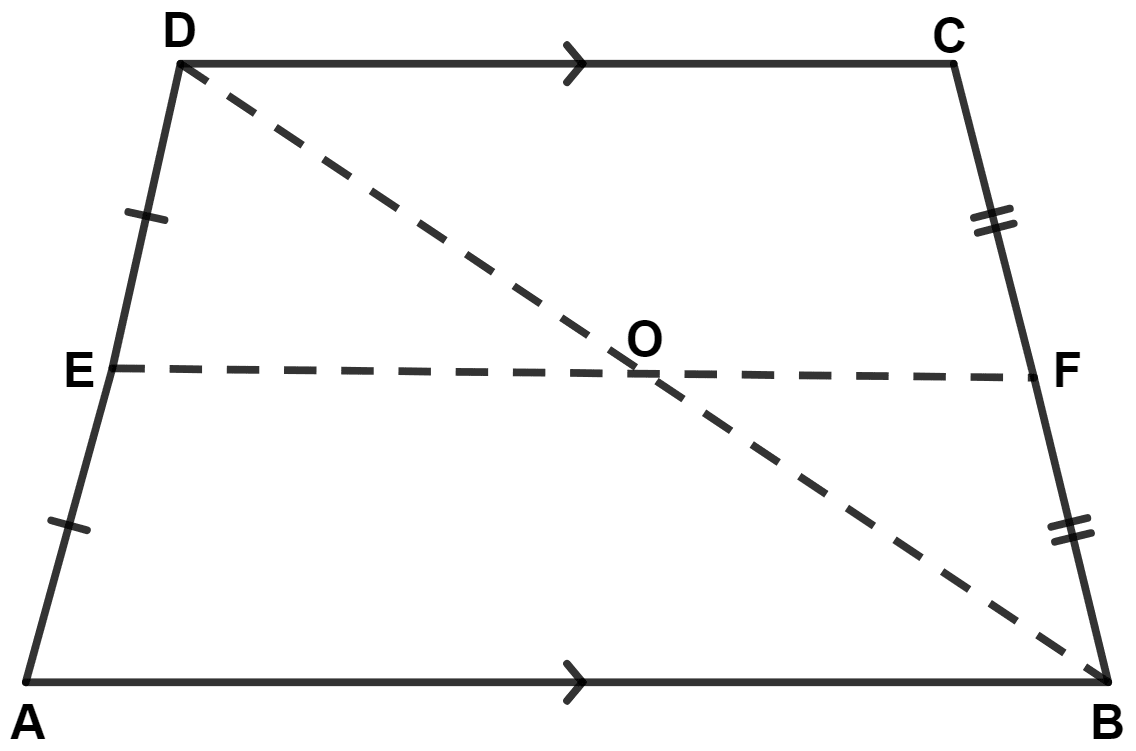
Statement 1: The diagonals of a quadrilateral are perpendicular to each other; P, Q, R and S are the midpoints of sides AB, BC, CD and DA respectively.

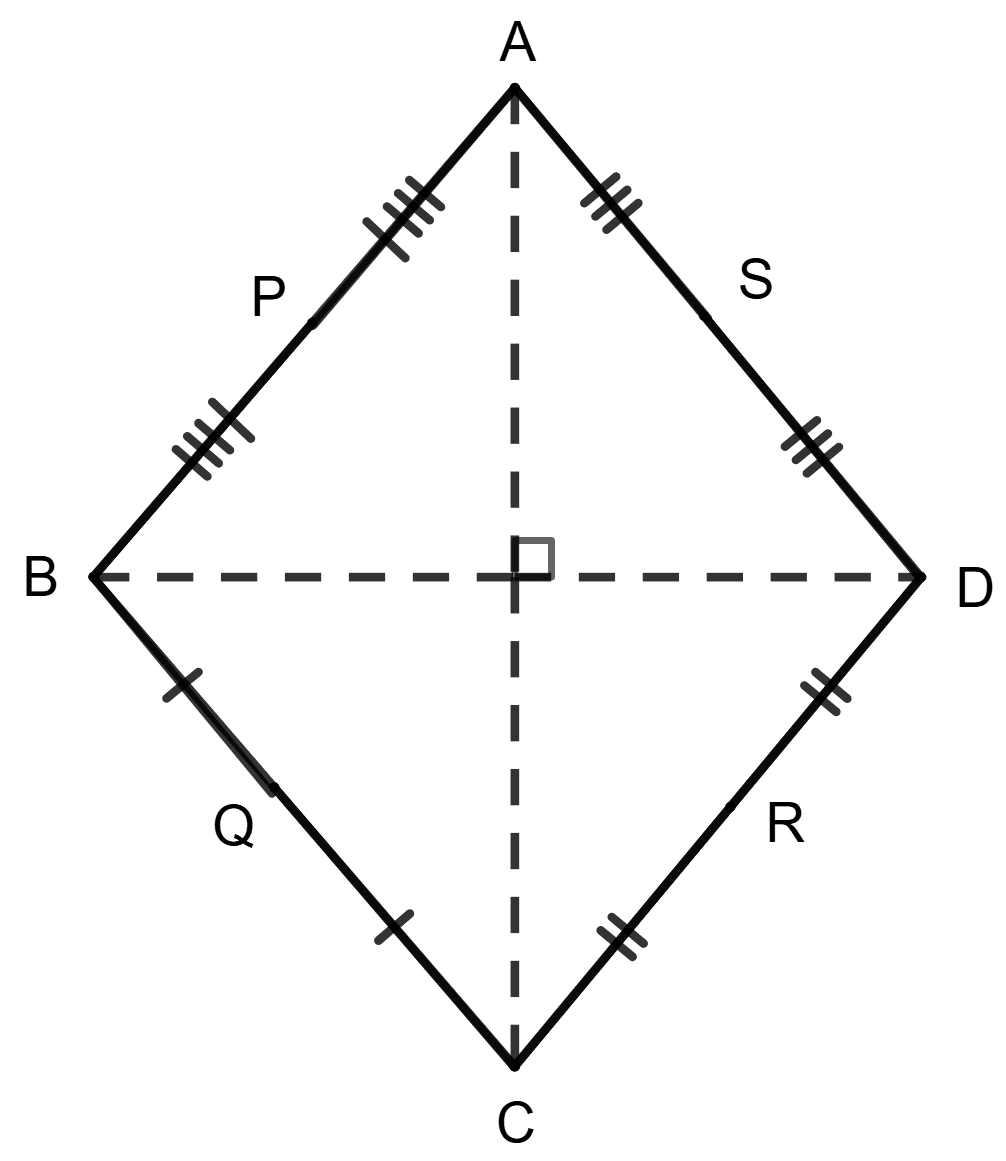
Statement 2: Quadrilateral PQRS is a square.

1. Both the statements are true.

2. Both the statements are false.

3. Statement 1 is true, and statement 2 is false.

4. Statement 1 is false, and statement 2 is true.

Answer

From figure,

PA = PB ⇒ P is mid-point of AB

SA = SD ⇒ S is mid-point of AD

BQ = CQ ⇒ Q is mid-point of BC

CR = RD ⇒ R is mid-point of CD

So, statement 1 is true.

By mid-point theorem,

The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and is equal to half of it.

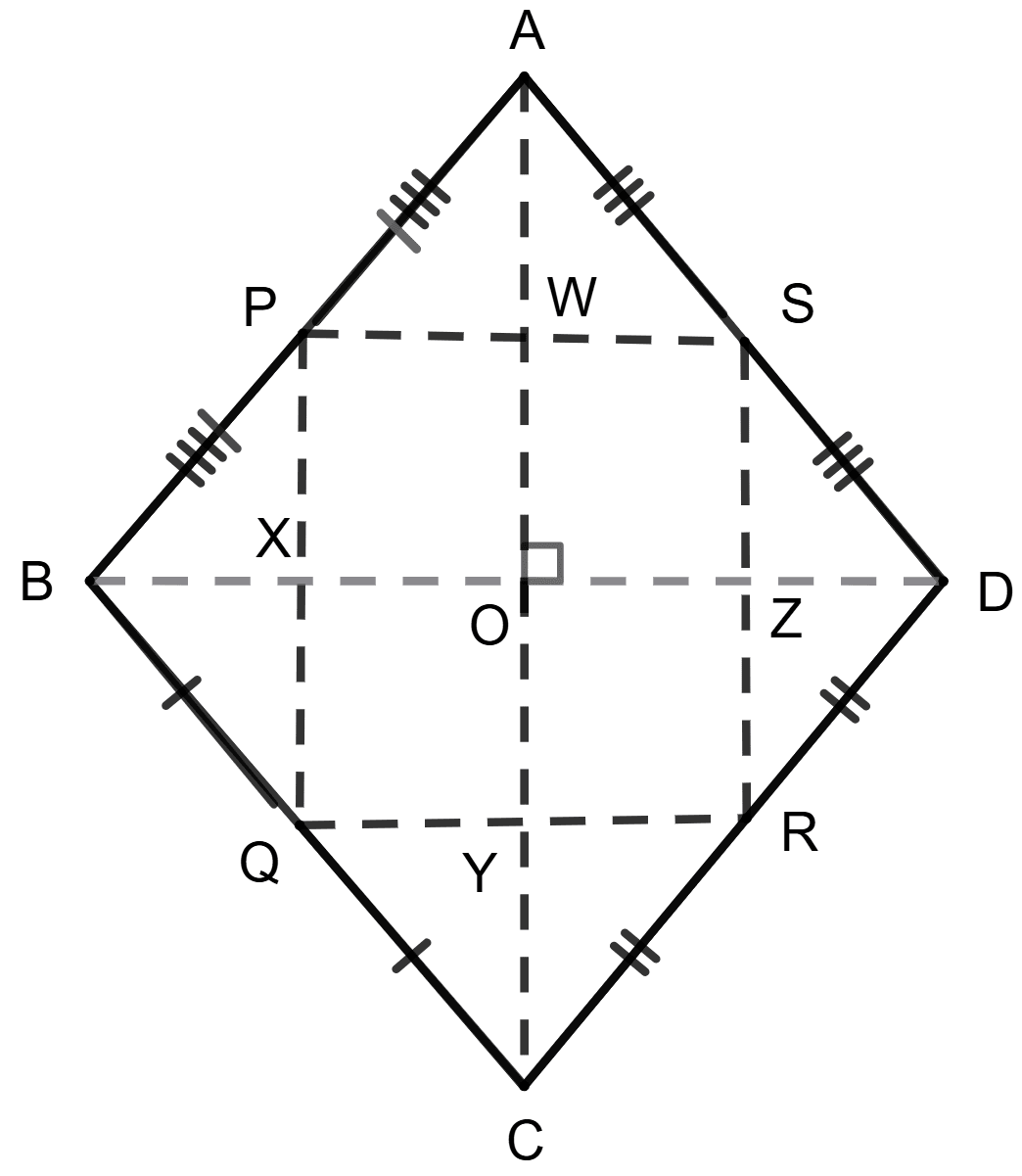
In △ ABC,

P and Q are mid-points of AB and BC respectively.

⇒ PQ = $\dfrac{1}{2}$ AC and PQ || AC. [By mid-point theorem] ................(1)

In △ ADC,

S and R are mid-points of AD and CD respectively.

⇒ SR = $\dfrac{1}{2}$ AC and SR || AC. [By mid-point theorem] .................(2)

From (1) and (2), we get :

PQ = SR and PQ || SR.

In △ BCD,

R and Q are mid-points of CD and BC respectively.

⇒ QR = $\dfrac{1}{2}$ BD and QR || BD. [By mid-point theorem] .................(3)

In △ ABD,

S and P are mid-points of AD and AB respectively.

⇒ PS = $\dfrac{1}{2}$ BD and PS || BD. [By mid-point theorem] .................(4)

From (3) and (4), we get :

QR = PS and QR || PS.

Since, diagonals of quadrilateral intersect at right angle.

∴ ∠AOD = ∠COD = ∠AOB = ∠BOC = 90°.

From figure,

PQ || AC

∴ ∠PXO = ∠AOD = 90° (Corresponding angles are equal)

∴ ∠QXO = ∠COD = 90° (Corresponding angles are equal)

SR || AC

∴ ∠SZO = ∠AOB = 90° (Corresponding angles are equal)

∴ ∠RZO = ∠BOC = 90° (Corresponding angles are equal)

PS || BD

∴ ∠S = ∠RZO = 90° (Corresponding angles are equal)

∴ ∠P = ∠QXO = 90° (Corresponding angles are equal)

QR || BD

∴ ∠R = ∠SZO = 90° (Corresponding angles are equal)

∴ ∠Q = ∠PXO = 90° (Corresponding angles are equal)

Since, in quadrilateral PQRS,

Each interior angle is equal to 90° and opposite sides are parallel and equal, and we can prove that PQRS is a rectangle but cannot prove that all sides are equal.

So, statement 2 is false.

∴ Statement 1 is true, and statement 2 is false.

Hence, option 3 is the correct option.

Statement 1: AD is median of triangle ABC and DE is parallel to BA.

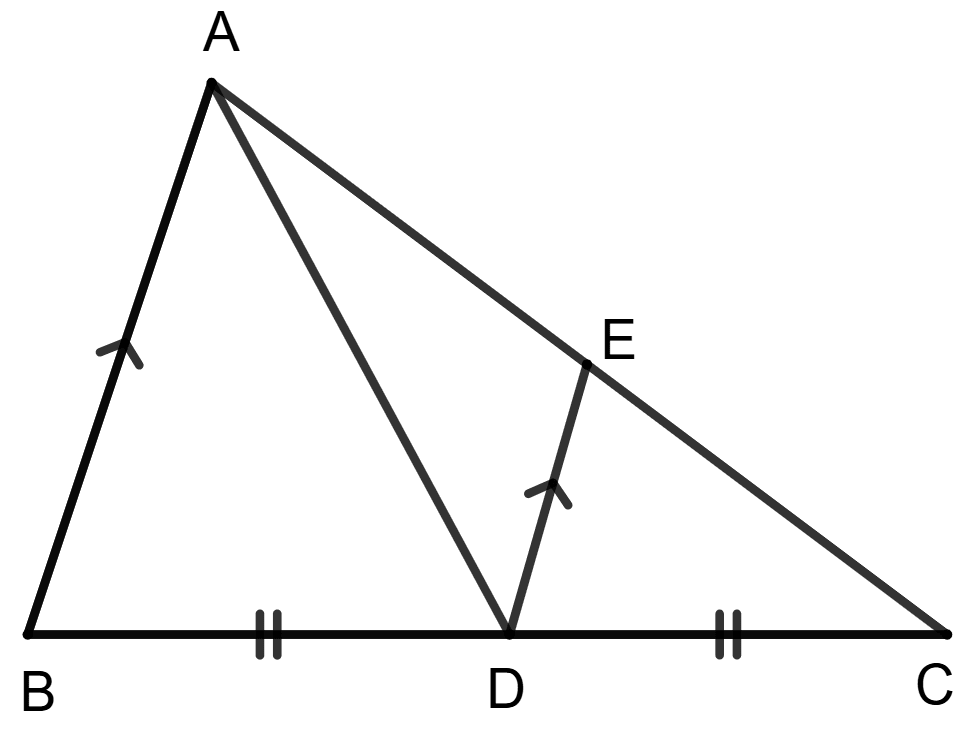
Statement 2: DE is median of triangle ADC.

1. Both the statements are true.

2. Both the statements are false.

3. Statement 1 is true, and statement 2 is false.

4. Statement 1 is false, and statement 2 is true.

Answer

In △ ABC,

From figure,

BD = DC.

∴ D is the mid-point of BC.

A median of a triangle is a line segment that connects a vertex of the triangle to the midpoint of the opposite side.

So, AD is the median of triangle ABC.

So, statement 1 is true.

By converse of mid-point theorem,

The straight line drawn through the mid-point of one side of a triangle parallel to another, bisects the third side.

Since, D is mid-point of BC and AB || DE

∴ E is the mid-point of AC.

Thus, DE is a median of triangle ADC.

So, statement 2 is true.

∴ Both the statements are true.

Hence, option 1 is the correct option.

Assertion (A): The figure formed by joining the mid-points of the sides of a quadrilateral ABCD is a square.

Reason (R): Diagonals of quadrilateral ABCD are not equal and are not perpendicular to each other.

1. A is true, but R is false.

2. A is false, but R is true.

3. Both A and R are true, and R is the correct reason for A.

4. Both A and R are true, and R is the incorrect reason for A.

Answer

For the figure formed by joining the midpoints of a quadrilateral to be a square, the diagonals of the original quadrilateral must be both equal and perpendicular to each other.

The reason states that the diagonals are not equal and not perpendicular.

∴ A is false, but R is true.

Hence, option 2 is the correct option.

Assertion (A): R, S, D and E are mid-points of OC, OB, AB and AC respectively, then DERS is a parallelogram.

Reason (R): DS ∥ AO ∥ ER and DS = ER = $\dfrac{1}{2}AO$.

1. A is true, but R is false.

2. A is false, but R is true.

3. Both A and R are true, and R is the correct reason for A.

4. Both A and R are true, and R is the incorrect reason for A.

Answer

By mid-point theorem,

The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and is equal to half of it.

In △ABO,

D and S are respective midpoints of AB and BO.

∴ DS || AO and DS = $\dfrac{1}{2}$ AO [By mid-point theorem].................(1)

In △ACO,

E and R are respective midpoints of AC and CO.

∴ ER || AO and ER = $\dfrac{1}{2}$ AO [By mid-point theorem]..................(2)

From (1) and (2) we get,

DS || ER and DS = ER = $\dfrac{1}{2}$ AO

So, reason (R) is true.

We know that,

If one pair of opposite sides of a quadrilateral are equal in length and parallel, then the quadrilateral is a parallelogram.

∴ DERS is a parallelogram.

So, assertion (A) is true.

∴ Both A and R are true, and R is the correct reason for A.

Hence, option 3 is the correct option.

In triangle ABC, D and E are mid-points of the sides AB and AC respectively. Through E, a straight line is drawn parallel to AB to meet BC at F. Prove that BDEF is a parallelogram. If AB = 8 cm and BC = 9 cm; find the perimeter of the parallelogram BDEF.

Answer

By mid-point theorem,

The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and is equal to half of it.

By converse of mid-point theorem,

The straight line drawn through the mid-point of one side of a triangle parallel to another, bisects the third side.

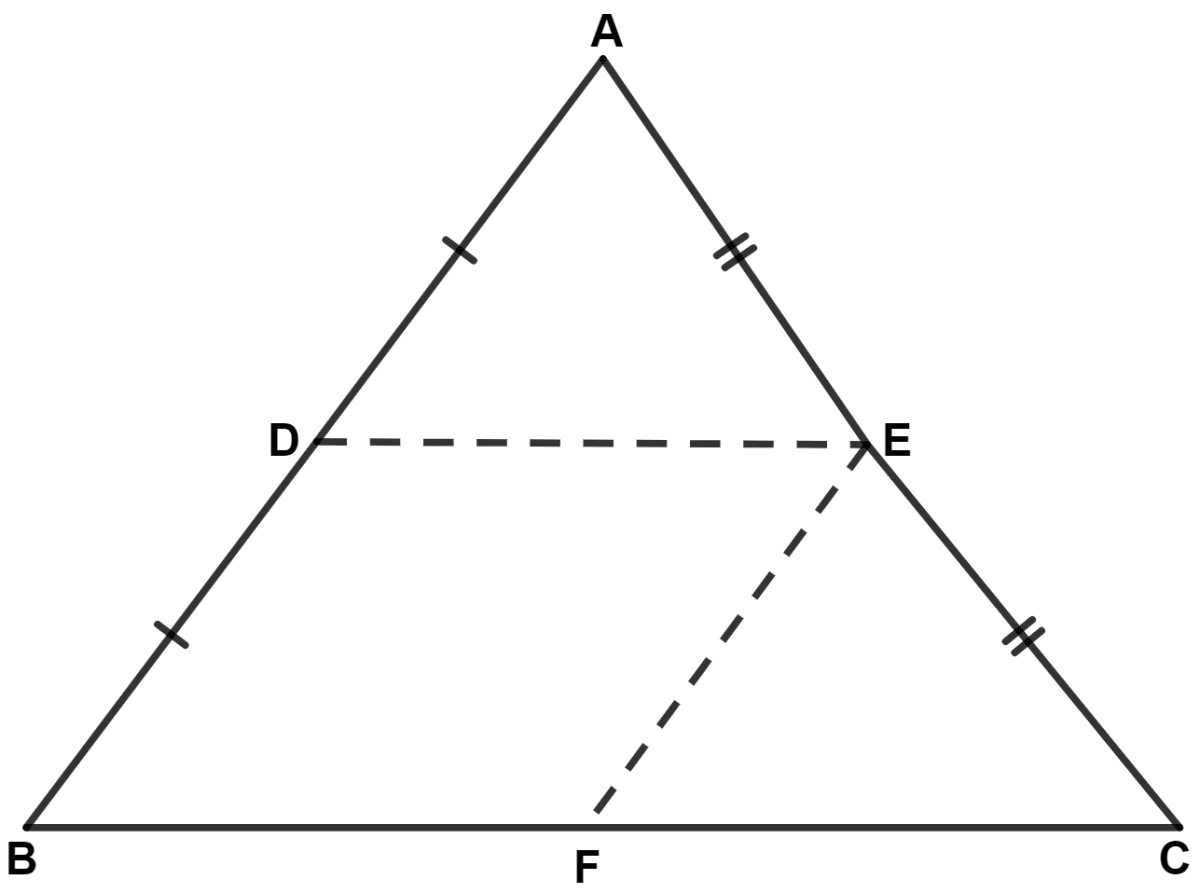
Given,

E is mid-point of AC and EF || AB.

∴ F is mid-point of BC (By converse of mid-point theorem).

Since, D and E are mid-points of sides AB and AC respectively.

∴ DE || BC and DE = $\dfrac{1}{2}BC$ (By mid-point theorem)

⇒ DE || BF and DE = BF (As F is mid-point of BC).

Given,

EF || AB

∴ EF || BD.

Since, E and F are mid-points of sides AC and BC respectively.

∴ EF = $\dfrac{1}{2}AB$ = BD. (By mid-point theorem)

Since, opposite sides of quadrilateral BDEF are parallel and equal.

∴ BDEF is a parallelogram.

From figure,

⇒ BD = $\dfrac{1}{2}AB = \dfrac{1}{2} \times 8$ = 4 cm,

⇒ BF = $\dfrac{1}{2}BC = \dfrac{1}{2} \times 9$ = 4.5 cm.

Perimeter of BDEF = BD + DE + EF + BF

= BD + BF + BD + BF (Since opposite sides of parallelogram are equal)

= 4 + 4.5 + 4 + 4.5

= 17 cm.

Hence, perimeter of parallelogram BDEF = 17 cm.

P, Q and R are mid-points of sides AB, BC and CD respectively of a rhombus ABCD. Show that PQ is perpendicular to QR.

Answer

Join diagonals of rhombus AC and BD.

We know that,

Diagonals of rhombus intersect at 90°.

By mid-point theorem,

The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and is equal to half of it.

In △ ABC,

P and Q are mid-points of sides AB and BC respectively.

∴ PQ || AC (By mid-point theorem)

In △ BCD,

R and Q are mid-points of sides CD and BC respectively.

∴ QR || BD (By mid-point theorem)

Since, AC ⊥ BD and PQ || AC and QR || BD.

∴ PQ ⊥ QR.

Hence, PQ is perpendicular to QR.

The diagonals of a quadrilateral ABCD are perpendicular to each other. Prove that the quadrilateral obtained by joining the mid-points of its adjacent sides is a rectangle.

Answer

By mid-point theorem,

The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and is equal to half of it.

Let ABCD be a quadrilateral where P, Q, R and S are the mid-point of AB, BC, CD and DA.

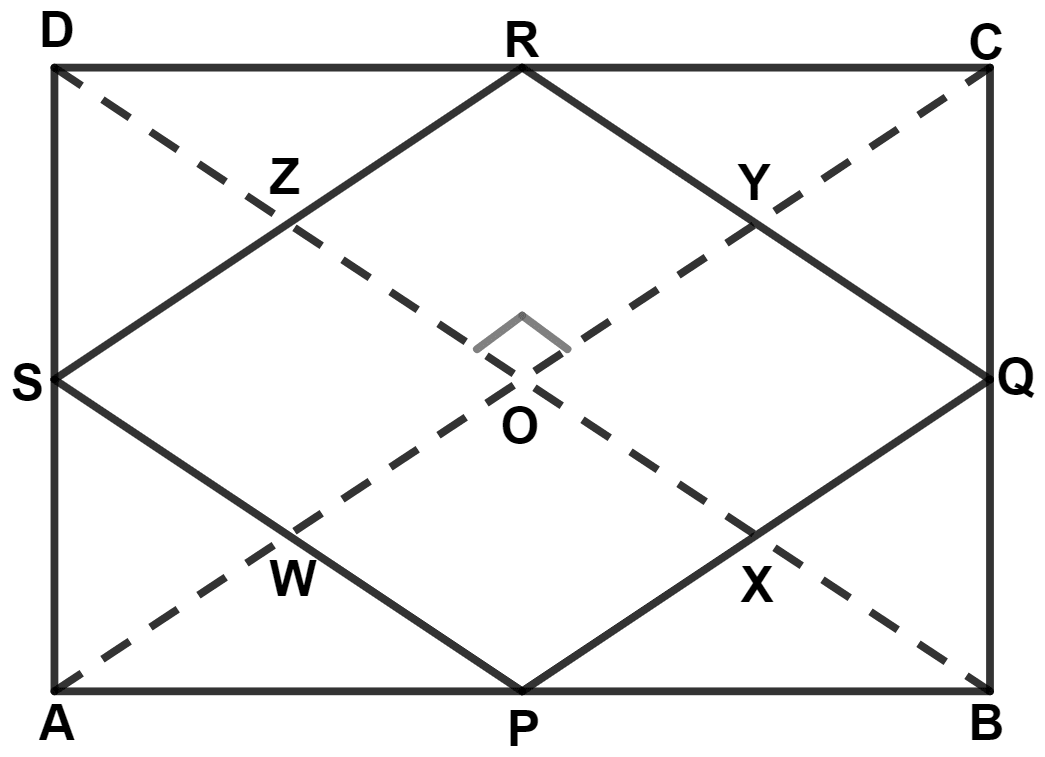
In △ ABC,

P and Q are mid-points of AB and BC respectively.

⇒ PQ = $\dfrac{1}{2}AC$ and PQ || AC. [By mid-point theorem] .......(1)

In △ ADC,

S and R are mid-points of AD and CD respectively.

⇒ SR = $\dfrac{1}{2}AC$ and SR || AC. [By mid-point theorem] .......(2)

From (1) and (2), we get :

PQ = SR and PQ || SR.

In △ BCD,

R and Q are mid-points of CD and BC respectively.

⇒ QR = $\dfrac{1}{2}BD$ and QR || BD. [By mid-point theorem] .......(3)

In △ ABD,

S and P are mid-points of AD and AB respectively.

⇒ PS = $\dfrac{1}{2}BD$ and PS || BD. [By mid-point theorem] .......(4)

From (3) and (4), we get :

QR = PS and QR || PS.

Since, diagonals of quadrilateral intersect at right angle.

∴ ∠AOD = ∠COD = AOB = ∠BOC = 90°.

From figure,

PQ || AC

∴ ∠PXO = ∠AOD = 90° (Corresponding angles are equal)

∴ ∠QXO = ∠COD = 90° (Corresponding angles are equal)

SR || AC

∴ ∠SZO = ∠AOB = 90° (Corresponding angles are equal)

∴ ∠RZO = ∠BOC = 90° (Corresponding angles are equal)

PS || BD

∴ ∠S = ∠RZO = 90° (Corresponding angles are equal)

∴ ∠P = ∠QXO = 90° (Corresponding angles are equal)

QR || BD

∴ ∠R = ∠SZO = 90° (Corresponding angles are equal)

∴ ∠Q = ∠PXO = 90° (Corresponding angles are equal)

Since, in quadrilateral PQRS,

Each interior angle is equal to 90° and opposite sides are parallel and equal.

∴ PQRS is a rectangle.

Hence, proved that the the figure obtained by joining the mid-points of the adjacent sides of the quadrilateral is a rectangle.

In △ ABC, E is mid-point of the median AD and BE produced meets side AC at point Q. Show that BE : EQ = 3 : 1.

Answer

Draw DY || BQ.

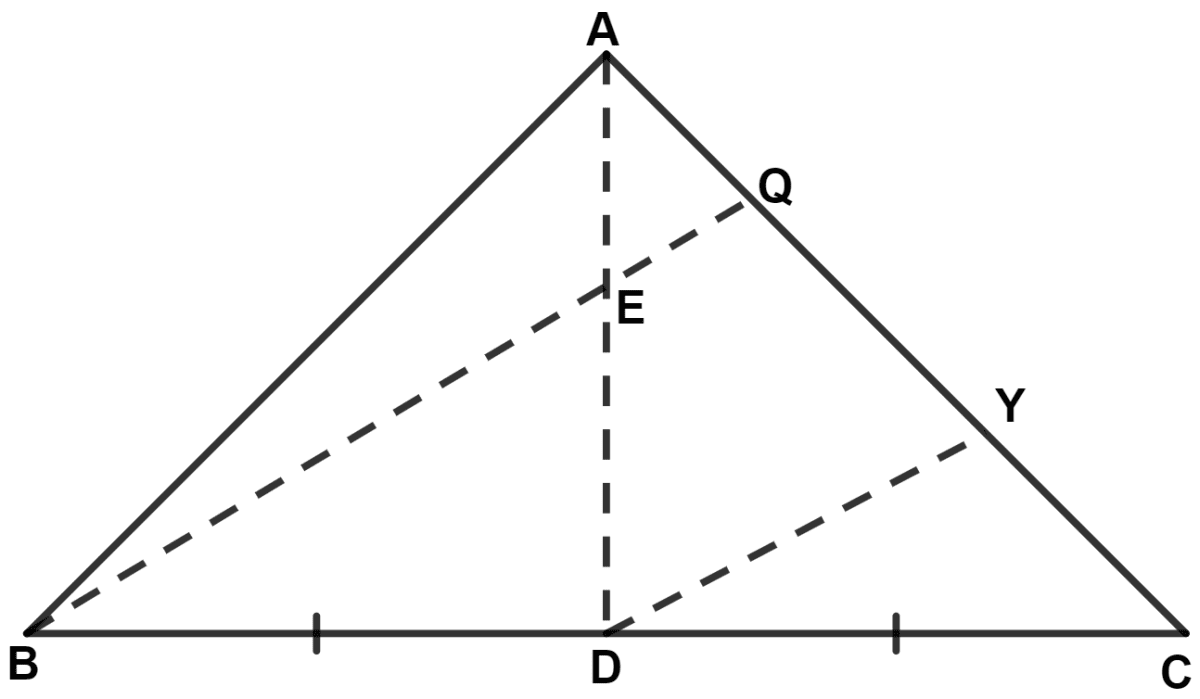
In △ BCQ and △ DCY,

⇒ ∠BCQ = ∠DCY (Common)

⇒ ∠BQC = ∠DYC (Corresponding angles are equal)

∴ △ BCQ ~ △ DCY (By A.A. axiom)

We know that,

Corresponding sides of similar triangle are proportional.

$\Rightarrow \dfrac{BQ}{DY} = \dfrac{BC}{DC} = \dfrac{CQ}{CY}$ ..........(1)

Since, D is the mid-point of BC.

∴ BC = 2CD

Considering L.H.S. of the equation (1), we get :

$\Rightarrow \dfrac{BQ}{DY} = \dfrac{2CD}{DC} \\[1em] \Rightarrow \dfrac{BQ}{DY} = 2 \text{ ........(1)}$

In △ AEQ and △ ADY,

⇒ ∠EAQ = ∠DAY (Common)

⇒ ∠AEQ = ∠ADY (Corresponding angles are equal)

∴ △ AEQ ~ △ ADY (By A.A. axiom)

We know that,

Corresponding sides of similar triangle are proportional.

$\Rightarrow \dfrac{EQ}{DY} = \dfrac{AE}{AD} = \dfrac{1}{2}$ (Since, E is the mid-point of AD)

$\Rightarrow \dfrac{EQ}{DY} = \dfrac{1}{2}$ ............(2)

Dividing equation (1) by (2), we get :

$\Rightarrow \dfrac{\dfrac{BQ}{DY}}{\dfrac{EQ}{DY}} = \dfrac{2}{\dfrac{1}{2}} \\[1em] \Rightarrow \dfrac{BQ \times DY}{EQ \times DY} = 4 \\[1em] \Rightarrow \dfrac{BQ}{EQ} = 4 \\[1em] \Rightarrow \dfrac{BE + EQ}{EQ} = 4 \\[1em] \Rightarrow BE + EQ = 4EQ \\[1em] \Rightarrow BE = 4EQ - EQ \\[1em] \Rightarrow BE = 3EQ \\[1em] \Rightarrow \dfrac{BE}{EQ} = \dfrac{3}{1}.$

Hence, proved that BE : EQ = 3 : 1.

In the given figure, M is the mid-point of AB and DE, whereas N is mid-point of BC and DF. Show that : EF = AC.

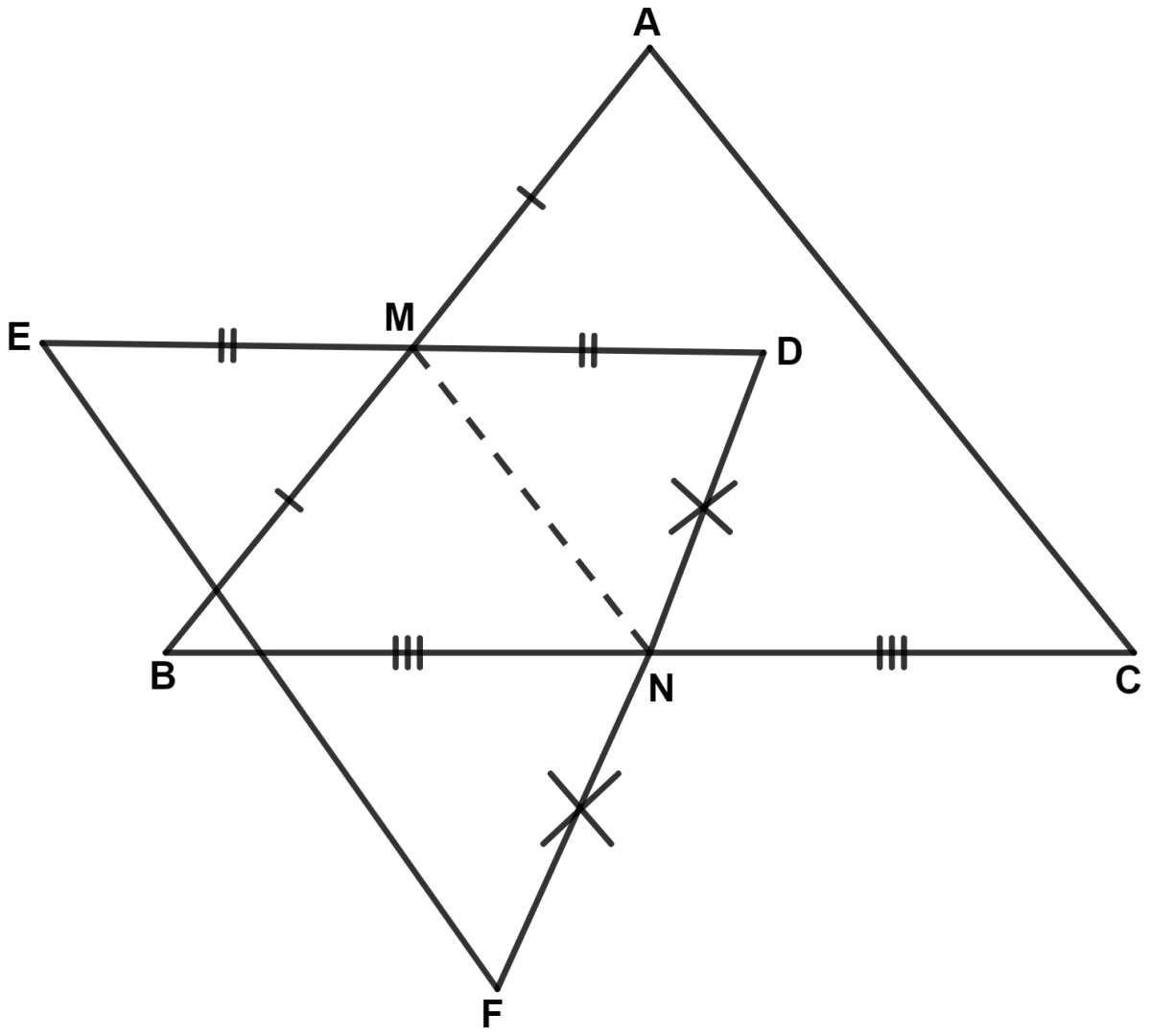
Answer

By mid-point theorem,

The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and is equal to half of it.

In △ EDF,

M is the mid-point of ED and N is the mid-point of DF.

∴ MN = $\dfrac{1}{2}EF$ (By mid-point theorem)

⇒ EF = 2MN .............(1)

In △ ABC,

M is the mid-point of AB and N is the mid-point of BC.

∴ MN = $\dfrac{1}{2}AC$ (By mid-point theorem)

⇒ AC = 2MN .............(2)

From (1) and (2), we get :

⇒ EF = AC.

Hence, proved that EF = AC.

In triangle ABC; D and E are mid-points of the sides AB and AC respectively. Through E, a straight line is drawn parallel to AB to meet BC at F. Prove that BDEF is a parallelogram. If AB = 16 cm, AC = 12 cm and BC = 18 cm, find the perimeter of the parallelogram BDEF.

Answer

By mid-point theorem,

The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and is equal to half of it.

By converse of mid-point theorem,

The straight line drawn through the mid-point of one side of a triangle parallel to another, bisects the third side.

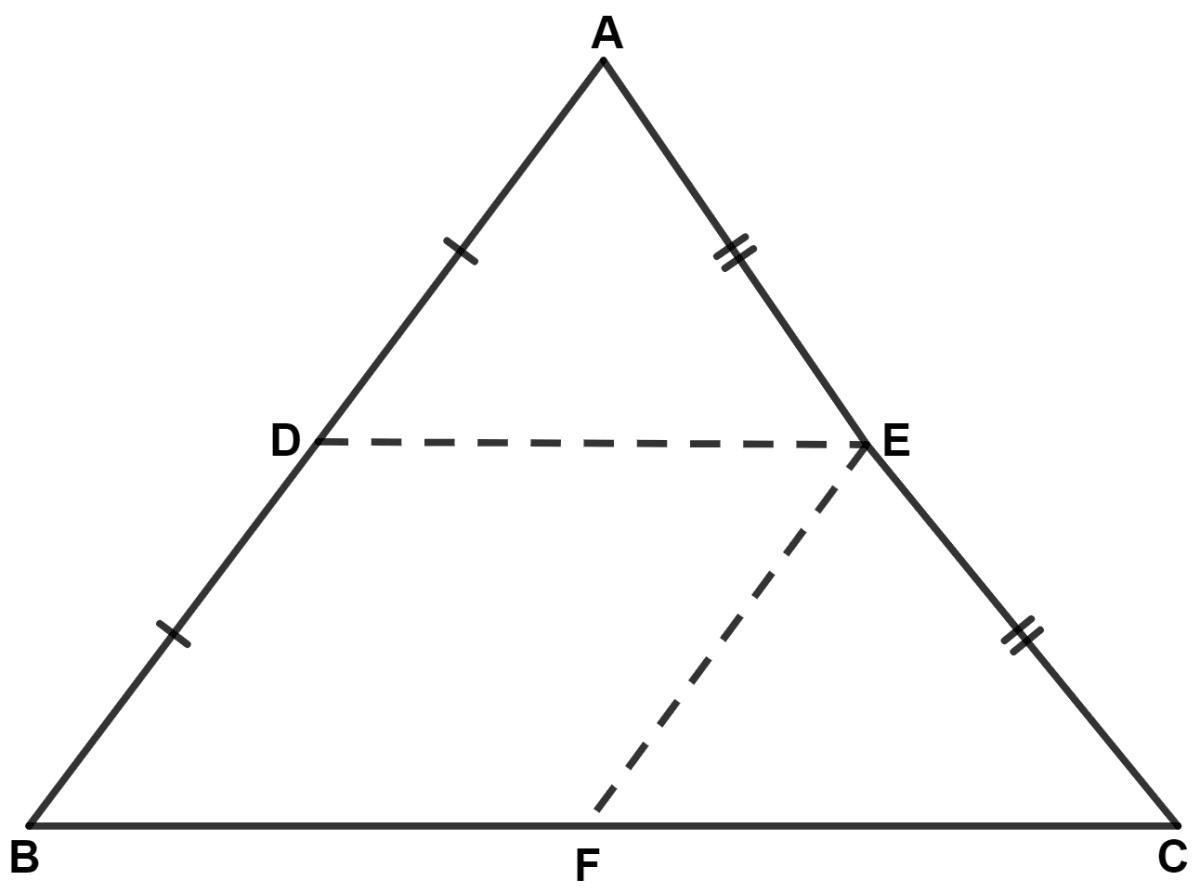
Given,

E is mid-point of AC and EF || AB.

∴ F is mid-point of BC (By converse of mid-point theorem).

Since, D and E are mid-points of sides AB and AC respectively.

∴ DE || BC and DE = $\dfrac{1}{2}BC$ (By mid-point theorem)

⇒ DE || BF and DE = BF (As F is mid-point of BC).

Given,

EF || BC

∴ EF || BD.

Since, E and F are mid-points of sides AC and BC respectively.

∴ EF = $\dfrac{1}{2}AB$ = BD. (By mid-point theorem)

Since, opposite sides of quadrilateral BDEF are parallel and equal.

∴ BDEF is a parallelogram.

From figure,

⇒ BD = $\dfrac{1}{2}AB = \dfrac{1}{2} \times 16$ = 8 cm,

⇒ BF = $\dfrac{1}{2}BC = \dfrac{1}{2} \times 18$ = 9 cm.

Perimeter of BDEF = BD + DE + EF + BF

= BD + BF + BD + BF (Since opposite sides of parallelogram are equal)

= 8 + 9 + 8 + 9

= 34 cm.

Hence, perimeter of parallelogram BDEF = 34 cm.

In the given figure, AD and CE are medians and DF // CE. Prove that : FB = $\dfrac{1}{4}AB$.

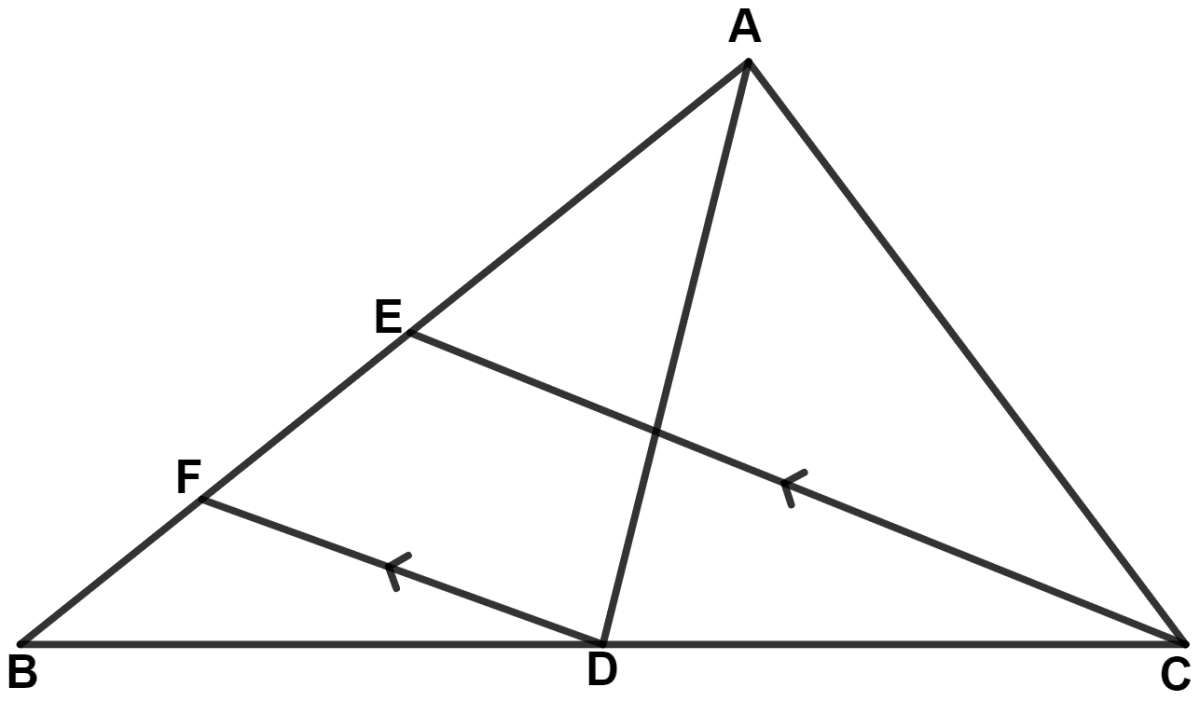
Answer

By mid-point theorem,

The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and is equal to half of it.

By converse of mid-point theorem,

The straight line drawn through the mid-point of one side of a triangle parallel to another, bisects the third side.

Since, AD and CE are medians.

∴ D is the mid-point of BC and E is the mid-point of AB.

In △ BEC,

DF || CE and D is the mid-point of BC.

∴ F is the mid-point of BE. (By converse of mid-point theorem)

∴ FB = $\dfrac{1}{2}BE$ .......(1)

Since, E is the mid-point of AB.

∴ BE = $\dfrac{1}{2}AB$ .......(2)

Substituting value of BE from equation (2) in (1), we get :

∴ FB = $\dfrac{1}{2} \times \dfrac{1}{2} \times AB = \dfrac{1}{4}AB$.

Hence, proved that FB = $\dfrac{1}{4}AB$.

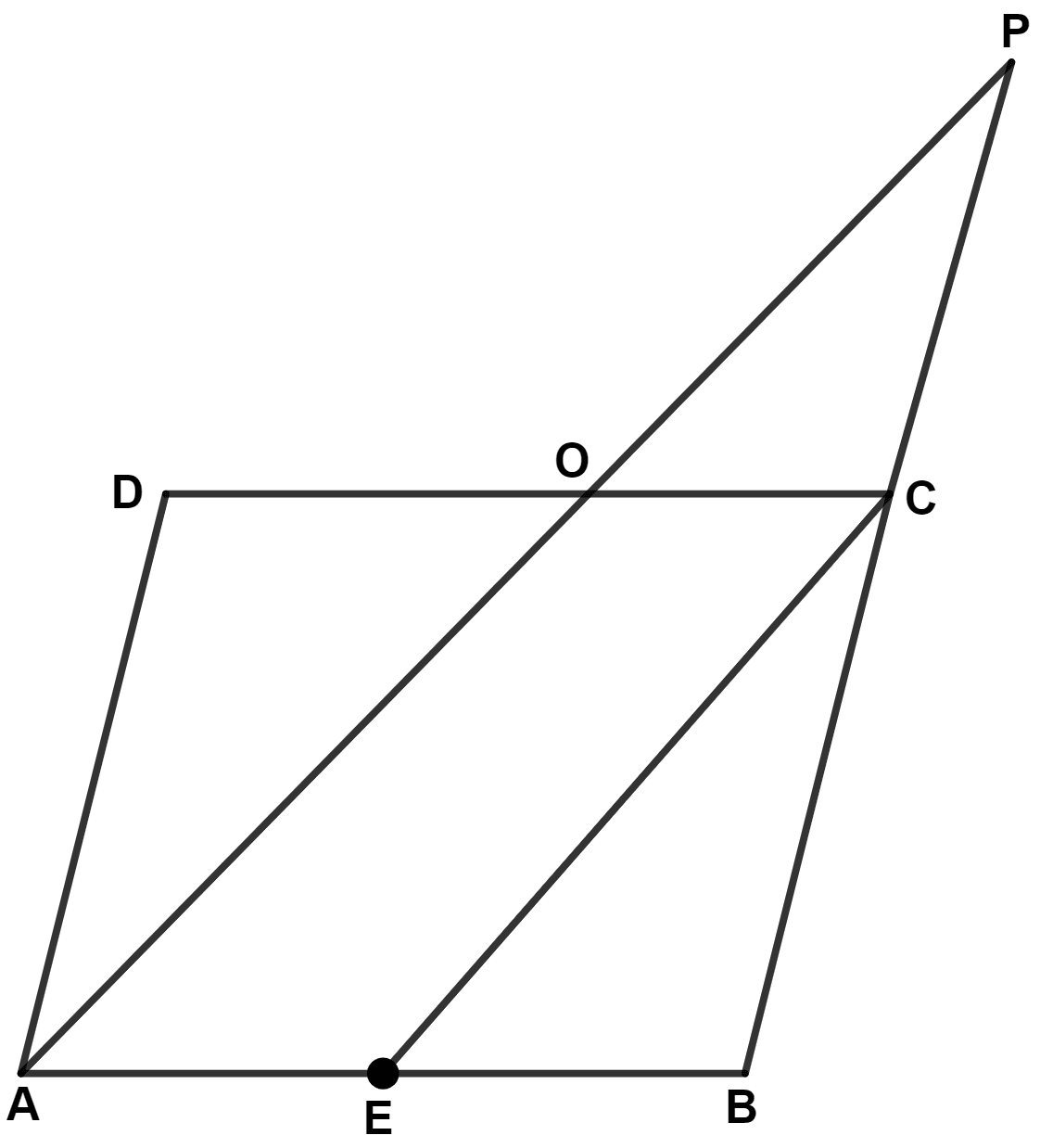
In parallelogram ABCD, E is the mid-point of AB and AP is parallel to EC which meets DC at point O and BC produced at P. Prove that :

(i) BP = 2AD

(ii) O is mid-point of AP.

Answer

By mid-point theorem,

The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and is equal to half of it.

By converse of mid-point theorem,

The straight line drawn through the mid-point of one side of a triangle parallel to another, bisects the third side.

(i) In △ ABP,

⇒ E is the mid-point of AB and EC || AP.

∴ C is the mid-point of BP. (By converse of mid-point theorem)

∴ BP = 2BC .........(1)

Since, ABCD is a parallelogram.

∴ AD = BC (Opposite sides of parallelogram are equal) .......(2)

From equation (1) and (2), we get :

⇒ BP = 2AD.

Hence, proved that BP = 2AD.

(ii) Since, opposite sides of parallelogram are parallel.

∴ AB || CD

⇒ AB || OC.

In △ ABP,

⇒ E is the mid-point of AB and OC || AB.

∴ O is the mid-point of AP. (By converse of mid-point theorem)

Hence, O is the mid-point of AP.

In a trapezium ABCD, sides AB and DC are parallel to each other. E is mid-point of AD and F is mid-point of BC.

Prove that :

AB + DC = 2EF.

Answer

Join BE and produce to meet CD produced at point P.

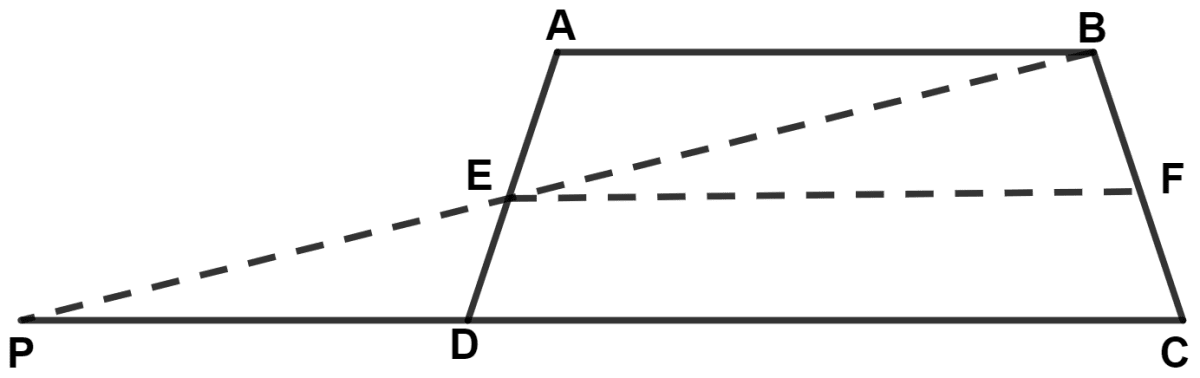
In △ PDE and △ BAE,

⇒ ∠PED = ∠BEF (Vertically opposite angles are equal)

⇒ AE = ED (Since, E is the mid-point of AD)

⇒ ∠EDP = ∠EAB (Alternate angles are equal)

∴ △ PDE ≅ △ BAE (By A.S.A. axiom)

We know that,

Corresponding parts of congruent triangle are equal.

∴ BE = EP and AB = PD.

In △ BPC,

Since, E and F are mid-points of sides BP and BC respectively.

∴ EF = $\dfrac{1}{2}PC$.

To prove :

AB + CD = 2EF ........(1)

Substituting value in L.H.S. of equation (1), we get :

⇒ AB + CD = PD + CD = PC.

Substituting value in R.H.S. of equation (2), we get :

⇒ 2EF = $2 \times \dfrac{1}{2}PC$ = PC.

Since, L.H.S. = R.H.S.

Hence, proved that AB + CD = 2EF.

In △ ABC, AD is the median and DE is parallel to BA, where E is a point in AC. Prove that BE is also a median.

Answer

By converse of mid-point theorem,

The straight line drawn through the mid-point of one side of a triangle parallel to another, bisects the third side.

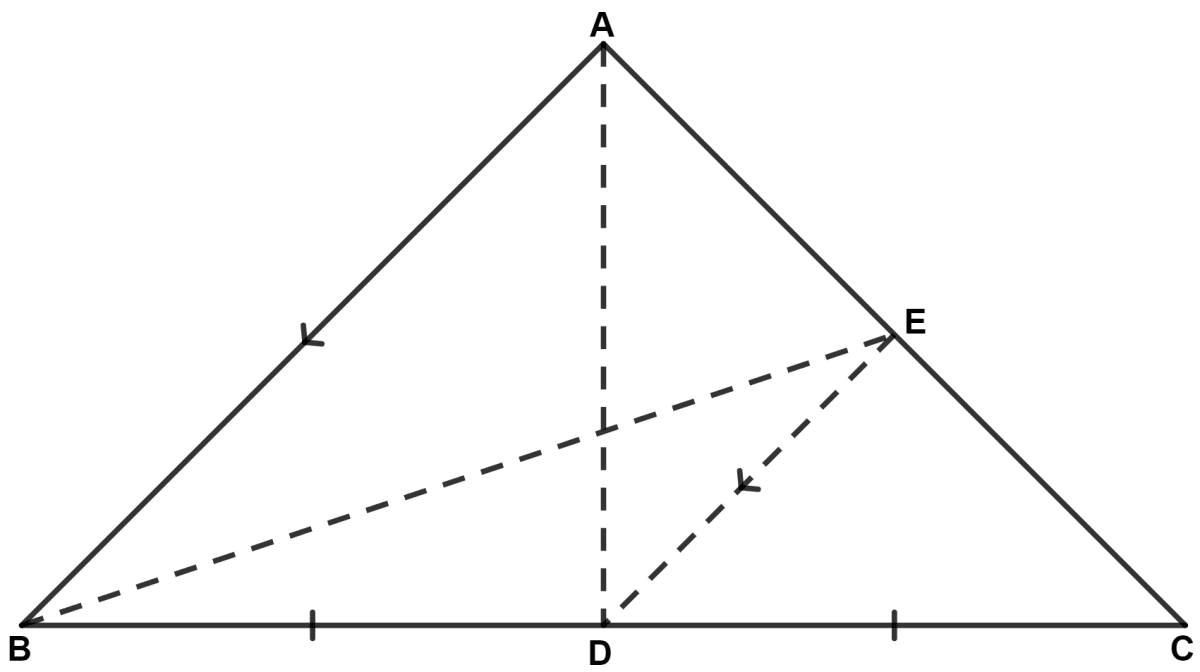
In △ ABC,

Since, AD is the median.

∴ D is the mid-point of BC.

Since, D is mid-point of BC and DE || AB.

∴ E is the mid-point of AC. (By converse of mid-point theorem)

Join BE.

Hence, proved that BE is also a median.

Adjacent sides of a parallelogram are equal and one of diagonals is equal to any one of the sides of this parallelogram. Show that its diagonals are in the ratio $\sqrt{3} : 1$.

Answer

Let ABCD be the required parallelogram.

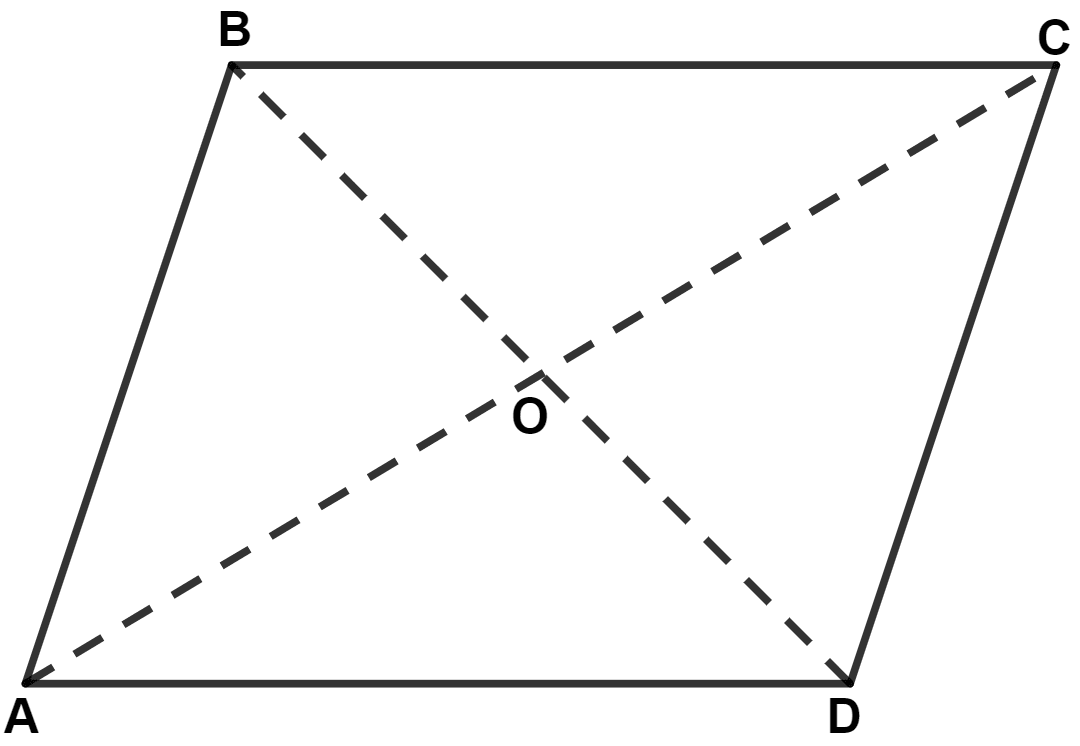
∴ AB = CD and BC = AD. (Opposite sides of parallelogram are equal)

Given,

Adjacent sides of a parallelogram are equal.

∴ AB = BC.

∴ AB = BC = CD = AD

Since, all sides of parallelogram are equal.

∴ ABCD is a rhombus.

Given, one of the diagonals is equal to its sides. Let diagonal BD be equal to sides.

∴ AB = BC = CD = AD = BD = a (let).

From figure,

⇒ BO = $\dfrac{BD}{2} = \dfrac{a}{2}$ (Since, in a rhombus diagonals bisect each other at right angle).

Hence, △ AOB is right-angled at O.

In △ AOB,

By pythagoras theorem,

⇒ AB² = BO² + AO²

⇒ a² = $\Big(\dfrac{a}{2}\Big)^2$ + AO²

⇒ AO² = $a^2 - \dfrac{a^2}{4}$

⇒ AO² = $\dfrac{4a^2 - a^2}{4}$

⇒ AO² = $\dfrac{3a^2}{4}$

⇒ AO = $\dfrac{\sqrt{3}a}{2}$,

⇒ AC = 2AO = $2 \times \dfrac{\sqrt{3}a}{2} = \sqrt{3}a$ units.

The ratio of the diagonals is:

$\Rightarrow \dfrac{AC}{BD} = \dfrac{\sqrt{3}a}{a} = \dfrac{\sqrt{3}}{1}$

∴ AC : BD = $\sqrt{3}$ : 1.

Hence, proved that diagonals are in the ratio $\sqrt{3}$ : 1.