Isosceles Triangles [Including Inequalities]

In the given figure, ∠B = ∠C and ∠BAD = ∠CAD, then :

1. AB = AC

2. AB ≠ AC

3. ∠ADB ≠ ∠ADC

4. ∠ADB ≠ 90°

Answer

We know that,

Sides opposite to equal angles are equal.

Since, ∠B = ∠C

∴ AC = AB.

Hence, Option 1 is the correct option.

In the given figure, AD ⊥ BC and AB = AC, then :

1. △ ABD ≇ △ ACD

2. BD = CD

3. ∠BAC = 90°

4. ∠CAD = 45°

Answer

We know that,

Angles opposite to equal sides are equal.

Since, AB = AC,

∴ ∠C = ∠B.

In △ ABD and △ ACD,

⇒ AB = AC (Given)

⇒ AD = AD (Common side)

⇒ ∠B = ∠C (Proved above)

∴ △ ABD ≅ △ ACD (By S.A.S. axiom)

We know that,

Corresponding sides of congruent triangles are equal.

∴ BD = CD.

Hence, Option 2 is the correct option.

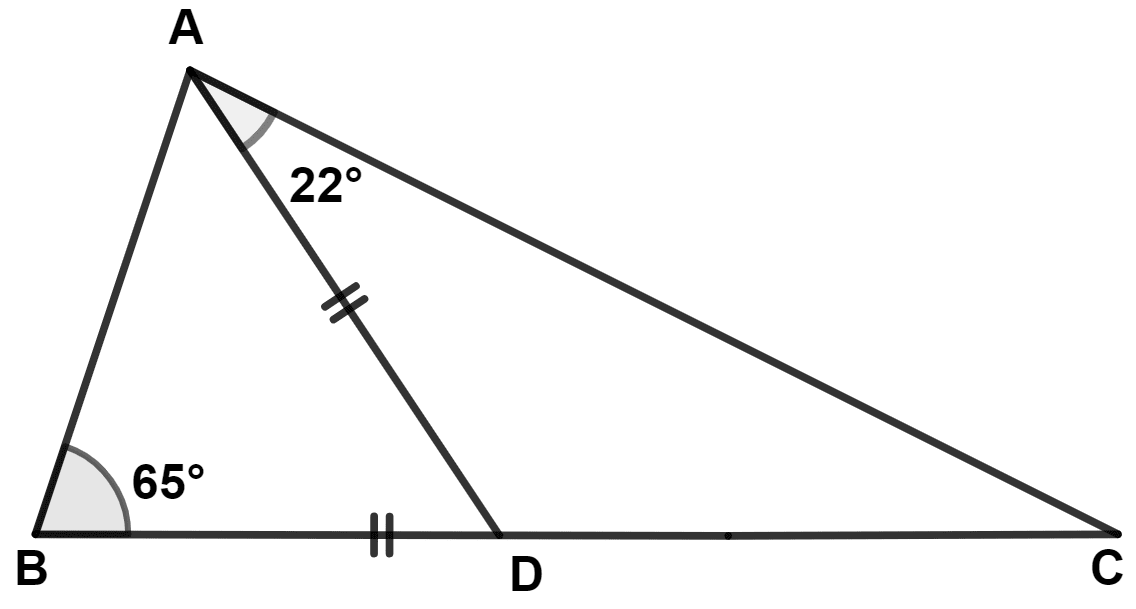
In the given figure, AD = BD, then angle ACD is :

1. 43°

2. 22°

3. 65°

4. 28°

Answer

Given,

AD = BD

In △ ABD,

⇒ ∠BAD = ∠ABD = 65° (Angles opposite to equal sides are equal)

In △ ABC,

⇒ ∠BAC = ∠BAD + ∠DAC = 65° + 22° = 87°.

By angle sum property of triangle,

⇒ ∠BAC + ∠ACB + ∠CBA = 180°

⇒ 87° + ∠ACB + 65° = 180°

⇒ ∠ACB + 152° = 180°

⇒ ∠ACB = 180° - 152° = 28°.

From figure,

⇒ ∠ACD = ∠ACB = 28°.

Hence, Option 4 is the correct option.

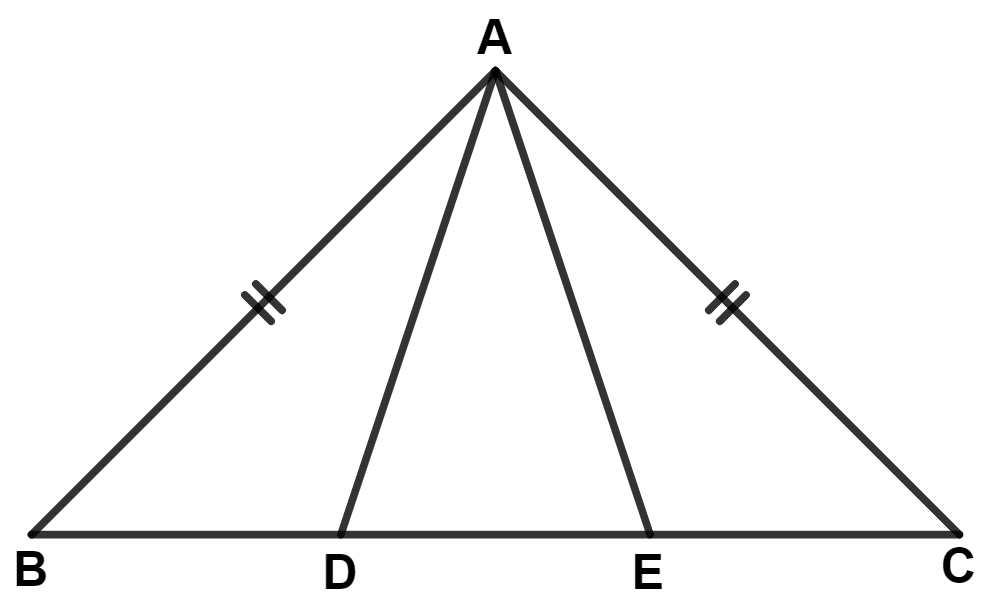
In the given figure; BE = DC, then :

1. AD = DC

2. AE = BE

3. AD = AE

4. ∠ABE = ∠DAC

Answer

From figure,

⇒ AB = AC

∴ ∠B = ∠C (Angles opposite to equal sides are equal)

Given,

⇒ BE = DC

⇒ BD + DE = DE + EC

⇒ BD = EC.

In △ ABD and △ AEC,

⇒ BD = EC (Proved above)

⇒ AB = AC (Given)

⇒ ∠B = ∠C (Proved above)

∴ △ ABD ≅ △ AEC (By S.A.S. axiom)

We know that,

Corresponding parts of congruent triangle are equal.

∴ AD = AE.

Hence, Option 3 is the correct option.

In △ ABC and △ PQR, AB = AC, ∠C = ∠P and ∠B = ∠Q; then triangles are :

1. isosceles but not congruent

2. isosceles and congruent

3. congruent but not isosceles

4. neither isosceles nor congruent.

Answer

△ ABC and △ PQR are shown below:

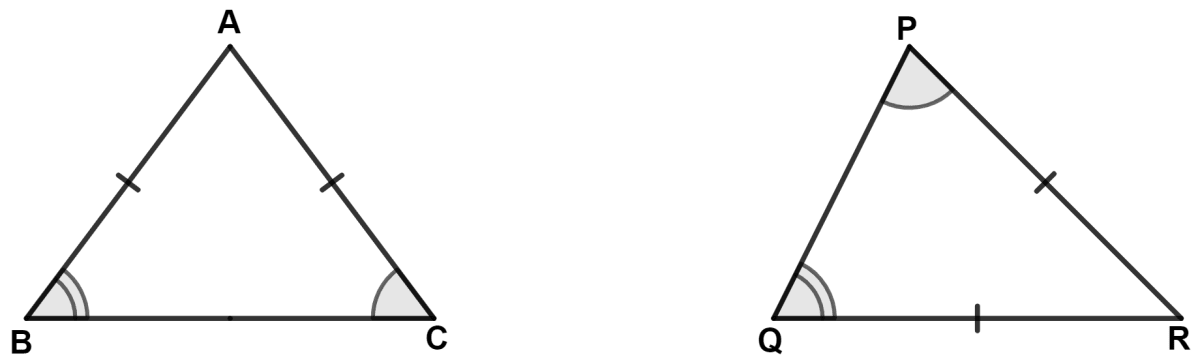
In △ ABC,

⇒ AB = AC (Given)

∴ ∠C = ∠B = x (let) (Angles opposite to equal sides are equal).

Given,

⇒ ∠P = ∠C

∴ ∠P = x.

⇒ ∠Q = ∠B

∴ ∠Q = x.

In △ PQR,

⇒ ∠P = ∠Q = x

⇒ QR = PR (Sides opposite to equal angles are equal).

∴ ABC and PQR are isosceles triangles.

Hence, Option 1 is the correct option.

In the figure alongside,

AB = AC

∠A = 48° and

∠ACD = 18°.

Show that : BC = CD.

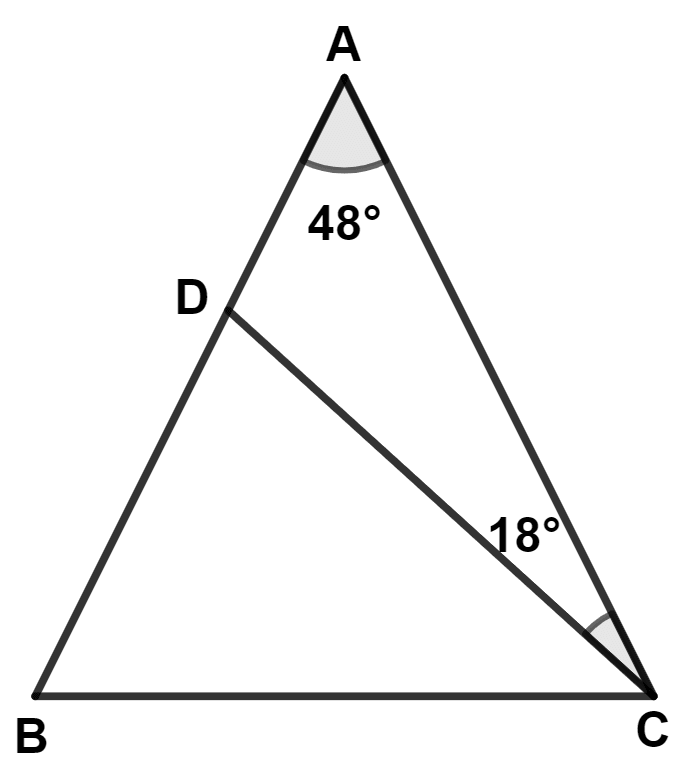
Answer

In △ ABC,

⇒ AB = AC (Given)

⇒ ∠C = ∠B = x (let) (Angles opposite to equal sides are equal)

By angle sum property of triangle,

⇒ ∠A + ∠B + ∠C = 180°

⇒ 48° + x + x = 180°

⇒ 48° + 2x = 180°

⇒ 2x = 180° - 48°

⇒ 2x = 132°

⇒ x = $\dfrac{132°}{2}$ = 66°.

∴ ∠B = ∠C = 66°.

From figure,

⇒ ∠DCB = ∠C - ∠ACD = 66° - 18° = 48°.

In △ BDC,

By angle sum property of triangle,

⇒ ∠BDC + ∠DCB + ∠CBD = 180°

⇒ ∠BDC + 48° + 66° = 180°

⇒ ∠BDC + 114° = 180°

⇒ ∠BDC = 180° - 114° = 66°.

Since, ∠BDC = ∠CBD

∴ BC = CD (Sides opposite to equal angles are equal).

Hence, proved that BC = CD.

Calculate :

(i) ∠ADC

(ii) ∠ABC

(iii) ∠BAC

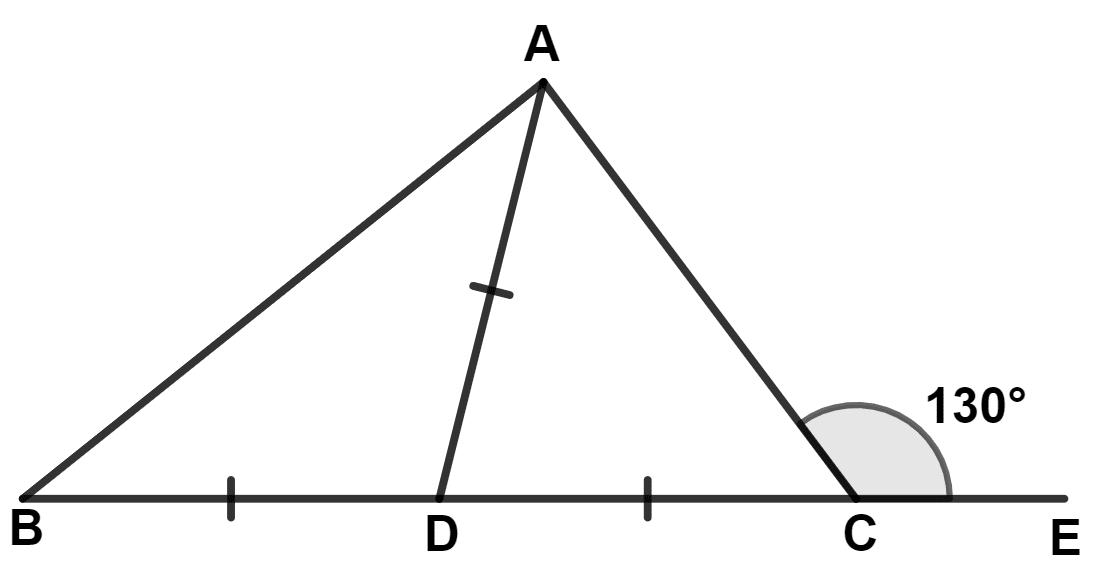
Answer

(i) Since, DCE is a straight line.

∴ ∠ACD + ∠ACE = 180°

⇒ ∠ACD + 130° = 180°

⇒ ∠ACD = 180° - 130° = 50°.

In △ ADC,

⇒ AD = DC (Given)

⇒ ∠DAC = ∠ACD = 50° (Angles opposite to equal sides are equal.)

By angle sum property of triangle,

⇒ ∠ADC + ∠DAC + ∠ACD = 180°

⇒ ∠ADC + 50° + 50° = 180°

⇒ ∠ADC + 100° = 180°

⇒ ∠ADC = 180° - 100° = 80°.

Hence, ∠ADC = 80°.

(ii) Since, BDC is a straight line.

∴ ∠ADB + ∠ADC = 180°

⇒ ∠ADB + 80° = 180°

⇒ ∠ADB = 180° - 80° = 100°.

In △ ABD,

⇒ AD = BD (Given)

⇒ ∠DBA = ∠BAD = x (let).

By angle sum property of triangle,

⇒ ∠BAD + ∠ADB + ∠DBA = 180°

⇒ x + 100° + x = 180°

⇒ 2x + 100° = 180°

⇒ 2x = 180° - 100°

⇒ 2x = 80°

⇒ x = $\dfrac{80°}{2}$ = 40°.

⇒ ∠DBA = ∠BAD = 40°.

From figure,

⇒ ∠ABC = ∠DBA = 40°.

Hence, ∠ABC = 40°.

(iii) From figure,

⇒ ∠BAC = ∠BAD + ∠DAC = 40° + 50° = 90°.

Hence, ∠BAC = 90°.

In the following figure, AB = AC; BC = CD and DE is parallel to BC. Calculate :

(i) ∠CDE

(ii) ∠DCE

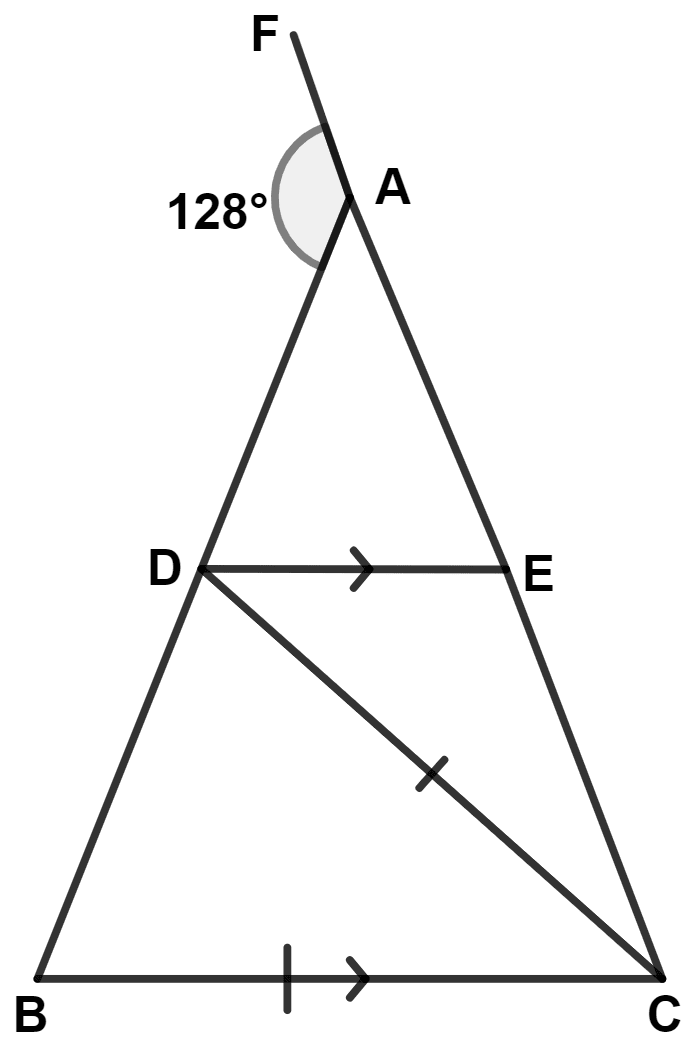
Answer

Since, FAC is a straight line.

∴ ∠BAC + ∠FAB = 180°

⇒ ∠BAC + 128° = 180°

⇒ ∠BAC = 180° - 128° = 52°.

In △ ABC,

⇒ ∠A = 52°

⇒ AB = AC (Given)

∴ ∠B = ∠C = x (let) [Angles opposite to equal sides are equal].

By angle, sum property of triangle,

⇒ ∠A + ∠B + ∠C = 180°

⇒ 52° + x + x = 180°

⇒ 52° + 2x = 180°

⇒ 2x = 180° - 52°

⇒ 2x = 128°

⇒ x = $\dfrac{128°}{2}$ = 64°

⇒ ∠B = ∠C = 64°.

In △ DBC,

⇒ BC = CD (Given)

⇒ ∠BDC = ∠DBC = 64° (Angles opposite to equal sides are equal)

From figure,

⇒ ∠ADE = ∠ABC = 64° (Corresponding angles are equal)

Since, ADB is a straight line.

∴ ∠ADE + ∠CDE + ∠BDC = 180°

⇒ 64° + ∠CDE + 64° = 180°

⇒ ∠CDE + 128° = 180°

⇒ ∠CDE = 180° - 128° = 52°.

Hence, ∠CDE = 52°.

(ii) Since,

DE || BC

⇒ ∠DCB = ∠CDE = 52° (Alternate angles are equal)

From figure,

⇒ ∠DCE = ∠ECB - ∠DCB

= 64° - 52° = 12°.

Hence, ∠DCE = 12°.

Calculate x :

(i)

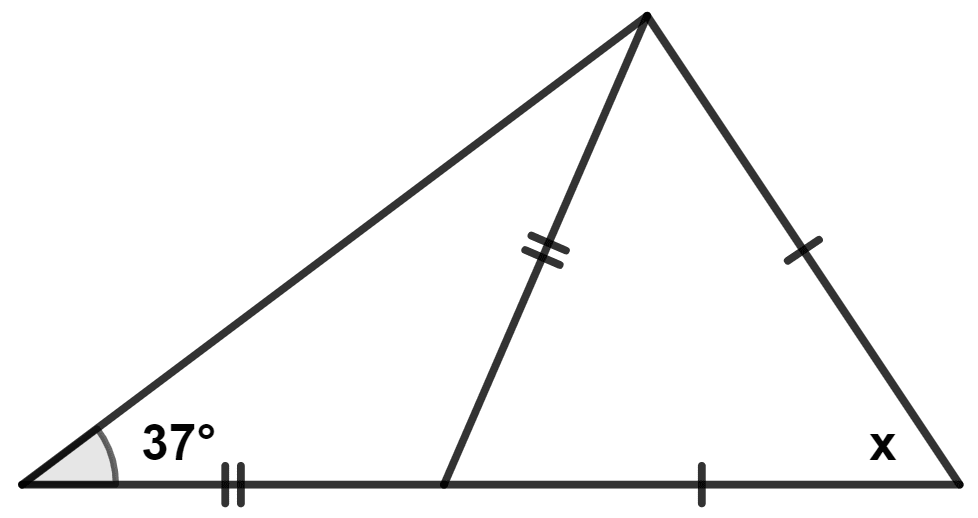
(ii)

Answer

(i) In △ ABC,

⇒ BC = AC (Given)

∴ ∠BAC = ∠CBA = 37° (Angles opposite to equal sides are equal)

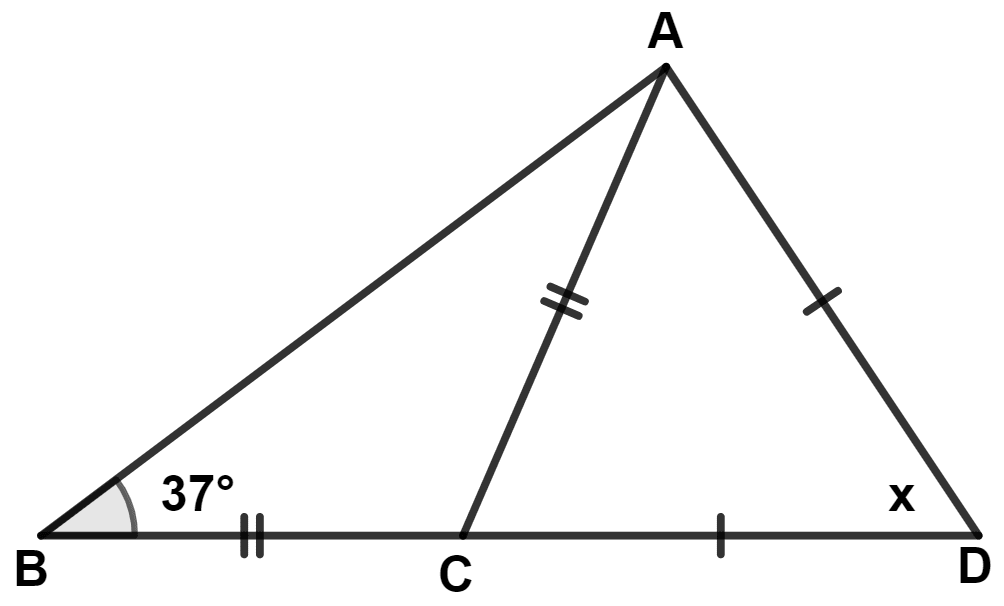
By angle sum property of triangle,

⇒ ∠BAC + ∠CBA + ∠ACB = 180°

⇒ 37° + 37° + ∠ACB = 180°

⇒ ∠ACB + 74° = 180°

⇒ ∠ACB = 180° - 74° = 106°.

From figure,

Since, BCD is a straight line,

∴ ∠ACB + ∠ACD = 180°

⇒ 106° + ∠ACD = 180°

⇒ ∠ACD = 180° - 106° = 74°.

In △ ACD,

⇒ CD = AD (Given)

∴ ∠CAD = ∠ACD = 74° (Angles opposite to equal sides are equal)

By angle sum property of triangle,

⇒ ∠CAD + ∠ACD + ∠ADC = 180°

⇒ 74° + 74° + x = 180°

⇒ 148° + x = 180°

⇒ x = 180° - 148° = 32°.

Hence, x = 32°.

(ii) In △ ABC,

⇒ BC = AC (Given)

∴ ∠BAC = ∠CBA = 50° (Angles opposite to equal sides are equal)

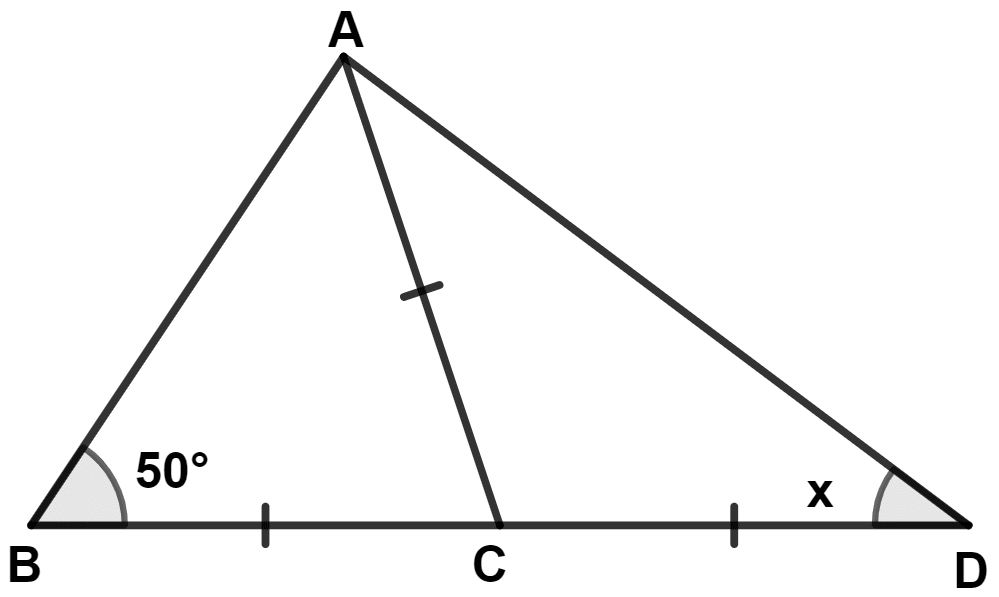
By angle sum property of triangle,

⇒ ∠BAC + ∠CBA + ∠ACB = 180°

⇒ 50° + 50° + ∠ACB = 180°

⇒ ∠ACB + 100° = 180°

⇒ ∠ACB = 180° - 100° = 80°.

From figure,

Since, BCD is a straight line,

∴ ∠ACB + ∠ACD = 180°

⇒ 80° + ∠ACD = 180°

⇒ ∠ACD = 180° - 80° = 100°.

In △ ACD,

⇒ CD = AC (Given)

∴ ∠CAD = ∠ADC = x (Angles opposite to equal sides are equal)

By angle sum property of triangle,

⇒ ∠CAD + ∠ACD + ∠ADC = 180°

⇒ x + x + 100° = 180°

⇒ 2x + 100° = 180°

⇒ 2x = 180° - 100°

⇒ 2x = 80°

⇒ x = $\dfrac{80°}{2}$ = 40°.

Hence, x = 40°.

In the figure, given below, AB = AC. Prove that : ∠BOC = ∠ACD.

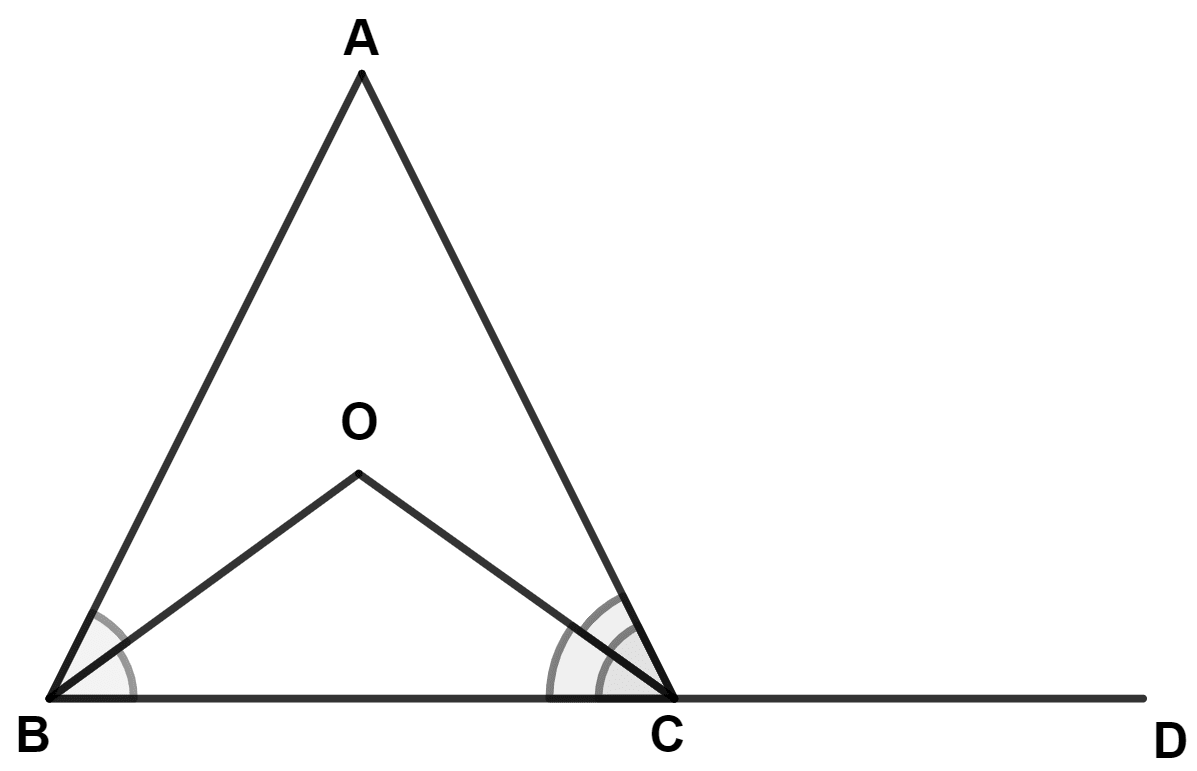
Answer

In △ ABC,

⇒ AB = AC (Given)

∴ ∠C = ∠B = x (let)

From figure,

OB and OC bisects angle ∠B and ∠C.

∴ ∠OBC = $\dfrac{∠B}{2} = \dfrac{x}{2}$ and ∠OCB = $\dfrac{∠C}{2} = \dfrac{x}{2}$.

In △ BOC,

By angle sum property of triangle,

⇒ ∠OBC + ∠OCB + ∠BOC = 180°

⇒ $\dfrac{x}{2} + \dfrac{x}{2}$ + ∠BOC = 180°

⇒ x + ∠BOC = 180°

⇒ ∠BOC = 180° - x.

From figure,

⇒ ∠OCA = $\dfrac{x}{2}$ (As OC is bisector of ∠C)

Since, BCD is a straight line.

∴ ∠OCB + ∠OCA + ∠ACD = 180°

⇒ $\dfrac{x}{2} + \dfrac{x}{2}$ + ∠ACD = 180°

⇒ x + ∠ACD = 180°

⇒ ∠ACD = 180° - x.

∴ ∠BOC = ∠ACD.

Hence, proved that ∠BOC = ∠ACD.

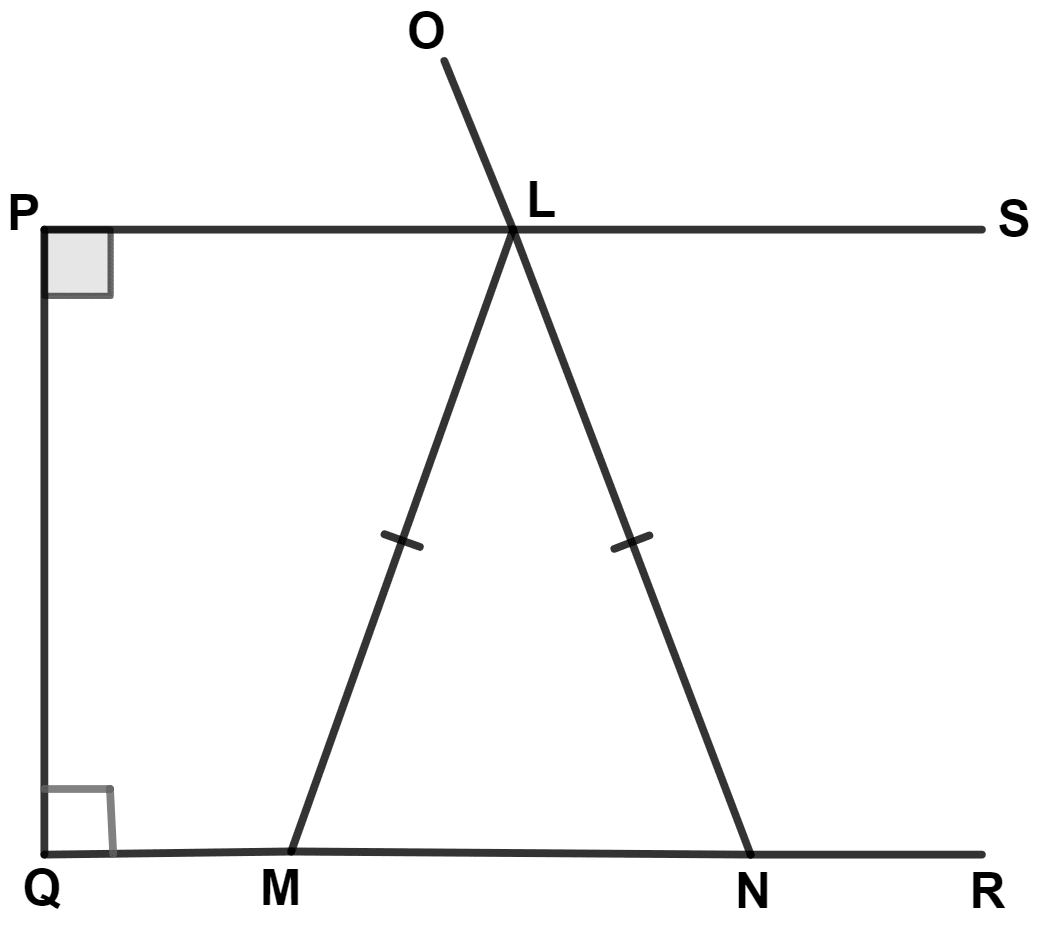
In the figure given below, LM = LN; angle PLN = 110°. Calculate :

(i) ∠LMN

(ii) ∠MLN

Answer

(i) In quadrilateral PQNL,

By angle sum property of quadrilateral,

⇒ ∠QPL + ∠PLN + ∠LNQ + ∠NQP = 360°

⇒ 90° + 110° + ∠LNQ + 90° = 360°

⇒ ∠LNQ + 290° = 360°

⇒ ∠LNQ = 360° - 290° = 70°.

From figure,

⇒ ∠LNM = ∠LNQ = 70°.

In triangle LMN,

⇒ LN = LM (Given)

⇒ ∠LMN = ∠LNM = 70°.

Hence, ∠LMN = 70°.

(ii) In triangle LMN,

By angle sum property of triangle,

⇒ ∠LMN + ∠LNM + ∠MLN = 180°

⇒ 70° + 70° + ∠MLN = 180°

⇒ ∠MLN + 140° = 180°

⇒ ∠MLN = 180° - 140° = 40°.

Hence, ∠MLN = 40°.

An isosceles triangle ABC has AC = BC. CD bisects AB at D and ∠CAB = 55°. Find :

(i) ∠DCB

(ii) ∠CBD

Answer

Isosceles triangle ABC is shown in the figure below:

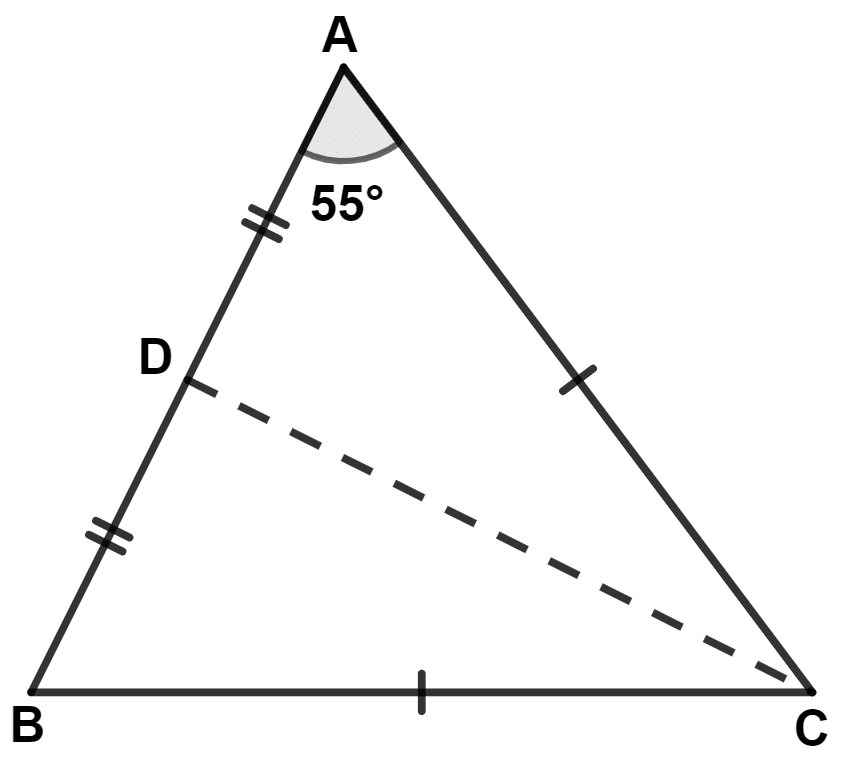
(i) In △ ACD and △ BCD,

⇒ ∠CAD = ∠CBD (Since, AC = BC and angles opposite to equal sides are equal.)

⇒ AD = BD (CD bisects AB)

⇒ AC = BC (Given)

∴ △ ACD ≅ △ BCD (By S.A.S. axiom)

We know that,

Corresponding sides of congruent triangle are equal.

∴ ∠ADC = ∠BDC = x (let)

Since, ADB is a straight line.

∴ ∠ADC + ∠BDC = 180°

⇒ x + x = 180°

⇒ 2x = 180°

⇒ x = $\dfrac{180°}{2}$ = 90°.

∴ ∠ADC = ∠BDC = 90°.

In △ BDC,

⇒ ∠BDC + ∠DCB + ∠CBD = 180°

⇒ 90° + ∠DCB + 55° = 180°

⇒ 145° + ∠DCB = 180°

⇒ ∠DCB = 180° - 145° = 35°.

Hence, ∠DCB = 35°.

(ii) From part (i), we get :

⇒ ∠CBD = 55°.

Hence, ∠CBD = 55°.

Find x :

Answer

In △ ADC,

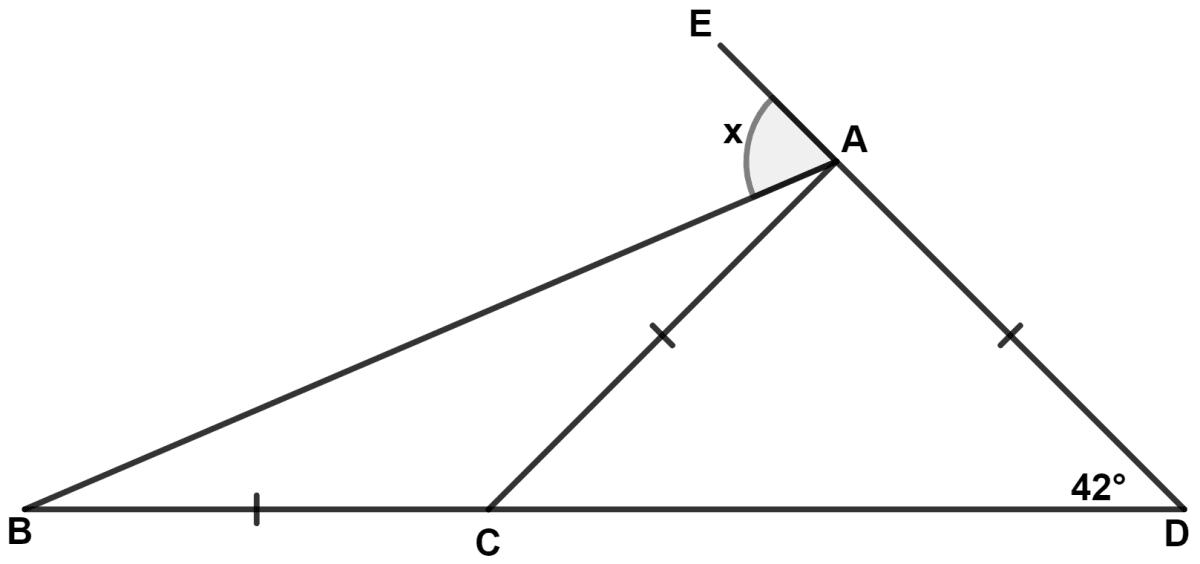
⇒ AC = AD (Given)

⇒ ∠ACD = ∠ADC = 42° (Angles opposite to equal sides are equal)

By angle sum property of triangle,

⇒ ∠ACD + ∠ADC + ∠CAD = 180°

⇒ 42° + 42° + ∠CAD = 180°

⇒ ∠CAD + 84° = 180°

⇒ ∠CAD = 180° - 84° = 96°.

Since, BCD is a straight line.

From figure,

⇒ ∠ACD + ∠ACB = 180°

⇒ 42° + ∠ACB = 180°

⇒ ∠ACB = 180° - 42° = 138°.

In △ ABC,

⇒ AC = BC (Given)

⇒ ∠ABC = ∠CAB = z (let) (Angles opposite to equal sides are equal)

By angle sum property of triangle,

⇒ ∠ABC + ∠CAB + ∠ACB = 180°

⇒ z + z + 138° = 180°

⇒ 2z + 138° = 180°

⇒ 2z = 180° - 138°

⇒ 2z = 42°

⇒ z = $\dfrac{42°}{2}$ = 21°.

⇒ ∠ABC = ∠CAB = 21°.

Since, EAD is a straight line.

From figure,

⇒ ∠EAB + ∠CAB + ∠CAD = 180°

⇒ x + 21° + 96° = 180°

⇒ x + 117° = 180°

⇒ x = 180° - 117° = 63°.

Hence, x = 63°.

In the triangle ABC, BD bisects angle B and is perpendicular to AC. If the lengths of the sides of the triangle are expressed in terms of x and y as shown, find the values of x and y.

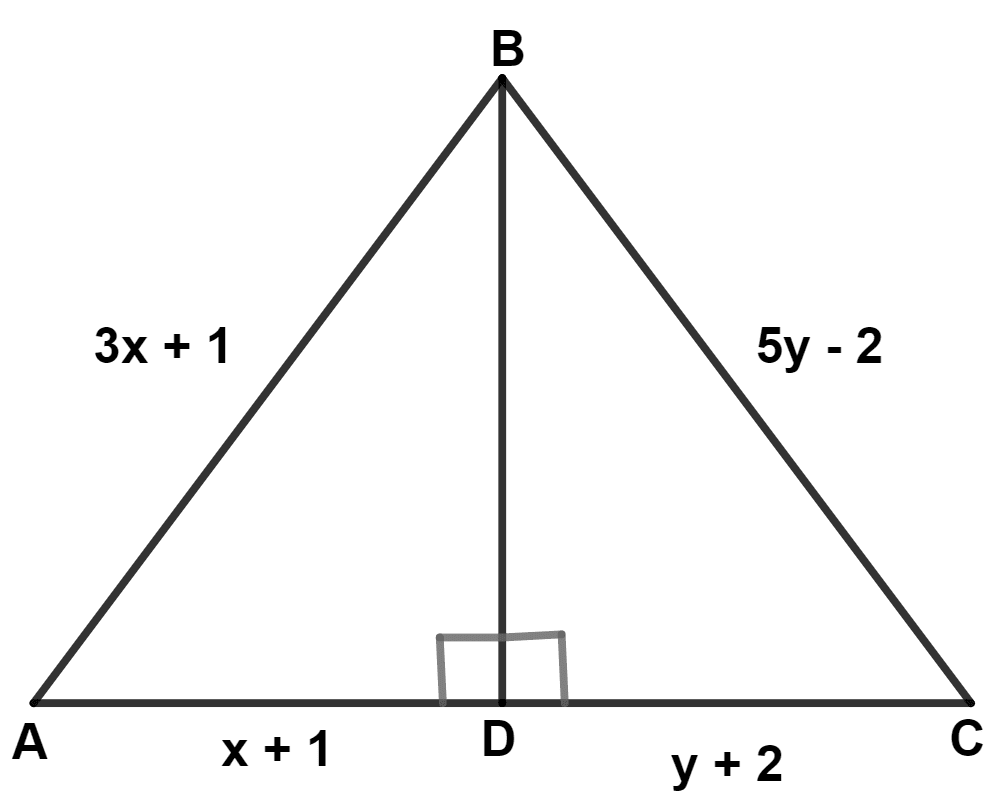
Answer

In △ ABD and △ CBD,

⇒ ∠ABD = ∠CBD (Since, BD bisects ∠B)

⇒ BD = BD (Common side)

⇒ ∠BDA = ∠BDC (Both equal to 90°)

∴ △ ABD ≅ △ CBD (By A.S.A. axiom)

We know that,

Corresponding sides of congruent triangle are equal.

∴ AB = BC and AD = CD

Considering, AB = BC

∴ 3x + 1 = 5y - 2

⇒ 3x + 1 + 2 = 5y

⇒ 5y = 3x + 3

⇒ y = $\dfrac{3x + 3}{5}$ ..........(1)

Considering, AD = CD

∴ x + 1 = y + 2

⇒ y = x + 1 - 2

⇒ y = x - 1 ...........(2)

Equating equations (1) and (2), we get :

⇒ x - 1 = $\dfrac{3x + 3}{5}$

⇒ 5(x - 1) = 3x + 3

⇒ 5x - 5 = 3x + 3

⇒ 5x - 3x = 3 + 5

⇒ 2x = 8

⇒ x = $\dfrac{8}{2}$ = 4.

Substituting value of x in equation (2), we get :

⇒ y = 4 - 1 = 3.

Hence, x = 4 and y = 3.

In triangle ABC; AB = AC and ∠A : ∠B = 8 : 5; find angle A.

Answer

Given,

⇒ ∠A : ∠B = 8 : 5

Let ∠A = 8x and ∠B = 5x.

In △ ABC,

⇒ AB = AC (Given)

⇒ ∠C = ∠B = 5x (Angles opposite to equal sides are equal)

By angle sum property of triangle,

⇒ ∠A + ∠B + ∠C = 180°

⇒ 8x + 5x + 5x = 180°

⇒ 18x = 180°

⇒ x = $\dfrac{180}{18}$ = 10°.

⇒ ∠A = 8x = 8 × 10° = 80°.

Hence, ∠A = 80°.

In triangle ABC; ∠A = 60°, ∠C = 40° and bisector of angle ABC meets side AC at point P. Show that BP = CP.

Answer

In △ ABC,

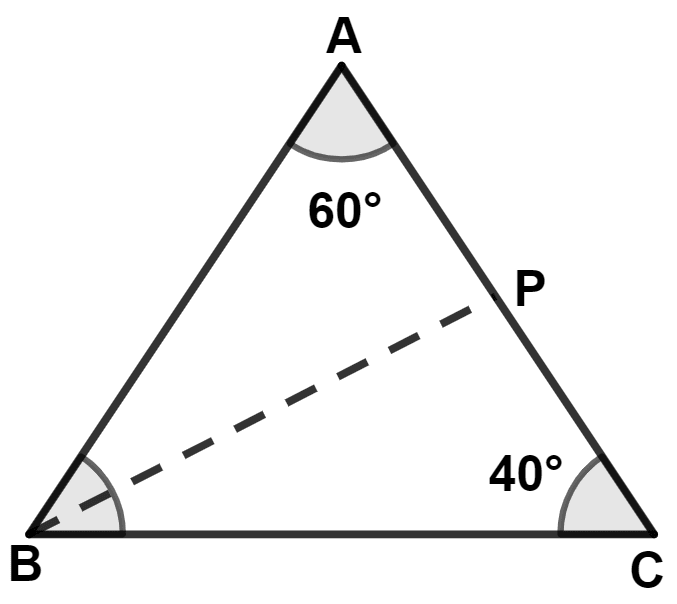
By angle sum property of triangle,

⇒ ∠A + ∠B + ∠C = 180°

⇒ 60° + ∠B + 40° = 180°

⇒ ∠B + 100° = 180°

⇒ ∠B = 180° - 100° = 80°.

Since, BP is bisector of ∠B,

∴ ∠PBC = $\dfrac{∠B}{2} = \dfrac{80°}{2}$ = 40°.

∵ ∠PBC = ∠PCB (Both equal to 40°)

∴ CP = BP (Sides opposite to equal angles are equal)

Hence, proved that BP = CP.

In the given figure, AB ⊥ BE, EF ⊥ BE, AB = EF and BC = DE, then :

1. △ ABD ≅ △ EFC

2. △ ABD ≅ △ FEC

3. △ ABD ≅ △ ECF

4. △ ABD ≅ △ CEF

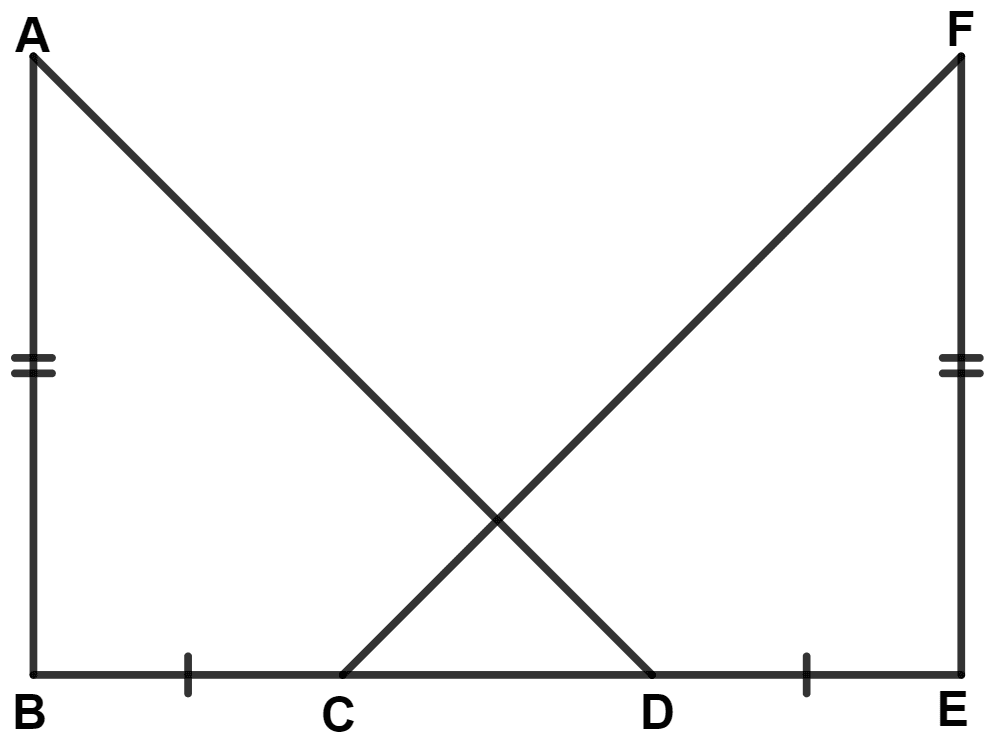
Answer

Since, AB ⊥ BE and EF ⊥ BE,

∴ ∠ABE = 90° and ∠FEB = 90°.

From figure,

⇒ ∠ABD = ∠ABE = 90°

⇒ ∠FEC = ∠FEB = 90°

Given,

⇒ BC = DE

⇒ BC + CD = CD + DE

⇒ BD = CE.

In △ ABD and △ FEC,

⇒ AB = FE (Given)

⇒ BD = CE (Proved above)

⇒ ∠ABD = ∠FEC (Both equal to 90°)

∴ △ ABD ≅ △ FEC (By S.A.S. axiom)

Hence, Option 2 is the correct option.

From the adjoining figure, we find :

1. OP = OR

2. OP = OQ

3. PQ = PR

4. PR ≠ PQ

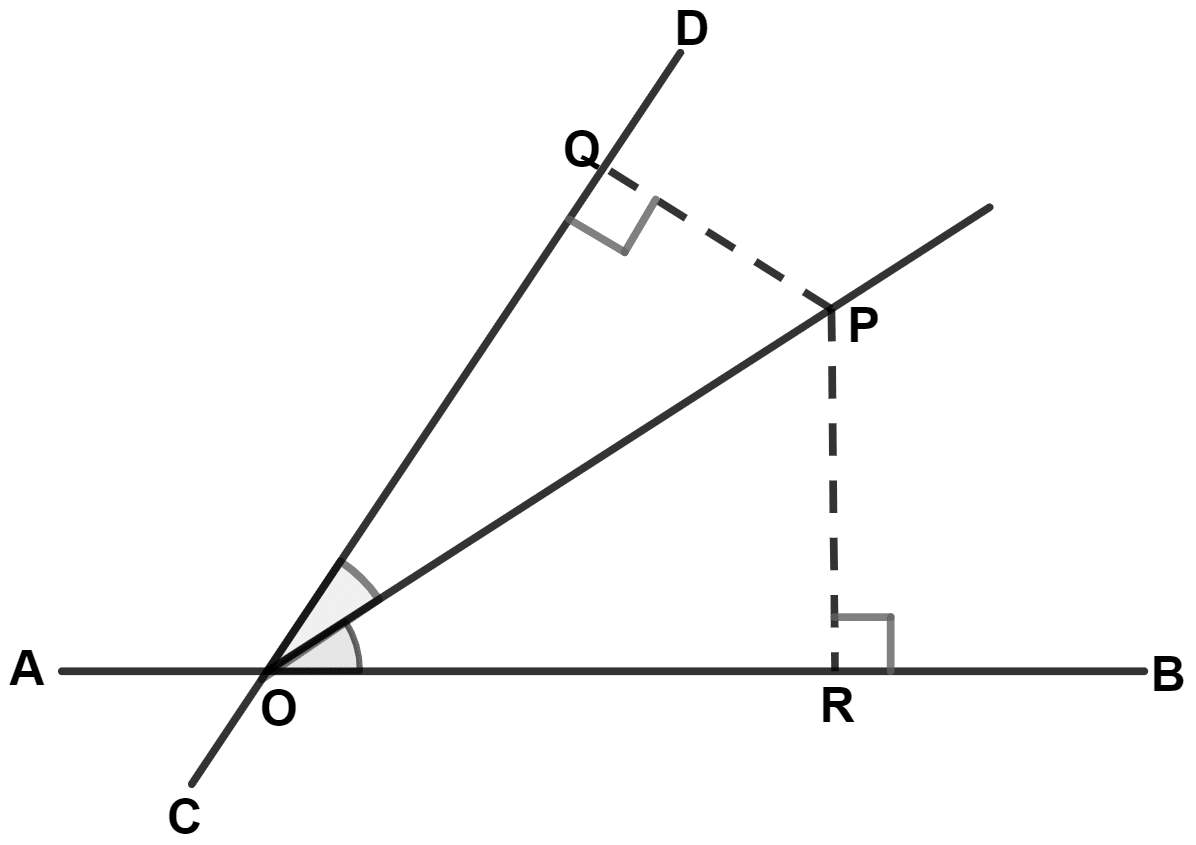
Answer

In △ OPQ and △ OPR,

⇒ OP = OP (Common side)

⇒ ∠POQ = ∠POR (Given)

⇒ ∠OQP = ∠ORP (Both equal to 90°)

∴ △ OPQ ≅ △ OPR (By A.A.S. axiom)

We know that,

Corresponding sides of congruent triangle are equal.

∴ PQ = PR.

Hence, Option 3 is the correct option.

From the given figure, if ∠A = ∠C, we get :

1. x = 8, y = 16

2. x = -8, y = 16

3. x = 16, y = -8

4. x = 16, y = 8

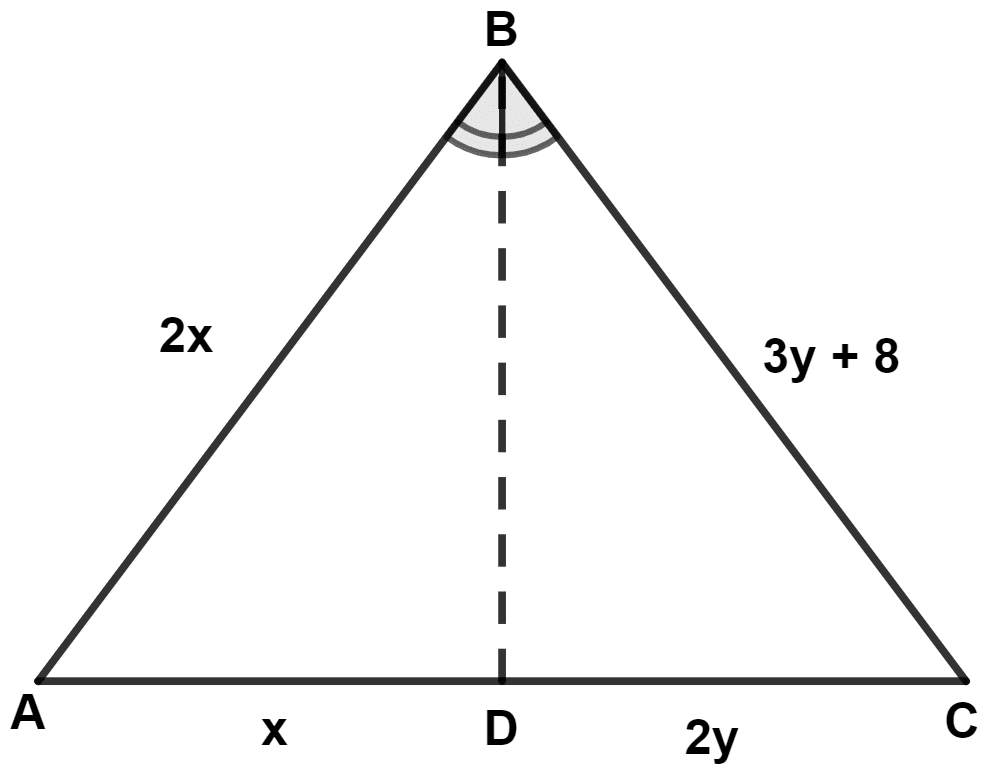
Answer

In △ ABD and △ CBD,

⇒ ∠A = ∠C (Given)

⇒ BD = BD (Common side)

⇒ ∠ABD = ∠CBD (Given)

∴ △ ABD ≅ △ CBD (By A.A.S. axiom)

We know that,

Corresponding sides of congruent triangle are equal.

∴ AB = BC and AD = CD.

Considering AD = CD,

⇒ x = 2y ......(1)

Considering AB = BC,

⇒ 2x = 3y + 8

Substituting value of x from equation (1) in above equation, we get :

⇒ 2(2y) = 3y + 8

⇒ 4y = 3y + 8

⇒ 4y - 3y = 8

⇒ y = 8

⇒ x = 2y = 2(8) = 16.

Hence, Option 4 is the correct option.

ABCD is a rectangle. X and Y are points on sides AD and BC respectively such that AX = BY, then :

1. AY ≠ BX

2. △ ABX ≅ △ BYA

3. △ ABX ≅ △ AYB

4. △ ABX ≅ △ BAY

Answer

Rectangle ABCD is shown in the figure below:

In △ ABX and △ BAY,

⇒ AX = BY (Given)

⇒ AB = AB (Common side)

⇒ ∠XAB = ∠YBA (Both equal to 90°)

∴ △ ABX ≅ △ BAY (By S.A.S. axiom)

Hence, Option 4 is the correct option.

In the given figure, P is mid-point of side AD of rectangle ABCD; then :

1. ∠PBC = ∠PBA

2. ∠PBC = ∠PCB

3. ∠BPA = ∠BPC

4. ∠PBC = ∠BPA

Answer

In △ PCD and △ PBA,

⇒ ∠D = ∠A (Both equal to 90°)

⇒ AP = PD (P is mid-point of AD)

⇒ DC = AB (Opposite sides of rectangle are equal)

∴ △ PCD ≅ △ PBA (By S.A.S. axiom)

We know that,

Corresponding sides of congruent triangle are equal.

∴ ∠PCD = ∠PBA

⇒ 90° - ∠PCD = 90° - ∠PBA

⇒ ∠PCB = ∠PBC.

Hence, Option 2 is the correct option.

In the given figure, AB = AC. Prove that :

(i) DP = DQ

(ii) AP = AQ

(iii) AD bisects angle A

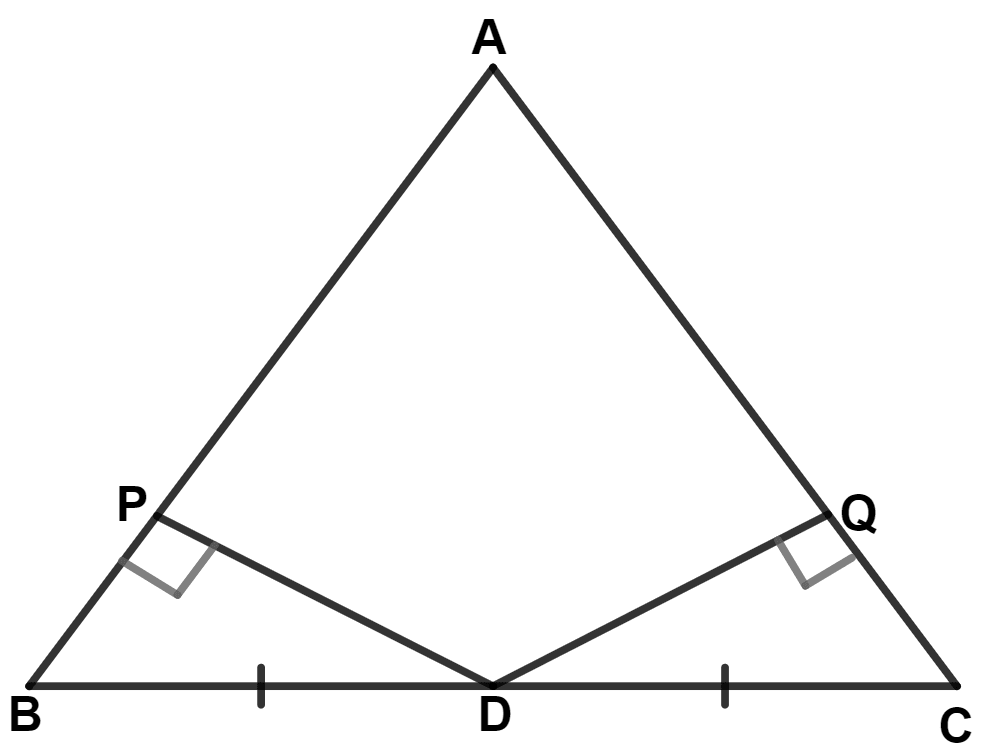
Answer

(i) In △ ABC,

⇒ AB = AC (Given)

∴ ∠B = ∠C (Angles opposite to equal sides are equal)

In △ PDB and △ QDC,

⇒ ∠P = ∠Q (Both equal to 90°)

⇒ ∠B = ∠C (Proved above)

⇒ BD = CD (Given)

∴ △ PDB ≅ △ QDC (By A.A.S. axiom)

We know that,

Corresponding sides of congruent triangle are equal.

∴ DP = DQ

Hence, proved that DP = DQ.

(ii) Since, △ PDB ≅ △ QDC

∴ BP = QC = y (let) [By C.P.C.T.C.]

⇒ AB = AC = x (let)

From figure,

⇒ AP = AB - BP = x - y

⇒ AQ = AC - QC = x - y

∴ AP = AQ.

Hence, proved that AP = AQ.

(iii) Join AD.

In △ ABD and △ ACD,

⇒ AB = AC (Proved above)

⇒ BD = CD (Given)

⇒ AD = AD (Common side)

∴ △ ABD ≅ △ ACD (By S.S.S. axiom)

We know that,

Corresponding sides of congruent triangle are equal.

∴ ∠BAD = ∠CAD.

Hence, proved that AD bisects angle A.

In triangle ABC, AB = AC; BE ⊥ AC and CF ⊥ AB. Prove that :

(i) BE = CF

(ii) AF = AE

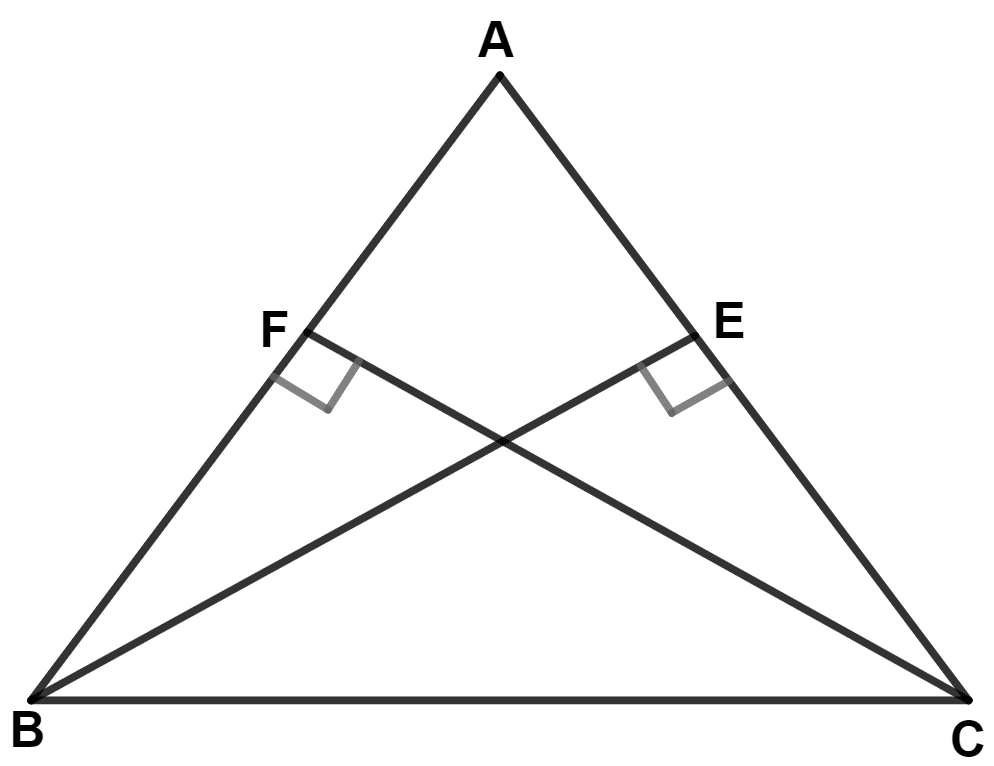
Answer

(i) In △ ABC,

⇒ AB = AC (Given)

∴ ∠B = ∠C (Angles opposite to equal sides are equal)

In △ BCF and △ CBE,

⇒ ∠B = ∠C (Proved above)

⇒ BC = BC (Common side)

⇒ ∠F = ∠E (Both equal to 90°)

∴ △ BCF ≅ △ CBE (By A.A.S. axiom)

We know that,

Corresponding sides of congruent triangle are equal.

∴ BE = CF.

Hence, proved that BE = CF.

(ii) Since, △ BCF ≅ △ CBE

∴ BF = CE = y (let) [By C.P.C.T.C.]

⇒ AB = AC = x (let)

From figure,

⇒ AF = AB - BF = x - y

⇒ AE = AC - AE = x - y

∴ AF = AE.

Hence, proved that AF = AE.

In isosceles triangle ABC, AB = AC. The side BA is produced to D such that BA = AD. Prove that : ∠BCD = 90°.

Answer

In △ ABC,

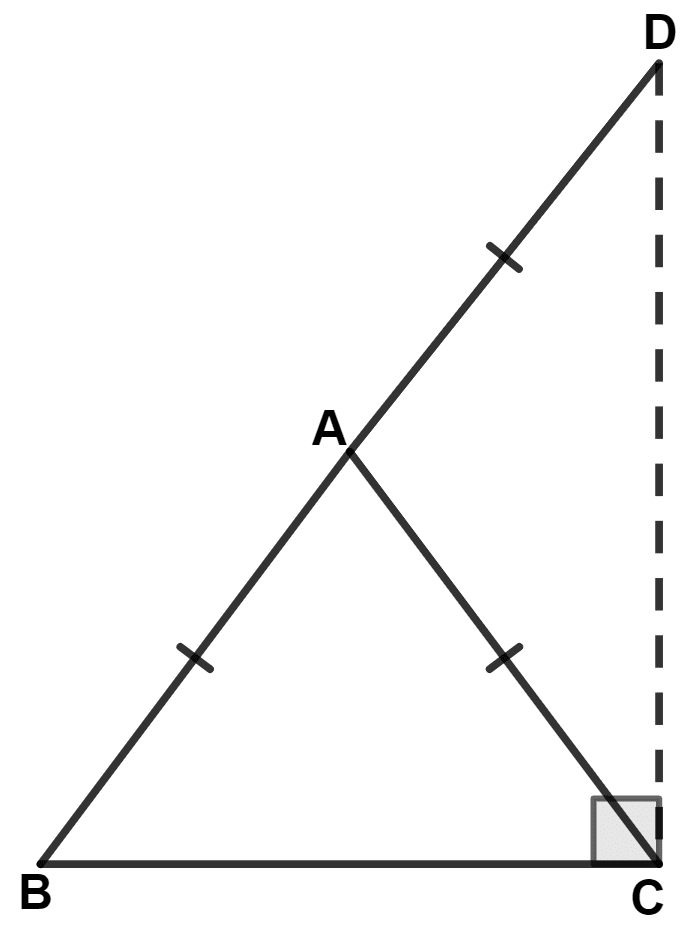
⇒ AB = AC (Given)

⇒ ∠B = ∠C (Angles opposite to equal sides are equal) .........(1)

In △ ACD,

⇒ AC = AD (Given)

⇒ ∠ADC = ∠ACD (Angles opposite to equal sides are equal) .......(2)

Adding equation (1) and (2), we get :

⇒ ∠B + ∠ADC = ∠C + ∠ACD

⇒ ∠B + ∠ADC = ∠BCD ....(3)

In △ BCD,

⇒ ∠B + ∠ADC + ∠BCD = 180° (By angle sum property of triangle)

⇒ ∠BCD + ∠BCD = 180°

⇒ 2∠BCD = 180°

⇒ ∠BCD = $\dfrac{180°}{2}$ = 90°.

Hence, proved that ∠BCD = 90°.

In a triangle ABC, AB = AC and ∠A = 36°. If the internal bisector of ∠C meets AB at point D, prove that AD = BC.

Answer

In △ ABC,

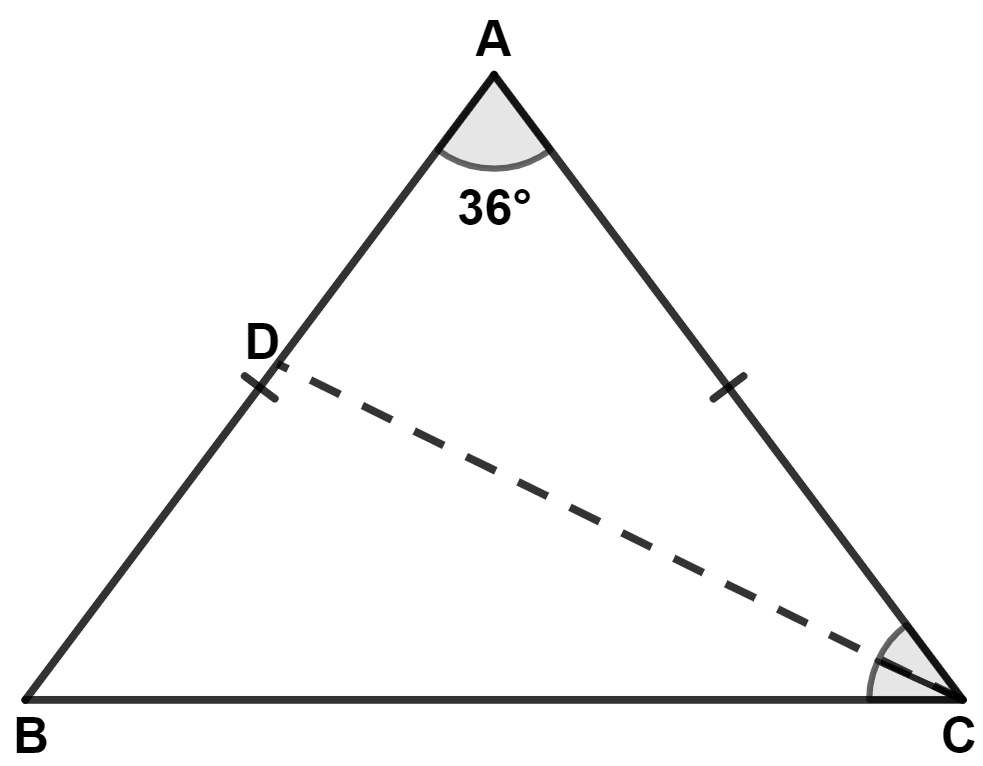
⇒ AB = AC (Given)

∴ ∠B = ∠C = x (let) [Angles opposite to equal sides are equal]

By angle sum property of triangle,

⇒ ∠A + ∠B + ∠C = 180°

⇒ 36° + x + x = 180°

⇒ 36° + 2x = 180°

⇒ 2x = 180° - 36°

⇒ 2x = 144°

⇒ x = $\dfrac{144°}{2}$ = 72°.

Since, CD is bisector of angle C,

∴ ∠ACD = ∠BCD = $\dfrac{72°}{2}$ = 36°.

In △ ACD,

⇒ ∠ACD = ∠DAC (Both equal to 36°)

∴ AD = DC [Sides opposite to equal angles are equal] ........(1)

In △ DCB,

By angle sum property of triangle,

⇒ ∠CDB + ∠DCB + ∠DBC = 180°

⇒ ∠CDB + 36° + 72° = 180°

⇒ ∠CDB + 108° = 180°

⇒ ∠CDB = 180° - 108° = 72°.

∴ ∠CDB = ∠DBC (Both equal to 72°)

∴ BC = CD (Sides opposite to equal angles are equal) ...........(2)

From equation (1) and (2), we get :

⇒ AD = BC.

Hence, proved that AD = BC.

If the bisector of an angle of a triangle bisects the opposite side, prove that the triangle is isosceles.

Answer

Let AD bisect BC and also the angle A.

In △ ABD and △ ACD,

⇒ BD = CD (Since, AD bisects BC)

⇒ AD = AD (Common side)

⇒ ∠BAD = ∠CAD (Since, AD bisects angle A)

∴ △ ABD ≅ △ ACD (By S.A.S. axiom)

We know that,

Corresponding sides of congruent triangle are equal.

∴ AB = AC

∴ ABC is an isosceles triangle.

Hence, proved that if the bisector of an angle of a triangle bisects the opposite side, the triangle is isosceles.

Prove that the bisectors of the base angles of an isosceles triangle are equal.

Answer

In isosceles triangle △ ABC,

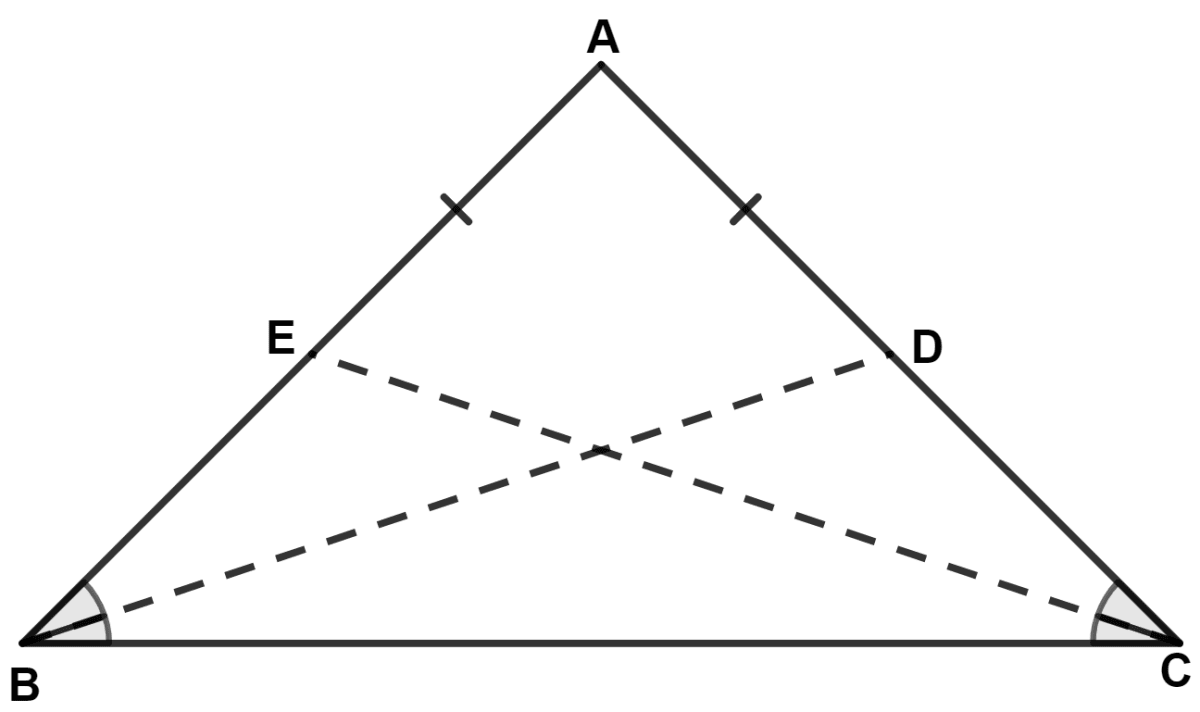
Let AB = AC,

∴ ∠C = ∠B = x (let) [Angles opposite to equal sides are equal]

From figure,

BD and CE are bisectors of angle B and C.

∴ ∠CBD = $\dfrac{∠B}{2} = \dfrac{x}{2}$ and ∠BCE = $\dfrac{∠C}{2} = \dfrac{x}{2}$.

∴ ∠CBD = ∠BCE.

In △ CBD and △ BCE,

⇒ ∠CBD = ∠BCE (Proved above)

⇒ ∠C = ∠B (Proved above)

⇒ BC = BC (Common side)

∴ △CBD ≅ △BCE (By A.S.A. axiom)

We know that,

Corresponding sides of congruent triangle are equal.

∴ BD = CE.

Hence, proved that the bisectors of the base angles of an isosceles triangle are equal.

In the given figure, AB = AC and ∠DBC = ∠ECB = 90°.

Prove that :

(i) BD = CE

(ii) AD = AE

Answer

(i) In △ ABC,

⇒ AB = AC (Given)

⇒ ∠ABC = ∠ACB (Angles opposite to equal sides are equal) .......(1)

From figure,

⇒ ∠DBC = ∠ECB (Both equal to 90°) .......(2)

Subtracting equation (1) from (2), we get :

⇒ ∠DBC - ∠ABC = ∠ECB - ∠ACB

⇒ ∠DBA = ∠ECA .........(3)

In △ DBA and △ ECA,

⇒ ∠DBA = ∠ECA (Proved above)

⇒ AB = AC (Given)

⇒ ∠DAB = ∠EAC (Vertically opposite angles are equal)

∴ △ DBA ≅ △ ∠ECA (By A.S.A. axiom)

We know that,

Corresponding sides of congruent triangle are equal.

∴ BD = CE.

Hence, proved that BD = CE.

(ii) Since,

△ DBA ≅ △ ∠ECA

∴ AD = AE (By C.P.C.T.C.)

Hence, proved that AD = AE.

In triangle ABC; AB = AC. P, Q and R are mid-points of sides AB, AC and BC respectively. Prove that :

(i) PR = QR

(ii) BQ = CP

Answer

(i) In triangle ABC,

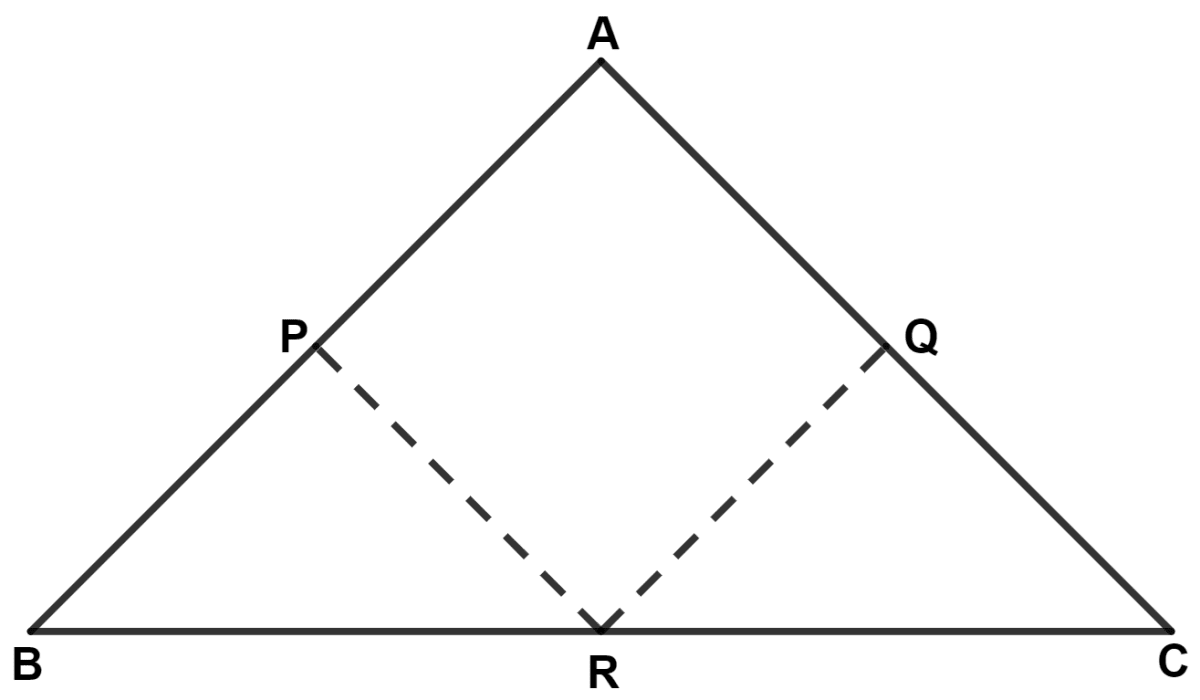
⇒ AB = AC (Given)

⇒ $\dfrac{AB}{2} = \dfrac{AC}{2}$

⇒ AP = AQ [Since P and Q are mid-points of AB and AC] ........(1)

By mid-point theorem,

The line segment in a triangle joining the midpoint of any two sides of the triangle is said to be parallel to its third side and is also half of the length of the third side.

Since, P and R are mid-points of sides AB and BC respectively.

∴ PR = $\dfrac{AC}{2}$

∴ PR = AQ .........(2)

From figure,

Q and R are mid-points of AC and BC respectively.

⇒ QR = $\dfrac{AB}{2}$ [By mid-point theorem]

⇒ QR = AP ........(3)

From equations (1), (2) and (3), we get :

⇒ PR = QR.

Hence, proved that PR = QR.

(ii) From figure,

In triangle ABC,

⇒ AB = AC

⇒ ∠B = ∠C (Angles opposite to equal sides are equal)

⇒ $\dfrac{1}{2}AB = \dfrac{1}{2}AC$ (As AB = AC)

⇒ BP = CQ.

In △ BPC and △ CQB,

⇒ BP = CQ (Proved above)

⇒ ∠B = ∠C (Proved above)

⇒ BC = BC (Common side)

∴ Δ BPC ≅ Δ CQB (By S.A.S. axiom)

We know that,

Corresponding parts of congruent triangle are equal.

⇒ BQ = CP.

Hence, proved that BQ = CP.

From the following figure, prove that :

(i) ∠ACD = ∠CBE

(ii) AD = CE

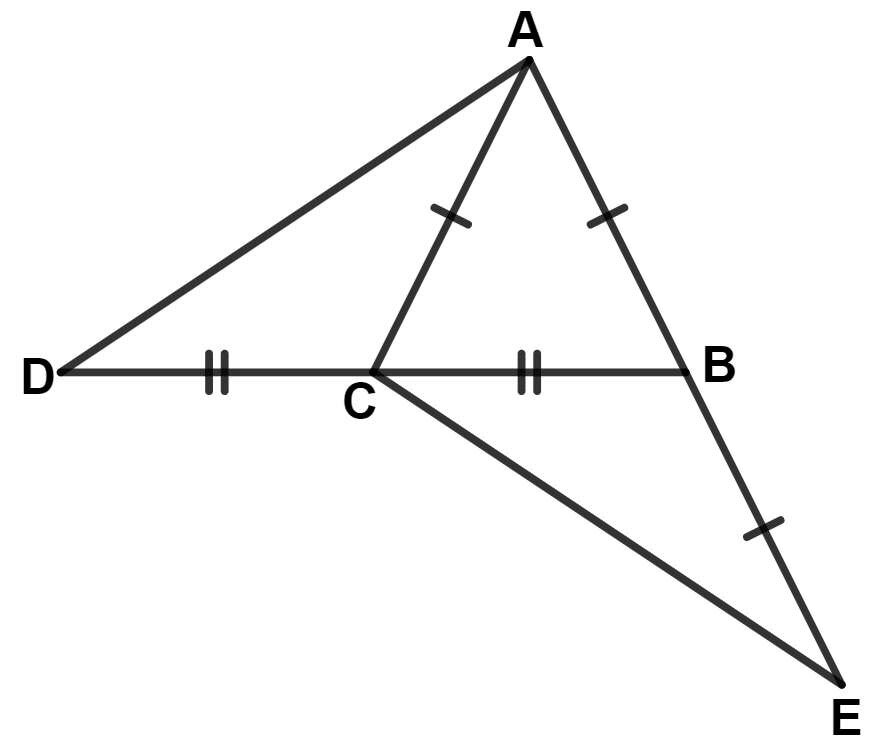
Answer

(i) In Δ ACB,

⇒ AC = AB (Given)

∴ ∠ABC = ∠ACB (Angles opposite to equal sides are equal) ........(1)

Since, DCB is a straight line.

∴ ∠ACD + ∠ACB = 180° ......(2)

Since, ABE is a straight line.

∴ ∠ABC + ∠CBE = 180° ......(3)

Equating equations (2) and (3), we get :

⇒ ∠ACD + ∠ACB = ∠ABC + ∠CBE

⇒ ∠ACD + ∠ACB = ∠ACB + ∠CBE [From equation (1)]

⇒ ∠ACD = ∠CBE.

Hence, proved that ∠ACD = ∠CBE.

(ii) In △ ACD and △ CBE,

⇒ DC = CB (Given)

⇒ AC = BE (Given)

⇒ ∠ACD = ∠CBE (Proved above)

∴ Δ ACD ≅ Δ CBE (By S.A.S. axiom)

We know that,

Corresponding parts of congruent triangles are equal.

⇒ AD = CE.

Hence, proved that AD = CE.

ABC is a triangle. The bisector of the angle BCA meets AB in X. A point Y lies on CX such that AX = AY.

Prove that : ∠CAY = ∠ABC.

Answer

In △ ABC,

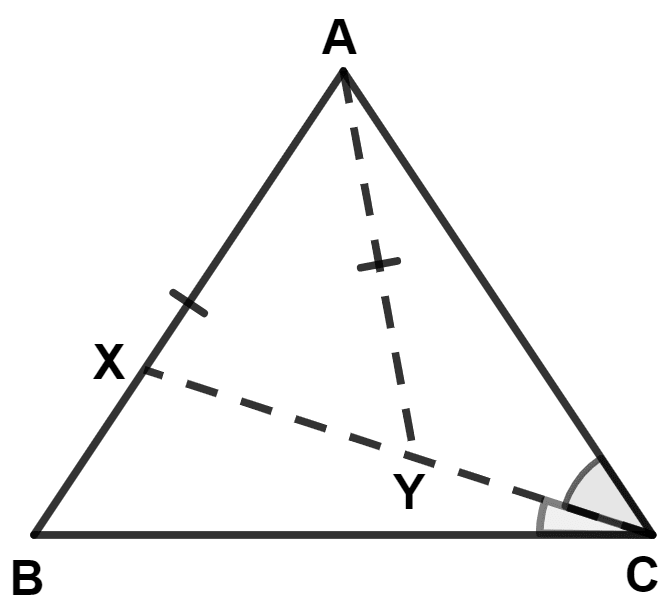
CX is the angle bisector of ∠C.

⇒ ∠ACX = ∠BCX

⇒ ∠ACY = ∠BCX ........(1)

In △ AXY,

⇒ AX = AY (Given)

⇒ ∠AXY = ∠AYX (Angles opposite to equal sides are equal) ...........(2)

From figure,

⇒ ∠XYC = ∠AXB = 180° (Since, XYC and AXB is a straight line)

⇒ ∠AYX + ∠AYC = ∠AXY + ∠BXY

⇒ ∠AXY + ∠AYC = ∠AXY + ∠BXY [From equation (2)]

⇒ ∠AYC = ∠AXY - ∠AXY + ∠BXY

⇒ ∠AYC = ∠BXY ..........(3)

By angle sum property of triangle AYC and BXC,

⇒ ∠AYC + ∠ACY + ∠CAY = ∠BXC + ∠BCX + ∠XBC

⇒ ∠BXY + ∠BCX + ∠CAY = ∠BXC + ∠BCX + ∠XBC [From equations (1) and (3)]

⇒ ∠BXC + ∠BCX + ∠CAY = ∠BXC + ∠BCX + ∠XBC [∵ From fig. ∠BXY = ∠BXC and ∠XBC = ∠ABC]

⇒ ∠CAY = ∠ABC.

Hence, proved that ∠CAY = ∠ABC.

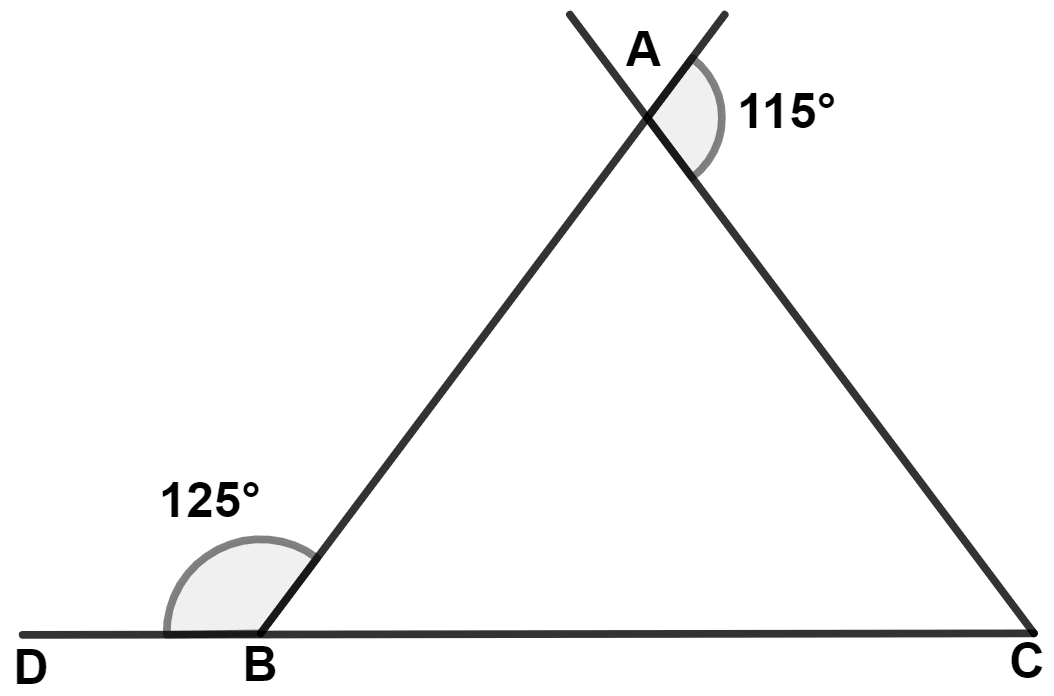
In the adjoining figure, we find :

1. AB = AC

2. BC > AB

3. AB > BC

4. AC = BC

Answer

From figure,

DBC is a straight line.

∴ ∠ABD + ∠ABC = 180°

⇒ 125° + ∠ABC = 180°

⇒ ∠ABC = 180° - 125° = 55°.

We know that,

Exterior angle is equal to the sum of two opposite interior angle.

∴ Ext. ∠A = ∠ABC + ∠ACB

⇒ 115° = 55° + ∠ACB

⇒ ∠ACB = 115° - 55° = 60°.

In △ ABC,

By angle sum property of triangle,

⇒ ∠ABC + ∠ACB + ∠BAC = 180°

⇒ 55° + 60° + ∠BAC = 180°

⇒ 115° + ∠BAC = 180°

⇒ ∠BAC = 180° - 115° = 65°.

Since, ∠BAC > ∠ACB,

∴ BC > AB (If two angles of a triangle are unequal, the greater angle has the greater side opposite to it.)

Hence, Option 2 is the correct option.

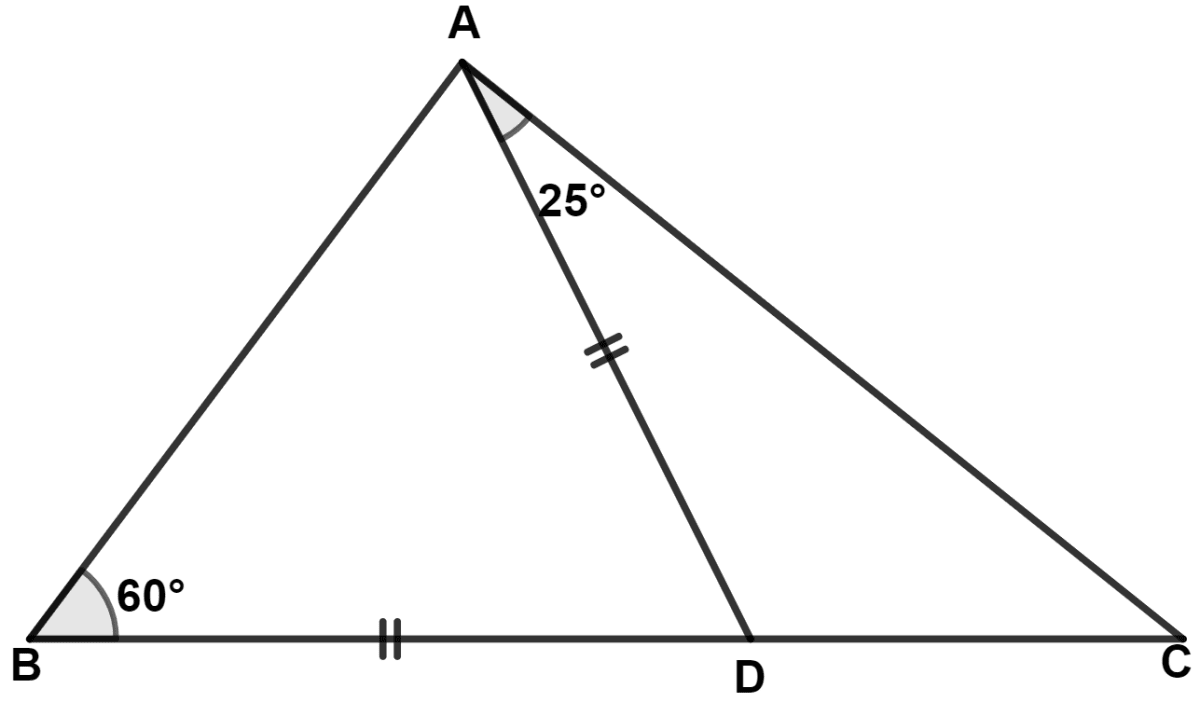
In the adjoining figure, we find :

1. BD = DC

2. BD < DC

3. BD > DC

4. AD = CD

Answer

In △ ABD,

⇒ AD = BD (Given)

⇒ ∠A = ∠B = 60° (Angles opposite to equal sides are equal)

By angle sum property of triangle,

⇒ ∠A + ∠B + ∠D = 180°

⇒ 60° + 60° + ∠D = 180°

⇒ 120° + ∠D = 180°

⇒ ∠D = 180° - 120° = 60°.

Since, each angle of triangle equals 60°.

∴ ABD is an equilateral triangle, AB = BD = DA.

From figure,

BDC is a straight line.

∴ ∠ADB + ∠ADC = 180°

⇒ 60° + ∠ADC = 180°

⇒ ∠ADC = 180° - 60° = 120°.

In △ ADC,

By angle sum property of triangle,

⇒ ∠DAC + ∠ADC + ∠DCA = 180°

⇒ 25° + 120° + ∠DCA = 180°

⇒ 145° + ∠DCA = 180°

⇒ ∠DCA = 180° - 145° = 35°.

Since, ∠DCA > ∠DAC

∴ AD > DC

Since, AD = BD,

∴ BD > DC. (If two angles of a triangle are unequal, the greater angle has the greater side opposite to it.)

Hence, Option 3 is the correct option.

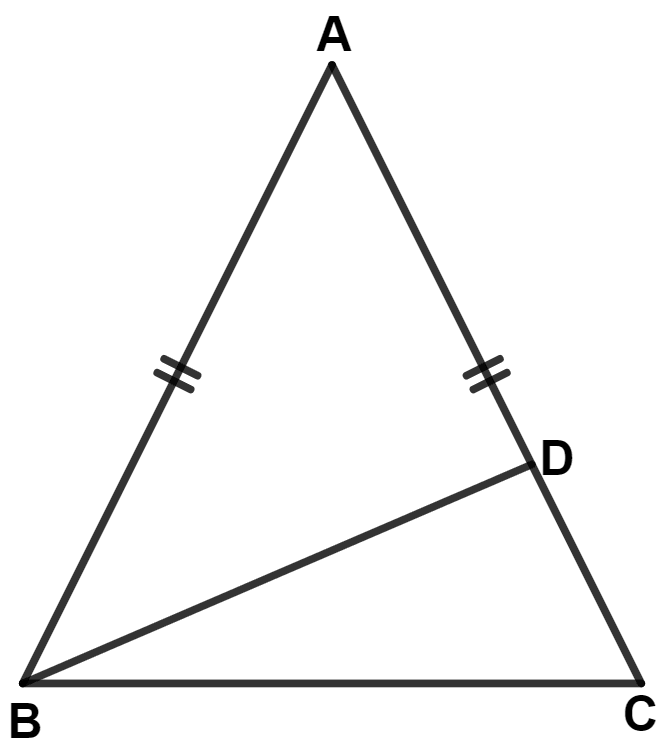
In the given figure, AB = AC, then :

1. BD = BC

2. BD = CD

3. BD < CD

4. BD > CD

Answer

In △ ABC,

⇒ AB = AC (Given)

⇒ ∠C = ∠B (Angles opposite to equal sides are equal)

In △ ABD,

⇒ AD = AC - CD

⇒ AD < AB

⇒ ∠ABD < ∠ADB (If two sides of a triangle are unequal, the greater side has the greater angle opposite to it.)

In △ BDC,

⇒ ∠DBC = ∠B - ∠ABD = ∠C - ∠ABD

∴ ∠DBC < ∠C

⇒ CD < BD

⇒ BD > CD.

Hence, Option 4 is the correct option.

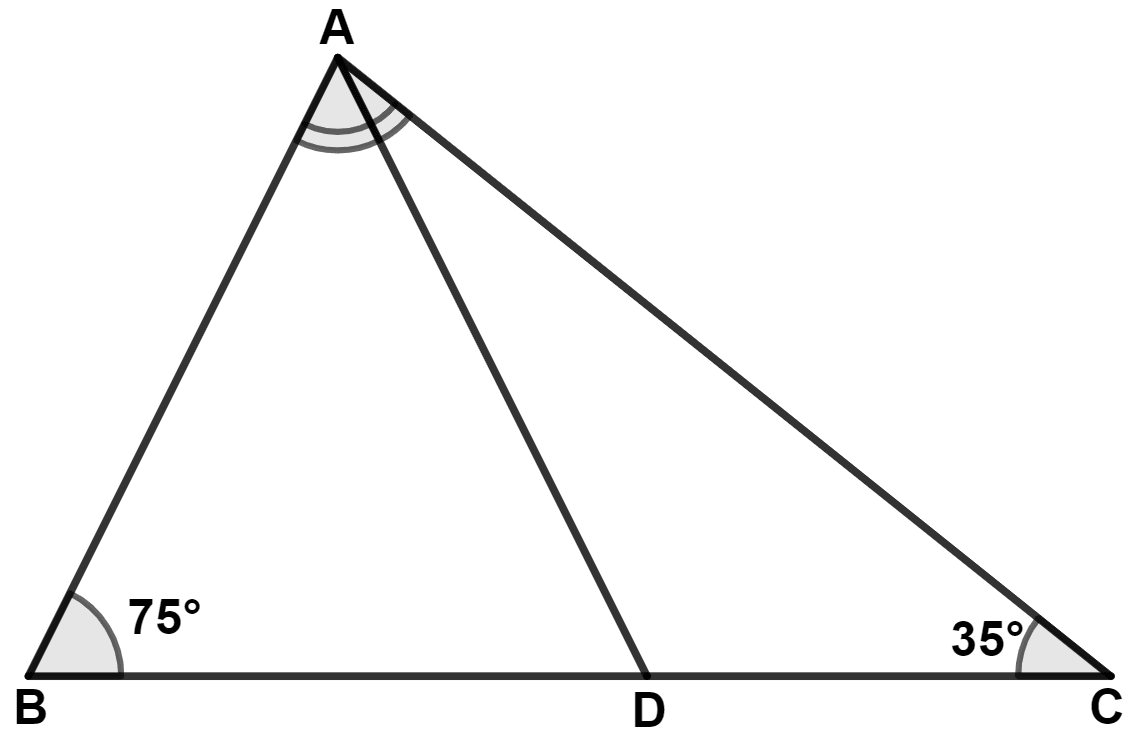
In the given figure, we find :

1. BD > AB

2. BD < AB

3. BD = AB

4. DC < AB

Answer

In △ ABC,

By angle sum property of triangle,

⇒ ∠A + ∠B + ∠C = 180°

⇒ ∠A + 75° + 35° = 180°

⇒ ∠A + 110° = 180°

⇒ ∠A = 180° - 110° = 70°.

From figure,

AD bisects angle A.

∴ ∠BAD = ∠DAC = $\dfrac{∠A}{2} = \dfrac{70°}{2}$ = 35°.

In △ ABD,

By angle sum property of triangle,

⇒ ∠ABD + ∠BAD + ∠ADB = 180°

⇒ 75° + 35° + ∠ADB = 180°

⇒ ∠ADB + 110° = 180°

⇒ ∠ADB = 180° - 110° = 70°.

Since, ∠BAD < ∠ADB

∴ BD < AB (If two angles of a triangle are unequal, the greater angle has the greater side opposite to it.)

Hence, Option 2 is the correct option.

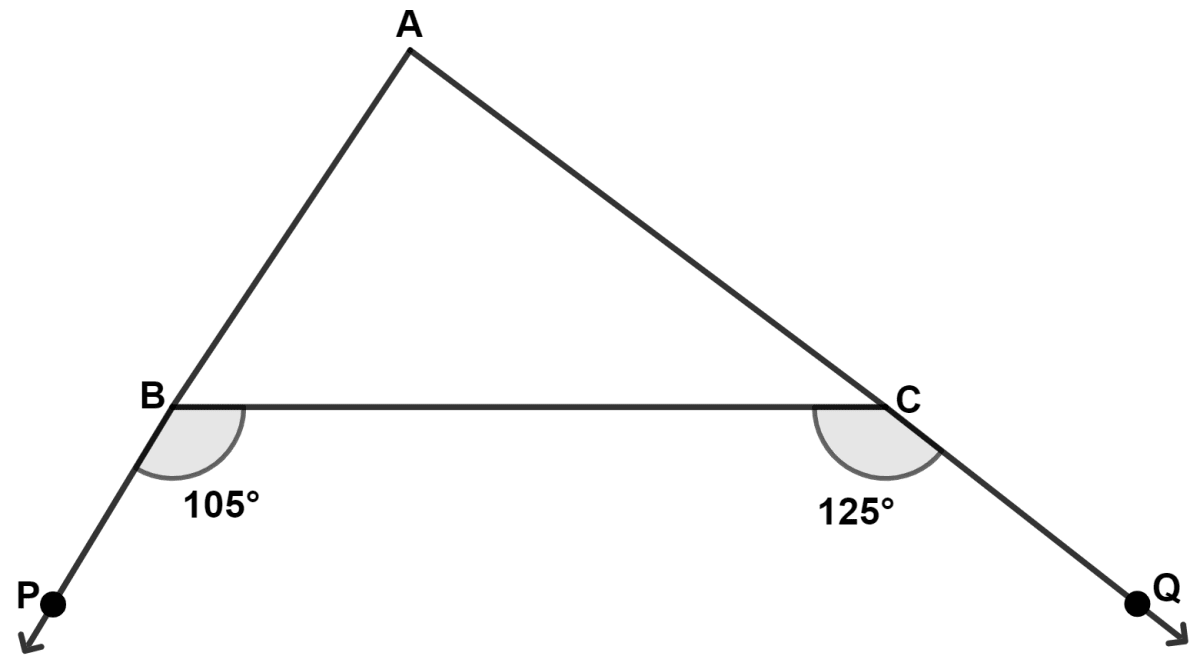
In the given figure, we find :

1. AB > AC

2. AC > AB

3. AB < BC

4. AC = AB

Answer

From figure,

ABP is a straight line.

∴ ∠PBC + ∠ABC = 180°

⇒ 105° + ∠ABC = 180°

⇒ ∠ABC = 180° - 105° = 75°.

ACQ is a straight line.

∴ ∠ACB + ∠BCQ = 180°

⇒ 125° + ∠ACB = 180°

⇒ ∠ACB = 180° - 125° = 55°.

Since, ∠ABC > ∠ACB

∴ AC > AB (If two angles of a triangle are unequal, the greater angle has the greater side opposite to it.)

Hence, Option 2 is the correct option.

In a quadrilateral ABCD,

1. AB + BC + CD + DA > AC + BD

2. AB + BC + CD + DA < AC + BD

3. AB + BC + CD + DA = AC + BD

4. AB + BC < AC

Answer

We know that,

The sum of lengths of two sides of a triangle is always greater than the third side.

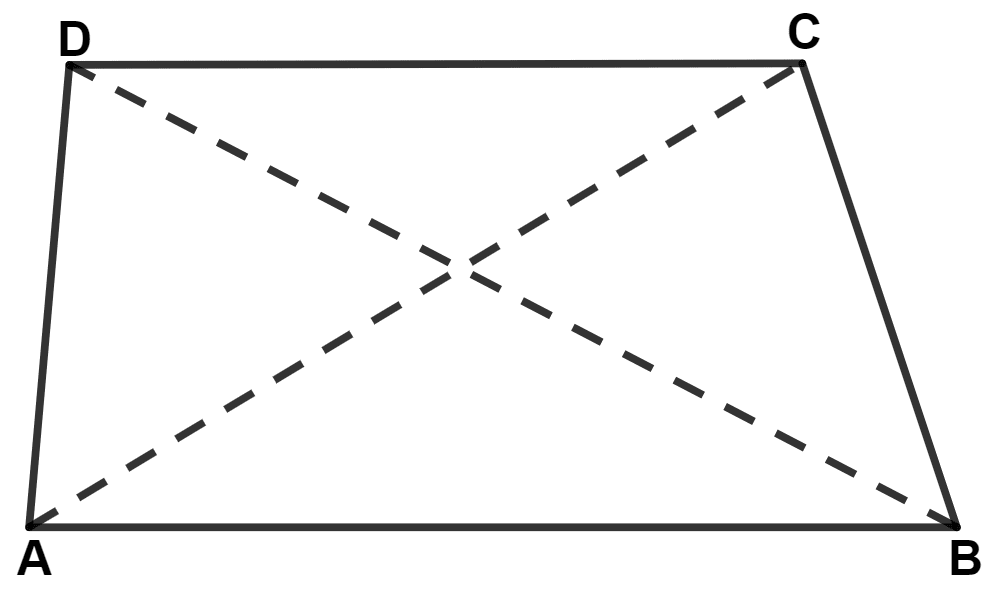
In △ ABC,

⇒ AB + BC > AC ........(1)

In △ ADC,

⇒ AD + CD > AC ........(2)

In △ ADB,

⇒ AD + AB > BD ........(3)

In △ DCB,

⇒ DC + CB > BD ........(4)

Adding equations (1), (2), (3) and (4) we get,

⇒ AB + BC + AD + CD + AD + AB + DC + CB > AC + AC + BD + BD

⇒ AB + AB + BC + BC + CD + CD + AD + AD > 2AC + 2BD

⇒ 2(AB + BC + CD + AD) > 2(AC + BD)

⇒ AB + BC + CD + AD > AC + BD.

Hence, Option 1 is the correct option.

From the following figure, prove that : AB > CD.

Answer

In △ ABC,

⇒ AB = AC (Given)

⇒ ∠C = ∠B = 70°

By angle sum property of triangle,

⇒ ∠BAC + ∠B + ∠C = 180°

⇒ ∠BAC + 70° + 70° = 180°

⇒ ∠BAC + 140° = 180°

⇒ ∠BAC = 180° - 140° = 40°.

In △ ABD,

By angle sum property of triangle,

⇒ ∠BAD + ∠B + ∠D = 180°

⇒ ∠BAD + 70° + 40° = 180°

⇒ ∠BAD + 110° = 180°

⇒ ∠BAD = 180° - 110° = 70°.

From figure,

⇒ ∠CAD = ∠BAD - ∠BAC = 70° - 40° = 30°.

In △ ACD,

Since, ∠CDA > ∠CAD

∴ AC > CD (If two angles of a triangle are unequal, the greater angle has the greater side opposite to it.)

Since, AB = AC

∴ AB > CD.

Hence, proved that AB > CD.

In a triangle PQR; QR = PR and ∠P = 36°. Which is the largest side of the triangle ?

Answer

In △ PQR,

⇒ PR = QR (Given)

⇒ ∠Q = ∠P = 36°

By angle sum property of triangle,

⇒ ∠Q + ∠P + ∠R = 180°

⇒ 36° + 36° + ∠R = 180°

⇒ 72° + ∠R = 180°

⇒ ∠R = 180° - 72° = 108°.

Since, ∠R is greatest angle.

∴ PQ is the largest side. (In a triangle, side opposite to greatest angle is largest.)

Hence, PQ is the largest side.

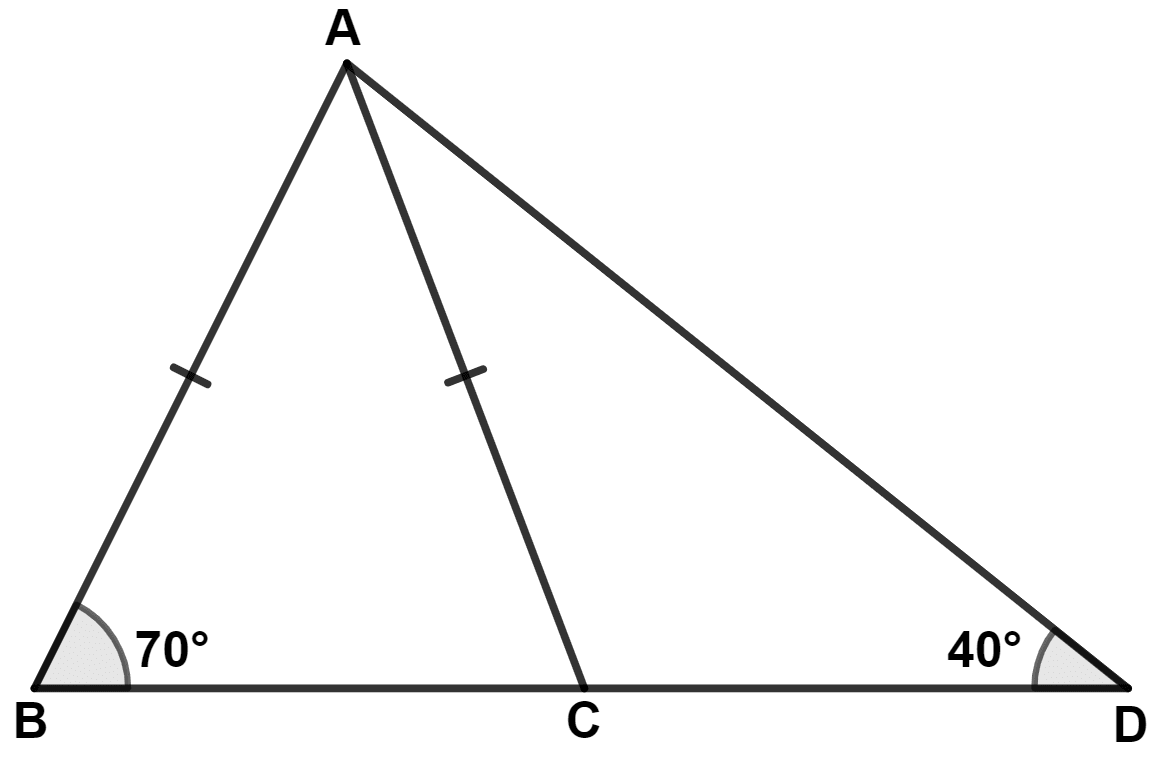
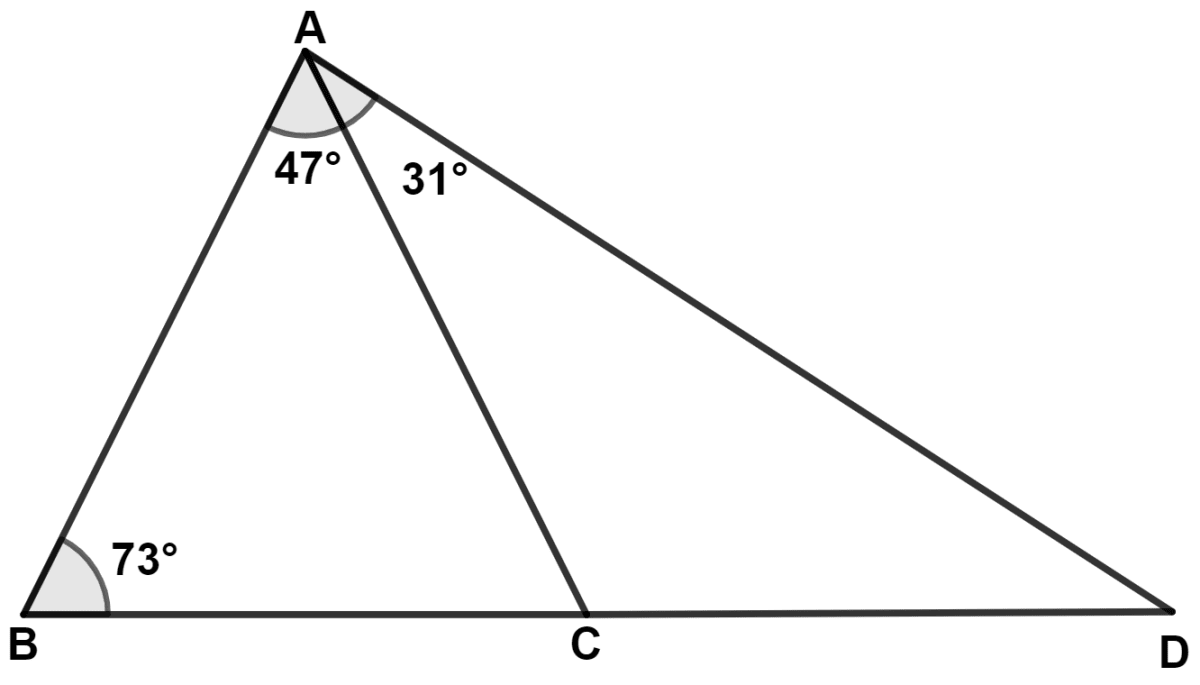
In each of the following figures, write BC, AC and CD in ascending order of their lengths.

Answer

(i) In △ ABC,

⇒ AC = AB (Given)

⇒ ∠B = ∠C = 67°.

By angle sum property of triangle,

⇒ ∠BAC + ∠B + ∠C = 180°

⇒ ∠BAC + 67° + 67° = 180°

⇒ ∠BAC + 134° = 180°

⇒ ∠BAC = 180° - 134° = 46°.

In △ ABD,

By angle sum property of triangle,

⇒ ∠BAD + ∠B + ∠D = 180°

⇒ ∠BAD + 67° + 33° = 180°

⇒ ∠BAD + 100° = 180°

⇒ ∠BAD = 180° - 100° = 80°.

From figure,

⇒ ∠CAD = ∠BAD - ∠BAC = 80° - 46° = 34°.

We know that,

If two angles of a triangle are unequal, the greater angle has the greater side opposite to it.

In △ ABC,

Since, ∠BAC < ∠ABC

⇒ BC < AC ........(1)

In △ ACD,

Since, ∠CDA < ∠CAD

⇒ AC < CD ........(2)

From equation (1) and (2), we get :

⇒ BC < AC < CD.

Hence, BC < AC < CD.

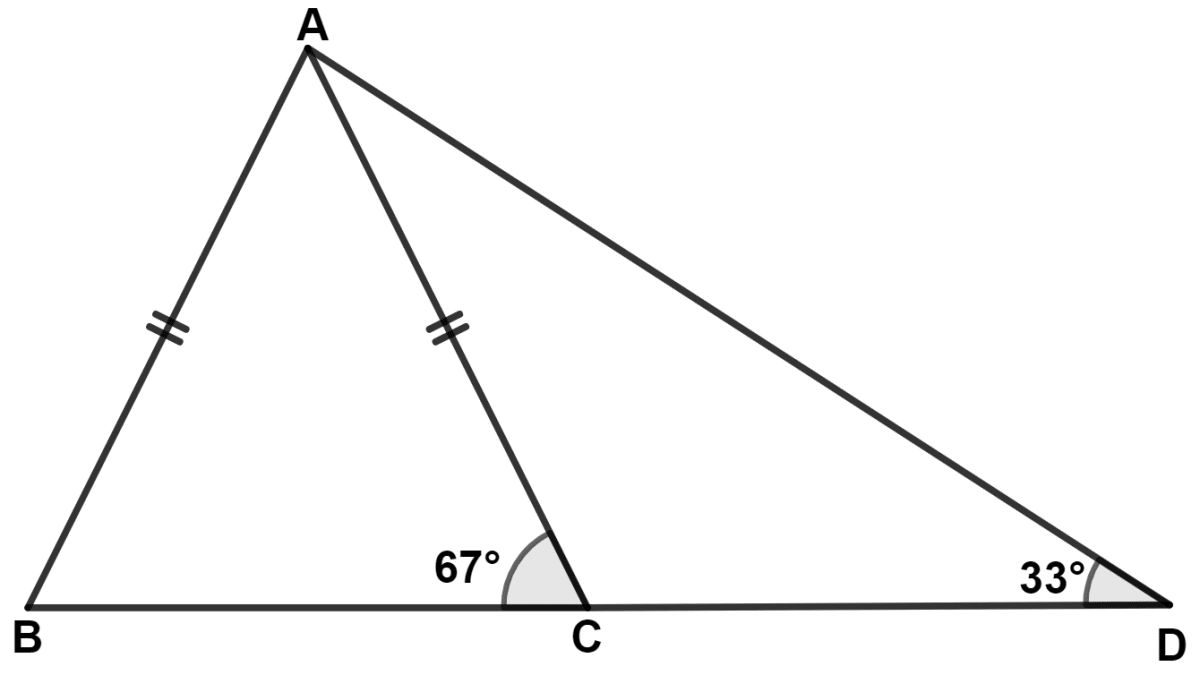
(ii) In △ ABC,

⇒ ∠BAC < ∠ABC

⇒ BC < AC [If two angles of a triangle are unequal, the greater angle has the greater side opposite to it.] .......(1)

By angle sum property of triangle,

⇒ ∠ACB + ∠BAC + ∠ABC = 180°

⇒ ∠ACB + 47° + 73° = 180°

⇒ ∠ACB + 120° = 180°

⇒ ∠ACB = 180° - 120° = 60°.

From figure,

As, BCD is a straight line.

⇒ ∠ACB + ∠ACD = 180°

⇒ 60° + ∠ACD = 180°

⇒ ∠ACD = 180° - 60° = 120°.

In △ ACD,

By angle sum property of triangle,

⇒ ∠ADC + ∠ACD + ∠CAD = 180°

⇒ ∠ADC + 120° + 31° = 180°

⇒ ∠ADC + 151° = 180°

⇒ ∠ADC = 180° - 151° = 29°.

Since, ∠ADC < ∠CAD, we get :

AC < CD [If two angles of a triangle are unequal, the greater angle has the greater side opposite to it.] .......(2)

From equations (1) and (2), we get :

⇒ BC < AC < CD.

Hence, BC < AC < CD.

Arrange the sides of △ BOC in descending order of their lengths. BO and CO are bisectors of angles ABC and ACB respectively.

Answer

From figure,

DAC is a straight line.

∴ ∠DAB + ∠BAC = 180°

⇒ 137° + ∠BAC = 180°

⇒ ∠BAC = 180° - 137° = 43°.

EBC is a straight line.

∴ ∠EBA + ∠ABC = 180°

⇒ 106° + ∠ABC = 180°

⇒ ∠ABC = 180° - 106° = 74°.

In △ ABC,

By angle sum property of triangle,

⇒ ∠ABC + ∠BAC + ∠ACB = 180°

⇒ 74° + 43° + ∠ACB = 180°

⇒ 117° + ∠ACB = 180°

⇒ ∠ACB = 180° - 117° = 63°.

Since, OB is the bisector of angle ABC.

∴ ∠OBC = $\dfrac{∠ABC}{2} = \dfrac{74°}{2}$ = 37°.

Since, OC is the bisector of angle ACB.

∴ ∠OCB = $\dfrac{∠ACB}{2} = \dfrac{63°}{2}$ = 31.5°.

In △ OBC,

By angle sum property of triangle,

⇒ ∠OBC + ∠OCB + ∠BOC = 180°

⇒ 37° + 31.5° + ∠BOC = 180°

⇒ 68.5° + ∠BOC = 180°

⇒ ∠BOC = 180° - 68.5° = 111.5°

∴ ∠BOC > ∠OBC > ∠OCB

∴ BC > CO > BO (If two angles of a triangle are unequal, the greater angle has the greater side opposite to it.)

Hence, sides of triangle BOC in descending order are BC > CO > BO.

D is a point in side BC of triangle ABC. If AD > AC, show that AB > AC.

Answer

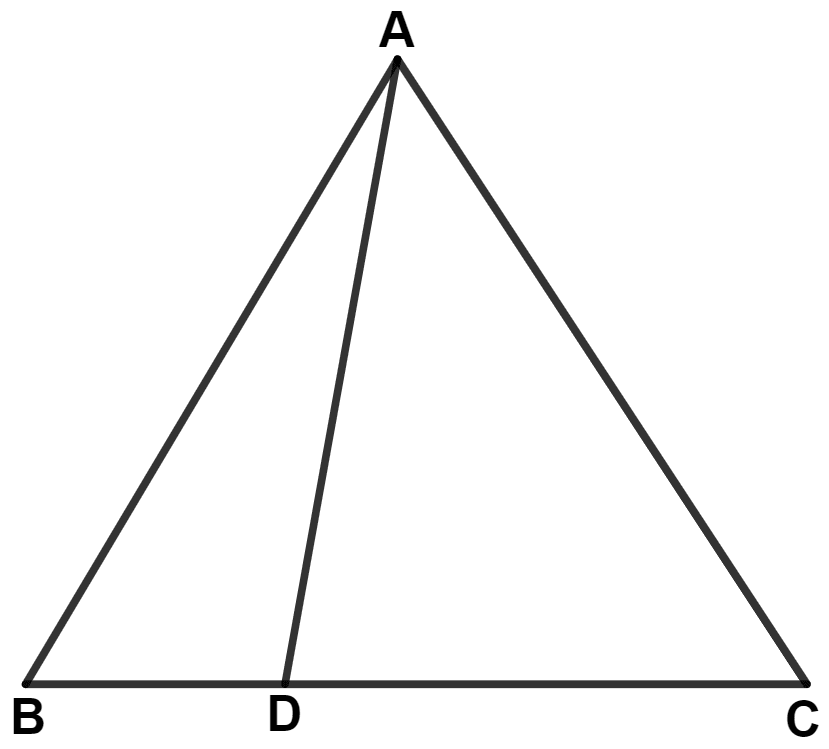
In △ ADC,

⇒ AD > AC (Given)

∴ ∠ACD > ∠ADC (If two sides of a triangle are unequal, the greater side has the greater angle opposite to it.) .......(1)

In △ ABD,

⇒ ∠ADC = ∠ABD + ∠BAD (An exterior angle is equal to sum of two opposite interior angles) .........(2)

Substituting value of ∠ADC from equation (2) in (1), we get :

⇒ ∠ACD > ∠ABD + ∠BAD ......(3)

∴ ∠ACD > ∠ABD .....(4)

From figure,

⇒ ∠ACD = ∠ACB and ∠ABD = ∠ABC

Substituting above values in equation (4), we get :

⇒ ∠ACB > ∠ABC

Thus, in △ ABC,

⇒ AB > AC (If two angles of a triangle are unequal, the greater angle has the greater side opposite to it.)

Hence, proved that AB > AC.

In the following figure, ∠BAC = 60° and ∠ABC = 65°. Prove that :

(i) CF > AF

(ii) DC > DF

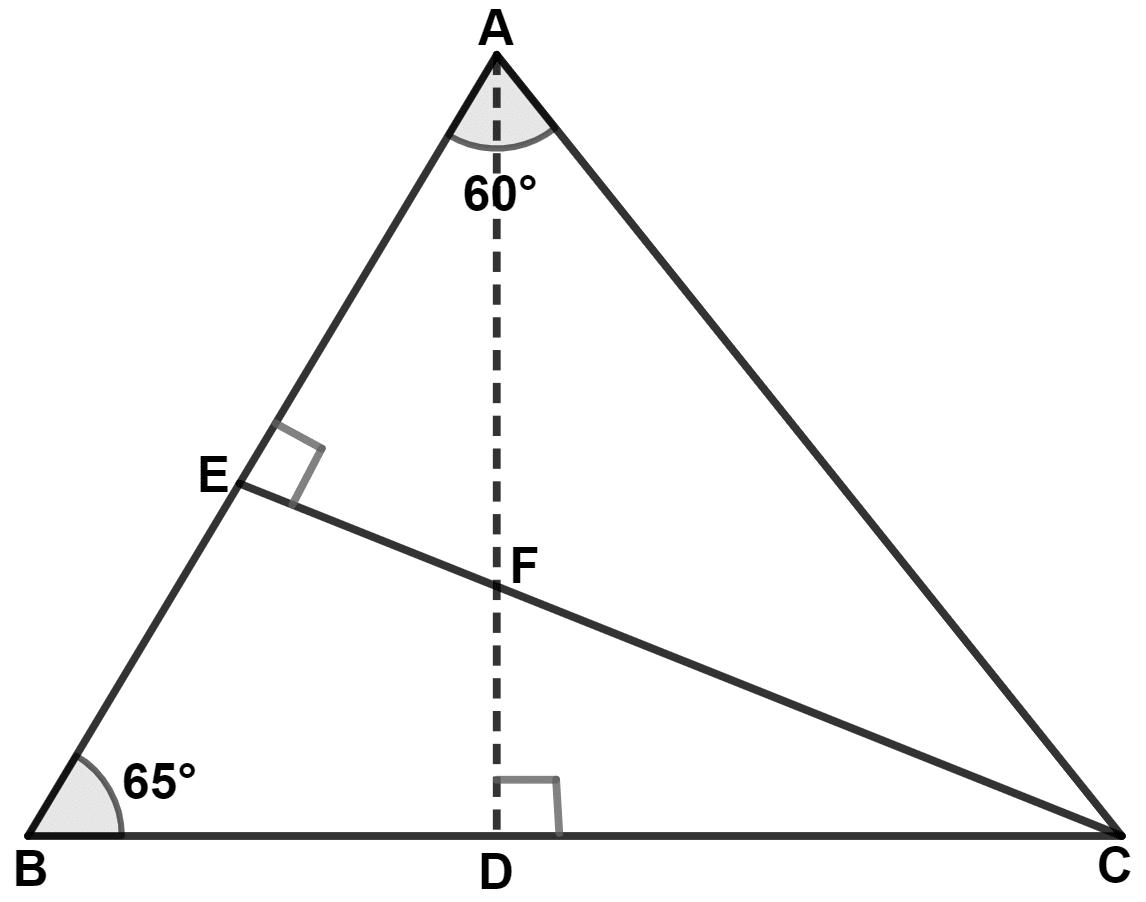
Answer

(i) In △ BEC,

⇒ ∠CBE + ∠BEC + ∠BCE = 180°

⇒ 65° + 90° + ∠BCE = 180°

⇒ ∠BCE = 180° - 90° - 65° = 25°.

From figure,

⇒ ∠DCF = ∠BCE = 25° .......(1)

In △ CDF,

⇒ ∠DCF + ∠FDC + ∠CFD = 180°

⇒ 25° + 90° + ∠CFD = 180°

⇒ ∠CFD = 180° - 90° - 25° = 65° .........(2)

From figure,

AFD is a straight line,

⇒ ∠AFC + ∠CFD = 180°

⇒ ∠AFC + 65° = 180°

⇒ ∠AFC = 180° - 65° = 115° ........(3)

In △ ACE,

By angle sum property of triangle,

⇒ ∠ACE + ∠CEA + ∠EAC = 180°

⇒ ∠ACE + ∠CEA + ∠BAC = 180° (From figure, ∠EAC = ∠BAC)

⇒ ∠ACE + 90° + 60° = 180°

⇒ ∠ACE + 150° = 180°

⇒ ∠ACE = 180° - 150° = 30° ........(4)

In △ AFC,

By angle sum property of triangle,

⇒ ∠AFC + ∠ACF + ∠FAC = 180°

⇒ 115° + ∠ACE + ∠FAC = 180° (From figure, ∠ACF = ∠ACE)

⇒ 115° + 30° + ∠FAC = 180°

⇒ ∠FAC + 145° = 180°

⇒ ∠FAC = 180° - 145° = 35° ........(5)

In △ AFC,

⇒ ∠FAC > ∠ACF

∴ CF > AF (If two angles of a triangle are unequal, the greater angle has the greater side opposite to it.)

Hence, proved that CF > AF.

(ii) In △ CDF,

⇒ ∠DCF = 25° ........[From equation (1)]

⇒ ∠CFD = 65° ........[From equation (2)]

⇒ ∠CFD > ∠DCF

∴ DC > DF (If two angles of a triangle are unequal, the greater angle has the greater side opposite to it.)

Hence, proved that DC > DF.

In the following figure;

AC = CD; ∠BAD = 110° and ∠ACB = 74°.

Prove that : BC > CD.

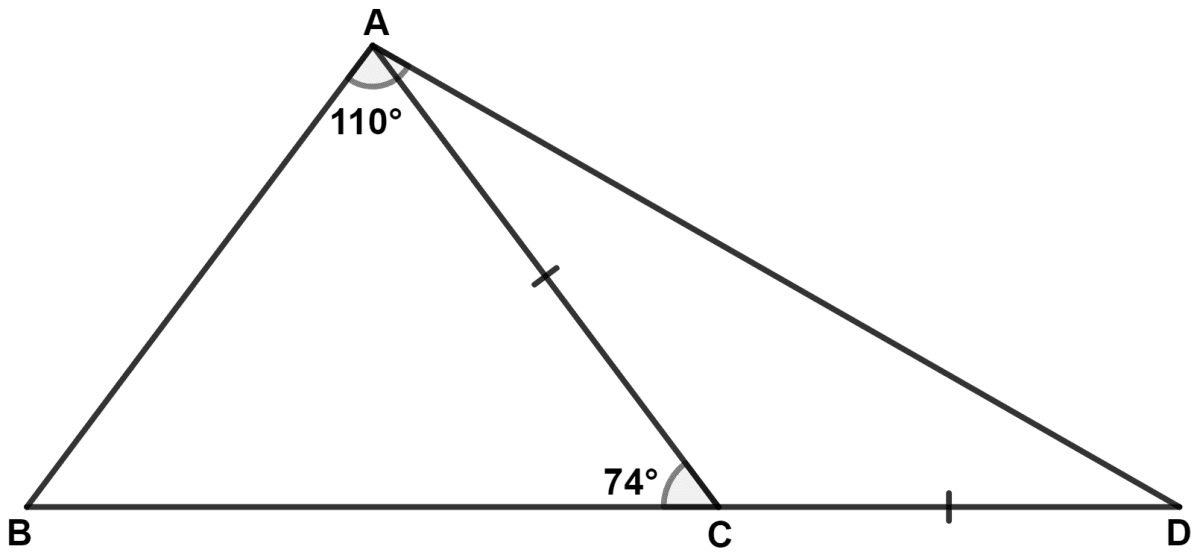
Answer

Since, BCD is a straight line.

∴ ∠BCA + ∠ACD = 180°

⇒ 74° + ∠ACD = 180°

⇒ ∠ACD = 180° - 74° = 106°.

In △ ACD,

AC = CD (Given)

∴ ∠CAD = ∠CDA = x (let) [Angles opposite to equal sides are equal]

By angle sum property of triangle,

⇒ ∠ACD + ∠CAD + ∠CDA = 180°

⇒ 106° + x + x = 180°

⇒ 106° + 2x = 180°

⇒ 2x = 180° - 106°

⇒ 2x = 74°

⇒ x = $\dfrac{74°}{2}$ = 37°.

From figure,

⇒ ∠BAC = ∠BAD - ∠CAD = 110° - 37° = 73°.

In △ ABC,

By angle sum property of triangle,

⇒ ∠BAC + ∠ABC + ∠ACB = 180°

⇒ 73° + ∠ABC + 74° = 180°

⇒ ∠ABC + 147° = 180°

⇒ ∠ABC = 180° - 147°

⇒ ∠ABC = 33°.

∴ ∠ACB > ∠BAC > ∠ABC

∴ AB > BC > AC [If two angles of a triangle are unequal, the greater angle has the greater side opposite to it.] .......(1)

Given,

AC = CD ......(2)

From equations (1) and (2), we get :

BC > CD.

Hence, proved that BC > CD.

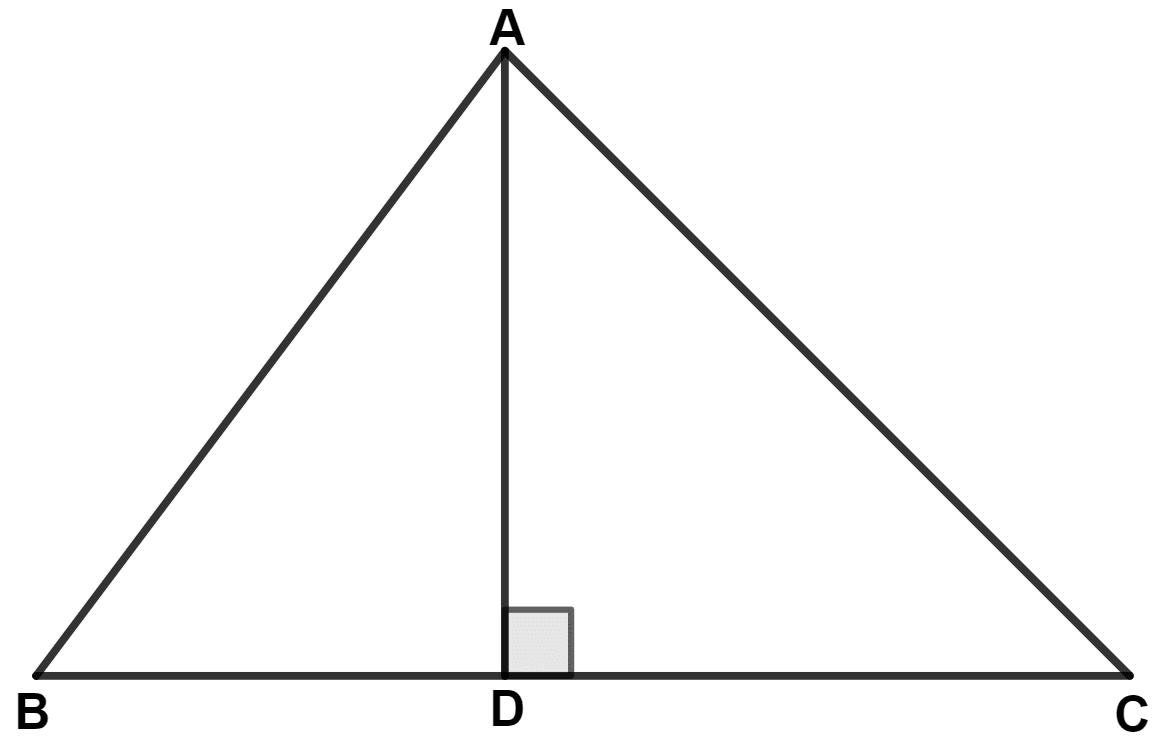
From the following figure; prove that :

(i) AB > BD

(ii) AC > CD

(iii) AB + AC > BC

Answer

(i) Since, BDC is a straight line.

∴ ∠ADB + ∠ADC = 180°

⇒ ∠ADB + 90° = 180°

⇒ ∠ADB = 180° - 90° = 90°.

In △ ABD,

∠BAD and ∠ABD will be definitely less than 90° as sum of angles of triangle equals to 180°.

∴ ∠ADB > ∠BAD

∴ AB > BD [If two angles of a triangle are unequal, the greater angle has the greater side opposite to it.] ...........(1)

Hence, proved that AB > BD.

(ii) From figure,

⇒ ∠ADC = 90°.

In △ ADC,

∠DAC and ∠DCA will be definitely less than 90° as sum of angles of triangle equals to 180°.

∴ ∠ADC > ∠DAC

∴ AC > CD [If two angles of a triangle are unequal, the greater angle has the greater side opposite to it.] ...........(2)

Hence, proved that AC > CD.

(iii) Adding equations (1) and (2), we get :

⇒ AB + AC > BD + CD

⇒ AB + AC > BC.

Hence, proved that AB + AC > BC.

In a quadrilateral ABCD; prove that :

(i) AB + BC + CD > DA

(ii) AB + BC + CD + DA > 2AC

(iii) AB + BC + CD + DA > 2BD

Answer

Let ABCD be the quadrilateral. Join AC and BD.

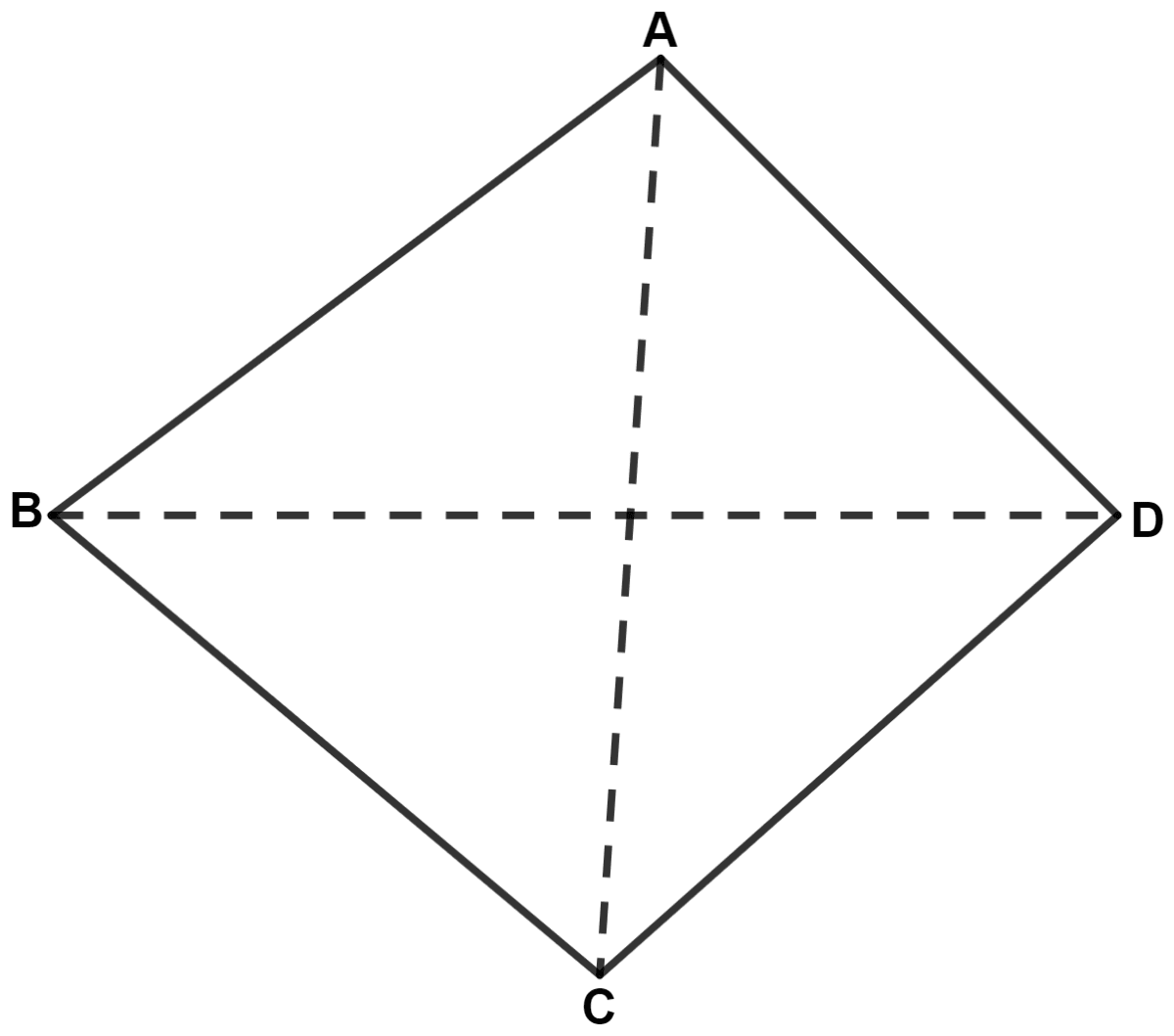
(i) In △ ABC,

⇒ AB + BC > AC (Sum of two sides in a triangle is greater tha the third triangle) ........(1)

In △ ACD,

⇒ AC + CD > DA (Sum of two sides in a triangle is greater tha the third triangle) ............(2)

Adding equations (1) and (2), we get :

⇒ AB + BC + AC + CD > AC + DA

⇒ AB + BC + CD > AC + DA - AC

⇒ AB + BC + CD > DA ........(3)

Hence, proved that AB + BC + CD > DA.

(ii) In △ ACD,

⇒ CD + DA > AC (Sum of two sides in a triangle is greater tha the third triangle) ............(4)

Adding equations (1) and (4), we get :

⇒ AB + BC + CD + DA > AC + AC

⇒ AB + BC + CD + DA > 2AC.

Hence, proved that AB + BC + CD + DA > 2AC.

(iii) In △ ABD,

⇒ AB + DA > BD (Sum of two sides in a triangle is greater tha the third triangle) .........(5)

In △ BCD,

⇒ BC + CD > BD (Sum of two sides in a triangle is greater tha the third triangle) .........(6)

Adding equations (5) and (6), we get :

⇒ AB + DA + BC + CD > BD + BD

⇒ AB + BC + CD + DA > 2BD.

Hence, proved that AB + BC + CD + DA > 2BD.

In the following figure, ABC is an equilateral triangle and P is any point in AC; prove that :

(i) BP > PA

(ii) BP > PC

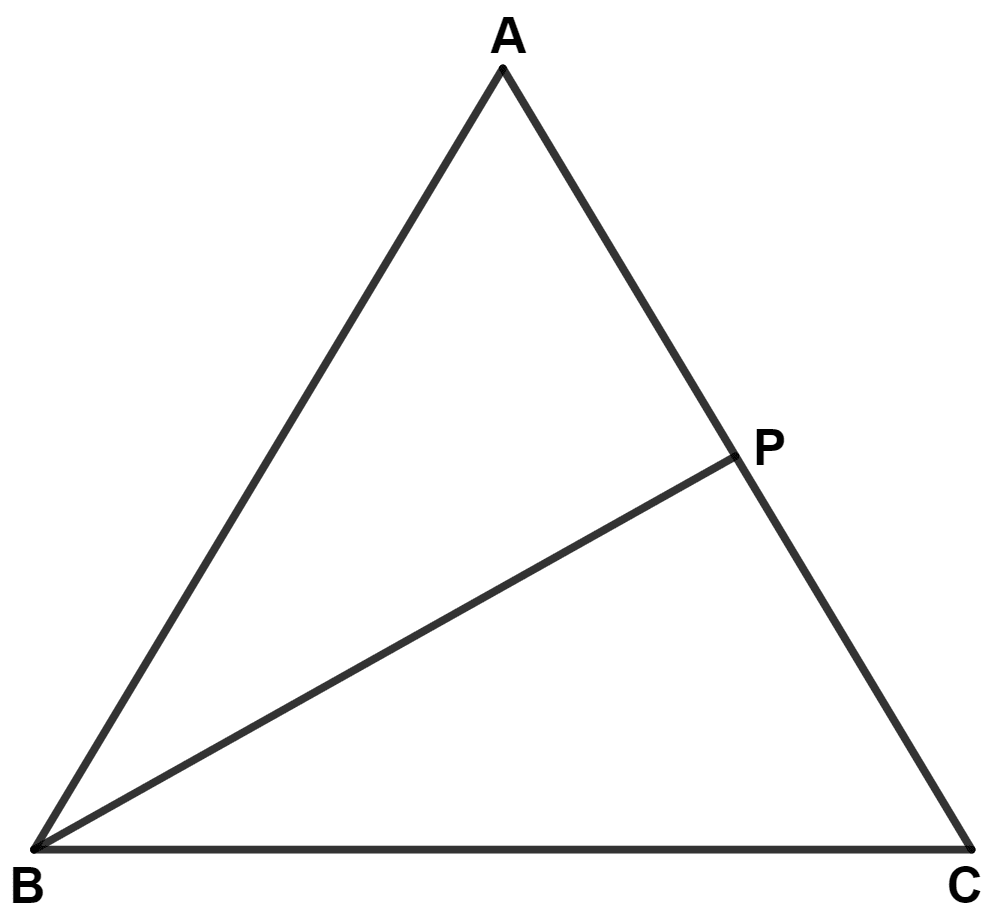
Answer

(i) Since, ABC is an equilateral triangle.

∴ ∠A = ∠B = ∠C = 60°.

In △ ABP,

∠ABP = ∠B - ∠PBC

∴ ∠ABP < ∠B

∴ ∠ABP < ∠A (Since, ∠B = ∠A)

∴ PA < BP or BP > PA [If two angles of a triangle are unequal, the greater angle has the greater side opposite to it.]

Hence, proved that BP > PA.

(ii) In △ BPC,

∠PBC = ∠B - ∠ABP

∴ ∠PBC < ∠B

∴ ∠PBC < ∠C (Since, ∠B = ∠C)

∴ PC < BP or BP > PC [If two angles of a triangle are unequal, the greater angle has the greater side opposite to it.]

Hence, proved that BP > PC.

In the following diagram; AD = AB and AE bisects angle A. Prove that :

(i) BE = DE

(ii) ∠ABD > ∠C

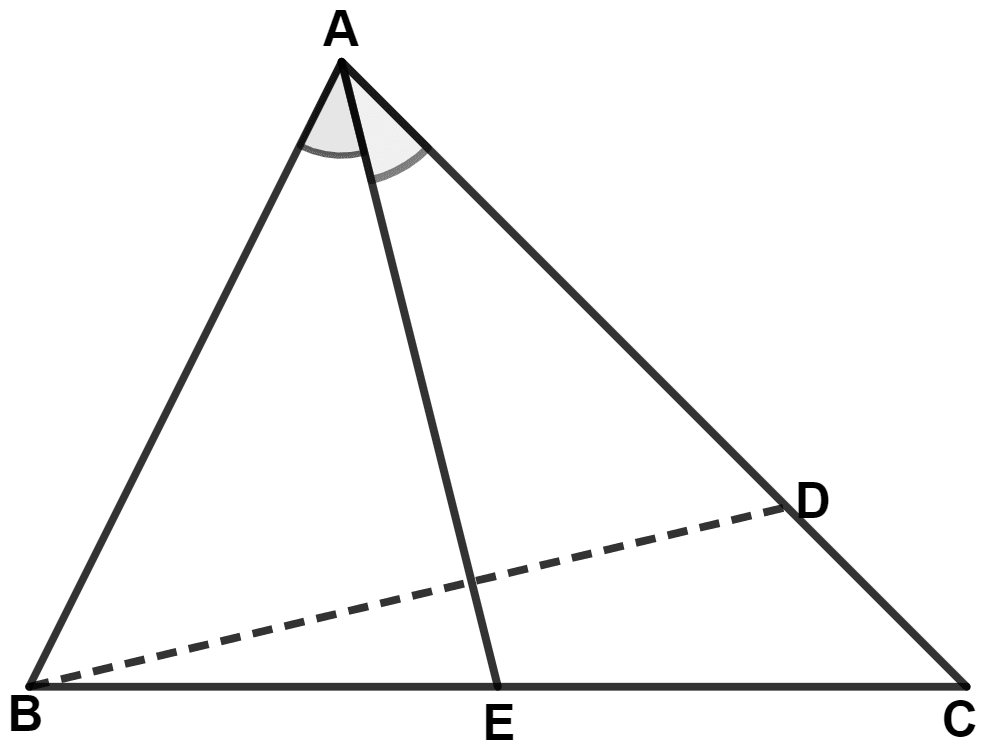
Answer

Join ED.

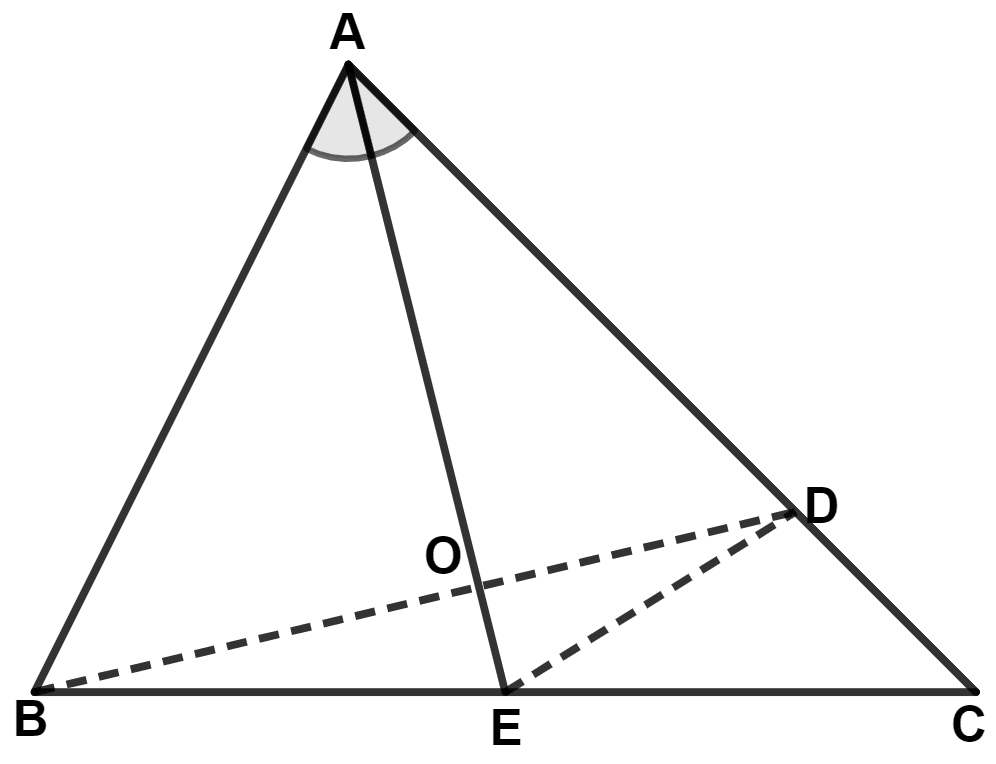
In △ AOB and △ AOD,

⇒ AB = AD (Given)

⇒ AO = AO (Common)

⇒ ∠BAO = ∠DAO (AO is the bisector of angle A)

∴ △ AOB ≅ △ AOD (By S.A.S. axiom)

We know that,

Corresponding parts of congruent triangle are equal.

⇒ BO = OD ..........(1) [By C.P.C.T.C.]

⇒ ∠AOB = ∠AOD .........(2) [By C.P.C.T.C.]

⇒ ∠ABO = ∠ADO [By C.P.C.T.C.]

⇒ ∠ABD = ∠ADB ..........(3)

From figure,

⇒ ∠AOB = ∠DOE and ∠AOD = ∠BOE (Vertically opposite angles are equal)

Substituting values of ∠AOB and ∠AOD from above equation in equation (2), we get :

⇒ ∠DOE = ∠BOE .............(4)

(i) In △ BOE and △ DOE,

⇒ BO = OD [From equation (1)]

⇒ OE = OE [Common side]

⇒ ∠BOE = ∠DOE [From equation (4)]

∴ △ BOE ≅ △ DOE (By S.A.S. axiom)

We know that,

Corresponding parts of congruent triangle are equal.

⇒ BE = DE.

Hence, proved that BE = DE.

(ii) In triangle BCD,

⇒ ∠ADB = ∠C + ∠CBD (An exterior angle is equal to sum of two opposite interior angles)

⇒ ∠ADB > ∠C

⇒ ∠ABD > ∠C (Since, ∠ABD = ∠ADB)

Hence, proved that ∠ABD > ∠C.

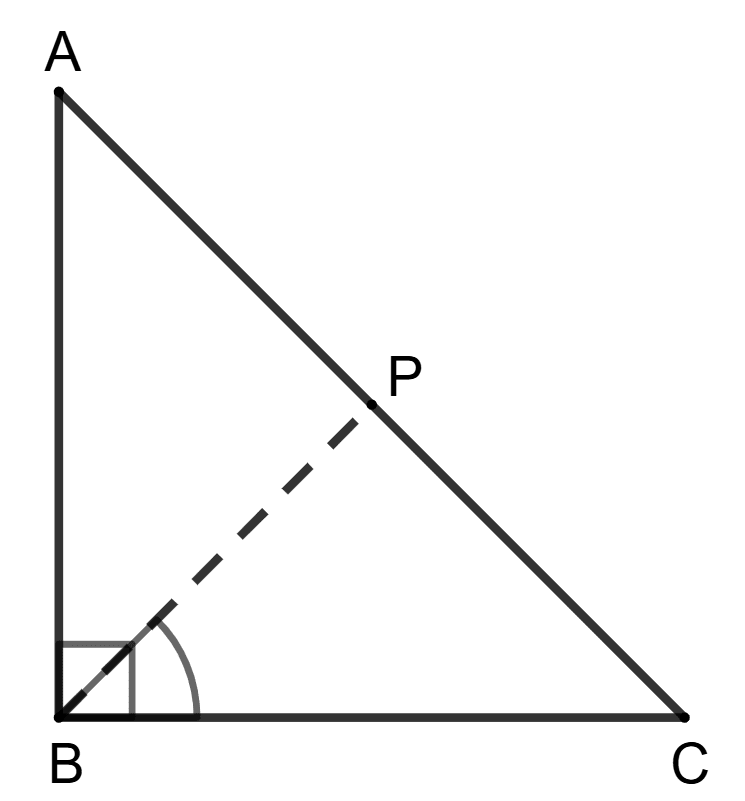
∠ABC = 90° and P is a point on side AC. Then:

1. PA = PB

2. PA > PB

3. PA < PB

4. none of these

Answer

In the right angled triangle ABC,

Let, ∠ACB = x

From figure,

⇒ ∠PCB = ∠ACB = x

⇒ ∠PBC = ∠PCB = x

By angle sum property of triangle,

⇒ ∠ABC + ∠ACB + ∠BAC = 180°

⇒ 90° + x + ∠BAC = 180°

⇒ ∠BAC = 180° - 90° - x = 90° - x

⇒ ∠BAP = ∠BAC = 90° - x.

From figure,

⇒ ∠ABP = ∠ABC - ∠PBC = 90° - x.

∴ ∠BAP = ∠ABP = 90° - x ...................(1)

In △ BAP,

⇒ ∠BAP = ∠ABP [From (1)]

∴ PB = PA (Sides opposite to equal angles in a triangle are equal)

Hence, option 1 is the correct option.

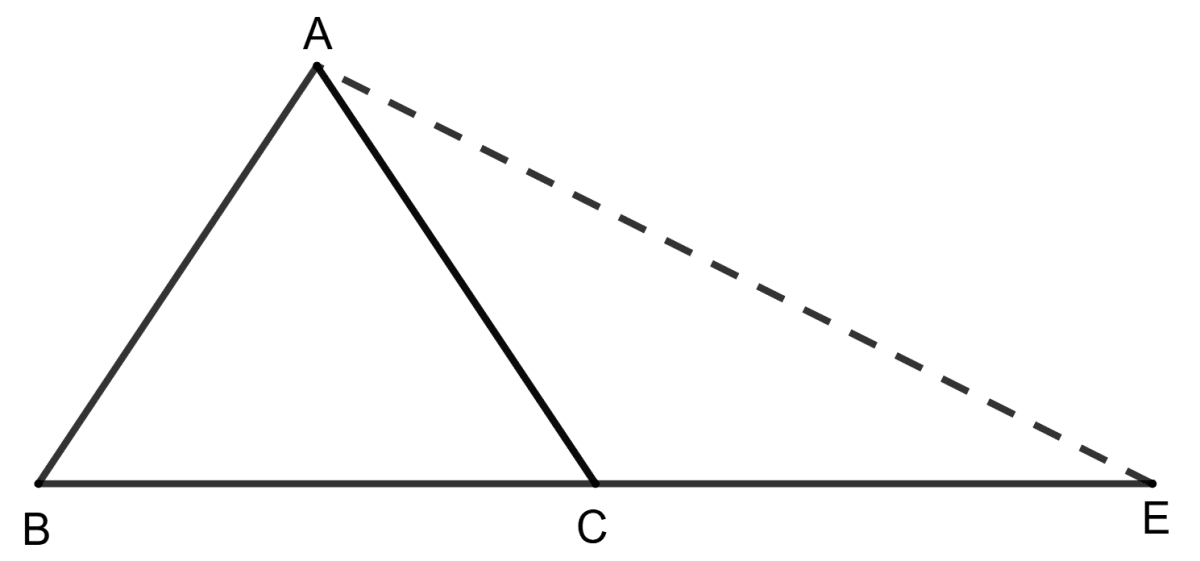
Triangles ABC is equilateral and BC = CE, then angle AEC is:

1. 60°

2. 45°

3. 30°

4. 120°

Answer

Since, ABC is an equilateral triangle, ∠A = ∠B = ∠C = 60°.

From figure,

⇒ ∠ACB + ∠ACE = 180° [Linear pairs]

⇒ 60° + ∠ACE = 180°

⇒ ∠ACE = 120°.

From figure, BC = CE (Given) ....................(1)

⇒ BC = AC (Side of equilateral triangle) ...................(2)

⇒ AC = CE (From equation (1) and (2))

⇒ ∠AEC = ∠CAE = y (let) [As angles opposite to equal sides of a triangle are equal]

By angle sum property in triangle AEC,

⇒ ∠AEC + ∠CAE + ∠ACE = 180°

⇒ y + y + 120° = 180°

⇒ 2y = 60°

⇒ y = 30°.

∴ ∠AEC = 30°.

Hence, option 3 is the correct option.

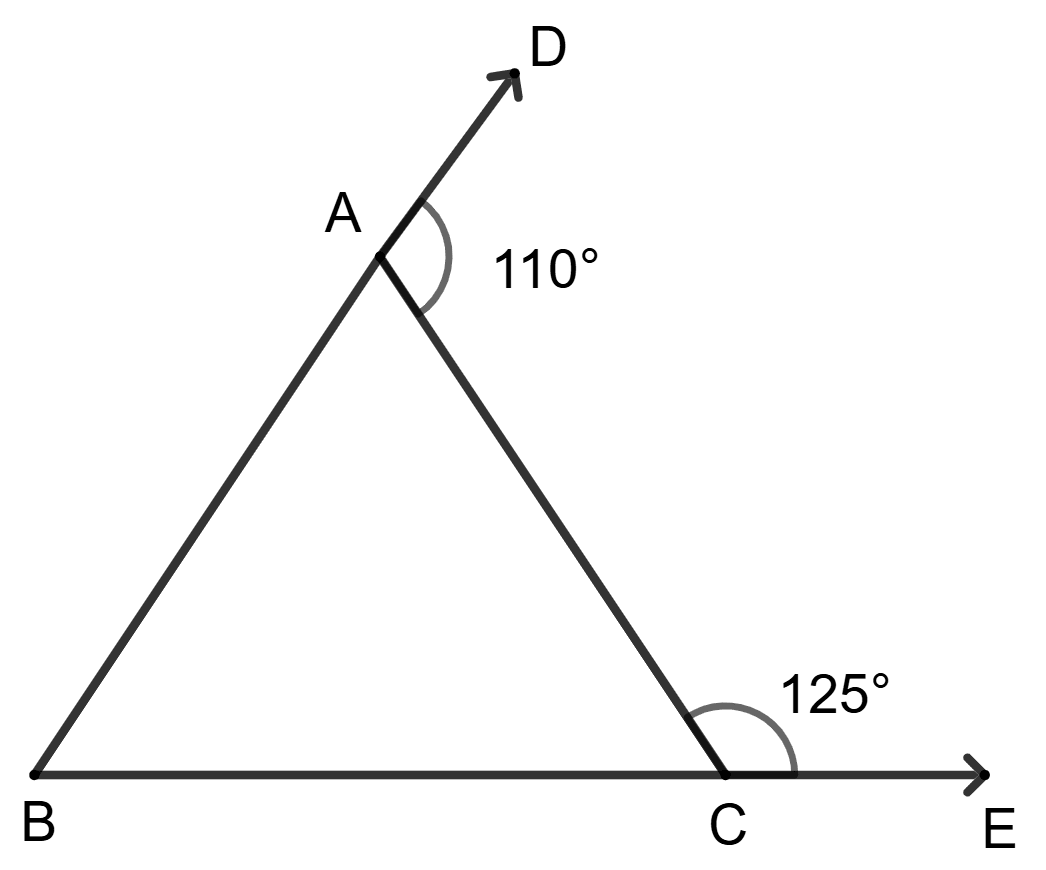
Side BA is produced upto point D and side BC upto point E such that ∠DAC = 110° and ∠ACE = 125°. Then the largest side of the triangle ABC is

1. AB

2. BC

3. AC

4. none of these

Answer

From figure, ∠DAC and ∠BAC forms linear pair.

⇒ ∠DAC + ∠BAC = 180°

⇒ 110° + ∠BAC = 180°

⇒ ∠BAC = 180° - 110°

⇒ ∠BAC = 70°

Similarly, ∠ACE and ∠ACB forms linear pair.

⇒ ∠ACE + ∠ACB = 180°

⇒ 125° + ∠ACB = 180°

⇒ ∠ACB = 180° - 125°

⇒ ∠ACB = 55°

In ΔABC, according to angle sum property,

⇒ ∠ABC + ∠ACB + ∠BAC = 180°

⇒ ∠ABC + 55° + 70° = 180°

⇒ ∠ABC + 125° = 180°

⇒ ∠ABC = 180° - 125°

⇒ ∠ABC = 55°

As we know that the side opposite to the largest angle in a triangle is the longest side.

Since, ∠BAC is the largest angle of the triangle.

So, BC is the largest side of the triangle ABC.

Hence, option 2 is the correct option.

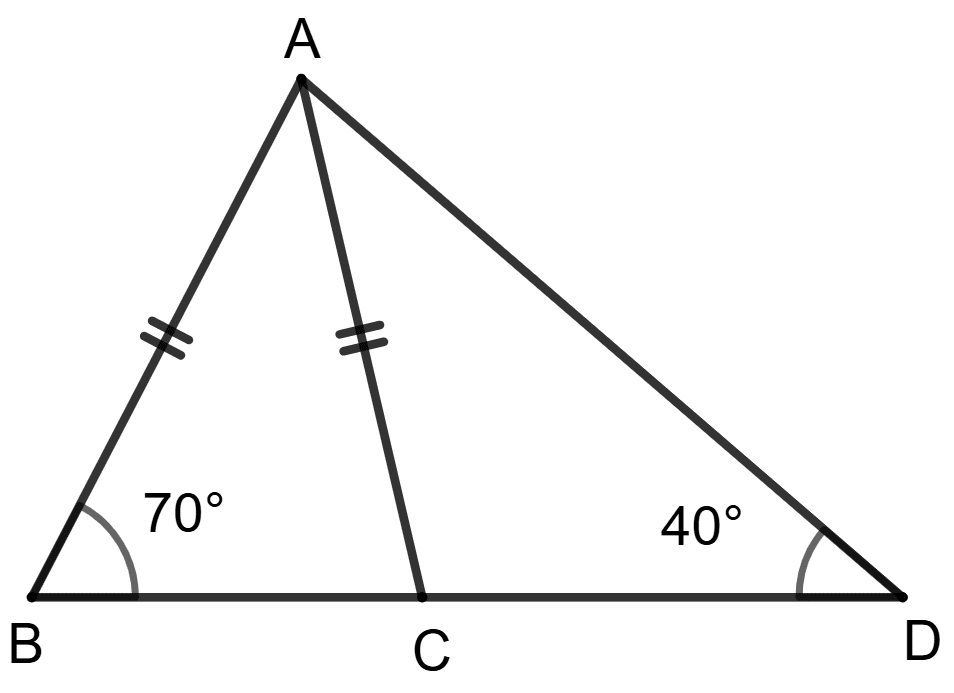
In the given figure,

1. AC = CD

2. AB > CD

3. AB < CD

4. none of these

Answer

Since, AB = AC.

∴ ∠ABC = ∠ACB = 70° (As angles opposite to equal sides of an isosceles triangle are equal.)

From figure,

⇒ ∠ACB + ∠ACD = 180° [Linear pairs]

⇒ 70° + ∠ACD = 180°

⇒ ∠ACD = 110°.

In △ACD,

⇒ ∠CAD + ∠ADC + ∠ACD = 180°

⇒ ∠CAD + 40° + 110° = 180°

⇒ ∠CAD + 150° = 180°

⇒ ∠CAD = 30°.

In △ACD,

∠ADC = 40°

∠CAD = 30°

∴ ∠ADC > ∠CAD

∴ AC > CD (As side opposite to greater angle is greater.)

Since, AB = AC,

∴ AB > CD.

Hence, option 2 is the correct option.

Statement (1): In the given figure, AC = DC = BD and ∠B = 30°.

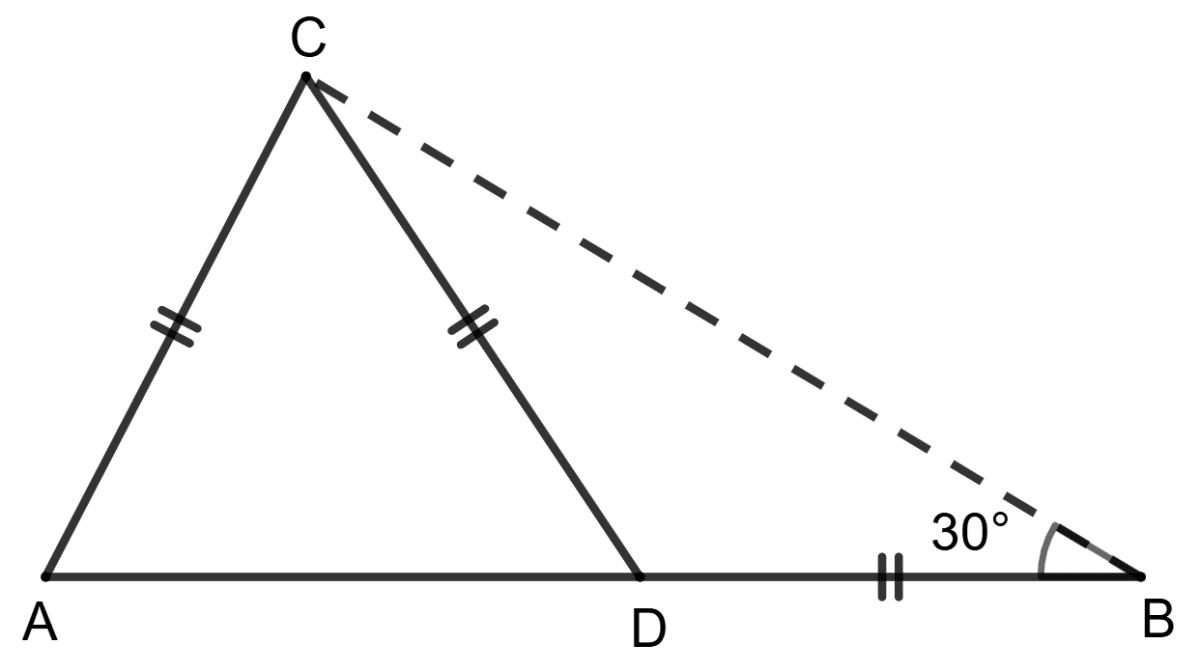
Statement (2): ΔCAD is equilateral.

1. Both the statements are true.

2. Both the statements are false.

3. Statement 1 is true, and statement 2 is false.

4. Statement 1 is false, and statement 2 is true.

Answer

In ΔBDC,

⇒ DC = DB

⇒ ∠DBC = ∠DCB = 30° (Angles opposite to equal sides of a triangle are always equal)

In ΔBDC, according to angle sum property,

⇒ ∠BDC + ∠DBC + ∠DCB = 180°

⇒ ∠BDC + 30° + 30° = 180°

⇒ ∠BDC + 60° = 180°

⇒ ∠BDC = 180° - 60°

⇒ ∠BDC = 120°

Since ∠BDC and ∠CDA forms linear pair.

⇒ ∠BDC + ∠CDA = 180°

⇒ 120° + ∠CDA = 180°

⇒ ∠CDA = 180° - 120°

⇒ ∠CDA = 60°

Since, AC = DC

⇒ ∠CDA = ∠CAD = 60° (Angles opposite to equal sides of a triangle is always equal)

In ΔACD, according to angle sum property,

⇒ ∠ACD + ∠CDA + ∠CAD = 180°

⇒ ∠ACD + 60° + 60° = 180°

⇒ ∠ACD + 120° = 180°

⇒ ∠ACD = 180° - 120°

⇒ ∠ACD = 60°

So, ΔCAD is equilateral.

∴ Both the statements are true.

Hence, option 1 is the correct option.

Statement (1): AB = AC and D is any point on side BC of triangle ABC.

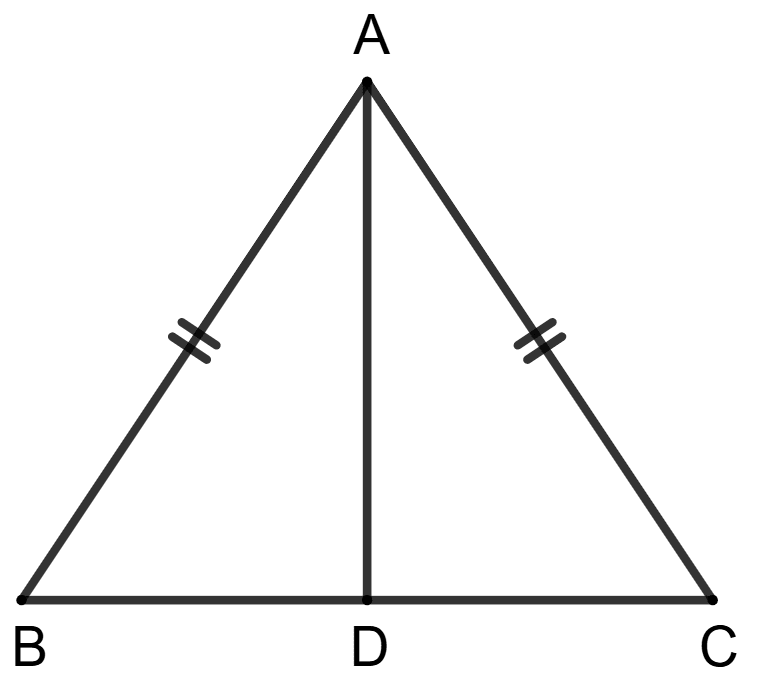
Statement (2): AB > AD.

1. Both the statements are true.

2. Both the statements are false.

3. Statement 1 is true, and statement 2 is false.

4. Statement 1 is false, and statement 2 is true.

Answer

Since AB = AC, ΔABC is an isosceles triangle.

The angles opposite to equal sides of a triangle are equal.

⇒ ∠B = ∠C

∠ADB is an exterior angle to ΔADC.

Therefore, ∠ADB > ∠C

⇒ ∠ADB > ∠B

⇒ AB > AD (Side opposite to the largest angle in a triangle is the longest side)

∴ Both the statements are true.

Hence, option 1 is the correct option.

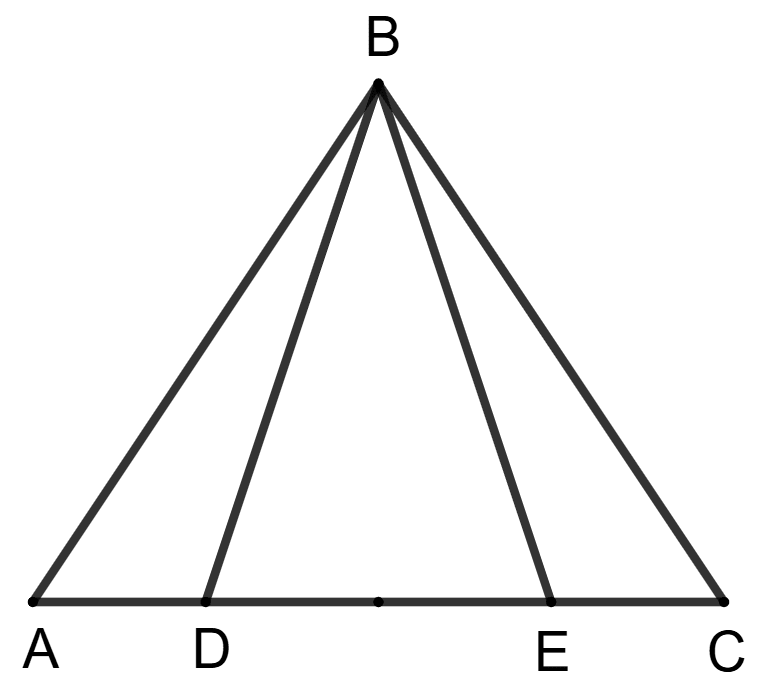
Assertion (A): In the given figure, AB = BC and AD = CE, then BD = CE.

Reason (R): ΔBAD ≅ ΔBCE by SAS.

1. A is true, but R is false.

2. A is false, but R is true.

3. Both A and R are true and R is the correct reason for A.

4. Both A and R are true and R is the incorrect reason for A.

Answer

It is given that AB = BC

⇒ ∠BAC = ∠BCA [Angles opposite to equal sides of the triangle are also equal]

⇒ ∠BAD = ∠BCE ..................(1)

In ΔBAD and ΔBCE,

⇒ AB = BC (Given)

⇒ AD = CE [Given]

⇒ ∠BAD = ∠BCE

∴ ΔBAD ≅ ΔBCE (By SAS congruency criterion)

By C.P.C.T.,

BE = BD

So, assertion (A) is false.

In ΔBAD and ΔBCE,

⇒ BD = BE (Proved above)

⇒ AB = BC (Given)

⇒ AD = EC (Given)

∴ ΔBAD ≅ ΔBCE (By SAS congruency criterion)

So, reason (R) is true.

Hence, option 2 is the correct option.

Assertion (A): In the given figure, S is any point on side QR.

∴ PQ + QR + RP > 2PS

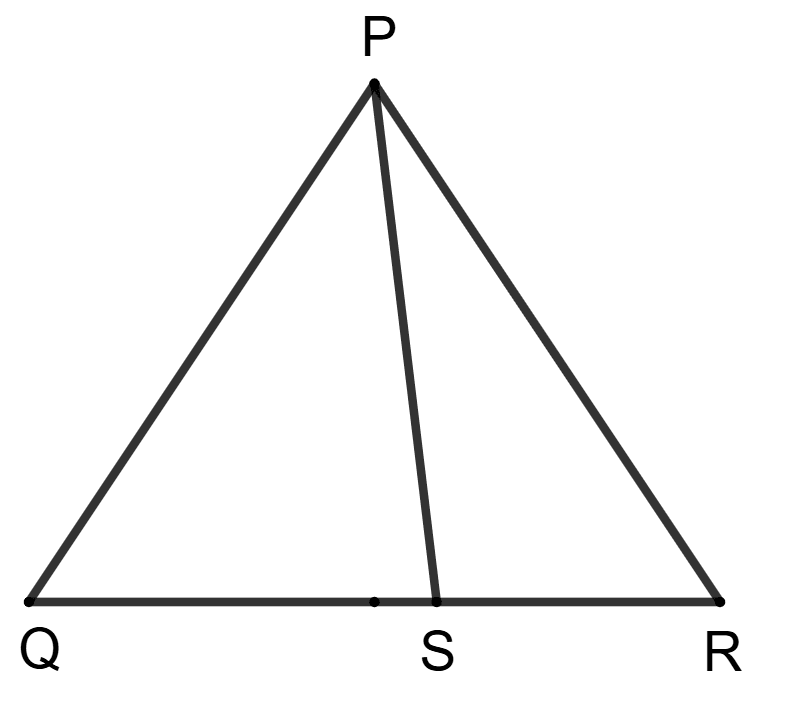
Reason (R): In ΔPQS, PQ + QS > PS and in ΔPRS, PR + SR > PS

1. A is true, but R is false.

2. A is false, but R is true.

3. Both A and R are true and R is the correct reason for A.

4. Both A and R are true and R is the incorrect reason for A.

Answer

In △ PQS,

⇒ PQ + QS > PS ......(1) [Sum of any two sides of a triangle is greater than the third side]

In △ PRS,

⇒ RP + RS > PS ......(2) [Sum of any two sides of a triangle is greater than the third side]

So, reason (R) is true.

Adding equations (1) and (2), we get :

⇒ PQ + QS + RP + RS > PS + PS

⇒ PQ + (QS + RS) + RP > 2PS

⇒ PQ + QR + RP > 2PS.

So, assertion (A) is true.

∴ Both A and R are true, and R is the correct reason for A.

Hence, option 3 is the correct option.

In the figure given alongside, AD = AB = AC, BD is parallel to CA and angle ACB = 65°. Find angle DAC.

Answer

From figure,

In △ ABC,

⇒ AB = AC (Given)

⇒ ∠ABC = ∠ACB = 65° (Angles opposite to equal sides are equal)

By angle sum property of triangle,

⇒ ∠ABC + ∠ACB + ∠BAC = 180°

⇒ 65° + 65° + ∠BAC = 180°

⇒ 130° + ∠BAC = 180°

⇒ ∠BAC = 180° - 130° = 50°.

Given,

BD || CA

∴ ∠DBA = ∠BAC = 50° (Alternate angles are equal)

In △ DAB,

⇒ AD = AB (Given)

⇒ ∠ADB = ∠DBA = 50° (Angles opposite to equal sides are equal)

By angle sum property of triangle,

⇒ ∠ADB + ∠DBA + ∠DAB = 180°

⇒ 50° + 50° + ∠DAB = 180°

⇒ 100° + ∠DAB = 180°

⇒ ∠DAB = 180° - 100° = 80°.

From figure,

⇒ ∠DAC = ∠DAB + ∠BAC = 80° + 50° = 130°.

Hence, ∠DAC = 130°.

Prove that a triangle ABC is isosceles, if :

(i) altitude AD bisects angle BAC or,

(ii) bisector of angle BAC is perpendicular to base BC.

Answer

Let AD be the altitude on side BC.

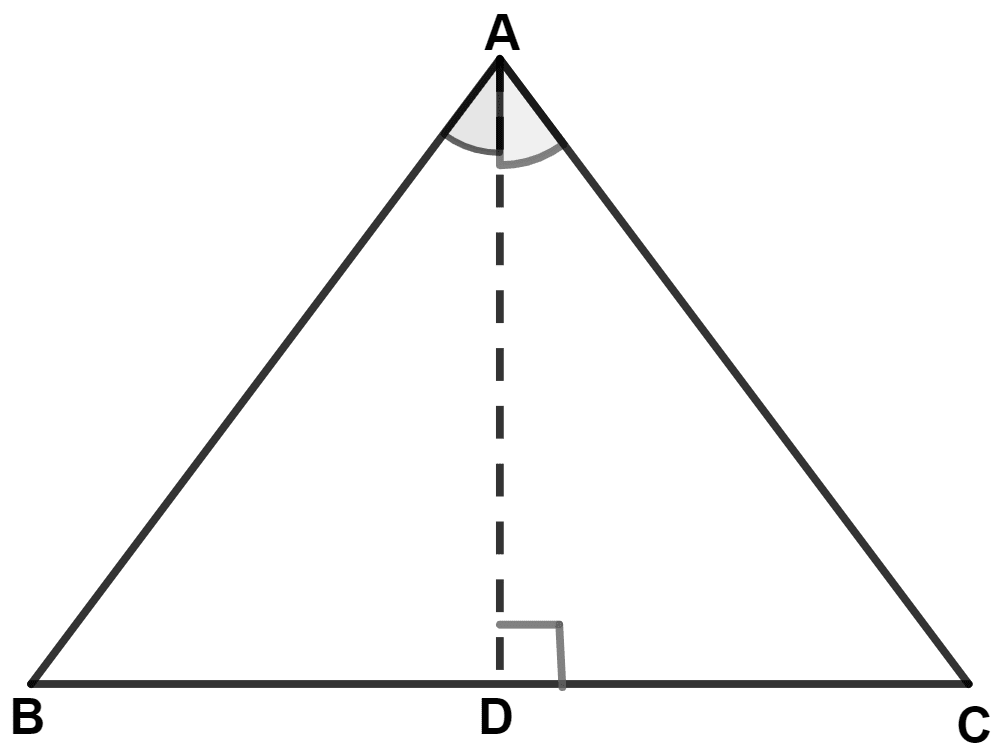
We know that,

Altitude from a point is always perpendicular to other side.

Let altitude AD bisect angle BAC.

Hence, segment AD satisfies both the conditions.

In △ ADB and △ ADC,

⇒ AD = AD (Common side)

⇒ ∠BAD = ∠CAD (Since, AD bisects angle BAC)

⇒ ∠ADB = ∠ADC (Since, AD is altitude to side BC)

∴ Δ ADB ≅ Δ ADC (By A.S.A. axiom)

We know that,

Corresponding parts of congruent triangle are equal.

⇒ AB = AC.

Hence, proved that ABC is an isosceles triangle.

In the given figure; AB = BC and AD = EC. Prove that : BD = BE.

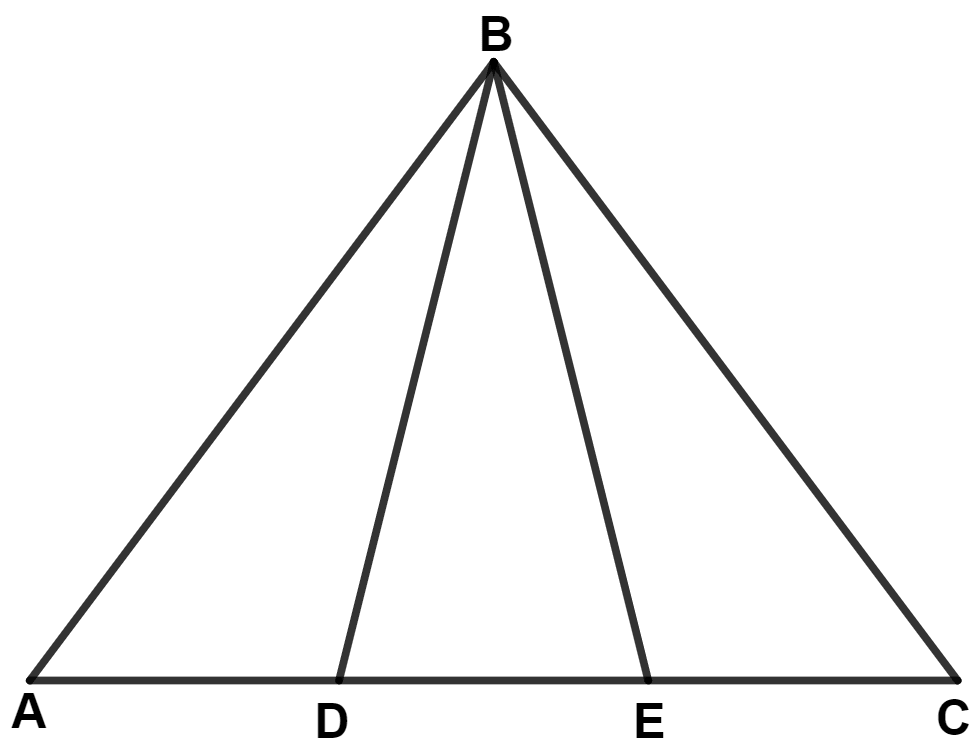
Answer

Given,

⇒ AD = EC

⇒ AD + DE = EC + DE

⇒ AE = DC

In △ ABE and △ BDC,

⇒ AB = BC (Given)

⇒ ∠A = ∠C (Since, AB = BC and angles opposite to equal angles are equal)

⇒ AE = DC (Proved above)

∴ Δ ABE ≅ Δ BDC (By S.A.S. axiom)

We know that,

Corresponding parts of congruent triangle are equal.

⇒ BE = BD.

Hence, proved that BD = BE.

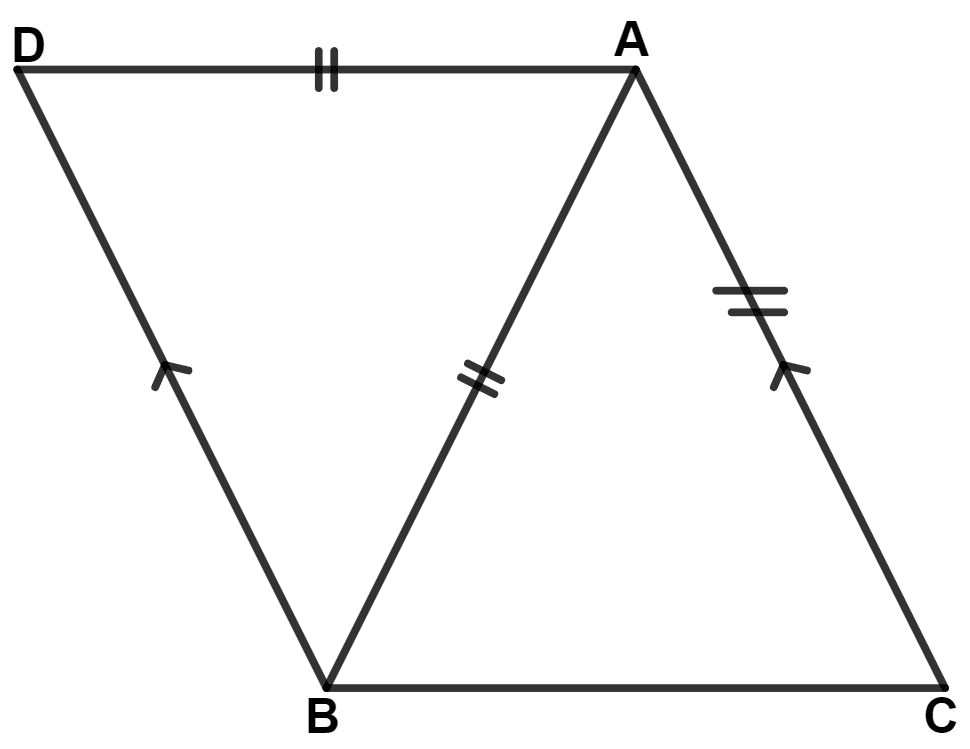
In the following figure; IA and IB are bisectors of angles CAB and CBA respectively. CP is parallel to IA and CQ is parallel to IB.

Prove that :

PQ = The perimeter of Δ ABC.

In the given figure; AB = BC and AD = EC. Prove that : BD = BE.

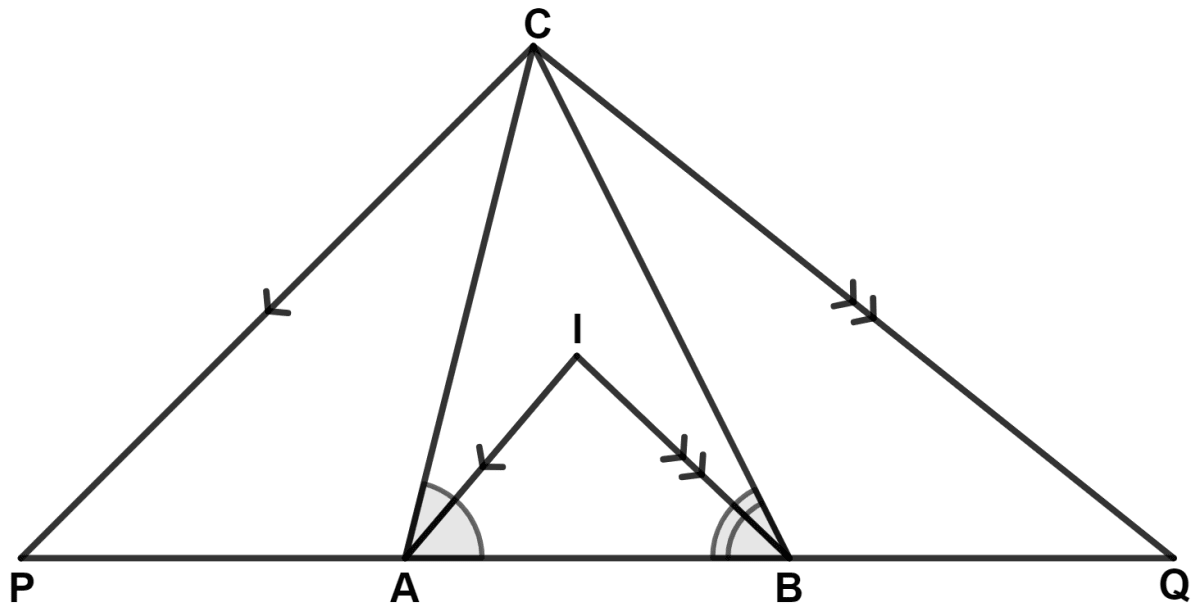
Answer

From figure,

IA || CP and CA is a transversal.

⇒ ∠CAI = ∠PCA (Alternate angles are equal) .........(1)

Also, IA || CP and AP is a transversal

⇒ ∠IAB = ∠APC (Corresponding angles are equal) ......(2)

Since, IA is the bisector of ∠CAB.

∴ ∠CAI = ∠IAB .........(3)

Substituting values from equation (1) and (2) in equation (3), we get :

⇒ ∠PCA = ∠APC

⇒ AC = AP (Sides opposite to equal angles are equal)

From figure,

IB || CQ and CB is a transversal.

⇒ ∠CBI = ∠QCB (Alternate angles are equal) .........(4)

Also, IB || CQ and BQ is a transversal

⇒ ∠IBA = ∠BQC (Corresponding angles are equal) ......(5)

Since, IB is the bisector of ∠CBA.

∴ ∠CBI = ∠IBA .........(6)

Substituting values from equation (4) and (5) in equation (6), we get :

⇒ ∠QCB = ∠BQC

⇒ BQ = BC (Sides opposite to equal angles are equal)

From figure,

PQ = AP + AB + BQ = AC + AB + BC

= Perimeter of △ ABC.

Hence, proved that PQ = Perimeter of △ ABC.

The given figure shows an equilateral triangle ABC with each side 15 cm. Also DE // BC, DF // AC and EG //AB. If DE + DF + EG = 20 cm, find FG.

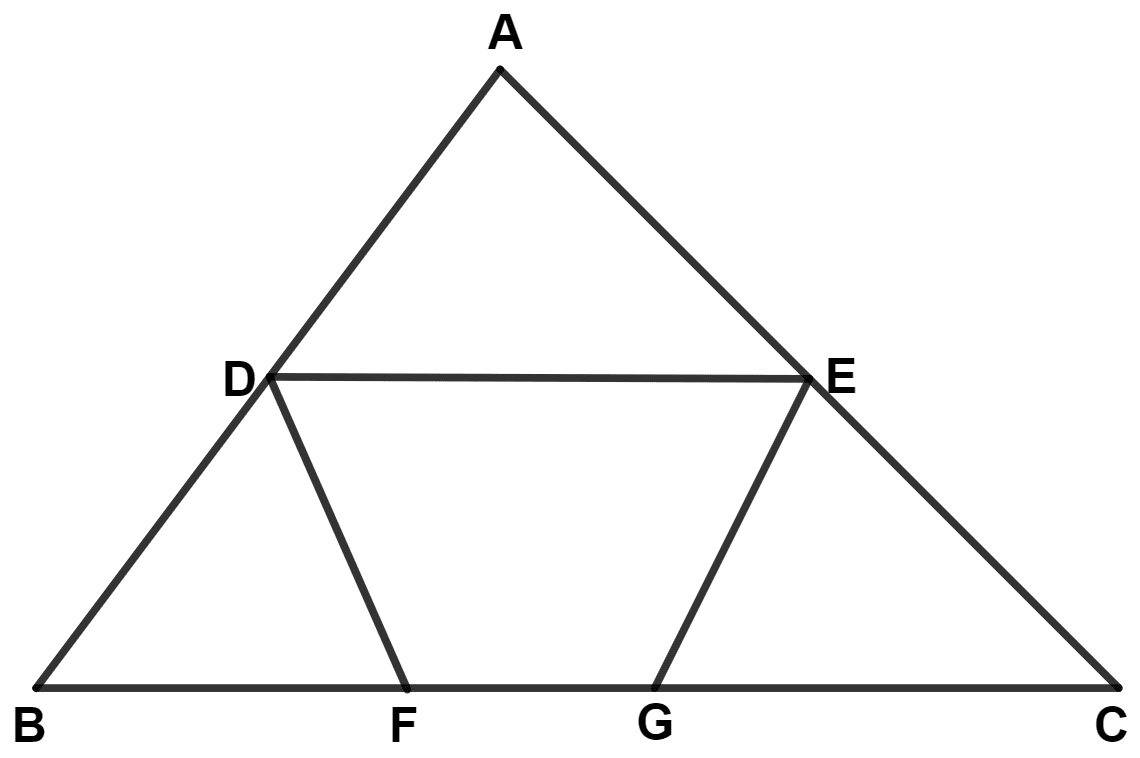
Answer

Given,

ABC is an equilateral triangle.

∴ AB = BC = AC = 15 cm and ∠A = ∠B = ∠C = 60°.

In △ ADE,

⇒ ∠ADE = ∠ABC = 60° (Corresponding angles are equal)

⇒ ∠AED = ∠ACB = 60° (Corresponding angles are equal)

By angle sum property of triangle,

⇒ ∠AED + ∠ADE + ∠DAE = 180°

⇒ 60° + 60° + ∠DAE = 180°

⇒ ∠DAE + 120° = 180°

⇒ ∠DAE = 180° - 120° = 60°.

∴ △ ADE is an equilateral triangle with each side equal to x cm.

∴ AD = DE = EA = x cm.

In △ BDF,

⇒ ∠BFD = ∠BCA = 60° (Corresponding angles are equal)

⇒ ∠DBF = ∠B = 60°

By angle sum property of triangle,

⇒ ∠BFD + ∠DBF + ∠BDF = 180°

⇒ 60° + 60° + ∠BDF = 180°

⇒ ∠BDF + 120° = 180°

⇒ ∠BDF = 180° - 120° = 60°.

∴ △ BDF is an equilateral triangle with each side equal to y cm.

∴ DB = BF = FD = y cm.

In △ EGC,

⇒ ∠EGC = ∠ABC = 60° (Corresponding angles are equal)

⇒ ∠ECG = ∠C = 60°

By angle sum property of triangle,

⇒ ∠EGC + ∠ECG + ∠GEC = 180°

⇒ 60° + 60° + ∠GEC = 180°

⇒ ∠GEC + 120° = 180°

⇒ ∠GEC = 180° - 120° = 60°.

∴ △ EGC is an equilateral triangle with each side equal to z cm.

∴ EG = GC = CE = z cm.

Given,

⇒ AB = 15

⇒ AD + BD = 15

⇒ x + y = 15 ..........(1)

⇒ AC = 15

⇒ AE + EC = 15

⇒ x + z = 15 ..........(2)

Given,

⇒ DE + DF + EG = 20

⇒ x + y + z = 20

⇒ 15 + z = 20 [From equation (1)]

⇒ z = 20 - 15 = 5 cm.

Substituting value of z in equation (2), we get :

⇒ x + 5 = 15

⇒ x = 15 - 5 = 10 cm.

Substituting value of x in equation (1), we get :

⇒ 10 + y = 15

⇒ y = 15 - 10 = 5 cm.

From figure,

⇒ BC = 15 cm

⇒ BF + FG + GC = 15

⇒ y + FG + z = 15

⇒ 5 + FG + 5 = 15

⇒ FG + 10 = 15

⇒ FG = 15 - 10 = 5 cm.

Hence, FG = 5 cm.

In triangle ABC, bisector of angle BAC meets opposite side BC at point D. If BD = CD, prove that △ ABC is isosceles.

Answer

Produce AD upto E such that AD = DE.

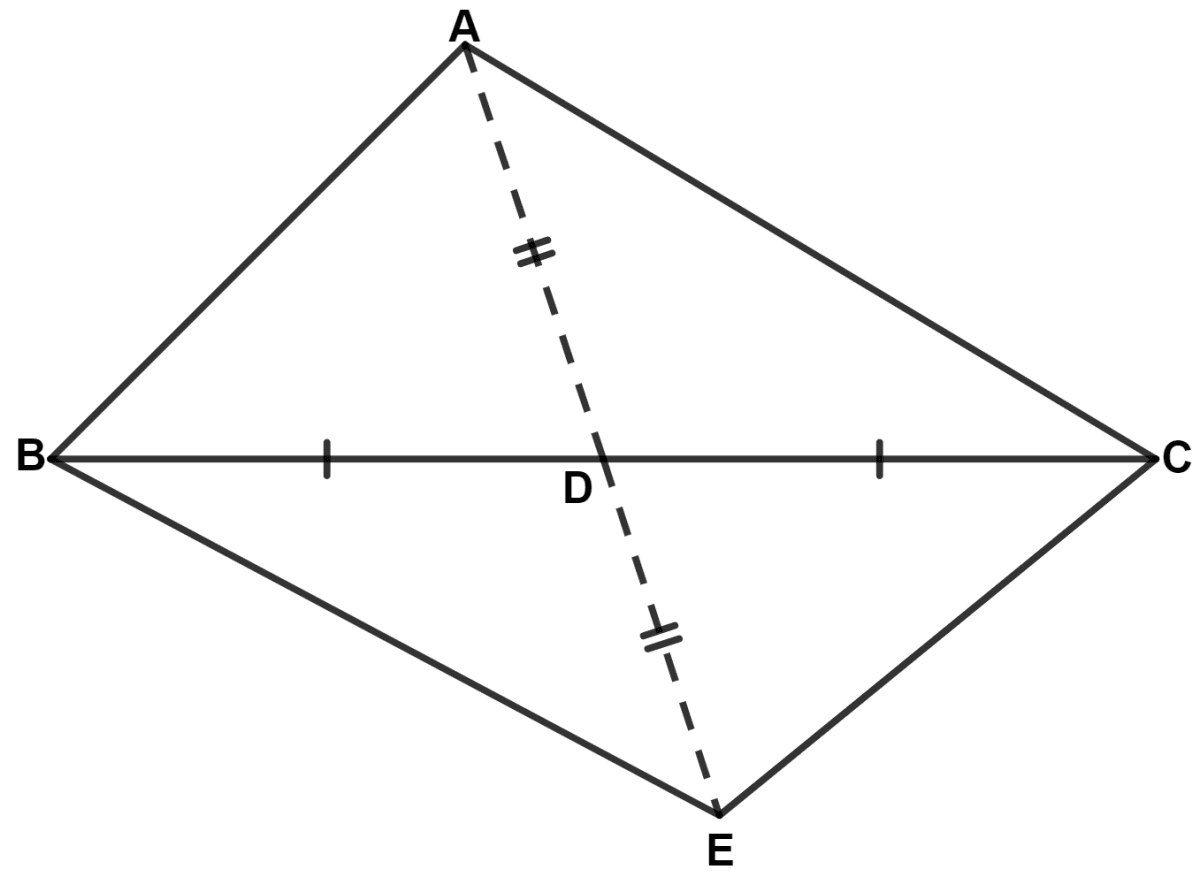
In △ ABD and △ EDC,

⇒ AD = DE (Given)

⇒ BD = CD (Given)

⇒ ∠ADB = ∠EDC (Vertically opposite angles are equal)

∴ △ ABD ≅ △ EDC (By S.A.S. axiom)

We know that,

Corresponding parts of congruent triangle are equal.

⇒ AB = CE .........(1)

⇒ ∠BAD = ∠CED

⇒ ∠BAD = ∠CAD (As AD is the bisector BAC)

∴ ∠CAD = ∠CED

∴ CE = AC (Sides opposite to equal angles are equal) ..........(2)

From equations (1) and (2), we get :

⇒ AB = AC.

Hence, proved that ABC is an isosceles triangle.

In Δ ABC, D is a point on BC such that AB = AD = BD = DC. Show that :

∠ADC : ∠C = 4 : 1.

Answer

Given,

AB = AD = BD

∴ Δ ABD is an equilateral triangle.

∴ ∠ABD = ∠ADB = ∠BAD = 60°.

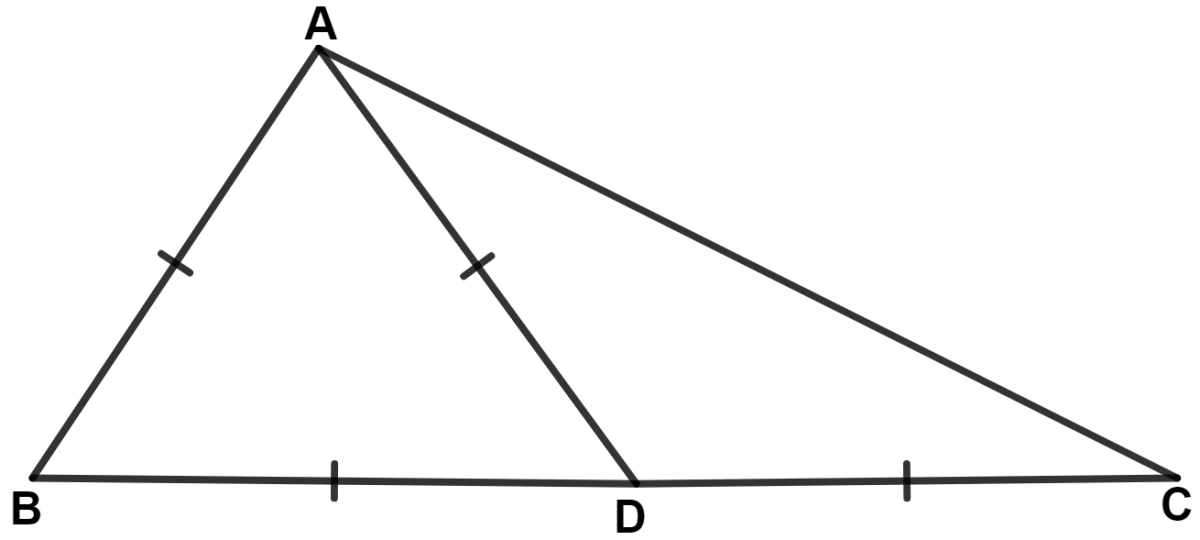
Since, BDC is a straight line.

∴ ∠ADB + ∠ADC = 180°

⇒ 60° + ∠ADC = 180°

⇒ ∠ADC = 180° - 60° = 120°.

In Δ ADC,

⇒ AD = DC (Given)

∴ ∠DAC = ∠DCA = x (let) [Angles opposite to equal sides are equal]

By angle sum property of triangle,

⇒ ∠DAC + ∠DCA + ∠ADC = 180°

⇒ x + x + 120° = 180°

⇒ 2x = 180° - 120°

⇒ 2x = 60°

⇒ x = $\dfrac{60°}{2}$ = 30°

⇒ ∠DCA = ∠C = 30°.

⇒ ∠ADC : ∠C = 120° : 30° = 4 : 1.

Hence, proved that ∠ADC : ∠C = 4 : 1.

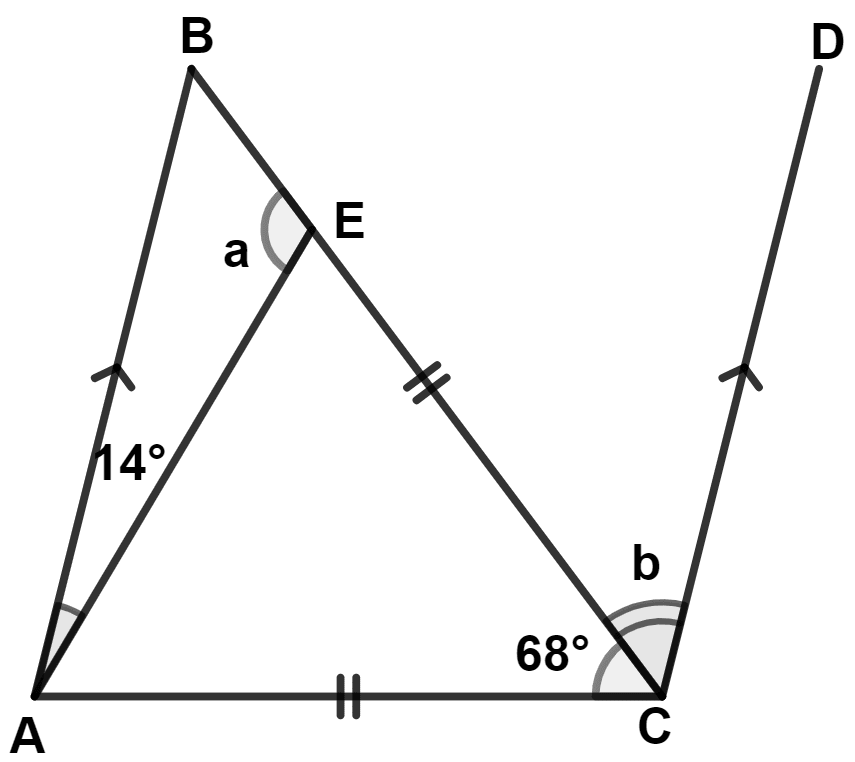
Using the information, given in each of the following figures, find the values of a and b.

Answer

In △ CAE,

⇒ AC = CE (Given)

∴ ∠AEC = ∠EAC = x (let) [Angles opposite to equal sides are equal]

By angle sum property of triangle,

⇒ ∠AEC + ∠EAC + ∠ACE = 180

⇒ x + x + 68° = 180°

⇒ 2x = 180° - 68°

⇒ 2x = 112°

⇒ x = $\dfrac{112°}{2}$ = 56°

⇒ ∠AEC = ∠EAC = 56°.

Since, B, E and C are in a straight line.

∴ ∠BEA + ∠AEC = 180°

⇒ a + 56° = 180°

⇒ a = 180° - 56° = 124°.

In △ ABE,

By angle sum property of triangle,

⇒ ∠ABE + ∠BEA + ∠EAB = 180°

⇒ ∠ABE + 124° + 14° = 180°

⇒ ∠ABE + 138° = 180°

⇒ ∠ABE = 180° - 138° = 42°.

Since, AB || CD

⇒ b = ∠ABE = 42°. (Alternate angles are equal)

Hence, a = 124° and b = 42°.

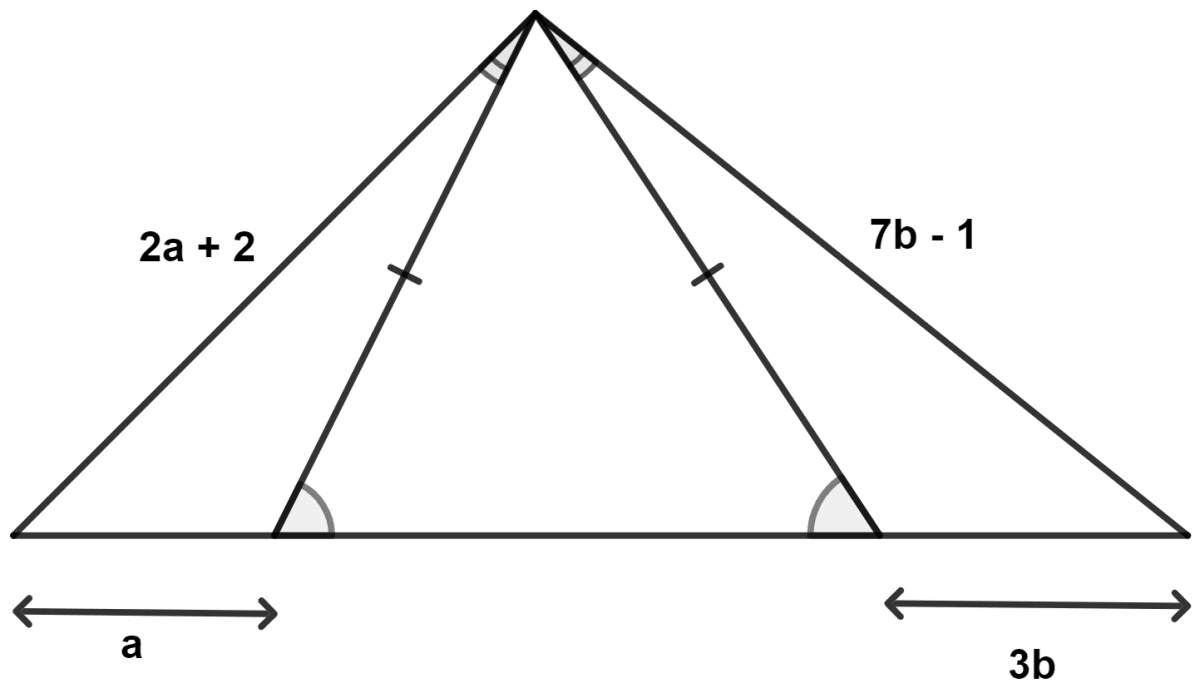
Using the information, given in each of the following figures, find the values of a and b.

Answer

In △ ADE,

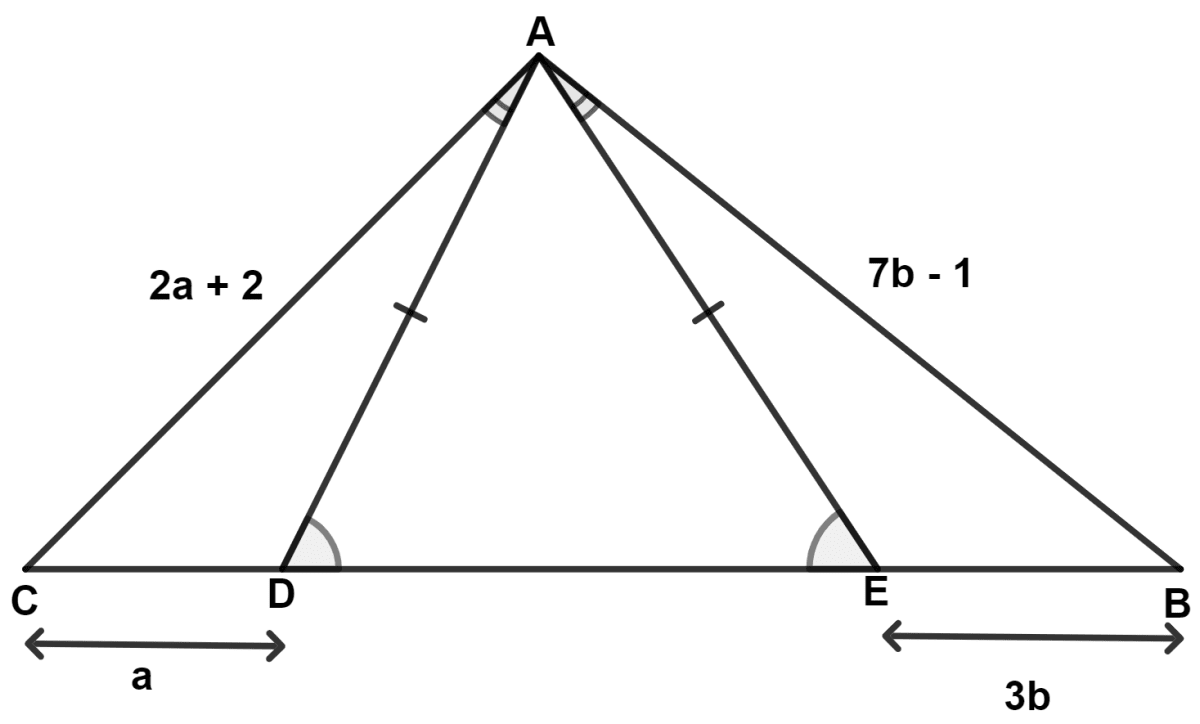
⇒ AD = AE (Given)

∴ ∠ADE = ∠AED (Angles opposite to equal sides are equal)

⇒ 180° - ∠ADE = 180° - ∠AED

⇒ ∠ADC = ∠AEB

In △ ABE and △ CAD,

⇒ ∠EAB = ∠CAB (Given)

⇒ ∠ADC = ∠AEB (Proved above)

⇒ AE = AD (Given)

∴ △ ABE ≅ △ CAD (By A.S.A. axiom)

We know that,

Corresponding sides of congruent triangle are equal.

∴ AC = AB and CD = EB.

Considering CD = EB,

⇒ a = 3b .........(1)

Considering AC = AB,

⇒ 2a + 2 = 7b - 1

Substituting value of a from equation (1) in above equation, we get :

⇒ 2(3b) + 2 = 7b - 1

⇒ 6b + 2 = 7b - 1

⇒ 7b - 6b = 2 + 1

⇒ b = 3.

Substituting value of b in equation (1), we get :

⇒ a = 3(3) = 9.

Hence, a = 9 and b = 3.

In the following figure; AB is the largest side and BC is the smallest side of triangle ABC.

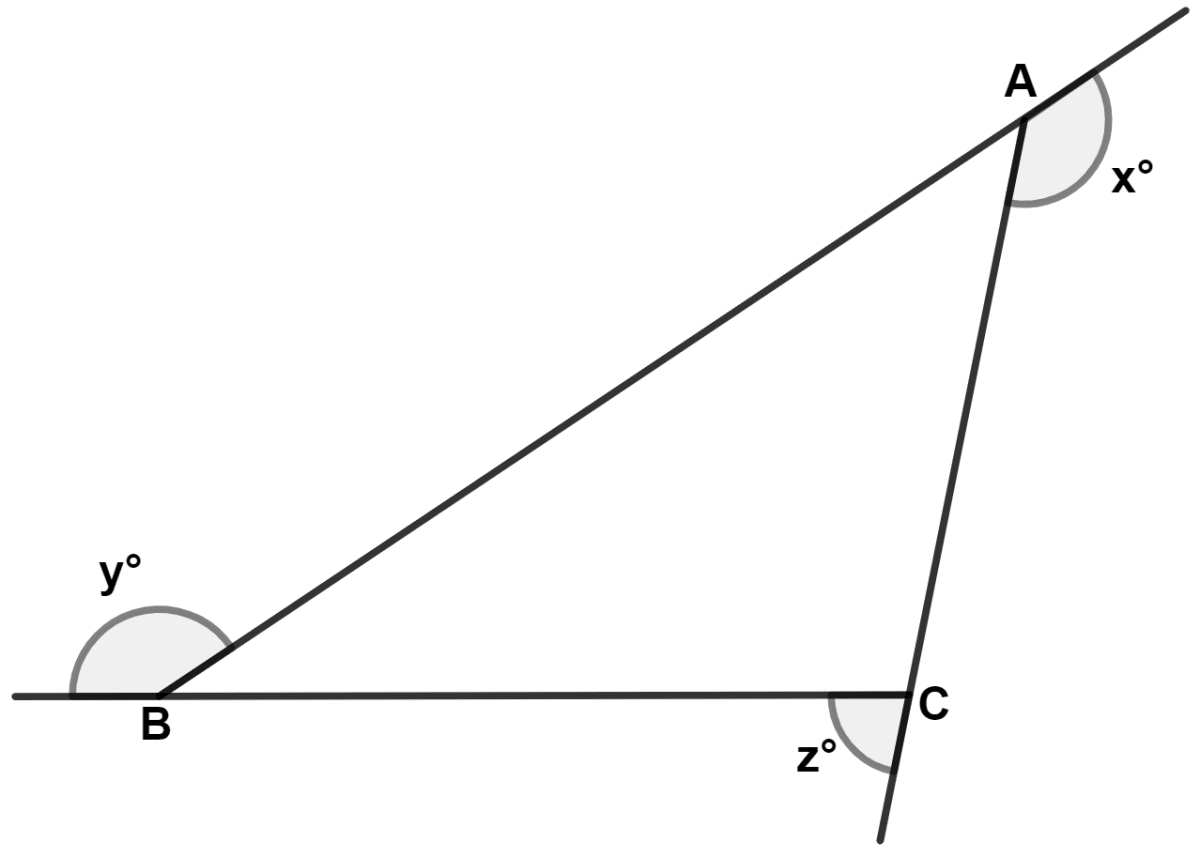
Write the angles x°, y° and z° in ascending order of their values.

Answer

Given,

AB is the largest side and BC is the smallest side of triangle ABC.

∴ AB > AC > BC

⇒ ∠C > ∠B > ∠A (If two sides of a triangle are unequal, the greater side has the greater angle opposite to it.)

⇒ 180° - ∠C < 180° - ∠B < 180° - ∠A

⇒ z° < y° < x°.

Hence, z° < y° < x°.

In quadrilateral ABCD, side AB is the longest and side DC is the shortest. Prove that :

(i) ∠C > ∠A

(ii) ∠D > ∠B

Answer

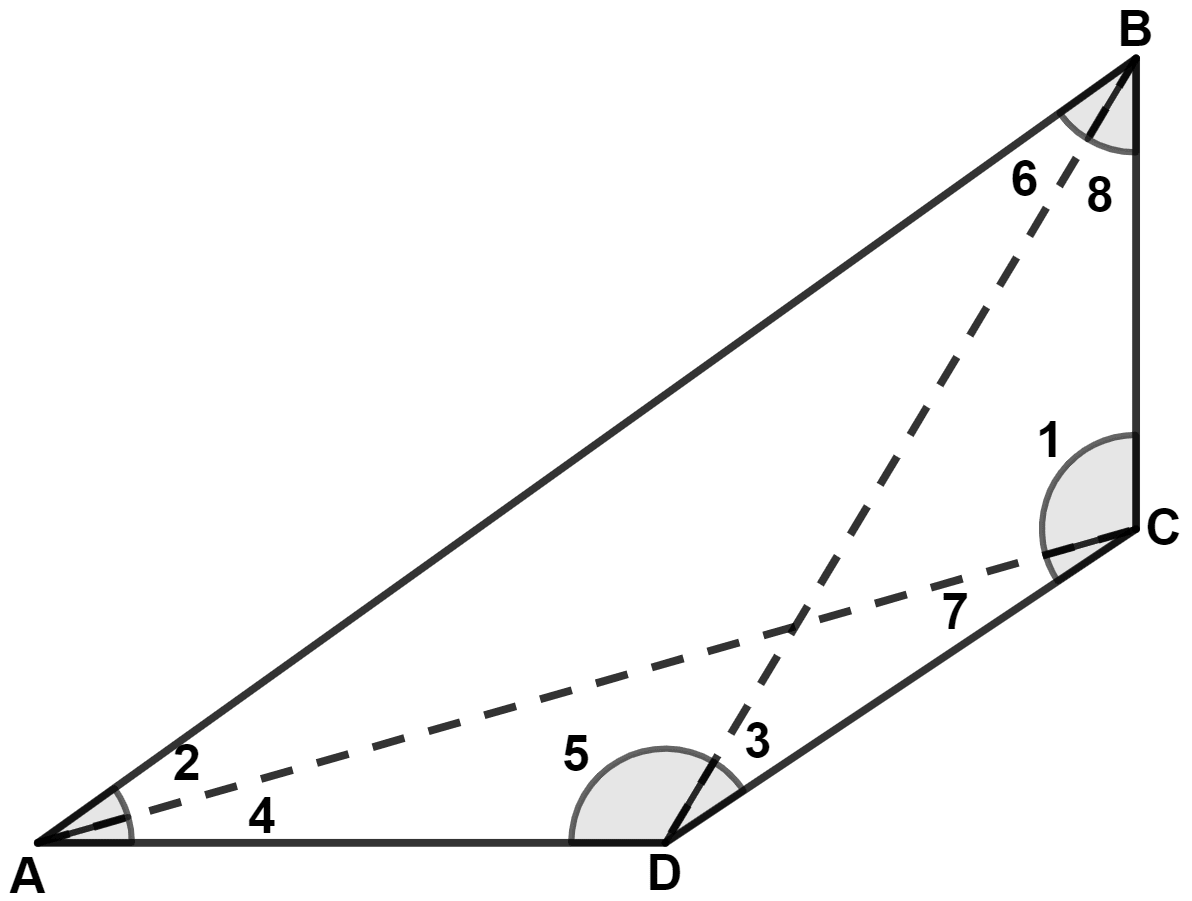
(i) Given,

In quadrilateral ABCD,

AB is the longest sides and DC is the shortest side.

Join BD and AC.

In △ ABC,

⇒ AB > BC

∴ ∠1 > ∠2 .......(1) [If two sides of a triangle are unequal, the greater side has the greater angle opposite to it.]

In △ ADC,

⇒ AD > DC

∴ ∠7 > ∠4 .......(2) [If two sides of a triangle are unequal, the greater side has the greater angle opposite to it.]

Adding equations (1) and (2), we get :

⇒ ∠1 + ∠7 > ∠2 + ∠4

⇒ ∠C > ∠A.

Hence, proved that ∠C > ∠A.

(ii) In △ ABD,

⇒ AB > AD

∴ ∠5 > ∠6 .......(1) [If two sides of a triangle are unequal, the greater side has the greater angle opposite to it.]

In △ BDC,

⇒ BC > CD

∴ ∠3 > ∠8 .......(2) [If two sides of a triangle are unequal, the greater side has the greater angle opposite to it.]

Adding equations (1) and (2), we get :

⇒ ∠5 + ∠3 > ∠6 + ∠8

⇒ ∠D > ∠B.

Hence, proved that ∠D > ∠B.

In triangle ABC, side AC is greater than side AB. If the internal bisector of angle A meets the opposite side at point D, prove that : ∠ADC is greater than ∠ADB.

Answer

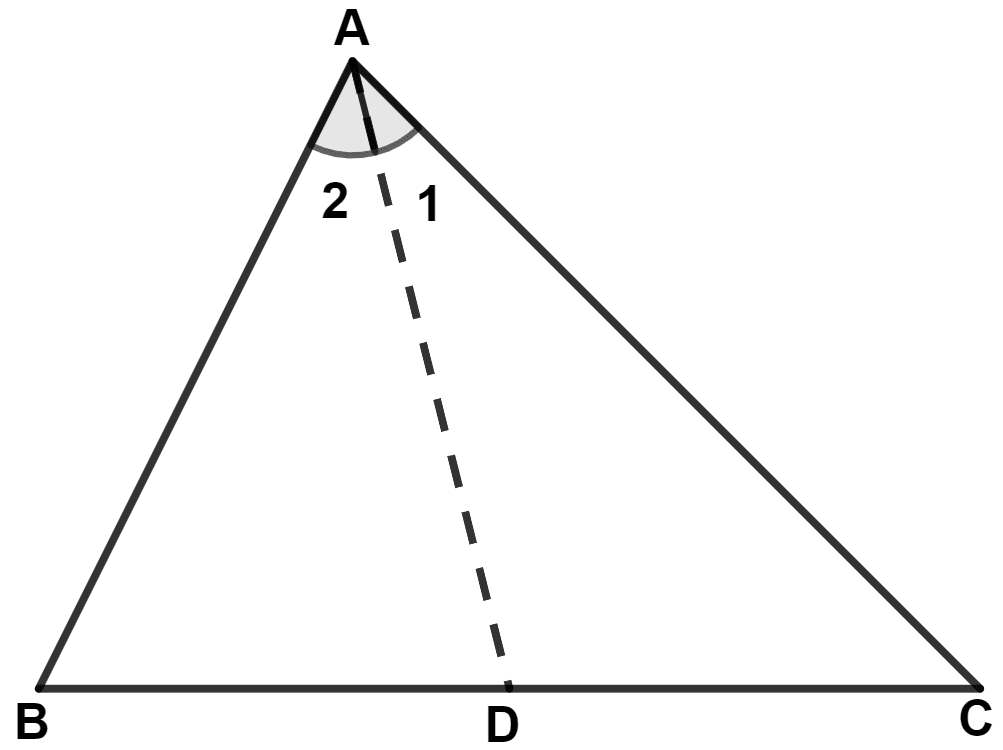
In △ ADC,

⇒ ∠ADB = ∠1 + ∠C [In a triangle an exterior angle is equal to the sum of two opposite interior angles.] .........(1)

In △ ADB,

⇒ ∠ADC = ∠2 + ∠B [In a triangle an exterior angle is equal to the sum of two opposite interior angles.] .........(2)

In △ ABC,

⇒ AC > AB (Given)

⇒ ∠B > ∠C [If two sides of a triangle are unequal, the greater side has the greater angle opposite to it.]

Since, AD is the bisector of angle A.

∴ ∠2 + ∠B > ∠1 + ∠C .........(3)

From equations (1), (2) and (3), we get :

⇒ ∠ADC > ∠ADB.

Hence, proved that ∠ADC is greater than ∠ADB.

In isosceles triangle ABC, sides AB and AC are equal. If point D lies in base BC and point E lies on BC produced (BC being produced through vertex C), prove that :

(i) AC > AD

(ii) AE > AC

(iii) AE > AD

Answer

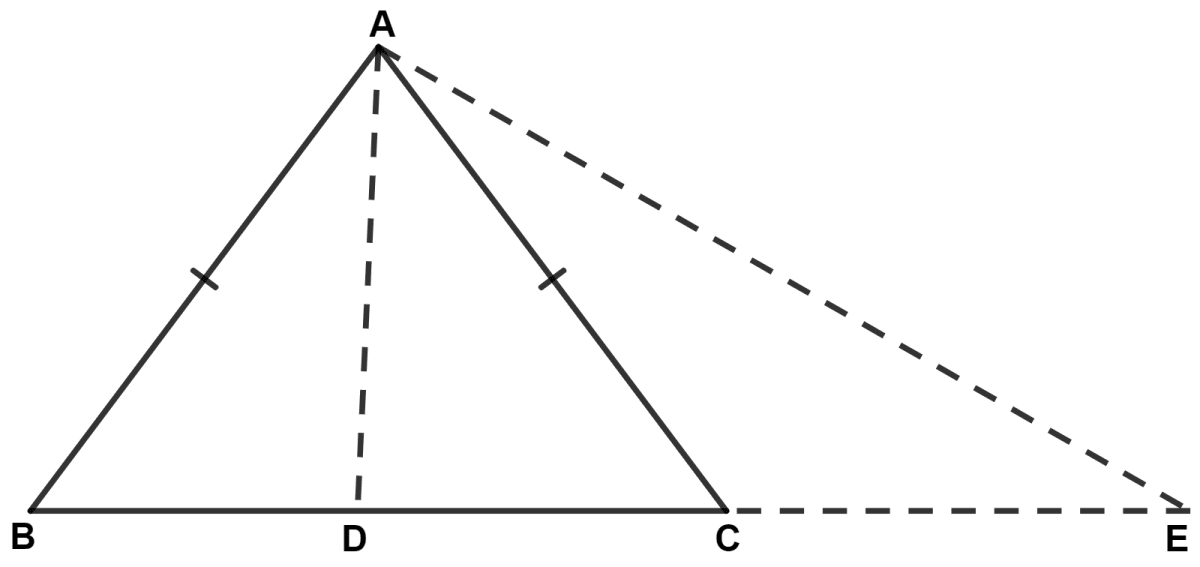
(i) In ∆ ABC,

⇒ AB = AC (Given)

⇒ ∠ACB = ∠ABC [Angles opposite to equal sides are equal] .......(1)

⇒ ∠ACD = ∠ABD [From figure, ∠ACB = ∠ACD and ∠ABC = ∠ABD] .........(2)

We know that exterior angle of a triangle is always greater than each of the interior opposite angle.

In ∆ ADC,

⇒ ∠ADB > ∠ACD

⇒ ∠ADB > ∠ABD [Using equation (2)]

⇒ AB > AD [If two angles of a triangle are unequal, the greater angle has the greater side opposite to it.]

⇒ AC > AD [As, AB = AC] .....(3)

Hence, proved that AC > AD.

(ii) We know that exterior angle of a triangle is always greater than each of the interior opposite angle.

In ∆ ACE,

⇒ ∠ACD > ∠AEC ........(4)

From equation (2),

⇒ ∠ACD = ∠ABD

From figure,

⇒ ∠ABD = ∠ABE

⇒ ∠ACD = ∠ABE

⇒ ∠AEC = ∠AEB

Substituting value of ∠ACD and ∠AEC in equation (4), we get :

⇒ ∠ABE > ∠AEB

In △ AEB,

⇒ AE > AB [If two angles of a triangle are unequal, the greater angle has the greater side opposite to it.]

As, AB = AC,

∴ AE > AC

Hence, proved that AE > AC.

(iii) Since, AE > AC and AC > AD,

∴ AE > AD.

Hence, proved that AE > AD.

Given : ED = EC

Prove : AB + AD > BC.

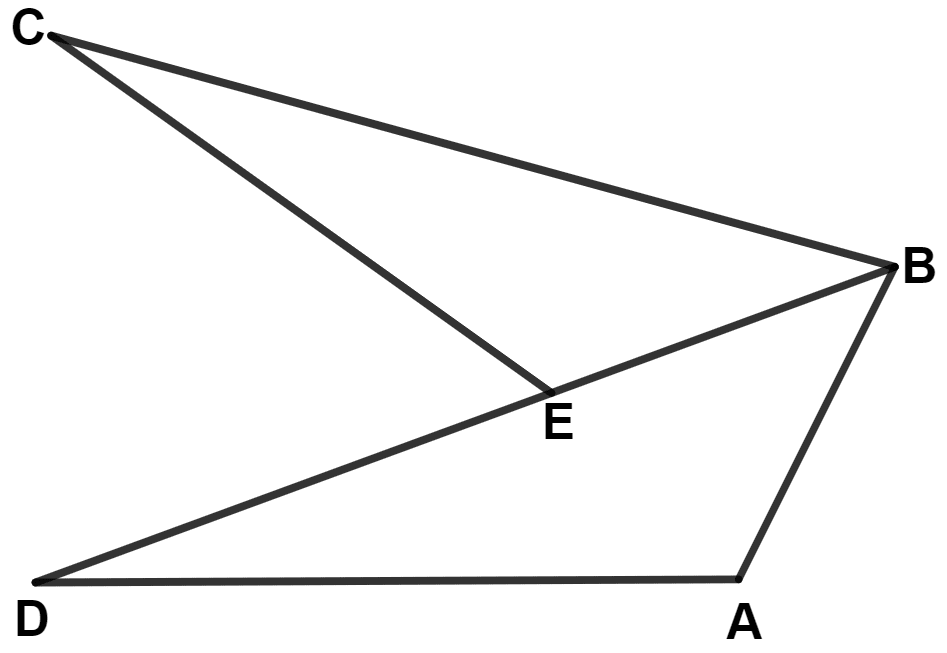
Answer

We know that,

The sum of any two sides of the triangle is always greater than the third side of the triangle.

In △ CEB,

⇒ EC + EB > BC

⇒ ED + EB > BC (As, EC = ED)

⇒ BD > BC

In △ ADB,

⇒ AD + AB > BD

Since, BD > BC and AD + AB > BD

∴ AD + AB > BC.

Hence, proved that AB + AD > BC.