It is given that △ABC ≅ △RPQ. Is it true to say that BC = QR? Why?
Answer
Given, △ABC ≅ △RPQ.
It means that A ↔ R, B ↔ P, C ↔ Q, therefore, BC = PQ (corresponding sides are equal).
Hence, BC ≠ QR as they are not corresponding sides.
"If two sides and an angle of one triangle are equal to two sides and an angle of another triangle, then the two triangles must be congruent." Is the statement true? Why?
Answer
Given, statement "If two sides and an angle of one triangle are equal to two sides and an angle of another triangle, then the two triangles must be congruent."
The statement is not true as the angles must be included angles.
In the adjoining figure, AB = AC and AP = AQ. Prove that
(i) △APC ≅ △AQB
(ii) CP = BQ
(iii) ∠APC = ∠AQB.

Answer
(i) In △APC and △AQB we have,
AB = AC (Given)
AP = AQ (Given)
∠PAC = ∠QAB (Common angles)
Hence, by SAS axiom △APC ≅ △AQB.
(ii) As, △APC ≅ △AQB.
We know that corresponding sides of congruent triangles are equal.
∴ CP = BQ.
Hence, proved that CP = BQ.
(iii) As, △APC ≅ △AQB.
We know that corresponding angles of congruent triangles are equal.
∴ ∠APC = ∠AQB.
Hence, proved that ∠APC = ∠AQB.
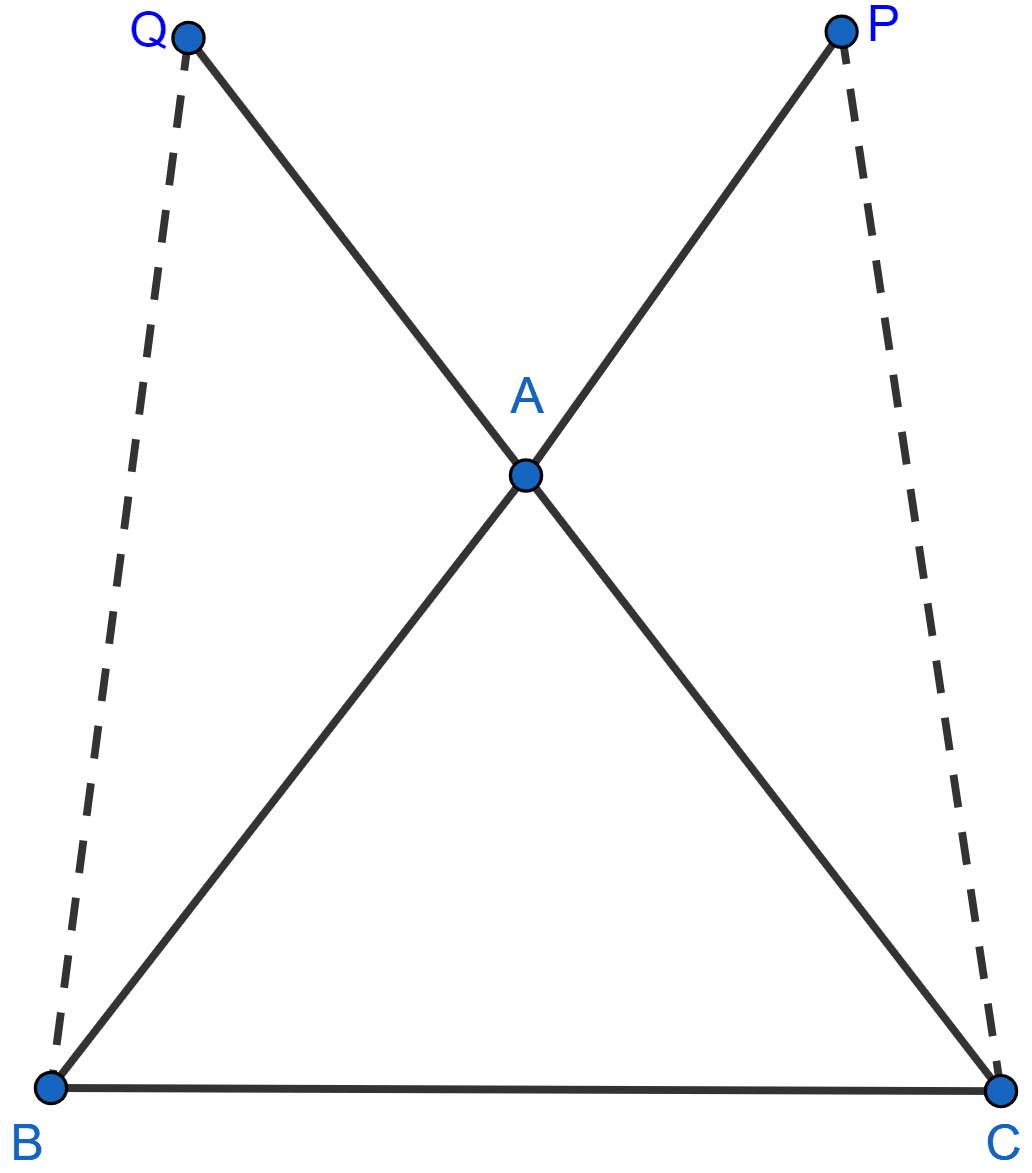
In the adjoining figure, AB = AC, P and Q are points on BA and CA respectively such that AP = AQ. Prove that
(i) △APC ≅ △AQB
(ii) CP = BQ
(iii) ∠ACP = ∠ABQ.
Answer
(i) In △APC and △AQB we have,
AP = AQ (Given)
AB = AC (Given)
∠PAC = ∠QAB (Vertically opposite angles)
Hence, by SAS axiom △APC ≅ △AQB.
(ii) As, △APC ≅ △AQB.
We know that corresponding sides of congruent triangles are equal.
∴ CP = BQ.
Hence, proved that CP = BQ.
(iii) As, △APC ≅ △AQB.
We know that corresponding angles of congruent triangles are equal.
∴ ∠ACP = ∠ABQ.
Hence, proved that ∠ACP = ∠ABQ.
In the adjoining figure, AD = BC and BD = AC. Prove that:
∠ADB = ∠BCA and ∠DAB = ∠CBA.

Answer
In △ABD and △BAC we have,
AD = BC (Given)
BD = AC (Given)
AB = AB (Common sides)
∴ △ABD ≅ △BAC. (By SSS axiom)
We know that corresponding angles of congruent triangles are equal.
∴ ∠ADB = ∠BCA and ∠DAB = ∠CBA.
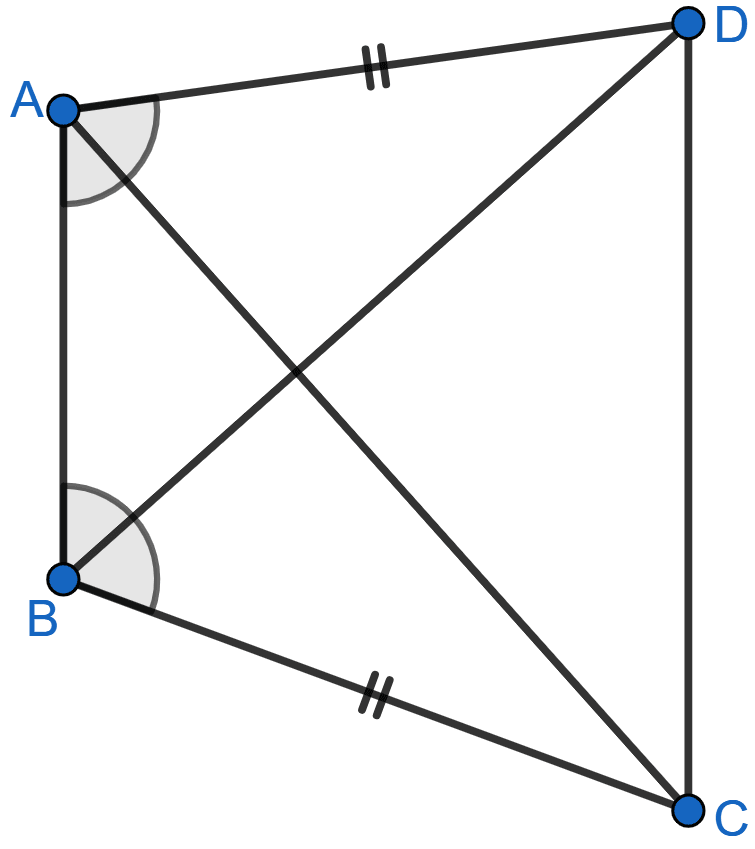
In the adjoining figure, ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA. Prove that
(i) △ABD ≅ △BAC
(ii) BD = AC
(iii) ∠ABD = ∠BAC
Answer
(i) In △ABD and △BAC,
AD = BC (Given)
∠BAD = ∠ABC (Given)
AB = AB (Common sides)
Hence, by SAS axiom △ABD ≅ △BAC.
(ii) As, △ABD ≅ △BAC.
We know that corresponding sides of congruent triangles are equal.
∴ BD = AC.
Hence, proved that BD = AC.
(iii) As, △ABD ≅ △BAC.
We know that corresponding angles of congruent triangles are equal.
∴ ∠ABD = ∠BAC.
Hence, proved that ∠ABD = ∠BAC.
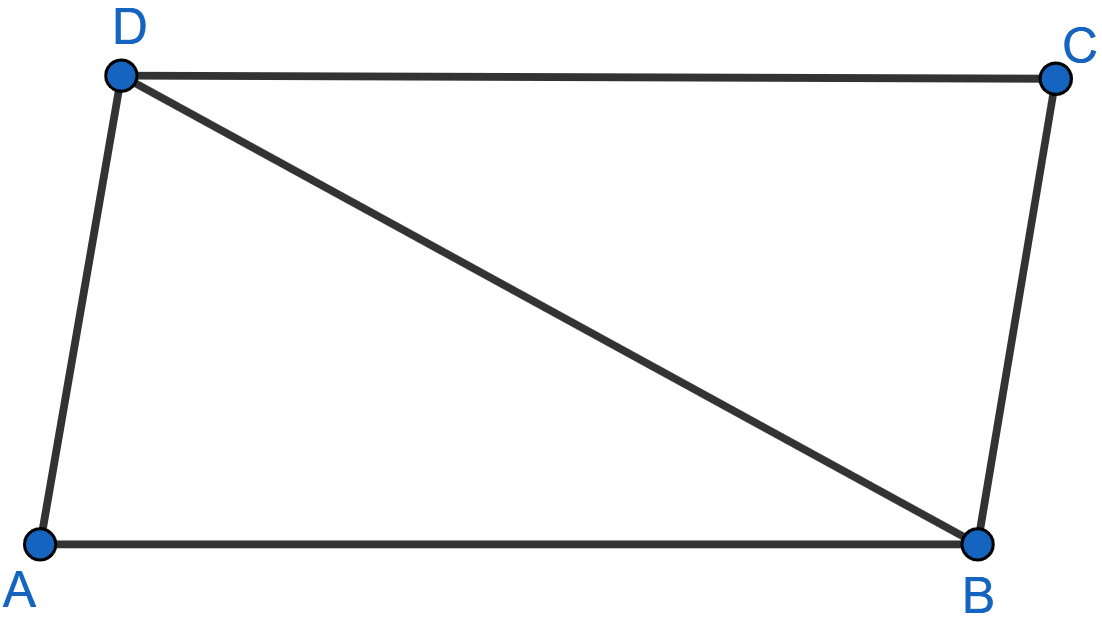
In the adjoining figure, AB = DC and AB || DC. Prove that AD = BC.
Answer
In △ABD and △CDB,
AD = BC (Given)
∠ABD = ∠CDB (Alternate angles are equal)
BD = BD (Common sides)
∴ △ABD ≅ △CDB. (By SAS axiom)
We know that corresponding sides of congruent triangles are equal.
∴ AD = BC.
Hence, proved that AD = BC.
In the adjoining figure AC = AE, AB = AD and ∠BAD = ∠CAE. Show that BC = DE.

Answer
Join DE.

Given,
⇒ ∠BAD = ∠CAE
∴ ∠BAD + ∠DAC = ∠CAE + ∠DAC
⇒ ∠BAC = DAE.
In △ABC and △ADE,
AC = AE (Given)
AB = AD (Given)
∠BAC = DAE (Proved)
∴ △ABC ≅ △ADE by SAS axiom.
We know that corresponding sides of congruent triangles are equal.
∴ BC = DE.
Hence, proved that BC = DE.
In the adjoining figure, AB = AC and D is the midpoint of BC. Use SSS rule of congruency to show that
(i) △ABD ≅ △ACD
(ii) AD is bisector of ∠A
(iii) AD is perpendicular to BC.

Answer
(i) In △ABD and △ACD,
Given,
AB = AC (Given)
BD = CD (As D is the midpoint of BC)
AD = AD (Common)
Hence, by SSS axiom △ABD ≅ △ACD.
(ii) Since, △ABD ≅ △ACD
We know that corresponding angles of congruent triangle are equal.
∴ ∠BAD = ∠CAD.
Hence, proved that AD is bisector of ∠A.
(iii) △ABD ≅ △ACD
We know that corresponding angles of congruent triangles are equal.
∠ADB = ∠ADC.
Let ∠ADB = ∠ADC = x.
We know that,
⇒ ∠ADB + ∠ADC = 180°
⇒ x + x = 180°
⇒ 2x = 180°
⇒ x = 90°.
Hence, ∠ADB = ∠ADC = 90°.
Hence, proved that AD is perpendicular to BC.
In the adjoining figure, AB = CD, CE = BF and ∠ACE = ∠DBF. Prove that
(i) △ACE ≅ △DBF
(ii) AE = DF.

Answer
(i) In △ACE and △DBF,
Given,
AB = CD
⇒ AB + BC = CD + BC
⇒ AC = BD.
∠ACE = ∠DBF (Given)
CE = BF (Given)
Hence, by SAS axiom △ACE ≅ △DBF.
(ii) We know that, △ACE ≅ △DBF.
We know that corresponding sides of congruent triangles are equal.
∴ AE = DF.
Hence, proved that AE = DF.
Two line segments AC and BD bisect each other at P. Draw the diagram and prove that
(i) AB = CD
(ii) ∠BAC = ∠DCA
Answer
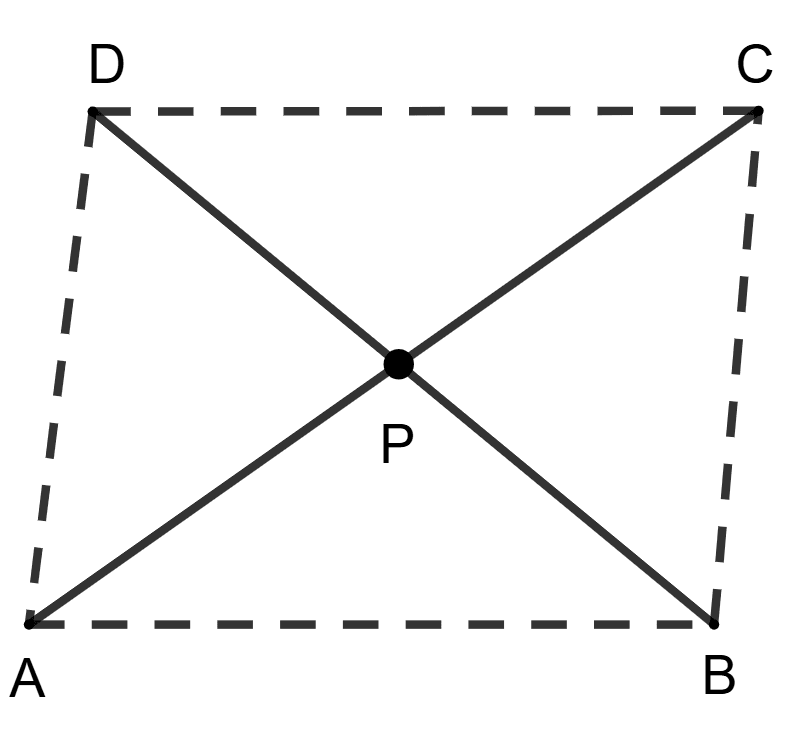
(i) Given, AC and BD bisect each other at P.
Join CD, BC, AB and AD.
In △BPA and △CPD,
As, P bisects AC and BD
⇒ PA = PC (P bisects AC and BD)
⇒ PB = PD (P bisects AC and BD)
⇒ ∠BPA = ∠CPD (Vertically opposite angles are equal).
∴ △BPA ≅ △CPD by SAS axiom.
We know that corresponding sides of congruent triangles are equal.
∴ AB = CD (By C.P.C.T.C.)
Hence, proved that AB = CD.
(ii) As proved in part (i),
△BPA ≅ △CPD by SAS axiom.
We know that corresponding angles of congruent triangles are equal.
∠DCP = ∠PAB ........................(1)
From figure we get,
∠DCP = ∠DCA and ∠PAB = ∠BAC.
Substituting above values in equation (1) we get,
∠DCA = ∠BAC.
Hence, proved that ∠BAC = ∠DCA.
Prove that the median drawn from the vertex P of an isosceles triangle △PQR with PQ = PR is perpendicular to QR and bisects ∠P.
Answer
Let PQR be an isosceles triangle with PQ = PR.
Draw a median from vertex P to the side QR. Let this median be PS, where S is the midpoint of QR.
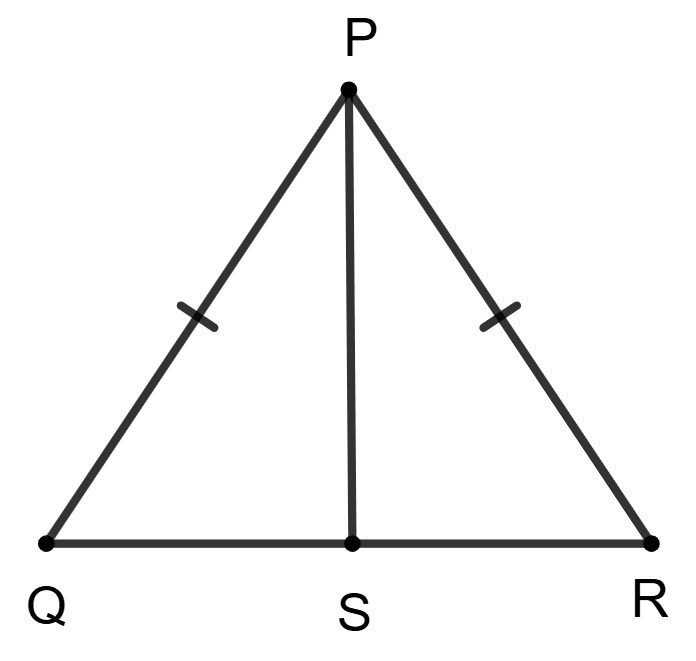
In △PQS and △PRS,
⇒ PQ = PR (△PQR is an isosceles triangle).
⇒ QS = RS (Since PS is the median, S is the midpoint of QR).
⇒ PS = PS (Common side to both triangles).
By the SSS (Side-Side-Side) congruence criterion,
△PQS ≅ △PRS
We know that,
Corresponding parts of congruent triangles are congruent.
⇒ ∠PSQ = ∠PSR = x (let)
From figure,
⇒ ∠PSQ + ∠PSR = 180° [Linear pair]
⇒ x + x = 180°
⇒ 2x = 180°
⇒ x = = 90°.
⇒ ∠PSQ = ∠PSR = 90°.
Thus, PS is perpendicular to QR.
So, PS ⊥ QR.
⇒ ∠QPS = ∠RPS (By C.P.C.T.C.)
Thus, PS bisects ∠P.
Hence, the median drawn from the vertex P of an isosceles triangle △PQR is perpendicular to QR and bisects ∠P.
In the adjoining figure, find the values of x and y.
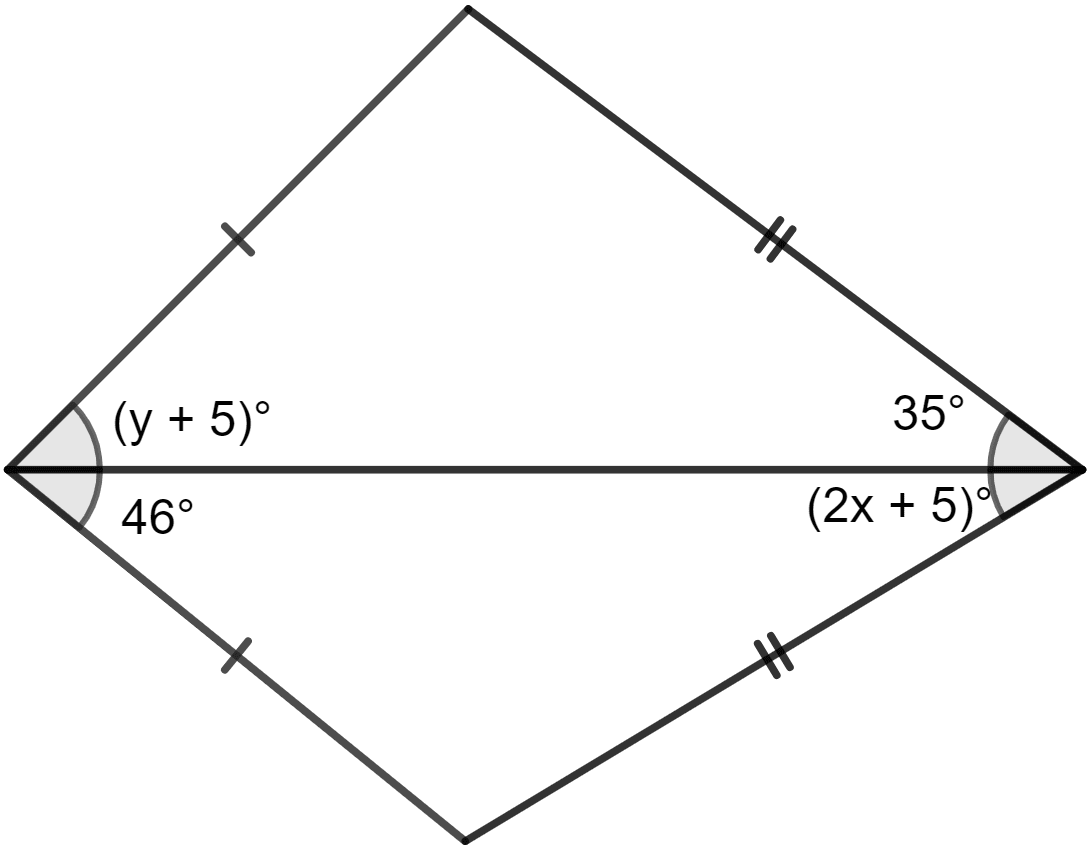
Answer
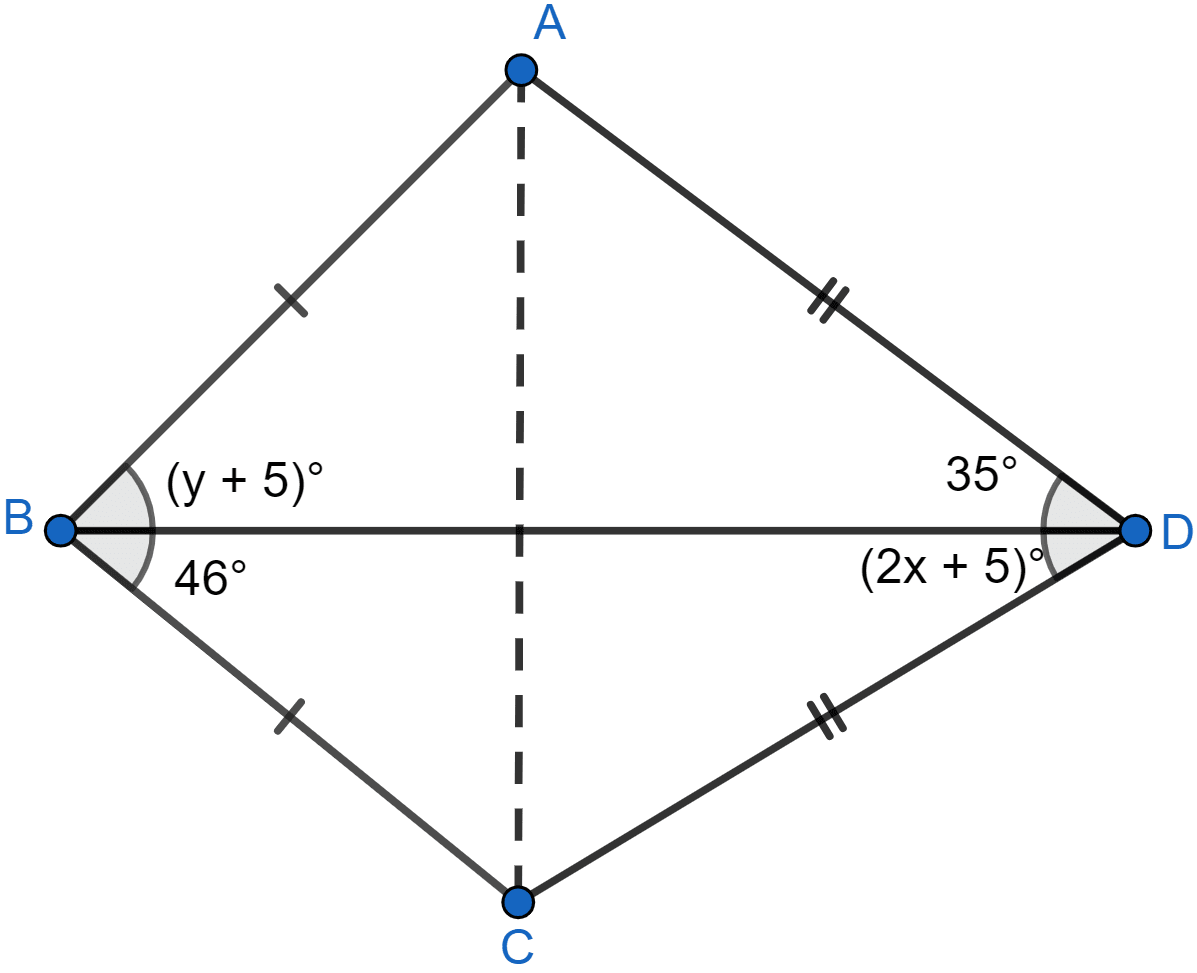
In △ABD and △CBD,
Given,
AB = BC (Given)
AD = CD (Given)
BD = BD (Common)
Hence, by SSS axiom △ABD ≅ △CBD.
We know that corresponding angles of congruent triangles are equal.
∴ (y + 5)° = 46° and (2x + 5)° = 35°
y° = 41° and 2x° = 30°
y = 41 and x = 15.
Hence, x = 15 and y = 41.
In triangles ABC and PQR, ∠A = ∠Q and ∠B = ∠R. Which side of △PQR should be equal to side AB of △ABC so that the two triangles are congruent? Give reason for your answer.
Answer
Given in triangles ABC and PQR,
∠A = ∠Q,
∠B = ∠R,
So, AB should be equal to QR. That will make, △ABC ≅ △QRP by ASA axiom.
Hence, AB = QR for △ABC ≅ △QRP by ASA axiom.
In triangles ABC and PQR, ∠A = ∠Q and ∠B = ∠R. Which side of △PQR should be equal to side BC of △ABC so that the two triangles are congruent? Give reason for your answer.
Answer
Given in triangles ABC and PQR,
∠A = ∠Q,
∠B = ∠R,
So BC should be equal to RP. That will make, △ABC ≅ △QRP by AAS axiom.
Hence, BC = RP for △ABC ≅ △QRP by AAS axiom.
"If two angles and a side of one triangle are equal to two angles and a side of another triangle, then the two triangles must be congruent". Is the statement true? Why?
Answer
"If two angles and a side of one triangle are equal to two angles and a side of another triangle, then the two triangles must be congruent".
The above statement is not true because the sides must be corresponding sides.
In the adjoining figure, AD is median of △ABC, BM and CN are perpendiculars drawn from B and C respectively on AD and AD produced. Prove that BM = CN.
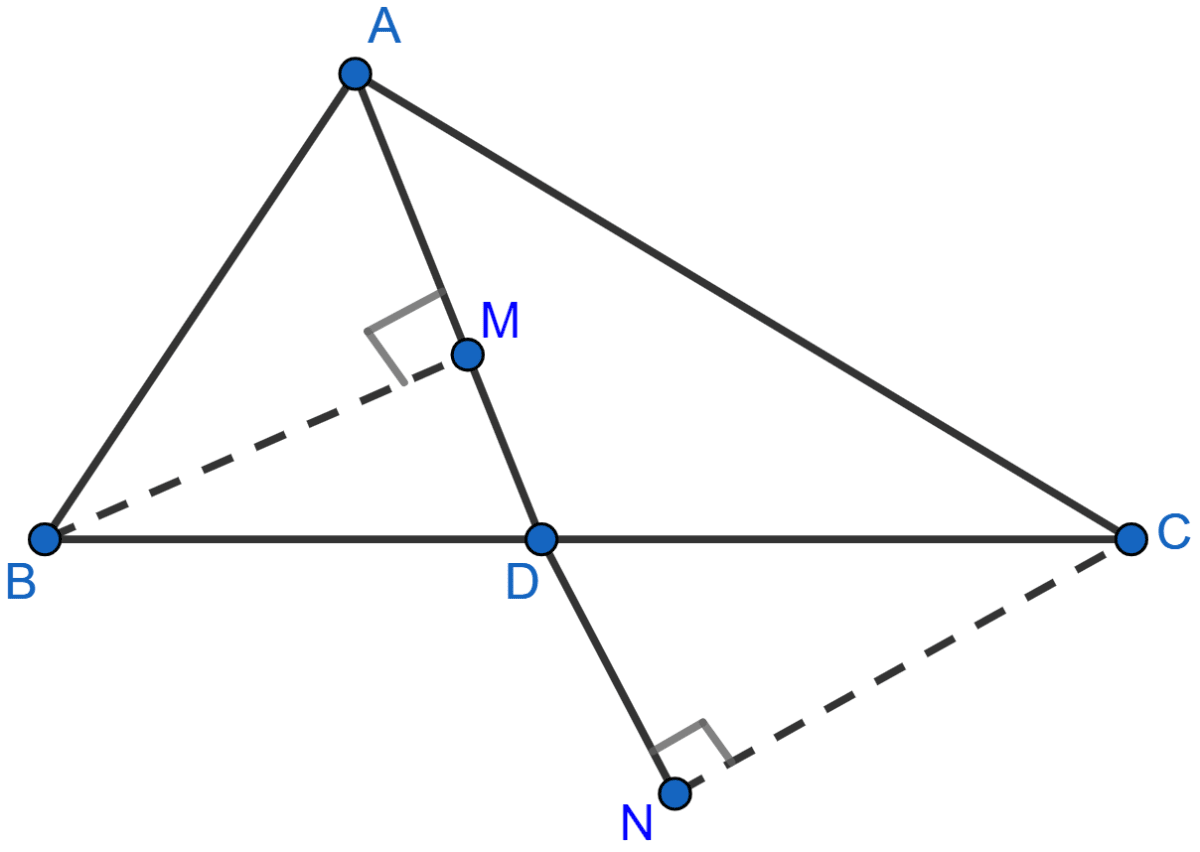
Answer
In △BMD and △CND,
BD = CD (As AD divides BC in two halves).
∠BMD = ∠CND (Both are equal to 90°)
∠BDM = ∠CDN (Vertically opposite angles)
∴ △BMD ≅ △CND by AAS axiom.
We know that corresponding sides of congruent triangles are equal.
∴ BM = CN.
Hence, proved that BM = CN.
In the adjoining figure, BM and DN are perpendiculars to the line segment AC. If BM = DN, prove that AC bisects BD.
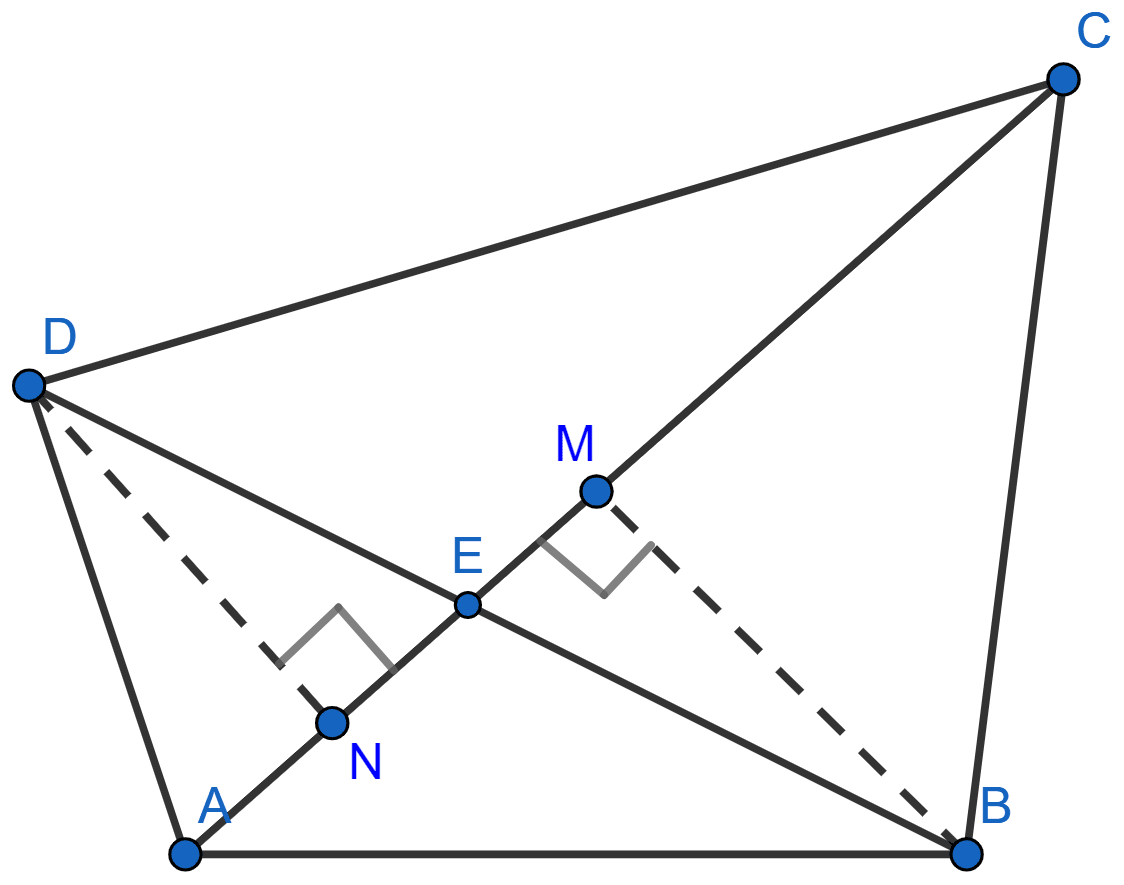
Answer
In △BEM and △DEN,
BM = DN (Given).
∠BME = ∠DNE (Both are equal to 90°)
∠BEM = ∠DEN (Vertically opposite angles)
∴ △BEM ≅ △DEN by AAS axiom.
We know that corresponding parts of congruent triangles are equal.
∴ DE = BE.
Since, DE = BE it means that AC bisects BD at E.
Hence, proved that AC bisects BD.
In the adjoining figure, l and m are two parallel lines intersected by another pair of parallel lines p and q. Show that △ABC ≅ △CDA.
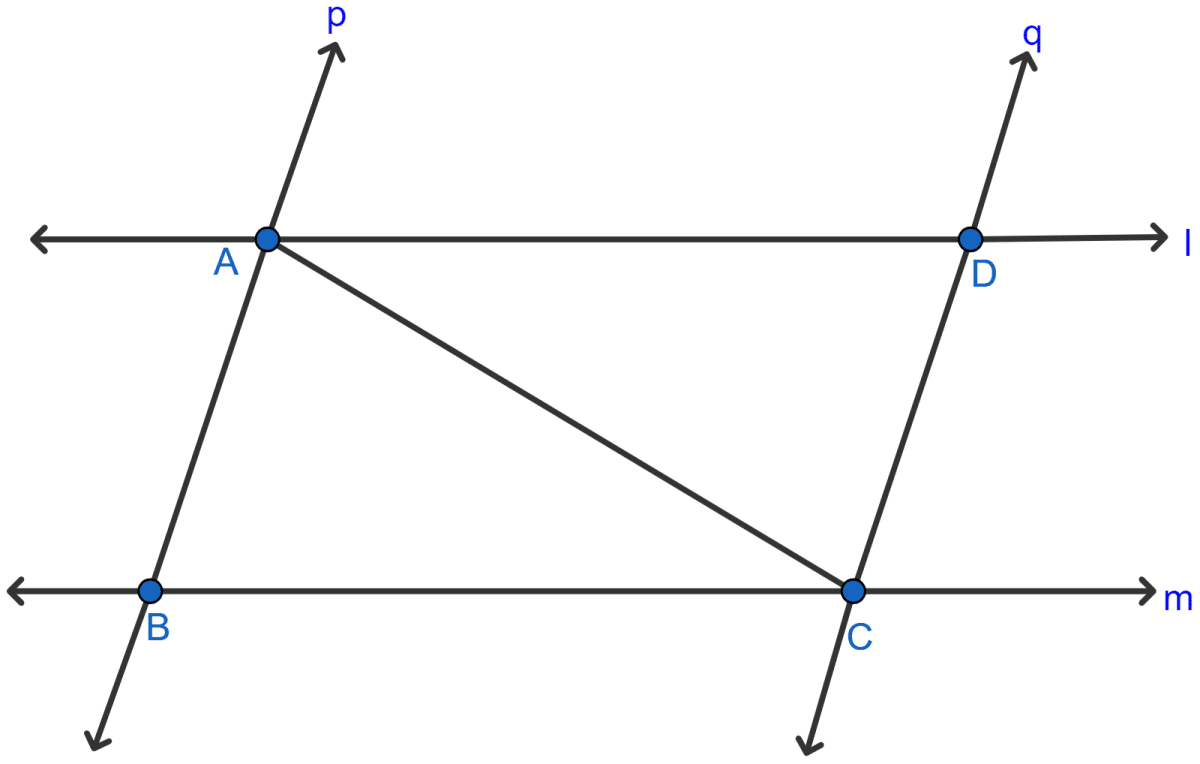
Answer
In △ABC and △CDA,
AC = AC (Common).
∠ACB = ∠CAD (Alternate angles)
∠BAC = ∠ACD (Alternate angles)
Hence, proved that △ABC ≅ △CDA by ASA axiom.
In the adjoining figure, two lines AB and CD intersect each other at the point O such that BC || DA and BC = DA. Show that O is the mid-point of both the line segments AB and CD.

Answer
In △BOC and △DOA,
BC = DA (Given).
∠CBO = ∠DAO (Alternate angles)
∠BOC = ∠DOA (Vertically opposite angles)
∴ △BOC ≅ △DOA by ASA axiom.
We know that corresponding parts of congruent triangles are equal.
∴ BO = AO and CO = DO.
Hence, proved that O is the mid-point of AB and CD.
In the adjoining figure, ∠BCD = ∠ADC and ∠BCA = ∠ADB. Show that
(i) △ACD ≅ △BDC
(ii) BC = AD
(iii) ∠A = ∠B

Answer
(i) In △ACD and △BDC,
Given,
∠BCD = ∠ADC
∠BCA = ∠ADB
∴ ∠BCD + ∠BCA = ∠ADC + ∠ADB
⇒ ∠ACD = ∠BDC
CD = CD (Common).
∠ADC = ∠BCD (Given)
Hence, proved that △ACD ≅ △BDC by ASA axiom.
(ii) We know that, △ACD ≅ △BDC.
We know that corresponding sides of congruent triangles are equal.
∴ BC = AD.
Hence, proved that BC = AD.
(iii) We know that, △ACD ≅ △BDC.
We know that corresponding angles of congruent triangles are equal.
∴ ∠A = ∠B.
Hence, proved that ∠A = ∠B.
In the adjoining figure, ∠ABC = ∠ACB, D and E are points on the sides AC and AB respectively such that BE = CD. Prove that
(i) △EBC ≅ △DCB
(ii) △OEB ≅ △ODC
(iii) OB = OC.

Answer
(i) Given, ∠ABC = ∠ACB.
∴ ∠EBC = ∠DCB.
In △EBC and △DCB,
∠EBC = ∠DCB (Proved)
BE = CD (Given)
BC = BC (Common)
Hence, proved △EBC ≅ △DCB by SAS axiom.
(ii) We know that, △EBC ≅ △DCB.
Subtracting common △OBC from both sides we get,
⇒ △EBC - △OBC ≅ △DCB - △OBC
⇒ △OEB ≅ △ODC
Hence, proved that △OEB ≅ △ODC.
(iii) We know that,
△OEB ≅ △ODC
We know that corresponding angles of congruent triangles are equal.
∴ OB = OC.
Hence, proved that OB = OC.
ABC is an isosceles triangle with AB = AC. Draw AP ⊥ BC to show that ∠B = ∠C.
Answer

In △APB and △APC,
AB = AC (Given).
∠APB = ∠APC (Both are equal to 90°)
AP = AP (Common)
∴ △APB ≅ △APC by RHS axiom.
We know that corresponding angles of congruent triangles are equal.
∴ ∠B = ∠C.
Hence, proved that ∠B = ∠C.
In the adjoining figure, BA ⊥ AC, DE ⊥ DF such that BA = DE and BF = EC. Show that △ABC ≅ △DEF.

Answer
In △ABC and △DEF,
BF = EC (Given)
⇒ BF + FC = EC + FC
∴ BC = FE.
BA = DE (Given)
∠BAC = ∠EDF (Both are equal to 90°)
∴ △ABC ≅ △DEF (By RHS axiom)
Hence, proved that △ABC ≅ △DEF.
ABCD is a rectangle. X and Y are points on sides AD and BC respectively such that AY = BX. Prove that BY = AX and ∠BAY = ∠ABX.
Answer

In △ABY and △ABX,
AB = AB (Common)
∠XAB = ∠YBA (Each angle in rectangle is equal to 90°)
AY = BX (Given)
∴ △ABY ≅ △ABX (By RHS axiom)
We know that corresponding parts of congruent triangles are equal.
∴ BY = AX and ∠BAY = ∠ABX.
Hence, proved that BY = AX and ∠BAY = ∠ABX.
In the figure (1) given below, QX, RX are bisectors of angles PQR and PRQ respectively of △PQR. If XS ⊥ QR and XT ⊥ PQ, prove that
(i) △XTQ ≅ △XSQ
(ii) PX bisects the angle P.
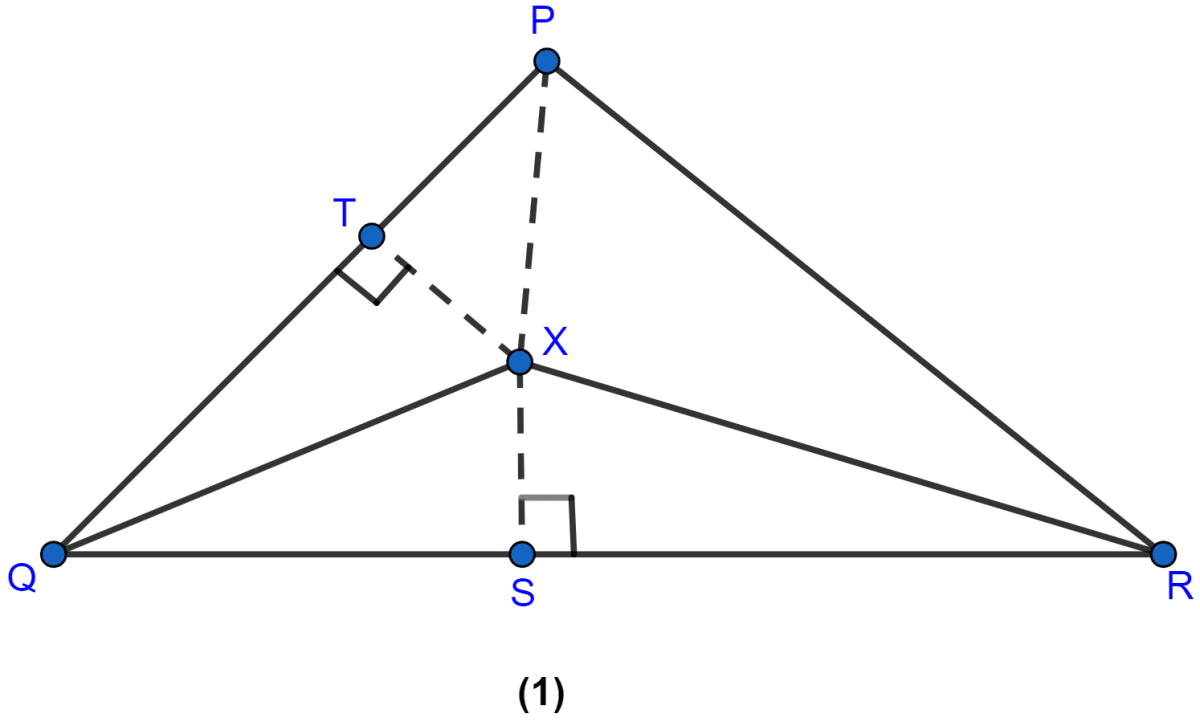
Answer
(i) Given, QX is the bisector of ∠PQR
∴ ∠PQX = ∠XQS
From figure,
∠XTQ = ∠XSQ (Both are equal to 90°)
XQ = XQ
Hence, △XTQ ≅ △XSQ by ASA axiom.
Hence, proved that △XTQ ≅ △XSQ.
(ii) Draw a perpendicular from X on PR i.e. XU.
In △XSR and △XUR,
∠XSR = ∠XUR (Both are equal to 90°)
∠XRS = ∠XRU (As XR is bisector)
XR = XR (Common)
Hence, △XSR ≅ △XUR by AAS axiom.
We know that corresponding parts of congruent triangle are equal.
∴ XU = XS ........(i)
As, △XTQ ≅ △XSQ
∴ XS = XT .......(ii)
In △XUP and △XTP,
From (i) and (ii) we get,
XU = XT
XP = XP (Common)
∠XTP = ∠XUP (Both are equal to 90°)
Hence, △XUP ≅ △XTP by SAS axiom.
We know that corresponding parts of congruent triangle are equal.
∴ ∠XPU = ∠XPT
Hence, proved that PX is bisector of ∠P.
In the figure (2) given below, AB || DC and ∠C = ∠D. Prove that
(i) AD = BC
(ii) AC = BD.

Answer
(i) Draw AE ⊥ CD, BF ⊥ CD.

Considering △ADE and △BCF we get,
∠ADE = ∠BCF (Given)
∠AED = ∠BFC = 90°
AE = BF (Distance between parallel lines are equal)
Hence, △ADE ≅ △BCF by AAS axiom.
We know that corresponding parts of congruent triangles are equal.
∴ AD = BC.
Hence, proved that AD = BC.
(ii) Join AC, BD.
Considering △ACD and △BDC we get,
∠ADC = ∠BCD (Given)
AD = BC (Proved)
DC = DC (Common)
Hence, △ACD ≅ △BDC by SAS axiom.
We know that corresponding parts of congruent triangles are equal.
∴ AC = BD.
Hence, proved that AC = BD.
In the figure (3) given below, BA || DF and CA || EG and BD = EC. Prove that
(i) BG = DF
(ii) EG = CF.

Answer
Given,
BD = EC
BD + DE = DE + EC
BE = DC.
Considering △BGE and △DFC,
∠GBE = ∠FDC (Corresponding angles)
∠GEB = ∠FCD (Corresponding angles)
BE = DC (Proved).
∴ △BGE ≅ △DFC by ASA axiom..
We know that corresponding parts of congruent triangles are equal.
∴ BG = DF.
Hence, proved that BG = DF.
(ii) We know,
△BGE ≅ △DFC.
We know that corresponding parts of congruent triangles are equal.
∴ EG = CF.
Hence, proved that EG = CF.
In the following figure, find the values of x and y.

Answer

In △ABC and △CDE,
∠ACB = ∠DCE (Vertically opposite angles)
∠BAC = ∠CED (Given)
BC = CD (Given)
∴ △ABC ≅ △CDE (By AAS axiom)
We know that corresponding parts of congruent triangles are equal.
∴ DE = AB
⇒ 2y + 3 = 25
⇒ 2y = 22
⇒ y = 11.
Given, BC = CD
⇒ 3x - 7 = 32
⇒ 3x = 32 + 7
⇒ 3x = 39
⇒ x = 13.
Hence, x = 13 and y = 11.
In the following figure, find the values of x and y.
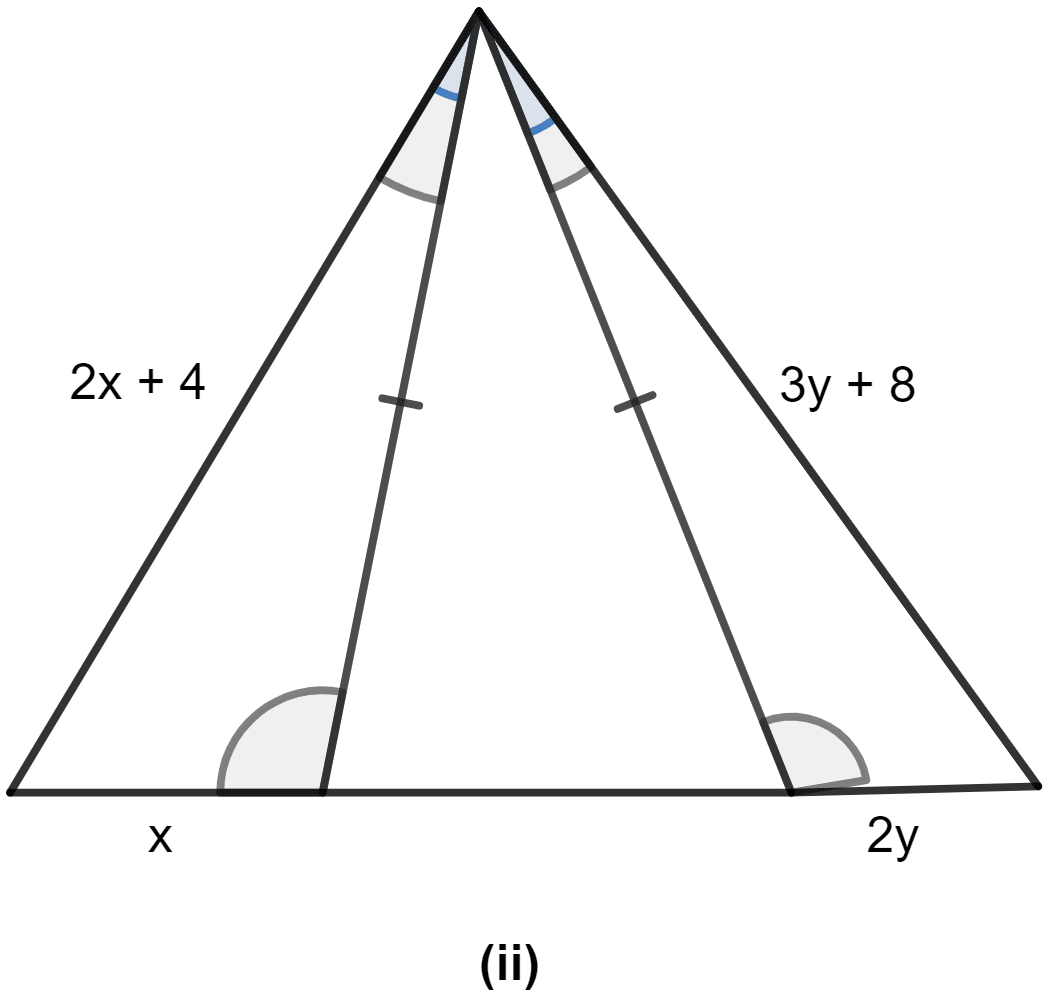
Answer
In △ABC and △ADE,
∠BAC = ∠DAE (Given)
∠BCA = ∠EDA (Given)
AC = AD (Given)
∴ △ABC ≅ △ADE (By ASA axiom)
We know that corresponding parts of congruent triangles are equal.
∴ BC = DE
⇒ x = 2y ......(i)
∴ AB = AE
⇒ 2x + 4 = 3y + 8
Substituting value of x from (i) in above equation we get,
⇒ 2(2y) + 4 = 3y + 8
⇒ 4y + 4 = 3y + 8
⇒ 4y - 3y = 8 - 4
⇒ y = 4.
∴ x = 2y = 2(4) = 8.
Hence, x = 8 and y = 4.
ABC is a right angled triangle in which ∠A = 90° and AB = AC. Find ∠B and ∠C.
Answer
Given,
AB = AC.

We know that angles opposite to equal sides of an isosceles triangle are equal.
∴ ∠B = ∠C = x°.
Sum of angles of triangle = 180°.
⇒ ∠A + ∠B + ∠C = 180°
⇒ 90° + x° + x° = 180°
⇒ 90° + 2x° = 180°
⇒ 2x° = 90°
⇒ x° = 45°.
Hence, ∠B = ∠C = 45°.
Show that the angles of an equilateral triangle are 60° each.
Answer
In equilateral triangle all sides are equal.
AB = BC = CA
∴ ∠C = ∠A = ∠B = x° (Angles opposite to equal sides are equal).
Sum of angles of triangle = 180°
∠A + ∠B + ∠C = 180°
x° + x° + x° = 180°
3x° = 180°
x = 60°.
Hence, proved that angles of an equilateral triangle are 60° each.
Show that every equiangular triangle is equilateral.
Answer
Let ABC be a triangle with, ∠A = ∠B = ∠C.
Considering, ∠A = ∠B
We get, BC = AC (Sides opposite to equal angles are equal.)
Considering, ∠B = ∠C
We get, AB = BC (Sides opposite to equal angles are equal.)
∴ AB = BC = AC.
Hence, proved that every equiangular triangle is equilateral.
In the following figure, find the value of x:

Answer
Since, △ABC is an isosceles triangle with AB = AC.
∴ ∠B = ∠C = y°
Sum of angles of triangle = 180°.
⇒ 50° + y° + y° = 180°
⇒ 50° + 2y° = 180°
⇒ 2y° = 180° - 50° = 130°.
⇒ y° = 65°.
From figure,
⇒ x° + y° = 180°
⇒ x° + 65° = 180°
⇒ x° = 180° - 65° = 115°.
Hence, x = 115°.
In the following figure, find the value of x:

Answer
From figure,
△PRS is an isosceles triangle with PR = SR.
∴ ∠S = ∠RPS = 30°.
∠QPS = ∠QPR + ∠RPS = 52° + 30° = 82°.
Since, sum of angles of triangle = 180°.
Considering △PQS we get,
⇒ ∠P + ∠Q + ∠S = 180°
⇒ 82° + x° + 30° = 180°
⇒ x° + 112° = 180°
⇒ x° = 180° - 112° = 68°.
Hence, x = 68°.
In the following figure, find the value of x:

Answer
△BDC is an isosceles triangle with BD = DC,
∴ ∠DBC = ∠DCB = 27°.
We know that,
An exterior angle is equal to the sum of two opposite interior angles,
Ext. ∠ADC = ∠DBC + ∠DCB = 27° + 27° = 54°.
△ADC is an isosceles triangle with AC = DC,
∴ ∠DAC = ∠ADC = 54°.
Since, sum of angles of triangle = 180°.
Considering △ADC we get,
⇒ ∠DAC + ∠ADC + ∠DCA = 180°
⇒ 54° + 54° + x = 180°
⇒ x + 108° = 180°
⇒ x = 180° - 108° = 72°.
Hence, x = 72°.
In the following figure, find the value of x:

Answer
△ABD is an isosceles triangle with BD = AD,
∴ ∠DBA = ∠BAD = 48°.
We know that,
An exterior angle is equal to the sum of two opposite interior angles,
Ext. ∠ADC = ∠BAD + ∠DBA = 48° + 48° = 96°.
△ADC is an isosceles triangle with AD = DC,
∴ ∠DAC = ∠DCA = x°.
Since, sum of angles of triangle = 180°.
Considering △ADC we get,
⇒ ∠DAC + ∠ADC + ∠DCA = 180°
⇒ x° + 96° + x° = 180°
⇒ 2x° + 96° = 180°
⇒ 2x° = 180° - 96° = 84°
⇒ x° = 42°
Hence, x = 42°.
In the following figure, find the value of x:

Answer
From figure,
∠ACD = 180° - 130° = 50°.
In △ADC, AD = CD.
∴ ∠DAC = ∠ACD = 50°.
∠ADC = 180° - (∠CAD + ∠DCA) = 180° - (50° + 50°) = 80°.
From figure,
∠ADB + ∠ADC = 180°
∠ADB = 180° - ∠ADC = 180° - 80° = 100°.
In △ADB,
∠DBA = ∠DAB = x° (As angles opposite to equal sides are equal)
∠DBA + ∠DAB + ∠ADB = 180°
x° + x° + 100° = 180°
2x° = 80°
x° = 40°
Hence, x = 40°.
In the following figure, find the value of x:

Answer
In △ADC,
DC = CA (Given)
∴ ∠ADC = ∠CAD = a.
∠ADC + ∠DCA + ∠CAD = 180°
⇒ a + 56° + a = 180°
⇒ 2a = 180° - 56°
⇒ 2a = 124°
⇒ a = 62°.
In △ABD,
AD = BD (Given)
∴ ∠ABD = ∠DAB = (x - a)°
In △ABD,
∠ABD + ∠BDA + ∠DAB = 180°
⇒ (x - a)° + (180 - a)° + (x - a)° = 180°
⇒ 2x° - 3a° + 180° = 180°
⇒ 2x° - 3(62°) = 0
⇒ 2x° - 186° = 0
⇒ 2x° = 186°
⇒ x° = 93°
⇒ x = 93.
Hence, x = 93.
In the figure (1) given below, AB = AD, BC = DC. Find ∠ABC.

Answer
Join BD.

In △ABD,
AB = AD
∴ ∠ABD = ∠ADB = a.
∠ABD + ∠ADB + ∠DAB = 180°
a + a + 54 = 180°
2a + 54° = 180°
2a = 126°
a = 63°.
In △BCD,
BC = CD
∴ ∠CDB = ∠DBC = b.
∠CDB + ∠DBC + ∠BCD = 180°
b + b + 116° = 180°
2b + 116° = 180°
2b = 64°
b = 32°.
From figure,
∠ABC = a + b = 63 + 32 = 95°.
Hence, ∠ABC = 95°.
In the figure (2) given below, BC = CD. Find ∠ACB.
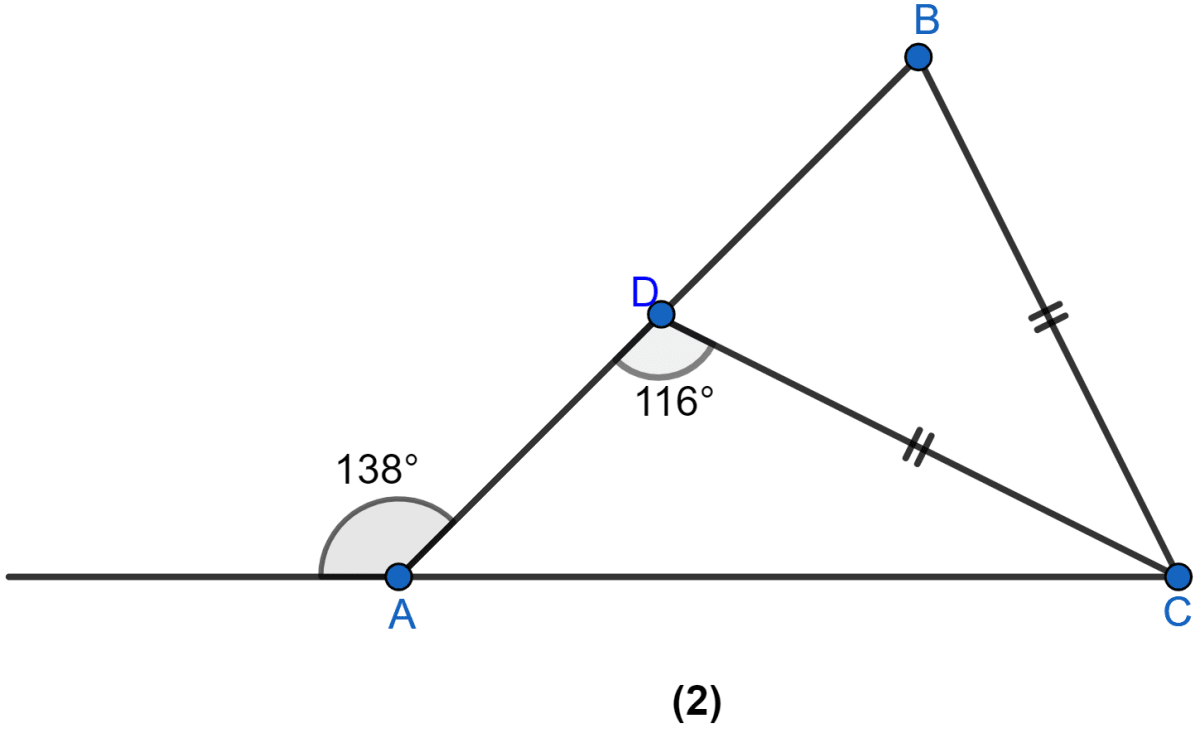
Answer
From figure,
∠DAC = 180° - 138° = 42°.
∠BDC = 180° - ∠ADC = 180° - 116° = 64°.
In △BCD,
∠CBD = ∠BDC = 64°.
∠DCB = 180° - (∠CBD + ∠BDC) = 180° - (64° + 64°)
= 180° - 128° = 52°.
In △ADC,
∠DCA = 180° - (∠CAD + ∠ADC) = 180° - (42° + 116°)
= 180° - 158° = 22°.
From figure,
∠ACB = ∠DCB + ∠DCA = 52° + 22° = 74°.
Hence, ∠ACB = 74°.
In the figure (3) given below, AB || CD and CA = CE. If ∠ACE = 74° and ∠BAE = 15°, find the values of x and y.
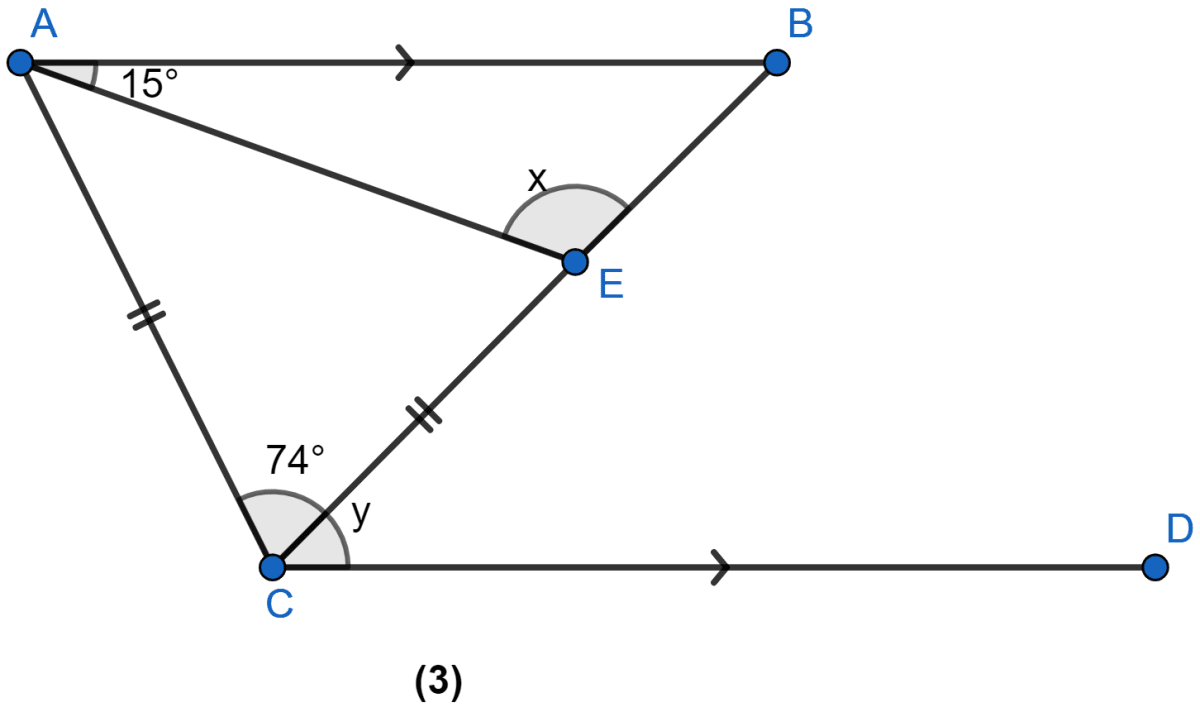
Answer
From figure,
∠CAE = ∠CEA = a (Angles opposite to equal side are equal.)
In △ACE
⇒ ∠CAE + ∠CEA + ∠ACE = 180°
⇒ a + a + 74° = 180°
⇒ 2a = 106°
⇒ a = 53°.
From figure,
∠CEA + ∠AEB = 180°
a + x = 180°
53° + x = 180°
x = 180° - 53° = 127°.
In △AEB,
⇒ ∠EAB + ∠AEB + ∠ABE = 180°
⇒ 15 + 127° + ∠ABE = 180°
⇒ 142° + ∠ABE = 180°
⇒ ∠ABE = 180° - 142° = 38°.
From figure,
y = ∠ABE (Alternate angles)
∴ y = 38°.
Hence, x = 127° and y = 38°.
In △ABC, AB = AC, ∠A = (5x + 20)° and each of the base angle is th of ∠A. Find the measure of ∠A.
Answer
Given, each of the base angle is th of ∠A.
∴ Each base angle = × (5x + 20) = (2x + 8)°

In △ABC,
∠A + ∠B + ∠C = 180°
(5x + 20)° + (2x + 8)° + (2x + 8)° = 180°
9x° + 36° = 180°
9x° = 144°
x° = 16°.
(5x + 20)° = 5(16°) + 20° = 80° + 20° = 100°.
Hence, ∠A = 100°.
In the figure (1) given below, ABC is an equilateral triangle. Base BC is produced to E, such that BC = CE. Calculate ∠ACE and ∠AEC.

Answer
Since, ABC is an equilateral triangle, ∠A = ∠B = ∠C = 60°.
From figure,
∠ACB + ∠ACE = 180°
60° + ∠ACE = 180°
∠ACE = 120°.
From figure,
∠AEC = ∠CAE (As angles opposite to equal sides are equal)
Let ∠AEC = ∠CAE = y.
From figure,
∠AEC + ∠CAE + ∠ACE = 180°
y + y + 120° = 180°
2y = 60°
y = 30°.
Hence, ∠ACE = 120° and ∠AEC = 30°.
In the figure (2) given below, prove that ∠BAD : ∠ADB = 3 : 1.

Answer
From figure,
∠ADC = ∠CAD (As angles opposite to equal sides of triangle are equal) ......(i)
From figure,
∠BAD = ∠BAC + ∠CAD = ∠BAC + ∠ADC = ∠BAC + ∠ADB .......(ii)
From △ABC,
∠BAC = ∠ACB (As angles opposite to equal sides of triangle are equal) ......(iii)
∠ACB = 180 - (∠ACD) = 180 - [180 - (∠CAD + ∠ADC)] = ∠CAD + ∠ADC ........(iv)
From figure,
∠ADC = ∠ADB
∴ ∠CAD = ∠ADB
From (iv)
∠ACB = ∠CAD + ∠ADC = ∠ADB + ∠ADB = 2∠ADB.
From (iii) we get,
∠BAC = ∠ACB = 2∠ADB.
Substituting value of ∠BAC in (ii) we get,
∠BAD = ∠BAC + ∠ADB = 2∠ADB + ∠ADB = 3∠ADB.
Hence, ∠BAD : ∠ADB = 3∠ADB : ∠ADB = 3 : 1.
Hence, proved that ∠BAD : ∠ADB = 3 : 1.
In the figure (3) given below, AB || CD. Find the values of x, y and z.
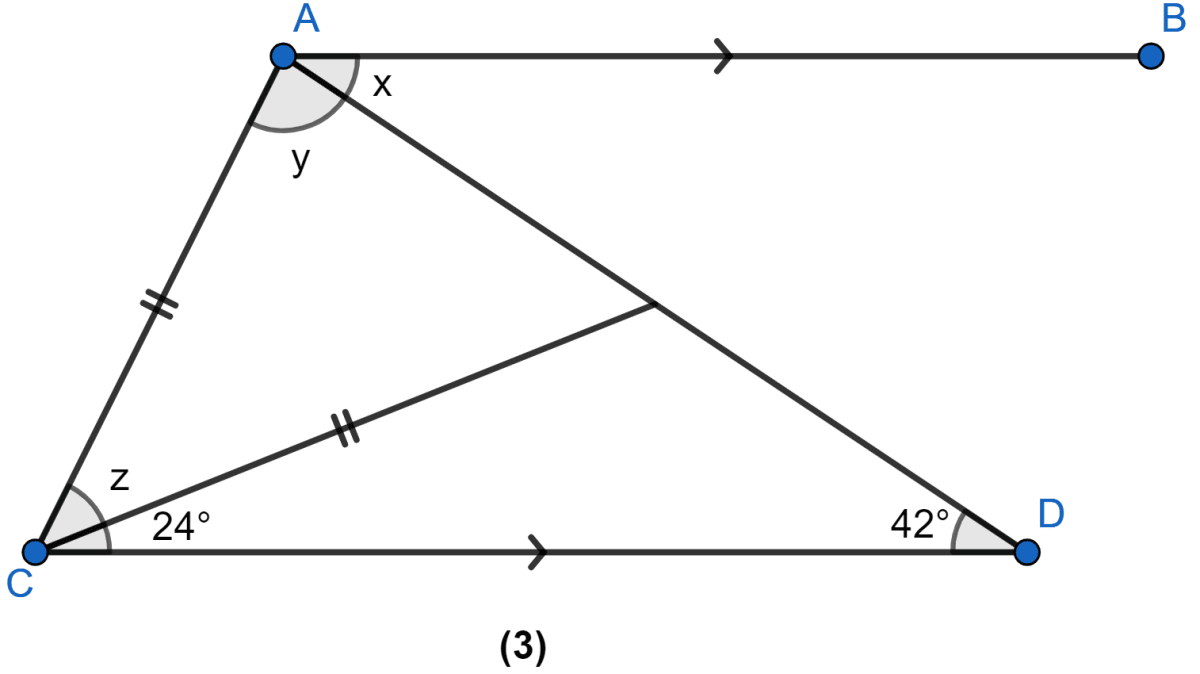
Answer
Add Answer fig
From figure,
∠BAD = ∠ADC (Alternate angles)
∴ x = 42°
In △CED,
⇒ 24° + ∠CED + 42° = 180°
⇒ ∠CED + 66° = 180°
⇒ ∠CED = 114°.
From figure,
⇒ ∠CEA + ∠CED = 180°
⇒ ∠CEA + 114° = 180°
⇒ ∠CEA = 66°.
In △CEA,
⇒ y = ∠CEA = 66° (As angles opposite to equal sides are equal)
In △CEA,
⇒ z + y + ∠CEA = 180°
⇒ z + 66° + 66° = 180°
⇒ z + 132° = 180°
⇒ z = 48°.
Hence, x = 42°, y = 66° and z = 48°.
In the adjoining figure, D is the midpoint of BC, DE and DF are perpendiculars to AB and AC respectively such that DE = DF. Prove that ABC is an isosceles triangle.
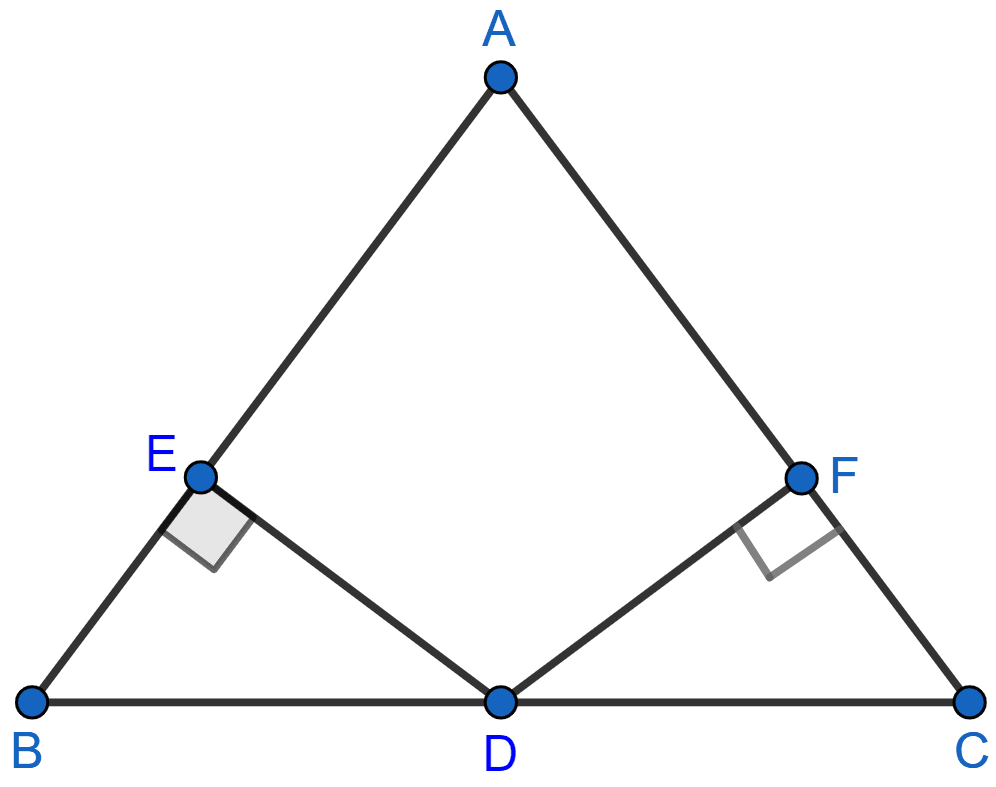
Answer
In △BED and △CFD,
∠BED = ∠CFD (Both are equal to 90°)
DE = DF (Given)
BD = DC (As D is the mid-point of BC.)
∴ △BED ≅ △CFD by RHS axiom.
We know that corresponding parts of congruent triangles are equal,
∴ ∠B = ∠C ⇒ AC = AB.
Hence, proved that ABC is an isosceles triangle.
In the adjoining figure, AD, BE and CF are altitudes of △ABC. If AD = BE = CF, prove that ABC is an equilateral triangle.
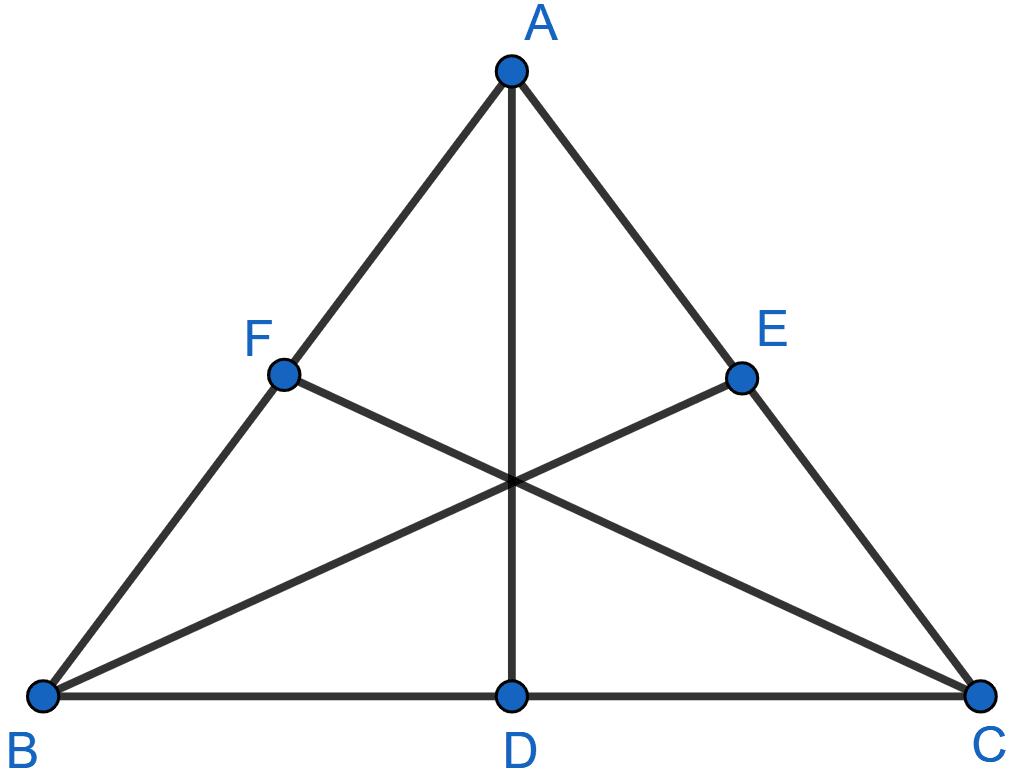
Answer
AD, BE and CF are altitudes of △ABC and
AD = BE = CF
Considering △BEC and △BFC,
Hypotenuse BC = BC (Common)
Side BE = CF (Given)
As altitudes are perpendicular to the sides,
∠CFB = ∠CEB = 90°
Hence, △BEC ≅ △BFC by RHS axiom.
We know that corresponding parts of congruent triangle are equal,
∴ ∠C = ∠B
⇒ AB = AC (Sides opposite to equal angles) .........(i)
Considering △CFA and △ADC,
AD = CF (Given)
∠ADC = ∠CFA = 90° (As altitudes are perpendicular to sides)
AC = AC (Common)
Hence, △CFA ≅ △ADC by RHS axiom.
We know that corresponding parts of congruent triangle are equal,
∴ ∠A = ∠C
⇒ AB = BC (Sides opposite to equal angles) .........(ii)
From (i) and (ii)
AB = BC = AC
△ABC is an equilateral triangle.
Hence, proved that △ABC is an equilateral triangle.
In a triangle ABC, AB = AC, D and E are points on the sides AB and AC respectively such that BD = CE. Show that:
(i) △DBC ≅ △ECB
(ii) ∠DCB = ∠EBC
(iii) OB = OC, where O is the point of intersection of BE and CD.
Answer
(i) From figure,
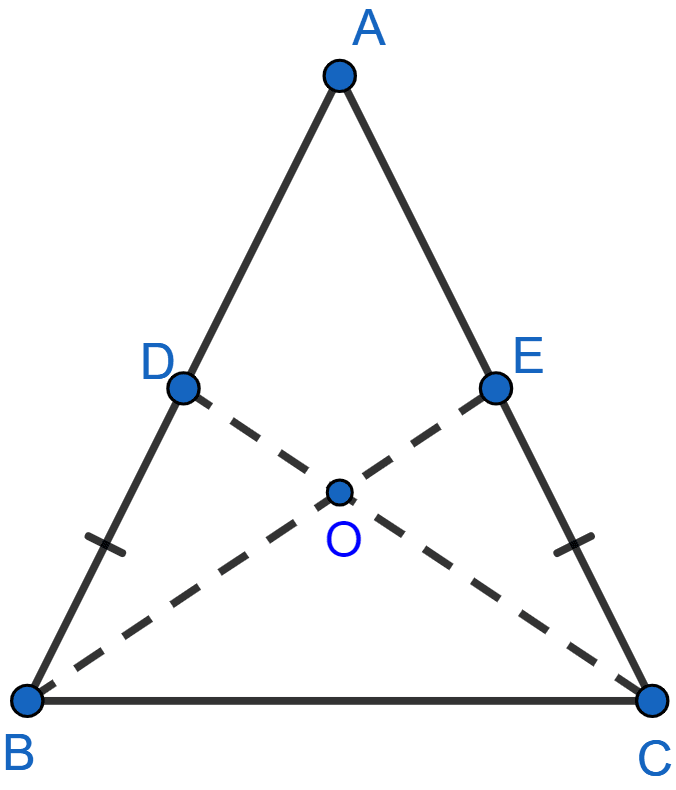
BD = CE (Given)
BC = BC (Common)
∠DBC = ∠ECB (as AB = AC).
∴ △DBC ≅ △ECB by SAS axiom.
Hence, proved △DBC ≅ △ECB.
(ii) We know that corresponding parts of congruent triangle are equal.
∴ ∠DCB = ∠EBC.
Hence, proved that ∠DCB = ∠EBC.
(iii) As △DBC ≅ △ECB,
∠BDO = ∠CEO (By c.p.c.t.)
∠DOB = ∠EOC (Vertically opposite angles)
BD = CE (Given)
Hence, △BOD ≅ △EOC by ASA axiom.
We know that corresponding parts of congruent triangles are equal.
∴ OB = OC.
Hence, proved that OB = OC.
ABC is an isosceles triangle in which AB = AC. P is any point in the interior of △ABC such that ∠ABP = ∠ACP. Prove that
(a) BP = CP
(b) AP bisects ∠BAC.
Answer
Below figure shows the isosceles triangle ABC with the points marked:
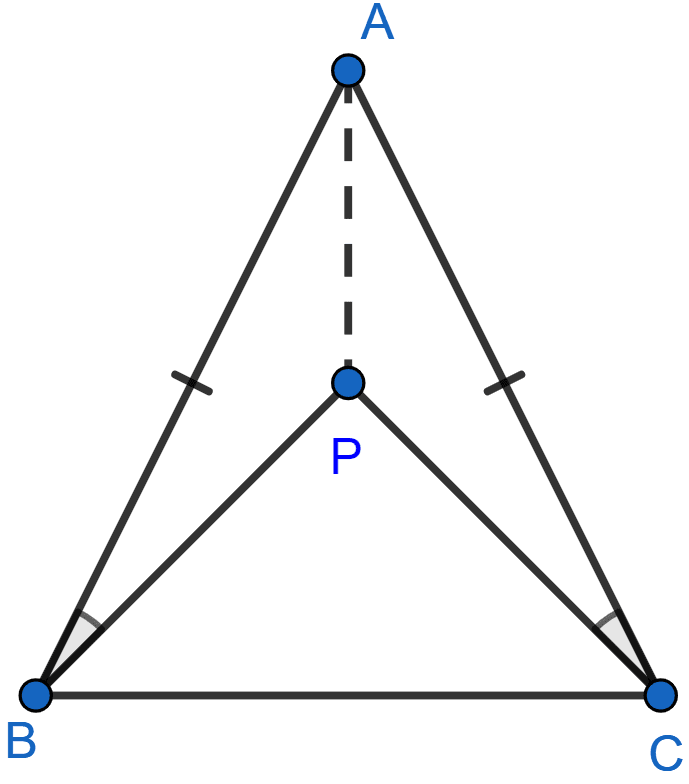
(a) Given,
AB = AC
∴ ∠B = ∠C ........(i)
Given, ∠ABP = ∠ACP ........(ii)
Subtracting (ii) from (i) we get,
∠B - ∠ABP = ∠C - ∠ACP
∠PBC = ∠PCB.
∴ BP = CP (As sides opposite to equal angles are equal)
Hence, proved that BP = CP.
(b) We know that,
BP = CP (Proved)
AB = AC (Given)
∠ABP = ∠ACP (Given)
Hence, △ABP ≅ △ACP by SAS axiom.
∠PAB = ∠PAC (Corresponding angles of congruent triangles are equal.)
Thus AP, bisects ∠BAC.
Hence, proved that AP bisects ∠BAC.
ΔPQR is an isosceles triangle such that PQ = QR. If S is a point on QR produced such that PR = RS and ∠QPS = 63°, find ∠PSQ.
Answer
ΔPQR is an isosceles triangle such that PQ = QR.
S is a point on QR produced such that PR = RS.
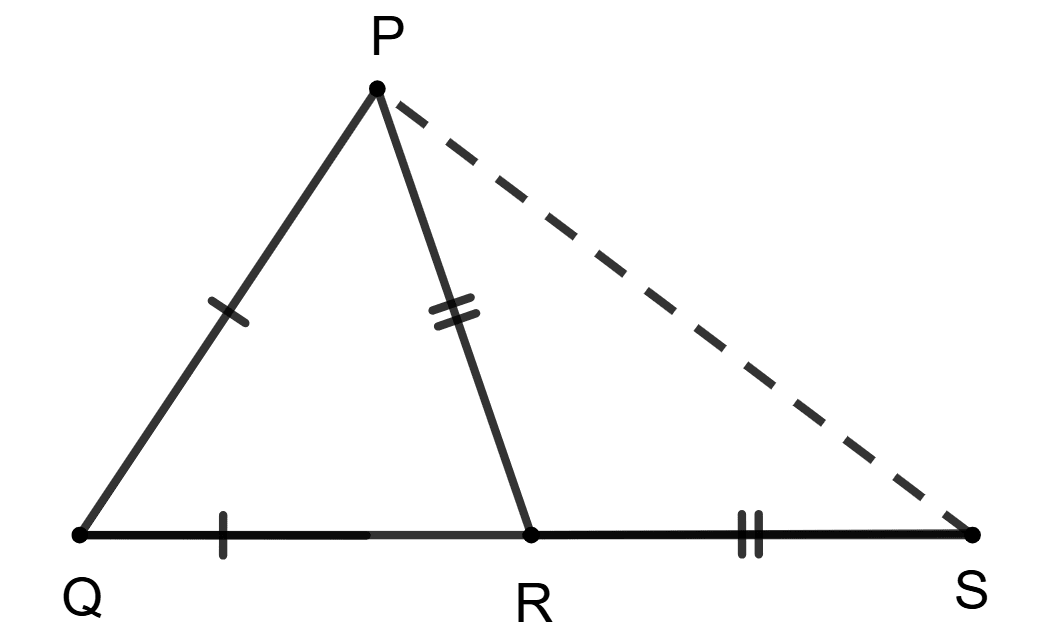
As we know that in an isosceles triangle, angles opposite to equal sides are equal.
In ΔPQR,
⇒ ∠QPR = ∠QRP = x° (let)....................(1)
In ΔPRS,
⇒ ∠PSR = ∠SPR = y° (let)....................(2)
Given,
⇒ ∠QPS = 63°
From figure,
⇒ ∠QPR + ∠SPR = 63°
⇒ x° + y° = 63° ..................(3)
We know that,
The exterior angle of a triangle is equal to the sum of the two opposite interior angles.
The angle ∠PRQ (which is x) is an exterior angle to △PRS at vertex R.
⇒ ∠PRQ = ∠SPR + ∠PSR.
⇒ x° = y° + y°
⇒ x° = 2y°
Substituting the above value of x in equation (1), we get :
⇒ 2y° + y° = 63°
⇒ 3y° = 63°
⇒ y° =
⇒ y° = 21°
⇒ ∠PSR = ∠SPR = 21°.
From figure,
⇒ ∠PSQ = ∠PSR = 21°
Hence, ∠PSQ = 21°.
In the adjoining figure, D and E are points on the side BC of △ABC such that BD = EC and AD = AE. Show that △ABD ≅ △ACE.

Answer
Given, AD = AE.
∴ ∠ADE = ∠AED (As angles opposite to equal sides are equal.)
⇒ 180 - ∠ADE = 180 - ∠AED
⇒ ∠ADB = ∠AEC.
BD = EC (Given)
∴ △ABD ≅ △ACE by SAS axiom.
Hence, proved that △ABD ≅ △ACE.
In the figure (i) given below, CDE is an equilateral triangle formed on a side CD of a square ABCD. Show that △ADE ≅ △BCE and hence, AEB is an isosceles triangle.
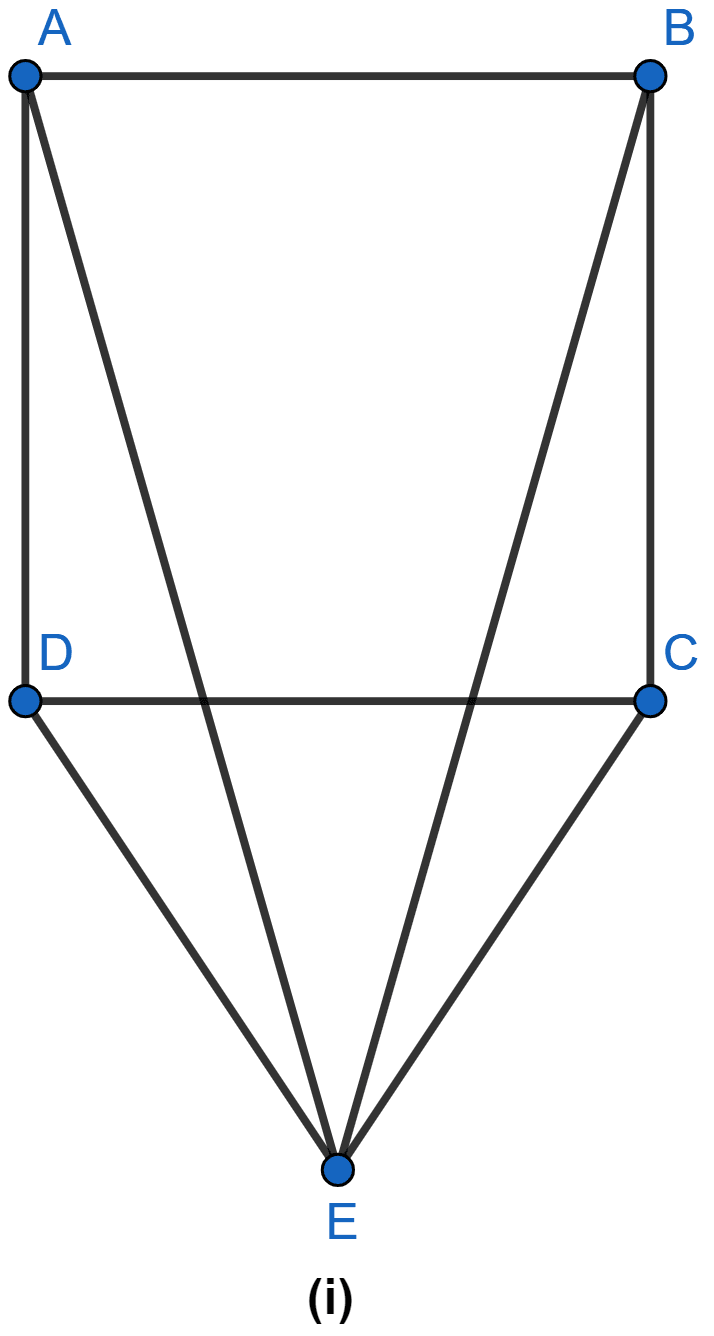
Answer
From figure,
∠ADE = ∠ADC + ∠CDE = 90° + 60° = 150°.
Similarly,
∠BCE = ∠BCD + ∠DCE = 90° + 60° = 150°.
⇒ ∠ADE = ∠BCE.
AD = BC (As sides of squares are equal)
DE = EC (As CDE is an equilateral triangle.)
∴ △ADE ≅ △BCE by SAS axiom.
We know that corresponding parts of congruent triangles are equal.
∴ AE = BE.
Hence, proved that AE = BE i.e. AEB is an isosceles triangle.
In the figure (ii) given below, O is the point in the interior of a square ABCD such that OAB is an equilateral triangle. Show that OCD is an isosceles triangle.
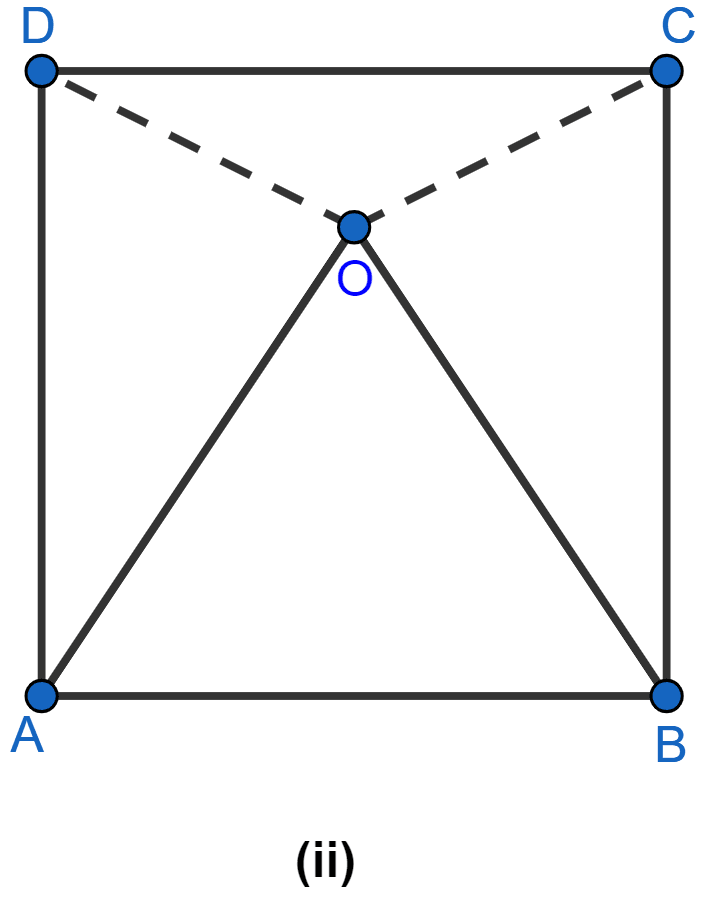
Answer
∠OAD = ∠DAB - ∠OAB = 90° - 60° = 30°.
Similarly,
∠OBC = ∠CBA - ∠OBA = 90° - 60° = 30°.
⇒ ∠OAD = ∠OBC.
AD = BC (As sides of squares are equal).
OA = OB (As OAB is equilateral triangle).
∴ △OAD ≅ △OBC by SAS axiom.
We know that corresponding parts of congruent triangles are equal.
∴ OD = OC.
Hence, proved that OD = OC i.e. OCD is an isosceles triangle.
In the adjoining figure, ABC is a right triangle with AB = AC. Bisector of ∠A meets BC at D. Prove that BC = 2AD.

Answer
In △ABC, ∠A = 90° and AB = AC.
⇒ ∠B = ∠C (As angles opposite to equal sides are equal)
We know,
∠A + ∠B + ∠C = 180°
90° + ∠B + ∠B = 180°
2∠B = 90°
∠B = 45° .
As AD is bisector of ∠A, ∠BAD = ∠CAD = 45°.
AD = AD (Common)
∠ACD = ∠ABD = 45°
Hence, △ABD ≅ △ACD by AAS axiom.
We know that corresponding parts of congruent triangles are equal.
∴ BD = CD .........(i)
In △ABD, ∠BAD = ∠ABD (each = 45°)
⇒ AD = BD (As sides opposite to equal angles are equal) ........(ii)
∴ BC = BD + CD
= BD + BD (Using (i))
∴ BC = 2BD
Using (ii),
BC = 2AD.
Hence, proved that BC = 2AD.
In △PQR, ∠P = 70° and ∠R = 30°. Which side of this triangle is longest? Give reason for your answer.
Answer
We know that,
Sum of angles of triangle = 180°.
∴ ∠P + ∠Q + ∠R = 180°
⇒ 70° + ∠Q + 30° = 180°
⇒ ∠Q + 100° = 180°
⇒ ∠Q = 80°.
We know that side opposite to the greatest angle is greatest side.
∴ PR is the greatest side, which is opposite to ∠Q.
Hence, PR is the greatest side because ∠Q = 80° and side opposite to the greatest angle is greatest side.
Show that in a right angled triangle, the hypotenuse is the longest side.
Answer
In △ABC,

∠B = 90°
∠A and ∠C are acute angles i.e. less that 90°.
∴ ∠B is the greatest angle.
∴ ∠B > ∠A and ∠B > ∠C
⇒ AC > BC and AC > AB.
Hence, proved that hypotenuse is the longest side in a right angled triangle.
PQR is a right angle triangle at Q and PQ : QR = 3 : 2. Which is the least angle?
Answer

Given,
PQR is a right angle triangle at Q and PQ : QR = 3 : 2.
PQ = 3x and QR = 2x.
Thus, QR is the smallest side and the angle opposite to the smallest side is smallest angle.
∴ ∠P is the least angle.
Hence, ∠P is the least angle.
In △ABC, AB = 8 cm, BC = 5.6 cm and CA = 6.5 cm. Which is
(i) the greatest angle?
(ii) the smallest angle?
Answer

(i) In △ABC,
AB is the greatest side, the greatest side has greatest angle opposite to it.
∴ ∠C is the greatest angle.
Hence, ∠C is the greatest angle.
(ii) In △ABC,
BC is the smallest side, the smallest side has smallest angle opposite to it.
∴ ∠A is the smallest angle.
Hence, ∠A is the smallest angle.
In a △ABC, ∠A = 50°, ∠B = 60°. Arrange the sides of the triangle in ascending order.
Answer
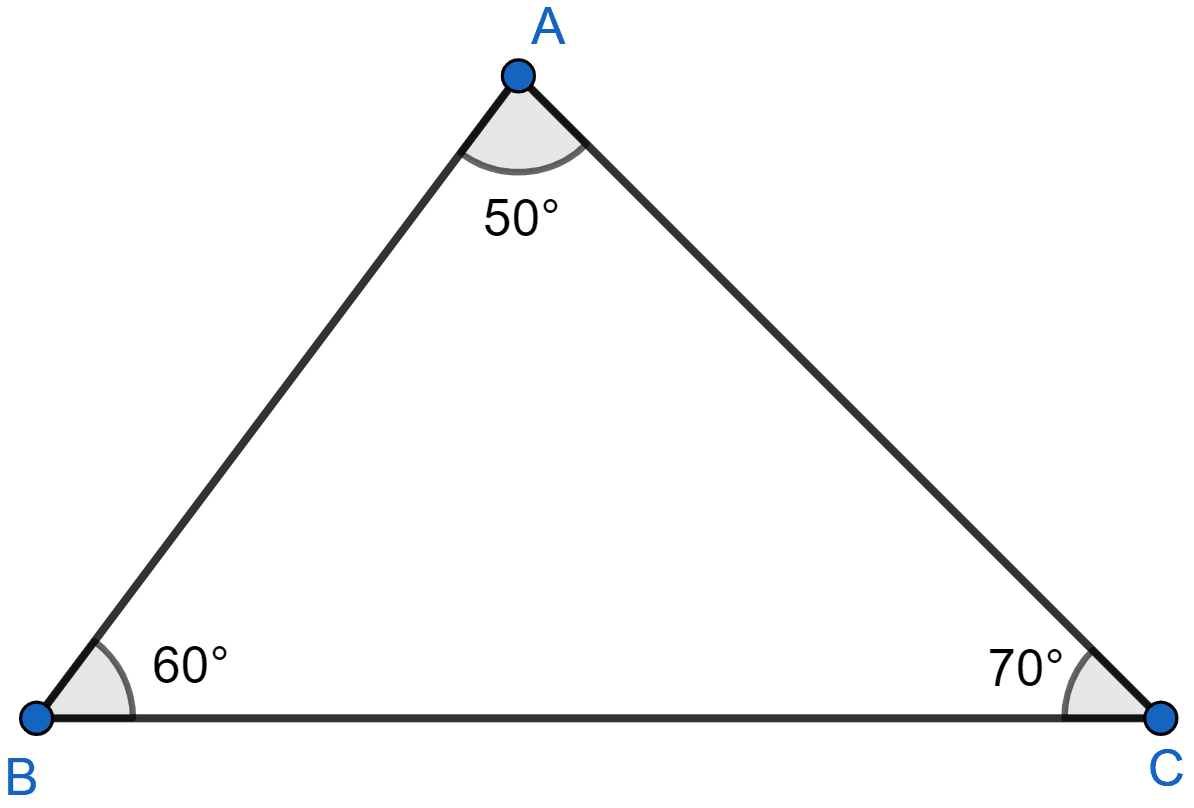
Sum of angles of triangle = 180°.
⇒ ∠A + ∠B + ∠C = 180°
⇒ 50° + 60° + ∠C = 180°
⇒ 110° + ∠C = 180°
⇒ ∠C = 70°.
So we get,
∠C > ∠B > ∠A.
We know that side opposite to greatest angle is greatest.
∴ AB > CA > BC or BC < CA < AB.
Hence, sides of the triangle in ascending order are BC < CA < AB.
In figure given alongside, ∠B = 30°, ∠C = 40° and the bisector of ∠A meets BC at D. Show that
(i) BD > AD
(ii) DC > AD
(iii) AC > DC
(iv) AB > BD.

Answer
In △ABC,
∠B = 30° and ∠C = 40°
∠BAC = 180° - (30° + 40°) = 180° - 70° = 110°.
As, AD is bisector of ∠A,
∴ ∠BAD = ∠CAD = .
(i) Now in △ABD,
∠BAD > ∠B
∴ BD > AD.
Hence, proved that BD > AD.
(ii) Now in △ACD,
∠CAD > ∠C
∴ DC > AD.
Hence, proved that DC > AD.
(iii) Now in △ACD,
∠ADC = 180° - (40° + 55°) = 180° - 95° = 85°.
In △ACD,
∠ADC > ∠CAD
∴ AC > DC.
Hence, proved that AC > DC.
(iv) In △ADB,
∠ADB = 180° - ∠ADC = 180° - 85° = 95°.
Thus, ∠ADB > ∠BAD
∴ AB > BD.
Hence, proved that AB > BD.
In the adjoining figure, AD bisects ∠A. Arrange AB, BD and DC in the descending order of their lengths.

Answer
∠A = 180° - 60° - 40° = 80°.
Since, AD bisects ∠A,
∠BAD = ∠DAC = = 40°.
∴ ∠ADB = ∠DAC + ∠C (As exterior angle is equal to sum of two opposite interior angles.)
∠ADB = 40° + 40° = 80°.
∴ In △ABD,
∠BAD < ∠ABD < ∠ADB
⇒ BD < AD < AB (side opp. to smaller angle is smaller) .......(i)
Also in △ADC, ∠DAC = 40° = ∠C ⇒ AD = DC .......(ii)
∴ BD < DC < AB or AB > DC > BD.
Hence, sides in descending order are AB > DC > BD.
In the figure (1) given below, prove that (i) CF > AF (ii) DC > DF.

Answer
(i) In △ABC,
⇒ ∠A + ∠B + ∠C = 180°
⇒ 60° + 65° + ∠C = 180°
⇒ ∠C = 180° - 125° = 55°.
In △BEC,
⇒ ∠B + ∠E + ∠C = 180°
⇒ 65° + 90° + ∠C = 180°
⇒ ∠C = 180° - 155° = 25°.
In △DFC,
⇒ ∠D + ∠C + ∠F = 180°
⇒ 90° + 25° + ∠F = 180°
⇒ ∠F = 180° - 115° = 65°.
From figure,
∠AFE = ∠DFC = 65° (Vertically opposite angles are equal.)
An exterior angle is equal to the sum of two opposite interior angles.
⇒ ∠AFE = ∠FAC + ∠FCA
⇒ 65° = ∠FAC + 30°
⇒ ∠FAC = 65° - 30° = 35°.
In △AFC,
∠FAC = 35°
∠FCA = 30°
∴ ∠FAC > ∠FCA
∴ CF > AF (As side opposite to greater angle is greater.)
Hence, proved that CF > AF.
(ii) In △DFC,
∠DFC = 65°
∠DCF = 25°
∴ ∠DFC > ∠DCF
∴ DC > DF (As side opposite to greater angle is greater.)
Hence, proved that DC > DF.
In the figure (2) given below, AB = AC. Prove that AB > CD.

Answer
Since, AB = AC.
∴ ∠ABC = ∠ACB = 70° (As angles opposite to equal sides of an isosceles triangle are equal.)
From figure,
⇒ ∠ACB + ∠ACD = 180°
⇒ 70° + ∠ACD = 180°
⇒ ∠ACD = 110°.
In △ACD,
⇒ ∠CAD + ∠ADC + ∠ACD = 180°
⇒ ∠CAD + 40° + 110° = 180°
⇒ ∠CAD + 150° = 180°
⇒ ∠CAD = 30°.
In △ACD,
∠ADC = 40°
∠CAD = 30°
∴ ∠ADC > ∠CAD
∴ AC > CD (As side opposite to greater angle is greater.)
Since, AB = AC,
∴ AB > CD.
Hence, proved that AB > CD.
In the figure (3) given below, AC = CD. Prove that BC < CD.

Answer
From figure,
⇒ ∠ACB + ∠ACD = 180°
⇒ 70° + ∠ACD = 180°
⇒ ∠ACD = 110°.
In △ACD,
AC = CD
∴ ∠CAD = ∠CDA (As angles opposite to equal sides are equal.)
Let ∠CAD = ∠CDA = x.
In △ACD,
⇒ ∠CAD + ∠CDA + ∠ACD = 180°
⇒ x + x + 110° = 180°
⇒ 2x + 110° = 180°
⇒ 2x = 70°
⇒ x = 35°.
⇒ ∠CAD = 35°.
From figure,
⇒ ∠CAD + ∠CAB = 70°
⇒ 35° + ∠CAB = 70°
⇒ ∠CAB = 35°
In △ABC,
⇒ ∠ABC + ∠ACB + ∠BAC = 180°
⇒ ∠ABC + 70° + 35° = 180°
⇒ ∠ABC + 105° = 180°
⇒ ∠ABC = 75°.
In △ABC,
∠ABC > ∠BAC
⇒ AC > BC (As side opposite to greater angle is greater)
∵ AC = CD
∴ CD > BC or BC < CD.
Hence, proved that BC < CD.
In the figure (i) given below, ∠B < ∠A and ∠C < ∠D. Show that AD < BC.

Answer
Given,
∠B < ∠A
∴ AO < BO (As side opposite to smaller angle is smaller.) ......(i)
∠C < ∠D
∴ OD < OC (As side opposite to smaller angle is smaller.) .......(ii)
From (i) and (ii) it can be concluded,
⇒ AO + OD < BO + OC
⇒ AD < BC.
Hence, proved that AD < BC.
In the figure (ii) given below, D is any point on the side BC of △ABC. If AB > AC, show that AB > AD.
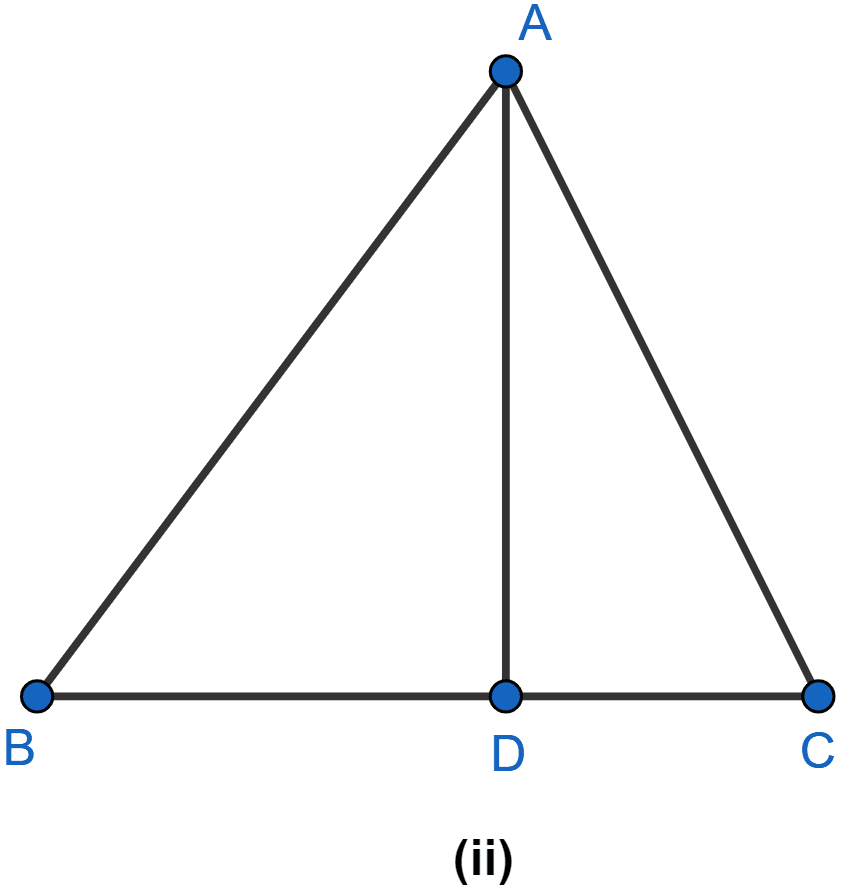
Answer
Given,
AB > AC
∴ ∠ACB > ∠ABC (As angle opposite to greater side is greater.)
From figure,
∠ADB = ∠ACB + ∠DAC (As exterior angle is equal to sum of two opposite interior angles.)
⇒ ∠ADB > ∠ACB
⇒ ∠ADB > ∠ABC [∵ ∠ACB > ∠ABC]
∴ AB > AD (As side opposite to greater angle is greater.)
Hence, proved that AB > AD.
Is it possible to construct a triangle with lengths of its sides as 4 cm, 3 cm and 7 cm? Give reason for your answer.
Answer
We know that sum of any two sides is greater than the third side.
Here,
4 cm + 3 cm = 7 cm, which is equal to third side.
Hence, construction of triangle with sides 4 cm, 3 cm and 7 cm is not possible.
Is it possible to construct a triangle with lengths of its sides as 9 cm, 7 cm and 17 cm? Give reason for your answer.
Answer
We know that sum of any two sides is greater than the third side.
Here,
9 cm + 7 cm = 16 cm, which is less than third side (i.e. 17 cm).
Hence, construction of triangle with sides 9 cm, 7 cm and 17 cm is not possible.
Is it possible to construct a triangle with lengths of its sides as 8 cm, 7 cm and 4 cm? Give reason for your answer.
Answer
Here,
⇒ 8 cm + 7 cm = 15 cm, which is 15 cm > 4cm,
⇒ 7 cm + 4 cm = 11 cm, which is 11 cm > 8 cm,
⇒ 8 cm + 4 cm = 12 cm, which is 12 cm > 7 cm.
We know that sum of any two sides is greater than the third side.
Hence, construction of triangle with sides 8 cm, 7 cm and 4 cm is possible.
Which of the following is not a criterion for congruency of triangles?
SAS
ASA
SSA
SSS
Answer
SSA is not a criterion for congruency of triangles.
Hence, Option 3 is the correct answer.
In the adjoining figure, AB = FC, EF = BD and ∠AFE = ∠CBD. Then the rule by which △AFE ≅ △CBD is
SAS
ASA
SSS
AAS

Answer
In △AFE and △CBD,
Given,
⇒ AB = CF
⇒ AB + BF = CF + BF
⇒ AF = BC.
BD = EF (Given)
∠AFE = ∠CBD (Given).
Hence, △AFE ≅ △CBD by SAS axiom.
Hence, Option 1 is the correct answer.
In the adjoining figure, AB ⊥ BE and FE ⊥ BE. If AB = FE and BC = DE, then
△ABD ≅ △EFC
△ABD ≅ △FEC
△ABD ≅ △ECF
△ABD ≅ △CEF

Answer
In △ABD and △FEC,
Given,
⇒ BC = ED
⇒ BC + CD = ED + CD
⇒ BD = EC.
AB = FE (Given)
∠ABD = ∠FEC (Both are equal to 90°)
Hence, △ABD ≅ △FEC by SAS axiom.
Hence, Option 2 is the correct answer.
In the adjoining figure, AB = AC and AD is median of △ABC, then ∠ADC is equal to
60°
120°
90°
75°

Answer
In △ADB and △ADC,
Given,
AB = AC (Given)
BD = DC (Given)
AD = AD (Common)
Hence, △ADB ≅ △ADC by SSS axiom.
We know that corresponding parts of congruent triangle are equal.
∴ ∠ADB = ∠ADC = x.
From figure,
⇒ ∠ADB + ∠ADC = 180°
⇒ x + x = 180°
⇒ 2x = 180°
⇒ x = 90°
∴ ∠ADC = 90°.
Hence, Option 3 is the correct option.
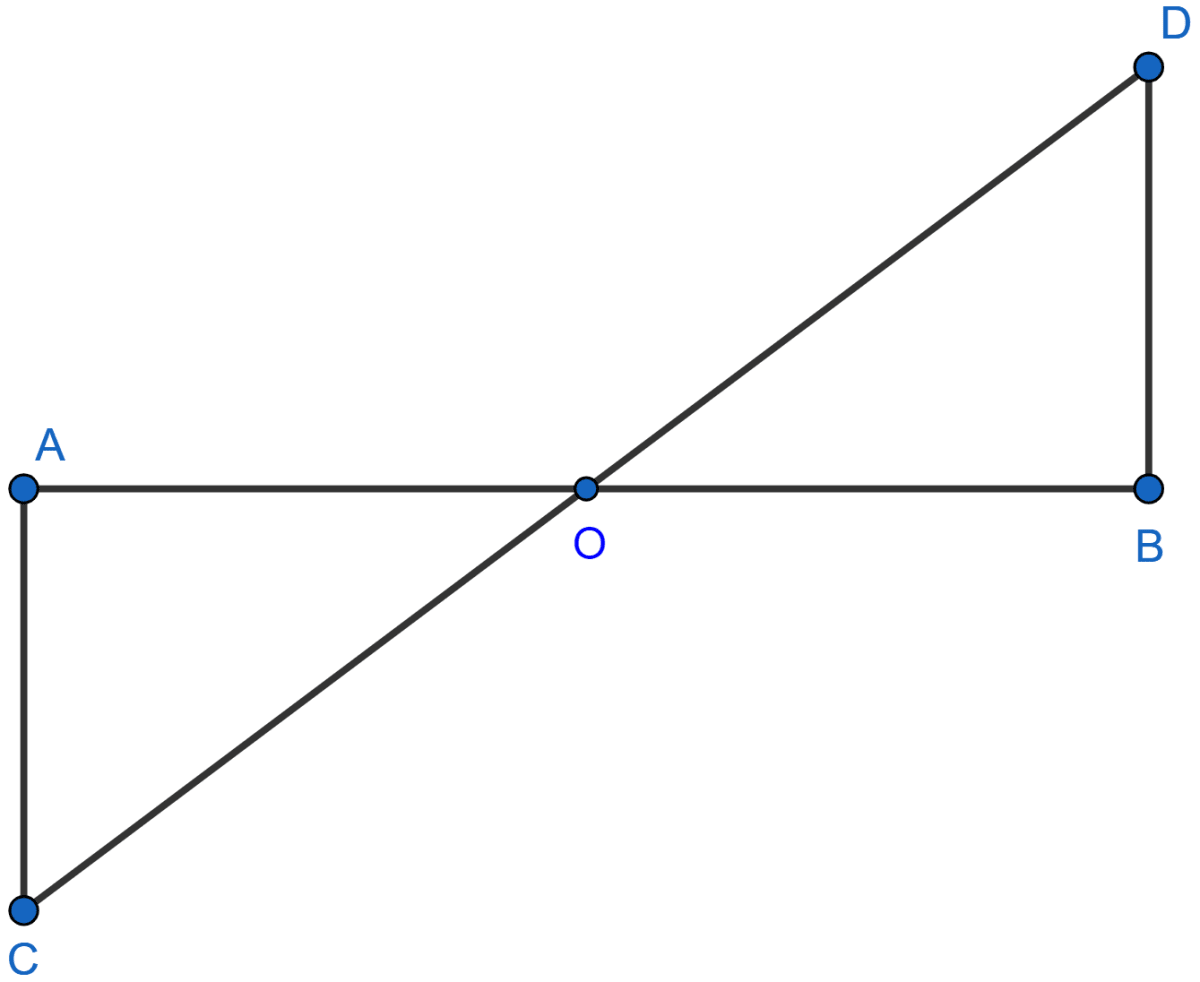
In the adjoining figure, O is the mid-point of AB. If ∠ACO = ∠BDO, then ∠OAC is equal to
∠OCA
∠ODB
∠OBD
∠BOD
Answer
In △AOC and △BOD,
AO = OB (As O is the mid-point of AB.)
∠ACO = ∠BDO (Given)
∠AOC = ∠BOD (Vertically opposite angles)
Hence, △AOC ≅ △BOD by AAS axiom.
We know that corresponding parts of congruent triangles are equal.
∴ ∠OAC = ∠OBD.
Hence, Option 3 is the correct answer.
In the adjoining figure, AC = BD. If ∠CAB = ∠DBA, then ∠ACB is equal to
∠BAD
∠ABC
∠ABD
∠BDA

Answer
In △CAB and △DBA,
AC = DB (Given)
AB = AB (Common)
∠CAB = ∠DBA (Given)
Hence, △CAB ≅ △DBA by SAS axiom.
We know that corresponding parts of congruent triangles are equal.
∴ ∠ACB = ∠BDA.
Hence, Option 4 is the correct answer.
In the adjoining figure, ABCD is a quadrilateral in which BN and DM are drawn perpendiculars to AC such that BN = DM. If OB = 4 cm, then BD is
6 cm
8 cm
10 cm
12 cm

Answer
∠MOD = ∠NOB (Vertically opposite angles)
∠DMO = ∠BNO (Each = 90°)
BN = DM (Given)
Hence, △MOD ≅ △NOB by AAS axiom.
We know that corresponding parts of congruent triangles are equal.
OD = OB = 4 cm.
BD = OB + OD = 4 + 4 = 8 cm.
Hence, Option 2 is the correct option.
In △ABC, AB = AC and ∠B = 50°. Then ∠C is equal to
40°
50°
80°
130°
Answer
Since in △ABC, AB = AC.
∴ ∠B = ∠C = 50°. (As angles opposite to equal sides in isosceles triangle are equal.)
Hence, Option 2 is the correct option.
In △ABC, BC = AB and ∠B = 80°. Then ∠A is equal to
80°
40°
50°
100°
Answer
Since in △ABC, BC = AB.
∴ ∠A = ∠C. (As angles opposite to equal sides in isosceles triangle are equal.)
Let ∠A = ∠C = x.
Sum of angles of triangle = 180°.
∠A + ∠B + ∠C = 180°
x + 80° + x = 180°
2x = 100°
x = 50°
∠A = 50°.
Hence, Option 3 is the correct option.
In △PQR, ∠R = ∠P, QR = 4 cm and PR = 5 cm. Then the length of PQ is
4 cm
5 cm
2 cm
2.5 cm
Answer
Since, ∠R = ∠P.
∴ PQ = QR = 4 cm.
Hence, Option 1 is the correct option.
In △ABC and △PQR, AB = AC, ∠C = ∠P and ∠B = ∠Q. The two triangles are
isosceles but not congruent
isosceles and congruent
congruent but isosceles
neither congruent nor isosceles
Answer
Given AB = AC hence ABC is isosceles.
∴ ∠B = ∠C
∠B = ∠P = ∠Q.
Since, ∠P = ∠Q so, PR = QR, hence PQR is isosceles.
Hence, Option 1 is the correct option.
Two sides of a triangle are of lengths 5 cm and 1.5 cm. The length of the third side of the triangle can not be
3.6 cm
4.1 cm
3.8 cm
3.4 cm
Answer
Given two sides are 5 cm and 1.5 cm then third side must be greater than the difference of two sides.
5 - 1.5 = 3.5 cm
Hence, third side must be greater than 3.5 cm.
Hence, Option 4 is the correct option.
If a, b, c are lengths of the sides of a triangle then,
a - b > c
c > a + b
c = a + b
c < a + b
Answer
We know that in a triangle, the sum of any two sides of a triangle is greater then the third side.
∴ c < a + b.
Hence, Option 4 is the correct option.
It is not possible to construct a triangle when the lengths of its sides are
6 cm, 7 cm, 8 cm
4 cm, 6 cm, 6 cm
5.3 cm, 2.2 cm, 3.1 cm
9.3 cm, 5.2 cm, 7.4 cm
Answer
We know that in a triangle, the sum of any two sides of a triangle is greater than the third side.
But, when sides are 5.3 cm, 2.2 cm, 3.1 cm.
2.2 + 3.1 = 5.3 cm.
Here, sum of two sides is equal to third side.
Hence, construction of triangle with sides 5.3 cm, 2.2 cm, 3.1 cm is not possible.
Hence, Option 3 is the correct option.
In △PQR, if ∠R > ∠Q, then
QR > PR
PQ > PR
PQ < PR
QR < PR
Answer
Given, ∠R > ∠Q
∴ PQ > PR (As side opposite to greater angle is greater.)
Hence, Option 2 is the correct option.
If triangle PQR is right angled at Q, then
PR = PQ
PR < PQ
PR < QR
PR > PQ
Answer
Since, PQR is a right angled triangle at Q.
So, PR is hypotenuse and hypotenuse is > perpendicular and base.
∴ PR > PQ.
Hence, Option 4 is the correct option.
If triangle ABC is obtuse angled and ∠C is obtuse, then
AB > BC
AB = BC
AB < BC
AC > AB
Answer
If ∠C is obtuse then ∠A will be acute,
∴ AB > BC (As side opposite to greater angle is greater.)
Hence, Option 1 is the correct option.
If the lengths of two sides of an isosceles triangle are 4 cm and 10 cm, then the length of the third side is
4 cm
10 cm
7 cm
14 cm
Answer
The length of third side can either be 4 cm or 10 cm.
If the third side is 4 cm then the sides are,
4, 4, 10.
Here, 4 + 4 = 8 < 10.
Since, the sum of two sides of a triangle must be greater than third side hence, these sides are not possible.
Hence, the length of third side is 10 cm.
Hence, Option 2 is the correct option.
Consider the following two statements :
Statement 1: If two angles and one side of a triangle is equal to two angles and one side of an other triangle then the two triangles are congruent.
Statement 2: The angle opposite to equal sides of an isosceles triangle are equal.
Which of the following is valid?
Both the statements are true.
Both the statements are false.
Statement 1 is true, and Statement 2 is false.
Statement 1 is false, and Statement 2 is true.
Answer
Given, according to statement 1 :
If two angles and one side of a triangle is equal to two angles and one side of an other triangle then the two triangles are congruent.
The above statement is true and the triangles are congruent by two axioms A.A.S. or A.S.A. axiom.
∴ Statement 1 is true.
In an isosceles triangle, the angles opposite to equal sides are equal.
∴ Statement 2 is true.
∴ Both statements are true.
Hence, option 1 is the correct option.
Assertion (A): If two triangles are congruent to each other then the ratio of corresponding side is 1 : 1.
Reason (R): Two triangles are congruent if and only if they have same shape and size.
Assertion (A) is true, Reason (R) is false.
Assertion (A) is false, Reason (R) is true.
Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).
Answer
The reason states, two triangles are congruent if and only if they have same shape and size.
This statement is the precise definition of congruent triangles. Congruence means that one triangle can be perfectly superimposed on the other, covering it exactly.
∴ Reason (R) is true.
If corresponding sides are equal, for example, if side AB of the first triangle corresponds to side DE of the second triangle, and they are equal in length (AB = DE), then their ratio is = 1. This applies to all pairs of corresponding sides.
Therefore, the ratio of corresponding sides is indeed 1 : 1.
∴ Assertion (A) is true.
∴ Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason (or explanation) for Assertion (A).
Hence, option 3 is the correct option.
Assertion (A): In the adjoining figure, Δ ABC ≅ Δ PQR.
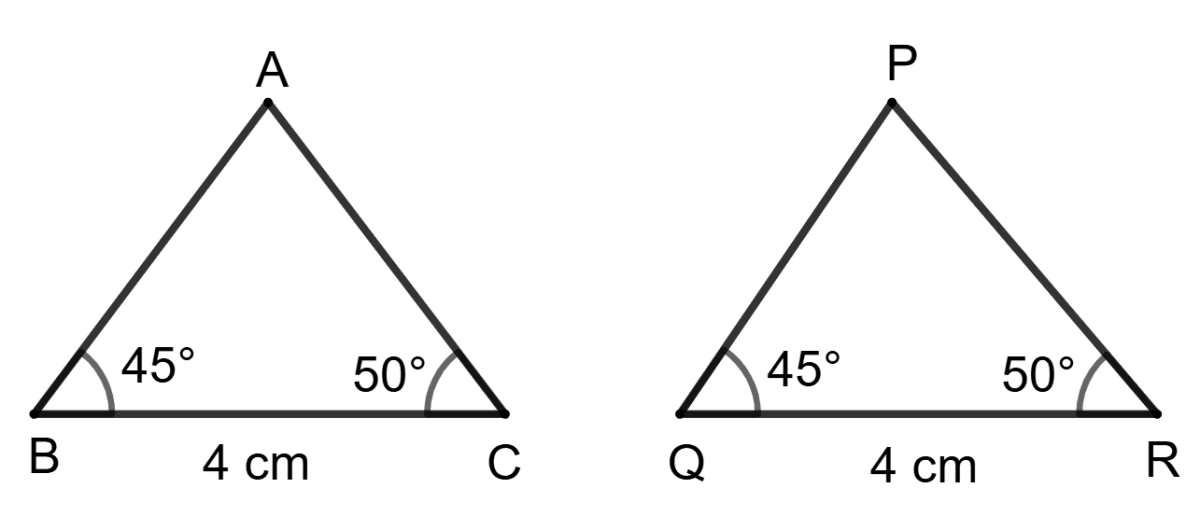
Reason (R): Two triangles are congruent if two angles and included side of One triangle are equal to two angles and the included side of other triangle.
Assertion (A) is true, Reason (R) is false.
Assertion (A) is false, Reason (R) is true.
Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).
Answer
The ASA (Angle-Side-Angle) Congruence rule states that if two angles and the included side (the side between those two angles) of one triangle are equal to the corresponding two angles and the included side of another triangle, then the two triangles are congruent.
∴ Reason (R) is true.
In △ABC and △PQR,
⇒ ∠B = ∠Q (Both equal to 45°)
⇒ BC = QR
⇒ ∠C = ∠R (Both equal to 50°)
∴ △ABC ≅ △PQR (By A.S.A. axiom)
∴ Assertion (A) is true.
∴ Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason (or explanation) for Assertion (A).
Hence, option 3 is the correct option.
Assertion (A): Two triangles are congruent to each other by RHS rule of congruency. The base of the one triangle is 6 cm and the height is 4 cm. The sum of area of two triangle is 24 cm2.
Reason (R): Two triangles are congruent if they have same shape and size. Congruent triangles have equal area.
Assertion (A) is true, Reason (R) is false.
Assertion (A) is false, Reason (R) is true.
Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).
Answer
Congruent figures are identical in every respect, meaning they have the same shape and occupy the same amount of space.
If two triangles have the same shape and size (i.e., they are congruent), then they must necessarily cover the same amount of space, meaning they have equal areas.
∴ Reason (R) is true.
Area of one triangle = x base x height
= x 6 x 4
= 3 x 4
= 12 cm2.
If two triangles are congruent, their areas must be equal.
So, the area of the second triangle is also 12 cm2.
The sum of the areas is 12 cm2 + 12 cm2 = 24 cm2.
∴ Assertion (A) is true.
∴ Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason (or explanation) for Assertion (A).
Hence, option 3 is the correct option.
Assertion (A): If ΔABC ≅ ΔPQR and AB = 4 units, then AB2 + PQ2 = 32.
Reason (R): When two triangles are congruent to each other, then their corresponding responding sides are equal in length.
Assertion (A) is true, Reason (R) is false.
Assertion (A) is false, Reason (R) is true.
Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).
Answer
When two triangles are congruent to each other, then their corresponding sides are equal in length.
It is a fundamental property of congruent triangles, better known as C.P.C.T.C.
∴ Reason (R) is true.
△ABC ≅ △PQR, this means triangle ABC is congruent to triangle PQR.
So, corresponding sides are equal.
This means AB corresponds to PQ, BC corresponds to QR, and AC corresponds to PR.
Therefore, AB = PQ.
Given AB = 4 units: Since AB = PQ, it implies PQ = 4 units.
AB2 + PQ2 = 42 + 42
= 16 + 16
= 32.
∴ Assertion (A) is true.
∴ Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason (or explanation) for Assertion (A).
Hence, option 3 is the correct option.
Assertion (A): Δ ABC ≅ Δ PQR
If 2AB = 3BC = 4CA = 12 cm, then the sum of perimeter of both triangle is 26 cm.
Reason (R): If two triangles are congruent to each other, then their corresponding sides are equal in length.
Assertion (A) is true, Reason (R) is false.
Assertion (A) is false, Reason (R) is true.
Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).
Answer
When two triangles are congruent to each other, then their corresponding sides are equal in length.
It is a fundamental property of congruent triangles, better known as C.P.C.T.C.
∴ Reason (R) is true.
Given,
△ABC ≅ △PQR.
If 2AB = 3BC = 4CA = 12 cm.
For side AB, 2AB = 12 cm ⇒ AB = = 6 cm,
For side BC, 3BC = 12 cm ⇒ BC = = 4 cm,
For side CA, 4CA = 12 cm ⇒ CA = = 3 cm.
Perimeter of △ABC = AB + BC + CA = 6 cm + 4 cm + 3 cm = 13 cm.
Since, △ABC ≅ △PQR their perimeters are equal.
Perimeter of △PQR = Perimeter of △ABC = 13 cm.
The sum of the perimeters of both triangles = Perimeter of △ABC + Perimeter of △PQR = 13 cm + 13 cm = 26 cm.
∴ Assertion (A) is true.
∴ Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason (or explanation) for Assertion (A).
Hence, option 3 is the correct option.
In triangles ABC and DEF, ∠A = ∠D, ∠B = ∠E and AB = EF. Will the two triangles be congruent? Give reasons for your answer.
Answer
Given,
In triangles ABC and DEF, ∠A = ∠D, ∠B = ∠E and AB = EF.
The two triangles will not be congruent as AB and EF are not corresponding sides.
In the adjoining figure, ABCD is a square. P, Q and R are points on the sides AB, BC and CD respectively such that AP = BQ = CR and ∠PQR = 90°. Prove that
(a) △PBQ ≅ △QCR
(b) PQ = QR
(c) ∠PRQ = 45°
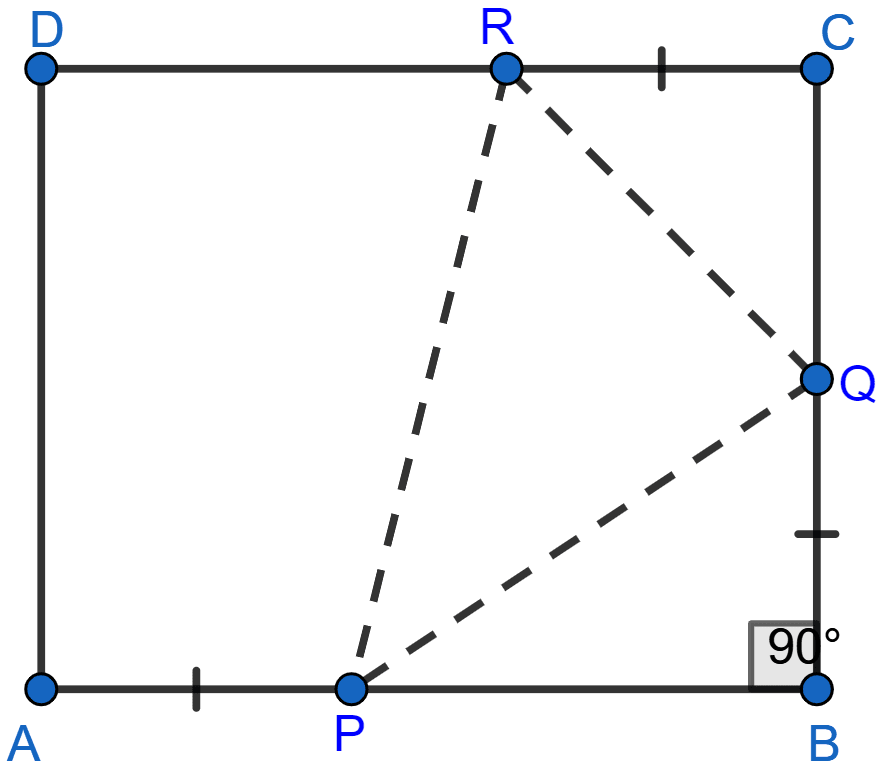
Answer
(a) Given, ABCD is a square.
∴ AB = BC.
Given, AP = BQ.
∴ AB - AP = BC - BQ .......(i)
In △PBQ and △QCR,
BQ = CR (Given)
From (i) we get,
PB = QC
∠PBQ = ∠QCR (Both are equal to 90°, as each angle in square = 90°.)
Hence, proved △PBQ ≅ △QCR by SAS axiom.
(b) We know that corresponding parts of congruent triangles are equal.
∴ PQ = QR.
Hence, proved that PQ = QR.
(c) Considering △PQR.
We know PQ = QR and ∠Q = 90°.
Hence, △PQR is an isosceles triangle with ∠P = ∠R = x.
Sum of angles of triangle = 180°.
⇒ ∠P + ∠Q + ∠R = 180°
⇒ x + 90° + x = 180°
⇒ 2x = 90°
⇒ x = 45°.
Hence, proved that ∠PRQ = 45°.
In the adjoining figure, OA ⊥ OD, OC ⊥ OB, OD = OA and OB = OC. Prove that AB = CD.

Answer
From figure,
∠AOD = ∠COB (Each 90°)
Adding ∠AOC to both sides,
⇒ ∠AOD + ∠AOC = ∠AOC + ∠COB
⇒ ∠COD = ∠AOB.
Now, in △AOB and △DOC
OA = OD (Given)
OB = OC (Given)
∠AOB = ∠COD (Proved)
∴ △AOB ≅ △DOC (SAS axiom)
We know that corresponding parts of congruent triangles are equal.
∴ AB = CD.
Hence, proved that AB = CD.
In the adjoining figure, PQ || BA and RS || CA. If BP = RC, prove that:
(i) △BSR ≅ △PQC
(ii) BS = PQ
(iii) RS = CQ.

Answer
Given, BP = RC
⇒ BR - PR = PC - PR
⇒ BR = PC.
Now, in △BSR and △PQC,
∠B = ∠P (Corresponding angles)
∠R = ∠C (Corresponding angles)
BR = PC (Proved)
Hence, proved △BSR ≅ △PQC by ASA axiom.
(ii) We know that corresponding parts of congruent triangles are equal.
∴ BS = PQ.
(iii) We know that corresponding parts of congruent triangles are equal.
∴ RS = CQ.
In the adjoining figure, AB = AC, D is a point in the interior of △ABC such that ∠DBC = ∠DCB. Prove that AD bisects ∠BAC of △ABC.
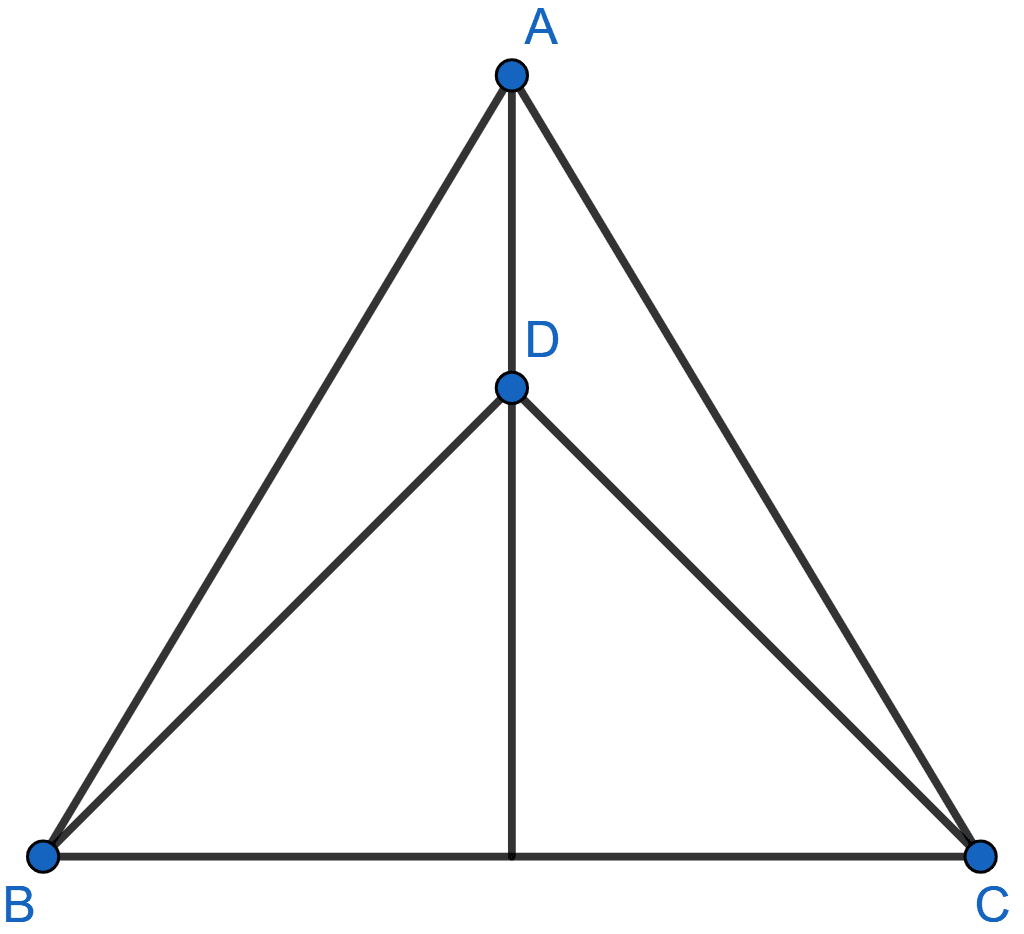
Answer
Given, AB = AC.
∴ ∠ABC = ∠ACB (As angles opposite to equal sides of isosceles triangle are equal.)
Given, ∠DBC = ∠DCB
∴ DB = DC. (Sides opposite to equal angles are equal.)
In △ABD and △ACD,
AB = AC (Given)
DB = DC (Proved)
AD = AD (Common)
Thus, △ABD ≅ △ACD by SSS axiom.
We know that corresponding parts of congruent triangle are equal.
∴ ∠BAD = ∠CAD.
Hence, proved that AD bisects ∠BAC.
In the adjoining figure, AB || DC. CE and DE bisects ∠BCD and ∠ADC respectively. Prove that AB = AD + BC.
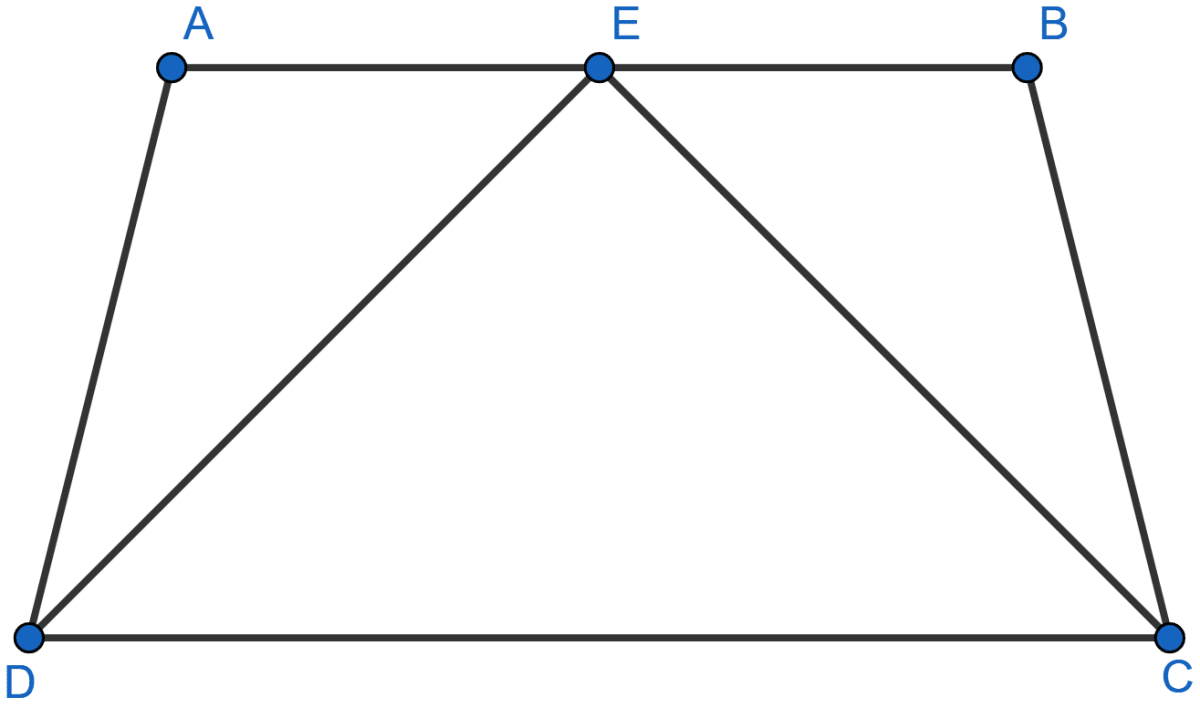
Answer
Given,
DE bisects ∠D.
∴ ∠EDA = ∠EDC = .
AB || CD and DE cuts these parallel lines.
∠DEA = ∠EDC = .
In △ADE,
∠ADE = ∠DEA = .
Hence, AD = AE.
Given,
CE bisects ∠C.
∴ ∠ECB = ∠ECD = .
AB || CD and CE cuts these parallel lines.
∠CEB = ∠ECD = .
In △BCE,
∠BEC = ∠BCE =
Hence, BE = BC.
⇒ AB = AE + BE = AD + BC
⇒ AB = AD + BC.
Hence, proved that AB = AD + BC.
In △ABC, D is a point on BC such that AD is the bisector of ∠BAC. CE is drawn parallel to DA to meet BD produced at E. Prove that △CAE is isosceles.
Answer
From figure,
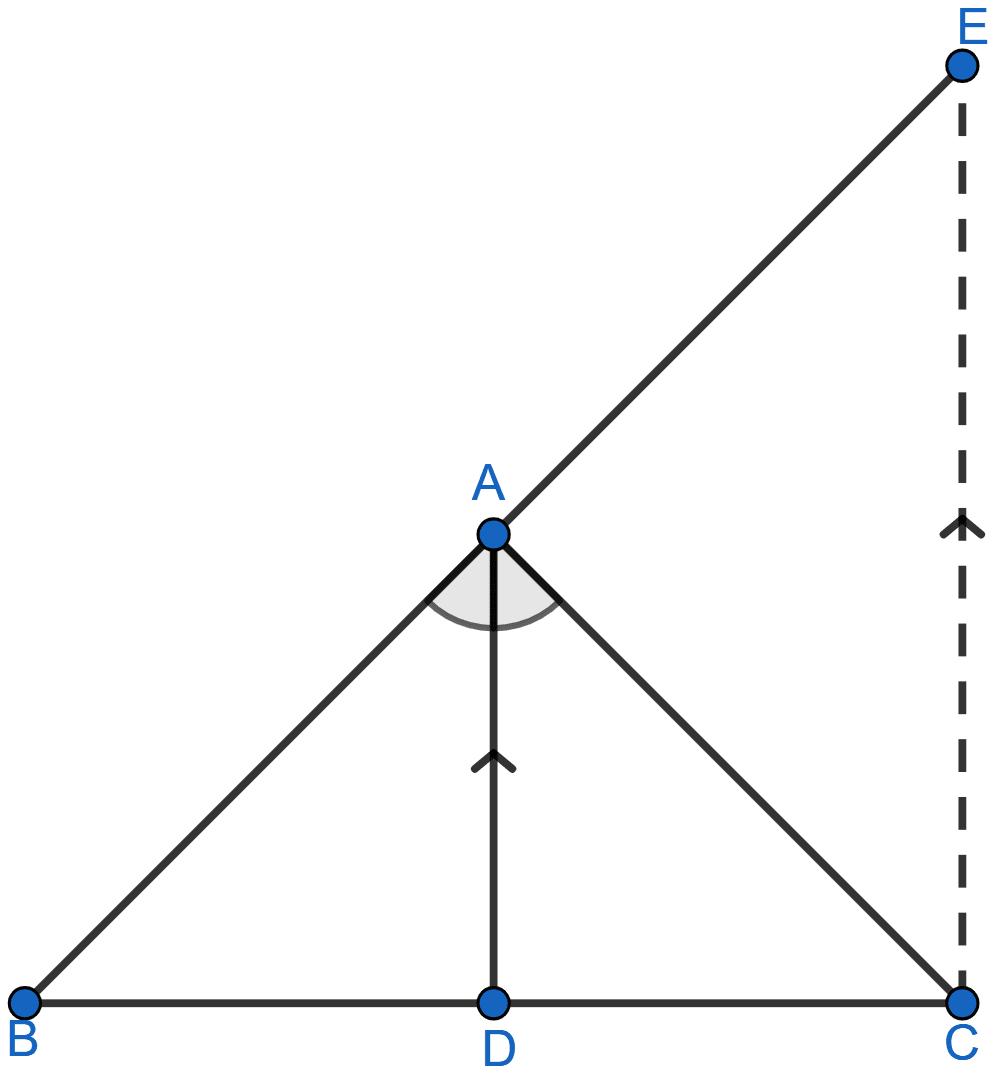
∠DAC= ∠ACE (Alternate angles)
∠BAD = ∠CEA (Corresponding angles)
But, ∠BAD = ∠DAC (as AD is bisector of ∠BAC)
∴ ∠ACE = ∠CEA
AE = AC (Sides opposite to equal angles are equal.)
∴ △CAE is isosceles triangle.
Hence, proved that △CAE is isosceles triangle.
In the adjoining figure, ABC is a right angled triangle at B. ADEC and BCFG are squares. Prove that AF = BE.

Answer
Given, ADEC and BCFG are squares.
Considering △BCE and FCA we get,
From figure,
∠BCE = ∠BCA + 90
∠ACF = ∠BCA + 90
∠BCE = ∠ACF
AC = CE (Sides of squares are equal)
BC = CF (Sides of squares are equal)
△BCE ≅ △FCA (By SAS axiom).
We know that corresponding parts of congruent triangles are equal.
∴ AF = BE.
Hence, proved that AF = BE.
In the adjoining figure, TR = TS, ∠1 = 2∠2 and ∠4 = 2∠3. Prove that RB = SA.

Answer
∠1 = ∠4 (Vertically opposite angles)
⇒ 2∠2 = 2∠3
⇒ ∠2 = ∠3.
TS = TR (Given)
⇒ ∠TRS = ∠TSR (As angle opposite to equal side are equal)
⇒ ∠TRS - ∠2 = ∠TSR - ∠3
⇒ ∠ARB = ∠BSA.
∠RTB = ∠STA (Common angle)
△RBT ≅ △SAT (By ASA axiom.)
We know that corresponding sides of congruent triangles are equal.
∴ RB = SA.
Hence, proved that RB = SA.
In the figure (1) given below, find the value of x.

Answer
From figure,

∠ABD = ∠BAD = 36° (As angles opposite to equal sides are equal.)
∠BDA = 180° - (36° + 36°) = 180° - 72° = 108°.
From figure,
∠BDA + ∠ADC = 180°
108° + ∠ADC = 180°
∠ADC = 72°.
In △ADC,
As AD = AC,
∴ ∠ADC = ∠ACD = 72° (As angles opposite to equal sides are equal.)
∠ADC + ∠ACD + ∠DAC = 180°
72° + 72° + ∠DAC = 180°
∠DAC = 180° - 144° = 36°.
From figure,
∠BAD + ∠DAC + x = 180°
36° + 36° + x = 180°
72° + x = 180°
x = 108°.
Hence, x = 108°.
In the figure (2) given below, AB = AC and DE || BC. Calculate
(i) x
(ii) y
(iii) ∠BAC
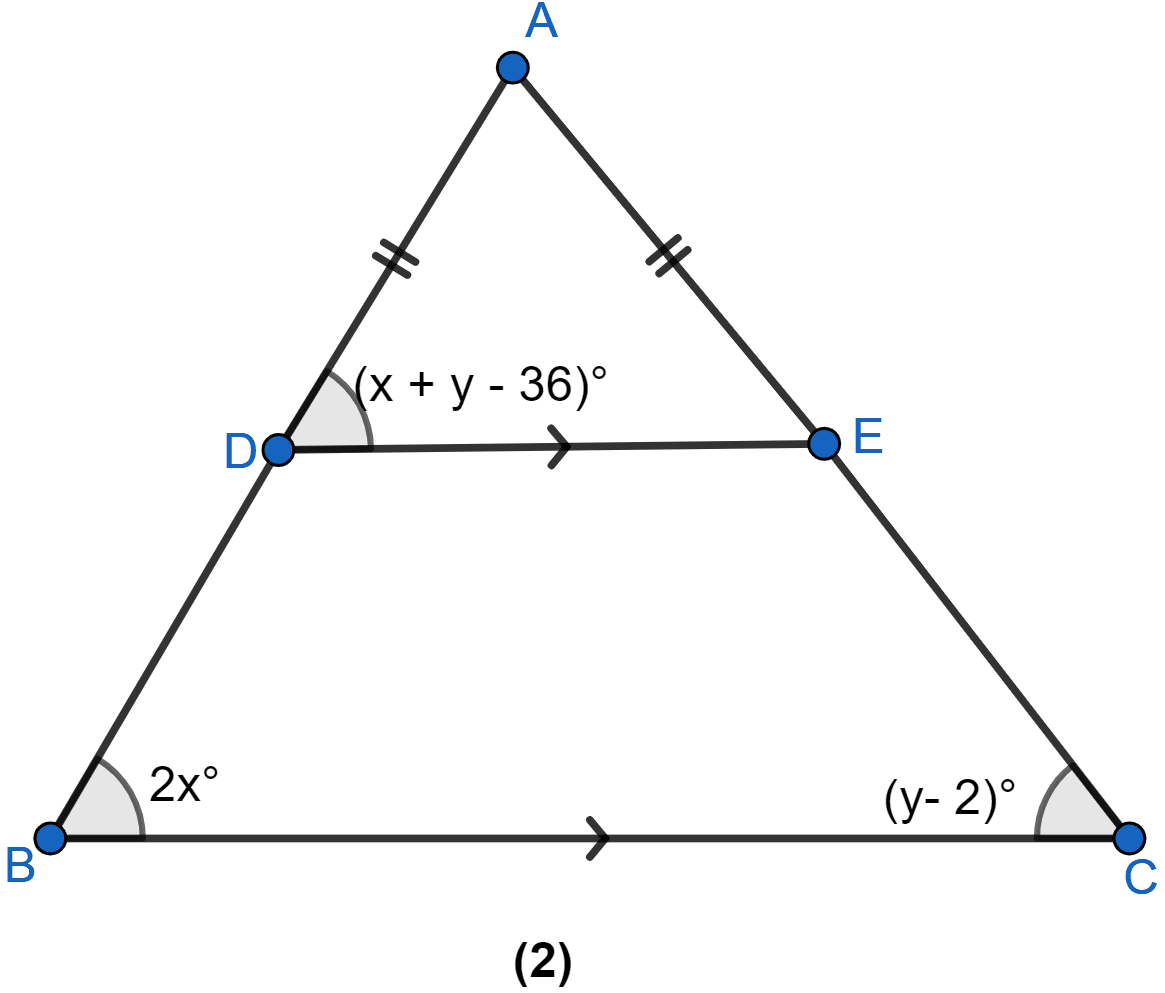
Answer
(i) Since, AB = AC
∠ABC = ∠ACB
⇒ 2x° = (y - 2)°
⇒ y° = 2x° + 2° .......(i)
From figure,
∠ADE = ∠ABC (Corresponding angles)
⇒ x° + y° - 36° = 2x°
⇒ y° - 36° = x°
Substituting value of y from (i) in above equation,
⇒ 2x° + 2° - 36° = x°
⇒ 2x° - x° = 34°
⇒ x° = 34°
⇒ x = 34.
Hence, x = 34.
(ii) Substituting value of x in (i),
⇒ y° = 2(34)° + 2°
⇒ y° = 68° + 2° = 70°.
⇒ y = 70.
Hence, y = 70.
(iii) From figure,
∠BAC = 180° - (2x° + y° - 2°)
= 180° - (2 × 34° + 70° - 2°)
= 180° - (68° + 68°)
= 180° - 136° = 44°.
Hence, ∠BAC = 44°.
In the figure (3) given below, calculate the size of each lettered angle.

Answer
From figure,

∠AEB = ∠DEC = 80° (Vertically opposite angles are equal).
In △AEB,
⇒ x + 54° + 80° = 180°
⇒ x + 134° = 180°
⇒ x = 46°.
AB = BC
⇒ ∠BAC = ∠ACB (As angles opposite to equal sides are equal.)
∴ ∠ACB = 54°
In △ABC,
∠ABC + ∠ACB + ∠BAC = 180°
⇒ (x + y)° + 54° + 54° = 180°
⇒ y° + 46° + 108° = 180°
⇒ y = 180° - 154° = 26°.
From figure,
∠ECD = ∠BAE = 54° (Alternate angles)
∠BCA + ∠ECD + z = 180°
54° + 54° + z = 180°
108° + z = 180°
z = 72°.
Hence, x = 46°, y = 26° and z = 72°.
In the figure (1) given below, AD = BD = DC and ∠ACD = 35°. Show that
(i) AC > DC
(ii) AB > AD.

Answer
From figure,
∠DAC = ∠ACD = 35° (As angles opposite to equal sides are equal.)
∠ADC = 180° - (35° + 35°) = 180° - 70° = 110°.
Since, ∠ADC > ∠DAC
∴ AC > DC (Side opposite to greater angle is greater.)
Hence, proved that AC > DC.
(ii) From figure,
∠ADB = 180° - ∠ADC = 180° - 110° = 70°.
Considering △ABD,
AD = BD.
∴ ∠BAD = ∠ABD = a.
⇒ a + a + ∠ADB = 180°
⇒ 2a + 70° = 180°
⇒ 2a = 110°
⇒ a = 55°.
Since, ∠ADB > ∠ABD
∴ AB > AD. (Side opposite to greater angle is greater.)
Hence, proved that AB > AD.
In the figure (2) given below, prove that
(i) x + y = 90°
(ii) z = 90°
(iii) AB = BC.
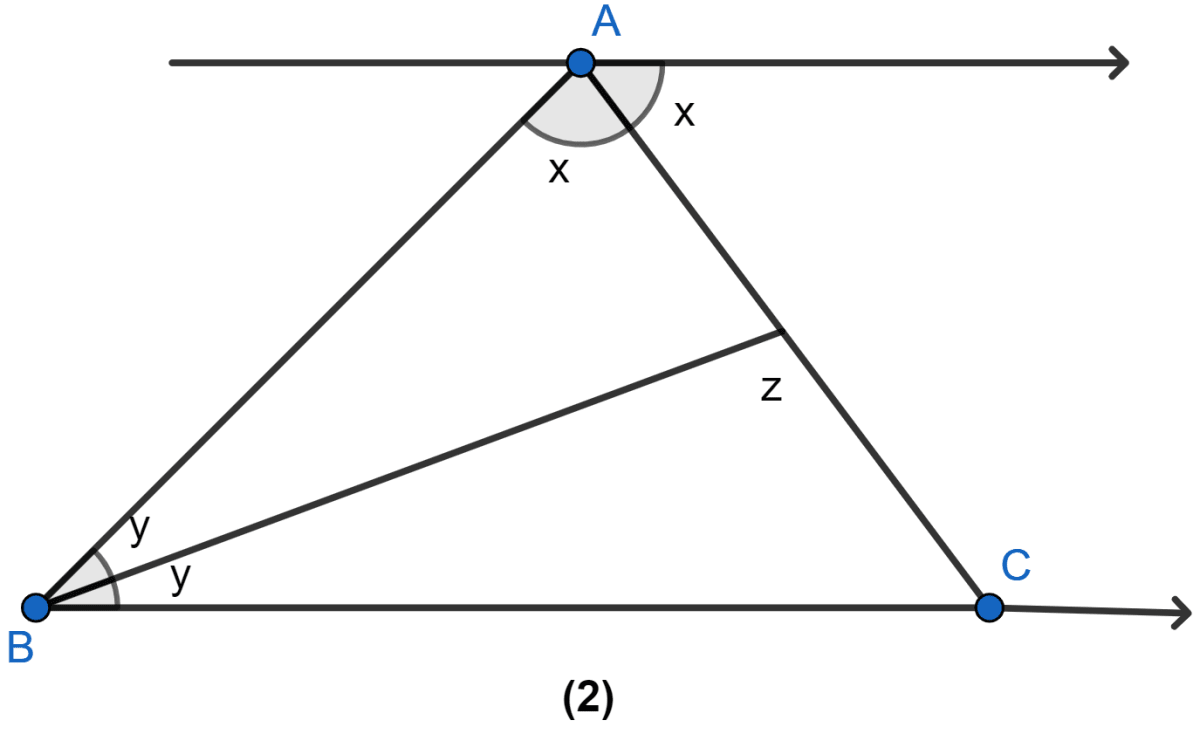
Answer
(i) From figure,
∠ACB = x (Alternate angles)
In △ABC,
⇒ x + (y + y) + ∠ACB = 180°
⇒ x + 2y + x = 180°
⇒ 2x + 2y = 180°
⇒ x + y = 90°.
Hence, proved that x + y = 90°.
(ii) Now in △BCD,
⇒ y + z + ∠BCD = 180° (Sum of all angles in a triangle is 180°)
⇒ y + z + x = 180°
⇒ 90° + z = 180° [∵ x + y = 90°]
⇒ z = 90°.
Hence, proved that z = 90°.
(iii) In △ABC,
∠ACB = ∠BAC = x
∴ AB = BC (As sides opposite to equal angles are equal.)
Hence, proved that AB = BC.
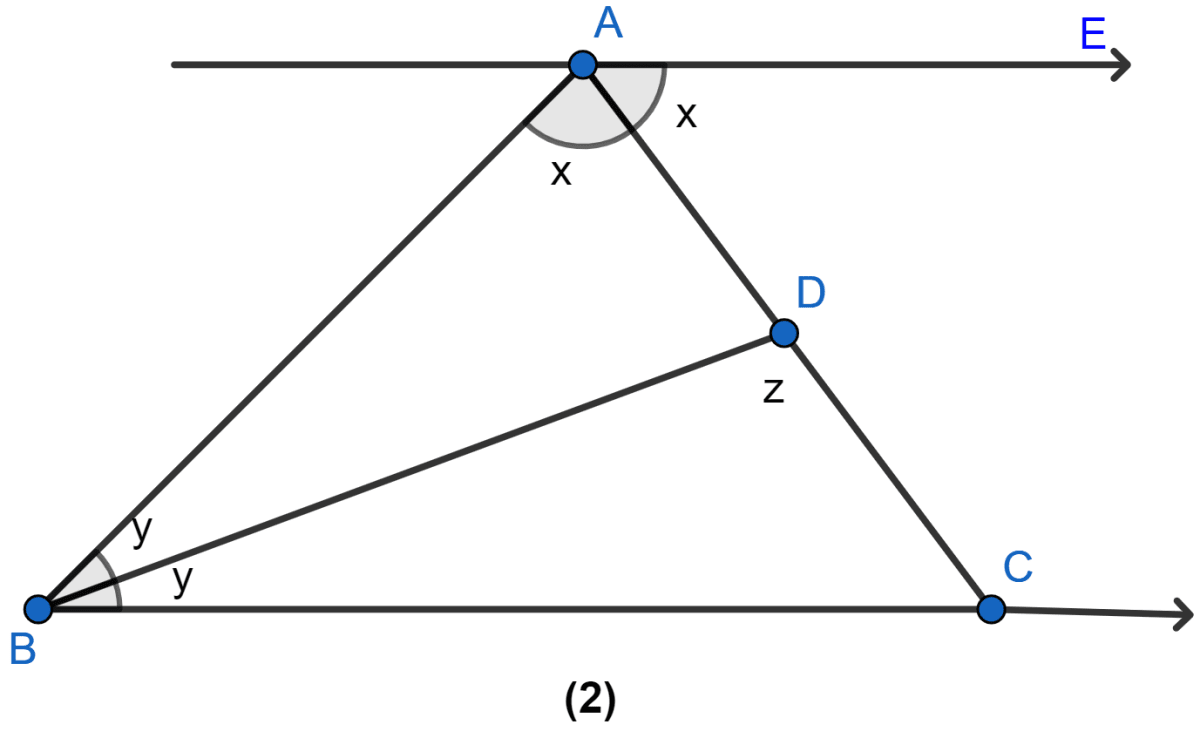
In the adjoining figure, ABC and DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at P, show that
(i) △ABD ≅ △ACD
(ii) △ABP ≅ △ACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC.
Answer
(i) AB = AC (as ABC is an isosceles triangle on base BC)
DB = DC (as DBC is an isosceles triangle on base BC)
AD = AD (Common)
∴ △ABD ≅ △ACD by SSS axiom.
Hence, proved that △ABD ≅ △ACD.
(ii) AB = AC (as ABC is an isosceles triangle on base BC)
AP = AP (Common)
∠ABP = ∠ACP (As angles opposite to equal sides are equal.)
∴ △ABP ≅ △ACP by AAS axiom.
Hence, proved that △ABP ≅ △ACP.
(iii) We know that,
△ABP ≅ △ACP.
As corresponding parts of congruent triangle are equal.
∴ ∠BAP = ∠CAP ......(i)
also ∠APB = ∠APC.
△DPB ≅ △DPC (By SAS axiom)
As corresponding parts of congruent triangle are equal.
∴ ∠BDP = ∠CDP ......(ii)
From (i) and (ii) we can say that AP bisects ∠A as well as ∠D.
Hence, proved that AP bisects ∠A as well as ∠D.
(iv) Since, ∠BPA = ∠CPA.
From figure,
∠BPA + ∠CPA = 180°
2∠BPA = 180°
∠BPA = 90°.
Hence, proved that AP is the perpendicular bisector of BC.
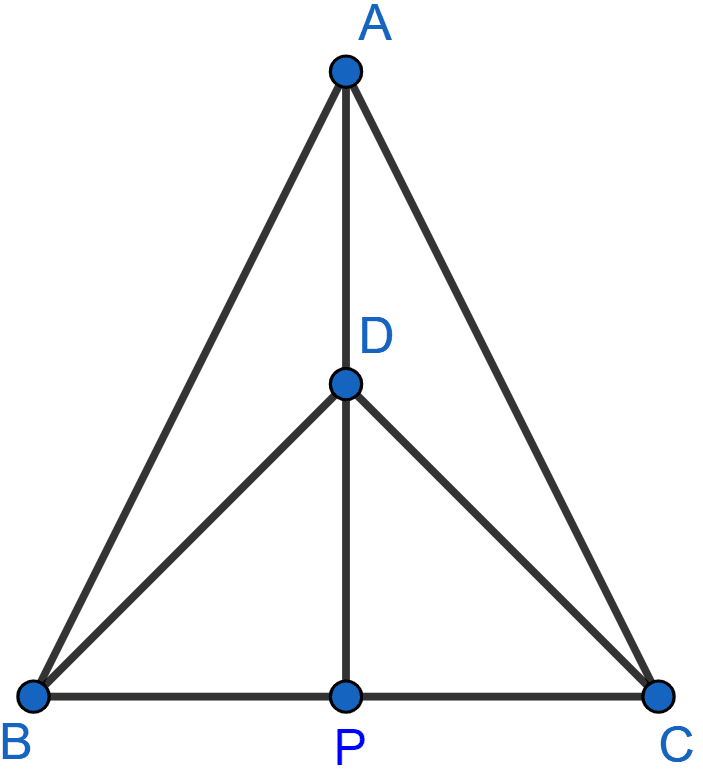
In the adjoining figure, AP ⊥ l and PR > PQ. Show that AR > AQ.
Answer
Take a point S on PR such that PS = PQ.
Join A and S. Mark angles as shown.
PQ = PS
AP = AP (Common)
∠APQ = ∠APS (Both are equal to 90°)
△APQ ≅ △APS (By SAS axiom)
We know that corresponding parts of congruent triangles are equal.
∠1 = ∠2.
In △ARS,
∠2 > ∠3 (As exterior angle is greater than each interior opposite angle.)
∴ ∠1 > ∠3
⇒ AR > AQ (As side opposite to greater angle is greater.)
Hence, proved that AR > AQ.
If O is any point in the interior of a triangle ABC, show that OA + OB + OC > (AB + BC + CA).
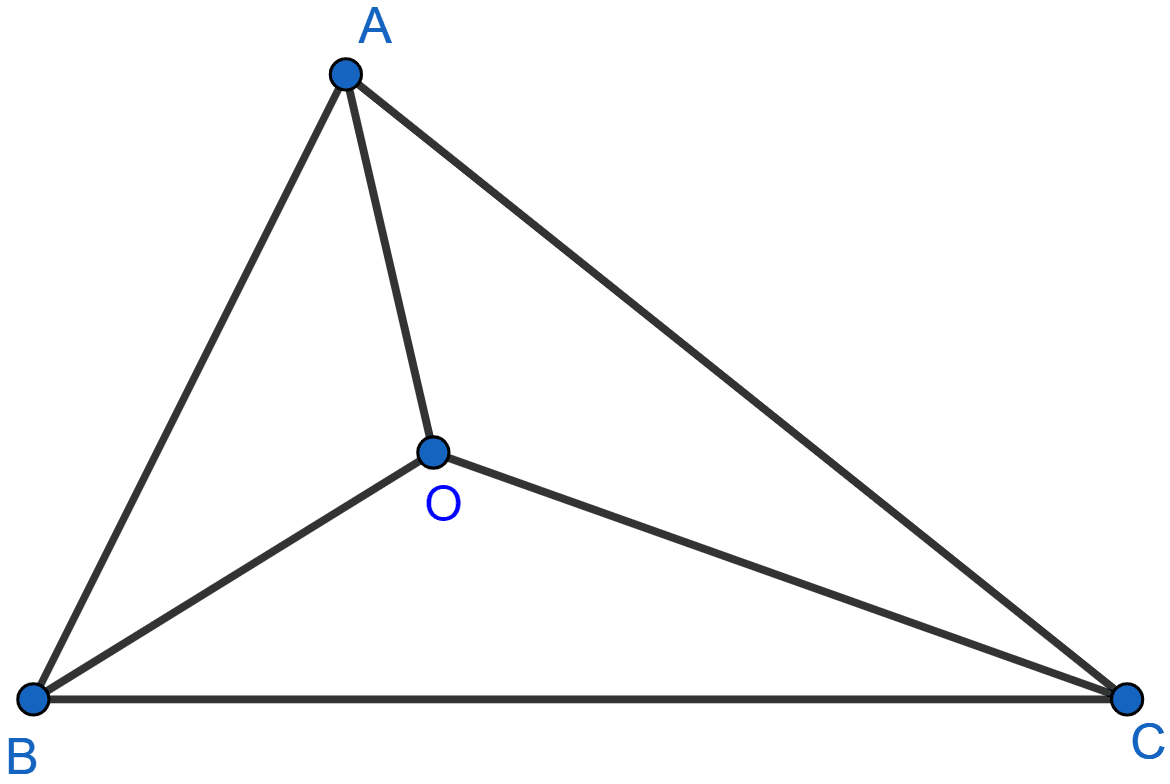
Answer
In △OBC, OB + OC > BC ......(i) (As sum of any two sides of triangle > third side)
Similarly OC + OA > CA .......(ii)
and, OA + OB > AB .......(iii)
On adding (i), (ii) and (iii), we get
⇒ OB + OC + OC + OA + OA + OB > BC + CA + AB
⇒ 2(OA + OB + OC) > AB + BC + CA
⇒ OA + OB + OC > (AB + BC + CA).
Hence, proved that OA + OB + OC > (AB + BC + CA).