Find the area of a triangle whose base is 6 cm and corresponding height is 4 cm.
Answer
Given,
Base of triangle = 6 cm
Height of triangle = 4 cm
We know that,
Area of triangle = × base × height
Substituting the values we get,
Area of triangle = × 6 × 4
= 6 × 2
= 12 cm2.
Hence, area of triangle = 12 cm2.
Find the area of a triangle whose sides are 3 cm, 4 cm and 5 cm.
Answer
Consider a = 3 cm, b = 4 cm and c = 5 cm
We know that
Semi perimeter (s) =
Substituting the values we get,
s = = 6 cm.
Area of triangle =
Substituting values we get,
Hence, area of triangle = 6 cm2.
Find the area of a triangle whose sides are 29 cm, 20 cm and 21 cm.
Answer
Consider a = 29 cm, b = 20 cm and c = 21 cm
We know that,
Semi perimeter (s) =
Substituting the values we get,
s = = 35 cm.
Area of triangle =
Substituting values we get,
Hence, area of triangle = 210 cm2.
Find the area of a triangle whose sides are 12 cm, 9.6 cm and 7.2 cm.
Answer
Consider a = 12 cm, b = 9.6 cm and c = 7.2 cm
We know that,
Semi perimeter (s) =
Substituting the values we get,
s = = 14.4 cm.
Area of triangle =
Substituting values we get,
Hence, area of triangle = 34.56 cm2.
Find the area of a triangle whose sides are 34 cm, 20 cm and 42 cm. Hence, find the length of the altitude corresponding to the shortest side.
Answer
Consider 34 cm, 20 cm and 42 cm as the sides of triangle.
a = 34 cm, b = 20 cm and c = 42 cm
We know that,
Semi perimeter (s) =
Substituting the values we get,
s = = 48 cm.
Area of triangle =
Substituting values we get,
Here the shortest side of the triangle is 20 cm. Let height = h cm be the corresponding altitude.
We know that,
Area of triangle = × base × height
Substituting the values we get,
⇒ 336 = × 20 × h
⇒ h =
⇒ h =
⇒ h = 33.6 cm.
Hence, area of triangle = 336 cm2 and length of the altitude corresponding to the shortest side = 33.6 cm.
The sides of a triangular field are 975 m, 1050 m and 1125 m. If this field is sold at the rate of ₹ 10 lakh per hectare, find its selling price. [1 hectare = 10000 m2]
Answer
Consider, a = 975 m, b = 1050 m and c = 1125 m.
We know that,
Semi perimeter (s) =
Substituting the values we get,
By formula,
Area of triangle (A) =
Substituting values we get :
We know that,
Selling price of 1 hectare field = ₹ 10 lakh.
∴ Selling price of 47.25 hectare field = ₹ 10,00,000 × 47.25 = ₹ 4,72,50,000.
Hence, selling price of the triangular field = ₹ 4,72,50,000.
The base of a right angled triangle is 12 cm and its hypotenuse is 13 cm long. Find its area and the perimeter.
Answer
It is given that,
ABC is a right angled triangle.
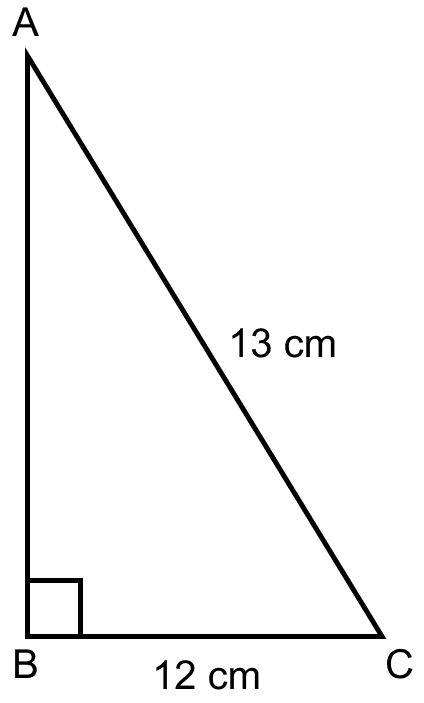
From figure,
BC = 12 cm and AC = 13 cm
Using the Pythagoras theorem,
AC2 = AB2 + BC2
Substituting the values we get,
⇒ 132 = AB2 + 122
⇒ AB2 = 132 – 122
⇒ AB2 = 169 – 144 = 25
⇒ AB = = 5 cm.
We know that,
Area of triangle ABC = × base × height.
Substituting the values we get,
A = = 30 cm2.
Perimeter of triangle ABC (P) = AB + BC + CA
Substituting the values we get,
= 5 + 12 + 13
= 30 cm.
Hence, area of triangle = 30 cm2 and perimeter = 30 cm.
Find the area of an equilateral triangle whose side is 8 m. Give your answer correct to two decimal places.
Answer
Given,
Side of equilateral triangle = 8 m.
We know that,
Area of equilateral triangle = (side)2
Substituting the values we get,
Hence, area of equilateral triangle = 27.71 m2.
If the area of an equilateral triangle is cm2, find its perimeter.
Answer
We know that,
Area of equilateral triangle = (side)2
Substituting the values,
So the perimeter of equilateral triangle = 3 × side
= 3 × 18 = 54 cm.
Hence, perimeter of equilateral triangle = 54 cm.
If the perimeter of an equilateral triangle is 36 cm, calculate its area and height.
Answer
We know that,
Perimeter of an equilateral triangle = 3 × side.
Substituting the values,
⇒ 36 = 3 × side
⇒ side = = 12 cm.
Area of equilateral triangle =
Substituting the values we get,
From figure,
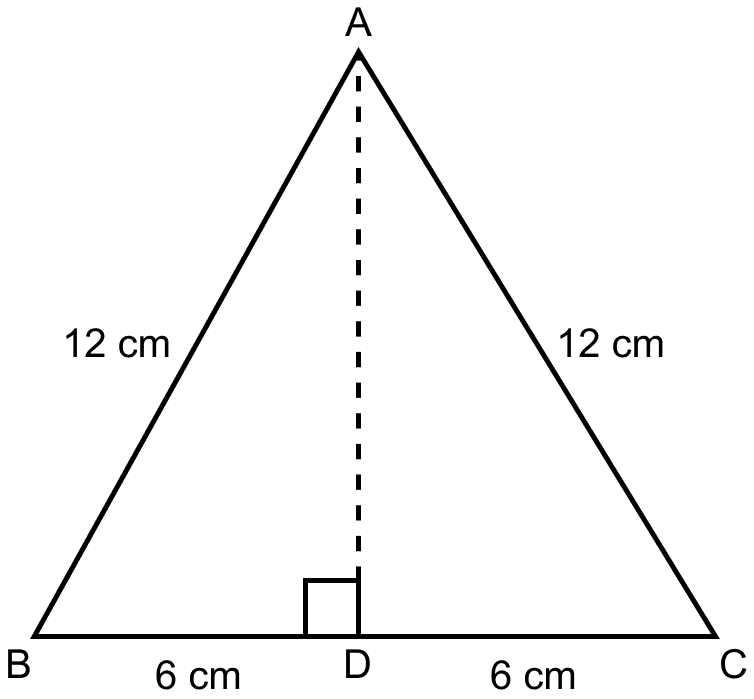
In triangle ABD,
Using Pythagoras Theorem,
AB2 = AD2 + BD2 .......(1)
The perpendicular from a vertex of an equilateral triangle to the opposite side, bisects it.
So, BD = = 6 cm.
Substituting the values in (1) we get,
⇒ 122 = AD2 + 62
⇒ 144 = AD2 + 36
⇒ AD2 = 144 – 36 = 108
⇒ AD = = 10.4 cm.
Hence, area of triangle = 62.4 cm2 and height = 10.4 cm.
If the lengths of the sides of a triangle are in the ratio 3: 4 : 5 and its perimeter is 48 cm, find its area.
Answer
Let a, b and c be the sides of the triangle.
Given,
Ratio of the sides are 3 : 4 : 5.
Let a = 3x cm, b = 4x cm and c = 5x cm.
Given,
⇒ Perimeter = 48 cm
⇒ a + b + c = 48
⇒ 3x + 4x + 5x = 48
⇒ 12x = 48
⇒ x = = 4.
Substituting value of x,
a = 3x = 3 × 4 = 12 cm,
b = 4x = 4 × 4 = 16 cm,
c = 5x = 5 × 4 = 20 cm.
We know that,
Semi perimeter (s) = .
Area of triangle =
Substituting values we get,
Hence, area of triangle = 96 cm2.
The sides of a triangular plot are in the ratio 3 : 5 : 7 and its perimeter is 300 m. Find its area. Take .
Answer
Given,
Sides of a triangle are in the ratio = 3 : 5 : 7
Perimeter = 300 m
Let a = 3x cm, b = 5x cm and c = 7x cm.
Given,
⇒ Perimeter = 300 m
⇒ a + b + c = 300
⇒ 3x + 5x + 7x = 300
⇒ 15x = 300
⇒ x = = 20.
Substituting value of x,
a = 3x = 3 × 20 = 60 m,
b = 5x = 5 × 20 = 100 m,
c = 7x = 7 × 20 = 140 m.
We know that,
Semi-perimeter (s) = = 150 m.
Area of triangle =
Substituting values we get,
Hence, area of triangle = 2598 m2.
ABC is a triangle in which AB = AC = 4 cm and ∠A = 90°. Calculate the area of △ABC. Also find the length of perpendicular from A to BC.
Answer
It is given that
AB = AC = 4 cm
From figure,
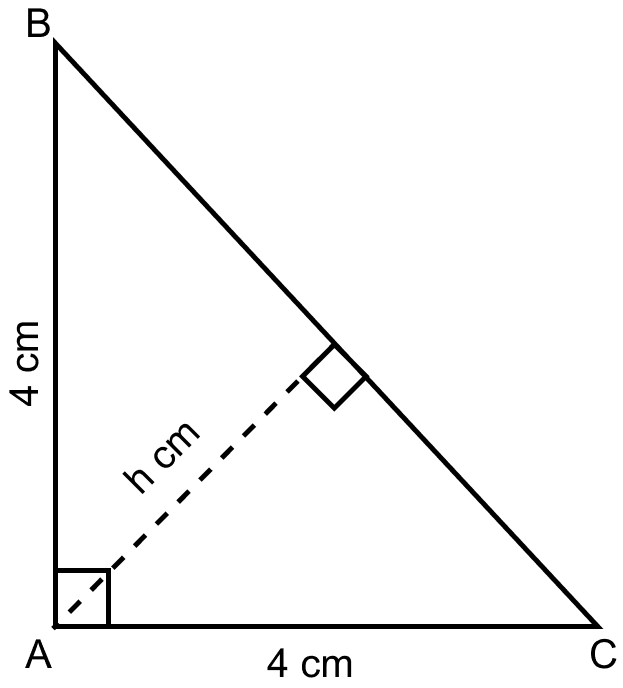
Using the Pythagoras theorem,
BC2 = AB2 + AC2
Substituting the values we get,
⇒ BC2 = 42 + 42
⇒ BC2 = 16 + 16 = 32
⇒ BC = cm.
Let perpendicular from A to BC be h cm.
Area of △ABC = × base × height
= × AC × AB
=
= 8 cm.
From figure,
Area of △ABC = × BC × h.
Hence, area of △ABC = 8 cm2 and length of perpendicular from A to BC = 2.83 cm.
Find the area of an isosceles triangle whose equal sides are 12 cm each and the perimeter is 30 cm.
Answer
Consider △ABC as the isosceles triangle.
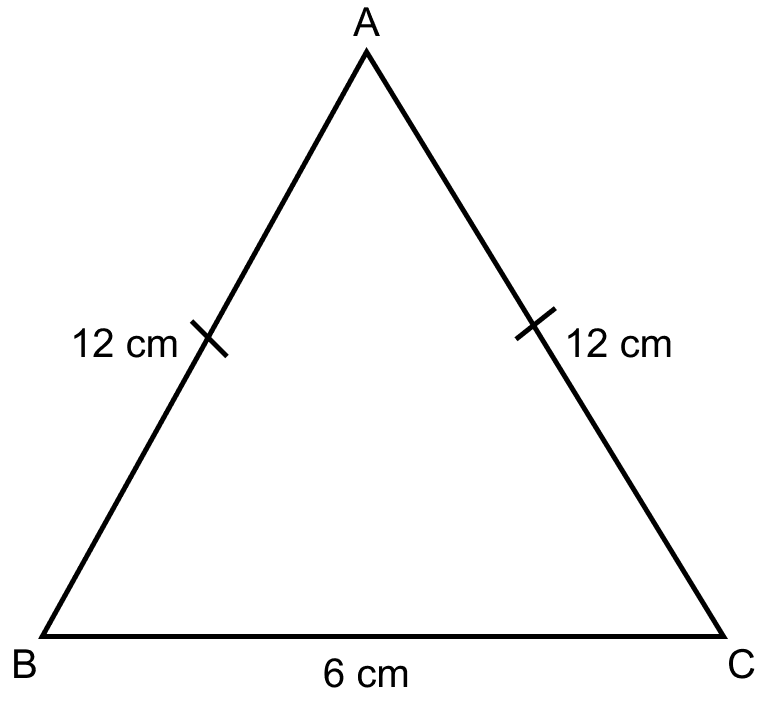
Here, AB = AC = 12 cm.
Perimeter = 30 cm
⇒ AB + AC + BC = 30
⇒ 12 + 12 + BC = 30
⇒ BC = 30 - 24 = 6 cm.
We know that,
Semi-perimeter (s) = = 15 cm.
Area of an isosceles triangle = , where a is length of equal sides and b is the length of other side.
Substituting values we get,
Hence, area of isosceles triangle = 34.86 cm2.
Find the area of an isosceles triangle whose base is 6 cm and perimeter is 16 cm.
Answer
Given,
base = 6 cm and perimeter = 16 cm
Consider △ABC as an isosceles triangle in which,
Let, AB = AC = x cm.
So, BC = 6 cm.
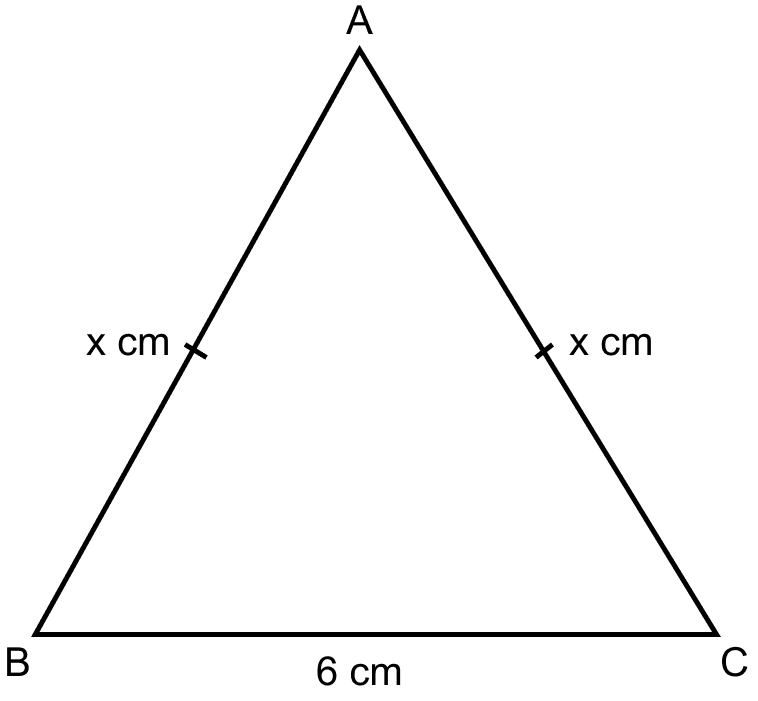
We know that,
Perimeter of △ABC = AB + BC + AC
Substituting the values we get,
⇒ 16 = x + 6 + x
⇒ 16 = 2x + 6
⇒ 16 – 6 = 2x
⇒ 10 = 2x
⇒ x = = 5 cm.
Area of an isosceles triangle = , where a is length of equal sides and b is the length of other side.
Substituting values we get,
Hence, area of isosceles triangle = 12 cm2.
The sides of a right-angled triangle containing the right angle are 5x cm and (3x – 1) cm. Calculate the length of the hypotenuse of the triangle if its area is 60 cm2.
Answer
Consider △ABC as a right angled triangle.
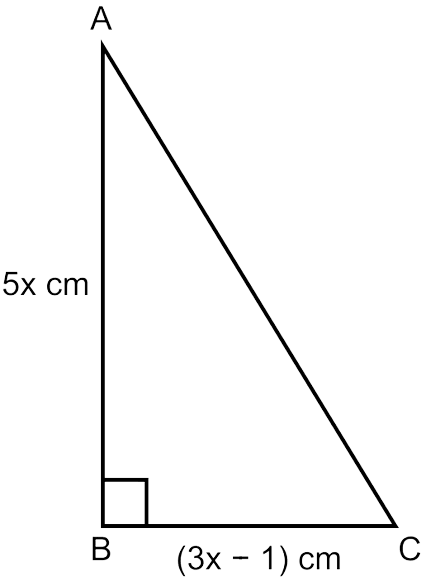
AB = 5x cm and BC = (3x – 1) cm
We know that,
Area of △ABC = × base × height = × BC × AB
Substituting the values we get,
⇒ 60 = × (3x – 1) × 5x
⇒ 120 = 5x(3x – 1)
⇒ 120 = 15x2 – 5x
⇒ 15x2 – 5x – 120 = 0
⇒ 5(3x2 – x – 24) = 0
⇒ 3x2 – x – 24 = 0
⇒ 3x2 – 9x + 8x – 24 = 0
⇒ 3x(x – 3) + 8(x - 3) = 0
⇒ (3x + 8)(x - 3) = 0
⇒ 3x + 8 = 0 or x - 3 = 0
⇒ 3x = -8 or x = 3
⇒ x = or x = 3
Since, x cannot be negative as length of a side cannot be negative. So, x = 3.
AB = 5 × 3 = 15 cm
BC = (3 × 3 – 1) = 9 – 1 = 8 cm
In right angled △ABC,
Using Pythagoras theorem,
⇒ AC2 = AB2 + BC2
Substituting the values we get,
⇒ AC2 = 152 + 82
⇒ AC2 = 225 + 64 = 289
⇒ AC2 = 172
So, AC = 17 cm.
Hence, the hypotenuse of the right angled triangle is 17 cm.
In △ABC, ∠B = 90°, AB = (2x + 1) cm and BC = (x + 1) cm. If the area of the △ABC is 60 cm2, find its perimeter.
Answer
Given,
AB = (2x + 1) cm
BC = (x + 1) cm

We know that,
Area of △ABC = × base × height
= × BC × AB
Substituting the values we get,
⇒ 60 = × (x + 1) × (2x + 1)
⇒ 60 × 2 = (2x + 1)(x + 1)
⇒ 120 = 2x2 + 3x + 1
⇒ 2x2 + 3x + 1 – 120 = 0
⇒ 2x2 + 3x – 119 = 0
⇒ 2x2 + 17x – 14x – 119 = 0
⇒ x(2x + 17) – 7(2x + 17) = 0
⇒ (x – 7)(2x + 17) = 0
⇒ x – 7 = 0 or 2x + 17 = 0
⇒ x = 7 or 2x = -17
⇒ x = 7 or x =
Since, x cannot be negative as length of a side cannot be negative. So, x = 7.
⇒ AB = (2x + 1) = 2 × 7 + 1 = 15 cm
⇒ BC = (x + 1) = 7 + 1 = 8 cm.
In right angled △ABC,
Using Pythagoras Theorem,
⇒ AC2 = AB2 + BC2
Substituting the values we get,
⇒ AC2 = 152 + 82
⇒ AC2 = 225 + 64
⇒ AC2 = 289
⇒ AC2 = 172
⇒ AC = 17 cm
Perimeter of △ABC = AB + BC + AC = 15 + 8 + 17 = 40 cm.
Hence, perimeter of △ABC = 40 cm.
If the perimeter of a right angled triangle is 60 cm and its hypotenuse is 25 cm, find its area.
Answer
Let △ABC be the right angle triangle.
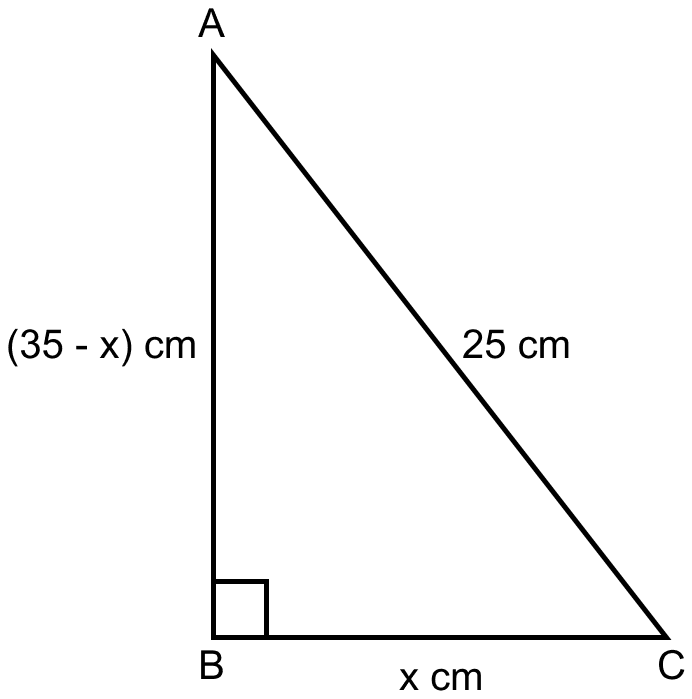
We know that,
Perimeter of a right-angled triangle = 60 cm
Hypotenuse = 25 cm
So, the sum of other two sides of triangle = 60 – 25 = 35 cm
Let base (BC) = x cm
So, AB = (35 - x) cm
Using the Pythagoras theorem,
⇒ AC2 = AB2 + BC2
⇒ 252 = (35 - x)2 + x2
⇒ 625 = 1225 + x2 - 70x + x2
⇒ 2x2 - 70x + 600 = 0
Dividing by 2 on both sides,
⇒ x2 - 35x + 300 = 0
⇒ x2 - 15x - 20x + 300 = 0
⇒ x(x – 15) - 20(x - 15) = 0
⇒ (x - 15)(x - 20) = 0
⇒ x - 15 = 0 or x - 20 = 0
⇒ x = 15 or x = 20.
If x = 15, then 35 - x = 35 - 15 = 20 cm.
If x = 20, then 35 - x = 35 - 20 = 15 cm.
So, length of other two sides apart from hypotenuse are 15 cm and 20 cm.
Area = × base × height
Substituting the values we get,
A = × 15 × 20 = 150 cm2.
Hence, area of triangle = 150 cm2.
The perimeter of an isosceles triangle is 40 cm. The base is two third of the sum of equal sides. Find the length of each side.
Answer
Let the length of equal sides be x cm.
Length of base = cm.
Given,
Perimeter = 40 cm
Length of Base = = = 16 cm
Hence, length of equal sides = 12 cm and length of base = 16 cm.
If the area of an isosceles triangle is 60 cm2 and the length of each of its equal sides is 13 cm, find its base.
Answer
Let the length of equal sides be a cm and length of base be b cm.
Area of isosceles △ABC = , where a is length of equal sides and b is the length of other side.
Substituting values in above equation we get,
Squaring both sides we get,
Hence, the length of base = 10 cm or 24 cm.
The base of a triangular field is 3 times its height. If the cost of cultivating the field at the rate of ₹25 per 100 m2 is ₹60000, find its base and height.
Answer
Given,
Cost of cultivating the field at the rate of ₹25 per 100 m2 = ₹ 60000
In ₹25, area of field cultivated = 100 m2
∴ In ₹60000, area of field cultivated = = 240000 m2.
∴ Area of field = 240000 m2.
Let base of field = b meters and height = 3b meters.
Area of triangle = base × height
Substituting values we get,
Hence, base = 400 m and height = 1200 m.
A triangular park ABC has sides 120 m, 80 m and 50 m (as shown in the adjoining figure). A gardner Dhania has to put a fence around it and also plant grass inside. How much area does she need to plant? Find the cost of fencing it with barbed wire at the rate of ₹ 200 per metre leaving a space 3 m wide for a gate on one side.
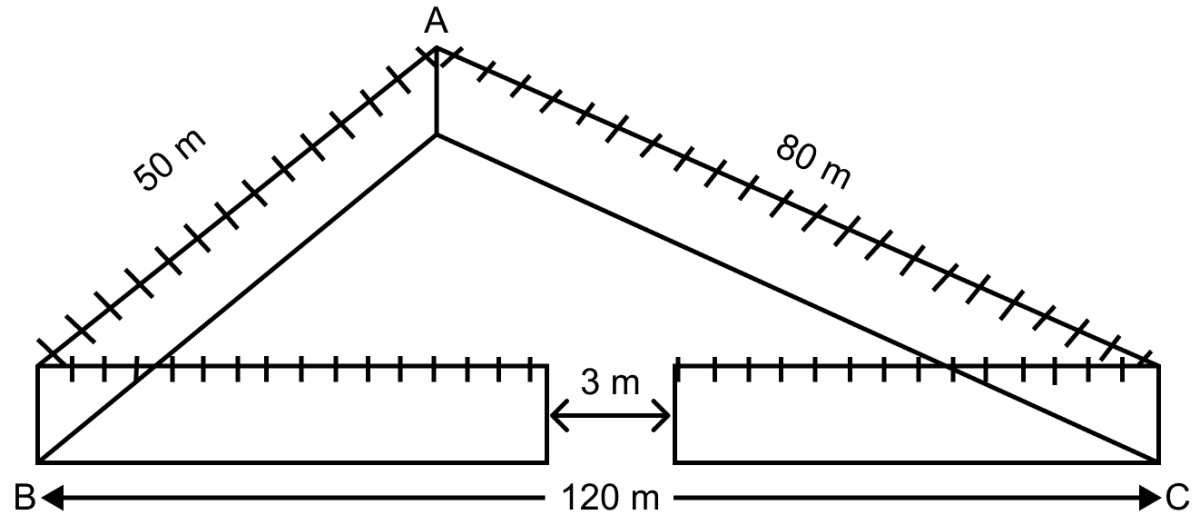
Answer
It is given that,
ABC is a triangular park with sides 120 m, 80 m and 50 m.
Here, the perimeter of △ABC = 120 + 80 + 50 = 250 m
Portion at which a gate is built = 3 m
Remaining perimeter = 250 – 3 = 247 m.
So, the length of the fence required around the park = 247 m.
Rate of fencing = ₹ 200 per metre
Total cost of fencing = 200 × 247 = ₹ 49,400.
We know that,
Semi perimeter (s) = = 125 m.
By formula,
Area of triangle (A) =
Substituting values we get,
Hence, area needed for plantation = m2 and cost of fencing = ₹49,400.
An umbrella is made by stitching 10 triangular pieces of cloth of two different colors (shown in the adjoining figure), each piece measuring 20 cm, 50 cm and 50 cm. How much cloth of each colour is required for the umbrella?

Answer
Semi-perimeter (s) = = 60 cm.
Total 10 triangular pieces of cloth are required. So, 5 of each colour.
Area of triangle =
Substituting values we get,
There are 5 triangular pieces. So area of 5 pieces = cm2.
Hence, cm2 of each colour cloth is required.
In the figure (i) given below, ABC is an equilateral triangle with each side of length 10 cm. In △BCD, ∠D = 90° and CD = 6 cm. Find the area of the shaded region. Give your answer correct to one decimal place.
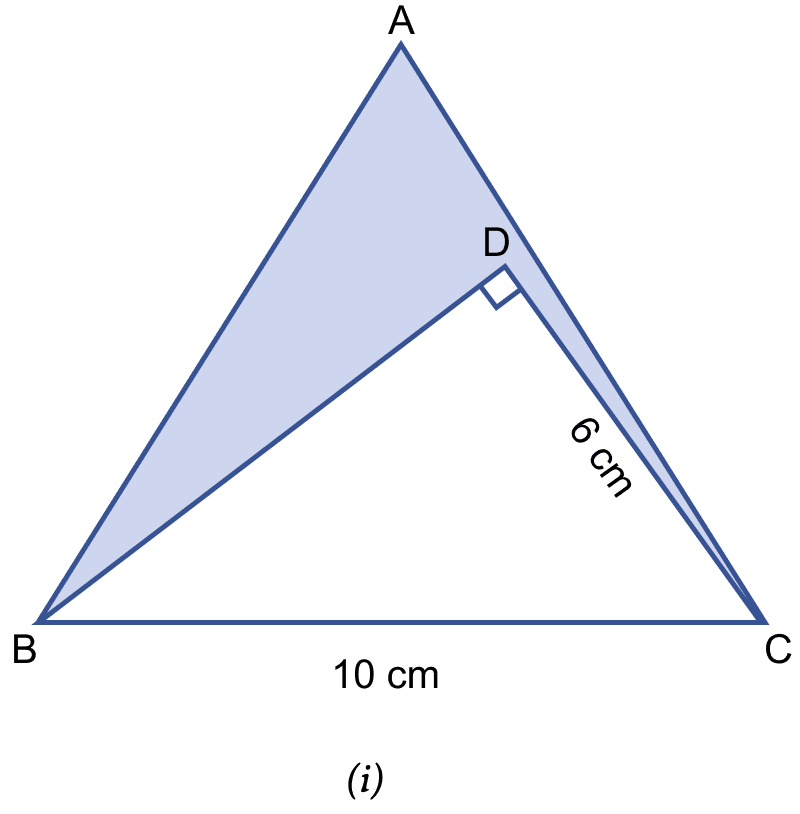
Answer
Given,
ABC is an equilateral triangle of side = 10 cm
We know that,
Area of equilateral triangle ABC =
Substituting the values we get,
In right angled triangle BCD,
⇒ BC2 = BD2 + CD2
⇒ 102 = BD2 + 62
⇒ BD2 = 100 - 36
⇒ BD2 = 64
⇒ BD = 8 cm.
We know that,
Area of right angled triangle = × base × height.
Area of △BCD = = 24 cm2
From figure,
Area of shaded portion = Area of triangle ABC - Area of triangle BCD
Substituting the values we get,
Area of shaded portion = 43.3 - 24 = 19.3 cm2.
Hence, area of shaded region = 19.3 cm2.
In the figure (ii) given, ABC is an isosceles right-angled triangle and DEFG is a rectangle. If AD = AE = 3 cm and DB = EC = 4 cm, find the area of the shaded region.
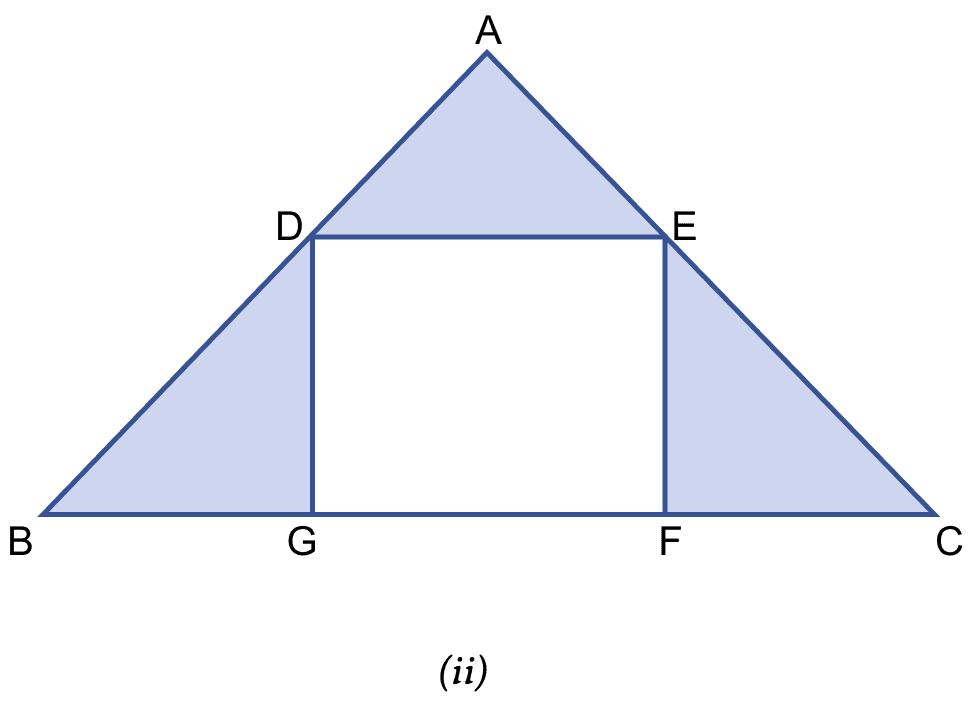
Answer
From figure,
In right angle triangle ADE,
Using pythagoras theorem,
⇒ DE2 = AD2 + AE2
⇒ DE2 = 32 + 32
⇒ DE2 = 9 + 9
⇒ DE2 = 18
⇒ DE = cm
Since, DEFG is a rectangle.
∴ GF = DE = cm.
In △DBG and △ECF,
DB = EC = 4 cm
DG = EF (Opposite sides of rectangle are equal)
∠DGB = ∠EFC = 90° (∵ DEFG is a rectangle)
Hence, by RHS axiom △DBG ≅ △ECF.
So, BG = FC (By C.P.C.T.)
Let BG = FC = x.
In right angle triangle ABC,
⇒ BC2 = AB2 + AC2
⇒ BC2 = 72 + 72
⇒ BC2 = 49 + 49
⇒ BC2 = 98
⇒ BC = cm
From figure,
BG + GF + FC = BC
⇒ BG + GF + FC =
⇒ x + + x =
⇒ 2x =
⇒ 2x =
⇒ x = cm.
In right angle triangle DBG,
⇒ DB2 = BG2 + DG2
⇒ 42 = 2 + DG2
⇒ 16 = 8 + DG2
⇒ DG2 = 16 - 8 = 8
⇒ DG = cm.
Area of right angle triangle DBG = x BG x DG
= x x
= x 8 = 4 cm2.
Since, △DBG ≅ △ECF.
∴ Areas of both triangle are equal.
Area of right angle triangle ADE = x AD x AE
= x 3 x 3
= = 4.5 cm2.
Area of shaded region = Area of (△ADE + △DBG + △ECF)
= 4.5 + 4 + 4 = 12.5 cm2.
Hence, area of shaded region = 12.5 cm2.
Find the area of quadrilateral whose one diagonal is 20 cm long and the perpendiculars to this diagonal from other vertices are of length 9 cm and 15 cm.
Answer
Consider ABCD as a quadrilateral in which BD = 20 cm, AY = 15 cm and CX = 9 cm.

Area of quadrilateral ABCD = Area of triangle ABD + Area of triangle BCD
Area of triangle = × base × height
∴ Area of quadrilateral ABCD = × BD × AY + × BD × CX
Substituting the values we get,
Area of quadrilateral ABCD = x BD x (AY + CX)
= x 20 x (15 + 9)
= 10 x 24
= 240 cm2
Hence, area of quadrilateral = 240 cm2.
Find the area of a quadrilateral whose diagonals are of length 18 cm and 12 cm and they intersect each other at right angles.
Answer
Consider ABCD as a quadrilateral in which the diagonals AC and BD intersect each other at M at right angles.

From figure,
AC = 18 cm and BD = 12 cm
When diagonals of a quadrilateral intersect at right angles,
Area of quadrilateral = x d1 x d2, where d1 and d2 are diagonals.
Substituting the values we get,
Area of quadrilateral ABCD = x 12 x 18
= 6 x 18
= 108 cm2
Hence, area of quadrilateral = 108 cm2.
Find the area of the quadrilateral field ABCD whose sides AB = 40 m, BC = 28 m, CD = 15 m, AD = 9 m and ∠A = 90°.
Answer
From figure,
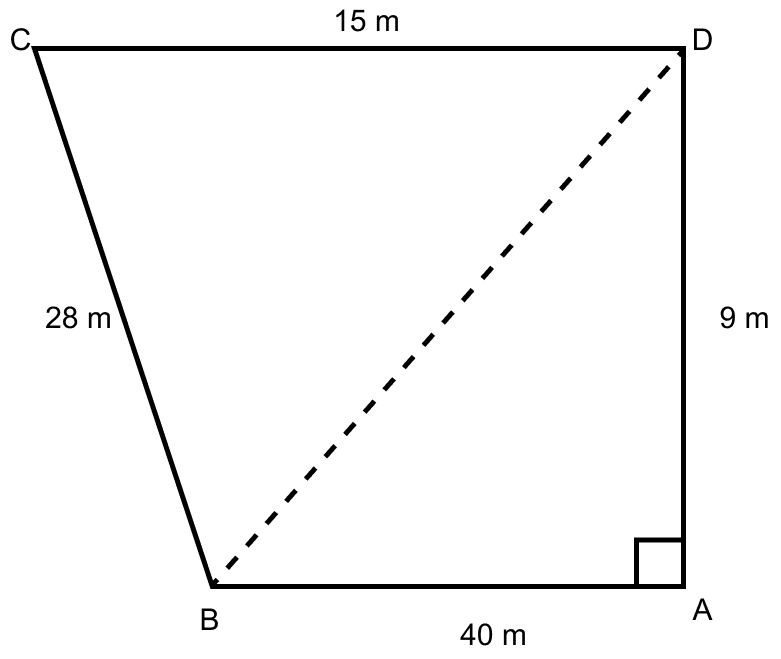
ABCD is a quadrilateral field.
In triangle BAD,
∠A = 90°
Using the Pythagoras Theorem
⇒ BD2 = AB2 + AD2
Substituting the values we get,
⇒ BD2 = 402 + 92
⇒ BD2 = 1600 + 81 = 1681
⇒ BD = = 41 m
We know that,
Area of quadrilateral ABCD = Area of △BAD + Area of △BDC
Calculating area of △BDC,
In △BDC,
Let a = BD = 41 m, b = BC = 28 m and c = CD = 15 m.
Semi-perimeter (s) = = 42 m.
By Heron's formula,
Area of triangle =
Substituting values we get,
Calculating area of △BAD,
Area of quadrilateral ABCD = Area of △BAD + Area of △BDC
= 180 + 126
= 306 m2.
Hence, area of quadrilateral ABCD = 306 m2.
Find the area of the quadrilateral ABCD in which ∠BCA = 90°, AB = 13 cm and ACD is an equilateral triangle of side 12 cm.
Answer
In right-angled △ABC,
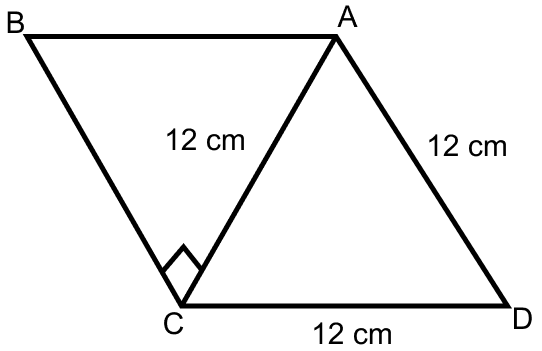
Using Pythagoras theorem,
⇒ AB2 = AC2 + BC2
Substituting the values we get,
⇒ 132 = 122 + BC2
⇒ BC2 = 132 – 122
⇒ BC2 = 169 – 144 = 25
⇒ BC = = 5 cm.
Calculating area of △BCA,
Calculating area of △ACD,
From figure,
Area of quadrilateral ABCD = Area of △BCA + Area of △ACD
= 30 cm2 + 62.35 cm2
= 92.35 cm2.
Hence, area of quadrilateral ABCD = 92.35 cm2.
Find the area of quadrilateral ABCD in which ∠B = 90° , AB = 6 cm, BC = 8 cm and CD = AD = 13 cm.
Answer
In △ABC,
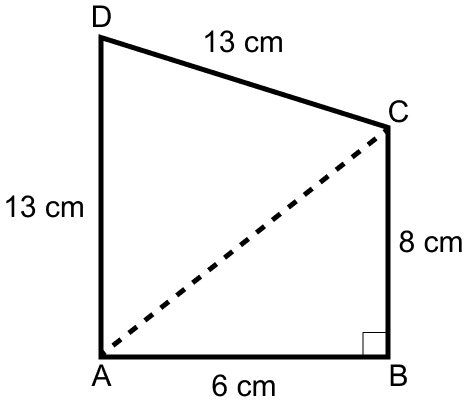
Using Pythagoras theorem,
AC2 = AB2 + BC2
Substituting the values we get,
⇒ AC2 = 62 + 82
⇒ AC2 = 36 + 64 = 100
⇒ AC2 = 102
⇒ AC = 10 cm
Calculating area of △ADC,
In △ADC,
Let a = AD = 13 cm, b = DC = 13 cm and c = AC = 10 cm.
Semi-perimeter (s) = = 18 cm.
By Heron's formula,
Area of triangle =
Substituting values we get,
Calculating area of △ABC,
From figure,
Area of quadrilateral ABCD = Area of △ADC + Area of △ABC
= 60 + 24
= 84 cm2.
Hence, area of quadrilateral ABCD = 84 cm2.
The perimeter of a rectangular cardboard is 96 cm; if its breadth is 18 cm, find the length and the area of the cardboard.
Answer
We know that,
Perimeter of rectangle = 2 × (l + b) = 96 cm
Substituting the values we get,
⇒ 2(l + 18) = 96
⇒ (l + 18) = 48
⇒ l = 48 - 18 = 30 cm.
Area of rectangular cardboard = l × b
Substituting the values we get,
Area = 30 × 18 = 540 cm2.
Hence, length = 30 cm and area of rectanglular cardboard = 540 cm2.
The length of a rectangular hall is 5 m more than its breadth. If the area of the hall is 594 m2, find its perimeter.
Answer
Let breadth = x meters
So, length = (x + 5) meters
We know that,
Area of rectangular hall = length × breadth
Substituting the values we get,
⇒ 594 = x(x + 5)
⇒ 594 = x2 + 5x
⇒ x2 + 5x – 594 = 0
⇒ x2 + 27x – 22x – 594 = 0
⇒ x(x + 27) – 22(x + 27) = 0
⇒ (x – 22)(x + 27) = 0
⇒ x – 22 = 0 or x + 27 = 0
⇒ x = 22 or x = -27.
Since, length of side cannot be negative so, x ≠ -27.
∴ Breadth = x = 22 m and Length = (x + 5) = 22 + 5 = 27 m.
Perimeter = 2(l + b)
Substituting the values we get,
Perimeter = 2(27 + 22) = 2 × 49 = 98 m.
Hence, perimeter of hall = 98 m.
The diagram (i) given below shows two paths drawn inside a rectangular field 50 m long and 35 m wide. The width of each path is 5 metres. Find the area of the shaded portion.

Answer
We know that,
Area of rectangle = length × breadth
Area of square = side × side.

From figure,
Area of shaded portion = Area of rectangle ABCD + Area of rectangle PQRS – Area of square LMNO
Substituting values we get,
Area of shaded portion = AB × AD + PR × RS - LM × MN
= 50 × 5 + 35 × 5 - 5 × 5
= 250 + 175 - 25
= 400 m2.
Hence, area of shaded region = 400 m2.
In the diagram (ii) given below, calculate the area of the shaded portion. All measurements are in centimetres.

Answer
We know that,
Area of rectangle = length × breadth
Area of square = side × side.
From figure,
Area of shaded portion = Area of large rectangle - 5 × Area of a small square.
Substituting values we get,
Area of shaded portion = (8 × 6) - (5 × 2 × 2)
= 48 - 20
= 28 cm2.
Hence, area of shaded region = 28 cm2.
A rectangular plot 20 m long and 14 m wide is to be covered with grass leaving 2 m all around. Find the area to be laid with grass.
Answer
Consider ABCD as a plot.

Length of plot = 20 m and breadth of plot = 14 m.
Let PQRS be the plot to be covered with grass.
From figure,
PQ = 20 - (2 × 2)
= 20 - 4
= 16 m
QR = 14 - (2 × 2)
= 14 - 4
= 10 m
Area of rectangular plot PQRS = length × breadth
Substituting the values we get,
Area = 16 × 10 = 160 m2.
Hence, area to be laid with grass = 160 m2.
The shaded region of the given diagram represents the lawn in front of a house. On three sides of the lawn there are flower beds of width 2 m.
(i) Find the length and the breadth of the lawn.
(ii) Hence, or otherwise, find the area of the flower–beds.

Answer
(i) Let PQRS be the lawn.
From figure,
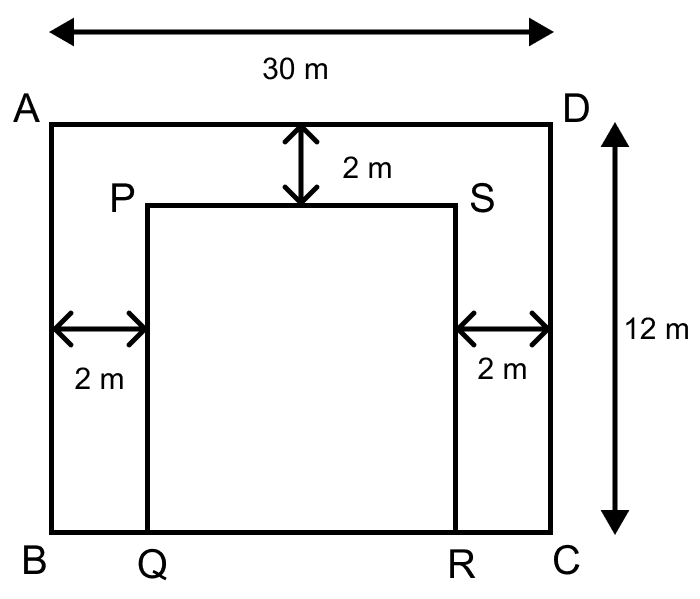
QR = BC - BQ - RC = 30 - 2 - 2 = 26 m.
SR = CD - DS = 12 - 2 = 10 m.
Length of PQRS = QR = 26 m and,
Breadth of PQRS = SR = 10 m.
Hence, length and breadth of lawn are 26 m and 10 m respectively.
(ii) From figure,
Area of flower beds = Area of rectangle ABCD - Area of rectangle PQRS
= (AD × DC) - (QR × SR)
= (30 × 12) - (26 × 10)
= 360 - 260
= 100 m2.
Hence, area of flower-beds = 100 m2.
A footpath of uniform width runs all around the inside of a rectangular field 50 m long and 38 m wide. If the area of the path is 492 m2, find its width.
Answer
Consider ABCD as a rectangular field having, length = 50 m and breadth = 38 m.
Let x meters be the width of foot path.
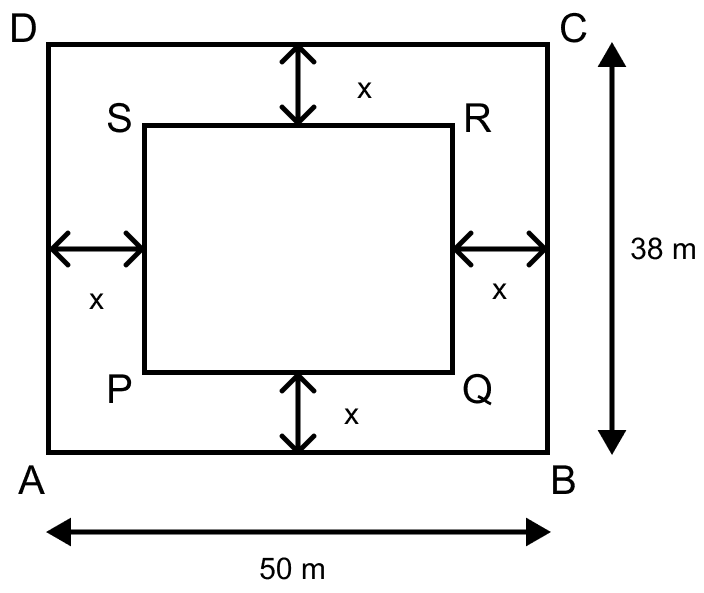
We know that,
Area of rectangular = l × b
From figure,
Area of path = Area of rectangle ABCD - Area of rectangle PQRS
Substituting the values we get,
Area of path = (AB × BC) - (PQ × QR) ........(1)
From figure,
PQ = AB - x - x = (50 - 2x) m,
QR = BC - x - x = (BC - 2x) m.
Substituting the values in equation 1 we get,
⇒ 492 = (50 × 38) - (50 - 2x) (38 - 2x)
⇒ 492 = 1900 - [50(38 - 2x) - 2x(38 - 2x)]
⇒ 492 = 1900 - (1900 - 100x - 76x + 4x2)
⇒ 492 = 1900 - 1900 + 100x + 76x - 4x2
⇒ 492 = 176x - 4x2
⇒ 492 = 4(44x - x2)
⇒ 123 = 44x - x2
⇒ x2 - 44x + 123 = 0
⇒ x2 - 41x - 3x + 123 = 0
⇒ x(x - 41) - 3(x - 41) = 0
⇒ (x - 3)(x - 41) = 0
⇒ x - 3 = 0 or x - 41 = 0
⇒ x = 3 m or x = 41 m.
Since, width of path cannot be greater than breadth of field,
So, x ≠ 41 m.
Hence, width of the footpath is 3 m.
The cost of enclosing a rectangular garden with a fence all around at the rate of ₹ 150 per metre is ₹ 54,000. If the length of the garden is 100 m, find the area of the garden.
Answer
Given,
Length = 100 m.
Let breadth = x meters.
By formula,
Perimeter of rectangle = 2(l + b)
Substituting the values we get,
Perimeter of rectangular garden = 2(100 + x) = (200 + 2x) m.
Given,
Cost of enclosing fence = ₹ 150 per meter.
∴ Cost of enclosing fence all round the rectangular garden = ₹150(200 + 2x) = ₹(30,000 + 300x).
Given, total cost of fencing = ₹ 54,000
∴ 30,000 + 300x = 54,000
⇒ 300x = 54,000 – 30,000
⇒ 300x = 24,000
⇒ x =
⇒ x = 80 m.
∴ Breadth of garden = 80 m.
So, the area of rectangular garden = length × breadth
= 100 × 80
= 8000 m2.
Hence, the area of rectangular garden = 8000 m2.
A rectangular floor which measures 15 m × 8 m is to be laid with tiles measuring 50 cm × 25 cm. Find the number of tiles required. Further, if a carpet is laid on the floor so that a space of 1 m exists between its edges and the edges of the floor, what fraction of the floor is uncovered?
Answer
Let ABCD be the rectangular floor and PQRS be the carpet.
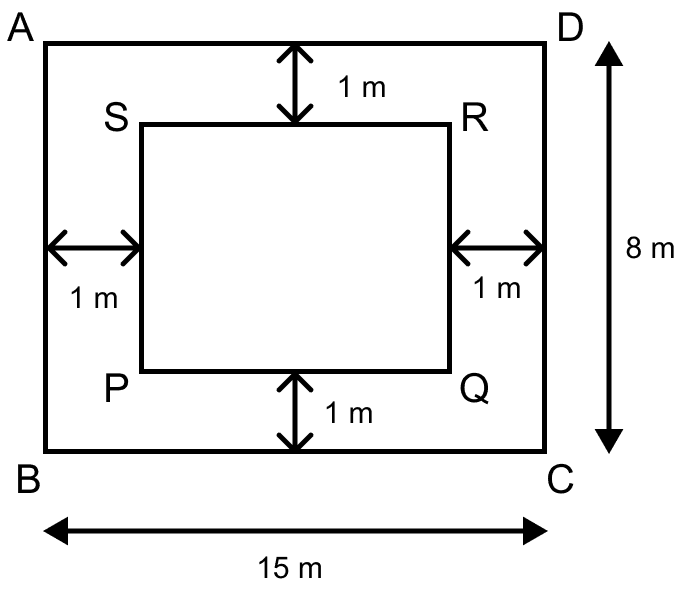
Area of floor = l × b = 15 × 8 = 120 m2 = 120 × (100 cm)2 = 1200000 cm2
Area of a tile = 50 cm × 25 cm = 1250 cm2
No. of required tiles =
Substituting the values we get,
No. of required tiles = = 960.
From figure,
Length of carpet (PQ) = 15 – 1 – 1
= 15 – 2
= 13 m
Breadth of carpet (QR) = 8 – 1 – 1
= 8 – 2
= 6 m
Area of carpet = l × b
= 13 × 6
= 78 m2.
Area of floor which is uncovered by carpet = Area of floor – Area of carpet
= 120 – 78
= 42 m2
Fraction of floor uncovered =
= .
Hence, number of tiles required to cover the floor = 960 tiles and is the fraction of floor uncovered.
The width of a rectangular room is of its length metres. If its perimeter is metres, write an equation connecting and . Find the floor area of the room if its perimeter is 32 m.
Answer
Given,
Length of rectangular room = x meters
Width of rectangular room = meters.
Perimeter = y meters.
We know that,
Perimeter = 2(l + b)
Substituting the values we get,
The above equation is the required relation between x and y.
Given, perimeter = y = 32 m.
Now substituting the value of y in equation (1)
⇒ 16x = 5 × 32
⇒ x = = 10 m,
⇒ Breadth = = 6 m.
Floor area of the room = l × b
= 10 × 6
= 60 m2.
Hence, 16x = 5y is the equation connecting x and y and the floor area of room = 60 m2.
A rectangular garden 10 m by 16 m is to be surrounded by a concrete walk of uniform width. Given that the area of the walk is 120 square metres, assuming the width of the walk to be x, form an equation in x and solve it to find the value of x.
Answer
Let ABCD be a rectangular garden.
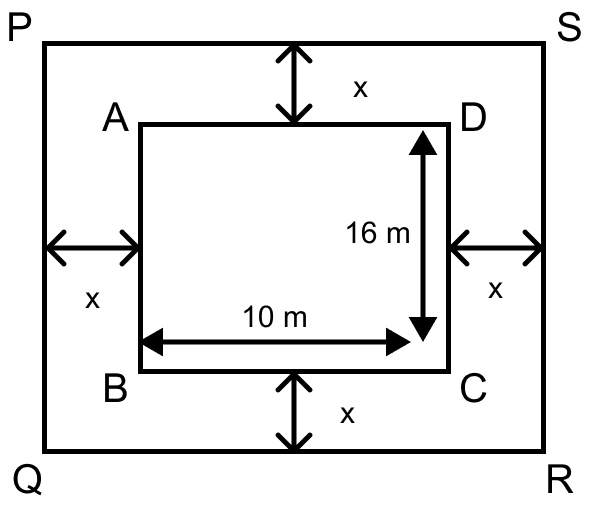
Length = 10 m and Breadth = 16 m.
Area of garden ABCD = l × b
= 10 × 16 = 160 m2
Given, width of the walk = x meters.
From figure,
Length of rectangular garden PQRS = 10 + x + x = (10 + 2x) m
Breadth of rectangular garden PQRS = 16 + x + x = (16 + 2x) m
From figure,
⇒ Area of walk = Area of rectangle PQRS - Area of rectangle ABCD
⇒ 120 = (10 + 2x)(16 + 2x) - 160
⇒ 120 = 160 + 20x + 32x + 4x2 - 160
⇒ 120 = 4x2 + 52x
⇒ 4x2 + 52x - 120 = 0
⇒ 4(x2 + 13x - 30) = 0
⇒ x2 + 13x - 30 = 0
The above equation is the equation in x.
Solving further,
⇒ x2 + 15x - 2x - 30 = 0
⇒ x(x + 15) - 2(x + 15) = 0
⇒ (x - 2)(x + 15) = 0
⇒ x = 2 or x = -15.
Since, length cannot be negative.
∴ x = 2.
Hence, equation is x2 + 13x - 30 = 0 and x = 2 metres.
A rectangular room is 6 m long, 4.8 m wide and 3.5 m high. Find the inner surface area of the four walls.
Answer
It is given that
Length of rectangular room = 6 m
Breadth of rectangular room = 4.8 m
Height of rectangular room = 3.5 m
By formula,
Inner surface area of four walls = 2(l + b) × h
= 2(6 + 4.8) × 3.5
= 2 × 10.8 × 3.5
= 21.6 × 3.5
= 75.6 m2.
Hence, inner surface area of four walls = 75.6 m2.
A rectangular plot of land measures 41 metres in length and 22.5 metres in width. A boundary wall 2 metres high is built all around the plot at a distance of 1.5 m from the plot. Find the inner surface area of the boundary wall.
Answer
Let ABCD be the rectangular plot.

Given,
Length of rectangular plot = 41 metres,
Breadth of rectangular plot = 22.5 metres.
Height of boundary wall = 2 metres.
Boundary wall is built at a distance of 1.5 m. It means wall is built on base PQRS.
From figure,
Length of plot PQRS = 41 + 1.5 + 1.5 = 44 m.
Breadth of plot PQRS = 22.5 + 1.5 + 1.5 = 25.5 m.
By formula,
Inner surface area of the boundary wall = 2(l + b) × h
= 2 (44 + 25.5) × 2
= 2 × 69.5 × 2
= 278 m2.
Hence, inner surface area of boundary wall = 278 m2.
Find the perimeter and area of the figure (i) given below in which all corners are right angles.

Answer
From figure,

Area of rectangle ABFG = l × b
= BF × AB
= (BC + CF) × AB
= (4 + 1.5) × 2
= 5.5 × 2
= 11 m2.
Area of rectangle CDEF = l × b
= CD × DE
= 4 × 1.5
= 6 m2.
Total Area = Area of rectangle ABFG + Area of rectangle CDEF
= 11 + 6 = 17 m2.
From figure,
AG = BF, GF = AB and FE = CD (As opposite sides of rectangle are equal.)
Perimeter of figure = AB + BC + CD + DE + EF + FG + AG
= 2 + 4 + 4 + 1.5 + 4 + 2 + 5.5
= 23 m.
Hence, perimeter = 23 m and area = 17 m2.
Find the perimeter and area of the figure (ii) given below in which all corners are right angles.

Answer
The points are labelled on the figure as shown below:

Area of rectangle ABIJ = l × b
= AB × BI
= AB × (BC + CI)
= 3 × (5 + 2)
= 3 × 7 = 21 m2.
Area of rectangle EFGH = l × b
= EF × FG
= 2 × 7 = 14 m2.
Area of rectangle CDHI = l × b
= CD × DH
= 8 × 2 = 16 m2.
Total area = Area of rectangle ABIJ + Area of rectangle EFGH + Area of rectangle CDHI
= 21 + 14 + 16
= 51 m2.
Perimeter of figure = AB + BC + CD + DE + EF + FG + GH + HI + IJ + JA
= 3 + 5 + 8 + 5 + 2 + 7 + 2 + 8 + 3 + 7
= 50 m.
Hence, perimeter = 50 m and area = 51 m2.
Find the area and perimeter of the figure (iii) given below in which all corners are right angles and all measurements are in cm.

Answer
The points are labelled on the figure as shown below:

Area of rectangle BCDE = l × b
= ED × CD
= 5 × 2
= 10 cm2.
Area of rectangle FGHI = l × b
= FG × GH
= 3 × 2
= 6 cm2.
Area of rectangle JKLM = l × b
= JK × KL
= 5 × 2
= 10 cm2.
Area of rectangle ABMN = l × b
= AB × AN
(From figure AB = AC - BC = 7 - 5 = 2 cm.)
= 2 × 12
= 24 cm2.
From figure,
Total area = Area of rectangle BCDE + Area of rectangle FGHI + Area of rectangle JKLM + Area of rectangle ABMN
= 10 + 6 + 10 + 24
= 50 cm2.
From figure,
The vertical distance between C and L will be equal to vertical distance between A and N,
So ignoring the vertical sides in right side and replacing it will CL.
Perimeter = AC + DE + FG + HI + JK + LN + NA + CL
= 7 + 5 + 3 + 3 + 5 + 7 + 12 + 12
= 54 cm.
Hence, area = 50 cm2 and perimeter = 54 cm.
The length and the breadth of a rectangle are 12 cm and 9 cm respectively. Find the height of a triangle whose base is 9 cm and whose area is one-third that of rectangle.
Answer
Area of rectangle = l × b = 12 × 9
= 108 cm2.
Given,
Area of triangle = one-third the area of rectangle.
Substituting the values we get,
Area of triangle = × 108 = 36 cm2.
Consider h cm as the height of triangle.
By formula,
Area of triangle = × base × height
Substituting the values we get,
⇒ 36 = × 9 × h
⇒ 36 × 2 = 9 × h
⇒ h =
⇒ h = 8 cm.
Hence, height of triangle is 8 cm.
The area of a square plot is 484 m2. Find the length of its one side and the length of its one diagonal.
Answer
Let ABCD be the square plot having area 484 m2.

Let length of each side of the plot be x meters.
We know that,
Area of square = side × side
Substituting the values we get,
⇒ 484 = (x)2
⇒ x = = 22 m.
Since, each angle = 90° in a square.
In right angle triangle ABC,
Using Pythagoras Theorem,
⇒ AC2 = AB2 + BC2
⇒ AC2 = 222 + 222
⇒ AC2 = 484 + 484 = 968
⇒ AC =
⇒ AC = 22 × 1.414 = 31.11 m.
Hence, length of side = 22 m and length of diagonal = 31.11 m.
A square has the perimeter 56 m. Find its area and the length of one diagonal correct up to two decimal places.
Answer
Let ABCD be a square with side x metres.

Perimeter of square = 4 × side
Substituting the values we get,
⇒ 56 = 4x
⇒ x = = 14 m.
Since, each angle = 90° in a square.
In right angle triangle ABC
Using Pythagoras theorem,
⇒ AC2 = AB2 + BC2
⇒ AC2 = 142 + 142
⇒ AC2 = 196 + 196 = 392
⇒ AC =
⇒ AC = = 14 × 1.414 = 19.80 m.
Area of square = (side)2
= 142 = 196 m2.
Hence, the area of square = 196 m2 and length of diagonal = 19.80 m.
A wire when bent in the form of an equilateral triangle encloses an area of cm2. Find the area enclosed by the same wire when bent to form:
(i) a square, and
(ii) a rectangle whose length is 2 cm more than its width.
Answer
Given,
Area of equilateral triangle = cm2
Consider x cm as the side of equilateral triangle
We know that,
Area of an equilateral triangle =
Substituting the values we get,
By formula,
Perimeter of equilateral triangle = 3 × side = 3 × 12 = 36 cm.
(i) As the same wire is now bent to form a square.
∴ Perimeter of equilateral triangle = Perimeter of square
36 = 4 × side
Side = = 9 cm.
Area of square = side × side = 9 × 9 = 81 cm2.
Hence, area enclosed by wire in form of square = 81 cm2.
(ii) As the same wire is now bent to form a rectangle.
∴ Perimeter of triangle = Perimeter of rectangle ........(1)
According to the condition given for rectangle,
Length is 2 cm more than its width
Let width of rectangle = x cm
∴ Length of rectangle = (x + 2) cm
Perimeter of rectangle = 2(l + b)
Substituting the values in equation 1 we get,
⇒ 36 = 2[(x + 2) + x]
⇒ 36 = 2[2x + 2]
⇒ 4x + 4 = 36
⇒ 4x = 32
⇒ x = 8 cm.
∴ Length of rectangle = x + 2 = 8 + 2 = 10 cm and Breadth of rectangle = x = 8 cm.
By formula,
Area of rectangle = length × breadth
= 10 × 8
= 80 cm2.
Hence, area enclosed by wire in form of square = 80 cm2.
Two adjacent sides of a parallelogram are 15 cm and 10 cm. If the distance between the longer sides is 8 cm, find the area of the parallelogram. Also find the distance between shorter sides.
Answer
Let ABCD be a parallelogram with side AB = 15 cm and side BC = 10 cm.

Distance between longer side DM = 8 cm
Consider DN as the distance between the shorter side
Area of parallelogram ABCD = base × height
= AB × DM = 15 × 8 = 120 cm2.
Considering base BC and height DN
Area of parallelogram = BC × DN
⇒ 120 = 10 × DN
⇒ DN = = 12 cm.
Hence, the area of parallelogram = 120 cm2 and the distance between shorter side = 12 cm.
ABCD is a parallelogram with sides AB = 12 cm, BC = 10 cm and diagonal AC = 16 cm. Find the area of the parallelogram. Also find the distance between its shorter sides.
Answer
In triangle ABC,
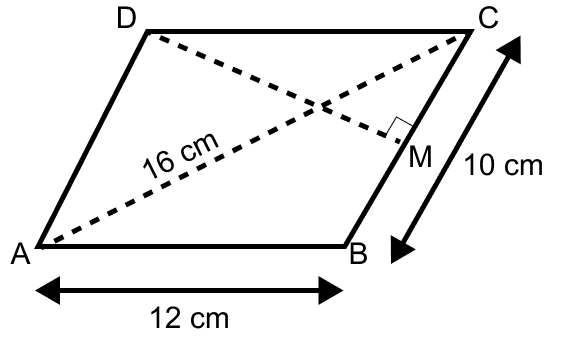
Let,
BC = a = 10 cm, AC = b = 16 cm and AB = c = 12 cm.
We know that,
Semi-perimeter (s) =
= = 19 cm.
By Heron's formula,
We know that,
Diagonal of a parallelogram divides it into two triangles of equal area.
∴ Area of triangle ABC = Area of triangle ADC
∴ Area of parallelogram = 2 × Area of triangle ABC.
= 2 × 59.9
= 119.8 cm2.
Let DM be the distance between the shorter sides of the parallelogram.
By formula,
Area of parallelogram = base × height = BC × DM
Substituting the values we get,
⇒ 119.8 = 10 × DM
⇒ DM =
⇒ DM = 11.98 cm.
Hence, the distance between shorter sides = 11.98 cm and area of parallelogram = 119.8 cm2.
Diagonals AC and BD of a parallelogram ABCD intersect at O. Given that AB = 12 cm and perpendicular distance between AB and DC is 6 cm. Calculate the area of the triangle AOD.
Answer
Let ABCD be a parallelogram with AC and BD the diagonals intersecting at O.
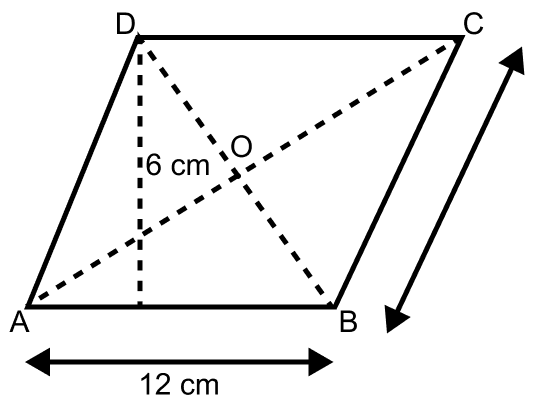
From figure,
AB = 12 cm and DM = 6 cm.
By formula,
Area of parallelogram ABCD = base × height = AB × DM
= 12 × 6
= 72 cm2.
Since, diagonals of parallelogram intersect each other so O is the mid-point of BD.
∴ AO is the median of the △ABD.
Since, median divides the triangle into two triangles of equal area,
∴ Area of △AOD = × Area of △ABD ......(1)
Since, diagonal of a parallelogram divides it into two triangles of equal area.
∴ Area of △ABD = × Area of || gm ABCD.
Substituting above value of △ABD in equation 1 we get,
Area of △AOD = Area of || gm ABCD
= = 18 cm2.
Hence, area of △AOD = 18 cm2.
ABCD is a parallelogram with side AB = 10 cm. Its diagonals AC and BD are of length 12 cm and 16 cm respectively. Find the area of the parallelogram ABCD.
Answer
Let ABCD be a parallelogram with diagonals intersecting at O.
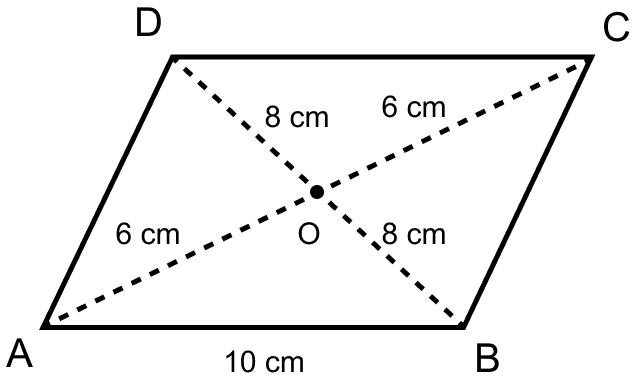
Since, diagonals of a parallelogram bisect each other.
∴ AO = = 6 cm and OB = = 8 cm.
In triangle AOB,
Let AB = a = 10 cm, BO = b = 8 cm and OA = c = 6 cm.
We know that,
Semi-perimeter (s) =
= = 12 cm.
By Heron's formula,
Since, diagonals of parallelogram intersect each other so O is the mid-point of BD.
∴ AO is the median of the △ABD.
Since, median divides the triangle into two triangles of equal area.
∴ Area of △AOB = × Area of △ABD ......(1)
Since, diagonal of a parallelogram divides it into two triangles of equal area.
∴ Area of △ABD = × Area of || gm ABCD.
Substituting above value of △ABD in equation 1 we get,
Area of △AOB = Area of || gm ABCD
Substituting values in above equation we get,
24 = Area of || gm ABCD
⇒ Area of || gm ABCD = 24 × 4 = 96 cm2.
Hence, area of || gm ABCD = 96 cm2.
The area of a parallelogram is p cm2 and its height is q cm. A second parallelogram has equal area but its base is r cm more than that of the first. Obtain an expression in terms of p, q and r for the height h of the second parallelogram.
Answer
By formula,
Area of a parallelogram = base × height ........(1)
Substituting values of 1st || gm in above equation,
⇒ p = base × q
⇒ base = cm.
Given,
Base of 2nd || gm is r cm more than the base of 1st || gm.
∴ Base of 2nd || gm = cm.
Given,
Height of second parallelogram = h cm
Substituting the values of 2nd || gm in equation 1,
Hence, h = cm.
What is the area of a rhombus whose diagonals are 12 cm and 16 cm?
Answer
By formula,
Area of rhombus = × d1 × d2, where d1 and d2 are diagonals.
Substituting the values we get,
Area of rhombus = × 16 × 12
= 8 × 12 = 96 cm2.
Hence, area of rhombus = 96 cm2.
The area of a rhombus is 98 cm2. If one of its diagonal is 14 cm, what is the length of the other diagonal?
Answer
By formula,
Area of rhombus = × d1 × d2, where d1 and d2 are diagonals.
Substituting the values we get,
⇒ 98 = × 14 × d2
⇒ d2 = = 14 cm.
Hence, the length of other diagonal = 14 cm.
The perimeter of a rhombus is 45 cm. If its height is 8 cm, calculate its area.
Answer
Let length of each side of rhombus = x cm.
Given,
Perimeter = 45 cm
⇒ x + x + x + x = 45
⇒ 4x = 45
⇒ x = cm
By formula,
Area of rhombus = base × height
Substituting the values we get,
Area of rhombus = × 8 = 90 cm2.
Hence, area of rhombus = 90 cm2.
PQRS is a rhombus. If it is given that PQ = 3 cm and the height of the rhombus is 2.5 cm, calculate its area.
Answer
From figure,
PQ is the base of rhombus PQRS and SM is the height of rhombus.

By formula,
Area of rhombus PQRS = base × height
= 3 × 2.5
= 7.5 cm2.
Hence, area of rhombus PQRS = 7.5 cm2.
If the diagonals of a rhombus are 8 cm and 6 cm, find its perimeter.
Answer
Let ABCD be a rhombus with AC and BD as two diagonals.

Let AC = 8 cm and BD = 6 cm.
Since, diagonals of a rhombus bisect each other at right angles.
∴ AO = 4 cm and BO = 3 cm.
In right angle triangle AOB,
Using Pythagoras theorem
⇒ AB2 = AO2 + BO2
⇒ AB2 = 42 + 32
⇒ AB2 = 16 + 9 = 25
⇒ AB = = 5 cm.
Side of rhombus ABCD = 5 cm
By formula,
Perimeter of rhombus = 4 × side = 4 × 5 = 20 cm.
Hence, perimeter of rhombus = 20 cm.
If the sides of a rhombus are 5 cm each and one diagonal is 8 cm, calculate
(i) the length of the other diagonal, and
(ii) the area of the rhombus.
Answer
(i) Let ABCD be a rhombus with AC and BD diagonals and each side = 5 cm.

Let AC = 8 cm.
Since, diagonals of rhombus bisect each other at right angles.
∴ AO = 4 cm.
In right angle triangle AOB
Using Pythagoras theorem,
⇒ AB2 = AO2 + BO2
⇒ 52 = 42 + BO2
⇒ 25 = 16 + BO2
⇒ BO2 = 25 – 16 = 9
⇒ BO = = 3 cm.
⇒ BD = 2 × BO = 2 × 3 = 6 cm.
Hence, length of other diagonal = 6 cm.
(ii) Area of rhombus = × product of diagonals
= × 8 × 6
= 4 × 6
= 24 cm2.
Hence, area of rhombus = 24 cm2.
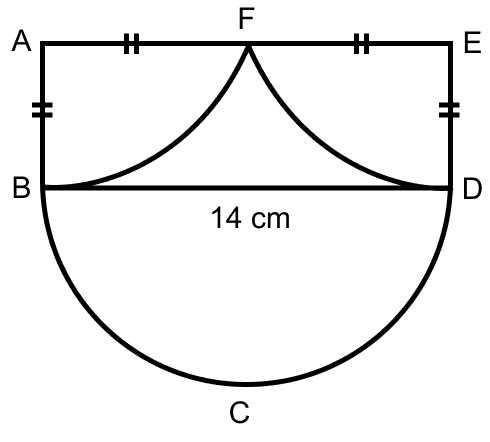
The figure (i) given below is a trapezium. Find the length of BC and the area of the trapezium. Assume AB = 5 cm, AD = 4 cm, CD = 8 cm.
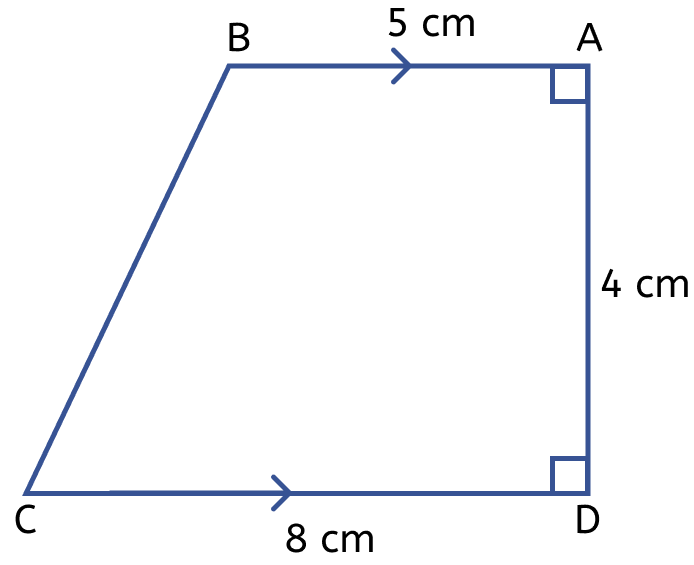
Answer
(a) Construct BN perpendicular to CD.
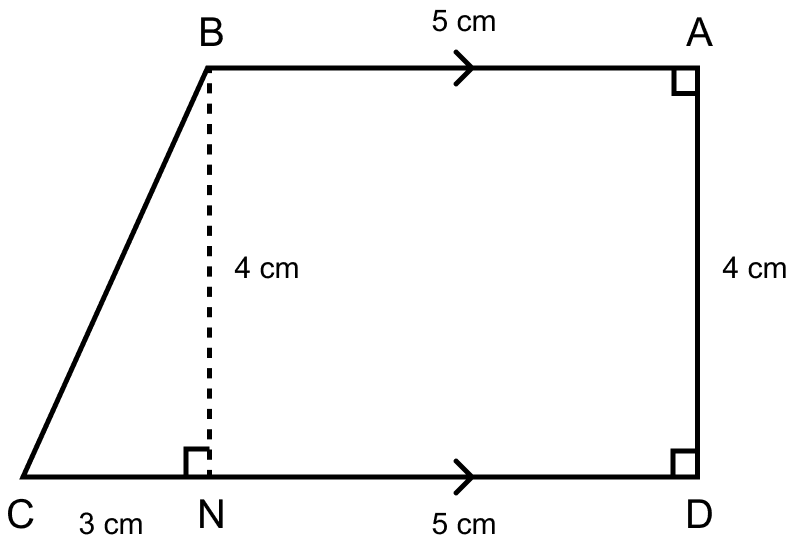
So, BADN is a rectangle.
As opposite sides of rectangle are equal.
∴ BN = AD = 4 cm and ND = BA = 5 cm.
From figure,
CN = CD – ND = 8 - 5 = 3 cm.
In right angle triangle BCN,
Using Pythagoras theorem,
⇒ BC2 = BN2 + CN2
⇒ BC2 = 42 + 32
⇒ BC2 = 16 + 9 = 25
⇒ BC = = 5 cm.
By formula,
Area of trapezium = × sum of parallel sides × height
= × (AB + CD) × AD
= × (5 + 8) × 4
= 13 × 2 = 26 cm2.
Hence, BC = 5 cm and area of trapezium = 26 cm2.
The figure (ii) given below is a trapezium. Find
(i) AB
(ii) area of trapezium ABCD.
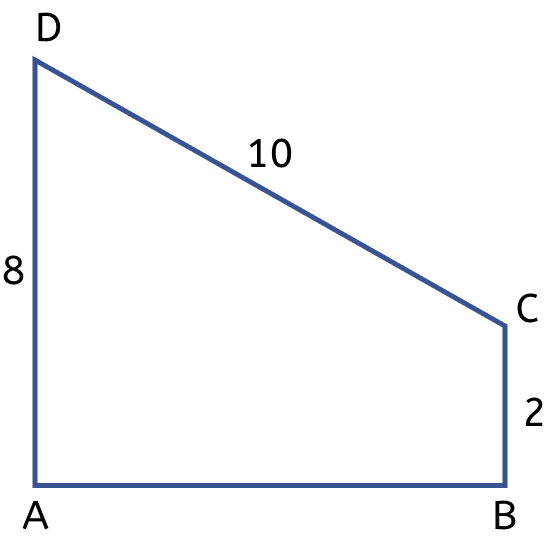
Answer
(i) Construct a perpendicular from C to AD parallel to AB.
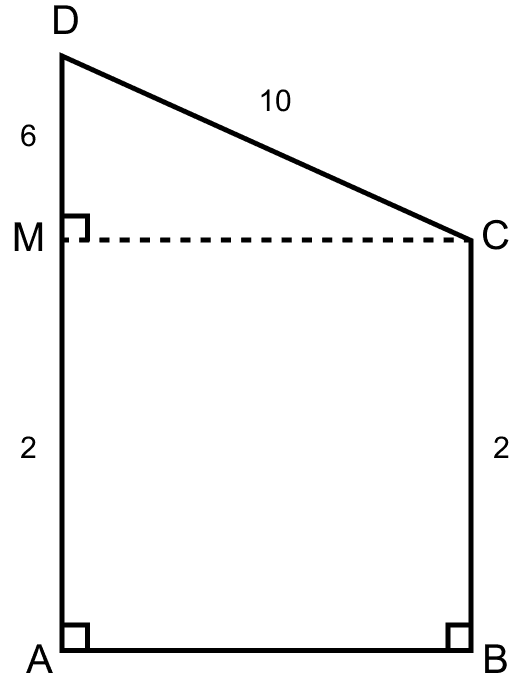
So, ABCM is a rectangle. Since, opposite sides of a rectangle are equal.
∴ AM = CB = 2 units.
From figure,
⇒ AD = AM + MD
⇒ MD = AD - AM = 8 - 2 = 6 units.
In right angle triangle MDC,
⇒ CD2 = MD2 + CM2
⇒ 102 = 62 + CM2
⇒ 100 = 36 + CM2
⇒ CM2 = 64
⇒ CM = = 8 units.
Since, ABCM is a rectangle.
∴ AB = CM = 8 units.
Hence, AB = 8 units.
(ii) Area of trapezium ABCD = × (sum of || sides) × distance between them
= × (AD + BC) × AB
= × (8 + 2) × 8
= 40 sq. units.
Hence, area of trapezium ABCD = 40 sq. units.
The cross-section of a canal is shown in figure (iii) given below. If the canal is 8 m wide at the top and 6 m wide at the bottom and the area of the cross-section is 16.8 m2, calculate its depth.

Answer
Consider ABCD as the cross section of canal in the shape of trapezium.
Draw a perpendicular AM from A to CD.
So, AM is the depth of canal.

Given, the area of cross-section of canal = 16.8 m2.
∴ × sum of parallel sides × depth = 16.8
⇒ × (AB + DC) × AM = 16.8
⇒ × (6 + 8) × AM = 16.8
⇒ × 14 × AM = 16.8
⇒ AM =
⇒ AM = = 2.4 m
Hence, depth of canal = 2.4 meters.
The distance between parallel sides of a trapezium is 12 cm and the distance between mid-points of other sides is 18 cm. Find the area of the trapezium.
Answer
Let ABCD be the trapezium in which AB || DC. Let E and F be mid-points of sides AD and BC respectively, then EF = 18 cm.

Given,
Distance between parallel sides of a trapezium is 12 cm.
∴ Height = 12 cm.
By formula,
Sum of the lengths of two parallel sides = 2 × Distance between mid-points of two non-parallel sides
⇒ AB + CD = 2 × EF = 2 × 18 = 36 cm.
Area of trapezium = × (Sum of parallel sides) × height
= × (AB + CD) × 12
= × 36 × 12
= 18 × 12
= 216 cm2.
Hence, area of trapezium = 216 cm2.
The area of a trapezium is 540 cm2. If the ratio of parallel sides is 7 : 5 and the distance between them is 18 cm, find the length of parallel sides.
Answer
Given,
Area of trapezium = 540 cm2
Ratio of parallel sides = 7 : 5
Let the sides be 7x and 5x cm.
Distance between the parallel sides = height = 18 cm
By formula,
Area of trapezium = × sum of parallel sides × height
⇒ 540 = × (7x + 5x) × 18
⇒ 540 = × 12x × 18
⇒ 540 = 6x × 18
⇒ 540 = 108x
⇒ x = = 5 cm.
⇒ 7x = 7 × 5 = 35 cm and 5x = 5 × 5 = 25 cm.
Hence, the length of parallel sides are 25 cm and 35 cm.
The parallel sides of an isosceles trapezium are in the ratio 2 : 3. If its height is 4 cm and area is 60 cm2, find the perimeter.
Answer
Since, ABCD is an isosceles trapezium so, BC = AD.
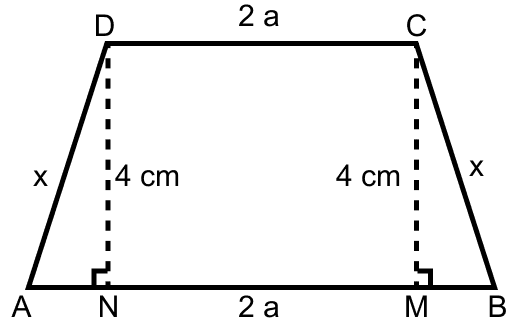
Since, parallel sides of an isosceles trapezium are in the ratio 2 : 3.
∴ CD = 2a and AB = 3a.
Construct perpendicular DN from D to AB and perpendicular CM from C to AB.
Given,
Area = 60 cm2
By formula,
Area of trapezium = × sum of parallel sides × height
⇒ 60 = × (AB + DC) × DN
⇒ 60 = × (3a + 2a) × 4
⇒ 60 = 2 × 5a
⇒ 10a = 60
⇒ a = 6 cm.
⇒ AB = 3a = 3 × 6 = 18 cm and CD = 2a = 2 × 6 = 12 cm.
In △ADN and △BCM,
⇒ ∠AND = ∠CMB = 90°
⇒ DN = CM = 4 cm
⇒ AD = CB = x cm (let) (As ABCD is an isosceles trapezium).
∴ △ADN ≅ △BCM by RHS axiom.
∴ AN = MB ........(1)
Since, DNMC is a rectangle.
∴ NM = DC = 12 cm. (As opposite sides of a rectangle are equal.)
From figure,
⇒ AN + NM + MB = 18
⇒ AN + 12 + MB = 18
⇒ AN + MB = 6
⇒ 2AN = 6 (As AN = MB)
⇒ AN = = 3 cm.
⇒ MB = 3 cm.
In right angle triangle AND,
⇒ AD2 = AN2 + DN2
⇒ x2 = 42 + 32
⇒ x2 = 16 + 9
⇒ x2 = 25
⇒ x = = 5 cm.
From figure,
Perimeter = AB + BC + CD + DA
= 18 + 5 + 12 + 5
= 40 cm.
Hence, perimeter of trapezium = 40 cm.
The area of a parallelogram is 98 cm2. If one altitude is half the corresponding base, determine the base and the altitude of the parallelogram.
Answer
Let base = x cm
Corresponding altitude = cm
By formula,
Area of parallelogram = base × altitude
Substituting the values we get,
⇒ 98 =
⇒ 98 =
⇒ x2 = 98 × 2 = 196
⇒ x = = 14 cm
⇒ Base = x = 14 cm
⇒ Altitude = = 7 cm.
Hence, base = 14 cm and altitude = 7 cm.
The length of a rectangular garden is 12 m more than its breadth. The numerical value of its area is equal to 4 times the numerical value of its perimeter. Find the dimensions of the garden.
Answer
Let breadth of rectangular garden = x meters,
∴ Length = (x + 12) meters.
Area of garden = length × breadth = x(x + 12) m2
Perimeter of garden = 2(l + b)
= 2[(x + 12) + x]
= 2[2x + 12] = (4x + 24) meters.
According to question,
⇒ Area of garden = 4 × Perimeter of garden
⇒ x(x + 12) = 4 × (4x + 24)
⇒ x2 + 12x = 16x + 96
⇒ x2 + 12x - 16x - 96 = 0
⇒ x2 - 4x - 96 = 0
⇒ x2 - 12x + 8x - 96 = 0
⇒ x(x - 12) + 8(x - 12) = 0
⇒ (x + 8)(x - 12) = 0
⇒ x + 8 = 0 or x - 12 = 0
⇒ x = -8 or x = 12.
Since, breadth cannot be negative.
∴ x ≠ -8.
Breadth = x = 12 m and Length = (x + 12) = (12 + 12) = 24 m.
Hence, length and breadth of garden are 24 m and 12 m respectively.
If the perimeter of a rectangular plot is 68 m and length of its diagonal is 26 m, find its area.
Answer
Let ABCD be a rectangular plot of length x m and breadth y m.
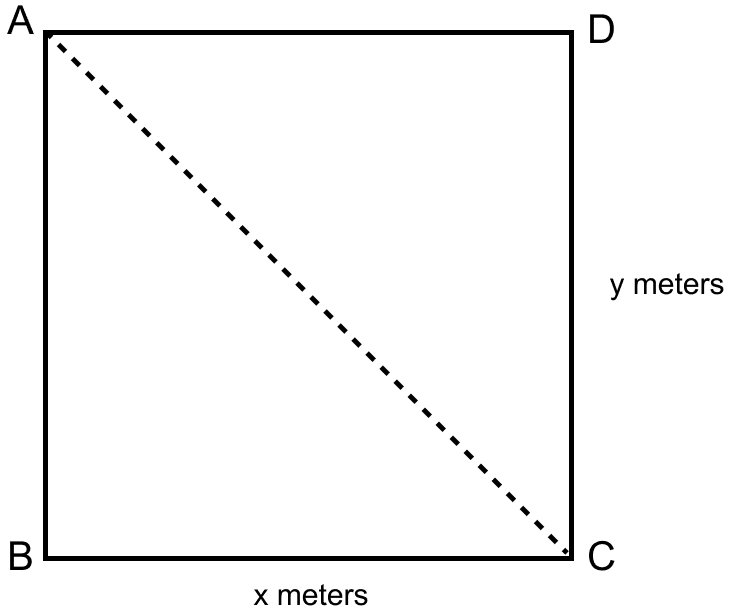
By formula,
Perimeter = 2(length + breadth)
Substituting the values we get,
⇒ 68 = 2(x + y)
⇒ 34 = x + y
⇒ x = 34 - y ......... (1)
In right angle triangle ABC
⇒ AC2 = AB2 + BC2 (By pythagoras theorem)
⇒ 262 = x2 + y2
⇒ x2 + y2 = 676
Substituting the value of x from equation (1),
⇒ (34 – y)2 + y2 = 676
⇒ 1156 + y2 – 68y + y2 = 676
⇒ 2y2 – 68y + 1156 – 676 = 0
⇒ 2y2 – 68y + 480 = 0
⇒ 2(y2 – 34y + 240) = 0
⇒ y2 – 34y + 240 = 0
⇒ y2 – 24y – 10y + 240 = 0
⇒ y(y – 24) – 10(y – 24) = 0
⇒ (y – 10)(y – 24) = 0
⇒ y – 10 = 0 or y – 24 = 0
⇒ y = 10 m or y = 24 m.
Now substituting the value of y in equation (1)
⇒ y = 10 m, x = 34 – 10 = 24 m
⇒ y = 24 m, x = 34 – 24 = 10 m
Area in both cases = xy
= 24 × 10 or 10 × 24
= 240 m2.
Hence, the area of the rectangular block is 240 m2.
A rectangle has twice the area of a square. The length of the rectangle is 12 cm greater and the width is 8 cm greater than a side of a square. Find the perimeter of the square.
Answer
Let length of a side of a square = x cm.
According to question,
Length of rectangle = (x + 12) cm
Breadth of rectangle = (x + 8) cm
Given,
⇒ Area of rectangle = 2 × area of square
⇒ (x + 12)(x + 8) = 2 × (x × x)
⇒ x(x + 8) + 12(x + 8) = 2x2
⇒ x2 + 8x + 12x + 96 = 2x2
⇒ x2 – 2x2 + 8x + 12x + 96 = 0
⇒ -x2 + 20x + 96 = 0
⇒ x2 – 20x – 96 = 0
⇒ x2 – 24x + 4x – 96 = 0
⇒ x(x - 24) + 4(x - 24) = 0
⇒ (x + 4)(x – 24) = 0
⇒ x + 4 = 0 or x - 24 = 0
⇒ x = -4 or x = 24 cm
Since, side of a square cannot be negative.
∴ x ≠ -4.
Side of square = 24 cm
Perimeter of square = 4 × side = 4 × 24
= 96 cm.
Hence, perimeter of square = 96 cm.
The perimeter of a square is 48 cm. The area of a rectangle is 4 cm2 less than the area of the square. If the length of the rectangle is 4 cm greater than its breadth, find the perimeter of the rectangle.
Answer
Perimeter of a square = 48 cm
Length of side of square = = 12 cm.
By formula,
Area = (side)2 = 122 = 144 cm2.
∴ Area of rectangle = 144 – 4 = 140 cm2
Let breadth of rectangle = x cm
∴ Length of rectangle = (x + 4) cm
Area of rectangle = l × b = x(x + 4) cm2
Substituting the values we get,
⇒ x(x + 4) = 140
⇒ x2 + 4x – 140 = 0
⇒ x2 + 14x – 10x – 140 = 0
⇒ x(x + 14) – 10(x + 14) = 0
⇒ (x + 14)(x – 10) = 0
⇒ x + 14 = 0 or x - 10 = 0
⇒ x = -14 or x = 10
Since, breadth cannot be negative.
∴ x ≠ -14.
Breadth = x = 10 cm and Length = x + 4 = 10 + 4 = 14 cm
Perimeter of rectangle = 2(l + b)
= 2(14 + 10)
= 2 × 24 = 48 cm.
Hence, perimeter of rectangle = 48 cm.
In the adjoining figure, ABCD is a rectangle with sides AB = 10 cm and BC = 8 cm. HAD and BFC are equilateral triangles; AEB and DCG are right angled isosceles triangles. Find the area of the shaded region and the perimeter of the figure.
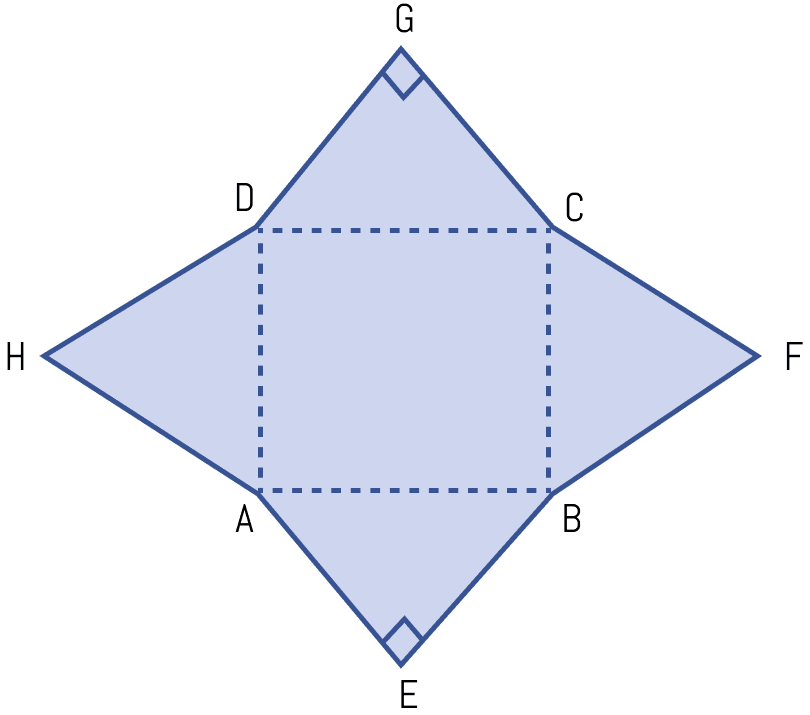
Answer
In △AEB,
Let AE = BE = x cm, then from right angled triangle AEB,
⇒ AB2 = AE2 + EB2
⇒ 102 = x2 + x2
⇒ 2x2 = 100
⇒ x2 = 50
⇒ x = cm.
Area of right angled △AEB = × base × height
In △DGC,
Let DG = GC = y cm, then from right angled triangle DGC,
⇒ DC2 = DG2 + GC2
⇒ 102 = y2 + y2
⇒ 2y2 = 100
⇒ y2 = 50
⇒ y = cm
Area of right angled △DCG = × base × height
Since, HAD and BFC are equilateral triangle with side = 8 cm.
Area of HAD = Area of BFC = × (side)2
=
= cm2
Area of rectangle ABCD = l × b = AB × CD
= 10 × 8 = 80 cm2
From figure,
Area of shaded region = Area of (△DGC + △BFC + △AEB + △HAD + rectangle ABCD)
= cm2.
Perimeter of figure = (AE + EB + BF + FC + CG + GD + DH + HA)
=
= cm.
Hence, area of shaded region = and perimeter = cm.
Find the area enclosed by the figure (i) given below, where ABC is an equilateral triangle and DEFG is an isosceles trapezium. All measurements are in centimeters.
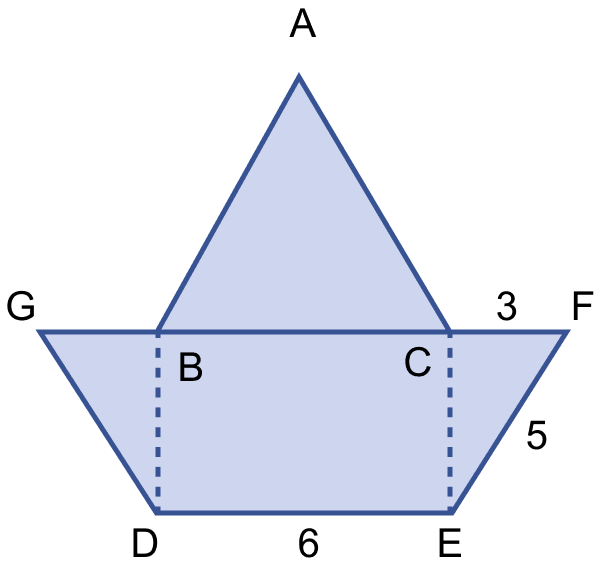
Answer
In right angle triangle ECF,
Using pythagoras theorem,
⇒ EF2 = EC2 + CF2
⇒ 52 = EC2 + 32
⇒ EC2 = 52 - 32
⇒ EC2 = 25 - 9 = 16
⇒ EC = = 4 cm.
Since, DEFG is an isosceles trapezium.
∴ GD = EF= 5 cm.
Since, BDEC is a rectangle,
∴ BD = EC = 4 cm and BC = DE = 6 cm.
In right angle triangle DBG,
Using pythagoras theorem,
⇒ GD2 = BD2 + GB2
⇒ 52 = 42 + GB2
⇒ GB2 = 52 - 42
⇒ GB2 = 25 - 16 = 9
⇒ GB = = 3 cm.
In trapezium,
GF = GB + BC + CF = 3 + 6 + 3 = 12 cm.
Area of trapezium DEFG = (sum of parallel sides) × distance between them
=
= 18 × 2
= 36 cm2.
Area of equilateral triangle ABC =
=
=
= 1.732 × 9
= 15.59 cm2
Area of figure = Area of trapezium DEFG + Area of equilateral triangle ABC
= 36 + 15.59 = 51.59 cm2.
Hence, area of figure = 51.59 cm2.
Find the area enclosed by the figure (ii) given below. All measurements are in centimeters.

Answer
From figure,

BJ = 2 + 2 + 2 + 2 = 8 cm.
Area of rectangle ABJK = l × b
= AB × BJ = 2 × 8
= 16 cm2.
From figure,
JH = KH - KI = 6 - 2 = 4 cm.
Area of trapezium FGHI = (sum of parallel sides) × distance between them
= × (FI + GH) × JH
= × (2 + 2) × 4
= × 4 × 4 = 8 cm2.
Area of trapezium CDEF = (sum of parallel sides) × distance between them
= × (CF + DE) × BD
= × (2 + 2) × 4
= × 4 × 4 = 8 cm2.
Total area enclosed = Area of rectangle ABJK + Area of trapezium FGHI + Area of trapezium CDEF
= 16 + 8 + 8
= 32 cm2.
Hence, area enclosed by figure = 32 cm2.
In the figure (iii) given below, from a 24 cm × 24 cm piece of cardboard, a block in the shape of letter M is cut off. Find the area of the cardboard left over, all measurements are in centimetres.

Answer
From figure,

Area of rectangle (I) = length × breadth
= 24 × 6
= 144 cm2.
Area of rectangle (II) = length × breadth
= 24 × 6
= 144 cm2.
Area of parallelogram (III) = base × height
= 8 × 6
= 48 cm2.
Area of parallelogram (IV) = base × height
= 8 × 6
= 48 cm2.
Area of figure M = Area of rectangle (I) + Area of rectangle (II) + Area of parallelogram (III) + Area of parallelogram (IV)
= 144 + 144 + 48 + 48
= 384 cm2.
Area of cardboard = 24 × 24
= 576 cm2.
Area of cardboard left = Area of cardboard - Area of figure M
= 576 - 384
= 192 cm2.
Hence, area of cardboard left = 192 cm2.
The figure (i) given below shows the cross-section of the concrete structure with the measurements as given. Calculate the area of cross-section.

Answer
From figure,

The figure consist of a trapezium and a rectangle.
Area of trapezium = (sum of parallel sides) × distance between them
= × (0.6 + 1.5) × (1.2 + 2.4)
= × 2.1 × 3.6
= 2.1 × 1.8
= 3.78 m2.
Area of rectangle = l × b
= 2.4 × 0.3 = 0.72 m2.
Area of cross section = Area of trapezium + Area of rectangle
= 3.78 + 0.72 = 4.5 m2.
Hence, area of cross-section = 4.5 m2.
The figure (ii) given below shows a field with the measurements given in metres. Find the area of the field.

Answer
From figure,
Area of right angled △AXB = × base × height
= × BX × AX
= × 30 × 12
= 180 m2.
Area of trapezium XZCB = (sum of parallel sides) × distance between them
= × (BX + CZ) × 15
= × (30 + 25) × 15
= × 55 × 15
= 412.5 cm2.
Area of right angled △CZD = × base × height
= × CZ × ZD
= × 25 × 10
= 125 m2.
Area of △AED = × base × height
= × AD × EY
= × 37 × 20
= 370 m2.
Area of field = Area of right angled △AXB + Area of trapezium XZCB + Area of right angled △CZD + Area of △AED
= 180 + 412.5 + 125 + 370 = 1087.5 m2.
Hence, area of field = 1087.5 m2.
Calculate the area of the pentagon ABCDE shown in fig (iii) below, given that AX = BX = 6 cm, EY = CY = 4 cm, DE = DC = 5 cm, DX = 9 cm and DX is perpendicular to EC and AB.
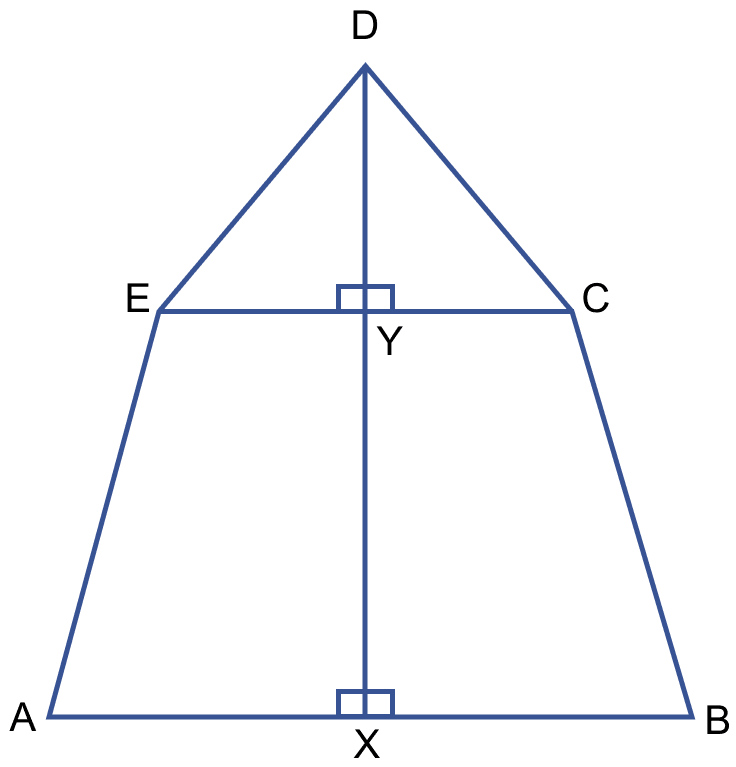
Answer
From figure,
In right angled △DEY,
⇒ DE2 = DY2 + EY2
⇒ 52 = DY2 + 42
⇒ DY2 = 52 - 42
⇒ DY2 = 25 - 16 = 9
⇒ DY = = 3 cm.
Area of right angled △DEY = × base × height
= × EY × DY
= × 4 × 3
= 6 cm2.
Area of right angle △DYC = × base × height
= × CY × DY
= × 4 × 3
= 6 cm2.
From figure,
XY = DX - DY = 9 - 3 = 6 cm.
Area of trapezium ECBA = (sum of parallel sides) × distance between them
= × (EC + AB) × XY
= × [(EY + CY) + (AX + BX)] × XY
= × [(4 + 4) + (6 + 6)] × 6
= × 20 × 6
= 60 cm2.
Area of pentagon = Area of right angled △DEY + Area of right angled △DYC + Area of trapezium ECBA
= 6 + 6 + 60
= 72 cm2.
Hence, area of trapezium = 72 cm2.
If the length and the breadth of a room are increased by 1 metre, the area is increased by 21 square metres. If the length is increased by 1 metre and breadth is decreased by 1 metre the area is decreased by 5 square metres. Find the perimeter of the room.
Answer
Let length = l metres and breadth = b metres.
Area = lb m2
Given,
If the length and the breadth of a room are increased by 1 metre, the area is increased by 21 square metres,
∴ (l + 1)(b + 1) - lb = 21
⇒ lb + l + b + 1 - lb = 21
⇒ l + b = 21 - 1
⇒ l + b = 20 ..........(1)
Given,
If the length is increased by 1 metre and breadth is decreased by 1 metre the area is decreased by 5 square metres.
∴ lb - (l + 1)(b - 1) = 5
⇒ lb - (lb - l + b - 1) = 5
⇒ lb - lb + l - b + 1 = 5
⇒ l - b = 4 ..........(2)
Adding equation (1) and (2) we get,
⇒ l + b + l - b = 20 + 4
⇒ 2l = 24
⇒ l = 12 m.
Substituting value of l in (2) we get,
⇒ 12 - b = 4
⇒ b = 12 - 4 = 8 m.
Perimeter of room = 2(l + b) = 2 × 20 = 40 m.
Hence, perimeter of room = 40 m.
A triangle and a parallelogram have the same base and same area. If the sides of the triangle are 26 cm, 28 cm and 30 cm, and the parallelogram stands on the base 28 cm, find the height of the parallelogram.
Answer
Let a = 26 cm, b = 28 cm and c = 30 cm.
Semi-perimeter (s) = = 42 cm.
Area of triangle =
Since, area of parallelogram = area of triangle.
∴ Area of parallelogram = 336
⇒ base × height = 336
⇒ 28 × height = 336
⇒ height = cm.
Hence, height of parallelogram = 12 cm.
A rectangle of area 105 cm2 has its length equal to x cm. Write down its breadth in terms of x. Given that its perimeter is 44 cm, write down an equation in x and solve it to determine the dimensions of the rectangle.
Answer
Given,
Area of rectangle = 105 cm2
Length of rectangle = x cm
By formula,
Area of rectangle = length × breadth
Substituting the values we get,
105 = x × breadth
Breadth = cm.
Perimeter of rectangle = 44 cm
If x = 7 cm,
Breadth = = 15 cm
If x = 15 cm,
Breadth = = 7 cm
Hence, breadth = , equation : 44 = and the required dimensions of rectangle are 15 cm and 7 cm.
The perimeter of a rectangular plot is 180 m and its area is 1800 m2. Take the length of plot as x m. Use the perimeter 180 m to write the value of the breadth in terms of x. Use the value of the length, breadth and the area to write an equation in x. Solve the equation to calculate the length and breadth of the plot.
Answer
Let length of rectangle be x meters.
Given,
Perimeter = 180 m
∴ 2(l + b) = 180
⇒ 2(x + b) = 180
⇒ x + b = 90
⇒ b = (90 - x) m.
Area = l × b
∴ x(90 - x) = 1800
⇒ 90x - x2 = 1800
⇒ x2 - 90x + 1800 = 0
⇒ x2 - 60x - 30x + 1800 = 0
⇒ x(x - 60) - 30(x - 60) = 0
⇒ (x - 30)(x - 60) = 0
⇒ x - 30 = 0 or x - 60 = 0
⇒ x = 30 or x = 60.
If x = 30, 90 - x = 60 and x = 60, 90 - x = 30.
Hence, breadth = (90 - x) m, equation : x(90 - x) = 1800 and length of rectangle = 60 m and breadth = 30 m.
Find the length of the diameter of a circle whose circumference is 44 cm.
Answer
Let radius = r cm.
By formula,
Circumference = 2πr
2πr = 44
Diameter = 2r = 2 × 7 = 14 cm.
Hence, length of the diameter of the circle = 14 cm.
Find the radius and area of a circle if its circumference is 18π cm.
Answer
Let radius = r cm.
By formula,
Circumference = 2πr
⇒ 2πr = 18π
⇒ 2r = 18
⇒ r = 9 cm.
Area of circle = πr2
=
= cm2.
Hence, radius = 9 cm and area = cm2.
Find the perimeter of a semicircular plate of radius 3.85 cm.
Answer
Perimeter of semicircular plate = (π + 2)r
Hence, perimeter of a semicircular plate = 19.8 cm.
Find the radius and circumference of a circle whose area is 144π cm2.
Answer
Let radius = r cm.
Area of circle = πr2
⇒ 144π = πr2
⇒ r2 = 144
⇒ r = = 12 cm.
Circumference of a circle = 2πr
=
= cm.
Hence, radius = 12 cm and circumference = cm.
A sheet is 11 cm long and 2 cm wide. Circular pieces 0.5 cm in diameter are cut from it to prepare discs. Calculate the number of discs that can be prepared.
Answer
Given,
Diameter of circle = 0.5 cm.

From figure,
Area of sheet required to cut a circle = area of a square with length of side equal to diameter.
∴ No. of discs prepared = No. of squares formed from sheet.
No. of squares that will be formed from sheet =
Hence, no. of discs that can be prepared = 88.
If the area of the semi-circular region is 77 cm2, find its perimeter.
Answer
Let radius = r cm.
Given,
Area of semi-circular region = 77 cm2
Perimeter of semi-circle = (π + 2) = πr + 2r
=
= 22 + 14
= 36 cm.
Hence, perimeter of circle = 36 cm.
In the figure (i) given below, AC and BD are two perpendicular diameters of a circle ABCD. Given that the area of shaded portion is 308 cm2, calculate :
(i) the length of AC and
(ii) the circumference of the circle.

Answer
(i) Let r be the radius of the circle. We know that,
Diameters of the circle divide circle into 4 equal quadrants.
Hence, area of each quadrant = πr2.
Since, 2 quadrants are shaded.
∴ Area of shaded region = πr2
⇒ 308 = r2
⇒ r2 =
⇒ r2 = 14 × 14 = 196
⇒ r = = 14 cm.
Since, AC is the diameter of circle so,
⇒ AC = 2r = 28 cm.
Hence, AC = 28 cm.
(ii) Circumference of circle = 2πr
=
= 88 cm.
Hence, circumference of circle = 88 cm.
In the figure (ii) given below, AC and BD are two perpendicular diameters of a circle with center O. If AC = 16 cm, calculate the area and perimeter of the shaded part. (Take π = 3.14)
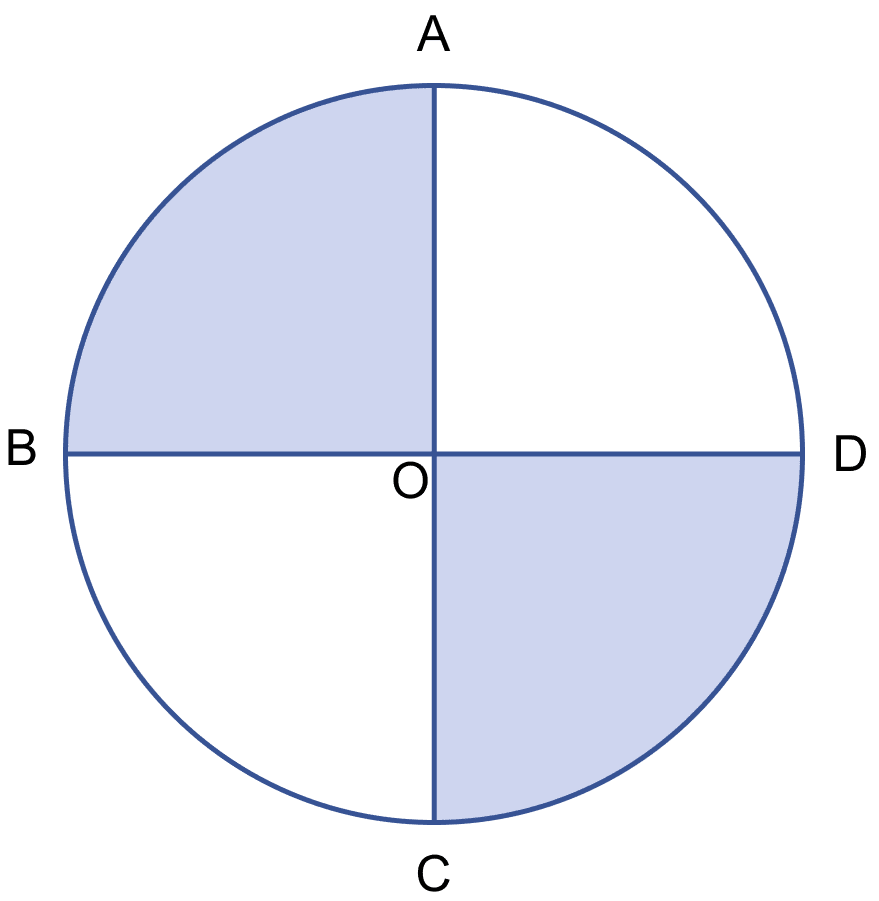
Answer
Given,
AC = 16 cm, AO = = 8 cm.
The diameters of the circle divide circle into 4 quadrants.
Area of each quadrant =
Area of quadrant AOD + Area of quadrant BOC = 50.24 + 50.24 = 100.48 cm2.
Perimeter of each quadrant =
Perimeter of both quadrants = 2 × 28.56 = 57.12 cm.
Hence, area of shaded region = 100.48 cm2 and perimeter of shaded region = 57.12 cm.
A bucket is raised from a well by means of a rope which is wound round a wheel of diameter 77 cm. Given that the bucket ascends in 1 minute 28 seconds with a uniform speed of 1.1 m/sec, calculate the number of complete revolutions the wheel makes in raising the bucket.
Answer
Time in which bucket ascends = 1 minute 28 seconds = 60 + 28 = 88 seconds.
Speed of bucket = 1.1 m/sec
Distance covered by bucket while ascending = Speed × Time = 1.1 × 88 = 96.8 m.
Radius of wheel = = 38.5 cm.
Circumference of circle = 2πr = = 242 cm = 2.42 m.
Let n be the no. of revolutions of wheel.
Distance covered by bucket = Distance covered by wheel
⇒ 96.8 = 2.42 × n
⇒ n = = 40.
Hence, wheel makes 40 revolutions in raising the bucket.
The wheel of a cart is making 5 revolutions per second. If the diameter of the wheel is 84 cm, find its speed in km/hr. Give your answer, correct to the nearest km.
Answer
Radius of wheel = = 42 cm.
Distance covered by wheel in 1 revolution = Circumference of wheel = 2πr
=
= 264 cm.
Distance covered by wheel in 5 revolutions = 5 × 264 = 1320 cm.
∴ Wheel covers 1320 cm in 1 second.
Hence, speed of wheel = 48 km/hr.
The circumference of a circle is 123.2 cm. Calculate :
(i) the radius of the circle in cm.
(ii) the area of the circle in cm2, correct to nearest cm2.
(iii) the effect on the area of the circle if the radius is doubled.
Answer
(i) Let radius = r cm.
By formula,
Circumference = 2πr
2πr = 123.2
Hence, radius = 19.6 cm.
(ii) By formula,
Area of circle = πr2
Hence, area of circle = 1207 cm2.
(iii) We know that,
Area of circle = πr2, where r is the radius.
If radius is doubled so new radius = 2r cm.
New area of circle = π(2r)2 = 4πr2.
Change in area =
Hence, area becomes 4 times.
In the figure (i) given below, the area enclosed between the concentric circles is 770 cm2. Given that the radius of the outer circle is 21 cm, calculate the radius of the inner circle.

Answer
Let radius of inner circle = r cm.
From figure,
Area of shaded region = Area of outer circle - Area of inner circle
⇒ 770 = π(21)2 - πr2
⇒ 770 = 441π - πr2
⇒ 770 = π(441 - r2)
⇒ 441 - r2 =
⇒ 441 - r2 =
⇒ 441 - r2 =
⇒ 441 - r2 = 245
⇒ r2 = 441 - 245
⇒ r2 = 196
⇒ r = = 14 cm.
Hence, radius of inner circle = 14 cm.
In the figure (ii) given below, the area enclosed between the circumferences of two concentric circles is 346.5 cm2. The circumference of the inner circle is 88 cm. Calculate the radius of the outer circle.

Answer
Let radius of inner circle = r cm.
Circumference = 2πr
⇒ 88 = 2πr
⇒ r =
⇒ r =
⇒ r =
⇒ r = 2 × 7 = 14 cm.
Let radius of outer circle = R cm.
From figure,
Area of shaded region = Area of outer circle - Area of inner circle
⇒ 346.5 = π(R)2 - πr2
⇒ 346.5 = π(R)2 - π(14)2
⇒ 346.5 = π(R2 - 196)
⇒ R2 - 196 =
⇒ R2 - 196 =
⇒ R2 - 196 =
⇒ R2 - 196 = 110.25
⇒ R2 = 110.25 + 196
⇒ R2 = 306.25
⇒ R =
⇒ R = 17.5 cm
Hence, radius of outer circle = 17.5 cm.
A road 3.5 m wide surrounds a circular plot whose circumference is 44 m. Find the cost of paving the road at ₹ 200 per m2.
Answer
Let the radius of circular plot = R meters.
Given,
Circumference of circular plot = 44 m
2πR = 44
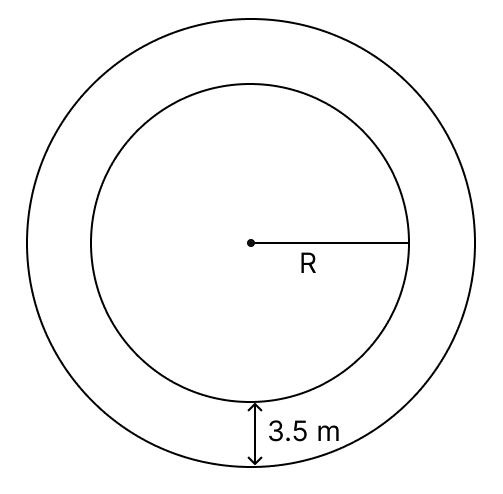
From figure,
Radius of outer circle = R + 3.5 = 7 + 3.5 = 10.5 m.
Area of road = Area of outer circle - Area of inner circle
= π(10.5)2 - π(7)2
= 110.25π - 49π
= 61.25π
= x 61.25
= 192.50 m2
Rate of paving the road = ₹ 200 per m2
Cost of paving road = Area of road × Rate of paving the road
= 192.5 × 200
= ₹ 38,500.
Hence, cost of paving the road = ₹ 38,500.
The sum of diameters of two circles is 14 cm and the difference of their circumferences is 8 cm. Find the circumferences of the two circles.
Answer
Let radius of larger circle be R cm and smaller circle r cm.
Diameter = 2R and 2r
Given, sum of diameters of two circles is 14 cm
⇒ 2r + 2R = 14
⇒ r + R = 7 ...........(1)
Given, difference in circumferences is 8 cm
⇒ 2πR - 2πr = 8
⇒ 2π(R - r) = 8
⇒ π(R - r) = 4
⇒
⇒ .........(2)
Adding equation 1 and 2,
Substituting value of R in Eq 2 we get,
Circumference of larger circle = 2πR
=
= 2 x 13
= 26 cm.
Circumference of smaller circle = 2πr
=
= 2 x 9
= 18 cm.
Hence, circumference of larger circle = 26 cm and smaller circle = 18 cm.
Find the circumference of the circle whose area is equal to the sum of the areas of three circles with radius 2 cm, 3 cm and 6 cm.
Answer
Let the radius of resultant circle be r cm.
Given,
Area of resultant circle is equal to the sum of the areas of three circles with radius 2 cm, 3 cm and 6 cm.
⇒ πr2 = π(2)2 + π(3)2 + π(6)2
⇒ πr2 = π[(2)2 + (3)2 + (6)2]
⇒ r2 = 22 + 32 + 62
⇒ r2 = 4 + 9 + 36
⇒ r2 = 49
⇒ r = = 7 cm.
Circumference of circle = 2πr
=
= 44 cm.
Hence, circumference of circle = 44 cm.
A copper wire when bent in the form of a square encloses an area of 121 cm2. If the same wire is bent into the form of a circle, find the area of the circle.
Answer
Area of square = (side)2
Given,
Area of square = 121 cm2
∴ (side)2 = 121
⇒ (side)2 = (11)2
⇒ side = 11 cm.
Perimeter of square = 4 × side = 4 × 11 = 44 cm.
Circumference of the circle of same wire = Perimeter of square of same wire
Let radius of circle formed = r cm.
∴ 2πr = 44
⇒ r =
= 7 cm.
Area of circle = πr2
=
= 154 cm2.
Hence, area of circle = 154 cm2.
A copper wire when bent in the form of an equilateral triangle has area cm2. If the same wire is bent in the form of a circle, find the area enclosed by the wire.
Answer
Area of equilateral triangle = (side)2
Given,
Area of equilateral triangle = cm2
Perimeter of equilateral triangle = 3 x side
= 3 x 22 = 66 cm.
Circumference of the circle of same wire = Perimeter of triangle of same wire
Let radius of circle formed = r cm.
∴ 2πr = 66
Area of circle = πr2
=
= 346.5 cm2.
Hence, area of circle = 346.5 cm2.
Find the circumference of the circle whose area is 16 times the area of the circle with diameter 7 cm.
Answer
Let area of larger circle be r cm.
Radius of circle with diameter 7 cm = = 3.5 cm.
Given,
Area of larger circle is 16 times the area of the circle with diameter 7 cm.
⇒ πr2 = 16 x π x (3.5)2
⇒ r2 = 196
⇒ r = = 14 cm.
Circumference = 2πr = = 88 cm.
Hence, circumference of circle = 88 cm.
In the given figure, find the area of the unshaded portion within the rectangle.
(Take π = 3.14)
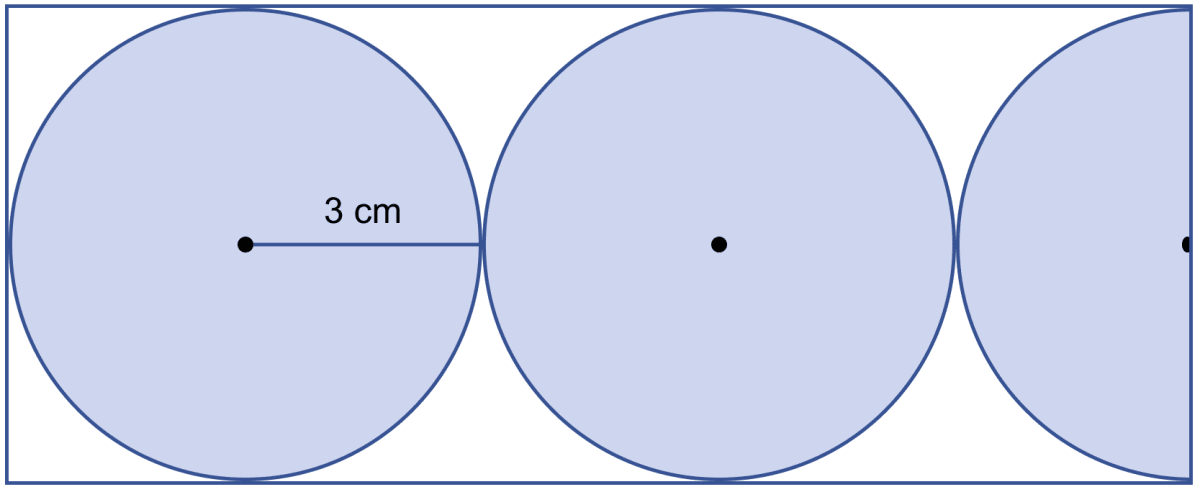
Answer
Let ABCD be a rectangle.
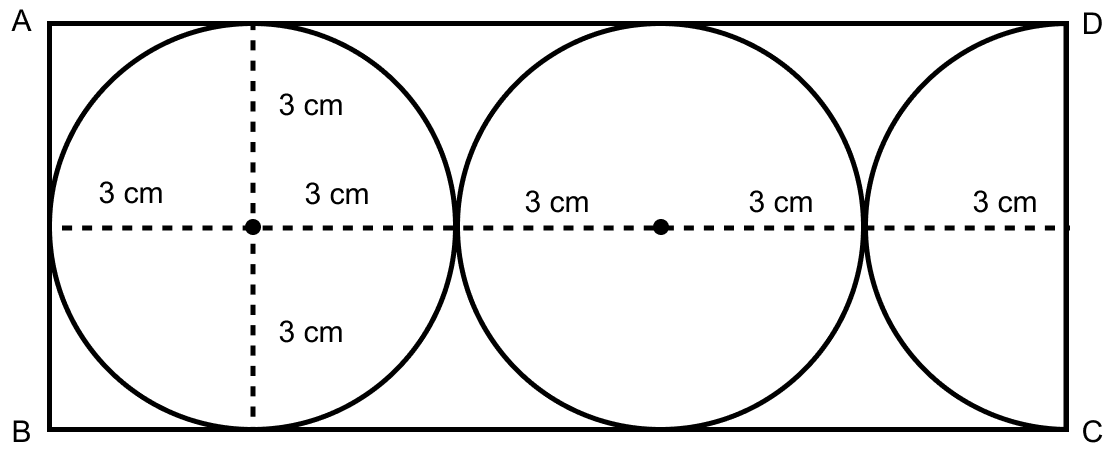
From figure,
AB = CD = 6 cm and,
AD = BC = 15 cm.
Area of rectangle = l × b = AD × AB = 15 × 6 = 90 cm2.
Area of shaded portion = π(3)2 + π(3)2 +
Area of unshaded region = Area of rectangle - Area of shaded region
= 90 - 70.65 = 19.35 cm2.
Hence, area of unshaded region = 19.35 cm2.
In the adjoining figure, ABCD is a square of side 21 cm. AC and BD are two diagonals of the square. Two semicircle are drawn with AD and BC as diameters. Find the area of the shaded region. Take π = .
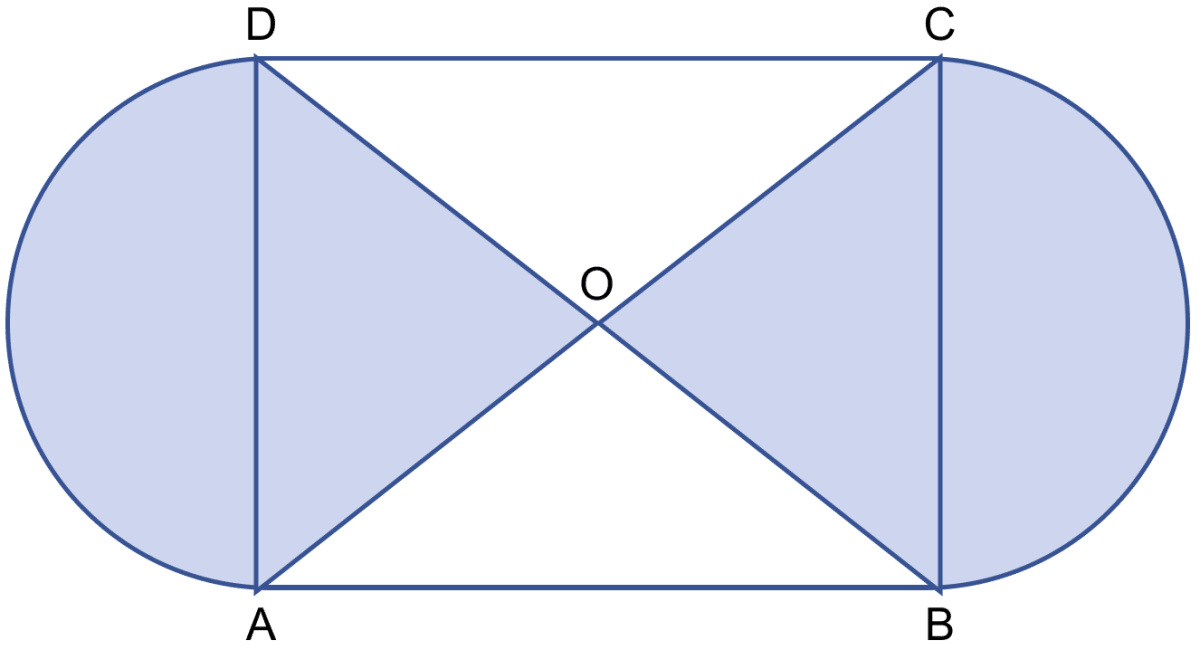
Answer
Area of square = (side)2 = 212 = 441 cm2.
We know that,
Diagonals of a square divide it into four triangles of equal area.
Area of a triangle = = 110.25 cm2.
Area of △AOD + Area of △BOC = 110.25 + 110.25 = 220.50 cm2
Diameter of each semicircle = 21 cm
∴ Radius = = 10.5 cm.
Area of each semicircle =
From figure,
Area of shaded region = Area of both semicircles + Area of △AOD + Area of △BOC
= (2 × 173.25) + 220.50
= 346.50 + 220.50
= 567 cm2.
Hence, area of shaded region = 567 cm2.
In the figure (i) given below, ABCD is a square of side 14 cm and APD and BPC are semicircles. Find the area and the perimeter of the shaded region.
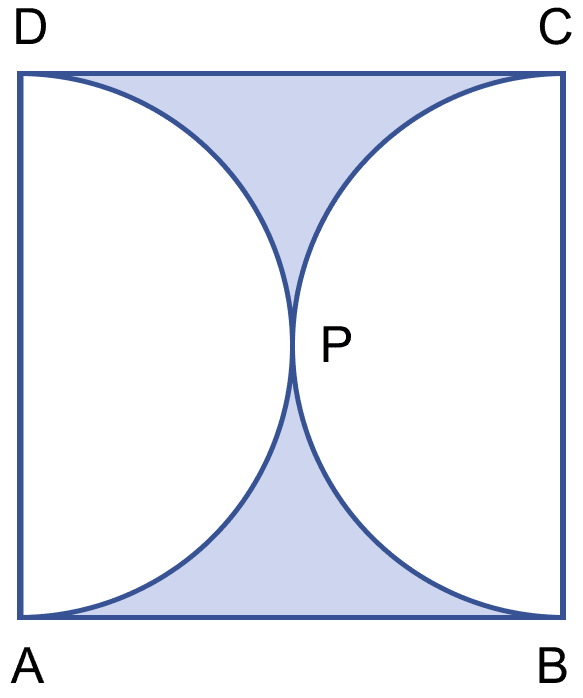
Answer
Area of square = (side)2 = 142 = 196 cm2.
From figure,
Diameter of both semicircle = side of square = 14 cm.
∴ Radius (r) = = 7 cm.
Area of both the semi-circles =
Area of shaded region = Area of square - Area of semi-circles
= 196 - 154 = 42 cm2.
From figure,
Perimeter = arc DPA + DC + arc CPB + AB
= πr + 14 + πr + 14
= 2πr + 28
= + 28
= 44 + 28 = 72 cm.
Hence, area of shaded region = 42 cm2 and perimeter = 72 cm.
In the figure (ii) given below, ABCD is a square of side 14 cm. Find the area of the shaded region.
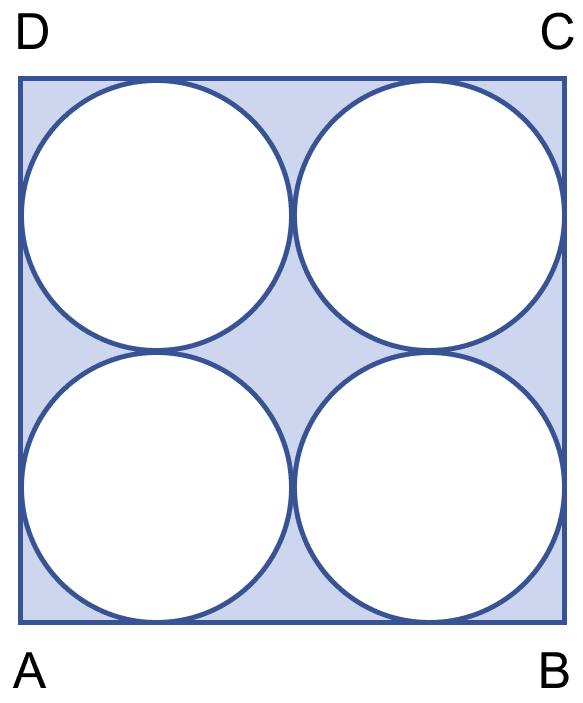
Answer
Let radius of each circle be r cm.
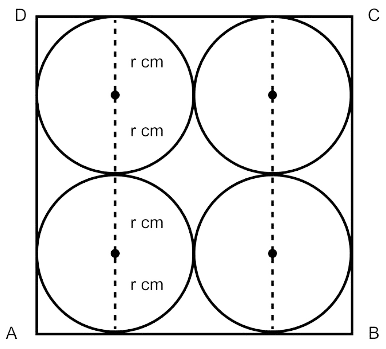
From figure,
⇒ r + r + r + r = 14
⇒ 4r = 14
⇒ r = 3.5 cm.
Since, radius is same so, each circle will have same area.
Area of each circle = πr2
=
=
= 22 × 0.5 × 3.5
= 38.5 cm2
Area of square = (side)2 = 142 = 196 cm2.
Area of shaded region = Area of square - Area of circles
= 196 - 4 × 38.5
= 196 - 154
= 42 cm2.
Hence, area of shaded region = 42 cm2.
In the figure (iii) given below, the diameter of the semicircle is equal to 14 cm. Calculate the area of the shaded region. Take π = .
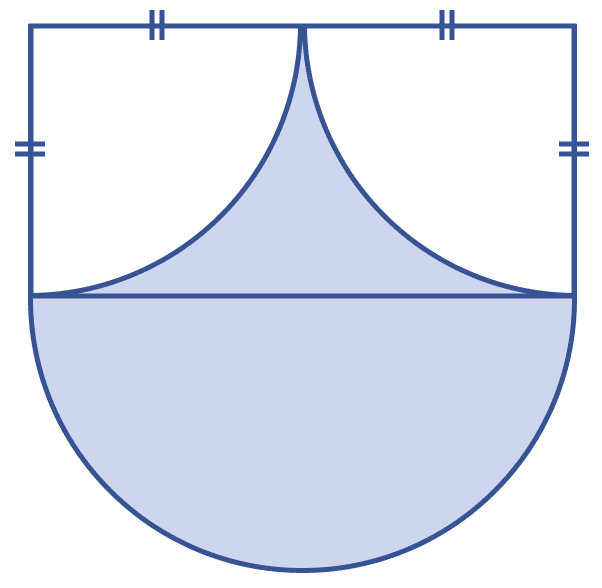
Answer
From figure,
BD = 14 cm (Diameter of semi-circle)
AF = FE = x (let)
⇒ BD = AF + FE
⇒ 14 = x + x
⇒ 2x = 14
⇒ x = 7 cm.
Area of semi-circle BCD =
Area of quadrant ABF = Area of quadrant EDF =
From figure, AB = ED = AF = FE = 7 cm.
Area of rectangle ABDE= AB × BD = 7 × 14 = 98 cm2.
Area of shaded region = Area of rectangle ABDE + Area of semi-circle BCD - Area of quadrant ABF - Area of quadrant EDF
= 98 + 77 - 38.5 - 38.5
= 98 cm2.
Hence, area of shaded region = 98 cm2.
Find the area and the perimeter of the shaded region in figure (i) given below. The diamensions are in centimeters.

Answer
From figure,
Radius of larger semi-circle (R) = 14 cm.
Area of larger semi-circle =
= 22 × 14
= 308 cm2.
Diameter of smaller semi-circle = 14 cm; radius (r) = = 7 cm.
Area of smaller semi-circle =
= 11 × 7
= 77 cm2.
From figure,
Area of shaded region = Area of larger semi-circle - Area of smaller semi-circle
= 308 - 77
= 231 cm2.
From figure,
Perimeter of shaded region = Circumference of larger semi-circle + Circumference of smaller circle + 14
= πR + πr + 14
=
= 44 + 22 + 14
= 80 cm.
Hence, area of shaded region = 231 cm2 and perimeter = 80 cm.
In the figure (ii) given below, area of △ABC = 35 cm2. Find the area of the shaded region.

Answer
From figure,
Area of △ABC = base × height
Substituting values we get,
⇒ AB × CD = 35
⇒ AB × 5 = 35
⇒ AB = = 14 cm.
From figure,
AB is the diameter of semicircle.
Radius = = 7 cm.
Area of semi-circle =
= 11 × 7
= 77 cm2.
Area of shaded region = Area of semi-circle - Area of △ABC
= 77 - 35
= 42 cm2.
Hence, area of shaded region = 42 cm2.
In the figure (i) given below, AOBC is a quadrant of a circle of radius 10 m. Calculate the area of the shaded portion. Take π = 3.14 and give your answer correct to two significant figures.
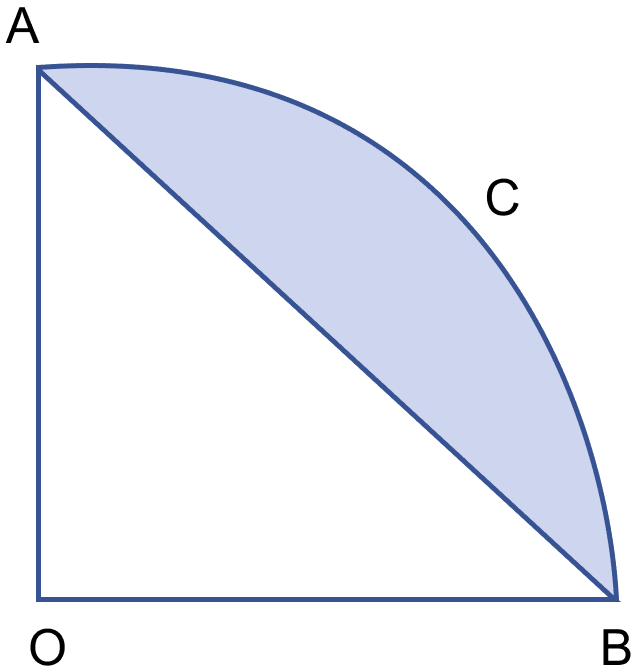
Answer
Area of quadrant =
Area of triangle AOB =
Area of shaded region = Area of quadrant - Area of triangle
= 78.5 - 50
= 28.5 ≈ 29 m2.
Hence, area of shaded region = 29 m2.
In the figure (ii) given below, OAB is a quadrant of a circle. The radius OA = 7 cm and OD = 4 cm. Calculate the area of the shaded portion.
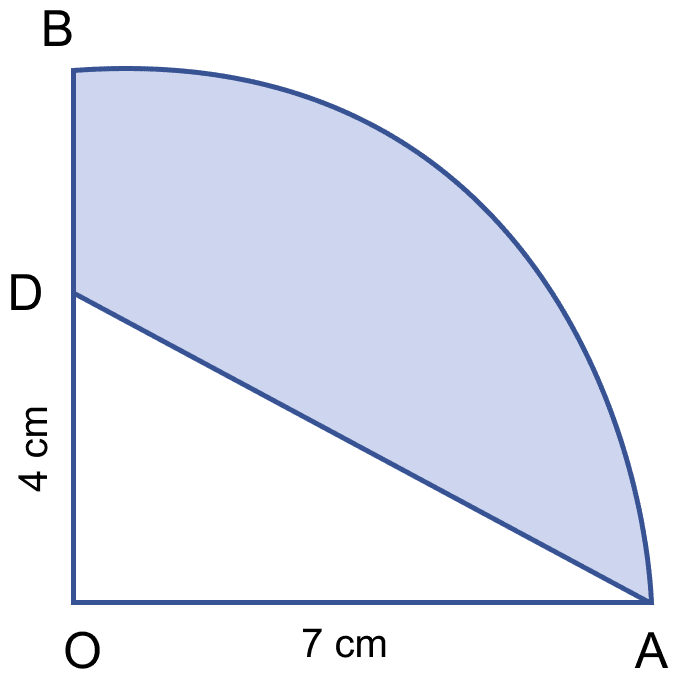
Answer
Area of quadrant =
Area of triangle AOD =
Area of shaded region = Area of quadrant - Area of triangle
= 38.5 - 14
= 24.5 cm2.
Hence, area of shaded region = 24.5 cm2.
A student takes a rectangular piece of paper 30 cm long and 21 cm wide. Find the area of the biggest circle that can be cut out from the paper. Also find the area of the paper left after cutting out the circle.
Answer
From figure,
Let ABCD be the rectangular piece.

Area of rectangular piece = 30 × 21 = 630 cm2
From figure,
Radius of the biggest circle that can be cut from the rectangular piece = = 10.5 cm
Area of circle = πr2
=
=
= 22 × 15.75
= 346.5 cm2.
Area of paper left = Area of rectangular piece - Area of circle
= 630 - 346.5
= 283.5 cm2.
Hence, the area of the biggest circle that can be cut from the rectangular piece = 346.5 cm2 and area of remaining paper = 283.5 cm2.
A rectangle with one side 4 cm is inscribed in a circle of radius 2.5 cm. Find the area of the rectangle.
Answer
Let ABCD be a rectangle with AB = 4 cm.

From figure,
Diameter of circle, AC = AO + OC = 2.5 + 2.5 = 5 cm.
In right angle triangle ABC,
⇒ AC2 = AB2 + BC2
⇒ 52 = 42 + BC2
⇒ BC2 = 52 - 42
⇒ BC2 = 25 - 16 = 9
⇒ BC = = 3 cm.
By formula,
Area of rectangle = l × b
= AB × BC
= 4 × 3
= 12 cm2.
Hence, area of rectangle = 12 cm2.
In the figure (i) given below, calculate the area of the shaded region correct to two decimal places. (Take π = 3.142)
Answer
From figure,
O is the center. In right angle triangle ABC,
Using pythagoras theorem,
⇒ AC2 = AB2 + BC2
⇒ AC2 = 52 + 122
⇒ AC2 = 25 + 144 = 169
⇒ AC = = 13 cm.
From figure,
AC is the diameter and OA is the radius = = 6.5 cm.
Area of circle = πr2
= 3.142 × (6.5)2
= 3.142 × 42.25
= 132.75 cm2.
Area of rectangle = l × b
= 12 × 5 = 60 cm2.
Area of shaded region = Area of circle - Area of rectangle
= 132.75 - 60
= 72.75 cm2.
Hence, area of shaded region = 72.75 cm2.
In the figure (ii) given below, ABC is an isosceles right angled triangle with ∠ABC = 90°. A semicircle is drawn with AC as diameter. If AB = BC = 7 cm, find the area of the shaded region. Take π = .
Answer
By formula,
Area of △ABC = × base × height
= × BC × AB
= × 7 × 7
= = 24.5 cm2.
In right angle triangle,
Using pythagoras theorem,
⇒ AC2 = AB2 + BC2
⇒ AC2 = 72 + 72
⇒ AC2 = 49 + 49 = 98
⇒ AC = cm.
From figure,
Radius of semi-circle (r) =
By formula,
Area of semi-circle =
Area of the shaded region = Area of the semi-circle – Area of △ABC
= 38.5 - 24.5
= 14 cm2.
Hence, area of the shaded region = 14 cm2.
A circular field has perimeter 660 m. A plot in the shape of a square having its vertices on the circumference is marked in the field. Calculate the area of the square field.
Answer
By formula,
Perimeter = 2πr
From figure,
BD = BO + OD = r + r = 2r = 2 × 105 = 210 m.
Let O be the center of the circle and ABCD be square of side x metres.
Area of square = (side)2 = x2.
In right angle triangle BCD,
⇒ BD2 = BC2 + CD2
⇒ 2102 = x2 + x2
⇒ 2x2 = 44100
⇒ x2 = = 22050 m2.
Hence, area of square = 22050 m2.
In the adjoining figure, ABCD is a square. Find the ratio between
(i) the circumferences
(ii) the areas of the incircle and the circumcircle of the square.
Answer
(i) Let side of the square be 2a units.
From figure,
AD = Diameter of incircle.
Radius of incircle (r) = = a units.
In right angle triangle ABC,
Using pythagoras theorem,
AC2 = AB2 + BC2
AC2 = (2a)2 + (2a)2
AC2 = 4a2 + 4a2
AC2 = 8a2
AC = units.
From figure,
AC is the diameter of circumcircle and AO is radius.
AO (R) = a units.
Hence, ratio between circumferences = .
(ii)
Hence, ratio between areas = 1 : 2.
The figure (i) given below shows a running track surrounding a grassed enclosure PQRSTU. The enclosure consists of a rectangle PQST with a semicircular region at each end. PQ = 200 m; PT = 70 m.
(i) Calculate the area of the grassed enclosure in m2.
(ii) Given that the track is of constant width 7 m, calculate the outer perimeter ABCDEF of the track.
Answer
Given,
PQ = 200 m and PT = 70 m.
(i) By formula,
Area of rectangle PQST = l × b
= 200 × 70
= 14000 m2.
Radius of each semi-circular part on either side of rectangle = = 35 m.
Area of both semi-circular parts = 2 × = πr2
=
= 22 × 5 × 35
= 3850 m2.
So, the total area of grassed enclosure = 14000 + 3850 = 17850 m2.
Hence, area of glassed enclosure = 17850 m2.
(ii) Given,
Width of track around the enclosure = 7 m.
From figure,
AB = PQ = 200 m
ED = ST = 200 m
EA = PT + ET + AP = 70 + 7 + 7 = 84 m
BD = DS + QS + BQ = 70 + 7 + 7 = 84 m
Outer radius of semi-circle (R) = = 42 m.
Circumference of both semi-circular part = πR + πR = 2πR.
=
= 264 m.
From figure,
Outer perimeter = Circumference of both semi-circular part + ED + AB
= 264 + 200 + 200
= 664 m.
Hence, perimeter of outer track ABCDEF = 664 m.
In the figure (ii) given below, the inside perimeter of a practice running track with semi-circular ends and straight parallel sides is 312 m. The length of the straight portion of the track is 90 m. If the track has a uniform width of 2 m throughout, find its area.
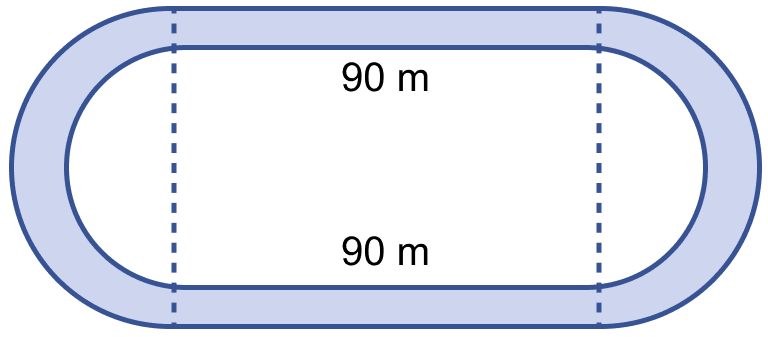
Answer
Given,
Perimeter of inside semi-circular track = 312 m.
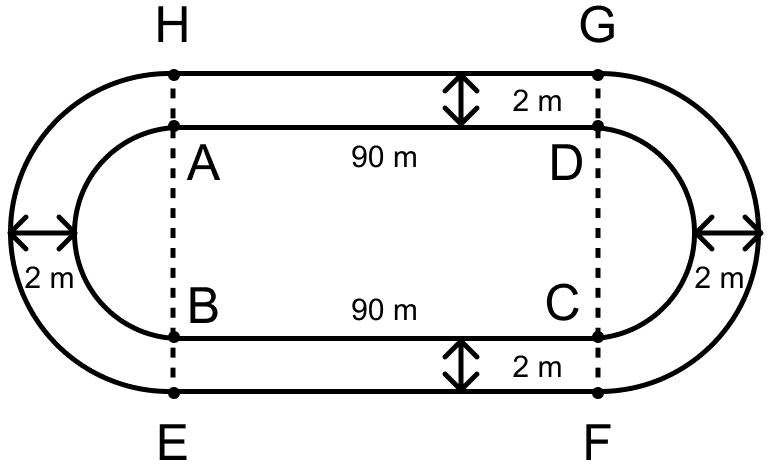
⇒ 90 + πr + 90 + πr = 312
⇒ 2πr + 180 = 312
⇒ 2πr = 312 - 180
⇒ 2πr = 132
⇒ πr =
⇒ πr = 66
⇒ r = m.
So, length of AB = 2r = 2 × 21 = 42 m.
Since, width of track = 2 m.
So, HE = GF = 42 + 2 + 2 = 46 m.
Radius of outer semi-circle (R) = = 23 m.
From figure,
Area of track = Area of outer semi-circle (with diametre HE) + Area of outer semi-circle( with diametre GF) + Area of outer rectangle (EFGH) - [Area of inner semi-circle (with diameter AB) + Area of inner semi-circle (with diameter DC) + Area of inner rectangle ABCD]
Hence, area of semi-circular track = m2.
In the figure (i) given below, two circles with centres A and B touch each other at the point C. If AC = 8 cm and AB = 3 cm, find the area of the shaded region.
Answer
Radius of circle with center A = AC = 8 cm.
Area of circle with center A = πr2
=
= = 201.14 cm2.
From figure,
BC = AC - AB = 8 - 3 = 5 cm.
Area of circle with center B = πr2
=
= = 78.57 cm2.
Area of shaded region = Area of circle with center A - Area of circle with center B
= 201.14 - 78.57
= 122.57 cm2.
Hence, area of shaded region = 122.57 cm2.
The quadrants shown in the figure (ii) given below are each of radius 7 cm. Calculate the area of the shaded portion.

Answer
Given,
Radius of each quadrant = 7 cm

From figure,
Area of shaded region = Area of square – 4 area of each quadrant
= (side)2 – 4 ×
= 142 –
= 196 – 154
= 42 cm2.
Hence, area of shaded region = 42 cm2.
In the figure (i) given below, two circular flower beds have been shown on the two sides of a square lawn ABCD of side 56 m. If the centre of each circular flower bed is the point of intersection O of the diagonals of the square lawn, find the sum of the areas of the lawn and the flower beds.
Answer
Area of lawn ABCD = (side)2
= (56)2 = 3136 m2.
In square,
Length of diagonal (AC) = side = m.
Since, diagonals of square are equal and bisect each other,
∴ AO = OC = OD = OB.
Radius of quadrant ODC = Radius of quadrant OAB = m.
Area of quadrant ODC = Area of quadrant OAB =
Since, diagonals of square divide it into four equal triangles.
Area of △ODC = Area of △OAB = = 784 m2.
From figure,
Area of flower bed = Area of quadrant ODC - Area of △ODC
= 1232 - 784 = 448 m2.
Since there are two flower beds so area = 2 × 448 = 896 m2.
Area of lawn and flower beds = 3136 + 896 = 4032 m2.
Hence, sum of the areas of the lawn and the flower beds = 4032 m2.
In the figure (ii) given below, a square OABC is inscribed in a quadrant OPBQ of a circle. If OA = 20 cm, find the area of the shaded region. (π = 3.14)

Answer
Given, length of each side of square = 20 cm.

We know that,
Length of diagonal of a square = side = cm.
∴ OB = cm.
From figure,
OB is the radius of the quadrant OPBQ.
Area of quadrant OPBQ =
Area of square OABC = (side)2
= (20)2 = 400 cm2.
Area of shaded region = Area of quadrant OPBQ - Area of square OABC
= 628 - 400
= 228 cm2.
Hence, area of shaded region = 228 cm2.
In the figure (i) given below, ABCD is a rectangle, AB = 14 cm and BC = 7 cm. Taking DC, BC and AD as diameters, three semicircles are drawn as shown in the figure. Find the area of the shaded portion.
Answer
Since, ABCD is a rectangle.
AD = BC = 7 cm.
CD = AB = 14 cm.
From figure,
AD and BC are diameters of smaller circles.
Radius = = 3.5 cm.
Area of each small semi-circle =
=
= 19.25 cm2.
From figure,
CD is the diameter of the larger semi-circle.
Radius = = 7 cm.
Area of larger semi-circle =
=
= 77 cm2.
Area of rectangle ABCD = AB × BC
= 14 × 7
= 98 cm2.
From figure,
Area of shaded region = Area of rectangle ABCD + 2 × Area of each smaller semi-circle - Area of larger semi-circle
= 98 + (2 × 19.25) - 77
= 98 + 38.5 - 77
= 59.5 cm2.
Hence, area of shaded region = 59.5 cm2.
In the figure (ii) given below, O is the centre of a circle with AC = 24 cm, AB = 7 cm and ∠BOD = 90°. Find the area of the shaded region. (Use π = 3.14)
Answer
We know that,
Angle in semi-circle = 90°.
∴ ∠A = 90°.
In right angle △ABC
Using Pythagoras theorem,
⇒ BC2 = AC2 + AB2
⇒ BC2 = 242 + 72
⇒ BC2 = (576 + 49) = 625
⇒ BC = = 25 cm.
From figure,
Radius of circle (OB) = = 12.5 cm.
By formula,
Area of △ABC = × AB × AC
= × 7 × 24
= 84 cm2.
Area of circle = πr2
= 3.14 × 12.5 × 12.5
= 490.63 cm2.
Area of quadrant COD = = 122.66 cm2.
Area of shaded portion = Area of circle – (Area of △ABC + Area of quadrant COD)
= 490.63 – (84 + 122.66)
= 490.63 – 206.66
= 283.97 cm2.
Hence, area of shaded portion = 283.97 cm2.
In the figure (i) given below, ABCD is a square of side 14 cm. A, B, C and D are centres of the equal circles which touch externally in pairs. Find the area of the shaded region.

Answer
Let r cm be the radius of each circle.
From figure,
⇒ r + r = AD
⇒ 2r = 14
⇒ r = 7 cm.
Hence, radius of each circle = 7 cm.
Area of each circle = πr2
=
=
= 22 x 7
= 154 cm2.
Area of 4 circles = 4 × 154 = 616 cm2.
From figure,
Radius of each quadrant in square ABCD = 7 cm.
Area of each quadrant =
=
= 38.5 cm2.
Area of 4 quadrants = 4 × 38.5 = 154 cm2.
Area of square = (side)2
= (14)2 = 196 cm2.
Area of shaded region = (Area of 4 circles - Area of 4 quadrants) + (Area of square - Area of 4 quadrants)
= (616 - 154) + (196 - 154)
= 462 + 42
= 504 cm2.
Hence, area of shaded region = 504 cm2.
In the figure (ii) given below, the boundary of the shaded region in the given diagram consists of three semicircular arcs, the smaller being equal. If the diameter of the larger one is 10 cm, calculate.
(i) the length of the boundary.
(ii) the area of the shaded region. (Take π to be 3.14)
Answer
From figure,
Diameter of big semi-circle = 10 cm.
Radius of big semi-circle (R) = = 5 cm,
Diameter of small semi-circle = 5 cm.
Radius of each smaller semi-circle (r) = = 2.5 cm.
(i) Length of boundary = Circumference of bigger semi-circle + 2 x circumference of smaller semi-circles
= πR + πr + πr
= π(R + 2r)
= 3.14(5 + 2 × )
= 3.14(5 + 5)
= 3.14 × 10
= 31.4 cm.
Hence, length of boundary = 31.4 cm.
(ii) From figure,
Area of shaded region = Area of bigger semi-circle + Area of one smaller semi-circle – Area of other smaller semi-circle
Hence, area of shaded region = 39.25 cm2.
In the figure (i) given below, the points A, B and C are centres of arcs of circles of radii 5 cm, 3 cm and 2 cm respectively. Find the perimeter and the area of the shaded region. (Take π = 3.14)
Answer
Let r1 = 5 cm, r2 = 3 cm and r3 = 2 cm.
Perimeter of shaded region = Circumference of largest semi-circle + Circumference of smaller semi-circle + Circumference of smallest semi-circle
= πr1 + πr2 + πr3
= π(5 + 3 + 2)
= 10π
= 10 x 3.14
= 31.4 cm.
Area of shaded region = Area of largest semi-circle - Area of smaller semi-circle + Area of smallest semi-circle
Hence, perimeter of shaded region = 31.4 cm and area of shaded region = 31.4 cm2.
In the figure (ii) given below, ABCD is a square of side 4 cm. At each corner of the square a quarter circle of radius 1 cm, and at the centre a circle of diameter 2 cm are drawn. Find the area of the shaded region. Take π = 3.14.
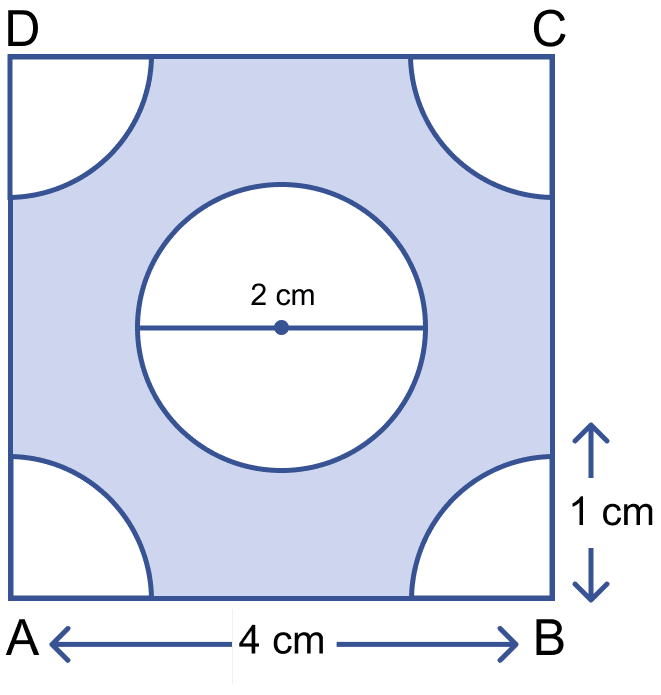
Answer
We know that,
Side of square ABCD = 4 cm
Radius of each quadrant circle (r) = 1 cm
Given,
Diameter of circle in the center = 2 cm
∴ Radius of circle in center (r1) = = 1 cm.
From figure,
Area of shaded region = Area of square – Area of 4 quadrants – Area of circle at center
Hence, area of shaded region = 9.72 cm2.
In the figure (i) given below, ABCD is a rectangle. AB = 14 cm, BC = 7 cm. From the rectangle, a quarter circle BFEC and a semicircle DGE are removed. Calculate the area of the remaining piece of the rectangle.

Answer
Area of rectangle = AB × BC = 14 × 7 = 98 cm2.
Since, ABCD is a rectangle.
∴ CD = AB = 14 cm.
BFEC is a quadrant of radius, BC = r1 = 7 cm.
∴ CE = 7 cm.
From figure,
DE = CD - CE = 14 - 7 = 7 cm.
From figure,
DE is the diameter of semi-circle DGE.
So, radius (r) = = 3.5 cm.
Area of semi-circle =
Area of quadrant BFEC =
Area of remaining piece of rectangle = Area of rectangle - Area of semicircle DGE - Area of quadrant BFEC
= 98 - 19.25 - 38.5
= 40.25 cm2.
Hence, area of remaining piece of rectangle = 40.25 cm2.
The figure (ii) given below shows a kite, in which BCD is in the shape of a quadrant of a circle of radius 42 cm. ABCD is a square and △CEF is an isosceles right angled triangle whose equal sides are 6 cm long. Find the area of the shaded region.
Answer
From figure,
∠ECF = ∠BCD = 90°.
Area of right angle △ECF = CF × EC
=
= 18 cm2.
Area of quadrant BCD =
Area of shaded region = Area of quadrant BCD + Area of right angle △ECF
= 18 + 1386 = 1404 cm2.
Hence, area of shaded region = 1404 cm2.
In the figure (i) given below, the boundary of the shaded region in the given diagram consists of four semicircular arcs, the smallest two being equal. If the diameter of the largest is 14 cm and of the smallest is 3.5 cm, calculate
(i) the length of the boundary.
(ii) the area of the shaded region.

Answer
(i) From figure,

OA = = 7 cm.
OB = OA - AB = 7 - 3.5 = 3.5 cm.
Radius of smallest semi-circle = = 1.75 cm.
Circumference of semi-circle = πr.
Length of boundary = Circumference of largest semi-circle + Circumference of smaller semi-circle + 2 × Circumference of smallest semi-circle
= 7π + 3.5π + (2 x 1.75π)
= 7π + 3.5π + 3.5π
= 14π
=
= 2 × 22
= 44 cm.
Hence, length of boundary = 44 cm.
(ii) Area of shaded region = Area of large semi-circle + Area of smaller semi-circle - 2 × Area of smallest semi-circle
Hence, area of shaded region = 86.625 cm2.
In the figure (ii) given below, a piece of cardboard, in the shape of a trapezium ABCD and AB || CD and ∠BCD = 90°, quarter circle BFEC is removed. Given AB = BC = 3.5 cm and DE = 2 cm. Calculate the area of the remaining piece of the cardboard.
Answer
From figure,
Radius of quadrant = BC = 3.5 cm.
EC = BC = 3.5 cm (As both equal to radius of quadrant BFEC)
By formula,
Area of trapezium = × (Sum of || sides) × distance between them
= × (AB + DC) × BC
= × (AB + EC + DE) × BC
= × (3.5 + 3.5 + 2) × 3.5
= × 9 × 3.5
= 4.5 × 3.5
= 15.75 cm2.
So, the area of quadrant BCEF =
Area of shaded portion = Area of trapezium - Area of quadrant
= 15.75 – 9.625 = 6.125 cm2.
Hence, area of shaded portion = 6.125 cm2.
In the figure (i) given below, ABC is a right angled triangle, ∠B = 90°, AB = 28 cm and BC = 21 cm. With AC as diameter a semi-circle is drawn and with BC as radius a quarter circle is drawn. Find the area of the shaded region correct to two decimal places.
Answer
In right angle △ABC,
Using Pythagoras theorem,
⇒ AC2 = AB2 + BC2
⇒ AC2 = 282 + 212
⇒ AC2 = 784 + 441
⇒ AC2 = 1225
⇒ AC = = 35 cm.
Radius of semi-circle (R) = = 17.5 cm.
Radius of quadrant (r) = BC = 21 cm.
From figure,
Area of shaded region = Area of △ABC + Area of semi-circle – Area of quadrant
Hence, area of shaded region = 428.75 cm2.
In the figure (ii) given below, ABC is an equilateral triangle of side 8 cm. A, B and C are the centers of circular arcs of equal radius. Find the area of the shaded region correct upto 2 decimal places.
Answer
We know that
△ABC is an equilateral triangle of side 8 cm
A, B, C are the centres of three circular arcs of equal radius
Radius = = 4 cm
By formula,
Area of △ABC =
= × 8 × 8
=
=
= 16 × 1.732
= 27.712 cm2.
So, the area of 3 equal sectors of 60° whose radius is 4 cm = 3 × πr2 ×
= 3 × 3.142 × 4 × 4 ×
= 3.142 × 8
= 25.136 cm2.
Area of shaded region = Area of equilateral triangle - Area of 3 sectors
= 27.712 – 25.136
= 2.576 ≈ 2.58 cm2.
Hence, area of shaded region = 2.58 cm2.
A circle is inscribed in a regular hexagon of side cm. Find
(i) the circumference of the inscribed circle
(ii) the area of the inscribed circle
Answer
(i) Side of the regular hexagon (a) = cm.
Now since a regular hexagon has 6 sides, hence we can say the central angle of a hexagon = = 60°.
From figure,
∠AOB = 60°.
Now in the ΔAOB,
Since the total sum of the angles of a triangle is equal to 180°
∴ ∠AOB + ∠OAB + ∠OBA = 180° .......(1)
Since, OA = OB = radius of circle,
So, ∠OAB = ∠OBA = x (let) (Angles opposite to equal sides are equal).
Substituting value in equation 1 we get,
⇒ 60° + x + x = 180°
⇒ 2x + 60° = 180°
⇒ 2x = 120°
⇒ x = 60°.
Now since all the angles of the triangle are equal hence we can say the triangle is an equilateral triangle. So, all the sides of the triangle will also be equal.
∴ AO = BO = AB = cm.
Draw perpendicular from O to AB.
From figure,
AT = BT = cm. (As altitude and median are same in equilateral triangle.)
From figure,
In right angle triangle OAT,
Hence, radius of circle = OT = 3 cm.
We know the circumference of a circle is given by the formula,
Circumference = 2πr
=
= cm.
Hence, circumference of inscribed circle = cm.
(ii) Area of inscribed circle = πr2
=
= cm2.
Hence, area of inscribed circle = cm2.
In the adjoining figure, a chord AB of a circle of radius 10 cm subtends a right angle at the centre O. Find the area of the sector OACB and of the major segment. Take π = 3.14.
Answer
Given,
Radius of the circle = 10 cm
Angle at the centre subtended by a chord AB = 90°.
We know that,
Area of sector OACB =
= 3.14 × 10 × 10 ×
=
= 78.5 cm2.
In right angle △OAB,
Area of △OAB = × OA × OB
= × 10 × 10
= 50 cm2.
Area of minor segment = Area of sector OACB – Area of △OAB
= 78.5 - 50
= 28.5 cm2.
Area of circle = πr2
= 3.14 × 10 × 10
= 314 cm2.
Area of major segment = Area of circle – Area of minor segment
= 314 - 28.5
= 285.5 cm2.
Hence, area of sector OACB = 78.5 cm2 and area of major segment = 285.5 cm2.
Find the surface area and volume of a cube whose one edge is 7 cm.
Answer
Given,
Length of edge of cube (a) = 7 cm
By formula,
Surface area of cube = 6a2
= 6 × (7)2
= 6 × 7 × 7
= 294 cm2.
Volume of cube = a3
= (7)3
= 7 × 7 × 7
= 343 cm3.
Hence, surface area and volume of cube = 294 cm2 and 343 cm3 respectively.
Find the surface area and the volume of a rectangular solid measuring 5 m by 4 m by 3 m. Also find the length of a diagonal.
Answer
In a rectangular solid,
Let l = 5 m, b = 4 m and h = 3 m
By formula,
Surface area of rectangular solid = 2(lb + bh + lh)
= 2(5 × 4 + 4 × 3 + 5 × 3)
= 2(20 + 12 + 15)
= 2 × 47
= 94 m2
Volume of rectangular solid = l × b × h
= 5 × 4 × 3
= 60 m3.
Diagonal of cuboid =
Hence, surface area = 94 m2, volume = 60 m3 and the length of diagonal is 7.07 m.
The length and breadth of a rectangular solid are respectively 25 cm and 20 cm. If the volume is 7000 cm3, find its height.
Answer
Given,
Length of rectangular solid = 25 cm
Breadth of rectangular solid = 20 cm
Volume of rectangular solid = 7000 cm3
Let height of rectangular solid = h cm.
By formula,
Volume = l × b × h
Substituting the values we get,
⇒ 7000 = 25 × 20 × h
⇒ 500 × h = 7000
⇒ h =
⇒ h = 14 cm.
Hence, height of rectangular solid is 14 cm.
A class room is 10 m long, 6 m broad and 4 m high. How many students can it accommodate if one student needs 1.5 m2 of floor area? How many cubic metres of air will each student have?
Answer
The given dimensions of class room are
Length (l) = 10 m
Breadth (b) = 6 m
Height (h) = 4 m
We know that,
Floor area of class room = l × b = 10 × 6 = 60 m2.
Given,
One student needs 1.5 m2 floor area.
So, the number of students = = 40.
By formula,
Volume of class room = l × b × h
= 10 × 6 × 4
= 240 m3.
Cubic metres of air for each student =
=
= 6 m3.
Hence, the classroom can accommodate 40 students and each student will have 6 m3 of air.
The volume of a cuboid is 1440 cm3. Its height is 10 cm and the cross-section is a square. Find the side of the square.
Answer
(a) Given,
Volume of cuboid = 1440 cm3
Height of cuboid = 10 cm.
Given, cross section is a square.
∴ length = breadth = x cm (let).
By formula,
Volume of cuboid = area of square × height
Substituting the values we get,
⇒ 1440 = × × 10
⇒ =
⇒ = 144
⇒ = = 12 cm.
Hence, the side of square is 12 cm.
The perimeter of one face of a cube is 20 cm. Find the surface area and the volume of the cube.
Answer
Given,
Perimeter of one face of a cube = 20 cm
Perimeter of one face of a cube = 4 × side (As it is a square)
⇒ 20 = 4 × side
⇒ Side = = 5 cm
Surface area of cube = 6(side)2
= 6(5)2
= 6 × 5 × 5 = 150 cm2
Volume of cube = side × side × side
= 5 × 5 × 5
= 125 cm3.
Hence, surface area of cube = 150 cm2 and volume = 125 cm3.
Mary wants to decorate her Christmas tree. She wants to place the tree on a wooden box covered with coloured papers with pictures of Santa Claus. She must know the exact quantity of paper to buy for this purpose. If the box has length 80 cm, breadth 40 cm and height 20 cm respectively, then how many square sheets of paper of side 40 cm would she require?
Answer
By formula,
Surface area of the cuboid (box) = 2(lh + bh + hl)
= 2(80 × 40 + 40 × 20 + 20 × 80)
= 2(3200 + 800 + 1600)
= 2 × 5600
= 11200 cm2.
Area of square sheet = (side)2
= 402
= 1600 cm2
Let no. of sheets required to cover be n.
So, total area of square sheets = 1600n cm2.
In order to cover the box with square sheets, their areas must be equal.
∴ 1600n = 11200
⇒ n = = 7.
Hence, 7 square sheets will be required.
The volume of a cuboid is 3600 cm3 and its height is 12 cm. The cross-section is a rectangle whose length and breadth are in the ratio 4 : 3. Find the perimeter of the cross-section.
Answer
Given,
Volume of a cuboid = 3600 cm3
Height of cuboid = 12 cm
Cross section is a rectangle with length and breadth in ratio 4 : 3.
Let length = 4x cm and breadth = 3x cm.
By formula,
Volume of cuboid = length × breadth × height
⇒ 3600 = 4x × 3x × 12
⇒ 144x2 = 3600
⇒ x2 =
⇒ x2 = 25
⇒ x = = 5 cm.
So.
Length of rectangle = 4x = 4 × 5 = 20 cm
Breadth of rectangle = 3x = 3 × 5 = 15 cm
Perimeter of the cross section = 2(l + b)
= 2(20 + 15)
= 2 × 35
= 70 cm.
Hence, perimeter of cross-section = 70 cm.
The volume of a cube is 729 cm3. Find its surface area and the length of a diagonal.
Answer
Given,
Volume of a cube = 729 cm3.
By formula,
Volume of a cube = (side)3
∴ (side)3 = 729
⇒ (side)3 = (9)3
⇒ side = 9 cm
By formula,
Surface area of cube = 6(side)2
= 6 × (9)2
= 6 × 9 × 9
= 486 cm2.
So the length of a diagonal = × side
= × 9
= 1.732 × 9
= 15.57 cm.
Hence, surface area = 486 cm2 and length of diagonal = 15.57 cm.
The length of the longest rod which can be kept inside a rectangular box is 17 cm. If the inner length and breadth of the box are 12 cm and 8 cm respectively, find its inner height.
Answer
The longest rod which can be kept inside a rectangular box will be equal to the diagonal of the box.
Let h cm be the inner height of box.
By formula,
Length of diagonal =
∴ 17 =
Squaring both sides,
⇒ 172 = 122 + 82 + h2
⇒ 289 = 144 + 64 + h2
⇒ 289 = 208 + h2
⇒ h2 = 289 - 208
⇒ h2 = 81
⇒ h = = 9 cm.
Hence, the inner height of rectangular box is 9 cm.
A closed rectangular box has inner dimensions 90 cm by 80 cm by 70 cm. Calculate its capacity and the area of tin-foil needed to line its inner surface.
Answer
Given,
Inner length of rectangular box = 90 cm
Inner breadth of rectangular box = 80 cm
Inner height of rectangular box = 70 cm
We know that
Capacity of rectangular box = volume of rectangular box = l × b × h
= 90 × 80 × 70
= 504000 cm3.
Area of tin foil = Surface area of box = 2(lb + bh + lh)
= 2(90 × 80 + 80 × 70 + 90 × 70)
= 2(7200 + 5600 + 6300)
= 2 × 19100
= 38200 cm2.
Hence, capacity of box = 504000 cm3 and area of tin-foil needed = 38200 cm2.
The internal measurements of a box are 20 cm long, 16 cm wide and 24 cm high. How many 4 cm cubes could be put into the box?
Answer
By formula,
Volume of cuboidal box = l × b × h
Substituting values we get,
Volume of box = 20 cm × 16 cm × 24 cm = 7680 cm3
By formula,
Volume of cube = (side)3
Substituting values we get,
Volume of cubes = 4 cm × 4 cm × 4 cm = 64 cm3
Let no. of cubes be n.
So, total volume of cubes = 64n cm3.
In order to fill the box with cubes,
Volume of cubes = Volume of box
∴ 64n = 7680
⇒ n = = 120.
Hence, 120 cubes can be put into the box.
The internal measurements of a box are 10 cm long, 8 cm wide and 7 cm high. How many cubes of side 2 cm can be put into the box?
Answer
Since the height of the box is 7 cm, so only 3 cubes can be put height-wise. (If we put 4 cubes, the height becomes 8 cm which is more than the height of the box.)
Height of 3 cubes = 3 x 2 = 6 cm
∴ We will only consider height of box up to 6 cm for placing the cubes inside it.
By formula,
Volume of cuboidal box = l × b × h
Substituting values we get,
Volume of box = 10 cm × 8 cm × 6 cm = 480 cm3
By formula,
Volume of cube = (side)3
Substituting values we get,
Volume of cubes = 2 cm × 2 cm × 2 cm = 8 cm3
Let no. of cubes be n.
So, total volume of cubes = 8n cm3.
In order to fill the box with cubes,
Volume of cubes = Volume of box
∴ 8n = 480
⇒ n = = 60.
Hence, 60 cubes can be put into the box.
A certain quantity of wood costs ₹ 25,000 per m3. A solid cubical block of such wood is bought for ₹ 18,225. Calculate the volume of the block and use the method of factor to find the length of one edge of the block.
Answer
Given,
Cost of 1 m3 wood = ₹ 25,000
Cost of a solid cubical block = ₹ 18,225
As we know that, cost of a solid cubical block = volume of block x cost of 1 m3 wood
By formula,
Volume of cuboidal block = (side)3
∴ (side)3 = 0.729 m3
On factorising 729 and 1000 we get,
Hence, volume of block = 0.729 m3 and the length of one edge of the block is 0.9 m.
A cube of 11 cm edge is immersed completely in a rectangular vessel containing water. If the dimensions of the base of the vessel are 15 cm × 12 cm, find the rise in the water level in centimeters correct to 2 decimal places, assuming that no water over flows.
Answer
Let rise in height of water be h cm.
The volume of water rising will be equal to volume of cube.
∴ 15 × 12 × h = 11 × 11 × 11
180h = 1331
h = = 7.39 cm.
Hence, the rise in the water level is 7.39 cm.
A rectangular container, whose base is a square of side 6 cm, stands on a horizontal table and holds water up to 1 cm from the top. When a cube is placed in the water and is completely submerged, the water rises to the top and 2 cm3 of water over flows. Calculate the volume of the cube.
Answer
Given, the base of rectangular container is a square
∴ l = 6 cm and b = 6 cm

When a cube is placed in it, water rises to top i.e. through height 1 cm and 2 cm3 of water overflows.
We know that,
Volume of cube = Volume of water displaced
= 6 × 6 × 1 + 2
= 36 + 2
= 38 cm3
Hence, volume of cube = 38 cm3.
Two cubes, each with 12 cm edge, are joined end to end. Find the surface area of the resulting cuboid.
Answer
From figure,

length of cuboid = 12 + 12 = 24 cm
breadth of cuboid = 12 cm
height of cuboid = 12 cm
By formula,
Total surface area of cuboid = 2(lb + bh + hl)
= 2(24 × 12 + 12 × 12 + 12 × 24)
= 2(288 + 144 + 288)
= 2 × 720
= 1440 cm2.
Hence, surface area of resulting cuboid = 1440 cm2.
A cube of a metal of 6 cm edge is melted and cast into a cuboid whose base is 9 cm × 8 cm. Find the height of the cuboid.
Answer
Side of a cube = 6 cm
Volume of cube = (side)3 = 63 = 216 cm3.
Since, the same metal is melted and casted into cuboid so,
Volume of cuboid = Volume of cube.
By formula,
Volume of cuboid = l × b × h
Substituting values we get,
⇒ 216 = 9 × 8 × h
⇒ h = = 3.
Hence, height of cuboid = 3 cm.
The area of a playground is 4800 m2. Find the cost of covering it with gravel 1 cm deep, if the gravel costs ₹260 per cubic metre.
Answer
Given,
Area of playground = 4800 m2
We can write it as,
l × b = 4800
Given,
Depth of level = 1 cm
∴ h = 1 cm = m
By formula,
Volume of gravel needed = l × b × h
= 4800 ×
= 48 m3
Cost of gravel = ₹260 per cubic metre
So the total cost = 260 × 48 = ₹12480
Hence, cost of covering the playground with 1 cm deep gravel = ₹12480.
A field is 30 m long and 18 m broad. A pit 6 m long, 4 m wide and 3 m deep is dug out from the middle of the field and the earth removed is evenly spread over the remaining area of the field. Find the rise in the level of the remaining part of the field in centimeters correct to two decimal places.
Answer
From figure,
ABCD is a field.
Volume of the earth dug out = 6 × 4 × 3 = 72 m3
Area of field ABCD = AB × BC = 18 × 30 = 540 m2.
Area of pit EFGH = EF × FG = 4 × 6 = 24 m2.
Area of remaining field = 540 - 24 = 516 m2.
Let h metres is the level raised over the field uniformly.
Volume of rise in level = Volume of earth dug out
∴ Area of remaining field × h = 72
516h = 72
h = m = 13.95 cm
Hence, the level of the remaining field has been raised by 13.95 cm.
A rectangular plot is 24 m long and 20 m wide. A cubical pit of edge 4 m is dug at each of the four corners of the field and the soil removed is evenly spread over the remaining part of the plot. By what height does the remaining plot get raised?
Answer
Let ABCD be the rectangular plot.

Given,
Length of plot (l) = 24 m
Width of plot (b) = 20 m
So, the area of plot = l × b = 24 × 20 = 480 m2.
We know that,
Side of cubical pit = 4 m
Volume of each pit = 43 = 64 m3.
Volume of 4 pits at the corners = 4 × 64 = 256 m3.
Surface area of each pit = 4(side)2
= 4 × 42
= 64 m2
So, the area of remaining plot = 480 – 64 = 416 m2.
Let height of soil be h meters spread over remaining land.
So, the volume of soil raised = Volume of soil dug
∴ 416 × h = 256
h = metre.
Hence, remaining plot gets raised by metre.
The inner dimensions of a closed wooden box are 2 m, 1.2 m and 0.75 m. The thickness of the wood is 2.5 cm. Find the cost of wood required to make the box if 1 m3 of wood costs ₹ 22,000.
Answer
Given,
Inner dimensions of wooden box are 2 m, 1.2 m and 0.75 m.
Thickness of the wood = 2.5 cm = = 0.025 m.
So the external dimensions of wooden box are,
⇒ (2 + 2 × 0.025), (1.2 + 2 × 0.025), (0.75 + 2 × 0.025)
⇒ (2 + 0.05), (1.2 + 0.05), (0.75 + 0.5)
⇒ 2.05 m, 1.25 m, 0.80 m.
By formula,
Volume of solid = External volume of box – Internal volume of box
Substituting the values we get,
Volume of solid = (2.05 × 1.25 × 0.80) – (2 × 1.2 × 0.75)
= 2.05 – 1.80
= 0.25 m3.
Cost of box = Cost per m3 × Volume of box
= ₹ 22,000 × 0.25
= ₹ 22,000 x
= ₹ 5,500.
Hence, cost of wood required to make the box is ₹ 5,500.
A cubical wooden box of internal edge 1 m is made of 5 cm thick wood. The box is open at the top. If the wood costs ₹ 28,800 per cubic metre, find the cost of the wood required to make the box. Calculate the cost to nearest hundred rupees.
Answer
Given,
Internal edge of cubical wooden box = 1 m
Thickness of wood = 5 cm = m = 0.05 m
We know that,
External length = (1 + 0.05 × 2) = 1.1 m
External Breadth = (1 + 0.05 × 2) = 1.1 m
External Height = (1 + 0.05) = 1.05 m [Since, box is open at top]
By formula,
Volume of the wood used = Outer volume – Inner volume
Substituting the values we get,
Volume of the wood used = 1.1 × 1.1 × 1.05 – 1 × 1 × 1
= 1.2705 – 1
= 0.2705 m3
Given,
Cost of 1 m3 of wood = ₹ 28,800
Cost of the wood required to make the box = Cost of wood per m3 × Volume of wood
= ₹ 28,800 × 0.2705
= ₹ 7,790.40
≈ ₹ 7,800 (to nearest hundred)
Hence, cost of wood required to make the box = ₹ 7,800.
A square brass plate of side x cm is 1 mm thick and weighs 4725 g. If one cc of brass weights 8.4 g, find the value of x.
Answer
Given,
Side of square brass plate = cm
Here, l = cm and b = cm
Thickness of plate = 1 mm = = 0.1 cm
We know that,
Volume of the plate = l × b × h
Substituting the values
= × × 0.1
= cm3
Given,
Weight of 1 cm3 of brass = 8.4 g
∴ Weight of cm3 of brass = 8.4 x g
But weight of square brass plate is given as 4725 g
Hence, x = 75.
Three cubes whose edges are x cm, 8 cm and 10 cm respectively are melted and recast into a single cube of edge 12 cm. Find x.
Answer
Since, cubes are melted and recasted into a single cube.
∴ Total volume of three cubes = Volume of new single cube
Substituting values we get,
Hence, x = 6.
The area of cross-section of a pipe is 3.5 cm2 and water is flowing out of pipe at the rate of 40 cm/s. How much water is delivered by the pipe in one minute?
Answer
It is given that
Area of cross-section of pipe = 3.5 cm2
Speed of water = 40 cm/s
Length of water column in 1 sec = 40 cm
We know that,
Volume of water flowing in 1 second = Area of cross section × length
= 3.5 × 40
= 140 cm3.
So, the volume of water flowing in 1 minute i.e., 60 sec = 140 × 60 = 8400 cm3.
1 cm3 = litre
∴ 8400 cm3 = = 8.4 litres.
Hence, 8.4 litres of water is delivered by the pipe in one minute.
The figure (i) given below shows a solid of uniform cross-section. Find the volume of the solid. All measurements are in cm and all angles in the figure are right angles.

Answer
(a) From figure,

The line AB divides the figure, into two cuboids vertical and horizontal.
Volume of solid = Volume of vertical cuboid + Volume of horizontal cuboid
= 4 × 2 × 6 + 4 × 4 × 2
= 48 + 32
= 80 cm3
Hence, volume of solid = 80 cm3.
The figure (ii) given below shows the cross section of a concrete wall to be constructed. It is 2 m wide at the top, 3.5 m wide at the bottom and its height is 6 m and its length is 400 m. Calculate
(i) the cross sectional area and
(ii) volume of concrete in the wall.

Answer
Figure (ii) is a trapezium with parallel sides 2 m and 3.5 m
(i) Area of cross section = (sum of parallel sides) × height
= (2 + 3.5) × 6
= × 5.5 × 6
= 5.5 × 3
= 16.5 m2.
Hence, area of cross-section = 16.5 m2.
(ii) Volume of concrete in the wall = Area of cross section × length
= 16.5 × 400
= 6600 m3.
Hence, volume of concrete wall = 6600 m3.
The figure (iii) given below show the cross-section of a swimming pool 10 m broad, 2 m deep at one end and 3 m deep at the other end. Calculate the volume of water it will hold when full, given that its length is 40 m.
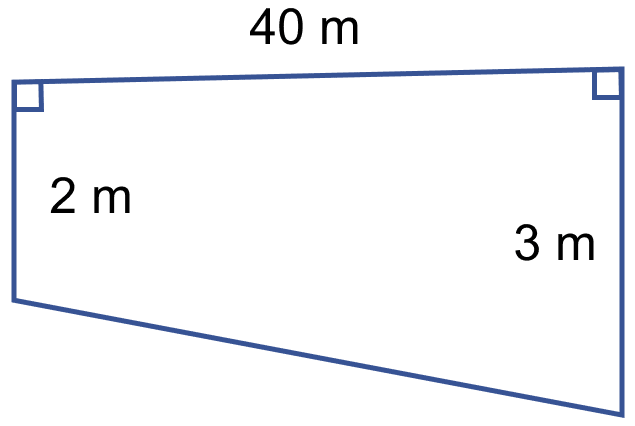
Answer
Figure (iii) is a trapezium with parallel sides 2 m and 3m.
By formula,
Area of cross section = (sum of parallel sides) × distance between them
= (2 + 3) × 40
= × 5 × 40
= 100 m2.
So, the volume of water it will hold when full = area of cross section × width
= 100 × 10
= 1000 m3.
Hence, swimming pool will hold 1000 m3 of water.
A swimming pool is 50 metres long and 15 metres wide. Its shallow and deep ends are metres and metres deep respectively. If the bottom of the pool slopes uniformly, find the amount of water required to fill the pool.
Answer
Given,
Length of swimming pool = 50 m
Width of swimming pool = 15 m
Its shallow and deep ends are 1.5 m and 4.5 m deep

By formula,
Area of cross section of swimming pool = (sum of parallel sides) × length
=
= × 6 × 50
= 150 m2.
Amount of water required to fill pool = Area of cross section × width
= 150 × 15
= 2250 m3.
Hence, amount of water required to fill pool 2250 m3.
Area of a triangle is 30 cm2. If its base is 10 cm, then its height is
5 cm
6 cm
7 cm
8 cm
Answer
By formula,
Area of triangle = × base × height.
Substituting values we get,
30 = × 10 × height
height = = 6 cm.
Hence, Option 2 is the correct option.
If the perimeter of a square is 80 cm, then its area is
800 cm2
600 cm2
400 cm2
200 cm2
Answer
By formula,
Perimeter of square = 4 × side
Substituting values we get,
80 = 4 × side
side = = 20 cm.
By formula,
Area of square = side × side = 20 × 20 = 400 cm2.
Hence, Option 3 is the correct option.
Area of a parallelogram is 48 cm2. If its height is 6 cm then its base is
8 cm
4 cm
16 cm
None of these
Answer
By formula,
Area of parallelogram = base × height
Substituting values we get,
⇒ 48 = base × 6
⇒ base = = 8 cm.
Hence, Option 1 is the correct option.
If d is the diameter of a circle, then its area is
πd2
2πd2
Answer
r = .
By formula,
Area of circle = πr2 =
Hence, Option 3 is the correct option.
If the area of trapezium is 64 cm2 and the distance between parallel sides is 8 cm, then sum of its parallel sides is
8 cm
4 cm
32 cm
16 cm
Answer
By formula,
Area of trapezium = × sum of parallel sides × distance between them
Substituting values we get,
⇒ 64 = × sum of parallel sides × 8
⇒ 64 = 4 × sum of parallel sides
⇒ sum of parallel sides = = 16 cm.
Hence, Option 4 is the correct option.
Area of a rhombus whose diagonals are 8 cm and 6 cm is
48 cm2
24 cm2
12 cm2
96 cm2
Answer
By formula,
Area of rhombus = × d1 × d2
Substituting values we get,
⇒ Area of rhombus = × 8 × 6 = 24 cm2.
Hence, Option 2 is the correct option.
If the lengths of diagonals of a rhombus is doubled, then area of rhombus will be
doubled
tripled
four times
remains same
Answer
Let diagonals be d1 and d2.
By formula,
Area of rhombus = × d1 × d2
If doubled, diagonals = 2d1 and 2d2.
Area of new rhombus = × 2d1 × 2d2
= 4 × × d1 × d2
= 4 × Area of rhombus.
Hence, Option 3 is the correct option.
If the length of a diagonal of a quadrilateral is 10 cm and lengths of the perpendiculars on it from opposite vertices are 4 cm and 6 cm, then area of quadrilateral is
100 cm2
200 cm2
50 cm2
None of these.
Answer
Let ABCD be the quadrilateral with diagonal BD.

Let AM and CN be the perpendiculars from A and C on diagonal BD.
From figure,
BD divides quadrilateral in two triangles.
Area of △ABD = × base × height
= × BD × AM
= × 10 × 4
= 20 cm2.
Area of △BCD = × base × height
= × BD × CN
= × 10 × 6
= 30 cm2.
Area of quadrilateral = Area of △ABD + Area of △BCD
= 20 + 30 = 50 cm2.
Hence, Option 3 is the correct option.
Area of a rhombus is 90 cm2. If the length of one diagonal is 10 cm then the length of other diagonal is
18 cm
9 cm
36 cm
4.5 cm
Answer
Let diagonals be d1 and d2.
By formula,
Area of rhombus = × d1 × d2
Substituting values we get,
⇒ 90 = × 10 × d2
⇒ d2 =
⇒ d2 = 18 cm.
Hence, Option 1 is the correct option.
In the adjoining figure, OACB is a quadrant of a circle of radius 7 cm. The perimeter of the quadrant is
11 cm
18 cm
25 cm
36 cm

Answer
Perimeter of quadrant =
Hence, Option 3 is the correct option.
In the adjoining figure, OABC is a square of side 7 cm. OAC is a quadrant of a circle with O as center. The area of the shaded region is
10.5 cm2
38.5 cm2
49 cm2
11.5 cm2

Answer
Area of square OABC = (7)2 = 49 cm2.
Area of quadrant OAC =
Area of shaded region = Area of square OABC - Area of quadrant OAC
= 49 - 38.5 = 10.5 cm2.
Hence, Option 1 is the correct option.
The adjoining figure shows a rectangle and a semicircle. The perimeter of the shaded region is
70 cm
56 cm
78 cm
46 cm

Answer
From figure,
Let length = 14 cm and breadth = 10 cm.
Diameter of semi-circle = 14 cm and radius = 7 cm.
Perimeter of shaded region = length + breadth + breadth + πr.
= 14 + 10 + 10 +
= 34 + 22 = 56 cm.
Hence, Option 2 is the correct option.
The area of the shaded region shown in the below figure is
140 cm2
77 cm2
294 cm2
217 cm2

Answer
Area of shaded region = Area of rectangle + Area of semi-circle
= length × breadth +
= 14 × 10 +
= 140 +
= 140 + 77
= 217 cm2.
Hence, Option 4 is the correct option.
In the adjoining figure, the boundary of the shaded region consists of semicircular arcs. The area of the shaded region is equal to
616 cm2
385 cm2
231 cm2
308 cm2
Answer
From figure,
Radius of larger circle (R) = 14 cm.
Area of shaded region = Area of larger circle - Area of 1st smaller circle + Area of 2nd smaller circle .......(1)
From figure,
Diameter of both the smaller semi-circles = 14 cm.
∴ Radius = 7 cm and area of both the circle are equal.
∴ Area of shaded region = Area of larger circle =
Hence, Option 4 is the correct option.
The perimeter of the shaded region shown in the below figure is
44 cm
88 cm
66 cm
132 cm

Answer
Radius of larger semi-circle (R) = 14 cm and radius of smaller semi-circle (r) = 7 cm.
From figure,
Perimeter of shaded region = Circumference of larger semi-circle + 2 × Circumference of smaller semi-circle
= πR + 2πr
=
= 44 + 44 = 88 cm.
Hence, Option 2 is the correct option.
In the adjoining figure, ABC is a right angled triangle at B. A semicircle is drawn on AB as diameter. If AB = 12 cm and BC = 5 cm, then the area of the shaded region is
(60 + 18π) cm2
(30 + 36π) cm2
(30 + 18π) cm2
(30 + 9π) cm2

Answer
Area of right angle triangle ABC = × base × height
= × AB × BC
= × 12 × 5
= 30 cm2.
From figure,
AB = 12 cm is the diameter of circle.
Radius = = 6 cm.
Area of semi-circle = = 18π cm2.
Area of shaded region = Area of right angle triangle ABC + Area of semi-circle
= (30 + 18π) cm2.
Hence, Option 3 is the correct option.
The perimeter of the shaded region shown in the below figure is
(30 + 6π) cm
(30 + 12π) cm
(18 + 12π) cm
(18 + 6π) cm

Answer
In right angle triangle ABC,
⇒ AC2 = AB2 + BC2
⇒ AC2 = (12)2 + (5)2
⇒ AC2 = 144 + 25
⇒ AC2 = 169
⇒ AC = = 13 cm.
From figure,
radius of semi-circle (r) = = 6 cm.
Perimeter of shaded region = AC + CB + Circumference of semi-circle
= 13 + 5 + πr
= (18 + 6π) cm.
Hence, Option 4 is the correct option.
If the volume of a cube is 729 m3, then its surface area is
486 cm2
324 cm2
162 cm2
None of these
Answer
By formula,
Volume of cube = (Side)3
∴ (Side)3 = 729
Side = = 9 cm.
⇒ Surface area of cube = 6(side)2
= 6(9)2
= 6 × 81 = 486 cm2.
Hence, Option 1 is the correct option.
If the total surface area of a cube is 96 cm2, then the volume of cube is
8 cm3
512 cm3
64 cm3
27 cm3
Answer
Let side of cube = x cm.
Given,
Surface area of cube = 96 cm2
By formula,
Surface area of a cube = 6x2
∴ 6x2 = 96
⇒ x2 = 16
⇒ x = = 4 cm.
Volume of cube = (side)3
= (x)3
= 43 = 64 cm3.
Hence, Option 3 is the correct option.
The length of the longest pole that can be put in a room of dimensions (10 m × 10 m × 5 m) is
15 m
16 m
10 m
12 m
Answer
The longest pole in a cuboid is equal to the diagonal of cuboid.
Diagonal of cuboid =
Hence, Option 1 is the correct option.
The lateral surface area of a cube is 256 m2. The volume of the cube is
512 m3
64 m3
216 m3
256 m3
Answer
By formula,
Lateral surface area of cube = 4(side)2
⇒ 4(side)2 = 256
⇒ (side)2 = 64
⇒ side = = 8 m.
Volume of cube = (side)3
= 83 = 512 m3.
Hence, Option 1 is the correct option.
If the perimeter of one face of a cube is 40 cm, then the sum of lengths of its edge is
80 cm
120 cm
160 cm
240 cm
Answer
Each face of cube is a square. Let length of each side = x cm.
Given, perimeter = 40 cm.
∴ 4x = 40 cm
⇒ x = 10 cm.
There are 12 edges in a cube.
Sum of edges = 12 × 10 = 120 cm.
Hence, Option 2 is the correct option.
A cuboid container has the capacity to hold 50 small boxes. If all the dimensions of the container are doubled, then it can hold (small boxes of same size)
100 boxes
200 boxes
400 boxes
800 boxes
Answer
Let l, b and h be the length, breadth and height of the cuboid container.
Volume = l × b × h = lbh.
If they are doubled then,
New Volume = 2l × 2b × 2h = 8lbh
Hence, volume becomes 8 times.
So, capacity becomes 8 times.
So, container can hold 50 × 8 = 400 boxes.
Hence, Option 3 is the correct option.
The number of planks of dimensions (4 m × 50 cm × 20 cm) that can be stored in a pit which is 16 m long, 12 m wide and 4 m deep is
1900
1920
1800
1840
Answer
Volume of plank = 4 m × 50 cm × 20 cm
= 4 m × 0.50 m × 0.20 m
= 0.4 m3.
Volume of pit = 16 m × 12 m × 4 m
= 768 m3.
No. of planks that can be stored in pit = = 1920.
Hence, Option 2 is the correct option.
Consider the following two statements:
Statement 1: If the circumference of a circle is 10π cm, then its area is 25π cm2.
Statement 2: The area of a circle is π times its circumference.
Which of the following is valid?
Both the statements are true.
Both the statements are false.
Statement 1 is true, and Statement 2 is false.
Statement 1 is false, and Statement 2 is true.
Answer
Given that the circumference is 10π cm.
⇒ 2πr = 10π
⇒ r =
⇒ r = 5 cm
Now, calculate the area using this radius,
⇒ A = πr2
= π.52
= 25π cm2.
∴ Statement 1 is true.
We know that,
Circumference of the circle = 2πr
2πr × π = 2π2r ≠ πr2.
∴ Statement 2 is false.
∴ Statement 1 is true, and Statement 2 is false.
Hence, option 3 is the correct option.
Assertion (A): Sides of a triangle are 9 cm, 12 cm and 15 cm. This triangle is both scalene triangle and right angle triangle.
Reason (R): Area of a right triangle = x base x height.
Assertion (A) is true, Reason (R) is false.
Assertion (A) is false, Reason (R) is true.
Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).
Answer
Given, sides of a triangle are 9 cm, 12 cm and 15 cm.
A scalene triangle is a triangle in which all three sides have different lengths.
The given side lengths are 9 cm, 12 cm, and 15 cm. All these lengths are distinct.
Therefore, it is a scalene triangle.
If the square of the longest side equals the sum of the squares of the other two sides, then it's a right-angled triangle.
The longest side is 15 cm.
Let's check: 152 = 92 + 122
⇒ 225 = 81 + 144
⇒ 225 = 225
Since the equality holds, the triangle is a right-angled triangle.
∴ Assertion (A) is true.
By formula,
Area of a right triangle = x base x height.
∴ Reason (R) is true.
∴ Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).
Hence, option 4 is the correct option.
Assertion (A): Heron's formula can be used to find the area of a scalene triangle only.
Reason (R): If ABC is a triangle with side a, b and c respectively, then its area = , where s = .
Assertion (A) is true, Reason (R) is false.
Assertion (A) is false, Reason (R) is true.
Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).
Answer
With the help of heron's formula, we can find the area of any triangle and not particularly scalene triangle.
∴ Assertion (A) is false.
If ABC is a triangle with side a, b and c respectively, then its area = , where s = .
This is the correct definition and formula for Heron's formula. The variable 's' represents the semi-perimeter of the triangle.
∴ Reason (R) is true.
∴ Assertion (A) is false, Reason (R) is true.
Hence, option 2 is the correct option.
Assertion (A): The volume of a cuboid having length, breadth and diagonal as 4 m, 3 m and 13 m is 144 m3.
Reason (R): Length of diagonal of a cuboid is .
Assertion (A) is true, Reason (R) is false.
Assertion (A) is false, Reason (R) is true.
Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).
Answer
Given: length, breadth and diagonal of cuboid = 4 m, 3 m and 13 m.
By formula,
Length of diagonal of a cuboid =
∴ Reason (R) is true.
Substituting the values, we get
Volume of cuboid = l x b x h
= 3 x 4 x 12
= 144 m3.
∴ Assertion (A) is true.
∴ Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).
Hence, option 3 is the correct option.
Calculate the area of the shaded region.

Answer
From figure,
Area of △AOB = × base × height
= × AO × OB
= × 12 × 5
= 30 cm2.
In right angle triangle AOB,
Using pythagoras theorem,
⇒ AB2 = AO2 + OB2
⇒ AB2 = 122 + 52
⇒ AB2 = 144 + 25
⇒ AB2 = 169
⇒ AB = = 13 cm.
In △ABC,
Let a = BC = 14 cm, b = AC = 15 cm and c = AB = 13 cm.
s = = 21 cm.
By Heron's formula,
Area =
Substituting values we get,
Area of shaded region = Area of △ABC - Area of △AOB
= 84 - 30 = 54 cm2.
Hence, area of shaded region = 54 cm2.
If the sides of a square are lengthened by 3 cm, the area becomes 121 cm3. Find the perimeter of the original square.
Answer
Let length of square be x cm.
New length = (x + 3) cm.
According to the question,
⇒ (x + 3)(x + 3) = 121
⇒ x2 + 3x + 3x + 9 = 121
⇒ x2 + 6x = 112
⇒ x2 + 6x - 112 = 0
⇒ x2 + 14x - 8x - 112 = 0
⇒ x(x + 14) - 8(x + 14) = 0
⇒ (x - 8)(x + 14) = 0
⇒ x - 8 = 0 or x + 14 = 0
⇒ x = 8 or x = -14.
Since, length cannot be negative.
∴ x ≠ -14.
Perimeter of original square = 4 × side = 4x
= 4 × 8 = 32 cm.
Hence, perimeter of original square = 32 cm.
Find the area enclosed by the figure (i) given below. All measurements are in centimeters.

Answer
From figure,

Area of shaded region = Area of square ABCD - Area of △EFG - Area of △HIJ ........(1)
In △EFG and △HIJ,
FG = HI
IJ = EF
∠HIJ = ∠GFE (Both equal to 90°).
Hence, △EFG ≅ △HIJ by SAS axiom.
∴ Area of △EFG = Area of △HIJ.
Area of △EFG = × base × height
= × EF × FG
= × 5 × 6 = 15 cm2.
Area of △HIJ = Area of △EFG = 15 cm2
Area of square ABCD = (side)2 = (9)2 = 81 cm2.
Substituting values in (1) we get,
Area of shaded region = 81 - 15 - 15 = 51 cm2.
Hence, area of shaded region = 51 cm2.
Find the area of the quadrilateral ABCD shown in figure (ii) given below. All measurements are in centimeters.

Answer
In right angle △ABD,
⇒ BD2 = AB2 + AD2
⇒ BD2 = 62 + 82
⇒ BD2 = 36 + 64
⇒ BD2 = 100
⇒ BD = = 10 cm.
In right angle △BDC,
⇒ BC2 = BD2 + DC2
⇒ 262 = 102 + DC2
⇒ DC2 = 676 - 100
⇒ DC2 = 576
⇒ DC = = 24 cm.
Area of △ABD = × base × height
= × AD × AB
= × 8 × 6
= 24 cm2.
Area of △BDC = × base × height
= × DC × BD
= × 24 × 10
= 120 cm2.
Area of quadrilateral ABCD = Area of △ABD + Area of △BDC
= 24 + 120 = 144 cm2.
Hence, area of quadrilateral ABCD = 144 cm2.
Calculate the area of the shaded region shown in figure (iii) given below. All measurements are in meters.

Answer
The points are labelled as shown in the figure below:

Area of right angle △AEH = × base × height
= × AH × AE
= × 5 × 5
= 12.5 m2.
Area of right angle △EBF = × base × height
= × BF × EB
= × 5 × 7
= 17.5 m2.
Area of trapezium GDCF = × (sum of parallel sides) × distance between them
= × (GD + FC) × DC
= × (3 + 7) × 12
= 60 m2.
Area of square ABCD = (side)2 = (12)2 = 144 m2.
From figure,
Area of shaded region = Area of square ABCD - (Area of right angle △AEH + Area of right angle △EBF + Area of trapezium GDCF)
= 144 - (12.5 + 17.5 + 60)
= 144 - 90 = 54 m2.
Hence, area of shaded region = 54 m2.
Asifa cut an aeroplane from a coloured chart paper (as shown in the adjoining figure). Find the total area of the chart paper used, correct to 1 decimal place.

Answer
The points are labelled as shown in the figure below:

In △ABK,
a = BK = 1 cm, b = AK = 5 cm and c = AB = 5 cm.
s = = 5.5 cm.
Area of △ABK =
Substituting values we get,
Area of △KIJ = base × height
= × KI × KJ
= × 1.5 × 6
= 4.5 cm2.
Area of △CBD = base × height
= × BD × CB
= × 1.5 × 6
= 4.5 cm2.
Area of rectangle BKHE = length × breadth
= BE × EH
= 6.5 × 1 = 6.5 cm2.
Let EL and HM be perpendicular to LM.
Since, EFGH is an isosceles trapezium so,
FL = MG = = 0.5 cm.
In right angle △EFL,
⇒ EF2 = EL2 + FL2
⇒ 12 = EL2 + (0.5)2
⇒ EL2 = 12 - (0.5)2
⇒ EL2 = 1 - 0.25
⇒ EL2 = 0.75
⇒ EL = = 0.87 cm.
Area of trapezium EFGH = × (sum of parallel sides) × distance between them
= × (EH + FG) × EL
= × (1 + 2) × 0.87
= 1.3 cm2.
Area of chart paper used = Area of aeroplane = Area of △ABK + Area of △KIJ + Area of △CBD + Area of rectangle BKHE + Area of trapezium EFGH
= 2.5 + 4.5 + 4.5 + 6.5 + 1.3
= 19.3 cm2.
Hence, area of chart paper used = 19.3 cm2.
If the area of a circle is 78.5 cm2, find its circumference. (Take π = 3.14)
Answer
By formula,
Area of circle = πr2
⇒ πr2 = 78.5
⇒ 3.14r2 = 78.5
⇒ r2 = = 25
⇒ r = = 5 cm.
Circumference = 2πr = 2 × 3.14 × 5 = 31.4 cm.
Hence, circumference = 31.4 cm.
From a square cardboard, a circle of biggest area was cut out. If the area of the circle is 154 cm2, calculate the original area of the cardboard.
Answer
Let radius of the circle be r cm.
Given,
Area of the circle = 154 cm2
πr2 = 154
The biggest circle that can be cut from a square has the diameter equal to the side of the square.
Side = 2r = 2 × 7 = 14 cm.
Area of cardboard = (side)2 = 142 = 196 cm2.
Hence, area of cardboard = 196 cm2.
From a sheet of paper of dimensions 2 m × 1.5 m, how many circles of radius 5 cm can be cut? Also find the area of the paper wasted. (Take π = 3.14)
Answer
Length of sheet = 2 m = 200 cm,
Breadth of sheet = 1.5 m = 150 cm.
Given,
Radius of each circle = 5 cm,
Diameter of each circle = 2 × 5 = 10 cm.
No. of circles lengthwise to be cut = = 20.
No. of circles breadthwise to be cut = = 15.
Total no. of circles that can be cut = 20 × 15 = 300.
Area of paper wasted = Area of sheet - Area of circles
= l × b - 300 × πr2
= 200 × 150 - 300 × 3.14 × (5)2
= 30000 - 23550
= 6450 cm2.
Hence, total no. of circles that can be cut = 300 and area of paper wasted = 6450 cm2.
If the diameter of a semi-circular protractor is 14 cm, then find its perimeter.
Answer
Diameter of semi-circular protractor = 14 cm
Radius = = 7 cm.
Perimeter of semi-circular protractor = πr + 2r = = 22 + 14 = 36 cm.
Hence, perimeter of semi-circular protractor = 36 cm.
A road 3.5 m wide surrounds a circular park whose circumference is 88 m. Find the cost of paving the road at the rate of ₹60 per square metre.
Answer
Given,
Circumference of circular park = 88 m
Let radius of circular park be r meters.

2πr = 88
From figure,
Radius of outer circle (R) = Radius of circular park + Width of road = 14 + 3.5 = 17.5 m
Area of road = Area of outer circle - Area of circular park
= πR2 - πr2
= π(17.5)2 - π(14)2
= π[306.25 - 196]
= 110.25π
= = 346.5 m2.
Cost of paving the road = Area of road × Rate = 346.5 × 60 = ₹ 20790.
Hence, cost of paving road = ₹ 20790.
The adjoining sketch shows a running track 3.5 m wide all around which consists of two straight paths and two semicircular rings. Find the area of the track.
Answer
From figure,
Length of inner rectangle ABCD = 140 m
Breadth of inner rectangle ABCD = 42 m
Diameter of inner semi-circle = 42 m
Radius of inner semi-circle (r) = = 21 m.
Length of outer rectangle = Length of inner rectangle = 140 m
Breadth of outer rectangle = Breadth of inner rectangle + 2 × Width of outer track = 42 + 2 × 3.5 = 42 + 7 = 49 m.
Diameter of outer semi-circle = 49 m
Radius of outer semi-circle (R) = = 24.5 m.
Area of track = Area of outer rectangle - Area of inner rectangle + 2(Area of outer semi-circle - Area of inner semi-circle)
Hence, area of track = 1480.5 m2.
In the adjoining figure, O is the center of a circular arc and AOB is a line segment. Find the perimeter and the area of the shaded region correct to one decimal place. (Take π = 3.142)
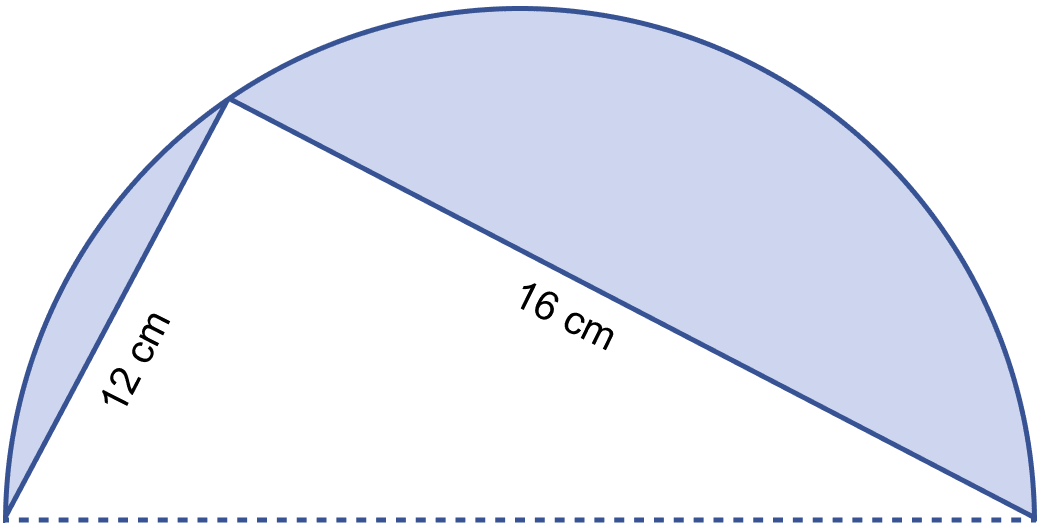
Answer
Angle in semi-circle = 90°
∴ ∠ACB = 90°
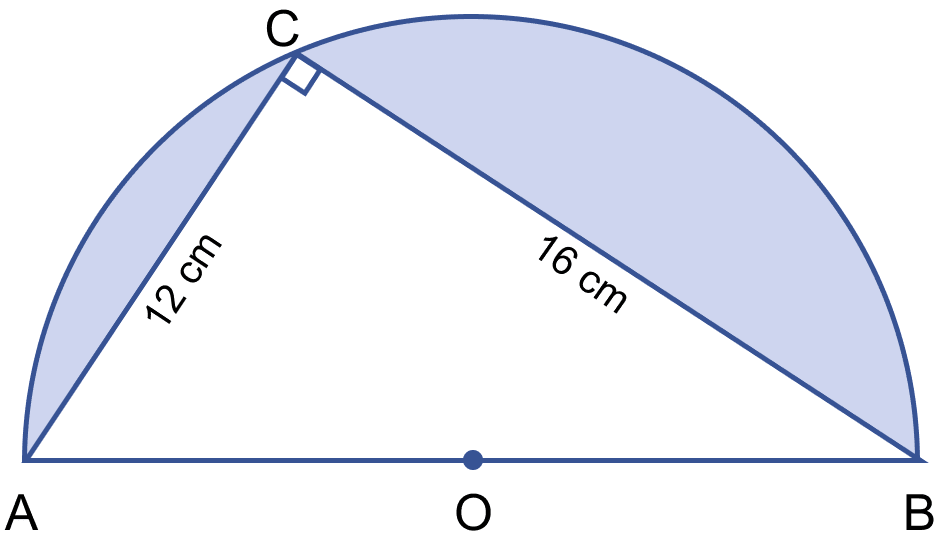
Using pythagoras theorem,
⇒ AB2 = AC2 + BC2
⇒ AB2 = 122 + 162
⇒ AB2 = 144 + 256
⇒ AB2 = 400
⇒ AB = = 20 cm.
AB is the diameter of circle,
∴ Radius = = = 10 cm.
Area of shaded region = Area of semi-circle - Area of triangle
Perimeter of shaded region = Circumference of semi-circle + AC + CB
= πr + 12 + 16
= 3.142 × 10 + 28
= 31.42 + 28
= 59.42 cm.
Hence, perimeter of shaded region = 59.42 cm and area of semi-circle = 61.1 cm2.
In the figure (i) given below, the radius is 3.5 cm. Find the perimeter of the quarter of the circle.

Answer
Perimeter of quarter of circle =
Substituting values we get,
Hence, perimeter of quarter of circle = 12.5 cm.
In the figure (ii) given below, there are five squares each of side 2 cm.
(i) Find the radius of the circle.
(ii) Find the area of the shaded region. (Take π = 3.14).

Answer
(i) Let O be the center of the circle.
B be the mid-point of side of square.
From figure,
OB = 2 + 1 = 3 cm
AB = 1 cm
Using Pythagoras theorem,
OA =
OA = .
So, the radius of the circle = cm.
Hence, the radius of circle = cm.
(ii) We know that,
Area of the circle = πr2.
= 3.14 ×
= 3.14 × 10
= 31.4 cm2.
Area of 5 square of side 2 cm each = 22 × 5
= 4 × 5
= 20 cm2.
So, the area of shaded portion = 31.4 – 20 = 11.4 cm2.
Hence, area of shaded portion = 11.4 cm2.
In the figure (i) given below, a piece of cardboard in the shape of a quadrant of a circle of radius 7 cm is bounded by the perpendicular radii OX and OY. Points A and B lie on OX and OY respectively such that OA = 3 cm and OB = 4 cm. The triangular part OAB is removed. Calculate the area and the perimeter of the remaining piece.

Answer
Area of quadrant =
Area of △OAB = × base × height
Area of shaded region = Area of quadrant - Area of △OAB
= 38.5 - 6 = 32.5 cm2.
From figure,
BY = OY - OB = 7 - 4 = 3 cm.
AX = OX - OA = 7 - 3 = 4 cm.
In right angle triangle OAB,
⇒ AB2 = OA2 + OB2
⇒ AB2 = 32 + 42
⇒ AB2 = 9 + 16
⇒ AB2 = 25
⇒ AB = = 5 cm.
Perimeter of shaded region = AB + BY + AX + Circumference of quadrant
= 5 + 3 + 4 +
= 12 +
= 12 + 11
= 23 cm.
Hence, area of shaded region = 32.5 cm2 and perimeter of remaining piece = 23 cm.
In the figure (ii) given below, ABCD is a square. Points A, B, C and D are centres of quadrants of circles of the same radius. If the area of the shaded portion is cm2, find the radius of the quadrants.
Answer
Let radius be r cm of each quadrant.
Area of each quadrant =
So, area of 4 quadrants =
From figure,
Side of square = r + r = 2r
Area of square ABCD = (Side)2 = (2r)2 = 4r2.
Area of shaded region = Area of square ABCD - Area of 4 quadrants
Hence, radius of quadrant = 5 cm.
In the adjoining figure, ABC is a right angled triangle right angled at B. Semicircles are drawn on AB, BC and CA as diameter. Show that the sum of areas of semicircles drawn on AB and BC as diameter is equal to the area of the semicircle drawn on CA as diameter.

Answer
Since, ABC is a right angled triangle.
Using pythagoras theorem,
AC2 = AB2 + BC2 .........(1)
Area of semi-circle with diameter AB =
= .........(2)
Area of semi-circle with diameter BC =
= ..........(3)
Area of semi-circle with diameter AC =
= ..........(4)
Adding equations (2) and (3) we get,
Area of semi-circle with diameter AB + Area of semi-circle with diameter BC =
=
From Eq 1,
Area of semi-circle with diameter AB + Area of semi-circle with diameter BC =
From Eq 4,
Area of semi-circle with diameter AB + Area of semi-circle with diameter BC = Area of semi-circle with diameter AC
Hence, proved that the sum of areas of semicircles drawn on AB and BC as diameter is equal to the area of the semicircle drawn on CA as diameter.
The length of minute hand of a clock is 14 cm. Find the area swept by the minute hand in 15 minutes.
Answer
Let minute hand be at A and after 15 minute it reaches B.
From figure,
Area of sector OAB =
Hence, area swept by minute hand in 15 minutes = 154 cm2.
Find the radius of a circle if a 90° arc has a length of 3.5π cm. Hence, find the area of the sector formed by this arc.
Answer
From figure,
AOB is a quadrant, with ∠AOB = 90°.
Let radius of circle be r cm,
Circumference of quadrant = .
Given,
Circumference of quadrant = 3.5π
Area of sector =
Hence, radius = 7 cm and area of sector = 38.5 cm2.
A cube whose each edge is 28 cm long has a circle of maximum radius on each of its face painted red. Find the total area of the unpainted surface of the cube.
Answer
Maximum diameter of circle can be 28 cm (Since, each edge is 28 cm).
So, radius = = 14 cm.
Area of each unpainted face = Area of square - Area of circle
= side2 - πr2
= 282 -
= 784 - 616
= 168 cm2.
Since, there are 6 faces in cube.
Total area of unpainted face = 6 × 168 = 1008 cm2.
Hence, total area of unpainted surface = 1008 cm2.
Can a pole 6.5 m long fit into the body of a truck with internal dimensions of 3.5 m, 3 m and 4 m?
Answer
Length of diagonal of cuboid =
Since, length of pole cannot be more than the length of diagonal.
Hence, 6.5 m pole cannot be fit into the body of a truck with internal dimensions of 3.5 m, 3 m and 4 m.
A car has a petrol tank 40 cm long, 28 cm wide and 25 cm deep. If the fuel consumption of the car averages 13.5 km per litre, how far can the car travel with a full tank of petrol?
Answer
Volume of tank = l × b × h
= 40 × 28 × 25
= 28000 cm3.
Since, 1 l = 1000 cm3.
∴ 28000 cm3 = 28 l.
Since, car travels 13.5 km per litre.
So, in 28 l car will travel 28 × 13.5 = 378 km.
Hence, car will travel 378 km in full tank of petrol.
An aquarium took 96 minutes to completely fill with water. Water was filling the aquarium at a rate of 25 litres every 2 minutes. Given that the aquarium was 2 m long and 80 cm wide, compute the height of the aquarium.
Answer
Let height of aquarium be h cm.
Volume of aquarium = l × b × h
= 2 m × 80 cm × h cm
= 200 cm × 80 cm × h cm
= 16000h cm3
= litres
= 16h litres.
Given,
Water was filling the aquarium at a rate of 25 litres every 2 minutes i.e., 12.5 litres per minute.
So, in 96 minutes, water filled = 96 × 12.5 = 1200 litres.
So, volume of aquarium = 1200 litres.
∴ 16h = 1200
h = = 75 cm.
Hence, height of aquarium = 75 cm.
The lateral surface area of a cuboid is 224 cm2. Its height is 7 cm and the base is a square. Find
(i) a side of the square, and
(ii) the volume of the cuboid.
Answer
(i) Since, base is a square.
Length = Breadth = x cm (let).
By formula,
Lateral surface area = 2(l + b) × h
⇒ 224 = 2(x + x) × 7
⇒ 224 = 2(2x) × 7
⇒ 28x = 224
⇒ x = = 8 cm.
Hence, the side of square = 8 cm.
(ii) Volume of cuboid = l × b × h
= 8 × 8 × 7
= 448 cm3.
Hence, volume of cuboid = 448 cm3.
If the volume of a cube is V m3, its surface area is S m2 and the length of a diagonal is d metres, prove that V = Sd.
Answer
Let side of cube = a m.
By formula,
Volume of cube (V) = (side)3 = a3,
Surface area (S) = 6(side)2 = 6a2.
Length of diagonal (d) = side = .
∴
Hence, proved that V = Sd.
The adjoining figure shows a victory stand, each face is rectangular. All measurements are in centimetres. Find its volume and surface area (the bottom of the stand is open).

Answer
By formula,
Volume of cuboid = l × b × h.
We know that,
Volume of part (3) = 50 × 40 × 12 = 24000 cm3
Volume of part (1) = 50 × 40 × (16 + 24)
= 50 × 40 × 40
= 80000 cm3.
Volume of part (2) = 50 × 40 × 24 = 48000 cm3.
So, the total volume = 24000 + 80000 + 48000 = 152000 cm3.
We know that
Total surface area = Area of front and back + Area of vertical faces + Area of top faces
Substituting the values we get,
= 2(50 × 12 + 50 × 40 + 50 × 24) cm2 + (12 × 40 + 28 × 40 + 16 × 40 + 24 × 40) cm2 + 3(50 × 40) cm2
= 2(600 + 2000 + 1200) cm2 + (480 + 1120 + 640 + 960) cm2 + (3 × 2000) cm2
= 2(3800) + 3200 + 6000 cm2
= 7600 + 3200 + 6000 cm2
= 16800 cm2.
Hence, volume = 152000 cm3 and surface area = 16800 cm2.
The external dimensions of an open rectangular wooden box are 98 cm by 84 cm by 77 cm. If the wood is 2 cm thick all around, find
(i) the capacity of the box
(ii) the volume of the wood used in making the box, and
(iii) the weight of the box in kilograms correct to one decimal place, given that 1 cm3 of wood weighs 0.8 g.
Answer
It is given that
External dimensions of open rectangular wooden box = 98 cm, 84 cm and 77 cm
Thickness = 2 cm
So, the internal dimensions of open rectangular wooden box = (98 - 2 × 2) cm, (84 - 2 × 2) cm and (77 - 2) cm
= (98 - 4) cm, (84 - 4) cm, 75 cm
= 94 cm, 80 cm, 75 cm.
(i) We know that,
Capacity of the box = Internal volume of box = 94 cm × 80 cm × 75 cm
= 564000 cm3.
Hence, capacity of the box = 564000 cm3.
(ii) Internal volume of box = 564000 cm3
External volume of box = 98 cm × 84 cm × 77 cm = 633864 cm3.
Volume of wood used in making the box = External volume - Internal volume
= 633864 – 564000 = 69864 cm3.
Hence, volume of box used in making the box = 69864 cm3.
(iii) Weight of 1 cm3 wood = 0.8 gm
So the weight of 69864 cm3 wood = 0.8 × 69864 gm
= kg
= kg
= 55.89 kg = 55.9 kg.
Hence, weight of box = 55.9 kg.
A cuboidal block of metal has dimensions 36 cm by 32 cm by 0.25 m. It is melted and recast into cubes with an edge of 4 cm.
(i) How many such cubes can be made?
(ii) What is the cost of silver coating the surfaces of the cubes at the rate of ₹1.25 per square centimeter?
Answer
(i) Given,
Dimensions of cuboidal block = 36 cm, 32 cm and 0.25 m.
Volume of cuboidal box = 36 cm × 32 cm × (0.25 × 100) cm
= (36 × 32 × 25) cm3
= 28800 cm3.
Volume of cube having edge 4 cm = 4 × 4 × 4 = 64 cm3.
We know that,
Number of cubes =
Hence, 450 cubes can be made.
(ii) By formula,
Total surface area of one cube = 6(side)2
= 6.(4)2
= 6 × 4 × 4
= 96 cm2.
So, the total surface area of 450 cubes = 450 × 96 = 43200 cm2
Cost of silver coating the surface for 1 cm2 = ₹1.25
Cost of silver coating the surface for 43200 cm2 = 43200 × 1.25 = ₹54000.
Hence, cost of silver coating the surface of cube = ₹54000.
Three cubes of silver with edges 3 cm, 4 cm and 5 cm are melted and recast into a single cube. Find the cost of coating the surface of the new cube with gold at the rate of ₹3.50 per square centimeter.
Answer
By formula,
Volume of cube = (edge)3
Volume of first cube = (3)3
= 3 × 3 × 3
= 27 cm3.
Volume of second cube = (4)3
= 4 × 4 × 4
= 64 cm3
Volume of third cube = (5)3
= 5 × 5 × 5
= 125 cm3.
Total volume = 27 + 64 + 125 = 216 cm3.
So, new cube's volume = 216 cm3
Let length of edge of new cube = x cm.
⇒ (x)3 = 216
⇒ (x)3 = (6)3
⇒ x = 6 cm.
Surface area of new cube = 6(x)2
= 6.(6)2
= 6 × 6 × 6
= 216 cm2.
Given,
Cost of coating the surface for 1 cm2 = ₹3.50
So, the cost of coating the surface for 216 cm2 = ₹3.50 × 216 = ₹756.
Hence, cost of coating the surface of new cube = ₹756.