Calculate the length of a chord which is at a distance 12 cm from the centre of a circle of radius 13 cm.
Answer
From figure,

AB is the chord which is at a distance 12 cm so,
OC = 12 cm and OA = radius = 13 cm.
In right angle triangle OAC,
⇒ OA2 = OC2 + AC2 (By pythagoras theorem)
⇒ 132 = 122 + AC2
⇒ AC2 = 132 - 122
⇒ AC2 = 169 - 144 = 25
⇒ AC = = 5 cm.
Since, the perpendicular to a chord from the centre of the circle bisects the chord,
∴ CB = AC = 5 cm.
AB = AC + CB = 5 + 5 = 10 cm.
Hence, length of chord = 10 cm.
A chord of length 48 cm is drawn in a circle of radius 25 cm. Calculate its distance from the centre of the circle.
Answer
From figure,

AB is the chord and radius = OA = 25 cm.
Since, the perpendicular to a chord from the centre of the circle bisects the chord,
∴ CB = AC = = 24 cm.
In right angle triangle OAC,
⇒ OA2 = OC2 + AC2 (By pythagoras theorem)
⇒ 252 = OC2 + 242
⇒ OC2 = 252 - 242
⇒ OC2 = 625 - 576 = 49
⇒ OC = = 7 cm.
Hence, chord is at a distance of 7 cm from the center.
A chord of length 8 cm is at a distance 3 cm from the centre of the circle. Calculate the radius of the circle.
Answer
From figure,

AB is the chord which is at a distance 3 cm from the center so OC = 3 cm.
Since, the perpendicular to a chord from the centre of the circle bisects the chord,
∴ CB = AC = = 4 cm.
In right angle triangle OAC,
⇒ OA2 = OC2 + AC2 (By pythagoras theorem)
⇒ OA2 = 32 + 42
⇒ OA2 = 9 + 16
⇒ OA2 = 25
⇒ OA = = 5 cm.
Hence, radius = 5 cm.
Calculate the length of a chord which is at a distance 6 cm from the center of a circle of diameter 20 cm.
Answer
Diameter = 20 cm,
∴ Radius = = 10 cm.
From figure,

AB is the chord which is at a distance 6 cm so,
OC = 6 cm and OA = radius = 10 cm.
In right angle triangle OAC,
⇒ OA2 = OC2 + AC2 (By pythagoras theorem)
⇒ 102 = 62 + AC2
⇒ AC2 = 102 - 62
⇒ AC2 = 100 - 36 = 64
⇒ AC = = 8 cm.
Since, the perpendicular to a chord from the centre of the circle bisects the chord,
∴ CB = AC = 8 cm.
AB = AC + CB = 8 + 8 = 16 cm.
Hence, length of chord = 16 cm.
A chord of length 16 cm is at a distance 6 cm from the center of the circle. Find the length of chord of the same circle which is at a distance of 8 cm from the center.
Answer
From figure,

AB is the chord which is at a distance 6 cm from the center so OC = 6 cm.
Since, the perpendicular to a chord from the centre of the circle bisects the chord,
∴ CB = AC = = 8 cm.
In right angle triangle OAC,
⇒ OA2 = OC2 + AC2 (By pythagoras theorem)
⇒ OA2 = 62 + 82
⇒ OA2 = 36 + 64
⇒ OA2 = 100
⇒ OA = = 10 cm.
Radius = 10 cm,
∴ OD = 10 cm.
From figure,
In right angle triangle ODF,
⇒ OD2 = OF2 + DF2 (By pythagoras theorem)
⇒ DF2 = OD2 - OF2
⇒ DF2 = 102 - 82
⇒ DF2 = 100 - 64 = 36
⇒ DF = = 6 cm.
Since, the perpendicular to a chord from the centre of the circle bisects the chord
∴ DE = DF + FE = 6 cm + 6 cm = 12 cm.
Hence, the length of chord which is at a distance of 8 cm from the center of the circle = 12 cm.
In a circle of radius 5 cm, AB and CD are two parallel chords of length 8 cm and 6 cm respectively. Calculate the distance between the chords, if they are on
(i) the same side of the centre
(ii) the opposite sides of the centre.
Answer
(i) From figure,

AB and CD are chords of length 8 cm and 6 cm, respectively.
Since, the perpendicular to a chord from the centre of the circle bisects the chord,
∴ AE = BE = = 4 cm and,
CF = FD = = 3 cm.
Radius = OA = OC = 5 cm.
In right angle triangle OAE,
⇒ OA2 = AE2 + OE2 (By pythagoras theorem)
⇒ OE2 = OA2 - AE2
⇒ OE2 = 52 - 42
⇒ OE2 = 25 - 16 = 9
⇒ OE = = 3 cm.
In right angle triangle OCF,
⇒ OC2 = CF2 + OF2 (By pythagoras theorem)
⇒ OF2 = OC2 - CF2
⇒ OF2 = 52 - 32
⇒ OF2 = 25 - 9 = 16
⇒ OF = = 4 cm.
Distance between two chords = EF = OF - OE = 4 - 3 = 1 cm.
Hence, distance between two chords = 1 cm.
(ii) From figure,

AB and CD are chords of length 8 cm and 6 cm respectively.
Since, the perpendicular to a chord from the centre of the circle bisects the chord,
∴ AE = BE = = 4 cm and,
CF = FD = = 3 cm.
Radius = OA = OC = 5 cm.
In right angle triangle OAE,
⇒ OA2 = AE2 + OE2 (By pythagoras theorem)
⇒ OE2 = OA2 - AE2
⇒ OE2 = 52 - 42
⇒ OE2 = 25 - 16 = 9
⇒ OE = = 3 cm.
In right angle triangle OCF,
⇒ OC2 = CF2 + OF2 (By pythagoras theorem)
⇒ OF2 = OC2 - CF2
⇒ OF2 = 52 - 32
⇒ OF2 = 25 - 9 = 16
⇒ OF = = 4 cm.
Distance between two chords = EF = OF + OE = 4 + 3 = 7 cm.
Hence, distance between two chords = 7 cm.
In figure (i) given below, O is the center of the circle. AB and CD are two chords of the circle. OM is perpendicular to AB and ON is perpendicular to CD. AB = 24 cm, OM = 5 cm, ON = 12 cm. Find the :
(i) radius of the circle
(ii) length of chord CD.

Answer
(i) Since, the perpendicular to a chord from the centre of the circle bisects the chord,
∴ AM = BM = = 12 cm.

In right angle triangle OAM,
⇒ OA2 = OM2 + AM2 (By pythagoras theorem)
⇒ OA2 = 52 + 122
⇒ OA2 = 25 + 144
⇒ OA2 = 169
⇒ OA = = 13 cm.
Hence, radius = 13 cm.
(ii) From figure,
OC = radius = 13 cm.
In right angle triangle OCN,
⇒ OC2 = ON2 + CN2 (By pythagoras theorem)
⇒ CN2 = OC2 - ON2
⇒ CN2 = 132 - 122
⇒ CN2 = 169 - 144 = 25
⇒ CN = = 5 cm.
Since, the perpendicular to a chord from the centre of the circle bisects the chord,
∴ ND = CN = 5 cm.
CD = CN + ND = 10 cm.
Hence, CD = 10 cm.
In the figure (ii) given below, CD is the diameter which meets the chord AB in E such that AE = BE = 4 cm. If CE = 3 cm, find the radius of the circle.
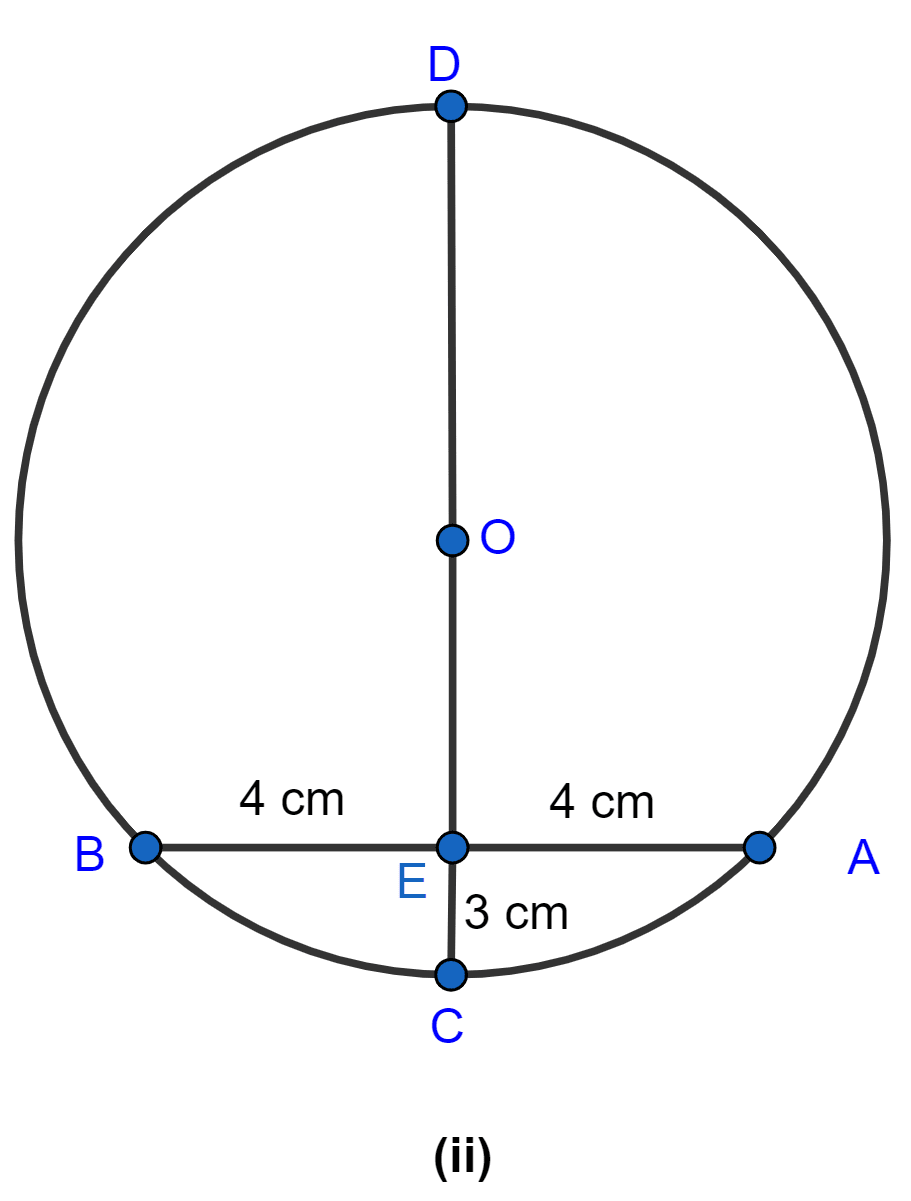
Answer
Given,
AB = 8 cm, EC = 3 cm
Let radius OB = OC = r
OE = (r - 3) cm.
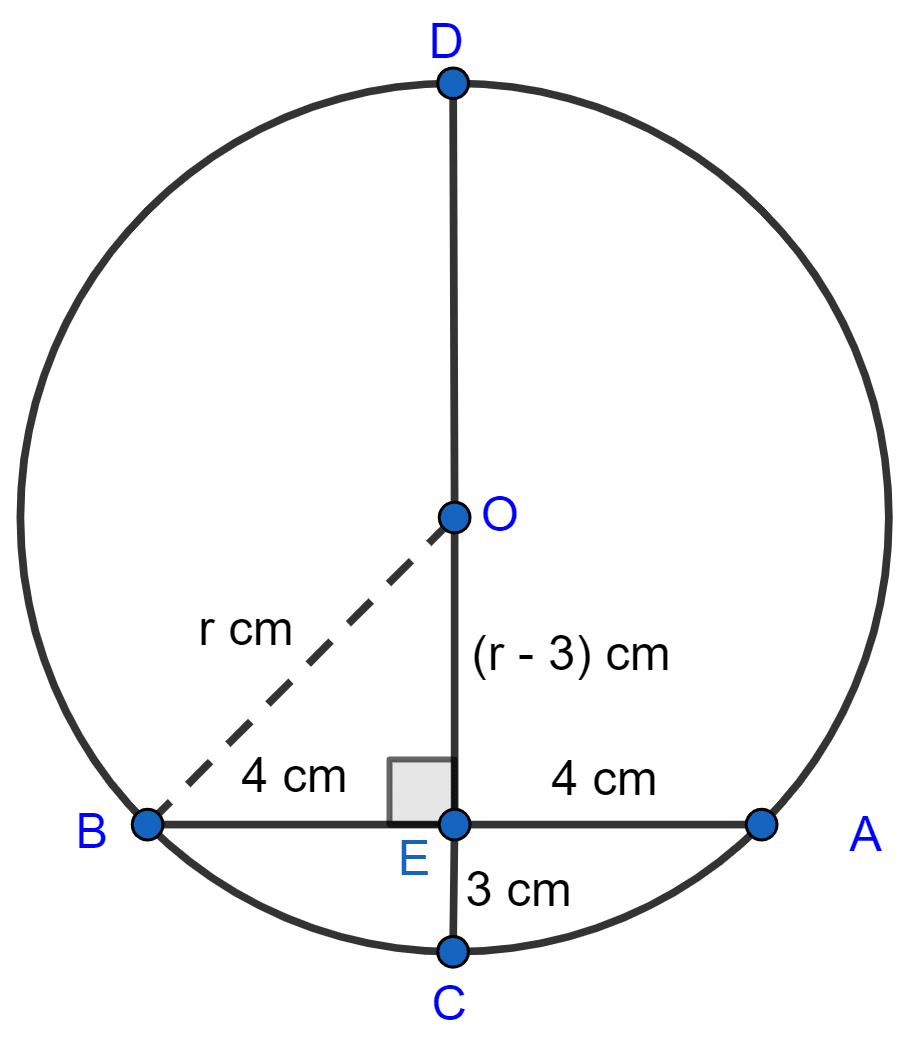
Since, chord AB is bisected by OE so OE ⊥ AB (As straight line drawn from the centre of circle to bisect a chord, is perpendicular to it.)
Now in right ∆OBE,
⇒ OB2 = BE2 + OE2
⇒ r2 = 42 + (r – 3)2
⇒ r2 = 16 + r2 – 6r + 9
⇒ r2 - r2 + 6r = 16 + 9
⇒ 6r = 25
⇒ r = cm.
Hence, radius = cm.
In the adjoining figure, AB and CD are two parallel chords and O is the centre. If the radius of the circle is 15 cm, find the distance MN between the two chords of length 24 cm and 18 cm respectively.
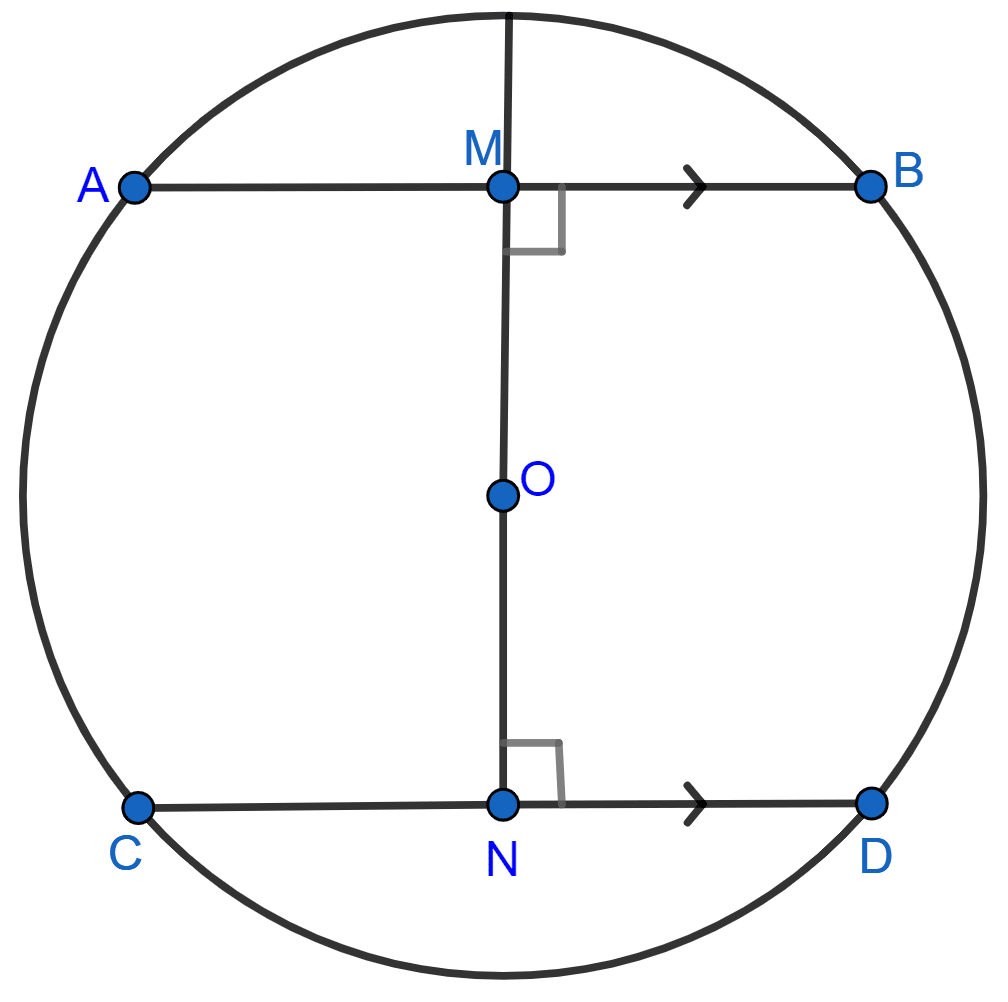
Answer
In the figure, chords AB ∥ CD and O is the centre of the circle.
Radius of the circle = 15 cm
Length of AB = 24 cm and CD = 18 cm.
Join OA and OC.
AB = 24 cm and OM ⊥ AB.
∴ AM = MB = = 12 cm (As perpendicular to a chord from the center of the circle bisects it)
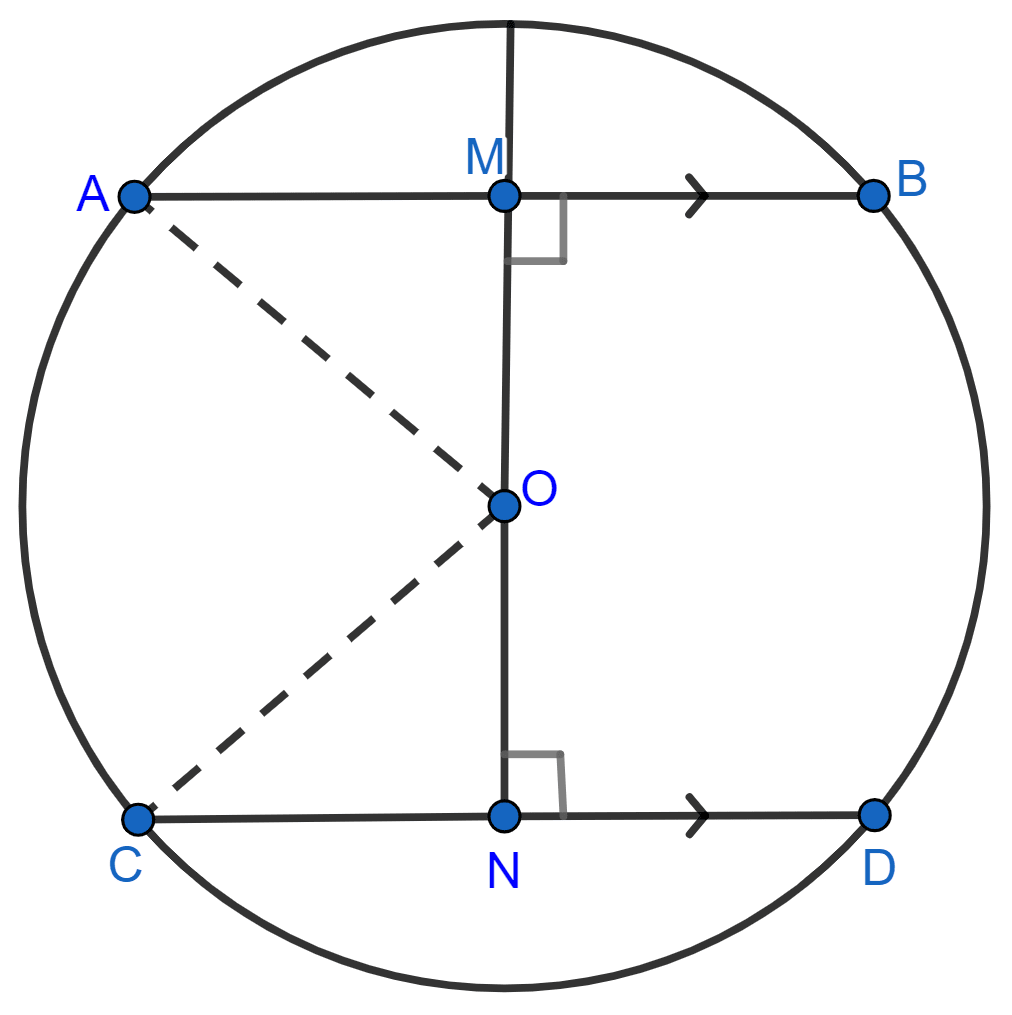
In right angle triangle OAM,
⇒ OA2 = OM2 + AM2 (By pythagoras theorem)
⇒ OM2 = OA2 - AM2
⇒ OM2 = 152 - 122
⇒ OM2 = 225 - 144
⇒ OM2 = 81
⇒ OM = = 9 cm.
Similarly ON ⊥ CD
CN = ND = = 9 cm
Similarly In right ∆CNO,
⇒ OC2 = ON2 + CN2 (By pythagoras theorem)
⇒ ON2 = OC2 - CN2
⇒ ON2 = 152 - 92
⇒ ON2 = 225 - 81
⇒ ON2 = 144
⇒ ON = = 12 cm.
MN = OM + ON = 9 + 12 = 21 cm.
Hence, MN = 21 cm.
AB and CD are two parallel chords of a circle of lengths 10 cm and 4 cm respectively. If the chords lie on the same side of the centre and the distance between them is 3 cm, find the diameter of the circle.
Answer
Let OE = x cm.
From figure,
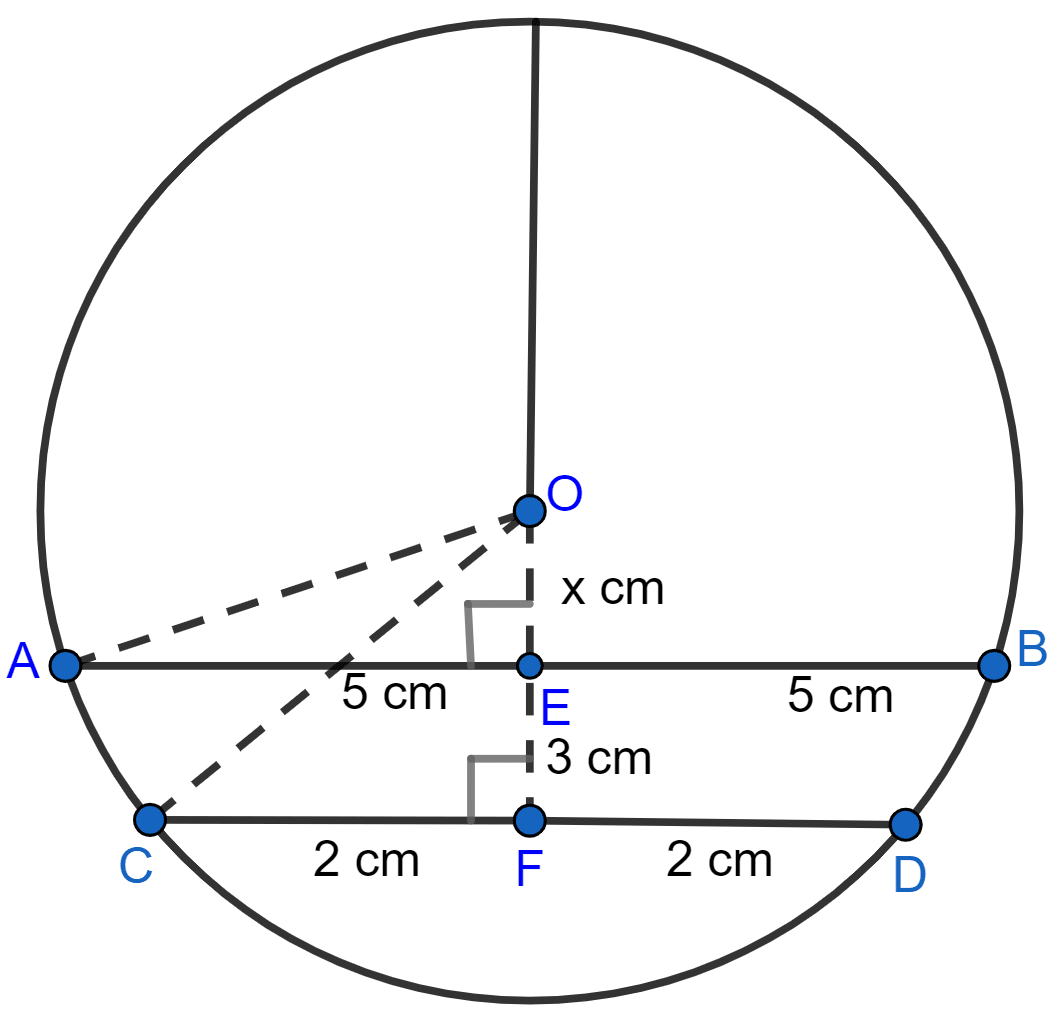
In right angle triangle OCF,
⇒ OC2 = OF2 + CF2 (By pythagoras theorem)
⇒ OC2 = (x + 3)2 + 22
⇒ OC2 = x2 + 9 + 6x + 4
⇒ OC2 = x2 + 6x + 13
Since, radius = OA = OC.
∴ OA2 = OC2 = x2 + 6x + 13.
In right angle triangle OAE,
⇒ OA2 = OE2 + AE2
⇒ x2 + 6x + 13 = x2 + 52
⇒ x2 - x2 + 6x = 25 - 13
⇒ 6x = 12
⇒ x = = 2 cm.
⇒ OC2 = x2 + 6x + 13
⇒ OC2 = 22 + 6(2) + 13
⇒ OC2 = 4 + 12 + 13
⇒ OC2 = 29
⇒ OC = cm.
Diameter = 2 × radius = 2 × cm.
Hence, diameter = cm.
ABC is an isosceles triangle inscribed in a circle. If AB = AC = cm and BC = 24 cm, find the radius of the circle.
Answer
From figure,
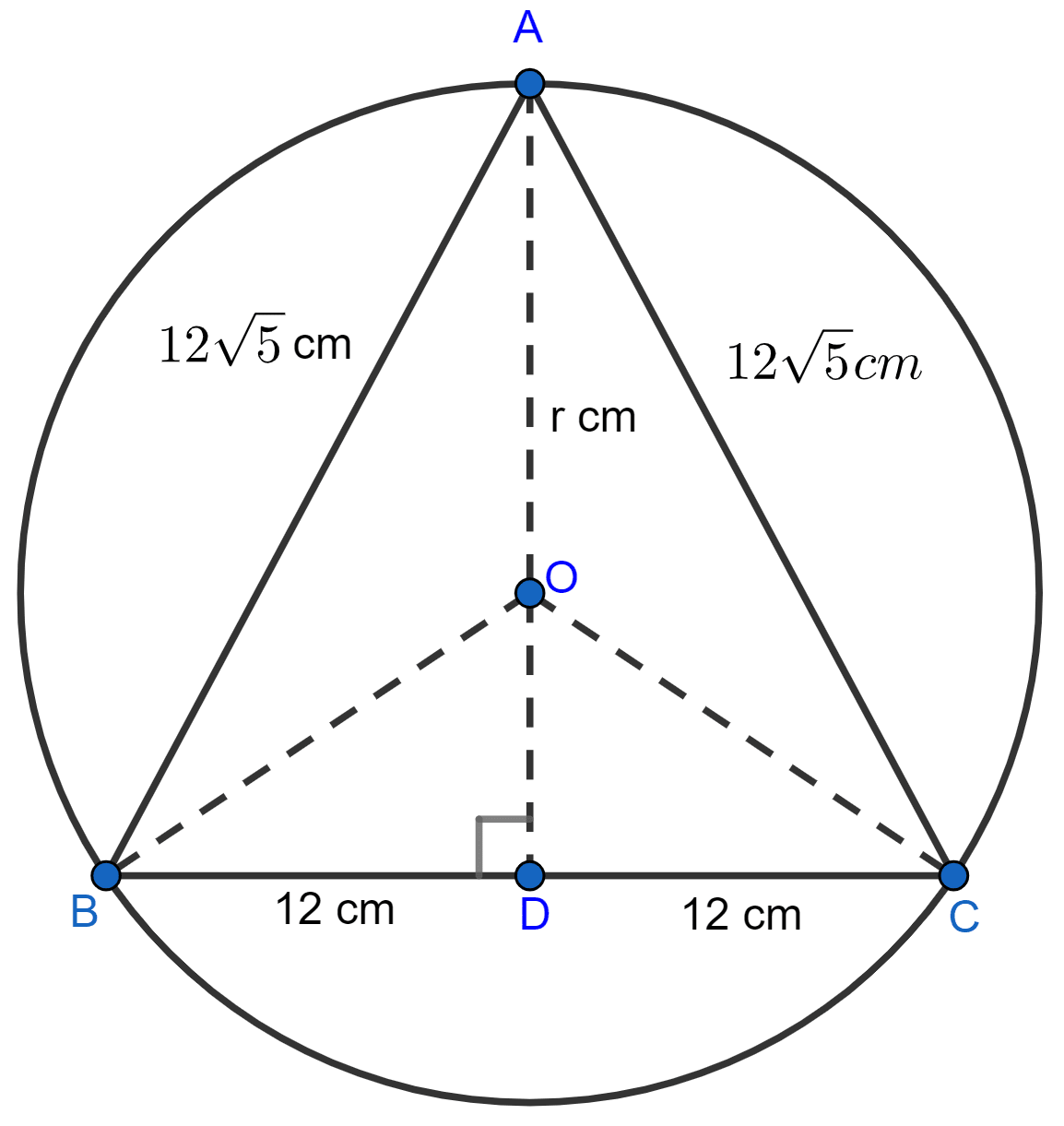
OA = radius = r cm.
BD = DC = = 12 cm (As perpendicular to a chord from the center of the circle bisects it)
In right angle triangle ABD,
OD = AD - OA = (24 - r) cm.
In right angle triangle OBD,
⇒ OB = radius = r cm.
⇒ OB2 = OD2 + BD2
⇒ r2 = (24 - r)2 + 122
⇒ r2 = 576 + r2 - 48r + 144
⇒ r2 - r2 + 48r = 720
⇒ 48r = 720
⇒ r = = 15 cm.
Hence, radius = 15 cm.
An equilateral triangle of side 6 cm is inscribed in a circle. Find the radius of the circle.
Answer
From figure,
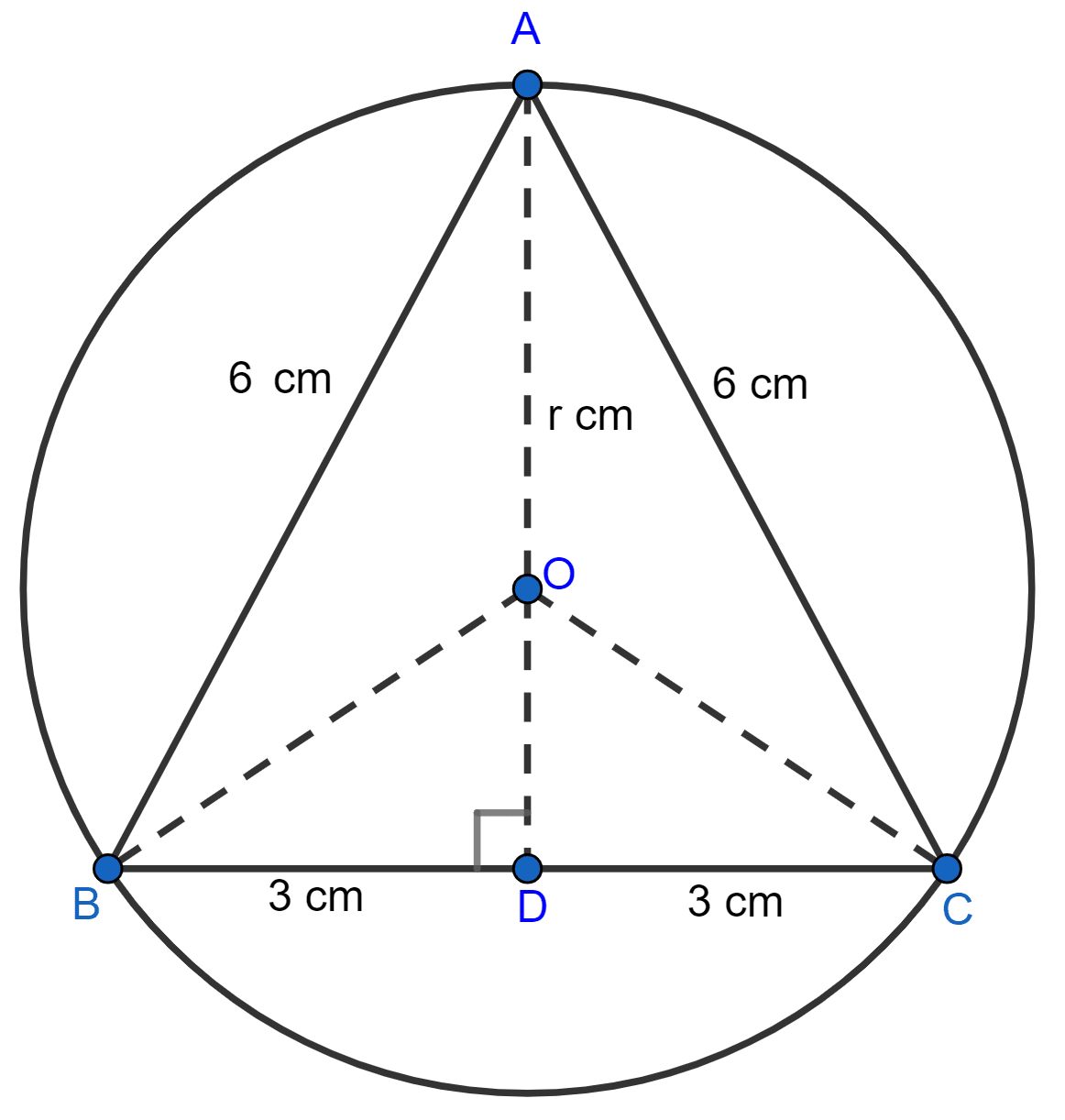
OA = radius = r cm.
BD = DC = = 3 cm (As perpendicular to a chord from the center of the circle bisects it)
In right angle triangle ABD,
⇒ AB2 = AD2 + BD2
⇒ 62 = AD2 + 32
⇒ AD2 = 36 - 9
⇒ AD2 = 27
⇒ AD = = cm.
OD = AD - AO = cm.
In right angle triangle OBD,
⇒ OB = radius = r cm.
⇒ OB2 = OD2 + BD2
⇒ r2 = 2 + 32
⇒ r2 = 27 + r2 - r + 9
⇒ r2 - r2 + r = 36
⇒ r = 36
⇒ r = cm.
Hence, radius = cm.
AB is a diameter of a circle. M is a point in AB such that AM = 18 cm and MB = 8 cm. Find the length of the shortest chord through M.
Answer
Given,
AM = 18 cm and MB = 8 cm
From figure,

AB = AM + MB = 18 + 8 = 26 cm
Radius of the circle = = 13 cm.
Let CD is the shortest chord drawn through M.
∴ CD ⊥ AB
From figure,
OM = AM - AO = 18 - 13 = 5 cm
OC (radius) = OA = 13 cm
Now in right ∆OMC,
OC2 = OM2 + MC2 (By pythagoras theorem)
132 = 52 + MC2
MC2 = 132 - 52
MC2 = 169 - 25 = 144
MC = = 12 cm.
M is Mid-Point of CD (As perpendicular from center to the chord bisects it.)
CD = 2 × MC = 2 × 12 = 24 cm.
Hence, length of shortest chord = 24 cm.
A rectangle with one side of length 4 cm is inscribed in a circle of diameter 5 cm. Find the area of rectangle.
Answer
Let side BC = 4 cm.
Since, the perpendicular to a chord from the centre of the circle bisects the chord,
∴ BM = MC = 2 cm.

Given,
Diameter = 5 cm, radius = = 2.5 cm.
In right ∆OBM,
⇒ OB2 = BM2 + OM2
⇒ (2.5)2 = 22 + OM2
⇒ 6.25 = 4 + OM2
⇒ OM2 = 2.25
⇒ OM = = 1.5 cm.
Similarly in right ∆OAN,
⇒ OA2 = AN2 + ON2
⇒ (2.5)2 = 22 + ON2
⇒ 6.25 = 4 + ON2
⇒ ON2 = 2.25
⇒ ON = = 1.5 cm.
From figure,
⇒ MN = OM + ON = 1.5 + 1.5 = 3 cm.
⇒ AB = DC = MN = 3 cm.
⇒ Area = length × breadth = 4 cm × 3 cm = 12 cm2.
Hence area of rectangle = 12 cm2.
The length of the common chord of two intersecting circles is 30 cm. If the radii of the two circles are 25 cm and 17 cm, find the distance between their centres.
Answer
Since, the perpendicular to a chord from the centre of the circle bisects the chord,
∴ AC = CB = = 15 cm.
From figure,
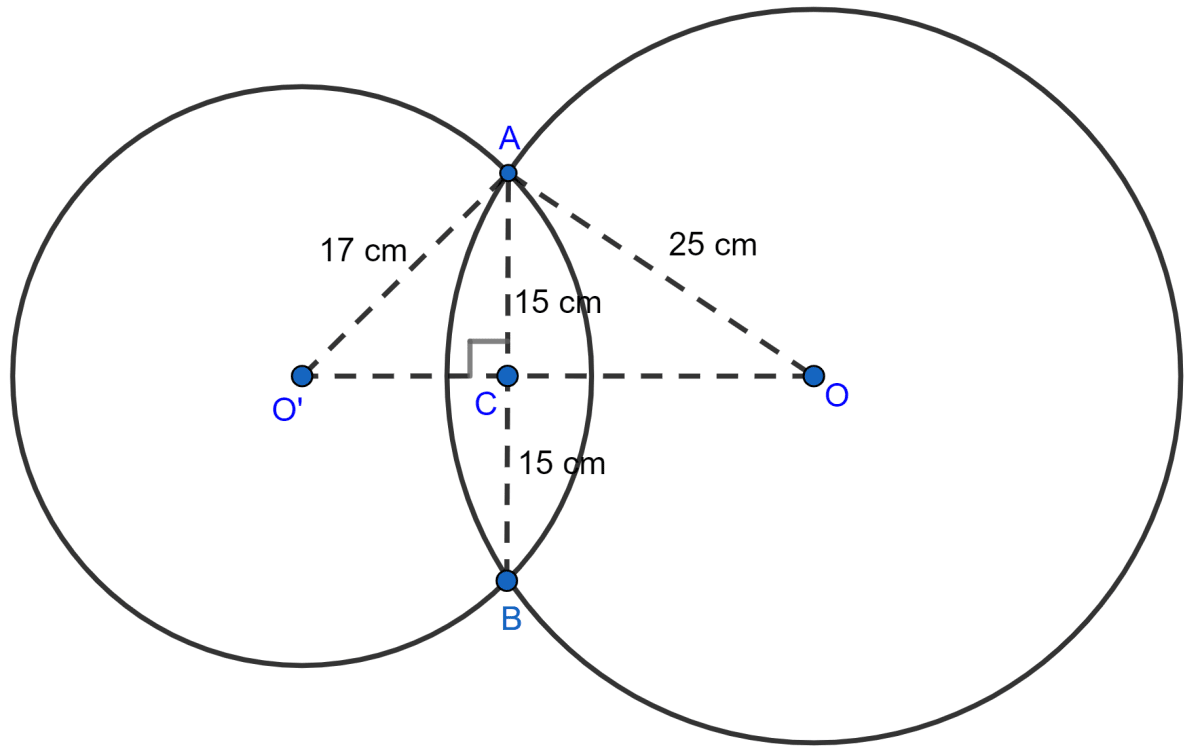
In right triangle OAC,
⇒ OA2 = OC2 + AC2 (By pythagoras theorem)
⇒ 252 = OC2 + 152
⇒ 625 = OC2 + 225
⇒ OC2 = 400
⇒ OC = = 20 cm.
In right triangle O'AC,
⇒ O'A2 = O'C2 + AC2 (By pythagoras theorem)
⇒ 172 = O'C2 + 152
⇒ 289 = O'C2 + 225
⇒ O'C2 = 64
⇒ O'C = = 8 cm.
Distance between centers = OO' = OC + O'C = 20 + 8 = 28 cm.
Hence, distance between their centres = 28 cm.
The line joining mid-points of two chords of a circle passes through its center. Prove that the chords are parallel.
Answer
In the figure, AB and CD are the two chords of a circle with center O. M and N are mid-points of AB and CD, respectively and MN is the line joining the mid-points of two chords and passing through center O.
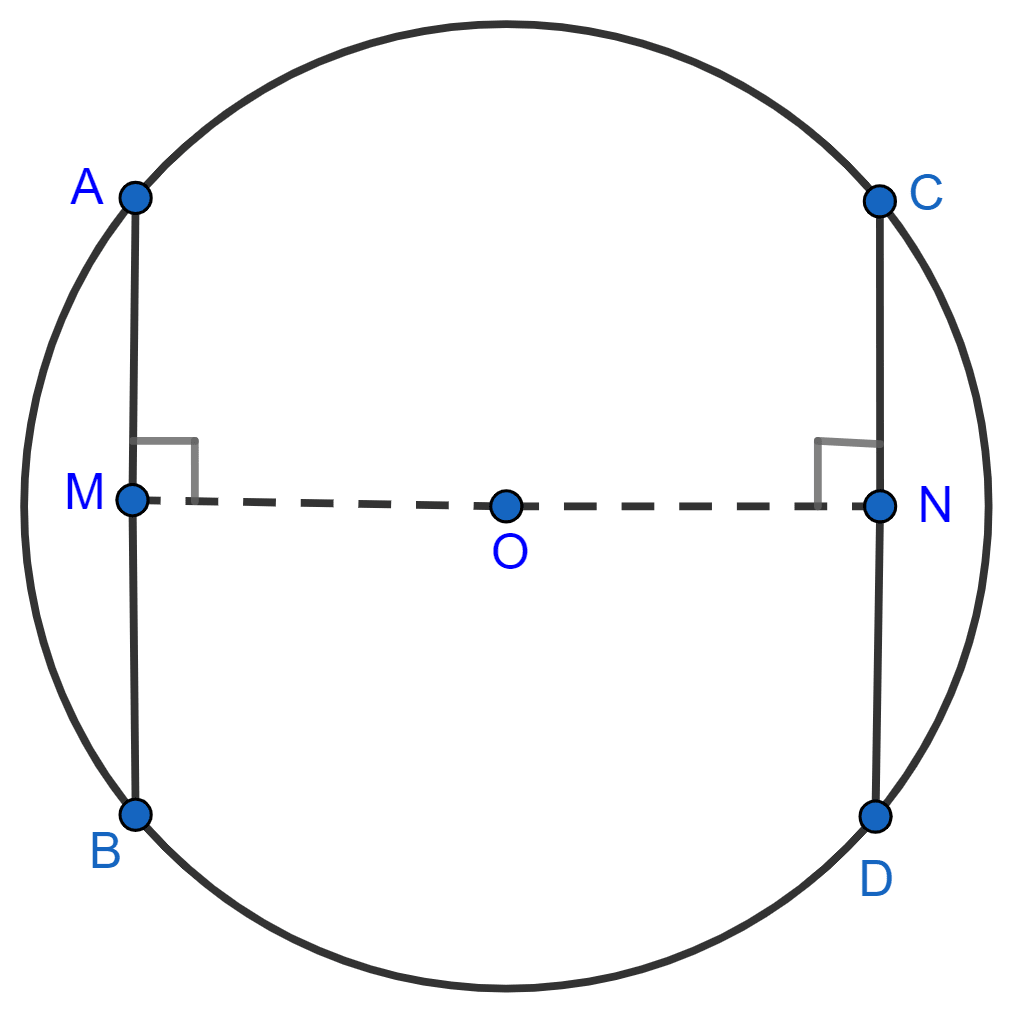
Since, the straight line drawn from the centre of a circle to bisect a chord is perpendicular to the chord,
∴ OM ⊥ AB and ON ⊥ CD.
So,
∠OMA = ∠OMB = 90° and ∠ONC = ∠OND = 90°
Since, ∠OMA = ∠OND = 90° (Alternate angles) and,
∠OMB = ∠ONC = 90° (Alternate angles)
Hence, proved that AB || CD.
If a diameter of a circle is perpendicular to one of two parallel chords of the circle, prove that it is perpendicular to the other and bisects it.
Answer
Since, AB || CD and ∠OMA = ∠OMB = 90°
From figure,

∠OMA = ∠OND = 90° (Alternate angles are equal)
∠OMB = ∠ONC = 90° (Alternate angles are equal)
∴ ON ⊥ CD or MN ⊥ CD
We know that,
The perpendicular to a chord from the center of the circle bisects the chord.
∴ NC = ND.
Hence, proved that diameter is perpendicular to other chord and bisects it.
In an equilateral triangle, prove that the centroid and the circumcentre of the triangle coincide.
Answer
From figure,
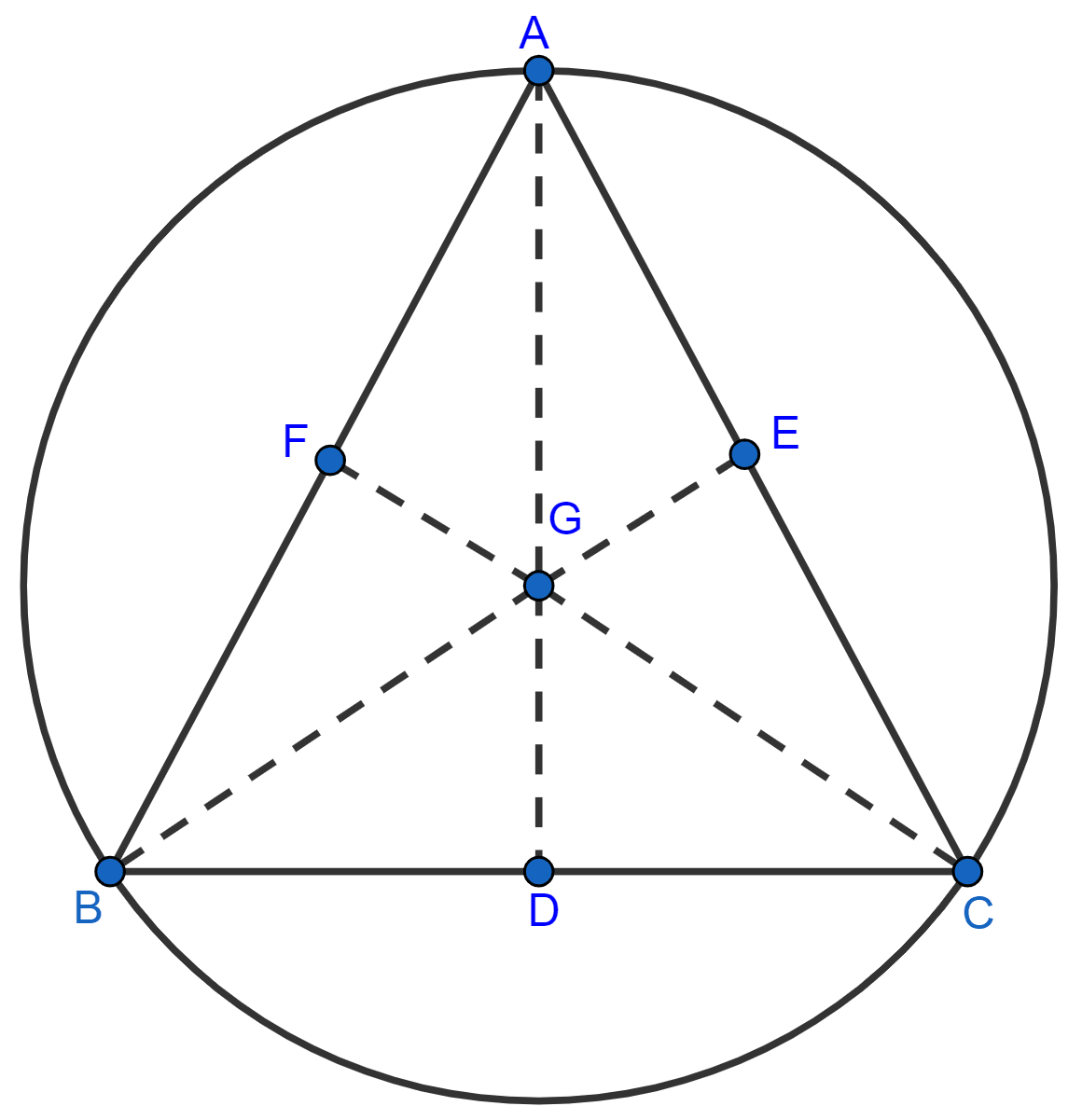
AD, BE and CF are medians of the triangle.
Let G be the centroid of triangle ABC.
Triangle ABC is an equilateral triangle,
∴ AB = BC = CA and ∠ABC = ∠BAC = ∠BCA = 60°
In △BFC and △BEC,
⇒ BC = BC (Common Side)
⇒ ∠FBC = ∠ECB = 60°.
⇒ BF = EC (As F is mid-point of AB and E is mid-point of AC and AB = AC.)
△BFC ≅ △BEC (By SAS axiom.)
∴ BE = CF (By C.P.C.T.) .........(1)
Now, in △ABE and △ABD
AB = AB (Common Side)
∠BAE = ∠ABD = 60°
BD = AE (As D is mid-point of BC and E is mid-point of AC and BC = AC.)
△ABE ≅ △ABD (By SAS axiom.)
∴ BE = AD (By C.P.C.T.) ............. (2)
From equation 1 and 2, we get:
⇒ AD = BE = CF
⇒
We know that G (the centroid) of the triangle divides the median in a 2 : 1 ratio.
∴ GA = GB = GC.
So, we can say that G is equidistant from the three vertices A. B and C.
G is circumcentre of ΔABC.
Hence, proved that the centroid and circumcentre are coincident.
In the figure (i) given below, OD is perpendicular to the chord AB of a circle whose center is O. If BC is a diameter, show that CA = 2OD.
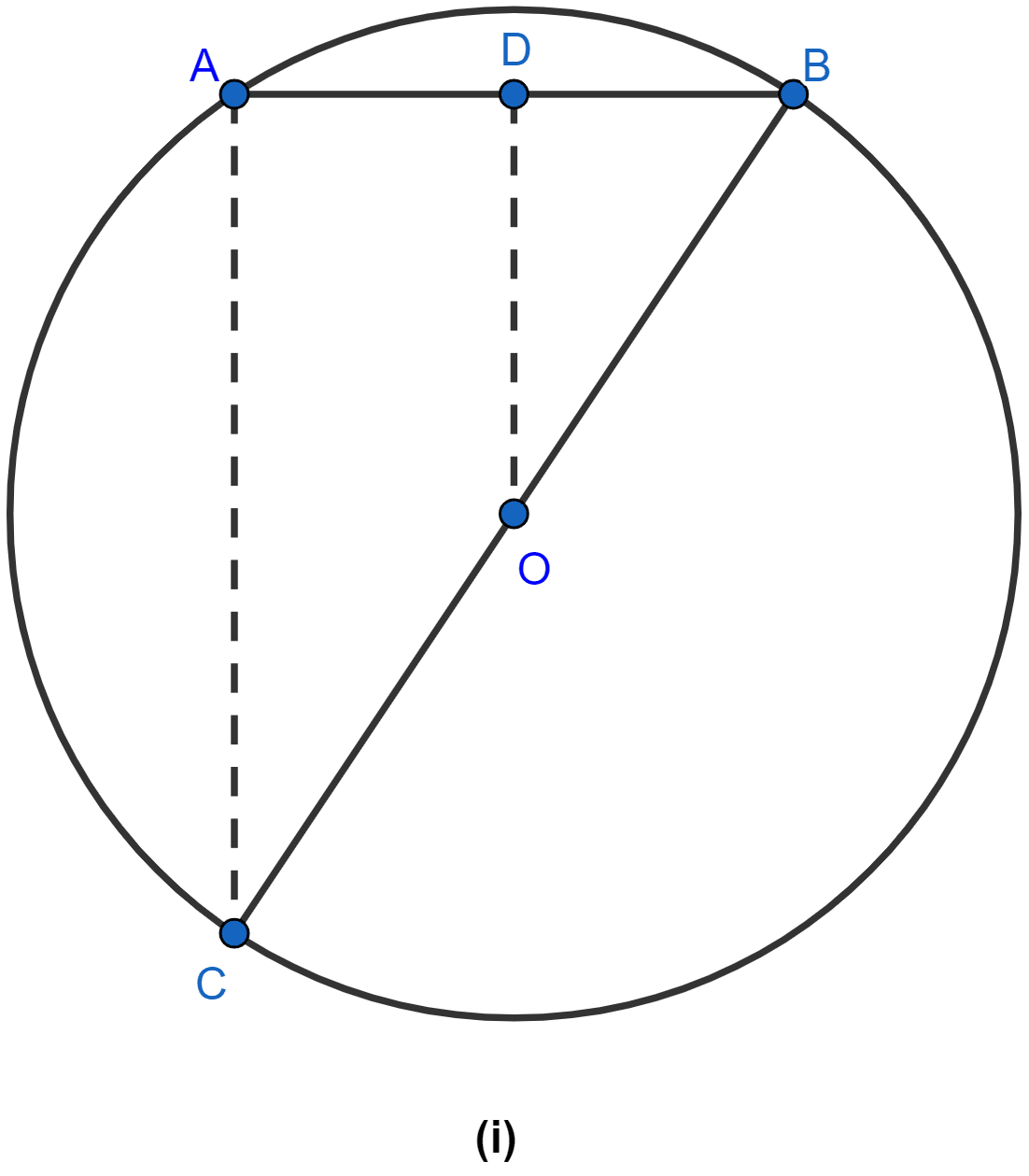
Answer
Since, the perpendicular to a chord from the centre of the circle bisects the chord,
∴ AD = DB
We can say that D is mid-point of AB.
Since, BC is diameter and O is center so, OB = OC = radius.
We can say that O is mid-point of BC.
In △ABC,
Since, D is mid-point of AB and O is mid-point of BC
By mid-point theorem,
⇒ OD || AC and OD =
⇒ AC = 2OD.
Hence, proved that CA = 2OD.
In the figure (ii) given below, O is the center of a circle. If AB and AC are chords of the circle such that AB = AC and OP ⊥ AB, OQ ⊥ AC, prove that PB = QC.
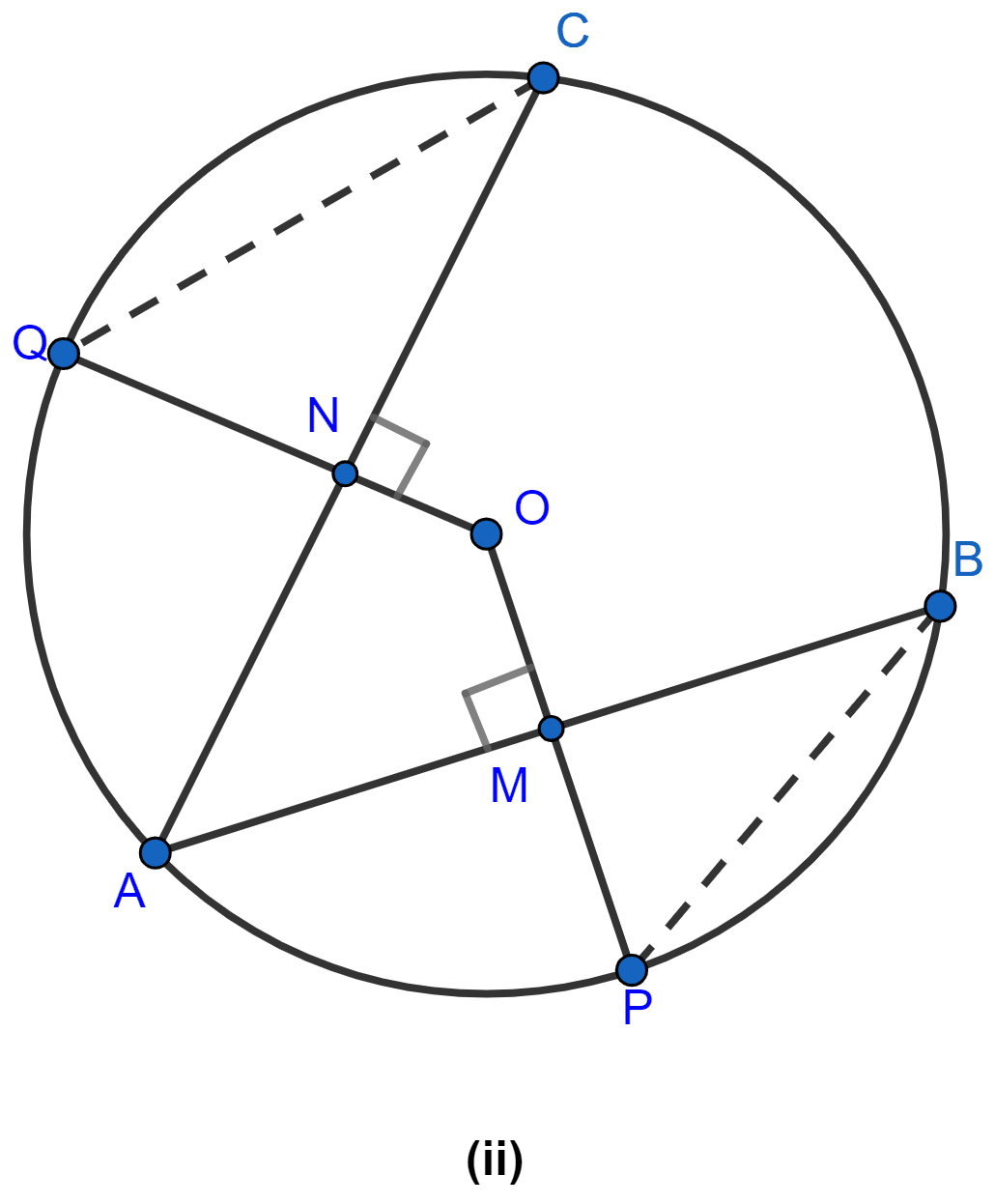
Answer
Let AB = AC = x
Given,
OM ⊥ AB and ON ⊥ AC
Since, the perpendicular to a chord from the centre of the circle bisects the chord,
∴ AM = MB =
and
AN = NC =
∴ MB = NC ..........(1)
Since, equal chords of a circle are equidistant from the centre,
∴ ON = OM = y (let).
Let radius of circle be r.
From figure,
OQ = OP = r
QN = OQ - ON = r - y
PM = OP - OM = r - y
∴ QN = PM ..........(2)
In △QNC and △PMB,
NC = MB [From (1)]
QN = PM [From (2)]
∠QNC = ∠PMB (Both equal to 90°)
△QNC ≅ △PMB by SAS axiom.
∴ PB = QC (By C.P.C.T.)
Hence, proved that PB = QC.
In the figure (i) given below, a line l intersects two concentric circles at the points A, B, C and D. Prove that AB = CD.
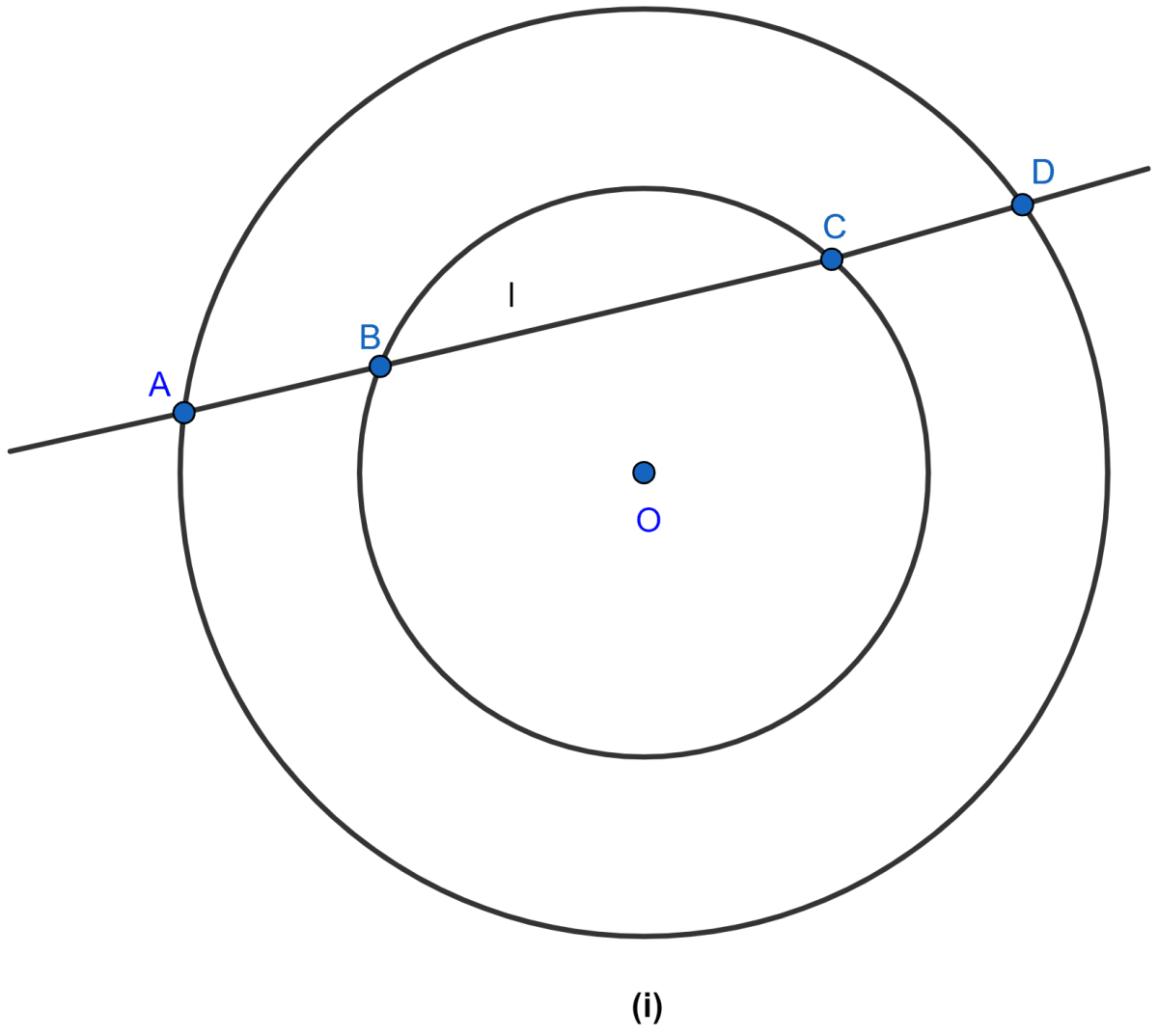
Answer
Draw OM perpendicular to BC.
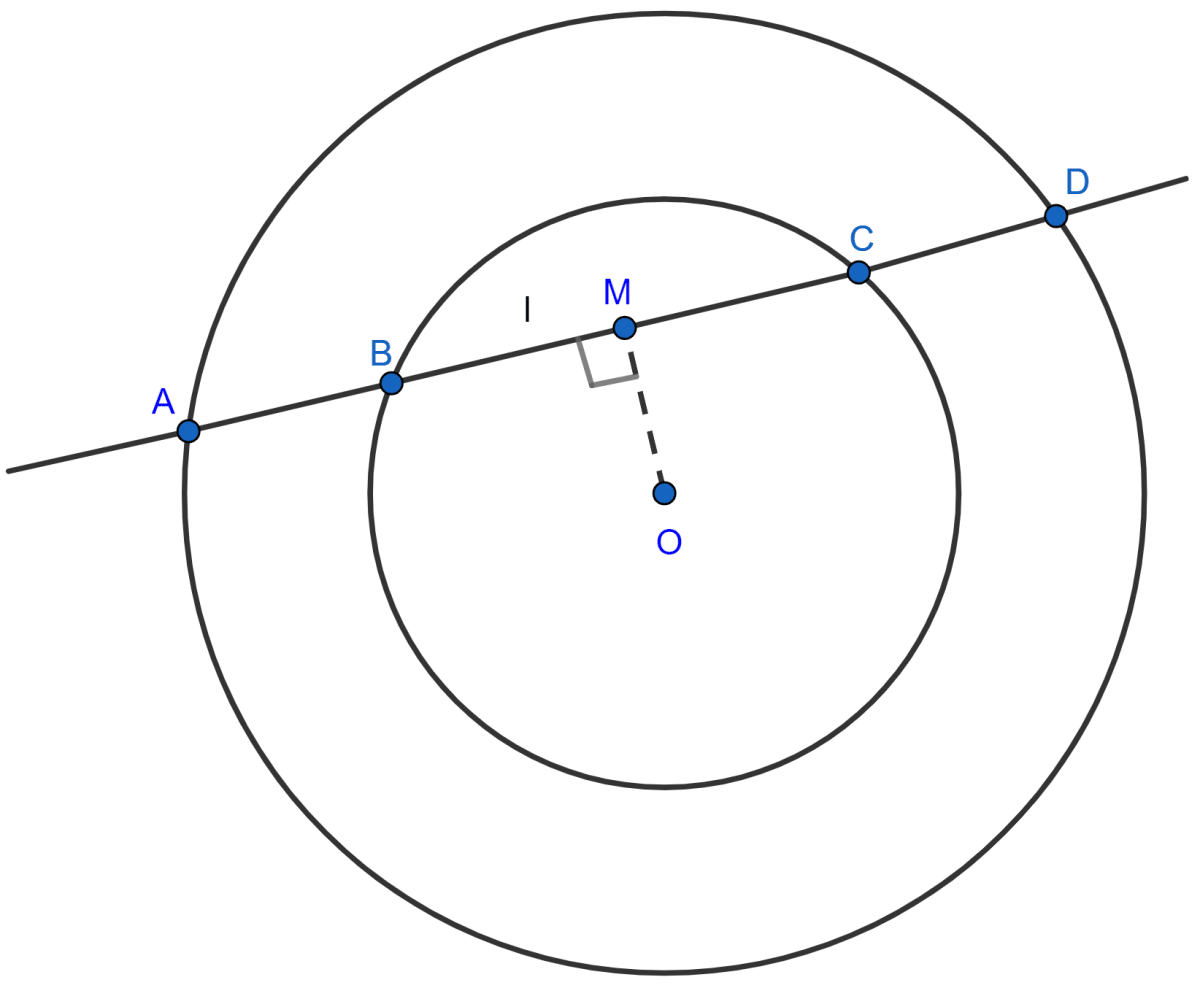
Since, the perpendicular to a chord from the centre of the circle bisects the chord,
So, in the smaller circle, M is mid-point of BC so,
BM = MC = x (let)
Similarly, in larger circle M is mid-point of AD so,
AM = MD = y (let)
From figure,
AB = AM - BM = (y - x)
CD = MD - MC = (y - x)
∴ AB = CD.
Hence, proved that AB = CD.
In the figure (ii) given below, chords AB and CD of a circle with centre O intersect at E. If OE bisects ∠AED, prove that AB = CD.

Answer
Draw perpendiculars from O to AB and CD.

In △OME and △ONE,
∠OME = ∠ONE = 90°
∠OEM = ∠OEN (As OE bisects ∠AED)
OE = OE (Common side)
∴ △OME ≅ △ONE (By A.A.S. axiom)
∴ OM = ON (By C.P.C.T.C.)
Hence, chords AB and CD are equidistant from the center of circle.
In the same circle, chords equidistant from the centre are equal.
∴ AB = CD.
Hence, proved that AB = CD.
In the figure (i) given below, AD is a diameter of a circle with center O. If AB || CD, prove that AB = CD.

Answer
Draw OM ⊥ AB and ON ⊥ CD,

In △OAM and △ODN,
OA = OD (Radius of circle)
∠AOM = ∠DON (Vertically opposite angles are equal)
∠OMA = ∠OND (Both equal to 90°)
∴ △OAM ≅ △ODN (By A.S.A. axiom).
∴ ND = AM (By C.P.C.T.) ........(1)
Since, the perpendicular to a chord from the centre of the circle bisects the chord,
so, equation 1 can be written as,
⇒
⇒ AB = CD.
Hence, proved that AB = CD.
In the figure (ii) given below, AB and CD are equal chords of a circle with center O. If AB and CD meet at E (outside the circle) prove that
(i) AE = CE
(ii) BE = DE.
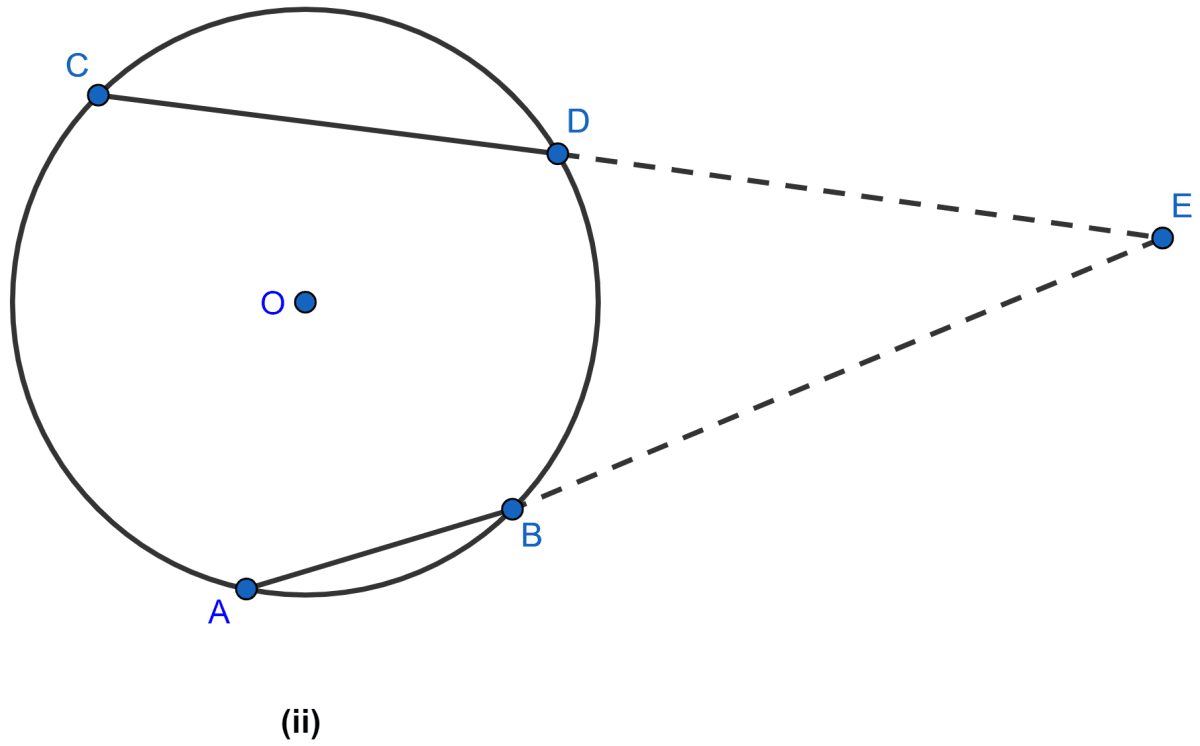
Answer
Draw ON ⊥ CD and OM ⊥ AB. Join OE.
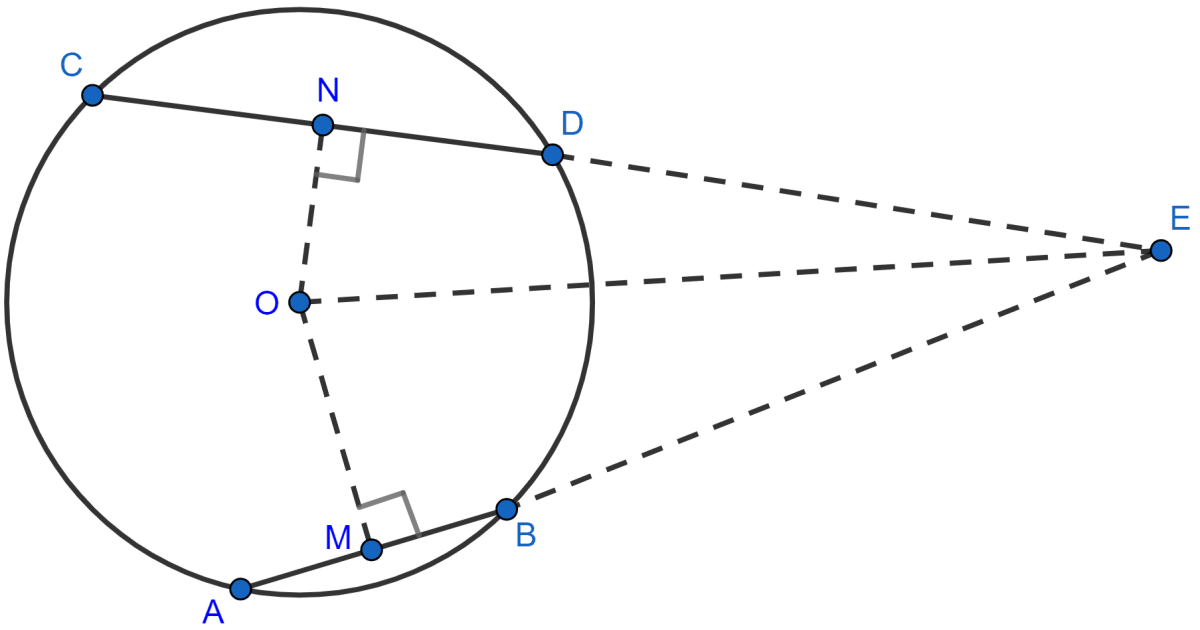
(i) Since, equal chords are equidistant from the center of the circle,
∴ ON = OM.
In △ONE and △OME,
ON = OM
∠ONE = ∠OME (Both equal to 90°)
OE = OE (Common side)
∴ △ONE ≅ △OME (By R.H.S. congruence rule).
∴ NE = ME = y (let) (By C.P.C.T.) ........(1)
Let AB = CD = x.
Since, the perpendicular to a chord from the centre of the circle bisects the chord,
∴ CN = ND = and
AM = MB = .
From figure,
AE = AM + ME =
CE = CN + NE =
Hence, proved that AE = CE.
(ii) From figure,
BE = ME - MB =
DE = NE - ND =
Hence, proved that BE = DE.
If arcs APB and CQD of a circle are congruent, then find the ratio of AB : CD.
Answer
arc APB = arc CQD (Given)
If two arcs are equal then chords are also equal.
∴ AB = CD = x (let).
Ratio =
Hence, AB : CD = 1 : 1.
A and B are points on a circle with center O. C is a point on the circle such that OC bisects ∠AOB, prove that OC bisects the arc AB.
Answer
The figure of the circle is shown below:

Given,
OC bisects ∠AOB.
∴ ∠AOC = ∠BOC
Since, equal arcs subtend equal angles at center.
∴ AC = BC
∴ C is mid-point of AB.
Hence, proved that OC bisects the arc AB.
Prove that the angle subtended at the center of a circle is bisected by the radius passing through the mid-point of arc.
Answer
The figure of the circle is shown below:

Let C be the mid-point of arc AB.
∴ AC = BC.
Since, equal arcs subtend equal angles at center.
∴ ∠AOC = ∠BOC.
Hence, proved that ∠AOC = ∠BOC.
In the adjoining figure, two chords AB and CD of a circle intersect at P. If AB = CD, prove that arc AD = arc CB.

Answer
Given AB = CD
Since, in a circle, equal chords cut off equal arcs.
∴ arc AB = arc CD
Subtracting arc BD from both sides we get,
⇒ arc AB - arc BD = arc CD - arc BD
⇒ arc AD = arc CB.
Hence, proved that arc AD = arc CB.
If P and Q are any two points on a circle, then the line segment PQ is called a
radius of the circle
diameter of the circle
chord of the circle
secant of the circle.
Answer
If P and Q are any two points on a circle, then the line segment PQ is called a chord.
Hence, Option 3 is the correct option.
If P is a point in the interior of a circle with center O and radius r, then
OP = r
OP > r
OP ≥ r
OP < r
Answer
If P is a point on circle and O is center then OP = r but since, P is in the interior of the circle, so it will be smaller than the radius.
OP < r
Hence, Option 4 is the correct option.
The circumference of a circle must be
a positive real number
a whole number
a natural number
an integer
Answer
Circumference of circle = 2πr
Since, π = and radius is always a positive no.
∴ Circumference of a circle must be a positive real number.
Hence, Option 1 is the correct option.
AD is a diameter of a circle and AB is a chord. If AD = 34 cm and AB = 30 cm, then the distance of AB from the center of circle is
17 cm
15 cm
4 cm
8 cm
Answer
Let OM be the distance of AB from the center of the circle.
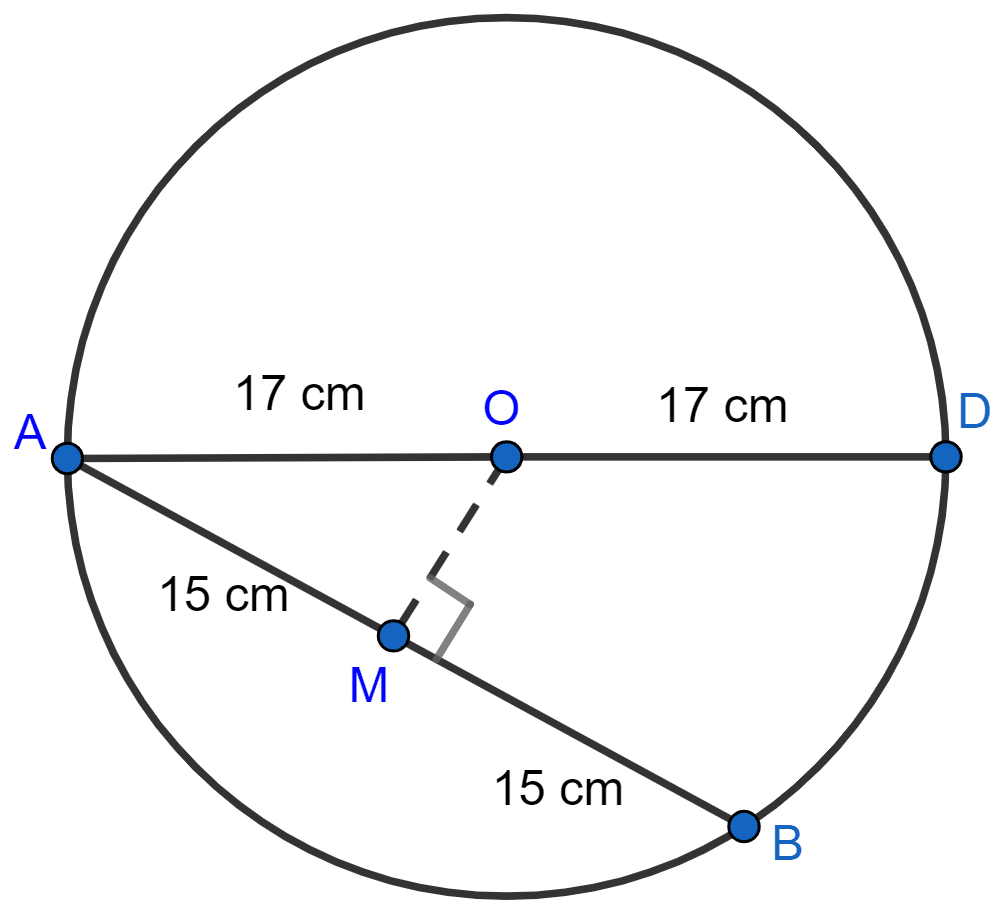
Since diameter = 34 cm, so radius = = 17 cm.
Since, the perpendicular to a chord from the centre of the circle bisects the chord,
∴ AM = MB = 15 cm.
In right triangle OAM,
⇒ OA2 = AM2 + OM2 (By pythagoras theorem)
⇒ OM2 = OA2 - AM2
⇒ OM2 = 172 - 152
⇒ OM2 = 289 - 225
⇒ OM2 = 64
⇒ OM = = 8 cm.
Hence, Option 4 is the correct option.
If AB = 12 cm, BC = 16 cm and AB is perpendicular to BC, then the radius of the circle passing through the points A, B and C is
6 cm
8 cm
10 cm
12 cm
Answer
Let r be the radius of the circle.
From figure,

AC = AO + OC = r + r = 2r.
In right △ABC,
⇒ AC2 = AB2 + BC2
⇒ (2r)2 = 122 + 162
⇒ 4r2 = 144 + 256
⇒ 4r2 = 400
⇒ r2 = = 100
⇒ r = = 10 cm.
Hence, Option 3 is the correct option.
In the adjoining figure, O is the center of the circle. If OA = 5 cm, AB = 8 cm and OD ⊥ AB, then length of CD is equal to
2 cm
3 cm
4 cm
5 cm

Answer
Since, the perpendicular to a chord from the centre of the circle bisects the chord,
∴ AC = CB = = 4 cm.
In right △OAC,
⇒ OA2 = OC2 + AC2
⇒ 52 = OC2 + 42
⇒ OC2 = 52 - 42
⇒ OC2 = 25 - 16
⇒ OC2 = 9
⇒ OC = = 3 cm.
From figure,
CD = OD - OC = 5 - 3 = 2 cm.
Hence, Option 1 is the correct option.
Consider the following two statements.
Statement 1: A line which meets a circle in two points is called a secant of the circle.
Statement 2: All radii of a circle are equal.
Which of the following is valid?
Both the statements are true.
Both the statements are false.
Statement 1 is true, and Statement 2 is false.
Statement 1 is false, and Statement 2 is true.
Answer
A secant is defined as a line that intersects a circle at exactly two distinct points.
∴ Statement 1 is true.
A radius is a line segment connecting the center of a circle to any point on its circumference.
By definition, all points on the circumference are equidistant from the center, meaning all radii have the same length.
∴ Statement 2 is true.
∴ Both the statements are true.
Hence, option 1 is correct option.
Assertion (A): Equal chords of a circle are equidistant from centre.
Reason (R): Chords of a circle that are equidistant from the centre of a circle are equal.
Assertion (A) is true, Reason (R) is false.
Assertion (A) is false, Reason (R) is true.
Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).
Answer
We know that,
Chords of equal length are equidistant from centre.
∴ Assertion (A) is true.
Also,
The chords which are equidistant from the centre of a circle are equal in length.
∴ Reason (R) is true.
Assertion is just the converse of reason.
∴ Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).
Hence, option 3 is the correct option.
Assertion (A): In a circle, equal arcs suspend equal angles at the centre.
Reason (R): In the same circle, equal chords cuts off equal arc.
Assertion (A) is true, Reason (R) is false.
Assertion (A) is false, Reason (R) is true.
Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).
Answer
We know that,
Arcs of equal lengths subtends equal angles at the center of the circle.
∴ Assertion (A) is true.
We know that,
The chords of equal length cut off equal arcs.
∴ Reason (R) is true.
∴ Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).
Hence, option 4 is the correct option.
Assertion (A): In adjoining figure, AB is diameter of the circle with centre O.
If chord AC = chord AD, then we can conclude that ars BC = arc DB.
Reason (R): In adjoining figure, we can conclude that if chord AC = chord AD, then arc AC = arc AD.
Assertion (A) is true, Reason (R) is false.
Assertion (A) is false, Reason (R) is true.
Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).
Answer
Given,
AB is the diameter of the circle with center O and, Chord AC = Chord AD.
We know that in a circle, equal chords subtend equal arcs.
⇒ arc AC = arc AD = x (let) ........................(1)
∴ Reason (R) is true.
AB is a diameter of the circle.
As we know that the diameter of a circle divides the circle into two equal arcs.
⇒ arc ACB = arc ADB.
⇒ arc AC + arc BC = arc AD + arc DB.
From equation (1), we get :
⇒ x + arc BC = x + arc DB.
⇒ arc BC = arc DB.
∴ Assertion (A) is true.
∴ Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).
Hence, option 3 is the correct option.
In the adjoining figure, a chord PQ of a circle with center O and radius 15 cm is bisected at M by a diameter AB. If OM = 9 cm, find the lengths of :
(i) PQ
(ii) AP
(iii) BP.
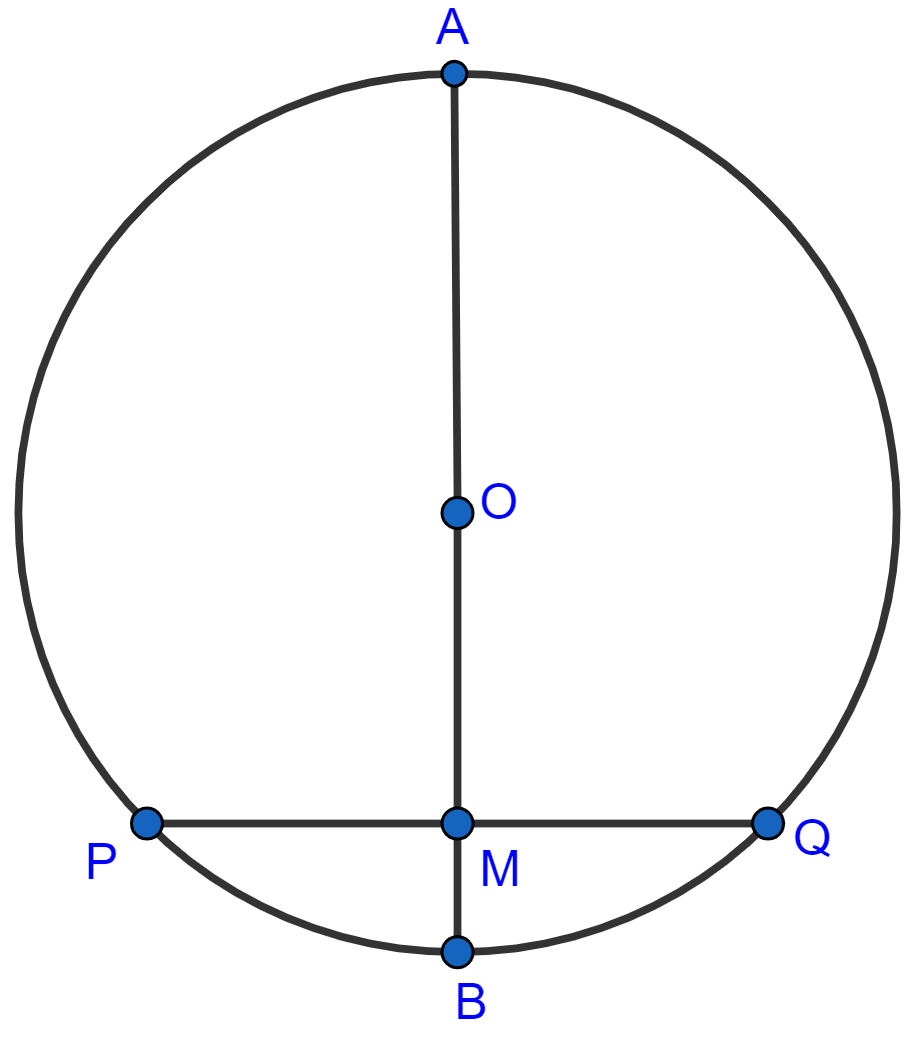
Answer
(i) Given,
AB bisects PQ.
∴ OM bisects PQ.
Since, the straight line drawn from the centre of a circle to bisect a chord, which is not a diameter, is perpendicular to the chord,
∴ OM ⊥ PQ.
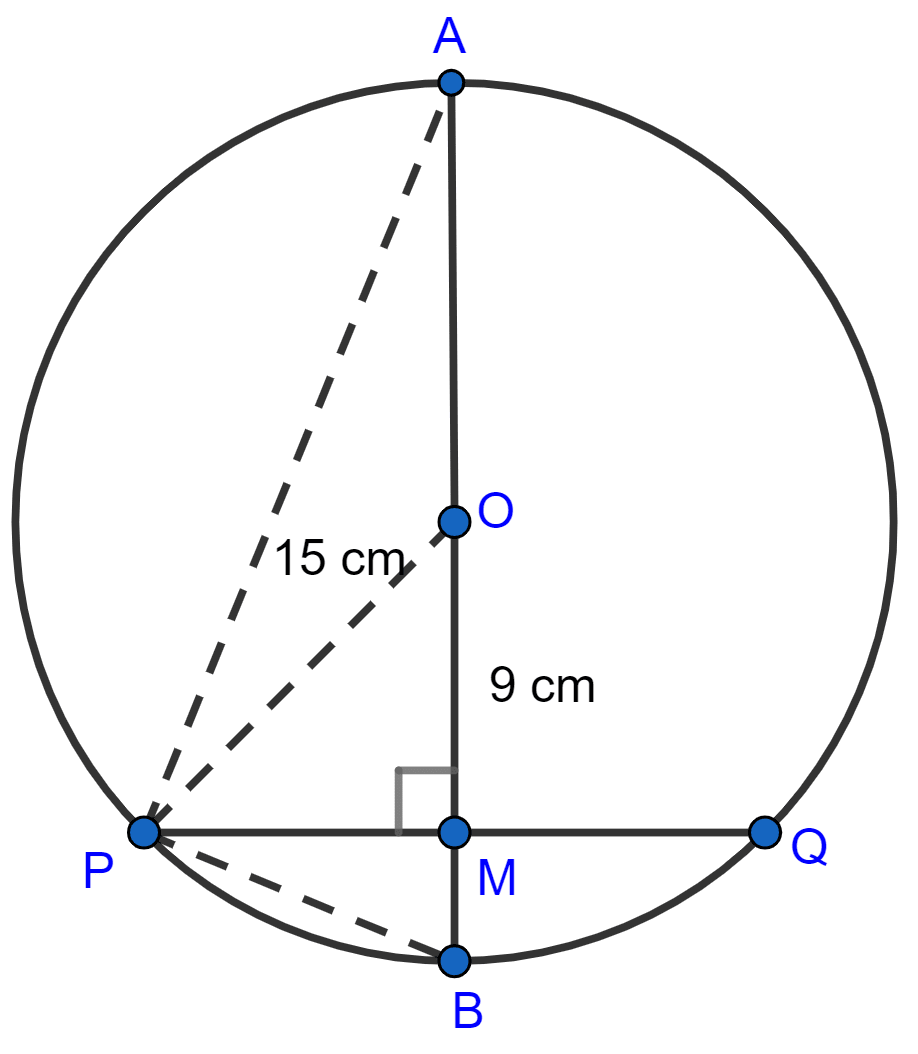
In right △OMP,
⇒ OP2 = OM2 + PM2 (By pythagoras theorem)
⇒ 152 = 92 + PM2
⇒ PM2 = 152 - 92
⇒ PM2 = 225 - 81
⇒ PM2 = 144
⇒ PM = = 12 cm.
PQ = 2PM = 24 cm.
Hence, PQ = 24 cm.
(ii) From figure,
AM = AO + OM = 15 + 9 = 24 cm.
In right △APM,
⇒ AP2 = AM2 + PM2 (By pythagoras theorem)
⇒ AP2 = 242 + 122
⇒ AP2 = 576 + 144
⇒ AP2 = 720
⇒ AP = = cm.
Hence, AP = cm.
(iii) From figure,
MB = OB - OM = 15 - 9 = 6 cm.
In right △MPB,
⇒ BP2 = PM2 + MB2 (By pythagoras theorem)
⇒ BP2 = 122 + 62
⇒ BP2 = 144 + 36
⇒ BP2 = 180
⇒ BP = = cm.
Hence, BP = cm.
The radii of two concentric circles are 17 cm and 10 cm; a line PQRS cuts the larger circle at P and S and the smaller circle at Q and R. If QR = 12 cm, calculate PQ.
Answer
Draw OM ⊥ QR.

In right △OQM,
⇒ OQ2 = OM2 + QM2
⇒ 102 = OM2 + 62
⇒ OM2 = 100 - 36
⇒ OM2 = 64
⇒ OM = = 8 cm.
In right △POM,
⇒ PO2 = OM2 + PM2
⇒ 172 = 82 + PM2
⇒ PM2 = 289 - 64
⇒ PM2 = 225
⇒ PM = = 15 cm.
From figure,
PQ = PM - QM = 15 - 6 = 9 cm.
Hence, PQ = 9 cm.
A chord of length 48 cm is at a distance of 10 cm from the centre of a circle. If another chord of length 20 cm is drawn in the same circle, find its distance from the center of the circle.
Answer
From figure,
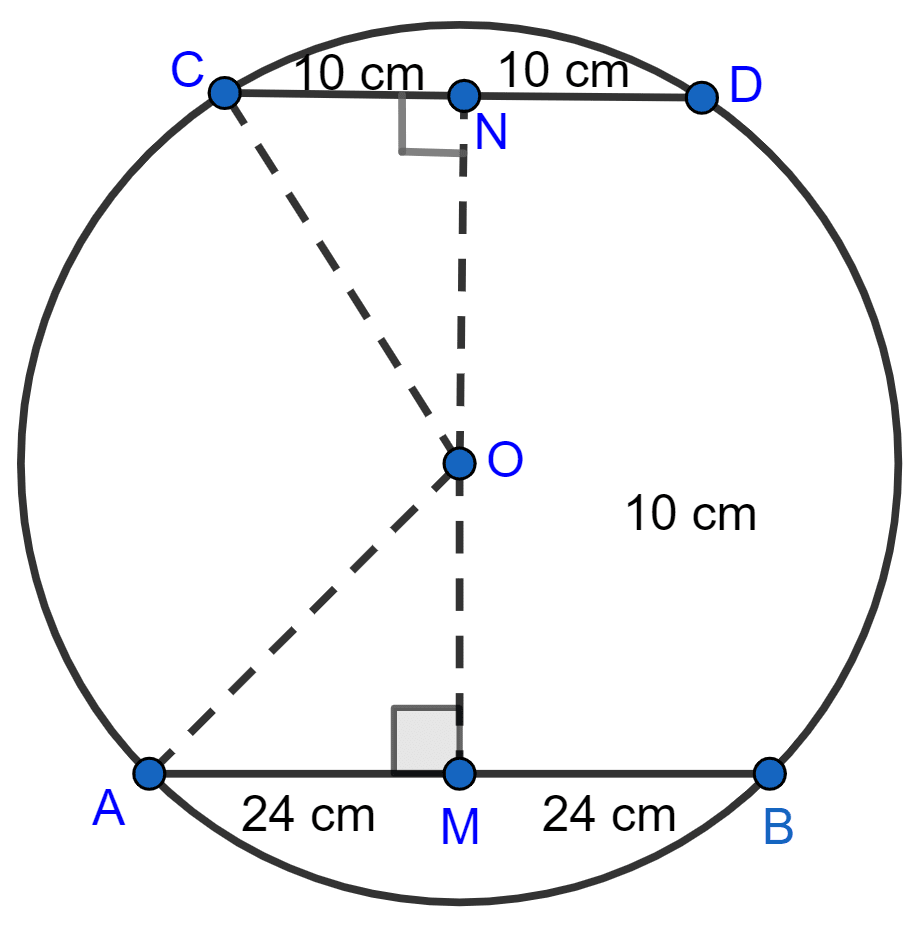
Since, OM ⊥ AB, it bisects it. (As perpendicular from center to chord bisects it)
∴ AM = MB = = 24 cm.
In right △AOM,
⇒ AO2 = OM2 + AM2 (By pythagoras theorem)
⇒ AO2 = 102 + 242
⇒ AO2 = 100 + 576
⇒ AO2 = 676
⇒ AO = = 26 cm.
Radius = 26 cm.
Since, ON ⊥ CD, it bisects it. (As perpendicular from center to chord bisects it)
∴ CN = ND = = 10 cm.
In right △CNO,
⇒ OC2 = ON2 + NC2 (By pythagoras theorem)
⇒ 262 = ON2 + 102
⇒ ON2 = 676 - 100
⇒ ON2 = 576
⇒ ON = = 24 cm.
Hence, the chord of length 20 cm is at a distance of 24 cm from the centre.
In the figure (i) given below, two circles with centers C, D intersect in points P, Q. If length of common chord is 6 cm and CP = 5 cm, DP = 4 cm, calculate the distance CD correct to two decimal places.
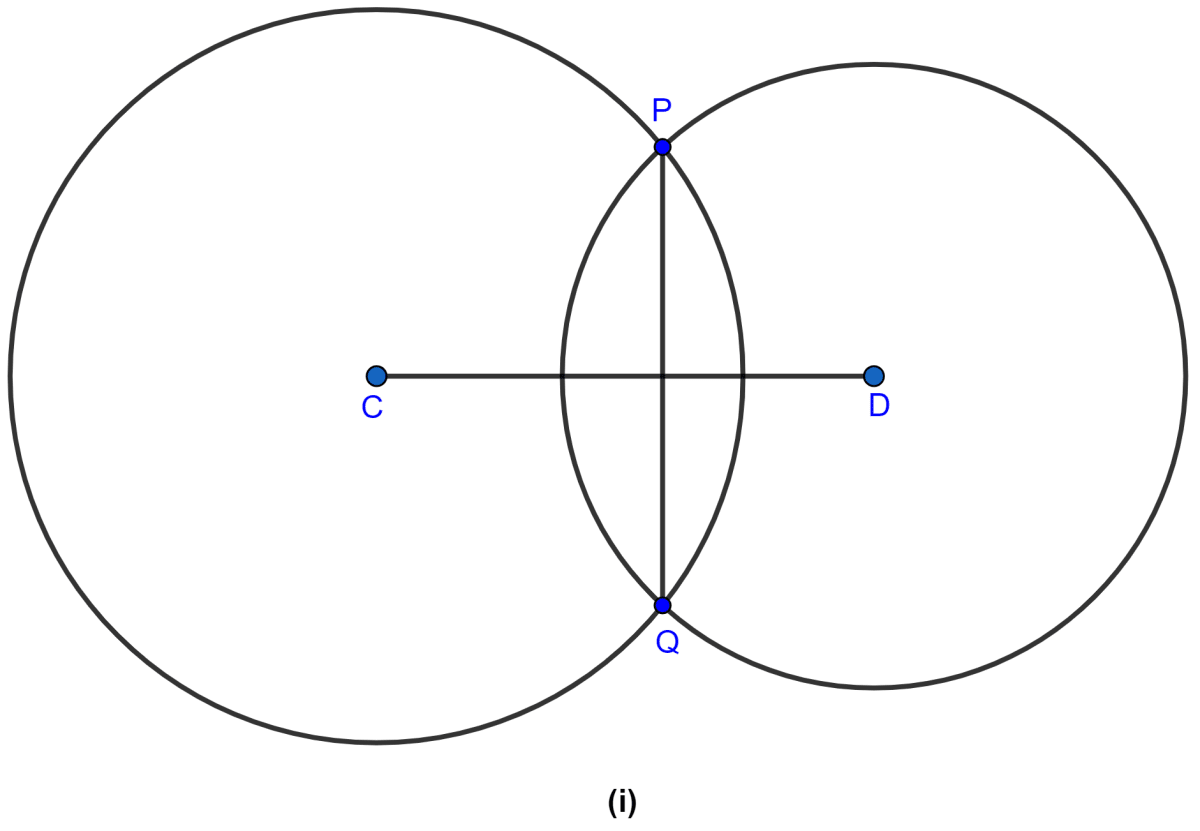
Answer
From figure,
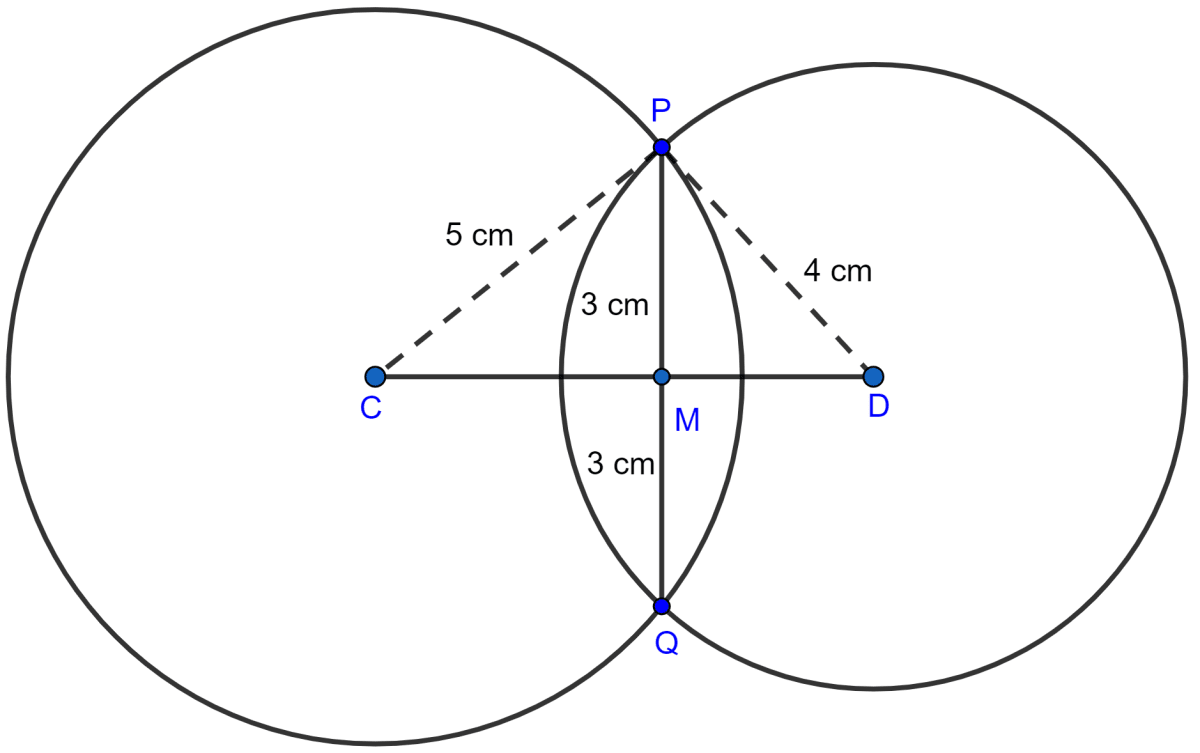
PM = MQ = = 3 cm.
In right △CMP,
⇒ CP2 = CM2 + PM2 (By pythagoras theorem)
⇒ 52 = CM2 + 32
⇒ CM2 = 25 - 9
⇒ CM2 = 16
⇒ CM = = 4 cm.
In right △DMP,
⇒ DP2 = DM2 + PM2 (By pythagoras theorem)
⇒ 42 = DM2 + 32
⇒ DM2 = 16 - 9
⇒ DM2 = 7
⇒ DM = = 2.65 cm.
CD = CM + MD = 4 + 2.65 = 6.65 cm.
Hence, CD = 6.65 cm.
In the figure (ii) given below, P is a point of intersection of two circles with centers C and D. If the st. line APB is parallel to CD, prove that AB = 2CD.
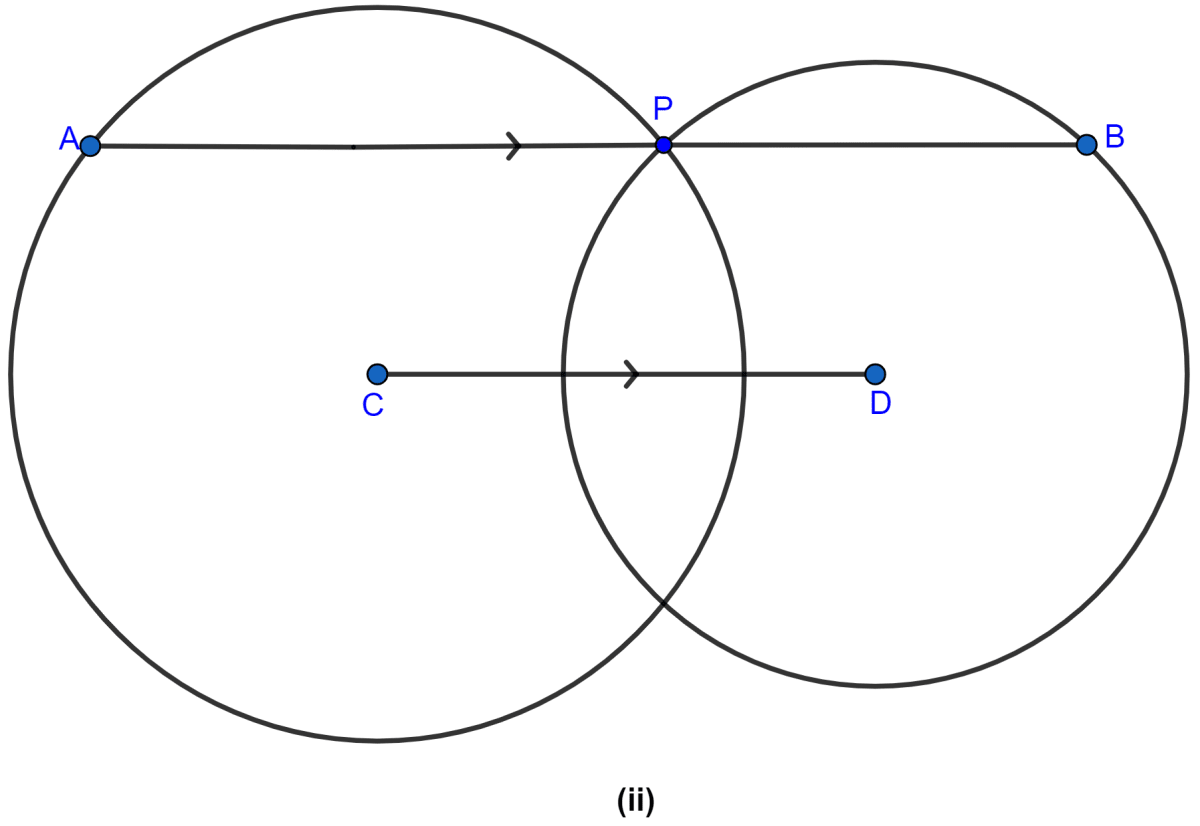
Answer
From C, D draw CM, DN perpendiculars to AB.
From figure,
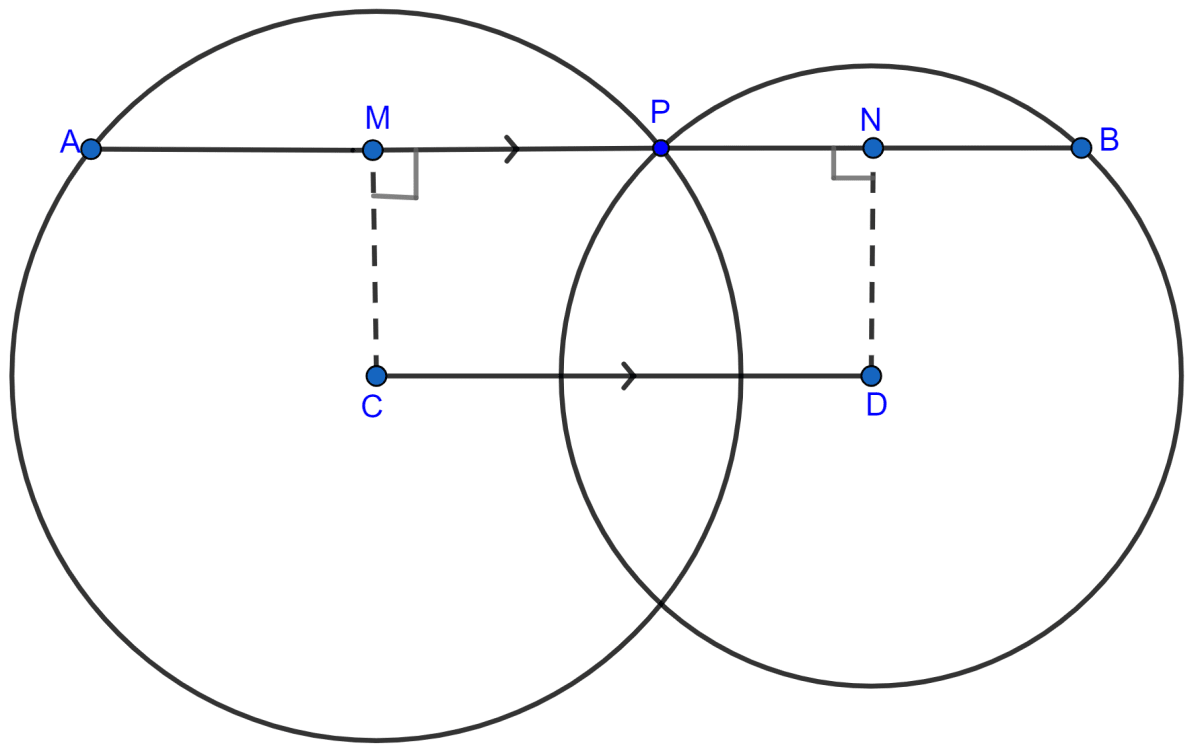
MCDN is a rectangle.
∴ MN = CD (Opposite sides of rectangle are equal).
Since, the perpendicular to a chord from the centre of the circle bisects the chord,
∴ MP = AP and NP = PB
From figure,
MN = MP + PN
= AP + PB
= (AP + PB)
= AB
∴ CD = AB [∵ MN = CD]
⇒ AB = 2CD
Hence, proved that AB = 2CD.
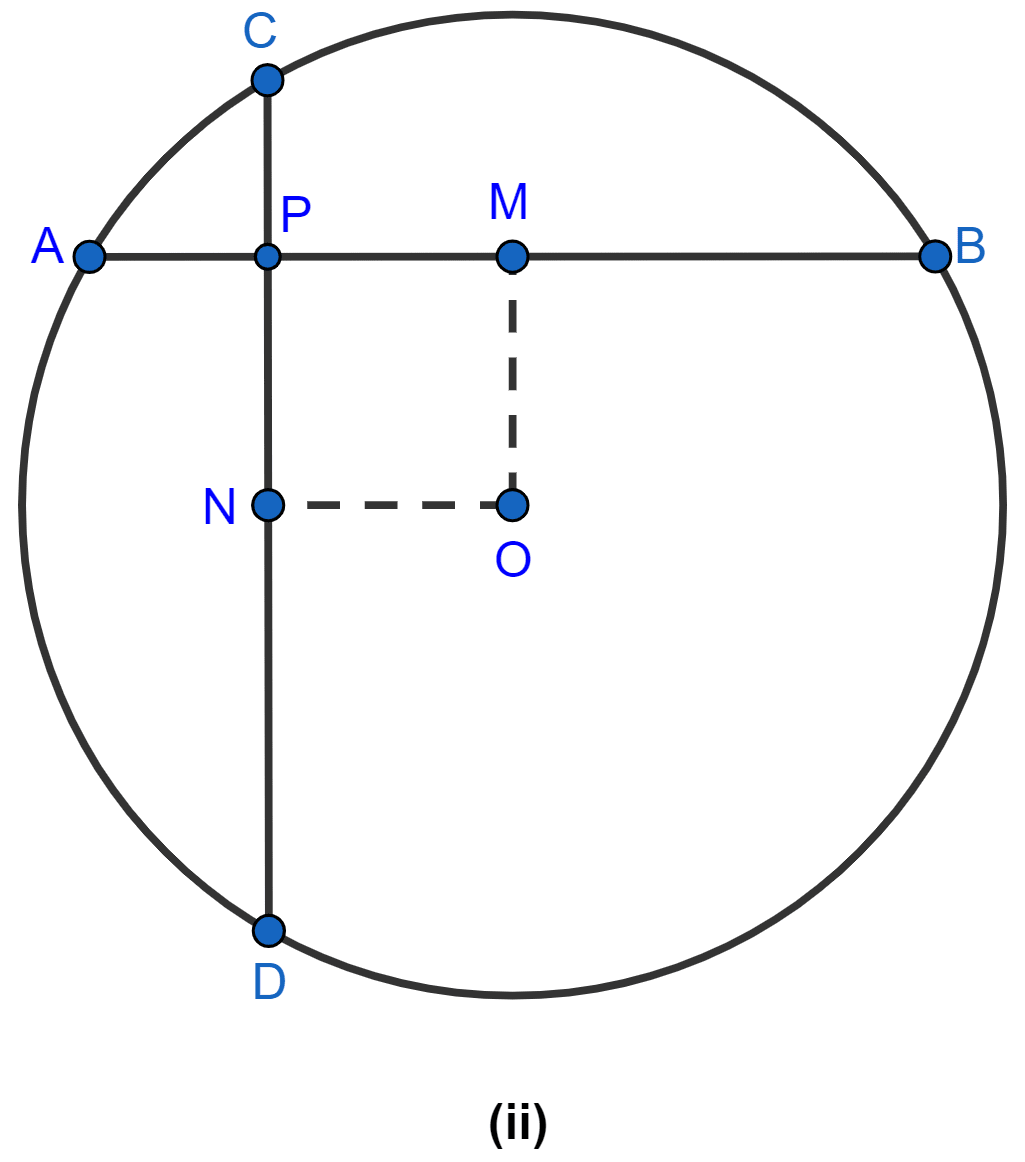
In the figure (i) given below, C and D are centers of two intersecting circles. The line APQB is perpendicular to the line of centers CD. Prove that
(i) AP = QB
(ii) AQ = BP.

Answer
Let M be the point of intersection of line CD and line APQB.

(i) Since, the perpendicular to a chord from the centre of the circle bisects the chord,
∴ In circle with center D,
PM = MQ .........(1)
and
In circle with center C,
AM = MB .........(2)
Subtracting equation (1) from (2),
⇒ AM - PM = MB - MQ
⇒ AP = QB
Hence, proved that AP = QB.
(ii) Let AP = QB = x.
From figure,
AQ = AB - QB = AB - x
BP = AB - AP = AB - x.
∴ AQ = BP.
Hence, proved that AQ = BP.
In the figure (ii) given below, two equal chords AB and CD of a circle with center O intersect at right angles at P. If M and N are mid-points of the chords AB and CD respectively, prove that NOMP is a square.
Answer
In NOMP,
∠P = 90° (As chords intersect at right angles)
∠M = ∠N = 90° (Straight lines from center bisecting the chord are perpendicular to it.)
∠O = 360° - (∠M + ∠N + ∠P)
= 360° - (90° + 90° + 90°)
= 90°
Since, equal chords are equidistant from center,
∴ OM = ON.
Since, all angles = 90° and all sides are equal.
Hence, NOMP is a square.
In the adjoining figure, AD is diameter of a circle. If the chord AB and AC are equidistant from its center O, prove that AD bisects ∠BAC and ∠BDC.
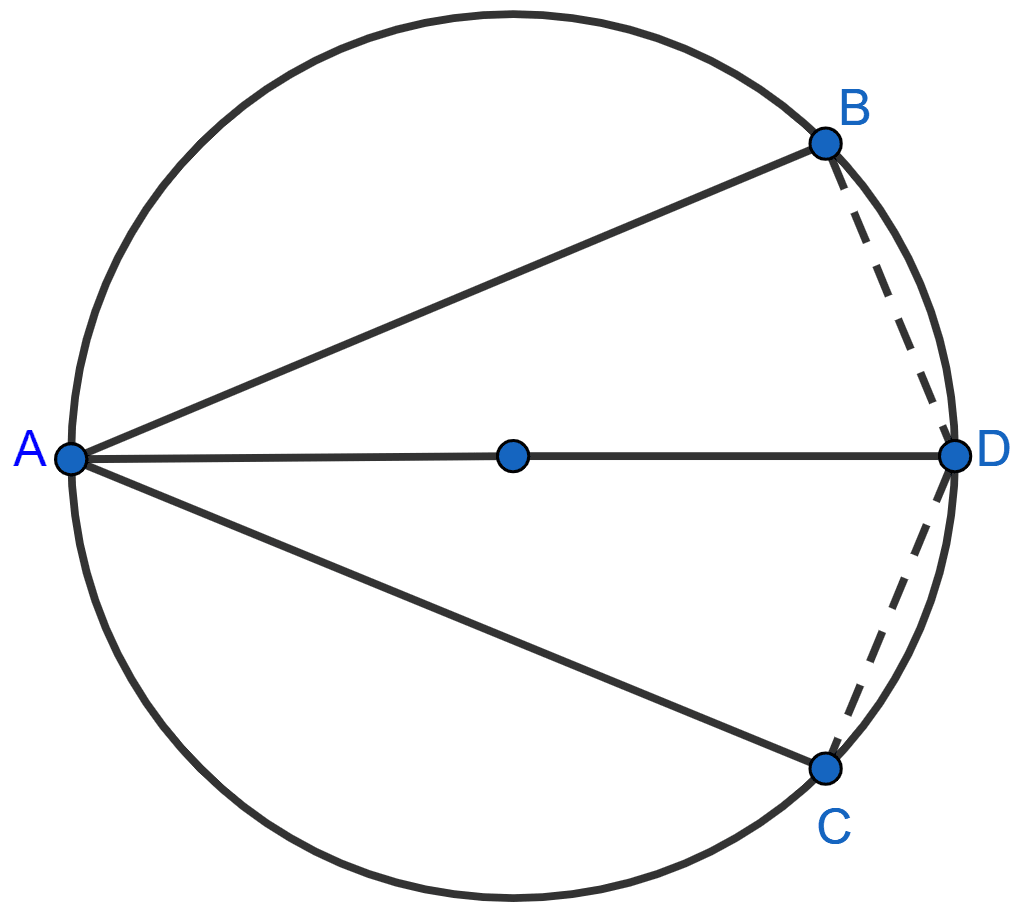
Answer
As chords AB and AC are equidistant from the center, so AB = AC. [∵ equal chords are equidistant from center]
Since, angle in a semicircle = 90°.
∠B = ∠C
In △ABD and △ACD,
∠B = ∠C (Both equal to 90°)
AD = AD (Common)
AB = AC (Proved above)
∴ △ABD ≅ △ACD (By R.H.S. congruence rule).
∴ ∠BAD = ∠CAD and ∠BDA = ∠CDA (By C.P.C.T.)
Hence, proved that AD bisects ∠BAC and ∠BDC.