Prove that the line segment joining the mid-points of a pair of opposite sides of a parallelogram divides it into two equal parallelograms.
Answer
Let us consider ABCD be a parallelogram in which E and F are mid-points of AB and CD. Join EF.
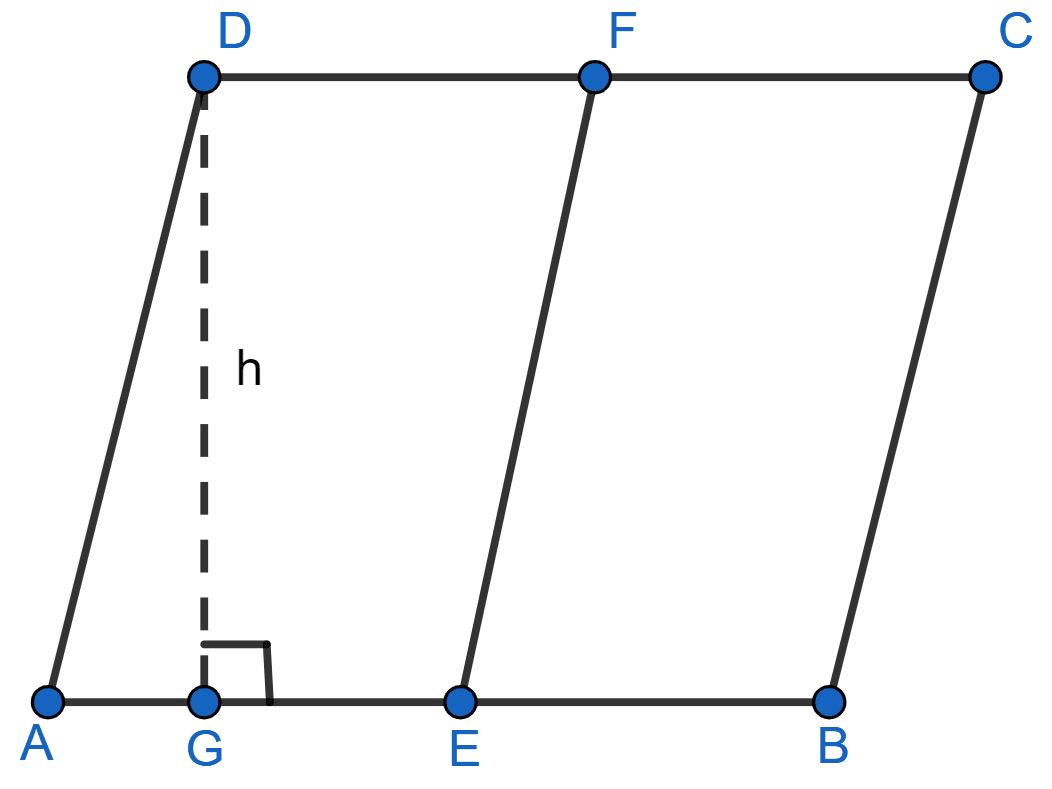
Let us construct DG ⊥ AB and let DG = h, where h is the altitude on side AB.
Area of ||gm ABCD = base × height = AB × h
Area of ||gm AEFD = AE × h = × h .......(i) [Since E is the mid-point of AB]
Area of ||gm EBCF = EB × h = × h .......(ii) [Since E is the mid-point of AB]
From (i) and (ii)
Area of ||gm AEFD = Area of ||gm EBCF.
Hence proved, that the line segment joining the mid-points of a pair of opposite sides of a parallelogram divides it into two equal parallelograms.
Prove that the diagonals of a parallelogram divide it into four triangles of equal area.
Answer
Let us consider a parallelogram ABCD, the diagonals AC and BD cut at point O.

In parallelogram ABCD, the diagonals bisect each other.
AO = OC
In ∆ACD, O is the mid-point of AC.
∴ OD is the median.
Area of ∆AOD = Area of ∆COD ....... (i) [Median of ∆ divides it into two triangles of equal areas.]
Similarly, in ∆ABC
O is the mid-point of AC.
∴ OB is the median.
Area of ∆AOB = Area of ∆COB ....... (ii) [Median of ∆ divides it into two triangles of equal areas.]
In ∆ADB,
O is the mid-point of BD.
∴ OA is the median.
Area of ∆AOD = Area of ∆AOB ....... (iii)
From (i), (ii) and (iii) we get,
Area of ∆AOB = ∆COB = ∆COD = ∆AOD
Hence proved, that the diagonals of a parallelogram divide it into four triangles of equal area.
In figure (1) given below, AD is the median of ∆ABC and P is any point on AD. Prove that
(i) Area of ∆PBD = area of ∆PDC.
(ii) Area of ∆ABP = area of ∆ACP.
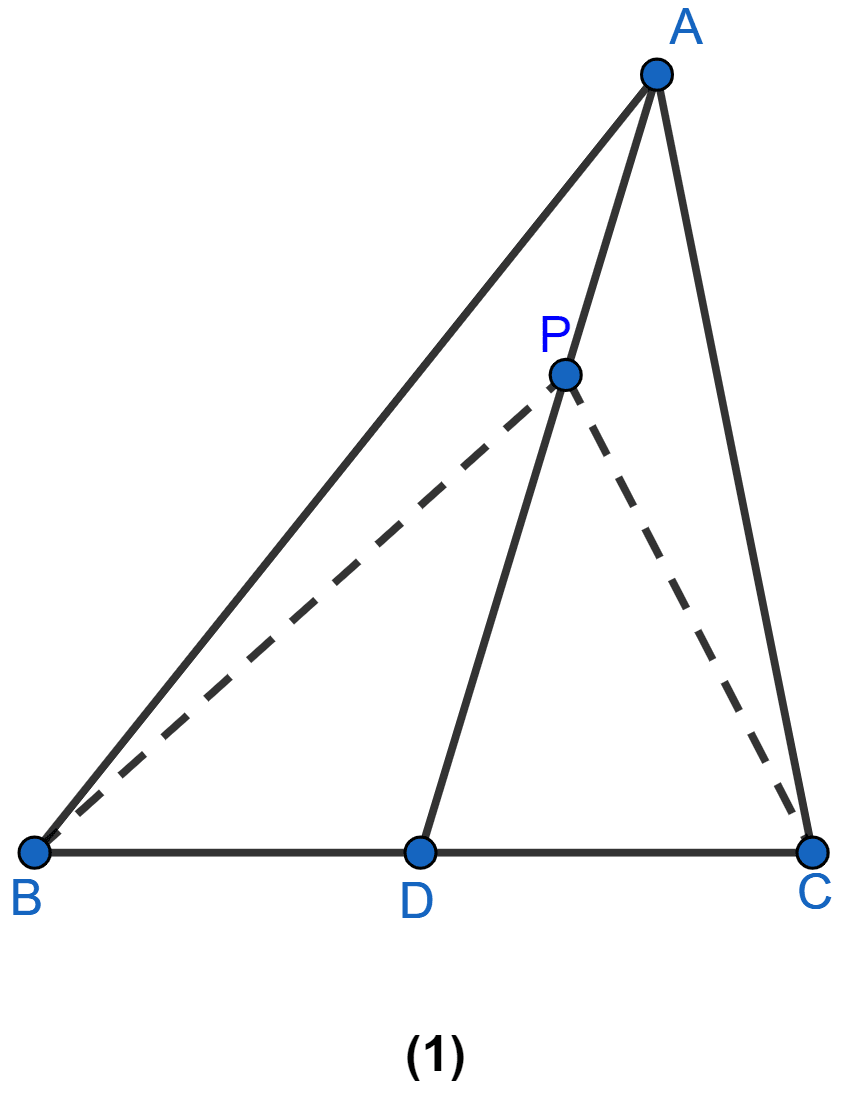
Answer
(i) In ∆ABC,
Area of ∆ABD = Area of ∆ADC [AD is the median] ......(1)
Since, PD is a straight line and base of ∆ABC and ∆PBC,
So PD is median of ∆PBC,
∴ Area of ∆PBD = Area of ∆PDC ........(2)
Hence, proved that Area of ∆PBD = Area of ∆PDC.
(ii) Subtracting eq. 1 from 2 we get,
⇒ Area of ∆ABD - Area of ∆PBD = Area of ∆ADC - Area of ∆PDC
⇒ Area of ∆ABP = Area of ∆ACP.
Hence proved that Area of ∆ABP = Area of ∆ACP.
In the figure (2) given below, DE || BC. Prove that
(i) area of ∆ACD = area of ∆ABE
(ii) area of ∆OBD = area of ∆OCE.

Answer
(i) We know that,
Triangles on the same base and between the same parallel lines are equal in area.
∆BCD and ∆BCE are on the same base BC and between the same || lines DE and BC.
⇒ Area of ∆BCD = Area of ∆BCE
Subtracting area of ∆BCD and ∆BCE from area of ∆ABC
⇒ Area of ∆ABC - Area of ∆BCD = Area of ∆ABC - Area of ∆BCE
⇒ Area of ∆ACD = Area of ∆ABE.
Hence proved, that Area of ∆ACD = Area of ∆ABE.
(ii) We know that,
⇒ Area of ∆BCD = Area of ∆BCE
Subtracting area of ∆OBC from above equation we get,
⇒ Area of ∆BCD - Area of ∆OBC = Area of ∆BCE - Area of ∆OBC
⇒ Area of ∆OBD = Area of ∆OCE.
Hence proved, that Area of ∆OBD = Area of ∆OCE.
In figure (1) given below, ABCD is a parallelogram and P is any point in BC. Prove that, Area of ∆ABP + area of ∆DPC = Area of ∆APD.
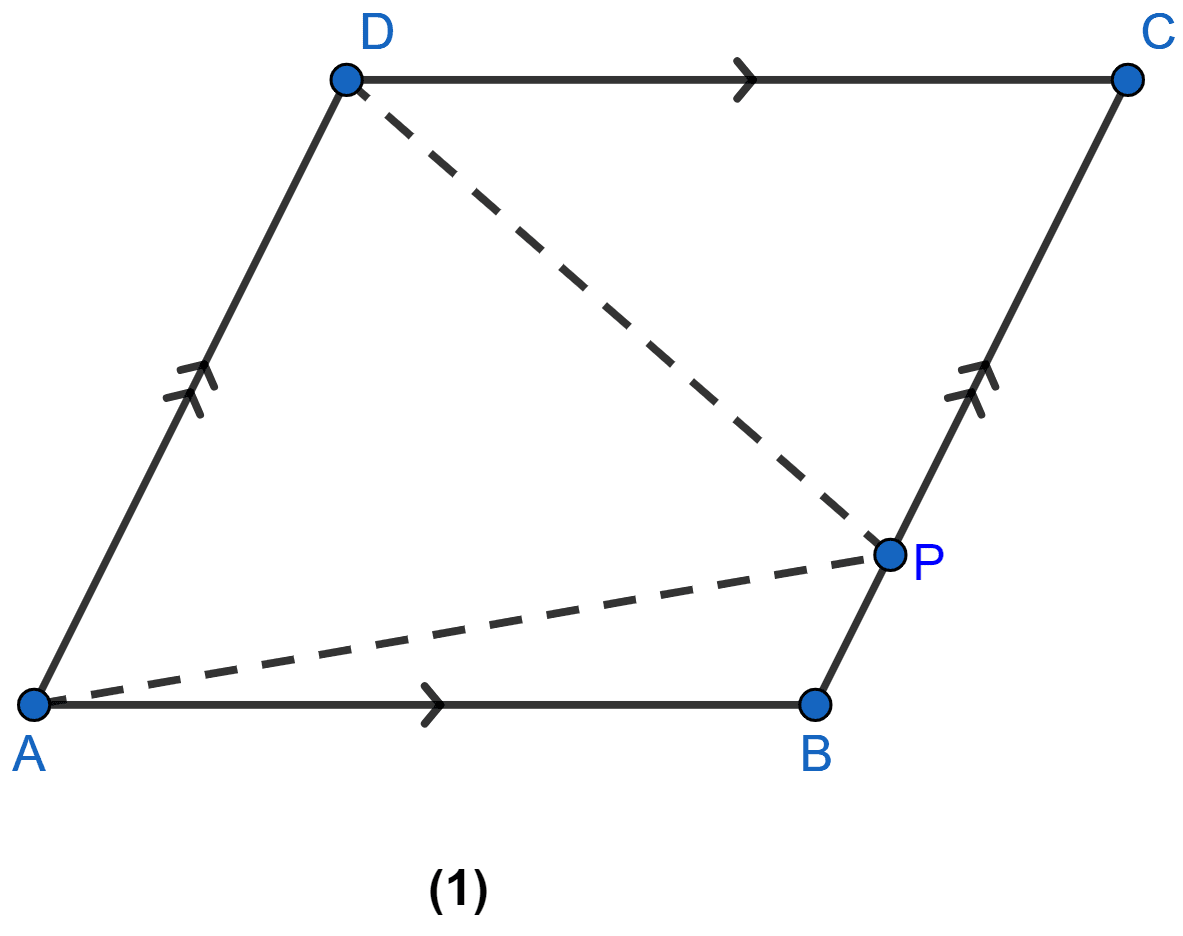
Answer
We know that,
Area of a triangle is half that of a parallelogram on the same base and between the same parallel lines.
∆APD and || gm ABCD are on the same base AD and between the same || lines AD and BC,
∴ Area of ∆APD = Area of || gm ABCD .......(i)
From figure,
Area of ||gm ABCD = Area of ∆APD + Area of ∆ABP + Area of ∆DPC
Dividing the above equation by 2 we get,
From (i),
Hence, proved that Area of ∆APD = Area of ∆ABP + Area of ∆DPC.
In the figure (2) given below, O is any point inside a parallelogram ABCD. Prove that
(i) area of ∆OAB + area of ∆OCD = area of || gm ABCD.
(ii) area of ∆OBC + area of ∆OAD = area of || gm ABCD.

Answer
(i) Draw a line PQ || to AB and CD from point O.

AB || PQ and AP || BQ (Since, AD || BC)
ABQP is a || gm
Similarly,
PD || CQ and PQ || DC
PQCD is a || gm
Now, ∆OAB and || gm ABQP are on the same base AB and between same || lines AB and PQ
Area of ∆OAB = Area of ||gm ABQP .....(1)
Similarly, ∆OCD and || gm PQCD are on the same base CD and between same || lines CD and PQ
Area of ∆OCD = Area of || gm PQCD ..... (2)
Now by adding (1) and (2),
Area of ∆OAB + Area of ∆OCD = Area of || gm ABQP + Area of || gm PQCD
= [Area of || gm ABQP + Area of || gm PQCD]
= Area of || gm ABCD
Hence, proved that Area of ∆OAB + Area of ∆OCD = Area of || gm ABCD.
(ii) From figure,
⇒ Area of ∆OAB + Area of ∆OBC + Area of ∆OCD + Area of ∆OAD = Area of || gm ABCD
⇒ Area of ∆OAB + Area of ∆OCD + Area of ∆OBC + Area of ∆OAD = Area of || gm ABCD
⇒ Area of || gm ABCD + Area of ∆OBC + Area of ∆OAD = Area of || gm ABCD
⇒ Area of ∆OBC + Area of ∆OAD = Area of || gm ABCD - Area of || gm ABCD
⇒ Area of ∆OBC + Area of ∆OAD = Area of || gm ABCD.
Hence, proved that Area of ∆OBC + Area of ∆OAD = Area of || gm ABCD.
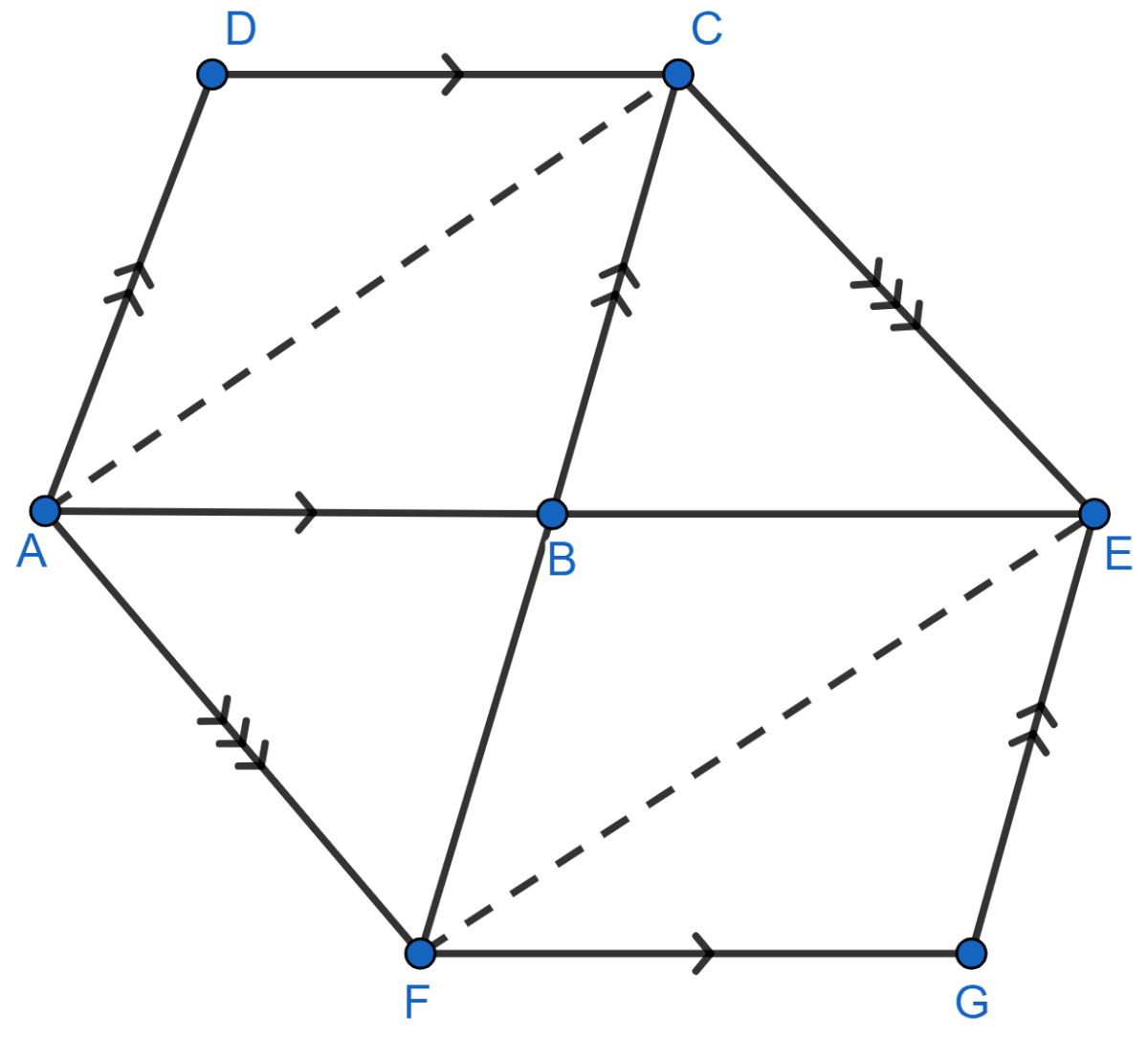
If E, F, G and H are mid-points of the sides AB, BC, CD and DA, respectively of a parallelogram ABCD, prove that area of the quad. EFGH = area of || gm ABCD.
Answer
Parallelogram ABCD with E, F, G and H as mid-points of the sides AB, BC, CD and DA, respectively is shown below:
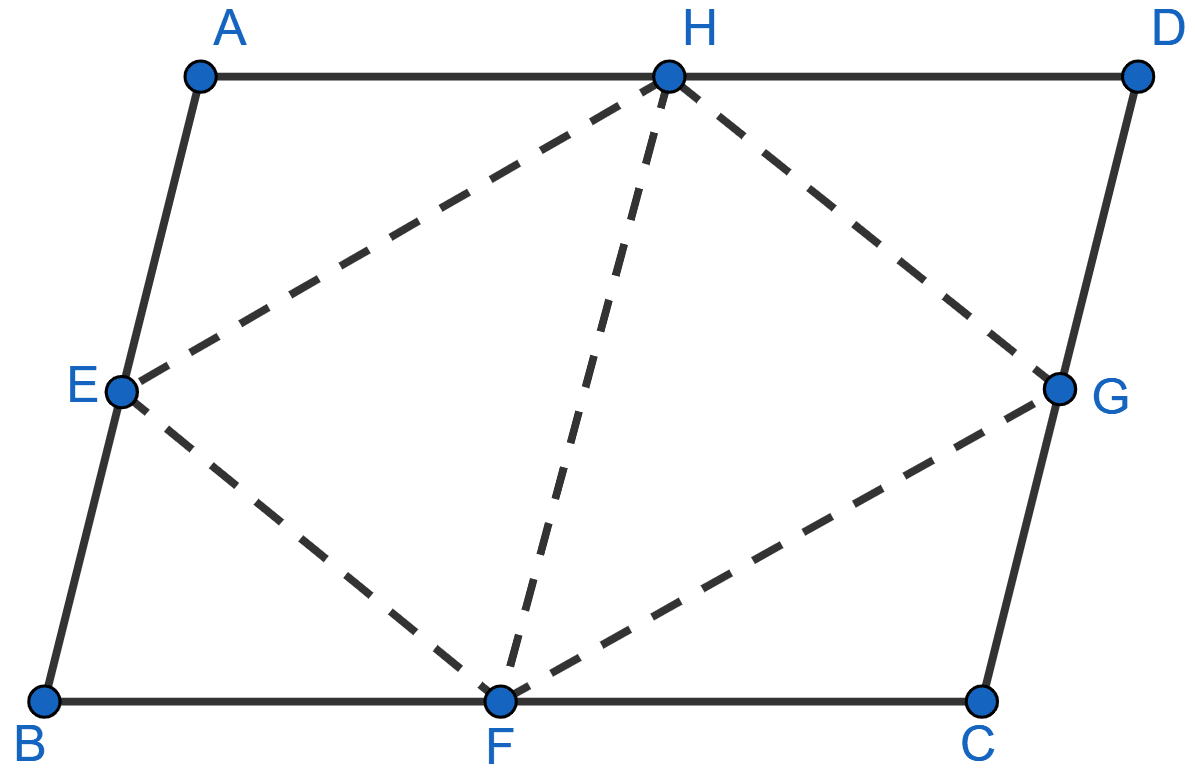
AH = AD (As H is the mid-point of AD)
BF = BC (As F is the mid-point of BC)
So, AH = BF and AH || BF (As AD || BC).
So, ABFH is a || gm.
Since, || gm ABFH and △EFH are on same base FH and between same parallel lines AB and FH so,
area of △EFH = area of || gm ABFH .......(i)
Similarly,
HD = AD (As H is the mid-point of AD)
FC = BC (As F is the mid-point of BC)
So, HD = FC and HD || FC (As AD || BC).
So, HFCD is a || gm.
Since, || gm HFCD and △HFG are on same base HF and between same parallel lines HF and DC so,
area of △HFG = area of || gm HFCD .......(ii)
Adding (i) and (ii) we get,
area of △EFH + area of △HFG = area of || gm ABFH + area of || gm HFCD
area of quad. EFGH = (area of || gm ABFH + area of || gm HFCD)
= (area of || gm ABCD).
Hence, proved that area of the quad. EFGH = area of || gm ABCD.
In figure (1) given below, ABCD is a parallelogram. P, Q are any two points on the sides AB and BC respectively. Prove that
area of ∆CPD = area of ∆AQD.
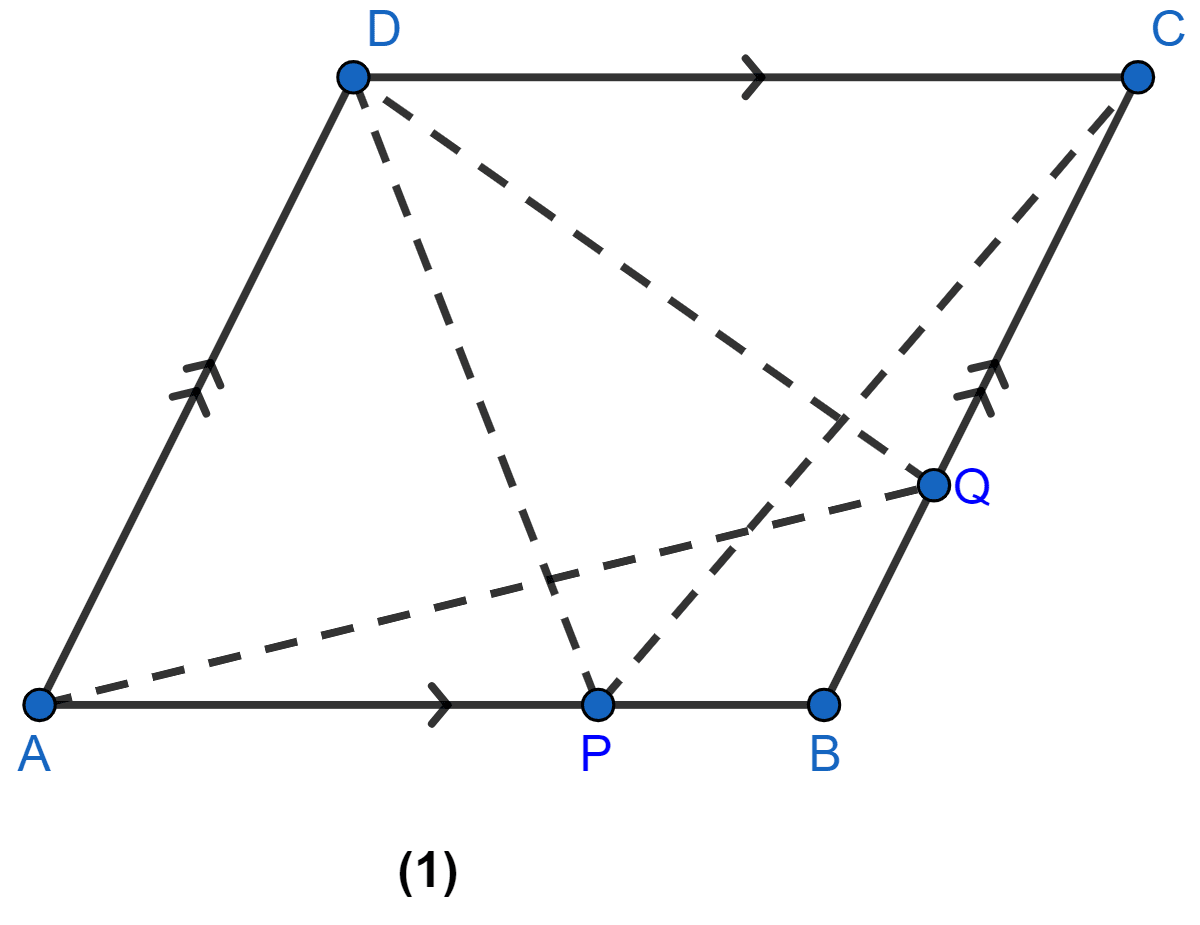
Answer
∆CPD and || gm ABCD are on the same base CD and between the same parallel lines AB and CD.
Area of ∆CPD = Area of ||gm ABCD .......(i)
∆AQD and || gm ABCD are on the same base AD and between the same parallel lines AD and BC.
Area of ∆AQD = Area of ||gm ABCD .......(ii)
From (i) and (ii)
Area of ∆CPD = Area of ∆AQD
Hence, proved that area of ∆CPD = area of ∆AQD.
In the figure (2) given below, PQRS and ABRS are parallelograms, and X is any point on the side BR. Show that
area of ∆AXS = area of || gm PQRS.

Answer
From figure,
Since, PB is a straight line and PQ || SR so,
PB || SR.
|| gm PQRS and ABRS are on the same base SR and between the same parallel lines PB and SR.
So, Area of ||gm PQRS = Area of ||gm ABRS .........(i)
∆AXS and || gm ABRS are on the same base AS and between the same parallel lines AS and BR.
So, Area of ∆AXS = Area of ||gm ABRS
= area of ||gm PQRS [From (i)]
Hence, proved that Area of ∆AXS = Area of || gm PQRS.
D, E and F are mid-points of the sides BC, CA and AB respectively of a ∆ABC. Prove that
(i) FDCE is a parallelogram
(ii) area of ∆DEF = area of ∆ABC
(iii) area of || gm FDCE = area of ∆ABC
Answer
∆ABC with D, E and F as mid-points of the sides BC, CA and AB, respectively is shown below:

(i) F and E are midpoints of AB and AC respectively.
So, by mid-point theorem,
FE || BC and FE = BC .........(1)
Also, D is the mid-point of BC
CD = BC ........ (2)
From (1) and (2),
FE || BC and FE = CD
Since, FE || BC so,
FE || CD and FE = CD ......... (3)
Similarly,
D and F are the midpoints of BC and AB.
So, by mid-point theorem,
DF || AC and DF = AC .........(4)
Also, E is the mid-point of AC
EC = AC ........ (5)
From (4) and (5),
DF || AC and DF = EC
Since, DF || AC so,
DF || EC and DF = EC ......... (6)
From 3 and 6,
FE || CD, FE = CD, DF || EC and DF = EC.
Since, opposite sides of FDCE are parallel and equal.
Hence proved FDCE is a parallelogram.
(ii) Since,
BD = CD (As D is mid-point of BC), FE = CD (Proved above) and FE || CD
So, BD = FE and BD || FE.
Hence, BDEF is a || gm.
Since,
FD = EC (Proved above) and AE = EC (As E is mid-point of AC) and FD || EC.
So, FD = AE and FD || AE.
Hence, AFDE is a || gm.
We know that, FDCE is a parallelogram and DE is a diagonal of || gm FDCE.
So, area of ∆DEF = area of ∆DEC (As diagonal divides || gm into two triangles with equal area) ........(1)
We know that, BDEF is a parallelogram and FD is a diagonal of || gm BDEF.
So, area of ∆DEF = area of ∆FBD (As diagonal divides || gm into two triangles with equal area) ........(2)
We know that, AFDE is a parallelogram and FE is a diagonal of || gm AFDE.
So, area of ∆DEF = area of ∆AFE (As diagonal divides || gm into two triangles with equal area) ........(3)
From 1, 2 and 3 we get,
area of ∆DEF = area of ∆DEC = area of ∆FBD = area of ∆AFE .........(4)
From figure,
area of ∆ABC = area of ∆DEF + area of ∆DEC + area of ∆FBD + area of ∆AFE
= area of ∆DEF + area of ∆DEF + area of ∆DEF + area of ∆DEF (From 4)
= 4 x area of ∆DEF.
∴ area of ∆ABC = 4 x area of ∆DEF
⇒ area of ∆DEF = area of ∆ABC
Hence, proved that area of ∆DEF = area of ∆ABC.
(iii) From figure,
Area of || gm FDCE = Area of ∆DEF + Area of ∆DEC
= Area of ∆DEF + Area of ∆DEF (From part (ii) eqn. 4)
= 2 area of ∆DEF
= area of ∆ABC [As area of ∆DEF = area of ∆ABC]
= area of ∆ABC.
Hence, proved that area of || gm FDCE = area of ∆ABC.
In the adjoining figure, D, E and F are midpoints of the sides BC, CA and AB respectively of ∆ABC. Prove that BCEF is a trapezium and area of the trap. BCEF = area of ∆ABC.

Answer
We know that D and E are the mid-points of BC and CA, respectively.
By mid-point theorem,
DE || AB and DE = AB = BF (As F is mid-point of AB)
From figure,
BF || DE and BF = DE.
Hence, BDEF is a || gm.
Similarly,
F and E are the mid-points of AB and CA.
By mid-point theorem,
EF || BC and EF = BC = DC (As D is mid-point of BC)
From figure,
EF || DC and EF = DC.
Hence, EFDC is a || gm.
Since, FE || BC and FB, EC are not parallel.
Hence, EFBC is a trapezium.
F and D are the mid-points of AB and BC.
By mid-point theorem,
FD || AC and FD = AC = AE (As E is mid-point of AC)
From figure,
FD || AE and FD = AE.
Hence, AFDE is a || gm.
We know that a diagonal divides a || gm in two triangles of equal area.
In || gm BDEF, FD is the diagonal,
∴ area of △DEF = area of △BDF .........(i)
In || gm EFDC, DE is the diagonal,
∴ area of △DEF = area of △EDC .........(ii)
In || gm AFDE, FE is the diagonal,
∴ area of △DEF = area of △AFE .........(iii)
From (i), (ii) and (iii) we get,
area of △DEF = area of △BDF = area of △EDC = area of △AFE .......(iv)
From figure,
area of △ABC = area of △DEF + area of △BDF + area of △EDC + area of △AFE
= area of △DEF + area of △DEF + area of △DEF + area of △DEF
= 4 x area of △DEF
∴ area of △ABC = 4 x area of △DEF
⇒ area of △DEF = area of △ABC ......(v)
From figure,
area of trapezium BCEF = area of △DEF + area of △BDF + area of △EDC
= area of △DEF + area of △DEF + area of △DEF
= 3 x area of △DEF
∴ area of trapezium BCEF = 3 x area of △DEF
⇒ area of △DEF = x area of trapezium BCEF .......(vi)
From (v) and (vi) we get,
⇒ area of △ABC = area of trapezium BCEF
⇒ area of trapezium BCEF = area of △ABC.
Hence, proved that area of trapezium BCEF = area of △ABC.
In figure (1) given below, point D divides the side BC of ∆ABC in the ratio m : n. Prove that area of ∆ABD : area of ∆ADC = m : n.
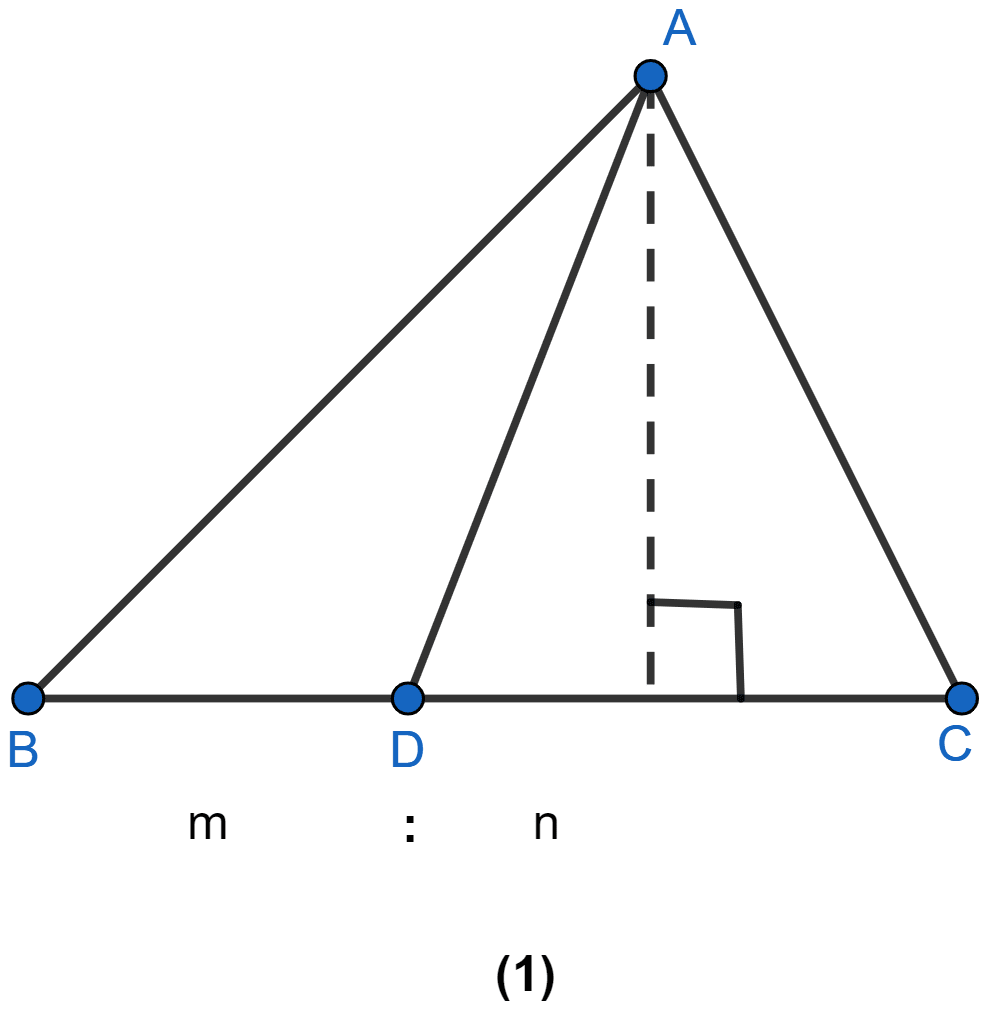
Answer
From fig (1)
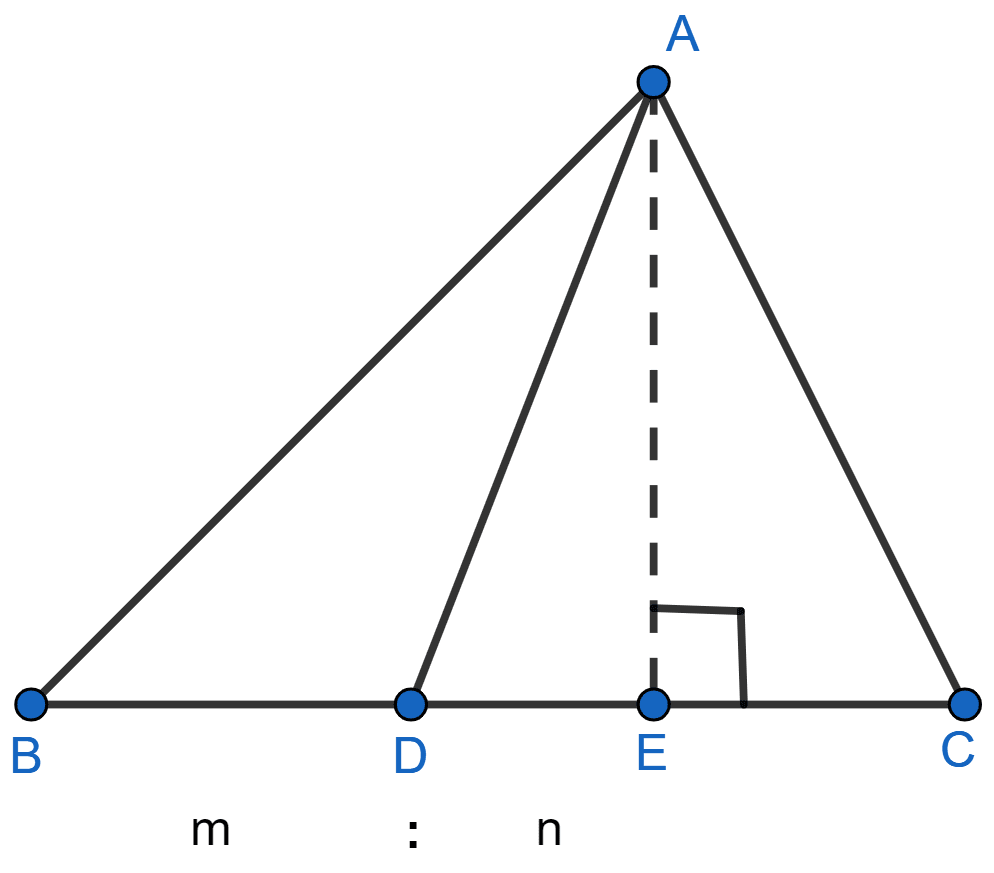
In ∆ABC, point D divides the side BC in the ratio m : n.
BD : DC = m : n
area of ∆ABD = × base × height
= × BD × AE ........ (i)
area of ∆ADC = × DC × AE ...... (ii)
Dividing (i) by (ii)
Hence, proved that area of ∆ABD : area of ∆ADC = m : n.
In the figure (2) given below, P is a point on the side BC of ∆ABC such that PC = 2BP, and Q is a point on AP such that QA = 5PQ, find area of ∆AQC : area of ∆ABC.
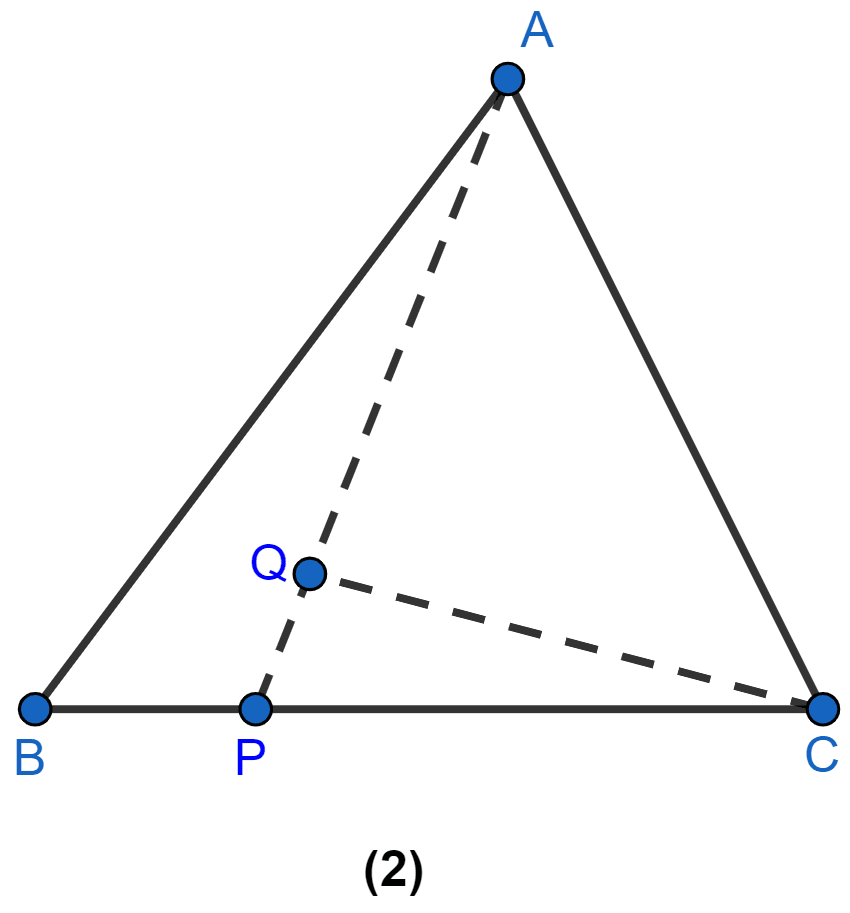
Answer
Given, PC = 2BP
From figure,
BC = BP + PC = BP + 2BP = 3BP.
PC = BC
Let AD be the altitude.
Area of △ABC = × BC × AD ......(i)
Area of △APC = × PC × AD
= ........(ii)
Dividing (ii) by (i) we get,
Given,
QA = 5PQ
From figure,
AP = AQ + QP = 5PQ + PQ = 6PQ.
.
AQ =
Let CE be the altitude.
Area of △AQC = × AQ × CE ......(iv)
Area of △APC = × AP × CE .......(v)
Dividing (iv) by (v) we get,
∴ area of △AQC : area of △ABC = 5 : 9.
Hence, area of △AQC : area of △ABC = 5 : 9.
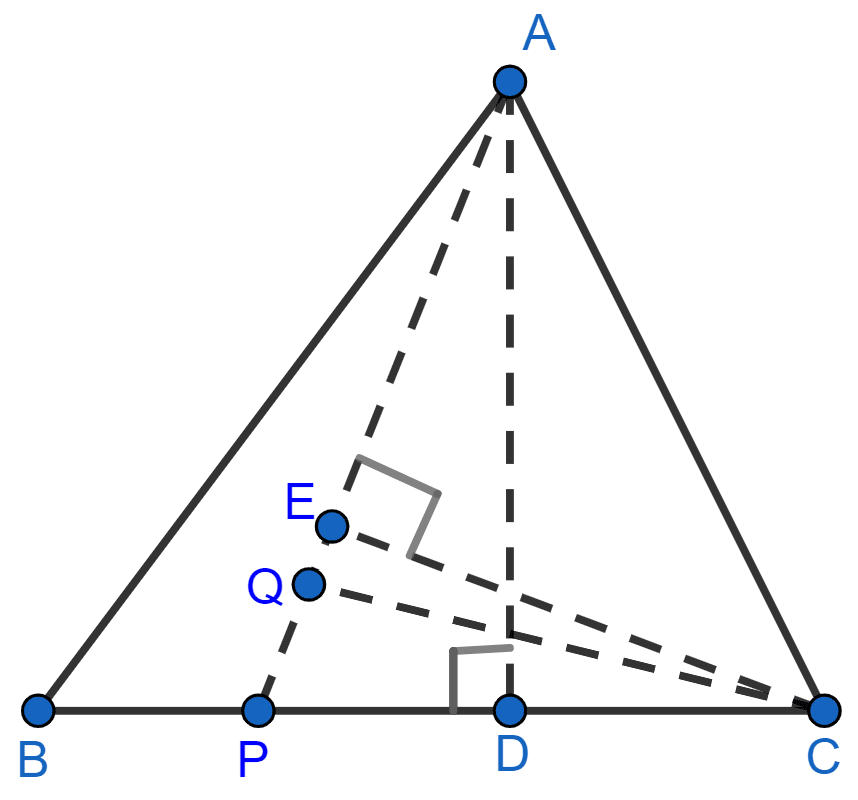
In the figure (3) given below, AD is a median of △ABC and P is a point in AC such that area of △ADP : area of △ABD = 2 : 3. Find
(i) AP : PC
(ii) area of △PDC : area of △ABC
Answer
(i) From figure,
Let DE be altitude on base AC.
Median divides a triangle into two triangles of equal area.
AD is the median of ∆ABC,
Area of ∆ABD = Area of ∆ADC = Area of ∆ABC .......(1)
It is given that,
⇒ area of ∆ADP : area of ∆ABD = 2 : 3
⇒ area of ∆ADP : area of ∆ADC = 2 : 3
Let AP = 2x and AC = 3x.
From figure,
PC = AC - AP = 3x - 2x = x.
Hence, AP : PC = 2 : 1
(ii) We know that,
PC : AC = x : 3x = 1 : 3
So,
Since, AD is median of ∆ABC so,
area of ∆ADC = area of ∆ABC
Substituting above value in 1 we get,
Hence, proved that area of △PDC : area of △ABC = 1 : 6.
In figure (1) given below, area of parallelogram ABCD is 29 cm2. Calculate the height of parallelogram ABEF if AB = 5.8 cm.

Answer
||gm ABCD and ||gm ABEF are on same base (AB) and between the same parallel lines AB and DE, so their areas are equal.
Area of ||gm ABEF = Area of ||gm ABCD = 29 cm2.
Area of ||gm ABEF = base × height
⇒ 29 = AB × height
⇒ 29 = 5.8 × height
⇒ Height =
= 5 cm.
The height of parallelogram ABEF is 5 cm.
In figure (2) given below, area of ∆ABD is 24 sq. units. If AB = 8 units, find the height of △ABC.

Answer
Given,
Area of ∆ABD = 24 sq. units
As ∆ABD and ∆ABC lie on same base AB and between same parallel lines AB and CD so,
Area of ∆ABC = Area of ∆ABD = 24 sq. units.
⇒ × AB × height = 24
⇒ × 8 × height = 24
⇒ 4 × height = 24
⇒ Height =
⇒ Height = 6 units.
Hence, height of ∆ABC = 6 units.
In figure (3) given below, E and F are midpoints of sides AB and CD, respectively, of parallelogram ABCD. If the area of parallelogram ABCD is 36 cm2,
(i) state the area of ∆APD.
(ii) Name the parallelogram whose area is equal to the area of ∆APD.
Answer
Join the diagonals AC and BD as shown below:
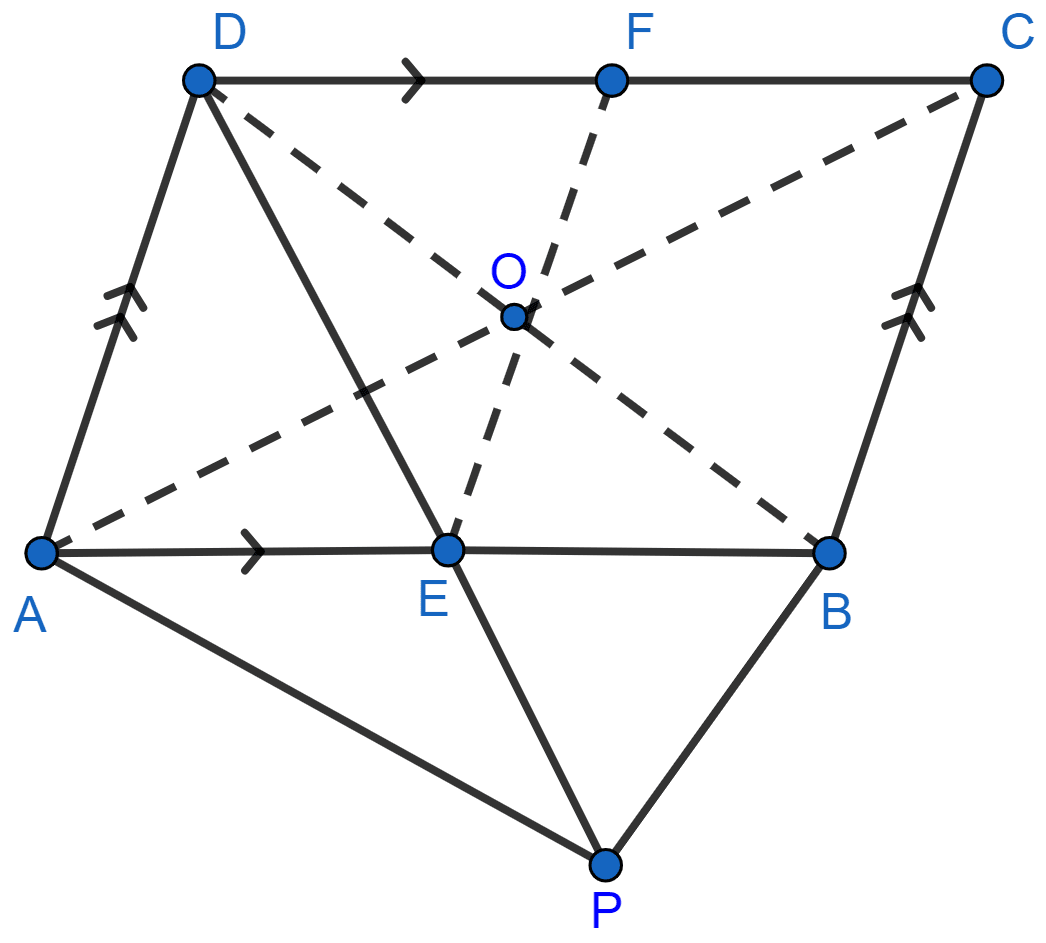
(i) ∆APD and || gm ABCD are on the same base AD and between the same parallel lines AD and BC.
Area of ∆APD = Area of ||gm ABCD
= × 36
= 18 cm2.
Hence, area of ∆APD = 18 cm2.
(ii) Let diagonals AC and BD meet at point O.
In ∆ABC,
Since, O is mid-point of AC (as diagonals bisect each other) and E is mid-point of AB so by mid-point theorem,
EO || BC
∴ EF || BC.
Since, BC || AD so,
⇒ EF || AD.
AB || DC (ABCD is a parallelogram)
⇒ AE || DF
Since, EF || AD and AE || DF.
∴ AEFD is a parallelogram.
EF bisects the parallelogram ABCD in two equal halves as E and F are mid-points of AB and CD and EF || BC || AD.
∴ Area of || gm AEFD = Area of || gm ABCD = × 36 = 18 cm2.
∴ Area of ∆APD = Area of || gm AEFD.
Hence, AEFD is the required parallelogram which has area equal to the area of ∆APD.
In figure (1) given below, ABCD is a parallelogram. Points P and Q on BC trisect BC into three equal parts. Prove that :
area of ∆APQ = area of ∆DPQ = (area of ||gm ABCD)
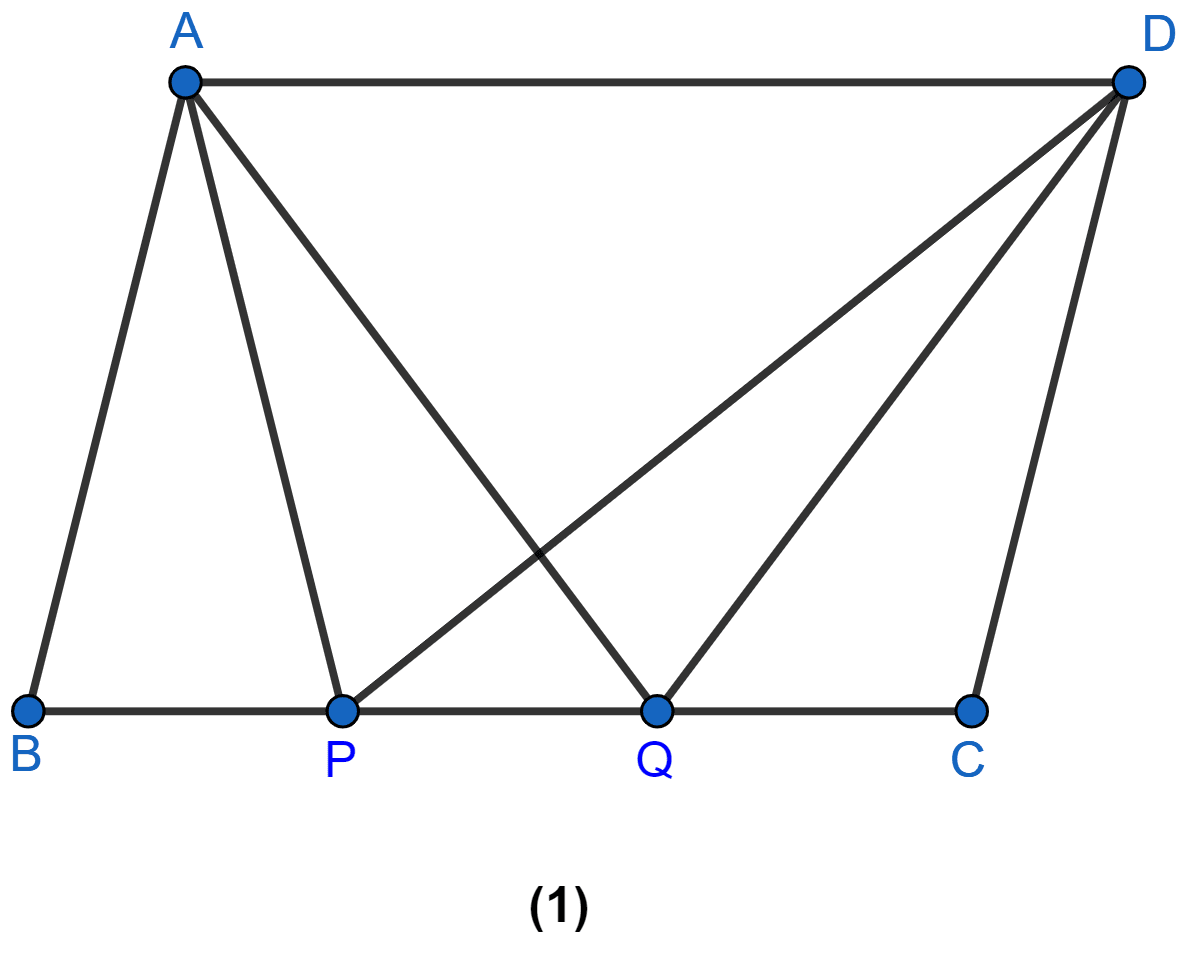
Answer
Construct: Through P and Q, draw PR and QS parallel to AB and CD.
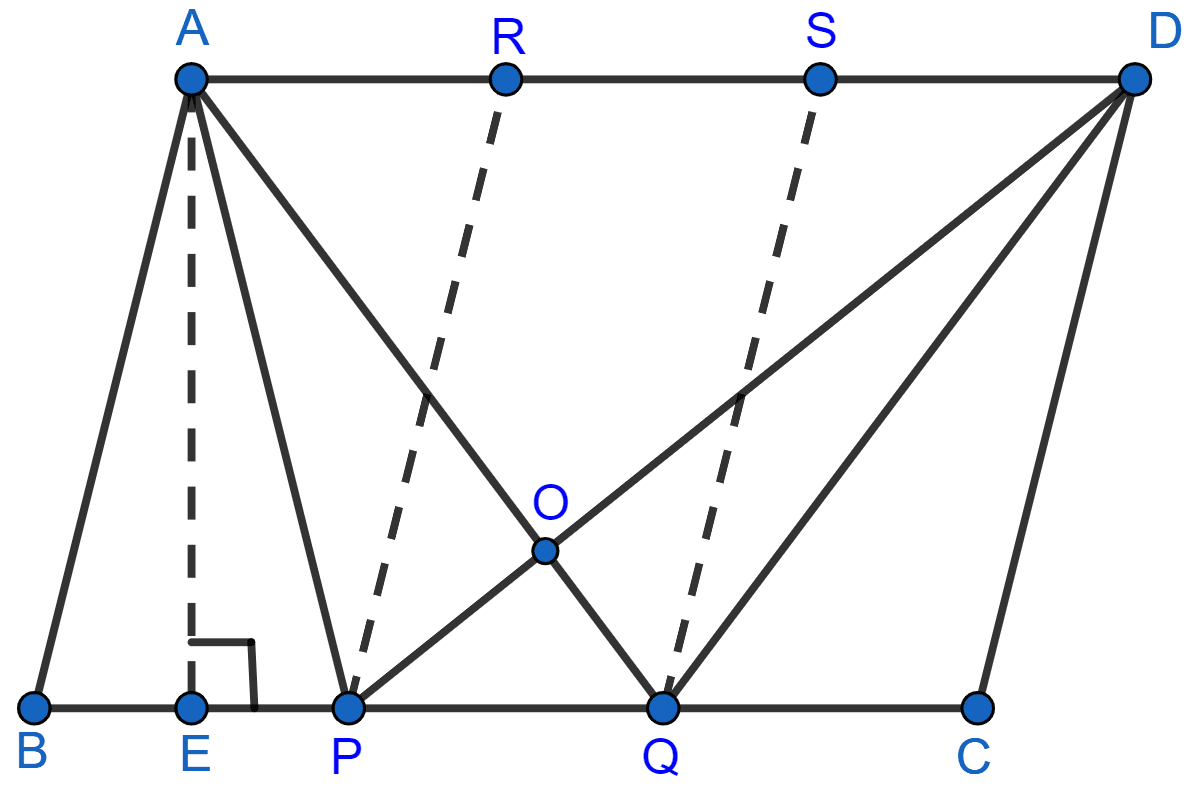
Area of ∆APD = Area of ∆AQD [Since ∆APD and ∆AQD lie on the same base AD and between the same parallel lines AD and BC]
Area of ∆APD – Area of ∆AOD = Area of ∆AQD – Area of ∆AOD [On subtracting ar ∆AOD on both sides]
Area of ∆APO = Area of ∆OQD ....... (i)
Area of ∆APO + Area of ∆OPQ = Area of ∆OQD + Area of ∆OPQ [On adding area of ∆OPQ on both sides]
Area of ∆APQ = Area of ∆DPQ ....... (ii)
We know that, ∆APQ and ||gm PQSR are on the same base PQ and between the same parallel lines PQ and AD.
Area of ∆APQ = Area of ||gm PQRS ....... (iii)
From figure,
Height of || gm ABCD = Height of || PQRS = AE
Since, P and Q trisect BC so,
⇒ PQ =
⇒ BC = 3PQ.
Substituting above value in (iii) we get,
⇒ Area of ∆APQ = Area of ||gm ABCD = Area of ||gm ABCD.
⇒ Area of ∆APQ = Area of ||gm ABCD ........(iv)
From (ii) and (iv) we get,
area of ∆APQ = area of ∆DPQ = (area of ||gm ABCD).
Hence, proved that area of ∆APQ = area of ∆DPQ = (area of ||gm ABCD).
In figure (2) given below, DE is drawn parallel to the diagonal AC of the quadrilateral ABCD to meet BC produced at point E. Prove that area of quad. ABCD = area of ∆ABE.

Answer
We know that, ∆ACE and ∆ADC are on the same base AC and between the same parallel lines AC and DE.
Area of ∆ACE = Area of ∆ADC
Now, adding ar (∆ABC) on both sides, we get
⇒ Area of ∆ACE + Area of ∆ABC = Area of ∆ADC + Area of ∆ABC
⇒ Area of ∆ABE = Area of quad. ABCD
Hence, proved that area of quad. ABCD = area of ∆ABE.
In the figure (3) given below, ABCD is a parallelogram. O is any point on the diagonal AC of the parallelogram. Show that the area of ∆AOB is equal to the area of ∆AOD.
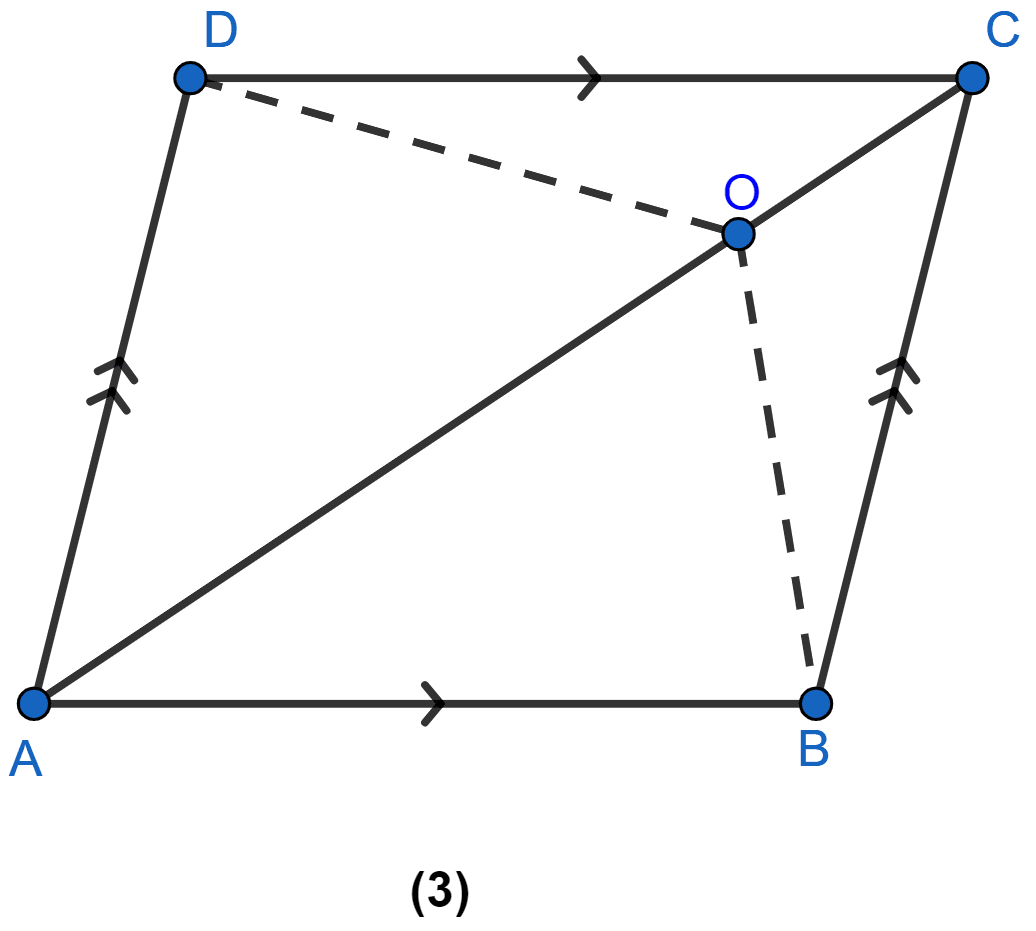
Answer
Join BD, which meets AC at P.
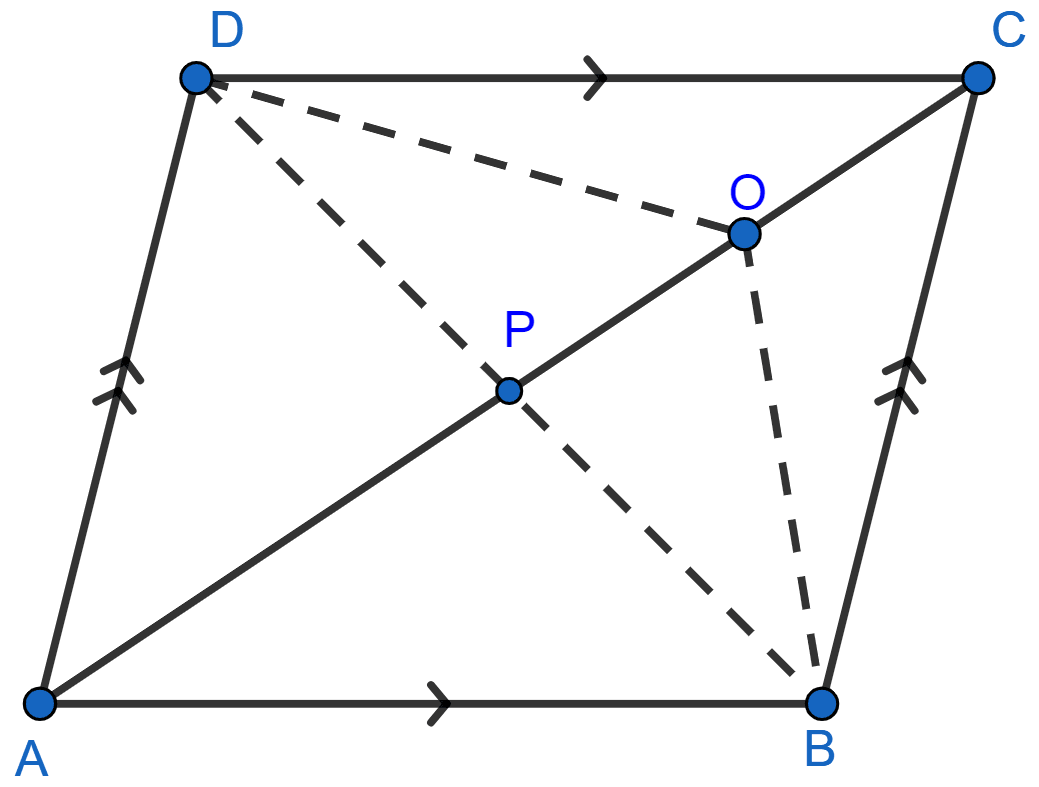
In ∆ABD, AP is the median (As P is mid-point of BD because diagonals of || gm bisect each other).
Since, median of triangle divides it into two triangles of equal area.
∴ Area of ∆ABP = Area of ∆ADP .......(i)
Similarly,
PO is median of ∆BOD,
∴ Area of ∆BOP = Area of ∆POD .......(ii)
Now, adding (i) and (ii), and we get
⇒ Area of ∆ABP + Area of ∆BOP = Area of ∆ADP + Area of ∆POD
⇒ Area of ∆AOB = Area of ∆AOD.
Hence, proved that area of ∆AOB = area of ∆AOD.
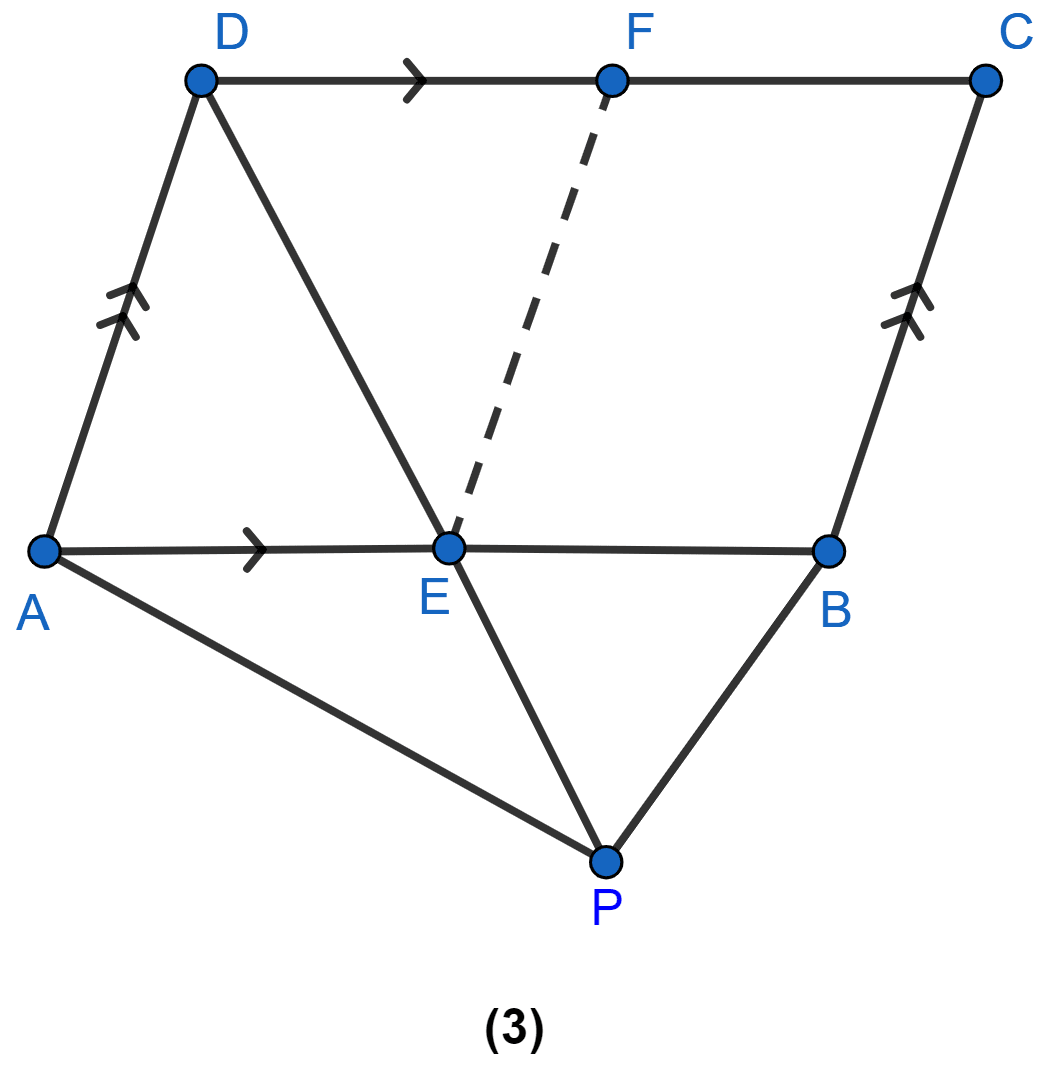
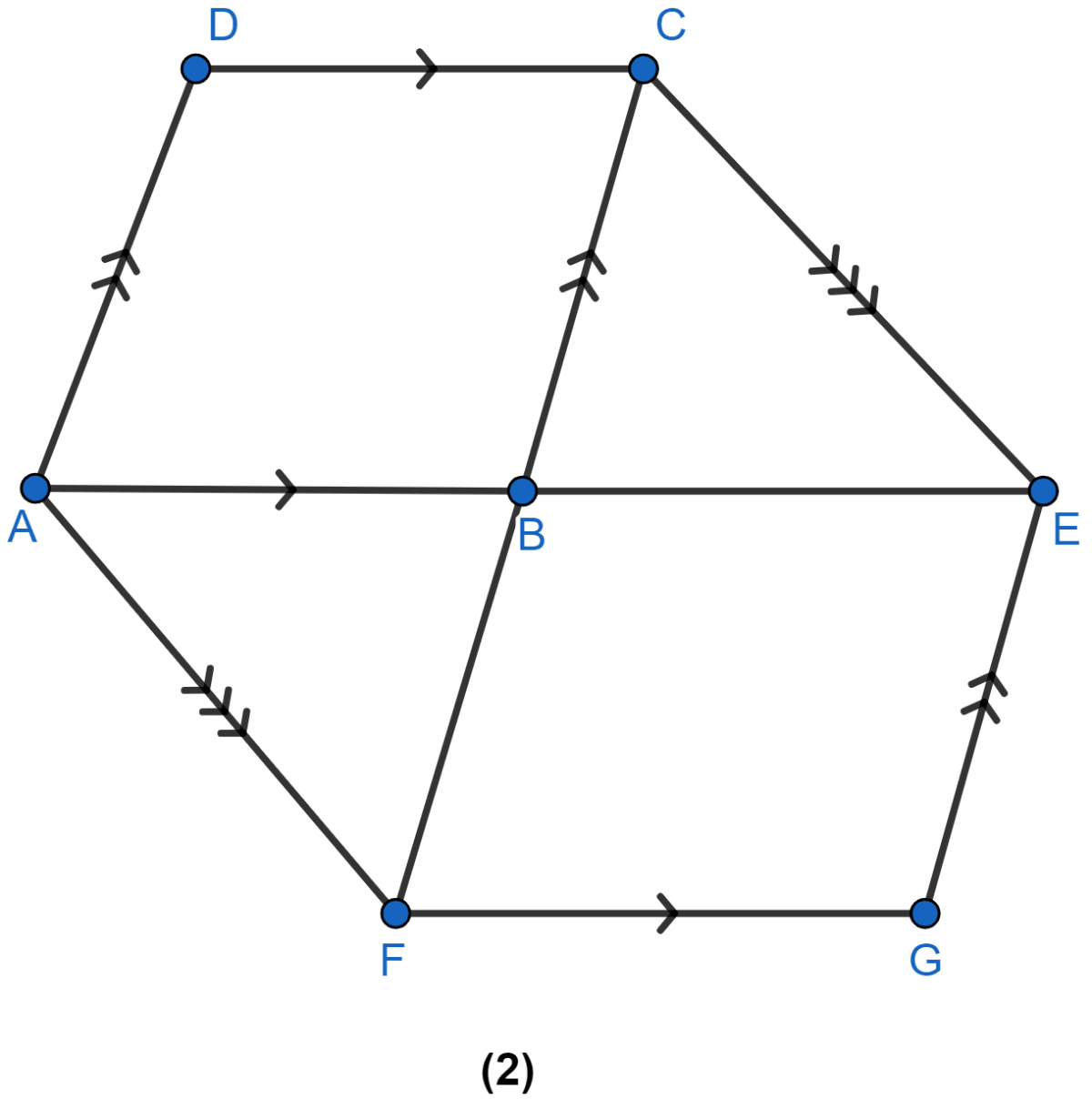
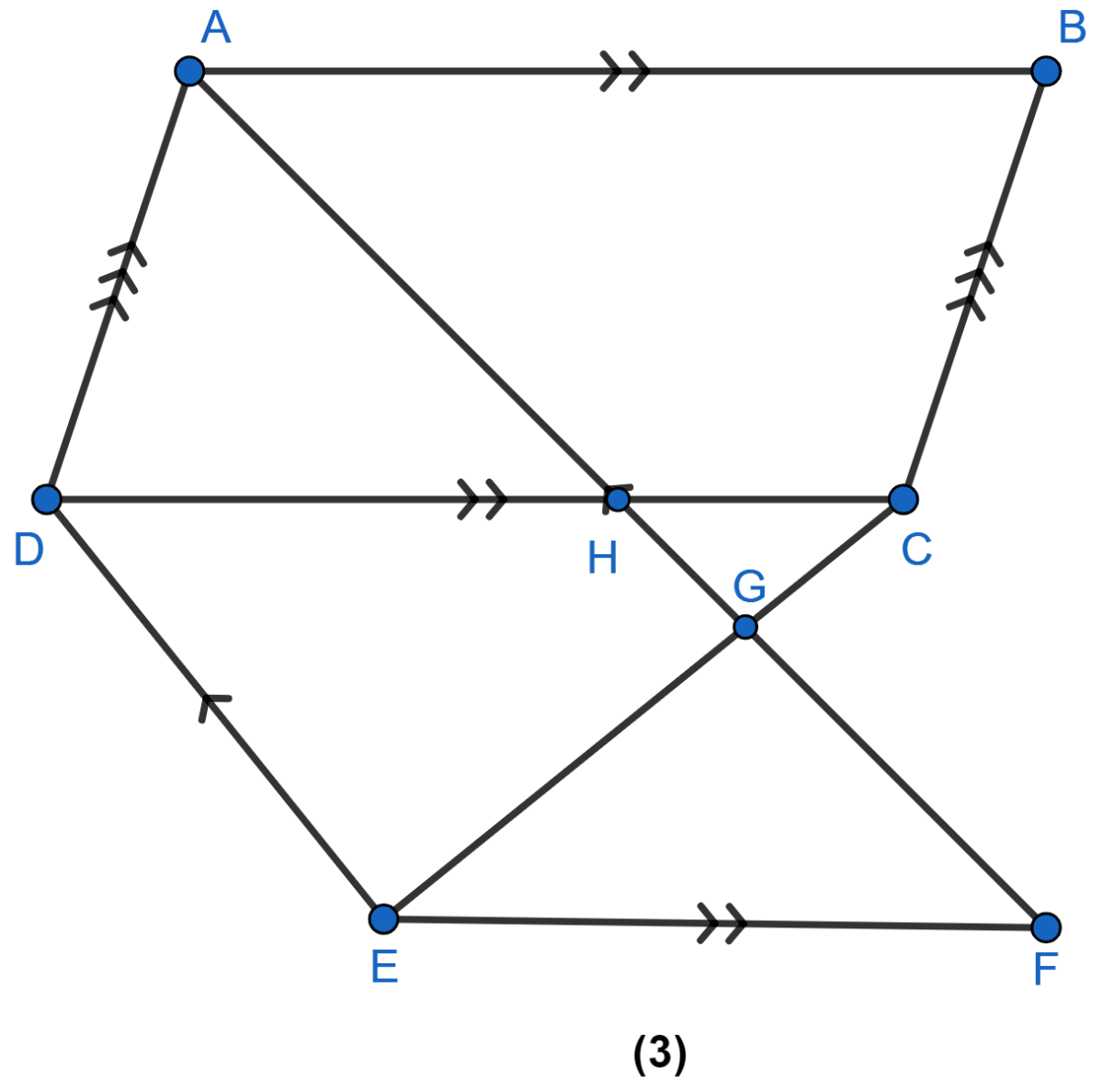
In the figure (1) given, ABCD and AEFG are two parallelograms. Prove that area of || gm ABCD = area of || gm AEFG.
Answer
(a) Join BG.
We know that,
Since, ∆ABG and || gm ABCD lie on same base AB and between same parallel lines AB and CD.
Area of ∆ABG = Area of ||gm ABCD ......(i)
Since, ∆ABG and || gm AEFG lie on same base AG and between same parallel lines AG and EF.
Area of ∆ABG = Area of ||gm AEFG ......(ii)
From (i) and (ii) we get,
Area of || gm ABCD = Area of || gm AEFG
⇒ Area of || gm ABCD = Area of || gm AEFG
Hence, proved that area of || gm ABCD = area of || gm AEFG.
In figure (2) given below, the side AB of the parallelogram ABCD is produced to E. A straight line through A is drawn parallel to CE to meet CB produced at F and parallelogram BFGE is completed. Prove that
area of || gm BFGE = area of || gm ABCD.
Answer
Join AC and EF.
Since, ∆AFC and ∆AFE lie on same base AF and between same parallel lines AF and CE so,
area of ∆AFC = area of ∆AFE
Now, subtract area of ∆ABF on both sides,
area of (∆AFC - ∆ABF) = area of (∆AFE – ∆ABF)
area of ∆ABC = area of ∆BEF
2 area of ∆ABC = 2 area of ∆BEF .......(i)
From figure,
As || gm ABCD and ∆ABC lie on same base AB and between same parallel lines AB and DC.
Area of ∆ABC = Area of || gm ABCD
Area of || ABCD = 2 Area of ∆ABC .........(ii)
As || gm BFGE and ∆BEF lie on same base BE and between same parallel lines FG and BE.
Area of ∆BEF = Area of || gm BFGE
Area of || BFGE = 2 Area of ∆BEF .........(iii)
Substituting value from (ii) and (iii) in (i) we get,
Area of || ABCD = Area of || BFGE.
Hence, proved that area of || ABCD = area of || BFGE.
In figure (3) given below, AB || DC || EF, AD || BE and DE || AF. Prove that the area of DEFH is equal to the area of ABCD.
Answer
We know that,
AD || BE ⇒ AD || EG
ED || FA ⇒ ED || GA
Since, opposite sides are parallel.
Hence, ADEG is a parallelogram.
Since || gm ABCD and || gm ADEG lie on same base AD and between same parallel lines AD and EB,
area of || gm ABCD = area of ||gm ADEG ....... (i)
We know that,
ED || FA ⇒ DE || FH
DH || EF
Since, opposite sides are parallel.
Hence, DEFH is a parallelogram.
Since || gm DEFH and || gm ADEG lie on same base DE and between same parallel lines DE and FA,
area of ||gm DEFH = area of ||gm ADEG ....... (ii)
From (i) and (ii) we get,
⇒ area of ||gm ABCD = area of ||gm DEFH
Hence, proved that area of ||gm ABCD = area of ||gm DEFH.
Any point D is taken on the side BC of a ∆ABC and AD is produced to E such that AD = DE, prove that area of ∆BCE = area of ∆ABC.
Answer
∆ABC with point D on the side BC and AD produced to E such that AD = DE is shown below:
In ∆ABE, it is given that AD = DE.
∴ BD is the median of ∆ABE
⇒ area of ∆ABD = area of ∆BED ........ (i)
Similarly,
In ∆ACE, it is given that AD = AE
∴ CD is the median of ∆ACE
⇒ area of ∆ACD = area of ∆CED ........ (ii)
By adding (i) and (ii), we get
⇒ area of ∆ABD + area of ∆ACD = area of ∆BED + area of ∆CED
⇒ area of ∆ABC = area of ∆BCE.
Hence, proved that area of ∆ABC = area of ∆BCE.
ABCD is a rectangle and P is the mid-point of AB. DP is produced to meet CB at Q. Prove that the area of rectangle ABCD = area of ∆DQC.
Answer
In ∆APD and ∆PQB,
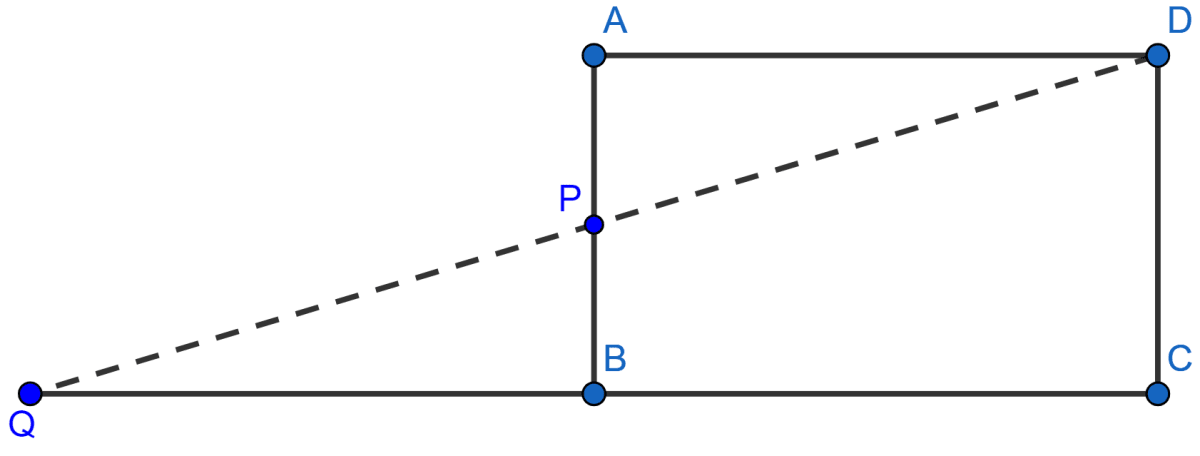
AP = BP [Since P is the mid-point of AB]
∠DAP = ∠QBP [each angle is 90° as ABCD is a rectangle]
∠APD = ∠BPQ [Vertically opposite angles are equal]
So, ∆APD ≅ ∆PQB [By using ASA axiom]
So, area of ∆APD = area of ∆PQB .......(i) (As both triangles are congruent.)
From figure,
area of rectangle ABCD = area of ∆APD + area of quad. PBCD
= area of ∆PQB + area of quad. PBCD ......(From i)
= area of ∆DQC.
Hence, proved that area of rectangle ABCD = area of ∆DQC..
In figure (1) given below, the perimeter of the parallelogram is 42 cm. Calculate the lengths of the sides of the parallelogram.
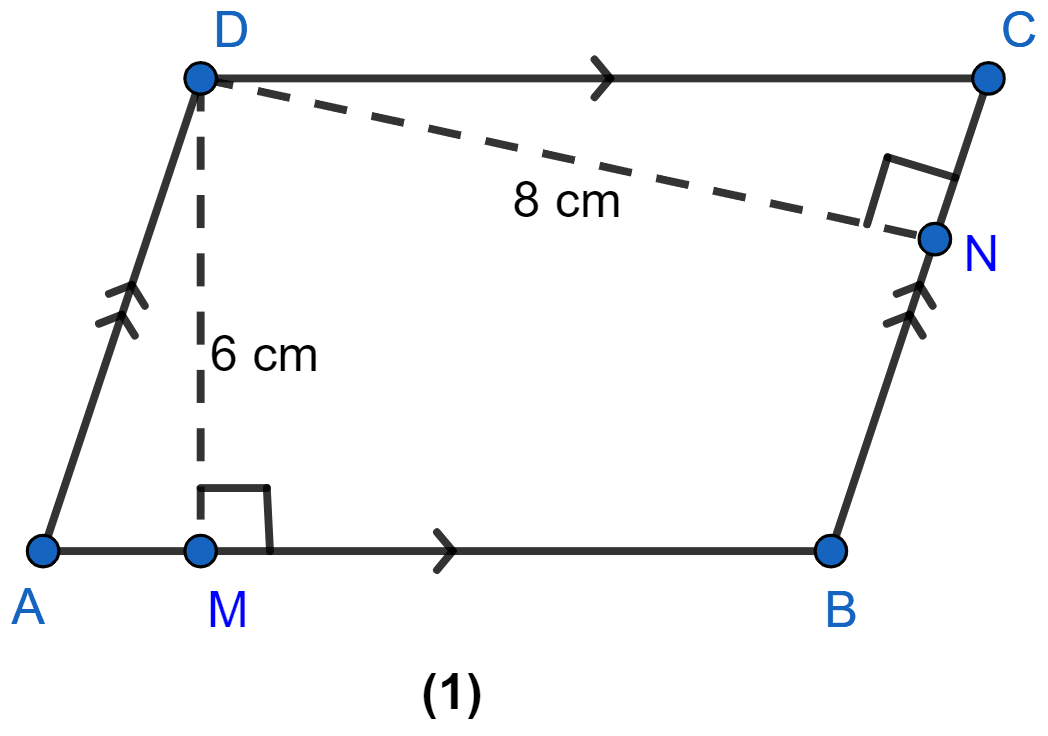
Answer
Let AB = p
Since, opposite sides of || gm are equal.
Perimeter of || gm ABCD = 2(AB + BC)
⇒ 42 = 2(p + BC)
⇒ p + BC =
⇒ p + BC = 21
⇒ BC = 21 – P
area of ||gm ABCD = base × height = AB × DM = p × 6 = 6p .......(i)
Also, area of ||gm ABCD = BC × DN
= (21 – p) × 8
= 8(21 – p) ............ (ii)
From (i) and (ii), we get
⇒ 6p = 8(21 – p)
⇒ 6p = 168 – 8p
⇒ 6p + 8p = 168
⇒ 14p = 168
⇒ p = = 12 cm.
⇒ 21 - p = 21 - 12 = 9 cm.
Hence, the sides of ||gm are AB = 12 cm and BC = 9 cm.
In the figure (2) given below, the perimeter of ∆ABC is 37 cm. If the lengths of the altitudes AM, BN and CL are 5x, 6x, and 4x respectively, calculate the lengths of the sides of ∆ABC.
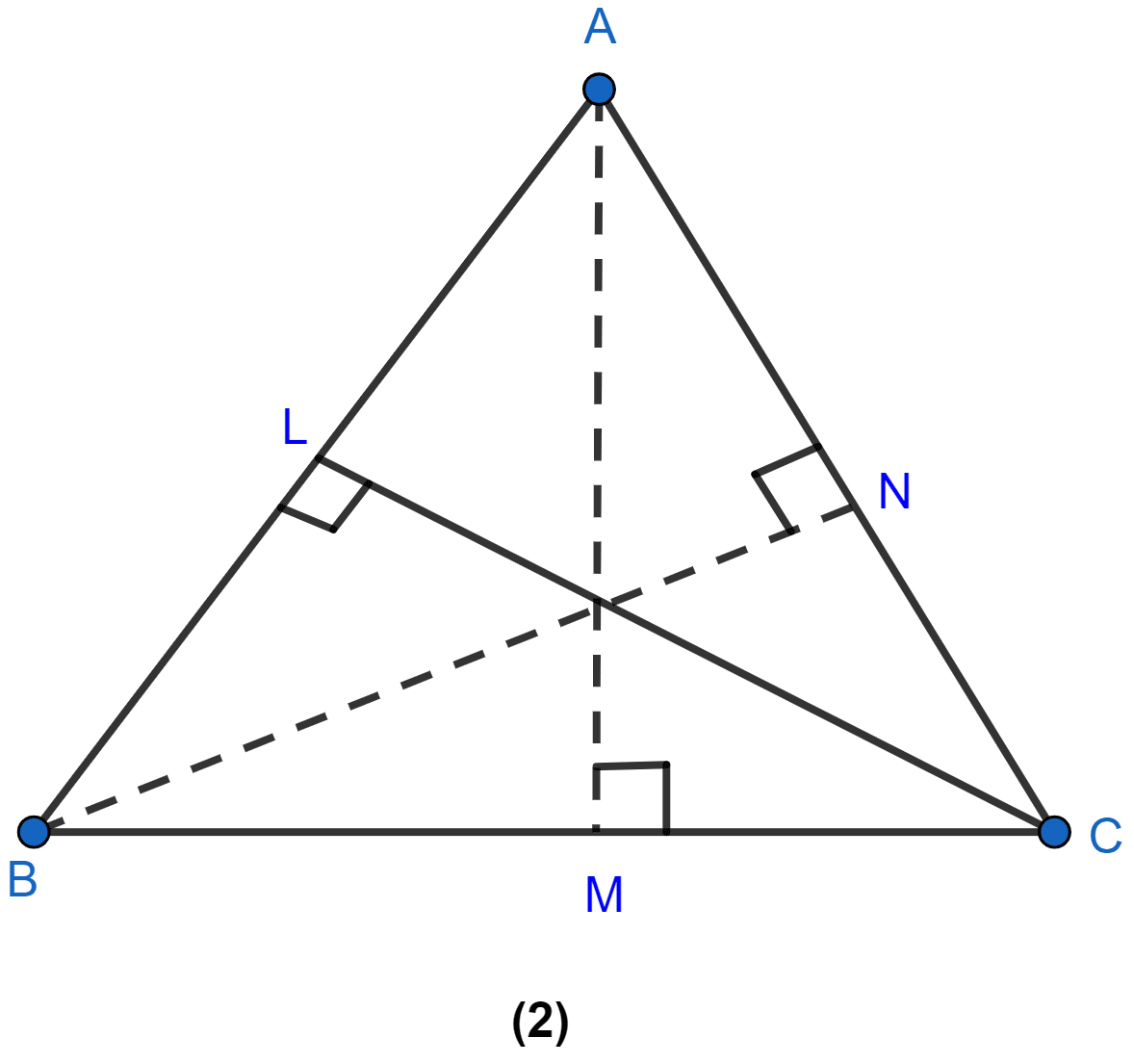
Answer
Let us consider BC = p, CA = q.
From figure,
Perimeter of ∆ABC = AB + BC + CA
⇒ 37 = AB + p + q
⇒ AB = 37 – (p + q)
Area of ∆ABC = × base × height
= × BC × AM
= × p ×
∴ Area of ∆ABC = × p × .........(i)
Also,
Area of ∆ABC = × CA × BN
= × q ×
∴ Area of ∆ABC = × q × .........(ii)
Also,
Area of ∆ABC = × AB × CL
= × (37 - p - q) ×
∴ Area of ∆ABC = × (37 - p - q) × .........(iii)
From equation (i) and (ii) we get,
From equation (ii) and (iii) we get,
⇒ CA = q = 10 cm.
⇒ BC = p = cm.
⇒ AB = (37 - p - q) = (37 - 12 - 10) = 15 cm.
Hence, AB = 15 cm, BC = 12 cm and CA = 10 cm.
In the figure(3) given below, ABCD is a parallelogram. P is a point on DC such that area of ∆DAP = 25 cm2 and the area of ∆BCP = 15 cm2. Find
(i) area of || gm ABCD
(ii) DP : PC.
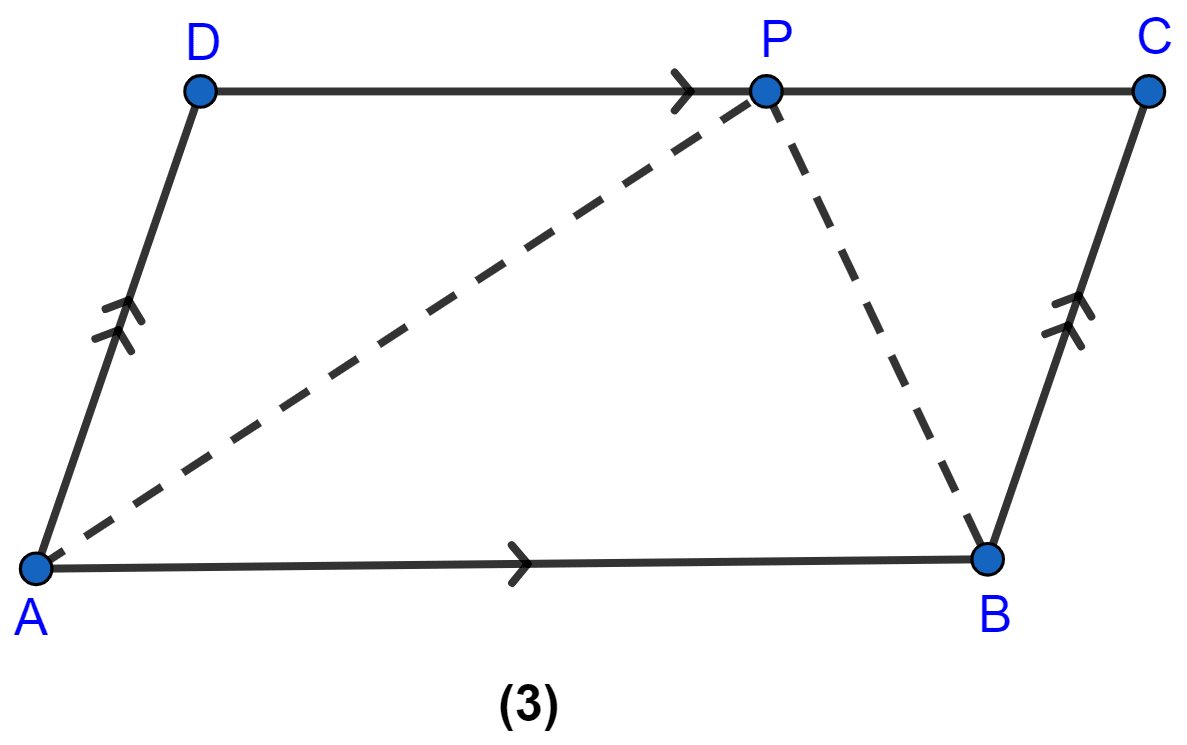
Answer
(i) Since,
∆APB and || gm ABCD have same base AB and are between same parallel lines AB and DC. So,
area of ∆APB = area of ||gm ABCD
From figure,
⇒ area of ||gm ABCD = area of (∆DAP + ∆BCP)
⇒ area of ||gm ABCD = 25 + 15 = 40
⇒ area of ||gm ABCD = 2 × 40 = 80 cm2.
Hence, area of ||gm ABCD = 80 cm2.
(ii) From figure,
∆DAP and ∆BCP are on the same base CD and between the same parallel lines CD and AB.
Hence, DP : PC = 5 : 3.
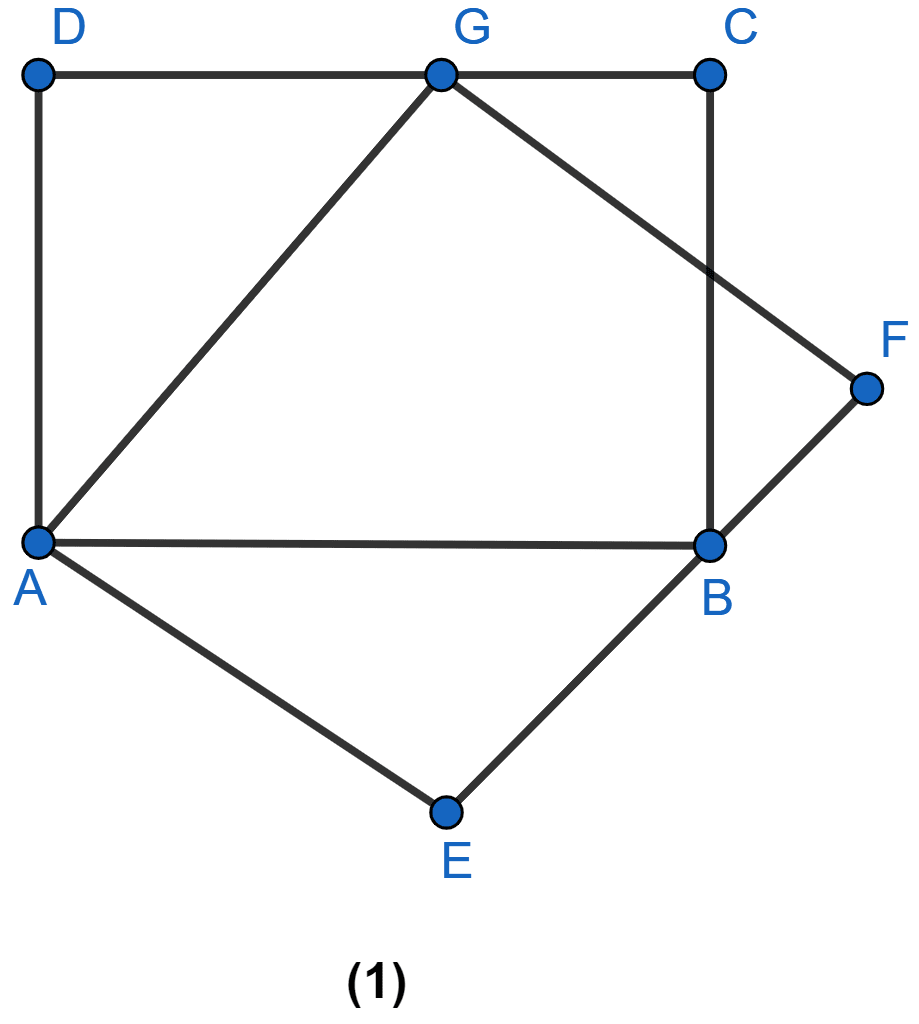
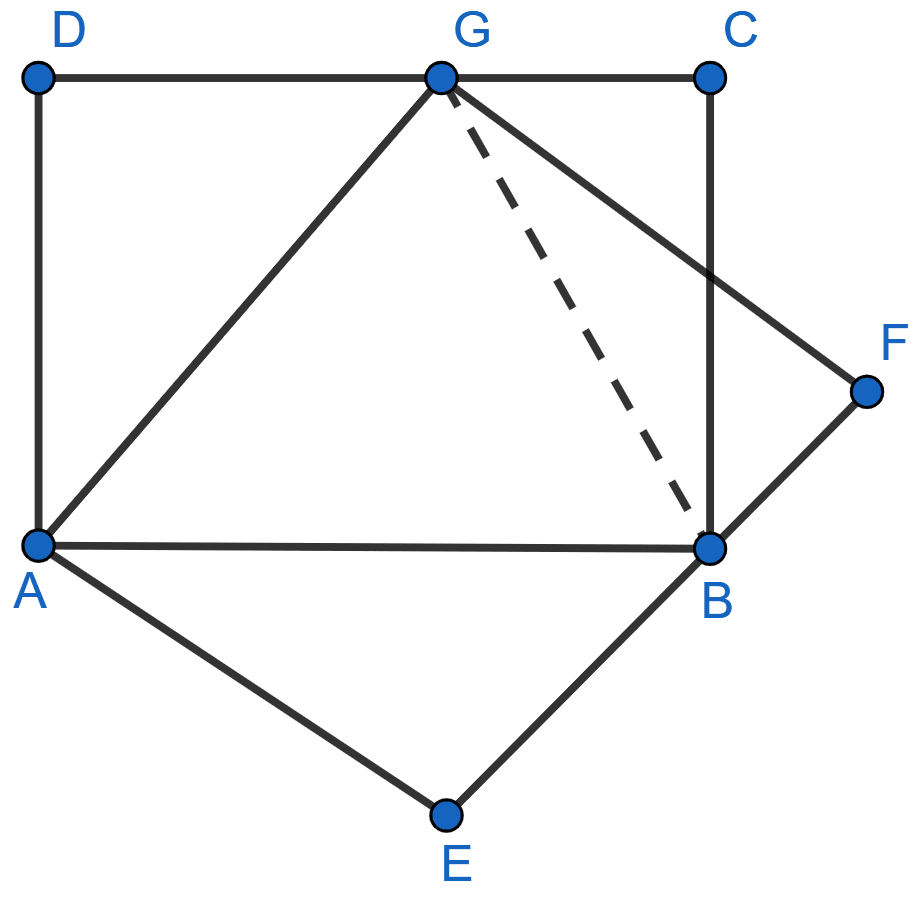
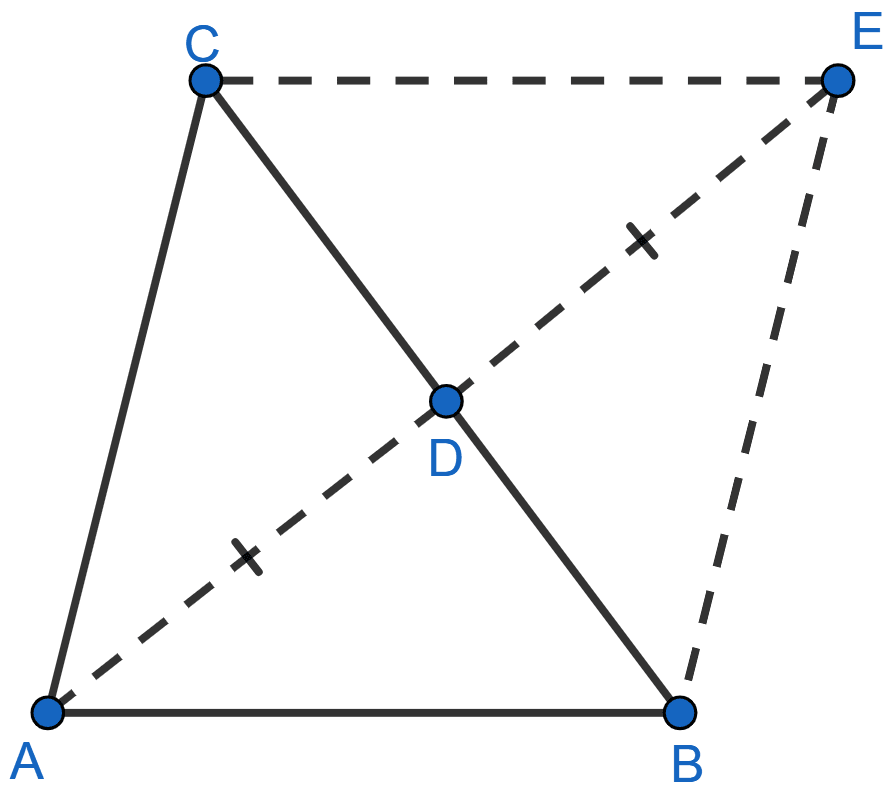
In the adjoining figure, E is the midpoint of the side AB of a triangle ABC and EBCF is a parallelogram. If the area of ∆ ABC is 25 sq. units, find the area of || gm EBCF.
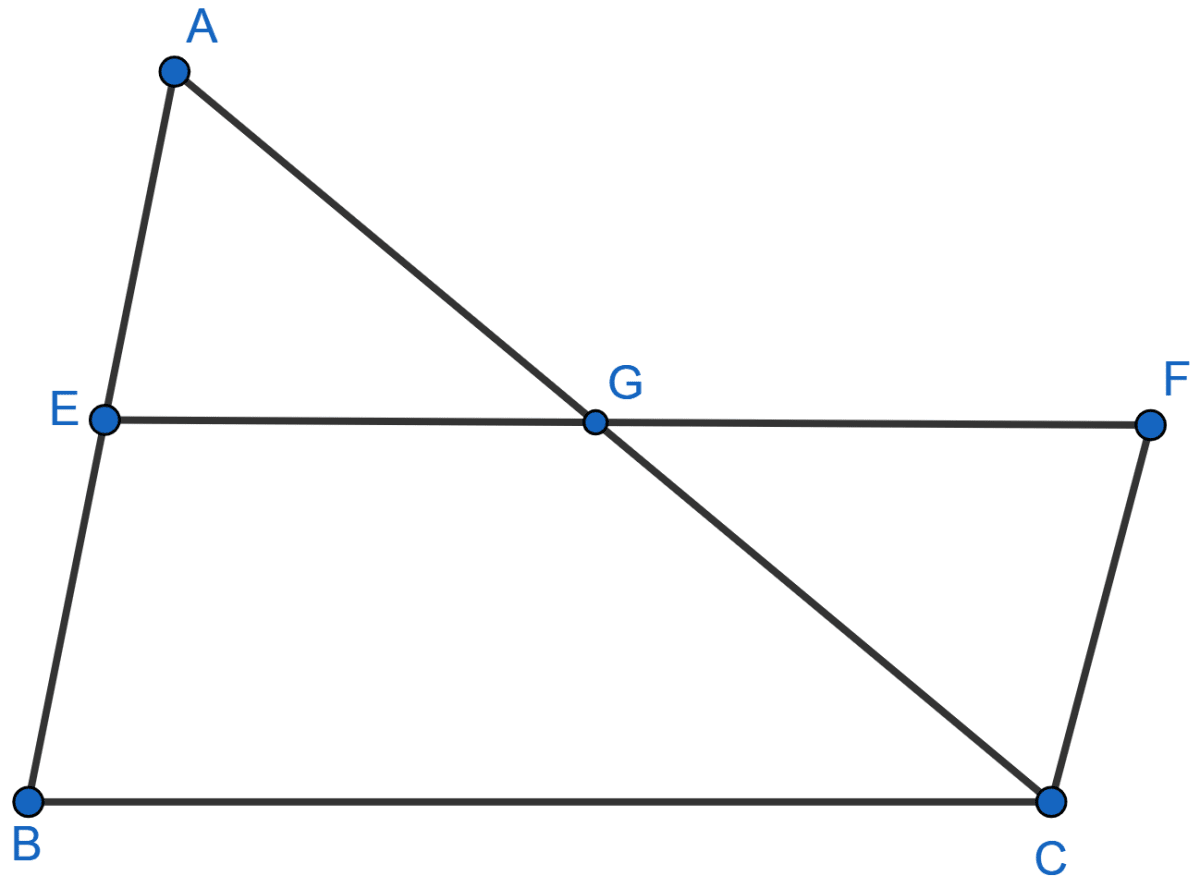
Answer
In △ABC,
As E is mid-point of AB and EF || BC so,
G is mid-point of AC (By mid-point theorem)
∴ AG = GC.
In ∆AEG and ∆CFG,
∠EAG = ∠GCF (Alternate angles are equal)
∠EGA = ∠CGF (Vertically opposite angles are equal)
AG = GC (Proved above)
Hence, ∆AEG ≅ ∆CFG (By ASA axiom)
∴ area of ∆AEG = area of ∆CFG ..........(i)
From figure,
area of || gm EBCF = area of quad. BCGE + area of ∆CFG
= area of quad. BCGE + area of ∆AEG ........(from i)
= area of ∆ABC = 25 sq. units.
Hence, area of ||gm EBCF = 25 sq. units.
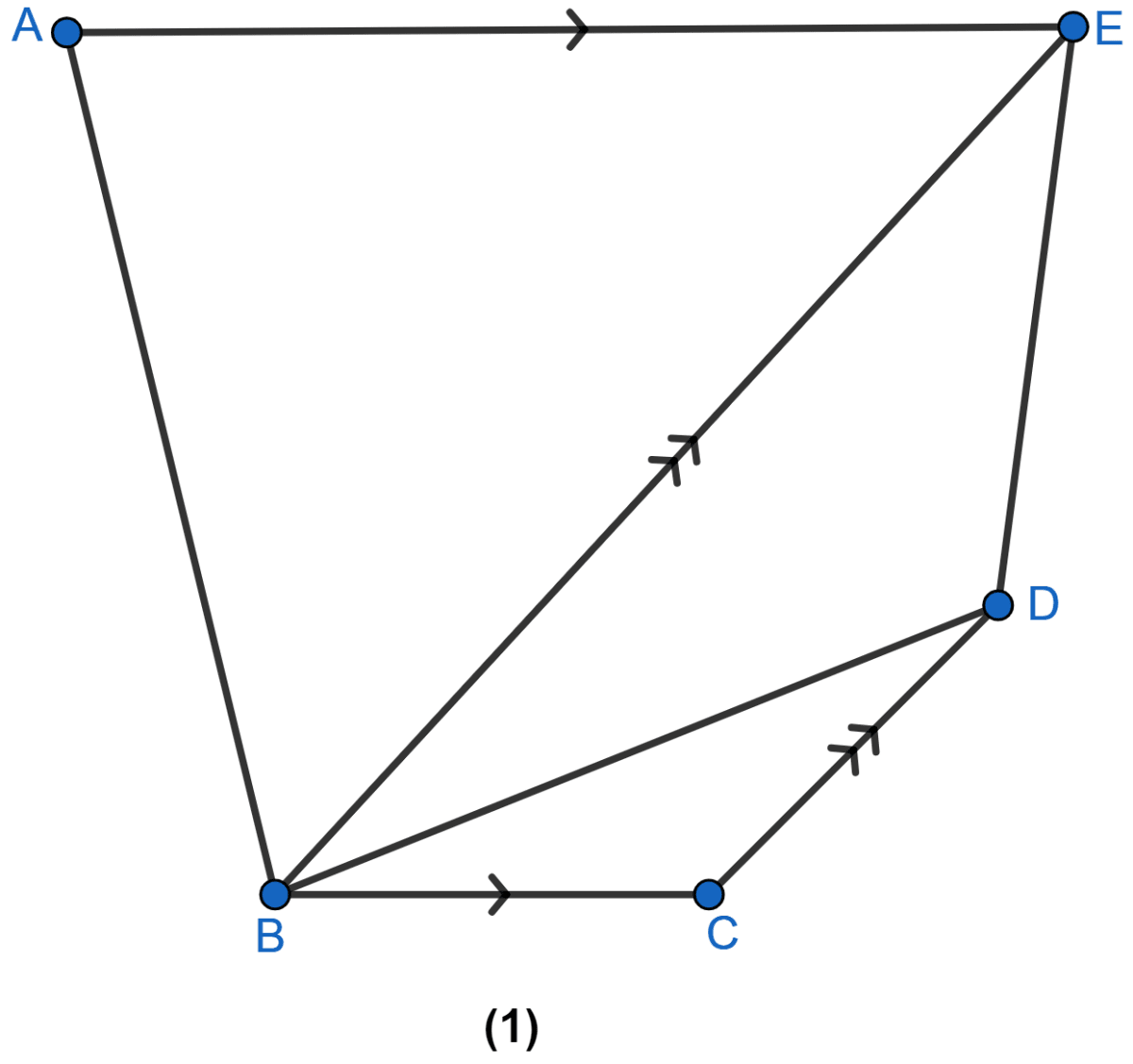
In the figure (1) given below, BC || AE and CD || BE. Prove that
area of ∆ABC= area of ∆EBD.
Answer
Join CE and AC.
From figure,
∆ABC and ∆EBC lie on same base BC and between same parallel lines BC and AE.
∴ area of ∆ABC = area of ∆EBC ....... (i)
From figure,
∆EBC and ∆EBD lie on same base BE and between same parallel lines CD and BE.
∴ area of ∆EBC = area of ∆EBD ....... (ii)
From (i) and (ii), we get
area of ∆ABC = area of ∆EBD.
Hence, proved that area of ∆ABC = area of ∆EBD.
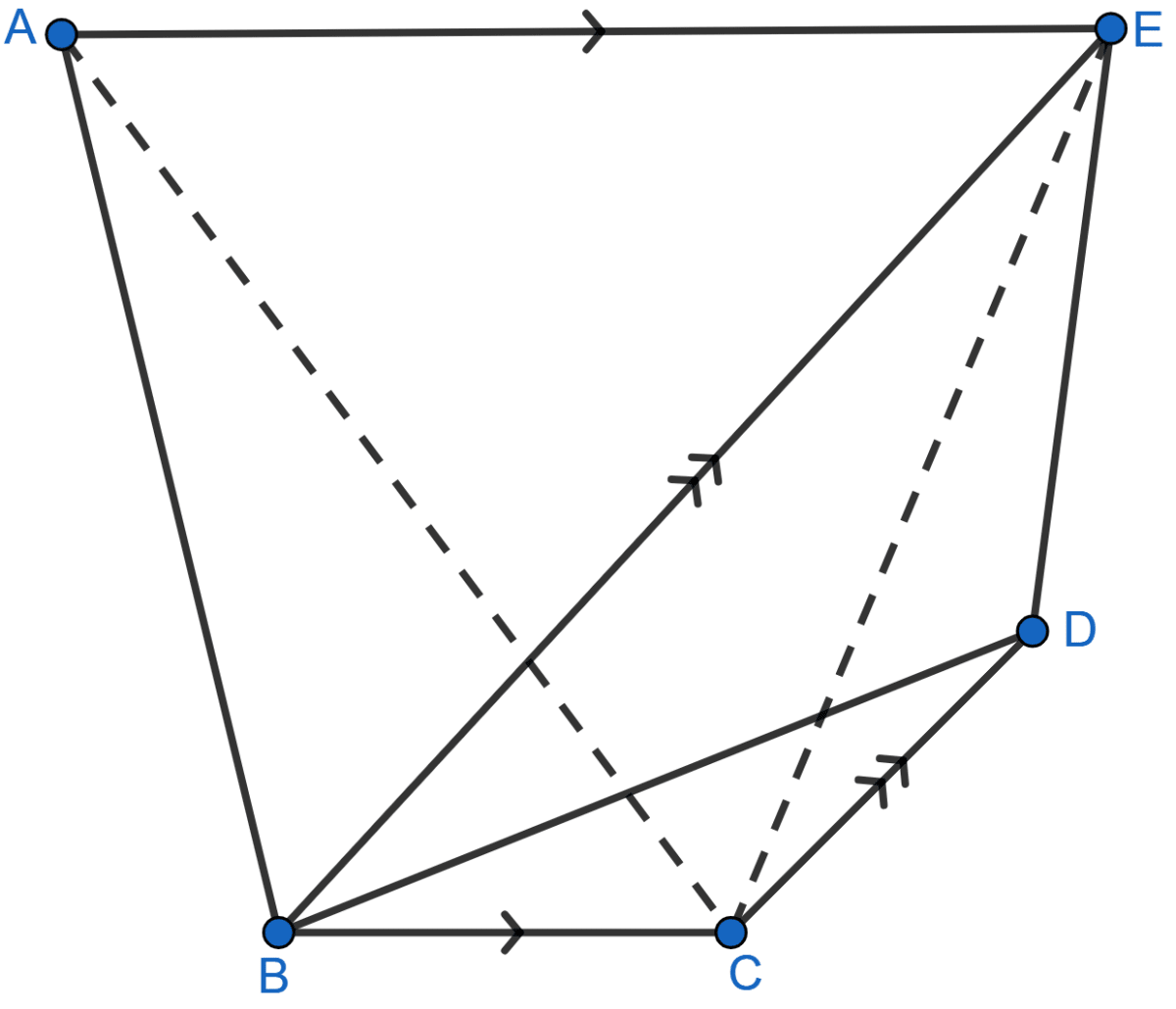
In figure (2) given below, ABC is a right-angled triangle at A. AGFB is a square on the side AB and BCDE is a square on the hypotenuse BC. If AN ⊥ ED, prove that
(i) ∆BCF ≅ ∆ABE.
(ii) area of square ABFG = area of rectangle BENM.
Answer
(i) From figure,
⇒ ∠FBC = ∠FBA + ∠ABC
∠FBA = 90° (As each angle of a square = 90°)
⇒ ∠FBC = 90° + ∠ABC ....... (1)
Also,
⇒ ∠ABE = ∠CBE + ∠ABC
∠CBE = 90° (As each angle of a square = 90°)
⇒ ∠ABE = 90° + ∠ABC .......(2)
From (1) and (2), we get
∠FBC = ∠ABE ........ (3)
Now, in ∆BCF and ∆ABE
BF = AB (As FBAG is a square)
∠FBC = ∠ABE (Proved above)
BC = BE (As BCDE is a square)
By using the SAS axiom rule of congruency,
∴ ∆BCF ≅ ∆ ABE.
Hence, proved that ∆BCF ≅ ∆ ABE.
(ii) We know that,
∆BCF ≅ ∆ABE
So, area of ∆BCF = area of ∆ABE ...... (4)
Since, ∆BCF and square AGFB have same base FB and are between same parallel lines FB and GC.
area of ∆BCF = area of square AGFB ........(5)
∆ABE and rectangle BENM are on same base BE and are between same parallel lines BE and AN.
area of ∆ABE = area of rectangle BENM ....... (6)
From (4), (5) and (6)
⇒ area of square AGFB = area of rectangle BENM
⇒ area of square AGFB = area of rectangle BENM
Hence, proved that area of square AGFB = area of rectangle BENM.
In the adjoining figure, if l || m, AF || BE, FC ⊥ m and ED ⊥ m, then the correct statement is
area of || ABEF = area of rect. CDEF
area of || ABEF = area of quad. CBEF
area of || ABEF = 2 area of △ACF
area of || ABEF = 2 area of △EBD
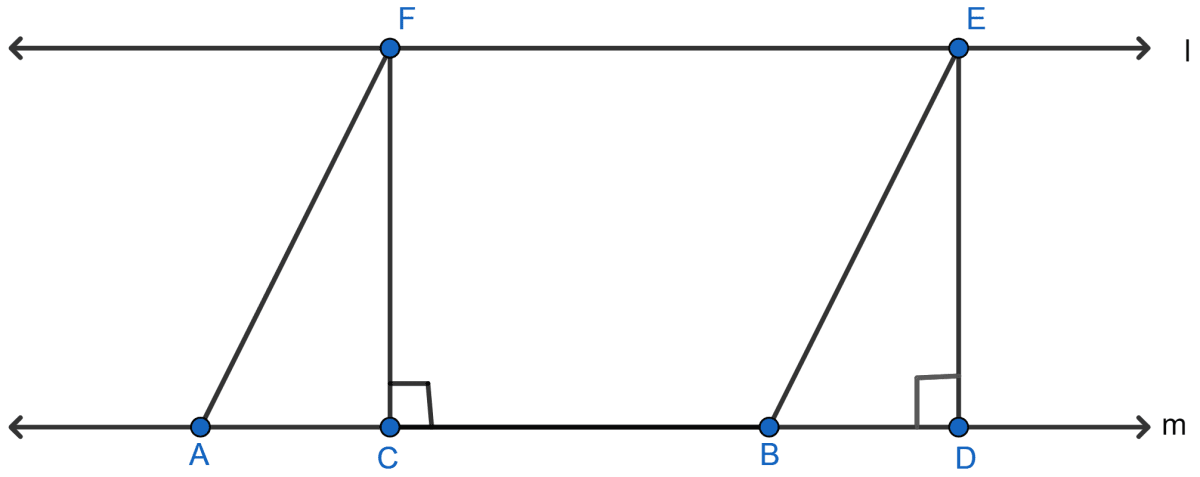
Answer
We know that,
A parallelogram and a rectangle on the same base and between the same parallel lines are equal in area.
Since, || ABEF and rectangle CDEF are on same base EF and between same parallel lines l and m.
∴ area of || ABEF = area of rect. CDEF.
Hence, Option 1 is the correct option.
Two parallelograms are on equal bases and between the same parallels. The ratio of their areas is
1 : 2
1 : 1
2 : 1
3 : 1
Answer
We know that,
Two parallelograms on equal bases and between the same parallel lines have equal areas.
So, ratio of their areas = 1 : 1.
Hence, Option 2 is the correct option.
If a triangle and a parallelogram are on the same base and between same parallels, then the ratio of area of the triangle to the area of parallelogram is
1 : 3
1 : 2
3 : 1
1 : 4
Answer
We know that,
Area of a triangle is half that of a parallelogram on the same base and between the same parallel lines.
Let area of parallelogram be x so area of triangle = .
Ratio of area of the triangle to the area of the parallelogram =
Hence, Option 2 is the correct option.
A median of a triangle divides it into two
triangles of equal area
congruent triangles
right triangles
isosceles triangles
Answer
A median of a triangle divides it into two triangles of equal area.
Hence, Option 1 is the correct option.
In the adjoining figure, area of parallelogram ABCD is
AB × BM
BC × BN
DC × DL
AD × DL

Answer
Area of || gm = base × height.
From figure,
Base = DC and Height = DL.
∴ Area of || gm = DC × DL.
Hence, Option 3 is the correct option.
The mid-points of the sides of a triangle along with any of the vertices as the fourth point make a parallelogram of area equal to
area of △ABC
area of △ABC
area of △ABC
area of △ABC
Answer
Let CDEF be a parallelogram.
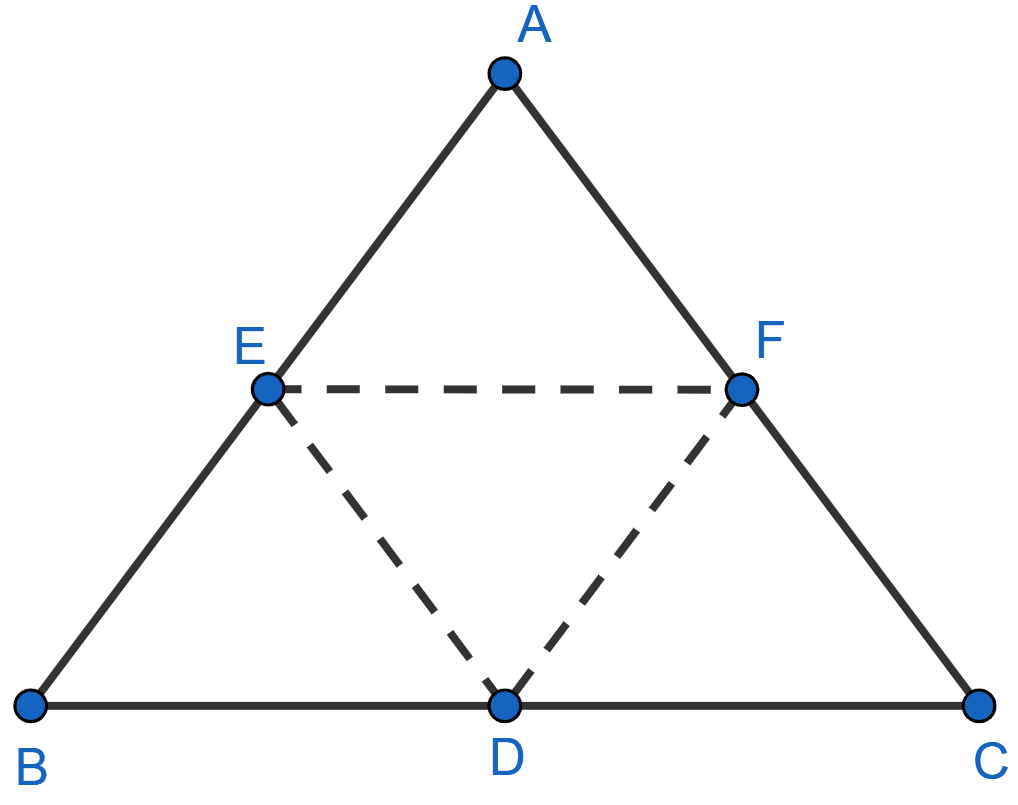
So, diagonal DF divides it into two triangles of equal area.
∴ area of △CDF = area of △EDF ........(i)
E and F are mid-points of side AB and AC respectively.
By mid-point theorem,
EF = BC = BD (As D is mid-point of BC) and EF || BC.
Since, FE || BC so from figure,
EF || BD and EF = BD.
So, EBDF is a paralleogram with diagonal ED dividing it into two triangles of equal area.
∴ area of △EBD = area of △EDF ........(ii)
E and D are mid-points of side AB and BC respectively.
By mid-point theorem,
ED = AC = AF (As F is mid-point of AC) and ED || AC.
Since, ED || AC so from figure,
ED || AF.
So, AEDF is a paralleogram with diagonal EF dividing it into two triangles of equal area.
∴ area of △AEF = area of △EDF ........(iii)
From (i), (ii) and (iii) we get,
area of △EDF = area of △CDF = area of △EBD = area of △AEF = x
From figure,
area of △ABC = area of △EDF + area of △CDF + area of △EBD + area of △AEF = 4x.
area of || gm EDCF = area of △EDF + area of △CDF = 2x.
So,
area of || gm EDCF = area of △ABC.
Hence, Option 1 is the correct option.
In the adjoining figure, ABCD is a trapezium with parallel sides AB = a cm and DC = b cm. E and F are mid-points of the non-parallel sides. The ratio of area of ABFE and area of EFCD is
a : b
(3a + b) : (a + 3b)
(a + 3b) : (3a + b)
(2a + b) : (3a + b)
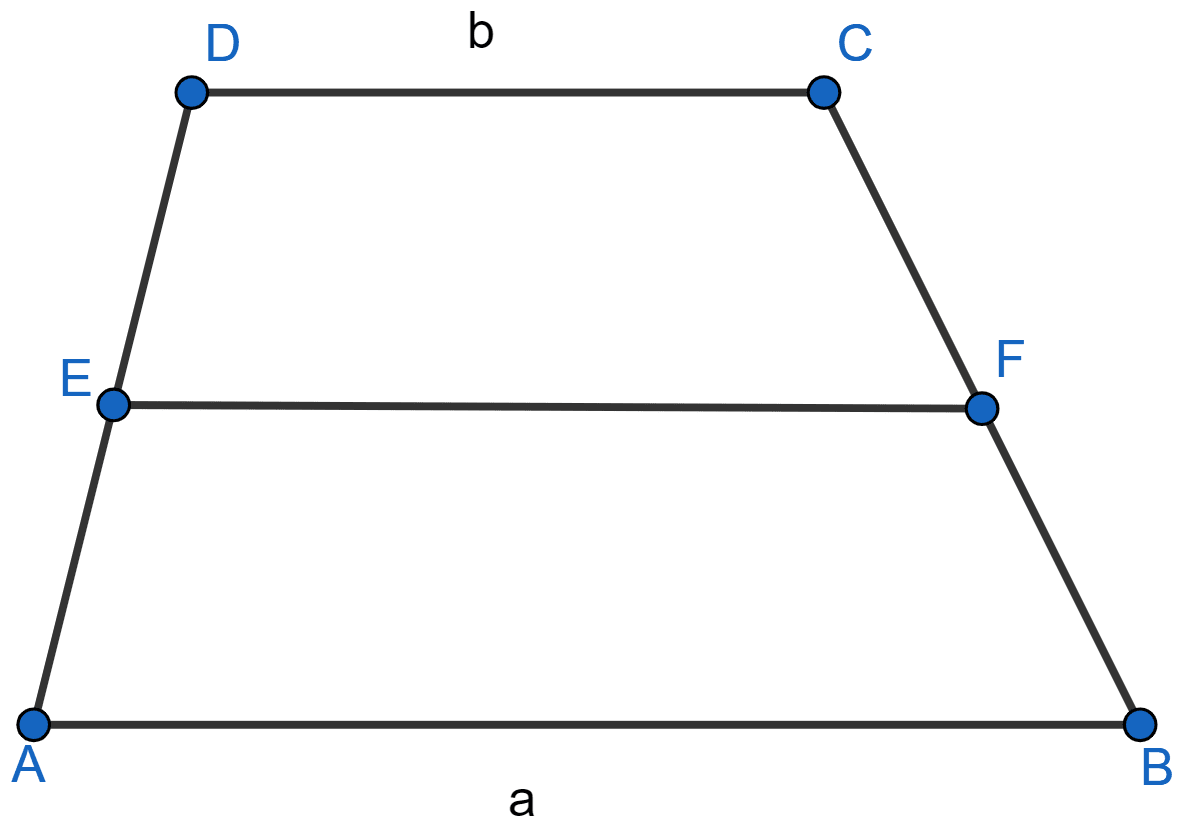
Answer
It is given that
AB = a cm
DC = b cm
AB || DC
E and F are the mid-points of AD and BC
Consider h as the distance between AB, CD and EF
Now join BD which intersects EF at M
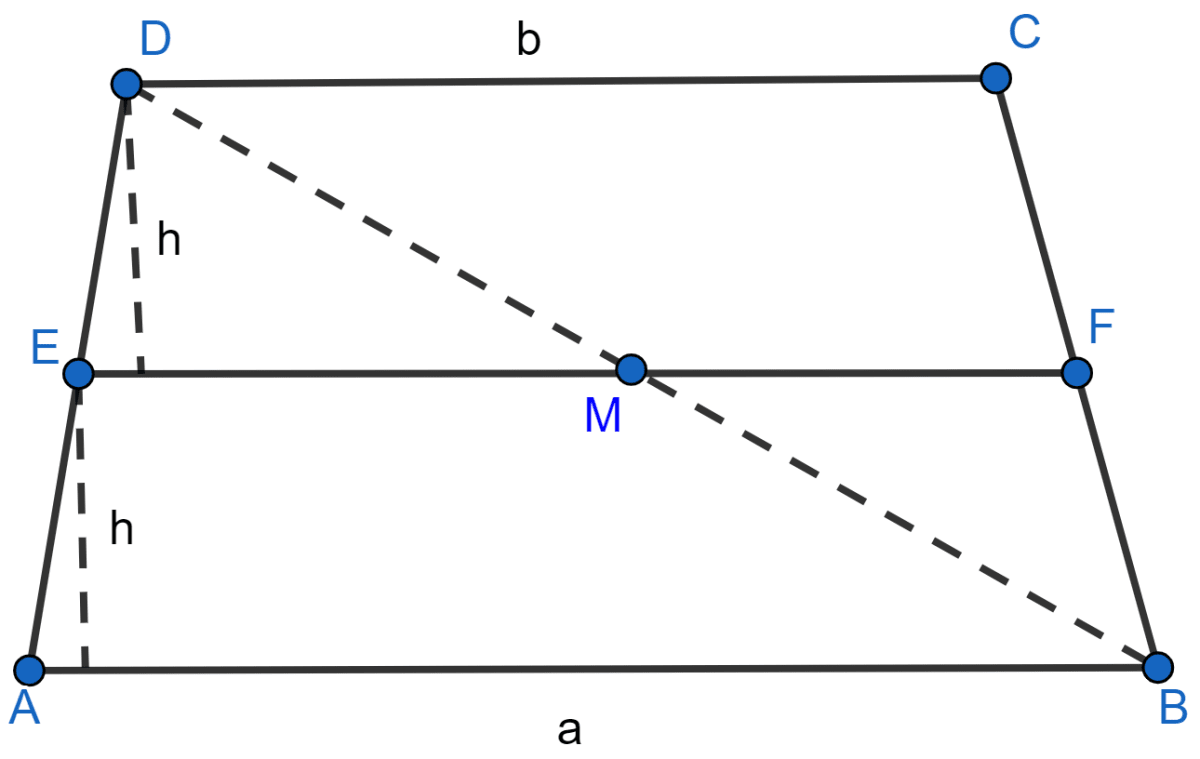
In ∆ABD,
E is the midpoint of AD and EM || AB
By midpoint theorem,
M is the midpoint of BD
and
EM = AB ........ (1)
In ∆CBD,
F is mid-point of BC and M is mid-point of BD so by mid-point theorem,
MF = CD ......... (2)
Adding equations (1) and (2)
EM + MF = AB + CD
EF = (AB + CD)
EF = (a + b)
Here,
Area of trapezium ABFE = [sum of parallel sides] × [distance between parallel sides]
Substituting the values,
Similarly,
Required ratio = Area of trapezium ABFE / Area of trapezium EFCD
By substituting the values,
Hence, Option 2 is the correct option.
In the adjoining figure, AB || DC and AB ≠ DC. If the diagonals AC and BD of the trapezium ABCD intersect at O, then which of the following statements is not true ?
area of △ABC = area of △ABD
area of △ACD = area of △BCD
area of △OAB = area of △OCD
area of △OAD = area of △OBC
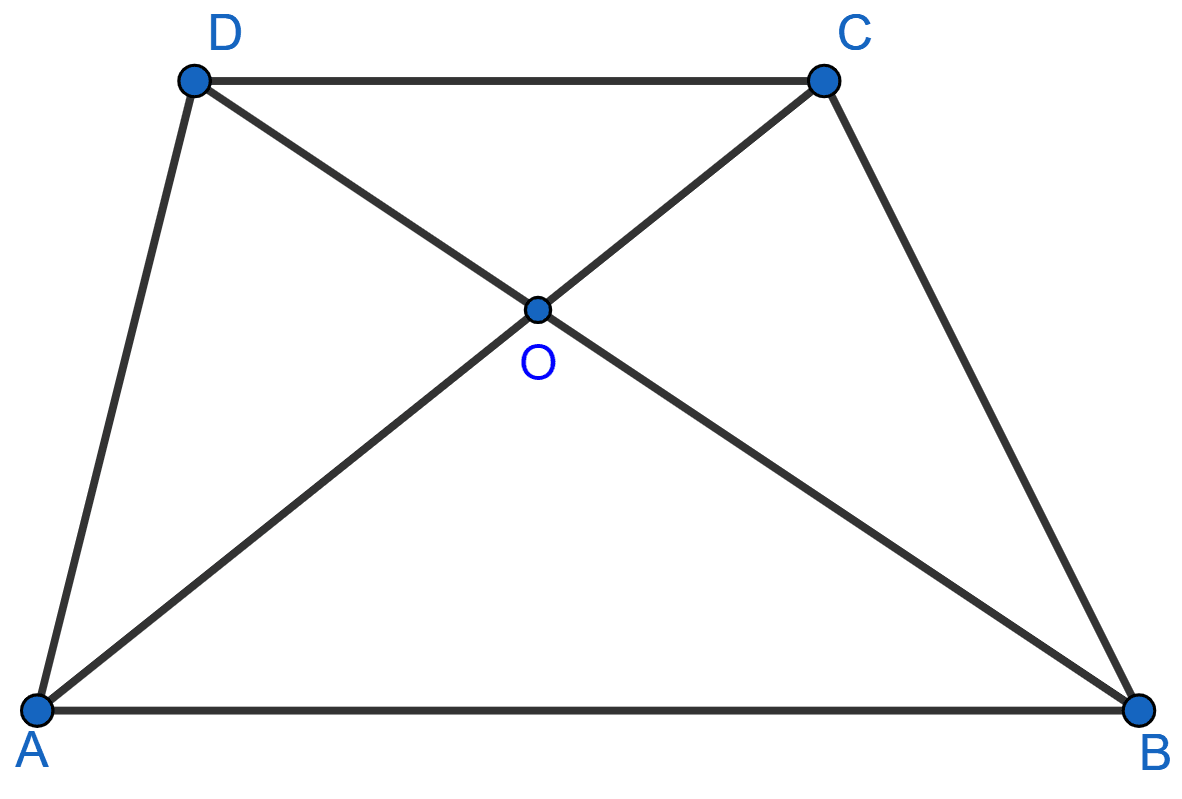
Answer
We know that,
Triangles on the same base and between same parallel lines are equal in area.
Hence,
⇒ area of △ABC = area of △ABD ........ (1)
⇒ area of △ACD = area of △BCD
From figure and eqn. (1),
area of (△AOB + △OAD) = area of (△AOB + △OBC)
⇒ area of △OAD = area of △OBC.
Hence, Option 3 is the correct option.
Consider the following two statements:
Statement 1: The line segment joining the mid-points of a pair of opposite sides of a parallelogram divides it into two equal parallelograms.
Statement 2: Diagonals of a parallelogram divide it into four triangles of equal area.
Which of the following is valid?
Both the statements are true.
Both the statements are false.
Statement 1 is true, and Statement 2 is false.
Statement 1 is false, and Statement 2 is true.
Answer
Let ABCD be a parallelogram in which E and F are mid-points of AB and CD respectively. Join EF.
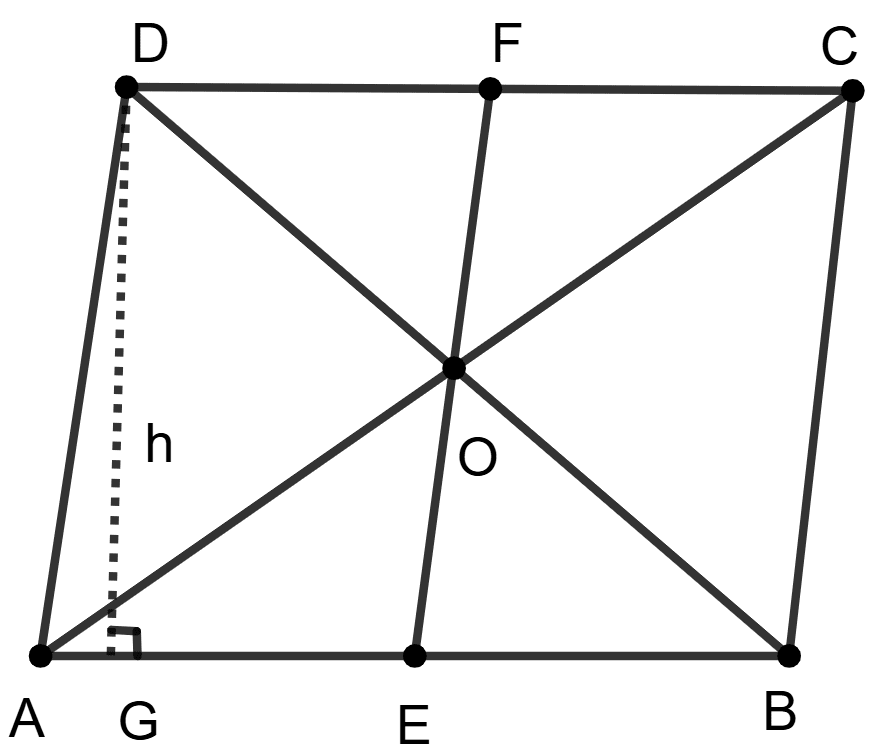
Let us construct DG ⊥ AB and let DG = h, where h is the altitude on side AB.
Area of || gm ABCD = base × height = AB × h
Area of ||gm AEFD = AE × h = × h ...................(1) [Since E is the mid-point of AB]
Area of ||gm EBCF = EB × h = × h ...................(2) [Since E is the mid-point of AB]
From (1) and (2),
Area of || gm AEFD = Area of || gm EBCF.
Thus, the line segment joining the mid-points of a pair of opposite sides of a parallelogram divides it into two equal parallelograms.
∴ Statement 1 is true.
From figure,
The diagonals AC and BD cut at point O.
In parallelogram, the diagonals bisect each other.
∴ AO = OC
In ∆ACD, O is the mid-point of AC.
∴ OD is the median.
Area of ∆AOD = Area of ∆COD ................. (3) [Median of ∆ divides it into two triangles of equal areas.]
Similarly, in ∆ABC
O is the mid-point of AC.
∴ OB is the median.
Area of ∆AOB = Area of ∆COB ................. (4) [Median of ∆ divides it into two triangles of equal areas.]
In ∆ADB,
O is the mid-point of BD.
∴ OA is the median.
Area of ∆AOD = Area of ∆AOB ................. (5)
From (3), (4) and (5) we get,
Area of ∆AOB = Area of ∆COB = Area of ∆COD = Area of ∆AOD
So proved, that the diagonals of a parallelogram divide it into four triangles of equal area.
∴ Statement 2 is true.
∴ Both the statements are true.
Hence, option 1 is the correct option.
Assertion (A): Area of trapezium = (sum of parallel sides) x height.
Reason (R): A parallelogram and a rectangle on the same base and between the same parallel lines are equal in area.
Assertion (A) is true, Reason (R) is false.
Assertion (A) is false, Reason (R) is true.
Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).
Answer
By formula,
Area of trapezium = (sum of parallel sides) x height.
∴ Assertion (A) is true.
We know that,
Parallelograms on the same base and between the same parallel lines are equal in area.
A rectangle is a special type of parallelogram.
Thus, a parallelogram and a rectangle on the same base and between the same parallel lines have equal areas.
∴ Reason (R) is true.
∴ Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).
Hence, option 4 is the correct option.
Assertion (A): In the adjoining figure, the two triangles are equal figures.
Reason (R): Two figures are called equal if and only if they have the same area.
Assertion (A) is true, Reason (R) is false.
Assertion (A) is false, Reason (R) is true.
Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).
Answer
When two figures are referred to as "equal figures," it specifically means that they have the same area. It does not imply that they are congruent.
∴ Reason (R) is true.
As we know that area of a triangle = x base x height
Area of first triangle = x 8 x 6
= x 48
= 24 cm2.
Area of second triangle = x 12 x 4
= x 48
= 24 cm2.
So, area of first triangle = area of second triangle.
∴ Assertion (A) is true.
∴ Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).
Hence, option 3 is the correct option.
Assertion (A): Two triangles having equal area are congruent.
Reason (R): Two congruent triangles have equal area.
Assertion (A) is true, Reason (R) is false.
Assertion (A) is false, Reason (R) is true.
Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).
Answer
Having equal areas does not necessarily mean two triangles are congruent.Congruent triangles must have the same shape and the same size.
Triangles with the same area can have different shapes.
∴ Assertion (A) is false.
Congruent triangles are identical in every aspect; they have the same shape and the same size.
If two figures are identical in size, they must occupy the same amount of space, and therefore, they must have the same area.
∴ Reason (R) is true.
∴ Assertion (A) is false, Reason (R) is true.
Hence, option 2 is the correct option.
In the figure (1) given below, ABCD is a rectangle (not drawn to scale) with side AB = 4 cm and AD = 6 cm. Find
(i) the area of parallelogram DEFC
(ii) area of △EFG.

Answer
(i) We know that,
A parallelogram and a rectangle on the same base and between the same parallel lines are equal in area.
From figure,
rectangle ABCD and parallelogram DEFC are on the same base DC and between same parallel lines DG and AF.
Hence, area of || gm DEFC = area of rectangle ABCD
= AB × AD
= 4 × 6
= 24 cm2.
Hence, area of || gm DEFC = 24 cm2.
(ii) We know that,
Area of a triangle is half that of a parallelogram on the same base and between the same parallel lines.
Since, triangle GEF and || gm DEFC are on same base EF and between same parallel lines DG and AF so,
area of △EFG = area of || gm DEFC
= cm2.
Hence, area of △EFG = 12 cm2.
In the figure (2) given below, PQRS is a parallelogram formed by drawing lines parallel to the diagonals of a quadrilateral ABCD through its corners. Prove that area of || gm PQRS = 2 × area of quad. ABCD.
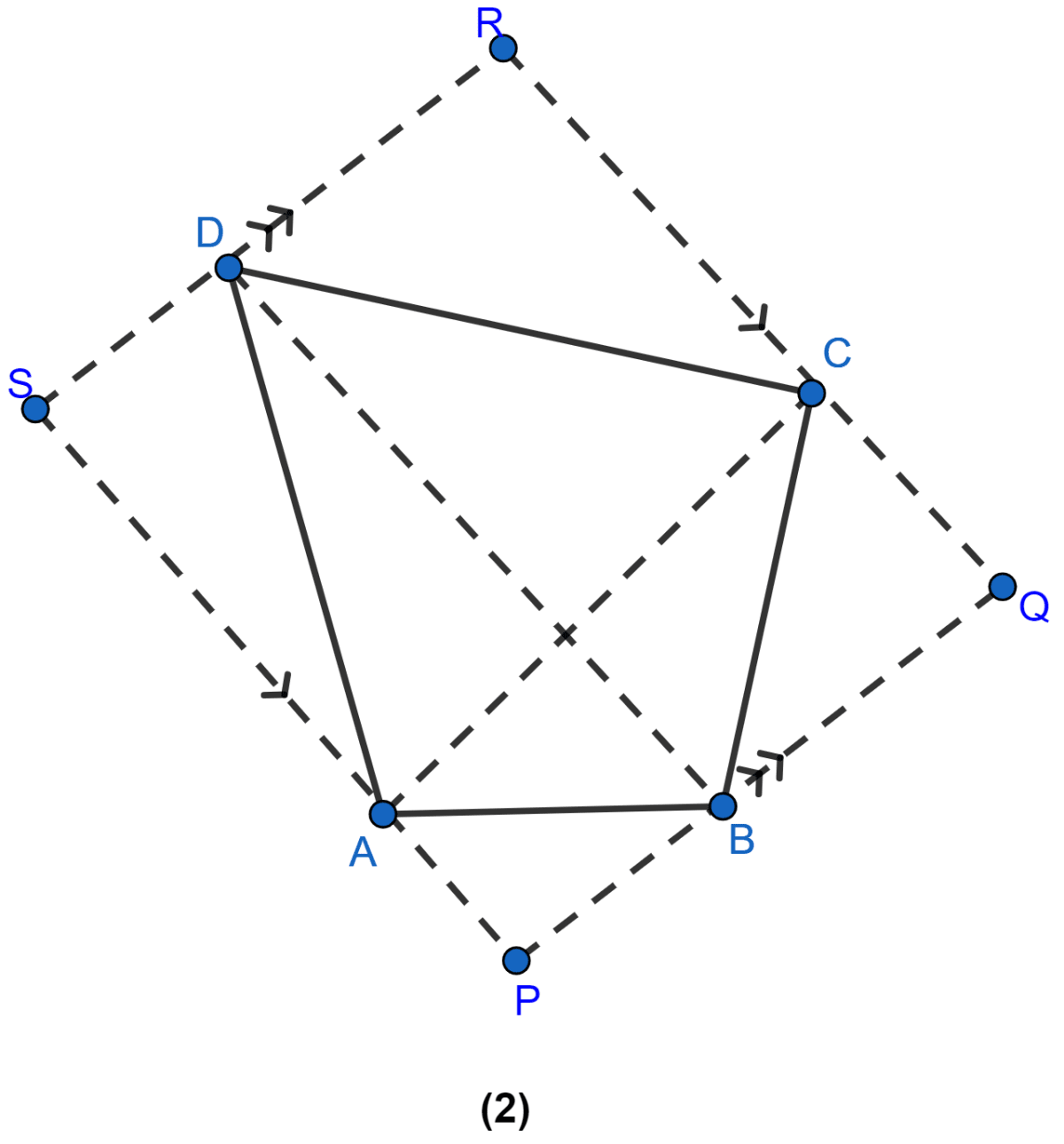
Answer
From figure,
Area of ∆ACD = Area of || gm ACRS [As both are on same base AC and between the same parallel lines AC and SR]
⇒ Area of || gm ACRS = 2 Area of ∆ACD .......(i)
Similarly,
Area of ∆ABC = Area of || gm ∆APQC [As both are on same base AC and between the same parallel lines AC and PQ]
⇒ Area of || gm APQC = 2 Area of ∆ABC .......(ii)
Adding (i) and (ii),
⇒ Area of || gm ACRS + Area of || gm APQC = 2 Area of ∆ACD + 2 Area of ∆ABC
⇒ Area of || gm PQRS = 2[Area of ∆ACD + Area of ∆ ABC]
⇒ Area of || gm PQRS = 2(Area of quad. ABCD)
Hence, proved that area of || gm PQRS = 2 x area of quad. ABCD.
In the parallelogram ABCD, P is a point on the side AB and Q is a point on the side BC. Prove that
(i) area of ∆CPD = area of ∆AQD
(ii) area of ∆ADQ = area of ∆APD + area of ∆CPB.
Answer
Parallelogram ABCD with point P on the side AB and Q on the side BC is shown below:

∆CPD and || gm ABCD are on the same base CD and between the same parallels lines AB and CD.
∴ Area of ∆CPD = Area of || gm ABCD ......(1)
∆AQD and || gm ABCD are on the same base AD and between the same parallel lines AD and BC,
∴ Area of ∆AQD = Area of || gm ABCD .......(2)
From (1) and (2),
Area of ∆CPD = Area of ∆AQD.
Hence, proved that area of ∆CPD = area of ∆AQD.
(ii) From part (i) we get,
Area of ∆CPD = Area of || gm ABCD
∴ Area of || gm ABCD - Area of ∆CPD = Area of || gm ABCD ........(3)
From figure,
Area of || gm ABCD - Area of ∆CPD = Area of ∆APD + Area of ∆CPB .........(4)
From (3) and (4) we get,
⇒ Area of ∆APD + Area of ∆CPB = Area of || gm ABCD
Since,
Area of ∆ADQ = Area of || gm ABCD (From eq 2)
⇒ Area of ∆APD + Area of ∆CPB = Area of ∆ADQ.
Hence, proved that area of ∆ADQ = area of ∆APD + area of ∆CPB.
In the adjoining figure, X and Y are points on the side LN of triangle LMN. Through X, a line is drawn parallel to LM to meet MN at Z. Prove that area of ∆LZY = area of quad. MZYX.
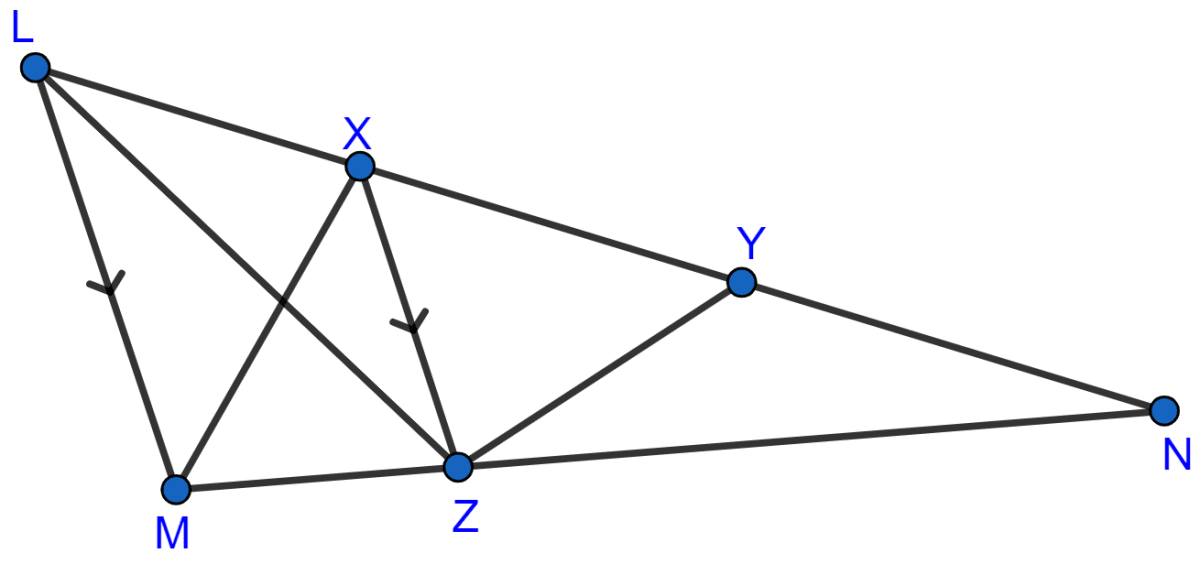
Answer
From figure,
∆LZX and ∆MZX are on the same base XZ and between the same parallel lines LM and XZ.
∴ Area of ∆LZX = Area of ∆MZX
Adding area ∆XZY to both sides of the above equation we get,
⇒ area of ∆LZX + area ∆XZY = area ∆MZX + area ∆XZY
From figure,
∆LZX + ∆XZY = ∆LZY and ∆MZX + ∆XZY = MZYX.
∴ Area of ∆LZY = Area of quadrilateral MZYX.
Hence, proved that area of ∆LZY = area of quadrilateral MZYX.
Perpendiculars are drawn from a point within an equilateral triangle to the three sides. Prove that the sum of the three perpendiculars is equal to the altitude of the triangle.
Answer
Since, ABC is an equilateral triangle. Let each side be x cm.
PN, PM, and PL are perpendicular on side AB, AC and BC respectively. AD is any altitude from point A on side BC.
Join PA, PB and PC.
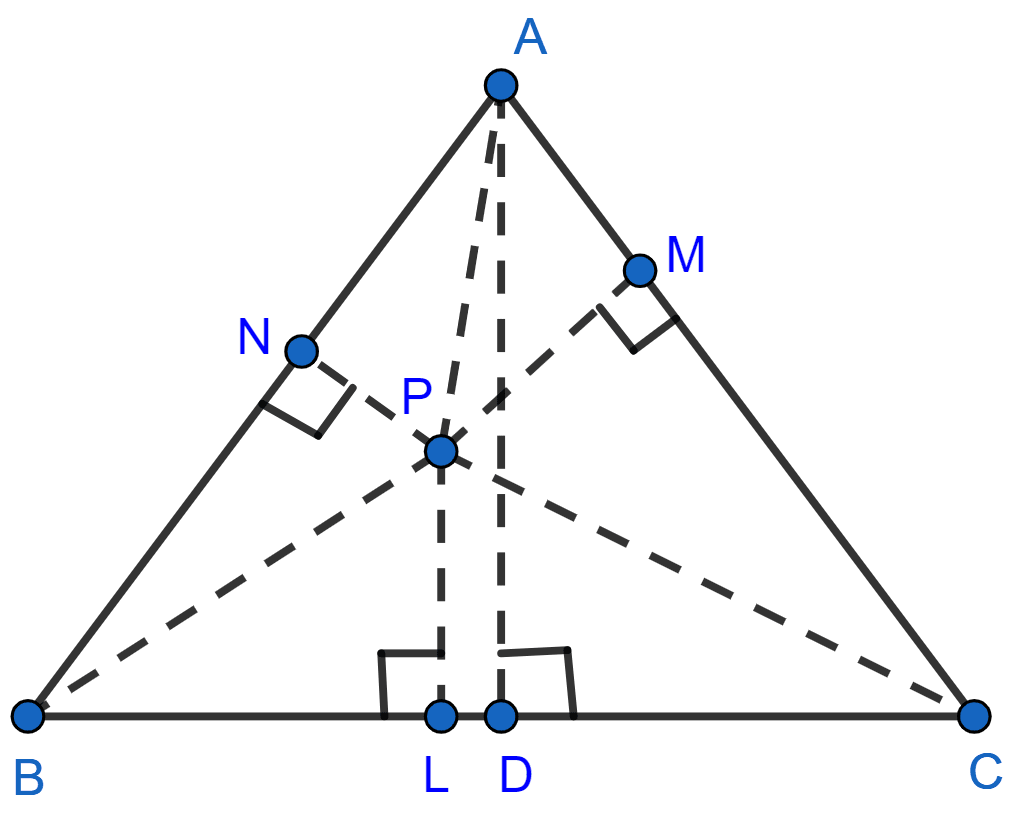
Area of ∆ABC = × Base × Altitude
= ........(1)
Area of ∆APB = × AB × NP ........(2)
Area of ∆APC = × AC × MP ........(3)
Area of ∆BPC = × BC × LP ........(4)
Adding (2), (3) and (4)
⇒ Area of (∆APB + ∆APC + ∆BPC) = × (AB × NP + AC × MP + BC × LP)
From figure,
∴ Area of ∆ABC = [NP + MP + LP] .......(5)
From (1) and (5),
× AD = × (NP + LP + MP)
⇒ AD = NP + LP + MP.
Hence, proved that the sum of three perpendiculars is equal to the altitude of the triangle.
If each diagonal of a quadrilateral divides it into two triangles of equal areas, then prove that the quadrilateral is a parallelogram.
Answer
Let ABCD be a quadrilateral such that each diagonal divides it into triangles of equal areas, then
area of △ABC = Area of ABCD, .......(1)
area of △ABD = Area of ABCD, ......(2)
area of △BCD = Area of ABCD, .......(3)
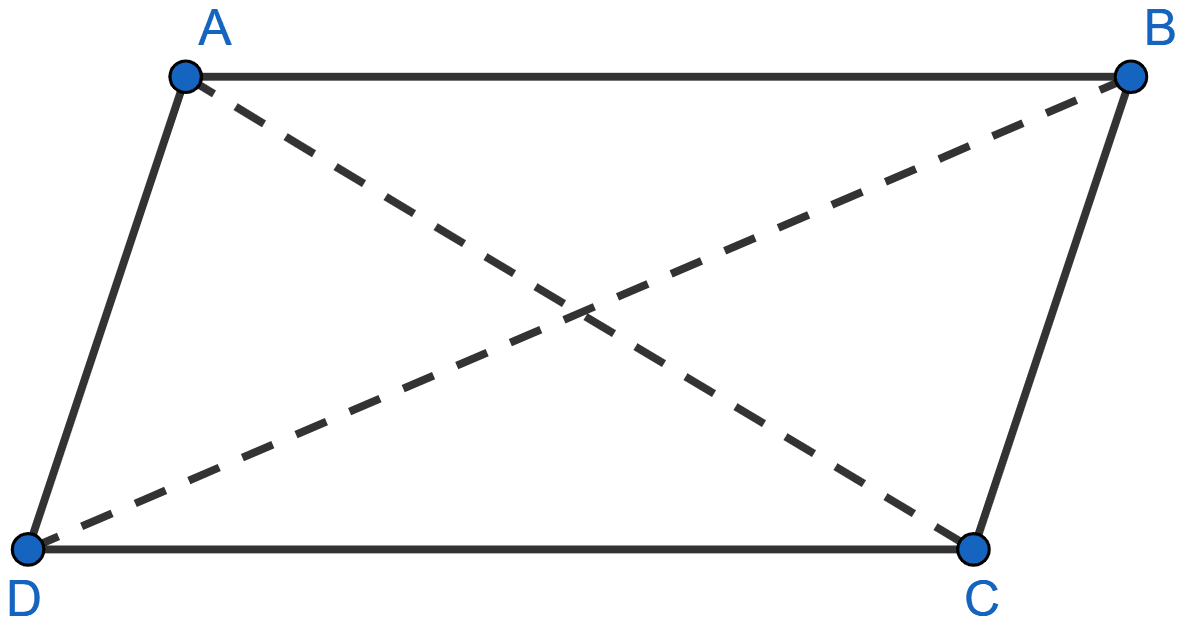
We know that,
Triangles on the same base and having equal areas lie between the same parallel lines.
From (1) and (2) we get,
Area of △ABC = Area of △ABD.
Since, △ABC and △ABD lie on same base AB and have equal area.
So, AB || CD.
From (1) and (3) we get,
∴ Area of △ABC = Area of △BCD.
Since, △ABC and △BCD lie on same base BC and have equal area.
So, BC || AD.
Since, AB || CD and BC || AD.
Hence, proved ABCD is a parallelogram.
In the adjoining figure, ABCD is a parallelogram in which BC is produced to E such that CE = BC. AE intersects CD at F. If area of ∆DFB = 3 cm2, find the area of parallelogram ABCD.

Answer
From figure,

BE is a straight line.
Since, BC || AD,
∴ CE || AD.
Hence, ACED is a parallelogram.
Diagonals AE and DC of || ACED bisect each other, so F is mid-point of DC.
So, BF is median of △BDC.
Since, median divides triangle into two triangles with equal areas.
∴ area of △BFC = area of △DFB = 3 cm2.
area of △BDC = area of △BFC + area of △DFB = 6 cm2.
From figure,
⇒ area of △BDC = area of || gm ABCD (As || gm ABCD and △BDC lie on same base CD and between same parallel lines AB and CD.)
⇒ 6 = area of || gm ABCD
⇒ area of || gm ABCD = 12 cm2.
Hence, area of || gm ABCD = 12 cm2.
In the adjoining figure, ABCD is a square. E and F are mid-points of sides BC and CD respectively. If R is mid-point of EF, prove that:
area of ∆AER = area of ∆AFR

Answer
In ∆ABE and ∆ADF,
AB = AD (Sides of a square)
∠B = ∠D (Each angle of a square = 90°)
BE = DF (E is mid-point of BC and F is mid-point of DC)
∴ ∆ABE ≅ ∆ADF (SAS axiom)
∴ AE = AF (c.p.c.t.)
Again in ∆AER and ∆AFR
AE = AF (Proved above)
AR = AR (Common)
ER = FR (R is mid-point of EF)
∴ ∆AER ≅ ∆AFR (SSS axiom)
∴ Area of ∆AER = Area of ∆AFR
Hence, proved that area of ∆AER = area of ∆AFR.
In the adjoining figure, X and Y are mid-points of the sides AC and AB respectively of ∆ABC. QP || BC and CYQ and BXP are straight lines. Prove that area of ∆ABP = area of ∆ACQ.
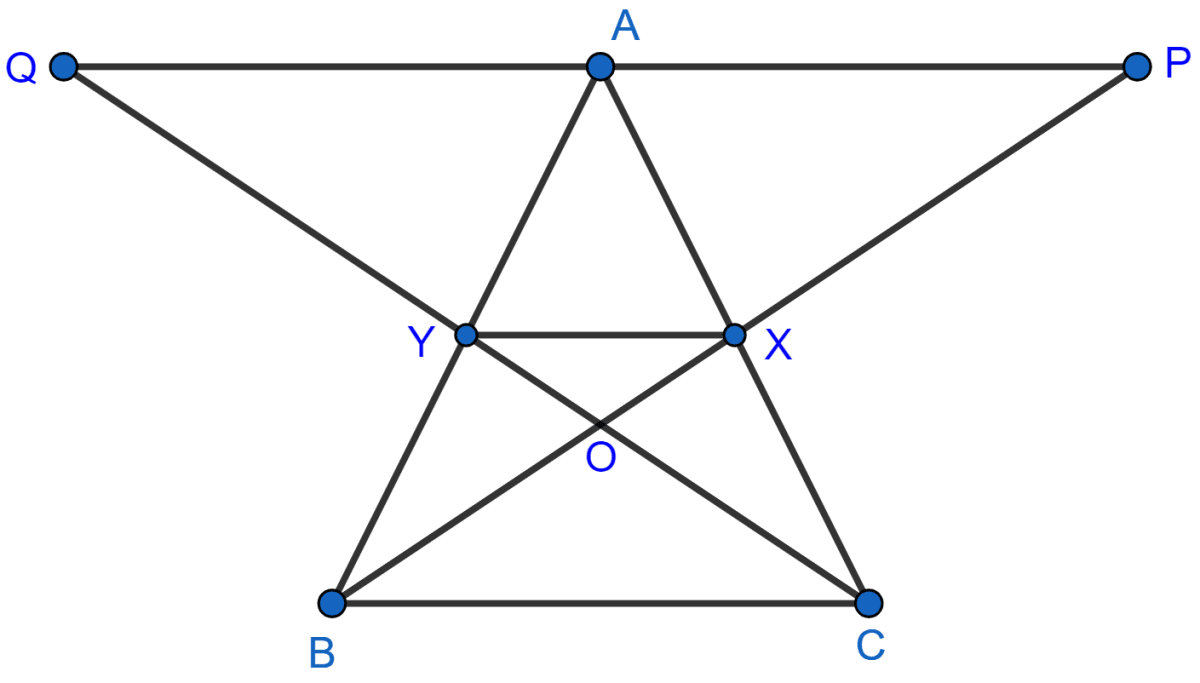
Answer
X and Y are the mid-points of sides AC and AB respectively.
Since, X and Y are midpoints of AC and AB respectively.
In ∆ABC,
XY || BC (By midpoint theorem).
Given, QP || BC
∴ QP || BC || XY
In ∆BAP, Y is mid of AB and XY || AP
∴ X is mid-point of BP (Converse of mid-point theorem)
∴ XY = AP .......(1)
Similarly we can prove in ∆AQC
X is mid-point of AC and XY is parallel to QA
∴ Y is mid-point of QC (Converse of mid-point theorem)
XY = QA .......(2)
From (1) and (2),
⇒
⇒ QA = AP.
Thus, ∆ABP and ∆ACQ are on the equal bases (QA = AP) and between the same parallel lines BC and QP
∴ Area of ∆ABP = Area of ∆ACQ.
Hence, proved that Area of ∆ABP = Area of ∆ACQ.