Mathematics
A footpath of uniform width runs all around the outside of a rectangular field 30 m long and 24 m wide. If the path occupies an area of 360 m2, find its width.
Answer
Given:
The length of the rectangular field = 30 m
The breadth of the rectangular field = 24 m
Area of path = 360 m2
Let the width of the path be x m.
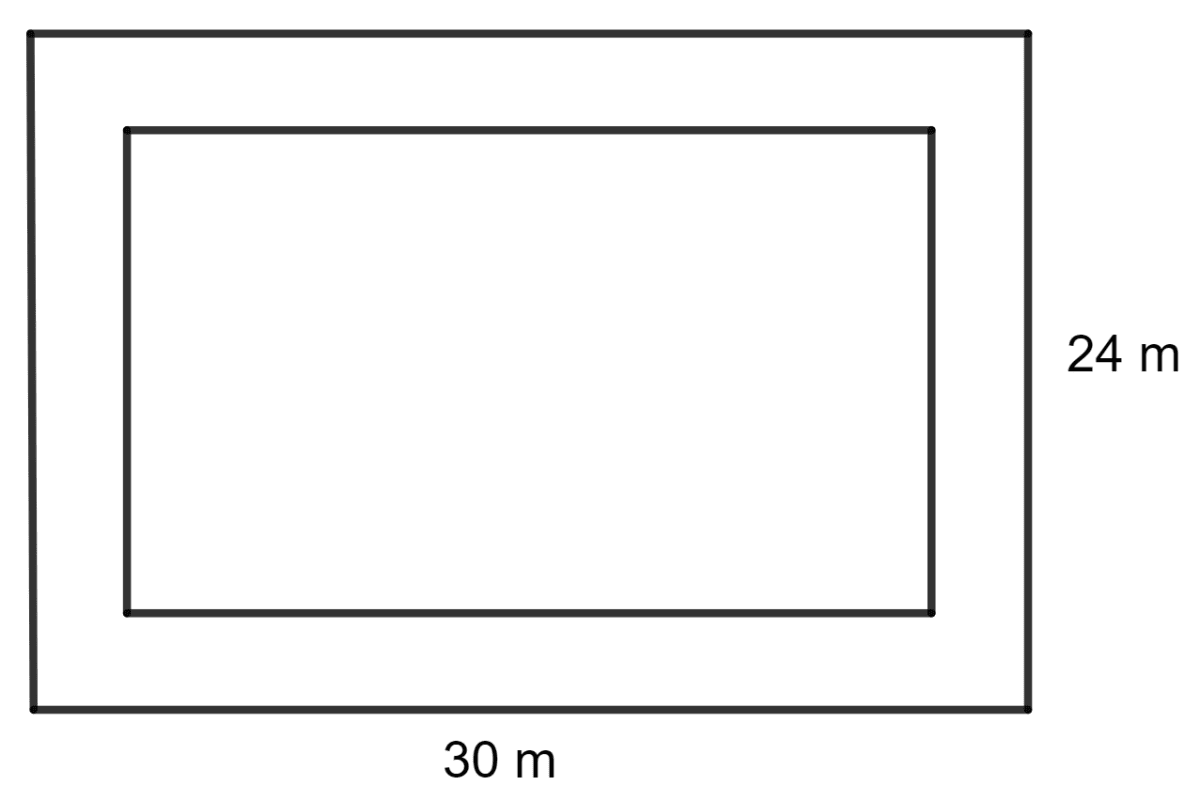
The length of the smaller rectangular field = 30 m - x m - x m
= 30 - 2x m
The breadth of the smaller rectangular field = 24 m - x m - x m
= 24 - 2x m
As we know, the area of a rectangle = length x breadth
⇒ Area of the larger rectangular field = 30 x 24 m2
= 720 m2
⇒ Area of the smaller rectangular field = (30 - 2x) x (24 - 2x) m2
= (720 - 108x - 4x2) m2
Area of the path = Area of larger rectangular field - Area of smaller rectangular field
⇒ 360 = 720 - (720 - 108x - 4x2)
⇒ 360 = 720 - 720 + 108x + 4x2
⇒ 4x2 + 108x - 360 = 0
⇒ x2 + 27x - 90 = 0
⇒ x2 + 30x - 3x - 90 = 0
⇒ x(x + 30) - 3(x + 30) = 0
⇒ (x + 30)(x - 3) = 0
⇒ x = - 30 or 3
Since the width of the path cannot be negative,
x = 3 m
Hence, the width of the path is 3 m.
Related Questions
Assertion (A): If BC = 14 cm, AB = 14 x 4 cm
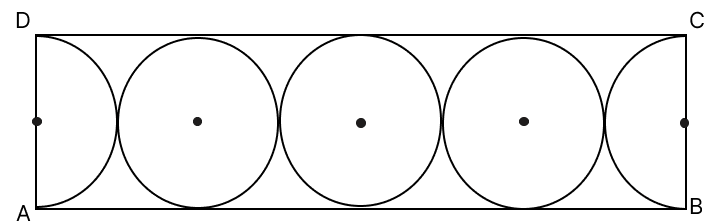
Reason (R): AB = 4 x 2r = 4 x 14 cm
A is true, but R is false.
A is false, but R is true.
Both A and R are true, and R is the correct reason for A.
Both A and R are true, and R is the incorrect reason for A.
AD is altitude of an isosceles triangle ABC in which AB = AC = 30 cm and BC = 36 cm. A point O is marked on AD in such a way that ∠BOC = 90°. Find the area of quadrilateral ABOC.
A wire when bent in the form of a square encloses an area of 484 m2. Find the largest area enclosed by the same wire when bent to form :
(i) an equilateral triangle.
(ii) a rectangle of breadth 16 m.
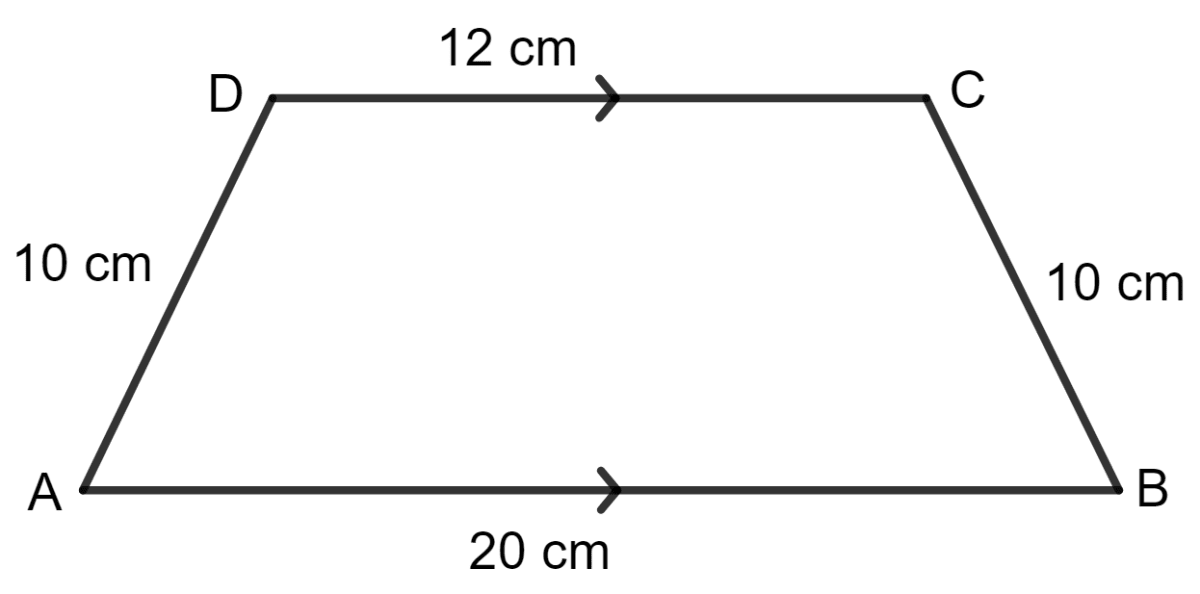
For the trapezium given below; find its area.