Mathematics
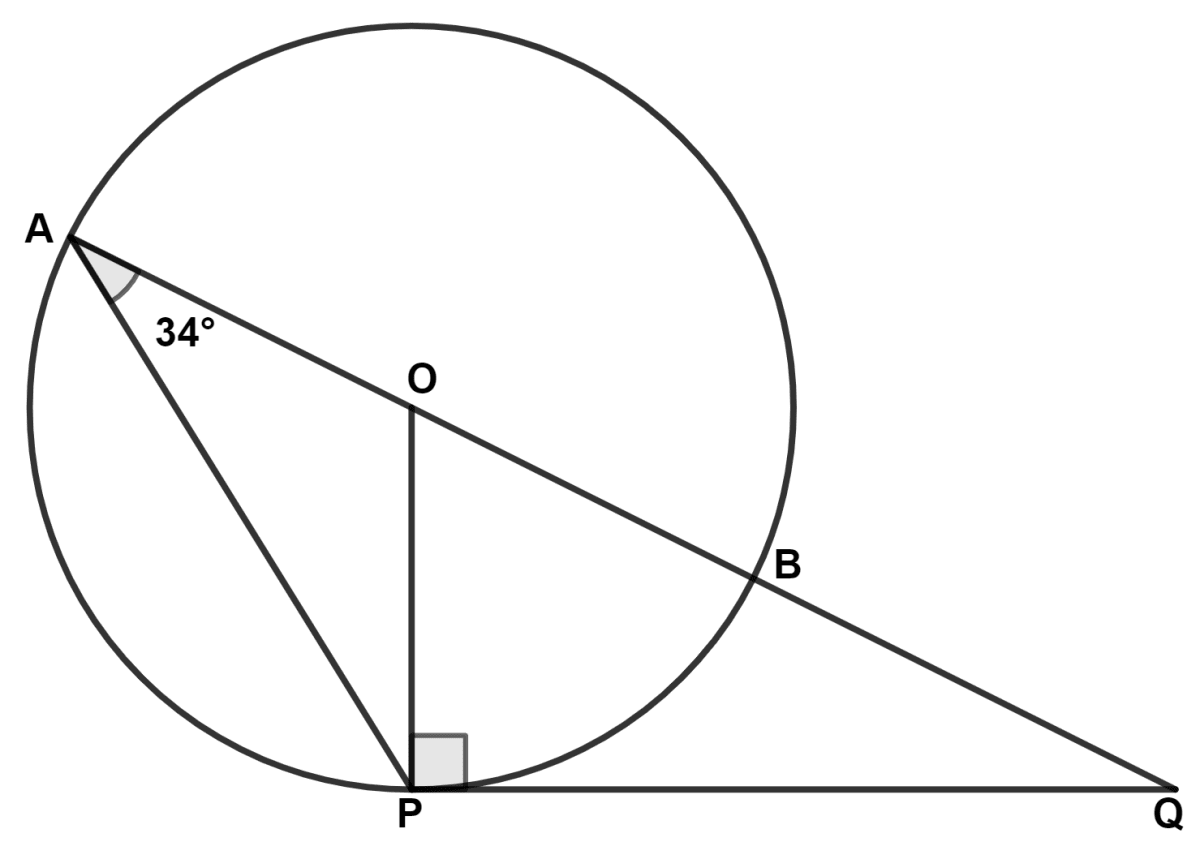
AB is a diameter of the circle with center O. The tangent at a point P meets AB produced in Q, ∠PAQ = 34°, find angles ∠PBA and ∠PQA.
Circles
9 Likes
Answer
We know that,
Angle in a semi-circle is a right angle.
∴ ∠APB = 90°
In △ APB,
⇒ ∠APB + ∠PAB + ∠PBA = 180°
⇒ 90° + 34° + ∠PBA = 180°
⇒ ∠PBA = 180° - 90° - 34° = 56°.
We know that,
Angle subtended by an arc at the center of the circle is twice the angle subtended by it on the circumference of the circle.
∴ ∠POB = 2∠PAB = 2 × 34° = 68°.
In △ POQ,
⇒ ∠OPQ + ∠PQO + ∠POQ = 180°
⇒ 90° + 68° + ∠PQO = 180°
⇒ 158° + ∠PQO = 180°
⇒ ∠PQO = 180° - 158° = 22°.
From figure,
⇒ ∠PQA = ∠PQO = 22°.
Hence, ∠PBA = 56° and ∠PQA = 22°.
Answered By
3 Likes
Related Questions
If M is the mean of six natural numbers x1, x2, x3, x4, x5 and x6. Show that :
(x1 - M) + (x2 - M) + (x3 - M) + (x4 - M) + (x5 - M) + (x6 - M) = 0
Items List price Rate of GST Discount A ₹ 800 12% 5% B ₹ 2,000 5% Nil C ₹ 600 18% 10% Find the total amount of bill for the above items.
The sum of first three terms of a G.P. is and their product is 1, find :
(i) the common ratio
(ii) the first three terms of this G.P.
Draw a histogram for the following distribution :
Marks out of 80 No. of students 40-44 2 45-49 8 50-54 12 55-59 10 60-64 8 Hence, estimate the mode.