Mathematics
If M is the mean of six natural numbers x1, x2, x3, x4, x5 and x6. Show that :
(x1 - M) + (x2 - M) + (x3 - M) + (x4 - M) + (x5 - M) + (x6 - M) = 0
Statistics
25 Likes
Answer
Given,
M is the mean of six natural numbers x1, x2, x3, x4, x5 and x6.
= M
⇒ x1 + x2 + x3 + x4 + x5 + x6 = 6M
⇒ x1 + x2 + x3 + x4 + x5 + x6 = M + M + M + M + M + M
⇒ (x1 - M) + (x2 - M) + (x3 - M) + (x4 - M) + (x5 - M) + (x6 - M) = 0
Hence, proved that (x1 - M) + (x2 - M) + (x3 - M) + (x4 - M) + (x5 - M) + (x6 - M) = 0.
Answered By
15 Likes
Related Questions
Without solving the equation = 0, find its nature of roots.
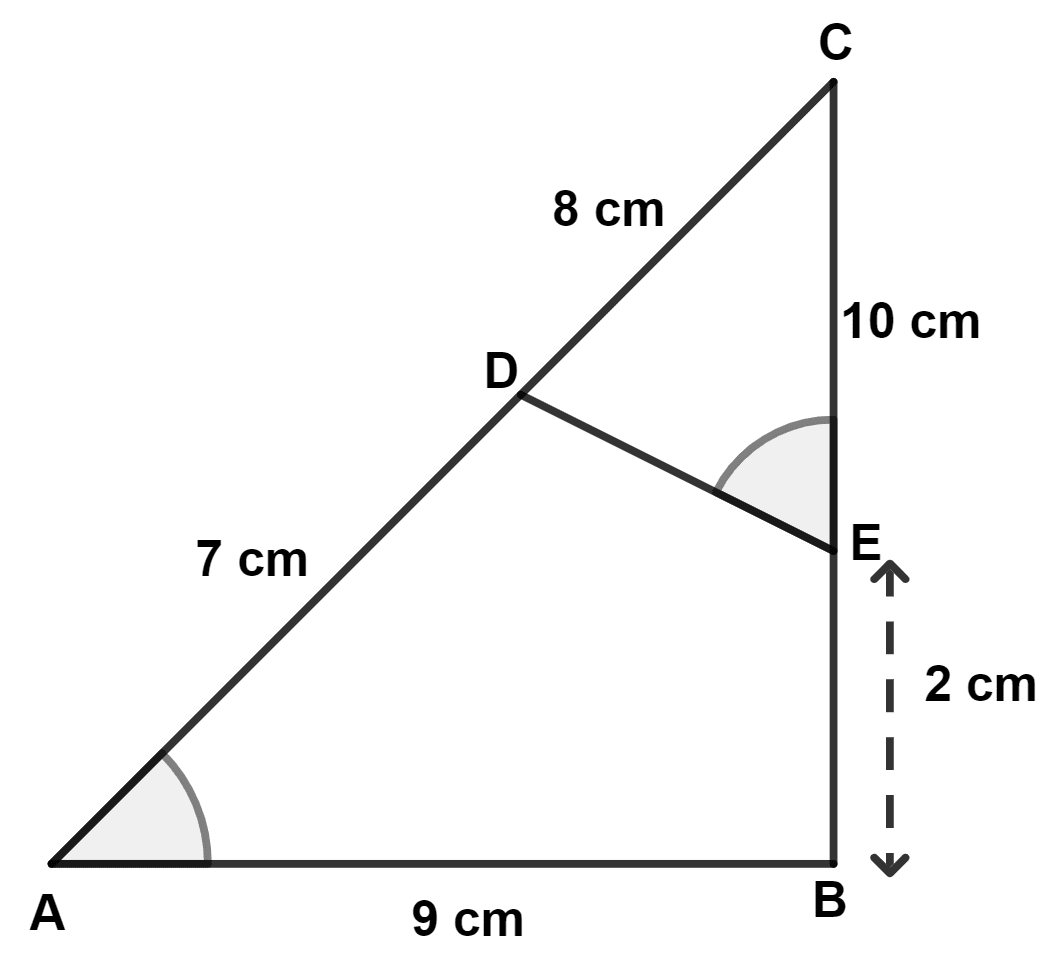
In the given figure, ∠CED = ∠CAB.
(i) Show that :
△CED is similar to triangle CAB.
(ii) Find DE.
Items List price Rate of GST Discount A ₹ 800 12% 5% B ₹ 2,000 5% Nil C ₹ 600 18% 10% Find the total amount of bill for the above items.
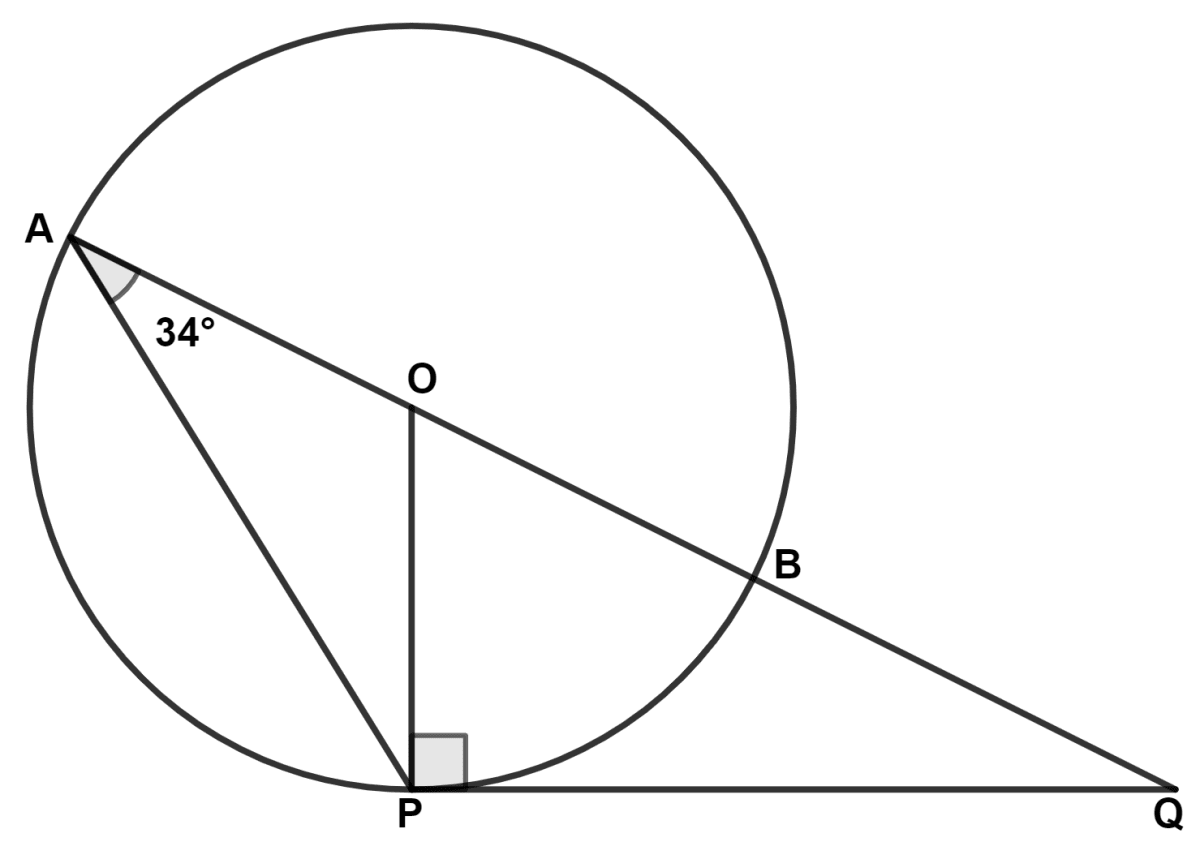
AB is a diameter of the circle with center O. The tangent at a point P meets AB produced in Q, ∠PAQ = 34°, find angles ∠PBA and ∠PQA.