Mathematics
Assertion (A): (2x - 3y, 8) = (2, x + 2y)
⇒ x = 1 and y = -2
Reason (R): 2x - 3y = 2 and 8 = x + 2y
A is true, but R is false.
A is false, but R is true.
Both A and R are true, and R is the correct reason for A.
Both A and R are true, and R is the incorrect reason for A.
Coordinate Geometry
1 Like
Answer
Given, (2x - 3y, 8) = (2, x + 2y)
Thus,
2x - 3y = 2 ……..(1)
x + 2y = 8 ……..(2)
So, reason (R) is true.
Multiplying equation (2) by 2, we get :
⇒ 2(x + 2y) = 2 × 8
⇒ 2x + 4y = 16 ……..(3)
Subtracting equation (1) from (3), we get :
⇒ 2x + 4y - (2x - 3y) = 16 - 2
⇒ 2x - 2x + 4y + 3y = 14
⇒ 7y = 14
⇒ y = = 2.
Substituting the value y = 2 in first equation,
⇒ 2x - 3 x 2 = 2
⇒ 2x - 6 = 2
⇒ 2x = 2 + 6
⇒ 2x = 8
⇒ x = = 4.
Hence, the value of x = 4 and y = 2.
∴ A is false, but R is true.
Hence, option 2 is the correct option.
Answered By
2 Likes
Related Questions
Statement 1: The vertex B of square OABC with each side 4 units lies in the fourth quadrant and its side are along the co-ordinate axes. The co-ordinate of vertex B are (4, -4).
Statement 2: B = (4, 4)
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Assertion (A): PQR is an equilateral triangle. The co-ordinates of point Q are (0, ).
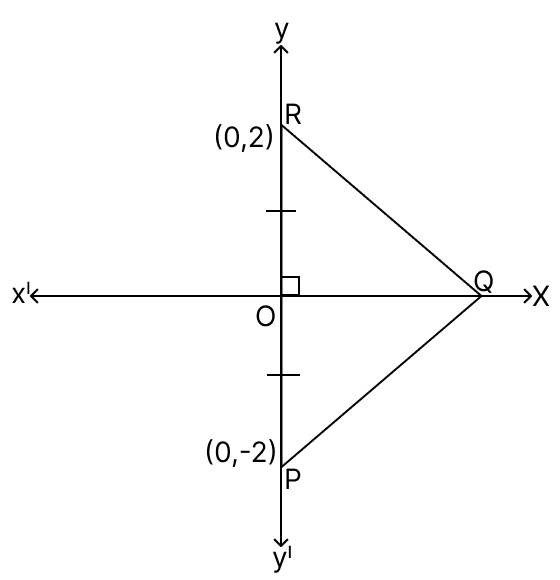
Reason (R): In ΔOPQ,
OQ2 = PQ2 - OP2 = 42 - 22 = 12.
A is true, but R is false.
A is false, but R is true.
Both A and R are true, and R is the correct reason for A.
Both A and R are true, and R is the incorrect reason for A.
By plotting the following points on the same graph paper, check whether they are collinear or not :
(3, 5), (1, 1) and (0, -1)
By plotting the following points on the same graph paper, check whether they are collinear or not :
(-2, -1), (-1, -4) and (-4, 1)