Mathematics
Assertion (A): PQR is an equilateral triangle. The co-ordinates of point Q are (0, ).
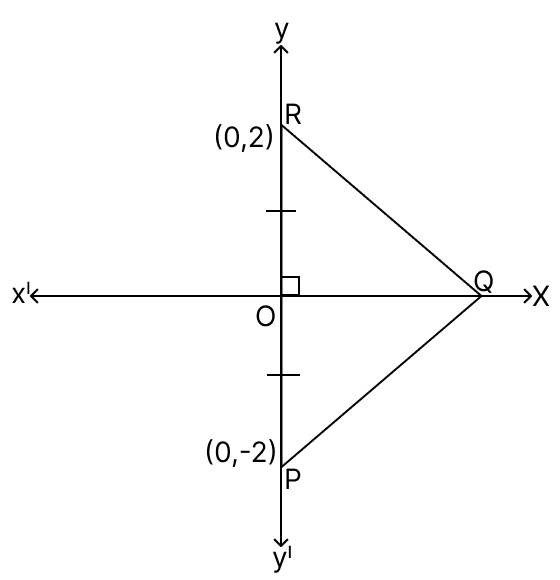
Reason (R): In ΔOPQ,
OQ2 = PQ2 - OP2 = 42 - 22 = 12.
A is true, but R is false.
A is false, but R is true.
Both A and R are true, and R is the correct reason for A.
Both A and R are true, and R is the incorrect reason for A.
Coordinate Geometry
3 Likes
Answer
The coordinates of R(0, 2) and P(0, -2).
Using distance formula,
Distance between two points =
PR = units.
Given equilateral triangle PQR.
∴ PQ = QR = PR = 4 units.
In an equilateral triangle, a perpendicular drawn from one of the vertices to the opposite side bisects the side.
∴ OP = x PR = x 4 = 2 units.
In right angle triangle OPQ,
By pythagoras theorem,
⇒ QP2 = OP2 + OQ2
⇒ OQ2 = QP2 - OP2
⇒ OQ2 = 42 - 22
⇒ OQ2 = 16 - 4
⇒ OQ2 = 12
⇒ OQ =
⇒ OQ =
Since, OQ = units and Q lies on x-axis.
Co-ordinates of Q = (, 0).
∴ A is false, but R is true.
Hence, option 2 is the correct option.
Answered By
1 Like
Related Questions
Statement 1: In the given diagram, OAB is an equilateral triangle.
Co-ordinates of the vertex B = (4, 4)
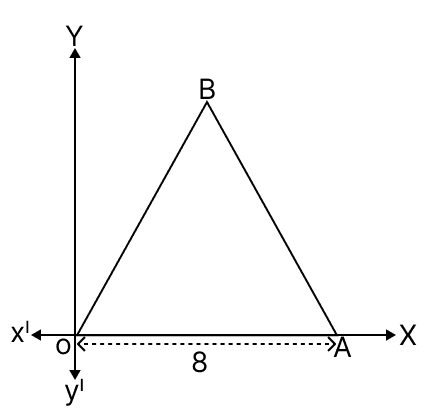
Statement 2: B = (4, )
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Statement 1: The vertex B of square OABC with each side 4 units lies in the fourth quadrant and its side are along the co-ordinate axes. The co-ordinate of vertex B are (4, -4).
Statement 2: B = (4, 4)
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Assertion (A): (2x - 3y, 8) = (2, x + 2y)
⇒ x = 1 and y = -2
Reason (R): 2x - 3y = 2 and 8 = x + 2y
A is true, but R is false.
A is false, but R is true.
Both A and R are true, and R is the correct reason for A.
Both A and R are true, and R is the incorrect reason for A.
By plotting the following points on the same graph paper, check whether they are collinear or not :
(3, 5), (1, 1) and (0, -1)