Mathematics
Statement 1: The vertex B of square OABC with each side 4 units lies in the fourth quadrant and its side are along the co-ordinate axes. The co-ordinate of vertex B are (4, -4).
Statement 2: B = (4, 4)
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Coordinate Geometry
2 Likes
Answer
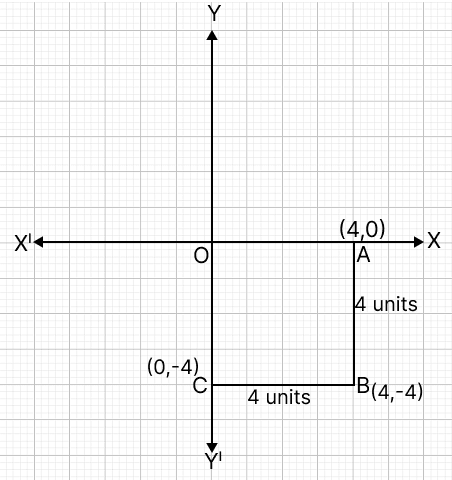
Vertex B lies in the fourth quadrant. The square's sides are along the coordinate axes, so one vertex, O, is at the origin (0, 0).
The side length is 4 units.
With O at (0, 0), the other two vertices on the axes must be A (4, 0) on the positive x-axis and C (0, -4) on the negative y-axis.
The fourth quadrant is where the x-coordinates are positive and the y-coordinates are negative.
Vertex B is located at the point where the line extending 4 units to the right from C (0, -4) intersects with the line extending 4 units down from A (4, 0), which is (4, -4).
⇒ B = (4, –4).
∴ Statement 1 is true, and statement 2 is false.
Hence, option 3 is the correct option.
Answered By
2 Likes
Related Questions
Three vertices of a square ABCD are A(2, 0), B(-3, 0) and C(-3, -5). Its fourth vertex D is:
(2, 5)
(2, -5)
(-2, 5)
(-2, -5)
Statement 1: In the given diagram, OAB is an equilateral triangle.
Co-ordinates of the vertex B = (4, 4)
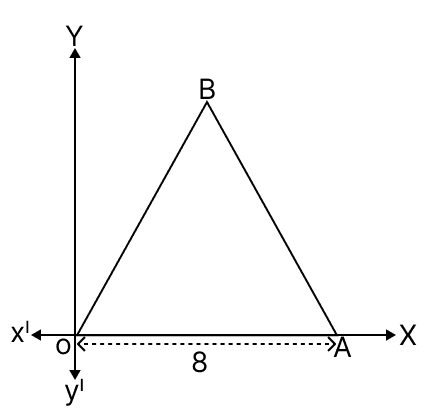
Statement 2: B = (4, )
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Assertion (A): PQR is an equilateral triangle. The co-ordinates of point Q are (0, ).
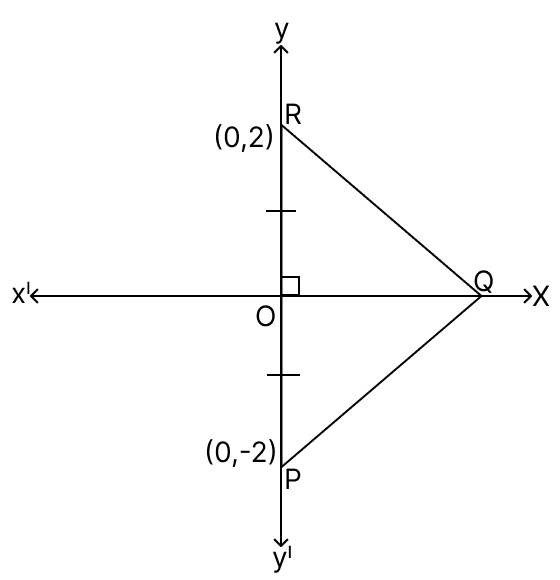
Reason (R): In ΔOPQ,
OQ2 = PQ2 - OP2 = 42 - 22 = 12.
A is true, but R is false.
A is false, but R is true.
Both A and R are true, and R is the correct reason for A.
Both A and R are true, and R is the incorrect reason for A.
Assertion (A): (2x - 3y, 8) = (2, x + 2y)
⇒ x = 1 and y = -2
Reason (R): 2x - 3y = 2 and 8 = x + 2y
A is true, but R is false.
A is false, but R is true.
Both A and R are true, and R is the correct reason for A.
Both A and R are true, and R is the incorrect reason for A.