Mathematics
Assertion (A): In the given figure, S is any point on side QR.
∴ PQ + QR + RP > 2PS
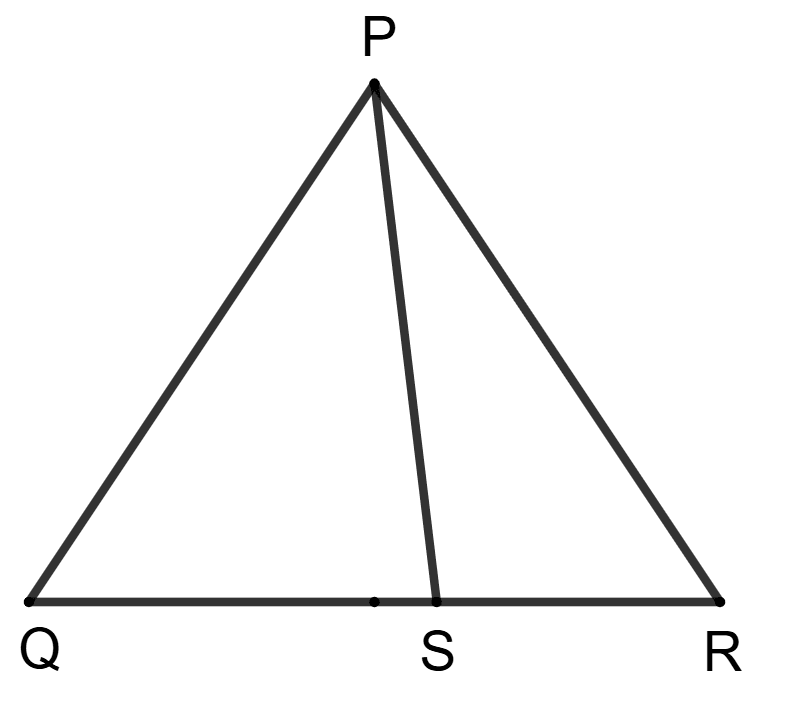
Reason (R): In ΔPQS, PQ + QS > PS and in ΔPRS, PR + SR > PS
A is true, but R is false.
A is false, but R is true.
Both A and R are true and R is the correct reason for A.
Both A and R are true and R is the incorrect reason for A.
Triangles
3 Likes
Answer
In △ PQS,
⇒ PQ + QS > PS ……(1) [Sum of any two sides of a triangle is greater than the third side]
In △ PRS,
⇒ RP + RS > PS ……(2) [Sum of any two sides of a triangle is greater than the third side]
So, reason (R) is true.
Adding equations (1) and (2), we get :
⇒ PQ + QS + RP + RS > PS + PS
⇒ PQ + (QS + RS) + RP > 2PS
⇒ PQ + QR + RP > 2PS.
So, assertion (A) is true.
∴ Both A and R are true, and R is the correct reason for A.
Hence, option 3 is the correct option.
Answered By
2 Likes
Related Questions
Statement (1): AB = AC and D is any point on side BC of triangle ABC.
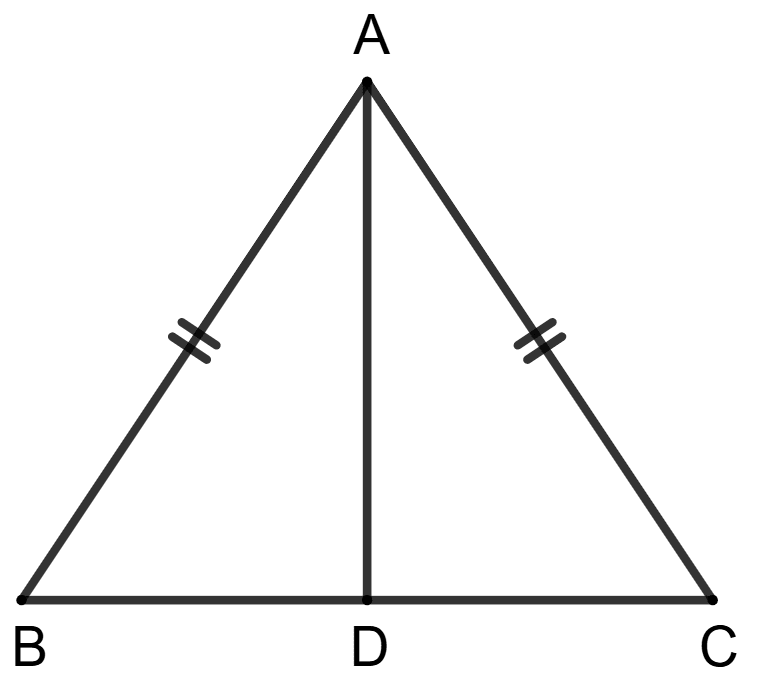
Statement (2): AB > AD.
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
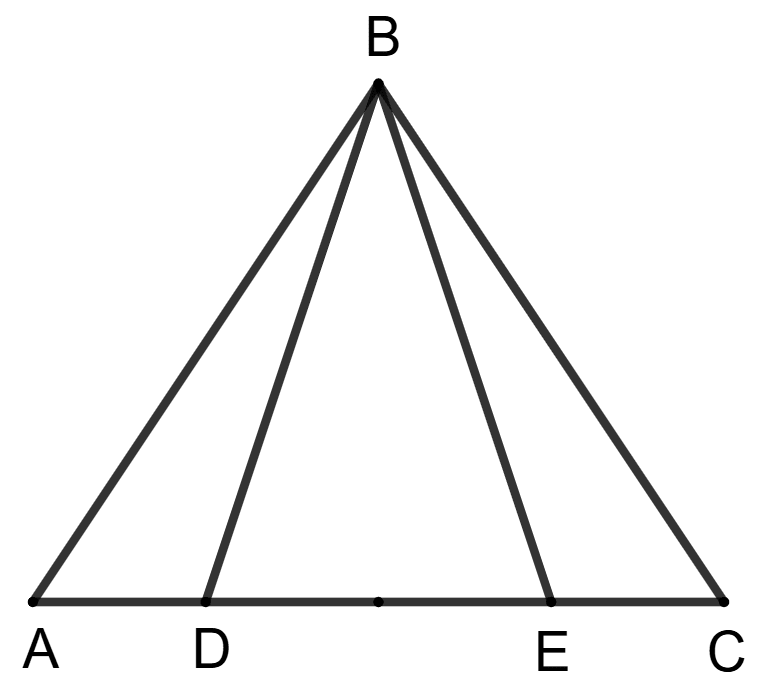
Assertion (A): In the given figure, AB = BC and AD = CE, then BD = CE.
Reason (R): ΔBAD ≅ ΔBCE by SAS.
A is true, but R is false.
A is false, but R is true.
Both A and R are true and R is the correct reason for A.
Both A and R are true and R is the incorrect reason for A.
In the figure given alongside, AD = AB = AC, BD is parallel to CA and angle ACB = 65°. Find angle DAC.
Prove that a triangle ABC is isosceles, if :
(i) altitude AD bisects angle BAC or,
(ii) bisector of angle BAC is perpendicular to base BC.