Mathematics
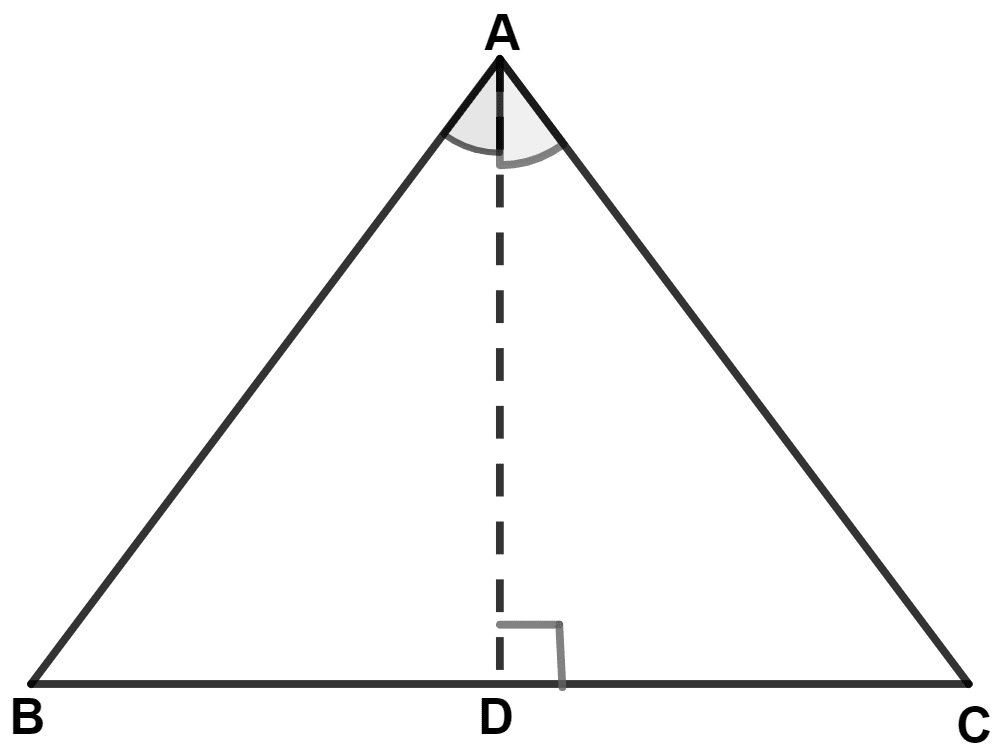
Prove that a triangle ABC is isosceles, if :
(i) altitude AD bisects angle BAC or,
(ii) bisector of angle BAC is perpendicular to base BC.
Triangles
1 Like
Answer
Let AD be the altitude on side BC.
We know that,
Altitude from a point is always perpendicular to other side.
Let altitude AD bisect angle BAC.
Hence, segment AD satisfies both the conditions.
In △ ADB and △ ADC,
⇒ AD = AD (Common side)
⇒ ∠BAD = ∠CAD (Since, AD bisects angle BAC)
⇒ ∠ADB = ∠ADC (Since, AD is altitude to side BC)
∴ Δ ADB ≅ Δ ADC (By A.S.A. axiom)
We know that,
Corresponding parts of congruent triangle are equal.
⇒ AB = AC.
Hence, proved that ABC is an isosceles triangle.
Answered By
3 Likes
Related Questions
Assertion (A): In the given figure, S is any point on side QR.
∴ PQ + QR + RP > 2PS
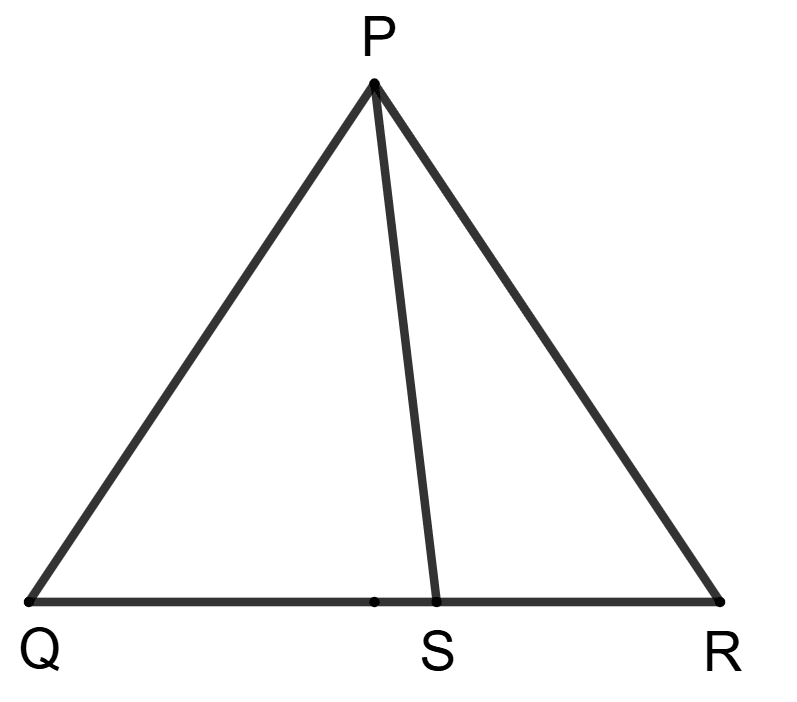
Reason (R): In ΔPQS, PQ + QS > PS and in ΔPRS, PR + SR > PS
A is true, but R is false.
A is false, but R is true.
Both A and R are true and R is the correct reason for A.
Both A and R are true and R is the incorrect reason for A.
In the figure given alongside, AD = AB = AC, BD is parallel to CA and angle ACB = 65°. Find angle DAC.
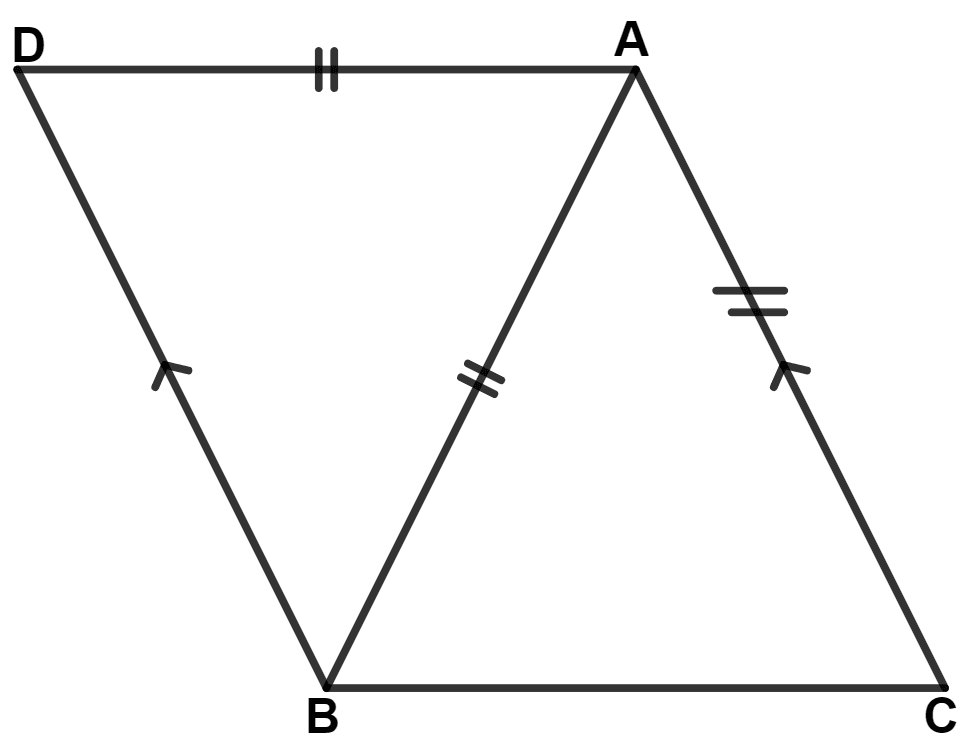
In the given figure; AB = BC and AD = EC. Prove that : BD = BE.
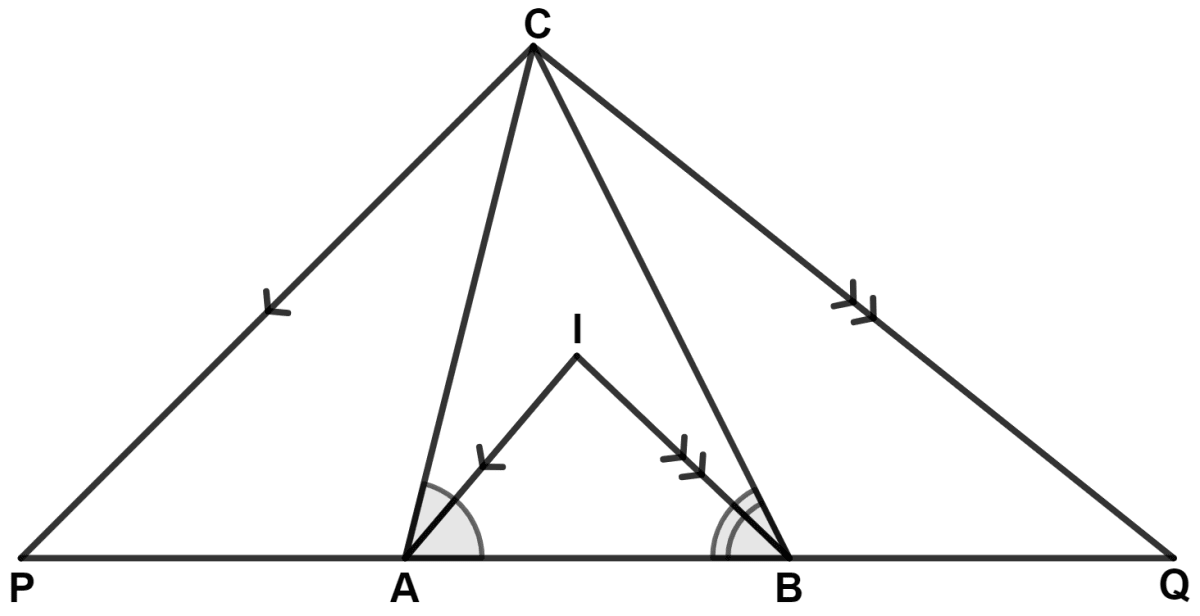
In the following figure; IA and IB are bisectors of angles CAB and CBA respectively. CP is parallel to IA and CQ is parallel to IB.
Prove that :
PQ = The perimeter of Δ ABC.
In the given figure; AB = BC and AD = EC. Prove that : BD = BE.