Mathematics
Assertion (A): In the given figure, square ABCD and △APB are equal in area.
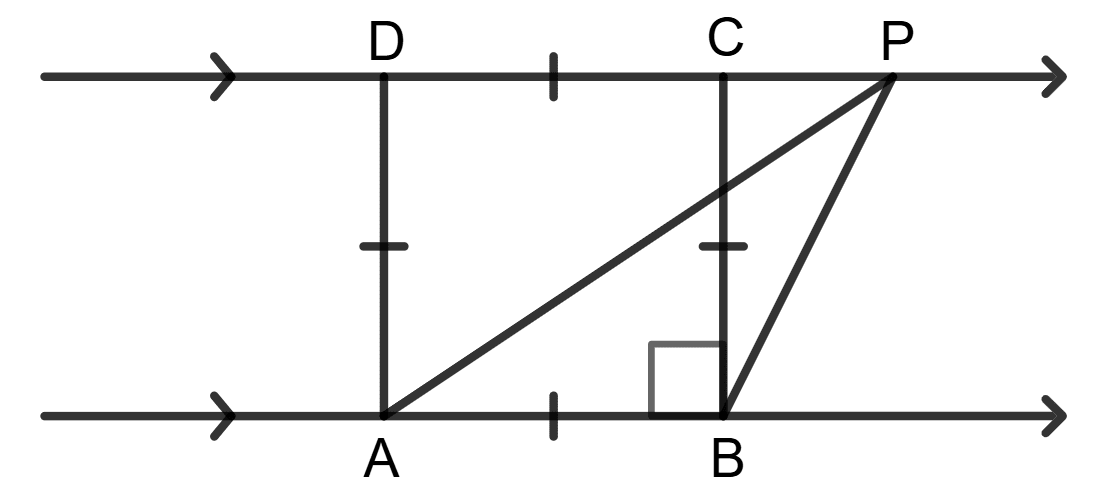
Reason (R): Square ABCD and △APB are on the same base (AB) and between the same parallels (AB//DP).
⇒ Area of △APB =
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Theorems on Area
3 Likes
Answer
A is false, R is true.
Explanation
Given,
ABCD is a square.
AB is parallel to CD.
△APB shares the base AB with square ABCD.
The height of △APB is equal to the side of the square (h).
Let BC = h (height of square)
Height of triangle = h (height of square)
Area of (Δ ABP) = x base x height
= x AB x h
= x h x h (∴ As all sides of square are equal)
= x h2 …………..(1)
Area of square ABCD = (side)2
= h2…………..(2)
From (1) and (2),
Area of (Δ ABP) = x Area of square ABCD
∴ Assertion (A) is false.
As proved above,
Area of (Δ ABP) = x Area of square ABCD
∴ Reason (R) is true.
Hence, Assertion (A) is false, Reason (R) is true.
Answered By
3 Likes
Related Questions
Assertion (A): The length of the side of a regular hexagon is equal to the radius of its circumcircle.
Reason (R):
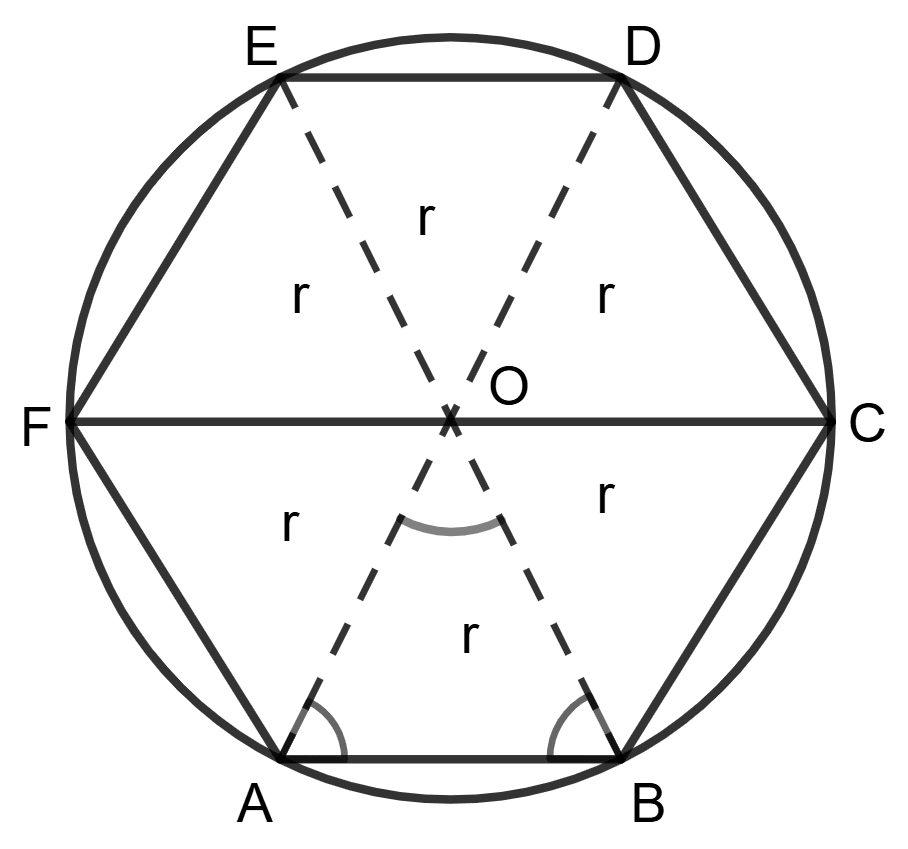
∠AOB =
∠OAB = ∠OBA =
⇒ OAB is an equilateral triangle
So, AB = OA = radius (r) of the circumcircle- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): Rhombus becomes square if its diagonals are equal.
Reason (R): OB = OD =
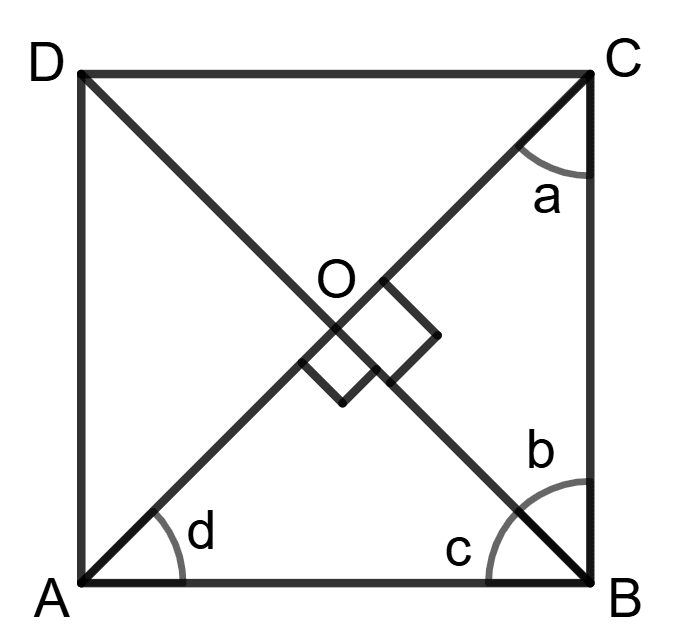
and OC = OA =
⇒ OB = OA = OC
OB = OC
⇒ ∠a = ∠b = 45°
Similarly, ∠c = ∠d = 45°
∠ABC = ∠b + ∠c = 45° + 45° = 90°- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): In △ABC, BD : DC = 1 : 2 and OA = OD
Area of △AOB : area of △ABC = 1 : 4
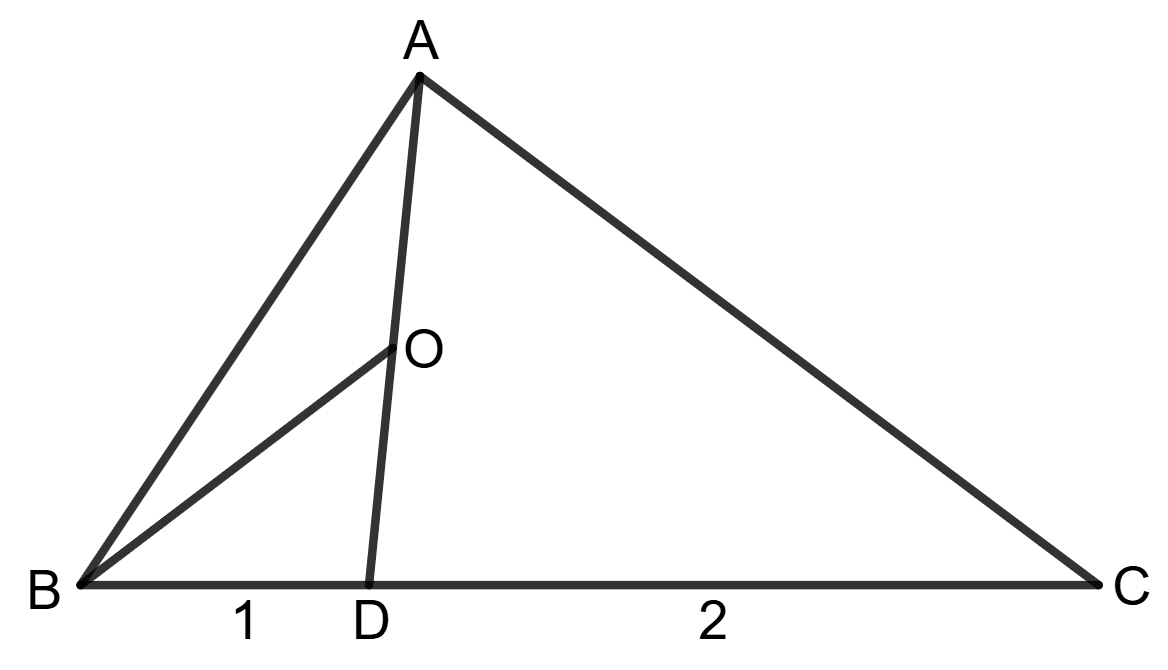
Reason (R):
Area of △AOB =
==
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.
Assertion (A): AM and BN are tangents to the same circle at points A and B respectively. Then AN = BM.
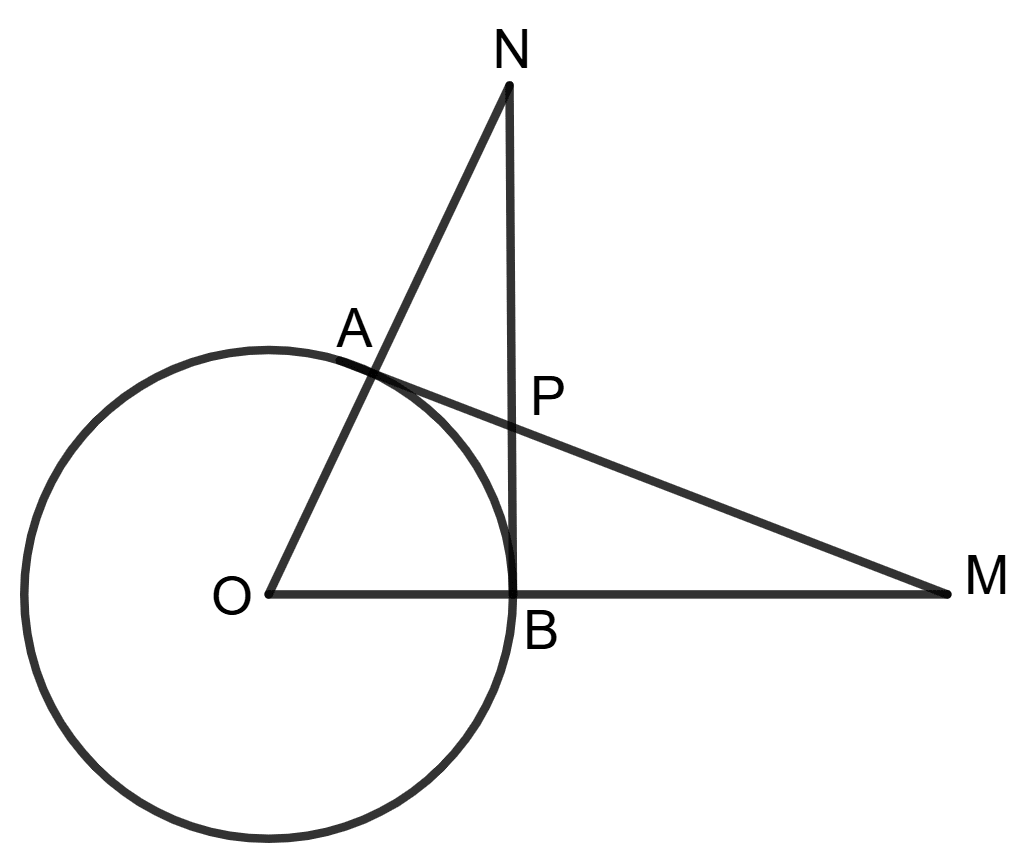
Reason (R): Since, tangents to a circle are equal in length
⇒ AM = BN
△APN ≅ △BPM ⇒ AN = BM
- A is true, R is false.
- A is false, R is true.
- Both A and R are true.
- Both A and R are false.