Mathematics
From a boat, 300 m away from a vertical pillar, the angles of elevation of the top and the foot of a vertical pillar at the edge of the cliff are 55°40' and 54°20' respectively. Find the height of the pillar correct to the nearest metre.
Heights & Distances
9 Likes
Answer
Let CD be the pillar and AD be the cliff.
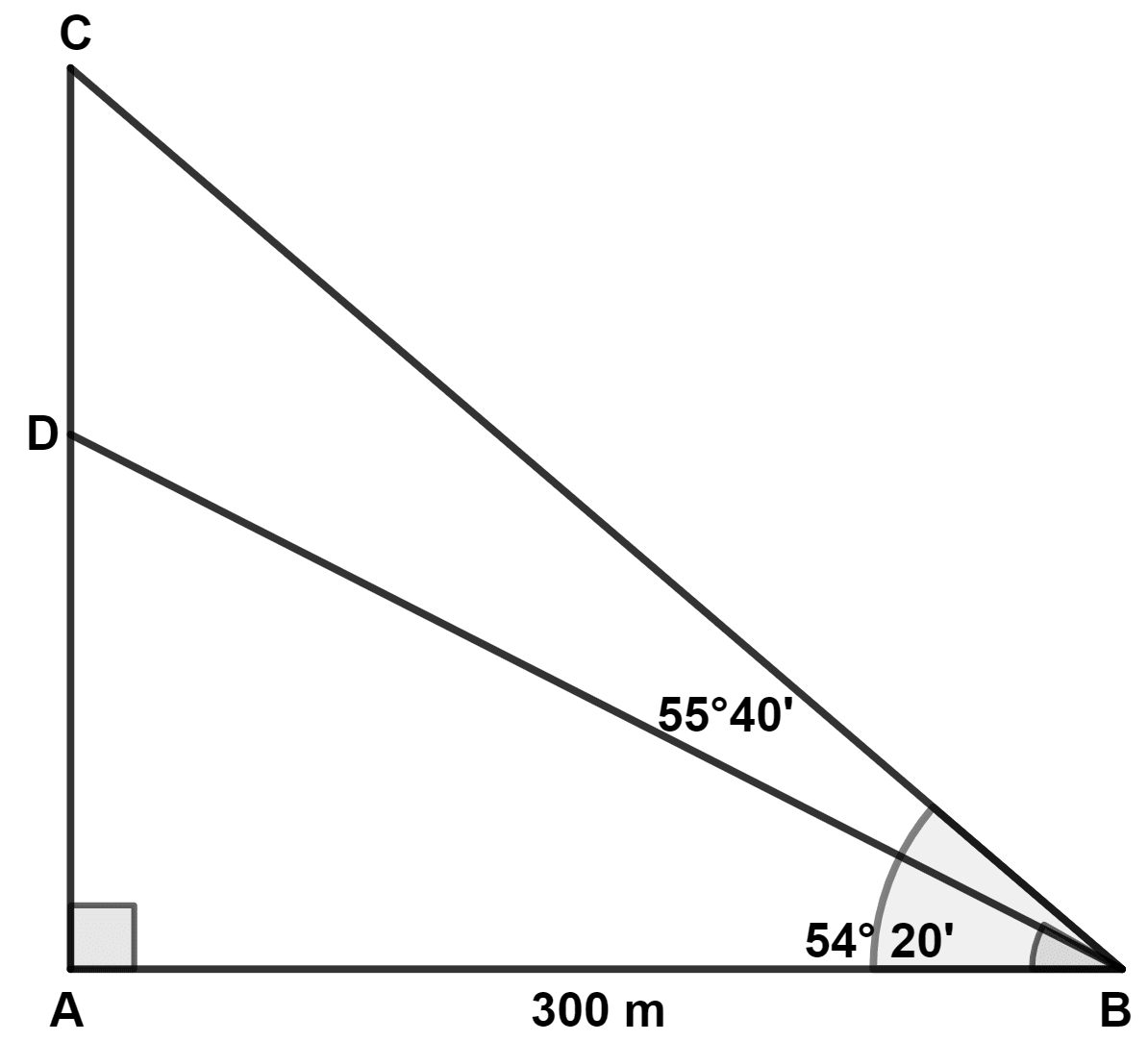
From figure,
From figure,
CD = AC - AD = 439 - 418 = 21 m.
Hence, height of the pillar = 21 m.
Answered By
4 Likes
Related Questions
A solid is in the form of right circular cylinder with a hemisphere at one end and a cone at the other end. The radius of the common base is 2.8 cm and heights of cylinder and conical portions are 14 cm and 7 cm respectively. Find :
(i) the total surface area of the solid
(ii) the volume of the solid
Take π = and find your answers correct to two decimal places.
In rhombus ABCD, A(7, 3) and C(0, -4) are two opposite vertices. Find :
(i) mid-point of diagonal AC
(ii) mid-point of diagonal BD
(iii) slope of diagonal AC
(iv) the equation of diagonal BD.
Solve the following inequation, write down the solution set and represent it on the real number line. -2 + 10x ≤ 13x + 10 < 24 + 10x, x ∈ R.
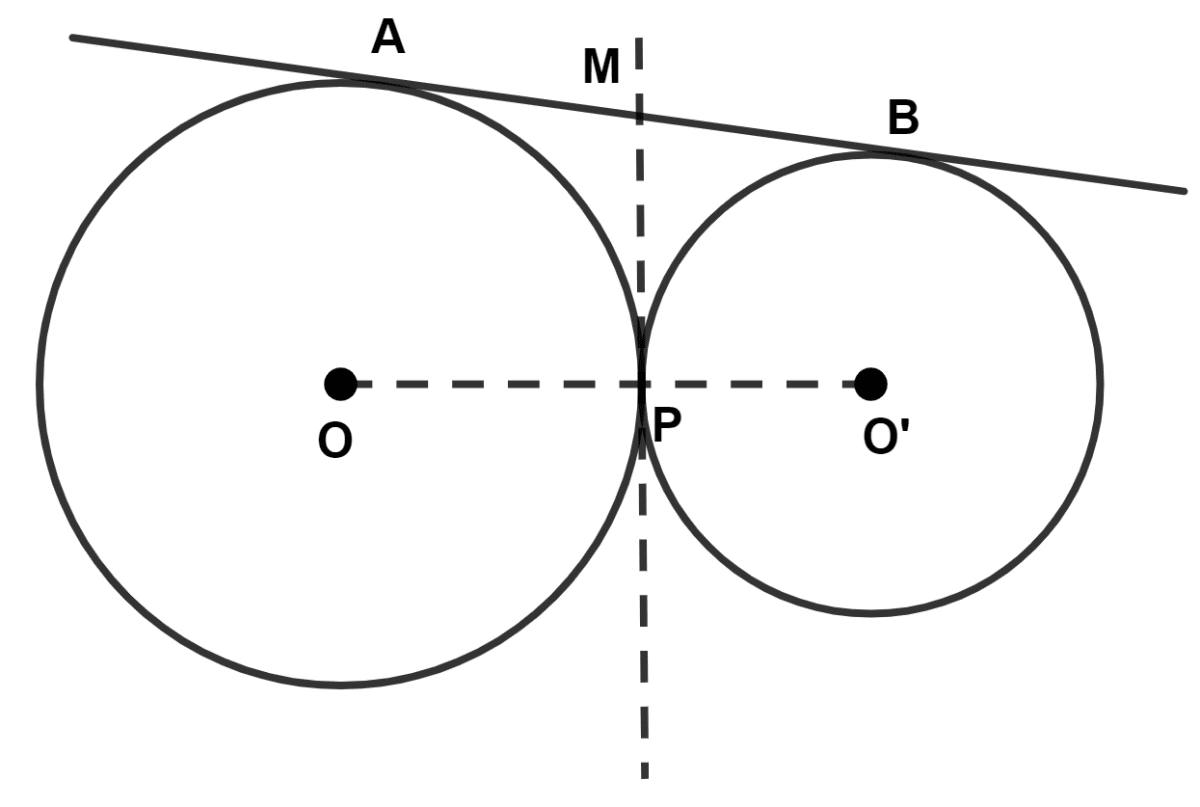
In the given figure, O and O' are centers of two circles, touching each other at point P. The common tangent at P meets a direct common tangent AB at M. Show that :
(i) M is mid-point of AB.
(ii) ∠APB = 90°