Mathematics
In the given figure, O and O' are centers of two circles, touching each other at point P. The common tangent at P meets a direct common tangent AB at M. Show that :
(i) M is mid-point of AB.
(ii) ∠APB = 90°
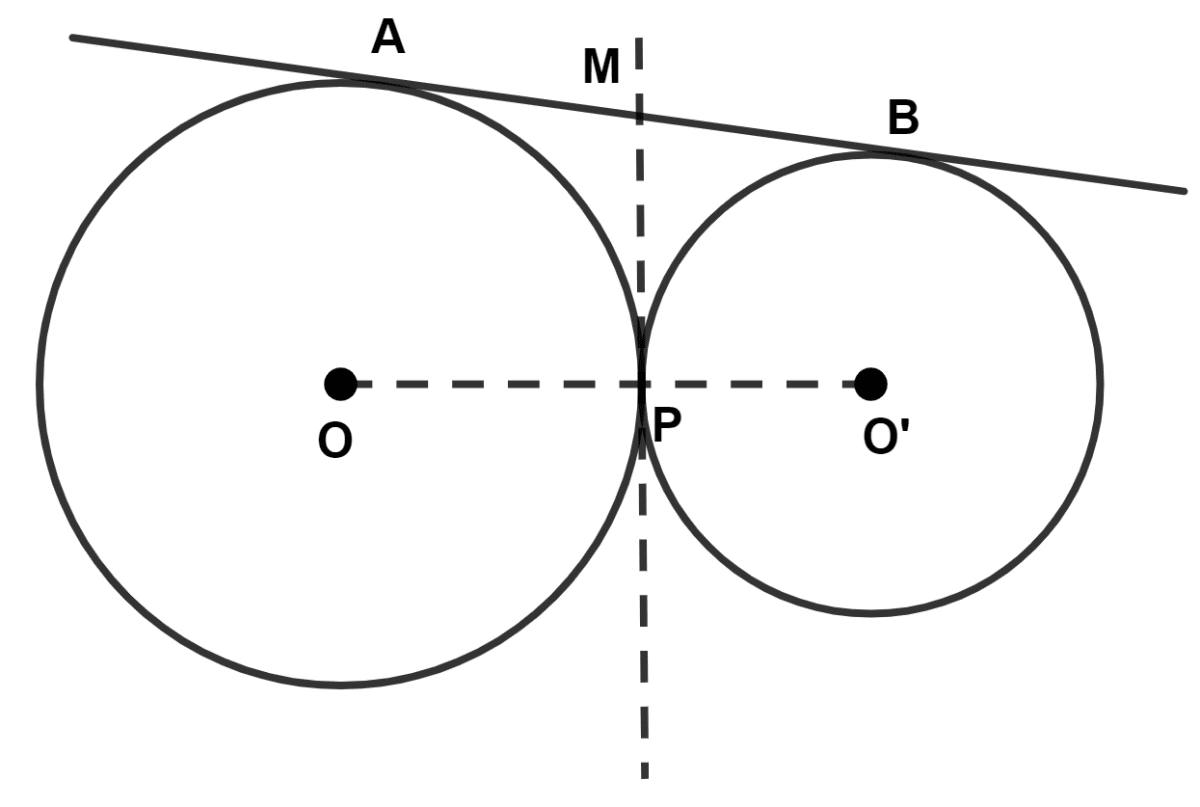
Circles
10 Likes
Answer
(i) From figure,
From M, MA and MP are the tangents.
∴ MA = MP …….(1) (∵ length of the different tangents to a circle from a single point are equal.)
Similarly,
From M, MB and MP are the tangents.
∴ MB = MP ………(2) (∵ length of the different tangents to a circle from a single point are equal.)
From (1) and (2),
MA = MB.
Hence, proved that M is the mid-point of AB.
(ii) Join AP and BP.
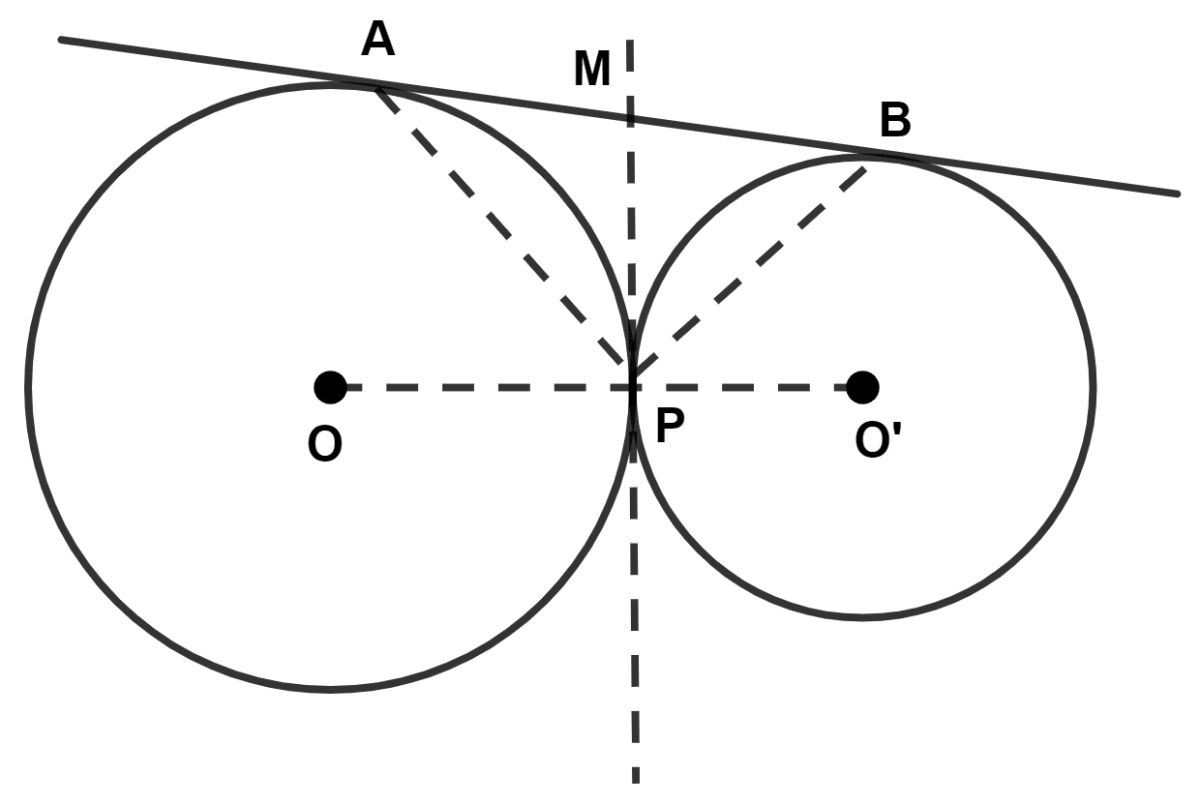
∵ MA = MP
∴ In Δ APM,
∠MAP = ∠MPA ……….(3) (∵ angles opposite to equal sides are equal.)
∵ MB = MP
∴ In Δ BPM,
∠MPB = ∠MBP ………(4) (∵ angles opposite to equal sides are equal.)
Adding equations (3) and (4)
⇒ ∠MAP + ∠MPB = ∠MPA + ∠MBP
⇒ ∠MAP + ∠MBP = ∠APB
Since sum of angles in a triangle = 180°
In Δ APB,
⇒ ∠APB + ∠BAP + ∠ABP = 180°
From figure,
∠BAP = ∠MAP
∠ABP = ∠MBP
Putting value of ∠MAP + ∠MBP = ∠APB in above equation
⇒ ∠APB + ∠APB = 180°
⇒ 2∠APB = 180°
⇒ ∠APB = = 90°.
Hence, proved that ∠APB = 90°.
Answered By
4 Likes
Related Questions
From a boat, 300 m away from a vertical pillar, the angles of elevation of the top and the foot of a vertical pillar at the edge of the cliff are 55°40' and 54°20' respectively. Find the height of the pillar correct to the nearest metre.
Solve the following inequation, write down the solution set and represent it on the real number line. -2 + 10x ≤ 13x + 10 < 24 + 10x, x ∈ R.
AB is a line segment joining the points A(3, 2) and B(4, 1). Find :
(i) the ratio in which AB is divided by point P on x-axis
(ii) the co-ordinates of point P
(iii) the equation of the line that passes through the point P and is perpendicular to AB.
If , show that : .