Mathematics
AB is a line segment joining the points A(3, 2) and B(4, 1). Find :
(i) the ratio in which AB is divided by point P on x-axis
(ii) the co-ordinates of point P
(iii) the equation of the line that passes through the point P and is perpendicular to AB.
Section Formula
3 Likes
Answer
(i) Let point P be (a, 0).
By section formula,
y =
Let ratio in which P divides AB be k : 1, substituting values we get :
Since, k is negative it means the division is external.
∴ k : 1 = 2 : 1 (externally)
Hence, point P on x-axis divides the line segment AB in the ratio 2 : 1.
(ii) By section-formula,
x =
Substituting values we get :
P = (a, 0) =
Hence, co-ordinates of P = .
(iii) By formula,
Slope =
Slope of AB = = -3.
We know that,
Product of slope of perpendicular lines = -1.
∴ -3 × Slope of AB = -1
⇒ Slope of AB = .
By point-slope form :
⇒ y - y1 = m(x - x1)
⇒ y - 0 =
⇒ y =
⇒ y =
⇒ 9y = 3x - 11
⇒ 3x - 9y - 11 = 0
Hence, required equation is 3x - 9y - 11 = 0.
Answered By
1 Like
Related Questions
Solve the following inequation, write down the solution set and represent it on the real number line. -2 + 10x ≤ 13x + 10 < 24 + 10x, x ∈ R.
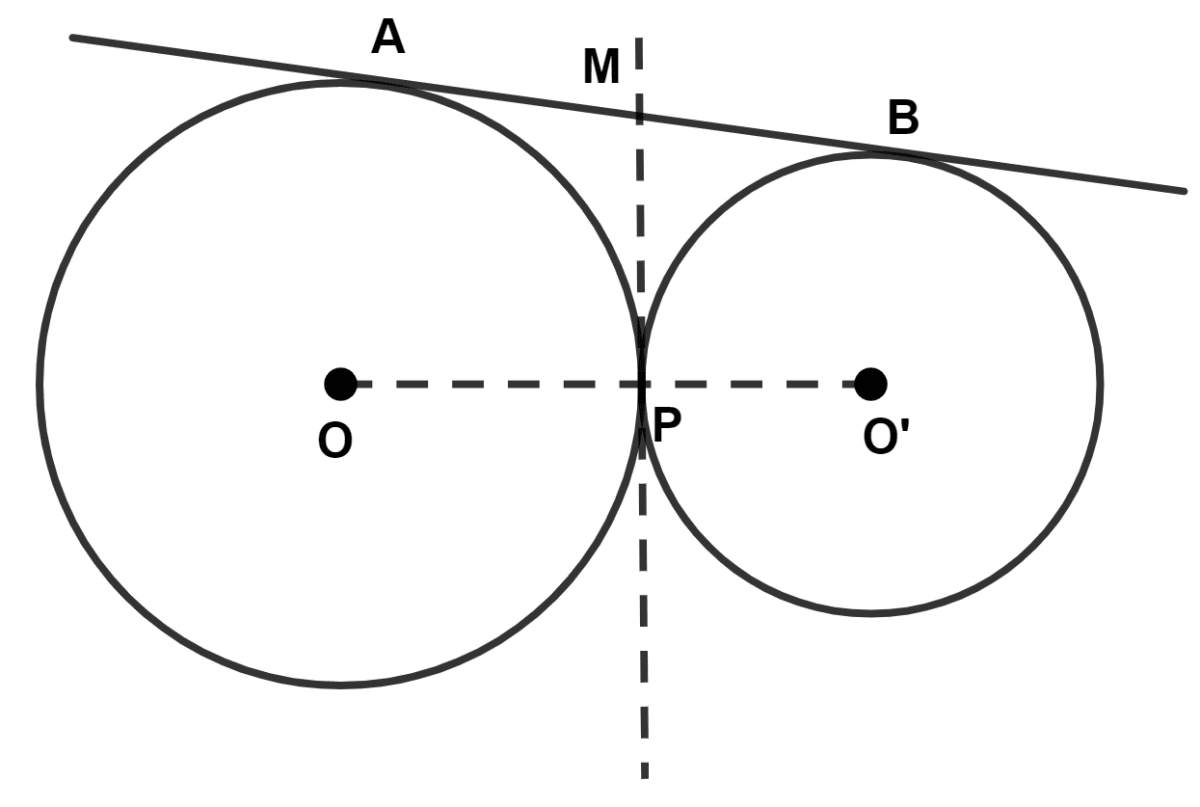
In the given figure, O and O' are centers of two circles, touching each other at point P. The common tangent at P meets a direct common tangent AB at M. Show that :
(i) M is mid-point of AB.
(ii) ∠APB = 90°
If , show that : .
An express train makes a run of 240 km at a certain speed. Another train whose speed is 12 km/h less takes an hour longer to cover the same distance. Find the speed of the express train.