A solid is in the form of right circular cylinder with a hemisphere at one end and a cone at the other end. The radius of the common base is 2.8 cm and heights of cylinder and conical portions are 14 cm and 7 cm respectively. Find :

(i) the total surface area of the solid

(ii) the volume of the solid

Take π = $3\dfrac{1}{7}$ and find your answers correct to two decimal places.

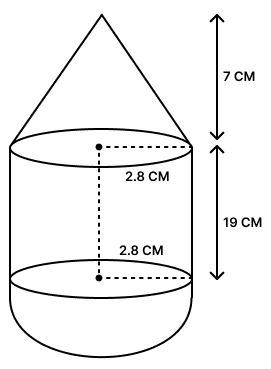
Height of cone (h) = 7 cm

Height of cylinder (H) = 14 cm

Radius of cone = Radius of cylinder = Radius of hemisphere = r = 2.8 cm

(i) By formula,

⇒ l² = r² + h²

⇒ l² = (2.8)² + 7²

⇒ l² = 7.84 + 49

⇒ l² = 56.84

⇒ l = $\sqrt{56.84}$ = 7.54 cm

Total surface area of solid = Surface area of cone + Surface area of cylinder + Surface area of hemisphere

= πrl + 2πrH + 2πr²

= πr(l + 2H + 2r)

= $\dfrac{22}{7} \times 2.8 \times (7.54 + 2 \times 14 + 2 \times 2.8)$

= 22 × 0.4 × (7.54 + 28 + 5.6)

= 22 × 0.4 × 41.14

= 362.032 cm².

Hence, total surface area of the solid = 362.032 cm².

(ii) From figure,

Volume of solid = Volume of cone + Volume of cylinder + Volume of hemisphere

$= \dfrac{1}{3}πr^2h + πr^2H + \dfrac{2}{3}πr^3 \\[1em] = πr^2\Big(\dfrac{h}{3} + H + \dfrac{2r}{3}\Big) \\[1em] = \dfrac{22}{7} \times (2.8)^2 \times \Big(\dfrac{7}{3} + 14 + \dfrac{2 \times 2.8}{3}\Big) \\[1em] = 22 \times 0.4 \times 2.8 \times \Big(\dfrac{7}{3} + 14 + \dfrac{5.6}{3}\Big) \\[1em] = 24.64 \times \Big(\dfrac{7 + 42 + 5.6}{3}\Big) \\[1em] = 24.64 \times \dfrac{54.6}{3} \\[1em] = 24.64 \times 18.2 \\[1em] = 448.44 \text{ cm}^3.$

Hence, volume of solid = 448.44 cm³.