Mathematics
The third term of a G.P. be one-fourth of fifth term and their sum is . If each term of this G.P. is positive, find its 10th term.
AP GP
19 Likes
Answer
Let first term of G.P. be a and common ratio be r.
Given,
The third term of a G.P. be one-fourth of fifth term.
∴ a3 =
⇒ ar2 =
⇒ 4ar2 = ar4
⇒ = 4
⇒ r2 = 4
⇒ r = .
Since, all terms of G.P. are positive, then r = 2.
Given,
Sum of third and fifth term = .
⇒ a3 + a5 =
⇒ ar2 + ar4 =
⇒ 4(ar2 + ar4) = 5
⇒ 4a(22 + 24) = 5
⇒ 4a(4 + 16) = 5
⇒ 4a × 20 = 5
⇒ a = .
⇒ a10 = ar9 = = 32.
Answered By
11 Likes
Related Questions
The following table shows the GST rates, the marked price and number of articles A, B and C brought.
Articles Marked price GST Rate No. of articles A ₹ 2,000 12% 2 B ₹ 5,000 5% 2 C ₹ 8,000 5% 1 Find the total amount to be paid.
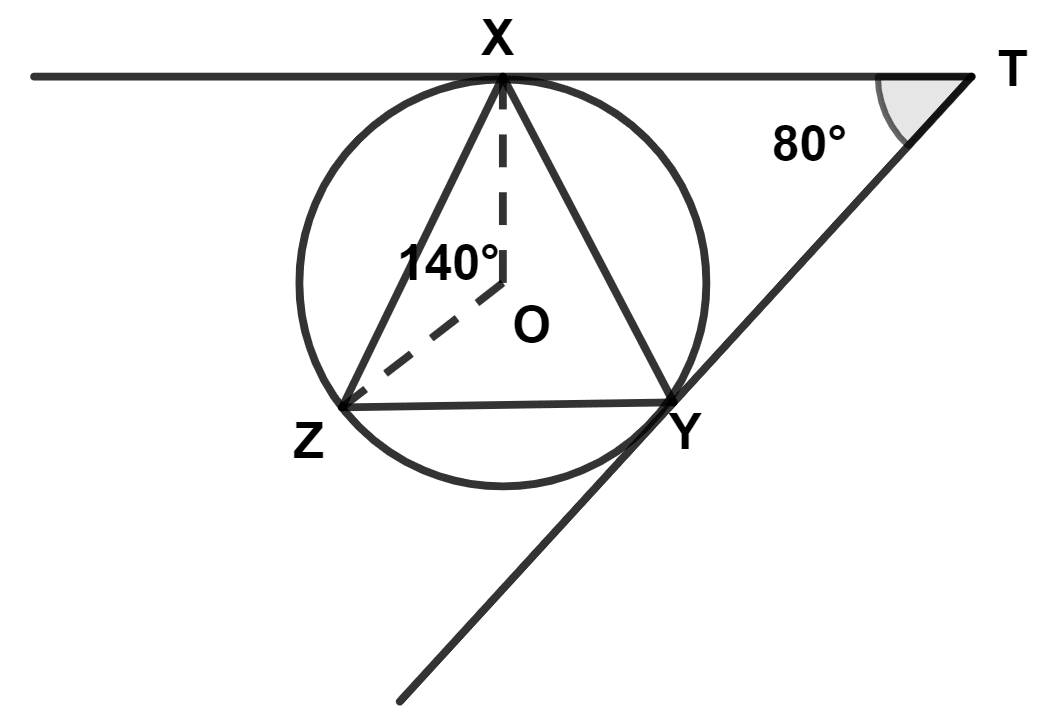
O is the center of the circumcircle of △ XYZ. Tangents at points X and Y meet each other at point T. If ∠XOZ = 140° and angle XTY = 80°, find angle ZXY.
Find the mode of the following distribution by drawing a histogram :
C.I. Frequency 1-6 6 7-12 12 13-18 20 19-24 15 25-30 9 A solid is in the form of right circular cylinder with a hemisphere at one end and a cone at the other end. The radius of the common base is 2.8 cm and heights of cylinder and conical portions are 14 cm and 7 cm respectively. Find :
(i) the total surface area of the solid
(ii) the volume of the solid
Take π = and find your answers correct to two decimal places.