Mathematics
In a circle with centre O and diameter AB; angle APB is the angle of semicircle. If PA = PB; find the measure of each angle of triangle APB.
Circles
16 Likes
Answer
Given, O is center of circle. AB is the diameter of the circle.
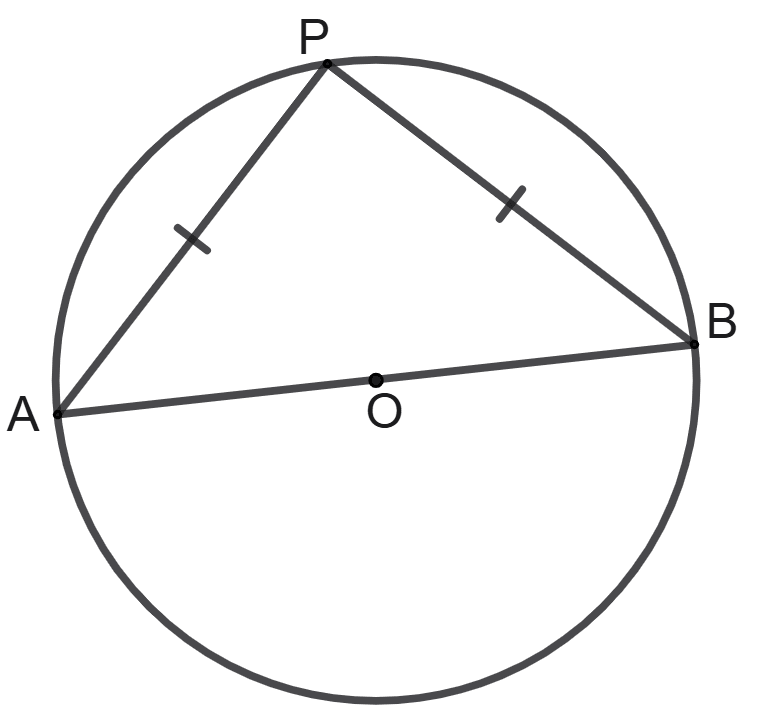
⇒ PA = PB (Given)
⇒ ∠PAB = ∠PBA = x (let) [Angles opposite to equal sides of a triangle are always equal]
We know that,
Angle in a semi-circle is a right angle.
⇒ ∠APB = 90°
In ΔAPB, using angle sum property
⇒ ∠PAB + ∠PBA + ∠APB = 180°
⇒ x + x + 90° = 180°
⇒ 2x = 180° - 90°
⇒ 2x = 90°
⇒ x =
⇒ x = 45°
⇒ ∠PAB = ∠PBA = 45°
Hence, all angles of the triangles are 45°, 45° and 90°.
Answered By
10 Likes
Related Questions
Draw a circle with radius 4 cm. Draw a chord AB of length 6 cm. Shade its minor segment by horizontal lines and major segment by vertical lines.
Draw a circle with centre at point P. Draw its radii PA and PB such that angle APB = 90°. Shade the minor sector of the circle by horizontal lines and its major sector by vertical lines.
In the following figure, O is the centre of the circle and AB is a diameter.
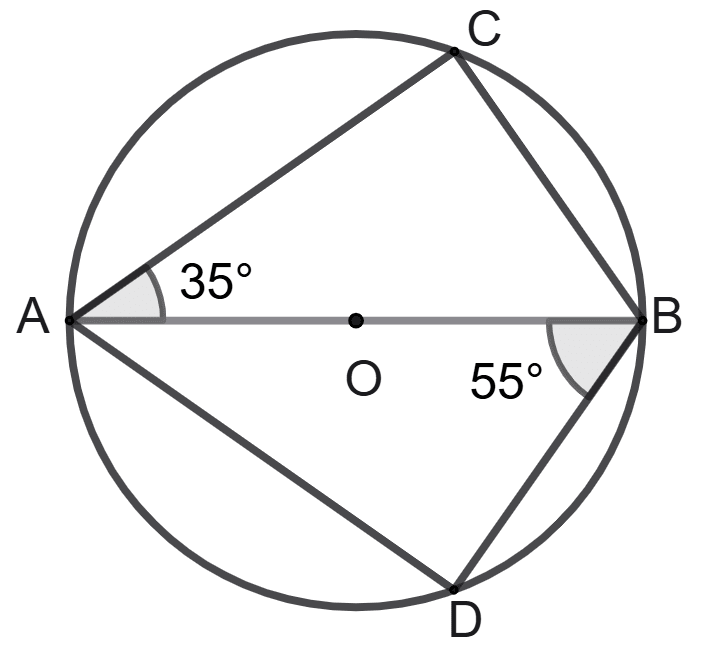
C and D are the points on the circumference of the circle such that ∠CAB = 35° and ∠ABD = 55°. Find the measures of angles CAD and CBD.
The following figure shows a circle with centre O and diameter PQ. Point R lies on the circumference of the circle such that PR = QR and PR = 4 cm.
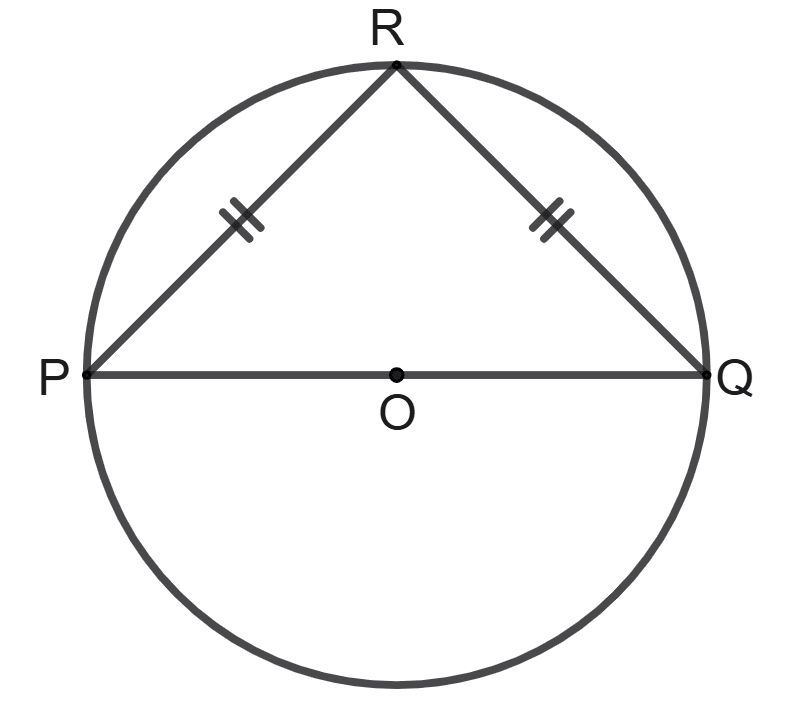
Calculate the radius of the given circle and state its value correct to two decimal places.