Mathematics
In the following figure, O is the centre of the circle and AB is a diameter.
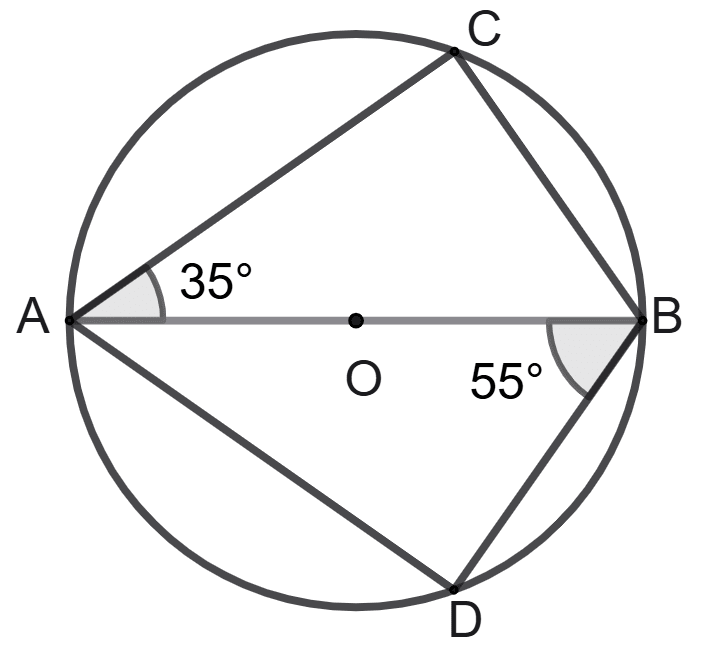
C and D are the points on the circumference of the circle such that ∠CAB = 35° and ∠ABD = 55°. Find the measures of angles CAD and CBD.
Circles
22 Likes
Answer
We know that,
Angle in a semi-circle is a right angle.
⇒ ∠ACB = ∠ADB = 90°
In ΔACB, using angle sum property
⇒ ∠CAB + ∠CBA + ∠ACB = 180°
⇒ 35° + ∠CBA + 90° = 180°
⇒ 125° + ∠CBA = 180°
⇒ ∠CBA = 180° - 125°
⇒ ∠CBA = 55°
From figure,
⇒ ∠CBD = ∠CBA + ∠ABD = 55° + 55° = 110°.
Similarly, in ΔADB, using angle sum property
⇒ ∠DAB + ∠DBA + ∠ADB = 180°
⇒ ∠DAB + 55° + 90° = 180°
⇒ ∠DAB + 145° = 180°
⇒ ∠DAB = 180° - 145°
⇒ ∠DAB = 35°
From figure,
⇒ ∠CAD = ∠CAB + ∠DAB = 35° + 35° = 70°.
Hence, angles CAD = 70° and angle CBD = 110°.
Answered By
12 Likes
Related Questions
Draw a circle with centre at point P. Draw its radii PA and PB such that angle APB = 90°. Shade the minor sector of the circle by horizontal lines and its major sector by vertical lines.
In a circle with centre O and diameter AB; angle APB is the angle of semicircle. If PA = PB; find the measure of each angle of triangle APB.
The following figure shows a circle with centre O and diameter PQ. Point R lies on the circumference of the circle such that PR = QR and PR = 4 cm.
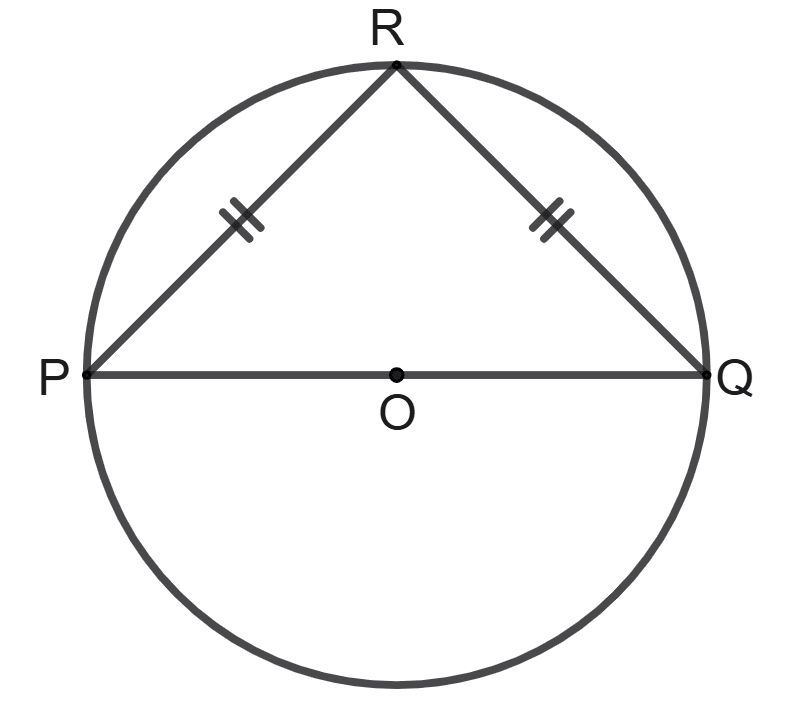
Calculate the radius of the given circle and state its value correct to two decimal places.
In the following figure, PQ and PR are the tangent to the circle with centre O. Line segment AC touch the circle at point B.
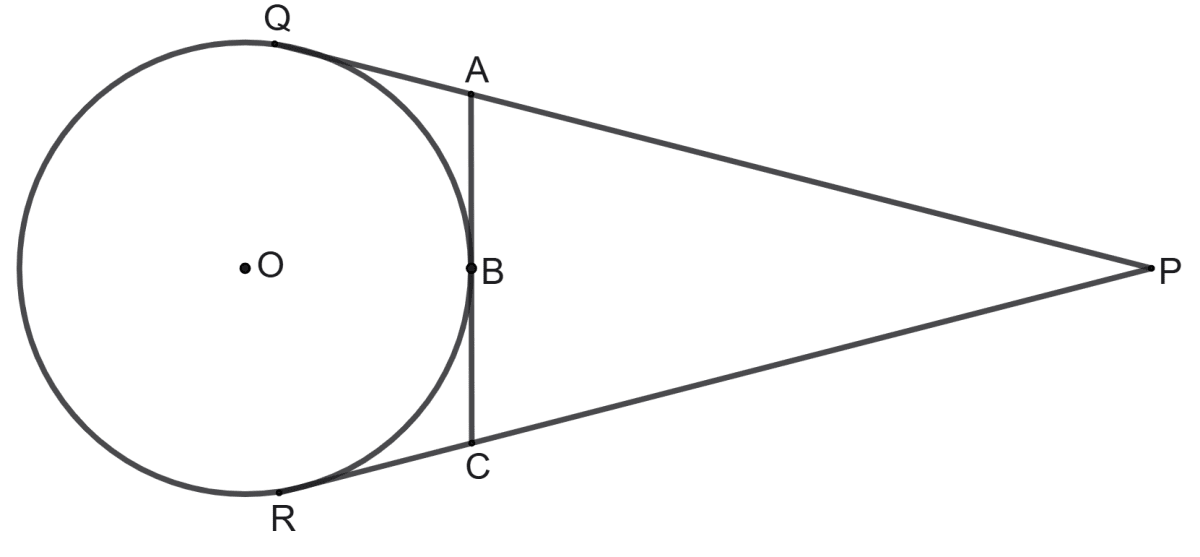
(i) State the relation between tangent PQ and PR.
Also show that:
(ii) PQ = PA + AB
(iii) PR = PC + CB
(iv) PQ + PR = Perimeter of ΔPAC.