Physics
(a) A coin lies at the bottom of a beaker. Water is poured into the beaker upto a height of 8 cm. Calculate the shift seen in the position of the coin.
(The refractive index of water is 4/3. The width of the glass wall of the beaker is negligible.)
(b) How will the apparent depth be affected if the temperature of water is increased?
Refraction Plane Surfaces
5 Likes
Answer
(a) Given,
- Real Depth = 8 cm
- Refractive index of water =
As we know,
where, aμw is the refractive index of the water with respect to air.
So, substituting the values in the formula we get,
Hence, the coin appears to be raised by a height of 2 cm when seen from vertically above.
(b) With increase in temperature, the refractive index of the medium decreases and lower the refractive index of the medium, less is the shift so on increasing the temperature of water, apparent depth decreases.
Answered By
4 Likes
Related Questions
Define background radiation. Give one internal source of this radiation.
Astatine (At) is a radioactive element. Study the graph given below showing the number of protons vs the number of neutrons of radioactive nuclei.
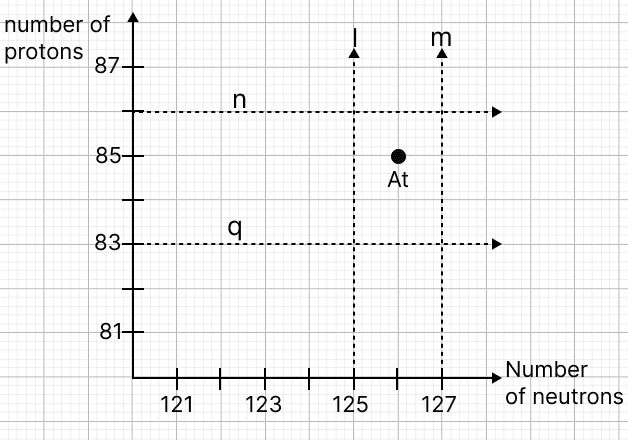
(a) Identify the mass number of the nucleus Astatine (At).
(b) Which line on the graph (l, m, n, or q) will never pass through the position of the daughter nuclei, regardless of any number of α, β, or γ emissions?
(c) Give a reason for your choice in (b).
Draw a ray diagram to invert the image without deviation of light using right angle isosceles prism.
Answer the following with respect to a concave lens (L).
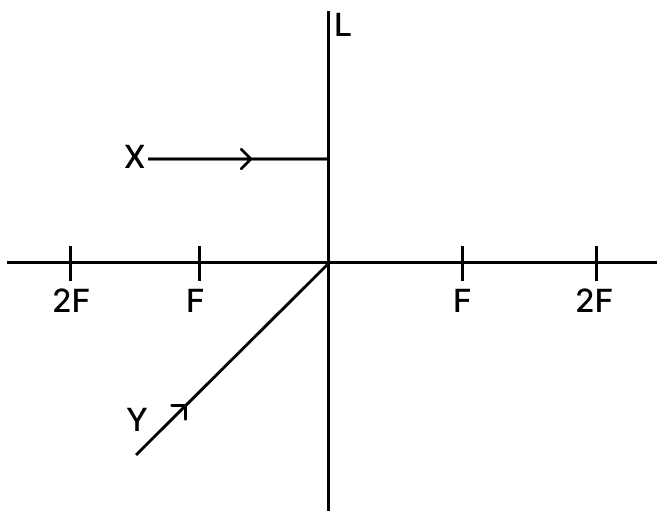
(a) Describe the path of the rays X and Y through the lens.
(b) Give one use of this lens.
(c) Calculate its power if the focal length of this lens is 20 cm.