Mathematics
The cross-section of a tunnel perpendicular to its length is a trapezium ABCD as shown in the following figure; also given that : AM = BN; AB = 7 m; CD = 5 m. The height of the tunnel is 2.4 m. The tunnel is 40 m long. Calculate :
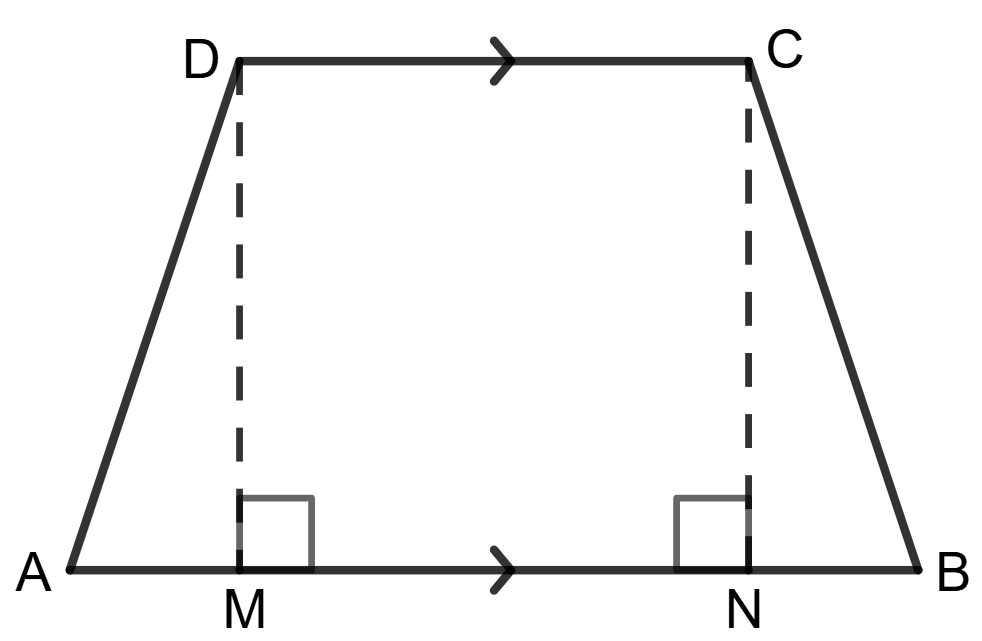
(i) the cost of painting the internal surface of the tunnel (excluding the floor) at the rate of ₹ 5 per m2 (sq. metre).
(ii) the cost of paving the floor at the rate of ₹ 18 per m2.
Mensuration
35 Likes
Answer
(i) Length of the tunnel = 40 m
Height of the tunnel = 2.4 m
Cross-section dimensions: AB = 7 m, CD = 5 m
AM = BN = = = = 1 m
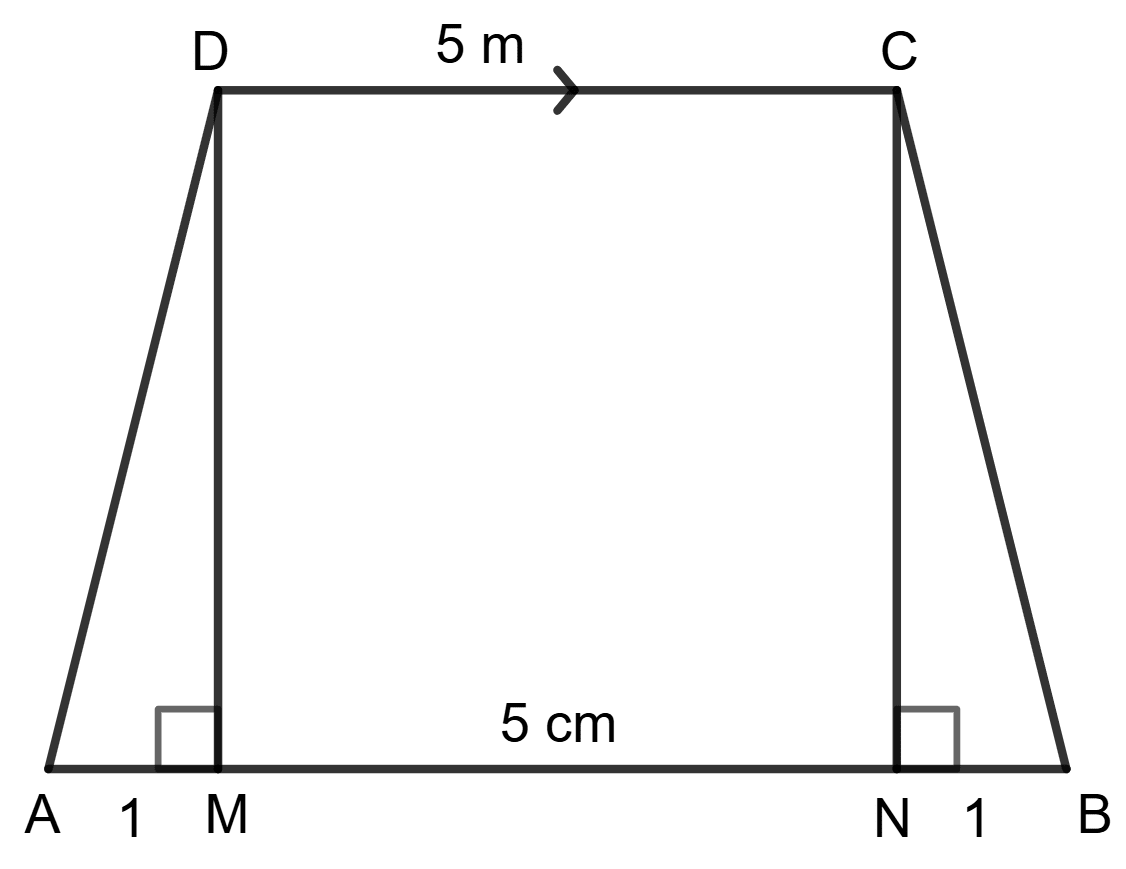
In Δ ADM,
Using the pythagorean theorem in triangle ADM,
Base2 + Height2 = Hypotenuse2
⇒ AM2 + DM2 = AD2
⇒ 12 + (2.4)2 = AD2
⇒ 1 + 5.76 = AD2
⇒ 6.76 = AD2
⇒ AD =
⇒ AD = 2.6 m
Area of the internal surface of the tunnel (excluding the floor) = Area of vertical walls - Area of floor
= 2.6 x 40 + 5 x 40 + 2.6 x 40 m2
= 104 + 200 + 104 m2
= 408 m2
Total cost of painting = Area of vertical walls x Cost of painting
= ₹ 408 x 5
= ₹ 2,040
Hence, total cost of painting the internal surface = ₹ 2,040.
(ii) Area of floor = 7 x 40 m2
= 280 m2
Total cost of paving = Area of floor x rate of paving
= ₹ (280 x 18)
= ₹ 5,040
Hence, total cost of paving = ₹ 5,040.
Answered By
21 Likes
Related Questions
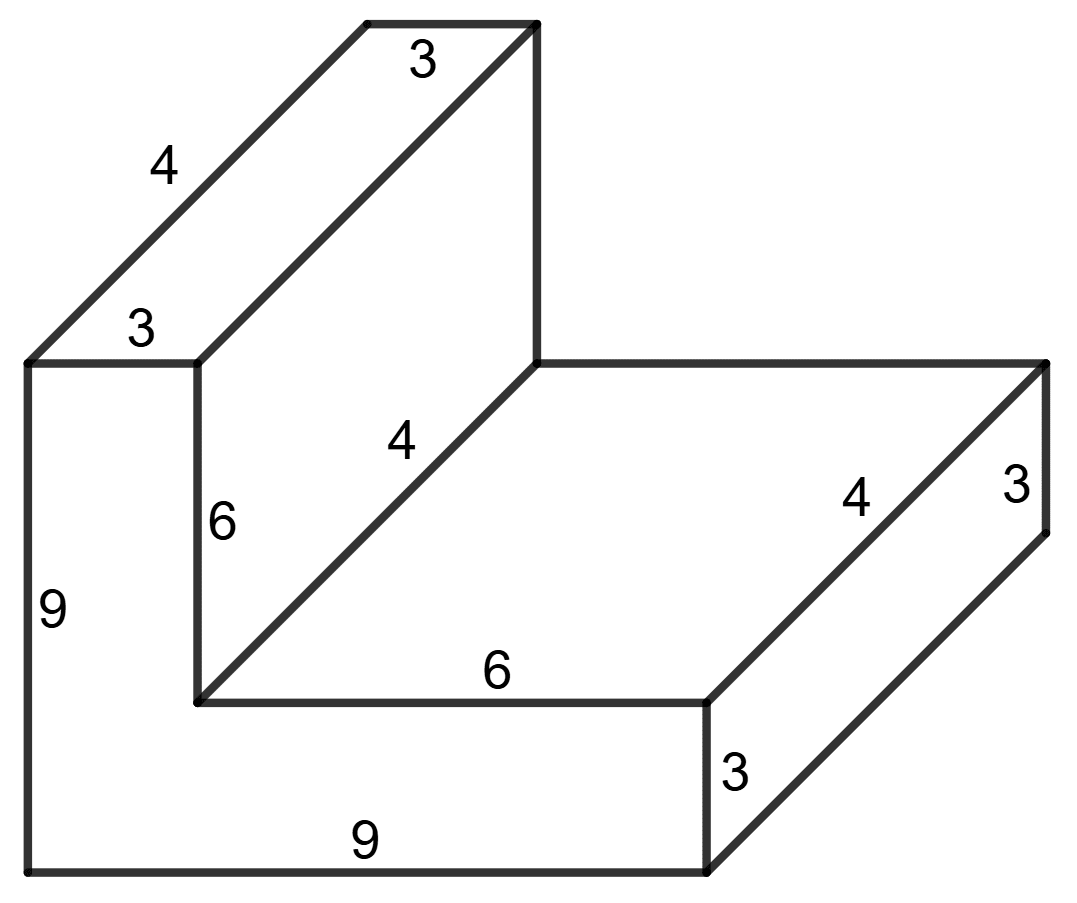
The following figure shows a solid of uniform cross-section. Find the volume of the solid. All measurements are in centimetres. Assume that all angles in the figure are right angles.
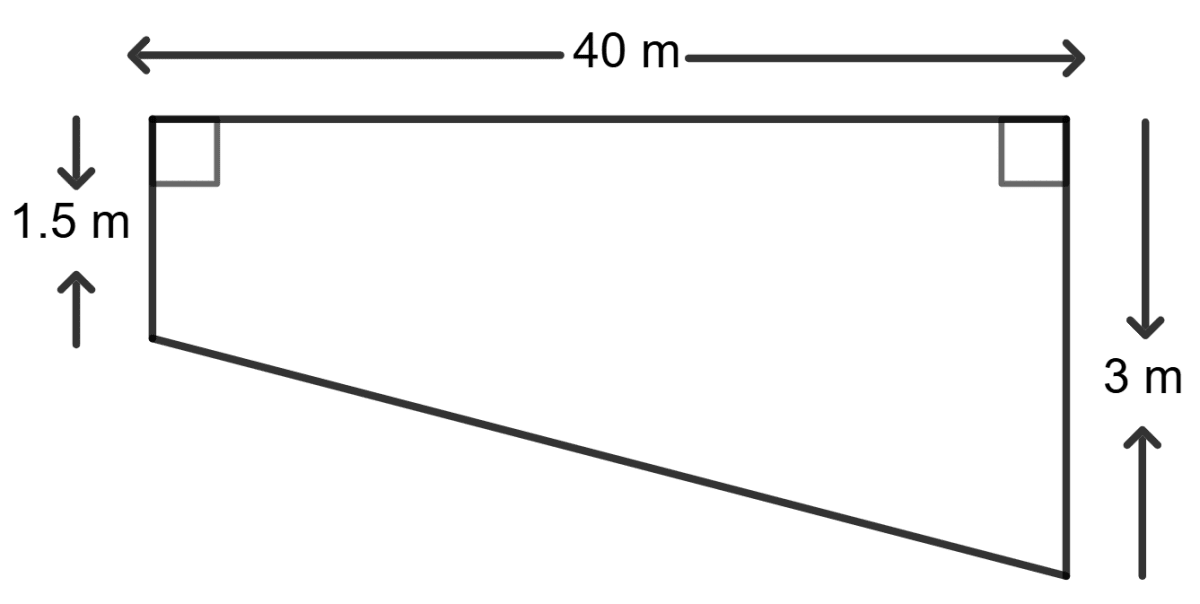
A swimming pool is 40 m long and 15 m wide. Its shallow and deep ends are 1.5 m and 3 m deep respectively. If the bottom of the pool slopes uniformly, find the amount of water in litres required to fill the pool.
Water is discharged from a pipe of cross-section area 3.2 cm2 at the speed of 5m/s. Calculate the volume of water discharged :
(i) in cm3 per sec.
(ii) in litres per minute.
A hose-pipe of cross-section area 2 cm2 delivers 1500 litres of water in 5 minutes. What is the speed of water in m/s through the pipe ?